| | | |
|
Яблоки
Система непересекающихся множеств
У Даши есть n друзей, у каждого ai яблок. Все друзья образуют непересекающиеся компании. В любой момент времени две компании могут объединиться. Даша тщательно запомнила все действия друзей. Теперь ей интересно узнать, сколько яблок было в каждой новообразовавшейся компании. Изначально все друзья тусят отдельно, т.е. нет компании, где больше одного человека. У Даши нет яблок и она не принимает участия в объединениях.
Входные данные:
В первой строке - целые числа n и k ( 2 <= n <= 300000, 0 <= k <= n - 1 ) - количество друзей Даши и количество событий. Во второй строке n чисел - ai (0 <= ai <= 10^9) - количество яблок у i-того друга Даши. В следующих k строках по два числа u, v ( 1 <= u, v <= n). Событие (u, v) означает, что компания с u-тым другом Даши присоединилась к компании с v-тым другом.
Выходные данные:
На каждый из k запросов выведите количество яблок в новой компании.
|
Ввод |
Вывод |
|
3 2
1 2 3
1 2
1 3
|
3
6
|
|
2 1
999999999 0
1 2
|
999999999 |
(с) Ибрахим Ахмад, 2018
| |
![]()
|
|
Острова
Система непересекающихся множеств
Одно разбросанное на островах Океании государство решило создать сеть автомобильных дорог (вернее, мостов). По каждому мосту можно перемещаться в обе стороны. Был разработан план очередности строительства мостов и известно, что после постройки всех мостов можно будет проехать по ним с каждого острова на каждый (возможно, через некоторые промежуточные острова
Однако, этот момент может наступить до того, как будут построены все мосты. Вам необходимо определить такое минимальное количество мостов, после строительства которых (в порядке, определенном планом), можно будет попасть с любого острова на любой другой.
Входные данные
Первая строка содержит два числа: число островов N (1≤N≤10000) и количество мостов в плане M (1≤M≤50000). Далее идет M строк, каждая содержит два числа x и y (1≤x,y≤N) - номера городов, которые соединяет очередной мост в плане.
Выходные данные
Программа должна вывести единственное число - минимальное количество построенных мостов, после которого можно будет попасть с любого острова на любой другой.
| Ввод |
Вывод |
|
4 5
1 2
1 3
2 3
3 4
4 1
|
4 |
| |
![]()
|
|
Остовное дерево
Система непересекающихся множеств
Требуется найти в связном графе остовное дерево минимально веса.
Входные данные
Первая строка входного файла содержит два натуральных числа n и m - количество вершин и ребер графа соответственно (1≤n≤20000, 0≤m≤100000). Следующие m строк содержат описание ребер по одному на строке. Ребро номер i описывается тремя натуральными числами bi, ei и wi - номера концов ребра и его вес соответственно (1≤bi,ei≤n, 0≤wi≤100000).
Граф является связным.
Выходные данные
Выведите единственное целое число - вес минимального остовного дерева.
| Ввод |
Вывод |
|
4 4
1 2 1
2 3 2
3 4 5
4 1 4
|
7 |
| |
![]()
|
|
Вес компоненты
Система непересекающихся множеств
В неориентированный взвешенный граф добавляют ребра. Напишите программу, которая в некоторые моменты находит сумму весов ребер в компоненте связности.
Входные данные
В первой строке записано два числа n и m (1 <= n, m <= 106) - количество вершин в графе и количество производимых добавлений и запросов. Далее следует m строк с описанием добавления или запроса. Каждая строка состоит из двух или четырех чисел. Первое из чисел обозначает код операции. Если первое число 1, то за ним следует еще три числа x, y, w. Это означает, что в граф добавляется ребро из вершины x в вершину y веса w. (1 <= x < y <= n, 1 <= w <= 103). Кратные ребра допустимы. Если первое число 2, то за ним следует ровно одно число x. Это означает, что необходимо ответить на вопрос, какова сумма ребер в компоненте связности, которой принадлежит вершина x (1 <= x <= n).
Выходные данные
Для каждой операции с кодом 2 выведите ответ на поставленную задачу. Ответ на каждый запрос выводите на отдельной строке.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6 10
2 1
1 1 2 1
2 1
1 2 4 2
2 1
1 1 4 3
2 1
1 3 5 3
2 5
2 6
|
0
1
3
6
3
0
|
| |
![]()
|
|
Ребра
Система непересекающихся множеств
Есть n вершин неориентированного графа, в нем же нет ребер. В граф постепенно добавляются m ребер.
После каждого добавления ребра требуется узнать количество компонент связности.
В графе могут быть петли и кратные ребра.
Входные данные:
В первой строке два числа - n и m (1 <= n <= 300000, 0 <= m <= 500000) - количество вершин графа и количество добавляемых ребер.
В следующих m строках по два числа u, v (1 <= u, v <= n) - они значат, что в граф добавили ребро (u, v).
Выходные данные:
После каждого добавления ребра выведите количество компонент связности графа.
|
Ввод |
Вывод |
|
3 2
1 2
2 3
|
2
1 |
|
3 6
1 1
2 2
3 3
1 1
2 2
1 2
|
3
3
3
3
3
2
|
(с) Ибрахим Ахмад, 2018
| |
![]()
|
|
Ася и котята
Система непересекающихся множеств
Ася очень любит животных. Недавно она приобрела n котят, дала им числовые идентификаторы от 1 до n и поселила в вольере. Вольер представляет собой ряд из n ячеек, также пронумерованных от 1 до n. Cоседние ячейки разделены сетчатыми перегородками, всего в вольере n−1 перегородок. Изначально в каждой ячейке поселился ровно один котёнок с некоторым номером.
Наблюдая за котятами, Ася заметила, что они очень дружелюбны и некоторые пары живущих в соседних ячейках котят очень хотят играть друг с другом. Чтобы не лишать их этого удовольствия, Ася стала вынимать перегородки между соседними ячейками, делая их более крупными.
В i-й день Ася делала следующее.
Обращала внимание, что какие-то котята xi и yi, в i-й день живущие в соседних ячейках, хотят играть.
Удаляла перегородку между этими ячейками, превращая их в одну, в которой оказывались все котята из двух прежних ячеек.
Поскольку Ася не возвращала перегородки, через n−1 день вольер стал единой ячейкой, в которой обитали все котята. Будучи очень педантичной, Ася записывала в специальный журнал идентификаторы котят xi и yi для каждого из n−1 дней.
Вам в руки попал журнал с этой информацией, однако вам неизвестно, как котята были поселены в ячейки изначально. Найдите любое расселение котят по n исходным ячейкам, не противоречащее данным в журнале.
Входные данные
В первой строке задано целое число n (\(2 \leq n \leq 150000\)) — количество котят.
В следующих n−1 строках заданы пары целых чисел xi , yi ( \(1 \leq x_i, y_i, \leq n,x_i \neq y_i\) ) — идентификаторы котят, между ячейками которых была удалена перегородка в день i. Гарантируется, что котята xi и yi не находятся в одной ячейке по итогам предыдущих объединений ячеек.
Выходные данные
Выведите n различных целых чисел pi (\(1 \leq p_i \leq n\)), где pi — идентификатор котёнка, который изначально жил в ячейке с номером i. Если возможных вариантов ответа несколько, выведите любой из них.
Примечание
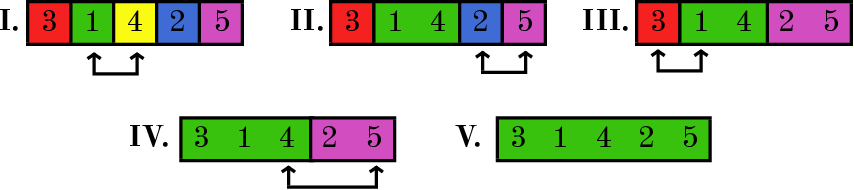
В ответе к примеру приведено одно из возможных изначальных расселений котят, существуют и другие варианты ответа. На изображении ниже показано, как происходило объединение ячеек для этого варианта исходного размещения котят. Обратите внимание, что при таком размещении котята, подружившиеся в каждый из дней согласно журналу Аси, находятся в соседних ячейках.
| Ввод |
Вывод |
5
1 4
2 5
3 1
4 5 |
3 1 4 2 5 |
| |
![]()
|
|
Минимальное остовное дерево c с данным ребром
Система непересекающихся множеств
Требуется найти в связном графе остовное дерево минимального веса в котором есть данное ребро.
Формат файла входных данных:
Первая строка входного файла содержит два натуральных числа N, M - количество вершин и ребер графа соответственно. Следующие m строк содержат описание ребер по одному на строке. Ребро номер i описывается тремя натуральными числами Bi, Ei, Wi номера концов ребра и его вес соответственно (1 <= Bi, Ei <= N, 0 <= Wi <= 2^32-1. N <= 10, M <= 10). В последней строке вводится данное ребро B, E, W.
Формат файла выходных данных:
Единственная строка выходного файла должна содержать одно натуральное число - вес минимального остовного дерева c данным ребром.
Ввод:
4 4
1 2 1
2 3 2
3 4 5
4 1 4
1 4 7
Вывод:
10
| |
![]()
|
|
Порталы
Система непересекающихся множеств
Древовидные структуры данных
Минимальный каркас
Беси расположена на сети из N (2≤N≤105) вершин помеченных 1…N и 2N порталов помеченных 1…2N. Каждый портал соединяет две различных вершины u и v (u≠v). Множество порталов может соединять некоторую пару вершин.
Каждая вершина v соседняя для четырёх различных порталов. Список порталов вершины v задаётся как pv=[pv,1,pv,2,pv,3,pv,4].
Ваше текущее положение может быть представлено упорядоченной парой (current vertex,current portal); то есть парой (v,pv,i) где 1≤v≤N и 1≤i≤4. Вы можете использовать одну из следующих операций для изменения своего текущего положения:
Изменить текущую вершину перемещением через текущий портал.
Переключить текущий портал. В каждой вершине первые два портала в списке объединены в пару и последние два портала в списке также объединены в пару. Поэтому если Ваше текущее состояние (v,pv,2), то Вы можете переключиться чтобы использовать портал (v,pv,1) и обратно. Аналогично, если Ваше текущее положение (v,pv,3) Вы можете переключиться на портал (v,pv,4) и обратно. никакие другие переключения не разрешены (например, Вы не можете переключиться с портала pv,2 на портал) pv,4).
Всего имеется 4N различных состояний. К несчастью, может не оказаться, что что любое состояние достижимо из любого с помощью последовательности заданных операций. Поэтому, за цену cv (1≤cv≤1000) мунов вы можете сделать перестановку списка порталов соседних вершине v, в любом желаемом Вами порядке. После этого первые два портала в списке объединяются в одну пару, а последние два портала - в другую пару.
Например, если Вы переставить порталы вершины v в порядке [pv,3,pv,1,pv,2,pv,4], Это означает. что если Вы в вершине v,
Если Вы в портале pv,1, Вы можете переключиться на портал pv,3 и обратно
Если Вы в портале pv,2, Вы можете переключиться на портал pv,4 и обратно
Теперь Вы не можете переключаться с портала pv,1 на pv,2, или с портала pv,3 на портал pv,4 и обратно.
Вычислите минимальное количество мунов, требуемых для модификации сети таким образом, чтобы сделать достижимым каждое состояние из каждого состояния. Гарантируется, что тестовые данные сконструированы таким образом, что существует хотя бы один способ такой модификации сети.
Входные данные:
Первая строка содержит N.
Каждая из следующих N строк описывает вершину. Строка v+1 содержит 5 разделённых одиночными пробелами целых чисел cv,pv,1,pv,2,pv,3,pv,4.
Гарантируется, что для каждой v все pv,1,pv,2,pv,3,pv,4 различны, и каждый портал появляется в списках ровно двух вершин.
Выходные данные:
Одна строка содержит минимальное количество мунов требуемых для модификации сети чтобы сделать возможным достижимость каждого состояния из другого состояния.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
5
10 1 4 8 9
11 1 2 5 6
12 9 10 2 3
3 4 3 6 7
15 10 8 7 5 |
13 |
Достаточно сделать перестановку списков вершин 1 и 4. Это требует c1+c4=13 мунов. Перестановки такие: p1=[1,9,4,8] и p4=[7,4,6,3]. |
| |
![]()
|
|
Выбор гурмана
Динамическое программирование на графах
Обход в глубину
Система непересекающихся множеств
Гурман Яблочков работает редактором известного гастрономического издания. Он разъезжает по всему миру, дегустируя новые изыски именитых шеф-поваров самых фешенебельных ресторанов высокой кухни. У Яблочкова есть свой фирменный способ ревью: в каждом заведении Яблочков заказывает два набора блюд в разные дни. Все заказанные блюда разные, так как Яблочков не любит есть одно и то же. Для каждой пары блюд из разных наборов он точно помнит, какое из них лучше по его ощущениям, или что они одинаковы по вкусовым качествам. Затем гурман оценивает каждое блюдо положительным целым числом.
Однажды, во время очередной ревизии, ресторан кельтской средневековой кухни «Пуассон», подающий суп из каштанов с пихтой, теплый содовый хлеб, пряный лимонный пирог и другую народную еду, очень приятно удивил гурмана своим разнообразным меню, и эксперт заказал слишком много. Поэтому ему нужна помощь в оценке блюд.
Гурман в первый день дегустировал набор из n блюд, во второй день набор из m блюд. Он составил таблицу ощущений a размером nm, в которой описал свои впечатления. Если по мнению эксперта блюдо i из первого набора лучше блюда j из второго набора, то aij равно « > », в противоположном случае aij равно « < ». Блюда также могут быть равны по уровню, тогда aij равно « = ».
Теперь Яблочков хочет, чтобы вы помогли ему оценить каждое блюдо в наборах целым положительным числом. Так как Яблочков очень строгий дегустатор, то постарается оценить блюда так, чтобы максимальная из оценок была как можно меньше. В то же время Яблочков очень справедливый, поэтому никогда не оценивает блюда так, чтобы это шло вразрез с его ощущениями. Другими словами, если aij равно « < », то оценка блюда i из первого набора должна быть меньше оценки блюда j из второго набора, если aij равно « > », то должна быть больше, а если aij равно « = », то должна совпадать.
Помогите Яблочкову выставить оценки каждому блюду из обоих наборов так, чтобы это согласовывалось с его ощущениями, или определите, что это невозможно.
Входные данные
В первой строке заданы два целых числа n и m (1 ≤ n, m ≤ 1000 ) — количества блюд в каждый из двух дней.
Каждая из следующих n строк содержит строку из m символов. j-й символ в i-й строке задаёт значение aij. Все строки состоят только из символов « < », « > » и « = ».
Выходные данные
В первой строке выведите « Yes » (без кавычек), если можно сделать корректную оценку всем блюдам и « No » (без кавычек), если иначе.
В случае, если сделать корректную оценку можно, во второй строке выведите n целых чисел — оценки блюд первого набора, а в третьей строке m целых чисел — оценки блюд второго набора.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснения |
| 1 |
3 4
>>>>
>>>>
>>>> |
Yes
2 2 2
1 1 1 1 |
Все блюда первого дня лучше всех блюд второго дня. Значит, самой высокой оценкой будет 2 для всех блюд первого дня. |
| 2 |
3 3
>>>
<<<
>>> |
Yes
3 1 3
2 2 2 |
|
| 3 |
3 2
==
=<
== |
No |
Таблица противоречива: нет ни одного набора оценок, который удовлетворял бы ей. |
| |
![]()
|
|
Перекраска клеток
Информатика
Система непересекающихся множеств
Двумерные массивы
Список
Дано клетчатое поле N x M, все клетки поля изначально белые. Автомат умеет:
закрасить клетку (i,j) в черный цвет.
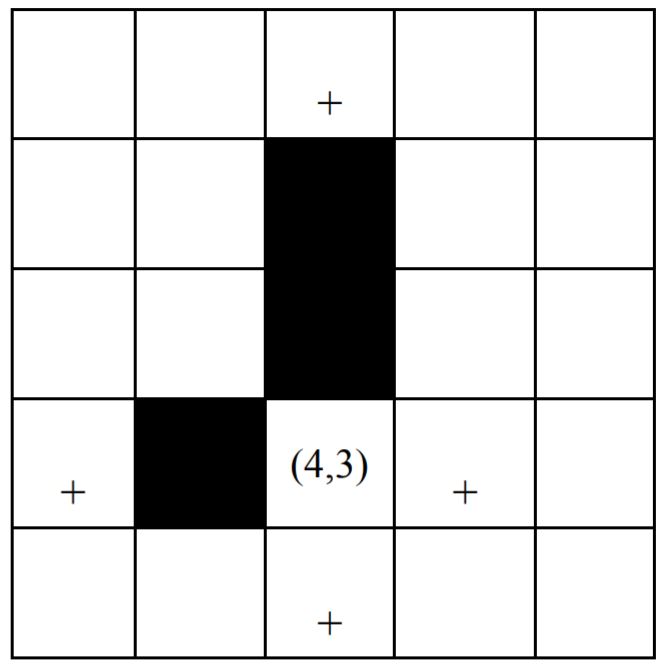
для клетки (i,j) узнать её ближайших белых соседей по вертикали и горизонтали.
Дана последовательность команд для автомата. Требуется выполнить эти команды в указанной последовательности, и для каждой команды запроса ближайших белых соседей указать результат ее выполнения.
Входные данные
Сначала вводятся размеры поля N и M (1 ≤ N ≤ 20, 1 ≤ M ≤ 50000), затем количество команд K (1 ≤ K ≤ 105), а затем сами команды. Команды записаны по одной в строке в следующем формате:
Color i j — окраска клетки (i,j) в черный цвет;
Neighbors i j — нахождение белых соседей для БЕЛОЙ клетки (i,j).
1 ≤ i ≤ N, 1 ≤ j ≤ M.
Выходные данные
На каждый запрос Neighbors требуется вывести сначала количество ближайших белых соседей (или 0, если ни с одной из сторон белых клеток не осталось), а затем их координаты (соседей можно перечислять в произвольном порядке). Если запросов Neighbors нет, ничего выводить не надо.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 5 6
Color 4 2
Neighbors 4 3
Color 2 3
Color 3 3
Neighbors 4 3
Neighbors 5 1 |
4
4 1
4 4
3 3
5 3
4
4 1
4 4
1 3
5 3
2
5 2
4 1 |
| |
![]()
|
|
Highways
Компоненты сильной связности
Система непересекающихся множеств
Остров народа Флатопии представляет собой часть плоскости. К сожалению, во Флатопии очень плохая система дорог. Правительство беспокоится об этой проблеме и уже построило несколько дорог, соединяющих наиболее важные города. Как всегда, остались города, до которых невозможно добраться по дорогам. Требуется построить новые дороги так, чтобы можно было проехать по дорогам от любого города до любого другого.
Города во Флатопии пронумерованы от 1 до N и город с номером i имеет декартовы координаты (xi, yi). Каждая дорога соединяет ровно два города. Все дороги (уже построенные и те, которые собираются построить) лежат на прямых линиях и их длина равна декартовому расстоянию между городами. Все дороги имеют двухстороннее движение. Дороги могут пересекаться, но водитель может переезжать с дороги на дорогу только в городах.
Правительство Флатопии хочет минимизировать стоимость постройки новых дорог. При этом, они хотят, чтобы все города были достижимы по дорогам. Так как Флатопия является плоской, то стоимость постройки дороги пропорциональна её длине. Поэтому, в целях экономии, требуется минимизировать суммарную длину построенных дорог.
Входные данные
Входной файл состоит из двух частей. Первая часть содержит информацию о городах Флатопии, а вторая о дорогах, которые уже построены.
Первая строка входного файла содержит единственное целое число N (1 <= N <= 750), обозначающее число городов. Следующие N строк содержат по два целых числа, xi и yi, разделённых пробелом. Эти числа являются координатами соответствующих городов (для i от 1 до N). Координаты по модулю не превосходят 10000. Никакие два города не совпадают.
Следующая строка содержит одно число M (0 <= M <= 1000), представляющее количество уже построенных дорог. Следующие M строк содержат по два целых числа, разделённых пробелом. Эти два числа обозначают пару городов, которые уже соединены дорогами. Каждая пара соединена не более чем одной дорогой.
Выходные данные
В выходной файл выведите дороги, имеющие минимальную возможную суммарную длину, которые требуется построить для соединения всех городов. Каждая дорога должна быть записана на отдельной строке в виде номеров соединённых городов, записанных через пробел. Если дорог строить не нужно, то выходной файл должен быть создан, но при этом остаться пустым.
| |
![]()
|