Запись арифметических операций

Напишите программу, которая вычисляет значение выражения по заданной формуле:

\({x + y\over {x +1}}-{x\cdot y-12 \over 34 + x}\)


Входные данные
С клавиатуры вводятся x и y - переменные целого типа.

Выходные данные
Программа должна вывести одно число - результат вычисления выражения.
 
 

Примеры

Встроенные функции

Делимость чисел

Принц Джеймс очень любит математику. Для своих исследований ему необходимо научиться быстро узнавать, делится ли одно из двух чисел на другое. Помогите Джеймсу написать программу, чтобы он мог мгновенно получать ответ.

Формат входных данных
На вход программа получает два натуральных числа, каждое не больше 100. Каждое число записано в отдельной строке.

Формат выходных данных
Программа должна выводить число 1, если одно из чисел делится на другое. В противном случае необходимо вывести любое другое число не равное 1, и не превосходящее \(10^9\).

Новый вопрос

Перекраска клеток

Дано клетчатое поле N x M, все клетки поля изначально белые. Автомат умеет:

закрасить клетку (i,j) в черный цвет.
для клетки (i,j) узнать её ближайших белых соседей по вертикали и горизонтали.
Дана последовательность команд для автомата. Требуется выполнить эти команды в указанной последовательности, и для каждой команды запроса ближайших белых соседей указать результат ее выполнения.

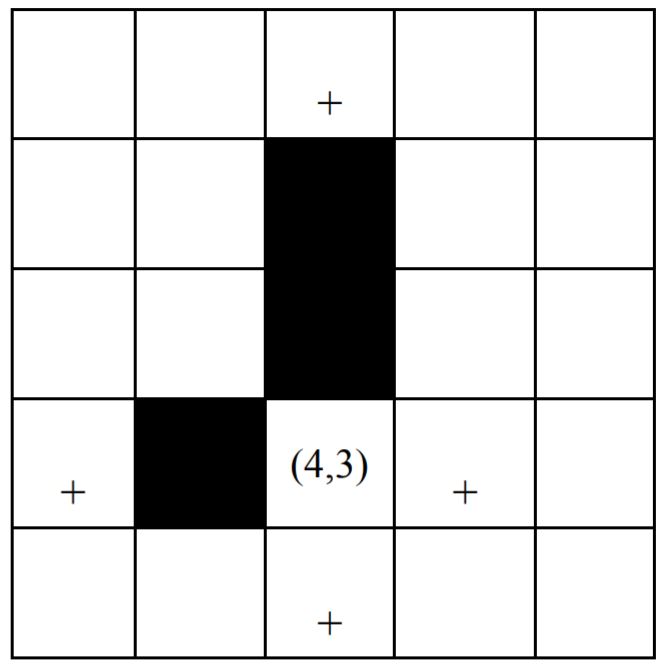
Входные данные
Сначала вводятся размеры поля N и M (1 ≤ N ≤ 20, 1 ≤ M ≤ 50000), затем количество команд K (1 ≤ K ≤ 10⁵), а затем сами команды. Команды записаны по одной в строке в следующем формате:

Color i j — окраска клетки (i,j) в черный цвет;
Neighbors i j — нахождение белых соседей для БЕЛОЙ клетки (i,j).

1 ≤ i ≤ N, 1 ≤ j ≤ M.

Выходные данные
На каждый запрос Neighbors требуется вывести сначала количество ближайших белых соседей (или 0, если ни с одной из сторон белых клеток не осталось), а затем их координаты (соседей можно перечислять в произвольном порядке). Если запросов Neighbors нет, ничего выводить не надо.

Примеры

Число в шестнадцатеричной системе счисления

Входные данные
Программа получает на вход натуральное число - N. 

Выходные данные
Выведите на экран представление числа в шестнадцатеричной системе счисления, в котором цифры числа записаны в обратном порядке, то есть с конца. Для представления цифр от 10 до 15 используйте большие английские буквы от  'A' до 'F'.
 

Примеры

39463

Алгоритм вычисления значения функции F(n), где n – целое неотрицательное число, задан следующими соотношениями:

F(0) = 8
F(n) = 5 + F(n / 3) если n > 0 и n делится на 3
F(n) = F(n // 3) в остальных случаях

39820

В системе счисления с основанием N запись числа 99 оканчивается на 4 и содержит не менее трёх цифр. Чему равно число N?

2(6)

От разведчика была получена следующая шифрованная радиограмма, переданная с использованием азбуки Морзе.
• – – – • • – – • • • • • – – •
При передаче радиограммы было потеряно разбиение на буквы, но известно, что в радиограмме использовались только следующие буквы.
 

(№ 5522) (А. Рогов)

В файле электронной таблицы 9-170.xls в каждой строке содержатся шесть натуральных чисел. Определите количество строк таблицы, для которых выполнены оба условия:
– в строке только одно число повторяется трижды (ровно 3 раза), остальные числа не повторяются;
– утроенная сумма неповторяющихся чисел строки не больше произведения повторяющихся чисел.

ege_06_000_Демо 2023

Р-00 (Демо-2023). Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n – целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись
Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 7 [Вперёд 10 Направо 120]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.
 

ege_06_053_квадрат с поворотом

Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n – целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает её голова, и Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись Повтори k [Команда1 Команда2 … КомандаS]
означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:
Направо 135
Повтори 25 [Вперёд 250 Направо 90]
Определите, сколько точек с целочисленными координатами будут находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии не следует учитывать.

ege-24_A01_33401

Текстовый файл состоит не более чем из 10⁶ символов английского алфавита (от A до Z). Определите длину самой длинной подцепочки, состоящей из одинаковых символов. В ответе укажите сначала символ, из которого строится данная подцепочка, затем, слитно без разделителей, длину данной подцепочки. Если таких подцепочек несколько, то укажите ту, в которой буква стоит раньше в алфавите.

Входные данные
Строка символов 
Выходные данные
Ответ на задачу
Примеры

Крылов 08

Ответы запишите через пробел
Файл

43410

В каждой строке электронной таблицы записаны четыре натуральных числа. Определите, сколько в таблице таких четвёрок, которые можно разбить на две пары с одинаковой нечётной суммой.

27_Обработка пар_01

Имеется набор данных, состоящий из троек натуральных чисел. Необходимо выбрать из каждой тройки два числа так, чтобы сумма всех выбранных чисел была кратна 4 и при этом была максимально возможной. Если получить требуемую сумму невозможно, в качестве ответа нужно выдать 0. 

Входные данные
На вход программе в первой строке подаётся количество троек N (1<=N<=100000). Каждая из следующих N строк содержит три натуральных числа, не превышающих 10 000.

Выходные данные
Выведите ответ на задачу

ege_25_П22-49_

Назовём маской числа последовательность цифр, в которой также могут встречаться следующие символы:
- символ «?» означает ровно одну произвольную цифру;
- символ «*» означает любую последовательность цифр произвольной длины; в том числе «*» может задавать и пустую последовательность.
Среди натуральных чисел, не превышающих 10⁸, найдите все числа, соответствующие маске 12*4?65, делящиеся на 161 без остатка. В ответе запишите в первом столбце таблицы все найденные числа в порядке возрастания, а во втором столбце – соответствующие им результаты деления этих чисел на 161.
 

EGE_09_CSV_P173

Дан набор строк. Количество строк заранее неизвестно.
Окончанием ввода является строка, не содержащая "знака разделителя чисел".
В каждой строке содержатся шесть натуральных чисел.

Задание 5

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.
1)??Строится двоичная запись числа N.
2)??К этой записи дописываются справа ещё два разряда по следующему правилу:
 -  если N  делится нацело на 4, в конец (справа) дописывается сначала ноль, а затем еще один ноль;
 -  если N при делении на 4 дает остаток 1, то в конец дописывается сначала ноль, а затем единица;
 -  если N при делении на 4 дает остаток 2, то в конец дописывается сначала один, а затем ноль;
 -  если N при делении на 4 дает остаток 3, то в конец дописывается сначала один, а затем еще один.
Например, двоичная запись 1001 числа 9 будет преобразована в 100101, а двоичная запись 1100 числа 12 будет преобразована в 110000.
Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа R.
Укажите минимальное число R, которое меньше 100 и может являться результатом работы алгоритма. В ответе это число запишите в десятичной системе.

 

ege-05_001_P301_d2023

На вход алгоритма подаётся натуральное число N.
Алгоритм строит по нему новое число R следующим образом.
1. Строится двоичная запись числа N.
2. Далее эта запись обрабатывается по следующему правилу:
а) если сумма цифр в двоичной записи числа чётная, то к этой записи справа дописывается 01, а затем три левых разряда заменяются на 101;
б) если сумма цифр в двоичной записи числа нечётная, то к этой записи справа дописывается 10, а затем три левых разряда заменяются на 110.
Полученная таким образом запись является двоичной записью искомого числа R.
Например, для исходного числа 6 = 110₂ результатом является число 10101₂ = 21,
а для исходного числа 4 = 100₂ результатом является число 11010₂ = 26.
Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число R, большее 99.
В ответе запишите это число в десятичной системе счисления.

 
 

Метро

Город имеет форму круга радиуса R с центром в точке (0,0).
Сеть метро состоит из N линий метро (часть линий или все проходят через город).
Линия метро - ломаная из отрезков прямых, вершины которых имеют целочисленные координаты. Линия метро не имеет самопересечений и может быть замкнутой. Во всех точках с целочисленными координатами, через которые проходят линии метро расположены станции метро .
Для каждой точки с целочисленными координатами определим параметр вес вершины. Вес вершины - это количество линий метро,  проходящих через данную точку (понятно, что точка с ненулевым весом  есть станция метро). 
Город разбит на кварталы. Квартал - это единичная клетка с целочисленными координатами вершин, хотя бы одна из которых находящаяся строго внутри города. 
Для каждого квартала определим "значимость", которая равна сумме весов вершин,  окружающих квартал (вершина квартала может быть вне города) 
Найдите значение "значимости" для каждого квартала. Для каждой полученной "значимости" определите количество кварталов имеющих эту значимость. 
Входные данные
В первой строке заданы значения R, N (4<R<201, 0<N<1000) 
В следующих N строках заданы описания линий метро.
Каждая линия описывается следующим образом:
первое число в строке M равно количеству вершин ломаной, далее даны координаты вершин (по два числа на вершину). 
Замкнутые ломаные определяются тем, что координаты начальной и конечной вершины совпадают.  
Выходные данные
В первой строке выведите число K - количество различных  значений "значимости" (включая нулевую).
В следующих K строках  выведите по два числа - значение "значимости" и количество кварталов, имеющих такое значение "значимости"

Примеры:

ege-22_Е09

В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первом столбце таблицы указан идентификатор процесса (ID), во втором столбце таблицы – время его выполнения в миллисекундах, в третьем столбце перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Типовой пример организации данных в файле:

ege-22_C01

В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первом столбце таблицы указан идентификатор процесса (ID), во втором столбце таблицы – время его выполнения в миллисекундах, в третьем столбце перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Определите максимальное количество процессов, которые выполнялись параллельно, при условии, что все независимые друг от друга процессы стартовали одновременно, а зависимые процессы стартовали одновременно с завершением всех процессов, от которых они зависят.
Типовой пример организации данных в файле:

ИН2210102 - 25

Маска числа – это последовательность цифр, в которой могут встречаться специальные символы «?» и «*». Символ «?» означает ровно одну произвольную цифру, символ «*» означает произвольную (в том числе пустую) последовательность цифр.

_St-23_02-kege-12(a)

Исполнитель Редактор получает на вход строку цифр и преобразует её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.
А) заменить (v,w).
Эта команда заменяет в строке первое слева вхождение цепочки v
на цепочку w.
Например, выполнение команды
заменить (111, 27)
преобразует строку 05111150 в строку 0527150.
Если в строке нет вхождений цепочки v, то выполнение команды
заменить (v,w) не меняет эту строку.
Б) нашлось (v).
Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.

Дана программа для Редактора:

Известно, что исходная строка A содержала ровно два нуля – на первом и на последнем месте, а также поровну единиц и двоек. После выполнения данной программы получилась строка B, содержащая 6 единиц и 9 двоек.
Какое наименьшее количество четвёрок может быть в строке B?

_St-23_03-kege-15(b)

Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n.
Например, 14&5 = 1110₂&0101₂ = 0100₂ = 4.
Для какого наименьшего неотрицательного целого числа А формула

            (x&116 ≠ 0 ∨ x&92 ≠ 0) → (x&69 = 0 → x&А ≠ 0)

Метро

Город имеет форму круга радиуса R с центром в точке (0,0).
Сеть метро состоит из N линий метро (часть линий или все проходят через город).
Линия метро - ломаная из отрезков прямых, вершины которых имеют целочисленные координаты. Линия метро не имеет самопересечений и может быть замкнутой. Во всех точках с целочисленными координатами, через которые проходят линии метро расположены станции метро .
Для каждой точки с целочисленными координатами определим параметр вес вершины. Вес вершины - это количество линий метро,  проходящих через данную точку (понятно, что точка с ненулевым весом  есть станция метро). 
Город разбит на кварталы. Квартал - это единичная клетка с целочисленными координатами вершин, хотя бы одна из которых находящаяся строго внутри города. 
Для каждого квартала определим "значимость", которая равна сумме весов вершин,  окружающих квартал (вершина квартала может быть вне города) 
Найдите значение "значимости" для каждого квартала. Для каждой полученной "значимости" определите количество кварталов имеющих эту значимость. 
Входные данные
В первой строке заданы значения R, N (4<R<201, 0<N<1000) 
В следующих N строках заданы описания линий метро.
Каждая линия описывается следующим образом:
первое число в строке M равно количеству вершин ломаной, далее даны координаты вершин (по два числа на вершину). 
Замкнутые ломаные определяются тем, что координаты начальной и конечной вершины совпадают.  
Выходные данные
В первой строке выведите число K - количество различных  значений "значимости" (включая нулевую).
В следующих K строках  выведите по два числа - значение "значимости" и количество кварталов, имеющих такое значение "значимости"

Примеры:

45877

Операнды арифметического выражения записаны в системе счисления с основанием 22.

97968х15₂₂ + 17x2433₂₂  – 75x273₂₂

В записи чисел переменной х обозначена неизвестная цифра из алфавита 22-ричной системы счисления. Определите значение х, при котором значение данного арифметического выражения кратно 17, при этом х - простое.  Если таких значений несколько, выберите наибольшее из них. Для найденного значения х вычислите частное от деления значения арифметического выражения на 17 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.

45879

Операнды арифметического выражения записаны в системе счисления с основанием 22.

97968х15₂₂ – 17x2433₂₂  + 75x273₂₂

В записи чисел переменной х обозначена неизвестная цифра из алфавита 22-ричной системы счисления. Определите значение х, при котором значение данного арифметического выражения кратно 15, при этом х - простое. Если таких значений несколько, выберите наименьшее из них.  Для найденного значения х вычислите частное от деления значения арифметического выражения на 15 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.

_St-23_04-kege-15(b)

На числовой прямой даны три отрезка: P = [13; 31], Q = [19; 80] и R = [48; 114].

(¬((x ∈ Q) → ((x ∈ P) ∨ (x ∈ R)))) → (¬(x ∈ A) → ¬(x ∈ Q))

тождественно истинна (т. е. принимает значение 1 при любом значении переменной х).

Задача 8

Имеется набор данных, состоящий из троек натуральных чисел. Необходимо выбрать из каждой тройки ровно одно число так, чтобы сумма всех выбранных чисел не была кратна 4 и при этом была максимально возможной.
Гарантируется, что искомую сумму получить можно. Программа должна напечатать одно число – максимально возможную сумму, соответствующую условиям задачи.

Входные данные
Даны два входных файла (файл А и файл В), каждый из которых содержит в первой строке количество троек n (n< 10⁵). Каждая из следующих n строк содержит три натуральных числа, не превышающих 10⁵.

Треугольник по медиане, высоте и биссектрисе

Для треугольника ABC известны длины высоты, медианы и биссектрисы, проведенных из вершины А к стороне BC.
Определите величину стороны BC с точностью не менее 5 знаков (относительная точность 10^-5). 
Входные данные:
три  различных числа - длины отрезков в произвольном порядке. Все значения не превосходят 10⁶
Выходные данные: значение стороны BC с точностью не менее 10^-5 
Пример:

Задание ЕГЭ № 7 Звук

Музыкальный фрагмент длительностью 2 минуты записали в формате стерео. Размер полученного файла составил 20 Мбайт. После чего музыкальный фрагмент перевели в формат моно, при этом уменьшив частоту дискретизации вдвое и удалив из фрагмента 24 секунды записи. Полученный фрагмент также сохранили в виде файла. Методы сжатия в обоих случаях не применялись.&lt;br /&gt; Найдите размер полученного после преобразования файла в МБайт.

Расширенный алгоритм Евклида

Даны два натуральных числа a и b.
Найдите их наибольший общий делитель d и два таких целых числа x и y,
что ax+by=d.
Программа должна вывести числа d?, x?, y?.

Вводятся два натуральных числа (формат ввода - в строку через пробел).

Выведите ответ на задачу - три числа (в строку, через пробел)

Паровозики на числовой прямой

Паровозики стоят на железной дороге параллельно друг другу на параллельных участках пути. Условно весь участок железной дороги можно представить в виде числовой прямой. В этом случае i-й паровозик на данной числовой прямой покрывает некоторое количество заданных целых точек (от точки starti до точки endi, включая данные точки).

Определите количество целых точек на числовой прямой, которые покрыты любой частью какого-либо паровозика.

Входные данные
В первой строке записано число N - количество паровозиков на железной дороге. В следующих N строках записаны по 2 числа (starti, endi)  - тоски начала и конца i-го паровозика. 

Ограничения

1 <= N <= 100
1 <= starti <= endi <= 100

Выходные данные
Выведите ответ на задачу.
 

Примеры

3
3 6
1 5
4 7

7

Буратино и бинарный поиск НОДа. Моделирование

Буратино стал использовать подсказку Пьеро по поиску наибольшего общего делителя для нечетных числел.
Однажды он применил этот способ  для чётного и нечётного числа и получил правильный ответ. Буратино выполнив ещё несколько примеров для четного и нечетного числа  и понял, что данный алгоритм работает для всех пар чисел, в которых хотя бы одно число нечётное. На уроке он рассказал об этом Мальвине. Мальвина похвалила его, дала мороженое и рассказала о некоторых свойствах НОД (см. теорию).
На основе этих правил  Буратино обновил свой алгоритм действий по поиску НОД:
gcd = 1
ПОКА (A чётное ) И (В чётное)  ДЕЛАЙ:
         А и В делим на 2
         gcd умножаем  на 2
Находим d=НОД (А. В) (одно из чисел нечётное - для этого случая уже умеем)
Умножаем gcd на d 
Промежуточные действия  Буратино записывал в тетрадь (смотри примеры)
Напишите программу, которая будет  выводить промежуточные результаты работы Буратино.
                   
Входные данные : натуральные чётные A, B (числа записаны в две строки, каждое не более 100000)
Выходные данные: Промежуточные записи поиска НОД, аналогичные выводу примеров.
Пояснения:
Первая строка содержит начальное значения чисел
Вторая строка содержит промежуточные значения - числа C, D и gcd (хотя бы одно из чисел A,B - нечётное; gcd  - степень числа 2)
Третья строка содержит НОД (C, D)
Четвертая  строка содержит НОД (A, B) 
 
Прмеры промежуточных записей из тетради Буратино:

Площадь треугольника на плоскости по координатам вершин

Найдите площадь треугольника с вершинами в точках с координатами   \(A,\ B,\ C\)
Напишите программу, которая по значениям координат точек  \(A,\ B,\ C\) (точки на плоскости)  определит значение площади \(\bigtriangleup ABC\)
\(A,\ B,\ C\ -\ списки(кортежи)\ со\ значениями\ координат\ вершин \\ area\ -\ площадь\ треугольника \)
Программа должна возвращать ответ на задачу - значение площади \(\bigtriangleup ABC\)

Среднее арифметическое числового вектора

Дан числовой вектор (список/кортеж чисел)  \(A.\) 
Напишите программу, которая определит среднее арифметическое вектора \(A.\)

Программа должна возвращать одно число m - среднее арифметическое.

Расстояние между векторами

Даны два числовых вектора одинакового размера (списоков/кортежей чисел)  \(A, B\).   
Напишите программу, которая "расстояние" между векторами  \(A\) и \(B\).

Для векторов \([a_1, a_2, \cdots , a_n] , [b_1, b_2, \cdots , b_n] \) расстоянием называется величина

\(\rho = \Sigma|a_i-b_i|\)

Программа должна возвращать одно число \(\rho\) - расстояние между векторами

Длина вектора

Дан числовой вектор \(A\).   
Напишите программу, которая определяет "длину" вектора  \(A\).

"Длиной" векторов \([a_1, a_2, \cdots , a_n] \)  называется величина \(||A||=\sqrt{\Sigma\ a_i\cdot a_i}\)

Программа должна возвращать одно число - квадрат "длины" вектора.

Косинусное сходство. Тип К

Даны два "ненулевых" числовых вектора одинакового размера (списоков/кортежей чисел)  \(A, B\).   
Напишите программу, которая "косинусное сходство" векторов  \(A\), \(B\).

Программа должна возвращать одно число  -  "косинусное сходство"  векторов  \(A\), \(B\)  

Центроид треугольника. Тип К

Треугольник на плоскости задан координатами вершин \(A,\ B,\ C\)
Используя "бариметрический" (средневзвешенное среднее) определите
координаты центроида треугольника (точки G)

Программа должна возвращать кортеж из координат точки G  

Делаем срезы 1-1

На вход программе подается одна строка. Напишите программу, которая выводит общее количество символов в строке;

Формат входных данных
На вход программе подается одна строка, длина которой больше $3$ символов.

Формат выходных данных
Программа должна вывести данные в соответствии с условием. Каждое значение выводится на отдельной строке.

Делаем срезы 1-3

На вход программе подается одна строка. Напишите программу, которая выводит строку с удаленным первым и последним символом.

Формат входных данных
На вход программе подается одна строка, длина которой больше $3$ символов.

Формат выходных данных
Программа должна вывести данные в соответствии с условием. Каждое значение выводится на отдельной строке.

Делаем срезы 2-2

На вход программе подается одна строка. Напишите программу, которая выводит всю строку, кроме последних двух символов.

Формат входных данных
На вход программе подается одна строка, длина которой больше $5$ символов.

Формат выходных данных
Программа должна вывести данные в соответствии с условием. Каждое значение выводится на отдельной строке.

Делаем срезы 2-4

На вход программе подается одна строка. Напишите программу, которая выводит все символы с нечетными индексами.

Формат входных данных
На вход программе подается одна строка, длина которой больше $5$ символов.

Формат выходных данных
Программа должна вывести данные в соответствии с условием. Каждое значение выводится на отдельной строке.

Праздничные ленты Летовца

На территории школы Летовца есть большой стадион. Стадион занимает прямоугольный участок, по длине которого через каждый метр отмечены точки. Каждая точка обозначена целым числом, обозначающим расстояние от начала участка. В начале участка нарисована точка с отметкой 0. 
Летовец со своими друзьями приготовили большие праздничные ленты, которыми будет украшаться стадион и его трибуны. Все ленты было решено сложить  друг на дружку на стадионе, вдоль отмеченных точек. При этом,  i-я лента на стадионе покрывает некоторое количество заданных целых точек (от точки starti до точки endi, включая данные точки). В ожидании праздника, Летовцу стало скучно и он решил посчитать количество точек на стадионе, которые покрыты любой частью какой-либо ленты.

Формат входных данных
В первой строке записано число N - количество лент, которые приготовили Летовец и его друзья. В следующих N строках записаны по 2 числа (starti, endi)  - точки начала и конца i-й ленты. 

Ограничения

1 <= N <= 100
1 <= starti <= endi <= 100

Формат выходных данных
Выведите ответ на задачу.

Примечание
В тестовом примере все точки от 1 до 7 покрыты хотя бы одной лентой. Поэтому ответ 7.

Префиксная сумма. Тип К

\(A\) - вектор/список данных \(a_1,\ a_2,\ \cdots\ ,\ a_n \).
"Постройте" \(B\) - вектор \(b_0,\ b_1,\ \cdots\ ,\ b_n \ такой\ что: b_0=0, b_j=\displaystyle\sum_{i=1}^{j} a_i\)
Напишите фрагмент программы, выполняющую это "построение".

Программа должна возвращать список   

Максимальная сумма подотрезка. Тип К

\(A\) - вектор/список данных \(a_1,\ a_2,\ \cdots\ ,\ a_n \).
\(B\) - вектор "префиксных сумм" от\(A\)   =   \(b_0,\ b_1,\ \cdots\ ,\ b_n \ такой\ что: b_0=0, b_j=\displaystyle\sum_{i=1}^{j} a_i\)
Для заданного  \(k \) "постройте" векто \(C\) =\(c_1,\ c_2,\ \cdots\ ,\ c_n \ такой\ что: \)

 \(c_t=0,\ для\ t<k \\ c_t=max(\displaystyle\sum_{i=j-k+1}^{j} a_i \ |\ k\leq j\leq t)\)

Напишите фрагмент программы, выполняющую это "построение" используя значения вектора \(B\).

Программа должна возвращать список   

Максимальная сумма подотрезка с "хвоста". Тип К

\(A\) - вектор/список данных \(a_1,\ a_2,\ \cdots\ ,\ a_n \).
\(B\) - вектор "префиксных сумм" от\(A\)   =   \(b_0,\ b_1,\ \cdots\ ,\ b_n \ такой\ что: b_0=0, b_j=\displaystyle\sum_{i=1}^{j} a_i\)
Для заданного  \(k \) "постройте" векто \(D\) =\(d_1,\ d_2,\ \cdots\ ,\ d_n \ такой\ что: \)

 \(d_t=0,\ для\ t>n-k \\ d_t=max(\displaystyle\sum_{i=j}^{j+k} a_i \ |\ t\leq j\leq n-k)\)

Напишите фрагмент программы, выполняющую это "построение" используя значения вектора \(B\).

Программа должна возвращать список   

Минимальный "махмимум". Тип К

\(C\) - вектор/список данных \(c_1,\ c_2,\ \cdots\ ,\ c_n \) длины \(n\).
\(D\) - вектор/список данных \(d_1,\ d_2,\ \cdots\ ,\ d_m \) длины \(m\).
\(l<m\) - длина "стены"
Найдите : \(x=min(max(c_i,d_{i+l})\ |\ 1\leq i\leq min(n,m-l))\)

Напишите фрагмент программы, выполняющий данный поиск.

Программа должна возвращать одно значение - число   

Значение функции

Для данного целого x найти значение функции f, принимающей значения целого типа:

Сделайте так, чтобы программа не упала

Напишите минимальный код, чтобы программа не упала

55861

Операнды арифметического выражения записаны в системе счисления с основанием 22.

97968х15₂₂ – 17x2433₂₂  - 75x273₂₂

В записи чисел переменной х обозначена неизвестная цифра из алфавита 22-ричной системы счисления. Определите значение х, при котором значение данного арифметического выражения кратно 15, при этом х - простое. Если таких значений несколько, выберите набольшее из них.  Для найденного значения х вычислите частное от деления значения арифметического выражения на 15 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.

_St-24_04-kege-15(a)

((y < 20) → (x > 70)) ∨ ¬((x < A) → (y > A)) 

_St-24_03-kege-15(b)

x&57665 = 0 → (x&83265 ≠ 0 → x&А ≠ 0) 

_St-24_02-kege-15(a)

x&20777 ≠ 0 → (x&12332 = 0 → x&А ≠ 0) 

_St-23_12-kege-15(a)

((x&57 > 0) \/ (x&99 > 0)) → (x&А > 0) 

_St-23_10-kege-15(a)

(x + 2y > 48) ∨ (y > x) ∨ (x + 3y < A) 

будет ложным?

_St-24_10-kege-15(a)

_St-24_12-kege-15(a)