| | | |
|
Подпоследовательность
Остатки
Напишите программу, которая в некоторой последовательности целых чисел находит подпоследовательность наименьшей длины, сумма элементов в которой является числом, оканчивающимся на 6 или более нулей (делится без остатка на 1000000).
Первая строка ввода содержит одно целое число N (2 ≤ N ≤ 100000). Вторая строка ввода содержит N целых чисел в диапазоне от 1 до 109, разделенных пробелами.
Вывести два целых числа – количество элементов в подпоследовательности и номер её первого элемента. Если существует несколько вариантов такой подпоследовательности с наименьшей длиной, выведите подпоследовательность с наименьшим номером первого элемента. Если такой подпоследовательности не существует – выведите одно число –1.
|
Ввод |
Вывод |
|
6
1 2 701000 299000 1000 999000
|
2 3 |
3
1 2 3 |
-1 |
| |
![]()
|
|
Разложение числа на 5 и 3
Остатки
На сколько пятерок и троек можно разложить число, чтобы количество разложений было минимально.
Входные данные
На вход подается одно натуральное число N (\(7 < N < 1000\)).
Выходные данные
Выведите два целых числа через пробел: число пятерок и число троек.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
8 |
1 1 |
| 2 |
11 |
1 2 |
| 3 |
15 |
3 0 |
| |
![]()
|
|
Тройной Фибоначчи
Остатки
Пятиклассник Лёня недавно прочитал статью о числах Фибоначчи.
Числами Фибоначчи называется числовая последовательность F1 , F2 , ..., Fn , ... , которая устроена следующим образом: F1 = 1 , F2 = 2 , а каждое следующие число вычисляется как сумма двух предыдущих: если i ≥ 3 , то Fi = Fi - 1 + Fi - 2 . Последовательность чисел Фибоначчи, таким образом, начинается с чисел 1, 2, 3, 5, 8, 13, 21, ... .
Сегодня Лёня изучает числа Фибоначчи с номерами от L до R , включительно. Так как Лёня очень любит число 3, ему стало интересно, сколько чисел Фибоначчи среди тех, которые он изучает сегодня, делятся на 3. Например, если L = 3 и R = 7 , то Лёня будет изучать числа F3 = 3 , F4 = 5 , F5 = 8 , F6 = 13 и F7 = 21 . Среди них на 3 делятся два числа: F3 = 3 и F7 = 21 .
Напишите программу, которая поможет Лёне найти ответ на волнующий его вопрос.
Входные данные
Первая строка входных данных содержит число L , а вторая — число R ( 1 ≤ L ≤ R ≤ 105 ).
Выходные данные
Выведите единственное число — количество чисел Фибоначчи с номерами от L до R , включительно, которые делятся на 3.
| № |
Входные данные |
Выходные данные |
| 1 |
3
7 |
2 |
| |
![]()
|
|
Конфеты детям
Остатки
Арифметические алгоритмы (Теория чисел)
На детском празднике дети водили хороводы. Как только музыка закончила играть, дети всё ещё стояли в кругу. Тут Лена вспомнила, что родители дали ей коробку с k конфетками «Wilky May». Лена не жадина, поэтому она решила раздать все свои конфетки друзьям из хоровода. Лена знает, что некоторые её друзья сладкоежки, а некоторые нет. Сладкоежки берут из коробки две конфетки, если в коробке есть хотя бы две конфетки, а иначе берут одну. Остальные друзья Лены всегда берут ровно одну конфетку из коробки.
Чтобы начать раздавать конфетки, Лена вышла из хоровода, после чего в хороводе остались n ее друзей. Чтобы раздавать конфетки было проще, Лена присвоила каждому другу в хороводе номер в порядке по часовой стрелке, начиная с её лучшего друга Ромы, который получил номер 1.
Лена дала коробку другу, который получил номер l, после чего каждый друг Лены, начиная с друга с номером l, брал конфетки из коробки и передавал коробку следующему в порядке по часовой стрелке другу. После того, как друг с номером r взял конфетки, в коробке конфеток не осталось. Обратите внимание, что возможно, что некоторые друзья Лены брали конфетки из коробки несколько раз, то есть коробка могла пройти несколько полных кругов по хороводу.
Лена не знает, кто из ее друзей сладкоежки, но ее интересует, сколько максимум из её друзей могут быть сладкоежками. Если же такой ситуации не могло случиться, и Лена ошиблась в своих наблюдениях, сообщите ей об этом.
Входные данные
В единственной строке задаются четыре целых числа n, l, r, k (1 ≤ n, k ≤ 1011 , 1 ≤ l, r ≤ n ) — количество детей в хороводе, номер друга, которому Лена отдала коробку конфет, номер друга, который взял последнюю конфетку, и количество конфет в коробке, соответственно.
Выходные данные
Выведите одно целое число — максимально возможное количество сладкоежек среди друзей Лены или « -1 » (без кавычек), если Лена ошиблась в своих наблюдениях.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
4 1 4 12 |
2 |
Любые два друга могут быть сладкоежками, тогда каждый два раза получит коробку конфет и последним, кто возьмёт конфету, будет четвёртый человек. |
| 2 |
5 3 4 10 |
3 |
Сладкоежками могут быть любые три друга, кроме друга, стоящего на третьем месте. |
| 3 |
10 5 5 1 |
10 |
Только один друг возьмёт одну конфетку, но он может быть сладкоежкой, просто он не может взять две конфеты. Все остальные в кругу тоже могут быть сладкоежками, но они не могут взять ни одной конфеты. |
| 4 |
5 4 5 6 |
-1 |
Лена ошиблась и такой ситуации быть не могло. |
| |
![]()
|
|
Раздача конфет
Остатки
ЕГЭ - вычислительные задачи
У Анны Николаевны есть N ящиков с конфетами. В i-м ящике лежит Ai количество конфет. Анна Николаевна достает конфеты из нескольких последовательных коробок и равномерно раздает их M детям. Найдите количество пар (l, r), удовлетворяющих следующим условиям:
- l и r целые числа и удовлетворяют условию 1<=l<=r<=N;
- Al + Al+1 + ... + Ar делится на M.
Входные данные
Программа получает на вход две строки. Первая строка содержит два целых числа N (1<=N<=105) и M (2<=M<=109). Вторая строка содержит N чисел Ai (1<=Ai<=109, 1<=i<=N).
Выходные данные
Выведите количество пар (l, r), удовлетворяющих условиям. Обратите внимание, что число может не соответствовать 32-битному целочисленному типу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 2
4 1 5 |
3 |
| 2 |
13 17
29 7 5 7 9 51 7 13 8 55 42 9 81 |
6 |
| |
![]()
|
|
Банды Фомина №2
Префиксные суммы(минимумы, ...)
Малая теорема Ферма
Остатки
Быстрое возведение в степень
Банда Фомина состоит из n групп, в каждой из которых ai человек. Планируется провести q рейдов. В i-ом рейде будет участвовать ровно один разбойник из каждой группы, номер которой лежит в отрезке \([l_i, r_i]\).
Мелехов тоскует, поэтому для каждого рейда он решил посчитать количество возможных отрядов по модулю \(10^9 + 7\). Однако Григорий постоянно находится в раздумьях о смысле жизни и поиске правды, поэтому он не может сконцентрироваться на расчетах и просит вас помочь.
Входные данные
В первой строке дано число n (\(1 <= n <= 10^5\)) – количество групп в банде Фомина.
Во второй строке дано n натуральных чисел ai (\(1 <= a_i <= 10^6\)) – количество человек в i-ой группе.
В третьей строке дано число q – количество рейдов.
Далее дано q строк, в каждой из которых дано два числа – li и ri (\(1 <= l_i <= r_i <= n\)) – номера групп, участвующих в i-ом рейде.
Выходные данные
Выведите q чисел, каждое в отдельной строке – ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6
1 3 7 1 4 100
3
1 3
3 4
2 6 |
21
7
8400 |
| |
![]()
|
|
Лесопилка
Динамическое программирование
Остатки
Недавно на лесопилку, где работает Вася, поступил новый заказ. Для постройки нового дома мэру соседнего города требуется a досок длины x футов и b досок длины y футов.
Поскольку на лесопилке имеется только неограниченный запас досок длины z футов, Васе поручили исполнить заказ клиента, распилив имеющиеся доски на меньшие. Вася хочет закончить работу как можно быстрее, поэтому он хочет выполнить заказ, сделав как можно меньше распилов. При этом количество использованных досок длины z роли не играет, кроме того, часть досок, образовавшихся в результате распила, может не требоваться для заказа и остаться на лесопилке.
Например, если на лесопилке имеются доски длины 80, а клиенту требуется две доски длины 30 и семь досок длины 20, то достаточно сделать семь распилов: одну доску распилить двумя распилами на доски длины 20, 30 и 30, одну тремя распилами на четыре доски длины 20 и одну двумя распилами на доски длины 20, 20 и 40. Доска длины 40 клиенту не нужна, она останется на лесопилке, остальные доски будут отправлены клиенту.
Входные данные
На вход программы поступают числа a, x, b, y и z. Все числа положительны и не превышают 300, x<=z, y<=z, x!=y.
Выходные данные
Выведите минимальное количество распилов, которые требуется сделать для того, чтобы выполнить заказ.
| Ввод |
Вывод |
| 2 30 7 20 80 |
7 |
| |
![]()
|
|
Контрольный блок
Остатки
Фирма Macrohard разработала новый протокол обмена данными по сети. Каждый блок данных при этом обмене состоит из N
чисел в диапазоне от 0 до M-1 включительно. Чтобы повысить надежность передачи, вместе с блоком данных пересылается контрольный блок такой же длины.
Предположим, что исходный блок состоит из чисел a1, a2,…,aN. Тогда, контрольный блок состоит из чисел b1, b2,…,bN, из диапазона от 0 до M-1 включительно таких, что выполняются следующие равенства: b1 = (aN + bN) mod M, b2 = (a1 + b1) mod M, ... , bN = (aN-1 + bN-1) mod M (обозначение X mod M обозначает остаток от деления X на M, например, 7 mod 4 = 3, 6 mod 2 = 0).
Блоки данных, для которых нельзя построить контрольный блок, удовлетворяющий указанному свойству, считаются подозрительными и их передача по сети не разрешается.
Ваня хочет поступить на работу программистом в фирму Macrohard, и в качестве вступительного задания ему поручили написать процедуру построения контрольного блока для заданного блока данных. Помогите ему!
Входные данные
В первой строке вводятся числа N и M (1 <= N <= 1000, 2 <= M <= 109). Следующая строка содержит блок данных, для которого следует построить контрольный блок, числа разделены пробелами.
Выходные данные
В первой строке выведите YES, если для данного блока данных можно построить контрольный блок, и NO, если нельзя. В случае, если контрольный блок построить можно, во второй строке выведите контрольный блок. Числа разделяйте пробелами. Если решений несколько, можно выдать любое из них.
| |
![]()
|
|
Похожие матрицы
Остатки
Обход в глубину
Рассмотрим таблицу, состоящую из N строк и M столбцов. Если в каждой ячейке такой таблицы стоит целое число, назовем такую таблицу целочисленной матрицей. Скажем, что эта матрица кратна чиcлу p, если все числа в ее ячейках кратны p.
Рассмотрим теперь суммы элементов матрицы по строкам и столбцам соответственно. Обозначим сумму чисел i-й строки за Hi, а сумму чисел j-го столбца за Vj. Упорядоченный набор чисел (H1, H2, …, HN, V1, V2, …, VM) назовем профилем матрицы. Скажем, что матрица почти кратна p, если все числа, входящие в ее профиль, кратны p. Почти кратная 5 матрица и ее профиль изображены на рисунке 1.
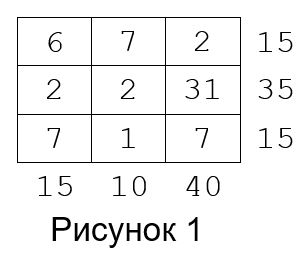
Если две матрицы A и B имеют одинаковый размер, причем элемент, стоящий на пересечении i-й строки и j
-го столбца в матрице A отличается от соответствующего элемента матрицы B не более чем на p, скажем, что A отличается от B не более чем на p. Скажем, что матрица B похожа на матрицу A относительно числа p, если
1. отличается от не более чем на p
2. профили B и A совпадают.
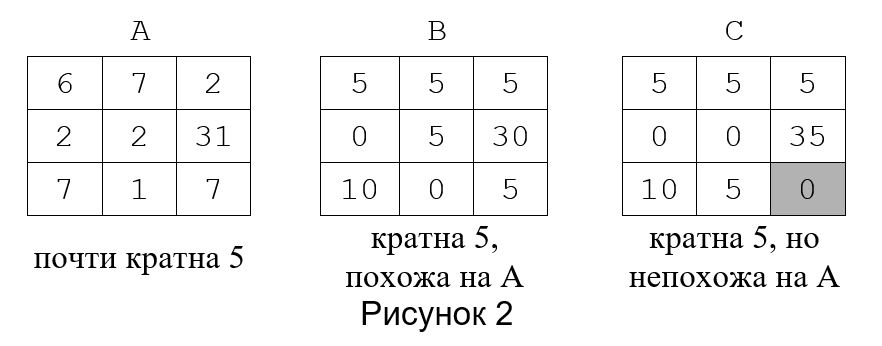
На рисунке 2 изображены две похожие относительно числа 5 матрицы, первая из них почти кратна 5, а вторая кратна 5. Третья матрица на рисунке 2 тоже кратна 5, но непохожа на первую (хотя похожа на вторую).
Дано число p и почти кратная p матрица A. Ваша задача - найти такую матрицу B, чтобы она была кратна p и похожа на A относительно p.
Входные данные
В первой строке входных данных задаются целые числа p (1 <= p <= 10), N и M (1 <= N, M <= 30). Следующие N строк содержат по M целых неотрицательных чисел, не превышающих 1000, которые являются элементами исходной матрицы A.
Выходные данные
Выведите матрицу B по строкам - сначала M элементов первой строки, затем M элементов второй, и т. д. Разделяйте числа пробелами и/или переводами строк. Заботиться о красивом форматировании таблицы не надо. Если искомой матрицы не существует, выведите единственное число - "-1". Если решений несколько, выведите любое из них.
| |
![]()
|
|
Игра с калькулятором
Остатки
В калькулятор вводится натуральное число K и нажимается клавиша "+". Калькулятор всё ещё показывает K. Цель игры: получить на экране число, состоящее из одинаковых цифр. Для её достижения можно производить только одно действие - нажимать на клавишу "=" (возможно, 0 раз). После первого нажатия получается результат K + K, после очередного нажатия результат увеличивается на K. Требуется определить, удастся ли достичь цели, а если удастся, то какое число, состоящее из одинаковых цифр, будет получено первым. Количество отображаемых калькулятором цифр считать неограниченным, время работы батареек - тоже.
1 <= K <= 999.
Входные данные
В первой строке находится одно число - K.
Выходные данные
Если цели достичь невозможно, вывести "Impossible", если возможно, вывести два числа через пробел: цифру, из которой состоит искомое число, и количество цифр в числе.
| |
![]()
|