| | | |
|
Игра с пешкой
Динамическое программирование на таблицах
Простые игры
В левой нижней клетке шахматной доски размера N×N стоит пешка. Двое игроков по очереди двигают её, причём каждый может подвинуть её на одну клетку вверх или на одну клетку вправо. На диагонали доски написаны числа a1, a2, …, aN. Когда пешка попадает на диагональ, игра кончается и выигрыш первого игрока равен значению числа, написанного в клетке с остановившейся пешкой. Напишите программу определения гарантированного выигрыша первого игрока.
Входные данные
В первой строке записано число N (1 ≤ N ≤ 100). Во второй строке записаны натуральные числа a1, a2, …, aN (1 ≤ ai ≤ 100).
Выходные данные
Выведите одно число – выигрыш первого игрока.
|
Ввод |
Вывод |
|
8
3 1 4 1 5 9 2 6
|
5 |
| |
![]()
|
|
Определите победителя
Динамическое программирование на таблицах
Простые игры
Вася и Петя играют в следующую игру. Они берут колоду из 36 карточек. На каждой карточке написано число от 1 до 9 и каждая карточка покрашена в один из 4 цветов так, что есть ровно по 9 карточек каждого цвета и они пронумерованы числами от 1 до 9. Карты перемешиваются, и игрокам раздается по 18 карт.
Дальше игроки по очереди делают ходы. За один ход игрок может выложить на стол одну карточку по следующим правилам. Карточку с цифрой 5 можно выкладывать на стол в любой момент. Карточку с другой цифрой можно выкладывать только если на стол уже выложена карточка того же цвета, на которой написано число на 1 большее или на 1 меньшее, чем на данной карточке (не важно, была ли эта карточка выложена вами или вашим противником, и была ли она выложена на предыдущем ходе или раньше). Если игрок может выложить хоть какую-то карточку, он обязан делать ход. Если ни одну карточку игрок выложить не может, он пропускает ход.
Выигрывает тот, кто первым выложит все свои карточки на стол.
Напишите программу, которая по информации о том, кому какие карточки достались, определяет, кто выиграет при оптимальной игре обоих игроков.
Входные данные
Во входном файле записаны 18 пар чисел, описывающих карточки, которые достались первому игроку. Каждая карточка описывается двумя числами — номером цвета (от 1 до 4) и цифрой, которая написана на карточке (от 1 до 9). Второму игроку, соответственно, достались все остальные карточки.
Выходные данные
В выходной файл выведите одно число (1 или 2) — номер игрока, который выиграет при оптимальной игре обоих игроков.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 1
1 2
1 3
1 4
1 5
1 6
1 7
1 8
1 9
2 1
2 2
2 3
2 4
2 5
2 6
2 7
2 8
2 9 |
1 |
| |
![]()
|
|
Энергичная черепаха
Динамическое программирование на таблицах
Дана сетка с N + 1 рядами и M + 1 столбцами. Черепаха находится на клетке (0, 0) и хочет попасть в клетку (N, M). Черепаха может идти только вверх или вправо. На сетке в K клетках находятся ловушки. Если черепаха пойдет в одну из этих клеток, то она перевернется. У черепашки есть силы для того, чтобы встать не более чем T раз. Посчитайте, сколькими различными путями черепаха может попасть в клетку (N, M). Так как это число может быть очень большим, выведите остаток от его деления на Z.
Входные данные
В первой строке входного файла задается 5 целых чисел: N, M, K, T и Z (1 ≤ N,M ≤ 300000, 0 ≤ K, T 20, 1 ≤ Z ≤ 109). В каждой из следующих K строк расположены координаты соответствующей клетки с ловушкой X, Y (0 ≤ X ≤ N, 0 ≤ Y ≤ M). Гарантируется, что все клетки с ловушками различные и в клетках (0, 0) и (N, M) ловушек нет.
Выходные данные
Выведите требуемое число.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 1 1 0 100
0 1 |
1 |
| 2 |
2 2 0 0 10 |
6 |
| |
![]()
|
|
K-й путь
Динамическое программирование на таблицах
У вас есть таблица c N строками и M столбцами. В каждой ячейке таблицы записана одна строчная буква английского алфавита. Рассмотрим все возможные пути от левого верхнего угла до правого нижнего угла, если вам разрешено идти только вправо и вниз. Конкатенация букв в порядке обхода составляют строку. Скажем, что эта строка - значение пути. Теперь рассмотрим все такие пути и отсортируем их значения в алфавитном порядке. Ваша задача найти значение K-го пути в этом отсортированном листе.
Входные данные
В первой строке задается два целых числа N - количество рядов и M - количество столбцов заданной таблицы (1 <= N, M <= 30). Каждая из следующих N строк содержит ровно M строчных букв английского алфавита. Последняя строка входного файла содержит целое число K (1 <= K <= 1018). Гарантируется, что для K ответ всегда существует.
Выходные данные
Выведите ответ на задачу
Пояснения к примеру
abcdgk, abcdgk, abcdjk, abfdgk, abfdjk, abfijk, aefdgk, aefdjk, aefijk, aehijk
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 4
abcd
efdg
hijk
4 |
abfdgk |
| |
![]()
|
|
Симпатичные узоры
Динамическое программирование на таблицах
Динамическое программирование по профилю
Компания BrokenTiles планирует заняться выкладыванием во дворах у состоятельных клиентов узоров из черных и белых плиток, каждая из которых имеет размер 1 х 1 метр. Известно, что дворы всех состоятельных людей имеют наиболее модную на сегодня форму прямоугольника N х M метров. Однако при составлении финансового плана у директора этой организации появилось целых две серьезных проблемы: во-первых, каждый новый клиент, очевидно, захочет, чтобы узор, выложенный у него во дворе, отличался от узоров всех остальных клиентов этой фирмы, а во-вторых, этот узор должен быть симпатичным.

Как показало исследование, узор является симпатичным, если в нем нигде не встречается квадрата 2 х 2 метра, полностью покрытого плитками одного цвета. Для составления финансового плана директору Васе необходимо узнать, сколько клиентов он сможет обслужить, прежде чем симпатичные узоры данного размера закончатся. Помогите ему!
Входные данные
Вводятся два положительных целых числа N и M (1 ≤ N · M ≤ 30).
Выходные данные
Выведите единственное число – количество различных симпатичных узоров, которые можно выложить во дворе размера N х M. Узоры, получающиеся друг из друга сдвигом, поворотом или отражением, считаются различными.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 2 |
4 |
| 2 |
2 3 |
50 |
| |
![]()
|
|
Количество маршрутов в прямоугольной таблице
Динамическое программирование на таблицах
В прямоугольной таблице NxM в левой верхней клетке стоит шашка. За один ход разрешается переместить шашку в соседнюю клетку либо вправо, либо вниз (влево и вверх перемещаться запрещено). Посчитайте, сколько есть вариантов переместить шашку в правую нижнюю клетку.
Входные данные
Вводятся два числа N и M - размеры таблицы (1<=N<=10, 1<=M<=10).
Выходные данные
Выведите искомое количество вариантов.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 3 |
3 |
| |
![]()
|
|
Биномиальные коэффициенты
Динамическое программирование на таблицах
Для биномиальных коэффициентов (числа сочетаний из n по k) хорошо известна рекуррентная формула: \(C^k_n=C^{k-1}_{n-1}+C^{k}_{n-1}\), \(C^0_n = C^n_n=1\).
Входные данные
Вводится 2 числа - n и k.
Выходные данные
Необходимо вывести значение \(С^k_n\) .
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 2 |
6 |
| |
![]()
|
|
Число сочетаний
Цикл for
Динамическое программирование на таблицах
По данным натуральным n и k вычислите значение \(C^k_n = {n! \over k!(n-k)!}\) (число сочетаний из n элементов по k).
Входные данные
Вводятся 2 числа - n и k (n, k ≤ 30 ).
Выходные данные
Необходимо вывести значение \(C^k_n\) (целое число).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2
1 |
2 |
| |
![]()
|
|
Ускорители для Деда Мороза
Динамическое программирование на таблицах
Алгоритмы на графах
Элементарная геометрия
Дед Мороз за ночь должен посетить N городов. У него есть двумерный план расположения всех городов. План нарисован в декартовой системе координат, в которой точкой (0, 0) обозначено место старта Деда Мороза. Каждый город на плане отмечен точкой с координатой (Xi, Yi). Также на карте обозначены M точек с координатами (Pi, Qi), в которых расположены ускорители. Чтобы успеть разнести все подарки, Дед Мороз может воспользоваться ускорителем, который увеличивает его скорость в два раза (а может им и не пользоваться).
Дед Мороз в Новогоднюю ночь начинает с места старта, посещает все N городов и возвращается обратно.
Начальная скорость Деда Мороза равна 1. Найдите наименьшее время, необходимое Деду Морозу, чтобы посетить все города и вернуться обратно. Временем, при котором он раскладывает все подарки будем пренебрегать!
Входные данные
Первая строка входных данных содержит два целых числа N и M (1 <= N <= 12, 0 <= M <=5). Следующие N строк содержат координаты городов (Xi, Yi). Далее идут M строк с координатами ускорителей (Pi, Qi). Все координаты различны и среди них нет координаты (0, 0).
Выходные данные
Выведите ответ на задачу, с точностью не менее 6 знаков после запятой.
Примеры
| № |
Входные данные |
Выходные данные |
Примечание |
| 1 |
2 1
1 1
0 1
1 0 |
2 1
1 1
0 1
1 0 |
Вот один из оптимальных способов разнести все подарки
- Пройти расстояние 1 от начала координат до ускорителя 1 со скоростью 1, затратив время 1.
- Пройти расстояние 1 от ускорителя 1 до города 1 со скоростью 2, затратив время 0,5.
- Пройти расстояние 1 от города 1 до города 2 со скоростью 2, затратив время 0,5.
- Пройти расстояние 1 от города 2 до начала координат со скоростью 2, затратив время 0,5.
|
| 2 |
2 1
1 1
0 1
100 0 |
3.4142135624 |
Вот один из оптимальных способов разнести все подарки
- Пройти расстояние 1.41... от начала координат до города 1 со скоростью 1, затратив время 1.41....
- Пройти расстояние 1 от города 1 до города 2 со скоростью 1, затратив время 1.
- Пройти расстояние 1 от города 2 до начала координат со скоростью 1, затратив время 1.
|
| 3 |
1 2
4 4
1 0
0 1 |
4.3713203436 |
Вот один из оптимальных способов разнести все подарки
- Пройти расстояние 1 от начала координат до ускорителя 1 со скоростью 1, затратив время 1.
- Пройти расстояние 1,41... от ускорителя 1 до ускорителя 2 со скоростью 2, затратив время 0,707....
- Пройти расстояние 5 от ускорителя 2 до города 1 со скоростью 4, затратив время 1,25.
- Пройти расстояние 5,65... от города 1 до начала координат со скоростью 4, затратив время 1,41....
|
| |
![]()
|
|
Черепаха
Динамическое программирование
Динамическое программирование на таблицах
Черепаха хочет переползти из левого верхнего угла поля размером N на M клеток ( 1 ≤ N , M ≤ 16 ) в правый нижний. За один шаг она может переместиться на соседнюю клетку вправо или на соседнюю клетку вниз. Определите, сколькими различными способами Черепаха может добраться до цели.
Входные данные
Входная строка содержит два натуральных числа: размеры поля N и M , разделённые пробелом ( 1 ≤ N , M ≤ 16 ).
Выходные данные
Программа должна вывести одно число: количество различных маршрутов из левого верхнего угла поля в правый нижний.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 3 |
6 |
| |
![]()
|
|
Маршрут максимальной стоимости
Динамическое программирование: два параметра
Динамическое программирование на таблицах
В прямоугольной таблице NxM (в каждой клетке которой записано некоторое число) в начале игрок находится в левой верхней клетке. За один ход ему разрешается перемещаться в соседнюю клетку либо вправо, либо вниз (влево и вверх перемещаться запрещено). При проходе через клетку с игрока берут столько у.е., какое число записано в этой клетке (деньги берут также за первую и последнюю клетки его пути).
Требуется найти наибольшую сумму у.е., заплатив которую игрок может попасть в правый нижний угол, а также маршрут, на котором достигается эта сумма.
Входные данные
В первой строке записаны два числа N и M - размеры таблицы (1<=N<=100, 1<=M<=100). Далее записаны N строк по M чисел в каждой - размеры штрафов в у.е. за прохождение через соответствующие клетки (каждое число от 0 до 100).
Выходные данные
Первая строка выходных данных содержит максимальную возможную сумму, вторая – маршрут, на котором достигается эта сумма. Маршрут выводится в виде последовательности, которая должна содержать N-1 букву D, означающую передвижение вниз и M-1 букву R, означающую передвижение направо. Если таких последовательностей несколько, необходимо вывести ровно одну (любую) из них.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 5
9 9 9 9 9
3 0 0 0 0
9 9 9 9 9
6 6 6 6 8
9 9 9 9 9
|
74
D D R R R R D D
|
| |
![]()
|
|
Дамка
Динамическое программирование
Динамическое программирование на таблицах
Домовой Кузьма очень любит играть в шашки на доске 8х8. Когда никто не хочет с ним играть, он просто сидит и думает. Например, сейчас он пытается посчитать сколько есть вариантов провести белую шашку в дамки, если она находится одна на доске?
(Белая шашка ходит по диагонали на одну клетку вверх-вправо или вверх-влево. Шашка проходит в дамки, если попадает на верхнюю горизонталь.)
Входные данные
Вводятся два числа от 1 до 8: номер номер столбца (считая слева) и строки (считая снизу), где изначально стоит шашка.
Выходные данные
Выведите одно число - количество вариантов.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 7 |
2 |
| 2 |
1 8 |
1 |
| 3 |
3 6 |
4 |
| |
![]()
|
|
Муравьиная ферма
Динамическое программирование
Динамическое программирование на таблицах
У мальчика Пети есть муравьиная ферма. На ферме есть участок прямоугольной формы, состоящий из NxM квадратов. В правом нижнем квадрате данной области имеется дырка, благодаря которой можно сбежать с фермы. Каждый день очередной муравьишка начинает свой путь с левой верхней клетки. Далее он перемещается в соседнюю клетку либо вправо, либо вниз (влево и вверх перемещаться он не может), и двигается так до достижения правой нижней клетки. Затем он выбирается наружу. Каждый муравьишка двигается своим уникальным путем (т.е. никакой муравей не повторяет ни один путь другого). Если муравей не может пойти по своему уникальному пути, то он остается на ферме. Посчитайте, сколько муравьев сбежит с фермы и поселится в комнате Пети.
Входные данные
Вводятся два числа N и M - размеры таблицы ( \(1<=N<=10\), \(1<=M<=10\)).
Выходные данные
Выведите искомое количество способов.
Примечание
При указанных ограничениях число способов входит в тип Longint.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 10 |
1 |
| |
![]()
|
|
Го
Динамическое программирование на таблицах
Петя играет с Васей в игру Го на доске размером NxM. По окончании игры вся доска была заполнена черными и белыми камешками. Петя играл черными камешками, а Вася - белыми. Теперь Петя хочет узнать квадрат с наибольшей площадью, который состоит только из его камешков.
Обозначим условно на доске черные камешки единицей, белые камешки - нулем. По заданному расположению камешков на доске, помогите Пете определить площадь такого квадрата.
Входные данные
В первой строке записаны 2 натуральных числа N и M - размер доски для игры в Го. Следующие N строк содержат по M чисел ai,j. Каждое число ai,j= 1 если на этой клетке расположен черный камушек и 0, если на ней расположен белый камушек.
Ограничения
n == количество строк в матрицеm == количество столбцов в матрице1 <= n, m <= 300a[i][j] это 0 или 1.
Выходные данные
Выведите максимальную площадь квадрата, состоящего из камушков Пети.
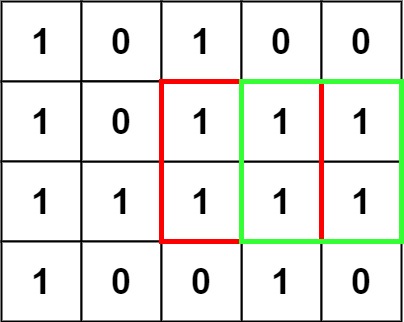
Рисунок выше относится к примеру № 1
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 5
1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0
|
4
|
| 2 |
2 2
0 1
1 0
|
1
|
| |
![]()
|
|
Приключение
Динамическое программирование на таблицах
Жадный алгоритм
Теплым весенним днем группа из N школьников-программистов гуляла в окрестностях города Кисловодска. К несчастью, они набрели на большую и довольно глубокую яму. Как это случилось — непонятно, но вся компания оказалась в этой яме.
Глубина ямы равна H. Каждый школьник знает свой рост по плечи hi и длину своих рук li. Таким образом, если он, стоя на дне ямы, поднимет руки, то его ладони окажутся на высоте hi + li от уровня дна ямы. Школьники могут, вставая друг другу на плечи, образовывать вертикальную колонну. При этом любой школьник может встать на плечи любого другого школьника. Если под школьником i стоят школьники j1, j2, …, jk, то он может дотянуться до уровня hj1 + hj2 + … + hjk + hi + li.
Если школьник может дотянуться до края ямы (то есть hj1 + hj2 + … + hjk + hi + li ≥ H), то он может выбраться из нее. Выбравшиеся из ямы школьники не могут помочь оставшимся.
Найдите наибольшее количество школьников, которые смогут выбраться из ямы до прибытия помощи, и перечислите их номера.
Формат входных данных
В первой строке входных данных задается натуральное число N (1 ≤ N ≤ 2000) — количество школьников, попавших в яму.
Далее в N строках содержится по два целых числа: рост i-го школьника по плечи hi (1 ≤ hi ≤ 105) и длина его рук li (1 ≤ li ≤ 105).
В последней строке указано целое число — глубина ямы H (1 ≤ H ≤ 105).
Формат выходных данных
В первой строке выведите K — максимальное количество школьников, которые смогут выбраться из ямы. Если K > 0, то во второй строке в произвольном порядке выведите их номера, разделяя их пробелами. Школьники нумеруются с единицы в том порядке, в котором они заданы во входных данных. Если существует несколько решений, выведите любое.
| |
![]()
|
|
Максимальная сумма
Динамическое программирование на таблицах
Сегодня на страницах газеты <<Математический досуг>> была опубликована необычная математическая головоломка. Одна из страниц газеты полностью занята прямоугольной таблицей, состоящей из \(m\) строк и \(n\) столбцов. В каждой ячейке таблицы записано некоторое целое число.
Для решения головоломки требуется найти такой невырожденный прямоугольник с вершинами в центрах ячеек таблицы, и сторонами, параллельными сторонам таблицы, чтобы сумма чисел, записанных в ячейках на границе получившегося прямоугольника, была максимальна.
Безуспешно потратив несколько часов на решение головоломки, Саша решил написать программу, которая сделала бы это за него. Но и тут его постигла неудача. Теперь ему ничего не остается, как обратиться за помощью к вам.
Напишите программу, которая по заданной таблице найдет искомый прямоугольник.
Формат входных данных
На первой строке записаны два целых числа \(m\) и \(n\) (\(2 \le m, n \le 300\)). Далее следует описание таблицы — \(m\) строк, каждая из которых содержит по \(n\) целых чисел \(a_{i,j}\) (\(-10^4 \le a_{i,j} \le 10^4\)).
Формат выходных данных
На первой строке выведите целое число \(s\) — максимальную сумму чисел на границе искомого прямоугольника. На второй строке выведите четыре натуральных числа: \(x_1, y_1, x_2, y_2\) — координаты левой верхней и правой нижней ячейки выбранного прямоугольника, соответственно (здесь \(x\) — номер строки, а \(y\) — номер столбца, строки нумеруются сверху вниз, начиная с единицы, столбцы нумеруются слева направо, начиная с единицы). Если оптимальных решений несколько, выведите любое.
| |
![]()
|
|
Игра
Динамическое программирование на таблицах
Поле для детской игры представляет собой последовательность кружков, первый из которых является стартом, а последний – финишем. На некоторых из кружков указано действие, которое нужно совершить фишке, попавшей на этот кружок: передвинуть фишку на несколько кружков вперед или назад, или сделать еще один ход. Изначально фишки всех K игроков ставятся на старт. Затем они по очереди делают ходы, которые заключаются в следующем. Игрок получает очередное "случайное" число, используя генератор псевдослучайных чисел, описанный ниже, и передвигает свою фишку на столько кружков вперед, какое число он получил (если это число больше количества кружков до финиша, то игрок останавливается на финише). Если на кружке, куда он попал в результате своего хода, написано, что требуется совершить некоторое действие, то игрок совершает это действие. После этого он совершает действие, указанное на кружке, куда он попал в результате предыдущего действия и т. д. до тех пор, пока он не попадет на кружок, на котором не указано никакого действия.
Игра заканчивается, как только фишка одного из игроков достигнет финиша. Этот игрок и считается победителем. Требуется написать программу, которая по описанию поля и по данным параметрам генератора псевдослучайных чисел определит, кто выиграет в данной игре.
Генератор псевдослучайных чисел устроен следующим образом. Его параметрами являются натуральные числа a, b, c и x0. Генератор порождает последовательность натуральных чисел x1, x2, x3, … по следующему правилу: xn+1 равно остатку от деления (axn+ b) на c (при n = 0, 1, 2, …). Для игры используются числа x1, x2, x3, … именно в этом порядке (число x0 не используется). Все игроки используют общий датчик, то есть, если, например, первый игрок использовал число x1 и передал ход второму, то тот будет использовать число x2, а если ему потребуется повторить ход, то x3 и т. д.
Входные данные
В первой строке входных данных содержатся числа a, b, c, x0, описывающие генератор псевдослучайных чисел. Все числа целые неотрицательные и не превосходят 1000; c > 0. В следующей строке записаны числа K – количество игроков и L – количество кружков поля, включая старт и финиш (1 ≤ K, L ≤ 1000). В следующих L–2 строках записаны команды во втором, третьем, …, L–1-м кружке (в кружках старта и финиша никаких команд нет и при попадании туда ничего делать не нужно). Каждая команда записывается парой чисел.
Если первое число равно единице, то это означает, что нужно сделать дополнительный ход. При этом, если второе число равно T и T > 0, то нужно сделать ход на T кружков вперед, если T < 0 – то на |T| кружков назад, а если T = 0, то нужно снова воспользоваться датчиком псевдослучайных чисел и сделать указанное им количество шагов вперед.
Если первое число равно нулю, то ничего делать не нужно. (Если первое число равно нулю, то второе число также равно нулю.)
Другие значения первое число принимать не может.
Число T целое, и всегда таково, что при соответствующем ходе фишка не окажется за пределами доски (но может оказаться на клетке Старт или Финиш). Если же T = 0 и очередное "случайное" число больше, чем количество кружков до финиша, то фишка останавливается на финише.
Выходные данные
Выведите одно число – номер игрока-победителя. Гарантируется, что одна из фишек обязательно достигнет финиша, причем за время игры будет совершено не более миллиона перемещений (на "случайное" число или число, указанное в кружке).
| |
![]()
|
|
Космический мусорщик
Динамическое программирование на таблицах
В околоземном космическом пространстве накопилось много мусора, поэтому ученые сконструировали специальный аппарат - ловушку для космического мусора. Для того, чтобы хорошо собирать мусор, этот аппарат должен двигаться по достаточно сложной траектории, сжигая собранный по пути мусор. Ловушка может передвигаться в пространстве по 6 направлениям: на север (N), на юг (S), на запад (W), на восток (E), вверх (U) и вниз (D). Движением ловушки управляет процессор. Программа движения задается шестью правилами движения, которые соответствуют каждому из указанных направлений. Каждое такое правило представляет собой строку символов из множества {N, S, W, E, U, D}.
Команда ловушки есть пара из символа направления и параметра - целого положительного числа M. При исполнении такой команды ловушка в соответствии со своей программой выполняет следующее. Если параметр больше 1, то она перемещается на один метр в направлении, которое указано в команде, а затем последовательно выполняет команды, заданные правилом для данного направления, с параметром меньше на 1. Если же параметр равен 1, то просто перемещается на один метр в указанном направлении.
Пусть, например, заданы следующие правила:
| Направление |
Правило |
| N |
N |
| S |
NUSDDUSE |
| W |
UEWWD |
| E |
|
| U |
U |
| D |
WED |
Тогда при выполнении команды S(3) мусорщик выполнит следующие действия:
1) переместится на 1 метр в направлении S
2) выполнит последовательно команды N(2), U(2), S(2), D(2), D(2), U(2), S(2), E(2).
Если далее проанализировать действия мусорщика при выполнении команд из пункта 2, получим, что в целом он совершит следующие перемещения:
SNNUUSNUSDDUSEDWEDDWEDUUSNUSDDUSEEПо заданной команде определите, какое общее количество перемещений на один метр совершит ловушка при выполнении заданной команды. В приведенном примере это количество равно 34.
Входные данные
Первые шесть строк входных данных задают правила для команд с направлением N, S, W, E, U и D соответственно. Каждая строка содержит не более 100 символов (и может быть пустой). Следующая строка содержит команду ловушки: сначала символ из множества {N, S, W, E, U, D}, затем пробел и параметр команды - целое положительное число, не превышающее 100.
Выходные данные
Выведите единственное число - количество перемещений, которое совершит ловушка. Гарантируется, что ответ не превышает 109.
| |
![]()
|
|
Пузырьки 1D
Динамическое программирование на таблицах
Сережа - большой любитель игр на сотовом телефоне. Недавно он скачал из интернета новую игру "Пузырьки 1D". Опишем правила игры.
Исходная позиция в игре представляет собой N пузырьков, расположенных вертикально в ряд. Каждый пузырек окрашен в один из четырех цветов - красный, зеленый, синий или желтый. Назовем группой несколько следующих подряд пузырьков одинакового цвета, непосредственно сверху и снизу от которых находятся либо пузырьки другого цвета, либо границы ряда пузырьков.
За один ход разрешается выбрать любую группу, состоящую хотя бы из двух пузырьков, и взорвать ее. За взрыв группы, содержащей K пузырьков, игрок получает K2 очков. После взрыва группы пузырьки, которые находились сверху, опускаются вниз.
Например, ниже на рисунке показана позиция, содержащая 10 пузырьков. В ней четыре группы, содержащие 3, 2, 4 и 1 пузырек, соответственно. Если взорвать группу, содержащую четыре пузырька, то игрок получит 16 очков, и верхние 5 пузырьков опустятся вниз. В получившейся позиции 6 пузырьков, и две группы по 3 пузырька в каждой.
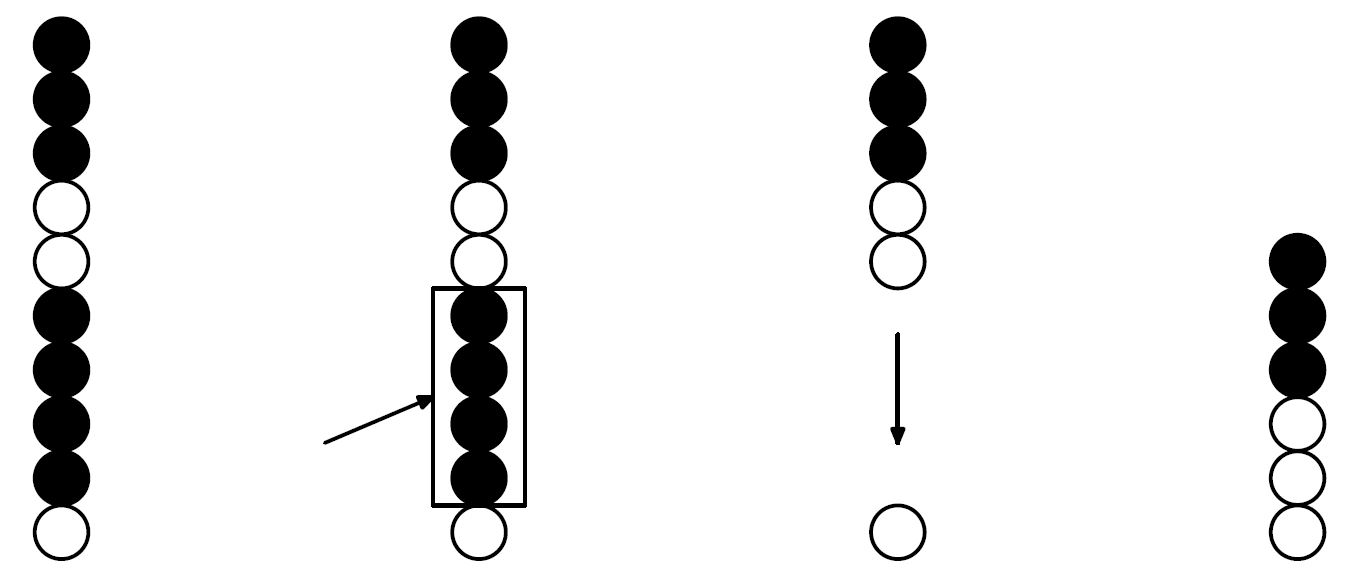
По заданной начальной позиции в игре выясните, сможет ли Сережа уничтожить все пузырьки, и если да, то какое максимальное количество очков он сможет заработать.
Входные данные
На вход программы поступает одна строка, состоящая из букв "R", "G", "B и "Y", описывающая начальную позицию. Буквы задают цвета пузырьков в порядке просмотра сверху вниз ("R" означает красный пузырек, "G" – зеленый, "B" – синий, а "Y" – желтый). В заданной позиции не менее двух и не более 100 пузырьков.
Выходные данные
Выведите одно число – максимальное количество очков, которое сможет заработать Сережа. Если уничтожить все пузырьки невозможно, выведите 0.
Пояснения
В первом примере следует действовать следующим образом: сначала надо взорвать группу из четырех красных пузырьков, получив 16 очков. Затем надо взорвать в любом порядке получившиеся две группы по 3 пузырька, получив по 9 очков за каждую.
| |
![]()
|
|
Движение по полосам
Динамическое программирование на таблицах
|
При организации движения по сложным перекресткам, для того, чтобы траектории водителей, выполняющих различные маневры не пересекались, вводят ограничения на возможные маневры водителей, в зависимости от того, по какой полосе движения водитель подъехал к перекрестку. Для этого используется знак <<движение по полосам>>, на рисунке справа приведен пример такого знака, установленного перед одним из перекрестков в Санкт-Петербурге.
|
|
Рассмотрим дорогу, подходящую к перекрестку, на котором сходится \(m\) дорог. Водитель, подъезжающий к перекрестку по этой дороге, потенциально может продолжить свое движение в \(m\) различных направлениях — обратно по дороге, по которой он приехал, а также по одной из оставшихся \(m - 1\) дорог. Пронумеруем возможные направления числами от 1 до \(m\) слева направо с точки зрения подъезжающего водителя, номер 1 получит разворот и возврат по дороге, по которой водитель подъезжал к перекрестку, номер 2 — поворот на самую левую из дорог, и т. д.
Пусть дорога содержит \(n\) полос для движения. Пронумеруем полосы от 1 до \(n\) слева направо, самая левая полоса получит номер 1, следующая номер 2, и т. д. Знак <<движение по полосам>> разрешает каждой из полос движение по некоторым из \(m\) возможных направлений. При этом должны выполняться следующие условия:
-
если с \(i\)-й полосы разрешено движение в \(a\)-м направлении, а с \(j\)-й полосы — в \(b\)-м направлении, причем \(i < j\), то \(a \le b\);
-
с каждой полосы разрешено движение хотя бы в одном направлении;
-
в каждом направлении разрешено движение хотя бы с одной полосы.
Инспекция по безопасности дорожного движения заинтересовалась, а сколько различных знаков <<движение по полосам>> можно установить перед таким перекрестком. Помогите им найти ответ на этот вопрос.
Формат входных данных
Строка содержит два целых числа: \(m\) и \(n\) (\(2 \le m \le 50\), \(1 \le n \le 15\)).
Формат выходных данных
Выведите одно число — количество возможных знаков <<движение по полосам>>, которые можно установить перед перекрестком.
В примере возможны следующие варианты знаков <<движение по полосам>>:
| разворот |
разворот, налево, прямо, направо |
| разворот |
налево, прямо, направо |
| разворот, налево |
налево, прямо, направо |
| разворот, налево |
прямо, направо |
| разворот, налево, прямо |
прямо, направо |
| разворот, налево, прямо |
направо |
| разворот, налево, прямо, направо |
направо |
| |
![]()
|
|
Представление числа
Динамическое программирование на таблицах
Учительница математики попросила школьников составить арифметическое выражение так, чтобы его значение было равно данному числу N, и записать его в тетради. В выражении могут быть использованы натуральные числа, не превосходящие K, операции сложения и умножения, а также скобки. Петя очень не любит писать, и хочет придумать выражение, содержащее как можно меньше символов. Напишите программу, которая поможет ему в этом.
Входные данные
В первой строке входных данных содержатся два натуральных числа: N (1 <= N <= 10000) - значение выражения и K (1 <= K <= 10000) - наибольшее число, которое разрешается использовать в выражении.
Выходные данные
В единственной строке выведите выражение с данным значением, записывающееся наименьшим возможным количеством символов. Если решений несколько, выведите любое из них.
Примечание
При подсчете длины выражения учитываются все символы: цифры, знаки операций, скобки. В приведенных ниже примерах для справки приводится длина получившейся строки. Выводить ее не нужно.
| |
![]()
|
|
Ломаные
Динамическое программирование на таблицах
На окружности отметили N точек и пронумеровали их последовательно числами от 1 до N. Требуется найти количество различных простых ломаных с вершинами в некоторых из отмеченных точек и с концами в точках с номерами i и j.
Ломаная называется простой, если она не проходит дважды через одну точку (и не содержит самокасаний и самопересечений).
Входные данные
Вводятся три натуральных числа N, i, j (2 ≤ N ≤ 2 000, 1 ≤ i < j ≤ N).
Выходные данные
Требуется вывести остаток от деления количества ломаных на 109.
| |
![]()
|
|
Маршрут
Динамическое программирование на таблицах
В таблице из N строк и N столбцов клетки заполнены цифрами от 0 до 9. Требуется найти такой путь из клетки (1, 1) в клетку (N, N), чтобы сумма цифр в клетках, через которые он пролегает, была минимальной; из любой клетки ходить можно только вниз или вправо.
Входные данные
В первой строке находится число N. В следующих N строках содержатся по N цифр без пробелов. 2 <= N <= 250.
Выходные данные
Выводятся N строк по N символов. Символ решётка показывает, что маршрут проходит через эту клетку, а минус - что не проходит. Если путей с минимальной суммой цифр несколько, вывести любой.
| |
![]()
|
|
Маршрут(2)
Динамическое программирование на таблицах
Дана матрица N*N, заполненная положительными числами. Путь по матрице начинается в левом верхнем углу. За один ход можно пройти в соседнюю по вертикали или горизонтали клетку (если она существует). Нельзя ходить по диагонали, нельзя оставаться на месте. Требуется найти максимальную сумму чисел, стоящих в клетках по пути длиной K (клетку можно посещать несколько раз).
Входные данные
В первой строке находятся разделенные пробелом числа N и K. Затем идут N строк по N чисел в каждой. 2 <= N <= 100, элементы матрицы имеют значения от 1 до 9999, 1 <= K <= 2000, все числа целые.
Выходные данные
Вывести одно число - максимальную сумму.
| |
![]()
|
|
Бегемот
Динамическое программирование на таблицах
Бегемот – это шахматная фигура, которая живет на доске размером 100x100 клеток. За один ход бегемот перемещается на n клеток по горизонтали или вертикали и на m клеток в перпендикулярном направлении. Например, шахматный конь – это бегемотик, у которого n=2, m=1 (или наоборот). Раскрасьте доску, на которой живет бегемот, в два цвета (каждую клетку – в один из двух цветов), так чтобы любой ход из любой клетки приводил бегемота в клетку другого цвета.
Входные данные
Вводятся два натуральных числа n и m, не превосходящие 99.
Выходные данные
Выведите 100 строк по 100 цифр – 1 или 0, обозначающих клетки разного цвета (через пробел).
| |
![]()
|
|
Cамый дешевый путь
Динамическое программирование на таблицах
В каждой клетке прямоугольной таблицы N×M записано некоторое число. Изначально игрок находится в левой верхней клетке. За один ход ему разрешается перемещаться в соседнюю клетку либо вправо, либо вниз (влево и вверх перемещаться запрещено). При проходе через клетку с игрока берут столько килограммов еды, какое число записано в этой клетке (еду берут также за первую и последнюю клетки его пути).
Требуется найти минимальный вес еды в килограммах, отдав которую игрок может попасть в правый нижний угол.
Входные данные
Вводятся два числа N и M — размеры таблицы (1≤N≤20, 1≤M≤20). Затем идет N строк по M чисел в каждой — размеры штрафов в килограммах за прохождение через соответствующие клетки (числа от 0 до 100).
Выходные данные
Выведите минимальный вес еды в килограммах, отдав которую можно попасть в правый нижний угол.
| |
![]()
|
|
Шашку - в дамки
Динамическое программирование на таблицах
На шахматной доске (8x8) стоит одна белая шашка. Сколькими способами она может пройти в дамки?
(Белая шашка ходит по диагонали. на одну клетку вверх-вправо или вверх-влево. Шашка проходит в дамки, если попадает на верхнюю горизонталь.)
Входные данные
Вводятся два числа от 1 до 8: номер столбца (считая слева) и номер строки (считая снизу), где изначально стоит шашка.
Выходные данные
Вывести одно число - количество путей в дамки.
| |
![]()
|
|
Еловая аллея
Динамическое программирование на таблицах
Мэр города Урюпинска решил посадить на главной аллее города, которая проходит с запада на восток, голубые ели. Причем сажать ели можно не во всех местах, а только на специально оставленных при асфальтировании аллеи клумбах.
Как оказалось, голубые ели бывают M различных сортов. Для ели каждого сорта известна максимальная длина ее тени в течение дня в западном и в восточном направлении (Wi и Ei соответственно). При этом известно, что ели растут гораздо лучше, если в течение дня они не оказываются в тени других елей.
Координатная ось направлена вдоль аллеи с запада на восток.
По заданным координатам клумб вычислите максимальное число елей, которое можно посадить, соблюдая условие о том, что никакая ель не должна попадать в тень от другой ели.
Входные данные
Во входном файле записано сначала натуральное число M — количество сортов елей (1<M<100). Затем идет M пар чисел Wi, Ei, описывающих максимальную длину тени в западном и восточном направлении в течение дня для каждого сорта ели (числа Wi, Ei — целые, из диапазона от 0 до 30000). Далее идет натуральное число N — количество клумб, в которых можно сажать ели (1<N<100). Далее идет N чисел, задающих координаты клумб (координаты — целые числа, по модулю не превышающие 30000). Клумбы перечислены с запада на восток (в порядке возрастания их координат).
Примечание
Если на клумбе с координатой X мы посадили ель, максимальная тень которой в восточном направлении равна E, то все клумбы с координатами от X+1 до X+E–1 попадают в тень от этой ели, а клумба с координатами X+E — уже нет. Аналогично для тени в западном направлении.
Выходные данные
В выходной файл выведите сначала число A — максимальное количество елей, которые удастся посадить, а затем A пар чисел, описывающих ели. Первое число каждой пары задает номер клумбы, в которую садится ель. Второе число определяет номер сорта этой ели.
| |
![]()
|
|
Левый лабиринт
Динамическое программирование на таблицах
Алгоритм Дейкстры
Обход в ширину
В спортзале размером NxM метров построили современный аттракцион под названием "Левый лабиринт". Для этого на полу спортзала с интервалом в 1 метр начертили линии, параллельные стенам спортзала. Таким образом, спортзал разбили на NxM клеток. Дальше некоторые из этих клеток покрасили в черный цвет.
Аттракцион заключается в том, что участника ставят в некоторой клетке спортзала и просят как можно быстрее добежать до некоторой другой клетки. При этом накладываются следующие условия:
- Участнику запрещено ходить по черным клеткам.
- Придя в какую-то клетку, участник может пойти либо прямо, либо налево, либо направо (если в соответствующем направлении клетка не покрашена в черный цвет): ходить назад, а также ходить по диагонали запрещается.
- За все время пути участнику разрешается повернуть направо (то есть пойти из текущей клетки направо относительно того, откуда он пришел в данную клетку) не более K раз.
- В начальной клетке участник может встать лицом в ту сторону, в какую ему захочется. С какой стороны участник прибежит в конечную клетку также не важно.
Известно, что на то, чтобы перебежать из клетки в соседнюю, участник тратит ровно 1 секунду. Требуется вычислить минимальное время, за которое участник сможет достичь конечной клетки.
Входные данные
Во входном файле сначала записано число K — количество разрешенных поворотов направо (целое число из диапазона от 0 до 5), затем записаны числа N и M, задающие размеры спортзала — натуральные числа, не превышающие 20. Далее записано N строк по M чисел в каждой. Число 0 обозначает непокрашенную клетку, число 1 — покрашенную, число 2 — клетку, откуда стартует участник и число 3 — клетку, куда нужно добежать (клетки, помеченные 2 и 3 являются непокрашенными). В лабиринте всегда есть ровно одна начальная клетка и ровно одна клетка, в которую нужно попасть.
Выходные данные
В выходной файл выведите минимальное время, за которое можно добраться в конечную клетку. Если попасть в конечную клетку с соблюдением всех условий нельзя, выведите –1.
| |
![]()
|
|
Поиск прямоугольников
Динамическое программирование на таблицах
Клеточная геометрия
На поле NxM клеток (N строк и M столбцов) положили K прямоугольников один поверх другого в случайном порядке. Длины сторон прямоугольников выражаются целым числом клеток. Прямоугольники не выходят за границы поля. Границы прямоугольников совпадают с границами клеток поля.
Получившуюся ситуацию записали в таблицу чисел (каждой клетке поля соответствует клетка таблицы). Если клетка поля не закрыта прямоугольником, то в соответствующую клетку таблицы записали число 0. Если же клетка закрыта одним или несколькими прямоугольниками, то в соответствующую клетку таблицы записали число, соответствующее номеру самого верхнего прямоугольника, закрывающего эту клетку.
По содержимому таблицы требуется определить положение и размеры прямоугольников.
Гарантируется, что во входных данных содержится информация, которой достаточно для однозначного определения размеров прямоугольников.
| 0 |
2 |
2 |
2 |
2 |
| 0 |
2 |
2 |
2 |
2 |
| 1 |
1 |
2 |
2 |
2 |
| 1 |
1 |
0 |
0 |
0 |
Входные данные
В первой строке входного файла записаны целые числа N, M, K (1≤N≤200, 1≤M≤200, 1≤K≤255). Далее следует N строк по M чисел в каждой — содержимое таблицы. Все числа в таблице целые, находятся в диапазоне от 0 до K включительно.
Выходные данные
В выходной файл необходимо выдать K строк. Каждая строка должна описывать соответствующий ее номеру прямоугольник четырьмя числами R C H W (R и C должны описывать координаты левого нижнего угла прямоугольника, а H и W — координаты правого верхнего угла). Числа должны разделяться пробелом.
Оси координат устроены следующим образом: начало координат находится в нижнем левом углу поля, а оси координат направлены вдоль сторон поля (ось Ox — вдоль нижней стороны, а ось Oy — вдоль левой стороны). Клетки поля имеют размер 1x1. Таким образом, координаты левого нижнего угла поля — (0,0), правого верхнего — (M,N). Заметьте, что вы должны вывести координаты углов прямоугольников (как точек) в этой системе координат, а не координаты угловых клеток, покрытых прямоугольниками.
| |
![]()
|