| Условие задачи | | Прогресс | Попытки, все/успешные |
ID 65811.
6
Темы:
Бинарный поиск по ответу
В королевстве Полерам расположен длинный линейный сад из N деревьев, стоящих в один ряд (по порядку с запада на восток). У каждого дерева i (нумерация от 1 до N) имеется некоторый урожай ai — количество собранных яблок (целое число, может быть положительным, нулевым или даже отрицательным, если учитывать затраты или потери).
Королевский интендант хочет упаковывать собранный урожай в большие ящики, рассчитанные ровно на K яблок. Для удобства он рассматривает непрерывные отрезки деревьев [L,R] и проверяет, делится ли сумма (aL )+ (aL+1) + … + (aR) на K без остатка. Если делится, то такой отрезок можно упаковать в ящики без недогруза и перегруза.
Требуется найти общее количество таких отрезков [L,R], для которых сумма урожая деревьев на этом участке кратно K, количество яблонь нечётное, а количество собранных яблок - положительное число.
Примечание:
В отрезке [L, R] должно быть выполнено неравенство 1<= L <= R <= N.
Формат входных данных
Первая строка: два целых числа N и K, (1 <= N <= 200000, 1 <= K <= 106).
Вторая строка: N целых чисел a1, a2, …, aN (-106 <= ai <= 106).
Формат выходных данных
Выведите одно число — количество всех пар (L, R) для которых (aL )+ (aL+1) + … + (aR) делится без остатка на K, количество яблонь нечётное, а количество собранных яблок - положительное число.
Пояснение: в данном примере есть четыре последовательности: (1 + 2), (1 + 2 + 3), (3), (6), в данном случае все с положительным количеством собранных яблок, но только 3 с нечётным количеством яблонь.
| |
![]()
|
20/
2
|
|
Темы:
Бинарный поиск по ответу
Фотографа попросили сделать фотосессию группы детей для выпускного альбома в детском саду. В числе прочих, он должен сделать групповой снимок, на котором должны присутствовать все дети одновременно. Фотограф считает, что для красивой фотографии группы требуется очень тщательно расставить детей в кадре. В частности, с его точки зрения, группа должна расположиться как можно компактнее по ширине, то есть количество людей в самом длинном ряду на фотографии должно быть как можно меньше.
Для гармоничного расположения детей фотограф размещает детей не более чем в четыре ряда. Девочек он располагает либо во втором ряду, сидящими на стульчиках, либо стоящими в третьем ряду. Мальчиков он размещает либо в первом ряду, сидящими на корточках, либо в четвёртом ряду, стоящими на стульчиках. Группа состоит из a мальчиков и b девочек. В студии есть стулья в количестве c штук. Какие-то ряды могут быть пустыми. Все стулья использовать не обязательно.
По заданным числам a, b и c требуется определить, какого наименьшего по ширине расположения группы сможет добиться фотограф.
Формат входных данных
Программа получает на вход три целых неотрицательных числа a, b и c, записанных в отдельных строках — количество мальчиков, девочек и стульев соответственно. Все числа не превосходят 1018 .
Обратите внимание, что значения переменных в этой задаче могут превышать возможные значения 32-битной целочисленной переменной, поэтому необходимо использовать 64-битные целочисленные типы данных (тип int64 в языке Pascal, тип long long в C++, тип long в Java и C#).
Формат выходных данных
Вывести одно целое число — минимальную ширину группы, которую сможет организовать фотограф.
Замечание
Во всех примерах в условии группа состоит из 9 мальчиков и 15 девочек.
В первом примере стульев нет, поэтому все девочки стоят, все мальчики сидят на корточках, общая ширина группы 15.
Во втором примере есть 4 стула. Можно посадить 4 девочек во втором ряду на эти стулья, остальные 11 девочек будут стоять в третьем ряду. Все мальчики будут сидеть на корточках в первом ряду. Общая ширина группы 11.
В третьем примере есть 7 стульев. Тогда есть два способа получить группу ширины 9. Например, можно посадить на все стулья девочек, тогда в первом ряду будет 9 мальчиков, во втором ряду будет 7 девочек, в третьем ряду 8 девочек. Либо можно посадить на стулья 6 девочек и поставить одного мальчика в четвёртый ряд. Тогда получим 8 мальчиков в первом ряду, 6 девочек во втором, 9 девочек в третьем и 1 мальчика в четвёртом. В любом из этих двух случаев ширина группы равна 9.
В четвёртом примере стульев много и есть несколько способов организовать группу ширины 8. Один из способов такой: посадим на корточки 4 мальчика в первом ряду, далее посадим 8 девочек на стулья во втором ряду, оставшиеся 7 девочек встанут в третьем и 5 мальчиков поставим на стульчики в четвёртом.
| |
![]()
|
33/
8
|
|
Темы:
Бинарный поиск по ответу
Аполлинария Прокофьевна и Белла Прокофьевна — две сестры-пенсионерки. Аполлинарии Прокофьевне каждый день необходимо принимать одну таблетку от забывчивости. К сожалению, этот режим она не соблюдает и вспоминает о лекарстве только раз в a дней (то есть приняв лекарство сначала в первый день, в следующий раз она примет его в день номер 1 + a). Белле Прокофьевне каждый день необходимо принимать одну таблетку от жадности. Ко всеобщему огорчению, и её болезнь сильнее лекарства, поэтому каждый день она глотает b таблеток. Внешне эти таблетки выглядят совершенно одинаково и каждая из сестёр считает, что вот этот пузырёк с n пилюлями именно её. На сколько дней им хватит этого количества лекарств?
Формат входных данных
Три строки входных данных содержат три целых числа a, b (1 ≤ a, b ≤ 100) и n (1 ≤ n ≤ 1018).
Обратите внимание, что значения переменных в этой задаче могут превышать возможные значения 32-битной целочисленной переменной, поэтому необходимо использовать 64-битные целочисленные типы данных (тип int64 в языке Pascal, тип long long в C++, тип long в Java и C#).
Формат выходных данных
Программа должна вывести одно число — ответ на задачу.
Замечание
В первом примере Аполлинария Прокофьевна принимает по одной таблетке раз в два дня (начиная с первого), Белла Прокофьевна принимает по три таблетки каждый день. В пузырьке 12 таблеток.
В первый день Аполлинария принимает одну таблетку, а Белла — три. В пузырьке осталось восемь пилюль.
Во второй день Аполлинария забывает принять таблетку, а Белла опять съедает три. В пузырьке осталось пять пилюль.
В третий день Аполлинария принимает одну таблетку, а Белла — три. В пузырьке осталась последняя пилюля, ещё на один день этого количества сёстрам не хватит.
Во втором примере начального количества таблеток не хватит даже на один день.
| |
![]()
|
468/
84
|
|
Темы:
Бинарный поиск по ответу
Вывод формулы
Трое друзей — Аня, Боря и Саша — пришли на детскую площадку, чтобы покачаться на качеляхбалансире. Качели представляют собой длинную балку, закреплённую в центре, на которую дети садятся с разных концов.

Массы детей равны A, B и C кг. Чтобы держать баланс на качелях, разница масс на двух концах качелей должна быть не более D кг. Друзьям повезло: рядом с площадкой оказалась груда достаточно тяжёлых камней. Один из детей может взять с собой любой камень, чтобы сделать разность масс на концах качелей допустимой. Помогите друзьям определить минимальную массу камня, благодаря которому они смогут покачаться на качелях.
Формат входных данных
Программа получает на вход три числа A, B, C, записанных в отдельных строках, — массы друзей. В четвёртой строке записано число D — наибольшая допустимая разница масс на концах качелей. Все числа — целые, положительные и не превосходящие 109 .
Формат выходных данных
Программа должна вывести одно целое число — минимальную необходимую массу камня, которую нужно добавить на одну из сторон качелей, чтобы друзья смогли покачаться на них, сев оптимально. Если камень им не понадобится, программа должна вывести число 0.
Замечание
В первом примере Аня и Саша сядут на одну сторону, их суммарная масса будет равна 65 кг. На другую сторону сядет Боря, взяв 15-килограммовый камень, тогда масса Бори с камнем составит 55 кг. Разница весов на концах качелей примет значение 10 кг. Во втором примере Аня и Боря сядут на одну сторону (50 кг), Саша — на другую сторону (45 кг). Разница весов будет равна 5 кг, поэтому камень не понадобится.
| |
![]()
|
262/
80
|
|
Темы:
Бинарный поиск в массиве
Бинарный поиск по ответу
Дано N упорядоченных по неубыванию последовательностей целых чисел (т.е. каждый следующий элемент больше либо равен предыдущему), в каждой из последовательностей ровно L элементов. Для каждых двух последовательностей выполняют следующую операцию: объединяют их элементы (в объединенной последовательности каждое число будет идти столько раз, сколько раз оно встречалось суммарно в объединяемых последовательностях), упорядочивают их по неубыванию и смотрят, какой элемент в этой последовательности из 2L элементов окажется на месте номер L (этот элемент называют левой медианой).
Напишите программу, которая для каждой пары последовательностей выведет левую медиану их объединения.
Входные данные
Сначала вводятся числа N и L (2≤N≤100, 1≤L≤300). В следующих N строках задаются параметры, определяющие последовательности.
Каждая последовательность определяется пятью целочисленными параметрами: x1, d1, a, c, m. Элементы последовательности вычисляются по следующим формулам: x1 нам задано, а для всех i от 2 до L: x1 = x1–1+di-1. Последовательность di определяется следующим образом: d1 нам задано, а для i≥2 di=((a*di-1+c) mod m), где mod – операция получения остатка от деления (a*di-1+c) на m.
Для всех последовательностей выполнены следующие ограничения: 1≤m≤40000, 0≤a<m, 0≤c<m, 0≤d1<m. Гарантируется, что все члены всех последовательностей по модулю не превышают 109.
Выходные данные
В первой строке выведите медиану объединения 1-й и 2-й последовательностей, во второй строке — объединения 1-й и 3-й, и так далее, в (N-1)-ой строке — объединения 1-й и N-ой последовательностей, далее медиану объединения 2-й и 3-й, 2-й и 4-й, и т.д. до 2-й и N-ой, затем 3-й и 4-й и так далее. В последней строке должна быть выведена медиана объединения (N–1)-й и N-ой последовательностей.
| |
![]()
|
1/
1
|
|
Темы:
Бинарный поиск по ответу
Наиболее известная игра, дошедшая до нас из Японии – это Судоку. Новая игра должна затмить ее славу. Про нее известно следующее. Нам дан квадрат, разделенный сеткой на n×n клеток, а каждая клетка содержит картинку одного из k типов. Игрок должен переместить их, чтобы получить максимально возможное число одинаковых первых рядов (два ряда считаются одинаковыми, если оба заполнены одинаковыми картинками и в одинаковом порядке). По виду таблицы определите, сколько одинаковых рядов в ней можно сложить (если менять картинки как угодно).
Например, если нам дана такая таблица:
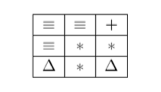
одно из результирующих состояний в игре будет:
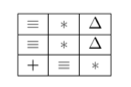
Входные данные
Первая строка входных данных содержит два числа n (1≤n≤40000) и k (1≤k≤50000). Каждая из следующих k строк содержит число картинок в таблице каждого из k типов. Все числа больше 0, их сумма в точности равна n2.
Выходные данные
Выведите в первой строке максимальное количество одинаковых рядов, которые можно построить из этих картинок. В следующих n строках выведите содержание таких рядов: в каждой строке должно находиться одно число – номер соответствующей картинке в порядке ее появления во входных данных. Если решений несколько, выведите любое из них.
| |
![]()
|
1/
1
|
|
Темы:
Бинарный поиск по ответу
Даша имеет n ювелирных украшений. Каждое украшение имеет стоимость wi и значимость для Даши vi. В связи с финансовым кризисом Даша решила продать некоторые украшения и сохранить только k из имеющихся. Чтобы решить, что именно сохранить, Даша вводит параметр важности для набора из выбранных k украшений, который вычисляет по следующей формуле:
\(\frac{\sum_{j=1}^k v_i}{\sum_{j=1}^k w_i}\)
Даша решает сохранить такие k украшений, для которых параметр важности будет максимально возможным. Помогите ей правильно выбрать украшения.
Входные данные
Первая строка ввода содержит числа n – количество ювелирных изделий у Даши и k – количество ювелирных изделий, которые планируется оставить (1 ≤ k ≤ n ≤ 100000).
В следующих n строках содержатся по два числа – vi и wi (0 ≤ vi ≤ 106,1≤wi≤106, обе суммы всех значений vi и wi не превосходят 107 каждая).
Выходные данные
Выведите k чисел – номера ювелирных украшений, которые следует оставить. Если существует несколько решений, то выведите любое из них.
| |
![]()
|
1/
1
|
|
Темы:
Бинарный поиск по ответу
Элементарная геометрия
Джо - электрик-ковбой. Как у всех ковбоев у него есть лассо, как всем электрикам ему иногда приходиться залезать на столбы, и как все он ленив.
Вот и сейчас ему поручили проверить два стоящих на расстоянии d друг от друга столба высоты h1 и h2 соответственно. Чтобы убедиться, что все хорошо, Джо должен побывать на вершинах обоих столбов.
Электрик-ковбой посещает столбы следующим образом: сначала он выбирает один из столбов и просто взбирается на него. Выполнив все работы на вершине, он спускается по этому столбу на некоторую высоту (возможно до самой земли), достает свое лассо и цепляется им за некоторую точку второго столба (это может быть произвольная точка). После этого Джо прыгает и двигается вниз по дуге окружности с центром в точке, за которую зацепилось лассо, пока не достигнет либо другого столба, либо земли.
При этом если от начальной позиции электрика до конца его полета высота изменяется более чем на l, то ковбой набирает слишком большую скорость, больно ударяется и попадает в больницу, так и не выполнив работу. Поэтому Джо всегда аккуратно выбирает параметры прыжка.
Если в результате прыжка Джо оказался на земле, он подходит к другому столбу и взбирается на него. Если же Джо оказался на столбе, то он взбирается на вершину из той точки, в которой он оказался.
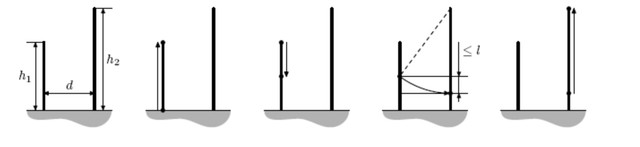
Джо просит вас помочь ему выполнить работу, сообщив какое минимальное расстояние ему придется лезть вверх по столбам.
Входные данные
Входной файл содержит четыре положительных целых числа: d, h1, h2 и l - расстояние между столбами, высоту первого и второго столбов и максимальный допустимый перепад высот при прыжке, соответственно. Все числа во входном файле не превышают 106.
Выходные данные
Выведите ответ с максимальной возможной точностью. Ответ будет проверяться с точностью до 10−5.
| |
![]()
|
15/
1
|
|
Темы:
Бинарный поиск в массиве
Бинарный поиск по ответу
Дано N упорядоченных по неубыванию последовательностей целых чисел (т.е. каждый следующий элемент больше либо равен предыдущему), в каждой из последовательностей ровно L элементов. Для каждых двух последовательностей выполняют следующую операцию: объединяют их элементы (в объединенной последовательности каждое число будет идти столько раз, сколько раз оно встречалось суммарно в объединяемых последовательностях), упорядочивают их по неубыванию и смотрят, какой элемент в этой последовательности из 2L элементов окажется на месте номер L (этот элемент называют левой медианой).
Напишите программу, которая для каждой пары последовательностей выведет левую медиану их объединения.
Входные данные
Сначала вводятся числа N и L (2≤N≤200, 1≤L≤50000). В следующих N строках задаются параметры, определяющие последовательности.
Каждая последовательность определяется пятью целочисленными параметрами: x1, d1, a, c, m. Элементы последовательности вычисляются по следующим формулам: x1 нам задано, а для всех i от 2 до L: x1 = x1–1+di-1. Последовательность di определяется следующим образом: d1 нам задано, а для i≥2 di=((a*di-1+c) mod m), где mod – операция получения остатка от деления (a*di-1+c) на m.
Для всех последовательностей выполнены следующие ограничения: 1≤m≤40000, 0≤a<m, 0≤c<m, 0≤d1<m. Гарантируется, что все члены всех последовательностей по модулю не превышают 109.
Выходные данные
В первой строке выведите медиану объединения 1-й и 2-й последовательностей, во второй строке — объединения 1-й и 3-й, и так далее, в (N-1)-ой строке — объединения 1-й и N-ой последовательностей, далее медиану объединения 2-й и 3-й, 2-й и 4-й, и т.д. до 2-й и N-ой, затем 3-й и 4-й и так далее. В последней строке должна быть выведена медиана объединения (N–1)-й и N-ой последовательностей.
| |
![]()
|
5/
1
|
|
Темы:
Бинарный поиск по ответу
Элементарная геометрия
N вражеских кораблей движутся прямолинейно с постоянными скоростями. Вакуумная бомба уничтожает все объекты в радиусе R от точки взрыва (то есть все объекты, расстояние от которых до точки взрыва не больше R). Взрывать бомбу можно только в целые моменты времени.
Требуется определить, за какое наименьшее количество взрывов можно уничтожить все корабли, а также в какие моменты времени и в каких точках для этого следует произвести взрывы. Время отсчитывается от момента, когда координаты движущихся кораблей были определены со спутника.
Входные данные
В первой строке входных данных задаются целые числа N (2 <= N <= 10) и R (0 < R ≤ 50. В следующих Nстроках содержится по 4 числа, описывающих движение кораблей. Первые два числа строки – координаты корабля в момент времени 0, по модулю не превосходящие 105. Следующие два числа – значения координат вектора скорости, по модулю не превосходящие 1000. Все эти числа целые.
Гарантируется, что никакие 2 корабля не имеют одинаковые векторы скорости.Однако вполне возможно, что в какой-то момент времени два корабля пройдут через одну точку.
Выходные данные
В первой строке выведите одно число – минимальное количество взрывов K. В следующих K строках для каждого взрыва выведите по три числа: целое время взрыва и вещественные координаты взрыва, указанные с точностью не менее трех значащих цифр после точки. Разрешается производить взрывы как в разные, так и в один и тот же момент времени. Разрешается взрывы производить как в различных точках, так и в одной точке в разные моменты времени.
Если решений несколько, выведите любое из них.
| |
![]()
|
1/
1
|
|
Темы:
Задачи на моделирование
Бинарный поиск по ответу
Сканирующая прямая
Организаторы детского праздника планируют надуть для него M воздушных шариков. С этой целью они пригласили N добровольных помощников, i-й среди которых надувает шарик за Ti минут, однако каждый раз после надувания Zi шариков устает и отдыхает Yi минут. Теперь организаторы праздника хотят узнать, через какое время будут надуты все шарики при наиболее оптимальной работе помощников, и сколько шариков надует каждый из них. (Если помощник надул шарик, и должен отдохнуть, но больше шариков ему надувать не придется, то считается, что он закончил работу сразу после окончания надувания последнего шарика, а не после отдыха).
Входные данные
В первой строке входных данных задаются числа M и N (0 <= M <= 15000, 1 <= N <= 1000). Следующие N строк содержат по три целых числа - Ti, Zi и Yi соответственно (1 <= Ti, Yi <= 100, 1 <= Zi <= 1000).
Выходные данные
Выведите в первой строке число T - время, за которое будут надуты все шарики. Во второй строке выведите N чисел - количество шариков, надутых каждым из приглашенных помощников. Разделяйте числа пробелами. Если распределений шариков несколько, выведите любое из них.
| |
![]()
|
28/
5
|
|
Темы:
Бинарный поиск по ответу
Элементарная геометрия
Квадродерево
Администрация одного института решила построить в холле фонтан. По плану администрации, фонтан должен иметь форму круга с максимально возможным радиусом. Дизайнеру сообщили, что холл института имеет вид прямоугольника, размером X×Y метров. Однако когда дизайнер стал выбирать место для фонтана, он столкнулся с серьезной проблемой: в холле института обнаружилось N круглых колонн, снести которые не представляется возможным.
Таким образом, у него появилась проблема: где следует поместить фонтан, чтобы он имел максимально возможный радиус и не имел ненулевого по площади пересечения с колоннами. Вам предстоит помочь ему в решении этой нелегкой задачи.
Входные данные
В первой строке входных данных содержатся вещественные числа X и Y, 1 <= X, Y <= 104 . Будем считать, что прямоугольник холла расположен на координатной сетке так, что его углы имеют координаты (0, 0), (X, 0), (X, Y) и (0, Y).
Во второй строке задается число N (0 <= N <= 10) - количество колонн. Следующие N строк содержат параметры колонн - i-я строка содержит три вещественных числа Xi, Yi и Ri - координаты центра и радиус i-й колонны (Ri <= Xi <= X-Ri, Ri <= Yi <= Y-Ri, 0.1 <= Ri <= min(X / 2, Y / 2); для любых i ≠ j sqrt( (Xi - Xj)2 + (Yi - Yj)2 )>= Ri + Rj). Все вводимые числа разделены пробелами.
Выходные данные
Выведите три вещественных числа: XF, YF и RF - координаты центра и радиус фонтана. Фонтан должен быть полностью расположен внутри холла (допускается касание стен) и не иметь ненулевого пересечения ни с одной из колонн (допускается касание). Радиус фонтана должен быть максимален. Разделяйте числа пробелами и/или переводами строки. Если решений несколько, выведите любое из них.
| |
![]()
|
1/
1
|
|
Темы:
Бинарный поиск по ответу
Сегодня день рождения Никиты. На празднование дня рождения приглашены n детей (включая самого Никиту). Все дети пронумерованы числами от 1 до n. Работники МакДональдса приготовили большой круглый стол и поставили вокруг него n стульев.
Как только дети приходят на день рождения, они рассаживаются за столом. Ребенок с номером 1 занимает одно из мест. Ребенок с номером 2 занимает место слева от ребенка с номером 1. Ребенок с номером 3 занимает следующее за ним место слева и так далее. Наконец, ребенок с номером n
займет оставшееся свободное место между детьми с номерами n – 1 и 1.
Работники МакДональдса хорошо знают, что некоторые из приглашенных детей ведут себя весьма шумно за столом, если сидят друг с другом. Поэтому работники ресторана собираются пересадить детей в некотором порядке. Этот порядок описывается перестановкой p1, p1,..., pn (p1, p2,..., pn — различные целые числа от 1 до n). То есть, ребенок p1 должен сидеть между pn и p2, ребенок pi (i = 2, 3, ... , n − 1) должен сидеть между pi-1 и pi+1; ребенок pn должен сидеть между pn-1 и p1.
К сожалению, все дети пришли и расселись так, как указано в первом абзаце. Поэтому для того, чтобы рассадить детей в нужном порядке, придется пересадить кого-то из детей на некоторое количество мест влево или вправо. Для каждого ребенка работникам ресторана необходимо решить, как он будет пересаживаться: они должны выбрать направление (влево или вправо) и расстояние (на сколько мест нужно переместиться). Затем, по заданному сигналу все дети должны одновременно встать и переместиться на места, определенные работниками МакДональдса.
Пересаживание детей вносит беспорядок в празднование дня рождения. Величина беспорядка пропорциональна максимальному из расстояний, на которые дети будут пересажены. Пересаживание детей можно организовать многими способами. Работники МакДональдса решили выбрать тот из них, при котором величина беспорядка будет минимальной, то есть тот способ, при котором максимальное из расстояний пересаживания будет минимальным. Помогите им найти такой способ.
Имейте в виду, что ребенок pi может сидеть как слева, так и справа от ребенка pn.
Задание
Ваша задача — написать программу, которая:
· читает из стандартного ввода количество детей и перестановку, определяющую желаемый порядок рассадки детей,
· вычисляет минимально возможную величину беспорядка,
· выводит результат в стандартный вывод.
Входные данные
В первой строке стандартного ввода содержится единственное целое число n (1 ≤ n ≤ 1 000 000). Во второй строке содержатся n целых чисел p1, p2,..., pn, разделенных одним пробелом. Числа p1, p2,..., pn образуют перестановку множества {1, 2, ... , n}, описывающую желаемый порядок рассадки детей. Кроме того, в 50% тестов число n не будет превышать 1 000.
Выходные данные
В первую и единственную строку стандартного вывода выведите единственное число — минимально возможное из максимальных расстояний, на которые придется пересесть детям.
Пояснения
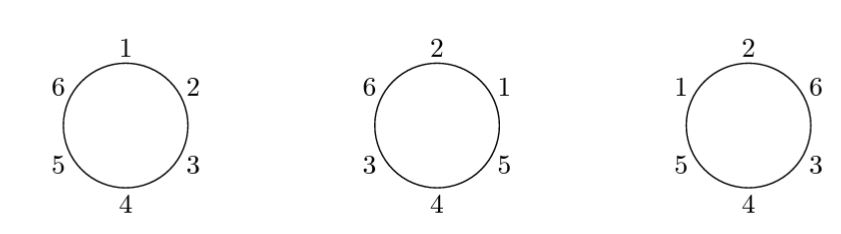
На рисунке слева изображена исходная рассадка детей. На рисунке в середине показан результат пересаживания, при котором дети с номерами 1 и 2 перемещаются на одно место, дети с номерами 3 и 5 перемещаются на два места и дети с номерами 4 и 6 не меняют своего положения. Требуемые условия рассадки выполнены, поскольку 3-й сидит между 6-м и 4-м, 4-й сидит между 3-м и 5-м, 5-й сидит между 4-м и 1-м, 1-й сидит между 5-м и 2-м, 2-й сидит между 1-м и 6-м и 6-й сидит между 2-м и 3-м. Также существует другой вариант конечной рассадки детей, изображенный на рисунке справа. В обоих вариантах величина беспорядка равна 2.
| |
![]()
|
1/
1
|
ID 54922.
Сад
Темы:
Бинарный поиск по ответу
Байтмен владеет красивейшим садом в Байттауне, в котором он посадил n роз. Пришло лето, и цветы выросли большими и красивыми. Байтмен понял, что он не в состоянии самостоятельно ухаживать за всеми розами, и решил нанять двух садовников в помощь. В этом случае ему нужно выбрать две прямоугольные области, чтобы каждый из садовников ухаживал за розами в одной их них. Области не должны пересекаться, и в каждой должно быть ровно k
роз.
Байтмен хочет установить забор, огораживающий прямоугольные области. Для экономии денег забор должен быть как можно короче. Ваша задача – помочь Байтмену выбрать две прямоугольные области.
Сад представляет собой прямоугольник длиной l метров и шириной w метров, который разделен на l·w одинаковых единичных квадратов размером 1x1 метр каждый. Зафиксируем координатную систему так, чтобы оси координат были параллельны сторонам сада. Все квадраты имеют целые координаты (x,y), удовлетворяющие ограничениям 1 <= x <= l, 1 <= y <= w. В каждом единичном квадрате может содержаться любое количество роз.
Стороны прямоугольных областей, которые выбираются, должны быть параллельны сторонам сада, а их угловые единичные квадраты – иметь целые координаты. Прямоугольная область с угловыми единичными квадратами (l1,w1), (l1 ,w2), (l2, w1) и (l2,w2) (для 1 <= l1 <= l2 <= l и 1 <= w1 <= w2 <= w):
• содержит все единичные квадраты с координатами (x,y), которые удовлетворяют условию l1 <= x <= l2 и w1 <= y <= w2, и
• имеет периметр 2 · (l2−l1+1)+ 2 · (w2−w1+1).
Две прямоугольных области не должны пересекаться, то есть, они не должны иметь ни одного общего квадрата. Даже если они имеют общую сторону или её часть, они ограждаются разными заборами.
Задание
Напишите программу, которая:
• читает из стандартного ввода размеры сада, общее количество роз в саду, количество роз, которое должно находиться в каждой прямоугольной области, и позицию каждой розы в саду, определяемую координатами единичного квадрата, в котором она находится;
• находит угловые единичные квадраты двух таких прямоугольных областей с минимальной суммой периметров, которые удовлетворяют заданным условиям;
• выводит в стандартный вывод минимальное значение суммы периметров двух непересекающихся прямоугольных областей, каждая из которых содержит точно заданное количество роз (или единственное слово NO, если такой пары прямоугольных областей не существует).
Входные данные
Первая строка стандартного ввода содержит два числа: l и w (1 <= l, w <= 250), разделенных одним пробелом – длину и ширину сада. Во второй строке задаются два числа: n и k (2 <= n <= 5000, 1 <= k <= n/2), записанных через пробел и обозначающих общее количество роз в саду и количество роз, которое должно быть в каждой из прямоугольных областей. Следующие n строк содержат позиции роз, по одной розе в строке. Каждая (i+2)-я строка содержит два числа li, wi (1 <= li <= l, 1 <= wi <= w), разделенных одним пробелом – координаты квадрата, содержащего i-ю розу.
В одном квадрате может содержаться две или большее количество роз.
Выходные данные
В первую и единственную строку стандартного вывода ваша программа должна вывести одно число – минимальную сумму периметров двух неперекрывающихся прямоугольных областей, каждая из которых содержит ровно k роз, или единственное слово NO, если таких прямоугольников нет.
Рисунок к тесту:
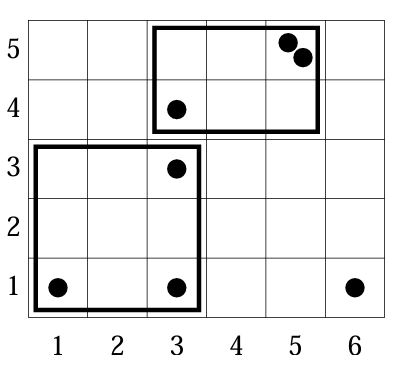
| |
![]()
|
1/
1
|
|
Темы:
Бинарный поиск по ответу
Петя каждый день ездит на работу на метро по одному и тому же маршруту с двумя пересадками. Он уже давно запомнил, сколько времени занимает проезд на нужном ему отрезке пути по каждой из трех линий. Также он выучил расписание поездов на всех трех линиях, по которым он ездит. Помогите Пете найти такое время входа в метро, чтобы поездка на работу занимала как можно меньше времени.
Входные данные
В первой строке вводятся времена поездки по первой, второй и третьей линии (до пересадки) в минутах. Все времена – натуральные числа и не превышают 1140 минут. Считается, что пересадка не занимает времени.
Во второй строке вводятся количество поездов на первой линии, на второй линии и на третьей линии – натуральные числа, не превосходящие 100.
В третьей строке вводятся времена отправления поездов первой линии со станции, на которой садится Петя (по два числа на каждый поезд – часы и минуты).
В четвертой строке в том же формате вводятся времена отправления поездов второй линии со станции, на которую Петя делает первую пересадку.
В пятой строке – аналогичное расписание поездов третьей линии со станции, на которую Петя делает вторую пересадку.
Находиться в метро с часу ночи до 6 часов утра запрещается (в 6 часов утра на поезд садиться можно). Расписание движения поездов таково, что Петя может добраться до работы, не выходя из метро.
Выходные данные
Выведите время (часы и минуты), в которое Петя может войти в метро, чтобы добраться до работы за наименьшее время. Если решений несколько, выведите любое из них.
| |
![]()
|
1/
1
|
|
Темы:
Бинарный поиск по ответу
Обход в глубину
В столице одной Очень Демократической Страны все жители в 8 часов утра одновременно выходят со станций метро, ближайших к месту своей работы, и дальше добираются до работы на автобусах. Мэр города хочет построить еще одну станцию метро так, чтобы после этого время, к которому все люди доберутся до места своей работы (то есть время, когда последний работник окажется на работе), было наименьшим возможным.
Автобусное сообщение в столице устроено следующим образом. Есть N автобусных остановок, в частности, возле каждой станции метро расположено по остановке. Между N – 1 парой остановок постоянно курсируют автобусы, время движения от одной остановки до другой – 1 минута. Временем ожидания и пересадки можно пренебречь. Автобусное сообщение в столице организовано так, что от любой автобусной остановки до любой другой можно добраться на автобусах (возможно, с пересадками).
Входные данные
В первой строке входных данных содержатся два числа N и M – количество автобусных остановок и станций метро соответственно (2 ≤ N ≤ 50 000, 1 ≤ M ≤ 1 000, M < N).
Во второй строке задаются через пробел M чисел – номера автобусных остановок, рядом с которыми есть станции метро (каждая – не более одного раза).
В следующих N – 1 строках записано по два числа – номера автобусных остановок, между которыми курсирует автобус. (Автобус ходит в обоих направлениях. Каждый маршрут указан один раз.)
Выходные данные
Выведите два числа – сначала наибольшее время за которое кто-то будет и после строительства добираться на работу, а затем номер автобусной остановки, рядом с которой следует построить новую станцию метро. (Строить можно возле тех автобусных остановок, возле которых еще нет станций метро). Если решений несколько, выведите одно из них.
| |
![]()
|
23/
1
|
Темы:
Бинарный поиск
Бинарный поиск по ответу
Быстрая сортировка
В одной демократической стране приближаются парламентские выборы. Выборы проходят по следующей схеме: каждый житель страны, достигший восемнадцатилетнего возраста, отдает свой голос за одну из политических партий. После этого партия, которая набрала максимальное количество голосов, считается победившей на выборах и формирует правительство. Если несколько партий набрали одинаковое максимальное количество голосов, то они должны сформировать коалиционное правительство, что обычно приводит к длительным переговорам.
Один бизнесмен решил выгодно вложить свои средства, и собрался поддержать на выборах некоторые партии. В результате поддержки он планирует добиться победы одной из этих партий, которая затем сформирует правительство, которое будет действовать в его интересах. При этом возможность формирования коалиционного правительства его не устраивает, поэтому он планирует добиться строгой победы одной из партий.
Чтобы повлиять на исход выборов, бизнесмен собирается выделить деньги на агитационную работу среди жителей страны. Исследование рынка показало, что для того чтобы один житель сменил свои политические воззрения, требуется потратить одну условную единицу. Кроме того, чтобы \(i\)-я партия в случае победы сформировала правительство, которое будет действовать в интересах бизнесмена, необходимо дать лидеру этой партии взятку в размере \(p_i\) условных единиц. При этом некоторые партии оказались идеологически устойчивыми и не согласны на сотрудничество с бизнесменом ни за какие деньги.
По результатам последних опросов известно, сколько граждан планируют проголосовать за каждую партию перед началом агитационной компании. Помогите бизнесмену выбрать, какую партию следует подкупить, и какое количество граждан придется убедить сменить свои политические воззрения, чтобы выбранная партия победила, учитывая, что бизнесмен хочет потратить на всю операцию минимальное количество денег.
Формат входных данных
Первая строка содержит целое число \(n\) — количество партий (\(1 \le n \le 10^5\)). Следующие \(n\) строк описывают партии. Каждая из этих строк содержит по два целых числа: \(v_i\) — количество жителей, которые собираются проголосовать за эту партию перед началом агитационной компании, и \(p_i\) — взятка, которую необходимо дать лидеру партии для того, чтобы сформированное ей в случае победы правительство действовало в интересах бизнесмена (\(1 \le v_i \le 10^6\), \(1 \le p_i \le 10^6\) или \(p_i = -1\)). Если партия является идеологически устойчивой, то \(p_i\) равно \(-1\). Гарантируется, что хотя бы одно \(p_i\) не равно \(-1\).
Формат выходных данных
На первой строке выведите минимальную сумму, которую придется потратить бизнесмену. На второй строке выведите номер партии, лидеру которой следует дать взятку. На третьей строке выведите \(n\) целых чисел — количество голосов, которые будут отданы за каждую из партий после осуществления операции. Если оптимальных решений несколько, выведите любое.
| |
![]()
|
20/
2
|
|
Темы:
Бинарный поиск по ответу
Мэр Цветочного города попросил лучшего плиточника Тайлера замостить квадратную зону площади плиткой. Тайлеру были выданы коробки, в каждой из которых содержится ai квадратных плиток размером 1х1. Тайлеру поставили условие, что он должен обязательно использовать все плитки, которые ему были выданы.
Помогите Тайлеру определить, сможет ли он использовать все плитки, чтобы замостить из всех них квадрат какого-либо размера или ему придется идти к мэру и просить еще плиток?
Считайте, что на площади можно замостить квадрат любого размера.
Формат входных данных
В первой строке вводится натуральное число n (1 ≤ n ≤ 2·105)- количество коробок, выданных Тайлеру. Во второй строке записаны n чисел ai (1 ≤ ai ≤ 109)- количество плиток в i-й коробке.
Формат выходных данных
Выведите YES, если Тайлер сможет из всех плиток замостить квадрат какого-либо размера на площади, в противном случае выведите NO.
| |
![]()
|
84/
21
|
|
Темы:
Бинарный поиск по ответу
Вы хотите построить лестницу и приготовили n блоков. Лестница строится путем наложения блоков друг на друга. В i-м ряду лестницы размещается ровно i блоков.
Определите количество полных рядов лестницы, которую вы сможете построить.
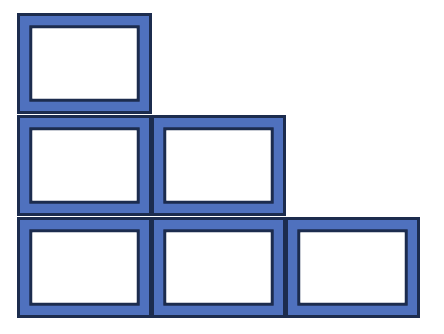
Решите задачу двоичным поиском.
Формат входных данных
Программа получает на вход натуральное число n (1 <= n <= 231 - 1) - количество блоков.
Формат выходных данных
Выведите ответ на задачу.
| |
![]()
|
507/
155
|
|
Темы:
Бинарный поиск по ответу
Вы - руководитель команды по разработке программных продуктов. В настоящее время вместе с командой занимаетесь выпуском нового релиза. К сожалению, последний релиз не прошел проверку качества. Поскольку каждый следующий релиз разрабатывается на основе предыдущих, все версии следующие за неудачной, также неуданы.
Вы уже выпустили n версий [1, 2, ..., n] и забыли проверить на качество все, кроме последней. Теперь, вы хотите найти первую плохую версию, которая приводит к тому, что все последующие становятся плохими.
Руководитель отдела качества очень хорошо к вам относится и написал для вас функцию isBadVersion(version), которая определяет является ли версия резила плохой (возвращает True, если версия плохая, и False если хорошая).
Теперь вам необходимо реализовать функцию для поиска первой плохой версии. Вы должны как можно быстрее определить с какой версии пошел плохой релиз, поэтому количество использования функции isBadVersion(version) должно быть минимальным.
Ваша функция должна вернуть номер первого плохого релиза.
| |
![]()
|
482/
68
|
|