| Условие задачи | | Прогресс |
|
Темы:
Динамическое программирование на таблицах
Простые игры
В левой нижней клетке шахматной доски размера N×N стоит пешка. Двое игроков по очереди двигают её, причём каждый может подвинуть её на одну клетку вверх или на одну клетку вправо. На диагонали доски написаны числа a1, a2, …, aN. Когда пешка попадает на диагональ, игра кончается и выигрыш первого игрока равен значению числа, написанного в клетке с остановившейся пешкой. Напишите программу определения гарантированного выигрыша первого игрока.
Входные данные
В первой строке записано число N (1 ≤ N ≤ 100). Во второй строке записаны натуральные числа a1, a2, …, aN (1 ≤ ai ≤ 100).
Выходные данные
Выведите одно число – выигрыш первого игрока.
|
Ввод |
Вывод |
|
8
3 1 4 1 5 9 2 6
|
5 |
| |
![]()
|
|
Темы:
Простые игры
В начальный момент времени Снарк находится в точке прямой с целой неотрицательной координатой X. За ход он может оказаться в любой точке с целой координатой Y при условии, что |X-Y| <= S. Кроме того, Снарк не любит булочки, поэтому он никогда не прыгнет в клетку, где одна из этих противных штук лежит. Булочник не хочет, чтобы Снарк попал домой. После каждого хода Снарка Булочник может положить булочку в любую точку прямой при условии, что это не начало координат (дом Снарка) и в этой клетке нет Снарка. Определите, сможет ли Булочник помешать Снарку оказаться дома. Изначально в некоторых клетках лежат булочки.
Входные данные
В первой строке задаются целые числа 0 <= X < 10000, 0 < S <= 100 и 0 <= N < max(X-1, 0) - количество булочек, которые уже лежат на прямой. Далее идут N различных чисел 0 < bi < X - координаты точек, где лежит гадость.
Выходные данные
Выведите "YES", если Булочник сможет реализовать свои грязные планы, "NO" - если при любых действиях врага Снарк сможет припрыгать домой.
|
Ввод |
Вывод |
|
1 1 0 |
NO |
|
10 3 3
7 8 9
|
YES |
| |
![]()
|
|
Темы:
Простые игры
Напомним содержание первой серии. Двое играют в такую игру: перед ними лежит шоколадка размера NxM. За ход можно разломить имеющийся кусок шоколадки вдоль одной из сторон на 2 "непустых".
Однако, нельзя разламывать куски размером не больше, чем 1k (куски можно поворачивать; мы считаем, что один кусок "не больше" другого, если он равен ему или его части). Таким образом, нельзя разламывать куски размером 11, 12, , 1k, а остальные куски разламывать можно.
Теперь куски, которые нельзя ломать, можно есть (не более одного за раз).
За один ход можно либо разламывать подходящий по размеру кусок, либо есть.
Проигрывает тот, кто не может сделать ход. Определите, кто же станет победителем в игре, если известны начальные размеры шоколадки.
Входные данные
Вводятся целые числа 0 < N, M, K <= 100.
Выходные данные
Выведите 1 или 2 - номер игрока, который выиграет при правильной игре.
|
Ввод |
Вывод |
|
1 1 1 |
1 |
|
1 1 100 |
1 |
| |
![]()
|
|
Темы:
Простые игры
Петя получил золотую медаль на IOI, за что от правительства ему положена благодарность в виде шоколадки. На данный момент имеется N видов шоколадок, которые производит государственная шоколадная фабрика. У каждой шоколадки есть стоимость. Кроме того, у каждого вида, кроме шоколадки "Юлька", есть вид-прародитель. Известно, что прародителем может быть только шоколадка, которая была выпушена хронологически раньше. Исторически самый первый вид - "Юлька". Чиновник и Петя выбирают шоколадку ему в подарок. При этом цель первого - сэкономить, второго - получить настолько дорогую шоколадку, насколько это возможно. Начинается выбор с "Юльки". Петя за ход либо берет текущую шоколадку, либо меняет свой выбор на шоколадку-потомка (если это возможно). Чиновнику же кажется, что позже выпущенные виды хуже и дешевле, поэтому он меняет выбор на шоколадку-потомка (если это возможно), либо покупает Пете шоколадку (если потомков нет). Они ходят по очереди, Петя - первый. Определите, на шоколадку какой стоимости может претендовать Петя.
Входные данные
Сначала вводится число 0 < N <= 200000 - количество видов. "Юлька" имеет номер 1. Далее идут N строк с парами чисел 0 <= Pi <= N - номер сорта-предка (для шоколадки "Юлька" указан 0, у остальных Pi > 0) и 0 < Ci <= 1000000000 - стоимость i-го сорта.
Выходные данные
Выведите стоимость шоколадки, которую Петя может себе гарантировать при правильных действиях.
|
Ввод |
Вывод |
|
8
0 4
5 3
1 2
5 1
1 5
4 8
3 6
3 7
|
6 |
| |
![]()
|
|
Темы:
Простые игры
Двое играют в игру. Есть несколько кучек спичек. За один ход разрешается взять любое ненулевое количество спичек из любой кучки, кто не может сделать ход, тот проиграл. Определите, кто выигрывает при правильной игре.
Формат входных данных
В первой строке входного файла записано натуральное число N — количество кучек. Во второй строке записаны N целых чисел — количество спичек в кучках. Все числа во входном файле не превосходят 100000.
Формат выходных данных
Выведите «1», если выигрывает первый игрок или «2», если выигрывает второй игрок.
| |
![]()
|
|
Темы:
Простые игры
Двое играют в игру. Есть несколько кучек спичек. За один ход разрешается взять любое ненулевое количество спичек из любой кучки, кто не может сделать ход, тот проиграл. Определите, кто выигрывает при правильной игре.
Входные данные
В первой строке входного файла записано натуральное число N — количество кучек. Во второй строке записаны N целых чисел — количество спичек в кучках. Все числа во входном файле не превосходят 100000.
Выходные данные
Выведите «1», если выигрывает первый игрок или «2», если выигрывает второй игрок. Если выигрывает первый игрок, во второй строке выведите число K — общее количество выигрышных ходов. В последующие K строк выведите информацию о выигрышных ходах — пары чисел, перечисленные в порядке возрастания первой координаты, а при равенстве в порядке возрастания второй координаты. В каждой такой паре первое число должно обозначать номер кучки, а второе — количество спичек, которые необходимо взять из этой кучки.
|
Ввод |
Вывод |
1
10 |
1
1
1 10
|
2
1 1 |
2 |
| |
![]()
|
|
Темы:
Динамическое программирование: один параметр
Простые игры
На столе лежат N камней. За ход игрок может взять:
- 1 или 2 камня, если N делится на 3;
- 1 или 3, если N при делении на 3 дает остаток один;
- 1, 2 или 3, если N при делении на 3 дает остаток два.
Каждый ход можно сделать при наличии достаточного количества камней. Проигрывает тот, кто хода сделать не может.
Входные данные: вводится целое число \(0 < N <= 100\).
Выходные данные: выведите 1 или 2 – номер игрока, который выиграет при правильной игре.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 |
1 |
| 2 |
3 |
2 |
| |
![]()
|
|
Темы:
Простые игры
Когда настала зима и дел в Простоквашино стало мало, Шарик и Матроскин все дни проводили за настольными играми. Но шахматы, шашки, крестики-нлоики и домино им быстро надоели, а других игр у них не было. Поэтому они придумали новую игру.
Они выписывают на печке угольком 100 чисел. Потом по очереди каждый из них выбирает число с правого или левого края, прибавляет его к своей сумме и стирает число. Начинает игру Матроскин. Он выигрывает, если сможет набрать сумму, не меньшую, чем Шарик. По заданным числам определите, кто выиграет при оптимальной игре.
Входные данные
В единственной строке записаны через пробел 100 чисел ai (1≤ai≤1000)
Выходные данные
В ответ выведите Matroskin, если выигрывает Матроскин, иначе выведите Sharik. Если выигрывает Матроскин, то на следующей строке выведите оптимальный первый ход Матроскина: если он должен взять самое левое число, то выведите «left», если он должен взять самое правое число — выведите «right». Если Матроскину не важно, какое из чисел взять, выведите любое из слов «left» и «right».
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 |
Matroskin
right |
| |
![]()
|
|
Темы:
Простые игры
Вася и Петя играют в следующую игру. Они берут колоду из 36 карточек. На каждой карточке написано число от 1 до 9 и каждая карточка покрашена в один из 4 цветов так, что есть ровно по 9 карточек каждого цвета, и они пронумерованы числами от 1 до 9. Карты перемешиваются, и игрокам раздается по несколько (не более чем по 18) карточек.
Дальше игроки по очереди делают ходы. За один ход игрок может выложить на стол одну или последовательно несколько карточек по следующим правилам. Карточку с цифрой 5 любого цвета можно выкладывать на стол без дополнительных условий. Карточку с другой цифрой можно выкладывать только если на стол уже выложена карточка того же цвета, на которой написано число на 1 большее или на 1 меньшее, чем на данной, или же карточка с той же цифрой, но другого цвета (не важно, была ли эта карточка выложена вами или вашим противником, и была ли она выложена на предыдущем ходе или раньше). Если ни одну карточку игрок выложить не может, он пропускает ход.
Напишите программу, которая по информации о том, какие карточки уже лежат на столе и какие есть у игрока, определит наибольшее число карточек, которое может быть выложено этим игроком на данном ходе.
Входные данные
Во входном файле записано сначала число K — количество уже выложенных на стол карточек. Далее идет K пар чисел, описывающих эти карточки. Затем записано число N — количество карточек на руках у игрока, который сейчас должен делать ход. Далее записано N пар чисел, описывающих эти карточки.
Каждая карточка описывается двумя числами — номером цвета (от 1 до 4) и цифрой, которая написана на карточке (от 1 до 9).
Ограничения: 0≤K≤35, 1≤N≤36, N+K≤36, все карточки различны.
Выходные данные
В выходной файл выведите одно число — наибольшее количество карточек, которые могут быть выложены на данном ходе.
Примеры
| № |
Входные данные |
Выходные данные |
Комментарии |
| 1 |
2
1 5
1 4
3
1 3
1 6
2 8 |
2 |
Это карты 1 3 (потому что на столе есть 1 4) и 1 6 (потому что на столе есть 1 5) |
| 2 |
0
4
2 8
1 5
3 6
1 6 |
3 |
Первым ходом можно выложить 1 5, после этого мы имеем право выложить и 1 6, после которой выкладываем 3 6 |
| 3 |
3
1 4
1 5
1 6
2
2 8
2 9 |
0 |
Нельзя выложить ни одной карточки |
| |
![]()
|
|
Темы:
Простые игры
Разбор случаев
Антонин, Бальбин и Цезарь играют в игру "Карты на троих", алгоритм которой следующий:
- сначала у каждого из трех игроков есть колода, состоящая из некоторого количества карт. На каждой карточке написана буква a, b или c. Порядок карт в колодах не может быть изменен;
- игроки ходят по очереди. Антонин ходит первым;
- если в колоде текущего игрока есть хотя бы одна карта, ему необходимо сбросить верхнюю карту в колоде;
- следующий ход переходит к игроку, имя которого начинается с буквы на сброшенной карте (a - Антонин, b - Бальбин, c - Цезарь);
- если колода текущего игрока пуста, игра заканчивается, и текущий игрок выигрывает игру.
Вам выдаются начальные колоды игроков (Sa, Sb, Sc). Состояние колоды Антонина записано в строке Sa, где i-й (\(1<=i<=len(S_a)\)) символ это буква в i-й карты в колоде. Строка Бальбина (Sb) и строка Цезаря (Sс) описываются таким же образом.
Определите победителя в игре.
Формат входных данных
На вход подаются три ненулевых строки Sa, Sb и Sc, каждая с новой строки. Длина каждой строки не более 100 символов. Каждая строка состоит только из букв a, b или c.
Формат выходных данных
Если выиграл Антонин. то выведите букву A, если Бальбин - букву B, если Цезарь - букву C.
Примечание
В первом тестовом примере игра будет развиваться следующим образом:
Антонин сбрасывает верхнюю карту своей колоды, a. Антонин делает следующий ход.
Антонин сбрасывает верхнюю карту своей колоды, с. Цезарь следующий.
Цезарь сбрасывает верхнюю карту своей колоды, с. Цезарь следующий.
Цезарь сбрасывает верхнюю карту своей колоды: a. Антонин делает следующий ход.
Антонин сбрасывает верхнюю карту своей колоды: a. Антонин делает следующий ход.
Колода Антонина пуста. Игра заканчивается, и Антонин выигрывает игру.
| |
![]()
|
|
Темы:
Игры и выигрышные стратегии
Простые игры
Древовидные структуры данных
В двусвязном списке, он же LinkedList, каждый элемент может быть связан максимум с двумя другими элементами — с предыдущим элементом (если он есть) и со следующим элементом (если он есть).
Билли и Рикардо проходят стажировку в компании FlexDex в группе поддержки внутреннего анонимного форума с возможностью деанонимизации. Для представления последовательных сообщений в теме необходимо использовать список, где элементами будут являться эти сообщения, и два товарища решили написать свою быструю реализацию двусвязного списка FlexList.
Но у них что-то пошло не так — в их списке новое сообщение может связываться не только с первым или последним сообщением, как должно быть, а с любым из уже существующих сообщений.
Если представить каждое сообщение как вершину графа, а связи между сообщениями как ребра графа, то гарантируется, что этот граф будет неориентированным, связным и ацикличным.
Говорится, что граф является корректным графом, если в этом графе у каждой вершины не более двух вершин, связанных с ней ребром. Изначально же FlexList связи между сообщениями могут выглядеть в виде любого связного ацикличного графа, не обязательно корректного.
Билли и Рикардо не растерялись и решили, что будут вручную исправлять все неясности в ходе работы программ, которые используют их изобретение. Тимлид дал им тестовый пример для проверки кода. Они получили на этом примере граф связей и вручную делают из него корректный граф, ведь связи между сообщениями в корректном двусвязном списке могут представлять собой только корректный граф.
Это выглядит так — сначала Билли проверяет, что граф корректный. Если это не так, то он выбирает и удаляет некоторый лист (вершина, у которой есть ровно одна связь с другими вершинами), и отдает граф Рикардо, затем Рикардо делает то же самое и отдает граф Билли, и так продолжается до тех пор, пока кто-то не получит от товарища корректный граф. Как только один из двух друзей получает такой граф, то тут же показывает его тимлиду, с надеждой на похвалу и повышение в должности.
Каждый хочет получить первым такой граф. Кто первым попадет к тимлиду, если оба товарища удаляют листья оптимально для себя?
Входные данные
В первой строке содержится одно целое число n (1 ≤ n ≤ 300000) — число сообщений в примере тимлида. Следующие n−1 строк задают связи между сообщениями. Каждая из них содержит два целых числа ai и bi (1 ≤ ai, bi ≤ n, ai ≠ bi), которые показывают, что сообщения с номерами ai и bi связаны.
Выходные данные
Выведите "Billy" (без кавычек), если первым попадет к тимлиду Билли, иначе выведите "Ricardo" (без кавычек).
Примечание
В первом примере Билли первым ходом может удалить одну из вершин с номерами 2, 4 или 5, так как они являются листьями. Он не будет удалять вершину с номером 4 или 5, так как в таком случае он передаст Рикардо корректный граф и проиграет. Значит, он удалит вершину 2. В свою очередь, Рикардо может удалить вершины 1, 4 или 5, и, в любом случае, Билли получит от него корректный граф.
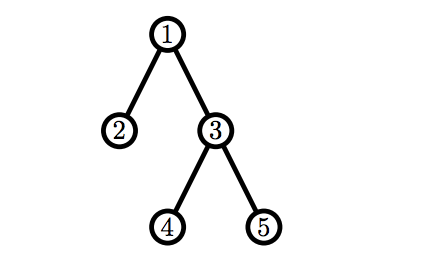
Во втором примере у Билли сразу есть корректный граф.
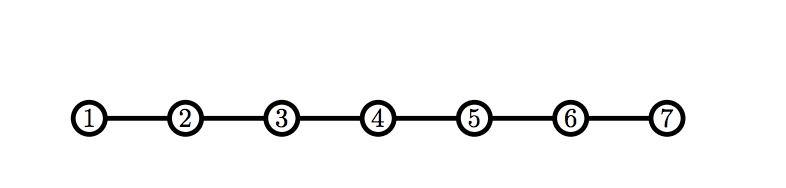
В третьем примере можно показать, что вне зависимости от ходов Билли, Рикардо получит корректный граф первым.
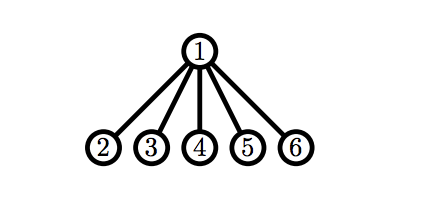
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
1 2
1 3
3 4
3 5 |
Billy |
| 2 |
7
1 2
2 3
3 4
4 5
5 6
6 7 |
Billy |
| 3 |
6
1 2
1 3
1 4
1 5
1 6 |
Ricardo |
| |
![]()
|
|
Темы:
Простые игры
Два игрока, Петя и Ваня, играют в следующую игру. Имеется строка s длиной 3 или больше символов. Никакие два соседних символа в s не равны. Игроки ходят по очереди. Петя ходит первым. За один ход нужно удалить один из символов из строки s, за исключением крайних (первого и последнего). Символ не может быть удален, если удаление символа приведет к появлению двух соседних одинаковых символов в строке. Игрок, который не может выполнить операцию, проигрывает игру. Определите, какой игрок выиграет, если они будут играть оптимально.
Входные данные
На вход подается строка s (\(3 <= len(s) <= 10^5\)). Строка состоит только из строчных английских букв (a-z). Никакие два соседних символа в s не равны.
Выходные данные
Если Петя выиграет, выведите First. Если выиграет Ваня, выведите Second.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
aba
|
Second
|
Петя не может выполнить операцию, так как удаление символа b, который является единственным символом, который можно удалить, приведет к тому, что s станет равной aa, два одинаковых символа будут соседними. |
| 2 |
abc
|
First
|
Когда Петя удаляет b из s, строка становится равной ac и Ваня не сможет выполнить операцию, поскольку в s нет других символов, за исключением крайних. |
| 3 |
abcab
|
First
|
|
| |
![]()
|
|
Темы:
Информатика
Простые игры
Алиса и капитан Буран играют в покер с одной картой. Однокарточный покер - это игра для двух игроков с игральными картами. Каждая карта в этой игре показывает целое число от 1 до 13 включительно. Сила карты определяется числом, написанным на ней, следующим образом:
Слабая 2 <3 <4 <5 <6 <7 <8 <9 <10 <11 <12 <13 <1 Сильная
В покер с одной картой играют следующим образом:
- Каждый игрок берет одну карту из колоды.
- Выбранная карта становится рукой игрока.
- Игроки раскрывают друг другу руки.
- Игрок с более сильной картой побеждает в игре.
- Если их карты одинаково сильны, игра заканчивается вничью.
Вы смотрите, как Алиса и капитан Буран играют в игру, и можете видеть их руки. Число, написанное на карточке Алисы, - A, а число, написанное на карточке капитана Бурана, - B.
Напишите программу для определения исхода игры.
| |
![]()
|
|
Темы:
Динамическое программирование на таблицах
Простые игры
Вася и Петя играют в следующую игру. Они берут колоду из 36 карточек. На каждой карточке написано число от 1 до 9 и каждая карточка покрашена в один из 4 цветов так, что есть ровно по 9 карточек каждого цвета и они пронумерованы числами от 1 до 9. Карты перемешиваются, и игрокам раздается по 18 карт.
Дальше игроки по очереди делают ходы. За один ход игрок может выложить на стол одну карточку по следующим правилам. Карточку с цифрой 5 можно выкладывать на стол в любой момент. Карточку с другой цифрой можно выкладывать только если на стол уже выложена карточка того же цвета, на которой написано число на 1 большее или на 1 меньшее, чем на данной карточке (не важно, была ли эта карточка выложена вами или вашим противником, и была ли она выложена на предыдущем ходе или раньше). Если игрок может выложить хоть какую-то карточку, он обязан делать ход. Если ни одну карточку игрок выложить не может, он пропускает ход.
Выигрывает тот, кто первым выложит все свои карточки на стол.
Напишите программу, которая по информации о том, кому какие карточки достались, определяет, кто выиграет при оптимальной игре обоих игроков.
Входные данные
Во входном файле записаны 18 пар чисел, описывающих карточки, которые достались первому игроку. Каждая карточка описывается двумя числами — номером цвета (от 1 до 4) и цифрой, которая написана на карточке (от 1 до 9). Второму игроку, соответственно, достались все остальные карточки.
Выходные данные
В выходной файл выведите одно число (1 или 2) — номер игрока, который выиграет при оптимальной игре обоих игроков.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 1
1 2
1 3
1 4
1 5
1 6
1 7
1 8
1 9
2 1
2 2
2 3
2 4
2 5
2 6
2 7
2 8
2 9 |
1 |
| |
![]()
|
|
Темы:
Двумерные массивы
Задача на реализацию
Простые игры
Пете и Васе стало очень скучно на уроке биологии, и они решили поиграть в любимую всеми школьниками игру в крестики-нолики до пяти в ряд на бесконечном поле.
Рассмотрим кратко правила игры. Игра происходит на бесконечном клетчатом поле, два игрока делают ходы по очереди, первый игрок ходит крестиками, а второй — ноликами. В свой ход игрок
выбирает свободную клетку поля и ставит туда свой символ. Если после хода очередного игрока на поле есть пять его символов подряд по вертикали, горизонтали или диагонали, то сделавший такой ход игрок объявляется победителем и игра заканчивается.
Петя и Вася уже довольно долго играют в игру. Сейчас должен ходить Петя, который играет крестиками. Петя надеется побыстрее завершить игру и хочет выиграть не более чем за два, а лучше
за один ход. Петя называет ход оптимальным, если для этого хода выполнено одно из двух:
• этот ход приводит к немедленной победе Пети;
• не существует хода, который приводит к немедленной победе Пети, но если Петя сделает этот ход, то Вася не выиграет следующим ходом и, вне зависимости от ответного хода Васи, у Пети
будет следующий ход, который приведет к его немедленной победе.
Помогите Пете найти количество оптимальных ходов.
Формат входных данных
В первой входного файла находятся два натуральных числа n, m (1 ≤ n,m ≤ 200) — размеры прямоугольника, содержащего все уже поставленные на поле крестики и нолики.
Следующие n строк содержат по m символов, каждый из которых равен одному из следующих:
«.» (точка), «X» (заглавная латинская буква «икс») или «0» (ноль). При этом «.» обозначает пустую клетку, «X» обозначает крестик, а «0» обозначает нолик. Гарантируется, что на поле находится
равное число крестиков и ноликов, и ни один игрок еще не одержал победу.
Формат выходных данных
Выведите одно число — количество оптимальных ходов Пети.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 3
...
000
XXX
...
...
|
2 |
| 2 |
4 4
..0.
.XX0
.0X.
....
|
0 |
| 3 |
5 6
......
.XXX..
.0000.
..X...
......
|
0 |
| |
![]()
|
|
Темы:
Простые игры
Аня и Боря играют в игру. Первый ход делает Аня. Изначально на доске записано натуральное число n. На каждом ходе игрока, этот игрок делает следующий ход:
- выбирает любое
x, не равное n, но кратное числу n (более формально 0 < x < n и n % x == 0)
- заменяет число
n на доске на n-x.
Если игрок не может сделать ход, то он проигрывает игру.
Определите, кто победит в этой игре, если оба будут следовать оптимальной стратегии.
Формат входных данных
Программа получает на вход натуральное число n (n <= 1000).
Формат выходных данных
Выведите 1, если Аня выигрывает игру, иначе выведите 0.
| |
![]()
|
|
Темы:
Простые игры
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее W. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу, в которой будет W или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ W-1.
Напишите программу, которая определяет:
задание 1) такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом.
задание 2) все значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
задание 3) все значение S, при котором одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
При написании программы будет считать, что все игроки действуют оптимально. Другими словами, игрок, у которого имеется выигрышная стратегия будет стремиться выиграть за наименьшее число ходов. Игрок, у которого отсутствует выигрышная стратегия (который проигрывает) будет стараться игру затянуть, т.е. проиграть за наибольшее число ходов.
Формат входных данных
Программа получает на вход целое число W (10 <= W <= 1000).
Формат выходных данных
В ответе должно быть три строки. В первой строке - ответ на задание 1, во второй - на задание 2, в третьей - на задание 3.
В каждой строке, в которой может быть больше одного значения, значения должны быть распечатаны в порядке возрастания, через один пробел
| |
![]()
|
|
Темы:
Простые игры
Двое играют в следующую игру: имеется дерево с отмеченной вершиной (корнем). За ход игрок рузрубает ветку (стирает ребро), причем из двух получившихся компонент связности остается только та, которая содержит корень - остальная отваливается вместе с корнем. Проигрывает тот, кто не может сделать ход. Определите, может ли выиграть первый игрок, и если да, то любой из его выигрышных ходов.
Входные данные
В первой строке вводится 2 числа - количество вершин 1 < N <= 100000 и номер корня 1 <= R <= N. В следующих N-1 строках идут пары чисел - описания ребер.
Выходные данные
Выведите 1 или 2 - номер победителя при правильной игре. Если побеждает первый игрок, то выведите порядковый номер ребра во входных данных, которое ему достаточно разрубить первым ходом (число от 1 до N-1).
| |
![]()
|
|
Темы:
Простые игры
То же, что и Дровосек - 1, только граф произвольный, после хода выживают те компоненты связности, которые содержат корни (изначально в каждой компоненте связности есть хотя бы один корень).
Входные данные
В первой строке задаются 3 числа - количество вершин 1 < N <= 10000, число ребер 0 <= M <= 100000 и количество корней 1 <= R <= N. В следующей строке идут различные числа 1 <= Ri <= N - номера вершин, являющихся корнями. В следующих M строках идут пары чисел - описания ребер.
Выходные данные
Выведите одно число - номер игрока-победителя.
| |
![]()
|
|
Темы:
Простые игры
Двое играют в следующую игру. Из кучки спичек за один ход игрок вытягивает либо 1, либо 2, либо 1000 спичек. Выигрывает тот, кто забирает последнюю спичку. Кто выигрывает при правильной игре?
Входные данные
Вводится одно натуральное число — N ( 1≤ N ≤ 10000) начальное количество спичек в кучке.
Выходные данные
Выведите 1, если выигрывает первый игрок (тот, кто ходит первым), или 2, если выигрывает второй игрок.
| |
![]()
|
|
Темы:
Простые игры
Слава и Оля играют в игру умножения - умножают целое число P на одно из чисел от 2 до 9. Слава всегда начинает с P = 1, делает умножение, затем число умножает Оля, затем Слава и т.д. Перед началом игры им задают случайное число N, и победителем считается тот, кто первым получит P >= N. Определить, кто выиграет при заданном N, если оба играют наилучшим образом.
Входные данные
В первой строке находится единственное число N. 2 <= N <= 4 294 967 295.
Выходные данные
Выводится одна строка - "Stan wins.", если победит Слава, или "Ollie wins.", если победит Оля.
| |
![]()
|
|
Темы:
Простые игры
Бумажная полоска разделена на N клеток. Двое играющих по очереди выбирают и зачёркивают ровно K пустых смежных клеток. Выигрывает сделавший последний ход. Оба игрока придерживаются правильной стратегии. Дана ситуация игры. Требуется определить, кто выиграет.
Входные данные
Ограничения: 1 <= K <= N <= 40.
В первой строке содержатся числа N и K, во второй строке N символов: латинская заглавная O - пустая клетка, латинская заглавная X - зачёркнутая клетка.
Выходные данные
Вывести одно число: 1, если выиграет первый, сделавший ход; 2, если выиграет второй; 0, если ход сделать нельзя.
| |
![]()
|
|
Темы:
Простые игры
После того, как к удивлению тётушки Полли, её забор был покрашен, она поручила Тому Сойеру обновить краску на плитках, которыми был вымощен их квадратный двор. Двор был покрыт NxN одинаковыми квадратными плитками, каждая из которых когда-то давно была покрашена в один из K цветов (K<N). Краска на плитках потускнела и Тому Сойеру поручили их покрасить, на этот раз в один любой цвет (из тех же К цветов). Покрасить нужно все плитки, в том числе и те, которые уже были покрашены в этот цвет раньше.
Окунув кисть в ведро с краской один раз, можно перекрасить один горизонтальный или вертикальный ряд плиток. Чтобы разнообразить свою работу, Том придумал, что ряд плиток можно красить только цветом, которым на данный момент уже покрашены (старой или новой краской) по крайней мере две плитки выбранного ряда (вертикального или горизонтального). За один раз Том собирается красить допустимым цветом весь ряд целиком, независимо от того, были ли уже перекрашены какие-либо его плитки ранее. Помогите Тому определить, какое минимальное число раз ему придется обмакнуть кисть, чтобы перекрасить все плитки, следуя придуманным правилам, и в какой цвет окажутся окрашены все плитки.
Входные данные
В первой строке записаны через пробел два числа: N — количество плиток в одном ряду (1<N≤200) и K (1≤K<N). В каждой из следующих N строк записаны N натуральных чисел, обозначающих номера цветов красок, в которые когда-то были выкрашены соответствующие плитки данного горизонтального ряда. Номера цветов — натуральные числа в диапазоне от 1 до K.
Выходные данные
Выведите два числа: L — какое минимальное число раз придется окунать кисть в ведро с краской, и номер краски С, в которую в результате окажутся перекрашены все плитки двора. Если таких красок может быть несколько, то выведите номер любой из них.
Если перекрасить все плитки, следуя придуманным Томом правилам, нельзя, выведите два раза число 0.
| |
![]()
|
|
Темы:
Простые игры
Алеша Попович и Добрыня Никитич сражаются со стаей двух- и трехголовых драконов. Они по очереди взмахивают мечами, и одним махом могут отрубить любое (по своему желанию) число голов, но только у одного дракона. Отрубивший последнюю голову у последнего дракона получает в жены прекрасную принцессу.
Кто из богатырей (начинающий или второй) может получить в жены принцессу независимо от действий другого?
Входные данные
Во входном файле записано два числа N и M — количество двух- и трехголовых драконов соответственно (оба числа целые из диапазона от 0 до 100).
Выходные данные
В выходной файл выведите сначала число 1 или 2 определяющее, кто из богатырей имеет все шансы получить в жены принцессу (1 — тот, кто начинает, 2 — второй). В случае 1 выведите также все варианты его первого хода, которые к этому приводят: сначала выведите количество различных выигрышных ходов (при этом отрубание одинакового количества голов у разных двухголовых драконов считается одним и тем же ходом, так же и для трехголовых), а затем сами ходы. Каждый ход задается парой чисел: первое число определяет у сколькиголового дракона нужно отрубать головы, а второе — сколько голов нужно отрубать.
| |
![]()
|