| Условие задачи | | Прогресс | Попытки, все/успешные |
|
Темы:
Топологическая сортировка
Применение обхода в глубину
Задан ориентированный ациклический граф с \(n\) вершинами и \(m\) ребрами. Также задана перестановка вершин графа. Необходимо проверить, является ли данная перестановка топологической сортировкой.
В первой строке даны два числа \(n\) и \(m\) — количество вершин и ребер в графе соответственно (\(1 \leq n, m \leq 10^5\)). В следующих \(m\) строках заданы пары чисел \(u_i, v_i\), означающие, что в графе есть ребро из вершины \(u_i\) в вершину \(v_i\). В последней строке задана перестановка из \(n\) элементов.
Выведите "YES" (без кавычек), если данная перестановка является топологической сортировкой и "NO" в противном случае.
| |
![]()
|
3/
2
|
|
Темы:
Применение обхода в глубину
Маша очень любила строить башенки из кубиков в детстве, но теперь она уже взрослая, потому башенки из простых кубиков её не интересуют. Она купила детали для башенки, которые представляют собой блок 3*3*1, который очень легко описать матрицей 3 на 3, так как толщина блока всего 1 кубик.
Маше точно известно, что:
- при использовании всех блоков, можно гарантированно построить башенку, которая не будет иметь пустот, включая нижнюю и верхнюю границы;
- используя все блоки, можно построить башенку только одним и не более способами;
- при строительстве башенки блоки нельзя вращать;
- только два блока во всём наборе имеют сплошную верхнюю или же нижнюю границу;
- глубина пустот в блоке может состоять из 1 или 2 элементов;
- блоков, имеющих пустоты, которые нельзя покрыть при сборе башенки не существует.
Напишите программу, помогающую Маше определить, в каком порядке нужно строить башню, исходя из всех ограничений, написанных выше.
Входные данные
В первой строке подаётся число N (1 <= N <= 10) – количество блоков для башенки, далее на 3*N строках вводится по 3 цифры через пробел(0 – у блока отсутствует элемент в этой позиции, 1 – сам блок), представляющие из себя N блоков, доступных для строительства.
Нумерация блоков начинается с 1 и увеличивается при описании каждого последующего блока (то есть первый блок, второй и так далее).
Выходные данные
Вывести в ответе в одну строку через пробел каждый элемент – номера блоков в порядке сбора башни снизу-вверх.
Пояснение
Пример №2

| |
![]()
|
2/
1
|
|
Темы:
Применение обхода в глубину
Алгоритмы на графах
Поиск компонент связности
В далёком заснеженном города Снежнокрибирске очень мало пеших тропинок, так как город просто не успевает их чистить, потому люди передвигаются в основном только на внедорожниках: ездят в магазин, отвозят детей в школу, ездят на работу и так далее.
В один из последних дней перед зимними каникулами ребятам в школе задали проект на каникулы, который можно делать как самому, так и в группе, но не более 3 человек. Но так как проект связан с совместной работой, а в городе нет никакой связи: ни телефонной, ни интернета, то ребята решили собираться у кого-нибудь дома, чтобы делать проект вместе. Так как проект может делать до трёх человек, то ученики составили карту своих домов в городе, а также отметили на них тропинки. У них встал вопрос о том, как делать большинство проектов максимальным возможным количеством человек, но так, чтобы как можно меньше учеников делали проект одни. Помогите ребятам по описанию карты их города и тропинкам составить возможный план, как им лучше распределить проекты между собой.
Формат входных данных
На первой строке подаются два числа N, M (1 <= N,M <= 100) – количество домов и тропинок между ними соответственно.
Далее на M строках подаются дорожки в виде номеров домов (если существует дорога 1-2, то значит существует дорожка и 2-1).
Формат выходных данных
Выведите на первой строке количество учеников, которые делают проект в одиночку.
На второй – количество групп учеников, делающих проект в паре.
На третьей – количество групп учеников, делающих проект втроём.
Примечание: ребята стараются разбиться на группы по максимуму человек (по 3), если остался кто-то один, но он мог делать проект не один, то стараемся минимизировать одиночек.
| |
![]()
|
88/
31
|
|
Темы:
Применение обхода в глубину
Неориентированный граф называется четно-нечетным, если найдутся две его вершины, между которыми существуют пути как из четного, так и из нечетного числа ребер. Напишите программу, которая:
- определяет, является ли заданный граф четно-нечетным;
- в случае отрицательного ответа на пункт 1 находит максимальное подмножество X вершин графа такое, что для любых двух вершин i и j из X выполняется следующее условие: все пути между i и j состоят из четного числа ребер.
Входные данные
Первая строка входного файла содержит число вершин графа N (1≤N≤100) и число ребер M (1≤M≤1000), а каждая последующая — пару чисел (i,j), означающих, что в графе присутствует ребро, соединяющее вершины с номерами i и j.
Выходные данные
Первая строка выходного файла должна содержать ответ на пункт 1 в форме «YES/NO». В случае отрицательного ответа на пункт 1 вторая строка должна содержать количество вершин в множестве X, а третья — номера вершин из этого множества в порядке возрастания, записанные через пробел. Если вариантов решений несколько, то достаточно вывести любое из них.
| |
![]()
|
1/
1
|
|
Темы:
Алгоритмы на графах
Арифметические алгоритмы (Теория чисел)
Применение обхода в глубину
Обход в глубину
Дано дерево на n вершинах (связный неориентированный ациклический граф c n−1 рёбрами), где у каждого ребра есть вес w. Назовём простой путь длины k возрастающим , если существует такое целое x>=2, что вес первого ребра пути делится на x, второго ребра — делится на x2, ……, вес k-го ребра делится на xk.
Требуется найти максимальную длину k возрастающего пути, где k — количество рёбер в нём.
Входные данные
В первой строке вводится единственное целое число n (1 <= n <= 100000) - число вершин в дереве.
В следующих n−1 строках вводятся по три целых числа u, v, w ( 1<= v <= n, 1<= w <= n, u ≠ v, 1 <= w <= 107) - номера вершин, которые соединяет очередное ребро, и его вес.
Выходные данные
Выведите одно целое число k - максимальную длину возрастающего пути.
Примечание
Простым путем называется такой путь, что все вершины в нем различны.
В 1-м примере есть путь длины 2: 3 — 1 — 2. Тогда для него подходящий x = 2. Можно показать, что возрастающего пути большей длины не существует.
Во 2-м примере есть путь длины 3: 3 — 4 — 5 — 6. Тогда для него подходящий x = 2. Можно показать, что возрастающего пути большей длины не существует.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4
1 2 8
1 3 6
1 4 3
|
2
|
| 2 |
6
1 2 2
2 3 4
3 4 2
4 5 4
5 6 8
|
3
|
| |
![]()
|
5/
2
|
|
Темы:
Применение обхода в глубину
Обход в глубину
Беси любит искать пути в лабиринтах и играть в "крестики-нолики". Фермер Джон придумал для неё способ играть в обе игры одновременно!
Первое - "крестики-нолики" - вместо размещения X и O на решётке 3×3, коровы играют с М и О на решётке 3×3. Во время хода корова может поставить М или О в любую пустую ячейку (в отличие от стандартной игры, где один игрок всегда ставит X, а другой всегда О). Победитель этой игры тот, кто первый получит слово 'MOO' горизонтально, вертикально или по диагонали. В обратном порядке тоже засчитывается, то есть 'OOM' тоже выигрышная комбинация. Как и в стандартной игре, возможно заполнить всё поле и никто не выиграл. Ход в игре указывается 3 символами 'Mij' или 'Oij', где i и j в интервале 1…3 и указывают строку и столбец, в которые ставится соответствующий символ 'M' или 'O'.
Фермер Джон спроектировал для Беси квадратный лабиринт, представляющий решётку из N×N ячеек (3≤N≤25). Некоторые ячейки, включая все граничные ячейки, содержат большие стоги сена, предотвращающие Беси от захода в эти ячейки. Беси может свободно двигаться во все другие ячейки лабиринта предпринимая шаги в в обычных направлениях -север, юг, запад, восток. Некоторые ячейки содержат листок бумаги, на котором написан ход для "крестиков ноликов". По ходу тго, как Беси двигается по лабиринту, каждый раз, когда она попадает на такую ячейку, она должна сделать соответствующий ход в игре "крестики-нолики", в которую она играет параллельно с движением по лабиринту. Если соответствующая ячейка в "крестиках-ноликах" уже занята, то она не предпринимает никаких действий. У неё нет противника в игре "крестики-нолики", но некоторые из ячеек лабиринта могут противоречить её цели составить слово 'MOO'.
Если Беси останавливает игру "крестики-нолики" сразу после победы, определите количество различных выигрышных конфигураций в "крестиках-ноликах", которые она может сгенерировать, двигаясь соответственно в лабиринте.
ФОРМАТ ВВОДА
Первая строка содержит N.
Лабиринт определяется следующими N строками, каждая из которых содержит 3N символов. Каждая ячейка описывается блоком из 3 символов: '###' для стены, '...' для пустой ячейки, 'BBB' для ячейки в которой стартует Беси, ход для "крестиков-ноликов". Ровно одна ячейка содержит 'BBB'.
ФОРМАТ ВЫВОДА
Выведите количество различных выигрышных комбинаций для "крестиков-ноликов" (возможно 0), которые Беси может сгенерировать движением по лабиринту, остановившись после победы.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
7
#####################
###O11###...###M13###
###......O22......###
###...######M22######
###BBB###M31###M11###
###...O32...M33O31###
#####################
|
8 |
В этом примере имеется 8 выигрышных комбинаций, которые Беси может достичь:
O.M
.O.
MOM
O..
.O.
.OM
O.M
.O.
.OM
O..
.O.
MOM
O..
...
OOM
..M
.O.
OOM
...
.O.
OOM
...
...
OOM
Пояснения к одной из них:
O..
...
OOM
Здесь Беси сначала посещает ячейку O11, затем двигается в нижний коридор, посещая O32, M33, O31. Игра прекращается, поскольку Беси выиграла. |
| |
![]()
|
2/
2
|
|
Темы:
Применение обхода в глубину
Граф называется двудольным, если его вершины можно раскрасить в два цвета так, что нет ребер, соединяющих вершины одинакового цвета (то есть каждое ребро идет из вершины 1-го цвета в вершину 2-го).
Дан граф. Требуется проверить, является ли он двудольным, и если да, то раскрасить его вершины.
Входные данные
В первой строке задано сначала число N - количество вершин графа (не превышает 100). Далее идет матрица смежности - матрица размером NxN из 0 и 1 (0 обозначает отсутствие ребра, 1 - наличие). Граф неориентированный, без петель.
Выходные данные
В первую строку выведите одно из сообщений YES или NO (в зависимости от того, является ли граф двудольным или нет). В случае ответа YES, во второй строке выведите N чисел - цвета, в которые нужно раскрасить вершины: для первого цвета используйте значение 1, для второго цвета - значение 2. Первая вершина должна иметь цвет 1.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
0 1 1
1 0 1
1 1 0
|
NO |
| 2 |
3
0 1 1
1 0 0
1 0 0
|
YES
1 2 2
|
| |
![]()
|
1993/
675
|
|
Темы:
Применение обхода в глубину
Во время контрольной работы профессор Флойд заметил, что некоторые студенты обмениваются записками. Сначала он хотел поставить им всем двойки, но в тот день профессор был добрым, а потому решил разделить студентов на две группы: списывающих и дающих списывать, и поставить двойки только первым.
У профессора записаны все пары студентов, обменявшихся записками. Требуется определить, сможет ли он разделить студентов на две группы так, чтобы любой обмен записками осуществлялся от студента одной группы студенту другой группы.
Входные данные: В первой строке находятся два числа N и M - количество студентов и количество пар студентов, обменивающихся записками (1<=N<=100, 0<=M<=(N(N−1))/2. Далее в M строках расположены описания пар студентов: два числа, соответствующие номерам студентов, обменивающихся записками (нумерация студентов идёт с 1). Каждая пара студентов перечислена не более одного раза.
Выходные данные: Необходимо вывести ответ на задачу профессора Флойда. Если возможно разделить студентов на две группы - выведите YES; иначе выведите NO.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 2
1 2
2 3
|
YES |
| 2 |
3 3
1 2
2 3
1 3
|
NO |
| |
![]()
|
1085/
553
|
|
Темы:
Обход в глубину
Применение обхода в глубину
Динамическое программирование
Динамическое программирование
Динамическое программирование на поддеревьях
В лаборатории теоретической пиротехники изучают новые технологии организации
фейерверков. Фейерверк представляется как корневое дерево, а поскольку в мощном
фейерверке его элементы также взрываются, порождая новые фейерверки, то ученые вводят
операцию возведения корневого дерева в степень.
Корневое дерево содержит одну или несколько вершин. Одна из вершин выделена и
называется корнем дерева, для каждой из остальных вершин ровно одна другая вершина
является родителем. При этом от любой вершины можно добраться до корня,
последовательно переходя от вершины к ее родителю. Вершина, которая не является
родителем никакой другой вершины, называется листом. Если вершина x является
родителем вершины y, то вершина y является ребенком вершины x. Будем говорить, что
вершина и ее родитель соединены ребром.
На рис. 1 показан пример корневого дерева с корнем в вершине 1. Родителем вершин
2 и 3 является вершина 1, родителем вершины 4 является вершина 2. Вершины 2 и 3 — дети
вершины 1, а вершина 4 — ребенок вершины 2. Листьями являются вершины 3 и 4.
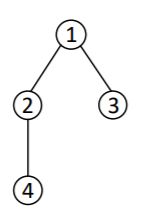
Рис. 1. Пример корневого дерева с корнем в вершине 1, листьями 3 и 4.
Фейерверк задается своим базовым деревом T и мощностью m. Фейерверк представляется деревом, которое получается в результате возведения дерева T в степень m. Операция возведения дерева в степень устроена следующим образом. Если m = 1, то результат T 1 — само дерево T. Для m > 1 рассмотрим дерево T m – 1 . Выполним следующую операцию: для каждого листа x дерева T m – 1 создадим копию дерева T и назначим лист x родителем корня соответствующей копии. Получившееся дерево будет деревом T m .
На рис. 2 показано дерево, представленное на рис. 1, в степенях 1, 2 и 3.
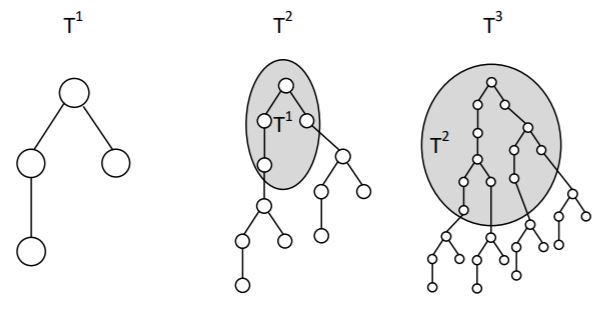
Рис. 2. Пример возведения дерева в степени 1, 2 и 3
Путем в дереве называется последовательность вершин, в которой две соседние
вершины соединены ребром. Все вершины в пути должны быть различны.
Для того, чтобы оценить красоту фейерверка, необходимо определить, какое
максимальное количество вершин может содержать путь в дереве, которым представляется
фейерверк. На рис. 3 приведен путь в дереве T2, содержащий максимальное количество
вершин. Таким образом, красота фейерверка с базовым деревом T и мощностью 2 равна 10.
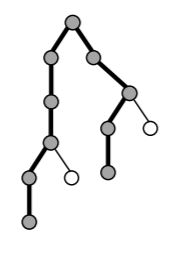
Рис. 3. Путь в дереве T 2 , содержащий максимальное количество вершин.
Требуется написать программу, которая по описанию дерева T и натуральному числу m определяет красоту фейерверка с базовым деревом T и мощностью m.
Формат входных данных
Первая строка входных данных содержит два натуральных числа n и m — количество
вершин в базовом дереве фейерверка T и его мощность (3 ≤ n ≤ 200 000, 1 ≤ m ≤ 200 000).
Вторая строка описывает дерево T и содержит (n – 1) целых чисел: p2, p3, …, pn —
номера родителей вершин 2, 3, …, n, соответственно (1 ≤ pi ≤ i – 1).
Формат выходных данных
Требуется вывести одно целое число — красоту фейерверка, представляемого
деревом Tm.
| |
![]()
|
24/
3
|
|
Темы:
Применение обхода в глубину
Обход в глубину
Деревья
Гномы продолжают искать золото предков в недрах Одинокой горы. Недра Одинокой горы представляют собой n пещер, некоторые из которых соединены двусторонними переходами. При этом из каждой пещеры в любую другую можно попасть по переходам, причем это можно сделать единственным способом.
Гномы разделились на два отряда, которые начали свои поиски с пещер u0 и v0, соответственно. Гномы каждого из отрядов перемещаются вместе. На обследование пещеры у отряда гномов уходит ровно одна минута, после чего каждый отряд быстро перемещается по переходу в одну из соседних пещер. При этом гномы никогда не заходят в пещеру, если они или другой отряд в ней уже побывали. Оба отряда никогда не заходят в одну и ту же пещеру. Если хотя бы один из отрядов гномов не может переместиться в соответствии с этими правилами, оба отряда сразу прекращают поиски сокровищ.
Чтобы как можно лучше обследовать недра Одинокой горы, гномы хотят, чтобы поиски продолжались как можно дольше. По заданной карте пещер в Одинокой горе и начальному положению отрядов гномов определите, какое максимальное время могут продолжаться поиски сокровищ.
Формат входных данных
В первой строке число n (2 ≤ n ≤ 200 000) — число пещер в Одинокой горе. В следующих n−1 строках заданы переходы между пещерами. В каждой строке записаны номера двух пещер v и u, соединенных переходом (1 ≤ v, u ≤ n). В следующей строке заданы номера пещер v0 и u0, в которых исходно находятся два отряда гномов (1 ≤ v0, u0 ≤ n, v0 != u0).
Формат выходных данных
Выведите максимальное число минут, которое могут продолжаться поиски сокровищ.
| Ввод |
Вывод |
Пояснение |
6
1 2
2 3
3 4
4 5
5 6
4 5 |
2 |
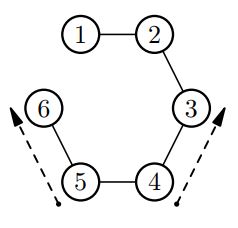 |
8
1 2
2 3
3 4
2 5
5 6
3 7
7 8
1 8 |
4 |
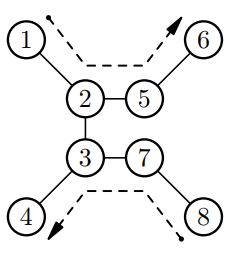 |
| |
![]()
|
2/
1
|
|
Темы:
Обход в глубину
Применение обхода в глубину
Разбор случаев
Олег очень любит двоичные последовательности — последовательности из нулей и единиц. Совсем недавно он написал в тетради очередную двоичную последовательность из n элементов.
Для выписанной последовательности Олег посчитал Z-функцию.
Z-функцией последовательности s1, . . . , sn называется массив z[1..n], в котором:
• z[1] = 0;
• Если i > 1, то z[i] равно длине наибольшего общего префикса последовательности s и суффикса последовательности s, начинающегося с i-й позиции. Иначе говоря, z[i] равно максимальному k, такому что s1 = si , s2 = si+1, . . . , sk = si+k−1.
Например, для последовательности s = h0, 0, 1, 1, 0, 0, 1i Z-функция следующая: z = h0, 1, 0, 0, 3, 1, 0i.
Записав в тетради последовательность и ее Z-функцию, Олег лег спать. Пока он спал, его младший брат Егор прокрался в комнату и закрасил фломастером последовательность и некоторые значения Z-функции. Проснувшись, Олег заинтересовался, сколько различных двоичных последовательностей он мог вечером написать в тетради, чтобы незакрашенные значения Z-функции были правильными.
Найдите число искомых последовательностей и выведите его по модулю 109 + 7. Заметьте, что Олег мог и ошибиться при вычислении Z-функции, в этом случае ни одна последовательность не подходит и ответ равен 0.
Формат входных данных
В первой строке входного файла находится целое число n — длина исходной двоичной последовательности (1 ≤ n ≤ 1000). Во второй строке входного файла находятся n целых чисел z[1], . . . , z[n], где z[i] — значение Z-функции в позиции i, или −1, если значение в i-й позиции было закрашено (−1 ≤ z[i] ≤ n).
Формат выходных данных
В выходной файл выведите единственное число — остаток от деления числа подходящих двоичных последовательностей на число 109 + 7.
| Ввод |
Вывод |
3
0 0 1 |
2 |
4
0 0 1 0 |
0 |
3
0 3 -1 |
0 |
3
-1 -1 -1 |
8 |
Пояснение
В первом примере подходят последовательности {0, 1, 0 } и { 1, 0, 1 }.
Во втором примере не существует ни одной двоичной последовательности длины 4 с заданной Z-функцией.
В третьем примере z[2] = 3, что противоречит определению Z-функции, поэтому ответ 0.
В четвертом примере подходит любая двоичная последовательность длины 3.
| |
![]()
|
1/
1
|