Плюсануть
Поделиться
Класснуть
Запинить


Олимпиадный тренинг

Вы можете самостоятельно решать эти задачи столько раз, сколько вам это понадобится.
   

Практический тест

Массивы Префиксные суммы(минимумы, ...) Динамическое программирование: один параметр

У нас есть сетка с H строками и W столбцами. Квадрат в i-й строке и j-м столбце будет называться Square(i, j). Целые числа от 1 до H·W записаны по всей сетке, а целое число, записанное в Square(i, j), равно Ai,j.
Вы - волшебник (волшебница), и можете телепортировать фигуру, помещенную на Square(i, j) в Square(x, y), потратив \(|x-i|+|y-j|\) маджиков (магических монет).
Теперь вам нужно пройти Q практических тестов на свои способности как волшебника (волшебницы). I-е испытание будет проводиться следующим образом:
- первоначально фигура располагается в квадрате, где записано целое число Li;
- пусть x будет целым числом, записанным в квадрате, занятом фигурой. Неоднократно переместите фигуру в квадрат, где написано целое число x+D, пока x не станет равен Ri. Тест заканчивается, когда x = Ri .
Гарантируется, что Ri- Li делится на D.
Для каждого теста найдите сумму маджиков, израсходованных во время этого теста.

Входные данные
В первой строке заданы три целых числа: H, W и D (\(1\leq H,W \leq 300\), \(1 \leq D \leq H \cdot W\)).
В следующих H строках записано по W чисел Ai,j (\(1 \leq A_{i,j} \leq H \cdot W\), \(A_{i,j} \neq A_{x,y} ((i,j) \neq (x,y))\).
В следующей строке записано целое число Q (\(1 \leq Q \leq 10^5\)).
В последних Q строках записано по 2 целых числа: Li и Ri (\(1 \leq L_i \leq R_i \leq H \cdot W\)), \((R_i-L_i)\) кратно D.

Выходные данные
Для каждого теста выведите сумму маджиков, израсходованных во время этого теста. Вывод должен быть в порядке проведения тестов.
 

 

Примеры
№ Входные данные Выходные данные Пояснения
1 3 3 2
1 4 3
2 5 7
8 9 6
1
4 8		 5 - 4 записано Square (1,2).
- 6 записано в Square (3,3).
- 8 записано in Square (3,1).

Таким образом, сумма магических очков, израсходованных во время одного теста, составляет:
 \((|3-1|+|3-2|)+(|3-3|+|1-3|)=5\).
 
2 4 2 3
3 7
1 4
5 2
6 8
2
2 2
2 2		 0
0		 Обратите внимание, что может быть тест, в котором фигура вообще не перемещается, и может быть несколько идентичных тестов.
3 5 5 4
13 25 7 15 17
16 22 20 2 9
14 11 12 1 19
10 6 23 8 18
3 21 5 24 4
3
13 13
2 10
13 13		 0
5
0		  

 

Радость Громозеки

Массивы Алгоритмы обработки "Два указателя"

Громозека имеет последовательность целых чисел A длины N. Он сделает три среза в последовательности A и разделит ее на четыре (непустые) смежные подпоследовательности B, C, D и E. Положения срезов он выбирает произвольно. Пусть P, Q, R, S - суммы элементов в B, C, D,  E соответственно. Громозека будет счастлив, когда абсолютная разница между максимумом и минимумом между P, Q, R, S будет минимальной. Найдите минимально возможную абсолютную разницу между максимумом и минимумом между P, Q, R, S.

Входные данные
В первой строке записано целое число N  (1 <= N <= 2·105). Во второй строке записано N целых чисел Ai (1 <= Ai <= 109).

Выходные данные
Выведите на экран минимально возможную абсолютную разницу между максимумом и минимумом между P, Q, R, S.
 

Примеры
№ Входные данные Выходные данные Пояснения
1 5
3 2 4 1 2		 2 Если разделить A на B, C, D, E = (3), (2), (4), (1,2), то P = 3, Q = 2, R = 4, S = 1 + 2 = 3.
Здесь максимум и минимум среди P, Q, R, S равны 4 и 2, с абсолютной разницей 2.
Мы не можем сделать абсолютную разницу между максимумом и минимумом меньше 2, поэтому ответ - 2.
2 10
10 71 84 33 6 47 23 25 52 64		 36  
3 7
1 2 3 1000000000 4 5 6		 999999994  

Путешествие Громозеки

Циклы Массивы

У Громозеки есть следующие два личных принципа: он никогда не преодолевает расстояние больше L за один день. Он никогда не спит под открытым небом. То есть он должен находться в отеле в конце дня.
На планете Блук N отелей и все расположены на одной улице. Координата i-го отеля (1<=i<=N) равна xi.
Путешествуя по планете Блук, Громозека запланировал Q переездов. Каждым переездом он планирует менять отель aj на bj (1<=j<=Q). Для каждого переезда найдите минимальное количество дней, которое нужно Громозеке, чтобы добраться от aj-го отеля до bj-го, следуя его принципам.
Гарантируется, что он всегда может поехать из aj-го отеля до bj-го отеля.

Входные данные
В первой строке задается целое число N (2<=N<=105) - количество отелей на планете Блук. Во второй строке - N чисел xi - координаты i-го отеля (1<=x1<x2<...<xN<=109 , xi+1−xi<=L). В третьей строке записано число L (1<=L<=109).  В четвертой строке - число Q (1<=N<=105). 
В последних Q строчках находится по два различных числа aj и bj (1<=aj,bj<=N). Все числа целые.

Выходные данные
Выведите Q строк. В j-й строке (1<=j<=Q) должно быть указано минимальное количество дней, которое Громозеке нужно, чтобы добраться из  aj-го отеля до bj -го отеля.

 

Примеры
№ Входные данные Выходные данные Пояснение
1 9
1 3 6 13 15 18 19 29 31
10
4
1 8
7 3
6 7
8 5		 4
2
1
2		 По 1-му переезду он может проехать от 1-го отеля до 8-го за 4 дня следующим образом:

День 1: Переезд из 1-го отеля во 2-й отель. Пройденное расстояние - 2.
День 2: Переезд из 2-го отеля в 4-й. Пройденное расстояние - 10.
День 3: Переезд из 4-го отеля в 7-й. Пройденное расстояние - 6.
День 4: Переезд из 7-го отеля в 8-й. Пройденное расстояние - 10.

 

Снежик Сугробович - 2

Циклы Массивы

В некотором мире сейчас 31 декабря и все веселье только начинается. Снежик Сугробович слепил N больших снежков и расположил их в ряд слева направо. На каждом i-м снежке, если считать слева (1 <= i <= N), он написал целое число ai. Он предлагает вам сыграть в игру. Снежик Сугробович разрешил сломать не более N − 1 снежков по вашему выбору. 

Допустим, осталось K снежков. Снежик Сугробович будет удовлетворен и подарит вам хороший подарок, если для каждого целого числа i (1<=i<=K) на i-м снежке, если считать слева оставшиеся снежки, будет написано целое число i.
Найдите минимальное количество снежков, которое вам нужно сломать, чтобы получить подарок. Если не получится, то выведите -1.

Входные данные
В первой строке программа получает на вход целое число N (1 <= N <= 200000). Во второй строке - N натуральных чисел ai (1<=ai<=N). 

Выходные данные
Выведите минимальное количество снежков, которые нужно сломать, чтобы получить подарок, или выведите -1, если это невозможно сделать.
 

Примеры
№ Входные данные Выходные данные Пояснение
1 3
2 1 2		 1 Сломайте первый снежок, числа на остальных снежках будут удовлетворять условию Снежика Сугробовича
2 3
2 2 2		 -1  
3 10
3 1 4 1 5 9 2 6 5 3		 7  
4 1
1		 0  

Vector: Начало

Массивы

Создайте вектор и заполните его только положительными элементами.


Входные данные
В первой строке вводится количество элементов в массиве. Во второй строке вводятся элементы массива.
 
Выходные данные
Выведите только положительные элементы из последовательности.

 
Примеры
№ Входные данные Выходные данные
1 4
2 -4 0 100		 2 100

Сортировка вектора: Начало

Массивы

Дана последовательность, состоящая из целых чисел. Напишите программу, которая создает и сортирует массив по убыванию.
 
Входные данные
Сначала задано число N — количество элементов в массиве (1<=N<=100). Далее через пробел записаны N чисел - элементы массива. Массив состоит из целых чисел.
 
Выходные данные
Необходимо вывести массив, отсортированный по убыванию.
 
Примеры
№ Входные данные Выходные данные
1 5
4 56 23 67 100		 100 67 56 23 4

Найти и посчитать

Массивы Алгоритмы обработки

Даны две целочисленные последовательности, каждая из которых имеет длину N: A = (A1, A2, ..., AN) и B = (B1, B2, ..., BN).
Все элементы A различны. Все элементы B тоже разные.

Выведите следующие два значения.

  1. Количество целых чисел, содержащихся в обоих A и B, появляющихся в одной и той же позиции в двух последовательностях. Другими словами, количество целых i чисел такое, что Ai = Bi.
  2. Количество целых чисел, содержащихся в обоих A и B, появляющихся в разных позициях в двух последовательностях. Другими словами, количество пар целых (i, j) чисел, таких, что Ai = Bj и i ≠ j.


Входные данные
Программа получает на вход три строки. В первой строке записано одно число N (1 <= N <= 1000) - количество чисел последовательности. Во второй строке записаны числа A1, A2, ..., AN, все числа различные. В третьей строке - числа B1, B2, ..., BN , все числа различные (1 <= Ai, Bi <= 109). 

Выходные данные
Выведите в первой строке ответ на первый вопрос, во второй строке - на второй.
 
 
Примеры
№ Входные данные Выходные данные
1 
4
1 3 5 2
2 3 1 4
 
1
2
2 
3
1 2 3
4 5 6
 
0
0

Мирные ладьи

Двумерные массивы Массивы

На шахматной доске размером N × N расставлено N шахматных ладей не бьющих друг друга, то есть на каждой вертикали и каждой горизонтали стоит ровно одна ладья.


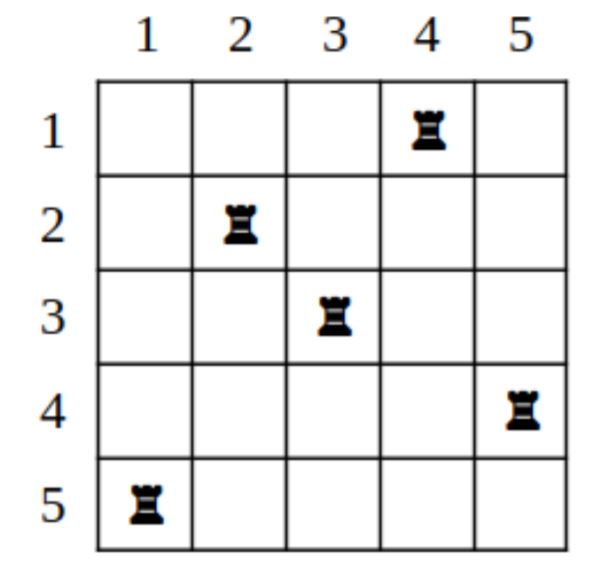
Шахматную доску повернули на 90° по часовой стрелке. Выведите получившуюся расстановку ладей.


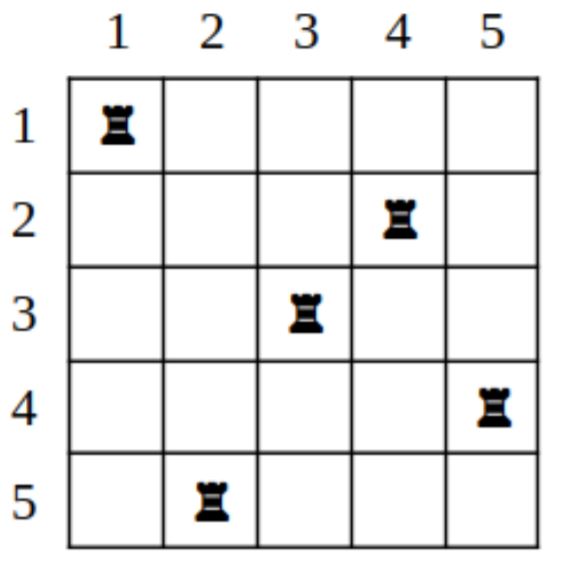
Входные данные
Первая строка входных данных содержит целое число N, 1 ≤ N ≤ 105 — размер доски. Следующие N строк содержат по одному числу от 1 до N, а именно, в i-й строке записано число ai — номер вертикали, в которой стоит ладья на i-й горизонтали. В этой задаче горизонтали нумеруются числами от 1 до N сверху вниз, вертикали нумеруются числами от 1 до N слева направо (см.рисунок).

Выходные данные
Программа должна вывести N чисел — расстановку ладей после поворота в таком же формате.

Примеры
№ Входные данные Выходные данные
1 5
4
2
3
5
1		 1
4
3
5
2

Замечание
Пример в условии соответствует рисункам. Первоначально ладьи стояли в столбцах 4, 2, 3, 5, 1
при перечислении их по строкам сверху вниз. После поворота ладьи стоят в столбцах 1, 4, 3, 5, 2.

 

Список делителей

Массивы

На вход программе подается натуральное число n >= 2, а затем n целых чисел. Напишите программу, которая создает из указанных чисел новый список, состоящий из сумм соседних чисел (0 и 1, 1 и 2, 2 и 3 и т.д.).

Входные данные
Программа получает на вход натуральное число n, а затем n целых чисел, каждое на отдельной строке.

Выходные данные
Программа должна вывести список, состоящий из сумм соседних чисел.

 

 
Примеры
№ Входные данные Выходные данные
1 5
1
2
3
4
5		 [3, 5, 7, 9]

12471

Массивы

Вводится сначала число N, а затем N чисел. Выведите эти N чисел в обратном порядке.
 
Входные данные
Вводится число N (0< N < 100), а затем N натуральных чисел, не превышающих 1000.
 
Выходные данные
Выведите N чисел в обратном порядке
 
 
Примеры
№ Входные данные Выходные данные
1
7
2 4 1 3 5 3 1
 1 3 5 3 1 4 2
 
 

Пара с максимальной суммой

Массивы

Напишите программу поиска номера первого из двух последовательных элементов в целочисленном массиве из 30 элементов, сумма которых максимальна (если таких пар несколько, то выбрать первую из них). Индексация элементов начинается с 0.


Входные данные
Программа получает на вход 30 строк, в каждой из которых записано по одному числу - элементу массива. Каждое число не превышает по модулю 109.

Выходные данные
Выведите одно число - ответ на задачу.
 
 

Максимус спасает Элстейд

Жадный алгоритм Массивы Алгоритмы сортировки

Одарённый невероятной магией и всезнанием Максимус заметил группу из n монстров, приближающихся к городку Элдстейд. Своими волшебными способностями он мгновенно определил расстояние в километрах от города до каждого монстра. Он также заметил, что все монстры двигаются с постоянной скоростью. У Максимуса есть оружие, способное уничтожить одного монстра после полной зарядки. Зарядка занимает ровно одну минуту. Чтобы победить монстра, оружие должно быть полностью заряжено к моменту приближения монстра к городу. Другими словами, невозможно убить монстра достигшего города, даже если в этот момент оружие закончило полную зарядку.
Максимус задается вопросом, сможет ли он сам спасти город от всех монстров или ему нужна помощь.
Напишите программу, которая поможет Максимусу мгновенно определить максимальное количество монстров, которое он сможет уничтожить до того момента, как хотя бы один монстр достигнет города.

Входные данные
Первая строка содержит число n - количество монстров. Во второй строке записано n чисел dist[i] - начальное расстояние в километрах от города для i-го монстра. Третья строка содержит n чисел speed[i] - скорость i-го монстра в километрах в минуту.

Ограничения

  • n == длина массива dist == длина массива speed
  • 1 <= n <= 105
  • 1 <= dist[i], speed[i] <= 105


Выходные данные
Выведите ответ на задачу.
 
 
Примеры
№ Входные данные Выходные данные Примечание
1 
3
1 3 4 
1 1 1
 
3
 Вначале расстояния между монстрами равны [1,3,4]. Максимус уничтожает первого монстра.
Через минуту расстояния между монстрами становятся [X,2,3]. Максимус уничтожает второго монстра.
Через минуту расстояния между монстрами будут [X,X,2]. Максимус уничтожает третьего монстра.
Все три монстра могут быть уничтожены.
 
2 
4
1 1 2 3
1 1 1 1
 
1
 Вначале расстояния между монстрами равны [1,1,2,3]. Максимус уничтожает первого монстра.
Через минуту расстояния между монстрами становятся равными [X,0,1,2], и второй монстр достиг города.
Максимус может уничтожить только 1 монстра.

 

Building a Ski Course

Двумерные массивы Конструктив Массивы

Фермер Джон помогает превратить его большое поле в лыжный маршрут для предстоящих Му-олимпийских игр. Поле имеет размеры M x N (1 <= M,N <=100) и его целевое финальное состояние описывается решеткой из M x N символов таких как:
 
RSRSSS
RSRSSS
RSRSSS
 
Каждый символ описывает состояние снега на этом участке R – грубый, S – гладкий (организаторы считают, что в таком случае - чередования грубых и гладких участков, гонка будет интересней).
 
Для выполнения этой задачи ФД планирует модифицировать свой трактор так, чтобы тот мог «отштамповать» любой фрагмент размером B x B (B<=M,B<=N) грубым снегом или гладким снегом.
ФД хочет сделать B как можно большим. С B=1 он может подготовить поле, штампуя индивидуально квадраты в соответствии с заданным финальным состоянием. Однако для бОльших значений B может оказаться невозможным выполнить задачу. Каждый квадрат поля должен быть обработан трактором. Невозможно оставить ячейку поля в исходном состоянии.
 
Помогите ФД определить максимально возможное значение B, которое он сможет успешно использовать.
 
INPUT FORMAT:
 
* Строка 1: Два разделённых пробелом целых числа M и N.
 
* Строки 2..M+1: M строк ровно по N символов (каждый R или S),
        описывающих желаемое финальное состояние поля.

 
OUTPUT FORMAT:
 
* Строка 1: Максимальное значение B, которое ФД может использовать, чтобы создать нужное поле.
 
 
Ввод Вывод
3 6
RSRSSS
RSRSSS
RSRSSS
 3


 
OUTPUT DETAILS:
 
ФД может отштамповать R колонках 1-3, затем S в колонках 2-4, затем R в колонках 3-5, и наконец,  S в колонках 4-6.
 

Симметричный подарок

ЕГЭ - вычислительные задачи Массивы

Максимус любит симметричные строки. В качестве новогоднего подарка, он попросил ему подарить несколько натуральных чисел.  При этом, Максимус будет доволен, если он сможет записать все значащие цифры шестнадцатеричной записи этих чисел так, чтобы полученная строка было симметричной (читалась одинаково как слева направо, так и справа налево). 
Дед Мороз выбрал для Максимуса N натуральных целых чисел, каждое из которых не больше 1000. Он просит вас помочь ему определить, будет ли доволен Максимус таким подарком.
Если Максимус будет доволен, то ваша программа должна вывести на экран число 1, а иначе - число 0.


Формат входных данных
На вход программе подаётся натуральное число N (N <= 105), а затем N натуральных чисел, каждое из которых не превышает 10000.

Формат выходных данных
Если Максимус будет доволен, то ваша программа должна вывести на экран число 0, а если возможно, то вывести число 1.

Примечание
1. В первом тестовом примере, если перевести все числа в шестнадцатеричную систему счисления, то получим цифры D, 1, 6, 2, 0. Из данных цифр невозможно составить симметричную строку. Ответ: 0.
2. Во втором тестовом примере, если перевести все числа в шестнадцатеричную систему счисления, то получим цифры A, B, 4, 4, A, B, D. Из данных цифр можем составить симметричную строку, например такую AB4D4BA. Ответ: 1.

 

Справедливая последовательность

Массивы

Последовательность из нулей и единиц четной длины назовем справедливой, если на четных местах этой последовательности столько же единиц, сколько на нечетных. Например, последовательность "011011" является справедливой, а последовательность "011101" – нет.

Задана некоторая последовательность нечетной длины из нулей и единиц. Из нее разрешается удалить одну цифру. Какую цифру следует удалить, чтобы последовательность стала справедливой?

Например, из последовательности "0111011" с этой целью можно удалить вторую цифру.

Входные данные
На вход программы поступает одна строка. Эта строка содержит последовательность нечетной длины из нулей и единиц. Длина последовательности не превышает 200001.

Выходные данные
Выведите одно число - номер цифры в последовательности, которую следует удалить, чтобы последовательность стала справедливой. Цифры нумеруются, начиная с 1.

Если это сделать невозможно, выведите 0. Если решений несколько, выведите любое.
Hallowen