| | | |
|
Проверка на простоту
Простые числа и разложение на множители
Проверьте, является ли число простым.
Входные данные
Вводится одно натуральное число n не превышающее 2000000000 и не равное 1.
Выходные данные
Необходимо вывести строку prime, если число простое, или composite, если число составное.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 |
prime |
| |
![]()
|
|
Разложение на простые - 1
Простые числа и разложение на множители
Требуется разложить целое число N на простые множители, представив его в виде произведения простых множителей и вывести результат в порядке возрастания.
Входные данные
На вход падается число N (\(2 <= N <= 10^9\)).
Выходные данные
Выведите список простых множителей числа N в порядке неубывания, разделенных знаком «*».
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 |
5 |
| 2 |
30 |
2*3*5 |
| |
![]()
|
|
Разложение на простые - 2
Простые числа и разложение на множители
Требуется разложить целое число N на простые множители, представив его в виде произведения степеней простых множителей и вывести результат в порядке возрастания.
Входные данные
На входе дано число N (\(2 <= N <= 10^9\)).
Выходные данные
Вывести разложение N на простые множители.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 |
2 |
| 2 |
1008 |
2^4*3^2*7 |
| |
![]()
|
|
Постулат Бертрана
Простые числа и разложение на множители
Постулат Бертрана (теорема Бертрана-Чебышева, теорема Чебышева) гласит, что для любого \(n > 1\) найдется простое число p в интервале \(n < p < 2n\). Такая гипотеза была выдвинута в 1845 году французским математиком Джозефом Бертраном (проверившим ее до \(n=3000000\)) и доказана в 1850 году Пафнутием Чебышевым. Раманужан в 1920 году нашел более простое доказательство, а Эрдеш в 1932 – еще более простое.
Ваша задача состоит в том, чтобы решить несколько более общую задачу – а именно по числу n найти количество простых чисел p из интервала \(n < p < 2n\).
Напомним, что число называется простым, если оно делится только само на себя и на единицу
Входные данные
Целое число n (\(2 <= n <= 50000\)).
Выходные данные
Выведите одно число – ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3000 |
353 |
| |
![]()
|
|
Простые числа - 1
Простые числа и разложение на множители
Найти количество всех четырехзначных простых чисел, оканчивающиеся на цифру k.
Входные данные
Число k.
Выходные данные
Вывести число - количество простых чисел, удовлетворяющих условию задачи. Если таких чисел нет то вывести слово Absent.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 |
266 |
| 2 |
0 |
Absent |
| |
![]()
|
|
Гипотеза Гольдбаха
Простые числа и разложение на множители
Гипотеза Гольдбаха (не доказанная до сих пор) утверждает, что любое четное число (кроме 2) можно представить в виде суммы двух простых чисел.
Входные данные
Программа получает на вход одно натуральное четное число n (\(3<n<2 \cdot 10^5\)).
Выходные данные
Программа должна вывести два числа, разделенные пробелом. Числа должны быть простыми и давать в сумме n.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 |
2 2 |
| 2 |
6 |
3 3 |
| |
![]()
|
|
Тройки чисел
Простые числа и разложение на множители
Напишите программу, находящую количество троек целых чисел a, c, p таких, что p — простое число, числа удовлетворяют равенству: $$ \sqrt{a} - \sqrt{c} = \sqrt{p}. $$ Каждое из чисел a, c и p лежит в промежутке от N до M (то есть \(N<=a<= M,\ N<=c<= M,\ N<=p<= M\)).
Входные данные
Вводятся два целых числа N и M (\(0<=N<=M<=100000\)).
Выходные данные
Выведите искомое количество троек чисел a, c, p.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 8 |
1 |
| 2 |
5 20 |
1 |
| 3 |
1 7 |
0 |
| |
![]()
|
|
Степень числа
Простые числа и разложение на множители
Для заданного натурального A найти минимальное натуральное N такое, что N в степени N (N, умноженное на себя N раз) делится на A.
Входные данные
На вход подается единственное число A (\(1 <= A <= 10^9\)).
Выходные данные
Необходимо вывести единственное число N.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
8 |
4 |
| 2 |
13 |
13 |
| |
![]()
|
|
Простые числа - 2
Простые числа и разложение на множители
Из заданного набора чисел выберите одно, имеющее максимальное количество простых делителей. Например, 30 имеет три простых делителя (2, 3 и 5), а 40 – только два (2 и 5).
Входные данные
Первая строка содержит число N – количество чисел в наборе. Во второй строке теста содержится N чисел, разделенных пробелом. Все числа во входных данных целые, принимающие значения от 2 до 1024.
Выходные данные
В ответе выведите число с максимальным количеством простых делителей. Если таких чисел несколько, выведите наименьшее из них.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
10
3 5 7 9 11 13 15 17 19 21
|
15 |
| 2 |
11
2 4 6 8 10 13 39 105 200 201 143
|
105 |
| |
![]()
|
|
2011
Целые числа
Простые числа и разложение на множители
Представьте число 2011 в виду суммы K последовательных простых чисел (то есть простых чисел, между которыми нет других простых чисел). Например, число 31 можно представить в виде суммы трех посдедовательных простых чисел следующим образом: 7 + 11 + 13 = 31.
Входные данные
Вводится одно натуральное число K (от 1 до 2011).
Выходные данные
Выведите слагаемые в порядке возрастания, разделяя их пробелом.
Если разложить в сумму K слагаемых невозможно, выведите NO SOLUTION (заглавными буквами).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 |
661 673 677 |
| 2 |
2 |
NO SOLUTION |
| |
![]()
|
|
Сломанный калькулятор
Простые числа и разложение на множители
У калькулятора есть две ячейки памяти: содержимое первой из них всегда отображается на табло, вторая является буфером. В начальный момент времени на табло калькулятора отображается целое число X, а в буфере записано число 0. У калькулятора работают только две клавиши: «+» и «=». При нажатии на «+» число, которое в данный момент отображено на табло, копируется в буфер. При нажатии на «=» число из буфера прибавляется к числу, отображенному на табло и результат отображается на табло, число в буфере при этом не меняется.
Требуется за наименьшее число нажатий клавиш на калькуляторе добиться того, чтобы на табло было отображено число Y.
Входные данные
Входной файл содержит два целых числа X и Y. Каждое из этих чисел по модулю не превышает 109.
Выходные данные
В первую строку выходного файла выведите одно число — количество нажатий клавиш, которое потребуется для получения числа Y. Если из числа X получить число Y с помощью указанных операций невозможно, в выходной файл выведите одно число –1.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
-1 -8 |
6 |
| 2 |
2 16 |
6 |
| 3 |
0 0 |
0 |
| |
![]()
|
|
Степень
Простые числа и разложение на множители
Для того чтобы проверить, как ее ученики умеют считать, Мария Ивановна каждый год задает им на дом одну и ту же задачу — для заданного натурального A найти минимальное натуральное N такое, что N в степени N (N, умноженное на себя N раз) делится на A. От года к году и от ученика к ученику меняется только число A.
Вы решили помочь будущим поколениям. Для этого вам необходимо написать программу, решающую эту задачу.
Формат входных данных
Во входном файле содержится единственное число A (1 ≤ A ≤ 1000000000 — на всякий случай; вдруг Мария Ивановна задаст большое число, чтобы кого-нибудь “завалить”).
Формат выходных данных
В выходной файл выведите единственное число N.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
8 |
4 |
| 2 |
13 |
13 |
| |
![]()
|
|
Псевдопростые числа
Простые числа и разложение на множители
Пусть a1 = 2, a2 = 3, an = a1·a2·...·an-1 – 1 при n ≥ 3. Назовем числа ai псевдопростыми. Для заданного натурального числа X нужно ответить на вопрос: можно ли X однозначно представить в виде произведения псевдопростых чисел (представления, отличающиеся только порядком множителей, считаются одинаковыми), и, если можно — выдать разложение.<
Входные данные
Вводится одно натуральное число X, 1 < X ≤ 109.
Выходные данные
Выведите псевдопростые числа, произведение которых равно X, в произвольном порядке. Если разложения не существует или оно не единственно, выдать 0.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6 |
2 3 |
| 2 |
5 |
5 |
| 3 |
7 |
0 |
| |
![]()
|
|
Минимальный делитель
Простые числа и разложение на множители
Цикл while
Найдите самый маленький натуральный делитель числа x, отличный от 1 (2 <= x <= 30000).
Входные данные
Вводится натуральное число x.
Выходные данные
Выведите наименьший делитель числа x, отличный от 1.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6 |
2 |
| |
![]()
|
|
Делители числа
Цикл for
Простые числа и разложение на множители
Условный оператор
Выведите все натуральные делители числа x в порядке возрастания (включая 1 и само число).
Входные данные
Вводится натуральное число x
Выходные данные
Выведите все делители числа x
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
32 |
1 2 4 8 16 32 |
| |
![]()
|
|
Количество делителей
Простые числа и разложение на множители
Цикл for
Подсчитайте количество натуральных делителей числа x (включая 1 и само число x).
Входные данные
Вводится натуральное число x (x < 30000).
Выходные данные
Выведите единственное число - количество делителей числа x.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
32 |
6 |
| |
![]()
|
|
Уравновесить подарки
НОД и алгоритм Евклида
Простые числа и разложение на множители
У Деда Мороза есть N мешков с подарками. Каждый мешок имеет вес a1, a2, ..., aN. Для равномерной нагрузки на сани Деду Морозу необходимо, чтобы вес всех мешков был одинаковым. Чтобы этого добиться, Дед Мороз своим волшебным посохом может выполнить одну из следующих операций любое количество раз, возможно ноль раз.
- Дед Мороз может выбрать любой мешок и если его вес кратен двум, то уменьшить вес в два раза.
- Дед Мороз может выбрать любой мешок и если его кратен трем, то уменьшить вес в три раза.
На каждую операцию у Деда Мороза уходит 1 секунда.
Найдите минимальное общее количество секунд, которое необходимо Деду Морозу, для достижения одинакового веса всех мешков с подарками. Если нет способа достичь цели, выведите вместо этого значение -1.
Входные данные
Программа получает на вход в первой строке целое число N (2 <= N <= 1000). Во второй строке записаны N чисел ai - вес i-го мешка с подарками (1 <= ai <= 109).
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
1 4 3 |
3 |
| 2 |
3
2 7 6 |
-1 |
| 3 |
6
1 1 1 1 1 1 |
0 |
| |
![]()
|
|
Выборы
Алгоритмы на графах
Простые числа и разложение на множители
Динамическое программирование
Динамическое программирование: один параметр
Скоро в Соединенных Штатах Берляндии пройдут выборы президента. На эту ответственную должность претендуют два кандидата: Дядя Сэм и Дядя Фродо. Вы работаете аналитиком в пред- выборном штабе Дяди Сэма, и вам поручено помочь ему победить конкурента. Раздуть газетный скандал из одержимости оппонента бросанием колец в жерла вулканов не получилось, так что при- дётся воспользоваться математикой.
Казалось бы, чтобы выиграть, необходимо убедить проголосовать за нашего кандидата более половины пришедших на выборы. Оказывается, что иногда нужно гораздо меньше! Для того чтобы понять, как это возможно, рассмотрим подробнее процедуру голосования.
Как вы знаете, Соединенные Штаты Берляндии разделены на несколько административных ре- гионов первого уровня — штатов. Сначала в каждом из штатов проходят местные выборы, по итогам которых каждый штат отдаёт свой голос за одного из кандидатов. Если не менее половины штатов выбрало Дядю Сэма, то выигрывает он (в случае равенства голосов Дядя Сэм имеет преимущество как действующий президент), иначе побеждает Дядя Фродо. Все штаты, в свою очередь, состоят из административных регионов второго уровня, каждый из которых представлен выборщиком из административных регионов третьего уровня и так далее. Последний уровень состоит из отдельных жителей Берляндии. Всего в Берляндии N жителей и K уровней административных единиц. Одним из ключевых принципов этой страны является равенство, так что любой регион i-го уровня делится на одинаковое число регионов следущего уровня (в том числе содержит одинаковое число граждан).
Так получилось, что делением на регионы поручили заняться именно вам, то есть в ваших руках назначить, на сколько именно административных единиц i-го уровня делится (i−1)-ая администра- тивная единица.
Также у вас есть сильный инструмент влияния на выбор людей — нефтяные бурли. Чтобы заста- вить одного избирателя отдать свой голос за Дядю Сэма, достаточно дать ему скромный подарок в размере одного нефтяного бурля.
К несчастью, изначально все N жителей Соединённых Штатов Берляндии собираются отдать свой голос за Дядю Фродо. Требуется определить минимальное количество нефтяных бурлей, ко- торое достаточно потратить для победы на выборах.
Формат входных данных
В единственной строке ввода находятся два целых числа N и K (1 <= N <= 1015 , 1 <= K <= 10).
Формат выходных данных
Требуется вывести единственное число — минимальное количество нефтяных бурлей, которое придётся потратить на предвыборные подарки при наилучшем разбиении на регионы.
Примеры
Замечание
Берляндские законы не запрещают, чтобы страна состояла из одного штата, а город — одного жителя. Аналогично с остальными типами регионов.
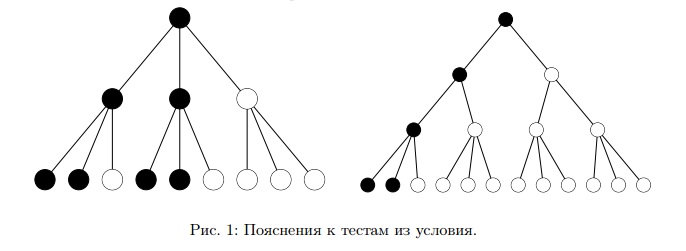
На рисунке 1 черным цветом отмечены те регионы, в которых победил Дядя Сэм. На нижнем уровне черными изображены вершины, соответствущие подкупленным конкретным жителям.
| |
![]()
|
|
Дробь
Разные комбинаторные структуры
Простые числа и разложение на множители
Известно, что сложение и умножение являются ассоциативными операциями. Это значит, что значение выражений вида \(a_1+a_2+\ldots +a_n\) и \(a_1\cdot a_2 \cdot \ldots \cdot a_n\) не зависит от порядка выполнения в них действий и следовательно не меняется при произвольной расстановке в этих выражениях скобок.
В отличии от сложения и умножения, деление — операция не ассоциативная. Так, значение выражения вида \(a_1/a_2/\cdots /a_n\) может меняться при расстановке в нем скобок.
Рассмотрим выражение вида \[p_1 / p_2 / \cdots / p_n,\] где все \(p_i\) — простые числа (не обязательно различные). Найдите количество возможных значений, которые может принять указанное выражение после расстановки в нем скобок, а также количество целых чисел среди этих значений.
Например, выражение \(3/2/2\) после расстановки скобок может принять два значения: \(3/4 = (3 / 2) / 2\) и \(3 = 3 / (2 / 2)\).
Формат входных данных
Первая строка содержит число \(n\) (\(1 \le n \le 200\)). Следующая строка содержат \(n\) натуральных чисел — \(p_1, p_2, \dots, p_n\). Все числа \(p_i\) простые и не превосходят \(10^4\).
Формат выходных данных
На первой строке выведите количество возможных значений, которые может принять выражение \(p_1 / p_2 / \cdots / p_n\) при заданных \(p_i\) после расстановки в нем скобок. На второй строке выведите количество целых чисел среди этих значений.
| |
![]()
|
|
Перестановки
Простые числа и разложение на множители
Одномерные массивы
Ваня и Петя играют в следующую игру. Ваня пишет на бумаге какую-либо перестановку чисел от 1 до N (то есть выписывает все числа от 1 до N в некотором порядке) и расставляет на столе в ряд N предметов. После этого Петя переставляет предметы в соответствии с Ваниной перестановкой. А именно, Петя выполняет следующие действия: если i-ое число в Ваниной перестановке равно ai, то Петя ставит предмет, который стоит на i-ом месте, на место с номером ai.
Обозначим предметы числами от 1 до N. Тогда начальное расположение предметов можно обозначить последовательностью чисел (1, 2, ..., N). К примеру, если N = 5, то начальное расположение предметов есть (1, 2, 3, 4, 5). Пусть Ваня написал перестановку <2, 5, 4, 3, 1>. Это значит, что после перемещения предметов они окажутся расставлены в следующем порядке: (5, 1, 4, 3, 2).
Однако, переставив предметы, Петя не останавливается на достигнутом и вновь переставляет их в соответствии с Ваниной перестановкой. Снова, если i-ое число в Ваниной перестановке равно ai, то Петя ставит предмет, который стоит на i-ом месте на место с номером ai. Так, если в приведенном выше примере повторно применить перестановку, предметы окажутся расположены в следующем порядке: (2, 5, 3, 4, 1).
Таким образом, Петя переставляет предметы в соответствии с Ваниной перестановкой, пока их расположение не окажется таким же, как исходное. В нашем примере Пете потребуется сделать еще 4 действия, порядок предметов после каждого из них будет следующим: (1, 2, 4, 3, 5), (5, 1, 3, 4, 2), (2, 5, 4, 3, 1), (1, 2, 3, 4, 5). Всего Пете потребовалось применить перестановку 6 раз.
Добрый Ваня хочет, чтобы Пете пришлось выполнить как можно больше действий. Помогите ему выбрать соответствующую перестановку.
Входные данные
Вводится единственное целое число N - количество предметов (1 <= N <= 100).
Выходные данные
Выведите перестановку чисел от 1 до N такую, что количество действий, которое придется сделать Пете, максимально. Если таких перестановок несколько, можно вывести любую.
| |
![]()
|
|
Марсианские факториалы
Простые числа и разложение на множители
Разные системы счисления
В 3141 году очередная экспедиция на Марс обнаружила в одной из пещер таинственные знаки. Они однозначно доказывали существование на Марсе разумных существ. Однако смысл этих таинственных знаков долгое время оставался неизвестным. Недавно один из ученых, профессор Очень-Умный, заметил один интересный факт: всего в надписях, составленных из этих знаков, встречается ровно K
различных символов. Более того, все надписи заканчиваются на длинную последовательность одних и тех же символов.
Вывод, который сделал из своих наблюдений профессор, потряс всех ученых Земли. Он предположил, что эти надписи являются записями факториалов различных натуральных чисел в системе счисления с основанием K. А символы в конце - это конечно же нули - ведь, как известно, факториалы больших чисел заканчиваются большим количеством нулей. Например, в нашей десятичной системе счисления факториалы заканчиваются на нули, начиная с 5!=1·2·3·4·5 . А у числа 100! в конце следует 24 нуля в десятичной системе счисления и 48 нулей в системе счисления с основанием 6 - так что у предположения профессора есть разумные основания!
Теперь ученым срочно нужна программа, которая по заданным числам N и K найдет количество нулей в конце записи в системе счисления с основанием K числа N!=1·2·3·...·(N-1)·N, чтобы они могли проверить свою гипотезу. Вам придется написать им такую программу!
Входные данные
В первой строке входных данных содержатся числа N и K, разделенные пробелом, (1 <= N <= 109, 2 <= K <= 1000).
Выходные данные
Выведите число X - количество нулей в конце записи числа N! в системе счисления с основанием K.
| |
![]()
|
|
Дом оригинальности и гармонии
Простые числа и разложение на множители
Строительная компания хочет построить дом, в котором будет n квадратных комнат. Каждая комната характеризуется своим размером — длиной стены. Обозначим размеры комнат в новом доме как a1, a2, …, an.
При этом для того, чтобы квартиры в доме активнее распродавались, компания объявила его «Домом оригинальности и гармонии». Оригинальность означает, что размер любой комнаты не должен делиться на размер никакой другой комнаты. Свойство гармонии требует, чтобы площадь любой комнаты делилась на размер каждой из комнат. Иначе говоря, для любых различных i и j должны выполняться условия: ai не делится на aj, а ai2 делится на aj.
Требуется по заданному числу n выбрать такие размеры комнат, чтобы выполнялись свойства оригинальности и гармонии. При этом с целью экономии строительных материалов размер каждой комнаты не должен превышать 263 – 1.
Входные данные
Строка содержит число n (1 ≤ n ≤ 1000).
Выходные данные
Выведите размеры комнат — n положительных целых чисел, не превосходящих 263 – 1. Разделяйте числа пробелами.
| |
![]()
|
|
Простые числа
Простые числа и разложение на множители
Одномерные массивы
Вывести все простые числа от M до N включительно.
Входные данные
В первой строке находятся разделённые пробелом M и N. 2 <= M <= N <= 300 000.
Выходные данные
Вывести числа в порядке возрастания, по одному в строке. Если между M и N включительно нет простых - вывести "Absent".
| |
![]()
|
|
Простые числа(2)
Простые числа и разложение на множители
Одномерные массивы
Вывести все простые числа от M до N включительно.
Входные данные
В первой строке находятся разделённые пробелом M и N. 2 <= M <= N <= 1 000 000.
Выходные данные
Вывести числа в порядке возрастания, по одному в строке. Если между M и N включительно нет простых - вывести "Absent".
| |
![]()
|
|
Разложение на простые множители
Простые числа и разложение на множители
Вывести представление целого числа N в виде произведения простых чисел.
Входные данные
В первой строке находится единственное число N. 2 <= N <= 231 - 1.
Выходные данные
Выводится список чисел в порядке неубывания, разделённых знаком "*".
| |
![]()
|
|
Заполните массив
Простые числа и разложение на множители
Динамическое программирование: один параметр
Требуется заполнить N элементов массива, пронумерованных числами от 1 до N (A[1]…A[N]), натуральными числами от 2 до N+1, использовав каждое число ровно один раз, так, чтобы значение каждого элемента массива делилось бы нацело на его номер (т.е. для каждого i A[i] делилось бы на i).
Напишите программу, которая для заданного N вычислит количество способов такого заполнения массива.
Входные данные
Вводится одно натуральное число N (1≤N≤60000).
Выходные данные
Выведите одно число — искомое количество способов заполнения массива.
Примечание
Массив можно заполнить единственным способом: 3 2
| |
![]()
|
|
Заполните массив
Простые числа и разложение на множители
Динамическое программирование: один параметр
Требуется заполнить N элементов массива, пронумерованных числами от 1 до N (A[1]…A[N]), натуральными числами от 2 до N+1, использовав каждое число ровно один раз, так, чтобы значение каждого элемента массива делилось бы нацело на его номер (т.е. для каждого i A[i] делилось бы на i).
Напишите программу, которая для заданного N вычислит количество способов такого заполнения массива.
Входные данные
Вводится одно натуральное число N (1≤N≤1000).
Выходные данные
Выведите одно число — искомое количество способов заполнения массива.
Примечание
Массив можно заполнить единственным способом: 3 2
| |
![]()
|
|
Призы победителям сборов
Простые числа и разложение на множители
Оргкомитет и жюри Московской олимпиады проводят очередные учебно-тренировочные сборы. Победители туров на сборах получают в качестве приза мороженое. Поскольку мороженое имеет тенденцию таять, то оно должно храниться в холодильнике. Холодильник, имеющийся в 179 школе слишком мал для хранения всего запаса мороженого. Поэтому организаторы решили заказать специальный супер-пупер-большой холодильник. Новый холодильник должен быть параллелепипедом A × B × C и хранить ровно N кубических баночек мороженого размером 1 × 1 × 1. Для уменьшения потерь холода, общая площадь поверхности холодильника должна быть как можно меньше.
Например, если размер холодильника должен быть 12, возможными вариантами являются:
| Размеры баночек |
Площадь поверхности |
| 3 × 2 × 2 |
32 |
| 4 × 3 × 1 |
38 |
| 6 × 2 × 1 |
40 |
| 12 × 1 × 1 |
50 |
Лучшим вариантом является 3 × 2 × 2.
Помогите организаторам сборов выбрать оптимальную форму холодильника.
Входные данные
Входной файл содержит одно число N (1 ≤ N ≤ 106).
Выходные данные
Выведите три числа A, B и C — оптимальные длины сторон холодильника. Если решений несколько — выведите любое из них.
| |
![]()
|
|
Простое число
Простые числа и разложение на множители
По введенному натуральному числу K, не превосходящему 1 000 000, выдать K-ое по счету простое число.
Входные данные
Во входном файле находится одно натуральное число K.
Выходные данные
В выходной файл выведите K-е простое число.
| |
![]()
|
|
Разность квадратов
Простые числа и разложение на множители
На доске были выписаны два квадрата натуральных чисел: \(x^2\) и \(y^2\), где \(l \le y^2 < x^2 \le r\). Числа \(x^2\) и \(y^2\) стерли и выписали на доске их разность \(d\).
По заданным \(l\), \(r\) и \(d\) выясните, сколько различных пар натуральных чисел \(x^2, y^2\) могло быть выписано на доске.
Формат выходных данных
В первой строке даны три числа \(d\), \(l\) и \(r\) (\(1 \le d \le 10^9, 1 \le l \le r \le 10^{18}\)).
Формат входных данных
Выведите количество подходящих пар квадратов.
Примечание
В первом примере подходят числа 100 и 36. Во втором примере также подходят числа 256 и 196.
| |
![]()
|
|
65959
Простые числа и разложение на множители
На уроке информатики Фоме задали задачу о проверке гипотезы Гольдбаха.
Условие задачи выглядело так:
Гипотеза Гольдбаха (не доказанная до сих пор) утверждает, что любое четное число (кроме 2) можно представить в виде суммы двух простых чисел.
Фома легко решил данную задачу методом поиска "первого решения".
Дома, Фома заметил, что во время отладки, он получал решения, в которых одно из чисел было не очень большим.
Так, для числа 1000000, он получил разложение 1000000=17+999983. Фома решил проверить, в чем сложность гипотезы Гольдбаха.
Для этого Фома придумал задачу:
Определим функцию g(n) = количеству разложений числа n в сумму двух простых чисел. (разложения, отличающиеся порядком слагаемых, считаются одинаковыми).
На отрезке натуральных чисел от A до B найдите чётное число x такое, что: g(x) кратно 5 и имеет минимальное значение среди всех g(x) кратных 5 на этом отрезке.
Решите задачу Фомы.
Входные данные
Границы отрезка A, B (два натуральных числа 5≤ A<B≤106 )
Выходные данные
- "Impossible" если для всех чётных x из отрезка [A;B] значение g(x) не кратно 5.
- два числа - x, g( x ) ( g(x) кратно 5 и минимальное для A≤ x≤B). Если таких x несколько, то выведите минимальное значение x.
Примеры
| № |
Входные данные |
Выходные данные |
Примечание |
| 1 |
5 10 |
Impossible |
На отрезке всего три четных числа (6, 8, 10)
Число 8 =3+5 и других представлений нет (5+3 считается таким же как 3+5)
Для 10 есть два представления (3+7 и 5+5)
Таким образом значений x, при которых g(x) кратно 5 нет. |
| 2 |
20 60 |
48 5 |
g(x) может принимать значения меньшие 3 (g(20)=2)
g(x)=5 для x из множества {48, 54}. 48 -минимальное значение |
| 3 |
2000 2005 |
Impossible |
|
| |
![]()
|
|
Марсианская колония
Простые числа и разложение на множители
*1000
Решето Эратосфена
На Марсе строится колония! Каждому жилому модулю присваивается номер от 1 до N. По марсианским законам, модули с простыми номерами получают улучшенную систему жизнеобеспечения.
Глава колонии хочет знать:
1. Сколько модулей получат улучшенную систему?
2. Какие именно это модули?
ВХОДНЫЕ ДАННЫЕ:
Одно число N (1 ≤ N ≤ 10^7) - количество модулей.
ВЫХОДНЫЕ ДАННЫЕ:
Первая строка: количество простых чисел от 2 до N.
Вторая строка: все простые числа от 2 до N через пробел (в порядке возрастания).
Если простых чисел нет, во второй строке ничего не выводить.
| |
![]()
|