| | | |
|
Степени вершин
Способы задания графа
Неориентированный граф задан матрицей смежности. Найдите степени всех вершин графа.
Формат входных данных
В первой строке вводится число n (1 ≤ n ≤ 100) – количество вершин в графе. Далее идет n строк по n чисел, каждое из которых равно 0 или 1, – его матрица смежности.
Формат выходных данных
Выведите n чисел – степени вершин графа (по одному числу в строке).
| |
![]()
|
|
Издевательство
Способы задания графа
Простые задачи на перебор
Штирлиц ехал на машине, увидел голосующего Бормана, и проехал мимо. Через некоторое время он снова увидел голосующего Бормана, и снова проехал мимо. Вскоре он опять увидел голосующего Бормана.
- Издевается! - подумал Борман.
- Кольцевая! - догадался Штирлиц.
В городе N площадей. Любые две площади соединены между собой ровно одной дорогой с двусторонним движением. В этом городе живет Штирлиц. У Штирлица есть хобби - он любит воскресным утром выйти из дома, сесть в машину, выбрать какой-нибудь кольцевой маршрут, проходящий ровно по трем площадям (то есть сначала он едет с какой-то площади на какую-то другую, потом - на третью, затем возвращается на начальную, и опять едет по этому маршруту). Он воображает, что где-то на этом пути стоит Борман. И так вот ездит Штирлиц все воскресенье, пока голова не закружится, и радуется...
Естественно, что Штирлицу хочется проезжать мимо точки, в которой, как он воображает, стоит Борман, как можно чаще. Для этого, естественно, выбранный Штирлицем маршрут должен быть как можно короче. Напишите программу, которая выберет оптимальный для Штирлица маршрут.
Входные данные
В первой строке задается число N (3 <= N <= 100). В последующих строках содержится матрица NxN расстояний между площадями (число в позиции i,j обозначает длину дороги, соединяющей i-ую и j-ую площади). Все числа в матрице (кроме стоящих на главной диагонали) - натуральные, не превышающие 1000. Матрица симметрична относительно главной диагонали, на главной диагонали стоят 0.
Выходные данные
Требуется вывести три числа — номера площадей в оптимальном маршруте. Если маршрутов несколько, выведите любой из них.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
0 1 9 9 2
1 0 9 9 9
9 9 0 9 9
9 9 9 0 9
2 9 9 9 0 |
1 2 5 |
| |
![]()
|
|
Схема дорог
Способы задания графа
Дед Мороз составляет схему дорог, по которой можно будет кратчайшим образом посетить N городов. Для простоты он пронумеровал все города номерами 1,..., N. Города соединены M количеством дорог. I-я дорога (1<=i<=M) соединяет город Ai и город Bi. Прежде чем построить оптимальный маршрут Дед Мороз хочет знать с какими городами связан каждый город. Помогите Деду Морозу.
Выведите N строк следующим образом.
- Пусть
di - количество городов, непосредственно связанных с городом i (1<=i<=N), и этими городами будут города ai,1, ..., ai,di,перечисленных в порядке возрастания.
I-я строка (1<=i<=N) должна содержать di+1 целое число: di, ai,1,...,ai,di в указанном порядке, разделенные пробелами.
Входные данные
Первая строка входных данных содержит два целых числа, разделенных одним пробелом N и M (2 <= N <= 105, 1 <= M <= 105). Далее следует M строк, каждая из которых содержит 2 числа Ai и Bi (1 <= Ai < Bi <= N, 1 <= i <= M).
Если i≠j, то (Ai, Bi)≠(Aj, Bj). Все числа целые.
Выходные данные
Выведите N строк по формату, описанному в условии задачи.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6 6
3 6
1 3
5 6
2 5
1 2
1 6 |
3 2 3 6
2 1 5
2 1 6
0
2 2 6
3 1 3 5 |
| 2 |
5 10
1 2
1 3
1 4
1 5
2 3
2 4
2 5
3 4
3 5
4 5 |
4 2 3 4 5
4 1 3 4 5
4 1 2 4 5
4 1 2 3 5
4 1 2 3 4 |
| |
![]()
|
|
Проверка на неориентированность
Способы задания графа
По заданной квадратной матрице n×n из нулей и единиц определите, может ли данная матрица быть матрицей смежности простого неориентированного графа.
Входные данные
На вход программы поступает число n (1≤n≤100) – размер матрицы, а затем n строк по n чисел, каждое из которых равно 0 или 1, – сама матрица.
Выходные данные
Выведите «YES», если приведенная матрица может быть матрицей смежности простого неориентированного графа, и «NO» в противном случае.
Примеры
| входные данные |
выходные данные |
5
0 0 1 0 0
0 0 1 0 1
1 1 0 0 0
0 0 0 0 0
0 1 0 0 0
|
YES |
| |
![]()
|
|
Петли
Способы задания графа
По заданной матрице смежности неориентированного графа определите, содержит ли он петли.
Входные данные
На вход программы поступает число n (1≤n≤100) – размер матрицы, а затем n строк по n чисел, каждое из которых равно 0 или 1, – сама матрица.
Выходные данные
Выведите «YES», если приведенная матрица может быть матрицей смежности простого неориентированного графа, и «NO» в противном случае.
Примеры
| входные данные |
выходные данные |
5
1 1 1 1 0
1 0 1 1 1
1 1 0 1 1
1 1 1 1 1
0 1 1 1 0 |
YES |
| |
![]()
|
|
Подсчет количества ребер неориентированного графа
Способы задания графа
Простой неориентированный граф задан матрицей смежности. Найдите количество ребер в графе.
Входные данные
На вход программы поступает число n (1≤n≤100) – размер матрицы, а затем n строк по n чисел, каждое из которых равно 0 или 1, – сама матрица.
Выходные данные
Выведите одно число – количество ребер заданного графа.
Примеры
| входные данные |
выходные данные |
5
0 0 1 0 0
0 0 1 0 1
1 1 0 0 0
0 0 0 0 0
0 1 0 0 0
|
3 |
| |
![]()
|
|
Подсчет количества ребер ориентированного графа
Способы задания графа
Ориентированный граф задан матрицей смежности. Найдите количество ребер в графе.
Входные данные
На вход программы поступает число n (1≤n≤100) – размер матрицы, а затем n строк по n чисел, каждое из которых равно 0 или 1, – сама матрица.
Выходные данные
Выведите одно число – количество ребер заданного графа.
Примеры
| входные данные |
выходные данные |
5
0 0 0 0 0
0 0 0 0 1
1 1 0 0 0
0 0 0 0 0
0 0 0 0 0
|
3 |
| |
![]()
|
|
От матрицы смежности к списку ребер, неориентированный вариант
Способы задания графа
Простой неориентированный граф задан матрицей смежности, выведите его представление в виде списка ребер.
Входные данные
На вход программы поступает число n (1≤n≤100) – размер матрицы, а затем n строк по n чисел, каждое из которых равно 0 или 1, – сама матрица.
Выходные данные
Выведите список ребер заданного графа. Каждое ребро выводить по возрастанию вершин ребра, ребра выводить в порядке возрастания вершин.
Примеры
| входные данные |
выходные данные |
5
0 0 1 0 0
0 0 1 0 1
1 1 0 0 0
0 0 0 0 0
0 1 0 0 0
|
1 3
2 3
2 5
|
| |
![]()
|
|
От списка ребер к матрице смежности, неориентированный вариант
Способы задания графа
Простой неориентированный граф задан списком ребер, выведите его представление в виде матрицы смежности.
Входные данные
На вход программы поступают числа n ( 1≤ n ≤100 ) – количество вершин в графе и m ( 1≤ m ≤ n(n−1)/2 ) – количество ребер. Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите матрицу смежности заданного графа.
Примеры
| входные данные |
выходные данные |
5 3
1 3
2 3
2 5
|
0 0 1 0 0
0 0 1 0 1
1 1 0 0 0
0 0 0 0 0
0 1 0 0 0
|
| |
![]()
|
|
От матрицы смежности к списку ребер, ориентированный вариант
Способы задания графа
Ориентированный граф задан матрицей смежности, выведите его представление в виде списка ребер.
Входные данные
На вход программы поступает число n (1≤n≤100) – размер матрицы, а затем n строк по n чисел, каждое из которых равно 0 или 1, – сама матрица.
Выходные данные
Выведите список ребер заданного графа. Ребра выводить в порядке возрастания вершин.
Примеры
| входные данные |
выходные данные |
5
0 0 0 0 0
0 0 0 0 1
1 1 0 0 0
0 0 0 0 0
0 0 0 0 0
|
2 5
3 1
3 2
|
| |
![]()
|
|
От списка ребер к матрице смежности, ориентированный вариант
Способы задания графа
Простой неориентированный граф задан списком ребер, выведите его представление в виде матрицы смежности.
Входные данные
На вход программы поступают числа n ( 1≤ n ≤100 ) – количество вершин в графе и m ( 1≤ m ≤ n(n−1) ) – количество ребер. Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите матрицу смежности заданного графа.
Примеры
| входные данные |
выходные данные |
5 3
1 3
2 3
5 2
|
0 0 1 0 0
0 0 1 0 0
0 0 0 0 0
0 0 0 0 0
0 1 0 0 0
|
| |
![]()
|
|
Проверка на наличие параллельных ребер, неориентированный вариант
Способы задания графа
Неориентированный граф задан списком ребер. Проверьте, содержит ли он параллельные ребра.
Входные данные
Сначала вводятся числа n ( 1≤ n ≤100 ) – количество вершин в графе и m ( 1≤ m ≤10000 ) – количество ребер.
Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите «YES», если граф содержит параллельные ребра, и «NO» в противном случае.
Примеры
| входные данные |
выходные данные |
5 3
1 3
2 3
2 5
|
NO
|
| |
![]()
|
|
Проверка на наличие параллельных ребер, ориентированный вариант
Способы задания графа
Ориентированный граф задан списком ребер. Проверьте, содержит ли он параллельные ребра.
Входные данные
Сначала вводятся числа n ( 1≤ n ≤100 ) – количество вершин в графе и m ( 1≤ m ≤10000 ) – количество ребер.
Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите «YES», если граф содержит параллельные ребра, и «NO» в противном случае.
Примеры
| входные данные |
выходные данные |
5 3
1 3
2 3
2 5
|
NO
|
| |
![]()
|
|
Степени вершин по спискам ребер
Способы задания графа
Неориентированный граф задан списком ребер. Найдите степени всех вершин графа.
Входные данные
Сначала вводятся числа n ( 1≤ n ≤ 100 ) – количество вершин в графе и m ( 1≤ m ≤ n(n−1)/2 ) – количество ребер.
Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите n чисел – степени вершин графа.
Примеры
| входные данные |
выходные данные |
5 3
1 3
2 3
2 5
|
1
2
2
0
1
|
| |
![]()
|
|
Полустепени вершин
Способы задания графа
Ориентированный граф задан матрицей смежности. Найдите полустепени захода и полустепени исхода всех вершин графа.
Входные данные
Сначала вводится число n ( 1≤ n ≤100 ) – количество вершин в графе, а затем n строк по n чисел, каждое из которых равно 0 или 1, – его матрица смежности.
Выходные данные
Выведите n пар чисел – для каждой вершины сначала выведите полустепень захода и затем полустепень исхода.
Примеры
| входные данные |
выходные данные |
5
0 0 0 0 0
0 0 0 0 1
1 1 0 0 0
0 0 0 0 0
0 0 0 0 0
|
1
0
1
1
0
2
0
0
1
0
|
| |
![]()
|
|
Полустепени вершин по спискам ребер
Способы задания графа
Ориентированный граф задан списком ребер. Найдите степени всех вершин графа.
Входные данные
Сначала вводятся числа n ( 1 ≤ n ≤ 100 ) – количество вершин в графе и m ( 1≤ m ≤ n(n−1) ) – количество ребер. Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите n пар чисел – для каждой вершины сначала выведите полустепень захода и затем полустепень исхода.
Примеры
| входные данные |
выходные данные |
5 3
2 5
3 1
3 2
|
1
0
1
1
0
2
0
0
1
0
|
| |
![]()
|
|
Истоки и стоки
Способы задания графа
Напомним, что вершина ориентированного графа называется истоком, если в нее не входит ни одно ребро и стоком, если из нее не выходит ни одного ребра.
Ориентированный граф задан матрицей смежности. Найдите все вершины графа, которые являются истоками, и все его вершины, которые являются стоками.
Входные данные
Сначала вводится число n ( 1≤ n ≤100 ) – количество вершин в графе, а затем n строк по n чисел, каждое из которых равно 0 или 1, – его матрица смежности.
Выходные данные
Вначале выведите k – число истоков в графе и затем k чисел – номера вершин, которые являются истоками, в возрастающем порядке.
Затем выведите информацию о стоках в том же порядке.
Примеры
| входные данные |
выходные данные |
5
0 0 0 0 0
0 0 0 0 1
1 1 0 0 0
0 0 0 0 0
0 0 0 0 0
|
2
3
4
3
1
4
5
|
| |
![]()
|
|
Регулярный граф
Способы задания графа
Неориентированный граф называется регулярным, если все его вершины имеют одинаковую степень.
Для заданного списком ребер графа проверьте, является ли он регулярным.
Входные данные
Сначала вводятся числа n ( 1≤ n ≤ 100 ) – количество вершин в графе и m ( 0≤ m ≤ n(n−1)/2 ) – количество ребер.
Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите «YES», если граф является регулярным, и «NO» в противном случае.
Примеры
| входные данные |
выходные данные |
5 0
|
YES
|
| |
![]()
|
|
Полный граф
Способы задания графа
Неориентированный граф с кратными рёбрами называется полным, если любая пара его различных вершин соединена хотя бы одним ребром.
Для заданного списком ребер графа проверьте, является ли он полным.
Входные данные
Сначала вводятся числа n ( 1≤ n ≤ 100 ) – количество вершин в графе и m ( 0≤ m ≤ n(n−1)/2 ) – количество ребер.
Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите «YES», если граф является полным, и «NO» в противном случае.
Примеры
| входные данные |
выходные данные |
5 18
1 2
1 3
1 3
1 4
1 4
1 4
1 5
1 5
2 3
2 4
2 4
2 5
3 4
3 4
3 4
3 5
3 5
4 5
|
YES
|
| |
![]()
|
|
Полуполный граф
Способы задания графа
Ориентированный граф называется полуполным, если между любой парой его различных вершин есть хотя бы одно ребро.
Для заданного списком ребер графа проверьте, является ли он полуполным.
Входные данные
Сначала вводятся числа n ( 1≤ n ≤ 100 ) – количество вершин в графе и m ( 0≤ m ≤ n(n−1)/2 ) – количество ребер.
Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите «YES», если граф является полуполным, и «NO» в противном случае.
Примеры
| входные данные |
выходные данные |
5 10
1 2
1 3
1 5
2 3
2 5
3 2
4 1
4 3
4 5
5 3
|
NO
|
| |
![]()
|
|
Турнир
Способы задания графа
Ориентированный граф называется турниром, если между любой парой его различных вершин существует ровно одно ребро.
Для заданного списком ребер графа проверьте, является ли он турниром.
Входные данные
Сначала вводятся числа n ( 1≤ n ≤ 100 ) – количество вершин в графе и m ( 0≤ m ≤ n(n−1)/2 ) – количество ребер.
Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите «YES», если граф является турниром, и «NO» в противном случае.
Примеры
| входные данные |
выходные данные |
5 10
1 2
1 3
1 5
2 3
2 5
4 1
4 2
4 3
4 5
5 3
|
YES
|
| |
![]()
|
|
Транзитивность неориентированного графа
Способы задания графа
Напомним, что граф называется транзитивным, если всегда из того, что вершины u и v соединены ребром и вершины v и w соединены ребром следует,
что вершины u и w соединены ребром.
Проверьте, что заданный неориентированный граф является транзитивным.
Входные данные
Сначала вводятся числа n ( 1≤ n ≤ 100 ) – количество вершин в графе и m ( 0≤ m ≤ n(n−1)/2 ) – количество ребер.
Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите «YES», если граф является транзитивным, и «NO» в противном случае.
Примеры
| входные данные |
выходные данные |
5 1
2 5
|
YES
|
| |
![]()
|
|
Транзитивность ориентированного графа
Способы задания графа
Напомним, что ориентированный граф называется транзитивным, если для любых трех различных вершин u, v и w из того,
что из u в вершину v ведет ребро и из вершины v в вершину w ведет ребро, следует, что из вершины u в вершину w ведет ребро.
Проверьте, что заданный ориентированный граф является транзитивным.
Входные данные
Сначала вводятся числа n ( 1≤ n ≤ 100 ) – количество вершин в графе, а затем n строк по n чисел,
каждое из которых равно 0 или 1, – его матрица смежности.
Выходные данные
Выведите «YES», если граф является транзитивным, и «NO» в противном случае.
Примеры
| входные данные |
выходные данные |
5
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
|
YES
|
| |
![]()
|
|
Обрати меня!
Способы задания графа
Мальчик Вася очень любит разворачивать ориентированные графы. Помогите ему в этом.
Входные данные
Во входном файле записано число N (1 ≤ N ≤ 50000) - количество вершин в графе.
В следующих N строках записан граф в виде списков смежности: в i-ой строке, в порядке возрастания, записаны номера вершин,
в которые идут ребра из i-ой вершины. Нумерация начинается с единицы. Гарантируется, что ребер в графе не более 50000.
Выходные данные
Выведите развернутый граф в том же формате, что и исходный.
Примеры
| входные данные |
выходные данные |
4
2 3
3
2
|
4
1 4
1 2
|
| |
![]()
|
|
Степени вершин
Способы задания графа
Неориентированный граф задан матрицей смежности. Найдите степени всех вершин графа.
Входные данные
Сначала вводятся числа n ( 1≤ n ≤ 100 ) – количество вершин в графе,
а затем n строк по n чисел, каждое из которых равно 0 или 1, – его матрица смежности.
Выходные данные
Выведите n чисел – степени вершин графа.
Примеры
| входные данные |
выходные данные |
5
0 0 1 0 0
0 0 1 0 1
1 1 0 0 0
0 0 0 0 0
0 1 0 0 0
|
1
2
2
0
1
|
| |
![]()
|
|
Матрица смежности из списков
Способы задания графа
Напишите программу, которая строит матрицу смежности графа на основе списков смежности для каждой вершины.
Входные данные
В первой строке вводится количество вершин графа N ( 1 ≤ N ≤ 1000 ).
В следующих N строках записаны списки смежности для каждой вершины – номера вершин, в которые существуют исходящие рёбра из данной вершины.
Выходные данные
Программа должна вывести матрицу смежности для заданного графа.
Примеры
| входные данные |
выходные данные |
5
2 3 4
1 3 5
1 2 4
0
2 4
|
0 1 1 1 0
1 0 1 0 1
1 1 0 1 0
0 0 0 0 0
0 1 0 1 0
|
| |
![]()
|
|
Списки смежности из матрицы
Способы задания графа
Способы задания графа
Напишите программу, которая строит списки смежности для каждой вершины графа на основе его матрицы смежности.
Входные данные
В первой строке вводится количество вершин графа N ( 1 ≤ N ≤ 1000 ).
В следующих N строках записано по N чисел, разделённых пробелами – элементы матрицы смежности графа.
Выходные данные
Программа должна вывести списки смежности для каждой вершины графа в порядке возрастания их номеров.
Номера вершин в каждом списке разделены пробелами и идут в порядке возрастания.
Нумерация начинается с единицы. Если из вершины не выходит ни одно ребро, вместо списка нужно вывести число 0.
Примеры
| входные данные |
выходные данные |
5
0 1 1 1 0
1 0 1 0 1
1 1 0 1 0
0 0 0 0 0
0 1 0 1 0
|
2 3 4
1 3 5
1 2 4
0
2 4
|
| |
![]()
|
|
Списки смежности из матрицы
Способы задания графа
Способы задания графа
Напишите программу, которая строит списки смежности для каждой вершины графа на основе его матрицы смежности.
Входные данные
В первой строке вводится количество вершин графа N ( 1 ≤ N ≤ 1000 ).
В следующих N строках записано по N чисел, разделённых пробелами – элементы матрицы смежности графа.
Выходные данные
Программа должна вывести списки смежности для каждой вершины графа в порядке возрастания их номеров.
Номера вершин в каждом списке разделены пробелами и идут в порядке возрастания.
Нумерация начинается с единицы. Если из вершины не выходит ни одно ребро, вместо списка нужно вывести число 0.
Примеры
| входные данные |
выходные данные |
5
0 1 1 1 0
1 0 1 0 1
1 1 0 1 0
0 0 0 0 0
0 1 0 1 0
|
2 3 4
1 3 5
1 2 4
0
2 4
|
| |
![]()
|
|
Мишина машина (В', В)
Кратчайшие пути в графе
Обход в ширину
Способы задания графа
Миша путешествует по стране на автомобиле. В стране есть несколько городов, соединенных дорогами, на каждой дороге может быть некоторое число ям.
Мише очень нравится ездить по дорогам на которых много ям, - он участвует в популярном телешоу "Неперсистентные машинки" и за каждую посещенную яму ему платят по одной монете.
Он начинает путь в любом из городов страны и затем путешествует по дорогам между городами. По каждой дороге Миша может проехать сколько угодно раз но ему платят за посещение любой ямы только один раз.
Помогите Мише найти самый выгодный маршрут.
Формат входных данных
В первой строке содержатся два целых числа n и m количество городов и дорог соединяющих города в стране соответственно (1 <= n <= 105 , 0<= m <= 105)
В следующих m строках содержится по три целых числа, разделенных пробелами номера, - городов, соединенных очередной дорогой и количество ям на этой дороге соответственно. Количество ям на каждой дороге неотрицательное число не превосходящее 106.
Гарантируется, что никакая дорога не соединяет город с самим собой и что нет двух дорог соединяющих одинаковые пары городов. Вершины нумеруются с единицы.
Формат выходных данных
Выведите одно число максимальное количество монет которое Миша сможет получить.
| Ввод |
Вывод |
4 4
1 2 1
2 3 1
1 4 1
4 3 0 |
3 |
4 2
1 3 5
2 4 4 |
5 |
Замечание
Все дороги двусторонние; проехав в любую сторону по дороге, Миша посещает все ямы на этой дороге. Обратите внимание, что между некоторыми парами городов может не существовать пути по имеющимся дорогам.
| |
![]()
|
|
От матрицы смежности к списку ребер, ориентированный вариант
Способы задания графа
Ориентированный граф задан матрицей смежности, выведите его представление в виде списка ребер.
Формат входных данных
На вход программы поступает число n (1 ≤ n ≤ 100) – количество вершин графа, а затем n строк по n чисел, каждое из которых равно 0 или 1, – его матрица смежности.
Формат выходных данных
Выведите список ребер заданного графа в порядке возрастания номеров вершин.
| |
![]()
|
|
От списка ребер к матрице смежности, ориентированный вариант
Способы задания графа
Простой ориентированный граф задан списком ребер, выведите его представление в виде матрицы смежности.
Формат входных данных
На вход программы поступают числа n ( 1 ≤ n ≤ 100) - количество вершин в графе и m (1 ≤ m ≤ n(n-1)) – количество ребер. Затем следует m пар чисел – ребра графа.
Формат выходных данных
Выведите матрицу смежности заданного графа.
| |
![]()
|
|
От списка ребер к матрице смежности, неориентированный вариант
Алгоритмы на графах
Способы задания графа
Простой неориентированный граф задан списком ребер, выведите его представление в виде матрицы смежности.
Формат входных данных
В первой строке задаются числа n (\(1<=n<=100\)) – количество вершин в графе и m (\(1<=m<=n(n - 1)/2\)) – количество ребер. Далее следует m пар чисел – ребра графа (каждая пара чисел в отдельной строке).
Формат выходных данных
Выведите матрицу смежности заданного графа.
| |
![]()
|
|
От матрицы смежности к списку ребер, неориентированный вариант
Алгоритмы на графах
Способы задания графа
Простой неориентированный граф задан матрицей смежности, выведите его представление в виде списка ребер.
Формат входных данных
Входные данные включают число n (\( 1<=n<=100\)) – количество вершин в графе, а затем n строк по n чисел, каждое из которых равно 0 или 1, – его матрицу смежности.
Формат выходных данных
Выведите список ребер заданного графа (в любом порядке).
| |
![]()
|
|
Петли
Алгоритмы на графах
Способы задания графа
По заданной матрице смежности неориентированного графа определите, содержит ли он петли.
Формат входных данных
В первой строке задается число n (\(1<=n<=100\)) – количество вершин графа. Затем задается матрица смежности - n строк по n чисел, каждое из которых равно 0 или 1.
Формат выходных данных
Выведите «YES», если граф содержит петли, и «NO» в противном случае.
| |
![]()
|
|
Проверка на неориентированность
Алгоритмы на графах
Способы задания графа
По заданной квадратной матрице n×n из нулей и единиц определите, может ли данная матрица быть матрицей смежности простого неориентированного графа.
Формат входных данных
В первой строке задается число n (\(1<=n<=100\)) – размер матрицы. Затем задается сама матрица - n строк по n чисел, каждое из которых равно 0 или 1.
Формат выходных данных
Выведите «YES», если приведенная матрица может быть матрицей смежности простого неориентированного графа, и «NO» в противном случае
| |
![]()
|
|
Города и дороги
Алгоритмы на графах
Способы задания графа
В галактике "Milky Way" на планете "Neptune" есть N городов, некоторые из которых соединены дорогами. Император "Maximus" галактики "Milky Way" решил провести инвентаризацию дорог на планете "Neptune". Но, как оказалось, он не силен в математике, поэтому он просит вас сосчитать количество дорог.
Формат входных данных
В первой строке задается число N (\(0<=N<=100\)). В следующих N строках записано по N чисел, каждое из которых является единичкой или ноликом. Причем, если в позиции (i,j) квадратной матрицы стоит единичка, то i-ый и j-ый города соединены дорогами, а если нолик, то не соединены.
Формат выходных данных
Вывести одно число - количество дорог на планете "Neptune".
Примечание
Все дороги двусторонние, то есть если есть дорога из города i в город j, то есть и дорога из города j в город i, и это та же самая дорога.
| |
![]()
|
|
Светофорчики-1
Алгоритмы на графах
Способы задания графа
В подземелье M тоннелей и N перекрестков, каждый тоннель соединяет какие-то два перекрестка. Мышиный король решил поставить по светофору в каждом тоннеле перед каждым перекрестком. Напишите программу, которая посчитает, сколько светофоров должно быть установлено на каждом из перекрестков. Перекрестки пронумерованы числами от 1 до N.
Формат входных данных
В первой строке записано два числа N и M (\(0<N<=100\), \(0<=M<=N*(N-1)/2\) ). В следующих M строках записаны по два числа i и j (\(1<=i,j<=N\)), которые означают, что перекрестки i и j соединены тоннелем.
Формат выходных данных
Вывести N чисел: k-ое число означает количество светофоров на k-ом перекрестке.
Примечание
Можно считать, что любые два перекрестка соединены не более, чем одним тоннелем. Нет тоннелей от перекрестка i до него самого.
| |
![]()
|
|
Цветной дождь
Алгоритмы на графах
Способы задания графа
В Банановой республике очень много холмов, соединенных мостами. На химическом заводе произошла авария, в результате чего испарилось экспериментальное удобрение "зован". На следующий день выпал цветной дождь, причем он прошел только над холмами, в некоторых местах падали красные капли, в некоторых - синие, а в остальных - зеленые, в результате чего холмы стали соответствующего цвета. Президенту Банановой республики это понравилось, но ему захотелось покрасить мосты между вершинами холмов так, чтобы мосты были покрашены в цвет холмов, которые они соединяют. К сожалению, если холмы разного цвета, то покрасить мост таким образом не удастся.
Посчитать количество таких "плохих" мостов.
Формат входных данных
В первой строке записано N (\(0<N<=100\)) - число холмов. Далее идет матрица смежности, описывающая наличие мостов между холмами (1-мост есть, 0-нет). В последней строке записано N чисел, обозначающих цвет холмов: 1 - красный; 2 - синий; 3 - зеленый.
Формат выходных данных
Вывести количество "плохих" мостов.
| |
![]()
|
|
Мафия
Способы задания графа
В городе Лост-Хевен произошла серия загадочных преступлений. Жители напуганы и не знают, кому можно доверять. Местный Шериф позвал на помощь знаменитого детектива Нормана, чтобы тот помог ему найти главаря мафии.
Норман принялся за дело и опросил всех жителей города. В итоге он теперь знает, кто кого боится.
Норман знает, что главным подозреваемым будет тот житель города, который удовлетворяет следующим условиям:
1) Подозреваемый никого не боится.
2) Все остальные жители боятся подозреваемого.
3) Существует ровно один такой человек, который удовлетворяет первым двум условиям.
Вы - программист, который помогает Норману. Норман дал вам информацию в виде списка, кто кого боится. Помогите Норману определить главного подозреваемого.
Формат входных данных
В первой строке записано натуральное число N - количество жителей города Лост-Хевен (1 <= N <= 1000). Во второй строке содержится неотрицательное число K (0 <= K <= 104) - количество записей сделанных Норманом после опроса всех жителей города. В следующих K строках записано по два числа (ai, bi) - обозначающие то, что i-й житель a боится жителя b (1 <= ai, bi <= n, ai не равно bi, каждая пара (ai, bi) уникальна).
Формат выходных данных
Выведите номер подозреваемого. Если выявить подозреваемого не представляется возможным, то в ответе укажите число -1.
| |
![]()
|
|
Вирус
Двумерные массивы
Задача на реализацию
Способы задания графа
Обход в ширину
Двумерные массивы
В лаборатории биоинформатики ученые проводят эксперименты по распространению искусственно созданных вирусов. Для эксперимента используется специальная лабораторная установка, представляющая собой таблицу из n × m ячеек. В каждую ячейку помещается живая клетка. Ученые заражают вирусом некоторые клетки, всего исходно заражается не более 8 клеток.
Каждую секунду среди незараженных клеток, имеющих зараженную клетку в соседней по стороне ячейке, ровно одна клетка заражается вирусом.
Ученые заинтересовались, какие конфигурации зараженных клеток могут получиться через t секунд. Для начала они хотят посчитать число таких конфигураций. Помогите им это сделать.
Формат входных данных
В первой строке входного файла находятся целые числа n, m и t (1 ≤ n, m ≤ 100, 1 ≤ t ≤ 6) — размеры таблицы и количество секунд. Каждая из следющих n строк содержит m символов. Символ «.» означает, что в изначальной конфигурации клетка не заражена, а символ «*» — что заражена. Количество «*» в таблице не превышает 8. Гарантируется, что незараженных клеток в исходной конфигурации не меньше t.
Формат выходных данных
Выведите количество различных возможных конфигураций таблицы после t секунд.
| Ввод |
Вывод |
2 2 1
*.
.. |
2 |
2 2 2
*.
.. |
3 |
2 2 3
*.
.. |
1 |
| |
![]()
|
|
Файловый менеджер
Алгоритм Дейкстры
Быстрая сортировка
Способы задания графа
Петя работает над очень большим проектом. Проект содержит N файлов. В процессе работы Пете часто приходится просматривать и редактировать файлы. Для ускорения работы Петя использует файловый менеджер Fur Manager, который отображает список имен файлов проекта в некотором порядке.
В текущей версии Fur Manager’a для перемещения по списку имен файлов есть следующие возможности:
можно нажать клавишу вниз, при этом курсор перемещается на следующий файл в списке, для последнего файла следующим считается первый;
можно нажать клавишу вверх, при этом курсор перемещается на предыдущий файл в списке, для первого файла предыдущим считается последний;
можно нажать клавишу Alt и, удерживая ее, набрать последовательность латинских букв. После этого клавишу Alt следует отпустить, и в этот момент курсор переместится на ближайший файл, имя которого начинается c заданной последовательности символов. Ближайший файл — это файл, на который можно переместиться за наименьшее количество нажатий клавиши вниз. Если заданная последовательность является началом имени текущего файла, или файла, имя которого начинается с этой последовательности, не существует, то курсор останется на месте.
Первая и вторая из описанных возможностей файлового менеджера требуют по одному нажатию клавиши, а третья — одного нажатия (нажатие клавиши Alt) плюс количество нажатий, равное длине набранной последовательности латинских букв.
Файлы пронумерованы от 1 до N в порядке их следования. После загрузки Fur Manager’а курсор находится на первом файле.
Петя знает, что ему сначала придется редактировать файл с номером a1, затем с номером a2 и так далее, а последним — файл с номером ak. В последовательности a1, a2, ..., ak один и тот же номер может встречаться несколько раз. При каждом перемещении от одного файла к другому Петя хочет нажимать как можно меньше клавиш.
Требуется написать программу, которая выдает искомую последовательность нажатий клавиш.
Входные данные
В первой строке входных данных содержится целое число N (1 ≤ N ≤ 1000) — количество файлов в проекте.
В следующих N строках записаны имена файлов, по одному в каждой строке. Файлы перечислены в том порядке, в котором они отображаются файловым менеджером. Имена состоят только из строчных латинских букв. Длина каждого имени не превосходит 2000 символов. Все имена файлов различны.
Далее в следующей строке записано целое число k (1 ≤ k ≤ 10).
Последняя строка входных данных содержит k целых чисел a1, a2, ..., ak (1 ≤ ai ≤ N) — номера редактируемых файлов. Редактирование файлов выполняется в том порядке, в котором они встречаются в последовательности a1, a2, ..., ak.
Выходные данные
Выведите описание искомой последовательности нажатий клавиш в виде k блоков информации:
первый блок информации описывает перемещение от файла с номером 1 к файлу с номером a1;
второй блок информации описывает перемещение от файла с номером a1 к файлу с номером a2;
…
k-ый блок информации описывает перемещение от файла с номером ak–1 к файлу с номером ak.
Каждый блок информации выглядит следующим образом.
В первой строке блока записывается число L — наименьшее количество нажатий клавиш, необходимое для перемещения от очередного файла последовательности к следующему.
Следующие L строк блока описывают нажимаемые клавиши. Каждая из строк содержит описание одной клавиши:
если нажимается клавиша вниз, то в строке записывается слово down;
если нажимается клавиша вверх, то в строке записывается слово up;
если нажимается клавиша Alt, то в строке записывается слово Alt;
при нажатии клавиши с латинской буквой выводится соответствующая ей латинская буква.
Если существует несколько оптимальных способов перемещения, то требуется вывести любой из них.
| Ввод |
Вывод |
|
6
a
b
c
d
e
f
4
4 3 1 6
|
2
Alt
d
1
up
2
Alt
a
1
up
|
| |
![]()
|
|
Электрички на перегонах не меняют
Способы задания графа
Обход в глубину
На пригородной железной дороге N станций и M соединяющих их перегонов. Любые две станции соединены не более чем одним перегоном. Сеть перегонов устроена так, что, отправившись от любой станции, можно вернуться на нее, только проехав хотя бы один перегон дважды. На железной дороге организовано движение электричек. Каждая электричка ходит в обоих направлениях по своему маршруту между двумя конечными станциями и останавливается на всех промежуточных станциях
Для удобства пассажиров руководство железной дороги решило ввести новую систему оплаты проезда. По этой системе каждой станции присваивается некоторое целое число, называемое тарифным номером этой станции. Стоимость проезда между двумя станциями без пересадок определяется модулем разности тарифных номеров этих станций. Тарифные номера станций вдоль маршрута каждой электрички должны изменяться монотонно, то есть при движении в каком-либо направлении строго возрастать и, следовательно, строго убывать при движении в обратном направлении. Это обеспечивает рост стоимости проезда с увеличением количества пройденных перегонов.
Требуется написать программу, которая назначит каждой станции тарифный номер.
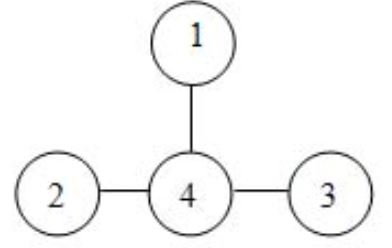 |
4 станции, 3 перегона: 1-4, 2-4, 3-4
Маршруты: 1-4-2, 2-4-3, 3-4-1.
Ответ: решения нет
|
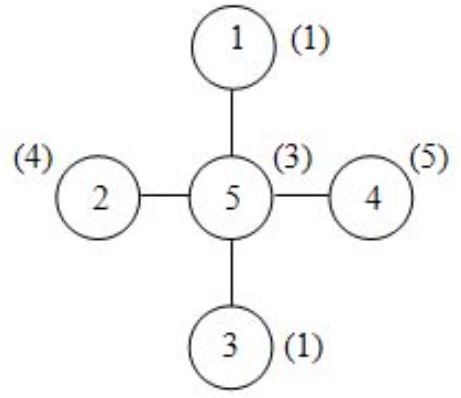 |
5 станций, 4 перегона: 1-5, 2-5, 3-5, 4-5
Маршруты: 1-5-2, 2-5-3, 3-5-4, 4-5-1.
Ответ: решение есть; например, следующее: номер станции: 1 2 3 4 5
тарифный номер: 1 4 1 5 3
Замечание: тарифные номера разных станций могут совпадать.
|
Формат входных данных
В первой строке входных данных содержатся два целых числа: N — количество станций (2 ≤ N ≤ 100 000), и M — количество перегонов между ними (1 ≤ M ≤ N – 1). В последующих M строках записаны пары целых чисел a, b (a ≠ b, 1 ≤ a ≤ N, 1 ≤ b ≤ N), означающие наличие перегона между станциями a и b. За ними в отдельной строке записано единственное целое положительное число K — количество маршрутов электричек. В последующих K строках идут описания маршрутов электричек, по одному на строке. Каждое описание представляет собой последовательность целых чисел — номеров всех станций маршрута в порядке одного из двух возможных направлений следования электрички. Описание маршрута заканчивается числом 0.
Все номера станций в описании маршрута различны. Количество станций в каждом маршруте не менее двух. Любые две последовательные станции в маршруте каждой электрички соединены перегоном. Суммарное количество станций в описаниях всех маршрутов не превосходит 200 000. Могут быть станции и перегоны, через которые не проходит ни одна электричка.
Формат выходных данных
В первую строку выведите «NO», если искомого назначения тарифных номеров не существует. В противном случае в первую строку выведите «YES», а в следующей строке — N целых положительных чисел, где i-е число — тарифный номер i-й станции. Тарифный номер каждой станции должен находиться в диапазоне от 1 до N.
Если существует несколько решений, необходимо вывести любое из них.
| |
![]()
|
|
Метро
Перебор с отсечением
Способы задания графа
Женя получил письмо от Леши со словесным описанием схемы метро в его городе. Метро содержит одну кольцевую линию. Каждая из остальных линий пересекается с кольцевой не более чем в двух местах, причем в точках пересечения организованы пересадочные станции. В одном месте кольцевую линию могут пересекать сразу несколько линий, имеющих общую пересадочную станцию.
Кроме этих пересадочных станций каждая из линий имеет не более одной пересадочной станции для перехода на другие, отличные от кольцевой, линии. На такой станции также может быть организована пересадка сразу на несколько линий.
Для каждой пересадочной станции Леша описал, какие линии на ней пересекаются, и указал порядок расположения пересадочных станций на кольцевой линии. Он утверждает, что все линии расположены на одной глубине и других пересечений, помимо пересадочных узлов, не имеют. Чтобы проверить это утверждение, Женя стал по словесному описанию рисовать схему метро, но у него не получилось.
Помогите Жене написать программу, которая будет проверять, действительно ли может существовать схема метро, соответствующая полученному описанию.
На рисунке приведена возможная схема метро, соответствующая второму примеру.
Формат входных данных
В первой строке содержится число \(k\) — количество линий метро в городе (\(1 \le k \le 10\)). Все линии пронумерованы от 0 до \(k - 1\), кольцевая линия имеет номер 0. Во второй строке записано число \(n\) — количество пересадочных станций. Каждая из следующих \(n\) строк описывает линии, пересекающиеся на соответствующей пересадочной станции, причем сначала следуют описания пересадочных станций, расположенных на кольцевой линии, в порядке их расположения на ней. Описание каждого узла начинается с количества пересекающихся в нем линий, затем следуют номера линий.
Формат выходных данных
Выведите слово YES, если по описанию можно построить схему метро, и NO в противном случае.
| |
![]()
|
|
Шоссе
Способы задания графа
Использование сортировки
Элементарная геометрия
Во Флатландии \(n\) городов, расположенных в различных точках плоскости. Известно, что никакие три города не лежат на одной прямой.
Правительство решило построить в стране сеть сверхскоростных шоссе. Сеть шоссе должна быть такой, чтобы из любого города можно было проехать в любой другой по построенным шоссе. А в целях экономии средств было решено, что путь, соединяющий любые два города, должен быть единственным. Каждое шоссе представляет собой отрезок, соединяющий некоторую пару городов.
Завод, выполняющий этот госзаказ, подготовил проект сети шоссе. Проект представляет собой описание \(n - 1\) шоссе. Каждое шоссе задается городами, которые оно соединяет. В целях секретности вместо названий городов в проекте были использованы коды — числа от 1 до \(n\).
Однако когда дело дошло до реализации проекта, выяснилось, что документ, в котором было указано соответствие номеров городам, утерян. Поскольку проект приурочен к пятисотлетию культурной столицы Флатландии, переделывать проект полностью оказалось невозможно. Поэтому было решено установить некоторое новое соответствие номеров городам.
При попытке это сделать разработчики проекта столкнулись со следующей проблемой. В соответствии с техническими нормами строительства, недопустимо, чтобы шоссе пересекались вне городов. Поэтому не любое сопоставление номеров городам допустимо. После пары бессонных ночей главный инженер завода решил поручить спасение проекта вам.
Ваша задача — таким образом сопоставить числам от 1 до \(n\) города, чтобы после реализации проекта шоссе не пересекались вне городов, которые они соединяют.
Формат входных данных
В первой строке содержится целое число \(n\) — количество городов во Флатландии (\(2 \le n \le 1500\)).
Далее следует \(n\) описаний городов. Описание каждого города состоит из двух строк. Первая строка содержит название города — строку, состоящую из символов с ASCII-кодами от 33 до 127. Названия различных городов не совпадают. Длина названия города не превышает 60 символов. Вторая строка описания города содержит два целых числа \(x\) и \(y\) — координаты города. Координаты не превышают \(10^4\) по абсолютной величине.
Далее следуют \(n - 1\) строк, которые описывают проект строительства сети шоссе в его текущем состоянии. Каждая строка содержит по два целых числа — номера городов, соединенных шоссе в проекте. Никакое шоссе в проекте не соединяет город сам с собой, никакие два города не соединены более чем одним шоссе.
Формат выходных данных
Выведите \(n\) строк, \(i\)-я из этих строк должна содержать название города, который следует сопоставить числу \(i\) в проекте. Если решений несколько, выведите любое.
Если решения не существует, выведите <<No solution>>.
Иллюстрация к примеру
| |
![]()
|
|
Подсчет количества ребер неориентированного графа
Способы задания графа
Простой неориентированный граф задан матрицей смежности. Найдите количество ребер в графе.
Входные данные
На вход программы поступает число n ( 1≤n≤100) – количество вершин в графе, а затем n строк по n чисел, каждое из которых равно 0 или 1, – его матрица смежности.
Выходные данные
Выведите одно число – количество ребер заданного графа.
| |
![]()
|
|
Подсчет количества ребер ориентированного графа
Способы задания графа
Ориентированный граф задан матрицей смежности. Найдите количество ребер в графе.
Входные данные
На вход программы поступает число n ( 1≤n≤100 ) – количество вершин в графе, а затем n строк по n чисел, каждое из которых равно 0 или 1, – его матрица смежности.
Выходные данные
Выведите одно число – количество ребер заданного графа.
| |
![]()
|
|
Проверка на наличие параллельных ребер, неориентированный вариант
Способы задания графа
Неориентированный граф задан списком ребер. Проверьте, содержит ли он параллельные ребра.
Входные данные
Сначала вводятся числа n ( 1≤n≤100) – количество вершин в графе и m ( 1≤m≤10,000 ) – количество ребер. Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите «YES», если граф содержит параллельные ребра, и «NO» в противном случае.
| |
![]()
|
|
Проверка на наличие параллельных ребер, ориентированный вариант
Способы задания графа
Ориентированный граф задан списком ребер. Проверьте, содержит ли он параллельные ребра.
Входные данные
Сначала вводятся числа n ( 1≤n≤1001≤𝑛≤100 ) – количество вершин в графе и m ( 1≤m≤10,0001≤𝑚≤10,000 ) – количество ребер. Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите «YES», если граф содержит параллельные ребра, и «NO» в противном случае.
| |
![]()
|
|
Степени вершин по спискам ребер
Способы задания графа
Неориентированный граф задан списком ребер. Найдите степени всех вершин графа.
Входные данные
Сначала вводятся числа n ( 1≤n≤100 ) – количество вершин в графе и \(m (1 \leq m \leq n (n - 1) / 2)\) – количество ребер. Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите n чисел – степени вершин графа.
| |
![]()
|
|
Полустепени вершин
Способы задания графа
Ориентированный граф задан матрицей смежности. Найдите полустепени захода и полустепени исхода всех вершин графа.
Входные данные
Сначала вводится число n ( 1≤n≤100) – количество вершин в графе, а затем n строк по n чисел, каждое из которых равно 0 или 1, – его матрица смежности.
Выходные данные
Выведите n пар чисел – для каждой вершины сначала выведите полустепень захода и затем полустепень исхода.
| |
![]()
|
|
Полустепени вершин по спискам ребер
Способы задания графа
Ориентированный граф задан списком ребер. Найдите степени всех вершин графа.
Входные данные
Сначала вводятся числа n ( 1≤n≤100 ) – количество вершин в графе и \(m (1 \leq m \leq n (n-1))\) – количество ребер. Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите n пар чисел – для каждой вершины сначала выведите полустепень захода и затем полустепень исхода.
| |
![]()
|
|
Истоки и стоки
Способы задания графа
Напомним, что вершина ориентированного графа называется истоком, если в нее не входит ни одно ребро и стоком, если из нее не выходит ни одного ребра.
Ориентированный граф задан матрицей смежности. Найдите все вершины графа, которые являются истоками, и все его вершины, которые являются стоками.
Входные данные
Сначала вводится число n ( 1≤n≤100) – количество вершин в графе, а затем n строк по n чисел, каждое из которых равно 0 или 1, – его матрица смежности.
Выходные данные
Вначале выведите k – число истоков в графе и затем k чисел – номера вершин, которые являются истоками, в возрастающем порядке. Затем выведите информацию о стоках в том же порядке.
| |
![]()
|
|
Регулярный граф
Способы задания графа
Неориентированный граф называется регулярным, если все его вершины имеют одинаковую степень. Для заданного списком ребер графа проверьте, является ли он регулярным.
Входные данные
Сначала вводятся числа n ( 1≤n≤100) – количество вершин в графе и \(m (0 \leq m \leq n (n - 1)/2)\) – количество ребер. Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите «YES», если граф является регулярным, и «NO» в противном случае.
| |
![]()
|
|
Полуполный граф
Способы задания графа
Ориентированный граф называется полуполным, если между любой парой его различных вершин есть хотя бы одно ребро. Для заданного списком ребер графа проверьте, является ли он полуполным.
Входные данные
Сначала вводятся числа n ( 1≤n≤100 ) – количество вершин в графе и \(m (1 \leq m \leq n (n-1))\) – количество ребер. Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите «YES», если граф является полуполным, и «NO» в противном случае.
| |
![]()
|
|
Полный граф
Способы задания графа
Неориентированный граф с кратными рёбрами называется полным, если любая пара его различных вершин соединена хотя бы одним ребром. Для заданного списком ребер графа проверьте, является ли он полным.
Входные данные
Сначала вводятся числа n ( 1≤n≤100 ) – количество вершин в графе и \(m ( 1 \leq m \leq n (n-1)/2)\) – количество ребер. Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите «YES», если граф является полным, и «NO» в противном случае.
| |
![]()
|
|
Турнир
Способы задания графа
Ориентированный граф называется турниром, если между любой парой его различных вершин существует ровно одно ребро. Для заданного списком ребер графа проверьте, является ли он турниром.
Входные данные
Сначала вводятся числа n ( 1≤n≤100 ) – количество вершин в графе и \(m ( 1 \leq m \leq n (n-1))\) – количество ребер. Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите «YES», если граф является турниром, и «NO» в противном случае.
| |
![]()
|
|
Транзитивность неориентированного графа
Способы задания графа
Напомним, что граф называется транзитивным, если всегда из того, что вершины u и v соединены ребром и вершины v и w соединены ребром следует, что вершины u и w соединены ребром.
Проверьте, что заданный неориентированный граф является транзитивным.
Входные данные
Сначала вводятся числа n ( 1≤n≤100 ) – количество вершин в графе и \(m (1 \leq m \leq n (n-1)/2)\) – количество ребер. Затем следует m пар чисел – ребра графа.
Выходные данные
Выведите «YES», если граф является транзитивным, и «NO» в противном случае.
| |
![]()
|
|
Транзитивность ориентированного графа
Способы задания графа
Напомним, что ориентированный граф называется транзитивным, если для любых трех различных вершин u, v и w из того, что из u в вершину v ведет ребро и из вершины v в вершину w ведет ребро, следует, что из вершины u в вершину w ведет ребро.
Проверьте, что заданный ориентированный граф является транзитивным.
Входные данные
Сначала вводится число n ( 1≤n≤100 ) – количество вершин в графе, а затем n строк по n чисел, каждое из которых равно 0 или 1, – его матрица смежности.
Выходные данные
Выведите «YES», если граф является транзитивным, и «NO» в противном случае.
| |
![]()
|
|
Метро
Способы задания графа
Метрополитен состоит из нескольких линий метро. Все станции метро в городе пронумерованы натуральными числами от 1 до N. На каждой линии расположено несколько станций. Если одна и та же станция расположена сразу на нескольких линиях, то она является станцией пересадки и на этой станции можно пересесть с любой линии, которая через нее проходит, на любую другую (опять же проходящую через нее).
Напишите программу, которая по данному вам описанию метрополитена определит, с каким минимальным числом пересадок можно добраться со станции A на станцию B. Если данный метрополитен не соединяет все линии в одну систему, то может так получиться, что со станции A на станцию B добраться невозможно, в этом случае ваша программа должна это определить.
Входные данные
Сначала вводится число N — количество станций метро в городе (2≤N≤100). Далее следует число M — количество линий метро (1≤M≤20). Далее идет описание M линий. Описание каждой линии состоит из числа Pi — количество станций на этой линии (2≤Pi≤50) и Pi чисел, задающих номера станций, через которые проходит линия (ни через какую станцию линия не проходит дважды).
Затем вводятся два различных числа: A — номер начальной станции, и B — номер станции, на которую нам нужно попасть. При этом если через станцию A проходит несколько линий, то мы можем спуститься на любую из них. Так же если через станцию B проходит несколько линий, то нам не важно, по какой линии мы приедем.
Выходные данные
Выведите минимальное количество пересадок, которое нам понадобится. Если добраться со станции A на станцию B невозможно, программа должна вывести одно число –1 (минус один).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
2
4 1 2 3 4
2 5 3
3 1 |
0 |
| 2 |
5
5
2 1 2
2 1 3
2 2 3
2 3 4
2 4 5
1 5 |
2 |
| 3 |
10
2
6 1 3 5 7 4 9
6 2 4 6 8 10 7
3 8 |
1 |
| 4 |
4
2
2 1 2
2 3 4
1 3 |
-1 |
| |
![]()
|
|
Яблоко от яблони…
Способы задания графа
Обход в глубину
У Пети в саду растет яблоня. Воодушевленный историей об Исааке Ньютоне, который, как известно, открыл закон всемирного тяготения после того, как ему на голову упало яблоко, Петя с целью повысить свою успеваемость по физике часто сидит под яблоней.
Однако, поскольку по физике у Пети твердая тройка, яблоки с его яблони падают следующим образом. В какой-то момент одно из яблок отрывается от ветки, на которой оно висит, и начинает падать строго вниз. Если в некоторый момент оно задевает другое яблоко, то то тоже отрывается от своей ветки и начинает падать вниз, при этом первое яблоко не меняет направление своего падения. Вообще, если любое падающее яблоко заденет другое яблоко на своем пути, то оно также начнет падать.
Таким образом, в любой момент каждое яблоко либо висит на ветке, либо падает строго вниз, причем все яблоки кроме первого, чтобы начать падать, должны сначала соприкоснуться с каким-либо другим падающим яблоком.
Выясните, какие яблоки упадут с Петиной яблони.
Входные данные
В первой строке вводится число N - количество яблок на Петиной яблоне (1 <= N <= 200). Следующие N строк содержат описания яблок. Будем считать все яблоки шарами. Каждое яблоко задается координатами своей самой верхней точки (той, где оно исходно прикреплено к дереву, длиной черенка пренебрежем) xi, yi и zi и радиусом ri ( -10000 <= xi, yi, zi <= 10000, 1 <= ri <= 10000, все числа целые). Гарантируется, что изначально никакие яблоки не пересекаются (даже не соприкасаются). Ось OZ направлена вверх.
Выходные данные
В первой строке выведите количество яблок, которые упадут с яблони, если начнет падать первое яблоко. В следующей строке выводите номера упавших яблок. Яблоки нумеруются, начиная с 1, в том порядке, в котором они заданы во входных данных.
| |
![]()
|
|
Развлечения с измерителем
Способы задания графа
Обход в глубину
Дима обнаружил у папы на столе специальный чертежный прибор, похожий на циркуль - измеритель. Измеритель отличается от обычного циркуля тем, что в обеих его ножках находятся иголки (у обычного циркуля в одной ножке находится иголка, а в другой - грифель).
Дима взял клетчатый лист бумаги, установил между иглами измерителя некоторое расстояние, прочно зафиксировав его, и начал втыкать измеритель в лист бумаги. Каждый раз Дима втыкал в лист обе иглы измерителя, при этом он всегда делал это так, что дырочки получались в точках пересечениях линий, которыми лист разлинован на клетки. При этом в одну и ту же дырку Дима мог вставлять измеритель несколько раз.
Вечером папа нашел лист, с которым развлекался Дима, и решил выяснить, какое расстояние между иглами измерителя Дима мог установить. Все, что знает папа - координаты дырок, проделанных иглами измерителя. Помогите Папе решить поставленную задачу.
Входные данные
В первой строке вводится число n
- количество дырок (2 <= n <= 1000). Следующие n строк содержат по два целых числа - координаты дырок. Координаты не превышают 104
по абсолютной величине.
Выходные данные
В первой строке выведите k
- количество различных расстояний, которые Дима мог установить между иглами измерителя. Следующие k строк должны содержать искомые расстояния, по одному вещественному числу в строке. Расстояния должны быть выведены в возрастающем порядке. Каждое число должно быть выведено с точностью не менее, чем 10-9.
Гарантируется, что существует по крайней мере одно расстояние, которое Дима мог установить между иглами измерителя.
| |
![]()
|
|
Свинки-копилки
Способы задания графа
Обход в глубину
У Васи есть N свинок-копилок, свинки занумерованы числами от 1 до N. Каждая копилка может быть открыта единственным соответствующим ей ключом или разбита.
Вася положил ключи в некоторые из копилок (он помнит, какой ключ лежит в какой из копилок). Теперь Вася собрался купить машину, а для этого ему нужно достать деньги из всех копилок. При этом он хочет разбить как можно меньшее количество копилок (ведь ему еще нужно копить деньги на квартиру, дачу, вертолет…). Помогите Васе определить, какое минимальное количество копилок нужно разбить.
Входные данные
В первой строке содержится число N — количество свинок-копилок (1≤N≤100000). Далее идет N строк с описанием того, где лежит ключ от какой копилки: в i-ой из этих строк записан номер копилки, в которой находится ключ от i-ой копилки.
Выходные данные
Выведите единственное число: минимальное количество копилок, которые необходимо разбить.
Примечание
Ключи от первой и третьей копилки лежат в копилке 2, ключ от второй — в первой, а от четвертой — в ней самой.
Чтобы открыть все копилки, достаточно разбить, например, копилки с номерами 1 и 4.
| |
![]()
|
|
Трехцветные таблицы
Способы задания графа
Обход в ширину
Обход в глубину
Прямоугольную таблицу, состоящую из N строк и M столбцов, раскрашивают следующим образом. Каждый столбец таблицы и каждую строку красят либо в синий, либо в желтый цвет. В итоге клетки, оказавшиеся на пересечении синего столбца и синей строки оказываются синими, желтого столбца и желтой строки — желтыми, а клетки на пересечении синего столбца и желтой строки, или, наоборот, желтого столбца и синей строки — зелеными.
Раскраска всех клеток таблицы (или просто сама таблица) называется правильной, если она может быть получена описанным выше способом.
Вам дана прямоугольная таблица, которую нужно раскрасить таким образом. Про некоторые клетки известно, какого цвета они должны быть, а остальные клетки могут в итоге быть любого цвета. Определите, сколько существует различных правильных таблиц, в которых нужные клетки покрашены в нужный цвет.
Входные данные
Вводятся числа N и M — количество строк и столбцов таблицы (1≤N≤30, 1≤M≤30). Далее записано N строк по M чисел в каждой, задающие цвета, в которые должны быть окрашены клетки:
0 — клетка может в итоге быть любого цвета
1 — клетка должна быть синей
2 — клетка должна быть желтой
3 — клетка должна быть зеленой
Выходные данные
Выведите одно число — количество различных правильных таблиц, в которых нужные клетки покрашены в нужный цвет. Обратите внимание, что если два или более способов раскраски столбцов и строк таблицы приводят к одинаковой раскраске самой таблицы, то это нужно считать как один вариант раскраски таблицы (см. пример 2).
| |
![]()
|
|
Свинки-копилки
Способы задания графа
Обход в глубину
У Васи есть N свинок-копилок, свинки занумерованы числами от 1 до N. Каждая копилка может быть открыта единственным соответствующим ей ключом или разбита.
Вася положил ключи в некоторые из копилок (он помнит, какой ключ лежит в какой из копилок). Теперь Вася собрался купить машину, а для этого ему нужно достать деньги из всех копилок. При этом он хочет разбить как можно меньшее количество копилок (ведь ему еще нужно копить деньги на квартиру, дачу, вертолет…). Помогите Васе определить, какое минимальное количество копилок нужно разбить.
Входные данные
В первой строке содержится число N — количество свинок-копилок (1≤N≤100000). Далее идет N строк с описанием того, где лежит ключ от какой копилки: в i-ой из этих строк записан номер копилки, в которой находится ключ от i-ой копилки.
Выходные данные
Выведите единственное число: минимальное количество копилок, которые необходимо разбить.
Примечание
Ключи от первой и третьей копилки лежат в копилке 2, ключ от второй — в первой, а от четвертой — в ней самой.
Чтобы открыть все копилки, достаточно разбить, например, копилки с номерами 1 и 4.
| |
![]()
|
|
Вырезанные фигуры
Обход в ширину
Способы задания графа
Эпидемия гриппа не обошла стороной семиклассника Алешу. Скучая дома, Алеша решил вырезать фигурки из листа клетчатой бумаги. Лист состоял из M строк и N столбцов клеточек. Сначала Алеша нарисовал на листе границы фигур. Количество фигур было не меньше 2. Чтобы фигуры получались ровными, границы фигур Алеша рисовал строго по линиям имеющейся клеточной разметки листа (при этом некоторые границы фигур могли пройти по границам листа). Форма фигур могла быть любой, но при этом все фигуры были связными (фигура называется связной, если из любой ее клетки можно добраться до любой другой, ходя только по клеткам фигуры и перемещаясь каждый раз в одну из 4-х соседних по стороне клеток). Никакие две фигуры не имели общих точек, в том числе не касались углами клеток.
<>Затем Алеша вырезал нарисованные фигуры, делая разрезы только по их границам. При этом оставшаяся часть листа осталась связной (то есть не распалась на несколько частей).
Лист с вырезами Алеша отсканировал. Сканер в своей памяти по результатам сканирования построил таблицу, состоящую из нулей и единиц, из M строк и N столбцов (строки нумеруются сверху вниз от 1 до M, столбцы — слева направо от 1 до N). Каждый элемент таблицы соответствовал клеточке исходного листа. Единица обозначала, что соответствующая клетка листа осталась на месте, ноль — соответствующая клетка была вырезана.
На рис. 1 приведен пример клетчатого листа, а на рис. 2 — соответствующая ему таблица в памяти сканера:
Рис 1.
Исходный клеточный лист с вырезанными фигурами
Размер листа: M=6, N=12.
Количество вырезанных фигур: 3 |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
| 1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
| 1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
| 1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
| 1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Рис 2.
Такая таблица строится в памяти сканера
|
После этого сканер представил полученную таблицу в специальном, описанном ниже формате и передал информацию на компьютер. Напишите программу, которая по полученной информации установит:
Пункт 1. Сколько клеток было вырезано из листа?
Пункт 2. Сколько фигур было вырезано? Описание формата представления таблицы Последовательность подряд идущих по горизонтали или вертикали единиц будем называть полосой. Полосу можно задаеть 4 числами:
- направление (0—горизонтальная, 1—вертикальная)
- (i, j) — координаты начальной клетки полосы (начальной является самая левая клетка для горизонтальной полосы, и самая верхняя — для вертикальной), i — номер строки клетки, j — номер столбца
- d — длина полосы (количество подряд стоящих единиц).
Всю таблицу разобьем на полосы, состоящие из единиц так, чтобы каждая единица принадлежала хотя бы одной полосе. При этом полосы могут пересекаться, а также накладываться. Таким образом, таблица представляется в виде описания всех полос, которое удовлетворяет трем дополнительным требованиям:
- В каждой клетке начинается не более одной полосы.
- Полосы перечислены в порядке следования их начальных клеток (клетки перечисляются по строкам сверху вниз, в строке — слева направо).
- Общее число полос не превышает 256000.
Заметим, что таблица может быть представлена в виде полос разными способами, но каждое представление позволяет однозначно восстановить таблицу.
Входные данные
Во входном файле записано сначала число P (1 или 2) — номер пункта задачи, ответ на который требуется получить. Далее записаны размеры исходного листа — числа M и N (1 ≤ M ≤ 4000,1 ≤ N ≤ 4000) . Затем записано число K (0 ≤ K ≤ 256000) — количество полос в описании полученной таблицы. Затем идет K четверок чисел, описывающих полосы (полосы перечисляются в порядке начальных клеток полос: по строкам сверху вниз, в строке — слева направо).
Выходные данные
В выходной файл выведите искомое количество (если P=1, то — количество клеток, вырезанных из листа, если P=2, то — количество фигур, вырезанных из листа).
| |
![]()
|
|
Юный поджигатель
Алгоритм Флойда
Способы задания графа
На клеточном поле введена система координат так, что центр координат находится в точке пересечения линий сетки и оси направлены вдоль линий сетки.
На этом поле выложили связную фигуру, состоящую из спичек. Использовались спички двух типов:
- Спички длины 1 выкладывались по сторонам клеток.
- Спички длины выкладывались по диагоналям клеток.
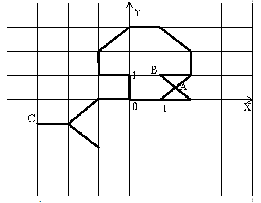
Ребенок хочет сжечь фигуру. При этом он может поджечь ее в одной точке, имеющей целочисленные координаты (например, в точке A на рисунке поджигать фигуру нельзя, а в точках B и C — можно).
Известно, что огонь распространяется вдоль спички равномерно (но по каждой спичке — со своей скоростью). Спичка может гореть в нескольких местах (например, когда она загорается с двух концов; или когда в середине диагональной спички огонь перекидывается с одной спички на другую — огонь расползается по вновь подожженной спичке в обе стороны).
Напишите программу, которая определит, в какой точке нужно поджечь фигуру, чтобы она сгорела за минимальное время.
Входные данные
Во входном файле записано сначала число N — количество спичек (1<N<40). Затем идет N пятерок чисел вида X1, Y1, X2, Y2, T, задающих координаты концов спички и время ее сгорания при условии, что она будет подожжена с одного конца (гарантируется, что каждая спичка имеет длину 1 или , все спички образуют связную фигуру, и положение никаких двух спичек не совпадает). Все координаты — целые числа, по модулю не превышающие 200, время сгорания — натуральное число, не превышающее 107.
Выходные данные
Выведите координаты целочисленной точки, в которой нужно поджечь фигуру, чтобы она сгорела за наименьшее время, а затем время, за которое в этом случае фигура сгорит. Время должно быть выведено с точностью не менее 2-х знаков после десятичной точки. Если решений несколько, выведите любое из них.
| |
![]()
|