| | | |
|
Раскраска кеглей
Циклы
Комбинаторика
В ряд ставятся N кеглей. Громозека красит каждую из них в один из K цветов из своих банок с краской. Из эстетических соображений любые две соседних кегли должны быть окрашены в разные цвета. Найдите количество возможных способов раскрасить кегли.
Входные данные
Входная строка содержит два целых числа N и K (\(1<=N<=1000\), \(2<=K<=1000\)).
Выходные данные
Выведите на экран ответ на задачу. Гарантируется, что верный ответ не превышает \(2^{31}-1\).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 2 |
2 |
| 1 |
1 10 |
10 |
| |
![]()
|
|
Март
Комбинаторика
Есть N человек. Имя i-го человека - Si . Мы хотим выбрать трех человек, чтобы выполнялись следующие условия:
- имя каждого выбранного человека начинается с M, А, R, С или Н;
- среди выбранных людей нет людей, имена которых начинаются с одной буквы.
Сколько существует таких способов выбрать трех человек, не обращая внимания на порядок?
Входные данные
В первой строке записано целое число N (\(1<=N<=10^5\)) В следующих N строках записаны имена Si - строка, состоящая только из английских заглавных букв, длина строки не более 10 символов. Все имена различные.
Выходные данные
Выведите ответ на задачу. Обратите внимание, что ответ может не соответствовать 32-битному целочисленному типу.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
5
MASHIKE
RUMOI
OBIRA
HABORO
HOROKANAI |
2 |
Трех людей можно выбрать такими способами:
- MASHIKE, RUMOI, HABORO
- MASHIKE, RUMOI, HOROKANAI
Ответ: 2
|
| 2 |
4
ZZ
ZZZ
Z
ZZZZZZZZZZ |
0 |
|
| 3 |
5
CHOKUDAI
RNG
MAKOTO
AOKI
RINGO |
7 |
|
| |
![]()
|
|
Числовые печеньки - 2
Динамическое программирование
Комбинаторика
У Громозеки N печенек. На i-й (1<=i<=N) печеньке написано целое число xi. Он выбирает одну или несколько из этих печенек, так чтобы среднее значение целых чисел, записанных на выбранных печеньках, было равно А.
Какими способами он может сделать свой выбор?
Входные данные
В первой строке вводятся два целых числа N (1<=N<=50) и A (1<=A<=50). Во второй строке N целых чисел - xi (1<=xi<=50).
Выходные данные
Выведите одно число - количество способов выбрать такие печеньки, чтобы среднее значение всех записанных чисел на печеньках было ровно A.
Примеры
| № |
Входные данные |
Выходные данные |
Примечение |
| 1 |
4 8
7 9 8 9 |
5 |
Ниже приведены 5 способов выбрать печеньки так, чтобы в среднем было 8.
1) Выберите 3-ю печеньку.
2) Выберите 1-ю и 2-ю печеньки.
3) Выберите 1-ю и 4-ю печеньки.
4) Выберите 1-ю, 2-ю и 3-ю печеньки.
5) Выберите 1-ю, 3-ю и 4-ю печеньки. |
| 2 |
3 8
6 6 9 |
0 |
|
| 3 |
8 5
3 6 2 8 7 6 5 9 |
19 |
|
| 4 |
33 3
3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 |
8589934591 |
Ответ может не соответствовать 32-битному целому числу. |
| |
![]()
|
|
Карты на троих
Комбинаторика
Молчун, Ворчун и Пилюлькин играют в карточную игру на троих. Правила игры следующие.
Сначала у каждого из трех игроков есть колода, состоящая из некоторого количества карт.
В колоде Пилюлькина N карт, в колоде Молчуна M карт, а в колоде Ворчуна K карт. На каждой карточке написана буква p, m или v. Порядок карт в колодах не может быть изменен. Игроки ходят по очереди. Пилюлькин ходит первым.
Если в колоде текущего игрока есть хотя бы одна карта, сбросьте верхнюю карту в колоде.
Затем следующий ход переходит к игроку, имя которого начинается с буквы на сброшенной карте.Например, если на карте написано «p», следующий ход переходит Пилюлькину.
Если колода текущего игрока пуста, игра заканчивается, и текущий игрок выигрывает игру.
Есть 3N + M + K возможных вариантов раскладки начальных колод трех игроков.
Сколько из этих шаблонов приведет к победе Пилюлькина? Поскольку ответ может быть большим, выведите его по модулю 1000000007 (= 109 +7).
Входные данные
На вход подается три целых числа N, M и K (2<=N, M, K <=3*105).
Выходные данные
Выведите количество победных для Пилюлькина шаблонов по модулю 1000000007 (= 109 +7).
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
1 1 1 |
17 |
Если карта Пилюлькина - p, то Пилюлькин выиграет независимо от карты Молчуна и Ворчуна. Таких вариантов 3 × 3 = 9.
Если карта Пилюлькина - m, Пилюлькин выиграет только тогда, когда карта Молчуна - p, или когда карта Молчуна - v, а карта Ворчуна - p. Всего таких шаблоно 3 + 1 = 4.
Если карта Пилюлькина - v, Пилюлькин выиграет только тогда, когда карта Ворчуна - p, или когда карта Ворчуна - m, а карта Ворчуна - p. Всего таких шаблонов 3 + 1 = 4.
Таким образом, всего 9 + 4 + 4 = 17 шаблонов, которые приведут к победе Пилюлькина. |
| 2 |
4 2 2 |
1227 |
|
| 3 |
1000 1000 1000 |
261790852 |
|
| |
![]()
|
|
До Нового года - 1
Циклы
Комбинаторика
Снежик Сугробович положил в ряд N ёлочных шаров, для того чтобы их покрасить. Он решил, что каждый шар будет одним из K цветов. При этом Снежик Сугробович хочет, чтобы любые два соседних ёлочных шара были окрашены в разные цвета. Найдите количество возможных способов раскрасить ёлочные шары.
Входные данные
Входная строка содержит два целых числа N и K (\(1<=N<=1000\), \(2<=K<=1000\)).
Выходные данные
Выведите на экран ответ на задачу. Гарантируется, что верный ответ не превышает \(2^{31}-1\).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 2 |
2 |
| 1 |
1 10 |
10 |
| |
![]()
|
|
Сенсор
Перебор
Комбинаторика
Артем создает интерактивный сенсор для игры в кости. Сенсор встроен в стол и может считать суммарное число точек на гранях всех брошенных костей, прилегающих к сенсору (то есть, на нижних гранях). Позже Артем понял, что для игры нужно считать сумму не на нижних, а на верхних гранях. Артем хочет написать программу, которая по сумме на нижних гранях сможет находить количество различных возможных сумм на верхних гранях. Но так как Артем не силен в программировании, он поручает эту задачу вам.
Сенсор выдает число s равное суммарному числу точек на нижних гранях игральных костей.
Все бросаемые кости шестигранные и удовлетворяют условию правильной игральной кости, то есть сумма точек на противоположных гранях кубика равна семи (1 и 6, 2 и 5, 3 и 4). Вам необходимо найти количество возможных сумм на верхних гранях кубиков.
Формат входных данных
В первой строке входного файла задано число s сумма на нижних гранях костей (s <= 105).
Формат выходных данных
Выведите одно число: количество различных всевозможных сумм на верхних гранях костей.
Пояснение к примеру
В первом примере на нижних гранях могло выпасть 1 + 1 или 2, суммы на верхних гранях 12 и
5, соответственно.
| |
![]()
|
|
Перестановки с другим началом (С', С)
Информатика
Комбинаторика
Перестановкой размера n называется упорядоченный набор из n чисел, в котором каждое число от 1 до n встречается ровно один раз. Например, (4, 2, 3, 5, 1) - это перестановка размера 5.
Нам дано число n и последовательность a, в которой k натуральных чисел.
Вычислите, сколько существует перестановок размера n, которые не начинаются на данную последовательность.
Формат входных данных
В первой строке содержатся два натуральных числа n и k (1 <= n <= 9, 1 <= k <= 100) .
Во второй строке содержатся k натуральных чисел, составляющие последовательность a. Каждое из этих чисел не превышает 100.
Формат выходных данных
Выведите количество перестановок размера n- которые не начинаются на данную последовательность a.
| Ввод |
Вывод |
3 2
2 1 |
5 |
5 2
4 4 |
120 |
5 6
2 3 9 5 6 6 |
120 |
| |
![]()
|
|
Boolean Satisfiability
Алгоритмы на графах
Конструктив
Комбинаторика
Boolean satisfiability problem (SAT) is known to be a very hard problem in computer science. In this problem you are given a Boolean formula, and you need to find out if the variables of a given formula can be consistently replaced by the values true or false in such a way that the formula evaluates to true. SAT is known to be NP-complete problem. Moreover, it is NP-complete even in case of 3-CNF formula (3-SAT). However, for example, SAT problem for 2-CNF formulae (2-SAT) is in P.
#SAT is the extension of SAT problem. In this problem you need to check if it is possible, and count the number of ways to assign values to variables. This problem is known to be #P-complete even for 2-CNF formulae. We ask you to solve #1-DNF-SAT, which is #SAT problem for 1-DNF formulae.
You are given a Boolean formula in 1-DNF form. It means that it is a disjunction (logical or) of one or more clauses, each clause is exactly one literal, each literal is either variable or its negation (logical not). Formally:
 Your task is to find the number of ways to replace all variables with values true and false (all occurrences of the same variable should be replaced with same value), such that the formula evaluates to true.
Input
The only line of the input file contains a logical formula in 1-DNF form (not longer than 1000 symbols). Logical operations are represented by ‘|’ (disjunction) and ‘~’ (negation). The variables are ‘A’ . . . ‘Z’ and ‘a’ . . . ‘z’ (uppercase and lowercase letters are different variables). The formula contains neither spaces nor other characters not mentioned in the grammar.
Output
Output a single integer — the answer for #SAT problem for the given formula
| Input |
Output |
| a |
1 |
| B|~B |
2 |
| c|~C |
3 |
| i|c|p|c |
7 |
| |
![]()
|
|
МАРШРУТЫ
Комбинаторика
В государстве Чудаков N городов ( 2 <=N <= 16 ), обозначаемых заглавными латинскими буквами, начиная с A, по порядку. Между некоторыми из них проложены дороги, которые могут быть как односторонними, так и двусторонними, причем не обязательно, что из каждого города можно проехать в любой другой.
В государстве всего один маршрут автобуса – 'Ч', который совершает только один рейс каждый день. Выходя из некоторого города, он совершает ровно N переездов между городами так, чтобы вернуться в тот, из которого выехал. Других ограничений на его маршрут нет. В течение дня автобус может несколько раз проезжать один и тот же город или дорогу. В каждом городе существуют автобусные парки, из которых могут выезжать автобусы маршрута 'Ч'. Так что, хотя автобус каждый день возвращается в город, из которого стартовал в этот день, на следующий день начало маршрута 'Ч' может быть из любого другого города. Но рейс каждый день только один.
Маршрут обозначается N буквами, начиная с города, из которого происходит выезд. Например, BCDCE – допустимый маршрут для государства из 5 городов ссоответствующими дорогами: выехать из B, проехать в C, затем в D, вернуться в C, проехать в E и вернуться в изначальный город B (последний пункт маршрута, совпадающий с первым, в маршруте не указывается).
Маршрут автобуса меняется каждый день так, что список маршрутов по дням расположен в словарном порядке и содержит все возможные маршруты. Когда список кончается, его обход начинается сначала. В первый день введения маршрута 'Ч' автобус шёл по первому по порядку маршруту. Выведите его маршрут на день K работы маршрута. Пример: В государстве четыре города: A, B, C, D. Наличие дорог между ними задано матрицей, где элемент равен 1, если из города, соответствующего строке, в город, соответствующий столбцу, есть дорога, и 0 – иначе (на главной диагонали нули – дорог, ведущих назад в тот же город, не бывает).
| откуда/куда |
A |
B |
C |
D |
| A |
0 |
0 |
1 |
1 |
| B |
1 |
0 |
1 |
1 |
| C |
0 |
1 |
0 |
0 |
| D |
0 |
1 |
1 |
0 |
Полное расписание маршрутов в таком государстве выглядит так:
ADCB
BADC
BCBC
BCBD
BDBC
BDBD
CBAD
CBCB
CBDB
DBCB
DBDB
DCBA
Таким образом, например, маршрут на день 30 – это BDBD.
Формат входных данных
В первой строке указывается количество городов N ( 2<= N <= 16 ). Далее следует N строк по N элементов (цифр), разделенных пробелом, содержащих матрицу, задающую дороги между городами. Далее следует строка содержащая целое число D – номер дня, маршрут которого требуется определить ( 1<= D <= 264 ).
Формат выходных данных
В единственной строке указывается маршрут, т.е. порядок посещения городов, например BDBD (см. предыдущий пример).
| Ввод |
Вывод |
3
0 1 1
1 0 1
1 1 0
4 |
BCA |
| |
![]()
|
|
Palindromic Paths
Строки
Динамическое программирование
Динамическое программирование: два параметра
Комбинаторика
Ферма Джона представлена решёткой N×N полей (1≤N≤500). Каждое поле представлено символом латинского алфавита. Например:
ABCD
BXZX
CDXB
WCBA
Каждый день корова Беси прогуливается из верхнего левого угла в правый нижний, каждый раз двигаясь на один шаг вправо или вниз. Беси записывает в строку буквы, по которым прошлась. Она огорчится, если у неё получится палиндром (слово, которое читается одинаково слева направо и справа налево), поскольку тогда она запутается, в каком направлении двигалась.
Пожалуйста, помогите Беси определить количество различных маршрутов которыми она может получить палиндромы. Различные пути, которыми получаются одинаковые палиндромы учитывать множество раз. Выведите свой ответ по модулю 1,000,000,007.
ФОРМАТ ВВОДА:
Первая строка ввода содержит N, и последующие N строк содержат N строк решётки, описывающей поля. Каждая строка содержит N символов в интервале A..Z.
ФОРМАТ ВЫВОДА:
Выведите количество различных путей Беси, формирующих палиндромы по модулю 1,000,000,007.
| Ввод |
Вывод |
|
4
ABCD
BXZX
CDXB
WCBA
|
12 |
Беси может сделать следующие палиндромы:
1 x "ABCDCBA"
1 x "ABCWCBA"
6 x "ABXZXBA"
4 x "ABXDXBA"
| |
![]()
|
|
Cow Hopscotch
Динамическое программирование
Динамическое программирование: один параметр
Динамическое программирование: два параметра
Комбинаторика
Фермер Джон придумал игру для своих коров
Она играется на решётке R*C (2 <= R <= 750, 2 <= C <= 750), где каждый квадрат помечен целым числом от 1 до K (1 <= K <= R*C). Коровы выполняют последовательность прыжков, начиная в левом верхнем квадрате и заканчивая в правом нижнем квадрате и прыжок является корректным если и только если:
1) Вы прыгаете на квадрат c другим числом
2) Квадрат, куда Вы прыгаете, как минимум на одну строку ниже квадрата, в котором Вы сейчас стоите
3) Квадрат, в который Вы прыгаете как минимум на одну колонку правее квадрата, в котором Вы сейчас стоите
Пожалуйста, помогите коровам вычислить количество возможных различных последовательностей корректных прыжков из левого верхнего квадрата в правый нижний.
INPUT FORMAT:
Первая строка ввода содержит целые числа R, C, K. Каждая из следующих R строк содержит C целых чисел, каждое в интервале 1..K.
OUTPUT FORMAT:
Выведите количество различных способов пропрыгать из левого верхнего угла в правый нижний, по модулю 1000000007.
| Ввод |
Вывод |
|
4 4 4
1 1 1 1
1 3 2 1
1 2 4 1
1 1 1 1
|
5 |
| |
![]()
|
|
Загадка у костра
Динамическое программирование
Алгоритмы на графах
Комбинаторика
Однажды Юрик оказался в лесу у костра, где собрались \(n\) человек. Оказалось, что некоторые из них знакомы друг с другом. Для удобства пронумеруем людей целыми числами от \(1\) до \(n\). Обозначим как \(d_i\) количество людей, сидящих у костра, с которыми знаком \(i\)-й человек. Неожиданно оказалось, что два человека с номерами \(i\) и \(j\) (\(i \ne j\)) знакомы друг с другом тогда и только тогда, когда \(d_i = d_j\).
Вернувшись домой, Юрик задумался, какое минимальное количество пар людей могли быть знакомы, чтобы выполнялось это условие?
Формат входных данных
Единственная строка содержит одно целое число \(n\) (\(1 \le n \le 5\,000\)) — количество людей.
Формат выходных данных
Выведите одно целое число — минимальное количество пар знакомых людей.
Замечание
Рассмотрим первый пример из условия. Возможны следующие варианты:
-
Любые два человека знакомы друг с другом. В этом случае количество пар знакомых людей равно \(\frac{4 \cdot 3}{2} = 6\).
-
Некоторые три человека попарно знакомы друг с другом, четвертый человек не знаком ни с кем. В этом случае количество пар знакомых людей равно \(3\).
| |
![]()
|
|
Клад
Динамическое программирование на графах
Комбинаторика
Однажды Юрик оказался в лесу у костра, где собрались \(n\) человек. Оказалось, что некоторые из них знакомы друг с другом. Для удобства пронумеруем людей целыми числами от \(1\) до \(n\). Обозначим как \(d_i\) количество людей, сидящих у костра, с которыми знаком \(i\)-й человек. Неожиданно оказалось, что два человека с номерами \(i\) и \(j\) (\(i \ne j\)) знакомы друг с другом тогда и только тогда, когда \(d_i = d_j\).
Вернувшись домой, Юрик задумался, какое минимальное количество пар людей могли быть знакомы, чтобы выполнялось это условие?
Формат входных данных
Единственная строка содержит одно целое число \(n\) (\(1 \le n \le 5\,000\)) — количество людей.
Формат выходных данных
Выведите одно целое число — минимальное количество пар знакомых людей.
Рассмотрим первый пример из условия. Возможны следующие варианты:
-
Любые два человека знакомы друг с другом. В этом случае количество пар знакомых людей равно \(\frac{4 \cdot 3}{2} = 6\).
-
Некоторые три человека попарно знакомы друг с другом, четвертый человек не знаком ни с кем. В этом случае количество пар знакомых людей равно \(3\).
| |
![]()
|
|
Похожие пары
Комбинаторика
Будем называть пару различных целых чисел похожими, если у них \(k\) последних цифр совпадает.
Дано число \(n\), найдите количество пар различных похожих чисел, состоящих из \(n\) цифр. Ведущие нули запрещены. Пары \((a, b)\) и \((b, a)\) считаются одинаковыми.
Формат входных данных
На первой строке находится целое число \(n\) (\(1 \le n \le 10\)).
На второй строке находится целое число \(k\) (\(1 \le k \le n\)).
Формат выходных данных
Выведите одно число — количество пар похожих чисел, состоящих из \(n\) цифр.
| |
![]()
|
|
Интересные числа
Динамическое программирование
Вывод формулы
Комбинаторика
Будем назвать натуральное число интересным, если в его десятичной записи первая цифра совпадает с последней.
Дано число \(n\). Найдите количество интересных чисел, не превышающих \(n\).
Формат входных данных
На ввод подается целое число \(n\) (\(1 \le n \le 10^{18}\)).
Обратите внимание, что для считывания этого числа вам может понадобиться 64-битный тип данных (<<long long>> в C++, <<long>> в Java, <<int64>> в Паскале).
Формат выходных данных
Выведите одно целое число — количество интересных натуральных чисел, не превышающих \(n\).
| |
![]()
|
|
Суммы модулей
Структуры данных
Вывод формулы
Комбинаторика
Для последовательности целых чисел \(a_1, a_2, \ldots, a_n\) и целого числа \(x\) обозначим через \(f(a, x)\) количество таких целых \(i\) от \(1\) до \(n\), что \(a_i \le x\).
Для пары последовательностей целых чисел \(a_1, a_2, \ldots, a_n\) и \(b_1, b_2, \ldots, b_n\) обозначим через \(g(a, b, c)\) сумму значений \(|f(a, x)-f(b, x)|\) по всем целым \(x\), лежащим в отрезке \([0, c]\). Более формально, \(g(a, b, c) = \sum_{x=0}^c |f(a, x)-f(b, x)|\).
Вам даны два целых числа \(n\) и \(c\), а также две последовательности целых чисел \(a_1, a_2, \ldots, a_n\) и \(b_1, b_2, \ldots, b_n\), все элементы которых лежат в отрезке \([-1, c]\). Известно, что ни в \(a\), ни в \(b\) нет двух подряд идущих элементов, равных \(-1\).
Скажем, что пара последовательностей целых чисел \(a_1', a_2', \ldots, a_n'\) и \(b_1', b_2', \ldots, b_n'\), все элементы которых лежат в отрезке \([0, c]\), соответствует шаблону \((a, b)\), если выполняются следующие условия:
-
Для всех \(i\) (\(1 \le i \le n\)), таких, что \(a_i \ne -1\), выполняется \(a_i'=a_i\).
-
Для всех \(i\) (\(1 \le i \le n\)), таких, что \(b_i \ne -1\), выполняется \(b_i'=b_i\).
-
Для всех \(i\) (\(1 \le i \le n-1\)) выполняется \(a_i' \le a_{i+1}'\).
-
Для всех \(i\) (\(1 \le i \le n-1\)) выполняется \(b_i' \le b_{i+1}'\).
Обозначим через \(h(a, b, c)\) сумму значений \(g(a', b', c)\) по всем парам последовательностей \((a', b')\), соответствующих шаблону \((a, b)\). Вы должны посчитать \(h(a, b, c)\). Также вы должны обработать \(q\) запросов изменения последовательностей \(a\) и \(b\) и посчитать \(h(a, b, c)\) после каждого изменения. Обратите внимание, что ни в \(a\), ни в \(b\) нет двух подряд идущих элементов, равных \(-1\), ни до всех запросов, ни после какого-либо запроса.
Формат входных данных
Первая строка содержит три целых числа \(n\), \(c\) и \(q\) (\(1 \le n \le 100\,000\), \(0 \le c \le 10^9\), \(0 \le q \le 100\,000\)) — длина последовательностей \(a\) и \(b\), ограничение на значения элементов \(a\) и \(b\) и количество запросов, соответственно.
Вторая строка содержит \(n\) целых чисел \(a_1, a_2, \ldots, a_n\) (\(-1 \le a_i \le c\)) — последовательность \(a\).
Третья строка содержит \(n\) целых чисел \(b_1, b_2, \ldots, b_n\) (\(-1 \le b_i \le c\)) — последовательность \(b\).
В следующих \(q\) строках заданы запросы изменения. Каждый запрос задается тройкой целых чисел \(t\), \(p\), \(x\) (\(1 \le t \le 2\), \(1 \le p \le n\), \(-1 \le x \le c\)). Если \(t=1\), то данный запрос меняет \(a_p\) на \(x\). Если \(t=2\), то данный запрос меняет \(b_p\) на \(x\).
Гарантируется, что до всех изменений и после каждого изменения ни в \(a\), ни в \(b\) нет двух подряд идущих элементов, равных \(-1\).
Формат выходных данных
Выведите \((q+1)\) строку. В \((i+1)\)-й строке (\(0 \le i \le q\)) выведите одно целое число — значение \(h(a, b, c)\) по модулю \(10^9+7\) после применения первых \(i\) запросов изменения.
Примечание
Рассмотрим первый тест из примера. В нем \(n=3\), \(c=4\), \(q=3\). До всех запросов \(a=[-1, 1, 3]\), \(b=[1, -1, 2]\). Шаблону \((a, b)\) соответствуют следующие пары последовательностей:
-
\(a'=[0, 1, 3], b'=[1, 1, 2]\), \(g(a, b, 4)=2\).
-
\(a'=[0, 1, 3], b'=[1, 2, 2]\), \(g(a, b, 4)=3\).
-
\(a'=[1, 1, 3], b'=[1, 1, 2]\), \(g(a, b, 4)=1\).
-
\(a'=[1, 1, 3], b'=[1, 2, 2]\), \(g(a, b, 4)=2\).
Таким образом, ответ на задачу до всех запросов равен \(h(a, b, 4)=2+3+1+2=8\).
В первом запросе \(t=1\), \(p=1\), \(x=2\). Этот запрос меняет \(a_1\) с \(-1\) на \(2\). Таким образом, после этого запроса \(a=[2, 1, 3]\), \(b=[1, -1, 2]\). В последовательности \(a\) нет \(-1\), поэтому в любой паре последовательностей \((a', b')\), соответствующей шаблону \((a, b)\), последовательность \(a'\) должна совпадать с \(a\). В последовательности \(a\) не выполняется условие \(a_1 \le a_2\), поэтому не существует ни одной пары последовательностей, соответствующей шаблону, а тогда \(h(a, b, 4)=0\) после первого запроса.
| |
![]()
|
|
D. Очередная задача на подпоследовательности
Комбинаторика
дп
*1900
Последовательность целых чисел \(a_1, a_2, \dots, a_k\) называется хорошим массивом, если \(a_1 = k - 1\) и \(a_1 > 0\). Например последовательности \([3, -1, 44, 0], [1, -99]\) — хорошие массивы, а последовательности \([3, 7, 8], [2, 5, 4, 1], [0]\) — нет. Последовательность целых чисел называется хорошей, если она состоит из положительного количества подряд идущих хороших массивов. Например последовательности \([2, -3, 0, 1, 4]\), \([1, 2, 3, -3, -9, 4]\) — хорошие, а последовательности \([2, -3, 0, 1]\), \([1, 2, 3, -3 -9, 4, 1]\) — нет. Для заданной последовательности чисел подсчитайте количество её подпоследовательностей, которые являются хорошими последовательностями, по модулю 998244353. Выходные данные В единственной строке выведите число — количество подпоследовательностей исходной последовательности, которые являются хорошими последовательностями, по модулю 998244353. Примечание В первом тестовом примере две хорошие подпоследовательности — \([a_1, a_2, a_3]\) и \([a_2, a_3]\). Во втором тестовом примере семь хороших подпоследовательностей — \([a_1, a_2, a_3, a_4], [a_1, a_2], [a_1, a_3], [a_1, a_4], [a_2, a_3], [a_2, a_4]\) и \([a_3, a_4]\). | |
![]()
|
|
A. Перестановка массива
Структуры данных
Комбинаторика
математика
сортировки
*1300
Дан массив целых чисел. Вася может переставлять его числа местами. При этом он хочет, чтобы как можно больше чисел стояли там, где раньше стояли меньшие числа. Помогите ему найти максимальное количество таких чисел. Например, если нам дан массив \([10, 20, 30, 40]\), мы можем переставить числа так, что массив станет \([20, 40, 10, 30]\). При этом на первой и второй позициях числа стали больше (\(20>10\), \(40>20\)), а на третьей и четвёртой — нет, значит для такой перестановки число, которое хочет максимизировать Вася, равно \(2\). Ознакомьтесь с примечанием к первому тестовому примеру, там разобран ещё один показательный тест. Помогите Васе так переставить числа, чтобы количество позиций, в которых в новом массиве числа больше, чем в изначальном, было максимальным. Выходные данные Выведите одно целое число — максимальное число элементов массива, которые после перестановки будут стоять на позициях, где изначально стоял меньший элемент. Примечание В первом тесте одна из оптимальных перестановок — \([1, 5, 5, 3, 10, 1, 1]\). На позициях со второй по пятую значения увеличились, значит ответ для этой перестановки — 4. Во втором тесте при любой перестановке ни на одной позиции элемент не может стать больше, значит, ответ — 0. | |
![]()
|
|
B. Замостите параллелепипед
Перебор
Комбинаторика
математика
теория чисел
*2400
битмаски
Вам дан прямоугольный параллелепипед с целыми положительными сторонами \(A\), \(B\) и \(C\). Найдите количество различных троек целых чисел (\(a\), \(b\), \(c\)) таких, что \(1\leq a\leq b\leq c\) и параллелепипед \(A\times B\times C\) можно замостить параллелепипедами \(a\times b\times c\). Обратите внимание, что все замощающие параллелепипеды должны быть ориентированы в одну сторону. Например, параллелепипед \(1\times 5\times 6\) можно разделить на параллелепипеды \(1\times 3\times 5\), но нельзя – на параллелепипеды \(1\times 2\times 3\). Выходные данные Для каждого теста выведите количество троек чисел, которые удовлетворяют всем условиям. Примечание В первом тесте параллелепипед со сторонами \((1, 1, 1)\) можно разделить только на параллелепипед со сторонами \((1, 1, 1)\). Во втором тесте параллелепипед со сторонами \((1, 6, 1)\) можно разделить на параллелепипеды со сторонами \((1, 1, 1)\), \((1, 1, 2)\), \((1, 1, 3)\) и \((1, 1, 6)\). В третьем тесте параллелепипед со сторонами \((2, 2, 2)\) можно разделить на параллелепипеды со сторонами \((1, 1, 1)\), \((1, 1, 2)\), \((1, 2, 2)\) и \((2, 2, 2)\). | |
![]()
|
|
E. Междугороднее путешествие
Теория вероятностей
Комбинаторика
математика
*2000
Леха собрался в путь из Москвы в Саратов. Он не любит ездить на поездах, поэтому решил отправиться из одного города в другой на машине. Путь из Москвы в Саратов может быть представлен, как прямая (пожалуй, она не столь ровная в действительности, но в данной задаче будем считать так), и расстояние между Москвой и Саратовом равно \(n\) км. Считаем, что Москва расположена в точке с координатой \(0\) км, а Саратов — в точке с координатой \(n\) км. Вести машину столь долгое время достаточно утомительно. Формально, если Леха преодолел \(i\) километров после того, как останавливался на отдых в прошлый раз, то сложностью преодоления \((i + 1)\)-го километра он считает величину \(a_{i + 1}\). Гарантируется, что для каждого \(i \in [1, n - 1]\) \(a_i \le a_{i + 1}\). Сложность пути определяется, как сумма сложностей по каждому километру пути. К счастью, между Москвой и Саратовом могут быть места для отдыха. Каждая целочисленная точка от \(1\) до \(n - 1\) может содержать место для отдыха. Когда Леха заезжает на место для отдыха, он (разумеется) отдыхает, и следующий километр для него становится сложности \(a_1\), километр после этого — сложности \(a_2\) и так далее. Например, если \(n = 5\) и есть место для отдыха в точке с координатой \(2\), то сложность пути получится \(2a_1 + 2a_2 + a_3\): первый километр будет иметь сложность \(a_1\), второй — \(a_2\), потом Леха отдохнет, и третий километр будет иметь сложность \(a_1\), четвертый — \(a_2\) и последний — \(a_3\). Другой пример: если \(n = 7\) и есть места для отдыха в точках с координатами \(1\) и \(5\), то сложность пути Лехи будет равна \(3a_1 + 2a_2 + a_3 + a_4\). Леха не знает, какие из целочисленных точек содержат места для отдыха. Поэтому он хочет предусмотреть любую возможную ситуацию. Очевидно, есть \(2^{n - 1}\) вариантов различных распределений точек отдыха (два распределения различны, когда существует такая точка \(x\), что место для отдыха есть ровно в одном из данных распределений). Леха считает все распределения равновероятными. Он хочет посчитать \(p\) — математическое ожидание сложности пути. Очевидно, \(p \cdot 2^{n - 1}\) — это целое число. Посчитайте его по модулю \(998244353\). Выходные данные Выведите одно число — \(p \cdot 2^{n - 1}\), взятое по модулю \(998244353\). | |
![]()
|
|
E. Противоположная раскраска
Комбинаторика
математика
*2100
дп
Дана квадратная доска, состоящая из \(n\) строк и \(n\) столбцов. Каждая клетка в ней должна быть раскрашена либо в белый, либо в черный цвет. Назовем некоторую раскраску красивой, если каждая пара соседних строк либо совпадает полностью, либо отличается в каждой позиции. Такое же условие накладывается и на столбцы. Назовем некоторую раскраску подходящей, если она красивая, и в ней нет ни одного прямоугольника одного цвета, состоящего не менее чем из \(k\) клеток. Ваша задача — подсчитать количество подходящих раскрасок доски заданного размера. Так как ответ может быть достаточно большим, выведите его по модулю \(998244353\). Выходные данные Выведите единственное целое число — количество подходящих раскрасок доски заданного размера по модулю \(998244353\). Примечание Доска размера \(1 \times 1\) — это либо единственная черная клетка, либо единственная белая клетка. Обе доски включают в себя прямоугольник одного цвета, состоящий из \(1\) клетки. Вот красивые раскраски доски размера \(2 \times 2\), которые не включают в себя прямоугольники одного цвета, состоящие не менее чем из \(3\) клеток:  Оставшиеся красивые раскраски доски \(2 \times 2\):  | |
![]()
|
|
D. Книга заявок
Структуры данных
Комбинаторика
*2100
жадные алгоритмы
Рассмотрим упрощенную версию книги заявок некоторой акции. Книга заявок — это список заявок (предложений) от людей, которые хотят купить или продать одну акцию, каждая заявка описывается направлением (BUY или SELL) и ценой. В каждый момент времени у любой SELL заявки цена больше, чем у любой BUY заявки. В этой задаче цены всех когда-либо существовавших заявок различны. Заявка с направлением SELL с наименьшей ценой и заявка с направлением BUY с наибольшей ценой называются лучшими предложениями и выделены черной рамкой на рисунке.  Данная книга заявок говорит, что кто-то хочет продать акцию по цене \(12\), и это лучшее предложение с направлением SELL, потому что у других двух заявок с этим направлением цена выше. У лучшего BUY предложения цена \(10\). Данная книга заявок говорит, что кто-то хочет продать акцию по цене \(12\), и это лучшее предложение с направлением SELL, потому что у других двух заявок с этим направлением цена выше. У лучшего BUY предложения цена \(10\). В книге заявок возможны два события: - Кто-то добавил новую заявку с некоторым направлением и некоторой ценой
- Кто-то принял лучшее SELL или BUY предложение (совершил сделку). Нельзя принять не лучшее предложение (совершать сделку по менее выгодной цене). После того, как лучшее предложение принято, оно навсегда удаляется из книги заявок.
Можно добавлять новые заявки BUY только с ценами ниже лучшего SELL предложения (если вы хотите купить по более высокой цене, то вместо постановки заявки нужно принять лучшее SELL предложение). Аналогично нельзя добавлять SELL заявки с ценами меньшими или равными лучшему предложению BUY. К примеру, нельзя добавить заявку "SELL \(20\)", если уже есть заявка "BUY \(20\)" или "BUY \(25\)" — в этом случае нужно просто принять лучшее предложение BUY. У вас есть поврежденный лог событий в книге заявок (в начале никаких заявок в книге нет). В логе есть события двух типов: - "ADD \(p\)" означает добавление новой заявки с ценой \(p\) и неизвестным направлением. Заявка не должна противоречить еще не удаленным заявкам в книге заявок.
- "ACCEPT \(p\)" означает принятие существующего лучшего предложения с ценой \(p\) и неизвестным направлением.
Направления всех заявок (BUY или SELL) в логе утеряны. Не всегда по имеющимся данным можно однозначно восстановить эти направления. Посчитайте количество способов корректно восстановить направления ADD заявок так, что описанные условия всегда выполнены. Ответ может быть очень большим, поэтому выведите его по модулю \(10^9 + 7\). Если невозможно корректно восстановить направления, то выведите \(0\). Выходные данные Выведите число способов восстановить направления всех заявок ADD по модулю \(10^9 + 7\). Примечание В первом примере каждая из заявок может быть и BUY, и SELL. Во втором примере заявка с ценой \(1\) должна иметь направление BUY, заявка с ценой \(3\) должна иметь направление SELL. | |
![]()
|
|
C. Разбиение на регионы
Деревья
Комбинаторика
дп
теория чисел
*2700
В королевстве Осени \(n\) городов, пронумерованных от \(1\) до \(n\). От любого города можно добраться до любого другого, используя некоторые из \(n-1\) дорог в королевстве. В этом году правительство приняло решение разбить королевство на регионы. После разбиения будут существовать регионы нескольких уровней, при этом само королевство будет являться регионом первого уровня. Любой регион уровня \(i\) должен быть разделен на несколько (хотя бы два) регионов уровня \(i+1\), если это не регион последнего уровня. Каждый город должен принадлежать ровно одному региону каждого уровня. Внутри одного региона, между любыми двумя городами в нем должен существовать путь, проходящий только по городам этого региона. Согласно исследованию, для каждого города \(i\) есть уровень важности — \(a_i\). Все регионы одного уровня должны иметь одинаковую сумму этих значений. Ваша задача состоит в том, чтобы узнать, сколько существует планов разбиения королевства на регионы, чтобы все условия выполнялись. Два плана считаются различными тогда и только тогда, когда количество уровней в них различно, или существует пара городов, которые для какого-то уровня находятся в одном регионе в одном плане, но в разных регионах того же уровня в другом. Поскольку ответ может быть очень большим, выведите его по модулю \(10^9+7\). Выходные данные Выведите одно число — количество различных планов по модулю \(10^9+7\). Примечание В первом примере существует \(4\) различных плана: План \(1\): Уровень \(1\): \(\{1,2,3,4\}\). План \(2\): Уровень \(1\): \(\{1,2,3,4\}\), Уровень \(2\): \(\{1,2\}\),\(\{3,4\}\). План \(3\): Уровень \(1\): \(\{1,2,3,4\}\), Уровень \(2\): \(\{1\}\),\(\{2\}\),\(\{3\}\),\(\{4\}\). План \(4\): Уровень \(1\): \(\{1,2,3,4\}\), Уровень \(2\): \(\{1,2\}\),\(\{3,4\}\), Уровень \(3\): \(\{1\}\),\(\{2\}\),\(\{3\}\),\(\{4\}\). Во втором примере существует \(2\) различных плана: План \(1\): Уровень \(1\): \(\{1,2,3,4\}\). План \(2\): Уровень \(1\): \(\{1,2,3,4\}\), Уровень \(2\): \(\{1\}\),\(\{2\}\),\(\{3\}\),\(\{4\}\). В третьем примере существует \(3\) различных плана: План \(1\): Уровень \(1\): \(\{1,2,3,4\}\). План \(2\): Уровень \(1\): \(\{1,2,3,4\}\), Уровень \(2\): \(\{1,2\}\),\(\{3,4\}\). План \(3\): Уровень \(1\): \(\{1,2,3,4\}\), Уровень \(2\): \(\{1,3\}\),\(\{2\}\),\(\{4\}\). | |
![]()
|
|
C. Шикарные числа
Комбинаторика
дп
*1900
Назовем некоторое положительное целое число шикарным, если в его десятичной записи встречается не более \(3\) ненулевых цифр. Например, числа \(4\), \(200000\), \(10203\) шикарные, а числа \(4231\), \(102306\), \(7277420000\) — нет. Задан отрезок \([L; R]\). Посчитайте количество таких шикарных чисел \(x\), что \(L \le x \le R\). В каждом тесте содержится несколько отрезков, для каждого из них необходимо решить задачу независимо. Выходные данные Выведите \(T\) строк — в \(i\)-й строке должно быть записано количество шикарных чисел на отрезке \([L_i; R_i]\). | |
![]()
|
|
F. Взаимно простые степени
Комбинаторика
математика
теория чисел
*2400
Рассмотрим некоторое положительное целое число \(x\). Его разложение на простые имеет вид \(x = 2^{k_1} \cdot 3^{k_2} \cdot 5^{k_3} \cdot \dots\) Назовем число \(x\) изящным, если наибольший общий делитель последовательности \(k_1, k_2, \dots\) равен \(1\). Например, числа \(5 = 5^1\), \(12 = 2^2 \cdot 3\), \(72 = 2^3 \cdot 3^2\) изящные, а числа \(8 = 2^3\) (\(GCD = 3\)), \(2500 = 2^2 \cdot 5^4\) (\(GCD = 2\)) — нет. Посчитайте количество изящных чисел от \(2\) до \(n\). В каждом тесте содержится несколько значений \(n\), для каждого из них необходимо решить задачу независимо. Выходные данные Выведите \(T\) строк — в \(i\)-й строке должно содержаться количество изящных чисел от \(2\) до \(n_i\). Примечание Приведен список не изящных чисел до \(10\): - \(4 = 2^2, GCD = 2\);
- \(8 = 2^3, GCD = 3\);
- \(9 = 3^2, GCD = 2\).
Для остальных \(GCD = 1\). | |
![]()
|
|
F. Максимальное упрощение
Структуры данных
Комбинаторика
математика
*2500
Вам дан массив \(a\) из \(n\) целых чисел и целое число \(k\) (\(2 \le k \le n\)), где элементы массива обозначаются как \(a_i\) (\(0 \le i < n\)). Выполните операцию \(z\) определённую ниже над \(a\) и выведите значение \(z(a,k)\) по модулю \(10^{9}+7\).
function z(array a, integer k):
if length(a) < k:
return 0
else:
b = empty array
ans = 0
for i = 0 .. (length(a) - k):
temp = a[i]
for j = i .. (i + k - 1):
temp = max(temp, a[j])
append temp to the end of b
ans = ans + temp
return ans + z(b, k)
Выходные данные Выведите одно целое число — значение \(z(a,k)\) взятое по модулю \(10^9+7\). Примечание В первом примере: - для \(a=(9,1,10)\), \(ans=19\) и \(b=(9,10)\),
- для \(a=(9,10)\), \(ans=10\) и \(b=(10)\),
- для \(a=(10)\), \(ans=0\).
Значит, ответ равен \(19+10+0=29\). Во втором примере: - для \(a=(5,8,7,1,9)\), \(ans=25\) и \(b=(8,8,9)\),
- для \(a=(8,8,9)\), \(ans=9\) и \(b=(9)\),
- для \(a=(9)\), \(ans=0\).
Значит, ответ равен \(25+9+0=34\). | |
![]()
|
|
D. Загадочное преступление
Перебор
Комбинаторика
математика
*1700
meet-in-the-middle
Ацингел — достаточно маленький городок. В этом городке был всего один доктор — Мисс Ада. Она была очень дружелюбной и никто никогда не говорил про неё ничего плохого. Так что кто мог подумать, что Аду найдут мёртвой в собственном доме? Мистер Гаври, известный во всём мире детектив, был назначен найти преступника. Он опросил \(m\) соседей Ады о клиентах, которые посетили её в тот злосчастный день. Давайте пронумеруем этих клиентов от \(1\) до \(n\). Свидетельством каждого соседа является перестановка этих чисел, которая описывает порядок, в котором этот сосед видел клиентов приходящими к Аде. Однако некоторые факты выглядят достаточно подозрительно — как могло быть, что, согласно некоторым перестановкам некоторые клиенты были замечены утром, а согласно другим — вечером? «Утром некоторые из соседей скорее всего спали! — подумал Гаври, — А вечером слишком темно, чтобы видеть лица людей...». Теперь он хочет удалить из каждой перестановки некоторый префикс и некоторый суффикс (возможно, пустые) так, что оставшиеся части будут не пусты и равны друг другу. Возможно, часть потенциальных преступников пропадёт, но хотя бы не будет противоречий в свидетельствах соседей. Сколькими способами он может это сделать? Два способа называются разными, если в них отличается оставшаяся общая часть. Выходные данные Выведите одно целое число — количество способов удалить из каждой перестановки некоторый префикс и суффикс (возможно, пустые) так, что оставшаяся часть была бы равной и непустой. Примечание В первом примере общей частью может быть \([1]\), \([2]\), \([3]\) и \([2, 3]\). Во втором и третьем примерах можно оставлять только общие части из \(1\) элемента. | |
![]()
|
|
F. Сделай единицу
Комбинаторика
математика
дп
теория чисел
кратчайшие пути
битмаски
*2500
Януш — бизнесмен. Он владеет компанией «Янушзекс», которая производит игры для школьников. Последним хитом Янушзекс является крутая игра для одного человека «Сделай единицу». Игроку дана последовательность из \(n\) целых чисел \(a_i\). Разрешается выбрать любое подмножество из них и количество очков равно наибольшему общему делителю выбранных чисел. Игроку нужно выбрать наименьшее количество элементов, получив количество очков, равное \(1\). Теперь Януш интересуется, какое минимальное количество элементов нужно выбрать игроку в таком случае? Выходные данные Если нет ни одного подмножества данной последовательности с наибольшим общим делителем равным \(1\), то выведите -1. Иначе выведите ровно одно целое число — размер минимального множества с наибольшим общим делителем равным \(1\). Примечание В первом примере подмножество, соответствующее всей последовательности даёт наибольший общий делитель равный \(1\). Все меньшие подмножества дают наибольший общий делитель больший \(1\). Во втором примере наибольший общий делитель любого подмножества хотя бы \(2\). | |
![]()
|
|
F. Сжимающееся дерево
Комбинаторика
дп
*2900
Рассмотрим дерево \(T\) (связный неориентированный граф без циклов) с \(n\) вершинами, пронумерованными целыми числами от \(1\) до \(n\). Запустим следующий процесс на \(T\): пока в \(T\) более одной вершины, делать следующее: - равновероятно выбрать случайное ребро \(T\);
- стянуть выбранное ребро: если ребро соединяло вершины \(v\) и \(u\), удалить и \(v\), и \(u\), и создать новую вершину, смежную со всеми вершинами, которые до этого были смежны или с \(v\), или с \(u\). Новая вершина равновероятно получает номер или \(v\), или \(u\).
Когда процесс завершится, \(T\) будет состоять из одной вершины, с номером из \(1, \ldots, n\). Найдите для каждого числа вероятность, что это число окажется номером финальной вершины. Выходные данные Выведите \(n\) вещественных чисел — описанные вероятности для номеров \(1, \ldots, n\), соответственно. Все числа должны быть правильными с точностью до абсолютной или относительной погрешности \(10^{-6}\). Примечание В первом примере, получившаяся вершина будет иметь номер 1 тогда и только тогда, когда для всех ребер вершина 1 выживет, соответственно вероятность равна \(1/2^3 = 1/8\). Все остальные числа имеют равную вероятность из-за симметрии, таким образом, каждое из них имеет вероятность \((1 - 1/8) / 3 = 7/24\). | |
![]()
|
|
E. Преобразования краев
Строки
Комбинаторика
*2300
Рассмотрим некоторое множество различных символов \(A\) и некоторую строку \(S\), состоящую ровно из \(n\) символов, где каждый символ присутствует в \(A\). Задан массив \(b\) из \(m\) целых чисел (\(b_1 < b_2 < \dots < b_m\)). Разрешено проводить следующую операцию над строкой \(S\): - Выбрать некоторый корректный \(i\) и выставить \(k = b_i\);
- Взять первые \(k\) символов \(S = Pr_k\);
- Взять последние \(k\) символов \(S = Su_k\);
- Заменить первые \(k\) символов \(S\) развернутой \(Su_k\);
- Заменить последние \(k\) символов \(S\) развернутой \(Pr_k\).
Например, рассмотрим строку \(S =\) «abcdefghi» и \(k = 2\). \(Pr_2 =\) «ab», \(Su_2 =\) «hi». Развернутые \(Pr_2 =\) «ba», \(Su_2 =\) «ih». Следовательно, полученная \(S\) равна «ihcdefgba». Данная операция может быть проведена произвольное количество раз (возможно, ноль). Любой \(i\) может быть выбран несколько раз в ходе проведения операций. Назовем строки \(S\) и \(T\) равными тогда и только тогда, когда существует такая последовательность операций, которая преобразовывает строку \(S\) в строку \(T\). Для приведенного выше примера «abcdefghi» и «ihcdefgba» равны. Обратите внимание, что это подразумевает и \(S = S\). Задача проста. Посчитайте количество различных строк. Ответ может быть достаточно велик, поэтому посчитайте его по модулю \(998244353\). Выходные данные Выведите единственное целое число — количество различных строк длины \(n\) с символами из множества \(A\) по модулю \(998244353\). Примечание Приведены все различные строки для первого примера. Выбранные буквы 'a' и 'b' только чтобы показать, что символы в \(A\) различны. - «aaa»
- «aab» = «baa»
- «aba»
- «abb» = «bba»
- «bab»
- «bbb»
| |
![]()
|
|
B. Баскетбольная команда
Теория вероятностей
Комбинаторика
математика
*1600
дп
Мистер Вафа учится в German University in Cairo (GUC) и любит играть в баскетбол. Он был приятно удивлен, когда узнал, что GUC планирует принять участие в Ежегодном Соревновании по Баскетболу (Annual Basketball Competition, ABC). Для соревнования будет собрана команда из n игроков — студентов GUC. Игроки будут случайным образом выбраны среди студентов играющих в баскетбол. Однако, в команде могут быть игроки с разных факультетов. Всего в GUC m факультетов, пронумерованных числами от 1 до m. Мистер Вафа учится на факультете номер h. Для каждого факультета i Мистер Вафа знает число si — сколько студентов с него играют в баскетбол, и соответственно могут оказаться членами команды GUC. Благодаря своим паранормальным способностям, Мистер Вафа знает, что он точно попадет в команду GUC. Теперь он хочет вычислить вероятность того, что вместе с ним в команде окажется хотя бы один студент с его факультета. Так как он очень не любит вычисления с дробными числами, эта задача поручается вам. Учтите, что все составы команды, в которых есть Мистер Вафа, могут быть выбраны с равной вероятностью. Считайте, что все студенты отличаются друг от друга. Выходные данные Выведите вероятность того, что кроме Мистера Вафы в команде GUC будет хотя бы один студент с его факультета. Если в GUC не хватит игроков чтобы выставить команду на ABC, выведите -1. Ответ считается верным, если абсолютная или относительная погрешность не превосходит 10 - 6. Примечание В первом примере все три игрока в баскетбол — два с факультета 1 и один с факультета 2 — будут членами команды GUC. Так как оба игрока с первого факультета будут членами команды, у Вафы гарантированно будет партнер по команде с его факультета. Во втором примере в GUC недостаточно игроков для того, чтобы выставить команду на ABC. В третьем примере команда, в состав которой входит Мистер Вафа, может быть составлена тремя способами, два состава из этих трех включают в себя второго игрока с факультета Мистера Вафы. | |
![]()
|
|
E. Сумма на отрезке
Комбинаторика
математика
дп
*2300
битмаски
Задано два целых числа \(l\) и \(r\) (\(l \le r\)). Ваша задача — посчитать сумму чисел от \(l\) до \(r\) (включая \(l\) и \(r\)) таких, что каждое число содержит не более \(k\) различных цифр, и вывести эту сумму по модулю \(998244353\). Например, если \(k = 1\), тогда вам необходимо посчитать все числа от \(l\) до \(r\) такие, что каждое число содержит только одинаковые цифры. Для \(l = 10, r = 50\) ответ равен \(11 + 22 + 33 + 44 = 110\). Выходные данные Выведите одно целое число — сумму чисел от \(l\) до \(r\) таких, что каждое число содержит не более \(k\) различных цифр, по модулю \(998244353\). Примечание В первом тестовом примере ответом является сумма чисел от \(l\) до \(r\), которая равна \(\frac{50 \cdot 51}{2} - \frac{9 \cdot 10}{2} = 1230\). Этот пример также разобран в условии задачи, но для \(k = 1\). Во втором тестовом примере ответом является просто сумма чисел от \(l\) до \(r\), которая равна \(\frac{2345 \cdot 2346}{2} = 2750685\). В третьем тестовом примере ответ равен \(101 + 110 + 111 + 112 + 113 + 114 + 115 + 116 + 117 + 118 + 119 + 121 + 122 + 131 + 133 + 141 + 144 + 151 = 2189\). | |
![]()
|
|
C. Цветные кирпичики
Комбинаторика
математика
дп
*1500
В свободное время Chouti любит выполнять работу по дому. У него есть одно новое задание — покрасить кирпичи во дворе. На земле выложен ряд из \(n\) кирпичей. У Chouti есть под рукой \(m\) ведер с красками разных цветов, поэтому он покрасил каждый кирпич в один из этих \(m\) цветов. Закончив красить все кирпичи, Chouti был доволен. Он решил узнать что-нибудь про эти кирпичики. После некоторых подсчетов он обнаружил, что существует ровно \(k\) кирпичей, у которых цвет отличается от цвета кирпича слева (конечно, мы не рассматриваем первый кирпич). Поэтому, как обычно, ему нужна ваша помощь в подсчёте количества способов так раскрасить кирпичи. Два способа покраски кирпичей различны, если хотя бы у одного кирпича отличаются цвета в этих двух способах. Поскольку ответ может быть довольно большим, вам нужно вывести его по модулю \(998\,244\,353\). Выходные данные Выведите одно целое число — количество способов покрасить кирпичи по модулю \(998\,244\,353\). Примечание В первом примере, так как \(k=0\), цвета всех кирпичей должны быть одинаковыми, поэтому есть ровно \(m=3\) способа покрасить кирпичи. Во втором примере, предположим в ведре находятся желтый и лаймовый цвета, на следующей картинке расположены все \(4\) раскраски.  | |
![]()
|
|
C. Орехус и строка
Комбинаторика
реализация
дп
*1500
Орехус нашел строку \(s\), состоящую из латинских букв нижнего регистра. Орехус любознательный парень, поэтому ему стал интересен следующий вопрос: сколько существует строго возрастающих последовательностей \(p_1, p_2, \ldots, p_k\) таких, что: - Для каждого \(i\) (\(1 \leq i \leq k\)), \(s_{p_i} =\) 'a'.
- Для каждого \(i\) (\(1 \leq i < k\)), существует \(j\), что \(p_i < j < p_{i + 1}\) и \(s_j =\) 'b'.
Удовлетворите любопытство Орехуса, или он расстроится. Это число должно быть посчитано по модулю \(10^9 + 7\). Выходные данные В единственной строке выведите ответ — число искомых последовательностей \(p_1, p_2, \ldots, p_k\) по модулю \(10^9 + 7\). Примечание В первом примере \(5\) допустимых последовательностей. \([1]\), \([4]\), \([5]\), \([1, 4]\), \([1, 5]\). Во втором примере \(4\) допустимых последовательности. \([2]\), \([3]\), \([4]\), \([5]\). В третьем примере \(3\) допустимых последовательности. \([1]\), \([3]\), \([4]\). | |
![]()
|
|
G. Красивая раскраска
Структуры данных
Комбинаторика
дп
*2900
Петя является коллекционером красивых матриц. Матрица размера \(n \times n\) является красивой, если: - Все элементы матрицы являются целыми числами от \(1\) до \(n\);
- В строке все элементы различные;
- В столбце нет двух соседних одинаковых элементов.
Сегодня Петя купил красивую матрицу \(a\) размера \(n \times n\) и хочет определить ее редкость. Редкость матрицы определяется, как ее номер в списке всех красивых матриц размера \(n \times n\), отсортированных в лексикографическом порядке. Сравнение матриц происходит построчно. (Нумерация начинается с нуля). Так как красивых матриц очень много, то Пете будет достаточно узнать редкость матрицы \(a\) по модулю \(998\,244\,353\). Выходные данные Выведите одно целое число — редкость матрицы \(a\) по модулю \(998\,244\,353\). Примечание Для матриц размера \(2 \times 2\) существует всего \(2\) красивые матрицы: 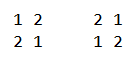 Красивых матриц \(3 \times 3\) довольно много, вот первые \(5\) в лексикографическом порядке:  | |
![]()
|
|
D. Новый год и конкатенация перестановок
Комбинаторика
математика
дп
*1700
Пусть \(n\) — целое число. Рассмотрим все перестановки целых чисел от \(1\) до \(n\) в лексикографическом порядке. Объедините их в одну большую последовательность \(p\). Например, если \(n = 3\), то \(p = [1, 2, 3, 1, 3, 2, 2, 1, 3, 2, 3, 1, 3, 1, 2, 3, 2, 1]\). Длина этой последовательности будет \(n \cdot n!\). Пусть \(1 \leq i \leq j \leq n \cdot n!\) — пара индексов. Мы называем последовательность \((p_i, p_{i+1}, \dots, p_{j-1}, p_j)\) подотрезком \(p\). Его длина определяется как количество элементов, то есть \(j - i + 1\). Его сумма определяется как сумма всех его элементов, то есть \(\sum_{k=i}^j p_k\). Дано \(n\). Найдите количество подотрезков \(p\) длины \(n\), имеющих сумму \(\frac{n(n+1)}{2}\). Поскольку это число может быть большим, выведите его по модулю \(998244353\) (простое число). Выходные данные Выведите одно число — количество подотрезков длины \(n\), в которых сумма равна \(\frac{n(n+1)}{2}\), по модулю \(998244353\). Примечание В первом примере есть \(16\) подотрезков длины \(3\). В порядке появления это: \([1, 2, 3]\), \([2, 3, 1]\), \([3, 1, 3]\), \([1, 3, 2]\), \([3, 2, 2]\), \([2, 2, 1]\), \([2, 1, 3]\), \([1, 3, 2]\), \([3, 2, 3]\), \([2, 3, 1]\), \([3, 1, 3]\), \([1, 3, 1]\), \([3, 1, 2]\), \([1, 2, 3]\), \([2, 3, 2]\), \([3, 2, 1]\). Их суммы равны \(6\), \(6\), \(7\), \(6\), \(7\), \(5\), \(6\), \(6\), \(8\), \(6\), \(7\), \(5\), \(6\), \(6\), \(7\), \(6\). Поскольку \(\frac{n(n+1)}{2} = 6\), то ответ — \(9\). | |
![]()
|
|
B. Удаление подстроки
Строки
Комбинаторика
математика
*1300
Задана строка \(s\) длины \(n\), состоящая только из строчных букв латинского алфавита. Подстрока строки — это последовательная подпоследовательность этой строки. Таким образом, строка «forces» является подстрокой «codeforces», а строка «coder» — нет. Ваша задача — посчитать количество способов удалить ровно одну подстроку из этой строки таким образом, чтобы все оставшиеся символы были равны между собой (количество различных символов было равно единице или нулю). Гарантируется, что в строке \(s\) существует хотя бы два различных символа. Заметьте, что вы можете удалить всю строку и это является корректным способом. Также заметьте, что вам необходимо удалить хотя бы один символ. Так как ответ может быть довольно большим (хотя не очень большим), выведите его по модулю \(998244353\). Если вы программируете на Python, рассмотрите возможность отправки решения на PyPy, а не на Python, когда будете отправлять свой код. Выходные данные Выведите одно целое число — количество способов по модулю \(998244353\) удалить ровно одну подстроку из \(s\) таким образом, чтобы все оставшиеся символы были равны. Примечание Пусть \(s[l; r]\) — подстрока строки \(s\) с позиции \(l\) по позицию \(r\) включительно. Тогда в первом тестовом примере вы можете удалить следующие подстроки: - \(s[1; 2]\);
- \(s[1; 3]\);
- \(s[1; 4]\);
- \(s[2; 2]\);
- \(s[2; 3]\);
- \(s[2; 4]\).
Во втором тестовом примере вы можете удалить следующие подстроки: - \(s[1; 4]\);
- \(s[1; 5]\);
- \(s[1; 6]\);
- \(s[1; 7]\);
- \(s[2; 7]\);
- \(s[3; 7]\).
В третьем тестовом примере вы можете удалить следующие подстроки: - \(s[1; 1]\);
- \(s[1; 2]\);
- \(s[2; 2]\).
| |
![]()
|
|
E. Супер-Бомбардир
Теория вероятностей
Комбинаторика
математика
дп
*2500
Хасан любит различные игры, и недавно его заинтересовала игра под названием Супер-Бомбардир. В этой игре (которая довольно похожа на футбол) \(p\) игроков бьют пенальти. Победитель — это тот игрок, который забил наибольшее число голов. В случае ничьи, один из игроков, забивших наибольшее число голов, объявляется победителем равновероятно. Игроки только закончили матч, и теперь ожидают результата. Однако закралась небольшая проблема! Судьи потеряли таблицу с счетом всех игроков! К счастью, до потери они успели посчитать сумму забитых голов, а также для каждого игрока они запомнили нижнюю границу на количество забитых им голов. Однако информация об этих границах конфиденциальна, поэтому Хасан смог узнать только свою нижнюю границу. Согласно предоставленной информации, он знает, что его счет не меньше \(r\), а сумма счета всех игроков — \(s\). Поэтому финальное состояние игры может быть записано в виде последовательности \(p\) целых чисел \(a_1, a_2, \dots, a_p\) (\(0 \le a_i\)) — счет игроков. Хасан — игрок номер \(1\), поэтому \(a_1 \ge r\). К тому же \(a_1 + a_2 + \dots + a_p = s\). Два состояния считаются различными, если существует такая позиция \(i\), что значение \(a_i\) различается в этих двух состояниях. Еще раз, Хасан не знает точного счета игроков (он не знает и свой точный счет). Поэтому он считает, что вероятность получить любое финальное состояние игры одинакова. Помогите Хасану найти вероятность его победы. Можно показать, что она может быть представлена в форме \(\frac{P}{Q}\), где \(P\) и \(Q\) — неотрицательные целые числа и \(Q \ne 0\), \(P \le Q\). Сообщите значение \(P \cdot Q^{-1} \pmod {998244353}\). Выходные данные Выведите единственное число — вероятность победы Хасана. Можно показать, что она может быть представлена в форме \(\frac{P}{Q}\), где \(P\) и \(Q\) — неотрицательные целые числа и \(Q \ne 0\), \(P \le Q\). Сообщите значение \(P \cdot Q^{-1} \pmod {998244353}\). Примечание В первом примере Хасан мог забить \(3\), \(4\), \(5\) или \(6\) голов. Если он забил \(4\) гола или больше, то его счет будет строго больше счета единственного соперника. Если он забил \(3\), то и его соперник забил \(3\), и вероятность победы Хасана равна \(\frac 1 2\). Следовательно, итоговая вероятность победы Хасана равна \(\frac 7 8\). Во втором примере даже нижняя граница на счет Хасана подразумевает, что он забил больше, чем любой из его соперников. Следовательно, итоговая вероятность победы Хасана равна \(1\). | |
![]()
|
|
F. Алексей и телешоу
Комбинаторика
теория чисел
битмаски
*2500
Алексей решил попытать счастья в телешоу. Однажды он сходил на викторину. После того, как он идеально ответил на вопросы «Как обычно называют псевдоним в интернете?» («Ум... может быть ник?»), «В честь какого известного изобретателя назвали единицу силы магнитного поля?» («Ум... Никола Тесла?»), он решил посетить гораздо более сложное телешоу: «Что в этом мультимножестве?!». Это телешоу устроено следующим образом: есть \(n\) мультимножеств, пронумерованных от \(1\) до \(n\). Каждое из них изначально пусто. Затем, происходят \(q\) запросов, где каждый запрос имеет один из четырёх следующих типов: - 1 x v — присвоить \(x\)-му мультимножеству мультимножество из одного элемента \(\{v\}\).
- 2 x y z — присвоить \(x\)-му мультимножеству объединение мультимножеств \(y\) и \(z\). For example: \(\{1, 3\}\cup\{1, 4, 4\}=\{1, 1, 3, 4, 4\}\).
- 3 x y z — присвоить \(x\)-му мультимножеству произведение \(y\)-го и \(z\)-го мультимножества. Произведение \(A \times B\) мультимножеств \(A\) и \(B\) определяется как \(\{ \gcd(a, b)\, \mid\, a \in A,\, b \in B \}\), где \(\gcd(p, q)\) обозначает наибольший общий делитель \(p\) и \(q\). Например, \(\{2, 2, 3\} \times \{1, 4, 6\}=\{1, 2, 2, 1, 2, 2, 1, 1, 3\}\).
- 4 x v — вас спрашивают, сколько раз число \(v\) встречается в мультимножестве \(x\). Так как викторина показал себя достаточно сложной в прошлом, то теперь нужно лишь сказать ответ на этот вопрос по модулю \(2\).
Обратите внимание, что \(x\), \(y\), и \(z\) в описании выше не обязательно различны. Для запросов \(2\)-го и \(3\)-го типа нужно сначала вычислить соответствующую сумму или произведение и лишь затем выполнить присвоение. Алексея смущают запутанные правила шоу. Помогите ему узнать ответы на все запросы \(4\)-го типа. Выходные данные Выведите строку из \(0\) и \(1\), имеющую длину равную количеству запросов \(4\)-го типа, \(i\)-й символ строки должен быть равен ответу на \(i\)-й запрос \(4\)-го типа. Примечание Мультимножества в тесте из примера выглядят следующим образом (\(i\) обозначает количество уже обработанных запросов). 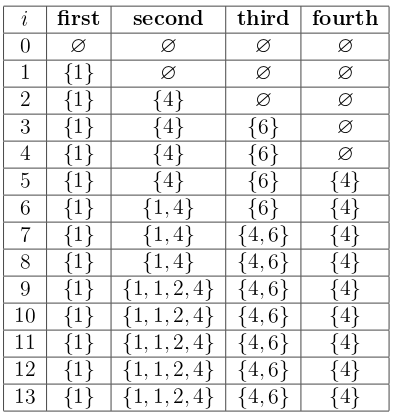
| |
![]()
|
|
G. Владислав и великая легенда
Деревья
Комбинаторика
дп
*3000
Однажды здесь была великая легенда, но один тролль взломал Codeforces и удалил его. Очень плохо для наc, но в сообществе троллей он заработал уважение и титул овер-супер-мега тролля. Пожалуй для них это что-то хорошее. А для нас, наверное, ещё лучше будет формальное условие. Вам дано дерево \(T\), содержащее \(n\) вершин, пронумерованных от \(1\) до \(n\). Для каждого непустого \(X\), являющемся подмножеством вершин \(T\), определим \(f(X)\) как количество рёбер в минимальном по размеру поддереве \(T\), содержащем все вершины из \(X\). Вам также дано целое число \(k\). Вам нужно вычислить сумму \((f(X))^k\) по всем непустым подмножествам вершин, то есть: \(\) \sum\limits_{X \subseteq \{1, 2,\: \dots \:, n\},\, X \neq \varnothing} (f(X))^k. \(\) Так как эта величина может быть очень большой, выведите её по модулю \(10^9 + 7\). Выходные данные Выведите одно целое число — требуемую сумму по модулю \(10^9 + 7\). Примечание В первых двух примерах значения \(f\) выглядят следующим образом: \(f(\{1\}) = 0\) \(f(\{2\}) = 0\) \(f(\{1, 2\}) = 1\) \(f(\{3\}) = 0\) \(f(\{1, 3\}) = 2\) \(f(\{2, 3\}) = 1\) \(f(\{1, 2, 3\}) = 2\) \(f(\{4\}) = 0\) \(f(\{1, 4\}) = 2\) \(f(\{2, 4\}) = 1\) \(f(\{1, 2, 4\}) = 2\) \(f(\{3, 4\}) = 2\) \(f(\{1, 3, 4\}) = 3\) \(f(\{2, 3, 4\}) = 2\) \(f(\{1, 2, 3, 4\}) = 3\) | |
![]()
|
|
E. Монотонная перенумерация
Комбинаторика
сортировки
*1700
Дан массив \(a\), состоящий из \(n\) целых чисел. Назовем монотонной перенумерацией массива \(a\) такой массив \(b\), состоящий из \(n\) целых чисел, что выполняются все следующие условия: - \(b_1 = 0\);
- для каждой пары индексов \(i\) и \(j\), такой, что \(1 \le i, j \le n\), если \(a_i = a_j\), то \(b_i = b_j\) (обратите внимание: если \(a_i \ne a_j\), все равно возможно \(b_i = b_j\));
- для каждого индекса \(i \in [1, n - 1]\) либо \(b_i = b_{i + 1}\), либо \(b_i + 1 = b_{i + 1}\).
Например, если \(a = [1, 2, 1, 2, 3]\), то две монотонные перенумерации \(a\) — следующие: \(b = [0, 0, 0, 0, 0]\) и \(b = [0, 0, 0, 0, 1]\). Посчитайте количество различных монотонных перенумераций \(a\). Ответ может быть большим, поэтому выведите его остаток от деления на \(998244353\). Выходные данные Выведите одно целое число — количество монотонных перенумераций \(a\) по модулю \(998244353\). | |
![]()
|
|
C. Аюб и утерянный массив
Комбинаторика
математика
дп
*1500
У Аюба был массив целых чисел \(a\) длины \(n\) и у этого массива было два необычных свойства: - Все целые числа в этом массиве были от \(l\) до \(r\) (включительно).
- Сумма всех элементов в массиве делилась на \(3\).
К сожалению, Аюб потерял свой массив, но он помнит размер массива \(n\), а также числа \(l\) и \(r\), так что он попросил вас посчитать количество способов восстановить массив по этим данным. Так как ответ может быть очень большим, выведите его по модулю \(10^9 + 7\) (то есть остаток при делении на \(10^9 + 7\)). В случае если не существует ни одного подходящего массива (Аюб что-то перепутал) — выведите \(0\). Выходные данные Выведите остаток при делении на \(10^9 + 7\) количества способов восстановить массив. Примечание В первом примере возможны массивы \([1,2], [2,1], [3, 3]\). Во втором примере единственный возможный массив — \([2, 2, 2]\). | |
![]()
|
|
D. Саша и интересный факт из теории графов
Деревья
Перебор
Комбинаторика
математика
дп
*2400
Однажды, во время пары Саше стало скучно и он решил поговорить со своими друзьями. Тут он увидел Кефу. О Кефе можно говорить бесконечно, поэтому делать мы этого не будем. Разговор ребят зашёл о графах. Кефа пообещал рассказать Саше один интересный факт из теории графов, если тот, в свою очередь, поможет Кефе посчитать количество красивых деревьев. В данной задаче деревом называется взвешенный связный граф, состоящий из \(n\) вершин и \(n-1\)-го ребра, такой, что веса всех рёбер — целые числа от \(1\) до \(m\). Красоту дерева Кефа оценивает следующим образом: он находит в дереве две свои любимые врешины — вершины с номерами \(a\) и \(b\), и считает расстояние между ними. Расстоянием между двумя вершинами \(x\) и \(y\) назовём сумму весов всех рёбер на простом пути из \(x\) в \(y\). Если расстояние от вершины \(a\) до вершины \(b\) равно \(m\), то дерево красивое. Саша очень любит теорию графов, а ещё больше Саша любит интересные факты, поэтому Саша согласился помочь. К счастью, Саша знаком с вами, лучшим программистом Байтландии. Помогите Саше посчитать количество красивых деревьев для Кефы. Два дерева считаются различными, если существует хотя бы одно ребро, принадлежащее одному из этих деревьев и не принадлежащее другому. Вес ребра имеет значение. Кефа предупредил Сашу, что красивых деревьев очень много, поэтому достаточно будет вычислить их количество по модулю \(10^9 + 7\). Выходные данные Выведите одно число — количество красивых деревьев по модулю \(10^9+7\). Примечание В первом примере существует \(5\) красивых деревьев: 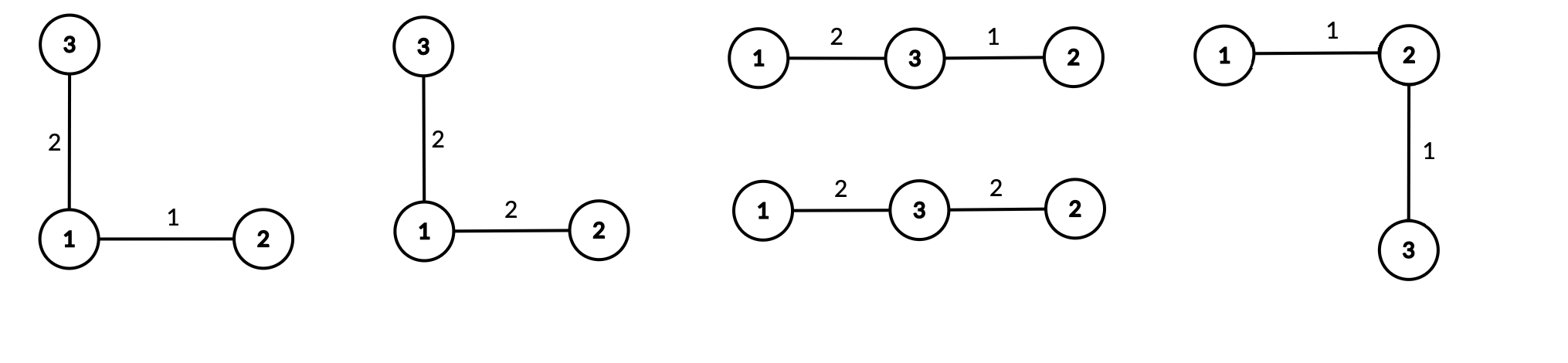
Во втором примере красивыми являются следующие деревья: 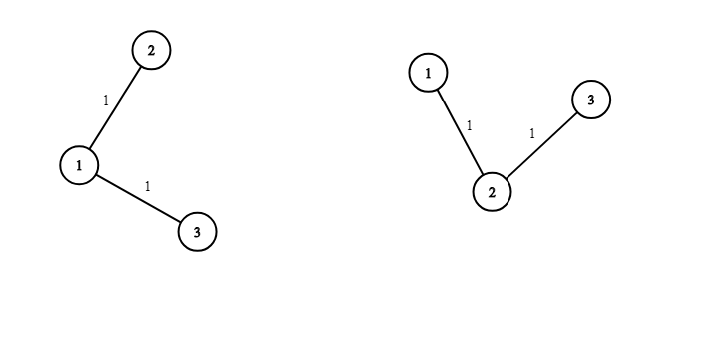
| |
![]()
|
|
D. Петя и раскраски
Комбинаторика
дп
*2300
Маленький Петя любит считать. Он хочет посчитать, сколько существует способов раскрасить прямоугольную клетчатую доску размера n × m (n строк, m столбцов) в k цветов. При этом раскраска должна обладать следующим свойством: для любой вертикальной прямой, проходящей по линиям сетки и делящей доску на две непустые части, количество различных цветов в обеих этих частях должно быть одинаковым. Помогите Пете посчитать количество таких раскрасок. Выходные данные Выведите ответ на задачу. Так как ответ может быть достаточно большим, нужно вывести его по модулю 109 + 7 (1000000007). | |
![]()
|
|
D. Уничтожить поселение
Комбинаторика
математика
дп
*2600
Поселение злодеев представляет из себя несколько логов, расположенных в линию. В каждом логове живет ровно один злодей. Каждое поселение можно представить как строку четной длины, где \(i\)-й символ строки определяет тип злодея, живущего в \(i\)-м логове. Железный человек может уничтожить поселение, если только все злодеи каждого типа живут либо только в первой половине поселения, либо только во второй половине. У его помощника Джарвиса есть суперспособность. Он может поменять местами жителей любых двух логов, иным словами, поменять местами любые две буквы строки. Он может выполнить эту операцию любое число раз. Железный человек задает Джарвису \(q\) вопросов. В каждом вопросе он дает Джарвису два номера \(x\) и \(y\). Джарвис должен ответить, сколько различных вариантов поселения он может сделать из исходного таких, что все злодеи, тип которых совпадает с типом злодея, находящегося изначально в \(x\)-м или \(y\)-м логове, живут в одной и той же половине, и Железный человек может уничтожить это поселение. Два варианта поселения считаются различными, если существует логово, в которых живут злодеи различного типа в этих двух вариантах. Выходные данные Для каждого вопроса выведите остаток от деления количества вариантов поселений на \(10^9+7\). Примечание Рассмотрим первый пример. В первом вопросе возможные варианты поселения это «aabb» и «bbaa». Во втором вопросе логово \(1\) содержит злодея типа «a», а логово \(2\) содержит злодея типа «b», и не существует варианта поселения, где все «a» и «b» находятся в одной половине. | |
![]()
|
|
F2. Разрезание дерева (сложная версия)
Деревья
Комбинаторика
дп
поиск в глубину и подобное
*2700
Задано неориентированное дерево из \(n\) вершин. Некоторые вершины покрашены в один из \(k\) цветов, а некоторые не покрашены совсем. Гарантируется, что дерево содержит хотя бы одну вершину каждого из \(k\) цветов. Может быть ноль непокрашенных вершин. Вы выбираете набор из ровно \(k - 1\) ребер и удаляете его из дерева. Дерево распадается на \(k\) связных компонент. Назовем набор хорошим, если ни в одной из полученных компонент не будет вершин различных цветов. Сколько хороших наборов ребер есть в данном дереве? Два набора считаются различными, если существует такое ребро, что оно присутствует в одном наборе и отсутствует в другом. Ответ может быть довольно большим, поэтому выведите его по модулю \(998244353\). Выходные данные Выведите одно целое число — количество хороших наборов ребер в данном дереве. Два набора считаются различными, если существует такое ребро, что оно присутствует в одном наборе и отсутствует в другом. Ответ может быть довольно большим, поэтому выведите его по модулю \(998244353\). Примечание Дерево из первого примера: 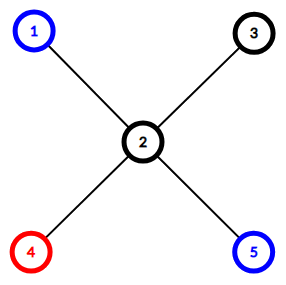 Единственный хороший набор — это ребро \((2, 4)\). После его удаления дерево распадается на компоненты \(\{4\}\) и \(\{1, 2, 3, 5\}\). В первой компоненте есть только вершина цвета \(1\), а во второй — только вершины цвета \(2\) и непокрашенные вершины. Дерево из второго примера: 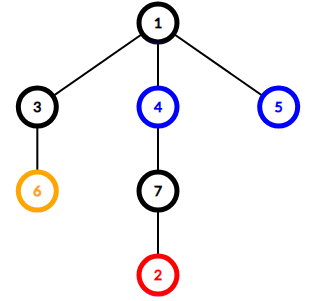 Хорошие наборы: \(\{(1, 3), (4, 7)\}\), \(\{(1, 3), (7, 2)\}\), \(\{(3, 6), (4, 7)\}\) и \(\{(3, 6), (7, 2)\}\). | |
![]()
|
|
E. Сон
Комбинаторика
математика
реализация
*2700
Однажды Вася лежал в кровати и для того, чтобы быстрее заснуть, наблюдал за своими электронными часами. Вася живет в странной стране, где в сутках h часов, а в каждом часе m минут. Часы показывают время в десятичной системе счисления в формате H:M, где строка H всегда имеет фиксированную длину, равную количеству цифр в десятичной записи числа h - 1, для этого, при необходимости, добавляются лидирующие нули. Строка M имеет аналогичный вид, и ее длина всегда равна количеству цифр в записи числа m - 1. Например, если h = 17, m = 1000, то время равное 13 часам и 75 минутам будет отображаться как «13:075». Вася наблюдал за часами с момента h1 часов m1 минут до h2 часов m2 минут включительно, а затем он заснул. Теперь он просит вас подсчитать, сколько раз он видел момент, в который на часах переключилось не менее k цифр одновременно. Например, при переключении 04:19 → 04:20 изменяется две цифры, при 23:59 → 00:00 — четыре цифры. Считайте, что Вася наблюдал за часами строго меньше суток. Обратите внимание, что последние значения, которые увидел Вася на часах до того, как заснуть, — это «h2:m2». То есть момент, в который время «h2:m2» переключается на следующее значение, Вася не видит. Выходные данные Выведите единственное число — сколько раз Вася увидел момент переключения не менее k цифр одновременно. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-х битовых чисел на С++. Рекомендуется использовать потоки cin, cout (также вы можете использовать спецификатор %I64d). Примечание В первом примере Вася увидит следующие моменты времени: 4:4  0:0 → 0:1 → 0:2 → 0:3 → 0:4 0:0 → 0:1 → 0:2 → 0:3 → 0:4  1:0 → 1:1 → 1:2 → 1:3 → 1:4 1:0 → 1:1 → 1:2 → 1:3 → 1:4  2:0 → 2:1 → 2:2 → 2:3 → 2:4. Двойной стрелкой ( 2:0 → 2:1 → 2:2 → 2:3 → 2:4. Двойной стрелкой ( ) обозначены искомые моменты времени (в данном примере — когда Вася видит переключение двух цифр одновременно). ) обозначены искомые моменты времени (в данном примере — когда Вася видит переключение двух цифр одновременно). Во втором примере k = 1. Нам подходит любое переключение времени, так как при каждом переключении меняется хотя бы одна цифра. Всего переключений 24·60 = 1440, но из них Вася не увидел одно переключение 23:59  00:00. 00:00. В третьем примере Вася уснул сразу после того, как начал смотреть на часы, значит он не увидел ни одного переключения. | |
![]()
|
|
E. Беспалиндромные массивы
Комбинаторика
дп
разделяй и властвуй
*2200
Назовем массив \(b\) плохим если он содержит последовательный отрезок \(b_l, b_{l+1}, \dots, b_{r}\) нечетной длины больше \(1\) (\(l < r\) и \(r - l + 1\) нечетно) такой что \(\forall i \in \{0, 1, \dots, r - l\}\) \(b_{l + i} = b_{r - i}\). Если массив не плохой, то он хороший. Вам задан массив \(a_1, a_2, \dots, a_n\). Некоторые его элементы равны \(-1\). Посчитайте количество хороших массивов, которое вы можете получить, заменив все \(-1\) на какие-то числа от \(1\) до \(k\). Так как ответ может быть большим, выведите его по модулю \(998244353\). Выходные данные Выведите единственное число — количество хороших массивов, которые вы можете получить по модулю \(998244353\). | |
![]()
|
|
E. Количество компонент
Структуры данных
Комбинаторика
математика
*2100
дп
Королевство Кремляндия представляет собой дерево (связный неориентированный граф без циклов), состоящее из \(n\) вершин. У каждой вершины \(i\) есть своя стоимость \(a_i\). Все вершины последовательно соединены рёбрами. Формально, для каждого \(1 \leq i < n\) существует ребро между вершинами \(i\) и \(i+1\). Введём понятие функции \(f(l, r)\), принимающую два целых числа \(l\) и \(r\) (\(l \leq r\)): - Оставим в дереве только вершины, стоимости которых находятся в пределах от \(l\) до \(r\).
- Значением функции будет количество компонент связности в новом графе.
Ваша задача состоит в том, чтобы посчитать следующую сумму: \(\)\sum_{l=1}^{n} \sum_{r=l}^{n} f(l, r) \(\) Выходные данные Выведите одно число — ответ на задачу. Примечание В первом примере значения функции будут такими: - \(f(1, 1)=1\) (остается только вершина под номером \(2\), которая образует одну компоненту)
- \(f(1, 2)=1\) (остаются вершины \(1\) и \(2\), которые образуют одну компоненту)
- \(f(1, 3)=1\) (все вершины остаются, получается одна компонента)
- \(f(2, 2)=1\) (только вершина под номером \(1\))
- \(f(2, 3)=2\) (остаются вершины \(1\) и \(3\), которые образуют две компоненты)
- \(f(3, 3)=1\) (только вершина \(3\))
Суммарно выходит \(7\). Во втором примере значения функции будут такими: - \(f(1, 1)=1\)
- \(f(1, 2)=1\)
- \(f(1, 3)=1\)
- \(f(1, 4)=1\)
- \(f(2, 2)=1\)
- \(f(2, 3)=2\)
- \(f(2, 4)=2\)
- \(f(3, 3)=1\)
- \(f(3, 4)=1\)
- \(f(4, 4)=0\) (никакой вершины не остаётся, а значит количество компонент равно \(0\))
Суммарно выходит \(11\). | |
![]()
|
|
F. Соня и информатика
Теория вероятностей
Комбинаторика
дп
*2300
матрицы
Девочка по имени Соня учится в научном лицее Королевства Кремляндия. Учитель информатики (любимого предмета Сони!) придумал для неё задачу. Даётся массив \(a\) длины \(n\), состоящий только из чисел \(0\) и \(1\), а также число \(k\). Ровно \(k\) раз происходит следующее: - Равновероятно выбираются два числа \(i\) и \(j\) такие, что (\(1 \leq i < j \leq n\)).
- Числа, стоящие на позициях \(i\) и \(j\), меняются местами.
Задача Сони найти вероятность того, что после выполнения всех операций массив \(a\) будет отсортирован по неубыванию. За помощью она обратилась к вам. Помогите Соне решить эту задачу. Можно показать, что искомая вероятность или равна \(0\), или её можно представить как \(\dfrac{P}{Q}\), где \(P\) и \(Q\) — взаимно простые числа и \(Q \not\equiv 0~\pmod {10^9+7}\). Выходные данные Если искомая вероятность равна \(0\), выведите \(0\), иначе выведите величину \(P \cdot Q^{-1}\) \(\pmod {10^9+7}\), где \(P\) и \(Q\) определены выше. Примечание В первом примере все возможные варианты конечного массива \(a\), после применения ровно двух операций: \((0, 1, 0)\), \((0, 0, 1)\), \((1, 0, 0)\), \((1, 0, 0)\), \((0, 1, 0)\), \((0, 0, 1)\), \((0, 0, 1)\), \((1, 0, 0)\), \((0, 1, 0)\). Следовательно ответ равен \(\dfrac{3}{9}=\dfrac{1}{3}\). Во втором примере массив не станет отсортированным по неубыванию после одной операции, следовательно ответ равен \(0\). | |
![]()
|
|
F. Сервал и бонусная задача
Теория вероятностей
Комбинаторика
математика
дп
*2600
Продвигаясь в своем пути к становлению математиком, Сервал стал студентом математического Университета Джапари. На уроке математики учитель научил его вычислять математическое ожидание длины случайного подотрезка данного отрезка. Затем он оставил бонусную задачу в качестве домашнего задания. Эта бонусная задача — расширить разобранную задачу на произвольный случай, как описано ниже. Задан отрезок длиной \(l\). Мы случайным образом выбираем \(n\) отрезков, выбирая равновероятно две точки (возможно, с нецелыми координатами) из данного отрезка и получая отрезок между двумя этими точками. Вам дано количество случайных отрезков \(n\) и еще одно целое число \(k\). \(2n\) концов выбранных отрезков делят исходный отрезок на \((2n+1)\) отрезков. Ваша задача — вычислить математическое ожидание суммарной длины тех из отрезков, которые покрыты хотя бы \(k\) отрезками из \(n\) случайных отрезков. Вам требуется вычислить ответ на эту задачу по модулю \(998244353\). Выходные данные Выведите одно целое число — математическое ожидание суммарной длины всех отрезков, покрытых хотя бы \(k\) отрезками из \(n\) случайных отрезков по модулю \(998244353\). Формально, пусть \(M = 998244353\). Можно показать, что ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Примечание В первом примере математическое ожидание равно \(\int_0^1 \int_0^1 |x-y| \,\mathrm{d}x\,\mathrm{d}y = {1\over 3}\), а \(3^{-1}\) по модулю \(998244353\) равно \(332748118\). | |
![]()
|
|
A. Тихий класс
Комбинаторика
*900
жадные алгоритмы
В первый класс школы в Нлогонии набрали \(n\) учеников. Директор хочет разделить их в два класса, каждый ученик должен оказаться ровно в одном из этих классов. Если в один класс попадут два школьника, имена которых начинаются с одной и той же буквы, то они будут слишком много болтать друг с другом (ведь наверняка у них много общего). Обозначим за \(x\) количество таких пар учеников в некотором разбиении на два класса. Пары \((a, b)\) и \((b, a)\) считаются одинаковыми и учитываются один раз. Например, если всего в классе \(6\) учеников — «olivia», «jacob», «tanya», «jack», «oliver» и «jessica», то: - разделение на два класса («jack», «jacob», «jessica», «tanya») и («olivia», «oliver») даст \(x=4\) (\(3\) пары будут болтать в первом классе, \(1\) пара будет болтать во втором классе),
- разделение на два класса («jack», «tanya», «olivia») и («jessica», «oliver», «jacob») даст \(x=1\) (\(0\) пар будут болтать в первом классе, \(1\) пара будет болтать во втором классе).
Вам дан список из \(n\) имен. Какое минимальное значение \(x\) мы можем получить, распределив этих школьников на два класса? Обратите внимание, не запрещается распределять всех учеников в один и тот же класс, оставив другой пустым. Выходные данные Выведите одно целое число \(x\) — минимально возможное количество пар учеников, которые будут болтать друг с другом. Примечание В первом примере минимально возможное число пар равно \(1\). Такого можно добиться, например, распределив всех кроме jose в один класс, а jose — в другой, так что болтать будут только jorge и jerry. Во втором примере минимально возможное число пар равно \(2\). Такого можно добиться, например, распределив kambei, gorobei, shichiroji и kyuzo в один класс, а heihachi, katsushiro и kikuchiyo в другой. В этом случае болтать будут kambei с kyuzo, а также katsushiro с kikuchiyo. В третьем примере минимально возможное число пар равно \(4\). Этого можно добиться, распределив трех школьников с именем mike в один класс, а остальных двух — в другой. Тогда в одном классе будет три болтающих пары, а в другом — одна. | |
![]()
|
|
E. Удаление отрезка
Бинарный поиск
Структуры данных
Комбинаторика
*2100
Вам задан массив, состоящий из \(n\) целых чисел \(a_1, a_2, \dots , a_n\) и целое число \(x\). Гарантируется, что для любого \(i\) выполняется \(1 \le a_i \le x\). Функция \(f(l, r)\) удаляет все числа из массива \(a\), для которых выполняется \(l \le a_i \le r\), и возвращает полученный массив. Например, если \(a = [4, 1, 1, 4, 5, 2, 4, 3]\), тогда \(f(2, 4) = [1, 1, 5]\). Вам нужно посчитать количество пар \((l, r)\), таких, что \(1 \le l \le r \le x\) и массив \(f(l, r)\) отсортирован в порядке неубывания. Обратите внимание, что пустой массив тоже считается отсортированным. Выходные данные Выведите количество пар \(1 \le l \le r \le x\), таких, что массив \(f(l, r)\) отсортирован в порядке неубывания. Примечание В первом тестовом примере подходящие пары — это \((1, 1)\), \((1, 2)\), \((1, 3)\) и \((2, 3)\). Во втором тестовом примере подходящие пары — это \((1, 3)\), \((1, 4)\), \((2, 3)\), \((2, 4)\), \((3, 3)\) и \((3, 4)\). | |
![]()
|
|
F. Скалярные запросы
Структуры данных
Комбинаторика
математика
сортировки
*2300
Вам задан массив \(a_1, a_2, \dots, a_n\). Все \(a_i\) попарно различные. Определим функцию \(f(l, r)\) следующим образом: - создадим массив \(b_1, b_2, \dots, b_{r - l + 1}\), где \(b_i = a_{l - 1 + i}\);
- отсортируем массив \(b\) в порядке возрастания;
- результатом функции \(f(l, r)\) назовем значение \(\sum\limits_{i = 1}^{r - l + 1}{b_i \cdot i}\).
Посчитайте \(\left(\sum\limits_{1 \le l \le r \le n}{f(l, r)}\right) \mod (10^9+7)\). Другими словами — сумму функций \(f\) для всех подотрезков массива \(a\) по модулю \(10^9+7\). Выходные данные Выведите единственное число — сумму функций \(f\) для всех подотрезков массива \(a\) по модулю \(10^9+7\). Примечание Описание первого примера: - \(f(1, 1) = 5 \cdot 1 = 5\);
- \(f(1, 2) = 2 \cdot 1 + 5 \cdot 2 = 12\);
- \(f(1, 3) = 2 \cdot 1 + 4 \cdot 2 + 5 \cdot 3 = 25\);
- \(f(1, 4) = 2 \cdot 1 + 4 \cdot 2 + 5 \cdot 3 + 7 \cdot 4 = 53\);
- \(f(2, 2) = 2 \cdot 1 = 2\);
- \(f(2, 3) = 2 \cdot 1 + 4 \cdot 2 = 10\);
- \(f(2, 4) = 2 \cdot 1 + 4 \cdot 2 + 7 \cdot 3 = 31\);
- \(f(3, 3) = 4 \cdot 1 = 4\);
- \(f(3, 4) = 4 \cdot 1 + 7 \cdot 2 = 18\);
- \(f(4, 4) = 7 \cdot 1 = 7\);
| |
![]()
|
|
B. Nauoo и окружность
Деревья
Комбинаторика
дп
поиск в глубину и подобное
*1900
Nauuo — девочка, которая любит рисовать окружности. Однажды она нарисовала окружность и захотела нарисовать на ней дерево. Дерево — это связный неориентированный граф из \(n\) вершин и \(n-1\) ребер. Вершины пронумерованы целыми числами от \(1\) до \(n\). Nauuo хочет нарисовать дерево на окружности, причем вершины должны лежать на \(n\) различных точках на окружности, а ребра — это отрезки, не пересекающиеся друг с другом. «Не пересекающиеся друг с другом» означает, что любые два ребра не должны иметь общих точек, кроме концов отрезков. Nauuo хочет нарисовать дерево, используя перестановку из \(n\) элементов. Перестановка из \(n\) элементов это последовательность целых чисел \(p_1,p_2,\ldots,p_n\), в которой каждое целое число от \(1\) до \(n\) встречается ровно один раз. После выбора перестановки Nauuo нарисует \(i\)-ю вершину в \(p_i\)-й точке на окружности, а затем нарисует ребра, основываясь на положении вершин. По данному дереву Nauuo хочет знать, сколько есть перестановок, подходящих под условие (ребра образуют непересекающиеся отрезки между вершинами). Она хочет узнать ответ по модулю \(998244353\), можете ли вы ей помочь? Очевидно, что корректность перестановки не зависит от выбранных \(n\) точек на окружности. Выходные данные Выведите одно целое число — количество перестановок, при которых возможно нарисовать дерево на окружности, не нарушая условия, по модулю \(998244353\). Примечание Пример 1 Корректные перестановки и их деревья. 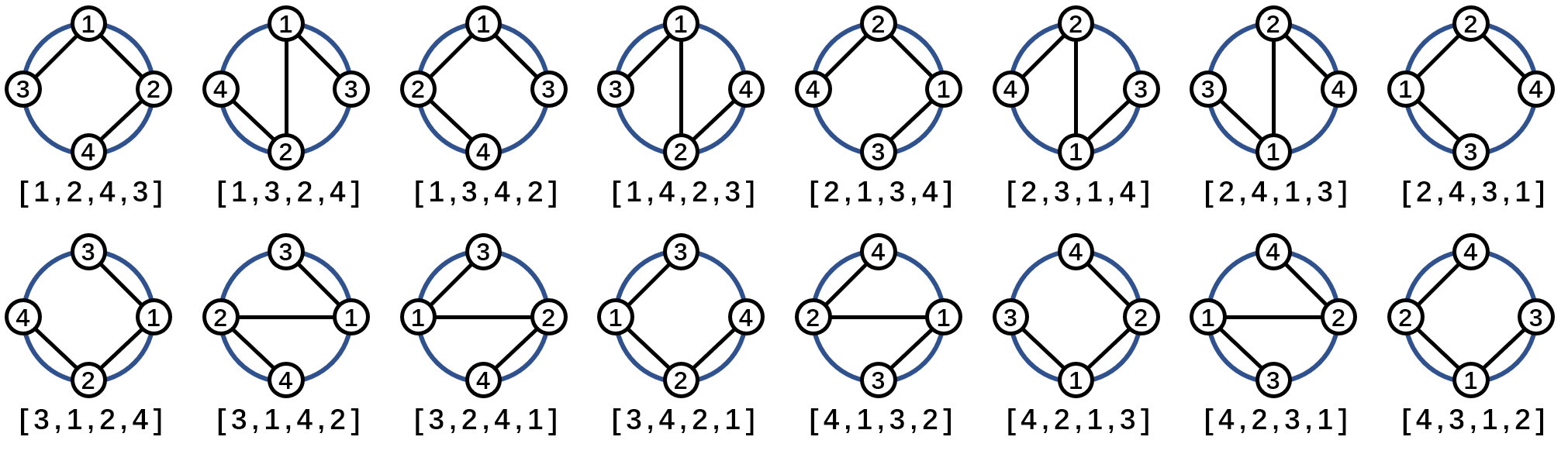
А вот пример некорректной перестановки: ребра \((1,3)\) и \((2,4)\) пересекаются. 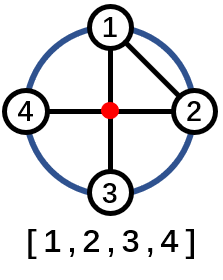
Example 2 Каждая перестановка приводит к корректному дереву, так что ответ равен \(4! = 24\). | |
![]()
|
|
E. Ихаб и обычная задача на OEIS
Комбинаторика
математика
дп
теория чисел
*2500
Определим функцию \(f(p)\) от перестановки \(p\) следующим образом. Пусть \(g_i\) — наибольший общий делитель (НОД) чисел \(p_1\), \(p_2\), ..., \(p_i\) (другими словами, НОД на префиксе длины \(i\)). Тогда \(f(p)\) равно числу различных значений среди \(g_1\), \(g_2\), ..., \(g_n\). Пусть \(f_{max}(n)\) — максимальное значение \(f(p)\) среди всех перестановок \(p\) чисел \(1\), \(2\), ..., \(n\). Вам дано число \(n\), подсчитайте число перестановок \(p\) чисел \(1\), \(2\), ..., \(n\) таких, что \(f(p)\) равно \(f_{max}(n)\). Так как ответ может быть большим, выведите остаток от деления этого числа на \(1000\,000\,007 = 10^9 + 7\). Выходные данные В единственной строке выведите ответ по модулю \(10^9+7\). Примечание Рассмотрим второй пример: ниже перечислены перестановки длины \(3\): - \([1,2,3]\), \(f(p)=1\).
- \([1,3,2]\), \(f(p)=1\).
- \([2,1,3]\), \(f(p)=2\).
- \([2,3,1]\), \(f(p)=2\).
- \([3,1,2]\), \(f(p)=2\).
- \([3,2,1]\), \(f(p)=2\).
Максимальное значение \(f_{max}(3) = 2\), и существуют \(4\) перестановки \(p\) такие, что \(f(p)=2\). | |
![]()
|
|
C. Плитки
Комбинаторика
математика
жадные алгоритмы
*1300
Боб украшает свою кухню, если точнее, то пол. Он уже выбрал, какую именно плитку будет использовать. Это — квадратные плитки, разделенные диагонально на белую и черную части. Вот так:  Размер этой плитки идеально подходит для кухни, так как Бобу нужно ровно \(w \times h\) плиток, чтобы покрыть всю кухню. То есть ширина кухни — \(w\) плиток, а длина — \(h\). Каждую плитку можно вращать, всего есть четыре способа, как можно это сделать. Бобу все еще нужно решить, как именно он будет покрывать кухню. Есть один обязательный эстетический критерий: любые две соседние плитки должны иметь разные цвета на той стороне, которая их соединяет. Другими словами, с одной стороны должен быть белый цвет, а с другой — черный.  На рисунке слева показан пример правильного покрытия кухни размером \(3 \times 2\). На рисунке справа показан пример неправильного покрытия, так как есть плитки, которые соприкасаются сторонами одного цвета. На рисунке слева показан пример правильного покрытия кухни размером \(3 \times 2\). На рисунке справа показан пример неправильного покрытия, так как есть плитки, которые соприкасаются сторонами одного цвета. Найдите количество способов покрыть кухню. Так как ответ может быть очень большим, выведите остаток от его деления на \(998244353\) (простое число). Выходные данные Выведите одно целое число \(n\) — остаток от деления количества способов покрыть кухню на \(998244353\). | |
![]()
|
|
F1. Короткая разноцветная полоска
Комбинаторика
дп
поиск в глубину и подобное
*2200
Это первая подзадача задачи F. Единственные различия между этой и второй подзадачами — это ограничения на значение \(m\) и ограничение по времени. Вам нужно решить обе подзадачи, чтобы взламывать эту подзадачу. Во вселенной всего есть \(n+1\) разных цветов, пронумерованных от \(0\) до \(n\). Есть полоска, длина которой \(m\) сантиметров, изначально покрашенная в цвет \(0\). Алиса взяла кисть и начала разукрашивать полоску. Для каждого \(i\) от \(1\) до \(n\) в таком порядке она выбирает два числа \(0 \leq a_i < b_i \leq m\) такие, что отрезок \([a_i, b_i]\) сейчас покрашен одним цветом, и красит его в цвет \(i\). Алиса выбрала такие отрезки, что сейчас каждый сантиметр имеет отличный от \(0\) цвет. Формально, отрезок \([i-1, i]\) покрашен в цвет \(c_i\) (\(c_i \neq 0\)). Каждый цвет, кроме \(0\), виден на полоске. Посчитайте количество пар последовательностей \(\{a_i\}_{i=1}^n\), \(\{b_i\}_{i=1}^n\), которые дадут заданную полоску. Так как это число может быть очень большим, выведите его по модулю \(998244353\). Выходные данные Выведите одно целое число — количество способов получить такую полоску по модулю \(998244353\). Примечание В первом примере всего есть \(5\) способов, все они показаны на рисунке ниже. Здесь \(0\) — белый цвет, \(1\) — красный, \(2\) — зеленый, а \(3\) — синий. 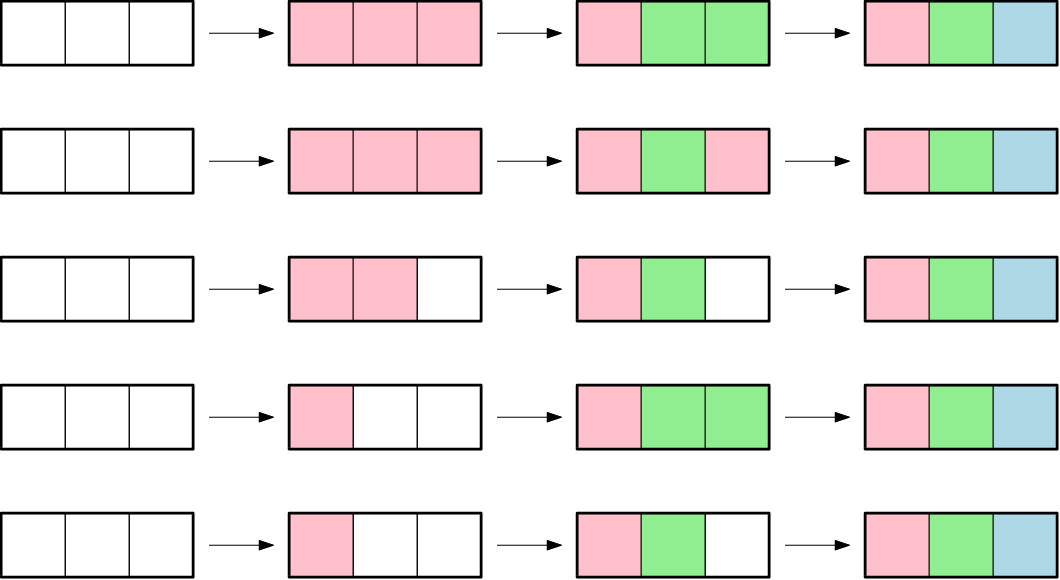
Ниже показан пример неправильной раскраски. Во второй операции отрезок 1 3 не покрашен ни в один цвет, поэтому он не может быть покрашен в цвет \(2\). 
| |
![]()
|
|
C. Флаг
Перебор
Комбинаторика
реализация
дп
*1900
Иннокентий работает на блошином рынке, продавая посетителям всякий хлам необычные вещи. Недавно он нашёл у себя на складе старое прямоугольное покрывало. Как оказалось, это покрывало имеет сетчатую форму, то есть покрывало состоит из \(n \cdot m\) цветных лоскутков, разбитых на \(n\) строк и \(m\) столбцов. Цветные лоскутки привлекли внимание Иннокентия, и он сразу же придумал, как можно заработать на своей находке. Если вырезать из покрывала подпрямоугольник, состоящий из трёх цветных полос, то потом этот подпрямоугольник можно будет продать как флаг какой-нибудь страны. В частности, Иннокентий считает, что подпрямоугольник будет достаточно похож на флаг какой-нибудь страны, если он будет состоять из трёх одноцветных полос одинаковой высоты, находящихся друг под другом. Разумеется, цвет верхней полосы не должен совпадать с цветом средней полосы, а цвет средней не должен совпадать с цветом нижней. Иннокентий пока не знает из какой части покрывала будет вырезать флаг, однако он точно решил, что будет вырезать флаг только по линиям сетки, при этом покрывало ни в коем случае нельзя поворачивать. Помогите Иннокентию и посчитайте количество различных подпрямоугольников, которые можно вырезать из покрывала и продать как флаг. Подпрямоугольники, образующие одинаковые флаги, однако расположенные в разных местах покрывала, считаются различными.    Примеры подпрямоугольников, являющихся флагами       Примеры подпрямоугольников, не являющихся флагами Выходные данные В единственной строке выведите одно целое число — количество подпрямоугольников, являющихся флагами. Примечание   Пояснение к примеру. Выделены подпрямоугольники, являющиеся флагами | |
![]()
|
|
G1. Плейлист для Поликарпа (упрощённая версия)
Комбинаторика
*2100
дп
битмаски
Единственное отличие этой версии от усложнённой — это ограничения. Поликарп очень любит слушать музыку, поэтому он никогда не расстается с плеером, даже по пути из университета домой. Поликарп преодолевает расстояние от университета до дома ровно за \(T\) минут. В плеере у Поликарпа хранится \(n\) песен, причем каждая из них характеризуется двумя параметрами: \(t_i\) и \(g_i\), где \(t_i\) — длительность песни в минутах (\(1 \le t_i \le 15\)), \(g_i\) — её жанр (\(1 \le g_i \le 3\)). Поликарп хочет составить такой плейлист, чтобы всё время в пути от университета до дома, он мог слушать музыку и в момент прибытия домой плейлист кончился. Поликарп никогда не прерывает песни и всегда слушает их от начала и до конца. Таким образом, если он начал слушать \(i\)-ю песню, то на её прослушивание он потратит ровно \(t_i\) минут. Также Поликарп не любит, когда подряд играют две песни одинакового жанра или когда песни в его плейлисте повторяются. Помогите Поликарпу посчитать количество различных последовательностей песен (их порядок имеет значение), суммарной длительностью ровно \(T\), таких, что в них нет двух подряд идущих песен одинакового жанра и все песни в плейлисте различны. Выходные данные Выведите одно целое число — количество различных последовательностей песен, суммарной длительностью ровно \(T\), таких, что в них нет двух подряд идущих песен одинакового жанра и все песни в плейлисте различны. Так как ответ может быть большим, выводите его по модулю \(10^9 + 7\) (то есть остаток при делении количества на число \(10^9 + 7\)). Примечание В первом примере Поликарп может составить любой из \(6\)-ти вариантов плейлист перестановкой имеющихся песен: \([1, 2, 3]\), \([1, 3, 2]\), \([2, 1, 3]\), \([2, 3, 1]\), \([3, 1, 2]\) и \([3, 2, 1]\) (указаны номера песен). Во втором примере первая и вторая песни не могут идти подряд (так как имеют одинаковый жанр). Таким образом, Поликарп может составить плейлист одним из \(2\)-х возможных способов: \([1, 3, 2]\) и \([2, 3, 1]\) (указаны номера песен). В третьем примере Поликарп может составить следующие плейлисты: \([1, 2, 3]\), \([1, 3, 2]\), \([2, 1, 3]\), \([2, 3, 1]\), \([3, 1, 2]\), \([3, 2, 1]\), \([1, 4]\), \([4, 1]\), \([2, 3, 4]\) и \([4, 3, 2]\) (указаны номера песен). | |
![]()
|
|
G2. Плейлист для Поликарпа (усложнённая версия)
Комбинаторика
дп
*2600
Единственное отличие этой версии от упрощённой — это ограничения. Поликарп очень любит слушать музыку, поэтому он никогда не расстается с плеером, даже по пути из университета домой. Поликарп преодолевает расстояние от университета до дома ровно за \(T\) минут. В плеере у Поликарпа хранится \(n\) песен, причем каждая из них характеризуется двумя параметрами: \(t_i\) и \(g_i\), где \(t_i\) — длительность песни в минутах (\(1 \le t_i \le 50\)), \(g_i\) — её жанр (\(1 \le g_i \le 3\)). Поликарп хочет составить такой плейлист, чтобы всё время в пути от университета до дома, он мог слушать музыку и в момент прибытия домой плейлист кончился. Поликарп никогда не прерывает песни и всегда слушает их от начала и до конца. Таким образом, если он начал слушать \(i\)-ю песню, то на её прослушивание он потратит ровно \(t_i\) минут. Также Поликарп не любит, когда подряд играют две песни одинакового жанра или когда песни в его плейлисте повторяются. Помогите Поликарпу посчитать количество различных последовательностей песен (их порядок имеет значение), суммарной длительностью ровно \(T\), таких, что в них нет двух подряд идущих песен одинакового жанра и все песни в плейлисте различны. Выходные данные Выведите одно целое число — количество различных последовательностей песен, суммарной длительностью ровно \(T\), таких, что в них нет двух подряд идущих песен одинакового жанра и все песни в плейлисте различны. Так как ответ может быть большим, выводите его по модулю \(10^9 + 7\) (то есть остаток при делении количества на число \(10^9 + 7\)). Примечание В первом примере Поликарп может составить любой из \(6\)-ти вариантов плейлист перестановкой имеющихся песен: \([1, 2, 3]\), \([1, 3, 2]\), \([2, 1, 3]\), \([2, 3, 1]\), \([3, 1, 2]\) и \([3, 2, 1]\) (указаны номера песен). Во втором примере первая и вторая песни не могут идти подряд (так как имеют одинаковый жанр). Таким образом, Поликарп может составить плейлист одним из \(2\)-х возможных способов: \([1, 3, 2]\) и \([2, 3, 1]\) (указаны номера песен). В третьем примере Поликарп может составить следующие плейлисты: \([1, 2, 3]\), \([1, 3, 2]\), \([2, 1, 3]\), \([2, 3, 1]\), \([3, 1, 2]\), \([3, 2, 1]\), \([1, 4]\), \([4, 1]\), \([2, 3, 4]\) и \([4, 3, 2]\) (указаны номера песен). | |
![]()
|
|
E. Задача от Red Pandы
Комбинаторика
*3300
На Moscow Workshops ICPC команды получают воздушные шарики за каждую задачу, которую они решили первыми. Команда MSU Red Panda получила так много шариков, что они не знали, что с ними делать. Тогда они придумали о них задачу. Есть несколько шариков, всего не более \(10^6\), каждый покрашен в один из \(k\) цветов. Мы можем делать следующую операцию: выбрать \(k-1\) шариков \(k-1\) различных цветов, и перекрасить их все в оставшийся цвет. Мы можем выполнять данную операцию любое конечное число раз (в частности, мы можем выполнить очередную операцию только если существует по крайней мере \(k-1\) различных цветов среди шариков в данный момент). Сколько различных конфигураций шариков мы можем получить? Играет роль только количество шариков каждого цвета, конфигурации, отличающиеся только порядком шариков, считаются одинаковыми. Так как это число может быть очень большим, выведите его по модулю \(998244353\). Выходные данные Выведите число возможных конфигураций по модулю \(998244353\). Примечание В первом примерe существуют \(3\) конфигурации которые мы можем получить: \([0, 1, 2]\), \([2, 0, 1]\), \([1, 2, 0]\). В втором примере мы можем применить операцию не более одного раза, и достижимыми являются : \([1, 1, 1, 1]\), \([0, 0, 0, 4]\), \([0, 0, 4, 0]\), \([0, 4, 0, 0]\), \([4, 0, 0, 0]\). В третьем примере мы не можем применить ни одной операции, поэтому единственная достижимая конфигурация - начальная. | |
![]()
|
|
F. Эксперт по кроссвордам
Теория вероятностей
Комбинаторика
дп
теория чисел
*2400
Сегодня у Адилбека тест по теории вероятности. К сожалению, к моменту, когда Адилбек пришел в университет, уже сформировалась огромная очередь из других желающих сдать этот же тест. Адилбек оценил, что он сможет приступить к тесту только через \(T\) секунд. К счастью, Адилбек может провести время ожидания более интересным образом, чем повторение скучных теорем и формул. У него на телефоне есть приложение с \(n\) японскими кроссвордами. Адилбек собрался решать их по одному, в том же порядке, в котором они перечислены в приложении, не пропуская ни одного кроссворда. Для каждого кроссворда известно время \(t_i\), за которое его в среднем может решить эксперт по кроссвордам (время также задано в секундах). Адилбек — настоящий эксперт по японским кроссвордам, но, к сожалению, ему иногда не везет с выбором стратегии решения. Поэтому решение \(i\)-го кроссворда будет занимать у него либо \(t_i\) секунд, либо \(t_i + 1\) секунд равновероятно (с вероятностью \(\frac{1}{2}\) он решает кроссворд ровно за \(t_i\) секунд, а с вероятностью \(\frac{1}{2}\) он потратит дополнительную секунду на решение кроссворда). Все эти события независимы. Ровно через \(T\) секунд (либо после решения последнего кроссворда, если он успевает их все решить меньше чем за \(T\) секунд) Адилбек закрывает приложение (если он заканчивает какой-то кроссворд в последний момент, то данный кроссворд считается решенным; иначе Адилбек бросает кроссворд не решенным до конца). Он считает, что будет очень интересно и по теме посчитать \(E\) — математическое ожидание количества кроссвордов, которые он успеет полностью решить. Можете ли вы посчитать данное матожидание? Напомним, что матожидание дискретной случайной величины — это вероятностно-взвешенное среднее всех ее возможных значений. В данной задаче это означает, что матожидание количества решенных кроссвордов может быть посчитано как как \(E = \sum \limits_{i = 0}^{n} i p_i\), где \(p_i\) — вероятность того, что Адилбек решит ровно \(i\) кроссвордов. Мы можем представить \(E\) как рациональную дробь \(\frac{P}{Q}\) с \(Q > 0\). В качестве ответа выведите \(P \cdot Q^{-1} \bmod (10^9 + 7)\). Выходные данные Выведите одно число — матожидание количества кроссвордов, решенных Адилбеком за \(T\) секунд, в форме \(P \cdot Q^{-1} \bmod (10^9 + 7)\). Примечание Ответ для первого примера равен \(\frac{14}{8}\). Ответ для второго примера равен \(\frac{17}{8}\). | |
![]()
|
|
D1. Подводная лодка в Рыбинском море (упрощённая редакция)
Комбинаторика
математика
*1500
теория чисел
Эта задача отличается от следующей исключительно наличием ограничения на равную длину всех чисел \(a_1, a_2, \dots, a_n\). На самом деле эта задача является подзадачей D2 из этого же контеста, и решение D2 решает эту подзадачу в том числе. Команда ЛКШ-ат собралась совершить путешествие на подводной лодке. Цель их плавания — древний клад на затонувшем судне, лежащем на дне Великого Рыбинского моря. К сожалению, ребята не знают координаты судна, и поэтому обратились за помощью к потомственному магу Мишане. Он согласился помочь команде, но только если они решат его задачку. Определим функцию, чередующую цифры двух чисел, \(f(a_1 a_2 \dots a_{p - 1} a_p, b_1 b_2 \dots b_{q - 1} b_q)\), где \(a_1 \dots a_p\) и \(b_1 \dots b_q\) — цифры двух чисел в десятичной системе счисления, записанные без ведущих нулей. Иными словами, функция \(f(x, y)\) перемешивает цифры чисел \(x\) и \(y\) выписывая их по очереди от младщих цифр к старшим, начиная с числа \(y\). Результат функции тоже строится справа налево (то есть от младших цифр к старшим). Если цифры одного из аргументов закончились, то выписываются оставшиеся цифры другого аргумента. Ознакомьтесь с примерами и формальным определением функции. Например: \(\)f(1111, 2222) = 12121212\(\) \(\)f(7777, 888) = 7787878\(\) \(\)f(33, 44444) = 4443434\(\) \(\)f(555, 6) = 5556\(\) \(\)f(111, 2222) = 2121212\(\) Формально: - если \(p \ge q\), то \(f(a_1 \dots a_p, b_1 \dots b_q) = a_1 a_2 \dots a_{p - q + 1} b_1 a_{p - q + 2} b_2 \dots a_{p - 1} b_{q - 1} a_p b_q\);
- если \(p < q\), то \(f(a_1 \dots a_p, b_1 \dots b_q) = b_1 b_2 \dots b_{q - p} a_1 b_{q - p + 1} a_2 \dots a_{p - 1} b_{q - 1} a_p b_q\).
Мишаня дал вам массив из \(n\) целых чисел \(a_i\). Все числа в этом массиве имеют равную длину (то есть состоят из одинакового количества цифр). Помогите ребятам посчитать \(\sum_{i = 1}^{n}\sum_{j = 1}^{n} f(a_i, a_j)\) по модулю \(998\,244\,353\). Выходные данные Выведите ответ по модулю \(998\,244\,353\). | |
![]()
|
|
D2. Подводная лодка в Рыбинском море (усложнённая редакция)
Комбинаторика
математика
теория чисел
*1800
Эта задача отличается от предыдущей исключительно отсутствием ограничения на равную длину всех чисел \(a_1, a_2, \dots, a_n\). Команда ЛКШ-ат собралась совершить путешествие на подводной лодке. Цель их плавания — древний клад на затонувшем судне, лежащем на дне Великого Рыбинского моря. К сожалению, ребята не знают координаты судна, и поэтому обратились за помощью к потомственному магу Мишане. Он согласился помочь команде, но только если они решат его задачку. Определим функцию, чередующую цифры двух чисел, \(f(a_1 a_2 \dots a_{p - 1} a_p, b_1 b_2 \dots b_{q - 1} b_q)\), где \(a_1 \dots a_p\) и \(b_1 \dots b_q\) — цифры двух чисел в десятичной системе счисления, записанные без ведущих нулей. Иными словами, функция \(f(x, y)\) перемешивает цифры чисел \(x\) и \(y\) выписывая их по очереди от младщих цифр к старшим, начиная с числа \(y\). Результат функции тоже строится справа налево (то есть от младших цифр к старшим). Если цифры одного из аргументов закончились, то выписываются оставшиеся цифры другого аргумента. Ознакомьтесь с примерами и формальным определением функции. Например: \(\)f(1111, 2222) = 12121212\(\) \(\)f(7777, 888) = 7787878\(\) \(\)f(33, 44444) = 4443434\(\) \(\)f(555, 6) = 5556\(\) \(\)f(111, 2222) = 2121212\(\) Формально: - если \(p \ge q\), то \(f(a_1 \dots a_p, b_1 \dots b_q) = a_1 a_2 \dots a_{p - q + 1} b_1 a_{p - q + 2} b_2 \dots a_{p - 1} b_{q - 1} a_p b_q\);
- если \(p < q\), то \(f(a_1 \dots a_p, b_1 \dots b_q) = b_1 b_2 \dots b_{q - p} a_1 b_{q - p + 1} a_2 \dots a_{p - 1} b_{q - 1} a_p b_q\).
Мишаня дал вам массив из \(n\) целых чисел \(a_i\), помогите ребятам посчитать \(\sum_{i = 1}^{n}\sum_{j = 1}^{n} f(a_i, a_j)\) по модулю \(998\,244\,353\). Выходные данные Выведите ответ по модулю \(998\,244\,353\). | |
![]()
|
|
E. Культурный код
Бинарный поиск
Структуры данных
Комбинаторика
дп
сортировки
*2300
кратчайшие пути
В магазине неподалеку продаются известные русские деревянные игрушки под названием «матрешки», и вы бы хотели приобрести несколько штук. В магазине продается \(n\) различных матрешек. Любая матрешка — это фигурка объема \(out_i\) с пустотой внутри объемом \(in_i\) (конечно, \(out_i > in_i\)). У вас не так много свободного места в сумке, но, к счастью, вы знаете, что матрешки можно вкладывать друг в друга. Формально, назовем набор матрешек вкладываемым, если мы можем переупорядочить их таким образом, что первая матрешка вкладывается во вторую, вторая — в третью и так далее. Матрешка \(i\) вкладывается в матрешку \(j\), если \(out_i \le in_j\). Только последняя игрушка из вкладываемого набора будет занимать место в вашей сумке. Назовем пустотой вкладываемого набора общий объем пустого места внутри данной структуры. Очевидно, что она равна \(in_{i_1} + (in_{i_2} - out_{i_1}) + (in_{i_3} - out_{i_2}) + \dots + (in_{i_k} - out_{i_{k-1}})\), где \(i_1\), \(i_2\), ..., \(i_k\) — индексы выбранных матрешек в порядке их вкладывания. Наконец, назовем вкладываемый поднабор заданного набора достаточно большим, если в него нельзя добавить ни одной матрешки из набора так, чтобы не нарушить его вкладываемость. Вы хотели бы купить много матрешек, а потому выбираете достаточно большой вкладываемый поднабор. Но автора задачи сильно расстроит, если в вашей сумке будет потрачено зря слишком много места, поэтому вы выбираете достаточно большой вкладываемый поднабор, пустота которого минимально возможная среди всех достаточно больших поднаборов. И вот возник вопрос: как много различных поднаборов удовлетворяют всем требованиям (поднаборы достаточно большие, и нет другого достаточно большого поднабора с пустотой меньше заданного). Два поднабора считаются различными, если существует хотя бы один индекс \(i\) такой, что один поднабор содержит \(i\)-ю матрешку, а другой — нет. Так как ответ может быть очень большим — выведите его по модулю \(10^9 + 7\). Выходные данные Выведите единственное число — количество достаточно больших вкладываемых поднаборов таких, что пустота каждого такого поднабора минимально возможная. Так как ответ может быть очень большим, выведите его по модулю \(10^9 + 7\). Примечание В первом примере есть ровно \(6\) достаточно больших вкладываемых поднаборов с минимальной пустотой: - \(\{1, 5\}\): мы не можем добавить в него другие матрешки, не нарушая вкладываемость; пустота поднабора равна \(1\);
- \(\{1, 6\}\);
- \(\{2, 4, 5\}\);
- \(\{2, 4, 6\}\);
- \(\{3, 4, 5\}\);
- \(\{3, 4, 6\}\).
Других «хороших» поднаборов нет, потому что, например, поднабор \(\{6, 7\}\) не достаточно большой (в него можно добавить \(4\)-ю матрешку), а поднабор \(\{4, 6, 7\}\) имеет пустоту, равную \(2\). | |
![]()
|
|
D. Выведите 1337-строку...
Строки
Конструктив
Комбинаторика
математика
*1900
Подпоследовательность — это последовательность, которую можно получить из другой последовательности путем удаления некоторых элементов, не меняя порядок оставшихся элементов. Вам задано число \(n\). Вам нужно найти такую последовательность \(s\), состоящую из цифр \(\{1, 3, 7\}\), что она имеет ровно \(n\) подпоследовательностей \(1337\). Например, последовательность \(337133377\) имеет \(6\) подпоследовательностей \(1337\): - \(337\underline{1}3\underline{3}\underline{3}7\underline{7}\) (нужно удалить второй и пятый символы);
- \(337\underline{1}\underline{3}3\underline{3}7\underline{7}\) (нужно удалить третий и пятый символы);
- \(337\underline{1}\underline{3}\underline{3}37\underline{7}\) (нужно удалить четверты и пятый символы);
- \(337\underline{1}3\underline{3}\underline{3}\underline{7}7\) (нужно удалить второй и шестой символы);
- \(337\underline{1}\underline{3}3\underline{3}\underline{7}7\) (нужно удалить третий и шестой символы);
- \(337\underline{1}\underline{3}\underline{3}3\underline{7}7\) (нужно удалить четвертый и шестой символы).
Обратите внимание, что длина последовательности \(s\) не должна превышать \(10^5\). Вам нужно ответить на \(t\) независимых запросов. Выходные данные На \(i\)-й запрос выведите строку \(s_i\) (\(1 \le |s_i| \le 10^5\)), состоящую из цифр \(\{1, 3, 7\}\). Строка \(s_i\) должна содержать ровно \(n_i\) подпоследовательностей \(1337\). Если подходящих строк несколько, выведите любую из них. | |
![]()
|
|
E. Наташа, Саша и префиксные суммы
Комбинаторика
математика
дп
теория чисел
*2300
Два любимых числа Наташи — это \(n\) и \(1\), а два любимых числа Саши — \(m\) и \(-1\). Однажды Саша и Наташа встретились и выписали все возможные массивы из \(n+m\) элементов, в которых \(n\) элементов равны \(1\), а другие \(m\) элементов равны \(-1\). Для каждого массива они посчитали его максимальную префиксную сумму, возможно пустую, равную \(0\) (т. е. если каждая непустая префиксная сумма меньше нуля, то она считается равной нулю). Более формально, обозначим за \(f(a)\) максимальную префиксную сумму массива \(a_{1, \ldots ,l}\) длины \(l \geq 0\). Тогда: \(\)f(a) = \max (0, \smash{\displaystyle\max_{1 \leq i \leq l}} \sum_{j=1}^{i} a_j )\(\) Теперь они хотят посчитать сумму максимальных префиксных сумм по всем выписанным массивам и просят вас в этом помочь. Так как эта сумма может быть очень большой, выведите её по модулю \(998\: 244\: 853\). Выходные данные Выведите ответ на задачу по модулю \(998\: 244\: 853\). Примечание В первом примере существует единственный возможный массив: [-1,-1], его максимальная префиксная сумма равна \(0\). Во втором примере существует единственный возможный массив: [1,1], его максимальная префиксная сумма равна \(2\). В третьем примере существуют \(6\) возможных массивов: [1,1,-1,-1], f([1,1,-1,-1]) = 2 [1,-1,1,-1], f([1,-1,1,-1]) = 1 [1,-1,-1,1], f([1,-1,-1,1]) = 1 [-1,1,1,-1], f([-1,1,1,-1]) = 1 [-1,1,-1,1], f([-1,1,-1,1]) = 0 [-1,-1,1,1], f([-1,-1,1,1]) = 0 Ответ для третьего примера равен \(2+1+1+1+0+0 = 5\). | |
![]()
|
|
E. Очередная задача на матожидание
Строки
Комбинаторика
*3100
Даны целые числа \(n\), \(k\). Рассмотрим алфавит из \(k\) различных символов. Назовем красотой \(f(s)\) строки \(s\) количество таких индексов \(i\), \(1\le i<|s|\), что префикс \(s\) длины \(i\) равен суфиксу \(s\) длины \(i\). К примеру, красота строки \(abacaba\) равна \(2\), так как для \(i = 1, 3\) префикс и суфикс длины \(i\) совпадают. Рассмотрим все слова длины \(n\) в данном алфавите. Найдите матожидание \(f(s)^2\) выбранного случайно и равновероятно слова алфавита. Можно показать, что ее можно представить в виде \(\frac{P}{Q}\), где \(P\) и \(Q\) взаимно простые, и \(Q\) не делится на \(10^9 + 7\). Выведите \(P\cdot Q^{-1} \bmod 10^9 + 7\). Выходные данные Выведите единственное число — \(P\times Q^{-1} \bmod 10^9 + 7\). Примечание В первом примере, существует \(9\) слов \(2\) в алфавите размера \(3\) — \(aa\), \(ab\), \(ac\), \(ba\), \(bb\), \(bc\), \(ca\), \(cb\), \(cc\). У \(3\) из них красота \(1\) и у \(6\) из них красота \(0\), поэтому среднее значение равно \(\frac{1}{3}\). В третьем примере, существует только одно такое слово, и его красота равна \(99\), поэтому среднее значение равно \(99^2\). | |
![]()
|
|
D. Количество перестановок
Комбинаторика
*1800
Вам задано \(n\) пар чисел: \((a_1, b_1), (a_2, b_2), \dots , (a_n, b_n)\). Последовательность считается плохой, если она отсортирована в порядке неубывания по первым элементам или если она отсортирована в порядке неубывания по вторым элементам. Иначе последовательность считается хорошей. Примеры хороших и плохих последовательностей: - \(s = [(1, 2), (3, 2), (3, 1)]\) — плохая, потому что последовательность первых элементов отсортирована: \([1, 3, 3]\);
- \(s = [(1, 2), (3, 2), (1, 2)]\) — плохая, потому что последовательность вторых элементов отсортирована: \([2, 2, 2]\);
- \(s = [(1, 1), (2, 2), (3, 3)]\) — плохая, потому что обе последовательности (последовательность первых элементов и последовательность вторых элементов) отсортированы;
- \(s = [(1, 3), (3, 3), (2, 2)]\) — хорошая, потому что обе последовательности (последовательность первых \(([1, 3, 2])\) и последовательность вторых элементов \(([3, 3, 2])\)) не отсортированы.
Посчитайте количество перестановок длины \(n\) таких, что после применения этой перестановки к последовательности \(s\) она станет хорошей последовательностью. Перестановка \(p\) длины \(n\) это последовательность \(p_1, p_2, \dots , p_n\) состоящая из \(n\) различных чисел от \(1\) до \(n\) (\(1 \le p_i \le n\)). Если вы примените перестановку \(p_1, p_2, \dots , p_n\) к последовательности \(s_1, s_2, \dots , s_n\) вы получите последовательность \(s_{p_1}, s_{p_2}, \dots , s_{p_n}\). Например, если \(s = [(1, 2), (1, 3), (2, 3)]\) и \(p = [2, 3, 1]\), то \(s\) превратится \([(1, 3), (2, 3), (1, 2)]\). Выходные данные Выведите количество перестановок длины \(n\) таких, что после применения этой перестановки к последовательности \(s\) она станет хорошей последовательностью. Так как количество таких перестановок может быть велико, выведите ответ по модулю \(998244353\). Примечание В первом тестовом примере есть шесть перестановок длины \(3\): - если \(p = [1, 2, 3]\), то \(s = [(1, 1), (2, 2), (3, 1)]\) — плохая последовательность (отсортирована по первым элементам);
- если \(p = [1, 3, 2]\), то \(s = [(1, 1), (3, 1), (2, 2)]\) — плохая последовательность (отсортирована по вторым элементам);
- если \(p = [2, 1, 3]\), то \(s = [(2, 2), (1, 1), (3, 1)]\) — хорошая последовательность;
- если \(p = [2, 3, 1]\), то \(s = [(2, 2), (3, 1), (1, 1)]\) — хорошая последовательность;
- если \(p = [3, 1, 2]\), то \(s = [(3, 1), (1, 1), (2, 2)]\) — плохая последовательность (отсортирована по вторым элементам);
- если \(p = [3, 2, 1]\), то \(s = [(3, 1), (2, 2), (1, 1)]\) — хорошая последовательность.
| |
![]()
|
|
C. Счастливая перестановка
Перебор
Комбинаторика
теория чисел
*1900
Петя любит счастливые числа. Всем известно, что счастливыми являются положительные целые числа, в десятичной записи которых содержатся только счастливые цифры 4 и 7. Например, числа 47, 744, 4 являются счастливыми, а 5, 17, 467 — не являются. Однажды во сне Петя увидел лексикографически k-ую перестановку целых чисел от 1 до n. Определите, сколько счастливых чисел стоит в этой перестановке на позициях, номера которых также являются счастливыми числами. Выходные данные Если не существует k-ой перестановки чисел от 1 до n, выведите одно число «-1» (без кавычек). Иначе выведите ответ на задачу: количество таких i, что одновременно и i, и ai являются счастливыми числами. Примечание Перестановка — это упорядоченный набор из n элементов, в котором каждое целое число от 1 до n встречается ровно один раз. Элемент перестановки в позиции i обозначается ai (1 ≤ i ≤ n). Перестановка a лексикографически меньше перестановки b, если существует такое i (1 ≤ i ≤ n), что ai < bi, и для любого j (1 ≤ j < i) aj = bj. Составим список из всех возможный перестановок из n элементов, и отсортируем его в порядке лексикографического возрастания. Тогда лексикографически k-ая перестановка — k-ый элемент этого списка перестановок. В первом примере перестановка имеет вид: 1 2 3 4 6 7 5 Единственная подходящая позиция — 4. Во втором примере перестановка имеет вид: 2 1 3 4 Единственная подходящая позиция — 4. | |
![]()
|
|
B. Количество произведений
Комбинаторика
реализация
дп
*1400
В данной задаче вам задана последовательность \(a_1, a_2, \dots, a_n\), состоящая из \(n\) ненулевых целых чисел (то есть \(a_i \ne 0\)). Перед вами стоит задача найти два числа: - количество таких пар индексов \((l, r)\) \((l \le r)\), что произведение \(a_l \cdot a_{l + 1} \dots a_{r - 1} \cdot a_r\) строго отрицательно;
- количество таких пар индексов \((l, r)\) \((l \le r)\), что произведение \(a_l \cdot a_{l + 1} \dots a_{r - 1} \cdot a_r\) строго положительно.
Выходные данные Выведите два целых числа — количество отрезков со строго отрицательным произведением и количество отрезков со строго положительным произведением. | |
![]()
|
|
G. Граф и числа
Перебор
Комбинаторика
дп
битмаски
meet-in-the-middle
*2900
Вам задан неориентированный граф из \(n\) вершин и \(m\) ребер. Вы должны написать число на каждой вершине графа, каждое число должно быть равно \(0\) или \(1\). После этого на каждом ребре будет записана сумма чисел на двух вершинах, инцидентных этому ребру. Вы должны выбрать числа таким образом, чтобы было хотя бы одно ребро с числом \(0\), хотя бы одно ребро с числом \(1\) и хотя бы одно ребро с числом \(2\). Сколько способов так расставить числа? Два способа различны, если существует хотя бы одна вершина, на которой в разных способах записаны разные числа. Выходные данные Выведите одно целое число — количество способов так записать числа на вершинах, что есть хотя бы одно ребро с числом \(0\), хотя бы одно ребро с числом \(1\) и хотя бы одно ребро с числом \(2\). | |
![]()
|
|
F2. Неправильный ответ на тесте 233 (усложненная версия)
Комбинаторика
математика
*2400
Ваша программа снова не работает, на этот раз она получает вердикт «Неправильный ответ на тесте 233» Это усложненная версия задачи, в этой версии \(1 \le n \le 2\cdot10^5\). Вы можете взламывать эту задачу, если вы ее заблокировали. Но вы можете взламывать предыдущую версию задачи, только если вы заблокировали обе версии. В задаче идёт речь о тесте из \(n\) вопросов. Каждый вопрос содержит \(k\) вариантов ответа, и только один из них правильный. Ответ на \(i\)-й вопрос это \(h_{i}\). Если ваш ответ на вопрос \(i\) равен \(h_{i}\), вы получите \(1\) балл, в противном случае вы получите \(0\) баллов за этот вопрос. В этой задаче значения \(h_1, h_2, \dots, h_n\) вам известны (заданы). Однако, вы допустили ошибку в вашей программе! Расположим все \(n\) ответов на окружности по часовой стрелке. Из-за ошибки в вашей программе, они сдвигаются на один по циклу в направлении часовой стрелки. Формально, ошибка двигает ответ на вопрос \(i\) к вопросу \(i \bmod n + 1\). Так она двигает ответ на вопрос \(1\) к вопросу \(2\), ответ на вопрос \(2\) к вопросу \(3\), ..., ответ на вопрос \(n\) к вопросу \(1\). Назовем все \(n\) ответов вместе набором ответов. Всего есть \(k^n\) возможных наборов ответов. Вас интересует количество наборов ответов удовлетворяющих следующему условию: после сдвига по часовой стрелки на \(1\), итоговое количество баллов нового набора ответов строго больше чем старого. Вам необходимо найти это количество по модулю \(998\,244\,353\). Например, если \(n = 5\) и ваш набор ответов \(a=[1,2,3,4,5]\), он будет изменен вашей программой на \(a'=[5,1,2,3,4]\) из-за ошибки. Если набор правильных ответов равен \(h=[5,2,2,3,4]\), тогда набор ответов \(a\) получит \(1\) балл, а набор ответов \(a'\) получит \(4\) балла. Так как \(4 > 1\), набор ответов \(a=[1,2,3,4,5]\) удовлетворяет условию и должен быть посчитан. Выходные данные Выведите одно целое число — количество наборов ответов, удовлетворяющих данному ограничению, по модулю \(998\,244\,353\). Примечание На первый пример, корректные наборы ответов — это \([2,1,1], [2,1,2], [2,1,3], [3,1,1], [3,1,2], [3,1,3], [3,2,1], [3,2,2], [3,2,3]\). | |
![]()
|
|
E. Другое заполнение таблицы
Комбинаторика
математика
дп
*2300
Дана квадратная таблица \(n \times n\) и целое число \(k\). Поставьте в каждую клетку по одному целому числу так, чтобы все условия были удовлетворены. - Все числа в таблице должны быть от \(1\) до \(k\) включительно.
- Минимальное число \(i\)-й строки должно быть равно \(1\) (\(1 \le i \le n\)).
- Минимальное число \(j\)-го столбца должно быть равно \(1\) (\(1 \le j \le n\)).
Найдите количество способов расставить числа в клетках. Так как ответ может быть очень большой, найдите его по модулю \((10^{9} + 7)\).  Пример правильной (слева) и неправильной (справа) таблицы, где \(n=k=2\). Пример правильной (слева) и неправильной (справа) таблицы, где \(n=k=2\). Выходные данные Выведите ответ по модулю \((10^{9} + 7)\). Примечание В первом примере есть \(7\) способов. 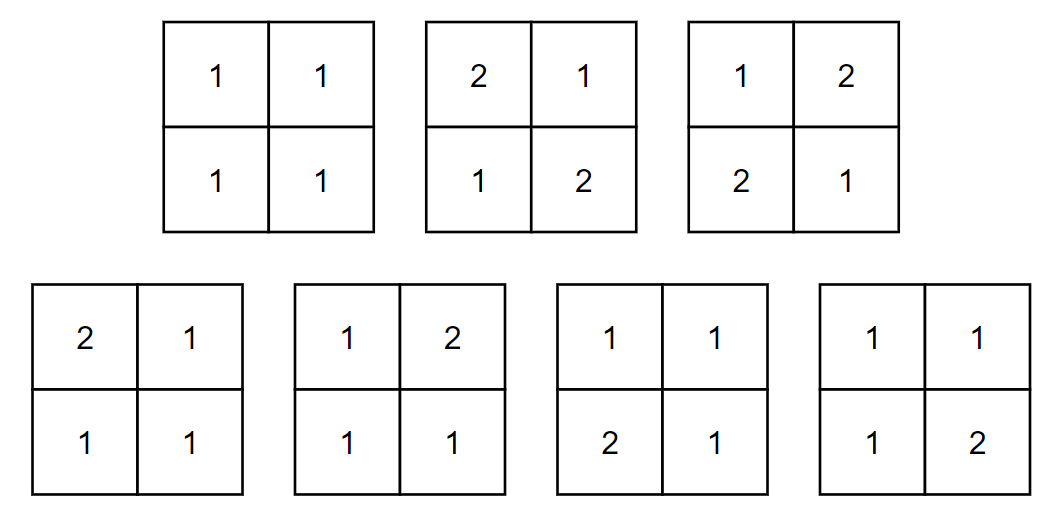 Во втором примере убедитесь, что вы выводите ответ по модулю \((10^{9} + 7)\). | |
![]()
|
|
C. Скобочки
Комбинаторика
дп
жадные алгоритмы
*2300
Двумерный массив называется скобочным массивом, если в каждой клетки находится одна из двух возможных скобочек — «(» или «)». Путь по клеткам двумерного массива называется монотонным, если любые две последовательные клетки в пути имеют общую сторону, и при этом каждая клетка пути находится либо ниже, либо правее предыдущей. Двумерный скобочный массив размером n × m называется правильным скобочным массивом, если любая строка, полученная выписыванием скобочек на каком-то монотонном пути из клетки (1, 1) в клетку (n, m), образует правильную скобочную последовательность. Определим операцию сравнения двух правильных скобочных массивов (a и b) следующим образом. Пусть задан двумерный массив приоритетов (p) — двумерный массив, заполненный различными целыми числами от 1 до nm. Найдем такую позицию (i, j) в двумерном массиве, что ai, j ≠ bi, j. Если таких позиций несколько, выберем ту, где число pi, j минимально. Если ai, j = «(», то a < b, иначе a > b. Если позиция (i, j) не найдена, то массивы считаются равными. Ваша задача — найти k-ый двумерный правильный скобочный массив. Гарантируется, что для заданных размеров n и m будет существовать не менее k двумерных правильных скобочных массивов. Выходные данные Выведите k-ый двумерный правильный скобочный массив. Примечание В первом примере существует лишь один правильный скобочный двумерный массив. Во втором и третьем примерах существует по два варианта. Напомним, что скобочная последовательность называется правильной, если путем вставки в нее символов «+» и «1» можно получить из нее корректное математическое выражение. Например, последовательности «(())()», «()» и «(()(()))» — правильные, в то время как «)(», «(()» и «(()))(» — нет. | |
![]()
|
|
B. Алиса и список подарков
Комбинаторика
математика
*1500
Недавно Алиса получила много подарков. Поэтому она решила упаковать некоторые из них в коробки и отправить своим друзьям. Всего есть \(n\) типов подарков. Подарки одного типа полностью одинаковые (то есть подарки одного типа неотличимы). Подарки разных типов отличаются между собой (то есть любые два подарка разных типов отличаются друг от друга). Количество подарков каждого типа, которое есть у Алисы, очень большое, поэтому мы можем считать его бесконечным. Также есть \(m\) коробок. Они все предназначены для разных людей, поэтому все попарно различны (предположим, что имена \(m\) ее друзей написаны на каждой коробке). Например, положить подарок первого типа в первую коробку, но не положить во вторую отличается от того, чтобы положить подарок первого типа во вторую коробку, но не положить в первую. Алиса хочет упаковать подарки по следующим правилам: - Она не будет класть больше одного подарка какого-то типа в одну и ту же коробку, поэтому в каждой коробке типы подарков должны быть различны (то есть каждая коробка содержит некоторое подмножество \(n\) типов подарков, пустые коробки разрешены);
- Подарок каждого типа должен быть упакован в хотя бы одну коробку.
Сейчас Алисе стало интересно, сколькими способами она может упаковать подарки. Помогите ей и посчитайте это количество. Поскольку ответ может быть слишком большим, найдите его по модулю \(10^9+7\). Посмотрите на примеры и их пояснение для лучшего понимания условия. Выходные данные Выведите одно целое число — количество способов упаковать подарки в коробки по правилам Алисы, взятое по модулю \(10^9+7\). Примечание В первом примере существует семь способов упаковать подарки: \(\{1\}\{\}\{\}\) \(\{\}\{1\}\{\}\) \(\{\}\{\}\{1\}\) \(\{1\}\{1\}\{\}\) \(\{\}\{1\}\{1\}\) \(\{1\}\{\}\{1\}\) \(\{1\}\{1\}\{1\}\) Во втором примере существует девять способов упаковать подарки: \(\{\}\{1,2\}\) \(\{1\}\{2\}\) \(\{1\}\{1,2\}\) \(\{2\}\{1\}\) \(\{2\}\{1,2\}\) \(\{1,2\}\{\}\) \(\{1,2\}\{1\}\) \(\{1,2\}\{2\}\) \(\{1,2\}\{1,2\}\) Например, способ упаковать подарки \(\{2\}\{2\}\) неправильный, потому что подарки первого типа должны быть упакованы в хотя бы одну коробку. | |
![]()
|
|
F. Сбалансированные расположения домино
Комбинаторика
дп
*2600
Рассмотрим прямоугольную доску из \(h\) строк и \(w\) столбцов, на которой расположены костяшки домино. Каждая костяшка покрывает ровно две клетки доски, которые имеют общую сторону. Каждая клетка покрыта не более чем одной костяшкой. Будем называть расположение домино на доске идеально сбалансированным, если никакая строка и никакой столбец не содержит пару клеток, покрытых разными костяшками. Другими словами, каждая строка и каждый столбец может не содержать ни одной покрытой клетки, содержать одну покрытую клетку либо содержать две покрытые клетки, принадлежащие одной костяшке. Вам дано идеально сбалансированное расположение домино на доске. Найдите число способов разместить ноль или более дополнительных костяшек на этой доске, чтобы расположение осталось идеально сбалансированным. Выведите это число по модулю \(998\,244\,353\). Выходные данные Выведите число способов разместить ноль или более дополнительных костяшек на доске, чтобы расположение осталось идеально сбалансированным, по модулю \(998\,244\,353\). Примечание В первом примере заданная доска выглядит так: 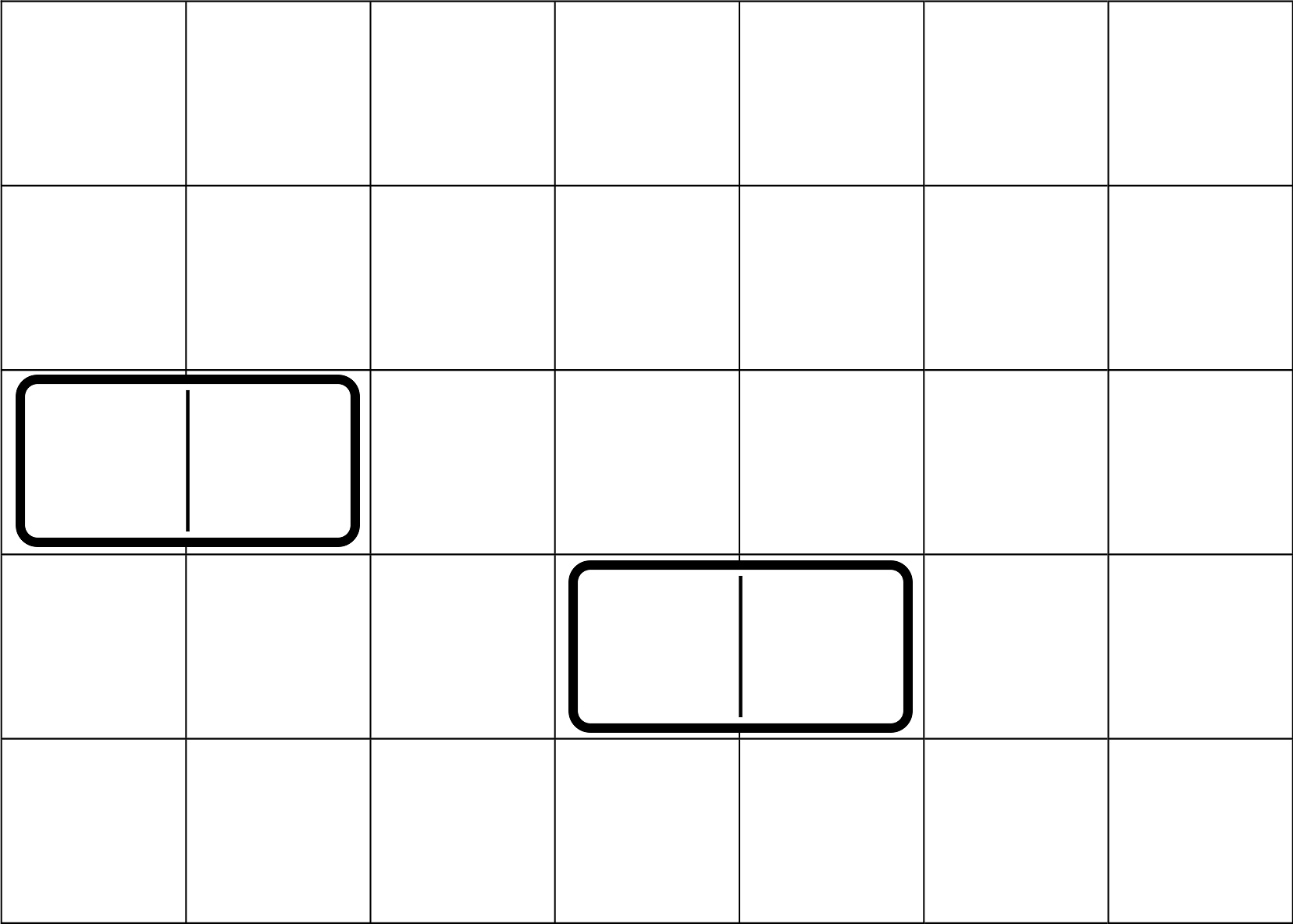
Вот \(8\) способов разместить ноль или более дополнительных костяшек, чтобы расположение осталось идеально сбалансированным: 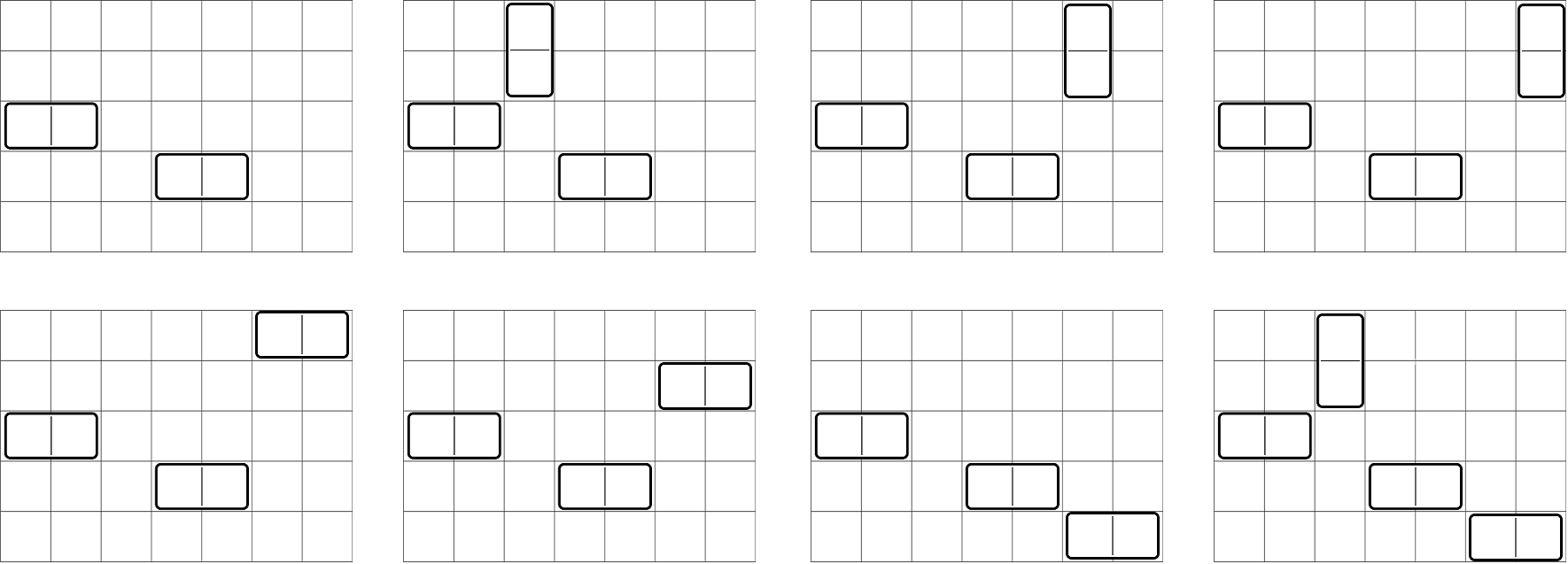
Во втором примере заданная доска выглядит так: 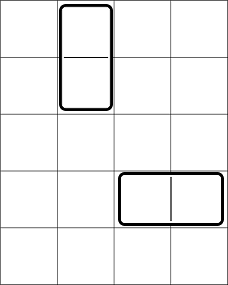
Ни одной дополнительной костяшки разместить нельзя. | |
![]()
|
|
D. AB-строка
Строки
Бинарный поиск
Комбинаторика
дп
*1900
Строка \(t_1t_2 \dots t_k\) является хорошей, если каждый символ этой строки принадлежит хотя бы одному палиндрому длины больше 1. Палиндром — это строка, читающаяся одинаково от первого символа к последнему и от последнего символа к первому. Например, строки A, BAB, ABBA, BAABBBAAB являются палиндромами, а строки AB, ABBBAA, BBBA — нет. Например, хорошим являются строки: - \(t\) = AABBB (символы \(t_1\), \(t_2\) принадлежат палиндрому \(t_1 \dots t_2\), а символы \(t_3\), \(t_4\), \(t_5\) — палиндрому \(t_3 \dots t_5\));
- \(t\) = ABAA (символы \(t_1\), \(t_2\), \(t_3\) принадлежат палиндрому \(t_1 \dots t_3\), а символ \(t_4\) — палиндрому \(t_3 \dots t_4\));
- \(t\) = AAAAA (все символы принадлежат палиндрому \(t_1 \dots t_5\));
Вам задана строка \(s\) длины \(n\), состоящая только из букв A и B. Посчитайте количество хороших подстрок строки \(s\). Выходные данные Выведите одно число — количество хороших подстрок строки \(s\). Примечание Первая строка содержит шесть хороших подстрок: \(s_1 \dots s_2\), \(s_1 \dots s_4\), \(s_1 \dots s_5\), \(s_3 \dots s_4\), \(s_3 \dots s_5\) и \(s_4 \dots s_5\). Вторая строка содержит две хороших подстроки: \(s_1 \dots s_2\), \(s_1 \dots s_3\) and \(s_2 \dots s_3\) | |
![]()
|
|
A. Иванушка-дурачок и теория вероятностей
Комбинаторика
математика
дп
*1700
Недавно Иванушка-дурачок захотел стать умнее и поэтому начал изучать теорию вероятностей. Он считает, что уже достаточно хорошо понимает данную тему, и стал этим хвастаться перед всеми. В качестве примера, Иванушка продемонстрировал окружающим концепцию случайного рисунка. Рисунок представляет собой клетчатое поле из \(n\) строкам и \(m\) столбцов, каждая клетка которого покрашена в белый или чёрный цвет. Иванушка считает, что рисунок случайный, если для любой клетки верно, что среди её соседей по стороне есть не более одной клетки такого же цвета, что и она. Его братья быстро выяснили, что задумал Иванушка. Они долго пытались объяснить ему, что он, дурачок, все ещё плохо понимает, что такое случайность. Но Иванушка так и не поверил им, поэтому они попросили помощи у вас. Они хотят найти количество различных случайных (по мнению Иванушки) рисунков. Два рисунка называются различными, если существует клетка, которая покрашена в разные цвета на этих рисунках. Так как число таких картинок может быть достаточно большим, выведите его по модулю \(10^9 + 7\). Выходные данные Выведите одно целое число — остаток от деления числа случайных рисунков на \(10^9 + 7\). Примечание На картинке ниже изображены все возможные случайные раскраски поля \(2\) на \(3\). 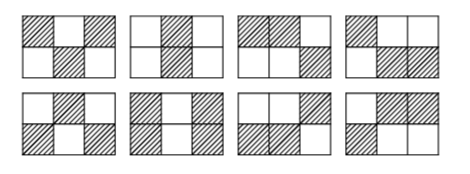 | |
![]()
|
|
B. Перестановки
Перебор
Комбинаторика
реализация
*1400
Дано n k-значных целых чисел. Требуется так переставить цифры в числах, чтобы разница между максимальным и минимальным числом была минимальна. Цифры во всех числах переставляются по одному и тому же правилу. Выходные данные Выведите одно число — минимальную возможную разницу между максимальным и минимальным числом после перестановки цифр во всех числах по одному и тому же правилу. Примечание В первом примере, если поменять порядок цифр в числах на (3,1,4,2), то 2-ое и 4-ое число будут равны 5237 и 2537 соответственно (они — максимальные и минимальные для такого порядка чисел). Во втором примере, поменяв вторые по порядку цифры с первыми, получим числа 100, 99 и 102. | |
![]()
|
|
F. Даниэль и весенняя уборка
Перебор
Комбинаторика
дп
*2300
битмаски
В ходе проведения очередной весенней уборки, Даниэль нашел старый калькулятор, который ему очень понравился. Однако кажется, что что-то в нем сломано. Когда он хочет посчитать \(1 + 3\) c помощью калькулятора, он получает \(2\) вместо \(4\). Но при вычислении \(1 + 4\) ответ получается правильный, \(5\). Озадаченный таким поведением, он вскрыл калькулятор и нашел разгадку: полные сумматоры стали полусумматорами! Теперь, когда он хочет посчитать \(a + b\) при помощи калькулатора, он получает ксор-сумму \(a \oplus b\) (определение можно прочитать по ссылке: https://ru.wikipedia.org/wiki/Сложение_по_модулю_2). Но как он уже заметил ранее, калькулятор иногда выдает правильные ответы. Поэтому его интересует, при данных \(l\) и \(r\) сколько существует таких пар целых чисел \((a, b)\), для которых выполняются следующие условия: \(\)a + b = a \oplus b\(\) \(\)l \leq a \leq r\(\) \(\)l \leq b \leq r\(\) Даниэль Бармен, однако, сейчас направляется в бар, а вернется только через пару часов. Он советует вам решить эту задачу до его возвращения, или же вы будете забанены. Выходные данные Выведите \(t\) целых чисел, \(i\)-е число должно быть ответом на \(i\)-й набор входных данных. Примечание \(a \oplus b\) обозначает побитовое исключающее ИЛИ \(a\) и \(b\). В первом примере подходящие пары: \((1, 2)\), \((1, 4)\), \((2, 1)\), \((2, 4)\), \((3, 4)\), \((4, 1)\), \((4, 2)\), и \((4, 3)\). | |
![]()
|
|
F. Красно-белый забор
Комбинаторика
*2500
бпф
Поликарп хочет построить забор возле дома. У него есть в запасе \(n\) белых досок и \(k\) красных досок, которые он может использовать. Каждая доска характеризуется своей длиной — целым числом. Хороший забор должен состоять из ровно одной красной доски и нескольких (возможно, нуля) белых досок. Красная доска должна быть самой длинной в заборе (каждая белая доска, использованная в заборе, должна быть строго короче), и последовательность длин досок забора должна быть возрастающей перед красной доской и убывающей после нее. Формально, если использовано \(m\) досок, и их длины \(l_1\), \(l_2\), ..., \(l_m\) в порядке их нахождения в заборе слева направо (назовем такой массив \([l_1, l_2, \dots, l_m]\) массивом длин), то должны выполняться следующие условия: - в заборе должна использоваться ровно одна красная доска (пусть она находится в позиции \(j\));
- для каждого \(i \in [1, j - 1]\) \(l_i < l_{i + 1}\);
- для каждого \(i \in [j, m - 1]\) \(l_i > l_{i + 1}\).
Поликарп построит свой забор следующим образом: он поставит все доски слева направо на землю (высоту \(0\)), без зазоров, то есть эти доски образуют многоугольник: 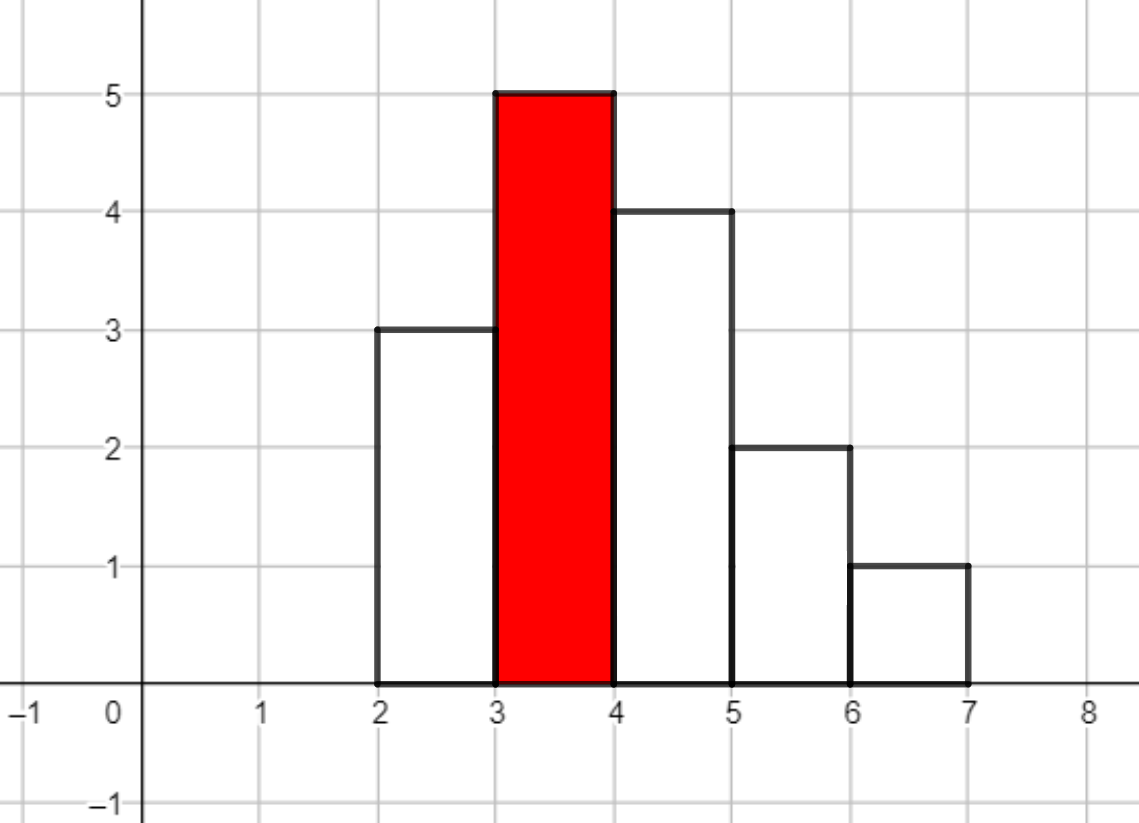 Пример: забор с массивом длин \([3, 5, 4, 2, 1]\). Вторая доска — красная. Периметр этого забора равен \(20\). Пример: забор с массивом длин \([3, 5, 4, 2, 1]\). Вторая доска — красная. Периметр этого забора равен \(20\). Поликарпу интересны только заборы особых периметров. У него есть \(q\) любимых четных целых чисел (назовем их \(Q_1\), \(Q_2\), ..., \(Q_q\)), и для каждого такого \(Q_i\), он хочет посчитать количество различных заборов с периметром \(Q_i\), которые возможно построить (два забора считаются различными, если их массивы длин различны). Можете ли вы помочь ему посчитать эти значения? Выходные данные Для каждого \(Q_i\), выведите одно число — количество хороших заборов с периметром \(Q_i\), которые может построить Поликарп, взятое по модулю \(998244353\). Примечание Возможные заборы для первого примера, заданные своими массивами высот (красная доска выделена): - с периметром \(6\): \([\textbf{2}]\);
- с периметром \(8\): \([1, \textbf{2}]\), \([\textbf{2}, 1]\);
- с периметром \(10\): \([1, \textbf{2}, 1]\), \([\textbf{4}]\);
- с периметром \(12\): \([1, \textbf{4}]\), \([3, \textbf{4}]\), \([\textbf{4}, 1]\), \([\textbf{4}, 3]\);
- с периметром \(14\): \([1, \textbf{4}, 1]\), \([1, \textbf{4}, 3]\), \([3, \textbf{4}, 1]\), \([3, \textbf{4}, 3]\), \([1, 3, \textbf{4}]\), \([\textbf{4}, 3, 1]\);
- с периметром \(16\): \([1, \textbf{4}, 3, 1]\), \([3, \textbf{4}, 3, 1]\), \([1, 3, \textbf{4}, 1]\), \([1, 3, \textbf{4}, 3]\);
- с периметром \(18\): \([1, 3, \textbf{4}, 3, 1]\).
| |
![]()
|
|
E. Отправьте дерево Чарли
Деревья
Комбинаторика
поиск в глубину и подобное
снм
*3300
Рождество постучало в дверь, и наш главный герой, Боб, готовил захватывающий подарок для своего давнего второго лучшего друга Чарли. Поскольку ему не нравится шоколад, он решил вместо этого украсить дерево. Дерево Боба можно представить в виде неориентированного связного графа с \(n\) вершинами (пронумерованными от \(1\) до \(n\)) и \(n-1\) ребрами. Первоначально Боб поместил украшение с номером \(i\) на вершину \(i\) для каждого \(1 \le i \le n\). Однако, поскольку такая простая композиция получилась некрасивой, он решил немного переместить украшения. Формально Боб сделал следующие шаги: - Сначала он выписал все \(n-1\) ребра в некотором порядке.
- Затем он рассмотрел все ребра один за другим в таком порядке. Для каждого ребра \((u, v)\) он поменял местами украшение вершины \(u\) с украшением вершины \(v\).
После этого Боб оказался довольным такой аранжировкой и пошел спать. На следующее утро Боб просыпается, только чтобы узнать, что его прекрасная аранжировка разрушена! Прошлой ночью младший брат Боба, Бобо, бросил некоторые украшения на пол, когда играл с деревом. К счастью, украшения не были потеряны, поэтому Боб может восстановить дерево в кратчайшие сроки. Однако он полностью забыл, как дерево выглядело вчера. Поэтому, учитывая номера украшений, которые все еще на дереве, Боб хочет узнать количество возможных конфигураций дерева. Поскольку результат может быть довольно большим, Боб будет рад, если вы сможете вывести результат по модулю \(1000000007\) (\(10^9+7\)). Обратите внимание, что, возможно, не существует никаких возможных конфигураций. Выходные данные Выведите количество конфигураций по модулю \(1000000007\) (\(10^9+7\)). Примечание В первом примере возможными конфигурациями дерева являются \([2, 4, 1, 3]\) и \([3, 4, 2, 1]\). Во втором примере обратите внимание, что есть \(4! = 24\) возможных перестановок ребер, но возможны только \(12\) различные финальные конфигурации. В третьем примере легко увидеть, что украшение с номером \(1\) не может оставаться в вершине \(1\) после перестановок. | |
![]()
|
|
D1. Красивая скобочная последовательность (простая версия)
Теория вероятностей
Комбинаторика
дп
*2600
Это простая версия этой задачи. Единственное отличие в ограничении на \(n\) — длине входной строки. В этой версии, \(1 \leq n \leq 2000\). Сложная версия этой задачи не предлагается в раунде для второго дивизиона. Определим правильную скобочную последовательность и ее глубину следующим образом: - Пустая строка это правильная скобочная последовательность глубины \(0\);
- Если «s» это правильная скобочная последовательность глубины \(d\) тогда «(s)» это правильная скобочная последовательность глубины \(d + 1\);
- Если «s» и «t» это две правильные скобочные последовательности тогда их конкатенация «st» это правильная скобочная последовательность с глубиной равной максимальной из глубин \(s\) и \(t\).
Для (не обязательно правильной) скобочной последовательности \(s\) мы определяем ее глубину как максимальную глубину любой правильной скобочной последовательности, которая может быть получена с помощью удаления некоторых символов из \(s\) (возможно нуля). Например, скобочная последовательность \(s = \)«())(())» имеет глубину \(2\), потому что при удалении третьего символа мы получим правильную скобочную последовательность «()(())» глубины \(2\). Дана строка \(a\), состоящая из символов '(', ')' и '?'. Рассмотрим все (не обязательно правильные) скобочные последовательности, получающиеся заменой всех символов '?' в строке \(a\) на '(' или ')'. Посчитайте сумму глубин всех таких скобочных последовательностей. Так как это число может быть очень большим, найдите его по модулю \(998244353\). Взломы в первом дивизионе по этой задачи могут быть сделаны, только если простая и сложная версия этой задачи сданы. Выходные данные Выведите ответ по модулю \(998244353\) в единственной строке. Примечание В первом тесте, мы можем получить \(4\) скобочные последовательности меняя все символы '?' на '(' или ')': - «((». Ее глубина \(0\);
- «))». Ее глубина \(0\);
- «)(». Ее глубина \(0\);
- «()». Ее глубина \(1\).
Поэтому, ответ равен \(1 = 0 + 0 + 0 + 1\). Во втором тесте, мы можем получить \(4\) скобочные последовательности меняя все символы '?' на '(' или ')': - «(((())». Ее глубина \(2\);
- «()()))». Ее глубина \(2\);
- «((()))». Ее глубина \(3\);
- «()(())». Ее глубина \(2\).
Поэтому, ответ равен \(9 = 2 + 2 + 3 + 2\). | |
![]()
|
|
D2. Красивая скобочная последовательность (сложная версия)
Теория вероятностей
Комбинаторика
*2900
Это сложная версия этой задачи. Единственное отличие в ограничении на \(n\) — длине входной строки. В этой версии, \(1 \leq n \leq 10^6\). Определим правильную скобочную последовательность и ее глубину следующим образом: - Пустая строка это правильная скобочная последовательность глубины \(0\);
- Если «s» это правильная скобочная последовательность глубины \(d\) тогда «(s)» это правильная скобочная последовательность глубины \(d + 1\);
- Если «s» и «t» это две правильные скобочные последовательности тогда их конкатенация «st» это правильная скобочная последовательность с глубиной равной максимальной из глубин \(s\) и \(t\).
Для (не обязательно правильной) скобочной последовательности \(s\) мы определяем ее глубину как максимальную глубину любой правильной скобочной последовательности, которая может быть получена с помощью удаления некоторых символов из \(s\) (возможно нуля). Например, скобочная последовательность \(s = \)«())(())» имеет глубину \(2\), потому что при удалении третьего символа мы получим правильную скобочную последовательность «()(())» глубины \(2\). Дана строка \(a\), состоящая из символов '(', ')' и '?'. Рассмотрим все (не обязательно правильные) скобочные последовательности, получающиеся заменой всех символов '?' в строке \(a\) на '(' или ')'. Посчитайте сумму глубин всех таких скобочных последовательностей. Так как это число может быть очень большим, найдите его по модулю \(998244353\). Взломы по этой задачи могут быть сделаны, только если простая и сложная версия этой задачи сданы. Выходные данные Выведите ответ по модулю \(998244353\) в единственной строке. Примечание В первом тесте, мы можем получить \(4\) скобочные последовательности меняя все символы '?' на '(' или ')': - «((». Ее глубина \(0\);
- «))». Ее глубина \(0\);
- «)(». Ее глубина \(0\);
- «()». Ее глубина \(1\).
Поэтому, ответ равен \(1 = 0 + 0 + 0 + 1\). Во втором тесте, мы можем получить \(4\) скобочные последовательности меняя все символы '?' на '(' или ')': - «(((())». Ее глубина \(2\);
- «()()))». Ее глубина \(2\);
- «((()))». Ее глубина \(3\);
- «()(())». Ее глубина \(2\).
Поэтому, ответ равен \(9 = 2 + 2 + 3 + 2\). | |
![]()
|
|
K. Key Storage
Комбинаторика
математика
*2100
Karl is developing a key storage service. Each user has a positive integer key. Karl knows that storing keys in plain text is bad practice. So, instead of storing a key, he decided to store a fingerprint of a key. However, using some existing fingerprint algorithm looked too boring to him, so he invented his own one. Karl's fingerprint is calculated by the following process: divide the given integer by 2, then divide the result by 3, then divide the result by 4, and so on, until we get a result that equals zero (we are speaking about integer division each time). The fingerprint is defined as the multiset of the remainders of these divisions. For example, this is how Karl's fingerprint algorithm is applied to the key 11: 11 divided by 2 has remainder 1 and result 5, then 5 divided by 3 has remainder 2 and result 1, and 1 divided by 4 has remainder 1 and result 0. Thus, the key 11 produces the sequence of remainders \([1, 2, 1]\) and has the fingerprint multiset \(\{1, 1, 2\}\). Ksenia wants to prove that Karl's fingerprint algorithm is not very good. For example, she found that both keys 178800 and 123456 produce the fingerprint of \(\{0, 0, 0, 0, 2, 3, 3, 4\}\). Thus, users are at risk of fingerprint collision with some commonly used and easy to guess keys like 123456. Ksenia wants to make her words more persuasive. She wants to calculate the number of other keys that have the same fingerprint as the keys in the given list of some commonly used keys. Your task is to help her. Output For each of the keys print one integer — the number of other keys that have the same fingerprint. Note The other key with the same fingerprint as 11 is 15. 15 produces a sequence of remainders \([1, 1, 2]\). So both numbers have the fingerprint multiset \(\{1, 1, 2\}\). | |
![]()
|
|
E. Общее число
Бинарный поиск
Комбинаторика
математика
*2100
дп
Введем определение функции \(f(x)\): \(\) \begin{matrix} f(x) & = & \left\{ \begin{matrix} \frac{x}{2} & \mbox{если } x \text{ четное} \\ x - 1 & \mbox{в противном случае } \end{matrix} \right. \end{matrix} \(\) Можно заметить, что если мы выбираем некоторое число \(v\) и применяем к нему функцию \(f\), затем применяем функцию \(f\) к числу \(f(v)\), и так далее, то рано или поздно мы получим значение \(1\). Выпишем все промежуточные значения на пути от \(v\) до \(1\) и назовем все выписанные значения \(path(v)\). Например, \(path(1) = [1]\), \(path(15) = [15, 14, 7, 6, 3, 2, 1]\), \(path(32) = [32, 16, 8, 4, 2, 1]\). Выпишем все \(path(x)\) для всех \(x\) от \(1\) до \(n\). Перед вами стоит задача: определить максимальное число \(m\) такое, что \(m\) встречается хотя бы в \(k\) различных \(path(x)\). Иначе говоря, нужно найти такое максимальное \(y\), что \(\left| \{ x ~|~ 1 \le x \le n, y \in path(x) \} \right| \ge k\). Выходные данные Выведите максимальное число \(m\) такое, что \(m\) встречается хотя бы в \(k\) различных \(path(x)\). Примечание В первом примере ответ равен \(5\), так как \(5\) встретится в \(path(5)\), в \(path(10)\) и в \(path(11)\). Во втором примере ответ равен \(4\), так как \(4\) встретится в \(path(4)\), в \(path(5)\), в \(path(8)\), в \(path(9)\), в \(path(10)\) и в \(path(11)\). В третьем примере \(n = k\), поэтому ответ равен \(1\), так как \(1\) это единственное число, содержащееся в путях всех чисел от \(1\) до \(20\). | |
![]()
|
|
C. Очередная сломанная клавиатура
Комбинаторика
реализация
дп
*1200
Недавно Norge нашел строку \(s = s_1 s_2 \ldots s_n\), состоящую из \(n\) строчных букв латинского алфавита. В качестве упражнения для улучшения скорости печатания он решил напечатать все подстроки \(s\). Да, все \(\frac{n (n + 1)}{2}\) из них! Подстрокой строки \(s\) называется непустая строка \(x = s[a \ldots b] = s_{a} s_{a + 1} \ldots s_{b}\) (\(1 \leq a \leq b \leq n\)). Например, «auto» и «ton» являются подстроками «automaton». Незадолго до начала упражнения Norge осознал, что его клавиатура сломана, а если говорить более точно, он может использовать только \(k\) латинских букв \(c_1, c_2, \ldots, c_k\) из \(26\). После этого Norge стало интересно, как много подстрок строки \(s\) он сможет написать, используя свою сломанную клавиатуру. Помогите ему найти это число. Выходные данные Выведите одно целое число — количество подстрок \(s\), которые можно написать, используя только доступные буквы \(c_1, c_2, \ldots, c_k\). Примечание В первом примере Norge может напечатать подстроки \(s[1\ldots2]\), \(s[2\ldots3]\), \(s[1\ldots3]\), \(s[1\ldots1]\), \(s[2\ldots2]\), \(s[3\ldots3]\), \(s[5\ldots6]\), \(s[6\ldots7]\), \(s[5\ldots7]\), \(s[5\ldots5]\), \(s[6\ldots6]\), \(s[7\ldots7]\). | |
![]()
|
|
F. Карты
Теория вероятностей
Комбинаторика
математика
дп
теория чисел
*2600
Рассмотрим следующий эксперимент. У вас есть колода из \(m\) карт, ровно одна из них — джокер. \(n\) раз вы производите следующие действия: перемешиваете колоду, берете верхнюю карту, просматриваете ее и возвращаете ее в колоду. Пусть \(x\) — количество раз, когда вы брали с вершины колоды джокера. Предполагая, что при каждом перемешивании колоды все \(m!\) перестановок карт равновероятны, чему равно математическое ожидание \(x^k\)? Выведите ответ по модулю \(998244353\). Выходные данные Выведите одно число — математическое ожидание \(x^k\), взятое по модулю \(998244353\) (ответ всегда можно представить в виде несократимой дроби \(\frac{a}{b}\), где \(b \mod 998244353 \ne 0\); выведите \(a \cdot b^{-1} \mod 998244353\)). | |
![]()
|
|
D. Робот Деда Мороза
Теория вероятностей
Комбинаторика
математика
*1700
Дед Мороз получил письма от \(n\) разных детей в течение всего этого года. Конечно, каждый ребенок хочет получить от Деда Мороза какие-то подарки: в частности, \(i\)-й малыш попросил подарить ему один из \(k_i\) различных предметов в качестве подарка. Некоторые предметы могли попросить несколько детей. Дед Мороз очень занят, поэтому он хочет, чтобы Новогодний Робот выбрал подарки для всех детей. К сожалению, алгоритм выбора подарков Роботом содержит ошибку. Чтобы выбрать подарок для какого-то малыша, Робот делает следующее: - равновероятно выбирает одного ребенка \(x\) среди всех \(n\) детей;
- равновероятно выбирает некоторый предмет \(y\) среди всех \(k_x\) предметов, которые хочет ребенок \(x\);
- равновероятно выбирает ребенка \(z\), который получит подарок, среди всех \(n\) детей (этот выбор не зависит от выбора \(x\) и \(y\)); результирующая тройка \((x, y, z)\) называется выбором Робота.
Если ребенок \(z\) хотел получить предмет \(y\), то выбор корректный. В противном случае, выбор Робота будет некорректным. Дед Мороз знает об ошибке, но он не может оценить, действительно ли эта ошибка серьезна. Для этого он хочет знать вероятность того, что один выбор, сгенерированный в соответствии с вышеупомянутым алгоритмом, корректен. Вы можете ему помочь? Выходные данные Выведите вероятность того, что Робот сделает корректный выбор следующим образом: Пусть эта вероятность представлена в виде неприводимой дроби \(\frac{x}{y}\). Вам необходимо вывести \(x \cdot y^{-1} \mod 998244353\), где \(y^{-1}\) является обратным элементом к \(y\) по модулю \(998244353\) (такое целое число, что \(y \cdot y^{-1}\) имеет остаток \(1\) по модулю \(998244353\)). | |
![]()
|
|
E. Новогодние перестановки
Комбинаторика
дп
*2700
Да, мы не смогли придумать новогоднюю легенду для этой задачи. Перестановка длины \(n\) — это массив \(n\) целых чисел, таких что каждое целое число от \(1\) до \(n\) появляется в нем ровно один раз. Элемент \(y\) перестановки \(p\) достижим из элемента \(x\), Если \(x = y\), или \(p_x = y\), или \(p_{p_x} = y\) и так далее. Определим декомпозицию перестановки \(p\) следующим образом: сначала у нас есть перестановка \(p\), все элементы которой не помечены, и пустой список \(l\). Затем мы делаем следующее: пока хотя бы один элемент не помечен в \(p\), находим самый левый такой элемент, перечисляем все элементы, которые достижимы из него в порядке их появления в \(p\), помечаем все эти элементы, затем циклически сдвигаем список этих элементов так, чтобы максимум появился в первой позиции, и добавляем этот список как элемент в \(l\). После того, как все элементы помечены, \(l\) является результатом этой декомпозиции. Например, если мы хотим построить декомпозицию \(p = [5, 4, 2, 3, 1, 7, 8, 6]\), мы делаем следующее: - изначально \(p = [5, 4, 2, 3, 1, 7, 8, 6]\) (жирным шрифтом выделены помеченные элементы), \(l = []\);
- самый левый не помеченный элемент — \(5\); \(5\) и \(1\) достижимы из него, поэтому список, который мы хотим сдвинуть, — \([5, 1]\); нет необходимости сдвигать его, так как максимум уже является первым элементом;
- \(p = [\textbf{5}, 4, 2, 3, \textbf{1}, 7, 8, 6]\), \(l = [[5, 1]]\);
- самый левый не помеченный элемент — \(4\), список достижимых элементов из него — это \([4, 2, 3]\); максимум уже первый элемент, поэтому сдвигать его не нужно;
- \(p = [\textbf{5}, \textbf{4}, \textbf{2}, \textbf{3}, \textbf{1}, 7, 8, 6]\), \(l = [[5, 1], [4, 2, 3]]\);
- самый левый не помеченный элемент — \(7\), список достижимых элементов из него — это \([7, 8, 6]\); мы должны сдвинуть его, чтобы он стал \([8, 6, 7]\);
- \(p = [\textbf{5}, \textbf{4}, \textbf{2}, \textbf{3}, \textbf{1}, \textbf{7}, \textbf{8}, \textbf{6}]\), \(l = [[5, 1], [4, 2, 3], [8, 6, 7]]\);
- все элементы помечены, так что \([[5, 1], [4, 2, 3], [8, 6, 7]]\) — результат декомпозиции.
Определим новогоднее преобразование перестановки следующим образом: построим декомпозицию этой перестановки; затем отсортируем все списки в декомпозиции по возрастанию первых элементов (мы не меняем местами элементы в этих списках, только сами списки); затем объединим списки в один список, который становится новой перестановкой. Например, новогоднее преобразование \(p = [5, 4, 2, 3, 1, 7, 8, 6]\) строится следующим образом: - декомпозиция равна \([[5, 1], [4, 2, 3], [8, 6, 7]]\);
- после сортировки, декомпозиция становится равна \([[4, 2, 3], [5, 1], [8, 6, 7]]\);
- \([4, 2, 3, 5, 1, 8, 6, 7]\) — результат преобразования.
Назовем перестановку хорошей, если результат ее преобразования совпадает с самой перестановкой. Например, \([4, 3, 1, 2, 8, 5, 6, 7]\) это хорошая перестановка; а \([5, 4, 2, 3, 1, 7, 8, 6]\) плохая, так как результатом преобразования является \([4, 2, 3, 5, 1, 8, 6, 7]\). Ваша задача состоит в следующем: при заданных \(n\) и \(k\) найти \(k\)-ю (лексикографически) хорошую перестановку длины \(n\). Выходные данные Для каждого набора входных данных выведите ответ на него следующим образом: если число хороших перестановок длины \(n\) меньше \(k\), выведите одно целое число \(-1\); в противном случае выведите \(k\)-ю (в лексикографическом порядке) хорошую перестановку из \(n\) элементов. | |
![]()
|
|
C. Игра с прямоугольниками
Комбинаторика
дп
*2000
В этой задаче Аня и Маша играют в игру. Изначально у них есть клетчатый лист бумаги, на котором нарисован прямоугольник n × m (только рамка, без внутренности). Аня и Маша делают ходы по очереди, первой ходит Аня. На каждом ходу надо внутри предыдущего прямоугольника нарисовать по линиям сетки прямоугольник, который не будет иметь с ним общих точек. Обратите внимание, что, опять же, рисуется только рамка, без внутренности. В этой игре никто не выигрывает — Аня и Маша просто играют, пока не сделают в сумме k ходов. Посчитайте, сколько в этой игре вариантов развития событий. Выходные данные Выведите единственное число — количество вариантов развития событий в этой игре. Поскольку это число может быть очень большим, выведите его значение по модулю 1000000007 (109 + 7). Примечание Два варианта развития событий считаются различными, если получившиеся в итоге картинки различны, то есть в одном варианте нарисован прямоугольник, который не нарисован в другом варианте. В первом примере у Ани, которая делает первый и единственный ход, есть единственный вариант хода — вставить квадратик 1 × 1 в данный квадрат 3 × 3. Во втором примере у Ани есть целых 9 вариантов: 4 способа нарисовать квадратик 1 × 1, 2 способа поставить прямоугольник 1 × 2 вертикально, еще 2 — поставить его горизонтально, и еще один способ нарисовать квадратик 2 × 2. | |
![]()
|
|
F. Межгалактическая головоломка
Конструктив
Комбинаторика
математика
*3400
Вы межгалактический хирург, и у вас есть инопланетный пациент. Для целей этой задачи мы будем моделировать тело этого пациента, используя прямоугольную сетку размером \(2 \times (2k + 1)\). Инопланетянин имеет \(4k + 1\) различных органов, пронумерованных целыми числами от \(1\) до \(4k + 1\). У здоровых инопланетян органы устроены особым образом. Например, вот как будут расположены органы здорового инопланетянина, если смотреть сверху, для \(k = 4\):  Здесь E обозначает пустое место. В общем случае у здорового инопланетянина первая строка содержит органы от \(1\) до \(2k + 1\) (в порядке слева направо) и вторая строка содержит органы от \(2k + 2\) до \(4k + 1\) (в порядке слева направо) и пустое место после этого, в конце второй строки. Органы вашего пациента целы, и находятся внутри его тела, но они каким-то образом перемешались! Ваша задача, как межгалактического хирурга, состоит в том, чтобы вернуть все органы свои места. Все органы пришельца должны находиться в его теле в течение всей процедуры. Это означает, что в любой момент времени во время процедуры есть ровно одна ячейка (в сетке), которая пуста. Кроме того, вы можете перемещать органы только одним из следующих способов: - Вы можете поменять пустую позицию E с любым органом непосредственно слева или справа от нее (если они существуют). Вы делаете это, перемещая рассматриваемый орган в пустое место;
- Вы можете поменять пустую позицию E с любым органом непосредственно сверху или снизу от нее (если они существуют). Это можно сделать только если пустая позиция в самой левой колонке, самой правой колонке или центральной колонке. Аналогично вы перемещаете рассматриваемый орган в пустое место.
Вашей задачей является получить последовательность шагов которые вы должны сделать при операции, чтобы вернуть все \(4k + 1\) органов пациента на правильные места. Если это сделать невозможно, вы должны сообщить об этом. Выходные данные Для каждого тестового случая выведите сначала строку, содержащую: - SURGERY COMPLETE если возможно вернуть все органы на изначальные места по правилам;
- SURGERY FAILED если это невозможно.
Если было невозможно, то это была единственная строка вывода для этого тестового случая. Если это возможно, выведите строку, описывающую последовательность ходов, чтобы вернуть все органы на изначальные места. Строкой ходов (возможно пустой) является строка из символов u, d, l или r, обозначающие действия замены пустой позиции с органом непосредственно сверху, снизу, слева или справа, соответсвенно. Выведите последовательность ходов в следующей строке в этом формате. Для удобства, вы можете использовать сокращения для уменьшения размера вывода. Вы можете использовать большие латинские буквы как сокращения последовательности команд. Например, вы можете использовать T для представления строки lddrr. Эти сокращения могут использоваться внутри других сокращений! Например, вы можете использовать E для того, чтобы обозначить TruT, и так далее. Вы можете использовать любое количество больших латинских букв (включая ноль) как сокращения. Единственные требования это: - Суммарная длина выведенных строк для одного тестового случая не превосходит \(10^4\);
- Не должно быть циклов на сокращениях, которые достижимы из главной последовательности;
- Итоговая последовательность конечна после раскрытия всех замен. Заметьте, что итоговая последовательность (после раскрытия) может быть длиннее чем \(10^4\), единственное ограничение это конечность.
Например, если T = lddrr, E = TruT и R = rrr, тогда TurTlER раскроется в: - TurTlER
- lddrrurTlER
- lddrrurlddrrlER
- lddrrurlddrrlTruTR
- lddrrurlddrrllddrrruTR
- lddrrurlddrrllddrrrulddrrR
- lddrrurlddrrllddrrrulddrrrrr
Для того, чтобы использовать сокращение выведите их по одному в строке как большой латинский символ, затем пробел, затем строка, которую сокращает этот символ. Вы можете выводить сокращения в любом порядке. После этого вы должны вывести строку содержащую слово DONE. Замечание: вам нужно вывести DONE даже если вы не собираетесь использовать сокращения. Ваша последовательность не обязана получиться кратчайшей. Любая подходящая последовательность перемещений (удовлетворяющая всем ограничениям) будет принята. Примечание Так три сокращения выглядят в первом тестовом случае: Тогда последовательность команд IR раскроется в: - IR
- lldllR
- lldllSrS
- lldllrrrS
- lldllrrrrr
| |
![]()
|
|
B. Новый год и восходящая последовательность
Бинарный поиск
Структуры данных
Комбинаторика
реализация
дп
*1400
сортировки
Последовательность \(a = [a_1, a_2, \ldots, a_l]\) длиной \(l\) имеет восход, если существует пара таких индексов \((i, j)\), что \(1 \le i < j \le l\) и \(a_i < a_j\). Например, последовательность \([0, 2, 0, 2, 0]\) имеет восход из-за пары индексов \((1, 4)\), но последовательность \([4, 3, 3, 3, 1]\) не имеет восхода. Назовем конкатенацией двух последовательностей \(p\) и \(q\) такую последовательность, которая получится при последовательной записи сначала \(p\), затем \(q\) друг за другом, не меняя порядок элементов в них. Например, конкатенация последовательностей \([0, 2, 0, 2, 0]\) и \([4, 3, 3, 3, 1]\) равна последовательности \([0, 2, 0, 2, 0, 4, 3, 3, 3, 1]\). Конкатенация последовательностей \(p\) и \(q\) обозначается как \(p+q\). Кенгун считает, что последовательность с восходом приносит удачу. Поэтому он хочет сделать много таких последовательностей на новый год. У Кенгун есть \(n\) последовательностей \(s_1, s_2, \ldots, s_n\), которые могут иметь разную длину. Кенгун рассмотрит \(n^2\) всевозможных пар последовательностей \(s_x\) и \(s_y\) (\(1 \le x, y \le n\)) и проверит содержит ли конкатенация \(s_x + s_y\) восход или нет. Обратите внимание, что порядок выбора последовательностей в пару имеет значение. Кроме того, он может выбирать последовательность в пару к самой себе. Пожалуйста, посчитайте количество пар последовательностей (\(x, y\)) для заданного набора \(s_1, s_2, \ldots, s_n\), конкатенация \(s_x + s_y\) которых имеет восход. Выходные данные Выведите одно целое число, количество пар последовательностей, конкатенация которых имеет восход. Примечание В первом примере, следующие \(9\) последовательностей имеют восход: \([1, 2], [1, 2], [1, 3], [1, 3], [1, 4], [1, 4], [2, 3], [2, 4], [3, 4]\). Одинаковые по содержимому последовательности учитываются столько раз, сколько раз они встречаются как результат конкатенации. | |
![]()
|
|
C. Новый год и перестановка
Комбинаторика
математика
*1600
Напомним, что перестановкой является массив, состоящий из \(n\) различных целых чисел от \(1\) до \(n\) в произвольном порядке. Например, \([2,3,1,5,4]\) — перестановка, но \([1,2,2]\) не перестановка (\(2\) встречается в массиве дважды) и \([1,3,4]\) тоже не перестановка (\(n=3\), но в массиве встречается \(4\)). Последовательность \(a\) является подотрезком \(b\), если \(a\) может быть получена из \(b\) удалением нескольких (возможно, ни одного или всех) элементов из начала и нескольких (возможно, ни одного или всех) элементов из конца. Обозначим подотрезок как \([l, r]\), где \(l, r\) — целые числа и \(1 \le l \le r \le n\). Это обозначает подотрезок, у которого убрали \(l-1\) элементов слева и \(n-r\) справа. Для перестановки \(p_1, p_2, \ldots, p_n\) назовём рамочным подотрезком такой подотрезок индексов \([l,r]\), в котором \(\max\{p_l, p_{l+1}, \dots, p_r\} - \min\{p_l, p_{l+1}, \dots, p_r\} = r - l\). Например, у перестановки \((6, 7, 1, 8, 5, 3, 2, 4)\) некоторые из рамочных подотрезков: \([1, 2], [5, 8], [6, 7], [3, 3], [8, 8]\). В частности, подотрезок \([i,i]\) всегда является рамочным подотрезком для любого \(i\) от \(1\) до \(n\) включительно. Для перестановки \(p\) определим счастье перестановки как количество таких пар \((l, r)\), что \(1 \le l \le r \le n\) и \([l, r]\) является рамочным подотрезком. Например, перестановка \([3, 1, 2]\) имеет счастье \(5\): Все подотрезки индексов кроме \([1, 2]\) являются рамочными. Даны два целых числа \(n\) и \(m\). Джонгвон хочет найти суммарное счастье всех перестановок длины \(n\) по модулю простого числа \(m\). Обратите внимание, что всего существует \(n!\) (факториал \(n\)) различных перестановок длины \(n\). Выходные данные Выведите \(r\) (\(0 \le r < m\)) — суммарное счастье всех перестановок длины \(n\) по модулю простого числа \(m\). Примечание Пусть \(n=3\), тогда рассмотрим все перестановки длиной \(3\): - \([1, 2, 3]\), все подотрезки являются рамочными подотрезками. Счастье равно \(6\).
- \([1, 3, 2]\), все подотрезки, кроме \([1, 2]\), являются рамочными подотрезками. Счастье равно \(5\).
- \([2, 1, 3]\), все подотрезки, кроме \([2, 3]\), являются рамочными подотрезками. Счастье равно \(5\).
- \([2, 3, 1]\), все подотрезки, кроме \([2, 3]\), являются рамочными подотрезками. Счастье равно \(5\).
- \([3, 1, 2]\), все подотрезки, кроме \([1, 2]\), являются рамочными подотрезками. Счастье равно \(5\).
- \([3, 2, 1]\), все подотрезки являются рамочными подотрезками. Счастье равно \(6\).
Поэтому суммарное счастье равно \(6+5+5+5+5+6 = 32\). | |
![]()
|
|
E. Новый год и строительство замком
Комбинаторика
математика
геометрия
сортировки
*2500
Любимая видеоигра Кивона теперь проводит новогоднее мероприятие, чтобы мотивировать пользователей! Игра о строительстве и защите замка, поэтому Кивон задумался над следующей загадкой. В двумерной плоскости у вас есть набор \(s = \{(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\}\), состоящий из \(n\) различных точек. В множестве \(s\) нет трех точек на одной прямой. Мы можем защитить точку \(p \in s\), построив замок. Замок — это простой четырехугольник (многоугольник с \(4\) вершинами), который строго покрывает точку \(p\) (то есть точка \(p\) строго внутри четырёхугольника). Кивона интересует количество подмножеств \(s\) из \(4\)-х точек, которые можно использовать для построения замка, защищающего точку \(p\). Обратите внимание, что если одно подмножество может быть соединено более чем одним способом, чтобы покрыть точку, то оно считается только один раз. Пусть \(f(p)\) будет количеством подмножеств из \(4\)-х точек, которые могут покрыть точку \(p\). Пожалуйста, посчитайте сумму \(f(p)\) по всем точкам \(p \in s\). Выходные данные Выведите сумму \(f(p)\) по всем точкам \(p \in s\). | |
![]()
|
|
F. Баян?
Бинарный поиск
Комбинаторика
теория чисел
*2900
Дан массив \(a\), состоящий из \(n\) целых чисел, найдите: \(\)\max\limits_{1 \le i < j \le n} LCM(a_i,a_j),\(\) где \(LCM(x, y)\) — это наименьшее положительное целое число, которое делится и на \(x\), и на \(y\). Например, \(LCM(6, 8) = 24\), \(LCM(4, 12) = 12\), \(LCM(2, 3) = 6\). Выходные данные Выведите одно целое число — максимальное значение наименьшее общего кратного двух чисел из массива \(a\). | |
![]()
|
|
C. Два массива
Комбинаторика
*1600
дп
Вам заданы два числа \(n\) и \(m\). Посчитайте количество таких пар массивов \((a, b)\), что: - длина обоих массивов равна \(m\);
- каждый элемент каждого массива — целое число от \(1\) до \(n\) (включительно);
- \(a_i \le b_i\) для любого индекса \(i\) от \(1\) до \(m\);
- массив \(a\) отсортирован в порядке неубывания;
- массив \(b\) отсортирован в порядке невозрастания.
Так как ответ может быть слишком большим, посчитайте его по модулю \(10^9+7\). Выходные данные Выведите одно число – количество массивов \(a\) и \(b\), удовлетворяющих условиям, описанным выше по модулю \(10^9+7\). Примечание В первом тесте существуют \(5\) подходящих вариантов: - \(a = [1, 1], b = [2, 2]\);
- \(a = [1, 2], b = [2, 2]\);
- \(a = [2, 2], b = [2, 2]\);
- \(a = [1, 1], b = [2, 1]\);
- \(a = [1, 1], b = [1, 1]\).
| |
![]()
|
|
C. Атака Ксенона
Деревья
Комбинаторика
дп
поиск в глубину и подобное
жадные алгоритмы
*2300
На другом этаже A.R.C. Markland-N, молодой человек Саймон "Ксенон" Джексон отдыхает, завершив свои работы по проекту быстрее запланированного (впрочем как всегда). Так как свободного времени достаточно много, он надевает свой легендарный хакерский "X" инстинкт и бежит сражаться против банд кибермира. Его целью является сеть из \(n\) небольших банд. Их сеть состоит из ровно \(n - 1\) прямых соединений, каждое из которых связывает какие-то две банды вместе. Соединения устроены таким образом, что любые две банды соединены через последовательность прямых соединений. Изучая данные, Ксенон понял, что банды используют для самозащиты следующую форму шифрования. Каждому соединению назначено целое число от \(0\) до \(n - 2\), таким образом, что все назначенные числа различны, а каждое число назначено какому-то соединению. Если атакующий пытается получить доступ к защищённым данным, то ему придётся прорваться через \(S\) слоёв с паролями, где \(S\) определяется как: \(\)S = \sum_{1 \leq u < v \leq n} mex(u, v)\(\) Здесь \(mex(u, v)\) обозначает наименьшее неотрицательное целое число, которое не встречается на соединениях на единственном простом пути между бандами \(u\) и \(v\). Ксенон не знает каким образом числа были назначены соединениям, но это не проблема. Он собирается поручить своим AI перебрать и взломать все пароли, но перед этим он хочет знать чему равно наибольшее возможное значение \(S\), чтобы настроить AI наиболее эффективно. Сейчас Ксенон ушёл писать скрипты для AI, и он собирается их закончить в течение двух часов. Не могли бы вы найти наибольшее значение \(S\) перед тем, как он вернётся? Выходные данные Выведите наибольшее возможное значение \(S\) — количества слоёв с паролями в сети банд. Примечание В первом примере можно достичь максимального \(S\) следующим образом:  В этой сети, \(mex(1, 2) = 0\), \(mex(1, 3) = 2\) и \(mex(2, 3) = 1\). Таким образом, \(S = 0 + 2 + 1 = 3\). Во втором примере можно достичь максимального \(S\) таким образом: 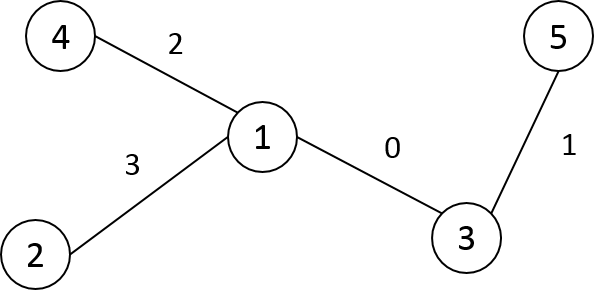 В этой сети все ненулевые значения mex перечислены ниже: - \(mex(1, 3) = 1\)
- \(mex(1, 5) = 2\)
- \(mex(2, 3) = 1\)
- \(mex(2, 5) = 2\)
- \(mex(3, 4) = 1\)
- \(mex(4, 5) = 3\)
Таким образом, \(S = 1 + 2 + 1 + 2 + 1 + 3 = 10\). | |
![]()
|
|
F. Игрушки Норы
Комбинаторика
дп
битмаски
*3500
Давным давно, семилетняя Нора любила играть в игрушки вместе со своим созданием ROBO_Head-02, не только для того чтобы развлечься, но и чтобы улучшить его способности. Однажды, приёмный отец Норы, Феникс Уайл, принёс Норе \(n\) коробок с игрушками. Перед тем как их распаковать, Нора решила устроить для ROBO небольшую игру. Она пронумеровала все \(n\) коробок используя \(n\) различных целых чисел \(a_1, a_2, \ldots, a_n\) и попросила ROBO выполнить ноль или более операций следующего вида: - Выбрать три различных индекса \(i\), \(j\) и \(k\), таких что \(a_i \mid a_j\) и \(a_i \mid a_k\). Иными словами, \(a_i\) делит и \(a_j\), и \(a_k\). Иначе говоря, \(a_j \bmod a_i = 0\), \(a_k \bmod a_i = 0\).
- Затем, Нора передаст \(k\)-ю коробку ROBO, а тот положит её наверх стопки с коробками рядом с ним. Изначально эта стопка пуста.
- После этого коробка \(k\) становится недоступной для любых дальнейших действий.
После девяти игр, это процесс весьма позабавил Нору. Она попросила ROBO посчитать количество возможных стопок с коробками, имеющие максимально возможный размер, которые могут получиться. Две стопки считаются различными, если существует хотя бы одна позиция, в которой они отличаются. Так как ROBO пока на очень ранней стадии развития, да и Нора достаточно молода, чтобы концентрироваться надолго, они оба заснули, не найдя ответа. Не могли бы вы им помочь? Так как количество таких стопок может быть достаточно большим, выведите его по модулю \(10^9 + 7\). Выходные данные Выведите количество различных максимальных по размеру стопок, которые могли получится у ROBO, по модулю \(10^9 + 7\). Примечание Обозначим содержимое стопки как последовательность \(b\), где самая нижняя коробка стопки находится на самой левой позиции. В первом примере возможно \(2\) различных стопки: - \(b = [6]\) (\([2, \mathbf{6}, 8] \xrightarrow{(1, 3, 2)} [2, 8]\))
- \(b = [8]\) (\([2, 6, \mathbf{8}] \xrightarrow{(1, 2, 3)} [2, 6]\))
Во втором примере возможно \(4\) различных стопки: - \(b = [9, 12]\) (\([2, 3, 4, \mathbf{9}, 12] \xrightarrow{(2, 5, 4)} [2, 3, 4, \mathbf{12}] \xrightarrow{(1, 3, 4)} [2, 3, 4]\))
- \(b = [4, 12]\) (\([2, 3, \mathbf{4}, 9, 12] \xrightarrow{(1, 5, 3)} [2, 3, 9, \mathbf{12}] \xrightarrow{(2, 3, 4)} [2, 3, 9]\))
- \(b = [4, 9]\) (\([2, 3, \mathbf{4}, 9, 12] \xrightarrow{(1, 5, 3)} [2, 3, \mathbf{9}, 12] \xrightarrow{(2, 4, 3)} [2, 3, 12]\))
- \(b = [9, 4]\) (\([2, 3, 4, \mathbf{9}, 12] \xrightarrow{(2, 5, 4)} [2, 3, \mathbf{4}, 12] \xrightarrow{(1, 4, 3)} [2, 3, 12]\))
В третьем примере ROBO не сможет сделать ничего. Поэтому возможна только \(1\) стопка, и это пустая стопка. | |
![]()
|
|
B. JOE на телевидении!
Комбинаторика
математика
*1000
жадные алгоритмы
Наш владелец Кафе JOE Миллер скоро примет участие в новом игровом телешоу «1 против \(n\)». Игра проходит в несколько раундов, где в каждом раунде ведущий задаёт JOE и его соперникам один общий вопрос. Все участники отвечающие неправильно выбывают из игры. Шоу заканчивается, когда остаётся только JOE (мы считаем, что JOE никогда не отвечает на вопрос неверно!). Для каждого вопроса, на который отвечает JOE, если у него оставалось \(s\) (\(s > 0\)) соперников и из них \(t\) (\(0 \le t \le s\)) ответили неверно, то JOE получает \(\displaystyle\frac{t}{s}\) долларов. Ну а в следующем раунде у него будет уже \(s - t\) соперников. JOE задумался, чему равен наибольший приз, который он может получить в лучшем случае. Однако шоу начинается достаточно скоро, и у него нет на это времени. Может быть вы сможете ответить на этот вопрос? Выходные данные Выведите наибольший возможный приз (в долларах), который может получить JOE. Ваш ответ будет засчитан, если его абсолютная или относительная погрешность будет не более \(10^{-4}\). Иначе говоря, если ваш ответ это \(a\), а ответ жюри \(b\), то должно выполняться \(\frac{|a - b|}{max(1, b)} \le 10^{-4}\). Примечание Во втором примере наилучший сценарий выглядит следующим образом: один участник ошибается на первом вопросе, а второй на втором, тогда итоговый приз составит \(\displaystyle \frac{1}{2} + \frac{1}{1} = 1.5\) долларов. | |
![]()
|
|
F. Хороший контест
Теория вероятностей
Комбинаторика
дп
*2700
На большой платформе по спортивному программированию ForceCoders скоро начнется очередной контест. Авторы подготовили \(n\) задач, и так как платформа очень популярна, аж \(998244351\) программист со всего мира будет принимать участие в контесте. Для каждой задачи авторы оценили количество участников, которые ее решат: по \(i\)-й задаче точно будет не менее \(l_i\) и не более \(r_i\) успешных решений. Создатель платформы ForceCoders использует различные критерии, чтобы определить, является ли контест хорошим. Один из этих критериев учитывает количество инверсий в порядке задач. Инверсией называется пара задач \((x, y)\), такая, что \(x\) расположена в контесте раньше (\(x < y\)), но количество успешных решений по задаче \(y\) строго больше. Очевидно, и создатель платформы, и авторы контеста хотят, чтобы контест получился хорошим. Поэтому сейчас они хотят посчитать вероятность того, что не будет ни одной инверсии в порядке задач. Можно предположить, что для каждой задачи \(i\) любое целочисленное количество решений (между \(l_i\) и \(r_i\)) равновероятно, и все эти значения независимы друг от друга. Выходные данные Вероятность, что в порядке задач не будет инверсий, можно выразить в виде несократимой дроби \(\frac{x}{y}\), где \(y\) взаимно просто с \(998244353\). Выведите одно целое число — значение \(xy^{-1}\), взятое по модулю \(998244353\), где \(y^{-1}\) — такое число, что \(yy^{-1} \equiv 1\) \((mod\) \(998244353)\). Примечание Ответ в первом тесте равен \(\frac{1}{2}\). | |
![]()
|
|
D. Вокруг света
Деревья
Комбинаторика
математика
дп
поиск в глубину и подобное
графы
графы
битмаски
*3000
Ги-Мануэль и Тома планируют \(144\) кругосветных путешествия. Вам дан простой взвешенный неориентированный связный граф из \(n\) вершин и \(m\) рёбер со следующим ограничением: не существует простого цикла (т. е. цикла, проходящего через каждую вершину не больше раза) длины больше \(3\), проходящего через вершину \(1\). Стоимостью пути (необязательно простого) в этом графе является XOR весов всех рёбер, входящих в этот путь, причём каждое ребро считается столько, сколько раз через него проходит путь. Однако, путешествия стоимостью \(0\) их не устраивают. Вы можете выбрать любое подмножество рёбер, инцидентных вершине \(1\), и удалить их. Сколько существует таких множеств, что при их удалении в полученном графе нет нетривиального цикла (необязательно простого) стоимостью \(0\), проходящего через вершину \(1\)? Цикл называется нетривиальным, если существует ребро, через которое он проходит нечётное количество раз. Так как ответ может быть большим, выведите его по модулю \(10^9+7\). Выходные данные В единственной строке выведите ответ по модулю \(10^9+7\). Примечание На рисунках представлены графы из примеров. 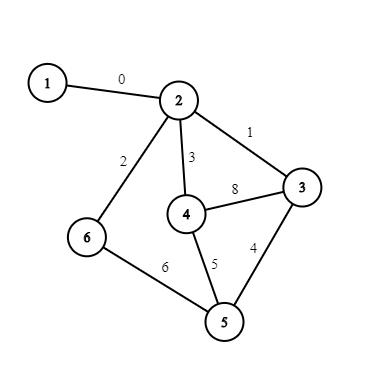 В первом примере в графе нет нетривиальных циклов со стоимостью \(0\), так что мы можем как удалить единственное ребро, инцидентное вершине \(1\), так и не удалять. В первом примере в графе нет нетривиальных циклов со стоимостью \(0\), так что мы можем как удалить единственное ребро, инцидентное вершине \(1\), так и не удалять.  Во втором примере если мы не удаляем ребро \(1-2\), то в графе будет цикл \(1-2-4-5-2-1\) со стоимостью \(0\); аналогично, если мы не удаляем ребро \(1-3\), то в графе будет цикл \(1-3-2-4-5-2-3-1\) со стоимостью \(0\). Единственный вариант — удалить оба ребра. Во втором примере если мы не удаляем ребро \(1-2\), то в графе будет цикл \(1-2-4-5-2-1\) со стоимостью \(0\); аналогично, если мы не удаляем ребро \(1-3\), то в графе будет цикл \(1-3-2-4-5-2-3-1\) со стоимостью \(0\). Единственный вариант — удалить оба ребра. 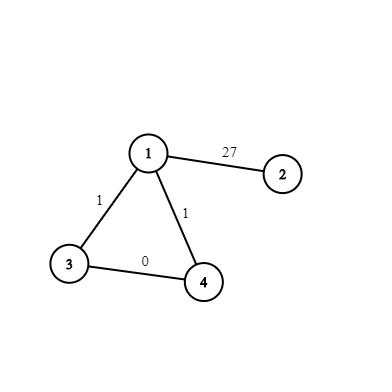 В третьем примере подходят все подмножества, кроме тех двух, при которых остаются оба ребра \(1-3\) и \(1-4\). В третьем примере подходят все подмножества, кроме тех двух, при которых остаются оба ребра \(1-3\) и \(1-4\). | |
![]()
|
|
C. Функция Айоуба
Строки
Бинарный поиск
Комбинаторика
математика
жадные алгоритмы
*1700
Айоуб думает, что он очень умный человек, поэтому он придумал функцию \(f(s)\), где \(s\) это бинарная строка (строка, содержащая только символы «0» и «1»). Функция \(f(s)\) равна количеству подстрок строки \(s\), которые содержат хотя бы один символ, равный «1». Более формально, \(f(s)\) равно количеству пар целых чисел \((l, r)\), таких что \(1 \leq l \leq r \leq |s|\) (где \(|s|\) равно длине строки \(s\)), таких что хотя бы один из символов \(s_l, s_{l+1}, \ldots, s_r\) равен «1». Например, если \(s = \)«01010», то \(f(s) = 12\), потому что есть \(12\) таких пар \((l, r)\): \((1, 2), (1, 3), (1, 4), (1, 5), (2, 2), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 4), (4, 5)\). Айоуб также думает, что он умнее Махмуда, поэтому дал ему два целых числа \(n\) и \(m\) и следующую задачу. По всем бинарным строкам \(s\) длины \(n\), которые содержат ровно \(m\) символов, равных «1», найдите максимальное значение \(f(s)\). У Махмуда не получилось решить эту задачу, поэтому он попросил вас о помощи. Можете ли вы помочь ему? Выходные данные Для каждого тестового случая выведите единственное целое число — максимальное значение \(f(s)\) по всем строкам \(s\) длины \(n\), которые содержат ровно \(m\) символов, равных «1». Примечание В первом тестовом случае, существует только \(3\) строки длины \(3\), которые содержат ровно \(1\) символ, равный «1». Эти строки это: \(s_1 = \)«100», \(s_2 = \)«010», \(s_3 = \)«001». Значения \(f\) для них это: \(f(s_1) = 3, f(s_2) = 4, f(s_3) = 3\), поэтому максимальное значение это \(4\) и ответ равен \(4\). Во втором тестовом случае, строка \(s\) для которой максимальное значение функции это «101». Во третьем тестовом случае, строка \(s\) для которой максимальное значение функции это «111». В четвертом тестовом случае, единственная строка \(s\) длины \(4\), которая содержит ровно \(0\) символов, равных «1» это «0000» и значение функции \(f\) для этой строки это \(0\), поэтому ответ равен \(0\). В пятом тестовом случае, строка \(s\) с максимальным значением функции это «01010» и она была подробно разобрана в качестве примера в тексте условия задачи. | |
![]()
|
|
C. Невозможное вычисление
Перебор
Комбинаторика
математика
*1600
теория чисел
Чтобы стать королем Codeforces, Курони должен решить следующую задачу. Ему даны \(n\) чисел \(a_1, a_2, \dots, a_n\). Помогите Курони посчитать \(\prod_{1\le i<j\le n} |a_i - a_j|\). Так как ответ может быть очень большим, посчитайте его по модулю \(m\). Если вы не знакомы с короткой формой записи, \(\prod_{1\le i<j\le n} |a_i - a_j|\) равно \(|a_1 - a_2|\cdot|a_1 - a_3|\cdot\) \(\dots\) \(\cdot|a_1 - a_n|\cdot|a_2 - a_3|\cdot|a_2 - a_4|\cdot\) \(\dots\) \(\cdot|a_2 - a_n| \cdot\) \(\dots\) \(\cdot |a_{n-1} - a_n|\). Другими словами, это произведение \(|a_i - a_j|\) по всем \(1\le i < j \le n\). Выходные данные Выведите единственное число — \(\prod_{1\le i<j\le n} |a_i - a_j| \bmod m\). Примечание В первом примере, \(|8 - 5| = 3 \equiv 3 \bmod 10\). Во втором примере, \(|1 - 4|\cdot|1 - 5|\cdot|4 - 5| = 3\cdot 4 \cdot 1 = 12 \equiv 0 \bmod 12\). В третьем примере, \(|1 - 4|\cdot|1 - 9|\cdot|4 - 9| = 3 \cdot 8 \cdot 5 = 120 \equiv 1 \bmod 7\). | |
![]()
|
|
E. Корова и угощения
Бинарный поиск
Комбинаторика
математика
реализация
дп
жадные алгоритмы
*2500
После удачного года по количеству удоя, Фермер Джон решил наградить своих коров их любимым угощением: вкусной травой! На поле располагается ряд из \(n\) единиц травы, каждая единица соответствующего уровня сладости \(s_i\). У Фермера Джона \(m\) коров, каждая обладает своим любимым уровнем сладости \(f_i\) и уровнем голода \(h_i\). Фермер Джон хочет выбрать непересекающиеся подмножества коров, чтобы разместить их с левой и правой стороны ряда травы. Нет никаких ограничений на количество коров с каждой стороны. Поведение коров описывается следующим образом: - Коровы с левой и правой сторон начинают кормиться по очереди в порядке, выбранном Фермером Джоном.
- Кормежка коровы выглядит следующим образом: корова начинает двигаться к противоположному концу ряда, не меняя своего направления, и поедает траву своего любимого уровня сладости, пока не съест \(h_i\) единиц.
- В тот момент, как корова съест \(h_i\) травы, она ложится спать прямо там, мешая проходу других коров с обоих сторон.
- Если же корова встречает на пути другую спящую корову или достигает конца ряда травы, она расстраивается. Фермер Джон ни при каких условиях не хочет расстраивать своих коров.
Заметим, что трава не отрастает обратно. Также, чтобы не расстраивать корову, Фермер Джон может просто не выбрать каких-то коров. Удивительно, но Фермер Джон решил, что спящие коровы — наиболее удовлетворенные. Если Фермер Джон будет выбирать порядок оптимально, то какое наибольшее количество спящих коров он сможет получить, и сколько способов существует выбрать два подмножества так, чтобы получить данное максимальное количество спящих коров (по модулю \(10^9+7\))? Порядок, в котором Фермер Джон посылает коров кормиться не важен пока ни одна корова не расстроена. Выходные данные Выведите два числа — максимальное количество спящих коров и количество способов его получить по модулю \(10^9+7\). Примечание В первом примере, Фермер Джон может выстроить коров следующим образом, чтобы получить в итоге \(2\) спящих коров: - Корова \(1\) стоит с левой стороны и корова \(2\) стоит справа.
- Корова \(2\) стоит с левой стороны и корова \(1\) стоит справа.
Во втором примере, Фермер Джон может выстроить коров следующим образом, чтобы получить в итоге \(1\) спящую корову: - Корова \(1\) стоит слева.
- Корова \(2\) стоит слева.
- Корова \(1\) стоит справа.
- Корова \(2\) стоит справа.
В третьем примере, Фермер Джон может выстроить коров следующим образом, чтобы получить в итоге \(2\) спящих коров: - Коровы \(1\) и \(2\) стоят слева.
- Коровы \(1\) и \(2\) стоят справа.
- Корова \(1\) стоит слева и корова \(2\) стоит справа.
- Корова \(1\) стоит справа и корова \(2\) стоит слева.
В четвертом примере, Фермер Джон не может получить ни одной спящей коровы, а потому не будет ни одной коровы стоящей с какой-либо стороны. | |
![]()
|
|
C. Весь мир театр
Комбинаторика
математика
*1400
В театральном кружке занимается n юношей и m девушек. Для постановки спектакля «Теория большого взрыва» им надо выбрать группу ровно из t актеров, которая содержит не менее 4 юношей и не менее одной девушки. Сколькими способами возможен выбор группы? Конечно, варианты отличающиеся только составом труппы считаются различными. Производите все вычисления в 64-битном типе: long long для С/С++, int64 для Delphi и long для Java. Выходные данные Выведите искомое количество способов. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-битных чисел на С++. Рекомендуется использовать потоки cin, cout или спецификатор %I64d. | |
![]()
|
|
D. Посчитайте массивы
Комбинаторика
математика
*1700
Посчитайте количество массивов, удовлетворяющих следующим условиям: - каждый массив состоит из \(n\) элементов;
- каждый элемент — целое число от \(1\) до \(m\);
- в каждом массиве есть ровно одна пара одинаковых элементов;
- в каждом массиве \(a\) существует такой индекс \(i\), что массив строго возрастает до \(i\)-го элемента и строго убывает после него (формально, \(a_j < a_{j + 1}\), если \(j < i\), и \(a_j > a_{j + 1}\), если \(j \ge i\)).
Выходные данные Выведите одно целое число — количество массивов, удовлетворяющих всем вышеописанным условиям, взятое по модулю \(998244353\). Примечание Массивы из первого примера: - \([1, 2, 1]\);
- \([1, 3, 1]\);
- \([1, 4, 1]\);
- \([2, 3, 2]\);
- \([2, 4, 2]\);
- \([3, 4, 3]\).
| |
![]()
|
|
C. Разбиения перестановки
Комбинаторика
математика
жадные алгоритмы
*1300
Вам дана перестановка \(p_1, p_2, \ldots, p_n\) целых чисел от \(1\) до \(n\) и целое число \(k\), такое что \(1 \leq k \leq n\). Перестановка обозначает, что каждое значение от \(1\) до \(n\) содержится в \(p\) ровно один раз. Рассмотрим все разбиения этой перестановки на \(k\) отрезков. Формально, такое разбиение это множество отрезков \(\{[l_1, r_1], [l_2, r_2], \ldots, [l_k, r_k]\}\), такое что: - \(1 \leq l_i \leq r_i \leq n\) для всех \(1 \leq i \leq k\).
- Для всех \(1 \leq j \leq n\) существует ровно один отрезок \([l_i, r_i]\), такой что \(l_i \leq j \leq r_i\).
Два разбиения считаются различными, если существует отрезок, лежащий в одном разбиении, но не лежащий в другом. Давайте посчитаем значение разбиения \(\sum\limits_{i=1}^{k} {\max\limits_{l_i \leq j \leq r_i} {p_j}}\) для всех возможных разбиений перестановки на \(k\) отрезков. Ваша задача найти максимальное значение разбиения по всем таким разбиениям и количество таких разбиений, значение которых равно максимально возможному. Поскольку второе число может быть слишком большим, вы должны найти его остаток при делении на \(998\,244\,353\). Выходные данные Выведите два целых числа — максимальное возможное значение разбиения по всем разбиениям перестановки на \(k\) отрезков и количество таких разбиений, для которых значение равно максимальному возможному значению по модулю \(998\,244\,353\). Обратите внимание, вы должны найти только второе число по модулю \(998\,244\,353\). Примечание В первом тесте, существует только два разбиения при \(k = 2\): \(\{[1, 1], [2, 3]\}\) и \(\{[1, 2], [3, 3]\}\). Для каждого из них значение разбиения равно \(2 + 3 = 5\). Поэтому максимальное возможное значение разбиения это \(5\) и количество разбиений равно \(2\). Во третьем тесте при \(k = 3\), разбиения, для которых значение равно максимальному возможному это \(\{[1, 2], [3, 5], [6, 7]\}\), \(\{[1, 3], [4, 5], [6, 7]\}\), \(\{[1, 4], [5, 5], [6, 7]\}\), \(\{[1, 2], [3, 6], [7, 7]\}\), \(\{[1, 3], [4, 6], [7, 7]\}\), \(\{[1, 4], [5, 6], [7, 7]\}\). Для всех этих разбиений их значение равно \(7 + 5 + 6 = 18\). Разбиение \(\{[1, 2], [3, 4], [5, 7]\}\), например, имеет значение \(7 + 3 + 6 = 16\), что меньше чем максимальное возможное, поэтому мы его не считаем. | |
![]()
|
|
E. Посчитайте блоки
Комбинаторика
математика
дп
*1800
Вы выписали все целые числа от \(0\) до \(10^n - 1\), добавляя к ним ведущие нули так, чтобы их длины были равны \(n\). Например, если \(n = 3\), то вы выпишете следующие числа: 000, 001, ..., 998, 999. Назовем блоком в числе \(x\) последовательный отрезок одинаковых цифр, который не может быть расширен ни влево, ни вправо. Например, в числе \(00027734000\) есть три блока длины \(1\), один блок длины \(2\) и два блока длины \(3\). Для всех чисел \(i\) от \(1\) до \(n\) посчитайте суммарное количество блоков длины \(i\) среди выписанных вами чисел. Так как эти числа могут быть слишком большими, выведите их по модулю \(998244353\). Выходные данные В единственной строке выведите \(n\) чисел. \(i\)-е число равно количеству блоков длины \(i\) среди выписанных вами чисел. Так как эти числа могут быть слишком большими, выведите их по модулю \(998244353\). | |
![]()
|
|
F. Отрезки И
Структуры данных
Комбинаторика
дп
битмаски
*2500
Даны три целых числа \(n\), \(k\), \(m\) и \(m\) условий \((l_1, r_1, x_1), (l_2, r_2, x_2), \dots, (l_m, r_m, x_m)\). Посчитайте количество различных массивов \(a\), состоящих из \(n\) целых чисел, таких что: - \(0 \le a_i < 2^k\) для всех \(1 \le i \le n\);
- побитовое И чисел \(a[l_i] \& a[l_i + 1] \& \dots \& a[r_i] = x_i\) для всех \(1 \le i \le m\).
Два массива \(a\) и \(b\) считаются различными, если существует такая позиция \(i\), что \(a_i \neq b_i\). Это число может быть довольно велико, поэтому выведите его по модулю \(998244353\). Выходные данные Выведите одно целое число — количество различных массивов \(a\), для которых выполняются все приведенные выше условия, по модулю \(998244353\). Примечание Можете вспомнить, что такое побитовое И по ссылке. В первом примере ответом являются следующие массивы: \([3, 3, 7, 6]\), \([3, 7, 7, 6]\) и \([7, 3, 7, 6]\). | |
![]()
|
|
B. K-я красивая строка
Бинарный поиск
Перебор
Комбинаторика
математика
реализация
*1300
Для заданного целого числа \(n\) (\(n > 2\)) выпишем все строки длины \(n\), которые содержат в себе \(n-2\) буквы 'a' и две буквы 'b', в лексикографическом (алфавитном) порядке. Напомним, что строка \(s\) длины \(n\) лексикографически меньше строки \(t\) длины \(n\), если существует такое \(i\) (\(1 \le i \le n\)), что \(s_i < t_i\), а для всех \(j\) (\(1 \le j < i\)) \(s_j = t_j\). Лексикографическое сравнение строк реализовано при помощи оператора < в современных языках программирования. Например, если \(n=5\), то получатся следующие строки (их порядок важен): - aaabb
- aabab
- aabba
- abaab
- ababa
- abbaa
- baaab
- baaba
- babaa
- bbaaa
Легко показать, что такой список строк будет содержать ровно \(\frac{n \cdot (n-1)}{2}\) строк. Вам задано \(n\) (\(n > 2\)) и \(k\) (\(1 \le k \le \frac{n \cdot (n-1)}{2}\)). Выведите \(k\)-ю строку из списка. Выходные данные Для каждого набора тестовых данных выведите \(k\)-ю строку из списка всех описанных выше строк длины \(n\). Строки в списке отсортированы лексикографически (в алфавитном порядке). | |
![]()
|
|
B. Dreamoon любит последовательности
Комбинаторика
математика
*1700
битмаски
Dreamoon очень любит последовательности. Поэтому он придумал задачу про последовательность, которую нельзя найти на OEIS: Вам дано два целых числа \(d, m\), вам нужно найти количество массивов \(a\), удовлетворяющих следующим ограничениям: - Длина \(a\) равна \(n\), \(n \ge 1\)
- \(1 \le a_1 < a_2 < \dots < a_n \le d\)
- Рассмотрим следующий массив \(b\) длины \(n\): \(b_1 = a_1\), \(\forall i > 1, b_i = b_{i - 1} \oplus a_i\), где \(\oplus\) это побитовое исключащее или (xor). После построения массива \(b\), должно выполняться ограничение \(b_1 < b_2 < \dots < b_{n - 1} < b_n\).
Так как количество возможных массивов может быть слишком большим, вам нужно найти его по модулю \(m\). Выходные данные Для каждого набора входных данных, выведите количество массивов \(a\), удовлетворяющих всем ограничениям, по модулю \(m\). | |
![]()
|
|
E. Все высоты равны
Конструктив
Комбинаторика
математика
*2100
матрицы
Алиса недавно подсела на игру, которая называется Сиртет. В игре Сиртет игроку дается поле \(n \times m\). В начале игры \(a_{i,j}\) кубиков поставлены друг на друга в клетке \((i,j)\). Две клетки называются соседними, если у них есть общая сторона. Игрок может делать следующие ходы: - поставить по одному кубику на две соседние клетки;
- поставить два кубика в одну клетку.
Упомянутые кубики все одинаковой высоты. Пример игры изображен на картинке. Состояния справа достигаются с помощью выполнения данных ходов из состояния слева, и после хода добавляются серые кубики. 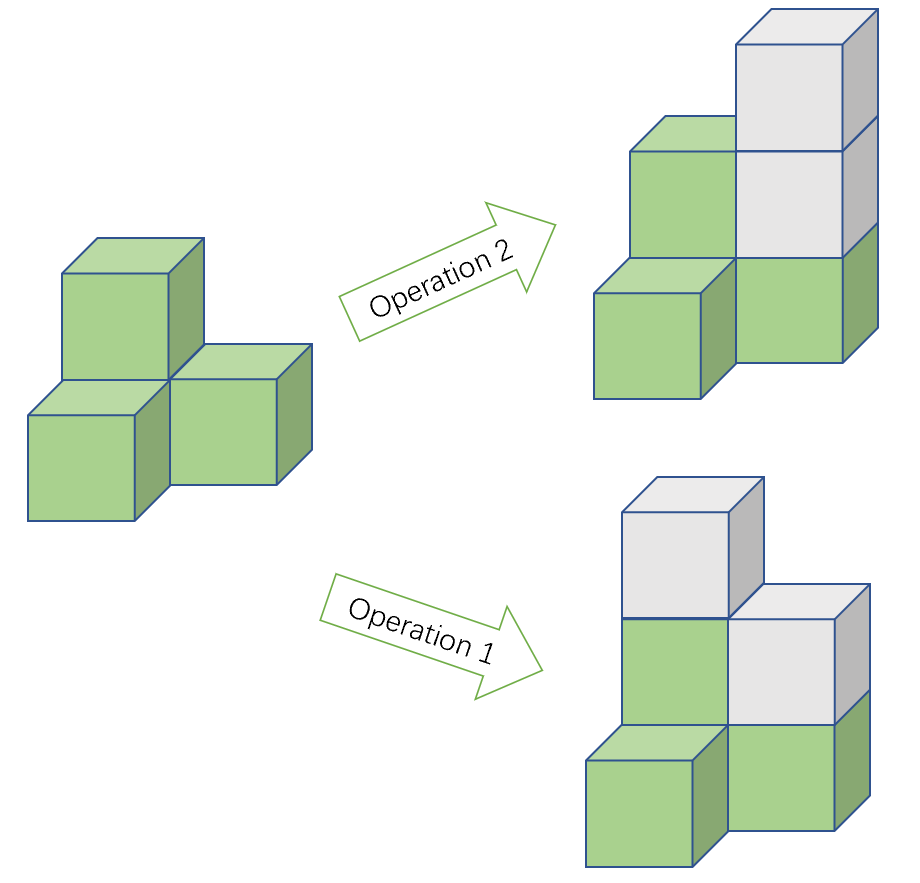 Цель игрока — сделать высоты всех клеток одинаковыми (то есть в каждой клетке должно быть одинаковое количество кубиков) при помощи данных ходов. Алиса обнаружила, что на некоторых начальных полях невозможно достичь цели, какие бы ходы игрок не делал. Поэтому ей стало интересно, сколько существует таких начальных полей, что - \(L \le a_{i,j} \le R\) для всех \(1 \le i \le n\), \(1 \le j \le m\);
- игрок может достичь цели, используя данные ходы.
Пожалуйста, помогите Алисе с этим. Обратите внимание, что ответ может быть довольно большой, поэтому выведите его по модулю \(998,244,353\). Выходные данные Выведите одно целое число, обозначающее ответ по модулю \(998,244,353\). Примечание В первом примере единственное поле, которое удовлетворяет условиям — это \(a_{1,1}=a_{2,1}=a_{1,2}=a_{2,2}=1\). Поэтому ответ \(1\). Во втором примере начальные поля, которые удовлетворяют условиям, — это \(a_{1,1}=a_{1,2}=1\) и \(a_{1,1}=a_{1,2}=2\). Поэтому ответ \(2\). | |
![]()
|
|
E. Пути по делителям
Комбинаторика
математика
теория чисел
жадные алгоритмы
графы
*2200
Задано целое положительное число \(D\). Построим из него следующий граф: - каждая вершина является делителем \(D\) (не обязательно простым, \(1\) и \(D\) тоже включаются);
- между двумя вершинами \(x\) и \(y\) (\(x > y\)) есть неориентированное ребро, если \(x\) делится на \(y\) и \(\frac x y\) — простое число;
- вес ребра — это количество делителей \(x\), которые не являются делителями \(y\).
Например, граф для \(D=12\): 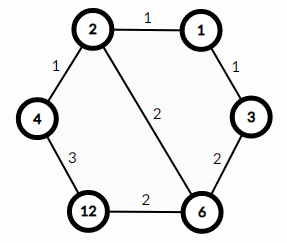 У ребра \((4,12)\) вес \(3\), потому что у \(12\) делители \([1,2,3,4,6,12]\), а у \(4\) делители \([1,2,4]\). Поэтому существует \(3\) делителя \(12\), которые не являются делителями \(4\) — \([3,6,12]\). Между \(3\) и \(2\) нет ребра, потому что \(3\) не делится на \(2\). Между \(12\) и \(3\) нет ребра, потому что \(\frac{12}{3}=4\) не простое число. Длина пути между некоторыми вершинами \(v\) и \(u\) в графе равна сумме весов ребер в нем. Например, длина пути \([(1, 2), (2, 6), (6, 12), (12, 4), (4, 2), (2, 6)]\) равен \(1+2+2+3+1+2=11\). Длина пустого пути равна \(0\). Тогда кратчайший путь между двумя вершинами \(v\) и \(u\) — это путь, длина которого минимальна. Два пути \(a\) и \(b\) различны, если либо содержат различное количество ребер, либо существует такая позиция \(i\), что ребра \(a_i\) и \(b_i\) различны. Даны \(q\) запросов вида: - \(v\) \(u\) — посчитайте количество кратчайших путей между вершинами \(v\) и \(u\).
Ответ может быть довольно большим, поэтому выведите его по модулю \(998244353\). Выходные данные Выведите \(q\) целых чисел — для каждого запроса выведите количество кратчайших путей между двумя данными вершинами по модулю \(998244353\). Примечание В первом примере: - на первый запрос только пустой путь — длина \(0\);
- на второй запрос пути \([(12, 4), (4, 2), (2, 1)]\) (длина \(3+1+1=5\)), \([(12, 6), (6, 2), (2, 1)]\) (длина \(2+2+1=5\)) и \([(12, 6), (6, 3), (3, 1)]\) (длина \(2+2+1=5\)).
- на третий запрос только путь \([(3, 1), (1, 2), (2, 4)]\) (длина \(1+1+1=3\)).
| |
![]()
|
|
E1. Chiori и выбор кукол (простая версия)
Перебор
Комбинаторика
математика
*2700
битмаски
Это простая версия этой задачи. Единственное различие между простой и сложной версиями заключается в ограничениях на \(m\). Вы можете делать взломы, только если обе версии задачи сданы. Chiori очень любит куклы и сейчас она собирается украсить свою спальню!  Так как Chiori коллекционирует куклы, всего у нее \(n\) кукол, \(i\)-я из этих кукол имеет неотрицательное целое число \(a_i\) (\(a_i < 2^m\), \(m\) дано). Chiori хочет выбрать некоторых кукол (возможно ноль) для украшения. Таким образом, всего существует \(2^n\) способов. Обозначим за \(x\) побитовую xor сумму значений у кукол, выбранных Chiori (в случае, если Chiori не выбрала ни одной куклы, \(x = 0\)). Значением способа выбора кукол назовем количество битов равных \(1\) в двоичном представлении \(x\). Более формально, это число также равно количеству индексов \(0 \leq i < m\), таких что \(\left\lfloor \frac{x}{2^i} \right\rfloor\) нечетно. Посчитайте для Chiori количество способов выбрать куклы со значением \(i\) для всех целых \(i\) от \(0\) до \(m\). Поскольку эти числа могут быть очень большими, вы должны посчитать их по модулю \(998\,244\,353\). Выходные данные Выведите \(m+1\) целое число \(p_0, p_1, \ldots, p_m\) — \(p_i\) равно количеству способов выбрать несколько кукол, так чтобы полученное значение выбора кукол оказалось равным \(i\) по модулю \(998\,244\,353\). | |
![]()
|
|
E2. Chiori и выбор кукол (сложная версия)
Перебор
Комбинаторика
математика
битмаски
*3500
Это сложная версия этой задачи. Единственное различие между простой и сложной версиями заключается в ограничениях на \(m\). Вы можете делать взломы, только если обе версии задачи сданы. Chiori очень любит куклы и сейчас она собирается украсить свою спальню!  Так как Chiori коллекционирует куклы, всего у нее \(n\) кукол, \(i\)-я из этих кукол имеет неотрицательное целое число \(a_i\) (\(a_i < 2^m\), \(m\) дано). Chiori хочет выбрать некоторых кукол (возможно ноль) для украшения. Таким образом, всего существует \(2^n\) способов. Обозначим за \(x\) побитовую xor сумму значений у кукол, выбранных Chiori (в случае, если Chiori не выбрала ни одной куклы, \(x = 0\)). Значением способа выбора кукол назовем количество битов равных \(1\) в двоичном представлении \(x\). Более формально, это число также равно количеству индексов \(0 \leq i < m\), таких что \(\left\lfloor \frac{x}{2^i} \right\rfloor\) нечетно. Посчитайте для Chiori количество способов выбрать куклы со значением \(i\) для всех целых \(i\) от \(0\) до \(m\). Поскольку эти числа могут быть очень большими, вы должны посчитать их по модулю \(998\,244\,353\). Выходные данные Выведите \(m+1\) целое число \(p_0, p_1, \ldots, p_m\) — \(p_i\) равно количеству способов выбрать несколько кукол, так чтобы полученное значение выбора кукол оказалось равным \(i\) по модулю \(998\,244\,353\). | |
![]()
|
|
E. Расстановка ладей
Комбинаторика
математика
*2300
бпф
Посчитайте количество способов расставить \(n\) ладей на доске \(n \times n\) так, что выполняются оба следующих условия: - все пустые клетки атакованы;
- ровно \(k\) пар ладей атакуют друг друга.
Пустая клетка считается атакованной, если хотя бы одна ладья находится в той же строке или в том же столбце. Две ладьи атакуют друг друга, если они находятся в одной и той же строке или в одном и том же столбце, и между ними нет других ладей. Например, на следующей картинке можно найти только две пары ладей, атакующих друг друга: 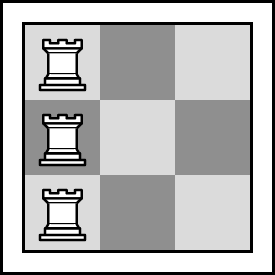 Один из способов расставить ладьи при \(n = 3\) и \(k = 2\) Один из способов расставить ладьи при \(n = 3\) и \(k = 2\) Два способа считаются различными, если существует хотя бы одна клетка, которая свободна в одном из способов и занята ладьей в другом способе. Ответ может быть очень большим, поэтому выведите его по модулю \(998244353\). Выходные данные Выведите одно число — количество способов расставить ладьи, взятое по модулю \(998244353\). | |
![]()
|
|
E. Слабая подпоследовательность
Комбинаторика
*3000
Маленький Петя очень любит строки. Недавно мама подарила ему ваучер на покупку строки в местном магазине. Можно считать, что в магазине присутствуют все возможные строки над алфавитом фиксированного размера. Размер алфавита равен k. Однако этот ваучер имеет ограничение на тип строк, которые можно приобрести при помощи него. А именно, строка s может быть приобретена, если длина самой длинной ее подстроки, которая также является ее слабой подпоследовательностью (см. определение ниже) равна w. Строка a длины n является слабой подпоследовательностью строки s длины m, если существует такой набор индексов 1 ≤ i1 < i2 < ... < in ≤ m, для которого выполняются два свойства: - ak = sik для всех k от 1 до n;
- существует хотя бы одно такое k (1 ≤ k < n), для которого ik + 1 – ik > 1.
Пете стало интересно, сколько различных строк доступны ему для покупки в магазине. Так как количество строк может быть очень велико, найдите его по модулю 1000000007 (109 + 7). В случае, если таких строк бесконечно много — выведите «-1». Выходные данные Выведите одно число — количество строк, которые доступны маленькому Пете для покупки по ваучеру, по модулю 1000000007 (109 + 7). Если таких строк бесконечно много — выведите «-1» (без кавычек). Примечание В первом примере по ваучеру доступны следующие строки: aaa, aab, abab, abb, abba, baa, baab, baba, bba, bbb. | |
![]()
|
|
E. Модульная стабильность
Комбинаторика
математика
теория чисел
*2000
Обозначим за \(x \bmod y\) остаток от целочисленного деления \(x\) на \(y\) (оператор \(\%\) в C++ или Java, mod в Pascal). Назовем массив целых чисел \([a_1, a_2, \dots, a_k]\) стабильным, если для каждой перестановки \(p\) целых чисел от \(1\) до \(k\), и для каждого неотрицательного целого числа \(x\) выполняется следующее условие: \( (((x \bmod a_1) \bmod a_2) \dots \bmod a_{k - 1}) \bmod a_k = (((x \bmod a_{p_1}) \bmod a_{p_2}) \dots \bmod a_{p_{k - 1}}) \bmod a_{p_k} \) Другими словами, для каждого неотрицательного целого \(x\) значение \((((x \bmod a_1) \bmod a_2) \dots \bmod a_{k - 1}) \bmod a_k\) не зависит от порядка элементов в массиве \(a\). Для двух заданных целых чисел \(n\) и \(k\) посчитайте количество стабильных массивов \([a_1, a_2, \dots, a_k]\), в которых \(1 \le a_1 < a_2 < \dots < a_k \le n\). Выходные данные Выведите количество стабильных массивов \([a_1, a_2, \dots, a_k]\), в которых \(1 \le a_1 < a_2 < \dots < a_k \le n\). Так как ответ может быть очень большим, выведите его по модулю \(998244353\). | |
![]()
|
|
G. Надежный пароль
Конструктив
Комбинаторика
математика
*2800
битмаски
интерактив
Это интерактивная задача. Ayush придумал еще один способ задать пароль для своего замка. В замке есть \(n\) слотов, в каждом слоте может находится любое неотрицательное целое число. Пароль \(P\) это последовательность из \(n\) целых чисел, \(i\)-й из которых соответствует \(i\)-му слоту замка. Чтобы задать пароль, Ayush придумал последовательность \(A\) из \(n\) целых чисел из отрезка \([0, 2^{63}-1]\). Затем, он определил \(i\)-й элемент \(P\) как побитовое ИЛИ всех чисел в массиве кроме \(A_i\). Вам нужно отгадать пароль. Чтобы задать запрос, вы можете выбрать непустое подмножество индексов массива и спросить побитовое ИЛИ всех элементов массива с индексами в этом подмножестве. Вы можете задать не более 13 запросов. Протокол взаимодействия Чтобы задать вопрос, в отдельной строке: - Сначала выведите «? c» (без кавычек), где \(c\) \((1 \leq c \leq n)\) обозначает размер подмножества запроса, после чего выведите \(c\) различных целых чисел из отрезка \([1, n]\), разделенных пробелами.
В ответ на каждый запрос, вы получите число \(x\) — побитовое ИЛИ чисел с выбранными индексами. Если вы спросили некорректное множество индексом или вы превысили количество запросов, тогда вы получите \(x = -1\). В таком случае вы должны немедленно завершить выполнение программы. Если вы угадали пароль, в отдельной строке выведите «!» (без кавычек), после чего выведите \(n\) целых чисел, разделенных пробелами — последовательность-пароль. Отгадывание пароля не считается в числе загаданных запросов. Интерактор не адаптивный. Массив \(A\) не меняется с запросами. После вывода запроса, не забывайте выводить конец строки и сбрасывать поток вывода. Иначе, вы получите верикт Превышен лимит бездействия. Чтобы сделать это, используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- читайте документацию для остальных языков.
Взломы Чтобы взломать решение, используйте следующий формат: В первой строке, выведите одно целое число \(n\) \((2 \le n \le 1000)\) — количество слотов в замке. Во второй строке выведите \(n\) целых чисел из отрезка \([0, 2^{63} - 1]\), разделенных пробелами — массив \(A\). Примечание Массив \(A\) в примере это \(\{{1, 2, 4\}}\). Первый элемент пароля это побитовое ИЛИ элементов \(A_2\) и \(A_3\), второй элемент это побитовое ИЛИ элементов \(A_1\) и \(A_3\), а третий элемент это побитовое ИЛИ элементов \(A_1\) и \(A_2\). Таким образом, пароль равен \(\{{6, 5, 3\}}\). | |
![]()
|
|
E. Два массива
Бинарный поиск
Перебор
Конструктив
Комбинаторика
*2100
дп
Вам даны два массива \(a_1, a_2, \dots , a_n\) и \(b_1, b_2, \dots , b_m\). Массив \(b\) отсортирован в порядке возрастания (\(b_i < b_{i + 1}\) верно для любого \(i\) от \(1\) до \(m - 1\)). Вам нужно разбить массив \(a\) на \(m\) непрерывных подмассивов так, чтобы для всех \(i\) от \(1\) до \(m\) минимум в \(i\)-м подмассиве был равен \(b_i\). Обратите внимание, что каждый элемент должен принадлежать ровно одному подмассиву, и они формируются следующим образом: первые несколько элементов массива \(a\) принадлежат первому подмассиву, следующие несколько элементов массива \(a\) принадлежат второму подмассиву, и так далее. Например, если \(a = [12, 10, 20, 20, 25, 30]\), а \(b = [10, 20, 30]\), то существует два подходящих разбиения массива \(a\): - \([12, 10, 20], [20, 25], [30]\);
- \([12, 10], [20, 20, 25], [30]\).
Вам нужно посчитать количество хороших разбиений массива \(a\). Так как это значение может быть слишком велико — выведите его по модулю 998244353. Выходные данные В единственной строке выведите число — количество хороших разбиений массива \(a\) по модулю 998244353. | |
![]()
|
|
E1. Астеризм (простая версия)
Бинарный поиск
Перебор
Комбинаторика
математика
теория чисел
сортировки
*1900
Это простая версия задачи. Различие между версиями заключается в ограничениях на \(n\) и \(a_i\). Вы можете делать взломы, только если обе версии этой задачи сданы. Сначала Aoi придумал следующую идею для задачи по программированию: Yuzu девочка, которая коллекционирует конфеты. Изначально, у нее есть \(x\) конфет. Также есть \(n\) врагов, пронумерованных целыми числами от \(1\) до \(n\). Враг \(i\) имеет \(a_i\) конфет. Yuzu хочет получить перестановку \(P\). Перестановкой называется массив, состоящий из \(n\) различных целых чисел от \(1\) до \(n\), расположенных в некотором порядке. Например, \(\{2,3,1,5,4\}\) это перестановка, а \(\{1,2,2\}\) это не перестановка (число \(2\) встречается в массиве дважды) и \(\{1,3,4\}\) тоже не является перестановкой (потому что \(n=3\), но в массиве есть число \(4\)). После этого, она проведет \(n\) дуэлей с врагами по следующим правилам: - Если Yuzu сейчас имеет не меньше конфет, чем враг \(P_i\), она побеждает в дуэли и получает \(1\) конфету. Иначе, она проигрывает дуэль и ничего не получает.
- Конфета, которую получает Yuzu в случае победы, будет использоваться в следующих дуэлях.
Yuzu хочет победить во всех дуэлях. Сколько существует возможных перестановок \(P\), для которых это произойдет? Эта задача была простой и неинтересной для Akari, друга Aoi. И Akari придумал следующую задачу, на основе описанной идеи: Давайте определим \(f(x)\) как количество возможных перестановок для целого числа \(x\). Вам дано число \(n\), массив \(a\) и простое число \(p \le n\). Назовем целое положительное число \(x\) хорошим, если значение \(f(x)\) не делится на \(p\). Найдите все хорошие числа \(x\). Решите задачу, предложенную Akari. Выходные данные В первой строке выведите количество хороших чисел \(x\). Во второй строке выведите все хорошие числа \(x\) в возрастающем порядке. Гарантируется, что количество хороших чисел \(x\) не превосходит \(10^5\). Примечание В первом тесте \(p=2\). - Если \(x \le 2\) тогда нет ни одной перестановки, подходящей для Yuzu. Поэтому \(f(x)=0\) для \(x \le 2\). Заметим, что \(0\) делится на \(2\), поэтому ни одно число \(x \leq 2\) не хорошее.
- Если \(x = 3\), то \(\{1,2,3\}\) единственная подходящая для Yuzu перестановка. Тогда, \(f(3)=1\), а значит число \(3\) хорошее.
- Если \(x = 4\), то \(\{1,2,3\} , \{1,3,2\} , \{2,1,3\} , \{2,3,1\}\) это все перестановки, подходящие для Yuzu. Тогда, \(f(4)=4\), значит число \(4\) не хорошее.
- Если \(x \ge 5\) , все \(6\) перестановок подходят Yuzu. Тогда, \(f(x)=6\) для всех \(x \ge 5\). Значит ни одно число \(x \ge 5\) не хорошее.
Значит единственное хорошее число это \(3\). В третьем тесте для всех целых положительных \(x\) значение \(f(x)\) делится на \(p = 3\). | |
![]()
|
|
E2. Астеризм (сложная версия)
Бинарный поиск
Комбинаторика
математика
дп
теория чисел
сортировки
*2300
Это сложная версия задачи. Различие между версиями заключается в ограничениях на \(n\) и \(a_i\). Вы можете делать взломы, только если обе версии этой задачи сданы. Сначала Aoi придумал следующую идею для задачи по программированию: Yuzu девочка, которая коллекционирует конфеты. Изначально, у нее есть \(x\) конфет. Также есть \(n\) врагов, пронумерованных целыми числами от \(1\) до \(n\). Враг \(i\) имеет \(a_i\) конфет. Yuzu хочет получить перестановку \(P\). Перестановкой называется массив, состоящий из \(n\) различных целых чисел от \(1\) до \(n\), расположенных в некотором порядке. Например, \(\{2,3,1,5,4\}\) это перестановка, а \(\{1,2,2\}\) это не перестановка (число \(2\) встречается в массиве дважды) и \(\{1,3,4\}\) тоже не является перестановкой (потому что \(n=3\), но в массиве есть число \(4\)). После этого, она проведет \(n\) дуэлей с врагами по следующим правилам: - Если Yuzu сейчас имеет не меньше конфет, чем враг \(P_i\), она побеждает в дуэли и получает \(1\) конфету. Иначе, она проигрывает дуэль и ничего не получает.
- Конфета, которую получает Yuzu в случае победы, будет использоваться в следующих дуэлях.
Yuzu хочет победить во всех дуэлях. Сколько существует возможных перестановок \(P\), для которых это произойдет? Эта задача была простой и неинтересной для Akari, друга Aoi. И Akari придумал следующую задачу, на основе описанной идеи: Давайте определим \(f(x)\) как количество возможных перестановок для целого числа \(x\). Вам дано число \(n\), массив \(a\) и простое число \(p \le n\). Назовем целое положительное число \(x\) хорошим, если значение \(f(x)\) не делится на \(p\). Найдите все хорошие числа \(x\). Решите задачу, предложенную Akari. Выходные данные В первой строке выведите количество хороших чисел \(x\). Во второй строке выведите все хорошие числа \(x\) в возрастающем порядке. Гарантируется, что количество хороших чисел \(x\) не превосходит \(10^5\). Примечание В первом тесте \(p=2\). - Если \(x \le 2\) тогда нет ни одной перестановки, подходящей для Yuzu. Поэтому \(f(x)=0\) для \(x \le 2\). Заметим, что \(0\) делится на \(2\), поэтому ни одно число \(x \leq 2\) не хорошее.
- Если \(x = 3\), то \(\{1,2,3\}\) единственная подходящая для Yuzu перестановка. Тогда, \(f(3)=1\), а значит число \(3\) хорошее.
- Если \(x = 4\), то \(\{1,2,3\} , \{1,3,2\} , \{2,1,3\} , \{2,3,1\}\) это все перестановки, подходящие для Yuzu. Тогда, \(f(4)=4\), значит число \(4\) не хорошее.
- Если \(x \ge 5\) , все \(6\) перестановок подходят Yuzu. Тогда, \(f(x)=6\) для всех \(x \ge 5\). Значит ни одно число \(x \ge 5\) не хорошее.
Значит единственное хорошее число это \(3\). В третьем тесте для всех целых положительных \(x\) значение \(f(x)\) делится на \(p = 3\). | |
![]()
|
|
E. Странная операция
Структуры данных
Комбинаторика
дп
*2800
Коала Коа имеет бинарную строку \(s\) длины \(n\). Коа может выполнить не более \(n-1\) (возможно, ноль) операций следующего вида: За одну операцию Коа выбирает позиции \(i\) и \(i+1\) для некоторого \(i\) с \(1 \le i < |s|\) и делает \(s_i\) равным \(max(s_i, s_{i+1})\). Затем Коа удаляет позицию \(i+1\) из \(s\) (после удаления оставшиеся части склеиваются). Обратите внимание, что после каждой операции длина \(s\) уменьшается на \(1\). Сколько разных бинарных строк может получить Коа, выполнив не более \(n-1\) (возможно, ноль) операций по модулю \(10^9+7\) (\(1000000007\))? Выходные данные В единственной строке выведите ответ на задачу по модулю \(10^9+7\) (\(1000000007\)). Примечание В первом примере Koa может получить следующие бинарные строки: \(0\), \(00\) и \(000\). Во втором примере Коа может получить следующие бинарные строки: \(1\), \(01\), \(11\), \(011\), \(101\) и \(0101\). Например: - для получения \(01\) из \(0101\) Коа может действовать следующим образом: \(0101 \rightarrow 0(10)1 \rightarrow 011 \rightarrow 0(11) \rightarrow 01\).
- для получения \(11\) от \(0101\) Коа может действовать следующим образом: \(0101 \rightarrow (01)01 \rightarrow 101 \rightarrow 1(01) \rightarrow 11\).
Круглые скобки обозначают две позиции, выбранные Коа в каждой операции. | |
![]()
|
|
C. Циклические перестановки
Комбинаторика
математика
дп
*1500
графы
Перестановка длины \(n\) — это массив, состоящий из \(n\) различных целых чисел от \(1\) до \(n\) в произвольном порядке. Например, \([2,3,1,5,4]\) — это перестановка, но \([1,2,2]\) — это не перестановка (\(2\) встречается дважды в массиве), а \([1,3,4]\) также не является перестановкой (\(n=3\), но в массиве встречается \(4\)). Рассмотрим перестановку \(p\) длины \(n\). Построим граф на \(n\) вершинах, используя перестановку следующим образом: - Для каждого \(1 \leq i \leq n\) найдите наибольшее значение \(j\), для которого \(1 \leq j < i\) и \(p_j > p_i\), и добавьте неориентированное ребро между вершинами \(i\) и \(j\).
- Для каждого \(1 \leq i \leq n\) найдите наименьшее значение \(j\), для которого \(i < j \leq n\) и \(p_j > p_i\), и добавьте неориентированное ребро между вершинами \(i\) и \(j\)
В тех случаях, когда таких \(j\) не существует, мы не добавляем ребер. Также обратите внимание, что мы проводим ребра между соответствующими индексами, а не значениями в этих индексах. Например, рассмотрим случай \(n = 4\) и \(p = [3,1,4,2]\); здесь ребрами графа являются \((1,3),(2,1),(2,3),(4,3)\). Перестановка \(p\) является циклической, если граф, построенный с использованием \(p\), имеет хотя бы один простой цикл. Для данного \(n\), найдите число циклических перестановок длины \(n\). Поскольку число может быть очень большим, выведите его по модулю \(10^9+7\). Пожалуйста, обратитесь к разделу Примечания для формального определения простого цикла. Выходные данные Выведите единственное целое число \(0 \leq x < 10^9+7\), количество циклических перестановок длины \(n\) по модулю \(10^9+7\). Примечание Для \(n = 4\) существует \(16\) циклических перестановок. \([4,2,1,3]\) — одна из таких перестановок, она содержит цикл длины четыре: \(4 \rightarrow 3 \rightarrow 2 \rightarrow 1 \rightarrow 4\). Вершины \(v_1\), \(v_2\), \(\ldots\), \(v_k\) образуют простой цикл, если выполняются следующие условия: - \(k \geq 3\).
- \(v_i \neq v_j\) для любой пары индексов \(i\) и \(j\). (\(1 \leq i < j \leq k\))
- Между \(v_i\) и \(v_{i+1}\) есть ребро для всех \(i\) (\(1 \leq i < k\)), как и между \(v_1\) и \(v_k\)
| |
![]()
|
|
H. ZS тасует карты
Теория вероятностей
Комбинаторика
математика
дп
*3000
У zscoder есть колода из \(n+m\) карт, изготовленная по индивидуальному заказу, которая состоит из \(n\) карт пронумерованных от \(1\) до \(n\) и \(m\) джокеров. Так как zscoder одинок, он хочет поиграть с сам с собой, используя эти карты. Изначально колода перетасовывается в случайном порядке и кладется на стол. У zscoder есть изначально пустое множество \(S\). Каждую секунду zscoder вытягивает верхнюю карту из колоды. - Если на карте написано число \(x\), zscoder снимает карту и добавляет \(x\) в множество \(S\).
- Если извлеченная карта является джокером, zscoder помещает все карты обратно в колоду и перетасовывает (равномерно случайным образом) все \(n+m\) карт, получая новую колоду (следовательно, новая колода также содержит все карты от \(1\) до \(n\) и \(m\) джокеров). Затем, если \(S\) в настоящее время содержит все элементы от \(1\) до \(n\), игра заканчивается. Перетасовка колоды не занимает времени.
Какое матожидание количества секунд до окончания игры? Можно показать, что ответ можно записать в виде \(\frac{P}{Q}\), где \(P, Q\) — взаимно простые целые числа, где \(Q \neq 0 \bmod 998244353\). Выведите значение \((P \cdot Q^{-1})\) по модулю \(998244353\). Выходные данные Выведите единственное целое число, значение \((P \cdot Q^{-1})\) по модулю \(998244353\). Примечание Для первого примера можно доказать, что ожидаемое время до окончания игры составляет \(5\) секунд. Для второго примера можно доказать, что ожидаемое время до окончания игры составляет \(\frac{28}{3}\)секунды. | |
![]()
|
|
E. Новогодняя гирлянда
Комбинаторика
дп
*2600
В то время как Геральд, Александр, Сергей и Геннадий уже занимаются привычными новогодними делами, Эдвард второпях наряжает новогоднюю елку. А какая елка без гирлянды? У Эдварда есть лампочки m цветов, и он хочет составить из них гирлянду — последовательность длины L. Елка Эдварда состоит из n ярусов, и Эдвард планирует расположить гирлянду таким образом, чтобы первые l1 лампочек гирлянды украшали первый ярус, следующие l2 лампочек — второй ярус и так далее, на последнем n-ом ярусе окажутся последние ln лампочек, 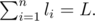 Эдвард — любитель математических головоломок, поэтому его неожиданно заинтересовал вопрос: сколько у него различных вариантов собрать гирлянду, чтобы выполнялись оба условия: Эдвард — любитель математических головоломок, поэтому его неожиданно заинтересовал вопрос: сколько у него различных вариантов собрать гирлянду, чтобы выполнялись оба условия: - Любые две подряд идущие лампочки на каждом ярусе должны иметь разные цвета.
- Множества цветов лампочек на каждых двух соседних ярусах должны быть различны. Здесь рассматриваются неупорядоченные множества (не мультимножества), в которых каждый цвет встречается не более одного раза. То есть количество лампочек значения не имеет.
Помогите Эдварду получить ответ на мучающий его вопрос, иначе он не успеет нарядить елку до Нового года. Считайте, что у Эдварда бесконечное количество лампочек каждого из m цветов, причем использовать все m цветов необязательно. Гирлянды считаются различными, если они как последовательности различаются хотя бы в одной позиции. Вычислите ответ на задачу по заданному модулю p. Выходные данные Выведите одно число — количество гирлянд по модулю p. Примечание В первом примере возможны следующие варианты: 121|1|12, 121|1|21, 121|2|12, 121|2|21, 212|1|12, 212|1|21, 212|2|12, 212|2|21. Во втором примере возможны варианты: 12|13, 12|23, 12|31, 12|32 и т.д. Рисунок к первому примеру:  | |
![]()
|
|
D. Зигзаги
Перебор
Структуры данных
Комбинаторика
математика
*1900
Вам задан массив \(a_1, a_2 \dots a_n\). Посчитайте количество таких четверок \((i, j, k, l)\), что: - \(1 \le i < j < k < l \le n\);
- \(a_i = a_k\) и \(a_j = a_l\);
Выходные данные Для каждого набора входных данных, выведите количество описанных четверок. Примечание В первом наборе входных данных, каждая четверка индексов \(i < j < k < l\) подходит, а потому ответ — это количество четверок. Во втором наборе, есть только \(2\) подходящих четверки: - \((1, 2, 4, 6)\): \(a_1 = a_4\) и \(a_2 = a_6\);
- \((1, 3, 4, 6)\): \(a_1 = a_4\) и \(a_3 = a_6\).
| |
![]()
|
|
G. Наемники
Перебор
Комбинаторика
математика
дп
*2600
битмаски
снм
Поликарп играет в (очередную) стратегическую компьютерную игру. В этой игре он управляет армией наемников. Поликарп хочет собрать свою армию для выполнения задания. Для найма доступны \(n\) наемников, и армия Поликарпа должна состоять из некоторого подмножества множества доступных наемников. \(i\)-го наемника можно выбрать только в том случае, если итоговое количество выбранных наемников не менее \(l_i\) (иначе этот наемник считает задание слишком опасным) и не более \(r_i\) (он не хочет делить добычу со слишком большим количеством других наемников). Кроме того, \(m\) пар наемников ненавидят друг друга, и из каждой такой пары можно взять на задание не более одного наемника. Сколько непустых подмножеств наемников Поликарп должен рассмотреть? Другими словами, посчитайте количество подмножеств наемников, которые не содержат пар наемников, ненавидящих друг друга, и размер которых принадлежит отрезку \([l_i, r_i]\) для каждого наемника из подмножества. Ответ может быть очень большим, поэтому посчитайте его по модулю \(998244353\). Выходные данные Выведите одно целое число — количество подмножеств, удовлетворяющих условию задачи, взятое по модулю \(998244353\). | |
![]()
|
|
C. Star Trek
Деревья
Комбинаторика
дп
*2600
*особая задача
поиск в глубину и подобное
графы
матрицы
игры
The United Federation of Planets is an alliance of \(N\) planets, they are indexed from \(1\) to \(N\). Some planets are connected by space tunnels. In a space tunnel, a starship can fly both ways really fast. There are exactly \(N-1\) space tunnels, and we can travel from any planet to any other planet in the Federation using these tunnels. It's well known that there are \(D\) additional parallel universes. These are exact copies of our universe, they have the same planets and space tunnels. They are indexed from \(1\) to \(D\) (our universe has index \(0\)). We denote the planet \(x\) in universe \(i\) by \(P_x^i\). We can travel from one universe to another using dimension portals. For every \(i\) (\(0\leq i \leq D-1\)), we will place exactly one portal that allows us to fly from \(P_{A_i}^i\) to \(P_{B_i}^{i+1}\), for some planet indices \(A_i\) and \(B_i\) (i.e. \(1 \leq A_i, B_i \leq N\)). Once all the portals are placed, Starship Batthyány will embark on its maiden voyage. It is currently orbiting around \(P_1^0\). Captain Ágnes and Lieutenant Gábor have decided to play the following game: they choose alternately a destination (a planet) to fly to. This planet can be in the same universe, if a space tunnel goes there, or it can be in another universe, if a portal goes there. Their aim is to visit places where no one has gone before. That's why, once they have visited a planet \(P_x^i\), they never go back there (but they can visit the planet \(x\) in another universe). Captain Ágnes chooses the first destination (then Gábor, then Ágnes etc.). If somebody can't choose a planet where they have not been before in his/her turn, he/she loses. Captain Ágnes and Lieutenant Gábor are both very clever: they know the locations of all tunnels and portals, and they both play optimally. For how many different placements of portals does Captain Ágnes win the game? Two placements are different if there is an index \(i\) (\(0\leq i \leq D-1\)), where the \(i\)th portal connects different pairs of planets in the two placements (i.e \(A_i\) or \(B_i\) differs). This number can be very big, so we are interested in it modulo \(10^9+7\). Output You should print a single integer, the number of possible placements of portals where Captain Ágnes wins modulo \(10^9+7\). Scoring \( \begin{array}{|c|c|c|} \hline \text{Subtask} & \text{Points} & \text{Constraints} \\ \hline 1 & 0 & \text{samples}\\ \hline 2 & 7 & N=2 \\ \hline 3 & 8 & N \leq 100 \: \text{and} \: D = 1 \\ \hline 4 & 15 & N \leq 1000 \: \text{and} \: D = 1\\ \hline 5 & 15 & D=1 \\ \hline 6 & 20 & N \leq 1000 \: \text{and} \: D \leq 10^5\\ \hline 7 & 20 & D \leq 10^5\\ \hline 8 & 15 & \text{no additional constraints}\\ \hline \end{array} \) Note There is only 1 portal and \(3 \cdot 3 = 9\) different placements. The following 4 placements are when the Captain wins. 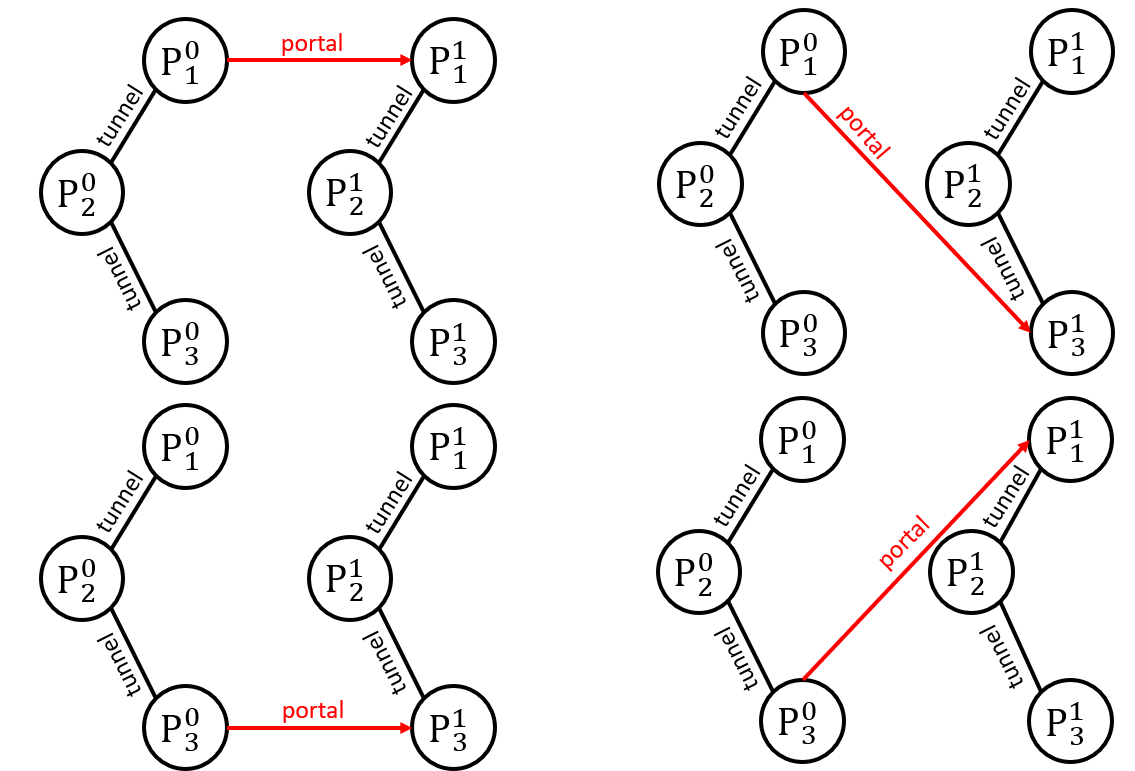
| |
![]()
|
|
C. Chess Rush
Комбинаторика
математика
реализация
дп
*особая задача
*3200
The mythic world of Chess Land is a rectangular grid of squares with \(R\) rows and \(C\) columns, \(R\) being greater than or equal to \(C\). Its rows and columns are numbered from \(1\) to \(R\) and \(1\) to \(C\), respectively. The inhabitants of Chess Land are usually mentioned as pieces in everyday language, and there are \(5\) specific types of them roaming the land: pawns, rooks, bishops, queens and kings. Contrary to popular belief, chivalry is long dead in Chess Land, so there are no knights to be found. Each piece is unique in the way it moves around from square to square: in one step, - a pawn can move one row forward (i.e. from row \(r\) to \(r+1\)), without changing columns;
- a rook can move any number of columns left/right without changing rows OR move any number of rows forward/backward without changing columns;
- a bishop can move to any square of the two diagonals intersecting at its currently occupied square;
- a queen can move to any square where a rook or a bishop could move to from her position;
- and a king can move to any of the \(8\) adjacent squares.
In the following figure, we marked by X the squares each piece can move to in a single step (here, the rows are numbered from bottom to top, and the columns from left to right). 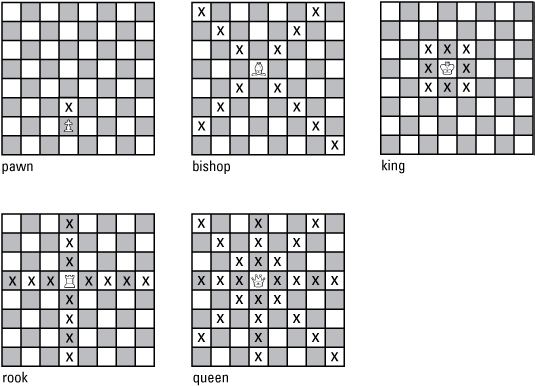 Recently, Chess Land has become a dangerous place: pieces that are passing through the land can get captured unexpectedly by unknown forces and simply disappear. As a consequence, they would like to reach their destinations as fast (i.e. in as few moves) as possible, and they are also interested in the number of different ways it is possible for them to reach it, using the minimal number of steps – because more paths being available could mean lower chances of getting captured. Two paths are considered different if they differ in at least one visited square. For this problem, let us assume that pieces are entering Chess Land in a given column of row \(1\), and exit the land in a given column of row \(R\). Your task is to answer \(Q\) questions: given the type of a piece, the column it enters row \(1\) and the column it must reach in row \(R\) in order to exit, compute the minimal number of moves it has to make in Chess Land, and the number of different ways it is able to do so. Output You have to print \(Q\) lines, the \(i\)-th one containing two space separated integers, the answer to the \(i\)-th question: the first one is the minimal number of steps needed, the second is the number of different paths available using this number of steps. Since the answer can be quite large, you have to compute it modulo \(10^9+7\). If it is impossible to reach the target square, output the line "0 0". Scoring \( \begin{array}{|c|c|l|} \hline \text{Subtask} & \text{Points} & \text{Constraints} \\ \hline 1 & 0 & \text{samples}\\ \hline 2 & 8 & T\in\{\text{'P','R','Q'}\}\text{, i.e. all pieces are pawns, rooks or queens} \\ \hline 3 & 15 & T=\text{'B' and } \: C,R\leq 100 \\ \hline 4 & 22 & T=\text{'B'} \\ \hline 5 & 5 & T=\text{'K' and }\:C,R\leq 100\:\text{and}\:Q\leq 50 \\ \hline 6 & 8 & T=\text{'K' and }\:C,R\leq 100\\ \hline 7 & 15 & T=\text{'K' and }\:C\leq 100\\ \hline 8 & 20 & T=\text{'K'}\\ \hline 9 & 7 & \text{no additional constraints}\\ \hline \end{array} \) | |
![]()
|
|
G. Подсчет кластеризаций
Деревья
Комбинаторика
дп
графы
*2700
снм
бпф
В сети компании есть \(n\) компьютеров. Они пронумерованы от \(1\) до \(n\). Для каждой пары компьютеров \(1 \leq i < j \leq n\) вы знаете значение \(a_{i,j}\): сложность отправки сообщения между компьютерами \(i\) и \(j\). Значения \(a_{i,j}\) для \(i<j\) различны. Вы хотите разделить компьютеры на \(k\) множеств \(A_1, A_2, \ldots, A_k\), чтобы следующие условия выполнялись: - для каждого компьютера \(1 \leq i \leq n\) есть ровно одно множество \(A_j\) такое, что \(i \in A_j\);
- для каждых двух пар компьютеров \((s, f)\) и \((x, y)\) (\(s \neq f\), \(x \neq y\)) таких, что \(s\), \(f\), \(x\) из одного множества, а \(x\) и \(y\) из разных, выполняется \(a_{s,f} < a_{x,y}\).
Для каждого \(1 \leq k \leq n\) найдите число способов разделить компьютеры на \(k\) групп так, чтобы все упомянутые условия соблюдались. Эти значения могут быть большими, так что вам нужно найти их по модулю \(998\,244\,353\). Выходные данные Выведите \(n\) целых чисел: \(k\)-е из них должно быть равно числу способов разбить компьютеры на \(k\) групп, соблюдая все описанные условия, по модулю \(998\,244\,353\). Примечание Ниже приведены все возможные разбиения компьютеров на \(4\) группы для второго примера: - \(\{1, 2\}, \{3, 4\}, \{5\}, \{6, 7\}\);
- \(\{1\}, \{2\}, \{3, 4\}, \{5, 6, 7\}\);
- \(\{1, 2\}, \{3\}, \{4\}, \{5, 6, 7\}\).
| |
![]()
|
|
E. Ожидаемый урон
Бинарный поиск
Теория вероятностей
Комбинаторика
*2400
Вы играете в компьютерную игру. В этой игре вам необходимо сразиться с \(n\) монстрами. Чтобы защищаться от монстров, вам нужен щит. У каждого щита есть два параметра: текущая прочность \(a\) и уровень защиты \(b\). У каждого монстра есть только один параметр: его сила \(d\). Если вы сражаетесь с монстром с силой \(d\), используя щит с текущей прочностью \(a\) и уровнем защиты \(b\), возможны три исхода: - если \(a = 0\), вы получаете \(d\) урона;
- если \(a > 0\) и \(d \ge b\), вы не получаете урона, но прочность щита уменьшается на \(1\);
- если \(a > 0\) и \(d < b\), ничего не происходит.
Сила \(i\)-го монстра равна \(d_i\), и вам придется сразиться со всеми монстрами в случайном порядке (все \(n!\) порядков равновероятны). Вы можете использовать один из \(m\) различных щитов, у \(i\)-го щита прочность изначально равна \(a_i\), а уровень защиты равен \(b_i\). Для каждого щита посчитайте математическое ожидание полученного урона, если вы сразитесь со всеми \(n\) монстрами в случайном порядке, используя этот щит. Выходные данные Выведите \(m\) целых чисел, \(i\)-е из которых соответствует математическому ожиданию урона, который вы получите, используя \(i\)-й щит, следующим образом: можно доказать, что для каждого щита ответ — это несократимая дробь \(\dfrac{x}{y}\), где \(y\) и \(998244353\) — взаимно простые числа. Выведите значение \(x \cdot y^{-1} \bmod 998244353\), где \(y^{-1}\) — обратный элемент к \(y\) (\(y \cdot y^{-1} \bmod 998244353 = 1\)). | |
![]()
|
|
D. Спасти Нибель!
Структуры данных
Комбинаторика
*1800
сортировки
Преодолев множество сложных испытаний, Ори и Сейн наконец-то зажгли Укрытый Светильник и нашли Печать Гумон, ключ к Руинам Форлорна! Когда же они наконец вставили Печать в дверь... ничего не произошло. Ори очень этому удивился, но Сейн быстро все объяснил: хитрые Гумон решили наложить дополнительную защиту на дверь. На двери расположено \(n\) светильников, наполненных светом Древа Духов. Сейн точно знает: \(i\)-й светильник горит в моменты времени с \(l_i\) по \(r_i\) включительно. Чтобы открыть дверь, необходимо выбрать такие \(k\) светильников, что они все горят одновременно в какой-то момент времени. Пока Сейн решает, какие же \(k\) светильников выбрать, Ори стало интересно: а сколько всего существует способов выбрать \(k\) светильников так, чтобы дверь открылась? Может получиться и так, что Сейн что-то напутал, и таких \(k\) светильников просто не существует. Так как это число может быть очень большим, выводите его остаток от деления на \(998\,244\,353\). Выходные данные Выведите одно целое число — ответ на задачу по модулю \(998\,244\,353\). Примечание В первом примере всего девять подходящих наборов из \(k\) ламп: \((1, 2, 3)\), \((1, 2, 4)\), \((1, 2, 5)\), \((1, 2, 6)\), \((1, 3, 6)\), \((1, 4, 6)\), \((2, 3, 6)\), \((2, 4, 6)\), \((2, 6, 7)\). Во втором примере \(k=1\), поэтому подходит каждый светильник. В третьем примере нет двух светильников, горящих одновременно, поэтому ответ 0. В четвертом примере все светильники горят в момент времени \(3\), поэтому ответ 1. В пятом примере всего семь наборов из \(k\) ламп: \((1, 2)\), \((1, 3)\), \((2, 3)\), \((2, 4)\), \((3, 4)\), \((3, 5)\), \((4, 5)\). | |
![]()
|
|
C. Торг
Комбинаторика
математика
дп
*1700
Порой сложно прийти к конечной цене в торге. Вот и Саша с Вовой никак не могут прийти к соглашению – Саша стремится назвать цену как можно больше, а Вова — вычеркнуть из нее как можно больше цифр. Т. е. получается так, что Саша называет какое-то целое число \(n\), Вова вычеркивает из него непустую последовательность подряд идущих цифр, а оставшиеся цифры схлопываются в одно число. Например, если из числа \(1213121\) вычеркнуть подстроку \(1312\), то получится число \(121\). Допустима, что итоговая цена содержит ведущие нули. Если Вова вычеркнет все цифры, то считается, что получился \(0\). Саша хочет как-то ограничить Вову, чтобы тот не вычеркнул все число, но, чтобы у него был правильные аргументы для убеждения, ему нужно знать сумму всех чисел, которые могут получиться после того, как Вова сделает вычеркивание. Помогите Саше посчитать. А так как число может получиться достаточно большим, то считайте его по модулю \(10^9 + 7\). Выходные данные В единственной строке выведите искомую сумму по модулю \(10^9 + 7\). Примечание Рассмотрим первый пример. Вова может вычеркнуть \(1\), \(0\), \(7\), \(10\), \(07\) или \(107\). Получившиеся числа равны \(07\), \(17\), \(10\), \(7\), \(1\), \(0\). Их сумма равна \(42\). | |
![]()
|
|
D. Danger of Mad Snakes
Комбинаторика
математика
дп
*2300
Mr. Chanek The Ninja is one day tasked with a mission to handle mad snakes that are attacking a site. Now, Mr. Chanek already arrived at the hills where the destination is right below these hills. The mission area can be divided into a grid of size \(1000 \times 1000\) squares. There are \(N\) mad snakes on the site, the i'th mad snake is located on square \((X_i, Y_i)\) and has a danger level \(B_i\). Mr. Chanek is going to use the Shadow Clone Jutsu and Rasengan that he learned from Lord Seventh to complete this mission. His attack strategy is as follows: - Mr. Chanek is going to make \(M\) clones.
- Each clone will choose a mad snake as the attack target. Each clone must pick a different mad snake to attack.
- All clones jump off the hills and attack their respective chosen target at once with Rasengan of radius \(R\). If the mad snake at square \((X, Y)\) is attacked with a direct Rasengan, it and all mad snakes at squares \((X', Y')\) where \(max(|X' - X|, |Y' - Y|) \le R\) will die.
- The real Mr. Chanek will calculate the score of this attack. The score is defined as the square of the sum of the danger levels of all the killed snakes.
Now Mr. Chanek is curious, what is the sum of scores for every possible attack strategy? Because this number can be huge, Mr. Chanek only needs the output modulo \(10^9 + 7\). Output A line with an integer that denotes the sum of scores for every possible attack strategy. Note Here is the illustration of all six possible attack strategies. The circles denote the chosen mad snakes, and the blue squares denote the region of the Rasengan: 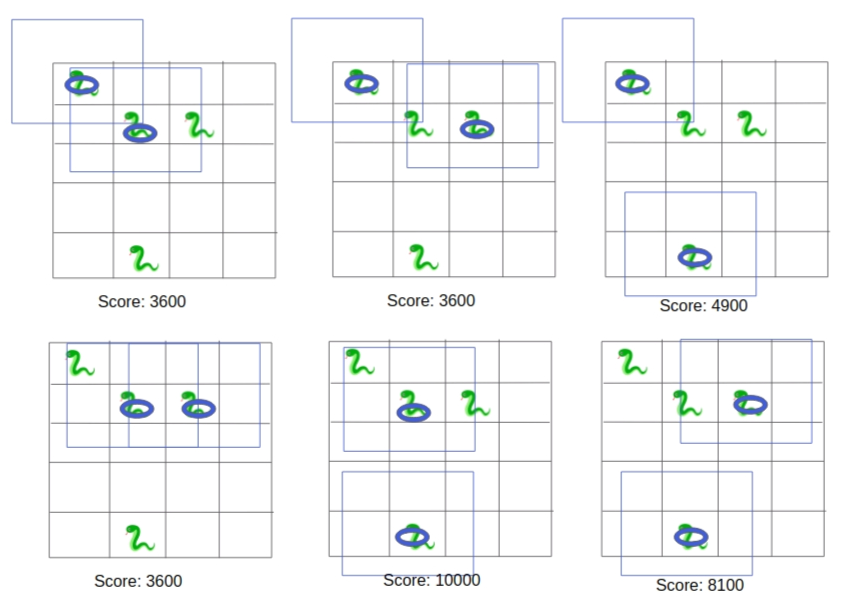 So, the total score of all attacks is: \(3.600 + 3.600 + 4.900 + 3.600 + 10.000 + 8.100 = 33.800\). | |
![]()
|
|
F. Количество подпоследовательностей
Строки
Комбинаторика
дп
*2000
Вам задана строка \(s\), состоящая из строчных букв «a», «b» и «c», а также из знаков вопроса «?». Пусть количество знаков вопроса в строке \(s\) равно \(k\). Заменим каждый знак вопроса на одну из букв «a», «b» и «c». Таким образом, мы получим \(3^{k}\) всевозможных строк, состоящих только из букв «a», «b» и «c». Например, если \(s = \)«ac?b?c» после замены знаков вопроса мы получим строки \([\)«acabac», «acabbc», «acabcc», «acbbac», «acbbbc», «acbbcc», «accbac», «accbbc», «accbcc»\(]\). Перед вами стоит задача определить количество подпоследовательностей «abc» во всех получившихся строках. Так как ответ может быть достаточно большим, выведите его по модулю числа \(10^{9} + 7\). Подпоследовательность строки \(t\) — это такая последовательность, которую можно получить из строки \(t\) путем удаления некоторого (возможно нулевого) количества букв, при этом порядок оставшихся букв должен быть неизменным. Например, в строке «baacbc» есть две подпоследовательности «abc». Это подпоследовательность, состоящая из букв в позициях \((2, 5, 6)\), и подпоследовательность, состоящая из букв в позициях \((3, 5, 6)\). Выходные данные Выведите суммарное количество подпоследовательностей вида «abc» во всех строках, которые можно получить путем замены знаков вопроса на буквы «a», «b» и «c», по модулю \(10^{9} + 7\). Примечание В первом примере после замены знаков вопроса получим \(9\) строк: - «acabac» — в этой строке \(2\) подпоследовательности «abc»,
- «acabbc» — в этой строке \(4\) подпоследовательности «abc»,
- «acabcc» — в этой строке \(4\) подпоследовательности «abc»,
- «acbbac» — в этой строке \(2\) подпоследовательности «abc»,
- «acbbbc» — в этой строке \(3\) подпоследовательности «abc»,
- «acbbcc» — в этой строке \(4\) подпоследовательности «abc»,
- «accbac» — в этой строке \(1\) подпоследовательность «abc»,
- «accbbc» — в этой строке \(2\) подпоследовательности «abc»,
- «accbcc» — в этой строке \(2\) подпоследовательности «abc».
Таким образом, во всех строках содержатся \(2 + 4 + 4 + 2 + 3 + 4 + 1 + 2 + 2 = 24\) подпоследовательности «abc». | |
![]()
|
|
E. Два хоровода
Комбинаторика
математика
*1300
Однажды \(n\) человек (\(n\) — чётное число) собрались на площади и организовали два хоровода, в каждом из которых танцевало по \(\frac{n}{2}\) человек ровно. Ваша задача — найти, сколькими способами \(n\) человек могут составить два хоровода размера \(\frac{n}{2}\). Каждый из человек должен танцевать ровно в одном из двух хороводов. Хоровод — это танцевальный круг, который составляют \(1\) или более человек. Два хоровода неотличимы, если один можно перевести в другой выбором начального участника хоровода. Например, хороводы \([1, 3, 4, 2]\), \([4, 2, 1, 3]\) и \([2, 1, 3, 4]\) — неотличимы. Например, если \(n=2\), то искомое количество способов равно \(1\): один хоровод будет составлен первым человеком, а второй — вторым. Например, если \(n=4\), то искомое количество способов равно \(3\). Возможные варианты: - один хоровод — \([1,2]\), другой — \([3,4]\);
- один хоровод — \([2,4]\), другой — \([3,1]\);
- один хоровод — \([4,1]\), другой — \([3,2]\).
Итак, ваша задача — найти, сколькими способами \(n\) человек могут составить два хоровода размера \(\frac{n}{2}\). Выходные данные Выведите единственное целое число — количество способов организовать хороводы. Гарантируется, что ответ помещается в \(64\)-битный целочисленный тип данных. | |
![]()
|
|
C. Бинарный поиск
Бинарный поиск
Комбинаторика
*1500
За свою долгую карьеру Андрей завоевал довольно много наград по программированию. Он считал себя действительно успешным программистом, но, к сожалению, он ничего не знал про алгоритм бинарного поиска. Прочитав уйму литературы, Андрей понял, что этот алгоритм позволяет довольно быстро найти в массиве некоторое число \(x\). Для некоторого массива \(a\), который нумеруются с нуля, и числа \(x\) псевдокод алгоритма выглядит следующим образом:  Обратите внимание, что в описанном выше алгоритме массив нумеруется с нуля, а деление является целочисленным (с округлением вниз). В книге, которую читал Андрей, было написано, что для корректной работы алгоритма массив обязательно должен быть отсортированным. Андрей не понял причину этого, ведь существуют неотсортированные массивы, для которых данный алгоритм найдёт число \(x\). Перед тем, как написать официальное письмо авторам книги, Андрею нужно проанализировать количество перестановок длины \(n\), для которых данный алгоритм найдёт число \(x\). Перестановкой длины \(n\) является массив, состоящий из \(n\) различных целых чисел от \(1\) до \(n\) в произвольном порядке. Помогите Андрею и выведите количество перестановок длины \(n\), в которых число \(x\) находится на позиции \(pos\) и для которых алгоритм бинарного поиска найдёт число \(x\) (вернёт true). Так как данное число может быть слишком большим, выведите остаток от деления этого числа на \(10^9+7\). Выходные данные Выведите единственное целое число — остаток от деления количества подходящих перестановок на \(10^9+7\). Примечание Все подходящие перестановки в первом тестовом примере: \((2, 3, 1, 4)\), \((2, 4, 1, 3)\), \((3, 2, 1, 4)\), \((3, 4, 1, 2)\), \((4, 2, 1, 3)\), \((4, 3, 1, 2)\). | |
![]()
|
|
F. Сумма по подмножествам
Комбинаторика
математика
теория чисел
*2800
В этой задаче вам дано мультимножество \(S\). Необходимо по всем парам подмножеств \(A\) и \(B\) таких, что: - \(B \subset A\);
- \(|B| = |A| - 1\);
- наибольший общий делитель элементов \(A\) равен единице;
найти сумму \(\sum_{x \in A}{x} \cdot \sum_{x \in B}{x}\) по модулю \(998\,244\,353\). Выходные данные В единственной строке выведите одно целое число — искомую сумму по модулю \(998\,244\,353\). Примечание Напомним, что мультимножество — это множество, в котором элементы могут повторяться несколько раз. \(|X|\) — мощность множества \(X\), количество элементов в нем. \(A \subset B\) — множество \(A\) является подмножеством множества \(B\). В первом примере \(B=\{1\}, A=\{1,2\}\) и \(B=\{2\}, A=\{1, 2\}\) дают произведение сумм \(1\cdot3 + 2\cdot3=9\). Все другие кандидаты на \(A\) и \(B\) не удовлетворяют требованиям. | |
![]()
|
|
F. Эмоциональные рыбаки
Комбинаторика
математика
дп
*2600
\(n\) рыбаков только что вернулись с рыбалки. \(i\)-й рыбак поймал рыбу веса \(a_i\). Рыбаки собираются похвастаться пойманной рыбой друг перед другом. Для этого они сначала выбирают порядок, в котором они показывают пойманную рыбу (каждый рыбак показывает свою рыбу ровно один раз, то есть, формально, порядок является перестановкой целых чисел от \(1\) до \(n\)). Затем они показывают свою рыбу в соответствии с выбранным порядком. Когда рыбак показывает свою рыбу, он может стать радостным, грустным, или остаться спокойным. Предположим, что рыбак показывает рыбу веса \(x\), и максимальный вес среди ранее показанных рыб равен \(y\) (\(y = 0\), если этот рыбак показывает свою рыбу первым). Тогда: - если \(x \ge 2y\), рыбак становится радостным;
- если \(2x \le y\), рыбак становится грустным;
- если ни одно из этих условий не выполняется, рыбак остается спокойным.
Назовем порядок, в котором рыбаки показывают свою рыбу, эмоциональным, если после того, как все рыбаки покажут свою рыбу, ни один из них не останется спокойным. Посчитайте количество эмоциональных порядков по модулю \(998244353\). Выходные данные Выведите одно число — количество эмоциональных порядков, взятое по модулю \(998244353\). | |
![]()
|
|
D. Финал INOI
Комбинаторика
дп
бпф
*3100
Сегодня финал INOI (Иранская национальная олимпиада по информатике). Зал для контеста представляет собой ряд из \(n\) компьютеров. Все компьютеры пронумерованы целыми числами от \(1\) до \(n\) слева направо. Всего будет \(m\) участников, пронумерованных целыми числами от \(1\) до \(m\). У нас есть массив \(a\) длины \(m\), где \(a_{i}\) (\(1 \leq a_i \leq n\)) — это компьютер, около которого \(i\)-й участник хочет сесть. Также у нас есть другой массив \(b\) длины \(m\), состоящий из символов «L» и «R». \(b_i\) — это сторона, с которой \(i\)-й участник заходит в зал. «L» обозначает, что участник заходит в зал левее \(1\)-го компьютера, и идет слева направо, а «R» обозначает, что участник заходит в зал правее \(n\)-го компьютера, и идет справа налево. Участники в порядке от \(1\) до \(m\) заходят в зал один за другим. \(i\)-й из них заходит в зал со стороны \(b_i\) и идет до компьютера \(a_i\). Если этот компьютер уже занят, он продолжает идти в том же направлении до первого не занятого компьютера. После этого он садится за этот компьютер. Если участник не встречает ни одного свободного компьютера, он расстраивается и покидает соревнование. Расстроенность \(i\)-о участника — это расстояние между его желаемым компьютером (\(a_i\)) и компьютером, за который он в итоге сел. Расстояние между компьютерами \(i\) и \(j\) равно \(|i - j|\). Числа в массиве \(a\) могут быть равны. Существует \(n^m \cdot 2^m\) возможных пар массивов \((a, b)\). Рассмотрим все пары массивов \((a, b)\) такие, что ни один участник не расстроится. Для каждой из них посчитаем сумму расстроенностей всех участников. Найдите сумму этих чисел. Вам будет дан некоторый простой модуль \(p\). Найдите эту сумму по модулю \(p\). Выходные данные Выведите единственное целое число — необходимую сумму по модулю \(p\). Примечание В первом тесте есть три возможных массива \(a\): \(\{1\}\), \(\{2\}\) и \( \{3\}\) и два возможных массива \(b\): \(\{\mathtt{L}\}\) и \(\{\mathtt{R}\}\). Для всех шести возможных пар массивов \((a, b)\) единственный участник сядет за компьютером \(a_1\) (потому что он точно окажется не занят), поэтому его расстроенность будет равна \(0\). Поэтому сумма всех расстоенностей будет равна \(0\). Во втором тесте все возможные пары массивов \((a, b)\) такие, что ни один участник не будет расстроен: - \((\{1, 1\}, \{\mathtt{L}, \mathtt{L}\})\), сумма расстроенностей \(1\);
- \((\{1, 1\}, \{\mathtt{R}, \mathtt{L}\})\), сумма расстроенностей \(1\);
- \((\{2, 2\}, \{\mathtt{R}, \mathtt{R}\})\), сумма расстроенностей \(1\);
- \((\{2, 2\}, \{\mathtt{L}, \mathtt{R}\})\), сумма расстроенностей \(1\);
- все возможные пары массивов \(a \in \{\{1, 2\}, \{2, 1\}\}\) и \(b \in \{\{\mathtt{L}, \mathtt{L}\}, \{\mathtt{R}, \mathtt{L}\}, \{\mathtt{L}, \mathtt{R}\}, \{\mathtt{R}, \mathtt{R}\}\}\), сумма расстроенностей \(0\).
Поэтому ответ равен \(1 + 1 + 1 + 1 + 0 \ldots = 4\). | |
![]()
|
|
B. Разбивай и суммируй
Комбинаторика
математика
сортировки
*1900
Вам задан массив \(a\) длины \(2n\). Рассмотрим разбиение массива \(a\) на две подпоследовательности \(p\) и \(q\) длины \(n\) (каждый элемент массива \(a\) должен попасть ровно в одну подпоследовательность: в \(p\) или в \(q\)). Отсортируем \(p\) по неубыванию, а \(q\) — по невозрастанию, и получим последовательности \(x\) и \(y\), соответственно. Тогда назовём стоимостью разбиения \(f(p, q) = \sum_{i = 1}^n |x_i - y_i|\). Вам необходимо найти сумму \(f(p, q)\) по всем корректным разбиениям массива \(a\). Так как это число может быть слишком большим, требуется посчитать остаток от деления его на \(998244353\). Выходные данные Выведите одно целое число — ответ на задачу по модулю \(998244353\). Примечание Два разбиения массива считаются различными, если отличаются наборы индексов элементов, входящих в подпоследовательность \(p\). В первом примере существует два корректных разбиения массива \(a\): - \(p = [1]\), \(q = [4]\), тогда \(x = [1]\), \(y = [4]\), \(f(p, q) = |1 - 4| = 3\)
- \(p = [4]\), \(q = [1]\), тогда \(x = [4]\), \(y = [1]\), \(f(p, q) = |4 - 1| = 3\).
Во втором примере существует шесть корректных разбиений массива \(a\): - \(p = [2, 1]\), \(q = [2, 1]\) (в подпоследовательность \(p\) выбраны элементы с индексами \(1\) и \(2\) исходного массива);
- \(p = [2, 2]\), \(q = [1, 1]\);
- \(p = [2, 1]\), \(q = [1, 2]\) (в подпоследовательность \(p\) выбраны элементы с индексами \(1\) и \(4\) исходного массива);
- \(p = [1, 2]\), \(q = [2, 1]\);
- \(p = [1, 1]\), \(q = [2, 2]\);
- \(p = [2, 1]\), \(q = [2, 1]\) (в подпоследовательность \(p\) выбраны элементы с индексами \(3\) и \(4\)).
| |
![]()
|
|
C. Счастливая подпоследовательность
Комбинаторика
математика
*2100
дп
Петя любит счастливые числа. Всем известно, что счастливыми являются положительные целые числа, в десятичной записи которых содержатся только счастливые цифры 4 и 7. Например, числа 47, 744, 4 являются счастливыми, а 5, 17, 467 — не являются. У Пети есть последовательность a из n целых чисел. Подпоследовательность последовательности a — это последовательность, которая получается из a путем удаления нуля или более ее элементов. Две подпоследовательности считаются различными, если множества индексов входящих в них чисел различны, то есть значения элементов не учитываются при сравнении подпоследовательностей. В частности, любая последовательность длины n имеет ровно 2n различных подпоследовательностей (считая пустую). Подпоследовательность называется счастливой, если она имеет длину ровно k, и не содержит двух одинаковых счастливых чисел (несчастливые числа могут повторяться сколько угодно раз). Помогите Пете найти количество различных счастливых подпоследовательностей последовательности a. Так как родители не разрешают Пете играть с большими числами, результат нужно вывести по модулю простого числа 1000000007 (109 + 7). Выходные данные В единственной строке выведите одно число — ответ на задачу по модулю простого числа 1000000007 (109 + 7). Примечание В первом примере все 3 подпоследовательности нужной длины являются счастливыми. Во втором примере есть 4 счастливые подпоследовательности, множества индексов для которых равны (индексация с 1): {1, 3}, {1, 4}, {2, 3} и {2, 4}. | |
![]()
|
|
D. Счастливая пара
Структуры данных
Комбинаторика
реализация
*2900
Петя любит счастливые числа. Всем известно, что счастливыми являются положительные целые числа, в десятичной записи которых содержатся только счастливые цифры 4 и 7. Например, числа 47, 744, 4 являются счастливыми, а 5, 17, 467 — не являются. У Пети есть массив a из n целых чисел. Числа в массиве нумеруются начиная с 1. К сожалению, в последнее время Петя плохо писал контесты, поэтому родители не разрешают ему играть с массивами, в которых много счастливых чисел. Гарантируется, что в массиве a не более 1000 элементов являются счастливыми. Пете нужно найти количество пар непересекающихся отрезков [l1;r1] и [l2;r2] (1 ≤ l1 ≤ r1 < l2 ≤ r2 ≤ n, все четыре числа — целые) таких, что нет такого счастливого числа, которое встречается одновременно и в подмассиве a[l1..r1], и в подмассиве a[l2..r2]. Помогите Пете посчитать количество таких пар. Выходные данные В единственной строке выведите одно число — ответ на задачу. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-х битовых чисел на С++. Рекомендуется использовать потоки cin, cout или спецификатор %I64d. Примечание Подмассив a[l..r] — массив из элементов al, al + 1, ..., ar. В первом примере есть 9 возможных пар, которые удовлетворяют условие: [1, 1] и [2, 2], [1, 1] и [2, 3], [1, 1] и [2, 4], [1, 1] и [3, 3], [1, 1] и [3, 4], [1, 1] и [4, 4], [1, 2] и [3, 3], [2, 2] и [3, 3], [3, 3] и [4, 4]. Во втором примере есть только одна возможная пара отрезков — [1;1] и [2;2] и она удовлетворяет условие. | |
![]()
|
|
H1. Соединение нитями (простая версия)
Комбинаторика
математика
бпф
*2900
Единственное различие между двумя версиями задачи состоит в том, что в простой версии задачи нет обновлений. Есть \(n\) катушек, расположенных вокруг круглого стола. Катушки бывают двух цветов: черного и белого. Любые две катушки одного цвета можно соединить нитью-отрезком того же цвета. Определим соответствие как способ соединить катушки так, что каждая катушка будет соединена ровно с одной другой катушкой. Раскраска это выбор цветов (белого или черного) для каждой катушки. Раскраска называется возможной, если для нее существует хотя бы одно соответствие. Это равносильно тому, что количества черных и белых катушек четные. Для соответствия можно посчитать количество раз, которое какая-то белая нить пересекает какую-то черную нить. Мы считаем не количество точек пересечения, а количество пар нитей разных цветов, которые пересекаются, поэтому одна точка пересечения может быть посчитана несколько раз, если несколько пар нитей пересекаются в одной и той же точке. Если \(c\) это возможная раскраска, обозначим за \(f(c)\) минимальное количество пересечений по всем возможным корректным соответствиям для этой раскраски. 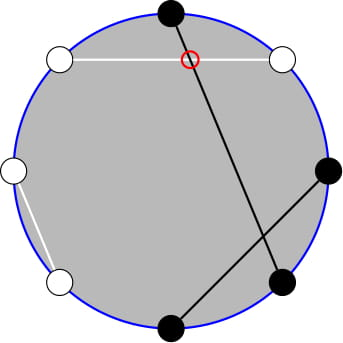 Картинка изображает раскраску bwbbbwww. Для нарисованного соответствия есть одно пересечение между нитями разного цвета. Можно показать, что это минимальное возможное количество по всем корректным соответствиям для этой раскраски, поэтому \(f(\text{bwbbbwww}) = 1\). Картинка изображает раскраску bwbbbwww. Для нарисованного соответствия есть одно пересечение между нитями разного цвета. Можно показать, что это минимальное возможное количество по всем корректным соответствиям для этой раскраски, поэтому \(f(\text{bwbbbwww}) = 1\). Вам дана строка \(s\) описывающая незавершенную раскраску с черными, белыми и непокрашенными катушками. Раскраска \(c\) называется \(s\)-достижимой, если ее можно получить, раскрасив все непокрашенные катушки в \(s\), не меняя цвета остальных. Раскраска \(c\) выбирается случайно равновероятно по всем возможным \(s\)-достижимым раскраскам. Найдите математическое ожидание \(f(c)\). Вы должны найти его по модулю \(998244353\). Можно показать, что ответ может быть записан в виде \(\frac{p}{q}\), где \(p\) и \(q\) некоторые взаимно простые целые числа и \(q\not\equiv 0\pmod{998244353}\). Тогда ответ по модулю \(998244353\) будет равен \((p\cdot q^{-1})\) modulo \(998244353\). Выходные данные Выведите математическое ожидание \(f(c)\) по модулю \(998244353\). Примечание Первый тест почти соответствует картинке. Нельзя покрасить '?' в 'w', потому что тогда получится не возможная раскраска, потому что количество черных катушек будет нечетным. Тогда единственная достижимая возможная раскраска это 'bwbbbwww'. Поскольку \(f(\text{bwbbbwww}) = 1\) математическое ожидание равно \(1\). Можно показать, что математическое ожидание для второго теста равно \(\frac{9}{16}\). | |
![]()
|
|
H2. Соединение нитями (сложная версия)
Комбинаторика
математика
реализация
*3300
Единственное различие между двумя версиями задачи состоит в том, что в простой версии задачи нет обновлений. Есть \(n\) катушек, расположенных вокруг круглого стола. Катушки бывают двух цветов: черного и белого. Любые две катушки одного цвета можно соединить нитью-отрезком того же цвета. Определим соответствие как способ соединить катушки так, что каждая катушка будет соединена ровно с одной другой катушкой. Раскраска это выбор цветов (белого или черного) для каждой катушки. Раскраска называется возможной, если для нее существует хотя бы одно соответствие. Это равносильно тому, что количества черных и белых катушек четные. Для соответствия можно посчитать количество раз, которое какая-то белая нить пересекает какую-то черную нить. Мы считаем не количество точек пересечения, а количество пар нитей разных цветов, которые пересекаются, поэтому одна точка пересечения может быть посчитана несколько раз, если несколько пар нитей пересекаются в одной и той же точке. Если \(c\) это возможная раскраска, обозначим за \(f(c)\) минимальное количество пересечений по всем возможным корректным соответствиям для этой раскраски. 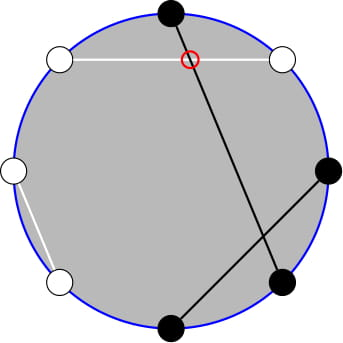 Картинка изображает раскраску bwbbbwww. Для нарисованного соответствия есть одно пересечение между нитями разного цвета. Можно показать, что это минимальное возможное количество по всем корректным соответствиям для этой раскраски, поэтому \(f(\text{bwbbbwww}) = 1\). Картинка изображает раскраску bwbbbwww. Для нарисованного соответствия есть одно пересечение между нитями разного цвета. Можно показать, что это минимальное возможное количество по всем корректным соответствиям для этой раскраски, поэтому \(f(\text{bwbbbwww}) = 1\). Вам дана строка \(s\) описывающая незавершенную раскраску с черными, белыми и непокрашенными катушками. Раскраска \(c\) называется \(s\)-достижимой, если ее можно получить, раскрасив все непокрашенные катушки в \(s\), не меняя цвета остальных. Раскраска \(c\) выбирается случайно равновероятно по всем возможным \(s\)-достижимым раскраскам. Найдите математическое ожидание \(f(c)\). Вы должны найти его по модулю \(998244353\). Также будет производиться \(m\) изменений одного символа в \(s\). После каждого изменения вы должны посчитать математическое ожидание \(f(c)\) снова. Можно показать, что каждый ответ может быть записан в виде \(\frac{p}{q}\), где \(p\) и \(q\) некоторые взаимно простые целые числа и \(q\not\equiv 0\pmod{998244353}\). Тогда ответ по модулю \(998244353\) будет равен \((p\cdot q^{-1})\) modulo \(998244353\). Выходные данные Выведите \(m+1\) строку: математическое ожидание \(f(c)\) изначально и после каждого изменения. Все значения должны быть найдены по модулю \(998244353\). Примечание Первый тест почти соответствует картинке. Нельзя покрасить '?' в 'w', потому что тогда получится не возможная раскраска, потому что количество черных катушек будет нечетным. Тогда единственная достижимая возможная раскраска это 'bwbbbwww'. Поскольку \(f(\text{bwbbbwww}) = 1\) математическое ожидание равно \(1\). Во втором тесте строка после каждого изменения будет: - ????w?wb??
- ??????wb??
- ?w????wb??
В третьем тесте строка после каждого изменения будет: - ww?b
- wb?b
- wb?b
| |
![]()
|
|
D. Радиовышки
Комбинаторика
математика
*1600
дп
На координатной прямой расположено \(n + 2\) города, с номерами от \(0\) до \(n + 1\). \(i\)-й город расположен в точке \(i\). В каждом из городов \(1, 2, \dots, n\) с вероятностью \(\frac{1}{2}\) строится радиовышка (эти события независимы). После этого вы хотите установить мощность сигнала каждой вышки равной целому числу от \(1\) до \(n\) (мощность сигнала не обязательно одинакова для всех вышек, но и не обязательно отличается). Сигнал с вышки, расположенной в городе \(i\) с мощностью сигнала \(p\), достигает каждого города \(c\), что \(|c - i| < p\). После постройки вышек вы хотите выбрать мощность сигнала таким образом, чтобы: - города \(0\) и \(n + 1\) не получали сигнал от радиовышек;
- города \(1, 2, \dots, n\) получали сигнал ровно от одной радиовышки каждый.
Например, если \(n = 5\), и вышки построены в городах \(2\), \(4\) и \(5\), вы можете установить мощность сигнала вышки в городе \(2\) равной \(2\), а мощность сигнала вышек в городах \(4\) и \(5\) равной \(1\). Таким образом, города \(0\) и \(n + 1\) не получат сигнал ни от одной вышки, города \(1\), \(2\) и \(3\) получат сигнал от вышки в городе \(2\), город \(4\) получит сигнал от вышки в городе \(4\), а город \(5\) получит сигнал от вышки в городе \(5\). Посчитайте вероятность того, что после постройки вышек у вас будет возможность установить мощность сигнала каждой из них, чтобы удовлетворить всем ограничениям. Выходные данные Выведите одно целое число — вероятность того, что найдется способ установить мощность сигнала так, чтобы все ограничения были выполнены, взятая по модулю \(998244353\). Вероятность можно выразить в виде несократимой дроби \(\frac{x}{y}\). Вы должны вывести значение \(x \cdot y^{-1} \bmod 998244353\), где \(y^{-1}\) — целое число, такое, что \(y \cdot y^{-1} \bmod 998244353 = 1\). Примечание Настоящий ответ для первого примера — \(\frac{1}{4}\): - с вероятностью \(\frac{1}{4}\) вышки построены в обоих городах \(1\) и \(2\), поэтому мы можем установить их мощность сигнала равной \(1\).
Настоящий ответ для второго примера — \(\frac{1}{4}\): - с вероятностью \(\frac{1}{8}\) вышки построены в городах \(1\), \(2\) и \(3\), поэтому мы можем установить их мощность сигнала равной \(1\);
- с вероятностью \(\frac{1}{8}\) построена только одна башня в городе \(2\), и мы можем установить ее мощность сигнала равной \(2\).
Настоящий ответ для третьего примера — \(\frac{5}{32}\). Обратите внимание, что даже если предыдущие пояснения использовали равные мощности сигнала для всех башен, это не обязательно так. Например, если \(n = 5\) и башни построены в городах \(2\), \(4\) и \(5\), вы можете установить мощность сигнала башни в городе \(2\) равной \(2\), а мощность сигнала башен в городах \(4\) и \(5\) равной \(1\). | |
![]()
|
|
E. Количество простых путей
Деревья
Комбинаторика
*2000
поиск в глубину и подобное
графы
Вам дан неориентированный граф, состоящий из \(n\) вершин и \(n\) ребер. Гарантируется, что заданный граф является связным (то есть возможно достичь любую вершину из любой другой вершины) и не содержит петель и кратных ребер. Ваша задача — посчитать количество простых путей длины хотя бы \(1\) в заданном графе. Заметьте, что пути, которые отличаются только направлением, являются одинаковыми (то есть вам необходимо посчитать количество неориентированных путей). Например, пути \([1, 2, 3]\) и \([3, 2, 1]\) являются одинаковыми. Вам необходимо ответить на \(t\) независимых наборов тестовых данных. Напомним, что путем в графе называется такая последовательность вершин \(v_1, v_2, \ldots, v_k\), что каждая пара соседних (последовательных) вершин в этой последовательности соединена ребром. Длиной пути является количество ребер в нем. Простым путем называется такой путь, что все вершины в нем различны. Выходные данные Выведите одно целое число для каждого набора тестовых данных: количество простых путей длины хотя бы \(1\) в заданном графе. Заметьте, что пути, которые отличаются только направлением, являются одинаковыми (то есть вам необходимо посчитать количество неориентированных путей). Примечание Рассмотрим второй набор тестовых данных примера. Он выглядит следующим образом: 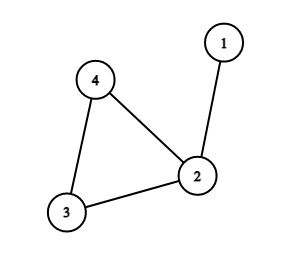
Здесь есть \(11\) различных простых путей: - \([1, 2]\);
- \([2, 3]\);
- \([3, 4]\);
- \([2, 4]\);
- \([1, 2, 4]\);
- \([1, 2, 3]\);
- \([2, 3, 4]\);
- \([2, 4, 3]\);
- \([3, 2, 4]\);
- \([1, 2, 3, 4]\);
- \([1, 2, 4, 3]\).
| |
![]()
|
|
E1. Близкие наборы (простая версия)
Бинарный поиск
Комбинаторика
математика
*1500
сортировки
Это простая версия этой задачи. Единственное различие между простой и сложной версиями заключается в ограничениях на \(k\) и \(m\) (в этой версии \(k=2\), \(m=3\)). Также в этой версии задачи НЕ НУЖНО выводить ответ по какому-либо модулю. Вам задана последовательность \(a\) длины \(n\), состоящая из целых чисел от \(1\) до \(n\). Среди чисел могут быть одинаковые. Найдите количество наборов из \(m = 3\) элементов, таких что максимальное число в наборе отличается от минимального не больше, чем на \(k = 2\). Формально, в этой задаче вам нужно найти количество троек индексов \(i < j < z\), таких что \(\)\max(a_i, a_j, a_z) - \min(a_i, a_j, a_z) \le 2.\(\) Например, если \(n=4\) и \(a=[1,2,4,3]\), то существуют две такие тройки (\(i=1, j=2, z=4\) и \(i=2, j=3, z=4\)). Если же \(n=4\) и \(a=[1,1,1,1]\), то все четыре возможные тройки подходят. Выходные данные Выведите \(t\) ответов на наборы входных данных. Каждый ответ — это количество упорядоченных троек элементов, таких что максимальное число в тройке отличается от минимального не больше, чем на \(2\). Обратите внимание, что в отличии от сложной версии задачи, здесь не нужно выводить ответ по какому-либо модулю. Необходимо вывести точное значение ответа. | |
![]()
|
|
E2. Близкие наборы (сложная версия)
Бинарный поиск
Комбинаторика
математика
реализация
сортировки
*1700
Это сложная версия этой задачи. Единственное различие между простой и сложной версиями заключается в ограничениях на \(k\) и \(m\). В этой версии задачи нужно выводить ответ по модулю \(10^9+7\). Вам задана последовательность \(a\) длины \(n\), состоящая из целых чисел от \(1\) до \(n\). Среди чисел могут быть одинаковые. Найдите количество наборов из \(m\) элементов, таких что максимальное число в наборе отличается от минимального не больше, чем на \(k\). Формально, вам нужно найти количество наборов из \(m\) индексов \(i_1 < i_2 < \ldots < i_m\), таких что \(\)\max(a_{i_1}, a_{i_2}, \ldots, a_{i_m}) - \min(a_{i_1}, a_{i_2}, \ldots, a_{i_m}) \le k.\(\) Например, если \(n=4\), \(m=3\), \(k=2\), \(a=[1,2,4,3]\), то существуют две такие тройки (\(i=1, j=2, z=4\) и \(i=2, j=3, z=4\)). Если же \(n=4\), \(m=2\), \(k=1\), \(a=[1,1,1,1]\), то все шесть возможных пар подходят. Поскольку ответ может быть достаточно большим, вам нужно посчитать его по модулю \(10^9 + 7\) (остаток при делении на число \(10^9 + 7\)). Выходные данные Выведите \(t\) ответов на наборы входных данных. Каждый ответ — это количество наборов из \(m\) элементов по модулю \(10^9 + 7\), таких что максимальное число в наборе отличается от минимального не больше, чем на \(k\). | |
![]()
|
|
G. Песни сирен
Строки
Комбинаторика
математика
*2600
разделяй и властвуй
хэши
строковые суфф. структуры
Кто по незнанию приближается к ним и слышит голос сирен, тот больше не возвращается.Гомер, Одиссея Во времена Ясона и Аргонавтов, было хорошо известно, что сирены используют свои песни, чтобы заманивать моряков к себе на погибель. Но немногие знали, что каждый раз сирены, когда зовут моряков по имени, те становятся слабее и более уязвимыми. Для целей этой задачи, и песни сирен, и имена моряков будем представлять строками, состоящими из строчных английских букв. Чем больше раз имя моряка появляется как непрерывная подстрока в песне, тем моряк в большей опасности. Ясон обнаружил, что сирены могут петь одну из \(n+1\) песен, которые имеют следующую структуру: пусть \(s_i\) (\(0 \leq i \leq n\)) будет \(i\)-й песней, а \(t\) — некоторой строкой длины \(n\), тогда для всех \(i < n\): \(s_{i+1} = s_i t_i s_i\). другими словами, \(i+1\)-я песня это конкатенация \(i\)-й песни, \(i\)-й буквы (в \(0\) индексации) строки \(t\), и \(i\)-й песни. К счастью, он также знает \(s_0\) и \(t\). Ясон интересуется, сколько раз имя моряка встречается в конкретной песне. Ответьте на \(q\) вопросов: дано имя моряка (\(w\)) и номер песни (\(i\)), выведите количество вхождений \(w\) в \(s_i\) как подстроки. Так как это число может быть довольно большим, выведите его по модулю \(10^9+7\). Выходные данные Выведите \(q\) строк, \(i\)-я из них должна содержать остаток по модулю \(10^9+7\) от числа вхождений \(w\) в \(s_k\). Примечание В первом примере песни сирен выглядят так: - Песня \(0\): aa
- Песня \(1\): aabaa
- Песня \(2\): aabaacaabaa
- Песня \(3\): aabaacaabaadaabaacaabaa
| |
![]()
|
|
H. Поиск удовлетворяющих решений
Комбинаторика
математика
дп
жадные алгоритмы
графы
*3300
Добраться до сюда в контесте было непросто. Решив все предыдущие задачи, вы произвели большое впечатление на богов. Поэтому, они решили избавить вас от истории в этой задаче и вместо этого дать вам формальное условие. Рассмотрим \(n\) агентов. У каждого из них изначально есть ровно один предмет, у \(i\)-го агента есть предмет номер \(i\). Мы хотим переназначить предметы между агентами. Назначение будет валидным, если каждый предмет назначен ровно одному агенту, и у каждого агента есть ровно один предмет. У каждого агента есть предпочтения одних предметов перед другими, которое может быть выражено перестановкой \(p\) элементов, отсортированных от наиболее желанных до наименее желанных. Другими словами, агент предпочитает предмет \(i\) предмету \(j\), если \(i\) появляется раньше в его перестановке \(p\). Профиль предпочтений это список из \(n\) перестановок длины \(n\) каждая, \(i\)-я перестановка описывает предпочтения \(i\)-го агента. Возможно, что некоторые агенты недовольны назначенными им предметами. Множество недовольных агентов может выбрать не кооперироваться с другими агентами. В таком случае, они обменяются теми предметами, которые у них были изначально (\(i\)-му агенту принадлежал \(i\)-й предмет), только между собой. Агенты из группы не волнуются об удовлетворенности агентов вне группы. Однако, они должны обменяться предметами так, чтобы как минимум один из них стал счастливее, и никто не стал менее счастливым (по сравнению с назначением, которое было сделано). Формально, рассмотрим валидное назначение элементов — \(A\). Скажем, что \(A(i)\) обозначает предмет, назначенный \(i\)-му агенту. Также, рассмотрим подмножество агентов. Пусть \(S\) будет множеством их индексов. Скажем, что это подмножество агентов недовольно, если существует такое валидное назначение элементов \(B(i)\), что: - Для всех \(i \in S\), \(B(i) \in S\).
- Ни один агент \(i \in S\) не предпочитает предмет \(A(i)\) предмету \(B(i)\) (ни один агент из \(S\) не менее счастлив).
- Как минимум один агент \(i \in S\) предпочитает предмет \(B(i)\) предмету \(A(i)\) (как минимум один агент из \(S\) более счастлив).
Назначение оптимально, если ни одно подмножество агентов не недовольно. Обратите внимание, что пустое подмножество не может быть недовольно. Можно доказать, что для каждого профиля предпочтений существует ровно одно оптимальное назначение. Пример: Рассмотрим \(3\) агентов со следующими профилями предпочтений: - \([2, 1, 3]\)
- \([1, 2, 3]\)
- \([1, 3, 2]\)
И следующее назначение: - Первый агент получает предмет \(2\)
- Второй агент получает предмет \(3\).
- Третий агент получает предмет \(1\).
Заметьте, что множество агентов \(\{1, 2\}\) является недовольным, потому что они могут переупорядочить их (исходные) предметы следующим образом: - Первый агент получает предмет \(2\).
- Второй агент получает предмет \(1\).
- Третий агент получает предмет \(3\).
Это назначение сделает второго агента более счастливым, и не имеет разницы для первого агента. В результате, третий агент получит предмет, который хуже для него, но это не влияет на то, что множество \(\{1,2\}\) будет недовольно (он не лежит в этом множестве). Следующее назначение будет оптимальным: - Первый агент получает предмет \(2\).
- Второй агент получает предмет \(1\).
- Третий агент получает предмет \(3\).
Дано назначение \(A\), вычислите количество различных профилей предпочтений, для которых это назначение \(A\) является оптимальным. Так как ответ может быть большим, выведите его по модулю \(10^9+7\). Два профиля предпочтений считаются различными, если есть агент, у которого различается перестановка предпочтений. Выходные данные Выведите одно целое число — количество профилей предпочтений, для который данное назначение является оптимальным, по модулю \(10^9+7\). Примечание Назначение в первом примере является оптимальным только для следующего профиля предпочтений: \(2, 1\) \(1, 2\) Если бы какой-то агент больше всего хотел получить не тот предмет, который ему дали, он мог бы сам по себе сформировать недовольное подмножество. Поэтому, для любого другого профиля предпочтений это назначение было бы не оптимально. | |
![]()
|
|
D. Сумма путей
Комбинаторика
математика
дп
*2200
Рассмотрим \(n\) клеток, пронумерованных числами \(1,2,\dots, n\) слева направо. Вы можете изначально в любую из этих клеток поставить робота, который затем должен сделать ровно \(k\) шагов. За один шаг робот перемещается в соседнюю клетку слева или справа, при этом он не может выходить за границы заданных клеток. Иными словами, если робот был в клетке \(i\), он должен переместиться либо в клетку \(i-1\), либо в клетку \(i+1\), при этом клетка, в которую он перемещается, должна иметь номер от \(1\) до \(n\) (включительно). Клетки в том порядке, в котором робот их посещает (включая стартовую клетку), вместе составляют хороший путь. В каждой клетке записано целое число — в клетке \(i\) записано число \(a_i\). Пусть \(c_0, c_1, \dots, c_k\) — последовательность клеток в хорошем пути в том порядке, в котором они были посещены (\(c_0\) — клетка, где был робот изначально, \(c_1\) — клетка, в которой он оказался после первого шага, и так далее; более формально, \(c_i\) — клетка, в которой оказался робот после \(i\) шагов). Тогда стоимость пути вычисляется по следующей формуле: \(a_{c_0} + a_{c_1} + \dots + a_{c_k}\). Ваша задача — посчитать суммарную стоимость всех хороших путей. Так как это число может быть очень большим, его надо выводить по модулю \(10^9 + 7\). Два хороших пути различны, если либо различается стартовая клетка, либо существует такое \(i \in [1, k]\), что местоположение робота после \(i\) шагов различается в этих путях. Также вам нужно обрабатывать \(q\) обновлений значений \(a\) и после каждого обновления вычислять требуемую суммарную стоимость. Каждое обновление меняет число, записанное ровно в одной клетке. Выходные данные Выведите \(q\) целых чисел, \(i\)-е из которых должно быть равно суммарной стоимости хороших путей после первых \(i\) обновлений. Так как эти числа могут быть большими, выводите их по модулю \(10^9 + 7\). Примечание Все хорошие пути в первом примере: \((1, 2), (2, 1), (2, 3), (3, 2), (3, 4), (4, 3), (4, 5), (5, 4)\). Изначально значения \(a\) равны \([3, 5, 1, 4, 2]\). После первого обновления — \([9, 5, 1, 4, 2]\). После второго обновления — \([9, 4, 1, 4, 2]\), и так далее. | |
![]()
|
|
E. Странная перестановка
Бинарный поиск
Структуры данных
Комбинаторика
реализация
дп
графы
*3200
У Игоря была перестановка \(p_1, p_2, \ldots, p_n\). К сожалению, перестановка выглядела достаточно скучно, так что он решил выбрать несколько непересекающихся подотрезков перестановки и развернуть каждый из них. Стоимость разворота одного отрезка \([l, r]\) (то есть элементов на позициях с \(l\) по \(r\) включительно) равна \(r - l\), а общая стоимость одной операции равна сумме стоимостей разворота для соответствующих отрезков. Игорю на Новый Год подарили целое число \(c\), поэтому его интересуют лишь те операции, стоимость которых не превосходит \(c\). Затем Игорю стало совсем скучно, и он решил выписать на листочек все перестановки, которые он может получить из исходной, проделав ровно одну операцию. Каждую перестановку он выписал ровно один раз, даже если какую-то перестановку можно было получить несколькими способами. Полученный список Игорь отсортировал лексикографически. Теперь Денис решил задать Игорю несколько вопросов про его список. Каждый вопрос выглядит следующим образом: чему равно \(i\)-е число в \(j\)-й перестановке в списке Игоря? Разумеется, Игорю слишком скучно заниматься ответами на эти вопросы, так что он обратился к вам за помощью. Выходные данные Для каждого вопроса в отдельной строке выведите ответ на этот вопрос или \(-1\), если Игорь ошибся и \(j\)-й перестановки не существует на листочке Игоря. Примечание В первом примере Игорь выписал на листочек следующие перестановки: \([1, 2, 3]\), \([1, 3, 2]\), \([2, 1, 3]\). Обратите внимание, что для получения перестановки \([3, 2, 1]\) Игорю пришлось бы развернуть весь массив, а стоимость такой операции равна \(2\), что больше указанного значения \(c=1\). Другие две перестановки не могут быть получены из исходной путем применением операции из условия задачи. | |
![]()
|
|
G. Плитки
Комбинаторика
математика
дп
*2800
бпф
Рассмотрим дорогу, состоящую из нескольких рядов. Каждый ряд разделен на несколько прямоугольных плиток, и все плитки в одном ряду одинаковы. Первый ряд содержит ровно одну прямоугольную плитку. Посмотрите на рисунок ниже, который показывает, как расположены плитки. Дорога построена следующим образом: - первый ряд состоит из \(1\) плитки;
- затем следует \(a_1\) рядов; каждый из этих рядов содержит на \(1\) плитку больше, чем предыдущий ряд;
- затем следует \(b_1\) рядов; каждый из этих рядов содержит на \(1\) плитку меньше, чем предыдущий ряд;
- затем следует \(a_2\) рядов; каждый из этих рядов содержит на \(1\) плитку больше, чем предыдущий ряд;
- затем следует \(b_2\) рядов; каждый из этих рядов содержит на \(1\) плитку меньше, чем предыдущий ряд;
- ...
- затем следует \(a_n\) рядов; каждый из этих рядов содержит на \(1\) плитку больше, чем предыдущий ряд;
- затем следует \(b_n\) рядов; каждый из этих рядов содержит на \(1\) плитку меньше, чем предыдущий ряд;
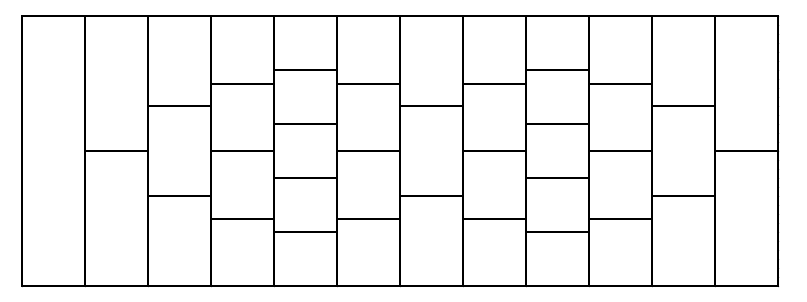 Пример дороги с \(n = 2\), \(a_1 = 4\), \(b_1 = 2\), \(a_2 = 2\), \(b_2 = 3\). Ряды расположены слева направо. Пример дороги с \(n = 2\), \(a_1 = 4\), \(b_1 = 2\), \(a_2 = 2\), \(b_2 = 3\). Ряды расположены слева направо. Вы начинаете с единственной плитки в первом ряду и хотите добраться до последнего ряда (любой плитки из нее). От вашей текущей плитки вы можете перейти к любой плитке в следующем ряду, которая касается с вашей текущей плиткой. Вычислите количество различных путей от первого ряда до последнего. Поскольку оно может быть большим, выведите его по модулю \(998244353\). Выходные данные Выведите одно целое число — количество путей от первого ряда до последнего, взятое по модулю \(998244353\). | |
![]()
|
|
C. Бал в Берляндии
Комбинаторика
математика
*1400
графы
В школе, в которой учится Вася, идет подготовка к проведению выпускного. Одно из запланированных выступлений — бал, в котором примут участие пары состоящие из мальчиков и девочек. Каждый класс должен представить на бал по две пары. В классе Васи \(a\) мальчиков и \(b\) девочек изъявили желание участвовать в мероприятии. Но не все мальчики и не все девочки готовы танцевать в паре. Формально, вам известно \(k\) возможных пар, состоящих из одного мальчика и одной девочки. Вам нужно выбрать из этих пар две так, чтобы ни один человек не состоял больше чем в одной паре. Например, если \(a=3\), \(b=4\), \(k=4\) и следующие пары готовы танцевать вместе \((1, 2)\), \((1, 3)\), \((2, 2)\), \((3, 4)\) (в каждой паре сначала идет номер мальчика, потом номер девочки), то возможны следующие комбинации из двух пар (ниже перечислены не все возможные варианты): - \((1, 3)\) и \((2, 2)\);
- \((3, 4)\) и \((1, 3)\);
Но следующие комбинации не возможны: - \((1, 3)\) и \((1, 2)\) — первый мальчик входит сразу в две пары;
- \((1, 2)\) и \((2, 2)\) — вторая девочка входит сразу в две пары;
Найдите количество способов выбрать две пары, походящие под условие выше. Два способа считаются различными, если состоят из разных пар. Выходные данные Для каждого набора входных данных в отдельной строке выведите одно целое число — количество способов выбрать две пары, походящие под условие выше. Примечание В первом наборе входных данных следующие комбинации из двух пар подходят: - \((1, 2)\) и \((3, 4)\);
- \((1, 3)\) и \((2, 2)\);
- \((1, 3)\) и \((3, 4)\);
- \((2, 2)\) и \((3, 4)\).
Во втором наборе входных данных есть всего одна пара. В третьем наборе входных данных следующие комбинации из двух пар подходят: - \((1, 1)\) и \((2, 2)\);
- \((1, 2)\) и \((2, 1)\).
| |
![]()
|
|
E. Рекламное агентство
Комбинаторика
математика
*1600
сортировки
Маша работает в рекламном агентстве. В целях продвижения нового бренда она хочет заключить договор с некоторыми блогерами. Всего у Маши есть контакты \(n\) разных блогеров. Блогер с номером \(i\) имеет \(a_i\) подписчиков. Так как бюджет у Маши ограничен, она может заключить договор только с \(k\) разными блогерами. Конечно же, Маша хочет, чтобы ее рекламу увидело как можно больше людей. Поэтому она должна нанять блогеров с максимальным суммарным количеством подписчиков. Помогите ей, найдите количество способов выбрать \(k\) блогеров так, чтобы суммарное количество их подписчиков было максимально. Два способа считаются разными, если в первом способе есть хотя бы один блогер, которого нет во втором способе. Маша считает, что у всех блогеров разная аудитория (то есть не существует подписчика, который был бы подписан на двух разных блогеров). Например, если \(n=4\), \(k=3\), \(a=[1, 3, 1, 2]\), то у Маши есть два способа выбрать \(3\)-х блогеров с максимальным суммарным количеством подписчиков: - заключить договор с блогерами с номерами \(1\), \(2\) и \(4\). В таком случае количество подписчиков будет равно \(a_1 + a_2 + a_4 = 6\).
- заключить договор с блогерами с номерами \(2\), \(3\) и \(4\). В таком случае количество подписчиков будет равно \(a_2 + a_3 + a_4 = 6\).
Так как ответ может быть достаточно большим, выведите его по модулю \(10^9+7\). Выходные данные Для каждого набора входных данных в отдельной строке выведите одно целое число — количество способов выбрать \(k\) блогеров так, чтобы суммарное количество их подписчиков было максимально. Примечание Первый набор входных данных разобран в условии. Во втором наборе входных данных следующие варианты являются подходящими: - заключить договор с блогерами с номерами \(1\) и \(2\). В таком случае количество подписчиков будет равно \(a_1 + a_2 = 2\);
- заключить договор с блогерами с номерами \(1\) и \(3\). В таком случае количество подписчиков будет равно \(a_1 + a_3 = 2\);
- заключить договор с блогерами с номерами \(1\) и \(4\). В таком случае количество подписчиков будет равно \(a_1 + a_4 = 2\);
- заключить договор с блогерами с номерами \(2\) и \(3\). В таком случае количество подписчиков будет равно \(a_2 + a_3 = 2\);
- заключить договор с блогерами с номерами \(2\) и \(4\). В таком случае количество подписчиков будет равно \(a_2 + a_4 = 2\);
- заключить договор с блогерами с номерами \(3\) и \(4\). В таком случае количество подписчиков будет равно \(a_3 + a_4 = 2\).
В третьем наборе входных данных следующие варианты являются подходящими: - заключить договор с блогера с номером \(2\). В таком случае количество подписчиков будет равно \(a_2 = 2\).
| |
![]()
|
|
F. Nezzar и шоколадные плитки
Теория вероятностей
Комбинаторика
математика
бпф
*3500
Nezzar купил свое любимое лакомство — \(n\) шоколадных плиток с длинами \(l_1,l_2,\ldots,l_n\). Однако некоторые из них могут быть слишком длинными, чтобы правильно их хранить! Чтобы решить эту проблему, Nezzar придумал интересный процесс разделения их на маленькие кусочки. Сначала Nezzar кладет свои шоколадные плитки в черный ящик. Затем он совершает следующую операцию, пока максимальная длина плитки превышает \(k\). - Nezzar выбирает случайную шоколадную плитку из ящика с вероятностью, пропроциональной ее длине \(x\).
- После шага \(1\) Nezzar равномерно выбирает вещественное число \(r \in (0,x)\) и делит выбранную шоколадную плитку на две плитки с длинами \(r\) и \(x-r\).
- Наконец, он кладет две новых шоколадных плитки обратно в черный ящик.
Nezzar интересуется, чему равно математическое ожидание количества операций, которое он сделает для того, чтобы разделить свои шоколадные плитки на маленькие кусочки. Можно показать, что ответ может быть представлен как \(\frac{P}{Q}\), где \(P\) и \(Q\) — взаимно простые числа и \(Q \not \equiv 0\) (\(\bmod 998\,244\,353\)). Выведите значение \(P\cdot Q^{-1} \mod 998\,244\,353\). Выходные данные Выведите единственное целое число — математическое ожидание количества операций, которое Nezzar сделает, чтобы разделить свои шоколадные плитки на маленькие кусочки, по модулю \(998\,244\,353\). | |
![]()
|
|
F. Копия или префиксная сумма
Структуры данных
Комбинаторика
дп
*2400
сортировки
Вам дан массив целых чисел \(b_1, b_2, \ldots, b_n\). Массив \(a_1, a_2, \ldots, a_n\) целых чисел смешанный, если для всех \(i\) (\(1 \leq i \leq n\)) хотя бы одно из этих двух условий выполнено: - \(b_i = a_i\), или
- \(b_i = \sum_{j=1}^{i} a_j\).
Найдите количество смешанных массивов \(a_1, a_2, \ldots, a_n\). Поскольку ответ может быть очень большим, найдите его по модулю \(10^9 + 7\). Выходные данные Для каждого набора входных данных выведите единственное целое число: количество смешанных массивов \(a_1, a_2, \ldots, a_n\) по модулю \(10^9 + 7\). Примечание В первом наборе входных данных смешанные массивы — это \([1, -2, 1]\), \([1, -2, 2]\), \([1, -1, 1]\). Во втором наборе входных данных смешанные массивы — это \([1, 1, 1, 1]\), \([1, 1, 1, 4]\), \([1, 1, 3, -1]\), \([1, 1, 3, 4]\), \([1, 2, 0, 1]\), \([1, 2, 0, 4]\), \([1, 2, 3, -2]\), \([1, 2, 3, 4]\). В четвертом наборе входных данных единственный смешанный массив — это \([0, 0, 0, 1]\). | |
![]()
|
|
F. Пары путей
Деревья
Структуры данных
Комбинаторика
дп
*2600
поиск в глубину и подобное
У вас есть дерево из \(n\) вершин, а также \(m\) простых вершинных путей. Ваша задача — найти, сколько пар этих путей пересекаются по ровно одной вершине. Более формально, вам нужно найти число пар \((i, j)\) \((1 \leq i < j \leq m)\) таких, что \(path_i\) и \(path_j\) имеют ровно одну общую вершину. Выходные данные Выведите единственное целое число — количество пар путей, которые пересекаются по ровно одной вершине. Примечание 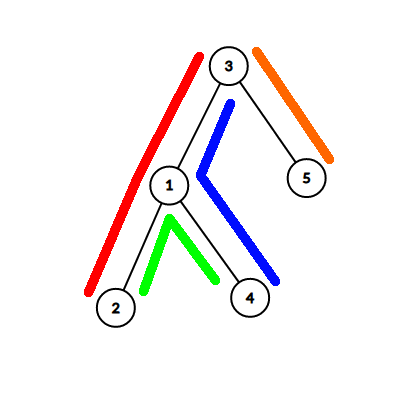
Дерево и пути в первом примере выглядят так. Пары \((1,4)\) и \((3,4)\) пересекаются по ровно одной вершине. Во втором примере все пути состоят из единственной одинаковой вершины, так что все пары \((1, 2)\), \((1, 3)\) и \((2, 3)\) пересекаются по одной вершине. Третий пример, такой же как первый, но с двумя дополнительными путями. Пары \((1,4)\), \((1,5)\), \((2,5)\), \((3,4)\), \((3,5)\), \((3,6)\) и \((5,6)\) пересекаются по ровно одной вершине. | |
![]()
|
|
G. Подсчет строк
Комбинаторика
математика
дп
*2700
бпф
У вас есть \(c_1\) букв 'a', \(c_2\) букв 'b', ..., \(c_{26}\) букв 'z'. Вы хотите построить красивую строку длины \(n\) из них (очевидно, \(i\)-я буква может быть использована не более \(c_i\) раз). Каждое значение \(c_i\) больше \(\frac{n}{3}\). Назовем строку красивой, если у нее нет ни одной палидромной непрерывной подстроки, длина которой нечетна и больше \(1\). Например, строка «abacaba» не является красивой, у нее есть несколько палиндромных подстрок, длина которых нечетна и больше \(1\) (одна из таких подстрок — «aca»). Другой пример: строка «abcaa» —- красивая. Посчитайте количество различных строк, которые можно построить, и выведите его по модулю \(998244353\). Выходные данные Выведите одно целое число — количество различных строк, которые можно построить, взятое по модулю \(998244353\). | |
![]()
|
|
H. Построй из суффиксов
Структуры данных
Комбинаторика
*2800
*особая задача
Задано целое число \(n\) и последовательность \(a\) из \(n-1\) целых чисел: каждый элемент равен либо \(0\), либо \(1\). Требуется построить такую строку длины \(n\), что: - каждая буква — одна из «abcd»;
- если \(a_i=1\), то \(i\)-й суффикс строки лексикографически меньше \((i+1)\)-го суффикса;
- если \(a_i=0\), то \(i\)-й суффикс строки лексикографически больше \((i+1)\)-го суффикса.
Будут заданы \(q\) запросов вида: - \(i\) (\(1 \le i \le n - 1\)) — сменить значение \(a_i\) на противоположное (если \(a_i=0\), то установить \(a_i\) в \(1\), и наоборот).
После каждого запроса выведите количество различных строк, удовлетворяющих данным ограничениям, по модулю \(998\,244\,353\). Выходные данные После каждого запроса выведите количество различных строк, удовлетворяющих данным ограничениям, по модулю \(998\,244\,353\). Примечание \(i\)-й суффикс строки — это последовательная подстрока, которая начинается в \(i\)-й позиции и заканчивается в последней позиции. Строка \(a\) лексикографически меньше строки \(b\), если и только если выполняется один из следующих пунктов: - \(a\) — префикс \(b\), но \(a \ne b\);
- в первой позиции, где \(a\) и \(b\) различны, в строке \(a\) находится буква, которая встречается в алфавите раньше, чем соответствующая буква в \(b\).
Две строки \(a\) и \(b\) длины \(n\) различаются, если существует такая позиция \(i\), что \(a_i \neq b_i\) | |
![]()
|
|
D. Деревья поиска в ширину
Деревья
Комбинаторика
математика
*2600
поиск в глубину и подобное
графы
кратчайшие пути
Будем говорить, что остовное дерево некоторого графа является деревом поиска в ширину с корнем в вершине \(s\), если и только если для всех вершин \(t\) кратчайшее расстояние между вершинами \(s\) и \(t\) в графе равно кратчайшему расстоянию между \(s\) и \(t\) в этом остовном дереве. Для фиксированного графа можно определить \(f(x,y)\) как число остовных деревьев в данном графе таких, что они являются деревьями поиска в ширину как с корнем в \(x\), так и с корнем в \(y\). Вам дан неориентированный связный граф с \(n\) вершинами и \(m\) ребрами. Вычислите \(f(i,j)\) для всех \(i\), \(j\) по модулю \(998\,244\,353\). Выходные данные Выведите \(n\) строк, каждая из которых содержит \(n\) целых чисел. Число в строке \(i\) на позиции \(j\) должно быть равно \(f(i,j) \bmod 998\,244\,353\). Примечание Изображения ниже описывают первый пример. 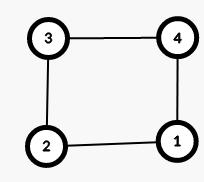
Дерево из красных ребер является деревом поиска в ширину с корнем как в \(1\), так и в \(2\). 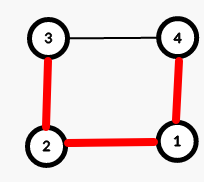
Похожим образом можно построить деревья поисков в ширину для любой пары соседних вершин. | |
![]()
|
|
A. Домино на подоконнике
Конструктив
Комбинаторика
математика
*800
У вас есть игральная доска, которую можно представить в виде поля из \(2 \times n\) клеток. Первые \(k_1\) клеток на первой строке и первые \(k_2\) клеток на второй строке покрашены в белый. Все остальные клетки окрашены в черный. У вас есть \(w\) белых доминошек (плитки \(2 \times 1\), обе клетки которых белые) и \(b\) черных доминошек (плитки \(2 \times 1\), обе клетки которых черные). Вы можете положить белую доминошку на доску, если обе клетки доски под ней белые и не заняты другими доминошками. Аналогично, вы можете положить черную доминошку на доску, если обе клетки доски под ней черные и не заняты другими доминошками. Можете ли вы положить все \(w + b\) доминошек на доску, если вы можете класть доминошки как вертикально, так и горизонтально? Выходные данные Для каждого набора входных данных, выведите YES, если возможно уложить все \(w + b\) доминошек на доску, или NO в противном случае. Вы можете вывести каждую букву в любом регистре (например, YES, Yes, yes, yEs будут распознаны как положительный ответ). Примечание В первом наборе входных данных, \(n = 1\), \(k_1 = 0\) и \(k_2 = 1\). Следовательно, у доски \(2 \times 1\) клетка \((1, 1)\) — черная, а \((2, 1)\) — белая. Таким образом, вы не можете положить ни одной белой доминошки, так как только одна клетка доски белая. Во втором наборе, доска того же размера \(2 \times 1\), но обе клетки — белые. Так как \(w = 0\) и \(b = 0\), то вы можете уложить \(0 + 0 = 0\) доминошек на доску. В третьем наборе, доска \(2 \times 3\), но полностью покрашена в черный (так как \(k_1 = k_2 = 0\)), а потому вы не можете уложить ни одной белой доминошки. В четвертом наборе, клетки \((1, 1)\), \((1, 2)\), \((1, 3)\) и \((2, 1)\) — белые, а все остальные — черные. Вы можете уложить \(2\) белые доминошки на позиции \(((1, 1), (2, 1))\) и \(((1, 2), (1, 3))\), и \(2\) черные доминошки на позиции \(((1, 4), (2, 4))\) \(((2, 2), (2, 3))\). | |
![]()
|
|
E. Хаотичное слияние
Строки
Комбинаторика
математика
дп
*2400
Заданы две строки \(x\) и \(y\), обе состоят из строчных латинских букв. Пусть \(|s|\) будет длиной строки \(s\). Назовем последовательность \(a\) последовательностью слияния, если она состоит из ровно \(|x|\) нулей и ровно \(|y|\) единиц в некотором порядке. Слияние \(z\) получается из последовательности \(a\) по следующим правилам: - если \(a_i=0\), то удалить букву из начала \(x\) и приписать ее в конец \(z\);
- если \(a_i=1\), то удалить букву из начала \(y\) и приписать ее в конец \(z\).
Две последовательности слияния \(a\) и \(b\) считаются различными, если существует такая позиция \(i\), что \(a_i \neq b_i\). Назовем строку \(z\) хаотичной, если для всех \(i\) от \(2\) до \(|z|\) \(z_{i-1} \neq z_i\). Пусть \(s[l,r]\) для некоторых \(1 \le l \le r \le |s|\) будет подстрокой последовательных букв \(s\), начинающейся с позиции \(l\) и заканчивающейся в позиции \(r\) включительно. Пусть \(f(l_1, r_1, l_2, r_2)\) будет количеством различных последовательностей слияния \(x[l_1,r_1]\) и \(y[l_2,r_2]\), которые производят хаотичные слияния. Обратите внимание, что рассматриваются только непустые подстроки \(x\) и \(y\). Посчитайте \(\sum \limits_{1 \le l_1 \le r_1 \le |x| \\ 1 \le l_2 \le r_2 \le |y|} f(l_1, r_1, l_2, r_2)\). Выведите ответ по модулю \(998\,244\,353\). Выходные данные Выведите одно число — сумму \(f(l_1, r_1, l_2, r_2)\) по \(1 \le l_1 \le r_1 \le |x|\) и \(1 \le l_2 \le r_2 \le |y|\) по модулю \(998\,244\,353\). Примечание В первом примере: - \(6\) пар подстрок «a» and «b», каждая с корректными последовательностями слияния «01» and «10»;
- \(3\) пары подстрок «a» and «bb», каждая с корректной последовательностью слияния «101»;
- \(4\) пары подстрок «aa» and «b», каждая с корректной последовательностью слияния «010»;
- \(2\) пары подстрок «aa» and «bb», каждая с корректными последовательностями слияния «0101» and «1010»;
- \(2\) пары подстрок «aaa» and «b», каждая без корректных последовательностей слияния;
- \(1\) пара подстрок «aaa» and «bb» с корректной последовательностью слияния «01010».
Поэтому ответ равен \(6 \cdot 2 + 3 \cdot 1 + 4 \cdot 1 + 2 \cdot 2 + 2 \cdot 0 + 1 \cdot 1 = 24\). | |
![]()
|
|
F. Разрезы диаметров
Деревья
Комбинаторика
дп
поиск в глубину и подобное
*2400
Задано целое число \(k\) и неориентированное дерево, состоящее из \(n\) вершин. Длина простого пути (пути, в котором каждая вершина встречается не более одного раза) между некоторой парой вершин равна количеству ребер в данном пути. Диаметр дерева равен максимальной длине пути между всеми парами вершин в дереве. Вы планируете удалить множество ребер из дерева. Когда ребра удаляются, дерево распадается на несколько меньших деревьев. Множество ребер считается корректным, если у всех полученных деревьев диаметр меньше либо равен \(k\). Два множества ребер считаются различными, если существует такое ребро, что оно встречается только в одном из множеств. Посчитайте количество корректных множеств ребер по модулю \(998\,244\,353\). Выходные данные Выведите одно целое число — количество корректных множеств ребер по модулю \(998\,244\,353\). Примечание В первом примере диаметр заданного дерева уже меньше либо равен \(k\). Поэтому можно выбрать любое множество ребер, и в полученных деревьях диаметры будут меньше либо равны \(k\). Всего есть \(2^3\) множеств, включая пустое. Во втором примере нужно удалить единственное ребро. Иначе диаметр будет \(1\), что больше \(0\). Деревья для третьего и четвертого примеров: 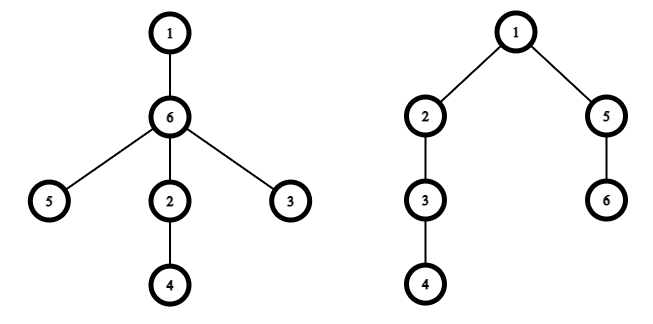 | |
![]()
|
|
E. Треугольники
Комбинаторика
дп
*2600
Летом Петя отдыхал у бабушки в селе, когда неподалеку на овец напал волк. Теперь Петя боится ходить через лес, боится обходить лес, боится даже выходить из дому. Объясняет свой страх Петя отнюдь не боязнью волка, а непонятным, на его взгляд, строением леса, который имеет n уровней, где n — четное число. В местном муниципалитете Вам предоставили карту местности, на которой бабушкин домик отмечен точкой H, а участки леса выделены заливкой серого цвета (см. рисунок для понимания того, как устроена местность). Но все же, после долгого сидения дома, Петя решил поддаться на уговоры бабушки и пойти подышать свежим воздухом. Как человек предусмотрительный, Петя заранее планирует прогулку, и ему необходимо выбрать маршрут. Маршрут, который Петя считает приемлемым для себя, обладает следующими свойствами: - маршрут замкнут, он начинается и заканчивается в домике у бабушки;
- маршрут проходит только по дорожкам леса (отрезки, выделенные черным на рисунке);
- маршрут имеет ненулевую длину (для того чтобы подышать свежим воздухом, Пете все же нужно выйти из дому);
- маршрут не может сам себя пересекать;
- участок земли, очерченный таким замкнутым маршрутом, не должен содержать внутри ни одного участка леса.
Необходимо посчитать количество таких приемлемых ориентированных маршрутов по модулю 1000000009.  На рисунке представлен пример карты местности для n = 12. Так как карта имеет регулярную структуру, для других значений n ее можно построить самостоятельно по аналогии. Выходные данные Выведите единственное число — количество путей Пети по модулю 1000000009. | |
![]()
|
|
B. Количество строк
Комбинаторика
математика
*1600
поиск в глубину и подобное
графы
Для тех, кто еще не понял: этой зимой в городе XXXводске реально холодно! Настолько холодно, что в голову порой лезут странные мысли. Например, сколько существует строк длины ровно n, над алфавитом размера m, таких, что любая подстрока длины в точности k является палиндромом. Ваша задача — найти это количество по модулю 1000000007 (109 + 7). Смотрите не упустите ни одной! Напоминаем, что подстрока является палиндромом, если она одинаково читается как слева направо, так и справа налево. Выходные данные Выведите одно целое число — количество строк описанного вида по модулю 1000000007 (109 + 7). Примечание В первом примере допустимой является только одна строка: «a» (обозначим как «a» единственную букву нашего алфавита). Во втором примере (если обозначить буквы алфавита как «a» и «b») допустимы следующие строки: «aaaaa» и «bbbbb». | |
![]()
|
|
E. 2-раскраска
Комбинаторика
математика
дп
*3100
Дана сетка с \(n\) строками и \(m\) столбцами. Каждая ячейка сетки должна быть окрашена в синий или желтый цвет. Раскраска сетки называется глупой, если в каждой строке есть ровно один отрезок синих ячеек, а в каждом столбце — ровно один отрезок желтых ячеек. Другими словами, каждая строка должна иметь хотя бы одну синюю ячейку, и все синие ячейки в строке должны быть последовательными. Точно так же каждый столбец должен иметь хотя бы одну желтую ячейку, а все желтые ячейки в столбце должны быть последовательными. 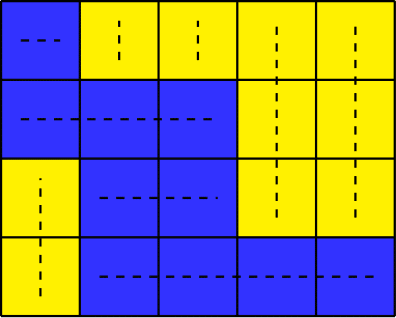 Пример глупой раскраски. Пример глупой раскраски.  Примеры умных раскрасок. В первой раскраске отсутствует синяя ячейка во втором ряду, а во второй раскраске есть два желтых отрезка во втором столбце. Примеры умных раскрасок. В первой раскраске отсутствует синяя ячейка во втором ряду, а во второй раскраске есть два желтых отрезка во втором столбце. Сколько всего существует глупых раскрасок сетки? Две раскраски считаются различными, если есть какая-то ячейка, которая раскрашена в них в разные цвета. Выходные данные Выведите единственное целое число — количество глупых раскрасок по модулю \(998244353\). Примечание Для первого примера единственные две глупые раскраски \(2\times 2\) изображены ниже. 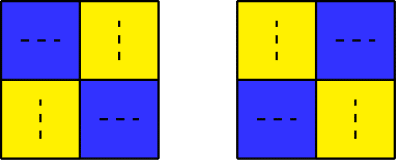 | |
![]()
|
|
B. Почти отсортированные
Бинарный поиск
Конструктив
Комбинаторика
реализация
*1800
Seiji Maki не только любит наблюдать за развитием отношений, он также любит наблюдать за последовательностями чисел, особенно перестановками. Сегодня он смотрит на почти отсортированные перестановки. Перестановка \(a_1, a_2, \dots, a_n\) чисел \(1, 2, \dots, n\) считается почти отсортированной, если условие \(a_{i + 1} \ge a_i - 1\) выполняется для всех \(i\) от \(1\) до \(n - 1\) включительно. Maki рассматривает список всех почти отсортированных перестановок чисел \(1, 2, \dots, n\), приведенных в лексикографическом порядке, и хочет найти в этом списке перестановку \(k\)-ю. Можете ли вы помочь ему найти такую перестановку? Перестановка \(p\) лексикографически меньше перестановки \(q\), если и только если выполняется следующее: - в первой позиции, где \(p\) и \(q\) различны, в перестановке \(p\) элемент меньше, чем соответствующий элемент в \(q\).
Выходные данные Для каждого набора входных данных выведите одну строку, содержащую \(k\)-ю почти отсортированную перестановку длины \(n\) в лексикографическом порядке, или \(-1\), если ее не существует. Примечание Для первого и второго набора входных данных список почти отсортированных перестановок с \(n = 1\) составляет \(\{[1]\}\). Для третьего и пятого набора входных данных список почти отсортированных перестановок с \(n = 3\) составляет \(\{[1, 2, 3], [1, 3, 2], [2, 1, 3], [3, 2, 1]\}\). | |
![]()
|
|
E. Раскраски и домино
Комбинаторика
математика
*2100
дп
жадные алгоритмы
У вас есть большая прямоугольная доска, разделенная на \(n \times m\) клетка (у доски \(n\) строк и \(m\) столбцов). Каждая клетка — либо белая, либо черная. Вы красите каждую белую клетку либо в красный цвет, либо в синий. Очевидно, количество различных вариантов раскраски доски равно \(2^w\), где \(w\) — количество белых клеток. После перекрашивания всех белых клеток вы начинаете класть на доску доминошки по следующим правилам: - каждая доминошка накрывает две соседние клетки;
- каждая клетка накрыта не более чем одной доминошкой;
- если доминошка расположена горизонтально (она накрывает две соседние клетки в строке), обе накрытые ею клетки должны быть красными;
- если доминошка расположена вертикально (она накрывает две соседние клетки в столбце), обе накрытые ею клетки должны быть синими.
Пусть ценность раскраски доски — максимальное количество доминошек, которое можно расположить. Посчитайте сумму ценностей по всем \(2^w\) способам раскрасить доску. Так как сумма может быть очень большой, выведите ее по модулю \(998\,244\,353\). Выходные данные Выведите одно целое число — сумму ценностей по всем \(2^w\) способам раскрасить доску, взятую по модулю \(998\,244\,353\). | |
![]()
|
|
B. Последовательности И
Конструктив
Комбинаторика
математика
*1400
битмаски
Последовательность \(n\) (\(n \ge 2\)) неотрицательных целых чисел \(a_1, a_2, \dots, a_n\) называется хорошей, если для всех \(i\) от \(1\) до \(n-1\) выполняется следующее условие: \(\)a_1 \: \& \: a_2 \: \& \: \dots \: \& \: a_i = a_{i+1} \: \& \: a_{i+2} \: \& \: \dots \: \& \: a_n,\(\) где \(\&\) обозначает операцию побитового И. Вам дан массив \(a\) размера \(n\) (\(n \geq 2\)). Найдите количество перестановок \(p\) чисел от \(1\) до \(n\), для которых последовательность \(a_{p_1}\), \(a_{p_2}\), ... ,\(a_{p_n}\) является хорошей. Так как это число может быть большим, выведите его по модулю \(10^9+7\). Выходные данные Выведите \(t\) строк, где \(i\)-я строка содержит количество хороших перестановок в \(i\)-м наборе входных данных по модулю \(10^9 + 7\). Примечание В первом наборе входных данных все числа равны, поэтому все перестановки являются хорошими. Всего есть \(6\) перестановок чисел от \(1\) до \(3\): \([1,2,3]\), \([1,3,2]\), \([2,1,3]\), \([2,3,1]\), \([3,1,2]\), \([3,2,1]\). Во втором наборе входных данных можно показать, что хороших перестановок нет. В третьем наборе входных данных существуют \(36\) хороших перестановок. Например, перестановка \([1,5,4,2,3]\) дает последовательность \(s=[0,0,3,2,0]\). Она хорошая, так как - \( s_1 = s_2 \: \& \: s_3 \: \& \: s_4 \: \& \: s_5 = 0\),
- \( s_1 \: \& \: s_2 = s_3 \: \& \: s_4 \: \& \: s_5 = 0\),
- \( s_1 \: \& \: s_2 \: \& \: s_3 = s_4 \: \& \: s_5 = 0\),
- \( s_1 \: \& \: s_2 \: \& \: s_3 \: \& \: s_4 = s_5 = 0\).
| |
![]()
|
|
E. Ценовой баланс
Конструктив
Комбинаторика
математика
сортировки
*2300
Массив называется красивым, если все его элементы равны. Вы можете преобразовать некоторый массив, выполнив следующие шаги любое количество раз: - Выберите два индекса \(i\) и \(j\) (\(1 \leq i,j \leq n\)), а также целое число \(x\) (\(1 \leq x \leq a_i\)). Назовем \(i\) истоком, а \(j\) — стоком.
- Уменьшите \(i\)-й элемент на \(x\), и увеличьте \(j\)-й элемент на \(x\). Итоговые значения на \(i\)-й и \(j\)-й позициях равны \(a_i-x\) и \(a_j+x\) соответственно.
- Стоимость такой операции равна \(x \cdot |j-i| \).
- После этой операции \(i\) больше не может стать стоком, а \(j\) больше не может стать истоком.
Общая стоимость преобразования равна сумме стоимостей на шаге \(3\). Например, массив \([0, 2, 3, 3]\) может быть преобразован в красивый массив \([2, 2, 2, 2]\) с общей стоимостью \(1 \cdot |1-3| + 1 \cdot |1-4| = 5\). Массив называется сбалансированным, если его можно преобразовать в красивый массив, и стоимость такого преобразования однозначно определена. Другими словами, минимальная стоимость преобразования в красивый массив равна максимальной стоимости. Вам дан массив \(a_1, a_2, \ldots, a_n\) длины \(n\), элементы которого — неотрицательные целые числа. Ваша задача — найти количество сбалансированных массивов, являющихся перестановками данного. Два массива считаются различными, если элементы на некоторых позициях отличаются. Так как ответ может быть большим, выведите его по модулю \(10^9 + 7\). Выходные данные Выведите одно целое число — количество сбалансированных перестановок по модулю \(10^9+7\). Примечание В первом примере \([1, 2, 3]\) является сбалансированным массивом, так как мы можем выбрать индекс \(3\) как исток, и индекс \(1\) как сток. После этой операции мы получим красивый массив \([2, 2, 2]\), итоговая стоимость преобразования равна \(2\). Можно показать, что это единственное возможная последовательность операций, приводящая к красивому массиву. Аналогично можно показать, что все другие перестановки тоже сбалансированные. Во втором примере сбалансированные перестановки — это \([0, 0, 4, 4]\) и \([4, 4, 0, 0]\). В третьем примере все перестановки являются сбалансированными. | |
![]()
|
|
B. AND 0, большая сумма
Комбинаторика
математика
*1200
битмаски
Первыми словами маленького Бадави были «AND 0 большая сумма», поэтому он решил решить следующую задачу. Даны два целых числа \(n\) и \(k\), вычислите количество массивов длины \(n\), таких что: - все элементы массива это целые числа от \(0\) до \(2^k-1\) (включительно);
- побитовое И всех его элементов это \(0\);
- сумма его элементов максимальная возможная.
Так как ответ может быть очень большим, выведите его остаток от деления на \(10^9+7\). Выходные данные Для каждого набора входных данных выведите количество массивов, удовлетворяющих всем условиям. Так как ответ может быть большим, выведите его остаток от деления на \(10^9+7\). Примечание В первом примере подходят \(4\) массива: - \([3,0]\),
- \([0,3]\),
- \([1,2]\),
- \([2,1]\).
| |
![]()
|
|
E. Феникс и компьютеры
Комбинаторика
математика
дп
*2200
В один ряд стоят \(n\) компьютеров, первоначально все выключены, и Феникс хочет всех их включить. Он будет лично включать их по одному. Однако в любой момент времени, если компьютеры \(i-1\) и \(i+1\) оказались включены, то компьютер \(i\) \((2 \le i \le n-1)\) включится сам автоматически (если он еще не включен). Заметим, что Феникс не может включить компьютер, который уже включился автоматически. Рассмотрим только последовательности компьютеров, включенных непосредственно Фениксом, сколько существует таких последовательностей, включающих все компьютеры? Две последовательности различны, если либо множество компьютеров, включенных лично Фениксом, различается, либо порядок их включения различен. Так как ответ может быть слишком большим, выведите его по модулю \(M\). Выходные данные Выведите одно число — количество способов включить все компьютеры по модулю \(M\). Примечание В первом примере, для Феникса есть \(6\) последовательностей, при которых он включит все компьютеры: - \([1,3]\). Включить компьютер \(1\), потом \(3\). Заметим, что компьютер \(2\) включится автоматически после того, как компьютер \(3\) будет включен Фениксом, но мы учитываем только компьютеры, включенные непосредственно Фениксом.
- \([3,1]\). Включить компьютер \(3\), потом \(1\).
- \([1,2,3]\). Включить компьютеры \(1\), потом \(2\), затем \(3\).
- \([2,1,3]\)
- \([2,3,1]\)
- \([3,2,1]\)
| |
![]()
|
|
E. Ехаб играет с перестановками
Комбинаторика
математика
дп
*2500
На этот раз Ехаб будет играть с перестановками. У него есть \(n\) кубиков, расположенных в ряд, с числами от \(1\) до \(n\), написанными на них. Он сделает ровно \(j\) операций. В ходе каждой из операций он выбирает \(2\) кубика и меняет их местами. Ехаб задался вопросом: сколько различных последовательностей кубиков я могу получить в конце? Так как Ехаб непостоянный человек, он не уверен, сколько операций хочет совершить. Поэтому он просит вас узнать ответ на его вопрос для всех \(j\) от \(1\) до \(k\). Выходные данные Выведите \(k\) целых чисел. \(i\)-е из них — это количество возможных последовательностей, которые можно получить после ровно \(i\) операций. Так как это число может быть очень большим, выведите его остаток от деления на \(10^9+7\). Примечание Во втором примере есть \(3\) последовательности, которые можно получить после \(1\) операции, потому что вы можете поменять местами \(3\) различные пары индексов. Также, есть ровно \(3\) последовательности, которые можно получить после \(2\) операций: - \([1,2,3]\),
- \([3,1,2]\),
- \([2,3,1]\).
| |
![]()
|
|
F. Воссоединение
Деревья
Комбинаторика
дп
*3200
Сообщается, что конференция 2050 пройдет в городе Юньци в Ханчжоу с 23 по 25 апреля. На ней будут тематические форумы, утренние пробежки, походы, и так далее. Отношения между \(n\) волонтерами конференции 2050 могут быть представлены как дерево (связный неориентированный граф с \(n\) вершинами и \(n-1\) ребром). \(n\) вершин дерева соответствуют \(n\) волонтерам и пронумерованы \(1,2,\ldots, n\). Определим расстояние между двумя волонтерами \(i\) и \(j\), dis\((i,j)\), как количество ребер на кратчайшем пути из вершины \(i\) в вершину \(j\) в дереве. dis\((i,j)=0\), если \(i=j\). Некоторые волонтеры смогут принять участие в очном воссоединении, а некоторые — нет. Если для некоторого волонтера \(x\) и неотрицательного целого числа \(r\), все волонтеры, чье расстояние до \(x\) не больше \(r\), смогут принять участие в очном воссоединении, то форум с радиусом \(r\) может состояться. Уровень очного воссоединения определяется как максимальный возможный радиус форума, который может состояться. Предположим, что каждый волонтер сможет принять участие в воссоединении с вероятностью \(\frac{1}{2}\), и все эти события независимы. Найдите математическое ожидание уровня очного воссоединения. Если ни один волонтер не сможет принять участие, уровень равен \(-1\). Если все волонтеры смогут принять участие, уровень равен \(n\). Выходные данные Выведите математическое ожидание уровня очного воссоединения по модулю \(998\,244\,353\). Формально, пусть \(M = 998\,244\,353\). Можно показать, что ответ может быть представлен как несократимая вещественная дробь \(\frac{p}{q}\), где \(p\) и \(q\) целые числа и \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Примечание В первом примере следующая таблица показывает возможные варианты. \(yes\) означает, что волонтер сможет принять участие, а \(no\) — что не сможет. \(\)\begin{array}{cccc} 1 & 2 & 3 & level\\ yes & yes & yes & 3\\ yes & yes & no & 1\\ yes & no & yes & 0\\ yes & no & no & 0\\ no & yes & yes & 1\\ no & yes & no & 0\\ no & no & yes & 0\\ no & no & no & -1\\ \end{array}\(\) Математическое ожидание уровня равно \(\frac{3+1+1+(-1)}{2^3}=\frac{1}{2}\). | |
![]()
|
|
C. Записная книжка
Комбинаторика
*1400
Однажды маленький Вася нашел записную книжку мамы. В ней были записаны n имен ее друзей, каждое из которых необыкновенным образом было длиной ровно m букв. Пронумеруем имена от 1 до n в том порядке, в котором они записаны. Так как мамы не было дома, Вася решил поиграть с именами: он выбирал три целых числа i, j, k (1 ≤ i < j ≤ n, 1 ≤ k ≤ m), и менял местами у имен с номерами i и j префиксы длиной ровно k символов. Например, если у имен «CBDAD» и «AABRD» поменять местами префиксы длиной 3, то получатся имена «AABAD» и «CBDRD». Вам интересно, сколько возможных различных имен могло быть записано на месте имени номер 1, если Васе разрешено делать любое количество описанных действий. Делая каждое действие, Вася выбирает числа i, j, k независимо от предыдущих ходов и исключительно по своему усмотрению. Искомое число может быть очень большим, поэтому необходимо найти только остаток от деления этого числа на 1000000007 (109 + 7). Выходные данные Выведите единственное целое число — остаток от деления на 1000000007 (109 + 7) количества различных имен, которые могли бы получиться на месте номер 1 после применений описанных действий. Примечание В первом примере Вася на месте имени номер 1 может получить следующие: «AAB», «AAA», «BAA» и «BAB». | |
![]()
|
|
E. Криптовалютные лампочки
Теория вероятностей
Комбинаторика
математика
дп
*2600
 Для отслеживания курса криптовалют трейдер Василий изобрел удивительный прибор, состоящий из \(n\) лампочек, расположенных в ряд. Прибор работает следующим образом: Изначально все лампочки в приборе Василия выключены. На очередной итерации прибор Василия равновероятно выбирает выключенную лампочку и включает её, подсказывая Василию, в какую криптовалюту ему стоит вложиться. Если после этой итерации среди каких-то \(k\) подряд идущих лампочек находится более одной включенной, то прибор Василия завершает свою работу. Василий не любит неопределенности, поэтому просит вас посчитать матожидание количества включенных лампочек в приборе после завершения его работы. Выходные данные Для каждого тестового примера выведите ответ по модулю \(10^9+7\). Формально, пусть \(M = 10^9+7\). Можно показать, что ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Примечание Объяснение первого тестового примера: Выпишем все возможные последовательности включений лампочек, которые завершают работу прибора: - \((1, 2)\) — включены \(2\) лампочки
- \((1, 3, 2)\) — включены \(3\) лампочки
- \((2, 1)\) — включены \(2\) лампочки
- \((2, 3)\) — включены \(2\) лампочки
- \((3, 2)\) — включены \(2\) лампочки
- \((3, 1, 2)\) — включены \(3\) лампочки
Тогда итоговое матожидание будет равняться \(\frac{2}{6}\) + \(\frac{3}{6}\) + \(\frac{2}{6}\) + \(\frac{2}{6}\) + \(\frac{2}{6}\) + \(\frac{3}{6}\) = \(\frac{14}{6}\) = \(\frac{7}{3}\). Тогда требуемый для вывода ответ это \(333333338\), так как \(333333338 \cdot 3 \equiv 7 \pmod{10^9+7}\). | |
![]()
|
|
E. Assimilation IV
Теория вероятностей
Комбинаторика
математика
*2100
дп
Монокарп играет в компьютерную игру Assimilation IV. В этой игре он управляет огромной империей: основывает города, отстраивает их и захватывает новые земли. Сейчас в империи Монокарпа \(n\) городов, и Монокарп планирует их развивать. Он собирается в каждом из этих городов построить по одному Монументу, и это поможет ему захватить новые территории. Игра пошаговая и, так как Монокарп еще не очень хорошо разбирается в игре, на каждом ходу он строит ровно один Монумент. Монокарпа интересуют \(m\) точек на карте, которые он хотел бы контролировать при помощи Монументов. Для каждой точки он знает расстояние от нее до каждого из своих городов. Монументы позволяют захватывать территорию следующим образом: в ход, в который Монокарп строит Монумент в некотором городе, строение позволяет ему контролировать все точки на расстоянии \(1\) до этого города. На следующий ход Монумент будет контролировать все точки на расстоянии не более \(2\), еще через ход — все точки на расстоянии \(3\), и так далее. Монокарп собирается построить \(n\) Монументов за \(n\) ходов, и после этого его империи будут принадлежать каждая интересующая его точка, которая контролируется хотя бы одним Монументом. Монокарп никак не может придумать оптимальную стратегию, и поэтому на каждом шагу он будет просто выбирать город случайно среди тех, в которых еще нет Монументов. Монокарп интересуется, сколько из \(m\) точек он сможет контролировать к концу хода под номером \(n\). Помогите Монокарпу посчитать математическое ожидание количества точек, которые он сможет контролировать! Выходные данные Можно показать, что математическое ожидание количества интересных точек, которые Монокарп сможет контролировать к концу хода \(n\), представимо в виде несократимой дроби \(\frac{x}{y}\). Выведите эту дробь по модулю \(998\,244\,353\) (значение \(x \cdot y^{-1} \bmod 998244353\), где \(y^{-1}\) — такое число, что \(y \cdot y^{-1} \bmod 998244353 = 1\)). Примечание Рассмотрим все возможные порядки городов постройки Монументов: - \([1, 2, 3]\):
- первый город контролирует все точки на расстоянии не более \(3\), другими словами, точки \(1\) и \(4\);
- второй город контролирует все точки на расстоянии не более \(2\), или же точки \(1\), \(3\) и \(5\);
- третий город контролирует все точки на расстоянии не более \(1\), или же точку \(1\).
В результате, \(4\) точки контролируются. - \([1, 3, 2]\): первый город контролирует точки \(1\) и \(4\); второй — точки \(1\) и \(3\); третий — точку \(1\). Суммарно, \(3\) точки.
- \([2, 1, 3]\): первый город контролирует точку \(1\); второй — точки \(1\), \(3\) и \(5\); третий — точку \(1\). Суммарно, \(3\) точки.
- \([2, 3, 1]\): первый город контролирует точку \(1\); второй — точки \(1\), \(3\) и \(5\); третий — точку \(1\). Суммарно, \(3\) точки.
- \([3, 1, 2]\): первый город контролирует точку \(1\); второй — точки \(1\) и \(3\); третий — точки \(1\) и \(5\). Суммарно, \(3\) точки.
- \([3, 2, 1]\): первый город контролирует точку \(1\); второй — точки \(1\), \(3\) и \(5\); третий — точки \(1\) и \(5\). Суммарно, \(3\) точки.
Матожидание количества контролируемых точек равно \(\frac{4 + 3 + 3 + 3 + 3 + 3}{6}\) \(=\) \(\frac{19}{6}\) или \(19 \cdot 6^{-1}\) \(\equiv\) \(19 \cdot 166374059\) \(\equiv\) \(166374062\) \(\pmod{998244353}\) | |
![]()
|
|
E. Oolimry и суффиксный массив
Конструктив
Комбинаторика
математика
*2400
Однажды Oolimry увидел суффиксный массив. Ему стало интересно, сколько строк могут дать этот суффиксный массив. Более формально, для данного суффиксного массив длины \(n\) и размера алфавита \(k\), подсчитайте количество строк, которые порождают такой суффиксный массив. Пусть \(s\) — строка длины \(n\). Тогда \(i\)-й суффикс \(s\) — это подстрока \(s[i \ldots n-1]\). Суффиксный массив — это массив целых чисел, которые представляют собой позиции начал всех суффиксов данной строки после сортировки этих суффиксов в лексикографическом порядке. Например, суффиксный массив oolimry — это \([3,2,4,1,0,5,6]\), так как отсортированный массив суффиксов — это \([\texttt{imry},\texttt{limry},\texttt{mry},\texttt{olimry},\texttt{oolimry},\texttt{ry},\texttt{y}]\). Строка \(x\) лексикографически меньше строки \(y\), если либо \(x\) является префиксом \(y\) (и \(x\neq y\)), либо существует такой \(i\), что \(x_i < y_i\), и для любого \(1\leq j < i\) , \(x_j = y_j\). Выходные данные Выведите, сколько строк порождают данный суффиксный массив. Поскольку число может быть очень большим, выведите ответ по модулю \(998244353\). Примечание В первом примере «abb» является единственным возможным решением. Во втором примере можно легко показать, что не существует возможных строк, так как все буквы должны быть одинаковыми. В четвертом примере одной из возможных строк является «ddbacef». Пожалуйста, не забывайте выводить свои ответы по модулю \(998244353\). | |
![]()
|
|
D. MEX дерево
Деревья
Комбинаторика
математика
реализация
поиск в глубину и подобное
*2400
Вам дано дерево из \(n\) вершин, в котором вершины пронумерованы от \(0\) до \(n-1\). Для каждого \(k\) от \(0\) до \(n\) включительно вам необходимо посчитать количество неупорядоченных пар \((u,v)\), \(u \neq v\), таких, что MEX всех номеров вершин на пути от \(u\) до \(v\) равен \(k\). MEX последовательности целых чисел равен наименьшему неотрицательному целому числу, которое в ней не встречается. Выходные данные Для каждого набора входных данных выведите \(n+1\) целое число: число путей в дереве таких, что MEX всех номеров вершин на нем равен \(k\), для всех \(k\) от \(0\) до \(n\). Примечание - В наборе входных данных \(1\):
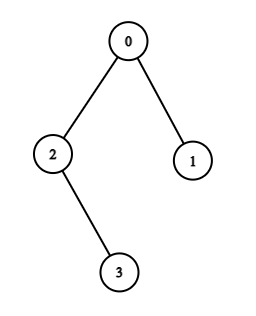 - Для \(k = 0\) существует только \(1\) путь из \(2\) в \(3\) с \(MEX([2, 3]) = 0\).
- Для \(k = 1\) существует \(2\) пути. Один из \(0\) в \(2\) с \(MEX([0, 2]) = 1\), и из \(0\) в \(3\) с \(MEX([0, 2, 3]) = 1\).
- Для \(k = 2\) существует \(1\) путь из \(0\) в \(1\) с \(MEX([0, 1]) = 2\).
- Для \(k = 3\) существует \(1\) путь из \(1\) в \(2\) с \(MEX([1, 0, 2]) = 3\)
- Для \(k = 4\) существует \(1\) путь из \(1\) в \(3\) с \(MEX([1, 0, 2, 3]) = 4\).
- В наборе входных данных \(2\):
 - Для \(k = 0\) не существует таких путей.
- Для \(k = 1\) не существует таких путей.
- Для \(k = 2\) существует \(1\) путь из \(0\) в \(1\) с \(MEX([0, 1]) = 2\).
| |
![]()
|
|
B. Kavi разбивает на пары
Комбинаторика
математика
дп
*1700
У Kavi есть \(2n\) точек, лежащих на оси \(OX\), \(i\)-я из которых расположена в точке \(x = i\). Kavi рассматривает все способы разбить эти \(2n\) точек на \(n\) пар. Среди этих способов его интересуют хорошие способы, которые определяются следующим образом: Рассмотрим \(n\) отрезков с концами в точках в соответствующих парах. Пара называется хорошей, если для каждых \(2\) различных отрезков \(A\) и \(B\) из этих, для них выполняется хотя бы одно из следующих условий: - Один из отрезков \(A\) и \(B\) полностью содержится внутри другого.
- \(A\) и \(B\) имеют одинаковую длину.
Рассмотрим следующий пример: 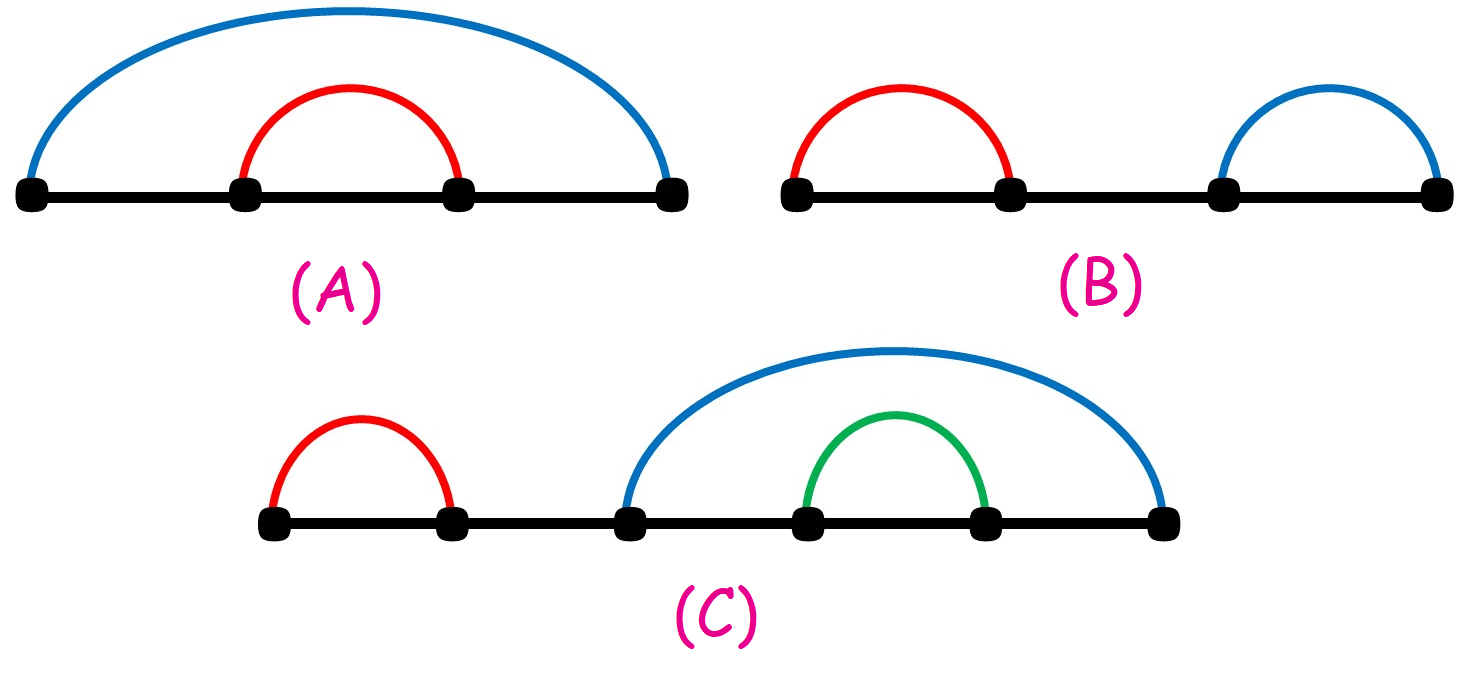 \(A\) — хорошее разбиение на пары, так как красный отрезок полностью лежит внутри синего отрезка. \(B\) — хорошее разбиение, так как красный и синий отрезки имеют одинаковую длину. \(C\) не является хорошим разбиением, так как ни один из красного и синего отрезков не лежит внутри другого, и они имеют разную длину. Kavi интересует количество хороших разбиений на пары, поэтому он хочет, чтобы вы нашли его для него. Поскольку результат может быть большим, найдите это число по модулю \(998244353\). Два разбиения на пары называются различными, если в одном из них какие-то две точки находятся в одной паре, а в другом — в разных парах. Выходные данные Выведите количество хороших пар по модулю \(998244353\). Примечание Хорошими разбиениями на пары для второго примера являются: 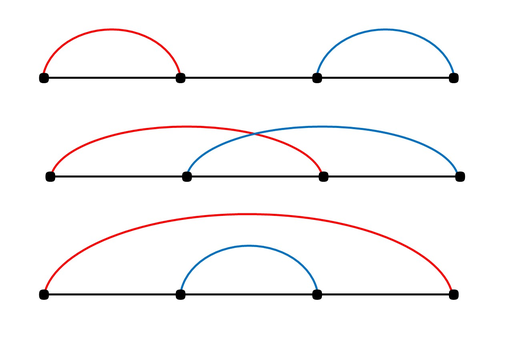 Хорошими разбиениями на пары для третьего примера являются: 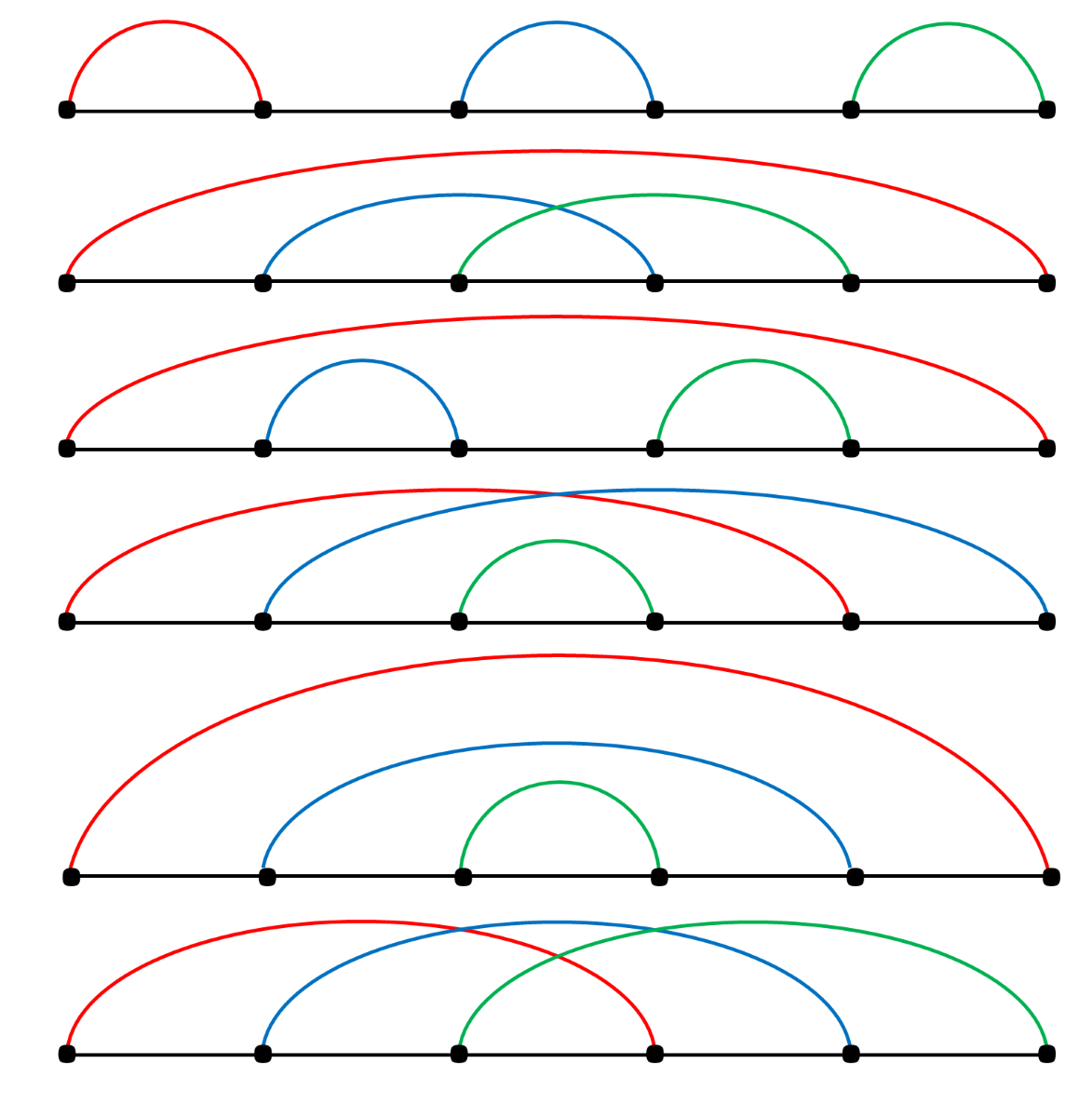 | |
![]()
|
|
E. Mashtali и деревья Hagh
Деревья
Комбинаторика
дп
*2900
Сегодня у Mashtali день рождения! Он получил в подарок от Haj Davood дерево Hagh! Ориентированное дерево называется деревом Hagh, если: - Длина самого длинного ориентированного пути в нем равна ровно \(n\).
- Каждая вершина имеет не более трех ребер, присоединенных к ней (исходящих и входящих вместе).
- Назовем вершины \(u\) и \(v\) друзьями, если из одной из них есть ориентированный путь к другой. Для каждой пары вершин \(u\) и \(v\), которые не являются друзьями, должна существовать вершина \(w\), которая дружит и с \(u\), и с \(v\) (общий друг).
Открыв свой подарок, Mashtali обнаружил, что номера вершин с вершин исчезли. Тогда он спросил себя: сколько существует различных непомеченных деревьев Hagh? Другими словами, сколько возможных деревьев он мог получить в подарок на день рождения? На первый взгляд, число таких деревьев кажется бесконечным, поскольку нет никакого ограничения на количество вершин; но затем он решил задачу и доказал, что непомеченых деревьев Hagh есть всего конечное число! Пораженный этим фактом, он поделился задачей с вами, чтобы вы тоже могли насладиться ее решением. Поскольку ответ может быть довольно большим, он попросил вас найти количество различных деревьев Hagh по модулю \(998244353\). Здесь два дерева считаются различными, если они не изоморфны: если нет способа поставить в соответствие вершины одного дерева вершинам второго дерева так, чтобы ребрам первого ставились в соответствие ребра второго, с сохранением ориентации. Некоторые примеры для \(n = 2\): 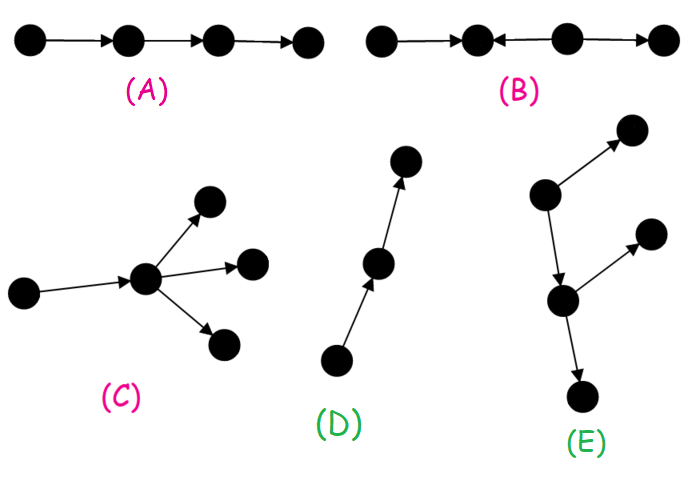 Ориентированные деревья \(D\) и \(E\) являются деревьями Hagh. \(C\) не является Hagh, потому что имеет вершину с \(4\) ребрами, присоединенными к ней. Деревья \(A\) и \(B\) не являются Hagh, потому что их самые длинные ориентированные пути не имеют длину \(n\). Также в \(B\) крайние левая и правая вершины не являются друзьями и не имеют общих друзей. Выходные данные Выведите одно целое число, ответ на задачу Mashtali по модулю \(998244353\). Примечание Вот все пять деревьев Hagh для \(n = 1\): 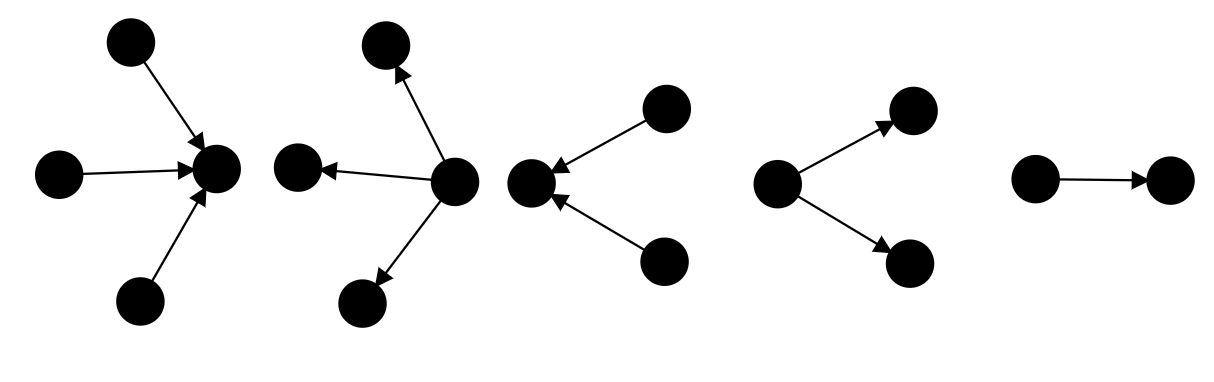 | |
![]()
|
|
F. Ферма AmShZ
Комбинаторика
математика
бпф
*3300
Для AmShZ все массивы равны, но некоторые массивы более равны, чем другие. А именно — массивы, состоящие из \(n\) элементов от \(1\) до \(n\), которые можно превратить в перестановки чисел от \(1\) до \(n\), добавив к каждому элементу по целому неотрицательному числу. Mashtali который хочет появиться в условии каждой задачи считает, что массив \(b\), состоящий из \(k\) элементов, совместим с более равным массивом \(a\), состоящим из \(n\) элементов, если для каждого \(1 \le i \le k\) выполняется \(1 \le b_i \le n\), а также \(a_{b_1} = a_{b_2} = \ldots = a_{b_k}\). Найдите количество пар массивов \(a\) и \(b\) таких, что \(a\) — более равный массив, состоящий из \(n\) элементов, а \(b\) — массив, совместимый с \(a\), состоящий из \(k\) элементов, по модулю \(998244353\). Заметим, что элементы \(b\) не обязательно разные, то же самое верно и для \(a\). Выходные данные Выведите одно целое число — ответ на задачу по модулю \(998244353\). Примечание Для второго примера существует восемь возможных пар: - \(a = \{1, 1\}, b = \{1, 1\}\)
- \(a = \{1, 1\}, b = \{1, 2\}\)
- \(a = \{1, 1\}, b = \{2, 1\}\)
- \(a = \{1, 1\}, b = \{2, 2\}\)
- \(a = \{1, 2\}, b = \{1, 1\}\)
- \(a = \{1, 2\}, b = \{2, 2\}\)
- \(a = \{2, 1\}, b = \{1, 1\}\)
- \(a = \{2, 1\}, b = \{2, 2\}\)
| |
![]()
|
|
F. Бинго
Теория вероятностей
Комбинаторика
математика
дп
*2600
битмаски
В предвкушении VK Fest 2021 вы составили себе табличку из \(n\) строк и \(n\) столбцов, и в каждую ячейку этой таблички записали некоторое событие, связанное с фестивалем, которое может произойти или нет — например, удастся ли вам выиграть на фестивале приз, или пойдёт ли дождь. Алгоритмы предсказания ВКонтакте уже оценили для каждого события вероятность того, что оно произойдёт. Событие в строке \(i\) и столбце \(j\) произойдёт с вероятностью \(a_{i, j} \cdot 10^{-4}\). При этом все события совместно независимы друг от друга. Назовём табличку с событиями выигрышной, если найдётся такая линия, на которой произойдут все \(n\) событий. Линией считается любая горизонталь (ячейки \((i, 1), (i, 2), \ldots, (i, n)\) для некоторого \(i\)), любая вертикаль (ячейки \((1, j), (2, j), \ldots, (n, j)\) для некоторого \(j\)), главная диагональ (ячейки \((1, 1), (2, 2), \ldots, (n, n)\)) и побочная диагональ (ячейки \((1, n), (2, n - 1), \ldots, (n, 1)\)). Определите вероятность того, что ваша табличка окажется выигрышной, и выведите её по модулю \(31\,607\) (см. формат вывода). Выходные данные Выведите вероятность того, что табличка окажется выигрышной, по модулю \(31\,607\). Формально, пусть \(M = 31\,607\). Можно показать, что ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Примечание В первом примере любые два события образуют линию, поэтому табличка будет выигрышной, если произойдут любые два события. Вероятность этого равна \(\frac{11}{16}\), а \(5927 \cdot 16 \equiv 11 \pmod{31\,607}\). | |
![]()
|
|
C. Головоломка маленького Алана
Комбинаторика
математика
дп
графы
*1300
снм
Во время перерывов в подготовке к Международной олимпиаде школьников по информатике маленький Алан любит решать различные головоломки, чтобы развивать мозги. Сегодня он решает головоломку, которая выглядит как таблица \(2 \times n\), где в каждом ряду записана перестановка чисел \(1,2,3,\ldots,n\). Задача головоломки — сделать так, чтобы ни в каком ряду и ни в каком столбце не было двух одинаковых чисел (назовем такие состояния решенными), а единственная разрешенная операция — поменять местами два числа в одном столбце. Когда маленький Алан решил головоломку много раз, он заскучал и начал размышлять, а сколько вообще существует различных решенных состояний в данной головоломке, которые он может получить из некоторого начального решенного состояния, применяя только разрешенные операции? Маленький Алан не справился с этой сложной задачей, поэтому он попросил вас помочь ему. Найдите ответ по модулю \(10^9+7\). Выходные данные Для каждого набора входных данных выведите одно целое число — количество решенных состояний головоломки, которые можно получить из данного, меняя местами числа в столбцах. Так как ответ может быть большим, выведите его по модулю \(10^9+7\). Примечание Два возможных решенный состояния в примере \(1\): - \([1,4,2,3]\) в первой строке, и \([3,2,1,4]\) во второй,
- \([3,2,1,4]\) в первой строке, и \([1,4,2,3]\) во второй.
| |
![]()
|
|
E. Омкар и лес
Комбинаторика
математика
графы
*2300
кратчайшие пути
Последний присоединившийся последователь Омкара, Ajit, вошел в Священный лес. Ajit понимает, что лес Омкара — это таблица размером \(n\) на \(m\) (\(1 \leq n, m \leq 2000\)), состоящая из целых неотрицательных чисел. Поскольку лес благословлен Омкаром, он удовлетворяет некоторым особым условиям: - Для любых двух соседних по стороне клеток абсолютное значение разности чисел в них не превышает \(1\).
- Если число в какой-то клетке строго больше \(0\), то оно должно быть строго больше, чем значение числа в по крайней мере одной клетке, примыкающей к ней по стороне.
К сожалению, Ajit еще не полностью достоин способностей Омкара. Он видит каждую клетку как "0" или "#". Если клетка обозначена как "0", то число в ней должно быть равно \(0\). Иначе число в ней может быть любым неотрицательным целым числом. Определите, сколько существует различных конфигураций элементов, при которых выполняются эти особые условия. Две конфигурации считаются различными, если существует хотя бы одна клетка такая, что числа, записанные в ней в этих конфигурациях, различны. Поскольку ответ может быть огромным, найдите ответ по модулю \(10^9+7\). Выходные данные Для каждого набора входных данных выведите одно целое число: количество допустимых конфигураций по модулю \(10^9+7\). Примечание Для первого набора входных данных есть две допустимых конфигурации: \(0000\\ 0000\\ 0000\) и \(0000\\ 0010\\ 0000\) | |
![]()
|
|
F. Омкар и Акмар
Конструктив
Комбинаторика
математика
геометрия
*2600
meet-in-the-middle
бпф
игры
строковые суфф. структуры
китайская теорема об остатках
Омкар и Акмар играют в игру на круговой доске с \(n\) (\(2 \leq n \leq 10^6\)) клетками. Клетки пронумерованы от \(1\) до \(n\), для каждой \(i\) (\(1 \leq i \leq n-1\)) клетка \(i\) соседствует с клеткой \(i+1\), а клетка \(1\) соседствует с клеткой \(n\). Изначально каждая клетка пуста. Омкар и Акмар по очереди выкладывают на доску букву A или B, причем Акмар ходит первым. Буква должна быть помещена на пустую клетку. Кроме того, буква не может быть помещена в такую клетку, что соседняя клетка содержит ту же букву. Игрок проигрывает, когда наступает его очередь и больше нет допустимых ходов. Выведите количество возможных различных игр, в которых оба игрока играют оптимально по модулю \(10^9+7\). Обратите внимание, что мы рассматриваем только те партии, в которых кто-то из игроков проиграл, и не осталось ни одного допустимого хода. Две игры считаются разными, если количества ходов в них отличаются, или на каком-то ходу буква или номер клетки, на которую ставится буква, были разными. Ход считается оптимальным, если он максимизирует шансы игрока на победу, предполагая, что другой игрок также играет оптимально. Более формально, если игрок, чья очередь ходить, имеет выигрышную стратегию, он должен сделать ход, после которого у него останется выигрышная стратегия. Если же у него ее нет, то он может сделать любой ход. Выходные данные Выведите одно целое число, — количество возможных различных игр, в которых оба игрока играют оптимально по модулю \(10^9+7\). Примечание В первом примере первый игрок имеет \(4\) возможных хода. Независимо от того, как ходит первый игрок, у второго игрока есть ровно \(1\) возможный ход, поэтому существует \(4\) возможных игры. | |
![]()
|
|
A. Старт олимпиады
Комбинаторика
математика
*1000
геометрия
жадные алгоритмы
В некоторой олимпиаде участвует \(n\) человек, причем они начинают олимпиаду с интервалом в \(x\) минут. Таким образом первый участник начнёт тур в момент времени \(0\), второй участник начнёт тур в момент времени \(x\), третий — в момент времени \(2 \cdot x\) и так далее. Длительность тура для каждого участника составляет ровно \(t\) минут, то есть первый участник закончит в момент времени \(t\), второй — в момент времени \(t + x\), и так далее. Когда участник заканчивает писать тур, величина его недовольства равна числу других участников, которые в текущий момент времени еще пишут или только начинают писать тур, но еще не закончили его. Определите, чему равно суммарное недовольство всех участников олимпиады. Выходные данные Выведите \(k\) строк, в \(i\)-й из них выведите суммарное недовольство всех участников олимпиады для \(i\)-го набора входных данных. Примечание В первом наборе входных данных первый участник начнёт писать тур в момент времени \(0\) и закончит в момент времени \(5\). К этому времени второй и третий участники уже начнут писать тур, поэтому недовольство первого участника будет равно \(2\). Второй участник начнёт писать в момент времени \(2\) и закончит в момент времени \(7\). К этому моменту третий и четвёртый участники уже начнут писать тур, поэтому недовольство второго будет равно \(2\). Третий участник начнёт писать тур в момент времени \(4\) и закончит в момент времени \(9\). К этому времени четвёртый уже начнёт писать тур, поэтому недовольство третьего будет равно \(1\). Четвёртый участник начнёт писать тур в момент времени \(6\) и закончит в момент времени \(11\). В момент времени \(11\) уже никто не будет писать тур, поэтому недовольство четвёртого будет равно \(0\). Во втором наборе входных данных первый участник начнёт писать тур в момент времени \(0\) и закончит в момент времени \(2\). К этому моменту второй уже будет писать тур, а третий как раз начнёт в момент времени \(2\). Поэтому недовольство первого участника будет равно \(2\). Второй начнёт в момент времени \(1\) и закончит в момент времени \(3\). К этому моменту только третий будет всё ещё писать тур. | |
![]()
|
|
B. Древесный массив
Деревья
Перебор
Теория вероятностей
Комбинаторика
математика
дп
графы
*2300
Вам задано дерево, состоящее из \(n\) вершин. По заданному дереву вы строите массив, отмечая вершины по одной. Первоначально, когда еще не помечено ни одной вершины, вы выбираете вершину равновероятно по всем вершинам дерева и отмечаете ее. После этого, пока еще остаются непомеченные вершины, вы выбираете и помечаете вершину равновероятно среди всех еще непомеченных, но связанных по ребру хотя бы с одной помеченной вершиной. Можно доказать, что данный процесс пометит все вершины в дереве. Финальный массив \(a\) — это список номеров вершин в порядке, в котором они были помечены. Определите математическое ожидание количества инверсий в массиве, полученном на основе заданного дереве с помощью описанного выше алгоритма. Количество инверсий в массиве \(a\) — это количество пар индексов \((i, j)\) таких, что \(i < j\) и \(a_i > a_j\). Например, в массиве \([4, 1, 3, 2]\) количество инверсий равно \(4\): \((1, 2)\), \((1, 3)\), \((1, 4)\), \((3, 4)\). Выходные данные Выведите математическое ожидание количества инверсий в построенном массиве по модулю \(10^9+7\). Формально, пусть \(M = 10^9+7\). Можно показать, что ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Примечание Изображение дерева из первого примера: 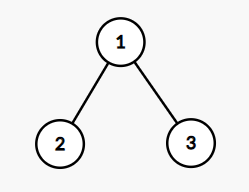 В первом примере получающиеся массивы почти фиксированы. Если первоначально выбрана вершина \(2\), то единственный возможный массив — это \([2, 1, 3]\) (\(1\) инверсия). Если первоначально выбрана вершина \(3\), то единственный возможный массив — это \([3, 1, 2]\) (\(2\) инверсии). Если первоначально выбрана вершина \(1\), то массивы \([1, 2, 3]\) (\(0\) инверсий) и \([1, 3, 2]\) (\(1\) инверсия) — это единственные варианты и они равновероятны. В результате математическое ожидание количества инверсий равно \(\frac{1}{3}\cdot 1 + \frac{1}{3} \cdot 2 + \frac{1}{3} \cdot (\frac{1}{2} \cdot 0 + \frac{1}{2} \cdot 1) = \frac{7}{6}\). \(166666669 \cdot 6 = 7 \pmod {10^9 + 7}\), то есть ответ равен \(166666669\). Изображение дерева из второго примера: 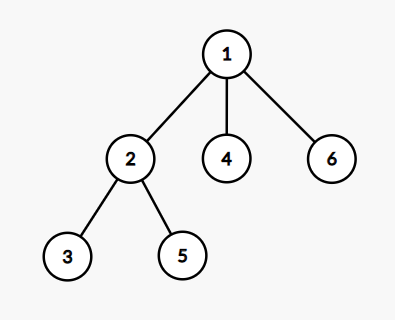 Изображение дерева из третьего примера:  | |
![]()
|
|
D. Очередь с приоритетом
Тернарный поиск
Комбинаторика
математика
реализация
дп
*2200
Дана последовательность \(A\), в которой каждый элемент записан в формате + x или -, где \(x\) — целое число. Для последовательности \(S\), в которой каждый элемент записан в формате + x или -, определим \(f(S)\) следующим образом: - Проходим по \(S\) от первого элемента до последнего и поддерживаем мультимножество \(T\), изначально пустое.
- Если элемент последовательности имеет вид + x, добавим \(x\) в \(T\). Иначе удалим наименьший элемент из \(T\) (если \(T\) пусто, ничего делать не нужно).
- После прохода по \(S\) посчитаем сумму всех элементов в \(T\). \(f(S)\) полагается равным этой сумме.
Последовательность \(b\) является подпоследовательностью последовательности \(a\), если \(b\) может быть получена из \(a\) удалением нуля или больше элементов без изменения порядка оставшихся элементов. Для всех подпоследовательностей \(B\) последовательности \(A\) посчитайте сумму \(f(B)\) по модулю \(998\,244\,353\). Выходные данные Выведите одно целое число, равное ответу на задачу по модулю \(998\,244\,353\). Примечание В первом примере все возможные пары \(B\) и \(f(B)\) выглядят так: - \(B=\) {}, \(f(B)=0\).
- \(B=\) {-}, \(f(B)=0\).
- \(B=\) {+ 1, -}, \(f(B)=0\).
- \(B=\) {-, + 1, -}, \(f(B)=0\).
- \(B=\) {+ 2, -}, \(f(B)=0\).
- \(B=\) {-, + 2, -}, \(f(B)=0\).
- \(B=\) {-}, \(f(B)=0\).
- \(B=\) {-, -}, \(f(B)=0\).
- \(B=\) {+ 1, + 2}, \(f(B)=3\).
- \(B=\) {+ 1, + 2, -}, \(f(B)=2\).
- \(B=\) {-, + 1, + 2}, \(f(B)=3\).
- \(B=\) {-, + 1, + 2, -}, \(f(B)=2\).
- \(B=\) {-, + 1}, \(f(B)=1\).
- \(B=\) {+ 1}, \(f(B)=1\).
- \(B=\) {-, + 2}, \(f(B)=2\).
- \(B=\) {+ 2}, \(f(B)=2\).
Сумма этих значений равна \(16\). | |
![]()
|
|
E1. Аномальные пары перестановок (простая версия)
Комбинаторика
математика
дп
*2400
бпф
Это простая версия задачи. Единственное различие между простой и сложной версиями заключается в ограничениях на \(n\). Вы можете делать взломы, только если решили обе версии этой задачи. Перестановка чисел \(1, 2, \ldots, n\) – это последовательность из \(n\) целых чисел, в которой каждое число от \(1\) до \(n\) встречается ровно один раз. Например, \([2,3,1,4]\) является перестановкой \(1, 2, 3, 4\), но \([1,4,2,2]\) – не перестановка, поскольку \(2\) встречается здесь дважды. Напомним, что количеством инверсий в перестановке \(a_1, a_2, \ldots, a_n\) называется число пар индексов \((i, j)\) таких, что \(i < j\) и \(a_i > a_j\). Пусть \(p\) и \(q\) – две перестановки чисел \(1, 2, \ldots, n\). Найдите количество пар перестановок \((p,q)\), удовлетворяющих следующим условиям: - \(p\) лексикографически меньше \(q\).
- Количество инверсий в \(p\) больше, чем в \(q\).
Выведите это количество пар по модулю \(mod\). Обратите внимание, что \(mod\) – не обязательно простое число. Выходные данные Выведите одно целое число — ответ на задачу по модулю \(mod\). Примечание Все возможные пары перестановок \((p,q)\) при \(n=4\): - \(p=[1,3,4,2]\), \(q=[2,1,3,4]\),
- \(p=[1,4,2,3]\), \(q=[2,1,3,4]\),
- \(p=[1,4,3,2]\), \(q=[2,1,3,4]\),
- \(p=[1,4,3,2]\), \(q=[2,1,4,3]\),
- \(p=[1,4,3,2]\), \(q=[2,3,1,4]\),
- \(p=[1,4,3,2]\), \(q=[3,1,2,4]\),
- \(p=[2,3,4,1]\), \(q=[3,1,2,4]\),
- \(p=[2,4,1,3]\), \(q=[3,1,2,4]\),
- \(p=[2,4,3,1]\), \(q=[3,1,2,4]\),
- \(p=[2,4,3,1]\), \(q=[3,1,4,2]\),
- \(p=[2,4,3,1]\), \(q=[3,2,1,4]\),
- \(p=[2,4,3,1]\), \(q=[4,1,2,3]\),
- \(p=[3,2,4,1]\), \(q=[4,1,2,3]\),
- \(p=[3,4,1,2]\), \(q=[4,1,2,3]\),
- \(p=[3,4,2,1]\), \(q=[4,1,2,3]\),
- \(p=[3,4,2,1]\), \(q=[4,1,3,2]\),
- \(p=[3,4,2,1]\), \(q=[4,2,1,3]\).
| |
![]()
|
|
E2. Аномальные пары перестановок (сложная версия)
Комбинаторика
математика
дп
*2700
бпф
Это сложная версия задачи. Единственное различие между простой и сложной версиями заключается в ограничениях на \(n\). Вы можете делать взломы, только если решили обе версии этой задачи. Перестановка чисел \(1, 2, \ldots, n\) – это последовательность из \(n\) целых чисел, в которой каждое число от \(1\) до \(n\) встречается ровно один раз. Например, \([2,3,1,4]\) является перестановкой \(1, 2, 3, 4\), но \([1,4,2,2]\) – не перестановка, поскольку \(2\) встречается здесь дважды. Напомним, что количеством инверсий в перестановке \(a_1, a_2, \ldots, a_n\) называется число пар индексов \((i, j)\) таких, что \(i < j\) и \(a_i > a_j\). Пусть \(p\) и \(q\) – две перестановки чисел \(1, 2, \ldots, n\). Найдите количество пар перестановок \((p,q)\), удовлетворяющих следующим условиям: - \(p\) лексикографически меньше \(q\).
- Количество инверсий в \(p\) больше, чем в \(q\).
Выведите это количество пар по модулю \(mod\). Обратите внимание, что \(mod\) – не обязательно простое число. Выходные данные Выведите одно целое число — ответ на задачу по модулю \(mod\). Примечание Все возможные пары перестановок \((p,q)\) при \(n=4\): - \(p=[1,3,4,2]\), \(q=[2,1,3,4]\),
- \(p=[1,4,2,3]\), \(q=[2,1,3,4]\),
- \(p=[1,4,3,2]\), \(q=[2,1,3,4]\),
- \(p=[1,4,3,2]\), \(q=[2,1,4,3]\),
- \(p=[1,4,3,2]\), \(q=[2,3,1,4]\),
- \(p=[1,4,3,2]\), \(q=[3,1,2,4]\),
- \(p=[2,3,4,1]\), \(q=[3,1,2,4]\),
- \(p=[2,4,1,3]\), \(q=[3,1,2,4]\),
- \(p=[2,4,3,1]\), \(q=[3,1,2,4]\),
- \(p=[2,4,3,1]\), \(q=[3,1,4,2]\),
- \(p=[2,4,3,1]\), \(q=[3,2,1,4]\),
- \(p=[2,4,3,1]\), \(q=[4,1,2,3]\),
- \(p=[3,2,4,1]\), \(q=[4,1,2,3]\),
- \(p=[3,4,1,2]\), \(q=[4,1,2,3]\),
- \(p=[3,4,2,1]\), \(q=[4,1,2,3]\),
- \(p=[3,4,2,1]\), \(q=[4,1,3,2]\),
- \(p=[3,4,2,1]\), \(q=[4,2,1,3]\).
| |
![]()
|
|
B. Настройка трассы
Комбинаторика
математика
*900
жадные алгоритмы
Шоссе 201 — самая оживлённая улица в Рокпорт-Сити. Машины, стоящие в пробках, создают помехи для гонок, особенно когда их много. Гоночная трасса, проходящая через это шоссе, разделена на \(n\) участков. Вам дан массив \(a\), в котором \(a_i\) равно количеству машин, стоящих в пробках на \(i\)-м участке. Положим неудобством гоночной трассы значение \(\sum\limits_{i=1}^{n} \sum\limits_{j=i+1}^{n} \lvert a_i-a_j\rvert\), где \(|x|\) — модуль числа \(x\). Вам разрешено проделывать следующую операцию любое (в том числе ноль) количество раз: выбрать машину, стоящую в пробке, и переместить ее из ее текущего участка в любой другой участок. Найдите минимальное неудобство, которого возможно достичь. Выходные данные Для каждого набора входных данных выведите строку, содержащую одно целое число — минимальное неудобство, которого возможно достичь, применяя указанную операцию любое (в том числе ноль) количество раз. Примечание В первом наборе входных данных вы можете переместить машину с \(3\)-го участка на \(1\)-й участок, чтобы получить неудобство, равное \(0\). Во втором наборе перемещение любой машины не уменьшит неудобство гоночной трассы. | |
![]()
|
|
B. AquaMoon и шахматы
Комбинаторика
математика
*1900
Cirno дала AquaMoon шахматную доску размера \(1 \times n\). Ее клетки пронумерованы целыми числами от \(1\) до \(n\) слева направо. Изначально в некоторых клетках находится одна пешка, а остальные клетки свободны. На каждой операции AquaMoon может выбрать клетку \(i\) с пешкой и сделать любую из следующих операций (если возможно): - Переместить пешку из нее в клетку \((i+2)\), если \(i+2 \leq n\), \((i+1)\)-я клетка занята пешкой, а \((i+2)\)-я клетка свободна.
- Переместить пешку из нее в клетку \((i-2)\), если \(i-2 \geq 1\), \((i-1)\)-я клетка занята пешкой, а \((i-2)\)-я клетка свободна.
Дано изначальное состояние шахматной доски. AquaMoon хочет посчитать количество состояний, которые достижимы из начального состояния с помощью некоторой последовательности операций. Но она не очень хороша в программировании. Можете ли вы помочь ей? Поскольку ответ может быть большим, найдите его по модулю \(998\,244\,353\). Выходные данные Для каждого набора входных данных выведите количество состояний, которое может быть получено из начального с помощью некоторой последовательности операций по модулю \(998\,244\,353\). Примечание В первом наборе входных данных строки «1100», «0110» и «0011» могут быть получены из изначального состояния с помощью некоторой последовательности операций. | |
![]()
|
|
C. AquaMoon и перестановки
Паросочетания
Перебор
Конструктив
Комбинаторика
*2800
графы
2-sat
Cirno подготовила \(n\) массивов длины \(n\) каждый. Каждый массив — это перестановка из \(n\) целых чисел от \(1\) до \(n\). Эти массивы специальные: для всех \(1 \leq i \leq n\), если мы возьмем \(i\)-й элемент каждого массива и построим другой массив длины \(n\), состоящий из этих элементов, получившийся массив также будет перестановкой \(n\) чисел от \(1\) до \(n\). Другими словами, если эти \(n\) массивов расположить друг под другом, образовав матрицу с \(n\) строками и \(n\) столбцами, эта матрица будет латинским квадратом. После этого Cirno добавила дополнительные \(n\) массивов, каждый массив также является перестановкой из \(n\) целых чисел от \(1\) до \(n\). Для всех \(1 \leq i \leq n\) существует хотя бы одна позиция \(1 \leq k \leq n\), такая что для \(i\)-го и \((n + i)\)-го массивов \(k\)-е элементы совпадают. Обратите внимание, что массивы с индексами от \(n + 1\) до \(2n\) не обязаны образовывать латинский квадрат. Также Cirno убедилась, что среди \(2n\) массивов никакие два не равны, то есть для всех пар индексов \(1 \leq i < j \leq 2n\) существует хотя бы одна позиция \(1 \leq k \leq n\), такая что в \(i\)-м и \(j\)-м массивах \(k\)-е элементы различны. В конце Cirno произвольно поменяла порядок, в котором расположены подготовленные \(2n\) массивов. AquaMoon называет подмножество всех \(2n\) массивов размера \(n\) хорошим, если эти массивы образуют латинский квадрат. AquaMoon хочет узнать, сколько хороших подмножеств существует. Поскольку это количество может быть очень большим, найдите его по модулю \(998\,244\,353\). Также она хочет найти любое хорошее подмножество. Можете ли вы помочь ей? Выходные данные Для каждого набора входных данных выведите две строки. В первой строке выведите количество хороших подмножеств по модулю \(998\,244\,353\). Во второй строке выведите \(n\) индексов от \(1\) до \(2n\) — индексы \(n\) массивов, которые образуют хорошее подмножество (вы можете вывести их в любом порядке). Если существует несколько возможных ответов — выведите любой. Примечание В первом наборе входных данных количество хороших подмножеств равно \(1\). Единственное такое подмножество это подмножество массивов с индексами \(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\). Во втором наборе входных данных количество хороших подмножеств равно \(2\). Эти подмножества это \(1\), \(3\), \(5\), \(6\), \(10\), а также \(2\), \(4\), \(7\), \(8\), \(9\). | |
![]()
|
|
C. Три поросенка
Комбинаторика
математика
дп
*2500
бпф
Делегации трех поросят со всего мира едут на конференцию! Каждую минуту новая тройка поросят прибывает в конференц-зал. После \(n\)-й минуты конференция завершается. Большой злой волк узнал об этой конференции и запланировал атаку. В определенную минуту конференции он ворвется в зал, съест ровно \(x\) поросят и убежит. Волк попросил Грегора помочь ему найти количество возможных планов для атаки, в которых он съест ровно \(x\) поросят, для различных значений \(x\) (\(1 \le x \le 3n\)). Два плана для атаки считаются различными, если атака происходит в различное время, или съедаются различные подмножества поросят. Обратите внимание, что все запросы независимы, то есть в действительности волк не ест поросят, а только строит планы! Выходные данные Вы должны вывести \(q\) строк. В \(i\)-й строке должно содержаться количество планов для атаки, если волк хочет съесть \(x_i\) поросят. Выведите каждый ответ по модулю \(10^9+7\). Примечание В приведенном примере \(n=2\). Таким образом, на минуте \(1\) в конференц-зале присутствуют \(3\) поросенка, на минуте \(2\) — \(6\) поросят. Даны три запроса: \(x=1\), \(x=5\) и \(x=6\). Если волк хочет съесть \(1\) поросенка, он может сделать это, используя \(3+6=9\) возможных планов для атаки в зависимости от того, на какой минуте (\(1\) или \(2\)) он прибудет. Если волк хочет съесть \(5\) поросят, он не может прибыть на минуте \(1\), поскольку в это время в зале недостаточно поросят. Поэтому волк должен прибыть на минуте \(2\) — тогда существует \(6\) возможных планов для атаки. Если волк хочет съесть \(6\) поросят, то его единственным планом является прибыть к концу конференции и поглотить всех. Не забудьте выводить ответы по модулю \(10^9+7\)! | |
![]()
|
|
D. Отличные массивы
Бинарный поиск
Конструктив
Комбинаторика
математика
реализация
сортировки
*2300
Назовем целочисленный массив \(a_1, a_2, \dots, a_n\) хорошим, если \(a_i \neq i\) для всех \(i\). Пусть \(F(a)\) — это количество пар \((i, j)\) (\(1 \le i < j \le n\)) таких, что \(a_i + a_j = i + j\). Назовем массив \(a_1, a_2, \dots, a_n\) отличным если: - \(a\) — хороший;
- \(l \le a_i \le r\) для всех \(i\);
- \(F(a)\) максимально возможное среди всех хороших массивов размера \(n\).
Для заданных \(n\), \(l\) и \(r\) посчитайте количество отличных массивов по модулю \(10^9 + 7\). Выходные данные Для каждого набора входных данных выведите количество отличных массивов по модулю \(10^9 + 7\). Примечание В первом наборе входных данных, можно показать, что максимальное \(F(a)\) среди всех хороших массивов \(a\) равно \(2\). Отличными являются следующие массивы: - \([2, 1, 2]\);
- \([0, 3, 2]\);
- \([2, 3, 2]\);
- \([3, 0, 1]\).
| |
![]()
|
|
F. Равноудалённые вершины
Деревья
Перебор
Комбинаторика
дп
поиск в глубину и подобное
*2200
Дерево — это неориентированный связный граф, в котором отсутствуют циклы. Задано дерево из \(n\) вершин. Необходимо посчитать количество способов выбрать в этом дереве ровно \(k\) вершин (т.е. \(k\)-элементное подмножество вершин), так чтобы все попарные расстояния между выбранными вершинами были равны. Иными словами, чтобы существовало такое число \(c\), что для всех \(u, v\) (\(u \ne v\), \(u, v\) — выбранные вершины) было верно \(d_{u,v}=c\), где \(d_{u,v}\) — расстояние от \(u\) до \(v\). Поскольку ответ может быть очень большим, необходимо вывести его по модулю \(10^9 + 7\). Выходные данные Для каждого набора входных данных выведите в отдельной строке одно целое число — количество способов выбрать в дереве ровно \(k\) вершин, так чтобы для любых двух пар вершин расстояние между вершинами в паре было одинаковым, по модулю \(10^9 + 7\) (иными словами, выведите остаток при делении на \(1000000007\)). | |
![]()
|
|
B. Забег за золотом
Комбинаторика
*1500
жадные алгоритмы
сортировки
графы
Олимпийские игры только что начались, и Федерико с нетерпением ждет начала марафонского забега. В марафоне будут участвовать \(n\) спортсменов, от \(1\) до \(n\), и все они в прошлом участвовали в \(5\) важных марафонах, пронумерованных от \(1\) до \(5\). Для каждого \(1\le i\le n\) и \(1\le j\le 5\) Федерико помнит, что спортсмен \(i\) занял место \(r_{i,j}\) в марафоне \(j\) (например, \(r_{2,4}=3\) означает, что спортсмен \(2\) был третьим в марафоне \(4\)). Федерико считает, что спортсмен \(x\) превосходит спортсмена \(y\), если спортсмен \(x\) занял лучшее место, чем спортсмен \(y\), по крайней мере в \(3\) прошлых марафонах, т.е. \(r_{x,j}<r_{y,j}\) по крайней мере для \(3\) различных значений \(j\). Федерико считает, что у спортсмена хорошие шансы получить золотую медаль на Олимпийских играх, если он превосходит всех остальных спортсменов. Найдите любого спортсмена, у которого хорошие шансы получить золотую медаль (то есть спортсмена, который превосходит всех остальных спортсменов), или определите, что такого спортсмена нет. Входные данные Первая строка содержит одно целое число \(t\) (\(1 \le t \le 1000\)) — количество наборов входных данных. Затем следуют \(t\) наборов входных данных. Первая строка каждого набора входных данных содержит одно целое число \(n\) (\(1\le n\le 50\,000\)) — количество спортсменов. Затем следуют \(n\) строк, каждая из которых описывает места одного спортсмена. \(i\)-я из этих строк содержит \(5\) целых чисел \(r_{i,1},\,r_{i,2},\,r_{i,3},\,r_{i,4},\, r_{i,5}\) (\(1\le r_{i,j}\le 50\,000\)) — места спортсмена \(i\) в последних \(5\) марафонах. Гарантируется, что в каждом из \(5\) прошедших марафонов \(n\) спортсменов заняли различные места, т.е. для каждого \(1\le j\le 5\), \(n\) значений \(r_{1,j},\, r_{2, j},\, \dots,\, r_{n, j}\) попарно различны. Гарантируется, что сумма \(n\) по всем наборам входных данных не превышает \(50\,000\). Выходные данные Для каждого набора входных данных выведите одно целое число — номер спортсмена, у которого хорошие шансы получить золотую медаль (то есть спортсмена, который превосходит всех остальных спортсменов). Если таких спортсменов нет, выведите \(-1\). Если таких спортсменов больше, чем один, выведите любого из них. Примечание Объяснение первого набора входных данных: Есть только один спортсмен, поэтому он превосходит всех остальных (так как больше никого нет), и поэтому у него хорошие шансы получить золотую медаль. Пояснение второго набора входных данных: Есть \(n=3\) спортсменов. - Спортсмен \(1\) превосходит спортсмена \(2\). Действительно, спортсмен \(1\) лучше спортсмена \(2\) в марафонах \(1\), \(2\) и \(3\).
- Спортсмен \(2\) превосходит спортсмена \(3\). Действительно, спортсмен \(2\) превосходит спортсмена \(3\) в марафонах \(1\), \(2\), \(4\) и \(5\).
- Спортсмен \(3\) превосходит спортсмена \(1\). Действительно, спортсмен \(3\) лучше, чем спортсмен \(1\) в марафонах \(3\), \(4\) и \(5\).
Объяснение третьего набора входных данных: Есть \(n=3\) спортсменов. - Спортсмен \(1\) превосходит спортсменов \(2\) и \(3\). Поскольку он превосходит всех остальных спортсменов, у него хорошие шансы получить золотую медаль.
- Спортсмен \(2\) превосходит спортсмена \(3\).
- Спортсмен \(3\) не превосходит ни одного другого спортсмена.
Пояснение четвертого набора входных данных: Есть \(n=6\) спортсменов. - Спортсмен \(1\) превосходит спортсменов \(3\), \(4\), \(6\).
- Спортсмен \(2\) превосходит спортсменов \(1\), \(4\), \(6\).
- Спортсмен \(3\) превосходит спортсменов \(2\), \(4\), \(6\).
- Спортсмен \(4\) не превосходит ни одного другого спортсмена.
- Спортсмен \(5\) превосходит спортсменов \(1\), \(2\), \(3\), \(4\), \(6\). Поскольку он превосходит всех остальных спортсменов, у него хорошие шансы получить золотую медаль.
- Спортсмен \(6\) превосходит только спортсмена \(4\).
| |
![]()
|
|
C. Максимизируйте пересечения
Конструктив
Комбинаторика
геометрия
*1800
жадные алгоритмы
сортировки
На окружности лежат \(2n\) различных точек, обладающих следующим свойством: как бы вы ни выбрали \(3\) хорды, соединяющие \(3\) непересекающиеся пары точек, ни одна точка строго внутри окружности не принадлежит всем \(3\) хордам. Точки нумеруются \(1, \, 2, \, \dots, \, 2n\) по часовой стрелке. Изначально \(k\) хорд соединяют \(k\) пар точек таким образом, что все \(2k\) концов этих хорд различны. Необходимо провести еще \(n - k\) хорд, которые соединят оставшиеся \(2(n - k)\) точек (каждая точка должна быть концом ровно одной хорды). Пусть \(x\) — это общее количество пересечений всех \(n\) хорд. Вычислите максимальное значение, которого может достичь \(x\) при оптимальном выборе \(n - k\) хорд. Обратите внимание, что точное расположение точек \(2n\) не имеет значения, пока выполняется свойство, указанное в первом предложении. Выходные данные Для каждого набора входных данных выведите максимальное количество пересечений, которое можно получить, проведя \(n - k\) дополнительных хорд. Примечание В первом наборе входных данных, есть три способа нарисовать \(2\) дополнительных хорд, показанных ниже (черные хорды — первоначально нарисованные, а красные — новые): 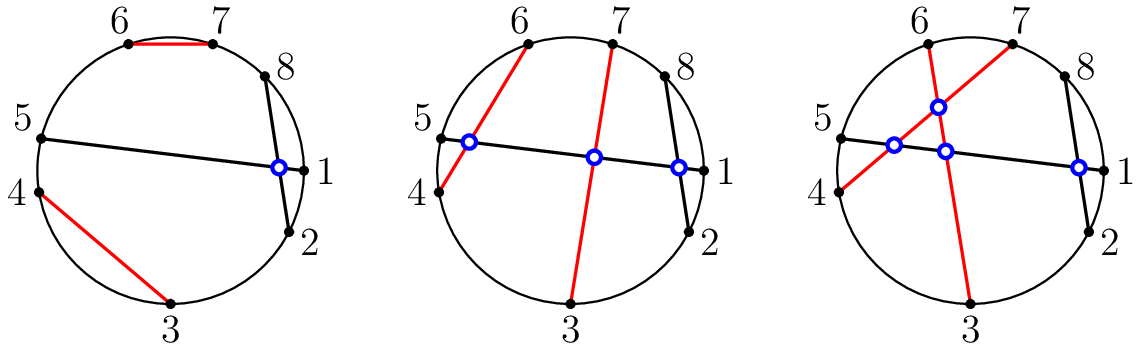 Мы видим, что третий способ дает максимальное количество пересечений, а именно \(4\). Во втором наборе входных данных, больше не нужно строить хорд. Конечно, при наличии только одной хорды пересечений нет. В третьем наборе входных данных, мы можем сделать не более одного пересечения, проведя хорды \(1-3\) и \(2-4\), как показано ниже: 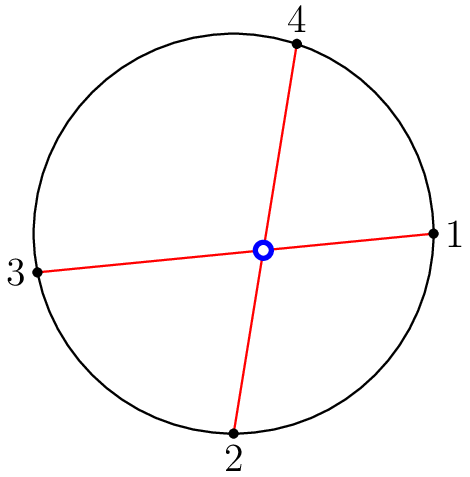 | |
![]()
|
|
E. Сдвиг перестановки
Перебор
Конструктив
Комбинаторика
математика
*2100
поиск в глубину и подобное
графы
снм
Тождественная перестановка длины \(n\) — это массив \([1, 2, 3, \dots, n]\). Мы применили следующие операции к тождественной перестановке длины \(n\): - Вначале мы циклически сдвинули ее вправо на \(k\) позиций, где \(k\) вам неизвестно (вы знаете только то, что \(0 \le k \le n - 1\)). При циклическом сдвиге массива вправо на \(k\) позиций необходимо взять \(k\) последних элементов исходного массива (не меняя их относительный порядок) и дописать \(n - k\) первых элементов исходного массива справа от них (также не меняя относительный порядок этих \(n - k\) элементов). Например, если бы мы циклически сдвинули тождественную перестановку длины \(6\) на \(2\) позиции вправо, мы бы получили массив \([5, 6, 1, 2, 3, 4]\);
- Далее мы выполнили следующую операцию не более \(m\) раз: выбрали два элемента массива и поменяли их местами.
Вам даны \(n\) и \(m\), а также полученный массив. Ваша задача — найти все возможные значения \(k\) в операции циклического сдвига. Выходные данные Для каждого набора входных данных выведите ответ следующим образом: - Вначале выведите одно целое число \(r\) (\(0 \le r \le n\)) — количество возможных значений \(k\) в операции циклического сдвига;
- Далее выведите \(r\) целых чисел \(k_1, k_2, \dots, k_r\) (\(0 \le k_i \le n - 1\)) — все возможные значения \(k\) в возрастающем порядке.
Примечание Рассмотрим примеры из условия. - В первом наборе входных данных единственное возможное значение для циклического сдвига это \(3\). Если мы сдвинем \([1, 2, 3, 4]\) на \(3\) позиции, мы получим \([2, 3, 4, 1]\). Далее мы можем поменять \(3\)-й и \(4\)-й элементы местами, чтобы получить массив \([2, 3, 1, 4]\);
- Во втором наборе единственное возможное значение для циклического сдвига это \(0\). Если мы сдвинем \([1, 2, 3]\) на \(0\) позиций, мы получим \([1, 2, 3]\). Далее мы не производим операций обмена (так как нам разрешено совершить не более \(1\)-го обмена), таким образом, полученный массив остается равным \([1, 2, 3]\);
- В третьем наборе все значения от \(0\) до \(2\) допустимы для циклического сдвига:
- если мы сдвинем \([1, 2, 3]\) на \(0\) позиций, мы получим \([1, 2, 3]\). Далее мы можем поменять \(1\)-й и \(3\)-й элементы, чтобы получить \([3, 2, 1]\);
- если мы сдвинем \([1, 2, 3]\) на \(1\) позицию, мы получим \([3, 1, 2]\). Далее мы можем поменять \(2\)-й и \(3\)-й элементы, чтобы получить \([3, 2, 1]\);
- если мы сдвинем \([1, 2, 3]\) на \(2\) позиции, мы получим \([2, 3, 1]\). Далее мы можем поменять \(1\)-й и \(2\)-й элементы, чтобы получить \([3, 2, 1]\);
- В четвертом наборе входных данных операции обмена запрещены, однако ни один циклический сдвиг не равен массиву \([1, 2, 3, 4, 6, 5]\).
| |
![]()
|
|
I. Лестницы
Комбинаторика
математика
дп
разделяй и властвуй
*3400
бпф
Для перестановки \(p\) чисел от \(1\) до \(n\) мы можем задать лестничный массив \(a\) следующим образом: \(a_i\) равняется длине наибольшего подотрезка перестановки, который содержит позицию \(i\) и состоит из последовательных чисел в отсортированном порядке: \([x, x+1, \ldots, y-1, y]\) или \([y, y-1, \ldots, x+1, x]\) для некоторых \(x \leq y\). Например, для перестановки \(p = [4, 1, 2, 3, 7, 6, 5]\) получается лестничный массив \(a = [1, 3, 3, 3, 3, 3, 3]\). Вам дан массив \(a\). Ваша задача — посчитать количество перестановок, лестничный массив которых равен \(a\). Так как это количество может быть достаточно большим, посчитайте его по модулю \(998\,244\,353\). Обратите внимание, что количество может быть равно нулю. Выходные данные Выведите количество перестановок, лестничный массив которых равен \(a\). Так как это число может быть довольно большим, выведите его по модулю \(998\,244\,353\). | |
![]()
|
|
F. Ставки на матчи
Теория вероятностей
Комбинаторика
математика
дп
графы
битмаски
*2500
 Василий увлекается не только трейдингом, но и ставками на спортивные матчи. В матче участвует \(n\) спортивных команд. Каждая команда характеризуется силой \(a_i\). Каждые две команды \(i < j\) играют друг с другом ровно один раз. С вероятностью \(\frac{a_i}{a_i + a_j}\) побеждает команда \(i\), с вероятностью \(\frac{a_j}{a_i + a_j}\) побеждает команда \(j\). Команда называется победителем, если она прямо или косвенно победила все остальные команды. Команда \(a\) победила (прямо или косвенно) команду \(b\), если существует последовательность команд \(c_1\), \(c_2\), ... \(c_k\) такая, что \(c_1 = a\), \(c_k = b\) и команда \(c_i\) выиграла матч у команды \(c_{i + 1}\) для всех \(i\) от \(1\) до \(k - 1\). Обратите внимание, что возможно, что команда \(a\) победила команду \(b\), и в то же время команда \(b\) победила команду \(a\). Василий хочет, чтобы вы помогли ему определить математическое ожидание количества победителей. Выходные данные Выведите единственное целое число — математическое ожидание количества победителей турнира по модулю \(10^9 + 7\). Формально, пусть \(M = 10^9+7\). Можно показать, что ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Примечание Чтобы лучше понять, в каких ситуациях возможно несколько победителей, рассмотрим второй тест: Одним из возможных результатов сыгранных матчей является следующий (\(a \rightarrow b\) означает, что \(a\) выиграла матч у \(b\)): - \(1 \rightarrow 2\)
- \(2 \rightarrow 3\)
- \(3 \rightarrow 1\)
- \(1 \rightarrow 4\)
- \(1 \rightarrow 5\)
- \(2 \rightarrow 4\)
- \(2 \rightarrow 5\)
- \(3 \rightarrow 4\)
- \(3 \rightarrow 5\)
- \(4 \rightarrow 5\)
Или более наглядно на рисунке: 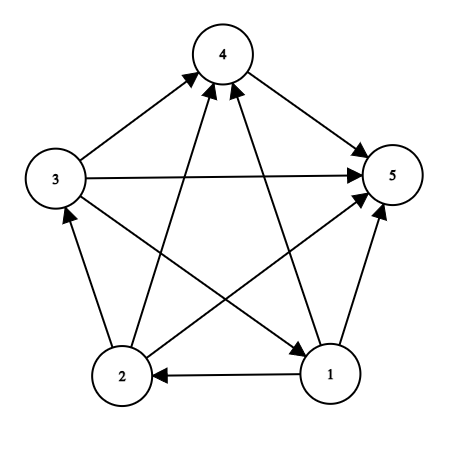 В данном варианте каждая команда из множества \(\{ 1, 2, 3 \}\) прямо или косвенно победила всех. То есть: - \(1\)-я победила всех, так как до остальных можно добраться следующим образом \(1 \rightarrow 2\), \(1 \rightarrow 2 \rightarrow 3\), \(1 \rightarrow 4\), \(1 \rightarrow 5\).
- \(2\)-я победила всех, так как до остальных можно добраться следующим образом \(2 \rightarrow 3\), \(2 \rightarrow 3 \rightarrow 1\), \(2 \rightarrow 4\), \(2 \rightarrow 5\).
- \(3\)-я победила всех, так как до остальных можно добраться следующим образом \(3 \rightarrow 1\), \(3 \rightarrow 1 \rightarrow 2\), \(3 \rightarrow 4\), \(3 \rightarrow 5\).
Следовательно, количество победителей равно \(3\). | |
![]()
|
|
C. Moamen и XOR
Комбинаторика
математика
дп
*1700
битмаски
матрицы
Moamen и Ezzat играют в игру. Они создают массив \(a\) длины \(n\), состоящий из неотрицательных целых чисел, где каждый элемент меньше \(2^k\). Moamen победит, если \(a_1 \,\&\, a_2 \,\&\, a_3 \,\&\, \ldots \,\&\, a_n \ge a_1 \oplus a_2 \oplus a_3 \oplus \ldots \oplus a_n\). Здесь \(\&\) обозначает операцию битового И, а \(\oplus\) обозначает операцию битового исключающего ИЛИ. Теперь Moamen хочет узнать, сколько существует таких массивов \(a\), где он побеждает? Так как ответ может быть очень большим, выведите его по модулю \(1\,000\,000\,007\) (\(10^9 + 7\)). Выходные данные Для каждого набора входных данных выведите одно целое число — количество различных массивов, в которых Moamen победит. Выведите результат по модулю \(1\,000\,000\,007\) (\(10^9 + 7\)). Примечание В первом примере \(n = 3\), \(k = 1\). В результате все возможные массивы — это \([0,0,0]\), \([0,0,1]\), \([0,1,0]\), \([1,0,0]\), \([1,1,0]\), \([0,1,1]\), \([1,0,1]\) и \([1,1,1]\). Moamen победит только в \(5\) из них: \([0,0,0]\), \([1,1,0]\), \([0,1,1]\), \([1,0,1]\), \([1,1,1]\). | |
![]()
|
|
D. Истинные вставки
Структуры данных
Комбинаторика
*2600
Рассмотрим алгоритм сортировки вставками целочисленной последовательности \([a_1, a_2, \ldots, a_n]\) длины \(n\) по неубыванию. Для каждого \(i\) в порядке от \(2\) до \(n\) делаем следующее. Если \(a_i \ge a_{i-1}\), ничего не делаем и переходим к следующему значению \(i\). В противном случае находим минимальный индекс \(j\) такой, что \(a_i < a_j\), и сдвигаем элементы на позициях с \(j\) по \(i-1\) на одну позицию вправо, а на позицию \(j\) записываем исходное значение \(a_i\). В таком случае мы будем говорить, что произошла вставка элемента с позиции \(i\) на позицию \(j\). Можно заметить, что после рассмотрения любого \(i\) префикс последовательности \([a_1, a_2, \ldots, a_i]\) отсортирован по неубыванию, следовательно, алгоритм действительно отсортирует любую последовательность. Например, сортировка последовательности \([4, 5, 3, 1, 3]\) происходит так: - \(i = 2\): \(a_2 \ge a_1\), ничего не делаем;
- \(i = 3\): \(j = 1\), вставка с позиции \(3\) на позицию \(1\): \([3, 4, 5, 1, 3]\);
- \(i = 4\): \(j = 1\), вставка с позиции \(4\) на позицию \(1\): \([1, 3, 4, 5, 3]\);
- \(i = 5\): \(j = 3\), вставка с позиции \(5\) на позицию \(3\): \([1, 3, 3, 4, 5]\).
Вам дано число \(n\) и список из \(m\) целочисленных пар \((x_i, y_i)\). Нас интересуют последовательности, при сортировке которых произойдёт ровно \(m\) вставок: сначала элемента с позиции \(x_1\) на позицию \(y_1\), потом элемента с позиции \(x_2\) на позицию \(y_2\), ..., наконец, элемента с позиции \(x_m\) на позицию \(y_m\). Сколько последовательностей длины \(n\) из (необязательно различных) целых чисел от \(1\) до \(n\) удовлетворяют этому условию? Выведите это число по модулю \(998\,244\,353\). Выходные данные Для каждого набора входных данных выведите число последовательностей длины \(n\) из целых чисел от \(1\) до \(n\), при сортировке которых алгоритмом из условия будет совершена заданная последовательность вставок, по модулю \(998\,244\,353\). Примечание В первом наборе входных данных алгоритм не совершил ни одной вставки — значит, исходная последовательность уже отсортирована по неубыванию. Есть \(10\) таких последовательностей: \([1, 1, 1], [1, 1, 2], [1, 1, 3], [1, 2, 2], [1, 2, 3], [1, 3, 3], [2, 2, 2], [2, 2, 3], [2, 3, 3], [3, 3, 3]\). Во втором наборе входных данных подходит только последовательность \([3, 2, 1]\). В третьем наборе входных данных \([4, 5, 3, 1, 3]\) является одной из подходящих последовательностей. | |
![]()
|
|
E. Mocha и звезды
Комбинаторика
математика
дп
теория чисел
*2200
бпф
Mocha хочет быть астрологом. В небе над Чжицзяном \(n\) звезд, яркость \(i\)-й звезды равна \(a_i\). Mocha считает, что \(n\) звезд образуют созвездие, и описывает его состояние массивом \((a_1,a_2,\ldots,a_n)\). Состояние называется математическим, если все три следующих условия выполнены: - Для всех \(i\) (\(1\le i\le n\)), \(a_i\) — целое число из отрезка \([l_i, r_i]\).
- \(\sum \limits _{i=1} ^ n a_i \le m\).
- \(\gcd(a_1,a_2,\ldots,a_n)=1\).
Здесь, \(\gcd(a_1,a_2,\ldots,a_n)\) обозначает наибольший общий делитель (НОД) чисел \(a_1,a_2,\ldots,a_n\). Mocha интересуется, сколько существует математических состояний этого созвездия. Так как ответ может быть большим, вы должны найти его по модулю \(998\,244\,353\). Два состояния \((a_1,a_2,\ldots,a_n)\) и \((b_1,b_2,\ldots,b_n)\) считаются различными, если существует индекс \(i\) (\(1\le i\le n\)) такой, что \(a_i \ne b_i\). Выходные данные Выведите одно целое число — количество различных математических состояний созвездия по модулю \(998\,244\,353\). Примечание В первом примере есть \(4\) различных математических состояния: - \(a_1=1\), \(a_2=1\).
- \(a_1=1\), \(a_2=2\).
- \(a_1=2\), \(a_2=1\).
- \(a_1=3\), \(a_2=1\).
| |
![]()
|
|
C. Шифр
Комбинаторика
дп
*2000
Шерлок Холмс обнаружил тайную переписку двух неких очень важных личностей и твердо вознамерился ее прочитать. Но не тут-то было! Оказалось, что переписка зашифрована. Он долго бился над этим шифром, но ничего не мог понять. Наконец, после некоторых раздумий, он осознал следующий факт. Пусть имеется слово s, состоящее из |s| строчных букв латинского алфавита. Тогда одной операцией можно выбрать некоторую позицию p (1 ≤ p < |s|) и сделать одно из двух: - либо букву sp заменить на следующую за ней в алфавитном порядке, и букву sp + 1 заменить на предшествующую ей в алфавитном порядке;
- либо букву sp заменить на предшествующую ей в алфавитном порядке, и букву sp + 1 заменить на следующую за ней в алфавитном порядке.
Заметим, что для буквы «z» не определена следующая буква, а для буквы «a» не определена предыдущая буква. Поэтому соответствующие замены не допустимы. Если операция требует выполнения хотя бы одной недопустимой замены, то такую операцию нельзя выполнить. Два слова совпадают по смыслу тогда и только тогда, когда одно можно получить из другого посредством выполнения нуля или более операций. Шерлоку Холмсу требуется научиться быстро определять, сколько всего может существовать слов, совпадающих по смыслу с данным словом, но отличающихся от него хотя бы одним символом. Посчитайте для него это количество по модулю 1000000007 (109 + 7). Выходные данные Для каждого слова надо вывести количество различных других слов, которые совпадают с ним по смыслу — не среди слов, указанных во входных данных, а среди всех возможных слов. Поскольку искомое количество может быть очень большим, выведите его значение по модулю 1000000007 (109 + 7). Примечание Некоторые пояснения касательно операции: - Обратите внимание, что для каждой буквы следующая за ней определена однозначно. Буква «b» является следующей в алфавитном порядке за буквой «a», буква «c» является следующей за «b», ..., «z» является следующей за буквой «y».
- Аналогичным образом определены и предшествующие буквы: буква «y» является предшествующей букве «z», ..., «a» является предшествующей букве «b».
- Заметьте, что операция никогда не меняет длину слова.
В первом примере можно получить единственную другую строку — «ba». Во втором примере нельзя получить такими действиями ни одной другой подстроки, поэтому правильный ответ — 0. Рассмотрим подробнее третий пример. Из слова «klmbfxzb» за одну операцию можно получить слово «klmcexzb»: нужно выбрать p = 4, и заменить четвертую букву на следующую («b» → «c»), а пятую — на предшествующую («f» → «e»). Также из этого слова можно получить много других слов за одну операцию. Из слова «ya» за одну операцию можно получить только одно другое слово — «xb». Слово «ya» совпадает по смыслу со словами «xb», «wc», «vd», ..., «ay» (всего 24 других слова). Для слова «klmbfxzb» вариантов гораздо больше — существует 3320092814 других слов, совпадающих с ним по смыслу. Ответ для первого слова 24, для второго 320092793 — это 3320092814 по модулю 109 + 7 | |
![]()
|
|
D. Улики
Комбинаторика
графы
*2500
Расследуя очередное дело, Шерлок Холмс нашел некоторое количество улик. Также он нашел прямые связи между некоторыми из этих улик. Прямые связи между уликами не направлены. То есть, прямая связь между уликами A и B и прямая связь между уликами B и A — это одно и тоже. Кроме того, между двумя уликами может существовать не более одной прямой связи. Конечно, Шерлок может найти прямые связи между всеми уликами. Но это займет слишком много времени — преступники могут успеть залечь на дно. Чтобы раскрыть дело, ему надо добиться того, чтобы каждая улика была связана со всеми остальными (возможно, не напрямую). Улики A и B считаются связанными, если есть прямая связь между ними или есть прямая связь между уликой A и некой уликой C, которая связана с B. Шерлок Холмс посчитал минимальное количество прямых связей между уликами, которые ему еще надо найти, чтобы раскрыть дело. Оно оказалось равно ровно T. Посчитайте, пожалуйста, количество различных способов найти ровно T прямых связей между уликами так, чтобы дело оказалось раскрытым. Два способа считаются различными, если существует хотя бы одна такая пара улик, что в одном способе между ними найдена прямая связь, а в другом — нет. Поскольку количество способов может оказаться очень большим, выведите его по модулю k. Выходные данные Выведите единственное целое число — ответ на задачу по модулю k. Примечание В первом примере есть всего две улики, и Шерлок пока не нашел между ними прямой связи. Есть единственный способ раскрыть дело — найти эту связь. Во втором примере есть три улики, И Шерлок пока не нашел никаких прямых связей между ними. Ему нужно найти две из трех возможных прямых связей между уликами, чтобы раскрыть дело — есть 3 способа это сделать. В третьем примере четыре улики, и уже найдена одна прямая связь, между первой и четвертой уликами. Есть 8 способов найти еще две прямых связи так, чтобы дело было раскрыто. | |
![]()
|
|
C. Проблемные переносы
Комбинаторика
математика
*1600
дп
битмаски
Алиса только недавно изучила сложение. Однако она еще не полностью освоила концепт «переноса»: вместо того, чтобы переносить цифру в следующий разряд, она переносит ее через один разряд. Например, обычный способ подсчета суммы \(2039 + 2976\) показан ниже: 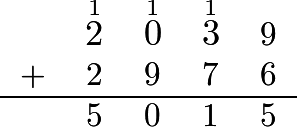 Однако Алиса подсчитывает сумму следующим образом: 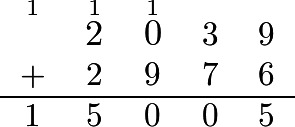 А именно, она делает следующее: - складывает \(9\) и \(6\), получая \(15\), и переносит \(1\) на два разряда левее, т. е. в столбец «\(0\) \(9\)»;
- складывает \(3\) и \(7\), получая \(10\), и переносит \(1\) на два разряда левее, т. е. в столбец «\(2\) \(2\)»;
- складывает \(1\), \(0\), и \(9\), получая \(10\), и переносит \(1\) на два разряда левее, т. е. в столбец над знаком плюс;
- складывает \(1\), \(2\) и \(2\), получая \(5\);
- складывает \(1\), получая \(1\).
Таким образом, она получает неправильный результат \(15005\). Алиса пришла к Бобу и рассказала, что она сложила два целых числа и получила в результате \(n\). Но Боб знает, что Алиса сложила числа как умеет. Помогите Бобу посчитать количество упорядоченных пар положительных целых чисел таких, что при сложении методом Алисы получается число \(n\). Обратите внимание, что пары \((a, b)\) и \((b, a)\) считаются различными при \(a \ne b\). Выходные данные Для каждого набора входных данных выведите одно целое число — количество упорядоченных пар положительных целых чисел, таких что при сложении своим методом Алиса получит в результате \(n\). Примечание В первом наборе входных данных при сложении Алисой любой из следующих пар: \(1 + 9\), \(2 + 8\), \(3 + 7\), \(4 + 6\), \(5 + 5\), \(6 + 4\), \(7 + 3\), \(8 + 2\) или \(9 + 1\), она получит \(100\) в результате. Изображение, показывающее как Алиса сложит \(6 + 4\), показано ниже:  | |
![]()
|
|
C. Заседание жюри
Комбинаторика
математика
*1500
\(n\) человек собрались, чтобы провести заседание жюри предстоящего соревнования, \(i\)-й член жюри придумал \(a_i\) задач, которыми он хочет поделиться с другими. Сначала жюри выбирает порядок, которому они будут следовать при обсуждении задач. Пусть это будет перестановка \(p\) чисел от \(1\) до \(n\) (массив размера \(n\), в котором каждое число от \(1\) до \(n\) встречается ровно один раз). Затем обсуждение происходит следующим образом: - если у члена жюри \(p_1\) остались задачи, которые нужно рассказать, то он рассказывает одну задачу. В противном случае он будет пропущен.
- если у члена жюри \(p_2\) остались задачи, которые нужно рассказать, то он рассказывает одну задачу. В противном случае он будет пропущен.
- ...
- если у члена жюри \(p_n\) остались задачи, которые нужно рассказать, то он рассказывает одну задачу. В противном случае он будет пропущен.
- если остались члены жюри, которые еще не рассказали все свои задачи, то процесс повторяется с самого начала. В противном случае обсуждение заканчивается.
Перестановка \(p\) хорошая, если никто из членов жюри не будет рассказывать две или более задач подряд. Подсчитайте количество хороших перестановок. Ответ может быть очень большим, поэтому выведите его по модулю \(998\,244\,353\). Выходные данные Для каждого набора входных данных выведите одно целое число — количество хороших перестановок, взятое по модулю \(998\,244\,353\). Примечание Объяснение первого примера: Существуют две возможные перестановки, \(p = [1, 2]\) и \(p = [2, 1]\). Для \(p = [1, 2]\) процесс происходит следующим образом: - первый член жюри рассказывает задачу;
- второй член жюри рассказывает задачу;
- у первого члена жюри не осталось задач, которые нужно было бы рассказать, поэтому он будет пропущен;
- второй член жюри рассказывает задачу.
Второй член жюри рассказал две задачи подряд, поэтому перестановка не является хорошей. Для \(p = [2, 1]\) процесс происходит следующим образом: - второй член жюри рассказывает задачу;
- первый член жюри рассказывает задачу;
- второй член жюри рассказывает задачу.
Эта перестановка является хорошей. | |
![]()
|
|
B. Домашнее задание
Комбинаторика
математика
*1100
жадные алгоритмы
Заданы четыре целых числа \(a\), \(b\), \(c\) и \(m\). Проверьте, существует ли строка, в которой: - \(a\) букв 'A';
- \(b\) букв 'B';
- \(c\) букв 'C';
- нет других букв;
- ровно \(m\) пар одинаковых соседних букв (ровно \(m\) таких позиций \(i\), что \(i\)-я буква совпадает с \((i+1)\)-й).
Выходные данные На каждый набор входных данных выведите «YES», если существует строка, которая удовлетворяет всем требованиям. Выведите «NO», если таких строк нет. Вы можете выводить ответ в любом регистре (например, строки yEs, yes, Yes и YES будут распознаны как положительный ответ). Примечание В первом наборе входных данных строки «ABCAB» или «BCABA» удовлетворяют требованиям. Существуют и другие подходящие строки. Во втором наборе нет способа получить пару соседних одинаковых букв, потому что никакая буква не встречается больше одного раза. В третьем наборе входных данных строка «CABBCC» удовлетворяет требованиям. Существуют и другие подходящие строки. | |
![]()
|
|
E. Раскраска
Конструктив
Комбинаторика
математика
реализация
*2500
Матрица размера \(n \times m\), состоящая только из цифр \(0\) или \(1\) считается красивой, если сумма в каждой подматрице размера \(2 \times 2\) ровно \(2\), т. е. каждый «квадрат» размера \(2 \times 2\) содержит ровно две цифры \(1\) и две цифры \(0\). Вам задана матрица размера \(n \times m\). Изначально все ячейки матрицы пусты. Обозначим ячейку стоящую на пересечении \(x\)-й строки \(y\)-го столбца как \((x, y)\). Вам нужно обрабатывать запросы трех типов: - \(x\) \(y\) \(-1\) — сделать ячейку \((x, y)\) пустой;
- \(x\) \(y\) \(0\) — записать цифру \(0\) в ячейку \((x, y)\), это перезапишет то, что там было;
- \(x\) \(y\) \(1\) — записать цифру \(1\) в ячейку \((x, y)\), это перезапишет то, что там было.
После каждого запроса выведите количество способов заполнить пустые ячейки матрицы так, чтобы матрица была красивой. Так как это значение может быть слишком велико, выведите его по модулю \(998244353\). Выходные данные После каждого запроса выведите число — количество способов заполнить пустые ячейки матрицы так, чтобы матрица была красивой по модулю \(998244353\). | |
![]()
|
|
F. Вхождения
Комбинаторика
дп
поиск в глубину и подобное
графы
*2700
снм
бпф
Подмассив массива \(a\) с индекса \(l\) по индекс \(r\) — это массив \([a_l, a_{l+1}, \dots, a_{r}]\). Количество вхождений массива \(b\) в массива \(a\) — это количество таких подмассивов массива \(a\), которые равны \(b\). Вам даны \(n\) массивов \(A_1, A_2, \dots, A_n\); их элементы — целые числа от \(1\) до \(k\). Вы должны построить массив \(a\) из \(m\) целых чисел от \(1\) до \(k\) таким образом, чтобы для каждого заданного массива \(A_i\) выполнялось следующее условие: количество вхождений массива \(A_i\) в массив \(a\) не меньше, чем количество вхождений каждого непустого подмассива \(A_i\) в \(a\) (по отдельности). Обратите внимание, что если \(A_i\) не входит в \(a\), и никакой подмассив \(A_i\) не входит в \(a\), это условие выполняется для \(A_i\). Ваша задача — посчитать количество различных массивов \(a\), удовлетворяющих этим условиям, и вывести его по модулю \(998244353\). Выходные данные Выведите одно целое число — количество различных массивов \(a\), удовлетворяющих данным условиям, по модулю \(998244353\). | |
![]()
|
|
B. Курс математики
Деревья
Перебор
Комбинаторика
дп
*2600
Пусть \(c_1, c_2, \ldots, c_n\) — перестановка чисел \(1, 2, \ldots, n\). Рассмотрим все подотрезки этой перестановки, содержащие число \(x\). Для фиксированного числа \(m\) скажем, что \(x\) хорошее, если среди максимумов на данных отрезках встречается ровно \(m\) различных значений. Cirno изучает математику, и учитель просит ее найти количество перестановок длины \(n\) с ровно \(k\) хорошими числами. К сожалению, Cirno не сильна в математике и не может ответить на этот вопрос. Поэтому она просит вас о помощи. Поскольку ответ может быть очень большим, вам нужно только сообщить ей количество перестановок по модулю \(p\). Перестановкой является массив, состоящий из \(n\) различных целых чисел от \(1\) до \(n\) в произвольном порядке. Например, \([2,3,1,5,4]\) — перестановка, но \([1,2,2]\) не перестановка (\(2\) встречается в массиве дважды) и \([1,3,4]\) тоже не перестановка (\(n=3\), но в массиве встречается \(4\)). Последовательность \(a\) является подотрезком \(b\), если \(a\) может быть получена из \(b\) удалением нескольких (возможно, ни одного или всех) элементов из начала и нескольких (возможно, ни одного или всех) элементов из конца. Выходные данные Выведите количество перестановок по модулю \(p\). Примечание В первом тестовом случае четырьмя перестановками являются \([1, 3, 2, 4]\), \([2, 3, 1, 4]\), \([4, 1, 3, 2]\) и \([4, 2, 3, 1]\). Возьмем перестановку \([1, 3, 2, 4]\) в качестве примера: Для числа \(1\) все подотрезки, содержащие его, являются: \([1]\), \([1, 3]\), \([1, 3, 2]\) и \([1, 3, 2, 4]\), и есть три разных максимума \(1\), \(3\) и \(4\). Аналогично, для числа \(3\) существуют два разных максимума \(3\) и \(4\). Для числа \(2\) существует три разных максимума \(2\), \(3\) и \(4\). А для числа \(4\) есть только один, то есть сам по себе \(4\). | |
![]()
|
|
F. Задачи для Codeforces
Комбинаторика
математика
бпф
*3300
XYMXYM и CQXYM готовят \(n\) задач для Codeforces. Сложность задачи \(i\) будет равна целому числу \(a_i\), где \(a_i \geq 0\). Сложности задач должны удовлетворять условиям: \(a_i+a_{i+1}<m\) (\(1 \leq i < n\)), а также \(a_1+a_n<m\), где \(m\) — фиксированное целое число. XYMXYM хочет узнать, сколько существует возможных последовательностей сложности задач по модулю \(998\,244\,353\). Два варианта распределения сложностей \(a\) и \(b\) различны, если существует такое \(i\) (\(1 \leq i \leq n\)), что \(a_i \neq b_i\). Выходные данные Выведите одно целое число — ответ на задачу. Примечание В первом примере допустимые распределения сложностей \(a\): \([0,0,0]\), \([0,0,1]\), \([0,1,0]\), \([1,0,0]\). \([1,0,1]\) некорректно, так как \(a_1+a_n \geq m\). | |
![]()
|
|
A. CQXYM считает перестановки
Комбинаторика
математика
теория чисел
*800
CQXYM считает перестановки длины \(2n\). Перестановкой является массив, состоящий из \(n\) различных целых чисел от \(1\) до \(n\) в произвольном порядке. Например, \([2,3,1,5,4]\) — перестановка, но \([1,2,2]\) не перестановка (\(2\) встречается в массиве дважды) и \([1,3,4]\) тоже не перестановка (\(n=3\), но в массиве встречается \(4\)). Перестановка \(p\)(длины \(2n\)) будет посчитана только в том случае, если количество \(i\), удовлетворяющих \(p_i<p_{i+1}\), не меньше \(n\). Например: - Перестановка \([1, 2, 3, 4]\) будет посчитана, так как количество таких \(i\) что \(p_i<p_{i+1}\) равно \(3\) (\(i = 1\), \(i = 2\), \(i = 3\)).
- Перестановка \([3, 2, 1, 4]\) не будет посчитана, так как количество таких \(i\) что \(p_i<p_{i+1}\) равно \(1\) (\(i = 3\)).
CQXYM хочет, чтобы вы помогли ему найти количество таких перестановок по модулю \(1000000007\)(\(10^9+7\)). Операцией по модулю называется взятие остатка от деления. Например: - \(7 \mod 3=1\), так как \(7 = 3 \cdot 2 + 1\),
- \(15 \mod 4=3\), так как \(15 = 4 \cdot 3 + 3\).
Выходные данные Для каждого примера выведите ответ в отдельной строке. Примечание \(n=1\), существует только одна перестановка, удовлетворяющая условию: \([1,2].\) В перестановке \([1,2]\), \(p_1<p_2\), только \(i=1\) подходит под условие. Так как \(1 \geq n\), Эта перестановка будет посчитана. В перестановке \([2,1]\), \(p_1>p_2\). Так как \(0<n\), эта перестановка не будет посчитана. \(n=2\), существует \(12\) перестановок: \([1,2,3,4],[1,2,4,3],[1,3,2,4],[1,3,4,2],[1,4,2,3],[2,1,3,4],[2,3,1,4],[2,3,4,1],[2,4,1,3],[3,1,2,4],[3,4,1,2],[4,1,2,3].\) | |
![]()
|
|
B. Лунтик и подпоследовательности
Комбинаторика
математика
*900
Лунтик вышел на утреннюю прогулку и нашел массив \(a\) длины \(n\). Он посчитал сумму \(s\) элементов массива (\(s= \sum_{i=1}^{n} a_i\)). Лунтик называет подпоследовательность массива \(a\) почти полной, если сумма чисел в этой подпоследовательности равна \(s-1\). Лунтик очень хочет узнать количество почти полных подпоследовательностей массива \(a\). Но ему надо возвращаться домой, поэтому он просит вас решить эту задачу! Напоминаем, что последовательность \(x\) является подпоследовательностью \(y\), если \(x\) может быть получена из \(y\) удалением нескольких (возможно, ни одного или всех) элементов. Выходные данные Для каждого набора входных данных выведите количество почти полных подпоследовательностей массива. Примечание В первом наборе входных данных \(s=1+2+3+4+5=15\), из всех подпоследовательностей почти полной будет только \((2,3,4,5)\), сумма в ней равна \(2+3+4+5=14=15-1\). Во втором наборе входных данных нет почти полных подпоследовательностей. В третьем наборе входных данных \(s=1+0=1\), почти полными будут подпоследовательности \((0)\) и \(()\) (пустая подпоследовательность имеет сумму \(0\)). | |
![]()
|
|
D. Угадай перестановку
Бинарный поиск
Комбинаторика
математика
*2000
интерактив
Это интерактивная задача. У жюри была тождественная перестановка \(a\) длины \(n\) (\(a_i = i\)). Жюри выбрало три целых числа \(i\), \(j\), \(k\) такие, что \(1 \leq i < j < k \leq n\), \(j - i > 1\). После этого жюри развернуло отрезки \([i, j - 1]\) и \([j, k]\) в последовательности \(a\). Разворачивание подотрезка \([l, r]\) последовательности \(a\) означает переворот подотрезка элементов \(a_l, a_{l+1}, \ldots, a_r\) в последовательности, то есть \(a_l\) меняется местами с \(a_r\), \(a_{l+1}\) с \(a_{r-1}\), и т. д.. Вам дано число \(n\). Вы должны найти \(i\), \(j\), \(k\) с помощью некоторых запросов. За один запрос вы можете выбрать два целых числа \(l\) и \(r\) (\(1 \leq l \leq r \leq n\)) и узнать количество инверсий на подотрезке \([l, r]\) последовательности \(a\). Жюри скажет вам количество пар \((i, j)\) таких, что \(l \leq i < j \leq r\) и \(a_i > a_j\). Найдите числа \(i\), \(j\), \(k\), выбранные жюри, сделав не более \(40\) запросов. Жюри фиксирует числа \(i\), \(j\) и \(k\) до запуска вашей программы и не меняет их в зависимости от ваших запросов. Протокол взаимодействия Чтобы спросить количество инверсий на отрезке \([l, r]\), выведите «? l r», где (\(1 \leq l \leq r \leq n\)). Вы можете сделать не более \(40\) таких запросов в каждом тестовом случае. В ответ вы получите целое число \(x\). - Если \(x = -1\), ваша программа сделала некорректный запрос или превысила допустимое количество запросов для данного набора. В таком случае ваша программа должна немедленно завершиться (иначе решение может получить произвольный вердикт вместо Неправильный ответ).
- Иначе \(x\) равен количеству инверсий на подотрезке \([l, r]\) последовательности \(a\).
Чтобы дать ответ, выведите «! i j k», где \(i\), \(j\), \(k\) — числа, которые, как вы считаете, загадало жюри. После этого вы должны перейти к следующему набору или завершить программу. После вывода запроса или ответа не забудьте вывести перевод строки и сбросить буфер выходного потока. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Взломы Чтобы сделать взлом, используйте следующий формат: Первая строка содержит единственное целое число \(t\) (\(1 \leq t \leq 100\)) — количество наборов входных данных. Каждая из следующих \(t\) строк содержит четыре целых числа \(n\), \(i\), \(j\), \(k\) (\(4 \leq n \leq 10^9\), \(1 \leq i < j < k \leq n\), \(j - i > 1\)). Примечание В первом наборе входных данных \(i = 1\), \(j = 3\), \(k = 5\), поэтому последовательность \(a\) равна \([2, 1, 5, 4, 3]\). Во втором наборе входных данных \(i = 2\), \(j = 4\), \(k = 5\), поэтому последовательность \(a\) равна \([1, 3, 2, 5, 4]\). | |
![]()
|
|
F. Неравные соседи
Комбинаторика
математика
дп
*2400
Вам дан массив \(a_1, a_2, \ldots, a_n\) длины \(n\), состоящий из положительных целых чисел. Ваша задача — посчитать количество массивов целых чисел \(b_1, b_2, \ldots, b_n\) длины \(n\) таких, что: - \(1 \le b_i \le a_i\) для всех \(i\) (\(1 \le i \le n\)), и
- \(b_i \neq b_{i+1}\) для всех \(i\) (\(1 \le i \le n - 1\)).
Количество таких массивов может быть очень большим, поэтому выведите это число по модулю \(998\,244\,353\). Выходные данные В единственной строке выведите ответ по модулю \(998\,244\,353\). Примечание В первом примере подходят массивы \([1, 2, 1]\) и \([2, 1, 2]\). Во втором примере допустимы массивы \([1, 2]\), \([1, 3]\), \([2, 1]\) и \([2, 3]\). | |
![]()
|
|
I. Омкар и мозаика
Конструктив
Комбинаторика
математика
*3500
Омкар создает мозаику, используя цветные квадратные плитки, которые он размещает в сетке \(n \times n\). Когда мозаика будет завершена, в каждой ячейке сетки будет либо глазурная, либо синоперная плитка. Однако в настоящее время он разместил плитки только в некоторых ячейках. Завершенная мозаика будет шедевром тогда и только тогда, когда каждая плитка примыкает ровно к \(2\) плиткам того же цвета (\(2\) плитки являются примыкающими, если у них есть общая сторона.) Омкар хочет заполнить оставшиеся плитки так, чтобы мозаика стала шедевром. Теперь ему интересно, правда ли, что есть ровно один способ это сделать, и если да, то какой? Выходные данные В первой строке выведите UNIQUE, если существует уникальный способ получить шедевр, NONE, если Омкар не может его создать, и MULTIPLE, если существует более одного способа. Все буквы должны быть заглавными. Если вы выведете UNIQUE, то после этого выведите \(n\) дополнительных строк с \(n\) символами в каждой строке, такими, что \(i\)-й символ в \(j^{\text{th}}\) строке будет \(S\), если плитка в строке \(i\) и столбце \(j\) шедевра — синоперная, и \(G\), если она глазурная. Примечание Для первого примера Омкар может получить шедевры SSSS SGGS SGGS SSSS и SSGG SSGG GGSS GGSS. Для второго примера можно доказать, что Омкар не может сложить плитки, чтобы создать шедевр. Для третьего примера можно доказать, что данный шедевр — единственный шедевр, который Омкар может создать, сложив плитки. Для четвертого примера очевидно, что единственная плитка в любой мозаике, которую создает Омкар, не может быть соседней с двумя плитками одного цвета, так как она будет соседней с \(0\) плитками. | |
![]()
|
|
E1. Раскраска кубика Рубика (простая версия)
Комбинаторика
математика
*1300
Это простая версия задачи. Различие состоит в том, что в этой версии нет вершин с уже зафиксированными цветами. Теофанис ужасно проголодался и хочет, наконец, отведать своего любимого блюда, шефталью. Но сначала ему нужно закончить с домашней работой. Поможете ли вы ему в решении данной задачи? Вам задано идеальное двоичное дерево из \(2^k - 1\) вершин — двоичное дерево, в котором у всех вершин \(i\) от \(1\) по \(2^{k - 1} - 1\) есть ровно два сына: вершины \(2i\) и \(2i + 1\). У вершин с \(2^{k - 1}\) по \(2^k - 1\) нет детей. Вы хотите покрасить его вершины в \(6\) цветов кубика Рубика (белый, зеленый, красный, синий, оранжевый и желтый). Назовем раскраску хорошей, если все ребра дерева соединяют вершины, цвета которых являются соседними цветами кубика Рубика. Изображение кубика Рубика и его развертка. Формально говоря: - соседними к белой вершине не могут быть белые и желтые вершины;
- соседними к желтой вершине не могут быть белые и желтые вершины;
- соседними к зеленой вершине не могут быть зеленые и синие вершины;
- соседними к синей вершине не могут быть зеленые и синие вершины;
- соседними к красной вершине не могут быть красные и оранжевые вершины;
- соседними к оранжевой вершине не могут быть красные и оранжевые вершины.
Вам нужно посчитать количество хороших раскрасок двоичного дерева. Две раскраски считаются различными, если существует вершина, цвет которой в них различается. Так как ответ может быть слишком большим, выведите его по модулю \(10^9+7\). Выходные данные Выведите одно целое число — количество различных раскрасок по модулю \(10^9+7\). Примечание На изображении ниже вы можете видеть одну из корректных раскрасок для первого примера.  | |
![]()
|
|
D. Тренировка
Структуры данных
Комбинаторика
математика
реализация
геометрия
*1700
Монокарп тренер команд Берляндского ГУ по программированию. Он решил собрать тренировку для своих команд перед квалификационным этапом. У Монокарпа есть \(n\) задач, которые еще не решал ни один из его студентов. У \(i\)-й задачи есть тема \(a_i\) (целое число от \(1\) до \(n\)) и сложность \(b_i\) (целое число от \(1\) до \(n\)), причем все задачи попарно различны, то есть нет двух задач, у которых одинаковы и тема, и сложность. Монокарп решил выбрать из \(n\) задач ровно \(3\) задачи для тренировки, при этом должно выполняться хотя бы одно из двух условий (возможно, оба): - темы всех трех выбранных задач различны;
- сложности всех трех выбранных задач различны.
Перед вами стоит задача определить количество способов, которыми Монокарп может выбрать три задачи для тренировки. Выходные данные Выведите количество способов выбрать три задачи для тренировки, которые удовлетворяют описанным в условии требованиям. Примечание В первом примере можно взять следующие наборы по три задачи: - задачи с номерами \(1\), \(2\), \(4\);
- задачи с номерами \(1\), \(3\), \(4\);
- задачи с номерами \(2\), \(3\), \(4\).
Таким образом, количество способов равно трем. | |
![]()
|
|
E. Лестницы
Перебор
Структуры данных
Комбинаторика
математика
реализация
*2100
дп
поиск в глубину и подобное
Дана матрица, состоящая из \(n\) строк и \(m\) столбцов. Строки пронумерованы сверху вниз, столбцы пронумерованы слева направо. Ячейки данной матрицы могут быть свободными или заблокированными. Назовем путь в матрице лестницей, если он: - начинается и заканчивается в свободной ячейке;
- посещает только свободные ячейки;
- имеет одну из двух возможных структур:
- вторая ячейка лежит на \(1\) справа от первой, третья — на \(1\) снизу от второй, четвертая — на \(1\) справа от третьей, и так далее;
- вторая ячейка лежит на \(1\) снизу от первой, третья — на \(1\) справа от второй, четвертая — на \(1\) снизу от третьей, и так далее.
В частности, путь, состоящий из одной ячейки, считается лестницей. Некоторые примеры лестниц:  Изначально все ячейки в матрице свободные. Требуется обработать \(q\) запросов, каждый из которых переключает состояние одной ячейки. То есть, если клетка в данный момент свободна, то делает ее заблокированной, а если заблокирована, то делает ее свободной. После каждого запроса требуется вывести количество различных лестниц. Две лестницы считаются различными, если существует такая ячейка, которая входит в один путь и не входит в другой. Выходные данные Выведите \(q\) целых чисел — \(i\)-е число должно быть равно количеству различных лестниц в матрице после \(i\) запросов. Две лестницы считаются различными, если существует такая ячейка, которая входит в один путь и не входит в другой. | |
![]()
|
|
C. Bubble Strike
Тернарный поиск
Теория вероятностей
Комбинаторика
математика
*2000
Little Johnny Bubbles enjoys spending hours in front of his computer playing video games. His favorite game is Bubble Strike, fast-paced bubble shooting online game for two players. Each game is set in one of the N maps, each having different terrain configuration. First phase of each game decides on which map the game will be played. The game system randomly selects three maps and shows them to the players. Each player must pick one of those three maps to be discarded. The game system then randomly selects one of the maps that were not picked by any of the players and starts the game. Johnny is deeply enthusiastic about the game and wants to spend some time studying maps, thus increasing chances to win games played on those maps. However, he also needs to do his homework, so he does not have time to study all the maps. That is why he asked himself the following question: "What is the minimum number of maps I have to study, so that the probability to play one of those maps is at least \(P\)"? Can you help Johnny find the answer for this question? You can assume Johnny's opponents do not know him, and they will randomly pick maps. Output Output contains one integer number – minimum number of maps Johnny has to study. | |
![]()
|
|
E. Идеальная задача
Комбинаторика
математика
дп
*3200
Последовательность целых чисел \(b_1, b_2, \ldots, b_m\) называется хорошей, если \(max(b_1, b_2, \ldots, b_m) \cdot min(b_1, b_2, \ldots, b_m) \ge b_1 + b_2 + \ldots + b_m\). Последовательность целых чисел \(a_1, a_2, \ldots, a_n\) называется идеальной, если каждая непустая подпоследовательность \(a\) является хорошей. У YouKn0wWho есть два целых числа \(n\) и \(M\), \(M\) — простое. Помогите ему найти количество, по модулю \(M\), идеальных последовательностей \(a_1, a_2, \ldots, a_n\) таких, что \(1 \le a_i \le n + 1\) для каждого \(i\) от \(1\) до \(n\). Последовательность \(d\) является подпоследовательностью последовательности \(c\), если \(d\) может быть получена из \(c\) путем удаления нескольких (возможно, нуля или всех) элементов. Выходные данные Выведите одно целое число — количество идеальных последовательностей по модулю \(M\). Примечание В первом примере идеальные последовательности — \([2, 2]\), \([2, 3]\), \([3, 2]\) и \([3, 3]\). Во втором примере, некоторые из идеальных последовательностей — \([3, 4, 3, 5]\), \([4, 5, 4, 4]\), \([4, 5, 5, 5]\) и т.д. Одним из примеров последовательности, которая не является идеальной, является \([2, 3, 3, 4]\), потому что, например, подпоследовательность \([2, 3, 4]\) не является хорошей, так как \(2 \cdot 4 < 2 + 3 + 4\). | |
![]()
|
|
F. 18 октября 2017
Комбинаторика
математика
реализация
дп
*2700
Это произошло 18 октября 2017 года. Shohag, меланхоличная душа, твердо решил, что будет серьезно заниматься спортивным программированием, поскольку оно показалось ему увлекательным. Прошло 4 года, и он счастлив, что выбрал этот путь. Сейчас он создает раунд на Codeforces. Он нашел выдающуюся задачу, но не имеет ни малейшего представления о том, как ее решить. Помогите ему решить финальную задачу раунда. Вам даны три целых числа \(n\), \(k\) и \(x\). Найдите количество, по модулю \(998\,244\,353\), последовательностей целых чисел \(a_1, a_2, \ldots, a_n\) таких, что выполняются следующие условия: - \(0 \le a_i \lt 2^k\) для каждого целого числа \(i\) от \(1\) до \(n\).
- Не существует непустой подпоследовательности в \(a\) такой, что побитовое исключающее ИЛИ элементов подпоследовательности равно \(x\).
Последовательность \(b\) является подпоследовательностью последовательности \(c\), если \(b\) может быть получена из \(c\) путем удаления нескольких (возможно, нуля или всех) элементов. Выходные данные Для каждого набора входных данных выведите одно целое число — ответ на задачу. Примечание В первом наборе входных данных допустимыми последовательностями являются \([1, 2]\), \([1, 3]\), \([2, 1]\), \([2, 3]\), \([3, 1]\) и \([3, 2]\). Во втором наборе входных данных единственной допустимой последовательностью является \([0, 0]\). | |
![]()
|
|
F. ПалиндORм
Комбинаторика
дп
*2900
Целочисленный массив \(a\) длины \(n\) называется палиндORмом, если (\(a_{1}\) \(|\) \(a_{2} \) \(|\) \( \ldots \) \(|\) \( a_{i}) = (a_{{n - i + 1}} \) \(|\) \( \ldots \) \(|\) \( a_{{n - 1}} \) \(|\) \( a_{n}) \) для всех \( 1 \leq i \leq n\), где \(|\) обозначает операцию побитового ИЛИ. Целочисленный массив \(a\) длины \(n\) считается хорошим, если его элементы могут быть переставлены так, чтобы образовать палиндORм. Формально, массив \(a\) является хорошим, если существует перестановка \(p_1, p_2, \ldots p_n\) (массив, в котором каждое целое число от \(1\) до \(n\) встречается ровно один раз), для которой \(a_{p_1}, a_{p_2}, \ldots a_{p_n}\) является палиндORмом. Найдите количество хороших массивов длины \(n\), состоящих только из целых чисел в диапазоне \([0, 2^{k} - 1]\), и выведите его по модулю некоторого простого числа \(m\). Два массива \(a_1, a_2, \ldots, a_n\) и \(b_1, b_2, \ldots, b_n\) считаются различными, если существует индекс \(i\) \((1 \leq i \leq n)\) такой, что \(a_i \ne b_i\). Выходные данные Выведите одно целое число — количество хороших массивов по модулю \(m\). Примечание В первом примере оба возможных массива \([0]\) и \([1]\) являются хорошими. Во втором примере есть несколько примеров хороших массивов: - \([2, 1, 2]\), потому что он уже является палиндORмом.
- \([1, 1, 0]\), потому что его можно перестроить в \([1, 0, 1]\), что является палиндORмом.
Обратите внимание, что \([1, 1, 0]\), \([1, 0, 1]\) и \([0, 1, 1]\) являются хорошими массивами и считаются разными в соответствии с определением в утверждении. В третьем примере примером хорошего массива является \([1, 0, 1, 4, 2, 5, 4]\). Его можно переставить в массив \(b = [1, 5, 0, 2, 4, 4, 1]\), который является палиндORмом, потому что: - \(\mathrm{OR}(1, 1)\) = \(\mathrm{OR}(7, 7)\) = \(1\)
- \(\mathrm{OR}(1, 2)\) = \(\mathrm{OR}(6, 7)\) = \(5\)
- \(\mathrm{OR}(1, 3)\) = \(\mathrm{OR}(5, 7)\) = \(5\)
- \(\mathrm{OR}(1, 4)\) = \(\mathrm{OR}(4, 7)\) = \(7\)
- \(\mathrm{OR}(1, 5)\) = \(\mathrm{OR}(3, 7)\) = \(7\)
- \(\mathrm{OR}(1, 6)\) = \(\mathrm{OR}(2, 7)\) = \(7\)
- \(\mathrm{OR}(1, 7)\) = \(\mathrm{OR}(1, 7)\) = \(7\)
Здесь \(\mathrm{OR}(l, r)\) обозначает \(b_{l}\) \(|\) \(b_{l+1} \) \(|\) \( \ldots \) \(|\) \( b_{r}\) | |
![]()
|
|
E. Арена
Комбинаторика
математика
*2100
дп
На арене сражаются \(n\) героев. Изначально у \(i\)-го героя \(a_i\) единиц здоровья. Бой на арене проходит в несколько раундов. В начале каждого раунда каждый еще живой герой наносит \(1\) урона всем остальным героям. Удары всех героев происходят одновременно. Герои, чье здоровье стало меньше \(1\) в конце раунда, считаются убитыми. Если после некоторого раунда в живых остается ровно \(1\) герой, то он объявляется победителем. В противном случае победителя нет. Ваша задача — посчитать количество способов выбрать начальное здоровье для каждого героя \(a_i\), где \(1 \le a_i \le x\), таким образом, чтобы не существовало победителя боя. Количество способов может быть очень большим, поэтому выведите его по модулю \(998244353\). Два способа считаются различными, если хотя бы у одного героя отличается количество здоровья. Например, способы \([1, 2, 1]\) и \([2, 1, 1]\) — разные. Выходные данные Выведите одно целое число — количество способов выбрать начальное здоровье для каждого героя \(a_i\), где \(1 \le a_i \le x\), таким образом, чтобы не существовало победителя боя, взятое по модулю \(998244353\). | |
![]()
|
|
D. Домино
Комбинаторика
математика
теория чисел
*2400
графы
бпф
Вам дано \(n\) домино. Каждое домино имеет левую и правую клетку. Каждая клетка может быть окрашена в черный или белый цвет. Некоторые клетки уже окрашены, а некоторые еще нет. Раскраска считается допустимой тогда и только тогда, когда можно переставить доминошки в некотором порядке так, чтобы для каждого \(1 \le i \le n\) цвет правой клетки \(i\)-го домино отличался от цвета левой клетки \(((i \bmod n)+1)\)-го домино. Обратите внимание, что домино нельзя вращать, поэтому левая клетка всегда остается левой, а правая — правой. Подсчитайте количество допустимых способов раскрасить еще не раскрашенные клетки домино. Два способа считаются разными, если есть клетка, которая в одном способе окрашивается в белый цвет, а во втором — в черный. В частности, раскраски BW WB и WB BW различны (и обе недопустимы). Поскольку это число может быть очень большим, выведите его по модулю \(998\,244\,353\). Выходные данные Выведите одно целое число — ответ на задачу. Примечание В первом примере есть только одна доминошка, и нам нужно, чтобы цвет ее правой клетки отличался от цвета ее левой клетки. Этого можно добиться только одним способом. Во втором примере существует только \(2\) таких раскраски: BB WW и WB WB. | |
![]()
|
|
F. MEX подсчет
Комбинаторика
реализация
дп
*3200
Для массива \(c\) неотрицательных целых чисел, \(MEX(c)\) обозначает наименьшее неотрицательное целое число, которое в нем не встречается. Например, \(MEX([0, 1, 3]) = 2\), \(MEX([42]) = 0\). Вам даны целые числа \(n, k\) и массив \([b_1, b_2, \ldots, b_n]\). Найдите количество массивов \([a_1, a_2, \ldots, a_n]\), для которых выполняются следующие условия: \(0 \le a_i \le n\) для каждого \(i\) для каждого \(i\) от \(1\) до \(n\). \(|MEX([a_1, a_2, \ldots, a_i]) - b_i| \le k\) для каждого \(i\) от \(1\) до \(n\).
Поскольку это число может быть очень большим, выведите его по модулю \(998\,244\,353\). Выходные данные Выведите одно целое число — количество массивов, удовлетворяющих ограничениям из условия, по модулю \(998\,244\,353\). | |
![]()
|
|
D. Ни кап Ли
Комбинаторика
математика
дп
теория чисел
*2000
В последнее время Ли не мог заснуть, потому что ему снились кошмары. В одном из своих кошмаров (который был о несбалансированном глобал раунде) он решил дать отпор и предложить задачу ниже (которую вы должны решить), чтобы сбалансировать раунд, надеясь освободить его от кошмаров. Непустой массив \(b_1, b_2, \ldots, b_m\) называется хорошим, если существует \(m\) целочисленных последовательностей, удовлетворяющих следующим свойствам: - \(i\)-я последовательность состоит из \(b_i\) последовательных целых чисел (например, если \(b_i = 3\), то \(i\)-я последовательность может быть \((-1, 0, 1)\) или \((-5, -4, -3)\), но не \((0, -1, 1)\) или \((1, 2, 3, 4)\)).
- Если сумма целых чисел в \(i\)-й последовательности равна \(sum_i\), то мы хотим, чтобы \(sum_1 + sum_2 + \ldots + sum_m\) было равно \(0\).
Вам дан массив \(a_1, a_2, \ldots, a_n\). У него есть \(2^n - 1\) непустых подпоследовательностей. Найдите, сколько из них являются хорошими. Поскольку это число может быть очень большим, выведите его по модулю \(10^9 + 7\). Массив \(c\) является подпоследовательностью массива \(d\), если \(c\) может быть получен из \(d\) путем удаления нескольких (возможно, нуля или всех) элементов. Выходные данные Выведите одно целое число — количество непустых хороших подпоследовательностей \(a\), по модулю \(10^9 + 7\). Примечание Для первого теста двумя примерами хороших подпоследовательностей являются \([2, 7]\) и \([2, 2, 4, 7]\): Для \(b = [2, 7]\) мы можем использовать \((-3, -4)\) в качестве первой последовательности и \((-2, -1, \ldots, 4)\) в качестве второй. Обратите внимание, что подпоследовательность \([2, 7]\) входит дважды в \([2, 2, 4, 7]\), поэтому мы должны считать ее дважды.  Зеленые круги обозначают \((-3, -4)\), а оранжевые квадраты - \((-2, -1, \ldots, 4)\). Зеленые круги обозначают \((-3, -4)\), а оранжевые квадраты - \((-2, -1, \ldots, 4)\). Для \(b = [2, 2, 4, 7]\) свойствам будут удовлетворять следующие последовательности: \((-1, 0)\), \((-3, -2)\), \((0, 1, 2, 3)\) и \((-3, -2, \ldots, 3)\). | |
![]()
|
|
G. Массив максимальной суммы
Конструктив
Комбинаторика
жадные алгоритмы
сортировки
*2500
Вам задан массив \(c = [c_1, c_2, \dots, c_m]\). Массив \(a = [a_1, a_2, \dots, a_n]\) строится по нему следующим образом: он состоит из чисел \(1, 2, \dots, m\), и для каждого \(i \in [1,m]\), \(i\) встречается в \(a\) строго \(c_i\) раз. Таким образом, количество элементов в \(a\) равно \(\sum\limits_{i=1}^{m} c_i\). Определим для данного массива \(a\) значение \(f(a)\) как \(\)f(a) = \sum_{\substack{1 \le i < j \le n\\ a_i = a_j}}{j - i}.\(\) Другими словами, \(f(a)\) — это суммарное расстояние между всеми парами одинаковых чисел. Ваша задача — определить наибольшее возможное значение \(f(a)\) и количество массивов с данным значением \(f(a)\). Два массива считаются различными, если элементы в какой-то позиции различаются. Выходные данные Выведите два целых числа — максимально возможное \(f(a)\) и количество массивов \(a\) с данным значением. Так как оба ответа могут быть очень большими, выведите их по модулю \(10^9 + 7\). Примечание В первом примере, все возможные массивы \(a\) — это перестановки \([1, 2, 3, 4, 5, 6]\). Так как у каждого такого \(a\) значение \(f(a) = 0\), то максимально возможное \(f(a) = 0\) и количество таких массивов равно \(6! = 720\). Во втором примере, единственный возможный массив состоит из \(10^6\) единиц и его \(f(a) = \sum\limits_{1 \le i < j \le 10^6}{j - i} = 166\,666\,666\,666\,500\,000\) и \(166\,666\,666\,666\,500\,000 \bmod{10^9 + 7} = 499\,833\,345\). | |
![]()
|
|
F. Раскраска дерева
Комбинаторика
*2600
разделяй и властвуй
бпф
Дано корневое дерево из \(n\) вершин, пронумерованных от \(1\) до \(n\). Корень дерева — вершина под номером \(1\). Необходимо раскрасить все вершины дерева в \(n\) цветов (также пронумерованных от \(1\) до \(n\)) так, чтобы в каждый цвет была покрашена ровно одна вершина. Пусть \(c_i\) — цвет вершины \(i\), а \(p_i\) — родитель вершины \(i\) в корневом дереве. Раскраска называется красивой, если не существует такого \(k\) (\(k > 1\)), что \(c_k = c_{p_k} - 1\), то есть не существует вершины, цвет которой меньше цвета ее родителя ровно на \(1\). Посчитайте количество красивых раскрасок и выведите его по модулю \(998244353\). Выходные данные Выведите одно целое число — количество красивых раскрасок, взятое по модулю \(998244353\). | |
![]()
|
|
C. Divan и битовые операции
Конструктив
Комбинаторика
математика
дп
*1500
битмаски
Однажды Divan проанализировал последовательность \(a_1, a_2, \ldots, a_n\), состоящую из \(n\) целых неотрицательных чисел, следующим образом. Он рассмотрел все непустые подпоследовательности последовательности \(a\), вычислил побитовое исключающее ИЛИ её элементов, после чего просуммировал все полученные результаты, получив удобство последовательности \(a\). Напомним, что последовательность \(c\) является подпоследовательностью последовательности \(d\), если \(c\) может быть получена из \(d\) путем удаления нескольких элементов (возможно, ни одного). Например, \([1, \, 2, \, 3, \, 4]\), \([2, \, 4]\) и \([2]\) являются подпоследовательностями \([1, \, 2, \, 3, \, 4]\), а \([4, \, 3]\) и \([0]\) не являются. Divan очень гордился проведенным анализом, но теперь потерял и последовательность \(a\), и значение ее удобства! Однако Divan помнит значение побитового ИЛИ на \(m\) непрерывных подотрезках последовательности \(a\). Оказалось, что каждый элемент последовательности входит хотя бы в один из этих \(m\) отрезков. Divan просит вас найти удобство последовательности \(a\), используя информацию, которую он помнит. Если возможны несколько значений удобства, выведите любое. Так как ответ может быть большим, выведите его по модулю \(10^9 + 7\). Выходные данные Для каждого набора входных данных выведите любое возможное удобство последовательности \(a\) по модулю \(10^9 + 7\). Примечание В первом примере одной из последовательностей, которая подходит под ограничения, является \([0, 2]\). Рассмотрим все её непустые подпоследовательности: - \([0]\): побитовое исключающее ИЛИ равно \(0\);
- \([2]\): побитовое исключающее ИЛИ равно \(2\);
- \([0, 2]\): побитовое исключающее ИЛИ равно \(2\).
Суммируя полученные числа, получаем \(4\), что является ответом. Во втором примере одной из последовательностей, которая подходит под ограничения, является \([0, \, 5, \, 5]\). В третьем примере одной из последовательностей, которая подходит под ограничения, является \([5, \, 6, \, 7, \, 0, \, 2]\). | |
![]()
|
|
F. ЛЕГОндарный гроссмейстер
Комбинаторика
математика
дп
*2800
Устав играть с мелками, вы решили перейти на Лего! Сегодня у вас есть длинная полоска высоты \(1\) и длины \(n\), в некоторых ячейках которой расположены детальки Лего \(1\) на \(1\). За одну секунду, вы можете либо убрать две последовательные детальки Лего с полоски (если таковые имеются), либо поставить две детальки Лего на последовательные позиции (если они пустые). Вы можете ставить и убирать Лего только по две штуки за раз, так как ваши пальцы слишком широкие для одной детальки. Вам интересно узнать, сколько времени вы потратите на игру с Лего. При этом, для вас крайне важна эффективность, а потому если вы хотите получить из некоторого стартового состояния некоторое финишное, то вы всегда потратите наименьшее количество секунд. Если же из стартового состояния невозможно получить финишное, то вы просто ничего не станете делать (то есть потратите \(0\) секунд). Проблема в том, что вы не помните, были ли детальки Лего в некоторых позициях (как в стартовом состоянии, так и в финишном). А потому вы хотите посчитать суммарное время получения финишного состояния из стартового для всех пар (стартовое состояние, финишное состояние), которые не противоречат вашей памяти. Так как время может оказаться очень большим, выведите его по модулю \(1\,000\,000\,007\) (\(10^9 + 7\)). Выходные данные Для каждого набора входных данных выведите одно число — ответ на задачу по модулю \(1\,000\,000\,007\) (\(10^9 + 7\)). Примечание В первом наборе входных данных, \(00\) — единственное возможное стартовое состояние, а \(11\) — единственное возможное финишное состояние. Потребуется одна операция, чтобы превратить \(00\) в \(11\). Во втором наборе, ниже приведены некоторые из возможных пар стартовых и финишных состояний: - \((000, 011)\) — потребуется \(1\) операция;
- \((001, 100)\) — потребуется \(2\) операции;
- \((010, 000)\) — потребуется \(0\) операций, так как невозможно получить из заданного стартового состояния заданное финишное.
| |
![]()
|
|
H. Следи за малостью XOR
Структуры данных
Комбинаторика
математика
дп
разделяй и властвуй
битмаски
*3000
Вам дан массив целых чисел \(a_1, a_2, \ldots, a_n\) и целое число \(x\). Найдите количество непустых подмножеств индексов этого массива \(1 \leq b_1 < b_2 < \ldots < b_k \leq n\) таких, что для всех пар \((i, j)\), где \(1 \leq i < j \leq k\), выполняется неравенство \(a_{b_i} \oplus a_{b_j} \leq x\). Здесь \(\oplus\) обозначает операцию побитового исключающего ИЛИ. Так как ответ может быть большим, выведите его по модулю \(998\,244\,353\). Выходные данные Выведите одно целое число: количество непустых подмножеств таких, что побитовое исключающее ИЛИ любых двух элементов не больше \(x\), по модулю \(998\,244\,353\). | |
![]()
|
|
G. Подпоследовательности повсюду
Комбинаторика
дп
*2400
битмаски
Для последовательности строк \([t_1, t_2, \dots, t_m]\) введем функцию \(f([t_1, t_2, \dots, t_m])\), которая равна кол-ву различных строк (включая пустую строку), которые являются подпоследовательностями хотя бы одной строки \(t_i\). \(f([]) = 0\) (то есть значение такой функции для пустой последовательности строк равно \(0\)). Вам задана последовательность строк \([s_1, s_2, \dots, s_n]\). Каждая строка в этой последовательности состоит из строчных латинских букв и является отсортированной (то есть каждая строка начинается с нескольких (возможно, ни одного) символов a, затем идут несколько (возможно, ноль) символов b, ..., в конце идут несколько (возможно, ноль) символов z). Для каждой из \(2^n\) подпоследовательностей \([s_1, s_2, \dots, s_n]\), посчитайте значение функции \(f\) по модулю \(998244353\). Выходные данные Так как выводить \(2^{23}\) чисел довольно долго, представьте ответ следующим образом: Для каждой из \(2^n\) подпоследовательностей (мы обозначим подпоследовательность как \([s_{i_1}, s_{i_2}, \dots, s_{i_k}]\)) посчитайте \(f([s_{i_1}, s_{i_2}, \dots, s_{i_k}])\), возьмите это значение по модулю \(998244353\), а затем умножьте на \(k \cdot (i_1 + i_2 + \dots + i_k)\). Выведите XOR всех \(2^n\) чисел, которые у вас получатся. Индексы \(i_1, i_2, \dots, i_k\) в описании подпоследовательности заданы в \(1\)-индексации (то есть они от \(1\) до \(n\)). | |
![]()
|
|
D. Перемешивание
Комбинаторика
математика
*2000
Вам задана бинарная строка (строка, состоящая из символов 0 и/или 1) \(s\) длины \(n\). Вы можете выполнить следующую операцию со строкой \(s\) не более одного раза: выбрать подстроку (непрерывную подпоследовательность) строки \(s\), в которой ровно \(k\) символов 1, и перемешать ее (переставить все символы подстроки в любом порядке). Посчитайте кол-во различных строк, которые могут быть получены из \(s\), если применить эту операцию не более одного раза. Выходные данные Выведите одно целое число — количество различных строк, которые могут быть получены из \(s\), если применить описанную в условии операцию не более одного раза. Так как ответ может быть очень большим, выведите его по модулю \(998244353\). Примечание Некоторые строки, которые вы можете получить в первом примере: - чтобы получить 0110110, вы можете выбрать подстроку с \(1\)-го символа по \(4\)-й символ. Эта подстрока — 1100, и ее перемешиванием можно получить 0110;
- чтобы получить 1111000, вы можете выбрать подстроку с \(3\)-го символа по \(7\)-й символ. Эта подстрока — 00110, и ее перемешиванием можно получить 11000;
- чтобы получить 1100101, вы можете выбрать подстроку с \(5\)-го символа по \(7\)-й символ. Эта подстрока —110, и ее перемешиванием можно получить 101.
Во втором примере \(k = 0\), поэтому можно выбирать только подстроки, состоящие только из символов 0. Перемешивание таких подстрок не меняет строку, поэтому единственная строка, которую можно получить — 10010. | |
![]()
|
|
F. Случайный код
Теория вероятностей
Комбинаторика
математика
дп
теория чисел
*2800
Дан массив целых чисел \(a_0, a_1, \dots, a_{n - 1}\) и целое число \(k\). Вы выполняете следующий код: long long ans = 0; // 64-битная знаковая целочисленная переменная, изначально равная 0
for(int i = 1; i <= k; i++)
{
int idx = rnd.next(0, n - 1); // генерирует случайное целое число от 0 до n - 1 включительно
// каждое целое число от 0 до n - 1 выбирается с одинаковой вероятностью
ans += a[idx];
a[idx] -= (a[idx] % i);
}
Ваша задача — посчитать матожидание значения переменной ans после выполнения этого кода. Обратите внимание, что входные данные генерируется специальным образом (подробнее в секции «Входные данные»). Выходные данные Пусть матожидание значения переменной ans после выполнения кода равно \(E\). Можно показать, что \(E \cdot n^k\) — целое число. Выведите остаток от деления этого числа на \(998244353\). Примечание Массив в первом примере — \([10, 35, 22]\). Во втором примере — \([15363, 1418543]\). | |
![]()
|
|
D1. Игра на сумму (Легкая версия)
Комбинаторика
математика
*2100
дп
игры
Это легкая версия задачи. Разница заключается в ограничениях на \(n\), \(m\) и \(t\). Делать взломы можно только в том случае, если решены обе задачи. Алисе и Бобу даются числа \(n\), \(m\) и \(k\), и они играют в следующую игру: В игре есть счет, который Алиса пытается максимизировать, а Боб старается минимизировать. Первоначально счет равен \(0\). Игра состоит из \(n\) ходов. Каждый ход Алиса выбирает число от \(0\) до \(k\) (необязательно целое), которое Боб либо прибавляет, либо вычитает из счета игры. Но на протяжении всей игры Боб должен прибавить не менее \(m\) из \(n\) ходов. Боб узнает, какое число выбрала Алиса, прежде чем решит, прибавить или вычесть это число из счета, а Алиса узнает, прибавил Боб или вычел число для предыдущего хода, прежде чем выбрать число для текущего хода (кроме первого хода, поскольку предыдущего хода не было). Если Алиса и Боб будут играть оптимально, каков будет окончательный счет игры? Выходные данные Для каждого тестового примера выведите одно число — результат оптимальной игры по модулю \(10^9 + 7\). Формально пусть \(M = 10^9 + 7\). Можно показать, что ответ может быть выражен в виде неприводимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Примечание В первом тестовом примере вся игра имеет \(3\) хода, и, поскольку \(m = 3\), Боб должен добавить в каждый из них. Следовательно, Алиса должна каждый ход выбирать самое большое число, которое она может, а именно \(k = 2\). В третьем тестовом примере у Алисы есть стратегия, гарантирующая оценку \(\frac{75}{8} \equiv 375000012 \pmod{10^9 + 7}\). В четвертом тестовом примере у Алисы есть стратегия, гарантирующая оценку \(\frac{45}{2} \equiv 500000026 \pmod{10^9 + 7}\). | |
![]()
|
|
D2. Игра на сумму (Сложная версия)
Комбинаторика
математика
дп
*2400
игры
Это сложная версия задачи. Разница заключается в ограничениях на \(n\), \(m\) и \(t\). Делать взломы можно только в том случае, если решены обе задачи. Алисе и Бобу даются числа \(n\), \(m\) и \(k\), и они играют в следующую игру: В игре есть счет, который Алиса пытается максимизировать, а Боб старается минимизировать. Первоначально счет равен \(0\). Игра состоит из \(n\) ходов. Каждый ход Алиса выбирает число от \(0\) до \(k\) (необязательно целое), которое Боб либо прибавляет, либо вычитает из счета игры. Но на протяжении всей игры Боб должен прибавить не менее \(m\) из \(n\) ходов. Боб узнает, какое число выбрала Алиса, прежде чем решит, прибавить или вычесть это число из счета, а Алиса узнает, прибавил Боб или вычел число для предыдущего хода, прежде чем выбрать число для текущего хода (кроме первого хода, поскольку предыдущего хода не было). Если Алиса и Боб будут играть оптимально, каков будет окончательный счет игры? Выходные данные Для каждого тестового примера выведите одно число — результат оптимальной игры по модулю \(10^9 + 7\). Формально пусть \(M = 10^9 + 7\). Можно показать, что ответ может быть выражен в виде неприводимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Примечание В первом тестовом примере вся игра имеет \(3\) хода, и, поскольку \(m = 3\), Боб должен добавить в каждый из них. Следовательно, Алиса должна каждый ход выбирать самое большое число, которое она может, а именно \(k = 2\). В третьем тестовом примере у Алисы есть стратегия, гарантирующая оценку \(\frac{75}{8} \equiv 375000012 \pmod{10^9 + 7}\). В четвертом тестовом примере у Алисы есть стратегия, гарантирующая оценку \(\frac{45}{2} \equiv 500000026 \pmod{10^9 + 7}\). | |
![]()
|
|
E. Ожидаемые компоненты
Теория вероятностей
Комбинаторика
математика
теория чисел
*2900
Дан кольцевой массив \(a\) размера \(n\), где \(a_i\) равно значению \(a\) в \(i\)-й позиции, значения могут повторяться. Пусть перестановка \(a\) равна другой перестановке \(a\) тогда и только тогда, когда их значения равны в каждой позиции \(i\) или можно сделать из одной перестановки другую циклическим сдвигом. Положим в качестве количества компонент циклического массива \(b\) количество компонент связности в графе, в котором вершины — это позиции \(b\), и между двумя соседними позициями \(b\) существует ребро, если значения в этих позициях равны (заметьте, что в кольцевом массиве первая и последняя позиции считаются соседними). Найдите математическое ожидание количества компонент перестановки \(a\), если мы равновероятно выбираем ее из множества всех различных перестановок \(a\). Выходные данные Для каждого набора входных данных напечатайте одно целое число — математическое ожидание количества компонент перестановки \(a\), если мы выбираем ее равновероятно из множества всех различных перестановок \(a\) по модулю \(998\,244\,353\). Формально, пусть \(M = 998\,244\,353\). Можно показать, что ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) – целые числа и \(q \not \equiv 0 \pmod{M}\). Напечатайте целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, напечатайте такое целое \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Примечание В первом наборе существует только \(1\) перестановка \(a\): - \([1, 1, 1, 1]\) содержит \(1\) компоненту.
- Поэтому математическое ожидание количества компонент равно \(\frac{1}{1} = 1\)
Во втором наборе есть \(4\) способа переставить кольцевой массив \(a\), но существует только \(1\) различная перестановка \(a\): - \([1, 1, 1, 2]\), \([1, 1, 2, 1]\), \([1, 2, 1, 1]\) и \([2, 1, 1, 1]\) — равные перестановки, содержащие \(2\) компоненты.
- Поэтому математическое ожидание количества компонент равно \(\frac{2}{1} = 2\)
Во третьем наборе есть \(6\) способов переставить кольцевой массив \(a\), но существует только \(2\) различные перестановки \(a\): - \([1, 1, 2, 2]\), \([2, 1, 1, 2]\), \([2, 2, 1, 1]\) и \([1, 2, 2, 1]\) — равные перестановки, содержащие \(2\) компоненты.
- \([1, 2, 1, 2]\) и \([2, 1, 2, 1]\) — равные перестановки, содержащие \(4\) компоненты.
- Поэтому математическое ожидание количества компонент равно \(\frac{2+4}{2} = \frac{6}{2} = 3\)
Во четвертом наборе есть \(120\) способов переставить кольцевой массив \(a\), но существует только \(24\) различные перестановки \(a\): - Любая перестановка \(a\) содержит \(5\) компонент.
- Поэтому математическое ожидание количества компонент равно \(\frac{24\cdot 5}{24} = \frac{120}{24} = 5\)
| |
![]()
|
|
D. Два массива
Перебор
Комбинаторика
математика
жадные алгоритмы
*2700
хэши
битмаски
Стас перешел в новую школу «75-угольник», и на первом же уроке биологии начал умничать, за что его учитель попросил решить задачу по генетике, решение которой сам не знает. Вам дано \(n\) массивов, \(i\)-й из которых содержит \(m\) различных целых чисел — \(a_{i,1}, a_{i,2},\ldots,a_{i,m}\). Также дан массив положительных целых чисел \(w\) длины \(n\). Вам надо найти минимальное возможное значение выражения \(w_i + w_j\) среди всех пар целых чисел \((i, j)\) (\(1 \le i, j \le n\)) таких, что среди чисел \(a_{i,1}, a_{i,2},\ldots,a_{i,m}, a_{j,1}, a_{j,2},\ldots,a_{j,m}\) все числа различны. Выходные данные Выведите единственное число — ответ на задачу. Если ни одной подходящей пары \((i, j)\) не существует, выведите \(-1\). Примечание В первом тесте минимальное значение это \(5 = w_3 + w_4\), так как среди чисел \(\{2, 3, 4, 5\}\) все различны. Во втором тесте нет ни одной подходящей пары \((i, j)\). | |
![]()
|
|
E. Особые позиции
Комбинаторика
математика
разделяй и властвуй
бпф
*3300
Будучи школьником Стас очень грустил, когда рассадка в школьном автобусе не позволяла ему сесть рядом с другом, поэтому сейчас он вырос и начал писать программу, решающую эту проблему, и ему потребовалось решить такую задачу. Дан массив \(a\) длины \(n\). Также даны \(m\) различных позиций \(p_1, p_2, \ldots, p_m\) (\(1 \leq p_i \leq n\)). Затем равновероятно выбирается непустое подмножество этих позиций \(T\) и вычисляется \(\)\sum_{i=1}^{n} (a_i \cdot \min_{j \in T} \left|i - j\right|).\(\) Иными словами, для каждого индекса массива перемножаются \(a_i\) и расстояние до ближайшей выбранной в подмножество позиции, и эти величины суммируются. Найдите математическое ожидание этой величины. Это число нужно найти по модулю \(998\,244\,353\). Формально, пусть \(M = 998\,244\,353\). Можно показать, что ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) целые числа и \(q \neq 0\) (mod \(M\)). Выведите целое число, равное \(p \cdot q^{-1}\) (mod \(M\)). Другими словами, выведите такое целое число \(x\), что \(0 \leq x < M\) и \(x \cdot q = p\) (mod \(M\)). Выходные данные Выведите единственное целое число — ответ на задачу. Примечание В первом примере: - Если взята только позиция \(1\), то итоговая величина равна \(1 \cdot 0 + 2 \cdot 1 + 3 \cdot 2 + 4 \cdot 3 = 20\).
- Если взята только позиция \(4\), то итоговая величина равна \(1 \cdot 3 + 2 \cdot 2 + 3 \cdot 1 + 4 \cdot 0 = 10\).
- Если взяты обе позиции, то итоговая величина равна \(1 \cdot 0 + 2 \cdot 1 + 3 \cdot 1 + 4 \cdot 0 = 5\).
Ответ на задачу \(\frac{20 + 10 + 5}{3} = \frac{35}{3} = 665\,496\,247\) (по модулю \(998\,244\,353\)). | |
![]()
|
|
E. Расширь маршрут
Перебор
Структуры данных
Комбинаторика
математика
реализация
*1900
Задана сетка размера \(n \times n\). Строки пронумерованы сверху вниз от \(1\) до \(n\), столбцы пронумерованы слева направо от \(1\) до \(n\). Робот расположен в клетке \((1, 1)\). Он может делать два типа ходов: - D — перейти на одну клетку вниз;
- R — перейти на одну клетку вправо.
Роботу запрещено выходить за пределы поля. Дана последовательность ходов \(s\) — изначальный маршрут робота. Этот маршрут не ведет робота за пределы поля. Вам разрешено провести произвольное количество изменений строки (возможно, ноль). За одно изменение можно раздвоить один ход в последовательности. То есть, заменить одно вхождение D на DD или одно вхождение R на RR. Посчитайте количество клеток таких, что существует хотя бы одна последовательность изменений, после применения которой робот посетит эту клетку на измененном маршруте и не выйдет за пределы поля. Выходные данные На каждый набор входных данных выведите одно целое число — количество клеток таких, что существует хотя бы одна последовательность изменений, после применения которой робот посетит эту клетку на измененном маршруте и не выйдет за пределы поля. Примечание В первом наборе входных данных достаточно рассмотреть следующие измененные маршруты: - RD \(\rightarrow\) RRD \(\rightarrow\) RRRD \(\rightarrow\) RRRDD \(\rightarrow\) RRRDDD — этот маршрут посещает клетки \((1, 1)\), \((1, 2)\), \((1, 3)\), \((1, 4)\), \((2, 4)\), \((3, 4)\) и \((4, 4)\);
- RD \(\rightarrow\) RRD \(\rightarrow\) RRDD \(\rightarrow\) RRDDD — этот маршрут посещает клетки \((1, 1)\), \((1, 2)\), \((1, 3)\), \((2, 3)\), \((3, 3)\) и \((4, 3)\);
- RD \(\rightarrow\) RDD \(\rightarrow\) RDDD — этот маршрут посещает клетки \((1, 1)\), \((1, 2)\), \((2, 2)\), \((3, 2)\) и \((4, 2)\).
Таким образом, клетки, которые посещены на хотя бы одном измененном маршруте: \((1, 1)\), \((1, 2)\), \((1, 3)\), \((1, 4)\), \((2, 2)\), \((2, 3)\), \((2, 4)\), \((3, 2)\), \((3, 3)\), \((3, 4)\), \((4, 2)\), \((4, 3)\) и \((4, 4)\). Во втором примере, нет способа изменить последовательность так, чтобы робот не вышел за пределы поля. Поэтому все посещенные клетки — это те, которые посещены на маршруте DRDRDRDR. В третьем примере клетки, которые посещены на хотя бы одном измененном маршруте: \((1, 1)\), \((2, 1)\) и \((3, 1)\). Клетки для всех наборов:  | |
![]()
|
|
F. Базис
Комбинаторика
математика
теория чисел
бпф
*2900
Для массива целых чисел \(a\) обозначим количество элементов в нем за \(|a|\). Давайте введем две функции: - \(F(a, k)\) — функция, принимающая массив целых чисел \(a\) и натуральное число \(k\). Результат этой функции — это массив, содержащий \(|a|\) первых элементов массива, который получается заменой каждого элемента \(a\) на \(k\) копий этого элемента.
Например, \(F([2, 2, 1, 3, 5, 6, 8], 2)\) считается следующим образом: сначала каждый элемент массива заменяется \(2\) копиями этого элемента, и получается массив \([2, 2, 2, 2, 1, 1, 3, 3, 5, 5, 6, 6, 8, 8]\). Затем от полученного массива берутся \(7\) первых элементов, поэтому результат функции — \([2, 2, 2, 2, 1, 1, 3]\). - \(G(a, x, y)\) — функция, которая принимает массив целых чисел \(a\) и два различных целых числа \(x\) и \(y\). Результат этой функции — массив \(a\), в котором каждое вхождение элемента \(x\) заменяется на \(y\), а каждое вхождение элемента \(y\) заменяется на \(x\).
Например, \(G([1, 1, 2, 3, 5], 3, 1) = [3, 3, 2, 1, 5]\).
Массив \(a\) — родитель массива \(b\), если: - либо существует положительное целое число \(k\), для которого \(F(a, k) = b\);
- либо существуют два различных целых числа \(x\) и \(y\), для которых \(G(a, x, y) = b\).
Массив \(a\) — предок массива \(b\), если существует последовательность массивов \(c_0, c_1, \dots, c_m\) (\(m \ge 0\)), в которой \(c_0\) — массив \(a\), \(c_m\) — массив \(b\), а для каждого \(i \in [1, m]\) массив \(c_{i-1}\) является родителем массива \(c_i\). А теперь — сама задача. Вам даны два целых числа \(n\) и \(k\). Ваша цель — построить последовательность массивов \(s_1, s_2, \dots, s_m\), удовлетворяющую следующим условиям: - каждый массив \(s_i\) содержит ровно \(n\) элементов, и все эти элементы — целые числа от \(1\) до \(k\);
- для каждого массива \(a\), состоящего из ровно \(n\) целых чисел от \(1\) до \(k\), последовательность содержит хотя бы один массив \(s_i\), такой, что \(s_i\) — предок \(a\).
Выведите минимальное количество массивов в такой последовательности. Выходные данные Выведите одно целое число — минимальное количество массивов в последовательности, удовлетворяющей условию задачи. Так как ответ может быть очень большим, выведите его по модулю \(998244353\). Примечание Давайте проанализируем первый пример. Один из возможных ответов для первого примера — последовательность \([[2, 1, 2], [1, 2, 2]]\). У каждого массива размера \(3\), элементы которого — числа от \(1\) до \(2\), есть предок в этой последовательности: - для массива \([1, 1, 1]\) предок — \([1, 2, 2]\): \(F([1, 2, 2], 13) = [1, 1, 1]\);
- для массива \([1, 1, 2]\) предок — \([1, 2, 2]\): \(F([1, 2, 2], 2) = [1, 1, 2]\);
- для массива \([1, 2, 1]\) предок — \([2, 1, 2]\): \(G([2, 1, 2], 1, 2) = [1, 2, 1]\);
- для массива \([1, 2, 2]\) предок — \([1, 2, 2]\);
- для массива \([2, 1, 1]\) предок — \([1, 2, 2]\): \(G([1, 2, 2], 1, 2) = [2, 1, 1]\);
- для массива \([2, 1, 2]\) предок — \([2, 1, 2]\);
- для массива \([2, 2, 1]\) предок — \([2, 1, 2]\): \(F([2, 1, 2], 2) = [2, 2, 1]\);
- для массива \([2, 2, 2]\) предок — \([1, 2, 2]\): \(G(F([1, 2, 2], 4), 1, 2) = G([1, 1, 1], 1, 2) = [2, 2, 2]\).
| |
![]()
|
|
A. Странная сумма
Структуры данных
Комбинаторика
математика
геометрия
*1400
сортировки
матрицы
У Егора есть табличка \(n \times m\), где строки пронумерованы от \(1\) до \(n\) сверху вниз, а столбцы пронумерованы с \(1\) до \(m\) слева направо. Каждая клетка таблички покрашена в некоторый цвет, где цвета пронумерованы целыми числами от \(1\) до \(10^5\). Будем обозначать клетку, которая находится на пересечении \(r\)-й строки и \(c\)-го столбца, как \((r, c)\). Определим манхэттенское расстояние между клетками \((r_1, c_1)\) и \((r_2, c_2)\) как длину кратчайшего пути между этими клетками, в котором любые две соседние клетки имеют общую сторону. Например, в таблице \(3 \times 4\) манхэттенское расстояние между клетками \((1, 2)\) и \((3, 3)\) равно \(3\), и один из кратчайших путей имеет вид \((1, 2) \to (2, 2) \to (2, 3) \to (3, 3)\). Обратите внимание, что путь может проходить по клеткам любого цвета. У Егора возникло желание посчитать сумму манхэттенских расстояний по всем парам клеток одного цвета. Помогите Егору — вычислите эту сумму. Выходные данные Выведите одно число — искомую сумму. Примечание В первом примере есть три пары клеток с одинаковым цветом: в координатах \((1, 1)\) и \((2, 3)\), в координатах \((1, 2)\) и \((2, 2)\), в координатах \((1, 3)\) и \((2, 1)\). Соответствующие манхеттенские расстояния равны \(3\), \(1\) и \(3\), их сумма равна \(7\). | |
![]()
|
|
C. Тайлер и строки
Структуры данных
Комбинаторика
реализация
*1900
Маленький Тайлер зашел на кухню и увидел, что на холодильнике магнитиками выложена строка \(s\). Он сразу увидел её безграничный потенциал! Тайлеру нравятся строки, особенно те, которые лексикографически меньше другой строки \(t\). Играя с магнитиками на холодильнике, он задумался, а сколько различных строк, лексикографически меньших строки \(t\), он может собрать, переставляя буквы в строке \(s\). Так как он учится всего лишь во втором классе, он не может этого посчитать, поэтому просит вас о помощи! Так как в алфавите языка Тайлера много букв, то для вашего удобства Тайлер уже заменил одинаковые буквы в строках \(s\) и \(t\) одинаковыми числами, а разные — разными. Напомним, что строка \(x\) лексикографически меньше строки \(y\), если выполнено одно из двух условий: - существует такая позиция символа \(m\), присутствующая в обеих строках, что до \(m\)-го символа строки совпадают, а \(m\)-й символ строки \(x\) меньше \(m\)-го символа \(y\),
- строка \(x\) является префиксом \(y\) и \(x \neq y\).
Так как ответ может быть слишком большим, выведите его по модулю \(998\,244\,353\). Выходные данные Выведите единственное число — количество строк, лексикографически меньших \(t\), которые можно получить, переставляя буквы в \(s\), по модулю \(998\,244\,353\). Примечание В первом примере интересующие нас строки это \([1\, 2\, 2]\) и \([2\, 1\, 2]\). Строка \([2\, 2\, 1]\) лексикографически больше строки \([2\, 1\, 2\, 1]\), поэтому её мы не считаем. Во втором примере подходят все строки, кроме \([4\, 3\, 2\, 1]\), так что их \(4! - 1 = 23\). В третьем примере подходит только строка \([1\, 1\, 1\, 2]\). | |
![]()
|
|
E. Сумма паросочетаний
Паросочетания
Перебор
Конструктив
Комбинаторика
математика
*2600
поиск в глубину и подобное
жадные алгоритмы
Обозначим размер максимального паросочетания в графе \(G\) как \(\mathit{MM}(G)\). Задан двудольный граф. Вершины первой доли пронумерованы от \(1\) до \(n\). Вершины второй доли пронумерованы от \(n+1\) до \(2n\). Степень каждой вершины равна \(2\). Для четверки целых чисел \((l, r, L, R)\), где \(1 \le l \le r \le n\) и \(n+1 \le L \le R \le 2n\), определим \(G'(l, r, L, R)\) как граф, который состоит из всех вершин заданного графа, которые находятся либо в отрезке \([l, r]\), либо в отрезке \([L, R]\), и всех ребер заданного графа таких, что вершины их концов принадлежат одному из этих отрезков. Другими словами, чтобы получить граф \(G'(l, r, L, R)\) из изначального графа, надо удалить все вершины \(i\) такие, что \(i \notin [l, r]\) и \(i \notin [L, R]\), и все инцидентные им ребра. Посчитайте сумму \(\mathit{MM}(G(l, r, L, R))\) по всем наборам целых чисел \((l, r, L, R)\) таких, что \(1 \le l \le r \le n\) and \(n+1 \le L \le R \le 2n\). Выходные данные Выведите одно целое число — сумму \(\mathit{MM}(G(l, r, L, R))\) по всем наборам целых чисел \((l, r, L, R)\), у которых \(1 \le l \le r \le n\) и \(n+1 \le L \le R \le 2n\). | |
![]()
|
|
H. Три минимума
Конструктив
Комбинаторика
математика
дп
разделяй и властвуй
бпф
*3500
Для набора различных чисел мы называем первым минимумом, вторым минимумом и третьим минимумом три наименьших значения (в возрастающем порядке). Перестановка \(p_1, p_2, \dots, p_n\) называется хорошей, если для всех пар \((l,r)\), удовлетворяющих \(1\le l < l+2 \le r\le n\), выполняется следующее условие. - Если \(\{p_l, p_r\}\) являются (не обязательно в таком порядке) первым и вторым минимумами среди \(p_l, p_{l+1}, \dots, p_r\), то третий минимум среди \(p_l, p_{l+1},\dots, p_r\) это либо \(p_{l+1}\), либо \(p_{r-1}\).
Вам дано целое число \(n\) и строка \(s\) длины \(m\), состоящая из символов «<» и «>». Вычислите количество хороших перестановок \(p_1, p_2,\dots, p_n\) таких, что для всех \(1\le i\le m\), - \(p_i < p_{i+1}\), если \(s_i =\) «<»;
- \(p_i > p_{i+1}\), если \(s_i =\) «>».
Так как ответ может быть большим, выведите его по модулю \(998\,244\,353\). Выходные данные Выведите одно целое число: количество хороших перестановок, удовлетворяющих ограничениям из условия, по модулю \(998\,244\,353\). Примечание В первом примере существуют \(5\) хороших перестановок, удовлетворяющих условиям, задаваемым строкой \(s\): \([4, 3, 2, 1, 5]\), \([5, 3, 2, 1, 4]\), \([5, 4, 2, 1, 3]\), \([5, 4, 3, 1, 2]\), \([5, 4, 3, 2, 1]\). Каждая из них - хорошая;
- удовлетворяет \(p_1 > p_2\);
- удовлетворяет \(p_2 > p_3\);
- удовлетворяет \(p_3 > p_4\).
Во втором примере существуют \(60\) перестановок таких, что \(p_1 < p_2\). Только \(56\) из них хорошие: перестановки \([1, 4, 3, 5, 2]\), \([1, 5, 3, 4, 2]\), \([2, 4, 3, 5, 1]\), \([2, 5, 3, 4, 1]\) не являются хорошими, потому что необходимое условие не выполнено для \((l, r)\) = \((1, 5)\). Например, для перестановки \([2, 4, 3, 5, 1]\), - первый и второй минимумы — это \(p_5\) и \(p_1\) соответственно (то есть \(\{p_l, p_r\}\) с точностью до порядка);
- третий минимум \(p_3\) (то есть ни \(p_{l+1}\), ни \(p_{r-1}\)).
В третьем примере есть \(23\) хорошие перестановки, удовлетворяющие ограничениям строки \(s\): \([1, 2, 4, 3, 6, 5]\), \([1, 2, 5, 3, 6, 4]\), \([1, 2, 6, 3, 5, 4]\), \([1, 3, 4, 2, 6, 5]\), \([1, 3, 5, 2, 6, 4]\), \([1, 3, 6, 2, 5, 4]\), \([1, 4, 5, 2, 6, 3]\), \([1, 4, 6, 2, 5, 3]\), \([1, 5, 6, 2, 4, 3]\), \([2, 3, 4, 1, 6, 5]\), \([2, 3, 5, 1, 6, 4]\), \([2, 3, 6, 1, 5, 4]\), \([2, 4, 5, 1, 6, 3]\), \([2, 4, 6, 1, 5, 3]\), \([2, 5, 6, 1, 4, 3]\), \([3, 4, 5, 1, 6, 2]\), \([3, 4, 5, 2, 6, 1]\), \([3, 4, 6, 1, 5, 2]\), \([3, 4, 6, 2, 5, 1]\), \([3, 5, 6, 1, 4, 2]\), \([3, 5, 6, 2, 4, 1]\), \([4, 5, 6, 1, 3, 2]\), \([4, 5, 6, 2, 3, 1]\). | |
![]()
|
|
H. Три минимума
Конструктив
Комбинаторика
математика
дп
разделяй и властвуй
бпф
*3500
Для набора различных чисел мы называем первым минимумом, вторым минимумом и третьим минимумом три наименьших значения (в возрастающем порядке). Перестановка \(p_1, p_2, \dots, p_n\) называется хорошей, если для всех пар \((l,r)\), удовлетворяющих \(1\le l < l+2 \le r\le n\), выполняется следующее условие. - Если \(\{p_l, p_r\}\) являются (не обязательно в таком порядке) первым и вторым минимумами среди \(p_l, p_{l+1}, \dots, p_r\), то третий минимум среди \(p_l, p_{l+1},\dots, p_r\) это либо \(p_{l+1}\), либо \(p_{r-1}\).
Вам дано целое число \(n\) и строка \(s\) длины \(m\), состоящая из символов «<» и «>». Вычислите количество хороших перестановок \(p_1, p_2,\dots, p_n\) таких, что для всех \(1\le i\le m\), - \(p_i < p_{i+1}\), если \(s_i =\) «<»;
- \(p_i > p_{i+1}\), если \(s_i =\) «>».
Так как ответ может быть большим, выведите его по модулю \(998\,244\,353\). Выходные данные Выведите одно целое число: количество хороших перестановок, удовлетворяющих ограничениям из условия, по модулю \(998\,244\,353\). Примечание В первом примере существуют \(5\) хороших перестановок, удовлетворяющих условиям, задаваемым строкой \(s\): \([4, 3, 2, 1, 5]\), \([5, 3, 2, 1, 4]\), \([5, 4, 2, 1, 3]\), \([5, 4, 3, 1, 2]\), \([5, 4, 3, 2, 1]\). Каждая из них - хорошая;
- удовлетворяет \(p_1 > p_2\);
- удовлетворяет \(p_2 > p_3\);
- удовлетворяет \(p_3 > p_4\).
Во втором примере существуют \(60\) перестановок таких, что \(p_1 < p_2\). Только \(56\) из них хорошие: перестановки \([1, 4, 3, 5, 2]\), \([1, 5, 3, 4, 2]\), \([2, 4, 3, 5, 1]\), \([2, 5, 3, 4, 1]\) не являются хорошими, потому что необходимое условие не выполнено для \((l, r)\) = \((1, 5)\). Например, для перестановки \([2, 4, 3, 5, 1]\), - первый и второй минимумы — это \(p_5\) и \(p_1\) соответственно (то есть \(\{p_l, p_r\}\) с точностью до порядка);
- третий минимум \(p_3\) (то есть ни \(p_{l+1}\), ни \(p_{r-1}\)).
В третьем примере есть \(23\) хорошие перестановки, удовлетворяющие ограничениям строки \(s\): \([1, 2, 4, 3, 6, 5]\), \([1, 2, 5, 3, 6, 4]\), \([1, 2, 6, 3, 5, 4]\), \([1, 3, 4, 2, 6, 5]\), \([1, 3, 5, 2, 6, 4]\), \([1, 3, 6, 2, 5, 4]\), \([1, 4, 5, 2, 6, 3]\), \([1, 4, 6, 2, 5, 3]\), \([1, 5, 6, 2, 4, 3]\), \([2, 3, 4, 1, 6, 5]\), \([2, 3, 5, 1, 6, 4]\), \([2, 3, 6, 1, 5, 4]\), \([2, 4, 5, 1, 6, 3]\), \([2, 4, 6, 1, 5, 3]\), \([2, 5, 6, 1, 4, 3]\), \([3, 4, 5, 1, 6, 2]\), \([3, 4, 5, 2, 6, 1]\), \([3, 4, 6, 1, 5, 2]\), \([3, 4, 6, 2, 5, 1]\), \([3, 5, 6, 1, 4, 2]\), \([3, 5, 6, 2, 4, 1]\), \([4, 5, 6, 1, 3, 2]\), \([4, 5, 6, 2, 3, 1]\). | |
![]()
|
|
H. Три минимума
Конструктив
Комбинаторика
математика
дп
разделяй и властвуй
бпф
*3500
Для набора различных чисел мы называем первым минимумом, вторым минимумом и третьим минимумом три наименьших значения (в возрастающем порядке). Перестановка \(p_1, p_2, \dots, p_n\) называется хорошей, если для всех пар \((l,r)\), удовлетворяющих \(1\le l < l+2 \le r\le n\), выполняется следующее условие. - Если \(\{p_l, p_r\}\) являются (не обязательно в таком порядке) первым и вторым минимумами среди \(p_l, p_{l+1}, \dots, p_r\), то третий минимум среди \(p_l, p_{l+1},\dots, p_r\) это либо \(p_{l+1}\), либо \(p_{r-1}\).
Вам дано целое число \(n\) и строка \(s\) длины \(m\), состоящая из символов «<» и «>». Вычислите количество хороших перестановок \(p_1, p_2,\dots, p_n\) таких, что для всех \(1\le i\le m\), - \(p_i < p_{i+1}\), если \(s_i =\) «<»;
- \(p_i > p_{i+1}\), если \(s_i =\) «>».
Так как ответ может быть большим, выведите его по модулю \(998\,244\,353\). Выходные данные Выведите одно целое число: количество хороших перестановок, удовлетворяющих ограничениям из условия, по модулю \(998\,244\,353\). Примечание В первом примере существуют \(5\) хороших перестановок, удовлетворяющих условиям, задаваемым строкой \(s\): \([4, 3, 2, 1, 5]\), \([5, 3, 2, 1, 4]\), \([5, 4, 2, 1, 3]\), \([5, 4, 3, 1, 2]\), \([5, 4, 3, 2, 1]\). Каждая из них - хорошая;
- удовлетворяет \(p_1 > p_2\);
- удовлетворяет \(p_2 > p_3\);
- удовлетворяет \(p_3 > p_4\).
Во втором примере существуют \(60\) перестановок таких, что \(p_1 < p_2\). Только \(56\) из них хорошие: перестановки \([1, 4, 3, 5, 2]\), \([1, 5, 3, 4, 2]\), \([2, 4, 3, 5, 1]\), \([2, 5, 3, 4, 1]\) не являются хорошими, потому что необходимое условие не выполнено для \((l, r)\) = \((1, 5)\). Например, для перестановки \([2, 4, 3, 5, 1]\), - первый и второй минимумы — это \(p_5\) и \(p_1\) соответственно (то есть \(\{p_l, p_r\}\) с точностью до порядка);
- третий минимум \(p_3\) (то есть ни \(p_{l+1}\), ни \(p_{r-1}\)).
В третьем примере есть \(23\) хорошие перестановки, удовлетворяющие ограничениям строки \(s\): \([1, 2, 4, 3, 6, 5]\), \([1, 2, 5, 3, 6, 4]\), \([1, 2, 6, 3, 5, 4]\), \([1, 3, 4, 2, 6, 5]\), \([1, 3, 5, 2, 6, 4]\), \([1, 3, 6, 2, 5, 4]\), \([1, 4, 5, 2, 6, 3]\), \([1, 4, 6, 2, 5, 3]\), \([1, 5, 6, 2, 4, 3]\), \([2, 3, 4, 1, 6, 5]\), \([2, 3, 5, 1, 6, 4]\), \([2, 3, 6, 1, 5, 4]\), \([2, 4, 5, 1, 6, 3]\), \([2, 4, 6, 1, 5, 3]\), \([2, 5, 6, 1, 4, 3]\), \([3, 4, 5, 1, 6, 2]\), \([3, 4, 5, 2, 6, 1]\), \([3, 4, 6, 1, 5, 2]\), \([3, 4, 6, 2, 5, 1]\), \([3, 5, 6, 1, 4, 2]\), \([3, 5, 6, 2, 4, 1]\), \([4, 5, 6, 1, 3, 2]\), \([4, 5, 6, 2, 3, 1]\). | |
![]()
|
|
H. Три минимума
Конструктив
Комбинаторика
математика
дп
разделяй и властвуй
бпф
*3500
Для набора различных чисел мы называем первым минимумом, вторым минимумом и третьим минимумом три наименьших значения (в возрастающем порядке). Перестановка \(p_1, p_2, \dots, p_n\) называется хорошей, если для всех пар \((l,r)\), удовлетворяющих \(1\le l < l+2 \le r\le n\), выполняется следующее условие. - Если \(\{p_l, p_r\}\) являются (не обязательно в таком порядке) первым и вторым минимумами среди \(p_l, p_{l+1}, \dots, p_r\), то третий минимум среди \(p_l, p_{l+1},\dots, p_r\) это либо \(p_{l+1}\), либо \(p_{r-1}\).
Вам дано целое число \(n\) и строка \(s\) длины \(m\), состоящая из символов «<» и «>». Вычислите количество хороших перестановок \(p_1, p_2,\dots, p_n\) таких, что для всех \(1\le i\le m\), - \(p_i < p_{i+1}\), если \(s_i =\) «<»;
- \(p_i > p_{i+1}\), если \(s_i =\) «>».
Так как ответ может быть большим, выведите его по модулю \(998\,244\,353\). Выходные данные Выведите одно целое число: количество хороших перестановок, удовлетворяющих ограничениям из условия, по модулю \(998\,244\,353\). Примечание В первом примере существуют \(5\) хороших перестановок, удовлетворяющих условиям, задаваемым строкой \(s\): \([4, 3, 2, 1, 5]\), \([5, 3, 2, 1, 4]\), \([5, 4, 2, 1, 3]\), \([5, 4, 3, 1, 2]\), \([5, 4, 3, 2, 1]\). Каждая из них - хорошая;
- удовлетворяет \(p_1 > p_2\);
- удовлетворяет \(p_2 > p_3\);
- удовлетворяет \(p_3 > p_4\).
Во втором примере существуют \(60\) перестановок таких, что \(p_1 < p_2\). Только \(56\) из них хорошие: перестановки \([1, 4, 3, 5, 2]\), \([1, 5, 3, 4, 2]\), \([2, 4, 3, 5, 1]\), \([2, 5, 3, 4, 1]\) не являются хорошими, потому что необходимое условие не выполнено для \((l, r)\) = \((1, 5)\). Например, для перестановки \([2, 4, 3, 5, 1]\), - первый и второй минимумы — это \(p_5\) и \(p_1\) соответственно (то есть \(\{p_l, p_r\}\) с точностью до порядка);
- третий минимум \(p_3\) (то есть ни \(p_{l+1}\), ни \(p_{r-1}\)).
В третьем примере есть \(23\) хорошие перестановки, удовлетворяющие ограничениям строки \(s\): \([1, 2, 4, 3, 6, 5]\), \([1, 2, 5, 3, 6, 4]\), \([1, 2, 6, 3, 5, 4]\), \([1, 3, 4, 2, 6, 5]\), \([1, 3, 5, 2, 6, 4]\), \([1, 3, 6, 2, 5, 4]\), \([1, 4, 5, 2, 6, 3]\), \([1, 4, 6, 2, 5, 3]\), \([1, 5, 6, 2, 4, 3]\), \([2, 3, 4, 1, 6, 5]\), \([2, 3, 5, 1, 6, 4]\), \([2, 3, 6, 1, 5, 4]\), \([2, 4, 5, 1, 6, 3]\), \([2, 4, 6, 1, 5, 3]\), \([2, 5, 6, 1, 4, 3]\), \([3, 4, 5, 1, 6, 2]\), \([3, 4, 5, 2, 6, 1]\), \([3, 4, 6, 1, 5, 2]\), \([3, 4, 6, 2, 5, 1]\), \([3, 5, 6, 1, 4, 2]\), \([3, 5, 6, 2, 4, 1]\), \([4, 5, 6, 1, 3, 2]\), \([4, 5, 6, 2, 3, 1]\). | |
![]()
|
|
H. Три минимума
Конструктив
Комбинаторика
математика
дп
разделяй и властвуй
бпф
*3500
Для набора различных чисел мы называем первым минимумом, вторым минимумом и третьим минимумом три наименьших значения (в возрастающем порядке). Перестановка \(p_1, p_2, \dots, p_n\) называется хорошей, если для всех пар \((l,r)\), удовлетворяющих \(1\le l < l+2 \le r\le n\), выполняется следующее условие. - Если \(\{p_l, p_r\}\) являются (не обязательно в таком порядке) первым и вторым минимумами среди \(p_l, p_{l+1}, \dots, p_r\), то третий минимум среди \(p_l, p_{l+1},\dots, p_r\) это либо \(p_{l+1}\), либо \(p_{r-1}\).
Вам дано целое число \(n\) и строка \(s\) длины \(m\), состоящая из символов «<» и «>». Вычислите количество хороших перестановок \(p_1, p_2,\dots, p_n\) таких, что для всех \(1\le i\le m\), - \(p_i < p_{i+1}\), если \(s_i =\) «<»;
- \(p_i > p_{i+1}\), если \(s_i =\) «>».
Так как ответ может быть большим, выведите его по модулю \(998\,244\,353\). Выходные данные Выведите одно целое число: количество хороших перестановок, удовлетворяющих ограничениям из условия, по модулю \(998\,244\,353\). Примечание В первом примере существуют \(5\) хороших перестановок, удовлетворяющих условиям, задаваемым строкой \(s\): \([4, 3, 2, 1, 5]\), \([5, 3, 2, 1, 4]\), \([5, 4, 2, 1, 3]\), \([5, 4, 3, 1, 2]\), \([5, 4, 3, 2, 1]\). Каждая из них - хорошая;
- удовлетворяет \(p_1 > p_2\);
- удовлетворяет \(p_2 > p_3\);
- удовлетворяет \(p_3 > p_4\).
Во втором примере существуют \(60\) перестановок таких, что \(p_1 < p_2\). Только \(56\) из них хорошие: перестановки \([1, 4, 3, 5, 2]\), \([1, 5, 3, 4, 2]\), \([2, 4, 3, 5, 1]\), \([2, 5, 3, 4, 1]\) не являются хорошими, потому что необходимое условие не выполнено для \((l, r)\) = \((1, 5)\). Например, для перестановки \([2, 4, 3, 5, 1]\), - первый и второй минимумы — это \(p_5\) и \(p_1\) соответственно (то есть \(\{p_l, p_r\}\) с точностью до порядка);
- третий минимум \(p_3\) (то есть ни \(p_{l+1}\), ни \(p_{r-1}\)).
В третьем примере есть \(23\) хорошие перестановки, удовлетворяющие ограничениям строки \(s\): \([1, 2, 4, 3, 6, 5]\), \([1, 2, 5, 3, 6, 4]\), \([1, 2, 6, 3, 5, 4]\), \([1, 3, 4, 2, 6, 5]\), \([1, 3, 5, 2, 6, 4]\), \([1, 3, 6, 2, 5, 4]\), \([1, 4, 5, 2, 6, 3]\), \([1, 4, 6, 2, 5, 3]\), \([1, 5, 6, 2, 4, 3]\), \([2, 3, 4, 1, 6, 5]\), \([2, 3, 5, 1, 6, 4]\), \([2, 3, 6, 1, 5, 4]\), \([2, 4, 5, 1, 6, 3]\), \([2, 4, 6, 1, 5, 3]\), \([2, 5, 6, 1, 4, 3]\), \([3, 4, 5, 1, 6, 2]\), \([3, 4, 5, 2, 6, 1]\), \([3, 4, 6, 1, 5, 2]\), \([3, 4, 6, 2, 5, 1]\), \([3, 5, 6, 1, 4, 2]\), \([3, 5, 6, 2, 4, 1]\), \([4, 5, 6, 1, 3, 2]\), \([4, 5, 6, 2, 3, 1]\). | |
![]()
|
|
H. Три минимума
Конструктив
Комбинаторика
математика
дп
разделяй и властвуй
бпф
*3500
Для набора различных чисел мы называем первым минимумом, вторым минимумом и третьим минимумом три наименьших значения (в возрастающем порядке). Перестановка \(p_1, p_2, \dots, p_n\) называется хорошей, если для всех пар \((l,r)\), удовлетворяющих \(1\le l < l+2 \le r\le n\), выполняется следующее условие. - Если \(\{p_l, p_r\}\) являются (не обязательно в таком порядке) первым и вторым минимумами среди \(p_l, p_{l+1}, \dots, p_r\), то третий минимум среди \(p_l, p_{l+1},\dots, p_r\) это либо \(p_{l+1}\), либо \(p_{r-1}\).
Вам дано целое число \(n\) и строка \(s\) длины \(m\), состоящая из символов «<» и «>». Вычислите количество хороших перестановок \(p_1, p_2,\dots, p_n\) таких, что для всех \(1\le i\le m\), - \(p_i < p_{i+1}\), если \(s_i =\) «<»;
- \(p_i > p_{i+1}\), если \(s_i =\) «>».
Так как ответ может быть большим, выведите его по модулю \(998\,244\,353\). Выходные данные Выведите одно целое число: количество хороших перестановок, удовлетворяющих ограничениям из условия, по модулю \(998\,244\,353\). Примечание В первом примере существуют \(5\) хороших перестановок, удовлетворяющих условиям, задаваемым строкой \(s\): \([4, 3, 2, 1, 5]\), \([5, 3, 2, 1, 4]\), \([5, 4, 2, 1, 3]\), \([5, 4, 3, 1, 2]\), \([5, 4, 3, 2, 1]\). Каждая из них - хорошая;
- удовлетворяет \(p_1 > p_2\);
- удовлетворяет \(p_2 > p_3\);
- удовлетворяет \(p_3 > p_4\).
Во втором примере существуют \(60\) перестановок таких, что \(p_1 < p_2\). Только \(56\) из них хорошие: перестановки \([1, 4, 3, 5, 2]\), \([1, 5, 3, 4, 2]\), \([2, 4, 3, 5, 1]\), \([2, 5, 3, 4, 1]\) не являются хорошими, потому что необходимое условие не выполнено для \((l, r)\) = \((1, 5)\). Например, для перестановки \([2, 4, 3, 5, 1]\), - первый и второй минимумы — это \(p_5\) и \(p_1\) соответственно (то есть \(\{p_l, p_r\}\) с точностью до порядка);
- третий минимум \(p_3\) (то есть ни \(p_{l+1}\), ни \(p_{r-1}\)).
В третьем примере есть \(23\) хорошие перестановки, удовлетворяющие ограничениям строки \(s\): \([1, 2, 4, 3, 6, 5]\), \([1, 2, 5, 3, 6, 4]\), \([1, 2, 6, 3, 5, 4]\), \([1, 3, 4, 2, 6, 5]\), \([1, 3, 5, 2, 6, 4]\), \([1, 3, 6, 2, 5, 4]\), \([1, 4, 5, 2, 6, 3]\), \([1, 4, 6, 2, 5, 3]\), \([1, 5, 6, 2, 4, 3]\), \([2, 3, 4, 1, 6, 5]\), \([2, 3, 5, 1, 6, 4]\), \([2, 3, 6, 1, 5, 4]\), \([2, 4, 5, 1, 6, 3]\), \([2, 4, 6, 1, 5, 3]\), \([2, 5, 6, 1, 4, 3]\), \([3, 4, 5, 1, 6, 2]\), \([3, 4, 5, 2, 6, 1]\), \([3, 4, 6, 1, 5, 2]\), \([3, 4, 6, 2, 5, 1]\), \([3, 5, 6, 1, 4, 2]\), \([3, 5, 6, 2, 4, 1]\), \([4, 5, 6, 1, 3, 2]\), \([4, 5, 6, 2, 3, 1]\). | |
![]()
|
|
H. Три минимума
Конструктив
Комбинаторика
математика
дп
разделяй и властвуй
бпф
*3500
Для набора различных чисел мы называем первым минимумом, вторым минимумом и третьим минимумом три наименьших значения (в возрастающем порядке). Перестановка \(p_1, p_2, \dots, p_n\) называется хорошей, если для всех пар \((l,r)\), удовлетворяющих \(1\le l < l+2 \le r\le n\), выполняется следующее условие. - Если \(\{p_l, p_r\}\) являются (не обязательно в таком порядке) первым и вторым минимумами среди \(p_l, p_{l+1}, \dots, p_r\), то третий минимум среди \(p_l, p_{l+1},\dots, p_r\) это либо \(p_{l+1}\), либо \(p_{r-1}\).
Вам дано целое число \(n\) и строка \(s\) длины \(m\), состоящая из символов «<» и «>». Вычислите количество хороших перестановок \(p_1, p_2,\dots, p_n\) таких, что для всех \(1\le i\le m\), - \(p_i < p_{i+1}\), если \(s_i =\) «<»;
- \(p_i > p_{i+1}\), если \(s_i =\) «>».
Так как ответ может быть большим, выведите его по модулю \(998\,244\,353\). Выходные данные Выведите одно целое число: количество хороших перестановок, удовлетворяющих ограничениям из условия, по модулю \(998\,244\,353\). Примечание В первом примере существуют \(5\) хороших перестановок, удовлетворяющих условиям, задаваемым строкой \(s\): \([4, 3, 2, 1, 5]\), \([5, 3, 2, 1, 4]\), \([5, 4, 2, 1, 3]\), \([5, 4, 3, 1, 2]\), \([5, 4, 3, 2, 1]\). Каждая из них - хорошая;
- удовлетворяет \(p_1 > p_2\);
- удовлетворяет \(p_2 > p_3\);
- удовлетворяет \(p_3 > p_4\).
Во втором примере существуют \(60\) перестановок таких, что \(p_1 < p_2\). Только \(56\) из них хорошие: перестановки \([1, 4, 3, 5, 2]\), \([1, 5, 3, 4, 2]\), \([2, 4, 3, 5, 1]\), \([2, 5, 3, 4, 1]\) не являются хорошими, потому что необходимое условие не выполнено для \((l, r)\) = \((1, 5)\). Например, для перестановки \([2, 4, 3, 5, 1]\), - первый и второй минимумы — это \(p_5\) и \(p_1\) соответственно (то есть \(\{p_l, p_r\}\) с точностью до порядка);
- третий минимум \(p_3\) (то есть ни \(p_{l+1}\), ни \(p_{r-1}\)).
В третьем примере есть \(23\) хорошие перестановки, удовлетворяющие ограничениям строки \(s\): \([1, 2, 4, 3, 6, 5]\), \([1, 2, 5, 3, 6, 4]\), \([1, 2, 6, 3, 5, 4]\), \([1, 3, 4, 2, 6, 5]\), \([1, 3, 5, 2, 6, 4]\), \([1, 3, 6, 2, 5, 4]\), \([1, 4, 5, 2, 6, 3]\), \([1, 4, 6, 2, 5, 3]\), \([1, 5, 6, 2, 4, 3]\), \([2, 3, 4, 1, 6, 5]\), \([2, 3, 5, 1, 6, 4]\), \([2, 3, 6, 1, 5, 4]\), \([2, 4, 5, 1, 6, 3]\), \([2, 4, 6, 1, 5, 3]\), \([2, 5, 6, 1, 4, 3]\), \([3, 4, 5, 1, 6, 2]\), \([3, 4, 5, 2, 6, 1]\), \([3, 4, 6, 1, 5, 2]\), \([3, 4, 6, 2, 5, 1]\), \([3, 5, 6, 1, 4, 2]\), \([3, 5, 6, 2, 4, 1]\), \([4, 5, 6, 1, 3, 2]\), \([4, 5, 6, 2, 3, 1]\). | |
![]()
|
|
H. Три минимума
Конструктив
Комбинаторика
математика
дп
разделяй и властвуй
бпф
*3500
Для набора различных чисел мы называем первым минимумом, вторым минимумом и третьим минимумом три наименьших значения (в возрастающем порядке). Перестановка \(p_1, p_2, \dots, p_n\) называется хорошей, если для всех пар \((l,r)\), удовлетворяющих \(1\le l < l+2 \le r\le n\), выполняется следующее условие. - Если \(\{p_l, p_r\}\) являются (не обязательно в таком порядке) первым и вторым минимумами среди \(p_l, p_{l+1}, \dots, p_r\), то третий минимум среди \(p_l, p_{l+1},\dots, p_r\) это либо \(p_{l+1}\), либо \(p_{r-1}\).
Вам дано целое число \(n\) и строка \(s\) длины \(m\), состоящая из символов «<» и «>». Вычислите количество хороших перестановок \(p_1, p_2,\dots, p_n\) таких, что для всех \(1\le i\le m\), - \(p_i < p_{i+1}\), если \(s_i =\) «<»;
- \(p_i > p_{i+1}\), если \(s_i =\) «>».
Так как ответ может быть большим, выведите его по модулю \(998\,244\,353\). Выходные данные Выведите одно целое число: количество хороших перестановок, удовлетворяющих ограничениям из условия, по модулю \(998\,244\,353\). Примечание В первом примере существуют \(5\) хороших перестановок, удовлетворяющих условиям, задаваемым строкой \(s\): \([4, 3, 2, 1, 5]\), \([5, 3, 2, 1, 4]\), \([5, 4, 2, 1, 3]\), \([5, 4, 3, 1, 2]\), \([5, 4, 3, 2, 1]\). Каждая из них - хорошая;
- удовлетворяет \(p_1 > p_2\);
- удовлетворяет \(p_2 > p_3\);
- удовлетворяет \(p_3 > p_4\).
Во втором примере существуют \(60\) перестановок таких, что \(p_1 < p_2\). Только \(56\) из них хорошие: перестановки \([1, 4, 3, 5, 2]\), \([1, 5, 3, 4, 2]\), \([2, 4, 3, 5, 1]\), \([2, 5, 3, 4, 1]\) не являются хорошими, потому что необходимое условие не выполнено для \((l, r)\) = \((1, 5)\). Например, для перестановки \([2, 4, 3, 5, 1]\), - первый и второй минимумы — это \(p_5\) и \(p_1\) соответственно (то есть \(\{p_l, p_r\}\) с точностью до порядка);
- третий минимум \(p_3\) (то есть ни \(p_{l+1}\), ни \(p_{r-1}\)).
В третьем примере есть \(23\) хорошие перестановки, удовлетворяющие ограничениям строки \(s\): \([1, 2, 4, 3, 6, 5]\), \([1, 2, 5, 3, 6, 4]\), \([1, 2, 6, 3, 5, 4]\), \([1, 3, 4, 2, 6, 5]\), \([1, 3, 5, 2, 6, 4]\), \([1, 3, 6, 2, 5, 4]\), \([1, 4, 5, 2, 6, 3]\), \([1, 4, 6, 2, 5, 3]\), \([1, 5, 6, 2, 4, 3]\), \([2, 3, 4, 1, 6, 5]\), \([2, 3, 5, 1, 6, 4]\), \([2, 3, 6, 1, 5, 4]\), \([2, 4, 5, 1, 6, 3]\), \([2, 4, 6, 1, 5, 3]\), \([2, 5, 6, 1, 4, 3]\), \([3, 4, 5, 1, 6, 2]\), \([3, 4, 5, 2, 6, 1]\), \([3, 4, 6, 1, 5, 2]\), \([3, 4, 6, 2, 5, 1]\), \([3, 5, 6, 1, 4, 2]\), \([3, 5, 6, 2, 4, 1]\), \([4, 5, 6, 1, 3, 2]\), \([4, 5, 6, 2, 3, 1]\). | |
![]()
|
|
E. Минимальная покрывающая звездочка
Паросочетания
Комбинаторика
математика
дп
*2200
В данной задаче мы рассматриваем полные неориентированные графы, состоящие из \(n\) вершин со взвешенными ребрами. Вес каждого ребра — это целое число от \(1\) до \(k\). Неориентированный граф называется красивым, если сумма весов всех ребер, инцидентных вершине \(1\), равна весу минимального покрывающего дерева в графе. Минимальное покрывающее дерево — это дерево, состоящее из \(n-1\) ребра графа, которое соединяет все \(n\) вершин и имеет наименьшую сумму среди всех таких деревьев; его вес равен сумме весов ребер в нем. Посчитайте количество полных красивых графов, в которых ровно \(n\) вершин и все веса ребер от \(1\) до \(k\). Так как ответ может быть большим, выведите его по модулю \(998244353\). Выходные данные Выведите одно целое число — количество полных красивых графов, в которых ровно \(n\) вершин и все веса ребер от \(1\) до \(k\). Так как ответ может быть большим, выведите его по модулю \(998244353\). | |
![]()
|
|
B. Марин и не взаимно простая перестановка
Комбинаторика
математика
теория чисел
*800
Марин хочет, чтобы вы посчитали количество красивых перестановок. Красивой перестановкой длины \(n\) называется перестановка, обладающая следующим свойством: \(\) \gcd (1 \cdot p_1, \, 2 \cdot p_2, \, \dots, \, n \cdot p_n) > 1, \(\) где \(\gcd\) — это наибольший общий делитель. Перестановка — это массив, состоящий из \(n\) различных целых чисел от \(1\) до \(n\) в произвольном порядке. К примеру, \([2,3,1,5,4]\) является перестановкой, а \([1,2,2]\) — не является (\(2\) встречается в массиве дважды), как и массив \([1,3, 4]\) (\(n=3\), но в массиве присутствует \(4\)). Выходные данные Для каждого набора входных данных выведите одно целое число — количество красивых перестановок. Так как ответ может быть очень большим, выведите его по модулю \(998\,244\,353\). Примечание В первом наборе существует единственная перестановка \([1]\), но она не является красивой, так как \(\gcd(1 \cdot 1) = 1\). Во втором наборе существует единственная красивая перестановка \([2, 1]\), так как \(\gcd(1 \cdot 2, 2 \cdot 1) = 2\). | |
![]()
|
|
N. Drone Photo
Комбинаторика
математика
сортировки
Today, like every year at SWERC, the \(n^2\) contestants have gathered outside the venue to take a drone photo. Jennifer, the social media manager for the event, has arranged them into an \(n\times n\) square. Being very good at her job, she knows that the contestant standing on the intersection of the \(i\)-th row with the \(j\)-th column is \(a_{i,j}\) years old. Coincidentally, she notices that no two contestants have the same age, and that everyone is between \(1\) and \(n^2\) years old. Jennifer is planning to have some contestants hold a banner with the ICPC logo parallel to the ground, so that it is clearly visible in the aerial picture. Here are the steps that she is going to follow in order to take the perfect SWERC drone photo. - First of all, Jennifer is going to select four contestants standing on the vertices of an axis-aligned rectangle.
- Then, she will have the two younger contestants hold one of the poles, while the two older contestants will hold the other pole.
- Finally, she will unfold the banner, using the poles to support its two ends. Obviously, this can only be done if the two poles are parallel and do not cross, as shown in the pictures below.
 Being very indecisive, Jennifer would like to try out all possible arrangements for the banner, but she is worried that this may cause the contestants to be late for the competition. How many different ways are there to choose the four contestants holding the poles in order to take a perfect photo? Two choices are considered different if at least one contestant is included in one but not the other. Output Print the number of ways for Jennifer to choose the four contestants holding the poles. Note In the first sample, there are \(4\) contestants, arranged as follows.  There is only one way to choose four contestants, with one pole held by contestants aged \(1\) and \(2\) and the other one by contestants aged \(3\) and \(4\). But then, as we can see in the picture, the poles cross.  Since there is no valid way to choose four contestants, the answer is \(0\). In the second sample, the \(4\) contestants are arranged as follows.  Once again, there is only one way to choose four contestants, but this time the poles don't cross.  Therefore, the answer is \(1\). In the third sample, the \(9\) contestants are arranged as follows.  There are \(6\) ways of choosing four contestants so that the poles don't cross, as shown in the following pictures.  | |
![]()
|
|
D. Is it rated - 3
Комбинаторика
математика
дп
*особая задача
| |
![]()
|
|
E. Центроидные вероятности
Комбинаторика
математика
дп
*3000
бпф
Рассмотрим все деревья (связные неориентированные ациклические графы) на \(n\) вершинах (\(n\) нечетное, вершины пронумерованы от \(1\) до \(n\)) такие, что для каждого \(2 \le i \le n\) \(i\)-я вершина смежна ровно одной вершине с меньшим номером. Для каждого \(i\) (\(1 \le i \le n\)) найдите количество деревьев, для которых \(i\)-я вершина является центроидом. Ответ может быть очень большим, поэтому выведите его по модулю \(998\,244\,353\). Центроидом называется вершина, после удаления которой дерево разбивается на поддеревья, каждое из которых состоит из не более чем \((n-1)/2\) вершин. Выходные данные В одну строку выведите \(n\) целых чисел, \(i\)-е из которых должно быть равно ответу для \(i\)-й вершины (по модулю \(998\,244\,353\)). Примечание Пример \(1\): существует два возможных дерева: с ребрами \((1-2)\), и \((1-3)\) — здесь центроидом является вершина \(1\); и с ребрами \((1-2)\), и \((2-3)\) — здесь центроидом является вершина \(2\). Таким образом, ответ равен \(1, 1, 0\). Пример \(2\): существует \(24\) возможных дерева. Например, подойдет дерево с ребрами \((1-2)\), \((2-3)\), \((3-4)\), и \((4-5)\). Здесь центроидом является вершина \(3\). | |
![]()
|
|
F. Джи, видишь?
Комбинаторика
дп
*2400
битмаски
Во время подготовки к ICPC команда «Jee You See» наткнулась на одну простую комбинаторную задачу. После большого количества вердиктов «Неправильный ответ» они решили сдаться и разбить выключить компьютер. Теперь они нуждаются в вашей помощи, чтобы дорешать задачу. Вам даны 4 целых числа \(n\), \(l\), \(r\) и \(z\). Вычислите количество массивов \(a\) длины \(n\), состоящих из неотрицательных целых чисел таких, что: - \(l\le a_1+a_2+\ldots+a_n\le r\), а также
- \(a_1\oplus a_2 \oplus \ldots\oplus a_n=z\), где \(\oplus\) обозначает операцию побитового исключающего ИЛИ.
Так как ответ может быть большим, выведите его по модулю \(10^9+7\). Выходные данные Выведите количество подходящих массивов \(a\) по модулю \(10^9+7\). Примечание Следующие массивы подходят в первом примере: - \([1, 0, 0]\);
- \([0, 1, 0]\);
- \([3, 2, 0]\);
- \([2, 3, 0]\);
- \([0, 0, 1]\);
- \([1, 1, 1]\);
- \([2, 2, 1]\);
- \([3, 0, 2]\);
- \([2, 1, 2]\);
- \([1, 2, 2]\);
- \([0, 3, 2]\);
- \([2, 0, 3]\);
- \([0, 2, 3]\).
Следующие массивы подходят во втором примере: - \([2, 0, 0, 0]\);
- \([0, 2, 0, 0]\);
- \([0, 0, 2, 0]\);
- \([0, 0, 0, 2]\).
| |
![]()
|
|
E. Прямой обход
Деревья
Комбинаторика
*2100
дп
сортировки
разделяй и властвуй
хэши
снм
Дано корневое дерево из \(2^n - 1\) вершин. У каждой вершины дерева либо \(0\) сыновей, либо \(2\). Все листья дерева расположены на одинаковой глубине, а у каждой внутренней вершины один из сыновей является левым, а другой — правым. Формально, вам задано совершенное бинарное дерево. Вершины дерева пронумерованы следующим образом: - номер корня — \(1\);
- если номер внутренней вершины — \(x\), то номер ее левого сына — \(2x\), а номер правого сына — \(2x+1\).
На каждой вершине дерева записана буква A или буква B. Пусть буква на вершине \(x\) — это \(s_x\). Назовем строкой прямого обхода вершины \(x\) строку, которая строится по следующим правилам: - если вершина \(x\) — лист, то строка прямого обхода \(x\) состоит из одного символа \(s_x\);
- в противном случае строка прямого обхода \(x\) равна \(s_x + f(l_x) + f(r_x)\), где \(+\) обозначает конкатенацию строк, \(f(l_x)\) — строка прямого обхода левого сына \(x\), а \(f(r_x)\) — строка прямого обхода правого сына \(x\).
Строка прямого обхода всего дерева — это строка прямого обхода его корня. А теперь — сама задача. Вы должны посчитать количество различных строк, которые могут быть получены как строка прямого обхода заданного дерева, если до построения строки прямого обхода можно применить следующую операцию любое количество раз: - выбрать любую вершину \(x\), не являющуюся листом, и поменять местами ее детей (то есть левый сын становится правым, и наоборот).
Выходные данные Выведите одно целое число — количество различных строк, которые можно получить в качестве строки прямого обхода дерева, если можно применить любое количество описанных в условии операций. Ответ может быть очень большим, поэтому выведите его по модулю \(998244353\). | |
![]()
|
|
F. Подсчет перестановок
Перебор
Комбинаторика
математика
дп
*2700
бпф
Посчитайте количество таких перестановок \(p\) размера \(n\), в которых ровно \(k\) инверсий (пар индексов \((i, j)\), для которых \(i < j\) и \(p_i > p_j\)) и ровно \(x\) индексов \(i\), для которых \(p_i > p_{i+1}\). Да, это вся задача. Удачи! Выходные данные Для каждого набора входных данных выведите одно целое число — количество перестановок, описанных в условии задачи. Так как ответ может быть очень большим, выведите его по модулю \(998244353\). | |
![]()
|
|
D. Потерянная арифметическая прогрессия
Комбинаторика
математика
теория чисел
*1900
Очень давно вы придумали две конечные арифметические прогрессии \(A\) и \(B\). Затем вы нашли другую последовательность \(C\), состоящую из всех элементов, принадлежащих одновременно и \(A\), и \(B\). Нетрудно заметить, что \(C\) также является конечной арифметической прогрессией. За долгие годы вы забыли \(A\), но помните \(B\) и \(C\). Вы по какой-то причине очень хотите найти эту забытую арифметическую прогрессию. Прежде чем начать этот поиск, вы хотите узнать, сколько существует различных конечных арифметических прогрессий, которые могут быть вашей забытой арифметической прогрессией \(A\). Две арифметические прогрессии считаются различными, если у них различается первый член, разность или количество членов. Возможно, существует бесконечно много таких арифметических прогрессий, в этом случае вы даже не будете пытаться их искать! Выведите \(-1\) в таком случае. Даже если существует конечное число таких арифметических прогрессий, ответ может быть очень большим. Поэтому вас интересует ответ по модулю \(10^9+7\). Выходные данные Для каждого набора входных данных выведите единственную строку, содержащую единственное число. Если существует бесконечно много конечных арифметических прогрессий, которые могут быть потерянной прогрессией \(A\), выведите \(-1\). Иначе, выведите количество конечных арифметических прогрессий, которые могут быть потерянной прогрессией \(A\), по модулю \(10^9+7\). В частности, если не существует таких арифметических прогрессий, выведите \(0\). Примечание В первом наборе входных данных \(B=\{-3,-2,-1,0,1,2,3\}\) и \(C=\{-1,1,3,5\}\). Не существует таких арифметических прогрессий, которые могли быть равны \(A\), поскольку \(5\) не находится в \(B\), и для любого \(A\), \(5\) не может находиться в \(C\) также. Во втором наборе входных данных \(B=\{-9,-6,-3,0,3,6,9,12,15,18,21\}\) и \(C=\{0,6,12\}\). Существует \(10\) возможных арифметических прогрессий, которые могут быть равны \(A\): - \(\{0,6,12\}\)
- \(\{0,2,4,6,8,10,12\}\)
- \(\{0,2,4,6,8,10,12,14\}\)
- \(\{0,2,4,6,8,10,12,14,16\}\)
- \(\{-2,0,2,4,6,8,10,12\}\)
- \(\{-2,0,2,4,6,8,10,12,14\}\)
- \(\{-2,0,2,4,6,8,10,12,14,16\}\)
- \(\{-4,-2,0,2,4,6,8,10,12\}\)
- \(\{-4,-2,0,2,4,6,8,10,12,14\}\)
- \(\{-4,-2,0,2,4,6,8,10,12,14,16\}\)
В третьем наборе входных данных \(B=\{2,7,12,17,22\}\) и \(C=\{7,12,17,22\}\). Существует бесконечно много конечных арифметических прогрессий, которые могут быть равны \(A\): - \(\{7,12,17,22\}\)
- \(\{7,12,17,22,27\}\)
- \(\{7,12,17,22,27,32\}\)
- \(\{7,12,17,22,27,32,37\}\)
- \(\{7,12,17,22,27,32,37,42\}\)
- \(\ldots\)
| |
![]()
|
|
E. Power или XOR?
Комбинаторика
математика
теория чисел
битмаски
*2500
Символ \(\wedge\) довольно неоднозначный, особенно когда используется без контекста. Иногда используется для обозначения возведения в степень (\(a\wedge b = a^b\)), а иногда используется для обозначения операции побитового исключающего ИЛИ (\(a\wedge b=a\oplus b\)). У вас неоднозначное выражение \(E=A_1\wedge A_2\wedge A_3\wedge\ldots\wedge A_n\). Вы можете заменить каждый \(\wedge\) символ на \(\texttt{Power}\) (возведение в степень) или на \(\texttt{XOR}\) (исключающее ИЛИ), чтобы получить однозначное выражение \(E'\). Значение выражения \(E'\) определяется по следующим правилам: - Все \(\texttt{Power}\) операции выполняются перед всеми \(\texttt{XOR}\) операциями. Иными словами, \(\texttt{Power}\) операция имеет приоритет перед \(\texttt{XOR}\) операциями. Например, \(4\;\texttt{XOR}\;6\;\texttt{Power}\;2=4\oplus (6^2)=4\oplus 36=32\).
- Последовательные возведения в степень выполняются слева направо. Например, \(2\;\texttt{Power}\;3 \;\texttt{Power}\;4 = (2^3)^4 = 8^4 = 4096\).
Вам дан массив \(B\) длины \(n\) и целое число \(k\). Массив \(A\) получается как \(A_i=2^{B_i}\) и выражение \(E\) получается как \(E=A_1\wedge A_2\wedge A_3\wedge\ldots\wedge A_n\). Вам нужно найти XOR значений всех возможных однозначных выражений \(E'\), которые могут быть получены из \(E\) и имеют хотя бы \(k\) \(\wedge\) символов, используемых как \(\texttt{XOR}\) операции. Поскольку ответ может быть очень большим, вам нужно найти его по модулю \(2^{2^{20}}\). Поскольку это число также может быть очень большим, вам нужно вывести его двоичное представление без лидирующих нулей. Если ответ равен \(0\), выведите \(0\). Выходные данные Выведите единственную строку, содержащую двоичную строку без лидирующих нулей, обозначающую ответ на задачу. Если ответ равен \(0\), выведите \(0\). Примечание Для всех примеров с \(1\) до \(3\), \(A = \{2^3,2^1,2^2\} = \{8,2,4\}\) и \(E=8\wedge 2\wedge 4\). В первом примере существует только одно возможное подходящее однозначное выражение \(E' = 8\oplus 2\oplus 4 = 14 = (1110)_2\). Во втором примере существуют три возможные подходящие однозначные выражения \(E'\): - \(8\oplus 2\oplus 4 = 14\)
- \(8^2\oplus 4 = 64\oplus 4= 68\)
- \(8\oplus 2^4 = 8\oplus 16= 24\)
XOR всех их значений равен \(14\oplus 68\oplus 24 = 82 = (1010010)_2\). Во третьем примере существуют четыре возможные подходящие однозначные выражения \(E'\): - \(8\oplus 2\oplus 4 = 14\)
- \(8^2\oplus 4 = 64\oplus 4= 68\)
- \(8\oplus 2^4 = 8\oplus 16= 24\)
- \((8^2)^4 = 64^4 = 2^{24} = 16777216\)
XOR всех их значений равен \(14\oplus 68\oplus 24\oplus 16777216 = 16777298 = (1000000000000000001010010)_2\). В четвёртом примере \(A=\{2,2\}\) и \(E=2\wedge 2\). Единственное возможное подходящее однозначное выражение \(E' = 2\oplus 2 = 0 = (0)_2\). | |
![]()
|
|
B. Словарь
Комбинаторика
математика
*800
Берляндский язык состоит из слов, образованных ровно двумя буквами. Более того, первая буква в слове отличается от второй буквы. Любое сочетание двух различных берляндских букв (которые, кстати, такие же, как и строчные буквы латинского алфавита) — это корректное слово в берляндском языке. В берляндском словаре записаны все слова этого языка. Слова упорядочены так же, как и обычно в словарях. Формально, слово \(a\) идет до слова \(b\) в словаре, если выполняется одно из следующих условий: - первая буква слова \(a\) меньше первой буквы слова \(b\);
- первые буквы в словах \(a\) и \(b\) одинаковые, а вторая буква слова \(a\) меньше второй буквы слова \(b\).
Поэтому словарь выглядит так: - Слово \(1\): ab
- Слово \(2\): ac
- ...
- Слово \(25\): az
- Слово \(26\): ba
- Слово \(27\): bc
- ...
- Слово \(649\): zx
- Слово \(650\): zy
Дано слово \(s\) из берляндского языка. Ваша задача — найти его позицию в словаре. Выходные данные На каждый набор входных данных выведите одно целое число — позицию слова \(s\) в словаре. | |
![]()
|
|
C. Бесконечная замена
Строки
Комбинаторика
*1000
реализация
Дана строка \(s\), состоящая только из латинских букв 'a', и строка \(t\), состоящая из строчных латинских букв. За один ход вы можете заменить любую букву 'a' в строке \(s\) на строку \(t\). Обратите внимание, что после замены в строке \(s\) могут оказаться буквы, отличные от 'a'. Можно проделать произвольное количество ходов (включая ноль). Сколько различных строк можно получить? Выведите это число или скажите, что оно бесконечно большое. Две строки считаются различными, если у них различается длина, или они различаются в какой-либо позиции. Выходные данные На каждый набор входных данных выведите количество различных строк \(s\), которые можно получить после применения произвольного количества ходов (включая ноль). Если это число бесконечно большое, то выведите -1. Иначе выведите это число. Примечание В первом примере можно заменить любую букву 'a' на строку «a», но это не изменит строку. Так что вне зависимости от того, сколько ходов вы проделаете, вы не сможете получить строку отличную от начальной. Во втором примере можно заменить вторую букву 'a' на «abc». Строка \(s\) становится равна «aabc». Затем снова вторую букву 'a'. Строка \(s\) становится равна «aabcbc». И так далее, производя бесконечно много различных строк. В третьем примере можно либо оставить строку \(s\) как есть, проделав ноль ходов, либо заменить единственную 'a' на «b». Строка \(s\) становится равна «b», так что над ней больше нельзя проделать ходы. | |
![]()
|
|
E. Типичная вечеринка в общаге
Строки
Комбинаторика
дп
*2400
битмаски
Сегодня в общаге праздник — приехал Олег, в честь чего девочки подарили ему строку. Олегу очень понравился подарок, поэтому он тут же придумал и предложил вам, лучшему его другу, следующую задачу. Вам дана строка \(s\) длины \(n\), которая состоит из первых \(17\) строчных букв латинского алфавита {\(a\), \(b\), \(c\), \(\ldots\), \(p\), \(q\)} и знаков вопроса. А также \(q\) запросов. Каждый запрос характеризуется набором попарно различных строчных первых \(17\) букв латинского алфавита, которые можно использовать чтобы заменить знаки вопроса в строке \(s\). Ответом на запрос является сумма количества различных подстрок, которые являются палиндромами, по всем строкам, которые можно получить из изначальной строки \(s\) путем замены знаков вопроса на разрешенные символы. Ответ необходимо посчитать по модулю \(998\,244\,353\). Обратите внимание! Две подстроки являются различными, когда отличаются их позиции начала и окончания в строке. Т. е. количество различных подстрок, которые являются палиндромами, для строки aba будет \(4\): a, b, a, aba. Рассмотрим примеры замены знаков вопроса на буквы. Например, из строки aba??ee при запросе {\(a\), \(b\)} можно получить строки ababaee или abaaaee но нельзя получить строки pizza, abaee, abacaba, aba?fee, aba47ee, или abatree. Напомним, что палиндромом называется строка, которая одинаково читается как слева направо, так и справа налево. Выходные данные На каждый запрос выведите одно число — суммарное количество подстрок-палиндромов во всех возможных строках, которые можно получить из строки \(s\), по модулю \(998\,244\,353\). Примечание Рассмотрим первый пример и первый запрос в нём. У нас может получится только одна строка по итогам замены знаков вопроса — abaaaba. В ней есть такие подстроки-палиндромы: - a — подстрока [\(1\); \(1\)].
- b — подстрока [\(2\); \(2\)].
- a — подстрока [\(3\); \(3\)].
- a — подстрока [\(4\); \(4\)].
- a — подстрока [\(5\); \(5\)].
- b — подстрока [\(6\); \(6\)].
- a — подстрока [\(7\); \(7\)].
- aa — подстрока [\(3\); \(4\)].
- aa — подстрока [\(4\); \(5\)].
- aba — подстрока [\(1\); \(3\)].
- aaa — подстрока [\(3\); \(5\)].
- aba — подстрока [\(5\); \(7\)].
- baaab — подстрока [\(2\); \(6\)].
- abaaaba — подстрока [\(1\); \(7\)].
В третьем запросе у нас может получится 4 строки: abaaaba, abababa, abbaaba, abbbaba. | |
![]()
|
|
E. Стань больше
Конструктив
Комбинаторика
математика
теория чисел
жадные алгоритмы
*3500
У Shinmyoumaru есть молоток, который может увеличивать или уменьшать предметы. Она проверяет это на последовательности \(a\) и числе \(v\), начальное значение которого равно \(1\). Она хочет получить \(v = \gcd\limits_{i\ne j}\{a_i\cdot a_j\}\), используя не более \(10^5\) операций (\(\gcd\limits_{i\ne j}\{a_i\cdot a_j\}\)обозначает \(\gcd\) всех произведений двух различных элементов последовательности \(a\)). В каждой операции она выбирает подпоследовательность \(b\) последовательности \(a\) и выполняет одно из следующих действий. - Увеличить: \(v = v \cdot \mathrm{lcm}(b)\)
- Уменьшить: \(v = \frac{v}{\mathrm{lcm}(b)}\)
Обратите внимание, что ей не нужно гарантировать, чтобы \(v\) являлось целым числом, то есть \(v\) не обязательно должно быть кратным \(\mathrm{lcm}(b)\) при выполнении операции уменьшать. Кроме того, она хочет гарантировать, чтобы суммарная длина \(b\), выбранных для операций, не превышала \(10^6\). Найдите возможную последовательность действий для нее. Вам не нужно ничего минимизировать. Выходные данные Первая строка содержит целое неотрицательное число \(k\) (\(0\leq k\leq 10^5\)) — количество операций. Следующие \(k\) строк содержат несколько целых чисел. В каждой строке первые два целых числа \(f\) (\(f\in\{0,1\}\)) и \(p\) (\(1\le p\le n\)) обозначают выбранный вами вариант (\(0\) для увеличения и \(1\) для уменьшения) и длину \(b\). Остальные целые числа \(p\) в строке \(i_1,i_2,\ldots,i_p\) (\(1\le i_1<i_2<\ldots<i_p\le n\)) представляют собой индексы подпоследовательности. Формально \(b_j=a_{i_j}\). Примечание В первом наборе входных данных \(\gcd\limits_{i\ne j}\{a_i\cdot a_j\}=\gcd\{60,90,150\}=30\). Выполните \(v = v\cdot \operatorname{lcm}\{a_1,a_2,a_3\}=30\). Во втором наборе входных данных \(\gcd\limits_{i\ne j}\{a_i\cdot a_j\}=8\). Выполните \(v = v\cdot \operatorname{lcm}\{a_4\}=16\). Затем выполните \(v = \frac{v}{\operatorname{lcm}\{a_1\}}=8\). | |
![]()
|
|
F. Дерево и k-подмножества
Деревья
Комбинаторика
математика
дп
поиск в глубину и подобное
*2500
Вам дано дерево \(G\) из \(n\) вершин, а также целое число \(k\). Вершины дерева пронумерованы от \(1\) до \(n\). Для некоторой вершины \(r\) и подмножества \(S\) вершин дерева \(G\) такого, что \(|S| = k\), определим \(f(r, S)\) как размер наименьшего корневого поддерева, содержащего все вершины \(S\) при условии, что корнем дерева является вершина \(r\). Множество вершин \(T\) называется корневым поддеревом, если все вершины в \(T\) связны и для любой вершины в \(T\) все ее потомки тоже принадлежат \(T\). Вам нужно вычислить сумму \(f(r, S)\) по всем различным комбинациям вершины \(r\) и подмножества \(S\), где \(|S| = k\). Формально, вычислите следующее: \(\)\sum_{r \in V} \sum_{S \subseteq V, |S| = k} f(r, S),\(\) где \(V\) — множество вершин дерева \(G\). Выведите ответ по модулю \(10^9 + 7\). Выходные данные Выведите ответ по модулю \(10^9 + 7\). Примечание Дерево во втором примере показано ниже: 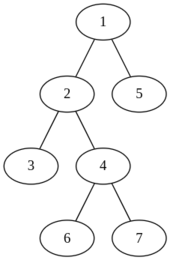 Всего в этом дереве \(21\) подмножество вершин размера \(2\). А именно, \(\)S \in \left\{\{1, 2\}, \{1, 3\}, \{1, 4\}, \{1, 5\}, \{1, 6\}, \{1, 7\}, \{2, 3\}, \{2, 4\}, \{2, 5\}, \{2, 6\}, \{2, 7\}, \{3, 4\}, \{3, 5\}, \{3, 6\}, \{3, 7\}, \{4, 5\}, \{4, 6\}, \{4, 7\}, \{5, 6\}, \{5, 7\}, \{6, 7\} \right\}.\(\) Так как в дереве \(7\) вершин, \(1 \le r \le 7\). Нужно найти сумму \(f(r, S)\) по всем парам \(r\) и \(S\). Ниже перечислены значения \(f(r, S)\) для некоторых комбинаций \(r\) и \(S\). - \(r = 1\), \(S = \{3, 7\}\). Значение \(f(r, S)\) равно \(5\), а соответствующее поддерево равно \(\{2, 3, 4, 6, 7\}\).
- \(r = 1\), \(S = \{5, 4\}\). Значение \(f(r, S)\) равно \(7\), а соответствующее поддерево равно \(\{1, 2, 3, 4, 5, 6, 7\}\).
- \(r = 1\), \(S = \{4, 6\}\). Значение \(f(r, S)\) равно \(3\), а соответствующее поддерево равно \(\{4, 6, 7\}\).
| |
![]()
|
|
E. Размещение кукол
Комбинаторика
математика
*2000
Будем говорить, что бесконечная последовательность \(a_{0}, a_{1}, a_2, \ldots\) является невозрастающей, если и только если \(a_i \ge a_{i+1}\) для всех \(i\ge 0\). Дано бесконечное вправо и вниз клетчатое поле. Верхняя левая клетка имеет координаты \((0,0)\). Строки пронумерованы от \(0\) до бесконечности сверху вниз, столбцы пронумерованы от \(0\) до бесконечности слева направо. Также дана невозрастающая бесконечная последовательность \(a_{0}, a_{1}, a_2, \ldots\). Вам заданы \(a_0\), \(a_1\), \(\ldots\), \(a_n\). Также известно, что \(a_i=0\) для всех \(i>n\). Для любой пары \(x\), \(y\) клетка с координатами \((x,y)\) (расположенная на пересечении \(x\)-й строки и \(y\)-го столбца) покрашена в белый цвет, если \(y<a_x\), а иначе покрашена в чёрный. Изначально на всём поле есть лишь одна кукла, расположенная в клетке \((0,0)\). Вы можете выполнять следующую операцию. - Выбрать одну куклу в клетке \((x,y)\). Затем удалить её и добавить по кукле в клетки \((x,y+1)\) и \((x+1,y)\).
Обратите внимание, что в одной клетке одновременно может находиться несколько кукол; за одну операцию вы удаляете только одну куклу. Ваша цель — сделать так, чтобы во всех белых клетках было ровно \(0\) кукол. Чему равно минимальное число операций, за которое можно достичь этой цели? Выведите ответ по модулю \(10^9+7\). Выходные данные Выведите одно число — ответ на задачу по модулю \(10^9+7\). Примечание Рассмотрим первый пример. На данном поле клетки \((0,0),(0,1),(1,0),(1,1)\) являются белыми, а все остальные — чёрными. Для описания поля будем использовать тройки: тройка \((x,y,z)\) означает, что в клетке \((x,y)\) расположено \(z\) кукол. Изначальное состояние поля: \((0,0,1)\). Одной из оптимальных последовательностей операций является следующая: - Выполнить операцию для \((0,0)\). Состояние поля станет таким: \((1,0,1),(0,1,1)\).
- Выполнить операцию для \((0,1)\). Состояние поля станет таким: \((1,0,1),(1,1,1),(0,2,1)\).
- Выполнить операцию для \((1,0)\). Состояние поля станет таким: \((1,1,2),(0,2,1),(2,0,1)\).
- Выполнить операцию для \((1,1)\). Состояние поля станет таким: \((1,1,1),(0,2,1),(2,0,1),(1,2,1),(2,1,1)\).
- Выполнить операцию для \((1,1)\). Состояние поля станет таким: \((0,2,1),(2,0,1),(1,2,2),(2,1,2)\).
После этого все белые клетки содержат по \(0\) кукол, так что цель достигнута за \(5\) операций. | |
![]()
|
|
H. Максимальное произведение?
Перебор
Комбинаторика
математика
реализация
дп
жадные алгоритмы
*3500
Вам дано положительное целое число \(k\). Для мультимножества целых чисел \(S\) определим \(f(S)\) следующим образом: - Если количество элементов в \(S\) меньше чем \(k\), то \(f(S)=0\).
- Иначе определим \(f(S)\) как максимально возможное произведение при выборе ровно \(k\) элементов из \(S\).
Более формально, пусть \(|S|\) означает число элементов в \(S\). Тогда, - Если \(|S|<k\), то \(f(S)=0\).
- Иначе \(f(S)=\max\limits_{T\subseteq S,|T|=k}\left(\prod\limits_{i\in T}i\right)\).
Вам дано мультимножество целых чисел \(A\). Вычислите \(\sum\limits_{B\subseteq A} f(B)\) по модулю \(10^9+7\). Обратите внимание, что в этой задаче элементы считаются различными, если они имеют различные индексы, но необязательно различные значения. То есть мультимножество, состоящее из \(n\) элементов, всегда содержит \(2^n\) различных подмножеств вне зависимости от того, равны ли в нём какие-то элементы или нет. Выходные данные Выведите \(\sum\limits_{B\subseteq A} f(B)\) по модулю \(10^9+7\). Примечание Рассмотрим первый тестовый пример. Из определения, - \(f(\varnothing)=0\)
- \(f(\{-1\})=0\)
- \(f(\{2\})=0\)
- \(f(\{4\})=0\)
- \(f(\{-1,2\})=-2\)
- \(f(\{-1,4\})=-4\)
- \(f(\{2,4\})=8\)
- \(f(\{-1,2,4\})=8\)
Таким образом, вывести необходимо \((0+0+0+0-2-4+8+8)\bmod (10^9+7)=10\). Во втором тестовом примере мультимножество, хоть и состоит из трёх равных элементов, содержит \(8\) различных подмножеств: \(\varnothing,\{1\},\{1\},\{1\},\{1,1\},\{1,1\},\{1,1\},\{1,1,1\}\). | |
![]()
|
|
E. Раскраска
Перебор
Конструктив
Комбинаторика
математика
реализация
геометрия
дп
жадные алгоритмы
*2400
графы
Заданы \(n\) точек на плоскости, координаты \(i\)-й из них — \((x_i, y_i)\). Ни у каких двух точек не совпадают координаты. Расстояние между точками \(i\) и \(j\) определено как \(d(i,j) = |x_i - x_j| + |y_i - y_j|\). Для каждой точки необходимо выбрать цвет — целое число от \(1\) до \(n\). Для каждой упорядоченной тройки различных точек \((a,b,c)\) должны выполняться следующие условия: - если \(a\), \(b\) и \(c\) покрашены в одинаковый цвет, то \(d(a,b) = d(a,c) = d(b,c)\);
- если \(a\) и \(b\) покрашены в одинаковый цвет, а цвет \(c\) отличен от цвета \(a\), то \(d(a,b) < d(a,c)\) и \(d(a,b) < d(b,c)\).
Посчитайте количество различных способов выбрать цвета, чтобы удовлетворить данные условия. Выходные данные Выведите одно целое число — количество различных способов выбрать цвета точек. Так как оно может быть довольно велико, выведите его остаток от деления на \(998244353\). Примечание В первом тесте подходят следующие способы выбрать цвета: - \([1, 1, 1]\);
- \([2, 2, 2]\);
- \([3, 3, 3]\);
- \([1, 2, 3]\);
- \([1, 3, 2]\);
- \([2, 1, 3]\);
- \([2, 3, 1]\);
- \([3, 1, 2]\);
- \([3, 2, 1]\).
| |
![]()
|
|
E. PermutationForces II
Деревья
Перебор
Комбинаторика
жадные алгоритмы
сортировки
*2300
Вам дана перестановка \(a\) длины \(n\). Напомним, что перестановкой называется массив из \(n\) различных чисел от \(1\) до \(n\) в произвольном порядке. Ваша сила равна \(s\). Вы можете выполнить \(n\) операций с перестановкой \(a\). \(i\)-я операция состоит в следующем: - Выберите два значения \(x\) и \(y\) такие, что \(i \leq x \leq y \leq \min(i+s,n)\), и поменяйте местами числа \(x\) и \(y\) в перестановке \(a\). Обратите внимание, что вы можете выбрать \(x=y\), в таком случае обмена не произойдет.
Вы хотите превратить \(a\) в другую перестановку \(b\) после \(n\) операций. Однако некоторые элементы \(b\) отсутствуют и заменены на \(-1\). Вычислите количество способов заменить каждую \(-1\) в \(b\) на некоторое целое число от \(1\) до \(n\) так, чтобы \(b\) была перестановкой, и можно было превратить \(a\) в \(b\) силой \(s\). Так как ответ может быть большим, выведите его по модулю \(998\,244\,353\). Выходные данные Для каждого набора входных данных выведите одно целое число — количество способов достроить перестановку \(b\) так, чтобы можно было превратить \(a\) в \(b\) силой \(s\), по модулю \(998\,244\,353\). Примечание В первом примере \(a=[2,1,3]\). Существуют два способа заменить \(-1\), чтобы \(b\) стала перестановкой: \([3,1,2]\) и \([3,2,1]\). Перестановку \(a\) можно превратить в \([3,1,2]\) силой \(1\) следующим образом: \(\)[2,1,3] \xrightarrow[x=1,\,y=1]{} [2,1,3] \xrightarrow[x=2,\,y=3]{} [3,1,2] \xrightarrow[x=3,\,y=3]{} [3,1,2].\(\) Можно показать, что невозможно превратить \([2,1,3]\) в \([3,2,1]\) силой \(1\). Поэтому только одна перестановка \(b\) подходит, поэтому ответ \(1\). Во втором примере \(a\) и \(b\) такие же, как в предыдущем примере, но теперь у нас сила \(2\). Перестановку \(a\) можно превратить в \([3,2,1]\) силой \(2\) следующим образом: \(\)[2,1,3] \xrightarrow[x=1,\,y=3]{} [2,3,1] \xrightarrow[x=2,\,y=3]{} [3,2,1] \xrightarrow[x=3,\,y=3]{} [3,2,1].\(\) Можно также превратить \(a\) в \([3,1,2]\) используя силу \(1\) как раньше, поэтому ответ \(2\). В третьем примере есть только одна перестановка \(b\). Можно показать, что невозможно превратить \(a\) в \(b\), поэтому ответ \(0\). | |
![]()
|
|
C. Третья задача
Конструктив
Комбинаторика
математика
*1700
Вам дана перестановка \(a_1,a_2,\ldots,a_n\) чисел от \(0\) до \(n - 1\). Вам нужно посчитать количество перестановок \(b_1,b_2,\ldots,b_n\), похожих на перестановку \(a\). Две перестановки \(a\) и \(b\) размера \(n\) называются похожими, если для всех отрезков \([l,r]\) (\(1 \le l \le r \le n\)) выполняется следующее условие: \(\)\operatorname{MEX}([a_l,a_{l+1},\ldots,a_r])=\operatorname{MEX}([b_l,b_{l+1},\ldots,b_r]),\(\) где \(\operatorname{MEX}\) набора чисел \(c_1,c_2,\ldots,c_k\) определяется как наименьшее неотрицательное целое число \(x\), которое не встречается в наборе чисел \(c\). Например, \(\operatorname{MEX}([1,2,3,4,5])=0\), а \(\operatorname{MEX}([0,1,2,4,5])=3\). Так как количество таких перестановок может быть очень большим, вам нужно вывести его остаток по модулю \(10^9+7\). В этой задаче перестановкой размера \(n\) является массив, состоящий из \(n\) различных целых чисел от \(0\) до \(n-1\) в произвольном порядке. Например, \([1,0,2,4,3]\) является перестановкой, а \([0,1,1]\) не является, так как \(1\) встречается в массиве дважды. \([0,1,3]\) также не является перестановкой, так как \(n=3\) и в массиве есть число \(3\). Выходные данные Для каждого набора входных данных выведите единственное целое число — количество перестановок, похожих на перестановку \(a\), взятое по модулю \(10^9+7\). Примечание В первом наборе входных данных единственными перестановками, похожими на \(a=[4,0,3,2,1]\), являются \([4,0,3,2,1]\) и \([4,0,2,3,1]\). Во втором и третьем наборах входных данных только данные перестановки похожи на себя. В четвёртом наборе входных данных есть \(4\) перестановки, похожие на \(a=[1,2,4,0,5,3]\): - \([1,2,4,0,5,3]\);
- \([1,2,5,0,4,3]\);
- \([1,4,2,0,5,3]\);
- \([1,5,2,0,4,3]\).
| |
![]()
|
|
F. Точки
Структуры данных
Комбинаторика
математика
реализация
*2500
матрицы
Тройка точек \(i\), \(j\) и \(k\) на координатной прямой считается красивой, если \(i < j < k\) и \(k - i \le d\). Вам задано множество точек на координатной прямой, изначально пустое. Вам нужно обрабатывать запросы трех типов: - добавить точку в множество;
- удалить точку из множества;
- посчитать количество красивых троек из точек, принадлежащих множеству.
Выходные данные Для каждого запроса выведите одно целое число — количество красивых троек после обработки запроса. | |
![]()
|
|
H1. Игра ИИ (простая версия)
Конструктив
Комбинаторика
математика
дп
*3200
бпф
Это упрощенная версия задачи. Разница между легкой и сложной версиями заключается в ограничении на \(k\) и ограничении по времени. Кроме того, в этой версии задачи вам нужно вычислить ответ только при \(n=k\). Вы можете делать взломы только в том случае, если обе версии задачи решены. Cirno играет в военный симулятор с \(n\) башнями (пронумерованными от \(1\) до \(n\)) и \(n\) ботами (пронумерованными от \(1\) до \(n\)). Первоначально \(i\)-я башня занята \(i\)-м ботом для всех \(1 \le i \le n\). Перед игрой Cirno сначала выбирает перестановку \(p = [p_1, p_2, \ldots, p_n]\) длины \(n\) (перестановкой длины \(n\) называется массив длины \(n\), где каждое целое число между \(1\) и \(n\) встречаются ровно один раз). После этого она может выбрать последовательность \(a = [a_1, a_2, \ldots, a_n]\) (\(1 \le a_i \le n\) и \(a_i \ne i\) для всех \(1 \le i \le n\) ). В игре есть \(n\) раундов-атак. В \(i\)-м раунде, если \(p_i\)-й бот все еще находится в игре, он начнет свою атаку, в результате чего \(a_{p_i}\)-я башня будет занята \(p_i\)-м ботом; бот, который ранее занимал \(a_{p_i}\)-ю башню, больше не будет ее занимать. Если \(p_i\)-го бота нет в игре, в этом раунде ничего не произойдет. После каждого раунда, если бот не занимает ни одной башни, он будет уничтожен и покинет игру. Обратите внимание, что ни одна башня не может быть занята более чем одним ботом, но один бот может занимать более одной башни во время игры. В конце игры Cirno запишет результат в виде последовательности \(b = [b_1, b_2, \ldots, b_n]\), где \(b_i\) — номер бота, занимающего \(i\)-ю башня в конце игры. Однако, как мастер математики, она хочет, чтобы вы решили следующую задачу на счет вместо того, чтобы играть в игры: Подсчитайте количество различных пар последовательностей \(a\) и \(b\), которые могут получиться из всех возможных выборов последовательности \(a\) и перестановки \(p\). Так как это число может быть большим, выведите его по модулю \(M\). Выходные данные Выведите одно целое число — количество различных пар последовательностей для \(n=k\) по модулю \(M\). Примечание Для \(n=1\) допустимой последовательности \(a\) не существует. Мы рассматриваем ответ как \(0\). При \(n=2\) возможен только один массив \(a\): \([2, 1]\). - Для массива \(a\) равного \([2, 1]\) и перестановки \(p\) равной \([1, 2]\), последовательность \(b\) будет \([1, 1]\) после всех раундов. Детали для каждого раунда:
- В первом раунде первый бот начнет атаку и успешно захватит башню \(2\). После этого раунда второй бот будет уничтожен и покинет игру, так как все его башни заняты другими ботами.
- Во втором раунде второго бота нет в игре.
- Для массива \(a\) равного \([2, 1]\) и перестановки \(p\) равной \([2, 1]\), последовательность \(b\) будет \([2, 2]\) после всех раундов. Детали для каждого раунда:
- В первом раунде второй бот начнет атаку и успешно захватит башню \(1\). После этого раунда первый бот будет уничтожен и покинет игру, так как все его башни заняты другими ботами.
- Во втором раунде первого бота нет в игре.
Таким образом, количество различных пар последовательностей \((a,b)\) равно \(2\) (\([2, 1]\), \([1, 1]\) и \([2, 1]\), \([2, 2]\)) при \(n=2\). | |
![]()
|
|
H2. Игра ИИ (сложная версия)
Комбинаторика
математика
бпф
*3500
Это сложная версия этой задачи. Разница между легкой и сложной версиями заключается в ограничении на \(k\) и ограничении по времени. Кроме того, в этой версии вам нужно вычислить ответ для всех положительных целых чисел \(n \in [1,k]\) в этой версии. Вы можете делать взломы только в том случае, если обе версии задачи решены. Cirno играет в военный симулятор с \(n\) башнями (пронумерованными от \(1\) до \(n\)) и \(n\) ботами (пронумерованными от \(1\) до \(n\)). Первоначально \(i\)-я башня занята \(i\)-м ботом для всех \(1 \le i \le n\). Перед игрой Cirno сначала выбирает перестановку \(p = [p_1, p_2, \ldots, p_n]\) длины \(n\) (перестановкой длины \(n\) называется массив длины \(n\), где каждое целое число между \(1\) и \(n\) встречаются ровно один раз). После этого она может выбрать последовательность \(a = [a_1, a_2, \ldots, a_n]\) (\(1 \le a_i \le n\) и \(a_i \ne i\) для всех \(1 \le i \le n\) ). В игре есть \(n\) раундов-атак. В \(i\)-м раунде, если \(p_i\)-й бот все еще находится в игре, он начнет свою атаку, в результате чего \(a_{p_i}\)-я башня будет занята \(p_i\)-м ботом; бот, который ранее занимал \(a_{p_i}\)-ю башню, больше не будет ее занимать. Если \(p_i\)-го бота нет в игре, в этом раунде ничего не произойдет. После каждого раунда, если бот не занимает ни одной башни, он будет уничтожен и покинет игру. Обратите внимание, что ни одна башня не может быть занята более чем одним ботом, но один бот может занимать более одной башни во время игры. В конце игры Cirno запишет результат в виде последовательности \(b = [b_1, b_2, \ldots, b_n]\), где \(b_i\) — номер бота, занимающего \(i\)-ю башня в конце игры. Однако, как мастер математики, она хочет, чтобы вы решили следующую задачу на счет вместо того, чтобы играть в игры: Подсчитайте количество различных пар последовательностей \(a\) и \(b\), которые могут получиться при всех возможных выборах последовательности \(a\) и перестановки \(p\). Вычислите ответ для всех значений \(n\) таких, что \(1 \le n \le k\). Так как эти числа могут быть большими, выведите их по модулю \(M\). Выходные данные Выведите \(k\) строк, где \(i\)-я строка содержит неотрицательное целое число, являющееся ответом для \(n=i\) по модулю \(M\). Примечание Для \(n=1\) допустимой последовательности \(a\) не существует. Мы рассматриваем ответ как \(0\). При \(n=2\) возможен только один массив \(a\): \([2, 1]\). - Для массива \(a\) равного \([2, 1]\) и перестановки \(p\) равной \([1, 2]\), последовательность \(b\) будет \([1, 1]\) после всех раундов. Детали для каждого раунда:
- В первом раунде первый бот начнет атаку и успешно захватит башню \(2\). После этого раунда второй бот будет уничтожен и покинет игру, так как все его башни заняты другими ботами.
- Во втором раунде второго бота нет в игре.
- Для массива \(a\) равного \([2, 1]\) и перестановки \(p\) равной \([2, 1]\), последовательность \(b\) будет \([2, 2]\) после всех раундов. Детали для каждого раунда:
- В первом раунде второй бот начнет атаку и успешно захватит башню \(1\). После этого раунда первый бот будет уничтожен и покинет игру, так как все его башни заняты другими ботами.
- Во втором раунде первого бота нет в игре.
Таким образом, количество различных пар последовательностей \((a,b)\) равно \(2\) (\([2, 1]\), \([1, 1]\) и \([2, 1]\), \([2, 2]\)) при \(n=2\). | |
![]()
|
|
D. Марк и лампочки
Конструктив
Комбинаторика
математика
*1800
жадные алгоритмы
сортировки
Марк только что купил светильник из \(n\) лампочек. Состояние лампочек можно описать бинарной строкой \(s = s_1s_2\dots s_n\), где \(s_i=\texttt{1}\) означает, что \(i\)-я лампочка включена, а \(s_i=\texttt{0}\) означает, что \(i\)-я лампочка выключена. К сожалению, лампочки сломаны, и Марк может выполнять единственную операцию, чтобы изменять состояние лампочек: - выбрать индекс \(i\) из чисел \(2,3,\dots,n-1\) такой, что \(s_{i-1}\ne s_{i+1}\);
- переключить \(s_i\): если \(s_i\) равно \(\texttt{0}\), установить для \(s_i\) значение \(\texttt{1}\), и наоборот.
Марк хочет, чтобы состояние лампочек описывалось другой бинарной строкой \(t\). Помогите Марку определить минимальное количество операций, чтобы достичь это состояние. Выходные данные Для каждого набора входных данных выведите строку, содержащую минимальное количество операций, которые должен выполнить Марк, чтобы преобразовать состояние лампочек из \(s\) в \(t\). Если такой последовательности операций не существует, выведите \(-1\). Примечание В первом наборе входных данных примера одна из последовательностей операций, обеспечивающая минимальное количество операций, следующая: - выбрать \(i=3\), заменив \(\texttt{01}\color{red}{\texttt{0}}\texttt{0}\) на \(\texttt{01}\color{red}{\texttt{1}}\texttt{0}\);
- выбрать \(i=2\), заменив \(\texttt{0}\color{red}{\texttt{1}}\texttt{10}\) на \(\texttt{0}\color{red}{\texttt{0}}\texttt{10}\).
Во втором наборе входных данных искомой последовательности операций не существует, потому что нельзя изменить ни первый, ни последний символ \(s\). В третьем наборе входных данных, хотя первые символы \(s\) и \(t\) совпадают и последние символы \(s\) и \(t\) одинаковы, можно показать, что не существует последовательности операций, которая удовлетворяет условию. В четвертом наборе входных данных одна из последовательностей, обеспечивающая минимальное количество операций, выглядит следующим образом: - выбрать \(i=3\), заменив \(\texttt{00}\color{red}{\texttt{0}}\texttt{101}\) на \(\texttt{00}\color{red}{\texttt{1}}\texttt{101}\);
- выбрать \(i=2\), заменив \(\texttt{0}\color{red}{\texttt{0}}\texttt{1101}\) на \(\texttt{0}\color{red}{\texttt{1}}\texttt{1101}\);
- выбрать \(i=4\), заменив \(\texttt{011}\color{red}{\texttt{1}}\texttt{01}\) на \(\texttt{011}\color{red}{\texttt{0}}\texttt{01}\);
- выбрать \(i=5\), заменив \(\texttt{0110}\color{red}{\texttt{0}}\texttt{1}\) на \(\texttt{0110}\color{red}{\texttt{1}}\texttt{1}\);
- выбрать \(i=3\), заменив \(\texttt{01}\color{red}{\texttt{1}}\texttt{011}\) на \(\texttt{01}\color{red}{\texttt{0}}\texttt{011}\).
| |
![]()
|
|
E. Марк и профессор Коро
Бинарный поиск
Перебор
Структуры данных
Комбинаторика
жадные алгоритмы
*2300
битмаски
После просмотра одного аниме перед сном Марку снится, что он стоит в старом классе с меловой доской, на которой записана последовательность из \(n\) положительных целых чисел \(a_1, a_2,\dots,a_n\). Затем в класс заходит профессор Коро. Он может выполнять следующую операцию: - выбрать целое число \(x\) которое присутствует на доске хотя бы \(2\) раза,
- стереть эти \(2\) вхождения,
- записать число \(x+1\) на доску.
После чего профессор Коро задает марку вопрос: «Какое максимально возможное число может появиться на доске после некоторого количества таких операций?» Марк быстро отвечает на этот вопрос, но он всё ещё медленнее профессора Коро. Поэтому профессор Коро решает задать Марку дополнительные вопросы. Он будет менять изначальную последовательность чисел на доске \(q\) раз. Каждый раз он будет выбирать положительные целые числа \(k\) и \(l\), затем менять \(a_k\) на \(l\). После каждого такого изменения он будет спрашивать у Марка ответ на тот же самый вопрос. Помогите Марку ответить на вопросы быстрее профессора Коро! Обратите внимание, что изменения начальной последовательности на доске сохраняются. Изменения, внесенные в последовательность \(a\), будут так же применяться при обработке следующих изменений. Выходные данные Выведите \(q\) строк, \(i\)-я строка должна содержать единственное целое число — ответ после \(i\)-го изменения. Примечание В первом примере программа должна обработать \(4\) изменения. После первого обновления последовательность на доске выглядит как \([2,3,2,4,5]\). Одна из возможных последовательностей операций, достигающих числа \(6\), такая: - Изначально, на доске числа \([2,3,2,4,5]\).
- Удаляем два вхождения числа \(2\) и записываем \(3\), получая \([3,4,5,\color{red}{3}]\).
- Удаляем два вхождения числа \(3\) и записываем \(4\), получая \([4,5,\color{red}{4}]\).
- Удаляем два вхождения числа \(4\) и записываем \(5\), получая \([5,\color{red}{5}]\).
- Удаляем два вхождения числа \(5\) и записываем \(6\), получая \([\color{red}{6}]\).
Затем, во время второго изменения, массив станет равным \([2,3,2,4,3]\). В этот раз Марк не может достичь числа \(6\). Однако одна из последовательностей операций, приводящая к числу \(5\), такая: - Изначально, на доске числа \([2,3,2,4,3]\).
- Удаляем два вхождения числа \(2\) и записываем \(3\), получая \([3,4,3,\color{red}{3}]\).
- Удаляем два вхождения числа \(3\) и записываем \(4\), получая \([3,4,\color{red}{4}]\).
- Удаляем два вхождения числа \(4\) и записываем \(5\), получая \([3,\color{red}{5}]\).
Во время третьего изменения массив станет равным \([2,3,2,1,3]\). Один из возможных вариантов достичь числа \(4\) такой: - Изначально, на доске числа \([2,3,2,1,3]\).
- Удаляем два вхождения числа \(3\) и записываем \(4\), получая \([2,2,1,\color{red}{4}]\).
| |
![]()
|
|
D. Частичные виртуальные деревья
Деревья
Комбинаторика
математика
дп
поиск в глубину и подобное
*3000
Каваширо Нитори — девушка, которой нравится спортивное программирование. Однажды она нашла корневое дерево из \(n\) вершин. Корень дерева был в вершине с номером \(1\). Как продвинутый автор, она сразу придумала задачу. У Каваширо Нитори есть множество вершин \(U=\{1,2,\ldots,n\}\). За одну операцию она будет выбирать множество вершин \(T\), где \(T\) является частичным виртуальным деревом множества \(U\), и заменять множество \(U\) на \(T\). Множество вершин \(S_1\) называется частичным виртуальным деревом множества вершин \(S_2\), если \(S_1\) — подмножество \(S_2\), \(S_1 \neq S_2\) и для любых пар вершин \(i\) и \(j\) из \(S_1\) \(\operatorname{LCA}(i,j)\) лежит внутри \(S_1\), где \(\operatorname{LCA}(x,y)\) обозначает наименьшего общего предка вершин \(x\) и \(y\) в дереве. Обратите внимание, что множество вершин может иметь много различных частичных виртуальных деревьев. Каваширо Нитори хочет узнать для каждого возможного \(k\), если применить операцию строго \(k\) раз, сколькими способами она может получить \(U=\{1\}\) в конце? Два способа считаются различными, если существует целое число \(z\) (\(1 \le z \le k\)) такое, что после \(z\) операций множества \(U\) различаются. Так как ответ может быть большим, найдите его по модулю \(p\). Гарантируется, что \(p\) — простое число. Выходные данные Выведите единственную строку, состоящую из \(n-1\) целых чисел — ответ по модулю \(p\) для всех \(k=1,2,\ldots,n-1\). Примечание В первом примере при \(k=1\) единственный возможный способ следующий: - \(\{1,2,3,4\} \to \{1\}\).
При \(k=2\) существуют \(6\) способов: - \(\{1,2,3,4\} \to \{1,2\} \to \{1\}\);
- \(\{1,2,3,4\} \to \{1,2,3\} \to \{1\}\);
- \(\{1,2,3,4\} \to \{1,2,4\} \to \{1\}\);
- \(\{1,2,3,4\} \to \{1,3\} \to \{1\}\);
- \(\{1,2,3,4\} \to \{1,3,4\} \to \{1\}\);
- \(\{1,2,3,4\} \to \{1,4\} \to \{1\}\).
При \(k=3\) существуют \(6\) возможных способов: - \(\{1,2,3,4\} \to \{1,2,3\} \to \{1,2\} \to \{1\}\);
- \(\{1,2,3,4\} \to \{1,2,3\} \to \{1,3\} \to \{1\}\);
- \(\{1,2,3,4\} \to \{1,2,4\} \to \{1,2\} \to \{1\}\);
- \(\{1,2,3,4\} \to \{1,2,4\} \to \{1,4\} \to \{1\}\);
- \(\{1,2,3,4\} \to \{1,3,4\} \to \{1,3\} \to \{1\}\);
- \(\{1,2,3,4\} \to \{1,3,4\} \to \{1,4\} \to \{1\}\).
| |
![]()
|
|
B. Звезда
Комбинаторика
*особая задача
*1300
Выходные данные Выведите единственное целое число output (1 ≤ output ≤ 2·109). | |
![]()
|
|
E1. Сумма НОК (простая версия)
Бинарный поиск
Перебор
Комбинаторика
математика
теория чисел
*2300
We are sum for we are many Some Number Это простая версия задачи. Разница между простой и сложной версиями задачи заключается только в ограничении на \(t\). Вы можете делать взломы только в том случае, если обе версии задачи решены. Вам даны два целых положительных числа \(l\) и \(r\). Посчитайте количество уникальных троек целых чисел \((i, j, k)\) таких, что \(l \le i < j < k \le r\) и \(\operatorname{lcm}(i,j,k) \ge i + j + k\). Здесь \(\operatorname{lcm}(i, j, k)\) означает наименьшее общее кратное (НОК) целых чисел \(i\), \(j\), и \(k\). Выходные данные Для каждого набора входных данных выведите единственное целое число — количество уникальных троек целых чисел, подходящих под условия задачи. Примечание В первом наборе входных данных существует \(3\) подходящих тройки: - \((1,2,3)\),
- \((1,3,4)\),
- \((2,3,4)\).
Во втором наборе входных данных существует только \(1\) подходящая тройка: | |
![]()
|
|
F. Потерянный массив
Конструктив
Комбинаторика
математика
дп
битмаски
*2900
Мои orz-дети, мы можем оптимизировать эту задачу с \(O(S^3)\) до \(O\left(T^\frac{5}{9}\right)\)! — Spyofgame, основатель религии Orz Давным-давно Spyofgame изобрел известный массив \(a\) (элементы которого нумеруются с \(1\)) длины \(n\), который содержал знания о мире и о жизни. После этого он превратил его в матрицу \(b\) (элементы которой нумеруются с \(0\)) размера \((n + 1) \times (n + 1)\), которая содержала знания о мире, о жизни, и о том, что за их пределами. Spyofgame превратил \(a\) в \(b\) по следующим правилам. - \(b_{i,0} = 0\) при \(0 \leq i \leq n\);
- \(b_{0,i} = a_{i}\) при \(1 \leq i \leq n\);
- \(b_{i,j} = b_{i,j-1} \oplus b_{i-1,j}\) при \(1 \leq i, j \leq n\).
Здесь \(\oplus\) обозначает операцию побитового исключающего ИЛИ. В наши дни археологи нашли знаменитую матрицу \(b\). Однако многие ее элементы утеряны. Удалось прочесть лишь значения \(b_{i,n}\) для всех \(1 \leq i \leq n\) (обратите внимание, это некоторые элементы последнего столбца, а не строки). Археологи хотят восстановить возможный массив \(a\). Можете помочь им найти любой массив, который может быть массивом \(a\)? Выходные данные Если какой-то массив \(a\) подходит под данную информацию, выведите строку, содержащую \(n\) целых чисел \(a_1, a_2, \ldots, a_n\). Если существуют несколько решений, выведите любое из них. Если решения не существует, выведите одно целое число \(-1\). Примечание Если \(a = [1,2,3]\), то \(b\) будет следующей: | \(\bf{0}\) | \(\bf{1}\) | \(\bf{2}\) | \(\bf{3}\) | | \(\bf{0}\) | \(1\) | \(3\) | \(0\) | | \(\bf{0}\) | \(1\) | \(2\) | \(2\) | | \(\bf{0}\) | \(1\) | \(3\) | \(1\) |
Значения \(b_{1,n}, b_{2,n}, \ldots, b_{n,n}\) равны \([0,2,1]\), что соответствует найденной археологами информации. | |
![]()
|
|
C. Моноблок
Структуры данных
Комбинаторика
математика
реализация
*1700
Сережа решил срочно купить новый моноблок. Сейчас он использует VPN и поэтому, чтобы попасть на сайт, надо решить вот такую капчу. Крутостью массива назовем минимальное количество блоков подряд идущих одинаковых чисел, на которые он разбивается. Например, крутость массива - \([1, 1, 1]\) это \(1\);
- \([5, 7]\) это \(2\), ведь его можно разбить на два блока: \([5]\) и \([7]\);
- \([1, 7, 7, 7, 7, 7, 7, 7, 9, 9, 9, 9, 9, 9, 9, 9, 9]\) это 3, потому что его можно разбить на блоки \([1]\), \([7, 7, 7, 7, 7, 7, 7]\) и \([9, 9, 9, 9, 9, 9, 9, 9, 9]\).
Вам дан массив \(a\) длины \(n\), а также \(m\) запросов, состоящих из двух целых чисел \(i\) и \(x\). Запрос \(i\), \(x\) означает, что теперь \(i\)-й элемент массива \(a\) равен \(x\). После каждого запроса выведите сумму крутостей всех непустых подотрезков массива \(a\). Другими словами, после каждого запроса вам надо вычислять \(\)\sum\limits_{l = 1}^n \sum\limits_{r = l}^n g(l, r),\(\) где \(g(l, r)\) это крутость массива \(b = [a_l, a_{l + 1}, \ldots, a_r]\). Выходные данные После каждого запроса выведите ответ на задачу в отдельной строке. Примечание После первого запроса массив \(a\) равен \([1, 2, 2, 4, 5]\), ответ равен \(29\), потому что подрезки массива можно разбить на блоки: - \([1; 1]\): \([1]\), 1 блок;
- \([1; 2]\): \([1] + [2]\), 2 блока;
- \([1; 3]\): \([1] + [2, 2]\), 2 блока;
- \([1; 4]\): \([1] + [2, 2] + [4]\), 3 блока;
- \([1; 5]\): \([1] + [2, 2] + [4] + [5]\), 4 блока;
- \([2; 2]\): \([2]\), 1 блок;
- \([2; 3]\): \([2, 2]\), 1 блок;
- \([2; 4]\): \([2, 2] + [4]\), 2 блока;
- \([2; 5]\): \([2, 2] + [4] + [5]\), 3 блока;
- \([3; 3]\): \([2]\), 1 блок;
- \([3; 4]\): \([2] + [4]\), 2 блока;
- \([3; 5]\): \([2] + [4] + [5]\), 3 блока;
- \([4; 4]\): \([4]\), 1 блок;
- \([4; 5]\): \([4] + [5]\), 2 блока;
- \([5; 5]\): \([5]\), 1 блок;
что в сумме равняется \(1 + 2 + 2 + 3 + 4 + 1 + 1 + 2 + 3 + 1 + 2 + 3 + 1 + 2 + 1 = 29\). | |
![]()
|
|
F. Мешки с шарами
Комбинаторика
математика
дп
теория чисел
*2500
Есть \(n\) мешков, в каждом лежат \(m\) шаров с числами от \(1\) до \(m\). В каждом мешке ровно один шар с числом \(i\) для каждого \(i \in [1, m]\). Из каждого мешка берется по одному шару (все мешки различные, так что, например, взять шар \(1\) из первого мешка и шар \(2\) из второго мешка — это не то же самое, что и взять шар \(2\) из первого мешка и шар \(1\) из второго мешка). После этого считается количество шаров с нечетными числами среди тех, которые достали. Пусть это количество будет равно \(F\). Ваша задача — посчитать сумму \(F^k\) по всем способам выбрать \(n\) шаров, по одному из каждого мешка. Выходные данные На каждый набор входных данных выведите одно целое число — сумму \(F^k\) по всем способам выбрать \(n\) шаров, по одному из каждого мешка. Так как это значение может быть достаточно велико, выведите его по модулю \(998244353\). | |
![]()
|
|
D. Мадока и коррупционная схема
Конструктив
Комбинаторика
математика
жадные алгоритмы
*1900
Мадоке решили доверить организацию крупного турнира по компьютерной игре «OSU»! В данном турнире матчи проходят по «олимпийской системе». Другими словами, в турнире участвуют \(2^n\) участников, пронумерованных целыми числами от \(1\) до \(2^n\). Всего в турнире происходит \(n\) раундов. В \(i\)-м раунде проходят \(2^{n - i}\) матчей между двумя игроками (один из которых правый, другой левый), после которых победители проходят дальше по турнирной сетке, а проигравшие участники выбывают из турнира. При этом относительный порядок в следующем раунде не меняется. А победитель в турнире — последний оставшийся участник. Но чем меньше номер участника, тем больше он заплатит Мадоке в случае победы, поэтому Мадока хочет, чтобы победил участник с наименьшим номером. Для этого она может как угодно расставить участников в первом раунде, а также для каждого матча определить кто победит — участник слева или справа. Но Мадока знает, что спонсоры турнира могут не более \(k\) раз поменять победителя в матчах. (То есть если до изменения побеждал участник слева, то после изменения будет побеждать участник справа, а если побеждал участник справа, то после изменения будет побеждать участник слева). 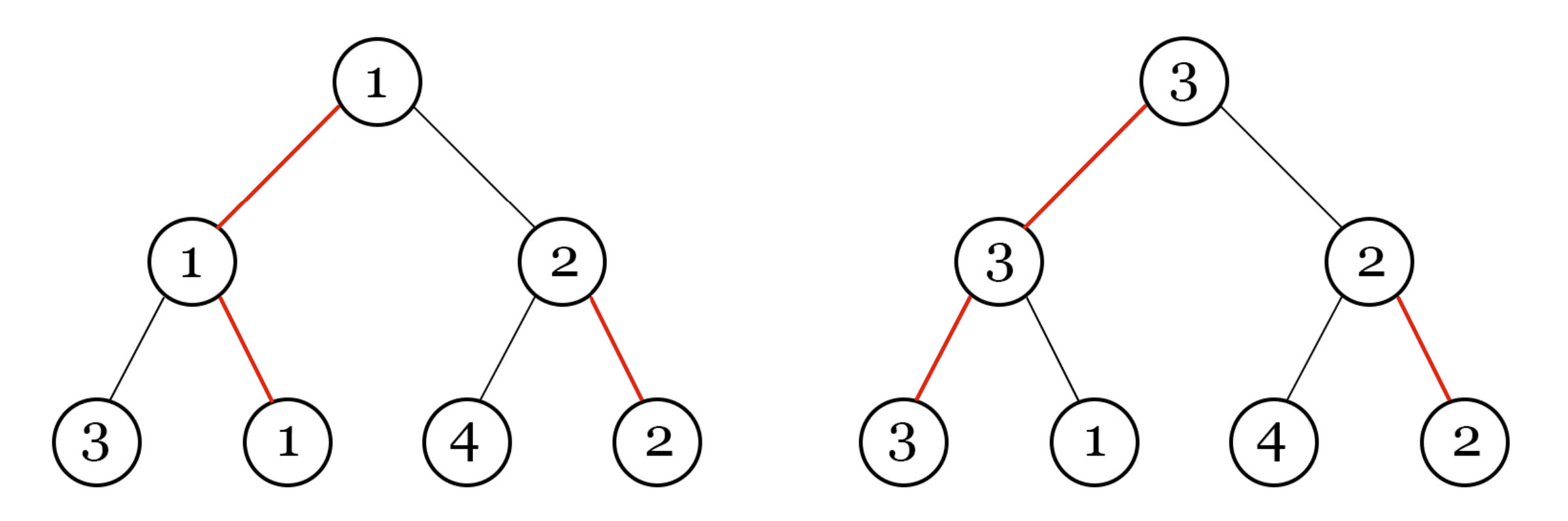 Так, на первом изображении показана турнирная сетка, которую сделала Мадока, где красные линии показывают, кто должен победить в матче. А на втором показана турнирная сетка, после одного измения исхода матча спонсорами (матч между игроками \(1\) и \(3\)). Так, на первом изображении показана турнирная сетка, которую сделала Мадока, где красные линии показывают, кто должен победить в матче. А на втором показана турнирная сетка, после одного измения исхода матча спонсорами (матч между игроками \(1\) и \(3\)). Выведите минимально возможный номер победителя в турнире, который Мадока может гарантированно получить вне зависимости от изменений спонсоров. Но так как ответ может быть очень большим выведите его по модулю \(10^9 + 7\). Обратите внимание, нам нужно минимизировать ответ, а только потом взять его по модулю. Выходные данные Выведите ровно одно целое число — минимальный номер победителя по модулю \(10^9 + 7\) Примечание В первом примере проходит всего один матч между игроками \(1\) и \(2\), поэтому спонсоры всегда смогут сделать так, чтобы выигрывал игрок \(2\). Схема турнира из второго примера изображена на картинке в условии. | |
![]()
|
|
C. Circular Mirror
Бинарный поиск
Комбинаторика
математика
геометрия
*2000
Pak Chanek has a mirror in the shape of a circle. There are \(N\) lamps on the circumference numbered from \(1\) to \(N\) in clockwise order. The length of the arc from lamp \(i\) to lamp \(i+1\) is \(D_i\) for \(1 \leq i \leq N-1\). Meanwhile, the length of the arc between lamp \(N\) and lamp \(1\) is \(D_N\). Pak Chanek wants to colour the lamps with \(M\) different colours. Each lamp can be coloured with one of the \(M\) colours. However, there cannot be three different lamps such that the colours of the three lamps are the same and the triangle made by considering the three lamps as vertices is a right triangle (triangle with one of its angles being exactly \(90\) degrees). The following are examples of lamp colouring configurations on the circular mirror. 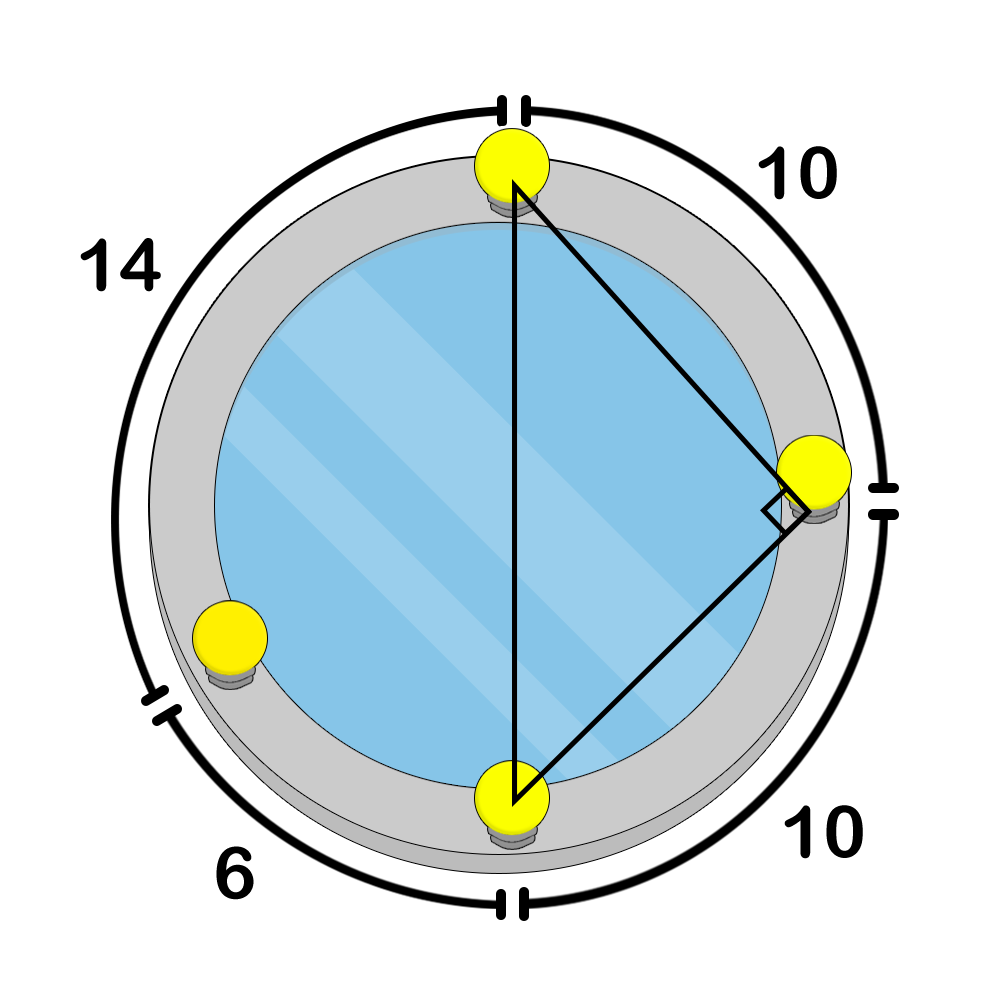 | 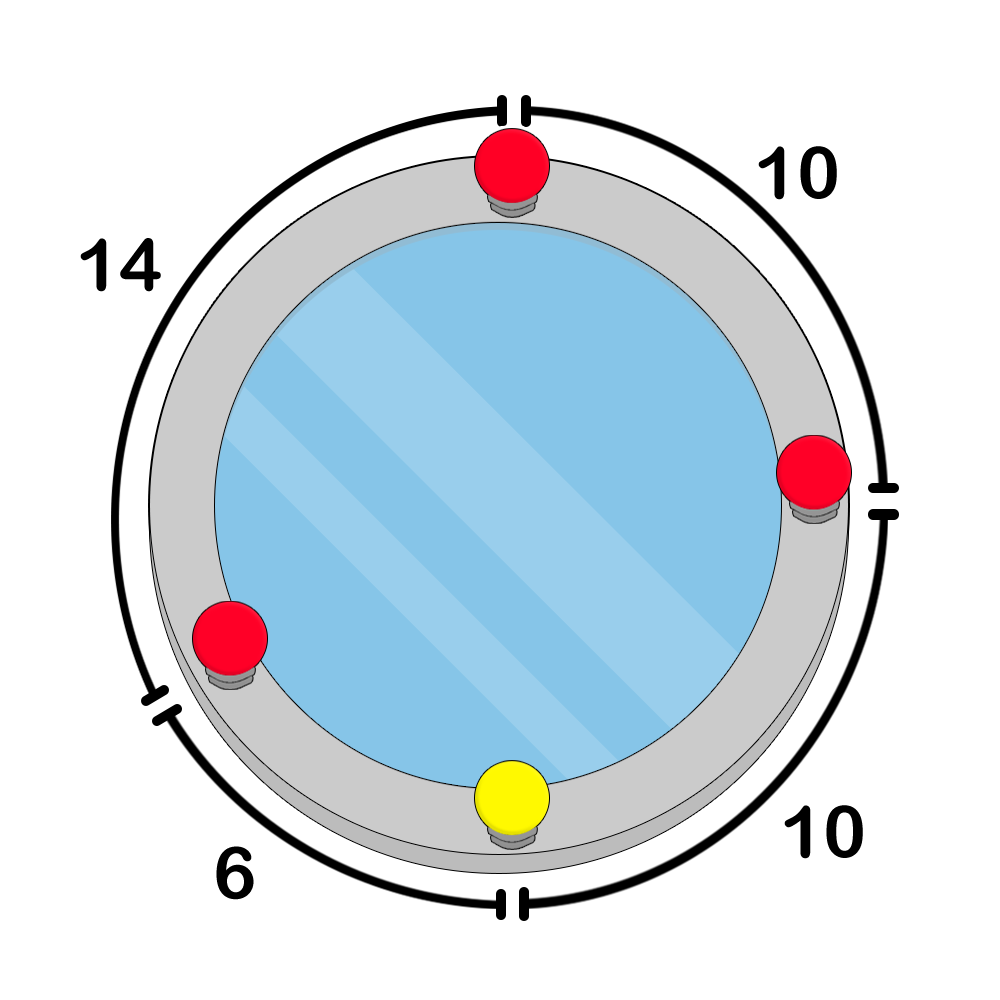 | 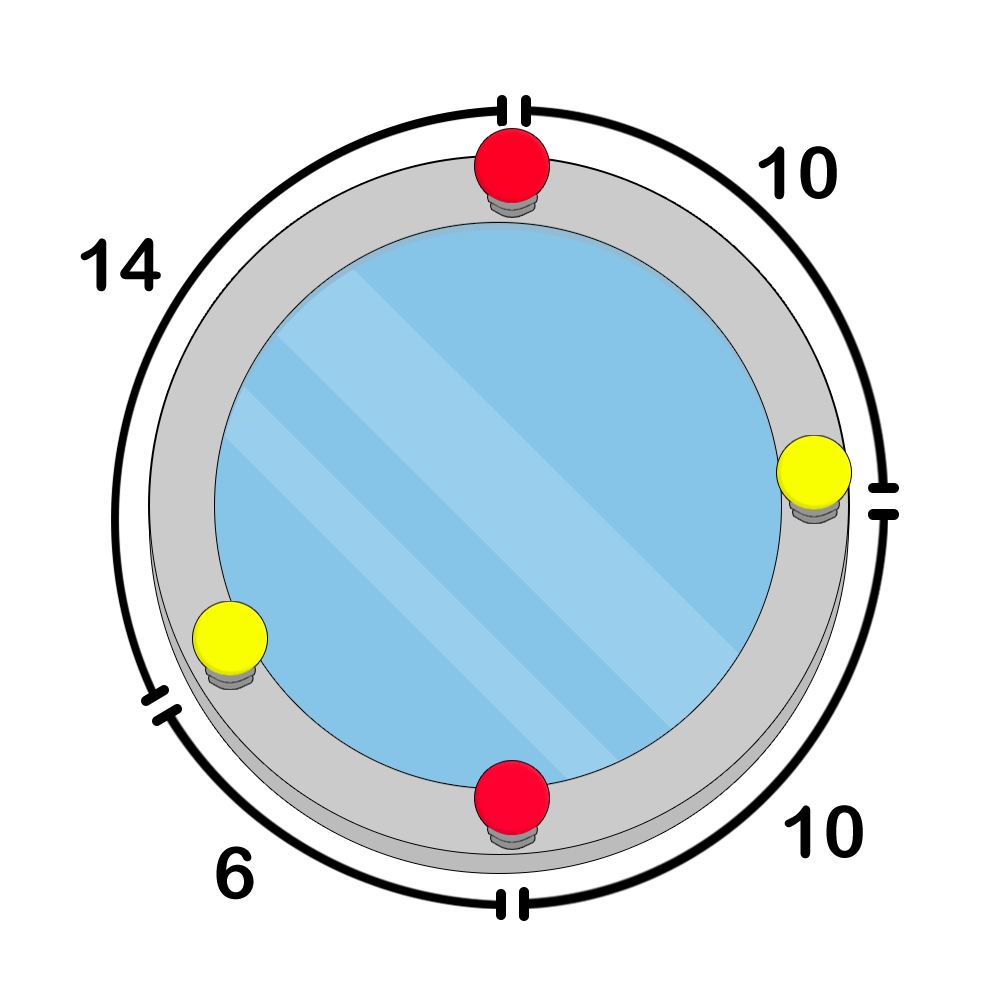 | | Figure 1. an example of an incorrect colouring because lamps \(1\), \(2\), and \(3\) form a right triangle | Figure 2. an example of a correct colouring | Figure 3. an example of a correct colouring |
Before colouring the lamps, Pak Chanek wants to know the number of distinct colouring configurations he can make. Count the number of distinct possible lamp colouring configurations, modulo \(998\,244\,353\). Output An integer representing the number of possible lamp colouring configurations, modulo \(998\,244\,353\). Note In the first example, all correct lamp colouring configurations are \([1, 1, 2, 1]\), \([1, 1, 2, 2]\), \([1, 2, 1, 2]\), \([1, 2, 2, 1]\), \([1, 2, 2, 2]\), \([2, 1, 1, 1]\), \([2, 1, 1, 2]\), \([2, 1, 2, 1]\), \([2, 2, 1, 1]\), and \([2, 2, 1, 2]\). | |
![]()
|
|
E. Electrical Efficiency
Деревья
Структуры данных
Комбинаторика
математика
дп
теория чисел
*2500
In the country of Dengkleknesia, there are \(N\) factories numbered from \(1\) to \(N\). Factory \(i\) has an electrical coefficient of \(A_i\). There are also \(N-1\) power lines with the \(j\)-th power line connecting factory \(U_j\) and factory \(V_j\). It can be guaranteed that each factory in Dengkleknesia is connected to all other factories in Dengkleknesia through one or more power lines. In other words, the collection of factories forms a tree. Each pair of different factories in Dengkleknesia can use one or more existing power lines to transfer electricity to each other. However, each power line needs to be turned on first so that electricity can pass through it. Define \(f(x, y, z)\) as the minimum number of power lines that need to be turned on so that factory \(x\) can make electrical transfers to factory \(y\) and factory \(z\). Also define \(g(x, y, z)\) as the number of distinct prime factors of \(\text{GCD}(A_x, A_y, A_z)\). To measure the electrical efficiency, you must find the sum of \(f(x, y, z) \times g(x, y, z)\) for all combinations of \((x, y, z)\) such that \(1 \leq x < y < z \leq N\). Because the answer can be very large, you just need to output the answer modulo \(998\,244\,353\). Note: \(\text{GCD}(k_1, k_2, k_3)\) is the greatest common divisor of \(k_1\), \(k_2\), and \(k_3\), which is the biggest integer that simultaneously divides \(k_1\), \(k_2\), and \(k_3\). Output An integer representing the sum of \(f(x, y, z) \times g(x, y, z)\) for all combinations of \((x, y, z)\) such that \(1 \leq x < y < z \leq N\), modulo \(998\,244\,353\) Note In the first example, the only \((x, y, z)\) possible is \((1, 2, 3)\). Because \(\text{GCD}(A_1, A_2, A_3) = \text{GCD}(1, 2, 3) = 1\) has \(0\) distinct prime factors, therefore \(f(x, y, z) \times g(x, y, z) = 2 \times 0 = 0\). In the second example, all triples \((x, y, z)\) that satisfy the condition are as follows: - \((1, 2, 3) \rightarrow f(1, 2, 3) \times g(1, 2, 3) = 2 \times 1 = 2\)
- \((1, 2, 4) \rightarrow f(1, 2, 4) \times g(1, 2, 4) = 2 \times 1 = 2\)
- \((1, 3, 4) \rightarrow f(1, 3, 4) \times g(1, 3, 4) = 3 \times 2 = 6\)
- \((2, 3, 4) \rightarrow f(2, 3, 4) \times g(2, 3, 4) = 2 \times 1 = 2\)
So the electrical efficiency is \(2 + 2 + 6 + 2 = 12\). | |
![]()
|
|
I. Imitating the Key Tree
Деревья
Комбинаторика
*2800
снм
Pak Chanek has a tree called the key tree. This tree consists of \(N\) vertices and \(N-1\) edges. The edges of the tree are numbered from \(1\) to \(N-1\) with edge \(i\) connecting vertices \(U_i\) and \(V_i\). Initially, each edge of the key tree does not have a weight. Formally, a path with length \(k\) in a graph is a sequence \([v_1, e_1, v_2, e_2, v_3, e_3, \ldots, v_k, e_k, v_{k+1}]\) such that: - For each \(i\), \(v_i\) is a vertex and \(e_i\) is an edge.
- For each \(i\), \(e_i\) connects vertices \(v_i\) and \(v_{i+1}\).
A circuit is a path that starts and ends on the same vertex. A path in a graph is said to be simple if and only if the path does not use the same edge more than once. Note that a simple path can use the same vertex more than once. The cost of a simple path in a weighted graph is defined as the maximum weight of all edges it traverses. Count the number of distinct undirected weighted graphs that satisfy the following conditions: - The graph has \(N\) vertices and \(2N-2\) edges.
- For each pair of different vertices \((x, y)\), there exists a simple circuit that goes through vertices \(x\) and \(y\) in the graph.
- The weight of each edge in the graph is an integer between \(1\) and \(2N-2\) inclusive. Each edge has distinct weights.
- The graph is formed in a way such that there is a way to assign a weight \(W_i\) to each edge \(i\) in the key tree that satisfies the following conditions:
- For each pair of edges \((i, j)\), if \(i<j\), then \(W_i<W_j\).
- For each pair of different vertex indices \((x, y)\), the cost of the only simple path from vertex \(x\) to \(y\) in the key tree is equal to the minimum cost of a simple circuit that goes through vertices \(x\) and \(y\) in the graph.
- Note that the graph is allowed to have multi-edges, but is not allowed to have self-loops.
Print the answer modulo \(998\,244\,353\). Two graphs are considered distinct if and only if there exists a triple \((a, b, c)\) such that there exists an edge that connects vertices \(a\) and \(b\) with weight \(c\) in one graph, but not in the other. Output An integer representing the number of distinct undirected weighted graphs that satisfy the conditions of the problem modulo \(998\,244\,353\). Note The following is an example of a graph that satisfies. 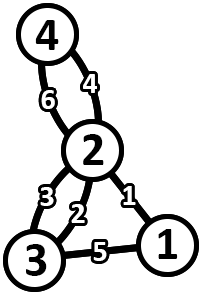
The following is an assignment of edge weights in the key tree that corresponds to the graph above. 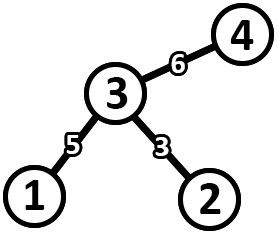
As an example, consider a pair of vertex indices \((1, 4)\). - The circuit in the graph for this pair of vertices is \(3 \xrightarrow{2} 2 \xrightarrow{4} 4 \xrightarrow{6} 2 \xrightarrow{1} 1 \xrightarrow{5} 3\) with a cost of \(6\).
- The path in the key tree for this pair of vertices is \(1 \xrightarrow{5} 3 \xrightarrow{6} 4\) with a cost of \(6\).
| |
![]()
|
|
E. Почти идеально
Комбинаторика
математика
*2400
бпф
Перестановка \(p\) длины \(n\) называется почти идеальной, если для всех целых \(1 \leq i \leq n\), выполняется условие \(\lvert p_i - p^{-1}_i \rvert \le 1\), где \(p^{-1}\) является перестановкой обратной \(p\) (т.е. \(p^{-1}_{k_1} = k_2\) тогда и только тогда, когда \(p_{k_2} = k_1\)). Посчитайте количество почти идеальных перестановок длины \(n\) по модулю \(998244353\). Выходные данные Для каждого набора входных данных выведите единственное число — количество почти идеальных перестановок длины \(n\) по модулю \(998244353\). Примечание Для \(n = 2\), обе перестановки \([1, 2]\) и \([2, 1]\) являются почти идеальными. Для \(n = 3\), есть только \(6\) перестановок. Взглянув на все из них, мы получаем: - \([1, 2, 3]\) является почти идеальной перестановкой.
- \([1, 3, 2]\) является почти идеальной перестановкой.
- \([2, 1, 3]\) является почти идеальной перестановкой.
- \([2, 3, 1]\) НЕ является почти идеальной перестановкой (\(\lvert p_2 - p^{-1}_2 \rvert = \lvert 3 - 1 \rvert = 2\)).
- \([3, 1, 2]\) НЕ является почти идеальной перестановкой (\(\lvert p_2 - p^{-1}_2 \rvert = \lvert 1 - 3 \rvert = 2\)).
- \([3, 2, 1]\) является почти идеальной перестановкой.
Поэтому мы получаем \(4\) почти идеальные перестановки. | |
![]()
|
|
G. Некая волшебная вечеринка
Структуры данных
Комбинаторика
жадные алгоритмы
сортировки
*3300
На вечеринке есть \(n\) человек. \(i\)-й человек имеет уровень счастья \(a_i\). У каждого человека есть определенный тип личности, который можно представить в виде двоичного целого числа \(b\). Если \(b = 0\), то счастье человека будет увеличиваться, если он рассказывает историю кому-то со строго меньшим счастьем, чем у него. Если \(b = 1\), то счастье человека будет увеличиваться, если он рассказывает историю кому-то со строго большим счастьем, чем у него. Давайте определим порядок выступления как порядок людей слева направо. Теперь происходит следующий процесс. Мы идем слева направо. Текущий человек говорит рассказывает историю всем остальным людям. Заметьте, что все уровни счастья остаются неизменными во время этого. После того, как человек закончил, он подсчитывает количество людей, которым он рассказывал историю и которые имеют строго меньший/больший уровень счастья, чем он, в соответствии с его типом личности, и его счастье увеличивается на это значение. Заметьте, что увеличивается уровень счастья только текущего человека. Как организатор вечеринки, вы не хотите, чтобы кто-то ушел грустным. Следовательно, вы хотите подсчитать количество порядков выступления, чтобы в конце процесса все \(n\) человек имели равные уровни счастья. Два порядка выступления считаются разными, если существует хотя бы один человек, не занимающий одинаковое положение в двух порядках выступления. Выходные данные Выведите количество различных допустимых последовательностей выступлений. Так как это число может быть большим, выведите его по модулю \(998244353\). Примечание Здесь объяснение для первого примера. Одним из корректных порядков выступлений является \([2,1,4,3]\) (здесь, мы написали индексы каждого человека). Каждый шаг показывает текущие уровни счастья и результаты. Шаг \(1\): \([1,2,4,4]\) \(\rightarrow\) Человек \(2\) рассказывает историю остальным. Так как его тип личности равен \(1\), его счастье увеличится на \(2\), так как люди \(3\) и \(4\) имеют строго большие уровни счастья. Шаг \(2\): \([1,4,4,4]\) \(\rightarrow\) Человек \(1\) рассказывает историю остальным. Так как его тип личности равен \(1\), его счастье увеличится на \(3\), так как люди \(2\), \(3\) и \(4\) имеют строго большие уровни счастья. Шаг \(3\): \([4,4,4,4]\) \(\rightarrow\) Человек \(4\) рассказывает историю остальным. Так кае его тип личности равен \(0\), его счастье увеличится на \(0\), так как ни у кого нет строго меньшего уровня счастья. Шаг \(4\): \([4,4,4,4]\) \(\rightarrow\) Человек \(3\) рассказывает историю остальным. Так как его тип личности равен \(0\), его счастье увеличится на \(0\), так как ни у кого нет строго меньшего уровня счастья. В итоге, у всех одинаковый уровень счастья. Заметьте, что \([2,1,3,4]\) также является корректным порядком для примера. Можно показать, что не существует корректных порядков во втором примере. | |
![]()
|
|
G. Освещение
Бинарный поиск
Перебор
Комбинаторика
математика
дп
*2700
битмаски
Рассмотрим отрезок \([0, d]\) координатной прямой. В этом отрезке \(n\) фонарей и \(m\) интересных точек. Для каждого фонаря вы должны выбрать его мощность — целое число от \(0\) до \(d\) (включительно). Фонарь с координатой \(x\) освещает интересную точку с координатой \(y\), если \(|x - y|\) меньше либо равно мощности фонаря. Способ выбрать мощности для всех фонарей является корректным, если каждая интересная точка освещена хотя бы одним фонарем. Вам нужно обработать \(q\) запросов. Каждый запрос обозначается одним целым числом \(f_i\). Чтобы ответить на \(i\)-й запрос, вам нужно: - добавить фонарь в точку \(f_i\);
- посчитать количество корректных способов назначить мощность каждому фонарю, и вывести это количество по модулю \(998244353\);
- удалить только что добавленный фонарь.
Выходные данные Для каждого запроса выведите ответ на него по модулю \(998244353\). | |
![]()
|
|
G. Вырежи подстроки
Строки
Комбинаторика
*2100
дп
хэши
Вам даны две непустые строки \(s\) и \(t\), состоящие из латинских букв. За один ход вы можете выбрать вхождение строки \(t\) в строку \(s\) и заменить его на точки. Ваша задача — за минимальное количество ходов убрать все вхождения строки \(t\) в строке \(s\), а также посчитать, сколько существует различных последовательностей ходов минимальной длины. Две последовательности ходов считаются различными, если множества индексов, в которых начинаются убираемые вхождения строки \(t\) в \(s\), различаются. Например, множества \(\{1, 2, 3\}\) и \(\{1, 2, 4\}\) считаются различными, множества \(\{2, 4, 6\}\) и \(\{2, 6\}\) — тоже, а множества \(\{3, 5\}\) и \(\{5, 3\}\) — нет. Например, пусть строка \(s =\) «abababacababa», а строка \(t =\) «aba». Мы можем убрать все вхождения строки \(t\) за \(2\) хода, заменив вхождения строки \(t\) на \(3\)-й и \(9\)-й позициях на точки. В этом случае строка \(s\) пример вид «ab...bac...ba». Также можно вырезать вхождения строки \(t\) на \(3\)-й и \(11\)-й позициях. Всего есть две различные последовательности ходов минимальной длины. Так как ответ может быть большим, выведите его по модулю \(10^9 + 7\). Выходные данные Для каждого набора входных данных выведите два целых числа — минимальное количество ходов и количество различных оптимальных последовательностей, взятое по модулю \(10^9 + 7\). Примечание Первый набор входных данных разобран в условии. Во втором наборе достаточно заменить любое из четырёх вхождений. В третьем наборе строка \(s\) является конкатенацией двух строк \(t =\) «xyz», поэтому существует единственная оптимальная последовательность из \(2\) ходов. В четвёртом и шестом наборах строка \(s\) изначально не содержит вхождений строки \(t\). В пятом наборе строка \(s\) содержит ровно одно вхождение строки \(t\). | |
![]()
|
|
E. Максимумы и минимумы
Структуры данных
Комбинаторика
теория чисел
разделяй и властвуй
*2700
Вам дан массив целых положительных чисел \(a_1, a_2, \ldots, a_n\). Найдите количество пар индексов \((l, r)\) (\(1 \le l \le r \le n\)), которые проходят проверку. Проверка пары чисел выполняется следующим образом: - Находятся минимум и максимум среди чисел \(a_l, a_{l+1}, \ldots, a_r\).
- Проверка считается пройденной, если максимум делится на минимум.
Выходные данные Для каждого набора входных данных выведите единственное целое число — количество проходящих проверку пар чисел. Примечание Ниже запись \(x \mid y\) означает, что \(y\) делится на \(x\). В первом наборе входных данных существует всего одна пара индексов \((1, 1)\), для нее максимум равен \(1\), минимум также \(1\), \(1 \mid 1\), поэтому эта пара проходит проверку, а ответ равен \(1\). Во втором наборе входных данных \(3\) пары индексов: - \((1, 1)\): максимум равен \(2\), минимум равен \(2\), \(2 \mid 2\), проверка пройдена.
- \((1, 2)\): максимум равен \(4\), минимум равен \(2\), \(2 \mid 4\), проверка пройдена.
- \((2, 2)\): максимум равен \(4\), минимум равен \(4\), \(4 \mid 4\), проверка пройдена.
В третьем наборе входных данных \(3\) пары индексов: - \((1, 1)\): максимум равен \(2\), минимум равен \(2\), \(2 \mid 2\), проверка пройдена.
- \((1, 2)\): максимум равен \(3\), минимум равен \(2\), \(3\) не делится на \(2\), поэтому проверка не пройдена.
- \((2, 2)\): максимум равен \(3\), минимум равен \(3\), \(3 \mid 3\), поэтому проверка пройдена.
| |
![]()
|
|
F. Сумма функций
Перебор
Комбинаторика
математика
дп
*2500
бпф
Предположим, вам задан целочисленный массив \(a_1, a_2, \dots, a_n\). Пусть \(\operatorname{lsl}(i)\) равно количеству индексов \(j\) (\(1 \le j < i\)) таких, что \(a_j < a_i\). Аналогично, пусть \(\operatorname{grr}(i)\) равно количеству индексов \(j\) (\(i < j \le n\)) таких, что \(a_j > a_i\). Назовем позицию \(i\) в массиве \(a\) хорошей, если \(\operatorname{lsl}(i) < \operatorname{grr}(i)\). Наконец, определим функцию \(f\) на массиве \(a\) \(f(a)\) как сумму всех \(a_i\) таких, что \(i\) — хорошая в \(a\). Для заданных целых чисел \(n\) и \(k\), посчитайте сумму \(f(a)\) по всем массивам \(a\) размера \(n\) таких, что \(1 \leq a_i \leq k\) для всех \(1 \leq i \leq n\), по модулю \(998\,244\,353\). Выходные данные Выведите единственное число — сумму \(f\) по всем массивам \(a\) размера \(n\) по модулю \(998\,244\,353\). Примечание В первом наборе входных данных: | \(f([1,1,1]) = 0\) | \(f([2,2,3]) = 2 + 2 = 4\) | | \(f([1,1,2]) = 1 + 1 = 2\) | \(f([2,3,1]) = 2\) | | \(f([1,1,3]) = 1 + 1 = 2\) | \(f([2,3,2]) = 2\) | | \(f([1,2,1]) = 1\) | \(f([2,3,3]) = 2\) | | \(f([1,2,2]) = 1\) | \(f([3,1,1]) = 0\) | | \(f([1,2,3]) = 1\) | \(f([3,1,2]) = 1\) | | \(f([1,3,1]) = 1\) | \(f([3,1,3]) = 1\) | | \(f([1,3,2]) = 1\) | \(f([3,2,1]) = 0\) | | \(f([1,3,3]) = 1\) | \(f([3,2,2]) = 0\) | | \(f([2,1,1]) = 0\) | \(f([3,2,3]) = 2\) | | \(f([2,1,2]) = 1\) | \(f([3,3,1]) = 0\) | | \(f([2,1,3]) = 2 + 1 = 3\) | \(f([3,3,2]) = 0\) | | \(f([2,2,1]) = 0\) | \(f([3,3,3]) = 0\) | | \(f([2,2,2]) = 0\) | |
Сложив все значения, получаем ответ, равный \(28\). | |
![]()
|
|
A. Bestie
Перебор
Конструктив
Комбинаторика
математика
*1000
реализация
теория чисел
Вам дан массив \(a\), состоящий из \(n\) целых чисел \(a_1, a_2, \ldots, a_n\). Друзья попросили вас сделать наибольший общий делитель (НОД) всех элементов массива равным \(1\). За одну операцию вы можете сделать следующее: - Выбрать произвольный индекс в массиве \(1 \leq i \leq n\);
- Сделать \(a_i = \gcd(a_i, i)\), где \(\gcd(x, y)\) обозначает НОД чисел \(x\) и \(y\). Стоимость такой операции равна \(n - i + 1\).
Вам нужно найти минимальную суммарную стоимость операций, которые нужно сделать, чтобы НОД всех элементов массива стал равен \(1\). Выходные данные Для каждого набора входных данных выведите единственное целое число — минимальную суммарную стоимость операций, которые нужно сделать, чтобы НОД всех элементов массива стал равен \(1\). Можно показать, что это всегда можно сделать. Примечание В первом наборе входных данных НОД всего массива уже равен \(1\), поэтому операции применять не нужно. Во втором наборе входных данных можно выбрать \(i = 1\). После этой операции \(a_1 = \gcd(2, 1) = 1\). Стоимость этой операции равна \(1\). В третьем наборе входных данных можно выбрать \(i = 1\), после этого массив \(a\) будет равен \([1, 4]\). НОД этого массива равен \(1\), а суммарная стоимость равна \(2\). В четвертом наборе входных данных можно выбрать \(i = 2\), после этого массив \(a\) будет равен \([3, 2, 9]\). НОД этого массива равен \(1\), а суммарная стоимость равна \(2\). В шестом наборе входных данных можно выбрать \(i = 4\) и \(i = 5\), после этого массив \(a\) будет равен \([120, 60, 80, 4, 5]\). НОД этого массива равен \(1\), а суммарная стоимость равна \(3\). | |
![]()
|
|
D. Мета-cет
Перебор
Структуры данных
Комбинаторика
математика
*1700
хэши
Вы любите настольную карточную игру «Сет». Каждая карта содержит \(k\) характеристик, каждая из которых может принимать значения из набора \(\{0, 1, 2\}\). В колоде содержатся все возможные варианты карт по одному разу, то есть всего \(3^k\) различных карт. Для тройки карт характеристика является хорошей, если она совпадает у всех трех карт, либо у всех трех попарно различается. Тройка карт называется сетом, если все \(k\) характеристик для них являются хорошими. Например, карты \((0, 0, 0)\), \((0, 2, 1)\) и \((0, 1, 2)\) образуют сет, а карты \((0, 2, 2)\), \((2, 1, 2)\) и \((1, 2, 0)\) — нет, так как, например, последняя характеристика не является хорошей. Группа из пяти карт называется мета-сетом, если среди этих карт строго больше одного сета. Сколько существует мета-сетов среди данных \(n\) различных карт? Выходные данные Выведите одно число — количество мета-сетов. Примечание Будем изображать карты из примеров, указывая первые четыре характеристики. Первая характеристика будет обозначать количество объектов на карте: \(1\), \(2\), \(3\). Вторая характеристика — цвет: красный, зеленый, фиолетовый. Третья — форму: овал, ромб, волну. Четвертая — заполнение: контур, штрихованная, закрашенная. Ниже нарисованы первые три теста. Для первых двух тестов выделены пятерки карт, которые являются мета-сетами. В первом тесте мета-сетом является пятерка карт \((0000,\ 0001,\ 0002,\ 0010,\ 0020)\). Сетами в нем являются тройки: \((0000,\ 0001,\ 0002)\) и \((0000,\ 0010,\ 0020)\). Также сетом является тройка \((0100,\ 1000,\ 2200)\), которая не принадлежит ни одному мета-сету. 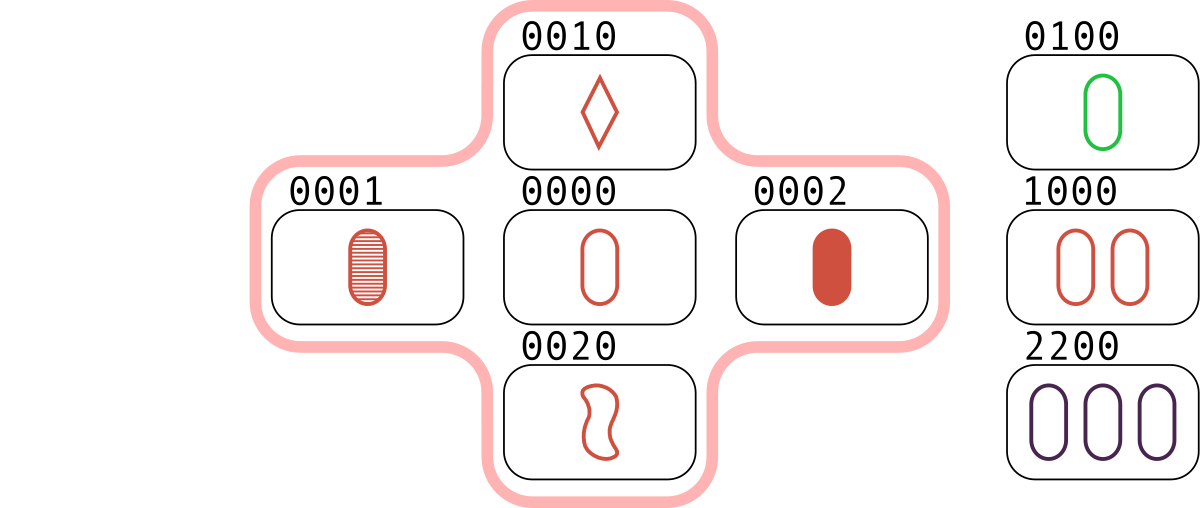 Во втором тесте мета-сетами являются пятерки: \((0000,\ 0001,\ 0002,\ 0010,\ 0020)\), \((0000,\ 0001,\ 0002,\ 0100,\ 0200)\), \((0000,\ 0010,\ 0020,\ 0100,\ 0200)\). 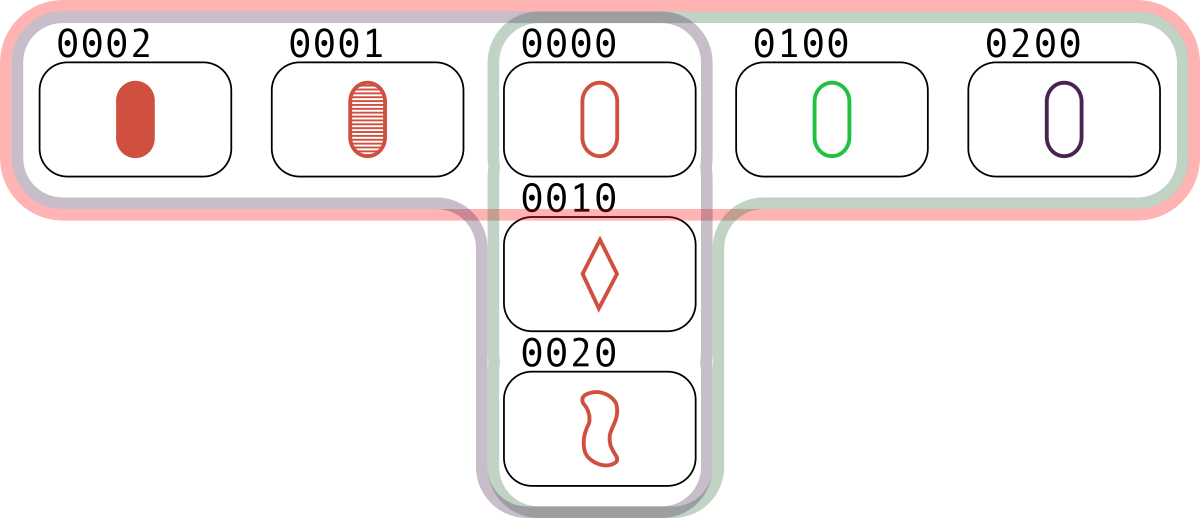 В третьем тесте \(54\) мета-сета. 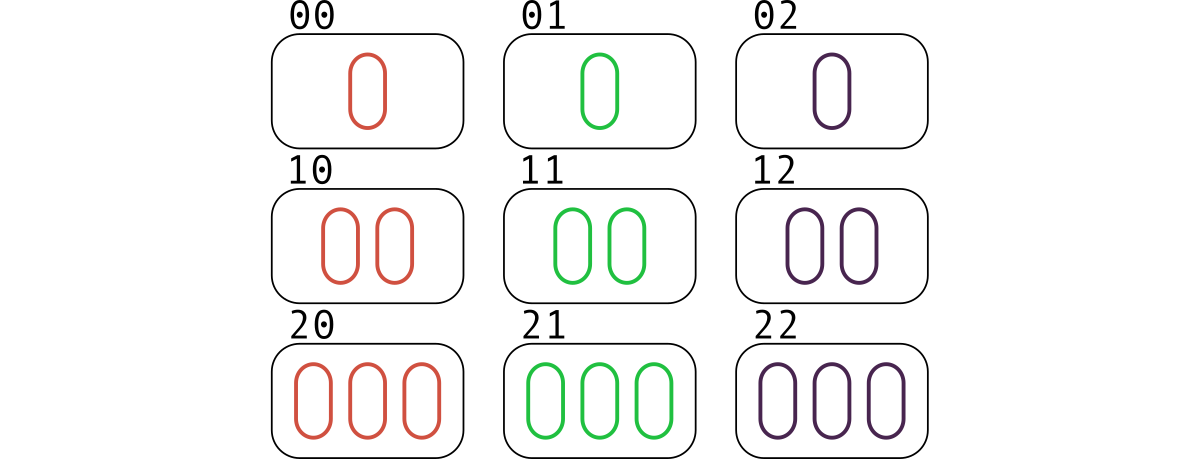 | |
![]()
|
|
E. Эла идет в поход
Теория вероятностей
Комбинаторика
математика
дп
*2500
 | Эла любит ходить в походы. Она любит природу и исследует различных животных. Однажды она увидела муравьев странного вида с каннибальскими наклонностями. В частности, муравей такого вида съест любого меньшего муравья, которого он увидит. Заинтересовавшись этой особенностью, Эла решила провести эксперимент. |
Она посадила \(n\) муравьев-каннибалов в ряд на длинной деревянной палке. Изначально все муравьи имеют одинаковый вес \(1\). Расстояние между любыми двумя соседними муравьями одинаково. Расстояния между первым муравьем в цепочке до левого конца палки и последним муравьем в цепочке до правого конца палки также одинаковы и равны расстоянию между двумя соседними муравьями. В какой-то момент каждый муравей начинает двигаться влево либо вправо равновероятно случайным образом с одной и той же постоянной для всех муравьев скоростью на протяжении всего эксперимента. Муравьи поворачиваются в обратную сторону сразу же, как только достигнут конца палки. Вскоре Эле удалось выяснить поведение муравьев в случае встречи. - Если два муравья разного веса встретятся, более тяжелый мгновенно съест более легкого и увеличит свой вес на вес более легкого. После этого он продолжит идти в том же направлении. Например, если более тяжелый муравей имеет вес \(x\) и идет вправо, а более легкий имеет вес \(y\) и идет влево (\(x > y\)), то после встречи более легкий будет съеден, а более тяжелый будет иметь вес \(x + y\) и продолжит идти вправо.
- Если два муравья одного веса встретятся, то тот, кто идет влево, мгновенно съест того, кто идет вправо, а затем продолжит идти в том же направлении. Другими словами, если один муравей веса \(x\), идущий влево, встретится с другим муравьем веса \(x\), идущим вправо, то муравей, идущий вправо, будет съеден, а идущий влево будет весить \(2x\) и продолжит двигаться влево.
Заметьте, что два муравья могут встретиться, только если идут в разные стороны Можно доказать, что через определенное время останется только один муравей. Изначально каждый муравей будет случайным образом равновероятно двигаться влево или вправо, что порождает \(2^n\) различных случаев начального движения. Для каждого муравья вычислите вероятность того, что он в итоге выживет. Выведите ее по модулю \(10^9 + 7\). Формально, пусть \(M = 10^9 + 7\). Можно показать, что ответ можно представить в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, а \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Выходные данные Для каждого теста выведите \(n\) строк. В \(i\)-й строке выведите единственное число, обозначающее вероятность выживания \(i\)-го муравья в строке по модулю \(10^9 + 7\). Примечание В примере на ветке находятся \(6\) муравьев. Движение муравья будет обозначаться для удобства либо символом \(L\), либо \(R\). Пусть муравьи на ветке будут двигаться как \(RLRRLR\). Вот как они ведут себя после этого:  Первоначально муравьи располагаются, как указано выше.  Через некоторое время муравей с индексом \(2\) (идущий влево) встретится с муравьем с индексом \(1\) (идущий вправо). Два муравья имеют одинаковый вес, поэтому муравей \(2\) съест муравья \(1\) и будет иметь вес \(2\). То же самое произойдет с муравьем \(5\) и муравьем \(4\). Муравей \(6\) дойдет до конца палки, тем самым изменив свое направление.  После этого муравей с индексом \(5\) встретится с муравьем с индексом \(3\). Поскольку муравей \(5\) тяжелее (вес \(2\)), чем муравей \(3\) (вес \(1\)), муравей \(5\) съест муравья \(3\) и будет иметь вес \(3\). Муравей \(2\) дойдет до конца палки, тем самым изменив свое направление. 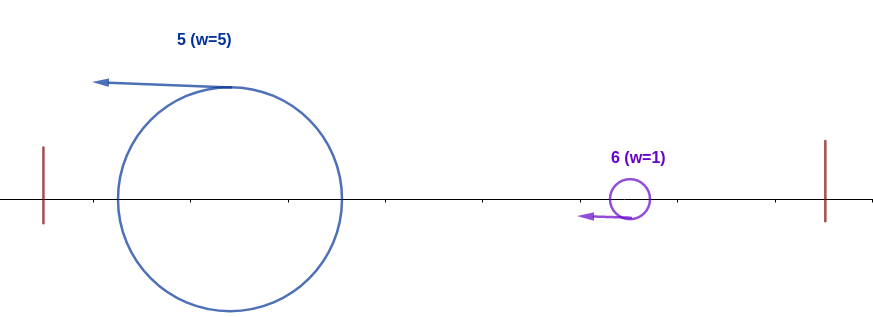 После этого муравей с индексом \(5\) встретится с муравьем с индексом \(2\). Поскольку муравей \(5\) тяжелее (вес \(3\)), чем муравей \(2\) (вес \(2\)), муравей \(5\) съест муравья \(2\) и наберет вес \(5\). 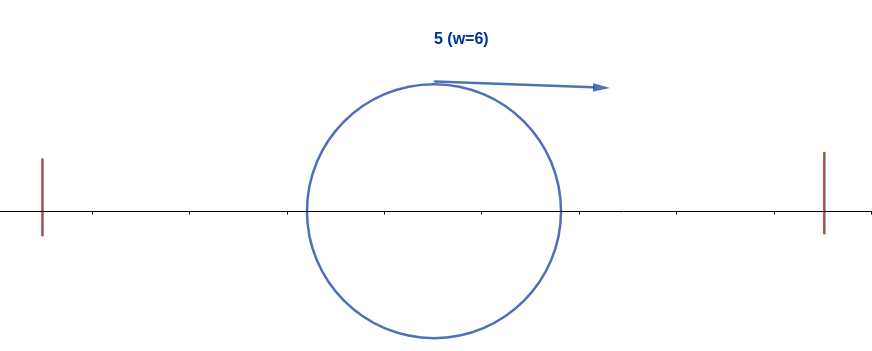 Наконец, после того, как муравей \(5\) дойдет до конца ветки и изменит направление, муравей \(5\) съест муравья \(6\) и останется последним оставшимся муравьем. | |
![]()
|
|
E. Упоротый баланс
Комбинаторика
математика
дп
*2300
Дана последовательность \(a_1, a_2, \dots, a_n\) длины \(n\), ваша задача посчитать число, по модулю \(998244353\), способов разбить ее на несколько не пустых непрерывных подпоследовательностей так, что сумма элементов в подпоследовательностях является сбалансированной последовательностью. Последовательность \(s_1, s_2, \dots, s_k\) длины \(k\) является сбалансированной, если \(s_{i} = s_{k-i+1}\) для всех \(1 \leq i \leq k\). Например, \([1, 2, 3, 2, 1]\) и \([1,3,3,1]\) сбалансированный, а \([1,5,15]\) нет. Формально, каждое разбиение может быть описано последовательностью индексов \(i_1, i_2, \dots, i_k\) длины \(k\) и \(1 = i_1 < i_2 < \dots < i_k \leq n\) такое, что - \(k\) является числом непустых непрерывных подпоследовательностей в разделении;
- Для каждого \(1 \leq j \leq k\), \(j\)-я непрерывная подпоследовательность начинается в \(a_{i_j}\), и заканчивается перед \(a_{i_{j+1}}\), где \(i_{k+1} = n + 1\). Значит, что \(j\)-я подпоследовательность это \(a_{i_j}, a_{i_j+1}, \dots, a_{i_{j+1}-1}\).
Всего \(2^{n-1}\) различных разбиений. Пусть \(s_1, s_2, \dots, s_k\) означает суммы элементов в подпоследовательностях относительно разбиения \(i_1, i_2, \dots, i_k\). Формально, для каждого \(1 \leq j \leq k\), \(\) s_j = \sum_{i=i_{j}}^{i_{j+1}-1} a_i = a_{i_j} + a_{i_j+1} + \dots + a_{i_{j+1}-1}. \(\) Например, разбиение \([1\,|\,2,3\,|\,4,5,6]\) последовательности \([1,2,3,4,5,6]\) задается последовательностью индексов \([1,2,4]\), и суммы элементов разбиения будут равны \([1,5,15]\). Два разбиения \(i_1, i_2, \dots, i_k\) и \(i'_1, i'_2, \dots, i'_{k'}\) (описанные последовательностью индексов) являются разными, если выполнено хотя бы одно из следующих условий. - \(k \neq k'\),
- \(i_j \neq i'_j\) для некоторого \(1 \leq j \leq \min\left\{ k, k' \right\}\).
Выходные данные Для каждого тестового примера выведите количество разделений, в которых сумма элементов в каждой подпоследовательности сбалансирована по модулю \(998244353\). Примечание В первом примере существует только один способ разделить последовательность длины \(1\), который, разумеется, сбалансированный. Для второго теста существует \(2\) способа разделить последовательность: - Сама последовательность \([1, 1]\) тогда \(s = [2]\) сбалансирована;
- Разделить на две последовательности \([1\,|\,1]\), тогда \(s = [1, 1]\) сбалансирована.
В третьем тесте существует \(3\) способа разделить последовательность: - Сама последовательность \([0, 0, 1, 0]\), тогда \(s = [1]\) сбалансирована;
- \([0 \,|\, 0, 1 \,|\, 0]\), тогда \(s = [0, 1, 0]\) сбалансирована;
- \([0, 0 \,|\, 1 \,|\, 0]\), тогда \(s = [0, 1, 0]\) сбалансирована.
В четвертом примере существует \(4\) способа разделить последовательность: - Сама последовательность \([1, 2, 3, 2, 1]\), тогда \(s = [9]\) сбалансирована;
- \([1, 2 \,|\, 3 \,|\, 2, 1]\), тогда \(s = [3, 3, 3]\) сбалансирована;
- \([1 \,|\, 2, 3, 2 \,|\, 1]\), тогда \(s = [1, 7, 1]\) сбалансирована;
- \([1 \,|\, 2 \,|\, 3 \,|\, 2 \,|\, 1]\), тогда \(s = [1, 2, 3, 2, 1]\) сбалансирована.
В пятом примере существует \(2\) способа разделить последовательность: - Сама последовательность \([1, 3, 5, 7, 9]\), тогда \(s = [25]\) сбалансирована;
- \([1, 3, 5 \,|\, 7 \,|\, 9]\), тогда \(s = [9, 7, 9]\) сбалансирована.
Для шестого примера любое разбиение подходит. Значит, ответ равен \(2^{32-1} \equiv 150994942 \pmod {998244353}\). | |
![]()
|
|
C. Карточная игра
Конструктив
Комбинаторика
дп
*1500
игры
Рассмотрим игру с \(n\) картами (\(n\) четное). На каждой карте написано число от \(1\) до \(n\). Числа на всех картах различны. Скажем, что карта с числом \(x\) сильнее карты с числом \(y\), если \(x > y\). Два игрока, Алексей и Борис играют в эту игру. В начале каждый из них получает ровно по \(\frac{n}{2}\) карт, так что каждая карта находится ровно у одного игрока. Затем они ходят по очереди. Сначала ходит Алексей, затем Борис, затем снова Алексей и так далее. На своем ходу игрок должен сыграть ровно одну из своих карт. Затем, если у соперника нет карт сильнее сыгранной карты, то соперник проигрывает, и игра заканчивается. Иначе соперник должен сыграть карту сильнее сыгранной (тоже ровно одну). Эти две карты удаляются из игры, и ход заканчивается. Если карт больше нет, то игра заканчивается вничью; иначе ход переходит к сопернику. Рассмотрим все способы распределить карты между двумя игроками так, чтобы у каждого была ровно половина всех карт. Вам надо посчитать три величины: - количество способов раздать карты так, чтобы выиграл Алексей;
- количество способов раздать карты так, чтобы выиграл Борис;
- количество способов раздать карты так, чтобы игра закончилась вничью.
Полагаем, что оба игрока играют оптимально (т. е. если игрок может выиграть вне зависимости от действий его соперника, то он выигрывает). Два способа раздать карты считаются различными, если есть хотя бы одна такая карта, что в одном из способов она у Алексея, а в другом — у Бориса. Например, пусть \(n = 4\), Алексей получает карты \([2, 3]\), а Борис получает карты \([1, 4]\). Игра может пойти следующим образом: - если Алексей играет карту \(2\), Борис должен ответить картой \(4\). Ход Алексея заканчивается, и начинается ход Бориса. У Бориса осталась только карта \(1\); он играет ее, и Алексей отвечает картой \(3\). Игра заканчивается ничьей;
- если Алексей играет карту \(3\), Борис должен ответить картой \(4\). Ход Алексея заканчивается, и начинается ход Бориса. У Бориса осталась только карта \(1\); он играет ее, и Алексей отвечает картой \(2\). Игра заканчивается ничьей.
Таким образом, в этом случае игра заканчивается вничью. Выходные данные На каждый набор входных данных выведите три числа: - количество способов раздать карты так, чтобы выиграл Алексей;
- количество способов раздать карты так, чтобы выиграл Борис;
- количество способов раздать карты так, чтобы игра закончилась вничью.
Так как ответ может быть достаточно большим, выведите его по модулю \(998244353\). Примечание В первом наборе входных данных Алексей выигрывает, если он получает карту \(2\) (он ее играет, а Борис не может ответить). Если Алексей получает карту \(1\), то игра заканчивается вничью. Во втором наборе входных данных: - Алексей выигрывает, если он получает карты \([3, 4]\), \([2, 4]\) или \([1, 4]\);
- Борис выигрывает, если Алексей получает карты \([1, 2]\) или \([1, 3]\);
- игра заканчивается вничью, если Алексей получает карты \([2, 3]\).
| |
![]()
|
|
F. Ограниченное смешивание
Комбинаторика
математика
дп
*2600
Паку Чанаку дан массив \(a\) из \(n\) целых чисел. Для каждого \(i\) (\(1 \leq i \leq n\)) Пак Чанак пишет на доске одноэлементное множество \(\{a_i\}\). После этого за одну операцию Пак Чанак может сделать следующее: - Выбрать два различных множества \(S\) и \(T\) на доске таких, что \(S \cap T = \varnothing\) (\(S\) и \(T\) не имеют общих элементов).
- Стереть \(S\) и \(T\) с доски и записать \(S \cup T\) (объединение \(S\) и \(T\)) на доску.
Выполнив ноль или более операций, Пак Чанак построит мультимножество \(M\), содержащее размеры всех множеств, написанных на доске. Другими словами, каждый элемент в \(M\) соответствует размеру некоторого множества после операций. Сколько различных\(^\dagger\) мультимножеств \(M\) может быть получено таким процессом? Так как ответ может быть большим, выведите его по модулю \(998\,244\,353\). \(^\dagger\) Мультимножества \(B\) и \(C\) различны тогда и только тогда, когда существует значение \(k\) такое, что количество элементов со значением \(k\) в \(B\) отличается от количества элементов со значением \(k\) в \(C\). Выходные данные Выведите количество различных мультимножеств \(M\) по модулю \(998\,244\,353\). Примечание В первом примере возможные мультимножества \(M\) таковы: \(\{1,1,1,1,1,1\}\), \(\{1,1,1,1,2\}\), \(\{1,1,1,3\}\), \(\{1,1,2,2\}\), \(\{1,1,4\}\), \(\{1,2,3\}\) и \(\{2,2,2\}\). В качестве примера рассмотрим возможную последовательность операций. - Вначале множества имеют вид \(\{1\}\), \(\{1\}\), \(\{2\}\), \(\{1\}\), \(\{4\}\) и \(\{3\}\).
- Применяем операцию ко множествам \(\{1\}\) и \(\{3\}\). Теперь множества на доске имеют вид \(\{1\}\), \(\{1\}\), \(\{2\}\), \(\{4\}\) и \(\{1,3\}\).
- Применяем операцию ко множествам \(\{2\}\) and \(\{4\}\). Теперь множества на доске имеют вид \(\{1\}\), \(\{1\}\), \(\{1,3\}\) и \(\{2,4\}\).
- Применяем операцию ко множествам \(\{1,3\}\) and \(\{2,4\}\). Теперь множества на доске имеют вид \(\{1\}\), \(\{1\}\) и \(\{1,2,3,4\}\).
- Полученное мультимножество \(M\) имеет вид \(\{1,1,4\}\).
| |
![]()
|
|
A. Пароль
Перебор
Комбинаторика
математика
реализация
*800
Монокарп забыл пароль от своего телефона. Пароль состоит ровно из \(4\) цифр от \(0\) до \(9\) (обратите внимание, что пароль может начинаться с цифры \(0\)). Монокарп помнит, что в его пароле были ровно две различные цифры, причем каждая из этих цифр встречалась в пароле ровно по два раза. Также Монокарп помнит, какие цифры точно не могли быть в его пароле. Посчитайте количество последовательностей из \(4\) цифр, которые могли бы быть паролем Монокарпа (то есть которые подходят под все описанные условия). Выходные данные На каждый набор входных данных выведите одно целое число — количество последовательностей из \(4\) цифр, которые подходят под все описанные условия. Примечание Возможные пароли в первом наборе входных данных: «3377», «3737», «3773», «7337», «7373», «7733». | |
![]()
|
|
G. Антифибоначчиевый разрез
Структуры данных
Конструктив
Комбинаторика
математика
дп
хэши
битмаски
*3000
Обратите внимание на нестандартное ограничение памяти. Введем последовательность строк Фибоначчи следующим образом: \(f_0\) — строка 0, \(f_1\) — строка 1, \(f_i\) строится по формуле \(f_{i-1} + f_{i-2}\) при \(i>1\) (\(+\) обозначает конкатенацию строк). Например, \(f_2\) — 10, \(f_3\) — 101, \(f_4\) — 10110. Для строки \(s\) обозначим за \(g(s)\) количество способов разрезать эту строку на строки, из которых ни одна не является строкой Фибоначчи. Например, если \(s\) — 10110101, \(g(s) = 3\), так как существуют три способа разрезать строку: - 101101 \(+\) 01;
- 1011 \(+\) 0101;
- 1011 \(+\) 01 \(+\) 01.
Вам дана последовательность строк \(s_1, s_2, \dots, s_n\). Посчитайте \(g(s_1), g(s_1 + s_2), \dots, g(s_1 + s_2 + \ldots + s_n)\). Так как эти значения могут быть очень большими, выведите их по модулю \(998244353\). Выходные данные Выведите \(n\) целых чисел, \(i\)-е из которых равно \(g(s_1 + s_2 + \ldots + s_i) \bmod 998244353\). | |
![]()
|
|
E. Генерация списков
Комбинаторика
математика
дп
*2900
Для заданных целых чисел \(n\) и \(m\) назовем пару массивов \(a\) и \(b\) целых чисел хорошей, если они удовлетворяют следующим условиям: - \(a\) и \(b\) имеют одинаковую длину, пусть их длина равна \(k\).
- \(k \ge 2\) и \(a_1 = 0, a_k = n, b_1 = 0, b_k = m\).
- Для каждого \(1 < i \le k\) имеет место следующее: \(a_i \geq a_{i - 1}\), \(b_i \geq b_{i - 1}\), и \(a_i + b_i \neq a_{i - 1} + b_{i - 1}\).
Найдите сумму \(|a|\) по всем хорошим парам массивов \((a,b)\). Поскольку ответ может быть очень большим, выведите его по модулю \(10^9 + 7\). Выходные данные Для каждого набора входных данных выведите одно целое число — сумму \(|a|\) по всем хорошим парам массивов \((a,b)\) по модулю \(10^9 + 7\). Примечание В первом наборе входных данных, хорошими парами массивов являются - \(([0, 1], [0, 1])\), длина = \(2\).
- \(([0, 1, 1], [0, 0, 1])\), длина = \(3\).
- \(([0, 0, 1], [0, 1, 1])\), длина = \(3\).
Следовательно, сумма длин будет \({2 + 3 + 3} = 8\). | |
![]()
|
|
D. ConstructOR
Конструктив
Комбинаторика
математика
*2100
теория чисел
битмаски
китайская теорема об остатках
Вам даны три целых числа \(a\), \(b\), \(d\). Найдите целое число \(x\), удовлетворяющее следующим требованиям, или сообщите, что такого числа не существует: - \(0 \le x \lt 2^{60}\);
- \(a|x\) делится на \(d\);
- \(b|x\) делится на \(d\).
Здесь \(|\) обозначает операцию побитового ИЛИ. Выходные данные Для каждого набора входных данных выведите одно число: - если существует число \(x\), удовлетворяющее требованиям из условия, выведите \(x\);
- иначе, выведите \(-1\).
Если существует несколько решений, выведите любое из них. Примечание В первом наборе входных данных одно из возможных решений \(x=18\). Оно корректно, так как \(39|18=55\) и \(12|18=30\) делятся на \(d=5\). Во втором наборе входных данных одно из возможных решений \(x=14\). Оно корректно, так как \(8|14=6|14=14\) делится на \(d=14\). Можно показать, что в третьем и четвёртом наборах входных данных решений не существует. | |
![]()
|
|
D. Подсчет массивов
Комбинаторика
математика
дп
теория чисел
*1900
Рассмотрим массив \(a\) длины \(n\), элементы которого пронумерованы от \(1\) до \(n\). Можно удалить \(i\)-й элемент из \(a\), если \(gcd(a_i, i) = 1\), где \(gcd\) обозначает наибольший общий делитель. После того, как элемент удаляется, те элементы, которые были справа от него, сдвигаются на одну позицию влево. Массив \(b\) из \(n\) элементов, для которых выполняется \(1 \le b_i \le n - i + 1\), называется последовательностью удалений для массива \(a\), если можно удалить все элементы \(a\) в следующем порядке: сначала удалить \(b_1\)-й элемент, затем \(b_2\)-й, ..., затем \(b_n\)-й. Например, пусть \(a = [42, 314]\): - \([1, 1]\) — последовательность удалений: когда вы удаляете \(1\)-й элемент массива, условие \(gcd(42, 1) = 1\) соблюдаются, и массив становится \([314]\); когда вы снова удаляете \(1\)-й элемент, условие \(gcd(314, 1) = 1\) соблюдается, и массив становится пустым.
- \([2, 1]\) не является последовательностью удалений: когда вы пытаетесь удалить \(2\)-й элемент, условие \(gcd(314, 2) = 1\) не выполняется.
Назовем массив неоднозначным, если у него хотя бы две последовательности удалений. Например, массив \([1, 2, 5]\) — неоднозначный: у него есть последовательности удалений \([3, 1, 1]\) и \([1, 2, 1]\). Массив \([42, 314]\) не является неоднозначным: единственная последовательность удалений для него — это \([1, 1]\). Вам даны два числа \(n\) и \(m\). Посчитайте количество неоднозначных массивов \(a\), таких, что длина \(a\) от \(1\) до \(n\), а элементы \(a_i\) — целые числа от \(1\) до \(m\). Выходные данные Выведите одно целое число — количество неоднозначных массивов \(a\), таких, что длина \(a\) от \(1\) до \(n\), а элементы \(a_i\) — целые числа от \(1\) до \(m\). Так как ответ может быть очень большим, выведите его по модулю \(998244353\). | |
![]()
|
|
D. Посчитайте НОД
Комбинаторика
математика
теория чисел
*1800
Вам даны два целых числа \(n\) и \(m\) и массив \(a\) из \(n\) целых чисел. Для каждого \(1 \le i \le n\) верно, что \(1 \le a_i \le m\). Ваша задача — посчитать количество различных массивов \(b\) длины \(n\) таких, что: - \(1 \le b_i \le m\) для каждого \(1 \le i \le n\), и при этом
- \(\gcd(b_1,b_2,b_3,...,b_i) = a_i\) для каждого \(1 \le i \le n\).
Здесь \(\gcd(a_1,a_2,\dots,a_i)\) обозначает наибольший общий делитель (НОД) целых чисел \(a_1,a_2,\ldots,a_i\). Так как это число может быть слишком большим, выведите его по модулю \(998\,244\,353\). Выходные данные Для каждого набора входных данных выведите единственное целое число — количество различных массивов, удовлетворяющих приведенным выше условиям. Так как это число может быть большим, выведите его по модулю \(998\,244\,353\). Примечание В первом наборе входных данных допустимыми массивами \(b\) являются: - \([4,2,1]\);
- \([4,2,3]\);
- \([4,2,5]\).
Во втором наборе входных данных единственным массивом, удовлетворяющим требованиям, является \([1,1]\). В третьем наборе входных данных можно доказать, что такого массива не существует. В третьем и четвертом тестовых примерах есть красивые объяснения, но, к сожалению, они слишком длинные, чтобы их писать, поэтому мы просим вас поверить нам. | |
![]()
|
|
F. Большинство
Строки
Комбинаторика
математика
дп
*2700
Ибти пытался придумать историю, которая придала бы смысл этой задаче. Он решил вставить грустную историю. Все были счастливы программировать, пока внезапно не случился перебой в электроснабжении, и лучший сайт спортивного программирования не вышел из строя. К счастью, системный администратор недавно купил новое оборудование, в том числе несколько ИБП. Таким образом, есть несколько серверов, которые всё ещё находятся в сети, но нам нужно, чтобы они все работали, чтобы раунд остался рейтинговым. Представьте, что серверы представляют собой бинарную строку \(s\) длины \(n\). Если \(i\)-й сервер находится онлайн, то \(s_i = 1\), иначе \(s_i = 0\). Системный администратор может выполнить следующую операцию под названием распределение электроэнергии, которая состоит из следующих этапов: - Выберите два сервера в позициях \(1 \le i < j \le n\) так, чтобы оба были подключены к сети (т. е. \(s_i=s_j=1\)). Распределение начинается только с онлайн-серверов.
- Проверьте, достаточно ли мощности для распространения. Мы считаем, что мощности достаточно, если количество включенных серверов в диапазоне \([i, j]\) не меньше количества выключенных серверов в диапазоне \([i, j]\). Более формально, проверьте, что \(2 \cdot (s_i + s_{i+1} + \ldots + s_j) \ge j - i + 1\).
- Если условие выше выполнено, включите все серверы в оффлайне в диапазоне \([i, j]\). Более формально, присвоить \(s_k := 1\) для всех \(k\) от \(i\) до \(j\).
Мы называем бинарную строку \(s\) длины \(n\) рейтинговой, если мы можем включить все серверы (т.е. сделать \(s_i = 1\) для \(1 \le i \le n\)) с помощью операции распределения электроэнергии произвольное количество раз (возможно, \(0\)). Ваша задача — найти количество рейтинговых строк длины \(n\) по модулю \(m\). Выходные данные Выведите единственное целое число — количество рейтинговых бинарных строк длины \(n\). Так как это число может быть большим, выведите его по модулю \(m\). Примечание В первом примере единственной рейтинговой строкой является 11. Таким образом, ответ \(1\). Во втором примере рейтинговыми строками являются: - 111;
- 101, потому что мы можем выполнить операцию с \(i = 1\) и \(j = 3\).
Таким образом, ответ равен \(2\). В третьем примере рейтинговые строки: Таким образом, ответ \(4\). | |
![]()
|
|
G. Допинг
Комбинаторика
математика
дп
*3300
Мы называем массив \(a\) длины \(n\) изысканным, если для каждого \(1 < i \le n\) верно, что \(a_i = a_{i-1} + 1\). Назовем \(f(p)\), применяемую к перестановке\(^\dagger\) длины \(n\), как минимальное количество подмассивов, на которые можно разбить перестановку так, чтобы каждый из них был изысканным. Например, \(f([1,2,3]) = 1\), а \(f([3,1,2]) = 2\) и \(f([3,2,1]) = 3\). Учитывая \(n\) и перестановку \(p\) длины \(n\), мы определяем перестановку \(p'\) длины \(n\) как \(k\)-специальную тогда и только тогда, когда: - \(p'\) лексикографически меньше\(^\ddagger\), чем \(p\), и
- \(f(p') = k\).
Ваша задача — посчитать для каждого \(1 \le k \le n\) количество \(k\)-специальных перестановок по модулю \(m\). \(^\dagger\) Перестановка — это массив, состоящий из \(n\) различных целых чисел от \(1\) до \(n\) в произвольном порядке. Например, \([2,3,1,5,4]\) — это перестановка, но \([1,2,2]\) — не перестановка (\(2\) встречается в массиве дважды) и \([1,3,4]\) тоже не перестановка (\(n=3\), но в массиве есть \(4\)). \(^\ddagger\) Перестановка \(a\) длины \(n\) лексикографически меньше перестановки \(b\) длины \(n\) тогда и только тогда, когда выполняется следующее: в первой позиции, где \(a\) и \(b\) различаются, перестановка \(a\) имеет меньший элемент, чем соответствующий элемент в \(b\). Выходные данные Выведите \(n\) целых чисел, где \(k\)-е число — это количество \(k\)-специальных перестановок по модулю \(m\). Примечание В первом примере перестановки, лексикографически меньшие, чем \([1,3,4,2]\), следующие: - \([1,2,3,4]\), \(f([1,2,3,4])=1\);
- \([1,2,4,3]\), \(f([1,2,4,3])=3\);
- \([1,3,2,4]\), \(f([1,3,2,4])=4\).
Таким образом, наш ответ \([1,0,1,1]\). Во втором примере перестановки, лексикографически меньшие, чем \([3,2,1]\), следующие: - \([1,2,3]\), \(f([1,2,3])=1\);
- \([1,3,2]\), \(f([1,3,2])=3\);
- \([2,1,3]\), \(f([2,1,3])=3\);
- \([2,3,1]\), \(f([2,3,1])=2\);
- \([3,1,2]\), \(f([3,1,2])=2\).
Таким образом, наш ответ равен \([1,2,2]\). | |
![]()
|
|
E. Тик-так
Комбинаторика
поиск в глубину и подобное
графы
снм
*2500
Танхаус, часовщик в городе Винден, делает необычные часы, измеряющие время в \(h\) часах, пронумерованных от \(0\) до \(h-1\). Однажды он решил сделать из таких часов загадку. Загадка состоит из таблицы размера \(n \times m\) с часами, где каждые часы показывают какой-то час ровно (то есть время не лежит между двумя ровными часами). За один ход он может выбрать строку или столбец и перевести все часы в строке или столбце на час вперед\(^\dagger\). Таблица с часами называется решаемой, если можно сделать так, чтобы все часы показывали одно и то же время. При создании закагки Танхаус вдруг забеспокоился, что, возможно, его загадка не получится решаемой. В некоторых клетках таблицы уже находятся часы, которые показывают определенное время, а некоторые клетки еще пустые. Вам дана частично заполненная таблица с часами, найдите количество способов\(^\ddagger\) заполнить пустые клетки часами так, чтобы таблица была решаемой. Так как ответ может быть большим, выведите его по модулю \(10^9 + 7\). \(^\dagger\) Если часы показывают \(t\) часов, и их переводят на час вперед, они будут показывать \((t+1) \bmod h\) часов. \(^\ddagger\) Два способа считаются различными, если существует клетка с часами, в двух способах показывающими различное время. Выходные данные Для каждого набора входных данных выведите число способов заполнить пустые клетки таблицы так, чтобы загадка была решаемой. Так как ответ может быть большим, выведите его по модулю \(10^9 + 7\). Примечание В первом примере например подходит следующая конфигурация часов: Она решаемая, например, так: - Перевести часы в среднем столбце на час.
- Перевести часы в третьем столбце на час.
- Перевести часы в третьем столбце на час.
- Перевести часы во второй строке на час.
После этого все часы показывают один час. Во втором примере можно показать, что нет решаемых конфигураций. | |
![]()
|
|
C. Игра с суперклеем
Конструктив
Комбинаторика
*2000
Два игрока играют в игру. Игра ведется на прямоугольной доске n × m клеток. В начале игры в двух различных клетках доски лежат две фишки. Цель первого игрока — сдвигая фишки, переместить их обе в одну клетку. Цель второго игрока — помешать первому при помощи тюбика с суперклеем. Опишем правила игры более подробно. Ходы делаются по очереди. Первым ходит первый игрок. Каждым своим ходом первый игрок выбирает одну из своих не приклеенных фишек и сдвигает ее влево, вправо, вверх или вниз на одну клетку. При этом не разрешается двигать фишку за границу доски. В момент начала хода некоторые клетки доски могут быть покрыты клеем. Первый игрок может передвинуть фишку в такую клетку, после чего фишка приклеивается намертво и ее больше нельзя двигать. Второй игрок на каждом своем ходу выбирает одну из свободных клеток (в которой нет фишки и клея) и намазывает ее суперклеем. Клей долго сохнет и все покрытые им клетки остаются липкими до конца игры. Если после какого-либо хода первого игрока обе фишки оказываются в одной клетке — выигрывает первый игрок. Если первый игрок не может сделать ход (обе его фишки приклеены), то выигрывает второй игрок. Заметим, что ситуации, когда второй игрок не может сделать ход, никогда не возникнет — он всегда может намазать клеем ту клетку, из которой первый игрок только что передвинул фишку. Стоит дополнительно пояснить случай, когда обе фишки оказываются приклеены и находятся в одной клетке. Тут выигрывает первый игрок, поскольку игра заканчивается сразу, как только фишки оказываются в одной клетке, и условие проигрыша (невозможность сделать хода) не возникает. Известны размеры доски и положения двух фишек на ней. В начале игры все клетки доски свободны от клея. Определите, кто выиграет при правильной игре. Выходные данные Если выигрывает первый игрок — выведите «First» без кавычек. Иначе выведите «Second» без кавычек. | |
![]()
|
|
D. Битовые переносы
Комбинаторика
математика
*2100
Пусть \(f(x,y)\) — число переносов при двоичном сложении \(x+y\) (т. е. \(f(x,y)=g(x)+g(y)-g(x+y)\), где \(g(x)\) — количество единиц в двоичном представлении \(x\)). Для данных двух целых чисел \(n\) и \(k\), найдите количество упорядоченных пар \((a,b)\) таких, что \(0 \leq a,b < 2^n\), а \(f(a,b)\) равно \(k\). Обратите внимание, что для \(a\ne b\), \((a,b)\) и \((b,a)\) считаются как две разные пары. Поскольку это число может быть большим, выведите его по модулю \(10^9+7\). Выходные данные Выведите одно целое число — ответ по модулю \(10^9+7\). Примечание Вот несколько примеров для понимания переносов: \(\) \begin{aligned} &\begin{array}{r} 1_{\ \ }1_{\ \ }1\\ +\ _{1}1_{\ \ }0_{\ \ }0\\ \hline \ 1_{\ \ }0_{\ \ }1_{\ \ }1 \end{array} &\begin{array}{r} \ 1_{\ \ }0_{\ \ }1\\ +\ _{\ \ }0_{\ \ }0_{1}1\\ \hline \ 0_{\ \ }1_{\ \ }1_{\ \ }0 \end{array} & &\begin{array}{r} \ 1_{\ \ }0_{\ \ }1\\ +\ _{1}0_{1}1_{1}1\\ \hline \ 1_{\ \ }0_{\ \ }0_{\ \ }0 \end{array} \end{aligned} \(\) Итак, \(f(7,4)=1\), \(f(5,1)=1\) и \(f(5,3)=3\). В первом примере все пары, удовлетворяющие ограничениям, это \((1,1),(1,5),(2,2),(2,3),(3,2),(4,4),(4,5),(4,6),(4,7),(5,1),(5,4),(5,6),(6,4),(6,5),(7,4)\). | |
![]()
|
|
F2. Анти-медианный (сложная версия)
Комбинаторика
математика
дп
*3500
Это сложная версия задачи. Единственное различие между двумя версиями — ограничение на \(n\). Вы можете делать взломы, только если все версии задачи решены. Назовем массив \(a\) нечетной длины \(2m+1\) (при \(m \ge 1\)) плохим, если элемент \(a_{m+1}\) равен медиане этого массива. Другими словами, массив является плохим, если после его сортировки элемент на \(m+1\)-й позиции остается неизменным. Назовем перестановку \(p\) целых чисел от \(1\) до \(n\) анти-медианной, если каждый ее подмассив нечетной длины \(\ge 3\) не является плохим. Вам уже даны значения некоторых элементов перестановки. Найдите количество способов задать неизвестные значения, чтобы получить анти-медианную перестановку. Поскольку это число может быть очень большим, найдите его по модулю \(10^9+7\). Выходные данные Для каждого наборам входных данных выведите одно целое число — количество способов установить неизвестные значения для получения анти-медианной перестановки, по модулю \(10^9+7\). Примечание В первом наборе входных данных анти-медианными являются как \([1, 2]\), так и \([2, 1]\). Во втором наборе входных данных перестановки \([1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2]\) являются анти-медианными. Оставшиеся две перестановки, \([1, 2, 3]\), \([3, 2, 1]\), сами по себе являются плохими массивами, так как их медиана, \(2\), находится в их середине. В третьем наборе входных данных \([1, 2, 3, 4]\) не является анти-медианным, поскольку содержит плохой подмассив \([1, 2, 3]\). В четвертом наборе входных данных единственный анти-медианный массив, который можно получить, это \([5, 6, 3, 4, 1, 2]\). | |
![]()
|
|
C. Бинарные строки это весело
Комбинаторика
математика
*1400
Бинарная строка\(^\dagger\) \(b\) нечетной длины \(m\) называется хорошей, если \(b_i\) — медиана\(^\ddagger\) строки \(b[1,i]^\S\) для всех нечетных индексов \(i\) (\(1 \leq i \leq m\)). Для бинарной строки \(a\) длины \(k\), бинарная строка \(b\) длины \(2k-1\) называется расширением \(a\), если \(b_{2i-1}=a_i\) для всех \(i\) таких, что \(1 \leq i \leq k\). Например, 1001011 и 1101001 являются расширениями строки 1001. строка \(x=\)1011011 не является расширением \(y=\)1001, так как \(x_3 \neq y_2\). Обратите внимание, что всего существует \(2^{k-1}\) различных расширений \(a\). Вам дана бинарная строка \(s\) длины \(n\). Найдите сумму количеств хороших расширений по всем префиксам \(s\). Другими словами, найдите \(\sum_{i=1}^{n} f(s[1,i])\), где \(f(x)\) — число хороших расширений строки \(x\). Так как ответ может быть большим, выведите его по модулю \(998\,244\,353\). \(^\dagger\) Бинарной строкой называется строка, состоящая только из символов \(\mathtt{0}\) и \(\mathtt{1}\). \(^\ddagger\) Для бинарной строки \(a\) длины \(2m-1\) медианой \(a\) называется (единственный) символ, который встречается не меньше \(m\) раз в \(a\). \(^\S\) \(a[l,r]\) обозначает строку длины \(r-l+1\), которая получается конкатенацией символов \(a_l,a_{l+1},\ldots,a_r\) в заданном порядке. Выходные данные Для каждого набора входных данных выведите ответ по модулю \(998\,244\,353\). Примечание В первом и во втором примерах \(f(s[1,1])=1\). В третьем примере ответ равен \(f(s[1,1])+f(s[1,2])=1+2=3\). В четвертом примере ответ равен \(f(s[1,1])+f(s[1,2])+f(s[1,3])=1+1+1=3\). \(f(\mathtt{11})=2\), так как существуют два хороших расширения: 101 и 111. \(f(\mathtt{01})=1\), так как существует только одно хорошее расширение: 011. | |
![]()
|
|
E. Сумма на дереве
Деревья
Комбинаторика
математика
*2600
Назовем реберно-взвешенное дерево из \(n\) вершин, пронумерованных от \(1\) до \(n\), хорошим, если вес каждого ребра равен либо \(1\), либо \(-1\), и для каждой вершины \(i\) произведение весов ребер, смежных с вершиной \(i\), равно \(-1\). Вам дано положительное целое число \(n\). Всего существует \(n^{n-2} \cdot 2^{n-1}\) различных\(^\dagger\) реберно-взвешенных деревьев на \(n\) вершинах, пронумерованных от \(1\) до \(n\), таких, что вес каждого ребра равен либо \(1\), либо \(-1\). Ваша задача — найти сумму \(d(1,n)^\ddagger\) по всем таким деревьям, которые являются хорошими. Так как ответ может быть большим, выведите его по модулю \(998\,244\,353\). \(^\dagger\) Два дерева называются различными, если: - существуют две вершины такие, что в одном дереве между ними есть ребро, а в другом нет; или
- существуют две вершины такие, что в обоих деревьях между ними есть ребро, но вес этого ребра в одном дереве отличается от веса этого ребра в другом дереве.
Обратите внимание, что по формуле Кэли число деревьев с \(n\) пронумерованными вершинами равно \(n^{n-2}\). Так как у нас \(n-1\) ребро, то для каждого дерева существует \(2^{n-1}\) способ выбрать веса ребер (которые могут быть либо \(1\), либо \(-1\)). Поэтому общее число различных реберно-взвешенных деревьев равно \(n^{n-2} \cdot 2^{n-1}\). \(^\ddagger\) \(d(u,v)\) обозначает сумму весов ребер на единственном простом пути от \(u\) до \(v\). Выходные данные Выведите одно целое число — ответ по модулю \(998\,244\,353\). Примечание В первом примере есть только \(1\) различное хорошее дерево. Значение \(d(1,2)\) для этого дерева равно \(-1\), что равно \(998\,244\,352\) по модулю \(998\,244\,353\). Во втором примере значение \(d(1,1)\) для любого дерева равно \(0\), поэтому ответ равен \(0\). В третьем примере \(16\) различных хороших деревьев. Значение \(d(1,4)\) равно: - \(-2\) для \(2\) деревьев;
- \(-1\) для \(8\) деревьев;
- \(0\) для \(4\) деревьев;
- \(1\) для \(2\) деревьев.
Сумма \(d(1,4)\) по всем деревьям равна \(2 \cdot (-2) + 8 \cdot (-1) + 4 \cdot (0) + 2 \cdot (1) = -10\), что равно \(998\,244\,343\) по модулю \(998\,244\,353\). | |
![]()
|
|
D. Допустимые битонические перестановки
Комбинаторика
математика
реализация
дп
теория чисел
*2200
Вам дано пять целых чисел \(n\), \(i\), \(j\), \(x\), и \(y\). Найдите количество битонических перестановок \(B\), чисел от \(1\) до \(n\), таких, что \(B_i=x\), и \(B_j=y\). Так как ответ может быть очень большим, выведите его по модулю \(10^9+7\). Битоническая перестановка — это перестановка чисел, такая, что элементы перестановки сначала увеличиваются до определенного индекса \(k\), \(2 \le k \le n-1\), а затем уменьшайте до конца. Обратитесь к примечаниям для получения дополнительных разъяснений. Выходные данные Для каждого набора входных данных выведите одну строку, содержащую количество битонических перестановок, удовлетворяющих вышеуказанным условиям по модулю \(10^9+7\). Примечание Перестановка — это массив, состоящий из \(n\) различных целых чисел от \(1\) до \(n\) в любом порядке. Например, \([2,3,1,5,4]\) это перестановка, но \([1,2,2]\) не перестановка (\(2\) встречается дважды) и \([1,3,4]\) тоже не перестановка (\(n=3\), но \(4\) встречается в массиве). Массив из \(n \ge 3\) элементов битонический, если его элементы сначала увеличиваются до индекса \(k\), \(2 \le k \le n-1\), а затем уменьшается до конца. Например, \([2,5,8,6,1]\) это битонический массив с \(k=3\), но \([2,5,8,1,6]\) не битонический массив (элементы сначала возрастают до \(k=3\), затем убывают, а затем возрастают снова). Битоническая перестановка — это перестановка, в которой элементы следуют вышеупомянутому битоническому свойству. Например, \([2,3,5,4,1]\) является битонической перестановкой, но \([2,3,5,1,4]\) не является битонической перестановкой (поскольку это не битонический массив) и \([2,3,4,4,1]\)также не является битонической перестановкой (поскольку это не перестановка). Объяснение примера из условий Для \(n=3\), возможные перестановки это \([1,2,3]\), \([1,3,2]\), \([2,1,3]\), \([2,3,1]\), \([3,1,2]\), и \([3,2,1]\). Среди приведенных перестановок битоническими перестановками являются \([1,3,2]\) и \([2,3,1]\). В первом тестовом примере ожидаемая перестановка должна иметь вид \([2,?,3]\), который не удовлетворяет ни одной из двух битонических перестановок с \(n=3\), следовательно, ответ равен 0. Во втором тестовом примере ожидаемая перестановка должна иметь вид \([?,3,2]\), который удовлетворяет только битонической перестановке \([1,3,2]\), следовательно, ответ 1. | |
![]()
|
|
D. Дореми и игра с колышками
Комбинаторика
математика
дп
*2000
У Дореми есть \(n+1\) колышек. \(n\) красных колышков расставлены в вершины правильного \(n\)-угольника и пронумерованы от \(1\) до \(n\) против часовой стрелки. Также есть синий колышек несколько меньшего диаметра по центру многоугольника. Вокруг красных колышков натянута резинка. Дореми сегодня очень скучно, поэтому она решила сыграть в игру. Изначально у нее есть пустой массив \(a\). До тех пор, пока резинка не коснется синего колышка, она будет повторять следующую операцию: - выбрать \(i\) (\(1 \leq i \leq n\)) такое, что красный колышек номер \(i\) еще не был убран;
- убрать красный колышек номер \(i\);
- добавить \(i\) в конец массива \(a\).
Дореми интересно, сколько различных массивов \(a\) может получиться как итог данного процесса. Так как ответ может быть большим, выведите его по модулю \(p\). Гарантируется, что \(p\) — простое число. 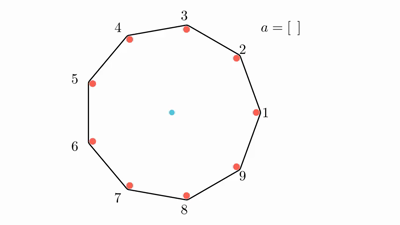 Игра с \(n=9\) и \(a=[7,5,2,8,3,9,4]\), а также игра с \(n=8\) и \(a=[3,4,7,1,8,5,2]\). Игра с \(n=9\) и \(a=[7,5,2,8,3,9,4]\), а также игра с \(n=8\) и \(a=[3,4,7,1,8,5,2]\). Выходные данные Выведите одно целое число — количество различных массивов \(a\), которые могут получиться как итог данной игры по модулю \(p\). Примечание В первом примере \(n=4\), в числе прочих могут получиться следующие массивы \(a\): \([4,2,3]\), \([1,4]\). Однако массив \(a\) не может быть равен \([1]\) или \([1,4,3]\). | |
![]()
|
|
C. Card Guessing
Теория вероятностей
Комбинаторика
дп
*2600
Consider a deck of cards. Each card has one of \(4\) suits, and there are exactly \(n\) cards for each suit — so, the total number of cards in the deck is \(4n\). The deck is shuffled randomly so that each of \((4n)!\) possible orders of cards in the deck has the same probability of being the result of shuffling. Let \(c_i\) be the \(i\)-th card of the deck (from top to bottom). Monocarp starts drawing the cards from the deck one by one. Before drawing a card, he tries to guess its suit. Monocarp remembers the suits of the \(k\) last cards, and his guess is the suit that appeared the least often among the last \(k\) cards he has drawn. So, while drawing the \(i\)-th card, Monocarp guesses that its suit is the suit that appears the minimum number of times among the cards \(c_{i-k}, c_{i-k+1}, \dots, c_{i-1}\) (if \(i \le k\), Monocarp considers all previously drawn cards, that is, the cards \(c_1, c_2, \dots, c_{i-1}\)). If there are multiple suits that appeared the minimum number of times among the previous cards Monocarp remembers, he chooses a random suit out of those for his guess (all suits that appeared the minimum number of times have the same probability of being chosen). After making a guess, Monocarp draws a card and compares its suit to his guess. If they match, then his guess was correct; otherwise it was incorrect. Your task is to calculate the expected number of correct guesses Monocarp makes after drawing all \(4n\) cards from the deck. Output Let the expected value you have to calculate be an irreducible fraction \(\dfrac{x}{y}\). Print one integer — the value of \(x \cdot y^{-1} \bmod 998244353\), where \(y^{-1}\) is the inverse to \(y\) (i. e. an integer such that \(y \cdot y^{-1} \bmod 998244353 = 1\)). | |
![]()
|
|
D. Плей-офф
Конструктив
Комбинаторика
математика
дп
*1500
жадные алгоритмы
\(2^n\) команд участвуют в плей-офф турнире. Турнир состоит из \(2^n - 1\) игры. Они проводятся следующим образом: на первом этапе команды делятся на пары: команда \(1\) играет против команды \(2\), команда \(3\) играет против команды \(4\) и так далее (таким образом, в этой фазе будет сыграно \(2^{n-1}\) игры). Когда команда проигрывает игру, она выбывает, и каждая игра приводит к выбыванию одной команды (нет ничьих). После этого остается \(2^{n-1}\) команд. Если остается только одна команда, она объявляется чемпионом; в противном начинается второй этап, где играется еще \(2^{n-2}\) игр: в первой из них победитель игры «\(1\) против \(2\)» играет против победителя игры «\(3\) против \(4\)», затем победитель игры «\(5\) против \(6\)» играет против победителя игры «\(7\) против \(8\)» и так далее. Этот процесс повторяется до тех пор, пока не останется только одна команда. Уровень навыков \(i\)-й команды равен \(p_i\), где \(p\) — перестановка чисел \(1\), \(2\), ..., \(2^n\) (перестановка — это массив, в котором каждый элемент от \(1\) до \(2^n\) встречается ровно один раз). Задана строка \(s\), состоящая из \(n\) символов. Эти символы обозначают результаты игр на каждом этапе турнира следующим образом: - если \(s_i\) равно 0, то на \(i\)-м этапе турнира (этапе с \(2^{n-i}\) играми) каждую игру выигрывает команда с меньшим уровнем навыков;
- если \(s_i\) равно 1, то на \(i\)-м этапе турнира (этапе с \(2^{n-i}\) играми) каждую игру выигрывает команда с большим уровнем навыков.
Назовем целое число \(x\) выигрышным, если существует такая перестановка \(p\), что команда с уровнем навыков \(x\) выиграет турнир. Найдите все выигрышные целые числа. Выходные данные Выведите все выигрышные целые числа \(x\) в порядке их возрастания. | |
![]()
|
|
E. Частичная сортировка
Комбинаторика
математика
теория чисел
*2300
Рассмотрим перестановку\(^\dagger\) \(p\) длины \(3n\). За один шаг вы можете выполнить одну из следующих операций: - Отсортировать первые \(2n\) элементов в возрастающем порядке.
- Отсортировать последние \(2n\) элементов в возрастающем порядке.
Можно показать, что любую перестановку можно отсортировать по возрастанию, используя только эти операции. Пусть \(f(p)\) — минимальное количество операций, необходимых для сортировки перестановки \(p\) в возрастающем порядке. По данному \(n\) найдите сумму \(f(p)\) по всем \((3n)!\) перестановкам \(p\) длины \(3n\). Так как ответ может быть очень большим, выведите его по модулю простого числа \(M\). \(^\dagger\) Перестановкой длины \(n\) называется массив, состоящий из \(n\) различных целых чисел от \(1\) до \(n\) в произвольном порядке. Например, \([2,3,1,5,4]\) является перестановкой, но \([1,2,2]\) не является перестановкой (\(2\) встречается дважды в массиве) и \([1,3,4]\) тоже не является перестановкой (\(n=3\), но в массиве присутствует \(4\)). Выходные данные Выведите ответ по модулю \(M\). Примечание В первом примере считается сумма по данным перестановкам: - \([1, 2, 3]\) требует \(0\) операций;
- \([1, 3, 2]\) требует \(1\) операцию;
- \([2, 1, 3]\) требует \(1\) операцию;
- \([2, 3, 1]\) требует \(2\) операции;
- \([3, 1, 2]\) требует \(2\) операции;
- \([3, 2, 1]\) требует \(3\) операции.
Таким образом, ответ \(0+1+1+2+2+3=9\). | |
![]()
|
|
E. Косия и дерево
Деревья
Теория вероятностей
Комбинаторика
математика
дп
поиск в глубину и подобное
*2400
снм
У Ими есть неориентированное дерево из \(n\) вершин, ребра которого пронумерованы от \(1\) до \(n-1\). \(i\)-е ребро соединят вершины \(u_i\) и \(v_i\). Также на дереве находятся \(k\) бабочек. Изначально \(i\)-я бабочка находится в вершине \(a_i\). Все значения \(a\) попарно различны. Косия играет в игру следующим образом. - Для \(i = 1, 2, \dots, n - 1\) Косия выбирает одно из направлений \(i\)-го ребра (\(u_i \rightarrow v_i\) или \(v_i \rightarrow u_i\)) с одинаковой вероятностью.
- Для \(i = 1, 2, \dots, n - 1\), если в начальной вершине \(i\)-го ребра есть бабочка, а в конечной вершине нет бабочки, то эта бабочка перелетает в конечную вершину. Обратите внимание, что операции выполняются для ребер \(1, 2, \dots, n - 1\) по порядку, а не одновременно.
- Косия выбирает две бабочки из \(k\) бабочек с равной вероятностью для всех \(\frac{k(k-1)}{2}\) способов выбрать две бабочки, затем она вычисляет расстояние\(^\dagger\) между двумя вершинами, и объявляет это своим счетом.
Косия хочет, чтобы вы вычислили математическое ожидание ее счета по модулю \(998\,244\,353^\ddagger\). \(^\dagger\) Расстоянием между двумя вершинами в дереве называется количество ребер на (единственном) простом пути между ними. \(^\ddagger\) Формально, пусть \(M = 998\,244\,353\). Можно показать, что ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Выходные данные Выведите одно целое число — математическое ожидание счета Косии по модулю \(998\,244\,353\). Примечание Дерево из первого примера показано ниже. Вершины с бабочками отмечены жирным. 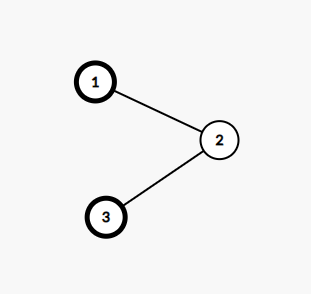 Существуют только \(2\) бабочки, поэтому выбор бабочек фиксирован. Рассмотрим следующие \(4\) случая: - Ориентация ребер \(1 \rightarrow 2\) и \(2 \rightarrow 3\): бабочка из вершины \(1\) перемещается в вершину \(2\), а бабочка в вершине \(3\) не двигается. Расстояние между вершинами \(2\) и \(3\) равно \(1\).
- Ориентация ребер \(1 \rightarrow 2\) и \(3 \rightarrow 2\): бабочка из вершины \(1\) перемещается в вершину \(2\), а бабочка в вершине \(3\) не двигается, потому что вершина \(2\) занята. Расстояние между вершинами \(2\) и \(3\) равно \(1\).
- Ориентация ребер \(2 \rightarrow 1\) и \(2 \rightarrow 3\): бабочки в вершинах \(1\) и \(3\) не двигаются. Расстояние между вершинами \(1\) и \(3\) равно \(2\).
- Ориентация ребер \(2 \rightarrow 1\) и \(3 \rightarrow 2\): бабочка в вершине \(1\) не двигается, а бабочка из вершины \(3\) перемещается в вершину \(2\). Расстояние между вершинами \(1\) и \(2\) равно \(1\).
Таким образом, математическое ожидание счета Косии равно \(\frac {1+1+2+1} {4} = \frac {5} {4}\), что есть \(748\,683\,266\) по модулю \(998\,244\,353\). Дерево из второго примера показано ниже. Вершины с бабочками отмечены жирным. Математическое ожидание счета Косии равно \(\frac {11} {6}\), что есть \(831\,870\,296\) по модулю \(998\,244\,353\).  | |
![]()
|
|
F. Кохиа и последовательность
Комбинаторика
математика
дп
теория чисел
битмаски
*3100
У Мари есть три целых числа \(n\), \(x\) и \(y\). Назовем массив \(a\) из \(n\) неотрицательных целых чисел хорошим, если он удовлетворяет следующим ограничениям: - \(a_1+a_2+\ldots+a_n=x\), и
- \(a_1 \, | \, a_2 \, | \, \ldots \, | \, a_n=y\), где \(|\) обозначает операцию побитового ИЛИ.
Значением хорошего массива называется значение \(a_1 \oplus a_2 \oplus \ldots \oplus a_n\), где \(\oplus\) обозначает операцию побитового исключающего ИЛИ. Косия хочет, чтобы вы нашли побитовое исключающее ИЛИ значений всех хороших массивов. Если хороших массивов не существует, выведите \(0\). Выходные данные Выведите одно целое число — побитовое исключающее ИЛИ значений всех хороших массивов. Примечание В первом примере есть \(12\) хороших массивов, они перечислены ниже. - \([0,2,3]\), \([0,3,2]\), \([2,0,3]\), \([2,3,0]\), \([3,0,2]\) и \([3,2,0]\): значение равно \(0 \oplus 2 \oplus 3 = 1\);
- \([1, 2, 2]\), \([2, 1, 2]\) and \([2, 2, 1]\): значение равно \(1 \oplus 2 \oplus 2 = 1\);
- \([1, 1, 3]\), \([1, 3, 1]\) and \([3, 1, 1]\): значение равно \(1 \oplus 1 \oplus 3 = 3\).
Поэтому побитовое исключющее ИЛИ значений всех хороших массивов равно \(\underbrace{1 \oplus \ldots \oplus 1}_{9\text{ раз}} \oplus 3 \oplus 3 \oplus 3 = 2\). Во втором примере нет хороших массивов. Ответ должен быть \(0\). | |
![]()
|
|
A. Хоссам и комбинации
Комбинаторика
математика
*900
сортировки
Хоссам проснулся, ему стало скучно, и поэтому он решил придумать интересный массив, позвав своего друга Хазема. Сейчас у них есть массив \(a\), состоящий из \(n\) положительных целых чисел. Хоссам выберет число \(a_i\), Хазем выберет число \(a_j\). Посчитайте количество интересных пар \((a_i, a_j)\), удовлетворяющих всем следующим условиям: - \(1 \le i, j \le n\);
- \(i \neq j\);
- Модуль разности \(|a_i - a_j|\) должен быть равен максимальному модулю разности по всем парам в массиве. Более формально: \(|a_i - a_j| = \max_{1 \le p, q \le n} |a_p - a_q|\).
Выходные данные Для каждого набора входных данных выведите одно число — количество интересных пар \((a_i, a_j)\) Примечание В первом наборе есть две интересные пары: - Хоссам выбирает четвертое число \(8\), Хазем выбирает пятое число \(1\).
- Хоссам выбирает пятое число \(1\), Хазем выбирает четвертое число \(8\).
Во втором наборе есть четыре интересные пары: - Хоссам выбирает второе число \(2\), Хазем выбирает шестое число \(10\).
- Хоссам выбирает шестое число \(10\), Хазем выбирает второе число \(2\).
- Хоссам выбирает пятое число \(2\), Хазем выбирает шестое число \(10\).
- Хоссам выбирает шестое число \(10\), Хазем выбирает пятое число \(2\).
| |
![]()
|
|
G. Покрытие отрезками
Деревья
Перебор
Структуры данных
Конструктив
Комбинаторика
дп
*3200
ChthollyNotaSeniorious дает DataStructures числовую ось с \(m\) различными отрезками на ней. Пусть \(f(l,r)\) — количество способов выбрать четное число отрезков так, чтобы их объединение было равно \([l,r]\), а \(g(l,r)\) — количество способов выбрать нечетное число отрезков так, чтобы их объединение было равно \([l,r]\). ChthollyNotaSeniorious задал DataStructures \(q\) вопросов. В каждом вопросе ChthollyNotaSeniorious дает DataStructures два числа \(l, r\), и хочет, чтобы вы помогли ему найти значение \(f(l,r)-g(l,r)\) по модулю \(998\,244\,353\), чтобы он не подвел ее. Выходные данные Для каждого запроса выведите одно целое число — \(f(l_i,r_i)-g(l_i,r_i)\) по модулю \(998\,244\,353\). Примечание В первом запросе мы должны найти \(f(1, 4) - g(1, 4)\). Единственное подмножество отрезков с объединением \([1, 4]\) это \(\{[1, 3], [2, 4]\}\), поэтому \(f(1, 4) = 1, g(1, 4) = 0\). Во втором запросе нам нужно найти \(f(1, 5) - g(1, 5)\). Единственными подмножествами отрезков с объединением \([1, 5]\) являются \(\{[1, 3], [2, 4], [3, 5]\}\) и \(\{[1, 3], [3, 5]\}\), поэтому \(f(1, 5) = 1, g(1, 5) = 1\). | |
![]()
|
|
G. Another Wine Tasting Event
Строки
Конструктив
Комбинаторика
математика
*2100
After the first successful edition, Gabriella has been asked to organize a second wine tasting event. There will be \(2n - 1\) bottles of wine arranged in a row, each of which is either red wine or white wine. This time, Gabriella has already chosen the type and order of all the bottles. The types of the wines are represented by a string \(s\) of length \(2n - 1\). For each \(1 \le i \le 2n - 1\), it holds that \(s_i = \texttt{R}\) if the \(i\)-th bottle is red wine, and \(s_i = \texttt{W}\) if the \(i\)-th bottle is white wine. Exactly \(n\) critics have been invited to attend. The critics are numbered from \(1\) to \(n\). Just like last year, each critic \(j\) wants to taste an interval of wines, that is, the bottles at positions \(a_j, \, a_j + 1, \, \dots, \, b_j\) for some \(1 \le a_j \le b_j \le 2n - 1\). Moreover, they have the following additional requirements: - each of them wants to taste at least \(n\) wines, that is, it must hold that \(b_j - a_j + 1 \ge n\);
- no two critics must taste exactly the same wines, that is, if \(j \ne k\) it must hold that \(a_j \ne a_k\) or \(b_j \ne b_k\).
Gabriella knows that, since the event is held in a coastal region of Italy, critics are especially interested in the white wines, and don't care much about the red ones. (Indeed, white wine is perfect to accompany seafood.) Thus, to ensure fairness, she would like that all critics taste the same number of white wines. Help Gabriella find an integer \(x\) (with \(0 \le x \le 2n - 1\)) such that there exists a valid assignment of intervals to critics where each critic tastes exactly \(x\) white wines. It can be proved that at least one such \(x\) always exists. Output Print an integer \(x\) — the number of white wines that each critic will taste. It can be proved that at least one solution exists. If multiple solutions exist, any of them will be accepted. Note In the first sample, there are \(5\) critics and \(2 \cdot 5 - 1 = 9\) bottles of wine. A possible set of intervals that makes each critic taste \(2\) white wines is the following: \([2, 6],\) \([1, 6],\) \([4, 8],\) \([1, 5],\) \([3, 7]\). Note that all intervals contain at least \(5\) bottles. In the second sample, there is \(1\) critic and \(2 \cdot 1 - 1 = 1\) bottle of wine. The only possible interval is \([1, 1]\), which gives \(x = 0\). | |
![]()
|
|
B. Морднилап
Комбинаторика
математика
*900
жадные алгоритмы
Перестановкой длины \(n\) является массив, состоящий из \(n\) различных целых чисел от \(1\) до \(n\) в произвольном порядке. Например, \([2,3,1,5,4]\) — перестановка, но \([1,2,2]\) не перестановка (\(2\) встречается в массиве дважды) и \([1,3,4]\) тоже не перестановка (\(n=3\), но в массиве встречается \(4\)). Всего существует \(n! = n \cdot (n-1) \cdot (n - 2) \cdot \ldots \cdot 1\) различных перестановок длины \(n\). По произвольной перестановке \(p\) длины \(n\) мы создаем массив \(a\) длины \(2n\), который равен конкатенации \(p\) и ее разворота. Далее, стоимостью \(p\) назовем число инверсий в \(a\). Число инверсий в массиве \(a\) определяется как количество пар индексов \(i\), \(j\), таких что \(i < j\) и \(a_i > a_j\). Например, если \(p = [1, 2]\), то \(a\) будет равно \([1, 2, 2, 1]\). В \(a\) всего две инверсии: \((2, 4)\) и \((3, 4)\) (нумерация элементов с 1). Значит, стоимость \(p\) равна \(2\). Ваша задача — найти сумму стоимостей всех \(n!\) перестановок длины \(n\). Выведите остаток от деления этой суммы на \(1\,000\,000\,007\) (\(10^9 + 7\)). Выходные данные Для каждого набора входных данных выведите одно число — сумму стоимостей всех перестановок длины \(n\) по модулю \(1\,000\,000\,007\) (\(10^9 + 7\)). Примечание В первом наборе входных данных \(p = [1]\) — единственная возможная перестановка. Тогда \(a = [1, 1]\), и в этом массиве \(0\) инверсий. Во втором наборе входных данных перестановки — это \([1, 2]\) и \([2, 1]\). Их соответствующие массивы \(a\) таковы: \([1, 2, 2, 1]\) и \([2, 1, 1, 2]\). В них обоих по \(2\) инверсии. | |
![]()
|
|
D. Цена дерева
Деревья
Теория вероятностей
Комбинаторика
математика
дп
поиск в глубину и подобное
*1900
битмаски
Дано дерево на \(n\) вершинах, корень дерева — вершина \(1\). В каждой вершине написано значение, изначально (в момент \(t=0\)) равное \(0\) или \(1\). В каждый целочисленный момент времени \(t>0\) значение вершины становится равно побитовому исключающему ИЛИ значений ее детей в момент времени \(t - 1\); значения листьев становятся равными \(0\), поскольку у них детей нет. Через \(S(t)\) обозначим сумму значений всех вершин в момент \(t\). Через \(F(A)\) обозначим сумму \(S(t)\) по всем значениям \(t\) в диапазоне \(0 \le t \le 10^{100}\), где \(A\) — некоторая изначальная расстановка \(0\) и \(1\) в дереве. Ваша задача — найти сумму \(F(A)\) по всем \(2^n\) изначальным расстановкам \(0\) и \(1\) в дереве. Выведите ответ по модулю \(10^9+7\). Выходные данные Для каждого набора входных данных выведите сумму по модулю \(10^9+7\). Примечание Найдём \(F(A)\) для расстановки \(A = [0,1,0,0,1,1]\) (\(A[i]\) означает значение вершины \(i\)). Состояние дерева в момент времени \(t = 0\) изображено ниже. В каждой вершине записаны два числа: ее номер, затем ее значение. \(S(0)\) в такой конфигурации равно \(3\). 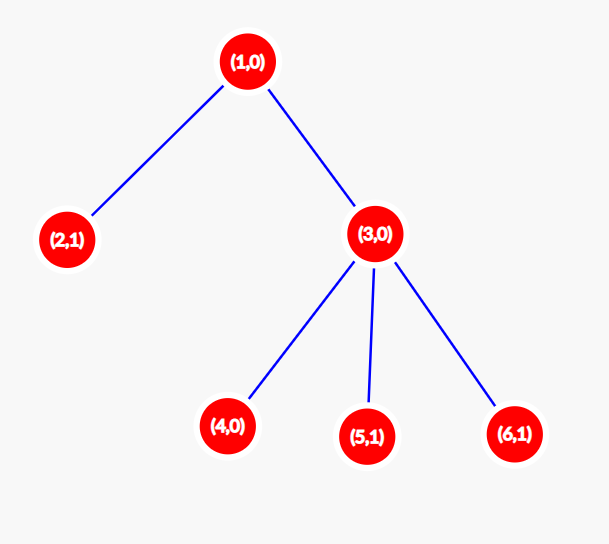 В момент \(t = 1\) конфигурация меняется на \([1,0,0,0,0,0]\). Дерево будет выглядеть так, как показано на рисунке ниже. Имеем \(S(1) = 1\). 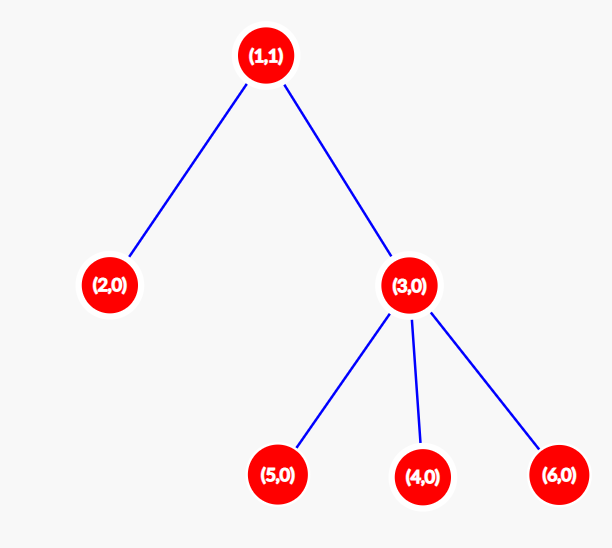 В момент \(t = 2\) конфигурация меняется на \([0,0,0,0,0,0]\). Дерево будет выглядеть так, как показано на рисунке ниже. Имеем \(S(2) = 0\).  Для всех \(t>2\) граф остаётся неизменным, то есть \(S(t)=0\) для всех \(t > 2\). Поэтому изначальная расстановка \(A = [0,1,0,0,1,1]\) имеет значение \(F(A) = 3 + 1 = 4\). Выполнив аналогичный процесс для всех \(2^{6}\) возможных стартовых расстановок, получим ответ \(\textbf{288}\). | |
![]()
|
|
D. Гибкая строка возвращается
Теория вероятностей
Комбинаторика
математика
*2100
дп
Вам даны две бинарные строки \(a\) и \(b\) длины \(n\). На каждом шаге строка \(a\) изменяется следующим образом. - Индекс \(i\) (\(1 \leq i \leq n\)) выбирается случайным образом. Символ \(a_i\) будет изменится на противоположный. То есть если символ \(a_i\) равен \(0\), то он становится \(1\), а если \(a_i\) равен \(1\), то он становится \(0\).
Чему равняется математическое ожидание количества шагов, необходимого для того, чтобы обе строки стали равными в первый раз? Бинарная строка — это строка, в которой каждый символ равен либо \(\tt{0}\), либо \(\tt{1}\). Выходные данные Для каждого набора входных данных выведите математическое ожидание количества ходов по модулю \(998\,244\,353\). Формально, пусть \(M = 998\,244\,353\). Можно показать, что ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Примечание В первом наборе индекс \(1\) выбирается случайным образом и \(a_1\) изменяется на противоположное значение. После этого строки \(a\) и \(b\) равны. Ожидаемое количество ходов — \(1\). Во втором наборе строки \(a\) и \(b\) уже равны. Таким образом, ожидаемое количество ходов равно \(0\). Ожидаемое количество ходов для третьего и четвертого наборов составляет \(\frac{56}{3}\) и \(\frac{125}{3}\) соответственно. | |
![]()
|
|
F. Три стула
Перебор
Структуры данных
Комбинаторика
дп
теория чисел
сортировки
*2300
битмаски
Как-то раз Кира нашел \(n\) друзей из Морио и решил собрать их за одним столом, чтобы провести мирный разговор. Рост друга \(i\) равен \(a_i\). Так получилось, что рост каждого из друзей уникален. Но вот незадача, в доме Киры всего \(3\) стула, и всех друзей усадить явно не удастся! Поэтому Кира должен позвать только \(3\) друзей. Но все не так просто! Если рост самого низкого и самого высокого из приглашенных друзей не взаимно просты, то друзья будут подшучивать друг над другом, что сильно разозлит Киру. Кира заинтересовался, сколько есть способов позвать \(3\) друзей так, чтобы они не стали подшучивать друг над другом? Два способа считаются различными, если существует такой друг, что он приглашен в одном случае, и не приглашен в другом. Формально, если Кира позовет друзей с номерами \(i\), \(j\) и \(k\), то должно выполняться \(\gcd(\min(a_i, a_j, a_k), \max(a_i, a_j, a_k)) = 1\), где \(\gcd(x, y)\) обозначает наибольший общий делитель (НОД) чисел \(x\) и \(y\). Кира не очень силен в информатике, поэтому просит вас посчитать количество различных способов позвать друзей. Выходные данные В единственной строке выведите количество способов позвать друзей. Примечание В первом примере подходит одна способ — позвать друзей \(1\), \(2\) и \(3\). Здесь \(1 < 2 < 3\), и числа \(1\) и \(3\) взаимно просты. | |
![]()
|
|
F. Вставка скобок
Деревья
Комбинаторика
математика
дп
*2700
Вика любит играть со скобочными последовательностями. Сегодня она хочет создать новую скобочную последовательность по следующему алгоритму. Исходно скобочная последовательность Вики — пустая строка, а дальше \(n\) раз она повторит следующие действия: - Выберет место в текущей скобочной последовательности, куда можно вставлять скобки, случайно равновероятно среди всех возможных позиций. Если длина текущей последовательности равна \(k\), то таких позиций \(k+1\): перед первой скобкой, между первой и второй скобками, \(\ldots\), после \(k\)-й скобки. В частности, в пустой скобочной последовательности одно такое место.
- Выберет строку «()» с вероятностью \(p\) или строку «)(» с вероятностью \(1 - p\) и вставит её в выбранное место. Длина скобочной последовательности увеличится на \(2\).
Скобочная последовательность называется правильной, если из неё возможно получить корректное арифметическое выражение путём вставки символов «+» и «1». Например, последовательности «(())()», «()» и «(()(()))» являются правильными, а «)(», «(()» и «(()))(» — нет. Вика хочет знать, с какой вероятностью ее итоговая скобочная последовательность будет правильной. Помогите ей и найдите эту вероятность по модулю \(998\,244\,353\) (см. формат вывода). Выходные данные Выведите вероятность того, что скобочная последовательность Вики окажется правильной, по модулю \(998\,244\,353\). Формально, пусть \(M = 998\,244\,353\). Можно показать, что ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Примечание В первом примере с вероятностью \(p = \frac{3}{4}\) получится правильная скобочная последовательность (), а с вероятностью \(1 - p = \frac{1}{4}\) получится неправильная скобочная последовательность )(. Искомая вероятность равна \(\frac{3}{4}\), а \(249\,561\,089 \cdot 4 \equiv 3 \pmod{998\,244\,353}\). Во втором примере искомая вероятность равна \(\frac{11}{25}\). | |
![]()
|
|
D. Деревянная ложка
Комбинаторика
дп
*2400
\(2^n\) человек, пронумерованных различными целыми числами от \(1\) до \(2^n\), играют в турнире по олимпийской системе. Сетка турнира представляет собой полное бинарное дерево высоты \(n\) с \(2^n\) листьями. Когда два игрока сходятся в матче, всегда выигрывает тот игрок, который имеет меньший номер. Победителем турнира становится игрок, выигравший все \(n\) своих матчей. Виртуальный утешительный приз «Деревянная ложка» вручается тому игроку, который удовлетворяет следующим \(n\) условиям: - он проиграл первый же свой матч;
- игрок, обыгравший его, проиграл свой следующий, второй матч;
- игрок, обыгравший этого игрока, проиграл свой третий матч;
- \(\ldots\);
- игрок, обыгравший игрока из предыдущего пункта, проиграл финальный матч турнира.
Можно показать, что этим условиям всегда удовлетворяет ровно один игрок. Рассмотрим все возможные \((2^n)!\) расстановок игроков в сетке турнира. Для каждого игрока найдите, в скольких из этих расстановок он получит «Деревянную ложку», и выведите эти числа по модулю \(998\,244\,353\). Выходные данные Выведите \(2^n\) целых чисел — число расстановок, при которых «Деревянную ложку» получает игрок номер \(1, 2, \ldots, 2^n\), по модулю \(998\,244\,353\). Примечание В первом примере «Деревянную ложку» всегда получает игрок \(2\). Во втором примере в \(8\) расстановках игроки \(1\) и \(4\) встречаются друг с другом в первом матче, и тогда «Деревянную ложку» получает игрок номер \(3\). В остальных \(16\) расстановках приз уходит игроку номер \(4\). | |
![]()
|
|
E. Бесконечная игра
Перебор
Теория вероятностей
Комбинаторика
дп
*3100
игры
Алиса и Боб играют в бесконечную игру, состоящую из сетов. Каждый сет состоит из раундов. В каждом раунде выигрывает один из игроков. В сете выигрывает тот, кто первым выиграет два раунда. Соответственно, сет всегда заканчивается со счётом \(2:0\) или \(2:1\) по раундам в пользу одного из игроков. Сценарием игры назовём конечную строку \(s\) из символов «a» и «b». Рассмотрим бесконечную строку, образованную повторениями строки \(s\): \(sss \ldots\) Пусть игроки играют раунды в соответствии с этой бесконечной строкой по порядку. Если очередной символ строки \(sss \ldots\) равен «a», то в текущем раунде выигрывает Алиса, если «b» — выигрывает Боб. Как только один из игроков выигрывает два раунда, сет завершается в его пользу, и со следующего раунда начинается новый сет. Пусть \(a_i\) равно числу выигранных Алисой сетов среди первых \(i\) сетов при игре по данному сценарию. Обозначим через \(r\) предел отношения \(\frac{a_i}{i}\) при \(i \rightarrow \infty\). Если \(r > \frac{1}{2}\), то строку \(s\) назовём выигрышным для Алисы сценарием. Если \(r = \frac{1}{2}\), то строку \(s\) назовём ничейным сценарием. Если \(r < \frac{1}{2}\), то строку \(s\) назовём выигрышным для Боба сценарием. Вам дана строка \(s\), состоящая из символов «a», «b» и «?». Рассмотрим все способы заменить каждый символ «?» на «a» или «b», чтобы получить строку, состоящую только из символов «a» и «b». Посчитайте, в скольких случаях получится выигрышный для Алисы сценарий, в скольких — ничейный, а в скольких — выигрышный для Боба, и выведите эти три числа по модулю \(998\,244\,353\). Выходные данные Выведите три числа: сколько способов замены приведут к выигрышному для Алисы сценарию, сколько — к ничейному, а сколько — к выигрышному для Боба. Все числа нужно вывести по модулю \(998\,244\,353\). Примечание В первом примере есть четыре варианта замены: - \(s = \mathtt{aa}\): Алиса выигрывает все сеты со счётом \(2:0\) — сценарий выигрышный для Алисы;
- \(s = \mathtt{ab}\): поочерёдно сначала Алиса, а потом Боб выигрывает сет со счётом \(2:1\) — сценарий ничейный;
- \(s = \mathtt{ba}\): поочерёдно сначала Боб, а потом Алиса выигрывает сет со счётом \(2:1\) — сценарий ничейный;
- \(s = \mathtt{bb}\): Боб выигрывает все сеты со счётом \(2:0\) — сценарий выигрышный для Боба.
| |
![]()
|
|
D. Игра на оси
Комбинаторика
реализация
поиск в глубину и подобное
*1900
графы
снм
Есть \(n\) точек \(1,2,\ldots,n\), у каждой точки \(i\) написано число \(a_i\). Вы играете в игру на этих точках. Изначально вы находитесь в точке \(1\). Когда вы находитесь в точке \(i\), выполните следующий шаг: - Если \(1\le i\le n\), перейдите к точке \(i+a_i\);
- В противном случае игра заканчивается.
Перед началом игры вы можете выбрать два целых числа \(x\) и \(y\), удовлетворяющих \(1\le x\le n\), \(-n \le y \le n\), и заменить число \(a_x\) на \(y\) (сделать \(a_x := y\)). Найдите количество различных пар \((x,y)\), при которых игра, которую вы начнете после замены, закончится за конечное число шагов. Обратите внимание, что вам не нужно удовлетворять условию \(a_x\not=y\). Выходные данные Для каждого набора входных данных выведите строку, содержащую одно целое число — количество различных пар \((x,y)\), игра с которыми конечна. Примечание В первом наборе входных данных парами \((x,y)\), с которыми игра конечна, являются \((1,-1)\) и \((1,1)\), соответствующие маршрутам \(1\rightarrow 0\) и \(1\rightarrow 2\). Обратите внимание, что пара \((1,2)\) не подходит, так как при \(n=1\) равенство \(y=2\) нарушает \(-n\le y\le n\). \((1,0)\) также не подходит, так как вы всегда переходите от \(1\) к \(1\), и игра не заканчивается. Во втором наборе входных данных подходящие пары равны \((1,-2),(1,-1),(1,2),(2,-2),(2,-1),(2,0),(2,1),(2,2)\). В четвертом наборе входных данных подходящие пары \((1,-2),(1,-1),(1,1),(1,2),(2,-2),(2,1),(2,2)\). | |
![]()
|
|
D. Движущиеся точки
Бинарный поиск
Перебор
Комбинаторика
математика
*2000
Вы играете в игру с \(n\) точками на числовой прямой. Изначальная координата \(i\)-й точки равна \(x_i\). Координаты всех точек различны. Каждая точка начинает двигаться одновременно с одинаковой постоянной скоростью. Каждая точка движется в направлении к ближайшей точке (отличной от нее самой), пока не встретится с какой-либо точкой. В случае равенства до ближайшей точки слева и справа, точка движется влево. Две точки встречаются, если их координаты совпадают, при этом они навсегда прекращают движение. Через некоторое время все точки перестанут двигаться. Результатом игры является количество различных координат, в которых остановятся точки. Поскольку эта игра слишком проста, подсчитайте сумму результатов игр для каждого подмножества из данных \(n\) точек, в котором есть хотя бы две точки. Так как ответ может быть очень большим, выведите его по модулю \(10^9+7\). Выходные данные Выведите сумму результатов по модулю \(10^9+7\). Примечание В первом примере для подмножества размером \(2\) две точки движутся навстречу друг другу, поэтому существует \(1\) координата, где точки останавливаются. Для подмножества размером \(3\) первая точка и третья точка движутся ко второй точке, поэтому существует \(1\) координата, где точки останавливаются, вне зависимости от направления движения второй точки. Для подмножества \([1, 2, 4, 6]\) первая и вторая точки движутся навстречу друг другу. Для третьей точки изначально вторая точка и четвертая точка являются ближайшими точками. Из-за этого равенства третья точка движется влево. Четвертая точка также движется влево. Таким образом, существует \(1\) координата, где точки останавливаются, которая равна \(1.5\). Поскольку существует \(6\) подмножеств размером \(2\), \(4\) подмножеств размером \(3\) и одно подмножество размером \(4\), ответ равен \(6 \cdot 1 + 4 \cdot 1 + 1 = 11\). Во втором примере для подмножества размером \(5\) (когда есть точки в координатах \(1\), \(3\), \(5\), \(11\), \(15\)) точки в координатах \(1\) и \(11\) будут двигаться вправо, а точки в координатах \(3\), \(5\), \(15\) — влево. Точки на \(1\), \(3\), \(5\) в конце концов встретятся в координате \(2\), а точки на \(11\) и \(15\) встретятся в координате \(13\), поэтому существует \(2\) координаты, где точки остановятся. | |
![]()
|
|
C. Serval и массивы Toxel
Комбинаторика
математика
реализация
дп
*1500
Toxel любит массивы. Перед поездкой в Paldea Serval подарил ему массив \(a\). Этот массив состоит из \(n\) попарно различных элементов. Чтобы получить больше массивов, Toxel выполнил \(m\) операций с исходным массивом. \(i\)-й операцией он изменил \(p_{i}\)-й элемент \((i-1)\)-го массива на \(v_{i}\), в результате чего получился \(i\)-й массив (исходный массив \(a\) имеет номер \(0\)). Во время изменений Toxel гарантировал, что элементы каждого массива по-прежнему попарно различны после каждой операции. Наконец, Toxel получил \(m+1\) массив и обозначил их как \(A_{0}=a, A_{1},\ldots,A_{m}\). Для каждой пары \((i,j)\) (\(0\le i<j\le m\)), Toxel определил её значение как количество различных элементов в конкатенации \(A_{i}\) и \(A_{j}\). Теперь Toxel задается вопросом, какова сумма значений для всех пар массивов? Пожалуйста, помогите ему вычислить ответ. Выходные данные Для каждого набора входных данных выведите единственное целое число — сумму значений для всех пар массивов. Примечание В первом наборе входных данных массив изменяется следующим образом: \([1,2,3]\to[\underline{4},2,3]\to[4,\underline{5},3]\). Конкатенацией \(0\)-го массива \(1\)-го массива является \(\require{cancel}[1,2,3,4,\cancel{2},\cancel{3}]\). Здесь есть \(4\) различных элемента. Конкатенацией \(0\)-го массива и \(2\)-го массива является \(\require{cancel}[1,2,3,4,5,\cancel{3}]\). Здесь есть \(5\) различных элементов. Конкатенацией \(1\)-го массива и \(2\)-го массива является \(\require{cancel}[4,2,3,\cancel{4},5,\cancel{3}]\). Здесь есть \(4\) различных элемента. Зачёркнутые элементы являются повторяющимися в массиве. Таким образом, ответ равен \(4+5+4=13\). Во втором наборе входных данных обратите внимание, что массив может оставаться без изменений после операций. | |
![]()
|
|
F1. Покраска графа (простая версия)
Комбинаторика
дп
графы
*2700
Единственное различие между простой и сложной версией — ограничение на \(n\). Дан полный неориентированный граф из \(n\) вершин. Полный граф — это такой граф, где между каждой парой вершин существует ровно одно ребро. Вы должны покрасить ребра этого графа в два цвета, синий и красный (каждое ребро должно быть покрашено в один из этих цветов). Назовем множество вершин \(S\) связным по красному цвету, если для каждой пары вершин \((v_1, v_2)\), такой, что \(v_1 \in S\) и \(v_2 \in S\), существует путь из \(v_1\) в \(v_2\), проходящий только по вершинам из \(S\) и по красным ребрам. Аналогично, назовем множество вершин \(S\) связным по синему цвету, если для каждой пары вершин \((v_1, v_2)\), такой, что \(v_1 \in S\) и \(v_2 \in S\), существует путь из \(v_1\) в \(v_2\), проходящий только по вершинам из \(S\) и по синим ребрам. Нужно раскрасить граф так, чтобы выполнялись следующие условия: - хотя бы одно ребро красное;
- хотя бы одно ребро синее;
- для каждого множества вершин \(S\), такого, что \(|S| \ge 2\), \(S\) связно по красному цвету или по синему цвету, но не по обоим цветам.
Посчитайте количество способов покрасить граф и выведите его по модулю \(998244353\). Выходные данные Выведите одно целое число — количество способов покрасить граф, взятое по модулю \(998244353\). | |
![]()
|
|
F2. Покраска графа (сложная версия)
Перебор
Комбинаторика
дп
графы
разделяй и властвуй
бпф
*2900
Единственное различие между простой и сложной версией — ограничение на \(n\). Дан полный неориентированный граф из \(n\) вершин. Полный граф — это такой граф, где между каждой парой вершин существует ровно одно ребро. Вы должны покрасить ребра этого графа в два цвета, синий и красный (каждое ребро должно быть покрашено в один из этих цветов). Назовем множество вершин \(S\) связным по красному цвету, если для каждой пары вершин \((v_1, v_2)\), такой, что \(v_1 \in S\) и \(v_2 \in S\), существует путь из \(v_1\) в \(v_2\), проходящий только по вершинам из \(S\) и по красным ребрам. Аналогично, назовем множество вершин \(S\) связным по синему цвету, если для каждой пары вершин \((v_1, v_2)\), такой, что \(v_1 \in S\) и \(v_2 \in S\), существует путь из \(v_1\) в \(v_2\), проходящий только по вершинам из \(S\) и по синим ребрам. Нужно раскрасить граф так, чтобы выполнялись следующие условия: - хотя бы одно ребро красное;
- хотя бы одно ребро синее;
- для каждого множества вершин \(S\), такого, что \(|S| \ge 2\), \(S\) связно по красному цвету или по синему цвету, но не по обоим цветам.
Посчитайте количество способов покрасить граф и выведите его по модулю \(998244353\). Выходные данные Выведите одно целое число — количество способов покрасить граф, взятое по модулю \(998244353\). | |
![]()
|
|
D. Подсчет факторизаций
Комбинаторика
математика
дп
теория чисел
*1900
разделяй и властвуй
Факторизация положительного целого числа \(m\) — это единственный способ записать его в виде \(\displaystyle m=p_1^{e_1}\cdot p_2^{e_2}\cdot \ldots \cdot p_k^{e_k}\), где \(p_1, p_2, \ldots, p_k\) — простые числа, \(p_1 < p_2 < \ldots < p_k\) и \(e_1, e_2, \ldots, e_k\) — положительные целые числа. Для каждого положительного целого числа \(m\), определим \(f(m)\) как мультимножество всех чисел в его факторизации, то есть \(f(m)=\{p_1,e_1,p_2,e_2,\ldots,p_k,e_k\}\) . Например, \(f(24)=\{2,3,3,1\}\), \(f(5)=\{1,5\}\) и \(f(1)=\{\}\). Вам задан список, состоящий из \(2n\) целых чисел \(a_1, a_2, \ldots, a_{2n}\). Подсчитайте, сколько положительных целых чисел \(m\) удовлетворяют условию \(f(m)=\{a_1, a_2, \ldots, a_{2n}\}\), поскольку это число может быть большим, выведите его по модулю \(998\,244\,353\). Выходные данные Выведите одно целое число — количество положительных целых чисел \(m\), удовлетворяющих условию \(f(m)=\{a_1, a_2, \ldots, a_{2n}\}\), по модулю \(998\,244\,353\). Примечание В первом примере два значения \(m\), такие что \(f(m)=\{1,2,3,3\}\): \(m=24\) и \(m=54\). Их факторизации: \(24=2^3\cdot 3^1\) и \(54=2^1\cdot 3^3\). Во втором примере пять значений \(m\), таких что \(f(m)=\{2,2,3,5\}\): \(200, 225, 288, 500\) и \(972\). В третьем примере не существует такого значения \(m\), что \(f(m)=\{1,4\}\). Ни \(1^4\), ни \(4^1\) не являются факторизациями, потому что \(1\) и \(4\) не являются простыми числами. | |
![]()
|
|
D. Раскраска треугольников
Комбинаторика
математика
*1600
Дан неориентированный граф из \(n\) вершин и \(n\) ребер, при этом \(n\) делится на \(6\). У каждого ребра есть вес — положительное целое число. Структура графа имеет следующий вид: граф разделен на \(\frac{n}{3}\) троек вершин, в первую тройку входят вершины \(1, 2, 3\), во вторую — \(4, 5, 6\), и так далее. Каждая пара вершин из одной и той же тройки соединена ребром. Ни одно ребро не соединяет две вершины из разных троек. Вершины этого графа надо раскрасить в два цвета, красный и синий. Каждая вершина должна быть покрашена в один из цветов; ровно \(\frac{n}{2}\) вершин должно быть покрашено в красный, и ровно \(\frac{n}{2}\) — в синий. Раскраски, отвечающие этим условиям, будем называть валидными. Вес раскраски — это суммарный вес всех ребер, соединяющих вершины разных цветов. Пусть \(W\) — максимальный вес валидной раскраски. Посчитайте количество валидных раскрасок с весом \(W\) и выведите результат по модулю \(998244353\). Выходные данные Выведите одно целое число — количество валидных раскрасок с максимальным весом, взятое по модулю \(998244353\). Примечание На картинке изображен граф из первого теста. 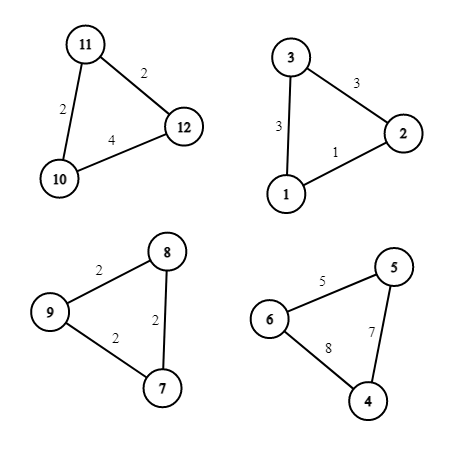 Максимальный вес валидной раскраски этого графа равен \(31\). | |
![]()
|
|
G. Подсчет голосов
Комбинаторика
математика
дп
*2600
\(n\) человек участвуют в голосовании. У каждого человека есть ровно один голос. \(i\)-й человек состоит в команде \(t_i\) (\(1 \leq t_i \leq n\)), где \(t_i = t_j\) означает что \(i\), \(j\) состоят в одной команде. По правилам человек может проголосовать только за человека из другой команды. Обратите внимание, что это автоматически означает, что каждый человек не может проголосовать за себя. Каждый человек знает количество голосов \(c_i\), которое он хочет получить. Сколько существует возможных способов провести голосование, так что каждый человек получит желаемое количество голосов? Поскольку это число может быть очень большим, найдите его по модулю \(998\,244\,353\). Выходные данные Выведите единственное целое число — количество способов провести голосование по модулю \(998\,244\,353\). Примечание В первом тесте есть два возможных способа провести голосование: \((2, 3, 1)\), \((3, 1, 2)\). В третьем тесте есть пять возможных способов провести голосование: \((3, 3, 2, 2, 1)\), \((2, 3, 2, 3, 1)\), \((3, 3, 1, 2, 2)\), \((3, 1, 2, 3, 2)\), \((2, 3, 1, 3, 2)\). | |
![]()
|
|
D. Мастер СНМ
Комбинаторика
математика
дп
снм
*2500
Вам дано целое число \(n\) и массив \(a\) длины \(n-1\), элементы которого либо \(0\), либо \(1\). Определим стоимость перестановки \(^\dagger\) \(p\) длины \(m-1\) (\(m \leq n\)) следующим образом. Пусть \(G\) - граф из \(m\) вершин с номерами от \(1\) до \(m\), не содержащий ребер. Для каждого \(i\) от \(1\) до \(m-1\) выполните следующие операции: - определим \(u\) и \(v\) как (различные) вершины с только входящими ребрами\(^{\dagger\dagger}\) в компонентах слабой связности \(^\ddagger\), содержащих вершины \(p_i\) и \(p_i+1\) соответственно
- в графе \(G\), добавим направленное ребро из вершины \(v\) в \(u\), если \(a_{p_i}=0\), иначе добавим направленное ребро из вершины \(u\) в \(v\) (если \(a_{p_i}=1\)).
Заметим, что после каждого шага можно показать, что каждая компонента слабой связности \(G\) имеет ровно одну вершину с только входящими рёбрами. Тогда, значение \(p\) — это количество входящих ребер \(G\) в вершину \(1\). Для каждого \(k\) от \(1\) до \(n-1\) найдите сумму стоимостей всех \(k!\) перестановок длины \(k\). Поскольку эта величина может быть большой, от вас требуется вычислить ее только по модулю \(998\,244\,353\).  Операции при \(n=3\), \(a=[0,1]\) и \(p=[1,2]\) Операции при \(n=3\), \(a=[0,1]\) и \(p=[1,2]\) \(^\dagger\) Перестановка длины \(n\) - это массив, состоящий из \(n\) различных целых чисел от \(1\) до \(n\) в произвольном порядке. Например, \([2,3,1,5,4]\) - перестановка, но \([1,2,2]\) - не перестановка (\(2\) встречается в массиве дважды), и \([1,3,4]\) - тоже не перестановка (\(n=3\), но в массиве есть \(4\)). \(^\ddagger\) Компоненты слабой связности направленного графа — это то же самое, что и компоненты неориентированной версии графа. Формально, для направленного графа \(G\) определите граф \(H\), где для всех ребер \(a \to b\) в \(G\) добавляется неориентированное ребро \(a \leftrightarrow b\) в \(H\). Тогда компоненты слабой связности \(G\) являются компонентами \(H\). \(^{\dagger\dagger}\) Заметим, что вершина, не имеющая ребер, считается имеющей только входящие ребра. Выходные данные Для каждого набора входных данных выведите \(n-1\) целых чисел в строке. \(i\)-е число является ответом для \(k=i\), по модулю \(998\,244\,353\). Примечание Рассмотрим первый набор входных данных. Когда \(k=1\), существует только \(1\) перестановка \(p\). - Когда \(p=[1]\), мы добавим одно ребро из вершины \(2\) в \(1\). Вершина \(1\) будет иметь \(1\) входящее ребро. Поэтому значение \([1]\) равно \(1\).
Поэтому, когда \(k=1\), ответ равен \(1\). Когда \(k=2\), существует \(2\) перестановки \(p\). - Когда \(p=[1,2]\), мы добавим ребро из вершины \(2\) в \(1\) и ребро из \(3\) в \(1\). Вершина \(1\) будет иметь \(2\) входящих ребер. Таким образом, значение \([1,2]\) равно \(2\).
- Когда \(p=[2,1]\), мы добавим ребро из вершины \(3\) в \(2\) и ребро из \(2\) в \(1\). Вершина \(1\) будет иметь входящее ребро \(1\). Таким образом, значение \([2,1]\) равно \(1\).
Поэтому, когда \(k=2\), ответ будет \(2+1=3\). | |
![]()
|
|
E1. Маршрутки на Венере (простая версия)
Комбинаторика
дп
разделяй и властвуй
*2200
Это простая версия задачи. Различия между версиями заключаются в ограничениях на \(n\) и \(k\). Вы можете делать взломы, только если все три версии задачи сданы. Максим — водитель маршрутки на планете Венера. Чтобы проехаться на маршрутке Максима, необходимо иметь билет. У каждого билета есть номер, состоящий из \(n\) цифр. Но, как известно, жители Венеры пользуются не десятичной системой счисления, а системой счисления по основанию \(k\). Поэтому можно считать, что номер билета — это последовательность из \(n\) целых чисел от \(0\) до \(k-1\) включительно. Жители Венеры считают билет счастливым, если на нем найдется цифра, равная сумме остальных цифр по модулю \(k\). Например, если \(k=10\), то билет \(7135\) является счастливым, поскольку \(7 + 1 + 5 \equiv 3 \pmod{10}\). С другой стороны, билет \(7136\) счастливым не является, поскольку ни одна цифра не равна сумме всех остальных по модулю \(10\). Однажды Максим, выполняя очередную поездку, задумался: а сколько всего существует счастливых билетов? При этом Максим понимает, что это число может быть очень велико, поэтому его интересует лишь остаток от деления ответа на некоторое простое число \(m\).  Выходные данные Выведите одно целое число — количество счастливых билетов по модулю \(m\), т. е. остаток от деления ответа на \(m\). Примечание В первом примере существует всего четыре счастливых билета: \(000\), \(011\), \(101\) и \(110\). | |
![]()
|
|
E2. Маршрутки на Венере (средняя версия)
Комбинаторика
дп
разделяй и властвуй
*2500
матрицы
Это средняя версия задачи. Различия между версиями заключаются в ограничениях на \(n\) и \(k\). Вы можете делать взломы, только если все три версии задачи сданы. Максим — водитель маршрутки на планете Венера. Чтобы проехаться на маршрутке Максима, необходимо иметь билет. У каждого билета есть номер, состоящий из \(n\) цифр. Но, как известно, жители Венеры пользуются не десятичной системой счисления, а системой счисления по основанию \(k\). Поэтому можно считать, что номер билета — это последовательность из \(n\) целых чисел от \(0\) до \(k-1\) включительно. Жители Венеры считают билет счастливым, если на нем найдется цифра, равная сумме остальных цифр по модулю \(k\). Например, если \(k=10\), то билет \(7135\) является счастливым, поскольку \(7 + 1 + 5 \equiv 3 \pmod{10}\). С другой стороны, билет \(7136\) счастливым не является, поскольку ни одна цифра не равна сумме всех остальных по модулю \(10\). Однажды Максим, выполняя очередную поездку, задумался: а сколько всего существует счастливых билетов? При этом Максим понимает, что это число может быть очень велико, поэтому его интересует лишь остаток от деления ответа на некоторое простое число \(m\).  Выходные данные Выведите одно целое число — количество счастливых билетов по модулю \(m\), т. е. остаток от деления ответа на \(m\). Примечание В первом примере существует всего четыре счастливых билета: \(000\), \(011\), \(101\) и \(110\). | |
![]()
|
|
E3. Маршрутки на Венере (сложная версия)
Перебор
Комбинаторика
математика
дп
*2800
Это сложная версия задачи. Различия между версиями заключаются в ограничениях на \(n\) и \(k\). Вы можете делать взломы, только если все три версии задачи сданы. Максим — водитель маршрутки на планете Венера. Чтобы проехаться на маршрутке Максима, необходимо иметь билет. У каждого билета есть номер, состоящий из \(n\) цифр. Но, как известно, жители Венеры пользуются не десятичной системой счисления, а системой счисления по основанию \(k\). Поэтому можно считать, что номер билета — это последовательность из \(n\) целых чисел от \(0\) до \(k-1\) включительно. Жители Венеры считают билет счастливым, если на нем найдется цифра, равная сумме остальных цифр по модулю \(k\). Например, если \(k=10\), то билет \(7135\) является счастливым, поскольку \(7 + 1 + 5 \equiv 3 \pmod{10}\). С другой стороны, билет \(7136\) счастливым не является, поскольку ни одна цифра не равна сумме всех остальных по модулю \(10\). Однажды Максим, выполняя очередную поездку, задумался: а сколько всего существует счастливых билетов? При этом Максим понимает, что это число может быть очень велико, поэтому его интересует лишь остаток от деления ответа на некоторое простое число \(m\).  Выходные данные Выведите одно целое число — количество счастливых билетов по модулю \(m\), т. е. остаток от деления ответа на \(m\). Примечание В первом примере существует всего четыре счастливых билета: \(000\), \(011\), \(101\) и \(110\). | |
![]()
|
|
G. Прогноз
Комбинаторика
математика
дп
*2800
Рассмотрим турнир, в котором участвуют \(n\) спортсменов. Рейтинг \(i\)-го спортсмена равен \(a_i\). Турнир проходит следующим образом. Сначала каждому спортсмену присваивается индекс — целое число от \(1\) до \(n\). Все индексы различны. Обозначим за \(p_i\) спортсмена с индексом \(i\). Затем организаторы проведут \(n-1\) игр. В первой игре будут соревноваться спортсмены \(p_1\) и \(p_2\). Во второй — победитель первой игры и спортсмен \(p_3\). В третьей — победитель второй игры и спортсмен \(p_4\), и так далее — в последней игре будут соревноваться победитель игры \((n-2)\) и спортсмен \(p_n\). Монокарп хочет спрогнозировать результаты каждой из \(n-1\) игр (конечно, он сформирует свой прогноз только после того, как все спортсмены получат свои индексы). Он знает, что когда в игре соревнуются спортсмены с рейтингами \(x\) и \(y\), и при этом \(|x - y| > k\), спортсмен с более высоким рейтингом обязательно побеждает. Но если \(|x - y| \le k\), победить может любой из двух спортсменов. Среди всех \(n!\) способов назначить индексы участникам посчитайте количество таких способов, что Монокарп может точно спрогнозировать результат каждой из \(n-1\) игр. Так как ответ может быть очень большим, выведите его по модулю \(998244353\). Выходные данные Выведите одно целое число — количество способов назначить участникам индексы так, чтобы Монокарп мог точно предсказать результат каждой из \(n-1\) игр. Примечание В первом примере Монокарп точно знает результат игры между любой парой игроков, поэтому все \(24\) способа назначить индексы игрокам подходят. Во втором примере подходящие способы назначить индексы — такие: \([1, 3, 2]\), \([2, 3, 1]\), \([3, 1, 2\)] и \([3, 2, 1]\). | |
![]()
|
|
H. Последнее число
Комбинаторика
математика
*2900
Вам дано мультимножество \(S\). Изначально \(S = \{1,2,3, \ldots, n\}\). Вы выполните следующую операцию \(n-1\) раз. - Выберите наибольшее число \(S_{\text{max}}\) в \(S\) и наименьшее число \(S_{\text{min}}\) в \(S\). Удалите эти два числа из \(S\) и добавьте \(S_{\text{max}} - S_{\text{min}}\) в \(S\).
Легко показать, что после \(n-1\) операций останется ровно одно число. Выведите это число. Выходные данные Для каждого набора входных данных выведите число, которое останется после \(n-1\) операции. Примечание Покажем, как изменится мультимножество \(S\) при \(n=4\). - Операция \(1\): \(S=\{1,2,3,4\}\), удаляем \(4\) и \(1\), добавляем \(3\).
- Операция \(2\): \(S=\{2,3,3\}\), удаляем \(3\) и \(2\), добавляем \(1\).
- Операция \(3\): \(S=\{1,3\}\), удаляем \(3\) и \(1\), добавляем \(2\).
- Получившееся мультимножество: \(S = \{2\}\).
Таким образом, при \(n = 4\) ответ равен \(2\). | |
![]()
|
|
G1. Влад и правильные пути (простая версия)
Комбинаторика
математика
*2100
дп
Это простая версия задачи, она отличается от сложной только ограничениями на \(n\) и \(k\). Влад нашёл ряд из \(n\) плиток и число \(k\). Плитки пронумерованы слева направо и \(i\)-я плитка имеет цвет \(c_i\). Немного подумав, он решил, что с этим делать. Вы можете начать с любой плитки и прыгать на любое количество плиток вправо, формируя при этом путь \(p\). Назовём путь \(p\) длины \(m\) правильным, если верно: - \(p\) разбивается на блоки длины ровно \(k\), то есть \(m\) делится на \(k\) без остатка;
- \(c_{p_1} = c_{p_2} = \ldots = c_{p_k}\);
- \(c_{p_{k+1}} = c_{p_{k+2}} = \ldots = c_{p_{2k}}\);
- \(\ldots\)
- \(c_{p_{m-k+1}} = c_{p_{m-k+2}} = \ldots = c_{p_{m}}\);
Ваша задача найти количество правильных путей максимальной длины. Так как это число может оказаться слишком большим, выведите его по модулю \(10^9 + 7\). Выходные данные Выведите \(t\) чисел, каждое из которых является ответом на соответствующий набор входных данных — количество правильных путей максимальной длины по модулю \(10^9 + 7\). Примечание В первом примере невозможно составить правильный путь, длины больше \(0\). Во втором примере нас интересуют следующие пути: - \(1 \rightarrow 3 \rightarrow 4 \rightarrow 5\)
- \(2 \rightarrow 4 \rightarrow 5 \rightarrow 7\)
- \(1 \rightarrow 3 \rightarrow 5 \rightarrow 7\)
- \(1 \rightarrow 3 \rightarrow 4 \rightarrow 7\)
В третьем примере подходит любой путь длины \(8\). | |
![]()
|
|
G2. Влад и правильные пути (сложная версия)
Бинарный поиск
Структуры данных
Комбинаторика
математика
дп
*2200
Это сложная версия задачи, она отличается от простой только ограничениями на \(n\) и \(k\). Влад нашёл ряд из \(n\) плиток и число \(k\). Плитки пронумерованы слева направо и \(i\)-я плитка имеет цвет \(c_i\). Немного подумав, он решил, что с этим делать. Вы можете начать с любой плитки и прыгать на любое количество плиток вправо, формируя при этом путь \(p\). Назовём путь \(p\) длины \(m\) правильным, если верно: - \(p\) разбивается на блоки длины ровно \(k\), то есть \(m\) делится на \(k\) без остатка;
- \(c_{p_1} = c_{p_2} = \ldots = c_{p_k}\);
- \(c_{p_{k+1}} = c_{p_{k+2}} = \ldots = c_{p_{2k}}\);
- \(\ldots\)
- \(c_{p_{m-k+1}} = c_{p_{m-k+2}} = \ldots = c_{p_{m}}\);
Ваша задача найти количество правильных путей максимальной длины. Так как это число может оказаться слишком большим, выведите его по модулю \(10^9 + 7\). Выходные данные Выведите \(t\) чисел, каждое из которых является ответом на соответствующий набор входных данных — количество правильных путей максимальной длины по модулю \(10^9 + 7\). Примечание В первом примере невозможно составить правильный путь, длины больше \(0\). Во втором примере нас интересуют следующие пути: - \(1 \rightarrow 3 \rightarrow 4 \rightarrow 5\)
- \(2 \rightarrow 4 \rightarrow 5 \rightarrow 7\)
- \(1 \rightarrow 3 \rightarrow 5 \rightarrow 7\)
- \(1 \rightarrow 3 \rightarrow 4 \rightarrow 7\)
В третьем примере подходит любой путь длины \(8\). | |
![]()
|
|
D. Подсчёт XOR
Комбинаторика
математика
дп
*2600
битмаски
Вам даны два положительных целых числа \(n\) и \(m\). Найдите сумму всех возможных значений \(a_1\bigoplus a_2\bigoplus\ldots\bigoplus a_m\), где \(a_1,a_2,\ldots,a_m\) являются неотрицательными целыми числами такими, что \(a_1+a_2+\ldots+a_m=n\). Обратите внимание, что все возможные значения \(a_1\bigoplus a_2\bigoplus\ldots\bigoplus a_m\) должны быть посчитаны в сумме ровно один раз. Так как ответ может быть очень большим, выведите его по модулю \(998244353\). Здесь \(\bigoplus\) обозначает операцию побитового исключающего ИЛИ. Выходные данные Для каждого набора входных данных выведите сумму всех возможных значений \(a_1\bigoplus a_2\bigoplus\ldots\bigoplus a_m\) по всем наборам неотрицательных целых чисел \(a_1,a_2,\ldots,a_m\) с \(a_1+a_2+\ldots+a_m=n\). Так как ответ может быть очень большим, выведите его по модулю \(998244353\). Примечание В первом наборе входных данных у нас должно быть \(a_1=69\), поэтому это единственное возможное значение \(a_1\), следовательно, наш ответ — \(69\). Во втором наборе входных данных \((a_1,a_2)\) может быть равно \((0,5), (1,4), (2,3), (3,2), (4,1)\) или \((5,0)\), в которых \(a_1\bigoplus a_2\) равно \(5,5,1,1,5,5\) соответственно. Поэтому \(a_1\bigoplus a_2\) может быть равно \(1\) или \(5\), поэтому ответ равен \(1+5=6\). В третьем наборе входных данных \(a_1,a_2,\ldots,a_{10}\) должны быть все равны \(0\), поэтому \(a_1\bigoplus a_2\bigoplus\ldots\bigoplus a_{10}=0\). Поэтому ответ равен \(0\). | |
![]()
|
|
C. Подобные многочлены
Комбинаторика
математика
*2400
Многочлен \(A(x)\) степени \(d\) — это выражение вида \(A(x) = a_0 + a_1 x + a_2 x^2 + \dots + a_d x^d\), где \(a_i\) — целые числа, и \(a_d \neq 0\). Два многочлена \(A(x)\) и \(B(x)\) называются подобными, если существует целое число \(s\), такое что для любого целого числа \(x\) выполняется условие \(\) B(x) \equiv A(x+s) \pmod{10^9+7}. \(\) Вам даны значения по модулю \(10^9+7\) двух подобных многочленов \(A(x)\) и \(B(x)\) степени \(d\) в точках \(x=0,1,\dots, d\). Найдите значение \(s\), такое что \(B(x) \equiv A(x+s) \pmod{10^9+7}\) для всех целых чисел \(x\). Выходные данные Выведите одно целое число \(s\) (\(0 \leq s < 10^9+7\)) такое, что \(B(x) \equiv A(x+s) \pmod{10^9+7}\) для всех целых чисел \(x\). Если существует несколько решений, выведите любое из них. Примечание В первом примере \(A(x) \equiv x-1 \pmod{10^9+7}\) и \(B(x)\equiv x+2 \pmod{10^9+7}\). Они подобны, потому что \(\)B(x) \equiv A(x+3) \pmod{10^9+7}.\(\) Во втором примере \(A(x) \equiv (x+1)^2 \pmod{10^9+7}\) и \(B(x) \equiv (x+10)^2 \pmod{10^9+7}\), следовательно, \(\)B(x) \equiv A(x+9) \pmod{10^9+7}.\(\) | |
![]()
|
|
A. Сопоставление
Комбинаторика
математика
*800
Целочисленный шаблон — это строка, состоящая из цифр и/или знаков вопроса. Положительное (строго больше \(0\)) целое число сопоставляется с шаблоном, если можно заменить каждый знак вопроса в шаблоне на цифру так, что мы получим десятичную запись этого числа без лишних нулей. Например: - \(42\) сопоставляется с 4?;
- \(1337\) сопоставляется с ????;
- \(1337\) сопоставляется с 1?3?;
- \(1337\) сопоставляется с 1337;
- \(3\) не сопоставляется с ??;
- \(8\) не сопоставляется с ???8;
- \(1337\) не сопоставляется с 1?7.
Вам дан целочисленный шаблон, состоящий из не более \(5\) символов. Посчитайте количество положительных (строго больших \(0\)) целых чисел, которые сопоставляются с ним. Выходные данные Для каждого набора входных данных выведите одно целое число — количество положительных (строго больших \(0\)) целых чисел, которые сопоставляются с заданным шаблоном. | |
![]()
|
|
F. Древесина
Комбинаторика
математика
дп
*2600
бпф
Перед торговым центром расположилась замечательная аллея с деревьями. Как жаль, что придется от нее избавиться, чтобы освободить место под парковку... Деревья на аллее растут в один ряд. Есть \(n\) мест под деревья: позиция \(0\) — это торговый центр, позиция \(n+1\) — это дорога, а позиции с \(1\) по \(n\) — это места под деревья. Некоторые из них заняты — в них растут деревья одинаковой высоты \(k\). Не более одного дерева растет на каждом месте. Когда вы срубаете дерево на месте \(x\), то вы можете его свалить либо налево, либо направо. Если оно падает налево, то занимает места с \(x-k\) по \(x\) включительно. Если оно падает направо, то занимает места с \(x\) по \(x+k\) включительно. Пусть \(m\) деревьев растут на аллее в каких-то местах \(x_1, x_2, \dots, x_m\). Назовем аллею неудачной, если все \(m\) деревьев можно срубить таким образом, чтобы: - ни одно дерево не упало на торговый центр или дорогу;
- ни одно место не было занято более чем одним упавшим деревом.
Посчитайте количество различных неудачных аллей с \(m\) деревьями высоты \(k\). Две аллеи считаются различными, если есть такое место \(y\), что дерево растет на месте \(y\) на первой аллее и не растет на месте \(y\) на второй аллее. Выведите это число по модулю \(998\,244\,353\). Выходные данные Выведите одно целое число — количество различных неудачных аллей с \(m\) деревьями высоты \(k\) по модулю \(998\,244\,353\). | |
![]()
|
|
A. A-характеристика
Конструктив
Комбинаторика
математика
*800
Рассмотрим массив \(a_1, a_2, \dots, a_n\) состоящий из чисел \(1\) и \(-1\). Назовем его \(A\)-характеристикой количество пар индексов \(1 \le i < j \le n\) таких, что \(a_i \cdot a_j = 1\). Вам необходимо найти любой массив \(a\) заданной длины \(n\), \(A\)-характеристика которого равна заданному \(k\). Выходные данные Для каждого набора входных данных, если нет массива \(a\) с \(A\)-характеристикой равной \(k\), выведите NO. Иначе выведите YES и \(n\) чисел \(1\) и \(-1\), которые формируют требуемый массив \(a\). Если есть несколько решений, выведите любой из них. Примечание В первом наборе есть лишь одна пара различных элементов в массиве, и их произведение \(a_1 \cdot a_2 = -1 \neq 1\), поэтому его \(A\)-характеристика равна \(0\). Во втором наборе есть лишь одна пара различных элементов в массиве, и их произведение \(a_1 \cdot a_2 = 1\), поэтому его \(A\)-характеристика равна \(1\). Во третьем наборе есть три пары различных элементов в массиве, и их произведение \(a_1 \cdot a_2 = -1\), \(a_1 \cdot a_3 = 1\), \(a_2 \cdot a_3 = -1\), поэтому его \(A\)-характеристика равна \(1\). В четвертом наборе можно показать что не существует массива длины \(3\), \(A\)-характеристика которого равна \(2\). | |
![]()
|
|
B1. LuoTianyi и летающие острова (простая версия)
Деревья
Теория вероятностей
Комбинаторика
математика
*1800
Это простая версия задачи. Единственное отличие в том, что в этой версии \(k\le\min(n,3)\). Вы можете делать взломы, только если обе версии задачи сданы.  Chtholly и летающие острова. Chtholly и летающие острова. LuoTianyi сейчас живёт в мире с \(n\) летающими островами. Летающие острова соединены \(n-1\) ненаправленной воздушной дорогой, и из любого из двух летающих островов можно добраться до другого, путешествуя по воздушным дорогам. Это означает, что \(n\) летающих островов образуют дерево. Однажды, LuoTianyi захотела встретиться со своими друзьями: Chtholly, Nephren, William, .... Всего она хочет встретиться с \(k\) людьми. Она не знает их точного расположения, но она знает, что они находятся на попарно различных островах. Она называет остров хорошим тогда и только тогда, когда сумма расстояний\(^{\dagger}\) от него до островов с \(k\) людьми минимально возможная среди всех \(n\) островов. Сейчас LuoTianyi хочет узнать, если \(k\) человек случайным образом находятся в \(k\) различных из \(n\) островов, чему равно математическое ожидание количества хороших островов? Вам нужно сказать ей математическое ожидание по модулю \(10^9+7\). \(^{\dagger}\)Расстоянием между двумя островами называется минимальное количество воздушных дорог, по которым нужно пройти, чтобы перейти с одного острова на другой. Выходные данные Выведите единственное целое число — математическое ожидание количества хороших островов по модулю \(10^9 + 7\). Формально, пусть \(M = 10^9 + 7\). Можно показать, что ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0\) (\(\operatorname{mod} M\)). Выведите целое число, равное \(p \cdot q^{-1}\) \(\operatorname{mod} M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p\) (\(\operatorname{mod} M\)). Примечание В первом примере дороги образуют следующее дерево: 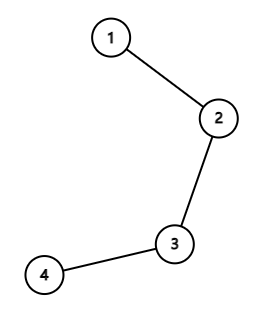 Если люди находятся на островах \(1\) и \(2\), тогда острова \(1\) и \(2\) являются хорошими. Сумма расстояний от острова \(1\) или \(2\) до всех людей равна \(1+0=1\), что минимально. В это время сумма расстояний от острова \(3\) до всех людей равна \(2+1=3\), что больше \(1\). Таким же образом, когда люди находятся на островах \(1\) и \(3\), тогда острова \(1,2\) и \(3\) являются хорошими. Когда люди находятся на островах \(1\) и \(4\), тогда острова \(1,2,3\) и \(4\) являются хорошими. Когда люди находятся на островах \(2\) и \(3\), тогда острова \(2\) и \(3\) являются хорошими. Когда люди находятся на островах \(2\) и \(4\), тогда острова \(2,3\) и \(4\) являются хорошими. Когда люди находятся на островах \(3\) и \(4\), тогда острова \(3\) и \(4\) являются хорошими. Поэтому математическое ожидание количества хороших островов равно \(\frac{16}{6}\), что равняется \(666666674\) по модулю \(10^9+7\). Во втором примере воздушные дороги образуют следующее дерево: 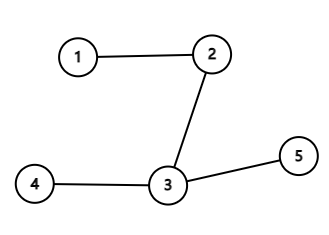 Всегда есть единственный хороший остров, поэтому математическое ожидание равно \(1\). | |
![]()
|
|
B2. LuoTianyi и летающие острова (сложная версия)
Деревья
Теория вероятностей
Комбинаторика
математика
поиск в глубину и подобное
*2300
Это сложная версия задачи. Единственное отличие в том, что в этой версии \(k\le n\). Вы можете делать взломы, только если обе версии задачи сданы.  Chtholly и летающие острова. Chtholly и летающие острова. LuoTianyi сейчас живёт в мире с \(n\) летающими островами. Летающие острова соединены \(n-1\) ненаправленной воздушной дорогой, и из любого из двух летающих островов можно добраться до другого, путешествуя по воздушным дорогам. Это означает, что \(n\) летающих островов образуют дерево. Однажды, LuoTianyi захотела встретиться со своими друзьями: Chtholly, Nephren, William, .... Всего она хочет встретиться с \(k\) людьми. Она не знает их точного расположения, но она знает, что они находятся на попарно различных островах. Она называет остров хорошим тогда и только тогда, когда сумма расстояний\(^{\dagger}\) от него до островов с \(k\) людьми минимально возможная среди всех \(n\) островов. Сейчас LuoTianyi хочет узнать, если \(k\) человек случайным образом находятся в \(k\) различных из \(n\) островов, чему равно математическое ожидание количества хороших островов? Вам нужно сказать ей математическое ожидание по модулю \(10^9+7\). \(^{\dagger}\)Расстоянием между двумя островами называется минимальное количество воздушных дорог, по которым нужно пройти, чтобы перейти с одного острова на другой. Выходные данные Выведите единственное целое число — математическое ожидание количества хороших островов по модулю \(10^9 + 7\). Формально, пусть \(M = 10^9 + 7\). Можно показать, что ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0\) (\(\operatorname{mod} M\)). Выведите целое число, равное \(p \cdot q^{-1}\) \(\operatorname{mod} M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p\) (\(\operatorname{mod} M\)). Примечание В первом примере дороги образуют следующее дерево: 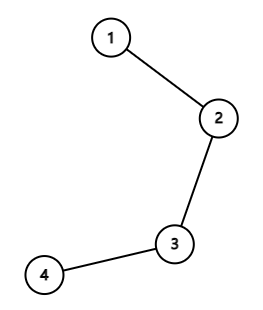 Если люди находятся на островах \(1\) и \(2\), тогда острова \(1\) и \(2\) являются хорошими. Сумма расстояний от острова \(1\) или \(2\) до всех людей равна \(1+0=1\), что минимально. В это время сумма расстояний от острова \(3\) до всех людей равна \(2+1=3\), что больше \(1\). Таким же образом, когда люди находятся на островах \(1\) и \(3\), тогда острова \(1,2\) и \(3\) являются хорошими. Когда люди находятся на островах \(1\) и \(4\), тогда острова \(1,2,3\) и \(4\) являются хорошими. Когда люди находятся на островах \(2\) и \(3\), тогда острова \(2\) и \(3\) являются хорошими. Когда люди находятся на островах \(2\) и \(4\), тогда острова \(2,3\) и \(4\) являются хорошими. Когда люди находятся на островах \(3\) и \(4\), тогда острова \(3\) и \(4\) являются хорошими. Поэтому математическое ожидание количества хороших островов равно \(\frac{16}{6}\), что равняется \(666666674\) по модулю \(10^9+7\). Во втором примере дороги образуют следующее дерево:  Мы можем заметить, что так как есть один человек на каждом острове, то только остров \(3\) является хорошим. Поэтому математическое ожидание количества хороших островов равно \(1\). | |
![]()
|
|
A. Подсчет порядка
Комбинаторика
математика
*1100
сортировки
Даны два массива \(a\) и \(b\), каждый из \(n\) целых чисел. Все элементы \(a\) попарно различны. Найдите количество способов переставить элементы массива \(a\) так, чтобы выполнялось \(a_i > b_i\) для всех \(1 \le i \le n\), по модулю \(10^9 + 7\). Два способа перестановки считаются разными, если полученные массивы различны. Выходные данные Для каждого набора входных данных выведите количество способов переставить элементы массива \(a\) так, чтобы выполнялось \(a_i > b_i\) для всех \(1 \le i \le n\), по модулю \(10^9 + 7\). | |
![]()
|
|
H. Не вините меня
Комбинаторика
математика
дп
*1700
битмаски
К сожалению, автор задачи не смог придумать интересную историю, поэтому он просто просит вас решить следующую задачу. Дан массив \(a\), состоящий из \(n\) положительных целых чисел. Посчитайте количество подпоследовательностей, для которых побитовое \(\mathsf{AND}\) элементов в подпоследовательности имеет ровно \(k\) единичных битов в двоичном представлении. Ответ может быть большим, поэтому выведите его по модулю \(10^9+7\). Напомним, что подпоследовательность массива \(a\) - это последовательность, которую можно получить из \(a\), удалив некоторые (возможно, ни одного) элементы. Например, \([1, 2, 3]\), \([3]\), \([1, 3]\) являются подпоследовательностями \([1, 2, 3]\), но \([3, 2]\) и \([4, 5, 6]\) - нет. Обратите внимание, что \(\mathsf{AND}\) обозначает логическую операцию AND. Выходные данные Для каждого тестового случая выведите одно целое число - количество подпоследовательностей, у которых в двоичном представлении значение побитового \(\mathsf{AND}\) имеет ровно \(k\) установленных битов. Ответ может быть большим, поэтому выведите его по модулю \(10^9+7\). | |
![]()
|
|
C. Гиперправильные скобочные последовательности
Комбинаторика
математика
теория чисел
жадные алгоритмы
*2400
сортировки
хэши
Вам дано целое число \(n\) и \(k\) отрезков. \(i\)-й отрезок имеет вид \([l_i,r_i]\), где \(1 \leq l_i \leq r_i \leq n\). Правильная скобочная последовательность\(^{\dagger,\ddagger}\) длины \(n\) называется гиперправильной, если для каждого \(i\) такого, что \(1 \leq i \leq k\), подстрока \(\overline{s_{l_i} s_{l_{i}+1} \ldots s_{r_i}}\) также является правильной скобочной последовательностью. Ваша задача — посчитать количество гиперправильных скобочных последовательностей. Так как это число может быть очень большим, требуется вывести его по модулю \(998\,244\,353\). \(^\dagger\) Скобочная последовательность — это строка, содержащая только символы «(» и «)». \(^\ddagger\) Последовательность скобок называется правильной, если её можно превратить в правильное математическое выражение путём добавления символов + и 1. Например, последовательности (())(), (), (()(())) и пустая строка являются правильными, а )(, (() и (())( — нет. Выходные данные Для каждого набора входных данных выведите количество гиперправильных скобочных последовательностей по модулю \(998\,244\,353\). Примечание - Для первого набора есть \(5\) гиперправильных скобочных последовательностей длины \(6\): ((())), (()()), (())(), ()(()) и ()()().
- Для второго набора нет правильных скобочных последовательностей длины \(5\), а следовательно, нет гиперправильных скобочных последовательностей длины \(5\).
- Для третьего набора нет гиперправильных скобочных последовательностей длины \(8\), для которых подстрока \([1 \ldots 3]\) является правильной скобочной последовательностью.
- Для четвертого набора существует \(4\) гиперправильные скобочные последовательности: ((())(())), ((())()()), ()()((())) и ()()(()()).
| |
![]()
|
|
E. Задачка на комбинаторику
Перебор
Комбинаторика
дп
*2200
Напомним, что биномиальный коэффициент \(\binom{x}{y}\) вычисляется следующим образом (\(x\) и \(y\) — неотрицательные целые числа): - если \(x < y\), то \(\binom{x}{y} = 0\);
- в противном случае \(\binom{x}{y} = \frac{x!}{y! \cdot (x-y)!}\).
Дан массив \(a_1, a_2, \dots, a_n\) и целое число \(k\). Вам нужно вычислить новый массив \(b_1, b_2, \dots, b_n\), где - \(b_1 = (\binom{1}{k} \cdot a_1) \bmod 998244353\);
- \(b_2 = (\binom{2}{k} \cdot a_1 + \binom{1}{k} \cdot a_2) \bmod 998244353\);
- \(b_3 = (\binom{3}{k} \cdot a_1 + \binom{2}{k} \cdot a_2 + \binom{1}{k} \cdot a_3) \bmod 998244353\), и так далее.
Формально, \(b_i = (\sum\limits_{j=1}^{i} \binom{i - j + 1}{k} \cdot a_j) \bmod 998244353\). Обратите внимание, что массив задан в измененном виде, и вы должны вывести его в измененном виде. Выходные данные Поскольку вывод \(10^7\) целых чисел может быть слишком медленным, вы должны выполнить следующее: Пусть \(c_i = b_i \cdot i\) (без взятия остатка от деления на \(998244353\) после умножения). Выведите целое число \(c_1 \oplus c_2 \oplus \dots \oplus c_n\), где \(\oplus\) обозначает оператор побитового исключающего ИЛИ. | |
![]()
|
|
F. Ира и фламенко
Структуры данных
Конструктив
Комбинаторика
математика
реализация
сортировки
*1700
Ира очень любит испанский танец фламенко. Она решила основать собственную танцевальную студию и нашла \(n\) учеников, \(i\)-й из которых имеет уровень \(a_i\). Ира может выбрать несколько своих учеников и поставить с ними танец. Таким образом она может поставить огромное количество танцев, но её интересуют только великолепные танцы. Танец называется великолепным, если выполнено следующее: - в танце участвуют ровно \(m\) учеников;
- уровни всех танцоров попарно различны;
- уровни любых двух танцоров отличаются строго меньше чем на \(m\).
Например, если \(m = 3\) и \(a = [4, 2, 2, 3, 6]\), следующие танцы являются великолепными (красным цветом выделены ученики, участвующие в танце): \([\color{red}{4}, 2, \color{red}{2}, \color{red}{3}, 6]\), \([\color{red}{4}, \color{red}{2}, 2, \color{red}{3}, 6]\). В то же время танцы \([\color{red}{4}, 2, 2, \color{red}{3}, 6]\), \([4, \color{red}{2}, \color{red}{2}, \color{red}{3}, 6]\), \([\color{red}{4}, 2, 2, \color{red}{3}, \color{red}{6}]\) не являются великолепными. В танце \([\color{red}{4}, 2, 2, \color{red}{3}, 6]\) участвуют \(2\) ученика, хотя \(m = 3\). В танце \([4, \color{red}{2}, \color{red}{2}, \color{red}{3}, 6]\) участвуют ученики с уровнями \(2\) и \(2\), хотя уровни всех танцоров должны быть попарно различны. В танце \([\color{red}{4}, 2, 2, \color{red}{3}, \color{red}{6}]\) участвуют ученики с уровнями \(3\) и \(6\), но \(|3 - 6| = 3\), хотя \(m = 3\). Помогите Ире посчитать количество великолепных танцев, которые она может поставить. Так как это число может быть очень большим, посчитайте его по модулю \(10^9 + 7\). Два танца считаются различными, если различны наборы учеников, участвующих в них. Выходные данные Для каждого набора входных данных выведите единственное число — количество великолепных танцев по модулю \(10^9 + 7\). Примечание В первом наборе входных данных Ира может поставить только такие великолепные танцы: \([\color{red}{8}, 10, 10, \color{red}{9}, \color{red}{6}, 11, \color{red}{7}]\), \([\color{red}{8}, \color{red}{10}, 10, \color{red}{9}, 6, 11, \color{red}{7}]\), \([\color{red}{8}, 10, \color{red}{10}, \color{red}{9}, 6, 11, \color{red}{7}]\), \([\color{red}{8}, 10, \color{red}{10}, \color{red}{9}, 6, \color{red}{11}, 7]\), \([\color{red}{8}, \color{red}{10}, 10, \color{red}{9}, 6, \color{red}{11}, 7]\). Второй набор входных данных разобран в условии. | |
![]()
|
|
E. Старый мобильник
Теория вероятностей
Комбинаторика
дп
*3500
Во время последней миссии звездолета U.S.S. Coder капитан Ян Битовский был случайно телепортирован на поверхность неизвестной планеты. Пытаясь найти обратную дорогу, Ян обнаружил артефакт древней цивилизации планеты Земля — мобильное устройство, способное осуществлять межзвездные звонки, созданное компанией Byterola. К сожалению, возникла другая проблема. Хотя Ян, как представитель людей, прекрасно знал старую нотацию номеров мобильных телефонов, символы на клавиатуре устройства были полностью стерты и невидимы человеческому глазу. На старых клавиатурах было ровно \(m + 1\) кнопок, по одной на каждую цифру из системы счисления по основанию \(m\), и одна кнопка backspace, позволяющая стереть последнюю написанную цифру (если на экране ничего не написано, то эта кнопка ничего не делает, но она нажатие все равно считается). Ян хочет связаться со своей командой. Ему нужно набрать определенное число (также из системы счисления по основанию \(m\), то есть цифры от \(0\) до \(m - 1\)). Он хочет знать математическое ожидание количества нажатий на кнопки, необходимое для связи с кораблем U.S.S. Coder. Ян всегда выбирает наиболее оптимальные кнопки с учетом своих текущих знаний. Кнопки неразличимы до тех пор, пока не будут нажаты. Помогите ему! Выходные данные Выведите ожидаемое количество нажатий на кнопки по модулю \(1\,000\,000\,007\). Формально, пусть \(M = 1\,000\,000\,007\). Можно показать, что ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Примечание В первом примере на клавиатуре имеются две цифры (\(0\) и \(1\)) и кнопка backspace. Ян не может знать, какая из них какая, поэтому он нажимает случайную. С вероятностью \(\frac{1}{3}\) он нажимает \(0\) и ему удается набрать номер экипажа. С вероятностью \(\frac{1}{3}\) он нажимает backspace, и ничего не происходит. Затем с вероятностью \(\frac{1}{2}\) ему удается нажать \(0\) (завершая процесс). В противном случае, с вероятностью \(\frac{1}{2}\), он набирает \(1\), который затем должен удалить с помощью backspace и нажать последнюю кнопку, которая должна быть \(0\). В этом случае ему потребуется \(4\) нажатий на кнопку. Наконец, он может нажать сначала кнопку \(1\), также с вероятностью \(\frac{1}{3}\). Затем, если он нажмет backspace с вероятностью \(50\%\), то все будет готово и ему останется только нажать последнюю кнопку (всего 3 нажатия). В худшем случае, он нажмет сначала кнопку \(0\) и должен будет удалить обе с помощью backspace, а затем, наконец, набрать число \(0\) (всего 5 нажатий). Мы получаем ожидаемое значение \(\frac{16}{6}\). Обратное к \(6\) по модулю \(1\;000\;000\;007\) равно \(166666668\), поэтому \(16 \cdot 166666668 = 666666674 \mod \; 1\;000\;000\;007\). | |
![]()
|
|
E. Договорной плей-офф
Деревья
Комбинаторика
*2200
\(2^k\) команд участвуют в плей-офф турнире. Команды пронумерованы от \(1\) до \(2^k\) в порядке убывания силы. То есть, команда \(1\) самая сильная, команда \(2^k\) самая слабая. Команда с меньшим номером всегда побеждает команду с большим номером. Сначала все команды располагаются в каком-то порядке. Каждой команде дается еще одно уникальное число от \(1\) до \(2^k\), называемое сид, которое обозначает ее стартовую позицию в плей-офф. Турнир состоит из \(2^k - 1\) игры. Они проводятся следующим образом: во-первых, команды делятся на пары: команда с сидом \(1\) играет против команды с сидом \(2\), команда с сидом \(3\) играет против команды с сидом \(4\) (именно в таком порядке) и так далее (таким образом, в этой фазе будет сыграно \(2^{k-1}\) игры). Когда команда проигрывает игру, она выбывает. После этого остается \(2^{k-1}\) команд. Если остается только одна команда, она объявляется чемпионом; в противном случае играется еще \(2^{k-2}\) игр: в первой из них победитель игры «сид \(1\) против сид \(2\)» играет против победителя игры «сид \(3\) против сид \(4\)», затем победитель игры «сид \(5\) против сид \(6\)» играет против победителя игры «сид \(7\) против сид \(8\)» и так далее. Этот процесс повторяется до тех пор, пока не останется только одна команда. Место команды в турнире зависит от того, в какой фазе турнира она выбыла: - команда-победитель турнира занимает место \(1\);
- команда, выбывшая в финале, занимает место \(2\);
- обе команды, выбывшие в полуфинале, занимают место \(3\);
- все команды, выбывшие в четвертьфинале, занимают место \(5\);
- все команды, выбывшие в 1/8 финала, занимают место \(9\), и так далее.
Теперь, когда мы установили правила, мы немножко подтасуем результаты. В частности, мы хотим, чтобы: - команда \(1\) (не команда с сидом \(1\)) заняла место \(1\);
- команда \(2\) заняла место \(2\);
- команды \(3\) и \(4\) заняли место \(3\);
- команды с \(5\) по \(8\) заняли место \(5\), и так далее.
Например, на этой картинке показан возможный ход турнира при \(k = 3\), а также итоговые места команд при таком ходе турнира: 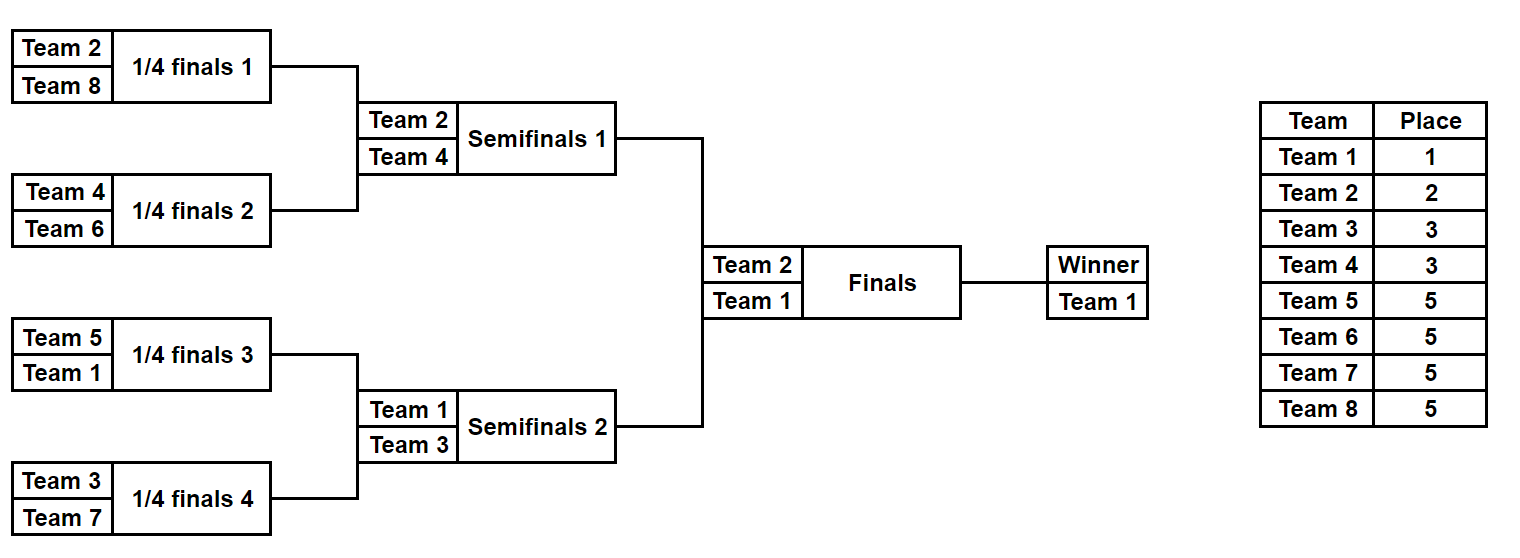 Некоторые сиды уже зарезервированы для некоторых команд (оказывается, не одни мы пытаемся повлиять на результаты). Требуется заполнить оставшиеся сиды оставшимися командами так, чтобы получить желаемые места для команд. Сколько есть способов это сделать? Так как это число может быть довольно большим, выведите его по модулю \(998\,244\,353\). Выходные данные Выведите одно целое число — количество способов заполнить незарезервированные сиды так, чтобы турнир прошел как мы хотим, по модулю \(998\,244\,353\). | |
![]()
|
|
E. Подсчет суперпоследовательностей
Комбинаторика
математика
дп
*2500
Вам дан массив \(a\) из \(n\) целых чисел, в котором все элементы \(a_i\) лежат в диапазоне \([1, k]\). Сколько различных массивов \(b\) из \(m\) целых чисел, где все элементы \(b_i\) лежат в диапазоне \([1, k]\), содержат \(a\) в качестве подпоследовательности? Два массива считаются различными, если они отличаются хотя бы в одной позиции. Последовательность \(x\) является подпоследовательностью последовательности \(y\), если \(x\) может быть получена из \(y\) путем удаления нескольких (возможно, нуля или всех) элементов. Поскольку ответ может быть очень большим, выведите его по модулю \(10^9 + 7\). Выходные данные Для каждого набора входных данных выведите одно целое число — количество подходящих массивов \(b\), по модулю \(10^9+7\). Примечание В первом примере, поскольку \(k=1\), существует только один массив размера \(m\), состоящий из целых чисел \([1, k]\). Этот массив (\([1, 1, \ldots, 1]\)) содержит исходный массив в качестве подпоследовательности, поэтому ответ - 1. Во втором примере есть \(9\) массивов: \([1, 1, 2, 2]\), \([1, 2, 1, 2]\), \([1, 2, 2, 1]\), \([1, 2, 2, 2]\), \([1, 2, 2, 3]\), \([1, 2, 3, 2]\), \([1, 3, 2, 2]\), \([2, 1, 2, 2]\), \([3, 1, 2, 2]\). В четвертом примере, поскольку \(m=n\), единственным массивом размера \(m\), который содержит \(a\) в качестве подпоследовательности, является сам \(a\). | |
![]()
|
|
B. Бинарная кофейня
Комбинаторика
математика
*1100
битмаски
Как-то раз Тёма оказался в бинарной кофейне. Это очень популярное и необычное место. Кофейня предлагает посетителям \(k\) разных вкусных десертов. Десерты нумеруются от \(0\) до \(k-1\). Стоимость \(i\)-о десерта составляет \(2^i\) монет, ведь это бинарная кофейня! Тёма готов потратить не более \(n\) монет на дегустацию десертов. При этом ему неинтересно покупать любой десерт более одного раза, ведь для оценки вкуса достаточно и одного. Сколькими различными способами он может купить несколько десертов (возможно ноль) для дегустации? Выходные данные Выведите \(t\) целых чисел, \(i\)-е из которых должно быть равно ответу на \(i\)-й набор входных данных — количеству способов купить десерты для дегустации. Примечание Варианты для первого набора входных данных: {}, {1} Варианты для второго набора входных данных: {}, {1} Варианты для третьего набора входных данных: {}, {1}, {2} Варианты для четвёртого набора входных данных: {}, {1}, {2}, {1, 2} | |
![]()
|
|
C. Горнолыжный курорт
Комбинаторика
математика
*1000
Дима Ватрушин работает учителем алгебры в школе. За хорошую работу его отправили в отпуск на \(n\) дней. Дима давно мечтал съездить на горнолыжный курорт, поэтому он хочет выделить несколько дней подряд и отправиться кататься на лыжах. Так как поездка требует тщательной подготовки, то он готов поехать минимум на \(k\) дней. Вам дан массив \(a\), содержащий прогноз погоды на курорте. То есть в \(i\)-й день температура будет равна \(a_i\) градусов. Дима родился в Сибири, поэтому он сможет отправиться отдохнуть, только если температура не поднимется выше \(q\) градусов на протяжении всей поездки. К сожалению, Дима настолько увлекся абстрактной алгеброй, что разучился считать. Он просит вас помочь ему и посчитать количество способов выбрать даты отдыха на курорте. Выходные данные Выведите \(t\) чисел, каждое из которых является ответом на соответствующий набор — количество способов Диме выбрать даты отдыха на курорте. Примечание В первом наборе входных данных примера Дима может поехать в любой день, поэтому ему подходят даты [1], [2], [3], [1, 2], [2, 3], [1, 2, 3]. Во втором и четвертом наборах входных данных примера Дима не может поехать ни в какой день из-за высокой температуры, поэтому подходящих дат нет. В третьем наборе входных данных примера Дима может поехать только в даты [1, 2, 3]. | |
![]()
|
|
G. Тенцинг и случайные операции
Теория вероятностей
Комбинаторика
математика
дп
*2800
Еще одна задача про случайность. У Тенцинга есть массив \(a\) длины \(n\) и целое число \(v\). Тенцинг выполняет следующую операцию \(m\) раз: - Выбрать целое число \(i\) такое, что \(1 \leq i \leq n\), равномерно случайным образом.
- Для всех \(j\) таких, что \(i \leq j \leq n\), присвоить \(a_j := a_j + v\).
Тенцинг хочет узнать ожидаемое значение \(\prod_{i=1}^n a_i\) после выполнения \(m\) операций, по модулю \(10^9+7\). Формально, пусть \(M = 10^9+7\). Можно показать, что ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Выходные данные Выведите ожидаемое значение \(\prod_{i=1}^n a_i\) по модулю \(10^9+7\). Примечание Существует три возможных значения \(a\) после выполнения всех \(m\) операций: 1. \(a_1=2,a_2=12\) с \(\frac{1}{4}\) вероятностью. 2. \(a_1=a_2=12\) с \(\frac{1}{4}\) вероятностью. 3. \(a_1=7,a_2=12\) с \(\frac{1}{2}\) вероятностью. Таким образом, ожидаемое значение \(a_1\cdot a_2\) равно \(\frac{1}{4}\cdot (24+144) + \frac{1}{2}\cdot 84=84\). | |
![]()
|
|
C. Сумма в бинарном дереве
Деревья
Комбинаторика
математика
*800
битмаски
Ване очень нравится математика. Однажды, когда он решал очередную задачу по математике, он придумал интересное дерево. Это дерево строится следующим образом. Изначально в дереве есть только одна вершина с номером \(1\) — корень дерева. Затем, Ваня добавляет к ней двух детей, присваивая им последовательные номера — \(2\) и \(3\) соответственно. После этого, он будет добавлять детей к вершинам по возрастанию их номеров, начиная с \(2\), присваивая их детям минимальные не занятые номера. В итоге, у Вани получится бесконечное дерево с корнем в вершине \(1\), где каждая вершина будет иметь ровно два ребенка, а номера вершин будут расположены последовательно по слоям. 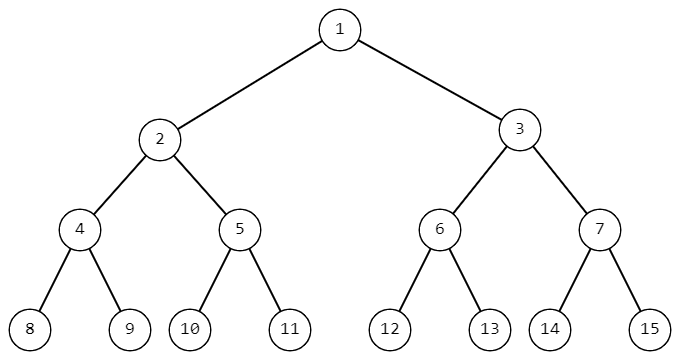 Часть дерева Вани. Часть дерева Вани. Ване стало интересно, чему равна сумма номеров вершин на пути от вершины с номером \(1\) до вершины с номером \(n\) в таком дереве. Так как Ваня не любит считать, он попросил Вас помочь ему узнать эту сумму. Выходные данные Для каждого набора входных данных выведите одно целое число — искомую сумму. Примечание В первом наборе данных примера на пути от корня до вершины \(3\) лежат две вершины \(1\) и \(3\), для них сумма равна \(4\). Во втором наборе данных примера на пути от корня до вершины с номером \(10\) лежат вершины \(1\), \(2\), \(5\), \(10\), сумма их номеров равна \(1+2+5+10 = 18\). | |
![]()
|
|
D. Яблоня
Деревья
Комбинаторика
математика
дп
поиск в глубину и подобное
*1200
У Тимофея в саду растёт яблоня, она представляет собой корневое дерево из \(n\) вершин с корнем в вершине \(1\) (вершины пронумерованы от \(1\) от \(n\)). Деревом называется связный граф без циклов, петель и кратных ребер. Это дерево очень необычное — оно растёт корнем вверх. Впрочем, в этом нет ничего необычного для деревьев в программировании. Яблоня достаточно молодая, поэтому на ней вырастет всего два яблока. Яблоки вырастут в определённых вершинах (эти вершины могу совпадать). После того как яблоки вырастут, Тимофей начнёт трясти яблоню, пока яблоки не упадут. Каждый раз, когда Тимофей трясёт яблоню, с каждым из яблок происходит следующее: Пусть яблоко сейчас находится в вершине \(u\). - Если у вершины \(u\) есть ребёнок, то яблоко перемещается в него (если таких вершин несколько, то яблоко может переместиться в любую из них).
- Иначе яблоко падает с дерева.
Можно показать, что через конечное время оба яблока упадут с дерева. У Тимофея есть \(q\) предположений, в каких вершинах могут вырасти яблоки. Он предполагает, что яблоки могут вырасти в вершинах \(x\) и \(y\), и хочет узнать количество пар вершин (\(a\), \(b\)), с которых яблоки могут упасть с дерева, где \(a\) — вершина, с которой упадёт яблоко из вершины \(x\), \(b\) — вершина, с которой упадёт яблоко из вершины \(y\). Помогите ему это сделать. Выходные данные Для каждого запроса Тимофея выведите количество упорядоченных пар вершин, с которых яблоки могут упасть с дерева, если предположение окажется верным, в отдельной строке. Примечание В первом примере: - Для первого запроса существует две возможные пары вершин, с которых яблоки могут упасть: \((4, 4), (5, 4)\).
- Для второго запроса также существует две пары: \((5, 4), (5, 5)\).
- Для третьего запроса есть всего одна пара: \((4, 4)\).
- Для четвертого запроса существует \(4\) пары: \((4, 4), (4, 5), (5, 4), (5, 5)\).
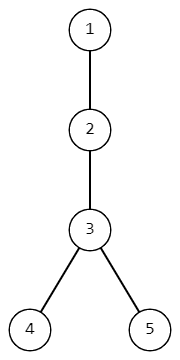 Дерево из первого примера. Дерево из первого примера. Во втором примере для первого предположения есть \(4\) возможных пар вершин, с которых могут упасть яблоки: \((2, 3), (2, 2), (3, 2), (3, 3)\). Для второго запроса есть всего одна возможная пара: \((2, 3)\). Для третьего запроса есть две пары: \((3, 2), (3, 3)\). | |
![]()
|
|
H. Циклы, кратные трём
Структуры данных
Комбинаторика
математика
дп
*3400
снм
Дана последовательность \(a_1,\dots,a_n\) длины \(n\), изначально все её элементы — пустые. Над последовательностью совершают \(n\) обновлений, в каждом из которых один из элементов \(a\) становится некоторым числом, таким образом, что после всех обновлений \(a\) становится перестановкой \(1,2,\dots,n\). После каждого обновления найдите число способов (по модулю \(998\,244\,353\)) заполнить остающиеся пустые места в \(a\) так, чтобы \(a\) стала перестановкой \(1,2,\dots,n\), причём длины всех циклов в \(a\) стали кратны \(3\). Перестановкой \(1,2,\dots,n\) является последовательность длины \(n\), состоящая из \(n\) различных целых чисел от \(1\) до \(n\) в произвольном порядке. Циклом в перестановке \(a\) называется последовательность попарно различных чисел \((i_1,\dots,i_k)\), такая что \(i_2 = a_{i_1},i_3 = a_{i_2},\dots,i_k = a_{i_{k-1}},i_1 = a_{i_k}\). Длина этого цикла равна числу \(k\), которое кратно \(3\), если и только если \(k \equiv 0 \pmod 3\). Выходные данные Выведите \(n\) строк: число способов (по модулю \(998\,244\,353\)) после \(1,2,\dots,n\) обновлений. Примечание В первом примере, скажем, после \(3\)-го обновления есть \(3\) способа заполнить последовательность \(a = [4,\_,2,5,\_,\_]\): - \([4,1,2,5,6,3]\): имеем один цикл \((1\,4\,5\,6\,3\,2)\) длины \(6\).
- \([4,6,2,5,1,3]\): имеем два цикла \((1\,4\,5)\) и \((2\,6\,3)\), с длинами \(3\) и \(3\).
- \([4,6,2,5,3,1]\): имеем один цикл \((1\,4\,5\,3\,2\,6)\) длины \(6\).
Во втором примере первое же обновление создаёт цикл длины \(1\), так что нет ни одного способа сделать так, чтобы длины всех циклов были кратны \(3\). | |
![]()
|
|
E. Платиновый треугольник?
Перебор
Теория вероятностей
Комбинаторика
математика
реализация
интерактив
*2900
Это интерактивная задача. Made in Heaven — довольно любопытный стенд. Конечно, это (возможно) самый сильный Стенд из всех существующих, но он также является ярым любителем головоломок. Например, недавно он задал Qtaro следующую задачу: Made in Heaven имеет \(n\) скрытых целых чисел \(a_1, a_2, \dots, a_n\) (\(3 \le n \le 5000\), \(1 \le a_i \le 4\)). Qtaro должен определить все \(a_i\), задав Made in Heaven несколько вопросов следующего вида: - В одном запросе Qtaro разрешается дать Made in Heaven три различных индекса \(i\), \(j\) и \(k\) (\(1 \leq i, j, k \leq n\)).
- Если \(a_i, a_j, a_k\) образуют стороны невырожденного треугольника \(^\dagger\), Made in Heaven выдаст площадь этого треугольника.
- В противном случае, Made in Heaven ответит \(0\).
Задав не более \(5500\) таких вопросов, Qtaro должен либо сказать Made in Heaven все значения \(a_i\), либо сообщить, что нет возможности однозначно определить их. К сожалению, из-за перезагрузки вселенной, Qtaro не так умен, как Jotaro. Пожалуйста, помогите Qtaro решить задачу Made In Heaven. —————————————————————— \(^\dagger\) Три целых положительных числа \(a, b, c\) образуют стороны невырожденного треугольника тогда и только тогда, когда выполняются все следующие три неравенства: - \(a+b > c\),
- \(b+c > a\),
- \(c+a > b\).
Протокол взаимодействия Взаимодействие начинается с чтения \(n\) (\(3 \le n \le 5000\)) — количества скрытых целых чисел. Чтобы задать вопрос, соответствующий тройке \((i, j, k)\) (\(1 \leq i < j < k \leq n\)), выведите «? \(i\) \(j\) \(k\)» без кавычек. После этого вы должны прочитать одно целое число \(s\). - Если \(s = 0\), то \(a_i\), \(a_j\) и \(a_k\) не являются сторонами невырожденного треугольника.
- Иначе, \(s = 16 \Delta^2\), где \(\Delta\) — площадь треугольника. Площадь предоставляется в таком формате для удобства, чтобы вам нужно было вводить только целые числа.
Если числа \(a_i\) не могут быть однозначно определены, выведите «! \(-1\)» без кавычек. Иначе, если вы определили все значения \(a_i\), выведите «! \(a_1\) \(a_2\) \(\dots\) \(a_n\)» в одну строку. Интерактор неадаптивный. Скрытый массив \(a_1, a_2, \dots, a_n\) фиксируется заранее и не изменяется в процессе взаимодействия. После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Взломы Для взлома используйте следующий формат. Первая строка содержат одно целое число \(n\) (\(3 \le n \le 5000\)) – количество скрытых целых чисел. Вторая строка содержат \(n\) целых чисел \(a_1, a_2, \ldots, a_n\) (\(1 \le a_i \le 4\)) – скрытый массив. Примечание В первом примере процесс взаимодействия происходит следующим образом: | Stdin | Stdout | Объяснение | | 3 | | Прочитаем \(n = 3\). Существует \(3\) скрытых целых чисел | | | ? 1 2 3 | | Попросим найти площадь, образованную \(a_1\), \(a_2\) и \(a_3\) | | | 63 | | Получено \(16\Delta^2 = 63\). Значит, площадь \(\Delta = \sqrt{\frac{63}{16}} \approx 1.984313\) | | | ! -1 | Ответим, что не существует однозначного массива, удовлетворяющего запросам. |
Из полученной площади можно сделать вывод, что числа, образующие треугольник, либо (\(4\), \(4\), \(1\)), либо (\(3\), \(2\), \(2\)) (в определенном порядке). Поскольку существует несколько массивов чисел, удовлетворяющих запросам, уникальный ответ не может быть найден. Во втором примере процесс взаимодействия происходит следующим образом: | Шаг | Stdin | Stdout | Объяснение | | 1 | 6 | | Прочитаем \(n = 6\). Значит, есть \(6\) скрытых чисел | | 2 | | ? 1 2 3 | Спросим площадь треугольника, образованного \(a_1\), \(a_2\) и \(a_3\) | | 3 | 0 | | Они не образуют невырожденный треугольник | | 4 | | ? 2 3 4 | Спросим площадь треугольника, образованного \(a_2\), \(a_3\) и \(a_4\) | | 5 | 0 | | Они не образуют невырожденный треугольник | | 6 | | ? 4 5 6 | Спросим площадь треугольника, образованного \(a_4\), \(a_5\) и \(a_6\) | | 7 | 0 | | Они не образуют невырожденный треугольник | | | 8 | | ? 1 5 6 | Спросим площадь треугольника, образованного \(a_1\), \(a_5\) и \(a_6\) | | 9 | 63 | | Получим \(16\Delta^2 = 63\). Тогда площадь \(\Delta = \sqrt{\frac{63}{16}} \approx 1.984313\) | | 10 | | ? 3 5 6 | Спросим площадь треугольника, образованного \(a_3\), \(a_5\) и \(a_6\) | | 11 | 15 | | Получим \(16\Delta^2 = 15\). Тогда площадь \(\Delta = \sqrt{\frac{15}{16}} \approx 0.968245\) | | 12 | | ? 1 2 4 | Спросим площадь треугольника, образованного \(a_3\), \(a_5\) и \(a_6\) | | 13 | 135 | | Получим \(16\Delta^2 = 135\). Тогда площадь \(\Delta = \sqrt{\frac{135}{16}} \approx 2.904738\) | | 14 | | ! 3 2 1 4 2 2 | Однозначный ответ найден, и он равен \(a = [3, 2, 1, 4, 2, 2]\). |
Из шагов \(10\) и \(11\) мы можем сделать вывод, что мультимножество \(\left\{a_3, a_5, a_6\right\}\) должно равняться \(\left\{2, 2, 1\right\}\). Из шагов \(8\) и \(9\), мультимножество \(\left\{a_1, a_5, a_6\right\}\) должно быть либо \(\left\{4, 4, 1\right\}\), либо \(\left\{3, 2, 2\right\}\). Так как \(\left\{a_3, a_5, a_6\right\}\) и \(\left\{a_1, a_5, a_6\right\}\) пересекаются по \(a_5\) и \(a_6\), делаем вывод, что \(a_5 = a_6 = 2\), а также \(a_1 = 3\), \(a_3 = 1\). Из шагов \(6\) и \(7\) известно, что \(a_5 = a_6 = 2\), а \(a_4\), \(a_5\) и \(a_6\) не могут образовать невырожденный треугольник, следовательно, \(a_4 = 4\). При всей известной информации, только \(a_2 = 2\) удовлетворяет запросам, сделанным на шагах \(2\), \(3\), \(4\), \(5\), \(12\) и \(13\). В третьем примере один массив, удовлетворяющий запросам, — \([1, 1, 1, 1, 3, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]\). | |
![]()
|
|
F. Вика и вики
Бинарный поиск
Комбинаторика
математика
дп
*2400
разделяй и властвуй
битмаски
На днях Вика изучала свой любимый интернет-ресурс — Википедию. На просторах Википедии она вычитала про интересную математическую операцию побитового исключающего ИЛИ, обозначаемую \(\oplus\). Вика стала изучать свойства этой загадочной операции. Для этого она взяла массив \(a\), состоящий из \(n\) целых неотрицательных чисел и применила одновременно ко всем его элементам следующую операцию: \(a_i = a_i \oplus a_{(i+1) \bmod n}\). Здесь \(x \bmod y\) обозначает остаток от деления \(x\) на \(y\). Элементы массива нумеруются, начиная с \(0\). Так как для полного изучения недостаточно проделать вышеописанные действия единожды, Вика повторяет их до тех пор, пока массив \(a\) не превратится в состоящий только из нулей. Определите, через сколько описанных выше действий все элементы массива \(a\) станут нулевыми. Если такой момент никогда не наступит, выведите \(-1\). Выходные данные Выведите единственное число — минимальное число действий, необходимое, чтобы сделать все элементы массива \(a\) нулевыми, или \(-1\), если массив \(a\) никогда не станет нулевым. Примечание В первом примере после одной операции массив \(a\) станет равен \([3, 3, 3, 3]\). Через ещё одну операцию он будет равен \([0, 0, 0, 0]\). Во втором примере массив \(a\) изначально состоит только из нулей. В третьем примере после одной операции массив \(a\) станет равен \([0]\). | |
![]()
|
|
G. The Morning Star
Структуры данных
Комбинаторика
математика
реализация
геометрия
*1500
сортировки
Компас указывает прямо на утреннюю звезду. Он может указывать только в одном из восьми направлений: четыре основных направления (N, S, E, W) или их комбинации (NW, NE, SW, SE). В противном случае, он сломается.  Направления, в которых может указывать компас. Направления, в которых может указывать компас. На плоскости находится \(n\) различных точек с целочисленными координатами. Сколько существует способов разместить компас в одной точке и утреннюю звезду в другой, чтобы компас не сломался? Выходные данные Для каждого набора входных данных выведите одно целое число — количество пар точек, которые не сломают компас. Примечание В первом примере, любая пара точек не сломает компас: - Компас находится в \((0,0)\), утренняя звезда находится в \((-1,-1)\): компас будет указывать \(\text{SW}\).
- Компас находится в \((0,0)\), утренняя звезда находится в \((1,1)\): компас будет указывать \(\text{NE}\).
- Компас находится в \((-1,-1)\), утренняя звезда находится в \((0,0)\): компас будет указывать \(\text{NE}\).
- Компас находится в \((-1,-1)\), утренняя звезда находится в \((1,1)\): компас будет указывать \(\text{NE}\).
- Компас находится в \((1,1)\), утренняя звезда находится в \((0,0)\): компас будет указывать \(\text{SW}\).
- Компас находится в \((1,1)\), утренняя звезда находится в \((-1,-1)\): компас будет указывать \(\text{SW}\).
Во втором примере, только две пары точек не сломают компас: - Компас находится в \((6,9)\), утренняя звезда находится в \((10,13)\): компас будет указывать \(\text{NE}\).
- Компас находится в \((10,13)\), утренняя звезда находится в \((6,9)\): компас будет указывать \(\text{SW}\).
| |
![]()
|
|
C. Ожидаемое разрушение
Теория вероятностей
Комбинаторика
математика
дп
*2500
У вас есть набор \(S\) из \(n\) различных целых чисел в диапазоне от \(1\) до \(m\). Каждую секунду вы выполняете следующие действия: - Выбираете элемент \(x\) из \(S\) равномерно случайным образом.
- Удаляете \(x\) из \(S\).
- Если \(x+1 \leq m\) и \(x+1\) не находится в \(S\), то добавляете \(x+1\) в \(S\).
Каково ожидаемое количество секунд до того момента, когда \(S\) не станет пустым? Выведите ответ по модулю \(1\,000\,000\,007\). Формально, пусть \(P = 1\,000\,000\,007\). Можно показать, что ответ может быть представлен в виде несократимой дроби \(\frac{a}{b}\), где \(a\) и \(b\) — целые числа, и \(b \not \equiv 0 \pmod{P}\). Выведите целое число, равное \(a \cdot b^{-1} \bmod P\). Другими словами, выведите такое целое число \(z\), что \(0 \le z < P\) и \(z \cdot b \equiv a \pmod{P}\). Выходные данные Выведите одно целое число — ожидаемое количество секунд до того момента, когда \(S\) станет пустым, по модулю \(1\,000\,000\,007\). Примечание Для теста 1 приведен список всех возможных сценариев и их вероятностей: - \([1, 3]\) (вероятность 50%) \(\to\) \([1]\) \(\to\) \([2]\) \(\to\) \([3]\) \(\to\) \([]\)
- \([1, 3]\) (вероятность 50%) \(\to\) \([2, 3]\) (вероятность 50%) \(\to\) \([2]\) \(\to\) \([3]\) \(\to\) \([]\)
- \([1, 3]\) (вероятность 50%) \(\to\) \([2, 3]\) (вероятность 50%) \(\to\) \([3]\) \(\to\) \([]\)
Сложив их, получим \(\frac{1}{2}\cdot 4 + \frac{1}{4} \cdot 4 + \frac{1}{4} \cdot 3 = \frac{15}{4}\). Мы видим, что \(750000009 \cdot 4 \equiv 15 \pmod{1\,000\,000\,007}\). | |
![]()
|
|
B. Наибольший интервал делителей
Перебор
Комбинаторика
математика
*900
теория чисел
жадные алгоритмы
Дано число \(n\). Найдите максимальный размер интервала \([l, r]\) из целых положительных чисел такого, что для каждого числа \(i\) из этого интервала (т.е. \(l \leq i \leq r\)) \(n\) кратно \(i\). Если вам даны два целых числа \(l\le r\), то размер интервала \([l, r]\) равен \(r-l+1\) (т.е. совпадает с количеством целых чисел, принадлежащих интервалу). Выходные данные Для каждого набора входных данных вывести одно целое число: максимальный размер допустимого интервала. Примечание В первом наборе входных данных допустимым интервалом с максимальным размером является \([1, 1]\) (он допустим, так как \(n = 1\) кратно \(1\)) и его размер равен \(1\). Во втором наборе входных данных допустимым интервалом с максимальным размером является \([4, 5]\) (он допустим, так как \(n = 40\) кратно \(4\) и \(5\)), а его размер равен \(2\). В третьем наборе входных данных допустимым интервалом с максимальным размером является \([9, 11]\). В четвертом наборе входных данных допустимым интервалом с максимальным размером является \([8, 13]\). В седьмом наборе входных данных допустимым интервалом с максимальным размером является \([327869, 327871]\). | |
![]()
|
|
G. Подсчет графов
Деревья
Комбинаторика
*2000
жадные алгоритмы
сортировки
графы
разделяй и властвуй
снм
Дано дерево, состоящее из \(n\) вершин. Дерево — это связный неориентированный граф без циклов. Каждое ребро дерева имеет свой вес, \(w_i\). Ваша задача — подсчитать количество различных графов, для которых одновременно выполняются четыре условия: - В графе нет петель и кратных ребер.
- Веса на ребрах графа целые числа и не превышают \(S\).
- Граф имеет ровно одно минимальное остовное дерево.
- Минимальное остовное дерево графа является заданным деревом.
Два графа считаются различными, если их наборы рёбер различны с учётом весов рёбер. Ответ может быть большим, выведите его по модулю \(998244353\). Выходные данные Для каждого теста выведите количество различных графов, удовлетворяющих условиям, по модулю \(998244353\). Примечание В первом примере существует единственный граф, который и является заданным деревом. Во втором примере заданное дерево выглядит так:  Ниже изображены все возможные графы для второго примера, красным цветом выделено минимальное остовное дерево: 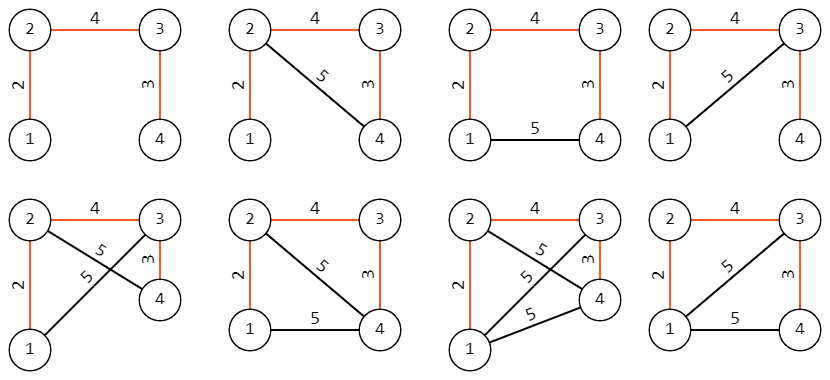 | |
![]()
|
|
E. Непересекающиеся подперестановки
Комбинаторика
математика
реализация
дп
*2300
Заданы два целых числа \(n\) и \(k\). Для массива длины \(n\) давайте определим его стоимость как максимальное количество непрерывных подмассивов этого массива, которые могут быть выбраны следующим образом: - каждый элемент массива принадлежит не более чем одному подмассиву;
- длина каждого подмассива ровно \(k\);
- каждый подмассив содержит каждое целое число от \(1\) до \(k\) ровно один раз.
Например, если \(n = 10\), \(k = 3\) и массив равен \([1, 2, 1, 3, 2, 3, 2, 3, 1, 3]\), его стоимость равна \(2\), потому что, например, мы можем выбрать два подмассива: от \(2\)-го элемента до \(4\)-го и от \(7\)-го элемента до \(9\)-го, и мы можем показать, что выбрать больше \(2\) подмассивов нельзя. Посчитайте сумму стоимостей по всем массивам длины \(n\), состоящих из целых чисел от \(1\) до \(k\), и выведите ее по модулю \(998244353\). Выходные данные Выведите одно целое число— сумму стоимостей по всем массивам длины \(n\), состоящих из целых чисел от \(1\) до \(k\), по модулю \(998244353\). | |
![]()
|
|
D. Шарики мороженого
Бинарный поиск
Конструктив
Комбинаторика
математика
*1300
Тёма решил увлечься приготовлением мороженого. Он достаточно преуспел в этом деле и научился хорошо делать мороженое в рожке ровно из двух шариков. До увлечения мороженым Тёма увлекался математикой. Поэтому он заинтересовался, какое минимальное количество шариков ему нужно иметь, чтобы из них можно было приготовить ровно \(n\) различных видов мороженого. Шарики мороженого бывают разных вкусов: \(1, 2, 3, \dots\). Тёма может приготовить мороженое из двух шариков любого вкуса (возможно, одинакового). Два мороженых считаются различными, если множества вкусов их шариков отличаются. Например \(\{1, 2\} = \{2, 1\}\), но \(\{1, 1\} \neq \{1, 2\}\). Например, имея следующие шарики мороженого: \(\{1, 1, 2\}\), можно приготовить всего два вида мороженого: \(\{1, 1\}\) и \(\{1, 2\}\). Обратите внимание, что Теме не нужно делать все стаканчики мороженого одновременно. Это означает, что он делает стаканчики мороженого независимо друг от друга. Также, чтобы сделать следующий стаканчик \(\{x, x\}\) для некоторого \(x\), Теме нужно иметь как минимум \(2\) шарика типа \(x\). Помогите Тёме ответить на этот вопрос. Можно показать, что ответ всегда существует. Выходные данные Для каждого набора входных данных выведите единственное число — минимальное количество шариков, которое необходимо купить Тёме. Примечание В первом примере достаточно иметь следующие типы шариков: \(\{1, 1\}\). Обратите внимание, что множество \(\{1\}\) недостаточно, так как нам нужно как минимум \(2\) шарика типа \(1\), чтобы сделать такой стаканчик \(\{1, 1\}\). Во втором примере невозможно сделать это с \(2\) шариками, но это можно сделать с помощью следующих шариков: \(\{1, 2, 3\}\). В третьем примере оптимальным ответом является \(\{1, 2, 3, 4\}\), поэтому мы можем получить следующие стаканчики мороженого: \(\{1, 2\}\), \(\{1, 3\}\), \(\{1, 4\}\), \(\{2, 3\}\), \(\{2, 4\}\), \(\{3, 4\}\). | |
![]()
|
|
G. Swaps
Комбинаторика
математика
дп
*2800
графы
Дан массив целых чисел \(a_1, a_2, \dots, a_n\) (\(1 \le a_i \le n\)). Вы можете выполнить следующую операцию несколько раз (возможно, ни одного): - выбрать произвольное \(i\) и выполнить swap\((a_i, a_{a_i})\).
Сколько различных массивов можно получить? Выведите ответ по модулю \((10^9 + 7)\). Выходные данные Выведите одно число — число достижимых массивов по модулю \((10^9 + 7)\). Примечание В первом примере изначально массив равен \([1, 1, 2]\). Если выполнить операцию с \(i = 3\), то местами поменяются значения \(a_3\) и \(a_2\), массив станет равен \([1, 2, 1]\). Можно показать, что других достижимых массивов нет. Во втором примере четыре достижимых массива суть \([2, 1, 4, 3]\), \([1, 2, 4, 3]\), \([1, 2, 3, 4]\), \([2, 1, 3, 4]\). Можно показать, что других достижимых массивов нет. | |
![]()
|
|
G. Волшебный квадрат
Конструктив
Комбинаторика
реализация
*3100
У Aquamoon есть квадратик Рубика, который можно представить как матрицу размера \(n \times n\), причём элементы матрицы составляют перестановку чисел \(1, \ldots, n^2\). Aquamoon можно производить над матрицей следующие операции: - Сдвиг строки, т.е. сдвиг некоторой строки матрицы на несколько позиций (хотя бы на \(1\) и не более чем на \(n-1\)) вправо. Элементы, выходящие за правую границу матрицы, сдвигаются в начало строки. Так, например, сдвиг строки \(\begin{pmatrix} a & b & c \end{pmatrix}\) на \(2\) позиции превратит её в \(\begin{pmatrix} b & c & a \end{pmatrix}\);
- Сдвиг столбца, т.е. сдвиг некоторого столбца матрицы на несколько позиций (хотя бы на \(1\) и не более чем на \(n-1\)) вниз. Элементы, выходящие за нижнюю границу матрицы, сдвигаются в начало столбца. Так, например, сдвиг столбца \(\begin{pmatrix} a \\ b \\ c \end{pmatrix}\) на \(2\) позиции превратит его в \(\begin{pmatrix} b\\c\\a \end{pmatrix}\).
Строки матрицы пронумерованы от \(1\) до \(n\) сверху вниз, столбцы пронумерованы от \(1\) до \(n\) слева направо. Клетку на пересечении \(x\)-й строки и \(y\)-го столбца обозначим как \((x, y)\). Aquamoon может выполнить несколько (возможно, ноль) операций, но она должна выполнять следующие ограничения: - каждая строка и каждый столбец могут быть сдвинуты не более чем по одному разу;
- каждое число матрицы может быть сдвинуто не более чем дважды;
- итоговые смещения любых двух чисел, сдвинутых дважды, должны быть попарно различны. Формально, пусть числа \(a\) и \(b\) были сдвинуты по два раза. Пусть \(a\) изменило свою позицию с \((x_1,y_1)\) на \((x_2,y_2)\), а \(b\) изменило позицию с \((x_3,y_3)\) на \((x_4,y_4)\). Тогда \(x_2-x_1 \not\equiv x_4-x_3 \pmod{n}\) или \(y_2-y_1 \not\equiv y_4-y_3 \pmod{n}\).
Aquamoon интересно, сколькими способами она может преобразовать исходное состояние квадратика в некоторое заданное конечно состояние. Два способа считаются различными, если последовательности применяемых операций в них различны. Поскольку ответ может быть очень большим, выведите его по модулю modulo \(998\,244\,353\). Выходные данные Для каждого набора входных данных, если возможно преобразовать начальное состояние в конечное, соблюдая все условия, то выведите одно число — число способов это сделать по модулю \(998\,244\,353\). Если решения не существует, выведите одно целое число \(0\). Примечание В первом наборе входных данных единственный способ преобразовать исходную матрицу в конечную — сдвинуть вторую строку на \(1\) вправо, а затем сдвинуть первый столбец на \(1\) вниз. Во втором наборе входных данных можно показать, что нет ни одного корректного способа преобразовать матрицу, так что ответ равен \(0\). | |
![]()
|
|
B. Battling with Numbers
Комбинаторика
математика
теория чисел
*1400
On the trip to campus during the mid semester exam period, Chaneka thinks of two positive integers \(X\) and \(Y\). Since the two integers can be very big, both are represented using their prime factorisations, such that: - \(X=A_1^{B_1}\times A_2^{B_2}\times\ldots\times A_N^{B_N}\) (each \(A_i\) is prime, each \(B_i\) is positive, and \(A_1<A_2<\ldots<A_N\))
- \(Y=C_1^{D_1}\times C_2^{D_2}\times\ldots\times C_M^{D_M}\) (each \(C_j\) is prime, each \(D_j\) is positive, and \(C_1<C_2<\ldots<C_M\))
Chaneka ponders about these two integers for too long throughout the trip, so Chaneka's friend commands her "Gece, deh!" (move fast) in order to not be late for the exam. Because of that command, Chaneka comes up with a problem, how many pairs of positive integers \(p\) and \(q\) such that \(\text{LCM}(p, q) = X\) and \(\text{GCD}(p, q) = Y\). Since the answer can be very big, output the answer modulo \(998\,244\,353\). Notes: - \(\text{LCM}(p, q)\) is the smallest positive integer that is simultaneously divisible by \(p\) and \(q\).
- \(\text{GCD}(p, q)\) is the biggest positive integer that simultaneously divides \(p\) and \(q\).
Output An integer representing the number of pairs of positive integers \(p\) and \(q\) such that \(\text{LCM}(p, q) = X\) and \(\text{GCD}(p, q) = Y\), modulo \(998\,244\,353\). Note In the first example, the integers are as follows: - \(X=2^2\times3^1\times5^1\times7^2=2940\)
- \(Y=3^1\times7^1=21\)
The following are all possible pairs of \(p\) and \(q\): - \(p=21\), \(q=2940\)
- \(p=84\), \(q=735\)
- \(p=105\), \(q=588\)
- \(p=147\), \(q=420\)
- \(p=420\), \(q=147\)
- \(p=588\), \(q=105\)
- \(p=735\), \(q=84\)
- \(p=2940\), \(q=21\)
In the third example, the integers are as follows: - \(X=2^1\times5^1=10\)
- \(Y=2^1\times3^1=6\)
There is no pair \(p\) and \(q\) that simultaneously satisfies \(\text{LCM}(p,q)=10\) and \(\text{GCD}(p,q)=6\). | |
![]()
|
|
H. Happy Sets
Комбинаторика
*2100
Define a set \(A\) as a child of set \(B\) if and only if for each element of value \(x\) that is in \(A\), there exists an element of value \(x+1\) that is in \(B\). Given integers \(N\) and \(K\). In order to make Chaneka happy, you must find the number of different arrays containing \(N\) sets \([S_1, S_2, S_3, \ldots, S_N]\) such that: - Each set can only contain zero or more different integers from \(1\) to \(K\). - There exists a way to rearrange the order of the array of sets into \([S'_1, S'_2, S'_3, \ldots, S'_N]\) such that \(S'_i\) is a child of \(S'_{i+1}\) for each \(1\leq i\leq N-1\). Print the answer modulo \(998\,244\,353\). Two sets are considered different if and only if there is at least one value that only occurs in one of the two sets. Two arrays of sets are considered different if and only if there is at least one index \(i\) such that the sets at index \(i\) in the two arrays are different. Output An integer representing the number of different arrays of sets that satisfy the problem condition, modulo \(998\,244\,353\). Note In the first example, there are \(11\) different arrays of sets possible, which are: - \([\{\}, \{\}]\)
- \([\{\}, \{1\}]\)
- \([\{\}, \{1, 2\}]\)
- \([\{\}, \{2\}]\)
- \([\{1\}, \{\}]\)
- \([\{1\}, \{1, 2\}]\)
- \([\{1\}, \{2\}]\)
- \([\{1, 2\}, \{\}]\)
- \([\{1, 2\}, \{1\}]\)
- \([\{2\}, \{\}]\)
- \([\{2\}, \{1\}]\)
| |
![]()
|
|
M. Mighty Rock Tower
Перебор
Теория вероятностей
Комбинаторика
математика
дп
*2400
Pak Chanek comes up with an idea in the midst of boredom to play a game. The game is a rock tower game. There is a big rock that is used as a base. There are also \(N\) small identical rocks that Pak Chanek will use to build a rock tower with a height of \(N\) above the base rock. Initially, there are no small rocks that are located above the base rock. In other words, the height of the tower above the base rock is initially \(0\). In one move, Pak Chanek can place one small rock onto the top of the tower which makes the height of the tower above the base rock increase by \(1\). Each time Pak Chanek place one small rock, the following will happen after the small rock is placed: - Let's say \(x\) is the height of the tower above the base rock right after the small rock is placed.
- There is a probability of \(P_x\) percent that the topmost rock falls.
- If \(x \geq 2\) and the topmost rock falls, then there is another probability of \(P_x\) percent that the \(2\)-nd topmost rock also falls.
- If \(x \geq 3\) and the \(2\)-nd topmost rock falls, then there is another probability of \(P_x\) percent that the \(3\)-rd topmost rock also falls.
- If \(x \geq 4\) and the \(3\)-rd topmost rock falls, then there is another probability of \(P_x\) percent that the \(4\)-th topmost rock also falls.
- And so on.
If the tower successfully reaches a height of \(N\) without any rocks falling after that, then the game is ended. If given an integer array \([P_1, P_2, \ldots, P_N]\), what is the expected value of the number of moves that Pak Chanek needs to do to end the game? It can be proven that the expected value can be represented as an simple fraction \(\frac{P}{Q}\) where \(Q\) is coprime to \(998\,244\,353\). Output the value of \(P \times Q^{-1}\) modulo \(998\,244\,353\). Output An integer representing the expected value of the number of moves that Pak Chanek needs to do to end the game, modulo \(998\,244\,353\). Note In the first example, the expected value of the number of moves that Pak Chanek needs to do to end the game is \(\frac{19}{2}\). | |
![]()
|
|
C. План путешествия
Деревья
Комбинаторика
математика
реализация
дп
*2400
Во время летних каникул после экзамена, Tom и Daniel планировали отправиться в путешествие. В их стране есть \(n\) городов, пронумерованных от \(1\) до \(n\). И система дорожного движения в стране особенная. Для любого города \(i\) (\(1 \le i \le n\)) есть: - дорога между городами \(i\) и \(2i\), если \(2i\le n\);
- дорога между городами \(i\) и \(2i+1\), если \(2i+1\le n\).
Составляя план путешествия, Daniel выбирает некоторое целое значение от \(1\) до \(m\) для каждого города, для \(i\)-го города обозначим его \(a_i\). Пусть \(s_{i,j}\) равно максимальному значению для городов на простом\(^\dagger\) пути между городами \(i\) и \(j\). Тогда оценка плана путешествия равна \(\sum_{i=1}^n\sum_{j=i}^n s_{i,j}\). Tom хочет знать сумму оценок всех возможных планов путешествия. Daniel просит вас помочь ему найти её. Вам нужно сказать ответ по модулю \(998\,244\,353\). \(^\dagger\) Простым путём между городами \(x\) и \(y\) называется путь между ними, который проходит по каждому городу не более одного раза. Выходные данные Для каждого набора входных данных выведите одно целое число — сумму оценок всех возможных планов путешествия по модулю \(998\,244\,353\). Примечание В первом наборе входных данных есть только один возможный план путешествия:  Путь \(1\rightarrow 1\): \(s_{1,1}=a_1=1\). Путь \(1\rightarrow 2\): \(s_{1,2}=\max(1,1)=1\). Путь \(1\rightarrow 3\): \(s_{1,3}=\max(1,1)=1\). Путь \(2\rightarrow 2\): \(s_{2,2}=a_2=1\). Путь \(2\rightarrow 1\rightarrow 3\): \(s_{2,3}=\max(1,1,1)=1\). Путь \(3\rightarrow 3\): \(s_{3,3}=a_3=1\). Оценка равна \(1+1+1+1+1+1=6\). Во втором наборе входных данных есть четыре возможных плана путешествия: 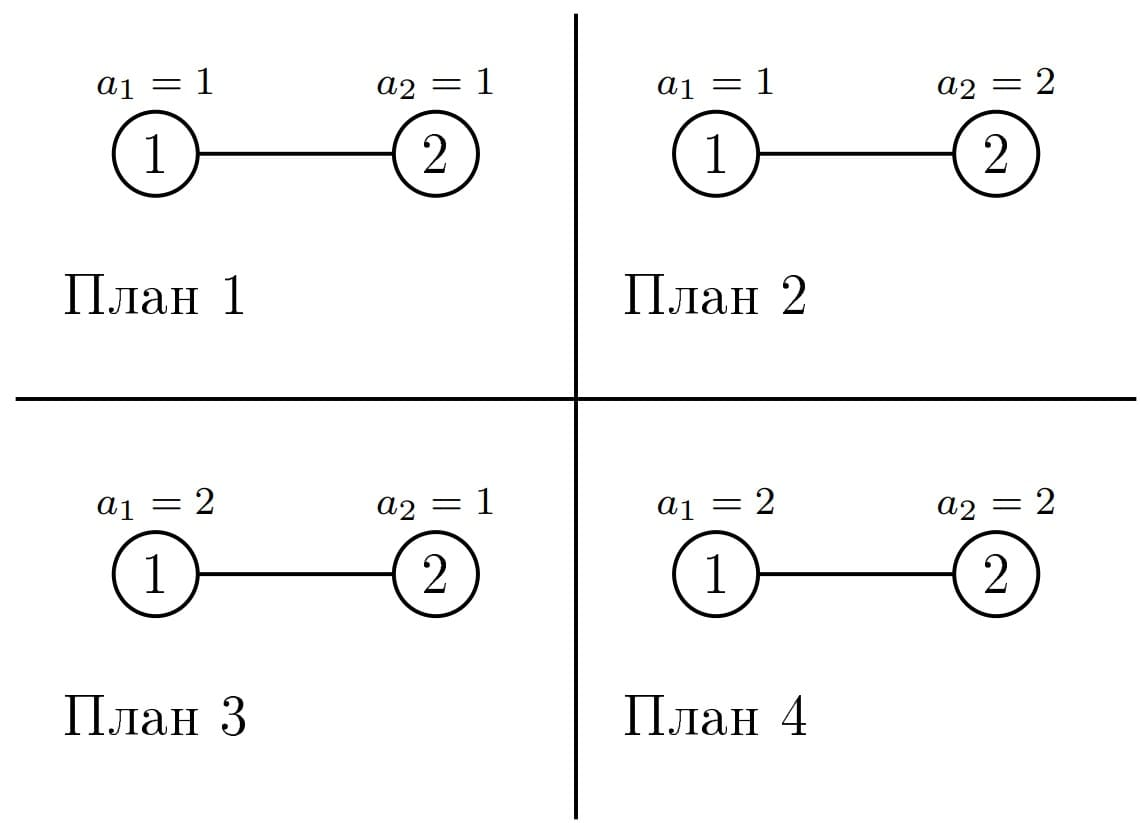 Оценка плана \(1\): \(1+1+1=3\). Оценка плана \(2\): \(1+2+2=5\). Оценка плана \(3\): \(2+2+1=5\). Оценка плана \(4\): \(2+2+2=6\). Таким образом, сумма оценок равна \(3+5+5+6=19\). | |
![]()
|
|
B. Эффект от крема против прыщей
Комбинаторика
*1500
теория чисел
сортировки
У Чанеки есть массив \([a_1,a_2,\ldots,a_n]\). Изначально все элементы покрашены в белый. Чанека выберет один или несколько различных индексов и покрасит элементы с этими индексами в черный цвет. Затем она выберет все белые элементы, чьи индексы кратны индексу по крайней мере одного черного элемента, и покрасит их в зеленый цвет. После этого ее оценка будет равна максимальному значению \(a_i\) среди всех черных и зеленых элементов. Существует \(2^n-1\) способов выбрать черные индексы. Найдите сумму оценок для всех возможных способов, которыми Чанека может выбрать черные индексы. Поскольку ответ может быть очень большим, выведите его по модулю \(998\,244\,353\). Выходные данные Выведите одно целое число — сумму оценок по всем способам выбрать черные индексы по модулю \(998\,244\,353\). Примечание В первом примере ниже перечислены \(15\) возможных вариантов выбора черных индексов: - Индекс \(1\) - черный. Индексы \(2\), \(3\) и \(4\) - зеленые. Максимальное значение среди них - \(19\).
- Индекс \(2\) - черный. Индекс \(4\) - зеленый. Максимальное значение среди них - \(14\).
- Индекс \(3\) - черный. Максимальное значение среди них - \(19\).
- Индекс \(4\) - черный. Максимальное значение среди них - \(9\).
- Индексы \(1\) и \(2\) - черные. Индексы \(3\) и \(4\) - зеленые. Максимальное значение среди них - \(19\).
- Индексы \(1\) и \(3\) - черные. Индексы \(2\) и \(4\) - зеленые. Максимальное значение среди них - \(19\).
- Индексы \(1\) и \(4\) - черные. Индексы \(2\) и \(3\) - зеленые. Максимальное значение среди них - \(19\).
- Индексы \(2\) и \(3\) - черные. Индекс \(4\) - зеленый. Максимальное значение среди них - \(19\).
- Индексы \(2\) и \(4\) - черные. Максимальное значение среди них - \(14\).
- Индексы \(3\) и \(4\) - черные. Максимальное значение среди них - \(19\).
- Индексы \(1\), \(2\) и \(3\) - черные. Индекс \(4\) - зеленый. Максимальное значение среди них - \(19\).
- Индексы \(1\), \(2\) и \(4\) - черные. Индекс \(3\) - зеленый. Максимальное значение среди них - \(19\).
- Индексы \(1\), \(3\) и \(4\) - черные. Индекс \(2\) - зеленый. Максимальное значение среди них - \(19\).
- Индексы \(2\), \(3\) и \(4\) - черные. Максимальное значение среди них - \(19\).
- Индексы \(1\), \(2\), \(3\) и \(4\) - черные. Максимальное значение среди них - \(19\).
Общая сумма составляет \(19+14+19+9+19+19+19+19+14+19+19+19+19+19+19 = 265\). | |
![]()
|
|
D. Лексихроматография
Комбинаторика
поиск в глубину и подобное
графы
снм
*2500
Пак Чанек любит свой факультет — факультет компьютерных наук Университета Индонезии (Fasilkom). Он хочет поиграть с цветами эмблемы факультета - синим и красным. Имеется массив \(a\), состоящий из \(n\) элементов, элемент \(i\) имеет значение \(a_i\). Пак Чанек хочет окрасить каждый элемент массива в синий или красный цвет так, чтобы выполнялись следующие условия: - Если все синие элементы складываются в подпоследовательность\(^\dagger\) и все красные элементы тоже, то синяя подпоследовательность строго меньше красной подпоследовательности лексикографически\(^\ddagger\).
- Массив \(a\) не имеет ни одного несбалансированного подмассива. Подмассив называется несбалансированным тогда и только тогда, когда существует такое значение \(k\), что количество красных элементов на этом подмассиве со значением \(k\) и количество синих элементов со значением \(k\) отличается хотя бы на \(2\).
- Заметим, что можно покрасить все элементы массива в один и тот же цвет.
Сколько различных раскрасок удовлетворяют всем этим условиям? Поскольку ответ может быть очень большим, выведите ответ по модулю \(998\,244\,353\). Две раскраски различны тогда и только тогда, когда существует хотя бы один элемент, который в одной раскраске является синим, а в другой - красным. \(^\dagger\) Подпоследовательность массива - это последовательность, которая может быть получена из массива путем удаления некоторых элементов (возможно, ни одного), без изменения порядка оставшихся элементов. \(^\ddagger\) Пусть \(p\) и \(q\) - две различные последовательности. Считается, что последовательность \(p\) лексикографически меньше последовательности \(q\) тогда и только тогда, когда \(p\) является префиксом \(q\) или существует индекс \(i\) такой, что \(p_j=q_j\) для всех \(1\leq j<i\), и \(p_i<q_i\). В частности, пустая последовательность всегда лексикографически меньше любой непустой последовательности. Выходные данные Выведите одно целое число — количество различных раскрасок, удовлетворяющих всем условиям задачи, по модулю \(998\,244\,353\). Примечание В первом примере \(3\) способа раскраски всех элементов с индекса \(1\) по индекс \(8\): - Синий, красный, красный, синий, синий, красный, красный, синий.
- Синий, красный, красный, красный, синий, синий, красный, синий.
- Красный, красный, синий, голубой, синий, красный, красный, синий.
Например, если мы раскрасим элементы с индекса \(1\) по индекс \(8\) в красный, красный, синий, красный, красный, красный, синий, синий, синий, то это не будет корректной раскраской, так как для подмассива \(a[2..6]\) существует \(0\) синих элементов со значением \(3\) и \(2\) красных элемента со значением \(3\), что делает подмассив \(a[2..6]\) несбалансированным подмассивом. | |
![]()
|
|
C. Чередуй!
Комбинаторика
дп
жадные алгоритмы
*1300
Дана двоичная строка \(s\). Двоичная строка — это строка, состоящая из символов 0 и/или 1. Вы можете производить следующую операцию со строкой \(s\) любое количество раз (даже ноль): - выбрать целое число \(i\) такое, что \(1 \le i \le |s|\), затем удалить символ \(s_i\).
Вам нужно сделать строку \(s\) чередующейся, т. е. после выполнения операций каждые два соседних символа в \(s\) должны быть разными. Ваша задача — вычислить два значения: - минимальное количество операций, необходимых для того, чтобы сделать строку \(s\) чередующейся;
- количество различных кратчайших последовательностей операций, которые делают строку \(s\) чередующейся. Две последовательности операций считаются различными, если хотя бы в одной операции выбранное целое число \(i\) отличается в этих двух последовательностях.
Выходные данные Для каждого набора входных данных выведите два целых числа: минимальное количество операций, которые вам нужно выполнить, и количество различных кратчайших последовательностей операций. Поскольку второе число может быть большим, выведите его остаток по модулю \(998244353\). Примечание В первом наборе входных данных примера кратчайшими последовательностями операций являются: - \([2]\) (удалить \(2\)-й символ);
- \([3]\) (удалить \(3\)-й символ).
Во втором наборе входных данных примера кратчайшими последовательностями операций являются: - \([2, 1]\) (удалить \(2\)-й символ, затем удалить \(1\)-й символ);
- \([2, 2]\);
- \([1, 1]\);
- \([1, 2]\);
- \([3, 1]\);
- \([3, 2]\).
В третьем наборе входных данных примера единственной кратчайшей последовательностью операций является \([]\) (пустая последовательность). | |
![]()
|
|
D. Сумма функций XOR
Комбинаторика
математика
дп
*1700
разделяй и властвуй
битмаски
Дан массив \(a\) длины \(n\), состоящий из неотрицательных целых чисел. Необходимо вычислить значение \(\sum_{l=1}^{n} \sum_{r=l}^{n} f(l, r) \cdot (r - l + 1)\), где \(f(l, r)\) равно \(a_l \oplus a_{l+1} \oplus \dots \oplus a_{r-1} \oplus a_r\) (символ \(\oplus\) обозначает побитовое исключающее ИЛИ). Так как ответ может быть очень большим, выведите его по модулю \(998244353\). Выходные данные Выведите одно целое число — значение \(\sum_{l=1}^{n} \sum_{r=l}^{n} f(l, r) \cdot (r - l + 1)\), взятое по модулю \(998244353\). Примечание В первом примере ответ равен \(f(1, 1) + 2 \cdot f(1, 2) + 3 \cdot f(1, 3) + f(2, 2) + 2 \cdot f(2, 3) + f(3, 3) = \) \(= 1 + 2 \cdot 2 + 3 \cdot 0 + 3 + 2 \cdot 1 + 2 = 12\). | |
![]()
|
|
D. Монокарп и множество
Структуры данных
Комбинаторика
математика
*2100
У Монокарпа есть \(n\) чисел \(1, 2, \dots, n\) и множество (изначально пустое). Он \(n\) раз добавляет свои числа в это множество в некотором порядке. Во время каждого шага он добавляет новое число (которого ранее не было в множестве). Другими словами, последовательность добавленных чисел является перестановкой длины \(n\). Каждый раз, когда Монокарп добавляет элемент в множество, кроме первого раза, он записывает символ: - если элемент, который Монокарп пытается добавить, становится максимальным элементом в множестве, Монокарп записывает символ >;
- если элемент, который Монокарп пытается добавить, становится минимальным элементом в множестве, Монокарп записывает символ <;
- если ни одно из вышеперечисленного не выполняется, Монокарп записывает символ ?.
Дана строка \(s\) из \(n-1\) символов, которая представляет записанные символы Монокарпом (в порядке их записи). Вам нужно обработать \(m\) запросов к строке. Каждый запрос имеет следующий формат: - \(i\) \(c\) — заменить \(s_i\) символом \(c\).
Перед всеми запросами и после каждого запроса вам нужно вычислить количество различных способов упорядочить числа \(1, 2, 3, \dots, n\) таким образом, что если Монокарп вставляет числа в множество в этом порядке, он получает строку \(s\). Поскольку ответы могут быть большими, выведите их по модулю \(998244353\). Выходные данные Перед всеми запросами и после каждого запроса выведите одно целое число — количество способов упорядочить числа \(1, 2, 3, \dots, n\) таким образом, чтобы, если Монокарп вставляет числа в множество в этом порядке, он получает строку \(s\). Поскольку ответы могут быть большими, выведите их по модулю \(998244353\). Примечание В первом примере до обработки запросов есть три способа упорядочить числа: - \(3, 1, 2, 5, 4, 6\);
- \(4, 1, 2, 5, 3, 6\);
- \(4, 1, 3, 5, 2, 6\).
После последнего запроса есть один способ упорядочить числа: | |
![]()
|
|
E. Симфония кактусов
Комбинаторика
дп
поиск в глубину и подобное
графы
*3500
Вам дан связный неориентированный граф, в котором любые два различных простых цикла не имеют общих вершин. Так как граф может быть очень большим, он дан вам в сжатом виде: для каждого ребра вам также дано некое число \(d\), обозначающее, что на этом ребре дополнительно находится \(d\) вершин. Требуется назначить каждой вершине и каждому ребру графа вес — целое число от \(1\) до \(3\). Ребро графа назовём хорошим, если побитовый XOR весов смежных ему вершин не равен \(0\) и не равен весу этого ребра. Аналогично вершину графа назовём хорошей, если побитовый XOR весов смежных ей рёбер не равен \(0\) и не равен весу этой вершины. Вам нужно определить, сколько существует способов назначить веса вершинам и рёбрам графа, чтобы все вершины и все рёбра были хорошими. Так как ответ может быть достаточно большим, нужно вычислить остаток от деления ответа на \(998\,244\,353\). Выходные данные Выведите единственное целое число — ответ на задачу по модулю \(998\,244\,353\). Примечание В первом тесте граф имеет вид простого цикла из \(3\) вершин. Можно показать, что есть ровно \(12\) способов назначить веса вершинам и рёбрам, чтобы все они были хорошими. Во втором тесте граф имеет вид двух простых циклов из \(3\) вершин, соединённых ребром. Можно показать, что для такого графа нет ни одного способа расставить веса, чтобы все вершины и рёбра были хорошими. | |
![]()
|
|
F. Красивые массивы
Комбинаторика
математика
дп
*2600
матрицы
Назовем массив \(a\) из \(n\) неотрицательных целых чиселкрасивым, если выполняются следующие условия: - массив содержит хотя бы одно из чисел \(x\), \(x + 1\), ..., \(x+k-1\);
- последовательные элементы массива отличаются не более чем на \(k\) (т.е. \(|a_i-a_{i-1}| \le k\) для каждого \(i \in [2, n]\)).
Даны значения \(n\), \(x\) и \(k\). Ваша задача — посчитать количество красивых массивов длины \(n\). Поскольку ответ может быть большим, выведите его по модулю \(10^9+7\). Выходные данные Для каждого набора входных данных выведите одно целое число — количество красивых массивов длины \(n\), взятое по модулю \(10^9+7\). Примечание В первом наборе входных данных примера следующие массивы являются красивыми: - \([0, 0, 0]\);
- \([0, 0, 1]\);
- \([0, 1, 0]\);
- \([0, 1, 1]\);
- \([0, 1, 2]\);
- \([1, 0, 0]\);
- \([1, 0, 1]\);
- \([1, 1, 0]\);
- \([2, 1, 0]\).
| |
![]()
|
|
E. One-X
Деревья
Комбинаторика
математика
дп
поиск в глубину и подобное
*2400
В этом грустном мире, полном недостатков, существуют уродливые деревья отрезков. Дерево отрезков — это дерево, где каждая вершина соответствует некоторому отрезку и имеет свой номер. Дерево отрезков для массива из \(n\) элементов можно построить рекурсивно. Пусть функция \(\operatorname{build}(v,l,r)\) строит дерево отрезков, корневая вершина которого имеет номер \(v\) и соответствует отрезку \([l,r]\). Теперь давайте определим \(\operatorname{build}(v,l,r)\): - Если \(l=r\), то вершина \(v\) является листом, поэтому мы прекращаем добавление новых рёбер;
- Иначе, мы добавляем рёбра \((v, 2v)\) и \((v, 2v+1)\). Пусть \(m=\lfloor \frac{l+r}{2} \rfloor\). Затем мы вызываем \(\operatorname{build}(2v,l,m)\) и \(\operatorname{build}(2v+1,m+1,r)\).
Таким образом, всё дерево строится путём вызова \(\operatorname{build}(1,1,n)\). Теперь Ибти построит дерево отрезков для массива из \(n\) элементов. Он хочет найти сумму всех \(\operatorname{lca}^\dagger(S)\), где \(S\) — непустое подмножество листьев. Обратите внимание, что существует ровно \(2^n - 1\) возможных подмножеств. Поскольку эта сумма может быть очень большой, выведите её по модулю \(998\,244\,353\). \(^\dagger\operatorname{lca}(S)\) — номер наименьшего общего предка для вершин, находящихся в \(S\). Выходные данные Для каждого набора входных данных выведите одно целое число — требуемую сумму по модулю \(998\,244\,353\). Примечание  В первом наборе входных данных: Давайте рассмотрим все подмножества листьев. - \(\operatorname{lca}(\{2\})=2\);
- \(\operatorname{lca}(\{3\})=3\);
- \(\operatorname{lca}(\{2,3\})=1\).
Таким образом, ответ равен \(2+3+1=6\). Во втором наборе входных данных: Давайте рассмотрим все подмножества листьев. - \(\operatorname{lca}(\{4\})=4\);
- \(\operatorname{lca}(\{5\})=5\);
- \(\operatorname{lca}(\{3\})=3\);
- \(\operatorname{lca}(\{4,5\})=2\);
- \(\operatorname{lca}(\{4,3\})=1\);
- \(\operatorname{lca}(\{5,3\})=1\);
- \(\operatorname{lca}(\{4,5,3\})=1\);
Таким образом, ответ равен \(4+5+3+2+1+1+1=17\). | |
![]()
|
|
H. Twin Friends
Комбинаторика
дп
*2200
You meet two new friends who are twins. The name of the elder twin is \(A\), which consists of \(N\) characters. While the name of the younger twin is \(B\), which consists of \(M\) characters. It is known that \(N \leq M\). You want to call each of them with a nickname. For the elder twin, you want to pick any permutation of \(A\) as the nickname. For the younger twin, you want to remove exactly \(M - N\) characters from any permutation of \(B\). Denote the nicknames of the elder twin and the younger twin as \(A'\) and \(B'\), respectively. You want the nicknames to satisfy the following requirement. For each \(i\) that satisfies \(1 \leq i \leq N\), \(B'_i\) must be equal to either \(A'_i\) or the next letter that follows alphabetically after \(A'_i\) (if such a next letter exists). Determine the number of different pairs of nicknames \((A', B')\) that satisfy the requirement. Two pairs of nicknames are considered different if at least one of the nicknames are different. As the result might be large, find the answer modulo \(998\,244\,353\). Output Output a single integer representing number of different pairs \((A', B')\) that satisfy the requirement, modulo \(998\,244\,353\). Note Explanation for the sample input/output #1 The \(9\) pairs are: - (AAM, AAN),
- (AAM, ABN),
- (AAM, BAN),
- (AMA, ANA),
- (AMA, ANB),
- (AMA, BNA),
- (MAA, NAA),
- (MAA, NAB), and
- (MAA, NBA).
Explanation for the sample input/output #2 The \(120\) pairs are the pairs where \(A'\) is a permutation of BINUS and \(B' = A'\). | |
![]()
|
|
J. Count BFS Graph
Комбинаторика
*2100
дп
You are currently researching a graph traversal algorithm called the Breadth First Search (BFS). Suppose you have an input graph of \(N\) nodes (numbered from \(1\) to \(N\)). The graph is represented by an adjacency matrix \(M\), for which node \(u\) can traverse to node \(v\) if \(M_{u, v}\) is \(1\), otherwise it is \(0\). Your algorithm will output the order the nodes are visited in the BFS. The pseudocode of the algorithm is presented as follows.
BFS(M[1..N][1..N]):
let A be an empty array
let Q be an empty queue
append 1 to A
push 1 to Q
while Q is not empty:
pop the front element of Q into u
for v = 1 to N:
if M[u][v] == 1 and v is not in A:
append v to A
push v to Q
return A
During your research, you are interested in the following problem. Given an array \(A\) such that \(A\) is a permutation of \(1\) to \(N\) and \(A_1 = 1\). How many simple undirected graph with \(N\) nodes and adjacency matrix \(M\) such that \(\text{BFS}(M) = A\)? Since the answer can be very large, calculate the answer modulo \(998\,244\,353\). A simple graph has no self-loop (\(M_{i, i} = 0\) for \(1 \leq i \leq N\)) and there is at most one edge that connects a pair of nodes. In an undirected graph, if node \(u\) is adjacent to node \(v\), then node \(v\) is also adjacent to node \(u\); formally, \(M_{u, v} = M_{v, u}\) for \(1 \leq u < v \leq N\). Two graphs are considered different if there is an edge that exists in one graph but not the other. In other words, two graphs are considered different if their adjacency matrices are different. Output Output an integer representing the number of simple undirected graphs with \(N\) nodes and adjacency matrix \(M\) such that \(\text{BFS}(M) = A\). Since the answer can be very large, output the answer modulo \(998\,244\,353\). Note Explanation for the sample input/output #1 The following illustration shows all graphs that satisfy the requirements.  Explanation for the sample input/output #2 The only graph that satisfies the requirements is a graph with two edges: one that connects nodes \(1\) and \(3\), and another one that connects nodes \(3\) and \(2\). | |
![]()
|
|
E. Хорошие тройки
Перебор
Комбинаторика
*1600
теория чисел
Дано неотрицательное целое число \(n\) (\(n \ge 0\)). Будем называть тройку неотрицательных целых чисел \((a, b, c)\) хорошей, если \(a + b + c = n\) и \(digsum(a) + digsum(b) + digsum(c) = digsum(n)\), где \(digsum(x)\) — это сумма цифр числа \(x\). Например, если \(n = 26\), то тройка \((4, 12, 10)\) является хорошей, потому что \(4 + 12 + 10 = 26\), и \((4) + (1 + 2) + (1 + 0) = (2 + 6)\). Ваша задача — найти количество хороших троек для заданного числа \(n\). Порядок чисел в тройке имеет значение. Например, тройки \((4, 12, 10)\) и \((10, 12, 4)\) считаются разными. Выходные данные Для каждого набора входных данных выведите одно целое число — количество хороших троек для заданного числа \(n\). Порядок чисел в тройке имеет значение. Примечание В первом примере хорошие тройки следующие: \((0, 0, 11)\), \((0, 1, 10)\), \((0, 10, 1)\), \((0, 11, 0)\), \((1, 0, 10)\), \((1, 10, 0)\), \((10, 0, 1)\), \((10, 1, 0)\), \((11, 0, 0)\). Во втором примере есть только одна хорошая тройка \((0, 0, 0)\). | |
![]()
|
|
F1. Небольшая задачка про перестановки (простая версия)
Перебор
Комбинаторика
математика
дп
*2200
В простой версии задачи \(a_i\) находятся в диапазоне \([0, n]\); в сложной версии \(a_i\) находятся в диапазоне \([-1, n]\) и определение хорошей перестановки немного отличается. Вы можете делать взломы, только если обе версии задачи решены. Вам дано целое число \(n\) и массив \(a_1, a_2 \dots, a_n\) целых чисел в диапазоне \([0, n]\). Перестановка \(p_1, p_2, \dots, p_n\) элементов \([1, 2, \dots, n]\) называется хорошей, если для каждого \(i\) верно следующее утверждение: - количество значений \(\leq i\) в \([p_1, p_2, \dots, p_i]\) в точности равно \(a_i\).
Посчитайте количество хороших перестановок \([1, 2, \dots, n]\) по модулю \(998\,244\,353\). Выходные данные Для каждого набора входных данных выведите одну строку, содержащую количество хороших перестановок по модулю \(998\,244\,353\). Примечание В первом наборе входных данных единственной хорошей перестановкой является \([1, 2, 3, 4, 5]\). Во втором наборе входных данных существует \(4\) хороших перестановки: \([2, 1, 5, 6, 3, 4]\), \([2, 1, 5, 6, 4, 3]\), \([2, 1, 6, 5, 3, 4]\), \([2, 1, 6, 5, 4, 3]\). Например, \([2, 1, 5, 6, 3, 4]\) — хорошая, потому что: - \(a_1 = 0\), и в \([p_1] = [2]\) есть \(0\) значений \(\leq 1\);
- \(a_2 = 2\), и есть \(2\) значения \(\leq 2\) в \([p_1, p_2] = [2, 1]\);
- \(a_3 = 2\), и есть \(2\) значения \(\leq 3\) в \([p_1, p_2, p_3] = [2, 1, 5]\);
- \(a_4 = 2\), и есть \(2\) значения \(\leq 4\) в \([p_1, p_2, p_3, p_4] = [2, 1, 5, 6]\);
- \(a_5 = 4\), и есть \(4\) значения \(\leq 5\) в \([p_1, p_2, p_3, p_4, p_5] = [2, 1, 5, 6, 3]\);
- \(a_6 = 6\), и есть \(6\) значений \(\leq 6\) в \([p_1, p_2, p_3, p_4, p_5, p_6] = [2, 1, 5, 6, 3, 4]\).
В третьем наборе входных данных нет хороших перестановок, потому что не существует перестановок с \(a_6 = 5\) значениями \(\leq 6\) в \([p_1, p_2, p_3, p_4, p_5, p_6]\). | |
![]()
|
|
F2. Небольшая задачка про перестановки (сложная версия)
Комбинаторика
математика
дп
*2500
В простой версии задачи \(a_i\) находятся в диапазоне \([0, n]\); в сложной версии \(a_i\) находятся в диапазоне \([-1, n]\) и определение хорошей перестановки немного отличается. Вы можете делать взломы, только если обе версии задачи решены. Вам дано целое число \(n\) и массив \(a_1, a_2, \dots, a_n\) целых чисел в диапазоне \([-1, n]\). Перестановка \(p_1, p_2, \dots, p_n\) в \([1, 2, \dots, n]\) называется хорошей, если для каждого \(i\) верно следующее утверждение: - если \(a_i \neq -1\), то количество значений \(\leq i\) в \([p_1, p_2, \dots, p_i]\) в точности равно \(a_i\).
Посчитайте количество хороших перестановок \([1, 2, \dots, n]\) по модулю \(998\,244\,353\). Выходные данные Для каждого набора входных данных выведите одну строку, содержащую количество хороших перестановок по модулю \(998\,244\,353\). Примечание В первом наборе входных данных все перестановки длины \(5\) являются хорошими, поэтому существует \(120\) хороших перестановок. Во втором наборе входных данных единственной хорошей перестановкой является \([1, 2, 3, 4, 5]\). В третьем наборе входных данных существует \(4\) хороших перестановки: \([2, 1, 5, 6, 3, 4]\), \([2, 1, 5, 6, 4, 3]\), \([2, 1, 6, 5, 3, 4]\), \([2, 1, 6, 5, 4, 3]\). Например, \([2, 1, 5, 6, 3, 4]\) — хорошая, потому что: - \(a_1 = 0\), и в \([p_1] = [2]\) есть \(0\) значений \(\leq 1\);
- \(a_2 = 2\), и есть \(2\) значения \(\leq 2\) в \([p_1, p_2] = [2, 1]\);
- \(a_3 = 2\), и есть \(2\) значения \(\leq 3\) в \([p_1, p_2, p_3] = [2, 1, 5]\);
- \(a_4 = 2\), и есть \(2\) значения \(\leq 4\) в \([p_1, p_2, p_3, p_4] = [2, 1, 5, 6]\);
- \(a_5 = -1\), поэтому на \([p_1, p_2, p_3, p_4, p_5]\) нет ограничений;
- \(a_6 = -1\), поэтому на \([p_1, p_2, p_3, p_4, p_5, p_6]\) нет ограничений;
| |
![]()
|
|
I. Короткая задача о перестановке
Комбинаторика
математика
дп
*1900
бпф
Вам дано целое число \(n\). Для каждой пары \((m, k)\) такой, что \(3 \leq m \leq n+1\) и \(0 \leq k \leq n-1\), посчитайте количество перестановок элементов \([1, 2, ..., n]\) таких, что \(p_i + p_{i+1} \geq m\) для ровно \(k\) индексов \(i\), по модулю \(998\,244\,353\). Выходные данные Пусть \(a_{m,k}\) - ответ для пары \((m, k)\), по модулю \(998\,244\,353\). Пусть \(\)\large S = \sum_{m=3}^{n+1} \sum_{k=0}^{n-1} a_{m,k}x^{mn+k}\phantom{0}.\(\) Выведите единственную строку с целым числом: \(S\) по модулю \(1\,000\,000\,007\). Обратите внимание, что использование двух разных модулей является намеренным. Мы хотим, чтобы вы вычислили все \(a_{m,k}\) по модулю \(998\,244\,353\), затем обработали их как целые числа в диапазоне \([0, 998\,244\,352]\), и хэшировали их по модулю \(1\,000\,000\,007\). Примечание В первом примеры ответы для всех \((m, k)\) приведены в следующей таблице: | \(k = 0\) | \(k = 1\) | \(k = 2\) | | \(m = 3\) | \(0\) | \(0\) | \(6\) | | \(m = 4\) | \(0\) | \(4\) | \(2\) |
- Ответ для \((m, k) = (3, 2)\) равен \(6\), потому что для каждой перестановки длины \(3\), \(a_i + a_{i+1} \geq 3\) ровно \(2\) раза.
- Ответ для \((m, k) = (4, 2)\) равен \(2\). Действительно, существует \(2\) перестановки длины \(3\) такие, что \(a_i + a_{i+1} \geq 4\) ровно \(2\) раза: \([1, 3, 2]\), \([2, 3, 1]\).
Таким образом, значение для вывода равно \(2^9 \cdot 0 + 2^{10} \cdot 0 + 2^{11} \cdot 6 + 2^{12} \cdot 0 + 2^{13} \cdot 4 + 2^{14} \cdot 2 \equiv 77\,824 \phantom{0} (\text{mod} \phantom{0} 1\,000\,000\,007)\). Во втором примере ответы для всех \((m, k)\) приведены в следующей таблице: | \(k = 0\) | \(k = 1\) | \(k = 2\) | \(k = 3\) | | \(m = 3\) | \(0\) | \(0\) | \(0\) | \(24\) | | \(m = 4\) | \(0\) | \(0\) | \(12\) | \(12\) | | \(m = 5\) | \(0\) | \(4\) | \(16\) | \(4\) |
- Ответ для \((m, k) = (5, 1)\) — \(4\). Действительно, существует \(4\) перестановки длины \(4\) такие, что \(a_i + a_{i+1} \geq 5\) ровно \(1\) раз: \([2, 1, 3, 4]\), \([3, 1, 2, 4]\), \([4, 2, 1, 3]\), \([4, 3, 1, 2]\).
В третьем примере ответы для всех \((m, k)\) представлены в следующей таблице: | \(k = 0\) | \(k = 1\) | \(k = 2\) | \(k = 3\) | \(k = 4\) | \(k = 5\) | \(k = 6\) | \(k = 7\) | | \(m = 3\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(40320\) | | \(m = 4\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(10080\) | \(30240\) | | \(m = 5\) | \(0\) | \(0\) | \(0\) | \(0\) | \(0\) | \(1440\) | \(17280\) | \(21600\) | | \(m = 6\) | \(0\) | \(0\) | \(0\) | \(0\) | \(480\) | \(8640\) | \(21600\) | \(9600\) | | \(m = 7\) | \(0\) | \(0\) | \(0\) | \(96\) | \(3456\) | \(16416\) | \(16896\) | \(3456\) | | \(m = 8\) | \(0\) | \(0\) | \(48\) | \(2160\) | \(12960\) | \(18240\) | \(6480\) | \(432\) | | \(m = 9\) | \(0\) | \(16\) | \(1152\) | \(9648\) | \(18688\) | \(9648\) | \(1152\) | \(16\) |
| |
![]()
|
|
I. Обратная задача
Комбинаторика
дп
*особая задача
*2700
Рассмотрим следующую задачу. Дана строка \(s\), состоящая из \(n\) строчных латинских букв, и целое число \(k\) (\(n\) не делится на \(k\)). Каждая буква — это одна из \(c\) первых букв алфавита. Вы применяете следующую операцию, пока длина строки больше \(k\): выбрать непрерывную подстроку строки длины ровно \(k\), удалить ее из строки и склеить полученные части вместе, не меняя порядка. Пусть полученная строка длины строго меньше \(k\) будет \(t\). Какую лексикографически наименьшую строку \(t\) можно получить? Вам же дается обратная задача. По двум целым числам \(n\) и \(k\) (\(n\) не делится на \(k\)) и строке \(t\), состоящей из (\(n \bmod k\)) строчных латинских букв, посчитайте количество строк \(s\), которые дают \(t\), как лексикографически наименьшее решение. Выведите это количество по модулю \(998\,244\,353\). Выходные данные Выведите одно целое число — количество строк \(s\), которые дают \(t\), как лексикографически наименьшее решение. Примечание Строки \(s\) в первом примере: «aaa», «aab», «aba», «abb», «baa», «bba». Строки \(s\) во втором примере: «bcabc», «bcacc», «bcbbc», «bcbcc», «bccbc», «bcccc», «caabc», «cabbc», «cacbc», «cbabc», «cbbbc», «cbcbc», «ccabc», «ccbbc», «cccbc». | |
![]()
|
|
G1. Лампочки (простая версия)
Деревья
Перебор
Комбинаторика
математика
*2100
дп
поиск в глубину и подобное
графы
снм
Простая и сложная версии этой задачи отличаются друг от друга только ограничениями на \(n\). В простой версии сумма значений \(n^2\) по всем наборам входных данных не превосходит \(10^6\). Кроме того, \(n\) не превосходит \(1000\) в каждом наборе входных данных. В ряд расположены \(2n\) лампочек. У каждой лампочки есть цвет от \(1\) до \(n\) (ровно по две лампочки каждого цвета). Изначально все лампочки выключены. Вы выбираете некоторое множество лампочек \(S\), которое вы изначально включите. После этого вы можете выполнять следующие операции в любом порядке любое количество раз: - выбрать две лампочки \(i\) и \(j\) одинакового цвета, ровно одна из которых включена, и включить вторую из них;
- выбрать три лампочки \(i, j, k\), такие, что обе лампочки \(i\) и \(k\) включены и имеют одинаковый цвет, а лампочка \(j\) находится между ними (\(i < j < k\)), и включить лампочку \(j\).
Вы хотите выбрать такое множество лампочек \(S\), которые вы изначально включаете, чтобы путем выполнения описанных операций можно было добиться того, чтобы все лампочки оказались включены. Посчитайте два числа: - минимальный размер множества \(S\), которое вы изначально включаете;
- количество множеств \(S\) минимального размера (по модулю \(998244353\)).
Выходные данные Для каждого набора входных данных выведите два целых числа: - минимальный размер множества \(S\), которое вы изначально включаете;
- количество множеств \(S\) минимального размера (по модулю \(998244353\)).
| |
![]()
|
|
G2. Лампочки (сложная версия)
Структуры данных
Комбинаторика
дп
поиск в глубину и подобное
графы
хэши
*2300
Простая и сложная версии этой задачи отличаются друг от друга только ограничениями на \(n\). В сложной версии сумма значений \(n\) по всем наборам входных данных не превосходит \(2 \cdot 10^5\). Кроме того, никаких дополнительных ограничений на значение \(n\) в одиночном наборе входных данных нет. В ряд расположены \(2n\) лампочек. У каждой лампочки есть цвет от \(1\) до \(n\) (ровно по две лампочки каждого цвета). Изначально все лампочки выключены. Вы выбираете некоторое множество лампочек \(S\), которое вы изначально включите. После этого вы можете выполнять следующие операции в любом порядке любое количество раз: - выбрать две лампочки \(i\) и \(j\) одинакового цвета, ровно одна из которых включена, и включить вторую из них;
- выбрать три лампочки \(i, j, k\), такие, что обе лампочки \(i\) и \(k\) включены и имеют одинаковый цвет, а лампочка \(j\) находится между ними (\(i < j < k\)), и включить лампочку \(j\).
Вы хотите выбрать такое множество лампочек \(S\), которые вы изначально включаете, чтобы путем выполнения описанных операций можно было добиться того, чтобы все лампочки оказались включены. Посчитайте два числа: - минимальный размер множества \(S\), которое вы изначально включаете;
- количество множеств \(S\) минимального размера (по модулю \(998244353\)).
Выходные данные Для каждого набора входных данных выведите два целых числа: - минимальный размер множества \(S\), которое вы изначально включаете;
- количество множеств \(S\) минимального размера (по модулю \(998244353\)).
| |
![]()
|
|
H1. Ранг матрицы (Простая версия)
Перебор
Комбинаторика
математика
дп
*2700
матрицы
Это простая версия задачи. Единственное отличие между двумя версиями этой задачи в ограничениях на \(k\). Вы можете делать взломы только если сданы обе версии задачи. Вам даны целые числа \(n\), \(p\) и \(k\). Гарантируется, что \(p\) является простым числом. Для каждого \(r\) от \(0\) до \(k\) найдите количество \(n \times n\) матриц \(A\) над полем\(^\dagger\) целых чисел по модулю \(p\), таких что ранг\(^\ddagger\) матрицы \(A\) в точности равен \(r\). Поскольку эти значения могут быть большими, вам требуется вывести их по модулю \(998\,244\,353\). \(^\dagger\) https://en.wikipedia.org/wiki/Field_(mathematics) \(^\ddagger\) https://en.wikipedia.org/wiki/Rank_(linear_algebra) Выходные данные Выведите \(k+1\) целое число, ответы для каждого \(r\) от \(0\) до \(k\). | |
![]()
|
|
H2. Ранг матрицы (сложная версия)
Комбинаторика
математика
дп
*2700
матрицы
строковые суфф. структуры
Это сложная версия задачи. Единственное различие между двумя версиями этой задачи в ограничениях на \(k\). Вы можете использовать взломы только если сданы обе версии задачи. Вам даны целые числа \(n\), \(p\) и \(k\). Гарантируется, что \(p\) является простым числом. Для каждого \(r\) от \(0\) до \(k\) найдите количество \(n \times n\) матриц \(A\) над полем\(^\dagger\) целых чисел по модулю \(p\), таких что ранг\(^\ddagger\) матрицы \(A\) в точности равен \(r\). Поскольку эти значения могут быть большими, вам требуется вывести их по модулю \(998\,244\,353\). \(^\dagger\) https://en.wikipedia.org/wiki/Field_(mathematics) \(^\ddagger\) https://en.wikipedia.org/wiki/Rank_(linear_algebra) Выходные данные Выведите \(k+1\) целое число, ответы для каждого \(r\) от \(0\) до \(k\). | |
![]()
|
|
B. Удалить первый или второй символ
Строки
Перебор
Структуры данных
Комбинаторика
дп
*1100
Вам дана строка \(s\) длины \(n\). Определим две операции, которые можно применить к строке: - удалить первый символ строки;
- удалить второй символ строки.
Ваша задача — найти количество различных непустых строк, которые можно получить, применяя заданные операции над исходной строкой любое количество раз (возможно, нулевое), в любом порядке. Выходные данные Для каждого набора входных данных выведите одно целое число: количество различных непустых строк, которые вы можете получить. Примечание В первом наборе входных данных мы можем получить следующие строки: \(a\), \(aa\), \(aaa\), \(aaaa\), \(aaaaa\). В третьем наборе входных данных, например, слово \(ba\) можно получить следующим образом: - удалить первый символ текущей строки \(ababa\), получив \(baba\);
- удалить второй символ текущей строки \(baba\), получив \(bba\);
- удалить второй символ текущей строки \(bba\), получив \(ba\).
| |
![]()
|
|
D. Очередная задача про инверсии
Структуры данных
Комбинаторика
математика
реализация
дп
теория чисел
*2300
Вам даны перестановка \(p_0, p_1, \ldots, p_{n-1}\) нечётных чисел от \(1\) до \(2n-1\) и перестановка \(q_0, q_1, \ldots, q_{k-1}\) целых чисел от \(0\) до \(k-1\). Определим массив \(a_0, a_1, \ldots, a_{nk-1}\) длины \(nk\) в соответствии со следующим правилом: \(a_{i \cdot k+j}=p_i \cdot 2^{q_j}\) для всех \(0 \le i < n\) и всех \(0 \le j < k\) Например, если \(p = [3, 5, 1]\) и \(q = [0, 1]\), то \(a = [3, 6, 5, 10, 1, 2]\). Обратите внимание, что все массивы в условии нумеруются с нуля. Также обратите внимание, что каждый элемент массива \(a\) определён однозначно. Найдите количество инверсий в массиве \(a\). Так как ответ может быть очень большим, выведите его по модулю \(998\,244\,353\). Инверсией в массиве \(a\) называется пара \((i, j)\) (\(0 \le i < j < nk\)), такая что \(a_i > a_j\). Выходные данные Для каждого набора входных данных выведите одно число — количество инверсий в массиве \(a\) по модулю \(998\,244\,353\). Примечание В первом наборе входных данных массив \(a\) равен \([3, 6, 5, 10, 1, 2]\). В нём есть \(9\) инверсий: \((0, 4)\), \((0, 5)\), \((1, 2)\), \((1, 4)\), \((1, 5)\), \((2, 4)\), \((2, 5)\), \((3, 4)\), \((3, 5)\). Обратите внимание, что здесь перечислены пары \((i, j)\), такие что \(i < j\) и \(a_i > a_j\). Во втором наборе входных данных массив \(a\) равен \([8, 4, 1, 2, 24, 12, 3, 6, 40, 20, 5, 10]\). В нём \(25\) инверсий. В третьем наборе входных данных массив \(a\) равен \([1, 2, 4, 8, 16]\). В нём нет инверсий. | |
![]()
|
|
E. Подсчёт префиксов
Конструктив
Комбинаторика
математика
реализация
дп
*2600
Есть неизвестный массив \(a\) длины \(n\), состоящий только из \(1\) и \(-1\). Пусть \(p\) — массив префиксных сумм массива \(a\). Более формально, \(p\) — это массив длины \(n\), в котором \(p_i = a_1 + a_2 + \ldots + a_i\). После этого массив \(p\) сортируется в неубывающем порядке. Например, если \(a = [1, -1, -1, 1, 1]\), то \(p = [1, 0, -1, 0, 1]\) до сортировки и \(p = [-1, 0, 0, 1, 1]\) после сортировки. Вам дан массив префиксных сумм \(p\) после сортировки, но вы не знаете, чему был равен массив \(a\). Ваша задача — посчитать количество исходных массивов \(a\), для которых в результате сортировки массива префиксных сумм получается заданный массив \(p\). Поскольку это число может быть большим, от вас требуется только найти его по модулю \(998\,244\,353\). Выходные данные Для каждого набора входных данных выведите ответ по модулю \(998\,244\,353\). Примечание В первых двух наборах входных данных единственными возможными массивами \(a\) для \(n = 1\) являются \(a = [1]\) и \(a = [-1]\). Соответствующие им отсортированные массивы префиксных сумм \(p\) — \(p = [1]\) и \(p = [-1]\). Следовательно, не существует массива \(a\), который может привести к отсортированному массиву префиксных сумм \(p = [0]\). Но существует ровно \(1\) массив \(a\), который может привести к отсортированному массиву префиксных сумм \(p = [1]\). В третьем наборе входных данных можно доказать, что не существует массива \(a\), который мог бы привести к отсортированному массиву префиксных сумм \(p = [-1, 1, 2]\). В четвертом наборе входных данных существует \(3\) возможных массива \(a\), которые могут привести к отсортированному массиву префиксных сумм \(p = [-1, 0, 0, 1, 1]\). - \(a = [1, -1, 1, -1, -1]\). Массив префиксных сумм до сортировки равен \(p = [1, 0, 1, 0, -1]\), а после сортировки \(p = [-1, 0, 0, 1, 1]\).
- \(a = [1, -1, -1, 1, 1]\). Массив префиксных сумм до сортировки равен \(p = [1, 0, -1, 0, 1]\), а после сортировки \(p = [-1, 0, 0, 1, 1]\).
- \(a = [-1, 1, 1, -1, 1]\). Массив префиксных сумм до сортировки равен \(p = [-1, 0, 1, 0, 1]\), а после сортировки \(p = [-1, 0, 0, 1, 1]\).
Для пятого набора входных данных единственным возможным массивом \(a\), который может привести к отсортированному массиву префиксных сумм \(p = [-4, -3, -3, -2, -1]\), является \(a = [-1, -1, -1, -1, 1]\). | |
![]()
|
|
E. Подсчёт бинарных строк
Комбинаторика
математика
*2100
дп
Патрик называет подстроку\(^\dagger\) бинарной строки\(^\ddagger\) хорошей, если эта подстрока содержит ровно одну 1. Помогите Патрику посчитать количество бинарных строк \(s\), таких что \(s\) содержит ровно \(n\) хороших подстрок и не имеет хороших подстрок длины строго больше \(k\). Обратите внимание, что подстроки различаются по их расположению в строке, например, если \(s =\) 1010, вы должны посчитать оба вхождения 10. \(^\dagger\) Строка \(a\) является подстрокой \(b\), если \(a\) может быть получена из \(b\) удалением нескольких (возможно, ни одного или всех) символов из начала и нескольких (возможно, ни одного или всех) символов из конца. \(^\ddagger\) Бинарная строка — это строка, которая содержит только символы 0 и 1. Выходные данные Для каждого набора входных данных выведите одно целое число — количество бинарных строк \(s\), таких что \(s\) содержит ровно \(n\) хороших подстрок и не имеет хороших подстрок длины строго больше \(k\). Поскольку это число может быть слишком большим, выведите его по модулю \(998\,244\,353\). Примечание В первом наборе входных данных единственной подходящей бинарной строкой является 1. Строка 01 не подходит, потому что она содержит подстроку 01 длины \(2 > 1\). Во втором наборе входных данных подходящими бинарными строками являются 011, 110 и 111. В третьем наборе входных данных подходящими бинарными строками являются 101, 0110, 0111, 1110, 1111. | |
![]()
|
|
B. Формирование треугольников
Конструктив
Комбинаторика
математика
*1200
сортировки
У вас есть \(n\) палочек, пронумерованных от \(1\) до \(n\). Длина \(i\)-й палочки равна \(2^{a_i}\). Вы хотите выбрать ровно \(3\) палочки из заданных \(n\) палочек и образовать из них невырожденный треугольник, используя палочки в качестве сторон треугольника. Треугольник называется невырожденным, если его площадь строго больше \(0\). Вам нужно посчитать количество способов выбрать ровно \(3\) палочки, чтобы из них можно было образовать треугольник. Обратите внимание, что порядок выбора палочек не имеет значения (например, выбрать \(1\)-ю, \(2\)-ю и \(4\)-ю палочку — это то же самое, что и выбрать \(2\)-ю, \(4\)-ю и \(1\)-ю палочку). Выходные данные Для каждого теста выведите одно целое число — количество способов выбрать ровно \(3\) палочки, чтобы из них можно было составить треугольник. Примечание В первом наборе входных данных примера можно выбрать любые три палочки из заданных \(7\). Во втором наборе входных данных примера можно выбрать \(1\)-ю, \(2\)-ю и \(4\)-ю палочку, или \(1\)-ю, \(3\)-ю и \(4\)-ю палочку. В третьем наборе входных данных примера нельзя образовать треугольник из заданных палочек длиной \(2\), \(4\) и \(8\). | |
![]()
|
|
D. Сбалансированные подпоследовательности
Комбинаторика
математика
дп
*2700
Последовательность скобок называется сбалансированной, если ее можно превратить в правильное математическое выражение, добавив символы '+' и '1'. Например, последовательности '(())()', '()', и '(()(()))' сбалансированы, в то время как ')(', '(()', и '(()))(' — нет. Подпоследовательность — это последовательность, которую можно получить из данной последовательности, удалив ноль или более элементов, и не меняя порядок оставшихся элементов. Даны три целых числа \(n\), \(m\) и \(k\). Найдите количество последовательностей, состоящих из \(n\) '(' и \(m\) ')', таких, что самая длинная сбалансированная подпоследовательность имеет длину \(2 \cdot k\). Поскольку ответ может быть большим, вычислите его по модулю \(1\,000\,000\,007\) (\(10^9 + 7\)). Выходные данные Для каждого тестового случая выведите одно целое число — ответ на задачу. Примечание Для первого тестового случая "()()", "(())" — \(2\) последовательности Для второго тестового случая невозможна ни одна последовательность. Для третьего тестового случая "))()(", "))(()", ")())(", "()))(" — \(4\) последовательности. | |
![]()
|
|
E. Снова режем бумагу
Теория вероятностей
Комбинаторика
*3100
Есть прямоугольный лист бумаги с начальной высотой \(n\) и шириной \(m\). Пусть текущая высота и ширина равны \(h\) и \(w\) соответственно. Мы вводим \(xy\)-координатную систему так, чтобы четыре угла листа были \((0, 0), (w, 0), (0, h)\) и \((w, h)\). Затем лист можно разрезать вдоль линий \(x = 1,2,\ldots,w-1\) и линий \(y = 1,2,\ldots,h-1\). На каждом шаге бумага режется случайным образом вдоль одной из этих \(h+w-2\) линий. После каждого вертикального и горизонтального разреза соответственно правая и нижняя часть бумаги отбрасывается. Найдите ожидаемое количество шагов, необходимых для того, чтобы сделать площадь листа бумаги строго меньше \(k\). Можно показать, что этот ответ всегда может быть выражен в виде дроби \(\dfrac{p}{q}\), где \(p\) и \(q\) — взаимно простые целые числа. Вычислите \(p\cdot q^{-1} \bmod (10^9+7)\). Выходные данные Для каждого набора входных данных выведите одно целое число — ответ на задачу. Примечание Для первого тестового случая площадь уже меньше \(10\), поэтому дополнительные разрезы не требуются. Для второго тестового случая площадь точно равна \(8\), поэтому любой из \(4\) возможных разрезов сделает площадь строго меньше \(8\). Для третьего тестового случая окончательный ответ равен \(\frac{17}{6} = 833\,333\,342\bmod (10^9+7)\). Для четвертого тестового случая окончательный ответ равен \(\frac{5}{4} = 250\,000\,003\bmod (10^9+7)\). | |
![]()
|
|
D. Хорошее путешествие
Теория вероятностей
Комбинаторика
математика
дп
*1900
В классе есть \(n\) детей, \(m\) пар среди них — друзья. \(i\)-я пара друзей имеет значение дружбы \(f_i\). Учитель должен посетить \(k\) экскурсий, на каждой из которых она выбирает пару детей случайно, равновероятно и независимо. Если выбрана пара друзей, их значение дружбы увеличивается на \(1\) для всех последующих экскурсий (учитель может выбрать пару детей более одного раза). Значение дружбы пары детей, не являющихся друзьями, остается \(0\), и не изменяется для следующих экскурсий. Найдите ожидаемое значение суммы значений дружбы по всем \(k\) парам, выбранным для экскурсий (в момент времени их выбора). Можно показать, что этот ответ всегда может быть выражен в виде дроби \(\dfrac{p}{q}\) где \(p\) и \(q\) взаимопростые целые числа. Посчитайте \(p\cdot q^{-1} \bmod (10^9+7)\). Выходные данные Для каждого набора входных данных выведите одно целое число — ответ на задачу. Примечание В первом наборе входных данных, нет пар друзей, а значит значение дружбы всегда равно \(0\) и остается \(0\) после выбора экскурсий, следовательно, сумма значений по всем экскурсиям равна \(0\). Во втором наборе входных данных, только одна возможная пара для выбора \((1, 2)\), и их значение дружбы изначально \(1\), значит их значение дружбы увеличивается каждую экскурсию на \(1\). Таким образом, сумма это \(1+2+3+\ldots+10 = 55\). В третьем наборе входных данных ответ это \(\frac{7}{9} = 777\,777\,784\bmod (10^9+7)\). | |
![]()
|
|
F. Цифровые узоры
Структуры данных
Комбинаторика
математика
реализация
*2900
Аня занимается рукоделием. Сегодня она решила связать платок из полупрозрачных ниток. Каждая нитка характеризуется единственным целым числом — коэффициентом прозрачности. Платок делается по следующей схеме: выбираются горизонтальные нитки с коэффициентами прозрачности \(a_1, a_2, \ldots, a_n\) и вертикальные с коэффициентами прозрачности \(b_1, b_2, \ldots, b_m\). Затем они переплетаются между собой, как показано на картинке снизу, и образуют кусок ткани размера \(n \times m\), состоящий ровно из \(nm\) узлов:  Пример куска ткани при \(n = m = 4\). Пример куска ткани при \(n = m = 4\). После того, как сплетение затянется и не будет видно зазоров между нитками, каждый узел, образованный горизонтальной ниткой с номером \(i\) и вертикальной ниткой с номером \(j\), превратится в клетку, которую мы будем обозначать как \((i, j)\). Клетка \((i, j)\) будет иметь коэффициент прозрачности \(a_i + b_j\). Интересностью полученного платка будем называть количество его подквадратов\(^{\dagger}\), в которых нет пары соседних\(^{\dagger \dagger}\) клеток с одинаковыми коэффициентами прозрачности. Аня ещё не решила, из каких ниток плести платок, поэтому вам будут даны также \(q\) запросов увеличения/уменьшения коэффициентов прозрачностей ниток на некоторых отрезках. После каждого запроса надо вывести интересность полученного платка. \(^{\dagger}\)Подквадратом куска ткани называется множество всех его клеток \((i, j)\), таких что \(x_0 \le i \le x_0 + d\) и \(y_0 \le j \le y_0 + d\) для некоторых целых чисел \(x_0\), \(y_0\) и \(d\) (\(1 \le x_0 \le n - d\), \(1 \le y_0 \le m - d\), \(d \ge 0\)). \(^{\dagger \dagger}\)Клетки \((i_1, j_1)\) и \((i_2, j_2)\) считаются соседними, если \(|i_1 - i_2| + |j_1 - j_2| = 1\). Выходные данные Выведите \((q+1)\) строку. В \((i + 1)\)-й строке (\(0 \le i \le q\)) выведите одно целое число — интересность платка после применения первых \(i\) запросов. Примечание В первом примере коэффициенты прозрачности клеток в получившемся платке равны: Тогда есть следующие подквадраты, не содержащие двух соседних по вертикали или по горизонтали клеток с одинаковым коэффициентом прозрачности: - Каждая из \(16\) клеток по отдельности;
- Подквадрат с левым верхним углом в клетке \((3, 1)\) и правым нижним углом в клетке \((4, 2)\);
- Подквадрат с левым верхним углом в клетке \((2, 3)\) и правым нижним углом в клетке \((3, 4)\);
- Подквадрат с левым верхним углом в клетке \((2, 1)\) и правым нижним углом в клетке \((3, 2)\);
- Подквадрат с левым верхним углом в клетке \((3, 3)\) и правым нижним углом в клетке \((4, 4)\).
Во втором примере после первого запроса коэффициенты прозрачности горизонтальных ниток равны \([1, 2, 2]\). После второго запроса коэффициенты прозрачности вертикальных ниток равны \([2, -4, 2]\). | |
![]()
|
|
D. Саша и прогулка по городу
Деревья
Комбинаторика
математика
дп
*1900
Саша хочет прогуляться со своей девушкой по городу. Город состоит из \(n\) перекрёстков, пронумерованных от \(1\) до \(n\). Некоторые из них соединены дорогами, причём от любого перекрёстка существует ровно один простой путь\(^{\dagger}\) до любого другого перекрёстка. Другими словами, перекрёстки и дороги между ними образуют дерево. Некоторые из перекрёстков являются опасными. И так как гулять одним по городу небезопасно, то Саша не хочет за время прогулки посещать три и более опасных перекрёстков. Саша называет множество перекрёстков хорошим, если выполняется следующее условие: - Если в городе опасными являются те и только те перекрёстки, которые содержатся в этом множестве, то любой простой путь в городе содержит не более двух опасных перекрёстков.
Однако Саша не знает, какие из перекрёстков являются опасными, поэтому его интересует количество различных хороших множеств перекрёстков, которые есть в городе. Поскольку это количество может быть очень большим, выведите его по модулю \(998\,244\,353\). \(^{\dagger}\)Простой путь — это путь, проходящий через каждый перекрёсток не более одного раза. Выходные данные Для каждого набора входных данных выведите одно целое число — количество хороших множеств перекрёстков по модулю \(998\,244\,353\). Примечание В первом наборе входных данных всего есть \(2^3 = 8\) множеств перекрёстков. Все из них являются хорошими, кроме множества \(\{1, 2, 3\}\), потому что, если перекрёстки \(1, 2\) и \(3\) являются опасными, то простой путь \(1 - 2 - 3\) содержит \(3\) опасных перекрёстка. Таким образом, всего есть \(7\) хороших множеств. Во втором наборе входных данных всего есть \(2^4 = 16\) множеств перекрёстков. При этом множества \(\{1, 2, 3, 4\}\), \(\{1, 2, 3\}\), \(\{1, 3, 4\}\), \(\{2, 3, 4\}\) не являются хорошими. Таким образом, всего есть \(12\) хороших множеств. Ниже изображена схема города:  | |
![]()
|
|
F. Саша и свадебное бинарное дерево поиска
Деревья
Перебор
Структуры данных
Комбинаторика
математика
поиск в глубину и подобное
*2300
Пройдя все трудности и невзгоды, Саша наконец решил жениться на своей девушке. Для этого нужно подарить ей обручальное кольцо. Однако его девушке не нравятся подобные романтические жесты, но нравятся бинарные деревья поиска\(^{\dagger}\). Поэтому Саша решил ей подарить такое дерево. Проведя немало времени на свадебных сайтах для программистов, он нашел идеальное бинарное дерево поиска с корнем в вершине \(1\). В нём значение в вершине \(v\) равно \(val_v\). Но спустя некоторое время он забыл значения в некоторых вершинах. Пытаясь вспомнить найденное дерево, Саша задался вопросом — сколько существует бинарных деревьев поиска, которые он мог найти на сайте, если известно, что значения во всех вершинах являются целыми числами и принадлежат отрезку \([1, C]\). Поскольку это число может быть очень большим, выведите его по модулю \(998\,244\,353\). \(^{\dagger}\)Бинарным деревом поиска называется корневое бинарное дерево, у которого для любой вершины \(x\) выполняется свойство: значения всех вершин в левом поддереве вершины \(x\) (если оно существует) меньше или равны значению в вершине \(x\) и значения всех вершин в правом поддереве вершины \(x\) (если оно существует) больше или равны значению в вершине \(x\). Выходные данные Для каждого набора входных данных выведите единственное целое число — количество подходящих бинарных деревьев поиска по модулю \(998\,244\,353\). Примечание В первом наборе входных данных, бинарное дерево поиска имеет следующий вид: 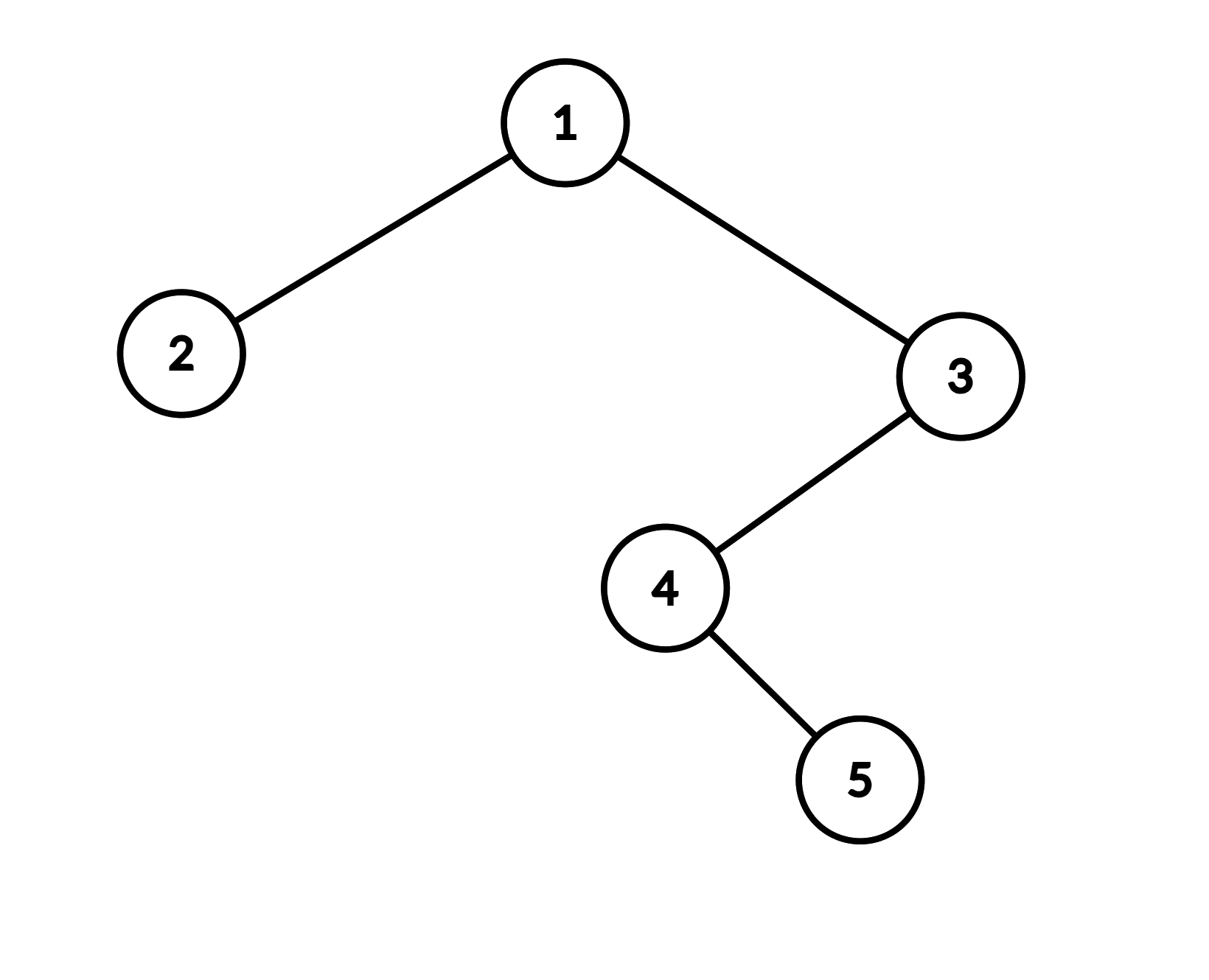 Тогда возможными значениями в вершинах являются: \([2, 2, 3, 2, 2]\), \([2, 2, 3, 2, 3]\), \([2, 2, 3, 3, 3]\) и \([3, 2, 3, 3, 3]\). Во втором наборе входных данных значения во всех вершинах известны, поэтому существует единственное подходящее бинарное дерево поиска. | |
![]()
|
|
E. 2...3...4.... Замечательно! Замечательно!
Комбинаторика
математика
дп
*2400
У Стека есть массив \(a\) длины \(n\) такой, что \(a_i = i\) для всех \(i\) (\(1 \leq i \leq n\)). Он выберет целое положительное число \(k\) (\(1 \leq k \leq \lfloor \frac{n-1}{2} \rfloor\)) и выполнит следующую операцию над \(a\) любое число раз (возможно, \(0\)): - Выбрать из \(a\) подпоследовательность\(^\dagger\) \(s\) длины \(2 \cdot k + 1\). Далее, удалить первые \(k\) элементов \(s\) из \(a\). Чтобы все было идеально сбалансировано (как и должно быть), также удалить последние \(k\) элементов \(s\) из \(a\).
Стеку стало интересно, сколько массивов \(a\) он может получить в итоге для каждого \(k\) (\(1 \leq k \leq \lfloor \frac{n-1}{2} \rfloor\)). Поскольку Стек плохо справляется с математическими задачами, ему нужна ваша помощь. Поскольку количество массивов может быть слишком большим, выведите его по модулю \(998\,244\,353\). \(^\dagger\) Последовательность \(x\) является подпоследовательностью \(y\), если \(x\) может быть получена из \(y\) удалением нескольких (возможно, ни одного или всех) элементов. Например, \([1, 3]\), \([1, 2, 3]\) и \([2, 3]\) являются подпоследовательностями \([1, 2, 3]\). С другой стороны, \([3, 1]\) и \([2, 1, 3]\) не являются подпоследовательностями \([1, 2, 3]\). Выходные данные Для каждого набора входных данных в отдельной строке выведите \(\lfloor \frac{n-1}{2} \rfloor\) целых чисел, разделенных пробелами, где \(i\)-е число равняется количеству (по модулю \(998\,244\,353\)) массивов, которые Стек может получить, если выберет \(k=i\). Примечание В первом наборе входных данных для \(k=1\) возможны два \(a\): Во втором наборе входных данных для \(k=1\) возможны четыре \(a\): - \([1,2,3,4]\);
- \([1,3]\);
- \([2,3]\);
- \([2,4]\).
В третьем наборе входных данных для \(k=2\) возможны два \(a\): - \([1,2,3,4,5]\);
- \([3]\).
| |
![]()
|
|
I. Считать всегда весело
Комбинаторика
*3500
Вам дан бинарный\(^\dagger\) шаблон \(p\) длины \(n\). Бинарная строка \(q\) той же длины \(n\) называется хорошей, если для каждого \(i\) (\(1 \leq i \leq n\)) существуют индексы \(l\) и \(r\) такие, что: - \(1 \leq l \leq i \leq r \leq n\), и
- \(p_i\) является модой\(^\ddagger\) строки \(q_lq_{l+1}\ldots q_r\).
Подсчитайте количество хороших бинарных строк по модулю \(998\,244\,353\). \(^\dagger\) Бинарная строка — это строка, состоящая только из символов \(\mathtt{0}\) и \(\mathtt{1}\). \(^\ddagger\) Символ \(c\) является модой строки \(t\) длины \(m\), если число вхождений \(c\) в \(t\) не меньше \(\lceil \frac{m}{2} \rceil\). Например, \(\mathtt{0}\) является модой \(\mathtt{010}\), \(\mathtt{1}\) не является модой \(\mathtt{010}\), и оба \(\mathtt{0}\) и \(\mathtt{1}\) являются модами \(\mathtt{011010}\). Выходные данные Выведите количество хороших строк по модулю \(998\,244\,353\). Примечание Во втором примере хорошими строками являются - \(\mathtt{010}\),
- \(\mathtt{011}\),
- \(\mathtt{101}\),
- \(\mathtt{110}\),
- \(\mathtt{111}\).
| |
![]()
|
|
D. Делимые пары
Комбинаторика
математика
теория чисел
*1300
У Поликарпа есть два любимых числа \(x\) и \(y\) (они могут быть равны), также он нашёл массив \(a\) длины \(n\). Поликарп считает пару индексов \(\langle i, j \rangle\) (\(1 \le i < j \le n\)) красивой, если: - \(a_i + a_j\) делится нацело на \(x\);
- \(a_i - a_j\) нацело делится на \(y\).
Например, если \(x=5\), \(y=2\), \(n=6\), \(a=\)[\(1, 2, 7, 4, 9, 6\)], то красивыми являются только пары: - \(\langle 1, 5 \rangle\): \(a_1 + a_5 = 1 + 9 = 10\) (\(10\) делится на \(5\)) и \(a_1 - a_5 = 1 - 9 = -8\) (\(-8\) делится на \(2\));
- \(\langle 4, 6 \rangle\): \(a_4 + a_6 = 4 + 6 = 10\) (\(10\) делится на \(5\)) и \(a_4 - a_6 = 4 - 6 = -2\) (\(-2\) делится на \(2\)).
Найдите количество красивых пар в массиве \(a\). Выходные данные Для каждого набора входных данных выведите единственное число — количество красивых пар в массиве \(a\). | |
![]()
|
|
F. Скриншоты чата
Комбинаторика
поиск в глубину и подобное
*1700
графы
В чате контестов по программированию состоит \(n\) человек. Участники чата упорядочены по активности, однако каждый человек видит самого себя в начале списка. Например, в чате \(4\) участника, и их порядок равен \([2, 3, 1, 4]\). Тогда - \(1\)-й пользователь видит порядок \([1, 2, 3, 4]\);
- \(2\)-й пользователь видит порядок \([2, 3, 1, 4]\);
- \(3\)-й пользователь видит порядок \([3, 2, 1, 4]\);
- \(4\)-й пользователь видит порядок \([4, 2, 3, 1]\).
\(k\) человек выложили в чат скриншоты, на которых виден порядок участников, показываемый данному пользователю. Скриншоты были сделаны в течение короткого промежутка времени, и порядок участников не изменился. Ваша задача — определить, существует ли некоторый порядок, которому соответствуют все скриншоты. Выходные данные Выведите \(t\) строк, каждая из которых является ответом на соответствующий набор входных данных. В качестве ответа выведите «YES», если существует хотя бы один порядок участников, при котором могли быть получены все \(k\) скриншотов. Иначе выведите «NO». Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Например, строки «yEs», «yes», «Yes» и «YES» будут приняты как положительный ответ. | |
![]()
|
|
G. Одномерный пазл
Комбинаторика
математика
теория чисел
*2000
У вас есть одномерный пазл, все элементы которого нужно сложить в один ряд, соединяя друг с другом. Все элементы пазла полностью белые и отличимы друг от друга, только если имеют разную форму. Каждый элемент имеет прямые границы сверху и снизу, а слева и справа имеет соединения, каждое из которых может быть выступом или углублением. Вращать элементы нельзя. Можно заметить, что существует ровно \(4\) типа элементов. Два элемента можно соединить, если правое соединение левого элемента противоположно левому соединению правого элемента.  Все возможные типы элементов. Все возможные типы элементов. Пазл содержит \(c_1, c_2, c_3, c_4\) элементов каждого типа. Пазл считается собранным, если вам удалось объединить все элементы в одну длинную цепочку. Вы хотите узнать, сколькими способами это можно сделать. Выходные данные Для каждого набора входных данных выведите одно целое число — количество возможных способов собрать пазл. Два способа считаются различными, если существует \(i\), такое, что типы элементов на \(i\)-й позиции в этих способах различаются. Так как ответ может быть очень большим, выведите его по модулю \(998244353\). Если пазл собрать невозможно, выведите \(0\). | |
![]()
|
|
G. Магический рисунок королевской черепахи
Перебор
Конструктив
Комбинаторика
математика
поиск в глубину и подобное
*2300
битмаски
Черепаха Алиса в настоящее время разрабатывает коробку для печенья с предсказаниями, и она хотела бы включить в нее теорию Лоушу. Коробку можно рассматривать как таблицу размера \(n \times m\) (\(n, m \ge 5\)), где строки нумеруются \(1, 2, \dots, n\), а столбцы нумеруются \(1, 2, \dots, m\). Каждая клетка может быть либо пустой, либо содержать одно печенье с предсказанием одной из следующих форм: круг или квадрат. Клетка на пересечении \(a\)-й строки \(b\)-го столбца обозначается как \((a, b)\). Изначально вся таблица пуста. Затем Алиса выполняет \(q\) операций с коробкой для печенья. \(i\)-я операция (\(1 \le i \le q\)) выполняется следующим образом: указывается в настоящее время пустая клетка \((r_i,c_i)\) и форма (круг или квадрат), затем ставится печенье с предсказанием указанной формы в клетку \((r_i,c_i)\). Обратите внимание, что после \(i\)-й операции клетка \((r_i,c_i)\) больше не является пустой. Перед всеми операциями и после каждой из \(q\) операций Алиса задается вопросом, сколько существует способов разместить печенья с предсказанием во всех оставшихся пустых клетках, так чтобы было удовлетворено следующее требование: Не существует трёх последовательных клеток с печеньем одинаковой формы в одной строке, одном столбце или на одной диагонали. Формально: - Не существует \((i,j)\), удовлетворяющих \(1 \le i \le n, 1 \le j \le m-2\), таких, что в клетках \((i,j), (i,j+1), (i,j+2)\) есть печенье одинаковой формы.
- Не существует \((i,j)\), удовлетворяющих \(1 \le i \le n-2, 1 \le j \le m\), таких, что в клетках \((i,j), (i+1,j), (i+2,j)\) есть печенье одинаковой формы.
- Не существует \((i,j)\), удовлетворяющих \(1 \le i \le n-2, 1 \le j \le m-2\), таких, что в клетках \((i,j), (i+1,j+1), (i+2,j+2)\) есть печенье одинаковой формы.
- Не существует \((i,j)\), удовлетворяющих \(1 \le i \le n-2, 1 \le j \le m-2\), таких, что в клетках \((i,j+2), (i+1,j+1), (i+2,j)\) есть печенье одинаковой формы.
Все ответы должны быть выведены по модулю \(998\,244\,353\). Также обратите внимание, что после некоторых операций требование уже может не быть удовлетворено с уже размещенными печеньями, в этом случае, вы должны выводить \(0\). Выходные данные Для каждого набора входных данных выведите \(q+1\) строк. Первая строка вывода должна содержать ответ до операций, \(i\)-я строка (\(2 \le i \le q+1\)) должна содержать ответ после первых \(i-1\) операций. Все ответы должны быть взяты по модулю \(998\,244\,353\). Примечание Во втором примере, после размещения печенья в форме круга в клетках \((1,1)\), \((1,2)\) и \((1,3)\), Требование уже не удовлетворено. Поэтому вы должны вывести \(0\). | |
![]()
|
|
D. Экзамен в ЦПМ
Бинарный поиск
Комбинаторика
математика
реализация
*1800
Центр Помощи Магистрам объявил вступительный экзамен, который заключается в следующем. Кандидату даётся множество \(s\) размера \(n\), а также некоторое странное число \(c\). Для этого множества нужно посчитать количество пар целых чисел \((x, y)\) таких, что \(0 \leq x \leq y \leq c\), \(x + y\) не содержится в множестве \(s\), а также \(y - x\) не содержится в множестве \(s\). Ваш друг хочет поступить в Центр. Помогите ему сдать экзамен! Выходные данные Для каждого набора входных данных выведите одно целое число — количество подходящих пар целых чисел. Примечание В первом наборе входных данных подходят следующие пары: \((0, 0)\), \((2, 2)\), \((3, 3)\). В третьем наборе входных данных подходят следующие пары: \((0, 1)\), \((0, 2)\), \((0, 4)\), \((1, 3)\), \((2, 6)\), \((3, 4)\), \((3, 5)\), \((4, 5)\), \((4, 6)\), \((5, 6)\). | |
![]()
|
|
E. Фермерская игра
Комбинаторика
*2300
игры
Фермер Нхой привел своих коров на ферму Фермера Джона, чтобы поиграть в игру! Ферма Фермера Джона может быть представлена в виде числовой прямой со стенами в точках \(0\) и \(l + 1\). На ферме есть \(2n\) коров, причем \(n\) коров принадлежат Фермеру Джону, а остальные \(n\) — Фермеру Нхою. Они размещают своих коров в различных точках так, чтобы никакие две коровы одного фермера не были соседними. Две коровы являются соседними, если между ними нет других коров. Формально, если \(a_1, a_2, \ldots, a_n\) представляют позиции коров фермера Джона, а \(b_1, b_2, \ldots, b_n\) представляют позиции коров фермера Нхоя, то \(0 < a_1 < b_1 < a_2 < b_2 < \ldots < a_n < b_n < l + 1\), или \(0 < b_1 < a_1 < b_2 < a_2 < \ldots < b_n < a_n < l + 1\). За один ход фермер выбирает число \(k\) \((1 \leq k \leq n)\) и направление (влево или вправо). Затем этот фермер выбирает \(k\) своих коров и перемещает их на одну позицию в выбранном направлении. Фермер не может переместить ни одну из своих коров на стены или на корову другого фермера. Если фермер не может переместить ни одной коровы, то он проигрывает. Фермер Джон начинает игру и делает первый ход. Учитывая \(l\) и \(n\), найдите количество возможных конфигураций игры, при которых Фермер Джон выиграет, если оба фермера играют оптимально. В случае, если при оптимальной игре она продолжается бесконечно долго, считается, что никто из фермеров не выигрывает. Конфигурация отличается от другой, если существует такое \(i\), что \(a_i\) или \(b_i\) отличаются. Выведите ответ по модулю \(998\,244\,353\). Выходные данные Для каждого набора входных данных выведите целое число: количество конфигураций игры, в которых Фермер Джон выигрывает, если оба фермера играют оптимально, по модулю \(998\,244\,353\). Примечание Пусть J обозначает корову Фермера Джона, N обозначает корову Фермера Нхоя, а _ обозначает пустое место. Для первого набора входных данных возможны две конфигурации: JN или NJ. В обоих случаях, поскольку Фермер Джон делает первый ход и не может сделать ни одного хода, он не может выиграть. Во втором случае есть две возможные конфигурации для победы Фермера Джона: N_J и J_N. | |
![]()
|
|
G. Бесси и карты
Комбинаторика
математика
дп
*2800
Бесси недавно начала играть в известную карточную игру. В игре участвует одна колода карт, состоящая из \(a\) карт «взять \(0\) карт», \(b\) карт «взять \(1\) карту», \(c\) карт «взять \(2\) карты» и \(5\) специальных карт. В начале игры все карты лежат в одной перемешанной случайным образом колоде. Бесси начинает игру, взяв верхние \(5\) карт из колоды. Затем она может играть с руки карты вида «взять \(x\) карт», чтобы взять следующие \(x\) карт с верха колоды. Обратите внимание, что каждая карта может быть сыграна только один раз, специальные карты играть нельзя, а если Бесси использует карту «взять \(2\) карты», когда в колоде осталось всего \(1\) карта, то она просто вытянет оставшуюся карту. Бесси выиграет, если вытянет все \(5\) специальных карт. Поскольку Бесси не очень хорошо разбирается в математических задачах, она хочет, чтобы вы нашли вероятность того, что она выиграет, учитывая, что колода тасуется случайным образом по всем \((a + b + c + 5)!\) возможным тасовкам. Можно показать, что ответ всегда можно выразить в виде дроби \(\frac{p}{q}\), где \(p\) и \(q\) — взаимно простые целые числа. Выведите \(p \cdot q^{-1}\) по модулю \(998\,244\,353\). Выходные данные Для каждого набора входных данных выведите одно целое число — вероятность того, что Бесси выиграет, по модулю \(998\,244\,353\). Примечание В первом наборе входных данных у нас есть по \(1\) карте каждого типа «взять» и \(5\) специальных карт. Существует \(30\,720\) стартовых колод, в которых Бесси выиграет, вытянув верхние \(5\) карт, и \(40\,320\) стартовых колод в целом. Таким образом, вероятность выигрыша Бесси равна \(\frac{30\,720}{40\,320} = \frac{16}{21}\). Одним из примеров выигрышной стартовой колоды является следующая (карты перечислены сверху вниз): - «Специальная»,
- «Взять \(1\) карту»,
- «Специальная»,
- «Специальная»,
- «Взять \(0\) карт»,
- «Взять \(2\) карты»,
- «Специальная»,
- «Специальная».
Одним из примеров проигрышной стартовой колоды является: - «Специальная»,
- «Взять \(1\) карту»,
- «Специальная»,
- «Специальная»,
- «Взять \(0\) карт»,
- «Специальная»,
- «Специальная»,
- «Взять \(2\) карты».
| |
![]()
|
|
D1. Считать всегда весело (простая версия)
Перебор
Комбинаторика
математика
дп
*2400
Это простая версия задачи. Единственное различие между двумя версиями — ограничение на \(n\). Вы можете делать взломы, только если обе версии задачи решены. Массив \(b\) из \(m\) целых неотрицательных чисел считается хорошим, если все элементы \(b\) можно сделать равными \(0\) с помощью применения следующей операции несколько (возможно, ноль) раз: - Выбрать два различных индекса \(l\) и \(r\) (\(1 \leq l \color{red}{<} r \leq m\)) и вычесть \(1\) из всех \(b_i\) таких, что \(l \leq i \leq r\).
Вам даны три целых положительных числа \(n\), \(k\) и простое число \(p\). Среди всех \((k+1)^n\) массивов длины \(n\), таких, что \(0 \leq a_i \leq k\) для всех \(1 \leq i \leq n\), посчитайте количество хороших массивов. Поскольку число может быть очень большим, от вас требуется найти его только по модулю \(p\). Выходные данные Для каждого набора входных данных в новой строке выведите количество хороших массивов по модулю \(p\). Примечание В первом наборе входных данных \(4\) хорошими массивами \(a\) являются: - \([0,0,0]\);
- \([0,1,1]\);
- \([1,1,0]\);
- \([1,1,1]\).
| |
![]()
|
|
D2. Считать всегда весело (сложная версия)
Комбинаторика
дп
*2800
Это сложная версия задачи. Единственное различие между двумя версиями — ограничение на \(n\). Вы можете делать взломы, только если обе версии задачи решены. Массив \(b\) из \(m\) целых неотрицательных чисел считается хорошим, если все элементы \(b\) можно сделать равными \(0\) с помощью применения следующей операции несколько (возможно, ноль) раз: - Выбрать два различных индекса \(l\) и \(r\) (\(1 \leq l \color{red}{<} r \leq m\)) и вычесть \(1\) из всех \(b_i\) таких, что \(l \leq i \leq r\).
Вам даны три целых положительных числа \(n\), \(k\) и простое число \(p\). Среди всех \((k+1)^n\) массивов длины \(n\), таких, что \(0 \leq a_i \leq k\) для всех \(1 \leq i \leq n\), посчитайте количество хороших массивов. Поскольку число может быть очень большим, от вас требуется найти его только по модулю \(p\). Выходные данные Для каждого набора входных данных в новой строке выведите количество хороших массивов по модулю \(p\). Примечание В первом наборе входных данных \(4\) хорошими массивами \(a\) являются: - \([0,0,0]\);
- \([0,1,1]\);
- \([1,1,0]\);
- \([1,1,1]\).
| |
![]()
|
|
E. Девочка-перестановочка
Комбинаторика
математика
дп
теория чисел
*2200
Загадана какая-то перестановочка длины \(n\). Вам даны индексы её префиксных максимумов и суффиксных максимумов. Напомним, что перестановка длины \(k\) — это такой массив размера \(k\), что в нем встречается каждое целое число от \(1\) до \(k\) ровно один раз. Префиксные максимумы — элементы, которые являются максимумом на префиксе, заканчивающемся в этом элементе. Более формально, элемент \(a_i\) является префиксным максимумом, если \(a_i > a_j\) для каждого \(j < i\). Аналогично определяются суффиксные максимумы, элемент \(a_i\) является суффиксным максимумом, если \(a_i > a_j\) для каждого \(j > i\). Требуется вывести количество различных перестановок, которые могли бы быть загаданы. Так как это число может быть очень большим, выведите ответ по модулю \(10^9 + 7\). Выходные данные Для каждого набора входных данных в отдельной строке выведите одно целое число — количество подходящих перестановок по модулю \(10^9 + 7\). Примечание Во втором наборе входных данных подходят следующие перестановки: - \([1, 4, 3, 2]\)
- \([2, 4, 3, 1]\)
- \([3, 4, 2, 1]\)
В шестом наборе входных данных подходят следующие перестановки: - \([2, 1, 6, 5, 3, 4]\)
- \([3, 1, 6, 5, 2, 4]\)
- \([3, 2, 6, 5, 1, 4]\)
- \([4, 1, 6, 5, 2, 3]\)
- \([4, 2, 6, 5, 1, 3]\)
- \([4, 3, 6, 5, 1, 2]\)
- \([5, 1, 6, 4, 2, 3]\)
- \([5, 2, 6, 4, 1, 3]\)
- \([5, 3, 6, 4, 1, 2]\)
- \([5, 4, 6, 3, 1, 2]\)
| |
![]()
|
|
F. Редкие монеты
Теория вероятностей
Комбинаторика
математика
*2500
В ряд расположено \(n\) мешков, пронумерованных от \(1\) до \(n\); \(i\)-й мешок содержит \(a_i\) золотых монет и \(b_i\) серебряных монет. Ценность золотой монеты равна \(1\). Ценность серебряной монеты равна \(0\) или \(1\), и определяется для каждой серебряной монеты независимо (\(0\) с вероятностью \(\frac{1}{2}\) и \(1\) с вероятностью \(\frac{1}{2}\)). Вам нужно ответить на \(q\) независимых запросов. Каждый запрос имеет следующий формат: - \(l\) \(r\) — посчитайте вероятность того, что суммарная ценность монет в мешках с \(l\) по \(r\) строго больше суммарной ценности во всех остальных мешках.
Выходные данные Для каждого запроса выведите одно целое число — вероятность того, что суммарная ценность монет в мешках с \(l\) по \(r\) строго больше суммарной ценности во всех остальных мешках, взятое по модулю \(998244353\). Вероятность можно выразить в виде несократимой дроби \(\frac{x}{y}\). Вы должны вывести значение \(x \cdot y^{-1} \bmod 998244353\), где \(y^{-1}\) — целое число, такое, что \(y \cdot y^{-1} \bmod 998244353 = 1\). Примечание В обоих запросах из первого примера ответ равен \(\frac{1}{4}\). | |
![]()
|
|
G. Клацанье шарами
Теория вероятностей
Комбинаторика
математика
*3100
По кругу расставлены \(m\) корзин, пронумерованных от \(1\) до \(m\) по часовой стрелке (корзина \(m\) находится рядом с корзиной \(1\)). Кроме того, имеется \(n\) шаров, причем шар \(i\) первоначально помещен в корзину \(a_i\), и ни одна корзина не содержит более одного шара. Алисе разрешено выполнять следующую операцию, которая всегда занимает ровно одну секунду, независимо от того, перемещаете/выбрасываете вы шар или нет: - Алиса выбирает целое число \(i\) между \(1\) и \(n\) равномерно случайным образом.
- Если шар \(i\) был выброшен ранее, ничего не делать.
- В противном случае, шар \(i\) перемещается из корзины, в которой он находится в данный момент, в следующую корзину (по часовой стрелке). Если в корзине, в которую перемещается шар, сейчас находится другой шар \(j\), выбросить шар \(j\).
Она повторяет эту операцию до тех пор, пока не останется ровно один шар. Вычислите математическое ожидание времени (в секундах), необходимого Алисе для завершения процесса. Можно доказать, что ответ можно представить в виде рационального числа \(\frac{p}{q}\) с простыми \(p\) и \(q\). Вам нужно вывести \(p \cdot q^{-1} \bmod 10^9 + 7\). Можно доказать, что \(10^9 + 7 \nmid q\). Выходные данные Для каждого набора входных данных выведите одно целое число: математическое ожидание времени (в секундах), необходимое Алисе для завершения процесса, по модулю \(10^9 + 7\). Примечание В первом наборе входных данных Алиса могла бы действовать следующим образом (мы определяем \(a_i = -1\), если шар \(i\) был выброшен): - Изначально \(a = [5, 1, 4]\).
- Алиса выбирает \(i = 2\) с вероятностью \(\frac{1}{3}\), и шар \(2\) перемещается в корзину \(2\). После этого \(a = [5, 2, 4]\).
- Алиса выбирает \(i = 2\) с вероятностью \(\frac{1}{3}\), и шар \(2\) перемещается в корзину \(3\). После этого \(a = [5, 3, 4]\).
- Алиса выбирает \(i = 2\) с вероятностью \(\frac{1}{3}\), и шар \(2\) перемещается в корзину \(4\). Поскольку в корзине \(4\) ранее находился шар \(3\), этот шар выбрасывается. После этого \(a = [5, 4, -1]\).
- Алиса выбирает \(i = 3\) с вероятностью \(\frac{1}{3}\). Шар \(3\) уже был выброшен, поэтому ничего не происходит. После этого \(a = [5, 4, -1]\).
- Алиса выбирает \(i = 2\) с вероятностью \(\frac{1}{3}\), и шар \(2\) перемещается в корзину \(5\), из которой выбрасывается шар \(1\). После этого \(a = [-1, 5, -1]\), и процесс завершается.
Ответ для этого набора входных данных равен \(\frac{189}{5}\). Ответ для второго набора входных данных равен \(14\) (обратите внимание, что эти два шара находятся рядом друг с другом). Ответ для третьего набора входных данных равен \(35\). Ответ для четвертого набора входных данных равен \(\frac{220}{3}\). В пятом наборе входных данных, поскольку изначально имеется только один шар, ответ равен \(0\). | |
![]()
|
|
E. Линейное сканирование
Комбинаторика
математика
*особая задача
игры
Будьте осторожны, чтобы не совершить ошибку. Вам, возможно, придется начать все сначала. — Кто-то, вероятно Выходные данные Выведите одно целое число — количество решений по модулю \(20240401\). Примечание В первом примере массив выглядит следующим образом: | \( \color{blue}{1} \) | \( \color{blue}{1} \) | \( \color{darkgreen}{2} \) | \( \color{blue}{1} \) | \( \color{blue}{1} \) | \( \color{darkgreen}{2} \) | \( \color{gray}{0} \) |
Очевидно, что ответ здесь равен \(1 \pmod{20240401}\). Во втором примере массив выглядит следующим образом: | \( \color{blue}{1} \) | \( \color{blue}{1} \) | \( \color{darkgreen}{2} \) | \( \color{blue}{1} \) | \( \color{blue}{1} \) | \( \color{blue}{1} \) | \( \color{gray}{0} \) |
Я не знаю, почему ответ здесь равен \(2 \pmod{20240401}\), мне пришлось догадаться. В третьем примере массив выглядит следующим образом: | \( \color{gray}{0} \) | \( \color{blue}{1} \) | \( \color{darkgreen}{2} \) | \( \color{blue}{1} \) | \( \color{blue}{1} \) | \( \color{blue}{1} \) | \( \color{gray}{0} \) |
Если ответ здесь не равен \(0 \pmod{20240401}\), я буквально взорвусь. | |
![]()
|
|
D. Цветные шары
Комбинаторика
математика
дп
*1800
сортировки
Существуют шары \(n\) различных цветов; количество шаров \(i\)-го цвета равно \(a_i\). Шары можно объединять в группы. Каждая группа должна содержать не более \(2\) шаров и не более \(1\) шара каждого цвета. Рассмотрим все \(2^n\) множеств цветов. Для множества цветов обозначим его значение как минимальное количество групп, на которые могут быть разделены шары этих цветов. Например, если есть три цвета с \(3\), \(1\) и \(7\) шарами соответственно, их можно объединить в \(7\) групп (и не менее \(7\)), поэтому значение этого множества цветов равно \(7\). Ваша задача — вычислить сумму значений по всем \(2^n\) возможным множествам цветов. Поскольку ответ может быть слишком большим, выведите его по модулю \(998\,244\,353\). Выходные данные Выведите одно целое число — сумму значений всех \(2^n\) множеств цветов, взятую по модулю \(998\,244\,353\). Примечание Рассмотрим первый пример. Есть \(8\) множеств цветов: - значение пустого множества равно \(0\);
- значение множества \(\{1\}\) равно \(1\);
- значение множества \(\{2\}\) равно \(1\);
- значение множества \(\{3\}\) равно \(2\);
- значение множества \(\{1,2\}\) равно \(1\);
- значение множества \(\{1,3\}\) равно \(2\);
- значение множества \(\{2,3\}\) равно \(2\);
- значение множества \(\{1,2,3\}\) равно \(2\).
Таким образом, сумма значений по всем \(2^n\) множествам цветов равна \(11\). | |
![]()
|
|
F. Уникальные строки
Комбинаторика
математика
дп
*3100
Назовем две строки \(a\) и \(b\) равными, если можно получить строку \(b\) циклическим сдвигом строки \(a\). Например, строки 0100110 и 1100100 — равны, а строки 1010 и 1100 — не равны. Вам задана бинарная строка \(s\) длины \(n\). Каждый из ее первых \(c\) символов — это 1, а каждый из последних \(n - c\) символов — это 0. За одну операцию вы можете заменить один 0 на 1. Посчитайте количество уникальных строк, которые вы можете получить, используя не более \(k\) операций. Поскольку ответ может быть слишком большим, выведите его по модулю \(10^9 + 7\). Выходные данные Выведите одно целое число — количество уникальных строк, которые вы можете получить, выполнив не более \(k\) операций, по модулю \(10^9 + 7\). Примечание В первом тесте возможная строка: 1. Во втором тесте возможные строки: 100, 110 и 111. Строка 101 равна 110, поэтому мы ее не учитываем. В третьем тесте возможные строки: 10000, 11000, 10100. Строка 10010 равна 10100, а 10001 равна 11000. | |
![]()
|
|
C. Как ходит ладья?
Комбинаторика
математика
*1600
дп
Вам дана шахматная доска размером \(n \times n\), на которой вы и компьютер поочередно расставляете белые и черные ладьи соответственно. Расставляя ладьи, вы должны следить за тем, чтобы никакие две ладьи не атаковали друг друга. Две ладьи атакуют друг друга, если они находятся в одной строке или столбце независимо от цвета. Правильный ход — установка ладьи на позиции (\(r\), \(c\)) так, чтобы она не атаковала никакую другую ладью. Вы начинаете первым, и когда вы в свой ход сделаете правильный ход, поставив белую ладью на позицию (\(r\), \(c\)), компьютер отзеркалит ваш ход и в свой ход поставит черную ладью на позицию (\(c\), \(r\)). Если \(r = c\), то компьютер не сможет отзеркалить ваш ход и пропустит его. Вы уже сыграли с компьютером \(k\) ходов (компьютер отразил и эти ходы), и вы должны продолжать игру, пока не останется ни одного правильного хода. Сколько различных конечных конфигураций можно получить, если продолжить игру после данных \(k\) ходов? Гарантируется, что \(k\) сделанных ходов были правильными. Так как ответ может быть большим, выведите его по модулю \(10^9+7\). Две конфигурации считаются различными, если существует координата (\(r\), \(c\)), в которой ладья есть в одной конфигурации, но нет в другой, или цвет ладьи на координате отличается. Выходные данные Для каждого набора входных данных выведите в отдельной строке одно число — общее количество возможных конечных конфигураций по модулю \(10^9+7\). Примечание В первом наборе входных данных у нас есть поле \(4 \times 4\), и вы уже сыграли \(1\) ход. После того как вы и компьютер сыграли по одному ходу, на поле есть белая ладья на (\(1\), \(2\)) и черная ладья на (\(2\), \(1\)). Из этого состояния возможны три конфигурации — - Вы ставите белую ладью на (\(3\), \(4\)), а компьютер в ответ ставит черную ладью на (\(4\), \(3\)).
- Вы ставите белую ладью на (\(4\), \(3\)), а компьютер в ответ ставит черную ладью на (\(3\), \(4\)).
- Вы ставите белую ладью на (\(3\), \(3\)), а затем на (\(4\), \(4\)), или наоборот. Оба варианта приводят к одной и той же конфигурации.
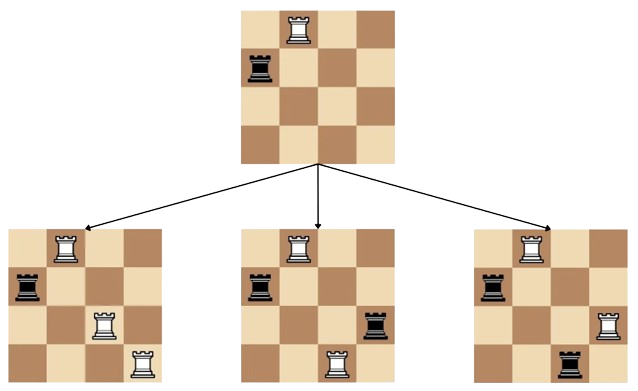 | |
![]()
|
|
E. Карусель комбинаций
Перебор
Комбинаторика
математика
дп
теория чисел
*2400
Вам дано целое число \(n\). Значение функции \(C(i,k)\) представляет собой количество различных способов, которыми можно выбрать \(k\) различных чисел из множества {\(1, 2, \ldots, i\)} и расположить их по кругу\(^\dagger\). Найдите значение \(\) \sum\limits_{i=1}^n \sum\limits_{j=1}^i \left( C(i,j) \bmod j \right). \(\) Здесь операция \(x \bmod y\) обозначает остаток от деления \(x\) на \(y\). Поскольку это значение может быть очень большим, найдите его по модулю \(10^9+7\). \(^\dagger\) Две последовательности считаются одинаковыми расстановками чисел по кругу, если одну из последовательностей можно циклически сдвинуть так, чтобы она совпала с другой. Например, \([1, 2, 3]\) и \([2, 3, 1]\) являются одинаковыми расстановками по кругу. Выходные данные Для каждого набора входных данных выведите на отдельной строке одно число — значение вычисляемого выражения по модулю \(10^9+7\). Примечание В первом наборе входных данных \(C(1,1) \bmod 1 = 0\). Во втором наборе входных данных: - \(C(1,1)=1\) (способы: \([1]\));
- \(C(2,1)=2\) (способы: \([1]\), \([2]\));
- \(C(2,2)=1\) (способы: \([1, 2]\));
- \(C(3,1)=3\) (способы: \([1]\), \([2]\), \([3]\));
- \(C(3,2)=3\) (способы: \([1, 2]\), \([2, 3]\), \([3, 1]\));
- \(C(3,3)=2\) (способы: \([1, 2, 3]\), \([1, 3, 2]\)).
Итого, \(\left(C(1,1) \bmod 1\right) + \left(C(2,1) \bmod 1\right) + \left(C(2,2) \bmod 2\right) + \left(C(3,1) \bmod 1\right) + \left(C(3,2) \bmod 2\right) + \left(C(3,3) \bmod 3\right) = 4\). | |
![]()
|
|
F. Узкие пути
Комбинаторика
*2000
*особая задача
Монокарп гуляет по матрице, состоящей из \(2\) строк и \(n\) столбцов. Будем обозначать клетку в \(i\)-й строке в \(j\)-м столбце \((i, j)\). Монокарп начинает в клетке \((1, 1)\) и хочет прийти в клетку \((2, n)\). За один ход Монокарп может перейти в одном из двух направлений: - направо — из клетки \((i, j)\) в клетку \((i, j + 1)\);
- вниз — из клетки \((i, j)\) в клетку \((i + 1, j)\).
Монокарп не может выходить за границы матрицы. Поликарп хочет помешать Монокарпу свободно гулять по матрице. Для этого он хочет выбрать ровно \(k\) различных клеток в матрице и заблокировать их. Он не может выбирать клетки \((1, 1)\) и \((2, n)\). Для каждого \(i\) от \(0\) до \(n\) Поликарп хочет знать, сколько способов заблокировать ровно \(k\) клеток у него есть, чтобы у Монокарпа было ровно \(i\) различных путей из \((1, 1)\) в \((2, n)\). Два пути считаются различными, если существует такая клетка, которую Монокарп посещает в одном пути, но не в другом. Так как число способов может быть достаточно большим, выведите его по модулю \(10^9 + 7\). Выходные данные Выведите \(n + 1\) целое число: для каждого \(i\) от \(0\) до \(n\) количество способов заблокировать ровно \(k\) клеток, чтобы у Монокарпа было ровно \(i\) различных путей из \((1, 1)\) в \((2, n)\). Все ответы выведите по модулю \(10^9 + 7\). | |
![]()
|
|
C. Дерево Фенвика
Деревья
Перебор
Структуры данных
Комбинаторика
математика
дп
*2300
битмаски
Пусть \(\operatorname{lowbit}(x)\) обозначает значение младшего двоичного бита \(x\), например, \(\operatorname{lowbit}(12)=4\), \(\operatorname{lowbit}(8)=8\). Для массива \(a\) длины \(n\), если массив \(s\) длины \(n\) удовлетворяет условию \(s_k=\left(\sum\limits_{i=k-\operatorname{lowbit}(k)+1}^{k}a_i\right)\bmod 998\,244\,353\) для всех \(k\), то \(s\) называется Деревом Фенвика массива \(a\). Обозначим его как \(s=f(a)\). Для целого положительного числа \(k\) и массива \(a\), \(f^k(a)\) определяется следующим образом: \(\) f^k(a)= \begin{cases} f(a)&\textrm{если }k=1\\ f(f^{k-1}(a))&\textrm{иначе.}\\ \end{cases} \(\) Вам дан массив \(b\) длины \(n\) и целое положительное число \(k\). Найдите массив \(a\), который удовлетворяет условию \(0\le a_i < 998\,244\,353\) и \(f^k(a)=b\). Можно доказать, что ответ всегда существует. Если существует несколько ответов, вы можете вывести любой из них. Выходные данные Для каждого набора входных данных выведите одну строку, содержащую корректный массив \(a\) длины \(n\). Примечание Из первого набора входных данных видно, что \(f^1([1,1,1,1,1,1,1,1])=[1,2,1,4,1,2,1,8]\). Во втором наборе входных данных видно, что \(f^2([1,2,3,4,5,6])=f^1([1,3,3,10,5,11])=[1,4,3,17,5,16]\). | |
![]()
|
|
E1. Снова считаем массивы (простая версия)
Комбинаторика
математика
дп
бпф
*3100
Это простая версия задачи. Разница между двумя версиями заключается в ограничениях на \(n, m, b_0\) и ограничении по времени. Вы можете делать взломы, только если обе версии решены. Малышка R уже посчитала множество множеств, и теперь она решила посчитать массивы. Малышка R считает, что массив \(b_0, \ldots, b_n\), состоящий из целых неотрицательных чисел, является непрерывным тогда и только тогда, когда для каждого \(i\), такого что \(1 \leq i \leq n\), выполняется \(\lvert b_i - b_{i-1} \rvert = 1\). Ей нравится непрерывность, поэтому она хочет генерировать только непрерывные массивы. Если малышке R даны \(b_0\) и \(a_1, \ldots, a_n\), то она попытается сгенерировать неотрицательный непрерывный массив \(b\), который не имеет сходства с \(a\). Более формально, для всех \(1 \leq i \leq n\), \(a_i \neq b_i\). Однако у малышки R нет никакого массива \(a\). Вместо этого она дала вам \(n\), \(m\) и \(b_0\). Она хочет посчитать количество различных целочисленных массивов \(a_1, \ldots, a_n\), удовлетворяющих условиям: - \(1 \leq a_i \leq m\);
- Можно сгенерировать хотя бы один неотрицательный непрерывный массив \(b_0, \ldots, b_n\).
Заметим, что \(b_i \geq 0\), но \(b_i\) может быть произвольно большим. Поскольку ответ может быть очень большим, выведите ответ по модулю \(998\,244\,353\). Выходные данные Для каждого набора входных данных выведите одну строку, содержащую целое число: количество различных массивов \(a_1, \ldots, a_n\), удовлетворяющих условиям, по модулю \(998\,244\,353\). Примечание В первом наборе входных данных, например, когда \(a = [1, 2, 1]\), мы можем задать \(b = [1, 0, 1, 0]\). Когда \(a = [1, 1, 2]\), мы можем задать \(b = [1, 2, 3, 4]\). Всего существует \(6\) допустимых вариантов \(a_1, \ldots, a_n\): можно доказать, что только \(a = [2, 1, 1]\) и \(a = [2, 1, 2]\) делают невозможным построение неотрицательной непрерывного \(b_0, \ldots, b_n\), поэтому ответ равен \(2^3 - 2 = 6\). | |
![]()
|
|
E2. Снова считаем массивы (сложная версия)
Комбинаторика
математика
дп
*3500
Это сложная версия задачи. Разница между двумя версиями заключается в ограничениях на \(n, m, b_0\) и ограничении по времени. Вы можете делать взломы, только если обе версии решены. Малышка R уже посчитала множество множеств, и теперь она решила посчитать массивы. Малышка R считает, что массив \(b_0, \ldots, b_n\), состоящий из целых неотрицательных чисел, является непрерывным тогда и только тогда, когда для каждого \(i\), такого что \(1 \leq i \leq n\), выполняется \(\lvert b_i - b_{i-1} \rvert = 1\). Ей нравится непрерывность, поэтому она хочет генерировать только непрерывные массивы. Если малышке R даны \(b_0\) и \(a_1, \ldots, a_n\), то она попытается сгенерировать неотрицательный непрерывный массив \(b\), который не имеет сходства с \(a\). Более формально, для всех \(1 \leq i \leq n\), \(a_i \neq b_i\). Однако у малышки R нет никакого массива \(a\). Вместо этого она дала вам \(n\), \(m\) и \(b_0\). Она хочет посчитать количество различных целочисленных массивов \(a_1, \ldots, a_n\), удовлетворяющих условиям: - \(1 \leq a_i \leq m\);
- Можно сгенерировать хотя бы один неотрицательный непрерывный массив \(b_0, \ldots, b_n\).
Заметим, что \(b_i \geq 0\), но \(b_i\) может быть произвольно большим. Поскольку ответ может быть очень большим, выведите ответ по модулю \(998\,244\,353\). Выходные данные Для каждого набора входных данных выведите одну строку, содержащую целое число: количество различных массивов \(a_1, \ldots, a_n\), удовлетворяющих условиям, по модулю \(998\,244\,353\). Примечание В первом наборе входных данных, например, когда \(a = [1, 2, 1]\), мы можем задать \(b = [1, 0, 1, 0]\). Когда \(a = [1, 1, 2]\), мы можем задать \(b = [1, 2, 3, 4]\). Всего существует \(6\) допустимых вариантов \(a_1, \ldots, a_n\): можно доказать, что только \(a = [2, 1, 1]\) и \(a = [2, 1, 2]\) делают невозможным построение неотрицательной непрерывного \(b_0, \ldots, b_n\), поэтому ответ равен \(2^3 - 2 = 6\). | |
![]()
|
|
C. Красивые пары троек
Структуры данных
Комбинаторика
*1400
Поликарпу подарили массив \(a\) из \(n\) целых чисел. Ему очень нравятся тройки чисел, поэтому для каждого \(j\) (\(1 \le j \le n - 2\)) он выписал тройку из элементов \([a_j, a_{j + 1}, a_{j + 2}]\). Поликарп считает пару из троек \(b\) и \(c\) красивой, если они различаются ровно в одной позиции, то есть выполняется одно из следующих условий: - \(b_1 \ne c_1\) и \(b_2 = c_2\) и \(b_3 = c_3\);
- \(b_1 = c_1\) и \(b_2 \ne c_2\) и \(b_3 = c_3\);
- \(b_1 = c_1\) и \(b_2 = c_2\) и \(b_3 \ne c_3\).
Найдите количество красивых пар троек среди выписанных троек \([a_j, a_{j + 1}, a_{j + 2}]\). Выходные данные Для каждого набора входных данных выведите одно целое число — количество красивых пар троек среди пар вида \([a_j, a_{j + 1}, a_{j + 2}]\). Обратите внимание, что ответ может не умещаться в 32-битные типы данных. Примечание В первом примере \(a = [3, 2, 2, 2, 3]\), Поликарп выпишет следующие тройки: - \([3, 2, 2]\);
- \([2, 2, 2]\);
- \([2, 2, 3]\).
Красивыми парами являются тройка \(1\) с тройкой \(2\) и тройка \(2\) с тройкой \(3\). В третьем примере \(a = [1, 2, 3, 2, 2, 3, 4, 2]\), Поликарп выпишет следующие тройки: - \([1, 2, 3]\);
- \([2, 3, 2]\);
- \([3, 2, 2]\);
- \([2, 2, 3]\);
- \([2, 3, 4]\);
- \([3, 4, 2]\);
Красивыми парами являются тройка \(1\) с тройкой \(4\), тройка \(2\) с тройкой \(5\), тройка \(3\) с тройкой \(6\). | |
![]()
|
|
F. Множество
Перебор
Комбинаторика
математика
дп
*2600
поиск в глубину и подобное
разделяй и властвуй
битмаски
Определим бинарное кодирование конечного множества целых неотрицательных чисел \(T \subseteq \{0,1,2,\ldots\}\) как \(f(T) = \sum\limits_{i \in T} 2^i\). Например, \(f(\{0,2\}) = 2^0 + 2^2 = 5\) и \(f(\{\}) = 0\). Обратите внимание, что \(f\) — это биекция от всех таких множеств ко всем неотрицательным целым числам. Таким образом, \(f^{-1}\) также определено. Дано целое число \(n\) и \(2^n-1\) множество \(V_1,V_2,\ldots,V_{2^n-1}\). Найдите все множества \(S\), которые удовлетворяют следующим ограничениям: - \(S \subseteq \{0,1,\ldots,n-1\}\). Заметим, что \(S\) может быть пустым.
- Для всех непустых \(T \subseteq \{0,1,\ldots,n-1\}\) выполнено \(|S \cap T| \in V_{f(T)}\).
Для экономии входные и выходные данные будут заданы в терминах двоичных кодировок множеств. Выходные данные Первая строка вывода должна содержать целое число \(k\), обозначающее количество подходящих \(S\). В следующих \(k\) строках вы должны вывести \(f(S)\) для всех подходящих \(S\) в порядке возрастания. Примечание В первом примере одним из возможных \(S\) является \(f^{-1}(3) = \{0,1\}\). Все непустые подмножества \(T \subseteq \{0,1,2\}\) и соответствующие им \(|S \cap T|\), \(f(T)\) и \(V_f(T)\) имеют следующий вид: | \(T\) | \(|S\cap T|\) | \(f(T)\) | \(V_{f(T)}\) | | \(\{0\}\) | \(1\) | \(1\) | \(\{0,1,2,3\}\) | | \(\{1\}\) | \(1\) | \(2\) | \(\{0,1,2,3\}\) | | \(\{2\}\) | \(0\) | \(4\) | \(\{0,1,2,3\}\) | | \(\{0,1\}\) | \(2\) | \(3\) | \(\{0,1,2,3\}\) | | \(\{0,2\}\) | \(1\) | \(5\) | \(\{0,1,2,3\}\) | | \(\{1,2\}\) | \(1\) | \(6\) | \(\{0,1,2,3\}\) | | \(\{0,1,2\}\) | \(2\) | \(7\) | \(\{2,3\}\) |
| |
![]()
|
|
D. Инвертируемые скобочные последовательности
Бинарный поиск
Структуры данных
Комбинаторика
реализация
*2000
разделяй и властвуй
Правильная скобочная последовательность — это скобочная последовательность, которую можно превратить в корректное арифметическое выражение, вставив символы '1' и '+' между исходными символами. Например: - скобочные последовательности «()()» и «(())» — правильные (из них можно получить выражения «(1)+(1)» и «((1+1)+1)»);
- скобочные последовательности «)(», «(» и «)» — неправильные.
Давайте определим инверсию скобочной последовательности следующим образом: заменить все скобки '(' на ')', и наоборот (все скобки ')' на '('). Например, строки «()((» и «)())» являются инверсиями друг друга. Задана правильная скобочная последовательность \(s\). Ваша задача — посчитать количество таких пар целых чисел \((l,r)\) (\(1 \le l \le r \le |s|\)), что если заменить всю подстроку \(s\) с \(l\)-го символа по \(r\)-й символ (включительно) на ее инверсию, \(s\) все еще будет правильной скобочной последовательностью. Выходные данные Для каждого набора входных данных выведите одно целое число — количество пар \((l,r)\), удовлетворяющих условию задачи. Примечание В первом примере есть только одна пара: - \((2, 3)\): (()) \(\rightarrow\) ()().
Во втором примере подходящих пар нет. В третьем примере есть три подходящих пары: - \((2, 3)\): ()()() \(\rightarrow\) (())();
- \((4, 5)\): ()()() \(\rightarrow\) ()(());
- \((2, 5)\): ()()() \(\rightarrow\) (()());
| |
![]()
|
|
E. Разделяемые перестановки
Деревья
Структуры данных
Комбинаторика
математика
поиск в глубину и подобное
жадные алгоритмы
*2500
Изначально у нас был один массив — перестановка размера \(n\) (массив размера \(n\), где каждое целое число от \(1\) до \(n\) встречается ровно один раз). Мы провели \(q\) операций. В ходе \(i\)-й операции мы сделали следующее: - выбрали любой из имеющихся у нас массивов размера хотя бы \(2\);
- разделили его на две непустых части (префикс и суффикс);
- записали два числа \(l_i\) и \(r_i\), где \(l_i\) — максимум в левой из полученных частей, а \(r_i\) — максимум в правой из полученных частей;
- удалили массив, который мы разделили, из набора массивов, которые мы можем использовать, а вместо него добавили две полученных части массива.
Например, пусть изначально у нас был массив \([6, 3, 4, 1, 2, 5]\), и мы провели следующие операции: - выбрали массив \([6, 3, 4, 1, 2, 5]\) и разделили его на \([6, 3]\) и \([4, 1, 2, 5]\). Затем мы записали \(l_1 = 6\) и \(r_1 = 5\), и в следующих операциях нам доступны массивы \([6, 3]\) и \([4, 1, 2, 5]\);
- выбрали массив \([4, 1, 2, 5]\) и разделили его на \([4, 1, 2]\) и \([5]\). Затем мы записали \(l_2 = 4\) и \(r_2 = 5\), и в следующих операциях нам доступны массивы \([6, 3]\), \([4, 1, 2]\) и \([5]\);
- выбрали массив \([4, 1, 2]\) и разделили его на \([4]\) и \([1, 2]\). Затем мы записали \(l_3 = 4\) и \(r_3 = 2\), и в следующих операциях нам доступны массивы \([6, 3]\), \([4]\), \([1, 2]\) и \([5]\).
Даны два целых числа \(n\) и \(q\), а также две последовательности \([l_1, l_2, \dots, l_q]\) и \([r_1, r_2, \dots, r_q]\). Перестановку размера \(n\) назовем подходящей, если можно провести на ней \(q\) операций и получить заданные последовательности \([l_1, l_2, \dots, l_q]\) и \([r_1, r_2, \dots, r_q]\). Посчитайте количество подходящих перестановок. Выходные данные Выведите одно целое число — количество подходящих перестановок, взятое по модулю \(998244353\). | |
![]()
|
|
C. Заработать на ставках
Бинарный поиск
Конструктив
Комбинаторика
теория чисел
*1200
Вам было предложено сыграть в игру. В данной игре возможно \(n\) исходов, на каждый из которых вы должны поставить некоторое целое количество монет. В случае, если \(i\)-й исход окажется выигрышным, вы получите обратно количество монет в размере вашей ставки на этот исход, умноженной на \(k_i\). Обратите внимание, что ровно один из \(n\) исходов окажется выигрышным. Ваша задача — сказать, как распределить монеты так, чтобы при любом выигрышном исходе выйти в плюс. Более формально, суммарное количество монет, которое вы поставили на все исходы, должно быть строго меньше числа монет, полученных обратно при каждом возможном выигрышном исходе. Выходные данные Для каждого набора входных данных выведите \(-1\), если требуемого способа распределить монеты не существует. Иначе выведите \(n\) целых чисел \(x_1, x_2,\ldots, x_n\) (\(1 \le x_i \le 10^{9}\)) — ваши ставки на исходы. Можно показать, что если какой-то ответ существует, то всегда существует ответ, удовлетворяющий данным ограничениям. Если существует несколько подходящих решений, выведите любое из них. Примечание В первом наборе входных данных можно распределить монеты следующим образом: \(27\) монет на первый исход, \(41\) монета на второй исход, \(12\) монет на третий исход. Тогда суммарное количество монет, которое будет поставлено на все исходы, равно \(27 + 41 + 12 = 80\) монет. Если первый исход окажется выигрышным, то вы получите обратно \(3 \cdot 27 = 81\) монету, если второй исход окажется выигрышным, то вы получите обратно \(2 \cdot 41 = 82\) монеты, если третий исход окажется выигрышным, то вы получите обратно \(7 \cdot 12 = 84\) монеты. Все эти значения строго больше \(80\). Во втором наборе входных данных одним из способов является поставить по одной монете на каждый из исходов. | |
![]()
|
|
E. Количество k-хороших подотрезков
Перебор
Комбинаторика
математика
дп
разделяй и властвуй
*2300
битмаски
meet-in-the-middle
Обозначим за \(bit(x)\) количество единичных бит в двоичной записи неотрицательного целого числа \(x\). Назовем подотрезок массива \(k\)-хорошим, если он состоит только из чисел, в которых не более \(k\) единичных бит, то есть подотрезок \((l, r)\) массива \(a\) хороший, если для любого \(i\), такого, что \(l \le i \le r\) выполняется \(bit(a_{i}) \le k\). У вас есть массив \(a\) длины \(n\), состоящий из последовательных неотрицательных целых чисел начиная с \(0\), то есть \(a_{i} = i\) для \(0 \le i \le n - 1\) (в \(0\)-индексации). Вам необходимо посчитать количество \(k\)-хороших подотрезков в этом массиве. Поскольку ответ может быть очень большим, выведите его по модулю \(10^{9} + 7\). Выходные данные Для каждого набора входных данных в отдельной строке выведите одно целое число — количество \(k\)-хороших подотрезков по модулю \(10^{9} + 7\). Примечание Для первого набора входных данных \(a = [0, 1, 2, 3, 4, 5]\), \(k = 1\). Чтобы найти ответ, давайте запишем все числа в двоичной записи: \(\)a = [\color{green}{000}, \color{green}{001}, \color{green}{010}, \color{red}{011}, \color{green}{100}, \color{red}{101}]\(\) Отсюда видно, что числа \(3\) и \(5\) имеют \(2 \ge (k = 1)\) единичных бита в двоичной записи, поэтому в ответ должны войти все подотрезки, в которых нет ни \(3\), ни \(5\), это отрезки (в \(0\)-индексации): (\(0\), \(0\)), (\(0\), \(1\)), (\(0\), \(2\)), (\(1\), \(1\)), (\(1\), \(2\)), (\(2\), \(2\)), (\(4\), \(4\)). | |
![]()
|
|
E. Я люблю шары
Теория вероятностей
Комбинаторика
математика
*2300
Алиса и Боб играют в игру. Имеется \(n\) шаров, из которых \(k\) — особенные. Каждый шар имеет свою стоимость. Игроки играют по очереди. В каждый ход игрок случайным образом выбирает шар и прибавляет его стоимость к своему счету, который в начале игры равен \(0\). Выбранный шар удаляется из игры. Если шар был особенным, следующий ход делает тот же игрок, если в игре остался хотя бы один шар. Если выбранный шар не был особенным, следующий игрок делает свой ход. Они играют так до тех пор, пока в игре не останется ни одного шара. Алиса ходит первой. Найдите ожидаемое количество очков, которое оба игрока получат в конце игры, по модулю \(10^9+7\). Формально, пусть \(M = 10^9+7\). Можно показать, что ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Выходные данные Для каждого набора входных данных выведите в отдельной строке по два целых числа: ожидаемый счёт Алисы и ожидаемый счёт Боба по модулю \(10^9+7\). Примечание В первом наборе входных данных ожидаемый счёт Алисы равен \(45\), а Боба — \(30\). | |
![]()
|
|
C2. Величина (сложная версия)
Комбинаторика
математика
дп
жадные алгоритмы
*1700
Две версии этой задачи отличаются друг от друга. Возможно, вы захотите прочитать обе версии. Вы сможете делать взломы, только если обе версии решены. Вам дан массив \(a\) длины \(n\). Изначально \(c = 0\). Для каждого \(i\) от \(1\) до \(n\) (в порядке возрастания) выполните ровно одно из следующих действий: - Вариант \(1\): сделать \(c\) равным \(c + a_i\).
- Вариант \(2\): сделать \(c\) равным \(|c + a_i|\), где \(|x|\) — абсолютное значение \(x\).
Пусть максимальное возможное конечное значение \(c\) после описанной выше процедуры равно \(k\). Найдите количество уникальных процедур, в результате которых получается \(c = k\). Две процедуры различны, если при каком-либо индексе \(i\) одна процедура выбрала вариант \(1\), а другая — вариант \(2\), даже если после этого хода значение \(c\) для обеих процедур одинаково. Поскольку ответ может быть большим, выведите его по модулю \(998\,244\,353\). Выходные данные Для каждого набора входных данных выведите одно целое число — количество уникальных процедур, в результате которых получается \(c = k\), по модулю \(998\,244\,353\). Примечание В первом наборе входных данных можно показать, что максимальное конечное значение \(c\) равно \(3\). Существует \(12\) способов достичь этого, потому что для получения \(3\) мы должны взять абсолютное значение при индексах \(2\) или \(4\), или при обоих, что дает \(3\) способа. Для двух других индексов значение не меняется от того, берем мы абсолютное значение или нет, поэтому для них у нас есть \(2 \cdot 2 = 4\) способа. Итого, у нас есть \(3 \cdot 4 = 12\) способов. Во втором наборе входных данных взятие абсолютного значения ничего не изменит, поэтому мы можем либо брать абсолютное значение, либо нет, для каждого индекса. Это дает нам \(2^8 = 256\) возможных способов. | |
![]()
|
|
H. Захват башни
Комбинаторика
геометрия
дп
*3300
В \(n\) различных точках \((x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\) существует \(n\) башен, причем никакие три из них не являются коллинеарными, а четыре — конциклическими. Изначально вы владеете башнями \((x_1, y_1)\) и \((x_2, y_2)\), и хотите захватить их все. Для этого вы можете проделать следующую операцию любое количество раз: - Выбрать две башни \(P\) и \(Q\), которыми вы владеете, и одну башню \(R\), которой вы не владеете, так, чтобы окружность, проходящая через точки \(P\), \(Q\) и \(R\) содержала все \(n\) башен внутри себя.
- После этого захватить все башни в или на треугольнике \(\triangle PQR\), включая сам \(R\).
План атаки — это последовательность выборов \(R\) (\(R_1, R_2, \ldots, R_k\)) в рамках вышеописанных операций, после которых вы захватываете все башни. Обратите внимание, что два плана атаки считаются различными, только если они отличаются выбором \(R\) в некоторой операции; в частности, два плана атаки с одинаковым выбором \(R\), но разными выборами \(P\) и \(Q\) считаются одинаковыми. Подсчитайте количество планов атаки минимальной длины. Обратите внимание, что захватить все башни может быть невозможно, и в этом случае ответ будет равен \(0\). Поскольку ответ может быть большим, выведите его по модулю \(998\,244\,353\). Выходные данные Для каждого набора входных данных выведите одно целое число — количество планов атаки минимальной длины, после которых вы захватите все башни, по модулю \(998\,244\,353\). Примечание В первом наборе входных данных существует только один возможный план атаки наименьшей длины, показанный ниже.  - Использовать операцию с башней \(P =\) \(1\), башней \(Q =\) \(2\) и башней \(R =\) \(5\). Окружность, проходящая через эти три башни, содержит все башни внутри себя, в результате чего башни \(3\) и \(5\) оказываются захваченными.
- Использовать операцию с башней \(P =\) \(5\), башней \(Q =\) \(1\) и башней \(R =\) \(4\). Окружность, проходящая через эти три башни, содержит все башни внутри себя, в результате чего башня \(4\) оказывается захваченной.
Во втором наборе входных данных, например, вы никогда не сможете захватить башню в точке \((3, 10\,000)\). | |
![]()
|
|
E. Секретный ящик
Перебор
Комбинаторика
математика
*1200
У Ntarsis есть ящик \(B\) с длиной сторон \(x\), \(y\) и \(z\). Он находится в трехмерной координатной плоскости, простираясь от \((0,0,0)\) до \((x,y,z)\). У Ntarsis есть секретный ящик \(S\). Он хочет выбрать его размеры так, чтобы все длины сторон были положительными целыми числами, и объем \(S\) был равен \(k\). Он может разместить \(S\) где-то внутри \(B\) так, что: - \(S\) параллелен всем осям.
- каждый угол \(S\) лежит на целочисленной координате.
\(S\) волшебный, поэтому, когда он размещен в целочисленных координатах внутри \(B\), он не упадет на землю. Среди всех возможных способов выбора размеров \(S\) определите максимальное количество различных мест, где он может разместить свой секретный ящик \(S\) внутри \(B\). Ntarsis не поворачивает \(S\), когда выбраны его длины сторон. Выходные данные Для каждого набора входных данных выведите ответ в виде целого числа на новой строке. Если нет способа выбрать размеры \(S\), чтобы он поместился в \(B\), выведите \(0\). Примечание Для первого примера оптимально выбрать \(S\) с длиной сторон \(2\), \(2\) и \(2\), что дает объем \(2 \cdot 2 \cdot 2 = 8\). Можно показать, что есть \(8\) способов поместить \(S\) внутри \(B\). Координаты с наименьшими значениями \(x\), \(y\) и \(z\) для каждого возможного расположения \(S\): - \((0, 0, 0)\)
- \((1, 0, 0)\)
- \((0, 1, 0)\)
- \((0, 0, 1)\)
- \((1, 0, 1)\)
- \((1, 1, 0)\)
- \((0, 1, 1)\)
- \((1, 1, 1)\)
Расположение \(S\) с координатой \((0, 0, 0)\) изображено ниже:  Для второго примера оптимально выбрать \(S\) с длиной сторон \(2\), \(3\) и \(3\). | |
![]()
|
|
G. D-Функция
Комбинаторика
математика
*1600
теория чисел
Пусть \(D(n)\) представляет собой сумму цифр числа \(n\). Для скольких целых чисел \(n\), \(10^{l} \leq n < 10^{r}\), выполняется условие \(D(k \cdot n) = k \cdot D(n)\)? Выведите ответ по модулю \(10^9+7\). Выходные данные Для каждого набора входных данных выведите целое число — ответ, по модулю \(10^9 + 7\). Примечание Для первого примера единственные значения \(n\), удовлетворяющие условию, — это \(1\) и \(2\). Для второго примера единственные значения \(n\), удовлетворяющие условию, — это \(1\), \(10\) и \(11\). Для третьего примера все значения \(n\) от \(10\) включительно до \(100\) исключительно удовлетворяют условию. | |
![]()
|
|
G1. Задача на перестановку (простая версия)
Бинарный поиск
Перебор
Структуры данных
Комбинаторика
математика
теория чисел
*2200
Это простая версия задачи. Единственное различие состоит в том, что в этой версии \(n \leq 10^5\) и сумма \(n\) по всем наборам входных данных не превосходит \(10^5\). Вам дана перестановка \(p\) длины \(n\). Посчитайте количество пар индексов \(1 \leq i < j \leq n\), таких что \(p_i \cdot p_j\) делится без остатка на \(i \cdot j\). Перестановка — это последовательность из \(n\) целых чисел, в которой каждое целое число от \(1\) до \(n\) встречается ровно по одному разу. Например, \([1]\), \([3,5,2,1,4]\), \([1,3,2]\) — перестановки, а \([2,3,2]\), \([4,3,1]\), \([0]\) — нет. Выходные данные Для каждого набора входных данных выведите количество пар индексов \(1 \leq i < j \leq n\), таких что \(p_i \cdot p_j\) делится без остатка на \(i \cdot j\). Примечание В первом наборе входных данных нет ни одной пары индексов, так как размер перестановки равен \(1\). Во втором наборе входных данных есть одна пара индексов \((1, 2)\) и она подходит. В третьем наборе входных данных подходит пара индексов \((1, 2)\). В четвертом наборе входных данных подходят пары индексов \((1, 2)\), \((1, 5)\) и \((2, 5)\). | |
![]()
|
|
F. Пульс
Комбинаторика
математика
дп
*3000
бпф
Для массива \(u_1, u_2, \ldots, u_n\) определим - префиксный максимум как такой индекс \(i\), что \(u_i>u_j\) для всех \(j<i\);
- суффиксный максимум как такой индекс \(i\), что \(u_i>u_j\) для всех \(j>i\);
- подъем как такой индекс \(i\) (\(i>1\)), что \(u_i>u_{i-1}\).
У вас есть три массива стоимостей: \([a_1, a_2, \ldots, a_n]\), \([b_1, b_2, \ldots, b_n]\) и \([c_0, c_1, \ldots, c_{n-1}]\). Определим стоимость массива, имеющего \(x\) префиксных максимумов, \(y\) суффиксных максимумов и \(z\) подъемов, как \(a_x\cdot b_y\cdot c_z\). Пусть сумма стоимости всех перестановок \(1,2,\ldots,n\) равна \(f(n)\). Найдите \(f(1)\), \(f(2)\), ..., \(f(n)\) по модулю \(998\,244\,353\). Выходные данные Выведите \(n\) целых чисел: \(i\)-е из них — \(f(i)\) по модулю \(998\,244\,353\). Примечание Во втором примере: - Рассмотрим перестановку \([1,2,3]\). Индексы \(1,2,3\) являются префиксными максимумами. Индекс \(3\) — единственный суффиксный максимум. Индексы \(2,3\) — подъемы. В итоге, у нее \(3\) префиксных максимума, \(1\) суффиксный максимум и \(2\) подъема. Поэтому ее стоимость равна \(a_3b_1c_2=12\).
- Перестановка \([1,3,2]\) имеет \(2\) префиксных максимума, \(2\) суффиксных максимума и \(1\) подъем. Ее стоимость равна \(6\).
- Перестановка \([2,1,3]\) имеет \(2\) префиксных максимума, \(1\) суффиксный максимум и \(1\) подъем. Ее стоимость равна \(4\).
- Перестановка \([2,3,1]\) имеет \(2\) префиксных максимума, \(2\) суффиксных максимума и \(1\) подъем. Ее стоимость равна \(6\).
- Перестановка \([3,1,2]\) имеет \(1\) префиксный максимум, \(2\) суффиксных максимума и \(1\) подъем. Ее стоимость равна \(3\).
- Перестановка \([3,2,1]\) имеет \(1\) префиксный максимум, \(3\) суффиксных максимума и \(0\) подъемов. Ее стоимость равна \(3\).
Сумма стоимостей всех перестановок равна \(34\), поэтому \(f(3)=34\). | |
![]()
|
|
E. Расстояние до различных
Комбинаторика
математика
дп
*2300
Рассмотрим массив \(a\) из \(n\) целых чисел, где каждый элемент находится в диапазоне от \(1\) до \(k\), и каждое целое число от \(1\) до \(k\) встречается как минимум один раз. Массив \(b\) строится следующим образом: для \(i\)-го элемента массива \(a\) значение \(b_i\) — это расстояние до ближайшего элемента в \(a\), который не равен \(a_i\). Другими словами, \(b_i = \min \limits_{j \in [1, n], a_j \ne a_i} |i - j|\). Например, если \(a = [1, 1, 2, 3, 3, 3, 3, 1]\), то \(b = [2, 1, 1, 1, 2, 2, 1, 1]\). Вычислите количество различных массивов \(b\), которые можно получить, если рассмотреть все возможные массивы \(a\), и выведите его по модулю \(998244353\). Выходные данные Выведите одно целое число — количество различных массивов \(b\), которые можно получить, взятое по модулю \(998244353\). | |
![]()
|
|
G. Ультра-мяу
Комбинаторика
математика
дп
*2000
K1o0n подарил вам массив \(a\) длины \(n\), состоящий из чисел \(1, 2, \ldots, n\). Принять? Конечно, да! Но что с ним делать? Конечно же посчитать \(\text{MEOW}(a)\). Пусть \(\text{MEX}(S, k)\) — \(k\)-е целое положительное число в порядке возрастания, отсутствующее в множестве \(S\). Обозначим за \(\text{MEOW}(a)\) сумму \(\text{MEX}(b, |b| + 1)\), по всем различным подмножествам \(b\) массива \(a\). Примеры значений \(\text{MEX}(S, k)\) для множеств: - \(\text{MEX}(\{3,2\}, 1) = 1\), т. к. \(1\) — первое целое положительное число, отсутствующее в множестве;
- \(\text{MEX}(\{4,2,1\}, 2) = 5\), т. к. первые два целые положительные числа, которых нет в множестве, это \(3\) и \(5\);
- \(\text{MEX}(\{\}, 4) = 4\), т. к. в пустом множестве нет никаких чисел, следовательно первые целые положительные \(4\) числа, которых в нём нет, это \(1, 2, 3, 4\).
Выходные данные Для каждого набора входных данных выведите одно число — \(\text{MEOW}(a)\). Поскольку оно может оказаться очень большим, выведите его по модулю \(10^9 + 7\). | |
![]()
|
|
H. Fortnite
Строки
Конструктив
Комбинаторика
математика
теория чисел
жадные алгоритмы
хэши
интерактив
игры
*3500
Это интерактивная задача! Тимофей пишет соревнование, которое называется Capture the flag (или сокращённо CTF). Ему осталась одна задача, в которой нужно взломать систему безопасности. Вся система основана на полиномиальных хеш-функциях\(^{\text{∗}}\). Тимофей может ввести в систему строку, состоящую из строчных латинских букв, и система выдаст её полиномиальный хеш. Чтобы взломать систему, Тимофею нужно узнать параметры полиномиального хеша, которые использует система (\(p\) и \(m\)). У Тимофея осталось очень мало времени, поэтому он успеет сделать только \(3\) запроса. Помогите ему решить задачу. Протокол взаимодействия Чтобы сделать запрос в систему выведите ? \(s\), где \(s\) — строка, длины не более \(50\), хеш которой вы хотите узнать. В ответ на этот запрос вы получите полиномиальный хеш строки \(s\). Чтобы вывести ответ, выведите ! \(p\) \(m\), где — \(p\) основание хеша, а \(m\) — модуль. После этого сразу же переходите к следующему набору входных данных. Вы должны сделать не более \(3\) запросов ?, в противном случае вы получите вердикт Wrong Answer. После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Примечание Ответом на первый запрос будет \((ord(a) \cdot 31^0 + ord(a) \cdot 31^1) \mod 59 = (1 + 1 \cdot 31) \mod 59 = 32\). Ответом на второй запрос является \((ord(y) \cdot 31^0 + ord(b) \cdot 31^1) \mod 59 = (25 + 2 \cdot 31) \mod 59 = 28\). | |
![]()
|
|
D. Веселье
Бинарный поиск
Перебор
Комбинаторика
математика
*1500
теория чисел
Подсчёт — это весело! — satyam343 Даны два целых числа \(n\) и \(x\), найдите количество троек (\(a,b,c\)) положительных целых чисел, таких, что \(ab + ac + bc \le n\) и \(a + b + c \le x\). Обратите внимание, что порядок имеет значение (например, (\(1, 1, 2\)) и (\(1, 2, 1\)) считаются разными) и \(a\), \(b\), \(c\) должны быть строго больше \(0\). Выходные данные Выведите одно целое число — количество троек (\(a,b,c\)) положительных целых чисел, таких, что \(ab + ac + bc \le n\) и \(a + b + c \le x\). Примечание В первом примере подходящие тройки это (\(1, 1, 1\)), (\(1, 1, 2\)), (\(1, 2, 1\)) и (\(2, 1, 1\)). Во втором примере подходящие тройки это (\(1, 1, 1\)), (\(1, 1, 2\)), (\(1, 1, 3\)), (\(1, 2, 1\)), (\(1, 2, 2\)), (\(1, 3, 1\)), (\(2, 1, 1\)), (\(2, 1, 2\)), (\(2, 2, 1\)) и (\(3, 1, 1\)). | |
![]()
|
|
E. Декодирование
Структуры данных
Комбинаторика
математика
реализация
*1600
В отчаянной попытке получить своего waifu любимого персонажа, вы взломали исходный код игры. После дней борьбы вы наконец нашли двоичную строку, которая кодирует систему гача в игре. Чтобы раскодировать ее, вам сначала нужно решить следующую задачу. Дана двоичная строка \(s\) длиной \(n\). Для каждой пары целых чисел \((l, r)\) \((1 \leq l \leq r \leq n)\) посчитайте количество пар \((x, y)\) \((l \leq x \leq y \leq r)\) таких, что количество \(\mathtt{0}\) равно количеству \(\mathtt{1}\) в подстроке \(s_xs_{x+1}...s_y\). Выведите сумму подсчетов для всех возможных \((l, r)\) по модулю \(10^9+7\). Выходные данные Для каждого набора входных данных выведите целое число — ответ по модулю \(10^9+7\). | |
![]()
|
|
F. Фишки на прямой
Перебор
Комбинаторика
математика
дп
жадные алгоритмы
*2700
У вас есть \(n\) фишек, и вы собираетесь разместить каждую из них в одной из \(x\) точек, пронумерованных от \(1\) до \(x\). В каждой точке может находиться несколько фишек. После размещения фишек вы можете выполнять следующие четыре операции (в любом порядке, любое количество раз): - выбрать фишку в точке \(i \ge 3\), удалить ее и разместить две новых фишки: одну в \(i-1\), одну в \(i-2\);
- выбрать две фишки в соседних точках \(i\) и \(i+1\), удалить их и разместить новую фишку в \(i+2\);
- выбрать фишку в точке \(1\) и переместить ее в \(2\);
- выбрать фишку в точке \(2\) и переместить ее в \(1\).
Обратите внимание, что координаты фишек, которые вы размещаете во время операций, не могут быть меньше \(1\), но могут быть больше \(x\). Обозначим стоимость размещения фишек как минимальное количество фишек, которое может остаться на прямой после выполнения этих операций, начиная с выбранного вами размещения. Например, стоимость размещения двух фишек в точках \(3\) и одной фишки в точке \(5\) равна \(2\), потому что вы можете уменьшить количество фишек до \(2\) следующим образом: - выбрать фишку в точке \(3\), удалить ее, разместить одну фишку в \(1\) и одну фишку в \(2\);
- выбрать по одной фишке в точках \(2\) и \(3\), удалить их и разместить фишку в \(4\);
- выбрать по одной фишке в точках \(4\) и \(5\), удалить их и разместить фишку в \(6\).
Вам даны три целых числа \(n\), \(x\) и \(m\). Вычислите количество размещений ровно \(n\) фишек в точках от \(1\) до \(x\), имеющих стоимость, равную \(m\), и выведите его по модулю \(998244353\). Два размещения считаются разными, если количество фишек в какой-либо точке отличается между этими размещениями. Выходные данные Выведите одно целое число — количество размещений со стоимостью, равной \(m\), взятое по модулю \(998244353\). Примечание В первом примере существует пять способов разместить \(2\) фишки в точках от \(1\) до \(3\), чтобы стоимость равнялась \(1\): - \((1, 1)\);
- \((1, 2)\);
- \((1, 3)\);
- \((2, 2)\);
- \((2, 3)\).
| |
![]()
|
|
F. Ожидаемая медиана
Комбинаторика
математика
*1500
Арул имеет бинарный массив\(^{\text{∗}}\) \(a\) длины \(n\). Он возьмет все подпоследовательности\(^{\text{†}}\) длины \(k\) (\(k\) — нечетное) этого массива и найдет их медиану.\(^{\text{‡}}\) Какова сумма всех этих значений? Поскольку эта сумма может быть очень большой, выведите ее по модулю \(10^9 + 7\). Другими словами, напечатайте остаток этой суммы при делении на \(10^9 + 7\). Выходные данные Для каждого набора входных данных выведите сумму по модулю \(10^9 + 7\). Примечание В первом наборе входных данных есть четыре подпоследовательности массива \([1,0,0,1]\) длины \(k=3\): - \([1,0,0]\): медиана \(= 0\).
- \([1,0,1]\): медиана \(= 1\).
- \([1,0,1]\): медиана \(= 1\).
- \([0,0,1]\): медиана \(= 0\).
Сумма результатов равна \(0+1+1+0=2\). Во втором наборе входных данных все подпоследовательности длины \(1\) имеют медиану \(1\), поэтому ответ равен \(5\). | |
![]()
|
|
E. Фотосессия для горилл
Структуры данных
Комбинаторика
математика
*1400
жадные алгоритмы
Вы очень любите горилл, поэтому решили устроить им фотосессию. Гориллы обитают в джунглях. Джунгли представляют собой клетчатое поле из \(n\) строк и \(m\) столбцов. В фотосессии согласились принять участие \(w\) горилл, горилла с номером \(i\) (\(1 \le i \le w\)) имеет рост \(a_i\). Вы хотите расставить всех горилл в клетки поля так, чтобы в каждой клетке стояло не более одной гориллы. Зрелищность расстановки равна сумме зрелищностей всех подквадратов поля с длиной стороны \(k\). Зрелищность подквадрата равна сумме ростов горилл в нём. Из всех подходящих расстановок выберите расстановку с максимальной зрелищностью. Выходные данные Для каждого набора входных данных выведите единственное целое число — максимальную зрелищность подходящей расстановки. Примечание В первом наборе входных данных первого теста суммируются зрелищности следующих подквадратов:  Жёлтый цвет соответствует подквадратам, зелёный — остальным клеткам поля. Жёлтый цвет соответствует подквадратам, зелёный — остальным клеткам поля. На картинке представлено оптимальное расположение горилл. Зрелищность расстановки равна \(4 + 4 + 3 + 3 + 4 + 3 = 21\). | |
![]()
|
|
E1. Детерминированная куча (простая версия)
Деревья
Комбинаторика
математика
дп
*2400
Это простая версия задачи. Разница между двумя версиями заключается в определении детерминированной max-кучи, ограничении на время и ограничениях на \(n\) и \(t\). Вы можете совершать взломы только в том случае, если решены обе версии задачи.. Рассмотрим полное бинарное дерево размером \(2^n - 1\), с вершинами, пронумерованными от \(1\) до \(2^n-1\), и корнем в \(1\). Для каждой вершины \(v\) (\(1 \le v \le 2^{n - 1} - 1\)) вершина \(2v\) является ее левым ребенком, а вершина \(2v + 1\) — ее правым ребенком. Каждой вершине \(v\) также присвоено значение \(a_v\). Определим операцию \(\mathrm{pop}\) следующим образом: - инициализировать переменную \(v\) как \(1\);
- повторять следующий процесс до тех пор, пока вершина \(v\) не станет листом (т.е. пока не выполняется \(2^{n - 1} \le v \le 2^n - 1\)):
- среди дочерних вершин \(v\) выбрать ту, значение которой больше, и обозначить такую вершину \(x\); если значения на них равны (то есть \(a_{2v} = a_{2v + 1}\)), то можно выбрать любую из них;
- присвоить \(a_x\) значению \(a_v\) (т.е. \(a_v := a_x\));
- присвоить \(x\) переменной \(v\) (т.е. \(v := x\));
- присвоить \(-1\) значению \(a_v\) (т.е. \(a_v := -1\)).
Мы говорим, что операция \(\mathrm{pop}\) является детерминированной, если существует единственный способ выполнить такую операцию. Другими словами, \(a_{2v} \neq a_{2v + 1}\) выполняется на каждом шаге операции. Бинарное дерево называется max-кучей, если для каждой вершины \(v\) (\(1 \le v \le 2^{n - 1} - 1\)) выполняется \(a_v \ge a_{2v}\) и \(a_v \ge a_{2v + 1}\). Максимальная куча является детерминированной, если операция \(\mathrm{pop}\) детерминирована для кучи, когда мы выполняем ее в первый раз. Изначально \(a_v := 0\) для каждой вершины \(v\) (\(1 \le v \le 2^n - 1\)), и ваша цель — посчитать количество различных детерминированных max-куч, которые можно получить в результате применения следующей операции \(\mathrm{add}\) ровно \(k\) раз: - Выбрать целое число \(v\) (\(1 \le v \le 2^n - 1\)), и для каждой вершины \(x\) на пути между \(1\) и \(v\) прибавить \(1\) к \(a_x\).
Две кучи считаются разными, если есть вершина, которая имеет разные значения в этих кучах. Поскольку ответ может быть очень большим, выведите его по модулю \(p\). Выходные данные Для каждого набора входных данных выведите единственную строку, содержащую целое число: количество различных детерминированных max-куч, которое можно получить в результате применения вышеупомянутой операции \(\mathrm{add}\) ровно \(k\) раз, по модулю \(p\). Примечание Для первого набора входных данных существует только один способ сгенерировать \(a\), и такая последовательность является детерминированной max-кучей, поэтому ответ — \(1\). Для второго набора входных данных, если мы выберем \(v = 1\) и выполним операцию, у нас будет \(a = [1, 0, 0]\), а поскольку \(a_2 = a_3\), мы можем выбрать любой из них при выполнении первой операции \(\mathrm{pop}\), поэтому такая куча не является детерминированной max-кучей. А если мы выберем \(v = 2\), у нас будет \(a = [1, 1, 0]\), то при выполнении первой операции \(\mathrm{pop}\) произойдет следующее: - инициализировать \(v\) как \(1\)
- поскольку \(a_{2v} > a_{2v + 1}\), выбрать \(2v\) как \(x\), тогда \(x = 2\)
- присвоить \(a_x\) значению \(a_v\), тогда \(a = [1, 1, 0]\)
- присвоить \(x\) переменной \(v\), тогда \(v = 2\)
- поскольку \(v\) является листом, присвоить \(-1\) значению \(a_v\), тогда \(a = [1, -1, 0]\)
Так как первая операция \(\mathrm{pop}\) детерминирована, то это детерминированная max-куча. Также, если мы выберем \(v = 3\), то \(a\) будет детерминированной max-кучей, так что ответ — \(2\). | |
![]()
|
|
E2. Детерминированная куча (сложная версия)
Деревья
Комбинаторика
дп
*2900
Это сложная версия задачи. Разница между двумя версиями заключается в определении детерминированной max-кучи, ограничении на время и ограничениях на \(n\) и \(t\). Вы можете совершать взломы только в том случае, если решены обе версии задачи.. Рассмотрим полное бинарное дерево размером \(2^n - 1\), с вершинами, пронумерованными от \(1\) до \(2^n-1\), и корнем в \(1\). Для каждой вершины \(v\) (\(1 \le v \le 2^{n - 1} - 1\)) вершина \(2v\) является ее левым ребенком, а вершина \(2v + 1\) — ее правым ребенком. Каждой вершине \(v\) также присвоено значение \(a_v\). Определим операцию \(\mathrm{pop}\) следующим образом: - инициализировать переменную \(v\) как \(1\);
- повторять следующий процесс до тех пор, пока вершина \(v\) не станет листом (т.е. пока не выполняется \(2^{n - 1} \le v \le 2^n - 1\)):
- среди дочерних вершин \(v\) выбрать ту, значение которой больше, и обозначить такую вершину \(x\); если значения на них равны (то есть \(a_{2v} = a_{2v + 1}\)), то можно выбрать любую из них;
- присвоить \(a_x\) значению \(a_v\) (т.е. \(a_v := a_x\));
- присвоить \(x\) переменной \(v\) (т.е. \(v := x\));
- присвоить \(-1\) значению \(a_v\) (т.е. \(a_v := -1\)).
Мы говорим, что операция \(\mathrm{pop}\) является детерминированной, если существует единственный способ выполнить такую операцию. Другими словами, \(a_{2v} \neq a_{2v + 1}\) выполняется на каждом шаге операции. Бинарное дерево называется max-кучей, если для каждой вершины \(v\) (\(1 \le v \le 2^{n - 1} - 1\)) выполняется \(a_v \ge a_{2v}\) и \(a_v \ge a_{2v + 1}\). Максимальная куча является детерминированной, если операция \(\mathrm{pop}\) детерминирована для кучи, когда мы выполняем ее в первый и второй раз. Изначально \(a_v := 0\) для каждой вершины \(v\) (\(1 \le v \le 2^n - 1\)), и ваша цель — посчитать количество различных детерминированных max-куч, которые можно получить в результате применения следующей операции \(\mathrm{add}\) ровно \(k\) раз: - Выбрать целое число \(v\) (\(1 \le v \le 2^n - 1\)), и для каждой вершины \(x\) на пути между \(1\) и \(v\) прибавить \(1\) к \(a_x\).
Две кучи считаются разными, если есть вершина, которая имеет разные значения в этих кучах. Поскольку ответ может быть очень большим, выведите его по модулю \(p\). Выходные данные Для каждого набора входных данных выведите единственную строку, содержащую целое число: количество различных детерминированных max-куч, которое можно получить в результате применения вышеупомянутой операции \(\mathrm{add}\) ровно \(k\) раз, по модулю \(p\). Примечание Для первого набора входных данных, если мы выберем \(v = 1\) и выполним операцию, у нас будет \(a = [1, 0, 0]\), а поскольку \(a_2 = a_3\), мы можем выбрать любой из них при выполнении первой операции \(\mathrm{pop}\), поэтому такая куча не является детерминированной max-кучей. А если мы выберем \(v = 2\), у нас будет \(a = [1, 1, 0]\), то при выполнении первой операции \(\mathrm{pop}\) произойдет следующее: - инициализировать \(v\) как \(1\)
- поскольку \(a_{2v} > a_{2v + 1}\), выбрать \(2v\) как \(x\), тогда \(x = 2\)
- присвоить \(a_x\) значению \(a_v\), тогда \(a = [1, 1, 0]\)
- присвоить \(x\) переменной \(v\), тогда \(v = 2\)
- поскольку \(v\) является листом, присвоить \(-1\) значению \(a_v\), тогда \(a = [1, -1, 0]\)
А во время второго \(\mathrm{pop}\) произойдет следующее: - инициализировать \(v\) как \(1\)
- поскольку \(a_{2v} < a_{2v + 1}\), выбрать \(2v + 1\) в качестве \(x\), тогда \(x = 3\)
- присвоить \(a_x\) значению \(a_v\), тогда \(a = [0, -1, 0]\)
- присвоить \(x\) переменной \(v\), тогда \(v = 3\)
- поскольку \(v\) является листом, присвоить \(-1\) значению \(a_v\), тогда \(a = [0, -1, -1]\)
Поскольку и первая, и вторая операция \(\mathrm{pop}\) детерминированы, это детерминированная max-куча. Также, если мы выберем \(v = 3\), то \(a\) будет детерминированной max-кучей, так что ответ — \(2\). | |
![]()
|
|
A. Простой палиндром
Конструктив
Комбинаторика
математика
*900
жадные алгоритмы
Нарек должен провести 2 часа с детьми в детском саду. Он хочет научить их спортивному программированию, и их первый урок посвящен палиндромам. Нарек выяснил, что дети знают только гласные буквы английского алфавита (буквы \(\mathtt{a}\), \(\mathtt{e}\), \(\mathtt{i}\), \(\mathtt{o}\) и \(\mathtt{u}\)), поэтому Нареку нужно составить строку, состоящую только из гласных. После составления строки он попросит детей посчитать количество подпоследовательностей, которые являются палиндромами. Нарек хочет, чтобы это было просто, поэтому он ищет строку, для которой количество палиндромных подпоследовательностей минимально. Помогите Нареку найти строку длины \(n\), состоящую из строчных гласных латинских букв (буквы \(\mathtt{a}\), \(\mathtt{e}\), \(\mathtt{i}\), \(\mathtt{o}\) и \(\mathtt{u}\)), которая минимизирует количество палиндромных\(^{\dagger}\) подпоследовательностей\(^{\ddagger}\) в ней. \(^{\dagger}\) Строка называется палиндромом, если она читается одинаково слева направо и справа налево. \(^{\ddagger}\) Строка \(t\) является подпоследовательностью строки \(s\), если \(t\) можно получить из \(s\) путем удаления нескольких (возможно, ни одного или всех) символов из \(s\) и конкатенации оставшихся, не меняя их порядок. Например, \(\mathtt{odocs}\) является подпоследовательностью \(\texttt{c}{\color{red}{\texttt{od}}}\texttt{ef}{\color{red}{\texttt{o}}}\texttt{r}{\color{red}{\texttt{c}}}\texttt{e}{\color{red}{\texttt{s}}}\). Выходные данные Для каждого набора входных данных выведите любую строку длины \(n\), которая удовлетворяет вышеуказанным условиям. Примечание В первом примере \(\texttt{uo}\) имеет только три палиндромные подпоследовательности: \(\texttt{u}\), \(\texttt{o}\) и пустую строку. Можно показать, что нет ответа лучше. В третьем примере \(\texttt{oeiiua}\) имеет только восемь палиндромных подпоследовательностей: \(\texttt{o}\), \(\texttt{e}\), \(\texttt{i}\), \(\texttt{i}\), \(\texttt{u}\), \(\texttt{a}\), \(\texttt{ii}\) и пустую строку. Можно показать, что нет ответа лучше. | |
![]()
|
|
F. Краски Доры
Перебор
Конструктив
Комбинаторика
реализация
графы
*3500
К сожалению, Дора пролила краску, когда рисовала мурал в классе. Дора рассматривает мурал как матрицу \(b\) размера \(n \times n\). Изначально \(b_{i,j} = 0\) для всех \(1 \le i, j \le n\). У Доры есть только две кисти, которые имеют два разных цвета. За одну операцию она может покрасить матрицу одной из двух кистей: - Первая кисть имеет цвет \(1\) и может покрасить один столбец матрицы. То есть, Дора выбирает целое число \(1 \leq j \leq n\) и присваивает \(b_{i,j} := 1\) для всех \(1 \leq i \leq n\);
- Вторая кисть имеет цвет \(2\) и может покрасить одну строку матрицы. То есть, Дора выбирает целое число \(1 \leq i \leq n\) и присваивает \(b_{i,j} := 2\) для всех \(1 \leq j \leq n\).
Дора раскрашивает матрицу так, чтобы полученная матрица \(b\) содержала только \(1\) и \(2\). Для матрицы \(b\) обозначим \(f(b)\) как минимальное количество операций, необходимых, чтобы превратить начальную матрицу (содержащую только \(0\)) в \(b\). Красота матрицы \(b\) равна количеству способов раскрасить начальную матрицу за ровно \(f(b)\) операций, чтобы превратить её в \(b\). Если нет способа превратить начальную матрицу в \(b\), то красота \(b\) равна \(0\). Однако Дора сделала случайную ошибку. В матрице \(a\), которую вы получили, ровно один элемент отличается от настоящей матрицы \(b\). То есть, существует ровно одна пара \((i, j)\) такая, что \(a_{i, j} = 3 - b_{i, j}\). Пожалуйста, помогите Доре вычислить ожидаемую красоту настоящей матрицы \(b\) по модулю \(998\,244\,353\) (все возможные \(n^2\) ошибок имеют равную вероятность). Поскольку размер матрицы слишком велик, Дора скажет вам только позиции \(m\) элементов цвета \(1\), а остальные \(n^2-m\) элементов имеют цвет \(2\). Выходные данные Для каждого набора входных данных выведите одно целое число — ожидаемую красоту настоящей матрицы \(b\), по модулю \(998\,244\,353\). Примечание В первом наборе входных данных матрица \(a = \left[\begin{matrix}1&1\\2&2\end{matrix}\right]\). Рассмотрим изменение элемента \((1,1)\) для вычисления ответа. Можно доказать, что минимальное количество операций для раскрашивания начальной матрицы в \(\left[\begin{matrix}2&1\\2&2\end{matrix}\right]\) равно \(3\). Сначала мы можем покрасить первую строку в цвет \(2\), затем покрасить второй столбец в цвет \(1\), и наконец покрасить вторую строку в цвет \(2\). Процесс выглядит следующим образом: \(\)\left[\begin{matrix}0&0\\0&0\end{matrix}\right]\Rightarrow\left[\begin{matrix}2&2\\0&0\end{matrix}\right]\Rightarrow\left[\begin{matrix}2&1\\0&1\end{matrix}\right]\Rightarrow\left[\begin{matrix}2&1\\2&2\end{matrix}\right]\(\) Можно доказать, что это единственный способ раскрасить матрицу за \(3\) операции. Таким образом, красота матрицы \(\left[\begin{matrix}2&1\\2&2\end{matrix}\right]\) равна \(1\). Аналогично, если изменить любой другой элемент матрицы, красота всегда равна \(1\), поэтому ожидаемая красота настоящей матрицы \(b\) равна \(1\). Во втором наборе входных данных матрица \(a = \left[\begin{matrix}1&2\\2&2\end{matrix}\right]\). Рассмотрим изменение элемента \((2, 2)\) для вычисления ответа. Можно доказать, что невозможно раскрасить начальную матрицу в \(\left[\begin{matrix}1&2\\2&1\end{matrix}\right]\), поэтому её красота равна \(0\). Если изменить любой другой элемент матрицы, красота всегда равна \(2\), поэтому ожидаемая красота равна \(\frac{0 + 2 + 2 + 2}{4} = \frac{6}{4} \equiv 499\,122\,178 \pmod {998\,244\,353}\). | |
![]()
|
|
F. Коробка Сакурако
Комбинаторика
математика
теория чисел
*1400
У Сакурако есть коробка, в которой \(n\) мячей. Каждый мяч имеет свою стоимость. Она хочет поспорить со своим другом, что если он наугад выберет из коробки два мяча (это могут быть два разных мяча, но они могут иметь одинаковое значение), то произведение их значений будет равно числу, которое загадала Сакурако. Так как Сакурако имеет докторскую степень по теории вероятностей, она знает, что наилучшее число для выбора — это математическое ожидание, но она забыла, как его вычислить. Помогите Сакурако и найдите математическое ожидание произведения двух элементов из массива. Можно показать, что математическое ожидание имеет вид \(\frac{P}{Q}\), где \(P\) и \(Q\) — неотрицательные целые числа, а \(Q \ne 0\). Сообщите значение \(P \cdot Q^{-1}(\bmod 10^9+7)\). Выходные данные Для каждого набора входных данных выведите значение \(P \cdot Q^{-1}(\bmod 10^9+7)\). Примечание Для первого теста друг Сакурако может выбрать такие пары шаров: \((a_1,a_2)\), \((a_1,a_3)\), \((a_2,a_3)\). Их произведение равно \(3\cdot 2=6\), \(3\cdot 3=9\), \(3\cdot 2=6\) соответственно, поэтому математическое ожидание равно \(\frac{6+9+6}{3}=7\). Для второго теста друг Сакурако может выбрать такие пары шаров: \((a_1,a_2)\), \((a_1,a_3)\), \((a_1,a_4)\), \((a_2,a_3)\), \((a_2,a_4)\), \((a_3,a_4)\). Их произведение равно \(2\cdot 2=4\), \(2\cdot 2=4\), \(2\cdot 4=8\), \(2\cdot 2=4\), \(2\cdot 4=8\), \(2\cdot 4=8\) соответственно, поэтому математическое ожидание равно \(\frac{4+4+8+4+8+8}{6}=\frac{36}{6}=6\). | |
![]()
|
|
E. Насквозь бюрократическая организация
Бинарный поиск
Комбинаторика
*2600
На прием в недавно открывшуюся, но уже насквозь бюрократическую организацию (сокращенно НБО) одновременно записались n человек. Поскольку организация насквозь бюрократическая, в каждый день она способна принять и обслужить ровно одного человека. Как следствие, каждому из n человек был назначен прием в один из последующих n дней, причем ни у каких двух людей день приема не совпадает. Однако работники организации подходят к работе весьма безответственно, поэтому ни одному из записавшихся людей не была сказана дата приема. Единственный способ узнать, в какие дни нужно приходить определенной группе людей — писать заявления-запросы в НБО. Бланк одного заявления-запроса состоит из m пустых строчек, в каждую из которых можно вписать имя некоторого человека из записавшихся на прием (а можно оставить пустой). При этом нельзя записывать одного и того же человека на одном заявлении дважды, иначе такой запрос игнорируется. На такие запросы в письменном виде НБО всегда отвечает очень быстро, зато некачественно — а именно, в ответ приходят верные даты приема указанных на бланке людей, однако в совершенно случайном порядке. При этом ответы на все поданные заявления-запросы приходят одновременно в конце дня (на каждом ответе указано, на какое именно заявление это ответ). К счастью, вы не входите в группу этих n счастливчиков. Ваша задача как стороннего наблюдателя — по заданным n и m определить, какое минимальное количество заявлений нужно подать в НБО, чтобы однозначно определить дату приема каждого человека. Выходные данные Выведите t строк, в каждой из которых расположен ответ на соответствующий тестовый случай (в порядке ввода) — минимальное количество заявлений, которое необходимо подать в НБО. Примечание В первом примере нужно сделать три запроса в НБО, указав в них трех разных людей. Узнав их даты приема, методом исключения можно узнать дату приема четвертого человека, поэтому четвертый запрос не нужен. Во втором примере достаточно двух заявлений. Пронумеруем людей от 1 до 4 и в первом укажем людей 1 и 2, а во втором — людей 1 и 3. Несложно убедиться, что дату приема каждого человека теперь можно однозначно определить независимо от того, какие ответы получены из НБО. В четвертом примере на прием записался всего один человек. Никаких заявлений ему подавать не надо — он записан на завтра. | |
![]()
|
|
F1. Сверхскоростной подсчёт (простая версия)
Комбинаторика
математика
дп
жадные алгоритмы
*2900
Это простая версия задачи. В трех версиях ограничения на \(n\) и ограничение по времени отличаются. Вы можете совершать взломы только в том случае, если решены все версии задачи. Это условие задачи D1B: - В ряд стоят \(n\) городов, пронумерованных \(1, 2, \ldots, n\) слева направо.
- В момент времени \(1\) вы захватываете ровно один город, называемый начальным городом.
- В моменты времени \(2, 3, \ldots, n\) вы можете выбрать город, соседний с уже захваченным, и захватить его.
Вы выиграете, если для каждого \(i\) вы захватите город \(i\) в момент времени не позже, чем \(a_i\). Выигрышная стратегия может существовать, а может и не существовать, в том числе в зависимости от стартового города. Сколько стартовых городов позволяют вам выиграть? Для каждого \(0 \leq k \leq n\) подсчитайте количество массивов целых положительных чисел \(a_1, a_2, \ldots, a_n\) таких, что - \(1 \leq a_i \leq n\) для каждого \(1 \leq i \leq n\);
- ответом на задачу D1B будет \(k\).
Ответ может быть очень большим, поэтому вы должны вычислить его по модулю заданного простого числа \(p\). Выходные данные Для каждого набора входных данных выведите \(n+1\) целых чисел: \(i\)-е целое число должно равняться количеству массивов, удовлетворяющих условиям для \(k = i-1\). Примечание В первом наборе входных данных, - массивы с \(1\) хорошим начальным городом: \([1]\).
Во втором наборе входных данных, - массивы с \(0\) хорошими начальными городами: \([1, 1]\);
- массивы с \(1\) хорошим начальным городом: \([1, 2]\), \([2, 1]\);
- массивы с \(2\) хорошими начальными городами: \([2, 2]\).
В третьем наборе входных данных, - массивы с \(0\) хороших начальных городов: \([1, 1, 1]\), \([1, 1, 2]\), \([1, 1, 3]\), \([1, 2, 1]\), \([1, 2, 2]\), \([1, 3, 1]\), \([1, 3, 2]\), \([2, 1, 1]\), \([2, 1, 2]\), \([2, 2, 1]\), \([2, 2, 2]\), \([2, 3, 1]\), \([2, 3, 2]\), \([3, 1, 1]\);
- массивы с \(1\) хорошим начальным городом: \([1, 2, 3]\), \([1, 3, 3]\), \([2, 1, 3]\), \([3, 1, 2]\), \([3, 1, 3]\), \([3, 2, 1]\), \([3, 3, 1]\);
- массивы с \(2\) хорошими начальными городами: \([2, 2, 3]\), \([2, 3, 3]\), \([3, 2, 2]\), \([3, 3, 2]\);
- массивы с \(3\) хорошими начальными городами: \([3, 2, 3]\), \([3, 3, 3]\).
| |
![]()
|
|
E1. Billetes MX (простая версия)
Бинарный поиск
Конструктив
Комбинаторика
поиск в глубину и подобное
графы
2-sat
снм
*2500
Это простая версия задачи. В этой версии гарантируется, что \(q = 0\). Вы можете совершать взломы только в том случае, если решены обе версии задачи. Целочисленная сетка \(A\) с \(p\) строками и \(q\) столбцами называется красивой, если: - Все элементы сетки являются целыми числами от \(0\) до \(2^{30}-1\), и
- Для любой подсетки XOR значений в углах равен \(0\). Формально, для любых четырех целых чисел \(i_1\), \(i_2\), \(j_1\), \(j_2\) (\(1 \le i_1 < i_2 \le p\); \(1 \le j_1 < j_2 \le q\)) должно выполняться \(A_{i_1, j_1} \oplus A_{i_1, j_2} \oplus A_{i_2, j_1} \oplus A_{i_2, j_2} = 0\), где \(\oplus\) обозначает операцию побитового исключающего ИЛИ.
Имеется частично заполненная целочисленная сетка \(G\) с \(n\) строками и \(m\) столбцами, в которой заполнены только \(k\) ячеек. Поликарп хочет узнать, сколькими способами он может распределить целые числа по незаполненным ячейкам, чтобы сетка стала красивой. Однако Монокарп считает, что эта задача слишком проста. Поэтому он выполнит \(q\) обновлений сетки. В каждом обновлении он будет выбирать незаполненную ячейку и присваивать ей целое число. Заметим, что эти обновления перманентны. То есть изменения, внесенные в сетку, будут применяться при обработке будущих обновлений. Для каждого из \(q + 1\) состояния сетки (начального состояния и после каждого из \(q\) запросов) определите количество способов, которыми Поликарп может присвоить целые числа незаполненным ячейкам, чтобы сетка стала красивой. Поскольку это число может быть очень большим, от вас требуется только вывести их значения по модулю \(10^9+7\). Выходные данные Для каждого набора входных данных выведите \(q + 1\) строку. В \(i\)-й строке вывода должен содержаться ответ для \(i\)-го состояния решетки по модулю \(10^9 + 7\). Примечание В первом наборе входных данных мы имеем следующую сетку: | \(0\) | \(6\) | \(10\) | | \(6\) | \(0\) | \(12\) | | \(10\) | \(12\) | \(?\) |
Можно доказать, что единственным допустимым значением для ячейки \((3, 3)\) является \(0\). | |
![]()
|
|
E2. Billetes MX (сложная версия)
Бинарный поиск
Структуры данных
Комбинаторика
*2600
графы
снм
Это сложная версия задачи. В этой версии гарантируется, что \(q \leq 10^5\). Вы можете совершать взломы только в том случае, если решены обе версии задачи. Целочисленная сетка \(A\) с \(p\) строками и \(q\) столбцами называется красивой, если: - Все элементы сетки являются целыми числами от \(0\) до \(2^{30}-1\), и
- Для любой подсетки XOR значений в углах равен \(0\). Формально, для любых четырех целых чисел \(i_1\), \(i_2\), \(j_1\), \(j_2\) (\(1 \le i_1 < i_2 \le p\); \(1 \le j_1 < j_2 \le q\)) должно выполняться \(A_{i_1, j_1} \oplus A_{i_1, j_2} \oplus A_{i_2, j_1} \oplus A_{i_2, j_2} = 0\), где \(\oplus\) обозначает операцию побитового исключающего ИЛИ.
Имеется частично заполненная целочисленная сетка \(G\) с \(n\) строками и \(m\) столбцами, в которой заполнены только \(k\) ячеек. Поликарп хочет узнать, сколькими способами он может распределить целые числа по незаполненным ячейкам, чтобы сетка стала красивой. Однако Монокарп считает, что эта задача слишком проста. Поэтому он выполнит \(q\) обновлений сетки. В каждом обновлении он будет выбирать незаполненную ячейку и присваивать ей целое число. Заметим, что эти обновления перманентны. То есть изменения, внесенные в сетку, будут применяться при обработке будущих обновлений. Для каждого из \(q + 1\) состояния сетки (начального состояния и после каждого из \(q\) запросов) определите количество способов, которыми Поликарп может присвоить целые числа незаполненным ячейкам, чтобы сетка стала красивой. Поскольку это число может быть очень большим, от вас требуется только вывести их значения по модулю \(10^9+7\). Выходные данные Для каждого набора входных данных выведите \(q + 1\) строку. В \(i\)-й строке вывода должен содержаться ответ для \(i\)-го состояния решетки по модулю \(10^9 + 7\). Примечание В первом наборе входных данных мы изначально имеем следующую сетку: | \(0\) | \(6\) | \(10\) | | \(6\) | \(0\) | \(12\) | | \(10\) | \(12\) | \(?\) |
Можно доказать, что единственным допустимым значением для ячейки \((3, 3)\) является \(0\), поэтому первый ответ — \(1\). Для второго запроса ячейка не удовлетворяет условию, поэтому ответ — \(0\). | |
![]()
|
|
B. Биномиальные коэффициенты, ну типа
Комбинаторика
математика
дп
*1100
Недавно акшиМ столкнулся с задачей, для решения которой нужны были биномиальные коэффициенты. Он написал код, который выглядел так: for (int n = 0; n < N; n++) { // цикл по n от 0 до N-1 включительно
C[n][0] = 1;
C[n][n] = 1;
for (int k = 1; k < n; k++) // цикл по k от 1 до n-1 включительно
C[n][k] = C[n][k - 1] + C[n - 1][k - 1];
}
К сожалению, он допустил ошибку, так как правильная формула следующая: C[n][k] = C[n - 1][k] + C[n - 1][k - 1];
Но его сокомандник, кеблидА, заинтересовался значениями, которые были получены с использованием неправильной формулы. Пожалуйста, помогите ему вычислить эти коэффициенты для \(t\) различных пар \((n_i, k_i)\). Обратите внимание: их необходимо вычислить в соответствии с первой (неправильной) формулой. Поскольку значения \(C[n_i][k_i]\) могут быть слишком большими, выводите их по модулю \(10^9 + 7\). Выходные данные Выведите \(t\) целых чисел \(C[n_i][k_i]\) по модулю \(10^9 + 7\). | |
![]()
|
|
E. Карточная игра
Комбинаторика
математика
дп
жадные алгоритмы
*2200
бпф
В самой популярной карточной игре в Берляндии используется колода из \(n \times m\) карт. У каждой карты есть два параметра: масть и ранг. Масти в игре пронумерованы от \(1\) до \(n\), а ранги пронумерованы от \(1\) до \(m\). Для каждой комбинации масти и ранга существует ровно одна карта в колоде. Карта с мастью \(a\) и рангом \(b\) может побить карту с мастью \(c\) и рангом \(d\) в одном из двух случаев: - \(a = 1\), \(c \ne 1\) (карта масти \(1\) может побить карту любой другой масти);
- \(a = c\), \(b > d\) (карта может побить любую другую карту той же масти, но ниже рангом).
В игру играют два игрока. Перед началом игры они получают ровно по половине колоды. Первый игрок выигрывает, если для каждой карты второго игрока он может выбрать свою карту, которая ее может побить, и при этом не будет выбирать свои карты повторно (то есть существует такое разбиение на пары карт первого игрока с картами второго игрока так, чтобы в каждой паре карта первого игрока била карту второго игрока). Иначе выигрывает второй игрок. Ваша задача — посчитать количество способов распределить карты так, чтобы выиграл первый игрок. Два способа считаются различными, если существует такая карта, что в одном она принадлежит первому игроку, а в другом — второму. Количество способов может быть очень большим, поэтому выведите его по модулю \(998244353\). Выходные данные Выведите единственное целое число — количество способов распределить карты так, чтобы выиграл первый игрок, взятое по модулю \(998244353\). | |
![]()
|
|
E. Приключения Алисы в кроличьей норе
Деревья
Теория вероятностей
Комбинаторика
математика
дп
поиск в глубину и подобное
жадные алгоритмы
*2300
игры
Алиса находится на дне кроличьей норы! Кроличья нора может быть смоделирована как дерево\(^{\text{∗}}\), у которого выход находится на вершине \(1\), а Алиса начинает с некоторой вершины \(v\). Она хочет выбраться из норы, но, к сожалению, Дама Червей приказала её казнить. Каждую минуту подбрасывается обычная монета. Если выпадает орёл, Алиса может переместиться в любую вершину, смежную со своим текущим положением, а если решка, Дама Червей может перетащить Алису на смежную вершину по своему выбору. Если Алиса когда-либо окажется на любом из некорневых листьев\(^{\text{†}}\) дерева, Алиса проигрывает. Предполагая, что они обе действуют оптимально, для каждой начальной вершины \(1\le v\le n\) вычислите вероятность того, что Алиса сможет убежать. Поскольку эти вероятности могут быть очень малыми, выведите их по модулю \(998\,244\,353\). Формально, пусть \(M = 998\,244\,353\). Можно показать, что точный ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Выходные данные Для каждого набора входных данных выведите \(n\) целых чисел в одной строке — вероятности того, что Алиса убежит, начиная с вершины \(1, 2, \ldots, n\). Поскольку эти вероятности могут быть очень малыми, выведите их по модулю \(998\,244\,353\). Примечание Для первого набора входных данных: - Алиса убегает из корня (вершина \(1\)) по определению с вероятностью \(1\).
- Алиса немедленно проигрывает из вершин \(4\) и \(5\), так как они являются листьями.
- Из других двух вершин Алиса убегает с вероятностью \(\frac 12\), так как Дама перетащит её к листьям.
| |
![]()
|
|
H. Распространение сообщения
Перебор
Комбинаторика
дп
битмаски
*3500
Дан неориентированный граф с \(n\) вершинами и \(m\) рёбрами. Каждое ребро соединяет две вершины \((u, v)\) и каждый день появляется с вероятностью \(\frac{p}{q}\). Изначально в вершине \(1\) есть сообщение. В конце дня вершина имеет сообщение тогда и только тогда, когда сама она или хотя бы одна из смежных с ней вершин имела сообщение в прошлый день. Обратите внимание, что каждый день ребро выбирает своё появление независимо. Вычислите математическое ожидание количества дней, прежде чем все вершины получат сообщение, по модулю \(998\,244\,353\). Выходные данные Выведите одно целое число в единственной строке вывода — математическое ожидание количества дней, по модулю \(998\,244\,353\). Формально, пусть \(M = 998\,244\,353\). Можно показать, что точный ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Примечание В первом тесте ответ равен математическому ожиданию количества дней, прежде чем появится единственное ребро в графе, и оно равно \(\frac{1}{0.1}=10\). Во втором тесте ответ равен \(\frac{20}{9}\), прежде чем он будет взят по модулю \(998\,244\,353\). В третьем тесте единственная вершина уже имеет сообщение, поэтому ответ равен \(0\). | |
![]()
|
|
B. Минимизируйте единичность
Конструктив
Комбинаторика
математика
*800
игры
Для произвольной бинарной строки \(t\)\(^{\text{∗}}\), пусть \(f(t)\) — количество непустых подпоследовательностей\(^{\text{†}}\) \(t\), которые содержат только символы \(\mathtt{0}\), и пусть \(g(t)\) — это количество непустых подпоследовательностей \(t\), которые содержат хотя бы одну \(\mathtt{1}\). Обратите внимание, что для \(f(t)\) и \(g(t)\) каждая подпоследовательность считается столько раз, сколько раз она встречается в \(t\). Например, \(f(\mathtt{000}) = 7, g(\mathtt{100}) = 4\). Назовём единичностью бинарной строки \(t\) значение \(|f(t)-g(t)|\), где \(|z|\) обозначает абсолютное значение \(z\) для любого числа \(z\). Вам дано целое положительное число \(n\). Найдите бинарную строку \(s\) длины \(n\), такую, чтобы её единичность была как можно меньше. Если строк несколько, вы можете вывести любую из них. Выходные данные Для каждого набора входных данных выведите \(s\) на отдельной строке. Если существует несколько ответов, выведите любой. Примечание В первом наборе входных данных \(f(t)=1\), потому что существует одна подпоследовательность, содержащая только \(\mathtt{0}\) (подпоследовательность \(\mathtt{0}\)), и \(g(t)=0\), потому что нет подпоследовательностей, содержащих хотя бы одну \(1\). Единичность равна \(|1-0|=1\). Строка \(\mathtt{1}\) также является корректным ответом, так как её единичность равна \(|0-1|=1\). Во втором наборе входных данных \(f(t)=1\), потому что существует одна непустая подпоследовательность, содержащая только \(\mathtt{0}\), и \(g(t)=2\), потому что существуют две непустые подпоследовательности, содержащие хотя бы одну \(\mathtt{1}\) (\(\mathtt{01}\) и \(\mathtt{1}\)). Таким образом, единичность равна \(|1-2|=1\). Можно показать, что \(1\) — это минимально возможное значение единичности среди всех бинарных строк длины \(2\). | |
![]()
|
|
E. MEXимизируйте счёт
Структуры данных
Комбинаторика
математика
реализация
дп
жадные алгоритмы
*2200
Предположим, что мы разбиваем элементы массива \(b\) на \(k\) непустых мультимножеств \(S_1, S_2, \ldots, S_k\), где \(k\) — произвольное целое положительное число. Определим счёт \(b\) как максимальное значение \(\operatorname{MEX}(S_1)\)\(^{\text{∗}}\)\( + \operatorname{MEX}(S_2) + \ldots + \operatorname{MEX}(S_k)\) среди всех возможных разбиений \(b\) для любого целого числа \(k\). Вашему завистнику дан массив \(a\) длины \(n\). Поскольку он знает, что вычислить счёт массива \(a\) для вас слишком просто, он просит вас вычислить сумму счётов всех \(2^n - 1\) непустых подпоследовательностей массива \(a\).\(^{\text{†}}\) Поскольку ответ может быть очень большим, выведите его по модулю \(998\,244\,353\). Выходные данные Для каждого набора входных данных выведите ответ по модулю \(998\,244\,353\). Примечание В первом наборе входных данных мы должны рассмотреть семь подпоследовательностей: - \([0]\): Счёт равен \(1\).
- \([0]\): Счёт равен \(1\).
- \([1]\): Счёт равен \(0\).
- \([0,0]\): Счёт равен \(2\).
- \([0,1]\): Счёт равен \(2\).
- \([0,1]\): Счёт равен \(2\).
- \([0,0,1]\): Счёт равен \(3\).
Ответ для первого набора входных данных составляет \(1+1+2+2+2+3=11\). В последнем наборе входных данных все подпоследовательности имеют счёт \(0\). | |
![]()
|
|
G1. Уничтожение Вселенной (простая версия)
Комбинаторика
математика
жадные алгоритмы
*2900
Это простая версия задачи. В этой версии \(n \leq 5000\). Вы можете совершать взломы только в том случае, если решены обе версии задачи. Орангутаны — могущественные существа — настолько могущественные, что им нужна всего \(1\) единица времени, чтобы уничтожить все уязвимые планеты во Вселенной! Во Вселенной существует \(n\) планет. Каждая планета имеет интервал уязвимости \([l, r]\), в течение которого она будет подвержена разрушению орангутанами. Орангутаны также могут расширять интервал уязвимости любой планеты на \(1\) единицу. В частности, предположим, что расширение происходит на планете \(p\) с интервалом уязвимости \([l_p, r_p]\). Тогда результирующий интервал уязвимости может быть либо \([l_p - 1, r_p]\), либо \([l_p, r_p + 1]\). При заданном множестве планет орангутаны могут уничтожить все планеты, если интервалы уязвимости всех планет из множества пересекаются хотя бы в одной общей точке. Назовём счётом такого набора минимальное количество расширений, которое необходимо выполнить. Орангутанов интересует сумма счётов всех непустых подмножеств планет во Вселенной. Поскольку ответ может быть очень большим, выведите его по модулю \(998\,244\,353\). Выходные данные Для каждого набора входных данных выведите целое число — сумму счётов всех непустых подмножеств планет во Вселенной, по модулю \(998\,244\,353\). Примечание В первом наборе входных данных есть семь непустых подмножеств планет, которые мы должны рассмотреть: - Для каждого из подмножеств \(\{[1,1]\}, \{[2,3]\}, \{[3,3]\}\), оценка равна \(0\).
- Для подмножества \(\{[2,3], [3,3]\}\) оценка равна \(0\), потому что точка \(3\) уже содержится в интервале уязвимости обеих планет.
- Для подмножества \(\{[1,1], [2,3]\}\) оценка равна \(1\). Используя одну операцию по изменению интервала уязвимости второй планеты на \([1,3]\), обе планеты теперь имеют точку \(1\) в своем интервале.
- Для подмножества \(\{[1,1], [3,3]\}\) оценка равна \(2\). С помощью двух операций по изменению интервала уязвимости первой планеты на \([1,3]\), обе планеты теперь имеют точку \(3\) в своем интервале.
- Для подмножества \(\{[1,1], [2,3], [3,3]\}\) оценка равна \(2\). С помощью одной операции по изменению интервала уязвимости первой планеты на \([1,2]\) и одной операции по изменению интервала уязвимости третьей планеты на \([2,3]\), все три планеты будут иметь точку \(2\) в своем интервале.
Сумма оценок всех непустых подмножеств первого набора входных данных равна \(0 \cdot 4 + 1 \cdot 1 + 2\cdot2 = 5\). | |
![]()
|
|
G2. Уничтожение Вселенной (сложная версия)
Комбинаторика
математика
*3100
Это сложная версия задачи. В этой версии \(n \leq 10^6\). Вы можете совершать взломы только в том случае, если решены обе версии задачи. Орангутаны — могущественные существа — настолько могущественные, что им нужна всего \(1\) единица времени, чтобы уничтожить все уязвимые планеты во Вселенной! Во Вселенной существует \(n\) планет. Каждая планета имеет интервал уязвимости \([l, r]\), в течение которого она будет подвержена разрушению орангутанами. Орангутаны также могут расширять интервал уязвимости любой планеты на \(1\) единицу. В частности, предположим, что расширение происходит на планете \(p\) с интервалом уязвимости \([l_p, r_p]\). Тогда результирующий интервал уязвимости может быть либо \([l_p - 1, r_p]\), либо \([l_p, r_p + 1]\). При заданном множестве планет орангутаны могут уничтожить все планеты, если интервалы уязвимости всех планет из множества пересекаются хотя бы в одной общей точке. Назовём счётом такого набора минимальное количество расширений, которое необходимо выполнить. Орангутанов интересует сумма счётов всех непустых подмножеств планет во Вселенной. Поскольку ответ может быть очень большим, выведите его по модулю \(998\,244\,353\). Выходные данные Для каждого набора входных данных выведите целое число — сумму счётов всех непустых подмножеств планет во Вселенной, по модулю \(998\,244\,353\). Примечание В первом наборе входных данных есть семь непустых подмножеств планет, которые мы должны рассмотреть: - Для каждого из подмножеств \(\{[1,1]\}, \{[2,3]\}, \{[3,3]\}\), оценка равна \(0\).
- Для подмножества \(\{[2,3], [3,3]\}\) оценка равна \(0\), потому что точка \(3\) уже содержится в интервале уязвимости обеих планет.
- Для подмножества \(\{[1,1], [2,3]\}\) оценка равна \(1\). Используя одну операцию по изменению интервала уязвимости второй планеты на \([1,3]\), обе планеты теперь имеют точку \(1\) в своем интервале.
- Для подмножества \(\{[1,1], [3,3]\}\) оценка равна \(2\). С помощью двух операций по изменению интервала уязвимости первой планеты на \([1,3]\), обе планеты теперь имеют точку \(3\) в своем интервале.
- Для подмножества \(\{[1,1], [2,3], [3,3]\}\) оценка равна \(2\). С помощью одной операции по изменению интервала уязвимости первой планеты на \([1,2]\) и одной операции по изменению интервала уязвимости третьей планеты на \([2,3]\), все три планеты будут иметь точку \(2\) в своем интервале.
Сумма оценок всех непустых подмножеств первого набора входных данных равна \(0 \cdot 4 + 1 \cdot 1 + 2\cdot2 = 5\). | |
![]()
|
|
F. Арахис
Комбинаторика
математика
дп
*2700
игры
Имея волшебную бобовую палку, Джек в последнее время собирал много арахисов. В конечном итоге он получил \(n\) мешков с арахисом, удобно пронумерованных от \(1\) до \(n\) слева направо. В \(i\)-м мешке находится \(a_i\) арахисов. Джек и его подруга детства Алиса решили сыграть в игру с арахисом. Сначала Алиса делит мешки на несколько коробок; каждая коробка будет содержать ненулевое количество последовательных мешков, и каждый мешок, очевидно, будет лежать в ровно одной коробке. При этом Алиса не меняет порядок коробок, то есть коробки пронумерованы в порядке возрастания номеров мешков в них. После этого Алиса и Джек будут по очереди делать ходы, при этом Алиса ходит первой. На каждом ходе текущий игрок будет забирать положительное количество арахисов из ровно одного мешка, который лежит в самой левой непустой коробке (т.е. самой левой коробке, содержащей хотя бы один непустой мешок). Другими словами, если мы пронумеруем коробки слева направо, то каждый игрок может забирать арахисы из мешка в \(j\)-й коробке (\(j \ge 2\)) только в том случае, если в \((j - 1)\)-й коробке не осталось арахисов. Игрок, который не может сделать допустимый ход, проигрывает. Алиса уверена, что она выиграет, так как у нее есть преимущество в том, что она сама делит мешки на коробки. Она хочет знать, сколько существует способов разделить мешки на коробки в начале игры, чтобы она выиграла, предполагая, что оба игрока играют оптимально. Можете помочь ей с расчетами? Поскольку результат может быть очень большим, выведите его по модулю \(998\,244\,353\). Выходные данные Для каждого набора входных данных выведите одно целое число — количество способов для Алисы разделить мешки на коробки в начале игры, чтобы гарантировать ее победу, предполагая, что оба игрока играют оптимально, по модулю \(998\,244\,353\). Примечание В первом наборе входных данных единственный способ для Алисы выиграть — это разделить мешки на две коробки следующим образом: \(([1, 2], [3])\) (первая коробка содержит первые два мешка, а вторая коробка содержит третий мешок). Алиса выигрывает, забирая оба арахиса из второго мешка, оставляя Джеку \(([1], [3])\). Джек вынужден забрать единственный оставшийся арахис в первой коробке, что позволяет Алисе забрать оставшиеся в второй коробке. Во втором наборе входных данных выигрышные разделения для Алисы — это \(([1], [2, 3, 1])\), \(([1, 2, 3, 1])\), \(([1, 2], [3], [1])\) и \(([1, 2], [3, 1])\). В третьем наборе входных данных Алиса всегда выигрывает, независимо от того, как она разделяет мешки на коробки. В четвертом наборе входных данных Алиса всегда проигрывает, независимо от того, как она разделяет мешки на коробки. | |
![]()
|
|
E. Гармония перестановок
Конструктив
Комбинаторика
математика
жадные алгоритмы
хэши
*2200
Райан хочет преподнести Рейхане подарок, чтобы завоевать её сердце. Однако Рейхане привередлива и примет только k-гармоничное множество перестановок. Определим k-гармоничное множество перестановок как набор \(k\) попарно различных перестановок \(p_1, p_2, \ldots, p_k\) такого размера \(n\), что для каждой пары индексов \(i\) и \(j\) (где \(1 \leq i, j \leq n\)) выполняется следующее условие: \(\) p_1[i] + p_2[i] + \ldots + p_k[i] = p_1[j] + p_2[j] + \ldots + p_k[j] \(\) Ваша задача состоит в том, чтобы помочь Райану, либо предоставив допустимое k-гармоничное множество перестановок для заданных значений \(n\) и \(k\), либо определив, что такого набора не существует. Мы называем последовательность длины \(n\) перестановкой, если она содержит каждое целое число от \(1\) до \(n\) ровно один раз. Выходные данные Для каждого набора входных данных, если k-гармоничное множество перестановок существует, выведите YES в первой строке. Затем выведите \(k\) строк, которые содержат различные перестановки целых чисел от \(1\) до \(n\). Если такого набора не существует, в единственной строке выведите NO. Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Например, строки «yEs», «yes», «Yes» и «YES» будут приняты как положительный ответ. Если существует несколько ответов, вы можете вывести любой из них. Примечание В 1 наборе входных данных мы имеем \(p_1 = [1, 2, 3]\), \(p_2 = [2, 3, 1]\), и \(p_3 = [3, 1, 2]\). Можно заметить, что \(p_1[1] + p_2[1] + p_3[1] = p_1[2] + p_2[2] + p_3[2] = p_1[3] + p_2[3] + p_3[3] = 6\). Во 2 наборе входных данных у нас есть \(p_1 = [1, 2, 3, 4]\) и \(p_2 = [4, 3, 2, 1]\). Можно заметить, что \(p_1[1] + p_2[1] = p_1[2] + p_2[2] = p_1[3] + p_2[3] = p_1[4] + p_2[4] = 5\). В 3 наборе входных данных, поскольку в \(p_1\) есть пять различных элементов, очевидно, что ответ — «No». | |
![]()
|
|
F1. Хайям и Королевский указ (простая версия)
Комбинаторика
математика
дп
сортировки
*2500
Это простая версия задачи. В двух версиях отличаются ограничения на \(k\) и на сумму \(k\). В древней Персии Хайям, умный купец и математик, играет в игру со своим драгоценным сундуком с сокровищами. Сундук содержит \(n\) красных рубинов стоимостью \(2\) динара каждый и \(m\) синих сапфиров стоимостью \(1\) динар каждый. У него также есть мешок, в котором изначально ничего нет, и \(k\) свитков с парами \((r_1, b_1), (r_2, b_2), \ldots, (r_k, b_k)\), описывающими особые состояния.  Игра состоит из \(n + m\) таких ходов: - Хайям случайно равновероятно достает драгоценный камень из сундука.
- Он кладет данный камень в свой мешок.
- Если существует свиток \(i\) (\(1 \leq i \leq k\)), для которого в сундуке находятся ровно \(r_i\) красных рубинов и \(b_i\) синих сапфиров, то по королевскому указу стоимость всех драгоценных камней в его мешке удваивается в качестве награды за достижение особого состояния.
Обратите внимание, что стоимость некоторых драгоценных камней может быть изменена несколькими указами, и тогда она удваивается несколько раз. Определите математическое ожидание стоимости камней в мешке Хайяма в конце игры по модулю \(998,244,353\). Формально, пусть \(M = 998,244,353\). Можно показать, что точный ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Выходные данные Для каждого набора входных данных выведите одно целое число: математическое ожидание стоимости камней в мешке Хайяма в конце процесса по модулю \(998,244,353\). Примечание В первом наборе входных данных, в конце процесса всегда будет \(3\) красных рубина и \(4\) синих сапфира. Ни одно из особых состояний, описанных в свитках, не соблюдено, поэтому стоимость мешка Хайяма остается неизменной. Общая стоимость мешка в конце всегда равна \(2 \cdot 3 + 1 \cdot 4 = 10\). Во втором наборе входных данных рассмотрим два случая: - С вероятностью \(1/2\) Хайям вытянет красный рубин, и стоимость его мешка станет равна \(2\). Затем, с вероятностью \(1\) он вытянет синий сапфир, и стоимость его мешка станет равной \(3\).
- С вероятностью \(1/2\) Хайям вытянет синий сапфир, и стоимость его мешка станет равной \(1\). На данный момент в сундуке находятся \(r_1 = 1\) красный рубин и \(b_1 = 0\) синих сапфиров, что соответствует особому состоянию, описанному в свитке. В результате стоимость мешка удваивается до \(2 \cdot 1 = 2\). Затем, с вероятностью \(1\), он вытянет красный рубин, и стоимость его мешка возрастёт до \(4\).
Таким образом, ожидаемая стоимость в конце равна \(\frac{1}{2} \cdot 3 + \frac{1}{2} \cdot 4 = \frac{7}{2}\), что равно \(499,122,180\) по модулю \(998,244,353\). | |
![]()
|
|
F2. Хайям и Королевский указ (сложная версия)
Комбинаторика
математика
дп
*2800
сортировки
Это сложная версия задачи. В двух версиях отличаются ограничения на \(k\) и на сумму \(k\). В древней Персии Хайям, умный купец и математик, играет в игру со своим драгоценным сундуком с сокровищами. Сундук содержит \(n\) красных рубинов стоимостью \(2\) динара каждый и \(m\) синих сапфиров стоимостью \(1\) динар каждый. У него также есть мешок, в котором изначально ничего нет, и \(k\) свитков с парами \((r_1, b_1), (r_2, b_2), \ldots, (r_k, b_k)\), описывающими особые состояния.  Игра состоит из \(n + m\) таких ходов: - Хайям случайно равновероятно достает драгоценный камень из сундука.
- Он кладет данный камень в свой мешок.
- Если существует свиток \(i\) (\(1 \leq i \leq k\)), для которого в сундуке находятся ровно \(r_i\) красных рубинов и \(b_i\) синих сапфиров, то по королевскому указу стоимость всех драгоценных камней в его мешке удваивается в качестве награды за достижение особого состояния.
Обратите внимание, что стоимость некоторых драгоценных камней может быть изменена несколькими указами, и тогда она удваивается несколько раз. Определите математическое ожидание стоимости камней в мешке Хайяма в конце игры по модулю \(998,244,353\). Формально, пусть \(M = 998,244,353\). Можно показать, что точный ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Выходные данные Для каждого набора входных данных выведите одно целое число: математическое ожидание стоимости камней в мешке Хайяма в конце процесса по модулю \(998,244,353\). Примечание В первом наборе входных данных, в конце процесса всегда будет \(3\) красных рубина и \(4\) синих сапфира. Ни одно из особых состояний, описанных в свитках, не соблюдено, поэтому стоимость мешка Хайяма остается неизменной. Общая стоимость мешка в конце всегда равна \(2 \cdot 3 + 1 \cdot 4 = 10\). Во втором наборе входных данных рассмотрим два случая: - С вероятностью \(1/2\) Хайям вытянет красный рубин, и стоимость его мешка станет равна \(2\). Затем, с вероятностью \(1\) он вытянет синий сапфир, и стоимость его мешка станет равной \(3\).
- С вероятностью \(1/2\) Хайям вытянет синий сапфир, и стоимость его мешка станет равной \(1\). На данный момент в сундуке находятся \(r_1 = 1\) красный рубин и \(b_1 = 0\) синих сапфиров, что соответствует особому состоянию, описанному в свитке. В результате стоимость мешка удваивается до \(2 \cdot 1 = 2\). Затем, с вероятностью \(1\), он вытянет красный рубин, и стоимость его мешка возрастёт до \(4\).
Таким образом, ожидаемая стоимость в конце равна \(\frac{1}{2} \cdot 3 + \frac{1}{2} \cdot 4 = \frac{7}{2}\), что равно \(499,122,180\) по модулю \(998,244,353\). | |
![]()
|
|
G. Исследование Натлана
Структуры данных
Комбинаторика
математика
дп
теория чисел
*2000
битмаски
Вы исследуете потрясающий регион Натлан! Этот регион состоит из \(n\) городов, и каждый город имеет рейтинг привлекательности \(a_i\). Направленное ребро существует от города \(i\) к городу \(j\) тогда и только тогда, когда \(i < j\) и \(\gcd(a_i,a_j)\neq 1\), где \(\gcd(x, y)\) обозначает наибольший общий делитель (НОД) целых чисел \(x\) и \(y\). Начав с города \(1\), ваша задача — определить общее количество различных путей, которыми вы можете добраться до города \(n\), по модулю \(998\,244\,353\). Два пути различны тогда и только тогда, когда множество посещённых городов различно. Выходные данные Выведите общее количество различных путей, которыми вы можете добраться до города \(n\), по модулю \(998\,244\,353\). Примечание В первом примере пять путей следующие: - Город \(1\rightarrow\) Город \(5\)
- Город \(1\rightarrow\) Город \(2\rightarrow\) Город \(5\)
- Город \(1\rightarrow\) Город \(2\rightarrow\) Город \(3\rightarrow\) Город \(5\)
- Город \(1\rightarrow\) Город \(2\rightarrow\) Город \(4\rightarrow\) Город \(5\)
- Город \(1\rightarrow\) Город \(4\rightarrow\) Город \(5\)
Во втором примере два пути следующие: - Город \(1\rightarrow\) Город \(3\rightarrow\) Город \(5\)
- Город \(1\rightarrow\) Город \(2\rightarrow\) Город \(3\rightarrow\) Город \(5\)
| |
![]()
|
|
F. Alternative Platforms
Структуры данных
Комбинаторика
математика
сортировки
*2500
бпф
Suppose you are working in the Ministry of Digital Development of Berland, and your task is to monitor the industry of video blogging. There are \(n\) bloggers in Berland. Recently, due to the poor state of the main video platform in Berland, two alternative platforms were introduced. That's why bloggers started to reupload their videos to these alternative platforms. You've got the statistics that the \(i\)-th blogger uploaded \(v_i\) videos to the first alternative platform and \(r_i\) videos to the second alternative platform. You think that a potential user will be upset if even at least one of his favorite bloggers doesn't upload anything. However, if a blogger uploads videos to both platforms, the user will watch that blogger on the platform where more videos are available. So, you've come up with the following function to estimate user experience. Suppose a user watches \(k\) bloggers \(b_1, b_2, \dots, b_k\); then, let user experience be \(\)E(b_1, \dots, b_k) = \max\left(\min_{i=1..k}{v[b_i]}, \min_{i=1..k}{r[b_i]}\right).\(\) In order to get some statistics, you want to calculate the value \(\mathit{avg}_k\) that is equal to an average experience among all subsets of bloggers of size \(k\). Also, you have to calculate \(\mathit{avg}_k\) for each \(k\) from \(1\) to \(n\). Since answers may be too large, print them modulo \(998\,244\,353\). Output Print \(n\) integers \(\mathit{avg}_1, \mathit{avg}_2, \dots, \mathit{avg}_n\). It can be proven that \(\mathit{avg}_k\) may be represented as an irreducible fraction \(\dfrac{x}{y}\) where \(y \not\equiv 0 \pmod{998\,244\,353}\). So, print \(\mathit{avg}_k\) in a form \(x \cdot y^{-1} \bmod 998\,244\,353\). Note In the first example, \(332748119\) is \(\frac{4}{3}\). In the third example, \(199648873\) is \(\frac{12}{5}\). | |
![]()
|
|
E. Shohag любит инверсии
Комбинаторика
математика
реализация
дп
*2200
У Shohag есть массив целых чисел \(a\). Изначально \(a = [0, 1]\). Он может выполнять следующую операцию любое количество раз: - Пусть \(k\) — количество инверсий\(^{\text{∗}}\) в текущем массиве \(a\).
- Вставить \(k\) на любую позицию в \(a\), в том числе возможно в начало или конец.
Например, если \(a = [4, 6, 2, 4]\), то количество инверсий равно \(k = 3\). Таким образом, после операции вы можете получить следующие массивы: \([\textbf{3}, 4, 6, 2, 4]\), \([4, \textbf{3}, 6, 2, 4]\), \([4, 6, \textbf{3}, 2, 4]\), \([4, 6, 2, \textbf{3}, 4]\), и \([4, 6, 2, 4, \textbf{3}]\). По заданному целому числу \(n\), помогите Shohag подсчитать количество различных массивов длины \(n\), которые можно получить после выполнения операций, по модулю \(998\,244\,353\). Выходные данные Для каждого набора входных данных выведите целое число — количество массивов по модулю \(998\,244\,353\). Примечание В первом наборе входных данных можно получить следующие \(5\) массивов (вставленное количество инверсий выделено жирным шрифтом): - \([0, 1] \rightarrow [0, \textbf{0}, 1] \rightarrow [0, 0, 1, \textbf{0}]\),
- \([0, 1] \rightarrow [0, \textbf{0}, 1] \rightarrow [0, 0, \textbf{0}, 1]\),
- \([0, 1] \rightarrow [0, 1, \textbf{0}] \rightarrow [0, 1, 0, \textbf{1}]\),
- \([0, 1] \rightarrow [0, 1, \textbf{0}] \rightarrow [0, 1, \textbf{1}, 0]\),
- \([0, 1] \rightarrow [0, 1, \textbf{0}] \rightarrow [\textbf{1}, 0, 1, 0]\).
| |
![]()
|
|
F1. Shohag любит считать (простая версия)
Комбинаторика
математика
дп
теория чисел
*2800
Это простая версия задачи. Единственные различия между двумя версиями этой задачи — ограничения на \(t\), \(m\) и сумму \(m\). Вы можете совершать взломы только в том случае, если решены обе версии задачи. Для массива целых чисел \(a\) длины \(n\) определим \(f(k)\) как наибольший общий делитель (НОД) максимальных значений всех подмассивов\(^{\text{∗}}\) длины \(k\). Например, если массив равен \([2, 1, 4, 6, 2]\), то \(f(3) = \operatorname{gcd}(\operatorname{max}([2, 1, 4]), \operatorname{max}([1, 4, 6]), \operatorname{max}([4, 6, 2])) = \operatorname{gcd}(4, 6, 6) = 2\). Массив является хорошим, если для всех пар \(1 \le i \lt j \le n\) выполняется \(f(i) \neq f(j)\). У Shohag есть целое число \(m\). Помогите ему подсчитать количество непустых хороших массивов произвольной длины, каждый элемент которых является целым числом от \(1\) до \(m\), по модулю \(998\,244\,353\). Выходные данные Для каждого набора входных данных выведите целое число — количество подходящих массивов по модулю \(998\,244\,353\). Примечание В первом наборе входных данных подходящими массивами являются \([1]\), \([1, 2]\), \([2]\) и \([2, 1]\). Во втором наборе входных данных всего \(29\) подходящих массивов. В частности, массив \([2, 1, 4]\) длины \(n = 3\) подходит, так как все его элементы принадлежат отрезку от \(1\) до \(m = 5\) и \(f(1)\), \(f(2)\) и \(f(n = 3)\) различны: - \(f(1) = \operatorname{gcd}(\operatorname{max}([2]), \operatorname{max}([1]), \operatorname{max}([4])) = \operatorname{gcd}(2, 1, 4) = 1.\)
- \(f(2) = \operatorname{gcd}(\operatorname{max}([2, 1]), \operatorname{max}([1, 4])) = \operatorname{gcd}(2, 4) = 2.\)
- \(f(3) = \operatorname{gcd}(\operatorname{max}([2, 1, 4])) = \operatorname{gcd}(4) = 4.\)
| |
![]()
|
|
A. Маленький Слоник и промежуток
Бинарный поиск
Комбинаторика
дп
*1500
Маленький Слоник очень любит суммы на промежутках. В этот раз у него есть пара целых чисел l и r (l ≤ r). Маленькому Слонику нужно найти количество таких целых чисел x (l ≤ x ≤ r), что первая цифра числа x равна последней (в десятичном представлении). Например, такие числа как 101, 477474 или 9 он будет включать в ответ, в то время как 47, 253 или 1020 — нет. Помогите ему, посчитайте описанное количество чисел x для заданной пары l и r. Выходные данные В единственной строке выведите одно целое число — ответ на задачу. Примечание В первом примере в ответ входят следующие числа: 2, 3, 4, 5, 6, 7, 8, 9, 11, 22, 33, 44. | |
![]()
|
|
C. Упорядоченные перестановки
Конструктив
Комбинаторика
математика
*1600
жадные алгоритмы
битмаски
Рассмотрим перестановку\(^{\text{∗}}\) \(p_1, p_2, \ldots, p_n\) чисел от \(1\) до \(n\). Введём следующую сумму\(^{\text{†}}\): \(\)S(p) = \sum_{1 \le l \le r \le n} \min(p_l, p_{l + 1}, \ldots, p_r)\(\) Рассмотрим все перестановки длины \(n\) с максимальным значением \(S(p)\). Необходимо вывести \(k\)-ю из них в лексикографическом\(^{\text{‡}}\) порядке, или сообщить, что их меньше \(k\). Выходные данные Для каждого набора входных данных, если подходящих перестановок меньше \(k\), выведите \(-1\). Иначе выведите \(k\)-ю подходящую перестановку. Примечание Посчитаем искомую сумму для всех перестановок длины \(3\) в лексикографическом порядке: | Перестановка | Значение \(S(p)\) | | \([1, 2, 3]\) | \(10\) | | \([1, 3, 2]\) | \(10\) | | \([2, 1, 3]\) | \(9\) | | \([2, 3, 1]\) | \(10\) | | \([3, 1, 2]\) | \(9\) | | \([3, 2, 1]\) | \(10\) |
В первом наборе необходимо вывести вторую подходящую перестановку длины \(3\). Посмотрев на таблицу, мы видим, что это перестановка \([1, 3, 2]\). Во втором наборе необходимо вывести третью подходящую перестановку длины \(3\). Посмотрев на таблицу, мы видим, что это перестановка \([2, 3, 1]\). | |
![]()
|
|
E. Контроль случайности
Деревья
Теория вероятностей
Комбинаторика
математика
*2100
дп
поиск в глубину и подобное
жадные алгоритмы
графы
Дано дерево с \(n\) вершинами. В некоторую вершину \(v \ne 1\) посадят робота. Пусть у вас изначально есть \(p\) монет. Рассмотрим следующий процесс, где в \(i\)-й шаг (начиная с \(i = 1\)): - Если \(i\) нечётное, робот передвинется в соседнюю вершину в сторону вершины \(1\);
- Иначе, \(i\) чётное. Можно либо заплатить одну монету (если остались), после чего робот передвинется в соседнюю вершину в сторону вершины \(1\), либо ничего не платить, после чего робот передвинется в равновероятно выбранную соседнюю вершину.
Процесс останавливается, как только робот попадает в вершину \(1\). Определим \(f(v, p)\) как минимально возможное математическое ожидание количества шагов процесса выше (количество использованных монет минимизировать не надо). Необходимо ответить на \(q\) запросов, в \(i\)-м из которых надо найти значение \(f(v_i, p_i)\) по модулю\(^{\text{∗}}\) \(998\,244\,353\). Выходные данные Для каждого набора входных данных выведите \(q\) целых чисел: значения \(f(v_i, p_i)\) по модулю \(998\,244\,353\). Формально, пусть \(M = 998\,244\,353\). Можно показать, что ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Примечание Дерево из первого набора показано ниже: 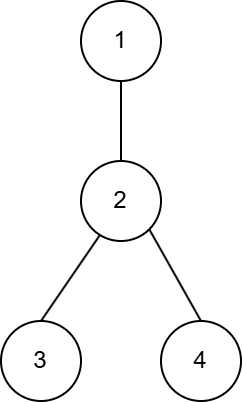 Для первого запроса значение математического ожидания равно \(1\), так как робот начинает движение с вершины \(2\) и первым ходом попадает в вершину \(1\) и завершает перемещение. Посчитаем значение математического ожидания для второго запроса (\(x\) это количество шагов в процессе): - \(P(x < 2) = 0\), расстояние до вершины \(1\) равно \(2\) и робот не может дойти до него за меньшее количество шагов.
- \(P(x = 2) = \frac{1}{3}\), так как есть только одна последовательность шагов, приводящая к \(x = 2\). Это \(3 \rightarrow_{1} 2 \rightarrow_{0.33} 1\) с вероятностью \(1 \cdot \frac{1}{3}\).
- \(P(x \bmod 2 = 1) = 0\), так как робот может достичь вершину \(1\) сделав только чётное количество шагов.
- \(P(x = 4) = \frac{2}{9}\): возможные пути \(3 \rightarrow_{1} 2 \rightarrow_{0.67} [3, 4] \rightarrow_{1} 2 \rightarrow_{0.33} 1\).
- \(P(x = 6) = \frac{4}{27}\): возможные пути \(3 \rightarrow_{1} 2 \rightarrow_{0.67} [3, 4] \rightarrow_{1} 2 \rightarrow_{0.67} [3, 4] \rightarrow_{1} 2 \rightarrow_{0.33} 1\).
- \(P(x = i \cdot 2) = \frac{2^{i - 1}}{3^i}\) в общем случае.
В результате \(f(v, p) = \sum\limits_{i=1}^{\infty}{i \cdot 2 \cdot \frac{2^{i - 1}}{3^i}} = 6\). Дерево из второго набора показано ниже:  | |
![]()
|
|
F. Количество кубов
Комбинаторика
математика
дп
теория чисел
*2700
Рассмотрим прямой параллелепипед с размерами сторон \(a\), \(b\) и \(c\), состоящий из единичных кубиков \(k\) различных цветов. Мы можем делать циклические сдвиги параллелепипеда в любом измерении и в любой комбинации\(^{\text{∗}}\). Имеется \(d_i\) кубиков \(i\)-го цвета (\(1 \le i \le k\)). Сколько можно составить из этих кубиков различных параллелепипедов с данными размерами сторон, никакие два из которых нельзя совместить комбинацией сдвигов? Выходные данные Для каждого набора входных данных выведите одно целое число — количество различных параллелепипедов по модулю \(998\,244\,353\). Примечание В первом наборе существует только один параллелепипед, состоящий из одного единичного куба. Возможные параллелепипеды во втором наборе 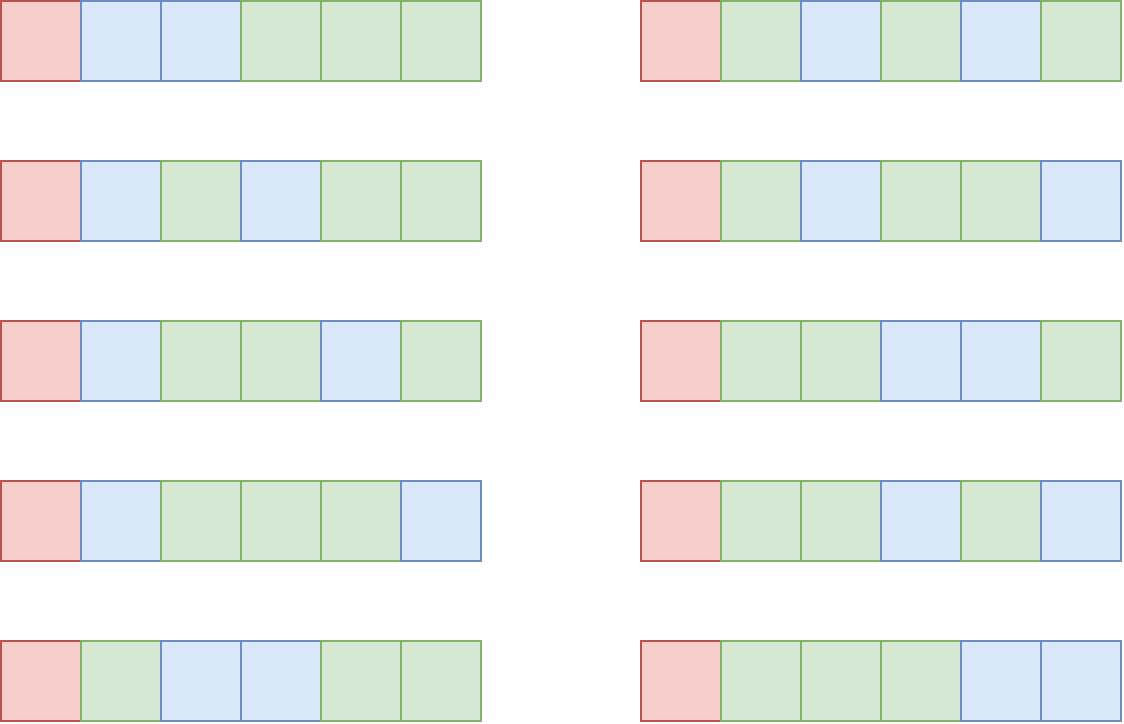 | |
![]()
|
|
H. Sheet Music
Комбинаторика
математика
дп
*2300
 Image generated by ChatGPT 4o. Image generated by ChatGPT 4o. Alice likes singing. As a singing enthusiast, Alice has listened to countless songs and has tried singing them many times. However, occasionally, some songs make Alice feel bored. After some research, Alice believes that this is because even though the songs she chose are all different, due to her instinctive preference, they all turn out to be musically similar to one another. To thoroughly analyze this, Alice decided to study the sheet music of the songs. For convenience, Alice represented a song of length \(n\) as an integer sequence \(a_1, a_2, \ldots, a_n\), where \(a_i\) is the pitch of the \(i\)-th note. Then she defined the musical equivalence between songs. Two songs \(a_1, a_2, \ldots, a_n\) and \(b_1, b_2, \ldots, b_n\) of length \(n\) are musically equivalent if for all \(1\leq i<n\), both \(a_i, a_{i+1}\) and \(b_{i}, b_{i+1}\) have the same pitch relationship. More specifically, \(a_i, a_{i+1}\) and \(b_i, b_{i+1}\) have the same pitch relationship if either - \(a_i < a_{i + 1}\) and \(b_i < b_{i + 1}\),
- \(a_i = a_{i + 1}\) and \(b_i = b_{i + 1}\), or
- \(a_i > a_{i + 1}\) and \(b_i > b_{i + 1}\).
For example, \(1, 2, 3, 3, 2\) and \(5, 9, 13, 13, 1\) are musically equivalent, while \(1, 2, 3, 2, 1\) and \(1, 2, 2, 2, 1\) are not. Having practiced consistently for a long time, Alice is able to sing any note in the range of \([1, k]\). She wants to know how many different songs of length \(n\) within her range there are, if we treat musically equivalent songs as the same one. Can you help her calculate the number? Since the answer might be large, print the answer modulo \(998244353\). Output Output the number of different songs modulo \(998244353\). | |
![]()
|
|
F. Ним
Перебор
Комбинаторика
реализация
дп
жадные алгоритмы
*2700
кратчайшие пути
битмаски
игры
Кратко напомним правила игры «Ним». Имеется \(n\) кучек камней, при этом в кучке \(i\) изначально лежит какое-то число камней. Два игрока по очереди выбирают непустую кучку и берут из нее произвольное положительное (строго больше \(0\)) количество камней. Проигрывает тот, кто не может сделать ход. Дан массив \(a\), состоящий из \(n\) целых чисел. Артем и Руслан решили играть в Ним на подотрезках массива. Каждый из \(q\) раундов определяется отрезком \((l_i, r_i)\), где элементы массива \(a_{l_i}, a_{l_i+1}, \dots, a_{r_i}\) рассматриваются как размеры кучек камней. До начала игры Руслан может удалить любое количество кучек из выбранного подотрезка. Однако хотя бы одна кучка должна остаться, поэтому в рамках одного раунда он может удалить не более \((r_i - l_i)\) кучек. Разрешается удалить \(0\) кучек. После удаления ребята играют в Ним на всех оставшихся кучках из этого отрезка. Все раунды независимы: удаления, произведенные в одном раунде, не влияют на исходный массив или другие раунды. Руслану нужно удалить как можно больше кучек так, чтобы Артем, который будет ходить первым, проиграл. Для каждого раунда определите: - максимальное количество кучек, которые Руслан может удалить;
- количество способов выбрать максимальное количество кучек для удаления.
Два способа считаются различными, если существует такая позиция \(i\), что в одном из способов кучка на позиции \(i\) удаляется, а во втором — нет. Поскольку количество способов может быть большим, выведите его по модулю \(998\,244\,353\). Если в каком-то раунде Руслан не может сделать так, чтобы Артем проиграл, выведите для этого раунда одно число -1. Выходные данные Для каждого раунда: - если Руслан может победить, выведите два целых числа — максимальное количество кучек, которые можно удалить, и количество способов удалить максимальное количество кучек, взятое по модулю \(998\,244\,353\);
- иначе выведите -1.
| |
![]()
|
|
E. Narrower Passageway
Структуры данных
Комбинаторика
*2700
You are a strategist of The ICPC Kingdom. You received an intel that there will be monster attacks on a narrow passageway near the kingdom. The narrow passageway can be represented as a grid with \(2\) rows (numbered from \(1\) to \(2\)) and \(N\) columns (numbered from \(1\) to \(N\)). Denote \((r, c)\) as the cell in row \(r\) and column \(c\). A soldier with a power of \(P_{r, c}\) is assigned to protect \((r, c)\) every single day. It is known that the passageway is very foggy. Within a day, each column in the passageway has a \(50\%\) chance of being covered in fog. If a column is covered in fog, the two soldiers assigned to that column are not deployed that day. Otherwise, the assigned soldiers will be deployed. Define a connected area \([u, v]\) (\(u \leq v\)) as a maximal set of consecutive columns from \(u\) to \(v\) (inclusive) such that each column in the set is not covered in fog. The following illustration is an example of connected areas. The grayed cells are cells covered in fog. There are \(4\) connected areas: \([1, 2]\), \([4, 6]\), \([9, 9]\), and \([11, 11]\).  The strength of a connected area \([u, v]\) can be calculated as follows. Let \(m_1\) and \(m_2\) be the maximum power of the soldiers in the first and second rows of the connected area, respectively. Formally, \(m_r = \max (P_{r, u}, P_{r, u + 1}, \dots, P_{r, v})\) for \(r \in \{ 1, 2\}\). If \(m_1 = m_2\), then the strength is \(0\). Otherwise, the strength is \(\min (m_1, m_2)\). The total strength of the deployment is the sum of the strengths for all connected areas. Determine the expected total strength of the deployment on any single day. Output Let \(M = 998\,244\,353\). It can be shown that the expected total strength can be expressed as an irreducible fraction \(\frac{x}{y}\) such that \(x\) and \(y\) are integers and \(y \not\equiv 0 \pmod{M}\). Output an integer \(k\) in a single line such that \(0 \leq k < M\) and \(k \cdot y \equiv x \pmod{M}\). Note Explanation for the sample input/output #1 There are \(8\) possible scenarios for the passageway. 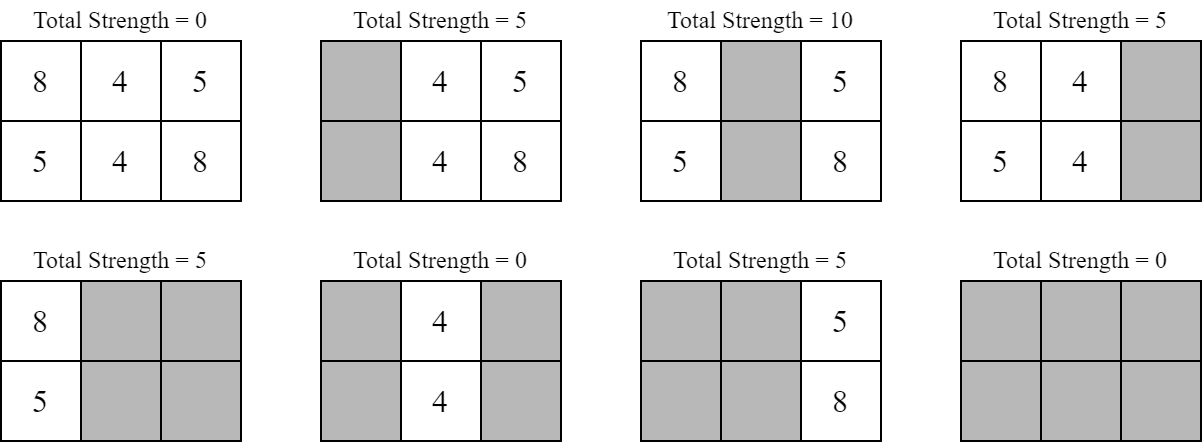 Each scenario is equally likely to happen. Therefore, the expected total strength is \((0 + 5 + 10 + 5 + 5 + 0 + 5 + 0) / 8 = \frac{15}{4}\). Since \(249\,561\,092 \cdot 4 \equiv 15 \pmod{998\,244\,353}\), the output of this sample is \(249\,561\,092\). Explanation for the sample input/output #2 The expected total strength is \(\frac{67}{16}\). | |
![]()
|
|
B. Замените символ
Строки
Перебор
Комбинаторика
*900
жадные алгоритмы
Вам дана строка \(s\) длиной \(n\), состоящая только из строчных латинских букв. Вы должны сделать ровно одну операцию следующего вида: - Выбрать любые два индекса \(i\) и \(j\) (\(1 \le i, j \le n\)). Вы можете выбрать \(i = j\).
- Установить \(s_i := s_j\).
Вам нужно минимизировать количество различных перестановок\(^\dagger\) строки \(s\). Выведите любую строку с наименьшим количеством различных перестановок после выполнения ровно одной операции. \(^\dagger\) Перестановка строки — это расположение её символов в любом порядке. Например, «bac» является перестановкой «abc», но «bcc» — нет. Выходные данные Для каждого набора входных данных выведите требуемую строку \(s\) после выполнения ровно одной операции. Если есть несколько решений, выведите любое из них. Примечание В первом наборе входных данных мы можем получить следующие строки за одну операцию: «abc», «bbc», «cbc», «aac», «acc», «aba» и «abb». Строка «abc» имеет \(6\) различных перестановок: «abc», «acb», «bac», «bca», «cab», и «cba». Строка «cbc» имеет \(3\) различных перестановки: «bcc», «cbc», и «ccb», что является наименьшим из всех получаемых строк. На самом деле, все получаемые строки, кроме «abc», имеют \(3\) перестановки, так что любая из них будет принята. | |
![]()
|
|
G. Кевин и матрицы
Перебор
Комбинаторика
математика
дп
*2800
Кевин был доставлен в больницу Святого Cердца, которая содержит все матрицы размером \( n \times m \) с целочисленными значениями из отрезка \( [1,v] \). Теперь Кевин хочет подружиться с некоторыми матрицами, но он готов подружиться с матрицей \( a \) только в том случае, если выполняется следующее условие: \(\) \min_{1\le i\le n}\left(\max_{1\le j\le m}a_{i,j}\right)\le\max_{1\le j\le m}\left(\min_{1\le i\le n}a_{i,j}\right). \(\) Пожалуйста, посчитайте, сколько матриц в больнице могут подружиться с Кевином. Поскольку Кевин очень дружелюбен, может быть много матриц, которые удовлетворяют этому условию. Поэтому вам нужно вывести результат по модулю \(998\,244\,353\). Выходные данные Для каждого набора выведите одно целое число — количество матриц, которые могут подружиться с Кевином по модулю \(998\,244\,353\). Примечание В первом наборе, кроме матриц \( a=\begin{bmatrix}1&2\\2&1\end{bmatrix} \) и \( a=\begin{bmatrix}2&1\\1&2\end{bmatrix} \), которые не удовлетворяют условию, оставшиеся \( 2^{2 \cdot 2} - 2 = 14 \) матриц могут подружиться с Кевином. | |
![]()
|
|
D. Равные медианы
Бинарный поиск
Перебор
Структуры данных
Комбинаторика
дп
разделяй и властвуй
*2200
Массив \(b\) из \(m\) целых чисел называется хорошим, если после его сортировки выполняется \(b_{\left\lfloor \frac{m + 1}{2} \right\rfloor} = b_{\left\lceil \frac{m + 1}{2} \right\rceil}\). Другими словами, \(b\) является хорошим, если обе его медианы равны. В частности, если \(m\) нечетно, то \(\left\lfloor \frac{m + 1}{2} \right\rfloor = \left\lceil \frac{m + 1}{2} \right\rceil\), поэтому \(b\) гарантированно будет хорошим, если он имеет нечетную длину. Вам дан массив \(a\) из \(n\) целых чисел. Вычислите количество хороших подмассивов\(^{\text{∗}}\) в \(a\). Выходные данные Для каждого набора входных данных выведите одно целое число — количество хороших подмассивов в \(a\). Примечание В первом наборе входных данных каждый подмассив является хорошим, поскольку все его элементы равны \(1\). Во втором наборе входных данных примером хорошего подмассива является \(b = [10, 2, 3, 3]\). Если его отсортировать, то \(b = [2, 3, 3, 10]\), значит, \(b_{\left\lfloor \frac{4 + 1}{2} \right\rfloor} = b_{\left\lceil \frac{4 + 1}{2} \right\rceil} = b_2 = b_3 = 3\). Другим примером может быть \(b = [1, 10, 2]\). С другой стороны, \(b = [1, 10]\) не подходит, поскольку его две медианы равны \(1\) и \(10\), и они не равны. | |
![]()
|
|
E. Вложенные отрезки
Комбинаторика
математика
дп
поиск в глубину и подобное
снм
*2500
Множество \(A\), состоящее из попарно различных отрезков \([l, r]\) с целочисленными концами, называется хорошим, если \(1\le l\le r\le n\), и для любой пары различных отрезков \([l_i, r_i], [l_j, r_j]\) из \(A\) выполняется ровно одно из следующих условий: - \(r_i < l_j\) или \(r_j < l_i\) (отрезки не пересекаются)
- \(l_i \le l_j \le r_j \le r_i\) или \(l_j \le l_i \le r_i \le r_j\) (один отрезок полностью содержится внутри другого)
Вам дано хорошее множество \(S\), состоящее из \(m\) попарно различных отрезков \([l_i, r_i]\) с целочисленными концами. Вы хотите добавить как можно больше дополнительных отрезков к набору \(S\), так, чтобы набор \(S\) остался хорошим. Поскольку эта задача слишком проста, вам нужно определить количество различных способов добавления максимального числа дополнительных отрезков к \(S\), так, чтобы набор остался хорошим. Два способа считаются разными, если существует отрезок, который добавляется одним из способов, но не другим. Формально, вам нужно найти количество хороших наборов различных отрезков \(T\), таких, чтобы \(S\) было подмножеством \(T\), и \(T\) имело максимально возможный размер. Поскольку ответ может быть очень большим, вычислите его по модулю \(998\,244\,353\). Выходные данные Для каждого набора входных данных выведите одно целое число — количество различных способов, которыми вы можете добавить максимальное количество дополнительных отрезков к набору \(S\), гарантируя при этом, что набор \(S\) останется хорошим, по модулю \(998\,244\,353\) Примечание В первом наборе входных данных единственным возможным отрезком является \([1, 1]\), поэтому \(T = \{[1, 1]\}\) имеет максимальный размер, и это единственное решение. Во втором наборе входных данных невозможно добавить какие-либо дополнительные отрезки к набору \(S\). Следовательно, единственный способ добавить отрезки к \(S\) — это ничего не добавлять. В третьем наборе входных данных можно добавить \(7\) дополнительных отрезков к \(S\), гарантируя, что набор останется хорошим. Можно доказать, что добавление более \(7\) дополнительных отрезков к \(S\) невозможно. Существует ровно \(2\) различных способа добавить эти \(7\) отрезков к \(S\), и соответствующие наборы \(T\) показаны ниже: - \(\{[1, 1], [1, 3], [1, 4], [1, 5], [2, 2], [2, 3], [3, 3], [4, 4], [5, 5]\}\)
- \(\{[1, 1], [1, 3], [1, 5], [2, 2], [2, 3], [3, 3], [4, 4], [4, 5], [5, 5]\}\).
В четвертом наборе входных данных существует ровно \(5\) различных способов добавить максимум \(6\) дополнительных отрезков к \(S\), соответствующие наборы \(T\) показаны ниже: - \(\{[1, 1], [1, 2], [1, 3], [1, 4], [2, 2], [3, 3], [4, 4]\}\)
- \(\{[1, 1], [1, 2], [1, 4], [2, 2], [3, 3], [3, 4], [4, 4]\}\)
- \(\{[1, 1], [1, 3], [1, 4], [2, 2], [2, 3], [3, 3], [4, 4]\}\)
- \(\{[1, 1], [1, 4], [2, 2], [2, 3], [2, 4], [3, 3], [4, 4]\}\)
- \(\{[1, 1], [1, 4], [2, 2], [2, 4], [3, 3], [3, 4], [4, 4]\}\)
| |
![]()
|
|
F1. Xor медиан (простая версия)
Перебор
Комбинаторика
математика
дп
*2700
битмаски
Это простая версия задачи. Отличие между версиями заключается в том, что в этой версии ограничения на \(t\), \(k\) и \(m\) ниже. Вы можете делать взломы только в том случае, если решили все версии этой задачи. Последовательность \(a\) из \(n\) целых чисел называется хорошей, если выполняется следующее условие: - Пусть \(\text{cnt}_x\) — количество вхождений \(x\) в последовательность \(a\). Для всех пар \(0 \le i < j < m\), по крайней мере одно из следующих условий должно быть истинным: \(\text{cnt}_i = 0\), \(\text{cnt}_j = 0\) или \(\text{cnt}_i \le \text{cnt}_j\). Другими словами, если и \(i\), и \(j\) присутствуют в последовательности \(a\), то число вхождений \(i\) в \(a\) меньше или равно числу вхождений \(j\) в \(a\).
Вам даны целые числа \(n\) и \(m\). Вычислите значение побитового XOR медиан\(^{\text{∗}}\) всех хороших последовательностей \(a\) длины \(n\), таких, что \(0\le a_i < m\). Обратите внимание, что значение \(n\) может быть очень большим, поэтому вместо него вам даётся его двоичное представление. Выходные данные Для каждого набора входных данных выведите одно целое число — побитовый XOR медиан всех хороших последовательностей \(a\) длины \(n\), где \(0\le a_i < m\) Примечание В первом наборе входных данных, \(n = 10_2 = 2\) и \(m = 3\). Существуют такие последовательности с элементами меньше \(m\): \([0, 0]\), \([0, 1]\), \([0, 2]\), \([1, 0]\), \([1, 1]\), \([1, 2]\), \([2, 0]\), \([2, 1]\), \([2, 2]\). Все они являются хорошими, поэтому ответ равен \(0 \oplus 0 \oplus 0 \oplus 0 \oplus 1 \oplus 1 \oplus 0 \oplus 1 \oplus 2 = 3\). Во втором наборе входных данных, \(n = 11_2 = 3\) и \(m = 3\). Некоторыми хорошими последовательностями являются \([2, 2, 2]\), \([1, 0, 1]\), и \([2, 0, 1]\). Однако последовательность \([2, 0, 0]\) не является хорошей, потому что \(\text{cnt}_0 = 2\), \(\text{cnt}_2 = 1\). Следовательно, если мы выберем \(i = 0\) и \(j = 2\), то \(i < j\) выполняется, а \(\text{cnt}_i \le \text{cnt}_j\) неверно. | |
![]()
|
|
F2. Xor медиан (сложная версия)
Перебор
Комбинаторика
математика
дп
битмаски
*3000
Это сложная версия задачи. Отличие между версиями заключается в том, что в этой версии ограничения на \(t\), \(k\) и \(m\) выше. Вы можете делать взломы только в том случае, если решили все версии этой задачи. Последовательность \(a\) из \(n\) целых чисел называется хорошей, если выполняется следующее условие: - Пусть \(\text{cnt}_x\) — количество вхождений \(x\) в последовательность \(a\). Для всех пар \(0 \le i < j < m\), по крайней мере одно из следующих условий должно быть истинным: \(\text{cnt}_i = 0\), \(\text{cnt}_j = 0\) или \(\text{cnt}_i \le \text{cnt}_j\). Другими словами, если и \(i\), и \(j\) присутствуют в последовательности \(a\), то число вхождений \(i\) в \(a\) меньше или равно числу вхождений \(j\) в \(a\).
Вам даны целые числа \(n\) и \(m\). Вычислите значение побитового XOR медиан\(^{\text{∗}}\) всех хороших последовательностей \(a\) длины \(n\), таких, что \(0\le a_i < m\). Обратите внимание, что значение \(n\) может быть очень большим, поэтому вместо него вам даётся его двоичное представление. Выходные данные Для каждого набора входных данных выведите одно целое число — побитовый XOR медиан всех хороших последовательностей \(a\) длины \(n\), где \(0\le a_i < m\) Примечание В первом наборе входных данных, \(n = 10_2 = 2\) и \(m = 3\). Существуют такие последовательности с элементами меньше \(m\): \([0, 0]\), \([0, 1]\), \([0, 2]\), \([1, 0]\), \([1, 1]\), \([1, 2]\), \([2, 0]\), \([2, 1]\), \([2, 2]\). Все они являются хорошими, поэтому ответ равен \(0 \oplus 0 \oplus 0 \oplus 0 \oplus 1 \oplus 1 \oplus 0 \oplus 1 \oplus 2 = 3\). Во втором наборе входных данных, \(n = 11_2 = 3\) и \(m = 3\). Некоторыми хорошими последовательностями являются \([2, 2, 2]\), \([1, 0, 1]\), и \([2, 0, 1]\). Однако последовательность \([2, 0, 0]\) не является хорошей, потому что \(\text{cnt}_0 = 2\), \(\text{cnt}_2 = 1\). Следовательно, если мы выберем \(i = 0\) и \(j = 2\), то \(i < j\) выполняется, а \(\text{cnt}_i \le \text{cnt}_j\) неверно. | |
![]()
|
|
F. Умножительные массивы
Комбинаторика
дп
теория чисел
*2200
Даны целые числа \(k\) и \(n\). Для каждого целого числа \(x\) от \(1\) до \(k\) посчитайте количество целых массивов \(a\), таких что выполняются все следующие условия: - \(1 \leq |a| \leq n\), где \(|a|\) обозначает длину массива \(a\).
- \(1 \leq a_i \leq k\) для всех \(1 \leq i \leq |a|\).
- \(a_1 \times a_2 \times \dots \times a_{|a|}=x\) (т.е. произведение всех элементов равно \(x\)).
Обратите внимание, что два массива \(b\) и \(c\) различны, если либо их длины различны, либо существует индекс \(1 \leq i \leq |b|\), такой что \(b_i\neq c_i\). Выведите ответ по модулю \(998\,244\,353\). Выходные данные Для каждого набора входных данных выведите \(k\) целых чисел, разделенных пробелом, на новой строке: количество массивов для \(x=1,2,\ldots,k\), по модулю \(998\,244\,353\). Примечание В первом наборе входных данных существует \(2\) массива \(a\) с \(|a|\leq 2\) и произведением элементов, равным \(1\): Существует \(3\) массива \(a\) с \(|a|\leq 2\) и произведением элементов, равным \(2\): - \([2]\)
- \([1,2]\)
- \([2,1]\)
| |
![]()
|
|
C. Кевин и головоломка
Комбинаторика
*1600
дп
2-sat
Кевин увлекается логическими головоломками. Он играет в игру с \(n\) одноклассниками, которые стоят в очереди. \(i\)-й человек слева заявляет, что слева от него (не включая его самого) находится \(a_i\) лжецов. Каждый одноклассник либо рыцарь, либо лжец, с тем ограничением, что два лжеца не могут стоять рядом друг с другом. Одноклассники-рыцари всегда говорят правду. Лжецы могут говорить либо правду, либо ложь, то есть их заявления недостоверны. Кевин хочет определить количество различных возможных конфигураций рыцарей и лжецов по модулю \(998\,244\,353\). Две конфигурации считаются различными, если по крайней мере один одноклассник является рыцарем в одной конфигурации и лжецом в другой. Выходные данные Для каждого набора входных данных выведите одно целое число — количество различных конфигураций по модулю \(998\,244\,353\). Примечание Мы будем использовать \(\color{red}{\text{красный}}\) для обозначения лжецов и \(\color{blue}{\text{синий}}\) для обозначения рыцарей. В первом наборе входных данных единственной возможной конфигурацией является \((\color{red}{0},\color{blue}{1},\color{red}{2})\). Во втором наборе входных данных возможны две конфигурации: \((\color{blue}{0},\color{blue}{0},\color{blue}{0},\color{blue}{0},\color{blue}{0})\) и \((\color{blue}{0},\color{blue}{0},\color{blue}{0},\color{blue}{0},\color{red}{0})\). В третьем наборе входных данных возможны три конфигурации: \((\color{blue}{0},\color{blue}{0},\color{red}{1},\color{blue}{1},\color{red}{2})\), \((\color{blue}{0},\color{red}{0},\color{blue}{1},\color{red}{1},\color{blue}{2})\) и \((\color{blue}{0},\color{red}{0},\color{blue}{1},\color{blue}{1},\color{red}{2})\). | |
![]()
|
|
H. Генератор галактик
Комбинаторика
дп
битмаски
*3500
В двумерной вселенной звезда может быть представлена как точка \((x,y)\) на двумерной плоскости. Две звезды соединены напрямую, если и только если их \(x\) или \(y\) координаты одинаковы, и между ними нет других звезд на отрезке. Определим галактику как связную компоненту, состоящую из звезд, соединенных напрямую или косвенно (через другие звезды). Для набора звезд его значение определяется как минимальное количество галактик, которое можно получить для этого набора, после выполнения следующей операции любое (возможно, нулевое) количество раз: в рамках операции вы можете выбрать точку \((x,y)\), в которой нет звезды. Если звезда, созданная в этой точке, может быть соединена напрямую как минимум с \(3\) звездами, то вы создаете в этой точке звезду. Вам дана матрица \(a\) размера \(n\times n\), состоящая из \(0\) и \(1\) и описывающая набор звёзд \(S\). Звезда находится в \((x,y)\) тогда и только тогда, когда \(a_{x,y}=1\). Вычислите сумму значений всех непустых подмножеств \(S\) по модулю \(10^9 + 7\). Выходные данные Для каждого набора входных данных выведите сумму значений всех непустых подмножеств \(S\) по модулю \(10^9 + 7\). Примечание В первом наборе входных данных \(S\) пусто. У \(S\) нет непустых подмножеств. Поэтому ответ \(0\). Во втором наборе входных данных \(S = \{(1,2),(2,1)\}\). У \(S\) есть \(3\) непустых подмножества. - \(\{(1,2)\}\) и \(\{(2,1)\}\) — в наборе только одна звезда, образующая \(1\) галактику.
- \(\{(1,2),(2,1)\}\) — две звезды в наборе не соединены, образуя \(2\) галактики.
Таким образом, ответ равен \(1+1+2=4\). В третьем наборе входных данных \(S = \{(1,2),(3,1),(3,3)\}\). У \(S\) есть \(7\) непустых подмножеств. - \(\{(1,2)\}\), \(\{(3,1)\}\) и \(\{(3,3)\}\) — в наборе только одна звезда, образующая \(1\) галактику.
- \(\{(1,2),(3,1)\}\) и \(\{(1,2),(3,3)\}\) — две звезды в наборе не соединены, образуя \(2\) галактики.
- \(\{(3,1),(3,3)\}\) — две звезды в наборе соединены, образуя \(1\) галактику.
- \(\{(1,2),(3,1),(3,3)\}\) — изначально звезда \((1,2)\) не входит в галактику, образованную \((3,1)\) и \((3,3)\). Вы можете выполнить операцию, создав звезду в \((3,2)\), соединяющую эти три звезды, образуя \(1\) галактику.
Таким образом, ответ равен \(1+1+1+2+2+1+1=9\). | |
![]()
|
|
F1. Считать не весело (Простая версия)
Деревья
Структуры данных
Комбинаторика
математика
реализация
дп
поиск в глубину и подобное
*2400
графы
хэши
снм
Это простая версия задачи. Отличие между версиями заключается в том, что в этой версии ограничения на \(t\) и \(n\) меньше. Вы можете делать взломы только в том случае, если решили все версии этой задачи. Теперь Маленький Джон богат, и поэтому он наконец-то покупает дом, достаточно большой, чтобы вместить его и его любимую скобочную последовательность. Но каким-то образом он оказался с большим количеством скобок! Разочарованный, он пробивает потолок с помощью «ладони Будды». Скобочная последовательность называется правильной, если она может быть построена по следующей формальной грамматике: - Пустая последовательность \(\varnothing\) сбалансирована.
- Если скобочная последовательность \(A\) правильная, то \(\mathtt{(}A\mathtt{)}\) также является правильной.
- Если скобочные последовательности \(A\) и \(B\) правильные, то и их конкатенированная последовательность \(A B\) также правильная.
Например, последовательности «(())()», «()», «(()(()))» и пустая последовательность являются правильными, в то время как «(()» и «(()))(» — нет. Дана правильная скобочная последовательность \(s\), пара индексов \((i,j)\) (\(i<j\)) называется хорошей, если \(s_i\) — это «(», а \(s_j\) — это «)», и две скобки добавляются одновременно в соответствии с правилом 2 при построении последовательности \(s\). Например, последовательность «(())()» имеет три разные хорошие пары: \((1,4)\), \((2,3)\) и \((5,6)\). Можно показать, что любая правильная скобочная последовательность из \(2n\) скобок содержит ровно \(n\) различных пар скобок, и использование любого порядка правил для построения одной и той же последовательности скобок приведет к одному и тому же набору пар скобок. Эмили будет играть в игру по угадыванию скобок с Джоном. Игра проходит следующим образом. Изначально у Джона есть правильная скобочная последовательность \(s\), содержащая \(n\) различных пар скобок, которая не известна Эмили. Джон говорит Эмили значение \(n\) и просит Эмили угадать последовательность. На протяжении \(n\) ходов Джон дает Эмили следующие подсказки на каждом ходе: - \(l\;r\): Последовательность \(s\) содержит пару скобок \((l,r)\).
Гарантируется, что подсказки, которые Джон дает Эмили, попарно различны и не противоречат друг другу. В какой-то момент Эмили может быть уверена, что правильная скобочная последовательность, удовлетворяющая подсказкам, данным до сих пор, уникальна. Например, предположим, что Эмили знает, что \(s\) имеет \(3\) хорошие пары, и она содержит пару скобок \((2,5)\). Из \(5\) правильных скобочных последовательностей с \(3\) хорошими парами существует только одна такая последовательность «((()))» с парой скобок \((2,5)\). Следовательно, можно увидеть, что Эмили не всегда нужно \(n\) ходов, чтобы угадать \(s\). Чтобы как можно раньше узнать содержимое \(s\), Эмили хочет знать количество различных правильных скобочных последовательностей, которые соответствуют подсказкам после каждого хода. Конечно, это не легкая задача для Эмили, особенно когда ей дано настолько много хороших пар. Теперь ваша очередь помочь Эмили. Учитывая подсказки, вы должны найти ответ до всех ходов и после каждого хода. Поскольку ответы могут быть огромными, вам нужно найти их по модулю \(998\,244\,353\). Выходные данные Для каждого набора выведите \(n+1\) целых числа в одной строке: - Первое целое число — это ответ до всех подсказок, по модулю \(998\,244\,353\).
- Для всех \(i \ge 1\), \(i+1\)-е целое число — это ответ после \(i\)-й подсказки, по модулю \(998\,244\,353\).
Примечание Первый пример из примера объясняется в описании задачи. Третий пример из примера объясняется следующим образом. Можно показать, что существует \(132\) сбалансированных последовательностей скобок с \(6\) парами скобок. Ответы после каждой подсказки следующие: - Вам дана хорошая пара \((2,3)\). Существует \(42\) правильных скобочных последовательностей, имеющих хорошую пару \((2,3)\).
- Вам дана хорошая пара \((1,6)\). Существует \(5\) правильных скобочных последовательностей, имеющих хорошие пары \((2,3)\), \((1,6)\).
- Вам дана хорошая пара \((7,8)\). Существуют \(2\) правильных скобочных последовательностей, имеющих три хорошие пары. Это строки «(()())()(())» и «(()())()()()», соответственно.
- Вам дана хорошая пара \((9,12)\). Существует только одна правильная скобочная последовательность, содержащая четыре хорошие пары. Таким образом, содержимое \(s\) имеет вид «(()())()(())».
Тогда количество правильных скобочных последовательностей после пятой и шестой подсказки равно \(1\), поскольку вы уже знаете содержимое \(s\). | |
![]()
|
|
F2. Считать не весело (Сложная версия)
Деревья
Структуры данных
Комбинаторика
реализация
поиск в глубину и подобное
графы
*2700
снм
Это сложная версия задачи. Отличие между версиями заключается в том, что в этой версии ограничения на \(t\) и \(n\) больше. Вы можете делать взломы только в том случае, если решили все версии этой задачи. Теперь Маленький Джон богат, и поэтому он наконец-то покупает дом, достаточно большой, чтобы вместить его и его любимую скобочную последовательность. Но каким-то образом он оказался с большим количеством скобок! Разочарованный, он пробивает потолок с помощью «ладони Будды». Скобочная последовательность называется правильной, если она может быть построена по следующей формальной грамматике: - Пустая последовательность \(\varnothing\) сбалансирована.
- Если скобочная последовательность \(A\) правильная, то \(\mathtt{(}A\mathtt{)}\) также является правильной.
- Если скобочные последовательности \(A\) и \(B\) правильные, то и их конкатенированная последовательность \(A B\) также правильная.
Например, последовательности «(())()», «()», «(()(()))» и пустая последовательность являются правильными, в то время как «(()» и «(()))(» — нет. Дана правильная скобочная последовательность \(s\), пара индексов \((i,j)\) (\(i<j\)) называется хорошей, если \(s_i\) — это «(», а \(s_j\) — это «)», и две скобки добавляются одновременно в соответствии с правилом 2 при построении последовательности \(s\). Например, последовательность «(())()» имеет три разные хорошие пары: \((1,4)\), \((2,3)\) и \((5,6)\). Можно показать, что любая правильная скобочная последовательность из \(2n\) скобок содержит ровно \(n\) различных пар скобок, и использование любого порядка правил для построения одной и той же последовательности скобок приведет к одному и тому же набору пар скобок. Эмили будет играть в игру по угадыванию скобок с Джоном. Игра проходит следующим образом. Изначально у Джона есть правильная скобочная последовательность \(s\), содержащая \(n\) различных пар скобок, которая не известна Эмили. Джон говорит Эмили значение \(n\) и просит Эмили угадать последовательность. На протяжении \(n\) ходов Джон дает Эмили следующие подсказки на каждом ходе: - \(l\;r\): Последовательность \(s\) содержит пару скобок \((l,r)\).
Гарантируется, что подсказки, которые Джон дает Эмили, попарно различны и не противоречат друг другу. В какой-то момент Эмили может быть уверена, что правильная скобочная последовательность, удовлетворяющая подсказкам, данным до сих пор, уникальна. Например, предположим, что Эмили знает, что \(s\) имеет \(3\) хорошие пары, и она содержит пару скобок \((2,5)\). Из \(5\) правильных скобочных последовательностей с \(3\) хорошими парами существует только одна такая последовательность «((()))» с парой скобок \((2,5)\). Следовательно, можно увидеть, что Эмили не всегда нужно \(n\) ходов, чтобы угадать \(s\). Чтобы как можно раньше узнать содержимое \(s\), Эмили хочет знать количество различных правильных скобочных последовательностей, которые соответствуют подсказкам после каждого хода. Конечно, это не легкая задача для Эмили, особенно когда ей дано настолько много хороших пар. Теперь ваша очередь помочь Эмили. Учитывая подсказки, вы должны найти ответ до всех ходов и после каждого хода. Поскольку ответы могут быть огромными, вам нужно найти их по модулю \(998\,244\,353\). Выходные данные Для каждого набора выведите \(n+1\) целых числа в одной строке: - Первое целое число — это ответ до всех подсказок, по модулю \(998\,244\,353\).
- Для всех \(i \ge 1\), \(i+1\)-е целое число — это ответ после \(i\)-й подсказки, по модулю \(998\,244\,353\).
Примечание Первый пример из примера объясняется в описании задачи. Третий пример из примера объясняется следующим образом. Можно показать, что существует \(132\) сбалансированных последовательностей скобок с \(6\) парами скобок. Ответы после каждой подсказки следующие: - Вам дана хорошая пара \((2,3)\). Существует \(42\) правильных скобочных последовательностей, имеющих хорошую пару \((2,3)\).
- Вам дана хорошая пара \((1,6)\). Существует \(5\) правильных скобочных последовательностей, имеющих хорошие пары \((2,3)\), \((1,6)\).
- Вам дана хорошая пара \((7,8)\). Существуют \(2\) правильных скобочных последовательностей, имеющих три хорошие пары. Это строки «(()())()(())» и «(()())()()()», соответственно.
- Вам дана хорошая пара \((9,12)\). Существует только одна правильная скобочная последовательность, содержащая четыре хорошие пары. Таким образом, содержимое \(s\) имеет вид «(()())()(())».
Тогда количество правильных скобочных последовательностей после пятой и шестой подсказки равно \(1\), поскольку вы уже знаете содержимое \(s\). | |
![]()
|
|
G. Скибидус и ложь
Комбинаторика
математика
теория чисел
*1700
Скибидус был похищен инопланетянами с Амога! Скибидус пытается выкрутиться, но инопланетяне с Амога не верят ему. Чтобы доказать, что он не врет, инопланетяне с Амога попросили его решить эту задачу: Целое число \(x\) считается полупростым, если его можно записать в виде \(p \cdot q\), где \(p\) и \(q\) — (не обязательно разные) простые числа. Например, \(9\) является полупростым, так как его можно записать как \(3 \cdot 3\), а \(3\) является простым числом. Скибидусу был дан массив \(a\), содержащий \(n\) целых чисел. Он должен сообщить количество пар \((i, j)\) таких, что \(i \leq j\) и \(\operatorname{lcm}(a_i, a_j)\)\(^{\text{∗}}\) является полупростым. Выходные данные Для каждого набора входных данных выведите количество упорядоченных пар индексов на новой строке. Примечание В первом наборе входных данных \(5\) пар индексов: \((1, 3)\), \((1, 4)\), \((2, 3)\), \((2, 4)\) и \((4, 4)\). | |
![]()
|
|
H. Бро считает себя избранным
Структуры данных
Комбинаторика
математика
дп
разделяй и властвуй
*2200
матрицы
Скибидус думает, что он избранный! Он доказал это, решив эту сложную задачу. Сможете ли вы? Дана двоичная строка\(^{\text{∗}}\) \(t\), \(f(t)\) определяется как минимальное количество смежных подстрок, каждая из которых состоит из одинаковых символов, на которые можно разбить \(t\). Например, \(f(\texttt{00110001}) = 4\), потому что \(t\) можно разбить как \(\texttt{[00][11][000][1]}\), где каждый сегмент в скобках состоит из одинаковых символов. Скибидус даёт вам двоичную строку \(s\) и \(q\) запросов. В каждом запросе один символ строки переворачивается (т.е. \(\texttt{0}\) меняется на \(\texttt{1}\), а \(\texttt{1}\) меняется на \(\texttt{0}\)), изменения сохраняются после обработки запроса. После каждого запроса выведите сумму по всем \(f(b)\), где \(b\) — это непустая подпоследовательность\(^{\text{†}}\) строки \(s\), по модулю \(998\,244\,353\). Выходные данные Для каждого набора входных данных выведите \(q\) целых чисел в одной строке — ответ после каждого запроса по модулю \(998\,244\,353\). Примечание В первом тестовом случае \(s\) становится \(\texttt{001}\) после первого запроса. Давайте посчитаем ответ для каждой подпоследовательности: - \(f(s_1) = f(\texttt{0}) = 1\)
- \(f(s_2) = f(\texttt{0}) = 1\)
- \(f(s_3) = f(\texttt{1}) = 1\)
- \(f(s_1 s_2) = f(\texttt{00}) = 1\)
- \(f(s_1 s_3) = f(\texttt{01}) = 2\)
- \(f(s_2 s_3) = f(\texttt{01}) = 2\)
- \(f(s_1 s_2 s_3) = f(\texttt{001}) = 2\)
Сумма этих значений равна \(10\), по модулю \(998\,244\,353\). | |
![]()
|
|
C. Битовые горки
Комбинаторика
математика
дп
*2300
битмаски
Вам дан массив \(a_1, a_2, \ldots, a_n\). А также три переменные \(P,Q,R\), изначально равные нулю. Вам необходимо поочерёдно обработать все числа \(a_1, a_2, \ldots, a_n\), в порядке от \(1\) до \(n\). Обрабатывая очередное \(a_i\), вы должны сделать ровно одно из трёх действий на выбор: - \(P := P \oplus a_i\)
- \(Q := Q \oplus a_i\)
- \(R := R \oplus a_i\)
\(\oplus\) обозначает операцию побитового исключающего ИЛИ. Выполняя действия, надо соблюдать главное правило: необходимо, чтобы после каждого действия все три числа \(P,Q,R\) не были попарно различны. Всего есть \(3^n\) способов произвести все \(n\) действий. Сколько из них не нарушают главное правило? Так как ответ может быть достаточно большим, найдите его по модулю \(10^9 + 7\). Выходные данные Для каждого набора входных данных выведите количество способов произвести все \(n\) действий, не нарушая главное правило, по модулю \(10^9 + 7\). Примечание В первом наборе входных данных 3 валидные последовательности операций: PPP, QQQ, RRR Во втором наборе входных данных 9 валидных последовательностей операций: PPPP, PPPQ, PPPR, QQQP, QQQQ, QQQR, RRRP, RRRQ, RRRR. | |
![]()
|
|
D1. Клуб юных авиастроителей (простая версия)
Комбинаторика
математика
дп
*2400
Это easy версия задачи. Отличие между версиями заключается в том, что в этой версии все \(a_i = 0\). Вы можете делать взломы только в том случае, если решили все версии этой задачи. Есть \(n\)-этажный дом, этажи пронумерованы от \(1\) до \(n\) снизу вверх. На каждом этаже живёт ровно один человек. У всех жителей дома сегодня есть очень важная цель: запустить всем домом суммарно хотя бы \(c\) бумажных самолётиков. Жители будут запускать самолётики поочерёдно. Когда человек с \(i\)-го этажа запускает самолётик, это видят все жители на этажах от \(1\) до \(i\), пока самолёт опускается на землю. Если с точки зрения жителя с \(i\)-го этажа уже было запущено хотя бы \(c\) самолётиков, сам он больше не будет запускать самолётики. Также известно, что в конце дня, с точки зрения каждого из жителей дома было запущено хотя бы \(c\) самолётиков, а всего было кинуто \(m\) самолётиков. Вы внимательно следили за данным флешмобом, и для каждого самолётика записывали, житель какого из этажей его кинул. Но, к сожалению, информация о том, кто именно кидал некоторые самолётики, была утеряна. Найдите количество способов заполнить пропуски, чтобы информация могла быть достоверной. Так как ответ может быть достаточно большим, выведите его по модулю \(10^9 + 7\). В этой версии задачи была утеряна вся информация, и весь массив состоит из пропусков. Также возможна ситуация, что вы ошиблись в своих записях, и не существует ни одного возможного способа восстановить пропуски. В таком случае ответ считается равным \(0\). Выходные данные Для каждого набора входных данных выведите количество способов заполнить пропуски числами от \(1\) до \(n\), чтобы хронология запуска самолётиков могла быть достоверной, по модулю \(10^9 + 7\). Примечание В первом тестовом примере все шесть возможных способов заполнить пропуски таковы: - \([1, 1, 3, 3]\)
- \([1, 2, 3, 3]\)
- \([1, 3, 2, 3]\)
- \([2, 1, 3, 3]\)
- \([2, 2, 3, 3]\)
- \([3, 1, 2, 3]\)
Обратите внимание, что массив \([2, 3, 1, 3]\) не является валидным способом заполнить пропуски, так как третий самолётик не мог быть запущен человеком с \(1\) этажа, так как с его точки зрения уже было запущено \(c = 2\) самолётика. Также массив \([1, 1, 2, 3]\) не является валидным способом заполнить пропуски, так как с точки зрения человека с \(3\) этажа всего был запущен только \(1\) самолётик, а \(c = 2\). | |
![]()
|
|
D2. Клуб юных авиастроителей (сложная версия)
Комбинаторика
математика
дп
*2900
Это hard версия задачи. Отличие между версиями заключается в том, что в этой версии не обязательно \(a_i = 0\). Вы можете делать взломы только в том случае, если решили все версии этой задачи. Есть \(n\)-этажный дом, этажи пронумерованы от \(1\) до \(n\) снизу вверх. На каждом этаже живёт ровно один человек. У всех жителей дома сегодня есть важная цель: запустить всем домом суммарно хотя бы \(c\) бумажных самолётиков. Жители будут запускать самолётики поочерёдно. Когда человек с \(i\)-го этажа запускает самолётик, это видят все жители на этажах от \(1\) до \(i\), пока самолёт опускается на землю. Если с точки зрения жителя с \(i\)-го этажа уже было запущено хотя бы \(c\) самолётиков, сам он больше не будет запускать самолётики. Также известно, что в конце дня, с точки зрения каждого из жителей дома, было запущено хотя бы \(c\) самолётиков, а всего было кинуто \(m\) самолётиков. Вы внимательно следили за данным флешмобом, и для каждого самолётика записывали, житель какого из этажей его кинул. Но, к сожалению, информация о том, кто именно кидал некоторые самолётики, была утеряна. Найдите количество способов заполнить пропуски, чтобы информация могла быть достоверной. Так как ответ может быть достаточно большим, выведите его по модулю \(10^9 + 7\). Также возможна ситуация, что вы ошиблись в своих записях, и не существует ни одного возможного способа восстановить пропуски. В таком случае ответ считается равным \(0\). Выходные данные Для каждого набора входных данных выведите количество способов заполнить пропуски числами от \(1\) до \(n\), чтобы хронология запуска самолётиков могла быть достоверной, по модулю \(10^9 + 7\). Примечание В первом тестовом примере все шесть возможных способов заполнить пропуски таковы: - \([1, 1, 3, 3]\)
- \([1, 2, 3, 3]\)
- \([1, 3, 2, 3]\)
- \([2, 1, 3, 3]\)
- \([2, 2, 3, 3]\)
- \([3, 1, 2, 3]\)
Обратите внимание, что массив \([2, 3, 1, 3]\) не является валидным способом заполнить пропуски, так как третий самолётик не мог быть запущен человеком с \(1\) этажа, так как с его точки зрения уже было запущено \(c = 2\) самолётика. Также массив \([1, 1, 2, 3]\) не является валидным способом заполнить пропуски, так как с точки зрения человека с \(3\) этажа всего был запущен только \(1\) самолётик, а \(c = 2\). | |
![]()
|
|
B. Числа
Комбинаторика
дп
*1900
Фурику нравится придумывать разные задачи, особенно те, которые он сам решить не может. Перед вами очередная задача Фурика, которую он дал Рубику. Рубик же просит вас решить ее. Имеется целое число n и массив a, состоящий из десяти целых чисел, проиндексированный номерами от 0 до 9. Нужно посчитать количество целых положительных чисел со следующими свойствами: - длина числа не превосходит n;
- число не содержит лидирующих нулей;
- количество вхождений цифры i (0 ≤ i ≤ 9) в число не меньше a[i].
Выходные данные В единственной строке выведите остаток от деления ответа на задачу на 1000000007 (109 + 7). Примечание В первом примере подходит число 9. Во втором примере подходит число 10. В третьем примере подходят числа: 10, 110, 210, 120, 103. Есть и другие подходящие числа, всего их 36. | |
![]()
|
|
E. Периодические числа
Комбинаторика
*2100
дп
теория чисел
Непустая строка s называется бинарной, если она состоит только из символов «0» и «1». Пронумеруем символы бинарной строки s от 1 до длины строки и обозначим i-й символ строки s как si. Бинарную строку s длины n будем называть периодической, если существует целое число 1 ≤ k < n такое, что: - k — делитель числа n
- для всех 1 ≤ i ≤ n - k выполняется si = si + k
Например, бинарные строки «101010» и «11» являются периодическими, а «10» и «10010» — нет. Целое положительное число x будем называть периодическим, если бинарная строка, являющаяся записью числа x в двоичной системе счисления (без лидирующих нулей), — периодическая. Ваша задача — найти количество периодических чисел в отрезке от l до r (оба конца включены). Выходные данные Выведите единственное целое число — количество периодических чисел в отрезке от l до r (оба конца включены). Примечание В первом примере периодическими числами являются 3, 7 и 10. Во втором примере периодическими числами являются 31 и 36. | |
![]()
|
|
D. Патруль Битоникса
Перебор
Комбинаторика
математика
поиск в глубину и подобное
битмаски
*2900
Байтляндия пытается отправить космическую миссию на планету Bit-X. Их задачу усложняет то, что орбита планеты регулярно патрулируется Капитаном Битониксом, возглавляющим космические подразделения планеты Bit-X. Вокруг Bit-X есть n станций пронумерованных по часовой стрелке от 1 до n. Станции равномерно расположены по круговой орбите, то есть станции с номерами i и i + 1 (1 ≤ i < n), а также станции с номерами 1 и n, являются соседними. Расстояние между любой парой соседних станций равняется m космическим милям. Патрулирование Капитана Битоникса заключается в том, что от запрыгивает в свою ракету на одной из станций и летает по кругу, пролетая по меньшей мере одну космическую милю перед тем, как приземлится на некоторой станции (возможно, той, с которой он взлетал). Ракета Битоникса движется на энергии, получаемой от сжигания баков с топливом. После того, как Битоникс использует x-литровый бак с топливом и выбирает направление (по или против часовой стрелки), ракета пролетает ровно x космических миль по круговой орбите в выбранном направлении. Обратите внимание, что у ракеты нет тормозов; ракета не может остановиться, пока не опустошится бак с топливом. Например, предположим, что n = 3, m = 60, а у Битоникса есть баки с топливом на 10, 60, 90 и 100 литров. Если Битоникс стартует со станции номер 1 и использует 100-литровый бак, чтобы лететь по часовой стрелке, затем использует 90-литровый бак, чтобы лететь по часовой стрелке, а затем использует 10-литровый бак, чтобы лететь против часовой стрелки, то он приземлится на станции номер 1, совершив корректный патруль. Обратите внимание, что Битоникс не обязан использовать все доступные баки с топливом. В данном примере Битоникс также может просто использовать 60-литровый бак, чтобы долететь до станции 2 или 3. Однако, если бы n равнялось 3, m равнялось бы 60, а Битониксу были доступны только один бак на 10 литров и один бак на 100 литров, то он никак не смог бы совершить корректный патруль (он бы не смог приземлиться ровно на странции). Космическое агентство Байтляндии хочет уничтожить некоторые топливные баки Капитана Битоникса таким образом, чтобы он не мог совершить ни одного корректного патруля. Сколькими способами можно уничтожить некоторое подмножество топливных баков Капитана Битоникса таким образом, чтобы он не мог совершить ни одного корректного патруля? Найдите описанное количество способов и выведите остаток от его деления на 1000000007 (109 + 7). Выходные данные Выведите единственное число — количество различных подмножеств топливных баков Капитана Битоникса таких, что их уничтожение не позвонит ему совершать корректные патрули, по модулю 1000000007 (109 + 7). Примечание Все топливные баки различны, даже если объемы некоторых из них совпадают. | |
![]()
|
|
C. Частичные суммы
Комбинаторика
математика
теория чисел
*1900
Дан массив a, состоящий из n целых чисел. Элементы массива проиндексированы от 1 до n. Определим операцию, которая состоит из двух шагов, следующим образом: - Сначала по массиву a строится массив s частичных сумм, состоящий из n элементов. Элемент номер i (1 ≤ i ≤ n) массива s равен
 . Операция x mod y обозначает взятие остатка от деления числа x на число y. . Операция x mod y обозначает взятие остатка от деления числа x на число y. - Затем содержимое массива s записывается в массив a. Элемент номер i (1 ≤ i ≤ n) массива s становится i-ым элементом массива a (ai = si).
Вам же нужно найти массив a после применения ровно k описанных операций. Выходные данные Выведите n целых чисел — элементы массива a после проделанных операций. Элементы выводите в порядке увеличения их индексов в массиве a. Выведенные числа разделяйте пробельными символами. | |
![]()
|
|
C. Треугольники
Комбинаторика
математика
*1900
графы
Алиса и Боб больше не играют ни в какие игры; теперь они дружно изучают свойства различных графов. Алиса придумала следующее занятие: из полного неориентированного графа с n вершинами она выбирает какие-то m ребер и оставляет их себе. Оставшиеся же 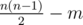 ребер достаются Бобу. ребер достаются Бобу. Алисе и Бобу очень нравятся «треугольники» в графах, то есть циклы длины 3. Поэтому они хотят узнать ответ на такой вопрос: какое суммарное количество треугольников находится в двух графах, образованных ребрами Алисы и ребрами Боба, соответственно? Выходные данные Выведите единственное число — суммарное количество циклов длины 3 в графах Алисы и Боба. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-битных чисел на С++. Рекомендуется использовать потоки cin, cout или спецификатор %I64d. Примечание В первом примере в графе Алисы есть 2 треугольника: (1, 2, 3) и (2, 3, 4). В графе Боба всего 1 треугольник: (1, 4, 5). Поэтому в двух графах всего 3 треугольника. Во втором примере в графе Алисы всего 1 треугольник: (1, 2, 3). В графе Боба находится 3 треугольника: (1, 4, 5), (2, 4, 5) и (3, 4, 5). В данном случае ответ на задачу — 4. | |
![]()
|
|
E. Дары
Теория вероятностей
Комбинаторика
математика
дп
*2600
Жил старик со своею старухой у самого синего моря. Однажды, закинув в море невод, старик поймал рыбку, да не простую, а золотую. Рыбка молвила: «Отпусти меня, старче! Взамен я откуплюсь n дарами, какие ты только пожелаешь!». Затем рыбка дала старику список с названиями даров и их ценностями. В списке некоторые дары могут иметь одинаковые названия, но разные ценности, однако не может быть двух даров с одинаковыми названием и ценностями. Также могут быть два дара с разными названиями, но одинаковыми ценностями. Старик может назвать рыбке n названий из этого списка. Если в списке, предоставленном рыбкой, некоторое название встречается ровно p раз, то старик не может среди своих n названий использовать это название более чем p раз. Старику известно, что если он попросит s даров одинакого названия, то золотая рыбка случайным образом (равновероятно среди всех возможных способов) выберет s даров различной ценности с таким названием из своего списка. Старик не хочет рассердить свою старуху; поэтому он выберет n названий таким способом, что будет иметь возможность получить n даров, имеющих наибольшую ценность. Причем он не очень дальновидный, поэтому, если таких способов несколько, то он выбирает один из них равновероятно. Старик задумался о том, с какой вероятностью он сможет получить n самых ценных даров. Так как старик не силен в теории вероятности, он просит вашей помощи. Выходные данные В единственной строке выведите вещественное число — вероятность получить n самых ценных даров. Ответ будет считаться правильным, если его относительная или абсолютная погрешность не превышает 10 - 9. | |
![]()
|
|
B. Таблица
Комбинаторика
математика
дп
*1900
битмаски
У Джона Доу есть таблица размером n × m. Джон Доу может нарисовать в некоторых ячейках таблицы точки, не более одной точки в одной ячейке таблицы. С помощью таких операций Джон Доу хочет добиться того, чтобы в любой квадратной подтаблице размера n × n количество точек было в точности равно k. Джону Доу стало интересно, сколькими различными способами можно заполнить эту таблицу точками так, чтобы описанное условие выполнялось. Поскольку это число может быть очень велико, Джон Доу просит узнать его остаток от деления на 1000000007 (109 + 7). Считайте, что Джон всегда рисует точку строго в центре некоторой ячейки. Два способа заполнения таблицы точками считаются различными, если существует ячейка таблицы, в которой в одном способе нарисована точка, а в другом — нет. Выходные данные В единственной строке выведите целое число — остаток от деления описанного количества способов на 1000000007 (109 + 7). Примечание Рассмотрим первый тестовый пример: 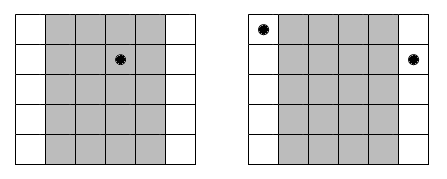 Серая область принадлежит обоим квадратам 5 × 5. Поэтому, если в ней есть одна точка, то больше нигде точек быть не может. Если в одной из белых областей есть точка, то в другой тоже должна быть точка. Таким образом есть 20 вариантов, в которых точка стоит в серой области и 25 вариантов в которых в каждой из белых областей стоит по точке. Всего 45 вариантов. | |
![]()
|
|
E. Задача с Числами
Комбинаторика
математика
реализация
дп
теория чисел
*2600
Обозначим количество делителей положительного целого числа n как d(n). Вам дано три числа a, b и c. Ваша задача — вычислить следующую сумму: 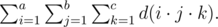 Найдите остаток от деления этой суммы на 1073741824 (230). Выходные данные Выведите единственное целое число — остаток от деления искомой суммы на 1073741824 (230). Примечание Пояснение к первому примеру. - d(1·1·1) = d(1) = 1;
- d(1·1·2) = d(2) = 2;
- d(1·2·1) = d(2) = 2;
- d(1·2·2) = d(4) = 3;
- d(2·1·1) = d(2) = 2;
- d(2·1·2) = d(4) = 3;
- d(2·2·1) = d(4) = 3;
- d(2·2·2) = d(8) = 4.
Следовательно, ответ — 1 + 2 + 2 + 3 + 2 + 3 + 3 + 4 = 20. | |
![]()
|
|
A. Точки на прямой
Бинарный поиск
Комбинаторика
*1300
Маленький Петя очень любит точки. Недавно мама подарила ему n точек, лежащих на прямой OX. Пете стало интересно, сколькими способами он может выбрать три различные точки так, чтобы расстояние между двумя самыми удаленными из выбранных точек не превышало d. Обратите внимание, что порядок точек внутри выбранной тройки значения не имеет. Выходные данные Выведите единственное целое число — количество троек точек, в которых расстояние между двумя самыми удаленными точками не превосходит d. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-х битовых чисел на С++. Рекомендуется использовать потоки cin, cout или спецификатор %I64d. Примечание В первом примере нам подходит любая тройка различных точек. Во втором примере нам подходят всего 2 тройки: {-3, -2, -1} и {-2, -1, 0}. В третьем примере нам подходит одна тройка: {1, 10, 20}. | |
![]()
|
|
B. Маленький Слоник и выборы
Перебор
Комбинаторика
дп
*1900
Недавно в Зоопарке прошли выборы. Всего в выборах участвовало 7 основных политических партий: одна из них Политическая партия Маленького Слоника, остальные 6 партий имеют менее запоминающиеся названия. Для политических партий очень важен их номер в избирательном бюллетене. Всего возможных номеров m: 1, 2, ..., m. Каждой из этих 7 партий будет каким-то образом присвоен ровно один номер, причем две разные партии не могут получить один и тот же номер. Члены Политической партии Маленького Слоника верят в счастливые цифры 4 и 7. Они хотят оценить свои шансы на выборах, для этого надо выяснить, сколько существует таких корректных присвоений номеров партиям, что количество счастливых цифр номера в бюллетене партии Маленького Слоника строго больше общего количества счастливых цифр в номерах остальных 6 партий. Помогите Политической партии Маленького Слоника, посчитайте это количество. Так как ответ может быть довольно большим, выведите остаток от его деления на 1000000007 (109 + 7). Выходные данные В единственной строке выведите целое число — ответ на задачу по модулю 1000000007 (109 + 7). | |
![]()
|
|
C. Маленький Слоник и НОК
Бинарный поиск
Комбинаторика
математика
дп
*2000
Маленький Слоник любит операцию НОК (наименьшее общее кратное) непустого множества целых положительных чисел. Результат операции НОК k целых положительных чисел x1, x2, ..., xk — это минимальное целое положительное число, которое делится на каждое из чисел xi. Пусть задана последовательность целых чисел b1, b2, ..., bn. Обозначим через lcm(b1, b2, ..., bn) их НОК, а через max(b1, b2, ..., bn) — максимальное из них. Маленький Слоник считает последовательность b хорошей, если lcm(b1, b2, ..., bn) = max(b1, b2, ..., bn). У Маленького Слоника есть последовательность целых чисел a1, a2, ..., an. Помогите ему найти количество хороших последовательностей целых чисел b1, b2, ..., bn таких, что для всех i (1 ≤ i ≤ n) выполняется 1 ≤ bi ≤ ai. Так как ответ может быть довольно большим, выведите остаток от его деления на 1000000007 (109 + 7). Выходные данные В единственной строке выведите одно целое число — ответ на задачу по модулю 1000000007 (109 + 7). | |
![]()
|
|
C. Паркет
Конструктив
Комбинаторика
реализация
*2000
жадные алгоритмы
Однажды Вася решил положить паркет у себя в гостиной, которая имела размеры n × m метров. У Васи были плитки трех типов: a плиток 1 × 2 метра, b плиток 2 × 1 метра и c плиток 2 × 2 метра. Помогите Васе выяснить, получится ли у него положить паркет в гостиной, и если получится, найдите один из возможных способов это сделать. Васе не обязательно использовать все имеющиеся плитки. Выходные данные Если положить паркет, используя имеющиеся плитки, невозможно, выведите IMPOSSIBLE. Иначе выведите один из возможных вариантов паркета в гостиной — выведите n строк по m строчных латинских букв в каждой. Две соседние по стороне клетки должны содержать одинаковые буквы, если эти клетки относятся к одной и той же плитке, и различные буквы в противном случае. Разные плитки могут обозначаться одной и той же буквой (см. примеры). Если решений несколько, выведите любое. | |
![]()
|
|
D. Билеты
Теория вероятностей
Комбинаторика
математика
*2400
Как большой фанат Формулы-1, Чарли очень рад организовывать продажу билетов на следующий Гран-при, который проходит в его городе. К сожалению, в связи с финансовым кризисом в его стране остались купюры только на 10 и 20 евро. Каждый билет на гонку стоит 10 евро, поэтому если кто-то хочет купить один билет на купюру на 20 евро, Чарли должен выдать ему сдачу купюрой на 10 евро. Чарли понимает, что при нехватке купюр на 10 евро, это может стать проблемой. У Чарли есть некоторая информация о покупателях, но он никак не может ее использовать, и ему нужна ваша помощь. Ровно n + m человек придут к нему за билетами. n из них придут с одной купюрой на 10 евро, и остальные m из них придут с одной купюрой на 20 евро. Сейчас у Чарли есть k купюр на 10 евро, которые, если понадобится, он может использовать для выдачи сдачи. Все n + m человек придут в магазин билетов в случайном порядке, все порядки равновероятны. Найдите вероятность того, что продажа всех билетов пройдет гладко, т. е. у Чарли будет сдача для каждого человека с купюрой на 20 евро. Выходные данные Выведите требуемую вероятность по крайней мере с 4 знаками после десятичной точки. | |
![]()
|
|
D. Дима и две последовательности
Комбинаторика
математика
*1600
сортировки
У маленького Димы есть две последовательности точек с целочисленными координатами: последовательность (a1, 1), (a2, 2), ..., (an, n) и последовательность (b1, 1), (b2, 2), ..., (bn, n). Теперь Дима хочет подсчитать сколько различных последовательностей точек длины 2·n можно собрать из этих последовательностей, таких что x-координаты точек в собранной последовательности будут не убывать. Помогите ему в этом. Обратите внимание, что каждый элемент каждой из начальных последовательностей должен быть использован ровно один раз в собранной последовательности. Две собранные последовательности (p1, q1), (p2, q2), ..., (p2·n, q2·n) и (x1, y1), (x2, y2), ..., (x2·n, y2·n) Дима считает различными, если найдется такое i (1 ≤ i ≤ 2·n), что (pi, qi) ≠ (xi, yi). Так как ответ может быть достаточно большим, выведите остаток от деления ответа на число m. Выходные данные В единственную строку выведите остаток от деления ответа на задачу на число m. Примечание В первом примере можно получить только одну последовательность: (1, 1), (2, 1). Во втором примере можно получить такие последовательности : (1, 1), (2, 2), (2, 1), (3, 2); (1, 1), (2, 1), (2, 2), (3, 2). Таким образом ответ 2. | |
![]()
|
|
E. Дима и кони
Конструктив
Комбинаторика
графы
*2200
Дима приехал в страну коней. В стране коней живет n коней. У каждого коня в стране коней есть несколько врагов (отношение вражды симметричное). Страна коней не очень враждебная, поэтому количество врагов каждого коня не превышает трех. Сейчас в стране коней выборы. Поэтому кони поручили Диме разделить их на две партии. При этом кони хотят, чтобы выполнялось следующее условие: у каждого коня не должно быть более одного врага в своей партии. Помогите Диме разделить коней на партии. Обратите внимание, что одна из партий может оказаться пустой. Выходные данные Выведите строку, состоящую из n символов: i-тый символ строки должен быть равен «0», если конь номер i будет принадлежать первой партии, иначе этот символ должен быть равен «1». Если не существует способа разделить коней требуемым образом выведите -1. | |
![]()
|
|
C. Очереди к умывальникам
Теория вероятностей
Комбинаторика
дп
*2200
В одном общежитии одного университета живет n студентов. Так как у всех пары начинаются в одно и то же время, расстояние до университета для всех одинаково и, как ни странно, все ходят на все пары, все n студентов просыпаются одновременно. Также на этаже находится m комнат с умывальниками и в i-ой комнате — ai умывальников. Утром, как только все просыпаются, каждый студент равновероятно и независимо от других выбирает одну из m комнат, в которую он пойдет умываться. После того, как студенты распределились по комнатам, внутри каждой комнаты студенты делятся на максимально равные очереди, по одной к каждому умывальнику. Т. е. они делятся на очереди так, чтобы размер самой длинной очереди был как можно меньше. Ваша задача выяснить математическое ожидание длины максимальной из очередей по всем комнатам, чтобы администрация могла улучшить общежитие и помочь студентам не опаздывать на пары. Выходные данные Выведите единственное число: математическое ожидание длины максимальной очереди. Ваш ответ должен иметь относительную или абсолютную погрешность меньше чем 10 - 9. | |
![]()
|
|
E. Коровки играют в теннис
Структуры данных
Комбинаторика
математика
*2800
Фермер Джон устраивает турнир по теннису среди своих n коровок. У каждой коровки есть умение si, и никакие две коровки не обладают одинаковым умением. На протяжении турнира, каждая коровка играет с каждой другой коровкой ровно один раз, в таком поединке коровка с большим умением побеждает коровку с меньшим умением. Однако Фермер Джон беспокоится, что турнир уничтожит самооценку самых слабых коровок, которые проиграют большую часть своих матчей... И вот он решил немного поменять результаты. Ровно k раз он возьмет два целых числа ai, bi (ai < bi) и поменяет все результаты матчей коровок с умениями от ai до bi, включительно. Таким образом, для каждой пары x, y 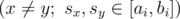 он поменяет результат матча между коровками x и y (то есть, если матч выиграла x, то после изменения будет считаться, что победила y и наоборот). Возможно, Фермер Джон поменяет результат какого-то одного матча несколько раз. Обратите внимание, что ai и bi могут быть не равны умению той или иной коровки. он поменяет результат матча между коровками x и y (то есть, если матч выиграла x, то после изменения будет считаться, что победила y и наоборот). Возможно, Фермер Джон поменяет результат какого-то одного матча несколько раз. Обратите внимание, что ai и bi могут быть не равны умению той или иной коровки. Фермер Джон хочет вычислить, насколько сбалансированными будут результаты турнира. Для этого он хочет посчитать количество троек коровок (p, q, r), для которых в итоге будет считаться, что коровка p выиграла у коровки q, коровка q выиграла у коровки r, а коровка r выиграла у коровки p. Помоги ему вычислить это количество. Обратите внимание, что две тройки считаются различными тогда, когда они не содержат одинаковый набор коровок (то есть, некоторая коровка есть в одной тройке и отсутствует в другой). Выходные данные Выведите единственное целое число — количество троек коровок (p, q, r), для которых в итоге будет считаться, что коровка p выиграла у коровки q, коровка q выиграла у коровки r, а коровка r выиграла у коровки p. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-битных чисел на С++. Рекомендуется использовать потоки cin, cout или спецификатор %I64d. Примечание В первом примере (коровка 3 > коровка 1), (коровка 3 > коровка 2), а (коровка 2 > коровка 1). Однако фермер подменит результаты матчей между коровками номер 1 и 2 и коровками номер 2 и 3, так что теперь результаты показывают, что (коровка 1 > коровка 2), (коровка 2 > коровка 3), а (коровка 3 > коровка 1). Таким образом, коровки номер 1, 2, и 3 формируют сбалансированный треугольник. | |
![]()
|
|
D. Сумма перестановок
Комбинаторика
реализация
дп
*1900
битмаски
meet-in-the-middle
Перестановкой p называется упорядоченный набор чисел p1, p2, ..., pn, состоящий из n различных целых положительных чисел, каждое из которых не больше чем n. Обозначим i-ый элемент перестановки p через pi. Число n будем называть размером или длиной перестановки p1, p2, ..., pn. Петя решил ввести операцию суммы на множестве перестановок длины n. Пусть заданы две перестановки длины n: a1, a2, ..., an и b1, b2, ..., bn. Суммой перестановок a и b Петя назвал такую перестановку c длины n, у которой ci = ((ai - 1 + bi - 1) mod n) + 1 (1 ≤ i ≤ n). Операция 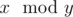 обозначает взятие остатка от деления числа x на число y. обозначает взятие остатка от деления числа x на число y. Очевидно, что не для всех перестановок a и b будет существовать перестановка c, являющаяся их суммой. Из-за этого Петя расстроился и попросил Вас для заданного n посчитать количество таких пар перестановок a и b длины n, что существует перестановка c, являющаяся суммой a и b. Пара перестановок x, y (x ≠ y) и пара перестановок y, x считаются различными парами. Так как ответ может получиться достаточно большим, выведите его остаток от деления на 1000000007 (109 + 7). Выходные данные В единственной строке выведите целое неотрицательное число — количество таких пар перестановок a и b, что существует перестановка c, которая является суммой a и b, по модулю 1000000007 (109 + 7). | |
![]()
|
|
E. Позиции в перестановке
Комбинаторика
математика
дп
*2600
Перестановкой p называется упорядоченный набор чисел p1, p2, ..., pn, состоящий из n различных целых положительных чисел, каждое из которых не больше чем n. Обозначим i-ый элемент перестановки p через pi. Число n будем называть размером или длиной перестановки p1, p2, ..., pn. Назовем позицию i (1 ≤ i ≤ n) в перестановке p1, p2, ..., pn хорошей, если |p[i] - i| = 1. Посчитайте количество перестановок размера n с ровно k хорошими позициями. Ответ выведите по модулю 1000000007 (109 + 7). Выходные данные Выведите количество перестановок размера n с ровно k хорошими позициями по модулю 1000000007 (109 + 7). Примечание Единственная перестановка размера 1 имеет 0 хороших позиций. Перестановка (1, 2) имеет 0 хороших позиций, а перестановка (2, 1) — 2 позиции. Перестановки размера 3: - (1, 2, 3) — 0 позиций
-
 — 2 позиции — 2 позиции -
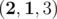 — 2 позиции — 2 позиции -
 — 2 позиции — 2 позиции -
 — 2 позиции — 2 позиции - (3, 2, 1) — 0 позиций
| |
![]()
|
|
B. Пингвин Поло и дома
Комбинаторика
*1500
Маленький пингвин Поло любит свою родную деревню. В этой деревне n домов, пронумерованных целыми числами от 1 до n. На каждом доме висит табличка с целым числом, на i-том доме висит табличка с целым числом pi (1 ≤ pi ≤ n). Маленький пингвин Поло очень любит гулять по этой деревне. Прогулка выглядит следующим образом. Сначала он стоит около дома с номером x. Потом пингвин идет к дому, номер которого написан на табличке дома x (то есть к дому px), затем к дому, номер которого написан на табличке дома px (то есть к дому ppx), и так далее. Известно, что: - Начав прогулку от любого дома с номером от 1 до k, включительно, он может дойти до дома с номером 1.
- Начав прогулку от любого дома с номером от k + 1 до n, включительно, он точно не может дойти до дома с номером 1.
- Начав прогулку от дома с номером 1, пингвин Поло может попасть обратно к дому с номером 1 через некоторое ненулевое количество переходов от дома к дому.
Вам нужно найти, сколькими способами можно написать числа на табличках домов, чтобы описанные выше три условия выполнялись. Выведите остаток от деления этого количества на 1000000007 (109 + 7). Выходные данные В единственной строке выведите целое число — ответ на задачу по модулю 1000000007 (109 + 7). | |
![]()
|
|
D. Пингвин Поло и дерево
Деревья
Комбинаторика
поиск в глубину и подобное
*2400
У маленького пингвина Поло есть дерево — неориентированный связанный ациклический граф, в котором n вершин и n - 1 ребро. Будем считать, что вершины дерева пронумерованы целыми числами от 1 до n. Сегодня Поло интересует следующая задача: найти количество пар путей, у которых нет ни одной общей вершины. Более формально, нужно найти количество четверок целых чисел a, b, c и d таких, что: - 1 ≤ a < b ≤ n;
- 1 ≤ c < d ≤ n;
- не существует такой вершины, которая одновременно лежит на кратчайшем пути от вершины a до вершины b и от вершины c до вершины d.
Под кратчайшим путем между двумя вершинами подразумевается путь, кратчайший по количеству ребер. Помогите Поло, решите эту задачу. Выходные данные В единственной строке выведите целое число — ответ на задачу. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-битных чисел на С++. Рекомендуется использовать потоки cin, cout или спецификатор %I64d. | |
![]()
|
|
B. Различные пути
Перебор
Комбинаторика
*2700
Дана прямоугольная доска, состоящая из n × m клеток. Некоторые из клеток уже покрашены в какой-то из k цветов. Требуется покрасить каждую непокрашенную клетку в один из k цветов таким образом, чтобы любой путь из верхней левой клетки в правую нижнюю (переходы возможны только по клеткам соседним по стороне и только вниз или вправо) не содержал в себе двух клеток одинакового цвета. Выведите остаток от деления количества возможных раскрасок на 1000000007 (109 + 7). Выходные данные Выведите остаток от деления количества возможных раскрасок на 1000000007 (109 + 7). | |
![]()
|
|
C. Шаасс и лампочки
Комбинаторика
теория чисел
*1900
В ряд выстроено n лампочек. Лампочки пронумерованы от 1 до n слева направо. Изначально некоторые лампочки включены. Шаасс хочет включить все лампочки. За один ход он может включить лампочку (которая на тот момент должна быть выключенной), если у нее есть хотя бы одна соседняя включенная лампочка. Юноша знает изначальное состояние лампочек и ему интересно, сколько есть различных способов включить все лампочки. Пожалуйста, посчитайте искомое количество способов по модулю 1000000007 (109 + 7). Выходные данные В единственной строке выведите количество различных возможных способов включить все лампочки по модулю 1000000007 (109 + 7). | |
![]()
|
|
C. Егор и друзья
Комбинаторика
*2100
дп
графы
кратчайшие пути
Егор с друзьями гуляли по лесу, всего, включая Егора, гуляло n человек. Очень скоро перед ними оказалась река. Ребята сразу же захотели перебраться через реку, тем более, что возле берега, к которому подошла компания стояла лодка. Известно, что эта лодка вмещает людей, суммарным весом не более k килограмм. Егор тут же выписал на листок бумаги список весов всех людей из его компании, включая свой вес. Оказалось, что каждый человек весит либо 50, либо 100 килограмм. Сейчас Егору нужно знать, за какое минимальное количество переправ на лодке через реку вся компания сможет оказаться на другом берегу. При переправе в лодке обязательно должен быть хотя бы один человек. При переправке в лодке может сидеть любое (ненулевое) количество человек, но их суммарный вес не должен превышать k. Так же Егора заинтересовал вопрос: сколько существует способов переправить всех людей на другую сторону за минимальное количество переправ на лодке. Два способа считаются различными, если при какой-либо переправе множество людей находящихся в лодке отличается. Помогите Егору с этой задачей. Выходные данные В первую строку выведите целое число — минимальное количество переправ. Если невозможно переправить всех людей на другой берег, то выведите целое число -1. Во вторую строку выведите остаток от деления количества способов переправить людей за минимальное количество переправ на число 1000000007 (109 + 7). Если невозможно переправить всех людей на другой берег, то выведите число 0. Примечание В первом тесте Егор гуляет один и соответственно требуется только одна переправа через реку. Во втором тесте нужно действовать по следующему плану: - переправить двух людей весом по 50 килограмм;
- переправить одного человека весом 50 килограмм обратно;
- переправить человека весом 100 килограмм;
- переправить человека весом 50 килограмм обратно;
- переправить двух людей весом по 50 килограмм.
Суммарно выходит 5 переправ. В зависимости от того, какого человека выбрать на шаге 2, получаются два различных способа. | |
![]()
|
|
D. Егор и пещеры
Комбинаторика
дп
*2400
У Егора есть планшет. Экран планшета представляет собой прямоугольник n × m клеток, каждая из которых может быть либо черной, либо белой. Будем считать, что строки планшета пронумерованы целыми числами от 1 до n сверху вниз. Аналогично, столбцы планшета пронумерованы целыми числами от 1 до m слева направо. Егор считает, что на экране планшета нарисована пещера, если выполнены следующие условия: - Найдется отрезок [l, r] (1 ≤ l ≤ r ≤ n), такой, что в каждой из строк l, l + 1, ..., r, будет ровно две черные клетки, а во всех остальных строках все клетки будут белыми.
- Найдется строка с номером t (l ≤ t ≤ r), такая, что для всех пар строк с номерами i и j (l ≤ i ≤ j ≤ t) множество столбцов, содержащихся между черными клетками в строке номер i (вместе со столбцами, в которых находятся черные клетки), будет подмножеством множества столбцов, содержащихся между черными клетками в строке номер j (вместе со столбцами, в которых находятся черные клетки). Аналогично, для всех пар строк с номерами i и j (t ≤ i ≤ j ≤ r) множество столбцов, содержащихся между черными клетками в строке номер j (вместе со столбцами, в которых находятся черные клетки), будет подмножеством множества столбцов, содержащихся между черными клетками в строке номер i (вместе со столбцами, в которых находятся черные клетки).
Егора заинтересовал вопрос: сколько существует способов изобразить пещеру на его планшете. Два изображения считаются различными, если существует клетка, цвет которой отличается в этих изображениях. Помогите Егору. Выходные данные В единственную строку выведите остаток от деления ответа на задачу на число 1000000007 (109 + 7). | |
![]()
|
|
B. Ярослав и две строки
Комбинаторика
дп
*2000
Ярослав считает, что две строки s и w, состоящие из цифр и имеющие длину n — несравнимы, если найдется два числа i и j (1 ≤ i, j ≤ n), таких, что si > wi, а sj < wj. Здесь запись si обозначает i-тую цифру строки s, аналогично, wj — j-тую цифру строки w. Шаблоном строки назовем строку, которая состоит из цифр и знаков вопроса («?»). У Ярослава есть два шаблона строк, каждый из которых длины n. Ярослав хочет посчитать, сколькими способами он может заменить все знаки вопроса в обоих шаблонах на некоторые цифры, так, чтобы полученные строки были несравнимы. Обратите внимание, что полученные строки могут содержать лидирующие нули и что разные знаки вопроса могут быть заменены на разные цифры, а могут и на одинаковые. Помогите Ярославу, посчитайте остаток от деления описанного количества способов на 1000000007 (109 + 7). Выходные данные В единственную строку выведите остаток от деления ответа на задачу на число 1000000007 (109 + 7). Примечание В первом тесте нет знаков вопроса и обе строки несравнимы, поэтому ответ — 1. Во втором тесте нет знаков вопроса, но заданные строки сравнимы, поэтому ответ — 0. | |
![]()
|
|
C. Прекрасные числа
Перебор
Комбинаторика
*1800
Виталий очень странный человек. У него есть две любимые цифры a и b. Виталий называет целое положительное число хорошим, если в десятичной записи этого числа используются только цифры a и b. Виталий называет хорошее число замечательным, если сумма его цифр является хорошим числом. Например, пусть у Виталия любимые цифры 1 и 3, тогда число 12 — не является хорошим, а числа 13 или 311 являются. Также число 111 — замечательное, а число 11 — нет. Теперь Виталий интересуется, сколько существует замечательных чисел длины ровно n. Так как количество таких чисел может быть довольно большим, он просит Вас посчитать остаток от деления этого количества на 1000000007 (109 + 7). Под длиной числа подразумевается количество цифр в его десятичной записи без лидирующих нулей. Выходные данные Выведите единственное целое число — ответ на задачу по модулю 1000000007 (109 + 7). | |
![]()
|
|
D. Оля и граф
Комбинаторика
математика
*2200
У Оли есть ориентированный невзвешенный граф, состоящий из n вершин и m ребер. Будем считать, что вершины графа пронумерованы от 1 до n некоторым способом. Тогда для каждого ребра графа, идущего от вершины v к вершине u, выполняется неравенство: v < u. Теперь Оле интересно, сколько существует способов добавить в граф произвольное (возможно нулевое) количество ребер так, чтобы для полученного графа были выполнены условия: - Из любой вершины с номером i (i < n) достижимы вершины с номерами i + 1, i + 2, ..., n.
- Для каждого ребра графа, идущего от вершины v к вершине u, выполняется неравенство: v < u.
- Между любыми двумя вершинами существует не более одного ребра.
- Кратчайшее расстояние между парой вершин i, j (i < j), для которых верно, что j - i ≤ k, равно j - i ребер.
- Кратчайшее расстояние между парой вершин i, j (i < j), для которых верно, что j - i > k, равно либо j - i, либо j - i - k ребер.
Два способа будем считать различными, если будет существовать пара вершин i, j (i < j) такая, что в первом полученном графе будет существовать ребро из i в j, а во втором — нет. Помогите Оле. Так как искомое количество способов может быть достаточно большим, выведите его остаток от деления на 1000000007 (109 + 7). Выходные данные Выведите единственное целое число — ответ на задачу по модулю 1000000007 (109 + 7). Примечание В первом примере есть два способа: первый — это ничего не добавлять, второй — добавить единственное ребро из вершины 2 в вершину 5. | |
![]()
|
|
C. Белое, черное и снова белое
Комбинаторика
*2100
теория чисел
Поликарп уверен, что жизнь его поддается описанию: «сначала идет белая полоса, потом черная, потом снова белая». Вот и в ближайшие n дней он уверен — это правило будет выполняться. Поликарп знает, что его ожидает w хороших событий и b не очень. Каждый день будет происходить хотя бы одно событие. Так как каждый из дней однозначно характеризуется как часть белой или черной полосы, в каждый из дней будут случаться события только одного типа (либо хорошие, либо не очень). Какое количество различных вариантов развития истории может быть в ближайшие n дней, если Поликарпа ждет сначала белая полоса (полоса из исключительно хороших событий, длина полосы не менее 1 дня), потом черная полоса (полоса из исключительно событий «не очень», длина полосы не менее 1 дня) и снова белая полоса (полоса из исключительно хороших событий, длина полосы не менее 1 дня). Каждый из n дней будет принадлежать ровно к одной из трех полос. Учтите, что события даже одного типа различимы между собой. Даже если события происходят в один день, они происходят в некотором порядке (одновременных событий не бывает). Напишите программу, которая выводит количество возможных конфигураций распределения событий по дням по модулю 1000000009 (109 + 9). Ознакомьтесь с примерами для уточнения того, какие способы следует различать. Выходные данные Выведите искомое количество способов по модулю 1000000009 (109 + 9). Примечание Будем обозначать хорошие события цифрами от 1, а события «не очень» буквами от 'a'. Вертикальными чертами будем разделять дни. В первом примере возможные варианты: «1|a|2» и «2|a|1». Во втором примере возможные варианты: «1|a|b|2», «2|a|b|1», «1|b|a|2» и «2|b|a|1». Во третьем примере возможные варианты: «1|ab|2», «2|ab|1», «1|ba|2» и «2|ba|1». | |
![]()
|
|
A. Танцевальный клуб Малека
Комбинаторика
математика
*1600
По традиции, каждый год перед международной олимпиадой по информатике все участники фан-клуба Наталии приглашаются в танц-клуб Малека для приятного времяпрепровождения. Танц-клуб Малека насчитывает 2n участников и по совпадению, фан-клуб Наталии также насчитывает 2n участников. Каждому участнику ТКМ приписывается уникальный номер i от 0 до 2n - 1. То же самое верно для каждого участника ФКН. Среди прочего, встречи традиционно включают парный танец, где каждый участник ТКМ танцует с участником ФКН. Пара в танце — это такая пара чисел (a, b), что участник номер a из ТКМ танцует с участником номер b из ФКН. Назовем сложностью распределения пар количество пар танцующих пар (a, b) и (c, d), таких, что a < c и b > d. Вам дано двоичное число x длины n. Мы знаем, что участник номер i из ТКМ танцует с участником номер  из ФКН. Ваша задача — высчитать сложность такого распределения по модулю 1000000007 (109 + 7). из ФКН. Ваша задача — высчитать сложность такого распределения по модулю 1000000007 (109 + 7). Выражение  обозначает применение операции «XOR» к числам x и y. Данная операция существует во всех современных языках программирования. Например, в C++ и Java она обозначается как «^», в языке Pascal — как «xor». обозначает применение операции «XOR» к числам x и y. Данная операция существует во всех современных языках программирования. Например, в C++ и Java она обозначается как «^», в языке Pascal — как «xor». Выходные данные Выведите сложность данного распределения по модулю 1000000007 (109 + 7). | |
![]()
|
|
B. Ciel и цветы
Комбинаторика
математика
*1600
У лисы Ciel есть некоторое количество цветов: r красных, g зеленых и b синих цветов. Она хочет сделать несколько букетов из этих цветов. Есть 4 типа букетов: - На «красный букет» надо 3 красных цветка.
- На «зеленый букет» надо 3 зеленых цветка.
- На «синий букет» надо 3 синих цветка.
- На «смешанный букет» надо 1 красный, 1 зеленый и 1 синий цветок.
Помогите лисе Ciel посчитать, какое максимальное количество букетов можно сделать из ее цветов. Выходные данные Выведите максимальное количество букетов, которое может сделать лиса Ciel. Примечание В тесте 1 можно сделать 1 красный букет, 2 зеленых букета и 3 синих букета. В тесте 2 можно сделать 1 красный, 1 зеленый, 1 синий и 1 смешанный букет. | |
![]()
|
|
A. Черно-белый куб
Конструктив
Комбинаторика
*1600
Вам дан куб размера k × k × k единичных кубиков. Два единичных кубика считаются соседними, если у них есть общая грань. Ваша задача — покрасить каждый из k3 единичных кубиков в один из двух цветов (черный или белый), так чтобы выполнялись два условия: - у каждого белого кубика есть ровно 2 соседних кубика белого цвета;
- у каждого черного кубика есть ровно 2 соседних кубика черного цвета.
Выходные данные Если решения не существует, то выведите -1. Иначе выведите искомую раскраску куба последовательно по слоям. В первых k строках выведите матрицу k × k — как должен быть раскрашен первый слой куба. В следующих k строках выведите матрицу k × k — как должен быть раскрашен второй слой куба. И так далее до последнего k-го слоя. Обратите внимание, что ориентация куба в пространстве не имеет значения. Единичный куб белого цвета обозначайте символом «w», черного — «b». Следуйте формату выходных данных, который указан в тестовых примерах. При проверке правильности ответа пустые строки никак не учитываются. | |
![]()
|
|
E. Тропинки и полянки
Комбинаторика
*2800
поиск в глубину и подобное
жадные алгоритмы
графы
снм
Красная Шапочка и Иван Дурак гуляют по лесу. Гуляя по лесу, они обнаружили, что в лесу есть тропинки и полянки. Всего в лесу n полянок, которым Иван Дурак назначил номера от 0 до n - 1. Иван Дурак заметил, что для каждой полянки i, из нее есть ровно две тропинки: одна ведет в полянку номер (2·i) mod n, вторая — в полянку ((2·i) + 1) mod n. Красная Шапочка, в свою очередь, заметила, что все тропинки однонаправленные (Красная Шапочка не может объяснить природу этого явления). Теперь, стоя в полянке с номером 0, Красная Шапочка задалась вопросом — если она начнет гулять по тропинкам, может ли она обойти все полянки ровно по одному разу и в конце вернуться на полянку с номером 0 опять (тем самым посетив ее дважды)? Запись x mod y обозначает операцию взятия остатка от деления числа x на число y. Выходные данные Выведите порядок, в котором следует обойти полянки. Каждая полянка должна быть выведена ровно один раз, кроме полянки 0, которая должна быть выведена ровно дважды: первой и последней в списке. Если решения не существует, выведите -1. Если решений несколько, выведите любое из них. | |
![]()
|
|
C. Волшебная пятерка
Комбинаторика
математика
*1700
Дана длинная табличка s с n цифрами, записанными на ней в ряд. Яхуб хочет удалить некоторое количество цифр (возможно, нулевое, но удалять все цифры не разрешается), чтобы получить на табличке «волшебное число», число, которое делится на 5. Обратите внимание, что итоговое число может содержать лидирующие нули. Теперь Яхуб хочет посчитать количество способов, которыми он может получить волшебное число, по модулю 1000000007 (109 + 7). Два способа различны тогда, когда набор удаленных позиций в s различается. Обратите внимание на описание входных данных, s задана в особой форме. Выходные данные Выведите единственное целое число — требуемое количество способов по модулю 1000000007 (109 + 7). Примечание В первом тесте есть четыре возможных способа получить число, делимое на 5: 5, 15, 25 и 125. Во втором тесте не забудьте выполнить конкатенацию копий a. Нужная табличка — 1399013990. В третьем тесте можно выбрать любой вариант (кроме удаления всех цифр). Следовательно, есть 26 - 1 = 63 возможных способов удалить цифры. | |
![]()
|
|
E. Идем по оси
Конструктив
Комбинаторика
дп
*2300
битмаски
meet-in-the-middle
Яхуб хочет встретиться со своей подружкой Яхубиной. Они оба живут на оси Ox (горизонтальной оси координат). Яхуб живет в точке 0, а Яхубина живет в точке d. У Яхуба есть n целых положительных чисел a1, a2, ..., an. Сумма этих чисел равняется d. Предположим, что p1, p2, ..., pn — это перестановка чисел {1, 2, ..., n}. Затем, пусть b1 = ap1, b2 = ap2 и так далее. Будем называть массив b — «путь». Существует n! различных путей, один путь для каждой перестановки p. Яхуб запланировал поход к своей подружке следующим образом. Сначала он проходит b1 шагов по оси Ox, затем делает привал в точке b1. Затем он проходит еще b2 шагов по оси Ox и устраивает привал в точке b1 + b2. Аналогично, в j-ый раз (1 ≤ j ≤ n) он проходит еще bj шагов по оси Ox и делает привал в точке b1 + b2 + ... + bj. Яхуб очень суеверный человек. У него есть k несчастливых целых чисел. Яхуб называет путь «хорошим», если он никогда не делает привала в точке, соответствующей хотя бы одному из этих k чисел. Просто из любопытства посчитайте, сколько существует хороших путей по модулю 1000000007 (109 + 7). Выходные данные Выведите единственное целое число — ответ на дилемму Яхуба. Примечание В первом тесте посмотрим на шесть возможных путей: - [2, 3, 5]. Яхуб остановится в точках 2, 5 и 10. Среди них несчастливое число — 5.
- [2, 5, 3]. Яхуб остановится в точках 2, 7 и 10. Среди них несчастливое число — 7.
- [3, 2, 5]. Остановка в несчастливой точке 5.
- [3, 5, 2]. Такое расположение подходит.
- [5, 2, 3]. Два несчастливых привала (5 и 7).
- [5, 3, 2]. Яхуб не согласится, так как здесь есть привал в точке 5.
Во втором тесте заметьте, что два разных способа могут иметь идентичные наборы привалов. В конкретном случае, все шесть возможных способов имеют одни и те же остановки: [2, 4, 6], так что тут неудача не грозит Яхубу. | |
![]()
|
|
D. Медведь Василий и красивые строки
Комбинаторика
математика
*2100
теория чисел
Медведь Василий любит красивые строки. Будем называть строку s красивой, если выполнены следующие условия: - Строка s состоит только из символов 0 и 1, причем символ 0 должен встречаться в строке s ровно n раз, а символ 1 — ровно m раз.
- За некоторое (возможно нулевое) количество модификаций из строки s можно получить любимый символ g, который равен либо нулю, либо единице.
Модификацией строки, длина которой не меньше двух, будем называть следующую операцию: из строки удаляются два последних символа, а на их место ставится ровно один другой символ, который будет равен единице, если оба удаленных символа были равны нулю, и нулю иначе. Например, в результате одной модификации из строки «01010» получится строка «0100», в результате двух — «011». Применять модификацию к строке длины меньше чем два запрещено. Помогите Медведю, посчитайте количество красивых строк. Так как количество красивых строк может быть очень большим, выведите остаток от деления этого количества на 1000000007 (109 + 7). Выходные данные Выведите единственное целое число — ответ на задачу по модулю 1000000007 (109 + 7). Примечание В первом примере красивыми являются строки «01», «10». Во втором примере красивыми являются строки «0011», «1001», «1010», «1100». В третьем примере красивых строк нет. | |
![]()
|
|
E. Медведь Василий и покраска квадрата
Комбинаторика
реализация
дп
*2700
битмаски
У медведя Василия есть два любимых целых числа n и k, а также карандаш. Кроме того, у него есть k банок с акварельными красками различных цветов. Все банки пронумерованы некоторым образом от 1 до k включительно. В банке с номером i находится краска i-ого цвета. Изначально на координатной плоскости медведь нарисовал карандашом четыре отрезка. Все они имеют в качестве конца точку (0, 0), а качестве начала они имеют следующие точки: (0, 2n), (0, - 2n), (2n, 0), ( - 2n, 0). Далее для каждого i = 1, 2, ..., n медведь нарисовал два квадрата. Первый квадрат имеет следующие координаты вершин: (2i, 0), ( - 2i, 0), (0, - 2i), (0, 2i). Второй квадрат имеет следующие координаты вершин: ( - 2i - 1, - 2i - 1), ( - 2i - 1, 2i - 1), (2i - 1, - 2i - 1), (2i - 1, 2i - 1). После всего этого медведь нарисовал еще один квадрат: (1, 0), ( - 1, 0), (0, - 1), (0, 1). Все точки, упомянутые выше, образуют множество точек A. 
Пример полученного рисунка при n = 0 
Пример полученного рисунка при n = 2 Медведь решил покрасить полученный рисунок за k ходов, i-ый ход состоит из следующих этапов: - Медведь выбирает 3 различных точки в множестве А так, чтобы между любой парой выбранных точек на рисунке существовал отрезок. Внутри области, ограниченной выбранными точками и отрезками между ними, не должно быть точек, уже покрашенных некоторой акварельной краской.
- Медведь закрашивает в i-ый цвет область, ограниченную выбранными точками и отрезками.
Отметим, что после k-ого хода некоторые части рисунка могут остаться непокрашенными. Медведь попросил Вас определить количество различных способов покраски его рисунка. Способом покраски Василий называет последовательность трехэлементных множеств точек, выбранных им на каждом из ходов. Две последовательности множеств считаются различными, если существует такое число i (1 ≤ i ≤ k), что i-ые члены этих последовательностей не совпадают как множества. Так как искомое количество способов покраски может быть довольно большим, требуется найти лишь остаток от деления его на число 1000000007 (109 + 7). Выходные данные Выведите ровно одно число — ответ на задачу по модулю 1000000007 (109 + 7). | |
![]()
|
|
C. Про туриста
Комбинаторика
математика
реализация
*1600
Яхуб — ярый поклонник туристов. Он и сам хочет стать туристом и поэтому запланировал поездку. На прямой дороге расположены n пунктов назначения, Яхуб хочет посетить их все. Он начинает экскурсию с километра номер 0. Яхубу известно как расположены пункты назначения на дороге. Он знает последовательность целых чисел a1, a2, ..., an, в которой число ak обозначает, что k-тый пункт назначения находится на расстоянии ak километров от точки начала экскурсии. Известно, что никакие два пункта не расположены в одном и том же месте. Яхуб хочет посетить каждый пункт ровно один раз. Обратите внимание, что если Яхуб пересекает какой-то пункт назначения по дороге к другому пункту, это не считается посещением. То есть, если Яхуб двигается к какому-то пункту, чтобы посетить его, и по дороге встречает непосещенный пункт, такое событие не считается посещением пункта. Также, после того как Яхуб посетит свой последний пункт назначения, он не возвращается на километр 0, то есть в последнем пункте путешествие заканчивается. Расстояние между пунктом, находящемся на километре x, и следующим пунктом, находящемся на километре y, считается равным |x - y| километров. «Путем» называется порядок прохождения пунктов назначения. Яхуб может посещать пункты в том порядке, в каком хочет, лишь бы он посетил все n пунктов назначения и при этом не посетил никакой пункт более одного раза. Яхуб начинает выписывать на бумаге все возможные пути. Для каждого пути он отмечает расстояние, которое надо будет пройти, если следовать этому пути. Яхуб хочет найти среднее количество километров в пути. Ему уже наскучило выписывать все пути, поэтому он просит Вас помочь ему. Выходные данные Выведите два целых числа — числитель и знаменатель дроби, равной требуемому среднему значению. Дробь должна быть несократимая. Примечание Рассмотрим 6 возможных путей: - [2, 3, 5]: суммарное пройденное расстояние равно |2 – 0| + |3 – 2| + |5 – 3| = 5;
- [2, 5, 3]: |2 – 0| + |5 – 2| + |3 – 5| = 7;
- [3, 2, 5]: |3 – 0| + |2 – 3| + |5 – 2| = 7;
- [3, 5, 2]: |3 – 0| + |5 – 3| + |2 – 5| = 8;
- [5, 2, 3]: |5 – 0| + |2 – 5| + |3 – 2| = 9;
- [5, 3, 2]: |5 – 0| + |3 – 5| + |2 – 3| = 8.
Таким образом средняя длина пути в километрах 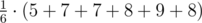 = = 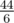 = = 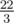 . . | |
![]()
|
|
E. Яхуб и перестановки
Комбинаторика
математика
*2000
Яхуб так обрадовался изобретению графов сортировки пузырьком, что он целый день сидит в офисе и выписывает перестановки. Яхубина вся извелась — ведь теперь Яхубу нет до нее дела. И вот, стоило Яхубу выйти, Яхубина зашла к нему в офис, чтобы саботировать его научную работу — и месть ее страшна. Девушка отыскала важную для исследования Яхуба перестановку. Перестановка состояла из n различных целых чисел a1, a2, ..., an (1 ≤ ai ≤ n). Найдя перестановку, она сразу же заменила некоторые элементы перестановки числами -1. Когда Яхуб вернулся, он обнаружил, что важная перестановка испорчена. Теперь Яхуб пытается ее восстановить. К сожалению, про изначальную перестановку он запомнил только то, что в перестановке не было ни одной неподвижной точки. Неподвижная точка перестановки — это такой элемент ak, значение которого равняется k (ak = k). Ваша задача — доказать Яхубу, что восстанавливать перестановку уже не стоит. Выведите количество перестановок, которые могут оказаться изначальной важной перестановкой Яхуба по модулю 1000000007 (109 + 7). Выходные данные Выведите единственное целое число — количество способов восстановления перестановки по модулю 1000000007 (109 + 7). Примечание В первом тестовом примере две перестановки, не имеющие неподвижных точек: [2, 5, 4, 3, 1] и [5, 1, 4, 3, 2]. У всех остальных перестановок была бы по крайней мере одна неподвижная точка. | |
![]()
|
|
B. Джефф и Фурик
Теория вероятностей
Комбинаторика
дп
*1900
Джефф — новый друг Фурика. Сейчас ребята собрались поиграть в одну увлекательную игру. В самом начале игры Джефф записывает на листке перестановку, состоящую из n чисел: p1, p2, ..., pn. Далее ребята по очереди делают ходы, первым ходит Джефф. На своем ходу Джефф выбирает два соседних элемента перестановки и меняет их местами. На своем ходу Фурик подбрасывает монетку, и если монетка выпадает «орлом», то Фурик выбирает случайную пару соседних элементов с номерами i и i + 1, для которых верно неравенство pi > pi + 1, и меняет их местами. Если же монетка выпала «решкой», то Фурик выбирает случайную пару соседних элементов с номерами i и i + 1, для которых верно неравенство pi < pi + 1, и меняет их местами. Если после того как монетка выпала «орлом» или «решкой» у Фурика есть несколько вариантов, какую пару соседних элементов взять, то он равновероятно выбирает один из вариантов. Если у Фурика нет ни одного варианта, то он подбрасывает монетку еще раз. Игра заканчивается, когда перестановка оказывается отсортированной по возрастанию. Джефф хочет, чтобы игра закончилась как можно быстрее (то есть было совершено как можно меньше ходов). Помогите Джеффу найти минимальное математическое ожидание количества ходов в игре, если он действует оптимально. Считайте, что монетка выпадает орлом (и решкой) с вероятностью 50 процентов. Выходные данные В единственную строку выведите вещественное число — ответ на задачу. Ответ будет считаться правильным, если его абсолютная или относительная погрешность не превышает 10 - 6. Примечание В первом тесте последовательность уже отсортирована, следовательно — ответ 0. | |
![]()
|
|
B. Две кучки
Конструктив
Комбинаторика
математика
реализация
жадные алгоритмы
сортировки
*1900
У Валеры имеется 2·n кубиков, на каждом из которых записано целое число от 10 до 99. Он произвольным образом выбирает n кубиков и откладывает в первую кучку. Оставшиеся кубики образуют вторую кучку. Валера решил поиграть с кубиками. Для этого он достает кубик из первой кучки и записывает число, изображенное на нем. Затем он достает кубик из второй кучки и дописывает к имеющимся двум цифрам справа двузначное число, изображенное на этом кубике. В итоге у Валеры получается четырехзначное число, первые две цифры которого записаны на кубике из первой кучки, а вторые две — на кубике из второй кучки. Валера увлекается арифметикой, поэтому он с легкостью посчитал количество различных четырехзначных чисел, которые можно получить в его забавной игре. Другой вопрос, а как разделить кубики на кучки так, чтобы можно было получить как можно больше различных четырехзначных чисел. Этого Валера не знает, поэтому хочет спросить у вас. Выходные данные В первой строке выведите целое число — максимально возможное количество различных четырехзначных чисел, которое может получить Валера. Во второй строке выведите 2·n целых чисел bi (1 ≤ bi ≤ 2), число bi обозначает номер кучки в которую Валера должен отнести i-ый кубик. Если существует несколько вариантов разбиения кубиков на кучки, дающих максимально возможное количество различных четырехзначных чисел, которое может получить Валера, выведите любой из них. Примечание В первом примере Валера может отложить первый кубик в первую кучку, а второй — во вторую. В этом случае он сможет получить число 1099. Если же он поместит в первую кучку второй кубик, а во вторую — первый, то он сможет получить число 9910. В обоих случаях максимальное количество различных чисел равно единице. Во втором тестовом примере Валера сможет получить числа 1313, 1345, 2413, 2445. Обратите внимание, что если бы Валера отложил в первую кучку первый и третий кубики, то он смог бы получить лишь два числа 1324 и 1345. | |
![]()
|
|
C. Купе
Конструктив
Комбинаторика
реализация
*2100
жадные алгоритмы
Команда школьников из города S направляется на Всеберляндскую олимпиаду по информатике. Традиционно, ребята едут на поезде. Всем школьникам купили билеты в один вагон, состоящий из n купе (в каждом купе едут ровно четыре человека). Известно, что если в купе едут один или два школьника-олимпиадника, то им становится скучно, а если едут три или четыре школьника-олимпиадника, то в этом купе весело на протяжении всей поездки. Школьники хотят поменяться с другими людьми так, чтобы ни в каком купе, где едут школьники, им не было скучно. Чтобы поменяться с другим человеком местами, нужно убедить его, что это действительно необходимо. Школьники не могут самостоятельно найти нужные аргументы, поэтому они обратились за помощью к сочувствующей им проводнице. Проводница, пользуясь своим жизненным опытом, может уговорить любого пассажира поменяться местами с кем-то из школьников. Однако, проводница не хочет терять время на уговоры зря, поэтому хочет узнать, какое минимальное количество людей ей надо уговорить поменяться местами со школьниками. Ваша задача — найти это количество. После всех обменов в каждом купе должно остаться либо ни одного школьника, либо три или четыре школьника. Выходные данные В случае, если никакая последовательность обменов местами остальных людей со школьниками не приведет к желаемому результату, выведите число «-1» (без кавычек). В противном случае, выведите наименьшее количество людей, которых нужно уговорить поменяться местами. | |
![]()
|
|
C. Левко и строки
Комбинаторика
дп
*2500
Левко очень любит строки длины n, состоящие из строчных латинских букв. У него есть одна такая строка s. Для каждой строки t длины n Левко определяет ее красоту относительно s, как количество пар индексов i, j (1 ≤ i ≤ j ≤ n) таких, что подстрока t[i..j] лексикографически больше подстроки s[i..j]. Мальчику стало интересно, сколько существует таких строк t, что их красота относительно s в точности равна k. Помогите ему — найдите остаток от деления этого количества на 1000000007 (109 + 7). Подстрокой s[i..j] строки s = s1s2... sn будем называть строку sisi + 1... sj. Строка x = x1x2... xp лексикографически больше строки y = y1y2... yp, если существует такое число r (r < p), что x1 = y1, x2 = y2, ... , xr = yr и xr + 1 > yr + 1. Символы строк сравниваются как их ASCII коды. Выходные данные Выведите единственное число — ответ на задачу по модулю 1000000007 (109 + 7). | |
![]()
|
|
A. Матрица
Структуры данных
Комбинаторика
реализация
*1600
Дана строка из десятичных цифр s. Определим bij = si·sj. Найдите в матрице b количество таких прямоугольников, что сумма bij для всех клеток (i, j), являющихся элементами прямоугольника, в каждом прямоугольнике равна a. Прямоугольником в матрице называется четверка чисел (x, y, z, t) (x ≤ y, z ≤ t). Элементами прямоугольника называются все клетки (i, j), такие, что x ≤ i ≤ y, z ≤ j ≤ t. Выходные данные Выведите единственное целое число — ответ на задачу. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-битных чисел на С++. Рекомендуется использовать потоки cin, cout или спецификатор %I64d. | |
![]()
|
|
E. Сережа и отрезки
Комбинаторика
дп
*2700
Сережа интересуется отрезками чисел, поэтому он приготовил для вас задачу про отрезки. Отрезок чисел — это пара целых чисел [l, r] (1 ≤ l ≤ r ≤ m). Отрезок [l1, r1] принадлежит отрезку [l2, r2], если выполняется условие: l2 ≤ l1 ≤ r1 ≤ r2. Сережа хочет записать на листке последовательность из n отрезков [l1, r1], [l2, r2], ..., [ln, rn]. Причем никакой отрезок в последовательности не должен принадлежать какому-то другому отрезку в последовательности. А еще Сережа очень любит число x, поэтому он хочет, что бы хотя бы один из отрезков имел левую границу li = x. Сережу интересует вопрос: сколько существует различных способов записать такие отрезки? Помогите Сереже, найдите описанное количество способов по модулю 1000000007 (109 + 7). Два способа считаются различными, если найдется такое j (1 ≤ j ≤ n), что j-ые отрезки в двух соответствующих последовательностях не равны. Выходные данные В единственную строку выведите ответ по модулю 1000000007 (109 + 7). Примечание В третьем примере подходят следующие последовательности отрезков: {[1, 1], [3, 3]}, {[1, 2], [3, 3]}, {[2, 2], [3, 3]}, {[3, 3], [1, 1]}, {[3, 3], [2, 2]}, {[3, 3], [1, 2]}. | |
![]()
|
|
D. Расписание занятий
Комбинаторика
математика
дп
*2300
В свободное от компьютерных игр время Петя ходит в университет на занятия. Каждый день занятия на факультете у Пети состоят из двух пар. Этаж на котором проходят занятия у Пети, представляет из себя длинный коридор, вдоль которого расположены M аудиторий, пронумерованных от 1 до M. Поток, на котором учится Петя, разбит на N групп. Недавно, Петя заметил, что расписание занятий у этих групп обладает следующей особенностью: номер аудитории, в которой проходит первое занятие у какой-то группы не превосходит номера аудитории для второго занятия этой группы. Как-то раз, Петя решил посчитать, сколькими способами можно составить расписание занятий для всех групп. Расписание — это набор из 2N чисел: для каждой группы номер аудитории для первого занятия, и номер аудитории для второго занятия. К сожалению, он быстро сбился со счета, и решил, считать только расписания, удовлетворяющие следующим условиям: 1) На первом занятии в i-ой аудитории должно находиться ровно Xi групп. 2) В i-ой аудитории может поместиться не более чем Yi групп. Помогите Пете посчитать количество расписаний удовлетворяющих всем этим условиям. Так как и таких расписаний может быть много, выведите ответ по модулю 109 + 7. Выходные данные В единственной строке выведите ответ на задачу по модулю 109 + 7. Примечание Во втором тесте из примера первое и второе занятия у каждой группы должны проходить в одной и той же аудитории, поэтому расписания будут отличаться только перестановкой номеров этих аудиторий для каждой группы, то есть 3! = 6. | |
![]()
|
|
E. Весело рисовать круги
Комбинаторика
геометрия
*3000
Дано множество из S точек на плоскости. Это множество не включает начала координат O(0, 0), а для каждых двух различных точек A и B из множества треугольник OAB имеет строго положительную площадь. Рассмотрим множество пар точек (P1, P2), (P3, P4), ..., (P2k - 1, P2k). Назовем такое множество хорошим тогда и только тогда, когда: - k ≥ 2.
- Все Pi различные и каждая точка Pi является элементом S.
- Для любых двух пар (P2i - 1, P2i) и (P2j - 1, P2j) описанные окружности треугольников OP2i - 1P2j - 1 и OP2iP2j имеют единственную общую точку, и описанные окружности треугольников OP2i - 1P2j и OP2iP2j - 1 имеют единственную общую точку.
Вычислите количество хороших множеств пар точек по модулю 1000000007 (109 + 7). Выходные данные Выведите единственное целое число — ответ на задачу по модулю 1000000007 (109 + 7). | |
![]()
|
|
B. Инна и девять
Комбинаторика
*1500
жадные алгоритмы
Инне очень нравится цифра 9. Поэтому она попросила Диму написать небольшое число, состоящее из девяток. Но Дима, видимо, что-то перепутал и написал очень большое число a, состоящее из цифр от 1 до 9. Инна хочет немного поменять число, написанное Димой, чтобы в итоге число содержало как можно больше девяток. За один ход Инна может взять две соседние цифры в числе, сумма которых равна 9, и заменить их на одну цифру 9. Например, Инна может изменить число 14545181 следующим образом: 14545181 → 1945181 → 194519 → 19919. Также из числа 14545181 описанным способом можно получить число 19991. Число 149591 Инна получать не станет, поскольку можно получить числа 19919 и 19991, а они содержат больше девяток. Дима — программист, поэтому он хочет узнать сколько различных чисел с максимальным количеством девяток может получить Инна из записанного им числа. Помогите ему с этой нелегкой задачей. Выходные данные В единственной строке выведите целое число — ответ на задачу. Гарантируется, что ответ на задачу не превосходит 263 - 1. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-битных чисел на С++. Рекомендуется использовать потоки cin, cout или спецификатор %I64d. Примечание Пояснения к примерам: В первом примере Инна может получить следующие числа: 369727 → 99727 → 9997, 369727 → 99727 → 9979. Во втором примере Инна может действовать следующим образом: 123456789987654321 → 12396789987654321 → 1239678998769321. | |
![]()
|
|
D. Сережа и кинотеатр
Комбинаторика
математика
*2500
Зал кинотеатра в городе, в котором живет Сережа, представляет собой n сидений, выстроенных в один ряд перед большим экраном. Слева и справа от каждого сиденья имеется отверстие для личных вещей. При этом у любых двух соседних сидений имеется ровно одно общее отверстие. На рисунке ниже изображено как расположены сиденья и отверстия для n = 4.  Сегодня состоится премьера фильма «Твердый Каштан». Билеты на все места в кинотеатре раскуплены. На входе в зал кинотеатра стоит очень строгий контролер, поэтому все n человек будут заходить в зал по очереди. Как только человек заходит в зал кинотеатра, он сразу (мгновенно) садится на свое место и занимает все свободные отверстия для вещей слева и справа от него. Если же свободных отверстий не оказалось, то человек очень сильно расстараивается и уходит. Люди очень непостоянны, поэтому сложно предугадать, в каком порядке будут заходить зрители в зал. Для некоторых мест Сережа знает, каким по номеру зайдет в зал зритель, сидящий на этом месте. Для остальных — порядок может быть любой. Сережу, как программиста и математика, очень волнует вопрос: сколько существует порядков захода людей в зал таких, что никто не будет расстроен. Так как это число может быть достаточно большим, выведите его по модулю 1000000007 (109 + 7). Выходные данные В единственную строку выведите остаток от деления ответа на число 1000000007 (109 + 7). | |
![]()
|
|
E. Ксения и комбинаторика
Комбинаторика
дп
*2600
У Ксюши — сессия, сегодня она учит комбинаторику. Вот одна из задач, которую ей нужно научиться решать. Сколько существует различных деревьев, состоящих из n вершин, каждое из которых обладает следующими свойствами: - дерево — помеченное, то есть вершины дерева пронумерованы от 1 до n;
- каждая вершина дерева связана не более чем с тремя другими вершинами, при этом вершина с номером 1 связана не более чем с двумя другими вершинами;
- мощность максимального паросочетания дерева равна k.
Два дерева считаются различными, если существуют такие две вершины u и v, что в одном дереве они соединены ребром, а в другом — нет. Помогите Ксюше решить задачу для заданных n и k. Так как ответ может быть достаточно большим, выведите его по модулю 1000000007 (109 + 7). Выходные данные Выведите единственное целое число — ответ на задачу по модулю 1000000007 (109 + 7). Примечание Если вы не знакомы с понятием максимальное паросочетание, почитайте статью по ссылке: http://ru.wikipedia.org/wiki/Паросочетание. | |
![]()
|
|
E. Гласные
Комбинаторика
дп
разделяй и властвуй
*2700
Яхубина устала от всех этих сложных языков, так что она решила изобрести новый, простой язык. Она уже составила словарь, сожержащий n 3-слов. 3-слово — это последовательность из ровно трех строчных букв из первых 24 букв английского алфавита (от a до x). Она решила, что некоторые буквы должны быть гласными, а остальные — согласными. Весь язык будет основываться на простом правиле: слово, которое содержит как минимум одну гласную, считается корректным. Яхубина забыла, какие буквы являются гласными, а какие — согласными, и хочет найти некоторые, возможно, корректные наборы гласных. Для этого она задает Яхубу вопросы. Каждый вопрос — это набор букв. Для каждого вопроса Яхубина хочет знать, сколько слов в словаре корректны, учитывая, что данный набор букв является гласными, а остальные буквы согласные. Яхубина хочет знать xor квадратов ответов на все возможные вопросы. Всего есть 224 вопросов (все подмножества множества первых 24 строчных букв английского алфавита). Помогите Яхубу найти это число. Выходные данные Выведите единственное число — xor квадратов ответов на все запросы. | |
![]()
|
|
C. Еще одна последовательность чисел
Комбинаторика
математика
матрицы
Все знают, что такое ряд чисел Фибоначчи. Это последовательность, которую можно определить следующим рекуррентным соотношением: F1 = 1, F2 = 2, Fi = Fi - 1 + Fi - 2 (i > 2).Определим новую последовательность чисел Ai(k) следующей формулой: Ai(k) = Fi × ik (i ≥ 1).В этой задаче вам требуется посчитать следующую сумму: A1(k) + A2(k) + ... + An(k). Ответ может быть очень большим, поэтому выведите его по модулю 1000000007 (109 + 7). Выходные данные Выведите единственное целое число — сумму первых n элементов последовательности Ai(k) по модулю 1000000007 (109 + 7). | |
![]()
|
|
A. О количестве разложений на множители
Комбинаторика
математика
теория чисел
Задано целое число m в виде произведения целых чисел a1, a2, ... an  . Требуется узнать, сколько существует различных разложений числа m в произведение n упорядоченных целых положительных чисел. . Требуется узнать, сколько существует различных разложений числа m в произведение n упорядоченных целых положительных чисел. Разложение на n множителей, заданное во входных данных, также должно считаться в ответе. Поскольку ответ может быть очень большим, выведите его по модулю 1000000007 (109 + 7). Выходные данные В единственной строке выведите целое число k — количество различных разложений числа m на n упорядоченных множителей по модулю 1000000007 (109 + 7). Примечание Во втором примере, чтобы получить разложение числа 2, нужно чтобы одно любое число из трех было равно 2, а остальные равны 1. В третьем примере возможные варианты разложения на упорядоченные множители — [7,5], [5,7], [1,35], [35,1]. Разложение целого положительного числа m на n упорядоченных множителей — это кортеж целых положительных чисел b = {b1, b2, ... bn}, такой что 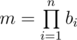 . Два разложения на упорядоченные множители b и c считаются различными, если существует индекс i, такой что bi ≠ ci. . Два разложения на упорядоченные множители b и c считаются различными, если существует индекс i, такой что bi ≠ ci. | |
![]()
|
|
D. О сумме количества инверсий в перестановках
Комбинаторика
математика
Вам дана перестановка p. Посчитайте суммарное количество инверсий во всех перестановках, лексикографически не больших данной. Поскольку это число может быть очень большим, выведите его по модулю 1000000007 (109 + 7). Выходные данные Выведите единственное число — ответ на задачу по модулю 1000000007 (109 + 7). Примечание Перестановкой p длины n называется последовательность, состоящая из n различных целых чисел, каждое из которых от 1 до n. Инверсией перестановки p1, p2, ..., pn называется пара индексов (i, j), такая что i < j и pi > pj. Перестановка a лексикографически не больше перестановки b, если a = b или существует такое число i, для которого выполняется логическое условие: 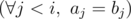 И (ai < bi). И (ai < bi). | |
![]()
|
|
E. Таблица из чисел
Комбинаторика
*2500
Недавно оказалось, что все экономическое состояние Берляндии на данный момент можно описать при помощи простой таблицы размера n × m. n — количество дней в каждом берляндском месяце, m — количество месяцев. Таким образом, клетка таблицы соответствует дню и месяцу берляндского года. В каждой клетке будет записано либо 1, либо -1, что означает доход государства в какой-то конкретный месяц и день, где 1 соответствует прибыли, -1 соответствует убытку. Для успешного развития оказалось важным проанализировать данные об экономическом состоянии прошлого года, но когда казначеи обратились в архив за данными, оказалось, что таблица была очень существенно испорчена. В некоторых клетках таблицы значения чисел стерлись, и теперь разобрать их невозможно. Известно, что количество клеток, где данные сохранились, строго меньше max(n, m). Однако, есть дополнительная информация — произведение чисел в каждой строке и в каждом столбце было равно -1. От вас требуется найти, сколько различных таблиц может соответствовать данным, которые сохранились. Так как ответ на задачу может быть достаточно большим, требуется найти его по модулю p. Выходные данные Вывести количество различных таблиц, которые могут соответствовать сохраненным данным, по модулю p. | |
![]()
|
|
D. Роман и числа
Перебор
Комбинаторика
дп
теория чисел
*2000
битмаски
Роман — юный, но уже довольно известный в Ужляндии, математик. К сожалению, Сережа так не считает. Чтобы переубедить Сережу, Роман готов решить любую математическую задачу. Сережа, не долго думая, попросил Рому найти количество близких чисел к числу n по модулю m. Число x называется близким к числу n по модулю m, если: - его можно получить перестановкой цифр числа n,
- оно не имеет лидирующих нулей,
- остаток от деления числа x на m равен 0.
Роман — хороший математик, но поскольку различных вариантов ответа может быть очень много, ему будет трудно найти ответ. Поэтому он просит помощи у вас. Выходные данные В единственной строке выведите целое число — количество близких чисел к числу n по модулю m. Примечание В первом примере нам подходят числа: 104, 140, 410. Во втором примере подходит единственное число 232. | |
![]()
|
|
D. Красивые пары чисел
Комбинаторика
дп
*2300
Последовательность пар целых чисел (a1, b1), (a2, b2), ..., (ak, bk) называется красивой, если выполнены два условия: - 1 ≤ a1 ≤ b1 < a2 ≤ b2 < ... < ak ≤ bk ≤ n, где n — заданное целое положительное число;
- все числа b1 - a1, b2 - a2, ..., bk - ak различные.
Для заданного числа n найдите количество красивых последовательностей длины k. Так как ответ может быть достаточно большим, выведите его остаток от деления на 1000000007 (109 + 7). Выходные данные Для каждого теста из входных данных выведите ответ на задачу по модулю 1000000007 (109 + 7). Ответы для тестов выводите в том порядке, в котором тесты заданы во входных данных. Примечание В первом тестовом примере ровно одна красивая последовательность: (1, 1). В втором тестовом примере следующие последовательности являются красивыми: В четвертом тестовом примере следующие последовательности являются красивыми: - (1, 1);
- (1, 2);
- (1, 3);
- (2, 2);
- (2, 3);
- (3, 3).
В пятом тестовом примере следующие последовательности являются красивыми: - (1, 1), (2, 3);
- (1, 2), (3, 3).
В третьем и шестом тестовых примерах красивых последовательностей нет. | |
![]()
|
|
C. Занимательный массив
Перебор
Комбинаторика
математика
реализация
*2500
Задан массив, состоящий из n целых чисел: a[1], a[2], ..., a[n]. Более того, заданы m запросов, каждый из которых характеризуется тремя числами li, ri, ki. Запрос li, ri, ki обозначает, что нужно добавить к каждому элементу a[j], где li ≤ j ≤ ri, число Ckij - li + ki. Запись Cxy обозначает биномиальный коэффициент, или количество сочетаний из y элементов по x элементов. Вам нужно выполнить последовательно все запросы и вывести, чему будут равны элементы массива в итоге, после всех запросов. Выходные данные Выведите n целых чисел: i-е число — это значение элемента a[i] после всех запросов. Так как значения могут быть достаточно большими выводите их по модулю 1000000007 (109 + 7). | |
![]()
|
|
B. Машмох и ACM
Комбинаторика
дп
теория чисел
*1400
Бимоху, начальнику Машмоха, Машмох не нравился. Вот он его и уволил. Решил тогда Машмох новую работу не искать, а поступить в университет и поучаствовать в ACM. Машмох хочет попасть в команду Бамоха. Для этого ему дали (в качестве испытания) несколько задач по программированию и неделю на их решение. Машмох не шибко умудренный программист. В общем-то, он и не программист вовсе. Так что ничего он не решил, а попросил вас помочь ему с этими заданиями. Одно из них такое: Последовательность из l целых чисел b1, b2, ..., bl (1 ≤ b1 ≤ b2 ≤ ... ≤ bl ≤ n) называется хорошей, если каждое число делит без остатка следующее число в последовательности. Более формально, 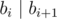 для всех i (1 ≤ i ≤ l - 1). для всех i (1 ≤ i ≤ l - 1). Вам даны n и k, найдите количество хороших последовательностей длины k. Так как ответ может быть достаточно большим, выведите его по модулю 1000000007 (109 + 7). Выходные данные Выведите единственное целое число — количество хороших последовательностей длины k по модулю 1000000007 (109 + 7). Примечание В первом примере хорошие последовательности такие: [1, 1], [2, 2], [3, 3], [1, 2], [1, 3]. | |
![]()
|
|
C. Машмох и операция реверс
Комбинаторика
*2100
разделяй и властвуй
Бимоху, начальнику Машмоха, Машмох не нравился. Вот он его и уволил. Решил тогда Машмох новую работу не искать, а поступить в университет и поучаствовать в ACM. Машмох хочет попасть в команду Бамоха. Для этого ему дали (в качестве испытания) несколько задач по программированию и неделю на их решение. Машмох не шибко умудренный программист. В общем-то, он и не программист вовсе. Так что ничего он не решил, а попросил вас помочь ему с этими заданиями. Одно из них такое: Вам дан массив a длины 2n, а также m запросов. Запрос номер i характеризуется целым числом qi. В ответ на i-й запрос вы должны выполнить последовательность операций: - разбить массив на 2n - qi частей, где каждая часть — подмассив, состоящий из 2qi чисел; j-й подмассив (1 ≤ j ≤ 2n - qi) должен содержать элементы a[(j - 1)·2qi + 1], a[(j - 1)·2qi + 2], ..., a[(j - 1)·2qi + 2qi];
- выполнить реверс элементов каждого подмассива;
- склеить все подмассивы в один массив в том же порядке (этот массив станет новым массивом a);
- вывести количество инверсий в новом массиве a.
Вам дан исходный массив a и все запросы. Ответьте на все запросы. Обратите внимание, что изменения от запроса сохраняются для последующих запросов. Выходные данные Выведите m строк. В i-й строке выведите ответ (количество инверсий) на i-й запрос. Примечание При выполнении реверса массива x[1], x[2], ..., x[n] получается новый массив y[1], y[2], ..., y[n], где y[i] = x[n - i + 1] для каждого i. Количество инверсий массива x[1], x[2], ..., x[n] — это количество пар индексов i, j, таких, что: i < j и x[i] > x[j]. | |
![]()
|
|
D. Случайное задание
Бинарный поиск
Комбинаторика
математика
*2100
дп
битмаски
Однажды после сложной лекции старательная студентка Саша увидела исписанную парту в аудитории. Присмотревшись, она прочитала следующее: «Найдите такое целое положительное n, что среди чисел n + 1, n + 2, ..., 2·n есть ровно m чисел, в двоичной записи которых ровно k единиц.» Ее заинтересовало это задание, и она просит вас помочь ей его решить. Саша знает, что вы боитесь больших чисел, поэтому она гарантирует, что существует ответ не превышающий 1018. Выходные данные Выведите искомое число n (1 ≤ n ≤ 1018). Если ответов несколько — выведите любой. | |
![]()
|
|
E. Ребенок и двоичное дерево
Комбинаторика
теория чисел
разделяй и властвуй
бпф
*3100
Наш ребенок обожает информатику, особенно двоичные деревья. Рассмотрим последовательность из n различных целых чисел: c1, c2, ..., cn. Ребенок называет двоичное корневое дерево со взвешенными вершинами хорошим тогда и только тогда, когда для каждой вершины v, вес v — это элемент множества {c1, c2, ..., cn}. Также наш ребенок считает, что вес дерева со взвешенными вершинами равняется сумме весов всех вершин. Задано число m, сможете ли вы для всех s (1 ≤ s ≤ m) посчитать количество хороших двоичных корневых деревьев со взвешенными вершинами с весом s? Для более глубокого понимания того, какие деревья считаются различными, пожалуйста, посмотрите примеры тестовых данных. Выведите ответ по модулю 998244353 (7 × 17 × 223 + 1, простое число). Выходные данные Выведите m строк, каждая строка должна содержать единственное целое число. В i-й строке должно быть записано количество хороших двоичных корневых деревьев со взвешенными вершинами с весом i. Выведите ответ по модулю 998244353 (7 × 17 × 223 + 1, простое число). Примечание В первом примере существует 9 хороших двоичных корневых деревьев со взвешенными вершинами, чей вес равняется ровно 3: 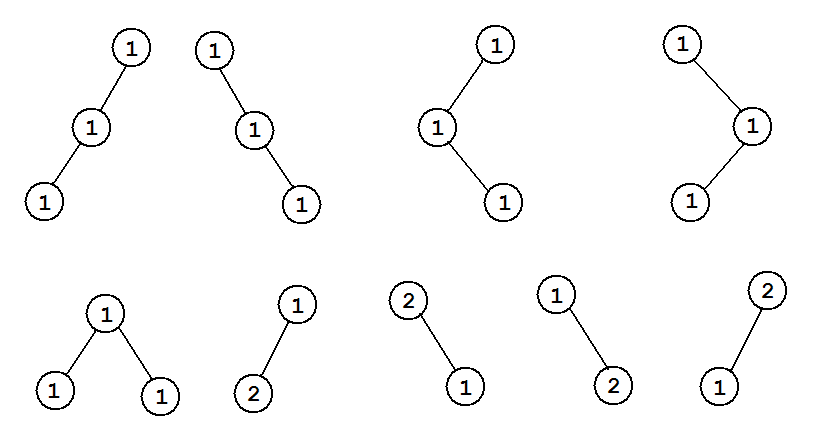 | |
![]()
|
|
E. Деву и праздник день рождения
Комбинаторика
математика
*2100
дп
Сегодня день рождения Деву. Чтобы отпраздновать это событие, он купил n конфет на рынке неподалеку и пригласил f своих друзей. Сейчас Деву хочет поделить конфеты между друзьями. Деву — добрый парень, и день сегодня особенный, так что он не хочет, чтобы кто-то грустил. Поэтому очень важно, чтобы каждый друг получил хотя бы одну конфету. Юноша хочет, чтобы день рождения прошел особенным образом, поэтому конфеты требуется разделить по особенному. Предположим, что он раздал n сладостей своим друзьям так, что i-му другу досталось ai конфет. Не должно существовать ни одного целого числа x (x > 1), которое делит все ai. Найдите количество способов распределения сладостей между друзьями, удовлетворяющих описанным ограничениям. Обратите внимание, что порядок имеет значение, например, [1, 2] и [2, 1] — различные распределения конфет. Так как ответ может быть достаточно велик, пожалуйста, выведите его по модулю 1000000007 (109 + 7). Чтобы задача была еще интереснее, вам дано q запросов. Каждый запрос содержит пару n, f. Для каждого запроса выведите необходимое количество способов по модулю 1000000007 (109 + 7). Выходные данные Для каждого запроса выведите единственное целое число в строке, соответствующее ответу на запрос. Примечание Для первого запроса: n = 6, f = 2. Возможные разделения: [1, 5] и [5, 1]. Для второго запроса: n = 7, f = 2. Возможные разделения: [1, 6] и [2, 5] и [3, 4] и [4, 3] и [5, 3] и [6, 1]. Таким образом, всего есть шесть возможных способов разделения. | |
![]()
|
|
I. Игрушки
Перебор
Комбинаторика
*2300
Маленькая девочка Маша любит раскладывать свои игрушки в кучки на полу. А еще она очень не любит, когда кто-нибудь трогает ее игрушки. Как-то раз Маша аккуратно разложила все свои n игрушек в несколько кучек, а затем ее старший брат Саша пришел и собрал все кучки в одну. Маша увидела это, страшно расстроилась и принялась плакать. У Саши никак не получается успокоить Машу, а скоро придет мама и ему влетит за то, что сестренка плачет. Поэтому он решает восстановить разложение игрушек по кучкам. Однако он совершенно не помнит, как лежали игрушки. Маша, конечно, помнит это, но она еще не умеет говорить и может помочь Саше лишь тем, что радостно завопит, когда он выложит игрушки именно так, как они и лежали. Значит, Саше придется раскладывать игрушки всеми возможными способами до тех пор, пока Маша не узнает нужное разложение. Взаимное расположение кучек и игрушек в каждой кучке не важно, поэтому два способа разложить игрушки считаются различными, если найдутся две такие игрушки, которые при одном из способов лежат в одной и той же кучке, а при другом нет. Саша ищет наиболее быстрый путь перебора всех способов, потому что скоро придет мама. За одно действие Саша может взять игрушку из любой кучки и переложить ее в любую другую кучку (возможно, при этом появится новая кучка или одна из кучек исчезнет). Саша хочет найти такую последовательность действий, что в процессе все способы разложить игрушки на кучки будут перебраны ровно по одному разу. Помогите Саше. Изначально, как мы помним, все игрушки находятся в одной кучке. Выходные данные В первой строке выведите количество различных способов разложить игрушки на кучки. Далее выведите все способы разложить игрушки на кучки в том порядке, в каком их должен перебирать Саша (т.е. каждый следующий способ должен получаться из предыдущего описанной в условии операцией). Каждый способ надо выводить следующим образом. В каждой кучке игрушки надо упорядочить по возрастанию номера. После этого надо упорядочить кучки по возрастанию номеров первых игрушек в них. Каждый способ выводите в отдельной строке. См. пример для уточнения формата выходных данных. Если решений несколько, выведите любое из них. | |
![]()
|
|
D. Jzzhu и числа
Комбинаторика
дп
*2400
битмаски
У Jzzhu есть n неотрицательных целых чисел a1, a2, ..., an. Назовем последовательность индексов i1, i2, ..., ik (1 ≤ i1 < i2 < ... < ik ≤ n) группой размера k. Jzzhu интересно, сколько существует таких групп, что ai1 & ai2 & ... & aik = 0 (1 ≤ k ≤ n)? Помогите ему найти их количество по модулю 1000000007 (109 + 7). Операция x & y обозначает операцию побитового И двух чисел. Выходные данные Выведите единственное целое число — количество требуемых групп по модулю 1000000007 (109 + 7). | |
![]()
|
|
E. Devu и цветы
Комбинаторика
теория чисел
*2300
битмаски
Devu хочет декорировать свой сад. Он приобрел n коробок с цветами, i-я коробка содержит fi цветов. Все цветы в одной коробке одного цвета (поэтому они неразличимы). Также среди коробок нет двух с одинаковыми цветами. Devu хочет выбрать ровно s цветов из коробок, чтобы украсить свой сад. Сколькими способами он может это сделать? Так как это число может быть очень большим, найдите его по модулю 1000000007 (109 + 7). Devu считает, что два способа различные, если в этих способах хотя бы из одной коробки выбрано разное количество цветов. Выходные данные Выведите целое число — количество способов выбрать s цветов по модулю 1000000007 (109 + 7). Примечание Пример 1. Есть два способа выбрать 3 цветка: {1, 2} и {0, 3}. Пример 2. Есть только один способ выбора 4 цветков: {2, 2}. Пример 3. Есть три способа выбора 5 цветков: {1, 2, 2}; {0, 3, 2}; {1, 3, 1}. | |
![]()
|
|
C. Фокус
Теория вероятностей
Комбинаторика
математика
*2100
Давид Пирожков (также известный как pieguy) любит показывать фокусы. В его репертуаре есть фокус, который использует колоду, состоящую из n карт. У него есть m одинаковых колод, каждая из которых состоит из n различных карт. Эти колоды были перемешаны вместе. Когда Давид показывает фокус, он берет n случайных карт из этих перемешанных колод, и показывает фокус, используя эти n карт. Получившаяся колода из n карт выглядит как обычная колода, но в ней теперь какие-то карты могут встречаться более одного раза. Сам фокус показывается следующим образом: сначала зритель вытягивает карту из колоды, и запоминает ее, после чего помещает ее обратно в колоду. Затем Давид тасует колоду, и достает из нее одну карту. Фокус считается выполненным успешно, если Давид достал ту же карту, которую запомнил зритель. Вы сильно подозреваете, что Давид на самом деле не очень хороший фокусник, и что он просто показывает случайную карту, надеясь, что она совпадет с картой, которую запомнил зритель. Посчитайте вероятность того, что фокус будет успешным, если вы правы. Выходные данные В единственной строке выведите одно число с плавающей точкой — вероятность того, что Давид сможет успешно выполнить фокус. Относительная или абсолютная погрешность ответа не должна превышать 10 - 6. Примечание В первом примере, с вероятностью  Давид будет показывать фокус, используя колоду с двумя одинаковыми картами. В этом случае фокус всегда будет успешным. Давид будет показывать фокус, используя колоду с двумя одинаковыми картами. В этом случае фокус всегда будет успешным. С вероятностью  карты будут различны, и вероятность успешного показа фокуса будет равна карты будут различны, и вероятность успешного показа фокуса будет равна  . . Итоговая вероятность: 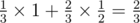 | |
![]()
|
|
D. Бинго!
Теория вероятностей
Комбинаторика
математика
*2700
Обычно в игру «Бинго!» играют на доске 5 × 5, заполненной различными целыми числами от 1 до 75. В этой задаче мы будем рассматривать обобщенную модель игры «Бинго!». Действие игры будет происходить на доске n × n, заполненной различными целыми числами от 1 до m (m ≥ n2). Рассмотрим следующий случайный процесс. Изначально генерируется случайная доска для игры (равновероятно среди всех досок). Затем случайным образом выбираются k различных чисел от 1 до m (равновероятно среди всех наборов из k различных чисел). Те из этих чисел, которые встречаются на сгенерированной доске, помечаются. Выигрышем будем называть число: два в степени [количество строк, целиком состоящих из помеченных чисел, плюс количество столбцов, целиком состоящих из помеченных чисел]. Ваша задача посчитать математическое ожидание выигрыша в описанном случайном процессе для заданных n, m, k. Полученное математическое ожидание может быть очень большим, поэтому если оно превышает 1099, выведите 1099 вместо ответа (например, можно вывести строку «1e99» без кавычек). Выходные данные Выведите математическое ожидание выигрыша или 1099, если математическое ожидание превышает это значение. Ответ будет считаться правильным, если его абсолютная или относительная погрешность не превышает 10 - 9. | |
![]()
|
|
B. Пашмак и цветы
Комбинаторика
реализация
сортировки
*1300
Пашмак решил подарить Пармиде пару цветов из своего сада. В саду растет n цветов, красота i-го из них равна bi. Пармида — девушка необычная, она необязательно хочет получить два самых красивых цветка. Она хочет получить такие два цветка, разница красот которых максимально возможная! Ваша задача — написать программу, которая посчитает два значения: - Максимальную разность красот двух цветов из сада Пашмака.
- Сколько существует способов выбрать два цветка из сада, чтобы разность их красот была максимально возможной. Два способа считаются различными тогда и только тогда, когда хотя бы один цветок выбран в одном из них и не выбран во втором.
Выходные данные В единственной строке выведите два целых числа — максимальную разность красот и количество способов ее получить. Примечание В третьем примере максимальная разность красот равна 2. Существует 4 способа ее получить: - выбрать первый и второй цветки;
- выбрать первый и пятый цветки;
- выбрать четвертый и второй цветки;
- выбрать четвертый и пятый цветки.
| |
![]()
|
|
C. Пашмак и автобусы
Конструктив
Комбинаторика
математика
*1900
Пашмак недавно устроился в транспортную компанию, которая владеет k автобусами. Недавно компания заключила договор со школой на перевозку школьников в течение d дней. Всего в школе учатся n ребят. Каждый день компания предоставляет школе все свои автобусы, Пашмак должен распределять детей по автобусам. Пашмак не хочет, чтобы кто-то из школьников подружился за эти d дней. Он считает, что два школьника сдружатся, если в течение всех d дней они будут ездить в одном автобусе. Помогите Пашмаку воплотить в жизнь его странную идею, найдите распределение, при котором никакие два школьника не сдружатся. Считайте, что автобусы имеют бесконечную вместимость. Выходные данные Если подходящего распределения не существует, выведите -1. В противном случае, выведите d строк, по n чисел в каждой строке: j-е число i-й строки обозначает номер автобуса, в котором поедет j-й школьник в i-й день. Считайте, что автобусы нумеруются от 1 до k. Примечание Обратите внимание, что два школьника становятся друзьями, если они находятся в одном автобусе каждый день. При этом автобус, в котором они едут вместе, может меняться день ото дня. | |
![]()
|
|
D. Увеличьте последовательность
Комбинаторика
*2100
дп
У Пети есть последовательность целых чисел a1, a2, ..., an. Петя хочет, чтобы все числа в ней были равны h. Он умеет выполнять операцию «прибавления единицы на отрезке [l, r]»: прибавить ко всем элементам последовательности с номерами от l до r (включительно) единицу. При этом Петя никогда не выбирает какое-то число в качестве начала отрезка повторно. Аналогично, Петя никогда не выбирает какое-то число в качестве конца отрезка повторно. Другими словами, для любых двух отрезков [l1, r1] и [l2, r2], на которых Петя выполнял прибавление единицы, верны следующие неравенства: l1 ≠ l2 и r1 ≠ r2. Сколько существует различных способов сделать все числа последовательности равными h? Выведите это количество способов по модулю 1000000007 (109 + 7). Два способа считаются различными, если в одном из них есть отрезок, которого нет в другом. Выходные данные Выведите единственное целое число — ответ на задачу по модулю 1000000007 (109 + 7). | |
![]()
|
|
B. Dreamoon и WiFi
Перебор
Теория вероятностей
Комбинаторика
математика
дп
*1300
битмаски
Dreamoon стоит на отметке 0 на числовой прямой. Drazil отправляет ему на смартфон список команд через Wi-Fi, а Dreamoon следует им. Каждая команда относится к одному из двух типов: - Пройти на 1 единицу в положительном направлении, обозначается как «+»
- Пройти на 1 единицу в отрицательном направлении, обозначается как «-»
Но так как уровень сигнала Wi-Fi очень слабый, смартфон Dreamoon'а сообщает, что некоторые команды не поддаются распознаванию. Более того, Dreamoon знает, что даже некоторые из рапознанных команд могут быть неверными. Dreamoon решил выполнять каждую распознанную команду, а для нераспознанных команд бросать монетку (это значит, что он пойдёт на 1 единицу в положительном или отрицательном направлении с одинаковой вероятностью 0.5). Вам дан изначальный список команд, которые выслал Drazil, и список, который получил Dreamoon. Какова вероятность того, что Dreamoon окажется в том положении, к которому привели бы команды Drazil'а? Выходные данные Выведите требуемую вероятность. Ответ будет сраниваться с относительной или абсолютной погрешностью 10 - 9. Примечание В первом примере как s1, так и s2 приведут Dreamoon'а к одной и той же позиции + 1. Во втором примере s1 приведет Dreamoon'а к позиции 0, в то время как для s2 есть четыре варианта: {"+-++", "+-+-", "+--+", "+---"} с конечными позициями {+2, 0, 0, -2}, соответственно. Таким образом, есть 2 подходящих случая из 4, так что вероятность окончить путь в верной позиции равна 0.5. Для третьего примера, s2 может привести только к позициям {+1, -1, -1, -3}, таким образом, вероятность окончить путь в позиции + 3 равна 0. | |
![]()
|
|
B. Случайные команды
Конструктив
Комбинаторика
математика
жадные алгоритмы
*1300
Для участия в соревнованиях n участников были разбиты некоторым образом на m команд так, чтобы в каждой команде был хотя бы один участник. После соревнований каждая пара участников из одной команды стала друзьями. Ваша задача — написать программу, которая определит, какое минимальное и какое максимальное количество пар друзей могло образоваться после соревнования. Выходные данные Требуется вывести два целых числа kmin и kmax — минимальное возможное количество пар друзей и максимальное возможное количество пар друзей соответственно. Примечание В первом примере все участники попадают в одну команду, поэтому в любом случае будет образовано ровно десять пар друзей. Во втором примере при любом разбиении в одной из команд будет два участника, а в другой — один. В таком случае количество пар друзей всегда будет равно одному. В третьем примере минимальное количество друзей выходит при разбиении на команды по 2 человека, а максимальное — при разбиении на команды размерами 1, 1 и 4 человек. | |
![]()
|
|
E. Катаемся на лифте
Комбинаторика
дп
*1900
Представьте себе, что вы находитесь в здании, в котором есть ровно n этажей. Для перемещения между этажами в здании есть лифт. Пронумеруем этажи снизу вверх целыми числами от 1 до n. Сейчас вы находитесь на этаже с номером a. Вам очень скучно, поэтому вы хотите покататься на лифте. На этаже с номером b находится секретная лаборатория, вход в которую вам запрещен. Однако вы уже настроились и решили последовательно совершить k поездок на лифте. Предположим, что в данный момент вы находитесь на этаже с номером x (изначально вы находились на этаже a). Для очередной поездки между этажами вы выбираете некоторый этаж с номером y (y ≠ x), и лифт везет вас на этот этаж. Поскольку вам нельзя посещать этаж b с секретной лабораторией, то вы решили, что расстояние от текущего этажа x до выбранного этажа y должно быть строго меньше, чем расстояние от текущего этажа x до этажа b с секретной лабораторией. Формально, это означает, что должно выполняться неравенство |x - y| < |x - b|. После того, как лифт успешно привез вас на этаж y, вы выписываете себе в блокнот число y. Ваша задача — определить количество различных последовательностей чисел, которые вы могли выписать себе в блокнот в результате k поездок на лифте. Поскольку искомое количество может быть очень большим, найдите остаток от деления этого количества на 1000000007 (109 + 7). Выходные данные Выведите единственное число — остаток от деления искомого количества последовательностей на 1000000007 (109 + 7). Примечание Две последовательности p1, p2, ..., pk и q1, q2, ..., qk называются различными, если существует такое целое число j (1 ≤ j ≤ k), что pj ≠ qj. Пояснения к примерам: - В первом примере после первой поездки вы можете оказаться либо на этаже 1, либо на этаже 3, поскольку |1 - 2| < |2 - 4| и |3 - 2| < |2 - 4|.
- Во втором примере всего две возможных последовательности: (1, 2); (1, 3). Вы не можете выбрать этаж 3 для первой поездки, потому что в этом случае никакой из этажей не подойдет для второй поездки.
- В третьем примере искомых последовательностей не существует, поскольку вы не можете выбрать этаж для первой поездки.
| |
![]()
|
|
D. Случайная функция и дерево
Деревья
Комбинаторика
дп
*2700
У вас есть корневое дерево, состоящее из n вершин. Пронумеруем вершины дерева целыми числами от 1 до n включительно. Корень дерева находится в вершине 1. Для каждого i > 1 непосредственным предком вершины i является вершина pi. Назовём вершину i ребёнком вершины pi. Изначально вы покрасили все вершины в красный цвет. Кроме этого, вы любите перекрашивать некоторые вершины дерева. Для этого вы используете функцию paint, которую вы вызываете от корня дерева. Ниже приведен псевдокод этой функции:
count = 0 // глобальная целочисленная переменная
rnd() { // эта функция используется в коде paint
вернуть 0 или 1 с равной вероятностью 50%
}
paint(s) {
if (count четное) then покрасить вершину s в белый цвет
else покрасить вершину s в черный цвет
count = count + 1
if rnd() = 1 then children = [массив из детей вершины s в порядке возрастания номеров]
else children = [массив из детей вершины s в порядке убывания номеров]
for child in chilren { // проходим по элементам массива child
if rnd() = 1 then paint(child) // выполняем рекурсивный вызов функции paint
}
}
В результате выполнения этой функции некоторые вершины могут изменить свой цвет на белый или чёрный, а некоторые — остаться красными. Ваша задача — определить количество различных возможных раскрасок вершин дерева. Будем считать раскраску возможной, если существует ненулевая вероятность получить эту раскраску с помощью одного вызова функции paint(1). Будем считать раскраски различными, если существует пара вершин, которые покрашены в различные цвета в этих раскрасках. Поскольку искомое количество может быть очень большим, найдите остаток от деления этого количества на 1000000007 (109 + 7). Выходные данные Выведите единственное целое число — ответ на задачу по модулю 1000000007 (109 + 7) Примечание Ниже приведены все возможные покраски первого примера. 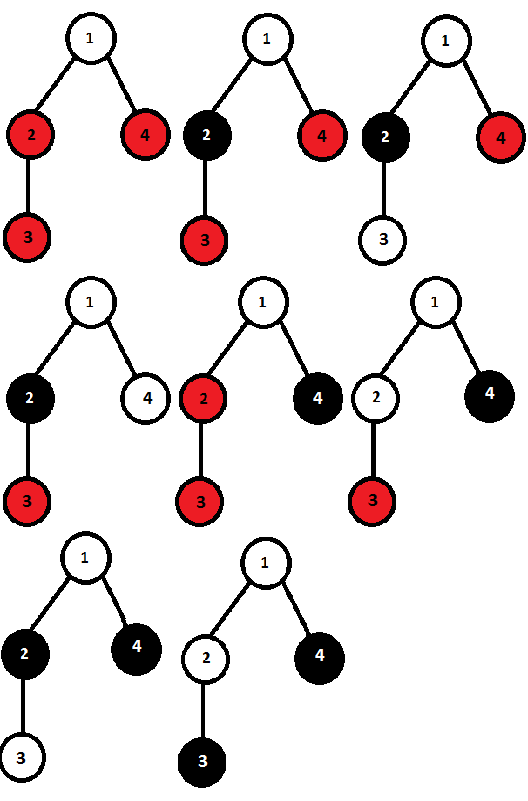 | |
![]()
|
|
D. Невыносимая запутанность бытия
Перебор
Комбинаторика
поиск в глубину и подобное
*1700
графы
Томаш постоянно плутает и теряется, гуляя по улицам столицы Берляндии. Еще бы, ведь он привык, что в его родном городе для любой пары перекрестков существует ровно один способ пройти от одного к другому. В столице Берляндии это совсем не так! Томаш подметил, что даже простые случаи неоднозначности перемещения его путают. Так, четверку различных перекрестков a, b, c и d таких, что существует два пути из a в c — один через b, а другой через d, он называет «чёртов ромб». Обратите внимание, пары перекрёстков (a, b), (b, c), (a, d), (d, c) должны быть непосредственно соединены дорогами. Схематично «чёртов ромб» изображен на рисунке ниже: 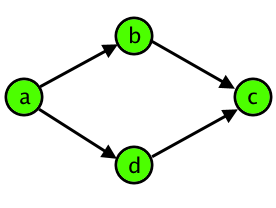 Наличие других дорог между любыми из перекрестков не делают ромб более привлекательным для Томаша, поэтому четверка перекрестков остается для него «чёртовым ромбом». Принимая во внимание, что в столице Берляндии n перекрестков и m дорог, все из которых являются односторонними и известны наперед, найдите количество «чёртовых ромбов» в городе. При сравнении ромбов порядок перекрестков b и d значения не имеет. Выходные данные Выведите искомое количество «чёртовых ромбов». | |
![]()
|
|
F. Особые матрицы
Комбинаторика
*2100
дп
Квадратная матрица n × n называется особой, если: - она бинарная, то есть в каждой ячейке стоит либо 0, либо 1;
- количество единиц в каждой строке и каждом столбце равно 2.
Вам заданы n и первые m строк матрицы. Выведите количество особых матриц n × n таких, первые m строк которых совпадают с заданными. Так как искомое значение может быть очень большим, то выведите остаток от деления значения на заданное число mod. Выходные данные Выведите остаток при делении искомого количества на число mod. Примечание Для первого теста искомые матрицы:
011
101
110
011
110
101
Во втором тесте особая матрица уже задана полностью, поэтому ответ 1. | |
![]()
|
|
D. Новогоднее взаимодействие Санта-Клаусов
Деревья
Комбинаторика
поиск в глубину и подобное
*1900
графы
В Древесном мире наступает Новый год! В этом мире, как понятно из названия, есть n городов, соединенных n - 1 дорогой, и между каждыми двумя различными городами всегда существует путь. Города пронумерованы целыми числами от 1 до n. Дороги пронумерованы целыми числами от 1 до n - 1. Определим d(u, v) как суммарную длину дорог на пути между городом u и городом v. Отдавая дань традиции, народ в Древесном мире ремонтирует ровно по дороге в год. В результате длина этой дороги уменьшается. Известно, что в i-м году длина ri-й дороги станет wi, что короче прежней длины этой же дороги. Предположим, что текущий год — это год 1. Три Санта-Клауса планируют раздавать подарки всем детям Древесного мира ежегодно. Для этого им надо подготовиться, в целях чего они выберут три различных города c1, c2, c3, и создадут в каждом из этих городов по одному складу: k-й (1 ≤ k ≤ 3) Санта-Клаус будет отвечать за склад в городе ck. Трем Санта-Клаусам очень скучно сидеть на складах поодиночке. Поэтому они решили построить сеть сообщения, предназначенную только для Сант! Затраты, необходимые для того, чтобы построить подобную сеть, равны d(c1, c2) + d(c2, c3) + d(c3, c1) долларам. Санты слишком заняты, чтобы искать лучшее место, так что они решили выбрать c1, c2, c3 случайно равновероятно среди всех троек различных чисел от 1 до n. Санты хотели бы знать математическое ожидание цены, необходимой для построения сети. Однако, как мы сказали, каждый год длина ровно одной дороги уменьшается. Таким образом, Санты хотят просчитать математическое ожидание после каждого изменения длины. Помогите им посчитать требуемые значения. Выходные данные Выведите q чисел. После каждого из изменений выведите строку с математическим ожиданием цены, необходимой для постройки сети сообщения в Древесном мире. Ответ будет считаться корректным, если его абсолютная или относительная погрешность не превышают 10 - 6. Примечание Рассмотрим первый пример. Есть 6 троек: (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1). Так как n = 3, затраты на построение сети всегда равны d(1, 2) + d(2, 3) + d(3, 1) для всех троек. Таким образом, матожидание стоимости равняется d(1, 2) + d(2, 3) + d(3, 1). | |
![]()
|
|
E. Миша и палиндромность
Бинарный поиск
Комбинаторика
реализация
*2500
У Миши есть массив из n целых чисел, проиндексированный целыми числами от 1 до n. Назовем палиндромностью массива a количество таких пар индексов (l, r)(1 ≤ l ≤ r ≤ n), что элементы с l-го по r-й включительно можно переставить так, что весь массив окажется палиндромом. Иными словами, для пары (l, r) должно выполняться, что после некоторой перестановки чисел на позициях от l до r включительно (разрешается не переставлять числа вовсе) для любого 1 ≤ i ≤ n будет выполняться что a[i] = a[n - i + 1]. Ваша задача — найти палиндромность Мишиного массива. Выходные данные В единственной строке выведите ответ на задачу. Примечание В первом примере подходит любая пара возможная пара (l, r). В третьем примере подходят пары (1, 3), (1, 4), (1, 5), (2, 5). | |
![]()
|
|
E. Подарок мистера Китаюта
Строки
Комбинаторика
дп
*3000
матрицы
Мистер Китаюта любезно предоставил Вам строку s из строчных букв латинского алфавита. Он просит вас вставить ровно n строчных букв латинского алфавита в s так, чтобы получился палиндром. Палиндром — это строка, которая читается одинаково в обоих направлениях. Например, «noon», «testset» и «a» — палиндромы, а «test» и «kitayuta» — нет. Вы можете выбрать любые n строчных букв латинского алфавита и вставить каждую из них в любую позицию s, в частности, можно вставить в начало или в конец s. Надо вставить ровно n букв, даже если данную строку можно сделать палиндромом, вставив менее n букв. Найдите количество палиндромов, которые можно получить таким способом, по модулю 10007. Выходные данные Выведите количество палиндромов, которые можно получить, по модулю 10007. Примечание В первом примере можно получить палиндром «reviver», вставив «r» в конец «revive». Во втором примере можно получить следующие 28 палиндромов: «adada», «adbda», ..., «adzda», «dadad» and «ddadd». | |
![]()
|
|
E. Пентагон
Комбинаторика
*2400
графы
матрицы
В соответствии с последним указом Президента Берляндии каждый город страны должен иметь собственное здание Министерства Обороны (свой собственный Пентагон). Мегаполис Бербург не стал исключением. В этом городе n перекрестков, некоторые пары из которых соединены двунаправленными дорогами. Всего в городе m дорог, между каждой парой перекрестков не более одной. В настоящий момент обсуждается выбор места расположения Пентагона в Бербурге. Решено, что Пентагон должен занимать территорию пяти различных перекрестков, которые соединены в цикл дорогами. В порядке цикла по дорогам будет построена специальная стена (как и положено — с высоким напряжением, колючей проволокой и т.п.). Таким образом, количество возможных способов построить Пентагон в городе равно количеству различных циклов длины 5, составленных из перекрестков и дорог. Ваша задача вывести количество способов построить Пентагон в Бербурге. Учтите, что в этой задаче пройдет только достаточно оптимизированное решение, так что обязательно протестируйте свой код на максимальном тесте. Выходные данные Выведите единственное число — искомое количество способов. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-х битовых чисел на С++. Рекомендуется использовать поток cout (также вы можете использовать спецификатор %I64d). | |
![]()
|
|
D. Илья и эскалатор
Теория вероятностей
Комбинаторика
математика
дп
*1700
Илья устал от олимпиадного программирования, ушел из университета и устроился на работу в метрополитен. Перед ним поставили задачу определения нагрузки на эскалатор. Пусть n человек стоят в очереди на эскалатор. В каждую секунду происходит одно из двух: либо первый человек в очереди с вероятностью p заходит на эскалатор, либо первый человек в очереди с вероятностью (1 - p) остается стоять на месте, не в силах совладать с боязнью эскалаторов, задерживая при этом всю очередь за ним. Формально говоря, i-й в очереди не сможет зайти на эскалатор, пока на него не зайдут люди с номерами от 1 до i - 1 включительно. За одну секунду может зайти только один человек. Так как эскалатор бесконечный, то единожды зайдя на него, человек никогда с него не сойдёт, т. е. будет ехать на нем в эту и любую последующую секунды. Илье нужно посчитать математическое ожидание количества людей, которые будут находиться на эскалаторе после t секунд. Вам необходимо помочь ему в решении этой непростой задачи. Выходные данные Выведите одно вещественное число — математическое ожидание количества людей, которые будут на эскалаторе через t секунд. Абсолютная или относительная погрешность не должна превышать 10 - 6. | |
![]()
|
|
F. Паша и труба
Бинарный поиск
Перебор
Комбинаторика
реализация
дп
*2300
На очередном заседании правящей партии «A» министр Павел предложил усовершенствовать систему водопровода и проложить в городе новую трубу. Город на карте представляет собой прямоугольное клетчатое поле размера n × m. Каждая клетка поля либо свободна (тогда труба может проходить по ней), либо занята (по такой клетке труба проходить не может). На карте свободные клетки обозначены символом '.', а занятые — '#'. Труба должна удовлетворят следующим свойствам: - труба имеет вид ломанной ширины 1,
- труба проходит по свободным клеткам,
- труба начинается с края поля, но не с угловой клетки,
- труба заканчивается на краю поля, но не в угловой клетке,
- труба имеет не более 2-х поворотов (на 90 градусов),
- на краях поля должно существовать ровно две клетки, по которым проходит труба,
- если труба представляет собой один отрезок, то концевые точки трубы должны лежать на разных краях поля,
- для каждой неконцевой клетки трубы существует ровно две соседние по стороне клетки, которые тоже принадлежат трубе,
- для каждой из концевых клеток трубы существует ровно одна соседняя по стороне клетка, которая тоже принадлежит трубе.
Примеры разрешенных маршрутов для прокладывания труб:
....# ....# .*..#
***** ****. .***.
..#.. ..#*. ..#*.
#...# #..*# #..*#
..... ...*. ...*.
Примеры запрещенных маршрутов для прокладывания труб:
.**.# *...# .*.*#
..... ****. .*.*.
..#.. ..#*. .*#*.
#...# #..*# #*.*#
..... ...*. .***.
В примерах трубы обозначены символами ' * '. Вам поручили написать программу, которая вычисляет количество различных способов проложить ровно одну трубу на территории города. Два способа прокладывания труб считаются различными, если они отличаются хотя бы в одной клетке. Выходные данные Выведите в первую строку выходных данных одно целое число — количество различных способов проложить ровно одну трубу. Примечание В первом примере существует 3 способа проложить трубу (клетки трубы обозначены символами ' * '):
.*. .*. ...
.*# **# **#
.*. ... .*.
| |
![]()
|
|
B. Прямоугольные треугольники
Комбинаторика
*1600
Дано прямоугольное поле n × m, состоящее из точек ('.') и звездочек ('*'). Ваша задача — посчитать количество прямоугольных треугольников, у которых две стороны параллельны сторонам поля, а вершины находятся в центрах клеток, помеченных звездочками. Выходные данные Выведите одно число — количество прямоугольных треугольников на поле. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-х битовых чисел на С++. Рекомендуется использовать поток cout (также вы можете использовать спецификатор %I64d). | |
![]()
|
|
E. Сплошные плюсы
Комбинаторика
математика
дп
теория чисел
*2200
Вася сидит на невыносимо скучном уроке математики. Чтобы развлечься, он выписал на листок бумаги n цифр в одну строку. После этого Вася стал выписывать разные способы поставить в строке между некоторыми цифрами плюсы («+») таким образом, чтобы получалось корректное арифметическое выражение; формально, никакие два плюса в таком разбиении не должны стоять рядом (между любыми двумя соседними плюсами должна стоять хотя бы одна цифра), и никакой плюс не может стоять в начале или в конце строки. Например, в строке 100500, способы 100500 (не ставить плюсов совсем), 1+00+500 или 10050+0 являются корректными, а способы 100++500, +1+0+0+5+0+0 или 100500+ являются некорректными. Урок был длинным, и Вася выписал все корректные способы расставить в своей строке из цифр ровно k плюсов. В этот момент его развлечение было замечено, и Вася получил задание до конца урока вычислить сумму значений всех получившихся арифметических выражений (при вычислении значения выражения ведущие нули в слагаемых следует игнорировать). Поскольку ответ может быть большим, Васе разрешили всего лишь получить остаток от деления ответа на 109 + 7. Выходные данные Выведите ответ на задачу по модулю 109 + 7. Примечание В первом примере результат равен (1 + 08) + (10 + 8) = 27. Во втором примере результат равен 1 + 0 + 8 = 9. | |
![]()
|
|
B. Тавас и СаДДас
Перебор
Комбинаторика
реализация
*1100
битмаски
Тавас снова начал есть сухой кофе ложками! Кейон пожаловался на ужасный запах, но юноша не остановился. Тогда Кейон попросил своего умного друга СаДДаса наказать Таваса! СаДДас забрал наушники Таваса и сказал ему: "Верну их, если ты решишь следующую задачу."  Задача звучит следующим образом: Вам дано счастливое число n. Счастливые числа — это положительные целые числа, содержащие в своей десятичной записи только счастливые цифры 4 и 7. Например, числа 47, 744, 4 счастливые, а 5, 17, 467 — нет. Если мы отсортируем все счастливые числа в возрастающем порядке, на какой позиции (при нумерации с единицы) будет стоять число n? Тавас не такой умный, как СаДДас, так что он попросил Вас сделать ему одолжение и решить эту задачу, чтобы он мог получить назад свои наушники. Выходные данные Выведите позицию, на которой n находится среди всех счастливых чисел. | |
![]()
|
|
C. Майк и пена
Комбинаторика
математика
дп
теория чисел
*2300
битмаски
Майк — бармен в баре Рико. В заведении Рико пивные стаканы кладутся на особую полку. Всего в баре n сортов пива, пронумерованных от 1 до n. Бокал с i-м сортом пива содержит ai миллилитров пены.  Максим — босс Майка. Сегодня он сказал Майку выполнить q запросов. Изначально полка пустая. Каждый запрос представляет собой целое число x. Если пиво номер x уже есть на полке, то Майк должен забрать его с полки, в противном случае — положить его на полку. После каждого запроса Майк должен определить качество полки. Медведи — те ещё гики, так что они считают, что качество полки — это количество пар (i, j) стаканов на полке, таких, что i < j и  , где , где  — наибольший общий делитель чисел a и b. — наибольший общий делитель чисел a и b. Майк устал. Поэтому он попросил вам помочь ему выполнить эти запросы. Выходные данные Для каждого запроса выведите ответ в отдельной строке. | |
![]()
|
|
D. GukiZ и двоичные операции
Комбинаторика
математика
реализация
*2100
теория чисел
матрицы
Все мы знаем, что GukiZ часто играет с массивами. Сейчас она размышляет над следующим вопросом: сколько существует массивов a длины n, состоящих из неотрицательных целых чисел строго меньше 2l, удовлетворяющих условию  ? Здесь операция ? Здесь операция 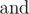 означает побитовое И (в языке Pascal она обозначается как and, на языке C/C++/Java/Python она обозначается как &), операция означает побитовое И (в языке Pascal она обозначается как and, на языке C/C++/Java/Python она обозначается как &), операция 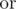 означает побитовое ИЛИ (на языке Pascal она обозначается как означает побитовое ИЛИ (на языке Pascal она обозначается как  , наC/C++/Java/Python она обозначается |). , наC/C++/Java/Python она обозначается |). Так как ответ может быть достаточно большим, посчитайте его по модулю m. В этот раз GukiZ не придумал решения и ему нужно, чтобы вы помогли ему! Выходные данные В единственной строке выведите количество массивов, удовлетворяющих данному выше условию, по модулю m. Примечание В первом примере подходящие массивы таковы: {1, 1}, {3, 1}, {1, 3}. Во втором примере единственный подходящий массив: {1, 1}. В третьем примере подходящие массивы: {0, 3, 3}, {1, 3, 2}, {1, 3, 3}, {2, 3, 1}, {2, 3, 3}, {3, 3, 0}, {3, 3, 1}, {3, 3, 2}, {3, 3, 3}. | |
![]()
|
|
D. Ваня и треугольники
Перебор
Структуры данных
Комбинаторика
математика
геометрия
сортировки
*1900
Ване было скучно и он нарисовал n различных точек на плоскости. После этого он соединил попарно все точки и увидел, что в итоге образовалось большое количество треугольников с вершинами в отмеченных точках. Он просит вас посчитать количество образовавшихся треугольников с ненулевой площадью. Выходные данные В первой строке выведите целое число — количество треугольников с ненулевой площадью среди отмеченных. Примечание Пояснение к первому тесту из условия. Образовано 3 треугольника: (0, 0) - (1, 1) - (2, 0); (0, 0) - (2, 2) - (2, 0); (1, 1) - (2, 2) - (2, 0). Пояснение ко второму тесту из усовия. Образован 1 треугольник: (0, 0) - (1, 1) - (2, 0). Пояснение к третьему тесту из условия. Одна точка не образует ни одного треугольника. | |
![]()
|
|
A. Кёя и цветные мячи
Комбинаторика
математика
дп
*1500
У Кёи Оотори есть сумка с n цветными мячиками, раскрашенными k различными цветами. Цвета пронумерованы от 1 до k. Мячики одного цвета неотличимы друг от друга. Юноша вынимает мячики из сумки один за другим, пока сумка не опустеет. Он заметил, что для всех i от 1 до k - 1 он вынул последний мяч цвета i до того, как он вынул последний мяч цвета i + 1. Теперь ему интересно, сколько существует различных последовательностей цветов вынутых мячей, удовлетворяющих данному условию. Выходные данные Выведите единственное целое число — остаток от деления на 1 000 000 007 количества различных последовательностей цветов мячей, удовлетворяющих условию. Примечание В первом примере у нас есть два мяча цвета 1, два мяча цвета 2, и один мяч цвета 3. Три возможных способа таковы:
1 2 1 2 3
1 1 2 2 3
2 1 1 2 3
| |
![]()
|
|
B. Кёя и перестановка
Бинарный поиск
Конструктив
Комбинаторика
математика
реализация
жадные алгоритмы
*1900
Определим перестановку длины n как последовательность p = [p1, p2, ..., pn], состоящую из n различных целых чисел от 1 до n. Мы говорим, что эта перестановка переводит число 1 в число p1, число 2 в число p2, и так далее. Кёя Оотори только что узнал про циклическое разложение перестановки. Цикл — это последовательность чисел, таких, что каждый элемент этой последовательности переводится перестановкой p в следующий элемент этой последовательности (а последний элемент цикла переводится в первый элемент цикла). Циклическое разложение — это представление p в виде набора циклов, образующих p. Например, перестановка p = [4, 1, 6, 2, 5, 3] имеет циклическое разложение, которое выглядит как (142)(36)(5): действительно, 1 переводится в 4, 4 переводится в 2, 2 переводится в 1, 3 и 6 меняются местами, и 5 остаётся на месте. Перестановка может иметь несколько циклических разложений, поэтому Кёя определяет стандартное циклическое разложение перестановки следующим образом. Сперва переставим элементы внутри каждого цикла таким образом, чтобы наибольший элемент был на первом месте. Затем переставим все циклы так, чтобы они были отсортированы по их первому элементу. Для данного выше примера стандартное циклическое разложение чисел [4, 1, 6, 2, 5, 3] равно (421)(5)(63). Кёя заметил, что если убрать скобки внутри стандартного циклического разложения, то мы получаем ещё одну перестановку! Например, [4, 1, 6, 2, 5, 3] превращается в [4, 2, 1, 5, 6, 3]. Кёя заметил, что некоторые перестановки не меняются после применения операции, описанной выше. Он выписал все перестановки длины n, которые не меняются в результате применения описанной операции, в лексикографическом порядке. К сожалению, его друг Тамаки Суо этот список потерял. Кёя хочет воспроизвести список и ему нужна ваша помощь. Вам даны целые числа n и k, выведите перестановку, которая была k-й в списке Кёи. Выходные данные Выведите через пробел n целых чисел, обозначающих перестановку, являющуюся ответом на вопрос. Примечание В первом тесте из условия стандартное циклическое разложение выглядит как (1)(32)(4), что дает нам изначальную перестановку после удаления скобок. Первая перестановка в списке равна [1, 2, 3, 4], а вторая перестановка равна [1, 2, 4, 3]. | |
![]()
|
|
D. Виталий и цикл
Комбинаторика
математика
*2000
поиск в глубину и подобное
графы
После того, как Виталий был отчислен из университета, он увлекся теорией графов. Особенно Виталию нравились циклы нечетной длины, в которых каждая вершина встречается не более одного раза. Виталию стало интересно, как решать следующую задачу. Задан неориентированный граф из n вершин и m ребер, необязательно связный, без кратных ребер и петель. Нужно найти t — минимальное количество ребер, которые нужно добавить в заданный граф таким образом, чтобы образовался простой цикл нечетной длины, состоящий из более чем одной вершины. Кроме того, ему надо найти w — количество способов добавить t ребер так, чтобы образовался цикл нечетной длины (состоящий из более чем одной вершины). Запрещается добавлять петли или кратные рёбра. Два способа добавить ребра в граф считаются одинаковыми, если в них совпадают множества добавляемых рёбер. Так как Виталий уже не учится в университете, он обратился к вам за помощью в решении этой задачи. Выходные данные Выведите в первую строку выходных данных через пробел два целых числа t и w — минимальное количество ребер, которое необходимо добавить в граф, чтобы образовался простой цикл нечетной длины, состоящий из более чем одной вершины, в котором каждая вершина встречается не более одного раза, и количество способов сделать это. Примечание Простой цикл это цикл, не проходящий дважды ни по какой вершине. | |
![]()
|
|
C. Геральд и гигантские шахматы
Комбинаторика
математика
дп
теория чисел
*2200
На Геральдионе очень распространены гигантские шахматы. Не будем углубляться в правила этой игры, скажем лишь, что игра происходит на поле размера h × w, и оно тоже раскрашено в два цвета, но не как в шахматах. Почти все клетки поля белые и только некоторые — чёрные. В данный момент Геральд заканчивает партию в гигантские шахматы против своего друга Полларда. Геральд почти выиграл, и для победы ему осталось только провести свою пешку из верхнего левого угла доски, где она сейчас стоит, в нижний правый. Геральд настолько уверен в победе, что ему стало интересно, сколькими способами он может выиграть? Пешка, которая осталась у Геральда, может ходить двумя способами: на одну клетку вниз или на одну клетку вправо. Кроме того, она не может ходить на чёрные клетки, иначе Геральд всё-таки проиграет. Никаких других пешек или фигур на поле не осталось, так что, согласно правилам гигантских шахмат, Геральд ходит своей пешкой, пока игра не закончится, а Поллард просто наблюдает за этим процессом. Выходные данные Выведите единственное число — остаток от деления количества способов провести пешку Геральда от верхней левой клетки до нижней правой на число 109 + 7. | |
![]()
|
|
D. Рандомизатор
Теория вероятностей
Комбинаторика
геометрия
*2800
Геральду надоело играть в настольные игры с обычным шестигранным кубиком и он купил себе игрушку, которая называется Рандомизатор. Он устроена следующим образом. У Рандомизатора есть своя собственная координатная плоскость, на которой нарисован строго выпуклый многоугольник, называющийся основным многоугольником. Если Рандомизатор потрясти, он рисует некоторый невырожденный (т. е. имеющий ненулевую площадь) выпуклый многоугольник с вершинами в каких-то вершинах основного многоугольника. Результатом броска (точнее говоря, результатом потряхивания) считается количество точек с целыми координатами, которые оказались строго внутри (точки на границе не считаются) выбранного многоугольника. Теперь Геральду интересно — каково математические ожидание результата потряхивания Рандомизатора? Во время потряхивания Рандомизатор рассматривает все возможные невырожденные выпуклые многоугольники с вершинами в вершинах основного многоугольника. Пусть оказалось k вариантов многоугольников. Тогда Рандомизатор выбирает каждый из них с вероятностью  . . Выходные данные Выведите искомое математическое ожидание с абсолютной или относительной погрешностью не более 10 - 9. Примечание Многоугольник называется строго выпуклым, если он выпуклый, и никакие три его вершины не лежат на одной прямой. Пусть случайная величина принимает значения x1, ..., xn с вероятностями p1, ..., pn соответственно. Тогда математическое ожидание этой случайной величины равняется  . . | |
![]()
|
|
B. Симметричное и транзитивное
Комбинаторика
математика
дп
*1900
Вовочка недавно занялся теорией множеств. Сейчас он проходит бинарные отношения. Вы, наверное, слышали термин «отношение эквивалентности». Такие отношения очень важны во многих разделах математики. Например, равенство двух чисел является отношением эквивалентности. Набор ρ пар (a, b) элементов некоторого множества A называется бинарным отношением на множестве A. Про два элемента a и b множества A говорят, что они находятся в отношении ρ, если пара 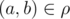 , в таком случае пишут , в таком случае пишут 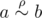 . . Бинарное отношение является отношением эквивалентности, если: - Оно рефлексивно (для любого a верно
 ); ); - Оно симметрично (для любых a, b верно, что если
 , то , то  ); ); - Оно транзитивно (если
 и и 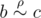 , то , то 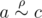 ). ).
Вовочка очень даже не дурак и заметил, что первое условие не нужно! Вот его «доказательство»: Возьмём любые два элемента a и b. Если 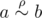 , то , то 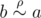 (по свойству (2)), а значит (по свойству (2)), а значит  (по свойству (3)). (по свойству (3)). Все очень просто, не правда ли? Однако, вы заметили, что «доказательство» Вовочки неверно, и решили предъявить ему множество примеров, доказывающих его неправоту. Вот ваше задание: посчитайте количество бинарных отношений над множеством размера n таких, что они симметричны, транзитивны, но не являются отношениями эквивалентности (то есть не являются рефлексивными). Так как их количество может быть очень большим (а не 0, как считает Вовочка), выведите остаток от деления их количества на 109 + 7. Выходные данные В единственной строке выведите ответ на задачу по модулю 109 + 7. Примечание При n = 1 есть только одно такое отношение — пустое, т.е.  . Иными словами, для единственного элемента x множества A выполнено . Иными словами, для единственного элемента x множества A выполнено  . . При n = 2 таких отношений уже три. Пусть множество A состоит из двух элементов x и y. Тогда подходящими элементами являются  , ρ = {(x, x)}, ρ = {(y, y)}. Нетрудно видеть, что три перечисленных бинарных отношения являются симметричными и транзитивными отношениями, но не являются отношениями эквивалентности. , ρ = {(x, x)}, ρ = {(y, y)}. Нетрудно видеть, что три перечисленных бинарных отношения являются симметричными и транзитивными отношениями, но не являются отношениями эквивалентности. | |
![]()
|
|
C. Массив
Комбинаторика
математика
*1900
Кролик Крис с детства увлекается массивами. Сейчас он занят исследованием массивов длиной n, которые содержат только целые числа от 1 до n. Он не силен в математике — поэтому некоторые простые вещи выводят его из себя. Вот, к примеру, вчера он задался целью вычислить, сколько всего есть разных красивых массивов? Крис считает, что массив красив, если выполняется одно из двух: - каждый элемент, начиная со второго, не больше предыдущего
- каждый элемент, начиная со второго, не меньше предыдущего
Крис, изрядно разозлившись на себя и на математику, пришел просить помощи у Стьюи и Брайана. Но те просто посмеялись и сказали, что ответ слишком прост и неинтересен. Помогите кролику Крису все же найти ответ. Выходные данные В единственной строке требуется вывести ответ. Так как он может быть достаточно большим — нужно вывести его по модулю 1000000007. | |
![]()
|
|
E. Свинка и палиндромы
Комбинаторика
дп
*2300
Свинка Пеппа во время прогулки попала в лес. По странному совпадению лес имеет форму прямоугольника, состоящего из n строк и m столбцов. Занумеруем строки прямоугольника сверху вниз числами от 1 до n, а столбцы — слева направо числами от 1 до m. Будем обозначать клетку на пересечении r-й строки и c-го столбца как (r, c). Исходно свинка стоит в клетке (1, 1), а в конце она хочет оказаться в клетке (n, m). Так как свинка торопится домой, из клетки (r, c) она может перейти только в клетку (r + 1, c) либо (r, c + 1), при этом выходить за пределы леса она не может. Лес, в котором оказалась свинка, очень необычный. Некоторые клетки леса похожи между собой, а некоторые выглядят совершенно по-разному. Пеппа любит фотографировать и на каждом шагу делает фотографию клетки, в которой она сейчас находится. Путь по лесу считается красивым, если фотографии, полученные на её пути, можно рассматривать как в прямом, так и в обратном порядке, будет получаться одна и та же последовательность фотографий. Более формально, строка, образованная клетками в порядке посещения, должна являться палиндромом (формальное определение палиндрома можете прочитать в условии предыдущей задачи). Посчитайте количество красивых путей из клетки (1, 1) в клетку (n, m). Так как это число может быть очень большим, определите остаток от деления его на 109 + 7. Выходные данные Выведите одно целое число — количество красивых путей по модулю 109 + 7. Примечание Пояснение к первому тесту из условия. 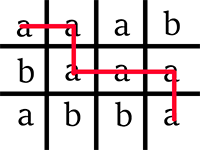 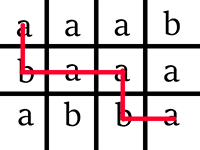
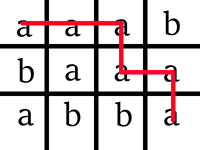
| |
![]()
|
|
A. Удлинение палочек
Комбинаторика
математика
реализация
*2100
Даны три палочки с целыми положительными длинами в a, b, и c сантиметров. Можно увеличить некоторые из них на целое положительное число сантиметров (разные палочки можно увеличивать на разную длину), но в сумме не больше, чем на l сантиметров. В частности, разрешается не увеличивать длину ни одной палочки. Определите количество способов увеличить длины некоторых палочек так, чтобы из них можно было сложить невырожденный (то есть, имеющий ненулевую площадь) треугольник. Два способа считаются различными, если в них длина какой-то из палочек увеличивается на разное число сантиметров. Выходные данные Выведите единственное целое число — количество способов увеличить размеры палочек в сумме не больше, чем на l сантиметров, так, чтобы из них можно было составить невырожденный треугольник. Примечание В первом тесте из условия можно не увеличивать ни одну из палочек, либо увеличить любые две палочки на 1 сантиметр. Во втором тесте из условия можно увеличить либо первую, либо вторую палочку на один сантиметр. Обратите внимание, что треугольник, составленный из исходных палочек, является вырожденным, и поэтому не подходит. | |
![]()
|
|
H. Боты
Комбинаторика
математика
дп
теория чисел
*1800
Саша и Ира — лучшие друзья. Они не просто друзья — они разработчики ПО и эксперты по искусственному интеллекту. Они разрабатывают алгоритм для двух ботов, играющих в игру для двух игроков. За каждый ход, один из игроков совершает ход (неважно, какой игрок, возможно, игроки делают ходы не по очереди). Алгоритм для ботов, разработанный Сашей и Ирой, работает за счет отслеживания состояния, в котором находится игра. Каждый раз, когда любой бот делает ход, состояние меняется. А так как игра очень динамичная, она никогда не вернется в то состояние, в котором она была на каком-либо этапе в прошлом. Саша и Ира — перфекционисты и они хотят, чтобы у их алгоритма была оптимальная выигрышная стратегия. Они заметили, что в оптимальной выигрышной стратегии оба бота делают ровно по N ходов каждый. Но для того, чтобы найти оптимальную стратегию, их алгоритму надо проанализировать все возможные состояния этой игры (они ещё не изучили альфа-бета отсечение) и выбрать лучшую последовательность ходов. Они беспокоятся насчет эффективности их алгоритма и им интересно, какое общее количество состояний в игре, которое необходимо проанализировать? Выходные данные Вывод должен содержать единственное целое число – количество возможных состояний по модулю 109 + 7. Примечание Начало: Игра в состоянии A. - Ход 1: Любой бот может ходить (первый бот красный, а второй бот синий), так что есть два возможных состояния после первого хода – B и C.
- Ход 2: В обоих состояниях, B и C, любой бот может снова сделать ход, так что список возможных состояний расширяется и включает в себя D, E, F и G.
- Ход 3: Красный бот уже совершил N=2 движений в состоянии D, так что отсюда он больше не может делать ходов. Он может совершать ходы в состояниях E, F и G, так что состояния I, K и M добавляются в список. Аналогичным образом, синий бот не может совершать ходы в состоянии G, но может в D, E и F, так что добавляются состояния H, J и L.
- Ход 4: Красный бот точка уже совершил N=2 шага в состояниях H, I и K, он может двигаться только в J, L и M, так что добавляются состояния P, R и S. Синий бот не может двигаться в состояниях J, L и M, а только в H, I и K, так что добавляются состояния N, O и Q.
Всего образуется 19 различных состояний игры, необходимых в анализе алгоритма. 
| |
![]()
|
|
B. Сумма по модулю
Структуры данных
Комбинаторика
дп
*1900
Дана последовательность чисел a1, a2, ..., an, а также число m. Проверьте, можно ли выбрать непустую подпоследовательность aij такую, что сумма чисел в этой подпоследовательности делится на m. Выходные данные В единственной строке выведите «YES» (без кавычек) в случае, если существует требуемая подпоследовательность, либо «NO» (без кавычек), если такой подпоследовательности не существует. Примечание В первом тесте из условия можно выбрать числа 2 и 3, сумма которых делится на 5. Во втором тесте из условия, единственная непустая подпоследовательность чисел — одно число 5. Число 5 не делится на 6, стало быть, искомой подпоследовательности не существует. В третьем тесте из условия нужно выбрать два числа 3 на концах. В четвертом тесте из условия можно взять целиком всю последовательность. | |
![]()
|
|
B. Коля и Таня
Комбинаторика
*1500
Коля любит рассаживать гномов по кругу и раздавать им монеты, а Таня любит изучать тройки гномов, сидящих в вершинах равностороннего треугольника. Более формально, в круге сидят 3n гномов. У каждого гнома может быть от 1 до 3 монет. Пронумеруем места в порядке следования по кругу числами от 0 до 3n - 1, пусть у гнома, сидящего на i месте, ai монет. Тогда если существует целое число i (0 ≤ i < n) такое, что ai + ai + n + ai + 2n ≠ 6, то Таня остается довольна. Посчитайте количество способов выбрать ai так, чтобы Таня осталась довольна. Так как способов раздачи монет может быть много, вычислите остаток от их деления на 109 + 7. Два способа a и b считаются различными, если существует индекс i (0 ≤ i < 3n) такой, что ai ≠ bi (то есть, какой-то гном получил разное количество монет в этих двух способах). Выходные данные Выведите единственное число — остаток от деления количества вариантов раздачи монет, устраивающих Таню на 109 + 7. Примечание 20 способов для для n = 1 (наверху каждого треугольника сидит гном с индексом 0, в правой нижней вершине - с индексом 1, в левой нижней - с индексом 2): 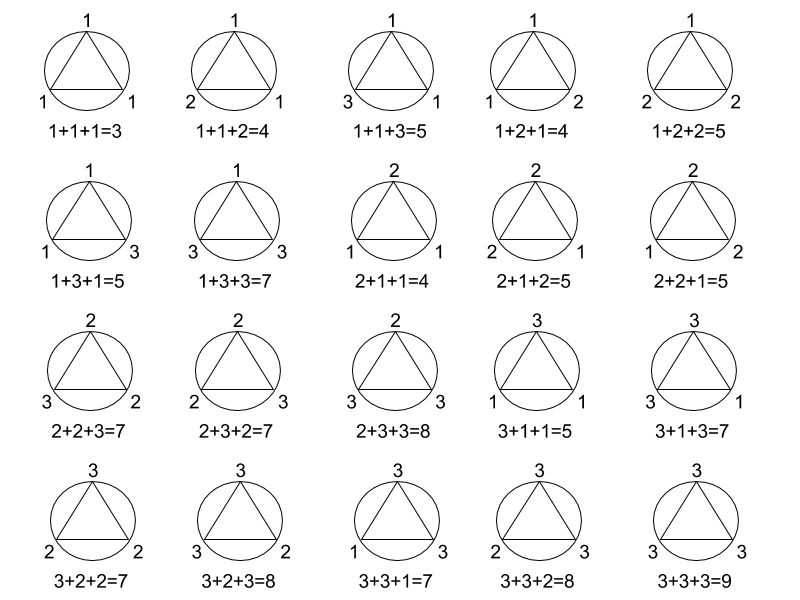 | |
![]()
|
|
E. Подарок для филателиста Виталика
Комбинаторика
математика
теория чисел
*2900
У филателиста Виталика сегодня день рождения! Как постоянному клиенту магазина почтовых марок «Робин Бобин», руководство магазина решило сделать ему подарок. Виталик хочет купить одну марку, а магазин, в свою очередь, подарит ему некоторый непустой набор из оставшихся марок, такой, что наибольший общий делитель (НОД) цен подаренных марок больше единицы. Если НОД цен купленной марки и цен марок из подаренного набора окажется равен 1, то Виталик уйдет из магазина абсолютно счастливым. Руководство магазина просит вас посчитать количество различных ситуаций, при которых Виталик уйдет из магазина абсолютно счастливым. Так как искомое количество ситуаций может оказаться очень большим, вам требуется найти остаток от деления этого количества на число 109 + 7. Ситуации считаются различными, если различаются марки, купленные Виталиком, или один из подарков содержит марку, которую не содержит другой. Выходные данные Выведите одно целое число — остаток от деления искомого количества ситуаций на число 109 + 7. Примечание В первом примере возможны следующие ситуации: - Виталик покупает 1-ю марку, магазин дарит 2-ю марку;
- Виталик покупает 3-ю марку, магазин дарит 2-ю марку;
- Виталик покупает 2-ю марку, магазин дарит 1-ю марку;
- Виталик покупает 2-ю марку, магазин дарит 3-ю марку;
- Виталик покупает 2-ю марку, магазин дарит 1-ю и 3-ю марки.
| |
![]()
|
|
C. Вилбур и точки
Комбинаторика
жадные алгоритмы
сортировки
*1700
Вилбур играет с множеством из n точек на координатной плоскости. Все точки имеют неотрицательные целочисленные координаты. Более того, если точка (x, y) принадлежит множеству Вилбура, то все точки (x', y'), такие, что 0 ≤ x' ≤ x и 0 ≤ y' ≤ y, также принадлежат этому множеству. Теперь Вилбур хочет пронумеровать точки в имеющемся множестве, то есть присвоить им различные целочисленные номера от 1 до n. Чтобы нумерация была эстетически приятна, Вилбур хочет выполнить такое условие: если некоторая точка (x, y) получает номер i, тогда всем (x',y') из этого множества, таким, что x' ≥ x и y' ≥ y, надо приписать номер не менее i. Например, для множества из четырех точек (0, 0), (0, 1), (1, 0) и (1, 1) есть две эстетически приятные нумерации: 1, 2, 3, 4, и 1, 3, 2, 4. Друг Вилбура увидел, как тот играет с точками, и решил усложнить ему задачу. Для любой точки он определяет её специальное значение как s(x, y) = y - x. Теперь он даёт Вилбуру последовательность w1, w2,..., wn и просит найти такую эстетически приятную нумерацию точек множества, что специальное значение точки, получившей номер i, будет равно wi, то есть s(xi, yi) = yi - xi = wi. Теперь Вилбур очень просит вас помочь ему с этой задачей. Выходные данные Если существует эстетически приятная нумерация точек множества, такая, что s(xi, yi) = yi - xi = wi, то выведите "YES" в первой строке выходных данных. В противном случае выведите "NO". Если решение существует, далее выведите n строк. В i-й из них строк выведите точку множества, которая получит номер i. Если существует несколько решений, выведите любое. Примечание В первом примере точка (2, 0) получает номер 3, точка (0, 0) получает номер 1, точка (1, 0) получает номер 2, точка (1, 1) получает номер 5 и точка (0, 1) получает номер 4. Легко проверить, что такая нумерация является эстетически прятной, и yi - xi = wi. Во втором примере специальные значения точек множества равны 0, - 1 и - 2, в то время как последовательность, которую Вилбуру даёт друг, равна 0, 1, 2. Следовательно, ответа не существует. | |
![]()
|
|
B. Муудулярная Арифметика
Комбинаторика
математика
теория чисел
*1800
поиск в глубину и подобное
снм
Как подобает любому порядочному школьнику, Кевин Сан изучает коровометрию, коровоматику и криптобычество в Буреновском государственном университете (БГУ) под руководством Фермера Ивана. На последнем занятии по математическому упрощению уравнений (МУУ) Кевин столкнулся со странным функциональным уравнением, для решения которого он нуждается в вашей помощи. Даны два целых числа k и p, при этом p — нечётное простое число и функциональное уравнение: 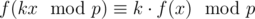 для некоторой функции  . (Равенство должно выполняться для любого целого x от 0 до p - 1 включительно). . (Равенство должно выполняться для любого целого x от 0 до p - 1 включительно). Кевин просит вас посчитать количество различных функций f, удовлетворяющих этому уравнению. Поскольку ответ может быть достаточно большим, вы должны вывести остаток от деления этого числа на 109 + 7. Выходные данные Выведите единственное целое число — количество различных функций f, удовлетворяющих уравнению, по модулю 109 + 7. Примечание В первом примере p = 3 и k = 2. Подходят следующие функции: - f(0) = 0, f(1) = 1, f(2) = 2.
- f(0) = 0, f(1) = 2, f(2) = 1.
- f(0) = f(1) = f(2) = 0.
| |
![]()
|
|
B. Сумма расстояний Хэмминга
Строки
Комбинаторика
*1500
Геносу нужна Ваша помощь. Сайтама попросил его решить следующую задачку по программированию: Обозначим как |s| длину некоторой строки s. Расстояние Хэмминга между двумя строками s и t одинаковой длины определяется как  , где si означает i-й символ строки s, а ti — i-й символ строки t. Например, расстояние Хэмминга между строкой "0011" и строкой "0110" равно |0 - 0| + |0 - 1| + |1 - 1| + |1 - 0| = 0 + 1 + 0 + 1 = 2. , где si означает i-й символ строки s, а ti — i-й символ строки t. Например, расстояние Хэмминга между строкой "0011" и строкой "0110" равно |0 - 0| + |0 - 1| + |1 - 1| + |1 - 0| = 0 + 1 + 0 + 1 = 2. Даны две строки a и b, найдите сумму расстояний Хэмминга между a и всеми подстроками b длины |a|. Выходные данные Выведите единственное целое число — сумму расстояний Хэмминга между a и всеми подстроками строки b длины |a|. Примечание В первом примере в строке b есть четыре подстроки длины |a|: "00", "01", "11", и "11". Расстояние между "01" и "00" равно |0 - 0| + |1 - 0| = 1. Расстояние между "01" и "01" равно |0 - 0| + |1 - 1| = 0. Расстояние между "01" и "11" равно |0 - 1| + |1 - 1| = 1. Последнее значение учитывается два раза, поскольку подстрока "11" встречается в b дважды. Сумма этих расстояний равна 1 + 0 + 1 + 1 = 3. Второй пример описан в условии задачи. | |
![]()
|
|
A. Паша и палка
Комбинаторика
математика
*1000
У Паши есть прямая деревянная палка целой положительной длины n. Он хочет сделать ровно три распила и получить четыре куска палки целой положительной длины, суммарная длина которых, очевидно, будет равна n. Паша любит прямоугольники, но в то же время очень не любит квадраты, поэтому хочет знать, сколько существует способов разрезать палку на четыре части таким образом, чтобы из получившихся кусков палки можно было сложить какой-нибудь прямоугольник, но нельзя было сложить квадрат. Перед вами стоит задача помочь Паше — посчитать количество таких способов. Два способа считаются различными, если отличаются наборы длин получившихся кусков, то есть для какой-то длины x количество палок длины x в одном способе не равно количеству палок такой же длины в другом способе. Выходные данные Выведите в первую строку выходных данных единственное целое число — количество способов разделить Пашину палку на четыре части ненулевой длины таким образом, чтобы можно было соединить концы получившихся частей и получить прямоугольник, но не квадрат. Примечание В первом тестовом примере существует одно корректное разделение с длинами {1, 1, 2, 2}. Во втором тестовом примере существует четыре корректных разделения с длинами {1, 1, 9, 9}, {2, 2, 8, 8}, {3, 3, 7, 7} и {4, 4, 6, 6}. Обратите внимание, что {5, 5, 5, 5} не подходит. | |
![]()
|
|
E. Корень квадратный из перестановки
Конструктив
Комбинаторика
математика
поиск в глубину и подобное
графы
*2200
Перестановка длины n — это такой массив длины n, который содержит каждое из чисел от 1 до n ровно по одному разу. Например, q = [4, 5, 1, 2, 3] — это перестановка. Для перестановки q ее квадратом называется такая перестановка p что p[i] = q[q[i]] для всех i = 1... n. Например, квадрат перестановки q = [4, 5, 1, 2, 3] равен p = q2 = [2, 3, 4, 5, 1]. Эта задача об обратном понятии — квадратном корне. Вам задана перестановка p ваша задача найти такую перестановку q, что q2 = p. Если искомых перестановок q несколько, найдите любую из них. Выходные данные Если перестановки q такой, что q2 = p не существует, выведите число "-1". Если же ответ существует, то нужно вывести его. Единственная строка должна содержать n различных чисел qi (1 ≤ qi ≤ n) — элементы перестановки q. Если существует несколько перестановок q, удовлетворяющих условию q·q = p, то разрешается вывести любую из них. | |
![]()
|
|
B. Шоколад
Комбинаторика
*1300
Вася обожает всё сладкое. Его любимый шоколад является палочкой, состоящей из кусочков, каждый из которых может содержать орешек. Вася хочет разломать шоколад на несколько частей так, чтобы любая часть содержала ровно один орешек, и любой разлом проходил между двумя соседними кусочками. Посчитайте количество способов, которыми Вася может это сделать. Два способа считаются различными, если в одном из них присутствует разлом в конкретной позиции, который отсутствует в другом способе. Обратите внимание, что если не сделать ни одного разлома, то вся шоколадка будет представлять собой один кусочек. В этом случае, в этом кусочке также должен быть ровно один орешек. Выходные данные Выведите количество способов разломать шоколад на несколько частей так, чтобы в каждой из них находился ровно один орешек. Примечание В первом примере есть ровно один орешек, поэтому количество способов равно 1 — не делать ни одного разлома. Во втором примере можно разломать шоколад четырьмя способами: 10|10|1 1|010|1 10|1|01 1|01|01 | |
![]()
|
|
B. Мокрая Акула и слоны
Комбинаторика
реализация
*1300
Сегодня у Мокрой Акулы есть n слонов на шахматной доске 1000 на 1000. Строки и столбцы пронумерованы от 1 до 1000, при этом строки пронумерованы сверху вниз, а столбцы пронумерованы слева направо. Мокрая Акула считает, что два слона атакуют друг друга, если они стоят на одной диагонали. Обратите внимание, в отличие от настоящих шахмат, наличие третьего слона между ними не является помехой. Теперь Мокрая Акула хочет посчитать количество пар слонов, которые атакуют друг друга. Выходные данные Выведите количество пар слонов, которые атакуют друг друга. Примечание В первом примере атакуют друг друга следующие пары слонов: (1, 3), (1, 5), (2, 3), (2, 4), (3, 4) и (3, 5). Пары (1, 2), (1, 4), (2, 5) и (4, 5) друг друга не атакуют, так как соответствующие слоны не находятся на одной диагонали. | |
![]()
|
|
C. Мокрая Акула и цветы
Теория вероятностей
Комбинаторика
математика
теория чисел
*1700
В подчинении у Мокрой Акулы находится n акул, сидящих за круглым столом. Таким образом, соседями являются акулы с номерами i и i + 1 для всех i от 1 до n - 1, а так же акулы с номерами 1 и n. Каждая акула в течение дня вырастит случайное количество цветков si — целое число от li до ri, при этом все варианты равновероятны. У Мокрой Акулы есть любимое простое число p, от которого он совершенно без ума! Если для какой-то пары соседних акул i и j произведение количества выращенных ими цветков si·sj делится на p, то Мокрая Акула радуется и даёт каждой из этих акул по 1000 бурлей. В конце дня акулы собираются вместе и складывают все подаренные бурли. Вычислите математическое ожидание этого количества. Выходные данные Выведите единственное вещественное число — математическое ожидание суммарного количества бурлей, которое получат акулы. Ваш ответ будет считаться правильным, если его абсолютная или относительная ошибка не будет превосходить 10 - 6. А именно: пусть ваш ответ равен a, а ответ жюри — b. Проверяющая программа будет считать ваш ответ правильным, если  . . Примечание Положительное целое число называется простым, если оно не делится ни на какое другое положительное целое число, кроме себя и 1. При этом число 1 простым не является. Рассмотрим первый пример из условия. Первая акула выращивает от 1 до 2 цветков, вторая от 420 до 421, а третья от 420420 до 420421. Возможны восемь вариантов количества выращенных цветков (s0, s1, s2): - (1, 420, 420420): 1·420 = 420, 420·420420 = 176576400 и 420420·1 = 420420. Каждая акула в каждой паре получит по 1000 бурлей, то есть в итоге каждая акула получит по 2000 бурлей, и сумма будет равна 6000 бурлей.
- (1, 420, 420421): В этом варианте 420421·1 не делится на 2, поэтому первая и третья акулы получат только по 1000 бурлей, а вторая всё ещё получит 2000. Итоговая сумма — 4000 бурлей.
- (1, 421, 420420): сумма 4000
- (1, 421, 420421): сумма 0.
- (2, 420, 420420): сумма 6000.
- (2, 420, 420421): сумма 6000.
- (2, 421, 420420): сумма 6000.
- (2, 421, 420421): сумма 4000.
Математическое ожидание равняется  . . Во втором примере никакая комбинация количества цветов не приносит акулам бурлей. | |
![]()
|
|
E. Преобразование последовательности
Комбинаторика
математика
дп
бпф
*3300
Определим преобразование P последовательности a1, a2, ..., an как b1, b2, ..., bn, где bi = a1 | a2 | ... | ai для всех i = 1, 2, ..., n. Символом | будем обозначать операцию побитового ИЛИ. Вася поочередно применяет преобразование P ко всем последовательностям длины n из целых чисел от 1 до 2k - 1 включительно. Он хочет знать, для скольких последовательностей результат преобразования будет строго возрастающей последовательностью. Помогите ему посчитать это число по модулю 109 + 7. Выходные данные В единственной строке выведите количество подходящих последовательностей по модулю 109 + 7. | |
![]()
|
|
D. Протест Джерри
Перебор
Теория вероятностей
Комбинаторика
дп
*1800
Эндрю и Джерри играют в игру, а Гарри ведёт счёт. Игра состоит из трёх раундов. В каждом раунде Эндрю и Джерри по очереди вынимают по одному шару из урны, содержащей n шаров, на которых написаны различные целые числа. Затем они передают шары Гарри, который добавляет очко тому, на чьём шаре было написано большее число, и кладёт их обратно в урну. Победителем игры объявляется тот, кто выиграл хотя бы в двух раундах из трёх. Известно, что Эндрю выиграл в раундах 1 и 2, а Джерри победил в раунде 3, так что победителем игры стал Эндрю. Однако Джерри недоволен способом определения победителя — по его словам, сумма чисел на вытянутых им шарах была строго больше суммы чисел на шарах, вытянутых Эндрю. Какова вероятность такого события? Выходные данные Выведите единственное вещественное число — вероятность того, что сумма чисел на всех шарах, вытянутых Джерри, была строго больше суммы чисел на всех шарах, вытянутых Эндрю, если известно, что Эндрю выиграл первые два раунда, а Джерри выиграл третий раунд. Ваш ответ будет считаться правильным, если его абсолютная или относительная погрешность не будет превосходить 10 - 6. А именно: пусть ваш ответ равен a, а ответ жюри — b. Проверяющая программа будет считать ваш ответ правильным, если 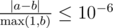 . . Примечание В первом примере имеется всего два шара. В первых двух раундах Эндрю обязательно доставал шар с числом 2, а Джерри доставал шар с числом 1, и наоборот в последнем раунде. Таким образом, сумма на всех шарах Эндрю обязательно равна 5, а на всех шарах Джерри — 4. Во втором примере у каждой игры могло быть три исхода: 10 - 2, 10 - 1 или 2 - 1. Чтобы выполнилось условие на сумму, Эндрю обязательно должен был оба раза победить с исходом 2 - 1, а в последнем раунде Джерри должен был достать 10. Вероятность такого события равняется 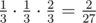 . . | |
![]()
|
|
A. Дальние родственники и торт
Перебор
Конструктив
Комбинаторика
реализация
*800
Семья Доров готовится праздновать день рождения Фомы Дора, для этого члены семьи приготовили ему весьма своеобразный торт. Торт представляет собой квадрат n × n, состоящий из одинаковых квадратиков со стороной 1. Каждый квадрат либо пустой, либо содержит шоколадку. Члены семьи испекли торт и разложили на нём шоколадки. Они думают, что радость Фомы будет равна количеству пар клеток с шоколадками, расположенных в одной строке или в одном столбце. Теперь они пытаются вычислить, чему же будет равно это значение для данного торта. Обратите внимание, что каждая пара может быть посчитана не более чем один раз, поскольку две различные клетки не могут быть одновременно расположены в одной строке и в одном столбце. Выходные данные Выведите, чему будет равна радость Фомы Дора, когда он увидит торт, то есть количество клеток с шоколадками, расположенных в одной строке или в одном столбце. Примечание Пронумеруем строки сверху вниз, а столбцы слева направо. Тогда в одной строке расположены: - (1, 2) и (1, 3)
- (3, 1) и (3, 3)
В одном столбце расположены следующие клетки с шоколадками: - (2, 1) и (3, 1)
- (1, 3) и (3, 3)
| |
![]()
|
|
E. Фома Дор и дороги
Деревья
Структуры данных
Теория вероятностей
Комбинаторика
дп
поиск в глубину и подобное
*2300
Карта города, в котором живёт Фома Дор, представляет собой дерево (неориентированный связный граф без простых циклов), поэтому гости зовут его Древоградом. В городе n перекрёстков, соединённых n - 1 дорогой. По всем дорогам можно перемещаться в обоих направлениях. В городе живёт m друзей Фомы Дора, i-й из них живёт рядом с перекрёстком ui, а работает рядом с перекрёстком vi. Все жители города несчастны, потому что между из домом и работой существует ровно один простой путь. Фома Дор хочет построить ровно одну новую дорогу, которую он выберет случайно среди всех n·(n - 1) / 2 возможных дорог. Обратите внимание, что он вполне может построить новую дорогу между какой-то парой перекрёстков, уже соединённых друг с другом дорогой. Фома знает, что каждый из его друзей будет счастлив, если после построения новой дороги будет путь из его дома до работы и обратно, который не проходит по одной дороге дважды. Формально, в графе будет существовать простой цикл, на котором лежат ui и vi. Более того, если какой-то друг становится счастлив, то уровень его радости определяется как длина этого пути (несложно заметить, что эта длина определяется однозначно). Для каждого своего друга Фома хочет вычислить математическое ожидание значения уровня радости, то есть математическое ожидание длины цикла, если этот цикл содержит ui и vi. Выходные данные Для каждого друга Фомы Дора вычислите математическое ожидание его уровня радости, при условии, что он будет счастлив. Ваш ответ будет считаться правильным, если его абсолютная или относительная ошибка не будет превосходить 10 - 6. А именно: пусть ваш ответ равен a, а ответ жюри — b. Проверяющая программа будет считать ваш ответ правильным, если 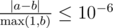 . . Примечание Рассмотрим второй пример. - Подходят дороги (1, 2) и (2, 3), поэтому математическое ожидание равняется
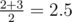 - Построение дорог (1, 3) и (2, 3) сделает второго друга счастливым. Как и для друга 1, ответ равен 2.5
- Единственный способ сделать третьего друга счастливым — это построить дорогу (2, 3), поэтому ответ равен 3
| |
![]()
|
|
C. Счастливые номера
Комбинаторика
математика
*1100
В новом здании налоговой инспекции ИТ-града было решено номера всех кабинетов сделать счастливыми. Счастливым называется номер, состоящий только из цифр 7 и 8. Найдите максимальное количество кабинетов в новом здании налоговой инспекции, если на табличку с номером кабинета помещается не более чем n-значное число. Выходные данные Выведите одно целое число — максимальное количество кабинетов, которые можно занумеровать различными счастливыми номерами длины не более n. | |
![]()
|
|
F. Подбор кадров
Комбинаторика
математика
*1300
В одной из компаний ИТ-града было принято решение создать группу инновационных разработок численностью от 5 до 7 человек и набрать для этого новых сотрудников. После размещения объявлений в компанию поступило n анкет. Теперь отделу кадров предстоит непростая задача оценить каждый возможный состав группы и выбрать один из них. Ваша задача — посчитать, сколько вариантов состава новой группы необходимо будет рассмотреть отделу кадров. Выходные данные Выведите одно целое число — количество различных вариантов состава новой группы. | |
![]()
|
|
G. Переходящие вымпелы
Комбинаторика
математика
*1600
В одной ИТ-компании ввиду урезания бюджета вместо премий была введена новая система нематериальных поощрений сотрудников. Особо отмечаются два вида действий: исправление критичных багов и предложение новых интересных фич. Человек, исправивший критичный баг, получает себе на стол вымпел «Исправил критичный баг». Человек, предложивший новую интересную фичу, получает себе на стол вымпел «Предложил новую фичу». Ввиду ограниченности бюджета новой системы поощрений было закуплено всего 5 вымпелов «Исправил критичный баг» и 3 вымпела «Предложил новую фичу». Чтобы этих вымпелов хватило надолго, их было решено сделать переходящими: когда человек исправляет новый критичный баг, один из ранее распределённых вымпелов «Исправил критичный баг» переходит ему на стол. Когда человек предлагает новую интересную фичу, один из ранее распределённых вымпелов «Предложил новую фичу» переходит ему на стол. У одного человека на столе может стоять несколько вымпелов одного типа и, разумеется, могут стоять вымпелы обоих типов. Всего в ИТ-компании n столов. Найдите количество способов распределения описанных вымпелов по этим столам, если известно, что каждый из вымпелов находится на каком-то из столов, и каждый стол достаточно велик, чтобы содержать любое количество вымпелов. Выходные данные Выведите одно целое число — количество способов расставить вымпелы по n столам. | |
![]()
|
|
H. Скамейки
Комбинаторика
математика
*1400
Городской парк ИТ-града содержит n дорожек, идущих с востока на запад и n дорожек, идущих с севера на юг. Каждая дорожка, идущая с севера на юг, пересекается с каждой дорожкой, идущей с востока на запад, таким образом, всего пересечений n2. Город выделил деньги на закупку пяти скамеек. Чтобы казалось, что скамеек много, было решено поставить их на как можно большее количество дорожек. Очевидно, такому условию удовлетворяет следующая схема размещения: каждая скамейка размещается на пересечении дорожек, на каждой дорожке находится не более одной скамейки. Помогите администрации парка сосчитать количество способов расставить скамейки. Выходные данные Выведите одно целое число — количество способов расставить скамейки. | |
![]()
|
|
I. Автостоянка
Комбинаторика
математика
*1700
Чтобы быстро набрать штат высококвалифицированных специалистов, одна из новых компаний ИТ-града пошла на беспрецедентный шаг. Она решила дарить каждому сотруднику автомобиль, причём сотрудник сам может выбрать одну из четырёх различных марок. Автостоянка перед офисом представляет собой одну линию из (2n - 2) парковочных мест. К сожалению, общее число машин оказалось больше, чем вместимость парковки. Более того, даже количество машин одной любой марки оказалось больше, чем количество парковочных мест! Поэтому свободных мест на стоянке не бывает никогда. Любуясь ровным рядом машин, директор подумал, что стоянка выглядела бы ещё красивее, если бы на ней нашлись ровно n подряд стоящих машин одинаковой марки. Помогите директору определить количество способов такого заполнения парковки. Выходные данные Выведите единственное целое число — количество способов заполнить стоянку машинами четырех марок требуемым образом Примечание Обозначим марки так: A — Астон Мартин, B — Бентли, M — Мерседес-Майбах, Z — запорожец. Для n = 3 подходят следующие варианты заполнения стоянки: AAAB AAAM AAAZ ABBB AMMM AZZZ BBBA BBBM BBBZ BAAA BMMM BZZZ MMMA MMMB MMMZ MAAA MBBB MZZZ ZZZA ZZZB ZZZM ZAAA ZBBB ZMMM Изначально планировалось раздавать спортивные автомобили марок Феррари, Ламборджини, Мазерати и Бугатти, но от этой идеи отказались, поскольку по разбитым дорогам ИТ-града на этих автомобилях с маленьким клиренсом невозможно проехать. | |
![]()
|
|
F. Ароматные эксперименты
Комбинаторика
математика
теория чисел
*2500
Чтобы отпраздновать установление мира, Бесси, Элси и Фермер Джон собираются посадить несколько грядок с цветами, что позволит им дополнительно украсить роскошные луга Бовинии. Как известно любому садоводу, на каждой грядке необходимо посадить одинаковые цветы в одинаковом порядке. Изначально у Фермера Джона есть n различных типов цветов, ai цветов типа i. В каждый из q последующих дней Фермер Джон получит некоторое количество цветов нового типа. В день j он получит cj цветов одного типа, отличного от всех типов, имевшихся у него до этого. Поскольку Фермер Джон знает баланс между экстравагантностью и минимализмом, он хочет посадить цветы ровно k различных типов. Кроме того, если какой-то тип был выбран для использования, то Джон хочет посадить все цветы этого типа. Дополнительно: цветы будут посажены на несколько грядок таким образом, что для каждого из k выбранных типов, количество цветов этого типа на каждой грядке одинаково. Поскольку Джон — фанат всеобщего равенства, он хочет, чтобы количество грядок при этом было максимально. Для каждого из q дней Фермер Джон хотел бы знать сумму по всем возможным способам выбрать k типов, максимального количества грядок, которое он может сделать для этого подмножества типов. Поскольку это число может быть достаточно большим, выведите его по модулю 109 + 7. Выходные данные Для каждого из q дней выведите сумму максимально возможного количества грядок по всем способам выбрать ровно k типов цветов. Ответ выводите по модулю 109 + 7. Примечание В первом примере k = 3. После первого дня у Фермера Джона есть (4, 6, 9, 8) цветов разных типов. Если выбрать (4, 6, 8), то можно разбить их на 2 грядки по 2, 3, 4 цветка соответствующего типа на каждой. Если выбрать (4, 6, 9), (4, 9, 8) или (6, 9, 8), то можно будет сделать только одну грядку. Таким образом, сумма по всем подмножествам размера k = 3 равняется 2 + 1 + 1 + 1 = 5. После второго дня у Фермера Джона (4, 6, 9, 8, 6) цветов. Сумма количества грядок по всем способам равняется 1 + 2 + 2 + 1 + 1 + 2 + 2 + 3 + 1 + 1 = 16. Во втором примере k = 1. Имея x цветов одного единственного типа, Фермер Джон всегда может разбить их на x грядок. Таким образом, ответы 6 + 5 + 4 + 3 + 2 = 20 для первого дня и 6 + 5 + 4 + 3 + 2 + 1 = 21 для второго. | |
![]()
|
|
C. Враждебные пары
Комбинаторика
*1800
сортировки
Вам задана перестановка p длины n. Также вам задано m враждебных пар (ai, bi) (1 ≤ ai, bi ≤ n, ai ≠ bi). Ваша задача посчитать количество различных интервалов (x, y) (1 ≤ x ≤ y ≤ n), которые не содержат никакие враждебные пары. Таким образом, вам не нужно считать интервалы (x, y), содержащие хотя бы одну враждебную пару (позиции и порядок значений из враждебной пары не имеют значения). Рассмотрим пример: p = [1, 3, 2, 4] и пары {(3, 2), (4, 2)} являются враждебными. Интервал (1, 3) не является корректным, поскольку содержит враждебную пару (3, 2). Интервал (1, 4) также не является корректным, поскольку содержит две враждебные пары (3, 2) и (4, 2). Но интервал (1, 2) является корректным, поскольку не содержит враждебных пар. Выходные данные Выведите одно целое число c — количество различных интервалов (x, y), не содержащих враждебных пар. Обратите внимание, что ответ может не поместиться в 32-битном типе данных. Для сохранения числа вы можете использовать, например, тип long long в языке C++ или тип long в языке Java. Примечание В первом примере, следующие интервалы являются корректными: (1, 1), (1, 2), (2, 2), (3, 3) и (4, 4). | |
![]()
|
|
G. Ход простым
Комбинаторика
математика
теория чисел
*3100
У кошечки Сони есть массив, состоящий из n целых положительных чисел. У этого массива есть 2n подпоследовательности. Для каждой подпоследовательности Соня вычисляет минимальное количество действий, которые необходимо совершить, чтобы сделать все элементы равными. Возможны следующие действия: - Выбрать один элемент подпоследовательности и умножить его на простое число;
- Выбрать какой-нибудь элемент подпоследовательности и поделить его на простое число. При этом данный элемент должен обязательно делиться на выбранное простое число.
Чему равна сумма минимального количества необходимых операций по всем 2n подпоследовательностям? Найдите и выведите это значение по модулю 109 + 7. Выходные данные Выведите сумму минимального количества операций, необходимых, чтобы уравнять все элементы подпоследовательности по всем подпоследовательностям данного массива. Значение выводите по модулю 109 + 7. Примечание В первом примере возможны 8 различных подпоследовательностей: (60, 60, 40), (60, 60), (60, 40), (60, 40), (60), (60), (40) и () (пустая подпоследовательность). Все элементы подпоследовательности (60, 60, 40) можно сделать одинаковыми за два действия: сперва разделить 40 на 2 и получить 20, а затем умножить 20 на 3 и получить 60. За меньшее количество действий сделать все элементы равными невозможно. Две подпоследовательности равны (60, 40), и для каждой из них придётся также сделать не меньше 2 операций. В каждой из оставшихся подпоследовательностей все элементы и так уже равны, поэтому на них мы потратим 0 операций. Таким образом, ответ равен 2 + 2 + 2 = 6. | |
![]()
|
|
G. Забористое разнообразие
Комбинаторика
дп
теория чисел
*2300
Давным-давно Василий Иванович соорудил на своей даче хороший забор. Василий Иванович называет забор хорошим, если он представляет собой ряд из n последовательно скреплённых вертикальных досок сантиметровой ширины, высота каждой из которых — целое положительное число сантиметров. Хозяин дачи прекрасно помнит, что высота i-й слева доски равна hi. Сегодня Василий Иванович решил изменить конструкцию сооружённого забора, спилив у него сверху связную часть таким образом, чтобы забор остался хорошим. Спиленная часть должна состоять только из верхних частей досок, причём соседние части должны быть соединены между собой (иметь ненулевую длину соприкосновения до выпиливания из забора). Вам, как любопытному соседу Василия Ивановича, предстоит посчитать количество возможных способов спилить ровно одну часть, как описано выше. Два способа спилить часть называются различными, если для оставшихся заборов существует такое i, что высоты i-х досок различаются. Поскольку забор Василия Ивановича может быть очень высоким и длинным, найдите остаток от деления искомого количества способов на 1 000 000 007 (109 + 7). Выходные данные Выведите остаток при делении r на 1 000 000 007, где r — количество способов спилить ровно одну связную часть так, чтобы часть состояла из верхних частей досок и оставшийся забор был хорошим. Примечание Из забора первого примера невозможно вырезать ровно одну часть таким образом, чтобы получившийся забор остался хорошим. Все возможные варианты получившегося забора из второго примера выглядят следующим образом (серым цветом выделена вырезаемая часть):  | |
![]()
|
|
E. Различные подмножества по всем кортежам
Комбинаторика
математика
*2300
Для последовательности a из n целых чисел от 1 до m, включительно, введём обозначение f(a) — количество различных подпоследовательностей a (включая пустую подпоследовательность). Вам заданы два положительных целых числа n и m. Пусть S это множество всех последовательностей длины n с элементами от 1 до m. Найдите значение суммы f(a) по всем a из S по модулю 109 + 7. Выходные данные Выведите одно целое число c — искомую сумму по модулю 109 + 7. | |
![]()
|
|
C. Кодовое слово
Строки
Комбинаторика
*2500
Знаменитый скульптор Кикассо — ребляндский шпион! Этим заголовком пестрят сегодня берляндские газеты. И теперь опальный скульптор находится в бегах. В этот раз маэстро нашёл убежище у вас, своего давнего друга. Как ни странно, у вас оказался защищённый бункер, который вы и предоставили скульптору. Вы установили для бункера такую систему защиты, что открыть его сможете лишь вы. Для этого необходимо решить задачу, простую для вас, но сложную для кого-либо ещё. Раз в день бункер формирует очередное кодовое слово s. Когда кто-нибудь пытается войти в бункер, на мониторе появляется целое число n. В ответ нужно ввести другое число — остаток от деления на 109 + 7 количества слов длины n, состоящих из строчных английских букв, таких, что они содержат строку s в качестве подпоследовательности. Подпоследовательностью строки a называют такую строку b, которая может быть получена из строки a удалением некоторого набора символов, возможно пустого. В частности, любая строка является своей подпоследовательностью. Например, строка «cfo» — это подпоследовательность строки «codeforces». Вы не успели реализовать алгоритм, который генерирует правильные ответы и это нужно срочно исправить. Займитесь этим. Выходные данные На каждый запрос типа 2 выведите в отдельной строке искомое количество по модулю 109 + 7. Примечание В тестовом примере к первому слову нам подходят слова вида "a?" и "?a", где ? — произвольный символ. Слов этих типов 26 в отдельности, но слово "aa" удовлетворяет обоим шаблонам, поэтому всего слов 51. | |
![]()
|
|
C. Ваня и надпись
Строки
Комбинаторика
реализация
*1500
битмаски
Ваня шёл по улице и увидел надпись «Hide&Seek». Поскольку Ваня — программист, ему сразу пришла идея воспользоваться операцией & (побитовое И) для этих двух слов в 64-ричной системе счисления (0..9A..Za..z-_) и получить новое слово. Теперь Ваня придумал некоторую строку s и задался вопросом, сколько существует различных пар слов длины |s| (длина строки s), побитовое И которых равно данному слову s? Поскольку ответ может быть очень большим, Ваня просит вас вычислить его по модулю 109 + 7. Для перевода букв слова в 64-ричную систему счисления Ваня использует следующее соответствие знаков и чисел: - цифрам от «0» до «9» соответствуют числа от 0 до 9;
- буквам от «A» до «Z» соответствуют числа от 10 до 35;
- буквам от «a» до «z» соответствуют числа от 36 до 61;
- символу «-» соответствует число 62;
- символу «_» соответствует число 63.
Выходные данные Выведите единственное целое число — количество возможных пар слов, побитовое И которых равняется строке s, по модулю 109 + 7. Примечание Для подробного описания функции побитовое И можно посмотреть соответствующую статью в Википедии. В первом примере возможны 3 варианта: - z&_ = 61&63 = 61 = z
- _&z = 63&61 = 61 = z
- z&z = 61&61 = 61 = z
| |
![]()
|
|
A. Разбойничьи часы
Перебор
Комбинаторика
математика
дп
*1700
Разбойники, напавшие на карету Герды, уже давным-давно успешно скрываются от королевских преследователей. Чтобы последним было сложнее догадаться о времени очередного нападения, разбойники используют собственные альтернативные часы. Во-первых, так как королевские воины плохо разбираются в математике, разбойники используют в своих цифровых часах семеричную систему счисления. Во-вторых, они делят сутки на n часов, а час — на m минут. Личные часы каждого разбойника поделены на две части: в первой из них ровно столько разрядов, чтобы показать все возможные значения часа (от 0 до n - 1), а во второй — все возможные значения минут (от 0 до m - 1). В-третьих, если значение часа или минуты умещается в меньшее число разрядов, чем есть в соответствующей части часов, то запись дополняется нулями слева. Обратите внимание, для записи числа 0 требуется один разряд. Маленькой разбойнице интересно, сколько в течение дня существует таких моментов времени (то есть фиксированных значений часов и минут), что все цифры на часах в этот момент различны. Помогите ей посчитать это значение. Выходные данные В первой строке выходного файла должно содержаться единственное число, записанное в десятичной системе счисления — количество пар значений часа и минуты, таких что все отображаемые на часах цифры различны. Примечание Для первого теста все возможные пары будут такими: (0: 1), (0: 2), (1: 0), (1: 2). Для второго теста все возможные пары будут такими: (02: 1), (03: 1), (04: 1), (05: 1), (06: 1). | |
![]()
|
|
A. Разбойничьи часы
Перебор
Комбинаторика
математика
дп
*1700
Разбойники, напавшие на карету Герды, уже давным-давно успешно скрываются от королевских преследователей. Чтобы последним было сложнее догадаться о времени очередного нападения, разбойники используют собственные альтернативные часы. Во-первых, так как королевские воины плохо разбираются в математике, разбойники используют в своих цифровых часах семеричную систему счисления. Во-вторых, они делят сутки на n часов, а час — на m минут. Личные часы каждого разбойника поделены на две части: в первой из них ровно столько разрядов, чтобы показать все возможные значения часа (от 0 до n - 1), а во второй — все возможные значения минут (от 0 до m - 1). В-третьих, если значение часа или минуты умещается в меньшее число разрядов, чем есть в соответствующей части часов, то запись дополняется нулями слева. Обратите внимание, для записи числа 0 требуется один разряд. Маленькой разбойнице интересно, сколько в течение дня существует таких моментов времени (то есть фиксированных значений часов и минут), что все цифры на часах в этот момент различны. Помогите ей посчитать это значение. Выходные данные В первой строке выходного файла должно содержаться единственное число, записанное в десятичной системе счисления — количество пар значений часа и минуты, таких что все отображаемые на часах цифры различны. Примечание Для первого теста все возможные пары будут такими: (0: 1), (0: 2), (1: 0), (1: 2). Для второго теста все возможные пары будут такими: (02: 1), (03: 1), (04: 1), (05: 1), (06: 1). | |
![]()
|
|
C. Майк и шоколадные воры
Бинарный поиск
Комбинаторика
математика
*1700
Плохие новости в деревне Майка — неизвестные воры украли много шоколадок с местного завода! Ужас! Кроме любви к сладкому, воры из окрестностей еще и известные жадины. Поэтому когда один из воров забирает несколько шоколадок для себя, следующий вор забирает ровно в k раз больше шоколадок. Значение k (k > 1) является секретным целым числом, известным только ворам. Также известно, что рюкзак любого вора выдерживает ограниченное количество шоколадок, однако и это целое число n остается в тайне между ворами. Кроме того, Майк знает, что всего в краже шоколадок участвовали четыре вора. Число n известно только ворам, однако по слухам, число способов, которыми воры могли разобрать шоколадки (при фиксированном n, но не фиксированном k) равно m. Два способа украсть шоколадки считаются различными, если найдется вор (а их следует нумеровать в порядке взятия ими шоколадок), что количество шоколадок, взятое им, различается в этих способах. Майк хочет поймать воров, поэтому ему важно знать больше об их сумках, и значение n поможет ему в этом. Помогите Майку найти наименьшее подходящее значение n или сообщите, что слухи ложны и подходящего n не существует. Выходные данные Выведите единственное целое число n — максимальное количество шоколадок, которое может выдержать портфель любого из воров. Если таких n несколько, выведите наименьшее из них. Если таких n не существует и слухи ложны, выведите - 1. Примечание В первом примере из условия наименьшим подходящим n является n = 8, и количества украденных каждым вором шоколадок равны (1, 2, 4, 8). Во втором примере из условия наименьшим подходящим n является n = 54 с количествами: (1, 2, 4, 8), (1, 3, 9, 27), (2, 4, 8, 16), (2, 6, 18, 54), (3, 6, 12, 24), (4, 8, 16, 32), (5, 10, 20, 40), (6, 12, 24, 48). В третьем примере подходящего к ровно десяти способам n не существует. | |
![]()
|
|
E. Майк и геометрическая задача
Структуры данных
Комбинаторика
реализация
геометрия
дп
*2000
Майк готовится к IMO, но плохо знаком с геометрией, поэтому его учитель дал ему занимательную геометрическую задачу. Пусть f([l, r]) = r - l + 1 — число целых точек в отрезке [l, r] (l ≤ r) (считаем, что 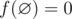 ). Даны два числа n и k и n отрезков [li, ri] на оси Ox, и требуется посчитать ). Даны два числа n и k и n отрезков [li, ri] на оси Ox, и требуется посчитать 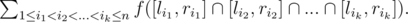 Другими словами, требуется посчитать сумму количеств целых точек в каждом из возможных пересечений любых k отрезков. Так как искомое значение может быть очень большим, выведите его остаток от деления на 1000000007 (109 + 7). Майк затрудняется решить эту задачу и нуждается в вашей помощи. Вы же не откажете ему в этом, не так ли? Выходные данные В единственной строке выведите одно целое число — ответ на задачу Майка по модулю 1000000007 (109 + 7). | |
![]()
|
|
D2. Стена (средняя)
Комбинаторика
*1800
Корова Хайди в шоке: в северной стене появились трещины? Зомби собираются и готовятся к нападению? Этого не должно произойти! Она быстро просмотрела свою методичку по безумным постройкам и нашла подходящую главу: Как построить стену: - Возьмите набор кирпичей.
- Выберите один из возможных дизайнов стены. Вычисление количества различных дизайнов оставлено читателю в качестве упражнения.
- Положите кирпичи друг на друга, чтобы образовать стену соответствующего дизайна.
Выглядит достаточно просто. Однако Хайди всё-таки кодящая корова, а не строящая корова. У неё из головы никак не идёт пункт 2b. Несмотря на серьёзную опасность и толпы зомби на подходе, она всё-таки хочет посчитать количество различных стен, которые она может построить с помощью n кирпичей. Стеной называется набор фрагментов стены, определяемый аналогично предыдущей задаче. Сколько различных стен может быть построено, состоящих из не менее чем 1 и не более чем n кирпичей? Две стены считаются различными, если существует столбец i и ряд j, такие что у одной стены есть кирпич в этом месте, а у другой нет. Помимо n вам также будет дано значение параметра c, определяющего ширину стены (аналогично лёгкой версии задачи). Выведите количество различных стен по модулю 106 + 3. Выходные данные Выведите количество различных стен, которые может построить Хайди, по модулю 106 + 3. | |
![]()
|
|
C. PLEASE
Комбинаторика
математика
реализация
дп
*2000
матрицы
Как известно, работа Барни это «PLEASE», и ему в целом нечем заняться на работе, и поэтому он решил сыграть в «чашки и ключ». В этой игре участвуют три одинаковые чашки, выставленные в ряд слева направо. Изначально ключ к сердцу Барни находится под стоящей посередине чашкой.  Затем, за один ход Барни меняет местами чашку посередине с одной из двух других чашек случайным образом (он выберет каждую с одинаковой вероятностью), так что выбранная чашка становится посередине. Игра длится n ходов, и в каждом из них Барни независимо выбирает чашку для обмена со средней на каждом ходу, а ключ всегда остается под чашкой, под которой был в самом начале. После n-го хода Барни просит девушку указать на чашку, содержащую ключ. Девушка указывает на стоящую посередине чашку, но Барни отвлекся во время игры и не знает, находится ли там ключ или нет. Поэтому Барни просит вас сообщить ему вероятность того, что девушка указала на правильную чашку. Число ходов n может быть очень большим, поэтому Барни не сообщил вам его. Вместо этого он дал вам массив a1, a2, ..., ak, такой, что 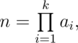 другими словами, n равно произведению чисел данного массива. Из-за проблем с точностью Барни просит вас сообщить ответ в виде несократимой дроби. Другими словами, найдите ответ в виде p / q, причем  , где , где  — наибольший общий делитель. Так как p и q могут быть очень большими, достаточно вывести остаток от деления каждого из них на 109 + 7. — наибольший общий делитель. Так как p и q могут быть очень большими, достаточно вывести остаток от деления каждого из них на 109 + 7. Заметьте, что мы хотим, чтобы наибольший общий делитель p и q был равен 1, а не наибольший общий делитель их остатков от деления на 109 + 7. Выходные данные В единственной строке выведите строку вида x / y, где x — остаток от деления p на 109 + 7, а y — остаток от деления q на 109 + 7. | |
![]()
|
|
D. Направленные дороги
Комбинаторика
математика
поиск в глубину и подобное
*1900
графы
Кодер ZS и Бабуин Крис довольно долго путешествовали по Удайлэнду. Они узнали, что он состоит из n городов, пронумерованных от 1 до n. В Удайлэнде существует ровно n направленных дорог. i-ая из них выходит из города с номером i и ведет в другой город с номером ai (ai ≠ i). Кодер ZS может поменять направление любой из дорог в Удайлэнде, то есть, если дорога вела от города A к городу B до смены направления, она будет вести от города B к городу A после него. Кодер ZS считает дороги в Удайлэнде запутанными, если существует последовательность различных городов A1, A2, ..., Ak (k > 1), таких, что для каждого 1 ≤ i < k существует дорога, ведущая из города Ai в город Ai + 1 и еще одна из города Ak в город A1. Другими словами, дороги запутанные, если некоторые из них образуют направленный цикл из каких-то городов. Теперь Кодеру ZS'у интересно, сколько наборов дорог изначальной конфигурации (всего их 2n) он может выбрать, таких, что после смены направления каждой из дорог в наборе ровно по одному разу, результирующая сеть дорог не будет запутанной. Заметьте, что после смены направления позволяется существовать городу, из которого выходит несколько дорог, или городу, из которого не выходит ни одной дороги, или нескольким дорогам между одной и той же парой городов. Выходные данные Выведите единственное целое число — количество способов поменять направление какого-нибудь набора дорог так, что весь набор дорог станет не запутанным. Так как ответ может быть очень большим, выведите остаток от его деления на 109 + 7. Примечание Рассмотрим первый пример из условия. Существует 3 города и 3 дороги. Города пронумерованы от 1 до 3, а дороги изначально имеют вид 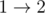 , ,  , , 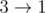 . Пронумеруем дороги от 1 до 3 в соответствующем порядке. . Пронумеруем дороги от 1 до 3 в соответствующем порядке. Наборы дорог, для которых Кодер ZS может сменить направление (чтобы сделать дороги не запутанными), это наборы {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}. Заметьте, что пустой набор дорог не подходит, поскольку, если не менять направление ни одной дороги, то города 1, 2, 3 образуют направленный цикл, так что дороги будут запутанными. Аналогично, смена направления каждой дороги приводит к запутанной конфигурации. Таким образом, всего существует 6 возможных наборов, для которых Кодер ZS может поменять направление. Следующий рисунок изображает всевозможные способы ориентации дорог из первого примера так, что сеть дорог не является запутанной: 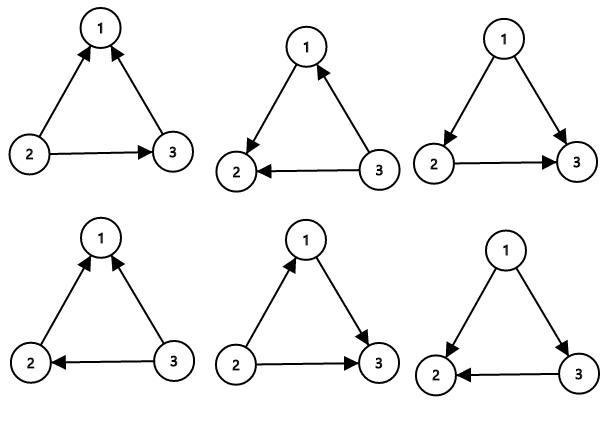
| |
![]()
|
|
D. Мемори и игра
Комбинаторика
математика
дп
*2200
Мемори и ее друг Лекс соревнуются, кто наберёт большее количество баллов в одной популярной игре. Изначально у Мемори a очков, а у Лекса b очков. За один ход и Мемори, и Лекс получают какое-то количество очков в диапазоне [ - k;k] (то есть одно целое число из множества - k, - k + 1, - k + 2, ..., - 2, - 1, 0, 1, 2, ..., k - 1, k) и прибавляют его к своему текущему счёту. Игра состоит ровно из t раундов. Однако, Мемори и Лекс играют довольно плохо, поэтому каждый из них просто получает в каждом из раундов случайное число. Мемори хочет знать количество различных сценариев игры, в которых у неё в конце будет строго больше очков, чем у Лекса. Два сценария игры считаются различными, если существует раунд, в котором хотя бы один из двух игроков получил разное количество очков. Таким образом, всего существует (2k + 1)2t различных сценариев игры. Поскольку ответ может быть очень большим, выведите остаток от его деления на 109 + 7. Выходные данные Выведите количество сценариев игры, интересных Мемори по модулю 1 000 000 007 (109 + 7). Примечание В первом примере Мемори начинает с 1, а Лекс с 2. Если Лекс получит - 2 очка, то Мемори может получить 0, 1 или 2, чтобы победить. Если Лекс получит - 1 очков, то Мемори для победы нужно 1 или 2. Если Лекс получит 0, то Мемори подойдёт только 2. Если же Лекс получит 1 или 2 очка, то Мемори уже не сможет победить. Таким образом, существует 3 + 2 + 1 = 6 возможных сценариев игры, в которых Мемори побеждает. | |
![]()
|
|
E. Дополни перестановки
Комбинаторика
математика
графы
*3400
бпф
Кодеру ZS'у даны две перестановки p и q множества {1, 2, ..., n}, но некоторые из их элементов заменены 0. Расстояние между двумя перестановками p и q определяется как минимальное количество обменов двух элементов, необходимое, чтобы превратить p в q. ZS может менять местами только любые два элемента перестановки p. Кодер ZS хочет найти количество способов заменить нули положительными целыми числами из множества {1, 2, ..., n} так, что p и q будут являться перестановками {1, 2, ..., n}, а расстояние между p и q в точности равно k. Кодер ZS хочет найти ответ для всех 0 ≤ k ≤ n - 1. Поможете ему? Выходные данные Выведите n целых чисел, i-е из них должно соответствовать ответу для k = i - 1. Так как ответ может быть довольно большим, а Кодер ZS любит странные простые числа, выведите ответы по модулю 998244353 = 223·7·17 + 1, который является простым. Примечание В первом примере из условия существует всего один способ заменить нули так, что потребуется 0 обменов для превращения p в q — это p = (1, 2, 3), q = (1, 2, 3). Существует два способа заменить нули так, что требуется 1 обмен для превращения p в q. Один из них — p = (1, 2, 3), q = (3, 2, 1), тогда обмен 1 и 3 в p превращает ее в q. Другой способ — p = (1, 3, 2), q = (1, 2, 3). В этом случае работает обмен 2 и 3. Наконец, существует всего один способ заменить нули так, что потребуется 2 обмена для превращения p в q — p = (1, 3, 2), q = (3, 2, 1). Тогда мы можем превратить p в q вот так:  . . | |
![]()
|
|
A. Организация фестиваля
Комбинаторика
математика
теория чисел
*2900
Прокопатели — известная музыкальная группа, поэтому уже 80 лет их приглашают на фестиваль ENTER, чтобы выступить в качестве неожиданных гостей. В начале своей карьеры они были не так успешны, поэтому зарабатывали на жизнь копанием каналов, откуда и произошло название группы. В любом случае, они очень любят ездить в турне, и их энергии хватает на невероятно долгие поездки. Однако, они терпеть не могут проводить два последовательных дня не давая концерта, поэтому стараются избегать такой ситуации. Турне определяется как последовательность концертов и выходных дней. Требуется посчитать количество способов выбрать k различных турне одинаковой длины между l и r. Например, пусть k = 2, l = 1 и r = 2. Будем обозначать день с концертом как {1}, а выходной как {0}. Возможными турами являются: {0}, {1}, {00}, {01}, {10}, {11}, но тур {00} не подходит, поскольку содержит два выходных дня подряд. Теперь найдём количество способов выбрать k = 2 тура одинаковой длины в диапазоне длин [1;2]. Перечислим их: {0,1}; {01,10}; {01,11}; {10,11}. Поскольку расписание Прокопателей уже достаточно плотно занято, то они просят вас посчитать ответ по модулю 1 000 000 007 (109 + 7). Выходные данные Выведите одно целое число: остаток от деления количества способов выбрать k различных туров одинаковой длины на 1 000 000 007. | |
![]()
|
|
E. Исследовательский зонд
Комбинаторика
дп
*2900
К сожалению, в этой задаче не удалось написать достаточно короткую формальную постановку, поэтому пришлось придумать легенду. Исследовательский зонд, наконец, достиг поверхности Марса и готов выполнить свою миссию. К сожалению, из-за сбоя навигационной системы, зонд приземлился не в той точке, в которой планировалось. Участок, на котором высадился зонд, можно представить в виде клетчатого поля, состоящего из n строк и m столбцов. Будем обозначать через (r, c) клетку, расположенную в строке r и столбце c. Из каждой клетки зонд может продолжить движение только в клетки по соседству с текущей по стороне. Зонд высадился в клетке с координатами (1, 1) и должен отправиться в клетку с координатами (n, m). Для этого зонд выберет произвольный кратчайший маршрут, соединяющий начальную и конечную клетки. Каждый возможный маршрут зонд выберет с равной вероятностью. В грузовом отсеке зонда находится батарея, которая понадобится зонду для проведения исследований в конечной точке его маршрута. Изначально заряд батареи равен s единицам энергии. В некоторых клетках данного поля находятся аномалии. Каждый раз, когда зонд оказывается в клетке с аномалией, батарея теряет половину своего заряда, округлённую вниз, то есть если до попадания в аномалию заряд был равен x, то после попадания он будет равен 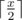 . . Пока зонд перебирает все возможные маршруты своего путешествия, посчитайте математическое ожидание заряда батареи в момент, когда робот достигнет клетки (n, m). Если в клетках (1, 1) и (n, m) также есть аномалии, то они тоже изменяют заряд батареи. Выходные данные Ответ всегда можно представить в виде несократимой дроби  . Выведите единственное число, равное P·Q - 1 по модулю 109 + 7. . Выведите единственное число, равное P·Q - 1 по модулю 109 + 7. Примечание В первом примере зонд может выбрать один из шести маршрутов: -
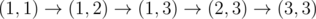 , после прохождения клетки (2, 3) заряд становится равным 6. , после прохождения клетки (2, 3) заряд становится равным 6. -
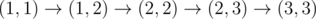 , после прохождения клетки (2, 3) заряд становится равным 6. , после прохождения клетки (2, 3) заряд становится равным 6. -
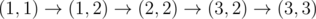 , заряд батареи остаётся равным 11. , заряд батареи остаётся равным 11. -
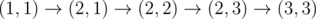 , после прохождения клеток (2, 1) и (2, 3) заряд становится равным сначала 6, а затем 3. , после прохождения клеток (2, 1) и (2, 3) заряд становится равным сначала 6, а затем 3. -
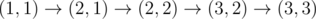 , после прохождения клетки (2, 1) заряд становится равным 6. , после прохождения клетки (2, 1) заряд становится равным 6. -
 , после прохождения клетки (2, 1) заряд становится равным 6. , после прохождения клетки (2, 1) заряд становится равным 6. Математическое ожидание заряда батареи в конце пути в данном случае считается по формуле: 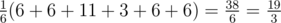 . . Таким образом, P = 19, а Q = 3. 3 - 1 по модулю 109 + 7 равно 333333336. 19·333333336 = 333333342 (mod 109 + 7) | |
![]()
|
|
F. Равномерно ветвистые деревья
Деревья
Комбинаторика
дп
*2700
Деревом называется связный граф без циклов. Два дерева, состоящих из n вершин, называются изоморфными, если существует перестановка p: {1, ..., n} → {1, ..., n} такая, что ребро (u, v) присутствует в первом дереве тогда и только тогда, когда ребро (pu, pv) присутствует во втором. Вершина дерева называется внутренней, если её степень больше либо равна двум. Посчитайте количество различных неизоморфных деревьев, состоящих из n вершин, таких что степень каждой внутренней вершины в точности равна d. Ответ выведите по заданному простому модулю mod. Выходные данные Выведите одно число — количество деревьев, удовлетворяющих условию задачи, взятое по модулю mod. | |
![]()
|
|
C. Теннисный Чемпионат
Конструктив
Комбинаторика
математика
*1600
жадные алгоритмы
Бразильский город Рио-де-Жанейро принимает крупный теннисный турнир, и Остап Бендер не намерен пропускать это событие. В турнире примут участие n теннисистов, причём с первого же матча будет идти игра на выбывание — проигравший сразу покидает турнир. Организаторы ещё не составили сетку чемпионата, но известно, что два игрока могут играть друг с другом, если и только если количество игр, уже проведённых одним из них, отличается от количества игр, проведённых другим, не более чем на одну игру (в любую сторону). Разумеется, оба игрока должны были выиграть все свои встречи, чтобы всё ещё участвовать в турнире. Пока турнир не начался и зрители ищут, чем занять себя в ожидании, Остап решил вычислить, в каком максимальном количестве партий может принять участие победитель турнира. Скорее всего, без вашей помощи ему не справиться. Выходные данные Выведите одно целое число — максимальное количество партий, в которых может принять участие победитель турнира. Примечание Во всех примерах будем считать, что турнир выигрывает участник с номером 1. В первом примере будет всего одна игра, поэтому ответ очевидно 1. Во втором примере первый игрок может последовательно обыграть игрока 2, а затем игрока 3. В третьем примере первый игрок не может последовательно обыграть всех остальных, так как если он сыграет с игроками 2 и 3, то у него будет уже две партии, а игрока номер 4 — ноль партий. Тогда они не смогут сыграть и турнир не завершится. Таким образом, ответ 2 и он достигается на сетке турнира, в которой сначала играют пары (1, 2) и (3, 4), а затем победители этих пар играют друг с другом. | |
![]()
|
|
F. Игорь и интересные числа
Перебор
Комбинаторика
математика
дп
*2500
Игорь очень любит 16-ричную систему счисления и считает целое положительное число в 16-ричной системе счисления интересным, если каждая цифра и буква в нём встречается не более t раз. Например, если t = 3, то числа 13a13322, aaa, abcdef0123456789 — интересные, а числа aaaa, abababab и 1000000 — нет. Перед вами стоит задача найти k-е по счёту интересное для Игоря число в 16-ричной системе счисления. Число не должно содержать лидирующих нулей. Выходные данные Выведите единственное целое число в 16-ричной системе счисления, которое является k-м по счёту интересным для Игоря числом в 16-ричной системе счисления. Примечание Первые 20 чисел, которые является интересными, если t = 1: 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, f, 10, 12, 13, 14, 15. Поэтому ответ на первый пример равен 12. | |
![]()
|
|
G. Новый год и пути в двоичном дереве
Перебор
Комбинаторика
дп
битмаски
*3200
Новогоднее дерево является бесконечным полным двоичным деревом, корнем которого является вершина с номером 1. У каждой вершины v есть ровно два сына: вершина с номером (2·v) и вершина с номером (2·v + 1). 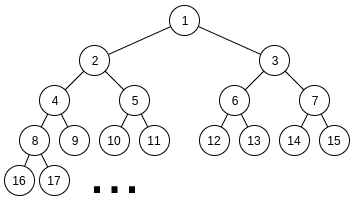 Полярные медведи очень любят украшать новогоднее дерево и Лимак конечно же не исключение. Поскольку он ещё только маленький медвежонок, ему разрешили украсить только некоторый простой путь между какой-то парой вершин. С другой стороны, ему разрешили самому выбрать какой именно путь украсить! Теперь он хочет знать количество неупорядоченных пар индексов (u, v) (u ≤ v), таких что сумма индексов на пути между u и v (включая крайние вершины) равняется s. Сможете ли вы помочь ему вычислить это количество? Выходные данные Выведите одно целое число, равное количеству неупорядоченных пар индексов вершин, определяющих простой путь с суммой индексов равной s. Примечание В примере из условия существует 4 пути с суммой индексов равной 10:  | |
![]()
|
|
G. Польшар и Много других шаров
Комбинаторика
математика
дп
теория чисел
разделяй и властвуй
*3200
бпф
Польшар стоит в ряд со многими другими шарами. Точнее, в ряд стоят ровно n шаров. Шары гордятся за свою родную землю — и хотят доказать, что она стронг. Шары решили начать с выборов ровно m групп шаров, каждая должна состоять либо из одного шара, либо из двух рядом стоящих. Каждый шар может состоять не более чем в одной группе. Шары хотят впечатлить своих врагов. Они просят вас посчитать количество таких разбиений на группы для каждого m, где 1 ≤ m ≤ k. Выведите отстаток от деления каждого из этих чисел на 998244353, враги все равно будут впечатлены. Выходные данные Выведите последовательность из k целых чисел. Число i должно быть равно искомому числу способов выбрать ровно i групп в соответствии с правилами Польшара. Примечание В первом примере можно разделить шары на группы следующим образом: {1}, {2}, {3}, {12}, {23}. {12}{3}, {1}{23}, {1}{2}, {1}{3}, {2}{3}. {1}{2}{3}. Поэтому нужно вывести 5 5 1. | |
![]()
|
|
D. Война бактерий
Перебор
Комбинаторика
дп
*2400
строковые суфф. структуры
Юля проводит эксперимент в своей лаборатории. Она поместила несколько колоний светящихся бактерий в горизонтальную пробирку. Бактерии разного типа можно отличить по цвету. Юля обозначает типы бактерий маленькими латинскими буквами «a», ..., «z». Пробирка разделена на n областей, расположенных в ряд друг за другом. В каждый момент времени любая область занята ровно одной колонией бактерий определенного типа. Таким образом, популяцию пробирки в любой момент можно описать строкой из n латинских букв. Иногда какая-то из колоний может решить захватить другую колонию в одной из соседних областей. В этом случае атакованная колония немедленно уничтожается и заменяется колонией того же типа, что и атакующая колония, при этом атакующая колония сохраняет свой тип. Колония может атаковать только соседей внутри пробирки. Одновременно может происходить не более одного нападения. В качестве примера рассмотрим пробирку с популяцией «babb». Для следующей атаки существует шесть вариантов: - первая колония атакует вторую (1 → 2), в результате популяция будет выглядеть как «bbbb»;
- 2 → 1, результат «aabb»;
- 2 → 3, результат «baab»;
- 3 → 2, результат «bbbb» (в данном случае результат такой же, как и в первом варианте);
- 3 → 4 или 4 → 3, популяция не меняется.
Предсказать последовательность нападений довольно трудно. Юля интересуется, сколько способов расположения бактерий в пробирке может получится после некоторой последовательности нападений (при этом возможно, что нападений не будет совсем). Поскольку ответ может быть большим, найдите его по модулю 109 + 7. Выходные данные Выведите одно число — ответ на задачу по модулю 109 + 7. Примечание В первом примере популяция не может измениться, поскольку все колонии имеют один и тот же тип. Во втором примере возможны три конфигурации: «ab» (нападений не было), «aa» (первая колония захватила вторую) и «bb» (вторая колония захватила первую). Для получения ответа на третий пример, помните, что могло произойти больше одного нападения. | |
![]()
|
|
E. Байтландские монеты
Комбинаторика
математика
дп
*3200
В Байтландии в ходу монеты n разных видов. Для удобства расчётов, достоинство монеты вида k обязательно делит достоинство монеты k + 1, а достоинство монеты вида 1 равно 1 тугрик. Отношение достоинств монет вида k + 1 и k равно ak. Также известно, что для любого x есть не более 20 видов монет, имеющих достоинство x. У Байтазара с собой есть ровно bk монет вида k, и сейчас ему нужно заплатить ровно m тугриков. Также известно, что Байтазар не носит с собой более 3·105 монет. Байтазар хочет узнать, сколько у него есть способов заплатить m тугриков. Способы считаются различными, если для некоторого k в способах различается количество монет вида k. Как и всех в Байтландии, Байтазара количество способов интересует исключительно по модулю 109 + 7. Выходные данные В единственной строке выведите одно число — количество способов заплатить ровно m тугриков по модулю 109 + 7. Примечание В первом примере у Байтазара есть 4 монеты достоинства 1, и нужно заплатить 2 тугрика. Способ единственен. Во втором примере у Байтазара есть по 4 монеты двух различных видов достоинства 1, и нужно заплатить 2 тугрика. Теперь способов 3: заплатить одну монету первого вида, одну — второго, заплатить две монеты первого вида, или заплатить две монеты второго вида. В третьем примере достоинства монет равны 1, 3, 9. | |
![]()
|
|
E. Баш играет с функциями
Перебор
Комбинаторика
дп
теория чисел
*2500
Баш решил сделать перерыв в своем пути к становлению величайшим мастером покемонов, и поиграть с функциями. Баш определил функцию f0(n), которая равна числу способов разложить число n на два множителя p и q такие, что gcd(p, q) = 1. Другими словами, f0(n) — число упорядоченных пар натуральных чисел (p, q) таких, что p·q = n и gcd(p, q) = 1. Но Баш почувствовал, что эту функцию слишком просто посчитать. Поэтому он определил набор функций, где fr + 1 определена как: 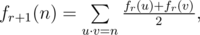 где (u, v) — упорядоченная пара натуральных чисел, при этом они не обязательно взаимно простые. Теперь Баш хочет узнать некоторые значения fr(n) для различных r и n. Так как эти значения могут быть большими, он хочет узнать остаток от деления этих значений на 109 + 7. Помогите ему! Выходные данные Выведите q чисел. Для каждой данной пары r и n выведите остаток от деления fr(n) на 109 + 7 на отдельной строке. | |
![]()
|
|
F. Вложение дерева
Деревья
Комбинаторика
*2800
графы
Даны два дерева (связных неориентированных графа без циклов) S и T. Требуется посчитать количество поддеревьев (связных подграфов) дерева S, изоморфных дереву T. Так как это число может быть достаточно большим, выведите его по модулю 109 + 7. Два поддерева дерева S считаются различными, если хотя бы одна вершина S входит ровно в одно из этих поддеревьев. Дерево G называется изоморфным дереву H, если существует биекция f из множества вершин дерева G в множество вершин дерева H, обладающая следующим свойством: если в дереве G есть ребро между вершинами A и B, то в дереве H должно быть ребро между вершинами f(A) и f(B), и наоборот — если в дереве H есть ребро между вершинами A и B, то в дереве G должно быть ребро между вершинами f - 1(A) и f - 1(B). Выходные данные На единственной строке выведите одно целое число — ответ на задачу по модулю 109 + 7. | |
![]()
|
|
F. Бочки и коробки
Перебор
Теория вероятностей
Комбинаторика
математика
теория чисел
*2300
Тарли имеет два различных типа предметов, коробки еды и бочки вина. Есть f коробок с едой и w бочек вина. Тарли хранит их в разных стеках, и каждый стек может содержать только либо коробки еды, либо бочки вина, но не оба типа предметов сразу. Стеки расположены в ряд так, что нет двух стеков еды рядом, и нет двух стеков вина рядом. Высота стека определена, как количество предметов в стеке. Два стека различны, если их высоты различны или один стек содержит еду, а другой вино. Джону Сноу не нравится когда, какой-нибудь стек с вином имеет высоту меньше либо равную h. Какова вероятность, что Джону Сноу понравится расстановка в стеки, если все расстановки равновероятны? Две расстановки стеков считаются разными, если существует такое i, что i-й стек одной расстановки не равен i-у стеку другой расстановки. Выходные данные Выведите вероятность того, что Джон Сноу понравится расстановка. Вероятность этого имеет форму  , вам необходимо вывести единственное целое число равное p·q - 1 mod (109 + 7). , вам необходимо вывести единственное целое число равное p·q - 1 mod (109 + 7). Примечание В первом тестовом примере f = 1, w = 1 и h = 1, здесь две возможных расстановки, и ни одна из них не нравится Джону Сноу. Во втором тестовом примере f = 1, w = 2 и h = 1, здесь три возможных расстановки. Джону нравятся расстановки (1) и (3). Поэтому вероятность равна  . . 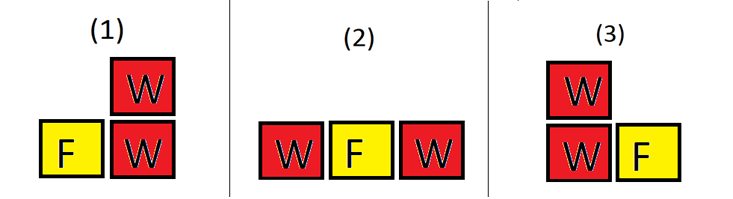 | |
![]()
|
|
F. Генерация тестов
Комбинаторика
математика
дп
теория чисел
разделяй и властвуй
*3400
бпф
Генерация тестов — непростое дело! Часто генерации случайных больших тестов недостаточно, чтобы обеспечить полноценную проверку решений на правильность. Например, рассмотрим задачу с одного из прошедших раундов Codeforces. Формат ее входных данных выглядит примерно так: В первой строке записано целое число n (1 ≤ n ≤ maxn) — количество элементов в множестве. Во второй строке в возрастающем порядке записано n различных целых чисел a1, a2, ..., an (1 ≤ ai ≤ maxa) — элементы множества. Если не обращать внимания на решение задачи, кажется, что сгенерировать хороший тест очень просто. Возьмем n = maxn, возьмем случайные различные ai от 1 до maxa, отсортируем... Далее вы поймете, что это не совсем так. Решение задачи выглядит следующим образом. Пусть g — наибольший общий делитель a1, a2, ..., an. Пусть x = an / g - n. Тогда правильное решение выводит «Alice», если x нечетно, и «Bob», если x четно. Рассмотрим два неверных решения задачи, отличающихся от правильного только формулой вычисления величины x. Первое вычисляет x по формуле x = an / g (без вычитания n). Второе вычисляет x по формуле x = an - n (без деления на g). Будем считать тест интересным, если на нем оба неверных решения выдают ответ, отличающийся от правильного. По данным значениям maxn, maxa и q найдите количество удовлетворяющих ограничениям интересных тестов к задаче и выведите его по модулю q. Выходные данные Выведите единственное число — количество удовлетворяющих ограничениям тестов, на которых оба приведенных неверных решения выдают ответ, отличающийся от правильного, по модулю q. Примечание В первом примере интересные тесты выглядят следующим образом:
1 1 1 3
2 4 6 2 4 6
| |
![]()
|
|
G. Шерлок и зашифрованные данные
Комбинаторика
дп
битмаски
*2900
Шерлок нашел зашифрованые данные, которые, как он считает, могут помочь поймать Мориарти. Зашифрованные данные состоят из двух целых чисел l и r. Шерлок заметил, что эти числа записаны в шестнадцатеричной системе счисления. Шерлок берет каждое целое число от l до r, и выполняет над ним следующие операции: - Выписывает все различные цифры, которые присутствуют в этом числе в шестнадцатеричной записи. Например, для 101416 он выпишет 1, 0, 4.
- Затем он складывает соответствующие степени двойки для каждой выписанной цифры. В примере выше sum = 21 + 20 + 24 = 1910.
- Затем Шерлок изменяет исходное число, выполняя операцию побитового xor над исходным числом и полученной суммой. Например,
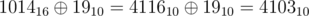 . Заметьте, что xor выполняется в двоичной системе счисления. . Заметьте, что xor выполняется в двоичной системе счисления.
Другой пример: для числа 1e сумма равна sum = 21 + 214. Буквами a, b, c, d, e, f обозначаются шестнадцатеричные цифры 10, 11, 12, 13, 14, 15, соответственно. Шерлок хочет найти количество чисел в диапазоне от l до r (включительно), которые уменьшатся после выполнения описанных четырех шагов. Он хочет, чтобы вы посчитали для него ответ для q различных вариантов l и r. Выходные данные Выведите q строк, строка i должна содержать ответ на i-й вопрос Шерлока (в десятеричной системе счисления). Примечание Во втором тесте из примера: 1416 = 2010 sum = 21 + 24 = 18 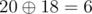
Это число уменьшается. Можно проверить, что это единственное число между 1 и 1e, которое уменьшается после выполнения операций. | |
![]()
|
|
D. Антон и школа - 2
Комбинаторика
математика
дп
теория чисел
*2300
Как вы уже, наверное, знаете, Антон учится в школе. Один из школьных предметов, который изучает Антон — скобкология. На уроках скобкологии школьники обычно изучают всякие последовательности, состоящие только из круглых скобок (символов «(» и «)» (без кавычек)). На прошлом уроке Антон изучал правильные простые скобочные последовательности (ППСП). Скобочная последовательность s длины n является ППСП, если соблюдаются следующие условия: - Она не является пустой (то есть n ≠ 0).
- Длина последовательности четна.
- Первые
 символов последовательности равны «(». символов последовательности равны «(». - Последние
 символов последовательности равны «)». символов последовательности равны «)». Например, последовательность «((()))» является ППСП, а вот последовательности «((())» и «(()())» — нет. На дом учитель Антона, Елена Ивановна, задала Антону такую задачу. Дана некоторая скобочная последовательность s. Необходимо найти количество ее различных подпоследовательностей таких, что они являются ППСП. Напомним, что подпоследовательностью строки s называется такая строка, которая была получена вычеркиванием из s некоторых символов. Две подпоследовательности считаются различными, если множества позиций вычеркнутых символов различаются. Так как ответ может быть очень большим, а учителю Антона не нравятся большие числа, то она просит Антона найти ответ по модулю 109 + 7. Антон долго думал над этой задачей, однако так и не придумал, как ее решить. Помогите Антону решить эту задачу и напишите программу, которая находит ответ на нее! Выходные данные Выведите одно целое число — ответ на задачу по модулю 109 + 7. Примечание В первом примере возможны следующие подпоследовательности: - Если вычеркнуть символы на позициях 1 и 5 (нумерация начинается с единицы), то получим подпоследовательность «(())».
- Если вычеркнуть символы на позициях 1, 2, 3 и 4, то получим подпоследовательность «()».
- Если вычеркнуть символы на позициях 1, 2, 4 и 5, то получим подпоследовательность «()».
- Если вычеркнуть символы на позициях 1, 2, 5 и 6, то получим подпоследовательность «()».
- Если вычеркнуть символы на позициях 1, 3, 4 и 5, то получим подпоследовательность «()».
- Если вычеркнуть символы на позициях 1, 3, 5 и 6, то получим подпоследовательность «()».
Остальные подпоследовательности не являются ППСП. Итого получили 6 различных подпоследовательностей, которые являются ППСП, поэтому ответ — 6. | |
![]()
|
|
B. Странное путешествие
Конструктив
Комбинаторика
*2100
поиск в глубину и подобное
графы
снм
Маленький мальчик Игорь решил стать путешественником. Сначала он решил обойти все города в своей родной стране Ужляндии. Как известно, в Ужляндии n городов, соединенных m двусторонними дорогами. Также известно, что между любыми двумя городами существует не больше одной дороги, но могут существовать дороги которые начинаются и заканчиваются в одном городе. Игорь решил спланировать свое путешествие заранее. Он называет хорошим путь, который посещает m - 2 дороги дважды, а остальные 2 дороги — по одному разу. Хороший путь начинается и заканчивается в любом городе. Не обязательно заканчивать путь в том же городе, в котором он начался. Теперь Игорю стало интересно, сколько же путей его устраивают? Он считает два хороших пути различными, если различаются множества дорог, по которым он пройдет один раз. Помогите Игорю — посчитайте количество различных хороших путей. Выходные данные Выведите одно целое число — количество различных хороших путей. Примечание В первом тестовом примере хорошими являются пути: - 2 → 1 → 3 → 1 → 4 → 1 → 5,
- 2 → 1 → 3 → 1 → 5 → 1 → 4,
- 2 → 1 → 4 → 1 → 5 → 1 → 3,
- 3 → 1 → 2 → 1 → 4 → 1 → 5,
- 3 → 1 → 2 → 1 → 5 → 1 → 4,
- 4 → 1 → 2 → 1 → 3 → 1 → 5.
Кроме того, существуют хорошие пути, которые совпадают с каким-то из перечисленных выше, потому что совпадают множества дорог, по которым Игорь пройдет один раз: - 2 → 1 → 4 → 1 → 3 → 1 → 5,
- 2 → 1 → 5 → 1 → 3 → 1 → 4,
- 2 → 1 → 5 → 1 → 4 → 1 → 3,
- 3 → 1 → 4 → 1 → 2 → 1 → 5,
- 3 → 1 → 5 → 1 → 2 → 1 → 4,
- 4 → 1 → 3 → 1 → 2 → 1 → 5,
- и все эти пути в обратную сторону.
Таким образом, ответ равен 6. Во втором примере Игорь не может пройти по всем дорогам. В третьем примере он пройдет по одному разу по каждой из дорог. | |
![]()
|
|
G. Заменить все
Комбинаторика
математика
дп
*3400
Аналитик Игорь недавно узнал о интересной функции в его текстовом редакторе, которая называется «Заменить все». Игорь заскучал на работе и придумал следующую задачу: Для двух заданных строк x и y, состоящих только из латинских букв «A» и «B», пара строк (s, t) называется хорошей, если: - s и t состоят из только из символов «0» и «1».
- 1 ≤ |s|, |t| ≤ n, где запись |z| обозначает длину строки z, а n — фиксированное натуральное число.
- Если заменить все буквы «A» в строках x и y на строку s, а все буквы «B» в строках x и y — на строку t, то две получившиеся строки из x и y будут равны.
Например, если x = AAB, y = BB, а n = 4, то (01, 0101) — одна из хороших пар строк, потому что обе получившиеся после замены строки будут равны «01010101». Назовем гибкостью пары строк x и y количество хороших пар строк (s, t). Пары считаются упорядоченными, то есть, например, пара (0, 1) и пара (1, 0) — различные. Вам даны две строки c и d. Они состоят только из латинских букв «A», «B» и символов «?». Найдите сумму гибкостей всех таких пар строк (c', d'), что c' и d' могут быть получены из c и d соответсвенно заменой знаков вопроса на буквы «A» и «B». Ответ нужно вывести по модулю 109 + 7. Выходные данные Выведите одно число: ответ на задачу по модулю 109 + 7. Примечание В первом примере возможно получить четыре различные пары (c', d'). Если (c', d') = (AA, A), то гибкость равна 0. Если (c', d') = (AB, A), то гибкость равна 0. Если (c', d') = (AA, B), то гибкость равна 2, так как пары строк (1, 11), (0, 00) — единственные хорошие пары. Если (c', d') = (AB, B), то гибкость равна 0. Таким образом, сумма гибкостей равна 2. Во втором примере существует 21 + 22 + ... + 210 = 2046 различных бинарных строк длины не более 10, а множество пар хороших строк в точности совпадает со множеством пар строк (s, s), где s — бинарная строка, длина которой не превосходит 10. | |
![]()
|
|
F. Взаимно простые подпоследовательности
Комбинаторика
теория чисел
*2000
битмаски
Назовём непустую последовательность натуральных чисел a1, a2... ak взаимно простой, если наибольший общий делитель всех элементов последовательности равен 1. Дан массив a, состоящий из n натуральных чисел. Найдите количество его взаимно простых подпоследовательностей. Так как ответ может быть очень большим, выведите его по модулю 109 + 7. Обратите внимание: две подпоследовательности считаются различными, если различны выбранные индексы. К примеру, в массиве [1, 1] 3 различных подпоследовательности: [1], [1] и [1, 1]. Выходные данные Выведите единственное число — количество взаимно простых подпоследовательностей a по модулю 109 + 7. Примечание В первом примере взаимно простыми являются следующие подпоследовательности: - 1
- 1, 2
- 1, 3
- 1, 2, 3
- 2, 3
Во втором примере все подпоследовательности являются взаимно простыми. | |
![]()
|
|
B. Минимальное число шагов
Комбинаторика
математика
реализация
*1400
жадные алгоритмы
Дана строка из букв «a» и «b». Мы хотим произвести над ней некоторые операции. На каждом шагу мы выбираем одну из подстрок «ab» в данной строке и заменяем ее на строку «bba». Если в строке нет подстрок «ab», то мы останавливаемся. Выведите минимальное число шагов, которое требуется нам сделать перед тем, как мы остановимся, по модулю 109 + 7. Строка «ab» встречается как подстрока, если где-то есть буква «b» сразу после буквы «a». Выходные данные Выведите минимальное число шагов по модулю 109 + 7. Примечание Первый пример: «ab» → «bba». Второй пример: «aab» → «abba» → «bbaba» → «bbbbaa». | |
![]()
|
|
F. Фальшивые слитки
Комбинаторика
дп
теория чисел
поиск в глубину и подобное
графы
*3400
В Исарте люди живут вечно. Среди них есть n банд злоумышленников. В i-й банде состоят si человек, пронумерованных от 0 до si - 1. Некоторые из них однажды приняли участие в большом ограблении шахты и украли каждый по одному золотому слитку (эти люди заданы во входных данных). Это произошло 10100 лет назад и с тех пор все банды уехали далеко от городов. Все эти годы бандиты копировали некоторые золотые слитки в соответствии с определенным планом, чтобы не быть пойманными. Они построили ориентированный граф-турнир (то есть граф, в котором между каждой парой вершин есть одно направленное ребро), вершины в котором — банды (граф задан во входных данных). В этом графе ребро из вершины u в вершину v означало, что в i-й час человек номер 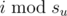 из банды u может послать фальшивый слиток человеку номер из банды u может послать фальшивый слиток человеку номер  из банды v. Он посылает слиток, только если у него есть какой-то слиток (настоящий или фальшивый), а у получателя нет слитков. Таким образом, в каждый момент времени каждый бандит имел один или ноль слитков. Некоторые из бандитов имели настоящие слитки, некоторые — фальшивые. из банды v. Он посылает слиток, только если у него есть какой-то слиток (настоящий или фальшивый), а у получателя нет слитков. Таким образом, в каждый момент времени каждый бандит имел один или ноль слитков. Некоторые из бандитов имели настоящие слитки, некоторые — фальшивые. В начале этого года полиции удалось найти банды, но, как всегда, поймать их она пока не может. Полиция решила открыть ювелирный магазин, чтобы бандиты попытались продать слитки. Теперь каждый бандит, у которого есть слиток (подлинный или фальшивый), попробует его продать. Если слиток подлинный, то он его без проблем продаст, а если фальшивый, то может случиться одна из двух ситуаций: - Бандит успешно продаст слиток.
- Бандит будет арестован полицией.
Сила банды равна числу бандитов, которые успешно продали свой слиток. После того, как все продажи завершены, полиция арестует b банд из самых сильных. Банда с силой p состоит в самых сильных бандах, если и только если не более чем a - 1 банда имеет силу строго больше p. Рассмотрим всевозможные результаты продажи фальшивых слитков и всевозможные способы выбрать b банд из самых сильных банд. Подсчитайте, сколько различных множеств могут образовать эти b банд по модулю 109 + 7. Два множества X и Y считаются различными, если некоторая банда есть в X, но ее нет в Y. Выходные данные Выведите одно число: количество различных множеств из b банд, которые полиция может арестовать по модулю 109 + 7. | |
![]()
|
|
C. Найти машину
Комбинаторика
дп
*2600
разделяй и властвуй
После прекрасного вечера в ресторане пришло время Нуре и Лехе ехать по домам. Хакер, как истинный джентльмен, предложил подвезти девушку к её дому. Нура, конечно же, с удовольствием согласилась. Но вот незадача: Леха никак не может найти свою машину на огромной стоянке близ ресторана. За помощью он решил обратиться к сторожу. Формально стоянку можно представить как матрицу 109 × 109. Во всех клетках матрицы стоят машины, в каждой клетке - ровно одна машина. У всех машин есть номер, выраженный целым положительным числом. Пронумеруем столбцы и строки матрицы от 1 до 109 слева направо и сверху вниз соответственно. По стечению странных обстоятельств оказалось, что для каждой клетки (x, y) матрицы номер машины, стоящей в этой клетке, равен минимальному числу, которое еще не встречалось среди номеров машин, стоящих на клетках (i, y) и (x, j), 1 ≤ i < x, 1 ≤ j < y.  Левый верхний фрагмент 5 × 5 парковки Левый верхний фрагмент 5 × 5 парковки Леха хочет задать сторожу q запросов, которые помогут хакеру найти свою машину. В каждом запросе Леха дает сторожу пять целых чисел x1, y1, x2, y2, k. После этого сторож должен рассмотреть все клетки (x, y) матрицы, такие что x1 ≤ x ≤ x2 и y1 ≤ y ≤ y2, и если номер машины, стоящей в клетке (x, y), не превышает k, то прибавить этот номер к ответу на запрос. Для каждого запроса Леха просит сказать ему получившуюся сумму. Из-за того, что сумма может получиться достаточно большой, он просит вычислить её по модулю 109 + 7. Однако сторожу запросы показались невыполнимыми. Помогите бедняге ответить на все запросы Лехи. Выходные данные Выведите q строк — в первой строке ответ на первый запрос, во второй — на второй и так далее. Примечание Разберем подробнее все запросы (в каждом случае запрашиваемая подматрица выделена синим). В первом запросе (k = 1) Леха спрашивает лишь про верхнюю левую клетку парковки. В ней находится автомобиль с номером 1 и, следовательно, ответ на этот запрос — 1. 
Во втором запросе (k = 5) подходящими номерами являются 4, 1, 2, 3, 2, 1, ответом на запрос является 4 + 1 + 2 + 3 + 2 + 1 = 13. 
Во третьем запросе (k = 10000) Леха спрашивает про левый верхний фрагмент 5 × 5, при том, что k достаточно велико, поэтому все номера из подматрицы удовлетворяют запросу Лехи, искомая сумма равна 93. 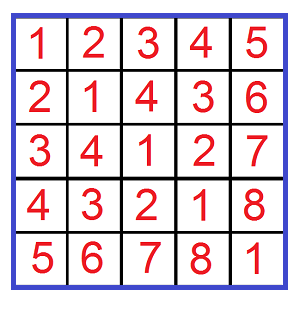
В четвертом запросе (k = 2) ни один из номеров автомобилей не удовлетворяет запросу Лехи, поэтому ответом на него является 0. 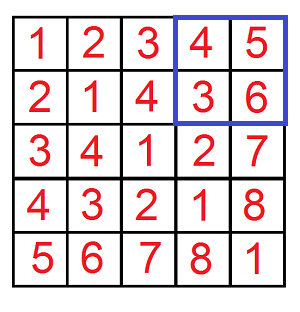
| |
![]()
|
|
E. Неизбежный объезд
Комбинаторика
дп
*2600
графы
кратчайшие пути
Те, кто не хотят возвращаться домой из дальнего путешествия, будут поражены болезнью улитки и потеряются. Майои, переносчик болезни, не хочет, чтобы такое случалось, но не может ничем помочь до того, как найдется лекарство. Сейчас она лишь хочет узнать, насколько сложно придется потерявшемуся. В регионе находятся n городов, пронумерованных от 1 до n, город номер 1 является столицей. Сеть дорог образована двусторонними дорогами равной длины, каждая из которых соединяет два города. Никакие две дороги не соединяют одинаковые пары городов, и никакая дорога не соединяет город сам с собой. Потерявшиеся не могут узнать, как устроена сеть, но жители могут предоставить следующую информацию: - Из любого города существует ровно один кратчайший (по числу дорог) путь до столицы;
- Пусть расстояние от города i до столицы равно li. Тогда li ≥ li - 1 выполняется для всех 2 ≤ i ≤ n;
- К городу i подходит ровно di дорог, и это число равно либо 2, либо 3.
Подсчитайте, сколько различных сетей дорог существует с заданными ограничениями и выведите ответ по модулю 109 + 7. Две сети считаются различными, если есть пара (u, v) (1 ≤ u, v ≤ n) такая, что в одной сети есть дорога между городами u и v, а в другой такой дороги нет. Выходные данные Выведите одно число — число различных графов по модулю 109 + 7. Примечание В первом примере следующая сеть — единственная, удовлетворяющая ограничениям. Все расстояния из столицы до городов 2, 3, 4 равны 1. 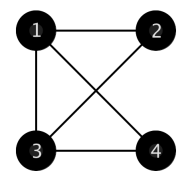 Во втором примере следующие две сети удовлетворяют условию: 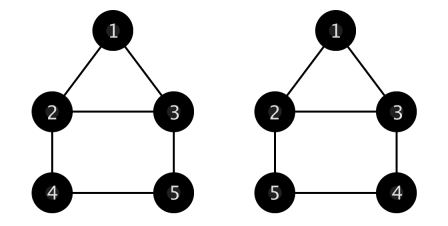 | |
![]()
|
|
B. Карен и тест
Перебор
Конструктив
Комбинаторика
математика
*2200
Карен только что пришла в школу, у нее сегодня тест по математике!  Тест проверяет умения складывать и вычитать числа. К сожалению, учителя были заняты подготовкой задач к раунду Codeforces, поэтому у них не было времени сделать тест. Поэтому они дали лишь одну задачу, которая стоит все баллы. В ряд записаны n целых чисел. Карен должна по очереди складывать и вычитать каждую пару соседних чисел, и записывать получающиеся суммы или разности в следующий ряд. Затем она должна повторить процесс со следующим рядом, и так далее, пока не останется ровно одно число. Первой операцией должно быть сложение. Заметьте, что, если она закончила предыдущий ряд, вычислив сумму чисел, то она должна начать новый ряд вычитанием, и наоборот. Учителя просто посмотрят на последнее число: если оно окажется верным, то Карен получит полный балл, иначе — ноль. Карен хорошо подготовилась к тесту, но боится сделать ошибку где-нибудь, что приведет ее к неправильному финальному ответу. Можете вычислить, какое число она должна получить в конце? Так как это число может быть большим, выведите неотрицательный остаток от его деления на 109 + 7. Выходные данные Выведите одно целое число: число в последнем ряду после выполнения всех операций. Так как оно может быть большим, выведите его неотрицательный остаток от деления на 109 + 7. Примечание В первом примере числа в первом ряду равны 3, 6, 9, 12 и 15. Карен выполняет операции как показано на рисунке: 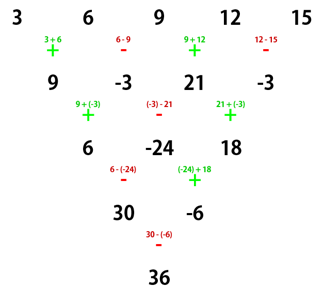 Неотрицательный остаток от деления итогового числа на 109 + 7 равен 36. Во втором примере числа в первом ряду равны 3, 7, 5 и 2. Карен выполняет следующие операции:  Неотрицательных остаток от деления итогового числа на 109 + 7 равен 109 + 6. | |
![]()
|
|
D. Карен и карты
Бинарный поиск
Структуры данных
Комбинаторика
геометрия
*2800
Карен пришла из супермаркета и собирается спать.  После принятия душа и переодевания в пижаму она заметила альбом на своей полке. Заинтересовавшись, она открыла его и увидела коллекцию карт. Она вспомнила, что играла в них, когда была ребенком, но, несмотря на то, что она уже выросла, ее по-прежнему интересует один вопрос. Каждая карта имеет три характеристики: сила, защита и скорость. Значения всех характеристик всех карт являются положительными целыми числами. Максимальное значение силы любой карты равно p, максимальное значение защиты равно q, максимальное значение скорости равно r. В коллекции Карен n карт. i-я из этих карт имеет силу ai, защиту bi и скорость ci, соответственно. Карта бьет другую карту, если хотя бы две ее характеристики строго больше соответствующих характеристик другой карты. Карен интересует, сколько существует различных карт таких, что каждая из них бьет все карты из ее коллекции. Две карты различны, если хотя бы одна характеристика этих карт различна. Выходные данные Выведите одно число — число различных карт, которые бьют все карты из коллекции Карен. Примечание В первом примере максимально возможная сила равна 4, максимально возможная защита равна 4, а максимально возможная скорость равна 5.У Карен есть три карты: - У первой карты сила 2, защита 2, скорость 5.
- У второй карты сила 1, защита 3, скорость 4.
- У третьей карты сила 4, защита 1, скорость 1.
Всего существуют 10 карт, которые бьют все карты из коллекции: - Карта с силой 3, защитой 3 и скоростью 5.
- Карта с силой 3, защитой 4 и скоростью 2.
- Карта с силой 3, защитой 4 и скоростью 3.
- Карта с силой 3, защитой 4 и скоростью 4.
- Карта с силой 3, защитой 4 и скоростью 5.
- Карта с силой 4, защитой 3 и скоростью 5.
- Карта с силой 4, защитой 4 и скоростью 2.
- Карта с силой 4, защитой 4 и скоростью 3.
- Карта с силой 4, защитой 4 и скоростью 4.
- Карта с силой 4, защитой 4 и скоростью 5.
Во втором примере максимально возможная сила равна 10, максимально возможная защита равна 10, максимально возможная скорость равна 10. У Карен пять карт, у всех из них сила 1, защита 1 и скорость 1. Каждая из 972 карт, у которых хотя бы две характеристики больше 1, бьет все карты из коллекции. | |
![]()
|
|
B. Макес и произведение
Комбинаторика
математика
реализация
*1500
сортировки
После возвращения из армии Макес получил в подарок массив a, состоящий из n целых положительных чисел. Так как он очень давно не решал задачи, его заинтересовал следующий вопрос: сколько существует таких упорядоченных троек (i, j, k), что i < j < k, а ai·aj·ak — минимально. Помогите ему в этом! Выходные данные Выведите единственное число — количество упорядоченных троек (i, j, k), что i, j и k — попарно различны, а ai·aj·ak — минимально. Примечание В первом тесте из условия Макес всегда выберет три единицы из четырёх, а количество способов их выбрать — 4. Во втором тесте выбирается тройка чисел (1, 2, 3). Так как 3 встречается в массиве дважды, а единица и двойка — единожды, то количество способов будет равно 2. В третьем тесте выбирается тройка (1, 1, 2), её можно выбрать единственным способом. | |
![]()
|
|
C. Прожорливая Кракозябра
Перебор
Комбинаторика
математика
жадные алгоритмы
*2700
 Недавно в Мармеладном замке поселилась самая настоящая Кракозябра. И она постоянно не прочь чем-нибудь поживиться. Любимым блюдом Кракозябры являются натуральные числа в медовом соусе, а точнее, нули в их десятичной записи. Другие цифры ей не по вкусу; мало того, от них у нее частенько случается несварение желудка. Поэтому прежде, чем приступить к трапезе, Кракозябра аккуратно раскладывает цифры числа в возрастающем порядке и съедает лишь нули (если они есть), а из оставшихся цифр формирует новое число, которое она презрительно отбрасывает как несъедобный хвост. Так, например, если Кракозябра предпочтет полакомиться числом 57040, то несъедобный хвост будет равняться 457. Сластене немного не по душе такое соседство, но ее природная гостеприимность не позволяет ей оставить Кракозябру без еды. У Сластены есть некоторый диапазон чисел от L до R, которыми она планирует накормить гостью. Помогите ей узнать, сколько различных несъедобных хвостов останется после ужина. Выходные данные Выведите одно число — ответ на задачу. Примечание В первом примере несъедобные хвосты — все числа от 1 до 9. Заметьте, что 10 и 1 дают одинаковые хвосты, равные 1. Во втором примере Кракозябра сформирует уникальные несъедобные хвосты из всех чисел диапазона, кроме пары 45, 54. Таким образом, ответ равен (57 - 40 + 1) - 1 = 17. | |
![]()
|
|
F. Префикс суммы
Бинарный поиск
Перебор
Комбинаторика
математика
*2400
матрицы
Дана функция p(x), где x — это массив из m целых чисел, которая возвращает массив y, состоящий из m + 1 целых чисел таких, что yi равно сумме первых i элементов массива x (0 ≤ i ≤ m). Дана бесконечная последовательность массивов A0, A1, A2..., где массив A0 дан во входных данных, и для всех i ≥ 1 Ai = p(Ai - 1). Кроме этого дано целое положительное число k. Найдите минимальное возможное i такое, что Ai содержит число не меньшее чем k. Выходные данные Выведите минимальное i такое, что массив Ai содержит число не меньшее чем k. | |
![]()
|
|
D. Зима пришла
Комбинаторика
математика
дп
теория чисел
*2200
Зима пришла на Севере и белые ходоки близко. Армия Джона Сноу состоит из n солдат. Пока остальная часть мира сражается за Железный трон, он собирается подготовиться к атаке белых ходоков. Он придумал метод оценки силы своей армии. Пусть сила i-го солдата ai. Для некоторого k он называет i1, i2, ..., ik кланом, если i1 < i2 < i3 < ... < ik и gcd(ai1, ai2, ..., aik) > 1. Он считает силой этого клана k·gcd(ai1, ai2, ..., aik). Тогда сила армии равна сумме сил всех кланов в армии. Ваша задача - найти силу его армии. Так как это число может быть очень большим, выведите его по модулю 1000000007 (109 + 7). Наибольшим общим делителем (greatest common divisor, gcd) последовательности целых чисел называется наибольшее целое число такое, что каждый элемент последовательности делится на это число. Выходные данные Выведите одно число — силу армии Джона Сноу по модулю 1000000007 (109 + 7). Примечание В первом примере кланы — {1}, {2}, {1, 2}, так что ответ 1·3 + 1·3 + 2·3 = 12 | |
![]()
|
|
A. Леха и функция
Комбинаторика
математика
теория чисел
жадные алгоритмы
сортировки
*1300
Леха очень любит всякие странности. Недавно ему понравилась функция F(n, k). Рассмотрим всевозможные k-элементные подмножества множества [1, 2, ..., n]. Для подмножества найдем минимальный элемент в нём. F(n, k) — это математическое ожидание минимального значения по всевозможным k-элементным подмножествам. Но одна только функция его не интересует. Он хочет делать с ней интересные вещи. Мама принесла ему два массива A и B, каждый состоит из m целых чисел. Для всех i, j таких, что 1 ≤ i, j ≤ m, выполняется условие Ai ≥ Bj. Помогите Лехе переупорядочить числа в массиве A так, чтобы сумма  была максимально возможной, где A' — уже переупорядоченный массив. была максимально возможной, где A' — уже переупорядоченный массив. Выходные данные Выведите m целых чисел a'1, a'2, ..., a'm — массив A', являющийся перестановкой массива A. | |
![]()
|
|
C. На скамейке
Комбинаторика
дп
*2500
Год назад на скамейке в общественном парке Леха нашёл массив из n чисел. Леха считает, что перестановка p называется правильной если для всех 1 ≤ i < n выполняется условие, что api·api + 1 не является квадратом целого числа. Леха хочет найти количество правильных перестановок по модулю 109 + 7. Выходные данные Выведите одно число — количество правильных перестановок по модулю 109 + 7. Примечание Разберём 1-й пример: [1, 2, 4] — хорошая перестановка, так как 2 и 8 не являются квадратами целого числа. [1, 4, 2] — плохая, так как 4 является квадратом 2. [2, 1, 4] — плохая, так как 4 является квадратом 2. [2, 4, 1] — плохая, так как 4 является квадратом 2. [4, 1, 2] — плохая, так как 4 является квадратом 2. [4, 2, 1] — хорошая перестановка, так как 8 и 2 не являются квадратами целого числа. | |
![]()
|
|
B. Прямоугольники
Комбинаторика
математика
*1300
Дана таблица размера n × m. Каждая клетка таблицы покрашена либо в белый, либо в черный цвет. Найдите количество непустых множеств клеток таких, что: - Все клетки в множестве имеют один и тот же цвет.
- Любые две клетки лежат в одной строке или в одном столбце.
Выходные данные Выведите одно целое число — искомое количество множеств. Примечание Во втором примере, кроме шести множеств, состоящих из одной клетки, существуют также два других подходящих множества: первое образовано крайними клетками первой строки, второе образовано крайними клетками второй строки. Суммарное количество множеств равно 8. | |
![]()
|
|
D. Shake It!
Потоки
Комбинаторика
дп
графы
*2900
Открывая тайную дверь, раскрой нескончаемый переменчивый сказочный мир. Назовем миром неориентированный граф G, во множестве вершин которого V(G) есть две особые вершины s(G) и t(G). Начальный мир имеет множество вершин {s(G), t(G)} и ребро между ними. С начальным миром произошло n изменений. В каждом изменении была добавлена новая вершина w во множество V(G), выбрано существующее ребро (u, v), и добавлены два новых ребра (u, w) и (v, w) во множество ребер E(G). Обратите внимание, некоторые ребра могут быть выбраны в более, чем одном изменении. Известно, что в итоговом графе минимальный s-t разрез равен m, то есть, нужно удалить хотя бы m ребер, чтобы s(G) и t(G) оказались в разных компонентах связности. Найдите число непохожих миров, которые могли получиться, по модулю 109 + 7. Два мира называются похожими, если они изоморфны и есть изоморфизм, который не переобозначает вершины s и t. Формально, два мира G и H считаются похожими, если между их множествами вершин существует биекция 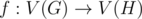 такая, что: такая, что: - f(s(G)) = s(H);
- f(t(G)) = t(H);
- Две вершины u и v в графе G соседние в G, если и только если f(u) и f(v) соседние в H.
Выходные данные Выведите одно число — число непохожих миров, которые могли получиться, по модулю 109 + 7. Примечание В первом примере следующие 6 миров попарно непохожи и удовлетворяют всем ограничениям, s(G) обозначена зеленым, t(G) обозначена синим, один из минимальных разрезов обозначен голубым. 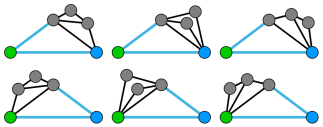 Во втором примере следующие 3 мира удовлетворяют ограничениям. 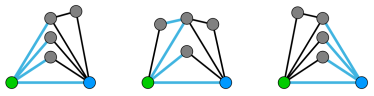 | |
![]()
|
|
E. Days of Floral Colours
Комбинаторика
математика
дп
разделяй и властвуй
*3400
бпф
Цветочные Часы находятся рядом с Зеркальным Озером много лет. Неспособные показывать время, они напоминают людям о его течении и о старых добрых днях. На окружности Цветочных Часов находятся 2n цветков, пронумерованных от 1 до 2n по часовой стрелке, каждый цветок имеет один из возможных n цветов. Есть ровно два цветка каждого цвета, расстояние между которыми либо не больше, чем 2, либо равняется n. Кроме того, если цветки u и v имеют одинаковый цвет, то цветок, расположенный напротив u, и цветок, расположенный напротив v, тоже имеют одинаковый цвет: симметрия — это прекрасно! Формально, расстояние между двумя цветками равно 1 плюс количество цветков на меньшей дуге между ними. Ниже показано возможная раскраска цветов при n = 6, которое описывает все возможные случаи.  Красотой раскраски называется произведение длин отрезков цветков, разделенных всеми цветами такими, что противоположный цветок имеет тот же цвет. Другими словами, чтобы вычислить красоту, нужно удалить из круга все цветки, которые имеют тот же цвет, что и цветок напротив них. Тогда красота равна произведению длин всех оставшихся отрезков. Обратите внимание, отрезки длины 0 тоже считаются. Если цветков, которые имеют тот же цвет, что и цветок напротив них, нет, то красота равна 0. Например, красота раскраски выше равна 1 × 3 × 1 × 3 = 9: отрезками являются {2}, {4, 5, 6}, {8} и {10, 11, 12}. Возможно большое число различных раскрасок, удовлетворяющих всем ограничениям. Найдите сумму всех красот по всем возможным раскраскам по модулю 998 244 353. Две раскраски различны, если существует пара (u, v) (1 ≤ u, v ≤ 2n) такая, что цветы u и v имеют один цвет в одной из них, но не имеют один цвет в другой. Выходные данные Выведите одно целое число — сумму красот по всем возможным раскраскам цветом по модулю 998 244 353. Примечание При n = 3, следующие шесть раскрасок каждая имеет красоту, равную 2 × 2 = 4.  Много других раскрасок, имею красоту, равную 0, например, изображенная на рисунке слева. Раскраска на рисунке справа некорректна, так как не выполняется условие симметричности.  | |
![]()
|
|
F. Преобразование произведения
Комбинаторика
математика
теория чисел
*2200
Рассмотрим массив A с N элементами, все из которых равны a. Определим преобразование произведение как одновременное обновление элементов массива Ai = Ai·Ai + 1, которое умножает каждый элементы на элемент справа от него для 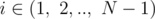 , а последний элемент AN остаётся неизменным. Например, если мы начнём с массива A с a = 2 и N = 4, после первого преобразования произведения A = [4, 4, 4, 2], а после двух A = [16, 16, 8, 2]. , а последний элемент AN остаётся неизменным. Например, если мы начнём с массива A с a = 2 и N = 4, после первого преобразования произведения A = [4, 4, 4, 2], а после двух A = [16, 16, 8, 2]. Ваша простая задача — найти массив A после M преобразований произведения. Так как числа могут стать очень большими, выведите ответ по модулю Q. Выходные данные Выведите массив A слева направо, разделённый пробелами. Примечание Мультипликативный порядок числа a по модулю Q 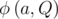 — это наименьшее положительное целое число x такое, что ax mod Q = 1. Например, — это наименьшее положительное целое число x такое, что ax mod Q = 1. Например,  . . | |
![]()
|
|
C. Одиннадцатилетие
Комбинаторика
математика
дп
*2400
На одиннадцатый день рождения Боре подарили n карточек с числами. На i-й карточке написано число ai. Боря хочет выложить карточки в один ряд так, чтобы получилось одно большое число. Например, если у Бори есть карточки с числами 1, 31 и 12, и он выложит их в этом порядке, он получит число 13112. В свои 11 он уже знает, что всего существует n! способов вызложить карточки, но сегодня его интересуют только те способы, в результате которых, он получит число, которое делится на одиннадцать. Так, приведенный выше способ подходит, поскольку 13112 = 1192 × 11, а вот если он выложит карточки в последовательности 31, 1, 12, то он получит число 31112, которое не делится на 11, этот способ Боре не подходит. Помогите Боре посчитать количество таких способов. Даже если на двух карточках написаны одинаковые числа, Боря считает способы, которые отличаются обменом этих двух карточек, различными, например, если у Бори есть две карточки с числом 1, то он может выложить их на стол двумя способами. Помогите Боре, найдите число подходящих способов выложить карточки. Поскольку это количество может быть слишком большим, требуется вывести остаток от его деления на 998244353. Выходные данные Для каждого теста в отдельной строке выведите остаток от деления на 998244353 количества способов выложить карточки таким образом, чтобы получившееся число делилось на 11. | |
![]()
|
|
E. Беспорядок на рабочих местах
Деревья
Комбинаторика
*2100
поиск в глубину и подобное
графы
снм
Привезли новые рабочие столы, и нужно с ними поскорее разобраться, так как в офисе стало очень тесно! Вам нужно составить новую рассадку инженеров в офисе. Столы пронумерованы, и вы провели опрос среди инженеров, выяснив, за каким столом они работают сейчас, и за каким столом они хотели бы работать (может совпадать с тем столом, за которым они сейчас работают). Каждый инженер должен либо остаться на своем месте, либо переместиться на то место, которое он обозначил как желаемое. Никакие два инженера не работают сейчас за одним столом, и после пересадки никакие два инженера также не должны работать за одним столом. Сколько существует способов рассадить инженеров так, чтобы удовлетворить описанным ограничениям? Ответ может быть большим, поэтому выведите его по модулю 1000000007 = 109 + 7. Выходные данные Выведите число способов рассадить всех инженеров по модулю 1000000007 = 109 + 7. Примечание Следующие рассадки возможны в первом примере: - 1 5 3 7
- 1 2 3 7
- 5 2 3 7
- 1 5 7 3
- 1 2 7 3
- 5 2 7 3
| |
![]()
|
|
G. Цветы и шоколад
Комбинаторика
математика
матрицы
*3300
Скоро день рождения Piegirl, поэтому Pieguy решил купить ей букет цветов и корзинку шоколадок. В цветочном магазине есть F различных видов цветов. Цветы i-го типа всегда имеют pi лепестков. Pieguy решил купить букет из ровно N цветов. Он может покупать цветы одного и того же типа несколько раз. Все N цветов составят букет. Важным обстоятельством является позиция цветка в букете. Вы можете считать, что букет — это упорядоченный список типов цветов. Шоколадный магазин продает шоколад в коробках. Всего есть B различных видов коробок. В коробке i-го типа находятся ci кусочков шоколада. Pieguy может купить сколько угодно коробок, в том числе несколько одного типа. Затем он положит все коробки в корзинку, при этом важен порядок. Вы можете считать, что корзинка описывается упорядоченным списком типов коробок. Pieguy знает, что Piegirl любит отрывать лепесток с цветка перед тем, как съесть кусочек шоколадки. Он хочет быть уверен, что она съест последний кусочек шоколадки из последней коробки сразу после того, как оторвет последний лепесток с последнего цветка. Другими словами, общее число лепестков в букете должно равняться общему числу кусочков шоколада в корзинке. Сколько различных комбинация букета и корзинки может купить Pieguy? Отрет может быть большим, поэтому выведите его по модулю 1000000007 = 109 + 7. Выходные данные Выведите число комбинаций букета и корзинки, которые может купить Pieguy по модулю 1000000007 = 109 + 7. Примечание В первом примере есть 1 способ сделать букет с 9 лепестками (3 + 3 + 3), и 1 способ сделать корзинку с 9 кусочками шоколада (3 + 3 + 3), итого 1 комбинация. Есть 3 способа сделать букет с 13 лепестками (3 + 5 + 5, 5 + 3 + 5, 5 + 5 + 3), и 5 способов сделать корзинку с 13 кусочками шоколада (3 + 10, 10 + 3, 3 + 3 + 7, 3 + 7 + 3, 7 + 3 + 3), что дает еще 15 комбинаций. Кроме того, если 1 способ сделать букет с 15 лепестками (5 + 5 + 5) и 1 способ сделать корзинку с 15 кусочками шоколада (3 + 3 + 3 + 3 + 3), что дает еще 1 комбинацию. Обратите внимание, что возможно существование нескольких типов цветов с одинаковым количеством лепестков. Такие типы все равно считаются различными. Аналогично, разные типы коробок тоже могут содержать равное число кусочков шоколада, но они считаются различными. | |
![]()
|
|
C. Интригующая одержимость
Комбинаторика
математика
дп
*1800
— Это не игра, а долг союзников справедливости, Нии-тян! — Не союзников, а самого правосудия, Онии-тян! Возьмитесь за руки и идите куда угодно, быстрее скорости мысли! На этот раз Сёстры Огня Карен и Цукихи направляются туда, где они ещё не были, — на окружённые водой острова! Есть три группы островов, покрашенные в красный, голубой и фиолетовый цвета. Группы состоят из a, b и c островов, соответственно. Мосты были построены между некоторыми парами островов. Возможно, что все пары островов соединены мостами или же нет ни одного моста. Мост соединяет два различных острова и имеет длину 1. По мосту можно перемещаться в обе стороны. Для каждой пары различных островов одного цвета должно быть выполнено, что расстояние между ними по мостам не менее 3 или же невозможно добраться с одного острова до другого по мостам. Сёстры Огня готовы к любым неожиданностям, но они также хотят проверить ваше мужество. От вас требуется узнать количество различных способов построить мосты между островами, чтобы они удовлетворяли данным ограничениям по модулю 998 244 353. Два способа считаются различными, если существует пара островов, такая, что между этими островами есть мост в одном способе и нет в другом. Выходные данные Выведите одно число — количество способов построить мосты по модулю 998 244 353. Примечание В первом примере могут быть построены 3 моста и любое их подмножество будет корректным способом. Поэтому ответ равен 23 = 8. Во втором примере два корректных способа постройки мостов изображены на картинке сверху, а два некорректных способа — на картинке снизу. 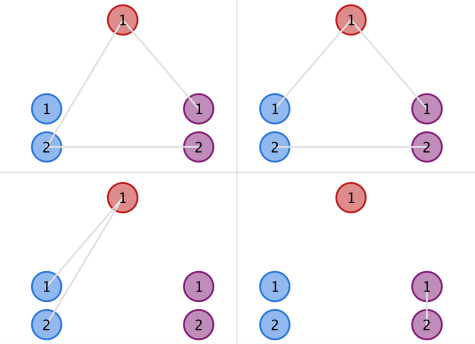 | |
![]()
|
|
D. Ор выше гор
Бинарный поиск
Структуры данных
Комбинаторика
разделяй и властвуй
*2200
битмаски
Рик и Морти очень любят ходить на горный хребет Высокоорный для того, чтобы поорать — эхо там просто невероятное. Не так давно они нашли интересное акустическое свойство этого хребта: если Рик и Морти начнут одновременно орать с разных гор, то их ор будет слышен между этими горами вплоть до высоты, равной побитовому ИЛИ высот гор, на которые они взошли, и всех гор между ними. Побитовое ИЛИ — это бинарная операция, которая определяется следующим образом. Рассмотрим записи чисел x и y в двоичной системе счисления (возможно с ведущими нулями) x = xk... x1x0 и y = yk... y1y0. Тогда z = x | y определяется следующим образом: z = zk... z1z0, где zi = 1, если xi = 1 или yi = 1, иначе zi = 0. Иными словами, нули в побитовом ИЛИ чисел находятся только в тех разрядах, в которых у обоих чисел находятся нули. Например, побитовое ИЛИ чисел 10 = 10102 и 9 = 10012 равняется 11 = 10112. В языках программирования C/C++/Java/Python данная операция обозначается как «|», а в Pascal как «or». Помогите Рику и Морти посчитать, сколькими способами они могут выбрать две различные горы так, что если они начнут орать с этих гор, ор их будет слышен выше этих гор и всех гор между ними. Формально говоря, требуется вычислить, сколько существует таких пар l и r (1 ≤ l < r ≤ n), что побитовое ИЛИ всех высот гор на отрезке от l до r включительно строго больше высоты любой горы на этом отрезке. Выходные данные Выведите одно число — искомое количество способов выбрать две различные горы. Примечание В первом примере все искомые способы — это пары гор со следующими номерами (горы нумеруются с единицы): (1, 4), (1, 5), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5)Во втором примере искомых пар не существует, поскольку для любой пары гор высота ора с них равна 3, и эта высота равна высоте любой из гор, следовательно она не выше их. | |
![]()
|
|
E. Числа на доске
Комбинаторика
дп
*3300
На доске написана последовательность из n целых чисел. Скоро к доске подойдёт Саша и начнёт делать следующую операцию: пусть x и y — два подряд идущих числа (x перед y), тогда он может их стереть и на их месте написать число x + 2y. Он делает такие операции, пока на доске не останется одно число. Саша очень любит большие числа и получит самое большое возможное число. Никита хочет успеть к доске раньше Саши и стереть часть чисел. У него есть q вариантов, в варианте i он стирает все числа левее позиции li и все числа правее позиции ri, то есть на доске остаются все числа от li-го до ri-го включительно. Для каждого из вариантов ему интересно, какое число в итоге получится у Саши. Так как ответ может быть большим, выведите его по модулю 109 + 7. Выходные данные Для каждого варианта Никиты выведите остаток от деления максимального числа, которое может получить Саша, на 109 + 7. Примечание Во втором примере Никита ничего не стирает. Саша первым действием сотрёт числа 1 и 2 и напишет 5. Потом он сотрёт 5 и -3 и получит -1. Остаток от деления -1 на 109 + 7 равен 109 + 6. | |
![]()
|
|
E. Максимум в массиве
Комбинаторика
математика
дп
*2400
Как-то раз Петя решал очень интересную задачу. Однако, какие бы оптимизации Петя ни применял, его решение всё равно получало вердикт Time limit exceeded. После тщательного анализа кода он обнаружил, что проблема заключается в его функции поиска максимума в массиве из n положительных чисел, которая работала слишком долго. В отчаянии Петя решил добавить весьма неожиданное отсечение с параметром k, после чего функция приняла следующий вид:
int fast_max(int n, int a[]) {
int ans = 0;
int offset = 0;
for (int i = 0; i < n; ++i)
if (ans < a[i]) {
ans = a[i];
offset = 0;
} else {
offset = offset + 1;
if (offset == k)
return ans;
}
return ans;
}
Таким образом, функция последовательно перебирает элементы массива, поддерживая текущий максимум, при этом если после k последовательных итераций этот максимум не изменился, то текущий максимум возвращается как ответ. Теперь Пете стало интересно, как часто его функция даёт неверный ответ. Он просит вас посчитать количество перестановок чисел от 1 до n таких, что результат работы его функции на этих перестановках не равен n. Так как ответ может быть большим, выведите его по модулю 109 + 7. Выходные данные Выведите количество перестановок, на которых функция Пети выдаёт неправильный ответ, взятое по модулю 109 + 7. Примечание Искомые перестановки из второго примера: [4, 1, 2, 3, 5], [4, 1, 3, 2, 5], [4, 2, 1, 3, 5], [4, 2, 3, 1, 5], [4, 3, 1, 2, 5], [4, 3, 2, 1, 5]. | |
![]()
|
|
D. Почти тождественные перестановки
Комбинаторика
математика
*1600
дп
Перестановка p размера n — такой массив, что каждое целое число от 1 до n встречается ровно один раз в этом массиве. Будем называть почти тождественными такие перестановки, что для каждой из них существует как минимум n - k индексов i (1 ≤ i ≤ n), таких, что pi = i. Вам необходимо подсчитать количество почти тождественных перестановок для заданных n и k. Выходные данные Выведите число почти тождественных перестановок для заданных n и k. | |
![]()
|
|
E. Похоть
Комбинаторика
математика
*3000
матрицы
Вам дана последовательность из n целых чисел. Также у вас есть переменная res, которая изначально равна 0. Следующая операция выполняется k раз. Выбирается индекс от 1 до n равновероятно случайным образом, назовем его x. К переменной res прибавляется произведение всех ai таких, что 1 ≤ i ≤ n, но i ≠ x. Затем из ax вычитается 1. Найдите математическое ожидание величины res в конце процесса. Можно показать, что ожидаемое значение величины res может быть представлено как несократимая дробь 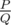 . Вам необходимо найти значение . Вам необходимо найти значение  . . Выходные данные Выведите одно целое число — значение  . . | |
![]()
|
|
E. Подсчет массивов
Комбинаторика
математика
дп
теория чисел
*2000
Вам заданы два целых положительных числа x и y. Массив F называется y-факторизацией числа x тогда и только тогда, когда выполняется следующие условия: - В массиве F ровно y элементов, все они являются целыми числами;
-
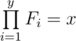 . . Посчитайте количество попарно различных массивов, являющихся y-факторизациями числа x. Два массива A и B считаются различными, если существует хотя бы одна позиция i (1 ≤ i ≤ y) такая, что Ai ≠ Bi. Так как ответ может быть очень большим, выведите его по модулю 109 + 7. Выходные данные Выведите q целых чисел. i-е число должно быть ровно количеству yi-факторизаций числа xi по модулю 109 + 7. Примечание Во втором запросе из примере есть 6 y-факторизаций: - { - 4, - 1};
- { - 2, - 2};
- { - 1, - 4};
- {1, 4};
- {2, 2};
- {4, 1}.
| |
![]()
|
|
B. Ральф и его магическое поле
Конструктив
Комбинаторика
математика
теория чисел
*1800
У Ральфа есть магическое поле, которое разделено на n × m блоков. А именно, на поле есть n строк и m столбцов. Ральф хочет в каждый блок поставить целое число. Однако, магическое поле не всегда работает правильно. Оно работает, только если произведение чисел в каждой строке и в каждом столбце равно k, где k может быть равно 1 или -1. Ральф хочет узнать количество способов поставить некоторые целые числа во все блоки так, чтобы магическое поле работало правильно. Два способа считаются различными, если и только если существует хотя бы один блок такой, что числа в нем в первом и втором способе различны. Вам необходимо вывести остаток от деления ответа на 1000000007 = 109 + 7. Обратите внимание, нет ограничения на целые числа, которые можно ставить в блоки, однако, можно показать, что ответ конечный. Выходные данные Выведите единственное число — остаток от деления ответа на 1000000007. Примечание В первом примере единственный способ — поставить -1 в единственный блок. Во втором примере единственный способ — поставить 1 в каждый блок. | |
![]()
|
|
C. Квадратные подмножества
Комбинаторика
математика
дп
*2000
битмаски
Как и Вася, Петя опоздал на пару. Преподаватель также дал ему дополнительное задание. Для некоторого массива a необходимо вычислить количество различных способов выбрать некоторое непустое подмножество его элементов так, чтобы их произведение было равно квадрату некоторого натурального числа. Два способа считаются различными если различаются множества индексов элементов, выбранных в первом и во втором способах. Так как ответ может быть очень большим, необходимо вычислить лишь остаток от деления ответа на 109 + 7. Выходные данные Выведите одно целое число — остаток от деления искомого количества способов на 109 + 7. Примечание В первом тесте произведение чисел выбираемых любым возможным способом равно 1. Так как 1 = 12, ответ равен 24 - 1 = 15. Во втором тесте можно получить произведение равное 16 одним способом и произведение равное 4 шестью способами. Поэтому ответ равен 6 + 1 = 7. | |
![]()
|
|
D. Оценочная строка
Строки
Комбинаторика
математика
*2100
В университете, где учится Вася, оценки представляют собой строки одинаковой длины, причем оценка x считается лучше чем y, если строка y лексикографически меньше строки x. Недавно в этом университете прошла важная контрольная, по которой Вася получил оценку a. Из-за большого количества студентов, преподаватель не может запомнить оценку каждого, но он точно помнит оценку b такую, что все студенты получили оценку строго меньше чем b. Вася недоволен своей оценкой и хочет её исправить. Для этого он может как угодно поменять местами символы в строке соответствующей его оценке. Сейчас Васю интересует количество различных способов улучшить свою оценку так, чтобы преподаватель не заподозрил неладного. Более формально: даны две строки одинаковой длины a и b, требуется вычислить количество различных строк c таких, что: 1) c может быть получена из a путем перестановки некоторых символов, то есть c является перестановкой a 2) a лексикографически меньше c 3) c лексикографически меньше b Если длина строки x равна длине строки y, то x лексикографически меньше y, если существует такое i, что x1 = y1, x2 = y2, ..., xi - 1 = yi - 1, xi < yi. Так как ответ может быть очень большим, вычислите только остаток от деления ответа на 109 + 7. Выходные данные Требуется вывести одно целое число — остаток от деления количества различных строк удовлетворяющих условию задачи на 109 + 7. Примечание В первом тесте из строки abc можно получить строки acb, bac, bca, cab, cba, все они больше строки abc, но меньше строки ddd. Поэтому ответ равен 5. Во втором тесте любая строка, которую можно получить из abcdef, будет больше строки abcdeg. Поэтому ответ равен 0. | |
![]()
|
|
D. Нефрен и кинотеатр
Комбинаторика
математика
теория чисел
*2900
китайская теорема об остатках
Лахеш любит снимать фильмы, поэтому Нефлен помогает ей организовать кинотеатр, который называется кинотеатр 68. 
Однажды в кинотеатре 68 кончились деньги (у них нет купюр достоинством в 50 юаней в данный момент), но Нефлен всё равно хочет открыть его. В кассу кинотеатра приходят три типа покупателей: одни приносят ровно одну купюру достоинством в 50 юаней, вторые приносят ровно одну купюру достоинством в 100 юаней, поэтому Нефлен должна дать им сдачу одной купюрой в 50 юаней, а третьи приходят с VIP картой, поэтому не должны платить за билет. Сейчас n посетителей стоят снаружи кинотеатра в очереди. Нефлен хочет узнать, сколько возможных очередей могут быть таких, чтобы все люди смогли купить билет (то есть каждый покупатель мог получить сдачу, если она требуется), и чтобы после продажи билетов всем покупателям в кассе осталось не менее l и не более r купюр достоинством 50 юаней. Две очереди называются различными, если существует позиция, на которой в этих очередях стоят покупатели разного типа. Так как ответ может быть большим, выведите его по модулю p. Выходные данные Выведите единственное число — ответ на задачу по модулю p. Примечание Обозначим буквами A, B и C покупателей с купюрой в 50 юаней, покупателей с купюрой в 100 юаней и покупателей с VIP картой, соответственно. В первом тестовом примере все возможные очереди, после которых в кассе останутся 2 купюры в 50 юаней выглядят так: AAAB, AABA, ABAA, AACC, ACAC, ACCA, CAAC, CACA и CCAA. Очереди, после которых в кассе останутся 3 купюры в 50 юаней выглядят так: AAAC, AACA, ACAA и CAAA. Таким образом, ответ в первом тестовом примере равен 13. Во втором тестовом примере существует 35 различных очередей. | |
![]()
|
|
D. Сколько деревьев?
Комбинаторика
дп
*1900
разделяй и властвуй
В одном старом-старом текстовом файле была записана Великая Мудрость. Эта Мудрость была настолько Великой, что расшифровать её не мог никто, даже Фонг, старейший из обитателей Мэйнфрейма. Но кое-что оттуда он сумел узнать. Например то, что Юзер запускает игры ради удовольствия — и тогда на город опускаются ужасные Игровые Кубы, несущие смерть тем модулям, которые не смогут в неё выиграть... Конечно, с появлением в Мэйнфрейме стража Боба многие модули перестали бояться Игровых Кубов. Ведь Боб (раз он ещё живой) ни разу не проиграл Юзеру, а он всегда лезет в Игровые Кубы, в силу того, что его так запрограммировали. Однако, бывают неприятные ситуации, когда Игровой Куб опускается на Затерянные Углы. Ведь именно там живёт злобный вирус Хексадесимал, которая... Ну... Очень странная. И очень любит поиграть. Вот и получается, что волей-неволей Бобу приходится сперва играть с ней, а потом ещё и с Юзером. В этот раз она придумала следующее развлечение: Боб должен прыгать через двоичные деревья поиска с n вершинами. Напомним, что двоичное дерево поиска — это такое двоичное дерево, у которого каждой вершине сопоставлен некоторый ключ, и для каждой вершины выполняется правило: ключ в текущем корне больше всех ключей в левом поддереве, но меньше всех ключей в правом поддереве. Все ключи — различные натуральные числа от 1 до n. У каждой вершины такого дерева может быть от нуля (в случае, когда вершина является листом) до двух потомков. В игре Хексадесимал все деревья различны, но высотой не менее h. В данной задаче под высотой подразумеватся максимальное количество вершин, лежащих на пути от корня к самому удалённому листу, включая корень и сам лист. Когда Боб перепрыгивает через дерево, дерево исчезает. Боб получит доступ к Кубу тогда, когда деревьев не останется. Он знает, сколько деревьев ему придётся перепрыгнуть в худшем случае. А Вы? Выходные данные Одно число — ответ на задачу. Гарантируется, что оно не превышает 9·1018. | |
![]()
|
|
D. Необычные последовательности
Комбинаторика
математика
дп
теория чисел
*2000
битмаски
Найдите количество различных последовательностей из строго положительных целых чисел a1, a2, ..., an (1 ≤ ai) таких, что gcd(a1, a2, ..., an) = x и  . Так как ответ может быть большим, выведите остаток от его деления на 109 + 7. . Так как ответ может быть большим, выведите остаток от его деления на 109 + 7. gcd здесь обозначает наибольший общий делитель. Выходные данные Выведите количество искомых последовательностей по модулю 109 + 7. Примечание В первом примере подходят последовательности: (3, 3, 3), (3, 6), (6, 3). Во втором примере не подходит ни одна последовательность. | |
![]()
|
|
E. Новый год и перечисление подходящих
Комбинаторика
математика
дп
битмаски
*2500
Вам дано целое число m. Пусть M = 2m - 1. Вам дано множество из n целых чисел, обозначим его за T. Эти целые числа будут даны в двоичной системе счисления как n бинарных строк длины m. Множество целых чисел S называется «хорошим», если следующие условия выполняются. - Если
 , то , то 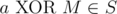 . . - Если
 , то , то  -
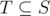 - Все элементы S меньше либо равны M.
Здесь  и и  обозначают побитовые операции исключающее ИЛИ и И, соответственно. обозначают побитовые операции исключающее ИЛИ и И, соответственно. Вычислите количество хороших множеств S по модулю 109 + 7. Выходные данные Выведите одно число: количество хороших множеств по модулю 109 + 7. Примечание Пример хорошего множества S: {00000, 00101, 00010, 00111, 11000, 11010, 11101, 11111}. | |
![]()
|
|
C. Лыжная база
Комбинаторика
графы
*2300
снм
В Моржландии собираются построить лыжную базу. Пока проект находится на стадии строительства. Под строительство базы был выбран большой участок земли, на котором находится n лыжных перекрестков. Изначально эти перекрестки никак не соединены. В процессе строительства будет проложено m двусторонних лыжных дорог. Дороги строятся по очереди: вначале будет построена дорога с номером 1, потом дорога с номером 2, и так далее. Дорога с номером i соединяет перекрестки с номерами ai и bi. Трасса — это маршрут, обладающий следующими свойствами: - Маршрут замкнут, то есть он начинается и заканчивается в одном и том же перекрестке.
- Маршрут содержит хотя бы одну дорогу.
- Маршрут не проходит по одной дороге более одного раза, но при этом может проходить через любой перекресток сколько угодно раз.
Будем называть лыжной базой непустое множество дорог, которое можно разбить на одну или более трасс так, чтобы по каждой дороге этого множества проходила ровно одна трасса, при этом каждая трасса может состоять только из дорог выбранного множества. Лыжная база может быть несвязной. Две лыжные базы считаются различными, если они состоят из разных множеств дорог. После постройки каждой новой дороги правительство Моржландии хочет знать количество вариантов выбрать лыжную базу на основе некоторого подмножества из уже построенных дорог. Правительство просит вашей помощи в решении данной задачи. Выходные данные Выведите m строк: i-ая строка должна обозначать количество способов построить лыжную базу после окончания строительства дороги с номером i. Числа следует выводить по модулю 1000000009 (109 + 9). Примечание Пусть у нас 3 перекрестка и уже построены 4 дороги между перекрестками (как после построки всех дорог в примере): 1 и 3, 2 и 3, 2 дороги между перекрестками 1 и 2. Участок под постройку будет выглядеть следующим образом: 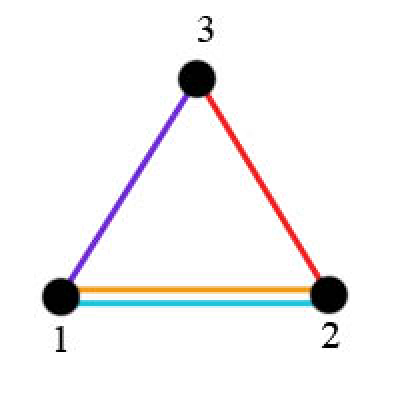 Можно выбрать подмножество дорог 3мя способами:  В первом и втором способах можно выбрать один маршрут, например, 1 - 2 - 3 - 1. В третьем случае можно выбрать один маршрут 1 - 2 - 1. | |
![]()
|
|
C. Комивояжёр и специальные числа
Перебор
Комбинаторика
дп
*1800
Комивояжёр проводит много времени в пути, поэтому часто скучает. Чтобы скоротать время, он любит производить операции с числами. Одна из таких операций заключается в том, что он берёт натуральное число x и уменьшает его до количества бит, которые установлены в 1 в двоичной записи числа x. Например, для числа 13 верно, что 1310 = 11012, значит, в нём есть 3 единичных бита, поэтому за одну операцию 13 уменьшится до 3. Он называет число специальным если минимальное количество операций, требуемых для уменьшения этого числа до 1 равно k. Комивояжёру интересно, сколько существует специальных чисел, не превосходящих n. Помогите ему. Так как ответ может быть большим, выведите его по модулю 109 + 7. Выходные данные Выведите одно целое число — количество специальных чисел, не превосходящих n, по модулю 109 + 7. Примечание В первом тестовом примере тремя специальными числами являются 3, 5 и 6. За одну операцию они уменьшаются до 2 (потому что в каждом из чисел 3, 5 и 6 два единичных бита), а затем до 1 (потому что в числе 2 один единичный бит) после применения ещё одной операции. | |
![]()
|
|
H. Деревянная игра Эмбера и Шторма
Деревья
Комбинаторика
дп
*3400
игры
Эмбер и Шторм играют в игру. Вначале, Эмбер выбирает помеченное дерево T на n вершинах, такое что степень каждой вершины не превосходит d. Затем Шторм выбирает две различные вершины u и v в этом дереве и выписывает номера вершин на пути из u в v как последовательность a1, a2... ak. Наконец Эмбер выбирает произвольный индекс i (1 ≤ i < k) и выполняет одну из следующих операций ровно один раз: - перевернуть подотрезок [i + 1, k] и прибавить ai ко всем числам на нём. После этого последовательность приобретает вид a1, ... ai, ak + ai, ak - 1 + ai, ... ai + 1 + ai
- Заменить все числа на подотрезке [i + 1, k] на противоположные и прибавить ai к ним. После этого последователньость приобретает вид a1, ... ai, - ai + 1 + ai, - ai + 2 + ai, ... - ak + ai
Эмбер выигрывает, если после произведённой операции массив монотонно возрастает или убывает, иначе выигрывает Шторм. Игра может быть представлена набором (T, u, v, i, op), где op — это «перевернуть» или «выполнить отрицаение» в зависимости от действия, которое Эмбер выполнил на последнем шаге. Найдите количество наборов, которые могут образоваться в результате оптимальной игры Эмбера и Шторма. Если они играют оптимально и у игрока есть несколько ходов, которые гарантируют победу, игрок может воспользоваться любым из них. Также если у игрока нет ни одного хода, гарантирующего победу, он может воспользоваться любым ходом. Выведите ответ по модулю m. Выходные данные Выведите единственное число — количество возможных наборов по модулю m. Примечание В первом тестовом примере существует только одно возможное дерево. Можно выбрать два пути: из 1 в 2 и из 2 в 1. Для обоих путей i может быть равно только 1, а op может принимать оба возможных значения. Поэтому ответ равен 4. Во втором тестовом примере подходящих деревьев нет. В третьем тестовом примере есть три возможных дерева. | |
![]()
|
|
C. Головастик
Комбинаторика
дп
матрицы
*2900
Как все знают, Дарт — это некое существо с Обратной стороны. Для простоты, мы называем их головастиками. Дарт и x - 1 других головастиков играют в игру. В ряд выложены n камней, пронумерованных от 1 до n слева направо. На одном камне одновременно может сидеть не более 1 головастика. Изначально головастики сидят на первых x камнях (по одному головастику на камне).  Дарт и его друзья хотят оказаться на последних x камнях. Каждую секунду самый левый головастик должен прыгнуть направо. Головастик может прыгнуть не более, чем на k камней; более конкретно, головастик может прыгнуть с камня i на камни i + 1, i + 2, ... i + k. Головастик не может прыгнуть на уже занятый камень. Прыжок на расстояние i отнимает ci единиц энергии у головастика. Кроме того, q камней являются специальными. Каждый раз, когда головастик попадает на специальный камень p, у него отнимается wp единиц энергии (в дополнении к энергии, затраченной на прыжок). wp может быть отрицательным, в таком случае головастик получает |wp| единиц энергии. Головастики хотят потратить как можно меньше энергии суммарно (эта величина может быть отрицательной). Так как они просто головастики, они просят вас посчитать, какую минимальную сумму изменений энергии они могут потратить. Выходные данные Выведите минимально возможное количество единиц энергии, которое нужно потратить головастикам. | |
![]()
|
|
G. Список чисел
Бинарный поиск
Перебор
Комбинаторика
математика
теория чисел
*2200
битмаски
Обозначим за L(x, p) бесконечную последовательность таких целых чисел y, что gcd(p, y) = 1 и y > x (где gcd — наибольший общий делитель двух чисел), расположенных в порядке возрастания. Элементы L(x, p) пронумерованы, начиная с 1; например, 9, 13 и 15 — соответственно первый, второй и третий элементы L(7, 22). Напишите программу, обрабатывающую t запросов. Каждый запрос задаётся тремя целыми числами x, p и k, а ответ на запрос — k-й элемент последовательности L(x, p). Выходные данные Выведите t чисел, где i-е число — ответ на i-й запрос. | |
![]()
|
|
C. Красивая команда
Комбинаторика
математика
*особая задача
*1700
Завтра у хоккейной команды, которой руководит Евгений, важный матч. Евгению нужно выбрать шесть игроков, которые выйдут на лед в стартовом составе: один вратарь, два защитника и три нападающих. Так как это стартовый состав, Евгения больше волнует, насколько красива будет команда на льду, чем способности игроков. А именно, Евгений хочет выбрать такой стартовый состав, чтобы номера любых двух игроков из стартового состава отличались не более, чем в два раза. Например, игроки с номерами 13, 14, 10, 18, 15 и 20 устроят Евгения, а если, например, на лед выйдут игроки с номерами 8 и 17, то это не устроит Евгения. Про каждого из игроков вам известно, на какой позиции он играет (вратарь, защитник или нападающий), а также его номер. В хоккее номера игроков не обязательно идут подряд. Посчитайте число различных стартовых составов из одного вратаря, двух защитников и трех нападающих, которые может выбрать Евгений, чтобы выполнялось его условие красоты. Выходные данные Выведите одно целое число — количество возможных стартовых составов. Примечание В первом примере всего один вариант для выбора состава, который удовлетворяет описанным условиям, поэтому ответ 1. Во втором примере подходят следующие игровые сочетания (в порядке вратарь-защитник-защитник-нападающий-нападающий-нападающий): - 16 20 12 13 21 11
- 16 20 12 13 11 10
- 16 20 19 13 21 11
- 16 20 19 13 11 10
- 16 12 19 13 21 11
- 16 12 19 13 11 10
Таким образом, ответ на этот пример — 6. | |
![]()
|
|
E. Командная работа
Комбинаторика
математика
дп
*2400
У вас в подчинении находится команда из N людей. Для определённой задачи вы можете выбрать непустое множество людей. Стоимость множества из x людей равна xk. Найдите сумму стоимостей по всем непустым подмножествам людей. Выходные данные Выведите сумму стоимостей по всем непустым подмножествам по модулю 109 + 7. Примечание В перовом тестовом примере есть одно непустое подмножество {1} со стоимостью 11 = 1. Во втором тестовом примере есть семь непустых подмножеств: - {1} со стоимостью 12 = 1 - {2} со стоимостью 12 = 1 - {1, 2} со стоимостью 22 = 4 - {3} со стоимостью 12 = 1 - {1, 3} со стоимостью 22 = 4 - {2, 3} со стоимостью 22 = 4 - {1, 2, 3} со стоимостью 32 = 9 Их суммарная стоимость равна 1 + 1 + 4 + 1 + 4 + 4 + 9 = 24. | |
![]()
|
|
D. Оригинальное вырезание
Перебор
Комбинаторика
математика
*2900
Все красное отпугивает монстра Ниана. Например, красная бумага и... вы, красные на Codeforces в будущем или уже сейчас. Большой Банбан приобрел кусочек бумаги с бесконечной целочисленной решеткой, точки решетки образуют квадраты равной площади. Его любимая замкнутая линия — окружность, т. к. окружность одновременно проста и красива. Он приготовился вырезать что-нибудь красивое, предварительно нарисовав несколько цветных окружностей.  Он нарисовал n концентрических окружностей и пронумеровал их от 1 до n таким образом, что центры всех окружностей совпадают с одной и той же точкой целочисленной решетки, а радиус k-й окружности равен 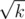 длинам кратчайшего периода решетки. длинам кратчайшего периода решетки. Определим красоту точки целочисленной решетки как сумму номеров окружностей, внутри или на границе которых лежит эта точка. Банбан хотел попросить вас определить суммарную красоту всех точек целочисленной решетки, но передумал. Определим суммарную красоту всех точек целочисленной решетки на ткани с n окружностями ка f(n). Вычислите 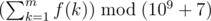 . . Выходные данные В единственной строка выведите одно целое число — 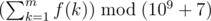 . . Примечание Решетка с 5 окружностями изображена на рисунке ниже.  Всего есть 5 типов точек целочисленной решетки, красота каждой красной точки равна 1 + 2 + 3 + 4 + 5 = 15, красота каждой оранжевой точки равна 2 + 3 + 4 + 5 = 14, красота каждой зеленой точки равна 4 + 5 = 9, красота каждой синей точки равна 5, а красота каждой серой точки равна 0. Итого, f(5) = 5·15 + 4·14 + 4·9 + 8·5 = 207. Аналогично, f(1) = 5, f(2) = 23, f(3) = 50, f(4) = 102, и поэтому  . . | |
![]()
|
|
E. История максимумов
Комбинаторика
математика
*2300
Задан массив a, состоящий из n элементов. Определим fa следующим образом: - Изначально fa = 0, M = 1;
- для каждого 2 ≤ i ≤ n если aM < ai, то установим fa = fa + aM и M = i.
Посчитайте сумму fa по всем n! перестановкам массива a по модулю 109 + 7. Обратите внимание, что два элемента считаются различными, если различаются их позиции, поэтому у любого массива a есть ровно n! перестановок. Выходные данные Выведите одно целое число, сумму fa по всем n! перестановкам массива a по модулю 109 + 7. Примечание Перестановки во втором примере: - p = [1, 2, 3] : fa равно 1;
- p = [1, 3, 2] : fa равно 1;
- p = [2, 1, 3] : fa равно 1;
- p = [2, 3, 1] : fa равно 1;
- p = [3, 1, 2] : fa равно 0;
- p = [3, 2, 1] : fa равно 0.
Где p — массив позиций оригинального массива a. Сумма fa равна 4. | |
![]()
|
|
F. Фибоначчиевы подпоследовательности
Комбинаторика
дп
*2400
матрицы
Дана бинарная строка s (каждый символ в строке равен либо 0, либо 1). Определим стоимость строки t как количество вхождений s в t. Например, если s равна 11 и t равна 111011, то стоимость t равна 3. Определим также фибоначчиевы строки следующим образом: - F(0) равна 0;
- F(1) равна 1;
- F(i) = F(i - 1) + F(i - 2) для i > 1, где + означает конкатенацию двух строк.
Ваша задача — посчитать сумму стоимостей всех подпоследовательностей строки F(x). Так как ответ может быть очень большим, выведите его по модулю 109 + 7. Выходные данные Выведите одно целое число — сумма стоимостей всех подпоследовательностей строки F(x) по модулю 109 + 7. | |
![]()
|
|
H. Подсчет путей
Комбинаторика
дп
*2500
Задано корневое дерево. Определим d(x) как высоту вершины x: высота корня равна 1, высоты любой другой вершины x равна d(y) + 1, где y — предок вершины x. У данного дерева есть следующее свойство: каждая вершина x с d(x) = i имеет ровно ai детей. Максимальная возможная глубина вершины равна n, an = 0. Определим fk как количество неупорядоченных пар вершин в дереве таких, что количество ребер на простом пути между ними равно k. Посчитайте fk по модулю 109 + 7 для всех 1 ≤ k ≤ 2n - 2. Выходные данные Выведите 2n - 2 чисел. В k-й строке выведите fk по модулю 109 + 7. Примечание Дерево из первого примера:  | |
![]()
|
|
E. Знакопеременное дерево
Деревья
Теория вероятностей
Комбинаторика
дп
поиск в глубину и подобное
разделяй и властвуй
*2300
Вам дано дерево с \(n\) вершинами, пронумерованными с \(1\) до \(n\). В вершине \(i\) записано значение \(V_i\). Если простой путь от вершины \(u_1\) до вершины \(u_m\) состоит из \(m\) вершин, а именно из \(u_1 \rightarrow u_2 \rightarrow u_3 \rightarrow \dots u_{m-1} \rightarrow u_{m}\), то знакопеременная сумма для этого пути \(A(u_{1},u_{m})\) определяется как \(A(u_{1},u_{m}) = \sum\limits_{i=1}^{m} (-1)^{i+1} \cdot V_{u_{i}}\). Путь может содержать \(0\) рёбер, т. е. \(u_{1}=u_{m}\). Вычислите сумму знакопеременных сумм для всех различных простых путей в дереве. Обратите внимание, пути ориентированны: два пути считаются различными, если у них различное начало или различный конец. Так как ответ может быть большим, выведите остаток от деления его на \(10^{9}+7\). Выходные данные Выведите сумму знакопеременных сумм по всем различным простым путям в дереве по модулю \(10^{9}+7\). Примечание Рассмотрим первый пример. Знакопеременная сумма для простого пути из вершины \(1\) в вершину \(2\): \(1 \rightarrow 2\) равна \(A(1,2) = 1 \cdot (-4)+(-1) \cdot 1 = -5\). Знакопеременная сумма для простого пути из вершины \(1\) в вершину \(3\): \(1 \rightarrow 3\) равна \(A(1,3) = 1 \cdot (-4)+(-1) \cdot 5 = -9\). Знакопеременная сумма для простого пути из вершины \(2\) в вершину \(4\): \(2 \rightarrow 1 \rightarrow 4\) равна \(A(2,4) = 1 \cdot (1)+(-1) \cdot (-4)+1 \cdot (-2) = 3\). Простой путь из вершины \(1\) в вершину \(1\) содержит только вершину \(1\), поэтому \(A(1,1) = 1 \cdot (-4) = -4\). Аналогично, \(A(2, 1) = 5\), \(A(3, 1) = 9\), \(A(4, 2) = 3\), \(A(1, 4) = -2\), \(A(4, 1) = 2\), \(A(2, 2) = 1\), \(A(3, 3) = 5\), \(A(4, 4) = -2\), \(A(3, 4) = 7\), \(A(4, 3) = 7\), \(A(2, 3) = 10\), \(A(3, 2) = 10\). Поэтому ответ равен \((-5) + (-9) + 3 + (-4) + 5 + 9 + 3 + (-2) + 2 + 1 + 5 + (-2) + 7 + 7 + 10 + 10 = 40\). | |
![]()
|
|
G. Бандитский блюз
Комбинаторика
математика
дп
бпф
*2900
Джапате, путешествуя через леса Мала, увидел N мешков с золотом, лежащих в ряд. У каждого мешка есть своя масса, отличная от масс других мешков, от 1 до N. Джапате может унести с собой только один мешок с золотом, поэтому он использует стратегию для выбора мешка: изначально он стартует с пустым мешком (массы 0), после чего начинает идти вдоль ряда мешков, и если он видит, что текущий мешок тяжелее мешка в его руках, он подбирает текущий мешок. Джапате понял, что если он пойдёт слева направо, то он подберёт A мешков, а если он пойдёт справа налево, он подберёт B мешков. Теперь ему интересно, сколько существует таких перестановок мешков, в которых он подбирает A мешков, идя слева направо и B мешков, идя справа налево, используя вышеупомянутую стратегию. Так как ответ может быть крайне велик, выведите его по модулю 998244353. Выходные данные Выведите одно целое число — число подходящих перестановок по модулю 998244353. Примечание В примере 1 единственная возможная перестановка — [1] В примерах 2 и 3 возможны всего две перестановки размера 2:{[1, 2], [2, 1]}. Величины a и b для первой перестановки равны 2 и 1 соответственно, а для второй перестановки эти величины равны 1 и 2 соответственно. В примере 4 из 120 возможных перестановок [1, 2, 3, 4, 5] всего 22 удовлетворяют заданным в примере a и b. | |
![]()
|
|
G. Разбиения
Комбинаторика
математика
теория чисел
*2700
Дано множество из n элементов, пронумерованных от 1 до n. Вес i-го объекта равен wi. Вес некоторого подмножества этого множества рассчитывается по формуле  . Вес разбиения R данного множества на k подмножеств равен . Вес разбиения R данного множества на k подмножеств равен  (напоминаем, разбиением называется множество таких подмножеств данного множества, что каждый элемент данного множества принадлежит ровно одному множеству из разбиения). (напоминаем, разбиением называется множество таких подмножеств данного множества, что каждый элемент данного множества принадлежит ровно одному множеству из разбиения). Посчитайте суммарный вес всех различных разбиений данного множества на k непустых подмножеств по модулю 109 + 7. Два разбиения считаются различными, если существуют два объекта x и y, такие, что в одном разбиении они принадлежат разным множествам, а в другом — одному и тому же. Выходные данные Выведите единственное число — суммарный вес всех различных разбиений на k непустых подмножеств по модулю 109 + 7. Примечание Возможные разбиения в первом тесте из условия: - {{1, 2, 3}, {4}}, W(R) = 3·(w1 + w2 + w3) + 1·w4 = 24;
- {{1, 2, 4}, {3}}, W(R) = 26;
- {{1, 3, 4}, {2}}, W(R) = 24;
- {{1, 2}, {3, 4}}, W(R) = 2·(w1 + w2) + 2·(w3 + w4) = 20;
- {{1, 3}, {2, 4}}, W(R) = 20;
- {{1, 4}, {2, 3}}, W(R) = 20;
- {{1}, {2, 3, 4}}, W(R) = 26;
Возможные разбиения в втором тесте из условия: - {{1, 2, 3, 4}, {5}}, W(R) = 45;
- {{1, 2, 3, 5}, {4}}, W(R) = 48;
- {{1, 2, 4, 5}, {3}}, W(R) = 51;
- {{1, 3, 4, 5}, {2}}, W(R) = 54;
- {{2, 3, 4, 5}, {1}}, W(R) = 57;
- {{1, 2, 3}, {4, 5}}, W(R) = 36;
- {{1, 2, 4}, {3, 5}}, W(R) = 37;
- {{1, 2, 5}, {3, 4}}, W(R) = 38;
- {{1, 3, 4}, {2, 5}}, W(R) = 38;
- {{1, 3, 5}, {2, 4}}, W(R) = 39;
- {{1, 4, 5}, {2, 3}}, W(R) = 40;
- {{2, 3, 4}, {1, 5}}, W(R) = 39;
- {{2, 3, 5}, {1, 4}}, W(R) = 40;
- {{2, 4, 5}, {1, 3}}, W(R) = 41;
- {{3, 4, 5}, {1, 2}}, W(R) = 42.
| |
![]()
|
|
H. K путей
Структуры данных
Комбинаторика
математика
дп
бпф
*3100
Дано дерево из \(n\) вершин. Требуется выбрать \(k\) (не обязательно различных) простых путей так, чтобы все ребра дерева можно было разбить на три множества: ребра, которые не принадлежит ни одному из путей, ребра, которые принадлежат ровно одному из этих пути, и ребра, которые принадлежат всем путям, причем последнее множество должно содержать хотя бы одно ребро. Посчитайте количество способов так выбрать \(k\) путей по модулю \(998244353\). Пути пронумерованы, иными словами, два способа считаются различными, если существует такое \(i\) (\(1 \leq i \leq k\)) и ребро, которое присутствует в \(i\)-м пути в одном способе и отсутствует в другом. Выходные данные Выведите количество способов выбрать \(k\) пронумерованных не обязательно различных простых путей так, чтобы по каждому ребру дерева проходило либо ни одного пути, либо проходил один путь, либо \(k\), и пересечение всех путей было непустым. Так как ответ может быть большим, выведите его по модулю \(998244353\). Примечание В первом примере подходят следующие последовательности путей: - \(((1,2), (1,2))\),
- \(((1,2), (1,3))\),
- \(((1,3), (1,2))\),
- \(((1,3), (1,3))\),
- \(((1,3), (2,3))\),
- \(((2,3), (1,3))\),
- \(((2,3), (2,3))\).
Во втором примере \(k=1\), поэтому подходят все \(n \cdot (n - 1) / 2 = 5 \cdot 4 / 2 = 10\) путей. В третьем примере ответ \(\geq 998244353\), поэтому он был взят по модулю \(998244353\), не забудьте про это! | |
![]()
|
|
G. Командные игроки
Комбинаторика
*2700
Есть \(n\) игроков, пронумерованных от \(0\) до \(n-1\). У каждого игрока есть ранг. Ранг \(i\)-го игрока равен \(i\). Игроки могут создавать команды: команда должна состоять ровно из трех игроков, и никакая пара игроков из этой команды не должна быть в ссоре друг с другом. Ранг команды подсчитывается следующим способом: пусть \(i\), \(j\), \(k\) — ранги игроков в команде и \(i < j < k\), тогда ранг команды будет равен \(A \cdot i + B \cdot j + C \cdot k\). Вам дана информация о парах поссорившихся игроков. Посчитайте сумму рангов всех возможных команд по модулю \(2^{64}\). Выходные данные Выведите единственное число — сумму рангов всех возможных команд по модулю \(2^{64}\). Примечание В первом примере все \(4\) возможные команды валидны, то есть возможными командами являются: {0, 1, 2}, {0, 1, 3}, {0, 2, 3} {1, 2, 3}. Во втором примере следующие команды валидны: {0, 2, 3}, {1, 2, 3}. В третьем примере следующие команды валидны: {0, 1, 2}, {0, 1, 4}, {0, 1, 5}, {0, 2, 4}, {0, 2, 5}, {1, 2, 3}, {1, 2, 4}, {1, 2, 5}. | |
![]()
|
|
B. Петя и перестановки
Комбинаторика
математика
*1800
Петя любит придумывать задачи со случайными данными. На этот раз ему понадобилась случайная перестановка. Он решил сгенерировать её следующим образом: он берет тождественную перестановку чисел от \(1\) до \(n\), а потом \(3n\) раз берёт случайную пару различных элементов и меняет их местами. Лёша очень завидует Пете, и пытается ему во всем подражать. Лёша тоже придумал задачу со случайной перестановкой, и генерирует её как Петя, но меняет местами случайную пару элементов не \(3n\) раз, а \(7n+1\). Потому что это более случайно, понятно?! Вам попал в руки тест, и вы хотите узнать, от какой он задачи. Выходные данные Если тест сгенерирован способом Пети, выведите «Petr» (без кавычек). Если тест сгенерирован способом Лёши, выведите «Um_nik» (без кавычек). Примечание Обратите внимание, что пример из условия не удовлетворяет ограничениям на \(n\) и приведён только для демонстрации формата ввода и вывода. Тем не менее, ваше решение должно проходить этот тест. Из-за случайности тестов в этой задаче запрещены взломы. | |
![]()
|
|
E. Номер автобуса
Перебор
Комбинаторика
математика
*1800
Вечер выдался не из легких... Вася играл безупречно, но, как это часто бывает, его подводила команда. Поражения следовали одно за другим, а Васе очень нужна была победа! Неудивительно, что в итоге Вася лёг спать чуть позже запланированного времени и совершенно не выспался. Утром Вася пришел на остановку стал ждать автобус до университета. Мысли путались в светлой голове Васи, поэтому он не смог вспомнить номер нужного ему автобуса и сел в первый попавшийся — им оказался автобус с номером \(n\). Сев в автобус, Вася подумал, что из-за своего состояния он мог перепутать порядок цифр в номере автобуса. Более того, некоторые цифры он мог «увидеть» несколько раз, но те цифры, которые он увидел, точно были в настоящем номере автобуса. Например, если Вася увидел номер 2028, то в оригинале номер автобуса мог быть 2028, 8022, 2820 или даже просто 820. При этом, например, номера 80, 22208, 52 точно не могли быть номером автобуса. Кроме того, разумеется, номер автобуса не начинался на цифру 0, поэтому, номер 082 тоже не мог быть настоящим номером автобуса. По заданному числу \(n\) необходимо определить, сколько существует вариантов исходного номера автобуса. Выходные данные Вывести единственное число — количество возможных вариантов настоящего номера автобуса. Примечание В первом примере возможны лишь варианты \(97\) и \(79\). Во втором примере возможные номера автобуса (в порядке возрастания): \(208\), \(280\), \(802\), \(820\), \(2028\), \(2082\), \(2208\), \(2280\), \(2802\), \(2820\), \(8022\), \(8202\), \(8220\). | |
![]()
|
|
F. Зарплаты в комуупании
Деревья
Комбинаторика
математика
дп
*2700
Аллен выпустился из Муусского техмулогоческого института (MIT) и основал стартап! Аллен — президент стартапа. Он нанял \(n-1\) работника, у каждого из которых есть один непосредственный начальник. Если \(u\) является начальником \(v\), а \(v\) является начальником \(w\), то \(u\) является начальником \(w\). Кроме того, нет таких \(u\) и \(v\), что \(u\) является начальником \(v\) и \(v\) является начальником \(u\). У Аллена нет начальников. Аллен — сотрудник номер \(1\), все остальные пронумерованы от \(2\) до \(n\). Наконец, Аллен должен назначить каждому в компании, включая себя, зарплату. Из-за бюджетных ограничений зарплата каждого из сотрудников должна быть между \(1\) и \(D\) включительно. Кроме того, никто не может получать больше, чем его начальник. Помогите Аллену найти количество способов назначить сотрудникам зарплаты. Эта величина может быть достаточно большой, поэтому выведите ее по модулю \(10^9 + 7\). Выходные данные Выведите одно целое число: количество способов назначить зарплаты по модулю \(10^9 + 7\). Примечание В первом примере сотрудники с номерами 2 и 3 подчиняются непосредственно Аллену. Три зарплаты по порядку могут быть \((1,1,1)\), \((2,1,1)\), \((2,1,2)\), \((2,2,1)\) или \((2,2,2)\). Во втором примере сотрудник 2 подчиняется Аллену, а сотрудник 3 подчиняется сотруднику 2. Возможные зарплаты равны \((1,1,1)\), \((2,1,1)\), \((2,2,1)\), \((2,2,2)\), \((3,1,1)\), \((3,2,1)\), \((3,2,2)\), \((3,3,1)\), \((3,3,2)\), \((3,3,3)\). | |
![]()
|
|
B. Римские цифры
Перебор
Комбинаторика
математика
дп
*2000
жадные алгоритмы
Рассмотрим систему счисления, основанную на упрощенных римских цифрах. Есть цифры I, V, X, L соответствующие значениям \(1\), \(5\), \(10\) и \(50\) соответственно. Другие римские цифры использовать нельзя. Числа в такой системе счисления записываются как последовательности из одной или более цифр. Определим значение записи просто как сумму всех цифр в ней. Например, запись XXXV соответствует числу \(35\), а запись IXI — числу \(12\). Заметим, что это отличается от традиционной римской системы счисления — например, любая последовательность цифр является корректной, а также порядок цифр не имеет значения (например, запись IX означает \(11\), а не \(9\)). Несложно заметить, что одно и то же число можно выразить несколькими способами. Вычислите сколько существует различных чисел, которые можно записать используя хотя бы одну запись из ровно \(n\) римских римских цифр I, V, X и L. Выходные данные Выведите одно число — количество различных чисел, которые можно выразить используя ровно \(n\) римских цифр I, V, X и L. Примечание В первом примере есть ровно \(4\) различных числа, которые можно получить — I, V, X и L. Во втором примере можно получить числа \(2\) (II), \(6\) (VI), \(10\) (VV), \(11\) (XI), \(15\) (XV), \(20\) (XX), \(51\) (IL), \(55\) (VL), \(60\) (XL) и \(100\) (LL). | |
![]()
|
|
C. Небо в огне
Комбинаторика
математика
*2500
На одной из планет Солнечной системы, в Атмосферном Университете, любят играть в бинго. Известно, что этой планете месяц состоит ровно из \(n^2\) дней, поэтому повсеместно используются календари, представляющие собой квадратную таблицу \(n\) на \(n\). Погодные условия на планете не менее необычны. Вследствие уникального состава атмосферы, при взаимодействии со солнечным светом небо каждый день принимает один из трёх цветов: синий, зелёный или красный. Для игры в бинго нужно в течении месяца наблюдать за погодными условиями — после каждого дня, его клетка в календаре расскрашивается в цвет неба в тот день, то есть в синий, зелёный или красный. В конце месяца студенты разглядывают календарь. Если хотя бы один столбец или строка состоит из клеток только одного цвета, то месяц называется удачным. Две раскраски календаря называются различными, если в них хотя бы одна из ячеек имеет разные цвета. Нетрудно заметить, что всего существует \(3^{n \cdot n}\) различных раскрасок. Посчитайте, сколько среди них удачных. Так как это количество может быть достаточно большим, выведите его по модулю \(998244353\). Выходные данные Выведите одно число — количество удачных раскрасок календаря по модулю \(998244353\) Примечание В первом примере любая раскраска является удачной, так как единственный столбец состоит только из одного цвета. Во втором примере удачными, в том числе, являются следующие раскраски: 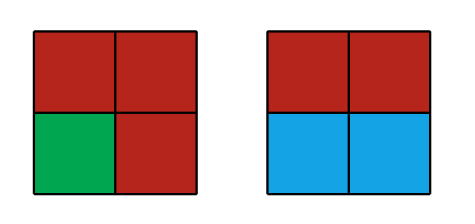 А вот эти раскраски удачными не являются: 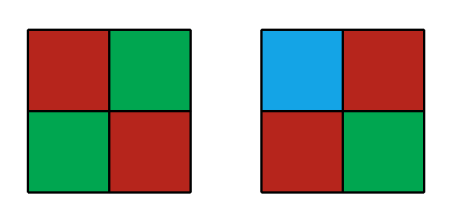 | |
![]()
|
|
D. Циклы в произведении
Деревья
Комбинаторика
разделяй и властвуй
*2900
Рассмотрим дерево (то есть неориентированный связный граф без циклов) \(T_1\) и дерево \(T_2\). Определим их декартово произведение \(T_1 \times T_2\) следующим образом. Пусть \(V\) — множество вершин \(T_1\), а \(U\) — множество вершин \(T_2\). Тогда множеством вершин \(T_1 \times T_2\) является \(V \times U\), то есть множество упорядоченных пар вершин, где первая вершина из \(V\), а вторая из \(U\). Проведём ребра следующего вида: - Между \((v, u_1)\) и \((v, u_2)\) есть неориентированное ребро, если \(u_1\) и \(u_2\) смежны в графе \(U\).
- Аналогично между \((v_1, u)\) и \((v_2, u)\) есть неориентированное ребро, если \(v_1\) и \(v_2\) смежны в графе \(V\).
Обратите внимание на пояснения к примерам, они содержат картинки для произведения деревьев для тестов из примеров. Рассмотрим граф \(T_1 \times T_2\). Вычислите количество циклов в этом графе (не обязательно простых) длины \(k\). Выведите остаток при делении найденного количества на \(998244353\). Циклом называется последовательность вершин \(w_1\), \(w_2\), ..., \(w_k\), где \(w_i \in V \times U\), такая что любые две соседние вершины смежны, а также \(w_1\) смежно с \(w_k\). Циклы отличающиеся только циклическим сдвигом или направлением обхода всё равно считаются различными. Выходные данные Выведите одно число — количество циклов по модулю \(998244353\). Примечание Следующие три картинки иллюстрируют графы, которые получаются в результате произведения в тестах из условия. В первом примере список циклов длины \(2\) следующий: - «AB», «BA»
- «BC», «CB»
- «AD», «DA»
- «CD», «DC»
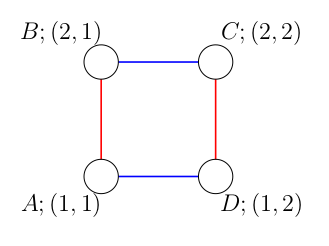 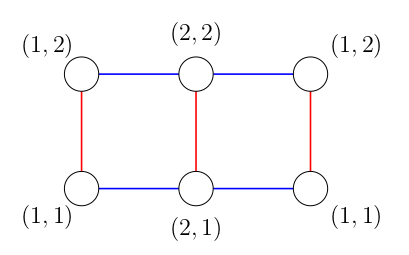 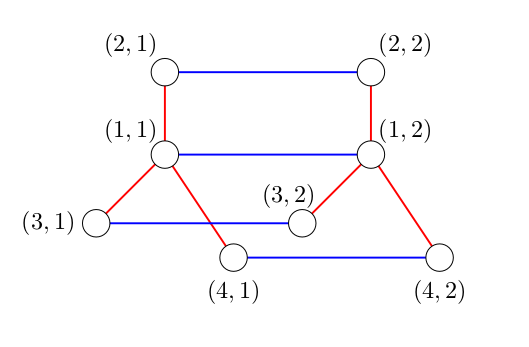 | |
![]()
|