| | | |
|
Лучшее место
Бинарный поиск
Сканирующая прямая
В зале ожидания на вокзале стоят N рядов из M кресел. Чтобы ожидающие не скучали, вместо некоторых кресел установлено K мощных Wi-Fi роутеров. Ожидающие стараются занять места ближе к роутерам, так как тогда они смогут смотреть ролики с Youtube или VK с более высоким разрешением, без задержек. Если пассажир сидит на месте с номером c в ряде r, а i-й роутер расположен на месте Ci в ряде Ri, то расстояние до i-го роутера вычисляется как max(|r−Ri|,|c−Ci|), где |x| – абсолютное значение x. Креслам в зале ожидания был присвоен приоритет от 1 до N⋅M−K, меньшие номера получили кресла с меньшим расстоянием до ближайшего роутера, среди кресел с одинаковым расстоянием до роутеров более удобными считаются кресла, стоящие в ряду с меньшим номером, а среди них — с меньшим номером места в ряду. На рисунке показан приоритет кресел в зале ожидания с 4 рядами из 7 кресел, в котором установлены 2 роутера (их позиции помечены черным цветом). Темно-серым цветом выделены кресла, стоящие на расстоянии 1 от роутеров, светло-серым — на расстоянии 2, белым — 3.

Напишите программу, которая вычисляет расстояние до ближайшего роутера от кресла с некоторым заданным приоритетом.
Первая строка ввода содержит четыре целых чисел — количество рядов N (2 ≤ N ≤ 109) и мест в ряду M (2 ≤ M ≤ 109), количество роутеров K (1 ≤ K ≤ 100, K < N⋅M), количество запросов Q (1 ≤ Q ≤ 100). Далее следует K строк, содержащих два целых числа — местонахождение роутеров: номер ряда Ri (1 ≤ Ri ≤ N) и номер места в ряду Ci (1 ≤ Сi ≤ M). Среди них нет совпадающих. Далее следует строка, содержащая Q целых чисел в диапазоне от 1 до N⋅M−K – приоритеты кресел.
Вывести для каждого запроса на отдельной строке одно целое число — расстояние до ближайшего роутера от кресла с заданным приоритетом.
| Ввод |
Вывод |
|
4 7 2 4
2 5
4 4
1 6 16 26
|
1
1
2
3
|
| |
![]()
|
|
Объединение прямоугольников
Сканирующая прямая
На плоскости задано N прямоугольников с вершинами в точках с целыми координатами и сторонами, параллельными осям координат. Необходимо найти площадь их объединения.
Входные данные
В первой строке входного файла указано число N (0≤N≤1500). В следующих N строках заданы по 4 целых числа x1, y1, x2, y2 — сначала координаты левого нижнего угла прямоугольника, потом правого верхнего (0≤x1≤x2≤109, 0≤y1≤y2≤109). Обратите внимание, что прямоугольники могут вырождаться в отрезки и даже в точки.
Выходные данные
В выходной файл выведите единственное число — ответ на задачу.
| Ввод |
Вывод |
|
3
1 1 3 5
5 2 7 4
2 4 6 7
|
23 |
|
2
0 0 2 2
1 3 2 4
|
5 |
| |
![]()
|
|
Покраска забора
Сканирующая прямая
Том Сойер уговорил n своих друзей помочь ему в нелегком деле покраски забора, окружающего дом тетушки Полли. Забор представляет собой k последовательных досок, пронумерованных от 1 до k, причем после k-й доски опять идет первая.
Друзья Тома очень привередливы, i-й друг согласен участвовать в покраске только в том случае, если ему дадут покрасить участок из ровно ai последовательных досок. Кисточка у Тома только одна, поэтому друзья будут красить по очереди и сразу весь отведенный им отрезок. Тому остается лишь выбрать порядок, в котором приглашать друзей, а также выбрать для каждого желаемое количество последовательных досок.
При этом каждый из друзей Тома готов красить как еще неокрашенную доску забора, так и доску, которую уже покрасил один из его предшественников. Тем не менее, друзья получают больше удовольствия от покраски неокрашенной доски. Том хочет выбрать число x и распределить отрезки забора для покраски таким образом, чтобы каждый из его друзей покрасил хотя бы x неокрашенных досок. Том очень любит своих друзей и хочет, чтобы каждый из них получил от процесса покраски забора максимальное удовольствие, поэтому он пытается максимизировать x.
Помогите Тому понять, сколько радости он сможет доставить своим друзьям.
Формат входных данных
Первая строка входного файла содержит два целых числа n (1 ≤ n ≤ 105 ) и k (1 ≤ k ≤ 109 ). Следующая строка содержит n целых чисел — значения ai (1 ≤ ai ≤ k).
Формат выходных данных
Выведите одно число — максимальное возможное значение x.
| Ввод |
Вывод |
2 100
5 10 |
5 |
4 10
7 8 3 5 |
2 |
Пояснение
В первом примере x = 5, так как один из друзей просто не хочет красить больше пяти досок. Он придет первым, покрасит свои пять, после чего еще 10 неокрашенных досок достанется второму другу Тома. Оставшиеся 85 досок Тому придется красить самому.
Во втором примере достичь x = 2 можно, например, так. Сначала третий друг красит доски с 4 по 6 (3 неокрашенных доски). Затем четвертый друг красит доски с 1 по 5 (3 неокрашенных доски). Затем второй друг красит доски с 1 по 8 (2 неокрашенных доски). Наконец, первый друг красит доски с 6 по 10 и с 1 по 2 (2 неокрашенных доски, заметим, что забор идет по циклу и эти доски образуют последовательный отрезок).
| |
![]()
|
|
Минимальное покрытие
Сканирующая прямая
На прямой задано некоторое множество отрезков с целочисленными координатами концов \([L_i, R_i]\). Выберите среди данного множества подмножество отрезков, целиком покрывающее отрезок \([0, M]\), (M — натуральное число), содержащее наименьшее число отрезков.
Входные данные
В первой строке указана константа M (\(1<=M<=5000\)). В каждой последующей строке записана пара чисел Li и Ri (\(|L_i|,|R_i| < 50000\)), задающая координаты левого и правого концов отрезков. Список завершается парой нулей. Общее число отрезков не превышает 100 000.
Выходные данные
В первой строке выходного файла выведите минимальное число отрезков, необходимое для покрытия отрезка \([0; M]\). Далее выведите список покрывающего подмножества, упорядоченный по возрастанию координат левых концов отрезков. Список отрезков выводится в том же формате, что и во входe. Завершающие два нуля выводить не нужно. Если покрытие отрезка \([0; M]\) исходным множеством отрезков \([L_i, R_i]\) невозможно, то следует вывести единственную фразу “ No solution”.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1
-1 0
-5 -3
2 5
0 0
|
No solution |
| 2 |
1
-1 0
0 1
0 0
|
1
0 1 |
| |
![]()
|
|
Автобусы
Сортировка подсчетом
Сканирующая прямая
Жадный алгоритм
Новый Президент Тридевятой республики начал свою деятельность с полной ревизии системы общественного транспорта страны. В результате на основе социологических опросов населения было составлено идеальное ежедневное расписание движения междугородних автобусов, утвержденное Парламентом республики.
Более того, было решено заменить весь автобусный парк одинаковыми новыми, очень дорогими, но гораздо более надежными, красивыми и удобными машинами.
Автобусная сеть страны охватывает N городов, занумерованных целыми числами от 1 до N.
Идеальное расписание содержит M ежедневных рейсов, i-й рейс начинается в городе Fi в момент времени Xi и заканчивается в некотором другом городе Gi в момент времени Yi. Продолжительность каждого рейса ненулевая и строго меньше 24 часов. Рейс i выполняется одним из автобусов, находящихся в момент времени Xi в городе Fi.
Новые автобусы не требуют ремонта и могут работать круглосуточно, поэтому автобус, прибывший в некоторый момент времени в некоторый город, всегда готов в тот же самый момент времени или позже отправиться в путь для обслуживания любого другого рейса из данного города. Автобус может выехать из города, только выполняя какой-либо рейс из расписания.
Предполагается, что расписание будет действовать неограниченное время, поэтому может оказаться так, что его невозможно обслужить никаким конечным числом автобусов.
Определите наименьшее количество новых автобусов, достаточное для обеспечения движения по расписанию в течение неограниченного периода времени.
Входные данные
В первой строке задаются целые числа N и М (1 ≤ N, M ≤ 100 000) — количество городов и рейсов автобусов соответственно.
В каждой из следующих M строк содержится описание рейса автобуса: номер города отправления Fi, время отправления Xi, номер города назначения Gi (Fi ≠ Gi), время прибытия Yi, отделенные друг от друга одним пробелом. Время прибытия и отправления задается в формате HH:MM, где HH — часы от 00 до 23, MM — минуты от 00 до 59.
Выходные данные
Выведите одно число — минимально необходимое количество автобусов. Если расписание невозможно обслуживать в течение неограниченного периода времени конечным числом автобусов, выведите число -1.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 6
1 10:00 2 12:00
1 10:00 3 09:00
3 12:00 4 23:00
2 11:00 4 13:00
4 12:00 1 11:00
4 12:00 1 10:30 |
8 |
| |
![]()
|
|
Новый аэропорт
Сортировка подсчетом
Сканирующая прямая
ЕГЭ_информатика
ЕГЭ-26. Обработка массива целых чисел. Сортировка
В аэропорту города Че начал работать новый аэропорт. В первые сутки работы был записан файл с временем прилета и вылета самолетов. Самолеты, которые улетали на следующие сутки в файл не были записаны. Определите максимальное число самолетов, которые находились в аэропорту одновременно и в течении какого максимального промежутка времени (в минутах) находилось в аэропорту такое число самолетов. Учитываются только самолеты, информация о которых записана в файле.
Входные данные
Первая строка содержит число N - общее количество самолетов за весь день. В каждой из следующих N строк содержится пара значений, где первое значение в паре показывает время прилета самолета, а второе значение - время вылета (время прилета и вылета находится в диапазоне от 00:00 до 23:59, причем гарантируется, что время прилета меньше времени вылета) . Все данные в строках разделены одним пробелом.
При совпадающем времени считается, что прилет происходит раньше вылета.
В ответе запишите два целых числа через пробел: сначала максимальное количество самолетов, которые находились в аэропорту одновременно, затем максимальный промежуток времени (в минутах), в течении которого в аэропорту было такое число транзитных самолетов.
Если самолет прилетел в 12:00, а вылетел в 12:01, то считается, что он пробыл в аэропорту 2 минуты.
Файл к заданию
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6
09:00 10:07
10:20 11:35
12:00 17:00
11:00 11:30
11:20 12:30
11:30 18:15 |
4 1 |
| |
![]()
|
|
Частица Му
Сканирующая прямая
Углубившись на карантине в изучение физики, коровы открыли "му-частицы"
В настоящий момент они проводят эксперимент с N "му-частицами" (1 ≤N ≤ 105). Частица i имеет "спин", описываемый двумя целыми числами xi и yi в диапазоне −109…109 включительно. Иногда две "му-частицы" взаимодействуют. Это может случиться только с такими частицами со спинами (xi,yi) и (xj,yj) у которых xi≤xj и yi≤yj. При этих условиях ровно одна из этих частиц исчезает (а с другой ничего не случится). В каждый момент времени может случиться не более одного взаимодействия.
Коровы хотят узнать минимальное количество "му-частиц", которые могут остаться после некоторой произвольной последовательности взаимодействий.
Входные данные
Первая строка содержит одно целое число N, начальное число "му-частиц". Каждая из последующих N строк содержит два разделённых пробелом целых числа, определяющих спин этой частицы. Все спины различны.
Выходные данные
Одно целое число, минимальное количество "му-частиц", которые могут остаться после некоторой произвольной последовательности взаимодействий.
Примеры
| № |
Входные данные |
Выходные данные |
Примечание |
| 1 |
4
1 0
0 1
-1 0
0 -1 |
1 |
Одна из возможных последовательностей взаимодействий:
Частицы 1 и 4 взаимодействуют, частица 1 исчезает.
Частицы 2 и 4 взаимодействуют, частица 4 исчезает.
Частицы 2 и 3 взаимодействуют, частица 3 исчезает.
Только частица 2 остаётся. |
| 2 |
3
0 0
1 1
-1 3 |
2 |
Частица 3 не может взаимодействовать ни с одной из других частиц, поэтому она должна остаться. Одна из частиц 1 и 2 тоже должна остаться. |
| |
![]()
|
|
Социальное дистанцирование II
Сканирующая прямая
Фермер Джон продолжает бороться за здоровье своих коров.
Имеется N cows (1≤N≤1000) коров, некоторые из которых больны. Коровы выстроены в ряд (на числовой прямой), корова i стоит на позиции xi. ФД знает что если другая корова находится в радиусе R от больной, то она тоже заболевает. А потом заболевают коровы, которые находятся в радиусе R от этой и т.д.
К несчастью, ФД не знает точное значение R. Однако он знает, какие из его коров больны. По этим данным определите минимальное количество изначально инфицированных болезнью коров.
Входные данные
Первая строка ввода содержит N. Каждая из последующих N строк описывает одну корову двумя числами x и s, где x - позиция коровы, а s равно 0 для здоровой коровы и 1 для больной. Как минимум 1 корова больна. И все коровы, которые могли стать больными от распространения болезни уже больны.
Выходные данные
Определите минимальное количество коров, которые изначально были больны, перед любым распространением болезни.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6
7 1
1 1
15 1
3 1
10 0
6 1 |
3 |
| |
![]()
|
|
Раскраска отрезков
Использование сортировки
Сканирующая прямая
У Джона Доу есть n отрезков на прямой. Отрезок (a, b) (a < b) — это множество точек x, таких, что a < x < b. Говорят, что отрезки (a1, b1) и (a2, b2) пересекаются, если существует такая точка c, что a1 < c < b1 и a2 < c < b2.
Джон хочет покрасить каждый отрезок в чёрный или белый цвет так, чтобы никакие два отрезка одного цвета не пересекались. Он хочет узнать, сколько существует различных способов покрасить отрезки таким образом.
Две покраски считаются различными, если существует отрезок, который в одной покраске покрашен в белый цвет, а в другой — в чёрный.
Пусть количество способов покрасить отрезки равно x. Выведите остаток от деления x на 106 + 3.
Входные данные
В первой строке записано целое число n (1 ≤ n ≤ 105) — количество отрезков у Джона. В следующих n строках находится описание отрезков. В i-й из них записано два числа li и ri (0 ≤ li < ri ≤ 109) — координаты концов i-го отрезка.
Выходные данные
Выведите остаток от деления x (количество способов покрасить отрезки) на 106 + 3.
Примеры тестов
Входные данные
Входные данные
3
1 2
1 3
1 4
Входные данные
4
1 2
2 3
3 4
4 5
Примечание
Тесты поделены на группы, но оцениваются отдельно.
- n ≤ 3 — 10 баллов
- n ≤ 15 — 30 баллов
- n ≤ 100 — 20 баллов
- ai ≤ 106 — 20 баллов
- Без дополнительных ограничений — 20 баллов
| |
![]()
|
|
Урок физкультуры
Словари
Сканирующая прямая
Структуры данных
Дерево отрезков, RSQ, RMQ
Феоктист Всеволодович — преподаватель физкультуры старой закалки, глубоко убеждённый, что в начале каждого урока школьников необходимо построить по росту. Для этого он сначала просит школьников построиться самостоятельно, после чего последовательно меняет местами про- извольную пару стоящих рядом учеников, пока шеренга не примет желанный вид.
Всего на урок пришло N детей, изначально построившихся таким образом, что рост стоящего на позиции i равен hi (используется нумерация c 1). Можно считать, что все числа hi различны и лежат в диапазоне от 1 до N. Шеренга считается упорядоченной, если на первой позиции стоит школьник ростом один, на второй позиции стоит школьник ростом два и так далее.
Феоктист Всеволодович получает большое удовольствие от процесса упорядочивания школьни- ков, поэтому он всегда выбирает наиболее длинную последовательность обменов. С другой стороны, он не хочет чтобы ученики догадались о том, что он умышленно затягивает построение, поэтому никогда не делает заведомо бессмысленных обменов. А именно, преподаватель никогда не меняет местами школьников на позициях i и j, если hi < hj . Очевидно, что данное ограничение делает процесс сортировки шеренги по росту конечным.
Староста Саша очень любит играть в волейбол и прекрасно понимает, что чем дольше препо- даватель будет расставлять всех по местам, тем меньше времени останется для игры. Ученики уже построились некоторым образом, а Феоктист Всеволодович вышел поговорить по телефону, так что Саша может успеть поменять местами ровно двух школьников, необязательно стоящих рядом в ше- ренге. Разумеется, он хочет сделать это таким образом, чтобы преподаватель как можно быстрее закончил упорядочивать шеренгу (Саша давно уже раскусил, как именно действует Феоктист Всево- лодович). С информатикой у старосты всегда были определённые проблемы, поэтому ему требуется ваша помощь.
Формат входных данных
В первой строке ввода содержится единственное число N — количество школьников на уроке (1 <= N <= 1 000 000). Во второй строке записано N различных целых чисел hi (1 <= hi <= N). i-е число соответствует росту школьника стоящего на i-й позиции.
Формат выходных данных
Выведите два числа — номера позиций школьников, которым необходимо поменяться местами, чтобы минимизировать количество действий преподавателя. Если таких пар несколько, то выведите любую из них. Если никому меняться местами не нужно, выведите -1 -1.
| Ввод |
Вывод |
5
2 4 3 5 1 |
2 5 |
| 4 1 2 3 4 |
-1 -1 |
10
2 3 7 1 5 10 4 6 9 8 |
3 7 |
| |
![]()
|
|
Тупики
Задачи на моделирование
Сканирующая прямая
Куча
На вокзале есть K тупиков, куда прибывают электрички. Этот вокзал является их конечной станцией, поэтому электрички, прибыв, некоторое время стоят на вокзале, а потом отправляются в новый рейс (в ту сторону, откуда прибыли).
Дано расписание движения электричек, в котором для каждой электрички указано время ее прибытия, а также время отправления в следующий рейс. Электрички в расписании упорядочены по времени прибытия. Поскольку вокзал — конечная станция, то электричка может стоять на нем довольно долго, в частности, электричка, которая прибывает раньше другой, отправляться обратно может значительно позднее.
Тупики пронумерованы числами от 1 до K. Когда электричка прибывает, ее ставят в свободный тупик с минимальным номером. При этом если электричка из какого-то тупика отправилась в момент времени X, то электричку, которая прибывает в момент времени X, в этот тупик ставить нельзя, а электричку, прибывающую в момент X+1 — можно.
Напишите программу, которая по данному расписанию для каждой электрички определит номер тупика, куда прибудет эта электричка.
Входные данные
Сначала вводятся число K — количество тупиков и число N — количество электропоездов (1≤K≤100000, 1≤N≤100000). Далее следуют N строк, в каждой из которых записано по 2 числа: время прибытия и время отправления электрички. Время задается натуральным числом, не превышающим 109. Никакие две электрички не прибывают в одно и то же время, но при этом несколько электричек могут отправляться в одно и то же время. Также возможно, что какая-нибудь электричка (или даже несколько) отправляются в момент прибытия какой-нибудь другой электрички. Время отправления каждой электрички строго больше времени ее прибытия.
Все электрички упорядочены по времени прибытия. Считается, что в нулевой момент времени все тупики на вокзале свободны.
Выходные данные
Выведите N чисел — по одному для каждой электрички: номер тупика, куда прибудет соответствующая электричка. Если тупиков не достаточно для того, чтобы организовать движение электричек согласно расписанию, выведите два числа: первое должно равняться 0 (нулю), а второе содержать номер первой из электричек, которая не сможет прибыть на вокзал.
| |
![]()
|
|
Формула - 3
Сканирующая прямая
Обход в глубину
Элементарная геометрия
В ежегодном чемпионате Флатландии (которая, естественно, является плоским миром) по космическим гонкам "Формула-3" участвуют N космических скутеров, имеющие форму треугольников. До начала гонок скутеры занимают положение в стартовой зоне согласно результатам жеребьевки.
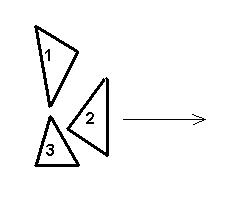
Скутеры стартуют строго по порядку. Каждый скутер,получив команду «старт», уезжает в положительном направлении оси Ox. Следующий скутер стартует лишь тогда, когда предыдущий покинет стартовую зону. Скутеры уезжают строго параллельно оси Ox, скутеры в стартовой зоне не поворачивают и не разворачиваются.
Естественно, что если в момент старта на пути скутера окажется другой скутер, то произойдет авария (даже если скутер заденет лишь угол другого скутера своим углом).
Для уменьшения опасности столкновения скутеров на старте строго соблюдается следующее правило: прямые, параллельные оси Ox и пересекающие какой-то скутер, должны в совокупности пересекать не более 100 других скутеров (прямая, проходящая через одну точку скутера также считается прямой, пересекающей скутер). Например, на приведенном рисунке прямые, параллельные Ox и пересекающие скутер 2, проходят через 2 других скутера (1 и 3), а прямые, проходящие через скутер 1, проходят только через один другой скутер (номер 2).
Главный Судья гонок хочет определить порядок, в котором должны стартовать скутеры, чтобы аварии не произошло. Например, в ситуации, приведенной на рисунке, сначала должен стартовать скутер номер 2 (если попытается стартовать скутер номер 1 или 3, то он столкнется со скутером номер 2). После этого скутеры 1 и 3 могут стартовать в любом порядке (они друг другу не мешают).
Помогите Главному Судье — напишите программу, которая определит какой-нибудь порядок старта скутеров, чтобы аварии не произошло.
Входные данные
В первой строке вводится натуральное число N( 1 ≤ N ≤ 30 000).
В каждой из следующих N строк содержится по 6 чисел: x1, y1, x2, y2, x3, y3 – координаты трех вершин скутера на старте, целые числа, не превосходящие по модулю 106. В начальный момент скутеры не задевают друг друга.
Выходные данные
Выведите через пробел N чисел – номера скутеров в том порядке, в котором они могут стартовать. Если решений несколько, выведите одно любое из них. Если решений нет, выведите одно число -1.
Примечание
Первый тест соответствует приведенному рисунку. Ответ 2 3 1 в этом тесте также является правильным
| |
![]()
|
|
Древние цивилизации
Быстрая сортировка
Сканирующая прямая
Недавно Петя занялся изучением древних цивилизаций. Он нашел в энциклопедии даты рождения и гибели N
различных древних цивилизаций и теперь хочет узнать о влиянии культуры одних цивилизаций на культуру других.
Петя предположил, что между цивилизациями A и B
происходил культурный обмен, если они сосуществовали в течение некоторого ненулевого промежутка времени. Например, если цивилизация A зародилась в 600 году до н.э. и существовала до 400 года до н.э., а цивилизация B зародилась в 450 году до н.э. и существовала до 300 года до н.э., то культура каждой из этих цивилизаций оказывала влияние на развитие другой цивилизации в течение 50 лет. В то же время, если цивилизация C зародилась в 400 году до н.э. и существовала до 50 года до н.э., то она не смогла осуществить культурного обмена с цивилизацией A, в то время как культурный обмен с цивилизацией B продолжался в течение 100 лет.
Теперь для выполнения своих исследований Петя хочет найти такую пару цивилизаций, культурный обмен между которыми имел место на протяжении наименьшего ненулевого промежутка времени. Помогите ему!
Входные данные
В первой строке вводится число N – количество цивилизаций, культура которых интересует Петю (1≤N≤100 000). Следующие N строк содержат описание цивилизаций – в каждой строке задаются два целых числа Si и Ei
– год зарождения и год гибели соответствующей цивилизации. Все числа не превосходят 109
по абсолютной величине, Si < Ei.
Выходные данные
Выведите два числа – номера цивилизаций, периоды существования которых имеют наименьшее ненулевое пересечение. Если никакие две цивилизации не пересекаются во времени, выведите единственное число 0.
| |
![]()
|
|
Выпуклая оболочка
Сканирующая прямая
Многоугольники. Выпуклые оболочки
Множество на плоскости называется выпуклым, если вместе с любыми двумя точками оно содержит также и отрезок, соединяющий эти точки. Минимальное по включению выпуклое множество, содержащее заданное множество точек \(X\), называется выпуклой оболочкой множества \(X\).
В этой задаче вам требуется найти выпуклую оболочку множества точек, принадлежащих заданному набору углов.
Углом называется геометрическая фигура, образованная двумя лучами, выходящими из одной точки. Эта точка называется вершиной угла.
На рисунке слева приведены два угла, на рисунке справа изображена их выпуклая оболочка.
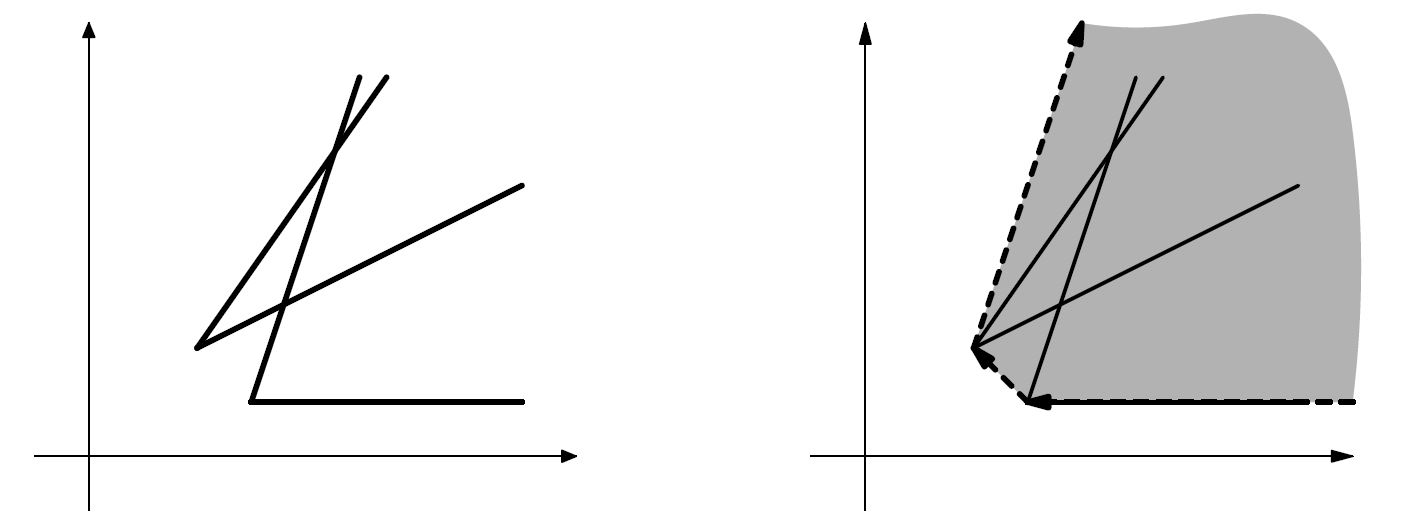
Формат входных данных
Первая строка содержит число \(n\) — количество углов (\(1 \le n \le 1000\)). Каждая из следующих \(n\) строк описывает углы. Каждый угол описывается координатами трех точек: вершины и двух отличных от вершины точек — по одной на каждом из лучей. Все координаты целые и не превышают \(10^4\) по абсолютной величине. Величина угла находится в диапазоне от 0 до 180 градусов, не включительно.
Формат выходных данных
Выведите границу выпуклой оболочки в виде последовательности направленных лучей, прямых и отрезков. Никакие два объекта в выходном файле не должны лежать на одной прямой. Все отрезки должны иметь длину больше нуля. Объекты должны быть перечислены в таком порядке, чтобы начало каждого следующего совпадало с концом предыдущего. Все числа должны быть целыми и не превосходить \(10^5\) по абсолютной величине. При проходе вдоль описанной границы выпуклая оболочка углов должна быть справа.
На первой строке выведите \(l\) — количество объектов в ответе. Следующие \(l\) строк должны содержать описание объектов. Объекты описываются следующим образом:
-
Отрезок: <<segment \(x_1\) \(y_1\) \(x_2\) \(y_2\)>>, где \((x_1, y_1)\) и \((x_2, y_2)\) — концы отрезка, отрезок считается направленным от \((x_1, y_1)\) к \((x_2, y_2)\).
-
Луч, направленный от начала: <<outray \(x_1\) \(y_1\) \(x_2\) \(y_2\)>>, где \((x_1, y_1)\) — начало луча, а \((x_2, y_2)\) — произвольная точка на луче, отличная от начала.
-
Луч, направленный к началу: <<inray \(x_1\) \(y_1\) \(x_2\) \(y_2\)>>, где \((x_2, y_2)\) — начало луча, а \((x_1, y_1)\) — произвольная точка на луче, отличная от начала.
-
Прямая: <<line \(x_1\) \(y_1\) \(x_2\) \(y_2\)>>, где \((x_1, y_1)\) и \((x_2, y_2)\) — две точки на прямой, причем при движении вдоль прямой в ее направлении точка \((x_1, y_1)\) следует ранее точки \((x_2, y_2)\).
Если выпуклой оболочкой является вся плоскость, то выведите \(l = 0\).
| |
![]()
|
|
Детский праздник
Задачи на моделирование
Бинарный поиск по ответу
Сканирующая прямая
Организаторы детского праздника планируют надуть для него M воздушных шариков. С этой целью они пригласили N добровольных помощников, i-й среди которых надувает шарик за Ti минут, однако каждый раз после надувания Zi шариков устает и отдыхает Yi минут. Теперь организаторы праздника хотят узнать, через какое время будут надуты все шарики при наиболее оптимальной работе помощников, и сколько шариков надует каждый из них. (Если помощник надул шарик, и должен отдохнуть, но больше шариков ему надувать не придется, то считается, что он закончил работу сразу после окончания надувания последнего шарика, а не после отдыха).
Входные данные
В первой строке входных данных задаются числа M и N (0 <= M <= 15000, 1 <= N <= 1000). Следующие N строк содержат по три целых числа - Ti, Zi и Yi соответственно (1 <= Ti, Yi <= 100, 1 <= Zi <= 1000).
Выходные данные
Выведите в первой строке число T - время, за которое будут надуты все шарики. Во второй строке выведите N чисел - количество шариков, надутых каждым из приглашенных помощников. Разделяйте числа пробелами. Если распределений шариков несколько, выведите любое из них.
| |
![]()
|
|
Триангуляция
Сортировка подсчетом
Сканирующая прямая
Вася нарисовал выпуклый N-угольник и провел в нем несколько диагоналей таким образом, что никакие две диагонали не пересекаются внутри N-угольника. Теперь он утверждает, что весь N-угольник оказался разбит на треугольники. Напишите программу, которая проверяет истинность Васиного утверждения.
Входные данные
Сначала вводятся числа N - количество вершин N-угольника (3 <= N <= 1000) и M - количество диагоналей, проведенных Васей. Далее на вход программы поступают M пар чисел, задающих диагонали (каждая диагональ задается парой номеров вершин, которые она соединяет). Гарантируется, что каждая пара чисел задает диагональ (то есть две вершины различны и не являются соседними), а также что никакие две пары не задают одну и ту же диагональ. Никакие две диагонали не пересекаются внутри N-угольника. Вершины N-угольника нумеруются числами от 1 до N.
Выходные данные
Если Васино утверждение верно, то программа должна выводить единственное число 0. В противном случае необходимо вывести сначала число K - количество вершин в какой-нибудь не треугольной части. Далее должно быть выведено K чисел - номера вершин исходного N-угольника, которые являются вершинами этой K-угольной части в порядке обхода этой части.
| |
![]()
|
|
Внутренние узлы
Сканирующая прямая
Рассмотрим бесконечную клетчатую бумагу. Покрасим некоторые узлы сетки в черный цвет, а остальные будем считать белыми. Узел V< называется внутренним, если он внутренний по вертикали и внутренний по горизонтали. Узел внутренний по горизонтали, если слева и справа от V расположены по крайней мере по одному черному узлу. Узел внутренний по вертикали, если сверху и снизу от V расположены по крайней мере по одному черному узлу.
На каждом шаге все внутренние белые узлы становятся черными, а остальные сохраняют свой цвет. Процесс прекращается, когда все внутренние вершины становятся черными. Напишите программу, которая вычисляет количество черных узлов после окончания процедуры перекраски.
Входные данные
Первая строка содержит одно целое число n (0 ≤ n≤ 100 000) – количество черных узлов в начале. Каждая из следующих n строк содержит два целых числа – координаты очередного черного узла, по модулю не превосходящие 109.
Выходные данные
Выведите число черных вершин после окончания всех перекрасок. Если процедура никогда не закончится, то выведите –1.
| |
![]()
|
|
Overplanting (Bronze)
Сканирующая прямая
Сжатие координат
Фермер Джон купил новую машину, которая умеет садить траву в прямоугольном регионе со сторонами, параллельными осям координат. К несчастью, эта машина однажды сломалась и посадила траву не в одном, а в N (1 <= N <= 10) различных регионах, некоторые из которых могут даже перекрываться.
По заданным прямоугольным регионам, засаженным травой, помогите ФД определить общую площадь, покрытую травой.
PROBLEM NAME: planting
Формат входных данных
* Строка 1: Целое число N.
* Строки 2..1+N: Каждая строка содержит четыре разделенных одиночными пробелами целых числа x1 y1 x2 y2 указывающих прямоугольный регион с верхним - левым углом (x1,y1) и нижним – правым углом (x2,y2). Все координаты – целые числа в диапазоне -10,000...10,000.
Формат выходных данных
* Строка 1: Общая площадь, покрытая травой.
| |
![]()
|