Плюсануть
Поделиться
Класснуть
Запинить


Олимпиадный тренинг

Вы можете самостоятельно решать эти задачи столько раз, сколько вам это понадобится.
   

Преобразуем четырехзначные

Обход в ширину

Витя хочет придумать новую игру с числами. В этой игре от игроков требуется преобразовывать четырехзначные числа не содержащие нулей при помощи следующего разрешенного набора действий:

1. Можно увеличить первую цифру числа на 1, если она не равна 9.
2. Можно уменьшить последнюю цифру на 1, если она не равна 1.
3. Можно циклически сдвинуть все цифры на одну вправо.
4. Можно циклически сдвинуть все цифры на одну влево.

Например, применяя эти правила к числу 1234 можно получить числа 2234, 1233, 4123 и 2341 соответственно. Точные правила игры Витя пока не придумал, но пока его интересует вопрос, как получить из одного числа другое за минимальное количество операций.


Входные данные: на вход подаются два различных четырехзначных числа, каждое из которых не содержит нулей. Каждое число с новой строки

Выходные данные: Программа должна вывести последовательность четырехзначных чисел, не содержащих нулей. Последовательность должна начинаться первым из данных чисел и заканчиваться вторым из данных чисел, каждое последующее число в последовательности должно быть получено из предыдущего числа применением одного из правил. Количество чисел в последовательности должно быть минимально возможным.

Примеры
№ Входные данные Выходные данные
1 1234
4321		 1234
2234
3234
4323
4322
4321

Длина пути

Обход в ширину Очередь

В неориентированном графе требуется найти длину кратчайшего пути между двумя вершинами.
 
Формат входных данных
В первой строке входных данных записано число N - количество вершин в графе (1 <= N <= 100). Далее с новой строки записана матрица смежности (0 обозначает отсутствие ребра, 1 - наличие ребра). В последней строке записаны номера двух вершин - начальной и конечной.
 
Формат выходных данных 
Выведите длину кратчайшего пути. Если пути не существует, выведите одно число -1.

Путь

Обход в ширину

В неориентированном графе требуется найти минимальный путь между двумя вершинами. 
 
Формат входных данных
В первой строке записано число N - количество вершин в графе (1 <= N <= 100). В следующих строках задана матрица смежности (0 обозначает отсутствие ребра, 1 - наличие ребра). В последней строке записаны номера двух вершин - начальной и конечной.
 
Формат выходных данных
Выведите сначала L - длину пути (количество ребер, которые нужно пройти). Затем выведите L+1 число - вершины в порядке следования вдоль этого пути. Если пути не существует, выведите одно число -1.
 
Примеры
№ Входные данные Выходные данные
1
5
0 1 0 0 1
1 0 1 0 0
0 1 0 0 0
0 0 0 0 0
1 0 0 0 0
3 5
 3
3 2 1 5

Один конь

Обход в ширину

На шахматной доске NxN в клетке (x1, y1) стоит голодный шахматный конь. Он хочет попасть в клетку (x2, y2), где растет вкусная шахматная трава. Какое наименьшее количество ходов он должен для этого сделать?
 
Формат входных данных
На вход программы поступает пять чисел: N, x1, y1, x2, y2 (\(5 <= N <= 20\), \(1 <= x_1,\ y_1,\ x_2,\ y_2 <= N\)). Левая верхняя клетка доски имеет координаты (1, 1), правая нижняя - (N, N).
 
Формат входных данных
Выведите единственное число K - наименьшее необходимое число ходов коня. 

Эвакуация

Обход в ширину

Одна из Сверхсекретных организаций, чье название мы не имеем право разглашать, представляет собой сеть из N подземных бункеров, соединенных равными по длине туннелями, по которым из любого бункера можно добраться до любого другого (не обязательно напрямую). Связь с внешним миром осуществляется через специальные засекреченные выходы, которые расположены в некоторых из бункеров.

Организации понадобилось составить план эвакуации персонала на случай экстренной ситуации. Для этого для каждого из бункеров необходимо узнать, сколько времени потребуется для того, чтобы добраться до ближайшего из выходов. Вам, как специалисту по таким задачам, поручено рассчитать необходимое время для каждого из бункеров по заданному описанию помещения Сверхсекретной организации. Для вашего же удобства бункеры занумерованы числами от 1 до N.

Формат входных данных
В первых двух строках вводятся два натуральных числа N, K (\(1 <= N <= 100000\), \(1 <= K <= N\)) — количество бункеров и количество выходов соответственно. В третьей строке через пробел записаны K различных чисел от 1 до N, обозначающих номера бункеров, в которых расположены выходы. В четвертой строке идёт число M (\(1 <= M <= 100000\)) — количество туннелей. В следующих M  строках вводятся пары чисел – номера бункеров, соединенных туннелем.
По каждому из туннелей можно двигаться в обе стороны. В организации не существует туннелей, ведущих из бункера в самого себя, зато может существовать более одного туннеля между парой бункеров.

Формат выходных данных
Выведите N чисел, разделенных пробелом — для каждого из бункеров минимальное время, необходимое чтобы добраться до выхода. Считайте, что время перемещения по одному туннелю равно 1.

Нью-Кэпитал

Обход в ширину Разбор случаев

В стране из предыдущей задачи много специалистов не только по защите детей, но и про проектированию городов. Поэтому, чтобы решить проблему пробок в перенаселенной столице раз и навсегда, было решено построить новую столицу и перенести все правительство туда. Сказано — сделано.

Улицы в новой столице образуют правильную прямоугольную сетку, в которой все улицы пересекаются ровно через одну местную единицу длины. Вертикально идущие улицы называются улицами, а горизонтально идущие — аллеями. Всего в городе получилось 2000 улиц и 2000 аллей, поэтому, чтобы не придумывать много новых названий, их все просто пронумеровали. Улицы пронумеровали с запада на восток числами от −1000 до 999, а аллеи — с юга на север, тоже числами от −1000 до 999. Центром города считаются кварталы на пересечении улиц и аллей с номерами от −100 до 100.

Чтобы увеличить пропускную способность дорог в городе, было решено сделать все улицы и аллеи односторонними. По улицам с четными номерами разрешается ехать только с севера на юг, а по улицам с нечетными номерами — только с юга на север. Аналогично, по аллеям с четными номерами можно ехать только с востока на запад, а с нечетными — только с запада на восток.

Сколько местных единиц длины придется проезжать мэру новой столицы каждый вечер, возвращаясь из мэрии города домой? И мэрия, и дом мэра находятся в центре города. Мэр едет домой кратчайшим путем, соблюдая, впрочем, правила дорожного движения.

Входные данные
В первой строке даны два числа x1 и y1 — номер улицы и номер аллеи, на пересечении которых находится мэрия. В второй строке даны два числа x2 и y2 — номер улицы и номер аллеи, на пересечении которых находится дом мэра. Все числа целые и не превосходят по модулю 100.

Выходные данные
Выведите одно число: длину кратчайшего пути от мэрии до дома мэра на автомобиле.-
 

Примеры
№ Входные данные Выходные данные
1 0 0
1 1		 4
2 3 5
2 4		 4

Игра с фишками

Обход в ширину Двумерные массивы

Вы являетесь одним из разработчиков новой компьютерной игры. Игра происходит на прямоугольной доске, состоящей из W×H клеток. Каждая клетка может либо содержать, либо не содержать фишку (см. рисунок).
Важной частью игры является проверка того, соединены ли две фишки путем, удовлетворяющим следующим свойствам:
1.    Путь должен состоять из отрезков вертикальных и горизонтальных прямых.
2.    Путь не должен пересекать других фишек.
При этом часть пути может оказаться вне доски. Например:

Фишки с координатами (1, 3) и (4, 4) могут быть соединены. Фишки с координатами (2, 3) и (5, 3) тоже могут быть соединены. А вот фишки с координатами (2, 3) и (3, 4) соединить нельзя — любой соединяющий их путь пересекает другие фишки.
Вам необходимо написать программу, проверяющую, можно ли соединить две фишки путем, обладающим вышеуказанными свойствами, и, в случае положительного ответа, определяющую минимальную длину такого пути (считается, что путь имеет изломы, начало и конец только в центрах клеток (или “мнимых клеток”, расположенных вне доски), а отрезок, соединяющий центры двух соседних клеток, имеет длину 1).

Формат входных данных
Первая строка входного файла содержит два натуральных числа: W — ширина доски, H — высота доски (1 ≤ W, H ≤ 75). Следующие H строк содержат описание доски: каждая строка состоит ровно из W символов: символ “X” (заглавная английская буква “экс”) обозначает фишку, символ “.” (точка) обозначает пустое место. Все остальные строки содержат описания запросов: каждый запрос состоит из четырех натуральных чисел, разделенных пробелами — X1, Y1, X2, Y2, причем 1 ≤ X1, X2 ≤ W, 1 ≤ Y1, Y2 ≤ H. Здесь (X1, Y1) и (X2, Y2) — координаты фишек, которые требуется соединить (левая верхняя клетка имеет координаты (1, 1)). Гарантируется, что эти координаты не будут совпадать (кроме последнего запроса). Последняя строка содержит запрос, состоящий из четырех чисел 0; этот запрос обрабатывать не надо. Количество запросов не превосходит 20.

Формат выходных данных
Для каждого запроса необходимо вывести одно целое число на отдельной строке — длину кратчайшего пути, или 0, если такого пути не существует.
Примеры
№ Входные данные Выходные данные
1 
5 4
XXXXX
X...X
XXX.X
.XXX.
2 3 5 3
1 3 4 4
2 3 3 4
0 0 0 0
5
6
0
2 
4 4
XXXX
.X..
..X.
X...
1 1 3 1
0 0 0 0
4

Роботы

Обход в ширину Задачи на моделирование

В подземелье есть N залов, соединенных туннелями. В некоторых залах находятся роботы, которые одновременно получили команду собраться в одном месте.

Роботы устроены так, что, получив команду, они все начали двигаться с такой скоростью, что туннель между двумя любыми залами преодолевают за 1 минуту. Роботы не могут останавливаться (в том числе и в залах), а также менять направление движения, находясь в туннелях (однако попав в зал, робот может из него пойти по тому же туннелю, по которому он пришел в этот зал).

Напишите программу, вычисляющую, через какое минимальное время все роботы смогут собраться вместе (в зале или в туннеле).

Входные данные
Сначала на вход программы поступают числа N — количество залов (1≤N≤400) и K — количество туннелей (1≤K≤20000). Далее вводится K пар чисел, каждая пара описывает номера залов, соединяемых туннелем (по туннелю можно перемещаться в обе стороны). Между двумя залами может быть несколько туннелей. Туннель может соединять зал с самим собой. Далее следует число M (1≤M≤400) — количество роботов. Затем вводятся M чисел, задающих номера залов, где вначале расположены роботы. В одном зале может быть несколько роботов.

Выходные данные
Выведите минимальное время в минутах, через которое роботы могут собраться вместе. Если роботы никогда не смогут собраться вместе, выведите одно число –1 (минус один).

Примеры
№ Входные данные Выходные данные
1 4 5
1 2
2 3
3 4
1 4
1 3
3
1 2 4		 1
2 3 2
1 2
2 3
2
1 3		 1

Транзитный путь

Алгоритмы на графах Кратчайшие пути в графе Обход в ширину

Вам дано дерево с N вершинами. Здесь дерево - это разновидность графа, а точнее, связный неориентированный граф с N−1 ребром, где N - количество его вершин. I-е ребро (\(1<=i<=N-1\)) соединяет вершины ai и bi и имеет длину ci.
Вам также дано Q запросов и целое число K. Для каждого j-го запроса (\(1<=j<=Q\)) найдите длину кратчайшего пути от вершины xj к вершине yj через вершину K.

Входные данные
В первой строке записано целое число N (\(3<=N<=10^5\)). В следующих N строках записаны вершины ai и bi (\(1<=a_i,b_i<=N\), \(1<=i<=N-1\)) и длина между ними ci (\(1<=c_i<=10^9\), \(1<=i<=N-1\))
Далее идут два числа Q и K (\(1<=Q<=10^5\), \(1<=K<=N\)). В последних Q строках записаны целые числа xj, yj (\(x_j \neq y_j\),\(x_j \neq K\), \(y_j \neq K\) \(1<=j<=Q\), ). 
Заданный граф является деревом.

Выходные данные
Выведите ответы на запросы в Q строках. В j-й строке выведите ответ на j-й запрос.

 

Примеры
№ Входные данные Выходные данные Пояснение
1 5
1 2 1
1 3 1
2 4 1
3 5 1
3 1
2 4
2 3
4 5		 3
2
4		 Кратчайшие пути для трех запросов следующие:

Запрос 1: Вершина 2 → Вершина 1 → Вершина 2 → Вершина 4: Длина 1 + 1 + 1 = 3
Запрос 2: Вершина 2 → Вершина 1 → Вершина 3: Длина 1 + 1 = 2
Запрос 3: Вершина 4 → Вершина 2 → Вершина 1 → Вершина 3 → Вершина 5: Длина 1 + 1 + 1 + 1 = 4
2 7
1 2 1
1 3 3
1 4 5
1 5 7
1 6 9
1 7 11
3 2
1 3
4 5
6 7		 5
14
22		 Путь для каждого запроса должен проходить через вершину K = 2.
3 10
1 2 1000000000
2 3 1000000000
3 4 1000000000
4 5 1000000000
5 6 1000000000
6 7 1000000000
7 8 1000000000
8 9 1000000000
9 10 1000000000
1 1
9 10		 17000000000  

 

Табличка

Обход в ширину

Дана таблица, состоящая из N строк и M столбцов. В каждой клетке таблицы записано одно из чисел: 0 или 1. Расстоянием между клетками (x1, y1) и (x2, y2) назовем сумму |x1-x2|+|y1-y2|. Вам необходимо построить таблицу, в клетке (i, j) которой будет записано минимальное расстояние между клеткой (i, j) начальной таблицы и клеткой, в которой записана 1. Гарантируется, что хотя бы одна 1 в таблице есть.

Формат входных данных
В первой строке вводятся два натуральных числа N и M, не превосходящих 500. Далее идут N строк по M чисел - элементы таблицы.

Формат выходных данных
Требуется вывести N строк по M чисел - элементы искомой таблицы.

Два коня

Обход в ширину

На стандартной шахматной доске (8х8) живут 2 шахматных коня: Красный и Зеленый. Обычно они беззаботно скачут по просторам доски, пощипывая шахматную травку, но сегодня особенный день: у Зеленого коня День Рождения. Зеленый конь решил отпраздновать это событие вместе с Красным. Но для осуществления этого прекрасного плана им нужно оказаться на одной клетке. Заметим, что Красный и Зеленый шахматные кони сильно отличаются от черного с белым: они ходят не по очереди, а одновременно, и если оказываются на одной клетке, никто никого не съедает. Сколько ходов им потребуется, чтобы насладиться праздником?

Входные данные
На вход программы поступают координаты коней, записанные по стандартным шахматным правилам (т.е. двумя символами - маленькая латинская буква (от a до h) и цифра (от 1 до 8), задающие столбец и строку соответственно).

Выходные данные
Требуется вывести наименьшее необходимое количество ходов, либо число -1, если кони не могут встретиться.

Примеры
№ Входные данные Выходные данные
1 a1 a3 1

BFS: Начало (Python)

Обход в ширину

Некоторые деревни соединены между собой дорогами, которые можно представить в виде неориентированного графа. Вершины данного графа - это деревни, а ребра - дороги между деревнями (граф может содержать циклы). Известно, что в деревне S основана артель коробейников. Каждое утро, чтобы продать свою мелкую галантерею, коробейники выходят в деревни, которые еще не посетили, и в которые есть дорога из текущей. Артель коробейников всегда делится на группы так, чтобы они могли за один день обойти все деревни, которые имеют дороги из текущей.
За сколько дней коробейники посетят все деревни?
Напишите функцию \(bfs()\), которая будет возвращать ответ на задачу.


Входные данные
В первой строке вводятся 3 целых числа n, m, s (\(1 <= n <= 10^5\), \(0 <= m <= 10^5\), \(1 <= s <= n\)) - количество деревень, количество дорог между ними и номер деревни, в которой основана артель коробейников. В следующих m строках содержится по 2 числа u, v(\(1 <= u, v <= n\)) - номера двух деревень, между которыми есть дорога. Индексация деревень ведется с 1.

Выходные данные
Выведите одно число - за сколько дней коробейники посетят все деревни.
 
 
Примеры
№ Входные данные Выходные данные
1 6 7 1
1 2
1 5
2 3
5 4
3 4
3 6
4 6		 4

Удаление клеток

Обход в ширину Обход в глубину

Из прямоугольного листа клетчатой бумаги (M строк, N столбцов) удалили некоторые клетки. На сколько кусков распадётся оставшаяся часть листа? Две клетки не распадаются, если они имеют общую сторону.


Входные данные

В первой строке находятся числа M и N, в следующих M строках - по N символов. Если клетка не была вырезана, этому соответствует знак #, если вырезана - точка. 1 <= M, N <= 100.


Выходные данные

Вывести одно число.
 

Примеры
№ Входные данные Выходные данные
1 
5 10
##..#####.
.#.#.#....
###..##.#.
..##.....#
.###.#####
 
5

Найти Дэйва

Обход в ширину

Беззработный Дэйв от скуки  соорудил в собственной гостиной лабиринт из картонных коробок. Лабиринт содержит  K входов. Когда его подружка Энни вернулась, лабиринт невероятным образом разросся изнутри, а сам горе-изобретатель там заблудился и не может выбраться.
Единственное, что нашла Энни в комнате это карту лабиринта, который имеет размеры NхM клеток. На карте было обозначено место, в котором находится Дэйв (как так вышло никто не знает). Клетки лабиринта либо пустые, по которым можно пройти, либо в них находится стена и по ним проходить нельзя. У клетки может быть до 4-х смежных клеток, в которую можно пройти из текущей.
Энни пригласила вас помочь ей определить, с какого входа нужно начать свой путь, чтобы побыстрее дойти до Дейва. Если таких входов несколько, Энни пойдет со входа с наименьшим номером.

Входные данные

Программа получает на вход несколько строк. В первой строке - 2 числа N и M (1<= N, M <= 100, NxM <= 100), размеры лабиринта. Далее следует N строк по M символов в каждой - описание лабиринта. 0 означает, что клетка свободна; 1, что в клетке находится стена. Символ * обозначает клетку с Дэйвом.
В (N+2)-й строке находится число K (1<=K<=NxM) -- количество входов в лабиринт. Далее в K строках содержатся координаты входов. В i-й строке содержатся числа xi и yi, означающие,что i-й вход расположен в xi-й строке и в yi-м столбце (1<=xi<=N,1<=yi<=M).
Координаты входов попарно различны, все входы расположены в пустых клетках. Ни один из входов не находится в клетке с Дэйвом.


Выходные данные

Выведите одно число - номер входа (нумерация начинается с 1). Если до Дэйва невозможно добраться, выведите -1.
 

 
Примеры
№ Входные данные Выходные данные
1 
5 5
00000
00000
10*00
01111
00000
4
1 1
1 5
4 1
5 5
 
1
2 
3 3
010
1*1
010
4
1 1
1 3
3 1
3 3
 
-1

Ананасы на Шешинеру

Обход в ширину

Аборигены с планеты Шешинера очень любят земные ананасы. Побывав у них в гостях, Алиса решила отправить несколько штук им в подарок. На то, чтобы доставить ананасы свежими есть всего 24 часа.

Алиса хочет хочет отправить как можно большее число ананасов. Капитан Полосков решил ей помочь и с радостью согласился слетать на своем космическом корабле. Но есть один нюанс: на некоторых космических маршрутах можно дозаправить корабль, не превышающий максимально установленный вес. А заправлять корабль в пути нужно всегда, иначе он просто не долетит. Поэтому если корабль заполнить ананасами по максимуму, то, его не получится дозаправить в пути и поэтому не удастся воспользоваться самым коротким маршрутов, и придётся лететь через другие планеты. Может случиться даже так, что корабль не успеет долететь до Шешинеры вовремя, и ананасы испортятся. 
Итак, сколько же ананасов можно погрузить в космический корабль, чтобы доставить груз вовремя?

Входные данные
Программа получает на вход несколько строк. В первой строке находятся числа n (1 <= n <= 500) и m - количество планет и количество космических маршрутов между планетми, соответственно. В следующих m строках записана информация о маршрутах. Каждый маршрут описывается в отдельной строке следующим образом. Сначала указаны номера планет, которые соединяются космическим маршрутом, потом время, которое тратится на перелет по этому маршруту, и, наконец, максимальный космического корабля, который можно заправить на этом маршруте. Известно, что все космические маршруты соединяют различные планеты, причем для каждой пары планет есть не более одного маршрута, непосредственно их соединяющий. Все числа разделены одним или несколькими пробелами. 

Планеты нумеруются числами от 1 до n. Планеты Земля имеет номер 1, а планета Шешинера - номер n. Время перелета по маршруту задано в минутах и не превосходит 1440 (24 часа). Ограничение на массу задано в граммах и не превосходит одного миллиарда. Кроме того, известно, что один ананас весит 100 грамм, а пустой корабль -  3 тонны.

Выходные данные
Выведите одно число - максимальное количество ананасов, которое можно доставить, потратив не более 24часов.
 

Примеры
№ Входные данные Выходные данные
1 
3 3
1 2 10 3000220
2 3 20 3000201
1 3 1 3000099
 
2

Игрушечный лабиринт

Обход в ширину

Игрушечный лабиринт представляет собой прозрачную плоскую прямоугольную коробку, внутри которой есть препятствия и перемещается шарик.
Лабиринт можно наклонять влево, вправо, к себе или от себя, после каждого наклона шарик перемещается в заданном направлении до ближайшего препятствия или до стенки лабиринта, после чего останавливается.
Целью игры является загнать шарик в одно из специальных отверстий – выходов. Шарик проваливается в отверстие, если оно встречается на его пути (шарик не обязан останавливаться в отверстии).
Первоначально шарик находится в левом верхнем углу лабиринта. Гарантируется, что решение существует и левый верхний угол не занят препятствием или отверстием.
Входные данные
В первой строке входного файла записаны числа N и M – размеры лабиринта (целые положительные числа, не превышающие 100).
Затем идет N строк по M чисел в каждой – описание лабиринта.
Число 0 в описании означает свободное место, число 1 – препятствие, число 2 – отверстие.
Выходные данные
Выведите единственное число – минимальное количество наклонов, которые необходимо сделать, чтобы шарик покинул лабиринт через одно из отверстий.

Примеры

входные данные выходные данные 
4 5
0 0 0 0 1
0 1 1 0 2
0 2 1 0 0
0 0 1 0 0
 
3

Издевательство

Обход в ширину

Штирлиц ехал на машине, увидел голосующего Бормана, и проехал мимо. Через некоторое время он снова увидел голосующего Бормана, и снова проехал мимо. Вскоре он опять увидел голосующего Бормана.
 - Издевается! - подумал Борман.
 - Кольцевая! - догадался Штирлиц.

В городе N площадей. Любые две площади соединены между собой ровно одной дорогой с двусторонним движением. В этом городе живет Штирлиц. У Штирлица есть хобби - он любит воскресным утром выйти из дома, сесть в машину, выбрать какой-нибудь кольцевой маршрут, проходящий ровно по трем площадям (то есть сначала он едет с какой-то площади на какую-то другую, потом - на третью, затем возвращается на начальную, и опять едет по этому маршруту). Он воображает, что где-то на этом пути стоит Борман. И так вот ездит Штирлиц все воскресенье, пока голова не закружится, и радуется...
Естественно, что Штирлицу хочется проезжать мимо точки, в которой, как он воображает, стоит Борман, как можно чаще. Для этого, естественно, выбранный Штирлицем маршрут должен быть как можно короче. Напишите программу, которая выберет оптимальный для Штирлица маршрут.
Входные данные
В первой строке задается  число N (3 <= N <= 100). В последующих строках содержится матрица NxN расстояний между площадями (число в позиции i,j обозначает длину дороги, соединяющей i-ую и j-ую площади). Все числа в матрице (кроме стоящих на главной диагонали) - натуральные, не превышающие 1000. Матрица симметрична относительно главной диагонали, на главной диагонали стоят 0.
Выходные данные
Требуется вывести три числа — номера площадей в оптимальном маршруте. Если маршрутов несколько, то выведите "наименьший" из них.
(то есть, на первом месте наименьшее возможное число, затем из возможных оставшихся наименьшее и т.д.)

Примеры

входные данные выходные данные 
5
0 1 9 9 2
1 0 9 9 9
9 9 0 9 9
9 9 9 0 9
2 9 9 9 0
 
1 2 5

Только направо

Обход в ширину

Змей Горыныч оказался в лабиринте и хочет выбраться из него как можно скорее. К сожалению, после вчерашнего употребления кефира, левая голова Змея соображает плохо.
Поэтому Змей Горыныч может поворачивать направо и идти прямо, но не может поворачивать налево и разворачиваться на месте.
Помогите Змею Горынычу определить длину кратчайшего пути до выхода из лабиринта.
Входные данные
В первой строке через пробел записаны числа r и c (4 ≤ r, c ≤ 20) -  количество строк и столбцов в карте лабиринта.
В каждой из следующих r строк записано по c символов, задающих эту карту.
Символ S обозначает положение Змея Горыныча, символ F - точку выхода из лабиринта, символ X - стенку. Пробелами обозначены проходимые клетки.
Гарантируется, что лабиринт окружен стенами. Перед началом движения Змей Горыныч может сориентироваться по любому из 4 направлений (вверх, вниз, влево или направо).
Выходные данные
Выведите единственное число - расстояние, которое придется пройти Змею Горынычу.
Гарантируется, что он всегда сможет выйти из лабиринта. 

Пояснение к примеру
Змей Горыныч начинает двигаться направо и его маршрут обозначен точками.

XXXXXXXXXXXXXX
X          XXX
X XFXXXXX    X
XXX·  XX  XX X
X S········  X
XX ·XXXXXX·X X
X  ·  ·· X·X X
X X····· X·X X
XXX XX·····  X
XXXXXXXXXXXXXX

Примеры

входные данные выходные данные 
10 14
XXXXXXXXXXXXXX
X          XXX
X XFXXXXX    X
XXX   XX  XX X
X S          X
XX  XXXXXX X X
X        X X X
X X      X X X
XXX XX       X
XXXXXXXXXXXXXX
 
29

Цивилизация (lite)

Обход в ширину

Карта мира в компьютерной игре “Цивилизация” версии 1 представляет собой прямоугольник, разбитый на квадратики. Каждый квадратик может иметь один из нескольких возможных рельефов, для простоты ограничимся тремя видами рельефов - поле, лес и вода. Поселенец перемещается по карте, при этом на перемещение в клетку, занятую полем, необходима одна единица времени, на перемещение в лес - две единицы времени, а перемещаться в клетку с водой нельзя.

У вас есть один поселенец, вы определили место, где нужно построить город, чтобы как можно скорее завладеть всем миром. Найдите маршрут переселенца, приводящий его в место строительства города, требующий минимального времени. На каждом ходе переселенец может перемещаться в клетку, имеющую общую сторону с той клеткой, где он сейчас находится.


Входные данные

Во входном файле записаны два натуральных числа N и M, не превосходящих 1000 - размеры карты мира (N - число строк в карте, M - число столбцов). Затем заданы координаты начального положения поселенца x и y, где x - номер строки, y - номер стролбца на карте (1 ≤ x ≤ N, 1 ≤ y ≤ M), строки нумеруются сверху вниз, столбцы - слева направо. Затем аналогично задаются координаты клетки, куда необходимо привести поселенца.

Далее идет описание карты мира в виде N строк, каждая из которых содержит M символов. Каждый символ может быть либо “.” (точка), обозначающим поле, либо “W”, обозначающим лес, либо “#”, обозначающим воду. Гарантируется, что начальная и конечная клетки пути переселенца не являются водой.


Выходные данные

В первой строке выходного файла выведите количество единиц времени, необходимое для перемещения поселенца (перемещение в клетку с полем занимает 1 единицу времени, перемещение в клетку с лесом - 2 единицы времени). Во второй строке выходного файла выведите последовательность символов, задающих маршрут переселенца. Каждый символ должен быть одним из четырех следующих: “N” (движение вверх), “E” (движение вправо), “S” (движение вниз), “W” (движение влево). Если таких маршрутов несколько, то выведите "наименьший" в лексико-графическом порядке.

Если дойти из начальной клетки в конечную невозможно, выведите число -1.

Примеры

входные данные выходные данные 
4 8 1 1 4 8
....WWWW
.######.
.#..W...
...WWWW.
 
13
SSSEENEEEEES
 
4 7 2 2 3 6
#######
#WW#..#
#WW#..#
#######
-1

Наименьшее кратное

Обход в ширину

Дано число X и множество цифр D. Требуется дописать к X минимальное количество цифр из D, чтобы получившееся число делилось на k. При этом получившееся число должно быть минимально возможным.


Входные данные

Первая строка входного файла содержит два натуральных числа X и k (1 ≤ X ≤ 101000, 2 ≤ k ≤ 105). Во второй строке записано количество цифр во множестве D. В третьей строке через пробел записаны эти цифры (если множество D пусто, то третьей строки во входных данных нет, что важно при считывании данных по строкам).


Выходные данные

Единственная строка должна содержать минимальное число, полученное из X дописыванием цифр из D и кратное k. Если такого числа не существует, выведите -1.

Примеры

входные данные выходные данные 
102 101
3
1 0 3
 
10201
 
202 101
3
1 0 3
 202

Цивилизация

Обход в ширину

Карта мира в компьютерной игре “Цивилизация” версии 1 представляет собой прямоугольник, разбитый на квадратики. Каждый квадратик может иметь один из нескольких возможных рельефов, для простоты ограничимся тремя видами рельефов - поле, лес и вода. Поселенец перемещается по карте, при этом на перемещение в клетку, занятую полем, необходима одна единица времени, на перемещение в лес - две единицы времени, а перемещаться в клетку с водой нельзя.

У вас есть один поселенец, вы определили место, где нужно построить город, чтобы как можно скорее завладеть всем миром. Найдите маршрут переселенца, приводящий его в место строительства города, требующий минимального времени. На каждом ходе переселенец может перемещаться в клетку, имеющую общую сторону с той клеткой, где он сейчас находится.


Входные данные

Во входном файле записаны два натуральных числа N и M, не превосходящих 1000 - размеры карты мира (N - число строк в карте, M - число столбцов). Затем заданы координаты начального положения поселенца x и y, где x - номер строки, y - номер стролбца на карте (1 ≤ x ≤ N, 1 ≤ y ≤ M), строки нумеруются сверху вниз, столбцы - слева направо. Затем аналогично задаются координаты клетки, куда необходимо привести поселенца.

Далее идет описание карты мира в виде N строк, каждая из которых содержит M символов. Каждый символ может быть либо “.” (точка), обозначающим поле, либо “W”, обозначающим лес, либо “#”, обозначающим воду. Гарантируется, что начальная и конечная клетки пути переселенца не являются водой.


Выходные данные

В первой строке выходного файла выведите количество единиц времени, необходимое для перемещения поселенца (перемещение в клетку с полем занимает 1 единицу времени, перемещение в клетку с лесом - 2 единицы времени). Во второй строке выходного файла выведите последовательность символов, задающих маршрут переселенца. Каждый символ должен быть одним из четырех следующих: “N” (движение вверх), “E” (движение вправо), “S” (движение вниз), “W” (движение влево). Если таких маршрутов несколько, то выведите "наименьший" в лексико-графическом порядке.

Если дойти из начальной клетки в конечную невозможно, выведите число -1.

Примеры

входные данные выходные данные 
4 8 1 1 4 8
....WWWW
.######.
.#..W...
...WWWW.
 
13
SSSEENEEEEES
 
4 7 2 2 3 6
#######
#WW#..#
#WW#..#
#######
-1

Кладоискатель

Алгоритм Флойда Обход в ширину

Кладоискателю Васе попалась карта древнего подземелья. Подземелье представляет собой лабиринт размера N×M (1 ≤ N, M ≤ 100 , N×M ≤ 100). Каждая клетка лабиринта либо пуста и по ней можно пройти, либо содержит стену. Из клетки можно переходить только в смежную по стене клетку (так, у каждой клетки может быть не более 4 смежных).
 
В одной из клеток находится клад, который и хочет достать Вася. В лабиринте есть K входов, из которых Вася может начать свой путь.
 
Требуется определить, с какого входа Васе нужно начать свой путь, чтобы пройденное расстояние до клада было наименьшим. Если таких входов несколько, нужно вывести вход с наименьшим номером.
 
Входные данные
Первая строка содержит 2 числа N и M, задающие размеры лабиринта. Далее следует описание лабиринта: N строк по M символов в каждой. 0 означает, что клетка свободна; 1, что в клетке находится стена. Символ * обозначает клетку с сокровищем (такая клетка в лабиринте ровно одна).
 
В (N+2)-й строке находится число K (1 ≤ K ≤ NxM) -- количество входов в лабиринт. Далее в K строках содержатся координаты входов. Так, в i-й строке содержатся числа xi и yi, означающие,что i-й вход расположен в xi-й строке и в yi-м столбце (1 ≤ xi ≤ N, 1 ≤ yi ≤ M). Гарантируется, что координаты входов попарно различны, и то, что все входы расположены в пустых клетках. Ни один из входов не находится в клетке с сокровищем.
 
Выходные данные
Необходимо вывести одно число - искомый номер входа (нумерация начинается с 1). Если до сокровища невозможно добраться, выведите -1.

Примеры
№ Входные данные Выходные данные
1
5 5
00000
00000
10*00
01111
00000
4
1 1
1 5
4 1
5 5
 1
2
3 3
010
1*1
010
4
1 1
1 3
3 1
3 3
 -1

Пожар в НИИЧАВО

Обход в ширину Структуры данных Алгоритмы на графах

В научно-исследовательском институте чародейства и волшебства пожар! Во время опыта Кор- неева В. П. по превращению всей морской и океанской воды планеты в живую воду произошло короткое замыкание, и теперь его кабинет объят пламенем. Задача первостепенной важности — спасти из огня ценные лабораторные приборы, в особенности единственный в своём роде диван- транслятор µ-поля. Ваша задача — перенести диван-транслятор из кабинета Корнеева в запасную лабораторию изучения µ-поля.

НИИЧАВО состоит из N кабинетов, соединённых M коридорами. Кабинеты пронумерованы це- лыми числами от 1 до N, при этом кабинет Корнеева имеет номер A, а лаборатория изучения µ-поля расположена в кабинете номер B. Благодаря специальному искажению пространства внутри инсти- тута, все коридоры имеют одинаковую длину, которую можно пройти за 1 минуту, если двигаться быстрым шагом.

Ситуация усугубляется тем, что диван-транслятор — прибор, очень чувствительный к резким пе- репадам температуры. Внутри каждого коридора НИИЧАВО поддерживается свой температурный режим. Если абсолютная величина разности температур в двух последовательных коридорах на пути из кабинета Корнеева в лабораторию окажется больше D градусов, то диван-транслятор пе- рейдёт в нестабильное состояние, что может привести к катастрофическим последствиям. Обратите внимание, что на своём пути вы не заходите в сами кабинеты, а только переходите из коридора в коридор, поэтому климат внутри кабинетов не влияет на диван-транслятор. В силу причин магиче- ского характера, войдя в коридор, вы обязаны дойти до его конца, иными словами, останавливаться или разворачиваться посреди коридора запрещено. По каждому коридору можно перемещаться в обоих направлениях.

Определите, за какое минимальное время можно добраться из кабинета Корнеева до запасной лаборатории, не допуская резкого перепада температур. В рамках данной задачи вам предлагается ответить на поставленный вопрос для нескольких пар значений A и B.

Формат входных данных
В первой строке входных данных следуют три целых числа N, M и D (2 <= N <= 100 000, 1 <= M <= 200 000, 0 <= D <= 2 · 108 ), обозначающие количество кабинетов, количество коридоров в НИИЧАВО и максимальный допустимый перепад температур для дивана-транслятора в граду- сах. В последующих M строках находятся описания коридоров. Каждая строка содержит по три целых числа ui , vi , ti — номера двух кабинетов, соединённых i-м коридором, и значение температуры в этом коридоре, выраженное в градусах (1 <= ui , vi <= N, −109 <= ti <= 109 ). Как вы уже могли понять, НИИЧАВО — весьма необычное заведение, поэтому между двумя кабинетами может пролегать несколько коридоров, возможно с разными температурами, а некоторые коридоры могут соединять кабинет с самим собой. Гарантируется, что коридоры перечислены во входном файле в порядке неубывания ti . В следующей строке находится целое число Q (1 <= Q <= 50) — количество пар A и B, которые вам требуется обработать. В каждой из последующих Q строк находятся по два целых числа Ai , Bi , обозначающих номер кабинета Корнеева и номер кабинета, в котором расположена лаборатория (1 <= Ai , Bi <= N, Ai != Bi).

Формат выходных данных
Для каждого набора данных выведите в отдельной строке минимальное количество минут, ко- торое требуется потратить, чтобы добраться из кабинета Корнеева до лаборатории, либо выведите −1, если сделать это, используя допустимый для дивана-транслятора маршрут, невозможно.

Примеры

Ввод Вывод
6 9 5
6 6 -42
1 2 4
2 3 6
3 2 7
2 5 11
6 1 12
1 3 15
3 4 16
5 6 18
2
1 5
4 2		 4
-1
6 9 7
6 6 -42
1 2 4
2 3 6
3 2 7
2 5 11
6 1 12
1 3 15
3 4 16
5 6 18
1
4 2		 5

Замечание
Пояснение к тестам из условия. В обоих тестах план НИИЧАВО выглядит следующим образом:

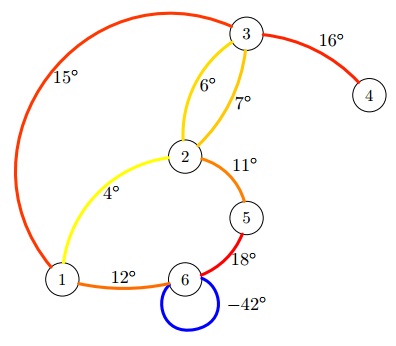
Рассмотрим первый тест, в нём D = 5. В первом наборе A = 1, B = 5. В качестве воз- можного маршрута может выступить следующая последовательность переходов по коридорам:
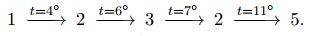Третьим шагом можно вернуться в кабинет 2 и по тому же коридору с t = 6 .
Во втором наборе A = 4, B = 2. Способа добраться из кабинета 4 в кабинет 2, ни разу не допустив перепад температуры больше, чем в 5 градусов, не существует.

Во втором тесте D = 7. В единственном наборе A = 4, B = 2 cтартовый и конечный кабинет те же, что и во втором наборе первого теста из условия, но допустимый перепад температур больше, благодаря чему подходит следующий маршрут: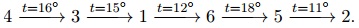 

Мишина машина (В', В)

Кратчайшие пути в графе Обход в ширину Способы задания графа

Миша путешествует по стране на автомобиле. В стране есть несколько городов, соединенных дорогами, на каждой дороге может быть некоторое число ям.
Мише очень нравится ездить по дорогам на которых много ям, -  он участвует в популярном телешоу "Неперсистентные машинки" и за каждую посещенную яму ему платят по одной монете.

Он начинает путь в любом из городов страны и затем путешествует по дорогам между городами. По каждой дороге Миша может проехать сколько угодно раз но ему платят за посещение любой ямы только один раз.
Помогите Мише найти самый выгодный маршрут.

Формат входных данных
В первой строке содержатся два целых числа n и m количество городов и дорог соединяющих города в стране соответственно (1 <= n <= 105 , 0<= m <= 105)
В следующих m строках содержится по три целых числа, разделенных пробелами номера, -  городов, соединенных очередной дорогой и количество ям на этой дороге соответственно. Количество ям на каждой дороге неотрицательное число не превосходящее 106.
 
Гарантируется, что никакая дорога не соединяет город с самим собой и что нет двух дорог соединяющих одинаковые пары городов. Вершины нумеруются с единицы.
 
Формат выходных данных
Выведите одно число максимальное количество монет которое Миша сможет получить.
 
Ввод Вывод
4 4
1 2 1
2 3 1
1 4 1
4 3 0		 3
4 2
1 3 5
2 4 4		 5
 
Замечание
Все дороги двусторонние; проехав в любую сторону по дороге, Миша посещает все ямы на этой дороге. Обратите внимание, что между некоторыми парами городов может не существовать пути по имеющимся дорогам.

Вирус

Двумерные массивы Задача на реализацию Способы задания графа Обход в ширину Двумерные массивы

В лаборатории биоинформатики ученые проводят эксперименты по распространению искусственно созданных вирусов. Для эксперимента используется специальная лабораторная установка, представляющая собой таблицу из n × m ячеек. В каждую ячейку помещается живая клетка. Ученые заражают вирусом некоторые клетки, всего исходно заражается не более 8 клеток.
Каждую секунду среди незараженных клеток, имеющих зараженную клетку в соседней по стороне ячейке, ровно одна клетка заражается вирусом.
Ученые заинтересовались, какие конфигурации зараженных клеток могут получиться через t секунд. Для начала они хотят посчитать число таких конфигураций. Помогите им это сделать.

Формат входных данных
В первой строке входного файла находятся целые числа n, m и t (1 ≤ n, m ≤ 100, 1 ≤ t ≤ 6) — размеры таблицы и количество секунд. Каждая из следющих n строк содержит m символов. Символ «.» означает, что в изначальной конфигурации клетка не заражена, а символ «*» — что заражена. Количество «*» в таблице не превышает 8. Гарантируется, что незараженных клеток в исходной конфигурации не меньше t.

Формат выходных данных
Выведите количество различных возможных конфигураций таблицы после t секунд.
 

Ввод Вывод
2 2 1
*.
..		 2
2 2 2
*.
..		 3
2 2 3
*.
..		 1

Открыть все комнаты

Обход в ширину

Магистр Максимус отправился в опасное путешествие в горы Ордена Магов. Внутри гор великими магами прошлого созданы комнаты, в каждой из которых хранятся магические артефакты. Максимус желает пройти через все n комнат, но, как оказалось, все комнаты заперты, за исключением комнаты 0, в которую Максимус уже вошел. 
В каждой комнате имеется набор уникальных заклинаний, открывающих двери других комнат. Магистр Максимус познал язык великих магов, поэтому он может легко прочитать эти заклинания и отпирать другие комнаты.

Максимус хочет посетить все комнаты и найти все магические артефакты. Однако, для этого ему необходимо найти заклинания открывающие каждую дверь.

По известному набору заклинаний, определите сможет ли Максимум получить все артефакты или нет.


Формат входных данных
В первой строке записано число n (2 <= n <= 1000), количество комнат. Далее идет n строк. В i-й строке описываются заклинания, хранящиеся в этой комнате. В каждой из этих строк первое число (m, 0 <= m <= 1000) обозначает количество уникальных заклинаний, которые открывают комнаты, далее записаны m уникальных чисел rooms[i](0 <= rooms[i][j] < n) -  номера комнат, которые открывают эти заклинания (0<=i<n,  1 <= общее количество заклинаний во всех комнатах <= 10000). 

 

Формат выходных данных
Выведите True, если Максимус может посетить все комнаты и найти все магические артефакты, или False в противном случае.

Количество кратчайших путей

Обход в ширину

В Сильвертауне  есть N районов с номерами от 1 до N и M дорог с номерами от 1 до M. Используя дорогу i, вы можете добраться из района Ai в район Bi или наоборот за один час.
Сколько существует путей, по которым можно добраться из района 1 в район N как можно быстрее?
Поскольку число может быть огромным, выведите его по модулю 109+7

Формат входных данных
Первая строка содержит два целых числа N и M. Далее идет M строк, в каждой из которых записано по 2 числа: Ai и Bi.

Ограничения 

  • 2 ≤ N ≤ 2×105
  • 0 ≤ M ≤ 2×105
  • 1 ≤ Ai < Bi ≤ N
  • Пары (Ai,Bi) уникальны.
  • Все значения во входных данных целые числа.
Формат выходных данных
Выведите ответ на задачу.

Маршрут кладоискателя

Алгоритм Флойда Обход в ширину

Вася из задачи A по-прежнему занят поиском кладов. Более того, у него появились последователи. Один из таких последователей попросил Васю помочь в своих поисках. Так, по карте сокровищ Васю просят восстановить кратчайший путь до клада. Конфигурация лабиринта совпадает с конфигурацией, описанной в задаче A (поле \(N \times M (1 \le N, M \le 100, N \times M \le 100))\), в одной клетке которого находится клад, в K
 клетках находятся входы в лабиринт).

Требуется вывести искомый путь.

Формат входных данных
Первая строка содержит 2 числа N<=100 и M<=100, задающие размеры лабиринта. Далее следует описание лабиринта: N
 строк по M символов в каждой. 0 означает, что клетка свободна; 1, что в клетке находится стена. Символ * обозначает клетку с сокровищем (такая клетка в лабиринте ровно одна).
В (N+2)-й строке находится число \(K (1 \le K \le N \times M)\) - количество входов в лабиринт. Далее в K строках содержатся координаты входов. Так, в i-й строке содержатся числа \(x_i\) и \(y_i\), означающие, что i-й вход расположен в \(x_i\)-й строке и в \(y_i\)-м столбце \((1 \le x_i \le N, 1\le y_i \le M)\). Гарантируется, что координаты входов попарно различны, и то, что все входы расположены в пустых клетках. Ни один из входов не находится в клетке с сокровищем.

Формат выходных данных
В первой строке вывести одно число - длину кратчайшего маршрута. В следующих строках необходимо вывести кратчайший маршрут. Каждую клетку маршрута (включая начальную и конечную) вывести на отдельной строке в формате \(x_i\) \(y_i\), где \(x_i\)  - строка клетки, а \(y_i\)  - столбец клетки.

Если существует несколько путей минимальной длины, выведите любой. Если до сокровища невозможно добраться, в единственной строке выведите -1.

Примеры
№ Входные данные Выходные данные
1 5 5
00000
00000
10*00
01111
00000
4
1 1
1 5
4 1
5 5		 4
1 1
2 1
2 2
3 2
3 3
2 3 3
010
1*1
010
4
1 1
1 3
3 1
3 3
 		 -1

Умывальники

Обход в ширину

Для того, чтобы отойти ко сну, живущему в ЛКШ мальчику Пете необходимо почистить зубы, вымыть ноги, принять душ и т.д., одним словом, посетить умывальник. Так случилось, что в корпусе, где он проживает, смонтировано лишь два умывальника. Вообще корпус представляет собой совокупность из N холлов, некоторые из которых соединены коридорами, причем, если по коридору можно пройти в одну сторону, это вовсе не означает, что можно пройти и в другую. Это фишка архитекторов.

Так как Петя идёт умываться после отбоя, он смертельно боится попасться на глаза воспитателям ЛКШ. Однако, как выяснилось, в каждом коридоре стоит ровно по одному воспитателю, причём каждый из них считает своим долгом при встрече Пети влепить ему наряд вне очереди.

Стоит отметить ещё одну немаловажную особенность корпуса, в котором живёт Петя: архитекторы оставили потайные ходы напрямую из каждого холла в оба умывальника, но т.к. существование этих ходов приравнивается руководством к красивой легенде, в случае пользования одним из них, Петя получит 10000 нарядов вне очереди.

Петя хочет узнать, получит ли он меньше нарядов вне очереди, если пойдёт в первый умывальник, нежели если он пойдёт во второй. Обратный путь его не интересует.

Входные данные
В первой строке входного файла четыре числа: N, S, V1, V2 (1 <= N <= 1000; 1 <= S, V1, V2 <= N), где N - общее количество холлов, S - номер холла, в котором Петя находится в начальный момент времени, V1, V2 - номера холлов, в которых располагаются умывальники. В следующих N строках по N чисел - 1 или 0. Стоящий в I-ой строке на J-ом месте 0 означает отсутствие коридора из I-го холла в J-ый, а стоящая 1 - присутствие.

Выходные данные
Вывести 1, если Петя сможет получить меньше нарядов вне очереди при использовании первого умывальника, нежели при использовании второго, или 0 в противном случае.

Витрина

Алгоритм Дейкстры Обход в ширину

Зал супермаркета имеет форму прямоугольника размером M x N, в котором расставлены витрины размером 1 x 1. Стороны витрин параллельны стенам супермаркета, а расстояния от витрин до стен – целые числа.

В супермаркет привезли новую супервитрину размером K  x 1 и выгрузили в одном из углов супермаркета. Требуется передвинуть ее в противоположный угол супермаркета. При этом ее нельзя поворачивать, а можно лишь передвигать параллельно стенам супермаркета. Напишите программу, которая по плану супермаркета поможет определить, какое наименьшее количество витрин нужно убрать, чтобы передвинуть супервитрину.




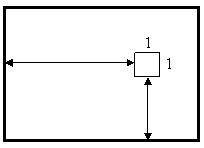
Входные данные
В первой строке вводятся три натуральных числа M, N и K (M, N ≤ 100, K ≤ M). Начальное и конечное расположение супервитрины такие, как указано на верхнем рисунке. В следующей строке записано целое неотрицательно число V – количество витрин (0 ≤ V ≤ N*M). В следующих V строках входных данных содержатся различные пары целых неотрицательных чисел, характеризующие положения витрин. Первое число (от 0 до M–1) – расстояние от левой стены супермаркета до витрины, второе (от 0 до N–1) – расстояние от нижней стены до витрины (см. нижний рисунок). Гарантируется, что там, где изначально поставили супервитрину, других витрин нет.

Выходные данные
В первой строке выведите минимальное количество витрин, которые необходимо убрать. Во второй строке выведите возможный маршрут передвижения супервитрины: одну строку из заглавных латинских букв, обозначающих следующее:

U – на 1 вверх,
D – на 1 вниз,
L – на 1 влево,
R – на 1 вправо.
Количество символов в строке не должно превышать N x M
.

Если возможных маршрутов несколько, то выведите любой из них.

Lines

Обход в ширину

В таблице из N строк и N столбцов некоторые клетки заняты шариками, другие свободны. Выбран шарик, который нужно переместить, и место, куда его нужно переместить. Выбранный шарик за один шаг перемещается в соседнюю по горизонтали или вертикали свободную клетку. Требуется выяснить, возможно ли переместить шарик из начальной клетки в заданную, и, если возможно, то найти путь из наименьшего количества шагов.

Входные данные
В первой строке находится число N, в следующих N строках - по N символов. Символом точки обозначена свободная клетка, латинской заглавной O - шарик, @ - исходное положение шарика, который должен двигаться, латинской заглавной X - конечное положение шарика. 2 <= N <= 40.

Выходные данные
В первой строке выводится Y, если движение возможно, или N, если нет. Если движение возможно, далее следует N строк по N символов - как и на вводе, но буква X, а также все точки по пути заменяются плюсами.

Покраска лабиринта

Обход в ширину

Лабиринт представляет собой квадрат, состоящий из NxN сегментов. Каждый из сегментов может быть либо пустым, либо заполненным монолитной каменной стеной. Гарантируется, что левый верхний и правый нижний сегменты пусты. Лабиринт обнесён сверху, снизу, слева и справа стенами, оставляющими свободными только левый верхний и правый нижний углы. Директор лабиринта решил покрасить стены лабиринта, видимые изнутри (см. рисунок). Помогите ему рассчитать количество краски, необходимой для этого.



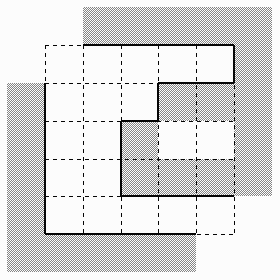
Входные данные
В первой строке находится число N, затем идут N строк по N символов: точка обозначает пустой сегмент, решётка - сегмент со стеной. 3 <= N <= 33, размер сегмента 3 x 3 м, высота стен 3 м.

Выходные данные
Вывести одно число - площадь видимой части внутренних стен лабиринта в квадратных метрах.

Lines(2)

Обход в ширину

В таблице из N строк и N столбцов некоторые клетки заняты шариками, другие свободны. Выбран шарик, который нужно переместить, и место, куда его нужно переместить. Выбранный шарик за один шаг перемещается в соседнюю по горизонтали или вертикали свободную клетку. Требуется выяснить, возможно ли переместить шарик из начальной клетки в заданную, и если возможно, то найти путь из наименьшего количества шагов.

Входные данные
В первой строке находится число N, в следующих N строках - по N символов. Символом точки обозначена свободная клетка, латинской заглавной O - шарик, @ - исходное положение шарика, который должен двигаться, латинской заглавной X - конечное положение шарика. 2 <= N <= 250.

Выходные данные
В первой строке выводится Y, если движение возможно, или N, если нет. Если движение возможно, далее следует N строк по N символов - как и на вводе, но X, а также все точки по пути заменяются плюсами +.

Путь коня

Обход в ширину

Дана шахматная доска, состоящая из N*N клеток, несколько из них вырезано. Провести ходом коня через невырезанные клетки путь минимальной длины из одной заданной клетки в другую.

Входные данные
В первой строке задано число N. В следующих N строках содержится по N символов. Символом # обозначена вырезанная клетка, точкой - невырезанная клетка, @ - заданные клетки (таких символов два). 2 <= N <= 50.

Выходные данные
Если путь построить невозможно, вывести "Impossible", в противном случае вывести такую же карту, как и на входе, но пометить все промежуточные положения коня символом @.

Прямоугольное деление

Элементарная геометрия Обход в ширину

Дано N прямоугольников со сторонами, параллельными осям координат. Требуется определить, на сколько частей эти прямоугольники разбивают плоскость (внутри частей не должно быть границ прямоугольников).

Входные данные
В первой строке содержится число прямоугольников N. Далее идут N строк, содержащих по 4 числа x1, y1, x2, y2 - координаты двух противоположных углов прямоугольника.

Ограничения: 1 <= N <= 100, координаты представляют собой целые числа и по абсолютной величине не превосходят 10 000.

Выходные данные
Вывести одно число - количество частей, на которые разбивается плоскость.

Путь спелеолога

Обход в ширину

Пещера представлена кубом, разбитым на N частей по каждому измерению (то есть на N 3 кубических клеток). Каждая клетка может быть или пустой, или полностью заполненной камнем. Исходя из положения спелеолога в пещере, требуется найти, какое минимальное количество перемещений по клеткам ему требуется, чтобы выбраться на поверхность. Переходить из клетки в клетку можно, только если они обе свободны и имеют общую грань.

Ограничения: 1 <= N <= 30.

Входные данные
В первой строке содержится число N. Далее следует N блоков. Блок состоит из пустой строки и N строк по N символов: # - обозначает клетку, заполненную камнями, точка - свободную клетку. Начальное положение спелеолога обозначено заглавной буквой S. Первый блок представляет верхний уровень пещеры, достижение любой свободной его клетки означает выход на поверхность. Выход на поверхность всегда возможен.

Выходные данные
Вывести одно число - длину пути до поверхности.

Дырявая ткань

Обход в ширину

На столе лежат несколько кусков ткани, не перекрывая друг друга. Эти куски могут иметь дыры, в том числе и настолько большие, что в них может поместиться целый кусок ткани. Был получен чёрно-белый образ поверхности стола, на котором области, покрытые тканью, представлены символами *, а свободные площади - точками. Один кусок ткани, таким образом, представлен 4-связной областью символов *, то есть группой *, соседствующих друг с другом горизонтально или вертикально, но не по диагонали.

.***..***
.*.*.**.*
.***.*.**
*...**.*.

На схеме три куска - один без дыр, а два - с одной дырой каждый: первый площадью 8, второй - площадью 12.
Ваша цель - найти кусок с наибольшим количеством дыр в нём. Дыра - это 4-связная область точек, полностью окружённых символами *. Если несколько кусков имеют одинаковое количество дыр, нужно выбрать кусок минимальной площади.

Входные данные
В первой строке содержатся два числа W и H, разделённые пробелами. Следующие H строк содержат по W символов каждая. Символы в этих строках - или * (ASCII 42), или точка (ASCII 46).

Ограничения: 1 <= W, H <= 100.

Выходные данные
Вывести одно целое число - площадь минимального из наиболее дырявых кусков. Если нет кусков с дырами, выходной файл должен содержать ноль.

Квас

Перебор Обход в ширину

На тропическом острове в разгар туристического сезона особой популярностью пользуется квас. Раньше весь квас импортировался из России, но с увеличением популярности этого напитка встал вопрос о производстве кваса прямо на месте. На острове расположено N курортных городов, все города расположены на побережье. Вдоль побережья проходит единственная на острове кольцевая дорога, соединяющая все города. Движение по дороге возможно в любом направлении. Для каждого города известно, сколько бочек кваса требуется ему ежедневно.

Планируется построить всего один завод в каком-нибудь городе, и развозить продукцию по остальным городам. Перевозка одной бочки в соседний город стоит один тугрик (местная валюта).

Ваша задача состоит в том, чтобы определить, в каком из городов следует построить завод, чтобы минимизировать транспортные расходы.

Входные данные
Первая строка входных данных содержит число N – количество городов ( N ≤ 10) и еще N чисел – количество кваса, требуемое ежедневно 1-м, 2-м, …, N -м городом (города нумеруются подряд вдоль кольцевой дороги).

Выходные данные
Выведите одно число – номер города, в котором следует построить завод. Если подходящих городов окажется несколько – выведите номер любого из них.

Примеры
№ Входные данные Выходные данные Пояснение
1 3 5 3 10 3  
2 6 4 4 1 5 1 3 2 На острове 6 городов, потребность каждого города указана в кружочках, номер города рядом с кружочком.

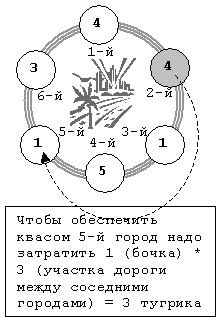
Если построить завод во 2-м городе (он выделен серым), то потребуется заплатить 4 + 1 (стоимость перевозки в 1-й и 3-й города) + 5*2 + 3*2 (в 4-й и 6-й) + 1*3 (в 5-й см. рисунок).
Во 2-й вообще ничего не везем. Это будет 24 тугрика. Легко проверить, что если построить завод в других городах, сумма будет больше. Например, если построить в 4-м городе, то сумма составит 1 + 1 + 3*2 + 4*2 + 4*3 = 28 тугриков.

Трехцветные таблицы

Способы задания графа Обход в ширину Обход в глубину

Прямоугольную таблицу, состоящую из N строк и M столбцов, раскрашивают следующим образом. Каждый столбец таблицы и каждую строку красят либо в синий, либо в желтый цвет. В итоге клетки, оказавшиеся на пересечении синего столбца и синей строки оказываются синими, желтого столбца и желтой строки — желтыми, а клетки на пересечении синего столбца и желтой строки, или, наоборот, желтого столбца и синей строки — зелеными.

Раскраска всех клеток таблицы (или просто сама таблица) называется правильной, если она может быть получена описанным выше способом.

Вам дана прямоугольная таблица, которую нужно раскрасить таким образом. Про некоторые клетки известно, какого цвета они должны быть, а остальные клетки могут в итоге быть любого цвета. Определите, сколько существует различных правильных таблиц, в которых нужные клетки покрашены в нужный цвет.

Входные данные
Вводятся числа N и M — количество строк и столбцов таблицы (1≤N≤30, 1≤M≤30). Далее записано N строк по M чисел в каждой, задающие цвета, в которые должны быть окрашены клетки:

0 — клетка может в итоге быть любого цвета

1 — клетка должна быть синей

2 — клетка должна быть желтой

3 — клетка должна быть зеленой

Выходные данные
Выведите одно число — количество различных правильных таблиц, в которых нужные клетки покрашены в нужный цвет. Обратите внимание, что если два или более способов раскраски столбцов и строк таблицы приводят к одинаковой раскраске самой таблицы, то это нужно считать как один вариант раскраски таблицы (см. пример 2).

Вырезанные фигуры

Обход в ширину Способы задания графа

Эпидемия гриппа не обошла стороной семиклассника Алешу. Скучая дома, Алеша решил вырезать фигурки из листа клетчатой бумаги. Лист состоял из M строк и N столбцов клеточек. Сначала Алеша нарисовал на листе границы фигур. Количество фигур было не меньше 2. Чтобы фигуры получались ровными, границы фигур Алеша рисовал строго по линиям имеющейся клеточной разметки листа (при этом некоторые границы фигур могли пройти по границам листа). Форма фигур могла быть любой, но при этом все фигуры были связными (фигура называется связной, если из любой ее клетки можно добраться до любой другой, ходя только по клеткам фигуры и перемещаясь каждый раз в одну из 4-х соседних по стороне клеток). Никакие две фигуры не имели общих точек, в том числе не касались углами клеток.

<>Затем Алеша вырезал нарисованные фигуры, делая разрезы только по их границам. При этом оставшаяся часть листа осталась связной (то есть не распалась на несколько частей).
Лист с вырезами Алеша отсканировал. Сканер в своей памяти по результатам сканирования построил таблицу, состоящую из нулей и единиц, из M строк и N столбцов (строки нумеруются сверху вниз от 1 до M, столбцы — слева направо от 1 до N). Каждый элемент таблицы соответствовал клеточке исходного листа. Единица обозначала, что соответствующая клетка листа осталась на месте, ноль — соответствующая клетка была вырезана.

На рис. 1 приведен пример клетчатого листа, а на рис. 2 — соответствующая ему таблица в памяти сканера:
 

 

 
 
 
 
 
 
 
 
 
 
 
 

 
 
 
 
 
 
 
 
 
 
 
 

 
 
 
 
 
 
 
 
 
 
 
 

 
 
 
 
 
 
 
 
 
 
 
 

 
 
 
 
 
 
 
 
 
 
 
 

 
 
 
 
 
 
 
 
 
 
 
 
 
Рис 1.
Исходный клеточный лист с вырезанными фигурами
Размер листа: M=6, N=12.
Количество вырезанных фигур: 3		  
1 1 1 1 1 1 1 1 1 1 1 1
1 0 0 1 1 1 0 0 0 0 0 1
1 0 0 1 1 1 1 0 0 1 1 1
1 1 1 1 1 0 0 0 0 0 1 1
1 1 0 0 1 1 1 0 1 0 1 1
1 1 0 0 1 1 1 1 1 1 1 1
 
Рис 2.
Такая таблица строится в памяти сканера
 


После этого сканер представил полученную таблицу в специальном, описанном ниже формате и передал информацию на компьютер. Напишите программу, которая по полученной информации установит:
Пункт 1. Сколько клеток было вырезано из листа?
Пункт 2. Сколько фигур было вырезано? Описание формата представления таблицы Последовательность подряд идущих по горизонтали или вертикали единиц будем называть полосой. Полосу можно задаеть 4 числами:
  • направление (0—горизонтальная, 1—вертикальная)
  • (i, j) — координаты начальной клетки полосы (начальной является самая левая клетка для горизонтальной полосы, и самая верхняя — для вертикальной), i — номер строки клетки, j — номер столбца
  • d — длина полосы (количество подряд стоящих единиц).
Всю таблицу разобьем на полосы, состоящие из единиц так, чтобы каждая единица принадлежала хотя бы одной полосе. При этом полосы могут пересекаться, а также накладываться. Таким образом, таблица представляется в виде описания всех полос, которое удовлетворяет трем дополнительным требованиям:
  • В каждой клетке начинается не более одной полосы.
  • Полосы перечислены в порядке следования их начальных клеток (клетки перечисляются по строкам сверху вниз, в строке — слева направо).
  • Общее число полос не превышает 256000.

Заметим, что таблица может быть представлена в виде полос разными способами, но каждое представление позволяет однозначно восстановить таблицу.

Входные данные
Во входном файле записано сначала число P  (1 или 2) — номер пункта задачи, ответ на который требуется получить. Далее записаны размеры исходного листа — числа M  и N  (1 ≤ M ≤ 4000,1 ≤ N ≤ 4000) . Затем записано число K  (0 ≤ K ≤ 256000)  — количество полос в описании полученной таблицы. Затем идет K четверок чисел, описывающих полосы (полосы перечисляются в порядке начальных клеток полос: по строкам сверху вниз, в строке — слева направо).

Выходные данные
В выходной файл выведите искомое количество (если P=1, то — количество клеток, вырезанных из листа, если P=2, то — количество фигур, вырезанных из листа).

Водостоки

Обход в ширину Обход в глубину

Карту местности условно разбили на квадраты, и посчитали среднюю высоту над уровнем моря для каждого квадрата.

Когда идет дождь, вода равномерно выпадает на все квадраты. Если один из четырех соседних с данным квадратом квадратов имеет меньшую высоту над уровнем моря, то вода с текущего квадрата стекает туда (и, если есть возможность, то дальше), если же все соседние квадраты имеют большую высоту, то вода скапливается в этом квадрате.

Разрешается в некоторых квадратах построить водостоки. Когда на каком-то квадрате строят водосток, то вся вода, которая раньше скапливалась в этом квадрате, будет утекать в водосток.

Если есть группа квадратов, имеющих одинаковую высоту и образующих связную область, то если хотя бы рядом с одним из этих квадратов есть квадрат, имеющий меньшую высоту, то вся вода утекает туда, если же такого квадрата нет, то вода стоит во всех этих квадратах. При этом достаточно построить водосток в любом из этих квадратов, и вся вода с них будет утекать в этот водосток.

Требуется определить, какое минимальное количество водостоков нужно построить, чтобы после дождя вся вода утекала в водостоки.

Входные данные
Во входном файле записаны сначала числа N и M, задающие размеры карты — натуральные числа, не превышающие 100. Далее идет N строк, по M чисел в каждой, задающих высоту квадратов карты над уровнем моря. Высота задается натуральным числом, не превышающим 10000. Считается, что квадраты, расположенные за пределами карты, имеют высоту 10001 (то есть вода никогда не утекает за пределы карты).

Выходные данные
В выходной файл выведите минимальное количество водостоков, которое необходимо построить.

Левый лабиринт

Динамическое программирование на таблицах Алгоритм Дейкстры Обход в ширину

В спортзале размером NxM метров построили современный аттракцион под названием "Левый лабиринт". Для этого на полу спортзала с интервалом в 1 метр начертили линии, параллельные стенам спортзала. Таким образом, спортзал разбили на NxM клеток. Дальше некоторые из этих клеток покрасили в черный цвет.

Аттракцион заключается в том, что участника ставят в некоторой клетке спортзала и просят как можно быстрее добежать до некоторой другой клетки. При этом накладываются следующие условия:

  • Участнику запрещено ходить по черным клеткам.
  • Придя в какую-то клетку, участник может пойти либо прямо, либо налево, либо направо (если в соответствующем направлении клетка не покрашена в черный цвет): ходить назад, а также ходить по диагонали запрещается.
  • За все время пути участнику разрешается повернуть направо (то есть пойти из текущей клетки направо относительно того, откуда он пришел в данную клетку) не более K раз.
  • В начальной клетке участник может встать лицом в ту сторону, в какую ему захочется. С какой стороны участник прибежит в конечную клетку также не важно.
Известно, что на то, чтобы перебежать из клетки в соседнюю, участник тратит ровно 1 секунду. Требуется вычислить минимальное время, за которое участник сможет достичь конечной клетки.

Входные данные
Во входном файле сначала записано число K — количество разрешенных поворотов направо (целое число из диапазона от 0 до 5), затем записаны числа N и M, задающие размеры спортзала — натуральные числа, не превышающие 20. Далее записано N строк по M чисел в каждой. Число 0 обозначает непокрашенную клетку, число 1 — покрашенную, число 2 — клетку, откуда стартует участник и число 3 — клетку, куда нужно добежать (клетки, помеченные 2 и 3 являются непокрашенными). В лабиринте всегда есть ровно одна начальная клетка и ровно одна клетка, в которую нужно попасть.

Выходные данные
В выходной файл выведите минимальное время, за которое можно добраться в конечную клетку. Если попасть в конечную клетку с соблюдением всех условий нельзя, выведите –1.

Побег с космической станции

Обход в ширину

Представьте, что вы состоите на службе во внешней разведке Межгалактического Альянса Республиканских Сил (МАРС). Одному из агентов разведки крупно не повезло, и он был захвачен на засекреченной космической базе. К счастью, внешней разведке МАРС удалось заполучить план этой базы. И вот теперь вам поручено разработать план побега.

База представляет собой прямоугольник размером NхM, со всех сторон окружённый стенами, и состоящий из квадратных отсеков единичной площади. База снабжена K выходами, до одного из которых агенту необходимо добраться. В некоторых отсеках базы находятся стены. Ваш агент может перемещаться из отсека в любой из четырех соседних с ним, если в том отсеке, куда он хочет переместиться, нет стены.

Кроме того, база снабжена системой гипертуннелей, способных перемещать агента из одного отсека базы (вход в гипертуннель) в другой (выход из гипертуннеля). Когда агент находится в отсеке, где есть вход в гипертуннель, он может (но не обязан) им воспользоваться.

Начальное положение вашего агента известно. Вам необходимо найти кратчайший путь побега (то есть путь, проходящий через минимальное количество отсеков).

Входные данные
В первой строке входного файла записаны числа N и M (2≤N≤100, 2≤M≤100), задающие размеры базы: N — количество строк в плане базы, M — количество столбцов. Во второй строке записаны начальные координаты агента XA,YA (1≤XA≤N, 1≤YA≤M). Первая координата задает номер строки, вторая — номер столбца. Строки нумеруются сверху вниз, столбцы слева направо.

Далее следуют N строк по M чисел, задающих описание стен внутри базы: 1 соответствует стенке, 0 — её отсутствию.

Далее в отдельной строке записано число H (0≤H≤1000) — количество гипертуннелей. В последующих H строках идут описания гипертуннелей. Каждый гипертуннель задается 4 числами: X1, Y1, X2, Y2 (1≤X1,X2≤N; 1≤Y1,Y2≤M) — координатами входа и выхода гипертуннеля. Никакие два гипертуннеля не имеют общего входа.

После этого в отдельной строке следует число K (1≤K≤10) — количество выходов с базы. В последующих K строках идут описания выходов с базы. Каждый выход задается двумя координатами X и Y (1≤X≤N; 1≤Y≤M).

Гарантируется, что начальные координаты агента не совпадают ни с одним из выходов и он не стоит в отсеке, занятом стеной. Никакие входы и выходы гипертуннелей, а также выходы с базы не находятся в отсеках, занятых стенами. Никакой вход в гипертуннель не совпадает с выходом с базы

Выходные данные
Если побег невозможен, выведите единственную строку с надписью "Impossible". В противном случае в первой строке выдайте число L - количество отсеков в кратчайшем пути побега. В последующих L строках последовательно выведите координаты отсеков кратчайшего пути побега. Если решений несколько, то выведите любое из них.

План эвакуации

Обход в ширину

Этаж здания представляет собой прямоугольник из \(n\times m\) квадратных комнат. Из каждой комнаты есть проходы в соседние комнаты. В двух комнатах находятся лестницы. Необходимо разработать план эвакуации — указать для каждой комнаты направление движения в одну из соседних комнат так, чтобы, передвигаясь по комнатам только в указанных направлениях, можно было бы достичь одной из двух лестниц, пройдя минимальное расстояние.

На рисунке изображён возможный план эвакуации для примера из условия. Комнаты с лестницами обозначены звёздочками.

image

Первая строка входных данных содержит число \(n\) — количество строк в плане эвакуации, \(1\le n\le 100\). Вторая строка входных данных содержит число \(m\) — количество столбцов в плане эвакуации, \(2\le m\le 100\). Следующие две строки содержат числа \(r_1\) и \(c_1\) — номера строки и столбца комнаты, в которой находится первая лестница, \(1\le r_1\le n\), \(1\le c_1\le m\). Следующие две строки содержат числа \(r_2\) и \(c_2\) — номера строки и столбца комнаты, в которой находится вторая лестница, \(1\le r_2\le n\), \(1\le c_2\le m\). Гарантируется, что \(r_1\ne r_2\) или \(c_1\ne c_2\). Строки нумеруются сверху вниз числами от 1 до \(n\), столбцы нумеруются слева направо числами от 1 до \(m\).

Программа должна вывести \(n\) строк, каждая строка должна содержать \(m\) символов. Каждый символ соответствует одной комнате. В двух комнатах с лестницами должен находиться символ <<S>> (прописная английская буква). В остальных комнатах находятся символы, указывающие направление движения:

<<<>> (символ <<меньше>>) — налево.

<<>>> (символ <<больше>>) — направо.

<<^>> (символ находится на клавише <<6>>) — вверх.

<<v>> (строчная английская буква) — вниз.

Никакие другие символы, например, пробелы, выводить не нужно. Вы можете вывести любой подходящий план эвакуации.

 

Решения, правильно работающие, когда \(n=1\), будут оцениваться в 20 баллов.

Решения, правильно работающие, когда \(c_1=c_2\), будут оцениваться в 20 баллов.

Решения, правильно работающие, когда лестницы находятся в двух противоположных углах здания, будут оцениваться в 20 баллов.

Cow Navigation

Обход в ширину

Амбар описывается решёткой \(N \times N\) (\(2 \leq N \leq 20\)) символов, некоторые из них пусты, некоторые заняты. Бесси начинает в левом нижнем углу (1,1) и должна пройти в правый верхний угол \(N,N\). Вы можете управлять ею посредством последовательности инструкций вида "вперёд", "повернись влево на 90 градусов", "повернись вправо на 90 градусов". Вы хотите задать кратчайшую последовательность, которая приведёт ее к цели. Есл инструкицю выполнить невозможно, Бесси пропускает её и переходит к следующей инструкции.

К несчастью, Бесси не знает, куда она смотрит вначале в клетку (1,2) или в клетку (2,1). Вы должны дать такую последовательность, которая приведёт её к цели кратчайшим образом вне зависимости от того, какой случай произошёл. Когда Беси достигает цели, она игнорирует остальные команды.

ФОРМАТ ВВОДА (файл cownav.in):

Первая строка ввода содержит \(N\).

Каждая из \(N\) последующих строк содержит ровно \(N\) символов, представляющих амбар. Первый символ последней строки есть ячейка (1,1). Поседний символ первой строки есть ячейка (N,N).

Каждый символ или H (непроходимы стог сена) или E - пустая ячейка.

Гарантируется, что ячейки 1,1 и \(N,N\) будут пустые, также гарантируется существование пути по пустым ячейкам из 1,1 в \(N, N\).

ФОРМАТ ВЫВОДА (файл cownav.out):

На единственной выводной строке выведите длину кратчайшей последовательности команд, которая приведёт Бесси к цели, вне зависимости куда она смотри вначале, вверх или вправо.

ФОРМАТ ВВОДА:

3
EHE
EEE
EEE

ФОРМАТ ВЫВОДА:

9

В этом примере Инструкции "Вперёд, Вправо, Вперёд, Вперёд, Влево, Вперёд, Влево, Вперёд, Вперёд" приведут Бесси к назначению вне зависимости от начальной ориентации.

Problem credits: Brian Dean

Lasers and Mirrors

Обход в ширину

Коровы Фермера Джона любят производить лазерные шоу.

Для своего последнего шоу, они купили огромный мощный лазер - такой большой, что они не смогли перместить его легко из того места, где он был приобретен. Он хотят послать свет от лазера в амбар ФД. И лазер, и амбра могут рассматриваться как точки на плоскости - карте фермы ФД. В панах коров направить лазер так, чтобы он послал лч света горизонтально или вертикально (то есть вдоль оси x или вдоль оси y). Затем они планируют ментяь направление луча посредством зеркал, чтобы направить луч в амбар.

На этой ферме есть \(N\) (\(1 \leq N \leq 100,000\)) точек изгороди, расположенных в различных точках на плоскости, (и отличающихся также от точек лазера и амбара), на которых могут крепится зеркала. Коровы могут выбрать не крепить зеркало к некоторым точкам, тогда луч просто проходит через эту точку без поворотов (не меняя направление). Если коровы монтируют зеркало в точке изгороди, они выравнивают его диагонально так / или так \, что соответсвенно пернаправляет горизонтальный в вертикальный и наоборот.

Вычислите минимально возможное количество зеркал, которое необходимо коровам, чтобы пернаправить лазер в амбар.

ФОРМАТ ВВОДА (файл lasers.in):

Первая строка ввода содержит 5 целых чисел, разделённых одиночными пробелами. \(N, x_L, y_L, x_B, y_B\), где \((x_L, y_L)\) - это размещение лазера, \((x_B, y_B)\) - размещение амбара. Все координаты между \(0\) и \(1,000,000,000\).

Каждая из следующих \(N\) строк содержит \(x\) и \(y\) - координаты точек изгороди - целые числа в интервале \(0 \ldots 1,000,000,000\).

ФОРМАТ ВЫВОДА (файл lasers.out):

Выведите минимальное колчиество зеркал, которое необходимо чтобы перенаправить лазер в амбар, или -1, если это невозможно сделать.

Switching on the Lights

Обход в ширину графы

Фермер Джон недавно построил огромный амбар, состоящий из \(N \times N\) решётки комнат, (\(2 \leq N \leq 100\)), пронумерованных от \((1,1)\) до \((N,N)\). Беси, будучи коровой которая боится темноты, хочет включить свет в как можно большем количестве комнат.

Беси начинает в комнате \((1,1)\), - единственной комнате, в которой изначально был включён свет. В некоторых комнатах она найдёт переключатели, которые могут переключать свет в других комнатах. Например, в комнате \((1,1)\) может находиться переключатель света в комнате \((1,2)\). Беси может ходить только в те комнаты, где уже горит свет. И также она может переходить из комнаты \((x,y)\) только в четыре соседние комнаты \((x-1,y)\), \((x+1,y)\), \((x,y-1)\), \((x,y+1)\) (или, возможно, в меньшее количество комнат, если она находится на границе решётки.

Определите максимальное количество комнат, в которые Беси может включить свет.

ФОРМАТ ВВОДА (файл lightson.in):

Первая строка ввода содержит целые числа \(N\) и \(M\) ($1 \leq M \leq 20,000$).

Каждая из следующих \(M\) строк описывает один переключатель четырьмя целыми числами \(x\), \(y\), \(a\), \(b\), означающими, что в комнате \((x,y)\) можно переключить свет в комнате \((a,b)\). Несколько переключателей могут находится в любой комнате и несколько переключателей могут переключать свет в любой комнате.

ФОРМАТ ВЫВОДА (файл lightson.out):

Одна строка, задающая максимальное количество комнат, в которых Беси может включить свет.

ПРИМЕР ВЫВОДА

5

Здесь Беси может использовать переключатель в комнате \((1,1)\), чтобы включить свет в комнатах \((1,2)\) и \((1,3)\). Затем она может перейти в комнату \((1,3)\) и включить свет в комнате \((2,1)\), где она может включить свет в комнате \((2,2)\). Переключатель в комнате \((2,3)\) недоступен для неё, поскольку он находится в комнате, где свет не включён. Поэтому Беси может посетить не более 5 комнат.

Авторы: Austin Bannister и Brian Dean

Switching on the Lights

Обход в ширину графы

Фермер Джон недавно построил огромный амбар, состоящий из \(N \times N\) решётки комнат, (\(2 \leq N \leq 100\)), пронумерованных от \((1,1)\) до \((N,N)\). Беси, будучи коровой которая боится темноты, хочет включить свет в как можно большем количестве комнат.

Беси начинает в комнате \((1,1)\), - единственной комнате, в которой изначально был включён свет. В некоторых комнатах она найдёт переключатели, которые могут переключать свет в других комнатах. Например, в комнате \((1,1)\) может находиться переключатель света в комнате \((1,2)\). Беси может ходить только в те комнаты, где уже горит свет. И также она может переходить из комнаты \((x,y)\) только в четыре соседние комнаты \((x-1,y)\), \((x+1,y)\), \((x,y-1)\), \((x,y+1)\) (или, возможно, в меньшее количество комнат, если она находится на границе решётки.

Определите максимальное количество комнат, в которые Беси может включить свет.

ФОРМАТ ВВОДА (файл lightson.in):

Первая строка ввода содержит целые числа \(N\) и \(M\) ($1 \leq M \leq 20,000$).

Каждая из следующих \(M\) строк описывает один переключатель четырьмя целыми числами \(x\), \(y\), \(a\), \(b\), означающими, что в комнате \((x,y)\) можно переключить свет в комнате \((a,b)\). Несколько переключателей могут находится в любой комнате и несколько переключателей могут переключать свет в любой комнате.

ФОРМАТ ВЫВОДА (файл lightson.out):

Одна строка, задающая максимальное количество комнат, в которых Беси может включить свет.

ПРИМЕР ВЫВОДА

5

Здесь Беси может использовать переключатель в комнате \((1,1)\), чтобы включить свет в комнатах \((1,2)\) и \((1,3)\). Затем она может перейти в комнату \((1,3)\) и включить свет в комнате \((2,1)\), где она может включить свет в комнате \((2,2)\). Переключатель в комнате \((2,3)\) недоступен для неё, поскольку он находится в комнате, где свет не включён. Поэтому Беси может посетить не более 5 комнат.

Авторы: Austin Bannister и Brian Dean

Bessie's Dream

Обход в ширину

После столь обильного поедания фруктов на кухне Фермера Джона, Беси посетили странные мечты. Она попала в лабиринт в форме решётки клеток \(N \times M\) (\(1 \le N, M \le 1,000\)). Она начинает в левой верхней клетке и хочет попасть в правую нижнюю. Когда она стоит в клетке, он может шагнуть в любом из четырёх направлений (вверх, вниз, вправо, вверх).

Однако подождите! Каждая клетка имеет свой цвет, и каждый цвет имеет различные свойства:

  • Если клетка red (красная), то в неё ходить нельзя
  • Если клетка pink (розовая), то в неё можно ходить
  • Если клетка orange (оранжевая), то в неё можно ходить, но Беси станет пахнуть как апельсин.
  • Если клетка blue (синяя) , то она содержит пираний, которые позволят Беси пройти только если она пахнет как апельсин.
  • Если клетка purple (пурпурная), то Беси проскальзывает в следующую клетку в этом направлении (если только в следующую клетку можно заходить). Если следующая клетка также пурпурная, Беси продолжает скользить, пока не попадёт в не пурпурную клетку или остановится перед непроходимой клеткой. Скольжение одной клетки засчитывается как один шаг. Пурпурные клетки также удаляют запах.

(Пример ниже подробнее поясняет "пурпурные" клетки)

Помогите Беси добраться из левого верхнего угла в правый нижний за минимально возможное количество ходов.

ФОРМАТ ВВОДА (файл dream.in):

Первая строка ввода содержит два целых числа \(N\) и \(M\), представляющие количество строк и столбцов лабиринта.

Каждая из следующих \(N\) строк имеет по \(M\) целых чисел, представляющих лабиринт:

  • Целое число '0' это красная клетка
  • Целое число '1' это розовая клетка
  • Целое число '2' это оранжевая клетка
  • Целое число '3' это синяя клетка
  • Целое число '4' это пурпурная клетка

Левая-верхняя и правая-нижняя клетки всегда будут '1'.

ФОРМАТ ВЫВОДА (файл dream.out):

Одно целое число, представляющее минимальное количество ходов, которое должна использовать Беси, чтобы пройти лабиринт, или -1, если невозможно пройти.

Bessie's Dream

Обход в ширину

После столь обильного поедания фруктов на кухне Фермера Джона, Беси посетили странные мечты. Она попала в лабиринт в форме решётки клеток \(N \times M\) (\(1 \le N, M \le 1,000\)). Она начинает в левой верхней клетке и хочет попасть в правую нижнюю. Когда она стоит в клетке, он может шагнуть в любом из четырёх направлений (вверх, вниз, вправо, вверх).

Однако подождите! Каждая клетка имеет свой цвет, и каждый цвет имеет различные свойства:

  • Если клетка red (красная), то в неё ходить нельзя
  • Если клетка pink (розовая), то в неё можно ходить
  • Если клетка orange (оранжевая), то в неё можно ходить, но Беси станет пахнуть как апельсин.
  • Если клетка blue (синяя) , то она содержит пираний, которые позволят Беси пройти только если она пахнет как апельсин.
  • Если клетка purple (пурпурная), то Беси проскальзывает в следующую клетку в этом направлении (если только в следующую клетку можно заходить). Если следующая клетка также пурпурная, Беси продолжает скользить, пока не попадёт в не пурпурную клетку или остановится перед непроходимой клеткой. Скольжение одной клетки засчитывается как один шаг. Пурпурные клетки также удаляют запах.

(Пример ниже подробнее поясняет "пурпурные" клетки)

Помогите Беси добраться из левого верхнего угла в правый нижний за минимально возможное количество ходов.

ФОРМАТ ВВОДА (файл dream.in):

Первая строка ввода содержит два целых числа \(N\) и \(M\), представляющие количество строк и столбцов лабиринта.

Каждая из следующих \(N\) строк имеет по \(M\) целых чисел, представляющих лабиринт:

  • Целое число '0' это красная клетка
  • Целое число '1' это розовая клетка
  • Целое число '2' это оранжевая клетка
  • Целое число '3' это синяя клетка
  • Целое число '4' это пурпурная клетка

Левая-верхняя и правая-нижняя клетки всегда будут '1'.

ФОРМАТ ВЫВОДА (файл dream.out):

Одно целое число, представляющее минимальное количество ходов, которое должна использовать Беси, чтобы пройти лабиринт, или -1, если невозможно пройти.

Piggyback

Обход в ширину


Беси и её сестра Эльза пасутся на различных полях в течение дня, а вечером обе хотят вернуться в амбар отдыхать. Будучи умными коровами, они хотят составить план, чтобы минимизировать суммарное количество энергии, которое они обе потратят на это путешествие.
Беси тратит B единиц энергии, когда она переходит с одного поля на соседнее поле, а Эльза тратит E единиц энергии при переходе на соседнее поле. Однако, если Беси и Эльза оказались на одном поле, то Беси может нести Эльзу на своих плечах, и тогда обе могут переместиться на соседнее поле, потратив только P единиц энергии, (где P может быть существенно меньше, чем B+E - количество энергии, которое затрачивается двумя коровами вместе, если они перемещаются на соседнее поле по отдельности). Если P очень маленькое, то коровам выгоднее перемещаться вместе, а если P очень большое - то по отдельности.
По заданным B, E, P и расположению полей на ферме, вычислите минимальное количество энергии, которое потребуется Беси и Эльзе, чтобы добраться до амбара.
Формат входных данных
Первая строка ввода содержит положительные числа B, E, P, N, M. Все они не превышают 40,000. B, E, P описаны выше. N - количество полей на ферме, пронумерованных от 1 до N, N>=3. M - количество дорожек между полями. Беси и Эльза начинают в полях 1 и 2 соответственно. Амбар расположен в поле N.
Каждая из следующих M строк ввода описывает дорожку между парой различных полей, указанную номерами этих полей. Дорожки двунаправленные. Всегда можно добраться от поля 1 до поля N и от поля 2 до поля N посредством некоторого количества дорожек.

Формат выходных данных
Одно целое число, указывающее минимальное количество энергии, которое суммарно потратят Беси и Эльза, чтобы добраться до амбара. В примере, приведенном выше, Беси перемещается от 1 к 4, Эльза перемещается от 2 к 3, затем к 4. Потом они перемещаются вместе от 4 к 7, затем к 8.

Telephone

графы Обход в ширину кратчайшие пути

\(N\) коров Фермера Джона, последовательно пронумерованные, \(1 \ldots N\) выстроены в ряд (\(1\le N\le 5\cdot 10^4\)). \(i\)-ая корова имеет идентификатор породы \(b_i\) в интервале \(1 \ldots K\), with \(1\le K\le 50\). Коровы нуждаются в Вашей помощи чтобы узнать, как быстрее передать сообщение от коровы \(1\) корове \(N\).

\(|i-j|\) минут требуется, чтобы передать сообщение от коровы \(i\) к корове \(j\). Однако не все породы готовы взаимодействовать друг с другом, что описано в матрице \(S\) размером \(K \times K\), где \(S_{ij} = 1\) если корова породы \(i\) готова передать сообщение корове породы \(j\) и 0 в противном случае. Необязательно истина то, что \(S_{ij}=S_{ji}\), и даже может быть случай, когда \(S_{ii} = 0\), то есть корова породы \(i\) не будет передавать сообщение корове своей породы.

Определите минимальное количество времени, которое потребуется для передачи сообщения.

ФОРМАТ ВВОДА (с клавиатуры / stdin):

Первая строка содержит \(N\) и \(K\).

Следующая строка содержит \(N\) разделённых пробелом целых чисел \(b_1,b_2,\ldots,b_N\).

Следующие \(K\) строк описывают матрицу \(S\). Каждая строка состоит из строки из K бит. \(S_{ij}\) \(j\)-ый бит \(i\)-ой строки сверху.

ФОРМАТ ВЫВОДА (на экран / stdout):

Выведите одно целое число - минимальное количество требуемого времени. Если невозможно передать сообщение от коровы \(1\) к корове \(N\), выведите \(-1\).

Bucket Brigade

Обход в ширину

На ферме пожар и коровы должны спасаться.

Ферма описывается решёткой \(10 \times 10\) символов: 

..........
..........
..........
..B.......
..........
.....R....
..........
..........
.....L....
..........

Символ 'B' представляет амбар, который горит. Символ 'L' представляет озеро, символ 'R' представляет огромную скалу.

Коровы хотят сформировать "ведерную бригаду", разместившись вдоль пути между озером и амбаром так, чтобы они могли передавать друг другу воду для тушения пожара. Ведро может передаваться между коровами, если они являются непосредственными соседями в направлении "север", "юг", "запад", "восток". Аналогично корова может набирать воду из озера, если она аналогично соседствует с ним. Наконец корова может поливать амбар из ведра, только если она аналогично непосредственно соседствует с ним.

Помогите определить минимальное количество квадратов '.', которые должны быть заняты коровами, чтобы сформировать успешную "ведерную бригаду".

Корова не может находится в квадрате, содержащем скалу, амбар или озеро. Гарантируется, что они не будут соседними друг другу.

ФОРМАТ ВВОДА (файл buckets.in):

Входной файл содержит 10 строк, каждая по 10 символов, описывающих план фермы.

ФОРМАТ ВЫВОДА (файл buckets.out):

Выведите одно целое число - минимальное количество коров, требуемых для того, чтобы сформировать "ведерную бригаду".

A Pie for a Pie

графы Обход в ширину кратчайшие пути

У Беси и Эльзы по N (\(1 \leq N \leq 10^5\)) пирогов. Каждый из \(2N\) пирогов имеет величину вкусности по мнению Беси и величину вкусности (возможно отличающуюся) по мнению Эльзы.

Беси хочет отдать один из своих пирогов Эльзе. Если Эльза получит пирог от Беси, она должна будет отдать один из своих пирогов Беси. Чтобы не оказаться ни скупой, ни щедрой, Эльза постарается выбрать пирог, как минимум, такой же вкусный (по мнению Эльзы) как она получила, но не более чем на \(D\) единиц вкуснее (\(0 \leq D \leq 10^9\)). Такой пирог может не существовать, в этом случае Эльза сбежит в Японию.

Но если Эльза отдаст Беси пирог взамен, то Беси аналогично постарается отдать Эльзе пирог, как минимум такой же вкусный (по мнению Беси), но не более чем на \(D\) единиц вкуснее, чем кусок, который она получила. Если Беси не сможет, то тоже сбежит. Иначе отдаст кусок Эльзе. Этот цикл продолжается, пока возможно, или пока одна из коров не получит кусок с величиной вкусности равной \(0\), в этом случае процесс заканчивается и обе коровы счастливы.

Заметим, что один и тот же кусок не может быть подарен дважды, и кусок не может вернуться той корове, которая его дарила.

Для каждого из \(N\) кусков Беси может выбрать его как начальный подарок Эльзе. Определите минимальное количество кусков, которые могут быть подарены так, чтобы обе коровы оказались счастливы.

ФОРМАТ ВВОДА (файл piepie.in):

Первая строка содержит два целых числа \(N\) и \(D\).

Следующие \(2N\) строк содержат по два целых числа, разделённых пробелом, соответственно обозначающие вкусность данного куска по мнению Беси и по мнению Эльзы.

Первые \(N\) строк о кусках Беси, а оставшиеся \(N\) строк о кусках Эльзы.

Гарантируется, что все величины вкусности в интервале \([0,10^9]\).

ФОРМАТ ВЫВОДА (файл piepie.out):

На выводе должно быть \(N\) строк. Строка \(i\) должна содержать одно целое число: минимальное количество кусков, которое может быть подарено при счастливом исходе, если Беси начнёт с куска \(i\). Если счастливый исход при начале с куска \(i\) невозможен, то строка \(i\) должна содержать \(-1\).

Cross Country Skiing

графы Бинарный поиск по ответу Обход в ширину


Лыжная трасса описана решёткой из M x N высот (1 <= M,N <= 500), каждая из высот в диапазоне 0 .. 1,000,000,000.
Некоторые из этих ячеек обозначены как точки маршрута гонки. Организаторы хотят назначить маршруту рейтинг трудности D так, чтобы корова могла попасть в любую точки маршрута из любой другой точки маршрута, последовательно перемещаясь между соседними ячейками, абсолютная разность высот которых не превышает D. Две ячейки считаются соседними, если они граничат по стороне (в направлении на север, юг, запад или восток одна от другой). Рейтинг трудности маршрута это минимальное значение D такое, что все точки маршрута взаимно достижимы при выполнении вышеописанного требования.
PROBLEM NAME: ccski
Формат входных данных
* Строка 1: Целые числа M и N.
* Строки 2..1+M: Каждая из этих M строк содержит N целых высот.
* Строки 2+M..1+2M: Каждая из этих M строк содержит N величин 0 или 1, 1 указывает, что данная высота – точка маршрута гонки.

Формат выходных данных
* Строка 1: Рейтинг трудности маршрута (минимальное значение D такое, что все точки маршрута взаимно достижимы)
Примечание
Если D = 21, то все 3 точки маршрута взаимно достижимы. Если D<21 верхняя правая точка не достижимы из других двух.

What's Up With Gravity

Обход в ширину


Капитан (C) должен спасти доктора (D). Все происходит на двумернйо решетке NxM (1<=N,M<=500). Некоторые из ячеек пусты (и по ним можно двигаться), а некоторые блокированы (и по ним нельзя двигаться).
Движение подчиняется следующим законам:
1) Если под Капитаном нет ячейки (он находится на краю решетки), то он падает в бездну и миссия спасения не выполнена 2) если под Капитаном есть пустая ячейка, но падает в нее. 3) Иначе a) Капитан может двигаться влево или вправо, если соответствующая ячейка существует и пуста. б) Капитан может переключить направление гравитации.
Когда капитан переключает направление гравитации, ячейка которая "под ним" (в смысле правил 1 и 2) переключается между ячейками с большим индексом и ячейками с меньшим индексом. Первая строка имеет индекс 1, последняя строка имеет индекс N.
Помогите Капитану найти Доктора используя минимальное количество переключений гравитации. Если Капитан не может добраться до клетки с Доктором - выведите -1.
PROBLEM NAME: gravity
Формат входных данных
* Строка 1: Два разделенных пробелом целых числа N и M.
* Строки 2..1+N: Строка i+1 описывает i-ую строку решетки: '.' обозначает пустую клетку, '#' обозначает блокированную клетку, 'C' обозначает стартовую позицию Капитана, 'D' обозначает позицию Доктора.
Формат выходных данных
* Строка 1: Одно целое число - минимальное количество раз, когда Капитан переключал гравитацию, или -1, если Капитану не возможно добраться до Доктора.
Примечание
Капитан начинает в позиции (4,2). Он переключает гравитацию и падает в позицию (2,2) затем двигается вправо дважды и попадает в точку (2,4). Переключает гравитацию снова и падает в позицию (4,4), затем двигается вправо в позицию (4,5). Переключает гравитацию опять и падает в позицию Доктора в клетке (3,5).

Island Travels

графы Минимальный каркас Обход в ширину


Фермер Джон отвез саоих коров на океан. Коровы живут на N (1<=N<=15) островах, которые расположены на решетке R x C (1 <= R, C <= 50). Остров - это максимальная связная группа квадратов на решетке, помеченная символами 'X', где два 'X' связны, только если они имеют общую сторону. Квадраты имеющие общий угол, не обязательно связны.
Беси опоздала, она прилетела с ФД на вертолете. Она может приземлиться на любом острове. Она хочет посетить все N островов хотя бы один раз.
Вокруг островов находится мелководье (обозначено буквой 'S'). Беси может плыть по нему в четырех направлениях (север, юг, запад, восток) для того, чтобы путешествовать между островами. Она также может путешествовать между островом и мелководьем и наоборот.
Определите минимальное расстояние, которое Беси должна проплыть, чтобы посетить все острова (гарантируется, что это возможно). Расстояние, которое проплывет Беси, равно количеству различных раз, когда Беси посетит клеточку 'S'.
PROBLEM NAME: island
Формат входных данных
* Строка 1: Два разделенных пробелом целых числа: R и C.
* Строки 2..R+1: Строка i+1 содержит C символов, определяющих i-ую строку решетки. Глубокая вода обозначена '.', острова 'X', мелководье 'S'.
Формат выходных данных
* Строка 1: Одно целое число, представляющее минимальное расстояние, которое должна проплыть Беси, чтобы посетить все острова.
Примечание
Бэси может проплыть от левого верхнего сотрова к среднему, проплыв 1 клеточку, а затем от среднего острова к правому нижнему, проплыв 2 клеточки - всего 3.

Tractor

Бинарный поиск по ответу Поиск компонент связности Обход в ширину


Одно из полей Фермера Джона весьма холмисто. И он хочет купить новый трактор для работы на этом поле. Поле описывается решеткой из N x N (1 <= N <= 500) неотрицательных целых высот ячеек. Трактор может перемещаться из ячейки в соседнюю (на один шаг на север, юг, запад или восток), с разницей их высот D ровно за D единиц денег.
ФД хочет заплатить достаточно, так чтобы его трактор, начиная с некоторой ячейки поля мог посетить как минимум половину ячеек поля. Если число ячеек в поле - нечетное, то половина, округленная вверх.
Определите минимальную стоимость покупки трактора способного выполнить эту задачу.

PROBLEM NAME: tractor
Формат входных данных
* Строка 1: Значение N.
* Строки 2..1+N: Каждая строка содержит N разделенных одиночными пробелами неотрицательных целых чисел (каждое не более миллиона), определяющих строку поля ФД.
Формат выходных данных
* Line 1: Минимальная стоимость трактора, который способен объехать не менее половины этого поля.
Примечание
Трактор стоимостью 3 способен перемещаться из ячейки с высотой 0 в ячейку с высотой 3. Поэтому он может посетить все ячейки с высотами 0 и 3. Вместе они представляют не менее половины фермы.

Unlocking Blocks (Silver)

Обход в ширину графы Задачи на моделирование


Коровы любят головоломки. Фермер Джон подарил Беси на день рождения новую головоломку. Она состоит из трех твердых объектов, каждый из которых состоит из склеенных вместе квадратиков размера 1 х 1. Каждый из этих объектов имеет «связную» форму в том смысле, что Вы можете перейти из одного квадратика в любой другой, двигаясь по квадратикам этого объекта в одном из четырех направлений: север, юг, запад, восток.
Объект может перемещаться последовательно скольжением на одну единицу в одном из четырех направлений: север, юг, запад, восток. Цель головоломки - переместить объекты так, чтобы они разделились – то есть, чтобы граничные квадратики отошли друг от друга. Ваша задача – по заданным трем объектам определить, можно их разделить, или нет. Конфигурация, которую разделить нельзя, называется заблокированной.

Замечание: программы, которые не делают ничего, кроме угадывания ответа, могут быть дисквалифицированы.
PROBLEM NAME: unlock
Формат входных данных
* Строка 1: Три разделенных одиночными пробелами целых числа: N1, N2, and N3, описывающих количество квадратов соответственно в фигурах 1, 2, и 3.
* Строки 2..1+N1: Каждая из этих строк описывает (x,y) координату юго-западного угла одного квадрата объекта 1. Все координаты в интервале 0..9.
* Строки 2+N1..1+N1+N2: Каждая из этих строк описывает (x,y) координату юго-западного угла одного квадрата объекта 2. Все координаты в интервале 0..9.
* Lines 2+N1+N2..1+N1+N2+N3: Каждая из этих строк описывает (x,y) координату юго-западного угла одного квадрата объекта 1. Все координаты в интервале 0..9.
Формат выходных данных
* Строка 1: Минимальное количество шагов, которое необходимо выполнить, чтобы разделить три объекта или -1, если объекты не могут быть разделены.
Примечание
Если мы сдвинем объект 3 на 4 позиции на восток, а затем объект 2 на одну позицию на север и затем на 3 позиции на восток, то границы трех фигур разъединятся.

Tractor

Обход в ширину


Фермер Джон оставил свой трактор в середине поля. Коровы решили подшутить над ФД. Они разместили N стогов сена (1 <= N <=50,000) в различных участках поля, так что ФД не может забрать трактор не удалив некоторые из них.
Местоположение трактора и стогов сена - это точки на декартовой плоскости с целочисленными координатами от 1 до 1000. Нет стогов сена в позиции трактора. Трактор ФД может двигаться только параллельно осям координат (на север, юг, запад и восток) на целое количество единиц. Трактор не может проходить через точку, в которой имеется стог сена.
Пожалуйста, помогите ФД определить минимальное количество стогов сена, которые придется убрать, чтобы он мог привести трактор в начало координат.
PROBLEM NAME: tractor
Формат входных данных
* Строка 1: Три разделенных пробелом целых числа N x y (x,y) - начальные координаты трактора
* Строки 2..1+N: Каждая строка содержит (x,y)-координаты стога сена


Формат выходных данных
* Строка 1: Минимальное количество стогов сена, которое ФД должен удалить для того, чтобы обеспечить путь своему трактору к началу координат.
Примечание
Достаточно удалить только 1 стог.

Cow Beauty Pageant (Silver Level)

Обход в ширину

Problem 1: Cow Beauty Pageant (Silver Level) [Brian Dean]
Прослышав, что модно иметь коров с тремя пятнами, Фермер Джон купил целое стадо таких коров. К несчастью, мода меняется очень быстро, и сейчас в моде коровы с одним пятном.
ФД теперь хочет подкрасить своих коров так, чтобы они стали с одним пятном. Раскраска коровы задается двумерным массивом символов (N*M), например, так:
................ ..XXXX....XXX... ...XXXX....XX... .XXXX......XXX.. ........XXXXX... ..XXX....XXX....
Здесь 'X' обозначает часть пятна. Два символа 'X' принадлежат одному и тому же пятну, если они соседние вертикально или горизонтально (диагональные соседними не являются). Все коровы ФДЖ имеют ровно 3 пятна.
ФД хочет потратить как можно меньше краски, чтобы объединить три пятна в одно. На примере выше, он может сделать это, покрасив только 4 позиции, они обозначены символом ‘*’ на рис. ниже.
................ ..XXXX....XXX... ...XXXX*...XX... .XXXX..**..XXX.. ...*....XXXXX... ..XXX....XXX....
Помогите ФД определить минимальное количество клеток(символов), которые нужно закрасить, чтобы объединить три пятна в одно.
PROBLEM NAME: pageant
Формат входных данных
* Строка 1: Два разделенных пробелом целых числа, N и M (1 <= N,M <= 50).
* Строки 2..1+N: Каждая содержит строку из M символов 'X' и '.', указывающих соответствующую линию раскраски коровы.
Формат выходных данных
* Line 1: Минимальное количество сиволов 'X', которые нужно добавить ко введенным данным, чтобы получить единое пятно.
Примечание
4 символа ‘X’ нужно добавить, чтобы получить одно пятно.

Водопровод

Перебор Обход в ширину битмаски

Город Восточный постоянно страдает от недостатка воды. Для устранения этой проблемы была построена новая водопроводная труба. Строительство трубы началось с обоих концов одновременно, и спустя некоторое время половины соединились. Ну, почти. Первая половина трубы заканчивалась в точке (x1, y1), а вторая - в точке (x2, y2).

К сожалению, осталось лишь несколько отрезков трубы различной длины. Более того, из-за специфики местной технологии трубы могут быть проложены только в направлении с севера на юг или с востока на запад и соединяются, образуя или прямую, или угол 90 градусов. Требуется, зная длины отрезков труб L1, L2, ..., LK и количество отрезков каждой длины C1, C2, ..., CK, сконструировать трубу, соединяющую две заданные точки, или определить, что это невозможно.

Ограничения: 1 <= K <= 4, 1 <= x1, y1, x2, y2, Li <= 1000, 1 <= Ci <= 10, все числа целые.



Входные данные
В первой строке находятся числа x1, y1, x2, y2, K, затем 2K чисел: L1, L2, ..., LK, C1, C2, ..., CK.

Выходные данные
Вывести одно число - минимальное количество нужных отрезков труб или -1, если соединение невозможно.

Нечестная игра

графы Обход в ширину Задачи на моделирование

На клетчатой доске размером \(n \times m\), состоящей из \(n\) строк и \(m\) столбцов, в клетке \((r, c)\), то есть на пересечении \(r\)-й сверху строки и \(c\)-го слева столбца, расположена фишка. На этой доске вам предстоит сыграть против компьютера в игру, в которой можно перемещать фишку и удалять клетки поля.

Каждый ход устроен следующим образом.

  1. Компьютер называет целое число \(k > 0\).

  2. Вы ровно \(k\) раз некоторым образом выбираете одну из еще не удаленных клеток, соседних по стороне (имеющих общую сторону) с той, в которой фишка находится в текущий момент, и перемещаете фишку в эту клетку. Вы можете перемещать фишку на клетку, в которой она уже была. Если не существует еще не удаленных клеток, соседних по стороне с текущей, перемещение не производится.

  3. Компьютер называет координаты \((i, j)\) произвольной еще не удаленной клетки поля, после чего она сразу же удаляется.

Если компьютер удаляет клетку, на которой находится фишка, игра заканчивается вашей победой. Ваша цель — победить как можно раньше. При этом вы не сообщаете компьютеру свои перемещения, поэтому можете играть нечестно: вместо реального перемещения фишки по полю вы можете следить за всеми возможными ее положениями. Иными словами, если в какой-то момент при удалении клетки \((i, j)\) существует последовательность перемещений фишки, при которой в данный момент фишка находится в точности в клетке \((i, j)\), вы можете сообщить компьютеру, что игра завершена, и вы победили.

Разумеется, компьютер следит за соблюдением правил, поэтому если вы сообщаете ему о своей победе при удалении клетки, на которой фишка не могла в этот момент находиться, вы автоматически проигрываете.

Определите как можно меньший номер хода, после которого вы можете сообщить комьютеру о своей победе, то есть после которого фишка могла оказаться на удаляемой клетке. Чем ближе ваш ответ к минимальному возможному, тем больше баллов вы получите.

Формат входных данных
В единственной строке ввода даны четыре целых числа \(n\), \(m\), \(r\) и \(c\) — размеры доски и координаты изначального расположения фишки (\(1 \le r \le n \le 1000\); \(1 \le c \le m \le 1000\)).

Во второй строке ввода дано максимальное количество баллов, которое можно получить за соответствующую группу тестов. Ваше решение это значение может игнорировать.

В следующих \(n \cdot m\) строках даны ходы, которые последовательно собирается сделать компьютер. Описание \(t\)-го хода задается тремя целыми числами \(k_t\), \(i_t\) и \(j_t\) — количеством перемещений фишки, которые вам понадобится совершить, и координатами клетки поля, которую после этого требуется удалить (\(1 \le k_t \le 10^9\); \(1 \le i_t \le n\); \(1 \le j_t \le m\)).

Гарантируется, что все удаляемые клетки различны, то есть никакая клетка не удаляется дважды.

Формат выходных данных
Выведите одно целое число от \(1\) до \(n \cdot m\) — номер хода, после которого вы сообщите компьютеру о своей победе.

 

Замечание

В первом примере можно, например, первым ходом передвинуть фишку из \((1, 1)\) в \((1, 2)\), а вторым — из \((1, 2)\) в \((2, 2)\) и затем в \((2, 1)\), тем самым поместив ее на удаляемую клетку.

Игрушечный лабиринт

Обход в ширину

Игрушечный лабиринт представляет собой прозрачную плоскую прямоугольную коробку, внутри которой есть препятствия и перемещается шарик. Лабиринт можно наклонять влево, вправо, к себе или от себя, после каждого наклона шарик перемещается в заданном направлении до ближайшего препятствия или до стенки лабиринта, после чего останавливается. Целью игры является загнать шарик в одно из специальных отверстий – выходов. Шарик проваливается в отверстие, если оно встречается на его пути (шарик не обязан останавливаться в отверстии).

Первоначально шарик находится в левом верхнем углу лабиринта. Гарантируется, что решение существует и левый верхний угол не занят препятствием или отверстием.


Входные данные

В первой строке входного файла записаны числа N и M – размеры лабиринта (целые положительные числа, не превышающие 100). Затем идет N строк по M чисел в каждой – описание лабиринта. Число 0 в описании означает свободное место, число 1 – препятствие, число 2 – отверстие.


Выходные данные

Выведите единственное число – минимальное количество наклонов, которые необходимо сделать, чтобы шарик покинул лабиринт через одно из отверстий.

 
Примеры
№ Входные данные Выходные данные
1 
4 5
0 0 0 0 1
0 1 1 0 2
0 2 1 0 0
0 0 1 0 0
 
3

Считаем графы

графы Обход в ширину Вывод формулы

У Маши есть связный ненаправленный граф G с N вершинами, помеченными 1…N и M ребрами (\(1 \leq N \leq10^2\), \(N-1 \leq M \leq \frac {N^2+N}{2}\)). G может содержать петли (ребра из вершины в неё же), но не имеет параллельных ребер (несколько ребер, соединяющих одни и те же конечные точки).
Пусть \(f_G(a,b)\) это булевская функция, которая отвечает истина, если существует путь от вершины 1 до вершины a, который проходит ровно b ребер, для \(1 \leq a \leq N\) и \(0 \leq b\), и ложь иначе. Если по ребру проходим множество раз, это число включается в ответ. 
Даша хочет повторить за Машей. В частности, она хочет сконструировать ненаправленный граф G′ такой, что \(f_{G'}(a,b)=f_G(a,b)\) для всех a и b.

Посчитайте количество различных графов G′, которые Даша может создать, по модулю \(10^9+7\). Как и G, G′ может содержать петли но не может иметь параллельные ребра (это означает, что имеется всего \(2^{ \frac {N^2+N} {2}}\) различных графов на N вершинах).
Каждый ввод содержит T (\(1 \leq T \leq \frac {10^5}{4}\)) тестов, которые должны решаться независимо. Гарантируется, что сумма \(N^2\) по всем тестам не превысит \(10^5\).

Входные данные
Первая строка ввода содержит T, количество тестов.
Первая строка каждого теста содержит два целых числа N и M.
Следующие M строк каждого теста содержат два целых числа x и y (\(1 \leq x \leq y \leq N\)), обозначающих ребро между x и y в G.

Тесты разделены пустой строкой для читабельности.

Выходные данные
Для каждого теста выведите количество различных G′ по модулю \(10^9+7\) на отдельной строке.
 
 

Примеры
№ Входные данные Выходные данные Примечание
1 1

5 4
1 2
2 3
1 4
3 5		 3 G′ может быть равен G′ или одному из двух следующих графов:
5 4
1 2
1 4
3 4
3 5

5 5
1 2
2 3
1 4
3 4
3 5
2 7

4 6
1 2
2 3
3 4
1 3
2 4
1 4

5 5
1 2
2 3
3 4
4 5
1 5

5 7
1 2
1 3
1 5
2 4
3 3
3 4
4 5

6 6
1 2
2 3
3 4
4 5
5 6
6 6

6 7
1 2
2 3
1 3
1 4
4 5
5 6
1 6

10 10
1 1
1 2
1 3
1 4
1 5
1 6
1 7
1 8
1 9
1 10

22 28
1 2
2 3
3 4
4 5
5 6
6 7
1 7
1 8
3 9
8 10
10 11
10 12
10 13
10 14
11 15
12 16
13 17
14 18
9 15
9 16
9 17
9 18
15 19
19 20
15 20
16 21
21 22
16 22		 45
35
11
1
15
371842544
256838540		 Это пример более крупного теста.
Обязательно выводите ответ по модулю \(10^9+7\).
Обратите внимание, что ответ для предпоследнего теста - \(2^{45}\ \ (mod\ 10^9 + 7)\).

 

Хакер

Обход в ширину графы

Однажды юный хакер Шалдыга Севин решил совершить дерзкое преступление - сменить имя своего друга Максима Никитина на сильвере, пока тот был в ЛКШ Зима (Ливневая Коробка Шредингера), чтобы Наталья Владимировна поставила ему двойку. Для этого Шалдыга решил заразить вирусом базу данных сильвера.
Однако юный хакер осознал одну проблему - он не знает, на каком именно компьютере лицея она хранится. Шалдыга не стал долго думать над этой проблемой и решил заразить все компьютеры в лицее (для надежности). Вирус работает так: раз в день он заражает все компьютеры, связанные с зараженными напрямую. Первый компьютер Шалдыге придется заразить лично, потому он может выбрать любой.
Хакер хочет узнать минимальное количество дней, которое понадобится для того, чтобы заразить все компьютеры лицея. Однако выяснилась еще одна проблема - эта задача легко решается с помощью БФСа, но написать его меньше чем за 15 дней невозможно, а Хакеру еще нужно сделать 200 номеров по математике. Поэтому Шалдыга попросил Вас сделать невозможное - написать программу, отвечающую на его вопрос, за время этого контеста.
 
Входные данные
В первой строке на вход подаются два числа N и M - количество компьютеров в лицее и соединений между ними соответственно. 1 <= N, M <= 100
В следущих M строках Вам даются описания соединений между компьютерами, а именно 2 чила U и V, которые означают, что компьютеры U и V соединены.
 
Выходные данные
Выведите ответ на вопрос Шалдыги

Ввод Вывод
6 9
1 2
1 3
2 4
2 6
3 4
3 5
4 5
4 6
5 6
 2



(с) Григорьев Е., 2017

Одуванчики

Обход в ширину

У Ани есть поле размером N×M клеток. На этом поле Аня разводит одуванчики. Аня заметила, что если в некоторой клетке поля растёт одуванчик, то на следующий день в четырёх клетках рядом с ним (севернее, восточнее, южнее и западнее) вырастает по одуванчику. Однако за пределами поля одуванчики не вырастают.

Сейчас на поле растёт несколько одуванчиков (не меньше одного). Определите, через сколько дней всё поле будет в одуванчиках. Известно, что Аня хорошо заботится о выросших одуванчиках, поэтому ни один из них не погибнет.
 
Формат входных данных
На первой строке находятся числа N и M (1<=N, M <= 100)  размеры поля. Далее идут N строк, каждая из которых по M элементов. Эти строки обозначают поле. Символ «.» в строке означает, что данная клетка поля пуста, а символ «*» что в клетке находится одуванчик. Других символов в строках быть не может.

Формат выходных данных
Выведите единственное число - количество дней, которое должно пройти, чтобы всё поле оказалось засеянным одуванчиками.
Частичные решения, работающие при случаях, когда N = 1 или M = 1, получат не менее 30 баллов.

Ввод Вывод
3 3
...
.*.
...
 2
4 3
...
...
...
*..
 5