Плюсануть
Поделиться
Класснуть
Запинить


Олимпиадный тренинг

Вы можете самостоятельно решать эти задачи столько раз, сколько вам это понадобится.
   

Суммы на подотрезках

Дерево отрезков, RSQ, RMQ

Реализуйте структуру данных для эффективного вычисления сумм подряд идущих элементов массива.

Входные данные
В первой строке вводится одно натуральное число N (1 ≤ N ≤ 100000) — количество чисел в массиве.

Во второй строке вводятся N чисел от 1 до 100000 — элементы массива.

В третьей строке вводится одно натуральное число K (1 ≤ K ≤ 30000) — количество запросов на вычисление суммы.

В следующих K строках вводится по два числа — номера левого и правого элементов отрезка массива (считается, что элементы массива нумеруются с единицы).

Выходные данные
Для каждого запроса выведите сумму чисел соответствующего участка массива. Числа выводите в одну строку через пробел.
 

Ввод Вывод
5
4 4 8 7 8
2
1 2
1 3		 8 16

33701

Дерево отрезков, RSQ, RMQ

Реализуйте эффективную структуру данных, позволяющую изменять элементы массивы и вычислять НОД нескольких подряд идущих элементов.

Входные данные
В первой строке вводится одно натуральное число N (1 ≤ N ≤ 100000) — количество чисел в массиве.
Во второй строке вводятся N чисел от 0 до 100000 — элементы массива.
В третьей строке вводится одно натуральное число M (1 ≤ M ≤ 30000) — количество запросов.
Каждая из следующих M строк представляет собой описание запроса. Сначала вводится одна буква, кодирующая вид запроса (s — вычислить НОД, u — обновить значение элемента).
Следом за s вводятся два числа — номера левой и правой границы отрезка.
Следом за u вводятся два числа — номер элемента и его новое значение.

Выходные данные
Для каждого запроса s выведите результат. Все числа выводите в одну строку через пробел.
 

Ввод Вывод
5
2 8 4 16 12
5
s 1 5
s 4 5
u 3 32
s 2 5
s 3 3		 2 4 4 32

Максимумы на подотрезках

Дерево отрезков, RSQ, RMQ sqrt декомпозиция

Реализуйте структуру данных для эффективного вычисления максимумов подряд идущих элементов массива.

Входные данные
В первой строке вводится одно натуральное число N (\(1 <= N <= 100000\)) — количество чисел в массиве. Во второй строке вводятся N чисел от 1 до 100000 — элементы массива. В третьей строке вводится одно натуральное число K (\(1 <= K <= 30000\)) — количество запросов на вычисление максимума. В следующих K строках вводится по два числа — номера левого и правого элементов отрезка массива (считается, что элементы массива нумеруются с единицы).

Выходные данные
Для каждого запроса выведите значение максимального элемента на указанном отрезке массива. Числа выводите в одну строку через пробел.

 

Примеры
№ Входные данные Выходные данные
1 5
2 2 2 1 5
2
2 3
2 5		 2 5

Организация коров фермера Джона 2

Дерево отрезков, RSQ, RMQ

Из N коров выбирается делегация (1≤N≤2⋅105). Они стоят в ряд, корова i имеет породу bi.

Делегация будет состоять из непрерывного участка коров не менее трёх, то есть коровы l…r для целых l и r удовлетворяющих условиям 1≤l<r≤N и r−l≥2. Три коровы в выбранном интервале помечаются как лидеры делегации. Две граничные коровы обязательно должны быть лидерами. Кроме того, каждый лидер должен иметь породу отличную от всех остальных коров в делегации (лидеры или не лидеры).

Определите количество способов которыми можно выбрать делегацию. Две делегации рассматриваются различными, если у них отличаются члены или лидеры.

Входные данные: 
Первая строка содержит N.
Вторая строка содержит N целых чисел b1,b2,…,bN, каждое в интервале [1,N].
Выходные данные: 
Количество возможных делегаций на одной строке.

Примеры
№ Входные данные Выходные данные Пояснение
1 7
1 2 3 4 3 2 5		 9 Каждая делегация соответствует одному из следующих триплетов лидеров:

(1,2,3),(1,2,4),(1,3,4),(1,4,7),(2,3,4),(4,5,6),(4,5,7),(4,6,7),(5,6,7).

Взвешивание камней

Алгоритмы сортировки Дерево отрезков, RSQ, RMQ Жадный алгоритм

Джек нашел N камней и упорядочил их в порядке возрастания их массы. Массы всех камней различны. Самый легкий камень получил номер 1, следующий ≤ 2 и так далее, самый тяжелый получил номер N.

У Джека есть чашечные весы и он решил положить все камни на них в каком-то порядке. Известен порядок, в котором он будет класть камни, и какой камень на какую чашу попадет.

Ваша задача — определить состояние весов после добавления каждого камня. Точные массы камней не известны — даются только их номера.

Входные данные
Первая строка содержит целое число N (1  N ≤ 100000).

Каждая из следующих N строк содержит по два целых числа: R (1 ≤ R ≤ N) и S (1 ≤ S ≤ 2). R - номер камня, который будет положен на чашу S. Все R будут различны.

Выходные данные
Выведите N строк -  по одной для каждого камня. Если после добавления соответствующего камня чаша 1 тяжелее, выведите “<”. Если сторона 2 тяжелее, выведите “>”. Если невозможно определить, в каком состоянии будут весы, выведите “?”.

Примеры
№ Входные данные Выходные данные
1 5
1 2
3 1
2 1
4 2
5 1		 
<
>
>
?
>

Подстроки подпоследовательностей

Динамическое программирование: один параметр Динамическое программирование Дерево отрезков, RSQ, RMQ Дерево Фенвика

Назовем подпоследовательностью массива a непустой массив b такой, что он может быть получен из массива a удалением нескольких (возможно, никаких) элементов массива a. Например, массив [1,3]  является попоследовательностью массива [1,2,3] , но [3,1]  не является.

Назовем подотрезком массива a непустой массив b такой, что он может быть получен путем удаления нескольких (возможно, никаких) первых и последних элементов массива a. Например, [1,2]  является подотрезком массива [1,2,3] , а [1,3]  не является. Несложно заметить, что у массива длины n ровно  \( {n(n+1) \over 2}\)  подотрезков.

Назовем массив a длины n возрастающим , если для любого 1 ≤ i ≤ n выполняется ai ≤ ai+1.

Монотонностью массива назовем количество его возрастающих подотрезков.

Дан массив a длины n. Посчитайте сумму монотонностей по всем его подпоследовательностям. Так как ответ может быть очень большим, выведите его по модулю 109+7.

Входные данные
В первой строке задано целое число n (1 ≤ n ≤ 200000) — длина массива a.
Во второй строке заданы n целых чисел (1 ≤ ai ≤ 200000) — элементы массива a.

Выходные данные
Выведите одно целое число — сумму монотонностей всех подпоследовательностей по модулю 109+7.

Примечание
В первом тестовом примере у массива есть 7 подпоследовательностей:

  • У массива [1]  есть ровно один подотрезок и он является возрастающим.
  • У массива [2]  есть ровно один подотрезок и он является возрастающим.
  • У массива [3]  есть ровно один подотрезок и он является возрастающим.
  • У массива [1,2]  есть три подотрезка ([1], [2], [1,2] ) и все они являются возрастающими.
  • У массива [1,3]  есть три подотрезка ([1], [3], [1,3] ) и все они являются возрастающими.
  • У массива [3,2]  есть три подотрезка ([3], [2], [3, 2] ), но только два из них ([3]  и [2] ) являются возрастающими.
  • У массива [1,3,2]  есть шесть подотрезков ([1], [3], [2], [1,3], [3,2], [1,3,2] ) и четыре из них ([1], [3], [2], [1,3] ) являются возрастающими.
Во втором тестовом примере все возрастающие подотрезки всех подпоследовательностей имеют длину 1.
Примеры
№ Входные данные Выходные данные
1 3
1 3 2		 15
2 3
6 6 6		 12

Путешествие по строке

Дерево отрезков, RSQ, RMQ sqrt декомпозиция Хеш Суффиксный массив Динамическое программирование Хеш

Скажем, что последовательность строк t1 , ..., tk является путешествием длины k , если для всех i > 1 ti является подстрокой ti - 1 строго меньшей длины. Например, { ab , b } является путешествием, а { ab , c } или { a , a } — нет.

Определим путешествие по строке s как путешествие t1 , ..., tk , все строки которого могут быть вложены в s так, чтобы существовали (возможно, пустые) строки u1 , ..., uk + 1 , такие, что s = u1t1u2 t2 ... uk tk uk + 1 . К примеру, { ab , b } является путешествием по строке для abb , но не для bab , так как соответствующие подстроки расположены справа налево.

Назовём длиной путешествия количество строк, из которых оно состоит. Определите максимально возможную длину путешествия по заданной строке s .

Входные данные
В первой строке задано целое число n ( 1 ≤ n ≤ 500 000 ) — длина строки s .

Во второй строке содержится строка s , состоящая из n строчных английских букв.

Выходные данные
Выведите одно число — наибольшую длину путешествия по строке s .

Примечание
В первом примере путешествием по строке наибольшей длины является { abcd , bc , c } .

Во втором примере подходящим вариантом будет { bb , b } .

Примеры
№ Входные данные Выходные данные
1 7
abcdbcc		 3
2 4
bbcb		 2

Сокровища

meet in the middle Дерево отрезков, RSQ, RMQ

Дочь короля Флатландии собирается выйти за прекрасного принца. 
Принц хочет подарить принцессе сокровища, но он не уверен какие именно бриллианты из своей коллекции выбрать.

В коллекции принца n бриллиантов, каждый характеризуется весом wi и стоимостью vi. 
Принц хочет подарить наиболее дорогие бриллианты, однако король умен и не примет бриллиантов суммарного веса больше R. С другой стороны, принц будет считать себя жадным всю оставшуюся жизнь, если подарит бриллиантов суммарным весом меньше L.

Помогите принцу выбрать набор бриллиантов наибольшей суммарной стоимости, чтобы суммарный вес был в отрезке [L, R].

Входные данные:
Первая строка содержит число n (1 <= n <= 32), L и R (0 <= L <= R <= 1018).
Следующие n строк описывают бриллианты и содержат по два числа - вес и стоимость соответствующего бриллианта (1 <= wi, vi <= 1015).

Выходные данные:
Первая строка вывода должна содержать k - количество бриллиантов, которые нужно подарить принцессе. 
Вторая строка должна содержать номера даримых бриллиантов.
Бриллианты нумеруются от 1 до n в порядке появление во входных данных.

Если составить подарок принцессе невозможно, то выведите 0 в первой строке вывода.

Примеры:
 

Входные данные Выходные данные
3 6 8
3 10
7 3
8 2		 1
2

Сумма минимумов

Динамическое программирование Дерево отрезков, RSQ, RMQ

Вам дан массив из n целых чисел. Вам необходимо разделить его на k непустых подотрезков (последовательность подряд идущих элементов) так, чтобы:
1) Каждый элемент массива входил ровно в один подотрезок.
2) Если для каждого подотрезка выбрать минимальное в нем число, то сумма всех минимумов должна быть максимально возможной.

Сообщите сумму минимумов значений в подотрезках этого разбиения.

Входные данные:
В первой строке дается два натуральных числа - n (1 <= n <= 500) и k (1 <= k <= n).
Во второй строке дается n целых чисел - элементы массива ai (1 <= ai <= 105).

Выходные данные:
Выведите одно число - ответ на задачу.

Пример:
 

Входные данные Выходные данные
5 3
4 2 5 1 3		 8

Пояснение:
Одно из подходящих разбиений: [4, 2], [5], [1, 3]. Сумма минимумов в каждом подотрезке равна 2 + 5 + 1 = 8.

Инверсии на отрезке

Алгоритм Мо Дерево отрезков, RSQ, RMQ

Дана перестановка из n элементов.
Ответьте на m запросов про число инверсий для подотрезка перестановки от l до r.
Инверсией называется пара индексов i, j такая, что i < j и ai > aj, где ai - это i-й элемент перестановки.

Входные данные:
В первой строке задано число n (1 <= n <= 105).
Во второй строке задана перестановка из n элементов (элементы перестановки - попарно различные целые числа от 1 до n).
В третьей строке задано число m (1 <= m <= 105).
В последующих m строках содержится по два числа l и r - границы запроса (1 <= l, r <= n).

Выходные данные:
Выведите m строк - ответы на данные запросы.

Примеры:
 

Входные данные Выходные данные
5
4 5 2 3 1
3
1 3
3 5
1 5		 2
2
8
6
5 2 4 3 1 6
3
4 6
2 5
1 5		 1
4
8

Урок физкультуры

Структуры данных Дерево отрезков, RSQ, RMQ Сканирующая прямая Словари

Феоктист Всеволодович — преподаватель физкультуры старой закалки, глубоко убеждённый, что в начале каждого урока школьников необходимо построить по росту. Для этого он сначала просит школьников построиться самостоятельно, после чего последовательно меняет местами про- извольную пару стоящих рядом учеников, пока шеренга не примет желанный вид.

Всего на урок пришло N детей, изначально построившихся таким образом, что рост стоящего на позиции i равен hi (используется нумерация c 1). Можно считать, что все числа hi различны и лежат в диапазоне от 1 до N. Шеренга считается упорядоченной, если на первой позиции стоит школьник ростом один, на второй позиции стоит школьник ростом два и так далее.

Феоктист Всеволодович получает большое удовольствие от процесса упорядочивания школьни- ков, поэтому он всегда выбирает наиболее длинную последовательность обменов. С другой стороны, он не хочет чтобы ученики догадались о том, что он умышленно затягивает построение, поэтому никогда не делает заведомо бессмысленных обменов. А именно, преподаватель никогда не меняет местами школьников на позициях i и j, если hi < hj . Очевидно, что данное ограничение делает процесс сортировки шеренги по росту конечным.

Староста Саша очень любит играть в волейбол и прекрасно понимает, что чем дольше препо- даватель будет расставлять всех по местам, тем меньше времени останется для игры. Ученики уже построились некоторым образом, а Феоктист Всеволодович вышел поговорить по телефону, так что Саша может успеть поменять местами ровно двух школьников, необязательно стоящих рядом в ше- ренге. Разумеется, он хочет сделать это таким образом, чтобы преподаватель как можно быстрее закончил упорядочивать шеренгу (Саша давно уже раскусил, как именно действует Феоктист Всево- лодович). С информатикой у старосты всегда были определённые проблемы, поэтому ему требуется ваша помощь.

Формат входных данных
В первой строке ввода содержится единственное число N — количество школьников на уроке (1 <= N <= 1 000 000). Во второй строке записано N различных целых чисел hi (1 <= hi <= N). i-е число соответствует росту школьника стоящего на i-й позиции.

Формат выходных данных
Выведите два числа — номера позиций школьников, которым необходимо поменяться местами, чтобы минимизировать количество действий преподавателя. Если таких пар несколько, то выведите любую из них. Если никому меняться местами не нужно, выведите -1 -1.

Ввод Вывод
5
2 4 3 5 1		 2 5
4 1 2 3 4 -1 -1
10
2 3 7 1 5 10 4 6 9 8		 3 7

Рассадка зверей

Дерево отрезков, RSQ, RMQ НОД и алгоритм Евклида НОД и алгоритм Евклида НОД и алгоритм Евклида

Сегодня Колобок созвал всех волков и лис к себе в гости на чаепитие. Чаепитие пройдет за круглым столом, за которым всего n мест. Колобок хочет рассадить зверей по-особенному — так, чтобы волки не сидели только с волками, а лисы только с лисами. Поэтому для каждого места он записал одно целое число — сколько лис должно сидеть на расстоянии не более d от этого места, включая это место.

Два места находятся на расстоянии не более d, если между ними встречаются не более d−1 места при движении по или против часовой стрелки от одного к другому. Таким образом, для заданного места всего существует 2d + 1 место, находящееся на расстоянии не более d от него.

Теперь он хочет придумать какую-нибудь рассадку зверей, удовлетворяющую этим ограничениям.

Входные данные
В первой строке находятся два натуральных числа n, d (3 ≤ n ≤ 105 , 3 ≤ 2d+1 ≤ n) — количество мест за круглым столом и расстояние d. В следующей строке находятся n неотрицательных целых чисел ai (0 ≤ ai ≤ 2d+1) — количество лис на расстоянии не более d от этого места, включая это место. Информация о местах перечислена в порядке их следования по кругу.

Выходные данные
Если решения не существует, выведите «NO», иначе в первой строке выведите «YES», а в следу- ющей n чисел: 1 в том случае, если на этом месте сидит лиса, и 0, если на этом месте сидит волк. Если ответов несколько, разрешается вывести любой.
 

Ввод Вывод
5
1 2 2 1 2 2		 YES
1 0 1 0 1
9
2 3 4 4 3 3 2 2 2 2		 YES
1 0 1 1 1 0 0 0 1
6
1 3 3 3 3 3 1		 NO

Switch Grass

Минимальный каркас Структуры данных Дерево отрезков, RSQ, RMQ Обход в глубину Алгоритмы на графах

Фермер Джон обнаружил, что разные типы коров любят разные типы травы. Однако он должен правильно их высаживать, чтобы не навредить.
Ферма Джона состоит из NN (1≤N≤200,000), полей, и MM пар полей соединены двунаправленными дорожками (1≤M≤200,000). Используя эти дорожки, можно пройти от любого поля к любому другому полю. Каждая дорожка имеет целочисленную длину в интервале 1…1,000,000. Любая пара полей соединена не более чем одной прямой дорожкой.
 
В каждом поле ФД изначально посадил один из KK типов травы (1≤K≤N). Через некоторое время, однако, он может решить изменить тип травы на некоторых из полей. Он называет это операцией "обновления".
 
После каждого обновления, ФД хочет знать длину кратчайшего пути между двумя полями, имеющими различные типы травы. То есть, среди всех пар полей, имеющих различные типы травы, он хочет узнать, какие два поля ближайшие друг к другу. Гарантируется, что всегда имеется как минимум одна пара полей с различными типами травы.
 
В 30 процентах тестов каждое поле непосредственно соединено не более чем с 10 дорожками.
 
ФОРМАТ ВВОДА:
 
Первая строка ввода содержит четыре целых числа N, M, K, Q, где Q - количество операций обновления (1≤Q≤200,000). Следующие M строк описывают дорожки. Каждая строка содержит три целых числа A, B, L, указывающих, что есть дорожка между полями A, B и её длина L. (A, B - целые числа в интервале 1…N). Следующая строка указывает начальный тип травы для каждого поля (N целых чисел в интервале 1…K). Затем идут Q строк, каждая из которых описывает одну операцию обновления двумя целыми числами A и B, означающими, что на поле A типе травы изменён на B.
 
ФОРМАТ ВЫВОДА:
 
Для каждой операции обновления выведите длину кратчайшего пути между двумя полями с различными типами травы, после применения этой операции обновления.
 
Ввод Вывод
3 2 3 4
1 2 3
2 3 1
1 1 2
3 3
2 3
1 2
2 2
 
1
3
3
1

Trapped in the Haybales

Динамическое программирование: один параметр Динамическое программирование Дерево отрезков, RSQ, RMQ Структуры данных

Фермер Джон получили груз из N больших стогов сена (1≤N≤100,000), и разметил их в различных положениях вдоль дороги, ведущей к амбару. К несчастью, он полностью забыл, что корова Беси пасётся вдоль дороги и может попасть в ловушку между стогами сена.
Каждый стог j имеет размер Sj и позицию Pj определяющую его положение вдоль дороги. Беси может двигаться вдоль дороги вплоть до позиции стога, но не может пересечь эту позицию. Исключение – если она прошла в этом направлении D единиц расстояния, тогда она набрала достаточно скорости, чтобы протаранить стог любого размера строго меньше чем D. Конечно после этого она может продолжить движение и таранить другие стога.
 
Беси может выйти на свободу если она в конце концов протаранит протаранит самый левый или самый правый стог. Вычислите общий размер участка дороги, состоящий из возможных точек старта Беси, из которых она не сможет выбраться.
 
ФОРМАТ ВООДА:
Первая строка ввода содержит N. Каждая из последующих N строк описывает стог, и содержит два целых числа определяющих размер и позицию в диапазоне 1…109. Все позиции различны.
ФОРМАТ ВЫВОДА:
Выведите одно целое число – размер области дороги, откуда Беси не сможет выбраться.
 
Ввод Вывод
5
8 1
1 4
8 8
7 15
4 20
 14


 

Load Balancing

Дерево Фенвика Дерево отрезков, RSQ, RMQ Структуры данных Тернарный поиск

Коровы Фермера Джона стоят в различных точках (x1,y1)…(xn,yn) его поля (1≤N≤100,000, все xi и yi - положительные нечётные целые числа, не превышающие 1,000,000. ФД хочет разделить своё поле изгородью бесконечной длины с севера на юг, описываемой уравнением x=a (a - чётное целое, так обеспечивается, что изгородь не пройдёт через позицию ни одной коровы). Также он хочет построить изгородь бесконечной длины с востока на запад, которая описывается уравнением y=b, где b - чётное целое. Эти две изгороди пересекаются в точке (a,b), и вместе делят поле на четыре региона.
ФД хочет выбрать a и b так, чтобы получить "сбалансированное" количество коров во всех регионах, т.е. чтобы не было региона, который содержит слишком много коров. Пусть M - максимальное количество коров в этих четырёх регионах, ФД хочет, чтобы M было как можно меньше. Помогите ФД определить это минимально возможное значение для M.
 
ФОРМАТ ВВОДА:
Первая строка ввода содержит одно целое число, N. Каждая из следующих n строк содержит местоположение одной коровы, указанное её координатами x и y.
ФОРМАТ ВЫВОДА:
Выведите минимально возможное значение M, которое может достичь ФД оптимальным расположением изгородей.
 
Ввод Вывод
7
7 3
5 5
7 13
3 1
11 7
5 3
9 1
 2

Башни 3.0

Структуры данных Дерево отрезков, RSQ, RMQ Дерево отрезков, RSQ, RMQ

В компьютерной игре есть n башен, высота i-й башни равна ai метров. Определим расстояние между двумя башнями с индексами i и j как |i−j|. Разрешается прыгнуть с i-й башни на j-ю башню тогда и только тогда, когда не существует такого индекса 1 <= k <= n, такого, что расстояние от i-й до j-й башни не меньше расстояния от i-й башни до k-й башни, и k-я башня имеет большую высоту, чем j-я. Башня j достижима из башни i если существует последовательность корректных прыжков, которая начинается в i-й башне и заканчивается в j-й.
 

Вам даны q запросов вида (u,v,l,r). Для каждого запроса посчитайте количество индексов l <= k <= r, таких, что k-я башня достижима из u-й башни и из v-й башни. Обратите внимание, что во многих подзадачах выполняется ограничение u=v, l=1, r=n, то есть ответом на запрос будет общее число башен, достижимых из u .

 

Входные данные
Первая строка входных данных содержит одно целое число n (1 <= n <= 500000) - количество башен.
Вторая строка входных данных содержит n чисел a1, a2, ..., an (1 <= an <= 109) - высоты башен.

Третья строка входных данных содержит одно целое число q (1 <= q  <= 500000) - количество запросов.

Следующие q строк описывают запросы. i-я из них описывает i-й запрос и содержит четыре целых числа ui, vi, li, ri (1<= ui, vi <= n, 1 <= li <= ri <= n) - индексы вершин запроса и границы отрезка запроса.

 

Выходные данные

Выведите n чисел, i-е из которых должно быть равным ответу на i-й запрос.

 

Примечание

В первых двух примерах запросы спрашивают количество достижимых из каждой башни башен.

В первом примере с 1-й башни можно прыгнуть на башни 1 и 5. Любая другая башня имеет меньшую высоту, чем башня 1, поэтому туда нельзя прыгнуть (в качестве k можно выбрать 1). Множество достижимых из 1-й башни также состоит из башен 1 и 5. Со второй башни можно прыгнуть на башни 1, 2, и 5, они же являются множеством достижимых. С третьей башни можно прыгнуть на башни 2, 3, 5. Однако, башня 1 также является достижимой, поскольку можно сделать два прыжка: 3→2→1. Таким образом, получается 4 достижимые башни. С 4-й башни можно прыгнуть на башни 4 и 5, они же являются единственными достижимыми. Из 5-й башни достижима только она сама.

Во втором примере из 1-й и из 2-й башни достижимы башни 1,2,3,4,5. Из 3-й башни достижимы башни 3,4,5. Из 4-й и 5-й башни достижимы башни 4,5. Из 6-й башни достижимы башни 4,5,6. Из 7-й башни достижимы башни 4,5,6,7.

Рассмотрим третий пример:

  • В первом запросе множество индексов башен k на отрезке [l,r], достижимых из u и из v — {3,6}.
  • Во втором запросе множество индексов башен k на отрезке [l,r], достижимых из u и из v — {6}.
  • В третьем запросе множество индексов башен k на отрезке [l,r], достижимых из u и из v — {3}.
  • В четвёртом запросе множество индексов башен k на отрезке [l,r], достижимых из u и из v пусто.
  • В пятом запросе множество индексов башен k на отрезке [l,r], достижимых из u и из v — {6}.
 
Примеры
№ Входные данные Выходные данные
1 
5
7 6 3 4 10
5
1 1 1 5
2 2 1 5
3 3 1 5
4 4 1 5
5 5 1 5
 
2
3
4
2
1
2 
7
1 1 1 2 2 1 1
7
1 1 1 7
2 2 1 7
3 3 1 7
4 4 1 7
5 5 1 7
6 6 1 7
7 7 1 7
 
5
5
3
2
2
3
4
3 
7
6 8 9 3 5 10 1
5
1 3 2 7
4 5 1 6
1 4 2 4
4 7 1 3
1 5 3 6
 
2
1
1
0
1

Башни 3.0

Структуры данных Дерево отрезков, RSQ, RMQ Дерево отрезков, RSQ, RMQ

В компьютерной игре есть n башен, высота i-й башни равна ai метров. Определим расстояние между двумя башнями с индексами i и j как |i−j|. Разрешается прыгнуть с i-й башни на j-ю башню тогда и только тогда, когда не существует такого индекса 1 <= k <= n, такого, что расстояние от i-й до j-й башни не меньше расстояния от i-й башни до k-й башни, и k-я башня имеет большую высоту, чем j-я. Башня j достижима из башни i если существует последовательность корректных прыжков, которая начинается в i-й башне и заканчивается в j-й.
 

Вам даны q запросов вида (u,v,l,r). Для каждого запроса посчитайте количество индексов l <= k <= r, таких, что k-я башня достижима из u-й башни и из v-й башни. Обратите внимание, что во многих подзадачах выполняется ограничение u=v, l=1, r=n, то есть ответом на запрос будет общее число башен, достижимых из u .

 

Входные данные
Первая строка входных данных содержит одно целое число n (1 <= n <= 500000) - количество башен.
Вторая строка входных данных содержит n чисел a1, a2, ..., an (1 <= an <= 109) - высоты башен.

Третья строка входных данных содержит одно целое число q (1 <= q  <= 500000) - количество запросов.

Следующие q строк описывают запросы. i-я из них описывает i-й запрос и содержит четыре целых числа ui, vi, li, ri (1<= ui, vi <= n, 1 <= li <= ri <= n) - индексы вершин запроса и границы отрезка запроса.

 

Выходные данные

Выведите n чисел, i-е из которых должно быть равным ответу на i-й запрос.

 

Примечание

В первых двух примерах запросы спрашивают количество достижимых из каждой башни башен.

В первом примере с 1-й башни можно прыгнуть на башни 1 и 5. Любая другая башня имеет меньшую высоту, чем башня 1, поэтому туда нельзя прыгнуть (в качестве k можно выбрать 1). Множество достижимых из 1-й башни также состоит из башен 1 и 5. Со второй башни можно прыгнуть на башни 1, 2, и 5, они же являются множеством достижимых. С третьей башни можно прыгнуть на башни 2, 3, 5. Однако, башня 1 также является достижимой, поскольку можно сделать два прыжка: 3→2→1. Таким образом, получается 4 достижимые башни. С 4-й башни можно прыгнуть на башни 4 и 5, они же являются единственными достижимыми. Из 5-й башни достижима только она сама.

Во втором примере из 1-й и из 2-й башни достижимы башни 1,2,3,4,5. Из 3-й башни достижимы башни 3,4,5. Из 4-й и 5-й башни достижимы башни 4,5. Из 6-й башни достижимы башни 4,5,6. Из 7-й башни достижимы башни 4,5,6,7.

Рассмотрим третий пример:

  • В первом запросе множество индексов башен k на отрезке [l,r], достижимых из u и из v — {3,6}.
  • Во втором запросе множество индексов башен k на отрезке [l,r], достижимых из u и из v — {6}.
  • В третьем запросе множество индексов башен k на отрезке [l,r], достижимых из u и из v — {3}.
  • В четвёртом запросе множество индексов башен k на отрезке [l,r], достижимых из u и из v пусто.
  • В пятом запросе множество индексов башен k на отрезке [l,r], достижимых из u и из v — {6}.
 
Примеры
№ Входные данные Выходные данные
1 
5
7 6 3 4 10
5
1 1 1 5
2 2 1 5
3 3 1 5
4 4 1 5
5 5 1 5
 
2
3
4
2
1
2 
7
1 1 1 2 2 1 1
7
1 1 1 7
2 2 1 7
3 3 1 7
4 4 1 7
5 5 1 7
6 6 1 7
7 7 1 7
 
5
5
3
2
2
3
4
3 
7
6 8 9 3 5 10 1
5
1 3 2 7
4 5 1 6
1 4 2 4
4 7 1 3
1 5 3 6
 
2
1
1
0
1

Индекс максимума на подотрезках

Дерево отрезков, RSQ, RMQ

Реализуйте структуру данных для эффективного вычисления номера максимального из нескольких подряд идущих элементов массива.

Входные данные
В первой строке вводится одно натуральное число N (\(1 <= N <= 100000\)) — количество чисел в массиве.

Во второй строке вводятся N чисел от 1 до 100000 — элементы массива.

В третьей строке вводится одно натуральное число K (\(1 <= K <= 30000\)) — количество запросов на вычисление максимума.

В следующих K строках вводится по два числа — номера левого и правого элементов отрезка массива (считается, что элементы массива нумеруются с единицы).

Выходные данные
Для каждого запроса выведите индекс максимального элемента на указанном отрезке массива. Если максимальных элементов несколько, выведите любой их них.

Числа выводите в одну строку через пробел.

Терминал

Дерево отрезков, RSQ, RMQ

Специальный терминал, разработанный в лаборатории, где работает Дима, представляет собой горизонтальный прямоугольник, состоящий из m×n ячеек, каждая из которых может содержать произвольное целое число. Ячейки занумерованы парами чисел, левая верхняя ячейка имеет номер (1, 1), правая нижняя – (m, n).

Специальное устройство ввода, сконструированное специально для этого терминала, позволяет отправлять терминалу две команды: A(r, c, d, v) и B(r1, c1, r2, c2, d, v).

Рассмотрим сначала команду A. Параметры r и c изменяются в пределах от 1 до m и от 1 до n соответственно и указывают, к какой ячейке применяется команда. Параметр d может принимать значение из множества {L, R, U, D} и задает направление, в котором применяется команда: влево, вправо, вверх или вниз соответственно. Параметр v представляет собой целое неотрицательное число. В результате выполнения команды значения во всех ячейках, находящихся в направлении d от ячейки (r, c), включая эту ячейку, увеличиваются на v.

Например, если терминал имеет размер 5×4, то после выполнения команды A(3, 2, R, 3) значения в ячейках (3, 2),(3,3) и (3, 4) увеличатся на 3, а после команды A(2, 1, U, 2) значения в ячейках (2, 1) и (1, 1) увеличатся на 2.

Рассмотрим теперь команду B. Первые четыре ее параметра являются целыми числами и удовлетворяют условиям 1≤ r1 ≤ r2 ≤ m и 1≤ c1 ≤ c2 ≤ n. Параметры d и v могут принимать те же значения, что и соответствующие параметры команды A. Команда B выполняется следующим образом: для всех пар (r, c), таких, что r1 ≤ r ≤ r2 и c1 ≤ c ≤ c2 выполняется команда A(r, c, d, v).

Исходно все ячейки терминала содержат нули. Выведите содержимое терминала после выполнения заданной последовательности команд.

Входные данные
В первой строке вводятся числа m и n, ( 1≤m, n≤200). В следующей строке задается число k – количество команд, которые следует обработать ( 0≤k≤40 000). Далее идут k строк, содержащих описания команд. Первый символ каждой строки задает тип команды, затем следует пробел и параметры команды, каждые два последовательных параметра разделены ровно одним пробелом. Параметр v каждой команды неотрицателен и не превышает 100.

Общее число команд A, которое потребуется выполнить на терминале, включая команды, которые придется выполнить при выполнении команд B, не превышает 5 * 106.

Выходные данные
Выведите m строк по n чисел в каждой – содержимое терминала после выполнения указанной последовательности команд.

Пирамида

Дерево отрезков, RSQ, RMQ

После победы в великой битве Король Ягуар хочет построить пирамиду, которая будет одновременно монументом в честь победы и гробницей для погибших солдат. Пирамида будет построена на поле боя. Она должна иметь прямоугольное основание, состоящее из a столбцов и b строк. Для сохранения останков и оружия павших солдат внутри основания пирамиды будет располагаться небольшая прямоугольная комната, состоящая из c столбцов и d строк.

Архитекторы Короля представили поле боя в виде прямоугольной сетки. Эта сетка состоит из квадратных клеток единичной площади и имеет m столбцов и n строк. Для каждой клетки они измерили ее высоту и получили некоторое целое число.

Основание пирамиды и комната должны покрывать включаемые ими клетки полностью, а их стороны должны быть параллельны сторонам поля боя. Высоты клеток, составляющих комнату, должны остаться неизменными, а высоты всех клеток основания пирамиды будут выровнены с помощью перемещения песка с более высоких клеток на более низкие. В результате этого высота основания пирамиды будет равна среднему арифметическому высот всех его клеток (за исключением клеток комнаты). Архитекторы могут выбрать любое местоположение для комнаты внутри пирамиды, но обязательно оставлять вокруг комнаты стену основания пирамиды толщиной хотя бы в одну клетку.

Помогите архитекторам выбрать наилучшее место для расположения пирамиды и комнаты внутри нее так, чтобы высота основания пирамиды была максимально возможной при заданных размерах. На рисунке показан пример поля боя, где число в каждой клетке обозначает ее высоту. Клетки, составляющие основание пирамиды, обозначены серым цветом, а белые клетки внутри основания пирамиды соответствуют расположению комнаты. На этом рисунке представлен пример оптимального решения.



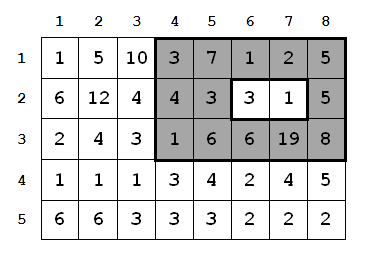
Задание
Напишите программу, которая по заданным размерам поля боя, пирамиды и комнаты, а также по заданным высотам всех клеток будет находить такое расположение пирамиды и комнаты внутри нее, что получившаяся высота основания пирамиды будет максимально возможной.

Ограничения
3 ≤ m ≤ 1000
3 ≤ n ≤ 1000
3 ≤ a ≤ m

3 ≤ b ≤ n

1 ≤ c ≤ a – 2
1 ≤ d ≤ b – 2
Все высоты – целые числа от 1 до 100.

Входные данные
Ваша программа получает входные данные в следующем формате:
СТРОКА 1: Содержит шесть целых чисел, разделенных пробелами, в следующем порядке: m, n, a, b, c и d.
СЛЕДУЮЩИЕ n СТРОК: Каждая из этих строк содержит m целых чисел, разделенных пробелами. Эти числа соответствуют высотам клеток в одной строке сетки. Первая из этих строк соответствует верхней строке (строке 1) сетки, а последняя – нижней строке (строке n). При этом m чисел в каждой строке соответствуют высотам клеток этой строки, начиная со столбца 1.

Выходные данные
Ваша программа должна вывести следующие данные:
СТРОКА 1: Должна содержать два целых числа, разделенные пробелом, – координаты левой верхней клетки основания пирамиды, при этом первое число соответствует столбцу, а второе – строке.
СТРОКА 2: Должна содержать два целых числа, разделенные пробелом, – координаты левой верхней клетки комнаты, при этом первое число соответствует столбцу, а второе – строке.

Замечание
Если существует несколько оптимальных положений пирамиды и комнаты, выведите любое из них.

Горы

Дерево отрезков, RSQ, RMQ

В Горном Парке Развлечений открылся новый аттракцион с американскими горками. Трек в аттракционе состоит из n рельсов, соединенных последовательно друг с другом, причем первый рельс начинается на высоте 0. Оператор Байтмэн может изменять конфигурацию трека по своему усмотрению, корректируя наклон некоторых последовательно соединенных рельсов. Наклон остальных рельсов при этом не изменяется. Всякий раз, когда наклон некоторых рельсов изменяется, все следующие за ними рельсы соответственно поднимаются или опускаются. При этом высота начала трека всегда остается равной 0.

На рисунках представлены изменения конфигурации трека в соответствии со входными данными, заданными в примере:

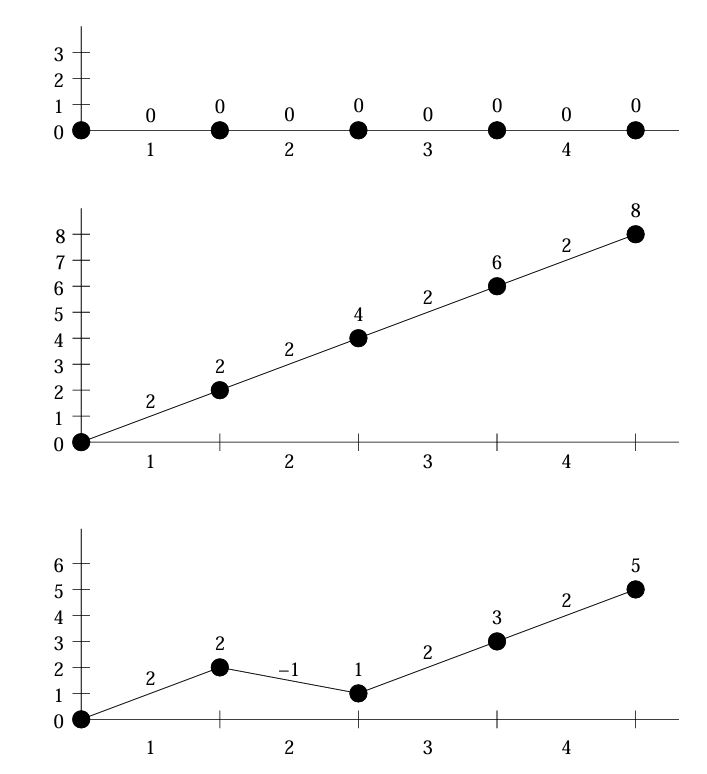
Каждый заезд начинается с того, что кабина запускается из начала трека с энергией, достаточной для достижения высоты h. Иными словами, кабина будет продолжать движение по рельсам, пока ее высота не превысит h или пока она не достигнет конца трека. Вычислите по записям о всех заездах и изменениях конфигураций трека число рельсов, которые были полностью пройдены кабиной в каждом из заездов до ее остановки.

В аттракционе трек описывается последовательностью из n наклонов, по одному для каждого рельса. i -е число d равно разнице высот (в сантиметрах) между концом i -го рельса и его началом. Иными словами, если после прохождения по первым i − 1 рельсам кабина оказывается на высоте h сантиметров, то после прохождения по i рельсам она будет на высоте h + di сантиметров. Изначально все рельсы горизонтальны, то есть di = 0 для всех i. Заезды и изменения конфигурации происходят в течение дня. Каждое изменение конфигурации описывается тремя числами: a, b
и D. Такое изменение затрагивает рельсы с a -го по b -й (включительно). Наклон каждого из этих рельсов устанавливается равным D. Иными словами, di = D для всех a <= i <= b. Каждый заезд задается одним числом h – максимальной высотой, на которую может подняться кабина.

Задание
Напишите программу, которая:
• читает из стандартного ввода последовательность описаний изменений конфигурации трека и заездов,
• для каждого заезда вычисляет количество рельсов, которые пройдены кабиной,
• выводит результаты в стандартный вывод.

Входные данные
Первая строка входных данных содержит одно положительное целое число n – количество рельсов в треке, 1 <= n
 <= 1000000000 . Последующие строки содержат описания изменений конфигурации и заездов. Последняя строка входных данных содержит признак окончания. Каждая строка, начиная со второй, может содержать:

• Описание изменения конфигурации трека – один символ ‘I’ и целые числа a , b и D, разделенные одним пробелом (1 <= a <= b <= n , − 1000000000 <= D <= 1000000000).
• Описание заезда – один символ ‘Q’ и целое число h ( 0 <= h <= 1000000000 ), разделенные одним пробелом.
• Один символ “E” – признак окончания входных данных.
Вы можете предполагать, что в каждый момент высота любой точки трека содержится в промежутке [0 , 1000000000] . Входные данные содержат не более 100000 строк.

Выходные данные
i-я строка выходных данных должна содержать единственное целое число – количество рельсов, которые пройдены кабиной в i-м заезде.

Берляндия атакует

Наименьший общий предок Дерево отрезков, RSQ, RMQ Разреженные таблицы (sparse table)

В этой задаче Вам вновь придется помочь Берляндии. Эта страна состоит из n городов, некоторые пары из которых соединены двусторонними дорогами, каждая дорога характеризуется своей длиной. Все города пронумерованы числами от 1 до n, столица имеет номер 1. Время от време ни Президент объезжает страну, посещая города страны. Целью каждой поездки является один из городов, к которому он едет из столицы вдоль дорог одним из кратчайших путей.

В далекие времена (когда задачи на алгоритм Дейкстры вызывали сложность) специальное ведомство составила такой набор дорог T, вдоль которого можно было проехать из столицы в любой город, причем единственным образом. Разумеется, путь по дорогам из набора T из столицы в каждый город являлся кратчайшим. Особо умные жители страны попросту называли этот набор дорог "деревом кратчайших путей". Известно, что Президент пользовался дорогами из T во время своих поездок. За прошедшие годы этот набор перестал быть секретным, и, поэтому, стал объектом повышенного внимания берляндских экстремистов. У специального ведомства новое задание. Для каждого города кроме столицы необходимо вычислить кратчайшее расстояние до него, при условии, что та дорога по которой Президент должен был закончить свой путь в этот город является атакованной и проезжать по ней нельзя.

Входные данные
В первой строке входного файла записана пара целых чисел n и m (2 ≤ n≤ 4000; n−1 ≤ m ≤100000), где n — количество городов в стране, а m— количество дорог в этой стране. Далее в m строках содержатся описания дорог, по одной дороге в строке. Каждая дорога задается четверкой целых чисел aj, bj, lj, tj , где aj, bj это номера городов, соединяемых дорогой (1 ≤ aj,bj ≤ n; aj≠bj), lj — ее длина (1 ≤ lj≤ 105), а tj равно 1 если дорога принадлежит дереву кратчайших путей и 0 в противном случае.

Гарантируется, что набор T удовлетворяет описанным выше свойствам. Между парой городов может быть более одной дороги. Все дороги двусторонние.

Выходные данные
Выведите n−1 число в строку через пробелы. i-ое число должно быть равно либо длине кратчайшго пути из столицы в город i+1, при условии, что по той дороге из T, которой Президент заканчивал свой путь в этот город, передвигаться нельзя, либо -1, если добраться до города i+1 вообще невозможно.

RMQ

Дерево отрезков, RSQ, RMQ

Реализуйте структуру данных, которая на данном массиве из N целых чисел позволяет узнать максимальное значение на этом массиве и индекс элемента, на котором достигается это максимальное значение.

Входные данные
В первой строке вводится натуральное число N (1 ≤  N ≤ 105) – количество элементов в массиве. В следующей строке содержатся N целых чисел, не превосходящих по модулю 109 – элементы массива. Далее идет число K  (0 ≤ K ≤ 105) – количество запросов к структуре данных. Каждая из следующих K строк содержит два целых числа l и r (1 ≤ l ≤ r ≤ N) – левую и правую границы отрезка в массиве для данного запроса.

Выходные данные
Для каждого из запросов выведите два числа: наибольшее значение среди элементов массива на отрезке от l до r и индекс одного из элементов массива, принадлежащий отрезку от l до r, на котором достигается этот максимум.

Непересекающиеся отрезки

Дерево отрезков, RSQ, RMQ

Отрезок целочисленной прямой длины N разбит на единичные отрезки, которые пронумерованы от 1 до N.

Их объединяют в группы по следующим правилам:
1. Несколько подряд идущих отрезков, ни один из которых не принадлежит ни одной из групп, могут быть объединены в группу.
2. Любая ранее созданная группа может быть уничтожена, при этом входившие в нее отрезки больше не относятся ни к какой группе и могут впоследствии быть отнесены к другим группам.

Видно, что любой отрезок всегда находится не более, чем в одной группе.

Каждую группу можно идентифицировать парой чисел: номером первого и номером последнего отрезка, входящего в группу.

Первоначально нет ни одной группы.

Входные данные
Первая строка входных данных содержит число N – количество отрезков и число K – количество запросов (1 ≤ N, K ≤105). Далее идет K строчек, содержащих запросы к структуре данных. Каждый запрос начинается с числа 1 (запрос на создание группы) или 2 (запрос на удаление группы). После числа 1 указывается два других числа l и r (1 ≤ l ≤ r ≤ N), после числа 2 указывается одно число i (1 ≤ i ≤ N).

Выходные данные
Для каждого запроса типа 1 необходимо отрезки с номерами от l до r объединить в группу. Если все эти отрезки не входят ни в одну группу, запрос считается удачным и программа должна вывести 1. Если хотя бы один из этих отрезков уже относится к какой-то группе, запрос считается неудачным, объединение не производится и программа выводит 0.

Для каждого запроса типа 2 необходимо удалить группу, в которую входит отрезок с номером i, при этом программа должна вывести два числа: номер первого и последнего отрезка, входящих в удаляемую группу. Если отрезок с номером i не относится ни к одной группе, программа должна вывести два нуля.

Хипуй!

Дерево отрезков, RSQ, RMQ Куча

В этой задаче вам необходимо организовать структуру данных Heap для хранения целых чисел, над которой определены следующие операции:

   a) Insert(k) – добавить в Heap число k (1 ≤  k ≤ 1000000) ;
   b) Extract достать из Heap наибольшее число (удалив его при этом).

Входные данные
В первой строке содержится количество команд N (1 ≤  N ≤ 100000), далее следуют N команд, каждая в своей строке.  Команда может иметь  формат: “0 <число>” или “1”, обозначающий, соответственно, операции Insert(<число>) и Extract. Гарантируется, что при выполенении команды Extract в структуре находится по крайней мере один элемент.

Выходные данные
Для каждой команды извлечения необходимо отдельной строкой вывести число, полученное при выполнении команды Extract.

Минимум на отрезке

Дерево отрезков, RSQ, RMQ Дек

Рассмотрим последовательность целых чисел длины N. По ней с шагом 1 двигается “окно” длины K, то есть сначала в “окне” видно первые K чисел, на следующем шаге в “окне” уже будут находиться K чисел, начиная со второго, и так далее до конца последовательности. Требуется для каждого положения “окна” определить минимум в нём.

Входные данные
В первой строке входных данных содержатся два числа N и K (1 ≤  N ≤  150000, 1 ≤ K ≤ 10000, K ≤  N) – длины последовательности и “окна”, соответственно. На следующей строке находятся N чисел – сама последовательность.

Выходные данные
Выходые данные должны содержать N − K + 1 строк – минимумы для каждого положения “окна”.

Контроль доступа

Бор Дерево отрезков, RSQ, RMQ

Вася разрабатывает новый веб-сервер. В настоящее время он работает над функцией, осебспечивающей поддержку списков контроля доступа. Список контроля доступа позволяет ограничить доступ к некоторым ресурсам веб-сайта, основываяь на основании IP-адреса запрашивающей стороны.

Каждый IP-адрес − это 4-байтный номер, который записан байт за байтом в десятичной записи. Байты разделены точками следующим образом: <<byte0.byte1.byte2.byte3>> (кавычки добавлены для ясности). Каждый байт записывается как десятичное число от 0 до 255 (включительно) без ведущих нулей. IP-адреса организованы в IP-сети. IP сети описывается двумя 4-байтовыми числами - сетевым адресом и маской сети. И сетевой адрес и маска сети записаны в той же форме, что и IP-адреса. Для того чтобы понять смысл сетевого адреса и маски сети рассмотрим их двоичное представление. Двоичное представление IP адреса, сетевого адреса и маски сети состоит из 32 бит: 8 бит для byte0 (от старших к младшим), затем по 8 бит для byte1, 8 бит для byte2 и 8 бит для byte3.

IP сеть содержит 2N IP-адресов, где 0≤N≤32. В маске сети первые 32–N бита установлены в единицы, и последние N бит установлены в ноль. Сетевой адрес имеет произвольные 32–N первых бит, а последние N бит установлен в ноль. IP сеть содержит все IP-адреса, первые 32−N бит которых равны 32–N
 первых бит сетевого адреса с произвольными N последними битами. Например, IP сеть с сетевым адресом 194.85.160.176 и сетевая маска 255.255.255.248 содержит 8 IP-адресов, с 194.85.160.176 по 194.85.160.183 (включительно).

IP сети, как правило, обозначается как <<byte0.byte1.byte2.byte3/S>>, где <<byte0.byte1.byte2.byte3>> − сетевой адрес, S − это число бит, установленных в единицу в маске сети. Например, IP сети из предыдущего абзаца обозначается как 194.85.160.176/29. Список контроля доступа содержит упорядоченный список правил. Каждое правило имеет одну из следующих форм:

deny from <IP network> − запрещает доступ к ресурсу для любого IP из заданной сети.

deny from <IP address> − запрещает доступ к ресурсу для указанного IP-адреса.

allow from <IP network> − разрешает доступ к ресурсу для любого IP из заданной сети.

allow from <IP address> − разрешает доступ к ресурсу для указанного IP-адреса.

Когда кто-нибудь обращается к какому-либо ресурсу, первым делом проверяется IP-адрес обращающегося по списку контроля доступа. Правила проверяются в том порядке, в котором они перечислены, и применяется первое выполняющееся правило. Если ни одно из правил не соответствует IP-адресу запрашивающей стороны, то доступ предоставляется.

По известному списку контроля доступа и списку запросов от IP-адресов, необходимо выяснить для каждого из запросов будет ли предоставлен доступ к ресурсу.

Входные данные
Первая строка ввода содержит число N − количество правил в списке контроля доступа (0≤N≤100000). Следующие N строк содержат правила по одному в строке. IP сеть всегда записывается как <<byte0.byte1.byte2.byte3/S>>. Следующая строка содержит число M − количество IP адресов, которые следует проверить (0≤M≤100000). Следующие M строк содержат по одному IP адресу в строке.

Выходные данные
Для каждого из M IP-адресов выведите <<A>>, если доступ будет предоставлен, и <<D>> иначе. Все символы следует выводить слитно, не разделяя пробелами.

Информационный стенд

Дерево отрезков, RSQ, RMQ sqrt декомпозиция

В холле 179 школы, есть информационный стенд размером H×W (H – высота, W – ширина). На этом стенде размещается информация о кружках, изменениях в расписании, победах в олимпиадах, а также другая важная информация.

Первого сентября стенд был пуст. Одно за другим на нем начали появляться объявления, которые потом не снимались.

Каждое объявление представляет собой полоску бумаги единичной высоты. I-ое объявление представляет собой прямоугольник размером 1×Wi.

Когда кто-либо вешает объявление на стенд, то он старается повесить объявление как можно выше. Среди возможных верхних мест всегда выбирается самое левое. Если подходящего места для объявления не нашлось, то объявление не вешается на стенд. Ваша задача состоит в том, чтобы для каждого объявления определить, как высоко оно будет располагаться (в каком ряду).

Входные данные
Первая строка содержит три целых числа H, W и N (1≤H,W≤109; 1≤N≤200000) — размеры стенда и количество объявлений. Каждая из следующих N строк содержит по одному целому числу Wi (1≤Wi≤109) — ширину i-го объявления.

Выходные данные
Для каждого из объявлений (в порядке следования во входном файле) выведите номер ряда, в котором оно будет размещено. Ряды занумерованы от 1 до H сверху вниз. Если объявление разместить нельзя — выведите «–1».
Hallowen