| | | |
|
HASH
Хеш
Программисту Васе не повезло - вместо отпуска его послали в командировку на научную конференцию. "Надо повышать уровень знаний", - сказал начальник, "Важная конференция по криптографии, проводится во Франции - а там шифровали еще во времена Ришелье и взламывали чужие шифры еще во времена Виета."
Вася быстро выяснил, что все луврские картины он уже где-то видел, вид Эйфелевой башни приелся ему еще раньше, чем мышка стерла его с коврика, а такие стеклянные пирамиды у нас делают надо всякими киосками и сомнительными забегаловками. Одним словом, смотреть в Париже оказалось просто не на что, рыбу половить негде, поэтому Васе пришлось посещать доклады на конференции.
Один из докладчиков, в очередной раз пытаясь разгадать шифры Бэкона, выдвинул гипотезу, что ключ к тайнам Бэкона можно подобрать, проанализировав все возможные подстроки произведений Бэкона. "Но их же слишком много!" - вслух удивился Вася. "Нет, не так уж и много!" - закричал докладчик, - "Подсчитайте, и вы сами убедитесь!"
Тем же вечером Вася нашел в интернете полное собрание сочинений Бэкона. Он написал программу, которая переработала тексты в одну длинную строку, выкинув из текстов все пробелы и знаки препинания. И вот теперь Вася весьма озадачен - а как же подсчитать количество различных подстрок этой строки?
Входные данные
На входе дана непустая строка, полученная Васей. Строка состоит только из строчных латинских символов. Ее длина не превосходит 2000 символов.
Выходные данные
Выведите количество различных подстрок этой строки.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
aaba |
8 |
| |
![]()
|
|
Красивые номера
Хеш
В одной маленькой стране разрешили открывать оффшорные компании, и туда тут же потянулись предприниматели с желанием открыть в ней свою фирму.
Поскольку все фирмы современные и идут в ногу со временем, им нужно связываться с клиентами и партнерами по бизнесу, а значит нужен и телефонный номер.
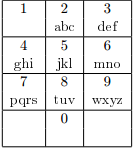
Таким образом, каждой букве соответствует некая цифра, и вместо телефонного номера достаточно знать слово, буквы которого соответствуют цифрам номера.
Каждая фирма хочет, чтобы ее телефонный номер было просто запомнить. Если набранное на телефоне название компании соответствует телефонному номеру компании, то номер очень легко запомнить, и ни один клиент его не забудет.
Поскольку фирм очень много, возможно, не все фирмы смогут получить удобный номер. Напишите программу, которая будет определять наибольшее количество фирм, которые смогут получить такой номер.
Входные данные
В первой строке вводится целое число N — количество новых фирм (1 ≤ N ≤ 103).
В последующих N строках вводятся названия фирм. Название каждой фирмы состоит из семи строчных латинских букв. Гарантируется, что названия всех фирм различны.
Выходные данные
Выведите одно число — максимальное количество фирм, которые смогут получить удобный номер.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4
lacoste
hyundai
renault
peugeot |
4 |
| 2 |
3
aaaaaaa
bbbbbbb
ccccccc |
1 |
| |
![]()
|
|
Волшебные грибы
Хеш
На планете Руук существует Большая Корпорация Маленьких Фей. Одним из видов деятельности, которым испокон веков занимаются ее сотрудницы, является посадка грядок с волшебными грибами. Каждый день, начиная с самого первого дня существования этой корпорации, феи создают одну новую грядку грибов. После этого с новой грядки два дня можно собирать споры, которыми размножаются эти грибы, а потом грядка будет поставлять уже только сам продукт — грибы.
Таким образом, если обозначить количество грибов, посаженных на грядке, созданной в день номер i, как ci, то оно будет считаться по формуле ci = ci - 1 + ci - 2. Так, в первый и второй дни было посажено по одному грибу, в третий — два, в четвертый — три, в пятый — пять и так далее.
Волшебные грибы являются самыми ценными сувенирами, которые путешественник может привезти с планеты Руук. Поэтому первым, что делает любой приезжий, становится поиск грядки с волшебными грибами. Однако, в последнее время все чаще стали появляться сообщения о поддельных волшебных грибах. Тщательное расследование показало, что это является следствием действий Маленькой Корпорации Больших Фей, которая сажает грядки с грибами, внешне не отличимыми, но далеко не такими ценными, как волшебные. Причем, создавая очередную грядку, эти феи сажают туда такое количество грибов, какое их соперницы никогда не сажали и не смогут посадить.
Казалось бы, после выяснения этого факта отличать волшебные грядки от поддельных стало просто. Но обе корпорации существуют достаточно давно, количество грядок и грибов на них давно превысило все разумные пределы. Вас попросили написать программу, по количеству грибов на грядке сообщающую, является ли эта грядка волшебной.
Входные данные
Первая строка входного файла содержит одно число N (1 ≤ N ≤ 1000000) — количество исследуемых грядок. Следующие n строк содержат по одному целому числу ai — количества грибов на исследуемых грядках. Размер входного файла не превышает 1 Мб.
Выходные данные
Для каждого числа, данного во входном файле, выведите «Yes», если грядка с таким количеством грибов является волшебной, и «No» — если не является. Ответы разделяйте переводами строк.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
8
1
2
3
4
5
6
7
8 |
Yes
Yes
Yes
No
Yes
No
No
Yes |
| |
![]()
|
|
Путешествие по строке
Динамическое программирование
Суффиксный массив
Дерево отрезков, RSQ, RMQ
sqrt декомпозиция
Хеш
Хеш
Скажем, что последовательность строк t1 , ..., tk является путешествием длины k , если для всех i > 1 ti является подстрокой ti - 1 строго меньшей длины. Например, { ab , b } является путешествием, а { ab , c } или { a , a } — нет.
Определим путешествие по строке s как путешествие t1 , ..., tk , все строки которого могут быть вложены в s так, чтобы существовали (возможно, пустые) строки u1 , ..., uk + 1 , такие, что s = u1t1u2 t2 ... uk tk uk + 1 . К примеру, { ab , b } является путешествием по строке для abb , но не для bab , так как соответствующие подстроки расположены справа налево.
Назовём длиной путешествия количество строк, из которых оно состоит. Определите максимально возможную длину путешествия по заданной строке s .
Входные данные
В первой строке задано целое число n ( 1 ≤ n ≤ 500 000 ) — длина строки s .
Во второй строке содержится строка s , состоящая из n строчных английских букв.
Выходные данные
Выведите одно число — наибольшую длину путешествия по строке s .
Примечание
В первом примере путешествием по строке наибольшей длины является { abcd , bc , c } .
Во втором примере подходящим вариантом будет { bb , b } .
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
7
abcdbcc |
3 |
| 2 |
4
bbcb |
2 |
| |
![]()
|
|
Путешествие по строке
Динамическое программирование
Суффиксный массив
Дерево отрезков, RSQ, RMQ
sqrt декомпозиция
Хеш
Хеш
Скажем, что последовательность строк t1 , ..., tk является путешествием длины k , если для всех i > 1 ti является подстрокой ti - 1 строго меньшей длины. Например, { ab , b } является путешествием, а { ab , c } или { a , a } — нет.
Определим путешествие по строке s как путешествие t1 , ..., tk , все строки которого могут быть вложены в s так, чтобы существовали (возможно, пустые) строки u1 , ..., uk + 1 , такие, что s = u1t1u2 t2 ... uk tk uk + 1 . К примеру, { ab , b } является путешествием по строке для abb , но не для bab , так как соответствующие подстроки расположены справа налево.
Назовём длиной путешествия количество строк, из которых оно состоит. Определите максимально возможную длину путешествия по заданной строке s .
Входные данные
В первой строке задано целое число n ( 1 ≤ n ≤ 500 000 ) — длина строки s .
Во второй строке содержится строка s , состоящая из n строчных английских букв.
Выходные данные
Выведите одно число — наибольшую длину путешествия по строке s .
Примечание
В первом примере путешествием по строке наибольшей длины является { abcd , bc , c } .
Во втором примере подходящим вариантом будет { bb , b } .
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
7
abcdbcc |
3 |
| 2 |
4
bbcb |
2 |
| |
![]()
|
|
Хэш двойной строки
Хеш
Вывод формулы
Вам дано t запросов, в каждом из которых вам дана строка s, состоящая из строчных латинских букв, число p и число mod.
Для каждого запроса вычислите полиномиальный хэш с основанием p по модулю mod от строки, являющейся строкой s, где каждая буква продублирована. То есть, если s = "isaac", то нужно посчитать хэш от строки "iissaaaacc".
Входные данные:
В первой строке дается число t - количество запросов.
Далее идет t строк, в каждой из которых через пробел даны s (1 <= |s| <= 20), p (1 <= p <= 105) и mod (1 <= mod <= 108).
Выходные данные:
Выведите ответы на запросы, каждый в отдельной строке.
Пример:
| Входные данные |
Выходные данные |
2
isaac 12345 87654321
newton 54321 12345678 |
8829000
9632318 |
| |
![]()
|
|
Странный сон Константина
Деревья
Деревья
Бор
Хеш
Однажды Константин, поучаствовав в очередной, уже 13-ой по счету международной олимпиаде, возвращался на поезде домой. Он как всегда сидел и размышлял о смысле жизни, попутно решая задачи по программированию. Через некоторое время Константин задремал, но вот беда, для того, чтобы проснуться, он должен решить всплывшую у него в голове задачу, не дающую ему покоя!
В этот раз Константину приснилось дерево, изначально состоящее всего из одной вершины с номером 1. В поставленной им задаче к дереву постепенно добавлялись новые вершины. В i-ую секунду в дерево добавлялась вершина с номером i+1, которая подвешивалась в качестве сына к вершине pi, а на ребре между вершинами i+1 и pi записывалась буква ci.
Каждому пути из корня дерева до вершины v соответствует некоторая строка, получающаяся путем выписывания символов, записанных на ребрах текущего пути в порядке следования от корня к вершине v. Перед Константином стояла нелегкая на первый взгляд задача - после каждого добавления новой вершины посчитать количество уникальных строк, начинающихся в корне дерева (вершине с номером 1), и заканчивающихся в какой-либо другой вершине.
В своем сне Константин вовсе не гений, поэтому решить эту задачу сам он не в силах. Помогите Константину решить задачу и тем самым проснуться.
Входные данные:
В первой строке записано число n - количество запросов на добавление новой вершины в дерево (1 <= n <= 300000).
В следующих n строках описаны запросы добавления вершин. i-ый запрос описывается параметрами pi (1 <= pi <= i) и ci, которые означают, что добавленная вершина с номером i+1 подвешивается к вершине с номером pi в качестве потомка, а на полученном ребре записывается символ ci - строчная буква латинского алфавита.
Выходные данные:
Выведите n строк. В i-ой строке выведите ответ на задачу Константина после добавления i+1-ой вершины.
Примеры:
| Входные данные |
Выходные данные |
2
1 b
2 p |
1
2 |
3
1 o
1 o
2 j |
1
1
2 |
| |
![]()
|
|
Подстроки в строке
Префиксные суммы(минимумы, ...)
Хеш
Дана строка S = s1s2...sn и множество запросов вида (l1, r1, l2, r2). Для каждого запроса требуется ответить, равны ли подстроки sl1...sr1 и sl2...sr2.
Входные данные:
В первой строке дана строка S (1 <= |S| <= 105), состоящая из строчных латинских букв.
Во второй строке дано натуральное число q (1 <= q <= 105) - количество запросов.
В следующих q строках дано по 4 натуральных числа - l1, r1, l2, r2 (1 <= l1 <= r1 <= |S|, 1 <=l2 <= r2 <= |S|).
Выходные данные:
Для каждого запроса выведите '+', если подстроки равны, и '-', в противном случае.
Примеры:
| Входные данные |
Выходные данные |
abacaba
4
1 1 7 7
1 3 5 7
3 4 4 5
1 7 1 7 |
++-+ |
| |
![]()
|
|
Том Сойер и слово на заборе
Префиксные суммы(минимумы, ...)
Хеш
Жадный алгоритм
Во время покраски забора Том Сойер написал на нем слово s. Однако затем он решил, что слова-палиндромы смотрятся красивее.
Теперь он хочет дописать к имеющемуся слову s справа другое слово g так, чтобы получившееся слово sg было палиндромом. Однако в целях экономии краски длина g должна быть как можно меньше.
Помогите Тому Сойеру определить слово g.
Входные данные:
В первой строке дано слово s (1 <= |s| <= 200000), состоящее из строчных латинских букв.
Выходные данные:
Выведите минимально возможное по длине слово g, которое нужно дописать, чтобы слово sg на заборе стало палиндромом. Если дописывать ничего не надо, то выведите '-'.
Примеры:
| Входные данные |
Выходные данные |
| abc |
ba |
| a |
- |
| |
![]()
|
|
Чтение вслух
Бинарный поиск
Бинарный поиск по ответу
Префиксные суммы(минимумы, ...)
Хеш
Том Сойер и Гекльберри Финн вместе читают вслух вырезку из газеты. Но получилось так, что Том Сойер начал читать с i-ого символа, а Гекльберри Финн с j-ого.
Сколько букв они смогут прочитать, прежде чем обнаружат, что начали читать с разных мест или пока оба не дочитают до конца?
Входные данные:
В первой строке дана строка S (1 <= |S| <= 105), состоящая из строчных латинских букв - надпись из газетной вырезки.
В следующей строке дано натуральное число q - количество запросов.
В следующих q строках дано по два натуральных числа i и j - позиции, с которых начинают читать Том Сойер и Гекльберри Финн соответственно.
Выходные данные:
Выведите q строк, в каждой из которых должно быть одно целое число - количество символов, совпадающих при чтении подстрок, начинающихся с i-ого и j-ого символа.
Примеры:
| Входные данные |
Выходные данные |
abacaba
4
1 5
3 5
4 2
2 6 |
3
1
0
2 |
| |
![]()
|
|
Гекльберри Финн и две строки
Перебор
Префиксные суммы(минимумы, ...)
Хеш
У Гекльберри Финна есть две строки s и t одинаковой длины n.
Гекльберри Финну нравится, когда у строк одинаковые префиксы (начала), поэтому он может поменять местами два символа в строке s, чтобы общий префикс строк s и t стал больше.
Однако этот трюк довольно утомительный, поэтому Гекльберри Финн либо совсем не будет его делать, либо сделает ровно один раз.
Помогите Гекльберри Финну определить наибольшую длину общего префикса строк s и t, которую он может получить.
Входные данные:
В первой строке дано натуральное число n (1 <= n <= 200000) - длина строк s и t
Во второй строке дана строка s, состоящая из строчных латинских букв.
В третьей строке дана строка t, состоящая из строчных латинских букв.
Выходные данные:
Выведите одно натуральное число - наибольшую длину общего префикса s и t, которую можно получить, применив операцию обмена двух символов в строке s не более одного раза.
Примеры:
| Входные данные |
Выходные данные |
3
wai
add |
1 |
5
qdyid
xreac |
0 |
| |
![]()
|
|
Культурный контакт
Перебор
Префиксные суммы(минимумы, ...)
Хеш
В начале XVIII века группа европейских исследователей прибыла на остров, населённый группой племён, никогда не вступавших в контакт с представителями европейской цивилизации.
Для успешного налаживания контактов с аборигенами руководитель группы планирует делать подарок вождю каждого встреченного племени. С этой целью он привёз длинную цепочку из стекляшек, похожих на драгоценные камни.
Представим цепочку как строку s, состоящую из маленьких букв английского алфавита, где каждая буква означает тип кусочка стекла на соответствующей позиции.
Исследователи собираются разрезать цепочку на некоторые фрагменты, после чего вручать ровно один фрагмент вождю каждого встреченного группой племени. Руководитель исследователей решил разделить цепочку на фрагменты согласно следующим правилами:
- Чтобы не тратить на разрезания много времени, каждый фрагмент должен являться группой соседних стекляшек цепочки, то есть подстрокой строки s.
- Все стекляшки должны быть использованы, то есть каждая стекляшка должна оказаться включённой ровно в один фрагмент.
- Поскольку исследователи не знают, как аборигены оценят те или иные виды стекляшек, они хотят, чтобы каждому вождю достался один и тот же набор стекляшек без учёта порядка. Иными словами, для любого типа стекляшек количество стекляшек этого типа должно быть одинаковым в каждом из фрагментов.
- Исследователи не знают, сколько племён обитает на острове, поэтому количество подготовленных фрагментов должно быть максимальным.
Помогите руководителю определить максимальное количество фрагментов, которое может получиться.
Входные данные:
В первой строке дана строка s (1 <= |s| <= 5000000).
Выходные данные:
Выведите одно число - максимально возможное количество фрагментов, на которое исследователи могут разрезать имеющуюся у них цепочку, не нарушая ни одного из условий, сформулированных руководителем группы.
Примеры:
| Входные данные |
Выходные данные |
| abbabbbab |
3 |
| aabb |
1 |
Пояснения:
В первом примере исследователи могут разбить цепочку 'abbabbbab' на фрагменты 'abb', 'abb', 'bab', тогда вождю каждого встреченного ими племени достанется по одной стекляшке типа 'a' и по две стекляшки типа 'b'.
Во втором примере строку невозможно поделить цепочку больше чем на один фрагмент, соблюдая все условия.
| |
![]()
|
|
Бункеры
Деревья
Хеш
Петя и Вася с упоением играют в шпионов. Сегодня они планируют, где будут
расположены их секретные бункеры и штаб-квартира.
Пока Петя и Вася решили, что им понадобится ровно n бункеров, которые для секретности будут пронумерованы числами от 1 до n.
Некоторые из них будут соединены двусторонними тоннелями, причем для надежности и секретности по тоннелям можно будет попасть из любого бункера в любой единственным образом.
Петя и Вася даже решили, какие из бункеров будут соединены тоннелями, но выбрать, какой из них будет штаб-квартирой, они не могут.
Мальчики хотят выбрать ее и разделить оставшиеся бункеры между собой таким образом, чтобы им досталось поровну бункеров к штаб-квартире вело бы ровно два тоннеля: один от бункера, принадлежащего Васе, другой - от бункера, принадлежащего Пете.
Уставший Петя пошел к себе домой, а утром Вася показал ему план, на котором бункеры были обозначены точками, а тоннели отрезками.
Кроме того, Вася выбрал штаб-квартиру таким образом, что нарисованный им план был симметричен относительно прямой, проходящей через точку, которая соответствовала штаб-квартире.
Хотя Петя почти сразу показал Васе, что тот ошибся и не нарисовал половину бункеров, ему стало интересно, можно ли выбрать штаб-квартиру и нарисовать такой симметричный план.
Входные данные:
В первой строке входного файла находится одно целое число n (1 <= n <= 105) - количество бункеров.
В следующих n - 1 строках находится по два целых числа ui и vi (1 <= ui, vi <= n, ui ≠ vi) - номера бункеров, которые соединяет i-ый тоннель.
Гарантируется, что между любыми двумя бункерами существует единственный путь.
Выходные данные:
В выходной файл выведите "YES", если можно выбрать штаб-квартиру и нарисовать такой план, или "NO" если это невозможно.
Примеры:
| Входные данные |
Выходные данные |
2
1 2 |
NO |
3
1 2
2 3 |
YES |
| |
![]()
|
|
Bovine Genomics
Строки
Множества
Хеш
У Фермера Джона NN коров с пятнами и NN коров без пятен. Пройдя курс генетики, ФД убеждён, что пятна у коров вызваны мутацией генов.
За большие деньги ФД зафиксировал геномы своих коров. Каждый геном это строка длиной MM, состоящая из символов A, C, G, T. Когда он выписал все геномы у него получилась такая таблица, N=3 и M=8:
Позиция : 1 2 3 4 5 6 7 8
Пятнистая корова 1: A A T C C C A T
Пятнистая корова 2: A C T T G C A A
Пятнистая корова 3: G G T C G C A A
Корова без пятен 1: A C T C C C A G
Корова без пятен 2: A C T C G C A T
Корова без пятен 3: A C T T C C A T
Посмотрев внимательно на эту таблицу, он заметил, что последовательность от позиции 2 до позиции 5 успешна, чтобы объяснять пятнистость. То есть, рассматривая символы в этих позициях (2…5), ФД может предсказать какие из его коров пятнистые, а какие нет. Например, если он видит символы GTCG в этих позициях, он знает, что корова будет пятнистая.
Помогите ФД определить длину кратчайшей последовательности позиций, которая может объяснить пятнистость.
ФОРМАТ ВВОДА:
Первая строка ввода содержит N (1≤N≤500) и M (3≤M≤500). Каждая из N следующих строк содержит по M символов. Эти символы описывают геномы пятнистых коров. Следующие N строк описывают геномы коров без пятен. Никакая пятнистая корова на имеет точно такой же геном, как корова без пятен.
ФОРМАТ ВЫВОДА:
Пожалуйста, выведите длину кратчайшей последовательности позиций, достаточной для объяснения пятнистости. Последовательность позиций объясняет пятнистость, если по ней можно предсказывать абсолютно точно пятнистая или нет любая из коров ФД.
| Ввод |
Вывод |
|
3 8
AATCCCAT
ACTTGCAA
GGTCGCAA
ACTCCCAG
ACTCGCAT
ACTTCCAT
|
4 |
| |
![]()
|
|
Censoring
Строки
Структуры данных
Хеш
Фермер Джон купил подписку журнала Good Hooveskeeping для своих коров. К сожалению, последний номер содержит неподходящую статью - как приготовить бифштекс. ФД не хочет, чтобы его коровы её читали.
ФД взял текст журнала, создал строку S длиной не более чем 10^5 символов. У него есть список слов t_1, t_2, ..., t_N, которые он хочет удалить из S. Поэтому ФД находит ближайшее вхождение слова из списка T (то есь с наименьшим индексом) и удаляет его из S. Затем он продолжает это процесс опять, пока в S не останется слов из T. Заметим, что удаление слова может создавать новое вхождение свлоа из T, которое не существовало ранее.
ФД заметил, что слова из списка T обладают таким свойством, что никакое из них не является подстрокой другого слова из T. В частности, это означает, что ранее вхождение слова из T в S всегда определено однозначно. Пожалуйста, помогите ФД определить финальное содержание строки S.
INPUT FORMAT:
Первая строка содержит S. Вторая строка содержит N - количество удаляемых слов. Последующие N строк содержат строки t_1, t_2, ..., t_N. Каждая строка содержит только маленькие латинские буквы (a..z) и суммарная длина всех строк не превысит 10^5.
OUTPUT FORMAT:
Строка S после всех удалений. Гарантируется, что S не станет пустой.
| Ввод |
Вывод |
|
begintheescapexecutionatthebreakofdawn
2
escape
execution
|
beginthatthebreakofdawn |
| |
![]()
|
|
Программа психологического исследования программистов
Хеш
Компания "Макрохард" заказала у одного известного психолога полное психологическое обследование всех работников компании. Психолог, привлеченный для проведения обследования, известен своим инновационным методом, позволяющим составить полную психологическую картину сотрудника по наиболее часто используемому им в программах идентификатору. Однако, к сожалению, программа, используемая в анализе, оказалась неожиданно испорчена вирусом, поэтому требуется срочно написать новую. Помогите известному психологу. Напишите программу, которая по приведенной программе выяснит наиболее часто используемый в ней идентификатор.
Поскольку разные сотрудники компании пишут программы на разных языках программирования, ваша программа должна уметь работать с произвольным языком. Поскольку в разных языках используются различные ключевые слова, то список ключевых слов в анализируемом языке предоставляется на вход программе. Все последовательности из латинских букв, цифр и знаков подчеркивания, которые не являются ключевыми словами и содержат хотя бы один символ, не являющийся цифрой, могут быть идентификаторами. При этом в некоторых языках идентификаторы могут начинаться с цифры, а в некоторых - нет. Если идентификатор не может начинаться с цифры, то последовательность, начинающаяся с цифры, идентификатором не является. Кроме этого, задано, является ли язык чувствительным к регистру символов, используемых в идентификаторах и ключевых словах.
Входные данные
В первой строке вводятся число n - количество ключевых слов в языке (0 <= n <= 50) и два слова C и D, каждое из которых равно либо "yes", либо "no". Слово C равно "yes", если идентификаторы и ключевые слова в языке чувствительны к регистру символов, и "no", если нет. Слово D равно "yes", если идентификаторы в языке могут начинаться с цифры, и "no", если нет.
Следующие n строк содержат по одному слову, состоящему из букв латинского алфавита и символов подчеркивания - ключевые слова. Все ключевые слова непусты, различны, при этом, если язык не чувствителен к регистру, то различны и без учета регистра. Длина каждого ключевого слова не превышает 50 символов.
Далее до конца входных данных идет текст программы. Он содержит только символы с ASCII-кодами от 32 до 126 и переводы строки.
Размер входных данных не превышает 10 килобайт. В программе есть хотя бы один идентификатор.
Выходные данные
Выведите идентификатор, встречающийся в программе максимальное число раз. Если таких идентификаторов несколько, следует вывести тот, который встречается в первый раз раньше. Если язык во входных данных не чувствителен к регистру, то можно выводить идентификатор в любом регистре.
| |
![]()
|
|
Цепочка слов
"Два указателя"
Хеш
Будем называть цепочкой слов длины n последовательность слов w1, w2, …, wn, такую, что для всех i от 1 до n – 1 слово wi является собственным префиксом слова wi+1.
Слово u длины k называется собственным префиксом слова v длины l, если l > k и первые k букв слова v совпадают со словом u. Например, «program» является собственным префиксом слова «programmer».
Задано множество слов S = {s1, s2, …, sm} и последовательность чисел x[1], x[2], …, x[k]. Требуется найти такие числа l и r (l ≤ r), что sx[l], sx[l + 1], …, sx[r – 1], sx[r] является цепочкой слов, и количество слов в цепочке (число r – l + 1) максимально.
Входные данные
Первая строка входного файла содержит целое число m (1 ≤ m ≤ 250 000). Каждая из следующих m строк содержит по одному слову из множества S.
Все слова не пусты, имеют длину, не превосходящую 250 000 символов, и состоят только из строчных букв латинского алфавита. Суммарная длина всех слов не превосходит 250 000.
Следующая строка содержит число k (1 ≤ k ≤ 250 000). Последняя строка входного файла содержит k чисел — последовательность чисел x[1], x[2], …, x[k] (для всех i выполнено 1 ≤ x[i] ≤ m).
Выходные данные
Выведите в первой строке выходного файла два числа: l и r. Если оптимальных ответов несколько, выведите любой из них. Разделяйте числа пробелом.
| |
![]()
|
|
Хеширование
Эвристические методы
Хеш
Реализуйте структуру данных типа “множество строк”. Хранимые строки – непустые последовательности длиной не более 10 символов, состоящие из строчных латинских букв. Структура данных должна поддерживать операции добавления строки в множество и проверки принадлежности данной строки множеству. Максимальное количество элементов в хранимом множестве не превосходит 106.
Входные данные
Каждая строка входных данных задает одну операцию над множеством. Запись операции состоит из типа операции и следующей за ним через пробел строки, над которой проводится операция. Тип операции – один из двух символов: + означает добавление данной строки в множество; ? означает проверку принадлежности данной строки множеству. Общее количество операций во входном файле не превосходит 106. Список операций завершается строкой, в которой записан один символ # – признак конца входных данных. При добавлении элемента в множество НЕ ГАРАНТИРУЕТСЯ, что он отсутствует в этом множестве.
Выходные данные
Программа должна вывести для каждой операции типа ? одну из двух строк YES или NO, в зависимости от того, встречается ли данное слово в нашем множестве.
| |
![]()
|
|
Хеширование с удалением
Эвристические методы
Хеш
Реализуйте структуру данных типа “множество строк”. Хранимые строки – непустые последовательности длиной не более 10 символов, состоящие из строчных латинских букв. Структура данных должна поддерживать операции добавления строки в множество, удаления строки из множества и проверки принадлежности данной строки множеству. Максимальное количество элементов в хранимом множестве не превосходит 106.
Входные данные
Каждая строка входных данных задает одну операцию над множеством. Запись операции состоит из типа операции и следующей за ним через пробел строки, над которой проводится операция. Тип операции – один из трех символов: + означает добавление данной строки в множество; - означает удаление строки из множества; ? означает проверку принадлежности данной строки множеству. Общее количество операций во входном файле не превосходит 106. Список операций завершается строкой, в которой записан один символ # – признак конца входных данных. При добавлении элемента в множество НЕ ГАРАНТИРУЕТСЯ, что он отсутствует в этом множестве. При удалении элемента из множества НЕ ГАРАНТИРУЕТСЯ, что он присутствует в этом множестве.
Выходные данные
Программа должна вывести для каждой операции типа ? одну из двух строк YES или NO, в зависимости от того, встречается ли данное слово в нашем множестве.
| |
![]()
|