| | | |
|
Кузнечик собирает монеты
Динамическое программирование: один параметр
Кузнечик прыгает по столбикам, расположенным на одной линии на равных расстояниях друг от друга. Столбики имеют порядковые номера от 1 до N . В начале Кузнечик сидит на столбике с номером 1. Он может прыгнуть вперед на расстояние от 1 до K столбиков, считая от текущего.
На каждом столбике Кузнечик может получить или потерять несколько золотых монет (для каждого столбика это число известно). Определите, как нужно прыгать Кузнечику, чтобы собрать наибольшее количество золотых монет. Учитывайте, что Кузнечик не может прыгать назад.
Входные данные
- в первой строке вводятся два натуральных числа: N и K (\(2 <= N ,\ K <= 10000\)), разделённые пробелом;
- во второй строке записаны через пробел N-2 целых числа – количество монет, которое Кузнечик получает на каждом столбике, от 2-го до N-1-го. Если это число отрицательное, Кузнечик теряет монеты.
Гарантируется, что все числа по модулю не превосходят 10000.
Выходные данные
- в первой строке программа должна вывести наибольшее количество монет, которое может собрать Кузнечик;
- во второй строке выводится число прыжков Кузнечика;
- в третьей строке – номера всех столбиков, которые посетил Кузнечик (через пробел в порядке возрастания).
Если правильных ответов несколько, выведите любой из них.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 3
2 -3 5
|
7
3
1 2 4 5
|
| |
![]()
|
|
Кузнечик-KMax
Динамическое программирование: один параметр
Кузнечик прыгает по столбикам, расположенным на одной линии на равных расстояниях друг от друга. Столбики имеют порядковые номера от 1 до N . В начале Кузнечик сидит на столбике с номером 1. Он может прыгнуть вперед на расстояние от 1 до K столбиков, считая от текущего. Требуется найти количество способов, которыми Кузнечик может добраться до столбика с номером N. Учитывайте, что Кузнечик не может прыгать назад.
Поскольку количество способов, которое нужно найти, может быть очень велико, вычислите его по модулю \(10^6 + 7\) , то есть найдите остаток от деления этого числа на \(10^6 + 7\) .
Входные данные: входная строка содержит натуральные числа N и K, разделённые пробелом. Гарантируется, что \(1 <= N ,\ K <= 10000\).
Выходные данные: программа должна вывести одно число: количество способов, которыми Кузнечик может добраться до столбика с номером N , вычисленное по модулю \(10^6+7\).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
10 5 |
236 |
| 2 |
100 50 |
934384 |
| |
![]()
|
|
Гвоздики
Динамическое программирование: один параметр
На прямой дощечке вбиты гвоздики. Любые два гвоздика можно соединить ниточкой. Требуется соединить какие-то пары гвоздиков ниточками так, чтобы к каждому гвоздику была привязана хотя бы одна ниточка, а суммарная длина всех ниточек была минимальна.
Входные данные:
- в первой строке записано число N - количество гвоздиков (\(2 <= N <= 100\));
- в следующей строке записано N чисел - координаты всех гвоздиков (неотрицательные целые числа, не превосходящие 10000).
Выходные данные: выведите единственное число - минимальную суммарную длину всех ниточек.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
4 10 0 12 2
|
6 |
| |
![]()
|
|
Покупка билетов
Динамическое программирование: один параметр
За билетами на премьеру нового мюзикла выстроилась очередь из N человек, каждый из которых хочет купить 1 билет. На всю очередь работала только одна касса, поэтому продажа билетов шла очень медленно, приводя "постояльцев" очереди в отчаяние. Самые сообразительные быстро заметили, что, как правило, несколько билетов в одни руки кассир продаёт быстрее, чем когда эти же билеты продаются по одному.
Поэтому они предложили нескольким подряд стоящим людям отдавать деньги первому из них, чтобы он купил билеты на всех.
Однако для борьбы со спекулянтами кассир продавала не более 3-х билетов в одни руки, поэтому договориться таким образом между собой могли лишь 2 или 3 подряд стоящих человека.
Известно, что на продажу i-му человеку из очереди одного билета кассир тратит Ai секунд, на продажу двух билетов - Bi секунд, трех билетов - Ci секунд. Напишите программу, которая подсчитает минимальное время, за которое могли быть обслужены все покупатели.
Обратите внимание, что билеты на группу объединившихся людей всегда покупает первый из них. Также никто в целях ускорения не покупает лишних билетов (то есть билетов, которые никому не нужны).
Входные данные:
- в первой строке записано число N - количество покупателей в очереди (\(1<=N<=5000\));
- далее идет N троек натуральных чисел Ai, Bi, Ci. Каждое из этих чисел не превышает 3600. Люди в очереди нумеруются начиная от кассы.
Выходные данные: выведите одно число - минимальное время в секундах, за которое могли быть обслужены все покупатели.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
5 10 15
2 10 15
5 5 5
20 20 1
20 1 1
|
12 |
| 2 |
2
3 4 5
1 1 1
|
4 |
| |
![]()
|
|
Ход конем
Динамическое программирование: один параметр
Шахматная ассоциация решила оснастить всех своих сотрудников такими телефонными номерами, которые бы набирались на кнопочном телефоне ходом коня. Например, ходом коня набирается телефон 340-4927. При этом телефонный номер не может начинаться ни с цифры 0, ни с цифры 8.
Клавиатура телефона выглядит так:
Напишите программу, определяющую количество телефонных номеров длины N, набираемых ходом коня.
Входные данные: на вход подается целое число N (\(1<=N<=50\)).
Выходные данные: выведите файл искомое количество телефонных номеров.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 |
16 |
| |
![]()
|
|
Камни
Динамическое программирование: один параметр
Простые игры
На столе лежат N камней. За ход игрок может взять:
- 1 или 2 камня, если N делится на 3;
- 1 или 3, если N при делении на 3 дает остаток один;
- 1, 2 или 3, если N при делении на 3 дает остаток два.
Каждый ход можно сделать при наличии достаточного количества камней. Проигрывает тот, кто хода сделать не может.
Входные данные: вводится целое число \(0 < N <= 100\).
Выходные данные: выведите 1 или 2 – номер игрока, который выиграет при правильной игре.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 |
1 |
| 2 |
3 |
2 |
| |
![]()
|
|
Слинки "Радуга"
Динамическое программирование: один параметр
 Слинки — игрушка-пружина, созданная в 1943 году в США Ричардом Джеймсом. В нашей стране она называлась просто Радуга. Все дети любили ее запускать со ступенек, считая у кого она спустится ниже. Слинки — игрушка-пружина, созданная в 1943 году в США Ричардом Джеймсом. В нашей стране она называлась просто Радуга. Все дети любили ее запускать со ступенек, считая у кого она спустится ниже.
Обычно "Радуга" в руках детей спускалась на следующую ступеньку, на ступеньку через одну или через 2. (Например, если Радугу запускали с 10-ой ступеньки, то она могла остановиться на 9-ой, 8-ой или 7-ой.)
Допустим на лестнице N ступенек. Определите число всевозможных "маршрутов" Радуги с вершины лестницы на землю.
Входные данные
Вводится одно число \(0 < N < 31\).
Выходные данные
Выведите одно число — количество "маршрутов" Радуги.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 |
7 |
| |
![]()
|
|
Хлебные крошки
Динамическое программирование: один параметр
Заботливые хозяева квартиры заботятся о таракане Василии. Вечером они выкладывают для него в ряд N хлебных крошек, которые он очень любит. Переходя от одной хлебной крошки к другой, таракан Василий может съесть ее, а может и не съесть. Но он никогда не ест две хлебные крошки подряд.
Посчитайте сколько различных вариантов полакомиться хлебными крошками есть у таракана Василия.
Входные данные
На вход программы поступает целое число N (\(1<=N<=100\) ).
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 |
2 |
| |
![]()
|
|
Играем в Камушки
Динамическое программирование: один параметр
Когда-то в далеком детстве мы все с удовольствием играли в игру "Камушки" или "Пять камешков", кто как называл. Для игры нужны были обычные камешки, которые можно было запросто найти на улице. Играть можно было в любом месте, Для игры нужна была небольшая ровная площадка утоптанной земли или ровный пол крыльца или беседки.
Первый шаг игры заключался в следующем. На землю перед собой бросаются все пять камешков. Выбирался один из них. Это биток. Этот камешек подбрасывается в воздух и, пока он летит, необходимо поднять один из оставшихся на земле камешков и успеть подхватить этой же рукой летящий. Подобранный камешек откладывается в сторону и действие повторяется для всех оставшихся камешков.
На следующих шагах количество камешков, которые надо подхватить увеличивается. Последним шагом был экзамен, когда необходимо было подбросить все собранные камешки в воздух и поймать их тыльной стороной ладони, а затем опять подбросить, и поймать открытой ладонью. Сколько камешков в итоге оставалось, столько баллов и получаешь. Ход переходит к следующему игроку, который также повторяет все шаги. Далее запускался новый тур игры. Выигрывал тот, кто набирал больше всего баллов за все туры.
Многие ребята усложняли игру самыми разными способами.
Допустим у ребят есть бесконечное число камешков лежащих на земле. В конце тура им необходимо поймать в ладони не все камешки, а ровно столько, чтобы общее число баллов у них увеличилось на 1 или удвоилось или утроилось. Перед началом игры у всех уже имеется 1 балл. Победителем будет считаться тот, кто быстрее наберет N баллов.
Будем считать, что у всех играющих достаточно опыта игры, и они всегда доходят до экзамена с нужным им числом камней (чтобы была возможность нужное число баллов увеличить на 1, удвоить или утроить).
Определите, какое наименьшее число туров необходимо отыграть для того, чтобы получить из 1 заданное число баллов N.
Входные данные
Программа получает на вход одно число, не превосходящее 106.
Выходные данные
Требуется вывести одно число: наименьшее количество искомых операций.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 |
0 |
| 2 |
5 |
3 |
| 3 |
32718 |
17 |
| |
![]()
|
|
Словарь
Динамическое программирование: один параметр
Бинарный поиск в массиве
У Васи на клавиатуре не работает клавиша пробел. Поэтому все тексты он теперь набирает слитно. Напишите программу, которая будет разделять набранный Васей текст на слова из данного словаря.
Входные данные
Сначала на вход программы поступает текст, введенный Васей – одна строка из не более чем 100 латинских строчных букв. В следующей строке входных данных задается значение N – количество слов в словаре (N – натуральное число, не превосходящее 2000). В следующих N строках записаны слова из словаря – по одному слову в строке, каждое слово содержит не более 20 латинских строчных букв. Слова записаны в алфавитном порядке.
Выходные данные
Выведите Васин текст с пробелами между словами (пробел после последнего слова допустим). Если возможно несколько вариантов разбиения строки на слова, выведите любой их них. Гарантируется, что хотя бы один способ разбиения строки на словарные слова существует.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
whatcanido
6
a
an
can
do
i
what |
what can i do |
| |
![]()
|
|
Распечатка условий
Динамическое программирование: один параметр
Популярность окружной олимпиады по информатике растет год от года. При этом организаторы должны заранее распечатать как условия задач, так и другие материалы олимпиады (анкеты, памятки и т.п). В этом году они оценили объем печатной продукции в N листов.
Фирма, готовая размножить печатные материалы, предлагает следующие финансовые условия. Один лист она печатает за A1 рублей, 10 листов — за A2 рублей, 100 листов — за A3 рублей, 1000 листов — за A4 рублей, 10 000 листов — за A5 рублей, 100 000 листов — за A6 рублей и 1 000 000 листов — за A7 рублей. При этом не гарантируется, что один лист в более крупном заказе обойдется дешевле, чем в более мелком. И даже может оказаться, что для любой партии будет выгодно воспользоваться тарифом для одного листа.
Печать конкретного заказа производится или путем комбинации нескольких тарифов, или путем заказа более крупной партии. Например, 980 листов можно распечатать, заказав печать 9 партий по 100 листов плюс 8 партий по 10 листов, сделав 98 заказов по 10 листов, 980 заказов по 1 листу или заказав печать 1000 (или даже 10 000 и более) листов, если это окажется выгоднее.
Требуется по заданному объему заказа в листах N определить минимальную сумму денег в рублях, которой будет достаточно для выполнения заказа.
Входные данные
На вход программе сначала подается число N (1 ≤ N ≤ 2 × 109) — количество листов в заказе. В следующих 7 строках ввода находятся натуральные числа A1, A2, A3, A4, A5, A6, A7 соответственно (1 ≤ Ai ≤ 106).
Выходные данные
Выведите одно число — минимальную сумму денег в рублях, которая нужна для выполнения заказа. Гарантируется, что правильный ответ не будет превышать 2 × 109.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
980
1
9
90
900
1000
10000
10000 |
882 |
| 2 |
980
1
10
100
1000
900
10000
10000 |
900 |
| |
![]()
|
|
Валютные махинации
Динамическое программирование: один параметр
Петя, изучая, как меняется курс рубля по отношению к доллару и евро, вывел закон, по которому происходят эти изменения (или думает, что вывел). По этому закону Петя рассчитал, каков будет курс рубля по отношению к доллару и евро в ближайшие N дней.
У Пети есть 100 рублей. В каждый из дней он может обменивать валюты друг на друга по текущему курсу без ограничения количества (при этом курс доллара по отношению к евро соответствует величине, которую можно получить, обменяв доллар на рубли, а потом эти рубли — на евро). Поскольку Петя будет оперировать не с наличной валютой, а со счетом в банке, то он может совершать операции обмена с любым (в том числе и нецелым) количеством единиц любой валюты.
Напишите программу, которая вычисляет, какое наибольшее количество рублей сможет получить Петя к исходу N-го дня.
Законы изменения курсов устроены так, что в течение указанного периода рублевый эквивалент той суммы, которая может оказаться у Пети, не превысит 108 рублей.
Входные данные
Первая строка входного файла содержит одно число N (1≤N≤5000). В каждой из следующих N строк записано по 2 числа, вычисленных по Петиным законам для соответствующего дня — сколько рублей будет стоить 1 доллар, и сколько рублей будет стоить 1 евро. Все эти значения не меньше 0.01 и не больше 10000. Значения заданы точно и выражаются вещественными числами не более, чем с двумя знаками после десятичной точки.
Выходные данные
В выходной файл выведите искомую величину с точностью не менее двух знаков после десятичной точки.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1
30.00 9999.99 |
100.00 |
| |
![]()
|
|
Подстроки подпоследовательностей
Динамическое программирование: один параметр
Динамическое программирование
Дерево отрезков, RSQ, RMQ
Дерево Фенвика
Назовем подпоследовательностью массива a непустой массив b такой, что он может быть получен из массива a удалением нескольких (возможно, никаких) элементов массива a. Например, массив [1,3] является попоследовательностью массива [1,2,3] , но [3,1] не является.
Назовем подотрезком массива a непустой массив b такой, что он может быть получен путем удаления нескольких (возможно, никаких) первых и последних элементов массива a. Например, [1,2] является подотрезком массива [1,2,3] , а [1,3] не является. Несложно заметить, что у массива длины n ровно \( {n(n+1) \over 2}\) подотрезков.
Назовем массив a длины n возрастающим , если для любого 1 ≤ i ≤ n выполняется ai ≤ ai+1.
Монотонностью массива назовем количество его возрастающих подотрезков.
Дан массив a длины n. Посчитайте сумму монотонностей по всем его подпоследовательностям. Так как ответ может быть очень большим, выведите его по модулю 109+7.
Входные данные
В первой строке задано целое число n (1 ≤ n ≤ 200000) — длина массива a.
Во второй строке заданы n целых чисел (1 ≤ ai ≤ 200000) — элементы массива a.
Выходные данные
Выведите одно целое число — сумму монотонностей всех подпоследовательностей по модулю 109+7.
Примечание
В первом тестовом примере у массива есть 7 подпоследовательностей:
- У массива [1] есть ровно один подотрезок и он является возрастающим.
- У массива [2] есть ровно один подотрезок и он является возрастающим.
- У массива [3] есть ровно один подотрезок и он является возрастающим.
- У массива [1,2] есть три подотрезка ([1], [2], [1,2] ) и все они являются возрастающими.
- У массива [1,3] есть три подотрезка ([1], [3], [1,3] ) и все они являются возрастающими.
- У массива [3,2] есть три подотрезка ([3], [2], [3, 2] ), но только два из них ([3] и [2] ) являются возрастающими.
- У массива [1,3,2] есть шесть подотрезков ([1], [3], [2], [1,3], [3,2], [1,3,2] ) и четыре из них ([1], [3], [2], [1,3] ) являются возрастающими.
Во втором тестовом примере все возрастающие подотрезки всех подпоследовательностей имеют длину 1.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
1 3 2 |
15 |
| 2 |
3
6 6 6 |
12 |
| |
![]()
|
|
Поход
Динамическое программирование: один параметр
Группа школьников решила сходить в поход вдоль Москвы-реки. У Москвы-реки существует множество притоков, которые могут впадать в нее как с правого, так и с левого берега.
Школьники хотят начать поход в некоторой точке на левом берегу и закончить поход в некоторой точке на правом берегу, возможно, переправляясь через реки несколько раз. Как известно, переправа как через реку, так и через приток представляет собой определенную сложность, поэтому они хотят минимизировать число совершенных переправ.
Школьники заранее изучили карту и записали, в какой последовательности в Москву-реку впадают притоки на всем их маршруте.
Помогите школьникам по данному описанию притоков определить минимальное количество переправ, которое им придется совершить во время похода.
Входные данные
Единственная строка содержит описание Москвы-реки между начальной и конечной точкой похода. Длина строки не превосходит 105 символов.
Каждый символ строки может быть одной из трех латинских букв L, R или B. Буква L означает, что очередной приток впадает в реку с левого берега, R - приток впадает в реку с правого берега и B - притоки впадают с обоих берегов реки в одном месте. Поход начинается на левом берегу перед описанной частью реки и заканчивается на правом берегу после описанной части.
Выходные данные
Выведите одно целое число - минимальное количество переправ.
Примечания
Рисунок к приведенному ниже примеру.
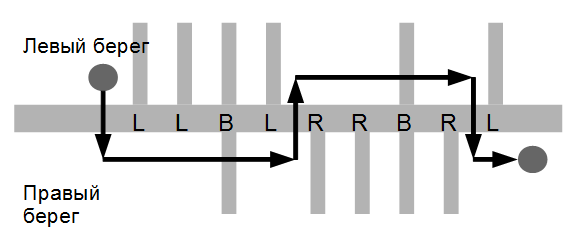
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
LLBLRRBRL |
5 |
| |
![]()
|
|
Количество треугольников
Динамическое программирование: один параметр
Рассмотрим фигуру, аналогичную показанной на рисунке (большой равносторонний треугольник, составленный из маленьких равносторонних треугольников). На рисунке приведена фигура, состоящая из 4-х уровней треугольников.
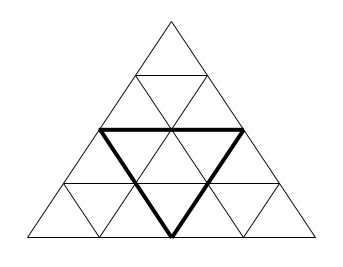
Напишите программу, которая будет определять, сколько всего в ней треугольников (необходимо учитывать не только "маленькие" треугольники, а вообще все треугольники — в частности, треугольник, выделенный жирным, а также вся фигура, являются интересующими нас треугольниками).
Входные данные
Вводится одно число N — количество уровней в фигуре (1 ≤ N ≤ 100000).
Выходные данные
Выведите количество треугольников в такой фигуре.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 |
1 |
| 2 |
2 |
5 |
| 3 |
4 |
27 |
| |
![]()
|
|
Практический тест
Массивы
Префиксные суммы(минимумы, ...)
Динамическое программирование: один параметр
У нас есть сетка с H строками и W столбцами. Квадрат в i-й строке и j-м столбце будет называться Square(i, j). Целые числа от 1 до H·W записаны по всей сетке, а целое число, записанное в Square(i, j), равно Ai,j.
Вы - волшебник (волшебница), и можете телепортировать фигуру, помещенную на Square(i, j) в Square(x, y), потратив \(|x-i|+|y-j|\) маджиков (магических монет).
Теперь вам нужно пройти Q практических тестов на свои способности как волшебника (волшебницы). I-е испытание будет проводиться следующим образом:
- первоначально фигура располагается в квадрате, где записано целое число Li;
- пусть x будет целым числом, записанным в квадрате, занятом фигурой. Неоднократно переместите фигуру в квадрат, где написано целое число x+D, пока x не станет равен Ri. Тест заканчивается, когда x = Ri .
Гарантируется, что Ri- Li делится на D.
Для каждого теста найдите сумму маджиков, израсходованных во время этого теста.
Входные данные
В первой строке заданы три целых числа: H, W и D (\(1\leq H,W \leq 300\), \(1 \leq D \leq H \cdot W\)).
В следующих H строках записано по W чисел Ai,j (\(1 \leq A_{i,j} \leq H \cdot W\), \(A_{i,j} \neq A_{x,y} ((i,j) \neq (x,y))\).
В следующей строке записано целое число Q (\(1 \leq Q \leq 10^5\)).
В последних Q строках записано по 2 целых числа: Li и Ri (\(1 \leq L_i \leq R_i \leq H \cdot W\)), \((R_i-L_i)\) кратно D.
Выходные данные
Для каждого теста выведите сумму маджиков, израсходованных во время этого теста. Вывод должен быть в порядке проведения тестов.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснения |
| 1 |
3 3 2
1 4 3
2 5 7
8 9 6
1
4 8 |
5 |
- 4 записано Square (1,2).
- 6 записано в Square (3,3).
- 8 записано in Square (3,1).
Таким образом, сумма магических очков, израсходованных во время одного теста, составляет:
\((|3-1|+|3-2|)+(|3-3|+|1-3|)=5\).
|
| 2 |
4 2 3
3 7
1 4
5 2
6 8
2
2 2
2 2 |
0
0 |
Обратите внимание, что может быть тест, в котором фигура вообще не перемещается, и может быть несколько идентичных тестов. |
| 3 |
5 5 4
13 25 7 15 17
16 22 20 2 9
14 11 12 1 19
10 6 23 8 18
3 21 5 24 4
3
13 13
2 10
13 13 |
0
5
0 |
|
| |
![]()
|
|
Крокрыс банк
Динамическое программирование: один параметр
Чтобы затруднить снятие денег, банк на планете Крокрыс разрешает своим клиентам снимать только одну из следующих сумм за одну операцию:
- 1 крокрыскоин (действующая монета на планете Крокрыс);
- 6 крокрыскоинов, 36 (=62) крокрыскоинов, 216(=63) крокрыскоинов , ...;
- 9 крокрыскоинов, 81 (=92) крокрыскоинов, 729(=93) крокрыскоинов , ...
Сколько минимум операций требуется, чтобы вывести ровно N крокрыскоинов?
Невозможно повторно внести снятые вами деньги.
Входные данные
На вход подается целое число N (\(1<=N<=100000\)).
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснения |
| 1 |
127 |
4 |
При снятии 1 + 9 + 36 + 81 получится снять 127 крокрыскоина за 4 операции. |
| 2 |
3 |
3 |
1+1+1 = 3, всего 3 операции |
| 3 |
44852 |
16 |
|
| |
![]()
|
|
Мячик на лесенке
Динамическое программирование: один параметр
Рекуррентные последовательности
На вершине лесенки, содержащей N ступенек, находится мячик, который начинает прыгать по ним вниз, к основанию. Мячик может прыгнуть на следующую ступеньку, на ступеньку через одну или через 2. (То есть, если мячик лежит на 8-ой ступеньке, то он может переместиться на 5-ую, 6-ую или 7-ую.) Определить число всевозможных "маршрутов" мячика с вершины на землю.
Входные данные
Вводится одно число 0 < N < 31.
Выходные данные
Выведите одно число — количество маршрутов.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 |
7 |
| |
![]()
|
|
Длина подстроки
Динамическое программирование: один параметр
Префиксные суммы(минимумы, ...)
У вас есть строка s. Вы хотите сделать новую строку, записывая в ней каждую букву количество раз равное порядковому номеру этой буквы в алфавите. Например, s = "abcdc", новая строка s_new = "abbcccddddccc". Нам стало интересно, какая получится у вас длина строки, если выписать все символы исходной строки, начиная с символа l и заканчивая символом r. Всего у нас k запросов к вам.
Входные данные
В первой строке программа получает на вход два числа n и k (1<=n<=106, 1<=k<=106), где n - длина строки, k - количество запросов. Во второй строке записана строка s длиной n. В следующих k строках расположены границы отрезков l и r (1 <= l <= r <= n). l, r - порядковые номера символов в строке, начиная с 1.
Выходные данные
Для каждого запроса выведите длину строки, которая у вас получилась. По одному числу в строке. Всего k строк.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 3
abcdc
1 5
2 3
3 5 |
13
5
10 |
| |
![]()
|
|
Ладья Громозеки
Динамическое программирование: один параметр
Любимая шахматная фигура Громозеки - это ладья. Но он любит ходить ей только по вертикали, причем либо на одну клетку, либо на две. Громозека заканчивает игру, когда ладья доходит до конца вертикали. Подумав над очередной позицией, он заметил, что некоторые клетки на пути ладьи находятся под ударом фигур соперника и ходить на эти клетки нельзя.
Помогите Громозеке посчитать сколькими способами он может перевести ладью c 1 горизонтали на другой конец шахматного поля, не попадая на клетки под ударом.
Входные данные
В первой строке вводится одно натуральное число N (N <= 40): размер шахматного поля. Во второй строке вводится одно натуральное число K (K <= N): количество клеток, находящихся под ударом. В третьей строке вводятся K различных натуральных чисел в диапазоне от 1 до N: номера клеток, находящихся под ударом фигур соперника.
Выходные данные
Выведите одно число - количество способов попасть на конец вертикали (на N-ю клетку).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
7
2
3 5 |
1 |
| 2 |
10
3
5 1 2 |
0 |
| 3 |
3
1
2 |
1 |
| |
![]()
|
|
Меняю конфеты на ноутбук
Одномерные массивы
Динамическое программирование
Использование сортировки
Порядковые статистики
Динамическое программирование: один параметр
Антон Б., суперспособный ученик 8 класса, обладает неудивительными математическими способностями. Побывав однажды на экскурсии в Колоколамске, он понял, что легко может написать программу, которая бы предсказывала стоимость его любимых конфет на любой промежуток дней вперед.
Используя эту программу, Антон Б. решил приобрести на все свои карманные деньги конфеты (а их у него было всего 10 рублей), затем, чуть позже, продать все купленные им конфеты. Таким образом, Антон Б. хочет заработать как можно больше денег на новый ноутбук.
Так как Антон Б. еще несовершеннолетний и один ездить в другие города не может, ему нужно понять, в какие из двух дней попросить старшего брата отвезти его в Колоколамск. Старший брат совершеннолетний и очень любит своего младшего брата, поэтому всегда готов ему помочь.
Так как Антон Б. очень торопится на кружок по информатике, он просит вас определить эти два дня в ближайшие N дней.
Входные данные
В первой строке записано число N (2 <= N <= 100000) количество дней, на которые Антон Б. делает прогноз. Вторая строка содержит N целых положительных чисел ai (1 <= i <= N , 1 <= ai <= 5000 ), где ai - предсказанная стоимость конфет в i-й день.
Выходные данные
Выведите два числа: первое число - номер дня, в который Антон Б. поедет покупать конфеты, второе - номер дня, в который он поедет продавать конфеты. В случае, если таких вариантов дней несколько, выведите любой из них. Если Антон Б. в итоге не сможет получить прибыль ни при каких вариантах, то выведите два нуля.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6
10 3 5 3 11 9
|
2 5
|
| 2 |
4
5 5 5 5
|
0 0
|
| |
![]()
|
|
Ограждение
Динамическое программирование: один параметр
Одним из хобби Летовца является выращивание различных растений. Для этого у него даже есть своя грядка, которая расположена на подоконнике в его комнате. Летовец решил оградить грядку. Для этого он вдоль одной стороны грядки, по одной прямой, вбил колышки. Летовец хочет любые два колышки соединить веревочкой. Причем, соединить колышки он хочет таким образом, чтобы веревочка была привязана к каждому колышку. Теперь Летовцу необходимо купить веревку, которую он сможет разрезать на маленькие веревочки и соединить ими колышками. Определите минимальную длину веревки, которую необходимо приобрести Летовцу.
Входные данные
В первой строке записано число N - количество колышков (\(2 <= N <= 100\));
В следующей строке записано N чисел - координаты всех колышков (неотрицательные целые числа, не превосходящие 10000).
Выходные данные
Выведите единственное число - минимальную длину веревки, которую необходимо приобрести Летовцу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
4 10 0 12 2
|
6 |
| |
![]()
|
|
MLG pro
Динамическое программирование
Динамическое программирование: один параметр
Bonkisilver очень хочет стать MLG pro и попасть в FaZe clan. Для этого он каждый день практикуется в стрельбе из снайперской винтовки. В качестве поощрения, за каждый noscope он получает 2 пачки doritos, а за каждый quickscope - одну. Сколько вариантов сделать выстрелы было у Bonkisilver, если в итоге у него была n-1 пачка.
Входные данные
На вход подается число n (1 <= n <= 50).
Выходные данные
Выведите одно число - количество вариантов сделать выстрелы.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 |
2 |
| |
![]()
|
|
Кузнечик и лягушки
Динамическое программирование
Динамическое программирование: один параметр
Рекуррентные последовательности
Кузнечик прыгает по столбикам, расположенным на одной линии на равных расстояниях друг от друга. Столбики имеют порядковые номера от 1 до N . В начале Кузнечик сидит на столбике с номером 1. Он может прыгнуть вперед на расстояние от 1 до K столбиков, считая от текущего.
На некоторых столбиках сидят лягушки, которые едят кузнечиков (Кузнечик не должен попадать на эти столбики!). Определите, сколькими способами Кузнечик может безопасно добраться до столбика с номером N. Учитывайте, что Кузнечик не может прыгать назад.
Входные данные
Входная строка содержит натуральные числа N и K , разделённые пробелом. Гарантируется, что 1 <= N, K <= 32 . Во второй строке записано число лягушек L ( 0 <= L <= N - 2 ). В третьей строка записано L натуральных чисел: номера столбиков, на которых сидят лягушки (среди них нет столбиков с номерами 1 и N ).
Выходные данные
Программа должна вывести одно число: количество способов, которыми Кузнечик может безопасно добраться до столбика с номером N .
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6 4
2
2 4 |
3 |
| |
![]()
|
|
Числа Фибоначчи: Мемоизация рекурсии (C++)
Динамическое программирование
Динамическое программирование: один параметр
Числа Фибоначчи, обозначаемые обычно F(n) образуют последовательность, называемую последовательностью Фибоначчи, такую, что каждое число является суммой двух предыдущих, начиная с 0 и 1. То есть,
F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), для n > 1.
По заданному n, вычислите F(n) (0 <= n <= 80).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 |
1 |
| 2 |
3 |
2 |
| 3 |
4 |
3 |
| |
![]()
|
|
Числа Фибоначчи: Мемоизация рекурсии (Python)
Динамическое программирование
Динамическое программирование: один параметр
Числа Фибоначчи, обозначаемые обычно F(n) образуют последовательность, называемую последовательностью Фибоначчи, такую, что каждое число является суммой двух предыдущих, начиная с 0 и 1. То есть,
F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), для n > 1.
По заданному n, вычислите F(n) (0 <= n <= 80).
(в коде программы длина одного отступа равна 4 пробелам!)
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 |
1 |
| 2 |
3 |
2 |
| 3 |
4 |
3 |
| |
![]()
|
|
N-е число Трибоначчи (рекурсивно)
Динамическое программирование
Динамическое программирование: один параметр
Последовательность чисел Трибоначчи (Tn) определяется следующим образом:
T0 = 0,
T1 = 1,
T2 = 1, и Tn+3 = Tn + Tn+1 + Tn+2 при n >= 0.
Для заданного числа n, определите значение Tn.
Входные данные
Программа получает на вход натуральное число n (0 <= n <= 37). Ответ гарантированно укладывается в рамки 32-разрядного целого числа, т.е. ответ <= 231 - 1.
Выходные данные
Выведите значение Tn.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 |
4 |
| 2 |
25 |
1389537 |
| |
![]()
|
|
Подняться на вершину горы (снизу-вверху)
Динамическое программирование
Динамическое программирование: один параметр
Робот Сильвер занимается терроформированием на планете Шелезяка. Сейчас робот находится перед лестницей, ведущей на вершину горы. Лестница состоит из n ступенек. Робот, поднимаясь вверх, может пойти на одну или сразу две ступеньки.
Пока робот поднимается на вершину, вы хотите определить, сколько существует различных способов, которыми он может добраться до последней ступеньки этой лестницы и тем самым оказаться на вершине горы.
Входные данные
Программа получает на вход одно целое число n - количество ступенек в лестнице (1 <= n <= 45).
Выходные данные
Выведите одно число - количество способов добраться до вершины горы.
Попробуйте решить эту задачу без использования массивов и других структур данных! Другими словами, ваша программа должна использовать фиксированный объем памяти, не зависящий от входных данных (О(1)).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 |
2 |
| 2 |
3 |
3 |
| |
![]()
|
|
Числа Фибоначчи. Динамика снизу вверх
Динамическое программирование
Динамическое программирование: один параметр
Числа Фибоначчи, обозначаемые обычно F(n) образуют последовательность, называемую последовательностью Фибоначчи, такую, что каждое число является суммой двух предыдущих, начиная с 0 и 1. То есть,
F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), для n > 1.
По заданному n, вычислите F(n) (0 <= n <= 80).
Попробуйте решить эту задачу без использования массивов и других структур данных! Другими словами, ваша программа должна использовать фиксированный объем памяти, не зависящий от входных данных (О(1)).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 |
1 |
| 2 |
3 |
2 |
| 3 |
4 |
3 |
| |
![]()
|
|
Подняться на вершину горы (рекурсивно)
Динамическое программирование
Динамическое программирование: один параметр
Робот Сильвер занимается терроформированием на планете Шелезяка. Сейчас робот находится перед лестницу, ведущей на вершину горы. Лестница состоит из n ступенек. Робот, поднимаясь вверх, может пойти на одну или сразу две ступеньки.
Пока робот поднимается на вершину, вы хотите определить, сколько существует различных способов, которыми он может добраться до последней ступеньки этой лестницы и тем самым оказаться на вершине горы.
Входные данные
Программа получает на вход одно целое число n - количество ступенек в лестнице (1 <= n <= 45).
Выходные данные
Выведите одно число - количество способов добраться до вершины горы.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 |
2 |
| 2 |
3 |
3 |
| |
![]()
|
|
N-е число Трибоначчи (снизу-вверх)
Динамическое программирование
Динамическое программирование: один параметр
Последовательность чисел Трибоначчи (Tn) определяется следующим образом:
T0 = 0,
T1 = 1,
T2 = 1, и Tn+3 = Tn + Tn+1 + Tn+2 при n >= 0.
Для заданного числа n, определите значение Tn.
Входные данные
Программа получает на вход натуральное число n (0 <= n <= 37). Ответ гарантированно укладывается в рамки 32-разрядного целого числа, т.е. ответ <= 231 - 1.
Выходные данные
Выведите значение Tn.
Попробуйте решить эту задачу без использования массивов и других структур данных! Другими словами, ваша программа должна использовать фиксированный объем памяти, не зависящий от входных данных (О(1)).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 |
4 |
| 2 |
25 |
1389537 |
| |
![]()
|
|
Стоимость проезда
Динамическое программирование
Динамическое программирование: один параметр
Робот Сильвер движется по платному шоссе на планете Шелезяка. На каждом километре шоссе расположен пункт оплаты. Всего на шоссе n пунктов оплаты. Первый пункт оплаты находится в самом начале шоссе, n-й пункт оплаты находится в начале последнего километра шоссе. Заплатив нужную сумму в i-м пункте оплаты, робот может двигаться дальше либо до следующего пункта оплаты, либо же до того, который находится через 2 километра (то есть, если робот находится в пункте i, то он может двигаться либо до пункта i+1, либо до пункта i+2). Первую оплату можно сделать либо в первом пункте, либо во втором (на выбор). Если оплаты была произведена в предпоследнем (n-1) пункте, то можно просто доехать до конца шоссе, не оплачивая проезд в последнем пункте.
Зная стоимость, которую необходимо заплатить в определенном пункте оплаты, помогите роботу Сильверу найти наименьшую сумму, которую он заплатит, проехав через все шоссе.
Формат входных дынных
В первой строке записано количество пунктов оплаты n (2 <= n <= 1000). Во второй строке записыны n целых чисел (costi) - стоимость проезда через i-й пункт оплаты (1 <= i <= n, 0 <= costi <= 999).
Формат выходных дынных
Выведите одно число - ответ на задачу.
| |
![]()
|
|
MTN DEW
Динамическое программирование
Рекуррентные последовательности
Динамическое программирование: один параметр
Чтобы подготовиться к предстоящей битве Bonkisilver должен прокачать свой скил, а, как известно, лучшим способом это сделать, является употребление mtn dew при прослушивании дабстепа в 4:20 по МСК. Полученный скилл вычисляется по формуле:
f(n) = f(n - 1) + f(n - 2) + f(n / 2),
где n - количество литров mtn dew, выражаемое целым числом. Операция n/2 означает целочисленное деление числа n на 2.
Также, известно, что
f(1) = 1 microCoinZ
f(x) = 0 microCoinZ, при x < 1.
Помогите Bonkisilver сосчитать полученное количество microCoinZ.
Входные данные
На вход подается число n (0 <= n <= 70).
Выходные данные
Выведите одно число - полученный скилл.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 |
1 |
PS: Mountain Dew, также MTN DEW — безалкогольный сильногазированный прохладительный напиток, торговая марка американской компании PepsiCo.
| |
![]()
|
|
Маршрут наименьшей стоимости
Динамическое программирование
Динамическое программирование: один параметр
Робот Сильвер движется по платному шоссе на планете Шелезяка. На каждом километре шоссе расположен пункт оплаты. Всего на шоссе n пунктов оплаты. Первый пункт оплаты находится в самом начале шоссе, n-й пункт оплаты находится в начале последнего километра шоссе. Заплатив нужную сумму в i-м пункте оплаты, робот может двигаться дальше либо до следующего пункта оплаты, либо же до того, который находится через 2 километра (то есть, если робот находится в пункте i, то он может двигаться либо до пункта i+1, либо до пункта i+2). Первую оплату можно сделать либо в первом пункте, либо во втором (на выбор). Если оплаты была произведена в предпоследнем (n-1) пункте, то можно просто доехать до конца шоссе, не оплачивая проезд в последнем пункте.
Зная стоимость проезда через определенный пункт оплаты, помогите роботу Сильверу найти наименьшую стоимость проезда через все шоссе, которую должен будет заплатить Сильвер, а также пункты оплаты, на которых ему необходимо будет остановиться.
Входные данные
В первой строке записано количество пунктов оплаты n (2 <= n <= 1000). Во второй строке записыны n целых чисел (costi) - стоимость проезда через i-й пункт оплаты (1 <= i <= n, 0 <= costi <= 999).
Выходные данные
Выведите в первой строке наименьшую стоимость проезда через шоссе.
Во второй строке выведите через пробел номера пунктов оплаты (по возрастанию), на которых роботу придется остановиться, чтобы оплатить проезд. Если вариантов маршрута с остановками в пунктах оплаты несколько, то выведите любой из них.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
10 15 20 |
15
2 |
| 2 |
10
1 100 1 1 1 100 1 1 100 1 |
6
1 3 5 7 8 10 |
| |
![]()
|
|
Калькулятор с восстановлением ответа
Динамическое программирование: один параметр
Динамическое программирование
Имеется калькулятор, который выполняет три операции:
- Прибавить к числу
X единицу.
- Умножить число
X на 2.
- Умножить число
X на 3.
Определите кратчайшую последовательность операций, необходимую для получения из числа 1 заданное число N.
Входные данные
Программа получает на вход одно число X, не превосходящее 10 6.
Выходные данные
Выведите строку, состоящую из цифр "1", "2" или "3", обозначающих одну из трех указанных операций, которая получает из числа 1 число N за минимальное число операций. Если возможных минимальных решений несколько, выведите любое из них.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 |
|
| 2 |
5 |
121 |
| 3 |
562340 |
3333312222122213312 |
| |
![]()
|
|
Магическая энергия
Динамическое программирование: один параметр
Вы - маг, который хочет собирать магическую энергию из домов вдоль улицы. В каждом доме сосредоточена определенная магическая энергия, и единственным ограничением является то, что если вы извлекаете магическую энергию из двух соседних домов в одну и ту же ночь, то это вызывает негативные последствия для вас и окружающей среды.
Зная уровень магической энергии в каждом доме, найдите максимальное количество магической энергии, которое вы можете собрать сегодня, избегая извлечения энергии из соседних домов в одну и ту же ночь. Кроме этого, определите заранее какие дома вы должны посетить?
Входные данные
В первой строке записано число n - количество домой вдоль улицы. Во второй строке - n целых чисел ai - количество магической энергии в i-м доме.
Ограничения на входные данные
1 <= n <= 1000 <= a[i] <= 4001 <= i <= n
Выходные данные
Выведите в первой строке максимальное количество магической энергии, которую вы сможете собрать. Во второй строке выведите номера домов (в порядке возрастания, через пробел), которые вы посетите.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4
3 2 2 1 |
5
1 3 |
| 2 |
5
2 7 9 3 1
|
12
1 3 5 |
| |
![]()
|
|
Опасные отходы
Динамическое программирование: один параметр
Рекуррентные последовательности
При переработке радиоактивных материалов образуются отходы двух типов: А (неопасные) и B (особо опасные). Отходы каждого типа упаковываются в контейнеры, а затем контейнеры складываются в стопки. Стопка считается взрывоопасной, если в ней есть три или больше контейнеров с особо опасными отходами (типа B) расположены рядом. Для заданного количества контейнеров N определите, сколько есть способов составить безопасную стопку.
Входные данные
Входная строка содержит натуральное число – количество контейнеров N в стопке (1 <= N <= 35).
Выходные данные
Программа должна вывести одно число – количество способов составить безопасную стопку из N контейнеров.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 |
7 |
| |
![]()
|
|
Магическая сила
Динамическое программирование: один параметр
Вы - маг, странствующий по волшебному лесу, в поисках своей утраченной магической силы. Эта магическая сила находится в волшебных кристаллах, которые растут на деревьях в этом волшебном лесу. На каждом дереве растет только один волшебный кристалл. Так как вы маг, то вы знаете какой силой обладает тот или иной кристалл, растущий на определенном дереве в этом лесу. Вы хотите получить в этом лесу как можно больше магической силы. Для этого вам следует выполнить следующее действие любое количество раз:
- Выберите любое дерево и соберите волшебный кристалл, который растет на нем, чтобы получить его магическую силу. Помните, что после того как был сорван кристалл с определенной силой, все кристаллы, чья сила на один меньше или на один больше, чем сила кристалла, который вы только что собрали, сами исчезают, оставляя вас с магической силой, равной силе собранного кристалла.
Определите максимальную магическую силу, которую вы можете получить, применяя вышеуказанное действие любое количество раз.
Входные данные
Первая строка входных данных содержит число n - количество деревьев в волшебном лесу. Вторая строка содержит n чисел ai - волшебная сила кристалла на i-м дереве.
Ограничения на входные данные
1 <= n <= 2 * 1041 <= a[i] <= 1041 <= i <= n
Выходные данные
Выведите максимальную магическую силу, которую вы можете получить.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
3 4 2 |
6 |
| 2 |
6
2 2 3 3 3 4 |
9 |
| |
![]()
|
|
Магическая энергия - 2
Динамическое программирование: один параметр
Вы - маг, который хочет собирать магическую энергию из домов вдоль улицы. Дома на этой улице расположены по кругу. Это означает, что первый дом является соседом последнего. В каждом доме сосредоточена определенная магическая энергия, и единственным ограничением является то, что если вы извлекаете магическую энергию из двух соседних домов в одну и ту же ночь, то это вызывает негативные последствия для вас и окружающей среды.
Зная уровень магической энергии в каждом доме, найдите максимальное количество магической энергии, которое вы можете собрать сегодня, избегая извлечения энергии из соседних домов в одну и ту же ночь.
Входные данные
В первой строке записано число n - количество домой вдоль улицы. Во второй строке - n целых чисел ai - количество магической энергии в i-м доме.
Ограничения на входные данные
1 <= n <= 1000 <= a[i] <= 10001 <= i <= n
Выходные данные
Выведите максимальное количество магической энергии, которую вы сможете собрать.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
2 3 2 |
3 |
| 2 |
4
1 2 3 1 |
4 |
| 3 |
3
1 2 3 |
3 |
| |
![]()
|
|
В фантастическом лесу
Динамическое программирование: один параметр
В фантастическом лесу живут различные существа, каждое из которых имеет свой уникальный номер, начинающийся с 1. Также у каждого существа есть свой уровень энергии, представленный целым числом. У первого существа уровень энергии равен 1. Каждое последующее существо имеет уровень энергии, который зависит от уникального номера существа. В общем виде уровень энергии существа можно выразиить следующим образом:
creature[1] = 1creature[2 * i] = creature[i], если 2 <= 2 * i <= ncreature[2 * i + 1] = creature[i] + creature[i + 1], при 2 <= 2 * i + 1 <= n
Чтобы понять, насколько могущественны существа в лесу, необходимо найти существо с максимальным уровенем энергии.
Входные данные
Программа получает на вход натуральное число n (1 <= n <= 100) - количество существ в фантастическом лесу.
Выходные данные
Выведите максимальный уровень энергии среди всех существ в данном фантастическом лесу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 |
1 |
| 2 |
7 |
3 |
| 3 |
3 |
2 |
| |
![]()
|
|
Кладовка из Простоквашино
Динамическое программирование: один параметр
Динамическое программирование
Префиксные суммы(минимумы, ...)
Сразу же после заселения в новый дом в Простоквашино кот Матроскин, Шарик и дядя Фёдор затеяли ремонт. Непосредственно перед его началом они обнаружили, что в доме отсутствует кла- довка для стройматериалов, и наспех пристроили её к дому. Как только вспомогательное строение было готово, встал вопрос о необходимости провести туда электричество и повесить лампочку.
Обсудив вопросы электрификации новых помещений с почтальоном Печкиным, наши герои узна- ли много полезной информации. Чтобы посетители не мучились с выбором, в деревенском магазине продаётся только один вид лампочек, зато в неограниченных количествах. Стоит одна лампочка ни дорого, ни дёшево, а ровно C рублей. Правда, лампочки в магазине не самые качественные, и вклю- чить каждую из них можно только K раз, а на K + 1 включение она перегорает. Недостаток этот компенсируется тем, что во включенном состоянии лампочка перегореть не может. К сожалению, электроэнергия в Простоквашино недешевая, и каждая минута работы лампочки обойдется дяде Фёдору и его друзьям в D рублей.
Узнав всё это, экономный Матроскин составил поминутный график из N предполагаемых посе- щений кладовки. Каждый визит в новое помещение задаётся моментом входа ai и моментом выхода bi . Таким образом, i-й визит продолжается ровно bi − ai минут.
Разумеется, во время посещения свет в кладовке должен быть включён. Если в начале очередного визита лампочка не горит, то посетитель сразу её включает, а вот уходя он может как выключить свет, так и оставить его включенным. Если во время очередного включения лампочка перегорает, то её приходится немедленно заменить. Теперь Матроскина интересует минимальное количество рублей, которое придётся потратить, чтобы выполнить все запланированные визиты в кладовку. Изначально в помещении уже висит новая лампочка в выключенном состоянии.
Формат входных данных
В первой строке входных данных записаны четыре целых числа N, K, C, D — количество пла- нируемых посещений кладовки, количество успешных включений для одной лампочки, стоимость покупки лампочки и стоимость минуты работы лампочки соответственно (1 <= N, K <= 200 000, 1 <= C, D <= 109 ). В следующих N строках даны по два целых положительных числа ai и bi , описывающих пред- полагаемые визиты в кладовку (1 <= ai < bi <= 109 ). Посещения не пересекаются по времени и упорядочены, то есть bi < ai+1.
Формат выходных данных
Выведите одно целое число — минимальное количество рублей, которое придётся потратить жителям дома, чтобы выполнить все запланированные визиты в кладовку при свете.
| Ввод |
Вывод |
1 2 5 6
3 5 |
12 |
3 1 15 10
1 3
4 5
30 35 |
105 |
Замечание
Замечание В первом примере достаточно заплатить только за электроэнергию: лампочка должна быть включена на третьей минуте и выключена на пятой, стало быть, суммарные затраты составляют (5 − 3) × 6 = 12.
Во втором примере выгодно не выключать лампочку между первым и вторым посетителем, а для третьего использовать уже новую лампочку
| |
![]()
|
|
Выборы
Алгоритмы на графах
Простые числа и разложение на множители
Динамическое программирование
Динамическое программирование: один параметр
Скоро в Соединенных Штатах Берляндии пройдут выборы президента. На эту ответственную должность претендуют два кандидата: Дядя Сэм и Дядя Фродо. Вы работаете аналитиком в пред- выборном штабе Дяди Сэма, и вам поручено помочь ему победить конкурента. Раздуть газетный скандал из одержимости оппонента бросанием колец в жерла вулканов не получилось, так что при- дётся воспользоваться математикой.
Казалось бы, чтобы выиграть, необходимо убедить проголосовать за нашего кандидата более половины пришедших на выборы. Оказывается, что иногда нужно гораздо меньше! Для того чтобы понять, как это возможно, рассмотрим подробнее процедуру голосования.
Как вы знаете, Соединенные Штаты Берляндии разделены на несколько административных ре- гионов первого уровня — штатов. Сначала в каждом из штатов проходят местные выборы, по итогам которых каждый штат отдаёт свой голос за одного из кандидатов. Если не менее половины штатов выбрало Дядю Сэма, то выигрывает он (в случае равенства голосов Дядя Сэм имеет преимущество как действующий президент), иначе побеждает Дядя Фродо. Все штаты, в свою очередь, состоят из административных регионов второго уровня, каждый из которых представлен выборщиком из административных регионов третьего уровня и так далее. Последний уровень состоит из отдельных жителей Берляндии. Всего в Берляндии N жителей и K уровней административных единиц. Одним из ключевых принципов этой страны является равенство, так что любой регион i-го уровня делится на одинаковое число регионов следущего уровня (в том числе содержит одинаковое число граждан).
Так получилось, что делением на регионы поручили заняться именно вам, то есть в ваших руках назначить, на сколько именно административных единиц i-го уровня делится (i−1)-ая администра- тивная единица.
Также у вас есть сильный инструмент влияния на выбор людей — нефтяные бурли. Чтобы заста- вить одного избирателя отдать свой голос за Дядю Сэма, достаточно дать ему скромный подарок в размере одного нефтяного бурля.
К несчастью, изначально все N жителей Соединённых Штатов Берляндии собираются отдать свой голос за Дядю Фродо. Требуется определить минимальное количество нефтяных бурлей, ко- торое достаточно потратить для победы на выборах.
Формат входных данных
В единственной строке ввода находятся два целых числа N и K (1 <= N <= 1015 , 1 <= K <= 10).
Формат выходных данных
Требуется вывести единственное число — минимальное количество нефтяных бурлей, которое придётся потратить на предвыборные подарки при наилучшем разбиении на регионы.
Примеры
Замечание
Берляндские законы не запрещают, чтобы страна состояла из одного штата, а город — одного жителя. Аналогично с остальными типами регионов.
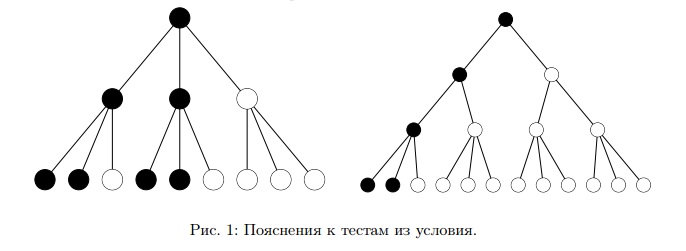
На рисунке 1 черным цветом отмечены те регионы, в которых победил Дядя Сэм. На нижнем уровне черными изображены вершины, соответствущие подкупленным конкретным жителям.
| |
![]()
|
|
Постройка забора
Динамическое программирование
Динамическое программирование: один параметр
После побега Колобка Дед и Баба решили построить забор вокруг своего дома, чтобы не допустить повторения истории.
Забор представляет собой многоугольник ненулевой площади, сторонами которого являются доски. Пилить или ломать доски нельзя. Например, из трех досок с длинами 10, 11 и 12 можно построить забор, а из четырех досок с длинами 100, 1, 2 и 3 — нельзя.
У Деда нашлось целых n досок, поэтому они с Бабой задались вопросом: а сколько различных способов выбрать несколько досок из имеющихся, чтобы из них затем можно было построить забор? Способы считаются различными, если существует доска, которая используется в одном из них, но не используется в другом.
Пожилым людям надо помогать, так что вам не составит труда решить для них эту задачу! Количество способов может быть довольно большим, поэтому выведите остаток от деления этого количества на число 109 + 7.
Формат входного файла
В первой строке входного файла находится одно натуральное число n (1 ≤ n ≤ 4000) — количе- ство досок. Во второй строке дано n чисел li (1 ≤ li ≤ 4000) — длины досок.
Формат выходного файла
В выходной файл выведите одно число — количество способов выбрать доски для постройки забора, взятое по модулю 109 + 7.
| Ввод |
Вывод |
3
10 11 12 |
1 |
4
100 1 2 3 |
0 |
4
5 5 5 5 |
5 |
| |
![]()
|
|
Trapped in the Haybales
Динамическое программирование: один параметр
Динамическое программирование
Дерево отрезков, RSQ, RMQ
Структуры данных
Фермер Джон получили груз из N больших стогов сена (1≤N≤100,000), и разметил их в различных положениях вдоль дороги, ведущей к амбару. К несчастью, он полностью забыл, что корова Беси пасётся вдоль дороги и может попасть в ловушку между стогами сена.
Каждый стог j имеет размер Sj и позицию Pj определяющую его положение вдоль дороги. Беси может двигаться вдоль дороги вплоть до позиции стога, но не может пересечь эту позицию. Исключение – если она прошла в этом направлении D единиц расстояния, тогда она набрала достаточно скорости, чтобы протаранить стог любого размера строго меньше чем D. Конечно после этого она может продолжить движение и таранить другие стога.
Беси может выйти на свободу если она в конце концов протаранит протаранит самый левый или самый правый стог. Вычислите общий размер участка дороги, состоящий из возможных точек старта Беси, из которых она не сможет выбраться.
ФОРМАТ ВООДА:
Первая строка ввода содержит N. Каждая из последующих N строк описывает стог, и содержит два целых числа определяющих размер и позицию в диапазоне 1…109. Все позиции различны.
ФОРМАТ ВЫВОДА:
Выведите одно целое число – размер области дороги, откуда Беси не сможет выбраться.
| Ввод |
Вывод |
|
5
8 1
1 4
8 8
7 15
4 20
|
14 |
| |
![]()
|
|
Cow Hopscotch
Динамическое программирование: один параметр
Динамическое программирование: два параметра
Динамическое программирование
Комбинаторика
Фермер Джон придумал игру для своих коров
Она играется на решётке R*C (2 <= R <= 750, 2 <= C <= 750), где каждый квадрат помечен целым числом от 1 до K (1 <= K <= R*C). Коровы выполняют последовательность прыжков, начиная в левом верхнем квадрате и заканчивая в правом нижнем квадрате и прыжок является корректным если и только если:
1) Вы прыгаете на квадрат c другим числом
2) Квадрат, куда Вы прыгаете, как минимум на одну строку ниже квадрата, в котором Вы сейчас стоите
3) Квадрат, в который Вы прыгаете как минимум на одну колонку правее квадрата, в котором Вы сейчас стоите
Пожалуйста, помогите коровам вычислить количество возможных различных последовательностей корректных прыжков из левого верхнего квадрата в правый нижний.
INPUT FORMAT:
Первая строка ввода содержит целые числа R, C, K. Каждая из следующих R строк содержит C целых чисел, каждое в интервале 1..K.
OUTPUT FORMAT:
Выведите количество различных способов пропрыгать из левого верхнего угла в правый нижний, по модулю 1000000007.
| Ввод |
Вывод |
|
4 4 4
1 1 1 1
1 3 2 1
1 2 4 1
1 1 1 1
|
5 |
| |
![]()
|
|
Ноутбук за печеньки
Одномерные массивы
Динамическое программирование
Использование сортировки
Порядковые статистики
Динамическое программирование: один параметр
Летовец обладает неудивительными математическими способностями. Его способности на столько велики, что он легко может просчитать стоимость его любимых печенек, которые продаются на другом конце города. К сожалению, Летовец не может по максимуму воспользоваться всеми своими способностями, потому что вчера у него сломался ноутбук и теперь он не может писать программы.
Чтобы купить себе новый ноутбук, Летовец решил потратить все свои карманные деньги (а это всего лишь 10 рублей) на покупку своих любимых печенек, а чуть позже, продать все купленные им печеньки.
Так как Летовец еще несовершеннолетний и один ездить на другой конец города не может, ему нужно понять, в какие из двух дней попросить маму отвезти его на другой конец города. Мама всегда готова ему помочь.
Отсутствие ноутбука очень угнетает юного Летовца, поэтому он просит вас определить эти два дня в ближайшие N дней.
Формат входных данных
В первой строке записано число N (2 <= N <= 100000) количество дней, на которые Летовец делает прогноз. Вторая строка содержит N целых положительных чисел ai (1 <= i <= N , 1 <= ai <= 5000 ), где ai - предсказанная стоимость печенек в i-й день.
Формат выходных данных
Выведите два числа: первое число - номер дня, в который Летовей поедет покупать печеньки, второе - номер дня, в который он поедет продавать печеньки. В случае, если таких вариантов дней несколько, выведите любой из них. Если Летовец в итоге не сможет получить прибыль ни при каких вариантах, то выведите два нуля.
| |
![]()
|
|
Обычные яблоки с необычной яблони
Динамическое программирование: один параметр
Летовец живет рядом с обычным лесом. В этом обычном лесу растет не совсем обычная яблоня. I-е яблоко весит ti грамм. Летовец обладает выдающимися математическими способностями и заранее знает, какое яблоко сколько весит. Он хочет собрать как можно больше грамм яблок. Для этого он может выполнить следующее действие любое количество раз:
- выбрать любое яблоко и сорвать его. Но! Так как яблоня не совсем обычная, то после того как было сорвано яблоко весом
ti грамм, все яблоки, чей вес на один грамм меньше или на один грамм больше, чем вес яблока, которое только что сорвали, исчезают.
Определите максимальный суммарный вес яблок, который Летовец может собрать, применяя вышеуказанное действие любое количество раз.
Формат входных данных
Первая строка входных данных содержит число n - количество яблок на яблоне. Вторая строка содержит n чисел ti - вес i-го яблока.
Ограничения на входные данные
1 <= n <= 2 * 1041 <= a[i] <= 1041 <= i <= n
Формат выходных данных
Выведите максимальный суммарный вес яблок, который Летовец может собрать.
| |
![]()
|
|
Призы
Динамическое программирование: один параметр
Миша участвует в процедуре награждения на интеллектуальном шоу. В процессе награждения ему последовательно предлагают призы. У каждого приза есть стоимость. Про каждый приз Миша должен заявить, хочет ли он его взять. После того, как Миша возьмет или пропустит приз, ему показывается следующий, и так далее, вернуться к предыдущим призам и изменить свое решение нельзя.
В качестве первого приза Миша может взять любой приз, а затем Миша может взять приз, если его стоимость строго больше стоимости предыдущего взятого им приза.
Миша подсмотрел сценарий шоу и знает стоимости призов, а также порядок, в котором они будут ему предлагаться. Помогите ему выбрать призы таким образом, чтобы их суммарная стоимость была как можно больше.
Формат входных данных
Первая строка ввода содержит целая число \(n\) — количество призов (\(1 \le n \le 1000\)). Вторая строка содержит \(n\) чисел \(a_1, a_2, \ldots, a_n\) — стоимости призов в том порядке, в котором их покажут Мише (\(1 \le a_i \le 10^9\)).
Формат выходных данных
Выведите одно число — максимальную суммарную стоимость призов, которые может получить Миша.
| |
![]()
|
|
Ударим мостом по бездорожью
Стек
Динамическое программирование: один параметр
Жадный алгоритм
Профиль Уральских гор задается ломаной (x1, y1), (x2, y2), …, (xN, yN), для координат вершин которой верны неравенства x1 < x2 < … < xN. Начальные и конечные точки профиля расположены на уровне моря (y1 = yN = 0).
На горном профиле заданы две различные точки A и B, между которыми требуется проложить дорогу. Эта дорога будет проходить по склонам гор и проектируемому горизонтальному мосту, длина которого не должна превышать L. Оба конца моста находятся на горном профиле. Дорога заходит на мост с одного конца и выходит с другого. Мост не может содержать точек, расположенных строго под ломаной (строительство тоннелей не предполагается).
Возможные примеры расположения моста Невозможное расположение моста

Достоверно известно, что строительство такого моста в данной местности возможно, причем позволит сократить длину дороги из точки A в точку B. Требуется написать программу, которая определит такое расположение горизонтального моста, что длина дороги от точки A до точки B будет наименьшей.
Формат входных данных
Первая строка входных данных содержит два целых числа N и L — количество вершин ломаной (2 ≤ N ≤ 100 000) и максимальную длину моста (1 ≤ L ≤ 106) соответственно. Вторая строка содержит координаты точки A, третья строка — координаты точки B. Точки A и B различны.
Последующие N строк содержат координаты вершин ломаной (x1, y1), (x2, y2), …, (xN, yN). Координаты вершин ломаной, а также точек A и B, задаются парой целых чисел, не превосходящих по абсолютному значению 106. Гарантируется, что x1 < x2 < … < xN и y1 = yN = 0, а также, что точки A и B принадлежат ломаной.
Формат выходных данных
В первой и второй строках выходных данных выведите координаты концов моста с точностью не менее 5 знаков после десятичной точки. В случае, когда решений несколько, выведите любое из них.
| |
![]()
|
|
Выражение
Динамическое программирование: один параметр
Петя - большой любитель математических головоломок. Недавно он прочитал в одном популярном журнале о новой головоломке. Он пытался ее решить несколько дней, но это ему так и не удалось. Помогите Пете справиться с неподдающейся задачей.
В ряд выписаны n чисел. Требуется поставить между каждой парой соседних чисел один из знаков "+" или "×" таким образом, чтобы значение получившегося выражения было как можно больше. Использовать скобки не разрешается.
Например, для последовательности чисел 1, 2, 3, 1, 2, 3 оптимально расставить знаки следующим образом: 1 + 2 × 3 × 1 × 2 × 3. Значение выражения в этом случае равно 37.
Входные данные
В первой строке вводится число n (2 <= n <= 200000). Вторая строка содержит n целых чисел - числа, между которыми следует расставить знаки. Все числа находятся в диапазоне от 0 до 109.
Выходные данные
Выведите оптимальное выражение. В качестве знака "×" выводите символ "*" (звездочку). Если оптимальных решений несколько, выведите любое из них.
| |
![]()
|
|
Сообщение
Динамическое программирование: один параметр
В сообщении, состоящем из одних русских букв и пробелов, каждую букву заменили её порядковым номером в русском алфавите (А - 1, Б - 2, ..., Я - 33), а пробел - нулем. Требуется по заданной последовательности цифр найти количество исходных сообщений, из которых она могла получиться.
Входные данные
В первой строке содержится последовательность цифр. Цифр не более 100.
Выходные данные
Вывести одно число.
| |
![]()
|
|
Перекраска N-угольника
Быстрая сортировка
Динамическое программирование: один параметр
В правильном N-угольнике провели некоторые диагонали так, что он оказался разбит на треугольники. Изначально стороны N-угольника и все его диагонали черные.
Разрешается выбрать четырехугольник, в котором ровно одна диагональ, и при этом эта диагональ черного цвета (сам четырехугольник не обязан быть полностью черным) и проделать с ним следующее: заменить диагональ на противоположную (т.е. если сам четырехугольник был ABCD и в нем была диагональ AC, то она меняется на диагональ BD), после чего перекрасить стороны этого четырехугольника и новую диагональ в красный цвет.
Требуется определить, можно ли с помощью таких операций сделать так, чтобы все отрезки (т.е. стороны N-угольника и изображенные диагонали) стали красными, и не осталось бы ни одного черного отрезка. А если это возможно, то какое минимальное количество операций для этого требуется.
Входные данные
Вводится сначала число N (3≤N≤30000). Далее идет описание N–3 проведенных диагоналей. Каждая диагональ описывается двумя натуральными числами — номерами вершин, которые она соединяет. Гарантируется, что проведенные диагонали внутри N-угольника не пересекаются.
Выходные данные
Выведите минимальное число действий, необходимое для того, чтобы перекрасить весь N-угольник и все его диагонали. Если перекрасить многоугольник указанным способом невозможно, выведите одно число –1 (минус один).
| |
![]()
|
|
Заполните массив
Простые числа и разложение на множители
Динамическое программирование: один параметр
Требуется заполнить N элементов массива, пронумерованных числами от 1 до N (A[1]…A[N]), натуральными числами от 2 до N+1, использовав каждое число ровно один раз, так, чтобы значение каждого элемента массива делилось бы нацело на его номер (т.е. для каждого i A[i] делилось бы на i).
Напишите программу, которая для заданного N вычислит количество способов такого заполнения массива.
Входные данные
Вводится одно натуральное число N (1≤N≤60000).
Выходные данные
Выведите одно число — искомое количество способов заполнения массива.
Примечание
Массив можно заполнить единственным способом: 3 2
| |
![]()
|
|
Заполните массив
Простые числа и разложение на множители
Динамическое программирование: один параметр
Требуется заполнить N элементов массива, пронумерованных числами от 1 до N (A[1]…A[N]), натуральными числами от 2 до N+1, использовав каждое число ровно один раз, так, чтобы значение каждого элемента массива делилось бы нацело на его номер (т.е. для каждого i A[i] делилось бы на i).
Напишите программу, которая для заданного N вычислит количество способов такого заполнения массива.
Входные данные
Вводится одно натуральное число N (1≤N≤1000).
Выходные данные
Выведите одно число — искомое количество способов заполнения массива.
Примечание
Массив можно заполнить единственным способом: 3 2
| |
![]()
|
|
Без трех единиц
Динамическое программирование: один параметр
Определите количество последовательностей из нулей и единиц длины N (длина - это общее количество нулей и едииниц), в которых никакие три единицы не стоят рядом.
Входные данные
Вводится натуральное число N, не превосходящее 40.
Выходные данные
Выведите количество искомых последовательностей. Гарантируется, что ответ не превосходит 231 − 1.
| |
![]()
|
|
Взрывоопасность
Динамическое программирование: один параметр
При переработке радиоактивных материалов образуются отходы двух видов — особо опасные (тип A) и неопасные (тип B). Для их хранения используются одинаковые контейнеры. После помещения отходов в контейнеры последние укладываются вертикальной стопкой. Стопка считается взрывоопасной, если в ней подряд идет более одного контейнера типа A. Стопка считается безопасной, если она не является взрывоопасной. Для заданного количества контейнеров N
определить количество возможных типов безопасных стопок.
Входные данные
Одно число 1 ≤ N ≤ 20.
Выходные данные
Одно число — количество безопасных вариантов формирования стопки.
Примечание
В примере из условия среди стопок длины 2 бывают безопасные стопки типов AB, BA и BB. Стопки типа AA являются взрывоопасными.
| |
![]()
|
|
Взрывоопасность-2
Динамическое программирование: один параметр
При переработке радиоактивных материалов образуются отходы трех видов — особо опасные (тип A), неопасные (тип B) и совсем не опасные (тип C). Для их хранения используются одинаковые контейнеры. После помещения отходов в контейнеры последние укладываются вертикальной стопкой. Стопка считается взрывоопасной, если в ней подряд идет более одного контейнера типа A. Стопка считается безопасной, если она не является взрывоопасной. Для заданного количества контейнеров N
определить число безопасных стопок.
Входные данные
Одно число 1≤N≤20.
Выходные данные
Одно число — количество безопасных вариантов формирования стопки.
Примечание
В примере из условия среди стопок длины 2 бывают безопасные стопки типов AB, AC, BA, BB, BC, CA, CB и CC. Стопки типа AA являются взрывоопасными.
| |
![]()
|
|
Самый дешевый путь
Динамическое программирование: один параметр
Мальчик подошел к платной лестнице. Чтобы наступить на любую ступеньку, нужно заплатить указанную на ней сумму. Мальчик умеет перешагивать на следующую ступеньку, либо перепрыгивать через ступеньку. Требуется узнать, какая наименьшая сумма понадобится мальчику, чтобы добраться до верхней ступеньки.

Входные данные
В первой строке входного файла вводится одно натуральное число 𝑁≤100 — количество ступенек.
В следующей строке вводятся 𝑁 натуральных чисел, не превосходящих 100 — стоимость каждой ступеньки (снизу вверх).
Выходные данные
Выведите одно число — наименьшую возможную стоимость прохода по лесенке.
| |
![]()
|
|
Летокоины
Динамическое программирование: один параметр
В деревне Летовецк, где живут мудрые старцы и их ученики, существует древний банк, который хранит богатства в виде ле́токоинов — особых монет, обладающих магической силой. Однако банк установил строгие правила: чтобы снять деньги, нужно использовать только определённые суммы за одну операцию:
-
за одну операцию можно снять только 1 ле́токоин,
-
за одну операцию можно снять сумму 6x, где x - любое натуральное число (можно снять сумму равную 6, 36, 216, и т.д.),
-
за одну операцию можно снять сумму 9x, где x - любое натуральное число (можно снять сумму равную 9, 81, 729, ...).
Старец Летовец спросил своих учеников: за какое минимальное количество операций вы сможете снять ровно N ле́токоинов?
Примечание: невозможно повторно вносить снятые деньги в банк!
Формат входных данных
На вход подается целое число N (\(1<=N<=100000\)).
Формат выходных данных
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснения |
| 1 |
127 |
4 |
При снятии 1 + 9 + 36 + 81 получится снять 127 летокоинов за 4 операции. |
| 2 |
3 |
3 |
1+1+1 = 3, всего 3 операции |
| 3 |
44852 |
16 |
|
| |
![]()
|