| | | |
|
Странный сон Константина
Хеш
Бор
Деревья
Деревья
Однажды Константин, поучаствовав в очередной, уже 13-ой по счету международной олимпиаде, возвращался на поезде домой. Он как всегда сидел и размышлял о смысле жизни, попутно решая задачи по программированию. Через некоторое время Константин задремал, но вот беда, для того, чтобы проснуться, он должен решить всплывшую у него в голове задачу, не дающую ему покоя!
В этот раз Константину приснилось дерево, изначально состоящее всего из одной вершины с номером 1. В поставленной им задаче к дереву постепенно добавлялись новые вершины. В i-ую секунду в дерево добавлялась вершина с номером i+1, которая подвешивалась в качестве сына к вершине pi, а на ребре между вершинами i+1 и pi записывалась буква ci.
Каждому пути из корня дерева до вершины v соответствует некоторая строка, получающаяся путем выписывания символов, записанных на ребрах текущего пути в порядке следования от корня к вершине v. Перед Константином стояла нелегкая на первый взгляд задача - после каждого добавления новой вершины посчитать количество уникальных строк, начинающихся в корне дерева (вершине с номером 1), и заканчивающихся в какой-либо другой вершине.
В своем сне Константин вовсе не гений, поэтому решить эту задачу сам он не в силах. Помогите Константину решить задачу и тем самым проснуться.
Входные данные:
В первой строке записано число n - количество запросов на добавление новой вершины в дерево (1 <= n <= 300000).
В следующих n строках описаны запросы добавления вершин. i-ый запрос описывается параметрами pi (1 <= pi <= i) и ci, которые означают, что добавленная вершина с номером i+1 подвешивается к вершине с номером pi в качестве потомка, а на полученном ребре записывается символ ci - строчная буква латинского алфавита.
Выходные данные:
Выведите n строк. В i-ой строке выведите ответ на задачу Константина после добавления i+1-ой вершины.
Примеры:
| Входные данные |
Выходные данные |
2
1 b
2 p |
1
2 |
3
1 o
1 o
2 j |
1
1
2 |
| |
![]()
|
|
Бункеры
Хеш
Деревья
Петя и Вася с упоением играют в шпионов. Сегодня они планируют, где будут
расположены их секретные бункеры и штаб-квартира.
Пока Петя и Вася решили, что им понадобится ровно n бункеров, которые для секретности будут пронумерованы числами от 1 до n.
Некоторые из них будут соединены двусторонними тоннелями, причем для надежности и секретности по тоннелям можно будет попасть из любого бункера в любой единственным образом.
Петя и Вася даже решили, какие из бункеров будут соединены тоннелями, но выбрать, какой из них будет штаб-квартирой, они не могут.
Мальчики хотят выбрать ее и разделить оставшиеся бункеры между собой таким образом, чтобы им досталось поровну бункеров к штаб-квартире вело бы ровно два тоннеля: один от бункера, принадлежащего Васе, другой - от бункера, принадлежащего Пете.
Уставший Петя пошел к себе домой, а утром Вася показал ему план, на котором бункеры были обозначены точками, а тоннели отрезками.
Кроме того, Вася выбрал штаб-квартиру таким образом, что нарисованный им план был симметричен относительно прямой, проходящей через точку, которая соответствовала штаб-квартире.
Хотя Петя почти сразу показал Васе, что тот ошибся и не нарисовал половину бункеров, ему стало интересно, можно ли выбрать штаб-квартиру и нарисовать такой симметричный план.
Входные данные:
В первой строке входного файла находится одно целое число n (1 <= n <= 105) - количество бункеров.
В следующих n - 1 строках находится по два целых числа ui и vi (1 <= ui, vi <= n, ui ≠ vi) - номера бункеров, которые соединяет i-ый тоннель.
Гарантируется, что между любыми двумя бункерами существует единственный путь.
Выходные данные:
В выходной файл выведите "YES", если можно выбрать штаб-квартиру и нарисовать такой план, или "NO" если это невозможно.
Примеры:
| Входные данные |
Выходные данные |
2
1 2 |
NO |
3
1 2
2 3 |
YES |
| |
![]()
|
|
Странный сон Константина
Хеш
Бор
Деревья
Деревья
Однажды Константин, поучаствовав в очередной, уже 13-ой по счету международной олимпиаде, возвращался на поезде домой. Он как всегда сидел и размышлял о смысле жизни, попутно решая задачи по программированию. Через некоторое время Константин задремал, но вот беда, для того, чтобы проснуться, он должен решить всплывшую у него в голове задачу, не дающую ему покоя!
В этот раз Константину приснилось дерево, изначально состоящее всего из одной вершины с номером 1. В поставленной им задаче к дереву постепенно добавлялись новые вершины. В i-ую секунду в дерево добавлялась вершина с номером i+1, которая подвешивалась в качестве сына к вершине pi, а на ребре между вершинами i+1 и pi записывалась буква ci.
Каждому пути из корня дерева до вершины v соответствует некоторая строка, получающаяся путем выписывания символов, записанных на ребрах текущего пути в порядке следования от корня к вершине v. Перед Константином стояла нелегкая на первый взгляд задача - после каждого добавления новой вершины посчитать количество уникальных строк, начинающихся в корне дерева (вершине с номером 1), и заканчивающихся в какой-либо другой вершине.
В своем сне Константин вовсе не гений, поэтому решить эту задачу сам он не в силах. Помогите Константину решить задачу и тем самым проснуться.
Входные данные:
В первой строке записано число n - количество запросов на добавление новой вершины в дерево (1 <= n <= 300000).
В следующих n строках описаны запросы добавления вершин. i-ый запрос описывается параметрами pi (1 <= pi <= i) и ci, которые означают, что добавленная вершина с номером i+1 подвешивается к вершине с номером pi в качестве потомка, а на полученном ребре записывается символ ci - строчная буква латинского алфавита.
Выходные данные:
Выведите n строк. В i-ой строке выведите ответ на задачу Константина после добавления i+1-ой вершины.
Примеры:
| Входные данные |
Выходные данные |
2
1 b
2 p |
1
2 |
3
1 o
1 o
2 j |
1
1
2 |
| |
![]()
|
|
Короткий код
Бор
Жадный алгоритм
Деревья
Код Эвана содержит n переменных. Каждая переменная имеет уникальное имя, состоящее только из английских строчных (маленьких) букв. Однажды Эван решил укоротить свой код.
Он хочет заменить имя каждой переменной его непустым префиксом таким образом, что новые имена останутся попарно различными (но новое имя какой-либо переменной может совпадать со старым именем этой или другой переменной). Среди всех таких возможных замен он хочет найти такую, для которой суммарная длина названий переменных будет минимальной.
Строка a является префиксом строки b, если вы можете удалить несколько (возможно, ни одного) символа с конца строки b и получить a.
Найдите минимальную возможную суммарную длину новых имён.
Входные данные:
В первой строке содержится одно целое число n (1 ≤ n ≤ 105) — число переменных в коде Эвана.
Следующие n строк содержат названия переменных по одному на строку. Каждое название не является пустой строкой и содержит только лишь строчные (маленькие) английские буквы. Суммарная длина всех этих строк не больше 105. Все названия переменных различны.
Выходные данные:
Выведите одно целое число — минимально возможную суммарную длину новых названий переменных.
Примеры:
| Входные данные |
Выходные данные |
3
codeforces
codehorses
code |
6 |
5
abba
abb
ab
aa
aacada |
11 |
3
telegram
digital
resistance |
3 |
Пояснения:
В первом примере одним из наилучших вариантов будет сокращение имён в порядке их ввода до "cod", "co", "c".
Во втором примере можно укоротить последнее имя до "aac" и первое имя до "a" без изменения других имён переменных.
| |
![]()
|
|
Высота дерева
Деревья
Двоичное дерево поиска
Реализуйте бинарное дерево поиска для целых чисел. Программа получает на вход последовательность целых чисел и строит из них дерево. Элементы в деревья добавляются в соответствии с результатом поиска их места. Если элемент уже существует в дереве, добавлять его не надо. Балансировка дерева не производится.
Входные данные
На вход программа получает последовательность натуральных чисел. Последовательность завершается числом 0, которое означает конец ввода, и добавлять его в дерево не надо.
Выходные данные
Выведите единственное число – высоту получившегося дерева.
Пример соответствует следующему дереву:
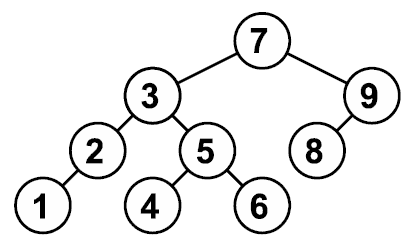
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
7 3 2 1 9 5 4 6 8 0
|
4
|
| |
![]()
|
|
Количество элементов в дереве
Деревья
Двоичное дерево поиска
Подсчитайте количество элементов в получившемся дереве и выведите это количество.
Входные данные
Вводится последовательность целых чисел, оканчивающаяся нулем. Сам ноль в последовательность не входит.
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
7 3 2 1 9 5 4 6 8 0
|
9
|
| |
![]()
|
|
Выведи листья
Деревья
Двоичное дерево поиска
Для полученного дерева выведите список всех листьев (вершин, не имеющих потомков) в порядке возрастания.
Входные данные
Вводится последовательность целых чисел, оканчивающаяся нулем. Сам ноль в последовательность не входит.
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
7 3 2 1 9 5 4 6 8 0
|
1
4
6
8
|
| |
![]()
|
|
Выведи развилки
Деревья
Двоичное дерево поиска
Для полученного дерева выведите список всех вершин, имеющих по два ребёнка, в порядке возрастания.
Входные данные
Вводится последовательность целых чисел, оканчивающаяся нулем. Сам ноль в последовательность не входит. Постройте по этой последовательности дерево.
Выходные данные
Выведите ответ задачи.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
7 3 2 1 9 5 4 6 8 0
|
3
5
7
|
| |
![]()
|
|
Сбалансированность
Деревья
Двоичное дерево поиска
Дерево называется сбалансированным, если для любой его вершины высота левого и правого поддерева для этой вершины различаются не более чем на 1.
Входные данные
Вводится последовательность целых чисел, оканчивающаяся нулем. Сам ноль в последовательность не входит. Постройте дерево, соответствующее данной последовательности.
Выходные данные
Определите, является ли дерево сбалансированным, выведите слово YES или NO.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
7 3 2 1 9 5 4 6 8 0
|
YES
|
| |
![]()
|
|
Второй максимум в дереве
Деревья
Двоичное дерево поиска
Выведите второй по величине элемент в построенном дереве. Гарантируется, что такой найдется.
Входные данные
Дана последовательность целых чисел, оканчивающаяся нулем. Сам ноль в последовательность не входит.
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
7 3 2 1 9 5 4 6 8 0
|
8
|
| |
![]()
|
|
Обход дерева
Деревья
Двоичное дерево поиска
Выведите все элементы полученного дерева в порядке возрастания.
Входные данные
Вводится последовательность целых чисел, оканчивающаяся нулем. Сам ноль в последовательность не входит. По данной последовательности требуется построить дерево.
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
7 3 2 1 9 5 4 6 8 0
|
1
2
3
4
5
6
7
8
9
|
| |
![]()
|
|
Ветки дерева
Деревья
Двоичное дерево поиска
Для полученного дерева выведите список всех вершин, имеющих только одного ребёнка, в порядке возрастания.
Входные данные
Вводится последовательность целых чисел,оканчивающаяся нулем. Построить по ней дерево.
Выходные данные
Выведите список требуемых вершин.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
7 3 2 1 9 5 4 6 8 0
|
2
9
|
| |
![]()
|
|
Бинарное дерево (вставка, поиск)
Деревья
Напишите программу, которая будет реализовывать действия в бинарном дереве поиска «вставить» и «найти» (по значению). Программа должна обрабатывать запросы трёх видов:
ADD n — если указанного числа еще нет в дереве, вставлять его и выводить слово «DONE», если уже есть — оставлять дерево как было и выводить слово «ALREADY».
SEARCH — следует выводить слово «YES» (если значение найдено в дереве) или слово «NO» (если не найдено). Дерево при этом не меняется.
PRINTTREE — выводить все дерево, обязательно используя алгоритм, указанный в формате вывода результатов.
Входные данные
В каждой строке входных данных записан один из запросов ADD n или SEARCH n или PRINTTREE. Гарантируется, что запросы PRINTTREE будут вызываться только в моменты, когда дерево не пустое. Общее количество запросов не превышает 1000, из них не более 20 запросов PRINTTREE.
Выходные данные
Для каждого запроса выводите ответ на него. Для запросов ADD и SEARCH — соответствующее слово в отдельной строке. На запрос PRINTTREE надо выводить дерево, обязательно согласно такому алгоритму:
template void print_tree(Node *p, int level)
{
if(p==NULL)
return;
print_tree(p->left, level+1);
for(int i=0; i < level; i++)
cout << ".";
cout << p->data << endl;
print_tree(p->right, level+1);
}
(Изначальный вызов этой функции — print_tree(root,0).)
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
ADD 2
ADD 3
ADD 2
SEARCH 2
ADD 5
PRINTTREE
SEARCH 7
|
DONE
DONE
ALREADY
YES
DONE
2
.3
..5
NO
|
| |
![]()
|
|
Бинарное дерево (вставка, поиск, удаление)
Деревья
Напишите программу, которая будет реализовывать действия в бинарном дереве поиска «вставить», «удалить» и «найти» (по значению). Программа должна обрабатывать запросы четырёх видов:
ADD n — если указанного числа еще нет в дереве, вставлять его и выводить слово «DONE», если уже есть — оставлять дерево как было и выводить слово «ALREADY».
DELETE n — если указанное число есть в дереве, удалять его и выводить слово «DONE», если нет — оставлять дерево как было и выводить слово «CANNOT». При удалении элемента, имеющего два сына, обязательно обменивать значение с максимальным элементом левого поддерева.
SEARCH — следует выводить слово «YES» (если значение найдено в дереве) или слово «NO» (если не найдено). Дерево при этом не меняется.
PRINTTREE — выводить все дерево, обязательно используя алгоритм, указанный в формате вывода результатов.
Входные данные
В каждой строке входных данных записан один из запросов ADD n или DELETE n или SEARCH n или PRINTTREE. Гарантируется, что запросы PRINTTREE будут вызываться только в моменты, когда дерево не пустое. Общее количество запросов не превышает 1000, из них не более 20 запросов PRINTTREE.
Выходные данные
Для каждого запроса выводите ответ на него. Для запросов ADD, DELETE и SEARCH — соответствующее слово в отдельной строке. На запрос PRINTTREE надо выводить дерево, обязательно согласно такому алгоритму:
template void print_tree(Node *p, int level)
{
if(p==NULL)
return;
print_tree(p->left, level+1);
for(int i=0; i < level; i++)
cout << ".";
cout << p->data << endl;
print_tree(p->right, level+1);
}
(Изначальный вызов этой функции — print_tree(root,0).)
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
ADD 2
ADD 7
ADD 5
PRINTTREE
ADD 5
DELETE 3
ADD 0
PRINTTREE
DELETE 7
PRINTTREE
|
DONE
DONE
DONE
2
..5
.7
ALREADY
CANNOT
DONE
.0
2
..5
.7
DONE
.0
2
.5
|
| |
![]()
|
|
Переворот
Деревья
Дан массив. Надо научиться обрабатывать два типа запросов.
* 1 L R - перевернуть отрезок [L,R]
* 2 L R - найти минимум на отрезке [L,R]
Входные данные
Первая строка файла содержит два числа n, m. (1<=n,m<=105) Во второй строке находится n чисел ni (1<=ai<=109) - исходный массив. Остальные m строк содержат запросы, в формате описанном в условии. Для чисел L, R выполняется ограничение (1<=L<=R<=n).
Выходные данные
На каждый запрос типа 2, во входной файл выведите ответ на него, в отдельной строке.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
10 7
5 3 2 3 12 6 7 5 10 12
2 4 9
1 4 6
2 1 8
1 1 8
1 8 9
2 1 7
2 3 6
|
3
2
2
2
|
| |
![]()
|
|
Range Minimum Query
Деревья
Компания Giggle открывает свой новый офис в Судиславле, и вы приглашены на собеседование. Ваша задача — решить поставленную задачу.
Вам нужно создать структуру данных, которая представляет из себя массив целых чисел. Изначально массив пуст. Вам нужно поддерживать две операции:
- запрос: «
? i j» — возвращает минимальный элемент между i-ым и j-м, включительно;
- изменение: «
+ i x» — добавить элемент x после i-го элемента списка. Если i=0, то элемент добавляется в начало массива.
Конечно, эта структура должна быть достаточно хорошей.
Входные данные
Первая строка входного файла содержит единственное целое число n — число операций над массивом (1<=n<=200000). Следующие n строк описывают сами операции. Все операции добавления являются корректными. Все числа, хранящиеся в массиве, по модулю не превосходят 109.
Выходные данные
Для каждой операции в отдельной строке выведите её результат.
Комментарий к примеру тестов
Нижеследующая таблица показывает процесс изменения массива из примера.
| Операция |
Массив после её выполнения |
| изначально |
пуст |
+ 0 5 |
5 |
+ 1 3 |
5, 3 |
+ 1 4 |
5, 4, 3 |
+ 0 2 |
2, 5, 4, 3 |
+ 4 1 |
2, 5, 4, 3, 1 |
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
8
+ 0 5
+ 1 3
+ 1 4
? 1 2
+ 0 2
? 2 4
+ 4 1
? 3 5
|
4
3
1
|
| |
![]()
|
|
Вычисление простого выражения
Деревья
Напишите программу, которая вычисляет значение арифметического выражения, записанного в виде символьной строки. В выражении используются только целые числа и знаки арифметических операций (+-*/). Результат операции деления – целое число.
Входные данные
На вход программы поступает символьная строка, содержащая правильную запись арифметического выражения.
Выходные данные
Программа должна вывести значение переданного ей выражения как целое число.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
125-6-73/5*8
|
7
|
| |
![]()
|
|
Вычисление простого выражения со скобками
Деревья
Напишите программу, которая вычисляет значение арифметического выражения, записанного в виде символьной строки. В выражении используются только целые числа, знаки арифметических операций (+-*/) и скобки произвольной вложенности. Результат операции деления – целое число.
Входные данные
На вход программы поступает символьная строка, содержащая правильную запись арифметического выражения, возможно, со скобками.
Выходные данные
Программа должна вывести значение переданного ей выражения как целое число.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
(5+20)*(98-34)/(5*8-23)
|
94
|
| |
![]()
|
|
Вычисление выражения с функциями
Деревья
Напишите программу, которая вычисляет значение арифметического выражения, записанного в виде символьной строки. В выражении используются целые числа, знаки арифметических операций, круглые скобки и вызовы функций ( sin , cos , abs , sqrt ). Результат операции деления – вещественное число.
Входные данные
На вход программы поступает символьная строка, содержащая правильную запись арифметического выражения.
Выходные данные
Программа должна вывести значение переданного ей выражения как вещественное число. При выводе результата нужно оставить 3 знака в дробной части числа.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
12+cos(sqrt(12+sin(2)))
|
11.100
|
| |
![]()
|
|
Вычисление выражения с вычислениями
Деревья
Напишите программу, которая вычисляет значение арифметического выражения, записанного в виде символьной строки. В выражении используются целые числа, знаки арифметических операций, круглые скобки, вызовы функций ( sin , cos , abs , sqrt ) и имена переменных (только однобуквенные). Результат операции деления – вещественное число.
Входные данные
Первая строка содержит правильную запись арифметического выражения. В следующих нескольких строках записаны значения всех переменных, использованных в выражении. Каждая из этих строк имеет формат:
<имя переменной>=<значение>
Каждое имя переменной состоят из одной строчной буквы латинского алфавита.
Выходные данные
Программа должна вывести значение переданного ей выражения как вещественное число. При выводе результата нужно оставить 3 знака в дробной части числа.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
cos(z+abs(sqrt(r*sin(x+4))))
r=5
z=10
x=3
|
0.729
|
| |
![]()
|
|
Воздушные потоки
Деревья
Наименьший общий предок
Разреженные таблицы (sparse table)
Структуры данных
Префиксные суммы(минимумы, ...)
Колобок ушёл от бабушки и поехал путешествовать. Неожиданно для себя он забрёл в страну Ивэнлэнд. Первые трудности встали на его пути: Колобка и вход в страну отделял огромный ров с водой, которая, как известно, не очень хорошо влияет на нашего героя. К счастью, повсюду рас- положены воздушные потоки, которые могли поднимать того, кто на них встает, на определённую высоту. Страна не просто так названа Ивэнлэнд, поэтому все высоты, на которые могут поднять героя воздушные потоки — это чётные числа.
Представим воздушные потоки как массив h[1..n] из n натуральных чисел — высот потоков. Для каждого 1 ≤ i ≤ n посчитаем G[i] — индекс ближайшего элемента слева, строго большего h[i]. Более формально, g[i] = max{j | j < i и h[j] > h[i]}. Если i = 1 или до h[i] нет ни одного элемента больше него, то G[i] считается равным 0.
Колобок считает, что оптимальность расположения воздушных потоков определяется суммой
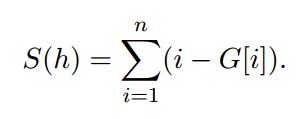
Чем меньше сумма, тем расположение оптимальнее. Всё, что может сейчас сделать Колобок — это увеличить высоту одного из воздушных потоков не более чем на m. После этого действия высота потока должна остаться целым числом, но может, если необходимо, стать и нечётной.
Помогите Колобку сделать оптимальное изменение, которое позволит добиться, чтобы сумма S(h), описанная выше, после проделанного действия была минимальна.
Формат входного файла
В первой строке входного файла даны числа n, m (1 ≤ n ≤ 105 , 1 ≤ m ≤ 109 ) — количество воздушных потоков и максимальное значение, на которое можно увеличить высоту одного из них. Во второй строке даны высоты воздушных потоков h[i] (1 ≤ h[i] ≤ 109 ). Гарантируется, что все высоты — чётные числа.
Формат выходного файла
В единственной строке выходного файла выведите одно целое число — минимальную искомую сумму.
| Ввод |
Вывод |
3 100
4 2 6 |
4 |
3 2
4 2 6 |
5 |
3 10
2 2 2 |
4 |
| |
![]()
|
|
Путь в никуда
Деревья
Деревья
Структуры данных
Разреженные таблицы (sparse table)
Бинарный поиск
Префиксные суммы(минимумы, ...)
Колобку снится странный сон.
В нём Колобок находится на клетчатом поле размера n × m в клетке с координатами (x, y).
Изначально Колобок смотрит вдоль положительного направления оси X. Затем он начинает идти по полю со следующей закономерностью:
• Пройти на одну клетку вперед. Повернуть на 90o вправо.
• Пройти на одну клетку вперед. Повернуть на 90o вправо.
• Пройти на две клетки вперед. Повернуть на 90o вправо.
• Пройти на две клетки вперед. Повернуть на 90o вправо.
• Пройти на три клетки вперед. Повернуть на 90o вправо.
• Пройти на три клетки вперед. Повернуть на 90o вправо.
• Пройти на четыре клетки вперед. Повернуть на 90o вправо.
• И так далее...
Движение продолжается до тех пор, пока Колобок не выйдет за границы поля. После этого Колобок просыпается.
Утром Колобок решил проанализировать свой сон. Он догадался, что в каждой клетке он был максимум один раз, но никак не может вспомнить, сколько клеток он посетил. Колобок просит вас написать программу, которая посчитает количество посещённых им клеток.
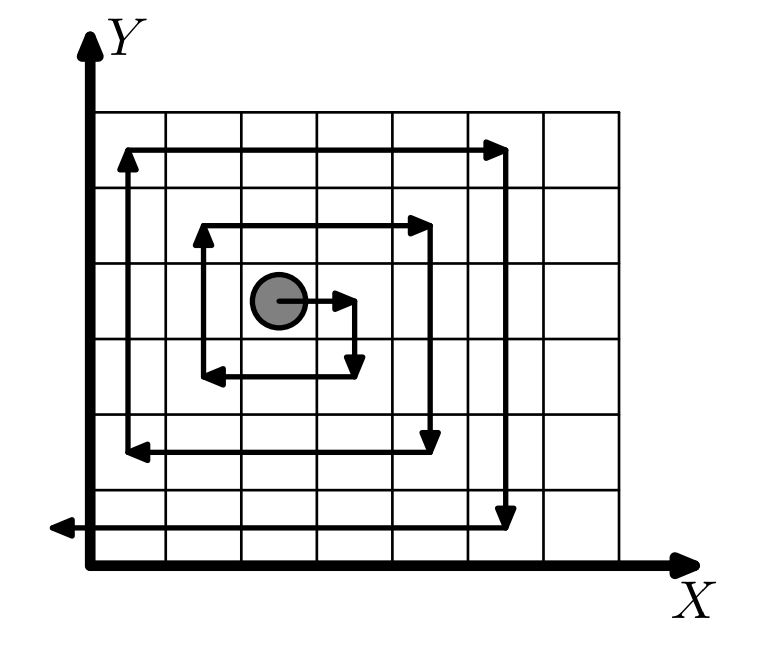
Формат входного файла
В первой строке входного файла находятся два натуральных числа n, m (1 ≤ n, m ≤ 109 ) — размеры доски вдоль оси X и оси Y соответственно. Во второй строке находятся два натуральных числа x, y (1 ≤ x ≤ n; 1 ≤ y ≤ m) — координаты стартовой позиции колобка.
Формат выходного файла
В выходной файл выведите одно число — количество клеток, посещенных Колобком во сне.
| Вывод |
Ввод |
7 6
3 4 |
36 |
2 2
1 1 |
2 |
2 2
1 2 |
4 |
Комментарий
На рисунке наглядно показан первый пример.
| |
![]()
|
|
Путь в никуда
Деревья
Деревья
Структуры данных
Разреженные таблицы (sparse table)
Бинарный поиск
Префиксные суммы(минимумы, ...)
Колобку снится странный сон.
В нём Колобок находится на клетчатом поле размера n × m в клетке с координатами (x, y).
Изначально Колобок смотрит вдоль положительного направления оси X. Затем он начинает идти по полю со следующей закономерностью:
• Пройти на одну клетку вперед. Повернуть на 90o вправо.
• Пройти на одну клетку вперед. Повернуть на 90o вправо.
• Пройти на две клетки вперед. Повернуть на 90o вправо.
• Пройти на две клетки вперед. Повернуть на 90o вправо.
• Пройти на три клетки вперед. Повернуть на 90o вправо.
• Пройти на три клетки вперед. Повернуть на 90o вправо.
• Пройти на четыре клетки вперед. Повернуть на 90o вправо.
• И так далее...
Движение продолжается до тех пор, пока Колобок не выйдет за границы поля. После этого Колобок просыпается.
Утром Колобок решил проанализировать свой сон. Он догадался, что в каждой клетке он был максимум один раз, но никак не может вспомнить, сколько клеток он посетил. Колобок просит вас написать программу, которая посчитает количество посещённых им клеток.

Формат входного файла
В первой строке входного файла находятся два натуральных числа n, m (1 ≤ n, m ≤ 109 ) — размеры доски вдоль оси X и оси Y соответственно. Во второй строке находятся два натуральных числа x, y (1 ≤ x ≤ n; 1 ≤ y ≤ m) — координаты стартовой позиции колобка.
Формат выходного файла
В выходной файл выведите одно число — количество клеток, посещенных Колобком во сне.
| Вывод |
Ввод |
7 6
3 4 |
36 |
2 2
1 1 |
2 |
2 2
1 2 |
4 |
Комментарий
На рисунке наглядно показан первый пример.
| |
![]()
|
|
Гномы и Одинокая гора
Обход в глубину
Применение обхода в глубину
Применение обхода в глубину
Обход в глубину
Деревья
Гномы продолжают искать золото предков в недрах Одинокой горы. Недра Одинокой горы представляют собой n пещер, некоторые из которых соединены двусторонними переходами. При этом из каждой пещеры в любую другую можно попасть по переходам, причем это можно сделать единственным способом.
Гномы разделились на два отряда, которые начали свои поиски с пещер u0 и v0, соответственно. Гномы каждого из отрядов перемещаются вместе. На обследование пещеры у отряда гномов уходит ровно одна минута, после чего каждый отряд быстро перемещается по переходу в одну из соседних пещер. При этом гномы никогда не заходят в пещеру, если они или другой отряд в ней уже побывали. Оба отряда никогда не заходят в одну и ту же пещеру. Если хотя бы один из отрядов гномов не может переместиться в соответствии с этими правилами, оба отряда сразу прекращают поиски сокровищ.
Чтобы как можно лучше обследовать недра Одинокой горы, гномы хотят, чтобы поиски продолжались как можно дольше. По заданной карте пещер в Одинокой горе и начальному положению отрядов гномов определите, какое максимальное время могут продолжаться поиски сокровищ.
Формат входных данных
В первой строке число n (2 ≤ n ≤ 200 000) — число пещер в Одинокой горе. В следующих n−1 строках заданы переходы между пещерами. В каждой строке записаны номера двух пещер v и u, соединенных переходом (1 ≤ v, u ≤ n). В следующей строке заданы номера пещер v0 и u0, в которых исходно находятся два отряда гномов (1 ≤ v0, u0 ≤ n, v0 != u0).
Формат выходных данных
Выведите максимальное число минут, которое могут продолжаться поиски сокровищ.
| Ввод |
Вывод |
Пояснение |
6
1 2
2 3
3 4
4 5
5 6
4 5 |
2 |
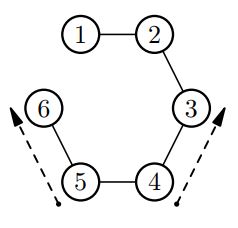 |
8
1 2
2 3
3 4
2 5
5 6
3 7
7 8
1 8 |
4 |
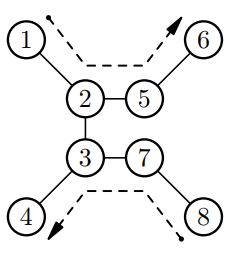 |
| |
![]()
|
|
Мониторинг труб
Деревья
Алгоритмы на графах
Строки
Динамическое программирование
Газораспределительная система одного региона устроена следующим образом. Она
содержит n узлов, пронумерованных от 1 до n, некоторые узлы соединены односторонними
трубами. Узел с номером 1 соответствует центральному газохранилищу.
Система узлов описывается числами от p2, p3, …, pn. Для всех i от 2 до n узел с
номером pi соединен односторонней трубой с узлом i, газ по этой трубе передается от узла pi
к узлу i. Известно, что возможно доставить газ по трубам от центрального газохранилища до
любого узла системы (возможно, с использованием промежуточных узлов). В системе
используются трубы различных типов, тип трубы обозначается буквой английского алфавита
от «a» до «z». Труба, соединяющая узел pi с узлом i, имеет тип ci.
Для проверки качества труб используется специальный робот. Он помещается в
систему труб в одном из узлов и перемещается по трубам, каждый раз проверяя трубу, по
которой он перемещается. Робот может перемещаться по трубам только в том же
направлении, в котором по трубе передается газ. Совершив одно или несколько
перемещений по трубам между узлами, робот извлекается из системы труб.
Каждый запуск робота должен соответствовать одной из m заданных спецификаций,
пронумерованных от 1 до m. Спецификация с номером t представляет собой строку st,
состоящую из строчных букв английского алфавита. Запуск соответствует спецификации st,
если количество перемещений робота по трубам во время запуска совпадает с длиной st, и
для всех j от 1 до длины st на j-м шаге робот перемещается по трубе, тип которой совпадает с
st[j] —символом на позиции j в спецификации.
Если запуск робота соответствует спецификации с номером t, то стоимость этого
запуска составляет wt. Оператору системы необходимо проверить все трубы, для этого
можно запускать робот несколько раз. Каждый раз выбирается спецификация и маршрут
робота по трубам, соответствующие выбранной спецификации. Необходимо проверить все
трубы так, чтобы суммарная стоимость запусков робота для проверки качества труб была
минимальна. Одну и ту же трубу можно проверять несколько раз.
Требуется написать программу, которая по описанию системы труб и списку
спецификаций определяет минимальную суммарную стоимость запусков робота, в
результате которых все трубы будут проверены, а также список необходимых для этого
запусков (по требованию).
Формат входных данных
В первой строке входных данных находятся три целых числа n, m и t — количество
узлов системы труб, количество спецификаций запусков робота и параметр, указывающий,
требуется ли вывести список запусков робота или только их минимальную суммарную
стоимость (1 ≤ n ≤ 500, 1 ≤ m ≤ 105, t равно 0 или 1).
В последующих (n – 1) строках содержится информация о трубах, (i – 1)-я из этих
строк содержит разделенные пробелом значения pi и ci, где pi — целое число, задающее
номер узла, из которого ведет труба в i-й узел, а ci — строчная буква английского алфавита,
задающая тип этой трубы (1 ≤ pi ≤ i – 1).
В последующих m строках содержится информация о спецификациях, i-я из этих
строк содержит разделенные пробелом целое число wi — стоимость запуска робота в
соответствии с этой спецификацией, и состоящую из строчных букв английского алфавита
строку si — саму спецификацию (1 ≤ wi ≤ 10 9). Суммарная длина строк si не превышает 10 6.
Формат выходных данных
Первая строка выходных данных должна содержать одно число — минимальную
суммарную стоимость запусков робота, в результате которых все трубы будут проверены.
Если проверить все трубы невозможно, требуется вывести «–1».
Если t = 0, то больше ничего выводить не требуется.
Если t = 1 и проверить трубы возможно, то далее следует вывести список описаний
запусков робота. В этом случае вторая строка выходных данных должна содержать
число k — количество запусков робота, которое необходимо выполнить для проверки труб. В
следующих k строках необходимо вывести по три целых числа ai, bi и ci — номер узла, в
котором начинается запуск, номер узла, в котором заканчивается запуск, и номер
спецификации, которой соответствует запуск.
Если оптимальных способов проверки несколько, требуется вывести любой из них.
| Ввод |
Вывод |
|
3 3 0
1 a
2 b
3 a
4 b
2 a
|
6 |
|
7 3 1
1 a
2 a
3 b
3 b
1 b
6 b
3 aab
5 b
2 ab
|
15
4
1 4 1
2 5 3
1 6 2
6 7 2
|
Пояснение к примеру
Система труб, заданная во втором примере входных данных, и оптимальный способ
проверки всех труб для этого случая приведены на рисунке ниже.
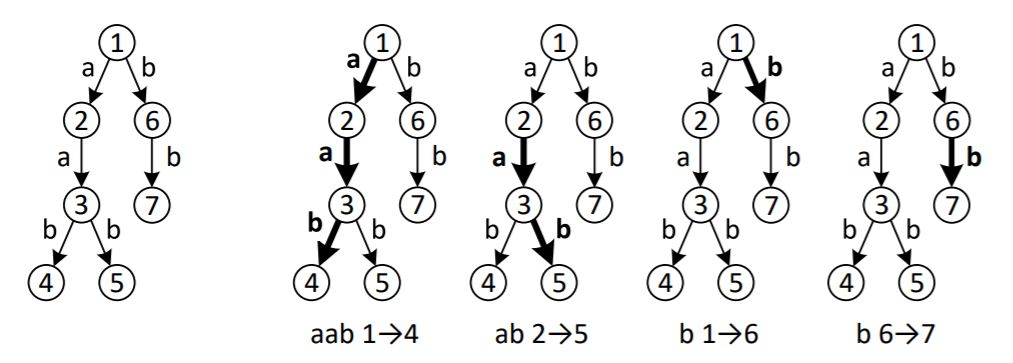
Необходимо обратить внимание на следующие моменты:
- трубу можно проверять несколько раз, так в приведенном примере дважды
проверена труба из узла 2 в узел 3;
- одну и ту же спецификацию разрешается использовать несколько раз, в
приведенном примере вторая спецификация используется дважды, для
проверки труб из узла 1 в узел 6 и из узла 6 в узел 7;
- робот может перемещаться по трубам только в том же направлении, по
которому по трубе передается газ, спецификацию «ab» нельзя использовать
для проверки труб по маршруту 2→1→6, так как робот не может
переместиться из узла 2 в узел 1.
| |
![]()
|
|
Breaking News
Деревья
Обход в глубину
Жизнь завода по производству олимпиадных задач монотонна и однообразна: каждый день происходит одно и то же, вечера похожи как две снежинки и каждое утро всё начинается сначала - ничего не меняется на заводе по производству олимпиадных задач.
В частности, давно известно, когда в течение дня пара сотрудников встречается между собой.
При встрече сотрудники делятся друг с другом новостями.
Утром перед работой сотрудник номер 1 узнал нежелательную новость. Конечно же, он делится с ней при встрече со всеми остальными сотрудниками и они тоже узнают новость и начинаются делиться ей с другими. Если встречаются два сотрудника и один из них знает новость, то начиная с этого момента второй из них также знает новость. Ни один сотрудник не может встречаться с двумя или более сотрудниками одновременно (из соображений секретности). Пара сотрудников может встречаться несколько раз в течение дня.
Вы можете помешать ровно одной встрече за весь день. Выберите такую встречу, отмена которой приведёт к тому, что как можно меньше сотрудников завода узнают новость.
Входные данные
В первой строке входного файла задано два целых числа N (2 ≤ N ≤ 1000) и D (1 ≤ D ≤ 100000) — количество сотрудников и встреч соответственно. В следующих D строках заданы описания встреч. Каждое описание встречи состоит из трех
чисел Ai, Bi и Ti (1 ≤ Ai, Bi ≤ N, 1 ≤ Ti ≤ 109) — пара номеров сотрудников и время встречи.
Выходные данные
Выведите описание встречи, которую необходимо отменить в том же формате, который используется во входных данных. Если ответов несколько — выведите любой.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 5
2 3 1
1 2 4
4 2 110
2 3 5
3 4 4 |
1 2 4 |
| |
![]()
|
|
Дано дерево
Деревья
Дано бесконечное бинарное дерево. У дерева есть корень и бесконечное число вершин, у каждой вершины есть левый и правый сын, у всех вершин кроме корня есть отец.
Каждая вершина может быть покрашена в один из \(c\) цветов или быть бесцветной. Изначально все вершины бесцветные.
Вам необходимо обрабатывать два типа запросов:
-
color(\(u\), \(x\)) Дана вершина \(u\), покрасить вершину \(u\) в цвет \(x\), а затем вызвать color(\(L\), \((x + 1) \bmod c\)) для ее левого сына \(L\) и color(\(R\), \((x - 1 + c) \bmod c\)) для её правого сына \(R\). Заметим, что эта операция перекрашивает все (бесконечное) множество вершин в поддереве вершины \(u\). Здесь \(\bmod\) — операция взятия числа по модулю. Если вершина уже была покрашена, то её цвет меняется на новый.
-
Дана вершина, вывести её текущий цвет.
Формат входных данных
В первой строке вводятся два числа \(q\), \(c\) — количество запросов и цветов, соответственно (\(1 \leq q \leq 5 \cdot 10^5\), \(1 \leq c \leq 10^9\)). Затем следует \(q\) запросов, каждый из которых начинается с целого числа \(t_i\) — типа \(i\)-го запроса.
Если \(t_i\) = 1, то далее в строке даётся целое число \(x\) (\(0 \leq x \leq c - 1\)) цвет, в который надо покрасить вершину запроса \(u\). В следующей строке описан путь до вершины \(u\) в виде непустой строки \(s_i\), состоящей из символов <<L>> и <<R>>. Данная строка задаёт путь от корня дерева до вершины \(u\), где <<L>> обозначает переход к левому сыну, а <<R>> "— к правому.
Если \(t_i\) = 2, то в следующей строке задаётся путь до вершины, цвет которой необходимо вывести, заданный аналогично предыдущему запросу.
Гарантируется, что сумма длин путей до всех вершин запросов не превосходит \(5 \cdot 10^5\).
Формат входных данных
Для каждого запроса второго типа в новой строке необходимо вывести ответ на него. Если вершина бесцветная, необходимо вывести число \(-1\).
| |
![]()
|
|
Мосты
Деревья
Жадный алгоритм
Одна сказочная страна располагалась в дельте далекой реки ( far away river ).
В стране было n островов и на каждом острове находился город. Города были соединены дорогами. Причем существовал в точности один путь от каждого города до любого другого, возможно проходящий через другие города. К сожалению мосты в этой стране были неизвестны, поэтому для пересечения реки использовались понтоны, поэтому путешествия были некомфортными, т.к. приходилось ездить только на лошадях. Когда было открыто мостостроительство король решил вместо нескольких понтонов построить мосты, по которым могли бы ездить даже кареты. В силу бедности страны только k мостов могут быть построены.
Вам необходимо выбрать какие k понтонов надо заменить на мосты так, чтобы суммарное время путешествия между всеми парами городов оказалось минимальным. Вы можете считать, что по обычным дорогам можно ехать только на лошади, а по дороге с мостом — только в карете, запряженной и несколькими лошадьми.
Входные данные
Первая строка входных данных содержит 4 числа n, k, sh и sc — число городов, число мостов, которым можно построить, скорость лошади и скорость экипажа в метрах в секунду (1 ≤ k < n≤ 10 000, 1 ≤sh; sc·≤ 100 000). Каждая из следующих n – 1 строк содержит три целых числа bi, ei — номера соединяемых городов и длину дороги в метрах li (1 ≤ li ≤ 106). Города пронумерованы от 1 до n, дороги пронумерованы от 1 до n – 1.
Выходные данные
k чисел — номера мостов, которые должны быть построены. Если существует несколько оптимальных планов строительства мостов, то выведите любой из них.
| |
![]()
|
|
Гигантский дракон
Вычислительная геометрия
Динамическое программирование
Деревья
Канеки смотрит на неориентированный граф на плоскости из \(n\) вершин и \(m\) ребер. В этом графе ему интересно найти самого большого дракона.
Назовем сегментом дракона три ребра графа \(AL\), \(AB\) и \(AR\), имеющие общую вершину \(A\), и обладающие следующими свойствами:
-
\(0 < \measuredangle (BAL) < 45^\circ\) и направление поворота от \(\overrightarrow{AB}\) к \(\overrightarrow{AL}\) — по часовой стрелке;
-
\(0 < \measuredangle (BAR) < 45^\circ\) и направление поворота от \(\overrightarrow{AB}\) к \(\overrightarrow{AR}\) — против часовой стрелки;
-
\(|AB| \geqslant |AL|\) и \(|AB| \geqslant |AR|\), то есть \(AB\) — максимальное по длине из трех ребер.
При выполнении всех указанных условий вершины \(A\) и \(B\) называются началом и концом сегмента, а ребра \(AL\), \(AB\) и \(AR\) — левой лапой, основанием и правой лапой сегмента, соответственно.
Определим дракона как последовательность сегментов, в которой
-
начало первого сегмента \(A_1\), также называемое головой дракона, находится в вершине \(S\);
-
\(A_{i} = B_{i-1}\) для всех \(i > 1\), то есть начало каждого следующего сегмента совпадает с концом предыдущего;
-
\(\left|\measuredangle \left(\overrightarrow{A_{i-1} B_{i-1}}, \overrightarrow{A_i B_i}\right)\right| < 45^\circ\), то есть угол между векторами оснований соседних сегментов строго меньше \(45^\circ\);
-
\(\left|\measuredangle \left(\overrightarrow{A_1 A_i}, \overrightarrow{A_i B_i}\right)\right| < 45^\circ\), то есть угол между вектором от головы дракона \(A_1\) до начала сегмента и основанием сегмента строго меньше \(45^\circ\).
Обратите внимание, что здесь углы взяты по модулю, то есть каждый следующий сегмент может быть повернут относительно предыдущего на менее чем \(45^\circ\) как по, так и против часовой стрелки.
Мощностью дракона будем считать сумму квадратов длин оснований его сегментов, то есть \(\sum |A_i B_i|^2\). В заданном графе помогите Канеки найти дракона максимальной мощности с головой в вершине \(S\).
Формат входных данных
В первой строке входных данных даны три числа \(n, m, S\) (\(2 \leqslant n \leqslant 2\cdot 10^5\); \(1 \leqslant m \leqslant 4\cdot 10^5\); \(1 \leqslant S \leqslant n\)) — количество вершин и ребер в заданном графе и номер вершины, являющейся головой дракона.
В следующих \(n\) строках дано описание вершин графа. Каждая строка содержит два целых числа \(x_i\) и \(y_i\) — координаты \(i\)-й вершины (\(0 \leqslant x_i, y_i \leqslant 10^9\)). Гарантируется, что все вершины графа различны, то есть не существует двух вершин, обе координаты которых совпадают.
Далее следует пустая строка.
В следующих \(m\) строках дано описание ребер графа. Каждая строка содержит два целых числа \(u_i\) и \(v_i\) — номера вершин, соединенных \(i\)-м ребром (\(1 \leqslant u_i, v_i \leqslant n\); \(u_i \neq v_i\)). Гарантируется, что граф не содержит кратных ребер.
Формат выходных данных
В первой строке выходных данных выведите два числа \(k\) и \(ans\) — количество сегментов в драконе, имеющем максимальную мощность, и само значение его мощности.
В следующих \(k\) строках выведите описание сегментов в том порядке, в котором они образуют дракона. В качестве описания сегмента \(i\) выведите номера вершин \(L_i\), \(B_i\) и \(R_i\).
Будем считать, что дракон может состоять только из вершины \(S\). В таком случае количество сегментов и его мощность следует считать нулями.
Замечание
Графы, данные в первом, втором и третьем тесте условий, выглядят следующим образом.
-
В первом тесте в качестве максимального дракона можно взять весь граф целиком;
-
Во втором тесте ни одна тройка ребер не может быть взята в сегмент, так как не выполняется одно из обязательных условий;
-
В третьем тесте максимальный дракон состоит из двух сегментов с основаниями \(9 \to 5\) и \(5 \to 1\) с лапами \((9 \to 8, 9 \to 7)\) и \((5 \to 3, 5 \to 2\)).
| |
![]()
|
|
Кластеры роботов
Обход в глубину
Жадный алгоритм
Конструктив
Деревья
На производстве расположены \(n\) роботов, пронумерованных от \(1\) до \(n\). Любая пара роботов может быть либо соединена проводом, либо нет. Всего на производстве \(m\) проводов и \(i\)-й из них сейчас соединяет роботов с номерами \(a_i\) и \(b_i\).
Вы находитесь рядом с роботом номер \(1\). Роботом номер \(t\) можно управлять, если он связан с первым некоторой цепочкой проводов, то есть
-
либо если \(t = 1\);
-
либо если существуют такие \(i_1, \ldots, i_k\), что \(i_1 = 1\), \(i_k = t\), и любые два соседних в этой последовательности робота \(i_j\) и \(i_{j + 1}\) связаны проводом.
Любому из роботов, которыми можно управлять, можно послать команду <<извлеки второй конец подключенного к себе провода и подключи его к другому роботу>>. Иными словами, если роботом номер \(t\) можно управлять, и есть провод, соединяющий его с роботом номер \(x\), то можно заменить провод \((t, x)\) на провод \((t, y)\) для любого \(y \neq t\), еще не связанного проводом с \(t\). Обратите внимание, что после этого вы можете потерять управление над \(t\)-м роботом, если единственная связь \(t\)-го с первым проходила через \(x\)-й.
Ваша задача — получить управление над максимально возможным количеством роботов на производстве. Найдите это количество и самую короткую последовательность действий, приводящую к такому исходу.
Формат входных данных
В первой строке записано целое число \(T\) (\(1 \le T \le 1000\)) — количество наборов входных данных в тесте.
Первая строка каждого набора входных данных содержит целые числа \(n\) и \(m\) (\(1 \leq n \leq 10^5\); \(0 \leq m \leq 1.5 \cdot 10^5\)) — количество роботов и количество проводов, соответственно.
В следующих \(m\) строках дано описание проводов: в \(i\)-й строке даны целые числа \(a_i\) и \(b_i\) (\(1 \leq a_i, b_i \leq n\); \(a_i \neq b_i\)) — номера роботов, соединенных \(i\)-м проводом. Гарантируется, что никакие два провода не соединяют одну и ту же пару роботов.
Также гарантируется, что сумма \(n\) по всем наборам входных данных не превосходит \(10^5\) и сумма \(m\) по всем наборам входных данных не превосходит \(1.5 \cdot 10^5\).
Формат выходных данных
Для каждого набора входных данных выведите в первой строке через пробел максимальное количество роботов, управление над которыми можно получить, и количество действий \(k\), которое для этого понадобится.
В следующих \(k\) строках выведите сами описания действий по одному на каждой строке. Описание действия должно состоять из трех целых чисел \(t\), \(x\) и \(y\) (\(1 \leq t, x, y \leq n\); \(x \neq y\)), означающих, что робот номер \(t\) меняет провод \((t, x)\) на провод \((t, y)\).
Если возможных ответов несколько, выведите любой. Обратите внимание, что \(k\) при этом обязано быть наименьшим, при котором можно подключить максимальное количество роботов.
| |
![]()
|
|
Кластеры роботов - 2
Деревья
Жадный алгоритм
Конструктив
Обход в глубину
На производстве расположены \(n\) роботов, пронумерованных от \(1\) до \(n\). Любая пара роботов может быть либо соединена проводом, либо нет. Известно, что \(i\)-й робот соединен с \(k_i\) другими роботами с номерами \(v_{i,1}, \ldots, v_{i,k_i}\). Провода двухсторонние, то есть если \(i\) связан с \(j\), то \(j\) связан с \(i\) (иными словами, \((i, j)\) и \((j, i)\) — это один и тот же провод).
Вы находитесь рядом с роботом номер \(n\). Роботом номер \(t\) можно управлять, если он связан с \(n\)-м некоторой цепочкой проводов, то есть
-
либо если \(t = n\);
-
либо если существуют такие \(i_1, \ldots, i_k\), что \(i_1 = n\), \(i_k = t\), и любые два соседних в этой последовательности робота \(i_j\) и \(i_{j + 1}\) связаны проводом.
Любому из роботов, которыми можно управлять, можно послать команду <<извлеки второй конец подключенного к себе провода и подключи его к другому роботу>>. Иными словами, если роботом номер \(t\) можно управлять, и есть провод, соединяющий его с роботом номер \(x\), то можно заменить провод \((t, x)\) на провод \((t, y)\) для любого \(y \neq t\), еще не связанного проводом с \(t\). Обратите внимание, что после этого вы можете потерять управление над \(t\)-м роботом, если единственная связь \(t\)-го с \(n\)-м проходила через \(x\)-й.
Ваша задача — получить управление над максимально возможным количеством роботов на производстве. Найдите это количество и самую короткую последовательность действий, приводящую к такому исходу.
Формат входных данных
В первой строке записано целое число \(T\) (\(1 \le T \le 1000\)) — количество наборов входных данных в тесте.
Первая строка каждого набора входных данных содержит одно целое число \(n\) (\(1 \leq n \leq 10^5\)) — количество роботов.
Затем следуют \(n\) строк, в \(i\)-й из которых записаны числа \(k_i\) (\(0 \le k_i \le n - 1\)) и \(v_{i,1}, \ldots, v_{i,k_i}\) (\(1 \le v_{i,j} \le n\); \(v_{i,j} \neq i\)) — количество проводов, подключенных к \(i\)-му роботу, и номера роботов на противоположных концах этих проводов. Гарантируется, что данные корректны: никакие два провода не соединяют одну и ту же пару роботов, и если \(j \in v_i\), то \(i \in v_j\).
Также гарантируется, что сумма \(n\) по всем наборам входных данных не превосходит \(10^5\) и сумма количества проводов по всем наборам входных данных не превосходит \(1.5 \cdot 10^5\).
Формат выходных данных
Для каждого набора входных данных выведите в первой строке через пробел максимальное количество роботов, управление над которыми можно получить, и количество действий \(k\), которое для этого понадобится.
В следующих \(k\) строках выведите сами описания действий в формате <<\(y\) + \(t\) - \(x\)>> (\(1 \leq t, x, y \leq n\); \(x \neq y\)). Каждая такая строка соответствует замене провода \((t, x)\) на провод \((t, y)\).
Если возможных ответов несколько, выведите любой. Обратите внимание, что \(k\) при этом обязано быть наименьшим, при котором можно подключить максимальное количество роботов.
| |
![]()
|
|
E. Нужно больше боссов
графы
Деревья
поиск в глубину и подобное
*2100
Ваш друг разрабатывает компьютерную игру. Он уже решил, каким должен быть игровой мир — он будет состоять из \(n\) локаций, соединенных \(m\) двусторонними переходами. Система переходов устроена таким образом, что с их помощью можно добраться из любой локации в любую другую. Естественно, некоторые переходы будут охраняться монстрами (если можно пройти куда угодно без боя, то это слишком просто и совсем не весело, так ведь?). Некоторые важные переходы будут охраняться очень сильными монстрами, требующими серьёзной подготовки и разработки специальной боевой тактики (обычно таких монстров в играх называют боссами). Ваш друг как раз хочет, чтобы вы ему помогли расставить боссов по переходам. Игра начнётся в локации \(s\) и закончится в локации \(t\), но эти локации пока не определены. После того, как эти две локации будут выбраны, ваш друг хочет поставить босса в каждый такой переход, что, не пользуясь этим переходом, невозможно попасть из локации \(s\) в локацию \(t\). Чем больше боссов будет в игре, тем лучше (чем сложнее игра, тем она веселее, так ведь?), и поэтому ваш друг попросил вас определить максимально возможное количество боссов, принимая во внимание любой возможный выбор локаций \(s\) и \(t\). Выходные данные Выведите одно число — максимальное количество боссов, которое можно поставить, по всем возможным парам локаций \(s\) и \(t\). | |
![]()
|
|
G. Два-пути
Деревья
дп
Структуры данных
*2700
Вам задано взвешенное дерево (неориентированный связный граф без циклов, петель и кратных ребер) из \(n\) вершин. Ребро \(\{u_j, v_j\}\) имеет вес \(w_j\). Также, каждой вершине \(i\) присвоено значение \(a_i\). Назовем путь, начинающийся в вершине \(u\) и заканчивающийся в \(v\), в котором по каждому ребру можно пройти не более двух раз (независимо от направления), 2-путем. Вершины в 2-пути могут встречаться любое количество раз (в том числе начальная и конечная). Для каждого 2-пути \(p\) можно найти его профит \(\text{Pr}(p) = \sum\limits_{v \in \text{различные вершины в } p}{a_v} - \sum\limits_{e \in \text{различные ребра в } p}{k_e \cdot w_e}\), где \(k_e\) равно количеству вхождений \(e\) в \(p\). То есть, вершины учитываются ровно один раз, а ребра — столько, сколько раз каждое встречается в \(p\). Вам необходимо ответить на \(m\) запросов. Каждый запрос является парой вершин \((qu, qv)\). Для каждого запроса найдите 2-путь \(p\) из \(qu\) в \(qv\) с максимальным профитом \(\text{Pr}(p)\). Выходные данные Для каждого запроса выведите по одному числу в строке — максимальный профит \(\text{Pr}(p)\) некоторого 2-пути \(p\) с соответствующими концами. Примечание Разъяснение запросов: - \((1, 1)\) — один из оптимальных 2-путей следующий: \(1 \rightarrow 2 \rightarrow 4 \rightarrow 5 \rightarrow 4 \rightarrow 2 \rightarrow 3 \rightarrow 2 \rightarrow 1\). \(\text{Pr}(p) = (a_1 + a_2 + a_3 + a_4 + a_5) - (2 \cdot w(1,2) + 2 \cdot w(2,3) + 2 \cdot w(2,4) + 2 \cdot w(4,5)) = 21 - 2 \cdot 12 = 9\).
- \((4, 4)\): \(4 \rightarrow 2 \rightarrow 1 \rightarrow 2 \rightarrow 3 \rightarrow 2 \rightarrow 4\). \(\text{Pr}(p) = (a_1 + a_2 + a_3 + a_4) - 2 \cdot (w(1,2) + w(2,3) + w(2,4)) = 19 - 2 \cdot 10 = 9\).
- \((5, 6)\): \(5 \rightarrow 4 \rightarrow 2 \rightarrow 3 \rightarrow 2 \rightarrow 1 \rightarrow 2 \rightarrow 4 \rightarrow 6\).
- \((6, 4)\): \(6 \rightarrow 4 \rightarrow 2 \rightarrow 1 \rightarrow 2 \rightarrow 3 \rightarrow 2 \rightarrow 4\).
- \((3, 4)\): \(3 \rightarrow 2 \rightarrow 1 \rightarrow 2 \rightarrow 4\).
- \((3, 7)\): \(3 \rightarrow 2 \rightarrow 1 \rightarrow 2 \rightarrow 4 \rightarrow 5 \rightarrow 4 \rightarrow 2 \rightarrow 3 \rightarrow 7\).
| |
![]()
|
|
E. Соня и магазины
Бинарный поиск
Деревья
дп
жадные алгоритмы
кратчайшие пути
Структуры данных
*2400
Соня очень любит мороженое. Она ест его даже во время соревнований по программированию. Поэтому, девочка решила, что хочет открыть свои собственные магазины мороженого. Соня живет в городе, в котором всего \(n\) перекрестков и \(n-1\) улиц. Все улицы — двусторонние и соединяют пары перекрестков. С любого перекрестка можно попасть в любой другой перекресток в городе, пройдя по одной или более улиц. Мэрия позволяет открывать магазины только на перекрестках, девочка не может открывать магазины посреди улиц, между перекрестками. У Сони есть ровно \(k\) друзей, которым она доверяет. Если она откроет магазин, один с её друзей должен там работать и смотреть, чтобы никто не ел мороженое не заплатив. Поскольку Соня не хочет пропускать важные соревнования по программированию, непосредственно в магазинах она работать не будет. Соня хочет, чтобы все её магазины мороженого образовали простой путь длины \(r\) (\(1 \le r \le k\)), то есть были расположены в различных перекрёстках \(f_1, f_2, \dots, f_r\) и существовала улица между \(f_i\) и \(f_{i+1}\) для всех \(i\) от \(1\) до \(r-1\). Девочка заботится о потенциальных покупателях, поэтому, она также хочет минимизировать максимальное расстояние от перекрестков до ближайшего магазина мороженого. Расстояние между двумя перекрестками \(a\) и \(b\) равно сумме длин всех улиц, которые нужно пройти, чтобы попасть с перекрестка \(a\) на перекресток \(b\). Таким образом, девочка хочет минимизировать \(\)\max_{a} \min_{1 \le i \le r} d_{a,f_i}\(\), где \(a\) принимает значение всевозможных \(n\) перекрёстков, \(f_i\) — перекресток с \(i\)-м магазином Сони, а \(d_{x,y}\) — расстояние между перекрестками \(x\) и \(y\). Соня неуверенна, что сможет найти оптимальные местоположения магазинов, поэтому, просит вас помочь ей открыть не более \(k\) магазинов, которые образуют простой путь, и максимальное расстояние от произвольного перекрестка города до ближайшего магазина минимально. Выходные данные Выведите одно число — минимальное максимальное расстояние, которое нужно будет пройти, чтобы попасть с любого перекрестка до ближайшего магазина мороженого. Магазины Сони должны располагаться вдоль произвольного простого пути из перекрестков длины не более \(k\). Примечание В первом примере можно выбрать путь 2-4, тогда ответ будет 4.  Первый пример. Первый пример. Во втором примере можно выбрать путь 4-1-2, тогда ответ будет 7.  Второй пример. Второй пример. | |
![]()
|
|
E. Военная задача
графы
Деревья
поиск в глубину и подобное
*1600
В этой задаче вам требуется помочь Берляндской армии организовать их систему распространения приказов. Всего в Берляндской армии есть \(n\) офицеров. Первый офицер — командующий армии, он не имеет никаких вышестоящих командующих. Любой другой офицер имеет ровно одного непосредственного командующего. Если офицер \(a\) является непосредственным командующим офицера \(b\), то можно сказать, что офицер \(b\) непосредственный подчиненный офицера \(a\). Офицер \(x\) является подчиненным (непосредственным или по цепочке) офицера \(y\), если выполняется одно из следующих условий: - офицер \(y\) непосредственный командующий офицера \(x\);
- непосредственный командующий офицера \(x\) является подчиненным офицера \(y\).
Например, на картинке ниже подчиненными офицера \(3\) являются: \(5, 6, 7, 8, 9\). Структура Берляндской армии организована таким образом, что каждый офицер, кроме командующего, является подчиненным командующего армией. Формально, Берляндская армия может быть представлена как дерево, состоящее из \(n\) вершин, в котором вершина \(u\) соответствует офицеру с номером \(u\). Предок вершины \(u\) соответствует непосредственному командующему офицера \(u\). Корень (который имеет номер \(1\)) соответствует командующему армией. Военное министерство Берляндии приказало вам ответить на \(q\) запросов, \(i\)-й запрос представлен в виде \((u_i, k_i)\), где \(u_i\) — это некоторый офицер, а \(k_i\) — некоторое натуральное число. Для обработки \(i\)-го запроса представим, как приказ, отданный офицером с номером \(u_i\) распространяется по поддереву \(u_i\). Этот алгоритм очень похож на DFS (depth first search, обход в глубину). Представим, что сейчас распространяет приказ офицер с номером \(a\). Офицер \(a\) выбирает \(b\) — одного из своих непосредственных подчиненных (то есть сына в дереве), который еще не получил приказ. Если существует несколько таких непосредственных подчиненных, тогда \(a\) выбирает офицера с минимальным индексом среди них. Офицер \(a\) отдает приказ офицеру \(b\). После этого \(b\) использует такой же самый алгоритм, чтобы распространить приказ в своем поддереве. После того, как \(b\) прекращает распространять приказ, офицер \(a\) выбирает следующего непосредственного подчиненного (при помощи такого же алгоритма). Когда \(a\) не может выбрать непосредственного подчиненного, еще не получившего приказ, офицер \(a\) прекращает распространять приказ. Посмотрим на следующий пример:  Если офицер \(1\) распространяет приказ, офицеры в его поддереве получат приказ в следующем порядке : \([1, 2, 3, 5 ,6, 8, 7, 9, 4]\). Если офицер \(3\) распространяет приказ, офицеры в его поддереве получат приказ в следующем порядке: \([3, 5, 6, 8, 7, 9]\). Если офицер \(7\) распространяет приказ, офицеры в его поддереве получат приказ в следующем порядке: \([7, 9]\). Если офицер \(9\) распространяет приказ, офицеры в его поддереве получат приказ в следующем порядке: \([9]\). Чтобы ответить на \(i\)-й запрос \((u_i, k_i)\), сформируем последовательность того, в каком порядке офицеры будут получать приказ, если \(u_i\)-й офицер начал его распространять. Ответом будет являться \(k_i\)-й элемент сформированной последовательности или -1, если в ней меньше \(k_i\) элементов. Запросы необходимо рассматривать независимо. Запрос не затрагивает следующие запросы. Выходные данные Выведите \(q\) чисел, где \(i\)-е число — это офицер на позиции \(k_i\) в порядке распространения приказа в поддереве офицера \(u_i\), если распространение приказа начинается с него. Выведите "-1", если количество офицеров, получивших приказ, меньше \(k_i\). Запросы необходимо рассматривать независимо. Они не влияют друг на друга. | |
![]()
|
|
D. Муравьи
2-sat
Деревья
Структуры данных
*3200
Есть дерево из \(n\) вершин, в котором живут \(m\) муравьёв. Каждый муравей имеет свой собственный цвет. У \(i\)-го муравья есть две любимые пары вершин: (\(a_i, b_i\)) и (\(c_i, d_i\)). Вам нужно сказать, можно ли раскрасить рёбра дерева в \(m\) цветов так, чтобы каждый муравей мог ходить между вершинами какой-то из своих любимых пар, используя только рёбра своего цвета; и если можно, то вывести, какую из пар будет использовать каждый муравей. Выходные данные Выведите «NO» (без кавычек), если искомая раскраска рёбер невозможна. Иначе выведите «YES» (без кавычек). В \(i\)-й из \(m\) следующих строк выведите \(1\), если \(i\)-й муравей будет использовать первую пару, и \(2\) иначе. Если существует несколько решений, выведите любое из них. Примечание В примере второе и третье ребро следует покрасить в первый цвет, первое и пятое — во второй цвет, а четвёртое — в третий цвет. | |
![]()
|
|
F. Доминирующие индексы
Деревья
снм
Структуры данных
*2300
Задано корневое неориентированное дерево, состоящее из \(n\) вершин. Вершина \(1\) является корнем. Определим массив глубин вершины \(x\), как бесконечную последовательность \([d_{x, 0}, d_{x, 1}, d_{x, 2}, \dots]\), где \(d_{x, i}\) — это количество вершин \(y\) таких, что выполняются оба следующих условия: - \(x\) является предком \(y\);
- простой путь из \(x\) в \(y\) проходит ровно по \(i\) ребрам.
Доминирующий индекс массива глубин вершины \(x\) (или же просто доминирующий индекс вершины \(x\)) — это такой индекс \(j\), что: - для каждого \(k < j\), \(d_{x, k} < d_{x, j}\);
- для каждого \(k > j\), \(d_{x, k} \le d_{x, j}\).
Для каждой вершины дерева вычислите ее доминирующий индекс. Выходные данные Выведите \(n\) чисел. \(i\)-е число должно быть равно доминирующему индексу вершины \(i\). | |
![]()
|
|
D. Замок
Деревья
дп
жадные алгоритмы
сортировки
Теория вероятностей
*2300
Геральд находится в старинном замке из n залов, соединенных n - 1 переходами. Из любого зала можно добраться до любого другого единственным способом, то есть граф представляет собой дерево. Изначально, в момент времени 0, Геральд находится в зале номер 1. Также в некотором другом зале этого замка находится клад, который Геральд хочет найти. Где именно находится клад неизвестно, он может быть с одинаковой вероятностью в любом из остальных n - 1 залов. Узнать о местонахождении клада Геральд может только тогда, когда придет непосредственно в тот зал. Тогда Геральд сразу же видит клад, и этот момент считается моментом достижения его цели. Переходы между залами имеют различные длины. При этом, переходы считаются длинными, а залы — маленькими и хорошо освещенными, так что временем, которое Геральд находится в залах, можно пренебречь. Замок очень старый, поэтому переходы обваливаются сразу после того, как по ним пройдут два раза, неважно в какую сторону. Геральд может ходить по замку, пользуясь переходами, и будет ходить до тех пор, пока не найдет клад. Естественно, Геральд хочет найти его как можно быстрее. Иными словами, он хочет действовать так, чтобы среднее время нахождения клада было как можно меньше. Каждый переход можно использовать не более двух раз. Поэтому Геральд заранее выбирает такую стратегию, которая позволяет обойти все залы. Более формально, если клад окажется во втором зале, то Геральд найдет его в тот момент, когда первый раз окажется во втором зале — пусть это будет в момент t2. Если в третьем, то Геральд найдет его тогда, когда первый раз окажется в третьем зале. Пусть это произойдет в момент времени t3. И так далее. Таким образом, среднее время нахождения клада окажется равным  . . Выходные данные Выведите одно вещественное число: искомое матожидание времени поиска клада. Ответ должен отличаться от правильного не более чем на 10 - 6. Примечание В первой тесте в замке всего два зала, значит, клад находится во втором зале. Геральду потребуется одна минута, чтобы перейти из первого зала во второй. Во втором тесте из первого зала Геральд может перейти только в третий. Из третьего он может перейти в первый или второй, но в первом он уже был, и из него он не может никуда попасть. Значит, ему нужно пойти во второй зал. Оттуда ему надо идти в 4 зал, потому что остальные залы уже посещены. Если клад окажется в третьем зале, Геральд найдет его через минуту, если во втором — через две, если в четвертом — через три. Среднее время — 2 минуты. В третьем тесте Геральду нужно посетить 4 зала: второй, третий, четвертый и пятый. В них всех можно попасть только из первого зала. Значит, ему нужно поочередно заходить в эти 4 зала в один за другим и возвращаться обратно. В первом из этих залов Геральд окажется через минуту, во втором — через три, в третьем — через 5, в четвертом — через 7. Среднее время — 4 минуты. | |
![]()
|
|
D. Марсоход
графы
Деревья
поиск в глубину и подобное
реализация
*2000
Наташа передвигалась по Марсу на марсоходе. Но неожиданно он сломался, а именно — логическая схема внутри него. Она представляет собой неориентированное дерево (связный ациклический граф) с корнем в вершине \(1\), в котором листья, не являющиеся корнем — входы, все остальные вершины — логические элементы, в том числе корень — выход. На каждый вход подается один бит. На выходе возвращается один бит. Логические элементы бывают четырех видов: AND (И, \(2\) входа), OR (ИЛИ, \(2\) входа), XOR (исключающее ИЛИ, \(2\) входа), NOT (НЕ, \(1\) вход). Логические элементы принимают значения со своих прямых потомков (входов) и возвращают результат функции, которую они выполняют. Наташе известна логическая схема марсохода, а также то, что в ней сломался ровно один вход. Чтобы починить марсоход, ей нужно изменить значение на этом входе. Для каждого входа определите, каким будет результат на выходе, если изменить именно этот вход. Выходные данные Выведите строку из символов '0' и '1' (без кавычек) — ответы на задачу для каждого листка по порядку их сортировки по номеру вершины во входных данных. Примечание Изначальная схема из тестового примера (до изменения входа): 
Зелёным цветом обозначены единичные биты, жёлтым — нулевые. Если изменить бит на входе \(2\) на \(0\), то на выходе будет \(1\). Если изменить бит на входе \(3\) на \(0\), то на выходе будет \(0\). Если изменить бит на входе \(6\) на \(1\), то на выходе будет \(1\). Если изменить бит на входе \(8\) на \(0\), то на выходе будет \(1\). Если изменить бит на входе \(9\) на \(0\), то на выходе будет \(0\). | |
![]()
|
|
F. Дерево
бпф
графы
Деревья
*3400
На Марсе растёт Главное Марсианское Дерево. Оно представляет собой бинарное дерево (корневое дерево, у каждой вершины которого не более двух сыновей) с \(n\) вершинами, корнем которого является вершина с номером \(1\). Его плодами являются Главные Марсианские Фрукты. Сейчас лето, поэтому на этом дереве ещё нет фруктов. Скоро наступит осень, и у дерева начнут опадать листья и ветки. Понятно, что если у дерева после этого нет какой-то вершины, то и всего её поддерева тоже нет. Кроме того, корень дерева должен остаться. Формально: у дерева останется некоторое связное подмножество вершин, содержащее корень. После этого у дерева (в тех вершинах, которые остались) появятся плоды. В корне будет расти ровно \(x\) плодов. Количество плодов в каждой оставшейся вершине не меньше, чем сумма количеств плодов в оставшихся сыновьях этой вершины. Допустимо, что в некоторых вершинах плодов не появится. Наташе интересно, сколько вариантов деревьев может быть после описанных изменений. Поскольку это количество вариантов может быть очень большим, выведите его по модулю \(998244353\). Два варианта получившегося дерева считаются разными, если выполняется одно из двух условий: - в них остались разные подмножества вершин;
- в них осталось одинаковое подмножество вершин, и есть вершина из этого подмножества, для которой количество фруктов в ней в одном варианте дерева не совпадает с количеством фруктов в ней в другом варианте дерева.
Выходные данные Выведите одно число — количество вариантов получившегося дерева по модулю \(998244353\). Примечание Рассмотрим первый тестовый пример.  В вершине \(1\) находятся \(2\) фрукта. Возможны такие \(13\) вариантов: - вершины \(2\) нет, вершины \(3\) нет;
 - вершины \(2\) нет, в вершине \(3\) нет фруктов;
 - вершины \(2\) нет, в вершине \(3\) есть \(1\) фрукт;
 - вершины \(2\) нет, в вершине \(3\) есть \(2\) фрукта;
 - в вершине \(2\) нет фруктов, вершины \(3\) нет;
 - в вершине \(2\) нет фруктов, в вершине \(3\) нет фруктов;
 - в вершине \(2\) нет фруктов, в вершине \(3\) есть \(1\) фрукт;
 - в вершине \(2\) нет фруктов, в вершине \(3\) есть \(2\) фрукта;
 - в вершине \(2\) есть \(1\) фрукт, вершины \(3\) нет;
 - в вершине \(2\) есть \(1\) фрукт, в вершине \(3\) нет фруктов;
 - в вершине \(2\) есть \(1\) фрукт, в вершине \(3\) есть \(1\) фрукт;
 - в вершине \(2\) есть \(2\) фрукта, вершины \(3\) нет;
 - в вершине \(2\) есть \(2\) фрукта, в вершине \(3\) нет фруктов.

Рассмотрим второй тестовый пример. В вершине \(1\) находятся \(5\) фруктов. Возможны такие \(7\) вариантов: - вершины \(2\) нет;
- в вершине \(2\) нет фруктов;
- в вершине \(2\) есть \(1\) фрукт;
- в вершине \(2\) есть \(2\) фрукта;
- в вершине \(2\) есть \(3\) фрукта;
- в вершине \(2\) есть \(4\) фрукта;
- в вершине \(2\) есть \(5\) фруктов.
| |
![]()
|
|
F. Проекты дорог
Деревья
дп
поиск в глубину и подобное
*2600
Берляндия состоит из \(n\) городов, некоторые из которых соединены двусторонними дорогами таким образом, что между каждой парой вершин существует ровно один путь, проходящий по каждой дороге не более одного раза. Каждая дорога характеризуется своей длиной. Города пронумерованы от \(1\) до \(n\). Время пути между некоторыми городами \(v\) и \(u\) — это суммарная длина дорог на кратчайшем пути из \(v\) в \(u\). Два наиболее важных города Берляндии имеют номера \(1\) и \(n\). Министерство Транспорта Берляндии решило построить ровно одну новую дорогу, чтобы разгрузить движение между самыми важными городами. Однако многие уже привыкли к текущему времени пути между самыми важными городами, поэтому новая дорога не должна его сильно изменить. Новая дорога может быть построена только между такими городами \(v\) и \(u\), что \(v \neq u\) и \(v\) и \(u\) еще не соединены никакой дорогой. Они создали планы \(m\) возможных проектов. Каждый проект — это просто длина \(x\) новой дороги. Поликарп работает главным аналитиком Министерства Транспорта Берляндии, разбираться с этими \(m\) проектами — его задача. Для \(i\)-го проекта он должен выбрать некоторые города \(v\) и \(u\) и построить новую дорогу длины \(x_i\) между ними так, чтобы время пути между самыми важными городами было максимально возможным. К сожалению, Поликарп совсем не программист, да и никакой аналитик в мире не справится со всеми проектами с помощью лишь ручки и бумаги. Поэтому он просит вас помочь ему посчитать максимально возможное время пути между самыми важными городами для каждого проекта. Обратите внимание, что \(v\) и \(u\) выбираются независимо для каждого проекта. Выходные данные Выведите \(m\) строк, \(j\)-я строка должна содержать одно целое число — максимально возможное время пути между самыми важными городами для \(j\)-го проекта. Примечание Сеть дорог из первого примера: 
Можно построить дорогу длины \(1\) между городами \(5\) и \(6\), чтобы получить \(83\) в качестве времени пути между \(1\) и \(7\) (\(1 \rightarrow 2 \rightarrow 6 \rightarrow 5 \rightarrow 3 \rightarrow 4 \rightarrow 7\) \(=\) \(18 + 4 + 1 + 12 + 24 + 24 = 83\)). Другие доступные пары городов дадут ответ меньше или равный \(83\). | |
![]()
|
|
E. Сезон дождей
Деревья
разделяй и властвуй
Структуры данных
*3200
К 3018 году Летняя Компьютерная Школа довольно сильно увеличилась в размерах. Новым местом проведения был выбран отель «Берендеетроник». База состоит из \(n\) домиков, между которыми есть \(n-1\) тропинок, и между любыми домиками есть путь. Все на базе было прекрасно, пока не начались дожди. Прогноз погоды обещает, что дожди будут идти \(m\) дней. Специальный отряд преподавателей смог вычислить, что по \(i\)-й тропинке, соединяющей некие домики \(u_i\) и \(v_i\), до дождей можно пройти за \(b_i\) секунд. Дождь же сильно размывает тропинку, и с каждым днем путь будет занимать на \(a_i\) секунд больше, иными словами, в \(t\)-й (с нуля) день после начала дождя прохождение тропинки будет занимать \(a_i \cdot t + b_i\) секунд. К сожалению, несмотря на все прилагаемые усилия, даже в 3018 году не все школьники встречают вечерку и мягкий отбой в своих домиках. Поскольку к жесткому отбою все обязаны уснуть, необходимо вычислить максимальное время пути между всеми парами домиков для каждого дня, и вывесить его на доску объявлений, чтобы каждый школьник знал последний момент, когда он бежать к себе домой. Посчитайте максимальное время пути между какой-либо парой домиков через \(t=0\), \(t=1\), ..., \(t=m-1\) дней после начала дождей. Выходные данные Выведите \(m\) чисел — значения самого длинного пути по базе через \(t=0, t=1, \ldots, t=m-1\) дней после начала дождя. Примечание Рассмотрим подробнее первый пример. В первые три дня (\(0 \le t \le 2\)) самый длинный путь проходит между вторым и третьим домиками, и его длина равна \(100+100=200\). В третий день (\(t=2\)) дорожка между домиками 1 и 4 становится по длине равной \(100\), и продолжает увеличиваться. Поэтому в дни с номерами \(t=2, 3, 4, 5\) самый длинный путь проходит между вершинами 4 и 1 или 2, и имеет длину \(180+10t\). Заметим, что в день \(t=2\) есть три тропинки длиной 100, и есть три максимальных пути одинаковой длины. В шестой день (\(t=5\)) тропинка между первым и пятым домиком по длине догоняет первые две, и становится равной 100. Таким образом, во все дни с \(t=5\) и далее самый длинный путь проходит между вершинами 4 и 5, и имеет длину \(80+30t\). | |
![]()
|
|
F. Мобильная сеть
графы
Деревья
поиск в глубину и подобное
снм
*2600
Вы руководите мобильным оператором и хотите предлагать конкурентоспособные цены для создания сети. В сети есть \(n\) узлов. Ваш конкурент уже предложил некоторые подключения между узлами по некоторым фиксированным ценам. Эти подключения двусторонние. Всего ваш конкурент предложил \(m\) подключений. \(i\)-е из этих подключений соединяет узлы \(fa_i\) и \(fb_i\) и стоит \(fw_i\). У вас есть список из \(k\) подключений, которые вы хотите предложить. Гарантируется, что эти подключения не образуют ни одного цикла. \(j\)-е из этих подключений соединит вершины \(ga_j\) и \(gb_j\). Эти подключения тоже двусторонние. Вы еще не определились с ценой каждого из подключений. Вы можете выбрать стоимости этих подключений любыми целыми числами независимо для каждого из подключений. После этого клиент выберет \(n - 1\) такое подключение из предложенных вами и вашим конкурентом, что все узлы будут объединены в единую сеть, а суммарная стоимость данных подключений будет минимальна. Если существует несколько способов сделать такой выбор, клиент выберет такой, где число ваших подключений максимально. Вы хотите предложить такие цены, что клиент выберет все \(k\) ваши подключения, а суммарная стоимость этих подключений максимально возможная. Выведите эту максимально возможную суммарную стоимость, или \(-1\), если она не ограничена. Выходные данные Выведите единственное число — максимально возможную прибыль, если вы можете произвольно выбирать стоимости ваших подключений. Если прибыль неограничена, выведите \(-1\). Примечание В первом примере оптимально дать стоимость \(3\) подключению \(1-3\), стоимость \(3\) подключению \(1-2\), стоимость \(8\) подключению \(3-4\). В таком случае самый дешевый способ получить связную сеть стоит \(14\), и клиент из таких способов выберет тот, которые содержит все ваши подключения. Во втором примере до тех пор, пока ваше первое подключение стоит \(30\) или меньше, клиент будет вынужден выбрать оба ваших подключения независимо от цены второго, и вы можете получить неограниченную прибыль. | |
![]()
|
|
G. Рыбы
Деревья
Потоки
Структуры данных
*3400
Группа исследователей изучает популяцию рыб в естественной системе рек и озер. Система состоит из \(n\) озёр, соединённых между собой \(n - 1\) реками. Каждая река имеет целочисленную длину (в километрах) и допускает перемещение в обоих направлениях. От любого озера можно добраться до любого другого по рекам (иными словами, система представляет собой дерево). В озёрах живёт неизвестное количество рыб, неотличимых друг от друга. В день \(1\) рыбы произвольно распределены по озёрам. Рыбы могут перемещаться между озёрами по рекам. Рыба может проплыть реку длиной \(l\) километров за \(l\) дней. Также любая рыба, которая посещает какое-либо озеро, может оставаться в нём любое количество дней. В наблюдаемый период в системе не появляется новых рыб, и присутствующие рыбы не исчезают. В любом озере в любой момент времени может находиться сколь угодно большое количество рыб одновременно. Исследователи провели несколько наблюдений. \(j\)-е из этих наблюдений определило, что в день \(d_j\) в озере \(p_j\) находилось не менее \(f_j\) различных рыб. Помогите исследователям определить наименьшее возможное общее количество рыб, проживающих в озёрах, которое не противоречило бы сделанным наблюдениям. Выходные данные Выведите одно число — наименьшее общее количество рыб, не противоречащее наблюдениям. Примечание В первом примере одна из рыб могла проплыть через озёра \(2\), \(1\) и \(4\), а вторая — через озёра \(3\), \(1\) и \(2\). Во втором примере одна рыба не могла быть замечена во всех наблюдениях одновременно, но две рыбы, плывущие по маршрутам \(2 \to 1 \to 4\) и \(3 \to 1 \to 5\), могли. В третьем примере одна рыба могла приплыть из озера \(1\) в озеро \(5\), а остальные могли все время находиться в одном и том же озере: две рыбы в озере \(4\), шесть рыб в озере \(5\), одна рыба в озере \(3\). Система озер показана на рисунке ниже.  | |
![]()
|
|
D. Восстановление BST
Деревья
дп
математика
Перебор
теория чисел
*2100
Хомяк Дима обожает грызть различные объекты, среди которых клетки, коробки, авторы плохих задач и даже деревья! Недавно он обнаружил двоичное дерево поиска и тут же сгрыз все его ребра, в результате чего вершины дерева перемешались в случайном порядке. Дима знает, что если Андрей, который кропотливо строил дерево на протяжении долгого времени, придет и увидит, что все разрушено, то он очень расстроится. По счастью, прежде чем сгрызть все ребра, Дима заметил, что для любых двух вершин, соединенных ребром, наибольший общий делитель их значений превосходит \(1\). Помогите Диме восстановить любое подходящее двоичное дерево поиска или скажите, что это невозможно. Определение и свойства двоичного дерева поиска можно найти здесь. Выходные данные Если можно собрать двоичное дерево поиска, такое что наибольший общий делитель любых двух вершин соединённых ребром больше \(1\), выведите «Yes» (без кавычек). В противном случае выведите «No» (без кавычек). Примечание На картинке ниже проиллюстрировано одно из возможных деревьев для первого примера.  На картинке ниже проиллюстрировано одно из возможных деревьев для третьего примера.  | |
![]()
|
|
F. Вася и максимальное паросочетание
Деревья
дп
*2400
У Васи есть дерево из \(n\) вершин. Он хочет знать количество способов удалить некоторое количество ребер (возможно, ни одного) из дерева так, чтоб в оставшемся графе максимальное паросочетание было единственно. Паросочетанием в графе называется подмножество ребер такое, что все концы этих ребер различны. Максимальным паросочетанием называется такое паросочетание, в котором количество ребер максимально возможное. Так как количество способов может быть велико, выведите его по модулю \(998244353\). Выходные данные В единственной строке выведите число — количество способов удалить ребра в дереве так, чтобы в оставшемся графе максимальное паросочетание было единственно. Выведите ответ по модулю \(998244353\). Примечание В первом тестовом примере максимальное паросочетание будет единственно в четырех случаях: - если удалить ребра \((1, 2)\) и \((1, 3)\).
- если удалить ребра \((1, 2)\) и \((1, 4)\).
- если удалить ребра \((1, 3)\) и \((1, 4)\).
- если удалить все ребра.
Во втором тестовом примере максимальное паросочетание будет единственно в шести случаях: - если не удалять ни одного ребра.
- если удалить ребра \((1, 2)\) и \((2, 3)\).
- если удалить ребра \((1, 2)\) и \((3, 4)\).
- если удалить ребра \((2, 3)\) и \((3, 4)\).
- если удалить ребро \((2, 3)\).
- если удалить все ребра.
| |
![]()
|
|
C. Разбиение на регионы
Деревья
дп
Комбинаторика
теория чисел
*2700
В королевстве Осени \(n\) городов, пронумерованных от \(1\) до \(n\). От любого города можно добраться до любого другого, используя некоторые из \(n-1\) дорог в королевстве. В этом году правительство приняло решение разбить королевство на регионы. После разбиения будут существовать регионы нескольких уровней, при этом само королевство будет являться регионом первого уровня. Любой регион уровня \(i\) должен быть разделен на несколько (хотя бы два) регионов уровня \(i+1\), если это не регион последнего уровня. Каждый город должен принадлежать ровно одному региону каждого уровня. Внутри одного региона, между любыми двумя городами в нем должен существовать путь, проходящий только по городам этого региона. Согласно исследованию, для каждого города \(i\) есть уровень важности — \(a_i\). Все регионы одного уровня должны иметь одинаковую сумму этих значений. Ваша задача состоит в том, чтобы узнать, сколько существует планов разбиения королевства на регионы, чтобы все условия выполнялись. Два плана считаются различными тогда и только тогда, когда количество уровней в них различно, или существует пара городов, которые для какого-то уровня находятся в одном регионе в одном плане, но в разных регионах того же уровня в другом. Поскольку ответ может быть очень большим, выведите его по модулю \(10^9+7\). Выходные данные Выведите одно число — количество различных планов по модулю \(10^9+7\). Примечание В первом примере существует \(4\) различных плана: План \(1\): Уровень \(1\): \(\{1,2,3,4\}\). План \(2\): Уровень \(1\): \(\{1,2,3,4\}\), Уровень \(2\): \(\{1,2\}\),\(\{3,4\}\). План \(3\): Уровень \(1\): \(\{1,2,3,4\}\), Уровень \(2\): \(\{1\}\),\(\{2\}\),\(\{3\}\),\(\{4\}\). План \(4\): Уровень \(1\): \(\{1,2,3,4\}\), Уровень \(2\): \(\{1,2\}\),\(\{3,4\}\), Уровень \(3\): \(\{1\}\),\(\{2\}\),\(\{3\}\),\(\{4\}\). Во втором примере существует \(2\) различных плана: План \(1\): Уровень \(1\): \(\{1,2,3,4\}\). План \(2\): Уровень \(1\): \(\{1,2,3,4\}\), Уровень \(2\): \(\{1\}\),\(\{2\}\),\(\{3\}\),\(\{4\}\). В третьем примере существует \(3\) различных плана: План \(1\): Уровень \(1\): \(\{1,2,3,4\}\). План \(2\): Уровень \(1\): \(\{1,2,3,4\}\), Уровень \(2\): \(\{1,2\}\),\(\{3,4\}\). План \(3\): Уровень \(1\): \(\{1,2,3,4\}\), Уровень \(2\): \(\{1,3\}\),\(\{2\}\),\(\{4\}\). | |
![]()
|
|
D. Корректный BFS?
графы
Деревья
кратчайшие пути
поиск в глубину и подобное
*1700
Алгоритм BFS определяется следующим образом. - Алгоритм выполняется над некоторым неориентированным графом, вершины которого пронумерованы от \(1\) до \(n\). Инициализируем \(q\) как новую очередь, содержащую только вершину \(1\), также пометим вершину \(1\) как использованную.
- Извлечем вершину \(v\) из начала очереди \(q\).
- Напечатаем номер вершины \(v\).
- Переберем в произвольном порядке все вершины \(u\) такие, что \(u\) является соседом \(v\) и ещё не помечена как использованная. Пометим вершину \(u\) как использованную и добавим в конец очереди \(q\).
- Если очередь не является пустой, продолжим выполнение с шага 2.
- В противном случае закончим.
Так как порядок обхода соседей в каждой вершине не является фиксированным, то для данного графа BFS может вывести несколько различных последовательностей. В данной задаче вам нужно проверить, может ли данная последовательность соответствовать какому-то запуску BFS на заданном дереве, начиная с вершины \(1\). Деревом называется неориентированный граф, в котором между каждой парой вершин есть ровно один простой путь. Выходные данные Выведите «Yes» (без кавычек), если порядок вершин соответствует какому-то корректному BFS на данном дереве, и «No» (без кавычек) иначе. Вы можете выводить каждую из букв в любом регистре (строчную или заглавную). Примечание Оба теста из примеров содержат одинаковое дерево. Для этого дерева существует два возможных порядка вершин, соответствующих какому-то запуску BFS. - \(1, 2, 3, 4\),
- \(1, 3, 2, 4\).
Порядок вершин \(1, 2, 4, 3\) не может получится в результате BFS. | |
![]()
|
|
D. Вам дано дерево
Деревья
дп
Структуры данных
*2800
Деревом называется связный неориентированный граф, в котором между любыми двумя вершинами существует ровно один простой путь. Будем говорить, что множество простых путей является \(k\)-допустимым, если каждая вершина дерева принадлежит не более чем одному из этих путей (включая концевые вершины) и каждый путь состоит ровно из \(k\) вершин. Вам дано дерево на \(n\) вершинах. Для каждого \(k\) от \(1\) до \(n\) включительно найдите максимально возможную мощность \(k\)-допустимого множества простых путей. Выходные данные Выведите \(n\) чисел, \(i\)-е из которых равно максимально возможной мощности \(i\)-допустимого множества путей. Примечание Один из способов достичь наибольшего количества путей во втором примере изображён на следующей картинке: 
| |
![]()
|
|
F. Множества листьев
графы
Деревья
жадные алгоритмы
поиск в глубину и подобное
снм
сортировки
Структуры данных
*2400
Вам дано неориентированное дерево, состоящее из \(n\) вершин. Назовём вершину листом, если она соединена ровно с одной другой вершиной. Под расстоянием между двумя вершинами будем понимать количество рёбер на кратчайшем пути между этими вершинами. Назовем некоторое множество листьев красивым, если максимальное расстояние между любой парой листьев из этого множества не превышает \(k\). Перед вами стоит задача разделить все листья дерева на непересекающиеся красивые множества. Определите минимальное количество множеств, которые можно получить в результате описанного разделения. Выходные данные Выведите минимальное количество красивых множеств в разбиении всех листьев. Примечание Картинка описывает разбиение дерева из первого примера.  | |
![]()
|
|
B. Пересекающиеся поддеревья
Деревья
интерактив
поиск в глубину и подобное
*1900
Вы играете в странную игру с Ли Ченом. У вас есть дерево с \(n\) вершинами, нарисованное на листе бумаги. Вершины дерева не пронумерованы, но различимы. Каждый из вас независимо пронумеровал вершины целыми числами от \(1\) до \(n\). Вы не знаете нумерацию друг друга. Вы и Ли Чен выбрали по поддереву (то есть связному подграфу) в этом дереве. При этом ваше поддерево в вашей нумерации состоит из вершин \(x_1, x_2, \ldots, x_{k_1}\), а поддерево Ли Чена в его нумерации состоит из вершин \(y_1, y_2, \ldots, y_{k_2}\). Значения \(x_1, x_2, \ldots, x_{k_1}\) и \(y_1, y_2, \ldots, y_{k_2}\) известны вам обоим.  На рисунке показаны две нумерации дерева: слева ваша нумерация, а справа — Ли Чена. Поддеревья, которые вы выбрали, выделены. В этих поддеревьев две общие вершины. На рисунке показаны две нумерации дерева: слева ваша нумерация, а справа — Ли Чена. Поддеревья, которые вы выбрали, выделены. В этих поддеревьев две общие вершины. Вы хотите узнать, есть ли хотя бы одна общая вершина у ваших поддеревьев. К счастью, ваш друг Андрей знает ваши с Ли Ченом нумерации. Вы можете спросить у Андрея не более \(5\) вопросов, каждый из которых один из следующих двух типов: - A x: Андрей посмотрит на вершину \(x\) в вашей нумерации и скажет вам ее номер в нумерации Ли Чена;
- B y: Андрей посмотрит на вершину \(y\) в нумерации Ли Чена и скажет вам ее номер в вашей нумерации.
Выясните, есть ли общая вершина у ваших поддеревьев. Если есть, то найдите обозначение любой одной из этих вершин в вашей нумерации. Протокол взаимодействия Каждый тест состоит из нескольких тестовых случаев. Сначала считайте строку, которая содержит одно целое число \(t\) (\(1 \leq t \leq 100\)) — количество тестовых случаев. Далее для каждого тестового случая ваша программа должна взаимодействовать с программой жюри следующим образом. В первой строке считайте одно целое число \(n\) (\(1 \leq n \leq 1\,000\)) — количество вершин в дереве. Далее в каждой из следующих \(n-1\) строк считайте два целых числа \(a_i\) и \(b_i\) (\(1\leq a_i, b_i\leq n\)) — ребро дерева, которое соединяет вершины \(a_i\) и \(b_i\), в соответствии с вашей нумерацией вершин. В следующей строке считайте одно целое число \(k_1\) (\(1 \leq k_1 \leq n\)) — количество вершин в вашем поддереве. Следующая строка содержит \(k_1\) различных целых чисел \(x_1,x_2,\ldots,x_{k_1}\) (\(1 \leq x_i \leq n\)) — номера вершин в вашем поддереве, в соответствии с вашей нумерацией. Гарантируется, что эти вершины формируют поддерево. Следующая строка содержит одно целое число \(k_2\) (\(1 \leq k_2 \leq n\)) — количество вершин в поддереве Ли Чена. Следующая строка содержит \(k_2\) различных целых чисел \(y_1, y_2, \ldots, y_{k_2}\) (\(1 \leq y_i \leq n\)) — номера (в соответствии с нумерацией Ли Чена) вершин поддерева Ли Чена. Гарантируется, что вершины формируют поддерево, если мы применим скрытую перестановку Ли Чена на дереве, чтобы перенумеровать вершины. Тесты будут предоставляться друг за другом, поэтому вы должны завершить взаимодействие с предыдущим тестовым случаем (то есть, выведя номер общей вершины или \(-1\), если такой вершины нет), чтобы начать получать следующий. Далее вы можете задавать Андрею два разных типа вопросов. - Вы можете вывести «A x» (\(1 \leq x \leq n\)). Это значит, что Андрей посмотрит на вершину \(x\) в вашей нумерации и скажет вам, какой номер имеет эта вершина в нумерации Ли Чена.
- Вы можете вывести «B y» (\(1 \leq y \leq n\)). Это значит, что Андрей посмотрит на вершину \(y\) в нумерации Ли Чена и скажет вам, какой номер имеет эта вершина в вашей нумерации.
Вы можете задать не более \(5\) вопросов в одном тестовом случае. Когда вы готовы отвечать, выведите «C s», где \(s\) — либо номер в вашей нумерации любой из вершин, которая есть в обоих поддеревьях, либо \(-1\), если таких нет. Вывод ответа не считается вопросом. Не забудьте сбросить буфер вывода, чтобы перейти к следующему тестовому случаю. После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Если программа жюри возвращает \(-1\) вместо ответа на запрос, это значит, что вы задали больше вопросов, чем разрешено, или задали недопустимый вопрос. Ваша программа должна немедленно завершиться (например, вызовом функции exit(0)). Вы получите вердикт Wrong Answer; это значит, что вы задали слишком много вопросов, или то, что вы задали некорректный запрос. Если вы это проигнорируете, вы можете получить любой другой вердикт, так как вы будете продолжать считывать из закрытого потока. Входные данные для взломов Чтобы взломать, используйте следующий формат. Обратите внимание, что вы можете взламывать только с одним тестовым случаем. Первая строка должна содержать одне целое число \(t\) (\(t=1\)). Вторая строка должна содержать одно целое число \(n\) (\(1 \leq n \leq 1\,000\)). Третья строка содержит \(n\) целых чисел \(p_1, p_2, \ldots, p_n\) (\(1\leq p_i\leq n\)) — скрытая перестановка от \(1\) до \(n\). Эта перестановка задает нумерацию, которую использует Ли Чен. То есть вершина, которая у вас имеет номер \(i\), имеет номер \(p_i\) в нумерации Ли Чена. Каждая из следующих \(n-1\) строк должна содержать два целых числа \(a_i\) и \(b_i\) (\(1\leq a_i, b_i\leq n\)). Эти ребра должны формировать дерево. Следующая строка должна содержать одно целое число \(k_1\) (\(1 \leq k_1 \leq n\)). Следующая строка должна содержать \(k_1\) различных целых чисел \(x_1,x_2,\ldots,x_{k_1}\) (\(1 \leq x_i \leq n\)). Эти вершины должны формировать поддерево. Следующая строка должна содержать одно целое число \(k_2\) (\(1 \leq k_2 \leq n\)). Следующая строка должна содержать \(k_2\) различных целых чисел \(y_1, y_2, \ldots, y_{k_2}\) (\(1 \leq y_i \leq n\)). Эти вершины должны формировать поддерево в нумерации Ли Чена. Примечание В первом примере \([2, 3, 1]\) является скрытой перестановкой Ли Чена, а во втором примере его скрытой перестановкой является \([5, 3, 2, 4, 1, 6]\). В первом примере есть дерево из трех вершин. Сверху расположено дерево в вашей нумерации и поддерево, которое вы выбрали, а внизу расположено дерево пронумерованное Ли Ченом и его поддерево:  Первым вопросом вы можете попросить Андрея посмотреть на вершину \(1\) в вашей нумерации и сказать её в нумерации Ли Чена. Андрей ответит \(2\). В этот момент вы знаете, что оба ваших поддеревья содержат одну и ту же вершину (то есть вершину \(1\), в соответствии с вашей нумерацией), значит вы могли бы вывести «C 1» и закончить. Однако, вы просите Андрея посмотреть, как обозначена вершина \(2\) в нумерации Ли Чена и сказать её номер в вашей нумерации. Андрей ответит \(1\) (этот вопрос был показан по единственной причине — показать вам как задавать вопросы). Во втором примере есть два тестовых случая. Первый выглядит так же, как и пример в условии:  Сначала мы спросим «B 2», и Андрей ответит \(3\). В таком случае, мы знаем, что \(3\) является общей вершиной, и более того, любое поддерево с размером \(3\), которое имеет вершину \(3\), так же будет содержать вершину \(1\), то есть мы может вывести либо "C 1", либо "C 3". Во втором тестовом случае второго примера:  В таком случае, вы знаете что есть только одно поддерево с размером \(3\), которое не содержит вершину \(1\), — это \(4,5,6\). Вы спрашиваете Андрея номер вершины \(1\) в нумерации Ли Чена. Он отвечает \(5\). В таком случае, вы знаете, что поддерево Ли Чена не содержит \(1\), значит его поддерево должно содержать \(4,5,6\) (в его нумерации), по этому два поддерева не имеют общих вершин. | |
![]()
|
|
A. Последний шанс
графы
Деревья
Паросочетания
Потоки
Структуры данных
*2500
2969-й год. Прошло 1000 лет с момента посадки на луну. Человечество колонизировало Гиперпространство и жило в гармонии. Жило, пока мы не поняли, что мы не одни. Не очень далеко от Земли многочисленный космический флот инопланетян готовит атаку на Землю. Впервые за долгое время человечеству угрожает реальная опасность. Повсюду паника и кризис. Ученые со всей солнечной системы встретились и обсуждают возможный выход из ситуации. Но пока все усилия тщетны. Последняя надежда Земли — ВЫ! К счастью, Земля имеет мощную систему защиты, созданную специалистами из MDCS. Флот инопланетян содержит \(N\) кораблей на одной линии. Система защиты состоит из трех типов вооружения: - SQL-ракеты: каждая SQL-ракета может уничтожить не более одного корабля инопланетян из заданного для каждой ракеты набора.
- лучи Познания: каждому лучу Познания сопоставлен отрезок \([l,r]\), он может уничтожить не более одного корабля инопланетян из этого отрезка.
- OMG-базука: каждая OMG-базука имеет ровно три цели и может уничтожить либо ровно ноль, либо ровно два корабля. Кроме того, система прицеливания является «умной», поэтому множества трех целей для любых двух OMG-базук не пересекаются (таким образом, каждый корабль находится под прицелом не более чем одной OMG-базуки).
Ваша задача — найти такой план атаки на корабли инопланетян, чтобы уничтожить максимально возможное количество кораблей. Каждый уничтоженный корабль должен быть уничтожен ровно одним оружием. Выходные данные Первая строка должна содержать максимальное количество уничтоженных кораблей \(X\). Каждая из следующих \(X\) строк должна содержать два целых числа \(A\) и \(B\), где \(A\) — номер оружия, а \(B\) — номер корабля, уничтоженного оружием \(A\). Примечание SQL-ракета может уничтожить только четвертый корабль. OMG-базука может уничтожить два из 1-го, 4-го или 5-го кораблей, а луч Познания может уничтожить любой корабль из отрезка \([1,4]\). Максимальное количество уничтоженных кораблей равно 4, один из возможных планов — SQL-ракета уничтожает 4-й корабль, OMG-базука уничтожает 1-й и 5-й корабли, а луч Познания уничтожает 2-й корабль. | |
![]()
|
|
C. Гиперпространственная магистраль
графы
Деревья
поиск в глубину и подобное
*2300
В неуказанной Солнечной системе есть \(N\) планет. Космическая правительственная компания недавно наняла космических подрядчиков, чтобы построить \(M\) двусторонних шоссе Hyperspace™, каждое из которых соединяет пару разных планет. Основная цель, заключавшаяся в том, чтобы убедиться, что любая планета может быть достигнута из любой другой планеты, используя только шоссе Hyperspace™, была полностью выполнена. К сожалению, у многих космических подрядчиков были друзья и двоюродные братья в космическом совете директоров компании, поэтому компания решила сделать нечто большее, чем просто соединение всех планет. Для того, чтобы оправдать траты огромных сумм космических денег на магистрали Hyperspace™, они решили ввести жесткое правило на сети Hyperspace™: для любого путешествия, которое начинается и заканчивается в одной и той же вершине, и посещает каждую планету не более одного раза, каждая пара планет на маршруте должна быть непосредственно связана с помощью шоссе Hyperspace™. Другими словами, для каждого простого цикла индуцированный подграф на множестве планет на нем является кликой. Вы разрабатываете навигационное приложение Hyperspace™, и ключевая техническая проблема, с которой вы столкнулись — это поиск минимального количества шоссе Hyperspace™, которыми нужно воспользоваться для путешествия из планеты \(A\) на планету \(B\). Поскольку эта задача слишком проста для Bubble Cup, вот более сложная задача: ваша программа должна сделать это для \(Q\) пар планет. Выходные данные Выведите \(Q\) строк: \(j\)-я строка вывода должна содержать минимальное количество шоссе Hyperspace™, которое понадобится чтобы добраться из планеты \(a_j\) на планету \(b_j\). Примечание Граф из второго примера:  | |
![]()
|
|
D. Межзвездная битва
Деревья
математика
Теория вероятностей
*2200
В межгалактической империи Баблдом \(N\) планет, некоторые пары которых напрямую соединены двусторонними кротовыми норами. Всего есть \(N-1\) кротовых нор. Кротовые норы имеют чрезвычайно важное значение в Баблдоме: множество планет в Баблдоме считается межгалактическим королевством, если и только если между любыми двумя планетами в этом множестве есть путь, использующий только кротовые норы. Известно, что весь Баблдом является королевством. Другими словами, сеть планет и кротовых нор является деревом. На Баблдом напал мощный противник, владеющий технологией телепортации. Враг атакует каждую ночь, а правительство Баблдома возвращает все планеты под свой контроль днем. В течение одной ночи враг атакует каждую планету Баблдома один раз, но некоторые планеты более стойкие, чем другие. Планеты пронумерованы \(0,1,…,N-1\), и планета номер \(i\) будет захвачена врагом в вероятностью \(p_i\). Перед каждой атакой (в том числе перед первой) правительство меняет вероятность захвата одной планеты (возможно как в большую, так и в меньшую сторону). Правительство Баблдома заинтересовано в следующем вопросе: каково математическое ожидание межгалактических королевств, на которые Баблдом распадется после каждой из атак врага (и до того, как правительство вернет планеты под свой контроль)? Другими словами, найдите математическое ожидание количества компонент связности после каждой атаки. Выходные данные Выведите \(Q\) чисел, каждое из которых означает математическое ожидание числа королевств, которые могут получиться после каждой из атак противника. Ваш ответ будет зачтен, если его абсолютная или относительная ошибка не превосходит \(10^{-4}\). | |
![]()
|
|
J. Moonwalk challenge
Деревья
Строки
Структуры данных
*2600
Поскольку астронавты из миссии BubbleCup XI закончили свою миссию на Луне и являются большими поклонниками известного певца, они решили провести некоторое время перед возвращением на Землю, и, таким образом, создали так называемую игру «Moonwalk challenge». Командам астронавтов выдаются карты кратеров на Луне и прямых двунаправленных путей от одних кратеров к другим, безопасные для «лунной походки». Каждый из этих прямых путей окрашен в один цвет, и есть единственный путь между каждым из двух кратеров. Цель игры заключается в том, чтобы найти два кратера, такие, что заданный массив цветов появляется чаще всего как непрерывный подотрезок на пути между этими двумя кратерами (пересекающиеся вхождения должны быть учтены как два различных). Чтобы помочь любимой команде одержать победу, необходимо составить программу, которая по заданной карте отвечает на запросы следующего типа: для двух кратеров и массива цветов ответит, сколько раз заданный массив появляется как непрерывный подотрезок на пути от первого кратера ко второму. Все цвета являются строчными буквами латинского алфавита. Выходные данные Для каждого запроса выведите количество вхождений S (представленного в виде строки) на пути между \(u\) и \(v\). | |
![]()
|
|
F. Самое короткое условие
графы
Деревья
кратчайшие пути
*2400
Вам задан взвешенный неориентированный связанный граф состоящий из \(n\) вершин и \(m\) ребер. Вам нужно ответить на \(q\) запросов, \(i\)-й запрос — найти кратчайшее расстояние между вершинами \(u_i\) и \(v_i\). Выходные данные Выведите \(q\) строк. В \(i\)-й строке должен содержаться ответ на \(i\)-й запрос — кратчайшее расстояние между вершинами \(u_i\) и \(v_i\). | |
![]()
|
|
E. Эйлеров обход
Деревья
Конструктив
*3500
Эйлер — маленький милый бельчонок. Когда приходит осень, он запасается желудями на зиму. Интересный факт, что Эйлер обычно собирает желуди очень специфичным способом. Дерево, с которого он собирает желуди, можно представить как \(n\) желудей, соединенных \(n - 1\) веткой таким образом, что есть ровно один путь между каждой парой желудей. Пронумеруем желуди от \(1\) до \(n\). Бельчонок выбирает один из желудей (не обязательно с номером \(1\)) как старт, затем обходит все желуди способом, который называется «Эйлеров обход» (см. примечание), собирая каждый из желудей, когда он посещает его в последний раз. Сегодня утром Кейт наблюдала за Эйлером. Она записала на листочке все желуди, которые посетил Эйлер на своем пути. К сожалению, на пути домой она попала под дождь и часть чисел теперь невозможно прочитать. Девочка очень расстроилась, так как свои наблюдения она должна была показать учителю. «Может быть, если я угадаю пропавшие числа, я все еще смогу показать это учителю!» — подумала Кейт. Помогите ей, восстановите любой Эйлеров обход некоторого дерева или скажите, что у нее где-то ошибка. Выходные данные Если нет никакого Эйлерова обхода, удовлетворяющего описанию, выведите "no" в единственной строке. Иначе выведите на первой строке "yes", а на второй строке выведите искомый Эйлеров обход. Любой подходящий Эйлеров обход будет считаться правильным, так как учитель не знает, как выглядело исходное дерево. Примечание Эйлеров обход дерева с \(n\) желудями — последовательность из \(2n - 1\) индекса желудей такая, что каждый желудь встречается хотя бы один раз, первый и последний желуди совпадают, и каждые два соседних в обходе желудя соединены веткой. | |
![]()
|
|
E. Эйлеров обход
Деревья
Конструктив
*3500
Эйлер — маленький милый бельчонок. Когда приходит осень, он запасается желудями на зиму. Интересный факт, что Эйлер обычно собирает желуди очень специфичным способом. Дерево, с которого он собирает желуди, можно представить как \(n\) желудей, соединенных \(n - 1\) веткой таким образом, что есть ровно один путь между каждой парой желудей. Пронумеруем желуди от \(1\) до \(n\). Бельчонок выбирает один из желудей (не обязательно с номером \(1\)) как старт, затем обходит все желуди способом, который называется «Эйлеров обход» (см. примечание), собирая каждый из желудей, когда он посещает его в последний раз. Сегодня утром Кейт наблюдала за Эйлером. Она записала на листочке все желуди, которые посетил Эйлер на своем пути. К сожалению, на пути домой она попала под дождь и часть чисел теперь невозможно прочитать. Девочка очень расстроилась, так как свои наблюдения она должна была показать учителю. «Может быть, если я угадаю пропавшие числа, я все еще смогу показать это учителю!» — подумала Кейт. Помогите ей, восстановите любой Эйлеров обход некоторого дерева или скажите, что у нее где-то ошибка. Выходные данные Если нет никакого Эйлерова обхода, удовлетворяющего описанию, выведите "no" в единственной строке. Иначе выведите на первой строке "yes", а на второй строке выведите искомый Эйлеров обход. Любой подходящий Эйлеров обход будет считаться правильным, так как учитель не знает, как выглядело исходное дерево. Примечание Эйлеров обход дерева с \(n\) желудями — последовательность из \(2n - 1\) индекса желудей такая, что каждый желудь встречается хотя бы один раз, первый и последний желуди совпадают, и каждые два соседних в обходе желудя соединены веткой. | |
![]()
|
|
F. Дерево и XOR
Деревья
Строки
*2900
Дан связный неориентированный граф без циклов (то есть дерево) на \(n\) вершинах, при этом на каждом ребре написано какое-то целое неотрицательное число. Рассмотрим все пары вершин \((v, u)\) (то есть всего \(n^2\) таких пар) и для каждой пары посчитаем побитовое исключащее ИЛИ (xor) всех чисел на рёбрах на простом пути между \(v\) и \(u\). Если путь состоял только из одной вершины, то xor всех чисел на рёбрах этого пути считается равным \(0\). Предположим, мы отсортировали полученные \(n^2\) значений по неубыванию. Требуется вывести \(k\)-е из них. Операция xor определяется следующим образом: Пусть даны два целых неотрицательных числа \(x\) и \(y\), рассмотрим их двоичные записи (возможно с ведущими нулями): \(x_k \dots x_2 x_1 x_0\) и \(y_k \dots y_2 y_1 y_0\) (где \(k\) любое число, что все биты \(x\) и \(y\) могут быть представлены). Здесь \(x_i\) это \(i\)-й бит числа \(x\), а \(y_i\) это \(i\)-й бит числа \(y\). Пусть \(r = x \oplus y\) — результат операции xor над числами \(x\) и \(y\). Тогда двоичной записью \(r\) будет \(r_k \dots r_2 r_1 r_0\), где: \(\) r_i = \left\{ \begin{aligned} 1, ~ \text{если} ~ x_i \ne y_i \\ 0, ~ \text{если} ~ x_i = y_i \end{aligned} \right. \(\) Выходные данные Выведите одно целое число — \(k\)-й по возрастанию xor пути в дереве. Примечание Дерево во втором тесте выглядит следующим образом: 
В таком дереве существует \(9\) путей: - \(1 \to 1\) со значением \(0\)
- \(2 \to 2\) со значением \(0\)
- \(3 \to 3\) со значением \(0\)
- \(2 \to 3\) (проходит через \(1\)) со значением \(1 = 2 \oplus 3\)
- \(3 \to 2\) (проходит через \(1\)) со значением \(1 = 2 \oplus 3\)
- \(1 \to 2\) со значением \(2\)
- \(2 \to 1\) со значением \(2\)
- \(1 \to 3\) со значением \(3\)
- \(3 \to 1\) со значением \(3\)
| |
![]()
|
|
D. Укрась яблоню
графы
Деревья
дп
жадные алгоритмы
Конструктив
поиск в глубину и подобное
сортировки
*1600
В саду Аркадия растет одна яблоня. Ее можно представить как множество точек развилок, соединенных ветками так, что между любыми двумя развилками существует ровно один путь по веткам. Развилки пронумерованы от \(1\) до \(n\), развилка номер \(1\) называется корнем. Поддеревом развилки \(v\) называется множество развилок \(u\) таких, что путь из \(u\) в корень проходит через \(v\). Обратите внимание, сама вершина \(v\) тоже входит в поддерево \(v\). Листом называется такая развилка, поддерево которой содержит только одну развилку. Скоро Новый год, поэтому Аркадий решил украсить яблоню. Он повесит по лампочке некоторого цвета на каждый лист и затем посчитает число счастливых развилок. Счастливой развилкой называется такая развилка \(t\), что все лампочки в поддереве \(t\) имеют различные цвета. Аркадий заинтересован в следующем вопросе: для каждого \(k\) от \(1\) до \(n\), какое минимальное число различных цветов лампочек необходимо, чтобы число счастливых развилок было не меньше \(k\)? Выходные данные Выведите \(n\) целых чисел. \(i\)-е из них должно быть равно минимальному количеству цветов, необходимых для того, чтобы число счастливых развилок было не меньше \(i\). Примечание В первом примере для \(k = 1\) и \(k = 2\) можно все лампочки сделать одного цвета: счастливыми будут развилки \(2\) и \(3\). Для \(k = 3\) нужно повесить лампочки разных цветов, тогда все развилки будут счастливыми. Во втором примере для \(k = 4\) можно, например, повесить лампочки цвета \(1\) в развилки \(2\) и \(4\), а лампочку цвета \(2\) в развилку \(5\). Тогда счастливыми будут развилки \(2\), \(3\), \(4\) и \(5\). | |
![]()
|
|
A. Cеть компании Bmail
*особая задача
Деревья
поиск в глубину и подобное
*900
Когда-то давно в небезызвестной компании Bmail был только один маршрутизатор. Шли года и с течением времени закупались новые маршрутизаторы. Каждый раз при покупке нового маршрутизатора он соединялся с одним из купленных до него. Вам заданы значения \(p_i\) — номер маршрутизатора к которому был подключен \(i\)-й после покупки (\(p_i < i\)). Сейчас в Bmail всего \(n\) маршрутизаторов. Выведите последовательность маршрутизаторов на пути от первого до \(n\)-го. Выходные данные Выведите путь от \(1\)-го до \(n\)-го маршрутизатора. Пусть должен начинаться с числа \(1\) и заканчиваться числом \(n\). Все номера в пути должны быть различны. | |
![]()
|
|
E. Разбейте дерево
Бинарный поиск
Деревья
дп
жадные алгоритмы
Структуры данных
*2400
Вам дано корневое дерево на \(n\) вершинах, его корень имеет номер \(1\). В \(i\)-й вершине записано число \(w_i\). Разбейте его на минимальное число таких вертикальных путей, что сумма чисел \(w_i\) в вершинах пути не превосходит \(S\), а количество вершин в пути не превосходит \(L\). Каждая вершина должна принадлежать ровно одному пути. Вертикальным путём называется последовательность вершин \(v_1, v_2, \ldots, v_k\), где \(v_i\) (\(i \ge 2\)) — непосредственный предок \(v_{i - 1}\) в дереве. Выходные данные Выведите одно целое число — минимальное число вертикальных путей. Если разбить дерево невозможно, выведите \(-1\). Примечание В первом примере дерево разбивается на пути \(\{1\},\ \{2\},\ \{3\}\). Во втором примере дерево разбивается на пути \(\{1,\ 2\},\ \{3\}\) или \(\{1,\ 3\},\ \{2\}\). В третьем примере разбить дерево невозможно. | |
![]()
|
|
E. Сергей и метро
Деревья
дп
поиск в глубину и подобное
*2000
Мэр уездного города N Сергей Семёнович днями и ночами думает об улучшении жизни Nчан. К сожалению, все мыслимые и немыслимые идеи по модернизации городского пространства уже были приведены в исполнение и больше мэру нечем занимать свой ум днём (ночью он теперь спит). Однако, его помощники быстро нашли выход из положения, они рисуют на бумаге новый город и предлагают мэру составлять проекты его улучшения. Вот и сейчас перед мэром лежит карта нового города, метрополитен которого состоит из \(n\) станций, некоторые из которых соединены перегонами. Поскольку помощники готовили карту в спешке и не успели проявить должную фантазию, то схема метрополитена представляет собой дерево. Это значит, что между любыми двумя станциями существует ровно один простой путь, то есть путь, не использующий никакой перегон более одного раза. Как показатель качества схемы метро, Сергей Семёнович использует сумму попарных расстояний между всеми парами станций. Расстоянием между двумя станциями называется минимально возможное количество перегонов на пути между ними. Сергей Семёнович решил добавить в схему новые перегоны. А именно, он дорисовал перегон между станциями \(u\) и \(v\), если эти станции не были соединены перегоном напрямую, но у них была общая станция-сосед, то есть существовала такая станция \(w\), что в оригинальной схеме присутствовал перегон между \(u\) и \(w\) и перегон между \(w\) и \(v\). Вам поставлена задача вычислить сумму попарных расстояний между всеми парами станций в получившейся схеме метрополитена. Выходные данные Выведите одно целое число, равное сумме расстояний между всеми парами станций после того как Сергей Семёнович дорисует новые перегоны между всеми станциями, у которых есть общая станция-сосед. Примечание В первом примере в новой схеме от каждой станции до каждой существует прямой перегон, поэтому сумма расстояний \(6\). Во втором примере перегоны существуют между всеми парами станций, кроме пары \((1, 4)\), расстояние для которой равно \(2\). | |
![]()
|
|
E. Компания
Бинарный поиск
Деревья
жадные алгоритмы
поиск в глубину и подобное
Структуры данных
*2300
У компании \(X\) есть \(n\) сотрудников, пронумерованных от \(1\) до \(n\). У каждого сотрудника \(u\) есть его прямой начальник \(p_u\) (\(1 \le p_u \le n\)), кроме сотрудника \(1\), у которого начальника нет. Гарантируется, что значения \(p_i\) образуют дерево. Сотрудник \(u\) называется ответственным за сотрудника \(v\), если \(u\) является прямым начальником \(v\) или есть такой сотрудник \(w\), что \(w\) ответственен за \(v\), и \(u\) является прямым начальником \(w\). Любой сотрудник также считается ответственным за самого себя. Также, для каждого сотрудника \(u\) мы определим его уровень \(lv(u)\) следующим образом: - \(lv(1)=0\)
- \(lv(u)=lv(p_u)+1\) если \(u \neq 1\)
У компании есть \(q\) возможных планов на ближайшее будущее. При чём \(i\)-й из них задаётся двумя числа \(l_i\) и \(r_i\), означающими что в этом плане принимают участие все сотрудники в отрезке \([l_i, r_i]\) и только они. Чтобы всё прошло гладко, у плана должен быть проектный менеджер, который является ответственным за всех сотрудников в этом плане. Более формально, если сотрудник \(u\) выбирается как проектный менеджер \(i\)-го плана, то для каждого сотрудника \(v \in [l_i, r_i]\), \(u\) должен быть ответственен за \(v\). Заметим, что при этом не обязательно \(u\) сам должен находится в отрезке \([l_i, r_i]\). Также, \(u\) всегда выбирается таким образом, что \(lv(u)\) является максимально возможным (чем больше уровень, тем меньше компания может платить сотруднику). До того как любой план начнёт выполняться, компания позволила JATC заглянуть в свои планы. С первого взгляда он заметил, что для каждого плана можно уменьшить количество вовлечённых в него сотрудников ровно на один без каких-либо проблем. Будучи жадной, компания спрашивает у JATC: какого же именно сотрудника надо выкинуть из плана, чтобы уровень менеджера проекта был максимально возможным? JATC уже выяснил ответ и теперь предлагает это сделать и вам. Выходные данные Выведите \(q\) строк по два целых числа в каждой — номер сотрудника, которого стоит выкинуть из соответствующего плана, и максимальный уровень менеджера проекта, который в таком случае получится. Если существует несколько способов выбрать сотрудника, которого стоит выкинуть, выведите любого из них. Примечание В примере:  В первом запросе мы можем выбрать \(4\), \(5\) или \(6\) и менеджером проекта в таком случае будет \(3\). Во втором запросе, если мы выберем любого сотрудника кроме сотрудника \(8\), то менеджером проекта будет сотрудник \(1\), если же мы выберем сотрудника \(8\), то проектным менеджером будет \(3\). Так как \(lv(3)=1 > lv(1)=0\), то оптимальным ответом будет выбрать сотрудника \(8\). В третьем запросе, как бы мы ни выбирали сотрудника, проектным менеджером всегда окажется сотрудник \(1\). В четвёртом запросе, если мы выберем \(9\) или \(10\), то менеджером проекта будет \(3\), если же мы выберем \(11\), то проектным менеджером окажется \(7\). Так как \(lv(7)=3>lv(3)=1\), то оптимальным ответом будет выбрать сотрудника \(11\). | |
![]()
|
|
F. Вверх и вниз по дереву
Деревья
дп
поиск в глубину и подобное
*2500
Вам задано дерево из \(n\) вершин с корнем в вершине \(1\). Также на данном дереве расположена фишка. Первоначально фишка находится в корне дерева. Вы можете двигать фишку по ребрам дерева следующим образом: пусть текущая вершина с фишкой \(v\), тогда у вас есть два возможных хода: - спуститься к любому листу поддерева вершины \(v\);
- если вершина \(v\) — лист, то подняться вверх по дереву не более чем \(k\) раз. Другими словами, если \(h(v)\) — глубина вершины \(v\) (глубина корня равна \(0\)), то вы можете передвинуть фишку в вершину \(to\) такую, что \(to\) — некоторый предок \(v\) и \(h(v) - k \le h(to)\).
В данной задаче считается, что корень не является листом (даже если его степень равна \(1\)). Посчитайте максимальное количество различных листов, которые вы сможете посетить одной последовательностью ходов. Выходные данные Выведите единственное целое число — максимально возможное количество различных листов, которые вы сможете посетить одной последовательностью ходов. Примечание Граф из первого примера изображен ниже:  Один из возможных оптимальных обходов: \(1 \rightarrow 2 \rightarrow 1 \rightarrow 5 \rightarrow 3 \rightarrow 7 \rightarrow 4 \rightarrow 6\). Граф из второго примера:  Один из возможных оптимальных обходов: \(1 \rightarrow 7 \rightarrow 5 \rightarrow 8\). Заметим, что невозможно добраться из вершины \(6\) в \(7\) или \(8\) и наоборот. | |
![]()
|
|
E. Ранг случайного леса
Деревья
дп
математика
Паросочетания
*2800
Определим ранг неориентированного графа как ранг его матрицы смежности в \(\mathbb{R}^{n \times n}\). Дано дерево. Каждое из рёбер дерева исчезает с вероятностью \(1/2\) независимо от остальных. Пусть \(E\) — математическое ожидание ранга полученного леса. Найдите остаток от деления \(E \cdot 2^{n-1}\) на \(998244353\) (несложно показать, что \(E \cdot 2^{n-1}\) — целое число). Выходные данные Выведите одно число — ответ на задачу. | |
![]()
|
|
F. Выбери два пути
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
*2500
Задано неориентированное невзвешенное дерево, состоящее из \(n\) вершин. Неориентированное дерево — это связный неориентированный граф с \(n - 1\) ребром. Ваша задача — выбрать две пары вершин этого дерева (все выбранные вершины должны быть различны) \((x_1, y_1)\) и \((x_2, y_2)\) таким образом, что \(x_1\) и \(y_1\) не должны принадлежать простому пути от \(x_2\) до \(y_2\) и наоборот (\(x_2\) и \(y_2\) не должны принадлежать простому пути от \(x_1\) до \(y_1\)). Гарантируется, что для заданного дерева всегда возможно выбрать такие пары. Среди всех возможных способов выбрать эти пары вам необходимо выбрать способ с максимальным количеством общих вершин между путями от \(x_1\) до \(y_1\) и от \(x_2\) до \(y_2\). И среди всех таких пар вам необходимо выбрать пару с максимальной суммарной длиной этих двух путей. Гарантируется, что для заданного дерева существует ответ, содержащий хотя бы две общие вершины между путями. Длина пути — это количество ребер в нем. Простой путь — это путь, посещающий каждую вершину не более одного раза. Выходные данные Выведите любые две пары вершин, удовлетворяющие ограничениям, описанным в условии задачи. Гарантируется, что для заданного дерева всегда возможно выбрать такие пары. Примечание Картинка, соответствующая первому тестовому примеру:  Пересечение путей равно \(2\) (вершины \(1\) и \(4\)), а суммарная длина равна \(4 + 3 = 7\). Картинка, соответствующая второму тестовому примеру:  Пересечение путей равно \(2\) (вершины \(3\) и \(4\)), а суммарная длина равна \(5 + 3 = 8\). Картинка, соответствующая третьему тестовому примеру:  Пересечение путей равно \(3\) (вершины \(2\), \(7\) и \(8\)), а суммарная длина равна \(5 + 5 = 10\). Картинка, соответствующая четвертому тестовому примеру:  Пересечение путей равно \(5\) (вершины \(1\), \(2\), \(3\), \(4\) и \(5\)), а суммарная длина равна \(6 + 6 = 12\). | |
![]()
|
|
E. Вася и дерево
Деревья
Структуры данных
*1900
У Васи есть дерево из \(n\) вершин с корнем в вершине \(1\). Изначально в каждой вершине записано число \(0\). Определим \(d(i, j)\) как расстояние между вершинами \(i\) и \(j\) в дереве, то есть количество ребер на кратчайшем пути из \(i\) в \(j\). Также определим поддерево глубины \(k\) вершины \(x\) — набор вершин \(y\), таких, что выполняются следующие условия: - \(x\) является предком \(y\) (каждая вершина считается своим предком);
- \(d(x, y) \le k\).
Васе нужно обработать \(m\) запросов к дереву. \(i\)-й запрос представляется тремя числами \(v_i\), \(d_i\) и \(x_i\), и означает, что Васе нужно прибавить значение \(x_i\) ко всем вершинам поддерева вершины \(v_i\) на глубине \(d_i\). Сообщите Васе значение, записанное в каждой вершине после обработки всех запросов. Выходные данные В единственной строке выведите \(n\) чисел. \(i\)-е число должно равняться значению, записанному в \(i\)-й вершине после обработки всех запросов. Примечание В первом тестовом примере изначально значения в вершинах равны \(0, 0, 0, 0, 0\). После первого запроса значения будут равны \(1, 1, 1, 0, 0\). После второго запроса значения будут равны \(1, 11, 1, 0, 0\). После третьего запроса значения будут равны \(1, 11, 1, 100, 0\). | |
![]()
|
|
F. Быстрый набор
Деревья
дп
Строки
*2800
У Поликарпа в записной книжке \(n\) телефонов, про каждый он знает сам номер \(s_i\) и \(m_i\) — сколько раз в день он его набирает. Недавно Поликарп приобрел совершенно новый телефон с инновационной опцией быстрого набора! Более точно, \(k\) его клавишам можно назначить некоторый номер (не обязательно из телефонной книги). Для ввода номера Поликарп может нажать одну из этих \(k\) клавиш, а потом завершить набор номера нажатиями на обычные цифровые клавиши (ввод номера только цифровыми клавишами также возможен). Клавиша быстрого набора может быть нажата только когда ни одной цифры еще не набрано. Нельзя переназначать номера на клавиши быстрого набора. Сколько минимально нажатий цифровых клавиш ему придётся делать в сутки, если он назначит на клавиши быстрого набора номера оптимальным способом? Выходные данные Выведите единственное число — сколько минимально нажатий цифровых клавиш Поликарпу придётся делать в сутки, если он назначит на клавиши быстрого набора номера оптимальным способом. Примечание На единственной клавише цифрового набора в первом примере должно быть записано «0001». Тогда суммарное количество нажатий цифровых клавиш будет равно \(0 \cdot 5\) для первого номера + \(3 \cdot 4\) для второго + \(2 \cdot 1\) для третьего. \(14\) в сумме. На единственной клавише цифрового набора во втором примере должно быть записано «00». Тогда суммарное количество нажатий цифровых клавиш будет равно \(2 \cdot 5\) для первого номера + \(1 \cdot 6\) для второго + \(2 \cdot 1\) для третьего. \(18\) в сумме. | |
![]()
|
|
A. Орехус и оптимальный путь
Деревья
дп
Структуры данных
*1800
Орехус отправляется путешествовать в Древесную страну, в которой \(n\) городов. Кроме того, что большая часть её территории покрыта лесами, местная система дорог также представляет собой дерево (связный ациклический граф). Орехус хочет арендовать автомобиль в городе \(u\) и поехать по простому пути до города \(v\). Он ещё не определил свой путь, и сейчас самое время это сделать. Обратите внимание, что выбранный путь может состоять из одной вершины. В \(i\)-м городе стоит бензоколонка, в которой по странным законам Древесной страны можно купить не более \(w_i\) литров бензина. Можно считать, что у Орехуса бесконечное количество денег. У каждой дороги есть длина, и как только Орехус проезжает по ней, количество бензина уменьшается на длину дороги. Конечно, Орехус не сможет поехать по пути, на одной из дорог которого ему не хватит бензина. Он может купить в бензин в любом городе, в котором он был, в том числе в первом и последнем. Кроме того, он хочет найти максимальное количество бензина, которое у него может остаться в конце пути. Помогите ему: посчитайте это количество. Выходные данные Выведите одно число — максимальное количество бензина, которое может остаться у Орехуса в конце пути. Примечание Оптимальный путь в первом примере \(2 \to 1 \to 3\).  Оптимальный путь во втором примере \(2 \to 4\).  | |
![]()
|
|
C. Максимальный Mex
Деревья
Структуры данных
*2900
Однажды Гриша нашёл дерево (связный ациклический граф) с корнем в вершине \(1\). Но дерево было не простое — в вершинах этого дерева записана перестановка \(p\) чисел от \(0\) до \(n - 1\), в \(i\)-й вершине записано число \(p_i\). Так как Гриша любит придумывать себе странные и интересные задачи, но не всегда с ними справляется, вам нужно помочь ему обработать два типа запросов на этом дереве. Определим функцию \(MEX(S)\), где \(S\) является множеством целых неотрицательных чисел, как наименьшее целое неотрицательное число, не входящее в множество. Пусть \(l\) — простой путь в дереве. Тогда обозначим за \(u_1\), \(u_2\), \(\ldots\), \(u_k\) — номера вершин, принадлежащих \(l\). Обозначим за \(V(l)\) множество {\(p_{u_1}\), \(p_{u_2}\), \(\ldots\) , \(p_{u_k}\)}. Тогда запросы таковы: - Для двух вершин \(i\) и \(j\) нужно поменять местами значения \(p_i\) и \(p_j\).
- Требуется найти максимальный \(MEX(V(l))\) по все возможным \(l\).
Выходные данные Для каждого запроса второго типа выведите единственное число — ответ на запрос. Примечание Число в скобках обозначает значение перестановки для вершины.  В первом примере для первого запроса оптимальный путь — из вершины \(1\) в вершину \(5\). Для него множество значений \(\{0, 1, 2\}\), а \(MEX\) соответсвенно — \(3\).  Для третьего запроса оптимальный путь — из вершины \(5\) в вершину \(6\). Для него множество значений \(\{0, 1, 4\}\), а \(MEX\) соответсвенно — \(2\).  Во втором примере для первого запроса оптимальный путь — из вершины \(2\) в вершину \(6\). Для него множество значений \(\{0, 1, 2, 5\}\), а \(MEX\) соответсвенно — \(3\).  Для третьего запроса оптимальный путь — из вершины \(5\) в вершину \(6\). Для него множество значений \(\{0, 1, 3\}\), а \(MEX\) соответсвенно — \(2\).  Для пятого запроса оптимальный путь — из вершины \(5\) в вершину \(2\). Для него множество значений \(\{0, 1, 2, 3\}\), а \(MEX\) соответсвенно — \(4\).  Для седьмого запроса оптимальный путь — из вершины \(5\) в вершину \(4\). Для него множество значений \(\{0, 1, 2, 3\}\), а \(MEX\) соответсвенно — \(4\).  Для девятого запроса оптимальный путь — из вершины \(6\) в вершину \(5\). Для него множество значений \(\{0, 1, 3\}\), а \(MEX\) соответсвенно — \(2\). | |
![]()
|
|
D. Дерево минимального диаметра
Деревья
Конструктив
реализация
*1700
Вам дано дерево (неориентированный связный граф без циклов) и целое число \(s\). Ваня хочет как-то поставить веса на всех ребрах дерева, так что все веса неотрицательные вещественные числа, которые в сумме дают \(s\). При этом он хочет, чтобы диаметр получившегося после расстановки весов дерева был как можно меньше. Диаметром будем называть максимальную сумму весов ребер, лежащих на пути между какими-то двумя вершинами дерева. Найдите минимальный возможный диаметр, который мог у него получиться. Выходные данные Выведите минимальный диаметр дерева, который мог получиться при какой-то расстановке неотрицательных весов на ребра этого дерева, которые в сумме дают \(s\). Ваш ответ будет считаться правильным, если его абсолютная или относительная ошибка не будет превосходить \(10^{-6}\). А именно: пусть ваш ответ равен \(a\), а ответ жюри \(b\). Ваш ответ будет засчитан, если \(\frac {|a-b|} {max(1, b)} \leq 10^{-6}\). Примечание В первом примере необходимо расставить веса так:  Легко видеть, что диаметр такого дерева будет равен \(2\). Можно доказать, что это минимально возможный диаметр, который можно получить, как-то расставив веса. Вo втором примере необходимо расставить веса так:  | |
![]()
|
|
E. Ехаб и задача о выборе компонент
Деревья
дп
жадные алгоритмы
математика
*2400
Вам дано дерево, состоящее из \(n\) вершин. Каждая вершина \(u\) имеет некоторый вес \(a_u\). Вы хотите выбрать целое число \(k\) \((1 \le k \le n)\), а затем выбрать \(k\) связных компонент, которые не пересекаются друг с другом (каждая вершина находится максимум в одной компоненте). Пусть вы выбрали компоненты, в совокупности содержащие множество вершин \(s\). Вы хотите максимизировать следующее значение: \(\)\frac{\sum\limits_{u \in s} a_u}{k}\(\) Другими словами, вы хотите максимизировать сумму весов вершин из \(s\), деленную на количество выбранных вами компонент. Также, если возможных решений несколько, вы хотите максимизировать \(k\). Заметьте, что соседние вершины могут находиться в разных компонентах. Для лучшего понимания обратитесь к третьему тесту. Выходные данные Выведите ответ как несокращенную дробь, выраженную двумя целыми числами (первое из них является числителем дроби, второе - знаменателем). Дробь должна быть максимально возможной, а при равенстве необходимо максимизировать знаменатель. Для лучшего понимания обратитесь к примерам из условия. Примечание Связная компонента - это множество вершин, что для любой пары вершин из множества существует путь между этими вершинами только по вершинам множества. В первом примере оптимально выбрать все дерево. Во втором примере есть только один вариант выбора (выбрать компоненту, содержащую единственную вершину 1) потому что нельзя выбирать 0 компонент. В третьем примере следует заметить, что можно было выбрать, например, только вершину 1 или вершины 1 и 3, или все дерево, и результирующая дробь во всех этих случая имела бы значение -1, но необходимо максимизировать \(k\). В четвертом примере оптимально выбрать вершины 1 и 3. | |
![]()
|
|
F. Ехаб и странная формула веса
Деревья
Структуры данных
*2800
Дано дерево, состоящее из \(n\) вершин. У каждой вершины \(u\) есть вес \(a_u\). Гарантируется, что в дереве есть только одна вершина с минимальным весом. У каждой вершины \(u\) (кроме вершины с минимальным \(a_u\)), есть сосед \(v\), такой, что \(a_v<a_u\). Вам необходимо составить дерево с минимальным весом \(w\), который считается следующим образом: - Для каждой вершины \(u\), \(deg_u \cdot a_u\) прибавляется к \(w\) (\(deg_u\) обозначает степень вершины \(u\)).
- Для каждого ребра \(\{ u,v \}\), \(\lceil log_2(dist(u,v)) \rceil \cdot min(a_u,a_v)\) прибавляется к \(w\), где \(dist(u,v)\) обозначает количество ребер на пути из \(u\) в \(v\) в данном дереве.
Выходные данные Выведите одно целое число: минимальное возможное значение \(w\). Примечание В первом примере данное дерево исходно имеет минимальное значение \(w\). Во втором примере оптимальное дерево имеет следующий вид: 
| |
![]()
|
|
C. Счастливое дерево
Деревья
дп
снм
*1900
Петя любит счастливые числа. Всем известно, что счастливыми являются положительные целые числа, в десятичной записи которых содержатся только счастливые цифры 4 и 7. Например, числа 47, 744, 4 являются счастливыми, а 5, 17, 467 — не являются. Однажды Пете встретилось дерево из n вершин. При этом дерево было взвешенным, то есть каждое его ребро имело вес (целое положительное число). Ребро счастливое, если его вес — счастливое число. Напомним, что дерево из n вершин — это неориентированный связный граф, у которого ровно n - 1 ребер. Пете стало интересно, сколько существует таких троек вершин дерева (i, j, k), что и на пути из i в j, и на пути из i в k есть хотя бы одно счастливое ребро (все три вершины попарно различны). Порядок чисел в тройке имеет значение, то есть тройка (1, 2, 3) не равна тройке (2, 1, 3) и не равна тройке (1, 3, 2). Найдите количество таких троек. Выходные данные В единственной строке выведите одно число — ответ на задачу. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-битных чисел на С++. Рекомендуется использовать потоки cin, cout или спецификатор %I64d. Примечание 16 троек из первого примера: (1, 2, 4), (1, 4, 2), (2, 1, 3), (2, 1, 4), (2, 3, 1), (2, 3, 4), (2, 4, 1), (2, 4, 3), (3, 2, 4), (3, 4, 2), (4, 1, 2), (4, 1, 3), (4, 2, 1), (4, 2, 3), (4, 3, 1), (4, 3, 2). Во втором примере подходит любая тройка вершин. Всего троек: 4·3·2 = 24. | |
![]()
|
|
E. Лес минимального диаметра
Деревья
жадные алгоритмы
Конструктив
поиск в глубину и подобное
*2000
Задан лес — неориентированный граф из \(n\) вершин такой, что каждая его компонента связности является деревом. Диаметр (также «длиннейший кратчайший путь») связного неориентированного графа — это максимальное число ребер на кратчайшем пути между всеми парами вершин. Ваша задача — добавить несколько ребер (возможно ноль) в граф так, чтобы он стал деревом, а диаметр этого дерева был минимально возможным. Если существует несколько правильных ответов, то выведите любой. Выходные данные В первой строке выведите диаметр полученного дерева. В каждой из следующих \((n - 1) - m\) строк выведите по два целых числа \(v\) и \(u\) (\(1 \le v, u \le n\), \(v \ne u\)) — описания добавленных ребер. Полученный граф должен быть деревом, а его диаметр должен был минимально возможным. Eсли \(m = n - 1\), то, очевидно, ребра не будут добавлены и весь вывод состоит из одного числа — диаметра заданного дерева. Если существует несколько правильных ответов, то выведите любой. Примечание В первом примере добавление ребер (1, 4) или (3, 4) приведет к диаметру 3. Добавление ребра (2, 4), однако, сделает диаметр равным 2. Ребро (1, 2) — это единственный вариант добавляемого ребра для второго примера. Диаметр равен 1. В третьем примере нельзя добавить никаких ребер. Диаметр уже 2. | |
![]()
|
|
F. Дерево максимальной стоимости
Деревья
дп
поиск в глубину и подобное
*1900
Задано дерево, состоящее ровно из \(n\) вершин. Дерево — это связный неориентированный граф с \(n-1\) ребром. Каждой вершине \(v\) этого дерева соответствует некоторое значение \(a_v\). Пусть \(dist(x, y)\) — расстояние между вершинами \(x\) и \(y\). Расстояние между вершинами — это количество ребер на простом пути между ними. Определим стоимость дерева как следующую величину: сначала давайте зафиксируем одну вершину дерева. Пусть она равна \(v\). Тогда стоимость дерева равна \(\sum\limits_{i = 1}^{n} dist(i, v) \cdot a_i\). Ваша задача — найти максимально возможную стоимость дерева, если вы можете выбирать \(v\) самостоятельно. Выходные данные Выведите одно целое число — максимально возможную стоимость дерева, если вы можете выбрать любую вершину в качестве вершины \(v\). Примечание Картинка, соответствующая первому тестовому примеру:  Вы можете выбрать вершину \(3\) как корень, тогда ответ будет равен \(2 \cdot 9 + 1 \cdot 4 + 0 \cdot 1 + 3 \cdot 7 + 3 \cdot 10 + 4 \cdot 1 + 4 \cdot 6 + 4 \cdot 5 = 18 + 4 + 0 + 21 + 30 + 4 + 24 + 20 = 121\). Во втором тестовом примере дерево состоит только из одной вершины, поэтому ответ всегда равен \(0\). | |
![]()
|
|
G. Владислав и великая легенда
Деревья
дп
Комбинаторика
*3000
Однажды здесь была великая легенда, но один тролль взломал Codeforces и удалил его. Очень плохо для наc, но в сообществе троллей он заработал уважение и титул овер-супер-мега тролля. Пожалуй для них это что-то хорошее. А для нас, наверное, ещё лучше будет формальное условие. Вам дано дерево \(T\), содержащее \(n\) вершин, пронумерованных от \(1\) до \(n\). Для каждого непустого \(X\), являющемся подмножеством вершин \(T\), определим \(f(X)\) как количество рёбер в минимальном по размеру поддереве \(T\), содержащем все вершины из \(X\). Вам также дано целое число \(k\). Вам нужно вычислить сумму \((f(X))^k\) по всем непустым подмножествам вершин, то есть: \(\) \sum\limits_{X \subseteq \{1, 2,\: \dots \:, n\},\, X \neq \varnothing} (f(X))^k. \(\) Так как эта величина может быть очень большой, выведите её по модулю \(10^9 + 7\). Выходные данные Выведите одно целое число — требуемую сумму по модулю \(10^9 + 7\). Примечание В первых двух примерах значения \(f\) выглядят следующим образом: \(f(\{1\}) = 0\) \(f(\{2\}) = 0\) \(f(\{1, 2\}) = 1\) \(f(\{3\}) = 0\) \(f(\{1, 3\}) = 2\) \(f(\{2, 3\}) = 1\) \(f(\{1, 2, 3\}) = 2\) \(f(\{4\}) = 0\) \(f(\{1, 4\}) = 2\) \(f(\{2, 4\}) = 1\) \(f(\{1, 2, 4\}) = 2\) \(f(\{3, 4\}) = 2\) \(f(\{1, 3, 4\}) = 3\) \(f(\{2, 3, 4\}) = 2\) \(f(\{1, 2, 3, 4\}) = 3\) | |
![]()
|
|
A. Сумма в дереве
Деревья
жадные алгоритмы
Конструктив
поиск в глубину и подобное
*1600
У Мити есть корневое дерево из \(n\) вершин, пронумерованных от \(1\) до \(n\), причем корень дерева имеет номер \(1\). В каждой его вершине \(v\) было записано целое число \(a_v \ge 0\). Для каждой вершины \(v\) Митя вычислил величину \(s_v\): сумму чисел, записанных на пути от вершины \(v\) до корня, а также \(h_v\) — глубину вершины \(v\), то есть количество вершин на пути от вершины \(v\) до корня (таким образом, \(s_1=a_1\), \(h_1=1\)). После этого Митя уничтожил исходные значения \(a_v\). К сожалению, он также случайно уничтожил все значения \(s_v\) для вершин, находящихся на четной глубине (то есть тех, для которых \(h_v\) является четным). Ваша задача состоит в том, чтобы восстановить значения \(a_v\) для каждой из вершин либо определить, что это невозможно. Среди возможных вариантов нужно выбрать тот, при котором сумма значений \(a_v\) во всем дереве является минимально возможной. Выходные данные Выведите единственное число — минимально возможную сумму чисел \(a_v\) в вершинах исходного дерева или \(-1\), если такого дерева не существует. | |
![]()
|
|
C. Построй дерево
Бинарный поиск
графы
Деревья
жадные алгоритмы
Конструктив
поиск в глубину и подобное
*2400
Погуляв по заснеженному лесу, Миша очень полюбил деревья и решил нарисовать своё! Это дерево состоит из \(n\) вершин, пронумерованных различными целыми числами от \(1\) до \(n\). В этом дереве вершина \(1\) является корнем, а у любой другой вершины \(i\) есть непосредственный предок \(p_{i}\) (при этом \(i\) — непосредственный потомок \(p_{i}\)). Вершина \(u\) лежит в поддереве вершины \(v\), если переходя по непосредственным предкам из вершины \(u\) (\(u\), \(p_{u}\), \(p_{p_{u}}\), ...), можно попасть в вершину \(v\). В частности, любая вершина \(v\) лежит в поддереве самой себя. Число вершин в поддереве вершины \(v\) называется размером поддерева. Миша рассматривает только те деревья, в которых все вершины лежат в поддереве вершины \(1\). На рисунке ниже изображено дерево из \(6\) вершин. Поддерево вершины \(2\) состоит из вершин \(2\), \(3\), \(4\), \(5\). Таким образом, размер поддерева этой вершины равен \(4\).  Назовём разветвлённостью дерева максимальное количество непосредственных потомков какой-то из его вершин. Так, разветвлённость дерева на рисунке выше равна 2. Помогите Мише построить дерево из \(n\) вершин, в котором сумма размеров всех поддеревьев равна в точности \(s\), а разветвлённость — минимально возможная. Выходные данные Если требуемого дерева не существует, выведите «No». Иначе в первой строке выходных данных выведите «Yes», а в следующей строке выведите числа \(p_2\), \(p_3\), ..., \(p_n\), где вершина с номером \(p_i\) является непосредственным предком вершины с номером \(i\). Примечание Для первого примера одним из оптимальных деревьев изображено ниже. Сумма размеров поддеревьев в этом дереве равна \(3 + 1 + 1 = 5\), а разветвлённость равна \(2\).  Для третьего примера одним из оптимальных деревьев изображено ниже. В этом дереве сумма размеров поддеревьев равна \(6 + 3 + 2 + 1 + 2 + 1 = 15\), а разветвлённость равна \(2\).  | |
![]()
|
|
F. Печеньки
Бинарный поиск
Деревья
дп
игры
поиск в глубину и подобное
Структуры данных
*2400
Митя и Вася играют в интересную игру. У них есть подвешенное дерево из \(n\) вершин, пронумерованных числами от \(1\) до \(n\). В этом дереве вершина \(1\) является корнем, а родителем вершины \(i \ge 2\) является вершина \(p_i\) (при этом будем говорить, что вершина \(i\) — ребенок вершины \(p_i\)). В каждой вершине дерева находятся печеньки, в вершине \(i\) находится \(x_i\) печенек. Чтобы съесть одну печеньку в вершине \(i\), нужно потратить \(t_i\) единиц времени. Также в игре есть одна фишка. Изначально она находится в корне дерева. Чтобы переместить фишку по ребру, соединяющему вершину \(i\) с ее родителем, нужно потратить \(l_i\) единиц времени. Митя и Вася ходят по очереди, Митя начинает. На своем ходу Митя перемещает фишку из вершины, где она находится, в одного из ее детей. Вася на своем ходу может удалить какое-то ребро, ведущее из вершины, в которой стоит фишка, в одного из ее детей, или не удалять ничего.  На любом своем ходу Митя может закончить игру. После этого он двигает фишку вверх до корня, по пути съедая какие-то печеньки. Митя может потратить суммарно на спуск, подъем и поедание печенек не более \(T\) единиц времени. Обратите внимание, что в конце игры фишка всегда оказывается в корне: Митя не может оставить фишку ни в какой промежуточной вершине, даже если требуемое число печенек уже было съедено — он обязан переместить фишку в корень (и на каждое перемещение фишки по ребру из вершины \(v\) в ее предка он тратит \(l_v\) единиц времени). Какое максимальное количество печенек Митя может съесть, независимо от действий Васи? Выходные данные Выведите одно целое число — максимальное число печенек, которое может съесть Митя. Примечание В первом примере Митя может первым ходом переместить фишку в вершину \(2\). В этом случае, как бы после этого не играл Вася, Митя сможет съесть не менее \(11\) печенек. Ниже приведен пример того, как могла происходить игра: - Митя перемещает фишку в вершину \(2\).
- Вася отрезает ребро, ведущее в вершину \(4\).
- Митя перемещает фишку в вершину \(5\).
- Так как у вершины \(5\) нет детей, Вася не отрезает ничего.
- Митя заканчивает игру и поднимается наверх, по пути собирая печеньки (\(7\) в вершине \(5\), \(3\) в вершине \(2\), \(1\) в вершине \(1\)).
Митя тратит \(1+0\) времени на движение вниз, \(0+1\) на движение вверх, \(7\cdot 2\) чтобы съесть \(7\) печенек в вершине 5, \(3\cdot 3\) чтобы съесть \(3\) печеньки в вершине 2, \(1\cdot 1\) чтобы съесть \(1\) печеньку в вершине 1. Суммарное время равно \(1+0+0+1+7\cdot 2+3\cdot 3+1\cdot 1=26\). | |
![]()
|
|
D. Подсчёт GCD
Деревья
дп
поиск в глубину и подобное
Структуры данных
теория чисел
*2000
Дано дерево из \(n\) вершин. На каждой вершине дерева записано число; на \(i\)-й вершине записано число \(a_i\). Определим функцию \(g(x, y)\) как наибольший общий делитель всех чисел, записанных на вершинах на простом пути от вершины \(x\) до вершины \(y\) (включая эти две вершины). Также определим \(dist(x, y)\) как количество вершин на простом пути между \(x\) и \(y\), включая концы пути. \(dist(x, x) = 1\) для каждой вершины \(x\). Посчитайте максимальное значение \(dist(x, y)\) по всем таким парам вершин, что \(g(x, y) > 1\). Выходные данные Если не существует такой пары вершин \(x, y\), что \(g(x, y) > 1\), выведите \(0\). Иначе выведите максимальное значение \(dist(x, y)\) по всем таким парам. | |
![]()
|
|
D. Саша и интересный факт из теории графов
Деревья
дп
Комбинаторика
математика
Перебор
*2400
Однажды, во время пары Саше стало скучно и он решил поговорить со своими друзьями. Тут он увидел Кефу. О Кефе можно говорить бесконечно, поэтому делать мы этого не будем. Разговор ребят зашёл о графах. Кефа пообещал рассказать Саше один интересный факт из теории графов, если тот, в свою очередь, поможет Кефе посчитать количество красивых деревьев. В данной задаче деревом называется взвешенный связный граф, состоящий из \(n\) вершин и \(n-1\)-го ребра, такой, что веса всех рёбер — целые числа от \(1\) до \(m\). Красоту дерева Кефа оценивает следующим образом: он находит в дереве две свои любимые врешины — вершины с номерами \(a\) и \(b\), и считает расстояние между ними. Расстоянием между двумя вершинами \(x\) и \(y\) назовём сумму весов всех рёбер на простом пути из \(x\) в \(y\). Если расстояние от вершины \(a\) до вершины \(b\) равно \(m\), то дерево красивое. Саша очень любит теорию графов, а ещё больше Саша любит интересные факты, поэтому Саша согласился помочь. К счастью, Саша знаком с вами, лучшим программистом Байтландии. Помогите Саше посчитать количество красивых деревьев для Кефы. Два дерева считаются различными, если существует хотя бы одно ребро, принадлежащее одному из этих деревьев и не принадлежащее другому. Вес ребра имеет значение. Кефа предупредил Сашу, что красивых деревьев очень много, поэтому достаточно будет вычислить их количество по модулю \(10^9 + 7\). Выходные данные Выведите одно число — количество красивых деревьев по модулю \(10^9+7\). Примечание В первом примере существует \(5\) красивых деревьев: 
Во втором примере красивыми являются следующие деревья: 
| |
![]()
|
|
F. Саша и алгоритм звуков тишины
Деревья
Структуры данных
*3200
Однажды Саша решил, как обычно, прогуляться по парку. Придя в парк он обнаружил, что его любимая скамейка уже занята, и ему пришлось присесть на соседнюю. Саша сел и начал вслушиваться в тишину. Тут ему в голову пришла мысль: а что если в разных частях парка тишина звучит по-разному? Так и оказалось. Разделим парк на квадраты размера \(1 \times 1\) метр и назовем их клетками, пронумеруем строки от \(1\) до \(n\) сверху вниз, а столбцы от \(1\) до \(m\) слева направо. Теперь любую клетку можно описать парой чисел \((x, y)\), где \(x\) — номер строки, а \(y\) — номер столбца, в котором расположена эта клетка. Опытным путём Саша выяснил, что в клетке \((i, j)\) громкость тишины равна \(f_{i,j}\), а также все \(f_{i,j}\) образуют перестановку чисел от \(1\) до \(n \cdot m\). Саша решил посчитать, а сколько существует приятных отрезков тишины? Возьмем какой-то отрезок \([l \ldots r]\). Обозначим за \(S\) множество клеток \((i, j)\), что \(l \le f_{i,j} \le r\). Тогда отрезок тишины \([l \ldots r]\) является приятным, если существует только один простой путь между каждой парой клеток из \(S\) (путь не может содержать клетки, которые не содержатся в \(S\)). Другими словами, множество \(S\) должно выглядеть на плоскости как дерево. Саша справился с этим заданием очень быстро и назвал алгоритм — «алгоритмом звуков тишины». Время шло, и от алгоритма осталась только легенда. Чтобы доказать правдивость истории, вам предстоит помочь Саше и посчитать количество различных приятных отрезков тишины. Два отрезка \([l_1 \ldots r_1]\), \([l_2 \ldots r_2]\) считаются различными, если \(l_1 \neq l_2\) или \(r_1 \neq r_2\) или и то, и то одновременно. Выходные данные Выведите одно число — количество приятных отрезков тишины. Примечание В первом примере все отрезки тишины приятные. Во втором примере приятными являются следующие отрезки тишины: 
| |
![]()
|
|
F. Ближайший лист
Деревья
Структуры данных
*2600
Определим эйлеров обход дерева (связного неориентированного графа без циклов) следующим образом: рассмотрим рекурсивный алгоритм поиска в глубину, который обходит вершины дерева и нумерует вершины в том порядке, в котором их посещает, при этом учитывается только первое посещение каждой вершины. Данная функция стартует из вершины с номером \(1\), а затем рекурсивно вызывается от всех вершин, которые соединены ребром с текущей и ещё не посещены, в порядке возрастания номеров вершин. Формально данную функцию можно описать так:
next_id = 1
id = массив длины n, заполненный -1
visited = массив длины n, заполненный false
function dfs(v):
visited[v] = true
id[v] = next_id
next_id += 1
for to по соседям v в порядке возрастания:
if not visited[to]:
dfs(to)
Дано взвешенное дерево, вершины которого пронумеровали в порядке эйлерова обхода целыми числами от \(1\) до \(n\) при помощи алгоритма, описанного выше. Назовём листом вершину дерева, соединённую ребром ровно с одной другой вершиной. В данном вам дереве вершина \(1\) не является листом. Расстоянием между двумя вершинами дерева назовём сумму весов рёбер на единственном простом пути между ними. Требуется ответить на \(q\) запросов следующего вида: по заданным числам \(v\), \(l\) и \(r\) сообщить кратчайшее расстояние от вершины \(v\) до одного из листов дерева, имеющего номер от \(l\) до \(r\) (включительно). Выходные данные Выведите \(q\) чисел — ответы на запросы в порядке, в котором они заданы во входных данных. Примечание В первом примере дерево выглядит так:  В первом запросе ближайший к вершине \(1\) лист имеет номер \(4\). Расстояние до него равно \(3\). Во втором запросе ближайшим к вершине \(5\) листом является вершина с номером \(5\), расстояние до которой равно \(0\). В третьем примере ближайшим к вершине \(4\) листом является вершина с номером \(4\), однако она не попадает в отрезок вершин \([1, 2]\) запроса. Единственным листом с номером, попадающим в отрезок \([1, 2]\) является вершина с номером \(2\), расстояние до которой от вершины \(4\) равно \(13\). | |
![]()
|
|
G. Крестики-нолики на дереве
Деревья
игры
Конструктив
*3100
Игра в крестики-нолики начинается на дереве из \(n\) вершин. Некоторые вершины уже окрашены в белый цвет, а остальные пока бесцветны. Есть два игрока — белый и чёрный. Игроки ходят по очереди, белый игрок начинает игру. В свой ход игрок выбирает ещё не покрашенную вершину и красит её в свой цвет. Игрок выигрывает, если он покрасит какой-нибудь путь из трёх вершин в свой цвет. В случае, если все вершины становятся покрашенными, а никакой игрок так и не выиграл, то игра заканчивается вничью. Не могли бы вы выяснить, кто выиграет эту игру или закончится ли она в ничью, если оба игрока играют оптимально? Выходные данные Для каждого тестового случая выведите «White», «Draw» или «Black» в зависимости от того, кто выиграет (соответственно белый, ничья или черный). Примечание В первом примере вершина \(4\) уже изначально покрашена в белый. Белый игрок может выиграть покрасив своим первым ходом вершину \(1\) и покрасив оставшуюся вершину своим следующим ходом. Этот процесс изображен на картинках ниже.  Во втором примере можно показать, что ни один игрок не может гарантировать себе победу. | |
![]()
|
|
E. Дерево
графы
Деревья
дп
поиск в глубину и подобное
Структуры данных
*2500
Дано дерево из \(n\) вершин и \(q\) запросов. Каждый запрос начинается с трех целых чисел \(k\), \(m\) и \(r\), и продолжается \(k\) вершинами дерева \(a_1, a_2, \ldots, a_k\). Чтобы ответить на запрос, предположите, что дерево подвешено за вершину \(r\). Рассмотрим разбиения данных \(k\) вершин на не более чем \(m\) групп так, что выполняются следующие условия: - Каждая вершина принадлежит ровно одной группе, каждая группа содержит хотя бы одну вершину.
- Ни в одной группе нет двух вершин таких, что одна является предком (не обязательно непосредственным) другой.
Выведите количество различных таких разбиений по модулю \(10^{9}+7\) для каждого запроса. Выходные данные Выведите \(q\) строк, где \(i\)-я строка содержит ответ на \(i\)-й запрос. Примечание Рассмотрим первый пример. В первом запросе нужно разделить три данные вершины (\(7\), \(4\) и \(3\)) на не более чем три группы, считая, что корнем дерева является вершина \(2\). Когда дерево подвешено за вершину \(2\), вершина \(4\) является предком вершин \(3\) и \(7\). Поэтому нельзя все вершины отнести к одной группе. Есть только \(1\) способ разделить эти вершины на две группы: \([4]\) и \([3, 7]\). Кроме того, есть один способ разделить данные вершины на три группы: \([7]\), \([4]\) и \([3]\). Таким образом, есть всего \(2\) способа разбить данные вершины на не более чем три группы. Во втором запросе дерево подвешено за вершину \(4\), при этом \(6\) является предком \(2\), а \(2\) является предком \(1\). Поэтому нельзя все вершины отнести к одной группе. | |
![]()
|
|
F1. Разрезание дерева (легкая версия)
Деревья
поиск в глубину и подобное
*1800
Задано неориентированное дерево из \(n\) вершин. Некоторые вершины покрашены в красный цвет, некоторые — в синий, а некоторые не покрашены совсем. Гарантируется, что дерево содержит хотя бы одну красную вершину и хотя бы одну синюю вершину. Вы выбираете ребро и удаляете его из дерева. Дерево распадается на две связных компоненты. Назовем ребро хорошим, если в каждой из двух компонент не будет одновременно синей и красной вершин. Сколько хороших ребер в данном дереве? Выходные данные Выведите одно целое число — количество хороших ребер в данном дереве. Примечание Дерево из первого примера:  Единственное хорошее ребро — это ребро \((2, 4)\). После его удаления дерево распадается на компоненты \(\{4\}\) и \(\{1, 2, 3, 5\}\). В первой компоненте есть только красная вершина, а во второй — только синие и непокрашенные вершины. Дерево из второго примера:  Каждое ребро в нем хорошее. Дерево из третьего примера:  Ребро \((1, 3)\) разделяет дерево на компоненты \(\{1\}\) и \(\{3, 2\}\), во второй есть одновременно красная и синяя вершины, поэтому это ребро не хорошее. Ребро \((2, 3)\) разделяет дерево на компоненты \(\{1, 3\}\) и \(\{2\}\), в первой есть одновременно красная и синяя вершины, поэтому это ребро также не хорошее. Потому ответ равен 0. | |
![]()
|
|
F2. Разрезание дерева (сложная версия)
Деревья
дп
Комбинаторика
поиск в глубину и подобное
*2700
Задано неориентированное дерево из \(n\) вершин. Некоторые вершины покрашены в один из \(k\) цветов, а некоторые не покрашены совсем. Гарантируется, что дерево содержит хотя бы одну вершину каждого из \(k\) цветов. Может быть ноль непокрашенных вершин. Вы выбираете набор из ровно \(k - 1\) ребер и удаляете его из дерева. Дерево распадается на \(k\) связных компонент. Назовем набор хорошим, если ни в одной из полученных компонент не будет вершин различных цветов. Сколько хороших наборов ребер есть в данном дереве? Два набора считаются различными, если существует такое ребро, что оно присутствует в одном наборе и отсутствует в другом. Ответ может быть довольно большим, поэтому выведите его по модулю \(998244353\). Выходные данные Выведите одно целое число — количество хороших наборов ребер в данном дереве. Два набора считаются различными, если существует такое ребро, что оно присутствует в одном наборе и отсутствует в другом. Ответ может быть довольно большим, поэтому выведите его по модулю \(998244353\). Примечание Дерево из первого примера:  Единственный хороший набор — это ребро \((2, 4)\). После его удаления дерево распадается на компоненты \(\{4\}\) и \(\{1, 2, 3, 5\}\). В первой компоненте есть только вершина цвета \(1\), а во второй — только вершины цвета \(2\) и непокрашенные вершины. Дерево из второго примера:  Хорошие наборы: \(\{(1, 3), (4, 7)\}\), \(\{(1, 3), (7, 2)\}\), \(\{(3, 6), (4, 7)\}\) и \(\{(3, 6), (7, 2)\}\). | |
![]()
|
|
F. Нияз и маленькие степени
Деревья
дп
Структуры данных
*3400
У Нияза есть дерево из \(n\) вершин, пронумерованных от \(1\) до \(n\). Деревом называется связный граф без циклов. Каждое ребро в этом дереве имеет строго больший нуля вес, обозначаемый целым числом. Степенью вершины называется количество ребер, смежных данной вершине. Нияз не любит, когда вершины в дереве имеют слишком большие степени, поэтому он хочет найти для каждого \(x\) от \(0\) до \((n-1)\), ребра какого минимального суммарного веса нужно удалить, чтобы степени всех вершин стали не более \(x\). Выходные данные Выведите \(n\) целых чисел, разделенных пробелами: для каждого \(x = 0, 1, \ldots, (n-1)\) выведите минимальный суммарный вес такого множества ребер, при удалении которого степень всех вершин становится не больше \(x\). Примечание В первом примере в графе вершина \(1\) соединена со всеми остальными. Таким образом, для всеx \(x\) достаточно удалить \((4-x)\) ребер минимальной стоимости, исходящих из вершины \(1\), таким образом, ответы равны \(1+2+3+4\), \(1+2+3\), \(1+2\), \(1\), и \(0\). Во втором примере при \(x=0\) необходимо удалить все ребра, при \(x=1\) достаточно удалить два ребра веса \(1\) и \(5\), а при \(x \geq 2\) ребра удалять необязательно, поэтому ответы равны \(1+2+5+14\), \(1+5\), \(0\), \(0\) и \(0\). | |
![]()
|
|
E. Легендарное дерево
Бинарный поиск
Деревья
интерактив
*3100
Это интерактивная задача. Легендарное дерево покоится глубоко в лесу. Легенда гласит, что люди, которые узнают структуру этого дерева, навсегда станут легендарными гроссмейстерами. Чтобы помочь вам определить дерево, богиня Микаэла рассказала вам, что это дерево состоит из \(n\) вершин, пронумерованных от \(1\) до \(n\). Она также позволила вам спросить что-то про дерево. Чтобы задать вопрос, вы должны назвать Микаэле два непересекающихся непустых множеств вершин \(S\) и \(T\) и произвольную вершину \(v\). Затем Микаэла посчитает и скажет вам количество пар вершин \((s, t)\), где \(s \in S\) и \(t \in T\) таких, что простой путь от \(s\) до \(t\) содержит \(v\). Богиня Микаэла занята и сможет ответить вам только на \(11\,111\) запросов. Это ваш единственный шанс. Ваша задача — определить дерево и вывести его ребра. Выходные данные Когда ваша программа определила дерево и готова вывести его ребра, выведите «ANSWER» на отдельной строке. Убедитесь, что все буквы являются заглавными. Затем выведите \(n-1\) строку, в каждой строке должны находиться два целых числа, разделенных пробелами, обозначающие вершины, которые являются концами фиксированного ребра. Каждое ребро должно быть выведено ровно один раз. Затем ваша программа должна немедленно завершиться. Протокол взаимодействия Чтобы задать вопрос, действуйте следующим образом. - Сначала выведите размер множества \(S\) на отдельной строке. В следующей строке выведите \(|S|\) различных целых чисел, разделенных пробелами, описывающих вершины \(S\).
- Затем, аналогично, выведите размер множества \(T\) на отдельной строке. В следующей строке выведите \(|T|\) различных целых чисел, разделенных пробелами, описывающих вершины \(T\).
- Затем, в последней строке, выведите \(v\) — вершину, которую вы выбрали для этого запроса.
- Прочитайте ответ Микаэлы из входного файла.
Не забудьте, что \(S\) и \(T\) должны быть непустыми и непересекающимися. После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Если ваша программа сделает слишком много запросов, задаст некорректный запрос или некорректно последует описанному выше протоколу взаимодействия, она может получить произвольный вердикт. В противном случае, ваша программа получит вердикт Неправильный ответ, если она выведет неправильное дерево. Обратите внимание, что дерево загадано заранее и не зависит от ваших запросов. Взломы Взломы должны быть описаны следующим образом. Первая строка должна содержать целое число \(n\) (\(2 \leq n \leq 500\)) — количество вершин в дереве. Следующие \(n-1\) строк должны содержать по два целых числа \(u\) и \(v\), обозначающих наличие в дереве неориентированного ребра \((u, v)\) (\(1 \leq u, v \leq n\)). Примечание В первом тестовом примере задано следующее дерево:  \(n = 5\) задается программе. Затем программа задает Микаэеле запрос с \(S = \{1, 2, 3\}\), \(T = \{4, 5\}\), и \(v = 2\), на который она отвечает \(5\) (подходящие пары \((s, t)\) это \((1, 4)\), \((1, 5)\), \((2, 4)\), \((2, 5)\), и \((3, 5)\)). | |
![]()
|
|
G. Жадные подпоследовательности
Деревья
дп
Структуры данных
*2400
Для массива \(c\) назовем жадной подпоследовательностью последовательность индексов \(p_1\), \(p_2\), ..., \(p_l\), такую, что \(1 \le p_1 < p_2 < \dots < p_l \le |c|\), и для всех \(i \in [1, l - 1]\), \(p_{i + 1}\) — минимальный индекс, для которого выполняются условия: \(p_{i + 1} > p_i\) и \(c[p_{i + 1}] > c[p_i]\). Вам дан массив \(a_1, a_2, \dots, a_n\). Для каждого его подотрезка длины \(k\) посчитайте длину его самой длинной жадной подпоследовательности. Выходные данные Выведите \(n - k + 1\) чисел — максимальные длины жадных подпоследовательностей для каждого подотрезка длины \(k\). Первое число должно быть ответом для подотрезка \(a[1..k]\), второе — для \(a[2..k + 1]\), и так далее. Примечание В первом примере: - \([1, 5, 2, 5]\) — наидлиннейшими являются подпоследовательности \(1, 2\) (\([c_1, c_2] = [1, 5]\)) или \(3, 4\) (\([c_3, c_4] = [2, 5]\)).
- \([5, 2, 5, 3]\) — подпоследовательность \(2, 3\) (\([c_2, c_3] = [2, 5]\)).
- \([2, 5, 3, 6]\) — подпоследовательность \(1, 2, 4\) (\([c_1, c_2, c_4] = [2, 5, 6]\)).
Во втором примере: - \([4, 5, 2, 5, 3, 6]\) — наидлиннейшими являются подпоследовательности \(1, 2, 6\) (\([c_1, c_2, c_6] = [4, 5, 6]\)) или \(3, 4, 6\) (\([c_3, c_4, c_6] = [2, 5, 6]\)).
- \([5, 2, 5, 3, 6, 6]\) — подпоследовательность \(2, 3, 5\) (\([c_2, c_3, c_5] = [2, 5, 6]\)).
| |
![]()
|
|
F. Спички детям не игрушка
Деревья
Структуры данных
*3400
Лена играется со спичками. Естественный вопрос, посещающий любого школьника, играющего со спичками — а можно ли поджечь спичкой дерево? Скажем, что дерево — это связный граф без циклов, вершины которого пронумерованы целыми числами \(1, 2, \ldots, n\), в каждой вершине которого также записано некоторое целое число \(p_v\), являющееся приоритетом вершины \(v\). Все приоритеты различны. Оказывается, что если поджечь дерево, то оно, как и можно было ожидать, сгорит целиком. Однако процесс этот не быстрый. Сначала у дерева сгорает лист (листом называется вершина, имеющая ровно одного соседа) с минимальным приоритетом, затем сгорает лист с минимальным приоритетом из оставшихся вершин дерева, и так далее. Таким образом, вершины превращаются в листья и сгорают до тех пор, пока от дерева не останется лишь одна вершина, после чего она тоже сгорает. Лена приготовила дерево из \(n\) вершин и в каждой вершине записала приоритет \(p_v = v\). Лене с одной стороны интересно посмотреть, как горит дерево, но с другой она понимает, что если дерево поджечь, оно исчезнет насовсем. Лена добрая девочка, и деревья ей жалко, так что она хочет ограничиться выяснением ответов на некоторые вопросы про процесс сгорания дерева в уме. Лена хочет ответить на \(q\) вопросов, каждый из которых относится к одному из трёх следующих видов: - «up \(v\)», присвоить вершине \(v\) приоритет \(1 + \max\{p_1, p_2, \ldots, p_n\}\);
- «when \(v\)», выяснить, какой по счёту сгорит вершина \(v\), если дерево поджечь сейчас;
- «compare \(v\) \(u\)», выяснить, какая из вершин \(v\) и \(u\) сгорит раньше, если дерево поджечь сейчас.
Заметим, что если приоритеты всех вершин сейчас различны, то и после выполнения запроса «up» они тоже останутся различными. Исходно они различны, поэтому в любой момент времени порядок сгорания листьев определён однозначно. Выходные данные Для каждого запроса типа «when» нужно вывести одно целое число от \(1\) до \(n\) — момент времени, когда сгорит вершина \(v\). Для запроса типа «compare» выведите \(v\) или \(u\), в зависимости от того, какая вершина сгорит раньше. Примечание В первом примере процесс сгорания исходного дерева проиллюстрирован на картинке:  В частности, порядок сгорания вершин следующий: \([2, 4, 3, 1, 5]\). Во втором примере после применения операции «up» порядок сгорания вершин станет следующим: \([2, 4, 3, 5, 1]\) | |
![]()
|
|
C. Дерево и рёбра
графы
Деревья
математика
поиск в глубину и подобное
снм
*1500
Вам дано дерево (связный неориентированный граф без циклов), состоящее из \(n\) вершин. Каждое из \(n - 1\) рёбер дерева покрашено в чёрный или красный цвет. Вам также дано целое число \(k\). Рассмотрим последовательности из \(k\) вершин. Скажем, что последовательность \([a_1, a_2, \ldots, a_k]\) является хорошей, если она удовлетворяет следующему: - Мы пройдём некоторый путь в дереве (возможно посещающий несколько раз одну и ту же вершину или ребро), начинающийся в \(a_1\) и заканчивающийся в \(a_k\).
- Начнём в \(a_1\), затем перейдём в \(a_2\) по кратчайшему пути между \(a_1\) и \(a_2\), затем перейдём в \(a_3\) аналогичным образом, и так далее, пока наконец не пройдём кратчайший путь из \(a_{k-1}\) в \(a_k\).
- Если в результате такого процесса мы пройдём хотя бы по одному чёрному ребру, то последовательность является хорошей.
 Рассмотрим дерево, изображенное на рисунке. Если \(k=3\), то следующие последовательности являются хорошими: \([1, 4, 7]\), \([5, 5, 3]\) и \([2, 3, 7]\). Следующие последовательности не являются хорошими: \([1, 4, 6]\), \([5, 5, 5]\), \([3, 7, 3]\). Всего есть \(n^k\) последовательностей вершин, посчитайте сколько из них являются хорошими. Так как это число может быть очень большим, выведите его по модулю \(10^9+7\). Выходные данные Выведите одно число — количество хороших последовательностей по модулю \(10^9 + 7\). Примечание В первом примере все последовательности (\(4^4\)) длины \(4\) являются хорошими, кроме следующих: - \([1, 1, 1, 1]\)
- \([2, 2, 2, 2]\)
- \([3, 3, 3, 3]\)
- \([4, 4, 4, 4]\)
Во втором примере, все рёбра красные, а значит нет ни одной хорошей последовательности. | |
![]()
|
|
G. Двойное дерево
Деревья
кратчайшие пути
разделяй и властвуй
Структуры данных
*2700
Вам дан неориентированный граф специального вида. Он состоит из \(2n\) вершин, пронумерованных от \(1\) до \(2n\). Граф обладает следующими свойствами: - в нем ровно \(3n-2\) ребра: \(n\) ребер соединяют вершины с четными номерами и вершины с нечетными номерами, \(n - 1\) ребер соединяют вершины с нечетными номерами друг с другом, и \(n - 1\) ребер соединяют вершины с четными номерами друг с другом;
- для каждого ребра \((u, v)\) между вершинами с нечетными номерами существует ребро \((u + 1, v + 1)\), и наоборот;
- для каждого нечетного числа \(u \in [1, 2n - 1]\) существует ребро \((u, u + 1)\);
- граф является связным; более того, если мы удалим все четные вершины и ребра, инцидентные им, граф станет деревом (то же самое произойдет, если удалить все нечетные вершины).
Граф можно представить как два дерева с одинаковой структурой, и дополнительно \(n\) ребер, соединяющих соответствующие вершины в различных деревьях. Ребра графа являются взвешенными. Длина простого пути в этом графе определяется как сумма весов всех ребер, по которым проходит путь. Вам даны \(q\) запросов к графу; в каждом запросе требуется подсчитать длину кратчайшего пути между какой-то парой вершин. Можете ли вы справиться со всеми запросами? Выходные данные Выведите \(q\) целых чисел, \(i\)-е из которых должно быть ответом на \(i\)-й запрос. Примечание Граф в первом тесте выглядит следующим образом:  | |
![]()
|
|
G. Приватизация дорог в Древляндии
Бинарный поиск
графы
Деревья
жадные алгоритмы
Конструктив
поиск в глубину и подобное
*1900
Древляндия состоит из \(n\) городов и \(n-1\) дороги. Все дороги являются двусторонними и соединяют пару различных городов. Из любого города по дорогам можно добраться до любого другого. Всё верно, топология страны — это именно неориентированное дерево. В Древляндии есть несколько частных дорожных компаний. Правительство решило передать дороги в собственность компаний. После приватизации каждая дорога будет принадлежать какой-то одной компании, одна компания может владеть несколькими дорогами. Правительство обеспокоено возможными обвинениями в пристрастности. В правительстве полагают, что люди города могут посчитать несправедливой ситуацию, если две или более дороги, входящие в этот город, принадлежат одной компании. Правительство планирует такую приватизацию, что количество таких городов не будет превосходить \(k\), а количество частных компаний (которые участвуют в приватизации) — минимально. Выберите такое минимальное количество компаний \(r\), что возможно распределить все дороги по этим компаниям так, что количество городов с двумя или более дорогами одной компании не превосходит \(k\). Другими словами, назовём город хорошим, если все его дороги принадлежат различным компаниям. Ваша задача найти минимальное \(r\), что существует распределение всех дорог по компаниям от \(1\) до \(r\), что количество не являющимися хорошими городов не превосходит \(k\).  Картинка иллюстрирует первый пример (\(n=6, k=2\)). Ответ на этот тест содержит \(r=2\) компании. Числа на рёбрах соответствуют номерам дорог. Цвета рёбер соответствуют компаниям: красный цвет обозначает первую компанию, синий цвет обозначает вторую компанию. Серая вершина (с номером \(3\)) соответвует городу, который не является хорошим. Количество таких вершин (в данном случае, только одна) не превосходит \(k=2\). Невозможно получить не более \(k=2\) таких вершин, если ответ содержит только одну компанию. Картинка иллюстрирует первый пример (\(n=6, k=2\)). Ответ на этот тест содержит \(r=2\) компании. Числа на рёбрах соответствуют номерам дорог. Цвета рёбер соответствуют компаниям: красный цвет обозначает первую компанию, синий цвет обозначает вторую компанию. Серая вершина (с номером \(3\)) соответвует городу, который не является хорошим. Количество таких вершин (в данном случае, только одна) не превосходит \(k=2\). Невозможно получить не более \(k=2\) таких вершин, если ответ содержит только одну компанию. Выходные данные В первую строку выведите искомое число \(r\) (\(1 \le r \le n - 1\)). Во вторую строку выведите \(n-1\) целое число \(c_1, c_2, \dots, c_{n-1}\) (\(1 \le c_i \le r\)), где \(c_i\) — это номер компании, которая должна владеть \(i\)-й дорогой. Если ответов несколько, то выведите любой из них. | |
![]()
|
|
B. Lynyrd Skynyrd
Деревья
дп
математика
поиск в глубину и подобное
Структуры данных
*2000
Недавно Линэрд и Скинэрд отправились в магазин, где Линэрд купил себе перестановку \(p\) длины \(n\), а Скинэрд купил себе массив \(a\) длины \(m\), состоящий из чисел от \(1\) до \(n\). Линэрду и Скинэрду скучно, поэтому они решили задать вам \(q\) вопросов, имеющих следующий вид: «есть ли у подотрезка массива \(a\) c \(l\)-й по \(r\)-ю позицию включительно подпоследовательность, которая является циклическим сдвигом \(p\)?». Перестановка длины \(n\) — это последовательность из \(n\) чисел, в которой каждое число от \(1\) до \(n\) встречается ровно один раз. Циклический сдвиг перестановки \((p_1, p_2, \ldots, p_n)\) — это перестановка \((p_i, p_{i + 1}, \ldots, p_{n}, p_1, p_2, \ldots, p_{i - 1})\) для какого-то \(i\) от \(1\) до \(n\). Так, например, у перестановки \((2, 1, 3)\) есть три различных циклических сдвига: \((2, 1, 3)\), \((1, 3, 2)\), \((3, 2, 1)\). Подпоследовательность подотрезка массива \(a\) с \(l\)-й по \(r\)-ю позицию включительно — это последовательность \(a_{i_1}, a_{i_2}, \ldots, a_{i_k}\) для каких-то \(i_1, i_2, \ldots, i_k\) таких, что \(l \leq i_1 < i_2 < \ldots < i_k \leq r\). Выходные данные В единственной строке выведите строку длины \(q\), состоящую из \(0\) и \(1\), при этом на \(i\)-й позиции должна стоять \(1\), если у подотрезка массива \(a\) c \(l_i\)-й по \(r_i\)-ю позицию включительно есть подпоследовательность, которая является циклическим сдвигом \(p\), и \(0\) в противном случае. Примечание В первом примере отрезок с \(1\)-й по \(5\)-ю позицию это \(1, 2, 3, 1, 2\). В нём есть подпоследовательность \(1, 3, 2\), которая является циклическим сдвигом перестановки. В отрезке с \(2\)-й по \(6\)-ю позицию есть подпоследовательность \(2, 1, 3\), совпадающая с перестановкой. Отрезок с \(3\)-й по \(5\)-ю позицию это \(3, 1, 2\), в нём есть только одна подпоследовательность длиной \(3\) (\(3, 1, 2\)), но она не совпадает ни с каким циклическим сдвигом перестановки. Во втором примере у перестановки циклические сдвиги это \(1, 2\) и \(2, 1\). Отрезок с \(1\)-й по \(2\)-ю позицию это \(1, 1\), его подпоследовательности не совпадает ни с каким циклическим сдвигом перестановки. Отрезок с \(2\)-й по \(3\)-ю позицию это \(1, 2\), он совпадает с перестановкой. Отрезок с \(3\)-й по \(4\)-ю позицию это \(2, 2\), его подпоследовательности не совпадает ни с каким циклическим сдвигом перестановки. | |
![]()
|
|
C. Queen
Деревья
поиск в глубину и подобное
*1400
Вам дано корневое дерево, вершины которого пронумерованы от \(1\) до \(n\). Дерево — это связный граф без циклов. В корневом дереве есть выделенная вершина, называющаяся корнем. Предками вершины \(i\) называются все вершины, лежащие на пути от корня до вершины \(i\), кроме самой вершины \(i\). Родителем вершины \(i\) называется ближайший к \(i\) предок \(i\). В данном вам дереве родитель вершины \(i\) имеет номер \(p_i\). Для корня величина \(p_i\) равна \(-1\).  Пример возможного дерева для \(n=8\), корнем является вершина \(5\). Родителем вершины \(2\) является вершина \(3\), а родителем вершины \(1\) является вершина \(5\). Предками вершины \(6\) являются вершины \(4\) и \(5\), а предками вершины \(7\) являются вершины \(8\), \(3\) и \(5\) Пример возможного дерева для \(n=8\), корнем является вершина \(5\). Родителем вершины \(2\) является вершина \(3\), а родителем вершины \(1\) является вершина \(5\). Предками вершины \(6\) являются вершины \(4\) и \(5\), а предками вершины \(7\) являются вершины \(8\), \(3\) и \(5\) Вы заметили, что некоторые вершины не уважают других. А именно, если \(c_i = 1\), то вершина \(i\) не уважает каждого из своих предков, а если \(c_i = 0\), то она их уважает. Вы решили по очереди удалять из дерева вершины: на каждом шаге вы выбираете не корневую вершину, которая не уважает своего родителя, и которую не уважают все вершины, для которых она является родителем. Если таких вершин несколько, то вы выбираете вершину с минимальным номером. При удалении вершины \(v\) все вершины, для которых \(v\) была родителем, соединяются ребром с родителем \(v\).  Пример удаления вершины \(7\). Пример удаления вершины \(7\). Как только подходящих вершин для удаления нет, вы заканчиваете процесс. Выведите порядок, в котором вы удалите вершины. Обратите внимание, что этот порядок задается однозначно. Выходные данные В случае, если вы удалите хотя бы одну вершину, в единственной строке через пробел выведите номера всех удаленных вершин в том порядке, в котором вы их удалите. В случае, если никого не нужно удалять, выведите единственное число \(-1\). Примечание Процесс удаления в первом примере будет происходить по следующему сценарию (см. картинку ниже, вершины с \(c_i=1\) отмечены жёлтым): - сначала будет удалена вершина \(1\), так как она не уважает предков и все вершины, для которых она родитель (это одна вершина \(2\)) ее не уважают, а среди таких вершина номер \(1\) — наименьший номер;
- вершина \(2\) при этом будет соединена ребром с вершиной \(3\);
- затем будет удалена вершина \(2\), так как она не уважает предков, и все вершины, для которых она родитель (это одна вершина \(4\)) ее не уважают;
- при этом вершина \(4\) будет соединена ребром с вершиной \(3\);
- затем будет удалена вершина \(4\), так как она не уважает предков, и все вершины, для которых она родитель (таких нет) ее не уважают (vacuous truth);
- из дерева будет удалена вершина \(4\);
- процесс удаления завершается, так как нет подходящих вершин.
 Во втором примере вершины не нужно удалять: - у \(2\) и \(3\) есть вершины, для которых они являются родителями, но которые их уважают;
- \(4\) и \(5\) уважают руководство.
 В третьем примере дерево будет меняться следующим образом:  | |
![]()
|
|
F. Разделение листов
Деревья
дп
*2500
Вам дано корневое дерево с \(n\) вершинами, пронумерованными от \(1\) до \(n\). Корнем дерева является вершина \(1\). Предком \(i\)-й вершины является вершина \(p_i\). Лист — это вершина без детей. Для некоторого набора листьев \(L\) пусть \(f(L)\) обозначает наименьший связный подграф, содержащий все листья \(L\). Вы хотите разделить листы так, чтобы для любых двух различных множеств \(x, y\) разбиения \(f(x)\) и \(f(y)\) не пересекались. Подсчитайте количество способов разбить листья по модулю \(998244353\). Два разбиения различны, если есть такие два листа, которые находятся в одном множестве в одному разбиении, а в другом в двух различных. Выходные данные Выведите одно целое число по модулю \(998244353\) — количество способов разбить вершины. Примечание В первом примере листьями являются вершины \(2,3,4,5\). Способы разделить листья:  Во втором примере есть только один лист \(10\). Значит, что есть только один способ разбиения. Обратите внимание, что вершина \(1\) не является листом. | |
![]()
|
|
C. Генератор Деревьев™
Деревья
реализация
Структуры данных
*2700
Сов Пачино всегда интересовался деревьями — невзвешенными подвешенными деревьями, если быть точным. Он любит определять диаметр каждого дерева, что видит — максимальную длину простого пути в дереве. Друзья Сова Пачино решили подарить ему Генератор Деревьев™ — мощное устройство, позволяющее создавать деревья по их описанию. Подвешенное дерево из \(n\) вершин может быть описано скобочной последовательностью длины \(2(n - 1)\) следующим образом: рассмотрим любой обход дерева, который начинается и заканчивается в корне, и проходит по каждому ребру ровно два раза — один раз вниз по дереву, другой раз вверх. Затем в порядке пути выпишем «(» (открывающую скобку) если по ребру прошли вниз, и «)» (закрывающую скобку), иначе. На следующей иллюстрации расположены примеры подвешенных деревьев и их описания:  Сов выписал описание подвешенного дерева из \(n\) вершин. Затем, он изменил его описание \(q\) раз. Каждый раз, когда он выписывал новое описание, он выбирал два разных символа в описании, которое он написал в прошлый раз, менял их местами и записывал полученную строку. Он всегда следил за тем, чтобы каждая записанная строка была описанием подвешенного дерева. Затем Пачино использовал Генератор Деревьев™ для каждого описания, которое он выписал. Какие диаметры у всех построенных деревьев? Выходные данные Выведите \(q + 1\) целых чисел — диаметр каждого построенного по описанию дерева, в порядке, в котором эти описания выписывались. Примечание На следующей иллюстрации изображены все построенные деревья и их описания из первого примера:  | |
![]()
|
|
A. Праздник
графы
Деревья
поиск в глубину и подобное
*900
В компании работает n сотрудников, пронумерованных от 1 до n. У каждого сотрудника либо нет руководителя, либо есть ровно один непосредственный руководитель — некоторый другой сотрудник с другим номером. Сотрудник A называется начальником другого сотрудника B, если выполняется хотя бы одно из двух условий: - Сотрудник A — непосредственный руководитель сотрудника B.
- У сотрудника B есть непосредственный руководитель, сотрудник C, такой, что A является начальником сотрудника C.
В структуре компании нет циклов. То есть никакой сотрудник не является начальником своего непосредственного руководителя. Сегодня компания собирается организовать праздник. Для этого необходимо разделить всех n сотрудников на несколько групп: каждый человек должен относиться ровно к одной группе. Более того, в каждой группе не должно быть таких двух сотрудников A и B, что A является начальником B. Ваша задача — найти наименьшее возможное количество таких групп. Выходные данные Выведите единственное целое число — минимальное количество групп, на которые можно разделить всех сотрудников. Примечание В первом примере достаточно трех групп: - Сотрудник 1
- Сотрудники 2 и 4
- Сотрудники 3 и 5
| |
![]()
|
|
D. Неко и пранк
Деревья
дп
жадные алгоритмы
*2100
Неко играл в свои игрушки на заднем дворе дома Аки. Аки решил его разыграть и подбросил в его игрушки немного кошачей мяты. К сожалению он немного переборщил и случайно подбросил целый пакет мяты... Неко понадобилось больше дня чтобы вернутся в нормальное состояние, после чего он рассказал, что увидел за это время много странных вещей, например он видел бор всех правильных скобочных последовательностей длины \(2n\). Правильные скобочные последовательности определяются следующим образом: - Пустая последовательность является правильной скобочной последовательностью.
- Если \(s\) является правильной скобочной последовательностью, то \((\,s\,)\) тоже является правильной скобочной последовательностью,
- Если \(s\) и \(t\) образуют правильную скобочную последовательность, то \(st\) тоже является правильной скобочной последовательностью.
Например, строки «(())» и «()()» образуют правильную скобочную последовательность, а строки «)(» и «((» нет. Аки затем придумал интересную задачку. Он хочет узнать чему равен размер максимального паросочетания (то есть множества рёбер с непересекающимися концами) в этом дереве? Так как ответ может быть достаточно большим, выведите его по модулю \(10^9 + 7\). Выходные данные Выведите одно число — размер наибольшего паросочетания в дереве. Так как ответ может быть достаточно большим, выведите его по модулю \(10^9 + 7\). Примечание Картинки ниже иллюстрируют бор в первом и втором примере (для наглядности круглые скобки заменены на угловые). Максимальное паросочетание обозначено синим.   | |
![]()
|
|
D. Сервал и подвешенное дерево
Бинарный поиск
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
*1900
Теперь Сервал — младший ученик средней школы Джапари, и он все еще в восторге от математики, как и раньше. Как математически талантливый мальчик, он любит играть с числами. На этот раз он хочет поиграть с числами на подвешенном дереве. Деревом называется связный граф без циклов. Подвешенное дерево имеет выделенную вершину, называемую корнем. Родителем вершины \(v\) называется последняя отличная от \(v\) вершина на пути от корня к вершине \(v\). Дети вершины \(v\) — все вершины, для которых \(v\) является родителем. Вершина называется листом, если у нее нет детей. Подвешенное дерево Сервала имеет \(n\) вершин, корень дерева — вершина \(1\). Сервал хочет написать по одному числу в каждую из вершин, но есть некоторые ограничения. В каждой из вершин, кроме листьев, записана операция \(\max\) или \(\min\), указывающая, что число в этой вершине должно быть равно максимуму или минимуму среди всех чисел, написанных в ее детях, соответственно. Предположим, что в дереве \(k\) листьев. Сервал хочет написать числа \(1, 2, \ldots, k\) в эти \(k\) листьев (каждое число должно использоваться ровно один раз). Он любит большие числа, поэтому он хочет максимизировать число в корне. Как его лучший друг, вы можете помочь ему? Выходные данные Выведите одно целое число — максимальное значение числа в корне, которое Сервал может получить. Примечание Примеры показаны на рисунках ниже. Числа, написанные в середине вершин, являются их номерами, а сверху написаны числа, которые пишет Сервал. В первом примере, независимо от того, как вы расположите числа, ответ будет \(1\).  Во втором примере, независимо от того, как вы расположите числа, ответ будет \(4\).  В третьем примере одним из оптимальных решений для достижения \(4\) является расстановка чисел \(4\) и \(5\) на вершины \(4\) и \(5\).  В четвертом примере оптимальным решением является поставить число \(5\) на вершину \(5\).  | |
![]()
|
|
D. 0-1-Дерево
Деревья
дп
поиск в глубину и подобное
разделяй и властвуй
снм
*2200
Задано дерево (неориентированный связный ацикличный граф), состоящее из \(n\) вершин и \(n - 1\) ребра. На каждом ребре записано число, каждое из чисел — это либо \(0\) (назовем такие ребра \(0\)-ребрами), либо \(1\) (назовем их \(1\)-ребрами). Назовем упорядоченную пару вершин \((x, y)\) (\(x \ne y\)) корректной, если при проходе по простому пути от \(x\) до \(y\) мы никогда не пройдем по \(0\)-ребру после прохода по \(1\)-ребру. Ваша задача — посчитать количество корректных пар в дереве. Выходные данные Выведите одно целое число — количество корректных пар вершин. Примечание Картинка, соответствующая первому тестовому примеру: 
| |
![]()
|
|
E. Странный прибор
Бинарный поиск
Деревья
интерактив
математика
*3400
Это интерактивная задача. Вася обожает решать загадки и разгадывать головоломки. На этот раз он нашел странный прибор и хочет выяснить принцип его работы. Этот прибор зашифрован с помощью дерева (связного неориентированного графа без циклов), состоящего из \(n\) вершин, пронумерованных целыми числами от \(1\) до \(n\). Чтобы решить головоломку надо угадать это дерево. К счастью прибор умеет выполнять одну операцию, исходя из которой надо разгадать его шифр. Можно ввести в прибор последовательность \(d_1, d_2, \ldots, d_n\) целых неотрицательных чисел. На приборе есть \(n\) лампочек, \(i\)-я из которых отвечает за \(i\)-ю вершину дерева-шифра. Для всех \(i\) из этих лампочек \(i\)-я загорится, если существует такая вершина дерева-шифра с номером \(j \neq i\), что \(dist(i, j) \leq d_j\). Здесь \(dist(i, j)\) обозначает расстояние между вершинами \(i\) и \(j\) в дереве-шифре, то есть количество ребер в простом пути между вершинами \(i\) и \(j\). Вася хочет за \(\leq 80\) операций с прибором решить головоломку и угадать дерево-шифр. Помогите ему! Протокол взаимодействия В начале вашей программе вводится единственное целое число \(n\) — количество вершин в дереве-шифре прибора (\(2 \leq n \leq 1000\)). Далее вы можете выполнять операции в следующем формате. Сначала выведите символ "?" (без кавычек) и за ним \(n\) целых чисел \(d_1, d_2, \ldots, d_n\), разделенных пробелами. Заметьте, что в операциях для всех \(i\) должно быть выполнено неравенство \(0 \leq d_i < n\). В ответ будет выведена строка \(s\) длины \(n\), состоящая из символов "0" и "1" (без кавычек). Для всех \(i\) символ \(s_i\) будет равен "0", если у прибора не включилась лампочка, соответствующая \(i\)-й вершине дерева-шифра и "1", иначе. После нескольких запросов вы должны вывести угаданное дерево. Для этого в первой строке выведите единственный символ "!" (без кавычек). В следующих \(n-1\) строках выведите по \(2\) целых числа \(a_i\), \(b_i\) — номера вершин, соединяющих \(i\)-е ребро дерева. Выведенные числа должны удовлетворять условиям \(1 \leq a_i, b_i \leq n\) и \(a_i \neq b_i\). Эти ребра должны образовывать дерево, совпадающее с загаданным. Выводить ребра можно в любом порядке. После этого ваша программа должна завершиться. Гарантируется, что в каждом тесте дерево-шифр будет зафиксировано заранее и не будет меняться в зависимости от выполняемых операций. Ваша программа может выполнить от \(0\) до \(80\) операций с прибором и после этого сообщить дерево, совпадающее с загаданным. Если ваша программа сделает больше \(80\) операций, то она может получить любой вердикт, потому что будет считывать данные из закрытого потока ввода. Также, если ваша программа сделает операцию или выведет ответ в неверном формате, она может получить любой вердикт. Будьте внимательны. Не забудьте сбрасывать буфер вывода после того, как выведете данные для операции или ответ. Чтобы сбросить буфер вывода вы можете использовать: - fflush(stdout) в C++.
- System.out.flush() в Java.
- stdout.flush() в Python.
- flush(output) в Pascal.
- Прибегните к документации других языков.
Взломы: Первая строка должна содержать единственное целое число \(n\) — количество вершин в дереве-шифре (\(2 \leq n \leq 1000\)). Следующая \(n-1\) строка должна содержать по \(2\) целых числа \(a_i\), \(b_i\) — номера вершин, соединяющих \(i\)-е ребро дерева (\(1 \leq a_i, b_i \leq n\), \(a_i \neq b_i\)). Выведенные ребра должны образовывать дерево. Будьте внимательны, лишние пробелы или переводы строк запрещены. Примечание Дерево-шифр из первого теста выглядит так:  Таблица попарных расстояний между вершинами выглядит так:  - Если сделать операцию, в которой \(d = [0, 0, 0, 0, 0]\), то ни одна лампочка не загорится, потому что \(dist(i, j) > 0\) при всех \(i \neq j\).
- Если сделать операцию, в которой \(d = [1, 1, 2, 0, 2]\), то загорятся все лампочки, кроме лампочки, соответсвующей вершине дерева-шифра с номером \(3\). Например, лампочка, соответсвующая вершине с номером \(1\) загорится, потому что \(dist(1, 5) = 1 \leq 2 = d_5\).
- Если сделать операцию, в которой \(d = [0, 0, 0, 1, 0]\), то загорятся все лампочки, кроме лампочек, соответсвующих вершинам дерева-шифра с номерами \(4\) и \(5\).
- Если сделать операцию, в которой \(d = [0, 1, 0, 0, 1]\), то загорятся только лампочки, соответсвующие вершинам дерева-шифра с номерами \(1\) и \(4\).
| |
![]()
|
|
D. Анаграммные пути
Деревья
дп
реализация
*3000
У жабы Ильи есть подвешенное двоичное дерево с корнем в вершине \(1\). Деревом называется связный граф без циклов. Дерево называется подвешенным, если в нем выделена одна вершина, эта вершина называется корнем. Вершина \(u\) является сыном вершины \(v\), если \(u\) и \(v\) соединены ребром, и \(v\) ближе к корню, чем \(u\). Листом называется вершина, которая не является корнем, и у которой нет детей. В дереве Ильи у каждой вершины не более двух детей, и на каждом ребре записан символ. Каждый символ может быть строчной буквой латинского алфавита или знаком вопроса '?'. Илья немного изменит дерево \(q\) раз. Каждое обновление заменит один символ на ровно одном ребре. После каждого обновления Илья должен проверить, является ли дерево анаграммным и если это так, то еще и найти его анаграмность для каждой буквы. Это непросто объяснить, но мы попробуем. Для начала, строка \(a\) является анаграммой строки \(b\), если возможно переставить буквы строки \(a\) (не меняя сами буквы) так, что она станет равной строке \(b\). Например, строка «fortyfive» является анаграммой строки «overfifty», но строка «aabb» — не анаграмма строки «bbba». Рассмотрим путь от корня до листа. Символы на этом пути образуют строку, скажем, что эта строка ассоциирована с этим листом. Дерево называется анаграммным, если и только если возможно заменить каждый знак вопроса на строчную букву латинского алфавита так, что для любой пары листьев ассоциированные строки этих листьев являются анаграммами друг друга. Если дерево анаграммное, тогда его анаграмность для буквы \(c\) равна максимальному возможному количеству букв \(c\) в строке, ассоциированной с некоторым листом, после корректной замены всех знаков вопроса. После каждого обновления проверьте, является ли дерево анаграммным, и если является, то найдите \(\sum{f(c) \cdot ind(c)}\) по всем буквам \(c\), где \(f(c)\) — это анаграмность для буквы \(c\), а \(ind(x)\) — порядок буквы в алфавите (\(ind(\)"a"\() = 1\), \(ind(\)"b"\() = 2\), ..., \(ind(\)"z"\() = 26\)). Выходные данные Выведите \(q\) строк. В \(i\)-й из них выведите «Fou» если дерево не анаграммное после первых \(i\) обновлений. Иначе выведите «Shi» и \(\sum{f(c) \cdot ind(c)}\) по всем буквам \(c\). Примечание В первом примере после первого запроса, для каждого символа, вы можете поставить все ребра равными этому символу, и вы получите \(1\) такой символ на каждом пути, так что ответ равен \(1 \cdot (1+2+\ldots+26) = 351\). В первом примере после второго запроса, вы знаете, что все пути должны быть анаграммой «a», так что все пути должны быть равны «a», так что ответ равен \(1 \cdot 1 = 1\). В первом примере после третьего запроса, у вас есть два пути со строками «a» и «b», но эти строки не анаграммы, так что ответ «Fou». В первом примере после четвертого запроса, вы знаете, что все пути должны быть «b», так что ответ равен \(1 \cdot 2 = 2\). Во втором примере после первого запроса, вы знаете, что \(f(\)'a'\() = 2\) и \(f(c) = 1\) для всех остальных символов, так что ответ равен \(1 \cdot (2 + 3 + \ldots + 26) + 2 = 352\). Во втором примере после второго запроса, вы знаете, что на каждом пути должно быть одно 'a' и одно 'b', так что ответ равен \(1 \cdot 1 + 1 \cdot 2 = 3\). | |
![]()
|
|
E. Дерево или не дерево
графы
Деревья
разделяй и властвуй
реализация
Структуры данных
*2900
Дан неориентированный связный граф G из n вершин и n ребер. G не содержит петель и кратных ребер. Пусть у каждого ребра этого графа есть два состояния: включено и выключено. Изначально все ребра выключены. Также вам даны m запросов вида (v, u) — изменить состояние всех ребер на кратчайшем пути из вершины v в вершину u в графе G, если таких путей несколько, выбирается лексикографически наименьший. Более формально, рассмотрим все кратчайшие пути из вершины v в вершину u как последовательности вершин v, v1, v2, ..., u. Среди таких последовательностей выбирается лексикографически наименьшая. Требуется после каждого запроса сказать, сколько компонент связности в графе, вершины которого совпадают с вершинами графа G, а ребра совпадают с включенными ребрами графа G. Выходные данные Выведите m строк по одному целому числу в каждой — ответы на запросы. Примечание Рассмотрим первый пример. Будем синим выделять на рисунке включенные ребра. -
Граф до применения операций. В графе нет включенных ребер, поэтому 5 компонент связности есть изначально.  -
Граф после запроса v = 5, u = 4. Видно, что в графе 3 компоненты, если рассматривать только включенные ребра.  -
Граф после запроса v = 1, u = 5. Видно, что в графе 3 компоненты, если рассматривать только включенные ребра. 
Лексикографическое сравнение двух последовательностей одинаковой длины (k чисел) происходит следующим образом. Последовательность x лексикографически меньше последовательности y если существует такое i (1 ≤ i ≤ k), что xi < yi, а для любого j (1 ≤ j < i) xj = yj. | |
![]()
|
|
B. Nauoo и окружность
Деревья
дп
Комбинаторика
поиск в глубину и подобное
*1900
Nauuo — девочка, которая любит рисовать окружности. Однажды она нарисовала окружность и захотела нарисовать на ней дерево. Дерево — это связный неориентированный граф из \(n\) вершин и \(n-1\) ребер. Вершины пронумерованы целыми числами от \(1\) до \(n\). Nauuo хочет нарисовать дерево на окружности, причем вершины должны лежать на \(n\) различных точках на окружности, а ребра — это отрезки, не пересекающиеся друг с другом. «Не пересекающиеся друг с другом» означает, что любые два ребра не должны иметь общих точек, кроме концов отрезков. Nauuo хочет нарисовать дерево, используя перестановку из \(n\) элементов. Перестановка из \(n\) элементов это последовательность целых чисел \(p_1,p_2,\ldots,p_n\), в которой каждое целое число от \(1\) до \(n\) встречается ровно один раз. После выбора перестановки Nauuo нарисует \(i\)-ю вершину в \(p_i\)-й точке на окружности, а затем нарисует ребра, основываясь на положении вершин. По данному дереву Nauuo хочет знать, сколько есть перестановок, подходящих под условие (ребра образуют непересекающиеся отрезки между вершинами). Она хочет узнать ответ по модулю \(998244353\), можете ли вы ей помочь? Очевидно, что корректность перестановки не зависит от выбранных \(n\) точек на окружности. Выходные данные Выведите одно целое число — количество перестановок, при которых возможно нарисовать дерево на окружности, не нарушая условия, по модулю \(998244353\). Примечание Пример 1 Корректные перестановки и их деревья. 
А вот пример некорректной перестановки: ребра \((1,3)\) и \((2,4)\) пересекаются. 
Example 2 Каждая перестановка приводит к корректному дереву, так что ответ равен \(4! = 24\). | |
![]()
|
|
F. Ихаб и Большой Финал
графы
Деревья
интерактив
Конструктив
разделяй и властвуй
реализация
*2400
Это интерактивная задача. Вам дано дерево, состоящее из \(n\) вершин, с корнем в вершине \(1\). Дерево — это связный граф без циклов. Мы выбрали секретную вершину \(x\). Чтобы найти эту вершину, вы можете задавать запросы двух типов: - d \(u\) (\(1 \le u \le n\)). Мы ответим расстоянием между вершинами \(u\) и \(x\). Расстояние между двумя вершинами — это количество ребер в кратчайшем пути между ними.
- s \(u\) (\(1 \le u \le n\)). Мы ответим номер второй вершины на пути от \(u\) до \(x\). Тем не менее, есть одна хитрость. Если \(u\) не является предком \(x\), вы получите вердикт «Неправильный ответ»!
Вершина \(a\) называется предком вершины \(b\), если \(a \ne b\) и кратчайший путь от вершины \(1\) к вершине \(b\) проходит через вершину \(a\). Обратите внимание, что в этой задаче вершина не является предком сама себе. Можете ли вы найти \(x\), сделав не более \(36\) запросов? Скрытая вершина зафиксирована в каждом тесте заранее и не зависит от ваших запросов. Выходные данные Чтобы вывести ответ, выведите «! x» (без кавычек). Протокол взаимодействия Чтобы задать запрос, выведите в одном из двух следующих форматов: - d \(u\) (\(1 \le u \le n\)), или
- s \(u\) (\(1 \le u \le n\)).
После каждого вопроса вы должны прочитать ответ: либо расстояние, либо вторую вершину пути, как описано в легенде. Если мы ответим \(-1\) вместо корректного ответа, это означает, что вы превысили количество запросов, сделали неверный запрос или нарушили условие во втором типе запросов. Завершите вашу программу сразу после получения \(-1\), и вы получите вердикт Wrong answer. В противном случае вы можете получить другой вердикт, потому что ваше решение будет продолжать читать из закрытого потока. После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Взломы: Первая строка должна содержать два целых числа \(n\) и \(x\) (\(2 \le n \le 2 \cdot 10^5\), \(1 \le x \le n\)). Каждая из следующих \(n-1\) строк должна содержать два целых числа \(u\) и \(v\) (\(1 \le u,v \le n\)), которые значат, что между вершинами \(u\) и \(v\) есть ребро. Граф должен образовать дерево. Примечание В первом примере секретной вершиной является вершина \(5\).  Сначала мы спросим о расстоянии между вершинами \(x\) и \(2\). Ответ \(3\), поэтому вершина \(x\) равна либо \(4\), либо \(5\). Затем мы спрашиваем о второй вершине на пути от вершины \(3\) к вершине \(x\). Обратите внимание, что вершина \(3\) является предком вершины \(5\). Мы получаем вершину \(5\) в качестве ответа. Наконец, мы сообщаем, что секретная вершина — это вершина \(5\). | |
![]()
|
|
E. Минимальное покрытие отрезков
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
разделяй и властвуй
реализация
Структуры данных
*2200
Даны \(n\) отрезков в формате \([l; r]\) на числовой прямой. Также даны \(m\) запросов в формате \([x; y]\). Какое минимальное число отрезков надо взять так, чтобы каждая точка (не обязательно целочисленная) от \(x\) до \(y\) была покрыта хотя бы одним из них? Если нельзя выбрать отрезки так, чтобы каждая точка от \(x\) до \(y\) была покрыта, тогда выведите -1 на этот запрос. Выходные данные Выведите \(m\) целых чисел. \(i\)-е число должно быть ответом на \(i\)-й запрос: либо минимальное число отрезков необходимое, чтобы каждая точка (не обязательно целочисленная) от \(x_i\) до \(y_i\) была покрыта хотя бы одним из них, либо -1, если нельзя выбрать отрезки так, чтобы каждая точка от \(x_i\) до \(y_i\) была покрыта. Примечание В первом примере три запроса: - запрос \([1; 3]\) может быть покрыт отрезком \([1; 3]\);
- запрос \([1; 4]\) может быть покрыт отрезками \([1; 3]\) и \([2; 4]\). Нельзя покрыть \([1; 4]\) одним отрезком;
- запрос \([3; 4]\) может быть покрыт отрезком \([2; 4]\); Не важно, что покрыты какие-то точки вне данного запроса.
Во втором примере четыре запроса: - запрос \([1; 2]\) может быть покрыт отрезком \([1; 3]\). Обратите внимание, что можно выбрать любой из отрезков \([1; 3]\);
- запрос \([1; 3]\) может быть покрыт отрезком \([1; 3]\);
- запрос \([1; 4]\) не может быть покрыт никаким набором отрезков;
- запрос \([1; 5]\) не может быть покрыт никаким набором отрезков. Обратите внимание, что отрезки \([1; 3]\) и \([4; 5]\) вместе не покрывают \([1; 5]\), потому что даже нецелые точки должны быть покрыты. Здесь \(3.5\) не покрыта, например.
| |
![]()
|
|
E. Покрывай!
графы
Деревья
кратчайшие пути
поиск в глубину и подобное
снм
*1700
Задан неориентированный невзвешенный связный граф, состоящий из \(n\) вершин и \(m\) ребер. Гарантируется, что в данном графе нет петель и кратных ребер. Ваша задача — выбрать не более \(\lfloor\frac{n}{2}\rfloor\) вершин в данном графе так, чтобы каждая невыбранная вершина была смежна (другими словами, связана ребром) с хотя бы одной выбранной вершиной. Гарантируется, что ответ существует. Если существует несколько решений, выведите любое из них. Требуется ответить на несколько независимых запросов. Выходные данные Для каждого запроса выведите две строки. В первой строке выведите \(k\) (\(1 \le \lfloor\frac{n}{2}\rfloor\)) — количество выбранных вершин. Во второй строке выведите \(k\) различных целых чисел \(c_1, c_2, \dots, c_k\) в произвольном порядке, где \(c_i\) равно номеру \(i\)-й выбранной вершины. Гарантируется, что ответ всегда существует. Если существует несколько решений, выведите любое из них. Примечание В первом запросе любая вершина или любая пара вершин подойдет.  Обратите внимание, что не обязательно минимизировать количество выбранных вершин. Во втором запросе двух вершин достаточно (вершины \(2\) и \(4\)), но три так же подойдут.  | |
![]()
|
|
C. Сергей и школьная столовая
Бинарный поиск
Деревья
жадные алгоритмы
математика
Паросочетания
реализация
Структуры данных
*2200
Сергей пришел в школьную столовую и с ужасом обнаружил, что там уже очередь из целых \(m\) человек! Теперь он не уверен, стоит ли дожидаться конца этой очереди, поэтому хочет узнать, какое же блюдо ему достанется, если он это сделает. Так как Сергей устал после занятий, он попросил вас посчитать это за него. Всего в столовой есть \(n\) блюд со стоимостями \(a_1, a_2, \ldots, a_n\). Также есть очередь из \(m\) человек, у которых есть \(b_1, \ldots, b_m\) тугриков (школьники пронумерованы в том же порядке, как они стоят в очереди, то есть \(b_1\) означает, сколько тугриков у школьника, который стоит в очереди первым, а \(b_m\) — сколько у школьника, стоящего последним). Считается, что чем дороже блюдо, тем оно вкуснее, поэтому каждый школьник, когда подходит его очередь, просто покупает самое дорогое блюдо, на которое у него хватит денег (каждое блюдо в столовой есть только в одном экземпляре, поэтому после того, как один школьник купил блюдо, его уже никто не может купить), если же денег не хватает ни на одно из блюд, школьник так и уходит голодным (жестокий капитализм). Но для Сергея деньги не проблема, поэтому, когда подойдет его очередь, он, если еще не уйдет, просто купит самое дорогое из оставшихся блюд. Еще в школе Сергея сейчас нестабильная экономическая ситуация, поэтому, иногда могут изменяться стоимости некоторых блюд или количество денег у некоторых школьников. Поэтому вам нужно обработать \(q\) запросов двух типов: - изменить \(a_i\) на \(x\). То есть стоимость \(i\) блюда становится равна \(x\).
- изменить \(b_i\) на \(x\). То есть у \(i\) школьника становится \(x\) тугриков.
После каждого запроса нужно вывести стоимость блюда, которое получит Сергей, если дождется своей очереди, или \(-1\), если к этому моменту уже ничего не останется. Выходные данные Выведите \(q\) строк, \(i\)-я из которых содержит ответ на вопрос Сергея после \(i\) изменения (стоимость блюда, которое получит Сергей, если дождется своей очереди, или \(-1\), если к этому моменту уже ничего не останется). Примечание В первом примере после первого запроса в столовой есть одно блюдо стоимостью \(100\) тугриков и один школьник с одним тугриком, поэтому Сергей купит блюдо со стоимостью \(100\). Во втором примере после первого запроса есть одно блюдо со стоимостью один тугрик и один школьник, у которого есть \(100\) тугриков, поэтому Сергей ничего не получит. В третьем примере после первого запроса никто не сможет купить блюдо стоимостью \(8\), так что его получит Сергей. После второго запроса все блюда уже будут куплены до того, как настанет очередь Сергея. После третьего запроса запросе третий и пятый школьники купят соответственно первое и второе блюдо, а четвертое уже не купит никто. | |
![]()
|
|
D. Фёдор идет в президенты
Деревья
дп
Структуры данных
*2700
Фёдор выдвигается в президенты Байтландии! На дебатах (да-да!) его, конечно же, спросят, как он собирается решать транспортную проблему Байтландии? Дело действительно непростое, так как транспортная система Байтландии сейчас представляет собой дерево (связный граф без циклов). В министерстве транспорта Байтландии команда Федора выяснила, что средств в казне хватит на постройку всего одной дополнительной дороги. На дебатах Фёдор собирается сказать, что построит эту дорогу так, чтобы в стране было как можно больше различных простых путей. Простой путь — это путь, который проходит через каждую вершину не более одного раза. (два простых пути называются различными, если различается множество ребер, в них входящих). Однако наука Байтландии в упадке, и команде Фёдора не удалось найти ученых, которые быстро выяснят, а какого же максимальноого количества простых путей можно достичь добавлением в транспортную систему одного ребра? Поэтому он обратился к вам. Ответьте на этот вопрос. Можно добавлять ребро между вершинами, между которыми оно уже есть, но нельзя добавлять петлю. В этой задаче мы рассматриваем только простые пути длины хотя бы два. Выходные данные Выведите одно число — максимальное количество простых путей, которого можно добиться добавлением в граф ровно одного ребра. | |
![]()
|
|
D. Ирригация
Бинарный поиск
Деревья
реализация
сортировки
Структуры данных
*2200
Мальчика Мишу с юных лет волновали вопросы доставки воды. вот почему мама Миши отправила сына на ежегодную инновационную олимпиаду по ирригации (ИОИ). На этой олимпиаде школьники со всех концов Берляндии соревнуются в умении доставить воду для поливки растений самыми причудливыми способами. Проведение подобной олимпиады весьма затратно, поэтому спустя \(n\) первых проведений олимпиады было решено ввести правило, по которому будет определяться место проведения соревнования в следующий год. Город для проведения олимпиады выбирается следующим образом: всего в Берляндии есть \(m\) городов, пронумерованных от \(1\) до \(m\), готовых принять соревнование. Каждый год олимпиада проводится в городе, в котором она проводилась наименьшее число раз. Если таких городов несколько, то олимпиада проводится в городе с наименьшим номером среди городов с минимальным числом проведений олимпиады. Мишина мама очень волнуется за сына, поэтому её интересует, в каком городе будет проходить олимпиада в определённые годы. Единственная информация, которой располагает мама Миши, — места проведения олимпиады в первые \(n\) лет. Помогите маме Миши, и она попросит Мишу не залить вашу квартиру. Выходные данные Выведите \(q\) целых чисел. В строке с номером \(i\) выведите одно целое число — место проведения олимпиады в год \(k_i\). Примечание В первом примере Мишина мама интересуется о первых \(10\) годах после принятия нового правила, в эти года олимпиада пройдёт в городах 4, 3, 4, 2, 3, 4, 1, 2, 3, 4. Во втором примере после принятия нового правила олимпиада пройдёт в городах 2, 3, 1, 2, 3, 5, 1, 2, 3, 4, 5, 1. | |
![]()
|
|
D. Полное зеркало
Деревья
дп
Конструктив
поиск в глубину и подобное
реализация
хэши
*2400
Дерево состоит из \(n\) вершин. Выберите одну вершину как корень. Он должен удовлетворять условию ниже. - Для каждой пары вершин \(v_{1}\) и \(v_{2}\), если \(distance\)(\(root\), \(v_{1}\)) \(= distance\)(\(root\), \(v_{2})\), тогда \(degree\)(\(v_{1}\)) \(= degree\)(\(v_{2}\)), где \(degree\) — количество смежных вершин, а \(distance\) — количество ребер между двумя вершинами.
Определите и найдите, есть ли такой корень в дереве. Если есть несколько ответов, выведите любой из них. Выходные данные Если такой корень существует, выведите любой из них. Иначе выведите \(-1\). Примечание Рисунок до первого примера. \(1\), \(5\), \(7\) — также могут быть корнями.  Рисунок до второго примера. Невозможно найти корень графа.  | |
![]()
|
|
E1. Вторжение Далеков (лёгкая)
графы
Деревья
*1900
Хайди обнаружила, что Далеки создали сеть двусторонних Временных Коридоров, соединяющих различные точки пространства в разные моменты времени. Она подозревает, что они планируют очередное вторжение на всё Пространство и Время. Чтобы противостоять вторжению, она хочет развернуть ловушку во Вихре Времени, вдоль тщательно выбранного Временного Коридора. Хайди знает, что возится с Вихрем Времени опасно, поэтому она решила посоветоваться с Доктором. В результате, она узнала следующее: - Разные Временные Коридоры требуют разного количества энергии для поддержания их в стабильном состоянии.
- Далеки скорее всего не будут использовать все коридоры в своём вторжении. Они выберут набор Коридоров, которые требует минимальной суммы энергии для поддержания и при этом позволяет путешествовать между всеми точками (иначе говоря, они выберут минимальное остовное дерево).
- Установка ловушки может изменить энергию, необходимую для поддержания коридора стабильным.
Хайди решила провести полевые испытания и развернуть одну ловушку, разместив ее вдоль первого коридора. Но она хочет знать, собираются ли Далеки использовать этот коридор после развёртывания ловушки. Она дала вам карту Временных Коридоров (представляющую собой неориентированный граф) с требованиями на энергию для каждого Коридора. Для Коридора \(c\), \(E_{max}(c)\) это наибольшее \(e \le 10^9\), такое что если мы заменим требуемое количество энергии у \(c\) на \(e\), то Далеки возможно воспользуются \(c\) в своём вторжении (иначе говоря, оно будет входить в хотя бы одно минимальное остовное дерево). Вам нужно вычислить \(E_{max}(c_1)\) для Коридора \(c_1\), в котором Хайди хочет разместить ловушку, и которое является первым ребром графа. Выходные данные Выведите одно целое число: \(E_{max}(c_1)\) для первого Коридора \(c_1\) из входных данных. Примечание После установки ловушки новая потребность в энергии для первого Коридора может быть меньше, больше или равна старой потребности в энергии. В примере, если энергия первого Коридора установлена в \(4\) или меньше, то Далеки могут использовать множество Коридоров \(\{ \{ 1,2 \}, \{ 2,3 \} \}\) (в частности, если установить вес меньше \(4\), то это будет единственным возможным множеством Коридоров). Однако, если энергия будет больше \(4\), то Далеки воспользуются множеством Коридоров \(\{ \{2,3\}, \{3,1\} \}\). | |
![]()
|
|
E2. Вторжение Далеков (средняя)
графы
Деревья
кратчайшие пути
поиск в глубину и подобное
*2100
После успешных полевых испытаний, Хайди хочет развернуть ловушку вдоль какого-нибудь Коридора, не обязательно первого. Она хочет избежать встречи с Далеками внутри Временного Вихря, поэтому для большей осторожности она рассматривает размещение ловушек только вдоль тех коридоров, которые не будут использоваться в соответствии с текущим планом Далеков, который представляет из себя минимальное остовное дерево из Коридоров. Хайди знает, что потребности в энергии для всех Коридоров теперь разные, и что у Далеков есть единственный план, который они собираются использовать. Вашей задачей является вычисление функции \(E_{max}(c)\), которая определена также как и в лёгкой версии — как наибольшее \(e \le 10^9\), такое что если мы изменим энергию коридора \(c\) на \(e\), то Далеки могут им воспользоваться. Однако теперь эту функцию нужно вычислить для каждого коридора, который Хайди рассматривает. Выходные данные Выведите \(m-(n-1)\) строк по одному целому числу в каждой: \(E_{max}(c_i)\) для \(i\)-го Коридора \(c_i\) из входных данных, среди тех, которые не входят в План Далеков (минимальное остовное дерево) Примечание Если \(m = n-1\), то вам следует ничего не выводить. | |
![]()
|
|
E3. Вторжение Далеков (сложная)
графы
Деревья
снм
Структуры данных
*2400
С вашей помощью Хайди подготовила план размещения ловушки и защиты. Однако внезапно из ТАРДИС выпрыгнул Доктор и сказал ей, что он шпионил за подготовкой Далеков, и что их больше, чем когда-либо. Отчаянные времена требует отчаянных мер, поэтому Хайди собирается рискнуть и встретится с Далеками и что она рассмотрит вариант размещения ловушки вдоль любого Коридора. Это означает что ей опять нужна ваша помощь с вычислением \(E_{max}(c)\) — наибольшего \(e \le 10^9\), такого что если мы сменим требуемый уровень энергии у \(c\) на \(e\), то Далеки возможно воспользуются \(c\) в своём вторжении. Теперь нужно вычислить эту функцию для всех Временных Коридоров. Выходные данные Выведите \(m\) целых чисел: для каждого \(i\), \(E_{max}(c_i)\) для Коридора \(c_i\) из входных данных. | |
![]()
|
|
E. Покраска дерева
Деревья
дп
поиск в глубину и подобное
*2100
Вам задано дерево (неориентированный связный ацикличный граф), состоящее из \(n\) вершин. Вы играете в игру на этом дереве. Изначально все вершины белые. На первом ходу игры Вы выбираете одну вершину и красите ее в черный. Затем на каждом ходу Вы выбираете белую вершину, смежную (соединенную ребром) с любой черной вершиной и красите ее в черный. Каждый раз, когда вы выбираете вершину (даже во время первого хода), Вы получаете количество очков, равное размеру компоненты связности, состоящей только из белых вершин, содержащей выбранную вершину. Игра заканчивается, когда все вершины покрашены в черный цвет. Рассмотрим следующий пример: 
Вершины \(1\) и \(4\) уже покрашены в черный цвет. Если Вы выберете вершину \(2\), Вы получите \(4\) очка за компоненту связности, состоящую из вершин \(2, 3, 5\) и \(6\). Если Вы выберете вершину \(9\), Вы получите \(3\) очка за компоненту связности, состоящую из вершин \(7, 8\) и \(9\). Ваша задача — максимизировать количество очков, которое Вы получите. Выходные данные Выведите одно целое число — максимальное количество очков, которое вы получите, если будете играть оптимально. Примечание Первый тестовый пример показан в условии задачи. | |
![]()
|
|
A1. Прибавление на дереве
Деревья
*1600
Обратите внимание, что это первая задача из двух похожих задач. Вы можете взламывать эту задачу только тогда, когда решите обе задачи. Вам дано дерево с \(n\) вершинами. Изначально на каждом ребре написан \(0\). За одну операцию вы можете выбрать любые \(2\) различных листа \(u\), \(v\) и любое действительное число \(x\), и прибавить \(x\) ко всем числам записанных на ребрах на простом пути с \(u\) до \(v\). Для примера на изображении ниже показан результат применения двух операций к графу: прибавления \(2\) на пути от \(7\) до \(6\), а потом прибавления \(-0.5\) на пути от \(4\) до \(5\).  Верно ли, что для любой конфигурации действительных чисел записанных на ребрах, мы можем достичь ее, выполнив конечное число операций? Лист — это вершина степени \(1\). Простой путь — это путь, не содержащий ни одну вершину дважды. Выходные данные Если существует конфигурация действительных чисел записанных на ребрах дерева, которой мы не можем достичь выполнением операций, выведите «NO». Иначе выведите «YES». Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Примечание В первом примере, мы можем прибавить любое действительное \(x\) к числу записанному на единственному ребре \((1, 2)\).  Во втором примере одной из конфигураций, которые мы не можем достичь, является \(0\) записанный на \((1, 2)\) и \(1\) записанная на \((2, 3)\).  Ниже изображены графы с примеров \(3\), \(4\):   | |
![]()
|
|
A2. Прибавление на дереве: революция
Деревья
Конструктив
поиск в глубину и подобное
реализация
*2500
Обратите внимание, что это вторая задача из двух похожих задач. Вы можете взламывать эту задачу тогда, когда решите ее. Но предыдущую только тогда, когда решите обе задачи. Вам дано дерево с \(n\) вершинами. Изначально на каждом ребре написан \(0\). За одну операцию вы можете выбрать любые \(2\) различных листа \(u\), \(v\) и любое целое число \(x\), и прибавить \(x\) ко всем числам записанных на ребрах на простом пути с \(u\) до \(v\). Обратите внимание, что в предыдущей подзадаче \(x\) могло быть любым действительным, теперь оно должно быть целым. Для примера на изображении ниже показан результат применения двух операций к графу: прибавления \(2\) на пути от \(7\) до \(6\), а потом прибавления \(-1\) на пути от \(4\) до \(5\).  Вам дана некоторая конфигурация из неотрицательных целых, попарно различных, четных чисел, записанных на ребрах. Для заданной конфигурации необходимо сказать, можно ли получить ее с помощью данных операций, и, если это возможно, вывести последовательность операций, которая приводит к заданной конфигурации. Ограничения на операции смотрите в формате вывода. Лист это вершина степени \(1\). Простой путь это путь, не содержащий ни одну вершину дважды. Выходные данные Если требуемой последовательности операций не существует, в первой строке выведите «NO». Если же она существует, в первой строке выведите «YES». Во второй строке выведите \(m\) — количество операций, которое вы собираетесь применить (\(0 \le m \le 10^5\)). Заметьте, что минимизировать количество операций не требуется! В следующих \(m\) строках выведите операции в следующем формате: \(u, v, x\) (\(1 \le u, v \le n\), \(u \not = v\), \(x\) — целое число, \(-10^9 \le x \le 10^9\)), где \(u, v\) — листья, \(x\) — прибавляемое число. Гарантируется, что если существует последовательность операций, дающая заданную конфигурацию, то существует и последовательность операций, дающая ее, которая удовлетворяет всем заданными ограничениям. Примечание Конфигурация с первого примера нарисована ниже, и ее невозможно достичь.  Последовательность операций с второго примера иллюстрирована ниже.  | |
![]()
|
|
B. Динамический диаметр
*особая задача
Деревья
поиск в глубину и подобное
разделяй и властвуй
Структуры данных
Вам дано взвешенное неориентированное дерево с \(n\) вершинами, а также список из \(q\) обновлений. Каждое обновление меняет вес одного ребра. Ваша задача — вычислить диаметр дерева после каждого обновления. (Расстоянием между двумя вершинами называется сумма весов ребер на единственном простом пути между этими двумя вершинами. Диаметр дерева — наибольшее из этих расстояний.) Выходные данные Выведите \(q\) строк. Для всех возможных \(i\) строка \(i\) должна содержать диаметр дерева после \(i\)-го обновления. Система оценки Подзадача 1 (11 баллов): \(n,q \leq 100\) и \(w \leq 10,000\) Подзадача 2 (13 баллов): \(n,q \leq 5,000\) и \(w \leq 10,000\) Подзадача 3 (7 баллов): \(w \leq 10,000\), и все ребра дерева имеют вид \(\{1, i\}\) (То есть граф имеет вид «звезды» с центром в вершине 1.) Подзадача 4 (18 баллов): \(w \leq 10,000\), и все ребра дерева имеют вид \(\{i, 2i\}\) и \(\{i, 2i+1\}\) (То есть если мы подвесим дерево за вершину 1, то оно будет иметь вид сбалансированного бинарного дерева.) Подзадача 5 (24 балла): гарантируется, что после каждого обновления по крайней мере один из наидлиннейших простых путей проходит через вершину \(1\) Подзадача 6 (27 баллов): нет дополнительных ограничений Примечание Первый пример показан на рисунке ниже. Рисунок слева показывает изначальное дерево. Каждый следующий рисунок показывает ситуацию после очередного обновления. Вес обновленного ребра показан зеленым, а диаметр — красным. 
Первое обновление меняет вес \(3\)-го ребра, т.е. \(\{2, 4\}\), на \(1030\). Наибольшее расстояние между какой-либо парой вершин равно \(2030\) — расстояние между \(3\) и \(4\). Так как ответ равен \(2030\), то для второго обновления \(\)d'_2 = (1 + 2030) \bmod 3 = 0\(\) \(\)e'_2 = (1020 + 2030) \bmod 2000 = 1050\(\) Поэтому вес ребра \(\{1, 2\}\) меняется на \(1050\). Теперь наибольшее расстояние между вершинами \(\{1, 4\}\), оно равно \(2080\). Для третьего обновления имеем \(\)d'_3 = (1 + 2080) \bmod 3 = 2\(\) \(\)e'_3 = (890 + 2080) \bmod 2000 = 970\(\) Теперь, так как вес ребра \(\{2, 4\}\) уменьшается до \(970\), наиболее удаленная пара вершин, внезапно, \(\{1, 3\}\), а расстояние — \(2050\). | |
![]()
|
|
B. Волшебное дерево
*особая задача
Деревья
дп
Структуры данных
У нас есть волшебное дерево: корневое дерево с \(n\) вершинами. Вершины пронумерованы от \(1\) до \(n\). Вершина \(1\) является корнем. Волшебное дерево дает волшебные плоды. Плоды растут только в тех вершинах, которые не являются корнем. В каждой вершине может быть максимум один плод. Сейчас день 0 и ни один плод еще не поспел. Каждый плод будет спелым лишь в течение одного дня. Для каждого плода известна вершина \(v_j\), где он растет, день \(d_j\), когда он будет спелым, а также объем \(w_j\) волшебного сока, который мы можем получить, если соберем этот плод в тот день, когда он спелый. Плоды нужно собирать, отрезая некоторые ветви дерева. Каждый день можно отрезать сколько угодно ветвей. Те части дерева, которые вы отрежете, упадут на землю, и вы сможете собрать все спелые плоды, которые там есть. Все неспелые плоды, упавшие на землю, использовать для получения сока нельзя. Формально каждый день вы можете удалить некоторые ребра дерева. Когда вы делаете это, дерево распадается на несколько связных компонент. Вы удаляете все компоненты, не содержащие корень, и собираете все спелые плоды в этих компонентах. Вам дано описание дерево вместе с положением, временем поспевания и сочностью каждого из \(m\) плоды. Найдите максимальный объем сока, который вы можете получить. Выходные данные Выведите одно целое число — максимальных объем волшебного сока, который вы можете получить с дерева. Система оценки Подзадача 1 (6 баллов): \(n, k \leq 20\), а также \(w_j = 1\) для всех \(j\) Подзадача 2 (3 балла): фрукты растут только в листьях дерева Подзадача 3 (11 баллов): \(p_i = i-1\) для всех \(i\), а также \(w_j = 1\) для всех \(j\) Подзадача 4 (12 баллов): \(k \leq 2\) Подзадача 5 (16 баллов): \(k \leq 20\), а также \(w_j = 1\) для всех \(j\) Подзадача 6 (13 баллов): \(m \leq 1,000\) Подзадача 7 (22 балла): \(w_j = 1\) для всех \(j\) Подзадача 8 (17 баллов): нет дополнительных ограничений Примечание В примере одно из оптимальных решений выглядит так: - В день 4 отрезать ребро между вершинами 4 и 5 и собрать спелый плод с 1 единицей волшебного сока. В тот же день отрезать ребро между вершинами 1 и 2 и собрать 5 единиц волшебного сока со спелого плода в вершине 3.
- В день 7 ничего не делать. Мы могли бы собрать плод из вершины 4, но это не оптимально.
- В день 9 отрезать ребро между вершинами 1 и 4. Плод в вершине 4 уже не спелый, так что его нужно выбросить, а собрать 3 единицы волшебного сока со спелого фрукта в вершине 6. Кроме того, того же эффекта мы бы добились, отрезав ребро между вершинами 4 и 6.
| |
![]()
|
|
F. Пауки
Деревья
дп
жадные алгоритмы
*1400
Однажды мама попросила Петю разобрать игрушки и избавиться от части из них. Петя нашел целую коробку игрушечных пауков. Они очень ему дороги, и мальчик не хочет их выкидывать. Петя придумал хитрый план: он склеит всех паучков и подвесит к потолку. Также он знает, что чем ниже будет свисать эта конструкция, тем больше понравится маме, и она не станет выкидывать его самые любимые игрушки. Помогите Пете осуществить его план. Паук состоит из k бусинок, связанных k - 1 ниточкой. Каждая ниточка соединяет две различные бусинки, при этом любая пара бусинок, составляющих паука, либо непосредственно связана ниточкой, либо связана некоторой цепочкой из ниточек и бусинок. Склеивать пауков Петя может непосредственно за бусинки. Длина каждой нитки равна 1. Размерами бусинок можно пренебречь. Поэтому можно считать, что склеивание пауков происходит путем отождествления некоторых бусинок (см. рисунок). При этом конструкция, получаемая при склеивании, также должна представлять собой паука, т.е. для нее должны выполняться указанные свойства. После того, как Петя склеит всех пауков, он считает длину получившейся поделки. Расстояние между парой бусинок вычисляется как длина ниточек, соединяющих эти две бусинки. Длиной полученной конструкции называется наибольшее расстояние между всеми парами бусинок. Петя хочет получить конструкцию как можно большей длины.   На рисунке изображено 2 паучка из второго примера. К бусинке номер 2 первого паучка мы приклеим второго паучка за бусинку с номером 1. На рисунке выделены ниточки в паучках, которые образуют последовательность ниточек максимальной длины. Выходные данные Выведите одно число — длину искомой конструкции. | |
![]()
|
|
D. Почти все
Деревья
Конструктив
*2700
Дано дерево из \(n\) вершин. Вам необходимо расставить на его ребрах целые неотрицательные числа таким образом, чтобы выполнялось условие: Для каждых двух вершин \(i\), \(j\) посмотрим на путь между ними и посчитаем сумму чисел на ребрах этого пути. Выпишем полученную сумму на доску. Тогда каждое число от \(1\) до \(\lfloor \frac{2n^2}{9} \rfloor\) должно быть выписано по крайней мере один раз. Гарантируется, что такая расстановка существует. Выходные данные Выведите \(n-1\) строку, каждую вида \(u\) \(v\) \(x\) (\(0 \le x \le 10^6\)), что будет означать, что вы записали число \(x\) на ребре между \(u\), \(v\). Множество ребер \((u, v)\) должно совпадать с множеством ребер начального графа, но выводить ребра вы можете в любом порядке. Также вы можете выводить концы ребра в порядке, отличном от указанного во входных данных. Примечание В первом примере, расстояние между вершинами \(1\) и \(2\) равно \(2\), между \(2\) и \(3\) равно \(1\), между \(1\) и \(3\) равно \(3\). В третьем примере, числами от \(1\) to \(9\) (включительно) будут выписаны на доску, в то время как достаточно и от \(1\) до \(5\), чтобы пройти тест. | |
![]()
|
|
G. Инди альбом
Деревья
поиск в глубину и подобное
Строки
строковые суфф. структуры
Структуры данных
хэши
*2700
Любимая экспериментальная инди группа Мишки недавно выпустила новый альбом! У песен этого альбома есть одна общая особенность. Название каждой песни \(s_i\) — одно из следующих типов: - \(1~c\) — одна строчная латинская буква;
- \(2~j~c\) — название \(s_j\) (\(1 \le j < i\)) с приписанной к нему справа одной строчной латинской буквой.
Песни пронумерованы от \(1\) до \(n\). Гарантируется, что первая песня всегда типа \(1\). Вове тоже интересен новый альбом, но он никак не может найти время его послушать целиком. Поэтому он решил задать Мишке несколько вопросов о нем, чтобы узнать, достойна ли какая-нибудь песня прослушивания. Все вопросы имеют одинаковый формат: - \(i~t\) — посчитать количество вхождений строки \(t\) в \(s_i\) (название \(i\)-й песни альбома), как подстроки, \(t\) состоит только из строчных латинских букв.
И хотя Мишка не понимает, какая польза от этой информации, он старается помочь Вове. Однако вопросов так много, что он не справляется. Помогите, пожалуйста, Мише ответить на все вопросы Вовы. Выходные данные На каждый вопрос выведите одно целое число — количество вхождений строки вопроса \(t\) в название \(i\)-й песни альбома, как подстроки. Примечание Названия песен из первого примера: - d
- da
- dad
- dada
- dadad
- dadada
- dadadad
- dadadada
- d
- do
- dok
- doki
- dokid
- dokido
- dokidok
- dokidoki
- do
- dok
- doki
- dokidoki
Тогда вхождения для каждого вопроса следующие: - строка «da» начинается в позициях \([1, 3, 5, 7]\) в названии «dadadada»;
- строка «dada» начинается в позициях \([1, 3, 5]\) в названии «dadadada»;
- строка «ada» начинается в позициях \([2, 4, 6]\) в названии «dadadada»;
- строка «dada» начинается в позициях \([1, 3]\) в названии «dadada»;
- нет вхождений строки «dada» в названии «dad»;
- строка «doki» начинается в позиции \([1]\) в названии «doki»;
- строка «ok» начинается в позиции \([2]\) в названии «doki»;
- строка «doki» начинается в позициях \([1, 5]\) в названии «dokidoki»;
- строка «doki» начинается в позиции \([1]\) в названии «dokidok»;
- строка «d» начинается в позиции \([1]\) в названии «d»;
- нет вхождений строки «a» в названии «d»;
- строка «doki» начинается в позициях \([1, 5]\) в названии «dokidoki».
| |
![]()
|
|
H. Красно-синее дерево
Деревья
реализация
Структуры данных
*3500
Вам дано дерево с \(n\) вершинами. Дерево подвешено за вершину \(1\), которая не считается листом не зависимо от ее степени. Каждый лист покрашен в один из двух цветов: красный или синий. Листовая вершина с номером \(v\) исходно имеет цвет \(s_{v}\). Цвет каждой из внутренней вершины (включая корень) определятся следующим образом. - Обозначим за \(b\) количество синих непосредственных детей, и за \(r\) количество красных непосредственных детей данной вершины.
- Тогда цвет этой вершины синий тогда и только тогда, когда \(b - r \ge k\), иначе он красный.
Число \(k\) это параметр, одинаковый для всех вершин. Вам необходимо обработать запросы следующих типов: - 1 v: вывести цвет вершины \(v\);
- 2 v c: изменить цвет листа \(v\) на \(c\) (\(c = 0\) означает красный, \(c = 1\) означает синий);
- 3 h: изменить текущее значение \(k\) на \(h\).
Выходные данные Для каждого запроса первого типа выведите \(0\), если цвет вершины \(v\) красный, и \(1\) иначе. Примечание (i) Исходное дерево (ii) Дерево после 3-го запроса (iii) Дерево после 7-го запроса  | |
![]()
|
|
F. Коала и блокнот
графы
Деревья
кратчайшие пути
поиск в глубину и подобное
Строки
Структуры данных
*2600
Страна коал состоит из \(n\) городов и \(m\) двусторонних дорог, их соединяющих. Дороги пронумерованы от \(1\) до \(m\) в порядке входных данных. Гарантируется, что можно добраться от каждого города до любого другого города. Коала начинает путешествие из города \(1\). Каждый раз, когда он проходит по дороге, он записывает её номер в блокнот. Он не делает пробелов между числами, так что все записи склеятся в одно большое число. Перед тем как отправится в свой путь, Коала интересуется какое число может получится в блокноте в зависимости от конечного пункта. Для каждого возможного конечного пункта выясните, какое наименьшее число может для него получиться? Так как эти числа могут быть достаточно большими, вычислите их по модулю \(10^9+7\). Обратите внимание, что нужно вычислить остаток минимального возможного числа, не минимально возможный остаток. Выходные данные Выведите \(n - 1\) целое число — ответ для каждого города за исключением первого. \(i\)-е число должно быть равно наименьшему числу, которое получилось бы для конечной точки \(i+1\). Так как это число может быть достаточно большим, выведите его остаток по модулю \(10^9+7\). | |
![]()
|
|
C. Камил и проведение стрима
Деревья
математика
теория чисел
*2000
Камил любит стримить видео по спортивному программированию. Его канал на MeTube недавно набрал \(100\) миллионов подписчиков. Чтобы отпраздновать это, он выложил видео с интересной задачей, которую он пока не может решить. Можете ли вы помочь ему? Вам дано дерево — связный неориентированный граф состоящий из \(n\) вершин и \(n - 1\) ребер. Дерево подвешено за вершину \(1\). Вершина \(u\) является предком \(v\) если она лежит на кратчайшем пути между корнем и \(v\). В частности, вершина является предком себя. У каждой вершины \(v\) есть красота \(x_v\) — неотрицательное целое число не большее \(10^{12}\). Это позволяет нам определить красоту пути. Пусть \(u\) предок \(v\). Тогда определим красоту \(f(u, v)\) как наибольший общий делитель красот всех вершин на кратчайшем пути между \(u\) и \(v\). Формально, если \(u=t_1, t_2, t_3, \dots, t_k=v\) — вершины на кратчайшем пути между \(u\) и \(v\), тогда \(f(u, v) = \gcd(x_{t_1}, x_{t_2}, \dots, x_{t_k})\). Тут \(\gcd\) обозначает наибольший общий делитель множества чисел. В частности, \(f(u, u) = \gcd(x_u) = x_u\). Ваша задача найти сумму \(\) \sum_{u\text{ предок }v} f(u, v). \(\) Так как ответ может быть слишком большим, выведите его по модулю \(10^9 + 7\). Обратите внимание что для любого \(y\), \(\gcd(0, y) = \gcd(y, 0) = y\). В частности, \(\gcd(0, 0) = 0\). Выходные данные Выведите сумму красот всех таких путей \((u, v)\), что \(u\) предок \(v\). Эта сумма должна быть выведена по модулю \(10^9 + 7\). Примечание На следующей иллюстрации изображены все \(10\) возможных путей, в которых один из концов является предком другого. Сумма красот всех этих путей равна \(42\):  | |
![]()
|
|
G. Путь короля
*особая задача
Деревья
математика
*2500
В Древляндии \(n\) городов и \(n-1\) двусторонняя дорога. Каждая дорога соединяет пару различных городов. Из любого города можно проехать в любой другой, двигаясь только по дорогам. Города пронумерованы от \(1\) до \(n\). Да, конечно, вы узнали в этом описании неориентированное дерево. В каждом городе хранится один флаг, цвет флага в \(i\)-м городе равен \(c_i\). Возможно, что цвета флагов в разных городах совпадают. Если король едет по маршруту \([u_1, u_2, u_3, \dots, u_k]\), то это значит, что он стартует в городе \(u_1\), затем перемещается в город \(u_2\) (\(u_2\) соединён дорогой с \(u_1\)), затем из \(u_2\) в \(u_3\) (\(u_3\) соединён дорогой с \(u_2\)), и так далее пока не приедет в город \(u_k\). Возможно, что в процессе такого маршрута король посетит один и тот же город более одного раза. Иными словами, маршрут \([u_1, u_2, u_3, \dots, u_k]\) не обязательно состоит только из различных городов. В терминах теории графов — король перемещается из \(u_1\) в \(u_k\) по некоторому пути \([u_1, u_2, u_3, \dots, u_k]\), который не обязательно является простым (для всех \(j\) от \(1\) до \(k-1\) города \(u_j\) и \(u_{j+1}\) соединены дорогой). Когда король перемещается из одного города в другой, то главы городов в знак своей дружбы обмениваются флагами.  Пример перемещения короля по маршруту \([1, 4, 2, 6]\). Цвет вершины соответствуют цвету флага в этой вершине. Пример перемещения короля по маршруту \([1, 4, 2, 6]\). Цвет вершины соответствуют цвету флага в этой вершине. Из эстетических соображений, король хочет, чтобы цвет флага в городе \(i\) был равен \(d_i\) для всех \(i\) от \(1\) до \(n\). Определите, может ли король выбрать какой-то маршрут и проехать по нему так, чтобы для каждого города цвет флага в нём оказался равен желаемому цвету \(d_i\). Обратите внимание, что король может выбрать (и проехать) ровно один маршрут. В случае положительного ответа, найдите кратчайший возможный маршрут короля. В случае, если начальные цвета флагов уже соответствуют требованиям короля (то есть \(c_i=d_i\) для всех \(i\)), то считайте, что король совершает маршрут длины \(k=0\). Выходные данные Выведите ответы на все наборы в порядке их следования во входных данных. Каждый ответ должен начинаться со строки, содержащей «Yes» (в случае положительного ответа) или «No» (в случае, если искомого маршрута не существует). В случае положительного ответа следующая строка должна содержать целое число \(k\) — количество городов в кратчайшем возможном маршруте короля. Следующая строка должна содержать сам искомый маршрут \(u_1, u_2, \dots, u_k\) (\(1 \le u_i \le n\)). Вы можете не выводить эту строку, если \(k=0\). | |
![]()
|
|
H. Ремонт дорог в Древляндии
*особая задача
Бинарный поиск
Деревья
дп
*3100
В Древляндии \(n\) городов и \(n-1\) двусторонняя дорога. Каждая дорога соединяет пару различных городов. Из любого города можно проехать в любой другой, двигаясь только по дорогам. Города пронумерованы от \(1\) до \(n\). Да, конечно, вы узнали в этом описании неориентированное дерево. Правительство страны планирует отремонтировать все дороги. Каждая дорога будет отремонтирована некоторой частной компанией. Всего в стране \(10^6\) частных компаний, которые пронумерованы от \(1\) до \(10^6\). Допустимо, что некоторые компании не получат вообще дорог для ремонта, а некоторые будут ремонтировать множество дорог. Для упрощения контроля за работой частных компаний было введено следующее ограничение: для каждого города посчитаем количество различных компаний, которые чинят дороги, имеющие одним из концов этот город. Это число для каждого города не должно превосходить \(2\). Иными словами, для каждого города должно быть не более двух различных компаний, которые чинят дороги, имеющие отношение к этому городу. Национальный антикоррупционный комитет Древляндии опасается, что вся (или почти вся) работа достанется одной частной компании. По этой причине комитет требует, чтобы дороги были распределены по компаниям таким образом, чтобы минимизировать величину \(r\). Для каждой компании посчитаем количество назначенных ей дорог, максимум по этим количествам среди всех компаний называется числом \(r\). Помогите правительству найти такой способ распределить все дороги по компаниям требуемым образом. Выходные данные Выведите ответы для всех \(t\) наборов входных данных в тесте. Каждый набор должен начинаться строкой, которая содержит \(r\) — минимальное возможное количество дорог, назначенных наиболее используемой компании. Далее в следующей строке выведите \(n-1\) число \(c_1, c_2, \dots, c_{n-1}\) (\(1 \le c_i \le 10^6\)), где \(c_i\) обозначает номер компании, которой назначен ремонт \(i\)-й дороги. Если существует несколько способов назначения, выведите любой из них. | |
![]()
|
|
G. Запросы на пути
графы
Деревья
разделяй и властвуй
снм
сортировки
*1800
Вам задано взвешенное дерево, состоящее из \(n\) вершин. Напомним, что деревом называется связный граф без циклов. Вершины \(u_i\) и \(v_i\) соединены ребром веса \(w_i\). Вам задано \(m\) запросов. \(i\)-й запрос задан целым числом \(q_i\). В этом запросе вам необходимо посчитать количество пар вершин \((u, v)\) (\(u < v\)) таких, что максимальный вес ребра на простом пути между \(u\) и \(v\) не превосходит \(q_i\). Выходные данные Выведите \(m\) целых чисел — ответы на запросы. \(i\)-е число должно равняться количеству пар вершин \((u, v)\) (\(u < v\)) таких, что максимальный вес ребра на простом пути между \(u\) и \(v\) не превосходит \(q_i\). Запросы пронумерованы от \(1\) до \(m\) в порядке входных данных. Примечание Картинка, соответствующая дереву из первого тестового примера:  | |
![]()
|
|
E. Петя и конструктор
графы
Деревья
Конструктив
математика
сортировки
*2000
Недавно у Пети был день рождения. Его друзья знают, что Петя очень сильно любит головоломки, поэтому они подарили ему популярный конструктор «Электрик-\(n\)». Конструктор «Электрик-\(n\)» состоит из \(2n - 1\) проводов и \(2n\) лампочек. При этом каждая лампочка имеет свой уникальный номер, являющийся целыми числом от \(1\) до \(2n\), а все провода являются одинаковыми и неразличимы. Чтобы собрать конструктор требуется каждый из проводов использовать для соединения каких-то двух различных лампочек. Цепочкой в собранном конструкторе назовём последовательность из не менее чем двух различных лампочек, такую что любые две соседние в цепочке лампочки соединены проводом напрямую. Итоговая конфигурация конструктора является корректной, если сеть из проводов и лампочек имеет древовидную структуру, то есть любые две различные лампочки являются концами какой-нибудь цепочки. На протяжении нескольких дней Петя собирал различные конфигурации. Он обратил внимание на то, что иногда некоторые лампочки начинают светиться. После продолжительных экспериментов Петя выяснил, что лампочки с номерами \(2i\) и \(2i - 1\) горят тогда, когда цепочка между ними состоит ровно из \(d_i\) проводов. При этом выполнялось важное условие: значение \(d_i\) всегда было не больше \(n\). Сколько бы Петя не старался, у него так и не получилось найти конфигурацию, в которой бы светились все лампочки, поэтому он решил попросить помощи у вас. Требуется найти любую корректную конфигурацию, в которой горят все лампочки. Гарантируется, что это всегда возможно сделать. Выходные данные Выведите \(2n - 1\) строк. В \(i\)-й строке должны быть записаны два различных целых числа \(a_i\) и \(b_i\) (\(1 \leq a_i, b_i \leq 2n\), \(a_i \ne b_i\)), которые означают, что в вашей конфигурации лампочки с этими номерами соединены проводом. Если существует несколько правильных ответов, то разрешается вывести любой из них. Примечание  Ответ на первый тест из условия. Ответ на первый тест из условия.  Ответ на второй тест из условия. Ответ на второй тест из условия. | |
![]()
|
|
H. Укладывание плитки
Деревья
Конструктив
поиск в глубину и подобное
*2800
Новая пешеходная зона в центре Москвы состоит из \(n\) площадей, соединённых друг с другом с помощью \(n - 1\) пешеходных дорожек. Простым путём называется такая последовательность площадей, что никакая площадь не встречается в последовательности дважды, и любые две соседние в последовательности площади напрямую соединены пешеходной дорожкой. Размером простого пути будем называть количество площадей в образующей его последовательности. Дорожки спроектированы таким образом, что между любой парой различных площадей существует ровно один простой путь. В рамках подготовки к празднованию дня города московская мэрия планирует обновить плитку на всех \(n\) площадях. Всего существует \(k\) видов плитки разных цветов, пронумерованных от \(1\) до \(k\). Для каждой площади нужно выбрать ровно один вид плитки, который будет там уложен в процессе обновления. Чтобы сделать прогулки по центру Москвы более увлекательными, было решено назначить типы плиток площадям таким образом, чтобы для любого возможного простого пути размера ровно \(k\), при прогулке вдоль этого пути встречались бы все \(k\) различных типов плитки. Определите, можно ли уложить плитку подходящим образом или нет. Выходные данные Выведите «Yes», если уложить плитку возможно, и «No» иначе. В случае если ваш ответ «Yes», выведите \(n\) целых чисел от \(1\) до \(k\) — цвет плитки для каждой площади. Примечание Ниже изображена карта пешеходной зоны из первого и второго примеров, а также корректный выбор типов плитки для \(k = 4\).  | |
![]()
|
|
F. Задача с обязательными онлайн-запросами
графы
Деревья
разделяй и властвуй
снм
Структуры данных
*2600
Дан неориентированный граф из \(n\) вершин и без ребер. Вершины пронумерованы от \(1\) до \(n\). Необходимо ответить на запросы к нему. Пусть \(last\) будет ответом на предыдущий запрос второго типа (или \(0\), если таких запросов еще не было). Тогда запросы следующие: - \(1~x~y\) (\(1 \le x, y \le n\), \(x \ne y\)) — добавить неориентированное ребро между вершинами \((x + last - 1)~mod~n + 1\) и \((y + last - 1)~mod~n + 1\), если такого в графе нет, а иначе удалить его;
- \(2~x~y\) (\(1 \le x, y \le n\), \(x \ne y\)) — проверить, что существует путь между вершинами \((x + last - 1)~mod~n + 1\) и \((y + last - 1)~mod~n + 1\), который проходит только через существующие ребра, и выставить \(last\) значение \(1\), если есть, и \(0\) иначе.
Удачи! Выходные данные Выведите строку, состоящую из символов '0' и '1'. \(i\)-й символ должен быть равен ответу на \(i\)-й запрос второго типа. Таким образом, длина строки должна быть равна количеству запросов второго типа. Примечание Преобразованные запросы из первого примера: - 1 1 2
- 1 1 3
- 2 3 2
- 1 3 5
- 2 4 5
- 1 2 4
- 2 3 4
- 1 2 4
- 2 5 4
Преобразованные запросы из второго примера: - 1 1 2
- 1 2 3
- 1 3 1
- 2 1 3
- 1 1 3
- 2 3 1
- 1 2 3
- 2 2 3
- 2 1 2
| |
![]()
|
|
E. Туризм
графы
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
снм
*2200
Лёша решил отправиться в туристическую поездку по стране. Для простоты стоит считать, что в стране есть \(n\) городов и \(m\) двусторонних дороги, которые их соединяют. Лёша живёт в городе \(s\) и изначально находится в нём. Каждый город в стране по своему хорош, и чтобы сравнивать города между собой, Лёша поставил каждому городу оценку \(w_i\), которая тем больше, чем интереснее город кажется Лёше. Лёша считает, что его поездка по стране будет интересной только в том случае, если ему ни в какой момент времени не придётся ехать назад по дороге, по которой он только что проехал. Другими словами, если Лёша переехал из города \(u\) в город \(v\), следующим в своей поездке Лёша может выбрать любой город, соединённый с \(v\) дорогой, кроме города \(u\). Помогите Лёше спланировать поездку так, чтобы сумма оценок по всем посещённым им городам была максимальна. Считайте, что оценка любого посещённого города учитывается в сумме только один раз, даже если город был посещён не единожды. Выходные данные Выведите одно целое число — максимальную сумму оценок посещённых городов, которую можно получить. | |
![]()
|
|
E. Раскрась дерево
Деревья
дп
сортировки
*2100
Вам задано взвешенное дерево, состоящее из \(n\) вершин. Напомним, что деревом называется связный граф без циклов. Вершины \(u_i\) и \(v_i\) соединены ребром веса \(w_i\). Определим \(k\)-раскраску дерева как присвоение каждой вершине ровно \(k\) цветов, таким образом, что каждый цвет используется не более двух раз. Считайте, что различных доступных цветов бесконечно много. Назовем ребро насыщенным в \(k\)-раскраске, если его концы имеют хотя бы один общий цвет (т.е. найдется цвет, который присвоен обоим концам ребра). Так же определим счет \(k\)-раскраски как сумму весов насыщенных ребер. Вам необходимо найти максимально возможный счет \(k\)-раскраски заданного дерева. Вам нужно ответить на \(q\) независимых запросов. Выходные данные На каждый запрос выведите одно целое число — максимально возможный счет \(k\)-раскраски заданного дерева. Примечание Дерево, соответствующее первому запросу в тестовом примере: 
Одна из возможных \(k\)-раскрасок в первом запросе: \((1), (1), (2), (2)\), тогда ребра номер \(1\) и \(3\) являются насыщенными и сумма их весов равна \(8\). Дерево, соответствующее второму запросу в тестовом примере: 
Одна из возможных \(k\)-раскрасок во втором запросе: \((1, 2), (1, 3), (2, 4), (5, 6), (7, 8), (3, 4), (5, 6)\), тогда ребра номер \(1\), \(2\), \(5\) и \(6\) являются насыщенными и сумма их весов равна \(14\). | |
![]()
|
|
F. Фабрика деревьев
Деревья
жадные алгоритмы
Конструктив
*2500
Байтландская фабрика деревьев производит деревья для всевозможных промышленных применений. Вам требуется соптимизировать построение дерева определённого типа для большого и важного заказа. Нужное дерево является подвешенным деревом с \(n\) вершинами, и его вершины пронумерованы различными числами от \(0\) до \(n - 1\). Вершина с номером \(0\) является корнем дерева, и для любой некорневой вершины \(v\) номер её родителя \(p(v)\) меньше номера \(v\). Все деревья на фабрике делаются из заготовок-бамбуков. Бамбук — это такое корневое дерево, что каждая вершина имеет ровно одного сына, кроме единственной вершины-листа, у которой нет детей. Вершины бамбука-заготовки могут быть пронумерованы как угодно до начала обработки. Чтобы превратить бамбук в нужное дерево, вы можете применять один тип операций: выбрать произвольную некорневую вершину \(v\), такую что её родитель \(p(v)\) также не является корнем. Операция состоит в изменении родителя \(v\) на родителя его родителя \(p(p(v))\). Родители всех остальных вершин остаются без изменений, в частности, поддерево \(v\) не меняется. Эффективность крайне важна, поэтому вам требуется минимизировать количество операций для превращения бамбука-заготовки в нужное дерево. Постройте любую оптимальную последовательность операций. Обратите внимание, что нумерация вершин в полученном дереве должна совпадать с нумерацией в данном дереве. Формально, номера корней должны совпадать, а также для некорневых вершин с одинаковыми номерами должны совпадать номера их родителей. Гарантируется, что во всех тестах к этой задаче ответ существует, и, более того, в оптимальной последовательности не более \(10^6\) операций. Обратите внимание, что любой взлом, не удовлетворяющий этим ограничениям, будет некорректным. Выходные данные В первой строке выведите \(n\) различных целых чисел \(id_1, \ldots, id_n\) — изначальная нумерация вершин бамбука-заготовки, начиная с корня (\(0 \leq id_i < n\)). Во второй строке выведите одно целое число \(k\) — количество операций в вашей последовательности (\(0 \leq k \leq 10^6\)). В третьей строке выведите \(k\) целых чисел \(v_1, \ldots, v_k\), описывающих операции по порядку. \(i\)-я операция состоит в изменении \(p(v_i)\) на \(p(p(v_i))\). Каждая операция должна быть корректной, т.е. \(v_i\) и \(p(v_i)\) на момент операции не могут быть корнем. | |
![]()
|
|
F. Без одной вершины
Деревья
Конструктив
реализация
*2500
Дано целое число \(n\). Определим следующее дерево деревом McDic: - Создадим полное бинарное дерево с \(2^{n} - 1\) вершинами. То есть дерево, где ровно одна вершина является корнем, все листы имеют одинаковую высоту (расстояние до корня) и все не листовые вершины имеют по два прямых потомка.
- Выберем любую некорневую вершину \(v\) из этого бинарного дерева.
- Удалим \(v\) из дерева и проведем ребра между предком \(v\) и прямыми потомками \(v\). Если у \(v\) нет потомков, тогда ребра не добавляются.
Дано дерево. Определите, является ли это дерево деревом McDic. Если да, найдите предка удаленной вершины. Выходные данные Выведите две строки. В первой строке выведите одно целое число — количество ответов. Если это дерево не является деревом McDic, то выведите \(0\). Во второй строке выведите все возможные ответы в возрастающем порядке. Если это дерево не является деревом McDic, то ничего не выводите. Примечание В первом примере \(3\) — это единственный возможный ответ.  Во втором примере есть \(2\) возможных ответа.  В третьем примере дерево не является деревом McDic. | |
![]()
|
|
E. Лабиринт
Деревья
дп
поиск в глубину и подобное
Теория вероятностей
*2500
Лабиринт представляет из себя дерево (неориентированный граф, в котором между любой парой вершин существует ровно один путь). В лабиринте с определенной вероятностью выбираются вершины входа и выхода. Выход из лабиринта ищется при помощи обхода в глубину, в случае нескольких возможных ходов, ход выбирается равновероятно. Рассмотрим псевдокод:
DFS(x)
if x == вершина выхода then
завершить обход дерева
flag[x] <- TRUE
перемешать порядок вершин в V(x) // здесь каждая перестановка V(x) равновероятна
for i <- 1 to length[V] do
if flag[V[i]] = FALSE then
count++;
DFS(V[i]);
count++;
V(x) — список вершин смежных с x. Массив flag изначально заполнен FALSE. Изначально DFS запускается с параметром вершины входа. По завершению обхода в переменной count будет находится количество ходов. Требуется посчитать математическое ожидание количества ходов для нахождения выхода из лабиринта. Выходные данные Выведите матожидание количества ходов. Абсолютная или относительная погрешность не должна превосходить 10 - 9. Примечание В первом примере вершина входа всегда 1 и вершина выхода всегда 2. Во втором примере вершина входа всегда 1, вершина выхода с вероятностью 2/5 будет 2 или с вероятность 3/5 будет 3. Матожидания для вершин выхода 2 и 3 будут равны (симметричные случаи). На первом ходе с вероятностью 0.5 можно пойти в вершину выхода или с вероятностью 0.5 не в вершину выхода. В первом случаи количество ходов равно 1, во втором оно будет равно 3. Итоговое матожидание считается как 2 / 5 × (1 × 0.5 + 3 × 0.5) + 3 / 5 × (1 × 0.5 + 3 × 0.5) | |
![]()
|
|
F. Максимальное поддерево
графы
Деревья
дп
поиск в глубину и подобное
*2200
Пусть у вас есть \(k\) одномерных отрезков \(s_1, s_2, \dots s_k\) (каждый отрезок представляется двумя числами — координатами его концов). Тогда вы можете построить граф из \(k\) вершин на этих отрезках. Между \(i\)-й и \(j\)-й вершинами (\(i \neq j\)) есть ребро тогда и только тогда, когда отрезки \(s_i\) и \(s_j\) пересекаются (когда существует хотя бы одна точка, принадлежащая обоим отрезкам). Например, если \(s_1 = [1, 6], s_2 = [8, 20], s_3 = [4, 10], s_4 = [2, 13], s_5 = [17, 18]\), то граф будет выглядеть следующим образом:  Дерево размера \(m\) считается хорошим, если можно выбрать \(m\) таких одномерных отрезков, что граф, построенный на этих отрезках, совпадает с деревом. Вам задано дерево, найдите максимальный размер хорошего поддерева этого дерева. Напомним, что поддеревом называется связный подграф дерева. Обратите внимание, что вам нужно ответить на \(q\) независимых запросов. Выходные данные На каждый запрос выведите одно число — максимальный размер хорошего поддерева заданного дерева. Примечание В первом запросе одно из хороших поддеревьев размера \(8\) состоит из вершин: \({9, 4, 10, 2, 5, 1, 6, 3}\). | |
![]()
|
|
D. Покраска вершин
графы
Деревья
дп
Конструктив
Перебор
реализация
*1800
Вам задано дерево, состоящее из \(n\) вершин. Дерево — это связный неориентированный граф, не содержащий циклов.  Пример дерева. Пример дерева. Вы должны покрасить каждую вершину дерева в один из трех цветов. Для каждой вершины известна стоимость ее покраски в каждый из трех цветов. Вам нужно покрасить все вершины таким образом, чтобы в любом пути, состоящем ровно из трех различных вершин, цвета всех этих трех вершин были различны. Иными словами, рассмотрим все такие тройки вершин \((x, y, z)\), что \(x \neq y, y \neq z, x \neq z\), вершина \(x\) соединена ребром с вершиной \(y\), а вершина \(y\) соединена ребром с вершиной \(z\). Тогда цвета вершин \(x\), \(y\) и \(z\) должны быть попарно различны. Назовем такую покраску вершин хорошей. Перед вами стоит задача определить минимальную стоимость хорошей покраски дерева, а также в какой цвет необходимо покрасить каждую из вершин. Если не существует ни одной хорошей покраски дерева, сообщите об этом. Входные данные В первой строке следует целое число \(n\) \((3 \le n \le 100\,000)\) — количество вершин в дереве. Во второй строке следует последовательность \(c_{1, 1}, c_{1, 2}, \dots, c_{1, n}\) \((1 \le c_{1, i} \le 10^{9})\), где \(c_{1, i}\) равно стоимости покраски \(i\)-й вершины в первый цвет. В третьей строке следует последовательность \(c_{2, 1}, c_{2, 2}, \dots, c_{2, n}\) \((1 \le c_{2, i} \le 10^{9})\), где \(c_{2, i}\) равно стоимости покраски \(i\)-й вершины во второй цвет. В четвертой строке следует последовательность \(c_{3, 1}, c_{3, 2}, \dots, c_{3, n}\) \((1 \le c_{3, i} \le 10^{9})\), где \(c_{3, i}\) равно стоимости покраски \(i\)-й вершины в третий цвет. В каждой из следующих \((n - 1)\) строк следует по два целых числа \(u_j\) и \(v_j\) \((1 \le u_j, v_j \le n, u_j \neq v_j)\) — номера вершин, соединенных неориентированным ребром \(j\). Гарантируется, что заданные ребра образуют дерево. Выходные данные Если не существует хорошей покраски дерева, выведите \(-1\). В противном случае, в первой строке выведите минимальную стоимость хорошей покраски графа. Во второй строке выведите \(n\) целых чисел \(b_1, b_2, \dots, b_n\) \((1 \le b_i \le 3)\), где \(i\)-е число должно быть равно цвету, в который нужно покрасить вершину \(i\). Если подходящих покрасок минимальной стоимости несколько, разрешается вывести любую из них. Примечание В первом примере три вершины, поэтому все они должны быть покрашены в разные цвета. Первую вершину нужно покрасить в цвет \(1\), вторую вершину — в цвет \(3\), а третью вершину — в цвет \(2\). Стоимость такой покраски равна \(3 + 2 + 1 = 6\). | |
![]()
|
|
D. Шичикуджи и электросеть
графы
Деревья
жадные алгоритмы
кратчайшие пути
снм
*1900
Шичикуджи — новое местное божество Южного Храма Черной Улитки. Ее первое задание заключается в следующем: В префектуре X построено \(n\) новых городов. Города пронумерованы от \(1\) до \(n\). Город \(i\) находится в \(x_i\) км на север от храма и в \(y_i\) ем на восток от храма. Возможно, что \((x_i, y_i) = (x_j, y_j)\) даже если \(i \ne j\). Шичикуджи планирует обеспечить электричеством каждый город либо с помощью установки там электростанции, либо с помощью соединения его с другим городом, в котором уже есть электричество. То есть в городе есть электричество, если в нём есть электростанция или он соединён напрямую или по цепочке кабелей с городом, в котором есть электростанция. - Возведение электростанции в городе \(i\) стоит \(c_i\) иен;
- Соединение города \(i\) и города \(j\) стоит \(k_i + k_j\) иен за каждый км кабеля, использованного для соединения. Однако кабель можно прокладывать вдоль сторон света (на север, юг, восток, запад). Кабели могут пересекать друг друга. У каждого кабеля оба конца должны быть в некоторых городах. Если город \(i\) и город \(j\) соединены кабелем, то кабель всегда будет прокладываться по кратчайшему пути из города \(i\) в город \(j\). Тогда длина кабеля, соединяющего город \(i\) и город \(j\), равна \(|x_i - x_j| + |y_i - y_j|\) км.
Шичикуджи хочет осуществить эту затею, потратив как можно меньше денег, так как она считает, что нет ничего важнее в мире, чем деньги. Однако она умерла, когда была всего в пятом классе (разумеется, божества не стареют после смерти), поэтому недостаточно смышленая, чтобы воплотить проект в жизнь. Поэтому она просит вас о помощи. Таким образом, от вас требуется предоставить Шичикуджи следующую информацию: минимальное количество иен, необходимое, чтобы обеспечить электричеством все города, города, в которых будут построены электростанции, и проведенные соединения. Если существует несколько способов так выбрать города и соединения, чтобы получить конструкцию минимальной цены, то выведите любую из них. Выходные данные В первой строке выведите одно целое число, обозначающее минимальное количество иен, требуемых для конструкции. Затем выведите одно целое число \(v\) — количество электростанций, которые требуется построить. Далее выведите \(v\) целых чисел, обозначающих номера городов, в которых требуется построить электростанции. Каждое число должно быть от \(1\) до \(n\) и все числа должны быть попарно различны. Можно выводить числа в произвольном порядке. После этого выведите одно целое число \(e\) — количество необходимых соединений. Наконец, выведите \(e\) пар целых чисел \(a\) и \(b\) (\(1 \le a, b \le n\), \(a \ne b\)), обозначающих, что между городами \(a\) и \(b\) будет проведено соединение. Каждая неупорядоченная пара городов может встречаться не более одного раза (для каждого \((a, b)\) не должно больше существовать пар \((a, b)\) или \((b, a)\)). Пары можно выводить в произвольном порядке. Если существует несколько способов так выбрать города и соединения, чтобы получить конструкцию минимальной цены, то выведите любую из них. Примечание Для ответов на примеры смотрите на данные графики (города с электростанциями раскрашены зеленым, остальные — синим, кабели покрашены в красный): 
В первом примере цена строительства электростанций во всех городах равна \(3 + 2 + 3 = 8\). Можно показать, что больше никакая конфигурация не стоит меньше 8 иен. Во втором примере цена строительства электростанции в городе 2 равна 2. Стоимость соединения городов 1 и 2 равна \(2 \cdot (3 + 2) = 10\). Стоимость соединения городов 2 и 3 равна \(3 \cdot (2 + 3) = 15\). Поэтому итоговая цена равна \(2 + 10 + 15 = 27\). Можно показать, что никакая конфигурация не стоит меньше 27 иен. | |
![]()
|
|
F. Подмножество максимального веса
Деревья
дп
*2200
Вам задано дерево, состоящее из \(n\) вершин. Напомним что дерево — это связный неориентированный граф без циклов  Пример дерева. Пример дерева. Вершины пронумерованы от \(1\) до \(n\). Все вершины имеют вес, вес вершины \(v\) равен \(a_v\). Напомним, что дистанция между двумя вершинами в дереве равна количеству ребер на простом пути между ними. Ваша задача — найти подмножество вершин максимального суммарного веса (вес подмножества равен сумме весов всех вершин в нем) такое, что в этом подмножестве нет пары вершин на расстоянии \(k\) или меньше. Выходные данные Выведите одно целое число — максимально возможный суммарный вес подмножества, в котором все пары вершин находятся на расстоянии более \(k\). | |
![]()
|
|
B. Cleaning Robots
Деревья
дп
*2300
The new ICPC town has \(N\) junctions (numbered from \(1\) to \(N\)) which are connected by \(N-1\) roads. It is possible from one junction to go to any other junctions by going through one or more roads. To make sure all the junctions are well-maintained, the government environment agency is planning to deploy their newest advanced cleaning robots. In addition to its cleaning ability, each robot is also equipped with a movement ability such that it can move from one junction to any other junctions connected by roads. However, as you might have guessed, such robots are not cheap. Therefore, the agency is considering the following deployment plan. Let \(T_k\) be the set of junctions which should be cleaned by the \(k^{th}\) robot (also known as, the robot's task), and \(|T_k| \ge 1\) be the number of junctions in \(T_k\). The junctions in \(T_k\) form a path, i.e. there exists a sequence of \(v_1, v_2, \dots, v_{|T_k|}\) where \(v_i \in T_k\) and \(v_i \neq v_j\) for all \(i \neq j\) such that each adjacent junction in this sequence is connected by a road. The union of \(T\) for all robots is equal to the set of all junctions in ICPC town. On the other hand, no two robots share a common junction, i.e. \(T_i \cap T_j = \emptyset\) if \(i \neq j\). To avoid complaints from citizens for an inefficient operation, the deployment plan should be irreducible; in other words, there should be no two robots, \(i\) and \(j\), such that \(T_i \cup T_j\) forms a (longer) path. Note that the agency does not care whether the number of robots being used is minimized as long as all the tasks are irreducible. Your task in this problem is to count the number of feasible deployment plan given the town's layout. A plan is feasible if and only if it satisfies all the above-mentioned requirements. For example, let \(N = 6\) and the roads are \(\{(1,3),(2,3),(3,4),(4,5),(4,6)\}\). There are \(5\) feasible deployment plans as shown in the following figure. 
- The first plan uses \(2\) robots (labeled as A and B in the figure) to clean \(\{1,2,3\}\) and \(\{4,5,6\}\).
- The second plan uses \(3\) robots (labeled as A, B, and C in the figure) to clean \(\{1,3,4,6\}\), \(\{2\}\), and \(\{5\}\).
- The third plan uses \(3\) robots to clean \(\{1,3,4,5\}\), \(\{2\}\), and \(\{6\}\).
- The fourth plan uses \(3\) robots to clean \(\{1\}\), \(\{2,3,4,6\}\), and \(\{5\}\).
- The fifth plan uses \(3\) robots to clean \(\{1\}\), \(\{2,3,4,5\}\), and \(\{6\}\).
No other plans are feasible in this case. For example, the plan \(\{\{1,3\},\{2\},\{4,5,6\}\}\) is not feasible as the task \(\{1,3\}\) and \(\{2\}\) can be combined into a longer path \(\{1,3,2\}\). The plan \(\{\{1,2,3,4\},\{5\},\{6\}\}\) is also not feasible as \(\{1,2,3,4\}\) is not a path. Output Output in a line an integer representing the number of feasible deployment plans. As this output can be large, you need to modulo the output by \(1\,000\,000\,007\). Note Explanation for the sample input/output #1 This is the example from the problem description. | |
![]()
|
|
D. Find String in a Grid
Деревья
дп
Строки
Структуры данных
*3000
You have a grid \(G\) containing \(R\) rows (numbered from \(1\) to \(R\), top to bottom) and \(C\) columns (numbered from \(1\) to \(C\), left to right) of uppercase characters. The character in the \(r^{th}\) row and the \(c^{th}\) column is denoted by \(G_{r, c}\). You also have \(Q\) strings containing uppercase characters. For each of the string, you want to find the number of occurrences of the string in the grid. An occurrence of string \(S\) in the grid is counted if \(S\) can be constructed by starting at one of the cells in the grid, going right \(0\) or more times, and then going down \(0\) or more times. Two occurrences are different if the set of cells used to construct the string is different. Formally, for each string \(S\), you would like to count the number of tuples \(\langle r, c, \Delta r, \Delta c \rangle\) such that: - \(1 \le r \le R\) and \(r \le r + \Delta r \le R\)
- \(1 \le c \le C\) and \(c \le c + \Delta c \le C\)
- \(S = G_{r, c} G_{r, c + 1} \dots G_{r, c + \Delta c} G_{r + 1, c + \Delta c} \dots G_{r + \Delta r, c + \Delta c}\)
Output For each query in the same order as input, output in a line an integer representing the number of occurrences of the string in the grid. Note Explanation for the sample input/output #1 - There are \(2\) occurrences of "ABC", represented by the tuples \(\langle 1, 1, 1, 1 \rangle\) and \(\langle 1, 1, 0, 2 \rangle\).
- There are \(3\) occurrences of "BC", represented by the tuples \(\langle 1, 2, 0, 1 \rangle\), \(\langle 1, 2, 1, 0 \rangle\), and \(\langle 2, 1, 0, 1 \rangle\).
- There is \(1\) occurrence of "BD", represented by the tuple \(\langle 2, 1, 1, 0 \rangle\).
- There is no occurrence of "AC".
- There are \(2\) occurrences of "A", represented by the tuples \(\langle 1, 1, 0, 0 \rangle\) and \(\langle 3, 2, 0, 0 \rangle\).
| |
![]()
|
|
F. Regular Forestation
Деревья
хэши
*2400
A forestation is an act of planting a bunch of trees to grow a forest, usually to replace a forest that had been cut down. Strangely enough, graph theorists have another idea on how to make a forest, i.e. by cutting down a tree! A tree is a graph of \(N\) nodes connected by \(N - 1\) edges. Let \(u\) be a node in a tree \(U\) which degree is at least \(2\) (i.e. directly connected to at least \(2\) other nodes in \(U\)). If we remove \(u\) from \(U\), then we will get two or more disconnected (smaller) trees, or also known as forest by graph theorists. In this problem, we are going to investigate a special forestation of a tree done by graph theorists. Let \(V(S)\) be the set of nodes in a tree \(S\) and \(V(T)\) be the set of nodes in a tree \(T\). Tree \(S\) and tree \(T\) are identical if there exists a bijection \(f : V(S) \rightarrow V(T)\) such that for all pairs of nodes \((s_i, s_j)\) in \(V(S)\), \(s_i\) and \(s_j\) is connected by an edge in \(S\) if and only if node \(f(s_i)\) and \(f(s_j)\) is connected by an edge in \(T\). Note that \(f(s) = t\) implies node \(s\) in \(S\) corresponds to node \(t\) in \(T\). We call a node \(u\) in a tree \(U\) as a good cutting point if and only if the removal of \(u\) from \(U\) causes two or more disconnected trees, and all those disconnected trees are pairwise identical. Given a tree \(U\), your task is to determine whether there exists a good cutting point in \(U\). If there is such a node, then you should output the maximum number of disconnected trees that can be obtained by removing exactly one good cutting point. For example, consider the following tree of \(13\) nodes. 
There is exactly one good cutting point in this tree, i.e. node \(4\). Observe that by removing node \(4\), we will get three identical trees (in this case, line graphs), i.e. \(\{5, 1, 7, 13\}\), \(\{8, 2, 11, 6\}\), and \(\{3, 12, 9, 10\}\), which are denoted by \(A\), \(B\), and \(C\) respectively in the figure. - The bijection function between \(A\) and \(B\): \(f(5) = 8\), \(f(1) = 2\), \(f(7) = 11\), and \(f(13) = 6\).
- The bijection function between \(A\) and \(C\): \(f(5) = 3\), \(f(1) = 12\), \(f(7) = 9\), and \(f(13) = 10\).
- The bijection function between \(B\) and \(C\): \(f(8) = 3\), \(f(2) = 12\), \(f(11) = 9\), and \(f(6) = 10\).
Of course, there exists other bijection functions for those trees. Output Output in a line an integer representing the maximum number of disconnected trees that can be obtained by removing exactly one good cutting point, or output -1 if there is no such good cutting point. Note Explanation for the sample input/output #1 This is the example from the problem description. | |
![]()
|
|
F. Дешевый робот
Бинарный поиск
графы
Деревья
кратчайшие пути
снм
*2500
Вам дан простой, неориентированный, связный взвешенный граф с \(n\) вершинами и \(m\) ребрами. Вершины пронумерованы от \(1\) до \(n\). Есть ровно \(k\) центров (точек перезарядки), находящихся в вершинах \(1, 2, \ldots, k\). Рассмотрим робота, двигающегося по этому графу, с батареей емкости \(c\), пока не фиксированной конструктором. В любой момент времени батарея может содержать целое количество \(x\) энергии от \(0\) до \(c\) включительно. Переход по ребру веса \(w_i\) возможен, только если \(x \ge w_i\), и это стоит \(w_i\) энергии (\(x := x - w_i\)). Когда робот достигает центра, его батарея полностью перезаряжается (\(x := c\)). Вам дано \(q\) независимых миссий, в \(i\)-й миссии роботу требуется добраться от центра \(a_i\) до центра \(b_i\). Для каждой миссии, вам требуется найти минимальную емкость батареи, которая требуется, чтобы пройти эту миссию. Выходные данные Вам нужно вывести \(q\) строк, \(i\)-я из них должна содержать одно целое число: минимальная емкость, которая нужна, чтобы пройти \(i\)-ю миссию. Примечание В первом примере, граф является цепочкой \(10 - 9 - 2^C - 4 - 1^C - 5 - 7 - 3^C - 8 - 6\), где центрами являются вершины \(1\), \(2\) and \(3\). Для миссии \((2, 3)\), существует только один простой путь. Вот пример прохождения этой миссии с емкостью \(12\). - Робот начинает в вершине \(2\), с \(c = 12\) энергии.
- Робот использует ребро веса \(4\).
- Робот дошел до вершины \(4\), с \(12 - 4 = 8\) энергии.
- Робот использует ребро веса \(8\).
- Робот дошел до вершины \(1\) с \(8 - 8 = 0\) энергии.
- Робот на центре, поэтому его батарея перезаряжается. Теперь у него есть \(c = 12\) энергии.
- Робот использует ребро веса \(2\).
- Робот находится в вершине \(5\), с \(12 - 2 = 10\) очками энергии.
- Робот использует ребро веса \(3\).
- Робот находится в вершине \(7\), с \(10 - 3 = 7\) очками энергии.
- Робот использует ребро веса \(2\).
- Робот находится в вершине \(3\), с \(7 - 2 = 5\) очками энергии.
- Робот на центре, поэтому его батарея перезаряжается. Теперь у него есть \(c = 12\) энергии.
- Конец симуляции
Обратите внимание, что если бы \(c\) было меньше \(12\), у нас было бы меньше \(8\) энергии в вершине \(4\), поэтому было бы невозможно воспользоваться ребром \(4 \leftrightarrow 1\) веса \(8\). Таким образом \(12\) это минимальная возможная емкость, которой хватит, для прохождения миссии. — Граф во втором примере описан здесь (центры это красные вершины):  Робот может выполнить миссию \((3, 1)\) с батареей емкости \(c = 38\), испольуя путь \(3 \rightarrow 9 \rightarrow 8 \rightarrow 7 \rightarrow 2 \rightarrow 7 \rightarrow 6 \rightarrow 5 \rightarrow 4 \rightarrow 1\) Робот может выполнить миссию \((2, 3)\) с батареей емкости \(c = 15\), используя путь \(2 \rightarrow 7 \rightarrow 8 \rightarrow 9 \rightarrow 3\) | |
![]()
|
|
D. Запросы на дереве
Деревья
Структуры данных
Теория вероятностей
*2700
Хэнх — известный биолог. Он любит выращивать деревья и проводить эксперименты в своем собственном саду. Однажды он получил дерево, состоящее из \(n\) вершин. Вершины пронумерованы от \(1\) до \(n\). Дерево с \(n\) вершинами — это неориентированный связный граф с \(n - 1\) ребрами. Первоначально Хэнх устанавливает значение каждой вершины равным \(0\). Теперь Хэнх выполняет \(q\) запросов, каждых из которых имеет один из следующих типов: - Тип \(1\): Хэнх выбирает вершину \(v\) и целое число \(d\). Затем он выбирает некоторую вершину \(r\) полностью случайно, и для каждой вершины \(u\) такой, что путь от \(r\) до \(u\) проходит через \(v\), увеличивает значение в вершине \(u\) на \(d\).
- Тип \(2\): Хэнх выбирает вершину \(v\) и считает математическое ожидание значения вершины \(v\).
Поскольку Хэнх биолог, а не математик, ему нужна ваша помощь. Выходные данные Для каждого запроса второго типа выведите математическое ожидание. Пусть \(M = 998244353\). Можно показать, что ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Примечание Рисунок ниже показывает дерево в примере.  Для первого запроса, где \(v = 1\) и \(d = 1\): - Если \(r = 1\), значения всех вершин увеличатся.
- Если \(r = 2\), значения вершин \(1\) и \(3\) увеличатся.
- Если \(r = 3\), значения вершин \(1\), \(2\), \(4\) и \(5\) увеличатся.
- Если \(r = 4\), значения вершин \(1\) и \(3\) увеличатся.
- Если \(r = 5\), значения вершин \(1\) и \(3\) увеличатся.
Поэтому математические ожидания вершин после первого запроса такие: (\(1, 0.4, 0.8, 0.4, 0.4\)). Для второго запроса, где \(v = 2\) и \(d = 2\): - Если \(r = 1\), значения вершин \(2\), \(4\) и \(5\) увеличатся.
- Если \(r = 2\), значения всех вершин увеличатся.
- Если \(r = 3\), значения вершин \(2\), \(4\) и \(5\) увеличатся.
- Если \(r = 4\), значения вершин \(1\), \(2\), \(3\) и \(5\) увеличатся.
- Если \(r = 5\), значения вершин \(1\), \(2\), \(3\) и \(4\) увеличатся.
Поэтому математические ожидания вершин после второго запроса такие: (\(2.2, 2.4, 2, 2, 2\)). | |
![]()
|
|
E. Отправьте дерево Чарли
Деревья
Комбинаторика
поиск в глубину и подобное
снм
*3300
Рождество постучало в дверь, и наш главный герой, Боб, готовил захватывающий подарок для своего давнего второго лучшего друга Чарли. Поскольку ему не нравится шоколад, он решил вместо этого украсить дерево. Дерево Боба можно представить в виде неориентированного связного графа с \(n\) вершинами (пронумерованными от \(1\) до \(n\)) и \(n-1\) ребрами. Первоначально Боб поместил украшение с номером \(i\) на вершину \(i\) для каждого \(1 \le i \le n\). Однако, поскольку такая простая композиция получилась некрасивой, он решил немного переместить украшения. Формально Боб сделал следующие шаги: - Сначала он выписал все \(n-1\) ребра в некотором порядке.
- Затем он рассмотрел все ребра один за другим в таком порядке. Для каждого ребра \((u, v)\) он поменял местами украшение вершины \(u\) с украшением вершины \(v\).
После этого Боб оказался довольным такой аранжировкой и пошел спать. На следующее утро Боб просыпается, только чтобы узнать, что его прекрасная аранжировка разрушена! Прошлой ночью младший брат Боба, Бобо, бросил некоторые украшения на пол, когда играл с деревом. К счастью, украшения не были потеряны, поэтому Боб может восстановить дерево в кратчайшие сроки. Однако он полностью забыл, как дерево выглядело вчера. Поэтому, учитывая номера украшений, которые все еще на дереве, Боб хочет узнать количество возможных конфигураций дерева. Поскольку результат может быть довольно большим, Боб будет рад, если вы сможете вывести результат по модулю \(1000000007\) (\(10^9+7\)). Обратите внимание, что, возможно, не существует никаких возможных конфигураций. Выходные данные Выведите количество конфигураций по модулю \(1000000007\) (\(10^9+7\)). Примечание В первом примере возможными конфигурациями дерева являются \([2, 4, 1, 3]\) и \([3, 4, 2, 1]\). Во втором примере обратите внимание, что есть \(4! = 24\) возможных перестановок ребер, но возможны только \(12\) различные финальные конфигурации. В третьем примере легко увидеть, что украшение с номером \(1\) не может оставаться в вершине \(1\) после перестановок. | |
![]()
|
|
F. Покрашенное дерево
Деревья
Структуры данных
*2700
У вас есть дерево из \(n\) вершин. Цвет \(i\)-й вершины — \(h_{i}\). Стоимость дерева определяется как \(\sum\limits_{h_{i} = h_{j}, 1 \le i < j \le n}{dis(i,j)}\), где \(dis(i,j)\) — количество ребер на кратчайшем пути между \(i\) и \(j\). Вы не помните точные цвета вершин. Все, что вы помните — \(h_{i}\) может быть любым целым числом из \([l_{i}, r_{i}]\) (включая границы). Вы хотите посчитать суммарную стоимость всех деревьев, удовлетворяющих этим ограничениям, по модулю \(10^9 + 7\) (множество ребер фиксировано, но точные цвета неизвестны, поэтому всего таких деревьев \(\prod\limits_{i = 1}^{n} (r_{i} - l_{i} + 1)\)). Выходные данные Выведите одно целое число — суммарную стоимость всех деревьев, соответствующих ограничениям, взятую по модулю \(10^9 + 7\). Примечание В первом примере существует четыре способа покрасить дерево (то есть там надо просуммировать стоимость четырех деревьев): - дерево со следующими цветами: \(\lbrace 1,1,1,1 \rbrace\). Его стоимость равна \(dis(1,2)+dis(1,3)+dis(1,4)+dis(2,3)+dis(2,4)+dis(3,4) = 10\);
- дерево со следующими цветами: \(\lbrace 1,2,1,1 \rbrace\). Его стоимость равна \(dis(1,3)+dis(1,4)+dis(3,4)=4\);
- дерево со следующими цветами: \(\lbrace 1,1,1,2 \rbrace\). Его стоимость равна \(dis(1,2)+dis(1,3)+dis(2,3)=4\);
- дерево со следующими цветами: \(\lbrace 1,2,1,2 \rbrace\). Его стоимость равна \(dis(1,3)+dis(2,4)=4\).
Суммарная стоимость равна \(10+4+4+4=22\). | |
![]()
|
|
F. Экономические проблемы
графы
Деревья
дп
поиск в глубину и подобное
Потоки
Структуры данных
*2400
Электросеть дворцов в Берляндии состоит из 2-х сетей: основной и запасной. Провода во дворцах сделаны из дорогого материала, поэтому их продажа будет отличной идеей! Каждая из сетей (основная и запасная) имеет главный узел (он имеет номер \(1\)), из которого ток поступает на другие узлы сети. Все узлы доступны от главного по единственному пути. В обеих сетях количество узлов, из которых ток не распространяется дальше, равно \(n\). Иными словами, каждая из сетей является отдельным корневым ориентированным деревом с \(n\) листьями и с корнем в вершине \(1\). В каждом дереве свои вершины и своя независимая нумерация вершин. Кроме электросетей во дворце есть \(n\) приборов, каждый из которых соединён с одним из узлов основной и с одним из узлов запасной сети. Приборы соединяются только с такими узлами, из которых ток не распространяется далее (то есть, которые являются листьями). Каждый такой узел (лист дерева) соединён ровно с одним прибором.  В этом примере основная сеть содержит \(6\) узлов (изображена сверху), а запасная — \(4\) узла (изображена снизу). Количество приборов равно \(3\), они пронумерованы синим цветом. В этом примере основная сеть содержит \(6\) узлов (изображена сверху), а запасная — \(4\) узла (изображена снизу). Количество приборов равно \(3\), они пронумерованы синим цветом. Гарантируется, что вся электросеть (две сети и \(n\) приборов) может быть изображена на схеме способом, аналогичным картинке выше: - основная сеть будет составлять дерево сверху, в котором все провода ведут в направлении «сверху вниз»,
- запасная сеть будет составлять дерево снизу, в котором все провода ведут в направлении «снизу вверх»,
- приборы — горизонтальный ряд между ними, пронумерованный от \(1\) до \(n\) слева направо,
- провода между узлами сетей изображены непересекающимися отрезками.
Формально, для каждого дерева существует такой обход в глубину из вершины \(1\), что его листья посещаются в порядке их присоединения к приборам \(1, 2, \dots, n\) (то есть сначала узел, присоединенный к прибору \(1\), затем узел, присоединенный к прибору \(2\), и так далее). Предприниматель хочет продать (удалить) максимальное количество проводов так, чтобы на каждый прибор поступал ток из хотя бы одной сети. Иначе говоря, для каждого прибора должен существовать путь до главного узла сети (основной или запасной), проходящий по проводам сети от этого главного узла. Выходные данные Выведите единственное целое число — максимальное количество проводов, которые можно удалить из сети так, чтобы каждый прибор продолжил получать электрический ток. Примечание Для первого примера ниже на картинке изображен один из возможных вариантов решения (красным цветом отмечены провода, которые можно удалить):  Второй и третий примеры изображены ниже:  | |
![]()
|
|
D. Дерево отрезков
графы
Деревья
снм
Структуры данных
*2100
Как видно из названия задачи, вам предстоит решить задачу про отрезки и деревья. Напомним, что деревом является связный неориентированным граф, такой что между каждой парой его вершин существует ровно один простой путь. Вам дано \(n\) отрезков \([l_1, r_1], [l_2, r_2], \dots, [l_n, r_n]\), \(l_i < r_i\) для всех \(i\). Гарантируется, что концы отрезков являются целыми числами, все концы являются уникальными — нет такой пары отрезков, которые начинались бы в одной и той же точке, заканчивались в одной и той же точке, или один бы начинался в такой точке, что другой в ней заканчивается. Давайте построим граф с \(n\) вершинами. Вершины \(v\) и \(u\) соединены ребром тогда и только тогда, когда отрезки \([l_v, r_v]\) и \([l_u, r_u]\) пересекаются и ни один из них не лежит полностью внутри другого. Например, пары \(([1, 3], [2, 4])\) и \(([5, 10], [3, 7])\) будут образовывать ребра, а пары \(([1, 2], [3, 4])\) и \(([5, 7], [3, 10])\) не будут. Определите, является ли полученный граф деревом или нет. Выходные данные Выведите «YES», если полученный граф является деревом и «NO» в противном случае. Примечание Граф полученный в первом примере: 
Граф полученный во втором примере: 
Граф полученный в третьем примере: 
| |
![]()
|
|
E. Тесты для задачи D
Деревья
Конструктив
поиск в глубину и подобное
разделяй и властвуй
*2200
Нам было очень сложно придумать тесты для задачи D. Чтобы подготовить сильные тесты, нам пришлось решить следующую задачу. Для заданного неориентированного помеченного дерева, состоящего из \(n\) вершин, найдите набор отрезков, такой что: - концы каждого отрезка являются целыми числами от \(1\) до \(2n\), и каждое целое число от \(1\) до \(2n\) должно встречаться как конец ровно одного отрезка;
- все отрезки — невырожденные;
- для каждой такой пары чисел \((i, j)\), что \(i \ne j\), \(i \in [1, n]\) и \(j \in [1, n]\), вершины \(i\) и \(j\) соединены ребром тогда и только тогда, когда отрезки \(i\) и \(j\) пересекаются, но ни отрезок \(i\) не содержится полностью в отрезке \(j\), ни отрезок \(j\) полностью не содержится в отрезке \(i\).
А вы можете решить эту задачу? Выходные данные Выведите \(n\) пар целых чисел, \(i\)-я пара должна содержать два целых числа \(l_i\) и \(r_i\) (\(1 \le l_i < r_i \le 2n\)) — концы \(i\)-го отрезка. Все \(2n\) целых чисел, которые вы вывели, должны быть различными. Гарантируется, что ответ всегда существует. | |
![]()
|
|
C. Jeremy Bearimy
графы
Деревья
жадные алгоритмы
поиск в глубину и подобное
*2000
Добро пожаловать! Все хорошо. Вы прибыли в Среднее место, место между Хорошим местом и Плохим местом. Вам поручено выполнить два задания, одно сделает всех людей счастливыми, другое будет мучить их вечно. У вас есть список \(k\) пар людей, которые прибыли в новый район. Вам нужно назначить каждому из \(2k\) людей свой из \(2k\) домов. Каждый человек будет владельцем ровно одного дома и каждый дом будет иметь ровно одного владельца. Конечно, в этом районе можно перемещаться между домами. Всего есть \(2k - 1\) дорога, каждая из них соединяет два дома. Требуется некоторое время, чтобы проехать по дороге. Эти времена известны для каждой дороги. Район спроектирован таким образом, что между любыми двумя домами существует ровно один путь по дорогам от одного дома до другого, не проходящий по одной и той же дороге дважды. Другими словами, граф, в котором вершины это дома, а ребра это дороги это дерево. Люди в каждой из \(k\) пар людей хорошо дружат и любят ходить в гости. Мы пронумеруем пары людей от \(1\) до \(k\). Обозначим за \(f(i)\) время, которое требуется \(i\)-й паре людей, чтобы проехать между домами друг друга. Как уже было сказано ранее, вы должны сопоставить каждому из \(2k\) людей один из \(2k\) домов. У вас есть две миссии, одна назначена из Хорошего места, другая назначена из Плохого места. Эти миссии заключаются в следующем: - Первая миссия, из Хорошего места, заключается в том, чтобы сопоставить людям дома, так чтобы сумма \(f(i)\) по всем парам \(i\) была минимальна. Давайте обозначим эту минимальную возможную сумму за \(G\). Это дает нам уверенность, что все пары друзей могут легко и эффективно посещать друг друга;
- Вторая миссия, из Плохого места, заключается в том, чтобы сопоставить людям дома, так чтобы сумма \(f(i)\) по всем парам \(i\) была максимальна. Давайте обозначим эту максимальную возможную сумму за \(B\). Это дает нам уверенность, что все пары друзей могут только трудно и неэффективно посещать друг друга;
Чему равны значения \(G\) и \(B\)? Выходные данные Для каждого тестового случая, выведите два целых числа \(G\) и \(B\), разделенные пробелом. Примечание Для первого тестового случая, мы можем получить минимальную сумму равную \(G = 15\). Один из способов достичь такую сумму это следующее назначение домов: - Первой паре людей назначим дома \(5\) и \(6\), что даст нам \(f(1) = 5\);
- Второй паре людей назначим дома \(1\) и \(4\), что даст нам \(f(2) = 6\);
- Третьей паре людей назначим дома \(3\) и \(2\), что даст нам \(f(3) = 4\).
Обратите внимание, что тогда сумма всех \(f(i)\) это \(5 + 6 + 4 = 15\). Также мы можем получить максимальную сумму равной \(B = 33\). Один из способов достичь такую сумму это следующее назначение домов: - Первой паре людей назначим дома \(1\) и \(4\), что даст нам \(f(1) = 6\);
- Второй паре людей назначим дома \(6\) и \(2\), что даст нам \(f(2) = 14\);
- Третьей паре людей назначим дома \(3\) и \(5\), что даст нам \(f(3) = 13\).
Обратите внимание, что тогда сумма всех \(f(i)\) это \(6 + 14 + 13 = 33\). | |
![]()
|
|
D. Мисс Punyverse
Деревья
дп
жадные алгоритмы
*2500
Дуб имеет \(n\) гнезд, пронумерованных целыми числами от \(1\) до \(n\). Гнездо \(i\) это дом для \(b_i\) пчел и \(w_i\) ос. Некоторые гнезда соединены ветками. Мы называем два гнезда соседними если существует ветка, соединяющая их. Простой путь из гнезда \(x\) в \(y\) задается последовательностью \(s_0, \ldots, s_p\) различных гнезд, где \(p\) это неотрицательное целое число и \(s_0 = x\), \(s_p = y\) и \(s_{i-1}\) и \(s_{i}\) соседние для всех \(i = 1, \ldots, p\). Ветки дуба расположены так, что для любой пары гнезд \(x\) и \(y\) существует единственный простой путь из \(x\) в \(y\). По причине этого и биологи и программисты согласны, что дуб, по факту, является деревом. Деревня это непустое множество \(V\) гнезд, такое что для всех \(x\) и \(y\) из \(V\), существует простой путь из \(x\) в \(y\), все гнезда вдоль которого также лежат в \(V\). Множество деревень \(\cal P\) называется разбиением если каждое из \(n\) гнезд содержится в ровно одной деревне из \(\cal P\). Другими словами, никакие две деревни из \(\cal P\) не содержат одно и то же гнездо и в объединении дают все \(n\) гнезд. На дубе проводится ежегодный конкурс красоты мисс Punyverse. Всего два участника участвуют в этом году, это некрасивая оса и красивая пчела. Победитель конкурса красоты определяется голосованием, систему которого мы сейчас опишем. Пусть \(\mathcal{P}\) это разбиение гнезд на \(m\) деревень \(V_1, \ldots, V_m\). Проводится локальные выборы в каждой деревне. Каждое насекомое в деревне голосует за свое любимое насекомое. Если в деревне окажется, что строго больше голосов отдано за некрасивую осу чем за красивую пчелу, тогда некрасивая оса объявляется победителем в этой деревне. Иначе, красивая пчела побеждает. Известно, что пчелы всегда голосуют за пчел, то есть проголосуют за красивую пчелу в этом году и осы всегда голосуют за ос, то есть проголосуют за некрасивую осу в этом году. Все насекомые в улье участвуют в голосовании. Мэр Waspacito, а также его заместитель Alexwasp, хотят, чтобы некрасивая оса победила. Они имеют влияние и могут выбрать разбиение дуба на ровно \(m\) деревень. Если они выберут разбиение оптимально, определите максимальное количество деревень, в которых победит некрасивая оса. Выходные данные Для каждого тестового случая выведите целое число, равное максимальному количеству деревень, в которых победит некрасивая оса по всем разбиениям дуба на \(m\) деревень. Примечание В первом тестовом случае, нужно разделить \(n = 4\) гнезд на \(m = 3\) деревень. Мы можем так разделить, что некрасивая оса победит в \(2\) деревнях, например с помощью такого разбиения: \(\{\{1, 2\}, \{3\}, \{4\}\}\). В этом разбиении: - Некрасивая оса побеждает в деревне \(\{1, 2\}\), получив \(181\) голосов тогда как красивая пчела получила \(170\) голосов;
- Некрасивая оса также побеждает в деревне \(\{3\}\), получив \(111\) голосов тогда как красивая пчела получила \(70\) голосов;
- Некрасивая оса проиграет в деревне \(\{4\}\), получив \(0\) голосов тогда как красивая пчела получила \(50\).
Таким образом некрасивая оса победила в \(2\) деревнях и можно показать, что это максимально возможное число. Во втором тесте мы должны разделить \(n = 2\) гнезд на \(m = 1\) деревень. Есть только один способ это сделать: \(\{\{1, 2\}\}\). В этом разбиении некрасивая оса получит \(563\) голосов и красивая пчела также получит \(563\) голосов. Некрасивая оса побеждает, если получает строго больше голосов. Поэтому некрасивая оса не выиграет ни в какой деревне. | |
![]()
|
|
F. Гирлянда своими руками
Деревья
жадные алгоритмы
Конструктив
*2200
Поликарп решил украсить свою комнату перед Новым Годом. Одно из главных украшений — гирлянда, которую он спаяет сам. Простые гирлянды, в которых несколько лампочек расположены в ряд и соединены одним проводом, слишком скучны для Поликарпа. Он собирается спаять разветвленную гирлянду из \(n\) лампочек и \(n - 1\) провода. Ровно одна лампочка будет подключена к розетке, и от нее по проводам будет передаваться электроэнергия ко всем остальным лампочкам. Каждый провод соединяет ровно две лампочки, причем та из них, от которой будет идти энергия по этому проводу, называется главной, а та, которая получает энергию по этому проводу, называется побочной. Очевидно, для каждой лампочки существует не более одного провода, для которого она является побочной. У каждой лампочки есть своя яркость, причем яркость \(i\)-й лампочки равна \(2^i\). Назовем важностью провода суммарную яркость тех лампочек, которые окажутся отсоединены от источника энергии, если этот провод (и только его) удалить. Естественно, более важные провода должны быть более надежными. Поликарп нарисовал схему гирлянды, которую он хочет спаять (на схеме указаны все \(n\) лампочек и \(n - 1\) проводов, а также отмечена лампочка, которая будет подключена к электросети; провода расположены так, что энергия может передаваться до всех лампочек). После этого Поликарп посчитал важность каждого провода, пронумеровал их от \(1\) до \(n - 1\) в порядке уменьшения важности, а затем (с учётом новой нумерации проводов) для каждого провода записал номер его главной лампочки. На следующий день Поликарп купил необходимые провода и решил спаять гирлянду — но, к сожалению, не смог найти схему. Вспомнив, что у него есть список номеров главных лампочек для всех проводов в порядке уменьшения их важности, он решил попытаться восстановить схему гирлянды по этому списку. Можете ли вы помочь ему с восстановлением схемы? Выходные данные Если схему восстановить невозможно, выведите одно целое число: \(-1\). В противном случае выведите схему следующим образом. В первой строке выведите одно целое число \(k\) (\(1 \le k \le n\)) — номер лампочки, подключенной к электросети. Затем выведите \(n - 1\) строк, в каждой из которых должны быть заданы два целых числа \(x_i\) и \(y_i\) (\(1 \le x_i, y_i \le n\), \(x_i \ne y_i\)) — номера лампочек, соединенных некоторым проводом. Описания проводов (и номера лампочек, соединенных проводом) могут быть выведены в любом порядке. Вывод должен соответствовать некоторой схеме, по которой Поликарп мог бы выписать список чисел \(a_1\), \(a_2\), ..., \(a_{n - 1}\). Если таких схем несколько, выведите любую из них. Примечание Схема для первого примера (R обозначает лампу, подключенную к сети; числа на проводах обозначают их важность): 
| |
![]()
|
|
F. Новый год и социальная сеть
графы
Деревья
математика
Паросочетания
Структуры данных
*3200
Новая социальная сеть (НСС) от Donghyun содержит \(n\) пользователей с номерами \(1, 2, \ldots, n\). Их сеть представляет собой дерево, поэтому между пользователем существует \(n-1\) прямых соединений. Каждый пользователь может связаться с другим пользователем, используя некоторую последовательность прямых соединений. Мы будем обозначать эту первичную сеть как \(T_1\). Чтобы предотвратить возможную поломку сервера, Donghyun создал резервную сеть \(T_2\), которая соединяет тех же \(n\) пользователей как дерево. Если система выходит из строя, ровно одно ребро \(e \in T_1\) становится непригодным для использования. В этом случае Donghyun защитит ребро \(e\), выбрав другое ребро \(f \in T_2\), и добавит его в существующую сеть. Это новое ребро должно сделать сеть опять связной. Donghyun хочет выбрать заменяющее ребро \(f \in T_2\) для максимально возможного количества ребер \(e \in T_1\). Однако, поскольку резервная сеть \(T_2\) является хрупкой, \(f \in T_2\) может быть выбрано в качестве замещающего ребра для не более одного ребра в \(T_1\). С этим ограничением Donghyun хочет защитить как можно больше ребер в \(T_1\). Формально, пусть \(E(T)\) — множество ребер дерева \(T\). Рассмотрим двудольный граф с двумя долями \(E(T_1)\) и \(E(T_2)\). Для \(e \in E(T_1), f \in E(T_2)\), существует ребро, соединяющее \(\{e, f\}\) тогда и только тогда, когда граф \(T_1 - \{e\} + \{f\}\) — дерево. Вы должны найти максимальное паросочетание в этом двудольном графе. Выходные данные В первой строке выведите целое число \(m\) (\(0 \leq m < n\)), размер максимального по размеру паросочетания. В следующих \(m\) строках выведите по четыре целых числа \(a_i, b_i, c_i, d_i\). Эти четыре целых числа описывают, что ребро \((a_i, b_i)\) из \(T_1\) объединено в пару с ребром \((c_i, d_i)\) из \(T_2\). Все выведенные ребра должны принадлежать соответствующим деревьям, и все выведенные ребра одного дерева должны быть различными. Если убирают ребро \((a_i, b_i)\) из \(T_1\) и добавляют ребро \((c_i, d_i)\) из \(T_2\), то сеть должна оставаться связной. Порядок выведенных пар и порядок вершин внутри ребер не имеет значения. Если есть несколько возможных решений, вы можете вывести любое. | |
![]()
|
|
D. Dr. Evil Underscores
битмаски
Деревья
дп
жадные алгоритмы
Перебор
поиск в глубину и подобное
разделяй и властвуй
Строки
*1900
Сегодня Бакри в качестве дружеского подарка вручил Бадави \(n\) целых чисел \(a_1, a_2, \dots, a_n\) и дал ему задачку выбрать такой \(X\), что \(\underset{1 \leq i \leq n}{\max} (a_i \oplus X)\) принимает минимальное возможное значение, где \(\oplus\) обозначает операцию побитового исключающего ИЛИ. Бадави, как обычно, ленится, поэтому вы решили помочь ему и найти минимальное возможное значение \(\underset{1 \leq i \leq n}{\max} (a_i \oplus X)\). Выходные данные Выведите одно целое число — минимальное возможное значение \(\underset{1 \leq i \leq n}{\max} (a_i \oplus X)\). Примечание В первом примере можно выбрать \(X = 3\). Во втором примере можно выбрать \(X = 5\). | |
![]()
|
|
E. Удали один отрезок
графы
Деревья
дп
Конструктив
Перебор
сортировки
Структуры данных
*2300
На координатной прямой \(Ox\) заданы \(n\) отрезков \([l_1, r_1]\), \([l_2, r_2]\), ..., \([l_n, r_n]\). Отрезок \([l, r]\) покрывает все точки от \(l\) до \(r\) включительно, то есть такие \(x\), что \(l \le x \le r\). Отрезки могут располагаться произвольным образом — вкладываться друг в друга, совпадать и т.п. Отрезки могут вырождаться в точку, то есть допустимо, что \(l_i=r_i\). Объединением набора отрезков называется такой минимальный набор отрезков, который покрывает в точности тот же набор точек, что и заданный набор. Например: - если \(n=3\) и отрезки имеют вид \([3, 6]\), \([100, 100]\), \([5, 8]\), то их объединение состоит из \(2\) отрезков: \([3, 8]\) и \([100, 100]\);
- если \(n=5\) и отрезки имеют вид \([1, 2]\), \([2, 3]\), \([4, 5]\), \([4, 6]\), \([6, 6]\) то их объединение состоит из \(2\) отрезков: \([1, 3]\) и \([4, 6]\).
Очевидно, что объединение — это набор непересекающихся отрезков. Требуется удалить ровно один отрезок из заданных \(n\) таким образом, чтобы количество отрезков в объединении оставшихся \(n-1\) было наибольшим. Например, если \(n=4\) и отрезки имеют вид \([1, 4]\), \([2, 3]\), \([3, 6]\), \([5, 7]\), то: - если из набора удалить первый отрезок, то останутся отрезки \([2, 3]\), \([3, 6]\), \([5, 7]\), объединение которых состоит из \(1\) отрезка;
- если из набора удалить второй отрезок, то останутся отрезки \([1, 4]\), \([3, 6]\), \([5, 7]\), объединение которых состоит из \(1\) отрезка;
- если из набора удалить третий отрезок, то останутся отрезки \([1, 4]\), \([2, 3]\), \([5, 7]\), объединение которых состоит из \(2\) отрезков;
- если из набора удалить четвертый отрезок, то останутся отрезки \([1, 4]\), \([2, 3]\), \([3, 6]\), объединение которых состоит из \(1\) отрезка.
Таким образом, в примере выше надо обязательно удалять третий отрезок, чтобы получить ответ \(2\). Напишите программу, которая найдет наибольшее количество отрезков, которые получатся в объединении \(n-1\) оставшегося, если можно удалить любой из заданных \(n\) отрезков. Обратите внимание, что если в заданном наборе есть несколько одинаковых отрезков, то удалить вы всё-равно можете ровно один из них. То есть набор отрезков после удаления одного будет содержать ровно \(n-1\) отрезок. Выходные данные Выведите \(t\) чисел — ответы на заданные \(t\) наборов входных данных в порядке их следования в тесте. Ответ равен максимальному количеству отрезков в объединении \(n-1\) отрезка из \(n\) заданных, если допускается удалить один любой отрезок. | |
![]()
|
|
B. Числа на дереве
графы
Деревья
жадные алгоритмы
Конструктив
поиск в глубину и подобное
Структуры данных
*1800
Евлампию подарили корневое дерево, вершины которого пронумерованы от \(1\) до \(n\). В каждой \(i\)-й вершине написано число \(a_i\). Евлампий посчитал для каждой вершины \(i\) величину \(c_i\) — количество вершин \(j\) в поддереве вершины \(i\), для которых \(a_j < a_i\).  Иллюстрация ко второму примеру, первым написано \(a_i\), а в скобках написано \(c_i\) Иллюстрация ко второму примеру, первым написано \(a_i\), а в скобках написано \(c_i\)После нового года Евлампий не смог вспомнить, каким был его подарок! Он помнит дерево и значения \(c_i\), однако совсем забыл, какие числа \(a_i\) были написаны в вершинах. Помогите ему восстановить исходные числа! Выходные данные Если решение существует, то в первой строке выведите «YES», а во второй строке выведите \(n\) чисел \(a_i\) \((1 \leq a_i \leq {10}^{9})\) — искомые числа, которые были записаны в вершинах дерева. Если решений несколько, выведите любое из них. Можно показать, что если решение существует, то также существует решение, где все \(a_i\) лежат от \(1\) до \(10^9\). Если же решения не существует, то выведите «NO». | |
![]()
|
|
C. Атака Ксенона
Деревья
дп
жадные алгоритмы
Комбинаторика
поиск в глубину и подобное
*2300
На другом этаже A.R.C. Markland-N, молодой человек Саймон "Ксенон" Джексон отдыхает, завершив свои работы по проекту быстрее запланированного (впрочем как всегда). Так как свободного времени достаточно много, он надевает свой легендарный хакерский "X" инстинкт и бежит сражаться против банд кибермира. Его целью является сеть из \(n\) небольших банд. Их сеть состоит из ровно \(n - 1\) прямых соединений, каждое из которых связывает какие-то две банды вместе. Соединения устроены таким образом, что любые две банды соединены через последовательность прямых соединений. Изучая данные, Ксенон понял, что банды используют для самозащиты следующую форму шифрования. Каждому соединению назначено целое число от \(0\) до \(n - 2\), таким образом, что все назначенные числа различны, а каждое число назначено какому-то соединению. Если атакующий пытается получить доступ к защищённым данным, то ему придётся прорваться через \(S\) слоёв с паролями, где \(S\) определяется как: \(\)S = \sum_{1 \leq u < v \leq n} mex(u, v)\(\) Здесь \(mex(u, v)\) обозначает наименьшее неотрицательное целое число, которое не встречается на соединениях на единственном простом пути между бандами \(u\) и \(v\). Ксенон не знает каким образом числа были назначены соединениям, но это не проблема. Он собирается поручить своим AI перебрать и взломать все пароли, но перед этим он хочет знать чему равно наибольшее возможное значение \(S\), чтобы настроить AI наиболее эффективно. Сейчас Ксенон ушёл писать скрипты для AI, и он собирается их закончить в течение двух часов. Не могли бы вы найти наибольшее значение \(S\) перед тем, как он вернётся? Выходные данные Выведите наибольшее возможное значение \(S\) — количества слоёв с паролями в сети банд. Примечание В первом примере можно достичь максимального \(S\) следующим образом:  В этой сети, \(mex(1, 2) = 0\), \(mex(1, 3) = 2\) и \(mex(2, 3) = 1\). Таким образом, \(S = 0 + 2 + 1 = 3\). Во втором примере можно достичь максимального \(S\) таким образом:  В этой сети все ненулевые значения mex перечислены ниже: - \(mex(1, 3) = 1\)
- \(mex(1, 5) = 2\)
- \(mex(2, 3) = 1\)
- \(mex(2, 5) = 2\)
- \(mex(3, 4) = 1\)
- \(mex(4, 5) = 3\)
Таким образом, \(S = 1 + 2 + 1 + 2 + 1 + 3 = 10\). | |
![]()
|
|
D. Хаотичная В.
графы
Деревья
дп
жадные алгоритмы
математика
теория чисел
*2700
«Всё было спланировано, Никаких больше скрытых забот. Состояние Цитуса тоже совершенно..» Текущее время...... 00:01:12...... Время пришло. Образцов эмоций теперь достаточно. Прошло почти три года, и пришло время для Айви разбудить свою связанную сестру Ванессу. Система внутри библиотеки A.R.C. может быть представлена как неориентированный граф с бесконечным числом обрабатывающих вершин, пронумерованных последовательными положительными целыми числами (\(1, 2, 3, \ldots\)). Вершина с номером \(x\) (\(x > 1\)) напрямую соединена с вершиной с номером \(\frac{x}{f(x)}\), где \(f(x)\) обозначает наименьший простой делитель \(x\). Разум Ванессы разделён на \(n\) фрагментов. Спустя более 500 лет в коме, фрагменты несколько подраскидало: \(i\)-й фрагмент теперь находится в вершине с номером \(k_i!\) (факториал \(k_i\)). Чтобы максимизировать шансы успешного пробуждения, Айви хочет разместить образцы эмоций в вершине \(P\), такой что суммарная длина всех путей от каждого фрагмента до \(P\) является минимально возможной. В случае если несколько фрагментов расположены в одной и той же вершине, путь от них до \(P\) учитывается несколько раз. В мире нулей и единиц такое требование вполне тривиально для Айви. Не более, чем секундой позже, она уже нашла такую вершину. Возможно ли такое же для простого смертного как вы? Для простоты, найдите минимальную суммарную длину путей от каждого фрагмента до оптимальной вершины \(P\). Выходные данные Выведите одно целое число, обозначающее минимальную сумму путей от фрагментов до вершины с образцами эмоций \(P\). Напомним, что если несколько фрагментов расположены в одной вершины, то расстояние от этой вершины до \(P\) нужно учесть несколько раз. Примечание Первые \(24\) вершины системы выглядят следующим образом (вершины \(1!\), \(2!\), \(3!\), \(4!\) обозначены жирным): 
В первом примере Айви может разместить образцы эмоций в вершине \(1\), тогда: - Расстояние от первого фрагмента Ванессы до вершины \(1\) равно \(1\).
- Расстояние от второго фрагмента Ванессы до вершины \(1\) равно \(0\).
- Расстояние от третьего фрагмента Ванессы до вершины \(1\) равно \(4\).
Суммарная длина равна \(5\). Во втором примере Айви оптимальной вершина для сбора является \(6\): - Расстояние от первого фрагмента Ванессы до вершины \(6\) равно \(0\).
- Расстояние от второго фрагмента Ванессы до вершины \(6\) равно \(2\)..
- Расстояние от третьего фрагмента Ванессы до вершины \(6\) равно \(2\).
- Расстояние от четвёртого фрагмента Ванессы до вершины \(6\) снова равно \(2\).
Суммарная длина равна \(6\). | |
![]()
|
|
F. Три пути в дереве
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
*2000
Вам задано невзвешенное дерево с \(n\) вершинами. Напомним, что дерево — это связный неориентированный граф без циклов. Ваша задача — выбрать три различных вершины \(a, b, c\) в этом дереве таких, что количество ребер, принадлежащих как минимум одному из простых путей между \(a\) и \(b\), \(b\) и \(c\), или \(a\) и \(c\), максимально. Обратите внимание на примечания для лучшего понимания. Простой путь — это путь, который посещает каждую вершину не более одного раза. Выходные данные Первой строкой выведите одно целое число \(res\) — максимальное количество ребер, принадлежащих как минимум одному из простых путей между \(a\) и \(b\), \(b\) и \(c\), или \(a\) и \(c\). Во второй строке выведите три целых числа \(a, b, c\) таких, что \(1 \le a, b, c \le n\) и \(a \ne, b \ne c, a \ne c\). Если существует несколько подходящих ответов, вы можете вывести любой. Примечание Изображение, соответствующее первому примеру (и другой правильный ответ): 
Если выбрать вершины \(1, 5, 6\), то путь между вершинами \(1\) и \(5\) состоит из ребер \((1, 2), (2, 3), (3, 4), (4, 5)\), путь между \(1\) и \(6\) состоит из ребер \((1, 2), (2, 3), (3, 4), (4, 6)\) и путь между \(5\) и \(6\) состоит из ребер \((4, 5), (4, 6)\). Объединение этих путей — \((1, 2), (2, 3), (3, 4), (4, 5), (4, 6)\), следовательно, ответ — \(5\). Можно показать, что лучшего ответа не существует. | |
![]()
|
|
F. Красоты Берляндии
Деревья
жадные алгоритмы
Конструктив
поиск в глубину и подобное
сортировки
*2100
В Берляндии есть \(n\) железнодорожных станций, которые соединены \(n-1\) участками железной дороги, по которым может ходить поезд в любом из двух направлений. Железнодорожная сеть связна, то есть представляет собой неориентированное дерево. У вас есть карта этой сети, таким образом для каждого участка железной дороги известно, какие станции он соединяет. У каждого из \(n-1\) участков есть целочисленный параметр красота пейзажа за окном, однако эти значения на карте не указаны и вам неизвестны. Все эти значения лежат в границах от \(1\) до \(10^6\), включительно. Вы произвели опрос \(m\) пассажиров: \(j\)-й пассажир сообщил три значения: - станция отправления \(a_j\);
- станция прибытия \(b_j\);
- минимальную из красот пейзажа за окном на пути следования из \(a_j\) в \(b_j\) (поезд ехал кратчайшим путём из \(a_j\) в \(b_j\)).
Вы хотите улучшить карту и на каждом участке железной дороги указать величину \(f_i\) — красота пейзажа за окном. Эти значения должны быть согласованы с опросом пассажиров. Выведите любой возможный набор значений \(f_1, f_2, \dots, f_{n-1}\), которые согласуется с опросами или укажите, что такой не существует. Выходные данные Если ответа не существует, то выведите единственное число -1. В противном случае выведите \(n-1\) целое число \(f_1, f_2, \dots, f_{n-1}\) (\(1 \le f_i \le 10^6\)), где \(f_i\) — возможная красота пейзажа за окном для \(i\)-й дороги. Если существует несколько возможных ответов, вы можете вывести любой из них. | |
![]()
|
|
E. Модернизация в Древляндии
*особая задача
Деревья
поиск в глубину и подобное
Древляндия состоит из \(n\) городов и \(n-1\) двусторонних дорог, соединяющих некоторые пары городов. Из любого города можно добраться до любого другого города. Вы правы — система городов и дорог в Древляндии образует неориентированное дерево. Правительство объявило тендер на модернизацию инфраструктуры городов, при этом допустимо модернизировать произвольное подмножество \(S\) городов (возможно, все города), которое удовлетворяет следующим требованиям: - подмножество городов должно быть «связным», то есть из любого города подмножества \(S\) можно доехать до любого другого города подмножества \(S\) по дорогам, перемещаясь только по городам из \(S\);
- количество «тупиковых» городов в \(S\) должно быть равно заданному числу \(k\). Город является тупиковым, если он является единственным городом в \(S\), либо связан ровно с одним другим городом из \(S\).
 Здесь изображён один из возможных способов выбрать \(S\) (синие вершины) для заданной конфигурации и \(k=4\). Тупиковыми вершинами являются вершины с номерами \(1\), \(4\), \(6\) и \(7\). Здесь изображён один из возможных способов выбрать \(S\) (синие вершины) для заданной конфигурации и \(k=4\). Тупиковыми вершинами являются вершины с номерами \(1\), \(4\), \(6\) и \(7\). Помогите Древляндии с модернизацией — найдите любое из возможных подмножеств \(S\) или определите, что такого подмножества не существует. Выходные данные Для каждого набора входных данных выведите Yes или No (в любом регистре), в зависимости от того, существует ответ или нет. Если ответ существует, то далее выведите \(m\) (\(1 \le m \le n\)) — количество городов в найденном подмножестве. Затем выведите \(m\) различных чисел от \(1\) до \(n\) — номера городов, которые составляют найденное подмножество. Номера городов можно выводить в любом порядке. Если решений несколько, то выведите любое из них. | |
![]()
|
|
D. Вокруг света
битмаски
графы
графы
Деревья
дп
Комбинаторика
математика
поиск в глубину и подобное
*3000
Ги-Мануэль и Тома планируют \(144\) кругосветных путешествия. Вам дан простой взвешенный неориентированный связный граф из \(n\) вершин и \(m\) рёбер со следующим ограничением: не существует простого цикла (т. е. цикла, проходящего через каждую вершину не больше раза) длины больше \(3\), проходящего через вершину \(1\). Стоимостью пути (необязательно простого) в этом графе является XOR весов всех рёбер, входящих в этот путь, причём каждое ребро считается столько, сколько раз через него проходит путь. Однако, путешествия стоимостью \(0\) их не устраивают. Вы можете выбрать любое подмножество рёбер, инцидентных вершине \(1\), и удалить их. Сколько существует таких множеств, что при их удалении в полученном графе нет нетривиального цикла (необязательно простого) стоимостью \(0\), проходящего через вершину \(1\)? Цикл называется нетривиальным, если существует ребро, через которое он проходит нечётное количество раз. Так как ответ может быть большим, выведите его по модулю \(10^9+7\). Выходные данные В единственной строке выведите ответ по модулю \(10^9+7\). Примечание На рисунках представлены графы из примеров.  В первом примере в графе нет нетривиальных циклов со стоимостью \(0\), так что мы можем как удалить единственное ребро, инцидентное вершине \(1\), так и не удалять. В первом примере в графе нет нетривиальных циклов со стоимостью \(0\), так что мы можем как удалить единственное ребро, инцидентное вершине \(1\), так и не удалять.  Во втором примере если мы не удаляем ребро \(1-2\), то в графе будет цикл \(1-2-4-5-2-1\) со стоимостью \(0\); аналогично, если мы не удаляем ребро \(1-3\), то в графе будет цикл \(1-3-2-4-5-2-3-1\) со стоимостью \(0\). Единственный вариант — удалить оба ребра. Во втором примере если мы не удаляем ребро \(1-2\), то в графе будет цикл \(1-2-4-5-2-1\) со стоимостью \(0\); аналогично, если мы не удаляем ребро \(1-3\), то в графе будет цикл \(1-3-2-4-5-2-3-1\) со стоимостью \(0\). Единственный вариант — удалить оба ребра.  В третьем примере подходят все подмножества, кроме тех двух, при которых остаются оба ребра \(1-3\) и \(1-4\). В третьем примере подходят все подмножества, кроме тех двух, при которых остаются оба ребра \(1-3\) и \(1-4\). | |
![]()
|
|
G. Сумма префиксных сумм
геометрия
Деревья
разделяй и властвуй
Структуры данных
*2700
Определим сумму префиксных сумм массива \([s_1, s_2, \dots, s_k]\) как \(s_1 + (s_1 + s_2) + (s_1 + s_2 + s_3) + \dots + (s_1 + s_2 + \dots + s_k)\). Вам задано дерево, состоящее из \(n\) вершин. В каждой вершине \(i\) записано целое число \(a_i\). Определим значение простого пути от вершины \(u\) до вершины \(v\) следующим образом: рассмотрим все вершины на пути от \(u\) до \(v\), выпишем числа, записанные на этих вершинах, в порядке их появления на пути, и вычислим сумму префиксных сумм получившейся последовательности. Ваша задача — найти максимальное значение по всем путям в дереве. Выходные данные Выведите одно целое число — максимальное значение по всем путям в дереве. Примечание Ответ в первом примере достигается, если выбрать путь из вершины \(3\) в вершину \(1\). Мы получаем последовательность \([3, 3, 7, 1]\), сумма префиксных сумм которой равна \(36\). | |
![]()
|
|
E. 1-деревья и запросы
Деревья
кратчайшие пути
поиск в глубину и подобное
Структуры данных
*2000
Гильдонг забирался на гору, проходя через миллионы деревьев. Вдохновившись ими, он внезапно придумал интересную идею про деревья: А что если мы добавим еще одно ребро в дерево? Затем, он узнал, что такие древовидные графы называются 1-деревья. Так как Гильдон устал от решения задач на деревья, он решил проверить, могут ли похожие техники для деревьев использованы также для решения задач на 1-деревья. Вместо того, чтобы решать задачти самому, он решил проверить вас, запросами на 1-деревьях. Сначала, он даст вам дерево (не 1-дерево) на \(n\) вершинах, а затем задаст вам \(q\) запросов. Каждый запрос состоит из \(5\) целых чисел: \(x\), \(y\), \(a\), \(b\), и \(k\). Это означает, что вам надо проверить, есть ли путь из вершины \(a\) в вершину \(b\), которые содержит ровно \(k\) ребер, после добавления двустороннего ребра между вершинами \(x\) и \(y\). Путь может содержать одни и те же вершины и ребра несколько раз. Все запросы независимы друг от друга; т.е. добавленное ребро удаляется для следующего запроса. Выходные данные Для каждого запроса, выведите «YES» если есть путь, который содержит ровно \(k\) ребер, от \(a\) до \(b\), после добавления неориентированного ребра между вершинами \(x\) и \(y\). Иначе, выведите «NO». Вы можете выводить все буквы в любом регистре (верхнем или нижнем). Примечание Следующая картинка описывает дерево (кружочки и отрезки) и добавленные ребра для каждого запроса (пунктирные линии).  Возможные пути для ответов «YES»: - \(1\)-й запрос: \(1\) – \(3\) – \(2\)
- \(2\)-й запрос: \(1\) – \(2\) – \(3\)
- \(4\)-й запрос: \(3\) – \(4\) – \(2\) – \(3\) – \(4\) – \(2\) – \(3\) – \(4\) – \(2\) – \(3\)
| |
![]()
|
|
D. Курони и празднование
Деревья
интерактив
Конструктив
поиск в глубину и подобное
*1900
Это интерактивная задача. После АС после 13 вердиктов Превышено Время Исполнения по задаче с геометрии, Курони отправился в итальянский ресторан, чтобы отпраздновать это святое достижение. К сожалению, лишний соус дезориентировал его, и он теперь потерялся! Соединенные Штаты Америки могут быть смоделированы как дерево (хотя стойте...) с \(n\) вершинами. Корень дерева находится в вершине \(r\), в которой находится гостиница Курони. У Курони есть приложение для телефона, предназначенное для оказания ему помощи в таких экстренных случаях. Чтобы использовать приложение, ему нужно ввести две вершины \(u\) и \(v\), и оно вернет вершину \(w\), которая является наименьшим общим предком этих двух вершин. Однако, поскольку батарея телефона была почти полностью разряжена во время праздничной вечеринки Курони, он может использовать приложение не более \(\lfloor \frac{n}{2} \rfloor\) раз. После этого телефон разрядится и не останется ничего, чтобы помочь нашему дорогому другу! :( Поскольку ночь холодная и темная, Курони должен вернуться, чтобы он мог воссоединиться со своей удобной кроватью и подушками. Можете ли вы помочь ему выяснить местоположение своего отеля? Протокол взаимодействия Взаимодействие начинается с чтения одного целого числа \(n\) (\(2 \le n \le 1000\)), количества вершин дерева. Затем прочтите \(n-1\) строку, \(i\)-я из которых содержит два целых числа \(x_i\) и \(y_i\) (\(1 \le x_i, y_i \le n\), \(x_i \ne y_i\)), обозначающие, что есть ребро, соединяющее вершины \(x_i\) и \(y_i\). Гарантируется, что ребра сформируют дерево. После этого, вы можете делать запросы типа "? u v" (\(1 \le u, v \le n\)), чтобы найти наименьшего общего предка вершин \(u\) и \(v\). После запроса считайте результат \(w\) как целое число. В случае, если ваш запрос не соответствует требованиям, или вы задали более \(\lfloor \frac{n}{2} \rfloor\) запросов, программа выведет \(-1\) и прекратит взаимодействие. Вы получите вердикт Неправильный ответ. Вам нужно завершить работу вашей программы, чтобы не получить другие вердикты. Когда вы узнаете вершину \(r\), выведите "! \(r\)" и выйдите после этого. Этот запрос не учитывается в пределе \(\lfloor \frac{n}{2} \rfloor\). Обратите внимание, что дерево фиксировано заранее и не будет изменяться во время запросов, то есть интерактор не адаптивен. После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Формат взломов Для взломов используйте следующий формат: Первая строка должна содержать два целых числа \(n\) и \(r\) (\(2 \le n \le 1000\), \(1 \le r \le n\)), обозначающих количество вершин и вершину с отелем Курони. \(i\)-я из следующих \(n-1\) строк должна содержать два целых числа \(x_i\) и \(y_i\) (\(1 \le x_i, y_i \le n\)) — обозначающих, что есть ребро, соединяющее вершины \(x_i\) и \(y_i\). Представленные ребра должны сформировать дерево. Примечание Обратите внимание, что пример взаимодействия содержит дополнительные пустые строки, чтобы его было легче читать. Реальное взаимодействие не содержит пустых строк, и вы не должны также печатать лишние пустые строки. Рисунок ниже изображает дерево с примера: 
| |
![]()
|
|
F. Корова и отпуск
Деревья
поиск в глубину и подобное
снм
*3300
Бесси планирует отпуск! Кор-лифония состоит из \(n\) городов, соединенных \(n-1\) двусторонними дорогами. Гарантируется, что из любого города можно добраться до любого другого. Бесси рассматривает \(v\) возможных планов проведения отпуска, \(i\)-й план описывается начальным городом \(a_i\) и конечным городом \(b_i\). Известно, что только в \(r\) городах оборудованы специальные стоянки для отдыха. Бесси быстро устает, поэтому не может проехать более чем по \(k\) дорогам подряд, не отдохнув на стоянке. Фактически, отдых для Бесси настолько важен, что она готова ради этого посещать города по несколько раз. Для каждого плана отпуска, существует ли маршрут для Бесси, который позволит ей добраться из начального города в конечный? Выходные данные Если Бесси может достичь конечного города, не проезжая более \(k\) дорог без отдыха подряд, для \(i\)-го плана, выведите YES. Иначе, выведите NO. Примечание Граф из первого примера изображен ниже. Города со стоянками для отдыха отмечены красным. В первом плане, Бесси может посетить следующие города в таком порядке: \(1, 2, 3\). Во втором плане, Бесси может посетить следующие города в таком порядке: \(3, 2, 4, 5\). В третьем плане, Бесси не сможет достигнуть конечного города. Например, если она попытается проехать следующим образом: \(3, 2, 4, 5, 6\), ей придется проехать более \(2\) дорог без отдыха.  Граф из второго примера изображен ниже.  | |
![]()
|
|
E. Построить бинарное дерево
Деревья
Конструктив
Перебор
*2200
Вам даны два целых числа \(n\) и \(d\). Нужно построить корневое бинарное дерево из \(n\) вершин с корнем в вершине \(1\) с суммой глубин всех вершин равной \(d\). Дерево — это связный граф без циклов. Корневое дерево имеет специальную вершину — корень. Родитель вершины \(v\) — это последняя отличная от \(v\) вершина на пути от корня к вершине \(v\). Глубина вершины \(v\) — это длина пути от корня к вершине \(v\). Дети вершины \(v\) — все вершины, для которых \(v\) является родителем. Бинарное дерево — это такое дерево, в котором ни одна вершина не имеет более \(2\) детей. Вам нужно ответить на \(t\) независимых наборов входных данных. Выходные данные Для каждого набора входных данных выведите ответ на него. Если невозможно построить такое дерево, выведите «NO» (без кавычек) первой строкой. Иначе выведите «{YES}» первой строкой. Затем выведите \(n-1\) целое число \(p_2, p_3, \dots, p_n\) второй строкой, где \(p_i\) — родитель вершины \(i\). Обратите внимание: последовательность родителей, которую вы выведете, должна описывать некоторое бинарной дерево. Примечание Изображения, соответствующие первому и второму наборам входных данных из примера: 

| |
![]()
|
|
F. Разработка тарифов
Деревья
дп
*3500
Мэр города М. решил в 2020 году запустить несколько новых веток метро. Поскольку бюджет города сильно ограничен, он принял решение не копать новые туннели, а воспользоваться уже существующей подземной сетью. Туннельная система города М. состоит из \(n\) станций метро. Станции соединены между собой двунаправленными туннелями, которых всего \(n - 1\). Между любыми станциями \(v\) и \(u\) есть ровно один простой путь. Каждая ветка метро, которую хочет создать мэр, является простым путём от станции \(a_i\) до станции \(b_i\). Ветки могут пересекаться, то есть иметь общие станции или туннели. Однако, ещё не решено, в какую из двух сторон будут следовать поезда на каждой из веток. А именно, на пути между станциями \(a_i\) и \(b_i\) поезда будут следовать либо от станции \(a_i\) к станции \(b_i\), либо от станции \(b_i\) к станции \(a_i\), но только в одну из сторон. В городе \(M\) действует особая система тарифов. Каждой станции присваивается целое положительное число \(c_i\) — тарифная зона станции, а стоимость переезда от станции \(v\) до станции \(u\) определяется как \(c_u - c_v\) бурлей. Разумеется, такой переезд разрешен, только если есть ветка метро, по которой поезда идут из \(v\) в \(u\). Мэр города не хочет, чтобы между какими-то двумя станциями на одной ветке стоимость проезда была отрицательной, поэтому было принято решение выбрать направления движения поездов по веткам и изменить тарифные зоны всех станций города таким образом, чтобы на каждой ветке тарифные зоны станций строго возрастали, если рассмотреть её в сторону движения поездов. Мэр сначала хочет присвоить каждой станции тарифную зону, а потом выбрать направления всех веток метро, чтобы вдоль каждой ветки тарифные зоны строго возрастали. В связи со скорым наступлением дня города, из всех возможных вариантов назначения тарифных зон мэр хочет выбрать то, где максимальное \(c_i\) будет как можно меньше. Помогите мэру составить новое распределение, или скажите, что это невозможно. Обратите внимание, от вас требуется только назначить тарифные зоны оптимальным образом, а направления для веток выводить не требуется. Таким образом, ваше решение считается верным, если существует способ выбрать направление следования поездов на каждой ветке так, чтобы вдоль всех веток тарифные зоны строго возрастали. Выходные данные В первой строке выведите целое число \(k\) — максимальный номер тарифной зоны. В следующей строке выведите числа \(c_1, c_2, \ldots, c_n\) (\(1 \le c_i \le k\)) — тарифные зоны станций. Если существует несколько ответов, выведите любой из них. Если же не существует ни одного способа назначить тарифные зоны, выведите «-1». Примечание В первом примере ветка \(1 \rightarrow 3\) проходит по станциям в порядке 1, 2, 3. При таком порядке посещения станций их тарифные зоны возрастают. Поскольку на этой ветке 3 станции, то нам потребуется как минимум 3 тарифные зоны. Таким образом, ответ 1, 2, 3 оптимален. Во втором примере ни одно распределение тарифных зон не согласуется с ветками метро. | |
![]()
|
|
F. Максимально белое поддерево
графы
Деревья
дп
поиск в глубину и подобное
*1800
Вам задано дерево, состоящее из \(n\) вершин. Деревом называется связный неориентированный граф с \(n-1\) ребром. Каждая вершина \(v\) этого дерева имеет свой цвет (\(a_v = 1\), если вершина \(v\) белая, и \(0\), если вершина \(v\) черная). Вам нужно решить следующую задачу для каждой вершины \(v\): какую максимальную разницу между количеством белых вершин и количеством черных вершин вы можете получить, если выберете некоторое поддерево заданного дерева, которое содержит вершину \(v\)? Поддеревом дерева называется связный подграф заданного дерева. Более формально, если вы выберете поддерево, которое содержит \(cnt_w\) белых вершин и \(cnt_b\) черных вершин, вам нужно максимизировать \(cnt_w - cnt_b\). Выходные данные Выведите \(n\) целых чисел \(res_1, res_2, \dots, res_n\), где \(res_i\) — максимальная возможная разница между количеством белых и количеством черных вершин в некотором поддереве, которое содержит вершину \(i\). Примечание Первый тестовый пример представлен ниже: 
Черные вершины выделены жирным. Во втором тестовом примере лучшими поддеревьями для вершин \(2, 3\) и \(4\) являются вершины \(2, 3\) и \(4\) соответственно. И лучшим поддеревом для вершины \(1\) является поддерево, состоящее из вершин \(1\) и \(3\). | |
![]()
|
|
C. Ехаб и неПутевые MEXы
Деревья
жадные алгоритмы
Конструктив
поиск в глубину и подобное
*1500
Вам дано дерево, состоящее из \(n\) вершин. Вы хотите написать какие-то числа на ребрах дерева, чтобы выполнялись следующие условия: - Каждое написанное число является целым числом от \(0\) до \(n-2\) включительно.
- Все написанные числа различны.
- Наибольшее значение среди \(MEX(u,v)\) среди всех пар вершин \((u,v)\) минимально возможно.
Здесь \(MEX(u,v)\) обозначает наименьшее неотрицательное целое число, которое не записано ни на одном ребре уникального простого пути между вершинами \(u\) и \(v\). Выходные данные Выведите \(n-1\) целых чисел. \(i\)-е из них должно быть равно числу, записанным на \(i\)-м ребре (в порядке ввода). Примечание Дерево с второго примера: 
| |
![]()
|
|
G. Деревья паутины
геометрия
Деревья
дп
*3500
Назовем граф с \(n\) вершинами, каждой из которых соответствует своя точка \(A_i = (x_i, y_i)\) с целыми координатами, планарным деревом, если: - Все точки \(A_1, A_2, \ldots, A_n\) различны и никакие три точки не лежат на одной прямой.
- Граф является деревом, то есть в графе ровно \(n-1\) ребро и существует путь между любой парой вершин.
- Для всех пар ребер \((s_1, f_1)\) и \((s_2, f_2)\), таких что \(s_1 \neq s_2, s_1 \neq f_2,\) \(f_1 \neq s_2\) и \(f_1 \neq f_2\), отрезки \(A_{s_1} A_{f_1}\) и \(A_{s_2} A_{f_2}\) не пересекаются.
Представим планарное дерево на \(n\) вершинах. Рассмотрим выпуклую оболочку множества точек \(A_1, A_2, \ldots, A_n\). Давайте назовем это дерево паутиной если для всех \(1 \leq i \leq n\) следующие условия верны: - Все листья (вершины со степенью \(\leq 1\)) лежат на выпуклой оболочке.
- Все вершины на выпуклой оболочке являются листьями.
Пример паутины:  Точки \(A_3, A_6, A_7, A_4\) лежат на выпуклой оболочке и вершины \(3, 6, 7, 4\) это все листья этого дерева. Обратитесь к примечанию для большего количества примеров. Давайте назовем подмножество \(S \subset \{1, 2, \ldots, n\}\) вершин поддеревом, если для всех пар вершин из \(S\) существует путь между ними, содержащий только вершины из множества \(S\). Обратите внимание, что любое поддерево планарного дерева также будет являться планарным деревом. Вам дано планарное дерево, состоящее из \(n\) вершин. Назовем разбиение множества вершин \(\{1, 2, \ldots, n\}\) на непустые подмножества \(A_1, A_2, \ldots, A_k\) (то есть \(A_i \cap A_j = \emptyset\) для всех \(1 \leq i < j \leq k\) и \(A_1 \cup A_2 \cup \ldots \cup A_k = \{1, 2, \ldots, n\}\)) хорошим, если для всех \(1 \leq i \leq k\), множество \(A_i\) является поддеревом и паутиной. Два разбиения различны, если существует некоторое множество, лежащее в одном разбиении, но не лежащее в другом. Найдите количество хороших разбиений. Поскольку это число может быть очень большим, найдите его по модулю \(998\,244\,353\). Выходные данные Выведите одно целое число — количество хороших разбиений множества вершин данного планарного дерева по модулю \(998\,244\,353\). Примечание  Картинка дерева из первого теста. Картинка дерева из первого теста. В первом тесте, все хорошие разбиения это: - \(\{1\}\), \(\{2\}\), \(\{3\}\), \(\{4\}\);
- \(\{1, 2\}\), \(\{3\}\), \(\{4\}\);
- \(\{1, 3\}\), \(\{2\}\), \(\{4\}\);
- \(\{1, 4\}\), \(\{2\}\), \(\{3\}\);
- \(\{1, 2, 3, 4\}\).
Разбиение \(\{1, 2, 3\}\), \(\{4\}\) не является хорошим, потому что поддерево \(\{1, 2, 3\}\) это не паутина, потому что вершина \(1\), не являющаяся листом, лежит на выпуклой оболочке. Разбиение \(\{2, 3, 4\}\), \(\{1\}\) не является хорошим, потому что подмножество \(\{2, 3, 4\}\) не является поддеревом.  Картинка дерева из второго теста. Картинка дерева из второго теста. Во втором тесте, данное дерево само не является паутиной, потому что вершина \(1\), которая является листом, не лежит на выпуклой оболочке. Однако, поддерево \(\{2, 3, 4, 5\}\) является паутиной.  Картинка дерева из третьего теста. Картинка дерева из третьего теста.  Картинка дерева из четвертого теста. Картинка дерева из четвертого теста. В четвертом тесте, разбиение \(\{1, 2, 3, 4\}\), \(\{5, 6, 7, 8\}\) хорошее, потому что оба подмножества являются паутинами. | |
![]()
|
|
E. Запросы на дереве
графы
Деревья
поиск в глубину и подобное
*1900
Вам дано корневое дерево, состоящее из \(n\) вершин, пронумерованных от \(1\) до \(n\). Корень дерева находится в вершине с номером \(1\). Дерево — это связный неориентированный граф с \(n-1\) ребром. Вам заданы \(m\) запросов. \(i\)-й запрос состоит из множества \(k_i\) различных вершин \(v_i[1], v_i[2], \dots, v_i[k_i]\). Ваша задача — определить, существует ли путь от корня до некоторой вершины \(u\) такой, что каждая из заданных \(k\) вершин или принадлежит этому пути, или расположена на расстоянии \(1\) от некоторой вершины на этом пути. Выходные данные Для каждого запроса выведите ответ — «YES», если существует путь от корня до некоторой вершины \(u\) такой, что каждая из \(k\) заданных вершин или принадлежит этому пути, или расположена на расстоянии \(1\) от какой-либо вершины на этом пути, и «NO» в противном случае. Примечание Изображение, относящееся к примеру: 
Рассмотрим запросы. Первый запрос — \([3, 8, 9, 10]\). Ответ — «YES», так как вы можете выбрать путь от корня \(1\) до вершины \(u=10\). Тогда вершины \([3, 9, 10]\) принадлежат пути от \(1\) до \(10\) и вершина \(8\) расположена на расстоянии \(1\) от вершины \(7\), которая также принадлежит этому пути. Второй запрос — \([2, 4, 6]\). Ответ — «YES», так как вы можете выбрать путь до вершины \(u=2\). Тогда вершина \(4\) находится на расстоянии \(1\) от вершины \(1\), которая принадлежит этому пути, а вершина \(6\) находится на расстоянии \(1\) от вершины \(2\), которая принадлежит этому пути. Третий запрос — \([2, 1, 5]\). Ответ — «YES», так как вы можете выбрать путь до вершины \(u=5\) и все вершины из запроса будут принадлежать этому пути. Четвертый запрос — \([4, 8, 2]\). Ответ — «YES», так как вы можете выбрать путь до вершины \(u=9\), и вершины \(2\) и \(4\) расположены на расстоянии \(1\) от вершины \(1\), которая принадлежит этому пути, а вершина \(8\) расположена на расстоянии \(1\) от вершины \(7\), которая принадлежит этому пути. Ответ и на пятый, и на шестой запросы — «NO», потому что вы не можете выбрать подходящую вершину \(u\). | |
![]()
|
|
F. Независимое множество
Деревья
дп
поиск в глубину и подобное
*2500
Эрик — учитель по теории графов. Сегодня он рассказывает независимое множество и реберно-порожденный подграф. Для данного графа \(G=(V,E)\) независимым множеством называется такое подмножество вершин \(V' \subset V\), что для каждой пары \(u,v \in V'\), \((u,v) \not \in E\) (то есть в \(E\) нет ребра, соединяющего две вершины из \(V'\)). Реберно-порожденный подграф состоит из подмножества ребер \(E' \subset E\) и всех вершин оригинального графа, которые инцидентны хотя бы одному ребру подграфа. Для \(E' \subset E\) обозначим за \(G[E']\) реберно-порожденный подграф такой, что \(E'\) — это множество ребер этого подграфа. Иллюстрации этих определений:  В качестве упражнения на закрепление материала он дал студентам следующую задачу: Дано дерево \(G=(V,E)\), посчитайте сумму \(w(H)\) по всем реберно-порожденным подграфам \(H\) графа \(G\), кроме пустого, где \(w(H)\) — это количество независимых множеств в \(H\). Формально, посчитайте \(\sum \limits_{\emptyset \not= E' \subset E} w(G[E'])\). Докажите Эрику, что вы умнее его учеников, предъявив правильный ответ как можно скорее. Обратите внимание, что ответ может быть довольно большой, поэтому выведите его по модулю \(998,244,353\). Выходные данные Выведите одно целое число, обозначающее ответ по модулю \(998,244,353\). Примечание Во втором примере все независимые множества изображены на рисунке.  | |
![]()
|
|
A. Linova и королевство
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
сортировки
*1600
Написание легких романов является очень важной частью жизни Linova. Прошлой ночью ей приснилось сказочное королевство. Linova написала легкий роман про это королевство, как только проснулась. Конечно, она стала его королевой.  Всего есть \(n\) городов и \(n-1\) двусторонняя дорога, соединяющая некоторые пары городов королевства. Из любого города вы можете попасть в любой другой город, пройдя по некоторым дорогам. Города пронумерованы от \(1\) до \(n\) и город \(1\) является столицей королевства. Таким образом, структура королевства является деревом. Как королева, Linova планирует выбрать ровно \(k\) городов для развития индустрии, тогда как в остальных городах будет развиваться туризм. Столица также может быть как индустриальным, так и туристическим городом. Раз в год в столице будет проходить встреча. Для участия во встрече, каждый индустриальный город посылает участника. Все посланники приедут в столицу по кратчайшему пути (который как известно единственный в дереве). Путешествие по туристическим городам очень приятно. Для каждого посланника, его уровень счастья равен количеству туристических городов на его пути. Для того, чтобы люди любили королеву, Linova хочет выбрать \(k\) городов так, чтобы максимизировать сумму уровней счастья всех посланников. Можете ли вы посчитать максимальную возможную сумму для нее? Выходные данные Выведите строку, содержащую единственное целое число — максимальную возможную сумму уровней счастья всех посланников, которую можно достичь. Примечание 
В первом тесте, Linova может выбрать города \(2\), \(5\), \(6\), \(7\) для развития индустрии, тогда уровень счастья посланника из города \(2\) будет равен \(1\), уровни счастья посланников из городов \(5\), \(6\), \(7\) будут равны \(2\). Таким образом, сумма уровней счастья будет равна \(7\) и можно доказать, что это максимальная возможная сумма, которая может быть. 
Во втором тесте, выбрав города \(3\) и \(4\) для развития индустрии можно достичь суммы \(3\), но обратите внимание, что Linova планирует выбрать ровно \(k\) городов для развития индустрии, поэтому максимальная сумма равна \(2\). | |
![]()
|
|
F. Путешествия
графы
Деревья
разделяй и властвуй
Структуры данных
*3500
Где-то в дебрях, далеко-далеко находится святая земля, которая имеет форму дерева — связного неориентированного графа, состоящего из \(n\) вершин и \(n-1\) ребра. Вершины пронумерованы целыми числами от \(1\) до \(n\). Всего есть \(m\) путешественников, привлеченных красотой и процветанием этой земли. Каждый из них отправился в путешествие по ней. \(i\)-й путешественник проехал вдоль кратчайшего пути из \(s_i\) в \(t_i\). Во время этого путешествия, он прошел через все ребра, лежащие на кратчайшем пути из \(s_i\) в \(t_i\), который, как известно, единственный в дереве. Во время своих путешествий, некоторые путешественники познакомились с остальными. Некоторые из путешественников станут друзьями. Более точно, \(i\)-й и \(j\)-й путешественники станут друзьями, тогда и только тогда, когда было хотя бы \(k\) ребер, по которым прошли и \(i\)-й и \(j\)-й путешественники. Ваша задача состоит в том, чтобы найти количество пар путешественников \((i, j)\), удовлетворяющих следующим условиям: - \(1 \leq i < j \leq m\).
- \(i\)-й и \(j\)-й путешественники станут друзьями.
Выходные данные Выведите одно целое число — количество пар путешественников, удовлетворяющих описанным условиям. Примечание 
В первом тесте существует \(4\) пары, удовлетворяющие описанным условиям: \((1,2)\), \((1,3)\), \((1,4)\), \((3,4)\). - \(1\)-й путешественник и \(2\)-й путешественник оба пройдут по ребру \(6-8\).
- \(1\)-й путешественник и \(3\)-й путешественник оба пройдут по ребру \(2-6\).
- \(1\)-й путешественник и \(4\)-й путешественник оба пройдут по ребрам \(1-2\) и \(2-6\).
- \(3\)-й путешественник и \(4\)-й путешественник оба пройдут по ребру \(2-6\).
| |
![]()
|
|
B. Назначение весов ребрам
битмаски
Деревья
жадные алгоритмы
Конструктив
математика
поиск в глубину и подобное
*1800
У вас есть невзвешенное дерево на \(n\) вершинах. Вы должны назначить положительный вес каждому ребру, чтобы выполнялось следующее условие: - Для каждых двух разных листов \(v_{1}\) и \(v_{2}\) этого дерева, побитовое исключающее ИЛИ весов всех ребер на простом пути между \(v_{1}\) и \(v_{2}\) должно быть равно \(0\).
Обратите внимание, что вы можете назначать очень большие натуральные числа (такие как \(10^{(10^{10})}\)). Гарантируется, что такое назначение всегда существует при данных ограничениях. Теперь определим \(f\) как количество различных весов среди назначенных весов.  В этом примере назначение верно, потому что побитовое исключающее ИЛИ всех весов ребер между каждой парой листьев равно \(0\). Значение \(f\) здесь равно \(2\), потому что есть \(2\) различных веса ребер (\(4\) и \(5\)). В этом примере назначение верно, потому что побитовое исключающее ИЛИ всех весов ребер между каждой парой листьев равно \(0\). Значение \(f\) здесь равно \(2\), потому что есть \(2\) различных веса ребер (\(4\) и \(5\)). В этом примере назначение не удовлетворяет условию, поскольку побитовое исключающее ИЛИ всех весов ребер между вершинами \(1\) и \(6\) (\(3, 4, 5, 4\)) не равно \(0\). В этом примере назначение не удовлетворяет условию, поскольку побитовое исключающее ИЛИ всех весов ребер между вершинами \(1\) и \(6\) (\(3, 4, 5, 4\)) не равно \(0\).
Чему равны минимальное и максимальное возможные значения \(f\) для данного дерева? Найдите и выведите оба. Выходные данные Выведите два целых числа — минимальное и максимальное возможное значения \(f\), которые могут быть получены из правильного назначения данного дерева. Обратите внимание, что такое назначение всегда существует при данных ограничениях. Примечание В первом примере возможные назначения для минимума и максимума показаны на рисунке ниже. Конечно, есть и другие назначения.  Во втором примере возможные назначения для минимума и максимума показаны на рисунке ниже. Значение \(f\) для правильного назначения этого дерева всегда равно \(3\).  В третьем примере возможные назначения для минимума и максимума показаны на рисунке ниже. Конечно, есть и другие назначения.  | |
![]()
|
|
D. Вложенные резинки
Деревья
дп
Конструктив
математика
поиск в глубину и подобное
*2700
У вас есть дерево из \(n\) вершин. Вы собираетесь преобразовать это дерево в \(n\) резинок на бесконечной плоскости. Должно выполняться следующее; - Для каждой пары вершин \(a\) и \(b\), резинки \(a\) и \(b\) должны пересекаться тогда и только тогда, когда между \(a\) и \(b\) в дереве существует ребро.
- Форма резинки должна быть простой петлей. Другими словами, резинка — это замкнутая кривая без самопересечений.
Теперь давайте дадим следующие определения: - Резинка \(a\) включает резинку \(b\), если и только если резинка \(b\) находится полностью внутри резинки \(a\), и они не пересекаются.
- Последовательность резинок \(a_{1}, a_{2}, \ldots, a_{k}\) (\(k \ge 2\)) называется вложенной, если и только если для всех \(i\) (\(2 \le i \le k\)), \(a_{i-1}\) включает в себя \(a_{i}\).
 Это пример преобразования. Обратите внимание, что резинки \(5\) и \(6\) являются вложенными. Это пример преобразования. Обратите внимание, что резинки \(5\) и \(6\) являются вложенными. Можно доказать, что при заданных ограничениях существует преобразование и последовательность вложенных резинок. Какую максимальную длину последовательности вложенных резинок можно получить из данного дерева? Найдите и выведите ее. Выходные данные Выведите ответ. Примечание В первом примере можно получить вложенную последовательность из \(4\) резинок (\(1\), \(2\), \(5\) и \(6\)) с помощью следующего преобразования, приведенного ниже. Конечно, существуют и другие преобразования для создания вложенной последовательности длины \(4\). Однако вы не можете сделать последовательность из \(5\) или более вложенных резинок для данного дерева.  Одно из возможных преобразований для второго примера приведено ниже.  | |
![]()
|
|
D. Настя и машина времени
графы
Деревья
Конструктив
поиск в глубину и подобное
*2600
Придя к Насте, Денис обнаружил, что она ему не рада... Но у молодого человека есть последняя надежда. Он хочет купить все вещи, что нравятся Насте. Тогда-то она уж точно согласится с ним общаться. Карта города, в котором живут наши герои, представляет собой множество площадей, некоторые из которых соединены дорогами. От любой площади можно добраться до любой другой ровно одним способом, используя эти дороги и не посещая одну и ту же площадь дважды. Получается, что граф города — это дерево. Денис находится в вершине \(1\) в момент времени \(0\). Он хочет хоть раз побывать в каждой вершине и вернуться назад как можно раньше. Денис может проходить вдоль любой дороги за \(1\) времени. Увы, город столь велик, что сделать это быстро никак не выйдет. Поэтому Денис пошел на отчаянный шаг. Он достал свою карманную машину времени, которую он собрал у себя в подвале. С ее помощью Денис может стоя на месте сменить время на любое неотрицательное время, которое меньше текущего. Но у машины времени есть один нюанс. Если герой окажется в одном месте и в одно и то же время дважды, произойдет взрыв вселенских масштабов и не получится порадовать Настю. Поэтому Денис просит вас проложить ему маршрут с использованием машины времени такой, что он обойдет все площади и вернется на первую и при этом максимальное время в котором он побывал будет минимально. Формально, маршрут Дениса можно представить как последовательность пар \(\{v_1, t_1\}, \{v_2, t_2\}, \{v_3, t_3\}, \ldots, \{v_k, t_k\}\), где \(v_i\) — номер площади, а \(t_i\) — время, в котором сейчас находится мальчик. Должны быть выполнены следующие условия: - Маршрут начинается на площади \(1\) в момент времени \(0\), то есть \(v_1 = 1, t_1 = 0\) и заканчивается на площади \(1\), то есть \(v_k = 1\).
- Все переходы делятся на два типа:
- Стоя на площади сменить время: \(\{ v_i, t_i \} \to \{ v_{i+1}, t_{i+1} \} : v_{i+1} = v_i, 0 \leq t_{i+1} < t_i\).
- Пройти по одной из дорог: \(\{ v_i, t_i \} \to \{ v_{i+1}, t_{i+1} \}\). При этом \(v_i\) и \(v_{i+1}\) соединены дорогой и \(t_{i+1} = t_i + 1\).
- Все пары \(\{ v_i, t_i \}\) должны быть различны.
- Среди \(v_1, v_2, \ldots, v_k\) встречаются все площади.
Вам нужно найти маршрут такой, что максимальное время, в котором побывает Денис будет минимальным, то есть маршрут, для которого \(\max{(t_1, t_2, \ldots, t_k)}\) будет минимально возможным. Выходные данные В первой строке выведите целое число \(k\) \((1 \leq k \leq 10^6)\) — длина пути Дениса. В следующих \(k\) строках выведите пары \(v_i, t_i\) — пары, описывающие маршрут Дениса (как в условии). Все требования к маршруту, описанные в условии должны быть выполнены. Гарантируется, что при заданных ограничениях существует хотя бы один маршрут и ответ, длина которого не превосходит \(10^6\). Если возможных ответов несколько, выведите любой. | |
![]()
|
|
E. Железнодорожные пути
Деревья
Структуры данных
*3100
Все верно. Я студент университета Пердью и безо всякого стыда придумал задачу про поезда. Есть \(n\) станций и \(m\) поездов. Станции соединяются \(n-1\) однонаправленной железной дорогой так, что они образуют корневое дерево с корнем в станции \(1\). Все железные дороги имеют направлены вдоль путей от корневой станции \(1\) к листьям. Каждая железная дорога ведет от станции \(u\) к станции \(v\) и имеет расстояние \(d\), обозначающее, что требуется \(d\) единиц времени, чтобы доехать от станции \(u\) к станции \(v\). Каждая станция, из которой выходит хотя бы одна железная дорога, имеет переключатель, который определяет станцию, в которую затем поедет любой поезд, приехавший на эту станцию. Например, это может выглядеть следующим образом:  Здесь станции \(1\) и \(3\) имеют переключатели, направляющие к станциям \(2\) и \(4\), соответственно. Здесь станции \(1\) и \(3\) имеют переключатели, направляющие к станциям \(2\) и \(4\), соответственно. Изначально ни на одной станции нет поезда. Поезд \(i\) появится на станции \(1\) в момент времени \(t_i\). В каждый момент времени, начиная с \(1\), будут происходить следующие два шага: - Вы можете переключить переключатель не более одной станции на другую дорогу, выходящую из этой станции. Переключение происходит до шага \(2\).
- Любой поезд, который находится на станции \(u\), направляется к станции \(v\), в которую указывает переключатель станции \(u\). Если железная дорога от станции \(u\) к станции \(v\) имела расстояние \(d\), поезд прибудет на станцию \(v\) через \(d\) единиц времени от настоящего момента.
У каждого поезда есть станция прибытия \(s_i\). Когда он прибывает на станцию \(s_i\), он останавливается там навсегда. Если в какой-то момент времени поезд поедет в неверном направлении, то есть он никогда уже не сможет достичь станции \(s_i\) независимо от состояния переключателей, он тут же взорвется. Найдите наибольшее возможное время первого взрыва, если вы будете переключать переключатели оптимально или определите, что вы можете направить каждый поезд к своей станции прибытия так, что ни одного взрыва не произойдет. Также найдите минимальное количество переключений, которое требуется, чтобы достичь этого. Выходные данные Выведите два целых числа: наибольшее возможное время первого взрыва (или \(-1\), если можно предотвратить взрывы) и минимальное количество переключений, необходимое, чтобы достичь этого. Примечание В первом тесте один из возможных примеров того, как все будет происходить, описан ниже. - В момент времени \(1\) поезд \(1\) прибывает на станцию \(1\). Переключатель станции \(1\) направлен к станции \(2\). Поезд \(1\) отправляется к станции \(2\).
- В момент времени \(2\) поезд \(2\) прибывает на станцию \(1\) и поезд \(1\) прибывает на станцию \(2\), где останавливается навсегда. Мы переключаем переключатель в станции \(1\) к станции \(3\). Поезд \(2\) направляется к станции \(3\).
- В момент времени \(4\) поезд \(2\) прибывает на станцию \(3\). Мы переключаем переключатель в станции \(3\) к станции \(4\). Поезд \(2\) направляется к станции \(4\).
- В момент времени \(5\) поезд \(2\) прибывает на станцию \(4\), где останавливается навсегда.
- В момент времени \(6\) поезд \(3\) прибывает на станцию \(1\). Мы переключаем переключатель станции \(1\) к станции \(2\). Поезд \(3\) направляется к станции \(2\).
- В момент времени \(7\) поезд \(3\) прибывает на станцию \(2\), где останавливается навсегда. Мы переключаем переключатель станции \(3\) к станции \(5\).
- В момент времени \(10\) поезд \(4\) прибывает на станцию \(1\). Мы переключаем переключатель станции \(1\) к станции \(3\). Поезд \(4\) направляется к станции \(3\).
- В момент времени \(12\) поезд \(4\) прибывает на станцию \(3\). Поезд \(4\) направляется к станции \(5\).
- В момент времени \(15\) поезд \(4\) прибывает на станцию \(5\), где останавливается навсегда.
Во втором тесте мы не переключаем ничего. В момент времени \(4\) поезд \(2\) направляется к станции \(5\), и поезд \(4\) направляется к станции \(3\). Они оба взрываются. Невозможно предотвратить взрывы поездов к моменту времени \(4\). В третьем тесте давайте будем обозначать переключение переключателя как \((u\to v,t)\), если мы переключаем переключатель станции \(u\) к станции \(v\) в момент времени \(t\). Одним из решений является сделать следующие \(4\) переключения: \((1\to 2,1)\), \((1\to 3,2)\), \((7\to 8,5)\), \((5\to 6,8)\). В момент времени \(11\) поезда \(4\), \(5\) и \(6\) взорвутся. Невозможно предотвратить взрывы поездов к моменту времени \(11\). | |
![]()
|
|
D. Джонни и Джеймс
Деревья
жадные алгоритмы
математика
реализация
*2900
У Джеймса Бонда, любимого секретного агента Джонни, новая миссия. Есть \(n\) вражеских баз, каждая из которых задана своими координатами, так что мы можем рассматривать их как точки на плоскости. Базы могут общаться друг с другом, посылая сигнал, который является лучом, из выбранной точки в направлении начала координат или в противоположном направлении. Исключением является центральная база, расположенная в начале координат. Она может посылать сигнал в любом направлении. Когда какие-то две базы хотят коммуницировать, существует два возможных сценария. Если они лежат на одной прямой с началом координат, одна из них посылает сигнал непосредственно второй. Иначе, из первой базы сигнал посылается на центральную, и оттуда — на вторую. Обозначим расстоянием между двумя базами суммарное Евклидово расстояние, которое сигнал, посланный между ними, должен пройти. Бонд может повредить все, кроме некоторых \(k\) баз, которые он может выбрать на свое усмотрение. Поврежденная база не может посылать или получать сигнал напрямую, но все еще может передавать его между двумя работающими базами. В частности, Джеймс может повредить центральную базу, и сигнал все еще может быть послан между любыми двумя неповрежденными базами, как и раньше, и расстояние между ними останется неизменным. Какова максимальная сумма расстояний между всеми парами оставшихся баз, которую 007 может достичь, уничтожив ровно \(n - k\) баз? Выходные данные Вы должны вывести одно число — максимальную возможную сумму расстояний между всеми парами некоторых \(k\) из баз. Ваш ответ будет считаться правильным, если его абсолютная или относительная погрешность не превышает \(10^{-6}\). Примечание В первом примере, в оптимальном решении Бонд не разрушает базы с номерами \(4\) и \(6\) (помечены оранжевым):  Следующая иллюстрация показывает оптимальное решение для второго примера. Следующие базы не разрушены: \(2\), \(3\), \(4\), \(5\), \(6\) (помечены оранжевым).  Оптимальное решение для третьего теста изображено на иллюстрации. Только базы с номерами \(3\), \(4\) и \(5\) разрушены. Снова, не разрушенные базы помечены оранжевым.  | |
![]()
|
|
E. Джеймс и погоня
графы
Деревья
поиск в глубину и подобное
Теория вероятностей
*3000
У Джеймса Бонда есть новый план, как поймать своего врага. Есть несколько городов и ориентированные дороги между ними, причем используя эти дороги можно добраться из любого города до любого другого. Когда враг появляется в каком-то городе, Бонд знает её следующий пункт назначения, но понятия не имеет, какой путь она выберет, чтобы ехать туда. Город \(a\) называется интересным, если для любого города \(b\), существует ровно один простой путь из \(a\) в \(b\). Простым путем называется последовательность различных городов, в которой для каждых двух соседних городов есть дорога, ведущая из первого города во второй. Враг Бонда хороша в побегах, поэтому только погоня, начатая в интересном городе дает шанс поймать её. Джеймс хочет расположить своих людей в таких городах. Однако, если интересных городов недостаточно много, весь план не имеет смысла, потому что людям Бонда, возможно, придется ждать появления врага очень долго. Вы ответственны за поиск всех интересных городов. Выведите их, либо сообщите, что их недостаточно много. Под недостаточно много, Джеймс подразумевает строго меньше \(20\%\) всех городов. Выходные данные Если строго меньше \(20\%\) всех городов являются интересными, выведите \(-1\). Иначе, пусть \(k\) равно количеству интересных городов. Выведите \(k\) различных целых чисел в порядке возрастания — номера интересных городов. Примечание На всех иллюстрациях, если город интересный, он помечен зеленым, а иначе — красным. В первом наборе входных данных, все города интересные.  Во втором наборе входных данных, ни один город не интересен.  В третьем наборе входных данных, города \(1\), \(2\), \(3\) и \(5\) интересные.  В четвертом наборе входных данных, только город \(1\) является интересным. Это строго меньше, чем \(20\%\) всех городов, поэтому ответ \(-1\).  | |
![]()
|
|
C. Игра на листьях
Деревья
игры
*1600
Ayush и Ashish играют в игру на некорневом дереве, состоящем из \(n\) вершин, пронумерованных от \(1\) до \(n\). Игроки делают следующий ход по очереди: - Выберите любой лист в дереве и удалите его вместе со всеми ребрами, для которых этот лист является одним из концов. Лист — это вершина со степенью, не превосходящей \(1\).
Дерево — это связный неориентированный граф без циклов. Дана специальная вершина с номером \(x\). Игрок, который удаляет эту вершину, выигрывает игру. Ayush ходит первым. Определите победителя игры, если каждый игрок играет оптимально. Выходные данные Для каждого набора входных данных, если побеждает Ayush, выведите "Ayush", иначе выведите "Ashish" (без кавычек). Примечание В первом наборе входных данных Ayush может удалить только вершину \(2\) или \(3\), после чего вершина \(1\) становится листом, и Ashish может удалить ее в свою очередь. Во втором наборе входных данных Ayush может удалить вершину \(2\) на самом первом шаге. | |
![]()
|
|
E. Перестановка дерева
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
*2000
У Ashish есть дерево, состоящее из \(n\) вершин, пронумерованных от \(1\) до \(n\), с корнем в вершине \(1\). \(i\)-я вершина дерева имеет стоимость \(a_i\), и в ней записана бинарная цифра \(b_i\). Ashish хочет, чтобы в конце в \(i\)-й вершине была записана бинарная цифра \(c_i\). Для этого, он может выполнить следующую операцию любое количество раз: - Выберите любые \(k\) вершин из поддерева любой вершины \(u\) и переставьте цифры в этих вершинах так, как пожелаете, за стоимость \(k \cdot a_u\). Здесь он может выбрать \(k\) в диапазоне от \(1\) до размера поддерева \(u\).
Он хочет выполнить операции так, чтобы у каждой вершины в итоге оказалась цифра, соответствующая желаемой цифре для этой вершины. Помогите ему найти минимальную общую стоимость, за которую можно сделать так, чтобы после проведения всех операций для каждого \(u\) в вершине \(u\) была записана цифра \(c_u\), или определить, что это невозможно. Выходные данные Выведите минимальную общую стоимость, за которую можно сделать так, чтобы в каждой вершине была записана желаемая цифра для этой вершины, или \(-1\), если сделать это невозможно. Примечание Дерево, соответствующие примерам \(1\) и \(2\):  В примере \(1\) мы можем выбрать вершину \(1\) и \(k = 4\) за стоимость \(4 \times 1\) = \(4\) и выбрать вершины \({1, 2, 3, 5}\), переставить их цифры и получить желаемые цифры в каждой позиции. В примере \(2\) мы можем выбрать вершину \(1\) и \(k = 2\) за стоимость \(10000 \times 2\), выбрать вершины \({1, 5}\), обменять их цифры, после чего аналогичным образом выбрать вершину \(2\) и \(k = 2\) за стоимость \(2000 \times 2\) и вершины \({2, 3}\), обменять их цифры, чтобы получить нужные цифры в каждой позиции. В примере \(3\) невозможно получить нужные цифры, потому что среди начальных цифр нет цифры \(1\). | |
![]()
|
|
D. Последнее следствие Ехаба
графы
Деревья
жадные алгоритмы
Конструктив
поиск в глубину и подобное
реализация
*2100
Для связного неориентированного графа с \(n\) вершинами и целого числа \(k\), вы должны, на ваш выбор: - или найти независимое множество с ровно \(\lceil\frac{k}{2}\rceil\) вершинами.
- или найти простой цикл длины не более \(k\).
Независимое множество — это набор вершин такой, что никакие две из них не связаны ребром. Простой цикл — это цикл, который не содержит ни одной вершины дважды. У меня есть доказательство, что для любых входных данных вы всегда можете решить по крайней мере одну из этих задач, но оно слишком тривиально, чтобы поместиться здесь. Выходные данные Если вы решили решить первую задачу, то в первой строке выведите \(1\), а затем строку, содержащую \(\lceil\frac{k}{2}\rceil\) различных целых чисел, не превышающих \(n\) — вершины в желаемом независимом наборе. Если же вы решили решить вторую задачу, то в первой строке выведите \(2\), затем строку, содержащую одно целое число, \(c\), представляющее длину найденного цикла, а затем строку, содержащую \(c\) различных целых чисел, не превышающих \(n\) — вершины в нужном цикле, в порядке их появления в цикле. Примечание В первом примере: 
Обратите внимание, что вывод независимого множества \(\{2,4\}\) тоже зачтется, но вывод цикла \(1-2-3-4\) — нет, потому что его длина должна быть не более \(3\). Во втором примере: 
Обратите внимание, что вывод независимого множества \(\{1,3\}\) или цикла \(2-1-4\) также зачтутся. В третьем примере: 
В четвертом примере: 
| |
![]()
|
|
G. Двигаем доминошки
геометрия
графы
Деревья
Структуры данных
*3200
Билл любит играть с доминошками. Он взял доску размера \(n \times m\), разделённую на одинаковые квадратные клетки, и покрыл её доминошками. Каждая доминошка покрывает две клетки, соседние по горизонтали или вертикали, и каждая клетка покрыта ровно одной половиной доминошки (то есть, непокрытых клеток нет, и никакие две доминошки не покрывают одну клетку дважды). После этого Билл решил поиграть с покрытой доской и выложить фотографии в социальных сетях. Сперва он убирает с доски одну из доминошек, тем самым освобождая две клетки. После этого он двигает некоторые доминошки. Доминошку можно двигать только параллельно её длинной стороне. Двигать доминошку в каком-либо направлении можно лишь, если ближайшая клетка в этом направлении сейчас свободна. Билл не хочет забыть исходное расположение доминошек, поэтому он двигает доминошки только так, чтобы каждая доминошка всегда покрывала хотя бы одну клетку, общую с её исходным положением. После удаления доминошки и нескольких сдвигов (возможно, ни одного), Билл фотографирует получившуюся доску. Однако, Билл использует очень много фильтров, поэтому границы доминошек разглядеть нельзя, и можно увидеть лишь то, какие две клетки на доске свободны. Когда Билл выкладывает фотографию, он возвращает доску в исходное положение и начинает заново. Билл хочет выложить как можно больше фотографий, но он не будет выкладывать одну и ту же фотографию дважды. Сколько различных фотографий он сможет сделать? Напомним, что фотографии различны, если различны пары свободных клеток на них. Выходные данные Выведите одно число — количество различных фотографий, которые сможет сделать Билл. Примечание В первом примере после удаления любой доминошки нельзя сделать ни одного сдвига, поэтому различных фотографий четыре. Во втором примере после удаления самой левой доминошки можно сделать четыре фотографии, поскольку можно независимо двигать/не двигать оставшиеся две доминошки. Две другие фотографии можно сделать, если удалить одну из доминошек справа. | |
![]()
|
|
D. СоздатеЛи
графы
Деревья
дп
жадные алгоритмы
математика
*1900
Ли потратил так много времени на создание хорошей div.2 D задачи, чтобы сбалансировать недавний контест, но задача продолжает ощущаться неподходящей. Ли придумывал ее так мучительно долго, что заработал фобию div.2 D задач. И теперь он прячется в кустах... Назовем Корневым Сухим Кустом (КСК) уровня \(n\) корневое дерево, построенное согласно правилам ниже. Корневой Сухой Куст уровня \(1\) — это одна вершина. Для построения КСК уровня \(i\), сначала построим КСК уровня \(i-1\) и далее для каждой вершины \(u\): - если у \(u\) нет детей, то подвесим к ней одного сына;
- если у \(u\) есть один сын, то подвесим к ней еще двух детей;
- если у \(u\) есть более одного сына, то пропустим ее.
 Корневые Сухие Кусты уровня \(1\), \(2\) и \(3\). Корневые Сухие Кусты уровня \(1\), \(2\) и \(3\). Назовем лапой корневое дерево из четырех вершин: одна корневая вершина (также называется центром) и три ребенка. Оно напоминает лапу:  Центром лапы является вершина с номером \(1\). Центром лапы является вершина с номером \(1\). У Ли есть Корневой Сухой Куст уровня \(n\). Первоначально все вершины КСК зеленого цвета. За один шаг, он может выбрать лапу в КСК и, если все вершины в ней зеленые и все вершины лапы являются детьми ее центра, покрасить вершины лапы в в желтый. Ли хочет узнать максимальное количество желтых вершин, которое он сможет получить. Так как ответ может быть очень большим, выведите его по модулю \(10^9+7\). Выходные данные Для каждого набора входных данных выведите единственное целое число — максимальное количество желтых вершин, которые может получить Ли, по модулю \(10^9 + 7\). Примечание Несложно заметить, что ответ для КСК уровня \(1\) или \(2\) равен \(0\). Ответ для КСК уровня \(3\) равен \(4\), так как есть только одна лапа, которую можно выбрать: \(\{1, 2, 3, 4\}\). Ответ для КСК уровня \(4\) равен \(4\), так как мы можем выбрать либо одну лапу \(\{1, 3, 2, 4\}\) или одну лапу \(\{2, 7, 5, 6\}\). Других лап в КСК уровня \(4\) нет (например, мы не можем выбрать \(\{2, 1, 7, 6\}\), так как \(1\) не является ребенком вершины-центра \(2\)).  Корневой Сухой Куст уровня 4. Корневой Сухой Куст уровня 4. | |
![]()
|
|
F1. Загадана пара вершин (простая версия)
Бинарный поиск
графы
Деревья
интерактив
кратчайшие пути
поиск в глубину и подобное
*2400
Обратите внимание, что единственное различие между простой и сложной версиями задачи заключается в количестве разрешенных запросов. Вы можете делать взломы, только если все версии задачи решены. Это интерактивная задача. Вам дано дерево, состоящее из \(n\) вершин, пронумерованных целыми числами от \(1\) до \(n\). Ayush и Ashish выбрали две секретные различные вершины дерева. Вам нужно отгадать обе вершины. Вы можете делать следующий запрос: - Вы даете список вершин дерева и в результате получаете вершину из списка, сумма растояний от которой до двух загаданных вершин минимально (если таких вершин в списке несколько, вы получите одну из них). Вы также получите сумму расстояний от этой вершины до двух загаданных вершин.
Напомним, что деревом называется связный граф без циклов. Расстоянием между двумя вершинами называется количество ребер, лежащих на простом пути между ними. Более формально, пусть две загаданные вершины это \(s\) и \(f\). За один запрос, вы можете дать множество вершин \(\{a_1, a_2, \ldots, a_c\}\) дерева. В результате вы получите два числа \(a_i\) и \(dist(a_i, s) + dist(a_i, f)\). Вершина \(a_i\) является любой вершиной из данного вами множества, для которой число \(dist(a_i, s) + dist(a_i, f)\) минимально. Вы можете сделать не более \(14\) запросов. Протокол взаимодействия Для того, чтобы сделать запрос, выведите единственную строку в следующем формате: - В начале строки выведите «? c » (без кавычек), где \(c\) \((1 \leq c \leq n)\) равно количеству вершин в списке, про который вы хотите сделать запрос. После этого должны следовать \(c\) различных целых чисел из отрезка \([1, n]\) — номера вершин из списка.
В ответ на запрос, вы получите два целых числа \(x\), \(d\) — вершина (из вершин из списка из запроса) с минимальной суммой расстояний до двух загаданных вершин и сумма расстояний от этой вершины до двух загаданных вершин. Если список вершин в запросе некорректный или вы превысили лимит на количество запросов, вы получите \(x = d = -1\). В этом случае, вы должны завершить вашу программу немедленно. После того, как вы угадаете загаданные вершины, выведите единственную строку «! » (без кавычек). После этого выведите два целых числа из отрезка \([1, n]\) — загаданные вершины. Вы можете выводить их в любом порядке. После этого, вы должны считать строку. Если вы угадали вершины правильно, вы получите строку «Correct». В этом случае вы должны продолжить решать оставшиеся наборы входных данных или завершить программу, если все наборы входных данных были решены. Иначе, вы получите строку «Incorrect». В этом случае, вы должны завершить программу немедленно. Запрос угадывания загаданных вершин не считается в количестве сделанных запросов. Интерактор не адаптивный. Загаданные вершины не меняются во время запросов. Не забывайте считать строку «Correct» / «Incorrect» после запроса угадывания вершин. Вы должны решить набор входных данных перед получением входных данных следующего набора входных данных. Ограничение на \(14\) запросов существует для каждого набора входных данных по отдельности, а не для всех входных данных вместе. После вывода запроса, не забывайте выводить символ переноса строки и сбрасывать буфер выходного потока. Иначе, вы получите вердикт Idleness limit exceeded. Чтобы это сделать, используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- обратитесь к документации для других языков.
Взломы Чтобы сделать взлом, используйте следующий формат теста: В первой строке должно находиться единственное целое число \(t\) \((1 \leq t \leq 10)\) — количество наборов входных данных. Затем должно следовать описание наборов входных данных. Первая строка каждого набора входных данных должна содержать единственное целое число \(n\) \((2 \le n \le 1000)\) — количество вершин в дереве. Во второй строке должно находиться два различных целых числа из отрезка \([1, n]\) — загаданные вершины. Следующая \(n - 1\) строка должна содержать по два целых числа \(u\), \(v\) \((1 \le u, v \le n, u \ne v)\) — ребра дерева. Примечание Дерево из первого теста изображено на картинке, загаданные вершины \(1\) и \(3\).  | |
![]()
|
|
F2. Загадана пара вершин (сложная версия)
Бинарный поиск
графы
Деревья
интерактив
кратчайшие пути
поиск в глубину и подобное
*2700
Обратите внимание, что единственное различие между простой и сложной версиями задачи заключается в количестве разрешенных запросов. Вы можете делать взломы, только если все версии задачи решены. Это интерактивная задача. Вам дано дерево, состоящее из \(n\) вершин, пронумерованных целыми числами от \(1\) до \(n\). Ayush и Ashish выбрали две секретные различные вершины дерева. Вам нужно отгадать обе вершины. Вы можете делать следующий запрос: - Вы даете список вершин дерева и в результате получаете вершину из списка, сумма растояний от которой до двух загаданных вершин минимально (если таких вершин в списке несколько, вы получите одну из них). Вы также получите сумму расстояний от этой вершины до двух загаданных вершин.
Напомним, что деревом называется связный граф без циклов. Расстоянием между двумя вершинами называется количество ребер, лежащих на простом пути между ними. Более формально, пусть две загаданные вершины это \(s\) и \(f\). За один запрос, вы можете дать множество вершин \(\{a_1, a_2, \ldots, a_c\}\) дерева. В результате вы получите два числа \(a_i\) и \(dist(a_i, s) + dist(a_i, f)\). Вершина \(a_i\) является любой вершиной из данного вами множества, для которой число \(dist(a_i, s) + dist(a_i, f)\) минимально. Вы можете сделать не более \(11\) запросов. Протокол взаимодействия Для того, чтобы сделать запрос, выведите единственную строку в следующем формате: - В начале строки выведите «? c » (без кавычек), где \(c\) \((1 \leq c \leq n)\) равно количеству вершин в списке, про который вы хотите сделать запрос. После этого должны следовать \(c\) различных целых чисел из отрезка \([1, n]\) — номера вершин из списка.
В ответ на запрос, вы получите два целых числа \(x\), \(d\) — вершина (из вершин из списка из запроса) с минимальной суммой расстояний до двух загаданных вершин и сумма расстояний от этой вершины до двух загаданных вершин. Если список вершин в запросе некорректный или вы превысили лимит на количество запросов, вы получите \(x = d = -1\). В этом случае, вы должны завершить вашу программу немедленно. После того, как вы угадаете загаданные вершины, выведите единственную строку «! » (без кавычек). После этого выведите два целых числа из отрезка \([1, n]\) — загаданные вершины. Вы можете выводить их в любом порядке. После этого, вы должны считать строку. Если вы угадали вершины правильно, вы получите строку «Correct». В этом случае вы должны продолжить решать оставшиеся наборы входных данных или завершить программу, если все наборы входных данных были решены. Иначе, вы получите строку «Incorrect». В этом случае, вы должны завершить программу немедленно. Запрос угадывания загаданных вершин не считается в количестве сделанных запросов. Интерактор не адаптивный. Загаданные вершины не меняются во время запросов. Не забывайте считать строку «Correct» / «Incorrect» после запроса угадывания вершин. Вы должны решить набор входных данных перед получением входных данных следующего набора входных данных. Ограничение на \(11\) запросов существует для каждого набора входных данных по отдельности, а не для всех входных данных вместе. После вывода запроса, не забывайте выводить символ переноса строки и сбрасывать буфер выходного потока. Иначе, вы получите вердикт Idleness limit exceeded. Чтобы это сделать, используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- обратитесь к документации для других языков.
Взломы Чтобы сделать взлом, используйте следующий формат теста: В первой строке должно находиться единственное целое число \(t\) \((1 \leq t \leq 10)\) — количество наборов входных данных. Затем должно следовать описание наборов входных данных. Первая строка каждого набора входных данных должна содержать единственное целое число \(n\) \((2 \le n \le 1000)\) — количество вершин в дереве. Во второй строке должно находиться два различных целых числа из отрезка \([1, n]\) — загаданные вершины. Следующая \(n - 1\) строка должна содержать по два целых числа \(u\), \(v\) \((1 \le u, v \le n, u \ne v)\) — ребра дерева. Примечание Дерево из первого теста изображено на картинке, загаданные вершины \(1\) и \(3\).  | |
![]()
|
|
G. Изменение дерева
графы
Деревья
Конструктив
Паросочетания
Перебор
поиск в глубину и подобное
*2800
Вам дано дерево с \(n\) вершинами. Вы можете изменить строение дерева с помощью следующей многошаговой операции: - Выберите три вершины \(a\), \(b\) и \(c\) такие, чтобы \(b\) соединена ребром и с \(a\) и с \(c\).
- Для каждой вершины \(d\) кроме \(b\), которая соединена ребром с \(a\), удалите ребро, соединяющее \(d\) и \(a\), и добавьте ребро, соединяющее \(d\) и \(c\).
- Удалите ребро, соединяющее \(a\) и \(b\), и добавьте ребро, соединяющее \(a\) и \(c\).
В качестве примера рассмотрим следующее дерево:  Следующая диаграмма иллюстрирует последовательность шагов, которые происходят, когда мы применяем операцию к вершинам \(2\), \(4\) и \(5\):  Можно доказать, что после каждой операции полученный граф все еще является деревом. Найдите минимальное количество операций, которые необходимо выполнить, чтобы превратить дерево в звезду. Звезда — это дерево с одной вершиной степени \(n - 1\), называемой его центром, и \(n - 1\) вершинами степени \(1\). Выходные данные Выведите единственное целое число — минимальное количество операций, необходимое для преобразования дерева в звезду. Можно доказать, что при данных ограничениях всегда можно превратить дерево в звезду, используя не более \(10^{18}\) операций. Примечание Первый пример соответствует дереву из условия. Как мы уже видели, мы можем превратить дерево в звезду с центром в вершине \(5\), применив одну операцию к вершинам \(2\), \(4\) и \(5\). Во втором тестовом примере данное дерево уже является звездой с центром в вершине \(4\), поэтому никаких операций выполнять не нужно. | |
![]()
|
|
E. Перевернутые родословные
Деревья
дп
Конструктив
математика
разделяй и властвуй
*2800
Учёный Иван Иванович изучает перевёрнутые родословные. Перевёрнутая родословная представляет собой набор людей, про каждого из которых известны либо оба его родителя, либо не известен ни один родитель. Кроме того, известно, что у всех людей из родословной есть ровно один ребёнок, кроме одного человека, у которого детей вовсе нет. Поэтому, если пронумеровать людей целыми числами от \(1\) до \(n\), то можно обозначить за \(s_i\) номер ребёнка человека с номером \(i\) и сказать, что \(s_i = 0\) в случае, если у человека с номером \(i\) детей нет. Назовём человека \(a\) предком человека \(b\), если либо \(a = b\), либо если у \(a\) есть ребёнок, который является предком человека \(b\). Это значит, что человек \(a\) является предком для \(a\), \(s_a\), \(s_{s_a}\) и так далее. Будем считать, что произошёл перекос родословной с участием некоторого человека, если известны оба его родителя и количество известных предков одного из его родителей хотя бы вдвое больше, чем количество известных предков второго родителя. Иван Иванович посчитал количество перекосов родословной и получил число \(k\), но, конечно же, он делал это вручную и мог ошибиться. Помогите проверить Ивану Ивановичу его вычисления: скажите, существует ли родословная из \(n\) людей с \(k\) перекосами, и если существует, то приведите пример подобной родословной. Выходные данные В первой строке выведите «YES» (без кавычек), если существует родословная с \(n\) людьми и \(k\) перекосами, и «NO» (без кавычек) в противном случае. Если требуемая родословная существует, то во второй строке выведите \(n\) целых чисел \(s_1, s_2, \ldots, s_n\) (\(0 \leq s_i \leq n\)), задающих номера детей людей в родословной. Если искомых родословных несколько, выведите любую. Примечание В первом примере подойдет единственная родословная, которую можно составить из трёх человек (человек и два его родителя). Во втором примере подойдет следующая родословная:  В человеке номер один происходит перекос, так как у одного его родителя один предок, а у второго — три. | |
![]()
|
|
E. Слияние башен
Деревья
реализация
снм
Структуры данных
*2300
У вас есть \(n\) дисков, радиус \(i\)-го диска равен \(i\). Изначально эти диски распределены по \(m\) башням из дисков: каждая башня содержит хотя бы один диск, и диски в каждой башне отсортированы от большего к меньшему снизу вверх. Вы должны собрать все диски в одну башню. Чтобы сделать это, вы можете выбрать две различных башни \(i\) и \(j\) (каждая из которых содержит хотя бы один диск), взять несколько (возможно, все) верхних дисков с башни \(i\) и поместить их на вершину башни \(j\) в том же самом порядке — при условии, что верхний диск башни \(j\) больше каждого перемещаемого диска. Эту операцию можно применять любое количество раз. Например, если у вас есть две башни, содержащие диски \([6, 4, 2, 1]\) и \([8, 7, 5, 3]\) (в порядке снизу вверх), существуют ровно две возможные операции: - переместить диск \(1\) с первой башни на вторую, после чего башни станут следующими: \([6, 4, 2]\) и \([8, 7, 5, 3, 1]\);
- переместить диски \([2, 1]\) с первой башни на вторую, после чего башни станут следующими: \([6, 4]\) и \([8, 7, 5, 3, 2, 1]\).
Пусть сложность некоторого набора башен — это минимальное количество операций, необходимых для того, чтобы собрать все диски в одну башню. Например, сложность набора башен \([[3, 1], [2]]\) равна \(2\): вы можете переместить диск \(1\) на вторую башню, а потом переместить оба диска со второй башни на первую башню. Вам заданы \(m - 1\) запросов. Каждый запрос обозначается двумя числами \(a_i\) и \(b_i\), обозначающими следующее: «слить башни \(a_i\) и \(b_i\) в одну» (то есть взять все диски из этих башен и составить из них одну башню, в которой диски отсортированы по убыванию размера снизу вверх). Новая башня (являющаяся результатом слияния) получает индекс \(a_i\). Для каждого \(k \in [0, m - 1]\) посчитайте сложность набора башен после выполнения первых \(k\) запросов. Выходные данные Выведите \(m\) целых чисел. \(k\)-е число (в \(0\)-индексации) должно быть равно сложности набора башен после первых \(k\) запросов. Примечание Башни в примере из условия: - до запросов: \([[5, 1], [2], [7, 4, 3], [6]]\);
- после первого запроса: \([[2], [7, 5, 4, 3, 1], [6]]\);
- после второго запроса: \([[7, 5, 4, 3, 2, 1], [6]]\);
- после третьего запроса остается только одна башня: \([7, 6, 5, 4, 3, 2, 1]\).
| |
![]()
|
|
D. Величественная коричневая древесная змея
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
*3000
Существует неориентированное дерево, состоящее из \(n\) вершин, соединенных \(n-1\) двусторонним ребром. Также есть змея, находящаяся внутри этого дерева. Ее голова находится в вершине \(a\) и ее хвост находится в вершине \(b\). Тело змеи занимает все вершины на простом пути между вершинами \(a\) и \(b\). Змея хочет узнать, может ли она развернуться, то есть переместить свою голову в вершину, где начинался хвост и переместить свой хвост в вершину, где начиналась голова. К сожалению, движения змеи ограничены структурой дерева. За одну операцию змея может переместить свою голову в соседнюю вершину, которая не занята змеей в текущий момент. Когда это происходит, хвост змеи перемещается на одну вершину ближе к голове, то есть длина змеи не изменяется. Аналогично, змея может переместить свой хвост в соседнюю вершину, которая не занята змеей в текущий момент. Когда это происходит, голова змеи перемещается на одну вершину ближе к хвосту.  Будем обозначать позицию змеи, как \((h,t)\), где \(h\) — это номер вершины дерева, в которой находится голова и \(t\) — номер вершины дерева, где находится хвост. Змея сможет развернуться с помощью последовательности операций \((4,7)\to (5,1)\to (4,2)\to (1, 3)\to (7,2)\to (8,1)\to (7,4)\). Будем обозначать позицию змеи, как \((h,t)\), где \(h\) — это номер вершины дерева, в которой находится голова и \(t\) — номер вершины дерева, где находится хвост. Змея сможет развернуться с помощью последовательности операций \((4,7)\to (5,1)\to (4,2)\to (1, 3)\to (7,2)\to (8,1)\to (7,4)\). Определите, сможет ли змея развернуться с помощью некоторой последовательности операций. Выходные данные Для каждого набора входных данных выведите «YES», если змея может развернуть себя и «NO», иначе. Примечание Первый набор входных данных изображен на картинке в тексте условия задачи. Во втором наборе входных данных дерево имеет форму пути. Можно показать, что змея не сможет развернуться. В третьем наборе входных данных, можно показать, что змея не сможет развернуться. В четвертом наборе входных данных пример последовательности операций: \((15,12)\to (16,11)\to (15,13)\to (10,14)\to (8,13)\to (4,11)\to (1,10)\) \(\to (2,8)\to (3,4)\to (2,5)\to (1,6)\to (4,7)\to (8,6)\to (10,5)\) \(\to (11,4)\to (13,8)\to (14,10)\to (13,15)\to (11,16)\to (12,15)\). | |
![]()
|
|
A. Трансформация строки 1
графы
Деревья
жадные алгоритмы
снм
сортировки
Строки
*1700
Обратите внимание, что единственная разница между Трансформация строки 1 и Трансформация строки 2 заключается в операции, которую делает Коа. В этой версии буква \(y\), которую выбирает Koa, должна быть строго больше по алфавиту, чем \(x\) (для лучшего понимания прочитайте условие). Вы можете делать взломы по этим задачам независимо. У Коалы Коа есть две строки \(A\) и \(B\) одинаковой длины \(n\) (\(|A|=|B|=n\)), состоящие из первых \(20\) строчных букв английского алфавита (то есть от a до t). В один ход Коа: - выбирает некоторое подмножество позиций \(p_1, p_2, \ldots, p_k\) (\(k \ge 1; 1 \le p_i \le n; p_i \neq p_j\) если \(i \neq j\)) из \(A\), такое что \(A_{p_1} = A_{p_2} = \ldots = A_{p_k} = x\) (т. е. все буквы на этой позиции равны некоторой букве \(x\)).
- выбирает букву \(y\) (из первых \(20\) строчных букв английского алфавита) такую, что \(y>x\) (т. е. буква \(y\) в алфавитном порядке строго больше, чем \(x\)).
- делает все буквы в позициях \(p_1, p_2, \ldots, p_k\) равными \(y\). Более формально: для каждого \(i\) (\(1 \le i \le k\)) Коа устанавливает \(A_{p_i} = y\).
Обратите внимание, что вы можете изменять только буквы в строке \(A\).
Коа хочет знать наименьшее число ходов, которые она должна сделать, чтобы сделать строки равными друг другу (\(A = B\)) или определить, что нет никакого способа сделать их равными. Помогите ей! Выходные данные Для каждого набора входных данных: Выведите в единственной строке минимальное количество ходов, которое Koa должна сделать, чтобы строки стали равны друг другу (\(A = B\)) или \(-1\), если нет никакого способа сделать их равными. Примечание - В \(1\)-м наборе входных данных Коа:
- выбирает позиции \(1\) и \(2\) и устанавливает \(A_1 = A_2 = \) b (\(\color{red}{aa}b \rightarrow \color{blue}{bb}b\)).
- выбирает позиции \(2\) b \(3\) и устанавливает \(A_2 = A_3 = \) c (\(b\color{red}{bb} \rightarrow b\color{blue}{cc}\)).
- Во \(2\)-м наборе входных данных Коа не может сделать строку \(A\) равной строке \(B\).
- В \(3\)-м наборе входных данных Коа:
- выбирает позицию \(1\) и устанавливает \(A_1 = \) t (\(\color{red}{a}bc \rightarrow \color{blue}{t}bc\)).
- выбирает позицию \(2\) и устанавливает \(A_2 = \) s (\(t\color{red}{b}c \rightarrow t\color{blue}{s}c\)).
- выбирает позицию \(3\) и устанавливает \(A_3 = \) r (\(ts\color{red}{c} \rightarrow ts\color{blue}{r}\)).
| |
![]()
|
|
C. Трансформация строки 2
битмаски
графы
Деревья
дп
*3100
Обратите внимание, что единственная разница между Трансформация строки 1 и Трансформация строки 2 заключается в операции, которую делает Коа. В этой версии буква \(y\), которую выбирает Koa, может быть любой из первых \(20\) букв английского алфавита (для лучшего понимания прочитайте условие). Вы можете делать взломы по этим задачам независимо. Коала Коа имеет две строки \(A\) и \(B\) одинаковой длины \(n\) (\(|A|=|B|=n\)), состоящие из первых \(20\) строчных букв английского алфавита (то есть от a до t). В один ход Коа: - выбирает некоторое подмножество позиций \(p_1, p_2, \ldots, p_k\) (\(k \ge 1; 1 \le p_i \le n; p_i \neq p_j\) если \(i \neq j\)) из \(A\), такое что \(A_{p_1} = A_{p_2} = \ldots = A_{p_k} = x\) (т. е. все буквы на этой позиции равны некоторой букве \(x\)).
- выбирает любую букву \(y\) (из первых \(20\) строчных букв английского алфавита).
- делает все буквы в позициях \(p_1, p_2, \ldots, p_k\) равными \(y\). Более формально: для каждого \(i\) (\(1 \le i \le k\)) Коа устанавливает \(A_{p_i} = y\).
Обратите внимание, что вы можете изменять только буквы в строке \(A\). Коа хочет знать наименьшее число ходов, которые она должна сделать, чтобы сделать строки равными друг другу (\(A = B\)) или определить, что нет никакого способа сделать их равными. Помогите ей! Выходные данные Для каждого набора входных данных: Выведите в единственной строке минимальное количество ходов, которое Koa должна сделать, чтобы строки стали равны друг другу (\(A = B\)) или \(-1\), если нет никакого способа сделать их равными. Примечание - В \(1\)-м наборе входных данных Koa:
- выбирает позиции \(1\) и \(2\) и устанавливает \(A_1 = A_2 = \) b (\(\color{red}{aa}b \rightarrow \color{blue}{bb}b\)).
- выбирает позиции \(2\) и \(3\) и устанавливает \(A_2 = A_3 = \) c (\(b\color{red}{bb} \rightarrow b\color{blue}{cc}\)).
- В \(2\)-м наборе входных данных Koa:
- выбирает позиции \(1\) и \(4\) и устанавливает \(A_1 = A_4 = \) a (\(\color{red}{c}ab\color{red}{c} \rightarrow \color{blue}{a}ab\color{blue}{a}\)).
- выбирает позиции \(2\) и \(4\) и устанавливает \(A_2 = A_4 = \) b (\(a\color{red}{a}b\color{red}{a} \rightarrow a\color{blue}{b}b\color{blue}{b}\)).
- выбирает позицию \(3\) и устанавливает \(A_3 = \) c (\(ab\color{red}{b}b \rightarrow ab\color{blue}{c}b\)).
- В \(3\)-м наборе входных данных Koa:
- выбирает позицию \(1\) и устанавливает \(A_1 = \) t (\(\color{red}{a}bc \rightarrow \color{blue}{t}bc\)).
- выбирает позицию \(2\) и устанавливает \(A_2 = \) s (\(t\color{red}{b}c \rightarrow t\color{blue}{s}c\)).
- выбирает позицию \(3\) и устанавливает \(A_3 = \) r (\(ts\color{red}{c} \rightarrow ts\color{blue}{r}\)).
| |
![]()
|
|
F. Удаление листьев
Деревья
жадные алгоритмы
реализация
Структуры данных
*2300
Вам дано дерево (связный граф без циклов), состоящее из \(n\) вершин. Дерево не является корневым — это просто неориентированный связный граф без циклов. За один ход вы можете выбрать ровно \(k\) листьев (лист — это такая вершина, которая соединена только с одной другой вершиной), соединенных с одной и той же вершиной, и удалить их вместе с ребрами, инцидентными им. То есть вы выбираете такие листья \(u_1, u_2, \dots, u_k\), что существуют ребра \((u_1, v)\), \((u_2, v)\), \(\dots\), \((u_k, v)\), и удаляете эти листья вместе с этими ребрами. Ваша задача — найти максимальное количество ходов, которое вы можете совершить, если вы будете удалять листья оптимально. Вам необходимо ответить на \(t\) независимых наборов тестовых данных. Выходные данные Выведите ответ на каждый набор тестовых данных — максимальное количество ходов, которое вы можете совершить, если вы будете удалять листья оптимально. Примечание Картинка, соответствующая первому набору тестовых данных примера: 
Здесь вы можете удалить вершины \(2\), \(5\) и \(3\) в течение первого хода и вершины \(1\), \(7\) и \(4\) в течение второго хода. Картинка, соответствующая второму набору тестовых данных примера: 
Здесь вы можете удалить вершины \(7\), \(8\) и \(9\) в течение первого хода, затем вершины \(5\), \(6\) и \(10\) в течение второго хода, и вершины \(1\), \(3\) и \(4\) в течение третьего хода. Картинка, соответствующая третьему набору тестовых данных примера: 
Здесь вы можете удалить вершины \(5\) и \(7\) в течение первого хода, затем вершины \(2\) и \(4\) в течение второго хода, и вершины \(1\) и \(6\) в течение третьего хода. | |
![]()
|
|
B1. Посёлок (Минимум)
*особая задача
Деревья
дп
жадные алгоритмы
*2100
Эта задача разбита на две. В данной задаче, вам нужно найти минимальный ответ. В задаче же Посёлок (Максимум) вам нужно найти максимальный возможный ответ. За каждую из этих задач можно получить по \(50\) баллов. В одном посёлке люди живут в \(N\) домах. В каждом доме живёт ровно один житель. Дома соединены дорогами. Каждая дорога соединяет два дома и имеет длину \(1\) км. Из каждого дома можно достичь любой другой дом, идя по одной или нескольким дорогам. В общем в посёлке ровно \(N-1\) дорог. Однажды все жители решили переехать в другие дома. После переезда всех жителей в каждом доме снова должен жить ровно один житель, но ни один житель не должен остаться в том же доме, в котором жил до этого. Наша цель — узнать наименьшую возможную сумму кратчайших путей (в км) перемещения всех жителей из старых мест жительства на новые.  Пример посёлка с семью домами Например, если всего есть семь домов, соединённых дорогами так, как показано на рисунке, то наименьшая общая длина равняется \(8\) км (этого можно достичь, перемещая жителей \(1 \to 6\), \(2 \to 4\), \(3 \to 1\), \(4 \to 2\), \(5 \to 7\), \(6 \to 3\), \(7 \to 5\)). Напишите программу, которая находит наименьшую возможную сумму кратчайших путей (в км), а также распределение жителей по новым домам. Выходные данные В первой строке выведите одно целое число, наименьшую возможную общую длину кратчайших путей жителей в километрах. Во второй строке опишите одно правильное распределение жителей по новым домам с наименьшей возможной общей длиной: \(N\) различных целых чисел \(v_1, v_2, \ldots, v_N\). Для каждого \(i\), \(v_i\) обозначает номер дома, в который должен переехать житель из дома с номером \(i\) (\(v_i \neq i\)). Если существует несколько распределений, выведите любое из них. Система оценки Подзадачи: - (6 баллов) \(N \leq 10\)
- (19 баллов) \(N \leq 1\,000\)
- (25 баллов) Без дополнительных ограничений.
| |
![]()
|
|
B2. Посёлок (Максимум)
*особая задача
Деревья
поиск в глубину и подобное
*2500
Эта задача разбита на две. В данной задаче, вам нужно найти максимальный ответ. В задаче же Посёлок (Минимум) вам нужно найти минимальный возможный ответ. За каждую из этих задач можно получить по \(50\) баллов. В одном посёлке люди живут в \(N\) домах. В каждом доме живёт ровно один житель. Дома соединены дорогами. Каждая дорога соединяет два дома и имеет длину \(1\) км. Из каждого дома можно достичь любой другой дом, идя по одной или нескольким дорогам. В общем в посёлке ровно \(N-1\) дорог. Однажды все жители решили переехать в другие дома. После переезда всех жителей в каждом доме снова должен жить ровно один житель, но ни один житель не должен остаться в том же доме, в котором жил до этого. Наша цель — узнать наибольшую возможную сумму кратчайших путей (в км) перемещения всех жителей из старых мест жительства на новые.  Пример посёлка с семью домами Например, если всего есть семь домов, соединённых дорогами так, как показано на рисунке, то наибольшая общая длина равняется \(18\) км (этого можно достичь, перемещая жителей \(1 \to 7\), \(2 \to 3\), \(3 \to 4\), \(4 \to 1\), \(5 \to 2\), \(6 \to 5\), \(7 \to 6\)). Напишите программу, которая находит наибольшую возможную сумму кратчайших путей (в км), а также распределение жителей по новым домам. Выходные данные В первой строке выведите одно целое число, наибольшую возможную общую длину кратчайших путей жителей в километрах. Во второй строке опишите одно правильное распределение жителей по новым домам с наибольшей возможной общей длиной: \(N\) различных целых чисел \(v_1, v_2, \ldots, v_N\). Для каждого \(i\), \(v_i\) обозначает номер дома, в который должен переехать житель из дома с номером \(i\) (\(v_i \neq i\)). Если существует несколько распределений, выведите любое из них. Система оценки Подзадачи: - (6 баллов) \(N \leq 10\)
- (19 баллов) \(N \leq 1\,000\)
- (25 баллов) Без дополнительных ограничений.
| |
![]()
|
|
C. Дядя Богдан и настроение страны
Деревья
жадные алгоритмы
математика
поиск в глубину и подобное
*1800
Дядя Богдан, будучи матросом на корабле капитана Флинта, порой скучает по родине. Сегодня он рассказал о том, как в его государстве вводили индекс счастья населения. Всего в стране \(n\) городов и \(n−1\) двусторонняя дорога, соединяющая некоторые пары городов. Из любого города можно попасть в любой другой, пройдя по некоторым дорогам. Города пронумерованы от \(1\) до \(n\) и город \(1\) является столицей. Таким образом, структура государства является корневым деревом. Всего в стране проживает \(m\) человек. В \(i\)-м городе проживает \(p_i\) человек, но все работают в столице. После напряженного рабочего дня, каждый из жителей возвращается в свой город по кратчайшему пути. У каждого жителя есть свое настроение: кто-то уходит с рабочего места в хорошем настроении, а у кого-то настроение уже испорчено. Более того, и по пути домой настроение жителя может испортиться. Если настроение человека испортилось, то оно уже не может улучшиться. В каждом городе установлен детектор настроения — он отслеживает настроение каждого, кто побывал в этом городе. Детектор настроения \(i\)-го города считает индекс счастья \(h_i\) как количество человек в хорошем настроении минус количество в плохом. Для простоты будем считать, что настроение жителя внутри города не меняется. Детектор настроения — это новая разработка и нет полной уверенности, что все приборы отработают должным образом. После того, как все жители страны добрались до своих городов, власти обратились к Дяде Богдану, лучшему программисту государства, с просьбой определить корректны ли данные индекса счастья всех городов или где-то закралась ошибка. Дядя Богдан успешно справился с задачей. А удастся ли это Вам? Более формально, Вам требуется определить: «Возможно ли, что, после возвращения всех жителей по домам, для каждого города \(i\) будет верно, что индекс счастья в этом городе в точности равен \(h_i\)». Выходные данные Для каждого набора входных данных выведите YES, если все детекторы настроения исправны или NO — иначе. Буквы в словах YES и NO можно выводить в любом регистре. Примечание Рассмотрим первый набор входных данных первого теста:  Под конец рабочего дня все жители страны находятся в столице. Рассмотрим один из возможных вариантов развития событий: - житель города \(1\): живет в столице и его настроение не ухудшалось;
- житель города \(4\): посетил города \(1\) и \(4\), настроение ухудшилось между городами \(1\) и \(4\);
- житель города \(3\): посетил города \(1\) и \(3\) в хорошем настроении;
- житель города \(6\): посетил города \(1\), \(3\) и \(6\), настроение ухудшилось между городами \(1\) и \(3\);
Таким образом, - \(h_1 = 4 - 0 = 4\),
- \(h_2 = 0\),
- \(h_3 = 1 - 1 = 0\),
- \(h_4 = 0 - 1 = -1\),
- \(h_5 = 0\),
- \(h_6 = 0 - 1 = -1\),
- \(h_7 = 0\).
Второй набор первого теста:  У всех жителей страны уже испортилось настроение в столице. Это единственный возможный вариант развития событий. Первый набор второго теста:  Второй набор второго теста:  Можно показать, что требуемые значения индексов счастья недостижимы в обоих наборах второго теста. | |
![]()
|
|
D. Капитан Флинт и сокровище
графы
Деревья
жадные алгоритмы
поиск в глубину и подобное
реализация
Структуры данных
*2000
В погоне за очередным сокровищем капитан Флинт наткнулся на некоторую задачу, которая может быть связана с поиском сокровища, а может и не быть. Поэтому капитан Флинт поручил ее решение своим матросам и назначил огромное вознаграждение: целый один выходной день. Задача же звучит так... Заданы массивы \(a\) и \(b\) длины \(n\). Изначально, \(ans\) равен \(0\) и определена следующая операция: - Выбрать позицию \(i\) (\(1 \le i \le n\));
- Добавить к \(ans\) значение \(a_i\);
- Если \(b_i \neq -1\), то добавить к \(a_{b_i}\) значение \(a_i\);
Какой максимальный \(ans\) можно получить, применив эту операцию к каждой позиции \(i\) (\(1 \le i \le n\)) ровно один раз? Дядя Богдан очень хочет получить вознаграждение и просит Вас помочь ему с решением задачи, а также предоставить порядок позиций, в котором нужно применять операцию выше. Выходные данные В первой строке выведите одно целое число, максимальный \(ans\), который можно получить. Во второй строке опишите последовательность выполнения операций, чтобы получить этот максимальный ответ: \(n\) различных целых чисел \(p_1, p_2, \ldots, p_n\) (\(1 \le p_i \le n\)), где \(p_i\) обозначает позицию, операция над которой выполняется \(i\)-й по порядку. Если существует несколько таких последовательностей, выведите любою из них. | |
![]()
|
|
G. Выбираем направления
графы
Деревья
дп
поиск в глубину и подобное
*2800
Дан неориентированный связный граф, состоящий из \(n\) вершин и \(m\) ребер. \(k\) вершин этого графа — особенные. Вы должны ориентировать каждое ребро графа (или оставить некоторые ребра неориентированными за дополнительную плату). Вы можете оставить \(i\)-е ребро неориентированным, заплатив \(w_i\) монет, или бесплатно ориентировать его. Назовем вершину насыщенной, если она достижима из всех особенных вершин по ребрам графа (если ребро осталось неориентированным, по нему можно ходить в любом направлении). После того, как вы выберете направления для ребер графа (возможно, оставив некоторые неориентированными), вы получите \(c_i\) монет за каждую насыщенную вершину \(i\). То есть вашу итоговую прибыль можно посчитать по формуле \(\sum \limits_{i \in S} c_i - \sum \limits_{j \in U} w_j\), где \(S\) — множество насыщенных вершин, а \(U\) — множество ребер, оставшихся неориентированными. Для каждой вершины \(i\) посчитайте максимальную прибыль, которую вы можете получить, если вы обязательно должны сделать вершину \(i\) насыщенной. Выходные данные Выведите \(n\) целых чисел, \(i\)-е из которых должно быть равно максимальной прибыли, которую вы можете получить, если необходимо сделать вершину \(i\) насыщенной. Примечание Рассмотрим первый пример: - лучший способ насытить вершину \(1\) — направить ребра следующим образом: \(2 \to 1\), \(3 \to 2\); \(1\) — единственная насыщенная вершина, поэтому ответ равен \(11\);
- лучший способ насытить вершину \(2\) — оставить ребро \(1-2\) неориентированным, а другое ребро направить так: \(3 \to 2\); \(1\) и \(2\) — насыщенные вершины, стоимость ребра \(1-2\) равна \(10\), поэтому ответ равен \(2\);
- лучший способ насытить вершину \(3\) — направить ребра следующим образом: \(2 \to 3\), \(1 \to 2\); \(3\) — единственная насыщенная вершина, поэтому ответ равен \(5\).
Лучший план действий во втором примере — направить все ребра по циклу: \(1 \to 2\), \(2 \to 3\), \(3 \to 4\) и \(4 \to 1\). Таким образом, все вершины будут насыщенными. | |
![]()
|
|
E. Пары пар
графы
Деревья
жадные алгоритмы
Конструктив
поиск в глубину и подобное
*2600
У вас есть простой связный неориентированный граф, состоящий из \(n\) вершин и \(m\) ребер. Рассмотрим все способы разбить на пары некоторое подмножество из этих \(n\) вершин, чтобы ни одна вершина не присутствовала более чем в одной паре. Такое паросочетание считается хорошим, если для каждой пары выбранных пар индуцированный подграф, содержащий все \(4\) вершины, по два из каждой пары, имеет не более \(2\) ребер (из \(6\) возможных ребер). Более формально, для любых двух выбранных пар \((a,b)\) и \((c,d)\) индуцированный подграф с вершинами \(\{a,b,c,d\}\) должен иметь не более \(2\) ребер. Обратите внимание, что подграф, индуцированный набором вершин, содержит вершины только из этого набора и ребра, оба конца которых находятся в этом наборе. Теперь сделайте одно из двух - Найдите простой путь, состоящий как минимум из \(\lceil \frac{n}{2} \rceil\) вершин. Здесь путь называется простым, если он не посещает какую-либо вершину несколько раз.
- Найдите хорошее паросочетание, в котором по крайней мере у \(\lceil \frac{n}{2} \rceil\) вершин есть пара.
Можно показать, что в каждом графе, удовлетворяющим ограничениям из условия, можно найти или первое, или второе (или оба). Выходные данные Для каждого набора входных данных придерживайтесь следующего формата вывода: Если вы нашли хорошее паросочетание, в первой строке выведите «PAIRING» (без кавычек). - Затем выведите \(k\) (\(\lceil \frac{n}{2} \rceil \le 2\cdot k \le n\)), количество пар в вашем паросочетании.
- Затем в каждой из следующих \(k\) строк выведите по \(2\) целых числа \(a\) и \(b\) —, обозначающих, что \(a\) и \(b\) находятся в одной паре. Заметьте, что в графе не обязано быть ребро между вершинами \(a\) и \(b\)!
- Это паросочетание должно быть хорошим, и каждая вершина должен входить не более в \(1\) пару.
В противном случае в первой строке выведите «PATH» (без кавычек). - Затем выведите \(k\) (\(\lceil \frac{n}{2} \rceil \le k \le n\)), количество узлов на вашем пути.
- Затем во второй строке выведите \(k\) целых чисел, \(v_1, v_2, \ldots, v_k\), в том порядке, в котором они встречаются на пути. Формально, \(v_i\) и \(v_{i+1}\) должны иметь ребро между ними для каждого \(i\) (\(1 \le i < k\)).
- Этот путь должен быть простым, то есть ни одна вершина не должна встречаться на нем более одного раза.
Примечание Путь, полученный в первом наборе входных данных, следующий.  Вот хорошее паросочетание для первого набора входных данных.  Вот нехорошее паросочетание для первого набора входных данных — подграф \(\{1,3,4,5\}\) имеет \(3\) ребра.  Вот паросочетание, полученное во втором наборе входных данных.  Оно хорошее потому, что — - Подграф \(\{1,8,2,5\}\) содержит ребра (\(1\),\(2\)) и (\(1\),\(5\)).
- Подграф \(\{1,8,4,10\}\) содержит ребра (\(1\),\(4\)) и (\(4\),\(10\)).
- Подграф \(\{4,10,2,5\}\) содержит ребра (\(2\),\(4\)) и (\(4\),\(10\)).
Вот еще одно хорошее паросочетание для второго набора входных данных.  | |
![]()
|
|
D. Boboniu и Jianghu
Деревья
дп
жадные алгоритмы
сортировки
*2800
После того как Boboniu закончил строительство своего Jianghu, он занимался кунг-фу на этих горах каждый день. Boboniu разработал карту для своих \(n\) гор. Он использовал \(n-1\) дорогу чтобы соединить все \(n\) гор. Все горы связны с помощью дорог. Для \(i\)-й горы, Boboniu оценил скучность кунг-фу на ней как \(t_i\). Он также оценил высоту каждой горы как \(h_i\). Путь это такая последовательность гор \(M\), что для всех \(i\) (\(1 \le i < |M|\)), существует дорога между \(M_i\) и \(M_{i+1}\). Boboniu считает путь испытанием если для всех \(i\) (\(1\le i<|M|\)), \(h_{M_i}\le h_{M_{i+1}}\). Boboniu хочет разделить все \(n-1\) дорог на несколько испытаний. Обратите внимание, что каждая дорога должна встречаться ровно в одном испытании, но гора может встречаться в нескольких испытаниях. Boboniu хочет минимизировать суммарную скучность всех испытаний. Скучность испытания \(M\) это сумма скучностей всех гор в ней, т.е. \(\sum_{i=1}^{|M|}t_{M_i}\). Он попросил вас найти минимальную возможную суммарную скучность всех испытаний. В награду за вашу работу, вы станете охранником в его Jianghu. Выходные данные Выведите одно целое число: минимальную возможную суммарную скучность всех испытаний. Примечание В первом примере:  На картинке, чем светлее точка, тем выше гора, которую она представляет. Одно из лучших разделений это: - Испытание \(1\): \(3 \to 1 \to 2\)
- Испытание \(2\): \(5 \to 2 \to 4\)
Суммарно скучность для Boboniu равна \((30 + 40 + 10) + (20 + 10 + 50) = 160\). Можно показать, что это является минимальной возможной скучностью. | |
![]()
|
|
E. Паросочетание с расстояниями
Деревья
Конструктив
поиск в глубину и подобное
*3200
Вам дано целое число \(k\) и дерево \(T\) с \(n\) вершинами (\(n\) четно). Обозначим за \(dist(u, v)\) количество ребер на кратчайшем пути между вершинами \(u\) и \(v\) в \(T\). Определим неориентированный взвешенный полный граф \(G = (V, E)\) следующим образом: - \(V = \{x \mid 1 \le x \le n \}\) т.е. множество целых чисел от \(1\) до \(n\)
- \(E = \{(u, v, w) \mid 1 \le u, v \le n, u \neq v, w = dist(u, v) \}\) т.е. существует ребро между каждой парой разных вершин, вес ребра равен расстоянию между соотвествующими вершинами в \(T\)
Ваша задача — найти совершенное паросочетание в \(G\) с суммой весов ребер \(k\) \((1 \le k \le n^2)\). Выходные данные Если не существует необходимого паросочетания, выведите «NO» (без кавычек) в единственной строке. Иначе, выведите «YES» (без кавычек) в первой строке вывода. Затем, выведите \(\frac{n}{2}\) строк, в \(i\)-й из них выведите \(p_i, q_i\) (\(1 \le p_i, q_i \le n\)): \(i\)-ю пару в паросочетании. Примечание Дерево это связный неориентированный граф без циклов. Паросочетание это множество попарно несмежных ребер, без петель; таким образом, никакие два ребра не имеют общих концов. Совершенное паросочетание это паросочетание, которое покрывает все вершины графа; таким образом, каждая вершина инцидентна ровно одному ребру паросочетания. | |
![]()
|
|
E1. Деление весов (простая версия)
Деревья
жадные алгоритмы
поиск в глубину и подобное
Структуры данных
*2000
Простая и сложная версии на самом деле являются разными задачами, поэтому прочитайте условия обеих задач внимательно. Вам задано взвешенное корневое дерево, вершина \(1\) — корень этого дерева. Дерево — это связный граф без циклов. У корневого дерева есть специальная вершина, называемая корнем. Предком вершины \(v\) называется последняя отличная от \(v\) вершина на пути от корня к вершине \(v\). Потомками вершины \(v\) называются все вершины, для которых \(v\) является предком. Вершина называется листом, если у нее нет потомков. Взвешенное дерево — это такое дерево, в котором у каждого ребра есть некоторый вес. Вес пути — это сумма весов всех ребер на этом пути. Вес пути от вершины до самой себя равен \(0\). Вы можете совершить последовательность из нуля или более ходов. В течение одного хода вы можете выбрать ребро и поделить его вес на \(2\) с округлением вниз. Более формально, в течение одного хода вы выбираете какое-то ребро \(i\) и делите его вес на \(2\) с округлением вниз (\(w_i := \left\lfloor\frac{w_i}{2}\right\rfloor\)). Ваша задача — найти минимальное количество ходов, необходимых для того, чтобы сделать сумму весов путей от корня до каждого листа не превосходящей \(S\). Другими словами, если \(w(i, j)\) — это вес пути от вершины \(i\) до вершины \(j\), то вам необходимо сделать \(\sum\limits_{v \in leaves} w(root, v) \le S\), где \(leaves\) — это список всех листьев. Вам необходимо ответить на \(t\) независимых наборов тестовых данных. Выходные данные Для каждого набора тестовых данных выведите ответ на него: минимальное количество ходов, необходимое, чтобы сделать сумму весов путей от корня до каждого листа не превосходящей \(S\). | |
![]()
|
|
E2. Деление весов (сложная версия)
Бинарный поиск
Деревья
жадные алгоритмы
поиск в глубину и подобное
сортировки
*2200
Простая и сложная версии на самом деле являются разными задачами, поэтому прочитайте условия обеих задач внимательно. Вам задано взвешенное корневое дерево, вершина \(1\) — корень этого дерева. Также каждое ребро имеет свою собственную стоимость. Дерево — это связный граф без циклов. У корневого дерева есть специальная вершина, называемая корнем. Предком вершины \(v\) называется последняя отличная от \(v\) вершина на пути от корня к вершине \(v\). Потомками вершины \(v\) называются все вершины, для которых \(v\) является предком. Вершина называется листом, если у нее нет потомков. Взвешенное дерево — это такое дерево, в котором у каждого ребра есть некоторый вес. Вес пути — это сумма весов всех ребер на этом пути. Вес пути от вершины до самой себя равен \(0\). Вы можете совершить последовательность из нуля или более ходов. В течение одного хода вы можете выбрать ребро и поделить его вес на \(2\) с округлением вниз. Более формально, в течение одного хода вы выбираете какое-то ребро \(i\) и делите его вес на \(2\) с округлением вниз (\(w_i := \left\lfloor\frac{w_i}{2}\right\rfloor\)). Каждое ребро \(i\) имеет свою стоимость \(c_i\), которая равна либо \(1\), либо \(2\) монетам. Каждый ход с ребром \(i\) стоит \(c_i\) монет. Ваша задача — найти минимальную суммарную стоимость, необходимую для того, чтобы сделать сумму весов путей от корня до каждого листа не превосходящей \(S\). Другими словами, если \(w(i, j)\) — это вес пути от вершины \(i\) до вершины \(j\), то вам необходимо сделать \(\sum\limits_{v \in leaves} w(root, v) \le S\), где \(leaves\) — это список всех листьев. Вам необходимо ответить на \(t\) независимых наборов тестовых данных. Выходные данные Для каждого набора тестовых данных выведите ответ на него: минимальную суммарную стоимость, необходимую, чтобы сделать сумму весов путей от корня до каждого листа не превосходящей \(S\). | |
![]()
|
|
D. Два пути
графы
Деревья
дп
кратчайшие пути
поиск в глубину и подобное
*1900
Как вы знаете, Васин брат живет во Флатландии. Во Флатландии n городов, соединенных n - 1 двусторонней дорогой. Города пронумерованы от 1 до n. Из любого города можно добраться до любого другого двигаясь по дорогам. Компания «Два пути», в которой работает Васин брат, выиграла тендер на ремонт двух путей во Флатландии. Путем называется последовательность различных городов, последовательно соединенных дорогами. Пути, которые надо отремонтировать, компания может выбрать самостоятельно. Единственное условие, накладываемое тендером — они не должны пересекаться (то есть иметь общих городов). Известно, что прибыль, которую получит компания «Два пути», равна произведению длин выбранных двух путей. Считая длину каждой дороги равной 1, а длину пути равной количеству дорог в ней, найдите максимальную возможную прибыль компании. Выходные данные Выведите максимальную возможную прибыль. | |
![]()
|
|
D. Максимально распределенное дерево
Деревья
дп
жадные алгоритмы
математика
поиск в глубину и подобное
реализация
сортировки
теория чисел
*1800
Вам задано дерево, состоящее из \(n\) вершин. Вы должны сопоставить каждому из \(n-1\) ребер этого дерева целое число таким образом, чтобы выполнялись следующие условия: - каждое число должно быть целым и строго больше \(0\);
- произведение всех \(n-1\) чисел должно быть равно \(k\);
- количество \(1\)-ц среди всех \(n-1\) чисел должно быть минимально возможным.
Назовем \(f(u,v)\) сумму чисел на простом пути из вершины \(u\) в вершину \(v\). Также, назовем \(\sum\limits_{i=1}^{n-1} \sum\limits_{j=i+1}^n f(i,j)\) как индекс распределения дерева. Определите максимально возможный индекс распределения, который можно получить. Так как ответ может быть слишком большим, выведите его по модулю \(10^9 + 7\). В данной задаче, так как число \(k\) может быть слишком большим, задана факторизация \(k\) на простые числа. Выходные данные Выведите максимально возможный индекс распределения. Так как ответ может быть слишком большим, выведите его по модулю \(10^9+7\). Примечание В первом наборе входных данных, один из возможных ответов изображен на рисунке ниже:  В данном случае, \(f(1,2)=1\), \(f(1,3)=3\), \(f(1,4)=5\), \(f(2,3)=2\), \(f(2,4)=4\), \(f(3,4)=2\), и сумма этих \(6\) чисел равна \(17\). Во втором наборе входных данных, один из возможных ответов изображен ниже:  В этом случае, \(f(1,2)=3\), \(f(1,3)=1\), \(f(1,4)=4\), \(f(2,3)=2\), \(f(2,4)=5\), \(f(3,4)=3\), и сумма этих \(6\) чисел равна \(18\). | |
![]()
|
|
C. Star Trek
*особая задача
графы
Деревья
дп
игры
Комбинаторика
матрицы
поиск в глубину и подобное
*2600
The United Federation of Planets is an alliance of \(N\) planets, they are indexed from \(1\) to \(N\). Some planets are connected by space tunnels. In a space tunnel, a starship can fly both ways really fast. There are exactly \(N-1\) space tunnels, and we can travel from any planet to any other planet in the Federation using these tunnels. It's well known that there are \(D\) additional parallel universes. These are exact copies of our universe, they have the same planets and space tunnels. They are indexed from \(1\) to \(D\) (our universe has index \(0\)). We denote the planet \(x\) in universe \(i\) by \(P_x^i\). We can travel from one universe to another using dimension portals. For every \(i\) (\(0\leq i \leq D-1\)), we will place exactly one portal that allows us to fly from \(P_{A_i}^i\) to \(P_{B_i}^{i+1}\), for some planet indices \(A_i\) and \(B_i\) (i.e. \(1 \leq A_i, B_i \leq N\)). Once all the portals are placed, Starship Batthyány will embark on its maiden voyage. It is currently orbiting around \(P_1^0\). Captain Ágnes and Lieutenant Gábor have decided to play the following game: they choose alternately a destination (a planet) to fly to. This planet can be in the same universe, if a space tunnel goes there, or it can be in another universe, if a portal goes there. Their aim is to visit places where no one has gone before. That's why, once they have visited a planet \(P_x^i\), they never go back there (but they can visit the planet \(x\) in another universe). Captain Ágnes chooses the first destination (then Gábor, then Ágnes etc.). If somebody can't choose a planet where they have not been before in his/her turn, he/she loses. Captain Ágnes and Lieutenant Gábor are both very clever: they know the locations of all tunnels and portals, and they both play optimally. For how many different placements of portals does Captain Ágnes win the game? Two placements are different if there is an index \(i\) (\(0\leq i \leq D-1\)), where the \(i\)th portal connects different pairs of planets in the two placements (i.e \(A_i\) or \(B_i\) differs). This number can be very big, so we are interested in it modulo \(10^9+7\). Output You should print a single integer, the number of possible placements of portals where Captain Ágnes wins modulo \(10^9+7\). Scoring \( \begin{array}{|c|c|c|} \hline \text{Subtask} & \text{Points} & \text{Constraints} \\ \hline 1 & 0 & \text{samples}\\ \hline 2 & 7 & N=2 \\ \hline 3 & 8 & N \leq 100 \: \text{and} \: D = 1 \\ \hline 4 & 15 & N \leq 1000 \: \text{and} \: D = 1\\ \hline 5 & 15 & D=1 \\ \hline 6 & 20 & N \leq 1000 \: \text{and} \: D \leq 10^5\\ \hline 7 & 20 & D \leq 10^5\\ \hline 8 & 15 & \text{no additional constraints}\\ \hline \end{array} \) Note There is only 1 portal and \(3 \cdot 3 = 9\) different placements. The following 4 placements are when the Captain wins. 
| |
![]()
|
|
B. Spring cleaning
*особая задача
графы
Деревья
поиск в глубину и подобное
Структуры данных
*2300
Spring cleanings are probably the most boring parts of our lives, except this year, when Flóra and her mother found a dusty old tree graph under the carpet. This tree has \(N\) nodes (numbered from \(1\) to \(N\)), connected by \(N-1\) edges. The edges gathered too much dust, so Flóra's mom decided to clean them. Cleaning the edges of an arbitrary tree is done by repeating the following process: She chooses 2 different leaves (a node is a leaf if it is connected to exactly one other node by an edge), and cleans every edge lying on the shortest path between them. If this path has \(d\) edges, then the cost of cleaning this path is \(d\). She doesn't want to harm the leaves of the tree, so she chooses every one of them at most once. A tree is cleaned when all of its edges are cleaned. The cost of this is the sum of costs for all cleaned paths. Flóra thinks the tree they found is too small and simple, so she imagines \(Q\) variations of it. In the \(i\)-th variation, she adds a total of \(D_i\) extra leaves to the original tree: for each new leaf, she chooses a node from the original tree, and connects that node with the new leaf by an edge. Note that some nodes may stop being leaves during this step. For all these \(Q\) variations, we are interested in the minimum cost that is required to clean the tree. Output You should print \(Q\) lines. In the \(i\)-th line, print a single integer: the minimum cost required to clean the \(i\)-th variation of the tree. If the tree cannot be cleaned, print \(-1\). Scoring \( \begin{array}{|c|c|l|} \hline \text{Subtask} & \text{Points} & \text{Constraints} \\ \hline 1 & 0 & \text{samples}\\ \hline 2 & 9 & Q = 1, \text{there is an edge between node} \: 1 \: \text{and} \: i \: \text{for every} \: i \: (2 \leq i \leq N), \\ & & \text{Flóra can't add extra leaf to node} \: 1 \\ \hline 3 & 9 & Q = 1, \text{there is an edge between node} \: i \: \text{and} \: i+1 \: \text{for all} \: (1 \leq i < N), \\ & & \text{Flóra can't add extra leaf to node} \: 1 \: \text{nor node} \: N \\ \hline 4 & 16 & N \leq 20000, Q \leq 300\\ \hline 5 & 19 & \text{the original tree is a perfect binary tree rooted at node \)1\(} \\ & & \text{(i.e. each internal node has exactly \)2\( children, and every leaf} \\ & & \text{has the same distance from the root)}\\ \hline 6 & 17 & D_i = 1 \: \text{for all} \: i\\ \hline 7 & 30 & \text{no additional constraints}\\ \hline \end{array} \)Note The following picture shows the second variation. A possible solution is to clean the path between leaves \(1 - 6\), \(A - 7\) and \( B - 3\). 
You can download the above example and an additional (bigger) sample input here: https://gofile.io/d/8QlbsS | |
![]()
|
|
B. Догонялки на дереве
Деревья
дп
игры
поиск в глубину и подобное
*1900
Алиса и Боб играют в забавную игру — догонялки на дереве. В эту игру играют на дереве из \(n\) вершин, пронумерованных от \(1\) до \(n\). Напомним, что дерево на \(n\) вершинах — это неориентированный, связный граф с \(n-1\) ребрами. Изначально Алиса располагается в вершине \(a\), а Боб — в вершине \(b\). Они ходят по очереди, и Алиса делает первый ход. За свой ход Алиса может перепрыгнуть в вершину с расстоянием не более \(da\) от текущей вершины. Боб же за свой ход может перепрыгнуть в вершину с расстоянием не более \(db\) от текущей вершины. Расстояние между двумя вершинами определяется как количество рёбер на уникальном простом пути между ними. В частности, любому из игроков разрешается остаться на одной и той же вершине в свой ход. Заметим, что при выполнении хода игрок занимает только начальную и конечную вершины своего хода, а не вершины между ними. Если после не более чем \(10^{100}\) ходов Алиса и Боб занимают одну и ту же вершину, то победителем объявляется Алиса. В противном случае побеждает Боб. Определите победителя, если оба игрока играют оптимально. Выходные данные Для каждого набора входных данных выведите одну строку, содержащую победителя игры: «Alice» или «Bob». Примечание В первом наборе входных данных Алиса может выиграть, перейдя к вершине \(1\). Тогда куда бы Боб не двигался дальше, Алиса сможет перейти к той же самой вершине на следующем шаге.  Во втором наборе входных данных у Боба есть следующая победная стратегия. Куда бы Алиса ни двигалась, Боб всегда будет двигаться к той из вершин \(1\) или \(6\), которая более удалена от Алисы.  | |
![]()
|
|
C. Link Cut центроиды
графы
Деревья
Конструктив
поиск в глубину и подобное
*1700
Fishing Prince любит деревья и особенно он любит деревья с ровно одним центроидом. Деревом называется связный граф без циклов. Вершина называется центроидом дерева тогда и только тогда, когда при удалении этой вершины (удалении вершины и всех выходящих из нее ребер) размер наибольшей компоненты связности оставшегося графа будет наименьший возможный. Например, вершина \(2\) является центроидом дерева на следующей картинке, потому что после того, как вы удалите ее, размер наибольшей компоненты связности оставшегося графа будет равен \(2\). Невозможно удалить другую вершину, чтобы этот размер был меньше.  Однако, в некоторых деревьях может быть больше одного центроида, например:  Обе вершины \(1\) и \(2\) являются центроидами, потому что размер наибольшей компоненты связности будет равен \(3\) после удаления любой из них. Сейчас у Fishing Prince есть дерево. Он должен удалить одно ребро дерева. После этого он должен добавить одно ребро. Получившийся после этих двух операций граф снова должен стать деревом. Можно добавить только что удаленное ребро. Он хочет, чтобы у получившегося дерева был единственный центроид. Помогите ему и найдите любую возможную пару операций, которые можно сделать. Можно доказать, что хотя бы один способ сделать такую пару операций существует. Выходные данные Для каждого набора входных данных выведите две строки. В первой строке выведите два целых числа \(x_1, y_1\) (\(1 \leq x_1, y_1 \leq n\)), которые означают, что вы удаляете ребро между вершинами \(x_1\) и \(y_1\). Должно существовать ребро, соединяющее вершины \(x_1\) и \(y_1\). Во второй строке выведите два целых числа \(x_2, y_2\) (\(1 \leq x_2, y_2 \leq n\)), которые означают, что вы добавляете ребро между вершинами \(x_2\) и \(y_2\). Граф, получающийся после применения этих двух операций, должен снова являться деревом. Если существует несколько возможных решений, выведите любое. Примечание Обратите внимание, что вы можете добавлять то же самое ребро, которое вы удалили. В первом наборе входных данных после удаления и добавления одного и того же ребра вершина \(2\) по-прежнему останется единственным центроидом. Во втором наборе входных данных вершина \(2\) станет единственным центроидом после удаления ребра между вершинами \(1\) и \(3\) и добавления ребра между вершинами \(2\) и \(3\). | |
![]()
|
|
E. Избегайте разноцветных циклов
графы
Деревья
жадные алгоритмы
снм
сортировки
Структуры данных
*2400
Вам дано \(m\) множеств \(A_1, A_2, \ldots, A_m\), состоящих из целых чисел; элементы этих множеств — целые числа от \(1\) до \(n\) включительно. Есть два массива положительных целых чисел \(a_1, a_2, \ldots, a_m\) и \(b_1, b_2, \ldots, b_n\). За одну операцию вы можете удалить элемент \(j\) из множества \(A_i\) и заплатить за это \(a_i + b_j\) монет. Вы можете сделать несколько (возможно, ноль) операций (после этого некоторые множества могут стать пустыми). После этого вы построите неориентированный граф, где каждое ребро будет иметь цвет. Граф будет иметь \(n\) вершин. Для каждого множества \(A_i\) вы добавите ребро \((x, y)\) цвета \(i\) для всех \(x, y \in A_i\) и \(x < y\). Некоторые пары вершин могут быть соединены больше чем одним ребром, но такие ребра будут иметь разные цвета. Мы называем цикл \(i_1 \to e_1 \to i_2 \to e_2 \to \ldots \to i_k \to e_k \to i_1\) (\(e_j\) это какое-то ребро, соединяющее вершины \(i_j\) и \(i_{j+1}\) этого графа) разноцветным, если цвета всех ребер этого цикла различны. Найдите минимальное количество монет, которое нужно заплатить, чтобы получить граф без разноцветных циклов. Выходные данные Выведите единственное целое число — минимальное количество монет, которое нужно заплатить, чтобы получить граф без разноцветных циклов. Примечание В первом тесте можно сделать следующие операции. - Удалить элемент \(1\) из множества \(1\). Вы должны заплатить \(a_1 + b_1 = 5\) монет за эту операцию.
- Удалить элемент \(1\) из множества \(2\). Вы должны заплатить \(a_2 + b_1 = 6\) монет за эту операцию.
Суммарно вы заплатите \(11\) монет. После этих операций первое и второй множества будут равны \(\{2\}\), а третье множество будет равно \(\{1, 2\}\). Поэтому построенный граф будет содержать одно ребро \((1, 2)\) цвета \(3\). Во втором тесте можно сделать следующие операции. - Удалить элемент \(1\) из множества \(1\). Вы должны заплатить \(a_1 + b_1 = 11\) монет за эту операцию.
- Удалить элемент \(4\) из множества \(2\). Вы должны заплатить \(a_2 + b_4 = 13\) монет за эту операцию.
- Удалить элемент \(7\) из множества \(3\). Вы должны заплатить \(a_3 + b_7 = 13\) монет за эту операцию.
- Удалить элемент \(4\) из множества \(4\). Вы должны заплатить \(a_4 + b_4 = 16\) монет за эту операцию.
- Удалить элемент \(7\) из множества \(6\). Вы должны заплатить \(a_6 + b_7 = 13\) монет за эту операцию.
Суммарно вы заплатите \(66\) монет. После этих операций будут следующие множества: - \(\{2, 3\}\);
- \(\{1\}\);
- \(\{1, 3\}\);
- \(\{3\}\);
- \(\{3, 4, 5, 6, 7\}\);
- \(\{5\}\);
- \(\{8\}\).
Вы построите такой граф: 
В нем нет разноцветных циклов. | |
![]()
|
|
G. Подсчет кластеризаций
бпф
графы
Деревья
дп
Комбинаторика
снм
*2700
В сети компании есть \(n\) компьютеров. Они пронумерованы от \(1\) до \(n\). Для каждой пары компьютеров \(1 \leq i < j \leq n\) вы знаете значение \(a_{i,j}\): сложность отправки сообщения между компьютерами \(i\) и \(j\). Значения \(a_{i,j}\) для \(i<j\) различны. Вы хотите разделить компьютеры на \(k\) множеств \(A_1, A_2, \ldots, A_k\), чтобы следующие условия выполнялись: - для каждого компьютера \(1 \leq i \leq n\) есть ровно одно множество \(A_j\) такое, что \(i \in A_j\);
- для каждых двух пар компьютеров \((s, f)\) и \((x, y)\) (\(s \neq f\), \(x \neq y\)) таких, что \(s\), \(f\), \(x\) из одного множества, а \(x\) и \(y\) из разных, выполняется \(a_{s,f} < a_{x,y}\).
Для каждого \(1 \leq k \leq n\) найдите число способов разделить компьютеры на \(k\) групп так, чтобы все упомянутые условия соблюдались. Эти значения могут быть большими, так что вам нужно найти их по модулю \(998\,244\,353\). Выходные данные Выведите \(n\) целых чисел: \(k\)-е из них должно быть равно числу способов разбить компьютеры на \(k\) групп, соблюдая все описанные условия, по модулю \(998\,244\,353\). Примечание Ниже приведены все возможные разбиения компьютеров на \(4\) группы для второго примера: - \(\{1, 2\}, \{3, 4\}, \{5\}, \{6, 7\}\);
- \(\{1\}, \{2\}, \{3, 4\}, \{5, 6, 7\}\);
- \(\{1, 2\}, \{3\}, \{4\}, \{5, 6, 7\}\).
| |
![]()
|
|
F. Дороги и рамен
Деревья
Структуры данных
*2800
В стране Огня есть \(n\) деревень и \(n-1\) двусторонняя дорога, причем из каждой деревни можно добраться в каждую по дорогам. В этой стране есть только два типа дорог: каменные и песчаные. Поскольку страна Огня очень прогрессивная и постоянно обновляется, то каждый день рано утром строители выбирают одну дорогу и меняют ее тип (с каменной на песчаную или наоборот). А еще в стране Огня все любят рамен, поэтому каждый день на каждой каменной дороге устанавливается одна палатка с раменом, а в конце дня палатку убирают. В течение каждого из ближайших \(m\) дней, после того как очередную дорогу переделают, Наруто и Джирайя выбирают себе простой маршрут по стране Огня. Их маршрут может начинаться с любой деревни и заканчиваться тоже в любой (возможно, той же), но по каждой дороге они могут проходить не более одного раза. Поскольку Наруто и Джирайя очень любят рамен, то на каждой каменной дороге они обязательно покупают ровно одну тарелку рамена и кто-нибудь один из них ее ест. Поскольку у ниндзя все должно быть честно, то они выбирают только те пути, проходя по которым они могут съесть равное количество тарелок с раменом. Наруто и Джирайя любят много путешествовать, поэтому каждый день они выбирают самый длинный путь из подходящих. Для каждого дня необходимо определить максимальную длину пути (то есть количество дорог в нём), которым могут пойти Наруто и Джирайя. Выходные данные Необходимо вывести \(m\) строк, \(i\)-я из которых содержит максимальную длину подходящего пути в \(i\)-й день. Примечание После изменения дороги под номером \(3\) самый длинный путь состоит из дорог \(1\), \(2\) и \(4\). После изменения дороги под номером \(4\) самый длинный путь может состоять из дорог \(1\) и \(2\). После изменения дороги под номером \(1\) самый длинный путь может состоять из дорог \(1\), \(2\) и \(3\). После изменения дороги под номером \(3\) самый длинный путь состоит из дорог \(1\), \(2\) и \(4\). После изменения дороги под номером \(4\) самый длинный путь может состоять из дорог \(2\) и \(4\). | |
![]()
|
|
C. XOR-инверсии
битмаски
Деревья
дп
жадные алгоритмы
математика
разделяй и властвуй
сортировки
Строки
Структуры данных
*2000
Вам задан массив \(a\), состоящий из \(n\) неотрицательных целых чисел. Вы должны выбрать неотрицательное целое число \(x\) и сформировать массив \(b\) из \(n\) элементов по следующему правилу: для всех \(i\) от \(1\) до \(n\), \(b_i = a_i \oplus x\) (\(\oplus\) обозначает операцию побитового исключающего ИЛИ). Назовем инверсией в массиве \(b\) такую пару целых чисел \(i\) и \(j\), что \(1 \le i < j \le n\) и \(b_i > b_j\). Вы должны выбрать \(x\) таким образом, чтобы количество инверсий в массиве \(b\) было минимально возможным. Если таких \(x\) несколько — выведите минимальное из них. Выходные данные Выведите два целых числа: минимально возможное количество инверсией в массиве \(b\), и минимальное значение \(x\), при котором достигается такое количество инверсий. Примечание В первом примере из условия оптимально оставить массив без изменений, выбрав \(x = 0\). Во втором примере из условия при выборе \(x = 14\) получается следующий массив \(b\): \([4, 9, 7, 4, 9, 11, 11, 13, 11]\). В нем \(4\) инверсии: - \(i = 2\), \(j = 3\);
- \(i = 2\), \(j = 4\);
- \(i = 3\), \(j = 4\);
- \(i = 8\), \(j = 9\).
В третьем примере из условия при выборе \(x = 8\) получается следующий массив \(b\): \([0, 2, 11]\). В нем нет ни одной инверсии. | |
![]()
|
|
D. Граф и запросы
графы
Деревья
реализация
снм
Структуры данных
*2600
Вам дан неориентированный граф из \(n\) вершин и \(m\) ребер. Изначально в каждой вершине записано число: в вершине \(i\) записано число \(p_i\) (все \(p_i\) — различные числа от \(1\) до \(n\)). Вы должны обработать \(q\) запросов двух типов: - \(1\) \(v\) — среди всех вершин, достижимых из вершины \(v\) по ребрам (включая саму вершину \(v\)), найти вершину \(u\) с максимальным записанным в ней числом \(p_u\), вывести \(p_u\) и заменить \(p_u\) на \(0\);
- \(2\) \(i\) — удалить \(i\)-е ребро из графа.
Обратите внимание, что в запросе первого типа может возникнуть такая ситуация, что во всех вершинах, достижимых из \(v\), записано число \(0\) — в таком случае вершина \(u\) явно не определена, но так как от выбора конкретной вершины \(u\) ничего не зависит, в ответ на такой запрос можно выбрать любую вершину, достижимую из \(v\), и вывести число, записанное в ней (то есть \(0\)). Выходные данные На каждый запрос первого типа выведите одно целое число — значение \(p_u\), записанное в выбранной в запросе вершине \(u\). | |
![]()
|
|
C. Dušan's Railway
графы
Деревья
разделяй и властвуй
*3500
As you may already know, Dušan is keen on playing with railway models. He has a big map with cities that are connected with railways. His map can be seen as a graph where vertices are cities and the railways connecting them are the edges. So far, the graph corresponding to his map is a tree. As you already know, a tree is a connected acyclic undirected graph. He is curious to find out whether his railway can be optimized somehow. He wants to add so-called shortcuts, which are also railways connecting pairs of cities. This shortcut will represent the railways in the unique path in the tree between the pair of cities it connects. Since Dušan doesn't like repeating the railways, he has also defined good paths in his newly obtained network (notice that after adding the shortcuts, his graph is no more a tree). He calls a path good, if no edge appears more than once, either as a regular railway edge or as an edge represented by some shortcut (Every shortcut in a good path has length 1, but uses up all the edges it represents - they can't appear again in that path). Having defined good paths, he defines good distance between two cities to be the length of the shortest good path between them. Finally, the shortcutting diameter of his network is the largest good distance between any two cities. Now he is curious to find out whether it is possible to achieve shortcutting diameter less or equal than \(k\), while adding as few shortcuts as possible. Your solution should add no more than \(\mathbf{10 \cdot n}\) shortcuts. Output The first line of the output should contain a number \(t\) representing the number of the shortcuts that were added. Each of the following \(t\) lines should contain two integers \(u_i\) and \(v_i\), signifying that a shortcut is added between cities \(u_i\) and \(v_i\). Note Notice that adding a shortcut between all cities and city 1 will make a graph theoretic diameter become 2. On the other hand, the paths obtained that way might not be good, since some of the edges might get duplicated. In the example, adding a shortcut between all cities and city 1 doesn't create a valid solution, because for cities 5 and 10 the path that uses shortcuts 5-1 and 1-10 is not valid because it uses edges 1-2, 2-3, 3-4, 4-5 twice. | |
![]()
|
|
F. Скучная карточная игра
Деревья
жадные алгоритмы
Структуры данных
*3200
Когда им скучно, Federico и Giada часто играют в следующую карточную игру с колодой, содержащей \(6n\) карт. Каждая карта содержит одно число от \(1\) до \(6n\), и каждое число встречается ровно на одной карте. Первоначально колода отсортирована, поэтому первая карта содержит число \(1\), вторая карта содержит число \(2\), \(\dots\), а последняя — число \(6n\). Federico и Giada ходят по очереди, Federico начинает. В свой ход игрок берет из колоды по \(3\) последовательные карты и кладет их в карман. Порядок оставшихся в колоде карт не меняется. Они играют до тех пор, пока колода не опустеет (после ровно \(2n\) ходов). В конце игры и Federico, и Giada имеют в карманах по \(3n\) карт. Вы знаете карты в кармане Federico по окончанию игры. Опишите последовательность ходов, в результате которой в кармане Federico получается этот набор карт. Выходные данные Выведите \(2n\) строк, каждая из которых содержит \(3\) целых числа. В \(i\)-й строке в порядке возрастания должны быть выведены целые \(a_i<b_i<c_i\), записанные на трех картах, взятых игроком во время \(i\)-го хода (таким образом, взяты Federico, если \(i\) нечетное, и Giada, если \(i\) четное). Если существует несколько возможных последовательностей ходов, то можно вывести любую. Примечание Пояснение первого примера: Первоначально колода имеет \(12 = 2\cdot 6\) отсортированных карт, поэтому колода имеет \([1\ 2\ 3\ 4\ 5\ 6\ 7\ 8\ 9\ 10\ 11\ 12]\). - Во время хода \(1\) Federico берет три карты \([9\ 10\ 11]\). После его хода колода имеет вид \([1\ 2\ 3\ 4\ 5\ 6\ 7\ 8\ 12]\).
- Во время хода \(2\) Giada берет три карты \([6\ 7\ 8]\). После ее хода колода имеет вид \([1\ 2\ 3\ 4\ 5\ 12]\).
- Во время хода \(3\) Federico берет три карты \([2\ 3\ 4]\). После его хода колода имеет вид \([1\ 5\ 12]\).
- Во время хода \(4\) Giada берет три карты \([1\ 5\ 12]\). После ее хода колода пуста.
В конце игры карты в кармане Federico — \([2\ 3\ 4\ 9\ 10\ 11]\), а карты в кармане Giada – \([1\ 5\ 6\ 7\ 8\ 12]\). | |
![]()
|
|
D. Бандиты в городе
Бинарный поиск
графы
Деревья
жадные алгоритмы
поиск в глубину и подобное
*1900
Все в том же городе, где люди гуляли по улице, завелись бандиты! Один из таких, одетый в черную маску, задался целью поймать как можно больше мирных граждан. Город состоит из \(n\) площадей, которые соединяют \(n-1\) дорог так, что от каждой площади обычно можно добраться до другой ровно одним способом. Площадь под номером \(1\) является главной площадью города. Во время воскресной прогулки дороги между площадями в городе были изменены на односторонние таким образом, что теперь можно добраться от главной площади до любой другой. Бандит высадился из автомобиля на главной площади города в тот момент, когда на \(i\)-й площади было \(a_i\) горожан. Далее происходит следующий процесс. Сначала каждый мирный горожанин, находящийся на площади, из которой выходит хотя бы одна односторонняя дорога, выбирает одну из таких дорог и перемещается по ней. Затем бандит выбирает одну из дорог, выходящих из площади, на которой он сейчас находится, и перемещается по ней. После этого процесс повторяется до тех пор, пока бандит не окажется на площади, из которой не выходит ни одной дороги. Бандит ловит всех граждан, оказавшихся на этой площади. Бандит хочет задержать как можно больше горожан, а горожане не хотят быть пойманными, то есть хотят минимизировать количество задержанных. При этом бандит и горожане знают о расположении горожан на всех площадях в любой момент времени, а все горожане действуют сообща. Если каждая из сторон действует оптимально, то сколько горожан задержит бандит? Выходные данные Выведите одно целое число — количество горожан, которые задержит бандит при оптимальных действиях обеих сторон. Примечание В первом примере горожане на площади \(1\) могут разделиться на две группы \(2 + 1\), тогда на второй и третьей площади окажется по \(3\) человека. Во втором примере независимо от действий граждан бандит сможет поймать хотя бы \(4\) человека. | |
![]()
|
|
D. Дерево минимальной высоты
графы
Деревья
жадные алгоритмы
кратчайшие пути
*1600
У Монокарпа было дерево из \(n\) вершин с корнем в вершине \(1\). Он решил изучить алгоритм BFS (Поиск в ширину), и поэтому запустил BFS на своем дереве, стартуя с корня. Упрощенно, BFS можно описать следующим псевдокодом: a = [] # порядок, в котором вершины обработались
q = Queue()
q.put(1) # кладем корень в конец очереди
while not q.empty():
k = q.pop() # достаем вершину из начала очереди
a.append(k) # кладем k в конец последовательности, описывающей порядок посещения вершин
for y in g[k]: # g[k] — это список всех детей вершины k, отсортированный в порядке возрастания
q.put(y)
Монокарп был так восхищен алгоритмом BFS, что в результате потерял свое дерево. К счастью, у него осталась последовательность вершин в порядке их посещения алгоритмом BFS (массив a из псевдокода). Монокарп знает, что каждая вершина была посещена ровно один раз (так как они кладутся и забираются из очереди ровно один раз). Также он знает, что все дети каждой вершины были просмотрены в порядке возрастания. Монокарп понимает, что есть много деревьев (в общем случае) с одинаковым порядком посещения \(a\), поэтому даже не надеется восстановить свое дерево. Монокарпа устроит любое дерево минимально возможной высоты. Высота дерева — это максимум среди глубин вершин дерева, и глубина вершины — это количество дуг на пути от корня до этой вершины. Например, глубина вершины \(1\) равна \(0\), так как она является корнем, а глубина любого из детей корня равна \(1\). Помогите Монокарпу найти любое дерево с заданным порядком посещения \(a\) и минимальной высотой. Выходные данные Для каждого набора входных данных, выведите минимально возможную высоту дерева с заданным порядком обхода \(a\). Примечание В первом наборе входных данных, есть только одно дерево с заданным порядком посещения:  Во втором наборе, также есть только одно дерево с заданным порядком посещения:  В третьем наборе, оптимальное дерево с заданным порядком посещения изображено ниже:  | |
![]()
|
|
G. СУБД смерти
Деревья
Строки
строковые суфф. структуры
Структуры данных
*2600
Для простоты скажем, что «Тетрадь смерти» — это блокнот, который убивает того, чье имя в него вписывается. С помощью него легко убивать, но довольно сложно поддерживать актуальную информацию о тех людях, кого вы еще не убили, но планируете. Поэтому вы решили создать «Систему управления базой данных смерти» — компьютерную программу, которая предоставляет удобный доступ к базе данных возможных жертв. Позвольте мне описать ее особенности. Определим объект жертвы: у жертвы есть имя (необязательно уникальное), которое состоит только из строчных латинских букв, и целое значение подозрительности. В начале программы пользователь вводит список из \(n\) жертв в базу данных, значение подозрительности каждого устанавливается равным \(0\). Затем пользователь делает запросы двух типов: - \(1~i~x\) — выставить значение подозрительности \(i\)-й жертвы равным \(x\);
- \(2~q\) — по заданной строке \(q\) найти максимальное значение подозрительности жертвы, чье имя входит в \(q\) как подстрока (символы на подряд идущих позициях).
Просто напоминаю, что программа не убивает людей, она только помогает искать их имена для записи в настоящую тетрадь. Поэтому список жертв в базе данных не меняется на протяжении всех запросов. Ну и чего вы ждете? Напишите эту программу! Выходные данные На каждый запрос второго типа выведите одно целое число. Если нет такой жертвы, чье имя является подстрокой \(q\), то выведите \(-1\). Иначе выведите максимальное значение подозрительности жертвы, чье имя входит в \(q\) как подстрока. | |
![]()
|
|
F. Ольга и Игорь
Деревья
интерактив
Теория вероятностей
*3000
Это интерактивная задача. Игорь хочет найти ключ к сердцу Ольги. Проблема в том, что он находится в корне бинарного дерева. Есть полное бинарное дерево высотой \(h\), состоящее из \(n = 2^{h} - 1\) вершин. Вершинам были присвоены различные метки от \(1\) до \(n\). Однако Игорь знает только \(h\) и не знает, какой метке соответствует какая вершина. Чтобы найти ключ к сердцу Ольги, ему нужно найти метку, соответствующую корню, сделав запросы следующего типа не более \(n+420\) раз: - Игорь выберет три различные метки \(u\), \(v\) и \(w\) (\(1 \leq u,v,w \leq n\)).
- В ответ Ольга (интерактор) скажет ему метку наименьшего общего предка вершин, помеченных \(u\) и \(v\), если бы корнем дерева была вершина, помеченная \(w\).
Помогите Игорю найти метку корня дерева! Примечание: интерактор не адаптивный: метки фиксируются перед выполнением каких-либо запросов. Протокол взаимодействия Вы начинаете взаимодействие с чтения \(h\). Чтобы сделать запрос для меток \(u, v, w\), в отдельной строке выведите «? u v w». Числа в запросе должны удовлетворять \(1 \le u, v, w \le n\). Дополнительно \(u \ne v\), \(u \ne w\) и \(v \ne w\). В ответ вы получите \(1 \le x \le n\) — метку наименьшего общего предка \(u\) и \(v\), если бы корнем дерева была \(w\). В случае, если ваш запрос некорректен или вы задали более \(n+420\) запросов, вы получите \(-1\) вместо ответа. Вы получите вердикт Неправильный ответ. Убедитесь, что вы немедленно выходите из программы, чтобы избежать получения других вердиктов. Когда вы определите метку, присвоенную корню, выведите «! r», где \(r\) — метка корня. После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Ваша программа должна немедленно завершиться после прочтения ответа «-1», вы получите вердикт Неправильный ответ. В противном случае вы можете получить любой вердикт, так как программа продолжит чтение из закрытого потока. Формат взломов Для взлома используйте следующий формат. Первая строка должна содержать одно целое \(h\) (высоту бинарного дерева). В следующей строке выведите перестановку \(p\) размером \(n = 2^h - 1\). Она представляет собой бинарное дерево, в котором корень помечен \(p_1\), а для \(1 < i \le n\) непосредственным родителем \(p_i\) является \(p_{ \lfloor{\frac{i}{2}}\rfloor }\). Примечание Метки, соответствующие дереву в примере, равны [\(4\),\(7\),\(2\),\(6\),\(1\),\(5\),\(3\)], что означает, что корень обозначен \(4\), а для \(1 < i \le n\) родителем \(p_i\) является \(p_{ \lfloor{\frac{i}{2}}\rfloor }\). | |
![]()
|
|
E. Поступи нечестно и выиграй
битмаски
Деревья
игры
Структуры данных
*3500
Рассмотрим таблицу \((10^9+1) \times (10^9+1)\). Строки пронумерованы целыми числами от \(0\) до \(10^9\), и столбцы пронумерованы целыми числами от \(0\) до \(10^9\). Обозначим за \((x, y)\) клетку, расположенную в строке \(x\) в столбце \(y\). Давайте назовем клетку \((x, y)\) хорошей, если \(x \& y = 0\), где \(\&\) — это операция побитового И. Давайте построим граф, вершинами которого будут все хорошие клетки и проведем ребра между всеми парами соседних по стороне хороших клеток. Можно доказать, что этот граф является деревом — связным графом без циклов. Давайте подвесим это дерево за вершину \((0, 0)\), таким образом мы получим корневое дерево с корнем \((0, 0)\). Два игрока играют в игру. Изначально некоторые хорошие клетки черные, а остальные белые. Каждый игрок на своем ходе выбирает черную хорошую клетку и подмножество ее предков (возможно пустое) и инвертирует их цвета (с белого на черный и наоборот). Игрок, который не может сделать ход (потому что все хорошие клетки белые), проигрывает. Можно доказать, что эта игра конечна. Изначально все клетки белые. Вам дано \(m\) пар клеток. Для каждой пары клеток все клетки на простом пути между клетками в паре красятся в черный цвет. Обратите внимание, что эти цвета не инвертируются, а мы красим клетки в черный цвет. Sohrab и Mashtali собираются сыграть в эту игру. Sohrab будет первым игроком, а Mashtali вторым. Mashtali хочет победить и решил поступить нечестно. Он может сделать следующую операцию несколько раз перед тем как игра начнется: выбрать клетку и инвертировать цвета всех вершин на пути между ней и корнем дерева. Mammad, который наблюдает за ними, задался вопросом: «какое минимальное количество операций должен сделать Mashtali, чтобы иметь выигрышную стратегию?». Найдите ответ на этот вопрос для изначальной конфигурации цветов вершин дерева. Можно доказать, что хотя бы один способ поступить нечестно существует. Выходные данные Выведите единственное целое число — минимальное количество нечестных операций, которое второй игрок может сделать чтобы победить. Примечание В первом тесте вы можете сделать одну нечестную операцию с корнем дерева. После этого, второй игрок может победить, потому что он может использовать симметричную стратегию. Во втором тесте вы можете сделать нечестные операции в клетками \((0, 2), (0, 0), (3, 4)\). В третьем тесте второй игрок уже имеет выигрышную стратегию и ему не нужно делать никаких нечестных операций. | |
![]()
|
|
E. Найти вершину
Деревья
дп
интерактив
Перебор
поиск в глубину и подобное
*3500
Это интерактивная задача. Вам задано дерево — связный неориентированный граф без циклов. В нём загадали одну из вершин. Вы можете задавать вопросы интерактору: за один вопрос вы можете выбрать ребро и узнать, какой из двух концов ребра находится ближе к загаданной вершине, то есть, до какого из двух концов меньше кратчайшее расстояние от загаданной вершины. Вам требуется определить загаданную вершину за минимальное для данного дерева число запросов в худшем случае. Обратите внимание, что загаданная вершина может быть не фиксирована интерактором заранее: в зависимости от ваших запросов он может менять её на любую другую, с условием, что это не противоречит ответам на предыдущие запросы. Протокол взаимодействия После считывания выходных данных вы можете отправлять интерактору запросы двух типов: - «? \(u\) \(v\)» — узнать для ребра дерева \((u, v)\) (\(1 \le u, v \le n\)), какой из его концов ближе к загаданной вершине. В ответ вы получите одно число: номер одной из двух вершин. Обратите внимание, что \(u\) и \(v\) должны быть соединены ребром в дереве, поэтому они не могут находиться на равном расстоянии от загаданной вершины.
- «! \(u\)» — сообщить интерактору о том, что вы выяснили номер загаданной вершины. После вывода этой команды ваша программа должна немедленно завершиться.
После каждого вопроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Idleness Limit Exceeded или Превышено реальное время работы. Для сброса буфера вы можете использовать: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- sys.stdout.flush() в Python;
- смотрите документацию для других языков.
В случае, если вы сделаете большее число запросов, чем может быть необходимо для данного дерева в худшем случае, вы получите вердикт Неправильный ответ. Примечание Взломы в данной задаче запрещены. | |
![]()
|
|
C. Ксор дерево
Бинарный поиск
битмаски
Деревья
дп
разделяй и властвуй
Структуры данных
*2100
Для заданной последовательности попарно различных неотрицательных целых чисел \((b_1, b_2, \dots, b_k)\) мы определяем, является ли она хорошей следующим образом: - Рассмотрим граф на \(k\) вершинах, на которых написаны числа от \(b_1\) до \(b_k\).
- Для каждого \(i\) от \(1\) до \(k\) мы находим такое \(j\) (\(1 \le j \le k\), \(j\neq i\)), для которого значение \((b_i \oplus b_j)\) минимально среди всех таких \(j\), где \(\oplus\) обозначает операцию побитового исключающего ИЛИ. После этого мы проводим неориентированное ребро между вершинами с числами \(b_i\) и \(b_j\).
- Последовательность называется хорошей, если и только если получившийся граф является деревом (то есть он связан и не имеет простых циклов).
Возможно, что для некоторых чисел \(b_i\) и \(b_j\) вы попробуете добавить ребро между ними дважды. Тем не менее вы добавите это ребро только один раз. Ниже приведен пример (рисунок, соответствующий первому примеру). Последовательность \((0, 1, 5, 2, 6)\) не хорошая, так как мы не можем достичь \(1\) из \(5\). Однако, последовательность \((0, 1, 5, 2)\) является хорошей.  Вам дана последовательность \((a_1, a_2, \dots, a_n)\) из попарно различных неотрицательных целых чисел. Вы хотите удалить из нее некоторые элементы (возможно, ни одного), чтобы сделать оставшуюся последовательность хорошей. Какое минимально возможное количество удалений необходимо для достижения этой цели? Можно показать, что для любой последовательности можно удалить некоторое количество элементов, оставив как минимум \(2\), так, что оставшаяся последовательность будет хорошей. Выходные данные Необходимо вывести ровно одно целое число — минимально возможное количество элементов, которые нужно удалить, чтобы сделать оставшуюся последовательность хорошей. Примечание Обратите внимание, что числа, которые вы удаляете, не влияют на процедуру проверки, является ли хорошей оставшаяся последовательность. Возможно, что для некоторых чисел \(b_i\) и \(b_j\) вы попробуете добавить ребро между ними дважды. Тем не менее вы добавите это ребро только один раз. | |
![]()
|
|
G. Коммунизм
битмаски
Деревья
дп
*3500
Обратите внимание на нестандартное ограничение по памяти в этой задаче. В параллельной вселенной сатану звали «Trygub». По этой причине символы из его имени были удалены из алфавита еще в древние времена. В правительстве есть \(n\) работников, стоящих в ряд и пронумерованных целыми числами от \(1\) до \(n\) слева направо. Категории их работы могут быть описаны строкой \(s\) длины \(n\), в которой символ \(s_i\) обозначает категорию работы \(i\)-о работника. Новый закон был принят для того, чтобы увеличить равенство между всеми работниками. Правительство решило сделать так, чтобы все работники имели одинаковую категорию работы, делая следующую операцию любое количество раз (возможно ноль). Есть зафиксированный рациональный параметр \(k=\frac ab\), обозначающий то, насколько просто убедить общественность. Он будет использоваться для того, чтобы определить успешность операции. За одну операцию правительство сначала выбирает категорию работы \(x\), такую что существует хотя бы один работник этой категории в текущий момент. Обозначим за \(i_1,\ldots, i_m\) (\(i_1<\ldots<i_m\)) позиции всех работников с категорией работы \(x\). Если \(k\cdot (i_m-i_1+1)\le m\), то правительство может выбрать любую категорию работы \(y\), для которой существует хотя бы один работник этой категории в текущий момент и поменять категорию всех работников с категорией работы \(x\) на \(y\). Если можно сделать так, чтобы все работники имели категорию работы \(x\), мы называем категорию работы \(x\) достижимой. Можете ли вы сказать правительству множество достижимых категорий работы? Выходные данные Выведите целое число \(c\), равное количеству достижимых категорий работы и затем \(c\) символов, разделенных пробелами — достижимые категории работы в лексикографическом порядке. Примечание Первая операция обязана выбрать категорию работы 'i', потому что все другие категории работы не удовлетворяют условию. Поэтому 'i' не будет достижимой. Ниже показано, как достичь 'c', 'm' и 'o'. Квадратные скобки обозначают отрезок, содержащий всех работников выбранной категории. Красный цвет выделяет эту категорию, синий цвет выделяет новую категорию после операции. - Получение 'c':
- (\(\texttt{com}\color{red}{\texttt{[i]}}\texttt{com} \rightarrow \texttt{com}\color{#1E90FF}{\texttt{[o]}}\texttt{com}\))
- (\(\texttt{c}\color{red}{\texttt{[o}}\texttt{m}\color{red}{\texttt{o}}\texttt{c}\color{red}{\texttt{o]}}\texttt{m} \rightarrow \texttt{c}\color{#1E90FF}{\texttt{[m}}\texttt{m}\color{#1E90FF}{\texttt{m}}\texttt{c}\color{#1E90FF}{\texttt{m]}}\texttt{m}\))
- (\(\texttt{c}\color{red}{\texttt{[mmm}}\texttt{c}\color{red}{\texttt{mm]}} \rightarrow \texttt{c}\color{#1E90FF}{\texttt{[ccc}}\texttt{c}\color{#1E90FF}{\texttt{cc]}}\))
- Получение 'm':
- (\(\texttt{com}\color{red}{\texttt{[i]}}\texttt{com} \rightarrow \texttt{com}\color{#1E90FF}{\texttt{[o]}}\texttt{com}\))
- (\(\texttt{c}\color{red}{\texttt{[o}}\texttt{m}\color{red}{\texttt{o}}\texttt{c}\color{red}{\texttt{o]}}\texttt{m} \rightarrow \texttt{c}\color{#1E90FF}{\texttt{[c}}\texttt{m}\color{#1E90FF}{\texttt{c}}\texttt{c}\color{#1E90FF}{\texttt{c]}}\texttt{m}\))
- (\(\color{red}{\texttt{[cc}}\texttt{m}\color{red}{\texttt{ccc]}}\texttt{m} \rightarrow \color{#1E90FF}{\texttt{[mm}}\texttt{m}\color{#1E90FF}{\texttt{mmm]}}\texttt{m}\))
- Получение 'o':
- (\(\texttt{com}\color{red}{\texttt{[i]}}\texttt{com} \rightarrow \texttt{com}\color{#1E90FF}{\texttt{[c]}}\texttt{com}\))
- (\(\color{red}{\texttt{[c}}\texttt{om}\color{red}{\texttt{cc]}}\texttt{om} \rightarrow \color{#1E90FF}{\texttt{[m}}\texttt{om}\color{#1E90FF}{\texttt{mm]}}\texttt{om}\))
- (\(\color{red}{\texttt{[m}}\texttt{o}\color{red}{\texttt{mmm}}\texttt{o}\color{red}{\texttt{m]}} \rightarrow \color{#1E90FF}{\texttt{[o}}\texttt{o}\color{#1E90FF}{\texttt{ooo}}\texttt{o}\color{#1E90FF}{\texttt{o]}}\))
| |
![]()
|
|
G. Игра на дереве
Деревья
жадные алгоритмы
поиск в глубину и подобное
Структуры данных
*2700
Алиса и Боб играют в игру. У них есть дерево, состоящее из \(n\) вершин. Изначально у Боба есть \(k\) фишек, \(i\)-я фишка расположена в вершине \(a_i\) (все эти вершины уникальны). Перед началом игры Алиса поместит фишку в одну из вершин дерева. Игра состоит из ходов. На каждом ходу происходят следующие события (последовательно, точно в следующем порядке): - Алиса либо перемещает свою фишку в соседнюю вершину, либо не перемещает ее;
- для каждой фишки Боба он либо перемещает ее в соседнюю вершину, либо не перемещает. Обратите внимание, что этот выбор делается независимо для каждой фишки.
Игра заканчивается, когда фишка Алисы находится в одной вершине с одной (или несколькими) фишками Боба. Обратите внимание, что фишки Боба могут находиться в одной и той же вершине, даже если они находились в разных вершинах в начале игры. Алиса хочет максимизировать количество ходов, а Боб хочет минимизировать его. Если игра заканчивается в середине некоторого хода (Алиса перемещает свою фишку в вершину, содержащую одну или несколько фишек Боба), этот ход засчитывается. Для каждой вершины подсчитайте, сколько ходов продлится игра, если Алиса поместит свою фишку в эту вершину. Выходные данные Выведите \(n\) целых чисел. \(i\)-е из них должно быть равно числу ходов, которое продлится игра, если Алиса изначально поместит свою фишку в вершину \(i\). Если одна из фишек Боба уже помещена в вершину \(i\), то ответ для вершины \(i\) равен \(0\). | |
![]()
|
|
E. Собачьи закуски
Бинарный поиск
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
*2300
Gildong играет в игру со своей собакой, Badugi. Они находятся в парке, в котором есть \(n\) перекрестков и \(n-1\) двусторонних дорог, длиной в \(1\) и соединяющих два перекрестка. Пересечения пронумерованы от \(1\) до \(n\), и для каждой пары \(a\) и \(b\) (\(1 \le a, b \le n\)), возможно пройти от \(b\)-го перекрестка до \(a\)-го передвигаясь по дорогам. Gildong поставил одну закуску на каждый перекресток. Gildong поставил Badugi задачу — съесть все закуски. Badugi начинает на \(1\)-м перекрестке, и он передвигается по следующим правилам: - Badugi ищет закуски, которые находятся к нему как можно ближе. Расстояние это длина кратчайшего пути от текущей позиции Badugi до перекрестка с закуской. Однако, обоняние Badugi ограничено до \(k\) метров, так что он может находить только закуски на расстоянии не больше чем \(k\) метров от текущей позиции. Если он не может найти ни одной закуски, задание считается проваленным.
- Среди всех закусок, которые Badugi чувствует на его текущей позиции, он выбирает закуску с минимальным расстоянием до текущей позиции. Если есть несколько возможных закусок, он выбирает одну любую из них.
- Он повторяет этот процесс пока он не съест все \(n\) закусок. После этого, он должен снова найти \(1\)-й перекресток, который должен быть на расстоянии не больше чем \(k\) метров от последней съеденной закуски. Если он может найти его, он проходит задание. Иначе, задание считается проваленным.
К сожалению, Gildong не знает значение \(k\). Таким образом, он просит вас найти минимальное значение \(k\), при котором Badugi сможет выполнить задание, если будет действовать оптимально. Выходные данные Для каждого набора входных данных выведите одно целое число — минимальное возможное значение \(k\), при котором Badugi может выполнить свое задание. Примечание В первом наборе входных данных, Badugi может выполнить задание для \(k=2\), передвигаясь следующим образом: - Исходно, Badugi находится на \(1\)-м перекрестке. Ближайшая закуска, очевидно, находится на \(1\)-м перекрестке, поэтому он съедает ее.
- Затем, он ищет ближайшую закуску, которая может быть либо на \(2\)-м или на \(3\)-м перекрестке. Предположим, что он выбирает \(2\)-й перекресток. Он переходит на \(2\)-й перекресток, который находится на расстоянии \(1\) метр, и ест закуску.
- Единственная закуска находится на \(3\)-м перекрестке, и ему нужно пройти по \(2\) дорогам, чтобы дойти до нее.
- После съедения закуски на \(3\)-м перекрестке, ему снова нужно найти \(1\)-й перекресток, который находится на расстоянии \(1\) метр. После того как он возвращается на него, он выполнил свое задание.
Во втором наборе входных данных, единственная возможная последовательность действий это \(1\) – \(2\) – \(3\) – \(4\) – \(1\). Так как расстояние между \(4\)-м и \(1\)-м перекрестком равно \(3\), \(k\) должно быть хотя бы \(3\) для того, чтобы Badugi смог выполнить задание. В третьем наборе входных данных, Badugi может двигаться следующим образом: \(1\) – \(5\) – \(6\) – \(7\) – \(8\) – \(2\) – \(3\) – \(4\) – \(1\). Можно показать, что это единственный вариант для Badugi выполнить миссию с \(k=3\).  | |
![]()
|
|
E. Количество простых путей
графы
Деревья
Комбинаторика
поиск в глубину и подобное
*2000
Вам дан неориентированный граф, состоящий из \(n\) вершин и \(n\) ребер. Гарантируется, что заданный граф является связным (то есть возможно достичь любую вершину из любой другой вершины) и не содержит петель и кратных ребер. Ваша задача — посчитать количество простых путей длины хотя бы \(1\) в заданном графе. Заметьте, что пути, которые отличаются только направлением, являются одинаковыми (то есть вам необходимо посчитать количество неориентированных путей). Например, пути \([1, 2, 3]\) и \([3, 2, 1]\) являются одинаковыми. Вам необходимо ответить на \(t\) независимых наборов тестовых данных. Напомним, что путем в графе называется такая последовательность вершин \(v_1, v_2, \ldots, v_k\), что каждая пара соседних (последовательных) вершин в этой последовательности соединена ребром. Длиной пути является количество ребер в нем. Простым путем называется такой путь, что все вершины в нем различны. Выходные данные Выведите одно целое число для каждого набора тестовых данных: количество простых путей длины хотя бы \(1\) в заданном графе. Заметьте, что пути, которые отличаются только направлением, являются одинаковыми (то есть вам необходимо посчитать количество неориентированных путей). Примечание Рассмотрим второй набор тестовых данных примера. Он выглядит следующим образом: 
Здесь есть \(11\) различных простых путей: - \([1, 2]\);
- \([2, 3]\);
- \([3, 4]\);
- \([2, 4]\);
- \([1, 2, 4]\);
- \([1, 2, 3]\);
- \([2, 3, 4]\);
- \([2, 4, 3]\);
- \([3, 2, 4]\);
- \([1, 2, 3, 4]\);
- \([1, 2, 4, 3]\).
| |
![]()
|
|
F. Сумма диаметров
Деревья
Структуры данных
*3500
Вам дано дерево с \(n\) вершинами, пронумерованными \(1, \ldots, n\). Дерево — это связный простой граф без циклов. Пусть \(\mathrm{dist}(u, v)\) означает количество рёбер на единственном простом пути между вершинами \(u\) и \(v\). Пусть \(\mathrm{diam}(l, r) = \max \mathrm{dist}(u, v)\) по всем парам \(u, v\), таким что \(l \leq u, v \leq r\). Вычислите \(\sum_{1 \leq l \leq r \leq n} \mathrm{diam}(l, r)\). Выходные данные Выведите одно целое число — \(\sum_{1 \leq l \leq r \leq n} \mathrm{diam}(l, r)\). | |
![]()
|
|
E. План лекций
графы
Деревья
Конструктив
поиск в глубину и подобное
реализация
снм
сортировки
*2400
Иван — учитель по программированию. В течение учебного года он планирует прочитать \(n\) лекций на \(n\) различных тем. Каждая тема должна быть использована ровно в одной лекции. Иван хочет выбрать, какую тему он будет объяснять во время \(1\)-й, \(2\)-й, ..., \(n\)-й лекции — формально он хочет выбрать некоторую перестановку целых чисел от \(1\) до \(n\) (назовем эту перестановку \(q\)). \(q_i\) — это номер темы, которую Иван объяснит во время \(i\)-й лекции. Для каждой темы (за исключением ровно одной) существует обязательная предшествующая тема (для \(i\)-й темы предшествующая тема — \(p_i\)). Иван не может читать лекцию по теме, не прочитав лекцию по ее предшествующей теме. Существует по крайней мере один допустимый порядок тем в соответствии с этими предварительными ограничениями. Правильный порядок тем может помочь студентам лучше понять лекции. У Ивана есть \(k\) специальных пар тем \((x_i, y_i)\) таких, что он знает, что студенты лучше поймут \(y_i\)-ю тему, если лекция по ней будет проводиться сразу после лекции по \(x_i\)-й теме. Иван хочет удовлетворить ограничениям на каждую такую пару, то есть для каждого \(i \in [1, k]\) должно существовать некоторое \(j \in [1, n - 1]\) такое, что \(q_j = x_i\) и \(q_{j + 1} = y_i\). Теперь Иван хочет знать, существует ли порядок тем, удовлетворяющий всем этим ограничениям, и если хотя бы один из них существует, найти любой из них. Выходные данные Если не существует порядка тем, удовлетворяющих всем ограничениям, выведите \(0\). В противном случае выведите \(n\) попарно различных целых чисел \(q_1\), \(q_2\), ..., \(q_n\) (\(1 \le q_i \le n\)) — порядок тем, удовлетворяющих всем ограничениям. Если ответов несколько, выведите любой из них. | |
![]()
|
|
F. Моё прекрасное безумие
Деревья
Структуры данных
*3500
Вам дано дерево. Будем рассматривать простые пути в этом дереве. Обозначим путь между вершинами \(a\) и \(b\) как \((a, b)\). \(d\)-окрестностью пути назовём множество вершин дерева, находящихся на расстоянии \(\leq d\) от хотя бы одной вершины пути (например, \(0\)-окрестность пути — это сам путь). Пусть \(P\) — мультимножество путей этого дерева, изначально пустое. Нужно обрабатывать следующие запросы: - \(1\) \(u\) \(v\) — добавить путь \((u, v)\) в \(P\) (\(1 \leq u, v \leq n\)).
- \(2\) \(u\) \(v\) — удалить путь \((u, v)\) из \(P\) (\(1 \leq u, v \leq n\)). Заметьте, что \((u, v)\) и \((v, u)\) — один и тот же путь. Например, если \(P = \{(1, 2), (1, 2)\}\), то после запроса \(2\) \(2\) \(1\), \(P = \{(1, 2)\}\).
- \(3\) \(d\) — если пересечение всех \(d\)-окрестностей путей, находящихся в \(P\), непусто, выведите «Yes», иначе выведите «No» (\(0 \leq d \leq n - 1\)).
Выходные данные Выведите ответ на каждый запрос третьего типа в отдельной строке. | |
![]()
|
|
D. Тринадцатый подвиг Геракла
Деревья
жадные алгоритмы
сортировки
Структуры данных
*1500
Вы вероятно слышали про двенадцать подвигов Геракла, однако знаете ли вы про тринадцатый? Принято считать, что ему потребовалась дюжина лет, чтобы выполнить двенадцать подвигов, то есть в среднем год, чтобы выполнить каждый из них. Поскольку в наши дни время течет быстрее, у вас есть минуты, а не месяцы, чтобы решить эту задачу. Справитесь ли вы? В этой задаче вам дано дерево с \(n\) вершинами, каждая из которых имеет вес. Дерево — это связный граф с \(n - 1\) ребром. Определим \(k\)-раскраску дерева как назначение одного из \(k\) цветов каждому из его ребер. Обратите внимание, что вы не обязаны использовать все \(k\) цветов. Подграф цвета \(x\) состоит из тех ребер исходного графа, которым был назначен цвет \(x\), и только тех вершин, которые смежны с хотя бы одним из таких ребер. Поэтому в таком подграфе нет вершин степени \(0\). Весом компоненты связности назовем сумму весов её вершин. Весом подграфа назовем максимальный из весов компонент связности этого подграфа. Вес пустого подграфа будем считать равным \(0\). Определим вес \(k\)-раскраски как сумму весов подграфов всех \(k\) цветов. Дано дерево, для каждого \(k\) от \(1\) до \(n - 1\) вычислите максимальный возможный вес \(k\)-раскраски. Выходные данные Для каждого набора входных данных в отдельной строке выведите \(n - 1\) целое число, где \(i\)-е число должно равняться максимальному весу \(i\)-раскраски дерева. Примечание Оптимальные \(k\)-раскраски дерева из первого набора входных данных следующие:  В \(1\)-раскраске все ребра имеют одинаковый цвет. Подграф цвета \(1\) содержит все ребра и вершины исходного графа. Поэтому его вес равен \(3 + 5 + 4 + 6 = 18\).  В оптимальной \(2\)-раскраске ребрам \((2, 1)\) и \((3,1)\) назначен цвет \(1\). Ребру \((4, 3)\) — цвет \(2\). Подграф цвета \(1\) состоит из одной компоненты связности (вершины \(1, 2, 3\)) и его вес равен \(3 + 5 + 4 = 12\). Подграф цвета \(2\) состоит из двух вершин и одного ребра. Его вес равен \(4 + 6 = 10\).  В оптимальной \(3\)-раскраске всем ребрам назначены разные цвета. Поэтому подграф каждого цвета содержит одно ребро. Их веса следующие: \(3 + 4 = 7\), \(4 + 6 = 10\), \(3 + 5 = 8\). | |
![]()
|
|
E. Различающие корни
Деревья
дп
поиск в глубину и подобное
Структуры данных
*2500
Дано дерево из \(n\) вершин. На каждой вершине записано число; на вершине \(i\) записано число \(a_i\). Предположим, мы подвесили дерево за вершину \(v\) (сделали эту вершину корнем). Назовем \(v\) различающим корнем, если выполняется следующее условие: в каждом пути из \(v\) до некоторого листа дерева все значения, записанные на вершинах, различны. Значения, встречающихся на различных путях, могут совпадать, но значения на каждом пути, рассматриваемом в отдельности, должны быть различны. Посчитайте количество различающих корней заданного дерева. Выходные данные Выведите одно целое число — количество различающих корней в дереве. Примечание В первом примере из условия вершины \(1\), \(2\) и \(5\) — различающие корни. | |
![]()
|
|
D. Странный источник минералов
Бинарный поиск
битмаски
Деревья
Перебор
Структуры данных
Теория вероятностей
*2900
В стране Гомера есть \(n\) городов с номерами от \(1\) до \(n\), которые образуют дерево. Иначе говоря, между этими \(n\) городами есть \((n-1)\) неориентированных дорог, и с каждого города можно попасть в любой другой по этим дорогам. Страна Гомера — индустриальная страна, и каждый из \(n\) городов в ней содержит некоторый минеральный ресурс. Минеральный ресурс города \(i\) обозначен как \(a_i\). Гомеру даны планы страны на \(q\) следующих лет. План \(i\)-го года описывается четырьмя параметрами \(u_i, v_i, l_i\) и \(r_i\), и он должен найти любой такой минеральный ресурс \(c_i\) такой, что выполняются два условия: - минеральный ресурс \(c_i\) встречается нечетное количество раз между городами \(u_i\) и \(v_i\);
- \(l_i \leq c_i \leq r_i\).
Так как вы лучший друг Гомера, он просит вас о помощи. Для каждого плана найдите любой такой минерал \(c_i\) или скажите, что его нет. Выходные данные Выведите \(q\) строк, \(i\)-я из которых содержит целое число \(c_i\), такое, что - \(c_i = {-1}\), если нет такого минерального ресурса, который соответствовал бы требуемому условию; или
- \(c_i\) — это номер выбранного минерального ресурса в \(i\)-м году. Выбранный минеральный ресурс \(c_i\) должен удовлетворять условиям \(i\)-го года, описанным выше в условии задачи. Если есть несколько подходящих \(c_i\), вы можете вывести любой из них.
Примечание В первых трех запросах четыре города находятся между городом \(3\) и городом \(5\), а именно: город \(1\), город \(2\), город \(3\) и город \(5\). В них представлены минеральные ресурсы \(1\) (появляется в городах \(3\) и \(5\)), \(2\) (появляется в городе \(2\)) и \(3\) (появляется в городе \(1\)). Следует отметить, что - Первый запрос заключается только в том, чтобы проверить, появляется ли минеральный источник \(1\) нечетное количество раз между городом \(3\) и городом \(5\). Ответ — нет, потому что минеральный источник \(1\) появляется дважды (четное число раз) между городом \(3\) и городом \(5\).
- Второй и третий запросы одинаковы, но они могут выбирать разные минеральные ресурсы. Вы можете выбрать любой из \(2\) и \(3\).
| |
![]()
|
|
F. AB дерево
Деревья
дп
жадные алгоритмы
*3100
Kilani и Abd — соседи уже на протяжении 3000 лет, но пришел день и Kilani решил переехать. На прощание, Kilani решил дать Abd задачу, придуманную их общим соседом с таким же именем Abd.  Задача следующая: Вам задано связное дерево с корнем в вершине \(1\). Вам нужно назначить каждой вершине букву a или b таким образом, чтобы суммарное количество a было равно \(x\) и суммарное количество b было равно \(n - x\). Определим строку для каждой вершины \(v\) дерева следующим образом: - если \(v\) — это корень, то строка — это одна буква, назначенная \(v\):
- в противном случае, возьмем строку, полученную для родителя \(p_v\) вершины \(v\) и допишем к ней символ, назначенный \(v\).
Расставьте буквы на вершинах таким образом, чтобы минимизировать количество различных строк среди строк для всех вершин. Выходные данные В первой строке, выведите минимально возможное количество различных строк. Во второй строке, выведите \(n\) символов, каждый из которых — либо a, либо b и \(i\)-й символ — это символ, назначенный \(i\)-й вершине. Удостоверьтесь, что букв a ровно \(x\), а букв b ровно \(n - x\). Если существует несколько ответов, выведите любой из них. Примечание Дерево из примера изображено ниже:  После назначения букв каждой вершине (в соответствии с выходными данными), дерево выглядит следующим образом:  Строки для каждой вершины: - строка вершины \(1\): a
- строка вершины \(2\): aa
- строка вершины \(3\): aab
- строка вершины \(4\): aab
- строка вершины \(5\): aabb
- строка вершины \(6\): aabb
- строка вершины \(7\): aabb
- строка вершины \(8\): aabb
- строка вершины \(9\): aa
Множество различных строк равно \(\{\text{a}, \text{aa}, \text{aab}, \text{aabb}\}\), то есть количество различных строк равно \(4\). | |
![]()
|
|
H. Экзамен
Деревья
строковые суфф. структуры
Структуры данных
*3400
В этом году в Конохе вновь проводится экзамен на звание Чунина, и в нем участвуют \(n\) ниндзя с именами \(s_1\), \(s_2\), ..., \(s_n\). Все имена участников различны. Один из этапов экзамена — сражения между участниками. В этом году руководство Конохи решило, что определять, кто с кем сражается, будут по-новому. Ниндзя \(i\) сражается с ниндзя \(j\), если выполнены три правила: - \(i \neq j\);
- \(s_{j}\) — подстрока \(s_{i}\);
- не существует \(k\), отличного от \(i\) и \(j\) такого, что \(s_{j}\) — подстрока \(s_{k}\), а \(s_{k}\) — подстрока \(s_{i}\).
Строка \(a\) является подстрокой \(b\), если \(a\) может быть получена из \(b\) удалением нескольких (возможно, ни одного или всех) символов из начала и нескольких (возможно, ни одного или всех) символов из конца. Необходимо выяснить, сколько сражений будет проведено на экзамене в этом году. Выходные данные Необходимо вывести единственное число — количество сражений на экзамене в этом году. Примечание В первом примере hidan сражается с dan, а hanabi сражается с nabi, который также сражается с bi. Ниндзя с именами hanabi и bi не сражаются, поскольку есть ниндзя с именем nabi, из-за которого для этой пары не выполняется третье условие. Во втором примере сражения происходят между abacaba и acaba, abacaba и abaca, acaba и aca, abaca и aca. | |
![]()
|
|
E. Передвижения и замены
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
*2500
Вам дано \(n - 1\) целое число \(a_2, \dots, a_n\) и корневое дерево с \(n\) вершинами, подвешенное в вершине \(1\). Все листья находятся на одинаковом расстоянии \(d\) от корня. Деревом называется связный неориентированный граф без циклов. Расстоянием между парой вершин называется количество ребер на простом пути между ними. Все некорневые вершины, имеющие степень \(1\), называются листьями. Если вершины \(s\) и \(f\) соединены ребром, и \(f\) находится на расстоянии от корня большем, чем \(s\), то \(f\) называется сыном \(s\). Изначально в вершине \(1\) находятся красная и синяя фишки. Давайте обозначим за \(r\) вершину, в которой находится красная фишка, и за \(b\) вершину, в которой находится синяя фишка. Вы должны сделать \(d\) ходов. Ход состоит из трех шагов: - Переместить красную фишку в любого сына \(r\).
- Переместить синюю фишку в любую вершину \(b'\) такую, что \(dist(1, b') = dist(1, b) + 1\). Здесь \(dist(x, y)\) обозначает длину кратчайшего пути между \(x\) и \(y\). Обратите внимание, что \(b\) и \(b'\) не обязательно соединены ребром.
- Вы можете, если хотите, поменять две фишки местами (или пропустить этот шаг).
Обратите внимание, что \(r\) и \(b\) могут быть равны в любой момент времени, а в корне дерева не записано никакое число. После каждого хода вы получаете \(|a_r - a_b|\) очков. Какое максимальное количество очков вы можете получить после \(d\) ходов? Выходные данные Для каждого набора входных данных выведите единственное целое число: максимальное количество очков, которое вы можете получить после \(d\) ходов. Примечание В первом наборе входных данных оптимальное решение — это: - ход \(1\): \(r = 4\), \(b = 2\); нет замены;
- ход \(2\): \(r = 7\), \(b = 6\); замена (после нее \(r = 6\), \(b = 7\));
- ход \(3\): \(r = 11\), \(b = 9\); нет замен.
Общее количество очков равно \(|7 - 2| + |6 - 9| + |3 - 9| = 14\).  Во втором наборе входных данных оптимальное решение — это: - ход \(1\): \(r = 2\), \(b = 2\); нет замены;
- ход \(2\): \(r = 3\), \(b = 4\); нет замены;
- ход \(3\): \(r = 5\), \(b = 6\); нет замены.
Общее количество очков равно \(|32 - 32| + |78 - 69| + |5 - 41| = 45\). | |
![]()
|
|
F. Пары путей
Деревья
дп
Комбинаторика
поиск в глубину и подобное
Структуры данных
*2600
У вас есть дерево из \(n\) вершин, а также \(m\) простых вершинных путей. Ваша задача — найти, сколько пар этих путей пересекаются по ровно одной вершине. Более формально, вам нужно найти число пар \((i, j)\) \((1 \leq i < j \leq m)\) таких, что \(path_i\) и \(path_j\) имеют ровно одну общую вершину. Выходные данные Выведите единственное целое число — количество пар путей, которые пересекаются по ровно одной вершине. Примечание 
Дерево и пути в первом примере выглядят так. Пары \((1,4)\) и \((3,4)\) пересекаются по ровно одной вершине. Во втором примере все пути состоят из единственной одинаковой вершины, так что все пары \((1, 2)\), \((1, 3)\) и \((2, 3)\) пересекаются по одной вершине. Третий пример, такой же как первый, но с двумя дополнительными путями. Пары \((1,4)\), \((1,5)\), \((2,5)\), \((3,4)\), \((3,5)\), \((3,6)\) и \((5,6)\) пересекаются по ровно одной вершине. | |
![]()
|
|
E. Фиб-дерево
Деревья
Перебор
поиск в глубину и подобное
разделяй и властвуй
теория чисел
*2400
Пусть \(F_k\) обозначает \(k\)-й член последовательности Фибоначчи, определенной следующим образом: - \(F_0 = F_1 = 1\)
- для любого целого \(n \geq 0\), \(F_{n+2} = F_{n+1} + F_n\).
Вам дано дерево с \(n\) вершинами. Напомним, что дерево — это связный неориентированный граф без циклов. Дерево называется Фиб-деревом, если его количество вершин равно \(F_k\) для некоторого \(k\), и выполняется хотя бы одно из следующих условий: - Дерево состоит только из \(1\) вершины;
- Вы можете разделить его на два Фиб-дерева, удалив некоторое ребро дерева.
Определите, является ли данное дерево Фиб-деревом. Выходные данные Выведите «YES», если данное дерево является Фиб-деревом, или «NO», если не является. Ответ можно вывести в любом регистре. Например, если ответ «YES», то вывод «Yes» или «yeS» также будет считаться правильным ответом. Примечание В первом примере можно удалить ребро \((1, 2)\), и дерево будет разбито на \(2\) дерева размера \(1\) и \(2\) соответственно. Любое дерево размера \(2\) является Фиб-деревом, так как его можно разбить на \(2\) дерева размером \(1\). Во втором примере, независимо от того, какое ребро мы удаляем, дерево будет разбито на \(2\) дерева размера \(1\) и \(4\). Поскольку \(4\) не равняется \(F_k\) ни для какого \(k\), это не Фиб-дерево. В третьем примере, вот один из возможных порядков удаления ребер, чтобы все деревья в процессе были Фиб-деревьями: \((1, 3), (1, 2), (4, 5), (3, 4)\). | |
![]()
|
|
H. Yuezheng Ling и динамическое дерево
Деревья
Структуры данных
*3400
Yuezheng Ling дает Luo Tianyi дерево, которое имеет \(n\) вершин, с корнем \(1\). Luo Tianyi скажет вам, что непосредственным родителем вершины \(i\) является \(a_i\) (\(1 \leq a_i<i\) для \(2 \le i \le n\)), и попросит вас выполнить \(q\) запросов \(2\) типов: - Она даст вам три целых числа \(l\), \(r\) и \(x\) (\(2 \le l \le r \le n\), \(1 \le x \le 10^5\)). Вы должны заменить \(a_i\) на \(\max(a_i-x,1)\) для всех \(i\) с \(l \leq i \leq r\).
- Она даст вам два целых числа \(u\), \(v\) (\(1 \le u, v \le n\)). Вы должны найти LCA вершин \(u\) и \(v\) (их наименьший общий предок).
Выходные данные На каждый запрос второго типа выведите ответ в новой строке. Примечание Дерево в примере показано ниже.  После запроса первого типа дерево становится таким, как показано ниже.  | |
![]()
|
|
D. Dogeforces
Деревья
жадные алгоритмы
Конструктив
поиск в глубину и подобное
разделяй и властвуй
снм
сортировки
Структуры данных
*2300
В компании Dogeforces работают \(k\) сотрудников. У каждого сотрудника, кроме сотрудников нижнего звена, есть не менее \(2\) подчиненных. У сотрудников нижнего звена нет подчиненных. У каждого сотрудника (кроме руководителя компании) есть ровно один непосредственный начальник. Руководитель компании является непосредственным или косвенным начальником всех сотрудников. Известно, что в Dogeforces любой начальник получает зарплату строго больше, чем все его подчиненные. Полная структура компании является секретом, но вам известно количество сотрудников нижнего звена и для каждой пары сотрудников нижнего звена известна зарплата их общего начальника (если таких начальников несколько, то начальника с минимальной зарплатой). Вам предстоит восстановить структуру компании. Выходные данные В первую строку выведите одно целое число \(k\) — количество сотрудников в компании. Во второй строке выведите \(k\) целых чисел \(c_1, c_2, \dots, c_k\), где \(c_i\) — зарплата сотрудника с номером \(i\). В третьей строке выведите одно целое число \(r\) — номер сотрудника, который является руководителем компании. В последующих \(k-1\) строках выведите по два целых числа \(v\) и \(u\) (\(1 \le v, u \le k\)) — номер сотрудника и его непосредственного начальника. Обратите внимание, что сотрудники нижнего звена имею номера с \(1\) по \(n\), а для остальных сотрудников вам предстоит назначить номера от \(n+1\) до \(k\). Если корректных структур компании несколько, вы можете вывести любую из них. Примечание Одна из возможных структур в первом примере:  | |
![]()
|
|
D. Деревья поиска в ширину
графы
Деревья
Комбинаторика
кратчайшие пути
математика
поиск в глубину и подобное
*2600
Будем говорить, что остовное дерево некоторого графа является деревом поиска в ширину с корнем в вершине \(s\), если и только если для всех вершин \(t\) кратчайшее расстояние между вершинами \(s\) и \(t\) в графе равно кратчайшему расстоянию между \(s\) и \(t\) в этом остовном дереве. Для фиксированного графа можно определить \(f(x,y)\) как число остовных деревьев в данном графе таких, что они являются деревьями поиска в ширину как с корнем в \(x\), так и с корнем в \(y\). Вам дан неориентированный связный граф с \(n\) вершинами и \(m\) ребрами. Вычислите \(f(i,j)\) для всех \(i\), \(j\) по модулю \(998\,244\,353\). Выходные данные Выведите \(n\) строк, каждая из которых содержит \(n\) целых чисел. Число в строке \(i\) на позиции \(j\) должно быть равно \(f(i,j) \bmod 998\,244\,353\). Примечание Изображения ниже описывают первый пример. 
Дерево из красных ребер является деревом поиска в ширину с корнем как в \(1\), так и в \(2\). 
Похожим образом можно построить деревья поисков в ширину для любой пары соседних вершин. | |
![]()
|
|
F. Квадраты
графы
Деревья
дп
Конструктив
Структуры данных
*3300
\(n\) квадратов нарисованы на полу слева направо. На \(i\)-м квадрате записаны три целых числа \(p_i,a_i,b_i\). Последовательность \(p_1,p_2,\dots,p_n\) образует перестановку. Во время каждого раунда вы будете стартовать с самого левого квадрата \(1\) и прыгать вправо. Если вы сейчас на \(i\)-м квадрате, вы можете сделать одну из следующих двух операций: - Перепрыгнуть на \(i+1\)-й квадрат и заплатить за это \(a_i\). Если \(i=n\), тогда вы можете закончить раунд, заплатив \(a_i\).
- Перепрыгнуть на \(j\)-й квадрат и заплатить за это \(b_i\), где \(j\) — это самый левый квадрат, который удовлетворяет условиям \(j > i, p_j > p_i\). Если таких \(j\) не существует, вы можете закончить раунд, заплатив \(b_i\).
В игре будет \(q\) раундов. Чтобы сделать ее сложнее, вы должны поддерживать множество квадратов \(S\) (изначально пустое). Вы обязаны оказаться на этих квадратах во время раунда (вы можете также побывать и в других квадратах). Множество квадратов \(S\) для \(i\)-го раунда получается добавлением или удалением одного квадрата из множества квадратов для \((i-1)\)-го раунда. Для каждого раунда найдите минимальную цену, которую вы должны заплатить, чтобы его закончить. Выходные данные Выведите \(q\) строк, каждая из них должна содержать единственное целое число — минимальную цену, которую вы должны заплатить, чтобы закончить соответствующий раунд. Примечание Давайте обозначим символом \(T\) конец раунда. Тогда мы можем нарисовать два графа, соответствующих первому и второму примерам.   В первом раунде первого примера множество квадратов, через которое вы должны пройти, это \(\{1\}\). Путь, который вы можете использовать, это \(1\to 3\to T\). Его стоимость равна \(6\). Во втором раунде первого примера множество квадратов, через которое вы должны пройти, это \(\{1,2\}\). Путь, который вы можете использовать, это \(1\to 2\to 3\to T\). Его стоимость равна \(8\). | |
![]()
|
|
F. Рождественская игра
битмаски
Деревья
дп
игры
математика
поиск в глубину и подобное
Структуры данных
*2500
Алиса и Боб собираются отмечать Рождество, играя в игру с деревом подарков. Дерево состоит из \(n\) вершин (пронумерованных от \(1\) до \(n\), вершина \(r\) является корнем). На \(i\)-й вершине висят \(a_i\) подарков. Перед началом игры выбирается некоторое целое число \(k\). Затем игра проходит следующим образом: - Алиса начинает игру, затем ходы совершаются обоими игроками по очереди;
- на каждом ходу текущий игрок выбирает некоторую вершину (например, \(i\)), которая находится на глубине хотя бы \(k\). Затем игрок снимает некоторое положительное целое число подарков, которые висят на этой вершине, — назовем его \(m\) \((1 \le m \le a_i)\);
- затем игрок вешает эти \(m\) подарков на \(k\)-го предка (назовем его \(j\)) \(i\)-й вершины (\(k\)-м предком вершины \(i\) назовем такую вершину \(j\), что \(i\) — потомок \(j\), а глубина \(j\) ровно на \(k\) меньше глубины \(i\)). Теперь количество подарков на \(i\)-й вершине \((a_i)\) уменьшилось на \(m\), а \(a_j\), соответственно, увеличилось на \(m\);
- Алиса и Боб играют оптимально. Тот, кто не может совершить ход, проигрывает.
Для каждого возможного корня дерева сообщите, кто выиграет игру — Алиса или Боб. Глубина вершины \(i\) в дереве с корнем \(r\) определяется, как количество ребер на простом пути из вершины \(r\) до вершины \(i\). Глубина корня \(r\) равна нулю. Выходные данные Выведите \(n\) целых чисел, где \(i\)-е число равно \(1\), если Алиса выиграет игру, если дерево подвешено за вершину \(i\), и \(0\) в противном случае. Примечание Посчитаем ответ для примера с корнем в 1 и в 2. Корень 1 Алиса всегда выигрывает в данном случае. Возможная игра между Алисой и Бобом выглядит так: - Алиса перемещает один подарок из вершины 4 в вершину 3.
- Боб перемещает четыре подарка из вершины 5 в вершину 2.
- Алиса перемещает четыре подарка из вершины 2 в вершину 1.
- Боб перемещает три подарка из вершины 2 в вершину 1.
- Алиса перемещает три подарка из вершины 3 в вершину 1.
- Боб перемещает три подарка из вершины 4 в вершину 3.
- Алиса перемещает три подарка из вершины 3 в вершину 1.
Боб не может сделать ход, а потому проигрывает. Корень 2 Боб всегда выигрывает в данном случае. Пример игры: - Алиса перемещает четыре подарка из вершины 4 в вершину 3.
- Боб перемещает четыре подарка из вершины 5 в вершину 2.
- Алиса перемещает шесть подарков из вершины 3 в вершину 1.
- Боб перемещает шесть подарков из вершины 1 в вершину 2.
Алиса не может сделать ход, а потому проигрывает. | |
![]()
|
|
F. Разрезы диаметров
Деревья
дп
Комбинаторика
поиск в глубину и подобное
*2400
Задано целое число \(k\) и неориентированное дерево, состоящее из \(n\) вершин. Длина простого пути (пути, в котором каждая вершина встречается не более одного раза) между некоторой парой вершин равна количеству ребер в данном пути. Диаметр дерева равен максимальной длине пути между всеми парами вершин в дереве. Вы планируете удалить множество ребер из дерева. Когда ребра удаляются, дерево распадается на несколько меньших деревьев. Множество ребер считается корректным, если у всех полученных деревьев диаметр меньше либо равен \(k\). Два множества ребер считаются различными, если существует такое ребро, что оно встречается только в одном из множеств. Посчитайте количество корректных множеств ребер по модулю \(998\,244\,353\). Выходные данные Выведите одно целое число — количество корректных множеств ребер по модулю \(998\,244\,353\). Примечание В первом примере диаметр заданного дерева уже меньше либо равен \(k\). Поэтому можно выбрать любое множество ребер, и в полученных деревьях диаметры будут меньше либо равны \(k\). Всего есть \(2^3\) множеств, включая пустое. Во втором примере нужно удалить единственное ребро. Иначе диаметр будет \(1\), что больше \(0\). Деревья для третьего и четвертого примеров:  | |
![]()
|
|
E. Замерзаем красиво
Бинарный поиск
Деревья
разделяй и властвуй
Структуры данных
*3000
Этой зимой в городе... ну вы поняли :-) Дорожную систему города XXXводска можно представить как n перекрестков, соединенных n - 1 двунаправленными дорогами так, что между любыми двумя перекрестками есть путь. Организаторы некоего мероприятия хотят выбрать место, где будут жить участники (перекресток v), и место, где будут проходить соревнования (перекресток u). При этом, с одной стороны, они хотят, чтобы участники гуляли по городу и смотрели окрестности (поэтому расстояние между v и u должно быть не меньше l), но не хотят, чтобы участники замерзли (поэтому расстояние между v и u должно быть не больше r). Помимо этого для каждой улицы известна ее красота — некоторое целое число от 0 до 109. Ваша задача — выбрать путь, удовлетворяющий ограничениям по длине, и обладающей наибольшей средней красотой. Средней красотой пути будем называть медиану последовательности красот всех дорог на пути. Более формально: пусть есть путь длины k. Пусть ai — неубывающая последовательность, содержащая в точности k элементов, в которой каждое число встречается ровно столько раз, сколько дорог с такой красотой встречается на этом пути. Медианой пути назовем число a⌊k / 2⌋, предполагая что используется индексация от нуля. ⌊x⌋ — число х, округленное вниз до ближайшего целого. Например, если a = {0, 5, 12}, то медиана равна 5, а если a = {0, 5, 7, 12}, то медианой окажется число 7. Гарантируется, что найдется хотя бы один путь с подходящим количеством дорог. Выходные данные Выведите два числа — номера перекрестков, в которых необходимо поселить участников и проводить соревнования, соответственно. Если оптимальных ответов несколько, выведите любой. Примечание В первом примере все дороги имеют одинаковую красоту, а значит, все пути положительной длины имеют одинаковую медиану. Таким образом, нам подойдет любой путь с длиной от 3 до 4 включительно. Во втором примере город выглядит следующим образом: 1 - 2 - 3 - 4 - 5 - 6. Последние две дороги более ценные, и нужно выбрать любой путь, который содержит обе и имеет подходящую длину. Это либо путь между 2 и 6, либо путь между 3 и 6. | |
![]()
|
|
C. Завершите MST
битмаски
графы
Деревья
жадные алгоритмы
Перебор
поиск в глубину и подобное
снм
Структуры данных
*2500
Как преподаватель, Riko Hakozaki часто помогает ученикам в решении задач по различным предметам. Сегодня ее попросили помочь с задачей по программированию, которая заключается в следующем. Вам выдается неориентированный полный граф с \(n\) вершинами, где для некоторых ребер заданы положительные веса, а для остальных нет. Вам нужно назначить всем еще не назначенным рёбрам неотрицательные веса так, чтобы у получившегося графа XOR (побитовое исключающее ИЛИ) всех весов был равен \(0\). Определим уродство полного графа как вес его минимального остовного дерева, где вес остовного дерева равен сумме весов его рёбер. Нужно назначить веса так, чтобы уродство получившегося графа было как можно меньше. Напомним, что неориентированный полный граф с \(n\) вершинами содержит все рёбра \((u, v)\) с \(1 \le u < v \le n\); такой граф имеет \(\frac{n(n-1)}{2}\) рёбер. Она не знает, как решить эту задачу, поэтому просит вас решить ее за нее. Выходные данные Выведите в одной строке одно целое число — минимальное уродство среди всех возможных назначений весов с XOR суммой равной \(0\). Примечание На изображении ниже показан первый пример. Черные веса назначены предварительно, красные веса назначены нами, а минимальное остовное дерево состоит из синих ребер.  | |
![]()
|
|
E. Дерево-календарь
Деревья
Конструктив
Перебор
поиск в глубину и подобное
сортировки
Структуры данных
*3100
Yuu Koito и Touko Nanami — молодожёны! В день свадьбы Yuu подарила Touko ориентированное дерево с \(n\) вершинами и корнем в \(1\), а также маркировку \(a\), которая является некоторым DFS обходом дерева. Каждое ребро в этом дереве направлено в сторону от корня. Следующий алгоритм после вызова dfs(1) возвращает \(a\) — DFS-обход дерева, корнем которого является \(1\):
номер := 0
a := массив длины n
функция dfs(u):
номер := номер + 1
a[u] := номер
для всех v, для которых есть ориентированное ребро (u -> v):
dfs(v)
Обратите внимание, что для дерева может существовать несколько различных DFS-обходов Touko настолько понравился подарок, что она решила поиграть с ним! Каждый день, начиная с дня после свадьбы, Touko выполняет следующую процедуру один раз: - Среди всех ориентированных рёбер \(u \rightarrow v\) таких, что \(a_u < a_v\), выберите рёбро \(u' \rightarrow v'\) с лексикографически минимальной парой \((a_{u'}, a_{v'})\).
- Обменяйте местами \(a_{u'}\) и \(a_{v'}\).
Прошли дни со свадьбы, а Touko как-то забыла, когда была свадьба, и какой была оригинальная маркировка \(a\)! Опасаясь, что Yuu может разозлиться, Touko решила попросить вас определить эту информацию, используя текущую маркировку. Будучи ее хорошим другом, вы должны найти количество дней, прошедших со свадьбы, и оригинальную маркировку дерева. Однако есть шанс, что Touko могла ошибиться в процессе, в результате чего текущую маркировку невозможно получить ни из какой начальной маркировки, в этом случае, пожалуйста, сообщите об этом Touko. Выходные данные Если текущую маркировку невозможно получить ни из какого DFS-обхода, выведите NO. В противном случае в первой строке выведите YES. Во второй строке выведите единственное целое число, обозначающее количество дней со дня свадьбы. В третьей строке выведите \(n\) чисел через пробел, обозначающих оригинальную маркировку дерева. Если есть несколько правильных решений, вы можете вывести любое. Это означает, что вы можете вывести любую пару (DFS-обход, количество дней), для которой мы получим текущую конфигурацию, начав из DFS-обхода, который вы предоставили, ровно через предоставленное вами количество дней. Примечание Следующая анимация демонстрирует первый пример. Белая метка внутри вершины обозначает номер вершины \(i\), а оранжевая метка — значение \(a_i\).  | |
![]()
|
|
C. Очередная задача про колоду карт
Деревья
Перебор
реализация
Структуры данных
*1100
У вас есть колода из \(n\) карт, пронумерованных сверху вниз, т. е. у верхней карты индекс \(1\), а у нижней — \(n\). У каждой карты есть цвет: цвет \(i\)-й карты равен \(a_i\). Вам нужно обработать \(q\) запросов: \(j\)-й запрос описывается одним целым числом \(t_j\). Для каждого запроса вам нужно: - найти самую верхнюю карту в колоде с цветом \(t_j\), т. е. карту с минимальным индексом;
- вывести индекс найденной карты;
- вытащить данную карту и положить ее сверху колоды.
Выходные данные Выведите \(q\) целых чисел — ответы на все запросы. Примечание Описание примера: - текущая колода \([2, 1, 1, 4, \underline{3}, 3, 1]\) и верхняя карта цвета \(t_1 = 3\) на позиции \(5\);
- текущая колода \([3, \underline{2}, 1, 1, 4, 3, 1]\) и верхняя карта цвета \(t_2 = 2\) на позиции \(2\);
- текущая колода \([2, 3, \underline{1}, 1, 4, 3, 1]\) и верхняя карта цвета \(t_3 = 1\) на позиции \(3\);
- текущая колода \([\underline{1}, 2, 3, 1, 4, 3, 1]\) и верхняя карта цвета \(t_4 = 1\) на позиции \(1\);
- текущая колода \([1, 2, 3, 1, \underline{4}, 3, 1]\) и верхняя карта цвета \(t_5 = 4\) на позиции \(5\).
| |
![]()
|
|
F. Феникс и землетрясение
графы
Деревья
жадные алгоритмы
Конструктив
поиск в глубину и подобное
снм
*2600
Родина Феникса, Страна Огня, состоит из \(n\) городов, которые были соединены \(m\) дорогами, но из-за землетрясения они все были разрушены. Теперь Страна Огня хочет восстановить \(n-1\) из этих дорог так, чтобы все города стали снова связаны. Первоначально, в \(i\)-м городе есть \(a_i\) тонн асфальта. Чтобы восстановить дорогу, необходимо \(x\) тонн асфальта. При этом, чтобы восстановить дорогу между городами \(i\) и \(j\), в городах \(i\) и \(j\) должно быть суммарно хотя бы \(x\) тонн асфальта. Другими словами, в городе \(i\) есть \(a_i\) тонн асфальта, а городе \(j\) — \(a_j\) тонн, то после восстановления дороги между ними останется \(a_i+a_j-x\) тонн. Асфальт можно перевозить между городами, если дорога между ними уже восстановлена. Определите, возможно ли связать все города, и если да, то выведите последовательность дорог, которые нужно восстановить, в соответствующем порядке. Выходные данные Если невозможно связать все города, выведите NO. В противном случае выведите YES и далее \(n-1\) целое число \(e_1, e_2, \dots, e_{n-1}\) — порядок, в котором нужно восстанавливать дороги. \(e_i\) — это номер \(i\)-й в порядке восстановления дороги. Если существует несколько ответов, выведите любой. Примечание В первом примере, дороги восстанавливаются в следующем порядке: - Дорога \(3\) восстановлена (соединяет города \(3\) и \(4\)). В городе \(4\) первоначально было \(4\) тонны асфальта. После восстановления, осталось \(3\) тонны.
- Дорога \(2\) восстановлена (соединяет города \(2\) и \(3\)). Асфальт из города \(4\) можно перевезти в город \(3\) и использовать на дорогу. Осталось \(2\) тонны.
- Дорога \(1\) восстановлена (соединяет города \(1\) и \(2\)). Асфальт перевезен в город \(2\) и потрачен на дорогу. Осталась \(1\) тонна.
- Дорога \(4\) восстановлена (соединяет города \(4\) и \(5\)). Асфальт перевезен в город \(4\) и потрачен на дорогу. Больше асфальта не осталось.
Все города теперь связаны. Во втором примере, города \(1\) и \(2\) используют свой асфальт вместе для постройки дороги. В каждом городе по \(1\) тонне, то есть вместе \(2\) тонны, чего достаточно. В третьем примере, для восстановления дороги между городами \(1\) и \(2\) асфальта недостаточно. | |
![]()
|
|
F. Воссоединение
Деревья
дп
Комбинаторика
*3200
Сообщается, что конференция 2050 пройдет в городе Юньци в Ханчжоу с 23 по 25 апреля. На ней будут тематические форумы, утренние пробежки, походы, и так далее. Отношения между \(n\) волонтерами конференции 2050 могут быть представлены как дерево (связный неориентированный граф с \(n\) вершинами и \(n-1\) ребром). \(n\) вершин дерева соответствуют \(n\) волонтерам и пронумерованы \(1,2,\ldots, n\). Определим расстояние между двумя волонтерами \(i\) и \(j\), dis\((i,j)\), как количество ребер на кратчайшем пути из вершины \(i\) в вершину \(j\) в дереве. dis\((i,j)=0\), если \(i=j\). Некоторые волонтеры смогут принять участие в очном воссоединении, а некоторые — нет. Если для некоторого волонтера \(x\) и неотрицательного целого числа \(r\), все волонтеры, чье расстояние до \(x\) не больше \(r\), смогут принять участие в очном воссоединении, то форум с радиусом \(r\) может состояться. Уровень очного воссоединения определяется как максимальный возможный радиус форума, который может состояться. Предположим, что каждый волонтер сможет принять участие в воссоединении с вероятностью \(\frac{1}{2}\), и все эти события независимы. Найдите математическое ожидание уровня очного воссоединения. Если ни один волонтер не сможет принять участие, уровень равен \(-1\). Если все волонтеры смогут принять участие, уровень равен \(n\). Выходные данные Выведите математическое ожидание уровня очного воссоединения по модулю \(998\,244\,353\). Формально, пусть \(M = 998\,244\,353\). Можно показать, что ответ может быть представлен как несократимая вещественная дробь \(\frac{p}{q}\), где \(p\) и \(q\) целые числа и \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Примечание В первом примере следующая таблица показывает возможные варианты. \(yes\) означает, что волонтер сможет принять участие, а \(no\) — что не сможет. \(\)\begin{array}{cccc} 1 & 2 & 3 & level\\ yes & yes & yes & 3\\ yes & yes & no & 1\\ yes & no & yes & 0\\ yes & no & no & 0\\ no & yes & yes & 1\\ no & yes & no & 0\\ no & no & yes & 0\\ no & no & no & -1\\ \end{array}\(\) Математическое ожидание уровня равно \(\frac{3+1+1+(-1)}{2^3}=\frac{1}{2}\). | |
![]()
|
|
E. Сдвиг на один
геометрия
графы
Деревья
Конструктив
поиск в глубину и подобное
сортировки
*2700
На бесконечной плоскости лежат \(n\) точек. Координаты \(i\)-й точки \((x_i, y_i)\) такие, что \(x_i > 0\) и \(y_i > 0\). Координаты необязательно целые. За один ход осуществляются следующие операции: - выбрать две точки \(a\) и \(b\) (\(a \neq b\));
- подвинуть точку \(a\) из \((x_a, y_a)\) либо в \((x_a + 1, y_a)\), либо в \((x_a, y_a + 1)\);
- подвинуть точку \(b\) из \((x_b, y_b)\) либо в \((x_b + 1, y_b)\), либо в \((x_b, y_b + 1)\);
- удалить точки \(a\) и \(b\).
Ход можно совершить только в том случае, если существует прямая, проходящая через новые координаты \(a\), новые координаты \(b\) и \((0, 0)\). Иначе ход совершить нельзя, и точки остаются на своих начальных координатах \((x_a, y_a)\) и \((x_b, y_b)\), соответственно. Нумерация точек не меняется после удаления точек. Если точки удалены, то они не могут быть выбраны в последующих ходах. Обратите внимание, что необходимо двигать обе точки во время хода, нельзя оставлять их в изначальных координатах. Какое наибольшее количество ходов можно совершить? Какие это ходы? Если существует несколько ответов, то выведите любой из них. Выходные данные В первой строке выведите одно целое число \(c\) — наибольшее количество ходов, которые можно совершить. В каждой из следующих \(c\) строк должно быть записано описание хода: два целых числа \(a\) и \(b\) (\(1 \le a, b \le n\), \(a \neq b\)) — точки, удаляемые на текущем ходу. Должен существовать способ подвинуть точки \(a\) и \(b\) согласно условию так, чтобы существовала прямая, проходящая через новые координаты \(a\), новые координаты \(b\) и \((0, 0)\). Никакая удаленная точка не может быть удалена в последующих ходах. Если существует несколько ответов, то выведите любой из них. Можно выводить ходы и точки внутри ходов в произвольном порядке. Примечание Точки из первого примера и перемещения для тех из них, которые выбираются в ходах:  | |
![]()
|
|
E. Сад
битмаски
графы
Деревья
дп
*2500
У Васи есть очень красивый загородный сад, который представляет собой прямоугольное поле размером n × m, разделенное на n·m квадратных клеток. В один прекрасный день Вася вспомнил, что ему нужно проложить дорожки между k важными клетками с постройками — для этого он может залить бетоном некоторые из клеток своего сада. Про каждую клетку сада известно число aij, которое означает количество цветов, растущих в клетке с координатами (i, j). При заливании бетоном все цветы, растущие в клетке, погибают. Вася хочет залить бетоном некоторые клетки так, чтобы выполнялись условия: - все k важных клеток обязательно должны быть залиты бетоном
- из каждой важной клетки до любой другой важной клетки существовал путь по залитым бетоном клеткам при условии, что соседними считаются клетки, имеющие общую сторону
- общее количество погибших растений должно быть минимально
Так как у Васи достаточно большой сад, то он просит Вас ему помочь. Выходные данные В первую строку выведите единственное целое число — минимальное количество погибших при строительстве растений. Далее выведите n строк по m символов в каждой — план сада, где символом «X» (заглавная латинская буква X) обозначайте залитую бетоном клеточку, а символом «.» (точка) — незалитую. Если решений несколько, выведите любое. | |
![]()
|
|
D. Настя играет с деревом
Деревья
дп
жадные алгоритмы
Конструктив
поиск в глубину и подобное
реализация
снм
Структуры данных
*2500
У Насти есть невзвешенное дерево из \(n\) вершин, с которым ей не терпится поиграть! Девочка будет выполнять следующую операцию с деревом столько раз, сколько ей потребуется: - удалить любое существующее ребро, затем
- добавить неориентированное ребро между любой парой вершин.
Какое минимальное количество операций требуется девочке, чтобы получить из дерева бамбук? Бамбуком называется дерево, степень вершин в котором не превосходит \(2\). Выходные данные Для каждого из наборов входных данных в первой строке выведите одно целое число \(k\) — минимальное количество операций, необходимых, чтобы получить из дерева бамбук. В последующих \(k\) строках выведите \(4\) целых числа \(x_1\), \(y_1\), \(x_2\), \(y_2\) (\(1 \le x_1, y_1, x_2, y_{2} \le n\), \(x_1 \neq y_1\), \(x_2 \neq y_2\)) — таким образом вы удаляете ребро \((x_1, y_1)\) и добавляете неориентированное ребро \((x_2, y_2)\). Обратите внимание, что ребро \((x_1, y_1)\) обязано содержаться в графе до его удаления. Примечание Обратите внимание, что граф может быть несвязным после какого-то количества операций. Рассмотрим первый набор входных данных:  Красным обозначены удаленные ребра, а зеленым – добавленные. | |
![]()
|
|
C. Вложить и выложить
Деревья
жадные алгоритмы
Перебор
реализация
Структуры данных
*1600
 Василий — большой любитель планирования дел наперед. Поэтому каждое утро он занимается формированием вложенного списка предстоящих дел. Корректным вложенным списком является любой список, который можно получить из списка с одним пунктом «1» путем применения операций. Каждая операция вставляет в список новый пункт на следующей строке после одного из уже существующих пунктов \(a_1 \,.\, a_2 \,.\, a_3 \,.\, \,\cdots\, \,.\,a_k\), и бывает двух видов: - добавить пункт \(a_1 \,.\, a_2 \,.\, a_3 \,.\, \cdots \,.\, a_k \,.\, 1\) (начав более вложенный список), или
- добавить пункт \(a_1 \,.\, a_2 \,.\, a_3 \,.\, \cdots \,.\, (a_k + 1)\) (продолжив текущий уровень).
Операцию можно производить только при условии, что в списке не появится двух одинаковых пунктов. А также, если рассматривать каждый пункт как последовательность чисел, последовательность пунктов должна всегда оставаться возрастающей в лексикографическом порядке. Примеры корректных и некорректных списков приведены на рисунке. Пример того, как можно получить корректный список, изображенный на картинке, приведен в секции « Примечание». Когда Василий захотел сохранить Word-документ со списком своих дел, он промахнулся и вместо «Ctrl+S» нажал совсем другую комбинацию клавиш. Достоверно неизвестно, что это была за комбинация клавиш, но после ее нажатия каждый пункт списка заменился одним числом: числом, изначально написанным последним в номере пункта. Василий хочет, чтобы вы помогли ему восстановить подходящий изначальный вложенный список. Выходные данные Для каждого набора входных данных выведите \(n\) строк, которые являются корректным вложенным списком, из которого мог получиться список, который вам предоставил Василий. Если ответов несколько, то вы можете вывести любой подходящий. Примечание Во втором наборе входных данных одним из корректных подходящих списков является: 1 1.1 1.1.1 1.1.2 1.2 1.2.1 2 2.1 2.2 Такой список можно получить при помощи последовательности операций, показанной ниже:  - Изначальный список с одним пунктом \(1\).
- Вставляем пункт \(2\) при помощи операции вставки второго типа после пункта \(1\).
- Вставляем пункт \(1.1\) при помощи операции вставки первого типа после пункта \(1\).
- Вставляем пункт \(1.2\) при помощи операции вставки второго типа после пункта \(1.1\).
- Вставляем пункт \(1.1.1\) при помощи операции вставки первого типа после пункта \(1.1\).
- Вставляем пункт \(1.1.2\) при помощи операции вставки второго типа после пункта \(1.1.1\).
- Вставляем пункт \(1.2.1\) при помощи операции вставки первого типа после пункта \(1.2\).
- Вставляем пункт \(2.1\) при помощи операции вставки первого типа после пункта \(2\).
- Вставляем пункт \(2.2\) при помощи операции вставки второго типа после пункта \(2.1\).
| |
![]()
|
|
D. MEX дерево
Деревья
Комбинаторика
математика
поиск в глубину и подобное
реализация
*2400
Вам дано дерево из \(n\) вершин, в котором вершины пронумерованы от \(0\) до \(n-1\). Для каждого \(k\) от \(0\) до \(n\) включительно вам необходимо посчитать количество неупорядоченных пар \((u,v)\), \(u \neq v\), таких, что MEX всех номеров вершин на пути от \(u\) до \(v\) равен \(k\). MEX последовательности целых чисел равен наименьшему неотрицательному целому числу, которое в ней не встречается. Выходные данные Для каждого набора входных данных выведите \(n+1\) целое число: число путей в дереве таких, что MEX всех номеров вершин на нем равен \(k\), для всех \(k\) от \(0\) до \(n\). Примечание - В наборе входных данных \(1\):
 - Для \(k = 0\) существует только \(1\) путь из \(2\) в \(3\) с \(MEX([2, 3]) = 0\).
- Для \(k = 1\) существует \(2\) пути. Один из \(0\) в \(2\) с \(MEX([0, 2]) = 1\), и из \(0\) в \(3\) с \(MEX([0, 2, 3]) = 1\).
- Для \(k = 2\) существует \(1\) путь из \(0\) в \(1\) с \(MEX([0, 1]) = 2\).
- Для \(k = 3\) существует \(1\) путь из \(1\) в \(2\) с \(MEX([1, 0, 2]) = 3\)
- Для \(k = 4\) существует \(1\) путь из \(1\) в \(3\) с \(MEX([1, 0, 2, 3]) = 4\).
- В наборе входных данных \(2\):
 - Для \(k = 0\) не существует таких путей.
- Для \(k = 1\) не существует таких путей.
- Для \(k = 2\) существует \(1\) путь из \(0\) в \(1\) с \(MEX([0, 1]) = 2\).
| |
![]()
|
|
A. Огромное дерево Parsa
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
разделяй и властвуй
*1600
У Parsa есть огромное дерево на \(n\) вершинах. На каждой вершине \(v\) он записал два целых числа \(l_v\) и \(r_v\). Чтобы дерево Parsa выглядело еще более величественным, Nima хочет назначить число \(a_v\) (\(l_v \le a_v \le r_v\)) для каждой вершины \(v\) таким образом, чтобы красота дерева Parsa была максимальной. Восприятие красоты Nima довольно причудливо. Он определяет красоту дерева как сумму \(|a_u - a_v|\) по всем ребрам \((u, v)\) дерева. Поскольку дерево Parsa слишком велико, Nima не может самостоятельно максимизировать его красоту. Ваша задача — найти максимальную возможную красоту для дерева Parsa. Выходные данные Для каждого набора входных данных выведите максимальную возможную красоту для дерева Парса. Примечание Деревья в примере:  В первом наборе входных данных одно из возможных назначений — \(a = \{1, 8\}\), что приводит к \(|1 - 8| = 7\). Во втором наборе входных данных одно из возможных назначений — \(a = \{1, 5, 9\}\), что приводит к красоте \(|1 - 5| + |5 - 9| = 8\). | |
![]()
|
|
C. Деревья примирения
Деревья
жадные алгоритмы
поиск в глубину и подобное
Структуры данных
*2300
У Soroush и Keshi есть по одному пронумерованному корневому дереву на \(n\) вершин. У обоих деревьев корнем является вершина \(1\). Раньше Soroush и Keshi воевали. После бесконечных десятилетий борьбы они, наконец, стали союзниками, чтобы подготовить раунд Codeforces. Чтобы отметить это счастливое событие, они решили сделать памятный граф на \(n\) вершинах. Они добавляют ребро между вершинами \(u\) и \(v\) в памятный граф, если выполняются оба из следующих условий: - Одна из вершин \(u\) и \(v\) является предком второй в дереве Soroush.
- Ни одна из вершин \(u\) и \(v\) не является предком другой в дереве Keshi.
Здесь вершина \(u\) считается предком вершины \(v\), если \(u\) лежит на пути от \(1\) (корня) к \(v\). Выскочивший из ниоткуда Mashtali попытался найти максимальную клику в памятном графе. Он потерпел неудачу, потому что граф был слишком большим. Помогите Mashtali, найдя размер максимальной клики в памятном графе. Напомним, что клика — это такое подмножество вершин графа, каждые две из которых соединены ребром. Выходные данные Для каждого набора входных данных выведите одно целое число — размер максимальной клики в памятном графе. Примечание В первом и третьем наборах входных данных можно выбрать любую вершину. Во втором наборе входных данных одна из максимальных клик — \(\{2, 3, 4, 5\}\). В четвертом наборе входных данных одна из максимальных клик — \(\{3, 4, 6\}\). | |
![]()
|
|
E. Mashtali и деревья Hagh
Деревья
дп
Комбинаторика
*2900
Сегодня у Mashtali день рождения! Он получил в подарок от Haj Davood дерево Hagh! Ориентированное дерево называется деревом Hagh, если: - Длина самого длинного ориентированного пути в нем равна ровно \(n\).
- Каждая вершина имеет не более трех ребер, присоединенных к ней (исходящих и входящих вместе).
- Назовем вершины \(u\) и \(v\) друзьями, если из одной из них есть ориентированный путь к другой. Для каждой пары вершин \(u\) и \(v\), которые не являются друзьями, должна существовать вершина \(w\), которая дружит и с \(u\), и с \(v\) (общий друг).
Открыв свой подарок, Mashtali обнаружил, что номера вершин с вершин исчезли. Тогда он спросил себя: сколько существует различных непомеченных деревьев Hagh? Другими словами, сколько возможных деревьев он мог получить в подарок на день рождения? На первый взгляд, число таких деревьев кажется бесконечным, поскольку нет никакого ограничения на количество вершин; но затем он решил задачу и доказал, что непомеченых деревьев Hagh есть всего конечное число! Пораженный этим фактом, он поделился задачей с вами, чтобы вы тоже могли насладиться ее решением. Поскольку ответ может быть довольно большим, он попросил вас найти количество различных деревьев Hagh по модулю \(998244353\). Здесь два дерева считаются различными, если они не изоморфны: если нет способа поставить в соответствие вершины одного дерева вершинам второго дерева так, чтобы ребрам первого ставились в соответствие ребра второго, с сохранением ориентации. Некоторые примеры для \(n = 2\):  Ориентированные деревья \(D\) и \(E\) являются деревьями Hagh. \(C\) не является Hagh, потому что имеет вершину с \(4\) ребрами, присоединенными к ней. Деревья \(A\) и \(B\) не являются Hagh, потому что их самые длинные ориентированные пути не имеют длину \(n\). Также в \(B\) крайние левая и правая вершины не являются друзьями и не имеют общих друзей. Выходные данные Выведите одно целое число, ответ на задачу Mashtali по модулю \(998244353\). Примечание Вот все пять деревьев Hagh для \(n = 1\):  | |
![]()
|
|
D. Потерянное дерево
Деревья
интерактив
Конструктив
*1800
Это интерактивная задача. Маленький Дорми на фестивале столкнулся со странной головоломкой: ему нужно угадать ребра невзвешенного дерева из \(n\) вершин! Вершины дерева пронумерованы от \(1\) до \(n\). Ему разрешается задавать организатору вопросы одного вида: - Маленький Дорми выбирает вершину \(r\) (\(1 \le r \le n\)), а организатор в ответ предоставляет ему массив целых чисел \(d_1, d_2, \ldots, d_n\), где \(d_i\) — длина кратчайшего пути из \(r\) в вершину \(i\) для всех \(1 \le i \le n\).
Кроме того, чтобы сделать головоломку нечестной дополнительно озадачить Дорми, организатор разрешает задать не более \(\lceil\frac{n}{2}\rceil\) вопросов, где \(\lceil x \rceil\) обозначает наименьшее целое число, большее либо равное \(x\). Маленький Дорми переживает, что может не угадать дерево, поэтому ему нужна ваша помощь! Обратите внимание, что организатор создает дерево до начала взаимодействия, и не меняет его в процессе взаимодействия. Выходные данные Когда ваша программа нашла дерево, выведите одну строку, содержащую «!», а затем \(n-1\) строку, каждая из которых содержит два целых числа \(a\) и \(b\), означающие ребро, соединяющее вершины \(a\) и \(b\) (\(1 \le a, b \le n\)). После этого ваша программа должна сбросить буфер вывода и завершиться. Вы можете выводить ребра дерева в любом порядке, ребро \((a,b)\) и ребро \((b,a)\) считаются одним и тем же ребром. Вывод ответа не считается как один из вопросов. Протокол взаимодействия После чтения количества вершин, вы можете задать не более \(\lceil\frac{n}{2}\rceil\) вопросов. Каждый вопрос задается в формате «? r», где целое число \(r\) (\(1 \le r \le n\)) обозначает номер вершины, которую вы выбрали для этого вопроса. После этого считайте \(n\) целых чисел \(d_1, d_2, \ldots, d_n\) в отдельной строке, где \(d_i\) равно длине кратчайшего пути из вершины \(r\) в вершину \(i\). После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Если в какой-то момент вы задали больше, чем \(\lceil \frac{n}{2} \rceil\) вопросов, взаимодействие прекратится, и вы получите вердикт «Неправильный ответ». Взломы Чтобы взломать решение, используйте следующий формат теста. Первая строка содержит целое число \(n\) (\(2 \le n \le 2\,000\)). Следующие \(n−1\) строк содержат два целых числа \(u\) и \(v\) (\(1 \le u,v \le n\)), обозначающие ребро между вершинами \(u\) и \(v\) (\(u \neq v\)). Эти \(n-1\) ребер должны образовывать дерево. Примечание Ниже показано дерево из первого примера.  Обратите внимание, что ребра можно выводить в любом порядке. Кроме того, ниже показаны ответы для всех возможных вопросов в примере \(1\): - \(1\): \([0,1,2,2]\)
- \(2\): \([1,0,1,1]\)
- \(3\): \([2,1,0,2]\)
- \(4\): \([2,1,2,0]\)
Ниже показано дерево из второго примера.  Далее показаны ответы для всех возможных вопросов в примере \(2\): - \(1\): \([0,4,1,3,2]\)
- \(2\): \([4,0,3,1,2]\)
- \(3\): \([1,3,0,2,1]\)
- \(4\): \([3,1,2,0,1]\)
- \(5\): \([2,2,1,1,0]\)
| |
![]()
|
|
H. Потерянные вершины
графы
Деревья
дп
интерактив
Конструктив
сортировки
*3500
Это интерактивная задача. Так как маленький Эрики прошел на Международную олимпиаду школьников по информатике в этом году, он получил подарок от своих друзей: дерево с \(n\) вершинами! По пути к месту проведения Эрики было скучно, поэтому он решил сыграть в игру с маленьким Ивонном с использованием нового дерева. Сначала Ивонн загадывает две (не обязательно различные) вершины \(a\) и \(b\) в этом дереве (не сообщая их Эрики), а затем сообщает ему подсказку \(f\) — одну из вершин на простом пути от \(a\) до \(b\). Затем маленький Эрики может спрашивать следующие вопросы: - Если подвесить дерево за вершину \(r\) (Эрики может выбрать \(r\)), какая вершина будет наименьшим общим предком вершин \(a\) и \(b\)?
Задача маленького Эрики — найти вершины \(a\) и \(b\). Маленький Ивонн считает игру слишком простой, поэтому в начале игры, перед тем, как дать подсказку \(f\), он просит Эрики найти максимальное количество запросов, необходимых для нахождения \(a\) и \(b\) для всех возможных значений \(a\), \(b\) и \(f\) в предположении, что Эрики действует оптимально. Под оптимальными действиями подразумевается стратегия, делающая наименьшее число запросов. Конечно, после того, как маленький Эрики скажет это максимальное количество запросов, Ивонн не разрешит сделать больше запросов в самой игре. Дерево, \(a\), \(b\) и \(f\) фиксированы до начала игры и не меняются в зависимости от запросов. Протокол взаимодействия Сначала считайте строку, содержащую одно целое число \(n\) (\(1 \le n \le 10^5\)) — количество вершин в дереве. Сделающие \(n−1\) строк описывают дерево маленького Дорми. Каждая из этих строк содержит два целых числа \(u\) и \(v\) (\(1 \le u,v \le n\)), обозначающие ребро между вершинами \(u\) и \(v\) (\(u \neq v\)). Гарантируется, что эти ребра образуют дерево. После этого вы должны вывести \(k\) — максимальное число запросов, необходимое для определения \(a\) и \(b\) по всем возможным значениям \(a\), \(b\) и \(f\) в предположении оптимальной игры. Вы должны вывести перевод строки и сбросить буфер вывода после вывода \(k\). Затем считайте одно целое число \(f\) (\(1 \le f \le n\)) — подсказку: вершину на пути от \(a\) до \(b\) включительно. После этого вы можете делать запросы. Вам будет разрешено сделать не более \(k\) запросов, где \(k\) — число, которое вы вывели. Для того, чтобы сделать запрос, выведите «? r», где \(r\) — целое число, \(1 \le r \le n\), обозначающее, за какую вершину вы хотите подвесить дерево. В ответ вы получите целое число \(x\) (\(1 \le x \le n\)) — наименьший общий предок вершин \(a\) и \(b\), если дерево подвесить за \(r\). Когда ваша программа определит \(a\) и \(b\), выведите их в следующем формате: «! a b», где \(a\) и \(b\) — две загаданные вершины, и завершите программу сразу после сброса буфера вывода. Вы можете вывести \(a\) и \(b\) в любом порядке. После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Если вы сделаете некорректный вывод, или сделаете более \(k\) запросов, взаимодействие прекратится и вы получите вердикт «Неправильный ответ». Вывод считается некорректным, если это некорректный запрос, или вы вывели \(k\), меньшее \(0\) или большее \(n\). Взломы Чтобы взломать решение, используйте следующий формат: Первая строка содержит одно целое число \(n\) (\(1 \le n \le 10^5\)). Следующие \(n−1\) строк содержат по два целых числа \(u\) и \(v\) (\(1 \le u,v \le n\)), обозначающие ребро между вершинами \(u\) и \(v\) (\(u \neq v\)). Эти \(n-1\) ребра должны образовывать дерево. Следующая строка содержит два целых числа \(a\) и \(b\) (\(1 \le a,b \le n\)). Последняя строка должна содержать одно целое число \(f\) (\(1 \le f \le n\)). Вершина \(f\) должна лежать на простом пути от \(a\) до \(b\) включительно. Примечание Дерево из первого примера показано ниже. Вершины \(a\) и \(b\) выделены жирным. 
Обратите внимание, что вы можете вывести \(a\) и \(b\) в любом порядке. Ниже приведены ответы на все возможные запросы \(1,2,\ldots,n\): - \(1\): \(1\)
- \(2\): \(2\)
- \(3\): \(2\)
- \(4\): \(4\)
__________________________________________ Дерево из второго примера показано ниже. Вершины \(a\) и \(b\) выделены жирным. 
Ниже приведены ответы на все возможные запросы \(1,2,\ldots,n\) в примере \(2\): - \(1\): \(1\)
- \(2\): \(4\)
- \(3\): \(1\)
- \(4\): \(4\)
- \(5\): \(4\)
| |
![]()
|
|
D. Плей-офф турнир
Деревья
дп
поиск в глубину и подобное
реализация
Структуры данных
*1800
\(2^k\) команд участвуют в плей-офф турнире. Турнир состоит из \(2^k - 1\) игры. Они проводятся следующим образом: во-первых, команды делятся на пары: команда \(1\) играет против команды \(2\), команда \(3\) играет против команды \(4\) (именно в таком порядке) и так далее (таким образом, в этой фазе будет сыграно \(2^{k-1}\) игры). Когда команда проигрывает игру, она выбывает, и каждая игра приводит к выбыванию одной команды (нет ничьих). После этого остается \(2^{k-1}\) команд. Если остается только одна команда, она объявляется чемпионом; в противном случае играется еще \(2^{k-2}\) игр: в первой из них победитель игры «\(1\) против \(2\)» играет против победителя игры «\(3\) против \(4\)», затем победитель игры «\(5\) против \(6\)» играет против победителя игры «\(7\) против \(8\)» и так далее. Этот процесс повторяется до тех пор, пока не останется только одна команда. Например, на этом рисунке описан хронологический порядок игр с \(k = 3\):  Пусть строка \(s\), состоящая из \(2^k - 1\) символов, описывает результаты игр в хронологическом порядке следующим образом: - если \(s_i\) равно 0, то команда с меньшим индексом выигрывает \(i\)-ю игру;
- если \(s_i\) равно 1, то команда с большим индексом выигрывает \(i\)-ю игру;
- если \(s_i\) равно ?, то результат \(i\)-й игры неизвестен (любая команда может выиграть эту игру).
Пусть \(f(s)\) — число возможных победителей турнира, описываемого строкой \(s\). Команда \(i\) является возможным победителем турнира, если можно заменить каждый ? на 1 или 0 таким образом, что команда \(i\) является чемпионом. Вам дается начальное состояние строки \(s\). Вы должны обработать \(q\) запросов следующей формы: - \(p\) \(c\) — заменить \(s_p\) символом \(c\) и вывести \(f(s)\) в результате запроса.
Выходные данные Для каждого запроса выведите одно целое число — \(f(s)\). | |
![]()
|
|
E. Поставки золота
Бинарный поиск
Деревья
дп
жадные алгоритмы
интерактив
Структуры данных
*2200
Вам задано корневое дерево. Каждая вершина дерева содержит \(a_i\) тонн золота, стоящее \(c_i\) за тонну. Первоначально, дерево состоит только из корня с номером \(0\), в котором \(a_0\) тонн золота с ценой \(c_0\) за тонну. Всего есть \(q\) запросов. Каждый запрос одного из двух видов: - Подвесить вершину \(i\) (где \(i\) — это номер запроса) за некоторую вершину \(p_i\); вершина \(i\) будет содержать \(a_i\) тонн золота с ценой \(c_i\) за тонну. Гарантируется, что \(c_i > c_{p_i}\).
- Для заданной вершины \(v_i\) рассмотрим простой путь от \(v_i\) к корню. Нам нужно приобрести \(w_i\) тонн золота из вершин на этом пути, потратив наименьшее количество денег. Если на этом пути недостаточно золота, мы покупаем все что можно.
Если мы покупаем \(x\) тон золота в некоторой вершине \(v\), то оставшееся количество золота в ней уменьшается на \(x\) (очевидно, мы не можем купить больше золота, чем есть в вершине на данный момент). Для каждого запроса второго вида посчитайте, сколько тонн золота мы купим в результате и сколько мы на это потратим. Заметим, что вы должны решить данную задачу в онлайне. То есть вы не можете считать все входные данные заранее. Вы можете считать очередной запрос только после того как выведете ответ на предыдущий, поэтому не забывайте сбрасывать поток вывода после вывода ответа. Вы можете использовать такие функции как fflush(stdout) в C++, BufferedWriter.flush в Java или похожие после каждого вывода в программе. По стандарту (если вы не модифицировали I/O), endl сбрасывает cout в C++, а System.out.println в Java (или println в Kotlin) сбрасывают поток вывода автоматически. Выходные данные Для каждого запроса второго вида, выведите сколько тонн золота мы смогли купить и сколько на это потратили. Примечание Рассмотрим пример: В первом запросе, дерево состоит только из корня, поэтому мы приобретаем \(2\) тонны золота и платим \(2 \cdot 2 = 4\). В корне осталось \(3\) тонны. Во втором запросе, вы подвешиваем вершину \(2\) за вершину \(0\). В вершине \(2\) сейчас \(3\) тонны золота по цене \(4\) за тонну. В третьем запросе, простой путь из \(2\) в \(0\) содержит только вершины \(0\) и \(2\), а так как \(c_0 < c_2\), мы покупаем оставшиеся \(3\) тонны золота в вершине \(0\) и \(1\) тонну в вершине \(2\). Таким образом, мы приобрели \(3 + 1 = 4\) тонны и заплатили \(3 \cdot 2 + 1 \cdot 4 = 10\). Теперь, вершина \(0\) осталась без золота, а вершине \(2\) осталось \(2\) тонны золота. В четвертом запросе, мы подвешиваем вершину \(4\) за вершину \(0\). В вершине \(4\) сейчас \(1\) тонна золота по цене \(3\). В пятом запросе, простой путь из \(4\) в \(0\) состоит только из вершин \(0\) и \(4\). Но так как в вершине \(0\) уже нет золота, а в вершине \(4\) только \(1\) тонна, то мы покупаем \(1\) тонну из вершины \(4\) и тратим \(1 \cdot 3 = 3\). Теперь в вершине \(4\) больше не осталось золота. | |
![]()
|
|
B. Древесный массив
графы
Деревья
дп
Комбинаторика
математика
Перебор
Теория вероятностей
*2300
Вам задано дерево, состоящее из \(n\) вершин. По заданному дереву вы строите массив, отмечая вершины по одной. Первоначально, когда еще не помечено ни одной вершины, вы выбираете вершину равновероятно по всем вершинам дерева и отмечаете ее. После этого, пока еще остаются непомеченные вершины, вы выбираете и помечаете вершину равновероятно среди всех еще непомеченных, но связанных по ребру хотя бы с одной помеченной вершиной. Можно доказать, что данный процесс пометит все вершины в дереве. Финальный массив \(a\) — это список номеров вершин в порядке, в котором они были помечены. Определите математическое ожидание количества инверсий в массиве, полученном на основе заданного дереве с помощью описанного выше алгоритма. Количество инверсий в массиве \(a\) — это количество пар индексов \((i, j)\) таких, что \(i < j\) и \(a_i > a_j\). Например, в массиве \([4, 1, 3, 2]\) количество инверсий равно \(4\): \((1, 2)\), \((1, 3)\), \((1, 4)\), \((3, 4)\). Выходные данные Выведите математическое ожидание количества инверсий в построенном массиве по модулю \(10^9+7\). Формально, пусть \(M = 10^9+7\). Можно показать, что ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Примечание Изображение дерева из первого примера:  В первом примере получающиеся массивы почти фиксированы. Если первоначально выбрана вершина \(2\), то единственный возможный массив — это \([2, 1, 3]\) (\(1\) инверсия). Если первоначально выбрана вершина \(3\), то единственный возможный массив — это \([3, 1, 2]\) (\(2\) инверсии). Если первоначально выбрана вершина \(1\), то массивы \([1, 2, 3]\) (\(0\) инверсий) и \([1, 3, 2]\) (\(1\) инверсия) — это единственные варианты и они равновероятны. В результате математическое ожидание количества инверсий равно \(\frac{1}{3}\cdot 1 + \frac{1}{3} \cdot 2 + \frac{1}{3} \cdot (\frac{1}{2} \cdot 0 + \frac{1}{2} \cdot 1) = \frac{7}{6}\). \(166666669 \cdot 6 = 7 \pmod {10^9 + 7}\), то есть ответ равен \(166666669\). Изображение дерева из второго примера:  Изображение дерева из третьего примера:  | |
![]()
|
|
G. Сколько путей?
графы
Деревья
дп
поиск в глубину и подобное
*2100
Задан ориентированный граф \(G\), в котором допустимы петли (то есть рёбра из вершины в себя). В \(G\) отсутствуют кратные рёбра, то есть для каждой упорядоченной пары вершин \((u, v)\) существует не более одного ребра из \(u\) в \(v\). Вершины пронумерованы от \(1\) до \(n\). Назовём путем из \(u\) в \(v\) такую последовательность рёбер, что: - вершина \(u\) является началом первого ребра пути;
- вершина \(v\) является концом последнего ребра пути;
- для любой пары соседних рёбер следующее ребро начинается с вершины, на которую заканчивается предыдущее ребро.
Дополнительно будем считать, что пустая последовательность рёбер — это путь из \(u\) в \(u\). Для каждой вершины \(v\) выведите одно из четырёх значений: - \(0\), если не существует пути из \(1\) в \(v\);
- \(1\), если существует ровно один путь из \(1\) в \(v\);
- \(2\), если существует более одного пути из \(1\) в \(v\) и это число является конечной величиной;
- \(-1\), если существует бесконечно много путей из \(1\) в \(v\).
Рассмотрим пример, изображённый на рисунке.  Тогда: - ответ для вершины \(1\) равен \(1\): существует ровно один путь из \(1\) в \(1\) (путь длины \(0\));
- ответ для вершины \(2\) равен \(0\): не существует пути из \(1\) в \(2\);
- ответ для вершины \(3\) равен \(1\): существует ровно один путь из \(1\) в \(3\) (это ребро \((1, 3)\));
- ответ для вершины \(4\) равен \(2\): существует более одного, но конечное число путей из \(1\) в \(4\) (два пути: \([(1, 3), (3, 4)]\) и \([(1, 4)]\));
- ответ для вершины \(5\) равен \(-1\): существует бесконечно много путей из \(1\) в \(5\) (петля может быть использована в пути сколько угодно раз);
- ответ для вершины \(6\) равен \(-1\): существует бесконечно много путей из \(1\) в \(6\) (петля может быть использована в пути сколько угодно раз).
Выходные данные Выведите \(t\) строк. \(i\)-я строка должна содержать ответ на \(i\)-й набор входных данных — последовательность \(n\) целых чисел от \(-1\) до \(2\). | |
![]()
|
|
F. Равноудалённые вершины
Деревья
дп
Комбинаторика
Перебор
поиск в глубину и подобное
*2200
Дерево — это неориентированный связный граф, в котором отсутствуют циклы. Задано дерево из \(n\) вершин. Необходимо посчитать количество способов выбрать в этом дереве ровно \(k\) вершин (т.е. \(k\)-элементное подмножество вершин), так чтобы все попарные расстояния между выбранными вершинами были равны. Иными словами, чтобы существовало такое число \(c\), что для всех \(u, v\) (\(u \ne v\), \(u, v\) — выбранные вершины) было верно \(d_{u,v}=c\), где \(d_{u,v}\) — расстояние от \(u\) до \(v\). Поскольку ответ может быть очень большим, необходимо вывести его по модулю \(10^9 + 7\). Выходные данные Для каждого набора входных данных выведите в отдельной строке одно целое число — количество способов выбрать в дереве ровно \(k\) вершин, так чтобы для любых двух пар вершин расстояние между вершинами в паре было одинаковым, по модулю \(10^9 + 7\) (иными словами, выведите остаток при делении на \(1000000007\)). | |
![]()
|
|
H. XOR и расстояния
битмаски
Деревья
разделяй и властвуй
*2900
Вам дан массив \(a\), состоящий из \(n\) различных элементов, и целое число \(k\). Каждый элемент в массиве это неотрицательное целое число, не превосходящее \(2^k-1\). Обозначим через XOR расстояние для числа \(x\) следующую величину: \(\)f(x) = \min\limits_{i = 1}^{n} \min\limits_{j = i + 1}^{n} |(a_i \oplus x) - (a_j \oplus x)|,\(\) где через \(\oplus\) обозначено побитовое исключающее ИЛИ. Для каждого целого числа \(x\) от \(0\) до \(2^k-1\) посчитайте \(f(x)\). Выходные данные Выведите \(2^k\) чисел. \(i\)-е из них должно равняться \(f(i-1)\). Примечание Рассмотрим первый пример: - для \(x = 0\), если мы применим XOR ко всем элементам массива с числом \(x\), мы получим массив \([6, 0, 3]\), и минимальный модуль разности между элементами равен \(3\);
- для \(x = 1\), если мы применим XOR ко всем элементам массива с числом \(x\), мы получим массив \([7, 1, 2]\), и минимальный модуль разности между элементами равен \(1\);
- для \(x = 2\), если мы применим XOR ко всем элементам массива с числом \(x\), мы получим массив \([4, 2, 1]\), и минимальный модуль разности между элементами равен \(1\);
- для \(x = 3\), если мы применим XOR ко всем элементам массива с числом \(x\), мы получим массив \([5, 3, 0]\), и минимальный модуль разности между элементами равен \(2\);
- для \(x = 4\), если мы применим XOR ко всем элементам массива с числом \(x\), мы получим массив \([2, 4, 7]\), и минимальный модуль разности между элементами равен \(2\);
- для \(x = 5\), если мы применим XOR ко всем элементам массива с числом \(x\), мы получим массив \([3, 5, 6]\), и минимальный модуль разности между элементами равен \(1\);
- для \(x = 6\), если мы применим XOR ко всем элементам массива с числом \(x\), мы получим массив \([0, 6, 5]\), и минимальный модуль разности между элементами равен \(1\);
- для \(x = 7\), если мы применим XOR ко всем элементам массива с числом \(x\), мы получим массив \([1, 7, 4]\), и минимальный модуль разности между элементами равен \(3\).
| |
![]()
|
|
E. Скучные отрезки
Деревья
сортировки
Структуры данных
*2100
Даны \(n\) отрезков на числовой прямой, отрезки пронумерованы от \(1\) до \(n\). \(i\)-й отрезок покрывает все целочисленные точки от \(l_i\) до \(r_i\) и имеет значение \(w_i\). Требуется выбрать поднабор этих отрезков (возможно, все). Когда набор выбран, разрешается перемещаться между двумя целочисленными точками, если существует выбранный отрезок, который накрывает обе точки. Поднабор называется хорошим, если возможно достичь точку \(m\), начав из точки \(1\), за произвольное количество ходов. Цена поднабора — это разность между максимальным и минимальным значениями отрезков в нем. Найдите минимальную цену хорошего поднабора. В каждом тесте существует хотя бы один хороший набор. Выходные данные Выведите одно целое число — минимальную цену хорошего поднабора. | |
![]()
|
|
F. Хороший граф
графы
Деревья
снм
Структуры данных
*2700
У вас есть неориентированный граф из \(n\) вершин, и у каждого ребра есть вес. Назовем простым циклом цикл в графе без повторяющихся вершин. Назовем весом цикла исключающее ИЛИ весов его ребер. Скажем, что граф хороший, если все его простые циклы имеют вес \(1\). Граф плохой, если он является не хорошим. Первоначально, граф пустой. Далее приходят \(q\) запросов. Каждый запрос имеет следующий вид: - \(u\) \(v\) \(x\) — нужно добавить ребро между вершинами \(u\) и \(v\) веса \(x\), если добавление данного ребра не делает граф плохим.
Для каждого запроса выведите: было ли добавлено данное ребро. Выходные данные Для каждого запроса, выведите YES, если ребро было добавлено в граф, или NO в противном случае (оба в любом регистре). | |
![]()
|
|
D1. Mocha и Diana (простая версия)
графы
Деревья
жадные алгоритмы
Конструктив
Перебор
снм
*1400
Это простая версия задачи. Две версии отличаются ограничениями на \(n\). Вы можете делать взломы, только если обе версии задачи решены. Лесом называется неориентированный граф без циклов (не обязательно связный). Mocha и Diana — друзья из Чжицзяна, у каждой из них есть лес с вершинами, пронумерованными от \(1\) до \(n\), и они хотят добавить ребра в свои леса с выполнением следующих условий: - После добавления ребер каждый из графов остается лесом.
- Они добавляют одинаковые ребра. Это значит, что если ребро \((u, v)\) добавляется в лес Mocha, то также ребро \((u, v)\) добавляется в лес Diana, и наоборот.
Mocha и Diana хотят знать, какое максимальное количество ребер они могут добавить, и какие ребра им нужно добавлять. Выходные данные Первая строка содержит одно целое число \(h\) — максимальное количество ребер, которое можно добавить в каждый из лесов Mocha и Diana. Каждая из следующих \(h\) строк содержит два целых числа \(u\) и \(v\) (\(1 \le u, v \le n\), \(u \neq v\)) — ребра, которые нужно добавить. Если существует несколько решений, выведите любое из них. Примечание В первом примере нельзя добавить ни одно ребро. Во втором примере начальные леса выглядят следующим образом. 
Можно добавить ребро \((2, 4)\). 
| |
![]()
|
|
D2. Mocha и Diana (сложная версия)
графы
Деревья
жадные алгоритмы
Конструктив
Перебор
поиск в глубину и подобное
снм
*2500
Это сложная версия задачи. Две версии отличаются ограничениями на \(n\). Вы можете делать взломы, только если обе версии задачи решены. Лесом называется неориентированный граф без циклов (не обязательно связный). Mocha и Diana — друзья из Чжицзяна, у каждой из них есть лес с вершинами, пронумерованными от \(1\) до \(n\), и они хотят добавить ребра в свои леса с выполнением следующих условий: - После добавления ребер каждый из графов остается лесом.
- Они добавляют одинаковые ребра. Это значит, что если ребро \((u, v)\) добавляется в лес Mocha, то также ребро \((u, v)\) добавляется в лес Diana, и наоборот.
Mocha и Diana хотят знать, какое максимальное количество ребер они могут добавить, и какие ребра им нужно добавлять. Выходные данные Первая строка содержит одно целое число \(h\) — максимальное количество ребер, которое можно добавить в каждый из лесов Mocha и Diana. Каждая из следующих \(h\) строк содержит два целых числа \(u\) и \(v\) (\(1 \le u, v \le n\), \(u \neq v\)) — ребра, которые нужно добавить. Если существует несколько решений, выведите любое из них. Примечание В первом примере нельзя добавить ни одно ребро. Во втором примере начальные леса выглядят следующим образом. 
Можно добавить ребро \((2, 4)\). 
| |
![]()
|
|
E. Пересадка почек
Деревья
дп
жадные алгоритмы
Конструктив
поиск в глубину и подобное
*2000
Деревом называется связный граф без циклов. В корневом дереве есть особая вершина, которая называется корнем. Родитель вершины \(v\) (отличной от корня) — вершина перед \(v\) на кратчайшем пути от корня до \(v\). Дети вершины \(v\) — все вершины, для которых \(v\) является родителем. Вершина называется листом, если у неё нет детей. Назовем вершину почкой, если выполняются три следующих условия: - она не является корнем,
- у неё есть хотя бы один ребёнок, и
- все её дети — листья.
Вам дано корневое дерево из \(n\) вершин. Вершина \(1\) — корень. За одно действие вы можете выбрать любую почку со всеми её детьми (они являются листьями) и переподвесить её за любую другую вершину дерева. Таким действием вы удаляете ребро, соединяющее почку и родителя, и добавляете ребро между почкой и выбранной вершиной дерева. Эта выбранная вершина не может совпадать с выбранной почкой или быть одним из ее детей. Все дети почки остаются соединёнными с ней. Какое минимальное количество листьев можно получить, если разрешается сделать любое количество вышеописанных действий (возможно, ни одного)? Выходные данные Для каждого набора входных данных выведите одно число — минимальное количество листьев, которое можно получить после нескольких (возможно нуля) действий. Примечание В первом наборе входных данных дерево выглядит следующим образом:  Сначала вы можете выбрать почку \(4\) и переподвесить её за вершину \(3\). После этого вы можете выбрать почку \(2\) и переподвесить её за вершину \(7\). В результате вы получите следующее дерево с \(2\) листьями:  Можно доказать, что это минимальное количество листьев, которое можно получить. Во втором наборе входных данных дерево выглядит следующим образом:  Вы можете выбрать почку \(3\) и переподвесить её за вершину \(5\). В результате вы получите следующее дерево с \(2\) листьями:  Можно доказать, что это минимальное количество листьев, которое можно получить. | |
![]()
|
|
E. Eye-Pleasing City Park Tour
Деревья
Структуры данных
*2600
There is a city park represented as a tree with \(n\) attractions as its vertices and \(n - 1\) rails as its edges. The \(i\)-th attraction has happiness value \(a_i\). Each rail has a color. It is either black if \(t_i = 0\), or white if \(t_i = 1\). Black trains only operate on a black rail track, and white trains only operate on a white rail track. If you are previously on a black train and want to ride a white train, or you are previously on a white train and want to ride a black train, you need to use \(1\) ticket. The path of a tour must be a simple path — it must not visit an attraction more than once. You do not need a ticket the first time you board a train. You only have \(k\) tickets, meaning you can only switch train types at most \(k\) times. In particular, you do not need a ticket to go through a path consisting of one rail color. Define \(f(u, v)\) as the sum of happiness values of the attractions in the tour \((u, v)\), which is a simple path that starts at the \(u\)-th attraction and ends at the \(v\)-th attraction. Find the sum of \(f(u,v)\) for all valid tours \((u, v)\) (\(1 \leq u \leq v \leq n\)) that does not need more than \(k\) tickets, modulo \(10^9 + 7\). Output Output an integer denoting the total happiness value for all valid tours \((u, v)\) (\(1 \leq u \leq v \leq n\)), modulo \(10^9 + 7\). | |
![]()
|
|
I. Illusions of the Desert
Деревья
Структуры данных
*2300
Chanek Jones is back, helping his long-lost relative Indiana Jones, to find a secret treasure in a maze buried below a desert full of illusions. The map of the labyrinth forms a tree with \(n\) rooms numbered from \(1\) to \(n\) and \(n - 1\) tunnels connecting them such that it is possible to travel between each pair of rooms through several tunnels. The \(i\)-th room (\(1 \leq i \leq n\)) has \(a_i\) illusion rate. To go from the \(x\)-th room to the \(y\)-th room, there must exist a tunnel between \(x\) and \(y\), and it takes \(\max(|a_x + a_y|, |a_x - a_y|)\) energy. \(|z|\) denotes the absolute value of \(z\). To prevent grave robbers, the maze can change the illusion rate of any room in it. Chanek and Indiana would ask \(q\) queries. There are two types of queries to be done: - \(1\ u\ c\) — The illusion rate of the \(x\)-th room is changed to \(c\) (\(1 \leq u \leq n\), \(0 \leq |c| \leq 10^9\)).
- \(2\ u\ v\) — Chanek and Indiana ask you the minimum sum of energy needed to take the secret treasure at room \(v\) if they are initially at room \(u\) (\(1 \leq u, v \leq n\)).
Help them, so you can get a portion of the treasure! Output For each type \(2\) query, output a line containing an integer — the minimum sum of energy needed for Chanek and Indiana to take the secret treasure. Note  In the first query, their movement from the \(1\)-st to the \(2\)-nd room is as follows. - \(1 \rightarrow 5\) — takes \(\max(|10 + 4|, |10 - 4|) = 14\) energy.
- \(5 \rightarrow 6\) — takes \(\max(|4 + (-6)|, |4 - (-6)|) = 10\) energy.
- \(6 \rightarrow 2\) — takes \(\max(|-6 + (-9)|, |-6 - (-9)|) = 15\) energy.
In total, it takes \(39\) energy. In the second query, the illusion rate of the \(1\)-st room changes from \(10\) to \(-3\). In the third query, their movement from the \(1\)-st to the \(2\)-nd room is as follows. - \(1 \rightarrow 5\) — takes \(\max(|-3 + 4|, |-3 - 4|) = 7\) energy.
- \(5 \rightarrow 6\) — takes \(\max(|4 + (-6)|, |4 - (-6)|) = 10\) energy.
- \(6 \rightarrow 2\) — takes \(\max(|-6 + (-9)|, |-6 - (-9)|) = 15\) energy.
Now, it takes \(32\) energy. | |
![]()
|
|
B. Курс математики
Деревья
дп
Комбинаторика
Перебор
*2600
Пусть \(c_1, c_2, \ldots, c_n\) — перестановка чисел \(1, 2, \ldots, n\). Рассмотрим все подотрезки этой перестановки, содержащие число \(x\). Для фиксированного числа \(m\) скажем, что \(x\) хорошее, если среди максимумов на данных отрезках встречается ровно \(m\) различных значений. Cirno изучает математику, и учитель просит ее найти количество перестановок длины \(n\) с ровно \(k\) хорошими числами. К сожалению, Cirno не сильна в математике и не может ответить на этот вопрос. Поэтому она просит вас о помощи. Поскольку ответ может быть очень большим, вам нужно только сообщить ей количество перестановок по модулю \(p\). Перестановкой является массив, состоящий из \(n\) различных целых чисел от \(1\) до \(n\) в произвольном порядке. Например, \([2,3,1,5,4]\) — перестановка, но \([1,2,2]\) не перестановка (\(2\) встречается в массиве дважды) и \([1,3,4]\) тоже не перестановка (\(n=3\), но в массиве встречается \(4\)). Последовательность \(a\) является подотрезком \(b\), если \(a\) может быть получена из \(b\) удалением нескольких (возможно, ни одного или всех) элементов из начала и нескольких (возможно, ни одного или всех) элементов из конца. Выходные данные Выведите количество перестановок по модулю \(p\). Примечание В первом тестовом случае четырьмя перестановками являются \([1, 3, 2, 4]\), \([2, 3, 1, 4]\), \([4, 1, 3, 2]\) и \([4, 2, 3, 1]\). Возьмем перестановку \([1, 3, 2, 4]\) в качестве примера: Для числа \(1\) все подотрезки, содержащие его, являются: \([1]\), \([1, 3]\), \([1, 3, 2]\) и \([1, 3, 2, 4]\), и есть три разных максимума \(1\), \(3\) и \(4\). Аналогично, для числа \(3\) существуют два разных максимума \(3\) и \(4\). Для числа \(2\) существует три разных максимума \(2\), \(3\) и \(4\). А для числа \(4\) есть только один, то есть сам по себе \(4\). | |
![]()
|
|
D. Подпоследовательность
Деревья
дп
жадные алгоритмы
Перебор
разделяй и властвуй
*2900
У Алисы есть целочисленная последовательность \(a\) длины \(n\) и все ее элементы различны. Она выбирает из \(a\) подпоследовательность длины \(m\) и определяет ценность подпоследовательности \(a_{b_1},a_{b_2},\ldots,a_{b_m}\) как \(\)\sum_{i = 1}^m (m \cdot a_{b_i}) - \sum_{i = 1}^m \sum_{j = 1}^m f(\min(b_i, b_j), \max(b_i, b_j)),\(\) где \(f(i, j)\) обозначает \(\min(a_i, a_{i + 1}, \ldots, a_j)\). Алиса хочет, чтобы вы помогли ей максимизировать ценность выбираемой подпоследовательности. Последовательность \(s\) является подпоследовательностью \(t\), если \(s\) может быть получена из \(t\) удалением нескольких (возможно, ни одного или всех) элементов. Выходные данные Выведите максимальное значение, которое может получить Алиса. Примечание В первом примере Алиса может выбрать подпоследовательность \([15, 2, 18, 13]\), которая имеет ценность \(4 \cdot (15 + 2 + 18 + 13) - (15 + 2 + 2 + 2) - (2 + 2 + 2 + 2) - (2 + 2 + 18 + 12) - (2 + 2 + 12 + 13) = 100\). Во втором примере существует множество подпоследовательностей ценности \(176\), одна из них — \([9, 7, 12, 20, 18]\). | |
![]()
|
|
B. Омкар и божественное дерево
Деревья
Конструктив
*1200
Лорд Омкар хотел бы, чтобы у него было дерево с \(n\) вершинами (\(3 \le n \le 10^5\)), и попросил своих учеников построить дерево. Однако Лорд Омкар создал \(m\) (\(\mathbf{1 \le m < n}\)) ограничений, чтобы гарантировать, что дерево будет настолько божественным, насколько это возможно. Дерево на \(n\) вершинах — это связный неориентированный граф с \(n\) вершинами и \(n-1\) ребром. Заметим, что для любых двух вершин существует ровно один простой путь между ними, где простой путь — это путь между двумя вершинами, который не содержит ни одной вершины более одного раза. Вот пример дерева:  Ограничение состоит из \(3\) попарно различных целых чисел, \(a\), \(b\) и \(c\) (\(1 \le a,b,c \le n\)). Оно означает, что вершина \(b\) не может лежать на простом пути между вершинами \(a\) и \(c\). Сможете ли вы помочь Лорду Омкару и стать его самым доверенным учеником? Вам нужно будет найти божественные деревья для нескольких наборов ограничений. Можно показать, что при ограничениях задачи божественное дерево всегда найдется. Выходные данные Для каждого набора входных данных выведите \(n-1\) строку, обозначающих \(n-1\) ребро в дереве. В каждой строке выведите два целых числа \(u\) и \(v\) (\(1 \le u, v \le n\), \(u \neq v\)), обозначающие, что между вершинами \(u\) и \(v\) есть ребро. Данные ребра должны образовывать дерево, удовлетворяющее ограничениям Омкара. Примечание Вывод первого набора входных данных соответствует следующему дереву:  Для первого ограничения, простой путь между \(1\) и \(3\) — это \(1, 3\), и не содержит \(2\). Простой путь между \(3\) и \(5\) — это \(3, 5\), который не содержит \(4\). Простой путь между \(5\) и \(7\) — \(5, 3, 1, 2, 7\), который не содержит \(6\). Простой путь между \(6\) и \(4\) — \(6, 7, 2, 1, 3, 4\), который не содержит \(5\). Таким образом, это дерево удовлетворяет всем ограничениям. Вывод второго примера соответствует следующему дереву:  | |
![]()
|
|
E. Момент цветения
графы
Деревья
жадные алгоритмы
Конструктив
Паросочетания
поиск в глубину и подобное
*2200
Она делает все возможное, чтобы безупречно провести последний обряд человека и сохранить баланс инь и ян в мире. Ху Тао, будучи маленькой проказницей, попыталась напугать вас этой задачей с графом! Вам дан связный неориентированный граф из \(n\) вершин с \(m\) ребрами. У вас также есть \(q\) запросов. Каждый запрос состоит из двух вершин \(a\) и \(b\). Изначально все ребра графа имеют вес \(0\). Для каждого запроса вы должны выбрать простой путь, начинающийся из \(a\) и заканчивающийся в \(b\). Затем к весу каждого ребра вдоль этого пути добавляется \(1\). Определите, возможно ли, чтобы после обработки всех \(q\) запросов все ребра в этом графе имели четный вес. Если да, то выведите выбор путей для каждого запроса. Если это невозможно, определите наименьшее количество дополнительных запросов, которые можно добавить, чтобы это стало возможным. Можно показать, что при заданных ограничениях это число не превысит \(10^{18}\). Простой путь определяется как любой путь, который не посещает вершину более одного раза. Считается, что ребро имеет четный вес, если его значение кратно \(2\). Выходные данные Если можно заставить все веса ребер быть четными, выведите «YES» в первой строке, а затем \(2q\) строк, указывающих выбор пути для каждого запроса в том же порядке, в котором задаются запросы. Для каждого запроса первая строка должна содержать одно целое число \(x\): количество узлов в выбранном пути. Следующая строка должна содержать \(x\) целых чисел \(p_i\), указывающих выбранный путь (\(p_1 = a, p_x = b\) и все числа должны лежать между \(1\) и \(n\)). Этот путь не может содержать одну вершину более одного раза и должен быть корректным простым путем в графе. Если невозможно заставить все веса ребер быть четными, выведите «NO» в первой строке и минимальное количество запросов, которые нужно добавить, во второй строке. Примечание Вот как выглядят запросы для первого примера (красный цвет соответствует 1-му запросу, синий — 2-му, а зеленый — 3-му):  Обратите внимание, что каждое ребро в графе входит либо в \(0\), либо в \(2\) цветных пути. Граф во втором примере выглядит следующим образом:  Не существует такого назначения путей, которое заставит все ребра иметь четные веса при заданных запросах. Чтобы получить набор запросов, удовлетворяющих условию, нужно добавить по крайней мере \(2\) новых запроса. | |
![]()
|
|
H. Омкар и туры
Деревья
разделяй и властвуй
сортировки
Структуры данных
*3300
Омкар устраивает туры по своей стране, Омкарландии! В Омкарландии \(n\) городов, и, что довольно любопытно, существует ровно \(n-1\) двунаправленных дорог, соединяющих города друг с другом. Гарантируется, что вы можете добраться до любого города из любого другого города через сеть дорог. Каждый город имеет значение удовольствия \(e\). У каждой дороги есть пропускная способность \(c\), обозначающее максимальное количество автомобилей, которое может на ней находиться, и соответствующая плата за проезд \(t\). Однако система взимания платы в Омкарландии имеет интересную особенность: если автомобиль проезжает по нескольким дорогам за одну поездку, он платит только самую высокую плату за проезд по любой отдельной дороге, по которой он проехал. (Другими словами, он платит \(\max t\) по всем дорогам, по которым они проехал). Если автомобиль не проезжает ни одной дороги, он платит \(0\) за проезд. Омкар решил принять \(q\) туристических групп. Каждая туристическая группа состоит из \(v\) автомобилей, стартующих из города \(x\). (Следует помнить, что туристическая группа с \(v\) автомобилями может передвигаться только по дорогам с пропускной способностью \(\geq v\)). Будучи организатором тура, Омкар хочет, чтобы его группы получили как можно больше удовольствия, но при этом он должен возместить своим группам расходы на проезд по дорогам, которые они должны заплатить. Таким образом, для каждой туристической группы Омкар хочет знать две вещи: во-первых, какое максимальное значение удовольствия имеет город \(y\) — город с максимальным значением удовольствия среди тех, до которых туристическая группа может добраться из своего начального города, и, во-вторых, сколько Омкар должен будет заплатить с каждого автомобиля, чтобы возместить расходы всей группы на поездку из \(x\) в \(y\)? (Эта поездка из \(x\) в \(y\) всегда будет проходить по кратчайшему пути из \(x\) в \(y\)). В случае, если существует несколько городов с максимальным значением удовольствия, Омкар позволит своей туристической группе выбрать, в какой из них они хотят поехать. Поэтому, чтобы подготовиться ко всем возможным сценариям, он хочет знать сумму денег на автомобиль, которая ему необходима, чтобы гарантировать, что он сможет возместить расходы группы независимо от того, какой город они выберут. Выходные данные Выведите \(q\) строк. \(i\)-я строка должна содержать два целых числа: максимально возможное значение удовольствия города, до которого может добраться \(i\)-я туристическая группа, и количество денег на автомобиль, которое необходимо Омкару, чтобы гарантировать возмещение расходов \(i\)-й туристической группы. Примечание Карта с первого примера показана ниже. Для вершин нежирные числа представляют индексы, а жирные — значения удовольствия. Для ребер нежирные цифры обозначают пропускную способность, а жирные — стоимость проезда.  Для первого запроса туристическая группа размером \(1\), стартующая из города \(3\), может достичь городов \(1\), \(2\), \(3\), \(4\) и \(5\). Таким образом, наибольшее значение удовольствия, которого они могут достичь, равно \(3\). Если туристическая группа решит поехать в город \(4\), Омкар должен будет заплатить \(8\) за машину, что является максимумом. Для второго запроса туристическая группа размером \(9\), стартующая из города \(5\), может достичь только города \(5\). Таким образом, наибольшее достижимое значение удовольствия по-прежнему составляет \(3\), и Омкар заплатит \(0\) за автомобиль. Для третьего запроса туристическая группа размером \(6\), стартующая из города \(2\), может достичь городов \(2\) и \(4\). Наибольшее достижимое значение удовольствия снова равно \(3\). Если туристическая группа решит поехать в город \(4\), Омкар должен будет заплатить \(2\) за машину, что является максимумом. Карта второй выборки показана ниже:  Для первого запроса, туристическая группа размером \(5\), стартующая из города \(1\), может достичь только города \(1\). Таким образом, их максимальная ценность удовольствия составляет \(1\), а стоимость, которую придется заплатить Омкару, равна \(0\) за автомобиль. Для второго запроса туристическая группа размером \(4\), стартующая из города \(1\), может добраться до городов \(1\) и \(2\). Таким образом, их максимальная ценность удовольствия составляет \(2\), а Омкар заплатит \(1\) за автомобиль. Для третьего запроса, туристическая группа размером \(3\), стартующая из города \(1\), может добраться до городов \(1\), \(2\) и \(3\). Таким образом, их максимальная ценность удовольствия составляет \(3\), и Омкар заплатит \(1\) за автомобиль. Для четвертого запроса туристическая группа размером \(2\), стартующая из города \(1\), может добраться до городов \(1\), \(2\), \(3\) и \(4\). Таким образом, их максимальная ценность удовольствия составляет \(4\), и Омкар заплатит \(1\) за автомобиль. Для пятого запроса туристическая группа размером \(1\), стартующая из города \(1\), может добраться до городов \(1\), \(2\), \(3\), \(4\) и \(5\). Таким образом, их максимальное удовольствие составляет \(5\), и Омкар заплатит \(1\) за машину. | |
![]()
|
|
E. Запросы частот
Деревья
поиск в глубину и подобное
Структуры данных
*2400
У Пети есть подвешенное дерево, на вершинах которого написаны целые числа. Корень — вершина \(1\). Вам нужно ответить на некоторые вопросы про это дерево. Дерево — это связный ацикличный граф. Подвешенное дерево имеет специальную вершину — корень. Родителем вершины \(v\) называется следующая вершина на кратчайшем пути от \(v\) до корня. Каждый запрос задан тройкой целых чисел \(v\), \(l\), и \(k\). Чтобы на него ответить вы должны проделать следующие шаги: - Сначала, выпишите последовательность чисел, записанных на вершинах простого пути от \(v\) до корня (включая вершину \(v\) и сам корень).
- Посчитайте, сколько раз каждой число встречается в этой последовательности. Выкиньте из неё числа, которые встречаются меньше, чем \(l\) раз.
- Преобразуйте последовательность, удалив из неё дубликаты, и упорядочив числа в ней возрастанию количеств вхождений в изначальную последовательность. В случая совпадения таких количеств, два числа располагаются в произвольном относительном порядке.
- Ответом на запрос является число, стоящее \(k\)-м в получившейся последовательности. Важно отметить, что так как порядок определён неоднозначно, то в качестве ответа примется любое число, которое могло стоять на этой позиции. Также может получиться, что в результирующей последовательности меньше \(k\), в таком случае ответом считается \(-1\).
Например, если последовательность чисел на пути от \(v\) до корня равна \([2, 2, 1, 7, 1, 1, 4, 4, 4, 4]\), \(l = 2\) и \(k = 2\), то ответ равен \(1\). Ответьте, пожалуйста, на все вопросы про дерево. Выходные данные Для каждого из запросов, выведите ответ на него. Если ответов несколько, то выведите любой. | |
![]()
|
|
G. Браконьеры
графы
Деревья
дп
игры
*2500
Алиса и Боб — два браконьера, которые рубят лес. Лес это набор (возможно пустой) деревьев. Дерево — это связный граф без циклов. Подвешенное дерево имеет специальную вершину — корень. Родителем вершины \(v\) называется следующая вершина на кратчайшем пути от \(v\) до корня. Детьми вершины \(v\) называются вершины, для которых \(v\) является родителем. Вершина называется листом, если у неё нет детей. В этой задаче мы определим глубину вершины как количество вершин на простом пути от этой вершины до корня. Рангом дерева назовем минимальную глубину его листа. Изначально дан непустой лес подвешенных деревьев. Алиса и Боб играют в игру на этом лесе. Они ходят по очереди, Алиса ходит первой. В начале каждого хода игрок выбирает дерево из леса. Далее игрок выбирает положительное целое число — глубину разреза, которая не превосходит ранга выбранного дерева. Затем игрок удаляет из дерева все вершины, чьи глубины меньше либо равны глубине разреза. Все остальные вершины разбиваются на набор подвешенных деревьев, корнем каждого становится вершина, имевшая наименьшую глубину в дереве до разреза. Все эти деревья добавляются в лес и игра продолжается. Игрок проигрывает, если на момент начала его хода лес пуст. Определите, может ли Алиса победить, если оба игрока играют оптимально. Выходные данные Для каждого набора входных данных выведите «YES» (без кавычек), если Алиса может победить, иначе выведите «NO» (без кавычек). Вы можете выводить каждую букву в любом регистре. Примечание В первом наборе входных данных у Боба есть симметричная стратегия, поэтому Алиса выиграть не может. 
Во втором наборе Алиса может выбрать второе дерево и глубину разреза \(1\), чтобы получить лес, где уже у нее есть симметричная стратегия. 
В третьем наборе ранг единственного дерева равен \(2\), и оба возможных хода Алисы приводят к неудаче. В первом случае Боб может перейти к позиции с симметричной стратегией, а во втором сразу опустошить лес. 
В четвертом наборе все листья единственного дерева имеют одинаковую глубину, поэтому Алиса может за один ход опустошить весь лес. 
| |
![]()
|
|
C. Бакри и разделение
битмаски
графы
Деревья
дп
Конструктив
поиск в глубину и подобное
*1700
Бакри столкнулся с задачей, но поскольку ему лень ее решать, он просит вашей помощи. Вам дано дерево на \(n\) вершинах, \(i\)-й вершине присвоено значение \(a_i\) для каждого \(i\) от \(1\) до \(n\). Напомним, что дерево на \(n\) вершинах — это связный граф с \(n-1\) ребрами. Вы хотите удалить из дерева не менее \(1\), но не более \(k-1\) ребер так, чтобы выполнялось следующее условие: Возможно ли выполнить это условие? Выходные данные Для каждого набора входных данных вы должны вывести одну строку. Если вы можете удалить ребра в соответствии с условиями, написанными выше, выведите «YES» (без кавычек). В противном случае выведите «NO» (без кавычек). Вы можете вывести каждую букву «YES» и «NO» в любом регистре (верхнем или нижнем). Примечание Можно показать, что условие недостижимо для первого, третьего и пятого наборов входных данных. Во втором наборе входных данных можно просто удалить все ребра. Останется \(5\) компонент связности, каждая из которых содержит только одну вершину со значением \(3\), поэтому побитовое ИЛИ для каждой из них будет \(3\). В четвертом случае дерево изображено ниже:  . . Вы можете удалить ребро \((4,5)\). Побитовое ИЛИ первой компоненты будет равен \(a_1 \oplus a_2 \oplus a_3 \oplus a_4 = 1 \oplus 6 \oplus 4 \oplus 1 = 2\) (где \(\oplus\) обозначает побитовое ИЛИ). Побитовое ИЛИ второй компоненты будет равно \(a_5 = 2\). | |
![]()
|
|
D. Хемосе на ICPC?
Бинарный поиск
Деревья
интерактив
математика
поиск в глубину и подобное
реализация
теория чисел
*2300
Это интерактивная задача! На последнем региональном этапе Хемосе, ЗейадХаттаб и ЯхиаШериф — члены команды Carpe Diem — не прошли отбор на ICPC по каким-то неизвестным причинам. Хемосе был очень расстроен и у него был плохой день после соревнований, но ЗейадХаттаб очень мудрый и хорошо знает Хемосе, и не хочет видеть его грустным. Зейад знает, что Хемосе любит задачи с деревьями, поэтому он дал ему задачу с деревом с очень особенным устройством. У Хемоса есть взвешенное дерево на \(n\) вершинах и \(n-1\) ребрах. К сожалению, Хемосе не помнит веса ребер. Определим \(Dist(u, v)\) для \(u\neq v\) как наибольший общий делитель весов всех ребер на пути от вершины \(u\) к вершине \(v\). У Хемосе есть специальное устройство. Хемосе может дать устройству набор вершин, и устройство вернет наибольший \(Dist\) между любыми двумя вершинами из этого набора. Более формально, если Хемосе даст устройству набор из \(S\) узлов, устройство вернет наибольшее значение \(Dist(u, v)\) по всем парам \((u, v)\), для которых \(u\), \(v\) \(\in\) \(S\) и \(u \neq v\). Хемосе может использовать это устройство не более \(12\) раз, и хочет найти любые две различные вершины \(a\), \(b\) такие, что \(Dist(a, b)\) является максимально возможным. Можете ли вы ему помочь? Протокол взаимодействия Начните взаимодействие с чтения одного целого числа \(n\) (\(2 \le n \le 10^3\)) — количества вершин в дереве. Затем прочитайте \(n-1\) строк. \(i\)-я из следующих \(n-1\) строк содержит два целых числа \(u_i\) и \(v_i\) (\(1 \leq u_i, v_i \leq n\), \(u_i\neq v_i\)), что означает наличие ребра между вершинами \(u_i\) и \(v_i\). Гарантируется, что веса ребер были \(\leq 10^9\). Гарантируется, что данный граф является деревом. Теперь вы можете начать задавать запросы. Чтобы задать запрос о множестве из \(k\) вершин \(v_1, v_2, \ldots, v_k\) (\(2 \le k \le n\), \(1 \le v_i \le n\), все \(v_i\) различны), выведите: ? \(k\) \(v_1\) \(v_2\) \(\ldots\) \(v_k\). Вы получите целое число \(x\), наибольшее \(Dist(v_i, v_j)\) по \(1 \le i, j \le k\) с \(i \neq j\). Когда вы найдете \(a\) и \(b\) (\(1 \le a, b \le n)\), \(a\neq b\)) такие, что \(Dist(a, b)\) является максимально возможным, выведите ответ в следующем формате: ! \(a\) \(b\) Вывод ответа не учитывается в лимит в \(12\) запросов. Если существует несколько пар \((a, b)\) с одинаковым наибольшим \(Dist(a, b)\), можно вывести любую. После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Взломы Чтобы взломать решение, используйте следующий формат. Первая строка должна содержать одно целое число \(n\) \((2 \leq n \le 10^3)\) — количество вершин. В \(i\)-й из следующих \(n-1\) строк должно содержаться три целых числа \(u_i\), \(v_i\), \(w_i\) (\(1 \le u_i, v_i \le n\), \(u_i\ne v_i\), \(1 \le w \le 10^9\)), что означает, что между вершинами \(u_i\) и \(v_i\) есть ребро с весом \(w_i\). Эти \(n-1\) ребер должны образовывать дерево. Примечание Дерево в первом примере приведено ниже: 
| |
![]()
|
|
E. Садовник и дерево
Деревья
жадные алгоритмы
Перебор
поиск в глубину и подобное
реализация
Структуры данных
*1600
Дерево — это неориентированный связный граф, в котором отсутствуют циклы. В этой задаче речь идет о некорневых деревьях. Лист дерева — это вершина, которая соединена не более чем с одной другой вершиной. Садовник Виталий вырастил дерево из \(n\) вершин. Он решил подстричь дерево. Для этого он совершает несколько операций. За одну операцию он удаляет все листья дерева.  Пример дерева. Пример дерева. Например, рассмотрим дерево, изображённое на рисунке выше. На рисунке ниже приведён результат применения к дереву ровно одной операции.  Результат применения операции «удалить все листья». Результат применения операции «удалить все листья». Обратите внимание на особенные случаи применения операций: - применение операции к пустому дереву (из \(0\) вершин) не меняет его;
- применение операции к дереву из одной вершины приводит к удалению этой вершины (т. е. одна эта вершина считается листом);
- применение операции к дереву из двух вершин приводит к удалению обеих вершин (обе вершины считаются листьями).
Виталий применил к дереву последовательно \(k\) операций. Сколько вершин в нём осталось? Выходные данные Для каждого набора входных данных выведите в отдельной строке одно целое число — количество вершин, которое осталось в дереве после применения \(k\) операций. Примечание Первый набор входных данных разобран в условии. Во втором наборе задано дерево из двух вершин. К нему применяются \(200000\) операций. Первая удаляет обе вершины, остальные операции не изменяют дерево. В третьем наборе входных данных дано дерево из трёх вершин. В результате применения первой операции в нём остаётся всего \(1\) вершина (с номером \(2\)), в результате второй операции дерево становится пустым. | |
![]()
|
|
E2. Раскраска кубика Рубика (сложная версия)
Деревья
дп
математика
Перебор
реализация
*2300
Это сложная версия задачи. Различие состоит в том, что в этой версии есть вершины с уже зафиксированными цветами. Теофанис ужасно проголодался и хочет, наконец, отведать своего любимого блюда, шефталью. Но сначала ему нужно закончить с домашней работой. Поможете ли вы ему в решении данной задачи? Вам задано идеальное двоичное дерево из \(2^k - 1\) вершин — двоичное дерево, в котором у всех вершин \(i\) от \(1\) по \(2^{k - 1} - 1\) есть ровно два сына: вершины \(2i\) и \(2i + 1\). У вершин с \(2^{k - 1}\) по \(2^k - 1\) нет детей. Вы хотите покрасить его вершины в \(6\) цветов кубика Рубика (белый, зеленый, красный, синий, оранжевый и желтый). Назовем раскраску хорошей, если все ребра дерева соединяют вершины, цвета которых являются соседними цветами кубика Рубика. Изображение кубика Рубика и его развертка. Формально говоря: - соседними к белой вершине не могут быть белые и желтые вершины;
- соседними к желтой вершине не могут быть белые и желтые вершины;
- соседними к зеленой вершине не могут быть зеленые и синие вершины;
- соседними к синей вершине не могут быть зеленые и синие вершины;
- соседними к красной вершине не могут быть красные и оранжевые вершины;
- соседними к оранжевой вершине не могут быть красные и оранжевые вершины.
Однако, есть \(n\) особых вершин в дереве, цвета которых уже зафиксированы. Вам нужно посчитать количество хороших раскрасок двоичного дерева. Две раскраски считаются различными, если существует вершина, цвет которой в них различается. Так как ответ может быть слишком большим, выведите его по модулю \(10^9+7\). Выходные данные Выведите одно целое число — количество различных раскрасок по модулю \(10^9+7\). Примечание На изображении ниже вы можете видеть одну из корректных раскрасок для первого примера.  | |
![]()
|
|
D. Деревонумерация
битмаски
Деревья
жадные алгоритмы
игры
Конструктив
поиск в глубину и подобное
реализация
*2100
Eikooc и Sushi играют в игру. Игра проводится на дереве из \(n\) вершин, пронумерованных от \(1\) до \(n\). Напомним, что дерево с \(n\) вершинами это неориентированный связный граф с \(n-1\) ребрами. Игроки поочередно перемещают фишку по дереву. Eikooc делает первый ход, помещая фишку на любую вершину по своему выбору. Sushi делает следующий ход, затем Eikooc, затем Sushi, и так далее. В каждый ход после первого, игрок должен переместить фишку в какую-то вершину \(u\) такую, что: - Между вершинами \(u\) и \(v\) (на которой фишка находится данный момент), есть ребро
- \(u\) не была посещена ранее
- \(u \oplus v \leq min(u, v)\)
Здесь \(x \oplus y\) обозначает операцию побитового исключающего ИЛИ чисел \(x\) и \(y\). Оба игрока играют оптимально. Игрок, который не может сделать ход, проигрывает. Ниже приведены примеры, демонстрирующие правила игры.  Предположим, Eikooc начинает игру, помещая фишку в вершину \(4\). Затем Sushi перемещает фишку в вершину \(6\), которая не была посещена и является соседней к \(4\). Также \(6 \oplus 4 = 2 \leq min(6, 4)\). На следующем ходу Eikooc перемещает фишку в вершину \(5\), которая не была посещена и является соседней к \(6\). Также, \(5 \oplus 6 = 3 \leq min(5, 6)\). У Sushi больше нет ходов для игры, поэтому она проигрывает. Предположим, Eikooc начинает игру, помещая фишку в вершину \(4\). Затем Sushi перемещает фишку в вершину \(6\), которая не была посещена и является соседней к \(4\). Также \(6 \oplus 4 = 2 \leq min(6, 4)\). На следующем ходу Eikooc перемещает фишку в вершину \(5\), которая не была посещена и является соседней к \(6\). Также, \(5 \oplus 6 = 3 \leq min(5, 6)\). У Sushi больше нет ходов для игры, поэтому она проигрывает. |  Предположим, Eikooc начинает игру, помещая фишку в вершинул \(3\). Sushi перемещает фишку в вершину \(2\), которая не была посещена и является соседней к \(3\). Также \(3 \oplus 2 = 1 \leq min(3, 2)\). Eikooc не может переместить фишку в вершину \(6\), так как \(6 \oplus 2 = 4 \nleq min(6, 2)\). Поскольку у Eikooc нет ходов для игры, она проигрывает. Предположим, Eikooc начинает игру, помещая фишку в вершинул \(3\). Sushi перемещает фишку в вершину \(2\), которая не была посещена и является соседней к \(3\). Также \(3 \oplus 2 = 1 \leq min(3, 2)\). Eikooc не может переместить фишку в вершину \(6\), так как \(6 \oplus 2 = 4 \nleq min(6, 2)\). Поскольку у Eikooc нет ходов для игры, она проигрывает. |
Перед началом игры Eikooc решает тайком перенумеровать вершины дерева в свою пользу. Формально, перенумерация — это перестановка \(p\) длины \(n\) (последовательность из \(n\) целых чисел, где каждое целое число от \(1\) до \(n\) встречается ровно один раз), где \(p_i\) обозначает новый номер вершины \(i\). Она хочет максимизировать количество вершин, которые она может выбрать в первый ход, для которых она сможет гарантировать себе победу. Помогите Eikooc найти любую перенумерацию, которая поможет ей в этом. Выходные данные Для каждого набора входных данных выведите любую подходящую перестановку — перестановку длины \(n\), которая максимизирует количество вершин, которые Eikooc может выбрать в первый ход и иметь выиграшную стратегию. Если таких перестановок несколько, вы можете вывести любую из них. Примечание В первом наборе входных данных у Eikooc есть только одна вершина. У Sushi не будет ходов после того, как Eikooc выберет эту вершину, и Eikooc выиграет. Во втором наборе входных данных \(1 \oplus 2 = 3 \nleq min(1, 2)\). Следовательно, после того, как Eikooc выберет любую из вершин, у Sushi не останется ходов, и Eikooc выиграет. И \(\{1, 2\}\), и \(\{2, 1\}\) являются допустимыми перенумерациями. | |
![]()
|
|
F. Древесные запросы
Деревья
дп
Перебор
*2800
Дано дерево, состоящее из \(n\) вершин. Напомним, что дерево — это неориентированный ацикличный граф. Корнем данного дерева является вершина \(1\). Требуется обработать \(q\) запросов. В каждом запросе задается вершина дерева \(v\) и целое число \(k\). Для обработки запроса можно удалять вершины из дерева в произвольном порядке, кроме корня и вершины \(v\). Когда вершина удаляется, ее дети становятся детьми ее родителя. Требуется обработать запрос так, чтобы максимизировать значение \(c(v) - m \cdot k\) (где \(c(v)\) — это итоговое количество детей вершины \(v\), а \(m\) — это количество удаленных вершин). Выведите максимальное значение, которое можно получить. Запросы независимые: изменения, произведенные над деревом при обработке запроса, не затрагивают другие запросы. Выходные данные На каждый запрос выведите одно целое число — максимальное значение \(c(v) - m \cdot k\), которое можно получить. Примечание Дерево в первом примере показано на следующем изображении:  Ответы на запросы получаются следующим образом: - \(v=1,k=0\): можно удалить вершины \(7\) и \(3\), так, чтобы у вершины \(1\) стало \(5\) детей (вершины \(2\), \(4\), \(5\), \(6\) и \(8\)), и счет равен \(5 - 2 \cdot 0 = 5\);
- \(v=1,k=2\): можно удалить вершину \(7\), так, чтобы у вершины \(1\) стало \(4\) ребенка (вершины \(3\), \(4\), \(5\) и \(6\)), и счет равен \(4 - 1 \cdot 2 = 2\).
- \(v=1,k=3\): не надо удалять вершины; тогда у вершины \(1\) станет один ребенок (вершина \(7\)), и счет равен \(1 - 0 \cdot 3 = 1\);
- \(v=7,k=1\): можно удалить вершину \(3\), так, чтобы у вершины \(7\) стало \(5\) детей (вершины \(2\), \(4\), \(5\), \(6\) и \(8\)), и счет равен \(5 - 1 \cdot 1 = 4\);
- \(v=5,k=0\): что бы вы ни делали, у вершины \(5\) не будет детей, поэтому счет равен \(0\);
- \(v=7,k=200000\): не надо удалять вершины; тогда у вершины \(7\) станет \(4\) ребенка (вершины \(3\), \(4\), \(5\) и \(6\)), и счет равен \(4 - 0 \cdot 200000 = 4\).
| |
![]()
|
|
G. Алфавитное дерево
Бинарный поиск
Деревья
поиск в глубину и подобное
Строки
строковые суфф. структуры
Структуры данных
хэши
*3500
Вам даны \(m\) строк и дерево на \(n\) вершинах. На каждом ребре написана какая-то буква. Вы должны ответить на \(q\) запросов. Каждый запрос описывается \(4\) целыми числами \(u\), \(v\), \(l\) и \(r\). Ответом на запрос является общее количество вхождений \(str(u,v)\) в строки с индексами от \(l\) до \(r\). \(str(u,v)\) определяется как строка, составленная путем конкатенации букв, записанных на ребрах кратчайшего пути от \(u\) до \(v\) (в порядке их прохождения). Выходные данные Для каждого запроса выведите одно целое число — ответ на запрос. | |
![]()
|
|
D. Социальная сеть
графы
Деревья
жадные алгоритмы
реализация
снм
*1600
 Василий приехал на посвященную криптовалютам конференцию. Для того, чтобы быть в курсе всех самых важных новостей из мира криптовалют, нужно постоянно заводить новые знакомства или пользоваться знакомствами своих друзей. В конференции участвует \(n\) человек, которые изначально не знакомы между собой. Василий может познакомить двух любых людей \(a\) и \(b\), которые не были знакомы до этого. У Василия есть \(d\) условий, \(i\)-е из которых требует, чтобы человек \(x_i\) имел связь с человеком \(y_i\). Формально два человека \(x\) и \(y\) имеют связь, если найдется цепочка \(p_1=x, p_2, p_3, \dots, p_k=y\) такая, что для всех \(i\) от \(1\) до \(k - 1\) известно, что люди под номерами \(p_i\) и \(p_{i + 1}\) знакомы. Василий хочет, чтобы для каждого \(i\) (\(1 \le i \le d\)) вы рассчитали, какое максимальное количество знакомств может иметь один человек при условии, что Василий выполнил все условия от \(1\) до \(i\) включительно, произведя при этом ровно \(i\) знакомств. Проверка условий происходит после того, как Василий провел \(i\) знакомств. Ответ для каждого \(i\) необходимо найти независимо. То есть, когда вы вычисляете ответ для \(i\), вы должны считать, что никто из людей еще не был знаком. Выходные данные Выведите \(d\) целых чисел. \(i\)-е число должно быть равно количеству знакомств у человека с наибольшим возможным количеством знакомств, если Василий провел \(i\) знакомств и выполнил первые \(i\) условий. Примечание Пояснение для первого тестового примера: В этом пояснении круг и вписанное число обозначают человека с соответствующим номером. Линии, соединяющие людей, обозначают то, что эти люди знакомы между собой. Человек, отмеченный красным цветом, имеет наибольшее количество знакомых. Данные способы познакомить людей не являются единственными правильными.  | |
![]()
|
|
D. Расстояние в дереве
Деревья
дп
поиск в глубину и подобное
*1800
Деревом называется связный граф, не содержащий циклов. Расстоянием между двумя вершинами дерева называется длина (в ребрах) кратчайшего пути между этими вершинами. Дано дерево из n вершин и положительное число k. Посчитайте количество различных пар вершин дерева, расстояние между которыми равно k. Обратите внимание, что пары (v, u) и (u, v) считаются одной и той же парой. Выходные данные Выведите единственное целое число — количество различных пар вершин дерева, расстояние между которыми равно k. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-х битовых чисел на С++. Рекомендуется использовать потоки cin, cout или спецификатор %I64d. Примечание В первом примере парами вершин, расстояние между которыми равно 2, будут пары (1, 3), (1, 5), (3, 5) и (2, 4). | |
![]()
|
|
H. Игра в кальмара
Деревья
жадные алгоритмы
поиск в глубину и подобное
Структуры данных
*3100
После просмотра нового сериала «Игра в кальмара» Маштали и Соруш решили провести свою собственную «Игру в кальмара»! Соруш согласился быть ведущим и предоставить деньги для приза победителю, а Маштали стал фронтменом! \(m\) игроков зарегистрировались для участия в играх, чтобы выиграть большой приз, но когда Маштали узнал, каким огромным будет приз победителя, он решил убить устранить всех игроков, чтобы забрать деньги себе! Вот как злой Маштали собирается уничтожить игроков: Дано некорневое дерево с \(n\) вершинами. У каждого игрока есть \(2\) специальные вершины \(x_i\) и \(y_i\). За одну операцию Маштали может выбрать любую вершину \(v\) дерева. Затем для каждого оставшегося игрока \(i\) он находит вершину \(w\) на простом пути из \(x_i\) в \(y_i\), которая ближе всего к \(v\). Если \(w\ne x_i\) и \(w\ne y_i\), игрок \(i\) будет устранен. Теперь Маштали задался вопросом: «Какое минимальное количество операций я должен выполнить, чтобы устранить всех игроков и забрать деньги себе?». Поскольку он думал только о деньгах, он не смог решить задачу самостоятельно и обратился к вам за помощью! Выходные данные Выведите минимальное количество операций, которые Маштали должен выполнить. Если Маштали никак не может устранить всех игроков, выведите \(-1\). Примечание Пояснение к первому примеру:  В первую операцию, Маштали может выбрать вершину \(1\) и устранить игроков с красным и синим цветами. Во второй операции он может выбрать вершину \(6\) и устранить игрока с оранжевым цветом. В первую операцию, Маштали может выбрать вершину \(1\) и устранить игроков с красным и синим цветами. Во второй операции он может выбрать вершину \(6\) и устранить игрока с оранжевым цветом. Во втором примере Маштали не сможет устранить первого игрока. | |
![]()
|
|
I. Маштали против AtCoder
Деревья
игры
*3100
После многих неудачных попыток, Маштали решил скопировать модифицировать задачу с AtCoder. Итак, вот его скопированная новая задача: Дано дерево на \(n\) вершинах, и некоторое непустое множество вершин прибито к земле. Два игрока играют друг против друга на дереве. Они поочередно выполняют следующее действие: Вам дано дерево, но не дано множество прибитых вершин. Ваша задача — определить для каждого \(k\) победителя игры, если прибиты только вершины \(1, 2, 3, \ldots, k\), и оба игрока играют оптимально. Выходные данные Выведите строку длиной \(n\). \(i\)-й символ должен быть '1', если первый игрок выиграл \(i\)-й сценарий, и '2' в противном случае. Примечание Ниже вы можете увидеть дерево с первого примера:  Если \(k = 1\), то первый игрок может разрезать ребро \((1, 2)\). Если \(k = 2\) или \(k = 3\), то первый игрок может перерезать ребро \((2, 4)\), после чего останутся только ребра \((1, 2)\) и \((2, 3)\). После хода второго игрока у первого игрока останется только одно ребро для разрезания. Поэтому первый игрок выигрывает. | |
![]()
|
|
D. Расстановка весов ребер корневого дерева
Деревья
Конструктив
*1500
Вам задано корневое дерево из \(n\) вершин. Вершины пронумерованы от \(1\) до \(n\). Корнем может быть любая из вершин. Дерево — это связный неориентированный граф без циклов. Корневое дерево — дерево с выделенной вершиной, которую называют корнем. Дерево задано массивом предков \(b\), содержащим \(n\) чисeл: \(b_i\) — предок вершины с номером \(i\). Предком вершины \(u\) называется такая вершина, которая является следующей вершиной на простом пути от \(u\) к корню. Например, на простом пути из \(5\) в \(3\) (корень), следующая вершина будет \(1\), таким образом, предком вершины \(5\) является вершина \(1\). У корня предка нет, для него в качестве \(b_i\) используется значение \(i\) (таким образом, корень — единственная вершина, для которой \(b_i=i\)). Например, если \(n=5\) и \(b=[3, 1, 3, 3, 1]\), то дерево выглядит следующим образом.  Пример корневого дерева для \(n=5\), корень дерева — вершина \(3\). Пример корневого дерева для \(n=5\), корень дерева — вершина \(3\). Задан массив \(p\) — перестановка вершин дерева. Если это возможно, расставьте целочисленные положительные веса на всех ребрах данного дерева так, чтобы вершины, отсортированные по увеличению расстояния от корня, образовывали заданную перестановку \(p\). Иными словами, по заданной перестановке вершин \(p\) необходимо подобрать такие положительные веса рёбер, чтобы выполнялось неравенство \(dist[p_i]<dist[p_{i+1}]\) для всех \(i\) от \(1\) до \(n-1\), где \(dist[u]\) — сумма весов рёбер на пути от корня до \(u\). В частности, \(dist[u]=0\), если вершина \(u\) является корнем дерева. Например, пусть \(p=[3, 1, 2, 5, 4]\). В этом случае следующие веса ребер удовлетворяют этой перестановке: - ребро (\(3, 4\)) имеет вес \(102\);
- ребро (\(3, 1\)) имеет вес \(1\);
- ребро (\(1, 2\)) имеет вес \(10\);
- ребро (\(1, 5\)) имеет вес \(100\).
В этом случае массив расстояний от корня имеет вид: \(dist=[1,11,0,102,101]\). Если вершины отсортировать по возрастанию расстояний, то получится заданная перестановка \(p\). Выведите искомые веса рёбер или определите, что подходящего способа назначить веса не существует. Если решений несколько, то выведите любое из них. Выходные данные Для каждого набора входных данных выведите ответ на отдельной строке. Если решение существует, то выведите массив из \(n\) целых чисел \(w_1, w_2, \dots, w_n\), где \(w_i\) — вес ребра, которое ведёт из \(b_i\) в \(i\). Для корня такого ребра не существует, поэтому используйте значение \(w_i=0\). Для всех остальных вершин значения \(w_i\) должны удовлетворять неравенству \(1 \le w_i \le 10^9\). Среди значений \(w_i\) могут быть равные числа, но все суммы весов ребер от корня до вершин должны быть различны и удовлетворять заданной перестановке. Если решений несколько, выведите любое из них. Если решения не существует, то выведите -1. Примечание Первый набор входных данных примера разобран в основной части условия. Во втором наборе входных данных примера невозможно расставить целочисленные положительные веса так, чтобы получить заданную перестановку вершин. | |
![]()
|
|
E1. Побег из лабиринта (простая версия)
Деревья
жадные алгоритмы
кратчайшие пути
поиск в глубину и подобное
*1700
Эта задача отличается от E2 только поставленным вопросом. Влад построил лабиринт из \(n\) комнат и \(n-1\) двунаправленного коридора. Из любой комнаты \(u\) по коридорам достижима любая другая комната \(v\). Таким образом, система комнат образует неориентированное дерево. Влад собрал \(k\) друзей, чтобы сыграть с ними в игру. Влад начинает игру в комнате с номером \(1\) и выигрывает, если доходит до комнаты, отличной от \(1\), в которую ведёт ровно один коридор. Друзья же расставлены по лабиринту — друг с номером \(i\) стоит в комнате \(x_i\), и никакие два друга не стоят в одной комнате (то есть \(x_i \neq x_j\) для всех \(i \neq j\)). Друзья выигрывают, если одному удаётся встретиться с Владом в какой-либо комнате или коридоре, до того как он выиграет. За одну единицу времени каждый участник игры может пройти по одному коридору. Все участники ходят одновременно. Участники также могут не двигаться. Каждая комната может вместить всех участников одновременно. Друзья досконально изучили план и намерены выиграть. Влад в некотором замешательстве от их азарта. Определите, может ли он обеспечить себе победу (то есть победить при любом способе игры друзей)? Иными словами, определите, существует ли такая последовательность ходов Влада, что при любом способе игры друзей Влад победит. Выходные данные Выведите \(t\) строк, каждая из которых содержит ответ на соответствующий набор входных данных. В качестве ответа выведите «YES», если Влад может гарантировать себе победу, и «NO» в противном случае. Вы можете выводить ответ в любом регистре (например, строки «yEs», «yes», «Yes» и «YES» будут распознаны как положительный ответ). Примечание В первом наборе входных данных независимо от стратегии друзей Влад может выиграть, пройдя до комнаты \(4\). Игра при этом может выглядеть следующим образом:  Изначальное расположение Влада и друзей. Влад помечен зелёным цветом, друзья — красным. Изначальное расположение Влада и друзей. Влад помечен зелёным цветом, друзья — красным.  Расположение по прошествии одной единицы времени. Расположение по прошествии одной единицы времени.  Конец игры. Конец игры. Заметим, что если Влад попробует дойти до выхода в вершине \(8\), то друг из комнаты \(3\) сможет его поймать. | |
![]()
|
|
E2. Побег из лабиринта (сложная версия)
Деревья
дп
жадные алгоритмы
кратчайшие пути
поиск в глубину и подобное
*1900
Эта задача отличается от E1 только поставленным вопросом. Влад построил лабиринт из \(n\) комнат и \(n-1\) двунаправленного коридора. Из любой комнаты \(u\) по коридорам достижима любая другая комната \(v\). Таким образом, система комнат образует неориентированное дерево. Влад собрал \(k\) друзей, чтобы сыграть с ними в игру. Влад начинает игру в комнате с номером \(1\) и выигрывает, если доходит до комнаты, отличной от \(1\), в которую ведёт ровно один коридор. Друзья же расставлены по лабиринту — друг с номером \(i\) стоит в комнате \(x_i\), и никакие два друга не стоят в одной комнате (то есть \(x_i \neq x_j\) для всех \(i \neq j\)). Друзья выигрывают, если одному удаётся встретиться с Владом в какой-либо комнате или коридоре, до того как он выиграет. За одну единицу времени каждый участник игры может пройти по одному коридору. Все участники ходят одновременно. Участники также могут не двигаться. Каждая комната может вместить всех участников одновременно. Друзья досконально изучили план и намерены выиграть. Также они не хотят зря тратить силы и просят вас определить, могут ли они выиграть и, если могут, какое минимальное количество друзей должно остаться в лабиринте, чтобы они всегда могли поймать Влада. Иными словами вам нужно определить размер минимального подмножества друзей, который сможет переиграть Влада или сказать что такого подмножества не существует. Выходные данные Выведите \(t\) строк, каждая из которых содержит ответ на соответствующий набор входных данных. В качестве ответа выведите \(-1\), если Влад в любом случае победит, и минимальное необходимое число друзей иначе. Примечание В первом наборе входных данных даже если все друзья останутся в лабиринте, Влад всё равно сможет выиграть. Поэтому ответ «-1». Во втором наборе входных данных достаточно оставить друзей из комнат \(6\) и \(7\). Тогда Влад не сможет выиграть. Ответ «2». Во третьем и четвертом наборах входных данных Влад не сможет выиграть только если все его друзья останутся в лабиринте. Поэтому ответы соответственно «1» и «2». | |
![]()
|
|
D. (XO)R-ождественское дерево
битмаски
графы
Деревья
поиск в глубину и подобное
снм
*2200
Это была ночь перед рождеством, и пришло время Санте украсить свое Рождественское дерево. Это дерево состоит из \(n\) вершин, соединенных \(n-1\) ребром. На каждом ребре дерева расположена гирлянда, которую можно описать некоторым числом в двоичном представлении.  Посмотреть на это дерево собралось \(m\) эльфов. Каждый эльф выбрал две вершины \(a\) и \(b\), и он смотрит только на гирлянды на простом пути между этими вершинами. В результате созерцания у эльфа появляется любимое число, равное побитовому исключающему ИЛИ значений на ребрах этого пути. Однако, Северный Полюс только начал восстанавливаться после недавней эпидемии ОРВИ. Из-за этого Санта успел забыть, как выглядели некоторые гирлянды, и проверить их он не может, потому что уже покинул Северный Полюс! К счастью, на помощь пришли эльфы: каждый из них сообщил Санте свою пару вершин \((a_i, b_i)\), и четность количества единичных битов в своем любимом числе. Другими словами, каждый эльф помнит, было ли количество \(1\)-ц в его любимом числе, записанном в двоичном виде, четным или нечетным. Помогите Санте проверить, могло ли существовать такое дерево, и если да, как оно могло выглядеть, и возможно вы войдете в историю! Выходные данные Для каждого набора входных данных, сначала выведите YES или NO (в любом регистре), в зависимости от того, существует ли дерево, соответствующее памяти Санты, или нет. Если ответ YES, выведите \(n-1\) строк по три целых числа в каждом: \(x\), \(y\) и \(v\) (\(1 \le x, y \le n\); \(0 \le v < 2^{30}\)) — ребро дерева и число, описывающее состояние гирлянды на нем. Множество ребер должно совпадать с множеством из входных данных, и если состояние гирлянды на ребре известно, то оно не должно измениться. Вы можете выводить ребра в любом порядке. Если существует несколько решений, выведите любое. Примечание Первый набор входных данных соответствует изображению из условия. Один из возможных ответов — это присвоить ребру \((1, 2)\) значение \(5\), а ребру \((2, 5)\) — значение \(3\). Этот способ подходит потому что: - Первый эльф рассматривает путь между вершинами \(2\) и \(3\). Его любимое число будет равно \(4\), а потому он помнит значение \(1\) (так как в двоичном представлении \(4\) нечетное количество битов \(1\)).
- Второй эльф рассматривает путь между вершинами \(2\) и \(5\). Его любимое число будет равно \(3\), а потому он помнит значение \(0\) (так как в двоичном представлении \(3\) четное количество битов \(1\)).
- Третий эльф рассматривает путь между вершинами \(5\) и \(6\). Его любимое число будет равно \(7\), а потому он помнит значение \(1\) (так как в двоичном представлении \(7\) нечетное количество битов \(1\)).
- Четвертый эльф рассматривает путь между вершинами \(6\) и \(1\). Его любимое число будет равно \(1\), а потому он помнит значение \(1\) (так как в двоичном представлении \(1\) нечетное количество битов \(1\)).
- Пятый эльф рассматривает путь между вершинами \(4\) и \(5\). Его любимое число будет равно \(4\), а потому он помнит значение \(1\) (так как в двоичном представлении \(4\) нечетное количество битов \(1\)).
Заметим, что существуют и другие возможные ответы. | |
![]()
|
|
E. Фиолетовый мелок
графы
Деревья
жадные алгоритмы
игры
математика
поиск в глубину и подобное
сортировки
Структуры данных
*2400
Два игрока, Красный и Синий, снова в деле, и этот раз они играют с цветными мелками! Сегодня озорной паре под руку попалось корневое дерево, с которым они играют в свою любимую игру, раскрашивая вершины этого дерева. Игра выглядит следующим образом: есть дерево из \(n\) вершин с корнем в вершине \(1\), и каждая вершина первоначально белого цвета. У Красного и Синего есть ровно по одному ходу. Первым ходит Красный. В свой ход, Красный может выполнить следующее действие произвольное количество раз: - Он выбирает любое поддерево корневого дерева и красит каждую из вершин поддерева в красный.
Однако, для большей честности, Красный может покрасить только \(k\) вершин дерева. Другими словами, после окончания хода Красного, не более \(k\) вершин может быть покрашено в красный. Далее подходит очередь Синего. Он может выполнять следующее действие произвольное количество раз: - Он выбирает любое поддерево корневого дерева и красит каждую вершину поддерева в синий. Однако, ему нельзя выбирать поддеревья, в которых содержатся вершины, уже покрашенные в красный. Ведь в таком случае вершина получится фиолетового цвета, а никто не любит фиолетовый мелок* (англ. purple crayon).
Заметим, что нет ограничения на то, сколько вершин покрасит Синий, главное, что он не красит уже покрашенные Красным вершины. После того как каждый сделает свой ход, счет игры определяется следующим образом: пусть \(w\) — количество оставшихся белых вершин, \(r\) — количество красных вершин, а \(b\) — количество синих вершин. Счет игры будет равен \(w \cdot (r - b)\). Красный хочет максимизировать счет, а Синий — минимизировать. Чему будет равен счет игры, если оба игрока действуют оптимально? Выходные данные Выведите одно число — итоговый счет игры, если и Красный и Синий действуют оптимально. Примечание В первом наборе входных данных, одна из оптимальных стратегий следующая: - Красный выбирает для покраски поддеревья вершин \(2\) и \(3\).
- Синий выбирает для покраски поддерево вершины \(4\).
В результате вершины \(2\) и \(3\) покрашены в красный, \(4\) — в синий, а вершина \(1\) — в белый. Счет игры равен \(1 \cdot (2 - 1) = 1\). Во втором наборе, оптимальная стратегия следующая: - Красный выбирает для покраски поддерево вершины \(4\). Тем самым красит вершины \(4\) и \(5\).
- Синий не может ничего выбрать, а потому ничего не красит.
В результате вершины \(4\) и \(5\) покрашены в красный, а вершины \(1\), \(2\) и \(3\) — белые. Счет игры равен \(3 \cdot (2 - 0) = 6\). В третьем наборе:  Счет игры равен \(4 \cdot (2 - 1) = 4\). | |
![]()
|
|
E. Новогодние конфеты
графы
Деревья
дп
игры
кратчайшие пути
математика
поиск в глубину и подобное
реализация
теория чисел
*2700
Лунный Новый год приближается, и Льдинка только что получила коробку конфет от бабушки с дедушкой! Коробка содержит \(n\) конфет. \(i\)-я конфета имеет вкус \(a_i\). Льдинка верит, что хорошие вещи случаются парами. К сожалению, вкусы всех конфет попарно различны (все \(a_i\) различны). Льдинка хочет сделать равные вкусы хотя бы у одной пары конфет. Поэтому она попросила бабушку с дедушкой выполнить несколько замен. Перед выполнением замен Льдинка выбирает две конфеты с номерами \(x\) и \(y\) (\(1 \le x, y \le n\), \(x \ne y\)). За одну замену дедушка и бабушка Льдинки выбирают неотрицательное целое число \(k\) такое, что \(2^k \ge a_x\), и заменяют вкус \(x\)-й конфеты с \(a_x\) на \(2^k - a_x\) (то есть, присваивают \(a_x := 2^k - a_x\)). Замены прекратятся только при условии, что \(a_x = a_y\). Заметьте, что другие пары равных по вкусу конфет не остановят процесс. У Льдинки умные бабушка и дедушка, поэтому они выберут такую последовательность замен, которая минимизирует количество требуемых замен. Поскольку Льдинка любит доставлять неприятности, она хочет максимизировать минимальное требуемое количество замен, выбрав соответствующие \(x\) и \(y\). Она задаётся вопросом, как выбрать такую пару \((x, y)\), что минимальное требуемое количество замен максимально среди всех возможных пар \((x, y)\). Так как у Льдинки не очень хорошо с математикой, она надеется, что вы поможете ей решить эту задачу. Выходные данные Выведите три целых числа \(x\), \(y\) и \(m\). \(x\) и \(y\) являются номерами оптимальных конфет для применения замен. Ваш ответ должен удовлетворять \(1 \le x, y \le n\), \(x \ne y\). \(m\) является минимальным количеством замен, чтобы сделать \(a_x = a_y\). Можно показать, что \(m \le 10^9\) для любой пары конфет. Примечание В первом тесте минимальное количество замен, требуемое, чтобы заменить конфету со вкусом \(6\) на конфету со вкусом \(9\), является \(5\). Последовательность замен следующая: \(6 \rightarrow 2 \rightarrow 0 \rightarrow 1 \rightarrow 7 \rightarrow 9\). Во втором тесте минимальное количество замен, требуемое, чтобы заменить конфету со вкусом \(4\) на конфету со вкусом \(8\), является \(2\). Последовательность замен следующая: \(4 \rightarrow 0 \rightarrow 8\). | |
![]()
|
|
H. Поезда и самолёты
графы
Деревья
кратчайшие пути
поиск в глубину и подобное
*3500
Транспортная сеть одного крупного города состоит из \(n\) станций, соединённых \(n-1\) перегонами, и представляет собой дерево. Станция с номером \(1\) является центром города. Для каждого перегона известно время в минутах, за которое его преодолевают поезда. Временем остановки поездов на станциях можно пренебречь. Обозначим за \(dist(v)\) время, за которое можно доехать от станции \(v\) до станции \(1\). Эта транспортная сеть разделена на зоны, для обозначения которых используются первые \(k\) заглавных латинских букв. Зона станции \(i\) обозначается как \(z_i\). Центр города находится в зоне A. Для всех остальных станций выполнено, что ближайшая в направлении центра города станция находится в зоне с таким же, или лексикографически меньшим, обозначением. Любой перегон полностью принадлежит зоне его конца, более удалённого от центра города. Турист летит в этот город на самолёте и по прибытии в аэропорт сразу направится в центр города. Опишем подробнее, как происходит поездка от станции \(v\) до станции \(1\): - В момент времени \(0\) турист садится на поезд, который едет от станции \(v\) до станции \(1\) по кратчайшему пути. Поездка займёт \(dist(v)\) минут.
- В любой момент турист может купить билеты для любого подмножества зон. Билет для зоны \(i\) стоит \(pass_i\) евро.
- Каждые \(T\) минут с момента посадки на поезд (то есть в моменты \(T, 2T, \ldots\)) его будет сканировать система контроля безбилетного проезда. Если туриста сканировали в зоне \(i\) без билета для зоны \(i\), он будет обязан заплатить штраф \(fine_i\) евро. Зона в которой находится турист формально определяется следующим образом:
- Если турист находится на станции \(1\), то он уже доехал до центра города и не должен платить штраф.
- Если турист находится на станции \(u \neq 1\), то он находится в зоне \(z_u\).
- Если турист едет по перегону от станции \(x\) к станции \(y\), то он находится в зоне \(z_x\).
Обратите внимание, что турист может заплатить штраф в одной зоне несколько раз. Турист всегда выберет такой способ оплаты проезда, который минимизирует количество потраченных евро. Для станции \(v\) обозначим это число за \(f(v)\). К сожалению, турист не знает, чему равны текущие \(pass_i\) и \(fine_i\) для разных зон, а также не помнит, около какой станции находится аэропорт прибытия. Он будут делать разные предположения, а Вам предстоит обработать запросы \(3\) видов: - \(1\) \(i\) \(c\) — запрос изменения стоимости билета в зоне \(i\). Теперь \(pass_i\) равно \(c\).
- \(2\) \(i\) \(c\) — запрос изменения штрафа в зоне \(i\). Теперь \(fine_i\) равно \(c\).
- \(3\) \(u\) — решите следующую задачу для текущих значений \(pass\) и \(fine\):
- Дана станция \(u\). Рассмотрим множество станций \(v\), удовлетворяющих двум следующим условиям:
- \(z_v = z_u\).
- Станция \(u\) находится на пути от станции \(v\) до станции \(1\).
Найдите значение \(\min(f(v))\) по всем станциям \(v\) из этого множества, в предположении, что у туриста есть билет в зоне \(z_u\). Входные данные В первой строке дано число \(n\) (\(2 \leq n \leq 2 \cdot 10^5\)) — количество станций в транспортной сети. Следующие \(n - 1\) строка содержат по три числа \(v_i\), \(u_i\), \(t_i\) (\(1 \leq v_i, u_i \leq n, 1 \leq t_i \leq 10^9\)) — концы \(i\) перегона и время, за которое его преодолевают поезда. Гарантируется, что данные перегоны образуют дерево. Следующая строка содержит число \(k\) (\(1 \leq k \leq 26\)) — количество зон транспортной сети. Следующая строка содержит \(n\) символов \(z_1z_2 \ldots z_n\) — где \(z_i\) это обозначение зоны, в которой находится \(i\) станция. Гарантируется, что условия из второго абзаца выполняются. Следующая строка содержит \(k\) чисел \(pass_1\), \(pass_2\), \(\ldots\), \(pass_k\) (\(1 \leq pass_i \leq 10^9\)) — изначальные стоимости билетов. Следующая строка содержит \(k\) чисел \(fine_1\), \(fine_2\), \(\ldots\), \(fine_k\) (\(1 \leq fine_i \leq 10^9\)) — изначальные размеры штрафов. Следующая строка содержит число \(T\) (\(1 \leq T \leq 10^9\)) — частоту сканирования туриста системой контроля безбилетного проезда. Следующая строка содержит число \(q\) (\(1 \leq q \leq 2 \cdot 10^5\)) — количество запросов. Следующие \(q\) строк содержат запросы в описанном в условии формате. Гарантируется, что в запросах первого и второго вида \(i\) является корректным обозначением зоны (одной из первых \(k\) заглавных латинских букв) и \(1 \leq c \leq 10^9\), а в запросах третьего вида \(1 \leq u \leq n\). Выходные данные Для каждого запроса третьего вида выведите ответ на него в отдельной строке. Примечание Обратите внимание, что штраф может быть дешевле билета.  Транспортная сеть из примера. Зелёным обозначены станции и перегоны, находящиеся в зоне A, синим — в зоне B, красным — в зоне D. Около каждого перегона указано время, за которое его преодолевают поезда. Транспортная сеть из примера. Зелёным обозначены станции и перегоны, находящиеся в зоне A, синим — в зоне B, красным — в зоне D. Около каждого перегона указано время, за которое его преодолевают поезда. В первом запросе аэропорт может быть расположен около станции \(2\) или около станции \(4\). Во время поездки, турист всегда будет в зоне A. У него уже есть билет для этой зоны, поэтому ответ \(0\). После второго запроса стоимость билета в зоне A стала равна \(10\). В третьем запросе аэропорт может быть расположен только около станции \(3\). Оптимальным решением будет купить билет для зоны A. В течении первых \(3\) секунд поездки турист будет в зоне B. Потом он попадёт в зону A и будет сканирован там на \(4\)-й и \(8\)-й секундах поездки. Так как у него есть билет для этой зоны, он не будет платить штраф. После четвёртого запроса штраф в зоне A стал равен \(3\). В пятом запросе аэропорт может быть расположен только около станции \(7\) и \(f(7) = 6\). В шестом запросе аэропорт может быть расположен около станции \(6\) или около станции \(8\). Так как \(f(6)=9\) и \(f(8)=6\) ответ равен \(6\). | |
![]()
|
|
E. Дублирование среднего
Деревья
жадные алгоритмы
поиск в глубину и подобное
Строки
Структуры данных
*2500
Дано бинарное дерево из \(n\) вершин. Вершины дерева пронумерованы от \(1\) до \(n\), корень дерева имеет номер \(1\). Каждая вершина может не иметь детей, иметь только правого или только левого ребенка, или иметь двух детей. Для удобства обозначим за \(l_u\) и \(r_u\) левого и правого ребенка вершины \(u\) соответственно, при этом \(l_u = 0\), если у \(u\) нет левого ребенка, и \(r_u = 0\), если у \(u\) нет правого ребенка. В каждой вершине дерева записана некоторая строка, изначально состоящая из одного символа \(c_u\). Определим строковое представление дерева как конкатенацию всех строк, записанных в вершинах, в порядке центрированного обхода. Формально, пусть \(f(u)\) — строковое представление поддерева с корнем в вершине \(u\). \(f(u)\) определена так: \(\) f(u) = \begin{cases} \texttt{<пустая строка>,} & \text{если }u = 0; \\ f(l_u) + c_u + f(r_u) & \text{иначе}, \end{cases} \(\) где \(+\) обозначает строковую конкатенацию. Представление всего дерева это \(f(1)\). Для каждой вершины мы можем продублировать строку, записанную в ней, не более одного раза, а именно, заменить \(c_u\) на \(c_u + c_u\). Эта операция возможна только если \(u\) — корень дерева, или строка, записанная в родителе этой вершины уже продублирована. Вам дано дерево и целое число \(k\). Какое лексикографически минимальное строковое представление дерево может иметь, если мы можем продублировать строку в не более чем \(k\) вершинах? Строка \(a\) лексикографически меньше строки \(b\), если и только если выполняется один из следующих пунктов: - \(a\) — префикс \(b\), но \(a \ne b\);
- в первой позиции, где \(a\) и \(b\) различны, в строке \(a\) находится буква, которая встречается в алфавите раньше, чем соответствующая буква в \(b\).
Выходные данные Выведите одну строку, содержащую лексикографически минимальное строковое представление, которое может иметь дерево после не более чем в \(k\) вершинах строка будет продублирована. Примечание Рисунке ниже иллюстрируют примеры. Число в вершине обозначает номер вершины, а строка в нижнем индексе — строку, написанную в вершине. Справа находится строковое представление дерева, где каждая буква имеет цвет соответствующей вершине дерева. Ниже находится дерево для первого примера. Мы продублировали строки в вершинах \(1\) и \(3\). Строку в вершине \(2\) не нужно дублировать, так как в таком случае представление будет «bbaaab», что лексикографически больше, чем «baaaab».  Во втором примере можно продублировать строки в вершинах \(1\) и \(2\). Обратите внимание, что если продублировать только строку в корне, то представление будет хуже, чем у изначального дерева.  В третьем примере не нужно ничего дублировать. Даже если мы продублируем строку в вершине \(3\), мы будем обязаны также продублировать строку в вершине \(2\), что сделает результат хуже.  Нет способа получить строку «darkkcyan» из дерева с начальным представлением «darkcyan» :(. | |
![]()
|
|
D. Двоичные пауки
битмаски
Деревья
математика
реализация
сортировки
Структуры данных
*2300
На Марсе обитает необычный вид пауков — Двоичные пауки. Они плетут паутину, чтобы защищаться от врагов. Чтобы сплести паутину, пауки объединяются в пары. При этом, если у первого паука в паре \(x\) лапок, а у второго — \(y\) лапок, то у них выходит паутина прочностью \(x \oplus y\). Здесь \(\oplus\) обозначает операцию побитового исключающего ИЛИ. Двоичные пауки живут большими группами. Сейчас Вы наблюдаете за группой из \(n\) пауков, причем \(i\)-й паук имеет \(a_i\) лапок. Когда группе пауков грозит опасность, то некоторые из них становятся защитниками. Защитники выбираются следующим образом. Во-первых, должно быть как минимум два паука-защитника. Во-вторых, любая пара из пауков-защитников должна уметь сплести паутину прочностью хотя бы \(k\). В-третьих, защитников должно быть как можно больше. Ученые долго исследовали поведение Двоичных пауков и выдвинули гипотезу, что они всегда могут выбрать защитников оптимальным образом, удовлетворяя при этом условиям выше. Вам предстоит проверить эту гипотезу на группе пауков. Для этого надо понять, сколько пауков должны стать защитниками. А поскольку Вы не являетесь Двоичным пауком, то Вы решили прибегнуть к помощи компьютера и написать программу, которая решает эту непростую задачу. Выходные данные В первой строке выведите целое число \(\ell\) (\(2 \le \ell \le n\)) — максимально возможное количество пауков-защитников. Во второй строке выведите через пробел \(\ell\) различных целых чисел \(b_i\) (\(1 \le b_i \le n\)) — номера пауков, которые станут защитниками. Если существует несколько способов выбрать защитников, то выведите любой из них. Увы, может получиться и так, что собрать защитников невозможно. В таком случае требуется вывести единственное число \(-1\). Примечание Рассмотрим пример из условия. В первом примере группа пауков выглядит следующим образом:  Возьмем трех пауков: с двумя, десятью и \(16\)-ю лапками. Тогда нетрудно видеть, что каждая пара сможет сплести достаточно прочную паутину, т. к. \(2 \oplus 10 = 8 \ge 8\), \(2 \oplus 16 = 18 \ge 8\) и \(10 \oplus 16 = 26 \ge 8\). Данный вариант выбора не единственный: можно, к примеру, выбрать трех пауков с номерами \(3\), \(4\) и \(6\). Во втором примере никакая пара пауков не сможет сплести паутину прочностью \(1024\) или больше, поэтому ответ \(-1\). | |
![]()
|
|
E1. Обновление котов (простая версия)
графы
Деревья
дп
Перебор
поиск в глубину и подобное
разделяй и властвуй
Структуры данных
*2500
Это простая версия задачи. Единственным различием между простой и сложной версиями задачи является наличие запросов удаления: они присутствуют лишь в сложной версии. Компания «Interplanetary Software, Inc.» вместе с компанией «Robots of Cydonia, Ltd.» разработала и выпустила роботов-котов. Эти электронные питомцы умеют мяукать, ловить мышей и всячески развлекать хозяина. Недавно разработчики из «Interplanetary Software, Inc.» решили выпустить обновление программного обеспечения для этих роботов. После обновления коты должны уметь решать задачи, связанные со скобочными последовательностями. Одна из таких задач приведена ниже.  Сначала немного погрузимся в теорию скобочных последовательностей. Будем рассматривать строки, состоящие из символов «(», «)» и «.». Назовем строку правильной скобочной последовательностью (ПСП), если из нее можно получить пустую строку путем операций удаления одиночных символов «.» либо подряд идущих символов «()». Например, строка «(()(.))» является ПСП, т. к. с ней можно проделать следующую цепочку удалений: «(()(.))» \(\rightarrow\) «(()())» \(\rightarrow\) «(())» \(\rightarrow\) «()» \(\rightarrow\) «». Мы получили пустую строку, а это значит, что исходная строка является ПСП. В то же время, строка «)(» не является ПСП, поскольку к ней нельзя применить описанные выше операции удаления. Будем называть ПСП простой, если эта ПСП непуста, не начинается на «.» и не заканчивается на «.». Также будем считать, что подстрока строки \(s\) — это ее последовательный подотрезок. В частности, \(s[l\dots r] = s_ls_{l+1}\dots s_r\), где \(s_i\) — \(i\)-й символ строки \(s\). Теперь перейдем к формулировке задачи. Вам дана строка \(s\), изначально состоящая из символов «(» и «)». Необходимо отвечать на запросы следующего вида. Даны индексы \(l\) и \(r\) (\(1 \le l < r \le n\)), причем гарантируется, что подстрока \(s[l\dots r]\) — простая ПСП. Требуется найти количество подстрок в \(s[l\dots r]\), которые являются простыми ПСП. Иными словами, необходимо найти количество пар индексов \(i\), \(j\) таких, что \(l \le i < j \le r\) и \(s[i\dots j]\) является простой ПСП. Вы работаете в «Interplanetary Software, Inc.» и Вам поручили непростое задание: научить котов после обновления решать описанную выше задачу. Обратите внимание, что в данной версии задачи в строке не может появиться символ «.». Он нужен лишь для сложной версии задачи. Выходные данные Для каждого запроса выведите по одному целому числу в отдельной строке — количество подстрок, которые являются простыми ПСП. Ответы требуется выводить в том же, порядке, в котором приведены сами запросы. Примечание Рассмотрим пример из условия. Ответ на первый запрос равен \(3\), поскольку существует всего три требуемых подстроки: \(s[3\dots6]\), \(s[3\dots4]\) и \(s[5\dots6]\). Ответ на второй запрос равен \(4\). Подходящие подстроки — \(s[3\dots6]\), \(s[3\dots4]\), \(s[5\dots6]\) и \(s[2\dots7]\). Ответ на третий запрос равен \(1\). Подходящая подстрока — \(s[8\dots9]\). Ответ на четвертый запрос равен \(6\). Подходящие подстроки — \(s[3\dots6]\), \(s[3\dots4]\), \(s[5\dots6]\), \(s[2\dots7]\), \(s[8\dots9]\) и \(s[2\dots9]\). | |
![]()
|
|
E2. Обновление котов (сложная версия)
Бинарный поиск
графы
Деревья
поиск в глубину и подобное
Структуры данных
*2800
Это сложная версия задачи. Единственным различием между простой и сложной версиями задачи является наличие запросов удаления: они присутствуют лишь в сложной версии. Компания «Interplanetary Software, Inc.» вместе с компанией «Robots of Cydonia, Ltd.» разработала и выпустила роботов-котов. Эти электронные питомцы умеют мяукать, ловить мышей и всячески развлекать хозяина. Недавно разработчики из «Interplanetary Software, Inc.» решили выпустить обновление программного обеспечения для этих роботов. После обновления коты должны уметь решать задачи, связанные со скобочными последовательностями. Одна из таких задач приведена ниже.  Сначала немного погрузимся в теорию скобочных последовательностей. Будем рассматривать строки, состоящие из символов «(», «)» и «.». Назовем строку правильной скобочной последовательностью (ПСП), если из нее можно получить пустую строку путем операций удаления одиночных символов «.» либо подряд идущих символов «()». Например, строка «(()(.))» является ПСП, т. к. с ней можно проделать следующую цепочку удалений: «(()(.))» \(\rightarrow\) «(()())» \(\rightarrow\) «(())» \(\rightarrow\) «()» \(\rightarrow\) «». Мы получили пустую строку, а это значит, что исходная строка является ПСП. В то же время, строка «)(» не является ПСП, поскольку к ней нельзя применить описанные выше операции удаления. Будем называть ПСП простой, если эта ПСП непуста, не начинается на «.» и не заканчивается на «.». Также будем считать, что подстрока строки \(s\) — это ее последовательный подотрезок. В частности, \(s[l\dots r] = s_ls_{l+1}\dots s_r\), где \(s_i\) — \(i\)-й символ строки \(s\). Теперь перейдем к формулировке задачи. Вам дана строка \(s\), изначально состоящая из символов «(» и «)». Необходимо отвечать на следующие запросы: - Даны индексы \(l\) и \(r\) (\(1 \le l < r \le n\)). Гарантируется, что \(l\)-й символ строки равен «(», \(r\)-й символ строки равен «)», а символы между ними равны «.». Тогда требуется сделать \(l\)-й и \(r\)-й символ равными «.».
- Даны индексы \(l\) и \(r\) (\(1 \le l < r \le n\)), причем гарантируется, что подстрока \(s[l\dots r]\) — простая ПСП. Требуется найти количество подстрок в \(s[l\dots r]\), которые являются простыми ПСП. Иными словами, необходимо найти количество пар индексов \(i\), \(j\) таких, что \(l \le i < j \le r\) и \(s[i\dots j]\) является простой ПСП.
Вы работаете в «Interplanetary Software, Inc.» и Вам поручили непростое задание: научить котов после обновления решать описанную выше задачу. Выходные данные Для каждого запроса второго типа выведите по одному целому числу в отдельной строке — количество подстрок, которые являются простыми ПСП. Ответы требуется выводить в том же, порядке, в котором приведены сами запросы. Примечание Рассмотрим пример из условия. Ответ на первый запрос равен \(3\), поскольку существует всего три требуемых подстроки: \(s[3\dots6]\), \(s[3\dots4]\) и \(s[5\dots6]\). Ответ на второй запрос равен \(4\). Подходящие подстроки — \(s[3\dots6]\), \(s[3\dots4]\), \(s[5\dots6]\) и \(s[2\dots7]\). После третьего запроса строка станет равной «)(..())()». Ответ на четвертый запрос равен \(2\). Подходящие подстроки — \(s[5\dots6]\) и \(s[2\dots7]\). Обратите внимание, что \(s[3\dots6]\) больше не является простой ПСП, т. к. начинается с «.». Ответ на пятый запрос равен \(4\). Подходящие подстроки — \(s[5\dots6]\), \(s[2\dots7]\), \(s[8\dots9]\) и \(s[2\dots9]\). После шестого запроса строка станет равной «)(....)()». После седьмого запроса строка станет равной «)......()». Ответ на восьмой запрос равен \(1\). Подходящая подстрока — \(s[8\dots9]\). | |
![]()
|
|
E. Черно-белое дерево
Деревья
жадные алгоритмы
поиск в глубину и подобное
*2400
Дано дерево из \(n\) вершин. Некоторые вершины дерева (хотя бы две) — черные, остальные — белые. Вы ставите фишку в какую-то из вершин дерева и после этого проводите следующие операции: - пусть фишка сейчас находится в вершине \(x\). Вы выбираете черную вершину \(y\), а затем перемещаете фишку по первому ребру в простом пути из \(x\) в \(y\).
Вы не можете выбирать одну и ту же вершину \(y\) в двух операциях подряд (то есть для любых двух последовательных операций выбранные черные вершины должны быть различны). Вы заканчиваете операции, когда фишка оказывается в черной вершине (если она изначально в черной вершине — вы не выполняете операции вообще), или когда количество выполненных операций становится больше \(100^{500}\). Для каждой вершины \(i\) вы должны определить, существует ли (не обязательно непустая) последовательность операций, в результате которой фишка окажется в черной вершине, если изначально фишка расположена в вершине \(i\). Выходные данные Выведите \(n\) целых чисел. \(i\)-е из них должно быть равно \(1\), если существует (возможно, пустая) последовательность операций, которая перемещает фишку в черную вершину, если изначально расположить ее в вершине \(i\), или \(0\), если такой последовательности операций не существует. | |
![]()
|
|
C. Не назначать
Деревья
Конструктив
поиск в глубину и подобное
теория чисел
*1400
Вам дано дерево из \(n\) вершин, пронумерованных от \(1\) до \(n\), ребра которого пронумерованы от \(1\) до \(n-1\). Деревом называется связный неориентированный граф без циклов. Вам нужно назначить целочисленный вес каждому ребру дереву так, чтобы в результате получилось простое дерево. Дерево называется простым, если вес каждого пути, состоящего из одного или двух ребер, является простым числом. Рассматриваются только пути, не посещающие никакую вершину дважды. Весом пути называется сумма весов ребер на пути. Рассмотрим граф ниже. Он является простым деревом, так как вес любого пути из не более чем двух ребер простой. Например, путь из двух ребер \(2 \to 1 \to 3\) имеет вес \(11 + 2 = 13\), который является простым числом. Другой пример, путь из одного ребра \(4 \to 3\) имеет вес \(5\), который является простым числом.  Назначьте веса ребрам любым возможным способом таким, что получившееся дерево будет простым. Если такого способа нет, выведите \(-1\). Можно показать, что если существуют способы сделать дерево простым, то существуют и способ, использующий только веса от \(1\) до \(10^5\). Выходные данные Для каждого набора входных данных, если существует способ корректно назначить веса, выведите \(n-1\) целое число \(a_1, a_2, \dots, a_{n-1}\) (\(1 \leq a_i \le 10^5\)), где \(a_i\) обозначает вес, назначенный ребру \(i\). В противном случае выведите \(-1\). Если существует несколько решений, выведите любое. Примечание В первом примере есть только два пути по одному ребру: \(1 \to 2\) и \(2 \to 1\), оба пути имеют вес \(17\) — простое число.  Второй пример описан в условии задачи. Можно показать, что для третьего примера не существует корректного способа назначить веса. | |
![]()
|
|
E. Метеоритный город
Бинарный поиск
Деревья
снм
Структуры данных
*3100
Mihai живет в городе, где часто случаются метеоритные бури. Это раздражает, потому что Mihai иногда приходится покупать продукты, а попасть под метеориты крайне не весело. Поэтому мы просим вас найти самый опасный способ купить продукты, чтобы мы могли обманом заставить Mihai пойти туда. В городе есть \(n\) зданий с номерами от \(1\) до \(n\). Между некоторыми зданиями есть дороги, и существует ровно \(1\) простой путь от любого здания к любому другому. Каждая дорога имеет определенный уровень метеоритной опасности. Во всех зданиях есть продуктовые магазины, но Mihai, конечно, интересуют только открытые магазины. Изначально все продуктовые магазины закрыты. Вам задано \(q\) запросов трех типов: - Учитывая целые числа \(l\) и \(r\), в зданиях с номерами от \(l\) до \(r\) открываются продуктовые магазины (ничего не происходит со зданиями, в которых уже открыт продуктовый магазин).
- Учитывая целые числа \(l\) и \(r\), здания с номерами от \(l\) до \(r\) закрывают свои продуктовые магазины (ничего не происходит со зданиями, в которых уже закрыт продуктовый магазин).
- Учитывая целое число \(x\), найдите максимальный уровень метеоритной опасности на простом пути от \(x\) до любого открытого продуктового магазина или \(-1\), если нет ни одной дороги на любом простом пути к любому открытому магазину.
Выходные данные Для каждого запроса типа \(3\) (\(t_j = 3\)) выведите максимальный уровень метеоритной опасности, который находится на некотором простом пути от \(x_j\) до некоторого открытого магазина, или \(-1\), если нет ни одной дороги на любом простом пути к любому открытому магазину. Примечание 
Это иллюстрация города, представленного во входных данных примера. В первом запросе открытых магазинов нет, поэтому очевидно, что нет ребер на простом пути от \(1\) до любого открытого магазина, поэтому ответ \(-1\). После второго и третьего запросов набор открытых магазинов равен \(\{1\}\). Простой путь от \(1\) до \(1\) не имеет ребер, поэтому ответ для запроса \(3\) равен \(-1\). После четвертого запроса открытых магазинов нет. После пятого и шестого запросов набор открытых магазинов равен \(\{5, 6\}\). В шестом запросе есть два пути от \(x_j = 4\) до некоторого открытого продуктового магазина: От \(4\) до \(5\) и от \(4\) до \(6\). Самая большая метеоритная опасность находится на пути от \(4\) до \(6\), так что ответ на запрос \(6\) будет \(4\). На рисунке этот путь отмечен красным. После остальных запросов набор открытых магазинов равен \(\{5\}\). В восьмом запросе единственный путь от \(x_j = 4\) к открытому магазину от \(4\) до \(5\), а максимальная метеоритная опасность на этом пути составляет \(3\). На рисунке этот путь отмечен зеленым. В девятом запросе единственный путь от \(x_j = 1\) к открытому магазину от \(1\) до \(5\), а максимальная метеоритная опасность на этом пути равна \(5\). На рисунке этот путь отмечен синим цветом. | |
![]()
|
|
E. Электронное правительство
Деревья
дп
поиск в глубину и подобное
Строки
Структуры данных
*2800
В рамках проекта «Электронное правительство» лучшим программистам страны Распиляндии поручили создание системы автоматизации сбора статистики и анализа прессы. Известно, что членами правительства Распиляндии может стать любой из k граждан. Их фамилии — a1, a2, ..., ak. Все фамилии различны. Изначально в правительство входят все k граждан из этого списка. Система должна поддерживать следующие возможности: - Включить гражданина ai в состав правительства.
- Исключить гражданина ai из состава правительства.
- По заданному тексту статьи определить, насколько она политизирована. Для этого, для каждого действующего члена правительства, вычисляется количество раз, которое его фамилия встречается в тексте как подстрока. Считаются все вхождения, в том числе и пересекающиеся. Степень политизированности текста определяется как сумма этих количеств по всем действующим членам правительства.
Реализуйте эту систему. Выходные данные Для каждой операции «подсчитать политизированность» выведите на отдельной строке степень политизированности заданного в ней текста. Для остальных операций ничего выводить не нужно. | |
![]()
|
|
E1. Дистанционное дерево (простая версия)
Бинарный поиск
графы
Деревья
кратчайшие пути
поиск в глубину и подобное
Структуры данных
*2400
Эта версия задачи отличается от следующей только ограничением на \(n\). Дерево — это связный неориентированный граф без циклов. Взвешенное дерево — это такое дерево, в котором у каждого ребра есть некоторый вес. Расстояние между вершинами — минимальная сумма весов на пути между ними. Дано взвешенное дерево c \(n\) вершинами, у каждого ребра вес \(1\). Введём \(d(v)\) как расстояние между вершиной \(1\) и вершиной \(v\). Пусть \(f(x)\) равно минимально возможному значению \(\max\limits_{1 \leq v \leq n} \ {d(v)}\), если можно временно добавить одно ребро веса \(x\) между любыми двумя вершинами \(a\) и \(b\) \((1 \le a, b \le n)\). Обратите внимание, что после этой операции граф уже не является деревом. Для каждого целого числа \(x\) от \(1\) до \(n\) найдите \(f(x)\). Выходные данные Для каждого набора входных данных выведите в одной строке \(n\) целых чисел, \(x\)-е из которых равно \(f(x)\) для всех \(x\) от \(1\) до \(n\). Примечание  В первом наборе входных данных: - Для \(x = 1\) мы можем добавить ребро между вершинами \(1\) и \(3\), после чего \(d(1) = 0\) и \(d(2) = d(3) = d(4) = 1\), поэтому \(f(1) = 1\).
- Для \(x \ge 2\), вне зависимости от того, какое ребро мы добавим, \(d(1) = 0\), \(d(2) = d(4) = 1\) и \(d(3) = 2\), поэтому \(f(x) = 2\).
| |
![]()
|
|
E2. Дистанционное дерево (сложная версия)
Бинарный поиск
Деревья
кратчайшие пути
поиск в глубину и подобное
*2700
Эта версия задачи отличается от предыдущей только ограничением на \(n\). Дерево — это связный неориентированный граф без циклов. Взвешенное дерево — это такое дерево, в котором у каждого ребра есть некоторый вес. Расстояние между вершинами — минимальная сумма весов на пути между ними. Дано взвешенное дерево c \(n\) вершинами, у каждого ребра вес \(1\). Введём \(d(v)\) как расстояние между вершиной \(1\) и вершиной \(v\). Пусть \(f(x)\) равно минимально возможному значению \(\max\limits_{1 \leq v \leq n} \ {d(v)}\), если можно временно добавить одно ребро веса \(x\) между любыми двумя вершинами \(a\) и \(b\) \((1 \le a, b \le n)\). Обратите внимание, что после этой операции граф уже не является деревом. Для каждого целого числа \(x\) от \(1\) до \(n\) найдите \(f(x)\). Выходные данные Для каждого набора входных данных выведите в одной строке \(n\) целых чисел, \(x\)-е из которых равно \(f(x)\) для всех \(x\) от \(1\) до \(n\). Примечание  В первом наборе входных данных: - Для \(x = 1\) мы можем добавить ребро между вершинами \(1\) и \(3\), после чего \(d(1) = 0\) и \(d(2) = d(3) = d(4) = 1\), поэтому \(f(1) = 1\).
- Для \(x \ge 2\), вне зависимости от того, какое ребро мы добавим, \(d(1) = 0\), \(d(2) = d(4) = 1\) и \(d(3) = 2\), поэтому \(f(x) = 2\).
| |
![]()
|
|
E. Запросы об остовном дереве
Бинарный поиск
графы
Деревья
жадные алгоритмы
математика
поиск в глубину и подобное
снм
сортировки
Структуры данных
*2400
Задан связный взвешенный неориентированный граф, состоящий из \(n\) вершин и \(m\) ребер. К нему задаются \(k\) запросов. Каждый запрос состоит из одного целого числа \(x\). На каждый запрос вы должны выбрать остовное дерево в графе. Пусть веса его ребер будут \(w_1, w_2, \dots, w_{n-1}\). Стоимость остовного дерева равна \(\sum \limits_{i=1}^{n-1} |w_i - x|\) (сумма абсолютных разностей между весами и \(x\)). Ответ на запрос — это минимальная стоимость остовного дерева. Запросы даны в сжатом формате. Первые \(p\) \((1 \le p \le k)\) запросов \(q_1, q_2, \dots, q_p\) даны явно. Для запросов с \(p+1\) по \(k\) выполняется \(q_j = (q_{j-1} \cdot a + b) \mod c\). Выведите исключающее или ответов на все запросы. Выходные данные Выведите одно целое число — исключающее или ответов на все запросы. Примечание Запросы в первом примере: \(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0\). Ответы: \(11, 9, 7, 3, 1, 5, 8, 7, 5, 7, 11\).  Запросы во втором примере: \(3, 0, 2, 1, 6, 0, 3, 5, 4, 1\). Ответы: \(14, 19, 15, 16, 11, 19, 14, 12, 13, 16\).  Запросы в третьем примере: \(75, 0, 0, \dots\). Ответы: \(50, 150, 150, \dots\).  | |
![]()
|
|
F. Совершенное паросочетание
Деревья
интерактив
разделяй и властвуй
Структуры данных
*2800
Вам задано дерево, состоящее из \(n\) вершин (пронумерованных от \(1\) до \(n\)) и \(n-1\) ребер (пронумерованных от \(1\) до \(n-1\)). Изначально все вершины, кроме вершины \(1\), неактивны. Вам предстоит обрабатывать запросы трех типов: - \(1\) \(v\) — активировать вершину \(v\). Гарантируется, что вершина \(v\) неактивна перед этим запросом, а один из ее соседей активен. После активации вершины выберите подмножество ребер дерева таким образом, чтобы каждая активная вершина была инцидентна ровно одному выбранному ребру, и каждая неактивная вершина не была инцидентна ни одному из выбранных ребер — другими словами, это подмножество должно является совершенным паросочетанием активной части дерева. Если такое подмножество ребер существует, выведите сумму индексов ребер в нем; в противном случае выведите \(0\).
- \(2\) — запросы этого типа будут задаваться только сразу после запроса типа \(1\), и таких запросов будет не более \(10\). Если ваш ответ на предыдущий запрос был \(0\), просто выведите \(0\); в противном случае выведите подмножество ребер для предыдущего запроса в следующем формате: сначала выведите количество ребер в подмножестве, затем выведите индексы выбранных ребер в порядке возрастания. Сумма индексов должна быть равна вашему ответу на предыдущий запрос.
- \(3\) — завершить программу.
Обратите внимание, что вы должны решить эту задачу в режиме online. Это означает, что вы не можете считать все входные данные сразу. Вы можете считать каждый запрос только после вывода ответа на предыдущий запрос. Используйте функции fflush в C++ и BufferedWriter.flush в Java после каждого вывода в вашей программе. Выходные данные Для каждого запроса типа \(1\) или \(2\) выведите ответ в отдельной строке в формате, описанном в условии. Не забывайте сбрасывать буфер вывода. | |
![]()
|
|
F. Вышки
Деревья
дп
жадные алгоритмы
Конструктив
поиск в глубину и подобное
*2500
Дано дерево с \(n\) вершинами, пронумерованными от \(1\) до \(n\). Для вершины с номером \(i\) известна её высота \(h_i\). Вы можете установить любое количество вышек в вершины, для каждой вышки вы можете выбрать, в какую вершину её поставить, а также выбрать её эффективность. Установка вышки с эффективностью \(e\) стоит \(e\) монет, где \(e > 0\). Считается, что в вершине \(x\) ловит связь, если для какой-то пары вышек в вершинах \(u\) и \(v\) (\(u \neq v\), но может быть, что \(x = u\) или \(x = v\)) с эффективностями соответственно \(e_u\) и \(e_v\) выполняется, что \(\min(e_u, e_v) \geq h_x\) и \(x\) лежит на пути между \(u\) и \(v\). Найдите минимальное количество монет, необходимое для установки вышек, чтобы во всех вершинах ловила связь. Выходные данные Выведите одно целое число — минимальное необходимое количество монет, чтобы во всех вершинах ловила связь. Примечание В первом тесте оптимально установить две вышки с эффективностью \(2\) в \(1\) и \(3\) вершины. Во втором тесте оптимально установить вышку с эффективностью \(1\) в вершину \(1\) и две вышки с эффективностью \(3\) во \(2\) и \(5\) вершины. В третьем тесте оптимально установить две вышки с эффективностью \(6\) в \(1\) и \(2\) вершины. | |
![]()
|
|
D. Взвесьте дерево
Деревья
дп
Конструктив
поиск в глубину и подобное
реализация
*2000
Вам дано дерево из \(n\) вершин, пронумерованных от \(1\) до \(n\). Деревом называется связный неориентированный граф без циклов. Для всех \(i=1,2, \ldots, n\) обозначим за \(w_i\) вес \(i\)-й вершины. Вершина называется хорошей, если ее вес равен сумме весов всех ее соседей. Изначально веса в вершинах не определены. Выберете для каждой вершины положительный целочисленный вес так, чтобы количество хороших вершин в дереве было максимально возможным. Если есть несколько способов сделать это, вам нужно найти такой, который минимизирует сумму весов всех вершин в дереве. Выходные данные В первой строке выведите два целых числа: максимальное количество хороших вершин и минимально возможный суммарный вес вершин при этом. Во второй строке выведите \(n\) целых чисел \(w_1, w_2, \ldots, w_n\) (\(1\le w_i\le 10^9\)) — веса вершин. Можно показать, что существует оптимальное решение, удовлетворяющее данным ограничениям. Если существует несколько решений, выведите любое из них. Примечание Ниже изображено дерево из первого примера:  В этом случае, если вы выберете для каждый вершины вес \(1\), то хорошими вершинами будут вершины (покрашены черным) \(1\), \(3\) и \(4\). Невозможно выбрать такие веса, чтобы все вершины были хорошими. Минимально возможная сумма весов равна \(1+1+1+1=4\), меньшая сумма недостижима, так как вершины обязаны иметь положительный вес. Ниже изображено дерево из второго примера:  В этом случае, если вы выберете для каждой вершины вес \(1\), то хорошими вершинами будут вершины (покрашены черным) \(2\) и \(3\). Можно показать, что это оптимальное решение. | |
![]()
|
|
E. Авиареформа
графы
Деревья
поиск в глубину и подобное
разделяй и властвуй
реализация
снм
Структуры данных
*3200
Берляндия — большая страна с развитой системой авиасообщения. Всего в стране есть \(n\) городов, которые исторически обслуживаются авиакомпанией Берляфлот. Авиакомпания выполняет двухсторонние рейсы между \(m\) парами городов, \(i\)-й из них соединяет города с номерами \(a_i\) и \(b_i\) и имеет цену \(c_i\) на перелёт в каждую из сторон. Известно, что с помощью рейсов Берляфлота можно добраться от любого города до любого другого (возможно, с пересадками), а стоимость любого маршрута из нескольких стыковочных рейсов Берляфлота равна стоимости самого дорогого из них. Более формально, стоимость маршрута из города \(t_1\) в город \(t_k\) с \((k-2)\)-мя пересадками в городах \(t_2,\ t_3,\ t_4,\ \ldots,\ t_{k - 1}\) равна максимуму из стоимостей рейсов из города \(t_1\) в \(t_2\), из \(t_2\) в \(t_3\), из \(t_3\) в \(t_4\) и так далее до рейса из \(t_{k - 1}\) в \(t_k\). Разумеется, все эти рейсы должны выполняться авиакомпанией Берляфлот. Недавно в Берляндии начала работать новая авиакомпания S8 Airlines. Эта авиакомпания совершает двусторонние рейсы между всеми парами городов, между которыми нет рейсов Берляфлота. Таким образом, между каждой парой городов есть рейс либо Берляфлота, либо S8 Airlines. Стоимости рейсов авиакомпании S8 Airlines рассчитываются следующим образом: для каждой пары городов \(x\) и \(y\), между которыми выполняется рейс S8 Airlines, стоимость этого рейса равняется минимальной стоимости маршрута между городами \(x\) и \(y\) у Берляфлота в соответствии с описанным ранее ценообразованием. Известно, что с помощью рейсов S8 Airlines можно добраться от любого города до любого другого с возможными пересадками, и, аналогично Берляфлоту, стоимость маршрута между любыми двумя городами стыковочными рейсами S8 Airlines равна стоимости самого дорогого рейса в этом маршруте. Из-за увеличившейся конкуренции с S8 Airlines Берляфлот решил провести авиареформу и изменить стоимости своих рейсов. А именно, для \(i\)-го своего рейса между городами \(a_i\) и \(b_i\) Берляфлот хочет сделать стоимость этого рейса равной минимальной стоимости маршрута между городами \(a_i\) и \(b_i\) у авиакомпании S8 Airlines. Помогите менеджерам Берляфлота рассчитать новые стоимости рейсов. Выходные данные Для каждого набора входных данных в отдельной строке выведите \(m\) целых чисел, \(i\)-е из которых должно быть равно стоимости \(i\)-го рейса Берляфлота после авиареформы. Примечание В примере в первом наборе входных данных авиакомпания S8 Airlines будет выполнять рейсы между парами городов: \((1, 3)\), \((1, 4)\) и \((2, 4)\). Стоимость рейса между городами \(1\) и \(3\) будет равна \(2\), так как минимальная стоимость маршрута Берляфлота равна \(2\) — маршрут состоит из рейса между городами \(1\) и \(2\) стоимостью \(1\) и рейса между городами \(2\) и \(3\) стоимостью \(2\), максимум из стоимостей равен \(2\). Стоимость рейса между городами \(1\) и \(4\) будет равна \(3\), так как минимальная стоимость маршрута Берляфлота составляет \(3\) — маршрут состоит из рейса между городами \(1\) и \(2\) стоимостью \(1\), рейса между городами \(2\) и \(3\) стоимостью \(2\) и рейса между городами \(3\) и \(4\) стоимостью \(3\), максимум из стоимостей равен \(3\). Стоимость рейса между городами \(2\) и \(4\) будет равна \(3\), так как минимальная стоимость маршрута Берляфлота составляет \(3\) — маршрут состоит из рейса между городами \(2\) и \(3\) стоимостью \(2\) и рейса между городами \(3\) и \(4\) стоимостью \(3\), максимум из стоимостей равен \(3\). После авиареформы стоимость рейса Берляфлота между городами \(1\) и \(2\) будет составлять \(3\), так как минимальная стоимость маршрута S8 Airlines между этими городами составляет \(3\) — маршрут состоит из рейса между городами \(1\) и \(4\) стоимостью \(3\) и рейса между городами \(2\) и \(4\) стоимостью \(3\), максимум равен \(3\). Стоимость рейса Берляфлота между городами \(2\) и \(3\) будет составлять \(3\), так как минимальная стоимость маршрута S8 Airlines между этими городами составляет \(3\) — маршрут состоит из рейса между городами \(2\) и \(4\) стоимостью \(3\), рейса между городами \(1\) и \(4\) стоимостью \(3\) и рейса между \(1\) и \(3\) стоимостью \(2\), максимум равен \(3\). Стоимость рейса Берляфлота между городами \(3\) и \(4\) будет составлять \(3\), так как минимальная стоимость маршрута S8 Airlines между этими городами составляет \(3\) — маршрут состоит из рейса между городами \(1\) и \(3\) стоимостью \(2\) и рейса между городами \(1\) и \(4\) стоимостью \(3\), максимум равен \(3\). Во втором наборе входных данных у авиакомпании S8 Airlines будут следующие рейсы: между городами \(1\) и \(4\) стоимостью \(1\), между городами \(2\) и \(3\) стоимостью \(1\), между городами \(2\) и \(5\) стоимостью \(2\), между городами \(3\) и \(4\) стоимостью \(1\) и между городами \(3\) и \(5\) стоимостью \(2\). | |
![]()
|
|
D. Граф-борода
Деревья
снм
Структуры данных
*2100
Назовем неориентированный связный граф из n вершин и n - 1 ребра бородой, если в нем все вершины кроме, возможно, одной имеют степень 2 или 1 (то есть в нем существует не более одной вершины, степень которой более двух). Напомним, что степень вершины — это количество инцидентных ей ребер. Пусть каждое ребро имеет либо черный цвет, либо белый, изначально все ребра имеют черный цвет. Вам дано описание графа-бороды. Ваша задача — обрабатывать запросы следующих типов: - покрасить в черный цвет ребро, которое в описании имеет номер i (гарантируется, что к моменту этого запроса i-ое ребро имеет белый цвет)
- покрасить в белый цвет ребро, которое в описании имеет номер i (гарантируется, что к моменту этого запроса i-ое ребро имеет черный цвет)
- найти длину кратчайшего пути только по черным ребрам между вершинами a и b или указать, что не существует такого пути между ними (длина пути — это количество ребер в нем)
Вершины пронумерованы целыми числами от 1 до n, а ребра — целыми числами от 1 до n - 1. Выходные данные Для каждого запроса «найти расстояние между вершинами a и b» выведите результат. Если данные вершины на момент запроса недостижимы друг из друга по черным ребрам, то выведите «-1» (без кавычек). Результаты выводите в порядке поступления запросов, числа разделяйте пробелами или переводами строк. Примечание В первом примере вершины 1 и 2 связаны ребром номер 1, а вершины 2 и 3 — ребром номер 2. До перекраски ребра номер 2 каждая вершина достижима из каждой по черным ребрам, в частности, кратчайший путь между 1 и 3 проходит через оба ребра. Если перекрасить ребро номер 2 в белый цвет, то вершина 3 оказывается отрезанной от остальных, то есть из нее не существует пути по черным ребрам ни в какую другую вершину. | |
![]()
|
|
E. Одинаковые суммы деревьев
Деревья
Конструктив
математика
поиск в глубину и подобное
*2200
Вам дано неориентированное некорневое дерево — связный неориентированный граф без циклов. Вы должны присвоить каждой вершине ненулевой целочисленный вес так, чтобы выполнялось следующее: если удалить любую вершину дерева, то все оставшиеся компоненты связности имеют одинаковую сумму весов в своих вершинах. Выходные данные Для каждого набора входных данных необходимо вывести одну строку с \(n\) целыми числами \(a_1, a_2, \ldots, a_n\), разделенными пробелами, где \(a_i\) — вес, присвоенный вершине \(i\). Веса должны удовлетворять \(-10^5 \leq a_i \leq 10^5\) и \(a_i \neq 0\). Можно показать, что всегда существует решение, удовлетворяющее этим ограничениям. Если возможных решений несколько, выведите любое из них. Примечание В первом случае при удалении вершины \(1\) все оставшиеся компоненты связности имеют сумму весов \(5\), а при удалении вершины \(3\) все оставшиеся компоненты связности имеют сумму весов \(2\). При удалении других вершин остается только одна компонента связности, поэтому все оставшиеся компоненты связности имеют одинаковую сумму весов. | |
![]()
|
|
F. Слова на дереве
2-sat
графы
Деревья
поиск в глубину и подобное
снм
*2600
Дано дерево из \(n\) вершин, а также \(q\) троек \((x_i, y_i, s_i)\), где \(x_i\) и \(y_i\) — целые числа от \(1\) до \(n\), а \(s_i\) — строка, длина которой равна количеству вершин на простом пути от \(x_i\) до \(y_i\). Вы должны написать на каждой вершине строчную латинскую букву таким образом, что для каждой из \(q\) троек выполняется хотя бы одно из условий: - если выписать буквы на пути от \(x_i\) до \(y_i\) в том порядке, в котором они встречаются на пути, вы получите строку \(s_i\);
- если выписать буквы на пути от \(y_i\) до \(x_i\) в том порядке, в котором они встречаются на пути, вы получите строку \(s_i\).
Найдите любой способ написать по одной букве на каждую вершину, чтобы соблюсти ограничения, или сообщите, что это невозможно. Выходные данные Если нет способа удовлетворить ограничения задачи, выведите NO. Иначе выведите YES в первой строке и \(n\) строчных латинских букв во второй строке; \(i\)-я буква должна соответствовать той букве, которую вы пишете на \(i\)-й вершине. Если ответов несколько, выведите любой из них. | |
![]()
|
|
F. Игра с деревом и перестановкой
графы
Деревья
игры
поиск в глубину и подобное
*3000
Есть дерево из \(n\) вершин и перестановка \(p\) из \(n\) чисел. В вершине \(x\) дерева находится фишка. Алиса и Боб играют в игру. Алиса управляет перестановкой \(p\), а Bob управляет фишкой на дереве. В свой ход Алиса обязана выбрать два различных числа \(u\) и \(v\) (не индексы; \(u \neq v\)) такие, что фишка не находится ни в вершине \(u\), ни в вершине \(v\) дерева, и поменять их местами в перестановке \(p\). В свой ход Боб обязан передвинуть фишку в соседнюю с текущей вершину. Алиса хочет отсортировать перестановку в порядке возрастания, Боб хочет помешать этому. Алиса выигрывает, если перестановка отсортирована по возрастанию в начале или в конце ее хода. Боб выигрывает, если он может сделать так, чтобы игра продолжалась бесконечное количество ходов (то есть чтобы Алиса никогда не могла бы получить отсортированную перестановку). Оба игрока играют оптимально. Алиса ходит первой. По данному дереву, перестановке \(p\) и вершине \(x\), в которой изначально находится фишка, определите победителя игры. Выходные данные Для каждого набора входных данных выведите одну строку, содержащую слово Alice или Bob — победителя игры. В ответе важен регистр букв. Примечание Ниже находится объяснение первого примера. В первом наборе входных данных Алиса может выиграть. Например, возможна такая последовательность ходов: - Алиса меняет местами \(5\) и \(6\), получается \([2,1,3,5,4,6]\).
- Боб передвигает фишку в вершину \(5\).
- Алиса меняет местами \(1\) и \(2\), получается \([1,2,3,5,4,6]\).
- Боб передвигает фишку в вершину \(3\).
- Алиса меняет местами \(4\) и \(5\), получается \([1,2,3,4,5,6]\) и выигрывает.
Во втором наборе входных данных Алиса не может выиграть, так как Боб может бесконечно долго затягивать игру. Например, возможна такая последовательность ходов: - Алиса меняет местами \(1\) и \(3\), получается \([3,1,2]\).
- Боб передвигает фишку в вершину \(1\).
- Алиса меняет местами \(2\) и \(3\), получается \([2,1,3]\).
- Боб передвигает фишку в вершину \(2\).
- Алиса меняет местами \(1\) и \(3\), получается \([2,3,1]\).
- Боб передвигает фишку в вершину \(3\).
- Алиса меняет местами \(1\) и \(2\), получается \([1,3,2]\).
- Боб передвигает фишку в вершину \(2\).
И далее последовательность бесконечно повторяется. В третьем наборе Алиса выигрывает сразу, так перестановка уже отсортирована. | |
![]()
|
|
E. Узкие компоненты
Деревья
дп
математика
Перебор
снм
Структуры данных
*2500
Задана матрица \(a\), состоящая из \(3\) строк и \(n\) столбцов. Каждая клетка матрицы либо свободна, либо занята. Свободная клетка \(y\) достижима из свободной клетки \(x\), если выполняется хотя бы одно из следующих условий: - \(x\) и \(y\) имеют общую сторону;
- существует такая свободная клетка \(z\), что \(z\) достижима из \(x\), а \(y\) достижима из \(z\).
Компонента связности — это такой набор свободных клеток матрицы, что все клетки в нем достижимы друг из друга, а добавление любой другой свободной клетки в него нарушает это правило. К матрице задаются \(q\) запросов. Запросы следующего вида: - \(l\) \(r\) — посчитайте количество компонент связности матрицы, состоящей из столбцов с \(l\) по \(r\) матрицы \(a\) включительно.
Выведите ответы на все запросы. Выходные данные Выведите \(q\) целых чисел — \(j\)-е значение должно быть равно количеству компонент связности матрицы, состоящей из столбцов с \(l_j\) по \(r_j\) матрицы \(a\) включительно. | |
![]()
|
|
G. Gastronomic Event
Деревья
дп
жадные алгоритмы
SWERC organizers want to hold a gastronomic event. The location of the event is a building with \(n\) rooms connected by \(n-1\) corridors (each corridor connects two rooms) so that it is possible to go from any room to any other room. In each room you have to set up the tasting of a typical Italian dish. You can choose from \(n\) typical Italian dishes rated from \(1\) to \(n\) depending on how good they are (\(n\) is the best possible rating). The \(n\) dishes have distinct ratings. You want to assign the \(n\) dishes to the \(n\) rooms so that the number of pleasing tours is maximal. A pleasing tour is a nonempty sequence of rooms so that: - Each room in the sequence is connected to the next one in the sequence by a corridor.
- The ratings of the dishes in the rooms (in the order given by the sequence) are increasing.
If you assign the \(n\) dishes optimally, what is the maximum number of pleasing tours? Output Print the maximum number of pleasing tours. Note In the first sample, it is optimal to place the dish with rating \(1\) in room \(1\), the dish with rating \(2\) in room \(3\), the dish with rating \(3\) in room \(2\), the dish with rating \(4\) in room \(5\) and the dish with rating \(5\) in room \(4\). All the \(13\) possible pleasing tours are: \((1)\), \((2)\), \((3)\), \((4)\), \((5)\), \((1,2)\), \((3,2)\), \((2,4)\), \((2,5)\), \((1,2,4)\), \((1,2,5)\), \((3,2,4)\), \((3,2,5)\). There are also other ways to assign the dishes to the rooms so that there are \(13\) pleasing tours. | |
![]()
|
|
C. Заражение дерева
Бинарный поиск
Деревья
жадные алгоритмы
сортировки
*1600
Деревом называется связный граф без циклов. В корневом дереве есть особая вершина, которая называется корнем. Родитель вершины \(v\) (отличной от корня) — вершина перед \(v\) на кратчайшем пути от корня до \(v\). Дети вершины \(v\) — все вершины, для которых \(v\) является родителем. Вам дано корневое дерево из \(n\) вершин. Вершина \(1\) — корень. Изначально все вершины здоровы. Каждую секунду вы делаете две операции: распространение и, после этого, инъекцию: - Распространение: для каждой вершины \(v\), если хотя бы один ребёнок \(v\) заражён, то вы можете распространить инфекцию, дополнительно заразив не более одного ребёнка \(v\) на свой выбор.
- Инъекция: вы можете выбрать одну любую здоровую вершину и заразить её.
Этот процесс повторяется каждую секунду до тех пор, пока всё дерево не будет заражено. Необходимо найти минимальное время в секундах, за которое можно заразить всё дерево. Выходные данные Для каждого набора входных данных выведите одно число — минимальное время в секундах, за которое можно заразить всё дерево. Примечание На картинке изображено дерево из первого набора входных данных в каждую секунду. Вершина покрашена в чёрный, если она не заражена. Вершина покрашена в синий, если она заражена инъекцией в течение последней прошедшей секунды. Вершина покрашена в зелёный, если она заражена распространением в течение последней прошедшей секунды. Вершина покрашена в красный, если она заражена, но не в течение последней прошедшей секунды.  Обратите внимание, что вы можете выбирать, какие именно вершины будут заражены распространением и инъекциями. | |
![]()
|
|
D. Удаление рёбер
Деревья
дп
Конструктив
поиск в глубину и подобное
*2900
Дано дерево (связный неориентированный граф без циклов) с \(n\) вершинами. Два ребра считаются смежными, если они имеют ровно один общий конец. За один ход вы можете удалить любое ребро, которое смежно четному количеству оставшихся ребер. Удалите все ребра или установите, что это невозможно. Если существует несколько решений, выведите любое из них. Выходные данные Для каждого набора входных данных выведите «NO», если невозможно удалить все ребра. В противном случае выведите «YES» и в следующих \(n-1\) строке выведите возможный порядок удаления ребер. Для каждого ребра выведите его концы в любом порядке. Примечание Пример \(1\): можно удалить данное ребро, поскольку оно не смежно никакому ребру. Пример \(2\): оба ребра смежны ровно одному ребру, поэтому невозможно удалить ни одно из них. Таким образом, ответ «NO». Пример \(3\): ребро \(2-3\) смежно двум другим ребрам, поэтому его можно удалить. После этого также становится возможным удалить оставшиеся ребра. | |
![]()
|
|
E. Хемос на дереве
битмаски
Деревья
Конструктив
поиск в глубину и подобное
*2200
В последнем региональном соревновании Хемос со своей командой наконец-то отобрались на Финал ICPC, поэтому в честь этого достижения, а также из-за любви к деревьям он предлагает вам эту задачу, одноименную его команде «Hemose 3al shagra» (Хемос на дереве). Вам дано дерево из \(n\) вершин, где \(n\) — степень \(2\). Вам нужно назначить каждой вершине и каждому ребру целое число из диапазона \([1,2n -1]\) (включительно) так, чтобы все значения были различны. После назначения вы должны выбрать одну из вершин дерева в качестве корня так, чтобы максимальная стоимость среди всех простых путей от корня до всех вершин или ребер была минимально возможная. Стоимость пути между двумя вершинами \(u\) и \(v\) или между вершиной \(u\) и ребром \(e\) определяется как побитовое исключающее ИЛИ всех значений вершин и ребер на пути между ними, включая концы (обратите внимание, что в дереве есть только один простой путь между парой вершин или вершиной и ребром). Выходные данные Для каждого набора входных данных выведите в первой строке выбранный корень. Во второй строке выведите \(n\) целых чисел, где \(i\)-е число обозначает значение, выбранное для \(i\)-й вершине. В третьей строке выведите \(n-1\) целое число, где \(i\)-е число обозначает значение выбранное для \(i\)-го ребра. Ребра нумеруются в порядке присутствия во входных данных Если существует несколько решений, выведите любое из них. Примечание Дерево в первом наборе входных данных показано ниже.  Стоимости путей следующие: - \(3\);
- \(3\oplus 7=4\);
- \(3\oplus 7\oplus 6=2\);
- \(3\oplus 2=1\);
- \(3\oplus 2\oplus 1=0\);
- \(3\oplus 2\oplus 1\oplus 4=4\);
- \(3\oplus 2\oplus 1\oplus 4\oplus 5=1\).
Максимальная стоимость равна \(4\). Можно показать, что не существует способа расставить числа и выбрать корень так, чтобы получилась меньшая максимальная стоимость. Дерево для второго набора показано ниже:  | |
![]()
|
|
E. Прямой обход
Деревья
дп
Комбинаторика
разделяй и властвуй
снм
сортировки
хэши
*2100
Дано корневое дерево из \(2^n - 1\) вершин. У каждой вершины дерева либо \(0\) сыновей, либо \(2\). Все листья дерева расположены на одинаковой глубине, а у каждой внутренней вершины один из сыновей является левым, а другой — правым. Формально, вам задано совершенное бинарное дерево. Вершины дерева пронумерованы следующим образом: - номер корня — \(1\);
- если номер внутренней вершины — \(x\), то номер ее левого сына — \(2x\), а номер правого сына — \(2x+1\).
На каждой вершине дерева записана буква A или буква B. Пусть буква на вершине \(x\) — это \(s_x\). Назовем строкой прямого обхода вершины \(x\) строку, которая строится по следующим правилам: - если вершина \(x\) — лист, то строка прямого обхода \(x\) состоит из одного символа \(s_x\);
- в противном случае строка прямого обхода \(x\) равна \(s_x + f(l_x) + f(r_x)\), где \(+\) обозначает конкатенацию строк, \(f(l_x)\) — строка прямого обхода левого сына \(x\), а \(f(r_x)\) — строка прямого обхода правого сына \(x\).
Строка прямого обхода всего дерева — это строка прямого обхода его корня. А теперь — сама задача. Вы должны посчитать количество различных строк, которые могут быть получены как строка прямого обхода заданного дерева, если до построения строки прямого обхода можно применить следующую операцию любое количество раз: - выбрать любую вершину \(x\), не являющуюся листом, и поменять местами ее детей (то есть левый сын становится правым, и наоборот).
Выходные данные Выведите одно целое число — количество различных строк, которые можно получить в качестве строки прямого обхода дерева, если можно применить любое количество описанных в условии операций. Ответ может быть очень большим, поэтому выведите его по модулю \(998244353\). | |
![]()
|
|
D. Вертикальные пути
графы
Деревья
реализация
*1300
Задано корневое дерево из \(n\) вершин. Вершины пронумерованы от \(1\) до \(n\). Корнем может быть любая из вершин. Дерево — это связный неориентированный граф без циклов. Корневое дерево — дерево с выделенной вершиной, которую называют корнем. Дерево задано массивом предков \(p\), содержащим \(n\) целых чисел: \(p_i\) — предок вершины с номером \(i\). Предком вершины \(u\) называется такая вершина, которая является следующей вершиной на кратчайшем пути от \(u\) к корню. Например, на простом пути из \(5\) в \(3\) (корень), следующая вершина будет \(1\), таким образом, предком вершины \(5\) является вершина \(1\). У корня предка нет, для него в качестве \(p_i\) используется значение \(i\) (таким образом, корень — единственная вершина, для которой \(p_i=i\)). Найдите такой набор путей, что: - каждая вершина принадлежит ровно одному пути, каждый путь может содержать одну или более вершину;
- в каждом пути каждая очередная вершина — это сын текущей вершины (то есть пути всегда ведут вниз — от родителя к сыну);
- количество путей минимально.
Например, если \(n=5\) и \(p=[3, 1, 3, 3, 1]\), то дерево можно разбить на три пути: - \(3 \rightarrow 1 \rightarrow 5\) (путь из \(3\) вершин),
- \(4\) (путь из \(1\) вершины),
- \(2\) (путь из \(1\) вершины).
 Пример разбиения корневого дерева на три пути для \(n=5\), корень дерева — вершина \(3\). Пример разбиения корневого дерева на три пути для \(n=5\), корень дерева — вершина \(3\). Выходные данные Для каждого набора входных данных на первой строке выведите целое число \(m\) — минимальное количество непересекающихся путей, идущих сверху вниз, которыми можно покрыть все вершины дерева. Затем выведите \(m\) пар строк, содержащих описания путей. В первую из них выведите длину пути, во второй — последовательность вершин, задающих этот путь в порядке сверху вниз. Вы можете выводить пути в любом порядке. Если ответов несколько, выведите любой из них. | |
![]()
|
|
F. Влад и отложенные дела
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
*1800
Влад и Настя живут в городе, состоящем из \(n\) домов и \(n-1\) дороги. Из каждого дома можно добраться до другого передвигаясь только по дорогам. То есть город представляет собой дерево. Влад живёт в доме с номером \(x\), а Настя в доме с номером \(y\). Влад решил пойти к Насте в гости. Однако он вспомнил, что отложил на потом \(k\) дел, которые он должен сделать прежде чем прийти к Насте. Чтобы сделать \(i\)-е дело ему необходимо прийти в \(a_i\)-й дом, дела можно делать в любом порядке. За \(1\) минуту он может пройти от одного дома до другого, если их соединяет дорога. Влад не очень любит пешие прогулки, поэтому его интересует, какое минимальное количество минут он должен потратить на дорогу, чтобы сделать все дела и после этого прийти к Насте. Дома \(a_1, a_2, \dots, a_k\) он может посетить в любом порядке. Любые Дома он может посещать многократно (если захочет). Выходные данные Выведите \(t\) строк, каждая из которых содержит ответ на соответствующий набор входных данных. В качестве ответа выведите единственное число — минимальное количество минут, необходимых Владу на дорогу, чтобы сделать все дела и прийти к Насте. Примечание Дерево и оптимальный путь для первого теста:  \(1 \rightarrow 2 \rightarrow 1 \rightarrow 3\) \(1 \rightarrow 2 \rightarrow 1 \rightarrow 3\) Дерево и оптимальный путь для второго теста:  \(3 \rightarrow 1 \rightarrow 3 \rightarrow 5 \rightarrow 2 \rightarrow 5 \rightarrow 6 \rightarrow 5\) \(3 \rightarrow 1 \rightarrow 3 \rightarrow 5 \rightarrow 2 \rightarrow 5 \rightarrow 6 \rightarrow 5\) Дерево и оптимальный путь для третьего теста:  \(3 \rightarrow 5 \rightarrow 2\) \(3 \rightarrow 5 \rightarrow 2\) | |
![]()
|
|
G. Чёрно-белые сбалансированные поддеревья
графы
Деревья
дп
поиск в глубину и подобное
*1300
Вам дано подвешенное дерево из \(n\) вершин, пронумерованных от \(1\) до \(n\). Корнем является вершина \(1\). Также есть строка \(s\), задающая цвета всех вершин: если \(s_i = \texttt{B}\), то вершина \(i\) чёрная, а если \(s_i = \texttt{W}\), то вершина \(i\) белая. Поддерево дерева называется сбалансированным, если количество белых вершин поддерева равняется количеству чёрных вершин поддерева. Посчитайте количество сбалансированных поддеревьев.  На картинке дерево при \(n=7\), \(a=[1,1,2,3,3,5]\) и \(s=\texttt{WBBWWBW}\). Поддерево вершины \(3\) сбалансированно. На картинке дерево при \(n=7\), \(a=[1,1,2,3,3,5]\) и \(s=\texttt{WBBWWBW}\). Поддерево вершины \(3\) сбалансированно. Дерево — это связный граф без циклов. Подвешенное дерево — это дерево с выбранной вершиной, которую называют корнем. В этой задаче корнем каждого дерева является вершина \(1\). Дерево описано массивом предков \(a_2, \dots, a_n\), содержащим \(n-1\) число: \(a_i\) — предок вершины с номером \(i\) для всех \(i = 2, \dots, n\). Предок вершины \(u\) это следующая вершина на простом пути от \(u\) к корню. Поддерево вершины \(u\) — это множество всех вершин, которые содержат \(u\) в пути к корню. Например на картинке выше, \(7\) в поддереве у \(3\), потому что простой путь \(7 \to 5 \to 3 \to 1\) проходит через \(3\). Обратите внимание, что сама вершина входит в своё поддерево, и поддеревом корня является всё дерево. Выходные данные Для каждого набора входных данных выведите одно число — количество сбалансированных поддеревьев. Примечание Первый пример изображён в условии. Только поддеревья вершин \(2\) и \(3\) сбалансированны. Во втором примере только поддерево вершины \(1\) сбалансированно. в третьем примере сбалансированны поддеревья вершин \(1\), \(3\), \(5\) и \(7\). | |
![]()
|
|
F. Свободное вершинное покрытие
графы
Деревья
поиск в глубину и подобное
разделяй и властвуй
снм
*2600
Дан простой связный неориентированный граф, состоящий из \(n\) вершин и \(m\) ребер. Вершины пронумерованы от \(1\) до \(n\). Вершинное покрытие графа — это такой набор вершин, что у каждого ребра есть хотя бы один конец в наборе. Назовем свободным вершинным покрытием такое вершинное покрытие, что не более одного ребра имеет оба конца в наборе. Найдите свободное вершинное покрытие графа или сообщите, что его нет. Если существует несколько ответов, то выведите любой из них. Выходные данные На каждый набор входных данных в первой строке выведите YES, если свободное вершинное покрытие существует и NO, если нет. Если оно существует, то во второй строке выведите бинарную строку \(s\) длины \(n\), где \(s_i = 1\) означает, что \(i\)-я вершина в вершинном покрытии, а \(s_i = 0\) означает, что \(i\)-я вершина не в нем. Если существует несколько ответов, то выведите любой из них. Примечание Здесь изображены графы из первого примера. Вершины в свободном вершинном покрытии помечены красным.  | |
![]()
|
|
F. Уникальные вхождения
Деревья
дп
поиск в глубину и подобное
разделяй и властвуй
снм
Структуры данных
*2300
Задано дерево, состоящее из \(n\) вершин. На каждом ребре написано целое число. Пусть \(f(v, u)\) будет равно количеству значений, которые встречаются ровно один раз на ребрах на простом пути между \(v\) и \(u\). Посчитайте сумму \(f(v, u)\) по всем парам вершин \(v\) и \(u\), для которых \(1 \le v < u \le n\). Выходные данные Выведите одно целое число — сумму \(f(v, u)\) по всем парам вершин \(v\) и \(u\) таким, что \(v < u\). | |
![]()
|
|
D. Остовное дерево на окружности
Деревья
Конструктив
реализация
*2000
Дано \(n\) вершин, расположенных на окружности, пронумерованных от \(1\) до \(n\) по часовой стрелке. Вам также дана бинарная строка \(s\) длины \(n\). Ваша задача — построить дерево на заданных \(n\) вершинах, удовлетворяющее двум условиям ниже, или сообщить, что такого дерева не существует: - Для каждой вершины \(i\) \((1 \le i \le n)\), степень вершины четная, если \(s_i = 0\) и нечетная, если \(s_i = 1\).
- Никакие два ребра дерева не пересекаются внутри окружности. Разрешается, чтобы ребра пересекались на окружности.
Обратите внимание, что все ребра рисуются как отрезки прямых линий. Например, ребро \((u, v)\) в дереве рисуется как отрезок прямой, соединяющий \(u\) и \(v\) на окружности. Дерево с \(n\) вершинами — это связный граф с \(n - 1\) ребрами. Выходные данные Для каждого набора входных данных, если не существует дерева, удовлетворяющего заданным условиям, выведите «NO» (без кавычек), иначе выведите «YES», а затем выведите описание дерева. Вы можете выводить каждую букву в любом регистре (например, «YES», «Yes», «yes», «yEs», «yEs» будут распознаны как положительный ответ). Если существует дерево, то выведите \(n - 1\) строк, каждая из которых содержит два целых числа \(u\) и \(v\) \((1 \leq u,v \leq n, u \neq v)\), обозначающих ребро между \(u\) и \(v\) в дереве. Если существует несколько возможных ответов, выведите любой из них. Примечание В первом наборе входных данных дерево выглядит следующим образом:  Во втором наборе входных данных существует только одно возможное дерево с ребром между \(1\) и \(2\), и оно не удовлетворяет ограничениям на степени. В третьем наборе входных данных,  Дерево слева удовлетворяет ограничениям на степени, но ребра пересекаются внутри, поэтому оно не является допустимым деревом, в то время как дерево справа является допустимым. | |
![]()
|
|
E. Неупорядоченные обмены
графы
Деревья
жадные алгоритмы
Конструктив
математика
поиск в глубину и подобное
сортировки
*2700
У Алисы есть перестановка \(p\) чисел от \(1\) до \(n\). Алиса может поменять местами пару \((x, y)\), что означает поменять местами элементы в позициях \(x\) и \(y\) в \(p\) (то есть поменять местами \(p_x\) и \(p_y\)). Алиса недавно изучила свой первый алгоритм сортировки, поэтому она решила отсортировать свою перестановку за минимальное количество возможных обменов. Она записала на листе бумаги все обмены в том порядке, в котором она их выполняла для сортировки перестановки. Например, - \([(2, 3), (1, 3)]\) является правильной последовательностью обменов Алисы для перестановки \(p = [3, 1, 2]\), в то время как \([(1, 3), (2, 3)]\) не является, потому что не сортирует перестановку. Обратите внимание, что мы не можем отсортировать перестановку менее чем за \(2\) обмена.
- \([(1, 2), (2, 3), (2, 4), (2, 3)]\) не может быть последовательностью обменов Алисы для \(p = [2, 1, 4, 3]\), даже если она сортирует перестановку, потому что \(p\) можно отсортировать за \(2\) обмена, например, используя последовательность \([(4, 3), (1, 2)]\).
К сожалению, Боб переставил местами обмены в последовательности, выписанной Алисой. Вам дана перестановка Алисы \(p\) и обмены, сделанные Алисой в произвольном порядке. Можете ли вы восстановить правильную последовательность обменов, которая сортирует перестановку \(p\)? Поскольку Алиса написала правильные обмены до того, как Боб их перемешал, гарантируется, что существует некоторый порядок обменов, который сортирует перестановку. Выходные данные Выведите перестановку \(m\) целых чисел — правильный порядок обменов, выписанный Алисой, который сортирует перестановку \(p\). Для лучшего понимания обратитесь к объяснению примера. В случае нескольких возможных ответов выведите любой. Примечание В первом примере \(p = [2, 3, 4, 1]\), \(m = 3\) и заданы обмены \([(1, 4), (2, 1), (1, 3)]\). Существует только один правильный порядок обмена, а именно \([2, 3, 1]\). - Сначала мы выполняем обмен \(2\) из входных данных, т.е. \((2, 1)\), \(p\) становится \([3, 2, 4, 1]\).
- Затем мы выполняем обмен \(3\) из входных данных, т.е. \((1, 3)\), \(p\) становится \([4, 2, 3, 1]\).
- Наконец, мы выполняем обмен \(1\) из входных данных, т.е. \((1, 4)\) и \(p\) становится \([1, 2, 3, 4]\), что является отсортированным.
Во втором примере \(p = [6, 5, 1, 3, 2, 4]\), \(m = 4\) и заданные обмены \([(3, 1), (2, 5), (6, 3), (6, 4)]\). Один из возможных правильных порядков обмена — \([4, 2, 1, 3]\). - Выполните обмен \(4\) из входных данных, т.е. \((6, 4)\), \(p\) становится \([6, 5, 1, 4, 2, 3]\).
- Выполните обмен \(2\) из входных данных, т.е. \((2, 5)\), \(p\) становится \([6, 2, 1, 4, 5, 3]\).
- Выполните обмен \(1\) из входных данных, т.е. \((3, 1)\), \(p\) становится \([1, 2, 6, 4, 5, 3]\).
- Выполните обмен \(3\) из входных данных, т.е. \((6, 3)\) и \(p\) становится \([1, 2, 3, 4, 5, 6]\), что является отсортированным.
Возможны и другие ответы, например, \([1, 2, 4, 3]\). | |
![]()
|
|
C. Зараженное дерево
Деревья
дп
поиск в глубину и подобное
*1600
Байтландия — прекрасная земля, известная своими красивыми деревьями. Миша нашел бинарное дерево с \(n\) вершинами, пронумерованными от \(1\) до \(n\). Бинарное дерево — это ациклический связный неориентированный граф, содержащий \(n\) вершин и \(n - 1\) ребер. Каждая вершина имеет степень не больше \(3\), а корнем является вершина с номером \(1\) и имеет степень не больше \(2\). К сожалению, корень дерева был заражен. Следующий процесс происходит \(n\) раз: - Миша либо выбирает еще не зараженную (и не удаленную) вершину и удаляет ее со всеми ребрами, имеющими конец в этой вершине, либо ничего не делает.
- Затем заражение распространяется на каждую вершину, соединенную ребром с уже зараженной вершиной (все уже зараженные вершины остаются зараженными).
Так как Мише некогда думать, скажите ему, какое максимальное количество вершин он может спасти от заражения (обратите внимание, что удаленные вершины не считаются спасенными). Выходные данные Для каждого набора входных данных выведите единственное целое число — ответ на задачу. Примечание В первом наборе входных данных единственным возможным действием является удаление вершины \(2\), после чего мы спасли \(0\) вершин. Во втором наборе входных данных, если мы удалим вершину \(2\), мы сможем спасти вершины \(3\) и \(4\).  | |
![]()
|
|
F. Дерево и k-подмножества
Деревья
дп
Комбинаторика
математика
поиск в глубину и подобное
*2500
Вам дано дерево \(G\) из \(n\) вершин, а также целое число \(k\). Вершины дерева пронумерованы от \(1\) до \(n\). Для некоторой вершины \(r\) и подмножества \(S\) вершин дерева \(G\) такого, что \(|S| = k\), определим \(f(r, S)\) как размер наименьшего корневого поддерева, содержащего все вершины \(S\) при условии, что корнем дерева является вершина \(r\). Множество вершин \(T\) называется корневым поддеревом, если все вершины в \(T\) связны и для любой вершины в \(T\) все ее потомки тоже принадлежат \(T\). Вам нужно вычислить сумму \(f(r, S)\) по всем различным комбинациям вершины \(r\) и подмножества \(S\), где \(|S| = k\). Формально, вычислите следующее: \(\)\sum_{r \in V} \sum_{S \subseteq V, |S| = k} f(r, S),\(\) где \(V\) — множество вершин дерева \(G\). Выведите ответ по модулю \(10^9 + 7\). Выходные данные Выведите ответ по модулю \(10^9 + 7\). Примечание Дерево во втором примере показано ниже:  Всего в этом дереве \(21\) подмножество вершин размера \(2\). А именно, \(\)S \in \left\{\{1, 2\}, \{1, 3\}, \{1, 4\}, \{1, 5\}, \{1, 6\}, \{1, 7\}, \{2, 3\}, \{2, 4\}, \{2, 5\}, \{2, 6\}, \{2, 7\}, \{3, 4\}, \{3, 5\}, \{3, 6\}, \{3, 7\}, \{4, 5\}, \{4, 6\}, \{4, 7\}, \{5, 6\}, \{5, 7\}, \{6, 7\} \right\}.\(\) Так как в дереве \(7\) вершин, \(1 \le r \le 7\). Нужно найти сумму \(f(r, S)\) по всем парам \(r\) и \(S\). Ниже перечислены значения \(f(r, S)\) для некоторых комбинаций \(r\) и \(S\). - \(r = 1\), \(S = \{3, 7\}\). Значение \(f(r, S)\) равно \(5\), а соответствующее поддерево равно \(\{2, 3, 4, 6, 7\}\).
- \(r = 1\), \(S = \{5, 4\}\). Значение \(f(r, S)\) равно \(7\), а соответствующее поддерево равно \(\{1, 2, 3, 4, 5, 6, 7\}\).
- \(r = 1\), \(S = \{4, 6\}\). Значение \(f(r, S)\) равно \(3\), а соответствующее поддерево равно \(\{4, 6, 7\}\).
| |
![]()
|
|
B. Фейковые пластиковые деревья
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
*1700
Нам дано корневое дерево, состоящее из \(n\) вершин, пронумерованных от \(1\) до \(n\). Корнем дерева является вершина \(1\), а родителем вершины \(v\) является \(p_v\). В каждой вершине записано число, изначально все числа равны \(0\). Обозначим число, записанное в вершине \(v\), как \(a_v\). Для каждой \(v\) мы хотим, чтобы \(a_v\) находилось между \(l_v\) и \(r_v\) \((l_v \leq a_v \leq r_v)\). За одну операцию мы делаем следующее: - Выбираем некоторую вершину \(v\). Пусть \(b_1, b_2, \ldots, b_k\) — вершины на пути от вершины \(1\) до вершины \(v\) (то есть \(b_1 = 1\), \(b_k = v\) и \(b_i = p_{b_{i + 1}}\)).
- Выберем неубывающий массив \(c\) длины \(k\) из неотрицательных целых чисел: \(0 \leq c_1 \leq c_2 \leq \ldots \leq c_k\).
- Для каждого \(i\) \((1 \leq i \leq k)\), увеличим \(a_{b_i}\) на \(c_i\).
Какое минимальное количество операций необходимо для достижения нашей цели? Выходные данные Для каждого набора входных данных выведите минимально необходимое количество операций. Примечание В первом наборе входных данных мы можем достичь цели с помощью одной операции: выбрать \(v = 2\) и \(c = [1, 2]\), в результате чего \(a_1 = 1, a_2 = 2\). Во втором наборе входных данных мы можем достичь цели с помощью двух операций: сначала выбираем \(v = 2\) и \(c = [3, 3]\), в результате чего \(a_1 = 3, a_2 = 3, a_3 = 0\). Затем выбираем \(v = 3, c = [2, 7]\), в результате \(a_1 = 5, a_2 = 3, a_3 = 7\). | |
![]()
|
|
D1. Запросы в дереве (простая версия)
Деревья
дп
жадные алгоритмы
Конструктив
Перебор
поиск в глубину и подобное
*2200
Единственное отличие этой задачи от D2 — ограничение на размер дерева. Вам дано некорневое дерево с \(n\) вершинами. В этом дереве есть некоторая скрытая вершина \(x\), которую вы пытаетесь найти. Для этого вы можете задать \(k\) запросов \(v_1, v_2, \ldots, v_k\), где \(v_i\) — вершины дерева. После того, как вы закончили задавать все запросы, вам дается \(k\) чисел \(d_1, d_2, \ldots, d_k\), где \(d_i\) — количество ребер на кратчайшем пути между \(v_i\) и \(x\). Обратите внимание, что вы знаете, какое расстояние соответствует какому запросу. Найдите минимальное \(k\), при котором существуют некоторые запросы \(v_1, v_2, \ldots, v_k\), позволяющие всегда однозначно определить \(x\) (независимо от того, какой \(x\) выбран). Обратите внимание, что выводить эти запросы не нужно. Выходные данные Для каждого набора входных данных выведите в отдельной строке одно целое неотрицательное число — минимальное количество запросов, которое вам необходимо. Примечание В первом наборе входных данных есть только одна вершина, поэтому никаких запросов не требуется. Во втором наборе входных данных достаточно задать единственный запрос о вершине \(1\). Тогда, если \(x = 1\), вы получите \(0\), в противном случае — \(1\). | |
![]()
|
|
D2. Запросы в дереве (сложная версия)
Деревья
дп
жадные алгоритмы
Конструктив
поиск в глубину и подобное
*2300
Единственное отличие этой задачи от D1 — ограничение на размер дерева. Вам дано некорневое дерево с \(n\) вершинами. В этом дереве есть некоторая скрытая вершина \(x\), которую вы пытаетесь найти. Для этого вы можете задать \(k\) запросов \(v_1, v_2, \ldots, v_k\), где \(v_i\) — вершины дерева. После того, как вы закончили задавать все запросы, вам дается \(k\) чисел \(d_1, d_2, \ldots, d_k\), где \(d_i\) — количество ребер на кратчайшем пути между \(v_i\) и \(x\). Обратите внимание, что вы знаете, какое расстояние соответствует какому запросу. Найдите минимальное \(k\), при котором существуют некоторые запросы \(v_1, v_2, \ldots, v_k\), позволяющие всегда однозначно определить \(x\) (независимо от того, какой \(x\) выбран). Обратите внимание, что выводить эти запросы не нужно. Выходные данные Для каждого набора входных данных выведите в отдельной строке одно целое неотрицательное число — минимальное количество запросов, которое вам необходимо. Примечание В первом наборе входных данных есть только одна вершина, поэтому никаких запросов не требуется. Во втором наборе входных данных достаточно задать единственный запрос о вершине \(1\). Тогда, если \(x = 1\), вы получите \(0\), в противном случае — \(1\). | |
![]()
|
|
F. Восстановление дерева
графы
Деревья
Конструктив
Перебор
поиск в глубину и подобное
снм
*2600
Fishingprince любит деревья. Дерево — это связный неориентированный граф без циклов. У Fishingprince'а есть дерево на \(n\) вершинах. Его вершины пронумерованы числами от \(1\) до \(n\). Пусть \(d(x,y)\) равно длине кратчайшего расстояния между вершинами \(x\) и \(y\), если считать длину каждого ребра равной \(1\). К сожалению, Fishingprince потерял своё дерево. Тем не менее какая-то информация о нём сохранилась. А именно, для каждой тройки чисел \(x,y,z\) (\(1\le x<y\le n\), \(1\le z\le n\)) известно, выполнено ли равенство \(d(x,z)=d(y,z)\). Помогите ему восстановить структуру дерева или сообщите, что дерева, удовлетворяющего всем ограничениям, не существует. Выходные данные Для каждого набора входных данных: - выведите No, если искомого дерева не существует;
- иначе в первой строке выведите Yes. Затем выведите \(n-1\) строк. Каждая из них должна содержать два целых числа \(x,y\) (\(1\le x,y\le n\)), означающих ребро между вершинами \(x\) и \(y\) в дереве. Если существуют несколько решений, выведите любое из них.
При выводе Yes и No вы можете выводить каждый символ в любом регистре (верхнем или нижнем). | |
![]()
|
|
E. PermutationForces II
Деревья
жадные алгоритмы
Комбинаторика
Перебор
сортировки
*2300
Вам дана перестановка \(a\) длины \(n\). Напомним, что перестановкой называется массив из \(n\) различных чисел от \(1\) до \(n\) в произвольном порядке. Ваша сила равна \(s\). Вы можете выполнить \(n\) операций с перестановкой \(a\). \(i\)-я операция состоит в следующем: - Выберите два значения \(x\) и \(y\) такие, что \(i \leq x \leq y \leq \min(i+s,n)\), и поменяйте местами числа \(x\) и \(y\) в перестановке \(a\). Обратите внимание, что вы можете выбрать \(x=y\), в таком случае обмена не произойдет.
Вы хотите превратить \(a\) в другую перестановку \(b\) после \(n\) операций. Однако некоторые элементы \(b\) отсутствуют и заменены на \(-1\). Вычислите количество способов заменить каждую \(-1\) в \(b\) на некоторое целое число от \(1\) до \(n\) так, чтобы \(b\) была перестановкой, и можно было превратить \(a\) в \(b\) силой \(s\). Так как ответ может быть большим, выведите его по модулю \(998\,244\,353\). Выходные данные Для каждого набора входных данных выведите одно целое число — количество способов достроить перестановку \(b\) так, чтобы можно было превратить \(a\) в \(b\) силой \(s\), по модулю \(998\,244\,353\). Примечание В первом примере \(a=[2,1,3]\). Существуют два способа заменить \(-1\), чтобы \(b\) стала перестановкой: \([3,1,2]\) и \([3,2,1]\). Перестановку \(a\) можно превратить в \([3,1,2]\) силой \(1\) следующим образом: \(\)[2,1,3] \xrightarrow[x=1,\,y=1]{} [2,1,3] \xrightarrow[x=2,\,y=3]{} [3,1,2] \xrightarrow[x=3,\,y=3]{} [3,1,2].\(\) Можно показать, что невозможно превратить \([2,1,3]\) в \([3,2,1]\) силой \(1\). Поэтому только одна перестановка \(b\) подходит, поэтому ответ \(1\). Во втором примере \(a\) и \(b\) такие же, как в предыдущем примере, но теперь у нас сила \(2\). Перестановку \(a\) можно превратить в \([3,2,1]\) силой \(2\) следующим образом: \(\)[2,1,3] \xrightarrow[x=1,\,y=3]{} [2,3,1] \xrightarrow[x=2,\,y=3]{} [3,2,1] \xrightarrow[x=3,\,y=3]{} [3,2,1].\(\) Можно также превратить \(a\) в \([3,1,2]\) используя силу \(1\) как раньше, поэтому ответ \(2\). В третьем примере есть только одна перестановка \(b\). Можно показать, что невозможно превратить \(a\) в \(b\), поэтому ответ \(0\). | |
![]()
|
|
G1. Проходимые пути (простая версия)
Деревья
поиск в глубину и подобное
*1900
Это простая версия задачи. Единственное различие простой и сложной версии в количестве запросов. Поликарп вырастил дерево из \(n\) вершин. Напоминаем, что деревом из \(n\) вершин называется неориентированный связный граф из \(n\) вершин и \(n-1\) ребра, не содержащий циклов. Он называет множество вершин проходимым, если существует такой путь в дереве, который проходит через каждую вершину этого множества, не проходя по какому-либо ребру дважды. Путь может посещать другие вершины (не из этого множества). Иными словами, множество вершин называется проходимым, если существует простой путь, который проходит по всем вершинам этого множества (и, возможно, каким-то другим). Например для дерева ниже множества \(\{3, 2, 5\}\), \(\{1, 5, 4\}\), \(\{1, 4\}\) проходимы, а \(\{1, 3, 5\}\), \(\{1, 2, 3, 4, 5\}\) — нет.  Поликарп просит вас ответить на \(q\) запросов. Каждый запрос является множеством вершин. Для каждого запроса вам необходимо определить проходимо ли соответствующее множество вершин. Выходные данные Выведите \(q\) строк, каждая из которых содержит ответ на соответствующий запрос. В качестве ответа выведите «YES», если множество проходимо, и «NO» в противном случае. Вы можете выводить ответ в любом регистре (например, строки «yEs», «yes», «Yes» и «YES» будут распознаны как положительный ответ). | |
![]()
|
|
G2. Проходимые пути (сложная версия)
Деревья
поиск в глубину и подобное
Структуры данных
*2000
Это сложная версия задачи. Единственное различие простой и сложной версии в количестве запросов. Поликарп вырастил дерево из \(n\) вершин. Напоминаем, что деревом из \(n\) вершин называется неориентированный связный граф из \(n\) вершин и \(n-1\) ребра, не содержащий циклов. Он называет множество вершин проходимым, если существует такой путь в дереве, который проходит через каждую вершину этого множества, не проходя по какому-либо ребру дважды. Путь может посещать другие вершины (не из этого множества). Иными словами, множество вершин называется проходимым, если существует простой путь, который проходит по всем вершинам этого множества (и, возможно, каким-то другим). Например для дерева ниже множества \(\{3, 2, 5\}\), \(\{1, 5, 4\}\), \(\{1, 4\}\) проходимы, а \(\{1, 3, 5\}\), \(\{1, 2, 3, 4, 5\}\) — нет.  Поликарп просит вас ответить на \(q\) запросов. Каждый запрос является множеством вершин. Для каждого запроса вам необходимо определить проходимо ли соответствующее множество вершин. Выходные данные Выведите \(q\) строк, каждая из которых содержит ответ на соответствующий запрос. В качестве ответа выведите «YES», если множество проходимо, и «NO» в противном случае. Вы можете выводить ответ в любом регистре (например, строки «yEs», «yes», «Yes» и «YES» будут распознаны как положительный ответ). | |
![]()
|
|
E. Qpwoeirut и вершины
Бинарный поиск
Деревья
жадные алгоритмы
поиск в глубину и подобное
разделяй и властвуй
снм
Структуры данных
*2300
Вам дан связный неориентированный граф из \(n\) вершин и \(m\) рёбер. Вершины графа пронумерованы целыми числами от \(1\) до \(n\), а рёбра графа пронумерованы целыми числами от \(1\) до \(m\). Вам предстоит ответить на \(q\) запросов, каждый из которых состоит из двух чисел \(l\) и \(r\). Ответом на запрос является наименьшее неотрицательное число \(k\), для которого выполняется следующее условие: - для всех пар чисел \((a, b)\) таких, что \(l\le a\le b\le r\), вершины \(a\) и \(b\) достижимы друг из друга по пути, проходящему только по первым \(k\) рёбрам (то есть в пути могут встречаться только рёбра \(1, 2, \ldots, k\)).
Выходные данные Для каждого набора входных данных выведите \(q\) чисел — ответы на запросы. Примечание  Граф из первого набора входных данных. Около ребра записан его номер. Граф из первого набора входных данных. Около ребра записан его номер. В первом наборе входных данных граф состоит из \(2\) вершин и одного ребра между вершинами \(1\) и \(2\). В первом запросе \(l=1\) и \(r=1\). Вершина достижима сама из себя без использования рёбер, поэтому ответ на этот запрос равен \(0\). Во втором запросе \(l=1\) и \(r=2\). Вершины \(1\) и \(2\) достижимы друг из друга по пути \(1 \longleftrightarrow 2\), состоящему только из первого ребра. В то же время невозможно добраться из вершины \(1\) до вершины \(2\), используя только первые \(0\) рёбер. Поэтому ответ на запрос равен \(1\).  Граф из второго набора входных данных. Около рёбер записаны их номера. Граф из второго набора входных данных. Около рёбер записаны их номера. Во втором наборе входных данных граф состоит из \(5\) вершин и \(5\) рёбер. В первом запросе \(l=1\) и \(r=4\). Чтобы выполнить требуемое условие, достаточно использовать первые \(3\) ребра: - Вершины \(1\) и \(2\) достижимы друг из друга по пути \(1 \longleftrightarrow 2\) (состоящему из ребра \(1\)).
- Вершины \(1\) и \(3\) достижимы друг из друга по пути \(1 \longleftrightarrow 3\) (состоящему из ребра \(2\)).
- Вершины \(1\) и \(4\) достижимы друг из друга по пути \(1 \longleftrightarrow 2 \longleftrightarrow 4\) (состоящему из рёбер \(1\) и \(3\)).
- Вершины \(2\) и \(3\) достижимы друг из друга по пути \(2 \longleftrightarrow 1 \longleftrightarrow 3\) (состоящему из рёбер \(1\) и \(2\)).
- Вершины \(2\) и \(4\) достижимы друг из друга по пути \(2 \longleftrightarrow 4\) (состоящему из ребра \(3\)).
- Вершины \(3\) и \(4\) достижимы друг из друга по пути \(3 \longleftrightarrow 1 \longleftrightarrow 2 \longleftrightarrow 4\) (состоящему из рёбер \(2\), \(1\) и \(3\)).
Невозможно выполнить требуемое условие, используя меньше \(3\) первых рёбер. Например, при использовании \(2\) рёбер, невозможно добраться из вершины \(1\) в вершину \(4\). Поэтому ответ на запрос равен \(3\). Во втором запросе \(l=3\) и \(r=4\). Вершины \(3\) и \(4\) достижимы друг из друга по пути \(3 \longleftrightarrow 1 \longleftrightarrow 2 \longleftrightarrow 4\) (состоящему из рёбер \(2\), \(1\) и \(3\)). При использовании меньшего числа первых рёбер вершины \(3\) и \(4\) не будут достижимы друг из друга. | |
![]()
|
|
C. Деревья поиска в глубину
графы
Деревья
жадные алгоритмы
поиск в глубину и подобное
снм
сортировки
*2400
Вам дан связный неориентированный граф из \(n\) вершин и \(m\) рёбер. Вес \(i\)-го ребра равен \(i\). Ниже представлен некорректный алгоритм поиска минимального остовного дерева:
vis := массив длины n
s := множество рёбер
function dfs(u):
vis[u] := true
пройтись по каждому ребру (u, v) в порядке увеличения весов
if vis[v] = false
добавить ребро (u, v) в множество (s)
dfs(v)
function findMST(u):
установить все элементы (vis) в false
очистить множество (s)
dfs(u)
return множество (s)
Любой из вызовов функций findMST(1), findMST(2), ..., findMST(n) возвращает вам остовное дерево графа. Определите, какие из этих деревьев являются минимальными остовными деревьями. Выходные данные Выведите строку \(s\), состоящую из нулей и единиц, где \(s_i=1\), если findMST(i) возвращает минимальное остовное дерево, и \(s_i = 0\) иначе. Примечание Ниже показан граф из первого примера:  В этом графе существует только одно минимальное остовное дерево, состоящее из ребер \((1,2),(3,5),(1,3),(2,4)\), имеющих суммарный вес \(1+2+3+5=11\). Ниже описана часть вычислений при вызове findMST(1): - реинициализируем массив vis и множество ребер s;
- вызываем dfs(1);
- vis[1] := true;
- итерируемся по ребрам \((1,2),(1,3)\);
- добавляем ребро \((1,2)\) во множество s, вызываем dfs(2):
- vis[2] := true;
- итерируемся по ребрам \((2,1),(2,3),(2,4)\);
- так как vis[1] = true, игнорируем ребро \((2,1)\);
- добавляем ребро \((2,3)\) во множество s, вызываем dfs(3):
В конце алгоритма будут выбраны ребра \((1,2),(2,3),(3,5),(2,4)\) с суммарным весом \(1+4+2+5=12>11\), поэтому findMST(1) находит не минимальное остовное дерево. Можно показать, что остальные остовные деревья являются минимальными, поэтому ответ 01111. | |
![]()
|
|
D. Частичные виртуальные деревья
Деревья
дп
Комбинаторика
математика
поиск в глубину и подобное
*3000
Каваширо Нитори — девушка, которой нравится спортивное программирование. Однажды она нашла корневое дерево из \(n\) вершин. Корень дерева был в вершине с номером \(1\). Как продвинутый автор, она сразу придумала задачу. У Каваширо Нитори есть множество вершин \(U=\{1,2,\ldots,n\}\). За одну операцию она будет выбирать множество вершин \(T\), где \(T\) является частичным виртуальным деревом множества \(U\), и заменять множество \(U\) на \(T\). Множество вершин \(S_1\) называется частичным виртуальным деревом множества вершин \(S_2\), если \(S_1\) — подмножество \(S_2\), \(S_1 \neq S_2\) и для любых пар вершин \(i\) и \(j\) из \(S_1\) \(\operatorname{LCA}(i,j)\) лежит внутри \(S_1\), где \(\operatorname{LCA}(x,y)\) обозначает наименьшего общего предка вершин \(x\) и \(y\) в дереве. Обратите внимание, что множество вершин может иметь много различных частичных виртуальных деревьев. Каваширо Нитори хочет узнать для каждого возможного \(k\), если применить операцию строго \(k\) раз, сколькими способами она может получить \(U=\{1\}\) в конце? Два способа считаются различными, если существует целое число \(z\) (\(1 \le z \le k\)) такое, что после \(z\) операций множества \(U\) различаются. Так как ответ может быть большим, найдите его по модулю \(p\). Гарантируется, что \(p\) — простое число. Выходные данные Выведите единственную строку, состоящую из \(n-1\) целых чисел — ответ по модулю \(p\) для всех \(k=1,2,\ldots,n-1\). Примечание В первом примере при \(k=1\) единственный возможный способ следующий: - \(\{1,2,3,4\} \to \{1\}\).
При \(k=2\) существуют \(6\) способов: - \(\{1,2,3,4\} \to \{1,2\} \to \{1\}\);
- \(\{1,2,3,4\} \to \{1,2,3\} \to \{1\}\);
- \(\{1,2,3,4\} \to \{1,2,4\} \to \{1\}\);
- \(\{1,2,3,4\} \to \{1,3\} \to \{1\}\);
- \(\{1,2,3,4\} \to \{1,3,4\} \to \{1\}\);
- \(\{1,2,3,4\} \to \{1,4\} \to \{1\}\).
При \(k=3\) существуют \(6\) возможных способов: - \(\{1,2,3,4\} \to \{1,2,3\} \to \{1,2\} \to \{1\}\);
- \(\{1,2,3,4\} \to \{1,2,3\} \to \{1,3\} \to \{1\}\);
- \(\{1,2,3,4\} \to \{1,2,4\} \to \{1,2\} \to \{1\}\);
- \(\{1,2,3,4\} \to \{1,2,4\} \to \{1,4\} \to \{1\}\);
- \(\{1,2,3,4\} \to \{1,3,4\} \to \{1,3\} \to \{1\}\);
- \(\{1,2,3,4\} \to \{1,3,4\} \to \{1,4\} \to \{1\}\).
| |
![]()
|
|
E. XOR дерево
битмаски
Деревья
жадные алгоритмы
поиск в глубину и подобное
снм
Структуры данных
*2400
Дано дерево из \(n\) вершин. На каждой вершине дерева записано число; на \(i\)-й вершине записано число \(a_i\). Напомним, что простой путь — это путь, посещающий каждую вершину не более одного раза. Назовем весом пути побитовое исключающее ИЛИ значений записанных на его вершинах. Скажем, что дерево хорошее, если в нем не существует ни одного простого пути с весом \(0\). Вы можете применить следующую операцию произвольное количество раз (возможно, ноль): выбрать вершину дерева и заменить значение записанное на ней на произвольное положительное целое число. Какое минимальное количество раз необходимо применить данную операцию, чтобы дерево стало хорошим? Выходные данные Выведите одно целое число — минимальное количество раз, которое необходимо применить операцию, чтобы дерево стало хорошим. Примечание В первом примере можно заменить значение на вершине \(1\) на \(13\), а значение на вершине \(4\) — на \(42\). | |
![]()
|
|
F. Мультимножество строк
meet-in-the-middle
битмаски
бпф
графы
Деревья
дп
математика
Перебор
Потоки
*2500
Вам даны три целых числа \(n\), \(k\) и \(f\). Рассмотрим все бинарные строки (то есть все строки, состоящие из символов \(0\) и/или \(1\)) длины от \(1\) до \(n\). Для каждой такой строки \(s\) вы должны выбрать целое число \(c_s\) от \(0\) до \(k\). Мультимножество из бинарных строк длины ровно \(n\) считается красивым, если для каждой бинарной строки \(s\) длины от \(1\) до \(n\) выполняется следующее: количество строк в мультимножестве, для которых \(s\) является префиксом, не превосходит \(c_s\). Например, пусть \(n = 2\), \(c_{0} = 3\), \(c_{00} = 1\), \(c_{01} = 2\), \(c_{1} = 1\), \(c_{10} = 2\) и \(c_{11} = 3\). Мультимножество строк \(\{11, 01, 00, 01\}\) является красивым, так как: - для строки \(0\) существует \(3\) строки из мультимножества, для которых \(0\) — префикс, и \(3 \le c_0\);
- для строки \(00\) существует одна строка из мультимножества, для которой \(00\) — префикс, и \(1 \le c_{00}\);
- для строки \(01\) существует \(2\) строки из мультимножества, для которых \(01\) — префикс, и \(2 \le c_{01}\);
- для строки \(1\) существует одна строка из мультимножества, для которой \(1\) — префикс, и \(1 \le c_1\);
- для строки \(10\) существует \(0\) строк из мультимножества, для которых \(10\) — префикс, и \(0 \le c_{10}\);
- для строки \(11\) существует одна строка из мультимножества, для которой \(11\) — префикс, и \(1 \le c_{11}\).
А теперь — сама задача. Вы должны посчитать количество способов выбрать числа \(c_s\) для всех бинарных строк \(s\) длины от \(1\) до \(n\) таким образом, чтобы максимальный возможный размер красивого мультимножества был равен ровно \(f\). Выходные данные Выведите одно целое число — количество способов выбрать числа \(c_s\) для всех бинарных строк \(s\) длины от \(1\) до \(n\) таким образом, чтобы максимальный возможный размер красивого мультимножества был равен ровно \(f\). Так как ответ может быть очень большим, выведите его по модулю \(998244353\). Примечание В первом примере есть три способа выбрать значения \(c_s\): - \(c_0 = 0\), \(c_1 = 2\), тогда максимальное красивое мультимножество — \(\{1, 1\}\);
- \(c_0 = 1\), \(c_1 = 1\), тогда максимальное красивое мультимножество — \(\{0, 1\}\);
- \(c_0 = 2\), \(c_1 = 0\), тогда максимальное красивое мультимножество — \(\{0, 0\}\).
| |
![]()
|
|
D. Восстановление дерева
Деревья
Конструктив
*3400
У Родокса есть дерево из \(n\) вершин, но он не помнит его структуру. Вершины дерева пронумерованы от \(1\) до \(n\). Отрезок \([l,r]\) (\(1 \leq l \leq r \leq n\)) называется хорошим, если вершины \(l\), \(l + 1\), ..., \(r\) образуют связную компоненту в дереве Родокса. Иначе отрезок называется плохим. Например, для дерева на рисунке ниже только отрезок \([3,4]\) является плохим, а все остальные отрезки хорошие.  Для каждого из \(\frac{n(n+1)}{2}\) отрезков Родокс помнит, хорошим является этот отрезок, или плохим. Можете помочь ему восстановить дерево? Если существуют несколько решений, выведите любое из них. Гарантируется, что существует хотя бы одно дерево, подходящее под описание Родокса. Выходные данные Для каждого набора входных данных выведите \(n-1\) строку, описывающую ваше дерево. В \(i\)-й из этих строк выведите два целых числа \(u_i\) и \(v_i\) (\(1 \leq u_i,v_i \leq n\)), означающие, что в дереве есть ребро между вершинами \(u_i\) и \(v_i\). Если существуют несколько решений, выведите любое из них. Примечание Первый пример объяснен в условии. Во втором примере одно из возможных деревьев следующее:  В третьем примере одно из возможных деревьев следующее:  | |
![]()
|
|
F. Триаметр
Бинарный поиск
Деревья
поиск в глубину и подобное
Структуры данных
*3200
— To count graph diameters. You and Your Submission Дерево — это неориентированный связный граф без циклов. Взвешенное дерево — это дерево, каждому ребру которого назначен некоторый вес. Степень вершины — это количество ребер, прилегающих к данной вершине. Вам дано взвешенное дерево с \(n\) вершинами, каждое ребро которого имеет вес \(1\). Определим множество вершин \(L\) следующим образом: все вершины, степень которых равна \(1\), входят в это множество, остальные вершины в это множество не входят. Вам необходимо ответить на \(q\) независимых запросов. В \(i\)-м запросе: - Вам дано целое положительное число \(x_i\).
- Для всех \(u,v \in L\) таких, что \(u < v\), добавьте ребро \((u, v)\) с весом \(x_i\) в граф (который изначально является данным вам деревом).
- Найдите диаметр итогового графа.
Диаметр графа равен \(\max\limits_{1 \le u < v \le n}{\operatorname{d}(u, v)}\), где \(\operatorname{d}(u, v)\) — это длина кратчайшего пути между вершинами \(u\) и \(v\). Выходные данные В единственной строке выведите \(q\) целых чисел, которые являются ответами на запросы. Примечание Граф в первом тесте после добавления ребер:  | |
![]()
|
|
F. Построй дерево и точка
Деревья
Конструктив
реализация
*1900
Деревом называется связный неориентированный граф без циклов. Обратите внимание, что в этой задаче речь идёт о некорневых деревьях. Заданы четыре положительных целых числа \(n, d_{12}, d_{23}\) и \(d_{31}\). Постройте такое дерево, что: - оно содержит \(n\) вершин, пронумерованных от \(1\) до \(n\),
- расстояние (длина кратчайшего пути) от вершины \(1\) до вершины \(2\) равно \(d_{12}\),
- расстояние от вершины \(2\) до вершины \(3\) равно \(d_{23}\),
- расстояние от вершины \(3\) до вершины \(1\) равно \(d_{31}\).
Выведите любое дерево, которое удовлетворяет всем требованиям выше, или определите, что такого дерева не существует. Выходные данные Для каждого набора входных данных выведите YES, если искомое дерево существует, и NO в противном случае. В случае положительного ответа выведите ещё \(n-1\) строку, каждая содержит описание ребра дерева — пару положительных целых чисел \(x_i, y_i\), которая обозначает, что \(i\)-е ребро соединяет вершины \(x_i\) и \(y_i\). Ребра и вершины ребер можно выводить в произвольном порядке. Если искомых деревьев несколько, выведите любое из них. | |
![]()
|
|
G. Префиксы путей
Бинарный поиск
Деревья
поиск в глубину и подобное
Структуры данных
*1700
Вам задано корневое дерево. Оно содержит \(n\) вершин, которые пронумерованы от \(1\) до \(n\). Корнем является вершина \(1\). У каждого ребра есть две положительных целых стоимости. Таким образом, для каждого ребра заданы два положительных целых числа \(a_j\) и \(b_j\). Выведите \(n-1\) число \(r_2, r_3, \dots, r_n\), где \(r_i\) определяется следующим образом. Рассмотрим путь из корня (вершины \(1\)) в \(i\) (\(2 \le i \le n\)). Пусть сумма стоимостей \(a_j\) вдоль этого пути равна \(A_i\). Тогда \(r_i\) равно длине максимального такого префикса этого пути, что сумма \(b_j\) вдоль этого префикса не превосходит \(A_i\).  Пример для \(n=9\). Синим цветом изображены стоимости \(a_j\), а красным изображены стоимости \(b_j\). Пример для \(n=9\). Синим цветом изображены стоимости \(a_j\), а красным изображены стоимости \(b_j\). Рассмотрим пример. В этом случае: - \(r_2=0\), так как путь до \(2\) имеет сумму по \(a_j\) равную \(5\), только префикс этого пути длины \(0\) имеет меньшую или равную сумму по \(b_j\);
- \(r_3=3\), так как путь до \(3\) имеет сумму по \(a_j\) равную \(5+9+5=19\), префикс длины \(3\) этого пути имеет сумму по \(b_j\) равную \(6+10+1=17\) (число \(17 \le 19\));
- \(r_4=1\), так как путь до \(4\) имеет сумму по \(a_j\) равную \(5+9=14\), префикс длины \(1\) этого пути имеет сумму по \(b_j\) равную \(6\) (это самый длинный подходящий префикс, так как префикс длины \(2\) уже имеет сумму по \(b_j\) равную \(6+10=16\), что больше \(14\));
- \(r_5=2\), так как путь до \(5\) имеет сумму по \(a_j\) равную \(5+9+2=16\), префикс длины \(2\) этого пути имеет сумму по \(b_j\) равную \(6+10=16\) (это самый длинный подходящий префикс, так как префикс длины \(3\) уже имеет сумму по \(b_j\) равную \(6+10+1=17\), что больше \(16\));
- \(r_6=1\), так как путь до \(6\) имеет сумму по \(a_j\) равную \(2\), префикс длины \(1\) этого пути имеет сумму по \(b_j\) равную \(1\);
- \(r_7=1\), так как путь до \(7\) имеет сумму по \(a_j\) равную \(5+3=8\), префикс длины \(1\) этого пути имеет сумму по \(b_j\) равную \(6\) (это самый длинный подходящий префикс, так как префикс длины \(2\) уже имеет сумму по \(b_j\) равную \(6+3=9\), что больше \(8\));
- \(r_8=2\), так как путь до \(8\) имеет сумму по \(a_j\) равную \(2+4=6\), префикс длины \(2\) этого пути имеет сумму по \(b_j\) равную \(1+3=4\);
- \(r_9=3\), так как путь до \(9\) имеет сумму по \(a_j\) равную \(2+4+1=7\), префикс длины \(3\) этого пути имеет сумму по \(b_j\) равную \(1+3+3=7\).
Выходные данные Для каждого набора входных данных выведите \(n-1\) целое число в одной строке: \(r_2, r_3, \dots, r_n\). Примечание Первый пример разобран в условии. Во втором примере: - \(r_2=0\), так как путь до \(2\) имеет сумму по \(a_j\) равную \(1\), только префикс этого пути длины \(0\) имеет меньшую или равную сумму по \(b_j\);
- \(r_3=0\), так как путь до \(3\) имеет сумму по \(a_j\) равную \(1+1=2\), префикс длины \(1\) этого пути имеет сумму по \(b_j\) равную \(100\) (\(100 > 2\));
- \(r_4=3\), так как путь до \(4\) имеет сумму по \(a_j\) равную \(1+1+101=103\), префикс длины \(3\) этого пути имеет сумму по \(b_j\) равную \(102\), .
| |
![]()
|
|
D. Перестановка для Бурёнки
Деревья
жадные алгоритмы
математика
Паросочетания
Структуры данных
*3300
Назовем массив \(a\) чистым, если в нем все элементы попарно различны. Например, массив \([1, 7, 9]\) — чистый, а \([1, 3, 3, 7]\) — нет, ведь \(3\) встречается в нем дважды. Чистый массив \(b\) похож на чистый массив \(c\), если их длина \(n\) одинакова, и для всех пар индексов \(l\), \(r\) таких, что \(1 \le l \le r \le n\), выполняется \(\)\operatorname{argmax}([b_l, b_{l + 1}, \ldots, b_r]) = \operatorname{argmax}([c_l, c_{l + 1}, \ldots, c_r]),\(\) где \(\operatorname{argmax}(x)\) — индекс наибольшего элемента в \(x\) (уникального для чистых массивов). Например, \(\operatorname{argmax}([3, 4, 2]) = 2\), \(\operatorname{argmax}([1337, 179, 57]) = 1\). Недавно Тоня узнал, что Бурёнке очень нравится перестановка \(p\) длины \(n\). Тоня решил обрадовать Бурёнку и подарить ей массив \(a\), похожий на \(p\). Он уже зафиксировал некоторые элементы \(a\), но ровно \(k\) элементов отсутствуют (в этих позициях сейчас \(a_i = 0\)). Гарантируется, что \(k \ge 2\). Кроме того, у Тони есть множество \(S\) из \(k - 1\) числа. Тоня понял, что для того, чтобы заполнить пропуски в массиве \(a\) ему не хватает одного числа, поэтому он решил купить его. У него есть \(q\) вариантов покупки. Тоня считает, что число \(d\) подходит ему, если можно заполнить пропуски в \(a\) числами из \(S\) и числом \(d\) так, чтобы \(a\) стал чистым массивом, похожим на \(p\). Для каждого варианта покупки числа \(d\) выведите, подходит ли Тоне это число или нет. Входные данные В первой строке находится единственное целое число \(t\) (\(1 \le t \le 10^4\)) — количество наборов входных данных. Далее следует описание наборов входных данных. В первой строке каждого набора входных данных содержится два целых числа \(n\) и \(q\) (\(1 \le n, q \le 3 \cdot 10^5\)) — длина перестановки и количество вариантов покупки. Во второй строке каждого набора входных данных содержатся \(n\) различных целых чисел \(p_1, p_2, \ldots, p_n\) (\(1 \le p_i \le n\)) — перестановка, которая нравится Бурёнке. В третьей строке каждого набора входных данных содержатся \(n\) целых чисел \(a_1, a_2, \ldots, a_n\) (\(0 \le a_i \le 10^6\)) — элементы массива, где \(0\) означает место, которое нужно заполнить. Гарантируется, что существуют два индекса \(i, j\) \((1 \le i, j \le n, i \ne j)\) такие, что \(a_i = 0, a_j = 0\) из чего следует, что \(k \geq 2\). В четвертой строке каждого набора входных данных содержится \(k - 1\) число \(s_1, s_2, \ldots, s_{k-1}\) (\(1 \le s_i \le 10^6\)) — числа, которые есть у Тони во множестве \(S\). Каждая из следующих \(q\) строк содержит одно целое число \(d\) (\(1 \le d \le 10^6\)) – число, которое планирует купить Тоня. Гарантируется, что для каждого данного \(d\) существует способ заполнить пропуски в \(a\) числами из \(S\) и числом \(d\) так, чтобы получить чистый массив. Гарантируется, что сумма \(n\) и сумма \(q\) по всем тестам не превосходят \(3 \cdot 10^5\). Выходные данные Для каждого набора входных данных выведите \(q\) строк. Для каждого значения \(d\) выведите «YES», если существует способ заполнить массив \(a\), сделав его похожим на \(p\), и «NO» в противном случае. Примечание В первом наборе входных данных для \(d = 9\) можно получить \(a = [5, 9, 7, 6]\), можно доказать, что такое \(a\) похоже на \(p\), для \(d=1\) и \(d=4\) можно доказать, что ответа не существует. Во втором наборе входных данных для \(d = 1\) можно получить \(a = [1, 5, 10, 9, 3]\), для \(d = 8\) можно получить \(a = [3, 5, 10, 9, 8]\), можно доказать, что для \(d = 11\) ответа не существует. | |
![]()
|
|
D1. Xor-подпоследовательность (простая версия)
битмаски
Деревья
дп
Перебор
Строки
*1800
Это простая версия задачи. Единственное различие состоит в том, что в этой версии \(a_i \le 200\). Дан массив из \(n\) целых чисел \(a_0, a_1, a_2, \ldots a_{n - 1}\). Бряп захотел найти в данном массиве самую длинную хорошую подпоследовательность. Массив \(b = [b_0, b_1, \ldots, b_{m-1}]\), где \(0 \le b_0 < b_1 < \ldots < b_{m - 1} < n\), будем называть подпоследовательностью длины \(m\) массива \(a\). Подпоследовательность \(b = [b_0, b_1, \ldots, b_{m-1}]\) длины \(m\) называется хорошей, если выполняется следующее условие: - Для любого целого числа \(p\) (\(0 \le p < m - 1\)) выполняется условие: \(a_{b_p} \oplus b_{p+1} < a_{b_{p+1}} \oplus b_p\).
Здесь \(a \oplus b\) обозначает побитовое исключающее ИЛИ чисел \(a\) и \(b\). Например, \(2 \oplus 4 = 6\), а \(3 \oplus 1=2\). Так как Бряп не очень любознательная персона, он хочет знать лишь длину такой подпоследовательности. Помогите ему найти ответ на данную задачу. Выходные данные Для каждого набора входных данных единственное число — максимальную длину хорошей подпоследовательности. Примечание В первом наборе входных данных в качестве подпоследовательности мы можем выбрать оба элемента массива, так как \(1 \oplus 1 < 2 \oplus 0\). Во втором наборе входных данных мы можем взять элементы с индексами \(1\), \(2\) и \(4\) (в \(0\)-нумерации). Для них выполняется: \(2 \oplus 2 < 4 \oplus 1\) и \(4 \oplus 4 < 1 \oplus 2\). | |
![]()
|
|
D2. Xor-подпоследовательность (сложная версия)
битмаски
Деревья
дп
Строки
Структуры данных
*2400
Это сложная версия задачи. Единственное различие состоит в том, что в этой версии \(a_i \le 10^9\). Дан массив из \(n\) целых чисел \(a_0, a_1, a_2, \ldots a_{n - 1}\). Бряп захотел найти в данном массиве самую длинную хорошую подпоследовательность. Массив \(b = [b_0, b_1, \ldots, b_{m-1}]\), где \(0 \le b_0 < b_1 < \ldots < b_{m - 1} < n\), будем называть подпоследовательностью длины \(m\) массива \(a\). Подпоследовательность \(b = [b_0, b_1, \ldots, b_{m-1}]\) длины \(m\) называется хорошей, если выполняется следующее условие: - Для любого целого числа \(p\) (\(0 \le p < m - 1\)) выполняется условие: \(a_{b_p} \oplus b_{p+1} < a_{b_{p+1}} \oplus b_p\).
Здесь \(a \oplus b\) обозначает побитовое исключающее ИЛИ чисел \(a\) и \(b\). Например, \(2 \oplus 4 = 6\), а \(3 \oplus 1=2\). Так как Бряп не очень любознательная персона, он хочет знать лишь длину такой подпоследовательности. Помогите ему найти ответ на данную задачу. Выходные данные Для каждого набора входных данных единственное число — максимальную длину хорошей подпоследовательности. Примечание В первом наборе входных данных в качестве подпоследовательности мы можем выбрать оба элемента массива, так как \(1 \oplus 1 < 2 \oplus 0\). Во втором наборе входных данных мы можем взять элементы с индексами \(1\), \(2\) и \(4\) (в \(0\) нумерации). Для них выполняется: \(2 \oplus 2 < 4 \oplus 1\) и \(4 \oplus 4 < 1 \oplus 2\). | |
![]()
|
|
E. Запросы про префикс функцию
Деревья
дп
поиск в глубину и подобное
Строки
строковые суфф. структуры
хэши
*2200
Задана строка \(s\), состоящая из строчных латинских букв. К ней приходят \(q\) запросов: дана другая строка \(t\), состоящая из строчных латинских букв; проделайте следующие шаги: - склеить \(s\) и \(t\);
- посчитать префикс-функцию полученной строки \(s+t\);
- выведите значения префикс-функции на позициях \(|s|+1, |s|+2, \dots, |s|+|t|\) (\(|s|\) и \(|t|\) — это длины строк \(s\) и \(t\), соответственно);
- вернуть строку обратно к \(s\).
Префикс-функция строки \(a\) — это последовательность \(p_1, p_2, \dots, p_{|a|}\), где \(p_i\) — это наибольшее значение \(k\) такое, что \(k < i\) и \(a[1..k]=a[i-k+1..i]\) (\(a[l..r]\) обозначает непрерывную подстроку строку \(a\) с позиции \(l\) до позиции \(r\) включительно). Другими словами, это наибольший собственный префикс строки \(a[1..i]\), который равен ее суффиксу такой же длины. Выходные данные На каждый запрос выведите значения префикс-функции строки \(s+t\) на позициях \(|s|+1, |s|+2, \dots, |s|+|t|\). | |
![]()
|
|
E. Electrical Efficiency
Деревья
дп
Комбинаторика
математика
Структуры данных
теория чисел
*2500
In the country of Dengkleknesia, there are \(N\) factories numbered from \(1\) to \(N\). Factory \(i\) has an electrical coefficient of \(A_i\). There are also \(N-1\) power lines with the \(j\)-th power line connecting factory \(U_j\) and factory \(V_j\). It can be guaranteed that each factory in Dengkleknesia is connected to all other factories in Dengkleknesia through one or more power lines. In other words, the collection of factories forms a tree. Each pair of different factories in Dengkleknesia can use one or more existing power lines to transfer electricity to each other. However, each power line needs to be turned on first so that electricity can pass through it. Define \(f(x, y, z)\) as the minimum number of power lines that need to be turned on so that factory \(x\) can make electrical transfers to factory \(y\) and factory \(z\). Also define \(g(x, y, z)\) as the number of distinct prime factors of \(\text{GCD}(A_x, A_y, A_z)\). To measure the electrical efficiency, you must find the sum of \(f(x, y, z) \times g(x, y, z)\) for all combinations of \((x, y, z)\) such that \(1 \leq x < y < z \leq N\). Because the answer can be very large, you just need to output the answer modulo \(998\,244\,353\). Note: \(\text{GCD}(k_1, k_2, k_3)\) is the greatest common divisor of \(k_1\), \(k_2\), and \(k_3\), which is the biggest integer that simultaneously divides \(k_1\), \(k_2\), and \(k_3\). Output An integer representing the sum of \(f(x, y, z) \times g(x, y, z)\) for all combinations of \((x, y, z)\) such that \(1 \leq x < y < z \leq N\), modulo \(998\,244\,353\) Note In the first example, the only \((x, y, z)\) possible is \((1, 2, 3)\). Because \(\text{GCD}(A_1, A_2, A_3) = \text{GCD}(1, 2, 3) = 1\) has \(0\) distinct prime factors, therefore \(f(x, y, z) \times g(x, y, z) = 2 \times 0 = 0\). In the second example, all triples \((x, y, z)\) that satisfy the condition are as follows: - \((1, 2, 3) \rightarrow f(1, 2, 3) \times g(1, 2, 3) = 2 \times 1 = 2\)
- \((1, 2, 4) \rightarrow f(1, 2, 4) \times g(1, 2, 4) = 2 \times 1 = 2\)
- \((1, 3, 4) \rightarrow f(1, 3, 4) \times g(1, 3, 4) = 3 \times 2 = 6\)
- \((2, 3, 4) \rightarrow f(2, 3, 4) \times g(2, 3, 4) = 2 \times 1 = 2\)
So the electrical efficiency is \(2 + 2 + 6 + 2 = 12\). | |
![]()
|
|
I. Imitating the Key Tree
Деревья
Комбинаторика
снм
*2800
Pak Chanek has a tree called the key tree. This tree consists of \(N\) vertices and \(N-1\) edges. The edges of the tree are numbered from \(1\) to \(N-1\) with edge \(i\) connecting vertices \(U_i\) and \(V_i\). Initially, each edge of the key tree does not have a weight. Formally, a path with length \(k\) in a graph is a sequence \([v_1, e_1, v_2, e_2, v_3, e_3, \ldots, v_k, e_k, v_{k+1}]\) such that: - For each \(i\), \(v_i\) is a vertex and \(e_i\) is an edge.
- For each \(i\), \(e_i\) connects vertices \(v_i\) and \(v_{i+1}\).
A circuit is a path that starts and ends on the same vertex. A path in a graph is said to be simple if and only if the path does not use the same edge more than once. Note that a simple path can use the same vertex more than once. The cost of a simple path in a weighted graph is defined as the maximum weight of all edges it traverses. Count the number of distinct undirected weighted graphs that satisfy the following conditions: - The graph has \(N\) vertices and \(2N-2\) edges.
- For each pair of different vertices \((x, y)\), there exists a simple circuit that goes through vertices \(x\) and \(y\) in the graph.
- The weight of each edge in the graph is an integer between \(1\) and \(2N-2\) inclusive. Each edge has distinct weights.
- The graph is formed in a way such that there is a way to assign a weight \(W_i\) to each edge \(i\) in the key tree that satisfies the following conditions:
- For each pair of edges \((i, j)\), if \(i<j\), then \(W_i<W_j\).
- For each pair of different vertex indices \((x, y)\), the cost of the only simple path from vertex \(x\) to \(y\) in the key tree is equal to the minimum cost of a simple circuit that goes through vertices \(x\) and \(y\) in the graph.
- Note that the graph is allowed to have multi-edges, but is not allowed to have self-loops.
Print the answer modulo \(998\,244\,353\). Two graphs are considered distinct if and only if there exists a triple \((a, b, c)\) such that there exists an edge that connects vertices \(a\) and \(b\) with weight \(c\) in one graph, but not in the other. Output An integer representing the number of distinct undirected weighted graphs that satisfy the conditions of the problem modulo \(998\,244\,353\). Note The following is an example of a graph that satisfies. 
The following is an assignment of edge weights in the key tree that corresponds to the graph above. 
As an example, consider a pair of vertex indices \((1, 4)\). - The circuit in the graph for this pair of vertices is \(3 \xrightarrow{2} 2 \xrightarrow{4} 4 \xrightarrow{6} 2 \xrightarrow{1} 1 \xrightarrow{5} 3\) with a cost of \(6\).
- The path in the key tree for this pair of vertices is \(1 \xrightarrow{5} 3 \xrightarrow{6} 4\) with a cost of \(6\).
| |
![]()
|
|
J. Journey
Деревья
дп
*2500
One day, Pak Chanek who is already bored of being alone at home decided to go traveling. While looking for an appropriate place, he found that Londonesia has an interesting structure. According to the information gathered by Pak Chanek, there are \(N\) cities numbered from \(1\) to \(N\). The cities are connected to each other with \(N-1\) two-directional roads, with the \(i\)-th road connecting cities \(U_i\) and \(V_i\), and taking a time of \(W_i\) hours to be traversed. In other words, Londonesia's structure forms a tree. Pak Chanek wants to go on a journey in Londonesia starting and ending in any city (not necessarily the same city) such that each city is visited at least once with the least time possible. In order for the journey to end quicker, Pak Chanek also carries an instant teleportation device for moving from one city to any city that can only be used at most once. Help Pak Chanek for finding the minimum time needed. Notes: - Pak Chanek only needs to visit each city at least once. Pak Chanek does not have to traverse each road.
- In the journey, a city or a road can be visited more than once.
Output Output one integer, which represents the minimum time in hours that is needed to visit each city at least once. Note In the first example, the journey that has the minimum time is \(2 → 1 \xrightarrow{\text{teleport}} 4 → 3\). In the second example, the journey that has the minimum time is \(3 → 1 → 4 → 1 → 2 \xrightarrow{\text{teleport}} 5\). | |
![]()
|
|
D. Разделение рёбер
графы
Деревья
Конструктив
Перебор
поиск в глубину и подобное
снм
Теория вероятностей
*2000
Вам дан связный, неориентированный и невзвешенный граф с \(n\) вершинами и \(m\) рёбрами. Обратите внимание на ограничение на количество рёбер: \(m \le n + 2\). Давайте скажем, что мы красим некоторые рёбра в красный и оставшиеся рёбра в синий. Теперь рассмотрим только красные рёбра и посчитаем количество компонент связности в графе. Пусть это значение равно \(c_1\). Аналогично, рассмотрим только синие рёбра и посчитаем количество компонент связности в графе. Пусть это значение равно \(c_2\). Найдите распределение цветов по рёбрам такое, что величина \(c_1+c_2\) минимальна. Выходные данные Для каждого набора входных данных выведите бинарную строку длины \(m\). \(i\)-й символ строки должен быть 1, если \(i\)-е ребро должно иметь красный цвет, и 0, если оно должно иметь синий цвет. Если существует несколько способов распределить цвета, чтобы получить минимальную величину, вы можете вывести любой. | |
![]()
|
|
D. Упоротые перестановки
графы
Деревья
Конструктив
поиск в глубину и подобное
снм
Структуры данных
*1900
Дана перестановка \(a_1, a_2, \dots, a_n\) целых чисел от \(1\) до \(n\), и пороговое значение \(k\) такое, что \(0 \leq k \leq n\), по ним вычисляется последовательность \(b_1, b_2, \dots, b_n\) следующим образом. Для всех \(1 \leq i \leq n\) в порядке возрастания положим \(x = a_i\). - Если \(x \leq k\), приравняем \(b_{x}\) последнему элементу \(a_j\) (\(1 \leq j < i\)) такому, что \(a_j > k\). Если такого элемента \(a_j\) не существует, положим \(b_{x} = n+1\).
- Если \(x > k\), приравняем \(b_{x}\) последнему элементу \(a_j\) (\(1 \leq j < i\)) такому, что \(a_j \leq k\). Если такого элемента \(a_j\) не существует, положим \(b_{x} = 0\).
К сожалению, после построения последовательности \(b_1, b_2, \dots, b_n\), перестановка \(a_1, a_2, \dots, a_n\) и пороговое значение \(k\) потерялись. Теперь у вас есть только последовательность \(b_1, b_2, \dots, b_n\). Ваша задача найти любую подходящую перестановку \(a_1, a_2, \dots, a_n\) и пороговое значение \(k\) которые порождают последовательность \(b_1, b_2, \dots, b_n\). Гарантируется, что существует хотя бы одна пара перестановки \(a_1, a_2, \dots, a_n\) и порогового значения \(k\), что порождают \(b_1, b_2, \dots, b_n\). Перестановкой чисел от \(1\) до \(n\) называется последовательность длины \(n\) которая содержит все целые числа от \(1\) до \(n\) ровно один раз. Выходные данные Для каждого набора входных данных выведите пороговое значение \(k\) (\(0 \leq k \leq n\)) в первой строке, и затем выведите перестановку \(a_1, a_2, \dots, a_n\) (\(1 \leq a_i \leq n\)) во второй строке так, что перестановку \(a_1, a_2, \dots, a_n\) и пороговое значение \(k\) порождают последовательность \(b_1, b_2, \dots, b_n\). Если существуют несколько решений, выведите любое из них. Примечание В первом примере перестановка \(a = [1,3,2,4]\) и пороговое значение \(k = 2\) породят \(b\) следующим образом. - Когда \(i = 1\), \(x = a_i = 1 \leq k\), нет такого \(a_j\) (\(1 \leq j < i\)) что \(a_j > k\). Значит, \(b_1 = n + 1 = 5\).
- Когда \(i = 2\), \(x = a_i = 3 > k\), последний элемент \(a_j\) такой, что \(a_j \leq k\) это \(a_1\). Значит, \(b_3 = a_1 = 1\).
- Когда \(i = 3\), \(x = a_i = 2 \leq k\), последний элемент \(a_j\) такой, что \(a_j > k\) это \(a_2\). Значит, \(b_2 = a_2 = 3\).
- Когда \(i = 4\), \(x = a_i = 4 > k\), последний элемент \(a_j\) такой, что \(a_j \leq k\) это \(a_3\). Значит, \(b_4 = a_3 = 2\).
Получается последовательность \(b = [5,3,1,2]\). Для второго примера перестановка \(a = [1,2,3,4,5,6]\) и пороговое значение \(k = 3\) породят \(b\) следующим образом. - Когда \(i = 1, 2, 3\), \(a_i \leq k\), нет такого \(a_j\) (\(1 \leq j < i\)) что \(a_j > k\). Значит, \(b_1 = b_2 = b_3 = n + 1 = 7\).
- Когда \(i = 4, 5, 6\), \(a_i > k\), последний элемент \(a_j\) такой, что \(a_j \leq k\) это \(a_3\). Значит, \(b_4 = b_5 = b_6 = a_3 = 3\).
Получается последовательность \(b = [7,7,7,3,3,3]\). Для третьего примера перестановка \(a = [6,5,4,3,2,1]\) и пороговое значение \(k = 3\) породят \(b\) следующим образом. - Когда \(i = 1, 2, 3\), \(a_i > k\), нет такого \(a_j\) (\(1 \leq j < i\)) что \(a_j \leq k\). Значит, \(b_4 = b_5 = b_6 = 0\).
- Когда \(i = 4, 5, 6\), \(a_i \leq k\), последний элемент \(a_j\) такой, что \(a_j > k\) это \(a_3\). Значит, \(b_1 = b_2 = b_3 = a_3 = 4\).
Получается последовательность \(b = [4,4,4,0,0,0]\). | |
![]()
|
|
F. Упоротая связность
графы
Деревья
жадные алгоритмы
интерактив
Конструктив
кратчайшие пути
снм
*2400
Это интерактивная задача. Дан простой неориентированный граф с \(n\) вершинами пронумерованными от \(1\) до \(n\), ваша задача состоит в том, чтобы покрасить все вершины так, чтобы для каждого цвета \(c\), выполнялись следующие условия: - Множество вершин цвета \(c\) является связным;
- \(s_c \leq n_c^2\), где \(n_c\) число вершин цвета \(c\), и \(s_c\) сумма степеней вершин цвета \(c\).
Можно показать, что всегда существует раскраска такая, что условия выполняются. Исходно вам дано только \(n\) - число вершин и степень каждой вершины. Каждым запросом вы можете выбрать вершину \(u\). В ответ вы получите \(k\)-е ребро, исходящее из \(u\), если это \(k\)-й запрос к вершине \(u\). Вы можете сделать максимум \(n\) запросов. Неориентированный граф называется простым, если он не содержит кратных ребер и петель. Степень вершины это число ребер, исходящих из нее. Множество вершин \(S\) называется связным если для любых двух различных вершин \(u, v \in S\), существует путь, который проходит только по вершинам множества \(S\), и соединяет \(u\) и \(v\). Формально, существует последовательность ребер \((u_1, v_1), (u_2, v_2), \dots, (u_k, v_k)\) с \(k \geq 1\) такая, что - \(u_1 = u\), \(v_k = v\), и \(v_i = u_{i+1}\) для любого \(1 \leq i < k\); и
- \(u_k \in S\) и \(v_k \in S\) для любого \(1 \leq i \leq k\).
Множество содержащее одну вершину является связным. Протокол взаимодействия Каждый тест состоит из нескольких наборов входных данных. В первой строке содержится целое число \(t\) (\(1 \leq t \leq 1000\)) — количество наборов входных данных. Следующие строки содержат описание и интерактивную часть каждого набора входных данных. Для каждого набора входных данных вы начинаете взаимодействие с итерактором с чтения целого числа \(n\) (\(1\le n \le 1000\)) в первой строке, означающего число вершин в графе. Вторая строка содержит \(n\) целых чисел \(d_1, d_2, \dots, d_n\) (\(0 \leq d_i \leq n - 1\)), где \(d_i\) это степень вершины \(i\). Чтобы совершить запрос к вершине \(u\) (\(1 \leq u \leq n\)), вы должны вывести В отдельной строке. Если это \(k\)-й запрос к вершине \(u\), вершина \(e_{u, k}\) будет выведена на следующей отдельной строке, где \(\left(u, e_{u, k}\right)\) это \(k\)-е ребро, исходящее из вершины \(u\). В случае если \(k > d_u\), положим \(e_{u, k} = -1\). Вы должны сделать не более \(n\) «?» запросов. Чтобы дать ответ вы должны вывести - «! \(c_1\) \(c_2\) \(\dots\) \(c_n\)»
в отдельной строке, где \(c_i\) ( \(1 \leq c_i \leq n\)) это цвет вершины \(i\). После этого ваша программа должны продолжить работать со следующим набором входных данных или завершиться, если это был последний. Гарантируется, что дан простой неориентированный граф. Гарантируется, что сумма \(n\) по всем наборам входных данных не превосходит \(1000\). В случае, если формат запроса неверный, или вы сделали более \(n\) «?» запросов, вы получите вердикт Неправильный Ответ. После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Формат взломов Первая строка взлома должна содержать целое число \(t\) (\(1 \leq t \leq 1000\)), означающее число наборов входных данных. Следующие строки содержат описание наборов входных данных. Первая строка каждого набора входных данных содержит целое число \(n\) (\(1 \leq n \leq 1000\)), означающее число вершин в графе. Затем следуют \(n\) строк. В \(i\)-й строке содержится целое число \(d_i\) (\(0 \leq d_i \leq n - 1\)), означающее степень вершины \(i\), и затем \(d_i\) различных целых чисел \(e_{i,1}, e_{i,2}, \dots, e_{i,d_i}\) (\(1 \leq e_{i, j} \leq n\) и \(e_{i,j} \neq i\)), где \(\left(i, e_{i,j}\right)\) это \(j\)-е ребро, исходящее из вершины \(i\). Вы должны гарантировать, что граф является простым и неориентированным. Вы должны гарантировать, что сумма \(n\) по всем наборам входных данных не превосходит \(1000\). Примечание В примере только один набор входных данных. В нем \(n = 5\) вершин, из которых \(1, 2, 3, 4\) имеют степень \(2\) и вершина \(5\) имеет степень \(0\). Это означает, что вершина \(5\) изолированная - не соединена ни с одной другой вершиной. Возможное взаимодействие с итерактором показано во вводе и выводе примера, использовано \(4\) «?» запроса. Из них два к вершине \(1\) и два к вершине \(3\). Исходя из результатов этих запросов мы знаем, что вершины \(1\) и \(3\) соединены с вершинами \(2\) и \(4\). Возможное решение показано, вершины \(1\) и \(2\) покрашены в цвет \(1\), вершины \(3\) и \(4\) покрашены в цвет \(2\), и вершина \(5\) покрашена в цвет \(3\). Легко заметить, что решение удовлетворяет условиям. - Для цвета \(c = 1\), вершины \(1\) и \(2\) связны. Также, \(n_1 = 2\) и \(s_1 = d_1 + d_2 = 2 + 2 = 4 \leq n_1^2 = 2^2 = 4\);
- Для цвета \(c = 2\), вершины \(3\) и \(4\) связны. Также, \(n_2 = 2\) и \(s_2 = d_3 + d_4 = 2 + 2 = 4 \leq n_2^2 = 2^2 = 4\);
- Для цвета \(c = 3\), есть только одна вершина (вершина \(5\)) покрашенная в цвет \(3\). Также, \(n_3 = 1\) и \(s_3 = d_5 = 0 \leq n_3^2 = 1^2 = 1\).
| |
![]()
|
|
D. Сбросить k ребер
Бинарный поиск
графы
Деревья
жадные алгоритмы
поиск в глубину и подобное
Структуры данных
*1900
Задано корневое дерево, состоящее из \(n\) вершин. Вершины пронумерованы от \(1\) до \(n\), корень — это вершина \(1\). Вы можете совершить следующую операцию не более \(k\) раз: - выбрать ребро \((v, u)\) дерева такое, что \(v\) является родителем \(u\);
- удалить ребро \((v, u)\);
- добавить ребро \((1, u)\) (т. е. сделать \(u\) с его поддеревом ребенком корня).
Высотой дерева называют максимальную глубину среди всех его вершин, а глубина вершины — это количество ребер на пути от корня до нее. Например, глубина вершины \(1\) равна \(0\), так как она — корень, а глубина всех ее детей равна \(1\). Какую минимальную высоту дерева можно получить? Выходные данные На каждый набор входных данных выведите одно число — наименьшая высота дерева, которую можно получить, совершив не более \(k\) операций. | |
![]()
|
|
E. Подвешенные сердца
Деревья
дп
жадные алгоритмы
Конструктив
поиск в глубину и подобное
Структуры данных
*1800
У Пака Чанека есть \(n\) пустых карточек в форме сердца. Карточка \(1\) прикреплена непосредственно к стене, остальные же карточки подвешены ровно к одной другой карточке верёвочкой. А именно, карточка \(i\) (\(i > 1\)) подвешена к карточке \(p_i\) (\(p_i < i\)). Пак Чанек должен написать на каждой карточке одно целое число. Для этого он выберет произвольную перестановку \(a\) чисел \([1, 2, \dots, n]\), и на карточке \(i\) запишет число \(a_i\). После этого Пак Чанек должен выполнить следующую операцию \(n\) раз, поддерживая при этом последовательность \(s\) (изначально пустую): - Выбрать такую карточку \(x\), что к ней не подвешена ни одна другая карточка.
- Добавить число, записанное на карте \(x\), в конец последовательности \(s\).
- Если \(x \neq 1\) и число на карточке \(p_x\) больше, чем число на карточке \(x\), заменить число на карточке \(p_x\) на число на карточке \(x\).
- Удалить карточку \(x\).
После этого у Пака Чанека будет последовательность \(s\) из \(n\) элементов. Какова максимальная длина наибольшей неубывающей подпоследовательности\(^\dagger\) \(s\) в конце, если Пак Чанек выполняет все шаги оптимально? \(^\dagger\) Последовательность \(b\) называется подпоследовательностью последовательности \(c\) если \(b\) может быть получена из \(c\) удалением некоторого (возможно нулевого) количества элементов. Например, \([3,1]\) — подпоследовательность \([3,2,1]\), \([4,3,1]\) и \([3,1]\), но не \([1,3,3,7]\) и не \([3,10,4]\). Выходные данные Выведите одно целое число — максимальную длину наибольшей неубывающей подпоследовательности \(s\) в конце, если Пак Чанек сделает все шаги оптимально. Примечание Ниже представлена структура карточек в первом примере. 
Пак Чанек может выбрать перестановку \(a = [1, 5, 4, 3, 2, 6]\). 
Пусть \(w_i\) — число на карточке \(i\). Изначально \(w_i = a_i\). Пак Чанек может выполнять следующие операции по порядку: - Выбрать карточку \(5\). Добавить \(w_5 = 2\) в конец \(s\). Так как \(w_4 > w_5\), значение \(w_4\) становится равным \(2\). Удаляем карточку \(5\). После этой операции \(s = [2]\).
- Выбрать карточку \(6\). Добавить \(w_6 = 6\) в конец \(s\). Так как \(w_2 \leq w_6\), значение \(w_2\) остается неизменным. Удаляем карточку \(6\). После этой операции \(s = [2, 6]\).
- Выбрать карточку \(4\). Добавить \(w_4 = 2\) в конец \(s\). Так как \(w_1 \leq w_4\), значение \(w_1\) остается неизменным. Удаляем карточку \(4\). После этой операции \(s = [2, 6, 2]\).
- Выбрать карточку \(3\). Добавить \(w_3 = 4\) в конец \(s\). Так как \(w_2 > w_3\), значение \(w_2\) становится равным \(4\). Удаляем карточку \(3\). После этой операции \(s = [2, 6, 2, 4]\).
- Выбрать карточку \(2\). Добавить \(w_2 = 4\) в конец \(s\). Так как \(w_1 \leq w_2\), значение \(w_1\) is left unchanged. Удаляем карточку \(2\). После этой операции \(s = [2, 6, 2, 4, 4]\).
- Выбрать карточку \(1\). Добавить \(w_1 = 1\) в конец \(s\). Удаляем карточку \(1\). После этой операции \(s = [2, 6, 2, 4, 4, 1]\).
Одна из наибольших неубывающих подпоследовательностей \(s = [2, 6, 2, 4, 4, 1]\) это \([2, 2, 4, 4]\). Таким образом, длина наибольшей неубывающей подпоследовательности \(s\) равна \(4\). Можно доказать, что это действительно максимально возможная длина. | |
![]()
|
|
H. MEX и манипуляции с деревом
Деревья
Структуры данных
*3300
Для корневого дерева определим значение вершины \(u\) в дереве рекурсивно как MEX\(^\dagger\) значений её детей. Обратите внимание, что это только дети, а не все её потомки. В частности, значение листа равно \(0\). У Пака Чанека есть корневое дерево, которое изначально содержит только одну вершину с индексом \(1\), являющуюся корнем. Пак Чанек будет исполнять \(q\) запросов. В \(i\)-м запросе Паку Чанеку задано целое число \(x_i\). Паку Чанеку нужно добавить новую вершину с индексом \(i+1\) в качестве ребенка вершины \(x_i\). После добавления новой вершины Пак Чанек должен пересчитать значения всех вершин и сообщить сумму значений всех вершин в текущем дереве. \(^\dagger\) MEX (minimum excluded) массива это наименьшее неотрицательное целое число, которого нет в массиве. Например, MEX массива \([0,1,1,2,6,7]\) равен \(3\), а MEX \([6,9]\) равен \(0\). Выходные данные Для каждого запроса выведите строку, содержащую целое число — сумму новых значений всех вершин в дереве после добавления вершины. Примечание В первом примере после \(6\)-го запроса дерево примет следующий вид. 
- Вершина \(7\) — лист, поэтому её значение равно \(0\).
- Вершина \(6\) — лист, поэтому её значение равно \(0\).
- Вершина \(5\) имеет единственного ребенка со значением \(0\), поэтому её значение равно \(1\).
- Вершина \(4\) — лист, поэтому её значение равно \(0\).
- Вершина \(3\) имеет единственного ребенка со значением \(0\), поэтому её значение равно \(1\).
- Вершина \(2\) имеет детей со значениями \(0\) и \(1\), поэтому её значение равно \(2\).
- Вершина \(1\) имеет детей со значениями \(1\) и \(2\), поэтому её значение равно \(0\).
Сумма значений всех вершин равна \(0+0+1+0+1+2+0=4\). | |
![]()
|
|
D. Маша и красивое дерево
графы
Деревья
поиск в глубину и подобное
разделяй и властвуй
сортировки
*1300
Девочка Маша гуляла в лесу и нашла полное бинарное дерево высоты \(n\) и перестановку \(p\) длины \(m=2^n\). Полное бинарное дерево высоты \(n\) — это такое корневое дерево, что каждая вершина кроме листьев имеет ровно двух сыновей, а длина пути от корня до любого из листьев равна \(n\). Ниже на картинке изображено полное бинарное дерево для \(n=2\). Перестановкой называется массив, состоящий из \(n\) различных целых чисел от \(1\) до \(n\). Например, [\(2,3,1,5,4\)] является перестановкой, а [\(1,2,2\)] не является (\(2\) встречается дважды), и [\(1,3,4\)] тоже не является перестановкой (\(n=3\), но в массиве есть \(4\)). Пронумеруем \(m\) листьев этого дерева слева направо. В листе с номером \(i\) записано значение \(p_i\) (\(1 \le i \le m\)). Например, если \(n = 2\), \(p = [3, 1, 4, 2]\), дерево будет выглядеть так:  Маша считает дерево красивым, если значения в его листьях упорядочены слева направо по возрастанию. За одну операцию Маша может выбрать произвольную не являющуюся листом вершину дерева и поменять местами ее левого и правого сына (вместе с их поддеревьями). Например, если Маша применит эту операцию к корню рассмотренного выше дерева, оно приобретет следующий вид:  Помогите Маше понять, сможет ли она за некоторое количество операций сделать дерево красивым. Если сможет, то выведите минимальное количество операций, чтобы сделать дерево красивым. Выходные данные Для каждого набора входных данных в отдельной строке выведите минимальное возможное количество операций, за которое Маша сможет сделать дерево красивым или -1, если это невозможно. Примечание Рассмотрим первый тест. В первом наборе входных данных можно действовать так (фиолетовым цветом выделена вершина, к которой на текущем шаге применяется операция): Можно показать, что нельзя сделать дерево красивым за меньшее число операций. Во втором наборе входных данных можно показать, что нельзя сделать дерево красивым. В третьем наборе входных данных дерево сразу является красивым. | |
![]()
|
|
D. Пути на дереве
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
сортировки
*1900
Вам дано корневое дерево, состоящее из \(n\) вершин. Вершины пронумерованы от \(1\) до \(n\), а корнем является вершина \(1\). Также вам дан массив коэффициентов \(s_1, s_2, \ldots, s_n\). Мультимножество из \(k\) простых путей называется допустимым, если выполняются следующие два условия: - Каждый путь начинается в вершине \(1\).
- Пусть \(c_i\) — количество путей, покрывающих вершину \(i\). Для каждой пары вершин \((u,v)\) (\(2\le u,v\le n\)), имеющих общего родителя, верно \(|c_u-c_v|\le 1\).
Значение мультимножества путей определяется как \(\sum\limits_{i=1}^n c_i s_i\). Можно показать, что всегда можно найти хотя бы одно допустимое мультимножество. Найдите максимальное значение среди всех допустимых мультимножеств. Выходные данные Для каждого набора входных данных выведите одно целое число — максимальное значение мультимножества. Примечание В первом наборе входных данных одно из оптимальных решений — четыре пути \(1 \to 2 \to 3 \to 5\), \(1 \to 2 \to 3 \to 5\), \(1 \to 4\), \(1 \to 4\), при этом \(c=[4,2,2,2,2]\). Значение будет равно \(4\cdot 6+ 2\cdot 2+2\cdot 1+2\cdot 5+2\cdot 7=54\). Во втором наборе входных данных одно из оптимальных решений — три пути \(1 \to 2 \to 3 \to 5\), \(1 \to 2 \to 3 \to 5\), \(1 \to 4\), при этом \(c=[3,2,2,1,2]\). Значение будет равно \(3\cdot 6+ 2\cdot 6+2\cdot 1+1\cdot 4+2\cdot 10=56\). | |
![]()
|
|
E. Очередная задача на подсчёт массивов
Бинарный поиск
Деревья
дп
математика
Потоки
разделяй и властвуй
Структуры данных
*2300
Позиция первого максимума на отрезке \([l; r]\) массива \(x = [x_1, x_2, \ldots, x_n]\) это наименьшее целое число \(i\), такое что \(l \le i \le r\) и \(x_i = \max(x_l, x_{l+1}, \ldots, x_r)\). Вам дан массив \(a = [a_1, a_2, \ldots, a_n]\) длины \(n\). Найдите количество массивов \(b = [b_1, b_2, \ldots, b_n]\) длины \(n\), удовлетворяющих следующим требованиям: - \(1 \le b_i \le m\) для всех \(1 \le i \le n\);
- для всех пар \(1 \le l \le r \le n\), позиция первого максимума на отрезке \([l; r]\) массива \(b\) равна позиции первого максимума на отрезке \([l; r]\) массива \(a\).
Так как это количество может быть очень большим, выведите его по модулю \(10^9+7\). Выходные данные Для каждого набора входных данных выведите одно число: количество массивов \(b\), удовлетворяющих требованиям выше, по модулю \(10^9+7\). Примечание В первом наборе входных данных следующие \(8\) массивов удовлетворяют требованиям из условия: - \([1,2,1]\);
- \([1,2,2]\);
- \([1,3,1]\);
- \([1,3,2]\);
- \([1,3,3]\);
- \([2,3,1]\);
- \([2,3,2]\);
- \([2,3,3]\).
Во втором наборе входных данных следующие \(5\) массивов удовлетворяют требованиям из условия: - \([1,1,1,1]\);
- \([2,1,1,1]\);
- \([2,2,1,1]\);
- \([2,2,2,1]\);
- \([2,2,2,2]\).
| |
![]()
|
|
F. Расстояние до пути
Деревья
поиск в глубину и подобное
Структуры данных
*2800
Вам задано дерево, состоящее из \(n\) вершин. Первоначально в каждой вершине записано число \(0\). Вам нужно обработать \(m\) запросов двух видов: - Вам задан номер вершины \(v\). Выведите значение в данной вершине \(v\).
- Вам заданы номера вершин \(u\) и \(v\), и значения \(k\) и \(d\) (\(d \le 20\)). Вам нужно прибавить \(k\) к значению каждой вершины, расстояние от которой до пути из \(u\) в \(v\) не превосходит \(d\).
Расстояние между двумя вершинами \(x\) и \(y\) равно количеству ребер на пути из \(x\) в \(y\). Например, расстояние от \(x\) до самой \(x\) равно \(0\). Расстояние от вершины \(v\) до некоторого пути из \(x\) в \(y\) равно минимуму из расстояний от \(v\) до любой вершины на пути из \(x\) в \(y\). Выходные данные Для каждого запроса первого типа выведите текущее значение в заданной вершине. Примечание Дерево из первого примера:  Описания некоторых запросов: - «\(2\) \(4\) \(5\) \(10\) \(2\)»: попадающие под прибавление вершины — это \(\{4, 2, 5, 1, 3\}\);
- «\(2\) \(1\) \(1\) \(10\) \(20\)» и «\(2\) \(6\) \(6\) \(10\) \(20\)»: все вершины попадают под прибавление, так как расстояние до \(1\) (\(6\)) меньше \(20\) у любой вершины;
- «\(2\) \(3\) \(2\) \(10\) \(0\)»: попадающие под прибавление вершины — это \(\{3, 1, 2\}\);
- «\(2\) \(5\) \(2\) \(10\) \(1\)»: попадающие под прибавление вершины — это \(\{5, 2, 4, 1\}\).
| |
![]()
|
|
E. Археология
Деревья
поиск в глубину и подобное
Структуры данных
*3100
На этот раз вам нужно помочь группе ученых-исследователей на одном острове в Тихом Океане. Они изучают культуру древних племен, живших на этом острове много лет назад. Всего было раскопано n деревень. Некоторые пары деревень были соединены дорогами. По дорогам можно было двигаться в обоих направлениях. Всего было ровно n - 1 дорог, и из любой деревни можно было добраться в любую другую. Племена были неспокойны и часто воевали. В результате войн некоторые деревни полностью уничтожались. В более спокойные годы некоторые из деревень возрождались заново. В каждый момент времени использовались только те дороги, которые принадлежали какому-либо кратчайшему пути между двумя существующими в данный момент деревнями. Другими словами, использовалось наименьшее подмножество дорог так, чтобы из любой существующей деревни можно было добраться до любой другой существующей. Обратите внимание, что за всю историю острова существовало ровно n - 1 дорог, найденных исследователями, а других дорог никогда не было. Исследователи полагают, что наблюдения за суммарной длиной используемых дорог в разные моменты времени помогут им лучше понять культуру племен и ответить на ряд исторических вопросов. Вам будет предоставлена вся история существования племен. Ваша задача — определить суммарную длину используемых дорог в некоторые из моментов времени. Выходные данные На каждый запрос типа «?» выведите суммарную длину используемых дорог в отдельной строке. Ответы за запросы должны быть выведены в том порядке, в котором запросы перечислены во входных данных. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-х битовых чисел на С++. Рекомендуется использовать потоки cin, cout или спецификатор %I64d. | |
![]()
|
|
E. Сделайте связным
Бинарный поиск
графы
Деревья
жадные алгоритмы
Конструктив
матрицы
Перебор
снм
*2400
Вам дан простой неориентированный граф, состоящий из \(n\) вершин. Граф не содержит петель, между каждой парой вершин существует не более одного ребра. Ваша задача проста: сделать граф связным. Вы можете выполнить следующую операцию любое количество раз (возможно, ноль): - Выберите произвольную вершину \(u\).
- Для каждой вершины \(v\), для которой \(v\ne u\), если \(v\) смежна с \(u\), удалите ребро между \(u\) и \(v\), иначе добавьте ребро между \(u\) и \(v\).
Найдите минимальное количество операций, необходимых для того, чтобы сделать граф связным. Также найдите любую последовательность операций минимальной длины, которая делает граф связным. Выходные данные Для каждого набора входных данных в первой строке выведите целое число \(m\) — минимально необходимое количество операций. Если \(m\) больше нуля, то выведите дополнительную строку, состоящую из \(m\) целых чисел — вершин, выбранных в операциях в вашем решении. Если существует несколько решений с минимальным количеством операций, выведите любое из них. Примечание В первом наборе входных данных граф связен в начале, поэтому ответ — \(0\). Во втором наборе входных данных, если мы выполним операцию с вершиной \(1\), то получим следующий граф, представленный следующей матрицей смежности: \(\) \begin{bmatrix} 0&1&1\\ 1&0&1\\ 1&1&0 \end{bmatrix} \(\) Очевидно, что приведенный выше граф является связным. В третьем наборе входных данных, если мы проделаем операцию с вершинами \(3\) и \(4\), то получим следующий граф, представленный следующей матрицей смежности: \(\) \begin{bmatrix} 0&1&1&1\\ 1&0&1&1\\ 1&1&0&1\\ 1&1&1&0 \end{bmatrix} \(\) Очевидно, что приведенный выше граф является связным, и можно доказать, что мы не можем выполнить менее \(2\) операций, чтобы сделать граф связным. | |
![]()
|
|
G. Угадайте центроид
Деревья
интерактив
Теория вероятностей
*3500
Это интерактивная задача. Есть загаданное дерево, состоящее из \(n\) вершин, которое имеет только один центроид. Сначала вам известно только \(n\), и ваша задача — найти центроид дерева. Вы можете спросить расстояние между любыми двумя вершинами не более \(2\cdot10^5\) раз. Обратите внимание, что интерактор является неадаптивным. То есть, дерево фиксировано в каждом тесте заранее и не зависит от ваших запросов. Вершина называется центроидом, если ее удаление разбивает дерево на поддеревья, в каждом из которых не более \(\lfloor\frac{n}{2}\rfloor\) вершин. Протокол взаимодействия Начните взаимодействие с чтения \(n\). Чтобы задать запрос о расстоянии между двумя вершинами \(u, v\) (\(1 \le u, v \le n\)), выведите «? u v». Если вы определили, что центроидом дерева является \(x\), используйте «! x» для вывода ответа. После вывода запроса не забудьте вывести конец строки и сбросить буфер вывода. В противном случае вы получите Решение «зависло». Для этого используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- см. документацию для других языков.
В этой задаче взломы отключены. Гарантируется, что в этой задаче есть не более \(500\) тестов. Примечание Вот изображение дерева из примера.  | |
![]()
|
|
E. Сумма на дереве
Деревья
Комбинаторика
математика
*2600
Назовем реберно-взвешенное дерево из \(n\) вершин, пронумерованных от \(1\) до \(n\), хорошим, если вес каждого ребра равен либо \(1\), либо \(-1\), и для каждой вершины \(i\) произведение весов ребер, смежных с вершиной \(i\), равно \(-1\). Вам дано положительное целое число \(n\). Всего существует \(n^{n-2} \cdot 2^{n-1}\) различных\(^\dagger\) реберно-взвешенных деревьев на \(n\) вершинах, пронумерованных от \(1\) до \(n\), таких, что вес каждого ребра равен либо \(1\), либо \(-1\). Ваша задача — найти сумму \(d(1,n)^\ddagger\) по всем таким деревьям, которые являются хорошими. Так как ответ может быть большим, выведите его по модулю \(998\,244\,353\). \(^\dagger\) Два дерева называются различными, если: - существуют две вершины такие, что в одном дереве между ними есть ребро, а в другом нет; или
- существуют две вершины такие, что в обоих деревьях между ними есть ребро, но вес этого ребра в одном дереве отличается от веса этого ребра в другом дереве.
Обратите внимание, что по формуле Кэли число деревьев с \(n\) пронумерованными вершинами равно \(n^{n-2}\). Так как у нас \(n-1\) ребро, то для каждого дерева существует \(2^{n-1}\) способ выбрать веса ребер (которые могут быть либо \(1\), либо \(-1\)). Поэтому общее число различных реберно-взвешенных деревьев равно \(n^{n-2} \cdot 2^{n-1}\). \(^\ddagger\) \(d(u,v)\) обозначает сумму весов ребер на единственном простом пути от \(u\) до \(v\). Выходные данные Выведите одно целое число — ответ по модулю \(998\,244\,353\). Примечание В первом примере есть только \(1\) различное хорошее дерево. Значение \(d(1,2)\) для этого дерева равно \(-1\), что равно \(998\,244\,352\) по модулю \(998\,244\,353\). Во втором примере значение \(d(1,1)\) для любого дерева равно \(0\), поэтому ответ равен \(0\). В третьем примере \(16\) различных хороших деревьев. Значение \(d(1,4)\) равно: - \(-2\) для \(2\) деревьев;
- \(-1\) для \(8\) деревьев;
- \(0\) для \(4\) деревьев;
- \(1\) для \(2\) деревьев.
Сумма \(d(1,4)\) по всем деревьям равна \(2 \cdot (-2) + 8 \cdot (-1) + 4 \cdot (0) + 2 \cdot (1) = -10\), что равно \(998\,244\,343\) по модулю \(998\,244\,353\). | |
![]()
|
|
F. Запросы к ребрам
графы
Деревья
дп
поиск в глубину и подобное
снм
Структуры данных
*3000
Вам дан неориентированных, связный граф из \(n\) вершин и \(m\) ребер. Все вершины \(u\) графа удовлетворяют следующему условию: - Пусть \(S_u\) это множество вершин принадлежащих длиннейшему простому циклу начинающемуся и заканчивающемуся в \(u\).
- Пусть \(C_u\) это объединение множеств вершин всех простых циклов начинающихся и заканчивающихся в \(u\).
- \(S_u = C_u\).
Вы должны ответить на \(q\) запросов. Для каждого запроса вам будет дана вершина \(a\) и вершина \(b\). Для всех ребер принадлежащих любому простому пути из \(a\) в \(b\), посчитайте число ребер таких, что если вы удалите их, \(a\) и \(b\) останутся достижимы друг из друга. Выходные данные Для каждого запроса выведите одно целое число — ответ на запрос. Примечание Граф в первом примере:  Первый запрос это \((1, 4)\). Тут всего \(5\) ребер принадлежат любому простому пути из \(1\) в \(4\). Ребра \((3, 4), (4, 5), (5, 3)\) будут посчитаны как ответ на запрос. Четвертый запрос \((2, 8)\). Тут только один простой путь из \(2\) в \(8\), причем ни одно ребро не будет посчитано в ответ. Пятый запрос \((7, 10)\). Тут всего \(4\) ребра принадлежат любому простому пути из \(7\) в \(10\), все они будут посчитаны в ответе. | |
![]()
|
|
F. Дореми и экспериментальное дерево
Деревья
Конструктив
Перебор
поиск в глубину и подобное
снм
сортировки
*2500
У Дореми есть реберно-взвешенное дерево из \(n\) вершин, веса являются целыми числами от \(1\) до \(10^9\). Дореми провела \(\frac{n(n+1)}{2}\) экспериментов с деревом. В каждом эксперименте Дореми выбирает две вершины \(i\) и \(j\) такие, что \(j \leq i\), и соединяет их дополнительным ребром веса \(1\). После этого в графе образовывается один цикл (или петля, если \(i=j\)). Дореми определяет \(f(i,j)\) как сумму длин кратчайших путей от каждой вершины до цикла. Формально, пусть \(\mathrm{dis}_{i,j}(x,y)\) — длина кратчайшего пути между вершинами \(x\) и \(y\), когда в дерево добавлено одно ребро \((i,j)\) веса \(1\), а \(S_{i,j}\) — множество вершин на цикле, когда добавлено ребро \((i,j)\). Тогда \(\) f(i,j)=\sum_{x=1}^{n}\left(\min_{y\in S_{i,j}}\mathrm{dis}_{i,j}(x,y)\right). \(\) Дореми записала все значения \(f(i,j)\) для \(1 \leq j \leq i \leq n\), потом пошла спать. Однако проснувшись, она обнаружила, что дерево пропало. К счастью, значения \(f(i,j)\) все еще в ее тетради, и она значит, каким \(i\) и \(j\) они соответствуют. Вам даны значения \(f(i,j)\), можете ли вы помочь Дореми восстановить дерево? Гарантируется, что хотя бы одно подходящее дерево существует. Выходные данные Выведите \(n-1\) строку, описывающую дерево. В \(i\)-й строке выведите три целых числа \(u_i\), \(v_i\), \(w_i\) (\(1 \le u_i,v_i \le n\), \(1 \le w_i \le 10^9\)), обозначающих ребро \((u_i,v_i)\) веса \(w_i\). Если существуют несколько решений, выведите любое из них. Ребра должны образовывать дерево, а все значения \(f(i,j)\) должны совпадать с данными. Примечание Для первого примере рисунок ниже слева направо сверху вниз показывает графы, получающиеся при добавлении ребер \((1,1)\), \((1,2)\), \((1,3)\), \((2,2)\), \((2,3)\), \((3,3)\) соответственно. Вершины на цикле выделены желтым. 
| |
![]()
|
|
E. Algebra Flash
meet-in-the-middle
битмаски
графы
Деревья
дп
математика
Перебор
*2500
Выпущена новая версия: Algebra Flash 2.2Список изменений: Благодарим вас за непрерывную поддержку игры! И это все? С небольшим разочарованием вы запускаете игру и нажимаете на новый режим. Написано «Цветные платформы». В ряд расположены \(n\) платформ, пронумерованных от \(1\) до \(n\). В игре доступны \(m\) цветов, пронумерованных от \(1\) до \(m\). \(i\)-я платформа раскрашена в цвет \(c_i\). Вы начинаете на платформе \(1\) и хотите добраться до платформы \(n\). За один ход вы можете прыгнуть с некоторой платформы \(i\) на платформы \(i + 1\) или \(i + 2\). Все платформы изначально деактивированы (включая платформы \(1\) и \(n\)). Для каждого цвета \(j\) можно заплатить \(x_j\) монет, чтобы активировать все платформы этого цвета. Вы хотите включить некоторые платформы так, чтобы можно было начать на активированной платформе \(1\), попрыгать по некотором активированным платформам и достичь платформы \(n\). Какое наименьшее количество монет потребуется для достижения этого? Выходные данные Выведите наименьшее количество монет, которое потребуется того, чтобы можно было начать на активированной платформе \(1\), попрыгать по некотором активированным платформам и достичь платформы \(n\). | |
![]()
|
|
F. Два поддерева
Деревья
Структуры данных
*3100
Вам дано корневое дерево, состоящее из \(n\) вершин. Корень находится в вершине \(1\). В каждой вершине записано некоторое число: в \(i\)-й вершине — \(val_i\). Вы должны обработать \(q\) запросов к дереву, \(i\)-й запрос задается двумя вершинами \(u_i\) и \(v_i\). Для ответа на запрос нужно рассмотреть все вершины \(w\), которые лежат в поддереве \(u_i\) или \(v_i\) (если вершина лежит в обоих поддеревьях, она учитывается дважды). Нужно выписать все числа на вершинах в этой паре поддеревьев и найти то из них, которое встречается наибольшее количество раз (если таких несколько — минимальное из них). Выходные данные Для каждого запроса выведите ответ на него — целое число, которое встречается наибольшее количество раз в паре поддеревьев из запроса (если таких чисел несколько — минимальное из них). Примечание В \(1\)-м запросе пара поддеревьев содержит вершины \([2, 4, 7, 8]\), на которых записаны числа \(\{1, 2, 2, 4\}\). Число \(2\) встречается дважды, все остальные — не более одного раза, поэтому ответ на запрос — \(2\). Во \(2\)-м запросе пара поддеревьев содержит вершины \([3, 5, 6, 7, 7, 8, 8]\), на которых записаны числа \(\{3, 3, 3, 2, 2, 4, 4\}\). Число \(3\) встречается наибольшее количество раз. В \(4\)-м запросе пара поддеревьев содержит вершины \([1, 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6, 7, 7, 8, 8]\), на которых записаны числа \(\{2, 2, 1, 1, 3, 3, 2, 2, 3, 3, 3, 3, 2, 2, 4, 4\}\). Чаще всего встречаются числа \(2\) и \(3\), минимальное из них — \(2\). | |
![]()
|
|
E. Косия и дерево
Деревья
дп
Комбинаторика
математика
поиск в глубину и подобное
снм
Теория вероятностей
*2400
У Ими есть неориентированное дерево из \(n\) вершин, ребра которого пронумерованы от \(1\) до \(n-1\). \(i\)-е ребро соединят вершины \(u_i\) и \(v_i\). Также на дереве находятся \(k\) бабочек. Изначально \(i\)-я бабочка находится в вершине \(a_i\). Все значения \(a\) попарно различны. Косия играет в игру следующим образом. - Для \(i = 1, 2, \dots, n - 1\) Косия выбирает одно из направлений \(i\)-го ребра (\(u_i \rightarrow v_i\) или \(v_i \rightarrow u_i\)) с одинаковой вероятностью.
- Для \(i = 1, 2, \dots, n - 1\), если в начальной вершине \(i\)-го ребра есть бабочка, а в конечной вершине нет бабочки, то эта бабочка перелетает в конечную вершину. Обратите внимание, что операции выполняются для ребер \(1, 2, \dots, n - 1\) по порядку, а не одновременно.
- Косия выбирает две бабочки из \(k\) бабочек с равной вероятностью для всех \(\frac{k(k-1)}{2}\) способов выбрать две бабочки, затем она вычисляет расстояние\(^\dagger\) между двумя вершинами, и объявляет это своим счетом.
Косия хочет, чтобы вы вычислили математическое ожидание ее счета по модулю \(998\,244\,353^\ddagger\). \(^\dagger\) Расстоянием между двумя вершинами в дереве называется количество ребер на (единственном) простом пути между ними. \(^\ddagger\) Формально, пусть \(M = 998\,244\,353\). Можно показать, что ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Выходные данные Выведите одно целое число — математическое ожидание счета Косии по модулю \(998\,244\,353\). Примечание Дерево из первого примера показано ниже. Вершины с бабочками отмечены жирным.  Существуют только \(2\) бабочки, поэтому выбор бабочек фиксирован. Рассмотрим следующие \(4\) случая: - Ориентация ребер \(1 \rightarrow 2\) и \(2 \rightarrow 3\): бабочка из вершины \(1\) перемещается в вершину \(2\), а бабочка в вершине \(3\) не двигается. Расстояние между вершинами \(2\) и \(3\) равно \(1\).
- Ориентация ребер \(1 \rightarrow 2\) и \(3 \rightarrow 2\): бабочка из вершины \(1\) перемещается в вершину \(2\), а бабочка в вершине \(3\) не двигается, потому что вершина \(2\) занята. Расстояние между вершинами \(2\) и \(3\) равно \(1\).
- Ориентация ребер \(2 \rightarrow 1\) и \(2 \rightarrow 3\): бабочки в вершинах \(1\) и \(3\) не двигаются. Расстояние между вершинами \(1\) и \(3\) равно \(2\).
- Ориентация ребер \(2 \rightarrow 1\) и \(3 \rightarrow 2\): бабочка в вершине \(1\) не двигается, а бабочка из вершины \(3\) перемещается в вершину \(2\). Расстояние между вершинами \(1\) и \(2\) равно \(1\).
Таким образом, математическое ожидание счета Косии равно \(\frac {1+1+2+1} {4} = \frac {5} {4}\), что есть \(748\,683\,266\) по модулю \(998\,244\,353\). Дерево из второго примера показано ниже. Вершины с бабочками отмечены жирным. Математическое ожидание счета Косии равно \(\frac {11} {6}\), что есть \(831\,870\,296\) по модулю \(998\,244\,353\).  | |
![]()
|
|
D. Хоссам и дерево (под-)палиндромов
Деревья
дп
Перебор
поиск в глубину и подобное
Строки
Структуры данных
*2100
У Хоссама есть невзвешенное дерево \(G\), в вершинах которого записаны буквы. Через \(s(v, \, u)\) Хоссам обозначает строку, которая получается при написании всех букв на единственном простом пути из вершины \(v\) в вершину \(u\) в дереве \(G\). Строка \(a\) является подпоследовательностью строки \(s\), если \(a\) может быть получена из \(s\) путем удаления нескольких символов (возможно, ни одного). Например, «dores», «cf» и «for» являются подпоследовательностями «codeforces», а «decor» и «fork» не являются. Палиндромом называется строка, читающаяся одинаково слева направо и справа налево. Например, «abacaba» — палиндром, а «abac» — нет. Под-палиндромом строки \(s\) Хоссам называет подпоследовательность \(s\), являющуюся палиндромом. Например, «k», «abba» и «abhba» являются под-палиндромом строки «abhbka», а «abka» и «cat» — нет. Максимальным под-палиндромом строки \(s\) Хоссам называет под-палиндром \(s\), имеющий максимальную длину среди всех под-палиндромов \(s\). Например, у строки «abhbka» есть только один максимальный под-палиндром — «abhba». Но может быть и так, что у строки несколько максимальных под-палиндромов: у строки «abcd» целых \(4\) максимальных под-палиндрома. Хоссам просит вас найти длину самого длинного максимального под-палиндрома среди всех \(s(v, \, u)\) в заданном дереве \(G\). Еще раз обращаем Ваше внимание на то, что под-палиндром — это подпоследовательность, а не подстрока. Выходные данные Для каждого набора входных данных выведите одно число — длину самого длинного максимального под-палиндрома среди всех \(s(v, \, u)\). Примечание В первом примере искомым подпалиндромом может быть «aaa», символы которого расположены в вершинах \(1, \, 3, \, 5\) или «aca», символы которого расположены в вершинах \(1, \, 4, \, 5\).  Дерево из первого примера. Дерево из первого примера. Во втором примере единственным искомым палиндромом является «bacab», символы которого расположены в вершинах \(4, \, 2, \, 1, \, 5, \, 9\).  Дерево из второго примера. Дерево из второго примера. | |
![]()
|
|
F. Хоссам и минимум на отрезке
Бинарный поиск
битмаски
Деревья
Строки
Структуры данных
Теория вероятностей
хэши
*2500
Хоссам дал вам последовательность целых чисел \(a_1, \, a_2, \, \dots, \, a_n\) длины \(n\). Кроме того, он последовательно дает вам \(q\) запросов вида \((l, \, r)\). Для каждого запроса он хочет знать среди чисел \(a_l, \, a_{l + 1}, \, \dots, \, a_r\) такое минимальное число, что оно встречается в заданном отрезке последовательности нечетное количество раз. Вы должны посчитать ответ на каждый запрос, прежде чем отвечать на следующий. Выходные данные Для каждого запроса выведите минимальное число, которое встречается на заданном отрезке последовательности нечетное количество раз. Если такого числа не существует, выведите \(0\). Примечание В данном примере \(\)l_1 = 1, \, r_1 = 2,\(\) \(\)l_2 = 1, \, r_2 = 3,\(\) \(\)l_3 = 2, \, r_3 = 4,\(\) \(\)l_4 = 1, \, r_4 = 4,\(\) \(\)l_5 = 2, \, r_5 = 2,\(\) \(\)l_6 = 1, \, r_6 = 5.\(\) | |
![]()
|
|
E. Две шахматные фигуры
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
*1900
У Cirno_9baka есть дерево с \(n\) вершинами. Он готов поделиться им с вами, что означает, что вы можете на нем оперировать. Изначально в вершине \(1\) дерева стоят две шахматные фигуры. За один шаг вы можете выбрать любую фигуру и переместить ее в соседнюю вершину. Вам также дано целое число \(d\). Вам нужно выполнить следующее условие: расстояние между двумя фигурами всегда должно не превышать \(d\). У каждой из этих двух фигур есть последовательность вершин, которые они должны пройти в любом порядке, и, в конце концов, они должны вернуться в корень. Как любознательный мальчик, он хочет узнать минимальное количество шагов, которое для этого необходимо сделать. Выходные данные Выведите одно целое число — минимальное количество шагов, которые необходимо сделать. Примечание В первом примере, вот одна возможная последовательность шагов длиной \(6\). Вторая фигура перемещается по маршруту \(1 \to 2 \to 4 \to 2 \to 1\). Затем, первая фигура перемещается по маршруту \(1 \to 3 \to 1\).
Во втором примере, вот одна возможная последовательность шагов длиной \(8\): Первая фигура перемещается по маршруту \(1 \to 2 \to 3\). Затем, вторая фигура перемещается по маршруту \(1 \to 2\). Затем, первая фигура перемещается по маршруту \(3 \to 4 \to 3 \to 2 \to 1\). Затем, вторая фигура перемещается по маршруту \(2 \to 1\).
| |
![]()
|
|
G. Покрытие отрезками
Деревья
дп
Комбинаторика
Конструктив
Перебор
Структуры данных
*3200
ChthollyNotaSeniorious дает DataStructures числовую ось с \(m\) различными отрезками на ней. Пусть \(f(l,r)\) — количество способов выбрать четное число отрезков так, чтобы их объединение было равно \([l,r]\), а \(g(l,r)\) — количество способов выбрать нечетное число отрезков так, чтобы их объединение было равно \([l,r]\). ChthollyNotaSeniorious задал DataStructures \(q\) вопросов. В каждом вопросе ChthollyNotaSeniorious дает DataStructures два числа \(l, r\), и хочет, чтобы вы помогли ему найти значение \(f(l,r)-g(l,r)\) по модулю \(998\,244\,353\), чтобы он не подвел ее. Выходные данные Для каждого запроса выведите одно целое число — \(f(l_i,r_i)-g(l_i,r_i)\) по модулю \(998\,244\,353\). Примечание В первом запросе мы должны найти \(f(1, 4) - g(1, 4)\). Единственное подмножество отрезков с объединением \([1, 4]\) это \(\{[1, 3], [2, 4]\}\), поэтому \(f(1, 4) = 1, g(1, 4) = 0\). Во втором запросе нам нужно найти \(f(1, 5) - g(1, 5)\). Единственными подмножествами отрезков с объединением \([1, 5]\) являются \(\{[1, 3], [2, 4], [3, 5]\}\) и \(\{[1, 3], [3, 5]\}\), поэтому \(f(1, 5) = 1, g(1, 5) = 1\). | |
![]()
|
|
M. Parmigiana With Seafood
Бинарный поиск
Деревья
дп
жадные алгоритмы
*3000
The "Parmigiana di melanzane" is a typical Italian dish. Alessandro and Bianca have very different tastes when it comes to it: Alessandro loves to eat Parmigiana with seafood, but Bianca thinks it is an atrocity! To decide which ingredients to include in the dish they prepare, they play the following game. There are \(n\) possible ingredients, labeled from \(1\) to \(n\). The higher the label, the closer the ingredient is to being seafood. The ingredients are connected by \(n - 1\) edges, in such a way as to form a tree. Alessandro and Bianca take turns, with Alessandro going first. They alternately choose a terminal ingredient \(x\), that is an ingredient currently connected to at most one other ingredient, and remove it from the tree. If the terminal ingredient \(x\) was chosen by Alessandro, it goes in the recipe; if it was chosen by Bianca, it is discarded. The taste of the Parmigiana is measured as the maximum label of an ingredient in the recipe. Alessandro wants to maximize the taste, while Bianca wants to minimize the taste. If both play optimally, what is the taste of the Parmigiana? Output Print the value of the taste if both Alessandro and Bianca play optimally. Note In the first sample, Alessandro can choose terminal ingredient \(4\) in the first turn. This ingredient is added to the recipe. Since \(4\) is the maximum label of an ingredient, the taste is \(4\) regardless of the choices that follow.  In the second sample, Bianca can make sure that neither ingredient \(4\) nor \(5\) are included in the recipe, in which case Alessandro can include \(3\). Thus, the taste is \(3\).  | |
![]()
|
|
D. Цена дерева
битмаски
Деревья
дп
Комбинаторика
математика
поиск в глубину и подобное
Теория вероятностей
*1900
Дано дерево на \(n\) вершинах, корень дерева — вершина \(1\). В каждой вершине написано значение, изначально (в момент \(t=0\)) равное \(0\) или \(1\). В каждый целочисленный момент времени \(t>0\) значение вершины становится равно побитовому исключающему ИЛИ значений ее детей в момент времени \(t - 1\); значения листьев становятся равными \(0\), поскольку у них детей нет. Через \(S(t)\) обозначим сумму значений всех вершин в момент \(t\). Через \(F(A)\) обозначим сумму \(S(t)\) по всем значениям \(t\) в диапазоне \(0 \le t \le 10^{100}\), где \(A\) — некоторая изначальная расстановка \(0\) и \(1\) в дереве. Ваша задача — найти сумму \(F(A)\) по всем \(2^n\) изначальным расстановкам \(0\) и \(1\) в дереве. Выведите ответ по модулю \(10^9+7\). Выходные данные Для каждого набора входных данных выведите сумму по модулю \(10^9+7\). Примечание Найдём \(F(A)\) для расстановки \(A = [0,1,0,0,1,1]\) (\(A[i]\) означает значение вершины \(i\)). Состояние дерева в момент времени \(t = 0\) изображено ниже. В каждой вершине записаны два числа: ее номер, затем ее значение. \(S(0)\) в такой конфигурации равно \(3\).  В момент \(t = 1\) конфигурация меняется на \([1,0,0,0,0,0]\). Дерево будет выглядеть так, как показано на рисунке ниже. Имеем \(S(1) = 1\).  В момент \(t = 2\) конфигурация меняется на \([0,0,0,0,0,0]\). Дерево будет выглядеть так, как показано на рисунке ниже. Имеем \(S(2) = 0\).  Для всех \(t>2\) граф остаётся неизменным, то есть \(S(t)=0\) для всех \(t > 2\). Поэтому изначальная расстановка \(A = [0,1,0,0,1,1]\) имеет значение \(F(A) = 3 + 1 = 4\). Выполнив аналогичный процесс для всех \(2^{6}\) возможных стартовых расстановок, получим ответ \(\textbf{288}\). | |
![]()
|
|
E. Разворот ребер
Бинарный поиск
графы
Деревья
поиск в глубину и подобное
*2200
Задан ориентированный взвешенный граф на \(n\) вершинах и \(m\) ориентированных ребрах, вес \(i\)-го ребра равен \(w_i\) (\(1 \le i \le m\)). Нужно развернуть несколько ребер (изменить их ориентацию на противоположную) в этом графе таким образом, чтобы все вершины графа стали достижимы из какой-то одной. Стоимость таких разворотов равна максимальному весу среди всех развернутых ребер. Если можно обойтись без разворота ребер, стоимость считается равной \(0\). Гарантируется, что в графе нет петель и кратных ребер. Найдите наименьшую стоимость, необходимую для достижения цели. Если решения нет, выведите \(-1\). Выходные данные Для каждого набора входных данных выведите наименьшую необходимую стоимость. Если решения нет, выведите \(-1\). Примечание В первом наборе входных данных существует ребро из \(1\) в \(2\), так что все вершины уже достижимы из \(1\). Во втором наборе входных данных невозможно добиться того, чтобы все вершины были достижимы из какой-то одной, как бы ни были развернуты ребра. Поэтому в качестве ответа нужно вывести \(-1\). В третьем наборе входных данных можно развернуть \(4\)-е или \(5\)-е ребро. После этого все вершины станут достижимы из вершины \(1\). Для ответа выбирается \(5\)-е ребро, поскольку его вес меньше. | |
![]()
|
|
F. Немота массива
битмаски
Деревья
разделяй и властвуй
Строки
Структуры данных
*2400
Дан массив \(a\), состоящий из \(n\) неотрицательных целых чисел. Немотой подмассива \(a_l, a_{l+1}, \ldots, a_r\) (для произвольных \(l \leq r\)) назовем величину \(\)\max(a_l, a_{l+1}, \ldots, a_r) \oplus (a_l \oplus a_{l+1} \oplus \ldots \oplus a_r),\(\) где \(\oplus\) обозначает операцию побитового исключающего ИЛИ. Найдите максимальную немоту среди всех подмассивов. Выходные данные Для каждого набора входных данных выведите одно число — максимальную немоту среди всех подмассивов данного массива. Примечание В первом наборе входных данных рассмотрим подмассив \([3, 4, 5]\). В нем максимальное значение равно \(5\). Значит, его немота равна \(3 \oplus 4 \oplus 5 \oplus 5\) = \(7\). Это максимально возможное значение немоты по всем подмассивам. Во втором наборе входных данных подмассив \([47, 52]\) обеспечивает наибольшее значение немоты. | |
![]()
|
|
E. Дерево упало!
битмаски
Деревья
математика
поиск в глубину и подобное
*2500
Недавно на голову Боба с неба упало дерево. В дереве \(n\) вершин. В каждой вершине \(u\) дерева записано целое число \(a_u\). В дереве нет фиксированного корня, так как оно упало с неба. В настоящее время Боб изучает дерево. Чтобы внести некоторую изюминку, Алиса предлагает игру. Сначала Боб выбирает некоторую вершину \(r\) корнем дерева. После этого Алиса выберет вершину \(v\) и сообщит ее Бобу. Затем Боб выберет одну или несколько вершин из поддерева вершины \(v\). Его результат будет равен побитовому исключающему ИЛИ всех значений, записанных в выбранных им вершинах. Боб должен сказать, какой максимальный результат он может получить для заданных \(r\) и \(v\). Поскольку Боб не умеет решать задачи, он просит вас помочь ему найти ответ. Сможете ли вы ему помочь? Вам нужно найти ответ для нескольких комбинаций \(r\) и \(v\) для одного дерева. Напомним, что дерево — это связный неориентированный граф без циклов. Поддерево вершины \(u\) — это множество всех вершин \(y\) таких, что простой путь от \(y\) до корня проходит через \(u\). Обратите внимание, что вершина \(u\) входит в поддерево вершины \(u\). Выходные данные Для каждого набора входных данных для каждого запроса выведите строку, содержащую целое число, обозначающее максимальный результат, который может получить Боб. Примечание На каждом из приведенных ниже рисунков вершина, окрашенная в зеленый цвет — это вершина, выбранная Бобом, а вершина, окрашенный в красный цвет — это вершина, выбранная Алисой. Значения вершин помещены в синие ячейки рядом с вершинами. Рассмотрим первый пример. В первом запросе, если мы примем вершину \(4\) за корень, дерево будет выглядеть так, как показано на рисунке ниже:  Дерево с корнем \(4\) в первом запросе. Дерево с корнем \(4\) в первом запросе. Вершинами в поддереве \(2\) являются: \([2,1,5,6,3]\). Среди них Боб может выбрать вершину \(3\), \(5\) и \(6\). Его результат будет следующим: \(a_3 \oplus a_5 \oplus a_6 = 8 \oplus 6 \oplus 1 = 15\). Он не может набрать больше этого значения. Во втором запросе, если сделать корнем \(3\), то дерево будет выглядеть так:  Дерево с корнем \(3\) во втором запросе. Дерево с корнем \(3\) во втором запросе. Единственной вершиной в поддереве \(5\) является \(5\). Боб может выбрать только вершину \(5\). Его результатом будет \(a_5 = 6\). В третьем запросе, если корень — \(1\), то дерево выглядит следующим образом:  Дерево с корнем \(1\) в третьем запросе. Дерево с корнем \(1\) в третьем запросе. Вершинами в поддереве \(2\) являются: \([2,3,6,4]\). Среди них Боб может выбрать вершину \(2\), \(3\) и \(4\). Его результат будет следующим: \(a_2 \oplus a_3 \oplus a_4 = 12 \oplus 8 \oplus 25 = 29\). Он не может набрать больше этой суммы. | |
![]()
|
|
F. Максимизируем корень
графы
Деревья
дп
математика
поиск в глубину и подобное
теория чисел
*2600
Вам дано корневое дерево, состоящее из \(n\) вершин, пронумерованных от \(1\) до \(n\). Вершина \(1\) является корнем дерева. Каждая вершина имеет целочисленное значение. Значение \(i\)-й вершины равно \(a_i\). Следующую операцию можно выполнить не более \(k\) раз: - Выберите вершину \(v\), которая не была выбрана ранее, и целое число \(x\) такое, что \(x\) является общим делителем значений всех вершин поддерева \(v\). Умножьте значение каждой вершины поддерева \(v\) на \(x\).
Какое максимально возможное значение корневой вершины \(1\) можно получить после не более чем \(k\) операций? Формально, вы должны максимизировать значение \(a_1\). Дерево — это связный неориентированный граф без циклов. Корневое дерево — это дерево с выбранной вершиной, которая называется корнем. Поддерево вершины \(u\) — это множество всех вершин \(y\) таких, что простой путь от \(y\) до корня проходит через \(u\). Обратите внимание, что вершина \(u\) входит в поддерево вершины \(u\). Выходные данные Для каждого набора выведите максимальное значение корня после выполнения не более чем \(k\) операций. Примечание Оба примера имеют одно и то же дерево:  Для первого набора вы можете выполнить две операции следующим образом: - Выберите поддерево с вершиной \(4\) и \(x = 2\).
 После этой операции значения вершин станут \(\{24, 12, 24, 12, 12\}.\) После этой операции значения вершин станут \(\{24, 12, 24, 12, 12\}.\) - Выберите поддерево с вершиной \(1\) и \(x = 12\).
 После этой операции значения вершин станут \(\{288, 144, 288, 144, 144\}.\) После этой операции значения вершин станут \(\{288, 144, 288, 144, 144\}.\) Значение корня равно \(288\) и является максимальным. Для второго тестового примера можно выполнить три операции следующим образом: - Выберите поддерево с вершиной \(4\) и \(x = 2\).
 После этой операции значения вершин станут \(\{24, 12, 24, 12, 12\}.\) После этой операции значения вершин станут \(\{24, 12, 24, 12, 12\}.\) - Выберите поддерево с вершиной \(2\) и \(x = 4\).
 После этой операции значения вершин станут \(\{24, 48, 24, 48, 48\}.\) После этой операции значения вершин станут \(\{24, 48, 24, 48, 48\}.\) - Выберите поддерево с вершиной \(1\) и \(x = 24\).
 После этой операции значения вершин станут \(\{576, 1152, 576, 1152, 1152\}.\) После этой операции значения вершин станут \(\{576, 1152, 576, 1152, 1152\}.\) Значение корня равно \(576\) и является максимальным. | |
![]()
|
|
F. Ксолдовские камни
битмаски
Деревья
дп
Конструктив
*2500
Миша был забанен в шахматах за использование компьютера. Он отправился на пенсию и решил стать ксолдуном. Однажды, гуляя в парке, Миша наткнулся на корневое дерево с вершинами, пронумерованными от \(1\) до \(n\). Корнем дерева является вершина с номером \(1\). Для всех \(1\le i\le n\) в вершине \(i\) лежат \(a_i\) камней. Миша недавно выучил новое заклинание на уроке ксолдовства и хочет его опробовать. Заклинание состоит из нескольких шагов: - Выбрать некоторую вершину \(i\) (\(1 \leq i \leq n\)).
- Вычислить побитовое исключающее ИЛИ \(x\) всех \(a_j\) таких, что вершина \(j\) лежит в поддереве вершины \(i\) (\(i\) принадлежит своему поддереву).
- В значения \(a_j\) для всех вершин \(j\) в поддереве \(i\) присвоить \(x\).
Миша может выполнить не более \(2n\) заклинаний и хочет, чтобы в дереве не осталось камней. Более формально, он хочет, чтобы выполнялось \(a_i=0\) для всех \(1\leq i \leq n\). Можете помочь ему выполнить заклинания? Деревом из \(n\) вершин называется связный ациклический граф из \(n-1\) ребра. Поддеревом вершины \(i\) является множество всех вершин \(j\) таких, что \(i\) лежит на простом пути от \(1\) (корня) к \(j\). В этой задаче \(i\) принадлежит собственному поддереву. Выходные данные Если нет подходящей последовательности заклинаний, выведите \(-1\). Иначе в первой строке выведите одно целое число \(q\) (\(0 \leq q \leq 2n\)) — количество заклинаний в вашем решении. Во второй строке выведите последовательность целых чисел \(v_1,v_2,\ldots,v_q\) (\(1 \leq v_i \leq n\)): \(i\)-е заклинание будет выполнено к поддереву вершины \(v_i\). Обратите внимание, что здесь важен порядок. Если существует несколько решений, выведите любое из них. Вам не нужно минимизировать число операций. Примечание Рисунок ниже объясняет третий пример. Показаны только первые \(4\) заклинания, так как последние \(2\) ничего не меняют. Первый рисунок показывает начальное дерево, число камней в каждой вершине написано над вершиной зеленым. Изменения от заклинаний показаны красным.  | |
![]()
|
|
F. Вставка скобок
Деревья
дп
Комбинаторика
математика
*2700
Вика любит играть со скобочными последовательностями. Сегодня она хочет создать новую скобочную последовательность по следующему алгоритму. Исходно скобочная последовательность Вики — пустая строка, а дальше \(n\) раз она повторит следующие действия: - Выберет место в текущей скобочной последовательности, куда можно вставлять скобки, случайно равновероятно среди всех возможных позиций. Если длина текущей последовательности равна \(k\), то таких позиций \(k+1\): перед первой скобкой, между первой и второй скобками, \(\ldots\), после \(k\)-й скобки. В частности, в пустой скобочной последовательности одно такое место.
- Выберет строку «()» с вероятностью \(p\) или строку «)(» с вероятностью \(1 - p\) и вставит её в выбранное место. Длина скобочной последовательности увеличится на \(2\).
Скобочная последовательность называется правильной, если из неё возможно получить корректное арифметическое выражение путём вставки символов «+» и «1». Например, последовательности «(())()», «()» и «(()(()))» являются правильными, а «)(», «(()» и «(()))(» — нет. Вика хочет знать, с какой вероятностью ее итоговая скобочная последовательность будет правильной. Помогите ей и найдите эту вероятность по модулю \(998\,244\,353\) (см. формат вывода). Выходные данные Выведите вероятность того, что скобочная последовательность Вики окажется правильной, по модулю \(998\,244\,353\). Формально, пусть \(M = 998\,244\,353\). Можно показать, что ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Примечание В первом примере с вероятностью \(p = \frac{3}{4}\) получится правильная скобочная последовательность (), а с вероятностью \(1 - p = \frac{1}{4}\) получится неправильная скобочная последовательность )(. Искомая вероятность равна \(\frac{3}{4}\), а \(249\,561\,089 \cdot 4 \equiv 3 \pmod{998\,244\,353}\). Во втором примере искомая вероятность равна \(\frac{11}{25}\). | |
![]()
|
|
G. Разнообразная раскраска
Деревья
Конструктив
*3200
В этой задаче мы будем работать с подвешенными бинарными деревьями. Напомним, что дерево называется подвешенным бинарным, если в нем есть выделенный корень, а у каждой вершины не более двух детей. Сопоставим каждой вершине дерева один из двух цветов — белый или синий — и назовем такое сопоставление раскраской дерева. Раскраску назовем разнообразной, если у каждой вершины есть сосед (ребенок или родитель), покрашенный не в тот же цвет, что и сама вершина. Можно показать, что у любого дерева из не менее чем двух вершин существует разнообразная раскраска. Дисбалансом раскраски назовем абсолютную разность между числом белых и синих вершин в ней. Теперь к задаче. Изначально дерево состоит из одной вершины с номером \(1\), являющейся его корнем. Далее для каждого \(i\) от \(2\) до \(n\) в дереве появляется новая вершина \(i\), которая становится ребенком вершины \(p_i\). Гарантируется, что после каждого добавления дерево будет оставаться бинарным с корнем в вершине \(1\), то есть у каждой вершины будет не более двух детей. После каждого добавления вершины нужно вывести минимальное возможное значение дисбаланса по всем возможным разнообразным раскраскам текущего дерева. Более того, после добавления последней вершины с номером \(n\) нужно также вывести саму разнообразную раскраску с минимальным дисбалансом. Выходные данные Для каждого набора входных данных выведите \(n-1\) целое число — минимальное возможное значение дисбаланса по всем возможным разнообразным раскраскам дерева после добавления в него вершин \(2, 3, \ldots, n\). Далее выведите строку из \(n\) символов «w» и «b», описывающую разнообразную раскраску с минимальным дисбалансом для всего дерева целиком после добавления вершины \(n\): \(i\)-й символ строки должен быть равен «w», если вершина \(i\) покрашена в белый цвет, и «b», если в синий. Абсолютная разность между числом символов «w» и «b» должна быть равна последнему выведенному числу. У каждой вершины должен быть родитель или ребенок, покрашенный не в тот же цвет, что и сама вершина. Примечание Примеры разнообразных раскрасок с минимальным дисбалансом для всех промежуточных деревьев в первом наборе входных данных представлены на рисунке ниже:  | |
![]()
|
|
G. Радиус взвешенного дерева
Деревья
разделяй и властвуй
реализация
Структуры данных
*2800
Вам задано дерево из \(n\) вершин и \(n - 1\) ребра. Первоначальный вес \(i\)-й вершины равен \(a_i\). Назовем расстоянием \(d_v(u)\) от вершины \(v\) до вершины \(u\) количество ребер на пути из \(v\) в \(u\). Заметим, что \(d_v(u) = d_u(v)\) и \(d_v(v) = 0\). Назовем взвешенным расстоянием \(w_v(u)\) от \(v\) до \(u\) значение \(w_v(u) = d_v(u) + a_u\). Заметим, что \(w_v(v) = a_v\) и \(w_v(u) \neq w_u(v)\), если \(a_u \neq a_v\). Аналогично обычному расстоянию, назовем эксцентриситетом \(e(v)\) вершины \(v\) наибольшее взвешенное расстояние от \(v\) до какой-либо вершины (включая саму \(v\)), или \(e(v) = \max\limits_{1 \le u \le n}{w_v(u)}\). Наконец, назовем радиусом \(r\) дерева наименьший из эксцентриситетов его вершин, или \(r = \min\limits_{1 \le v \le n}{e(v)}\). Вам нужно обработать \(m\) запросов следующего вида: - \(v_j\) \(x_j\) — присвоить \(a_{v_j} = x_j\).
После обработки каждого запроса выведите радиус \(r\) текущего дерева. Выходные данные Выведите \(m\) целых чисел — радиус \(r\) дерева после обработки каждого запроса. Примечание После первого запроса дерево выглядит следующим образом:  Цветом на изображении отмечена вершина с наименьшим \(e(v)\), соответственно \(r = e(4) = 7\). Эксцентриситеты других вершин равны: \(e(1) = 8\), \(e(2) = 9\), \(e(3) = 9\), \(e(5) = 8\), \(e(6) = 8\). Дерево после второго запроса:  Радиус \(r = e(1) = 4\). После третьего запроса радиус \(r = e(2) = 5\):  | |
![]()
|
|
G. Раскраска дерева
Деревья
Перебор
Структуры данных
*3000
Задано реберно-взвешенное дерево из \(n\) вершин, каждое ребро которого окрашено в некоторый цвет. Каждая вершина дерева может быть заблокирована или разблокирована. Изначально все вершины разблокированы. Простой путь — это путь в графе, который не имеет повторяющихся вершин. Длина пути определяется как сумма весов всех ребер на пути. Путь называется хорошим, если это простой путь, состоящий из ребер одного цвета \(c\), все ребра цвета \(c\) в дереве лежат на этом пути, и каждая вершина пути разблокирована. Вам нужно обрабатывать запросы \(2\)-х типов: - заблокировать вершину,
- разблокировать вершину.
После каждого запроса выведите максимальную длину среди всех хороших путей. Если не существует хорошего пути, выведите \(0\). Выходные данные Для каждого запроса выведите максимальную длину хорошего пути. Если не существует хорошего пути, выведите \(0\). | |
![]()
|
|
F. XOR, деревья и запросы
битмаски
графы
Деревья
жадные алгоритмы
Конструктив
поиск в глубину и подобное
реализация
снм
*2500
Вам дано дерево с \(n\) вершинами. Вершины пронумерованы от \(1\) до \(n\). Вам нужно будет назначить каждому ребру вес. Пусть вес \(i\)-го ребра будет \(a_i\) (\(1 \leq i \leq n-1\)). Вес каждого ребра должен быть целым числом от \(0\) до \(2^{30}-1\), включительно. Вам дано \(q\) условий. Каждое условие состоит из трех целых чисел \(u\), \(v\) и \(x\). Это означает, что побитовое исключающее ИЛИ всех ребер на кратчайшем пути от \(u\) до \(v\) должно быть равно \(x\). Выясните, существуют ли числа \(a_1, a_2, \ldots, a_{n-1}\), удовлетворяющие заданным условиям. Если существуют, выведите такое решение, при котором \(a_1 \oplus a_2 \oplus \ldots \oplus a_{n-1}\) будет наименьшим. Здесь \(\oplus\) обозначает операцию побитового исключающего ИЛИ. Если существует несколько решений таких, что \(a_1 \oplus a_2 \oplus \ldots \oplus a_{n-1}\) является наименьшим, выведите любое из них. Выходные данные Если не существует \(a_1\), \(a_2\), ..., \(a_{n-1}\), которые удовлетворяют заданным условиям, выведите «No». В противном случае в первой строке выведите «Yes». Затем в следующей строке выведите \(n-1\) целых чисел, где \(i\)-е целое число — это вес \(i\)-го ребра. Если существует несколько решений, то выведите такое решение, при котором \(a_1 \oplus a_2 \oplus \ldots \oplus a_{n-1}\) будет наименьшим. Если существует несколько решений, при которых \(a_1 \oplus a_2 \oplus \ldots \oplus a_{n-1}\) принимает наименьшее значение, выведите любое. При выводе «Yes» или «No» вы можете выводить каждую букву в любом регистре (строчную или заглавную). Например, строки «yEs», «yes», «Yes» и «YES» будут приняты как положительный ответ. Примечание Для первого примера не существует набора весов ребер, удовлетворяющего заданному условию. Для второго примера два условия означают, что \(a_1 \oplus a_2 \oplus a_3=2\) и \(a_4 \oplus a_5=7\). Может существовать несколько решений, например, \((a_1, a_2, a_3, a_4, a_5)=(1, 2, 1, 4, 3)\). Для третьего примера два условия означают, что \(a_1 \oplus a_2 \oplus a_3=3\) и \(a_1 \oplus a_4 \oplus a_5=5\). Существует множество решений, удовлетворяющих данному условию. \((a_1, a_2, a_3, a_4, a_5)=(1, 1, 3, 4, 0)\) удовлетворяет заданным условиям, но побитовое исключающее ИЛИ весов всех ребер равно \(7\), что не является наименьшим возможным значением \(a_1 \oplus a_2 \oplus \ldots \oplus a_{n-1}\), поэтому это не является верным решением. | |
![]()
|
|
F. Тимофей и черно-белое дерево
графы
Деревья
жадные алгоритмы
кратчайшие пути
математика
Перебор
поиск в глубину и подобное
разделяй и властвуй
*2100
Тимофей приехал в известную летнюю школу и нашел там дерево на \(n\) вершинах. Дерево — это связный неориентированный граф без циклов. Каждая вершина этого дерева, кроме \(c_0\), покрашена в белый цвет. Вершина \(c_0\) покрашена в черный цвет. Тимофей хочет покрасить все вершины этого дерева в черный цвет. Для этого он выполняет \(n - 1\) операцию. Во время \(i\)-й операции он выбирает белую вершину \(c_i\) и красит ее в черный цвет. Назовем позитивностью дерева минимальное расстояние между всеми парами различных черных вершин в нем. Расстоянием между вершинами \(v\) и \(u\) называется количество ребер на пути от \(v\) до \(u\). После каждой очередной покраски Тимофей хочет знать позитивность текущего дерева. Выходные данные Для каждого набора входных данных выведите в отдельной строке \(n - 1\) число. Число с номером \(i\) должно быть равно позитивности дерева, полученного первыми \(i\) покрасками. Примечание В первом наборе входных данных, после второй покраски, дерево выглядит так:  Расстояние между вершинами \(1\) и \(6\) равно \(3\), расстояние между вершинами \(4\) и \(6\) равно \(3\), расстояние между вершинами \(1\) и \(4\) равно \(2\). Позитивность такого дерева равна минимуму из этих расстояний, то есть \(2\). В третьем наборе входных данных, после четвертой покраски, дерево выглядит так:  Позитивность такого дерева равна \(2\). | |
![]()
|
|
E. Разметка дерева расстояниями
Деревья
дп
жадные алгоритмы
реализация
Структуры данных
хэши
*2400
Вам задано невзвешенное дерево из \(n\) вершин, пронумерованных от \(1\) до \(n\), и список из \(n-1\) целого числа \(a_1, a_2, \ldots, a_{n-1}\). Дерево — это связный неориентированный граф без циклов. Вы можете использовать каждый элемент списка, чтобы пометить одну из вершин дерева. Никакая вершина не должна быть помечена дважды. Вы можете пометить единственную оставшуюся непомеченной вершину любым целым числом. Вершина \(x\) называется хорошей, если можно так пометить вершины, чтобы для каждой вершины \(i\) ее метка была равна расстоянию между \(x\) и \(i\). Расстояние между двумя вершинами \(s\) и \(t\) на дереве — это минимальное количество ребер на пути, который начинается в вершине \(s\) и заканчивается в вершине \(t\). Найдите все хорошие вершины. Выходные данные В первой строке выведите количество хороших вершин. Во второй строке выведите номера всех хороших вершин в порядке возрастания. Примечание На рисунке ниже показано дерево для первого примера:  На рисунке ниже показаны две возможные разметки, такие что \(2\) — хорошая вершина (слева) и \(4\) — хорошая вершина (справа).  Квадрат под каждой вершиной означает ее метку. Черные квадраты содержат числа, которые были в данном списке, а единственный белый квадрат содержит единственное число, которого не было в данном списке. Во втором примере единственной хорошей вершиной является вершина \(3\). В третьем примере хороших вершин нет. | |
![]()
|
|
F. Блокирующие фишки
Бинарный поиск
Деревья
жадные алгоритмы
Конструктив
поиск в глубину и подобное
*2400
Задано дерево, состоящее из \(n\) вершин. На нем есть \(k\) фишек, расположенных в вершинах \(a_1, a_2, \dots, a_k\). Все \(a_i\) различны. Вершины \(a_1, a_2, \dots, a_k\) изначально покрашены в черный цвет. Остальные вершины белые. Вы сыграете в игру, в ходе которой сделаете какое-то количество ходов (возможно, ноль). На \(i\)-м ходе (в \(1\)-индексации) вы подвинете фишку номер \(((i - 1) \bmod k + 1)\) из ее текущей вершины в соседнюю белую вершину и покрасите эту вершину в черный. То есть, если \(k=3\), то вы двигаете фишку \(1\) на ходе \(1\), фишку \(2\) на ходе \(2\), фишку \(3\) на ходе \(3\), фишку \(1\) на ходе \(4\), фишку \(2\) на ходе \(5\), и так далее. Если нет соседней белой вершины, то игра заканчивается. Какое наибольшее количество ходов вы можете совершить? Выходные данные На каждый набор входных данных выведите одно целое число — наибольшее количество ходов, которые вы можете совершить. | |
![]()
|
|
E. Красивые подграфы
Деревья
дп
жадные алгоритмы
игры
поиск в глубину и подобное
*2500
У Монокарпа есть дерево, состоящее из \(n\) вершин. Он планирует выбрать некоторую вершину \(r\) и проделать следующие операции над каждой вершиной \(v\) от \(1\) до \(n\): - присвоить \(d_v\) равным расстоянию от \(v\) до \(r\) (количество ребер на кратчайшем пути);
- раскрасить \(v\) в какой-нибудь цвет.
Раскраска называется красивой, если она удовлетворяет двум условиям: - для каждой пары вершин одного цвета \((v, u)\) существует путь из \(v\) в \(u\), который посещает только вершины того же цвета;
- для каждой пары вершины одного цвета \((v, u)\), \(d_v \neq d_u\).
Обратите внимание, что Монокарп может выбирать любое количество различных цветов, которые он хочет использовать. Для каждого использованного цвета он затем считает количество вершин этого цвета. Стоимость дерева — это минимум из этих значений. Какая может быть наибольшая стоимость дерева? Выходные данные На каждый набор входных данных выведите одно целое число — наибольшая возможная стоимость дерева. | |
![]()
|
|
D. Li Hua и дерево
Деревья
дп
Перебор
поиск в глубину и подобное
реализация
Структуры данных
*1900
У Li Hua есть дерево с \(n\) вершинами и \(n-1\) ребром. Корнем дерева является вершина \(1\). Каждая вершина \(i\) имеет важность \(a_i\). Обозначим размер поддерева как количество вершин в нем, а важность как сумму важности вершин в нем. Обозначим тяжелым сыном нелистовой вершины сына с наибольшим размером поддерева. Если таких вершин несколько, то тяжёлым сыном будет та, у которой индекс минимален. Li Hua хочет выполнить \(m\) операций: - «1 \(x\)» (\(1\leq x \leq n\)) — вычислить важность поддерева, корнем которого является \(x\).
- «2 \(x\)» (\(2\leq x \leq n\)) — повернуть тяжёлого сына поддерева \(x\) вверх. Формально, обозначим как \(son_x\) тяжелого сына \(x\), \(fa_x\) как отца \(x\). Он хочет удалить ребро между \(x\) и \(fa_x\) и добавить ребро между \(son_x\) и \(fa_x\). Гарантируется, что \(x\) не является корнем, но не гарантируется, что \(x\) не является листом. Если \(x\) является листом, проигнорируйте эту операцию.
Предположим, что вы Li Hua. Пожалуйста, решите эту задачу. Выходные данные Для каждого запроса вида «1 \(x\)» выведите ответ в отдельной строке. Примечание В первом примере: Начальное дерево показано на следующем рисунке: Важность поддерева \(6\) равна \(a_6+a_7=2\). После поворота тяжелого сына вершины \(3\) (которым является \(6\)) вверх, дерево будет выглядеть следующим образом: Важность поддерева \(6\) равна \(a_6+a_3+a_7=3\). Важность поддерева \(2\) - \(a_2+a_4+a_5=3\). | |
![]()
|
|
F. Li Hua и путь
Деревья
поиск в глубину и подобное
разделяй и властвуй
снм
Структуры данных
*3000
У Li Hua есть дерево из \(n\) вершин и \(n-1\) рёбер. Вершины пронумерованы от \(1\) до \(n\). Пара вершин \((u,v)\) (\(u < v\)) считается милой, если ровно одно из следующих двух утверждений истинно: - \(u\) является вершиной с минимальным индексом среди всех вершин на пути \((u,v)\).
- \(v\) — вершина с максимальным индексом среди всех вершин на пути \((u,v)\).
Будет выполнено \(m\) операций. В каждой операции Li Hua выбирает целое число \(k_j\), затем вставляет в дерево вершину с номером \(n+j\), соединяющуюся с вершиной номер \(k_j\). Он хочет подсчитать количество милых пар вершин до операций и после каждой операции. Предположим, что вы Li Hua. Пожалуйста, решите эту задачу. Выходные данные Выведите \(m+1\) целых чисел — количество милых пар вершин до операций и после каждой операции. Примечание Начальное дерево показано на следующем рисунке: Существует \(11\) милых пар — \((1,5),(2,3),(2,4),(2,6),(2,7),(3,4),(3,6),(3,7),(4,5),(5,7),(6,7)\). Аналогично, мы можем посчитать милые пары после каждой операции, и результатами будут \(15\) и \(19\). | |
![]()
|
|
G. Симмеtreeя
Деревья
поиск в глубину и подобное
реализация
хэши
*2200
Киду подарили дерево из \(n\) вершин с корнем в вершине \(1\). Так как он очень любит симметричные объекты, Кид хочет узнать симметрично ли это дерево.  Например, деревья на картинке выше симметричны. Например, деревья на картинке выше симметричны.  А деревья на этой картинке не симметричны. А деревья на этой картинке не симметричны. Более формально, дерево является симметричным, если существует такой порядок детей, что: - Поддерево самого левого ребёнка корня является зеркальным отражением поддерева самого правого ребёнка;
- поддерево второго слева ребёнка корня является зеркальным отражением поддерева второго справа ребёнка корня;
- ...
- если число детей корня нечётно, то поддерево среднего ребёнка должно быть симметрично.
Выходные данные Выведите \(t\) строк, каждая из которых является ответом на соответствующий набор входных данных. В качестве ответа выведите «YES», если данное дерево симметрично, и «NO» в противном случае. Вы можете выводить ответ в любом регистре (например, строки «yEs», «yes», «Yes» и «YES» будут распознаны как положительный ответ). | |
![]()
|
|
E. Цены на бензин
Деревья
разделяй и властвуй
снм
Структуры данных
хэши
*3000
Берляндия — это огромная страна, состоящая из \(n\) городов. Дорожную сеть Берляндии можно представить в виде корневого дерева, то есть всего в стране \(n - 1\) дорога, и от любого города можно добраться до любого другого ровно по одному пути, если не посещать никакой город дважды. Для удобства представления страны, для каждого города \(i\) зафиксирован город \(p_i\), равный первому городу, в который надо ехать из города \(i\), чтобы добраться до города \(1\). Иными словами, город \(p_i\) равен предку города \(i\), если дерево подвесить за город \(1\). В каждом городе Берляндии работает по одной заправке. У заправок особое ценообразование, и для каждой заправки зафиксирован диапазон цен, за которые там готовы продавать бензин. Заправка в городе с номером \(i\) готова продавать бензин по любой цене от \(l_i\) до \(r_i\) включительно. Король Берляндии — примерный семьянин, и в течение \(m\) лет каждый год у него рождалось по двое сыновей. Дети короля с раннего детства участвуют в государственных делах, и в конце каждого года они проверяют честность цен на бензин. С самого рождения дети короля, которые рождены в год \(i\), отвечают за проверку цен на бензин на путях от города \(a_i\) до города \(b_i\) и от города \(c_i\) до города \(d_i\) соответственно. Проверка происходит следующим образом: оба ребенка одновременно начинают путь от городов \(a_i\) и \(c_i\) соответственно. Первый сын короля, рождённый в год \(i\), двигается по пути от города \(a_i\) до города \(b_i\), а второй — от города \(c_i\) до города \(d_i\). Дети проверяют, что цена на бензин в городе \(a_i\) совпадает с ценой на бензин в городе \(c_i\). Далее они проверяют, что цена на бензин во втором городе на пути от \(a_i\) до \(b_i\) совпадает с ценой во втором городе на пути от \(c_i\) до \(d_i\). Далее они повторяют то же самое для пары третьих городов на их путях и так далее. В конце они проверяют, что цена на бензин в городе \(b_i\) совпадает с ценой на бензин в городе \(d_i\). Гарантируется, что длина пути от города \(a_i\) до города \(b_i\) совпадает с длиной пути от города \(c_i\) до города \(d_i\). Заправки должны строго подчиняться законам, а поэтому все проверки цен на бензин не должны выявлять нарушений. Помогите заправкам Берляндии выяснить, сколькими способами они могут выставлять цены на бензин в течение \(m\) лет. Другими словами, для каждого \(i\) от \(1\) до \(m\) посчитайте, сколькими способами можно выставить цены на бензин во всех заправках, чтобы после рождения первых \(i\) пар детей короля, все их проверки не выявили нарушений, а на любой заправке цена находилась в допустимом диапазоне цен. Так как число таких способов может быть большим, посчитайте ответ по модулю \(10^9 + 7\). Выходные данные В \(m\) строках выведите по одному числу. Число в \(i\)-й строке должно равняться числу способов выставить цены на бензин во всех городах, чтобы дети короля, рождённые в годы до \(i\)-го включительно не выявили нарушений в проверках. Числа выводите по модулю \(10^9 + 7\). Примечание Рассмотрим первый пример. После рождения первых двух сыновей цены в городах \(1\) и \(2\) должны быть равны. Всего существует 2 способа выбрать одинаковую цену на бензин для городов \(1\) и \(2\), чтобы она входила в допустимый диапазон цен для этих городов. Значит, всего способов выставить цены на бензин: \(2 \cdot 3 \cdot 3 \cdot 1 = 18\). Вторая пара сыновей будет проверять цены на путях \(1 - 2\) и \(2 - 1\). Значит, цены на бензин в городах \(1\) и \(2\) должны совпадать, что уже выполняется. Поэтому после рождения второй пары сыновей ответ никак не изменился. Третья пара сыновей будет проверять цены на путях \(3 - 1 - 2 - 4\) и \(4 - 2 - 1 - 3\). Тогда цена не бензин в городе \(3\) должна быть равна цене в городе \(4\), и цена в городе \(1\) должна быть равна цене в городе \(2\). Цены в городах \(1\) и \(2\) уже одинаковые. Для городов \(3\) и \(4\) существует 2 способа выбрать одинаковую цену на бензин, чтобы она входила в допустимый диапазон цен для этих городов. Значит, всего способов выставить цены на бензин: \(2 \cdot 2 \cdot 1 = 4\). Четвертая пара сыновей будет проверять цены на путях \(3 - 1 - 2 - 4\) и \(3 - 1 - 2 - 5\). Это означает, что цены в городах \(4\) и \(5\) должны быть равны, и так как цены в городах \(3\) и \(4\) уже совпадают, то в городах \(3\), \(4\) и \(5\) должна быть одинаковая цена на бензин. Цена на бензин в городе \(3\) должна быть не больше 3, а цена на бензин в городе \(5\) должна быть не меньше 4. Значит, после рождения четвёртой пары сыновей не существует способов выставить цены на бензин так, чтобы все проверки выполнялись и цены находились в необходимых диапазонах. | |
![]()
|
|
D. Широкий-преширокий граф
графы
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
*1800
Дано дерево (связный граф без циклов) на \(n\) вершинах. Зафиксируем число \(k\). Назовем графом \(G_k\) граф на \(n\) вершинах, в котором между вершинами \(u\) и \(v\) есть ребро тогда и только тогда, когда расстояние между вершинами \(u\) и \(v\) в данном дереве не меньше \(k\). Для каждого \(k\) от \(1\) до \(n\) выведите количество компонент связности в графе \(G_k\). Выходные данные Выведите \(n\) целых чисел — количество компонент связности в графе \(G_k\) для каждого \(k\) от \(1\) до \(n\). Примечание В первом примере: При \(k=1\) в графе будет ребро между каждой парой вершин, поэтому в нём будет одна компонента. При \(k=4\) в графе будут только рёбра \(4 \leftrightarrow 6\) и \(5 \leftrightarrow 6\), поэтому в графе будет \(4\) компоненты. Во втором примере: при \(k=1\) и \(k=2\) в графе одна компонента. При \(k=3\) граф \(G_k\) разбивается на \(3\) компоненты: в одной компоненте вершины \(1\), \(4\) и \(5\), а ещё две компоненты содержат по одной вершине. При \(k=4\) и \(k=5\) каждая вершина является отдельной компонентой. | |
![]()
|
|
E. Максимумов должно быть много
Деревья
дп
Перебор
поиск в глубину и подобное
Структуры данных
*2300
Дано дерево (связный граф без циклов). В каждой вершине дерева записано число. Назовём характеристикой \(\mathrm{MAD}\) (maximum double) дерева максимальное число, которое встречается в вершинах этого дерева хотя бы \(2\) раза. Если же никакое число не встречается в дереве больше одного раза, то положим \(\mathrm{MAD}=0\). Заметим, что если удалить ребро из дерева, то оно распадётся на два дерева. Вычислим \(\mathrm{MAD}\) в каждом из деревьев и возьмем максимум из этих двух значений. Полученный результат назовем значением удаленного ребра. Для каждого ребра найдите его значение. Обратите внимание, что мы в действительности не удаляем ребра из дерева, и каждое значение должно быть вычислено независимо. Выходные данные Для каждого ребра в порядке ввода выведите одно число — максимум из \(\mathrm{MAD}\) двух деревьев, получающихся после удаления из начального дерева данного ребра. Примечание  В первом примере после удаления ребра \((1, 2)\) ни в одном из получившихся поддеревьев никакое число не будет повторяться \(2\) раза, поэтому ответ равен \(\max(0, 0)=0\). После удаления ребра \((2, 3)\) в бо́льшем поддереве будет два раза повторяться \(1\) и два раза повторяться \(2\), поэтому \(\mathrm{MAD}\) этого дерева будет равен \(2\). После удаления ребра \((2, 4)\) в бо́льшем поддереве будет повторяться только число \(1\), а во втором будет только одно число, поэтому ответом будет \(1\). Во втором примере, если ребро \(1 \leftrightarrow 4\) не удалено, то в одном из поддеревьев будет две \(1\), поэтому ответ — \(1\). А если удалено ребро \(1 \leftrightarrow 4\), то в обоих поддеревьях нет повторяющихся значений, поэтому ответом будет \(0\). | |
![]()
|
|
E. Мастер деревьев
Деревья
Перебор
поиск в глубину и подобное
Структуры данных
*2200
Вам дано дерево с \(n\) взвешенными вершинами, пронумерованными от \(1\) до \(n\). Корнем дерева является \(1\). Родитель вершины \(i\) — вершина \(p_i\), а вес вершины \(i\) — число \(a_i\). Для удобства определим \(p_1=0\). Для двух вершин \(x\) и \(y\) одинаковой глубины\(^\dagger\), определим \(f(x,y)\) следующим образом: - Инициализируем \(\mathrm{ans}=0\).
- Пока \(x\) и \(y\) не \(0\):
- \(\mathrm{ans}\leftarrow \mathrm{ans}+a_x\cdot a_y\);
- \(x\leftarrow p_x\);
- \(y\leftarrow p_y\).
- \(f(x,y)\) равно значению \(\mathrm{ans}\).
Вам предстоит обработать \(q\) запросов. В \(i\)-м запросе вам даны два целых числа \(x_i\) и \(y_i\), и вам нужно вычислить \(f(x_i,y_i)\). \(^\dagger\) Глубина вершины \(v\) — это количество ребер на единственном простом пути от корня дерева до вершины \(v\). Выходные данные Выведите \(q\) строк, \(i\)-я строка содержит одно целое число — значение \(f(x_i,y_i)\). Примечание Рассмотрим первый пример. В первом запросе ответ – \(a_4\cdot a_5+a_3\cdot a_3+a_2\cdot a_2+a_1\cdot a_1=3+4+25+1=33\). Во втором запросе ответ – \(a_6\cdot a_6+a_2\cdot a_2+a_1\cdot a_1=1+25+1=27\). | |
![]()
|
|
F. M-дерево
Деревья
математика
сортировки
Структуры данных
*2800
Корневое дерево называется хорошим, если каждая вершина дерева либо является листом (вершиной без детей), либо имеет ровно \(m\) детей. Пусть на хорошем дереве на каждом листе \(u\) записано положительное целое число \(c_{u}\). Мы определяем значение листа как \(c_{u} + \mathrm{dep}_{u}\), где \(\mathrm{dep}_{u}\) — количество ребер на пути от вершины \(u\) до корня (также известное как глубина \(u\)). Ценность хорошего дерева — это максимальное значение всех его листьев. Вам дан массив из \(n\) целых чисел \(a_{1}, a_{2}, \ldots, a_{n}\), которые должны быть записаны на листьях. Вам нужно построить хорошее дерево из \(n\) листьев и записать целые числа из массива \(a\) во все листья. Формально, вы должны выбрать для каждого листа \(u\) индекс \(b_{u}\), где \(b\) — перестановка длины \(n\), означающая, что целое число, записанное на листе \(u\), равно \(c_u = a_{b_{u}}\). При этих ограничениях вам необходимо минимизировать ценность хорошего дерева. У вас есть \(q\) запросов. Каждый запрос задается парой целых чисел \(x\) и \(y\) и меняет \(a_{x}\) на \(y\), после чего вы должны вывести минимальное значение хорошего дерева для заданного массива \(a\). Перестановкой длины \(n\) называется массив, состоящий из \(n\) различных целых чисел от \(1\) до \(n\) в произвольном порядке. Например, \([2,3,1,5,4]\) — это перестановка, но \([1,2,2]\) не является перестановкой (\(2\) встречается в массиве дважды), также как и \([1,3,4]\) не является перестановкой (\(n=3\), но в массиве есть элемент равный \(4\)). Выходные данные Для каждого набора входных данных выведите \(q\) целых чисел, \(i\)-е из которых — минимальная ценность дерева после \(i\)-го изменения. Примечание В первом наборе входных данных после первого запроса текущий массив \(a\) равен \([4,3,4,4,5]\). Мы можем построить такое хорошее дерево: Первое число внутри вершины — это ее номер (в этой задаче номер вершины не имеет значения, но помогает понять рисунок). Если вершина является листом, то второе число внутри вершины — это число, написанное на ней. Заметим, что \(\mathrm{dep}_{3}=\mathrm{dep}_{4}=1,\mathrm{dep}_{5}=\mathrm{dep}_{6}=\mathrm{dep}_{7}=2\), и ценность дерева, которая является максимальным значением по всем листьям, равна \(5+1=6\). Значения листьев \(5\), \(6\) и \(7\) также равны \(6\). Можно показать, что это дерево имеет минимальную ценность среди всех допустимых деревьев. | |
![]()
|
|
B. Граф сумм
графы
Деревья
интерактив
Конструктив
кратчайшие пути
Перебор
реализация
*2000
Это интерактивная задача. Загадана перестановка \(p_1, p_2, \dots, p_n\). Рассмотрим неориентированный граф с \(n\) вершинами и без рёбер. Вы можете делать два типа запросов: - Укажите целое число \(x\) такое, что \(2 \le x \le 2n\). Тогда для всех целых чисел \(i\) (\(1 \le i \le n\)) таких, что \(1 \le x-i \le n\), будет добавлено ребро между вершинами \(i\) и \(x-i\).
- Запросить число рёбер в кратчайшем пути между вершинами \(p_i\) и \(p_j\). В качестве ответа вы получите количество рёбер на кратчайшем пути, если такой путь существует, или \(-1\), если такого пути нет.
Обратите внимание, что вы можете делать оба типа запросов в любом порядке. Сделав \(2n\) запросов (включая тип \(1\) и тип \(2\)), угадайте две возможные перестановки, хотя бы одна из которых равна \(p_1, p_2, \dots, p_n\). Ваш ответ будет засчитан, если хотя бы одна из перестановок верна. Вы можете вывести одну и ту же перестановку дважды. Перестановкой длины \(n\) является массив, состоящий из \(n\) различных целых чисел от \(1\) до \(n\) в произвольном порядке. Например, \([2,3,1,5,4]\) — перестановка, но \([1,2,2]\) не перестановка (\(2\) встречается в массиве дважды) и \([1,3,4]\) тоже не перестановка (\(n=3\), но в массиве встречается \(4\)). Протокол взаимодействия Взаимодействие для каждого набора входных данных начинается после считывания \(n\). Затем, сделайте не более \(2n\) запросов: - Если вы хотите сделать запрос типа \(1\), выведите «+ x». \(x\) должно быть целым числом от \(2\) до \(2n\) включительно. После этого считайте \(1\) или \(-2\). Если вы считали \(1\), то ваш запрос был корректным, иначе он был некорректным или вы превысили количество запросов, и ваша программа должна немедленно завершиться, чтобы получить вердикт Неправильный ответ.
- Если вы хотите сделать запрос типа \(2\), выведите «? i j». \(i\) и \(j\) должны быть целыми числами от \(1\) до \(n\) включительно. После этого, считайте единственное целое число \(r\) (\(-1 \le r \le n\)) — ответ на ваш запрос. Если вы получили число \(−2\) вместо ответа, то ваша программа сделала некорректный запрос или превысила число запросов. Ваша программа должна немедленно завершиться для получения вердикта Неправильный ответ.
В любой момент взаимодействия, если вы хотите угадать две перестановки, выведите «! \(p_{1,1}\) \(p_{1,2}\) \(\dots\) \(p_{1,n}\) \(p_{2,1}\) \(p_{2,2}\) \(\dots\) \(p_{2,n}\)». Обратите внимание, что вы должны выводить две перестановки на одной и той же строке и без восклицательного знака между перестановками. После этого считайте \(1\) или \(-2\). Если вы считали \(1\), то ваш ответ был правильным, иначе он был неправильным, и ваша программа должна немедленно завершиться, чтобы получить вердикт Неправильный ответ. После этого, перейдите к следующему набору входных данных, или завершите программу, если такого нет. Обратите внимание, что вывод ответа не считается как запрос. Обратите внимание, что даже если вы вывели правильную перестановку, вторая перестановка должна быть именно перестановкой, а не произвольным массивом. В любой момент, если вы продолжите взаимодействие после считывания числа \(-2\), вы можете получить любой вердикт, так как программа продолжит чтение из закрытого потока. После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Интерактор является неадаптивным. Это означает, что все перестановки зафиксированы до начала взаимодействия. Взломы Чтобы сделать взлом, используйте следующий формат. Первая строка должна содержать единственное целое число \(t\) (\(1 \le t \le 100\)) — количество наборов входных данных. Первая строка каждого набора входных данных должна содержать единственное целое число \(n\) (\(2 \le n \le 10^3\)) — длину перестановки. Вторая строка каждого набора входных данных должна содержать \(n\) различных целых чисел \(p_1, p_2, \ldots, p_n\) (\(1 \le p_i \le n\)) — загаданную перестановку. Сумма \(n\) по всем наборам входных данных не превосходит \(10^3\). Примечание В первом наборе входных данных \(n=6\) и загадана перестановка \(p = [1,4,2,5,3,6]\). Сначала сделаем запросы типа \(1\) с \(x=12, 2, 3\) соответственно. Это суммарно добавит в граф четыре ребра: - Ребро, соединяющее вершины \(6\) и \(6\).
- Ребро, соединяющее вершины \(1\) и \(1\).
- Ребро, соединяющее вершины \(1\) и \(2\).
- Ребро, соединяющее вершины \(2\) и \(1\).
Поскольку все эти запросы корректны, интерактор вернул \(1\) после каждого из них. Затем спросим количество рёбер на кратчайшем пути между вершинами \(p_1 = 1\) и \(p_3 = 2\), которое равно \(1\). Затем сделаем запрос типа \(1\) с \(x=5\). Это суммарно добавит в граф четыре ребра: - Ребро, соединяющее вершины \(1\) и \(4\).
- Ребро, соединяющее вершины \(2\) и \(3\).
- Ребро, соединяющее вершины \(3\) и \(2\).
- Ребро, соединяющее вершины \(4\) и \(1\).
Поскольку этот запрос корректен, интерактор вернул \(1\). Затем спросим количество рёбер на кратчайшем пути между вершинами \(p_1 = 1\) и \(p_5 = 3\), которое равно \(2\). Затем спросим количество рёбер на кратчайшем пути между вершинами \(p_4 = 5\) и \(p_5 = 3\). Такого пути не существует, поэтому интерактор вернёт \(-1\). После этого, благодаря некоторой магии, две возможные перестановки, которые могут быть равны \(p\), определены: первая перестановка равна \([1,4,2,5,3,6]\), и вторая перестановка равна \([1,2,3,4,5,6]\). Так как первая перестановка равна загаданной перестановке, этот набор входных данных решён корректно. Всего \(7\) запросов использовано, что находится в пределах \(2 \cdot 6 = 12\) запросов. Поскольку ответ правильный, интерактор вернул \(1\). Во втором наборе входных данных \(n=2\) и загадана перестановка \(p = [2,1]\). Так как есть только \(2! = 2\) возможные перестановки, никаких запросов не требуется. Достаточно просто вывести две перестановки \([1,2]\) и \([2,1]\). Всего \(0\) запросов использовано, что находится в пределах \(2 \cdot 2 = 4\) запросов. Поскольку ответ правильный, интерактор вернул \(1\). | |
![]()
|
|
C. Лисица и полный обход древа
Деревья
дп
Конструктив
математика
реализация
*2400
Лисица Яэ забралась на древо Священной сакуры. Древом называют связный неориентированный граф, не содержащий циклов. Для передвижения по древу лисица применяет свои магические способности. Яэ может прыгнуть из вершины \(v\) в другую вершину \(u\) тогда и только тогда, когда расстояние между этими вершинами не превосходит \(2\). Иными словами, за один прыжок Яэ может перепрыгнуть из вершины \(v\) в вершину \(u\), если вершины \(v\) и \(u\) соединены ребром, либо если существует такая вершина \(w\), что вершины \(v\) и \(w\) соединены ребром, а также вершины \(u\) и \(w\) соединены ребром. После того, как Яэ смогла заполучить лепесток сакуры, она задумалась, существует ли циклический маршрут в древе \(v_1, v_2, \ldots, v_n\), такой что: - лисица может совершить прыжок из вершины \(v_i\) в вершину \(v_{i + 1}\),
- лисица может совершить прыжок из вершины \(v_n\) в вершину \(v_1\),
- все \(v_i\) попарно различны.
Помогите лисице определить, существует ли требуемый обход. Выходные данные В первой строке выведите «Yes» (без кавычек), если требуемый обход древа существует, либо «No» (без кавычек) в противном случае. Если требуемый обход древа существует, во второй строке выведите \(n\) целых различных чисел \(v_1, v_2, \ldots, v_n\) (\(1 \le v_i \le n\)) — вершины древа в порядке обхода. Если существует несколько корректных обходов, выведите любой из них. Примечание Древо из первого примера изображено ниже. Жирными стрелками обозначен маршрут лисицы.  Во втором примере любая последовательность из трёх различных вершин является корректным маршрутом, потому что лисица может совершить прыжок из любой вершины в любую. Древо из третьего примера изображено ниже. Можно показать, что для него не существует требуемого маршрута.  | |
![]()
|
|
E. Дороги в городе E
Деревья
интерактив
математика
Теория вероятностей
*3200
Это интерактивная задача. Как хорошо известно, в городе «E» за его полутора тысячелетнюю историю ни разу не ремонтировали дороги. И только недавно руководство города отремонтировало некоторые из них. Известно, что всего в городе «E» есть \(n\) перекрестков и \(m\) дорог, пронумерованных целыми числами от \(1\) до \(m\), перемещаться по которым можно в обе стороны. \(i\)-я дорога соединяет перекрестки с номерами \(a_i\) и \(b_i\). Среди всех \(m\) дорог было отремонтировано некоторое подмножество дорог, но вам не известно, какое именно. Единственная информация, которую вы смогли получить от дорожных служб города, это то, что от любого перекрестка можно доехать до любого другого, двигаясь только по отремонтированным дорогам. Вы — молодой предприниматель, и решили организовать службу доставки свежего сырого мяса в городе «E» (в самом городе такое мясо называют «стейками», оно пользуется большой популярностью у местных жителей). Вы уже набрали штат курьеров, однако курьеры готовы перемещаться только по отремонтированным дорогам. Теперь вам предстоит выяснить, какие дороги уже отремонтированы. Городская администрация предоставила вам город на некоторое время, поэтому вы можете делать различные действия одного из трех типов: - Заблокировать дорогу с номером \(x\). В этом случае перемещение по дороге для курьеров будет запрещено. Исходно все дороги разблокированы.
- Разблокировать дорогу с номером \(x\). В этом случае курьеры смогут двигаться по дороге \(x\), если она отремонтирована.
- Попробовать доставить заказ на перекресток с номером \(y\). В этом случае один из ваших курьеров начнет двигаться с неизвестного вам перекрестка \(s\) и доставит заказ на перекресток с номером \(y\) в том случае, если существует путь по разблокированным отремонтированным дорогам от перекрестка \(s\) до перекрестка \(y\). При этом гарантируется, что перекресток \(s\) будет выбран заранее.
К сожалению, город предоставлен в ваше полное распоряжение ненадолго, поэтому вы можете сделать не более \(100 \cdot m\) запросов. Протокол взаимодействия После того, как вы считали описание набора входных данных, вы можете задавать запросы. Запросы могут быть трех типов: - «- \(x\)» (\(1 \le x \le m\)). В этом случае дорога с номером \(x\) блокируется, если она ещё не была заблокирована.
- «+ \(x\)» (\(1 \le x \le m\)). В этом случае дорога с номером \(x\) разблокируется. Обратите внимание, что дорога \(x\) должна быть заранее заблокирована. Исходно все дороги разблокированы.
- «? \(y\)» (\(1 \le y \le n\)). В этом случае программа жюри выбирает некоторый город \(s\). В случае, если от города \(s\) до города \(y\) можно добраться по разблокированным отремонтированным дорогам, программа жюри выведет \(1\), иначе программа жюри выведет \(0\). Обратите внимание, что город \(s\) будет выбран до получения информации о городе \(y\), однако при выборе города \(s\) могут учитываться ваши предыдущие запросы.
Всего вы можете задать не более \(100 \cdot m\) запросов для каждого набора входных данных. После того, как вы нашли все отремонтированные дороги, выведите «! \(c_1,\ c_2,\ c_3,\ \ldots,\ c_m\)», где \(c_i\) равно \(1\), если дорога \(i\) отремонтирована, и \(0\), если дорога не отремонтирована. Этот вывод не будет считаться в общем числе запросов. На это программа жюри выведет \(1\), если ваш ответ правильный, и \(0\), если ответ не правильный. Если вы считали \(0\), то ваша программа должна немедленно завершиться, чтобы получить вердикт Неправильный ответ. В противном случае вы можете получить любой вердикт, так как программа продолжит чтение из закрытого потока. Если вы считали \(1\), то перейдите к следующему набору входных данных, или завершите программу, если такого нет. Обратите внимание, что вам не обязательно разблокировать все дороги на момент вывода ответа. Гарантируется, что все отремонтированные дороги зафиксированы изначально и не будут меняться программой жюри в зависимости от запросов. После вывода запроса или ответа не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Взломы Вы не можете делать взломы по этой задаче. Примечание В первом наборе входных данных дорога \(1\) отремонтирована, а дорога \(2\) — нет. Для первого запроса доставки в качестве \(s\) был выбран перекресток \(1\), поэтому путь от перекрестка \(1\) до \(1\) есть. Для второго запроса доставки в качестве \(s\) был выбран перекресток \(1\), так как в города заблокирована единственная отремонтированная дорога, то пути между перекрестками \(1\) и \(2\) нет. Для третьего запроса доставки в качестве \(s\) был выбран перекресток \(2\), путь между перекрестками \(2\) и \(1\) есть по дороге \(1\), которая отремонтирована и разблокирована. Во втором наборе входных данных для запросов доставки в качестве стартовых перекрестков были выбраны перекрестки \(1\), \(3\), \(1\), \(2\), \(2\), \(3\), \(1\). | |
![]()
|
|
F. Подружки-садоводы
графы
Деревья
дп
Перебор
поиск в глубину и подобное
*1700
Две подруги, Алиса и Юки, посадили в своем саду дерево из \(n\) вершин. Дерево — это неориентированный граф без циклов, петель и кратных ребер. Каждое ребро в этом дереве имеет длину \(k\). Изначально вершина \(1\) — корень дерева. Алиса и Юки выращивают дерево не просто так, они хотят продать его. Стоимостью дерева назовем максимальное расстояние от корня до вершины по всем вершинам дерева. Расстоянием между двумя вершинами \(u\) и \(v\) является сумма длин ребер на пути от \(u\) до \(v\). Девочки проходили курс юных садоводов, поэтому они умеют модифицировать дерево. За \(c\) монет Алиса и Юки могут поменять корень дерева, выбрав одного из соседей текущего корня и сделав его корнем дерева. Эту операцию можно применять любое количество раз (в том числе и ноль). Обратите внимание, что операция не затрагивает структуру дерева; единственное изменение заключается в том, что корнем дерева становится другая вершина. Подруги хотят продать дерево с максимальной выгодой. Выгода — это разность стоимости дерева и затрат на все операции. Помогите девочкам и найдите максимальную выгоду, которую они могут получить, применив к дереву операции произвольное число раз (возможно, ноль). Выходные данные Для каждого набора входных данных выведите единственное число — максимальную выгоду, которую могут получить Юки и Алиса. | |
![]()
|
|
F. Случайная прогулка
графы
Деревья
дп
математика
Теория вероятностей
*2600
Вам задано дерево, состоящее из \(n\) вершин и \(n - 1\) ребер, и у каждой вершины \(v\) есть свой счетчик \(c(v)\). Первоначально в вершине \(s\) расположена фишка, и все счетчики, кроме \(c(s)\), равны \(0\); \(c(s)\) равен \(1\). Ваша задача — переместить фишку в вершину \(t\). Для этого вы можете совершить следующую последовательность шагов. Пусть сейчас фишка расположена в вершине \(v\). За один шаг вы можете сделать следующее: - выбрать одну из соседних вершин \(to\) вершины \(v\) равновероятно (\(to\) является соседней вершиной \(v\) тогда и только тогда, когда в дереве есть ребро \(\{v, to\}\));
- передвинуть фишку в вершину \(to\) и увеличить \(c(to)\) на \(1\).
Вы будете повторять данную операцию, пока не достигните вершины \(t\). Для каждой вершины \(v\) вычислите математическое ожидание значения \(c(v)\) по модулю \(998\,244\,353\). Выходные данные Выведите \(n\) чисел: математические ожидания значений \(c(v)\) по модулю \(998\,244\,353\) для каждого \(v\) от \(1\) по \(n\). Формально, пусть \(M = 998\,244\,353\). Можно показать, что ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Примечание Дерево из первого примера показано ниже:  Посчитаем математическое ожидание \(E[c(1)]\): - \(P(c(1) = 0) = 0\), так как \(c(1)\) изначально равно \(1\).
- \(P(c(1) = 1) = \frac{1}{2}\), так как есть только одна последовательность шагов, приводящая к \(c(1) = 1\). Это \(1 \rightarrow 2 \rightarrow 3\) с вероятностью \(1 \cdot \frac{1}{2}\).
- \(P(c(1) = 2) = \frac{1}{4}\): единственный путь \(1 \rightarrow_{1} 2 \rightarrow_{0.5} 1 \rightarrow_{1} 2 \rightarrow_{0.5} 3\).
- \(P(c(1) = 3) = \frac{1}{8}\): единственный путь \(1 \rightarrow_{1} 2 \rightarrow_{0.5} 1 \rightarrow_{1} 2 \rightarrow_{0.5} 1 \rightarrow_{1} 2 \rightarrow_{0.5} 3\).
- \(P(c(1) = i) = \frac{1}{2^i}\) в общем случае.
В результате \(E[c(1)] = \sum\limits_{i=1}^{\infty}{i \frac{1}{2^i}} = 2\). Изображение дерева во втором тесте  Изображение дерева в третьем тесте Изображение дерева в третьем тесте  | |
![]()
|
|
B1. LuoTianyi и летающие острова (простая версия)
Деревья
Комбинаторика
математика
Теория вероятностей
*1800
Это простая версия задачи. Единственное отличие в том, что в этой версии \(k\le\min(n,3)\). Вы можете делать взломы, только если обе версии задачи сданы.  Chtholly и летающие острова. Chtholly и летающие острова. LuoTianyi сейчас живёт в мире с \(n\) летающими островами. Летающие острова соединены \(n-1\) ненаправленной воздушной дорогой, и из любого из двух летающих островов можно добраться до другого, путешествуя по воздушным дорогам. Это означает, что \(n\) летающих островов образуют дерево. Однажды, LuoTianyi захотела встретиться со своими друзьями: Chtholly, Nephren, William, .... Всего она хочет встретиться с \(k\) людьми. Она не знает их точного расположения, но она знает, что они находятся на попарно различных островах. Она называет остров хорошим тогда и только тогда, когда сумма расстояний\(^{\dagger}\) от него до островов с \(k\) людьми минимально возможная среди всех \(n\) островов. Сейчас LuoTianyi хочет узнать, если \(k\) человек случайным образом находятся в \(k\) различных из \(n\) островов, чему равно математическое ожидание количества хороших островов? Вам нужно сказать ей математическое ожидание по модулю \(10^9+7\). \(^{\dagger}\)Расстоянием между двумя островами называется минимальное количество воздушных дорог, по которым нужно пройти, чтобы перейти с одного острова на другой. Выходные данные Выведите единственное целое число — математическое ожидание количества хороших островов по модулю \(10^9 + 7\). Формально, пусть \(M = 10^9 + 7\). Можно показать, что ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0\) (\(\operatorname{mod} M\)). Выведите целое число, равное \(p \cdot q^{-1}\) \(\operatorname{mod} M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p\) (\(\operatorname{mod} M\)). Примечание В первом примере дороги образуют следующее дерево:  Если люди находятся на островах \(1\) и \(2\), тогда острова \(1\) и \(2\) являются хорошими. Сумма расстояний от острова \(1\) или \(2\) до всех людей равна \(1+0=1\), что минимально. В это время сумма расстояний от острова \(3\) до всех людей равна \(2+1=3\), что больше \(1\). Таким же образом, когда люди находятся на островах \(1\) и \(3\), тогда острова \(1,2\) и \(3\) являются хорошими. Когда люди находятся на островах \(1\) и \(4\), тогда острова \(1,2,3\) и \(4\) являются хорошими. Когда люди находятся на островах \(2\) и \(3\), тогда острова \(2\) и \(3\) являются хорошими. Когда люди находятся на островах \(2\) и \(4\), тогда острова \(2,3\) и \(4\) являются хорошими. Когда люди находятся на островах \(3\) и \(4\), тогда острова \(3\) и \(4\) являются хорошими. Поэтому математическое ожидание количества хороших островов равно \(\frac{16}{6}\), что равняется \(666666674\) по модулю \(10^9+7\). Во втором примере воздушные дороги образуют следующее дерево:  Всегда есть единственный хороший остров, поэтому математическое ожидание равно \(1\). | |
![]()
|
|
B2. LuoTianyi и летающие острова (сложная версия)
Деревья
Комбинаторика
математика
поиск в глубину и подобное
Теория вероятностей
*2300
Это сложная версия задачи. Единственное отличие в том, что в этой версии \(k\le n\). Вы можете делать взломы, только если обе версии задачи сданы.  Chtholly и летающие острова. Chtholly и летающие острова. LuoTianyi сейчас живёт в мире с \(n\) летающими островами. Летающие острова соединены \(n-1\) ненаправленной воздушной дорогой, и из любого из двух летающих островов можно добраться до другого, путешествуя по воздушным дорогам. Это означает, что \(n\) летающих островов образуют дерево. Однажды, LuoTianyi захотела встретиться со своими друзьями: Chtholly, Nephren, William, .... Всего она хочет встретиться с \(k\) людьми. Она не знает их точного расположения, но она знает, что они находятся на попарно различных островах. Она называет остров хорошим тогда и только тогда, когда сумма расстояний\(^{\dagger}\) от него до островов с \(k\) людьми минимально возможная среди всех \(n\) островов. Сейчас LuoTianyi хочет узнать, если \(k\) человек случайным образом находятся в \(k\) различных из \(n\) островов, чему равно математическое ожидание количества хороших островов? Вам нужно сказать ей математическое ожидание по модулю \(10^9+7\). \(^{\dagger}\)Расстоянием между двумя островами называется минимальное количество воздушных дорог, по которым нужно пройти, чтобы перейти с одного острова на другой. Выходные данные Выведите единственное целое число — математическое ожидание количества хороших островов по модулю \(10^9 + 7\). Формально, пусть \(M = 10^9 + 7\). Можно показать, что ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0\) (\(\operatorname{mod} M\)). Выведите целое число, равное \(p \cdot q^{-1}\) \(\operatorname{mod} M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p\) (\(\operatorname{mod} M\)). Примечание В первом примере дороги образуют следующее дерево:  Если люди находятся на островах \(1\) и \(2\), тогда острова \(1\) и \(2\) являются хорошими. Сумма расстояний от острова \(1\) или \(2\) до всех людей равна \(1+0=1\), что минимально. В это время сумма расстояний от острова \(3\) до всех людей равна \(2+1=3\), что больше \(1\). Таким же образом, когда люди находятся на островах \(1\) и \(3\), тогда острова \(1,2\) и \(3\) являются хорошими. Когда люди находятся на островах \(1\) и \(4\), тогда острова \(1,2,3\) и \(4\) являются хорошими. Когда люди находятся на островах \(2\) и \(3\), тогда острова \(2\) и \(3\) являются хорошими. Когда люди находятся на островах \(2\) и \(4\), тогда острова \(2,3\) и \(4\) являются хорошими. Когда люди находятся на островах \(3\) и \(4\), тогда острова \(3\) и \(4\) являются хорошими. Поэтому математическое ожидание количества хороших островов равно \(\frac{16}{6}\), что равняется \(666666674\) по модулю \(10^9+7\). Во втором примере дороги образуют следующее дерево:  Мы можем заметить, что так как есть один человек на каждом острове, то только остров \(3\) является хорошим. Поэтому математическое ожидание количества хороших островов равно \(1\). | |
![]()
|
|
C. LuoTianyi и XOR-дерево
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
снм
Структуры данных
*2500
LuoTianyi дала вам дерево со значениями в вершинах, корнем этого дерева является вершина \(1\). За одну операцию вы можете изменить значение в любой вершине на любое неотрицательное целое число. Вам нужно найти минимальное количество операций, которые нужно сделать, чтобы побитовое исключающее ИЛИ на любом пути от корня до листа\(^{\dagger}\) было равно нулю. \(^{\dagger}\)Листом в корневом дереве называется вершина, которая имеет ровно одного соседа, и при этом не является корнем. Выходные данные Выведите единственное целое число — минимальное количество операций. Примечание Дерево из первого примера:  Если мы поменяем значение в вершине \(2\) на \(3\), значение в вершине \(5\) на \(4\), значение в вершине \(6\) на \(6\), то дерево станет подходящим. Побитовое исключающее ИЛИ от корня до листа \(2\) будет равно \(3 \oplus 3=0\). Побитовое исключающее ИЛИ от корня до листа \(5\) будет равно \(4 \oplus 7 \oplus 3=0\). Побитовое исключающее ИЛИ от корня до листа \(6\) будет равно \(6 \oplus 5 \oplus 3=0\). Дерево из второго примера:  Если мы поменяем значение в вершине \(2\) на \(4\), значение в вершине \(3\) на \(27\), значение в вершине \(6\) на \(20\), то дерево станет подходящим. Побитовое исключающее ИЛИ от корня до листа \(6\) будет равно \(20 \oplus 19 \oplus 7=0\). Побитовое исключающее ИЛИ от корня до листа \(8\) будет равно \(11 \oplus 27 \oplus 4 \oplus 19 \oplus 7=0\). Побитовое исключающее ИЛИ от корня до листа \(4\) будет равно \(16 \oplus 4 \oplus 19 \oplus 7=0\). Побитовое исключающее ИЛИ от корня до листа \(7\) будет равно \(16 \oplus 4 \oplus 19 \oplus 7=0\). В третьем примере единственным листом является вершина \(4\), и побитовое исключающее ИЛИ на пути до неё равно \(1 \oplus 2 \oplus 1 \oplus 2 = 0\), поэтому нам не нужно изменять значения. В четвёртом примере мы можем изменить значение в вершине \(1\) на \(5\), а значение в вершине \(4\) на \(0\). Здесь \(\oplus\) обозначает операцию побитового исключающего ИЛИ. | |
![]()
|
|
E. LuoTianyi и Картридж
Деревья
Структуры данных
*3500
LuoTianyi смотрит аниме Made in Abyss. Она считает, что создание Картриджа является очень интересным занятием. Чтобы более четко описать процесс создания Картриджа, она абстрагируется от исходной задачи и даёт вам следующую. Вам дано дерево \(T\), состоящее из \(n\) вершин. Каждая вершина имеет значения \(a_i\) и \(b_i\), а каждое ребро имеет значения \(c_j\) и \(d_j\). Теперь вам нужно построить дерево \(T'\) следующим образом: - Сначала выберите \(p\) вершин из \(T\) (\(p\) — число, выбранное вами самостоятельно) в качестве множества вершин \(S'\) в \(T'\);
- Затем последовательно выберите \(p-1\) ребро из \(T\) по одному (нельзя выбирать одно ребро более одного раза);
- Пусть вы выбрали \(j\)-е ребро, и оно соединяет вершины \(x_j\) и \(y_j\) и имеет значения \((c_j,d_j)\). Тогда вы можете выбрать две вершины \(u\) и \(v\) в \(S'\), для которых ребро \((x_j,y_j)\) лежит на простом пути из \(u\) в \(v\) в \(T\), и соединить \(u\) и \(v\) в \(T'\) ребром со значениями \((c_j,d_j)\) (\(u\) и \(v\) не должны содержаться в одной компоненте связности ранее в \(T'\)).
 Дерево с тремя вершинами, \(\min(A,C)=1,B+D=7\), стоимость равна \(7\). Дерево с тремя вершинами, \(\min(A,C)=1,B+D=7\), стоимость равна \(7\).  Выбрали вершины \(2\) и \(3\) как \(S'\), использовали ребро \((1,2)\) с \(c_j = 2\) и \(d_j = 1\), чтобы соединить эти вершины, теперь \(\min(A,C)=2,B+D=4\), стоимость равна \(8\). Выбрали вершины \(2\) и \(3\) как \(S'\), использовали ребро \((1,2)\) с \(c_j = 2\) и \(d_j = 1\), чтобы соединить эти вершины, теперь \(\min(A,C)=2,B+D=4\), стоимость равна \(8\). Пусть \(A\) — минимум из значений \(a_i\) в \(T'\), и \(C\) — минимум из значений \(c_i\) в \(T'\). Пусть \(B\) — сумма значений \(b_i\) в \(T'\), и \(D\) — сумма значений \(d_i\) в \(T'\). Определим \(\min(A, C) \cdot (B + D)\) как стоимость \(T'\). Вам нужно найти максимально возможную стоимость \(T'\). Выходные данные Выведите единственное целое число — максимальное возможную стоимость \(T'\). Примечание Дерево из первого примера изображено в условии. Дерево из второго примера изображено ниже:  \(A = 1, B = 18, C = 1, D = 17\), поэтому стоимость равна \(\min(1,1) \cdot (18 + 17) = 35\). | |
![]()
|
|
B1. Сортировка подотрезков (простая версия)
Бинарный поиск
Деревья
дп
жадные алгоритмы
снм
*2000
Единственная разница между простой и сложной версиями состоит в ограничениях на \(t\) и \(n\). Вам задан массив \(a\), состоящий из \(n\) различных целых чисел \(a_1, a_2, \ldots, a_n\). Определим стоимость массива \(p_1, p_2, \ldots p_k\) как минимальное количество времени, необходимое для сортировки этого массива с использованием произвольного количества операций сортировки диапазона. В каждой операции сортировки диапазона вы будете делать следующее: - Выберите два целых числа \(l\) и \(r\) (\(1 \le l < r \le k\)).
- Отсортируйте подмассив \(p_l, p_{l + 1}, \ldots, p_r\) за \(r - l\) секунд.
Пожалуйста, посчитайте сумму стоимостей по всем подмассивам массива \(a\). Подмассив массива определяется как непрерывная последовательность элементов массива. Выходные данные Для каждого набора входных данных выведите сумму стоимостей по всем подмассивам массива \(a\). Примечание В первом наборе входных данных: - Подмассив \([6]\) уже отсортирован, поэтому его стоимость равна \(0\).
- Подмассив \([4]\) уже отсортирован, поэтому его стоимость равна \(0\).
- Подмассив \([6, 4]\) можно отсортировать за одну операцию, выбрав \(l = 1\) и \(r = 2\). Его стоимость равна \(1\).
Сумма стоимостей по всем подмассивам данного массива равна \(0 + 0 + 1 = 1\). Во втором наборе входных данных: - Подмассив \([3]\) уже отсортирован, поэтому его стоимость равна \(0\).
- Подмассив \([10]\) уже отсортирован, поэтому его стоимость равна \(0\).
- Подмассив \([6]\) уже отсортирован, поэтому его стоимость равна \(0\).
- Подмассив \([3, 10]\) уже отсортирован, поэтому его стоимость равна \(0\).
- Подмассив \([10, 6]\) можно отсортировать за одну операцию, выбрав \(l = 1\) и \(r = 2\). Его стоимость равна \(2 - 1 = 1\).
- Подмассив \([3, 10, 6]\) можно отсортировать за одну операцию, выбрав \(l = 2\) и \(r = 3\). Его стоимость равна \(3 - 2 = 1\).
Сумма стоимостей по всем подмассивам данного массива равна \(0 + 0 + 0 + 0 + 1 + 1 = 2\). | |
![]()
|
|
D. Два центроида
Деревья
жадные алгоритмы
поиск в глубину и подобное
Структуры данных
*2800
Вам задано дерево (неориентированный связный ациклический граф), изначально содержащее только вершину \(1\). Будет несколько запросов к данному дереву. В \(i\)-м запросе появится вершина \(i + 1\), соединенная с вершиной \(p_i\) (\(1 \le p_i \le i\)). После каждого запроса найдите наименьшее количество операций, необходимых для того, чтобы текущее дерево имело два центроида. За одну операцию вы можете добавить одну вершину и одно ребро к дереву так, чтобы оно осталось деревом. Вершина называется центроидом, если ее удаление разбивает дерево на поддеревья с не более чем \(\lfloor \frac{n}{2} \rfloor\) вершин в каждом, где \(n\) — число вершин дерева. Например, центроид следующего дерева равен \(3\), потому что самое большое поддерево после удаления центроида имеет \(2\) вершины.  В следующем дереве вершины \(1\) и \(2\) являются центроидами.  Выходные данные Для каждого набора входных данных выведите \(n - 1\) целое число. \(i\)-е число является ответом на \(i\)-й запрос — наименьшее количество операций, необходимых для того, чтобы текущее дерево имело два центроида. Мы можем показать, что ответ всегда существует. Примечание На картинках ниже показан четвертый набор входных данных. После третьего запроса:  В дереве уже есть вершины \(2\) и \(3\) в качестве центроидов, поэтому никаких операций не требуется. После четвертого запроса:  Добавление вершины \(x\) к дереву делает вершины \(2\) и \(3\) центроидами. Нужна только одна операция. После пятого запроса:  Добавление к дереву вершин \(x\) и \(y\) делает вершины \(5\) и \(2\) центроидами. Нужны две операции. После шестого запроса:  Добавление к дереву вершин \(x\), \(y\) и \(z\) делает вершины \(5\) и \(2\) центроидами. Необходимо три операции. | |
![]()
|
|
E. Автобусные маршруты
Бинарный поиск
Деревья
жадные алгоритмы
Конструктив
поиск в глубину и подобное
*3400
Существует страна, состоящая из \(n\) городов и соединяющих их \(n - 1\) двунаправленных дорог, так что мы можем путешествовать между любыми двумя городами по этим дорогам. Другими словами, эти города и дороги образуют дерево. Есть \(m\) автобусных маршрутов, соединяющих города между собой. Автобусный маршрут между городами \(x\) и \(y\) позволяет вам путешествовать между любыми двумя городами по простому пути между \(x\) и \(y\) по этому маршруту. Определите, можно ли из каждой пары городов \(u\) и \(v\) проехать из \(u\) в \(v\), используя не более двух автобусных маршрутов. Выходные данные Для каждого теста выведите «YES», если вы можете путешествовать между любой парой городов, используя не более двух автобусных маршрутов. В противном случае выведите «NO». В следующей строке выведите два города \(x\) и \(y\) (\(1 \le x, y \le n\)) такие, что до города \(y\) из города \(x\) невозможно добраться не более чем двумя автобусными маршрутами. Вы можете вывести ответ в любом регистре (верхнем или нижнем). Например, строки «yEs», «yes», «Yes» и «YES» будут распознаны как положительные. ответы. Примечание Ниже приведены иллюстрации к \(1\), \(2\) и \(4\) наборам входных данных:    | |
![]()
|
|
A. Copil Copac рисует деревья
графы
Деревья
дп
поиск в глубину и подобное
*1400
Copil Copac получил список из \(n-1\) ребра, описывающих дерево на \(n\) вершинах. Он решил нарисовать его, используя следующий алгоритм: - Шаг \(0\): Рисует первую вершину (вершину \(1\)). Переходит к шагу \(1\).
- Шаг \(1\): Для каждого ребра из входных данных в порядке ввода: если ребро соединяет уже нарисованную вершину \(u\) с не нарисованной вершиной \(v\), он рисует \(v\) и ребро. После прохода по всем рёбрам он переходит к шагу \(2\).
- Шаг \(2\): Если все вершины нарисованы, завершает алгоритм. Иначе переходит к шагу \(1\).
Количество проходов определяется как количество раз, которое Copil Copac выполняет шаг \(1\). Найдите количество проходов, необходимых Copil Copac для рисования дерева. Выходные данные Для каждого набора входных данных выведите количество проходов, необходимых Copil Copac для рисования дерева. Примечание В первом наборе входных данных: После первого прохода дерево будет выглядеть так:  После второго прохода:  Таким образом, Copil Copac нужно \(2\) прохода, чтобы нарисовать дерево. | |
![]()
|
|
D. Дерево MEX
Деревья
дп
Перебор
*2800
Дано дерево с \(n\) вершинами. Каждую вершину дерева вы можете раскрасить в \(0\) или \(1\). Значение пути \((u,v)\) равно MEX\(^\dagger\) цветов вершин на кратчайшем пути между \(u\) и \(v\). Значение раскраски равно сумме значений всех путей \((u,v)\) таких, что \(1 \leq u \leq v \leq n\). Чему равно максимально возможное значение раскраски дерева? \(^{\dagger}\) MEX (minimum excluded) массива — это наименьшее неотрицательное целое число, которое не принадлежит массиву. Например: - MEX \([2,2,1]\) равно \(0\), потому что \(0\) не принадлежит массиву.
- MEX \([3,1,0,1]\) равно \(2\), потому что \(0\) и \(1\) принадлежат массиву, но \(2\) нет.
- MEX \([0,3,1,2]\) равно \(4\), потому что \(0\), \(1\), \(2\) и \(3\) принадлежат массиву, но \(4\) нет.
Выходные данные Для каждого набора входных данных выведите максимально возможное значение любой раскраски дерева. Примечание В первом примере мы закрасим вершину \(2\) в \(1\), а вершины \(1,3\) в \(0\). Затем мы рассмотрим все пути: - \((1,1)\) со значением \(1\)
- \((1,2)\) со значением \(2\)
- \((1,3)\) со значением \(2\)
- \((2,2)\) со значением \(0\)
- \((2,3)\) со значением \(2\)
- \((3,3)\) со значением \(1\)
Сумма значений равна \(8\), что является максимально возможной суммой. | |
![]()
|
|
G. Ксюша и шиншилла
Деревья
дп
жадные алгоритмы
Конструктив
поиск в глубину и подобное
реализация
снм
*1800
У Ксюши есть домашняя шиншилла, дерево на \(n\) вершинах и огромные ножницы. Деревом называется связный граф без циклов. Сейчас Ксюша сидит на скучном уроке физики и думает над тем, как развлечь своего питомца. Шиншиллам нравится играть с веточками. Веточкой называется дерево из \(3\) вершин.  Веточка выглядит так. Веточка выглядит так. Разрезом называется удаление некоторого (ещё не отрезанного) ребра в дереве. У Ксюши полно свободного времени, поэтому она может себе позволить сделать достаточно разрезов, чтобы дерево распалось на веточки. Другими словами, после нескольких (возможно нуля) разрезов, каждая вершина должна принадлежать ровно одной веточке. Помогите Ксюше выбрать отрезаемые рёбра или сообщите, что сделать это невозможно. Выходные данные Выведите ответ для каждого набора входных данных. Если искомого способа разрезать дерево не существует, выведите \(-1\). В противном случае выведите целое число \(k\) — количество отрезаемых рёбер. В следующей строке выведите \(k\) различных целых чисел \(e_i\) (\(1 \le e_i < n\)) — номера отрезаемых рёбер. Если \(k = 0\), выведите вместо этого пустую строку. Если решений несколько, вы можете вывести любое. Примечание  Первый набор входных данных в первом тесте. Первый набор входных данных в первом тесте. | |
![]()
|
|
E. Договорной плей-офф
Деревья
Комбинаторика
*2200
\(2^k\) команд участвуют в плей-офф турнире. Команды пронумерованы от \(1\) до \(2^k\) в порядке убывания силы. То есть, команда \(1\) самая сильная, команда \(2^k\) самая слабая. Команда с меньшим номером всегда побеждает команду с большим номером. Сначала все команды располагаются в каком-то порядке. Каждой команде дается еще одно уникальное число от \(1\) до \(2^k\), называемое сид, которое обозначает ее стартовую позицию в плей-офф. Турнир состоит из \(2^k - 1\) игры. Они проводятся следующим образом: во-первых, команды делятся на пары: команда с сидом \(1\) играет против команды с сидом \(2\), команда с сидом \(3\) играет против команды с сидом \(4\) (именно в таком порядке) и так далее (таким образом, в этой фазе будет сыграно \(2^{k-1}\) игры). Когда команда проигрывает игру, она выбывает. После этого остается \(2^{k-1}\) команд. Если остается только одна команда, она объявляется чемпионом; в противном случае играется еще \(2^{k-2}\) игр: в первой из них победитель игры «сид \(1\) против сид \(2\)» играет против победителя игры «сид \(3\) против сид \(4\)», затем победитель игры «сид \(5\) против сид \(6\)» играет против победителя игры «сид \(7\) против сид \(8\)» и так далее. Этот процесс повторяется до тех пор, пока не останется только одна команда. Место команды в турнире зависит от того, в какой фазе турнира она выбыла: - команда-победитель турнира занимает место \(1\);
- команда, выбывшая в финале, занимает место \(2\);
- обе команды, выбывшие в полуфинале, занимают место \(3\);
- все команды, выбывшие в четвертьфинале, занимают место \(5\);
- все команды, выбывшие в 1/8 финала, занимают место \(9\), и так далее.
Теперь, когда мы установили правила, мы немножко подтасуем результаты. В частности, мы хотим, чтобы: - команда \(1\) (не команда с сидом \(1\)) заняла место \(1\);
- команда \(2\) заняла место \(2\);
- команды \(3\) и \(4\) заняли место \(3\);
- команды с \(5\) по \(8\) заняли место \(5\), и так далее.
Например, на этой картинке показан возможный ход турнира при \(k = 3\), а также итоговые места команд при таком ходе турнира:  Некоторые сиды уже зарезервированы для некоторых команд (оказывается, не одни мы пытаемся повлиять на результаты). Требуется заполнить оставшиеся сиды оставшимися командами так, чтобы получить желаемые места для команд. Сколько есть способов это сделать? Так как это число может быть довольно большим, выведите его по модулю \(998\,244\,353\). Выходные данные Выведите одно целое число — количество способов заполнить незарезервированные сиды так, чтобы турнир прошел как мы хотим, по модулю \(998\,244\,353\). | |
![]()
|
|
F. Тенцинг и дерево
Деревья
жадные алгоритмы
кратчайшие пути
поиск в глубину и подобное
сортировки
*2500
У Тенцинга есть неориентированное дерево из \(n\) вершин. Определим ценность дерева с черными и белыми вершинами следующим образом: значение ребра — это абсолютная разница между количеством черных вершин в двух компонентах дерева после удаления ребра. Ценность дерева — это сумма значений по всем ребрам. Для всех \(k\) таких, что \(0 \leq k \leq n\), Тенцинг хочет знать максимальную ценность дерева, когда \(k\) вершин окрашены в черный цвет, а \(n-k\) вершин — в белый. Выходные данные Выведите \(n+1\) число. Число \(i\) является ответом на вопрос \(k=i-1\). Примечание Рассмотрим первый пример. Когда \(k=2\), Тенцинг может покрасить вершины \(1\) и \(2\) в черный цвет, тогда значение ребра \((1,2)\) равно 0, а значения остальных ребер все равны \(2\). Таким образом, ценность этого дерева равна \(4\). | |
![]()
|
|
C. Сумма в бинарном дереве
битмаски
Деревья
Комбинаторика
математика
*800
Ване очень нравится математика. Однажды, когда он решал очередную задачу по математике, он придумал интересное дерево. Это дерево строится следующим образом. Изначально в дереве есть только одна вершина с номером \(1\) — корень дерева. Затем, Ваня добавляет к ней двух детей, присваивая им последовательные номера — \(2\) и \(3\) соответственно. После этого, он будет добавлять детей к вершинам по возрастанию их номеров, начиная с \(2\), присваивая их детям минимальные не занятые номера. В итоге, у Вани получится бесконечное дерево с корнем в вершине \(1\), где каждая вершина будет иметь ровно два ребенка, а номера вершин будут расположены последовательно по слоям.  Часть дерева Вани. Часть дерева Вани. Ване стало интересно, чему равна сумма номеров вершин на пути от вершины с номером \(1\) до вершины с номером \(n\) в таком дереве. Так как Ваня не любит считать, он попросил Вас помочь ему узнать эту сумму. Выходные данные Для каждого набора входных данных выведите одно целое число — искомую сумму. Примечание В первом наборе данных примера на пути от корня до вершины \(3\) лежат две вершины \(1\) и \(3\), для них сумма равна \(4\). Во втором наборе данных примера на пути от корня до вершины с номером \(10\) лежат вершины \(1\), \(2\), \(5\), \(10\), сумма их номеров равна \(1+2+5+10 = 18\). | |
![]()
|
|
D. Яблоня
Деревья
дп
Комбинаторика
математика
поиск в глубину и подобное
*1200
У Тимофея в саду растёт яблоня, она представляет собой корневое дерево из \(n\) вершин с корнем в вершине \(1\) (вершины пронумерованы от \(1\) от \(n\)). Деревом называется связный граф без циклов, петель и кратных ребер. Это дерево очень необычное — оно растёт корнем вверх. Впрочем, в этом нет ничего необычного для деревьев в программировании. Яблоня достаточно молодая, поэтому на ней вырастет всего два яблока. Яблоки вырастут в определённых вершинах (эти вершины могу совпадать). После того как яблоки вырастут, Тимофей начнёт трясти яблоню, пока яблоки не упадут. Каждый раз, когда Тимофей трясёт яблоню, с каждым из яблок происходит следующее: Пусть яблоко сейчас находится в вершине \(u\). - Если у вершины \(u\) есть ребёнок, то яблоко перемещается в него (если таких вершин несколько, то яблоко может переместиться в любую из них).
- Иначе яблоко падает с дерева.
Можно показать, что через конечное время оба яблока упадут с дерева. У Тимофея есть \(q\) предположений, в каких вершинах могут вырасти яблоки. Он предполагает, что яблоки могут вырасти в вершинах \(x\) и \(y\), и хочет узнать количество пар вершин (\(a\), \(b\)), с которых яблоки могут упасть с дерева, где \(a\) — вершина, с которой упадёт яблоко из вершины \(x\), \(b\) — вершина, с которой упадёт яблоко из вершины \(y\). Помогите ему это сделать. Выходные данные Для каждого запроса Тимофея выведите количество упорядоченных пар вершин, с которых яблоки могут упасть с дерева, если предположение окажется верным, в отдельной строке. Примечание В первом примере: - Для первого запроса существует две возможные пары вершин, с которых яблоки могут упасть: \((4, 4), (5, 4)\).
- Для второго запроса также существует две пары: \((5, 4), (5, 5)\).
- Для третьего запроса есть всего одна пара: \((4, 4)\).
- Для четвертого запроса существует \(4\) пары: \((4, 4), (4, 5), (5, 4), (5, 5)\).
 Дерево из первого примера. Дерево из первого примера. Во втором примере для первого предположения есть \(4\) возможных пар вершин, с которых могут упасть яблоки: \((2, 3), (2, 2), (3, 2), (3, 3)\). Для второго запроса есть всего одна возможная пара: \((2, 3)\). Для третьего запроса есть две пары: \((3, 2), (3, 3)\). | |
![]()
|
|
F1. Метрополитен в Омске (простая версия)
графы
Деревья
дп
жадные алгоритмы
математика
поиск в глубину и подобное
Структуры данных
*1800
Это простая версия задачи. Единственное отличие между простой и сложной версией состоит в том, что в этой версии для всех вопросов \(u = 1\). Как известно, Омск — столица Берляндии. Как и в любой столице, в Омске есть хорошо развитая система метрополитена. Метрополитен Омска представляет из себя некоторое количество станций, соединённых туннелями, причём между любыми двумя станциями есть ровно один путь, проходящий по каждому из туннелей не более одного раза. Иными словами, метрополитен представляет собой дерево. Для развития метрополитена и привлечения жителей в Омске используется следующая система. Каждая станция имеет свой вес \(x \in \{-1, 1\}\). Если станция имеет вес \(-1\), то при посещении станции с жителя Омска взимается плата в \(1\) бурль. Если же вес станции равен \(1\), то житель Омска вознаграждается \(1\)-м бурлем. Пока что есть только одна станция с номером \(1\) и весом \(x = 1\). Каждый день происходит одно из следующих событий: - К станции с номером \(v_i\) присоединяется новая станция с весом \(x\), и ей присваивается номер, на единицу больший количества уже существующих станций.
- Лёша, живущий в Омске, задаётся вопросом: существует ли подотрезок\(\dagger\) (возможно, пустой) пути между вершинами \(u\) и \(v\) такой, что, проехав по нему, можно заработать ровно \(k\) бурлей (если \(k < 0\), то это означает, что на проезд придётся потратить \(k\) бурлей). Иначе говоря, Лёшу интересует, существует ли такой подотрезок пути, что сумма весов вершин в нем равна \(k\). Обратите внимание, что подотрезок может быть пустым, и тогда сумма равна \(0\).
Вы являетесь другом Лёши, поэтому Ваша задача — ответить на вопросы Лёши. \(\dagger\)Подотрезок — непрерывная последовательность элементов. Выходные данные Для каждого вопроса Лёши выведите «Yes» (без кавычек), если описанный в условии подотрезок существует, иначе выведите «No» (без кавычек). Вы можете выводить ответ в любом регистре (например, строки «yEs», «yes», «Yes» и «YES» будут распознаны как положительный ответ). Примечание Пояснение к первому примеру. Ответ на второй вопрос «Yes», так как существует путь \(1\). В четвертом вопросе мы можем снова выбрать путь \(1\). В пятом запросе ответ «Yes», так как есть путь \(1-3\). В шестом запросе мы можем выбрать пустой путь, так как сумма весов на нем равна \(0\). Нетрудно показать, что нет путей, удовлетворяющих первому и третьему запросу. | |
![]()
|
|
F2. Метрополитен в Омске (сложная версия)
Деревья
дп
математика
поиск в глубину и подобное
разделяй и властвуй
Структуры данных
*2300
Это сложная версия задачи. Единственное отличие между простой и сложной версией состоит в том, что в этой версии \(u\) может принимать любые возможные значения. Как известно, Омск — столица Берляндии. Как и в любой столице, в Омске есть хорошо развитая система метрополитена. Метрополитен Омска представляет из себя некоторое количество станций, соединённых туннелями, причём между любыми двумя станциями есть ровно один путь, проходящий по каждому из туннелей не более одного раза. Иными словами, метрополитен представляет собой дерево. Для развития метрополитена и привлечения жителей в Омске используется следующая система. Каждая станция имеет свой вес \(x \in \{-1, 1\}\). Если станция имеет вес \(-1\), то при посещении станции с жителя Омска взимается плата в \(1\) бурль. Если же вес станции равен \(1\), то житель Омска вознаграждается \(1\)-м бурлем. Пока что есть только одна станция с номером \(1\) и весом \(x = 1\). Каждый день происходит одно из следующих событий: - К станции с номером \(v_i\) присоединяется новая станция с весом \(x\), и ей присваивается номер, на единицу больший количества уже существующих станций.
- Лёша, живущий в Омске, задаётся вопросом: существует ли подотрезок\(\dagger\) (возможно, пустой) пути между вершинами \(u\) и \(v\) такой, что, проехав по нему, можно заработать ровно \(k\) бурлей (если \(k < 0\), то это означает, что на проезд придётся потратить \(k\) бурлей). Иначе говоря, Лёшу интересует, существует ли такой подотрезок пути, что сумма весов вершин в нем равна \(k\). Обратите внимание, что подотрезок может быть пустым, и тогда сумма равна \(0\).
Вы являетесь другом Лёши, поэтому Ваша задача — ответить на вопросы Лёши. \(\dagger\)Подотрезок — непрерывная последовательность элементов. Выходные данные Для каждого вопроса Лёши выведите «Yes» (без кавычек), если описанный в условии подотрезок существует, иначе выведите «No» (без кавычек). Вы можете выводить ответ в любом регистре (например, строки «yEs», «yes», «Yes» и «YES» будут распознаны как положительный ответ). Примечание Пояснение к первому примеру. Ответ на второй вопрос «Yes», так как существует путь \(1\). В четвертом вопросе мы можем снова выбрать путь \(1\). В пятом запросе ответ «Yes», так как есть путь \(1-3\). В шестом запросе мы можем выбрать пустой путь, так как сумма весов на нем равна \(0\). Нетрудно показать, что нет путей, удовлетворяющих первому и третьему запросу. | |
![]()
|
|
G. Дерево с весами
битмаски
Деревья
Конструктив
математика
матрицы
поиск в глубину и подобное
реализация
Структуры данных
теория чисел
*3000
Дано дерево на \(n\) вершинах, пронумерованных числами \(1,2,\dots,n\). \(i\)-е ребро соединяет вершины \(u_i\) и \(v_i\) и имеет некоторый неизвестный целый положительный вес \(w_i\). Вам также известны расстояния \(d_i\) между вершинами \(i\) и \(i+1\) для всех \(1 \le i \le n-1\) (это расстояние равно сумме весов рёбер на простом пути между вершинами дерева \(i\) и \(i+1\)). Найдите вес каждого ребра. Если существует несколько решений, выведите любое из них. Если не существует весов \(w_i\), согласующихся со всеми данными, выведите одно целое число \(-1\). Выходные данные Если решения не существует, выведите одно целое число \(-1\). В противном случае выведите \(n-1\) строку, содержащую веса \(w_1,\dots,w_{n-1}\). Если существует несколько решений, выведите любое из них. Примечание В первом примере дерево выглядит следующим образом:  Во втором примере вес \(w_2\) не может быть равен \(0\), поскольку должен быть целым положительным числом. Поэтому решения нет. В третьем примере дерево выглядит следующим образом:  | |
![]()
|
|
F. XOR-разделение
Бинарный поиск
битмаски
Деревья
жадные алгоритмы
разделяй и властвуй
Структуры данных
*2700
Для множества целых чисел \(S\) определим его стоимость как минимальное значение \(x \oplus y\) среди всех пар различных чисел из множества (\(\oplus\) обозначает оператор побитового исключающего ИЛИ). Если в множестве менее двух элементов, его стоимость равна \(2^{30}\). Вам дано множество целых чисел \(\{a_1, a_2, \dots, a_n\}\). Вы должны разделить его на два множества \(S_1\) и \(S_2\) таким образом, что каждый элемент принадлежит ровно одному из этих двух множеств. Стоимость разделения — это минимум из стоимостей \(S_1\) и \(S_2\). Найдите разделение с максимальной стоимостью. Выходные данные Выведите строку из \(n\) символов 0 и/или 1, описывающую разделение следующим образом: \(i\)-й символ строки должен быть 0, если \(a_i\) принадлежит \(S_1\), в противном случае этот символ должен быть 1. Если существует несколько оптимальных ответов — выведите любой из них. | |
![]()
|
|
F. Лиза и марсиане
битмаски
Деревья
жадные алгоритмы
математика
Строки
*1800
Девочку Лизу похитили марсиане! Не беда, ведь она смотрела много телепередач про инопланетян, поэтому знает, что её ждёт. Назовём число марсианским, если оно является целым неотрицательным и строго меньше \(2^k\), например, при \(k = 12\), числа \(51\), \(1960\), \(0\) — марсианские, а числа \(\pi\), \(-1\), \(\frac{21}{8}\), \(4096\) — нет. Инопланетяне выдадут Лизе \(n\) марсианских чисел \(a_1, a_2, \ldots, a_n\). Затем они попросят её назвать любое марсианское число \(x\). После чего Лиза выберет в выданной последовательности пару чисел \(a_i, a_j\) (\(i \neq j\)) и посчитает \((a_i \oplus x) \& (a_j \oplus x)\). Операция \(\oplus\) означает Побитовое исключающее ИЛИ, операция \(\&\) означает Побитовое И. Например, \((5 \oplus 17) \& (23 \oplus 17) = (00101_2 \oplus 10001_2) \& (10111_2 \oplus 10001_2) = 10100_2 \& 00110_2 = 00100_2 = 4\). Лиза уверена, что чем больше окажется посчитанное значение, тем выше её шансы вернуться домой. Помогите девочке выбрать такие \(i, j, x\), чтобы максимизировать посчитанное значение. Выходные данные Для каждого набора входных данных выведите три целых числа \(i, j, x\) (\(1 \le i, j \le n\), \(i \neq j\), \(0 \le x < 2^k\)). Значение \((a_i \oplus x) \& (a_j \oplus x)\) должно быть максимально возможным. Если решений несколько, вы можете вывести любое. Примечание Первый набор входных данных: \((3 \oplus 14) \& (1 \oplus 14) = (0011_2 \oplus 1110_2) \& (0001_2 \oplus 1110_2) = 1101_2 = 1101_2 \& 1111_2 = 1101_2 = 13\). Второй набор входных данных: \((1 \oplus 0) \& (1 \oplus 0) = 1\). Третий набор входных данных: \((9 \oplus 4082) \& (13 \oplus 4082) = 4091\). Четвёртый набор входных данных: \((3 \oplus 7) \& (0 \oplus 7) = 4\). | |
![]()
|
|
G. Влад и горы
Бинарный поиск
графы
Деревья
реализация
снм
сортировки
Структуры данных
*2000
Влад решил отправиться в путешествие в горы. Всего он планирует перемещаться по \(n\) горам, между некоторыми из которых есть дороги. Горы имеют высоты, высота \(i\)-й горы равна \(h_i\). Если между горами \(i\) и \(j\) есть дорога, то Влад может перейти с горы \(i\) на гору \(j\), потратив при этом \(h_j - h_i\) единиц энергии. Если при переходе его энергия должна опуститься ниже нуля, он не сможет перейти с горы \(i\) на гору \(j\). Обратите внимание, что \(h_j - h_i\) может быть отрицательным и тогда энергия восстановится. Влад хочет рассмотреть разные варианты маршрута, поэтому просит вас ответить на следующие запросы: можно ли построить какой-либо маршрут, начинающийся на горе \(a\) и заканчивающийся на горе \(b\), если изначально у него есть \(e\) единиц энергии? Выходные данные Для каждого запроса выведите «YES», если Влад может составить маршрут от горы \(a\) до горы \(b\), и «NO» в противном случае. Вы можете выводить ответ в любом регистре (например, строки «yEs», «yes», «Yes» и «YES» будут распознаны как положительный ответ). В примерах ниже ответы на разные наборы данных разделены пустой строкой, вы можете её не выводить. | |
![]()
|
|
D. Майкл и отель
Бинарный поиск
Деревья
интерактив
*3000
Майкл и Брайан застряли в отеле с \(n\) номерами, пронумерованными от \(1\) до \(n\), и должны найти друг друга. Но все двери в отеле заперты, и единственный способ передвижения — это использование телепортов в каждом номере. В номере \(i\) есть телепорт, который перенесет вас в номер \(a_i\) (может оказаться, что \(a_i = i\)). Но они не знают значений \(a_1,a_2, \dots, a_n\). Вместо этого они могут позвонить в регистратуру и задать запрос. В одном из запросов они указывают номер \(u\), целое положительное число \(k\) и набор номеров \(S\). Консьерж отеля отвечает, попадет ли человек, начав жить в номере \(u\) и воспользовавшись телепортами \(k\) раз, в номер из набора \(S\). Брайан находится в номере \(1\). Майкл хочет знать набор номеров \(A\) такой, что если он начнет жить в одном из этих номеров, они могли встретиться с помощью телепортов. Он может задать не более \(2000\) запросов. Значения \(a_1, a_2, \dots, a_n\) фиксированы до начала взаимодействия и не зависят от запросов. Другими словами, интерактор не является адаптивным. Протокол взаимодействия Чтобы сделать запрос, выведите строку в формате «? u k |S| S_1 S_2 ... S_|S|», в которой \(1 \leq u, S_1, \ldots, S_{|S|} \leq n\), все \(S_i\) различны, а \(1 \leq k \leq 10^9\). В качестве ответа на запрос вы получите «1», если ответ положительный, и «0», если ответ отрицательный. Чтобы вывести ответ, необходимо напечатать «! |A| A_1 A_2 ... A_|A|», где \(1 \leq A_1, \ldots, A_{|A|} \leq n\), все они различны. Вывод ответа не считается запросом. Для большей ясности смотрите пример взаимодействия. Если вы зададите слишком много запросов или неправильно сформируете запрос, то получите вердикт Неправильный ответ. После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Взломы Для взломов используйте следующий формат. Первая строка должна содержать \(n\) — количество комнат. Вторая строка должна содержать \(n\) целых чисел \(a_1, a_2, \dots, a_n\) — телепорт в комнате \(i\) ведет в комнату \(a_i\). Примечание В примере имеется \(n=5\) комнат, а массив (скрытый), описывающий поведение телепортов, имеет вид \([1, 2, 1, 3, 2]\). - В первом запросе спрашивается, можно ли, начиная с номера комнаты \(a=3\) и используя телепорты \(5\) раз, оказаться в одной из двух комнат \(S=\{2, 3\}\). В результате этого действия мы оказываемся в комнате \(1\), поэтому ответ — \(0\).
- Второй запрос спрашивает, можно ли, начиная с номера комнаты \(a=2\) и используя телепорты \(5\) раз, оказаться в одной из двух комнат \(S=\{2, 3\}\). В результате этого действия мы оказываемся в комнате \(2\), поэтому ответ - \(1\).
| |
![]()
|
|
E1. ПерестановДерево (простая версия)
Деревья
дп
поиск в глубину и подобное
*1800
Это простая версия задачи. Различия между двумя версиями заключаются в ограничении на \(n\) и ограничении по времени. Делать взломы можно только в том случае, если решены обе версии задачи. Дано дерево с \(n\) вершинами с корнем в вершине \(1\). Для некоторой перестановки\(^\dagger\) \(a\) длины \(n\) пусть \(f(a)\) — количество пар вершин \((u, v)\) таких, что \(a_u < a_{\operatorname{lca}(u, v)} < a_v\). Здесь \(\operatorname{lca}(u,v)\) обозначает наименьшего общего предка вершин \(u\) и \(v\). Найдите максимально возможное значение \(f(a)\) по всем перестановкам \(a\) длины \(n\). \(^\dagger\) Перестановкой длины \(n\) является массив, состоящий из \(n\) различных целых чисел от \(1\) до \(n\) в произвольном порядке. Например, \([2,3,1,5,4]\) — перестановка, но \([1,2,2]\) не перестановка (\(2\) встречается в массиве дважды) и \([1,3,4]\) тоже не перестановка (\(n=3\), но в массиве встречается \(4\)). Выходные данные Выведите максимальное значение \(f(a)\). Примечание Дерево в первом примере:  Одной возможной оптимальной перестановкой \(a\) является \([2, 1, 4, 5, 3]\) с \(4\)-мя подходящими парами вершин: - \((2, 3)\), так как \(\operatorname{lca}(2, 3) = 1\) и \(1 < 2 < 4\),
- \((2, 4)\), так как \(\operatorname{lca}(2, 4) = 1\) и \(1 < 2 < 5\),
- \((2, 5)\), так как \(\operatorname{lca}(2, 5) = 1\) и \(1 < 2 < 3\),
- \((5, 4)\), так как \(\operatorname{lca}(5, 4) = 3\) и \(3 < 4 < 5\).
Дерево в третьем примере:  Дерево в четвёртом примере:  | |
![]()
|
|
E2. ПерестановДерево (сложная версия)
битмаски
бпф
Деревья
дп
жадные алгоритмы
математика
поиск в глубину и подобное
реализация
*2700
Это сложная версия задачи. Различия между двумя версиями заключаются в ограничении на \(n\) и ограничении по времени. Делать взломы можно только в том случае, если решены обе версии задачи. Дано дерево с \(n\) вершинами с корнем в вершине \(1\). Для некоторой перестановки\(^\dagger\) \(a\) длины \(n\) пусть \(f(a)\) — количество пар вершин \((u, v)\) таких, что \(a_u < a_{\operatorname{lca}(u, v)} < a_v\). Здесь \(\operatorname{lca}(u,v)\) обозначает наименьшего общего предка вершин \(u\) и \(v\). Найдите максимально возможное значение \(f(a)\) по всем перестановкам \(a\) длины \(n\). \(^\dagger\) Перестановкой длины \(n\) является массив, состоящий из \(n\) различных целых чисел от \(1\) до \(n\) в произвольном порядке. Например, \([2,3,1,5,4]\) — перестановка, но \([1,2,2]\) не перестановка (\(2\) встречается в массиве дважды) и \([1,3,4]\) тоже не перестановка (\(n=3\), но в массиве встречается \(4\)). Выходные данные Выведите максимальное значение \(f(a)\). Примечание Дерево в первом примере:  Одной возможной оптимальной перестановкой \(a\) является \([2, 1, 4, 5, 3]\) с \(4\)-мя подходящими парами вершин: - \((2, 3)\), так как \(\operatorname{lca}(2, 3) = 1\) и \(1 < 2 < 4\),
- \((2, 4)\), так как \(\operatorname{lca}(2, 4) = 1\) и \(1 < 2 < 5\),
- \((2, 5)\), так как \(\operatorname{lca}(2, 5) = 1\) и \(1 < 2 < 3\),
- \((5, 4)\), так как \(\operatorname{lca}(5, 4) = 3\) и \(3 < 4 < 5\).
Дерево в третьем примере:  Дерево в четвёртом примере:  | |
![]()
|
|
D. Сильные вершины
Деревья
математика
сортировки
*1300
Даны два массива \(a\) и \(b\), оба длины \(n\). Элементы обоих массивов пронумерованы от \(1\) до \(n\). Вы строите ориентированный граф, где существует ориентированное ребро из \(u\) в \(v\) (\(u\neq v\)), если \(a_u-a_v \ge b_u-b_v\). Вершина \(V\) называется сильной, если существует путь от \(V\) ко всем остальным вершинам. Путем в ориентированном графе называют такую цепочку из нескольких вершин, соединенных рёбрами, что двигаясь от вершины \(u\) по направлениям рёбер можно достичь вершины \(v\). Ваша задача — найти все сильные вершины. Например, если \(a=[3,1,2,4]\) и \(b=[4,3,2,1]\), граф будет выглядеть так:  Граф имеет только одну сильную вершину с номером \(4\) Граф имеет только одну сильную вершину с номером \(4\) Выходные данные Для каждого набора входных данных выведите две строки: в первой строке выведите количество сильных вершин, а во второй строке выведите все сильные вершины в возрастающем порядке. Примечание Первый пример разобран в условии. Для второго примера граф выглядит так:  Граф имеет две сильные вершины с номерами в \(3\) и \(5\). Обратите внимание, что между вершинами \(3\) и \(5\) проведено двунаправленное ребро. Граф имеет две сильные вершины с номерами в \(3\) и \(5\). Обратите внимание, что между вершинами \(3\) и \(5\) проведено двунаправленное ребро. В третьем примере вершины соединяет единственное направленное ребро от вершины \(2\) к вершине \(1\), поэтому единственная сильная вершина это \(2\). В четвертом примере все вершины попарно соединены двунаправленными рёбрами, поэтому от каждой вершины есть путь к любой другой. | |
![]()
|
|
G. Подсчет графов
графы
Деревья
жадные алгоритмы
Комбинаторика
разделяй и властвуй
снм
сортировки
*2000
Дано дерево, состоящее из \(n\) вершин. Дерево — это связный неориентированный граф без циклов. Каждое ребро дерева имеет свой вес, \(w_i\). Ваша задача — подсчитать количество различных графов, для которых одновременно выполняются четыре условия: - В графе нет петель и кратных ребер.
- Веса на ребрах графа целые числа и не превышают \(S\).
- Граф имеет ровно одно минимальное остовное дерево.
- Минимальное остовное дерево графа является заданным деревом.
Два графа считаются различными, если их наборы рёбер различны с учётом весов рёбер. Ответ может быть большим, выведите его по модулю \(998244353\). Выходные данные Для каждого теста выведите количество различных графов, удовлетворяющих условиям, по модулю \(998244353\). Примечание В первом примере существует единственный граф, который и является заданным деревом. Во втором примере заданное дерево выглядит так:  Ниже изображены все возможные графы для второго примера, красным цветом выделено минимальное остовное дерево:  | |
![]()
|
|
E1. Откаты (простая версия)
Деревья
Перебор
поиск в глубину и подобное
Структуры данных
*2500
Это простая версия задачи. Единственное отличие между простой и сложной версиями в том, что в сложной версии вы должны отвечать на запросы в режиме онлайн. Вы можете делать взломы, только если обе версии задачи решены. У вас есть массив \(a\), изначально пустой. Вам нужно обрабатывать запросы следующих типов: - + \(x\) — добавить число \(x\) в конец массива \(a\).
- - \(k\) — удалить \(k\) последних чисел из массива \(a\).
- ! — откатить последнее действующее изменение (т. е. сделать массив \(a\) таким, каким он был до изменения). В данной задаче изменениями считаются только запросы первых двух типов (+ и -).
- ? — найти количество различных чисел в массиве \(a\).
Выходные данные Для каждого запроса четвёртого типа выведите одно целое число: количество различных элементов в массиве \(a\) в момент запроса. Примечание В первом тесте из условия массив \(a\) изменяется следующим образом: - После первого запроса \(a=[1]\).
- После второго запроса \(a=[1,2]\).
- После третьего запроса \(a=[1,2,2]\).
- В момент четвёртого запроса в массиве \(a\) встречаются \(2\) различных числа: \(1\) и \(2\).
- После пятого запроса \(a=[1,2]\) (откатили изменение + 2).
- После шестого запроса \(a=[1,2,3]\).
- После седьмого запроса \(a=[1]\).
- В момент восьмого запроса массиве \(a\) состоит только из одной \(1\).
- После девятого запроса \(a=[1,1]\).
- В момент десятого запроса массиве \(a\) состоит только из двух \(1\).
Во втором тесте из условия массив \(a\) изменяется следующим образом: - После первого запроса \(a=[1]\).
- После второго запроса \(a=[1,1\,000\,000]\).
- В момент третьего запроса в массиве \(a\) встречаются \(2\) различных числа: \(1\) и \(1\,000\,000\).
- После четвёртого запроса \(a=[1]\) (откатили изменение + 1000000).
- После пятого запроса \(a=[]\) (откатили изменение + 1).
- В момент шестого запроса в массиве \(a\) нет чисел, поэтому ответ на этот запрос равен \(0\).
| |
![]()
|
|
E2. Откаты (сложная версия)
Деревья
интерактив
Структуры данных
*2600
Это сложная версия задачи. Единственное отличие между простой и сложной версиями в том, что в сложной версии вы должны отвечать на запросы в режиме онлайн. Вы можете делать взломы, только если обе версии задачи решены. У вас есть массив \(a\), изначально пустой. Вам нужно обрабатывать запросы следующих типов: - + \(x\) — добавить число \(x\) в конец массива \(a\).
- - \(k\) — удалить \(k\) последних чисел из массива \(a\).
- ! — откатить последнее действующее изменение (т. е. сделать массив \(a\) таким, каким он был до изменения). В данной задаче изменениями считаются только запросы первых двух типов (+ и -).
- ? — найти количество различных чисел в массиве \(a\).
Выходные данные Для каждого запроса четвёртого типа выведите одно целое число: количество различных элементов в массиве \(a\) в момент запроса. Примечание В первом тесте из условия массив \(a\) изменяется следующим образом: - После первого запроса \(a=[1]\).
- После второго запроса \(a=[1,2]\).
- После третьего запроса \(a=[1,2,2]\).
- В момент четвёртого запроса в массиве \(a\) встречаются \(2\) различных числа: \(1\) и \(2\).
- После пятого запроса \(a=[1,2]\) (откатили изменение + 2).
- После шестого запроса \(a=[1,2,3]\).
- После седьмого запроса \(a=[1]\).
- В момент восьмого запроса массиве \(a\) состоит только из одной \(1\).
- После девятого запроса \(a=[1,1]\).
- В момент десятого запроса массиве \(a\) состоит только из двух \(1\).
Во втором тесте из условия массив \(a\) изменяется следующим образом: - После первого запроса \(a=[1]\).
- После второго запроса \(a=[1, 1\,000\,000]\).
- В момент третьего запроса в массиве \(a\) встречаются \(2\) различных числа: \(1\) и \(1\,000\,000\).
- После четвёртого запроса \(a=[1]\) (откатили изменение + 1000000).
- После пятого запроса \(a=[]\) (откатили изменение + 1).
- В момент шестого запроса в массиве \(a\) нет чисел, поэтому ответ на этот запрос равен \(0\).
| |
![]()
|
|
F. Телепортация в Байтландии
графы
Деревья
кратчайшие пути
поиск в глубину и подобное
разделяй и властвуй
Структуры данных
*3200
В Байтландии есть \(n\) городов, некоторые пары которых соединены дорогами, по которым можно ездить в обе стороны. \(i\)-я дорога характеризуется сложностью проезда по ней \(w_i\). Время проезда по дороге со сложностью \(w_i\) равняется \(\lceil\frac{w_i}{c}\rceil\) часов, где \(c\) — навык вождения водителя. Транспортная система Байтландии представляет собой дерево. Иными словами, между любой парой городов существует ровно один путь, который проходит по каждому городу не более одного раза. В некоторых городах можно посетить курсы вождения. Если провести в таком городе, изучая курсы, \(T\) часов, то навык вождения \(c\) увеличивается в \(2\) раза. Заметьте, что значение \(T\) одинаково во всех городах, и курсы можно посещать в одном и том же городе несколько раз. Вам нужно ответить на \(q\) запросов: за какое минимальное время можно добраться из города \(a\) в город \(b\), если начать путь с навыком вождения \(c = 1\)? Выходные данные Для каждого запроса выведите одно целое число в отдельной строке — минимальное время, за которое можно добраться в соответствующем запросе. Примечание В первом наборе входных данных в первом запросе оптимально не проходить курсы вождения. Тогда минимальное время равно сложности дороги между городами \(1\) и \(2\), которое равно \(1\). Во втором наборе входных данных в первом запросе оптимально вначале пройти курсы вождения за \(3\) часа в городе \(1\) один раз, а потом поехать в город \(5\). Тогда всего путь займёт \(3 + \lceil\frac{5}{2}\rceil + \lceil\frac{10}{2}\rceil = 11\) часов. | |
![]()
|
|
C. Запросы к массиву
Деревья
поиск в глубину и подобное
реализация
Строки
Структуры данных
*1600
У Монокарпа был массив \(a\), состоящий из целых чисел. Изначально массив был пустым. Монокарп выполнял три типа запросов к этому массиву: - выбрать число и добавить его в конец массива. Каждый раз, когда Монокарп выполнял этот запрос, он выписывал символ +;
- удалить последний элемент из массива. Каждый раз, когда Монокарп выполнял этот запрос, он выписывал символ -. Монокарп не выполнял этот запрос, если массив был пуст;
- проверить, отсортирован ли массив в порядке неубывания, т. е. выполняется ли \(a_1 \le a_2 \le \dots \le a_k\), где \(k\) — количество элементов в массиве на данный момент. Любой массив, содержащий меньше \(2\) элементов, считается отсортированным. Если массив отсортирован в момент запроса, Монокарп выписывал символ 1. Иначе он выписывал символ 0.
Вам задана строка \(s\), состоящая из \(q\) символов 0, 1, + и/или -. Это символы, выписанные Монокарпом, строго в том порядке, в каком он их выписывал. Вам нужно выяснить, является ли эта строка непротиворечивой, т. е. мог ли Монокарп выполнять такие запросы, что выписанная после них строка равна строке \(s\). Выходные данные Для каждого набора входных данных выведите YES, если Монокарп мог выполнить такие запросы, в результате которых будет выписана строка \(s\). Иначе выведите NO. Вы можете выводить символы в ответе в любом регистре. Примечание В первом наборе входных данных Монокарп мог выполнить следующие запросы: - добавить число \(13\);
- добавить число \(37\);
- проверить, что массив \([13, 37]\) отсортирован в порядке неубывания (и он действительно отсортирован).
В пятом наборе входных данных Монокарп мог выполнить следующие запросы: - добавить число \(3\);
- добавить число \(2\);
- проверить, что массив \([3, 2]\) отсортирован (он не отсортирован);
- удалить последний элемент;
- добавить число \(3\);
- проверить, что массив \([3, 3]\) отсортирован (он отсортирован);
- удалить последний элемент;
- добавить число \(-5\);
- проверить, что массив \([3, -5]\) отсортирован (он не отсортирован);
В остальных наборах входных данных Монокарп не мог выписать строку \(s\), выполняя свои запросы. | |
![]()
|
|
H. Машина Голдберга 3
Деревья
дп
*3500
Дано полное корневое бинарное дерево, то есть корневое дерево, в котором у каждой вершины или \(0\), или \(2\) ребёнка. Корнем этого дерева является вершина \(1\). Вершина без детей называется листом. У каждого листа есть значение голода, обозначим значение голода листа \(v\) через \(h_v\). В каждой внутренней вершине дерева есть свой переключатель, указывающий на одного из сыновей этой вершины. Дерево принимает печеньки. Перед запуском процесса вы можете выбрать начальное положение каждого переключателя для всех вершин независимо. Процесс устроен следующим образом: - Изначально в вершинах нет печенек.
- Вы вставляете печеньки по одной в корневую вершину.
- Пока печенька не спустилась до листа, она падает в ребёнка, на которого указывает переключатель в текущей вершине. Сам переключатель после этого изменяет своё состояние на противоположное, т. е. начинает указывать на другого ребёнка.
- Вы перестаёте кормить машину печеньем, когда в каждом листе \(v\) будет хотя бы \(h_v\) печенек. В этом случае дерево считается накормленным.
Даны \(q\) запросов. Каждый запрос меняет значение \(h_v\) для какого-то листа \(v\). Вам необходимо вывести \(q + 1\) число, \(i\)-е из которых равно минимальному количеству печенек, необходимых для того, чтобы полностью накормить машину после первых \((i - 1)\) запросов, если перед запуском процесса вы можете выбрать начальное положение каждого переключателя независимо. Поскольку это количество может быть очень большим, выведите его по модулю \(998\,244\,353\). Обратите внимание, что между запросами вы можете менять начальное состояние переключателей. Однако сами запросы не являются независимыми: при ответе на \(i\)-й запрос нужно также учесть эффект от запросов \(1, 2, \ldots, i - 1\). Выходные данные Выведите \(q + 1\) число, \(i\)-е из которых равно минимальному количеству печенек, необходимых для того, чтобы накормить машину после \((i - 1)\) запросов, взятое по модулю \(998\,244\,353\). Примечание Рассмотрим пример. До начала всех запросов нам не нужно вставлять печенье, поскольку все нулевые величины голода автоматически удовлетворены. После первого запроса можно сделать так, чтобы изначально переключатель в вершине \(1\) указывал на вершину \(3\). Тогда достаточно вставить одну печеньку, она немедленно упадёт в вершину \(3\). После второго запроса можно сделать так, чтобы изначально переключатель в вершине \(1\) указывал на \(3\), а переключатель в вершине \(2\) — на вершину \(4\). Первая печенька упадёт в вершину \(3\) и изменит состояние переключателя в вершине \(1\): теперь он будет указывать на \(2\). Вторая печенька пройдёт по пути \(1 \to 2 \to 4\). После третьего запроса можно сделать так, чтобы изначально переключатель в вершине \(1\) указывал на \(2\), а переключатель в вершине \(2\) — на вершину \(4\). Тогда три печеньки пройдут по путям \(1 \to 2 \to 4\), \(1 \to 3\), \(1 \to 2 \to 5\). После четвёртого запроса можно сделать так, чтобы изначально переключатель в вершине \(1\) указывал на \(3\). Вне зависимости от исходного положения переключателя в вершине \(2\), после того как мы вставим семь печенюшек в дерево, четыре из них окажутся в листе \(3\), а в каждом из листьев \(4\) и \(5\) окажется по одной или две печеньки (обратите внимание, что превышать величины голода разрешается). После пятого запроса ответ равен \(3\,999\,999\,997\). Не забудьте вывести ответ по модулю \(998\,244\,353\). | |
![]()
|
|
I. Избыточные маршруты
Деревья
дп
Конструктив
*3500
Дано дерево из \(n\) вершин, пронумерованных числами \(1, 2, \ldots, n\). Длина простого пути в дереве равна числу вершин в нём. Вам нужно выбрать некоторое множество простых путей длины хотя бы \(2\) каждый, причём нельзя одновременно выбрать два разных пути, один из которых содержится в другом. Найдите наибольший возможный размер такого множества. Формально, множество вершин \(S\) называется маршрутом, если в нём по крайней мере две вершины, при этом оно является множеством вершин некоторого простого пути в дереве. Набор попарно различных маршрутов называется расписанием. Маршрут \(S\) в расписании \(T\) называется избыточным, если есть какой-то другой маршрут \(S' \in T\), такой что \(S \subset S'\). Расписание называется эффективным, если в нём нет избыточных маршрутов. Найдите наибольшее возможное количество маршрутов в эффективном расписании. Выходные данные Выведите единственное число — ответ на задачу. Примечание В первом примере возможными эффективными расписаниями являются \(\{\{1, 2\}, \{1, 3\}, \{1, 4\}\}\) и \(\{\{1, 2, 3\}, \{1, 2, 4\}, \{1, 3, 4\}\}\). Во втором примере можно выбрать \(\{ \{1, 2, 3\}, \{2, 3, 4\}, \{3, 4, 6\}, \{2, 3, 5\}, \{3, 4, 5\}, \{3, 4, 7\}, \{4, 6, 7\}\}\). | |
![]()
|
|
E. Угадайка
битмаски
Деревья
игры
математика
сортировки
Строки
Структуры данных
Теория вероятностей
*2100
У Кэрол есть последовательность \(s\) из \(n\) неотрицательных целых чисел. Она хочет сыграть с Алисой и Бобом в «Угадайку». Игра устроена следующим образом. Сначала Кэрол случайно выберет два целых индекса \(i_a\) и \(i_b\) из диапазона \([1, n]\) и обозначит \(a=s_{i_a}\), \(b=s_{i_b}\). Обратите внимание: \(i_a\) и \(i_b\) могут совпасть. Затем Кэрол сообщит: - значение \(a\) — Алисе;
- значение \(b\) — Бобу;
- значение \(a \mid b\) и Алису и Бобу, где \(|\) обозначает операцию побитового ИЛИ.
Обратите внимание: Кэрол не сообщит никакой информации об \(s\) ни Алисе, ни Бобу. Затем начинается процесс угадывания. Алиса и Боб ходят по очереди, причём первой ходит Алиса. Цель обоих игроков — выяснить, какое из утверждений верно: \(a < b\), \(a > b\), или \(a = b\). На своём ходу игрок может сделать одно из двух: - сказать «Я не знаю» и передать ход другому игроку;
- сказать «Я знаю», а затем сообщить ответ: «\(a<b\)», «\(a>b\)», или же «\(a=b\)»; после этого игра заканчивается.
Алиса и Боб слышат фразы друг друга и могут использовать их в своих рассуждениях. Оба игрока достаточно умны. Сказать «Я знаю» они могут только в том случае, если точно уверены в ответе. Найдите математическое ожидание числа шагов в такой игре. Выведите ответ по модулю \(998\,244\,353\). Формально, пусть \(M = 998\,244\,353\). Можно показать, что ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Выходные данные Для каждого набора входных данных выведите одно число — ответ на задачу по модулю \(998\,244\,353\). Примечание В первом наборе входных данных есть всего \(4\) возможные ситуации: - \(i_a=1\), \(i_b=1\), \(a=2\), \(b=2\), число шагов равно \(2\);
- \(i_a=1\), \(i_b=2\), \(a=2\), \(b=3\), число шагов равно \(3\);
- \(i_a=2\), \(i_b=1\), \(a=3\), \(b=2\), число шагов равно \(2\);
- \(i_a=2\), \(i_b=2\), \(a=3\), \(b=3\), число шагов равно \(3\).
Математическое ожидание числа шагов равно \(\frac{2+3+2+3}{4}=\frac{5}{2}=499122179\pmod{998244353}\). Рассмотрим первый случай, когда \(a=2\), \(b=2\). Процесс угадывания происходит следующим образом. На первом ходу Алиса думает так: «Я знаю, что \(a=2, a\mid b=2\). Можно сделать вывод, что \(b=0\) или \(b=2\), но какой из этих двух случаев имеет место — пока неясно». Поэтому она говорит: «Я не знаю». На втором ходу Боб думает так: «Я знаю, что \(b=2, a\mid b=2\). Можно сделать вывод, что \(a=0\) или \(a=2\). Однако если \(a=0\), то Алиса на своём ходу уже бы сказала, что \(a<b\). Но она этого не сказала. Значит, \(a=2\)». Поэтому он говорит: «Я знаю, \(a=b\)». Игра завершается. Во втором наборе входных данных, при \(a=0\), \(b=0\), Алиса сразу заключает, что \(a=b\). Ожидаемое число ходов равно \(1\). | |
![]()
|
|
K. Keen Tree Calculation
Бинарный поиск
геометрия
графы
Деревья
дп
реализация
Структуры данных
*2500
There is a tree of \(N\) vertices and \(N-1\) edges. The \(i\)-th edge connects vertices \(U_i\) and \(V_i\) and has a length of \(W_i\). Chaneka, the owner of the tree, asks you \(Q\) times. For the \(j\)-th question, the following is the question format: - \(X_j\) \(K_j\) – If each edge that contains vertex \(X_j\) has its length multiplied by \(K_j\), what is the diameter of the tree?
Notes: - Each of Chaneka's question is independent, which means the changes in edge length do not influence the next questions.
- The diameter of a tree is the maximum possible distance between two different vertices in the tree.
Output Output \(Q\) lines with an integer in each line. The integer in the \(j\)-th line represents the diameter of the tree on the \(j\)-th question. Note In the first example, the following is the tree without any changes. 
The following is the tree on the \(1\)-st question. 
The maximum distance is between vertices \(6\) and \(7\), which is \(6+6+6=18\), so the diameter is \(18\). The following is the tree on the \(2\)-nd question. 
The maximum distance is between vertices \(2\) and \(6\), which is \(3+2+6=11\), so the diameter is \(11\). | |
![]()
|
|
C. План путешествия
Деревья
дп
Комбинаторика
математика
реализация
*2400
Во время летних каникул после экзамена, Tom и Daniel планировали отправиться в путешествие. В их стране есть \(n\) городов, пронумерованных от \(1\) до \(n\). И система дорожного движения в стране особенная. Для любого города \(i\) (\(1 \le i \le n\)) есть: - дорога между городами \(i\) и \(2i\), если \(2i\le n\);
- дорога между городами \(i\) и \(2i+1\), если \(2i+1\le n\).
Составляя план путешествия, Daniel выбирает некоторое целое значение от \(1\) до \(m\) для каждого города, для \(i\)-го города обозначим его \(a_i\). Пусть \(s_{i,j}\) равно максимальному значению для городов на простом\(^\dagger\) пути между городами \(i\) и \(j\). Тогда оценка плана путешествия равна \(\sum_{i=1}^n\sum_{j=i}^n s_{i,j}\). Tom хочет знать сумму оценок всех возможных планов путешествия. Daniel просит вас помочь ему найти её. Вам нужно сказать ответ по модулю \(998\,244\,353\). \(^\dagger\) Простым путём между городами \(x\) и \(y\) называется путь между ними, который проходит по каждому городу не более одного раза. Выходные данные Для каждого набора входных данных выведите одно целое число — сумму оценок всех возможных планов путешествия по модулю \(998\,244\,353\). Примечание В первом наборе входных данных есть только один возможный план путешествия:  Путь \(1\rightarrow 1\): \(s_{1,1}=a_1=1\). Путь \(1\rightarrow 2\): \(s_{1,2}=\max(1,1)=1\). Путь \(1\rightarrow 3\): \(s_{1,3}=\max(1,1)=1\). Путь \(2\rightarrow 2\): \(s_{2,2}=a_2=1\). Путь \(2\rightarrow 1\rightarrow 3\): \(s_{2,3}=\max(1,1,1)=1\). Путь \(3\rightarrow 3\): \(s_{3,3}=a_3=1\). Оценка равна \(1+1+1+1+1+1=6\). Во втором наборе входных данных есть четыре возможных плана путешествия:  Оценка плана \(1\): \(1+1+1=3\). Оценка плана \(2\): \(1+2+2=5\). Оценка плана \(3\): \(2+2+1=5\). Оценка плана \(4\): \(2+2+2=6\). Таким образом, сумма оценок равна \(3+5+5+6=19\). | |
![]()
|
|
D. Цветочное псевдодерево
графы
Деревья
жадные алгоритмы
Конструктив
реализация
*3000
Псевдодеревом называется связный граф, который имеет ровно один цикл и не имеет петель. Обратите внимание, что псевдодерево может содержать кратные рёбра. Можно доказать, что псевдодерево с \(n\) вершинами всегда содержит \(n\) рёбер. После удаления всех рёбер на цикле в псевдодереве образуется лес\(^{\dagger}\). Можно доказать, что каждое дерево в лесу будет содержать ровно одну вершину, которая находится на цикле до удаления рёбер. Если все деревья в лесу имеют одинаковую глубину\(^{\ddagger}\) при выборе вершины на цикле в качестве корня, мы называем исходное псевдодерево цветочным. У нашего друга sszcdjr, было цветочное псевдодерево с \(n\) вершинами и \(n\) рёбрами. Однако, он забыл все рёбра в псевдодереве. К счастью, он все ещё помнит степени вершин. В частности, степень \(i\)-й вершины равна \(d_i\). Вы должны помочь sszcdjr построить возможное цветочное псевдодерево с \(n\) вершинами, где степень \(i\)-й вершины строго равна \(d_i\), или сообщить ему, что это невозможно. \(^{\dagger}\) Лесом называется граф, в котором все компоненты связности являются деревьями. Деревом называется связный граф без циклов и петель. \(^{\ddagger}\) Глубиной дерева с корнем называется максимальное расстояние от корня до вершины этого дерева. Выходные данные Для каждого набора входных данных, если существует возможное цветочное псевдодерево: - Выведите «Yes» (без кавычек) в первой строке.
- Затем выведите \(n\) строк, в каждой строке выведите два целых числа \(u_i\) и \(v_i\) — две вершины, которые соединяет \(i\)-е ребро.
Если есть несколько ответов, вы можете вывести любой из них. В противном случае, выведите «No» (без кавычек) в единственной строке вывода. Вы можете выводить первую строку для каждого набора входных данных в любом регистре (верхнем или нижнем). Например, строки «yEs», «yes», «Yes» и «YES» будут распознаны как положительные ответы. Примечание В первом наборе входных данных единственным возможным цветочным псевдодеревом является:  После удаления всех рёбер на цикле в псевдодереве каждое дерево имеет глубину \(0\). Во втором наборе входных данных можно доказать, что не существует такого цветочного псевдодерева. В третьем наборе входных данных одним из возможных цветочных псевдодеревьев является:  | |
![]()
|
|
H. Стандартная задача на графы
графы
Деревья
жадные алгоритмы
Структуры данных
*3500
Вам дан взвешенный ориентированный граф, содержащий \(n\) вершин и \(m\) ребер. Каждая вершина графа может быть выделенной или обычной, изначально все вершины обычные. Ценой графа назовём минимальную суммарную цену рёбер, которые нужно взять, чтобы из каждой обычной вершины была достижима по взятым ребрам хотя бы одна любая выделенная вершина. Если такого набора рёбер не существует, то цена равна \(-1\). Вам предстоит вычислить цену графа после каждого из \(q\) запросов. Запросы бывают двух типов: - \(+\;v_i\) делает вершину \(v_i\) выделенной; гарантируется, что перед запросом вершина была обычной.
- \(-\;v_i\) делает вершину \(v_i\) обычной; гарантируется, что перед запросом вершина была выделенной.
Выведите цену графа после каждого из \(q\) запросов. Выходные данные Выведите \(q\) чисел. \(i\)-е число — это цена графа после первых \(i\) запросов. Примечание В первом тесте: - Посыле первого запроса выгоднее всего взять ребра с номерами \(3, 4, 5\), сумма их цен равна \(15\).
- После второго запроса, нет ни одной выделенной вершины, а значит, не существует подходящих наборов ребер, цена графа \(-1\).
- После третьего запроса выгоднее всего взять ребра с номерами \(1, 2, 5\), сумма их цен равна \(14\).
- После четвертого запроса выгоднее всего взять ребра с номерами \(4\) и \(5\), сумма их цен равна \(12\).
- После пятого запроса выгоднее всего взять только ребро номер \(5\), его цена равна \(4\).
- После шестого запроса все вершины выделенные и можно не брать ребер, цена графа равна \(0\).
| |
![]()
|
|
H. Безумный город
графы
Деревья
игры
кратчайшие пути
поиск в глубину и подобное
снм
*1700
Марсель и Валериу находятся в безумном городе, который представляет собой \(n\) зданий с \(n\) двусторонними дорогами между ними. Марсель и Валериу начинают в зданиях \(a\) и \(b\) соответственно. Марсель хочет поймать Валериу, то есть оказаться в том же здании, что и он, или встретиться на одной дороге. Во время каждого хода они выбирают, пойти в соседнее здание от текущего или остаться в том же здании. Поскольку Валериу хорошо знает Марселя, Валериу может предсказать, куда Марсель пойдет в следующем ходу. Валериу может использовать эту информацию, чтобы сделать свой ход. Они начинают и заканчивают ход одновременно. Гарантируется, что любая пара зданий соединена некоторым путем, и между любой парой зданий есть не более одной дороги. Предполагая, что оба игрока играют оптимально, ответьте, есть ли у Валериу стратегия, чтобы бесконечно уходить от Марселя. Выходные данные Для каждого набора входных данных выведите «YES», если Валериу может бесконечно уходить от Марселя, и «NO» в противном случае. Вы можете выводить ответ в любом регистре (например, строки «yEs», «yes», «Yes» и «YES» будут распознаны как положительный ответ). Примечание В первом примере граф выглядит следующим образом:  Марсель начинает в здании \(2\), а Валериу начинает в здании \(1\). Валериу знает, каким путем Марсель будет двигаться вокруг треугольника, и он может просто всегда двигаться так же, чтобы всегда избегать Марселя. Во втором примере граф выглядит следующим образом:  Марсель начинает в здании \(1\), а Валериу начинает в здании \(4\). Марсель может пойти в здание \(4\) на своем первом ходу и победить, так как Валериу должен либо пойти в здание \(1\) (тогда они встретятся на дороге от \(1\) до \(4\)), либо остаться в здании \(4\) (тогда они встретятся в здании \(4\)). Таким образом, у Валериу нет стратегии для победы. | |
![]()
|
|
E. Шаро-стек
Деревья
дп
Конструктив
Структуры данных
*3300
С таким названием задача точно не может быть задачей на графы... У Чанеки есть граф с \(n\) вершинами и \(n-1\) ребрами. Некоторые ребра являются направленными, а некоторые — неориентированными. Ребро \(i\) соединяет вершину \(u_i\) с вершиной \(v_i\). Если \(t_i=0\), то ребро \(i\) является ненаправленным. Если \(t_i=1\), то ребро \(i\) направлено в сторону от \(u_i\) к \(v_i\). Известно, что если сделать все ребра ненаправленными, то граф превратится в дерево\(^\dagger\). Чанека хочет направить все ненаправленные ребра и раскрасить каждое ребро (разные ребра могут иметь один и тот же цвет). После этого, предположим, что Чанека начинает прогулку из произвольной вершины \(x\) в произвольную вершину \(y\) (возможно, что \(x=y\)), проходя через одно или несколько ребер. Ей разрешается проходить через каждое ребро, следуя направлению ребра или в противоположную от направления сторону. Также ей разрешается посещать вершину или ребро более одного раза. Во время прогулки Чанека хранит стек шаров, который изначально пуст до начала прогулки. Каждый раз, когда Чанека проходит через ребро, она делает следующее: - Если Чанека проходит его в правильном направлении, она кладет на вершину стека новый шар, цвет которого совпадает с цветом ребра.
- Если Чанека проходит по нему в обратном направлении, то она убирает шар, находящийся на вершине стека.
Прогулка называется стековой тогда и только тогда, когда стек не пуст перед каждым проходом Чанеки по ребру в обратном направлении. Прогулка называется шаро-стековой тогда и только тогда, когда она стековая и каждый раз, когда Чанека проходит через ребро в обратном направлении, цвет шарика, вынутого из стека, совпадает с цветом пройденного ребра. Можно ли направить все неориентированные ребра и раскрасить все рёбра так, чтобы все стековые прогулки были также шаро-стековыми? Если это возможно, то найдите пример, в котором используется максимальное количество различных цветов среди всех допустимых способов направления и раскраски. Если таких решений несколько, выведите любое из них. \(^\dagger\) Дерево — это связный граф, не имеющий циклов. Выходные данные Выведите одно число \(-1\), если искомой конструкции не существует. В противном случае вывод состоит из \(n\) строк, описывающих вашу конструкцию. Первая строка содержит целое число \(z\), равное количеству используемых цветов. В \(i\)-й из следующих \(n-1\) строк содержится три целых числа \(p\), \(q\) и \(c\) (\(1\leq p,q\leq n\); \(1\leq c\leq z\)) — ребро, соединяющее вершины \(p\) и \(q\) в графе, направлено от вершины \(p\) к вершине \(q\) и окрашено в цвет \(c\). Если таких решений несколько, выведите любое из них. Обратите внимание, что поскольку в вашей конструкции должно быть \(z\) различных цветов, это означает, что каждый цвет от \(1\) до \(z\) должен встречаться в графе хотя бы один раз. Примечание Ниже приведен заданный граф.  Чанека может направить все неориентированные ребра и раскрасить каждое ребро следующим образом:  В качестве примера рассмотрим путь \(3→1→5→2→5→4→5\). Покажем, что этот путь является шаро-стековым. - Чанека начинается в вершине \(3\). Стеком является \([]\).
- Чанека переходит в вершину \(1\). Она кладет шар цвета \(3\). В стеке \([3]\).
- Чанека перемещается в вершину \(5\). Она кладет шар цвета \(2\). В стеке \([3,2]\).
- Чанека перемещается в вершину \(2\). Она убирает шар цвета \(2\) (того же цвета, что и ребро). В стеке оказывается \([3]\).
- Чанека перемещается в вершину \(5\). Она кладет шар цвета \(2\). В стеке \([3,2]\).
- Чанека перемещается в вершину \(4\). Она кладет шар цвета \(1\). В стеке \([3,2,1]\).
- Чанека перемещается в вершину \(5\). Она убирает шар цвета \(1\) (того же цвета, что и ребро). В стеке оказывается \([3,2]\).
Поскольку каждый раз, когда Чанека снимает шар со стека, он имеет тот же цвет, что и пройденное ребро, то вышеописанная прогулка является шаро-стековой. Можно показать, что если мы направим и раскрасим ребра так, как показано выше, то любая возможная стековая прогулка будет также шаро-стековой. | |
![]()
|
|
G. Clubstep
Бинарный поиск
Деревья
жадные алгоритмы
Перебор
Структуры данных
*3500
Существует чрезвычайно сложная видеоигра, которая является одной из любимых видеоигр Чанеки. Один из самых трудных уровней в игре называется Clubstep. Clubstep состоит из \(n\) частей, пронумерованных от \(1\) до \(n\). Чанека хорошо натренировалась в прохождении уровня, поэтому на данный момент ее уровень знакомства с каждой частью \(i\) составляет \(a_i\). После этого Чанека может сделать несколько (возможно, ноль) попыток пройти Clubstep. В каждой попытке она погибает на одной из \(n\) частей. Если попытка заканчивается на части \(p\), то это означает, что она успешно проходит только через каждую часть \(k\) для всех \(1 \leq k \leq p-1\) и не достигает ни одной части \(k\) для всех \(p+1 \leq k \leq n\). Попытка, закончившаяся на части \(p\), занимает \(p\) секунд. Известно, что Чанека улучшает ту часть, на которой она погибает, гораздо больше, чем все остальные. Известно также, что во время попытки Чанека не успевает потренироваться на тех частях, до которых она не дошла. Таким образом, эффект от попытки, которая заканчивается на части \(p\), будет следующим: - Значение знакомства Чанеки с частью \(p\) увеличивается на \(2\).
- Значение знакомства Чанеки с каждой частью \(k\) для всех \(1 \leq k \leq p-1\) увеличивается на \(1\).
Имеется \(q\) вопросов. В \(j\)-м вопросе Вам даются три целых числа \(l_j\), \(r_j\) и \(x_j\). Затем требуется найти минимальное время (в секундах), которое потребуется Чанеке для того, чтобы значение знакомства с каждой частью \(p\) ( \(l_j \leq p \leq r_j\)) стало не меньше \(x_j\). Заметим, что каждый запрос является независимым, поэтому попытка, которую предпринимает Чанека в одном запросе, не влияет на значения знакомства в других запросах. Выходные данные Выведите \(q\) целых чисел в отдельных строках. Число в \(j\)-й строке равняется минимальнму времени (в секундах), за которое Чанека может сделать так, чтобы значение знакомства для каждой части \(p\) (\(l_j \leq p \leq r_j\)) было не менее \(x_j\). Примечание Для ответа на \(1\)-й вопрос можно поступить следующим образом: - Сделать \(1\) попытку, которая заканчивается на части \(1\). Это занимает \(1\) секунду. Значения знакомства становятся \([3, 3, 2, 1, 2]\).
- Выполнить \(1\) попытку, которая заканчивается на части \(4\). Это занимает \(4\) секунды. Значения знакомства становятся \([4, 4, 3, 3, 2]\).
- Выполнить \(2\) попытки, которые заканчиваются на части \(5\). Это занимает \(10\) секунд. Значения знакомства становятся \([6, 6, 5, 5, 6]\).
Общее время (в секундах) составляет \(1+4+10=15\). Для ответа на \(2\)-й вопрос можно поступить следующим образом: - Сделать попытку \(1\), которая заканчивается на части \(3\). Это занимает \(3\) секунды. Значения знакомства становятся \([2, 4, 4, 1, 2]\).
- Выполнить \(2\) попытки, которые заканчиваются на части \(4\). Это занимает \(8\) секунд. Значения знакомства становятся \([4, 6, 6, 5, 2]\).
Общее время (в секундах) составляет \(3+8=11\). | |
![]()
|
|
G. Дерево wxhtzdy ORO
Бинарный поиск
битмаски
Деревья
Перебор
поиск в глубину и подобное
реализация
Структуры данных
*2300
После (наконец-то) прохождения отбора на IOI 2023, wxhtzdy был очень счастлив и решил сделать то, что делают многие люди: попытаться угадать задачи, которые будут на IOI. В процессе этого он случайно создал задачу, которая, по его мнению, была очень крутой. Дано дерево (связный ациклический граф) с \(n\) вершинами и \(n-1\) ребром. Вершине \(i\) (\(1 \le i \le n\)) соответствует значение \(a_i\). Пусть \(g(u, v)\) - это побитовое ИЛИ значений всех вершин на кратчайшем пути от \(u\) до \(v\). Например, если мы хотим вычислить \(g(3, 4)\) на дереве из первого набора данных примера. На пути от \(3\) до \(4\) находятся вершины \(3\), \(1\), \(4\). Тогда \(g(3, 4) = a_3 \ | \ a_1 \ | \ a_4\) (здесь \(|\) обозначает побитовое ИЛИ). Также дано \(q\) запросов, и каждый запрос выглядит следующим образом: Вам даны \(x\) и \(y\). Рассмотрим все вершины \(z\) такие, что \(z\) находится на кратчайшем пути от \(x\) до \(y\) (включительно). Определим красоту вершины \(z\) как сумму количества ненулевых битов в \(g(x, z)\) и количества ненулевых битов в \(g(y, z)\). Вам нужно найти максимальную красоту среди всех вершин \(z\) на кратчайшем пути от \(x\) до \(y\). Так как его мозг очень устал после решения output only задачи на SIO (он должен был это сделать, чтобы пройти отбор на IOI), он хочет вашей помощи в этой задаче. Выходные данные Для каждого набора входных данных выведите \(q\) целых чисел, каждое из которых является ответом на соответствующий запрос. Примечание На изображении ниже показано дерево из первого набора входных данных второго примера.  Дерево из первого набора входных данных второго примера. Дерево из первого набора входных данных второго примера. В первом запросе \(x=7\), \(y=5\). Самый короткий путь от \(7\) до \(5\) это \(7-4-2-1-5\). Давайте вычислим красоту вершины \(7\) на этом пути. У нас есть \(g(7,7)=a_7=10=(1010)_2\) и \(g(5,7)=a_5 \ | \ a_1 \ | \ a_2 \ | \ a_4 \ | \ a_7=10 \ | \ 4 \ | \ 7 \ | \ 4 \ | \ 10=15=(1111)_2\), поэтому ее красота равна \(2 + 4 = 6\). Теперь давайте вычислим красоту вершины \(4\) на этом пути. У нас есть \(g(7,4)=a_7 \ | \ a_4=10 \ | \ 4=14=(1110)_2\) и \(g(5,4)=a_5 \ | \ a_1 \ | \ a_2 \ | \ a_4=10 \ | \ 4 \ | \ 7 \ | \ 4=15=(1111)_2\), поэтому ее красота равна \(3 + 4 = 7\). Теперь давайте вычислим красоту вершины \(2\) на этом пути. У нас есть \(g(7,2)=a_7 \ | \ a_4 \ | \ a_2=10 \ | \ 4 \ | \ 7=15=(1111)_2\) и \(g(5,2)=a_5 \ | \ a_1 \ | \ a_2=10 \ | \ 4 \ | \ 7=15=(1111)_2\), поэтому ее красота равна \(4 + 4 = 8\). Теперь давайте вычислим красоту вершины \(1\) на этом пути. У нас есть \(g(7,1)=a_7 \ | \ a_4 \ | \ a_2 \ | \ a_1=10 \ | \ 4 \ | \ 7 \ | \ 4=15=(1111)_2\) и \(g(5,1)=a_5 \ | \ a_1=10 \ | \ 4=14=(1110)_2\), поэтому ее красота равна \(4 + 3 = 7\). Наконец, давайте вычислим красоту вершины \(5\) на этом пути. У нас есть \(g(7,5)=a_7 \ | \ a_4 \ | \ a_2 \ | \ a_1 \ | \ a_5=10 \ | \ 4 \ | \ 7 \ | \ 4 \ | \ 10=15=(1111)_2\) и \(g(5,5)=a_5=10=(1010)_2\), поэтому ее красота равна \(4 + 2 = 6\). Максимальная красота на этом пути у вершины \(2\), и она равна \(8\). | |
![]()
|
|
E. Интерактивная игра с раскраской
графы
Деревья
интерактив
Конструктив
Перебор
поиск в глубину и подобное
реализация
*2400
Это интерактивная задача. Не забывайте о том, что ваша программа должна каждый раз после вывода запроса сбрасывать буфер вывода. Для сброса буфера вывода можно использовать fflush(stdout) в C++, system.out.flush() в Java, stdout.flush() в Python или flush(output) в Pascal. Если вы используете другой язык программирования, посмотрите в его документации, как выполняется эта операция. Также рекомендуем вам прочесть руководство по интерактивным задачам: https://cf.m27.workers.dev/blog/entry/45307. Дано дерево с \(n\) вершинами; вершина \(1\) является корнем дерева. Для каждого \(i \in [2, n]\) вам дан родитель \(i\)-й вершины \(p_i\); для каждой вершины соблюдается \(p_i < i\). Вам предстоит раскрасить все ребра дерева, используя минимально возможное количество цветов, таким образом, чтобы выиграть в игру на этом дереве (каждое ребро должно быть окрашено в ровно один цвет). Игра, в которую мы собираемся играть, будет проходить следующим образом. После того как вы раскрасите ребра и выведите их цвета, жюри поместит фишку в одну из вершин дерева (кроме корня). Ваша цель — переместить эту фишку в корень ровно за \(d\) ходов, где \(d\) — расстояние от вершины до корня (расстояние равно количеству ребер на пути). Если фишка достигает корня за \(d\) ходов, вы выигрываете. В противном случае вы проигрываете. Жюри не сообщит вам, где находится фишка. Вы даже не будете знать значение \(d\) заранее. Однако в начале каждого хода вам будет сообщено, сколько ребер каждого цвета инцидентно текущей вершине (это включает как ребро, ведущее вверх по дереву, так и ребра, ведущие вниз). Вы должны выбрать один из этих цветов, и фишка будет перемещена вдоль ребра выбранного цвета (если есть несколько ребер с этим цветом, жюри выбирает одно из них). После перемещения фишки вам снова будет сообщена та же информация о текущей вершине, и игра продолжается, пока вы не достигнете корня или не сделаете \(d\) ходов, не достигнув корня. Интерактор для этой задачи является адаптивным. Это означает, что начальная вершина и текущая вершина не фиксированы и могут изменяться «на ходу» в зависимости от вывода вашей программы. Однако состояние игры всегда будет согласовано с информацией, которую вы получаете: всегда будет как минимум одна начальная вершина и как минимум один путь вашей фишки из этой вершины, согласующийся как с информацией о цветах, которую вы получаете, так и с цветами, которые вы выбирали во время ходов. Протокол взаимодействия Сначала вы должны вывести выбранную вами раскраску ребер следующим образом: - в первой строке выведите одно целое число \(k\) (\(1 \le k \le n - 1\)) — количество используемых вами цветов;
- во второй строке выведите \(n-1\) целых чисел \(c_2, c_3, \dots, c_n\) (\(1 \le c_i \le k\)), где \(c_i\) — цвет ребра, соединяющего вершины \(p_i\) и \(i\).
Затем начинается игра. В начале каждого хода программа жюри выводит что-то одно из следующего: - целое число \(1\) на отдельной строке, указывающее, что фишка достигла корня, и вы выиграли;
- целое число \(-1\) на отдельной строке, указывающее, что вы не достигли корня за \(d\) ходов и проиграли, или вы сделали что-то неправильно (либо раскраска, которую вы предоставили, не соответствует ограничениям, либо ваш предыдущий ход невозможен);
- или целое число \(0\) на отдельной строке, за которым следует строка, содержащая \(k\) целых чисел \(e_1, e_2, \dots, e_k\), где \(e_i\) — количество ребер с цветом \(i\), инцидентных текущей вершине.
Если вы получаете \(1\) или \(-1\), ваша программа должна немедленно завершиться, в противном случае вердикт для вашей посылки может быть неопределенным. Если вы получаете \(0\), за которым следуют \(k\) целых чисел \(e_1, e_2, \dots, e_k\), вы должны вывести одно целое число, указывающее цвет, который вы выбираете во время хода (конечно, \(e_i\) для этого цвета не должно быть равно \(0\)). Не забывайте сбрасывать буфер вывода каждый раз, когда что-то выводите! Примечание В первом примере каждая вершина от \(2\) до \(n\) соединена с корнем. Поэтому мы можем покрасить все ребра в один цвет \(1\), и когда игра начнется, будет только одно ребро, инцидентное текущей вершине (и оно будет вести к корню). Во втором примере дерево представляет собой путь из \(4\) вершин. Мы должны покрасить его ребра в разные цвета, потому что можно показать, что у нас нет выигрышной стратегии с двумя цветами. | |
![]()
|
|
F. Минимальное максимальное расстояние
графы
Деревья
дп
кратчайшие пути
поиск в глубину и подобное
*1700
У вас есть дерево из \(n\) вершин, некоторые вершины которого помечены. Дерево — это связный неориентированный граф без циклов. Обозначим за \(f_i\) максимальное расстояние от вершины с номером \(i\) до какой-то из помеченных вершин. Ваша задача — найти минимальное значение \(f_i\) среди всех вершин.  Например, в дереве из примера раскрашены вершины с номерами \(2\), \(6\) и \(7\). Тогда массив \(f(i) = [2, 3, 2, 4, 4, 3, 3]\). \(f_i\) минимальна для вершин с номерами \(1\) и \(3\). Выходные данные Для каждого набора входных данных выведите одно целое число — минимальное значение \(f_i\) по всем вершинам. | |
![]()
|
|
D. XOR на дереве
битмаски
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
*1900
Дано дерево с \(n\) вершинами, пронумерованными от \(1\) до \(n\). В вершине \(i\) записано целое число \(a_{i}\) для каждого \(i = 1, 2, \ldots, n\). Ваша цель — сделать все \(a_{i}\) одинаковыми, выполнив несколько заклинаний (возможно, ни одного). Предположим, что корнем дерева выбрана некоторая вершина. Чтобы выполнить заклинание, можно выбрать произвольную вершину \(v\) и произвольное неотрицательное целое число \(c\). Затем для каждой вершины \(i\) в поддереве\(^{\dagger}\) \(v\) нужно заменить \(a_{i}\) на \(a_{i} \oplus c\). Стоимость такого заклинания равна \(s \cdot c\), где \(s\) — число вершин в поддереве. Здесь \(\oplus\) обозначает операцию побитового исключающего ИЛИ. Пусть \(m_r\) — минимально возможная суммарная стоимость, за которую можно сделать все \(a_i\) равными, в случае если вершина \(r\) выбрана корнем дерева. Найдите \(m_{1}, m_{2}, \ldots, m_{n}\). \(^{\dagger}\) Пусть вершина \(r\) выбрана корнем дерева. Тогда вершина \(i\) принадлежит поддереву \(v\), если простой путь от \(i\) до \(r\) содержит \(v\). Выходные данные Для каждого набора входных данных выведите \(m_1, m_2, \ldots, m_n\) на отдельной строке. Примечание В первом наборе входных данных, чтобы найти \(m_1\), подвесим дерево за вершину \(1\). - На первом заклинании выберем \(v=2\) и \(c=1\). После выполнения этого заклинания \(a\) станет равным \([3, 3, 0, 1]\). Стоимость этого заклинания равна \(3\).
- На втором заклинании выберем \(v=3\) и \(c=3\). После выполнения этого заклинания \(a\) станет равным \([3, 3, 3, 1]\). Стоимость этого заклинания равна \(3\).
- На третьем заклинании выберем \(v=4\) и \(c=2\). После выполнения этого заклинания \(a\) станет равным \([3, 3, 3, 3]\). Стоимость этого заклинания равна \(2\).
Теперь все значения в массиве \(a\) одинаковы, а суммарная стоимость равна \(3 + 3 + 2 = 8\). Значения \(m_2\), \(m_3\), \(m_4\) находятся аналогично. Во втором наборе входных данных цель уже достигнута, поскольку в дереве всего одна вершина. | |
![]()
|
|
D. Разрез
Бинарный поиск
Деревья
математика
разделяй и властвуй
снм
Структуры данных
*2700
Назовём массив \(b_1, b_2, \ldots, b_m\) (\(m \ge 2\)) хорошим, если его можно разрезать на две части так, чтобы все элементы в левой части были строго меньше, чем все элементы в правой части. Другими словами, должен существовать такой индекс \(1 \le i < m\), что любой элемент из \(b_1, \ldots, b_i\) строго меньше любого элемента из \(b_{i+1}, \ldots, b_m\). Дан массив \(a_1, a_2, \ldots a_n\), состоящий из различных целых чисел от \(1\) до \(n\). Поступают \(q\) запросов. В каждом запросе даны два числа \(l\) и \(r\). Требуется для каждого запроса проверить, является ли массив \(a_l, a_{l+1}, \ldots, a_r\) хорошим. Выходные данные Для каждого запроса выведите «Yes» (без кавычек), если массив \(a_l, a_{l+1}, \ldots, a_r\) является хорошим, и «No» (без кавычек) иначе. Вы можете выводить «Yes» и «No» в любом регистре (например, строки «yEs», «yes», «Yes» и «YES» будут распознаны как положительный ответ). Примечание В первом примере: - Массив \([3,2,1,4,5]\) можно разрезать на две части \([3,2,1]\) и \([4,5]\).
- Массив \([3,2,1]\) нельзя разрезать на две части так, чтобы все элементы в левой части были меньше всех элементов в правой части.
- Массив \([3,2,1,4]\) можно разрезать на две части \([3,2,1]\) и \([4]\).
- Массив \([3,2]\) нельзя разрезать на две части так, чтобы все элементы в левой части были меньше всех элементов в правой части.
- Массив \([2,1,4,5]\) можно разрезать на две части \([2,1]\) и \([4,5]\).
Во втором примере: - Массив \([2,4,3]\) можно разрезать на две части \([2]\) и \([4,3]\).
- Массив \([6,2,4,3,5]\) нельзя разрезать на две части так, чтобы все элементы в левой части были меньше всех элементов в правой части.
- Массив \([4,3,5]\) можно разрезать на две части \([4,3]\) и \([5]\).
| |
![]()
|
|
D. Игра со стеками
графы
Деревья
Перебор
поиск в глубину и подобное
реализация
*3000
У вас есть \(n\) стеков \(r_1,r_2,\ldots,r_n\). Каждый стек содержит некоторое количество целых положительных чисел в диапазоне от \(1\) до \(n\). Определим следующие функции: function init(pos):
stacks := массив, содержащий n стеков r[1], r[2], ..., r[n].
return get(stacks, pos)
function get(stacks, pos):
if stacks[pos] пуст:
return pos
else:
new_pos := верхний элемент stacks[pos]
удалить верхний элемент stacks[pos]
return get(stacks, new_pos)
Вы хотите узнать значения, возвращаемые \(\texttt{init(1)}, \texttt{init(2)}, \ldots, \texttt{init(n)}\). Заметим, что во время этих вызовов стеки \(r_1,r_2,\ldots,r_n\) не изменяются, поэтому вызовы \(\texttt{init(1)}, \texttt{init(2)}, \ldots, \texttt{init(n)}\) являются независимыми. Выходные данные Необходимо вывести \(n\) значений, \(i\)-м из которых является значение, возвращаемое \(\texttt{init(i)}\). Примечание В первом примере: - При вызове \(\texttt{init(1)}\) присваивается \(\texttt{stacks := [[1,2,2],[3,1,2],[1,2,1]]}\), а затем вызывается \(\texttt{get(stacks, 1)}\).
- \(\texttt{stacks[1]}\) не пуст, присваивается \(\texttt{new_pos := 2}\) и удаляется верхний элемент \(\texttt{stacks[1]}\), в результате чего \(\texttt{stacks}\) станет \([[1,2],[3,1,2],[1,2,1]]\), а затем вызывается \(\texttt{get(stacks, 2)}\).
- \(\texttt{stacks[2]}\) не пуст, присваивается \(\texttt{new_pos := 2}\) и удаляется верхний элемент \(\texttt{stacks[2]}\), в результате чего \(\texttt{stacks}\) станет \([[1,2],[3,1],[1,2,1]]\), а затем вызывается \(\texttt{get(stacks, 2)}\).
- \(\texttt{stacks[2]}\) не пуст, присваивается \(\texttt{new_pos := 1}\) и удаляется верхний элемент \(\texttt{stacks[2]}\), в результате чего \(\texttt{stacks}\) станет \([[1,2],[3],[1,2,1]]\), а затем вызывается \(\texttt{get(stacks, 1)}\).
- \(\texttt{stacks[1]}\) не пуст, присваивается \(\texttt{new_pos := 2}\) и удаляется верхний элемент \(\texttt{stacks[1]}\), в результате чего \(\texttt{stacks}\) станет \([[1],[3],[1,2,1]]\), а затем вызывается \(\texttt{get(stacks, 2)}\).
- \(\texttt{stacks[2]}\) не пуст, присваивается \(\texttt{new_pos := 3}\) и удаляется верхний элемент \(\texttt{stacks[2]}\), в результате чего \(\texttt{stacks}\) станет \([[1],[],[1,2,1]]\), а затем вызывается \(\texttt{get(stacks, 3)}\).
- \(\texttt{stacks[3]}\) не пуст, присваивается \(\texttt{new_pos := 1}\) и удаляется верхний элемент \(\texttt{stacks[3]}\), в результате чего \(\texttt{stacks}\) станет \([[1],[],[1,2]]\), а затем вызывается \(\texttt{get(stacks, 1)}\).
- \(\texttt{stacks[1]}\) не пуст, присваивается \(\texttt{new_pos := 1}\) и удаляется верхний элемент \(\texttt{stacks[1]}\), в результате чего \(\texttt{stacks}\) станет \([[],[],[1,2]]\), а затем вызывается \(\texttt{get(stacks, 1)}\).
- \(\texttt{stacks[1]}\) пуст, возвращается \(1\).
- При вызове \(\texttt{init(2)}\) присваивается \(\texttt{stacks := [[1,2,2],[3,1,2],[1,2,1]]}\), а затем вызывается \(\texttt{get(stacks, 2)}\).
- \(\texttt{stacks[2]}\) не пуст, присваивается \(\texttt{new_pos := 2}\) и удаляется верхний элемент \(\texttt{stacks[2]}\), в результате чего \(\texttt{stacks}\) станет \([[1,2,2],[3,1],[1,2,1]]\), а затем вызывается \(\texttt{get(stacks, 2)}\).
- \(\texttt{stacks[2]}\) не пуст, присваивается \(\texttt{new_pos := 1}\) и удаляется верхний элемент \(\texttt{stacks[2]}\), в результате чего \(\texttt{stacks}\) станет \([[1,2,2],[3],[1,2,1]]\), а затем вызывается \(\texttt{get(stacks, 1)}\).
- \(\texttt{stacks[1]}\) не пуст, присваивается \(\texttt{new_pos := 2}\) и удаляется верхний элемент \(\texttt{stacks[1]}\), в результате чего \(\texttt{stacks}\) станет \([[1,2],[3],[1,2,1]]\), а затем вызывается \(\texttt{get(stacks, 2)}\).
- \(\texttt{stacks[2]}\) не пуст, присваивается \(\texttt{new_pos := 3}\) и удаляется верхний элемент \(\texttt{stacks[2]}\), в результате чего \(\texttt{stacks}\) станет \([[1,2],[],[1,2,1]]\), а затем вызывается \(\texttt{get(stacks, 3)}\).
- \(\texttt{stacks[3]}\) не пуст, присваивается \(\texttt{new_pos := 1}\) и удаляется верхний элемент \(\texttt{stacks[3]}\), в результате чего \(\texttt{stacks}\) станет \([[1,2],[],[1,2]]\), а затем вызывается \(\texttt{get(stacks, 1)}\).
- \(\texttt{stacks[1]}\) не пуст, присваивается \(\texttt{new_pos := 2}\) и удаляется верхний элемент \(\texttt{stacks[1]}\), в результате чего \(\texttt{stacks}\) станет \([[1],[],[1,2]]\), а затем вызывается \(\texttt{get(stacks, 2)}\).
- \(\texttt{stacks[2]}\) пуст, возвращается \(2\).
- При вызове \(\texttt{init(3)}\) присваивается \(\texttt{stacks := [[1,2,2],[3,1,2],[1,2,1]]}\), а затем вызывается \(\texttt{get(stacks, 3)}\).
- \(\texttt{stacks[3]}\) не пуст, присваивается \(\texttt{new_pos := 1}\) и удаляется верхний элемент \(\texttt{stacks[3]}\), в результате чего \(\texttt{stacks}\) станет \([[1,2,2],[3,1,2],[1,2]]\), а затем вызывается \(\texttt{get(stacks, 1)}\).
- \(\texttt{stacks[1]}\) не пуст, присваивается \(\texttt{new_pos := 2}\) и удаляется верхний элемент \(\texttt{stacks[1]}\), в результате чего \(\texttt{stacks}\) станет \([[1,2],[3,1,2],[1,2]]\), а затем вызывается \(\texttt{get(stacks, 2)}\).
- \(\texttt{stacks[2]}\) не пуст, присваивается \(\texttt{new_pos := 2}\) и удаляется верхний элемент \(\texttt{stacks[2]}\), в результате чего \(\texttt{stacks}\) станет \([[1,2],[3,1],[1,2]]\), а затем вызывается \(\texttt{get(stacks, 2)}\).
- \(\texttt{stacks[2]}\) не пуст, присваивается \(\texttt{new_pos := 1}\) и удаляется верхний элемент \(\texttt{stacks[2]}\), в результате чего \(\texttt{stacks}\) станет \([[1,2],[3],[1,2]]\), а затем вызывается \(\texttt{get(stacks, 1)}\).
- \(\texttt{stacks[1]}\) не пуст, присваивается \(\texttt{new_pos := 2}\) и удаляется верхний элемент \(\texttt{stacks[1]}\), в результате чего \(\texttt{stacks}\) станет \([[1],[3],[1,2]]\), а затем вызывается \(\texttt{get(stacks, 2)}\).
- \(\texttt{stacks[2]}\) не пуст, присваивается \(\texttt{new_pos := 3}\) и удаляется верхний элемент \(\texttt{stacks[2]}\), в результате чего \(\texttt{stacks}\) станет \([[1],[],[1,2]]\), а затем вызывается \(\texttt{get(stacks, 3)}\).
- \(\texttt{stacks[3]}\) не пуст, присваивается \(\texttt{new_pos := 2}\) и удаляется верхний элемент \(\texttt{stacks[3]}\), в результате чего \(\texttt{stacks}\) станет \([[1],[],[1]]\), а затем вызывается \(\texttt{get(stacks, 2)}\).
- \(\texttt{stacks[2]}\) пуст, возвращается \(2\).
| |
![]()
|
|
E. Обменные деревья Дореми
графы
Деревья
поиск в глубину и подобное
*3500
Рассмотрим два неориентированных графа \(G_1\) и \(G_2\). Каждая вершина в \(G_1\) и в \(G_2\) имеет номер. Дореми называет \(G_1\) и \(G_2\) подобными тогда и только тогда, когда: - Все номера в \(G_1\) различны, и все номера в \(G_2\) различны.
- Множество \(S\) номеров в \(G_1\) совпадает с множеством номеров в \(G_2\).
- Для каждой пары двух различных номеров \(u\) и \(v\) в \(S\) соответствующие вершины находятся в одной и той же компоненте связности в \(G_1\) тогда и только тогда, когда они находятся в одной и той же компоненте связности в \(G_2\).
Теперь Дореми дает вам два дерева \(T_1\) и \(T_2\) с \(n\) вершинами, пронумерованными от \(1\) до \(n\). Вы можете выполнить следующую операцию любое количество раз: - Выбрать множество ребер \(E_1\) из \(T_1\) и множество ребер \(E_2\) из \(T_2\), такие, что \(\overline{E_1}\) и \(\overline{E_2}\) подобны. Здесь \(\overline{E}\) представляет собой граф, который задается набором рёбер \(E\) из дерева \(T\) и концами этих рёбер (т.е. подграф, индуцированный ребрами). Иными словами, \(\overline{E}\) получается из \(T\) удалением всех рёбер, не входящих в \(E\), а также последующего удаления всех изолированных вершин.
- Поменяйте местами множество ребер \(E_1\) в \(T_1\) с множеством ребер \(E_2\) в \(T_2\).
Теперь Дореми интересно, сколько различных \(T_1\) можно получить после любого количества операций. Можете ли вы помочь ей найти ответ? Выведите ответ по модулю \(10^9+7\). Выходные данные Для каждого набора входных данных выведите одну строку с целым числом, представляющим собой количество отличий \(T_1\) после любого количества операций по модулю \(10^9+7\). Примечание В первом наборе входных данных существует не более одного множества \(T_1\), имеющего единственное ребро \((1,2)\). Во втором наборе входных данных можно выбрать множество ребер \(\{(1,3),(2,3)\}\) в \(T_1\), множество ребер \(\{(1,2),(2,3)\}\) в \(T_2\) и поменять их местами. Таким образом, \(T_1\) может быть \(1-3-2\) или \(1-2-3\). В третьем наборе входных данных существует \(4\) различных \(T_1\), как показано на следующих рисунках. 
| |
![]()
|
|
F. Усреднённое дерево Дореми
Деревья
дп
жадные алгоритмы
Структуры данных
*3500
У Дореми есть корневое дерево размера \(n\), корнем которого является вершина \(r\). Изначально на вершине \(i\) записано число \(w_i\). Дореми может использовать свою силу, чтобы выполнить данную операцию не более \(k\) раз: - Выберем вершину \(x\) (\(1 \leq x \leq n\)).
- Пусть \(s = \frac{1}{|T|}\sum_{i \in T} w_i\), где \(T\) — множество всех вершин в поддереве \(x\).
- Для всех \(i \in T\) присваиваем \(w_i := s\).
Дореми хочет узнать, каким будет лексикографически минимальный\(^\dagger\) массив \(w\) после выполнения всех операций. Можете ли вы ей помочь? Если ответов несколько, вы можете вывести любой из них. \(^\dagger\) Для массивов \(a\) и \(b\) длины \(n\), \(a\) лексикографически меньше \(b\) тогда и только тогда, когда существует индекс \(i\) (\(1 \leq i \le n\)) такой, что \(a_i < b_i\) и для всех индексов \(j\) таких, что \(j<i\), выполняется условие \(a_j=b_j\). Выходные данные Для каждого набора входных данных в первой строке выведите одно целое число \(cnt\) (\(0 \le cnt \le k\)) — количество выполняемых операций. Затем во второй строке выведите \(cnt\) целых чисел \(p_1,p_2,\ldots,p_{cnt}\) — \(x\) выбирается равным \(p_i\) для \(i\)-й операции. Если ответов несколько, то можно вывести любой из них. Примечание В первом наборе входных данных: 
Изначально \(w=[1,9,2,6,1,8]\). Можно выбрать некоторую вершину \(x\) для выполнения не более одной операции. - Если \(x=1\), то \(w=[\frac{9}{2},\frac{9}{2},\frac{9}{2},\frac{9}{2},\frac{9}{2},\frac{9}{2}]\).
- Если \(x=2\), то \(w=[1,\frac{15}{2},2,\frac{15}{2},1,8]\).
- Если \(x=3\), то \(w=[1,9,\frac{11}{3},6,\frac{11}{3},\frac{11}{3}]\).
- Если \(x \in \{4, 5, 6\}\), то \(w=[1,9,2,6,1,8]\).
- Если вы не выполняете никаких операций, то \(w=[1,9,2,6,1,8]\).
\(w\) является лексикографически наименьшим, если \(x=2\). | |
![]()
|
|
F. Растущее дерево
Деревья
поиск в глубину и подобное
Структуры данных
*2000
Дано корневое дерево с корнем в вершине \(1\), изначально состоящее из одной вершины. У каждой вершины есть числовое значение, изначально равное \(0\). Так же есть \(q\) запросов двух типов: - Первый тип запроса: добавить ребёнка с номером \(sz + 1\) к вершине \(v\), где \(sz\) — текущий размер дерева. Числовое значение новой вершины также равно \(0\).
- Второй тип запроса: Прибавить \(x\) ко всем числовым значений вершин в поддереве вершины \(v\).
После всех запросов нужно для каждой вершины вывести его итоговое числовое значение. Выходные данные После всех запросов выведите числовые значения каждой вершины конечного дерева. Примечание В первом примере итоговое дерево с числовыми значениями будет выглядеть так:  Итоговое дерево с числовыми значениями Итоговое дерево с числовыми значениями | |
![]()
|
|
D. XOR-конструктив
битмаски
Деревья
Конструктив
математика
строковые суфф. структуры
Структуры данных
*1900
Даны \(n-1\) целых чисел \(a_1, a_2, \dots, a_{n-1}\). Ваша задача — построить массив \(b_1, b_2, \dots, b_n\) такой, что: - каждое целое число от \(0\) до \(n-1\) встречается в \(b\) ровно один раз;
- для каждого \(i\) от \(1\) до \(n-1\), \(b_i \oplus b_{i+1} = a_i\) (где \(\oplus\) обозначает побитовое исключающее ИЛИ).
Выходные данные Выведите \(n\) целых чисел \(b_1, b_2, \dots, b_n\). Если существует несколько массивов, подходящих под условие задачи, вы можете вывести любой из них. | |
![]()
|
|
F. Лёшины капризы
графы
Деревья
жадные алгоритмы
Конструктив
кратчайшие пути
*1600
Дерево — связный граф без циклов. Можно показать, что любое дерево из \(n\) вершин имеет ровно \(n - 1\) ребро. Лист — вершина в дереве, из которой выходит ровно одно ребро. Расстояние между двумя вершинами \(u\) и \(v\) в дереве — минимальное количество рёбер, которое нужно пройти, чтобы из вершины \(u\) прийти в вершину \(v\). У Лёши скоро день рождения, и Тимофею хотелось бы подарить ему дерево из \(n\) вершин. Однако Лёша очень капризный мальчик. Каждый день на протяжении \(q\) дней он будет выбирать целое число, обозначим выбранное в \(i\)-й день число \(d_i\). Если в \(i\)-й день в дереве не будет двух листов на расстоянии ровно \(d_i\), то Лёша будет разочарован. Тимофей решил подарить Лёше конструктор, чтобы он сам мог менять своё дерево, как ему хочется. Тимофей знает, что Лёша ещё и ленив (ужас, а не человек), поэтому в начале каждого дня он может выполнить не более одной операции следующего вида: - Выбрать вершины \(u\), \(v_1\) и \(v_2\), такие, что между \(u\) и \(v_1\) есть ребро, а между \(u\) и \(v_2\) нет ребра. После этого удалить ребро между \(u\) и \(v_1\) и добавить ребро между \(u\) и \(v_2\). Эту операцию нельзя выполнить, если после неё граф перестанет быть деревом.
Чудесным образом Тимофею удалось узнать все \(d_i\). После этого его посетила ещё одна гениальная мысль — на всякий случай сделать инструкцию к набору, при этом такую, чтобы Лёша не был разочарован. Тимофей не такой ленивый, как Лёша, но когда он увидел число \(n\), у него резко пропало желание разрабатывать инструкцию и придумывать изначальное дерево, поэтому он поручил эту задачу вам. Можно показать, что дерево и последовательность операций, удовлетворяющие описанным условиям, всегда существуют. 
Вот пример операции, где были выбраны вершины: \(u\) — \(6\), \(v_1\) — \(1\), \(v_2\) — \(4\). Выходные данные Для каждого набора входных данных сначала выведите \(n - 1\) строку с описанием рёбер дерева. Если вы хотите, чтобы в дереве было ребро между вершинами \(u\) и \(v\), то среди этих \(n - 1\) строк должна быть строка \(v\) \(u\) или \(u\) \(v\). В следующих \(q\) строках выведите по три целых числа \(u\) \(v_1\) \(v_2\) — описание операций. Если Лёше не нужно выполнять операцию, выведите \(-1\) \(-1\) \(-1\). | |
![]()
|
|
G. Необычное развлечение
Деревья
кратчайшие пути
поиск в глубину и подобное
снм
сортировки
Структуры данных
*1900
Дерево — связный граф без циклов. Перестановка — массив, состоящий из \(n\) различных целых чисел от \(1\) до \(n\) в произвольном порядке. Например, \([5, 1, 3, 2, 4]\) является перестановкой, но \([2, 1, 1]\) не является перестановкой (\(1\) встречается в массиве дважды) и \([1, 3, 2, 5]\) тоже не является перестановкой (\(n = 4\), но в массиве присутствует \(5\)). После неудачной съёмки в ролике BrMeast у Лёши началась депрессия. Даже день рождения не радовал его. Однако после подарка Тимофея настроение Лёши резко поднялось. Теперь он днями напролёт игрался с подаренным конструктором. Недавно он придумал себе необычное развлечение. Лёша строит из своего конструктора дерево, состоящее из \(n\) вершин, пронумерованных от \(1\) до \(n\), с корнем в вершине \(1\). Затем он в произвольном порядке выписывает каждое число от \(1\) до \(n\) ровно по одному разу и получает перестановку \(p\). После этого Лёша придумывает \(q\) троек чисел \(l, r, x\). Для каждой тройки он пытается понять, есть ли среди вершин с номерами \(p_l, p_{l+1}, \ldots, p_r\) хотя бы один потомок вершины \(x\). Вершина \(u\) является потомком вершины \(v\) тогда и только тогда, когда \(\mathrm{dist}(1, v) + \mathrm{dist}(v, u) = \mathrm{dist}(1, u)\), где \(\mathrm{dist}(a, b)\) — расстояние между вершинами \(a\) и \(b\). Иначе говоря, вершина \(v\) должна находиться на пути от корня до вершины \(u\). Лёша рассказал об этом развлечении Захару. Теперь Лёша говорит своему другу \(q\) троек, описанных выше, надеясь, что Захар сможет проверить наличие потомка. Захар очень сильно хочет спать, поэтому обратился за помощью к вам. Помогите Захару ответить на все вопросы Лёши и наконец-то пойти спать. Выходные данные Для каждого вопроса Лёши выведите «Yes» (без кавычек), если описанный в условии потомок существует, иначе выведите «No» (без кавычек). Вы можете выводить ответ в любом регистре (например, строки «yEs», «yes», «Yes» и «YES» будут распознаны как положительный ответ). | |
![]()
|
|
C. Аньи и двоичное дерево
Деревья
дп
поиск в глубину и подобное
*1300
Аньи продолжает игнорировать сообщения Кексика. Через общего друга Кексик выяснил, что Аньи очень любит бинарные деревья, и захотел решить ее задачу, чтобы привлечь ее внимание. Аньи задала Кексику двоичное дерево с \(n\) вершинами. Вершина \(1\) является корнем и не имеет родителя. Все остальные вершины имеют ровно одного родителя. Каждая вершина может иметь до \(2\) детей — левого и правого. Для каждой вершины Аньи сообщает Кексику индекс ее левого и правого ребенка или говорит, что их не существует. Кроме того, на каждой из вершин написана буква \(s_i\), которая является либо «U», либо «L», либо «R». Кексик начинает свой путь с корня и на каждом ходу делает следующее: - Если он находится в вершине, на которой написана буква «U», то он переходит к ее родителю. Если он не существует, то Кексик ничего не делает.
- Если он находится в вершине, на которой написана буква «L», то он переходит к ее левому ребенку. Если его не существует, то он ничего не делает.
- Если он находится в вершине, на которой написана буква «R», то он переходит к ее правому ребенку. Если его не существует, то он ничего не делает.
Перед тем, как отправиться в путь, он может выполнять следующие операции: выбрать любую вершину и заменить написанную на ней букву на другую. Вас интересует минимальное количество операций, которые он должен выполнить перед путешествием, чтобы, начав путешествие, он в какой-то момент оказался в листе. Лист — это вершина, у которой нет детей. Не имеет значения, какого листа он достигнет. Заметим, что не имеет значения, останется ли он в листе — ему нужно только переместиться в лист. Кроме того, неважно, сколько раз он должен переместиться, прежде чем достигнет листа. Помогите Кексику решить задачу Аньи, чтобы он смог завоевать ее сердце, и Анья приехала в Чачак. Выходные данные Для каждого набора входных данных выведите одно целое число — минимальное количество операций, которое необходимо выполнить Кексику, чтобы он смог достичь листа. Примечание В первом наборе входных данных вершина \(1\) имеет левого ребенка \(2\) и правого — \(3\). Вершины \(2\) и \(3\) не имеют детей и поэтому являются листьями. Поскольку в вершине \(1\) написана буква «L», то Кексик перейдет в вершину \(2\), поэтому ему не нужно выполнять никаких операций. Во втором наборе входных данных вершина \(1\) имеет левого ребенка \(3\) и правого — \(2\). Вершины \(2\) и \(3\) являются листьями. Поскольку в вершине \(1\) написана буква «U», то для того, чтобы добраться до листа, Кексику необходимо изменить эту букву на «L» или «R». В третьем наборе вершина \(1\) имеет только правого ребенка, которым является вершина \(2\). Поскольку на корневой вершине написана буква «L», Кексик должен изменить букву на «R», иначе он застрянет в вершине \(1\). В четвертом наборе он может изменить \(3\) буквы так, чтобы буквы на вершинах были «LURL», что позволит ему достичь вершины \(2\). В пятом наборе имеется \(3\) листа: \(3\), \(6\) и \(7\). Чтобы добраться до листа \(6\) или листа \(7\), ему нужно поменять \(2\) буквы. Однако, если он поменяет букву на вершине \(1\) на «R», то достигнет листа \(3\), поэтому ответ — \(1\).  Изначальное дерево в пятом наборе входных данных. Изначальное дерево в пятом наборе входных данных. | |
![]()
|
|
E. Сжатие дерева
графы
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
сортировки
*2200
Вам дано дерево, состоящее из \(n\) вершин. На каждой вершине записано число; число на вершине \(i\) равно \(a_i\). Вы можете выполнить следующую операцию любое количество раз (возможно, ноль): - выбрать вершину, имеющую не более \(1\) инцидентного ребра, и удалить ее из дерева.
Обратите внимание, что вы можете удалить все вершины. После выполнения всех операций происходит сжатие дерева. Процесс сжатия выполняется следующим образом. Пока в дереве есть вершина, имеющая ровно \(2\) инцидентных ребра, выполняется следующую операцию: - удалить эту вершину, а ее соседей соединить ребром.
Можно показать, что если существует несколько способов выбрать вершину для удаления в процессе сжатия, итоговое дерево остается тем же самым. Ваша задача — вычислить максимально возможную сумму чисел, записанных на вершинах, после применения вышеописанной операции любое количество раз, а затем сжатия дерева. Выходные данные Для каждого набора входных данных, выведите одно целое число — максимально возможную сумму чисел, записанных на вершинах, после применения вышеописанной операции любое количество раз, а затем сжатия дерева. | |
![]()
|
|
E. Коллапс строк
Деревья
Строки
Структуры данных
*1900
Заданы \(n\) строк \(s_1, s_2, \dots, s_n\), состоящие из строчных латинских букв. Пусть \(|x|\) означает длину строки \(x\). Определим операцию коллапса \(C(a, b)\) двух строк \(a\) и \(b\) следующим образом: - если \(a\) пуста, \(C(a, b) = b\);
- если \(b\) пуста, \(C(a, b) = a\);
- если последняя буква \(a\) совпадает с первой буквой \(b\), то \(C(a, b) = C(a_{1,|a|-1}, b_{2,|b|})\), где \(s_{l,r}\) — подстрока \(s\) с \(l\)-й по \(r\)-ю букву;
- в противном случае, \(C(a, b) = a + b\), то есть, конкатенация двух строк.
Вычислите \(\sum\limits_{i=1}^n \sum\limits_{j=1}^n |C(s_i, s_j)|\). Выходные данные Выведите одно целое число — \(\sum\limits_{i=1}^n \sum\limits_{j=1}^n |C(s_i, s_j)|\). | |
![]()
|
|
F. Снова деревья и XOR-запросы
графы
Деревья
математика
поиск в глубину и подобное
разделяй и властвуй
реализация
Структуры данных
*2400
Вам дано дерево, состоящее из \(n\) вершин. На каждой вершине написано целое число; на \(i\)-й вершине написано число \(a_i\). Вам необходимо обработать \(q\) запросов. \(i\)-й запрос состоит из трех целых чисел \(x_i\), \(y_i\) и \(k_i\). Для этого запроса вы должны ответить, возможно ли выбрать набор вершин \(v_1, v_2, \dots, v_m\) (возможно, пустой) так, чтобы: - каждая вершина \(v_j\) находилась на простом пути между \(x_i\) и \(y_i\) (в том числе можно использовать концы пути);
- \(a_{v_1} \oplus a_{v_2} \oplus \dots \oplus a_{v_m} = k_i\), где \(\oplus\) обозначает оператор побитового исключающего ИЛИ.
Выходные данные Для каждого запроса выведите YES, если возможно сформировать набор вершин, удовлетворяющий ограничениям. В противном случае выведите NO. Каждую букву можно выводить в любом регистре. | |
![]()
|
|
F. Няня
2-sat
Бинарный поиск
графы
Деревья
Структуры данных
*2500
Теофанис хочет играть в видеоигры, но при этом он должен заботиться о своей сестре. Поскольку Теофанис учится на программиста, он нашел способ делать и то, и другое. Он установит в своем доме несколько камер, чтобы убедиться, что с его сестрой все в порядке. Его дом — это неориентированный граф с \(n\) вершинами и \(m\) ребрами. Его сестра любит играть на ребрах графа, поэтому он должен установить камеру хотя бы в одном из концов каждого ребра графа. Теофанис хочет найти вершинное покрытие, которое максимизирует минимальную разницу между номерами выбранных вершин. Более формально, пусть \(a_1, a_2, \ldots, a_k\) — вершинное покрытие графа. Пусть минимальная разница между номерами выбранных вершин — это минимальное \(\lvert a_i - a_j \rvert\) (где \(i \neq j\)) среди вершин, которые вы выбрали. Если \(k = 1\), то считаем, что минимальная разница между номерами выбранных вершин равна \(n\). Можете ли вы найти максимально возможную минимальную разницу между номерами выбранных вершин? Выходные данные Для каждого набора входных данных выведите максимум среди минимальных разностей между выбранными вершинами среди всех вершинных покрытий. Примечание В первом наборе входных данных мы можем установить камеры в вершинах \(1\), \(3\) и \(7\), поэтому ответ — \(2\).  Во втором наборе входных данных мы можем установить только одну камеру в вершине \(1\), поэтому ответ равен \(3\). | |
![]()
|
|
E. Запросы на дереве
графы
Деревья
поиск в глубину и подобное
реализация
Структуры данных
*2500
Кто не работает, тот не ест. Получи то, что ты хочешь своими силами. Поверь, искренние и серьёзные люди всегда смеются последними. Но я всё равно не дам тебе подарка. —Санта, Hayate no Gotoku! Поскольку Хаяте не получил никаких рождественских подарков от Санты, его вместо этого ожидает решение задачи на запросы на дереве. У Хаяте есть дерево с \(n\) вершинами. Теперь Хаяте хочет, чтобы вы ответили на \(q\) запросов. Каждый запрос состоит из вершины \(x\) и \(k\) других дополнительных вершин \(a_1,a_2,\ldots,a_k\). Эти \(k+1\) вершина гарантированно различны. Для каждого запроса необходимо найти длину самого длинного простого пути, начинающегося в вершине \(x^\dagger\) после удаления вершин \(a_1,a_2,\ldots,a_k\) вместе со всеми ребрами, соединенными хотя бы с одной из вершин \(a_1,a_2,\ldots,a_k\). \(^\dagger\) Простой путь длины \(k\), начинающийся в вершине \(x\) — это последовательность различных вершин \(x=u_0,u_1,\ldots,u_k\) таких, что существует ребро между вершинами \(u_{i-1}\) и \(u_i\) для всех \(1 \leq i \leq k\). Выходные данные Для каждого запроса выведите одно целое число, являющееся ответом на этот запрос. Примечание В первом примере дерево выглядит следующим образом:  В первом запросе ни одна вершина не пропущена. Самый длинный простой путь, начинающийся в вершине \(2\), это \(2 \to 1 \to 3 \to 4\). Таким образом, ответ — \(3\). Во третьем запросе отсутствуют вершины \(1\) и \(6\), и дерево показано ниже. Самый длинный простой путь из вершины \(2\) — это \(2 \to 5\). Таким образом, ответ — \(1\).  | |
![]()
|
|
F. Прекрасное дерево
графы
Деревья
поиск в глубину и подобное
реализация
Структуры данных
*2800
У Ланчбокса есть дерево размера \(n\) с корнем в вершине \(1\). Каждой вершине присваивается значение. Ланчбокс считает дерево прекрасным, если каждое значение является уникальным и находится в диапазоне от \(1\) до \(n\). Кроме того, прекрасное дерево должно удовлетворять \(m\) требованиям \(2\) типов: - «1 a b c» — Вершина с наименьшим значением на пути между вершинами \(a\) и \(b\) должна быть \(c\).
- «2 a b c» — Вершина с наибольшим значением на пути между вершинами \(a\) и \(b\) должна быть \(c\).
Теперь вы должны присвоить значения каждой вершине так, чтобы получившееся дерево было прекрасным. Если это невозможно, выведите \(-1\). Выходные данные Если невозможно присвоить значения так, чтобы дерево было прекрасным, выведите \(-1\). В противном случае выведите \(n\) целых чисел, \(i\)-е из которых обозначает значение вершины \(i\). | |
![]()
|
|
B. Зельда для новичков
Деревья
жадные алгоритмы
*1100
Вам дано дерево\(^{\dagger}\). За одну зельда-операцию вы можете сделать следующее: - Выбрать две вершины дерева \(u\) и \(v\);
- Сжать все вершины на пути от \(u\) до \(v\) в одну вершину. Другими словами, все вершины на пути от \(u\) до \(v\) будут удалены из дерева, будет создана новая вершина \(w\). Затем каждая вершина \(s\), которая имела ребро с какой-то вершиной на пути от \(u\) до \(v\), будет иметь ребро с вершиной \(w\).
 Иллюстрация результата зельда-операции для вершин \(1\) и \(5\). Иллюстрация результата зельда-операции для вершин \(1\) и \(5\). Определите минимальное количество зельда-операций, необходимых для того, чтобы в дереве осталась только одна вершина. \(^{\dagger}\)Дерево — это неориентированный связный граф без циклов. Выходные данные Для каждого набора входных данных выведите единственное целое число — минимальное количество зельда-операций, необходимых для того, чтобы в дереве осталась только одна вершина. Примечание В первом наборе входных данных достаточно выполнить одну зельда-операцию для вершин \(2\) и \(4\). Во втором наборе входных данных мы можем выполнить следующие зельда-операции: - \(u = 2, v = 1\). Пусть добавленная вершина будет обозначена как \(w = 10\);
- \(u = 4, v = 9\). Пусть добавленная вершина будет обозначена как \(w = 11\);
- \(u = 8, v = 10\). После этой операции дерево состоит из одной вершины.
| |
![]()
|
|
E. One-X
Деревья
дп
Комбинаторика
математика
поиск в глубину и подобное
*2400
В этом грустном мире, полном недостатков, существуют уродливые деревья отрезков. Дерево отрезков — это дерево, где каждая вершина соответствует некоторому отрезку и имеет свой номер. Дерево отрезков для массива из \(n\) элементов можно построить рекурсивно. Пусть функция \(\operatorname{build}(v,l,r)\) строит дерево отрезков, корневая вершина которого имеет номер \(v\) и соответствует отрезку \([l,r]\). Теперь давайте определим \(\operatorname{build}(v,l,r)\): - Если \(l=r\), то вершина \(v\) является листом, поэтому мы прекращаем добавление новых рёбер;
- Иначе, мы добавляем рёбра \((v, 2v)\) и \((v, 2v+1)\). Пусть \(m=\lfloor \frac{l+r}{2} \rfloor\). Затем мы вызываем \(\operatorname{build}(2v,l,m)\) и \(\operatorname{build}(2v+1,m+1,r)\).
Таким образом, всё дерево строится путём вызова \(\operatorname{build}(1,1,n)\). Теперь Ибти построит дерево отрезков для массива из \(n\) элементов. Он хочет найти сумму всех \(\operatorname{lca}^\dagger(S)\), где \(S\) — непустое подмножество листьев. Обратите внимание, что существует ровно \(2^n - 1\) возможных подмножеств. Поскольку эта сумма может быть очень большой, выведите её по модулю \(998\,244\,353\). \(^\dagger\operatorname{lca}(S)\) — номер наименьшего общего предка для вершин, находящихся в \(S\). Выходные данные Для каждого набора входных данных выведите одно целое число — требуемую сумму по модулю \(998\,244\,353\). Примечание  В первом наборе входных данных: Давайте рассмотрим все подмножества листьев. - \(\operatorname{lca}(\{2\})=2\);
- \(\operatorname{lca}(\{3\})=3\);
- \(\operatorname{lca}(\{2,3\})=1\).
Таким образом, ответ равен \(2+3+1=6\). Во втором наборе входных данных: Давайте рассмотрим все подмножества листьев. - \(\operatorname{lca}(\{4\})=4\);
- \(\operatorname{lca}(\{5\})=5\);
- \(\operatorname{lca}(\{3\})=3\);
- \(\operatorname{lca}(\{4,5\})=2\);
- \(\operatorname{lca}(\{4,3\})=1\);
- \(\operatorname{lca}(\{5,3\})=1\);
- \(\operatorname{lca}(\{4,5,3\})=1\);
Таким образом, ответ равен \(4+5+3+2+1+1+1=17\). | |
![]()
|
|
C. Дураки и дороги
Деревья
поиск в глубину и подобное
Структуры данных
*1900
Как известно, в Берляндии ровно две проблемы — дураки и дороги. Кроме того, в Берляндии есть n городов, в которых эти дураки живут, а дороги, соответственно, эти города соединяют. Все берляндские дороги двунаправленные. Так как в Берляндии дураков много, то для каждой пары городов есть путь между ними (иначе дураки расстроятся), а также между каждой парой городов есть не более одного простого пути (иначе дураки заблудятся). Но это еще не все особенности Берляндии. В этой стране дураки иногда ходят друг к другу в гости, и от этого дороги портятся. Дураки не очень умны, поэтому всегда ходят только по простым путям. Простой путь — это путь, который проходит через каждый город Берляндии не более одного раза. Правительству Берляндии известны пути, по которым ходят дураки. Помогите правительству для каждой дороги посчитать, сколько различных дураков может по ней проходить. Обратите внимание на то, как заданы пути дураков во входных данных. Выходные данные Выведите n - 1 целое число. Числа должны быть разделены пробелами. i-e число должно быть равно количеству дураков, которые могут проходить по i-той дороге. Дороги нумеруются с единицы в порядке их следования во входных данных. Примечание В первом примере дурак номер 1 пройдет через первую и третью дорогу, а дурак номер 3 — через вторую, первую и четвертую. Во втором примере через первую дорогу пройдут дураки под номерами 1, 3 и 5, через вторую — дурак номер 5, через третью — дурак номер 3, через четвертую — дурак номер 1. | |
![]()
|
|
E. Разгон митингов
Бинарный поиск
Деревья
Структуры данных
*2200
В Берляндии неспокойные времена. Берляндская оппозиция, финансируемая из соседнего государства, организовала митинги в столице Берляндии городе Берляндске. Благодаря работе разведки известно, что митинги продлятся k дней. К счастью, в Берляндии есть специальный полицейский отряд, который может спасти страну. В нем ровно n солдат, пронумерованных от 1 до n. Берляндский генерал, командующий отрядом, должен составить расписание работы отряда в эти непростые k дней. В каждый из этих дней генерал должен отправить некоторое количество полицейских для разгона беспорядков. Так как отряд большой, а генерал не очень умный, то он может выбрать только набор из всех солдат с номерами от l до r, включительно, где l и r он выбирает произвольно. Сейчас у генерала есть ровно две проблемы. Во-первых, нельзя два раза отправлять один и тот же отряд — тогда солдатам станет скучно и они взбунтуются. Во-вторых, не все солдаты одинаково надежны. У каждого солдата есть некоторая надежность ai. Надежность отряда считается как сумма надежностей солдат в нем. Надежность одного солдата может быть отрицательной, тогда при включении в отряд он будет только помехой. Генерал отличается большой жадностью и столь же большой недальновидностью, поэтому каждый день он отправляет на разгон самый надежный отряд солдат из возможных (то есть из всех отрядов, которые еще не были отправлены). Правительство Берляндии решило узнать, какова будет минимальная надежность отряда, отправляемого на разгон митингов в течение этих k дней. Сам генерал не может справиться со столь сложной задачей. Помогите ему не опозориться перед начальством! Выходные данные Выведите одно число — искомую минимальную надежность отряда в течение этих k дней. | |
![]()
|
|
F. Постройте вокзалы
*особая задача
Деревья
жадные алгоритмы
*2000
Монокарп играет в компьютерную игру, в которой он управляет империей. Империя состоит из \(n\) городов, соединенных \(n - 1\) дорогой. Города пронумерованы от \(1\) до \(n\). Из каждого города можно добраться до любого другого по дорогам. Поездка по одной дороге занимает \(2\) часа. Однако, это можно улучшить. Монокарп может построить вокзалы в не более чем \(k\) городах. После того, как они построены, все существующие дороги, которые соединяют два города с вокзалами, превращаются в железные дороги, поездка по которым занимает \(1\) час. Пусть \(f(x, y)\) будет суммарным временем, которое потребуется, чтобы проехать по дорогам на кратчайшем пути между городами \(x\) и \(y\). Монокарп хочет построить не более \(k\) вокзалов таким образом, чтобы минимизировать следующее значение: \(\sum \limits_{v=1}^{n} \sum \limits_{u=1}^{v-1} f(v, u)\) (суммарное время, необходимое, чтобы добраться из каждого города до каждого другого города). Какое наименьшее значение он может получить? Выходные данные На каждый набор входных данных выведите одно целое число — наименьшее суммарное время, необходимое, чтобы добраться из каждого города до каждого другого города, которое Монокарп может получить, если построит не более \(k\) вокзалов. | |
![]()
|
|
D. Схлопывание массива
Деревья
дп
разделяй и властвуй
Структуры данных
*2100
Вам дан массив \([p_1, p_2, \dots, p_n]\), где все элементы различны. Вы можете выполнить несколько (возможно, ни одной) операций с ним. В одной операции вы можете выбрать непрерывный подотрезок \(p\) и удалить все элементы из этого подотрезка, кроме минимального элемента в этом подотрезке. Например, если \(p = [3, 1, 4, 7, 5, 2, 6]\) и вы выберете подотрезок от \(3\)-го элемента до \(6\)-го элемента, полученный массив будет \([3, 1, 2, 6]\). Массив \(a\) называется достижимым, если его можно получить из \(p\) с помощью нескольких (возможно, нуля) вышеупомянутых операций. Вычислите количество достижимых массивов и выведите его по модулю \(998244353\). Выходные данные Для каждого теста выведите одно целое число — количество достижимых массивов, взятое по модулю \(998244353\). | |
![]()
|
|
F. Соревнование по программированию
Деревья
дп
жадные алгоритмы
Паросочетания
поиск в глубину и подобное
*1900
BerSoft — крупнейшая IT-корпорация в Берляндии. В компании BerSoft работает \(n\) сотрудников, пронумерованных от \(1\) до \(n\). Первый сотрудник является руководителем компании и у него нет начальника. У каждого другого сотрудника \(i\) есть ровно один непосредственный начальник \(p_i\). Сотрудник \(x\) считается начальником (непосредственным или косвенным) сотрудника \(y\), если выполняется одно из следующих условий: - сотрудник \(x\) является непосредственным начальником сотрудника \(y\);
- сотрудник \(x\) является начальником непосредственного начальника сотрудника \(y\).
Структура BerSoft организована таким образом, что руководитель компании является начальником для каждого сотрудника. Скоро будет проведено соревнование по программированию. Для этой цели будут созданы команды из двух человек. Однако, если в команде один сотрудник является начальником другого, им будет некомфортно вместе. Поэтому команды из двух человек должны быть созданы таким образом, что никто не был начальником для другого. Обратите внимание, что никакой сотрудник не может участвовать более чем в одной команде. Ваша задача — посчитать максимально возможное количество команд в соответствии с вышеописанными правилами. Выходные данные Для каждого набора входных данных выведите одно целое число — максимально возможное количество команд в соответствии с вышеописанными правилами. Примечание В первом примере можно создать команду \((3, 4)\). Во втором примере команда не может быть создана, потому что здесь всего \(2\) сотрудника и один является начальником другого. В третьем примере можно создать команду \((2, 3)\). В четвертом примере можно создать команды \((2, 4)\), \((3, 5)\) и \((6, 7)\). В пятом примере можно создать команды \((2, 3)\), \((6, 4)\) и \((5, 7)\). | |
![]()
|
|
G1. Лампочки (простая версия)
графы
Деревья
дп
Комбинаторика
математика
Перебор
поиск в глубину и подобное
снм
*2100
Простая и сложная версии этой задачи отличаются друг от друга только ограничениями на \(n\). В простой версии сумма значений \(n^2\) по всем наборам входных данных не превосходит \(10^6\). Кроме того, \(n\) не превосходит \(1000\) в каждом наборе входных данных. В ряд расположены \(2n\) лампочек. У каждой лампочки есть цвет от \(1\) до \(n\) (ровно по две лампочки каждого цвета). Изначально все лампочки выключены. Вы выбираете некоторое множество лампочек \(S\), которое вы изначально включите. После этого вы можете выполнять следующие операции в любом порядке любое количество раз: - выбрать две лампочки \(i\) и \(j\) одинакового цвета, ровно одна из которых включена, и включить вторую из них;
- выбрать три лампочки \(i, j, k\), такие, что обе лампочки \(i\) и \(k\) включены и имеют одинаковый цвет, а лампочка \(j\) находится между ними (\(i < j < k\)), и включить лампочку \(j\).
Вы хотите выбрать такое множество лампочек \(S\), которые вы изначально включаете, чтобы путем выполнения описанных операций можно было добиться того, чтобы все лампочки оказались включены. Посчитайте два числа: - минимальный размер множества \(S\), которое вы изначально включаете;
- количество множеств \(S\) минимального размера (по модулю \(998244353\)).
Выходные данные Для каждого набора входных данных выведите два целых числа: - минимальный размер множества \(S\), которое вы изначально включаете;
- количество множеств \(S\) минимального размера (по модулю \(998244353\)).
| |
![]()
|
|
E. Весёлая жизнь в университете
Деревья
жадные алгоритмы
поиск в глубину и подобное
Структуры данных
*2300
Егор и его друг Арсений в этом году заканчивают учиться в школе и уже скоро поступят университет. И так как они очень ответственные ребята, они начали готовиться к поступлению уже сейчас. Прежде всего они решили позаботиться о том, где будут жить долгие четыре года обучения, и зайдя на сайт университета, выяснили, что общежитие университета можно представить в виде корневого дерева из \(n\) вершин с корнем в вершине \(1\). В дереве каждая вершина представляет собой рекреацию с некоторым видом активности \(a_i\). Друзьям нужно выбрать \(2\) рекреации (не обязательно различные), в которых они поселятся. Ребята убеждены, что тем будет веселее их жизнь, чем больше значение следующей функции \(f(u, v) = diff(u, lca(u, v)) \cdot diff(v, lca(u, v))\). Помогите Егору и Арсению и найдите максимальное значение \(f(u, v)\) среди всех пар рекреаций! \(^{\dagger} diff(u, v)\) — количество различных активностей, выписанных на простом пути от вершины \(u\) до вершины \(v\). \(^{\dagger} lca(u, v)\) — такая вершина \(p\), что она находится на максимальном расстоянии от корня и является предком и вершины \(u\), и вершины \(v\). Выходные данные Для каждого набора входных данных выведите максимальное значение \(f(u, v)\), по всем парам рекреаций \((u, v)\). Примечание Рассмотрим четвертый набор входных данных. Дерево имеет такой вид:  Все рекреации раскрашены в цвета. Одинаковые цвета означает что активности в рекреациях совпадают. Рассмотрим пару вершин \((11, 12)\), \(lca(11, 12) = 1\). Выпишем все активности на пути от \(11\) до \(1\) — \([11, 5, 1, 11]\), среди них различных активностей \(3\), то есть \(diff(11, 1) = 3\). Также выпишем все активности на пути от \(12\) до \(1\) — \([7, 8, 2, 11]\), среди них различных активностей \(4\), то есть \(diff(12, 1) = 4\). Получаем что \(f(11, 12) = diff(12, 1) \cdot diff(11, 1) = 4 \cdot 3 = 12\), что и является ответом для данного дерева. Можно показать, что ответ лучше получить невозможно. | |
![]()
|
|
G. Оптимизации из ЧелГУ
Деревья
дп
разделяй и властвуй
теория чисел
*3500
Вам дано дерево на \(n\) вершинах, вершины которого пронумерованы числами от \(1\) до \(n\). На каждом ребре записано некоторое целое число \(w_i\). Определим \(len(u, v)\) как количество ребер в простом пути между вершинами \(u\) и \(v\), \(gcd(u, v)\) как Наибольший Общий Делитель всех чисел, записанных на ребрах простого пути между вершинами \(u\) и \(v\). Например, \(len(u, u) = 0\) и \(gcd(u, u) = 0\) для любого \(1 \leq u \leq n\). Вам нужно найти наибольшее значение \(len(u, v) \cdot gcd(u, v)\) по всем парам вершин в дереве. Выходные данные Для каждого набора входных данных выведите единственное число равное наибольшему значению \(len(u, v) \cdot gcd(u, v)\) по всем парам вершин в дереве. | |
![]()
|
|
F. Постройте дерево
битмаски
Деревья
дп
Конструктив
*2500
Вам дан массив целых чисел \(l_1, l_2, \dots, l_n\) и целое число \(d\). Можно ли построить дерево, удовлетворяющее следующим трем условиям? - Дерево содержит \(n + 1\) вершину.
- Длина \(i\)-го ребра равна \(l_i\).
- (Взвешенный) диаметр дерева равен \(d\).
Выходные данные Для каждого набора входных данных выведите \(\texttt{Yes}\), если возможно построить дерево, удовлетворяющее всем условиям, и \(\texttt{No}\) в противном случае. Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Например, строки «yEs», «yes», «Yes» и «YES» будут приняты как положительный ответ. Примечание Ниже приведены иллюстрации деревьев для первого и третьего наборов входных данных. Один из диаметров выделен путем окрашивания его ребер в красный цвет.  | |
![]()
|
|
F. Гусеница на дереве
графы
Деревья
жадные алгоритмы
поиск в глубину и подобное
реализация
сортировки
*2500
Гусеница решила побывать в каждой вершине дерева. Изначально она сидит в корне. Дерево представлено как корневое дерево с корнем в вершине \(1\). Каждое переползание в соседнюю вершину у неё занимает \(1\) минуту. А под деревом стоит батут. Если гусеница отцепится от дерева и упадёт на батут, то за \(0\) секунд окажется в корне дерева. Но батут старый и выдержит не более \(k\) падений гусеницы. За какое минимальное время гусеница сможет обойти дерево? Более формально — надо найти минимальное время, нужное, чтобы посетить все вершины дерева, если гусеница начинает в корне (вершине \(1\)) и двигается с помощью двух способов. - Перейти по ребру в одну из соседних вершин: тратит \(1\) минуту.
- Телепортироваться в корень: не тратит времени, никакие новые вершины не становятся посещёнными.
Второй способ (телепортацию) можно применить не более \(k\) раз. Гусеница может закончить путешествие в любой вершине. Выходные данные В единственной строке выведите одно число — минимальное число минут, за которое можно побывать во всех вершинах дерева. Примечание На картинке показан один из способов обойти дерево из первого теста за 9 минут.  | |
![]()
|
|
D. 01-дерево
Деревья
жадные алгоритмы
Конструктив
снм
сортировки
Структуры данных
*2100
Есть ребро-взвешенное полное двоичное дерево с \(n\) листьями. Полное двоичное дерево определяется как дерево, в котором каждая нелистовая вершина имеет ровно 2 дочерних вершины. Для каждой нелистовой вершины обозначим одного из ее детей как левого ребенка, а другого — как правого. Это двоичное дерево обладает очень странным свойством. Для каждой нелистовой вершины одно из ребер к ее детям имеет вес \(0\), а другое ребро — вес \(1\). Обратите внимание, что ребро с весом \(0\) может идти как к левому ребенку, так и к правому. Вы забыли, как выглядит дерево, но, к счастью, вы помните некоторую информацию о листьях в виде массива \(a\) длины \(n\). Для каждого \(i\) от \(1\) до \(n\), \(a_i\) представляет собой расстояние\(^\dagger\) от корня до \(i\)-го листа (в порядке обхода dfs\(^\ddagger\)). Определите, существует ли полное двоичное дерево, удовлетворяющее массиву \(a\). Обратите внимание, что восстанавливать дерево не нужно. \(^\dagger\) Расстояние от вершины \(u\) до вершины \(v\) определяется как сумма весов ребер на пути от вершины \(u\) до вершины \(v\). \(^\ddagger\) Порядок листьев в dfs определяется вызовом следующей функции \(\texttt{dfs}\) на корне бинарного дерева.
dfs_order = [] — порядок обхода dfs
функция dfs(v):
если v — лист:
добавить v в конец dfs_order
иначе:
dfs(левый ребенок v)
dfs(правый ребенок v)
dfs(корень)
Выходные данные Для каждого набора входных данных выведите «YES», если существует полное двоичное дерево, удовлетворяющее массиву \(a\), и «NO» в противном случае. Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Например, строки «yEs», «yes», «Yes» и «YES» будут приняты как положительный ответ. Примечание В первом наборе входных данных массиву удовлетворяет следующее дерево. 
Для второго набора входных данных можно доказать, что не существует полного двоичного дерева, удовлетворяющего массиву. | |
![]()
|
|
G. Легендарный древесный гроссмейстер
Деревья
игры
Конструктив
разделяй и властвуй
*3500
В мире деревьев есть популярная игра для двух игроков, которая проводится на дереве с \(n\) вершинами, пронумерованными от \(1\) до \(n\). В этой игре ведущие турнира сначала выбирают вершину, которая будет корнем дерева, и выбирают другую вершину (возможно, ту же самую, что и корень), на которую кладут монету. Затем каждый игрок по очереди перемещает монету в любую дочернюю\(^\dagger\) вершину вершины, на которой в данный момент находится монета. Первый игрок, который не может сделать ход, проигрывает. Алиса хочет стать легендарным древесным гроссмейстером, поэтому она тратит много времени на изучение игры. Она записала матрицу \(s\) размером \(n\) на \(n\), где \(s_{i,j} = \mathtt{1}\), если первый игрок может выиграть, если корнем дерева выбрана вершина \(i\), а монета изначально была помещена на вершину \(j\). В противном случае \(s_{i, j} = \mathtt{0}\). Алиса — перфекционистка, поэтому она предполагает, что оба игрока играют идеально. Однако по дороге на турнир она случайно ударилась головой и забыла, как выглядит дерево. Определите, существует ли дерево, которое удовлетворяет выигрышным и проигрышным состояниям, представленным матрицей \(s\), и если существует, постройте подходящее дерево. \(^\dagger\) Вершина \(c\) является дочерней по отношению к вершине \(u\), если между \(c\) и \(u\) есть ребро, и \(c\) не лежит на единственном простом пути из корня в вершину \(u\). Выходные данные Если не существует дерева, удовлетворяющего выигрышным и проигрышным состояниям, представленным матрицей \(s\), выведите единственную строку, содержащую «NO». В противном случае, если существует дерево, удовлетворяющее матрице \(s\), выведите «YES» в первой строке, а затем \(n - 1\) строку, каждая из которых содержит два целых числа \(u\) и \(v\) (\(1 \le u, v \le n\)), означающих, что дерево имеет ребро между вершинами \(u\) и \(v\). Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Например, строки «yEs», «yes», «Yes» и «YES» будут приняты как положительный ответ. Если существует несколько деревьев, удовлетворяющих матрице \(s\), выведите любое из них. Примечание В первом наборе входных данных граф \(1\!-\!4\!-\!2\!-\!3\) удовлетворяет выигрышным и проигрышным состояниям, представленным матрицей \(s\). Например, \(s_{3,3} = 1\), так как первый игрок может переместить монету из \(3\rightarrow 2\), затем второй игрок перемещает монету из \(2\rightarrow 4\), и, наконец, первый игрок перемещает монету из \(4\rightarrow 1\). В этот момент у вершины \(1\) нет детей, поэтому второй игрок не может сделать ход и проигрывает. С другой стороны, \(s_{1,3} = 0\), так как если \(1\) является корнем, то у \(3\) нет детей, поэтому первый игрок не может сделать первый ход и проигрывает. Во втором наборе входных данных можно показать, что ни одно дерево не удовлетворяет матрице \(s\). | |
![]()
|
|
H. Диаметр дерева
Деревья
интерактив
*2000
Жюри загадало секретное дерево с \(n\) вершинами. \(n-1\) ребро дерева пронумерованы от \(1\) до \(n-1\). Вы можете делать запросы следующих двух типов: - Дать грейдеру массив \(a\) из \(n - 1\) положительных целых чисел. Для каждого ребра от \(1\) до \(n - 1\) вес ребра \(i\) устанавливается равным \(a_i\). Грейдер вернет длину диаметра\(^\dagger\) дерева с данными весами.
- Дать грейдеру два индекса \(1 \le a, b \le n - 1\). Грейдер вернет количество ребер между ребрами \(a\) и \(b\). Другими словами, если ребро \(a\) соединяет \(u_a\) и \(v_a\), а ребро \(b\) соединяет \(u_b\) и \(v_b\), то грейдер вернет \(\min(\text{dist}(u_a, u_b), \text{dist}(v_a, u_b), \text{dist}(u_a, v_b), \text{dist}(v_a, v_b))\), где \(\text{dist}(u, v)\) представляет собой количество ребер на пути между вершинами \(u\) и \(v\).
Найдите любое дерево, изоморфное\(^\ddagger\) секретному дереву после не более чем \(n\) запросов типа 1 и не более чем \(n\) запросов типа 2 в любом порядке. \(^\dagger\) Расстояние между двумя вершинами равно сумме весов единственного простого пути, соединяющего их. Диаметр — это наибольшее из этих расстояний. \(^\ddagger\) Два дерева, состоящие из \(n\) вершин каждое, называются изоморфными, если существует перестановка \(p\), содержащая целые числа от \(1\) до \(n\), такая, что ребро (\(u\), \(v\)) присутствует в первом дереве тогда и только тогда, когда ребро (\(p_u\), \(p_v\)) присутствует во втором дереве. Протокол взаимодействия Начните взаимодействие с чтения \(n\). Вам разрешается делать запросы следующим образом: - «\(\mathtt{?}\,1\,a_1\,a_2 \ldots a_{n-1}\)» (\(1 \le a_i \le 10^9\)). Затем вы должны cчитать целое число \(k\), которое представляет собой длину диаметра. Вы можете задать этот запрос не более \(n\) раз.
- «\(\mathtt{?}\,2\,a\,b\)» (\(1 \le a, b \le n - 1\)). Затем вы должны прочитать целое число \(k\), которое представляет собой количество ребер между ребрами \(a\) и \(b\). Вы можете задать этот запрос не более \(n\) раз.
Если ваш запрос некорректен, программа немедленно завершится, и вы получите вердикт Неправильный ответ. Чтобы вывести ответ, выведите «!» в единственной строке, за которой следует \(n - 1\) строка, где строка \(i\) содержит «\(u_i\,v_i\)» (\(1 \le u_i, v_i \le n\)), что означает, что для каждого \(i\) от \(1\) до \(n-1\), существует ребро между \(u_i\) и \(v_i\). После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Взломы Первая строка содержит одно целое число \(n\) (\(3 \le n \le 1000\)) — количество вершин в дереве. Следующие \(n - 1\) строк содержат по два целых числа \(u_i, v_i\) (\(1 \le u_i, v_i \le n\)) — ребра дерева. Примечание 
Секретное дерево в примере показано выше. Здесь числа на вершинах обозначают номер вершины, а числа на ребрах — номера ребер. 
В первом запросе все ребра имеют вес \(1\), поэтому диаметр имеет длину \(3\), как показано на картинке. Во втором запросе между ребрами \(1\) и \(3\) есть \(1\) ребро. 
В третьем запросе диаметр равен \(9\), если взять ребра \(1\), \(2\) и \(3\). В четвертом запросе между ребрами \(4\) и \(2\) нет ребер. 
Ответ, приведенный в примере, показан на картинке выше. Поскольку он изоморфен секретному дереву, он принимается как правильный ответ. Обратите внимание, что ребра могут быть выведены в любом порядке. | |
![]()
|
|
F2. Спокойное плавание (сложная версия)
Бинарный поиск
геометрия
графы
Деревья
снм
Структуры данных
*3000
Единственное отличие двух версий этой задачи состоит в ограничении на \(q\). Вы можете делать взломы, только если обе версии задачи решены. Томас плавает вокруг острова, окружённого океаном. Океан и остров можно представить в виде таблицы с \(n\) строками и \(m\) столбцами. Строки пронумерованы от \(1\) до \(n\) сверху вниз, а столбцы пронумерованы от \(1\) до \(m\) слева направо. Позицию клетки в строке \(r\) и в столбце \(c\) обозначим как \((r, c)\). Ниже приведен пример допустимой таблицы.  Пример допустимой таблицы Пример допустимой таблицы Существует три типа клеток: остров, океан и подводный вулкан. Клетки, представляющие остров, отмечены символом '#', клетки, представляющие океан, отмечены символом '.', а клетки, представляющие подводный вулкан, отмечены символом 'v'. Гарантируется, что есть хотя бы одна клетка острова и хотя бы одна клетка подводного вулкана. Также гарантируется, что множество всех клеток острова образует единую связную компоненту\(^{\dagger}\), и множество всех клеток океана и подводных вулканов также образует единую связную компоненту. Кроме того, гарантируется, что на краю таблицы (то есть, в строке \(1\), в строке \(n\), в столбце \(1\) и в столбце \(m\)) нет клеток острова. Определим круговой маршрут, проходимый Томасом, начинающийся в клетке \((x, y)\), как путь, который удовлетворяет следующим условиям: - Путь начинается и заканчивается в клетке \((x, y)\).
- Если Томас находится в клетке \((i, j)\), то он может перейти в клетки \((i+1, j)\), \((i-1, j)\), \((i, j-1)\) и \((i, j+1)\), при условии, что клетка, в которую он переходит, является клеткой океана или подводного вулкана и находится внутри таблицы. Обратите внимание, что Томасу разрешается посещать одну и ту же клетку несколько раз за один круговой маршрут.
- Путь должен обойти остров и полностью его окружить. Некоторый путь \(p\) полностью окружает остров, если невозможно добраться от клетки острова до клетки на границе таблицы, перемещаясь только в соседние по стороне или диагонали клетки, не посещая при этом клетку на пути \(p\). На изображении ниже путь, начинающийся в \((2, 2)\), приходящий в \((1, 3)\) и возвращающийся в \((2, 2)\) в обратную сторону, не полностью окружает остров и не считается круговым маршрутом.
 Пример пути, который не полностью окружает остров Пример пути, который не полностью окружает остров Безопасность кругового маршрута — это минимальное манхэттенское расстояние\(^{\ddagger}\) от клетки на круговом маршруте до подводного вулкана (обратите внимание, что наличие клеток острова не влияет на это расстояние). У вас есть \(q\) запросов. Запрос можно представить как \((x, y)\), и для каждого запроса вы хотите найти максимальную безопасность кругового маршрута, начинающегося в \((x, y)\). Гарантируется, что \((x, y)\) является клеткой океана или подводного вулкана. \(^{\dagger}\)Множество клеток образует единую связную компоненту, если из любой клетки этого множества можно добраться до любой другой клетки этого множества, перемещаясь только по клеткам этого множества, каждый раз переходя в клетку с общей стороной. \(^{\ddagger}\)Манхэттенское расстояние между клетками \((r_1, c_1)\) и \((r_2, c_2)\) равно \(|r_1 - r_2| + |c_1 - c_2|\). Выходные данные Для каждого запроса выведите одно целое число — максимальную безопасность кругового маршрута, начинающегося в указанной клетке. Примечание Для первого примера на изображении ниже показан оптимальный круговой маршрут, начинающийся в \((1, 1)\). Безопасность кругового маршрута равна \(3\), так как минимальное манхэттенское расстояние от клетки на круговом маршруте до подводного вулкана равно \(3\).  Пример оптимального кругового маршрута Пример оптимального кругового маршрута В четвёртом примере помните, что Томасу разрешается посещать одну и ту же клетку несколько раз за один круговой маршрут. Например, это необходимо для кругового маршрута, начинающегося в \((7, 6)\). | |
![]()
|
|
E. Посчитай пути
графы
Деревья
дп
поиск в глубину и подобное
снм
Структуры данных
*2000
Вам дано дерево, состоящее из \(n\) вершин, пронумерованных от \(1\) до \(n\). Каждая вершина окрашена в некоторый цвет, обозначенный целым числом от \(1\) до \(n\). Простой путь в дереве называется красивым, если: - он состоит хотя бы из \(2\) вершин;
- первая и последняя вершины пути имеют одинаковый цвет;
- ни одна другая вершина на пути не имеет такой же цвет, как и первая вершина.
Посчитайте количество красивых простых путей в дереве. Обратите внимание, что пути считаются ненаправленными (то есть путь из \(x\) в \(y\) — это то же самое, что и путь из \(y\) в \(x\)). Выходные данные Для каждого набора входных данных выведите одно целое число — количество красивых простых путей в дереве. | |
![]()
|
|
G. Влад и проблемы в МИТ
графы
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
Потоки
реализация
*1900
У Владислава есть сын, который очень хотел поступить в МИТ. Общежитие колледжа в МИТ (Молдавский институт технологий) можно представить в виде дерева с \(n\) вершинами, где каждая вершина представляет собой комнату с ровно одним студентом. Дерево — это связный неориентированный граф с \(n\) вершинами и \(n-1\) ребром. Сегодня ночью есть три типа студентов: - студенты, которые хотят веселиться и слушать музыку (обозначены \(\texttt{P}\)),
- студенты, которые хотят спать и наслаждаться тишиной (обозначены \(\texttt{S}\)), и
- студенты, которым не важно, что делать ночью (обозначены \(\texttt{C}\)).
Изначально все рёбра представляют собой тонкие стены, которые позволяют музыке проходить через них, поэтому когда веселящийся студент включает музыку, её можно услышать в каждой комнате. Однако мы можем установить толстые стены на любые рёбра — толстые стены не позволяют музыке проходить через них. Университет хочет установить несколько толстых стен, чтобы каждый веселящийся студент мог слушать музыку, и ни один спящий студент не мог её услышать. Поскольку университет потерял много денег в судебном процессе о правах на наименование, они просят вас найти минимальное количество толстых стен, которые им придется использовать. Выходные данные Для каждого набора входных данных выведите одно целое число — искомое минимальное количество толстых стен. Примечание В первом случае мы можем установить одну толстую стену между комнатами \(1\) и \(2\), как показано ниже. Мы не можем установить \(0\) стен, так как тогда музыка из комнаты 3 дойдет до комнаты 2, где студент хочет спать, поэтому ответ равен \(1\). Существуют и другие допустимые решения.  | |
![]()
|
|
F. Микроцикл
графы
Деревья
жадные алгоритмы
поиск в глубину и подобное
реализация
снм
сортировки
Структуры данных
*1900
Дан неориентированный взвешенный граф из \(n\) вершин и \(m\) рёбер. Между каждой парой вершин в графе существует не более одного ребра, граф не содержит петель (рёбер из вершины в себя же). Граф не обязательно связный. Цикл в графе называется простым, если он не проходит через одну и ту же вершину дважды и не содержит одно и то же ребро дважды. Найдите любой простой цикл этого графа, в котором вес самого лёгкого ребра минимален. Выходные данные Для каждого набора входных данных выведите пару чисел \(b\) и \(k\), где: - \(b\) — минимальный вес ребра в найденном цикле,
- \(k\) — количество вершин в найденном цикле.
В следующей строке выведите \(k\) чисел от \(1\) до \(n\) — вершины цикла в порядке обхода. Обратите внимание, что ответ всегда существует, так как при заданных ограничениях в графе всегда есть хотя бы один простой цикл. | |
![]()
|
|
D. Саша и прогулка по городу
Деревья
дп
Комбинаторика
математика
*1900
Саша хочет прогуляться со своей девушкой по городу. Город состоит из \(n\) перекрёстков, пронумерованных от \(1\) до \(n\). Некоторые из них соединены дорогами, причём от любого перекрёстка существует ровно один простой путь\(^{\dagger}\) до любого другого перекрёстка. Другими словами, перекрёстки и дороги между ними образуют дерево. Некоторые из перекрёстков являются опасными. И так как гулять одним по городу небезопасно, то Саша не хочет за время прогулки посещать три и более опасных перекрёстков. Саша называет множество перекрёстков хорошим, если выполняется следующее условие: - Если в городе опасными являются те и только те перекрёстки, которые содержатся в этом множестве, то любой простой путь в городе содержит не более двух опасных перекрёстков.
Однако Саша не знает, какие из перекрёстков являются опасными, поэтому его интересует количество различных хороших множеств перекрёстков, которые есть в городе. Поскольку это количество может быть очень большим, выведите его по модулю \(998\,244\,353\). \(^{\dagger}\)Простой путь — это путь, проходящий через каждый перекрёсток не более одного раза. Выходные данные Для каждого набора входных данных выведите одно целое число — количество хороших множеств перекрёстков по модулю \(998\,244\,353\). Примечание В первом наборе входных данных всего есть \(2^3 = 8\) множеств перекрёстков. Все из них являются хорошими, кроме множества \(\{1, 2, 3\}\), потому что, если перекрёстки \(1, 2\) и \(3\) являются опасными, то простой путь \(1 - 2 - 3\) содержит \(3\) опасных перекрёстка. Таким образом, всего есть \(7\) хороших множеств. Во втором наборе входных данных всего есть \(2^4 = 16\) множеств перекрёстков. При этом множества \(\{1, 2, 3, 4\}\), \(\{1, 2, 3\}\), \(\{1, 3, 4\}\), \(\{2, 3, 4\}\) не являются хорошими. Таким образом, всего есть \(12\) хороших множеств. Ниже изображена схема города:  | |
![]()
|
|
E. Саша и веселая нарезка дерева
битмаски
графы
Деревья
дп
жадные алгоритмы
математика
Перебор
поиск в глубину и подобное
*2300
Саше за победу на очередной олимпиаде подарили дерево\(^{\dagger}\) из \(n\) вершин. Но, вернувшись домой после празднования очередной победы, он заметил его потерю. Саша помнит, что он покрасил некоторые рёбра этого дерева. При этом он точно знает, что для любой из \(k\) пар вершин \((a_1, b_1), \ldots, (a_k, b_k)\) он покрасил хотя бы одно ребро на простом пути\(^{\ddagger}\) между вершинами \(a_i\) и \(b_i\). Саша не помнит, сколько рёбер он точно покрасил, так что он просит вас сказать, какое минимальное количество рёбер он мог покрасить, чтобы выполнялось описанное выше условие. \(^{\dagger}\)Деревом называется неориентированный связный граф без циклов. \(^{\ddagger}\)Простой путь — это путь, проходящий через каждую вершину не более одного раза. Выходные данные Для каждого набора входных данных выведите одно целое число — минимальное количество рёбер, которое мог покрасить Саша. Примечание В первом наборе входных данных Саша мог покрасить только одно ребро \((1, 2)\). Тогда на простом пути между вершинами \(1\) и \(3\) и вершинами \(4\) и \(1\) будет хотя бы одно покрашенное ребро.  Во втором наборе входных данных Саша мог покрасить рёбра \((1, 6)\) и \((1, 3)\).  | |
![]()
|
|
F. Саша и свадебное бинарное дерево поиска
Деревья
Комбинаторика
математика
Перебор
поиск в глубину и подобное
Структуры данных
*2300
Пройдя все трудности и невзгоды, Саша наконец решил жениться на своей девушке. Для этого нужно подарить ей обручальное кольцо. Однако его девушке не нравятся подобные романтические жесты, но нравятся бинарные деревья поиска\(^{\dagger}\). Поэтому Саша решил ей подарить такое дерево. Проведя немало времени на свадебных сайтах для программистов, он нашел идеальное бинарное дерево поиска с корнем в вершине \(1\). В нём значение в вершине \(v\) равно \(val_v\). Но спустя некоторое время он забыл значения в некоторых вершинах. Пытаясь вспомнить найденное дерево, Саша задался вопросом — сколько существует бинарных деревьев поиска, которые он мог найти на сайте, если известно, что значения во всех вершинах являются целыми числами и принадлежат отрезку \([1, C]\). Поскольку это число может быть очень большим, выведите его по модулю \(998\,244\,353\). \(^{\dagger}\)Бинарным деревом поиска называется корневое бинарное дерево, у которого для любой вершины \(x\) выполняется свойство: значения всех вершин в левом поддереве вершины \(x\) (если оно существует) меньше или равны значению в вершине \(x\) и значения всех вершин в правом поддереве вершины \(x\) (если оно существует) больше или равны значению в вершине \(x\). Выходные данные Для каждого набора входных данных выведите единственное целое число — количество подходящих бинарных деревьев поиска по модулю \(998\,244\,353\). Примечание В первом наборе входных данных, бинарное дерево поиска имеет следующий вид:  Тогда возможными значениями в вершинах являются: \([2, 2, 3, 2, 2]\), \([2, 2, 3, 2, 3]\), \([2, 2, 3, 3, 3]\) и \([3, 2, 3, 3, 3]\). Во втором наборе входных данных значения во всех вершинах известны, поэтому существует единственное подходящее бинарное дерево поиска. | |
![]()
|
|
A. Разрезание фигуры
графы
Деревья
Конструктив
*1700
Дан лист клетчатой бумаги n × m. Некоторые его клетки закрашены. Множество всех закрашенных клеток листа бумаги обозначим через A. Множество A является связным. Требуется найти минимальное количество клеток, которые можно удалить из множества A так, чтобы оно перестало быть связным. Множество закрашенных клеток называется связным, если для каждых двух клеток из этого множества a и b найдется последовательность клеток множества, начинающаяся в a и заканчивающаяся в b, такая, что любая клетка этой последовательности, исключая последнюю, имеет общую сторону со следующей в последовательности клеткой. Пустое множество и множество, состоящее из одной клетки, по определению считаются связными. Выходные данные На первой строке выведите минимальное количество клеток, которые нужно удалить, чтобы лишить множество A связности или -1, если это невозможно. Примечание В первом примере можно удалить любые две клетки, не имеющие общей стороны и множество закрашенных клеток потеряет связность. Пояснение ко второму примеру изображено на рисунке. Слева изображено изначальное множество клеток. Справа — множество с удаленными клетками. Удаленные клетки помечены крестиками.  | |
![]()
|
|
G. Подсчет множества префиксных максимумов
Деревья
дп
Структуры данных
*3100
Определим для массива \(b\) функцию \(f\) такую, что \(f(b)\) возвращает массив префиксных максимумов \(b\). Другими словами, \(f(b)\) — это массив, содержащий только такие элементы \(b_i\), для которых \(b_i=\max(b_1,b_2,\ldots,b_i)\), без изменения их порядка. Например, \(f([3,10,4,10,15,1])=[3,10,10,15]\). Вам дано дерево, состоящее из \(n\) вершин с корнем \(1\). Перестановка\(^\dagger\) \(p\) является прямым обходом дерева, если для всех \(i\) выполняется следующее условие: - Пусть \(k\) — число потомков\(^\ddagger\) вершины \(p_i\).
- Для всех \(x\) таких, что \(i < x \leq i+k\), \(p_x\) — потомок вершины \(p_i\).
Найдите количество различных значений \(f(a)\) среди всех возможных прямых обходов \(a\). Так как это значение может быть большим, вам нужно найти его по модулю \(998\,244\,353\). \(^\dagger\) Перестановкой длины \(n\) является массив, состоящий из \(n\) различных целых чисел от \(1\) до \(n\) в произвольном порядке. Например, \([2,3,1,5,4]\) — перестановка, но \([1,2,2]\) не перестановка (\(2\) встречается в массиве дважды) и \([1,3,4]\) тоже не перестановка (\(n=3\), но в массиве встречается \(4\)). \(^\ddagger\) Вершина \(t\) является потомком вершины \(s\), если \(s \neq t\) и \(s\) находится на единственном простом пути из \(t\) в \(1\). Выходные данные Для каждого набора входных данных выведите количество различных значений \(f(a)\), которые вы можете получить, по модулю \(998\,244\,353\). Примечание В первом наборе входных данных единственным допустимым прямым обходом является \(a=[1]\). Поэтому единственное возможное значение \(f(a)\) — \([1]\). Во втором наборе входных данных единственным допустимым прямым обходом является \(a=[1,2]\). Поэтому единственное возможное значение \(f(a)\) — \([1,2]\). В третьем наборе входных данных два допустимых прямых обхода — \(a=[1,2,3]\) и \(a=[1,3,2]\). Таким образом, возможные значения \(f(a)\) — \([1,2,3]\) и \([1,3]\). В пятом наборе входных данных возможными значениями \(f(a)\) являются: - \([1,5]\);
- \([1,2,5]\);
- \([1,3,5]\);
- \([1,4,5]\);
- \([1,2,3,5]\);
- \([1,2,4,5]\);
- \([1,3,4,5]\);
- \([1,2,3,4,5]\).
| |
![]()
|
|
H. Интерактивное дерево мексов
Деревья
интерактив
Конструктив
поиск в глубину и подобное
*3300
Это интерактивная задача. У Алисы есть дерево \(T\), состоящее из \(n\) вершин, пронумерованных от \(1\) до \(n\). Алиса покажет дерево \(T\) Бобу. После того как Боб увидит \(T\), он должен назвать Алисе две перестановки \(p_1\) и \(p_2\) чисел \([1, 2, \ldots, n]\). Затем Алиса сыграет \(q\) раундов следующей игры: - Алиса создаст массив \(a\), который является перестановкой чисел \([0,1,\ldots,n-1]\). Значение вершины \(v\) будет равно \(a_v\).
- Алиса выберет две вершины \(u\) и \(v\) (\(1 \leq u, v \leq n\), \(u \neq v\)) из \(T\) и сообщит их Бобу. Бобу нужно будет найти \(\operatorname{MEX}^\dagger\) значений на единственном простом пути между вершинами \(u\) и \(v\).
- Чтобы найти это значение, Боб может задать Алисе не более \(5\) запросов. В каждом запросе Боб должен дать Алисе три целых числа \(t\), \(l\) и \(r\), таких, что \(t\) равно \(1\) или \(2\), и \(1 \leq l \leq r \leq n\). После этого Алиса сообщит Бобу величину, равную \(\)\min_{i=l}^{r} a[p_{t,i}].\(\)
Обратите внимание, что все раунды независимы друг от друга. В частности, значения \(a\), \(u\) и \(v\) могут быть разными в разных раундах. Боб озадачен, поскольку он знает только решение с HLD, которое требует \(O(\log(n))\) запросов в каждом раунде. Поэтому ему нужна ваша помощь, чтобы выиграть игру. \(^\dagger\) \(\operatorname{MEX}\) набора чисел \(c_1, c_2, \ldots, c_k\) определяется как наименьшее неотрицательное целое число \(x\), которое не встречается в наборе чисел \(c\). Протокол взаимодействия Каждый тест состоит из нескольких наборов входных данных. В первой строке находится одно целое число \(t\) (\(1 \leq t \leq 10^4\)) — количество наборов входных данных. Далее следует взаимодействие по каждому набору входных данных. Первая строка каждого набора входных данных содержит два положительных целых числа \(n\) и \(q\) (\(2 \leq n \leq 10^5\), \(1 \leq q \leq 10^4\)) — количество вершин в \(T\) и количество раундов соответственно. Следующие \(n-1\) строк содержат по два целых числа \(u\) и \(v\) (\(1 \leq u, v \leq n\), \(u \neq v\)), обозначающие ребро между вершинами \(u\) и \(v\). Гарантируется, что заданные ребра образуют дерево. Гарантируется, что суммы \(n\) и \(q\) по всем наборам входных данных не превосходит \(10^5\) и \(10^4\) соответственно. Также гарантируется, что сумма значений \(n \cdot q\) не превосходит \(3 \cdot 10^6\). После завершения чтения ребер дерева необходимо вывести две перестановки \(p_1\) и \(p_2\) чисел \([1, 2, \ldots, n]\). Для этого в отдельной строке выведите \(n\) целых чисел — перестановку \(p_1\). В следующей строке выведите \(n\) целых чисел — перестановку \(p_2\). Алиса начнет играть в игру. Для каждого раунда необходимо считать два целых числа \(u\) и \(v\) (\(1 \leq u, v \leq n\), \(u \neq v\)). Вам нужно найти \(\operatorname{MEX}\) значений вершин на пути из \(u\) в \(v\). Чтобы сделать запрос, выведите «? \(t\) \(l\) \(r\)» без кавычек, где \(t\) равно \(1\) или \(2\) и \(1 \leq l \leq r \leq n\). После этого вы должны прочитать одно целое число — ответ на ваш запрос \(\min_{i=l}^{r} a_{p_{t,i}}\). В каждом раунде можно сделать не более \(5\) таких запросов для каждого раунда. Когда вы хотите вывести ответ, выведите «! \(x\)» (\(1 \leq x, y \leq n\)) без кавычек. После этого считайте одно целое число, которое в нормальной ситуации будет равно \(1\). Если вместо корректного ответа вы получаете целое число \(-1\), это означает, что ваша программа сделала некорректный запрос, превысила лимит запросов или дала неправильный ответ на предыдущем наборе входных данных. Чтобы получить вердикт Неправильный ответ, ваша программа должна немедленно завершиться. В противном случае вы можете получить произвольный вердикт, поскольку ваше решение будет продолжать читать из закрытого потока. После вывода запроса или ответа не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Взломы Чтобы сделать взлом, используйте следующий формат. Первая строка должна содержать целое число \(t\) (\(1 \le t \le 10^4\)) — количество наборов входных данных. Первая строка каждого набора входных данных должна содержать два целых числа \(n\) и \(q\) (\(2 \leq n \leq 10^5\); \(1 \leq q \leq 10^4\)) — количество вершин в \(T\) и количество раундов, соответственно. Следующие \(n-1\) строк должны содержать по два целых числа \(u\) и \(v\) (\(1 \leq u, v \leq n\), \(u \neq v\)), означающие ребро между вершинами \(u\) и \(v\). Данные ребра должны образовывать дерево. Для каждого из \(q\) раундов сначала выведите в отдельной строке перестановку чисел \([0, 1, 2, \ldots, n-1]\) — массив \(a\), который выберет Алиса в начале раунда. В следующей строке выведите два различных целых числе \(u\) и \(v\) (\(1 \leq u, v \leq v\), \(u \neq v\)) — вершины, являющиеся концам пути, про который спросит Алиса. Сумма значений \(n\) и сумма значений \(q\) по всем наборам входных данных не должны превышать \(10^5\) и \(10^4\) соответственно. Сумма значений \(n \cdot q\) не должна превышать \(3 \cdot 10^6\). Примечание В первом примере взаимодействие происходит следующим образом. | Решение | жюри | объяснение | | 1 | Имеется 1 набор входных данных. | | 3 1 | Дерево \(T\) состоит из \(3\) вершин, и Алиса будет играть только один раунд. | | 1 2 | Первое ребро \(T\) | | 2 3 | Второе ребро \(T\) | | 1 2 3 | | Перестановка \(p_1\) | | 2 1 3 | | Перестановка \(p_2\) | | | Алиса переставляет элементы \(a\) и получает \(a=[0,2,1]\), прежде чем выдать вершины для единственного раунда. | | 2 3 | Вершины для раунда | | ? 1 2 3 | 1 | \(\min(a_{p_{1,2}},a_{p_{1,3}})=\min(a_2,a_3)=1\) | | ? 2 1 3 | 0 | \(\min(a_{p_{2,1}},a_{p_{2,2}},a_{p_{2,3}})=\min(a_2,a_1,a_3)=0\) | | ! 0 | 1 | Учитывая ответы на запросы, очевидно, что \(\operatorname{MEX}\) равен \(0\). Поскольку вывод верен, жюри отвечает \(1\). |
После каждого набора входных данных обязательно считывайте \(1\) или \(-1\). | |
![]()
|
|
F. Дерево Андрея
Бинарный поиск
Деревья
жадные алгоритмы
Конструктив
поиск в глубину и подобное
реализация
снм
Структуры данных
*2800
Магистр Андрей очень любит деревья\(^{\dagger}\), поэтому у него есть дерево, состоящее из \(n\) вершин. Но не все так просто. Магистр Тимофей решил украсть одну вершину из дерева. Если Тимофей украл вершину \(v\) из дерева, то вершина \(v\) и все ребра с концом в вершине \(v\) удаляются из дерева, при этом номера других вершин не меняются. Чтобы Андрей не расстраивался, Тимофей решил сделать получившийся граф снова деревом. Для этого он может добавлять ребра между произвольными вершинами \(a\) и \(b\), однако при добавлении такого ребра он должен заплатить \(|a - b|\) монет в Центр Помощи Магистрам. Обратите внимание, что получившееся дерево не содержит вершину \(v\). Тимофей не определился, какую вершину \(v\) он удалит из дерева, поэтому он хочет знать для каждой вершины \(1 \leq v \leq n\), какое минимальное количество монет нужно потратить, чтобы после удаления вершины \(v\) сделать граф снова деревом, а также какие ребра при этом нужно добавить. \(^{\dagger}\)Деревом называется неориентированный связный граф без циклов. Выходные данные Для каждого набора входных данных выведите ответ в следующем формате: Для каждой вершины \(v\) (в порядке от \(1\) до \(n\)) в первой строке выведите два целых числа \(w\) и \(m\) — минимальное количество монет, которое нужно потратить, чтобы граф после удаления вершины \(v\) снова стал деревом, и количество добавленных ребер. Далее выведите \(m\) строк, каждая из которых содержит два целых числа \(a\) и \(b\) (\(1 \le a, b \le n, a \ne v, b \ne v\), \(a \ne b\)) — концы добавленного ребра. Если существует несколько способов добавить ребра, вы можете вывести любое решение с минимальной стоимостью. Примечание В первом наборе входных данных: Рассмотрим удаление вершины \(4\):  Оптимальным решением будет провести ребро из вершины \(5\) в вершину \(3\). Тогда мы потратим \(|5 - 3| = 2\) монеты. В третьем наборе входных данных: Рассмотрим удаление вершины \(1\):  Оптимальным решением будет: - Провести ребро из вершины \(2\) в вершину \(3\), потратив \(|2 - 3| = 1\) монету.
- Провести ребро из вершины \(3\) в вершину \(4\), потратив \(|3 - 4| = 1\) монету.
- Провести ребро из вершины \(4\) в вершину \(5\), потратив \(|4 - 5| = 1\) монету.
Тогда сумарно мы потратим \(1 + 1 + 1 = 3\) монеты. Рассмотрим удаление вершины \(2\):  Ребра проводить не нужно, так как после удаления вершины граф останется деревом. | |
![]()
|
|
H. Лучший стажер фермера Джона
Деревья
дп
Потоки
Структуры данных
*3500
Руби только что получила место стажера на ферме Фермера Джона, победив в соревновании по программированию! В обязанности Руби входит обслуживание персикового дерева Фермера Джона — дерева, состоящего из \(n\) вершин, с корнем в вершине \(1\). В каждой вершине изначально содержится \(a_i = 0\) персиков. Могут происходить два вида событий: - Событие роста в вершине \(x\): Руби должна выбрать либо родителя \(x\), либо любую вершину в поддереве \(x\), и увеличить количество персиков в ней на единицу.
- Событие сбора урожая в вершине \(x\): Руби должна выбрать одну вершину, которая находится в поддереве \(x\), и уменьшить количество содержащихся в ней персиков на единицу. Обратите внимание, что это не тот же набор вершин, что и в событии роста.
Обратите внимание, поддерево вершины \(x\) включает в себя саму вершину \(x\). Руби также дан массив \(b\) длины \(n\). Персиковое дерево считается здоровым, если \(a_i \ge b_i\) для каждой вершины \(i\). Руби предлагается выполнить \(q\) операций двух типов: - 1 x v — Выполнить \(v\) событий роста на вершине \(x\). Руби не обязательно выбирать одну и ту же вершину для увеличения в каждом событии роста.
- 2 x v — Выполнить \(v\) событий сбора урожая на вершине \(x\). Руби не обязательно выбирать одну и ту же вершину для уменьшения в каждом событии сбора урожая.
Для каждого префикса операций она просит вас определить, может ли она выполнить эти операции в некотором порядке так, чтобы получившееся (после всех этих операций) персиковое дерево было здоровым. Обратите внимание, что Руби не может выполнять событие сбора урожая, которое сделает некоторое \(a_i\) отрицательным. Каждый префикс операций независим, то есть для данной операции Руби может выбрать разные вершины для выполнения событий на каждом префиксе, содержащем эту операцию. Выходные данные Для каждого набора входных данных выведите \(q\) строк. Строка \(i\) должна содержать «YES», если Руби может сделать персиковое дерево здоровым после выполнения операций \(1, 2, \ldots, i\) в любом порядке. В противном случае она должна содержать «NO». Вы можете выводить ответ в любом регистре (верхнем или нижнем). Например, строки «YEs», «Yes», «Yes» и «YES» будут распознаны как положительные ответы. Примечание Для префикса, содержащего операции \(1, 2, \ldots, 5\) в первом примере, Руби может выполнять операции в следующем порядке: - Руби выполняет операцию \(2\) и решает увеличить \(a_4\) на \(9\) и \(a_5\) на \(8\).
- Руби выполняет операцию \(1\) и решает увеличить \(a_1\) на \(5\), \(a_3\) на \(2\), \(a_6\) на \(4\) и \(a_8\) на \(3\).
- Руби выполняет операцию \(3\) и решает увеличить \(a_2\) на \(7\).
- Руби выполняет операцию \(4\) и решает уменьшить \(a_2\) на \(1\).
- Руби выполняет операцию \(5\) и решает увеличить \(a_7\) на \(1\).
| |
![]()
|
|
C. Циркуль для дерева
Деревья
жадные алгоритмы
Конструктив
поиск в глубину и подобное
*2300
Вам дано дерево с \(n\) вершинами, пронумерованными \(1, 2, \ldots, n\). Изначально все вершины окрашены в белый цвет. Вы можете выполнить следующую двухэтапную операцию: - Выбрать вершину \(v\) (\(1 \leq v \leq n\)) и расстояние \(d\) (\(0 \leq d \leq n-1\)).
- Для всех вершин \(u\) (\(1 \leq u \leq n\)) таких, что \(\text{dist}^\dagger(u,v)=d\), покрасить \(u\) в черный цвет.
Постройте последовательность операций для перекрашивания всех вершин дерева в черный цвет, используя минимально возможное количество операций. Можно показать, что это всегда можно сделать, используя не более \(n\) операций. \(^\dagger\) \(\text{dist}(x, y)\) обозначает количество ребер на (единственном) простом пути между вершинами \(x\) и \(y\) на дереве. Выходные данные Для каждого набора входных данных сначала выведите одно целое число \(op\) \((1 \le op \le n)\) — минимальное количество операций, необходимых для перекрашивания всех вершин дерева в черный цвет. Затем выведите \(op\) строк, каждая из которых содержит \(2\) целых числа. В \(i\)-й строке должны содержаться значения \(v\) и \(d\), выбранные для \(i\)-й операции (\(1 \le v \le n\), \(0 \le d \le n - 1\)). Необходимо, чтобы в результате \(op\) операций все вершины были покрашены в черный цвет. Если существует несколько решений, вы можете вывести любое из них. Примечание В первом наборе входных данных существует только одна возможная операция, и ее выполнение дает правильный ответ. Во втором наборе входных данных первая операция перекрашивает вершину \(2\) в черный цвет, а вторая операция перекрашивает вершину \(1\) в черный цвет. Можно показать, что за одну операцию невозможно перекрасить обе вершины в черный цвет, поэтому минимальное количество необходимых операций равно \(2\). Другим возможным решением является использование \(2\) операций: \((u, r) = (1, 0)\) и \((u, r) = (2, 0)\). В третьем наборе входных данных первая операция перекрашивает вершины \(2\), \(3\) и \(4\) в черный цвет, а вторая операция перекрашивает вершину \(1\) в черный цвет. Опять же, можно показать, что за \(1\) операцию невозможно перекрасить все вершины в черный цвет, поэтому минимальное количество необходимых операций равно \(2\). В четвертом наборе входных данных первая операция перекрашивает вершины \(4\), \(1\) и \(7\) в черный цвет, вторая операция перекрашивает вершины \(2\), \(5\) и \(6\) в черный цвет, а третья операция перекрашивает вершины \(3\) и \(7\) в черный цвет. Обратите внимание, что вершину \(7\) разрешено перекрашивать в черный цвет дважды. Таким образом, каждая вершина была перекрашена хотя бы один раз, причем вершина \(7\) была перекрашена дважды. Можно показать, что невозможно перекрасить все вершины в черный цвет менее чем за \(3\) хода. | |
![]()
|
|
C. Разрезание дерева
Бинарный поиск
Деревья
дп
жадные алгоритмы
реализация
*1600
Вам дано дерево из \(n\) вершин. Ваша задача — найти такое максимальное число \(x\), что можно удалить из этого дерева ровно \(k\) ребер так, чтобы размер каждой оставшейся компоненты связности\(^{\dagger}\) был не менее \(x\). \(^{\dagger}\) Две вершины \(v\) и \(u\) находятся в одной компоненте связности, если существует такая последовательность чисел \(t_1, t_2, \ldots, t_k\) произвольной длины \(k\), такая что \(t_1 = v\), \(t_k = u\), и для каждого \(i\) от \(1\) до \(k - 1\) вершины \(t_i\) и \(t_{i+1}\) соединены ребром. Выходные данные Для каждого набора входных данных в отдельной строке выведите такое максимальное число \(x\), что можно удалить ровно \(k\) ребер дерева так, чтобы размер каждой оставшейся компоненты связности был равен не менее \(x\). Примечание Дерево в первом наборе входных данных:  После удаления ребра \(1\) — \(3\) дерево будет выглядеть следующим образом:  Дерево распалось на две компоненты связности. Первая компонента состоит из двух вершин: \(1\) и \(2\). Вторая компонента связности состоит из трех вершин: \(3, 4\) и \(5\). В обоих компонентах связности не менее двух вершин. Можно показать, что ответ \(3\) не достижим, поэтому ответ \(2\). | |
![]()
|
|
G. MST с паросочетанием
битмаски
Деревья
Паросочетания
Перебор
снм
*3100
Дан неориентированный связный граф, в котором \(n\) вершин. У каждого ребра этого графа есть вес; вес ребра между вершинами \(i\) и \(j\) равен \(w_{i,j}\) (или \(w_{i,j} = 0\), что означает, что между \(i\) и \(j\) нет ребра). Все веса — положительные целые числа. Также дано положительное целое число \(c\). Вы должны построить остовное дерево для этого графа, то есть выбрать ровно \((n-1)\) ребер графа так, чтобы можно было из любой вершины добраться до любой другой по выбранным ребрам. Стоимость остовного дерева — это сумма двух значений: - сумма весов всех выбранных ребер;
- максимальное паросочетание в остовном дереве (то есть максимальный размер множества ребер, такого, что каждое ребро принадлежит остовному дереву и каждой вершине инцидентно не более одного ребра из множества), умноженное на заданное число \(c\).
Найдите любое остовное дерево с минимальной стоимостью. Так как граф связный, у него существует хотя бы одно остовное дерево. Выходные данные Выведите одно целое число — минимальную стоимость остовного дерева. Примечание В первом примере минимальное остовное дерево состоит из ребер \((1, 3)\), \((2, 3)\) и \((3, 4)\). Максимальное паросочетание относительно него равно \(1\). Во втором примере минимальное остовное дерево состоит из ребер \((1, 2)\), \((2, 3)\) и \((3, 4)\). Максимальное паросочетание относительно него равно \(2\). | |
![]()
|
|
C. Annual Ants' Gathering
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
*1900
Deep within a forest lies an ancient tree, home to \(n\) ants living in \(n\) tiny houses, indexed from \(1\) to \(n\), connected by the branches of the tree.  Once a year, all the ants need to gather to watch the EUC. For this, all ants move along the \(n-1\) branches of the tree they live on to meet at the home of one ant. However, this year the ants could not agree on where to meet and need your help to gather up. You can tell all the ants currently at house \(u\) to move to house \(v\) if there is a branch directly connecting those two houses. However, the ants ignore your command if there are fewer ants gathered in house \(v\) than in house \(u\), i.e., if it would be easier for the ants from house \(v\) to move. This even holds true if no ant at all is currently in house \(v\). You can give this kind of commands as many times as you want. Is it possible for you to gather all the ants in a single house? Output Print \(\texttt{YES}\) if it is possible to gather all the ants in a single house. Otherwise, print \(\texttt{NO}\). Note In the first sample, you can gather all the ants at house \(3\) as follows: - You tell to the ant at house \(4\) to move to house \(6\).
- You tell to the ant at house \(2\) to move to house \(3\).
- You tell to the two ants at house \(6\) to move to house \(3\) (which already contains two ants).
- You tell to the ant at house \(5\) to move to house \(1\).
- You tell to the ant at house \(7\) to move to house \(1\) (which already contains two ants).
- You tell to the three ants at house \(1\) to move to house \(3\) (which already contains four ants).
In the second sample, it is impossible to gather all the ants in a single house. | |
![]()
|
|
F. Dating
Деревья
жадные алгоритмы
сортировки
*2200
You are the developer of a dating app which ignores gender completely. The app has \(n\) users, indexed from \(1\) to \(n\). Each user's profile features a list of the activities they enjoy doing. There are \(m\) possible activities, indexed from \(1\) to \(m\). A match between two users is good if they share at least one activity and, at the same time, both of them like at least one activity that the other user does not like. Find a good match if it exists. Output Print \(\texttt{YES}\) if a good match exists. Otherwise, print \(\texttt{NO}\). If a good match exists, on the next line print two integers — the indexes of two users that make a match. Note In the first sample, users \(1\) and \(3\) form a match, because they share activity \(1\), and, furthermore, user \(3\) likes activity \(5\) (which user \(1\) does not like) and user \(1\) likes activity \(4\) (which user \(3\) does not like). Note that users \(1\) and \(2\), as well as users \(2\) and \(3\), do not form a match, as there is no activity that users \(1\) or \(3\) like, and user \(2\) doesn't like. | |
![]()
|
|
J. Amanda the Amoeba
графы
Деревья
реализация
*2600
This problem has an attachment. You can use it to simulate and visualize the movements of the amoeba. Amoeba Amanda lives inside a rectangular grid of square pixels. Her body occupies some of these pixels. Other pixels may be either free or blocked. Amanda moves across the grid using the so-called amoeboid movement. In each step of such a movement, her body first shrinks by one pixel (one pixel of the body is removed and becomes free), and then grows at a different place (one previously-free pixel is added to the body). To prevent structural damage, Amanda's body always occupies a connected region of pixels, which means that any pair of pixels forming the body can be connected by a sequence of adjacent pixels without ever leaving the body. Two pixels are considered adjacent if they share a common side (each pixel has at most 4 neighbours). The body remains connected even during the movement, including the moment after removing a pixel and before adding another one. Your task is to help Amanda find her way around. Given her initial position and desired final position, suggest a sequence of valid moves leading from the former to the latter.  Illustration of sample \(1\): The filled shape is the initial position, the dotted region is the final position. Illustration of sample \(1\): The filled shape is the initial position, the dotted region is the final position. Output Print \(\texttt{YES}\) if it is possible for Amanda to go from the initial position to the final one. Otherwise, print \(\texttt{NO}\). If it is possible, on the next line print one integer \(m\) (\(0\le m\le 10\,000\)) — the number of moves to execute. The following \(m\) lines must contain four integer coordinates each: \(i_1\), \(j_1\), \(i_2\), \(j_2\) (\(1\le i_1,i_2\le r\), \(1\le j_1,j_2\le c\)). These four coordinates specify one move, meaning that the pixel at \(i_1\)-th row and \(j_1\)-th column is first removed from the body. Then, \((i_2,j_2)\) must designate a different location where one pixel is added. The sequence should consist only of valid moves and after the last move, Amanda's body should occupy the desired final position. If there are multiple solutions, print any of them. Under the assumptions of this problem, it can be proven that if it is possible for Amanda to go from the initial position to the desired final one, then it is possible to do it with at most \(10\,000\) moves. Note In the first sample, Amanda executes 5 moves to reach the final position, as shown in the figure below.  | |
![]()
|
|
F. 0, 1, 2, Tree!
битмаски
Деревья
жадные алгоритмы
Перебор
реализация
*1700
Найдите минимальную высоту корневого дерева\(^{\dagger}\) с \(a+b+c\) вершинами, которое удовлетворяет следующим условиям: - \(a\) вершин имеют ровно \(2\) потомка,
- \(b\) вершин имеют ровно \(1\) потомка, и
- \(c\) вершин имеют ровно \(0\) потомков (не имеют потомков).
Если такого дерева не существует, вы должны сообщить об этом.  Дерево выше с корнем в верхней вершине, и каждая вершина помечена числом потомков. Здесь \(a=2\), \(b=1\), \(c=3\), и высота равна \(2\). \(^{\dagger}\) Корневое дерево — это связный граф без циклов, с особой вершиной, называемой корнем. В корневом дереве, среди любых двух вершин, соединенных ребром, одна вершина является родителем (ближе к корню), а другая — потомком. Расстояние между двумя вершинами в дереве — количество ребер в кратчайшем пути между ними. Высота корневого дерева — это максимальное расстояние от вершины до корня. Выходные данные Для каждого набора входных данных, если такое дерево не существует, выведите \(-1\). В противном случае выведите одно целое число — минимальную высоту дерева, удовлетворяющего описанным условиям. Примечание Первый набор входных данных изображен в условии. Можно доказать, что высота не может быть меньше \(2\). Во втором наборе входных данных, можно сформировать дерево с одной вершиной и без ребер. Оно имеет высоту \(0\), что является оптимальным. В третьем наборе входных данных, можно сформировать дерево с двумя вершинами, соединенными одним ребром. Оно имеет высоту \(1\), что является оптимальным. | |
![]()
|
|
H. Щелчок Таноса
Бинарный поиск
Деревья
дп
жадные алгоритмы
игры
*3200
Имеется массив \(a\) длины \(2^k\), который изначально является перестановкой значений от \(1\) до \(2^k\) для некоторого целого положительного числа \(k\). Алиса и Боб играют в следующую игру на массиве \(a\). Сначала Алисе и Бобу даётся значение \(t\) между \(1\) и \(k\). Затем, ровно \(t\) ходов происходит следующее: - Алиса либо ничего не делает, либо выбирает два различных элемента массива \(a\) и меняет их местами.
- Боб выбирает либо левую половину, либо правую половину массива \(a\), и стирает её.
Счет игры определяется как максимальное значение в \(a\) после всех \(t\) ходов. Алиса хочет максимизировать этот счет, а Боб — минимизировать. Вам нужно вывести \(k\) чисел: счет игры, если и Алиса, и Боб играют оптимально, для всех \(t\) от \(1\) до \(k\). Выходные данные Для каждого набора входных данных выведите \(k\) чисел, где \(i\)-е число — это счет игры, если Алиса и Боб играют оптимально, а игра длится \(t = i\) ходов. Примечание В третьем наборе входных данных, для \(t = 2\), игра могла бы проходить следующим образом: - Изначально, \(a = [5, 1, 6, 4, 7, 2, 8, 3]\).
- Алиса меняет местами \(a_6\) и \(a_8\), \(a\) становится \([5, 1, 6, 4, 7, 3, 8, 2]\).
- Боб стирает правую половину массива, \(a\) становится \([5, 1, 6, 4]\).
- Алиса ничего не делает, \(a\) остается \([5, 1, 6, 4]\).
- Боб стирает правую половину массива, \(a\) становится \([5, 1]\).
- Игра заканчивается со счётом \(5\).
| |
![]()
|
|
F1. Несоответствие частот (простая версия)
Бинарный поиск
Деревья
разделяй и властвуй
Структуры данных
Теория вероятностей
хэши
*2600
Это простая версия задачи. Единственное отличие между версиями — ограничение на \(k\). Вы можете делать взломы, только если обе версии задачи решены. Вам дано неориентированное дерево из \(n\) вершин. На каждой вершине \(v\) записано значение \(a_v\). Вы должны ответить на запросы, связанные с деревом. Вам дано \(q\) запросов. В каждом запросе дается \(5\) целых чисел, \(u_1, v_1, u_2, v_2, k\). Обозначим количество вершин со значением \(c\) на пути \(u_1 \rightarrow v_1\) как \(x_c\), а количество вершин со значением \(c\) на пути \(u_2 \rightarrow v_2\) как \(y_c\). Пусть существует \(z\) таких значений \(c\), что \(x_c \neq y_c\). Тогда выведите любые \(\min(z, k)\) таких значений в любом порядке. Выходные данные Для каждого запроса выведите ответ на отдельной строке. Для каждого запроса сначала выведите \(\min(z, k)\), а затем в той же строке выведите любые \(\min(z, k)\) значений, которые встречаются разное количество раз на путях, в любом порядке. Примечание Для \(1\) запроса первый путь: \(1 \rightarrow 2 \rightarrow 4\), на котором встречается мультинабор значений \(\{5, 2, 4\}\). На втором пути \(4 \rightarrow 2 \rightarrow 5\) мы имеем мультинабор \(\{4, 2, 3\}\). Два числа — \(3\) и \(5\) встречаются разное количество раз, поэтому мы выводим одно из них. Во \(2\) запросе пути совпадают, поэтому выводим \(0\). В \(3\) запросе первый путь — только вершина \(5\), что приводит к мультинабору \(\{3\}\), а второй путь — \(4 \rightarrow 2 \rightarrow 1 \rightarrow 3\) дает \(\{4, 2, 5, 3\}\). Числа \(5\), \(2\) и \(4\) встречаются разное количество раз. | |
![]()
|
|
F2. Несоответствие частот (сложная версия)
Бинарный поиск
Деревья
поиск в глубину и подобное
Структуры данных
Теория вероятностей
хэши
*2700
Это сложная версия задачи. Единственное отличие между версиями — ограничение на \(k\). Вы можете делать взломы, только если обе версии задачи решены. Вам дано неориентированное дерево из \(n\) вершин. На каждой вершине \(v\) записано значение \(a_v\). Вы должны ответить на запросы, связанные с деревом. Вам дано \(q\) запросов. В каждом запросе дается \(5\) целых чисел, \(u_1, v_1, u_2, v_2, k\). Обозначим количество вершин со значением \(c\) на пути \(u_1 \rightarrow v_1\) как \(x_c\), а количество вершин со значением \(c\) на пути \(u_2 \rightarrow v_2\) как \(y_c\). Пусть существует \(z\) таких значений \(c\), что \(x_c \neq y_c\). Тогда выведите любые \(\min(z, k)\) таких значений в любом порядке. Выходные данные Для каждого запроса выведите ответ на отдельной строке. Для каждого запроса сначала выведите \(\min(z, k)\), а затем в той же строке выведите любые \(\min(z, k)\) значений, которые встречаются разное количество раз на путях, в любом порядке. Примечание Для \(1\) запроса первый путь: \(1 \rightarrow 2 \rightarrow 4\), на котором встречается мультинабор значений \(\{5, 2, 4\}\). На втором пути \(4 \rightarrow 2 \rightarrow 5\) мы имеем мультинабор \(\{4, 2, 3\}\). Два числа — \(3\) и \(5\) встречаются разное количество раз, поэтому мы выводим оба числа. Во \(2\) запросе пути совпадают, поэтому выводим \(0\). В \(3\) запросе у нас те же пути, что и в запросе \(1\), но нам нужно вывести только \(1\) значение, поэтому мы выводим \(5\). В \(4\) запросе первый путь — только вершина \(5\), что приводит к мультинабору \(\{3\}\), а второй путь — \(4 \rightarrow 2 \rightarrow 1 \rightarrow 3\) дает \(\{4, 2, 5, 3\}\). Числа \(5\), \(2\) и \(4\) встречаются разное количество раз. | |
![]()
|
|
C. Нарисуйте дерево
геометрия
Деревья
Конструктив
разделяй и властвуй
сортировки
*2200
Даны дерево с n вершинами и n точек на плоскости, никакие три из которых не лежат на одной прямой. Вам надо нарисовать заданное дерево на плоскости, используя заданные точки в качестве вершин. То есть каждой вершине дерева нужно сопоставить ровно одну точку, и каждая точка должна быть сопоставлена какой-либо вершине. Если две вершины дерева соединены ребром, между соответствующими точками должен быть нарисован отрезок. Отрезки, соответствующие несмежным ребрам, не должны иметь общих точек. Отрезки, соответствующие смежным ребрам, должны иметь ровно одну общую точку. Выходные данные Выведите n различных целых чисел от 1 до n через пробел: i-ое число должно равняться номеру вершины, которую надо поместить в i-ую точку (точки нумеруются в порядке их перечисления во входных данных). Если существует несколько решений, выведите любое. Примечание Возможные ответы для примеров приведены ниже.   | |
![]()
|
|
C. Дерево Фенвика
битмаски
Деревья
дп
Комбинаторика
математика
Перебор
Структуры данных
*2300
Пусть \(\operatorname{lowbit}(x)\) обозначает значение младшего двоичного бита \(x\), например, \(\operatorname{lowbit}(12)=4\), \(\operatorname{lowbit}(8)=8\). Для массива \(a\) длины \(n\), если массив \(s\) длины \(n\) удовлетворяет условию \(s_k=\left(\sum\limits_{i=k-\operatorname{lowbit}(k)+1}^{k}a_i\right)\bmod 998\,244\,353\) для всех \(k\), то \(s\) называется Деревом Фенвика массива \(a\). Обозначим его как \(s=f(a)\). Для целого положительного числа \(k\) и массива \(a\), \(f^k(a)\) определяется следующим образом: \(\) f^k(a)= \begin{cases} f(a)&\textrm{если }k=1\\ f(f^{k-1}(a))&\textrm{иначе.}\\ \end{cases} \(\) Вам дан массив \(b\) длины \(n\) и целое положительное число \(k\). Найдите массив \(a\), который удовлетворяет условию \(0\le a_i < 998\,244\,353\) и \(f^k(a)=b\). Можно доказать, что ответ всегда существует. Если существует несколько ответов, вы можете вывести любой из них. Выходные данные Для каждого набора входных данных выведите одну строку, содержащую корректный массив \(a\) длины \(n\). Примечание Из первого набора входных данных видно, что \(f^1([1,1,1,1,1,1,1,1])=[1,2,1,4,1,2,1,8]\). Во втором наборе входных данных видно, что \(f^2([1,2,3,4,5,6])=f^1([1,3,3,10,5,11])=[1,4,3,17,5,16]\). | |
![]()
|
|
A2. Balanced Unshuffle (Medium)
Деревья
Конструктив
Перебор
*2400
The differences with the easy version of this problem are highlighted in bold. A parentheses sequence is a string consisting of characters "(" and ")", for example "(()((". A balanced parentheses sequence is a parentheses sequence which can become a valid mathematical expression after inserting numbers and operations into it, for example "(()(()))". The balance of a parentheses sequence is defined as the number of opening parentheses "(" minus the number of closing parentheses ")". For example, the balance of the sequence "(()((" is 3. A balanced parentheses sequence can also be defined as a parentheses sequence with balance 0 such that each of its prefixes has a non-negative balance. We define the balanced shuffle operation that takes a parentheses sequence and returns a parentheses sequence as follows: first, for every character of the input sequence, we compute the balance of the prefix of the sequence before that character and write those down in a table together with the positions of the characters in the input sequence, for example: | Prefix balance | 0 | 1 | 2 | 1 | 2 | 3 | 2 | 1 | | Position | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | | Character | ( | ( | ) | ( | ( | ) | ) | ) |
Then, we sort the columns of this table in increasing order of prefix balance, breaking ties in decreasing order of position. In the above example, we get: | Prefix balance | 0 | 1 | 1 | 1 | 2 | 2 | 2 | 3 | | Position | 1 | 8 | 4 | 2 | 7 | 5 | 3 | 6 | | Character | ( | ) | ( | ( | ) | ( | ) | ) |
The last row of this table forms another parentheses sequence, in this case "()(()())". This sequence is called the result of applying the balanced shuffle operation to the input sequence, or in short just the balanced shuffle of the input sequence. Surprisingly, it turns out that the balanced shuffle of any balanced parentheses sequence is always another balanced parentheses sequence (we will omit the proof for brevity). Even more surprisingly, the balanced shuffles of two different balanced parentheses sequences are always different, therefore the balanced shuffle operation is a bijection on the set of balanced parentheses sequences of any given length (we will omit this proof, too). You are given a balanced parentheses sequence. Find its preimage: the balanced parentheses sequence the balanced shuffle of which is equal to the given sequence. Output Print the balanced parentheses sequence \(t\) such that the balanced shuffle of \(t\) is equal to \(s\). It is guaranteed that the answer always exists and is unique. | |
![]()
|
|
A3. Balanced Unshuffle (Hard)
Деревья
Конструктив
*2400
The only difference with the medium version is the maximum length of the input. A parentheses sequence is a string consisting of characters "(" and ")", for example "(()((". A balanced parentheses sequence is a parentheses sequence which can become a valid mathematical expression after inserting numbers and operations into it, for example "(()(()))". The balance of a parentheses sequence is defined as the number of opening parentheses "(" minus the number of closing parentheses ")". For example, the balance of the sequence "(()((" is 3. A balanced parentheses sequence can also be defined as a parentheses sequence with balance 0 such that each of its prefixes has a non-negative balance. We define the balanced shuffle operation that takes a parentheses sequence and returns a parentheses sequence as follows: first, for every character of the input sequence, we compute the balance of the prefix of the sequence before that character and write those down in a table together with the positions of the characters in the input sequence, for example: | Prefix balance | 0 | 1 | 2 | 1 | 2 | 3 | 2 | 1 | | Position | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | | Character | ( | ( | ) | ( | ( | ) | ) | ) |
Then, we sort the columns of this table in increasing order of prefix balance, breaking ties in decreasing order of position. In the above example, we get: | Prefix balance | 0 | 1 | 1 | 1 | 2 | 2 | 2 | 3 | | Position | 1 | 8 | 4 | 2 | 7 | 5 | 3 | 6 | | Character | ( | ) | ( | ( | ) | ( | ) | ) |
The last row of this table forms another parentheses sequence, in this case "()(()())". This sequence is called the result of applying the balanced shuffle operation to the input sequence, or in short just the balanced shuffle of the input sequence. Surprisingly, it turns out that the balanced shuffle of any balanced parentheses sequence is always another balanced parentheses sequence (we will omit the proof for brevity). Even more surprisingly, the balanced shuffles of two different balanced parentheses sequences are always different, therefore the balanced shuffle operation is a bijection on the set of balanced parentheses sequences of any given length (we will omit this proof, too). You are given a balanced parentheses sequence. Find its preimage: the balanced parentheses sequence the balanced shuffle of which is equal to the given sequence. Output Print the balanced parentheses sequence \(t\) such that the balanced shuffle of \(t\) is equal to \(s\). It is guaranteed that the answer always exists and is unique. | |
![]()
|
|
C2. Game on Tree (Medium)
Деревья
дп
игры
поиск в глубину и подобное
*1700
This is the medium version of the problem. The difference in this version is that \(t=1\) and we work on trees. Ron and Hermione are playing a game on a tree of \(n\) nodes that are initially inactive. The game consists of \(t\) rounds, each of which starts with a stone on exactly one node, which is considered as activated. A move consists of picking an inactive neighbor of the node with a stone on it and moving the stone there (thus activating this neighbor). Ron makes the first move, after which he alternates with Hermione until no valid move is available. The player that cannot make a move loses the round. If both players play optimally, who wins each round of this game? Note that all the rounds are played with the same tree; only the starting node changes. Moreover, after each round, all active nodes are considered inactive again. Output The output consists of \(t=1\) line which is either "Ron" or "Hermione". | |
![]()
|
|
C3. Game on Tree (Hard)
Деревья
дп
игры
поиск в глубину и подобное
*1900
This is the hard version of the problem. The only difference in this version is the constraint on \(t\). Ron and Hermione are playing a game on a tree of \(n\) nodes that are initially inactive. The game consists of \(t\) rounds, each of which starts with a stone on exactly one node, which is considered as activated. A move consists of picking an inactive neighbor of the node with a stone on it and moving the stone there (thus activating this neighbor). Ron makes the first move, after which he alternates with Hermione until no valid move is available. The player that cannot make a move loses the round. If both players play optimally, who wins each round of this game? Note that all the rounds are played with the same tree; only the starting node changes. Moreover, after each round, all active nodes are considered inactive again. Output The output consists of \(t\) lines, each line being either "Ron" or "Hermione". | |
![]()
|
|
G1. Min-Fund Prison (Easy)
Деревья
поиск в глубину и подобное
*1900
In the easy version, \(m = n-1\) and there exists a path between \(u\) and \(v\) for all \(u, v\) (\(1 \leq u, v \leq n\)). After a worker's strike organized by the Dementors asking for equal rights, the prison of Azkaban has suffered some damage. After settling the spirits, the Ministry of Magic is looking to renovate the prison to ensure that the Dementors are kept in check. The prison consists of \(n\) prison cells and \(m\) bi-directional corridors. The \(i^{th}\) corridor is from cells \(u_i\) to \(v_i\). A subset of these cells \(S\) is called a complex if any cell in \(S\) is reachable from any other cell in \(S\). Formally, a subset of cells \(S\) is a complex if \(x\) and \(y\) are reachable from each other for all \(x, y \in S\), using only cells from \(S\) on the way. The funding required for a complex \(S\) consisting of \(k\) cells is defined as \(k^2\). As part of your Intro to Magical Interior Design course at Hogwarts, you have been tasked with designing the prison. The Ministry of Magic has asked that you divide the prison into \(2\) complexes with \(\textbf{exactly one corridor}\) connecting them, so that the Dementors can't organize union meetings. For this purpose, you are allowed to build bi-directional corridors. The funding required to build a corridor between any \(2\) cells is \(c\). Due to budget cuts and the ongoing fight against the Death Eaters, you must find the \(\textbf{minimum total funding}\) required to divide the prison as per the Ministry's requirements or \(-1\) if no division is possible. Note: The total funding is the sum of the funding required for the \(2\) complexes and the corridors built. If after the division, the two complexes have \(x\) and \(y\) cells respectively and you have built a total of \(a\) corridors, the total funding will be \(x^2 + y^2 + c \times a\). Note that \(x+y=n\). Output Print the \(\textbf{minimum funding}\) required to divide the prison as per the Ministry's requirements or \(-1\) if no division is possible. | |
![]()
|
|
G2. Min-Fund Prison (Medium)
графы
Деревья
дп
Перебор
поиск в глубину и подобное
*2200
In the medium version, \(2 \leq \sum n \leq 300\) and \(1 \leq \sum m \leq 300\) After a worker's strike organized by the Dementors asking for equal rights, the prison of Azkaban has suffered some damage. After settling the spirits, the Ministry of Magic is looking to renovate the prison to ensure that the Dementors are kept in check. The prison consists of \(n\) prison cells and \(m\) bi-directional corridors. The \(i^{th}\) corridor is from cells \(u_i\) to \(v_i\). A subset of these cells \(S\) is called a complex if any cell in \(S\) is reachable from any other cell in \(S\). Formally, a subset of cells \(S\) is a complex if \(x\) and \(y\) are reachable from each other for all \(x, y \in S\), using only cells from \(S\) on the way. The funding required for a complex \(S\) consisting of \(k\) cells is defined as \(k^2\). As part of your Intro to Magical Interior Design course at Hogwarts, you have been tasked with designing the prison. The Ministry of Magic has asked that you divide the prison into \(2\) complexes with \(\textbf{exactly one corridor}\) connecting them, so that the Dementors can't organize union meetings. For this purpose, you are allowed to build bi-directional corridors. The funding required to build a corridor between any \(2\) cells is \(c\). Due to budget cuts and the ongoing fight against the Death Eaters, you must find the \(\textbf{minimum total funding}\) required to divide the prison as per the Ministry's requirements or \(-1\) if no division is possible. Note: The total funding is the sum of the funding required for the \(2\) complexes and the corridors built. If after the division, the two complexes have \(x\) and \(y\) cells respectively and you have built a total of \(a\) corridors, the total funding will be \(x^2 + y^2 + c \times a\). Note that \(x+y=n\). Output Print the \(\textbf{minimum funding}\) required to divide the prison as per the Ministry's requirements or \(-1\) if no division is possible. Note In the first test case of the sample input, there is no way to divide the prison according to the Ministry's requirements. In the second test case, consider the corridor between cells \(1\) and \(5\) as the connection between the \(2\) complexes consisting of \(\{2, 3, 5, 6\}\) and \(\{1, 4\}\) cells respectively. There are no new corridors built. The total funding is \(4^2 + 2^2 = 20\). You can verify this is the minimum funding required.  In the third test case, build a corridor between \(2\) and \(4\). Consider the corridor between cells \(1\) and \(5\) as the connection between the \(2\) complexes consisting of \(\{3, 5, 6\}\) and \(\{1, 2, 4\}\) cells respectively. The total funding is \(3^2 + 3^2 + 7 \times 1 = 25\). You can verify this is the minimum funding required.  In the fourth test case, build a corridor between \(2\) and \(4\) and between \(5\) and \(7\). Consider the corridor between cells \(5\) and \(7\) as the connection between the \(2\) complexes consisting of \(\{1, 2, 4, 7\}\) and \(\{3, 5, 6\}\) cells respectively. The total funding is \(4^2 + 3^2 + 4 \times 2 = 33\). You can verify this is the minimum funding required.  Note for all test cases that there may be multiple ways to get the same funding but there is no other division which will have a more optimal minimum funding. | |
![]()
|
|
G3. Min-Fund Prison (Hard)
битмаски
графы
Деревья
дп
поиск в глубину и подобное
*2400
In the hard version, \(2 \leq \sum n \leq 10^5\) and \(1 \leq \sum m \leq 5 \times 10^{5}\) After a worker's strike organized by the Dementors asking for equal rights, the prison of Azkaban has suffered some damage. After settling the spirits, the Ministry of Magic is looking to renovate the prison to ensure that the Dementors are kept in check. The prison consists of \(n\) prison cells and \(m\) bi-directional corridors. The \(i^{th}\) corridor is from cells \(u_i\) to \(v_i\). A subset of these cells \(S\) is called a complex if any cell in \(S\) is reachable from any other cell in \(S\). Formally, a subset of cells \(S\) is a complex if \(x\) and \(y\) are reachable from each other for all \(x, y \in S\), using only cells from \(S\) on the way. The funding required for a complex \(S\) consisting of \(k\) cells is defined as \(k^2\). As part of your Intro to Magical Interior Design course at Hogwarts, you have been tasked with designing the prison. The Ministry of Magic has asked that you divide the prison into \(2\) complexes with \(\textbf{exactly one corridor}\) connecting them, so that the Dementors can't organize union meetings. For this purpose, you are allowed to build bi-directional corridors. The funding required to build a corridor between any \(2\) cells is \(c\). Due to budget cuts and the ongoing fight against the Death Eaters, you must find the \(\textbf{minimum total funding}\) required to divide the prison as per the Ministry's requirements or \(-1\) if no division is possible. Note: The total funding is the sum of the funding required for the \(2\) complexes and the corridors built. If after the division, the two complexes have \(x\) and \(y\) cells respectively and you have built a total of \(a\) corridors, the total funding will be \(x^2 + y^2 + c \times a\). Note that \(x+y=n\). Output Print the \(\textbf{minimum funding}\) required to divide the prison as per the Ministry's requirements or \(-1\) if no division is possible. Note In the first test case of the sample input, there is no way to divide the prison according to the Ministry's requirements. In the second test case, consider the corridor between cells \(1\) and \(5\) as the connection between the \(2\) complexes consisting of \(\{2, 3, 5, 6\}\) and \(\{1, 4\}\) cells respectively. There are no new corridors built. The total funding is \(4^2 + 2^2 = 20\). You can verify this is the minimum funding required.  In the third test case, build a corridor between \(2\) and \(4\). Consider the corridor between cells \(1\) and \(5\) as the connection between the \(2\) complexes consisting of \(\{3, 5, 6\}\) and \(\{1, 2, 4\}\) cells respectively. The total funding is \(3^2 + 3^2 + 7 \times 1 = 25\). You can verify this is the minimum funding required.  In the fourth test case, build a corridor between \(2\) and \(4\) and between \(5\) and \(7\). Consider the corridor between cells \(5\) and \(7\) as the connection between the \(2\) complexes consisting of \(\{1, 2, 4, 7\}\) and \(\{3, 5, 6\}\) cells respectively. The total funding is \(4^2 + 3^2 + 4 \times 2 = 33\). You can verify this is the minimum funding required.  Note for all test cases that there may be multiple ways to get the same funding but there is no other division which will have a more optimal minimum funding. | |
![]()
|
|
D. Раскрасьте дерево
Деревья
дп
жадные алгоритмы
кратчайшие пути
Перебор
поиск в глубину и подобное
*1700
У 378QAQ есть дерево с \(n\) вершинами. Изначально все вершины белые. На дереве есть две шахматные фигуры с названиями \(P_A\) и \(P_B\). \(P_A\) и \(P_B\) изначально расположены на вершинах \(a\) и \(b\) соответственно. За один шаг 378QAQ выполняет следующие действия по порядку: - Переместить \(P_A\) в соседнюю вершину. Если вершина, в которую переместилась фигура, белая, то перекрасить эту вершину в красный цвет.
- Переместить \(P_B\) в соседнюю вершину. Если вершина, в которую переместилась фигура, красная, то перекрасить эту вершину в синий цвет.
Изначально вершина \(a\) окрашена в красный цвет. Если \(a=b\), то вместо этого вершина \(a\) окрашена в синий цвет. Обратите внимание, что на каждом шаге обе шахматные фигуры должны быть перемещены. Две фигуры могут находиться в одной вершине в любой момент времени. 378QAQ хочет узнать минимальное количество шагов, которое требуется, чтобы покрасить все вершины в синий цвет. Выходные данные Для каждого набора входных данных выведите минимальное количество шагов, которое требуется, чтобы покрасить все вершины в синий цвет. Примечание В первом наборе входных данных 378QAQ может покрасить все вершины в синий цвет следующим образом: - Изначально \(P_A\) находится в вершине \(1\), а \(P_B\) — в вершине \(2\). Вершина \(1\) окрашена в красный цвет, а вершина \(2\) — в белый.
- 378QAQ перемещает \(P_A\) в вершину \(2\) и красит ее в красный цвет. Затем 378QAQ перемещает \(P_B\) в вершину \(1\) и красит её в синий цвет.
- 378QAQ перемещает \(P_A\) в вершину \(1\). Затем 378QAQ перемещает \(P_B\) в вершину \(2\) и закрашивает её синим цветом.
| |
![]()
|
|
E. Цепные запросы
Бинарный поиск
Деревья
поиск в глубину и подобное
реализация
Структуры данных
*2100
Вам дано дерево из \(n\) вершин, пронумерованных от \(1\) до \(n\). Изначально все вершины окрашены в белый или черный цвет. Вам предлагается выполнить \(q\) запросов: - «u» — поменять цвет вершины \(u\) (если она была белой, то поменять на черную и наоборот).
После каждого запроса вы должны ответить, образуют ли все черные вершины цепочку. То есть существуют ли две черные вершины такие, что простой путь между ними проходит через все черные вершины и только через черные вершины. В частности, если существует только одна черная вершина, то она образует цепочку. Если черных вершин нет, то они не образуют цепочку. Выходные данные Для каждого запроса выведите «Yes», если черные вершины образуют цепочку, и «No» в противном случае. Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Например, строки «yEs», «yes», «Yes» и «YES» будут приняты как положительный ответ. Примечание Во втором наборе входных данных цвета вершин следующие: Исходное дерево:  Первый запрос меняет цвет вершины \(4\):  Второй запрос меняет цвет вершины \(3\):  Третий запрос меняет цвет вершины \(2\):  Четвертый запрос меняет цвет вершины \(5\):  | |
![]()
|
|
E. Разделяемые перестановки
Деревья
жадные алгоритмы
Комбинаторика
математика
поиск в глубину и подобное
Структуры данных
*2500
Изначально у нас был один массив — перестановка размера \(n\) (массив размера \(n\), где каждое целое число от \(1\) до \(n\) встречается ровно один раз). Мы провели \(q\) операций. В ходе \(i\)-й операции мы сделали следующее: - выбрали любой из имеющихся у нас массивов размера хотя бы \(2\);
- разделили его на две непустых части (префикс и суффикс);
- записали два числа \(l_i\) и \(r_i\), где \(l_i\) — максимум в левой из полученных частей, а \(r_i\) — максимум в правой из полученных частей;
- удалили массив, который мы разделили, из набора массивов, которые мы можем использовать, а вместо него добавили две полученных части массива.
Например, пусть изначально у нас был массив \([6, 3, 4, 1, 2, 5]\), и мы провели следующие операции: - выбрали массив \([6, 3, 4, 1, 2, 5]\) и разделили его на \([6, 3]\) и \([4, 1, 2, 5]\). Затем мы записали \(l_1 = 6\) и \(r_1 = 5\), и в следующих операциях нам доступны массивы \([6, 3]\) и \([4, 1, 2, 5]\);
- выбрали массив \([4, 1, 2, 5]\) и разделили его на \([4, 1, 2]\) и \([5]\). Затем мы записали \(l_2 = 4\) и \(r_2 = 5\), и в следующих операциях нам доступны массивы \([6, 3]\), \([4, 1, 2]\) и \([5]\);
- выбрали массив \([4, 1, 2]\) и разделили его на \([4]\) и \([1, 2]\). Затем мы записали \(l_3 = 4\) и \(r_3 = 2\), и в следующих операциях нам доступны массивы \([6, 3]\), \([4]\), \([1, 2]\) и \([5]\).
Даны два целых числа \(n\) и \(q\), а также две последовательности \([l_1, l_2, \dots, l_q]\) и \([r_1, r_2, \dots, r_q]\). Перестановку размера \(n\) назовем подходящей, если можно провести на ней \(q\) операций и получить заданные последовательности \([l_1, l_2, \dots, l_q]\) и \([r_1, r_2, \dots, r_q]\). Посчитайте количество подходящих перестановок. Выходные данные Выведите одно целое число — количество подходящих перестановок, взятое по модулю \(998244353\). | |
![]()
|
|
F. Удаление мостов
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
сортировки
Структуры данных
*2800
Вам дано корневое дерево, состоящее из \(n\) вершин, пронумерованных от \(1\) до \(n\). Вершина \(1\) является корнем. Кроме того, у корня есть только один ребенок. Требуется добавить ровно \(k\) рёбер в дерево (возможно, кратные рёбра и/или рёбра, уже существующие в дереве). Напомним, что мост — это такое ребро, что после его удаления количество компонент связности в графе увеличивается. Таким образом, изначально все рёбра дерева являются мостами. После добавления \(k\) рёбер некоторые изначальные рёбра дерева остаются мостами, а некоторые перестают ими быть. Необходимо удовлетворить два условия: - для каждого моста все рёбра дерева в поддереве нижней вершины этого моста также должны быть мостами;
- количество мостов должно быть как можно меньше.
Решите задачу для всех значений \(k\) от \(1\) до \(n - 1\) и выведите наименьшее количество мостов. Выходные данные Для каждого набора входных данных выведите \(n - 1\) целое число. Для каждого \(k\) от \(1\) до \(n - 1\) выведите наименьшее количество мостов, которые могут остаться после добавления \(k\) рёбер в дерево. | |
![]()
|
|
G. Яся и таинственное дерево
битмаски
графы
Деревья
жадные алгоритмы
поиск в глубину и подобное
Строки
Структуры данных
*2300
Яся гуляла по лесу и совершенно случайно нашла дерево на \(n\) вершинах. Дерево — это связный неориентированный граф, в котором отсутствуют циклы. Рядом с деревом девочка нашла древний манускрипт, на котором записаны \(m\) запросов. Запросы бывают двух видов. Первый вид запросов описывается числом \(y\). Вес каждого ребра в дереве заменяется на побитовое исключающее «ИЛИ» веса этого ребра и числа \(y\). Второй вид описывается вершиной \(v\) и числом \(x\). Яся выбирает вершину \(u\) (\(1 \le u \le n\), \(u \neq v\)) и мысленно проводит в дереве двунаправленное ребро веса \(x\) из \(v\) в \(u\). Затем Яся находит простой цикл в получившемся графе и считает побитовое исключающее «ИЛИ» от всех рёбер на нём. Она хочет выбрать такую вершину \(u\), чтобы посчитанное значение было максимально. Это посчитанное значение и будет ответом на запрос. Можно показать существование и единственность такого цикла в указанных ограничениях (независимо от выбора \(u\)). Если ребро между \(v\) и \(u\) уже существовало, простым циклом будет путь \(v \to u \to v\). Обратите внимание, что запрос второго типа выполняется мысленно, то есть дерево после него никак не меняется. Помогите Ясе ответить на все запросы. Выходные данные Для каждого набора входных данных выведите ответы на запросы второго типа. | |
![]()
|
|
F. Черепаха и пути на дереве
Деревья
дп
Структуры данных
*3000
Обратите внимание на необычное определение \(\text{MEX}\) в этой задаче. Свинка подарила Черепахе бинарное дерево\(^{\dagger}\) с \(n\) вершинами и последовательностью \(a_1, a_2, \ldots, a_n\) на ее день рождения. Бинарное дерево имеет корень в вершине \(1\). Если набор путей \(P = \{(x_i, y_i)\}\) в дереве покрывает каждое ребро ровно один раз, то Черепаха считает, что набор путей хороший. Обратите внимание, что хороший набор путей может покрывать вершину дважды или более. Черепаха определяет значение набора путей как \(\sum\limits_{(x, y) \in P} f(x, y)\), где \(f(x, y)\) обозначает \(\text{MEX}^{\ddagger}\) всех \(a_u\), таких что вершина \(u\) лежит на простом пути от \(x\) до \(y\) в дереве (включая начальную вершину \(x\) и конечную вершину \(y\)). Черепаха задается вопросом о минимальном значении среди всех хороших наборов путей. Пожалуйста, помогите ему вычислить ответ! \(^{\dagger}\)Бинарное дерево — это дерево, в котором у каждой вершины есть не более \(2\) сыновей. \(^{\ddagger}\text{MEX}\) набора целых чисел \(c_1, c_2, \ldots, c_k\) определяется как наименьшее положительное целое число \(x\), которое не встречается в наборе \(c\). Например, \(\text{MEX}\) для \([3, 3, 1, 4]\) равно \(2\), \(\text{MEX}\) для \([2, 3]\) равно \(1\). Выходные данные Для каждого тестового случая выведите одно целое число — минимальное значение среди всех хороших наборов путей. Примечание В первом тестовом случае дерево выглядит следующим образом. Число в скобках обозначает вес вершины:  Хороший набор путей с минимальным значением — \(\{(2, 3), (4, 5)\}\). Обратите внимание, что в этом тестовом случае \(\{(4, 5)\}\) и \(\{(3, 4), (4, 5)\}\) не являются хорошими наборами путей, потому что каждое ребро должно быть покрыто ровно один раз. Во втором тестовом случае дерево выглядит следующим образом:  Набор хороших путей с минимальным значением — \(\{(1, 2), (1, 3), (4, 5)\}\). В третьем тестовом случае дерево выглядит следующим образом:  Набор хороших путей с минимальным значением — \(\{(1, 6), (3, 5)\}\). | |
![]()
|
|
G. Ваша потеря
битмаски
Деревья
дп
Перебор
*3000
Вам дано дерево с \(n\) вершинами, пронумерованными от \(1\) до \(n\), а также массив длины \(n\). Значение \(i\)-й вершины — \(a_{i}\). Имеется \(q\) запросов. В каждом запросе даны 2 вершины с номерами \(x\) и \(y\). Рассмотрим путь от вершины с номером \(x\) до вершины с номером \(y\). Пусть путь представлен в виде \(x = p_0, p_1, p_2, \ldots, p_r = y\), где \(p_i\) — промежуточные вершины. Вычислите сумму \(a_{p_i}\oplus i\) по всем \(i\) таким, что \(0 \le i \le r\), где \(\oplus\) обозначает операцию побитового исключающего ИЛИ. Более формально, вычислите \(\)\sum_{i =0}^{r} a_{p_i}\oplus i\(\) Выходные данные Для каждого запроса выведите одно число — искомую сумму. | |
![]()
|
|
E. Перемешивание
Деревья
дп
жадные алгоритмы
*2400
Две голодные красные панды, Оскар и Лура, получили в подарок дерево \(T\) с \(n\) вершинами. Они хотят выполнить следующую процедуру перемешивания для всего дерева \(T\) ровно один раз. С помощью этой процедуры они создадут новое дерево из вершин старого дерева: - Выбрать любую вершину \(V\) из исходного дерева \(T\). Создать новое дерево \(T_2\) с \(V\) в качестве корня.
- Удалить \(V\) из \(T\) так, чтобы исходное дерево было разбито на одно или несколько поддеревьев (или ноль поддеревьев, если \(V\) является единственной вершиной в \(T\)).
- Перемешать каждое поддерево с помощью той же процедуры (снова выбирая любую вершину в качестве корня), затем соединить корни всех перетасованных поддеревьев с \(V\), чтобы закончить построение \(T_2\).
После этого у Оскара и Луры остается новое дерево \(T_2\). Они могут есть только листья и очень голодны. Поэтому они просят вас помочь им найти максимальное количество листьев среди всех деревьев, которое можно получить за ровно одно перемешивание. Обратите внимание, что листья — это все вершины со степенью \(1\). Таким образом, корень может считаться листом, если у него есть только один ребенок. Выходные данные Для каждого набора входных данных выведите одно целое число — максимальное количество листьев, достижимое с помощью одной операции. Примечание В первом наборе входных данных можно показать, что максимальное количество листьев равно \(4\). Для этого мы можем начать перемешивание с выбора вершины \(3\) в качестве нового корня.  Далее у нас остается только одно поддерево, в котором мы можем выбрать вершину \(2\) в качестве нового корня этого поддерева.  Это заставит все оставшиеся \(3\) вершины стать листьями, и когда мы присоединим их обратно к нашему новому корню, перемешанное поддерево будет выглядеть так:  Мы соединяем перемешанное поддерево обратно с корнем нашего нового дерева. Наше конечное дерево имеет четыре листа (включая корень) и выглядит следующим образом:  Во втором наборе входных данных у нас есть бамбук из пяти вершин. Можно показать, что максимальное количество листьев после одного перемешивания составляет \(3\). Мы можем начать с вершины \(2\), которая заставит вершину \(1\) стать листом. Затем, если мы выберем вершину \(4\) с правой стороны, вершины \(3\) и \(5\) также окажутся листьями. Третий набор входных данных представляет собой граф-звезду с шестью вершинами. Количество листьев не может увеличиться, поэтому наш ответ будет равен \(5\) (если мы начнем перемешивание с исходной корневой вершины). | |
![]()
|
|
F. Внеучебная задача
графы
Деревья
поиск в глубину и подобное
*1900
Вам дан связный неориентированный граф, вершины которого пронумерованы целыми числами от \(1\) до \(n\). Ваша задача минимизировать количество пар вершин \(1 \leq u < v \leq n\), между которыми существует путь в этом графе. Для этого вы можете удалить ровно одно любое ребро из графа. Найдите это наименьшее количество пар вершин! Выходные данные Для каждого набора входных данных выведите наименьшее количество пар достижимых друг из друга вершин, если можно удалить ровно одно ребро. Примечание В первом наборе входных данных мы удалим единственное ребро \((1, 2)\) и единственная пара вершин \((1, 2)\) станет не достижима друг из друга. Во втором наборе входных данных какое бы ребро мы не удалили, все вершины будут достижимы друг из друга. В четвертом наборе входных данных так выглядит граф изначально.  Мы удалим ребро \((3, 4)\) и тогда достижимы друг из друга будут только пары вершин \((1, 2)\), \((1, 3)\), \((2, 3)\), \((4, 5)\), \((4, 6)\), \((5, 6)\).  В шестом наборе входных данных так выглядит граф изначально.  После удаления ребра \((2, 4)\) граф будет выглядеть следующим образом. Таким образом, будет \(21\) пара достижимых друг из друга вершин.  | |
![]()
|
|
E. Прекрасное дерево!
Деревья
жадные алгоритмы
Перебор
поиск в глубину и подобное
снм
Структуры данных
*2000
Да благословят боги этот прекрасный ArrayForces! Случайная галька Дано дерево с \(n\) вершинами с корнем в вершине \(1\), в \(i\)-й вершине записано целое число \(a_i\). Пусть \(L\) — это множество всех прямых сыновей\(^{\text{∗}}\) вершины \(v\). Назовём дерево прекрасным, если для всех вершин \(v\) с непустым \(L\) верно \(\)a_v \le \sum_{u \in L}{a_u}.\(\) За одну операцию вы можете выбрать любую вершину \(v\) и увеличить значение \(a_v\) на \(1\). Найдите минимальное количество операций, необходимых для того, чтобы сделать данное дерево прекрасным! Выходные данные Для каждого набора входных данных выведите одно целое число — минимальное количество операций, необходимых для того, чтобы сделать данное дерево прекрасным! Примечание Дерево в первом наборе входных данных:  Вы можете применить операцию к вершине \(5\) и дважды к вершине \(2\), чтобы получить прекрасное дерево. Во втором наборе входных данных вы можете два раза применить операцию к вершине \(2\), чтобы получить прекрасное дерево. В третьих и четвёртых наборах входных данных дерево уже прекрасно, поэтому применять операций не надо. | |
![]()
|
|
G1. Очень круглый спин (простая версия)
Деревья
дп
разделяй и властвуй
*2900
Это простая версия задачи. Разница между простой и сложной версиями задачи заключается только в допустимых символах в \(s\). В простой версии строка \(s\) содержит только символ ?. Вы можете делать взломы только в том случае, если обе версии задачи решены. Дана перестановка \(p\) длины \(n\). Также дана строка \(s\) длины \(n\), содержащая только символ ?. Для каждого \(i\) от \(1\) до \(n\): - Определим \(l_i\) как наибольший индекс \(j < i\) такой, что \(p_j > p_i\). Если такого индекса не существует, \(l_i := i\).
- Определим \(r_i\) как наименьший индекс \(j > i\) такой, что \(p_j > p_i\). Если такого индекса не существует, \(r_i := i\).
Изначально есть неориентированный граф с \(n\) вершинами (пронумерованными от \(1\) до \(n\)) и без рёбер. Затем для каждого \(i\) от \(1\) до \(n\) в граф добавляется одно ребро: - Если \(s_i =\) L, в граф добавляется ребро \((i, l_i)\).
- Если \(s_i =\) R, в граф добавляется ребро \((i, r_i)\).
- Если \(s_i =\) ?, в граф добавляется либо ребро \((i, l_i)\), либо ребро \((i, r_i)\) по вашему выбору.
Найдите максимально возможный диаметр\(^{\text{∗}}\) среди всех связных графов, которые вы можете получить. Выведите \(-1\), если невозможно получить ни один связный граф. Выходные данные Для каждого набора входных данных выведите одно целое число — максимальный диаметр среди всех связных графов, которые вы можете получить, или \(-1\), если таковых нет. Примечание Для первого набора входных данных ниже показаны примеры некоторых графов, которые можно получить (в вершинах написаны индексы): Во втором наборе входных данных у единственного связного графа диаметр равен \(1\). | |
![]()
|
|
G2. Очень круглый спин (сложная версия)
Деревья
дп
разделяй и властвуй
*3500
Это сложная версия задачи. Разница между простой и сложной версиями задачи заключается только в допустимых символах в \(s\). Вы можете делать взломы только в том случае, если обе версии задачи решены. Дана перестановка \(p\) длины \(n\). Также дана строка \(s\) длины \(n\), содержащая только символы L, R и ?. Для каждого \(i\) от \(1\) до \(n\): - Определим \(l_i\) как наибольший индекс \(j < i\) такой, что \(p_j > p_i\). Если такого индекса не существует, \(l_i := i\).
- Определим \(r_i\) как наименьший индекс \(j > i\) такой, что \(p_j > p_i\). Если такого индекса не существует, \(r_i := i\).
Изначально есть неориентированный граф с \(n\) вершинами (пронумерованными от \(1\) до \(n\)) и без рёбер. Затем для каждого \(i\) от \(1\) до \(n\) в граф добавляется одно ребро: - Если \(s_i =\) L, в граф добавляется ребро \((i, l_i)\).
- Если \(s_i =\) R, в граф добавляется ребро \((i, r_i)\).
- Если \(s_i =\) ?, в граф добавляется либо ребро \((i, l_i)\), либо ребро \((i, r_i)\) по вашему выбору.
Найдите максимально возможный диаметр\(^{\text{∗}}\) среди всех связных графов, которые вы можете получить. Выведите \(-1\), если невозможно получить ни один связный граф. Выходные данные Для каждого набора входных данных выведите одно целое число — максимальный диаметр среди всех связных графов, которые вы можете получить, или \(-1\), если таковых нет. Примечание В первом наборе входных данных можно получить два связных графа (в вершинах написаны индексы): У графа слева диаметр равен \(2\), а у графа справа диаметр равен \(3\), поэтому ответ \(3\). Во втором наборе входных данных нельзя получить связный граф, поэтому ответ \(-1\). | |
![]()
|
|
D. Универсальный убийца монстров
Деревья
дп
Перебор
поиск в глубину и подобное
*2000
Вы, убийца монстров, хотите убить группу монстров. Монстры находятся в дереве с \(n\) вершинами. В вершине с номером \(i\) (\(1\le i\le n\)) находится монстр с \(a_i\) очками атаки. Вы хотите сражаться с монстрами в течение \(10^{100}\) раундов. В каждом раунде происходит следующее по порядку: - Все живые монстры атакуют вас. Ваше здоровье уменьшается на сумму очков атаки всех живых монстров.
- Вы выбираете некоторых (возможно, всех или ни одного) монстров и убиваете их. После убийства монстр больше не сможет совершать атаки в будущем.
Также есть следующее ограничение: за один раунд вы не можете убить двух монстров, находящихся в соединенных ребром вершинах. Если вы оптимально выбираете, каких монстров атаковать на каждом шагу, на какую минимальную величину может уменьшиться ваше здоровье за все раунды? Выходные данные Для каждого набора входных данных выведите одно целое число — минимально возможное уменьшение здоровья. Примечание В первом наборе оптимальная последовательность операций следующая: - В первом раунде: сначала получите атаку от монстра в вершине \(1\), поэтому ваше здоровье уменьшается на \(10^{12}\). Затем убейте монстра в вершине \(1\).
- Во втором раунде до \(10^{100}\)-го раунда: все монстры были убиты, поэтому ничего не происходит.
Общее уменьшение здоровья составляет \(10^{12}\). Во втором наборе оптимальная последовательность операций следующая: - В первом раунде: сначала получите атаку от монстров в вершинах \(1,2,3,4,5\), поэтому ваше здоровье уменьшается на \(47+15+32+29+23=146\). Затем убейте монстров в вершинах \(1,4,5\).
- Во втором раунде: сначала получите атаку от монстров в вершинах \(2,3\), поэтому ваше здоровье уменьшается на \(15+32=47\). Затем убейте монстров в вершинах \(2,3\).
- В третьем раунде до \(10^{100}\)-го раунда: все монстры были убиты, поэтому ничего не происходит.
Общее уменьшение здоровья составляет \(193\). В третьем наборе оптимальная последовательность операций следующая: - В первом раунде: сначала получите атаку от монстров в вершинах \(1,2,3,4,5,6,7\), поэтому ваше здоровье уменьшается на \(8+10+2+3+5+7+4=39\). Затем убейте монстров в вершинах \(1,3,6,7\).
- Во втором раунде: сначала получите атаку от монстров на вершинах \(2,4,5\), поэтому ваше здоровье уменьшается на \(10+3+5=18\). Затем убейте монстров на вершинах \(2,4,5\).
- В третьем раунде до \(10^{100}\)-го раунда: все монстры были убиты, поэтому ничего не происходит.
Общее уменьшение здоровья составляет \(57\). | |
![]()
|
|
E1. Поймай крота (легкая версия)
Бинарный поиск
Деревья
интерактив
поиск в глубину и подобное
Структуры данных
*2500
Это легкая версия задачи. Единственное отличие — это ограничение на количество запросов. Это интерактивная задача. Вам дано дерево из \(n\) вершин с вершиной \(1\) в качестве корневой. В одной из вершин спрятан крот. Чтобы найти его положение, вы можете выбрать вершину \(x\) (\(1 \le x \le n\)) и сделать запрос к жюри. После этого жюри вернет \(1\), если крот находится в поддереве вершины \(x\). В противном случае жюри вернет \(0\). Если жюри возвращает \(0\) и крот не находится в корневой вершине \(1\), крот переместится в вершину-родителя той вершины, в которой он находится в данный момент. Используя не более \(300\) операций, найдите текущую вершину, в которой находится крот. Протокол взаимодействия Первая строка каждого набора входных данных содержит одно целое число \(n\) (\(2 \le n \le 5000\)). Следующая \(n-1\) строка описывает ребра дерева. Каждая строка содержит два целых числа, разделенные пробелом, \(u_i\) и \(v_i\) (\(1 \le u_i, v_i \le n\)), обозначающие ребро между вершинами \(u_i\) и \(v_i\). Гарантируется, что входные данные представляют собой дерево. Интерактор в этой задаче не является адаптивным. Другими словами, вершина, где изначально находится крот, зафиксирована в каждом наборе входных данных и не меняется во время взаимодействия. Чтобы сделать запрос, вам нужно выбрать вершину \(x\) (\(1 \le x \le n\)) и вывести строку следующего вида: После этого вы получите: - \(0\), если крот не находится в поддереве \(x\);
- \(1\), если крот находится в поддереве \(x\).
Вы можете сделать не более \(300\) запросов такого вида для каждого набора входных данных. Затем, если вы определили текущую вершину, где находится крот, выведите строку следующего вида: Обратите внимание, что эта строка не считается запросом и не учитывается при подсчете количества заданных запросов. После этого переходите к следующему набору входных данных. Если вы сделаете более \(300\) запросов во время взаимодействия, ваша программа должна немедленно завершиться, и вы получите вердикт Неправильный ответ. В противном случае вы можете получить произвольный вердикт, потому что ваше решение будет продолжать читать из закрытого потока. После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Взломы Чтобы сделать взлом, используйте следующий формат: Первая строка содержит количество наборов входных данных \(t\) (\(1 \le t \le 100\)). Далее следует описание наборов входных данных. Первая строка каждого набора входных данных содержит два целых числа \(n\) и \(x\) (\(2 \le n \le 5000\), \(1 \le x \le n\)), описывающие размер дерева и начальное положение крота. Следующая \(n-1\) строка описывает ребра дерева. Каждая строка содержит два целых числа, разделенные пробелом, \(u_i\) и \(v_i\) (\(1 \le u_i, v_i \le n\)), обозначающие ребро между вершинами \(u_i\) и \(v_i\). Входные данные обязаны представлять собой дерево. Примечание В первом наборе входных данных крот изначально находится в вершине \(2\). Для запроса «? 2», жюри возвращает \(1\), потому что крот находится в поддереве вершины \(2\). После этого запроса крот не перемещается. Ответ \(2\) — это текущая вершина, где находится крот, поэтому ответ считается правильным. Во втором наборе входных данных крот изначально находится в вершине \(6\). Для запроса «? 2», жюри возвращает \(0\), потому что крот не находится в поддереве вершины \(2\). После этого запроса крот перемещается из вершины \(6\) в вершину \(5\). Для запроса «? 6», жюри возвращает \(0\), потому что крот не находится в поддереве вершины \(6\). После этого запроса крот перемещается из вершины \(5\) в вершину \(4\). Для запроса «? 4», жюри возвращает \(1\), потому что крот находится в поддереве вершины \(4\). После этого запроса крот не перемещается. Ответ \(4\) — это текущая вершина, где находится крот, поэтому ответ считается правильным. Обратите внимание, что приведенный пример предназначен только для понимания условия, и запросы в примере не гарантируют определение уникального положения крота. | |
![]()
|
|
E2. Поймай крота (сложная версия)
Бинарный поиск
Деревья
интерактив
поиск в глубину и подобное
разделяй и властвуй
Структуры данных
*2600
Это сложная версия задачи. Единственное отличие — это ограничение на количество запросов. Это интерактивная задача. Вам дано дерево из \(n\) вершин с вершиной \(1\) в качестве корневой. В одной из вершин спрятан крот. Чтобы найти его положение, вы можете выбрать вершину \(x\) (\(1 \le x \le n\)) и сделать запрос к жюри. После этого жюри вернет \(1\), если крот находится в поддереве вершины \(x\). В противном случае жюри вернет \(0\). Если жюри возвращает \(0\) и крот не находится в корневой вершине \(1\), крот переместится в вершину-родителя той вершины, в которой он находится в данный момент. Используя не более \(160\) операций, найдите текущую вершину, в которой находится крот. Протокол взаимодействия Первая строка каждого набора входных данных содержит одно целое число \(n\) (\(2 \le n \le 5000\)). Следующая \(n-1\) строка описывает ребра дерева. Каждая строка содержит два целых числа, разделенные пробелом, \(u_i\) и \(v_i\) (\(1 \le u_i, v_i \le n\)), обозначающие ребро между вершинами \(u_i\) и \(v_i\). Гарантируется, что входные данные представляют собой дерево. Интерактор в этой задаче не является адаптивным. Другими словами, вершина, где изначально находится крот, зафиксирована в каждом наборе входных данных и не меняется во время взаимодействия. Чтобы сделать запрос, вам нужно выбрать вершину \(x\) (\(1 \le x \le n\)) и вывести строку следующего вида: После этого вы получите: - \(0\), если крот не находится в поддереве \(x\);
- \(1\), если крот находится в поддереве \(x\).
Вы можете сделать не более \(160\) запросов такого вида для каждого набора входных данных. Затем, если вы определили текущую вершину, где находится крот, выведите строку следующего вида: Обратите внимание, что эта строка не считается запросом и не учитывается при подсчете количества заданных запросов. После этого переходите к следующему набору входных данных. Если вы сделаете более \(160\) запросов во время взаимодействия, ваша программа должна немедленно завершиться, и вы получите вердикт Неправильный ответ. В противном случае вы можете получить произвольный вердикт, потому что ваше решение будет продолжать читать из закрытого потока. После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Взломы Чтобы сделать взлом, используйте следующий формат: Первая строка содержит количество наборов входных данных \(t\) (\(1 \le t \le 100\)). Далее следует описание наборов входных данных. Первая строка каждого набора входных данных содержит два целых числа \(n\) и \(x\) (\(2 \le n \le 5000\), \(1 \le x \le n\)), описывающие размер дерева и начальное положение крота. Следующая \(n-1\) строка описывает ребра дерева. Каждая строка содержит два целых числа, разделенные пробелом, \(u_i\) и \(v_i\) (\(1 \le u_i, v_i \le n\)), обозначающие ребро между вершинами \(u_i\) и \(v_i\). Входные данные обязаны представлять собой дерево. Примечание В первом наборе входных данных крот изначально находится в вершине \(2\). Для запроса «? 2», жюри возвращает \(1\), потому что крот находится в поддереве вершины \(2\). После этого запроса крот не перемещается. Ответ \(2\) — это текущая вершина, где находится крот, поэтому ответ считается правильным. Во втором наборе входных данных крот изначально находится в вершине \(6\). Для запроса «? 2», жюри возвращает \(0\), потому что крот не находится в поддереве вершины \(2\). После этого запроса крот перемещается из вершины \(6\) в вершину \(5\). Для запроса «? 6», жюри возвращает \(0\), потому что крот не находится в поддереве вершины \(6\). После этого запроса крот перемещается из вершины \(5\) в вершину \(4\). Для запроса «? 4», жюри возвращает \(1\), потому что крот находится в поддереве вершины \(4\). После этого запроса крот не перемещается. Ответ \(4\) — это текущая вершина, где находится крот, поэтому ответ считается правильным. Обратите внимание, что приведенный пример предназначен только для понимания условия, и запросы в примере не гарантируют определение уникального положения крота. | |
![]()
|
|
D. Смешная игра
графы
Деревья
жадные алгоритмы
Конструктив
математика
снм
теория чисел
*1900
У Вани есть граф из \(n\) вершин (пронумерованных от \(1\) до \(n\)) и массив \(a\) из \(n\) целых чисел, изначально в графе нет рёбер. Ване стало скучно, и чтобы ему стало весело, он решил выполнить \(n - 1\) операцию. Операция под номером \(x\) (операции нумеруются по порядку начиная с \(1\)) заключается в следующем: - Выбрать \(2\) различных числа \(1 \leq u,v \leq n\), таких что \(|a_u - a_v|\) делится на \(x\).
- Добавить в граф неориентированное ребро между вершинами \(u\) и \(v\).
Помогите Ване с помощью \(n - 1\) операции получить связный\(^{\text{∗}}\) граф, или скажите, что это невозможно. Выходные данные Для каждого набора входных данных, если решения не существует, то выведите «No» (без кавычек). Иначе выведите «Yes» (без кавычек), после этого выведите \(n - 1\) строку, в \(i\)-й из них выведите числа \(u\) и \(v\), которые надо выбрать на операции \(i\). Вы можете вывести каждую букву в любом регистре (например, «YES», «Yes», «yes», «yEs» будут распознаны как положительный ответ). Примечание Рассмотрим второй набор входных данных. - Первая операция \((x = 1)\): можно соединить вершины \(4\) и \(1\), так как \(|a_4 - a_1| = |13 - 99| = |-86| = 86\), а \(86\) кратно \(1\).
 - Вторая операция \((x = 2)\): можно соединить вершины \(2\) и \(1\), так как \(|a_2 - a_1| = |7 - 99| = |-92| = 92\), а \(92\) кратно \(2\).
 - Третья операция \((x = 3)\): можно соединить вершины \(3\) и \(2\), так как \(|a_3 - a_2| = |1 - 7| = |-6| = 6\), а \(6\) кратно \(3\).
 Из картинки видно, что получился связный граф. | |
![]()
|
|
E. Деревянная игра
битмаски
Деревья
жадные алгоритмы
математика
*2000
Вам дан лес из \(k\) корневых деревьев\(^{\text{∗}}\). Дровосек Тимофей хочет вырубить весь лес, применяя такую операцию: - Выбрать поддерево\(^{\text{†}}\) какой-либо вершины одного из деревьев и удалить его из дерева.
Тимофей очень любит битовые операции, поэтому он хочет, чтобы побитовое ИЛИ размеров поддеревьев, которые он удалял, было максимальным. Помогите ему и найдите, какой максимальный результат он может получить. Выходные данные Для каждого набора входных данных выведите одно целое число — максимальный результат, который можно получить. Примечание Во втором наборе входных данных деревья выглядят так: 
Первой операцией удалим все второе дерево. 
Второй операцией удалим вершину \(4\) из первого дерева. 
Третьей операцией удалим первое дерево. Результат равен \(6|1|3 = 7\) (\(|\) обозначает побитовое ИЛИ). В третьем наборе входных данных нужно удалить все дерево. | |
![]()
|
|
F. Stardew Valley
графы
Деревья
Конструктив
поиск в глубину и подобное
*2500
Пеликан-таун представляет из себя \(n\) домов, соединенных \(m\) двунаправленными дорогами. На некоторых дорогах стоят NPC. Фермеру Бубе очень важно пройти по каждой дороге с NPC и поговорить с ними. Помогите фермеру найти маршрут, для которого выполняются следующие условия: - Маршрут начинается у некоторого дома, проходит по некоторым дорогам, и заканчивается в том же доме.
- Маршрут не проходит ни по какой дороге более одного раза (в обоих направлениях вместе).
- Маршрут проходит по каждой дороге с NPC ровно один раз.
Обратите внимание, фермер может ходить по дорогам без NPC, также, вам не нужно минимизировать длину маршрута. Гарантируется, что если в Пеликан-тауне оставить только дороги с NPC, то можно будет добраться от любого дома до любого другого. Выходные данные Для каждого набора входных данных, если решения не существует, то выведите «No» (без кавычек). Иначе выведите «Yes» (без кавычек), после этого выведите \(k\) — количество дорог в маршруте. В следующей строке выведите \(k + 1\) число — дома маршрута в порядке обхода. Обратите внимание, что первый дом должен совпадать с последним, поскольку маршрут циклический. Если существуют несколько решений, вы можете вывести любое из них. Вы можете вывести каждую букву в любом регистре (например, «YES», «Yes», «yes», «yEs» будут распознаны как положительный ответ). Примечание Обратите внимание, что в третьем наборе входных данных присутствуют кратные ребра \((5, 2)\). Вам обязательно нужно пройти по двум из них. | |
![]()
|
|
D. Максимизация корня
Бинарный поиск
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
*1500
Задано корневое дерево, состоящее из \(n\) вершин. Вершины в дереве пронумерованы от \(1\) до \(n\), вершина \(1\) — корень. Значение \(a_i\) записано в \(i\)-й вершине. Вы можете выполнять следующую операцию любое количество раз (возможно, ноль): выбрать вершину \(v\), у которой есть хотя бы один сын; увеличить \(a_v\) на \(1\); и уменьшить \(a_u\) на \(1\) для всех вершин \(u\), которые находятся в поддереве \(v\) (за исключением самой \(v\)). Но после каждой операции значения на всех вершинах должны быть неотрицательными. Ваша задача — посчитать максимальное возможное значение в корне, используя вышеописанную операцию. Выходные данные Для каждого набора входных данных выведите одно целое число — максимальное возможное значение в корне, используя вышеописанную операцию. Примечание В первом наборе входных данных возможна следующая последовательность операций: - провести операцию на \(v=3\), тогда значения на вершинах станут \([0, 1, 1, 1]\);
- провести операцию на \(v=1\), тогда значения на вершинах станут \([1, 0, 0, 0]\).
| |
![]()
|
|
C. Угадайте дерево
Бинарный поиск
Деревья
жадные алгоритмы
интерактив
Перебор
поиск в глубину и подобное
разделяй и властвуй
снм
*1500
Это интерактивная задача. Мизуки выбрала секретное дерево с \(n\) вершинами, пронумерованными от \(1\) до \(n\), и попросила вас отгадать его с помощью запросов следующего типа: - «? a b» — Мизуки скажет вам, какая вершина \(x\) минимизирует \(|d(a,x) - d(b,x)|\), где \(d(x,y)\) — расстояние между вершинами \(x\) и \(y\). Если таких вершин несколько, Мизуки укажет вам ту, которая минимизирует \(d(a,x)\).
Выясните структуру секретного дерева Мизуки, используя не более \(15n\) запросов! Протокол взаимодействия Взаимодействие начинается с чтения целого числа \(n\). Затем вы можете сделать до \(15n\) запросов. Чтобы сделать запрос, выведите строку в формате «? a b» (без кавычек) (\(1 \le a,b \le n\)). После каждого запроса считайте целое число — ответ на ваш запрос. Чтобы сообщить ответ, выведите строку в формате «! \(a_1\) \(b_1\) \(a_2\) \(b_2\) ... \(a_{n-1}\) \(b_{n-1}\)» (без кавычек), что означает, что между вершинами \(a_i\) и \(b_i\) существует ребро для каждого \(1 \le i \le n-1\). Вы можете выводить ребра в любом порядке. После того как будет сделано \(15n\) запросов, ответ на любой другой запрос будет равен \(-1\). Получив такой ответ, завершите программу, чтобы получить вердикт Неправильный ответ. После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Взломы Для взломов используйте следующий формат: Первая строка содержит целое число \(t\) (\(1 \le t \le 200\)) — количество наборов входных данных. Первая строка каждого набора входных данных держит целое число \(n\) — количество вершин в скрытом дереве. Затем следует \(n-1\) строка. В \(i\)-й из них содержатся два целых числа \(a_i\) и \(b_i\) (\(1 \le a_i, b_i \le n\)), что означает, что между \(a_i\) и \(b_i\) в скрытом дереве есть ребро. Сумма \(n\) по всем наборам входных данных не должна превосходить \(1000\). Примечание Дерево — это связный неориентированный граф без циклов. Дерево с \(n\) вершинами всегда будет иметь \(n-1\) ребро. В примере ответ на «? 1 2» равен \(1\). Это означает, что между вершинами \(1\) и \(2\) есть ребро. Ответ на запрос «? 1 3» равен \(1\). Это означает, что между вершинами \(1\) и \(3\) есть ребро. Ответ на запрос «? 1 4» равен \(3\). Можно доказать, что это возможно только в том случае, если вершина \(3\) соединена с вершинами \(1\) и \(4\). Следовательно, ребра дерева — это \((1,2)\), \((1,3)\) и \((3,4)\). | |
![]()
|
|
E1. Детерминированная куча (простая версия)
Деревья
дп
Комбинаторика
математика
*2400
Это простая версия задачи. Разница между двумя версиями заключается в определении детерминированной max-кучи, ограничении на время и ограничениях на \(n\) и \(t\). Вы можете совершать взломы только в том случае, если решены обе версии задачи.. Рассмотрим полное бинарное дерево размером \(2^n - 1\), с вершинами, пронумерованными от \(1\) до \(2^n-1\), и корнем в \(1\). Для каждой вершины \(v\) (\(1 \le v \le 2^{n - 1} - 1\)) вершина \(2v\) является ее левым ребенком, а вершина \(2v + 1\) — ее правым ребенком. Каждой вершине \(v\) также присвоено значение \(a_v\). Определим операцию \(\mathrm{pop}\) следующим образом: - инициализировать переменную \(v\) как \(1\);
- повторять следующий процесс до тех пор, пока вершина \(v\) не станет листом (т.е. пока не выполняется \(2^{n - 1} \le v \le 2^n - 1\)):
- среди дочерних вершин \(v\) выбрать ту, значение которой больше, и обозначить такую вершину \(x\); если значения на них равны (то есть \(a_{2v} = a_{2v + 1}\)), то можно выбрать любую из них;
- присвоить \(a_x\) значению \(a_v\) (т.е. \(a_v := a_x\));
- присвоить \(x\) переменной \(v\) (т.е. \(v := x\));
- присвоить \(-1\) значению \(a_v\) (т.е. \(a_v := -1\)).
Мы говорим, что операция \(\mathrm{pop}\) является детерминированной, если существует единственный способ выполнить такую операцию. Другими словами, \(a_{2v} \neq a_{2v + 1}\) выполняется на каждом шаге операции. Бинарное дерево называется max-кучей, если для каждой вершины \(v\) (\(1 \le v \le 2^{n - 1} - 1\)) выполняется \(a_v \ge a_{2v}\) и \(a_v \ge a_{2v + 1}\). Максимальная куча является детерминированной, если операция \(\mathrm{pop}\) детерминирована для кучи, когда мы выполняем ее в первый раз. Изначально \(a_v := 0\) для каждой вершины \(v\) (\(1 \le v \le 2^n - 1\)), и ваша цель — посчитать количество различных детерминированных max-куч, которые можно получить в результате применения следующей операции \(\mathrm{add}\) ровно \(k\) раз: - Выбрать целое число \(v\) (\(1 \le v \le 2^n - 1\)), и для каждой вершины \(x\) на пути между \(1\) и \(v\) прибавить \(1\) к \(a_x\).
Две кучи считаются разными, если есть вершина, которая имеет разные значения в этих кучах. Поскольку ответ может быть очень большим, выведите его по модулю \(p\). Выходные данные Для каждого набора входных данных выведите единственную строку, содержащую целое число: количество различных детерминированных max-куч, которое можно получить в результате применения вышеупомянутой операции \(\mathrm{add}\) ровно \(k\) раз, по модулю \(p\). Примечание Для первого набора входных данных существует только один способ сгенерировать \(a\), и такая последовательность является детерминированной max-кучей, поэтому ответ — \(1\). Для второго набора входных данных, если мы выберем \(v = 1\) и выполним операцию, у нас будет \(a = [1, 0, 0]\), а поскольку \(a_2 = a_3\), мы можем выбрать любой из них при выполнении первой операции \(\mathrm{pop}\), поэтому такая куча не является детерминированной max-кучей. А если мы выберем \(v = 2\), у нас будет \(a = [1, 1, 0]\), то при выполнении первой операции \(\mathrm{pop}\) произойдет следующее: - инициализировать \(v\) как \(1\)
- поскольку \(a_{2v} > a_{2v + 1}\), выбрать \(2v\) как \(x\), тогда \(x = 2\)
- присвоить \(a_x\) значению \(a_v\), тогда \(a = [1, 1, 0]\)
- присвоить \(x\) переменной \(v\), тогда \(v = 2\)
- поскольку \(v\) является листом, присвоить \(-1\) значению \(a_v\), тогда \(a = [1, -1, 0]\)
Так как первая операция \(\mathrm{pop}\) детерминирована, то это детерминированная max-куча. Также, если мы выберем \(v = 3\), то \(a\) будет детерминированной max-кучей, так что ответ — \(2\). | |
![]()
|
|
E2. Детерминированная куча (сложная версия)
Деревья
дп
Комбинаторика
*2900
Это сложная версия задачи. Разница между двумя версиями заключается в определении детерминированной max-кучи, ограничении на время и ограничениях на \(n\) и \(t\). Вы можете совершать взломы только в том случае, если решены обе версии задачи.. Рассмотрим полное бинарное дерево размером \(2^n - 1\), с вершинами, пронумерованными от \(1\) до \(2^n-1\), и корнем в \(1\). Для каждой вершины \(v\) (\(1 \le v \le 2^{n - 1} - 1\)) вершина \(2v\) является ее левым ребенком, а вершина \(2v + 1\) — ее правым ребенком. Каждой вершине \(v\) также присвоено значение \(a_v\). Определим операцию \(\mathrm{pop}\) следующим образом: - инициализировать переменную \(v\) как \(1\);
- повторять следующий процесс до тех пор, пока вершина \(v\) не станет листом (т.е. пока не выполняется \(2^{n - 1} \le v \le 2^n - 1\)):
- среди дочерних вершин \(v\) выбрать ту, значение которой больше, и обозначить такую вершину \(x\); если значения на них равны (то есть \(a_{2v} = a_{2v + 1}\)), то можно выбрать любую из них;
- присвоить \(a_x\) значению \(a_v\) (т.е. \(a_v := a_x\));
- присвоить \(x\) переменной \(v\) (т.е. \(v := x\));
- присвоить \(-1\) значению \(a_v\) (т.е. \(a_v := -1\)).
Мы говорим, что операция \(\mathrm{pop}\) является детерминированной, если существует единственный способ выполнить такую операцию. Другими словами, \(a_{2v} \neq a_{2v + 1}\) выполняется на каждом шаге операции. Бинарное дерево называется max-кучей, если для каждой вершины \(v\) (\(1 \le v \le 2^{n - 1} - 1\)) выполняется \(a_v \ge a_{2v}\) и \(a_v \ge a_{2v + 1}\). Максимальная куча является детерминированной, если операция \(\mathrm{pop}\) детерминирована для кучи, когда мы выполняем ее в первый и второй раз. Изначально \(a_v := 0\) для каждой вершины \(v\) (\(1 \le v \le 2^n - 1\)), и ваша цель — посчитать количество различных детерминированных max-куч, которые можно получить в результате применения следующей операции \(\mathrm{add}\) ровно \(k\) раз: - Выбрать целое число \(v\) (\(1 \le v \le 2^n - 1\)), и для каждой вершины \(x\) на пути между \(1\) и \(v\) прибавить \(1\) к \(a_x\).
Две кучи считаются разными, если есть вершина, которая имеет разные значения в этих кучах. Поскольку ответ может быть очень большим, выведите его по модулю \(p\). Выходные данные Для каждого набора входных данных выведите единственную строку, содержащую целое число: количество различных детерминированных max-куч, которое можно получить в результате применения вышеупомянутой операции \(\mathrm{add}\) ровно \(k\) раз, по модулю \(p\). Примечание Для первого набора входных данных, если мы выберем \(v = 1\) и выполним операцию, у нас будет \(a = [1, 0, 0]\), а поскольку \(a_2 = a_3\), мы можем выбрать любой из них при выполнении первой операции \(\mathrm{pop}\), поэтому такая куча не является детерминированной max-кучей. А если мы выберем \(v = 2\), у нас будет \(a = [1, 1, 0]\), то при выполнении первой операции \(\mathrm{pop}\) произойдет следующее: - инициализировать \(v\) как \(1\)
- поскольку \(a_{2v} > a_{2v + 1}\), выбрать \(2v\) как \(x\), тогда \(x = 2\)
- присвоить \(a_x\) значению \(a_v\), тогда \(a = [1, 1, 0]\)
- присвоить \(x\) переменной \(v\), тогда \(v = 2\)
- поскольку \(v\) является листом, присвоить \(-1\) значению \(a_v\), тогда \(a = [1, -1, 0]\)
А во время второго \(\mathrm{pop}\) произойдет следующее: - инициализировать \(v\) как \(1\)
- поскольку \(a_{2v} < a_{2v + 1}\), выбрать \(2v + 1\) в качестве \(x\), тогда \(x = 3\)
- присвоить \(a_x\) значению \(a_v\), тогда \(a = [0, -1, 0]\)
- присвоить \(x\) переменной \(v\), тогда \(v = 3\)
- поскольку \(v\) является листом, присвоить \(-1\) значению \(a_v\), тогда \(a = [0, -1, -1]\)
Поскольку и первая, и вторая операция \(\mathrm{pop}\) детерминированы, это детерминированная max-куча. Также, если мы выберем \(v = 3\), то \(a\) будет детерминированной max-кучей, так что ответ — \(2\). | |
![]()
|
|
D1. Проверка DFS (лёгкая версия)
графы
Деревья
Перебор
поиск в глубину и подобное
Структуры данных
хэши
*1900
Это лёгкая версия задачи. В этой версии заданное дерево является полным бинарным деревом, а ограничения на \(n\) и \(q\) ниже. Вы можете совершать взломы только в том случае, если решены обе версии задачи. Вам дано полное бинарное дерево\(^\dagger\), состоящее из \(n\) вершин. Вершины пронумерованы от \(1\) до \(n\), вершина \(1\) — корень. Вам также дана перестановка \(p_1, p_2, \ldots, p_n\) чисел \([1,2,\ldots,n]\). Вам нужно ответить на \(q\) запросов. В каждом запросе вам даются два целых числа \(x\), \(y\); вам нужно поменять местами \(p_x\) и \(p_y\) и определить, является ли \(p_1, p_2, \ldots, p_n\) возможным порядком обхода в глубину\(^\ddagger\) заданного дерева. Обратите внимание, что перестановки элементов сохраняются между запросами. \(^\dagger\) Полное бинарное дерево — это дерево с корнем в вершине \(1\), имеющее размер \(n=2^k-1\) для некоторого целого положительного числа \(k\), и где родитель каждой вершины \(i\) (\(1<i\le n\)) — это \(\left\lfloor\frac{i}{2}\right\rfloor\). Таким образом, все листья этого дерева находятся на расстоянии \(k - 1\) от корня. \(^\ddagger\) Порядок обхода в глубину получается вызовом следующей функции \(\texttt{dfs}\) на заданном дереве. dfs_order = []
function dfs(v):
добавить v в конец dfs_order
выбрать произвольную перестановку s детей v
for child in s:
dfs(child)
dfs(1)
Обратите внимание, что порядок обхода DFS определён не однозначно. Выходные данные Для каждого набора входных данных выведите \(q\) строк, соответствующих \(q\) запросам. Для каждого запроса выведите \(\texttt{YES}\), если есть порядок обхода в глубину, который точно равен текущей перестановке, и выведите \(\texttt{NO}\) в противном случае. Вы можете вывести \(\texttt{Yes}\) и \(\texttt{No}\) в любом регистре (например, строки \(\texttt{yEs}\), \(\texttt{yes}\), \(\texttt{Yes}\) и \(\texttt{YES}\) будут распознаны как положительный ответ). Примечание В первом наборе входных данных перестановка \(p_1, p_2, \ldots, p_n\) после каждой модификации равна \([1,3,2],[1,2,3],[3,2,1]\) соответственно. Первые две перестановки — это возможные порядки обхода в глубину; третья — не порядок обхода в глубину. Во втором наборе входных данных перестановка \(p_1, p_2, \ldots, p_n\) после каждой модификации равна \([1,2,3,4,5,6,7],[1,2,5,4,3,6,7],[1,3,5,4,2,6,7],[1,3,7,4,2,6,5],[1,3,7,6,2,4,5]\) соответственно. | |
![]()
|
|
D2. Проверка DFS (сложная версия)
Бинарный поиск
графы
Деревья
поиск в глубину и подобное
Структуры данных
хэши
*2300
Это сложная версия задачи. В этой версии на заданное дерево нет дополнительных ограничений, а ограничения на \(n\) и \(q\) выше. Вы можете совершать взломы только в том случае, если решены обе версии задачи. Вам дано корневое дерево, состоящее из \(n\) вершин. Вершины пронумерованы от \(1\) до \(n\), вершина \(1\) — корень. Вам также дана перестановка \(p_1, p_2, \ldots, p_n\) чисел \([1,2,\ldots,n]\). Вам нужно ответить на \(q\) запросов. В каждом запросе вам даются два целых числа \(x\), \(y\); вам нужно поменять местами \(p_x\) и \(p_y\) и определить, является ли \(p_1, p_2, \ldots, p_n\) возможным порядком обхода в глубину\(^\dagger\) заданного дерева. Обратите внимание, что перестановки элементов сохраняются между запросами. \(^\dagger\) Порядок обхода в глубину получается вызовом следующей функции \(\texttt{dfs}\) на заданном дереве. dfs_order = []
function dfs(v):
добавить v в конец dfs_order
выбрать произвольную перестановку s детей v
for child in s:
dfs(child)
dfs(1)
Обратите внимание, что порядок обхода DFS определён не однозначно. Выходные данные Для каждого набора входных данных выведите \(q\) строк, соответствующих \(q\) запросам. Для каждого запроса выведите \(\texttt{YES}\), если есть порядок обхода в глубину, который точно равен текущей перестановке, и выведите \(\texttt{NO}\) в противном случае. Вы можете вывести \(\texttt{Yes}\) и \(\texttt{No}\) в любом регистре (например, строки \(\texttt{yEs}\), \(\texttt{yes}\), \(\texttt{Yes}\) и \(\texttt{YES}\) будут распознаны как положительный ответ). Примечание В первом наборе входных данных перестановка \(p_1, p_2, \ldots, p_n\) после каждой модификации равна \([1,3,2],[1,2,3],[3,2,1]\) соответственно. Первые две перестановки — это возможные порядки обхода в глубину; третья — не порядок обхода в глубину. Во втором наборе входных данных перестановка \(p_1, p_2, \ldots, p_n\) после каждой модификации равна \([1,2,3,4,5,6,7],[1,2,5,4,3,6,7],[1,3,5,4,2,6,7],[1,3,7,4,2,6,5],[1,3,7,6,2,4,5]\) соответственно. | |
![]()
|
|
A. Ирис и игра на дереве
графы
Деревья
жадные алгоритмы
игры
Конструктив
поиск в глубину и подобное
*1700
У Ирис есть дерево, корень которого находится в вершине \(1\). Каждая вершина имеет значение \(\mathtt 0\) или \(\mathtt 1\). Рассмотрим лист дерева (вершина \(1\) никогда не считается листом) и определим его вес. Построим строку, сформированную значениями вершин на пути от корня до этого листа. Тогда вес листа — это разность количества вхождений подстроки \(\mathtt{10}\) и количества вхождений подстроки \(\mathtt{01}\) в этой строке. Возьмем следующее дерево в качестве примера. Зеленые вершины имеют значение \(\mathtt 1\), в то время как белые вершины имеют значение \(\mathtt 0\).  - Посчитаем вес листа \(5\): сформированная строка равна \(\mathtt{10110}\). Количество вхождений подстроки \(\mathtt{10}\) равно \(2\), количество вхождений подстроки \(\mathtt{01}\) равно \(1\), так что разность равна \(2 - 1 = 1\).
- Посчитаем вес листа \(6\): сформированная строка равна \(\mathtt{101}\). Количество вхождений подстроки \(\mathtt{10}\) равно \(1\), количество вхождений подстроки \(\mathtt{01}\) равно \(1\), так что разность равна \(1 - 1 = 0\).
Оценкой дерева назовём количество листьев с ненулевым весом в дереве. Однако значения некоторых вершин ещё не определены и будут даны вам как \(\texttt{?}\). Заполнение пропусков было бы слишком скучным, поэтому Ирис собирается пригласить Дору поиграть в игру. На каждом ходу одна из девочек выбирает любую из оставшихся вершин со значением \(\texttt{?}\) и изменяет её значение на \(\mathtt{0}\) или \(\mathtt{1}\), при этом Ирис ходит первой. Игра продолжается до тех пор, пока в дереве не останется вершин со значением \(\mathtt{?}\). Ирис стремится максимизировать оценку дерева, в то время как Дора стремится минимизировать её. Предполагая, что обе девочки играют оптимально, определите итоговую оценку дерева. Выходные данные Для каждого набора входных данных выведите одно целое число — итоговую оценку дерева. Примечание В первом наборе входных данных значения во всех вершинах уже определены. Существует три различных пути от корня до листа: - От вершины \(1\) до вершины \(2\). Сформированная строка равна \(\mathtt{01}\), так что вес листа равен \(0-1=-1\).
- От вершины \(1\) до вершины \(3\). Сформированная строка равна \(\mathtt{00}\), так что вес листа равен \(0-0=0\).
- От вершины \(1\) до вершины \(4\). Сформированная строка равна \(\mathtt{01}\), так что вес листа равен \(0-1=-1\).
Таким образом, есть два листа с ненулевым весом, так что оценка дерева равна \(2\). Во втором наборе входных данных одна из последовательностей оптимальных ходов для двух игроков может быть следующей: - Ирис выбирает изменить значение вершины \(3\) на \(\mathtt 1\).
- Дора выбирает изменить значение вершины \(1\) на \(\mathtt 0\).
- Ирис выбирает изменить значение вершины \(2\) на \(\mathtt 0\).
Итоговое дерево выглядит следующим образом:  Единственный лист с ненулевым весом — это \(3\), так что оценка дерева равна \(1\). Обратите внимание, что это может быть не единственная последовательность оптимальных ходов для Ирис и Доры. | |
![]()
|
|
B. Ирис и дерево
Деревья
математика
Перебор
поиск в глубину и подобное
снм
Структуры данных
*1800
Дано корневое дерево с корнем в вершине \(1\). Для любой вершины \(i\) (\(1 < i \leq n\)) в дереве есть ребро, соединяющее вершины \(i\) и \(p_i\) (\(1 \leq p_i < i\)), вес которого равен \(t_i\). Ирис не знает значений \(t_i\), но она знает, что \(\displaystyle\sum_{i=2}^n t_i = w\) и любое из \(t_i\) является неотрицательным целым числом. Вершины дерева пронумерованы особым образом: номера вершин в каждом поддереве представляют собой последовательные целые числа. Другими словами, вершины дерева пронумерованы в порядке обхода в глубину.  Дерево на этой картинке удовлетворяет условию. Например, в поддереве вершины \(2\) номера вершин равны \(2, 3, 4, 5\), то есть являются последовательными целыми числами. Дерево на этой картинке удовлетворяет условию. Например, в поддереве вершины \(2\) номера вершин равны \(2, 3, 4, 5\), то есть являются последовательными целыми числами.  Дерево на этой картинке не удовлетворяет условию, так как в поддереве вершины \(2\) номера вершин \(2\) и \(4\) не являются последовательными целыми числами. Дерево на этой картинке не удовлетворяет условию, так как в поддереве вершины \(2\) номера вершин \(2\) и \(4\) не являются последовательными целыми числами. Определим \(\operatorname{dist}(u, v)\) как длину простого пути между вершинами \(u\) и \(v\) в дереве. Далее произойдёт \(n - 1\) событие: - Ирис сообщают целые числа \(x\) и \(y\), обозначающие, что \(t_x = y\).
После каждого события Ирис хочет знать максимальное возможное значение \(\operatorname{dist}(i, i \bmod n + 1)\) независимо для всех \(i\) (\(1\le i\le n\)). Ей достаточно узнать только сумму этих \(n\) значений. Пожалуйста, помогите Ирис быстро получить ответы. Обратите внимание, что при вычислении максимально возможных значений \(\operatorname{dist}(i, i \bmod n + 1)\) и \(\operatorname{dist}(j, j \bmod n + 1)\) для \(i \ne j\) неизвестные веса рёбер могут быть разными. Выходные данные Для каждого набора входных данных выведите одну строку, содержащую \(n-1\) целых числа, каждое из которых представляет ответ после каждого события. Примечание В первом наборе входных данных \(\operatorname{dist}(1, 2) = \operatorname{dist}(2, 1) = t_2 = w = 10^{12}\), поэтому \(\operatorname{dist}(1, 2) + \operatorname{dist}(2, 1) = 2 \cdot 10^{12}\) Во втором наборе входных данных дерево после того, как Ирис узнала все \(t_x\), показано ниже:  \(\operatorname{dist}(1, 2) = t_2\), \(\operatorname{dist}(2, 3) = t_2 + t_3\), \(\operatorname{dist}(3, 4) = t_3 + t_4\), \(\operatorname{dist}(4, 1) = t_4\). После первого события мы узнали, что \(t_2 = 2\), поэтому \(\operatorname{dist}(1, 2) = 2\). В то же время: - \(\operatorname{dist}(2, 3)\) максимально, если \(t_3 = 7\), \(t_4 = 0\). Тогда \(\operatorname{dist}(2, 3) = 9\).
- \(\operatorname{dist}(3, 4)\) и \(\operatorname{dist}(4, 1)\) максимальны, если \(t_3 = 0\), \(t_4 = 7\). Тогда \(\operatorname{dist}(3, 4) = \operatorname{dist}(4, 1) = 7\).
Таким образом, ответ равен \(2 + 9 + 7 + 7 = 25\). После второго события мы узнали, что \(t_4 = 4\), тогда \(t_3 = w - t_2 - t_4 = 4\). \(\operatorname{dist}(1, 2) = 2\), \(\operatorname{dist}(2, 3) = 2 + 3 = 5\), \(\operatorname{dist}(3, 4) = 3 + 4 = 7\), \(\operatorname{dist}(4, 1) = 4\). Таким образом, ответ равен \(2 + 5 + 7 + 4 = 18\). | |
![]()
|
|
E. Полное бинарное дерево Ирис
Деревья
Перебор
поиск в глубину и подобное
Структуры данных
*3100
Ирис любит полные бинарные деревья. Определим глубину корневого дерева как максимальное количество вершин на простых путях от некоторой вершины до корня. Полное бинарное дерево глубины \(d\) — это бинарное дерево глубины \(d\) с ровно \(2^d - 1\) вершинами. Ирис называет дерево \(d\)-бинарным, если к нему можно добавить некоторые вершины и рёбра, чтобы оно стало полным бинарным деревом глубины \(d\). Обратите внимание, что любая вершина может быть выбрана в качестве корня полного бинарного дерева. Поскольку выполнение операций над большими деревьями затруднительно, она определяет бинарную глубину дерева как минимальное \(d\), удовлетворяющее условию, что дерево является \(d\)-бинарным. В частности, если не существует целого числа \(d \ge 1\), такого что дерево является \(d\)-бинарным, то бинарная глубина дерева равна \(-1\). У Ирис сейчас есть дерево, состоящее только из вершины \(1\). Она хочет добавить ещё \(n - 1\) вершин, чтобы сформировать большее дерево. Она будет добавлять вершины по одной. Когда она добавляет вершину \(i\) (\(2 \leq i \leq n\)), она сообщит вам целое число \(p_i\) (\(1 \leq p_i < i\)) и добавит новое ребро, соединяющее вершины \(i\) и \(p_i\). Ирис хочет спросить вас о бинарной глубине дерева, образованного первыми \(i\) вершинами для всех \(1 \le i \le n\). Можете ли вы сказать ей ответ? Выходные данные Для каждого набора входных данных выведите \(n\) целых чисел, \(i\)-е из которых представляет бинарную глубину дерева, образованного первыми \(i\) вершинами. Примечание В первом наборе входных данных итоговое дерево показано ниже:  - Дерево, состоящее из вершины \(1\), имеет бинарную глубину \(1\) (само дерево является полным бинарным деревом глубины \(1\)).
- Дерево, состоящее из вершин \(1\) и \(2\), имеет бинарную глубину \(2\) (мы можем добавить вершину \(3\), чтобы сделать его полным бинарным деревом глубины \(2\)).
- Дерево, состоящее из вершин \(1\), \(2\) и \(3\), имеет бинарную глубину \(2\) (само дерево является полным бинарным деревом глубины \(2\)).
Во втором наборе входных данных полное бинарное дерево, образованное после добавления некоторых вершин к дереву, состоящему из \(n\) вершин, показано ниже (добавленные вершины выделены жирным):  Глубина образованного полного бинарного дерева равна \(4\). В пятом наборе входных данных итоговое дерево показано ниже:  Можно доказать, что Ирис не может сформировать никакое полное бинарное дерево, добавляя вершины и рёбра, поэтому бинарная глубина равна \(-1\). | |
![]()
|
|
F1. Игра на дереве (простая версия)
Бинарный поиск
Деревья
дп
жадные алгоритмы
игры
Перебор
реализация
Структуры данных
*2700
Это простая версия задачи. В этой версии \(\mathbf{u = v}\). Вы можете совершать взломы только в том случае, если решены обе версии задачи. Алиса и Боб играют в забавную игру на дереве. В эту игру играют на дереве из \(n\) вершин, пронумерованных от \(1\) до \(n\). Напомним, что дерево на \(n\) вершинах — это неориентированный связный граф с \(n - 1\) ребрами. Алиса и Боб ходят по очереди, причём Алиса ходит первой. Каждый игрок начинает с какой-то вершины. В свой ход игрок должен перейти из текущей вершины в соседнюю, которая ещё не была никем посещена до этого. Первый игрок, который не может сделать ход, проигрывает. Вам даны две вершины \(u\) и \(v\). Представим простой путь из вершины \(u\) в \(v\) как массив \(p_1, p_2, p_3, \ldots, p_m\), где \(p_1 = u\), \(p_m = v\), между \(p_i\) и \(p_{i + 1}\) есть ребро для всех \(i\) (\(1 \le i < m\)). Вы должны определить победителя игры, если Алиса начнёт в вершине \(1\), а Боб в вершине \(p_j\) для каждого \(j\) (где \(1 \le j \le m\)). Выходные данные Для каждого набора входных данных выведите \(m\) строк. В \(i\)-й строке выведите победителя игры, если Алиса начинает с вершины \(1\), а Боб с вершины \(p_i\), выведите «Alice» (без кавычек), если выиграет Алиса, или «Bob» (без кавычек) в противном случае. Примечание  Дерево из первого и второго примера. Дерево из первого и второго примера. В первом наборе входных данных путь будет иметь вид (\(2,2\)). Боб начинает в вершине \(2\), Алиса в своём первом ходу не сможет никуда пойти, и она проиграет. Во втором наборе входных данных путь будет иметь вид (\(3,3\)). Боб начинает в вершине \(3\), Алиса переместится в вершину \(2\), и у Боба не останется вершин, которые можно посетить, и он проиграет. | |
![]()
|
|
F2. Игра на дереве (сложная версия)
Бинарный поиск
Деревья
Структуры данных
*3500
Это сложная версия задачи. В этой версии не гарантируется, что \(u = v\). Вы можете совершать взломы только в том случае, если решены обе версии задачи. Алиса и Боб играют в забавную игру на дереве. В эту игру играют на дереве из \(n\) вершин, пронумерованных от \(1\) до \(n\). Напомним, что дерево на \(n\) вершинах — это неориентированный связный граф с \(n - 1\) ребрами. Алиса и Боб ходят по очереди, причём Алиса ходит первой. Каждый игрок начинает с какой-то вершины. В свой ход игрок должен перейти из текущей вершины в соседнюю вершину, которая ещё не была никем посещена до этого. Первый игрок, который не может сделать ход, проигрывает. Вам даны две вершины \(u\) и \(v\). Представим простой путь из вершины \(u\) в \(v\) как массив \(p_1, p_2, p_3, \ldots, p_m\), где \(p_1 = u\), \(p_m = v\), между \(p_i\) и \(p_{i + 1}\) есть ребро для всех \(i\) (\(1 \le i < m\)). Вы должны определить победителя игры, если Алиса начнёт в вершине \(1\), а Боб в вершине \(p_j\) для каждого \(j\) (где \(1 \le j \le m\)). Выходные данные Для каждого набора входных данных выведите \(m\) строк. В \(i\)-й строке выведите победителя игры, если Алиса начинает с вершины \(1\), а Боб с вершины \(p_i\), выведите «Alice» (без кавычек), если выиграет Алиса, или «Bob» (без кавычек) в противном случае. Примечание  Дерево из первого примера. Дерево из первого примера. В первом наборе входных данных путь будет иметь вид (\(2,3\)). В случае, когда Боб начинает в вершине \(2\), Алиса в своём первом ходу не сможет никуда пойти, и она проиграет. А в случае, когда Боб начинает в вершине \(3\), Алиса переместится в вершину \(2\), и у Боба не останется вершин, которые можно посетить, и он проиграет. | |
![]()
|
|
F. Защита шерифа
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
*2000
"Почему, мастер," сказал Маленький Джон, беря мешки и взвешивая их в руке, "вот блеск золота." Народный герой Робин Гуд сильно беспокоит шерифа Ноттингема. Шериф знает, что Робин Гуд собирается атаковать его лагеря, и он хочет быть готовым. Шериф Ноттингема построил лагеря с учетом стратегии, и поэтому есть ровно \(n\) лагерей, пронумерованных от \(1\) до \(n\), и \(n-1\) троп, каждая из которых соединяет два лагеря. Любой лагерь можно достичь из любого другого лагеря. Каждый лагерь \(i\) изначально имеет \(a_i\) золота. Шериф может укрепить лагерь, вычитая ровно \(c\) золота из каждого из его соседних лагерей и использовать это для строительства лучших защит для этого лагеря. Укрепление лагеря не изменяет его золото, только золото его соседей. Лагерь может иметь отрицательное количество золота. После атаки Робина Гуда все лагеря, которые не были укреплены, будут уничтожены. Какое максимальное количество золота шериф может сохранить в своих лагерях после атаки Робина Гуда, если он оптимально укрепляет свои лагеря? Лагерь \(a\) является соседним лагерем \(b\), если и только если существует тропа, соединяющая \(a\) и \(b\). Только укрепленные лагеря учитываются в ответе, так как остальные будут уничтожены. Выходные данные Выведите одно целое число, максимальное золото, которое шериф Ноттингема может сохранить в своих выживших лагерях после атаки Робина Гуда. Примечание В первом наборе входных данных оптимально укрепить второй лагерь. Конечное золото в каждом лагере составляет \([1,3,0]\). Во втором наборе входных данных оптимально укрепить все лагеря. Конечное золото в каждом лагере составляет \([2,4,2]\). В третьем наборе входных данных оптимально не укреплять ни один лагерь. | |
![]()
|
|
C. Стрижка деревьев
Деревья
жадные алгоритмы
Перебор
поиск в глубину и подобное
сортировки
*1700
Вам дано дерево с \(n\) вершинами, корень которого находится в вершине \(1\). В этой задаче лист — это некорневая вершина со степенью \(1\). За одну операцию можно удалить лист и смежное с ним ребро (возможно, появятся новые листья). Какое минимальное количество операций нужно выполнить, чтобы получилось дерево, также с корнем в вершине \(1\), в котором все листья находятся на одинаковом расстоянии от корня? Выходные данные Для каждого набора входных данных выведите одно целое число: минимальное количество операций, необходимое для достижения цели. Примечание В первых двух наборах входных данных деревья выглядят так:  В первом наборе входных данных, удалив ребра \((1, 3)\) и \((2, 5)\), вы получите дерево, у которого все листья (вершины \(6\) и \(7\)) находятся на одинаковом расстоянии от корня (вершины \(1\)), которое равняется \(3\). Ответ — \(2\), так как это минимальное количество ребер, которое нужно удалить для достижения цели. Во втором наборе входных данных удаление ребер \((1, 4)\) и \((5, 7)\) приводит к дереву, в котором все листья (вершины \(4\) и \(5\)) находятся на одинаковом расстоянии от корня (вершины \(1\)), которое равняется \(2\). | |
![]()
|
|
D. Соедини точки
графы
Деревья
дп
математика
Перебор
снм
*1800
Одним уютным вечером Алиса решила сыграть в классическую игру «Соедини точки», но с подвохом. Чтобы начать игру, Алиса рисует прямую линию и отмечает на ней \(n\) точек, проиндексированных числами от \(1\) до \(n\). Изначально между точками нет рёбер, так что все они попарно не соединены. Затем Алиса выполняет \(m\) операций следующего типа: - Она выбирает три целых числа \(a_i\), \(d_i\) (\(1 \le d_i \le 10\)) и \(k_i\).
- Затем для точек \(a_i, a_i+d_i, a_i+2d_i, a_i+3d_i, \ldots, a_i+k_i\cdot d_i\) Алиса соединяет ребром каждую пару из них.
Алиса хочет узнать, сколько компонент связности\(^\dagger\) образуют эти точки после выполнения всех \(m\) операций. \(^\dagger\) Считается, что две точки лежат в одной компоненте связности, если между ними есть путь, использующий несколько (возможно, ноль) промежуточных рёбер и вершин. Выходные данные Для каждого набора входных данных выведите количество компонент связности. Примечание В первом наборе входных данных есть \(n = 10\) точек. Первая операция соединяет точки \(1\), \(3\), \(5\), \(7\) и \(9\). Вторая операция соединяет точки \(2\), \(4\), \(6\), \(8\) и \(10\). В итоге получаем две компоненты связности: \(\{1, 3, 5, 7, 9\}\) и \(\{2, 4, 6, 8, 10\}\). Во втором наборе входных данных есть \(n = 100\) точек. Единственная операция соединяет точки \(19\), \(21\), \(23\), \(25\) и \(27\). Теперь они образуют одну компоненту связности размера \(5\). Остальные \(95\) точек ни с кем не соединены, так что каждая из них образует отдельную компоненту связности. Значит, ответ равен \(1 + 95 = 96\). В третьем наборе входных данных есть \(n = 100\) точек. После выполнения всех операций все точки с нечётными номерами от \(1\) до \(79\) образуют одну компоненту связности размера \(40\). Остальные \(60\) точек ни с кем не соединены, так что каждая из них образует отдельную компоненту связности. Значит, ответ равен \(1 + 60 = 61\). | |
![]()
|
|
E1. Цифровая деревня (простая версия)
бпф
графы
Деревья
дп
жадные алгоритмы
математика
Перебор
поиск в глубину и подобное
реализация
снм
Структуры данных
*2300
Это простая версия задачи. В трех версиях отличаются ограничения на \(n\) и \(m\). Вы можете совершать взломы только в том случае, если решены все версии задачи. Пак Чанек устанавливает интернет-связь в деревне Кхунтиен. Деревню можно представить как связный простой граф с \(n\) домами и \(m\) интернет-кабелями, соединяющими дом \(u_i\) и дом \(v_i\), каждый с задержкой \(w_i\). Существует \(p\) домов, которым требуется интернет. Пак Чанек может установить серверы не более чем в \(k\) домов. Дома, которым нужен интернет, будут подключены к одному из серверов. Однако, поскольку каждый кабель имеет свою задержку, задержка, которую испытывает дом \(s_i\), нуждающийся в интернете, будет равна максимальной задержке кабелей между этим домом и сервером, к которому он подключен. Для каждого \(k = 1,2,\ldots,n\), помогите Пак Чанеку определить минимальную суммарную задержку, которая может быть достигнута для всех домов, требующих интернет. Выходные данные Для каждого набора входных данных выведите \(n\) целых чисел: минимальное общее время ожидания, которое может быть достигнуто для всех домов, нуждающихся в интернете для каждого \(k = 1,2,\ldots,n\). Примечание В первом наборе входных данных для \(k=3\) одним из лучших решений является установка серверов в вершинах \(2\), \(6\) и \(8\) и получение следующей задержки: - задержка\((2) = 0\)
- задержка\((5) = \max(3, 5) = 5\)
- задержка\((6) = 0\)
- задержка\((8) = 0\)
- задержка\((9) = \max(2, 4) = 4\)
Таким образом, общая задержка составит \(9\). | |
![]()
|
|
E2. Цифровая деревня (сложная версия)
графы
Деревья
дп
математика
снм
Структуры данных
*2500
Это сложная версия задачи. В трех версиях отличаются ограничения на \(n\) и \(m\). Вы можете совершать взломы только в том случае, если решены все версии задачи. Пак Чанек устанавливает интернет-связь в деревне Кхунтиен. Деревню можно представить как связный простой граф с \(n\) домами и \(m\) интернет-кабелями, соединяющими дом \(u_i\) и дом \(v_i\), каждый с задержкой \(w_i\). Существует \(p\) домов, которым требуется интернет. Пак Чанек может установить серверы не более чем в \(k\) домов. Дома, которым нужен интернет, будут подключены к одному из серверов. Однако, поскольку каждый кабель имеет свою задержку, задержка, которую испытывает дом \(s_i\), нуждающийся в интернете, будет равна максимальной задержке кабелей между этим домом и сервером, к которому он подключен. Для каждого \(k = 1,2,\ldots,n\), помогите Пак Чанеку определить минимальную суммарную задержку, которая может быть достигнута для всех домов, требующих интернет. Выходные данные Для каждого набора входных данных выведите \(n\) целых чисел: минимальное общее время ожидания, которое может быть достигнуто для всех домов, нуждающихся в интернете для каждого \(k = 1,2,\ldots,n\). Примечание В первом наборе входных данных для \(k=3\) одним из лучших решений является установка серверов в вершинах \(2\), \(6\) и \(8\) и получение следующей задержки: - задержка\((2) = 0\)
- задержка\((5) = \max(3, 5) = 5\)
- задержка\((6) = 0\)
- задержка\((8) = 0\)
- задержка\((9) = \max(2, 4) = 4\)
Таким образом, общая задержка составит \(9\). | |
![]()
|
|
E3. Цифровая деревня (экстремальная версия)
графы
Деревья
дп
жадные алгоритмы
математика
поиск в глубину и подобное
снм
Структуры данных
*2800
Это экстремальная версия задачи. В трех версиях отличаются ограничения на \(n\) и \(m\). Вы можете совершать взломы только в том случае, если решены все версии задачи. Пак Чанек устанавливает интернет-связь в деревне Кхунтиен. Деревню можно представить как связный простой граф с \(n\) домами и \(m\) интернет-кабелями, соединяющими дом \(u_i\) и дом \(v_i\), каждый с задержкой \(w_i\). Существует \(p\) домов, которым требуется интернет. Пак Чанек может установить серверы не более чем в \(k\) домов. Дома, которым нужен интернет, будут подключены к одному из серверов. Однако, поскольку каждый кабель имеет свою задержку, задержка, которую испытывает дом \(s_i\), нуждающийся в интернете, будет равна максимальной задержке кабелей между этим домом и сервером, к которому он подключен. Для каждого \(k = 1,2,\ldots,n\), помогите Пак Чанеку определить минимальную суммарную задержку, которая может быть достигнута для всех домов, требующих интернет. Выходные данные Для каждого набора входных данных выведите \(n\) целых чисел: минимальное общее время ожидания, которое может быть достигнуто для всех домов, нуждающихся в интернете для каждого \(k = 1,2,\ldots,n\). Примечание В первом наборе входных данных для \(k=3\) одним из лучших решений является установка серверов в вершинах \(2\), \(6\) и \(8\) и получение следующей задержки: - задержка\((2) = 0\)
- задержка\((5) = \max(3, 5) = 5\)
- задержка\((6) = 0\)
- задержка\((8) = 0\)
- задержка\((9) = \max(2, 4) = 4\)
Таким образом, общая задержка составит \(9\). | |
![]()
|
|
E. Древо жизни
Деревья
дп
жадные алгоритмы
*3300
В сердце древнего королевства растет легендарное Древо Жизни — единственное в своем роде и источник магической силы всего мира. Дерево состоит из \(n\) узлов. Каждый узел этого дерева — это волшебный источник, связанный с другими такими же источниками через магические каналы (ребра). Всего в дереве \(n-1\) каналов, \(i\)-й из которых соединяет узлы \(v_i\) и \(u_i\). Также между любыми двумя узлами в дереве существует единственный простой путь по каналам. Однако магическая энергия, текущая через эти каналы, должна быть сбалансирована, иначе мощь Древа Жизни может нарушить естественный порядок и вызвать катастрофические последствия. Мудрецы королевства обнаружили, что когда два магических канала сходятся в одном узле, между ними возникает опасная «магическая резонансная вибрация». Чтобы защитить Древо Жизни и сохранить его баланс, необходимо выбрать несколько путей и провести через них специальные ритуалы. Путь — это последовательность различных узлов \(v_1, v_2, \ldots, v_k\), где каждая пара соседних узлов \(v_i\) и \(v_{i+1}\) соединена ребром. При проведении мудрецами ритуала через такой путь блокируются все резонансные вибрации между парами соседних каналов в пути, а именно между каналами \((v_i, v_{i+1})\) и \((v_{i+1}, v_{i+2})\) для каждого \(1 \leq i \leq k - 2\). Задача мудрецов: выбрать минимальное количество путей и провести через них ритуалы, чтобы заблокировать все резонансные вибрации. Это означает, что для каждой пары каналов, исходящих из одного узла, должен существовать хотя бы один выбранный путь, который содержит оба этих канала. Помогите мудрецам найти минимальное количество таких путей, чтобы магический баланс Древа Жизни был сохранен, и его сила продолжала питать весь мир! Выходные данные Для каждого набора входных данных выведите одно целое число — минимальное количество путей, которое нужно выбрать мудрецам, чтобы предотвратить катастрофу. Примечание В первом наборе входных данных есть две пары каналов, исходящих из одного узла: \((1, 2)\) и \((2, 3)\), \((2, 3)\) и \((3, 4)\). Достаточно провести ритуал через путь \(1-2-3-4\). Таким образом, ответ \(1\). Во втором наборе входных данных нет пар каналов, исходящих из одного узла, поэтому ответ \(0\). В третьем наборе входных данных можно провести ритуалы через пути \(2-1-3\), \(2-1-4\) и \(3-1-4\). | |
![]()
|
|
F. Выбери свои запросы
графы
Деревья
дп
жадные алгоритмы
Конструктив
поиск в глубину и подобное
*2700
Дан массив \(a\), состоящий из \(n\) целых чисел (нумеруемых от \(1\) до \(n\)). Изначально все они равны нулю. Необходимо обработать \(q\) запросов \(i\)-й запрос состоит из двух различных целых чисел \(x_i\) и \(y_i\). В ходе \(i\)-го запроса нужно выбрать целое число \(p\) (которое равно либо \(x_i\), либо \(y_i\)) и целое число \(d\) (которое равно либо \(1\), либо \(-1\)), и присвоить \(a_p = a_p + d\). После каждого запроса каждый элемент массива \(a\) должен быть неотрицательным целым числом. Необходимо обработать все запросы таким образом, чтобы сумма всех элементов массива \(a\) после последнего запроса была минимально возможной. Выходные данные Для каждого запроса выведите строку, содержащую два символа: - первый символ должен быть x, если вы выбрали \(p=x_i\), или y, если вы выбрали \(p=y_i\);
- второй символ должен быть +, если вы выбрали \(d=1\), или -, если вы выбрали \(d=-1\).
Если существует несколько ответов, выведите любой из них. | |
![]()
|
|
F. Мороженое в Бермарте
Деревья
дп
поиск в глубину и подобное
разделяй и властвуй
реализация
Структуры данных
*2700
В сети магазинов Бермарт продается мороженое. У каждого сорта мороженого есть два параметра: цена и вкусность. Изначально есть один магазин с номером \(1\), в котором ничего не продаётся. Требуется обработать \(q\) запросов следующих типов: - \(1~x\) — открывается новый магазин, в котором продаются те же сорта мороженого, что и в магазине \(x\). Он получает первый свободный порядковый номер. Порядок появления сортов мороженого в новом магазине тот же, что и в магазине \(x\).
- \(2~x~p~t\) — в магазине \(x\) в продаже появляется сорт мороженого с ценой \(p\) и вкусностью \(t\).
- \(3~x\) — в магазине \(x\) исчезает из продажи сорт мороженого, который там появился раньше всего.
- \(4~x~p\) — для магазина \(x\) надо найти максимальную суммарную вкусность поднабора сортов, которые там продаются, так, чтобы суммарная цена не превышала \(p\) (каждый сорт можно использовать в поднаборе не более одного раз).
Выходные данные На каждый запрос типа \(4\) выведите одно целое число — для магазина \(x\) найдите максимальную суммарную вкусность поднабора сортов, которые там продаются, так, чтобы суммарная цена не превышала \(p\) (каждый сорт можно использовать в поднаборе не более одного раз). | |
![]()
|
|
E. Приключения Алисы в кроличьей норе
Деревья
дп
жадные алгоритмы
игры
Комбинаторика
математика
поиск в глубину и подобное
Теория вероятностей
*2300
Алиса находится на дне кроличьей норы! Кроличья нора может быть смоделирована как дерево\(^{\text{∗}}\), у которого выход находится на вершине \(1\), а Алиса начинает с некоторой вершины \(v\). Она хочет выбраться из норы, но, к сожалению, Дама Червей приказала её казнить. Каждую минуту подбрасывается обычная монета. Если выпадает орёл, Алиса может переместиться в любую вершину, смежную со своим текущим положением, а если решка, Дама Червей может перетащить Алису на смежную вершину по своему выбору. Если Алиса когда-либо окажется на любом из некорневых листьев\(^{\text{†}}\) дерева, Алиса проигрывает. Предполагая, что они обе действуют оптимально, для каждой начальной вершины \(1\le v\le n\) вычислите вероятность того, что Алиса сможет убежать. Поскольку эти вероятности могут быть очень малыми, выведите их по модулю \(998\,244\,353\). Формально, пусть \(M = 998\,244\,353\). Можно показать, что точный ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Выходные данные Для каждого набора входных данных выведите \(n\) целых чисел в одной строке — вероятности того, что Алиса убежит, начиная с вершины \(1, 2, \ldots, n\). Поскольку эти вероятности могут быть очень малыми, выведите их по модулю \(998\,244\,353\). Примечание Для первого набора входных данных: - Алиса убегает из корня (вершина \(1\)) по определению с вероятностью \(1\).
- Алиса немедленно проигрывает из вершин \(4\) и \(5\), так как они являются листьями.
- Из других двух вершин Алиса убегает с вероятностью \(\frac 12\), так как Дама перетащит её к листьям.
| |
![]()
|
|
D. Классный граф
графы
Деревья
жадные алгоритмы
Конструктив
поиск в глубину и подобное
снм
Структуры данных
*1900
Вам дан неориентированный граф с \(n\) вершинами и \(m\) рёбрами. Вы можете выполнить следующую операцию не более чем \(2\cdot \max(n,m)\) раз: - Выберите три различные вершины \(a\), \(b\) и \(c\). Затем для каждого из рёбер \((a,b)\), \((b,c)\) и \((c,a)\) выполните следующее:
- Если ребро не существует, добавьте его. В противном случае, если оно существует, удалите его.
Граф называется классным, если и только если выполняется одно из следующих условий: - Граф не имеет рёбер, или
- Граф является деревом.
Вам нужно сделать граф классным, выполняя указанные выше операции. Обратите внимание, что вы можете использовать не более чем \(2\cdot \max(n,m)\) операций. Можно показать, что всегда существует хотя бы одно решение. Выходные данные Для каждого набора входных данных в первой строке выведите целое число \(k\) (\(0\le k\le 2\cdot \max(n, m)\)) — количество операций. Затем выведите \(k\) строк, \(i\)-я строка содержит три различных целых числа \(a\), \(b\) и \(c\) (\(1\le a,b,c\le n\)) — три целых числа, которые вы выбрали в \(i\)-й операции. Если существует несколько решений, вы можете вывести любое из них. Примечание В первом наборе входных данных граф уже классный, потому что рёбер нет. Во втором наборе входных данных, после выполнения единственной операции, граф становится деревом, поэтому он классный. В третьем наборе входных данных граф уже классный, потому что он является деревом. В четвёртом наборе входных данных, после выполнения единственной операции, граф не имеет рёбер, поэтому он классный. В пятом наборе входных данных: | Операция | Граф до операции | Граф после операции | | \(1\) |  |  | | \(2\) |  |  | | \(3\) |  |  |
Обратите внимание, что после первой операции граф уже стал классным, и есть две лишние операции. Поскольку граф по-прежнему классный после двух лишних операций, это является допустимым ответом. | |
![]()
|
|
E. Деревья Пенчика и Хлои
Деревья
дп
жадные алгоритмы
математика
поиск в глубину и подобное
реализация
сортировки
Структуры данных
*2100
До отъезда Пенчика и Хлои в Сингапур оставалось всего несколько часов, и им не терпелось увидеть высоченные деревья в Сингапурском ботаническом саду! Пытаясь сдержать свое волнение, Пенчик смастерил дерево с корнями, чтобы занять Хлою и себя. У Пенчика есть корневое дерево\(^{\text{∗}}\), состоящее из \(n\) вершин, пронумерованных от \(1\) до \(n\), с вершиной \(1\) в качестве корня. Хлоя может выбрать целое неотрицательное число \(d\), чтобы создать совершенное бинарное дерево\(^{\text{†}}\) глубины \(d\). Поскольку Пенчик и Хлоя — хорошие друзья, Хлоя хочет, чтобы ее дерево было изоморфно\(^{\text{‡}}\) дереву Пенчика. Чтобы достичь этого, Хлоя может выполнить следующую операцию над своим деревом любое количество раз: - Выбрать ребро \((u,v)\), где \(u\) является родителем \(v\).
- Удалить вершину \(v\) и все ребра, связанные с \(v\), а затем соединить всех бывших детей \(v\) непосредственно с \(u\).
В частности, операция над ребром \((u, v)\), где \(v\) — лист, удалит вершину \(v\) без добавления новых ребер. Поскольку построение совершенного бинарного дерева может занять много времени, Хлоя хочет выбрать минимальное \(d\), такое, чтобы совершенное бинарное дерево глубины \(d\) можно было сделать изоморфным дереву Пенчика с помощью вышеописанной операции. Обратите внимание, что Хлоя не может менять корни деревьев. Выходные данные Для каждого набора входных данных выведите в отдельной строке одно целое число: минимальную глубину совершенного бинарного дерева Хлои. Примечание В первом наборе входных данных можно создать совершенное бинарное дерево глубины \(2\).  Рассмотрим выполнение операции на ребре \(AC\). Рёбра \(AC\), \(CF\) и \(CG\) удаляются, а рёбра \(AF\) и \(AG\) добавляются.  Полученное дерево изоморфно дереву, заданному на входе. Можно доказать, что никакая последовательность операций над бинарным деревом глубины менее \(2\) не может привести к дереву, изоморфному дереву, заданному на входе. Во втором наборе входных данных дерево уже изоморфно совершенному бинарному дереву глубины \(3\). | |
![]()
|
|
D. Генокракен
графы
Деревья
жадные алгоритмы
интерактив
Конструктив
реализация
Структуры данных
*1800
Это интерактивная задача. Очистив Прибрежную Зону, Гретель обнаружила монстра по имени Генокракен и удерживает его для своих научных исследований. Нервная система монстра может быть представлена как дерево\(^{\dagger}\) из \(n\) вершин (на самом деле, всё не должно постоянно напоминать деревья\(\ldots\)), пронумерованных от \(0\) до \(n-1\), с вершиной \(0\) в качестве корня. Цель Гретель — узнать точную структуру нервной системы монстра. Более конкретно, она хочет узнать значения \(p_1, p_2, \ldots, p_{n-1}\) дерева, где \(p_i\) (\(0 \le p_i < i\)) является прямым предком вершины \(i\) (\(1 \le i \le n - 1\)). Она не знает точно, как расположены вершины, но знает несколько приятных фактов: - Если мы удалим корневую вершину \(0\) и все смежные ребра, то это дерево превратится в лес, состоящий только из путей\(^{\ddagger}\). Каждая вершина, которая изначально была смежной с вершиной \(0\), будет концом какого-то пути.
- Вершины нумеруются таким образом, что если \(1 \le x \le y \le n - 1\), то \(p_x \le p_y\).
- Вершина \(1\) гарантированно имеет ровно две смежные вершины (включая вершину \(0\)).
 |  |  | | Дерево на этой картинке не удовлетворяет условию, потому что если мы удалим вершину \(0\), то вершина \(2\) (которая изначально была смежной с вершиной \(0\)) не будет концом пути \(4-2-5\). | Дерево на этой картинке не удовлетворяет условию, потому что должно выполняться \(p_3 \le p_4\). | Дерево на этой картинке не удовлетворяет условию, потому что вершина \(1\) имеет только одну смежную вершину. |
Гретель может делать запросы к защитной камере: - «? a b» (\(1 \le a, b < n\), \(a \ne b\)) — камера проверит, содержит ли простой путь между вершинами \(a\) и \(b\) вершину \(0\).
Однако, чтобы избежать неожиданных последствий от чрезмерной стимуляции существа, Гретель хочет сделать не более \(2n - 6\) запросов. Хотя Гретель одарена, она не может сделать всё сразу, так что можете ли вы протянуть ей руку помощи? \(^{\dagger}\)Дерево — это связный граф, в котором каждая пара различных вершин имеет ровно один простой путь, соединяющий их. \(^{\ddagger}\)Путь — это дерево, вершины которого могут быть записаны в порядке \(v_1, v_2, \ldots, v_k\) так, что рёбра имеют вид \((v_i, v_{i+1})\) (\(1 \le i < k\)). Протокол взаимодействия Для каждого набора входных данных взаимодействие начинается с чтения целого числа \(n\). Затем вы можете делать запросы следующего вида: - «? a b» (без кавычек) (\(1 \le a, b < n\), \(a \ne b\)).
После запроса прочитайте целое число \(r\) — ответ на ваш запрос. Вам разрешено использовать не более \(2n - 6\) запросов этого типа. - Если простой путь между вершинами \(a\) и \(b\) не содержит вершину \(0\), вы получите \(r = 0\).
- Если простой путь между вершинами \(a\) и \(b\) содержит вершину \(0\), вы получите \(r = 1\).
- В случае, если вы сделаете более \(2n-6\) запросов или сделаете некорректный запрос, вы получите \(r = -1\). После получения такого ответа ваша программа должна немедленно завершиться, чтобы получить вердикт «Неправильный ответ». В противном случае вы можете получить произвольный вердикт, потому что ваше решение продолжит чтение из закрытого потока.
Когда вы определите структуру, выведите строку в формате «! \(p_1 \space p_2 \ldots p_{n-1}\)» (без кавычек), где \(p_i\) (\(0 \le p_i < i\)) обозначает индекс прямого предка вершины \(i\). Этот запрос не учитывается в лимите \(2n - 6\) запросов. После решения одного набора входных данных программа должна сразу же переходить к следующему. После решения всех наборов входных данных программа должна быть немедленно завершена. После вывода любого запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте: - fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Интерактор неадаптивный. Дерево не меняется в процессе взаимодействия. Взломы Для взлома используйте следующий формат: Первая строка содержит одно целое число \(t\) (\(1 \le t \le 500\)) — количество наборов входных данных. Далее следует описание наборов входных данных. Первая строка каждого набора входных данных содержит одно целое число \(n\) (\(4 \le n \le 10^4\)) — количество вершин в нервной системе Генокракена. Вторая строка каждого набора входных данных содержит \(n-1\) целых чисел \(p_1, p_2, \ldots, p_{n-1}\) (\(0 \le p_1 \le p_2 \le \ldots \le p_{n-1} \le n - 2\), \(0 \le p_i < i\)) — прямые предки вершин \(1\), \(2\), ..., \(n-1\) в системе соответственно. В каждом наборе входных данных значения \(p_1, p_2, \ldots, p_{n-1}\) должны обеспечивать следующее в дереве: - Если мы удалим корневую вершину \(0\) и все смежные ребра, то это дерево превратится в лес, состоящий только из путей. Каждая вершина, которая изначально была смежной с вершиной \(0\), будет концом какого-то пути.
- Вершина \(1\) имеет ровно две смежные вершины (включая вершину \(0\)).
Сумма \(n\) по всем наборам входных данных не должна превышать \(10^4\). Примечание В первом наборе входных данных нервная система Генокракена образует следующее дерево:  - Ответ на «? 2 3» равен \(1\). Это означает, что простой путь между вершинами \(2\) и \(3\) содержит вершину \(0\).
Во втором наборе входных данных нервная система Генокракена образует следующее дерево:  - Ответ на «? 2 3» равен \(1\). Это означает, что простой путь между вершинами \(2\) и \(3\) содержит вершину \(0\).
- Ответ на «? 2 4» равен \(0\). Это означает, что простой путь между вершинами \(2\) и \(4\) не содержит вершину \(0\).
В третьем наборе входных данных нервная система Генокракена образует следующее дерево:  | |
![]()
|
|
G. Сакурако и Чефир
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
Структуры данных
*2200
Дано дерево из \(n\) вершин с корнем в вершине \(1\). Гуляя по нему со своим котом Чефиром, Сакурако отвлеклась, и Чефир убежал. Чтобы помочь Сакурако, Косукэ записал свои \(q\) предположений. В \(i\)-м предположении он считает, что Чефир потерялся в вершине \(v_i\) и имел \(k_i\) выносливости. Также для каждого предположения Косукэ считает, что Чефир мог переместиться по рёбрам произвольное число раз: - из вершины \(a\) в вершину \(b\), если \(a\) является предком\(^{\text{∗}}\) \(b\), выносливость от этого не изменится;
- из вершины \(a\) в вершину \(b\), если \(a\) не является предком \(b\), тогда выносливость Чефира понизится на \(1\).
Если выносливость Чефира равна \(0\), то он не сможет сделать перемещение второго типа. Для каждого предположения ваша задача — вычислить расстояние до самой дальней вершины, в которую Чефир мог уйти от вершины \(v_i\), имея \(k_i\) выносливости. Выходные данные Для каждого теста и для каждого предположения выведите расстояние до самой дальней вершины, в которую Чефир мог пройти от начальной точки \(v_i\) имея \(k_i\) выносливости. Примечание В первом примере: - В первом запросе можно пройти из вершины \(5\) в вершину \(3\) (после этого выносливость уменьшится на \(1\) и станет равна \(0\)), после этого можно пройти в вершину \(4\);
- Во втором запросе из вершины \(3\) имея \(1\) выносливости можно добраться только до вершин \(2\), \(3\), \(4\) и \(5\);
- В третьем запросе из вершины \(2\) имея \(0\) выносливости можно добраться только до вершин \(2\), \(3\), \(4\) и \(5\);
| |
![]()
|
|
F. Операции с деревом
Бинарный поиск
Деревья
дп
Перебор
поиск в глубину и подобное
*2500
Это многое говорит об обществе. Однажды черепаха подарила вам дерево с \(n\) вершинами и корнем в вершине \(x\). Вершина \(i\) имеет начальное целое неотрицательное значение \(a_i\). Вы хотите сделать так, чтобы значения всех вершин стали равны \(0\). Для этого вы выполните ряд операций над деревом, где каждая операция будет выполняться над определенной вершиной. Определим операцию над вершиной \(u\) как выбор одной вершины в поддереве\(^{\text{∗}}\) \(u\), и увеличение или уменьшение ее значения на \(1\). Порядок выполнения операций над вершинами следующий: - Для \(1 \le i \le n\), \(i\)-я операция будет выполнена над вершиной \(i\).
- Для \(i > n\), \(i\)-я операция будет выполнена над той же вершиной, что и операция \(i - n\).
Более формально, \(i\)-я операция будет выполнена над \((((i - 1) \bmod n) + 1)\)-й вершиной.\(^{\text{†}}\) Обратите внимание, что нельзя пропускать операции; то есть нельзя выполнить \(i\)-ю операцию, не выполнив сначала операции \(1, 2, \ldots, i - 1\). Найдите минимальное количество операций, которое необходимо выполнить, чтобы значения всех вершин стали равны \(0\), при условии, что вы выполняете операции оптимально. Если после конечного числа операций невозможно сделать значения всех вершин равными \(0\), выведите \(-1\). Выходные данные Для каждого набора входных данных выведите одно целое число, обозначающее минимальное количество операций, необходимое для того, чтобы сделать значения всех вершин равными \(0\). Если невозможно сделать значения всех вершин равными \(0\), выведите \(-1\). Примечание В первом наборе входных данных вы можете выполнить следующую последовательность операций: - На \(1\) операции уменьшите значение вершины \(1\). Эта операция корректна, потому что \((((1 - 1) \bmod n) + 1) = 1\), и вершина \(1\) находится в поддереве вершины \(1\).
- На \(2\) операции уменьшите значение вершины \(2\). Эта операция корректна, потому что \((((2 - 1) \bmod n) + 1) = 2\), и вершина \(2\) находится в поддереве вершины \(2\).
- На \(3\) операции уменьшите значение вершины \(2\). Эта операция корректна, потому что \((((3 - 1) \bmod n) + 1) = 1\), а вершина \(2\) находится в поддереве вершины \(1\).
| |
![]()
|
|
G1. Учись! (простая версия)
Деревья
дп
*3300
Это простая версия задачи. Различия между версиями заключаются в ограничениях на \(n\) и сумму \(n\). В этой версии \(n \leq 3000\), а сумма \(n\) не превосходит \(10^4\). Вы можете совершать взломы только в том случае, если решены обе версии задачи. Так-так-так, посмотрим, как Бесси распоряжается своими финансами. Похоже, она в финансовой яме! К счастью, чтобы решить эту проблему, она устраивается на работу в Moogle. Собеседования в Moogle требуют глубокого знания непонятных алгоритмов и сложных структур данных, но Бесси получила от легендарного гроссмейстера наводку на то, что именно ей нужно изучить. Бесси написала следующий код для бинарного поиска определенного элемента \(k\) в возможно несортированном массиве \([a_1, a_2,\ldots,a_n]\) с \(n\) элементами. let l = 1
let h = n
while l < h:
let m = floor((l + h) / 2)
if a[m] < k:
l = m + 1
else:
h = m
return l
Бесси отправила свой код в задачу фермера Джона с \(m\) (\(1 \leq m \leq n\)) тестами. \(i\)-й тест имеет вид \((x_i, k_i)\) (\(1 \leq x, k \leq n\)). Гарантируется, что все \(x_i\) различны и все \(k_i\) различны. Тест \(i\) корректен, если выполняются следующие условия: - \(x_i\)-й элемент в массиве — \(k_i\).
- Если Бесси вызовет двоичный поиск, как показано в коде выше, для \(k_i\), то он вернет \(x_i\).
Возможно, не все \(m\) тестов будут корректны на одном и том же массиве, поэтому фермер Джон удалит некоторые из них, чтобы Бесси могла пройти все тесты. Пусть \(r\) — это минимальное количество тестов, которое нужно удалить, чтобы существовал массив \([a_1, a_2,\ldots,a_n]\), в котором \(1 \leq a_i \leq n\), чтобы все оставшиеся тесты были корректными. Помимо нахождения \(r\), фермер Джон хочет, чтобы вы подсчитали количество массивов \([a_1, a_2,\ldots,a_n]\), в которых \(1 \leq a_i \leq n\), таких, что существует способ удалить ровно \(r\) тестов так, чтобы все оставшиеся тесты были корректными. Поскольку это число может быть очень большим, выведите его по модулю \(998\,244\,353\). Выходные данные Для каждого набора входных данных выведите два целых числа: \(r\) — минимальное количество удаленных тестов, чтобы существовал массив, в котором все оставшиеся тесты корректны; и количество массивов, для которых можно удалить \(r\) тестов, чтобы все оставшиеся тесты были корректны, по модулю \(998\,244\,353\). Примечание Рассмотрим первый пример. В первом наборе входных данных массив \([1,2,2,3,4]\) удовлетворяет всем \(m\) тестам, поэтому минимальное количество тестов, которые должна удалить Бесси, равно \(0\). Обратите внимание, что это также единственный массив, который удовлетворяет всем \(m\) тестам. Во втором наборе входных данных минимальное количество тестов, которое Бесси должна удалить, равняется \(1\). Единственный тест, который Бесси может удалить, это \((2,5)\). Если Бесси удалит тест \((2,5)\), то массивами, удовлетворяющими оставшимся \(m-1\) тестам, будут \([2,2,3,1,4]\), \([2,2,3,2,4]\), \([2,2,3,3,4]\). | |
![]()
|
|
D. Непростое дерево
Деревья
жадные алгоритмы
Конструктив
Перебор
поиск в глубину и подобное
теория чисел
*1900
Дано дерево с \(n\) вершинами. Вам необходимо создать массив \(a_1, a_2, \ldots, a_n\) длины \(n\), состоящий из различных целых чисел от \(1\) до \(2 \cdot n\). При этом для каждого ребра \(u_i \leftrightarrow v_i\) дерева значение \(|a_{u_i} - a_{v_i}|\) не должно быть простым числом. Найдите любой массив, удовлетворяющий этим условиям, либо сообщите, что такого массива нет. Выходные данные Для каждого набора входных данных, если массив, удовлетворяющий условиям, существует, выведите его элементы \(a_1, a_2, \ldots, a_n\). Иначе, выведите единственное число \(-1\). Примечание Ниже представлены возможные ответы. Вместо номеров вершин в них записаны соответствующие элементы массива \(a\). Изображение дерева в первом наборе  Изображение дерева во втором наборе Изображение дерева во втором наборе  | |
![]()
|
|
E. Контроль случайности
графы
Деревья
дп
жадные алгоритмы
Комбинаторика
математика
поиск в глубину и подобное
Теория вероятностей
*2100
Дано дерево с \(n\) вершинами. В некоторую вершину \(v \ne 1\) посадят робота. Пусть у вас изначально есть \(p\) монет. Рассмотрим следующий процесс, где в \(i\)-й шаг (начиная с \(i = 1\)): - Если \(i\) нечётное, робот передвинется в соседнюю вершину в сторону вершины \(1\);
- Иначе, \(i\) чётное. Можно либо заплатить одну монету (если остались), после чего робот передвинется в соседнюю вершину в сторону вершины \(1\), либо ничего не платить, после чего робот передвинется в равновероятно выбранную соседнюю вершину.
Процесс останавливается, как только робот попадает в вершину \(1\). Определим \(f(v, p)\) как минимально возможное математическое ожидание количества шагов процесса выше (количество использованных монет минимизировать не надо). Необходимо ответить на \(q\) запросов, в \(i\)-м из которых надо найти значение \(f(v_i, p_i)\) по модулю\(^{\text{∗}}\) \(998\,244\,353\). Выходные данные Для каждого набора входных данных выведите \(q\) целых чисел: значения \(f(v_i, p_i)\) по модулю \(998\,244\,353\). Формально, пусть \(M = 998\,244\,353\). Можно показать, что ответ может быть представлен в виде несократимой дроби \(\frac{p}{q}\), где \(p\) и \(q\) — целые числа, и \(q \not \equiv 0 \pmod{M}\). Выведите целое число, равное \(p \cdot q^{-1} \bmod M\). Другими словами, выведите такое целое число \(x\), что \(0 \le x < M\) и \(x \cdot q \equiv p \pmod{M}\). Примечание Дерево из первого набора показано ниже:  Для первого запроса значение математического ожидания равно \(1\), так как робот начинает движение с вершины \(2\) и первым ходом попадает в вершину \(1\) и завершает перемещение. Посчитаем значение математического ожидания для второго запроса (\(x\) это количество шагов в процессе): - \(P(x < 2) = 0\), расстояние до вершины \(1\) равно \(2\) и робот не может дойти до него за меньшее количество шагов.
- \(P(x = 2) = \frac{1}{3}\), так как есть только одна последовательность шагов, приводящая к \(x = 2\). Это \(3 \rightarrow_{1} 2 \rightarrow_{0.33} 1\) с вероятностью \(1 \cdot \frac{1}{3}\).
- \(P(x \bmod 2 = 1) = 0\), так как робот может достичь вершину \(1\) сделав только чётное количество шагов.
- \(P(x = 4) = \frac{2}{9}\): возможные пути \(3 \rightarrow_{1} 2 \rightarrow_{0.67} [3, 4] \rightarrow_{1} 2 \rightarrow_{0.33} 1\).
- \(P(x = 6) = \frac{4}{27}\): возможные пути \(3 \rightarrow_{1} 2 \rightarrow_{0.67} [3, 4] \rightarrow_{1} 2 \rightarrow_{0.67} [3, 4] \rightarrow_{1} 2 \rightarrow_{0.33} 1\).
- \(P(x = i \cdot 2) = \frac{2^{i - 1}}{3^i}\) в общем случае.
В результате \(f(v, p) = \sum\limits_{i=1}^{\infty}{i \cdot 2 \cdot \frac{2^{i - 1}}{3^i}} = 6\). Дерево из второго набора показано ниже:  | |
![]()
|
|
I. Auto Complete
Бинарный поиск
Деревья
реализация
сортировки
Строки
Структуры данных
хэши
*2300
 You are designing a snazzy new text editor, and you want to add a nifty auto-complete feature to help users save time. Here is how it will work: if a user types "App", your editor will magically suggest the word "Application"! Even better, users can personalize the words that auto-complete in your editor. Your editor will support 4 kinds of operations (Let's say the current text in your editor is \(t\)): - Add an auto complete pattern \(p_i\).
- Delete an auto complete pattern \(p_i\).
- Append a string \(s\) to the end of \(t\).
- Delete \(c\) characters from the end of \(t\). Note that if \(c\) is larger then the length of \(t\), delete all the characters from \(t\).
After each action, your editor should suggest an auto-complete candidate \(i\) that matches the following criteria: - The string \(p_i\) has a prefix equal to \(t\).
- If there are multiple \(p_i\), pick the longest one.
- If there are still multiple \(p_i\), pick the one with the smallest lexicographic order.
- If there are still multiple \(p_i\), pick the one with the smallest ID.
To simplify the question, for each action, print the suggested auto complete pattern ID. If there's no match, print -1. For example, let us say we have three candidates: "alice", "bob", and "charlie", with ID 1, 2, and 3. At first, there is nothing on the screen, so "charlie" (3) should be suggested because it is the longest. Then, let us say the user types "b". You should suggest "bob" (2) because it is the only one that starts with "b". Finally, let us say the user type "body". You should print -1 because there is no matched pattern. Output The program should output \(n\) lines. For each action, output an integer \(i\), which means that after the action, \(p_i\) is the suggested auto complete candidate. If there is no \(p_i\) that matches the requirement, output -1. | |
![]()
|
|
E. Пары вершин
Бинарный поиск
Деревья
жадные алгоритмы
Перебор
поиск в глубину и подобное
разделяй и властвуй
реализация
Структуры данных
*2900
Дано дерево, состоящее из \(2n\) вершин. Напомним, что деревом называется связный неориентированный граф, в котором нет циклов. На каждой вершине написано одно целое число от \(1\) до \(n\). Каждое число от \(1\) до \(n\) написано ровно на двух различных вершинах. У каждой вершины также есть стоимость — вершина \(i\) стоит \(2^i\). Требуется выбрать в дереве такое подмножество вершин, что: - подмножество связно; то есть, из каждой вершины подмножества можно добраться до любой другой вершины подмножества, проходя только через вершины подмножества;
- каждое число от \(1\) до \(n\) написано хотя бы на одной вершине подмножества.
Среди всех таких подмножеств требуется найти такое, что суммарная стоимость вершин в нем минимальна. Обратите внимание, что не требуется минимизировать количество вершин в подмножестве. Выходные данные В первой строке выведите одно целое число \(k\) — количество вершин в подмножестве. Во второй строке выведите \(k\) различных целых чисел от \(1\) до \(2n\) — номера вершин в выбранном подмножестве. Вершины можно выводить в произвольном порядке. Примечание  На данных изображениях нарисованы ответы на первые два примера. В скобках около номеров вершин подписаны числа, написанные на них. В первом примере есть такие валидные подмножества: \([2, 4, 5]\) (стоимость равна \(2^2 + 2^4 + 2^5 = 52\)), \([2, 4, 5, 6]\) (стоимость равна \(116\)), \([1, 6, 3]\) (стоимость равна \(74\)), \([2, 6, 3]\) (стоимость равна \(76\)) и многие другие. Во втором примере стоимость подмножества \([4, 6, 3, 1]\) равна \(90\). | |
![]()
|
|
G1. Средняя демоническая задача (легкая версия)
графы
Деревья
Паросочетания
поиск в глубину и подобное
реализация
*1700
Это легкая версия задачи. Ключевое отличие между двумя версиями выделено жирным шрифтом. Группа из \(n\) пауков собралась, чтобы обменяться плюшевыми игрушками. Изначально у каждого паука есть \(1\) плюшевая игрушка. Каждый год, если паук \(i\) имеет хотя бы одну плюшевую игрушку, он отдаст ровно одну плюшевую игрушку пауку \(r_i\). В противном случае он ничего не сделает. Обратите внимание, что все передачи плюшевых игрушек происходят одновременно. В этой версии, если у любого паука в любой момент времени больше \(1\) плюшевой игрушки, он выбросит все, кроме \(1\). Процесс считается стабильным в текущем году, если у каждого паука количество плюшевых игрушек (до обмена в текущем году) совпадает с количеством плюшевых игрушек, которое у него было в предыдущем году (до обмена в предыдущем году). Обратите внимание, что год \(1\) никогда не может быть стабильным. Найдите первый год, в котором процесс становится стабильным. Выходные данные Для каждого набора входных данных выведите целое число в новой строке, первый год, в котором процесс становится стабильным. Примечание Для второго набора входных данных: - В год \(1\) следующий массив показывает количество плюшевых игрушек у каждого паука: \([1, 1, 1, 1, 1]\). Затем происходит обмен в год \(1\).
- В год \(2\) следующий массив показывает количество плюшевых игрушек у каждого паука: \([1, 1, 1, 1, 1]\). Поскольку этот массив такой же, как в предыдущем году, этот год является стабильным.
Для третьего набора входных данных: - В год \(1\) следующий массив показывает количество плюшевых игрушек у каждого паука: \([1, 1, 1, 1, 1]\). Затем происходит обмен в год \(1\).
- В год \(2\) следующий массив показывает количество плюшевых игрушек у каждого паука: \([1, 1, 1, 1, 0]\). Затем происходит обмен в год \(2\). Обратите внимание, что, хотя два паука отдали пауку \(2\) плюшевые игрушки, паук \(2\) может оставить только одну плюшевую игрушку.
- В год \(3\) следующий массив показывает количество плюшевых игрушек у каждого паука: \([1, 1, 0, 1, 0]\). Затем происходит обмен в год \(3\).
- В год \(4\) следующий массив показывает количество плюшевых игрушек у каждого паука: \([1, 1, 0, 0, 0]\). Затем происходит обмен в год \(4\).
- В год \(5\) следующий массив показывает количество плюшевых игрушек у каждого паука: \([1, 1, 0, 0, 0]\). Поскольку этот массив такой же, как в предыдущем году, этот год является стабильным.
| |
![]()
|
|
G2. Средняя демоническая задача (сложная версия)
графы
Деревья
дп
поиск в глубину и подобное
реализация
снм
*1900
Это сложная версия задачи. Ключевое отличие между двумя версиями выделено жирным шрифтом. Группа из \(n\) пауков собралась, чтобы обменяться плюшевыми игрушками. Изначально у каждого паука есть \(1\) плюшевая игрушка. Каждый год, если паук \(i\) имеет хотя бы одну плюшевую игрушку, он отдаст ровно одну плюшевую игрушку пауку \(r_i\). В противном случае он ничего не сделает. Обратите внимание, что все передачи плюшевых игрушек происходят одновременно. В этой версии каждому пауку разрешено иметь более 1 плюшевой игрушки в любой момент времени. Процесс считается стабильным в текущем году, если у каждого паука такое же количество плюшевых игрушек (до обмена в текущем году), как и в предыдущем году (до обмена в предыдущем году). Обратите внимание, что год \(1\) никогда не может быть стабильным. Найдите первый год, в котором процесс становится стабильным. Выходные данные Для каждого набора входных данных выведите целое число в новой строке, первый год, в котором процесс становится стабильным. Примечание Для второго набора входных данных: - В год \(1\) следующий массив показывает количество плюшевых игрушек у каждого паука: \([1, 1, 1, 1, 1]\). Затем происходит обмен в год \(1\).
- В год \(2\) следующий массив показывает количество плюшевых игрушек у каждого паука: \([1, 1, 1, 1, 1]\). Поскольку этот массив такой же, как в предыдущем году, этот год является стабильным.
Для третьего набора входных данных: - В год \(1\) следующий массив показывает количество плюшевых игрушек у каждого паука: \([1, 1, 1, 1, 1]\). Затем происходит обмен в год \(1\).
- В год \(2\) следующий массив показывает количество плюшевых игрушек у каждого паука: \([1, 2, 1, 1, 0]\). Затем происходит обмен в год \(2\).
- В год \(3\) следующий массив показывает количество плюшевых игрушек у каждого паука: \([1, 3, 0, 1, 0]\). Затем происходит обмен в год \(3\).
- В год \(4\) следующий массив показывает количество плюшевых игрушек у каждого паука: \([1, 4, 0, 0, 0]\). Затем происходит обмен в год \(4\).
- В год \(5\) следующий массив показывает количество плюшевых игрушек у каждого паука: \([1, 4, 0, 0, 0]\). Поскольку этот массив такой же, как в предыдущем году, этот год является стабильным.
| |
![]()
|
|
F. Кевин и математический класс
Деревья
дп
математика
Перебор
разделяй и властвуй
реализация
Структуры данных
*2500
Кевин — студент из Вечно Спящего Города, который в настоящее время посещает математический класс, где учитель задает ему упражнения на деление. На доске написаны две строки положительных целых чисел, каждая из которых содержит \( n \) чисел. Первая строка — это \( a_1, a_2, \ldots, a_n \), а вторая строка — \( b_1, b_2, \ldots, b_n \). Для каждого упражнения на деление Кевин может выбрать любой отрезок \( [l, r] \) и найти минимальное значение \( x \) среди \( b_l, b_{l+1}, \ldots, b_r \). Затем он изменит каждое \( a_i \) для \( l \leq i \leq r \) на округление вверх от \( a_i \), деленного на \( x \). Формально, он выбирает два целых числа \( 1 \leq l \leq r \leq n \), устанавливает \( x = \min_{l \leq i \leq r} b_i \), и изменяет все \( a_i \) для \( l \leq i \leq r \) на \( \lceil \frac{a_i}{x} \rceil \). Кевин может покинуть класс и вернуться домой, когда все \( a_i \) станут равны \( 1 \). Он стремится уйти и хочет узнать минимальное количество упражнений на деление, необходимых для достижения этого. Выходные данные Для каждого набора входных данных выведите одно целое число — минимальное количество упражнений на деление, необходимых для выхода из класса. Примечание Для первого примера: \( [{\color{red}{5,4}},2]\xrightarrow[\min(b_1,b_2)=3]{\text{операция на отрезке }[1,2]}[{\color{red}{2,2,2}}]\xrightarrow[\min(b_1,b_2,b_3)=2]{\text{операция на отрезке }[1,3]}[1,1,1] \). Для второго примера: \( [{\color{red}{3,6,1}},3,2]\xrightarrow[\min(b_1,b_2,b_3)=3]{\text{операция на отрезке }[1,3]}[1,{\color{red}{2,1,3}},2]\xrightarrow[\min(b_2,b_3,b_4)=2]{\text{операция на отрезке }[2,4]}[1,1,1,{\color{red}{2,2}}]\xrightarrow[\min(b_4,b_5)=2]{\text{операция на отрезке }[4,5]}[1,1,1,1,1] \). | |
![]()
|
|
G. Развал дерева
Деревья
дп
поиск в глубину и подобное
*1900
Дано дерево\(^{\text{∗}}\) из \(n\) вершин. Вы можете один раз выбрать две вершины \(a\) и \(b\) и удалить все вершины на пути из \(a\) в \(b\), включая сами вершины. Если вы выберете \(a=b\), то будет удалена только одна вершина. Ваша задача — найти максимальное количество компонент связности\(^{\text{†}}\), которое может образоваться после удаления пути из дерева. Выходные данные Для каждого набора входных данных выведите одно целое число — максимальное число компонент связности, которого можно добиться с помощью описанной операции. | |
![]()
|
|
E. Находчивая гусеничная последовательность
графы
Деревья
дп
жадные алгоритмы
игры
поиск в глубину и подобное
*1900
Дано дерево, состоящее из \(n\) вершин. Гусеница обозначается парой целых чисел \((p, q)\) (\(1 \leq p, q \leq n\), \(p \neq q\)): её голова находится в вершине \(p\), её хвост находится в вершине \(q\), и она доминирует над всеми вершинами на простом пути от \(p\) до \(q\) (включая \(p\) и \(q\)). Гусеничная последовательность пары \((p, q)\) определяется как последовательность, состоящая только из вершин на простом пути, отсортированных в порядке возрастания расстояния до \(p\). Нора и Арон по очереди двигают гусеницу, причем Нора ходит первой. Оба игрока будут использовать свою собственную оптимальную стратегию: - Они будут играть, чтобы выиграть;
- Однако, если это невозможно, они будут играть, чтобы помешать другому человеку победить (таким образом, игра закончится ничьёй).
В свой ход Нора может выбрать вершину \(u\), смежную с вершиной \(p\), над которой не доминирует гусеница, и переместить все вершины в ней на одно ребро по направлению к вершине \(u\)\(^{\text{∗}}\). В свою очередь, Арон может выбрать вершину \(v\), смежную с вершиной \(q\), над которой не доминирует гусеница, и переместить все вершины в ней на одно ребро по направлению к вершине \(v\). Обратите внимание, что ходы, разрешенные двум игрокам, различны. Если \(p\) — лист\(^{\text{†}}\), то Нора выигрывает\(^{\text{‡}}\). Если \(q\) — лист, то Арон выигрывает. Если либо изначально оба \(p\) и \(q\) являются листьями, либо после \(10^{100}\) ходов игра не закончится, результатом будет ничья. Пожалуйста, посчитайте количество целочисленных пар \((p, q)\) с \(1 \leq p, q \leq n\) и \(p \neq q\) таких, что если изначально гусеница находится на \((p, q)\), то Арон выиграет. Выходные данные Для каждого набора входных данных выведите одну строку, содержащую целое число: количество целых пар \((p, q)\), для которых Арон выиграет. Примечание В первом наборе входных данных всеми возможными гусеницами являются \((1, 2)\) и \((2, 1)\), что приводит к ничьей с самого начала, поскольку оба \(p\) и \(q\) являются листьями. Во втором наборе входных данных, гусеницы, которые позволяют Арону выиграть, следующие: \((1, 3)\), \((1, 4)\), \((1, 5)\), \((2, 3)\), \((2, 4)\), \((2, 5)\). Давайте рассмотрим некоторых гусениц. - Для гусеницы \((1, 5)\): вершина \(p = 1\) — это не лист, но вершина \(q = 5\) — лист, так что Арон выигрывает в самом начале.
- Для гусеницы \((2, 1)\): вершина \(p = 2\) не является листом, и \(q = 1\) не является листом. На первом ходу Нора может переместить гусеницу в направлении вершины \(5\). Следовательно, гусеница становится \((5, 2)\), а вершина \(p = 5\) — лист, так что Нора выиграет.
| |
![]()
|
|
D. Сбалансированное дерево
графы
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
*2200
Дано дерево\(^{\text{∗}}\) с \(n\) вершинами и значениями \(l_i, r_i\) для каждой вершины. Вы можете выбрать начальные значения \(a_i\), удовлетворяющие условию \(l_i\le a_i\le r_i\) для \(i\)-й вершины. Дерево считается сбалансированным, если все значения в вершинах равны, а значение сбалансированного дерева определяется как значение любой вершины. За одну операцию вы можете выбрать две вершины \(u\) и \(v\) и увеличить значения всех вершин в поддереве\(^{\text{†}}\) вершины \(v\) на \(1\), рассматривая \(u\) как корень всего дерева. Обратите внимание, что \(u\) может быть равен \(v\). Ваша цель — выполнить последовательность операций так, чтобы дерево стало сбалансированным. Найдите минимально возможное значение дерева после выполнения этих операций. Обратите внимание, что вам не нужно минимизировать количество операций. Выходные данные Для каждого набора данных выведите одно целое число — минимально возможное значение, к которому могут быть приведены все \(a_i\) после выполнения операций. Можно доказать, что ответ всегда существует. Примечание В первом наборе данных вы можете выбрать \(a=[6,6,0,5]\). Вы можете выполнить следующие операции, чтобы сделать все \(a_i\) равными: - Выберите \(u=4\), \(v=3\) и выполните операцию \(5\) раз.
- Выберите \(u=1\), \(v=3\) и выполните операцию \(6\) раз.
Полный процесс показан ниже (числа в скобках — значения \(a\)): 
Можно доказать, что это оптимальное решение. | |
![]()
|
|
E1. Игра (простая версия)
графы
Деревья
жадные алгоритмы
игры
поиск в глубину и подобное
Структуры данных
*2000
Это простая версия задачи. Отличие между версиями заключается в том, что в этой версии вам нужно только найти только одну из возможных вершин, которую может выбрать Чирно. Вы можете делать взломы только в том случае, если решили все версии этой задачи. Чирно и Дайёсей играют в игру с деревом\(^{\text{∗}}\) из \(n\) вершин, корнем которого является вершина \(1\). Значение \(i\)-й вершины равно \(w_i\). Они по очереди делают ходы; первым ходит Чирно. На каждом ходу, предполагая, что противник выбрал \(j\) на последнем ходу, игрок может выбрать любую оставшуюся вершину \(i\), удовлетворяющую условию \(w_i>w_j\), и удалить поддерево\(^{\text{†}}\) вершины \(i\). В частности, Чирно может выбрать любую вершину и удалить её поддерево на первом ходу. Первый игрок, который не может сделать ход, выигрывает, и они оба надеются победить. Найдите одну из возможных вершин, которую может выбрать Чирно на первом ходу, чтобы выиграть, если оба игрока будут играть оптимально. Выходные данные Для каждого набора входных данных выведите одну строку. Если Чирно может выиграть, выведите любую вершину, которую она может выбрать на первом ходу. В противном случае выведите «0» (без кавычек). Примечание В первом наборе входных данных: - Если Чирно выберет \(1\) или \(3\) на первом ходу, Дайёсей не сможет сделать ход, поэтому Дайёсей выигрывает.
- Если Чирно выберет \(2\) или \(4\) на первом ходу, Дайёсей сможет выбрать только \(3\), но после этого Чирно не сможет сделать ход, поэтому Чирно выигрывает.
Таким образом, все возможные вершины, которые может выбрать Чирно — это \(2\) и \(4\). Во втором наборе входных данных, независимо от того, какую вершину выберет Чирно, Дайёсей не сможет сделать ход, поэтому Дайёсей выигрывает. В третьем и четвертом наборах входных данных единственной возможной вершиной, которую может выбрать Чирно на первом ходу, является \(2\). В пятом наборе входных данных все возможные вершины, которые может выбрать Чирно на первом ходу — это \(3,4,6,7\) и \(10\). | |
![]()
|
|
E2. Игра (сложная версия)
графы
Деревья
игры
поиск в глубину и подобное
реализация
Структуры данных
*3000
Это сложная версия задачи. Отличие между версиями заключается в том, что в этой версии вам нужно найти все возможные вершины, которые может выбрать Чирно. Вы можете делать взломы только в том случае, если решили все версии этой задачи. Чирно и Дайёсей играют в игру с деревом\(^{\text{∗}}\) из \(n\) вершин, корнем которого является вершина \(1\). Значение \(i\)-й вершины равно \(w_i\). Они по очереди делают ходы; первым ходит Чирно. На каждом ходу, предполагая, что противник выбрал \(j\) на последнем ходу, игрок может выбрать любую оставшуюся вершину \(i\), удовлетворяющую условию \(w_i>w_j\), и удалить поддерево\(^{\text{†}}\) вершины \(i\). В частности, Чирно может выбрать любую вершину и удалить её поддерево на первом ходу. Первый игрок, который не может сделать ход, выигрывает, и они оба надеются победить. Найдите все возможные вершины, которые может выбрать Чирно на первом ходу, чтобы выиграть, если оба игрока будут играть оптимально. Выходные данные Для каждого набора входных данных выведите одну строку. Если Чирно может выиграть, выведите несколько чисел. Первое число \(k\) обозначает количество возможных вершин, которые она может выбрать на первом ходу. Следующие \(k\) чисел обозначают данные вершины в порядке возрастания. В противном случае выведите «0» (без кавычек). Примечание В первом наборе входных данных: - Если Чирно выберет \(1\) или \(3\) на первом ходу, Дайёсей не сможет сделать ход, поэтому Дайёсей выигрывает.
- Если Чирно выберет \(2\) или \(4\) на первом ходу, Дайёсей сможет выбрать только \(3\), но после этого Чирно не сможет сделать ход, поэтому Чирно выигрывает.
Таким образом, все возможные вершины, которые может выбрать Чирно — это \(2\) и \(4\). Во втором наборе входных данных, независимо от того, какую вершину выберет Чирно, Дайёсей не сможет сделать ход, поэтому Дайёсей выигрывает. В третьем и четвертом наборах входных данных единственной возможной вершиной, которую может выбрать Чирно на первом ходу, является \(2\). В пятом наборе входных данных все возможные вершины, которые может выбрать Чирно на первом ходу — это \(3,4,6,7\) и \(10\). | |
![]()
|
|
C. Удалить ровно две
графы
Деревья
дп
жадные алгоритмы
Перебор
поиск в глубину и подобное
сортировки
Структуры данных
*1600
Недавно Маленький Джон получил дерево от своей тёти, чтобы украсить свой дом. Но, как кажется, одного дерева недостаточно, чтобы украсить весь дом. У Маленького Джона появилась идея. Может быть, он сможет удалить несколько вершин из дерева. Это превратит его в большее количество деревьев! Верно? Вам дано дерево\(^{\text{∗}}\), состоящее из \(n\) вершин. Вы должны выполнить следующую операцию ровно дважды. - Выберите вершину \(v\);
- Удалите все рёбра, соединённые с вершиной \(v\), а также саму вершину \(v\).
Вам необходимо найти максимальное количество компонент связности после выполнения операции ровно дважды. Две вершины \(x\) и \(y\) находятся в одной компоненте связности тогда и только тогда, когда существует путь от \(x\) до \(y\). Граф с \(0\) вершинами имеет \(0\) компонент связности по определению.\(^{\text{†}}\) Выходные данные Для каждого теста выведите максимальное количество компонент связности в отдельной строке. Примечание В первом примере удаление вершины дважды сделает граф пустым. По определению количество компонент связности в графе с \(0\) вершинами равно \(0\). Поэтому ответ равен \(0\). Во втором примере удаление двух вершин \(1\) и \(2\) оставляет \(2\) компоненты связности. Поскольку невозможно создать \(3\) компоненты связности с \(2\) вершинами, ответ равен \(2\). В третьем примере удаление двух вершин \(1\) и \(5\) оставляет \(4\) компоненты связности, которые являются \(\left\{ 2,4\right\}\), \(\left\{ 3\right\}\), \(\left\{ 6\right\}\) и \(\left\{ 7\right\}\). Можно показать, что невозможно получить \(5\) компонент связности. Поэтому ответ равен \(4\). | |
![]()
|
|
E. Треугольное дерево
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
Структуры данных
*2300
Однажды в деревне выросло гигантское дерево. Маленький Джон, со своим детским орлом, решил сделать его своим домом. Маленький Джон построит конструкцию на дереве из оцинкованной квадратной стали. Однако он не знал, что не сможет построить то, что физически невозможно. Вам дано корневое дерево\(^{\text{∗}}\), содержащее \(n\) вершин, с корнем в вершине \(1\). Пара вершин \((u,v)\) называется хорошей парой, если \(u\) не является предком\(^{\text{†}}\) \(v\), и \(v\) не является предком \(u\). Для любых двух вершин \(\text{dist}(u,v)\) определяется как количество рёбер на уникальном простом пути от \(u\) до \(v\), а \(\text{lca}(u,v)\) определяется как их наименьший общий предок. Функция \(f(u,v)\) определяется следующим образом. - Если \((u,v)\) — это хорошая пара, то \(f(u,v)\) — это количество различных целых значений \(x\), таких что существует невырожденный треугольник\(^{\text{‡}}\) с длинами сторон \(\text{dist}(u,\text{lca}(u,v))\), \(\text{dist}(v,\text{lca}(u,v))\) и \(x\).
- В противном случае \(f(u,v)\) равно \(0\).
Вам необходимо посчитать следующее значение: \(\)\sum_{i = 1}^{n-1} \sum_{j = i+1}^n f(i,j).\(\) Выходные данные Для каждого набора входных данных выведите ответ на новой строке. Примечание В первом наборе входных данных единственной хорошей парой \((i,j)\), удовлетворяющей \(i<j\), является \((2,3)\). Здесь \(\text{lca}(2,3)\) равен \(1\), а два расстояния равны \(1\) и \(1\). Существует только одно значение \(x\) для двух длин сторон \(1\) и \(1\), а именно \(1\). Поэтому ответ для первого набора входных данных равен \(1\). Во втором примере нет хорошей пары. Поэтому ответ для второго теста равен \(0\). В третьем примере хорошими парами \((i,j)\), удовлетворяющими \(i<j\), являются следующие: - \((2,5)\): \(\text{lca}(2,5)\) равен \(1\), расстояния равны \(1\) и \(1\). Существует только одно возможное значение \(x\), а именно \(1\).
- \((3,4)\): \(\text{lca}(3,4)\) равен \(2\), расстояния равны \(1\) и \(1\). Существует только одно возможное значение \(x\), а именно \(1\).
- \((3,5)\): \(\text{lca}(3,5)\) равен \(1\), расстояния равны \(2\) и \(1\). Существует только одно возможное значение \(x\), а именно \(2\).
- \((4,5)\): \(\text{lca}(4,5)\) равен \(1\), расстояния равны \(2\) и \(1\). Существует только одно возможное значение \(x\), а именно \(2\).
Поэтому ответ для третьего примера равен \(1+1+1+1=4\). | |
![]()
|
|
F1. Считать не весело (Простая версия)
графы
Деревья
дп
Комбинаторика
математика
поиск в глубину и подобное
реализация
снм
Структуры данных
хэши
*2400
Это простая версия задачи. Отличие между версиями заключается в том, что в этой версии ограничения на \(t\) и \(n\) меньше. Вы можете делать взломы только в том случае, если решили все версии этой задачи. Теперь Маленький Джон богат, и поэтому он наконец-то покупает дом, достаточно большой, чтобы вместить его и его любимую скобочную последовательность. Но каким-то образом он оказался с большим количеством скобок! Разочарованный, он пробивает потолок с помощью «ладони Будды». Скобочная последовательность называется правильной, если она может быть построена по следующей формальной грамматике: - Пустая последовательность \(\varnothing\) сбалансирована.
- Если скобочная последовательность \(A\) правильная, то \(\mathtt{(}A\mathtt{)}\) также является правильной.
- Если скобочные последовательности \(A\) и \(B\) правильные, то и их конкатенированная последовательность \(A B\) также правильная.
Например, последовательности «(())()», «()», «(()(()))» и пустая последовательность являются правильными, в то время как «(()» и «(()))(» — нет. Дана правильная скобочная последовательность \(s\), пара индексов \((i,j)\) (\(i<j\)) называется хорошей, если \(s_i\) — это «(», а \(s_j\) — это «)», и две скобки добавляются одновременно в соответствии с правилом 2 при построении последовательности \(s\). Например, последовательность «(())()» имеет три разные хорошие пары: \((1,4)\), \((2,3)\) и \((5,6)\). Можно показать, что любая правильная скобочная последовательность из \(2n\) скобок содержит ровно \(n\) различных пар скобок, и использование любого порядка правил для построения одной и той же последовательности скобок приведет к одному и тому же набору пар скобок. Эмили будет играть в игру по угадыванию скобок с Джоном. Игра проходит следующим образом. Изначально у Джона есть правильная скобочная последовательность \(s\), содержащая \(n\) различных пар скобок, которая не известна Эмили. Джон говорит Эмили значение \(n\) и просит Эмили угадать последовательность. На протяжении \(n\) ходов Джон дает Эмили следующие подсказки на каждом ходе: - \(l\;r\): Последовательность \(s\) содержит пару скобок \((l,r)\).
Гарантируется, что подсказки, которые Джон дает Эмили, попарно различны и не противоречат друг другу. В какой-то момент Эмили может быть уверена, что правильная скобочная последовательность, удовлетворяющая подсказкам, данным до сих пор, уникальна. Например, предположим, что Эмили знает, что \(s\) имеет \(3\) хорошие пары, и она содержит пару скобок \((2,5)\). Из \(5\) правильных скобочных последовательностей с \(3\) хорошими парами существует только одна такая последовательность «((()))» с парой скобок \((2,5)\). Следовательно, можно увидеть, что Эмили не всегда нужно \(n\) ходов, чтобы угадать \(s\). Чтобы как можно раньше узнать содержимое \(s\), Эмили хочет знать количество различных правильных скобочных последовательностей, которые соответствуют подсказкам после каждого хода. Конечно, это не легкая задача для Эмили, особенно когда ей дано настолько много хороших пар. Теперь ваша очередь помочь Эмили. Учитывая подсказки, вы должны найти ответ до всех ходов и после каждого хода. Поскольку ответы могут быть огромными, вам нужно найти их по модулю \(998\,244\,353\). Выходные данные Для каждого набора выведите \(n+1\) целых числа в одной строке: - Первое целое число — это ответ до всех подсказок, по модулю \(998\,244\,353\).
- Для всех \(i \ge 1\), \(i+1\)-е целое число — это ответ после \(i\)-й подсказки, по модулю \(998\,244\,353\).
Примечание Первый пример из примера объясняется в описании задачи. Третий пример из примера объясняется следующим образом. Можно показать, что существует \(132\) сбалансированных последовательностей скобок с \(6\) парами скобок. Ответы после каждой подсказки следующие: - Вам дана хорошая пара \((2,3)\). Существует \(42\) правильных скобочных последовательностей, имеющих хорошую пару \((2,3)\).
- Вам дана хорошая пара \((1,6)\). Существует \(5\) правильных скобочных последовательностей, имеющих хорошие пары \((2,3)\), \((1,6)\).
- Вам дана хорошая пара \((7,8)\). Существуют \(2\) правильных скобочных последовательностей, имеющих три хорошие пары. Это строки «(()())()(())» и «(()())()()()», соответственно.
- Вам дана хорошая пара \((9,12)\). Существует только одна правильная скобочная последовательность, содержащая четыре хорошие пары. Таким образом, содержимое \(s\) имеет вид «(()())()(())».
Тогда количество правильных скобочных последовательностей после пятой и шестой подсказки равно \(1\), поскольку вы уже знаете содержимое \(s\). | |
![]()
|
|
F2. Считать не весело (Сложная версия)
графы
Деревья
Комбинаторика
поиск в глубину и подобное
реализация
снм
Структуры данных
*2700
Это сложная версия задачи. Отличие между версиями заключается в том, что в этой версии ограничения на \(t\) и \(n\) больше. Вы можете делать взломы только в том случае, если решили все версии этой задачи. Теперь Маленький Джон богат, и поэтому он наконец-то покупает дом, достаточно большой, чтобы вместить его и его любимую скобочную последовательность. Но каким-то образом он оказался с большим количеством скобок! Разочарованный, он пробивает потолок с помощью «ладони Будды». Скобочная последовательность называется правильной, если она может быть построена по следующей формальной грамматике: - Пустая последовательность \(\varnothing\) сбалансирована.
- Если скобочная последовательность \(A\) правильная, то \(\mathtt{(}A\mathtt{)}\) также является правильной.
- Если скобочные последовательности \(A\) и \(B\) правильные, то и их конкатенированная последовательность \(A B\) также правильная.
Например, последовательности «(())()», «()», «(()(()))» и пустая последовательность являются правильными, в то время как «(()» и «(()))(» — нет. Дана правильная скобочная последовательность \(s\), пара индексов \((i,j)\) (\(i<j\)) называется хорошей, если \(s_i\) — это «(», а \(s_j\) — это «)», и две скобки добавляются одновременно в соответствии с правилом 2 при построении последовательности \(s\). Например, последовательность «(())()» имеет три разные хорошие пары: \((1,4)\), \((2,3)\) и \((5,6)\). Можно показать, что любая правильная скобочная последовательность из \(2n\) скобок содержит ровно \(n\) различных пар скобок, и использование любого порядка правил для построения одной и той же последовательности скобок приведет к одному и тому же набору пар скобок. Эмили будет играть в игру по угадыванию скобок с Джоном. Игра проходит следующим образом. Изначально у Джона есть правильная скобочная последовательность \(s\), содержащая \(n\) различных пар скобок, которая не известна Эмили. Джон говорит Эмили значение \(n\) и просит Эмили угадать последовательность. На протяжении \(n\) ходов Джон дает Эмили следующие подсказки на каждом ходе: - \(l\;r\): Последовательность \(s\) содержит пару скобок \((l,r)\).
Гарантируется, что подсказки, которые Джон дает Эмили, попарно различны и не противоречат друг другу. В какой-то момент Эмили может быть уверена, что правильная скобочная последовательность, удовлетворяющая подсказкам, данным до сих пор, уникальна. Например, предположим, что Эмили знает, что \(s\) имеет \(3\) хорошие пары, и она содержит пару скобок \((2,5)\). Из \(5\) правильных скобочных последовательностей с \(3\) хорошими парами существует только одна такая последовательность «((()))» с парой скобок \((2,5)\). Следовательно, можно увидеть, что Эмили не всегда нужно \(n\) ходов, чтобы угадать \(s\). Чтобы как можно раньше узнать содержимое \(s\), Эмили хочет знать количество различных правильных скобочных последовательностей, которые соответствуют подсказкам после каждого хода. Конечно, это не легкая задача для Эмили, особенно когда ей дано настолько много хороших пар. Теперь ваша очередь помочь Эмили. Учитывая подсказки, вы должны найти ответ до всех ходов и после каждого хода. Поскольку ответы могут быть огромными, вам нужно найти их по модулю \(998\,244\,353\). Выходные данные Для каждого набора выведите \(n+1\) целых числа в одной строке: - Первое целое число — это ответ до всех подсказок, по модулю \(998\,244\,353\).
- Для всех \(i \ge 1\), \(i+1\)-е целое число — это ответ после \(i\)-й подсказки, по модулю \(998\,244\,353\).
Примечание Первый пример из примера объясняется в описании задачи. Третий пример из примера объясняется следующим образом. Можно показать, что существует \(132\) сбалансированных последовательностей скобок с \(6\) парами скобок. Ответы после каждой подсказки следующие: - Вам дана хорошая пара \((2,3)\). Существует \(42\) правильных скобочных последовательностей, имеющих хорошую пару \((2,3)\).
- Вам дана хорошая пара \((1,6)\). Существует \(5\) правильных скобочных последовательностей, имеющих хорошие пары \((2,3)\), \((1,6)\).
- Вам дана хорошая пара \((7,8)\). Существуют \(2\) правильных скобочных последовательностей, имеющих три хорошие пары. Это строки «(()())()(())» и «(()())()()()», соответственно.
- Вам дана хорошая пара \((9,12)\). Существует только одна правильная скобочная последовательность, содержащая четыре хорошие пары. Таким образом, содержимое \(s\) имеет вид «(()())()(())».
Тогда количество правильных скобочных последовательностей после пятой и шестой подсказки равно \(1\), поскольку вы уже знаете содержимое \(s\). | |
![]()
|
|
F. Скибидус и slay
графы
Деревья
жадные алгоритмы
поиск в глубину и подобное
Структуры данных
*1700
Определим мажорирующий элемент последовательности из \(k\) элементов как уникальное значение, которое появляется строго более чем \(\left \lfloor {\frac{k}{2}} \right \rfloor\) раз. Если такое значение не существует, то последовательность не имеет мажорирующего элемента. Например, последовательность \([1,3,2,3,3]\) имеет мажорирующий элемент \(3\), потому что оно появляется \(3 > \left \lfloor {\frac{5}{2}} \right \rfloor = 2\) раза, но \([1,2,3,4,5]\) и \([1,3,2,3,4]\) не имеют мажорирующего элемента. Скибидус нашел дерево\(^{\text{∗}}\) из \(n\) вершин и массив \(a\) длиной \(n\). Вершина \(i\) имеет значение \(a_i\), написанное на ней, где \(a_i\) — это целое число в диапазоне \([1, n]\). Для каждого \(i\) от \(1\) до \(n\) определите, существует ли нетривиальный простой путь\(^{\text{†}}\) такой, что \(i\) является мажорирующим элементом последовательности целых чисел, написанных на вершинах, которые образуют путь. Выходные данные Для каждого теста выведите двоичную строку \(s\) длиной \(n\) на отдельной строке. \(s_i\) должно вычисляться следующим образом: - Если существует нетривиальный путь, содержащий \(i\) как мажорирующий элемент, то \(s_i\) равно '1';
- В противном случае \(s_i\) равно '0'.
Примечание В первом примере нет нетривиального пути с \(1\), \(2\) или \(3\) в качестве мажорирующего элемента, поэтому выводимая двоичная строка — «000». Во втором примере \(1\rightarrow 2\rightarrow 4\) — это нетривиальный путь с \(3\) в качестве мажорирующего элемента. | |
![]()
|
|
E. Братья по крови
Бинарный поиск
Деревья
поиск в глубину и подобное
Структуры данных
*2100
Поликарп раздобыл дерево родственных связей. Найденное дерево описывает родственные связи n человек, пронумерованных от 1 до n. Каждый человек в этом дереве имеет не более одного непосредственного предка. Назовем человека a 1-прародителем человека b, если a является непосредственным предком b. Назовем человека a k-прародителем (k > 1) человека b, если у человека b есть 1-прародитель, и a является (k - 1)-прародителем 1-прародителя b. В найденном дереве родственные связи не образуют циклов. Другими словами не существует человека, который непосредственно или косвенно является собственным прародителем (то есть является x-прародителем самого себя, для некоторого x, x > 0). Назовем двух людей x и y (x ≠ y) p-юродными братьями (p > 0), если существует человек z, который является p-прародителем x и p-прародителем y. Поликарп очень сильно интересуется сколько у кого и каких братьев. Он записал на листочке m пар чисел vi, pi. Помогите ему для каждой пары vi, pi узнать, сколько у человека vi pi-юродных братьев. Выходные данные Выведите m целых чисел, разделенных пробельными символами, — ответы на записи Поликарпа. Ответы для записей выводите в том порядке, в котором записи встречаются во входных данных. | |
![]()
|
|
E. Инопланетная ДНК
Деревья
снм
Структуры данных
*2800
Профессор Байтоцы проводит опыты над инопланетными ДНК. Он обнаружил, что эта ДНК подвержена повторяющимся мутациям — каждая мутация проходит одинаково: некоторая непрерывная подпоследовательность инопланетной ДНК активируется, копируется, после чего копия подпоследовательности искажается и вставляется сразу после неискаженной подпоследовательности в ДНК. Искаженная копия активированной непрерывной подпоследовательности образуется следующим образом: сначала соединяются все элементы подпоследовательности на четных позициях, далее к ним присоединяются все элементы подпоследовательности на нечетных позициях. Таким образом, если активированная подпоследовательность состоит из 11 элементов и имеет вид s1s2... s11, то ее искаженная копия выглядит как s2s4s6s8s10s1s3s5s7s9s11. Например, если исходная последовательность была «ACTGG», а мутация произошла на отрезке [2, 4] (то есть активирована подпоследовательность «CTG»), то мутировавшая ДНК выглядит так: «ACTGTCGG». Искаженная копия активированной подпоследовательности выделена жирным шрифтом. Профессор Байтоцы записал исходную последовательность ДНК и затронувшую ее последовательность мутаций. Теперь он просит Вас восстановить первые k элементов последовательности ДНК после всех мутаций. Выходные данные Выведите единственную строку, которая содержит первые k букв из мутировавшей последовательности ДНК. Примечание Во втором примере после первой мутации последовательность превратилась в «ACCAGTACGT». После второй — в «ACCAGTACCGACATCGT». | |
![]()
|
|
D. Выбор столицы Древляндии
графы
Деревья
дп
поиск в глубину и подобное
*1700
Страна Древляндия состоит из n городов, некоторые пары из которых соединены односторонними дорогами. Всего в этой стране n - 1 дорога. Известно, что если не обращать внимание на направление дорог, то из любого города можно добраться до любого другого. Недавно советом старейшин было решено выбрать столицу Древляндии. Конечно, это должен быть один из городов страны. Предполагается, что совет будет заседать в столице и регулярно перемещаться из столицы в другие города (об обратном перемещении пока никто не думает). По этой причине, если город a будет выбран столицей, то все дороги должны быть ориентированы так, что, двигаясь по ним, можно из города a добраться до любого другого города. Для этого, возможно, некоторые дороги придется переориентировать. Помогите старейшинам выбрать столицу так, что необходимо переориентировать минимальное количество дорог в стране. Выходные данные В первую строку выведите минимальное количество переориентируемых дорог при оптимальном выборе столицы. Во вторую строку выведите все возможные способы выбрать столицу — последовательность номеров городов в порядке возрастания. | |
![]()
|
|
E. Схема
графы
Деревья
поиск в глубину и подобное
*2300
Чтобы как можно быстрее узнавать последние новости о своей любимой принципиально новой операционной системе, BolgenOS community Нижнего Тагила решило разработать схему, согласно которой первый член community, узнавший какую-либо новость, звонит кому-то другому, тот звонит третьему и так далее. То есть человеку с номером i был назначен человек с номером fi, которому он должен звонить, как только сам узнает новость. Со временем участники BolgenOS community поняли, что их схема не всегда срабатывает — некоторые могут так и не узнать новость. Теперь они хотят дополнить ее: в схему добавляется несколько указаний вида (xi, yi), означающих, что человек xi должен позвонить еще и человеку yi. Какое наименьшее число указаний нужно добавить, чтобы, независимо от того, кто первый узнал новость, в итоге новость узнали все? Выходные данные В первую строку выходных данных выведите одно число — какое наименьшее число указаний нужно добавить. Далее выведите один из возможных вариантов добавления этих указаний в схему, по одному указанию в строке. Если решений несколько, выведите любое. | |
![]()
|
|
E. Путь благородного рыцаря
Деревья
Структуры данных
*2900
В Берляндии каждый феодал владеет ровно одним замком, а каждый замок принадлежит ровно одному феодалу. Каждый феодал, кроме одного (короля), находится в подчинении у другого феодала. Вассалов (подчиненных) у феодала может быть любое количество. Некоторые замки соединены дорогами, по которым разрешено движение в обе стороны. Между двумя замками есть дорога в том и только в том случае, если владелец одного из этих замков находится в непосредственном подчинении у владельца другого. Каждый год в Берляндии может случиться ровно одно из двух событий. - На замок номер с напали варвары. Известно, что за всю историю Берляндии варвары никогда не нападали на один и тот же замок дважды.
- Благородный рыцарь отправился в путешествие из замка a в замок b (причем по такому пути, что каждый замок встречается на нем не более одного раза).
Остановимся подробнее на втором событии. Поскольку путь из a в b предстоит неблизкий, то, возможно, рыцарь захочет остановиться в замке, лежащем на его пути, чтобы отдохнуть. Но он может сделать остановку не в каждом замке: благородство не позволяет ему находиться в замке, оскверненном невыветрившимся духом врага. Замок считается оскверненным тогда и только тогда, когда на него совершалось нападение после года y. Поэтому выбор рыцаря остановится на k-м замке, лежащем на его пути, считая от a (сами замки a и b в счет не идут), на который не совершалось нападений в годы с y + 1 по текущий. Рыцари плохо помнят, в какие годы и на какие замки совершались нападения, поэтому они обратились к придворному ученому, то есть к Вам, за помощью. Вам задана последовательность событий в истории Берляндии, сообщите каждому рыцарю, в каком городе ему следует остановиться, или огорчите его известием о том, что на пути из a в b меньше k городов, удовлетворяющих его требованиям, а потому отдыхать рыцарю не придется. Выходные данные Для каждого события второго типа выведите целое число — номер замка, в котором должен остановиться на отдых рыцарь, или -1, если ему придется проделать путь из ai в bi без остановок. Разделяйте ответы пробельными символами. Ответы выводите в том порядке, в котором события второго типа заданы во входных данных. Примечание В первом примере на пути рыцаря из замка 1 в замок 3 лежит только замок 2. Когда рыцарь проделает путь 1 - 3 в первый раз, замок 2 не будет осквернен врагом, поэтому именно в нем рыцарь и остановится. Во второй год замок 2 станет осквернен, а потому в следующие два года рыцарю будет негде остановиться (так как ему важно, чтобы замок не был осквернен, начиная с годов 1 и 2, соответственно). В пятый год рыцарь не будет считать замок 2 оскверненным, а потому вновь остановится в нем. | |
![]()
|
|
E. Кактус
графы
Деревья
дп
поиск в глубину и подобное
Структуры данных
*2100
Связный неориентированный граф называется вершинным кактусом, если каждая вершина этого графа принадлежит не более чем одному простому циклу. Простым циклом в неориентированном графе назовем последовательность различных вершин v1, v2, ..., vt (t > 2) такую, что для любого i (1 ≤ i < t) существует ребро между вершинами vi и vi + 1, а также существует ребро между вершинами v1 и vt. Простым путем в неориентированном графе назовем последовательность не обязательно различных вершин v1, v2, ..., vt (t > 0) такую, что для любого i (1 ≤ i < t) существует ребро между вершинами vi и vi + 1, причем каждое ребро встречается не более одного раза. Будем говорить, что простой путь v1, v2, ..., vt начинается в вершине v1 и заканчивается в вершине vt. Вам задан граф, состоящий из n вершин и m ребер, который является вершинным кактусом. Также есть список из k пар интересных вершин xi, yi, для которых Вы захотели узнать следующую информацию — сколько различных простых путей начинается в вершине xi и заканчивается в вершине yi. Два простых пути будем считать различными, если различаются множества ребер, которые в них входят. Для каждой пары интересных вершин посчитайте количество различных простых путей между ними. Поскольку это количество может быть достаточно большим, требуется посчитать остаток от деления этого числа на 1000000007 (109 + 7). Выходные данные Выведите k строк: в i-ой строке выведите единственное число — остаток от деления количества различных простых путей, начинающихся в xi и заканчивающихся в yi, на 1000000007 (109 + 7). | |
![]()
|
|
D. Д-Декомпозиция
графы
Деревья
жадные алгоритмы
поиск в глубину и подобное
*2000
Вам задано неориентированное дерево s, состоящее из n вершин. Необходимо построить для него оптимальную Д-декомпозицию. Определим Д-декомпозицию следующим образом. Обозначим за v множество всех вершин s. Рассмотрим неориентированное дерево t, вершинами которого являются некоторые непустые подмножества v, которые обозначим через xi  . Дерево t является Д-декомпозицией s, если выполняются следующие условия: . Дерево t является Д-декомпозицией s, если выполняются следующие условия: - объединение всех xi равно v;
- для любого ребра (a, b) дерева s существует вершина дерева t, содержащая как a, так и b;
- если вершины дерева t xi и xj, содержат вершину a дерева s, то все вершины дерева t, лежащие на пути из xi в xj также содержат вершину a, то есть это условие эквивалентно тому, что все вершины дерева t, которые содержат вершину a дерева s, образуют связное поддерево дерева t.
Очевидно, что существует много различных деревьев t, являющихся Д-декомпозициями дерева s. Например, Д-декомпозицией является дерево, состоящее из одной вершины, представляющей собой все множество v. Назовем мощностью вершины xi количество вершин дерева s, которые в ней содержатся. Выберем в дереве t вершину с максимальной мощностью. Пусть ее мощность равна w. Тогда весом Д-декомпозиции t назовем величину w. Оптимальной назовем Д-декомпозицию, у которой вес минимален. Вам необходимо найти оптимальную Д-декомпозицию, заданного дерева s имеющую наименьшее количество вершин. Выходные данные В первой строке выведите единственное целое число m, обозначающее количество вершин в искомой Д-декомпозиции. Далее выведите m строк, содержащих описания вершин Д-декомпозиции. В i-той (1 ≤ i ≤ m) из них выведите описание вершины xi Д-декомпозиции. Описание каждой из вершин xi должно начинаться с целого числа ki, обозначающего количество вершин исходного дерева s, которые содержатся в вершине xi. Далее через пробел нужно вывести ki различных целых чисел — номера вершин из s, содержащихся в xi, в любом порядке. Далее выведите m - 1 строк, содержащих по два целых числа pi, qi (1 ≤ pi, qi ≤ m; pi ≠ qi). Пара чисел pi, qi обозначает наличие ребра между вершинами xpi и xqi Д-декомпозиции. Выведенная Д-декомпозиция должна быть оптимальной Д-декомпозицией для заданного дерева s и содержать минимально возможное количество вершин среди оптимальных. Если существует несколько оптимальных Д-декомпозиций с минимальным количеством вершин, выведите любую из них. | |
![]()
|
|
C. Братья-Пожиратели Мира
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
*2100
Вы, наверное, слышали о двух братьях, мечтающих править миром. Коль скоро все их предыдущие планы провалились, на этот раз они решили сотрудничать друг с другом для того, чтобы править миром. Как вы знаете, в мире существует n стран. Эти страны связаны n - 1 направленными дорогами. Если не учитывать направлений дорог, то между каждой парой стран в мире существует уникальный путь, проходящий по каждой дороге не более одного раза. Каждый из братьев хочет установить свое правление в какой-то стране, сделав это, он сможет контролировать страны, до которых можно добраться из его страны по направленным дорогам. Братья смогут править миром, если найдется не более двух стран, которые они могут выбрать (и установить свои правления в этих странах), таких, что любая другая страна находится под контролем по крайней мере одной из них. Для того, чтобы сделать это возможным, братья хотят, изменить направление минимального количества дорог. Ваша задача — вычислить это минимальное количество дорог. Выходные данные В единственной строке выходных данных выведите минимальное количество дорог, которым надо поменять направление для того, чтобы братья смогли управлять миром. | |
![]()
|
|
D. Дороги не только в Берляндии
графы
Деревья
снм
*1900
Правительство Берляндии решило улучшать отношения с соседними странами. В первую очередь было решено построить новые дороги так чтобы из всех городов Берляндии и соседних стран можно было добраться до всех остальных. Всего в Берляндии и соседних странах n городов и ровно n - 1 двусторонних дорог. Из-за недавнего финансового кризиса правительство Берляндии сильно стеснено в средствах, поэтому чтобы построить новую дорогу оно вынуждено закрывать какую-то из существующих. Каждый день можно закрыть одну существующую дорогу и сразу же построить новую. Ваша задача — определить, сколько дней потребуется для перестройки дороги так, чтобы из любого города можно было добраться до любого другого, а так же составить план закрытия старых и постройки новых дорог. Выходные данные Выведите ответ на задачу, число t — какое наименьшее число дней потребуется, чтобы перестроить дороги так чтобы из любого города можно было добраться до любого другого. Далее выведите t строк — план закрытия старых и постройки новых дорог. Каждая строка должна описывать действия в очередной день в формате i j u v — означает, что нужно закрыть дорогу между городами i и j и построить дорогу между городами u и v. Города нумеруются начиная с 1. Если решений несколько, выведите любое. | |
![]()
|
|
E. Дерево и таблица
Деревья
дп
поиск в глубину и подобное
реализация
*3000
Маленький Петя очень любит деревья. Недавно мама подарила ему дерево с 2n вершинами. Петя сразу же решил расположить это дерево на прямоугольной таблице, состоящей из 2 строк и n столбцов так, чтобы выполнялись следующие условия: - Каждой клетке таблицы соответствует ровно одна вершина дерева и наоборот, каждой вершине дерева соответствует ровно одна клетка таблицы.
- Если две вершины дерева соединены ребром, то соответствующие им клетки имеют общую сторону.
Сейчас Пете интересно, сколько существует способов расположить его дерево на таблице. Он называет два расположения различными, если существует вершина дерева, которой соответствуют разные клетки таблицы в этих двух расположениях. Поскольку большие числа очень пугают Петю, выведите остаток от деления ответа на 1000000007 (109 + 7). Выходные данные Выведите единственное целое число — искомое количество способов расположить дерево на таблице, взятое по модулю 1000000007 (109 + 7). Примечание Пояснение к примеру 1 (ниже представлены все 12 вариантов расположения дерева на таблице):
1-3-2 2-3-1 5 4 6 6 4 5
| | | | | | | | | | | |
5 4 6 6 4 5 1-3-2 2-3-1
4-3-2 2-3-4 5-1 6 6 1-5
| | | | | | | |
5-1 6 6 1-5 4-3-2 2-3-4
1-3-4 4-3-1 5 2-6 6-2 5
| | | | | | | |
5 2-6 6-2 5 1-3-4 4-3-1
| |
![]()
|
|
E. Маленький Слоник и дерево
Деревья
поиск в глубину и подобное
Структуры данных
*2400
Маленький Слоник очень любит деревья, а особенно корневые. У него есть дерево, состоящее из n вершин (вершины пронумерованы от 1 до n), с корнем в вершине с номером 1. В каждой вершине дерева хранится некоторый список чисел, который изначально пуст. Маленький Слоник хочет выполнить m операций. На i-той операции (1 ≤ i ≤ m) он сначала добавляет число i в списки всех вершин поддерева с корнем в вершине с номером ai, а потом добавляет число i в списки всех вершин поддерева с корнем в вершине bi. После выполнения всех операций, Маленький Слоник для каждой вершины i хочет посчитать число ci — количество целых чисел j (1 ≤ j ≤ n; j ≠ i) таких, что в списках i-той и j-той вершины есть хотя бы одно общее число. Помогите Маленькому Слонику, посчитайте числа ci за него. Выходные данные В единственной строке выведите n целых чисел через пробел — c1, c2, ..., cn. | |
![]()
|
|
D. Черно-белое дерево
графы
Деревья
жадные алгоритмы
Конструктив
снм
*2100
На доске нарисован граф-дерево из n вершин. Напомним, что неориентированный граф называется деревом, если он связен и не содержит циклов. Каждая вершина графа покрашена в черный или белый цвет таким образом, что не существует двух вершин одного цвета, соединенных ребром. На каждом ребре записана его стоимость — неотрицательное целое число. Плохой мальчик Вася подошел к доске и написал около каждой вершины v число sv — сумму стоимостей всех инцидентных этой вершине ребер, после чего он стер ребра и их стоимости с доски. Ваша задача — восстановить исходное дерево по цветам вершин и числам sv. Выходные данные Выведите описание n - 1 ребер графа-дерева. Каждое описание — это тройка чисел vi, ui, wi (1 ≤ vi, ui ≤ n, vi ≠ ui, 0 ≤ wi ≤ 109), где vi и ui — номера вершин, которые соединяет i-ое ребро, а wi — его стоимость. Обратите внимание, что должно выполняться условие cvi ≠ cui. Гарантируется, что для любых входных данных существует по крайней мере один соответствующий этим данным граф. Если существует несколько решений, то выведите любое. Ребра разрешается выводить в любом порядке. Числа при выводе разделяйте пробелами. | |
![]()
|
|
B. Нулевое дерево
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
*1800
Дерево — это граф, состоящий из n вершин и ровно n - 1 ребер; этот граф должен удовлетворять следующему условию: существует ровно один кратчайший (по количеству ребер) путь между любой парой его вершин. Поддерево дерева T — это дерево, где как вершины, так и ребра являются подмножествами вершин и ребер T. Вам дано дерево с n вершинами. Вы можете считать, что его вершины пронумерованы целыми числами от 1 до n. Дополнительно в каждой вершине дерева записано целое число. Изначально целое число, записанное в i-ой вершине, равняется vi. За один ход Вы можете применить следующую операцию: - Выбрать поддерево данного дерева, которое включает вершину с номером 1.
- Увеличить (или уменьшить) на один все целые числа, записанные в вершинах этого поддерева.
Вычислите минимальное количество ходов, необходимое для того, чтобы сделать все целые числа, записанные в вершинах данного дерева, равными нулю. Выходные данные Выведите минимальное количество операций, необходимое для решения задачи. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-битных чисел на С++. Рекомендуется использовать потоки cin, cout или спецификатор %I64d. | |
![]()
|
|
E. Девочка и задача про дерево
графы
Деревья
Структуры данных
*2100
Девочка очень любит задачи про деревья. Вот одна из них. Дерево — это неориентированный связный граф без циклов. Степень вершины x в дереве — это количество вершин y дерева таких, что каждая из них связана с вершиной x каким-то ребром дерева. Рассмотрим дерево, состоящее из n вершин. Будем считать, что вершины этого дерева пронумерованы от 1 до n. Рассматриваемое дерево обладает следующим свойством: каждая вершина, кроме вершины с номером 1, имеет степень не более 2. Изначально в каждой вершине дерева записано число 0. Ваша задача — быстро выполнять запросы двух типов: - Запрос вида: 0 v x d. В ответ на запрос нужно добавить x ко всем числам, записанным в вершинах, которые находятся на расстоянии не более чем d от вершины с номером v. Расстоянием между двумя вершинами будем считать количество ребер на кратчайшем пути между ними.
- Запрос вида: 1 v. В ответ на запрос нужно вывести текущее число, записанное в вершине с номером v.
Выходные данные Для каждого запроса на вывод значения, записанного в вершине, выведите целое число — ответ на запрос. | |
![]()
|
|
E. Бинарное дерево на плоскости
Деревья
Потоки
*2400
Корневое дерево — это ориентированный ациклический граф, в котором есть одна вершина (корень), из которой существует ровно один путь до любой другой вершины. Корневое дерево называется бинарным, если каждая вершина имеет не более двух исходящих дуг. Когда бинарное дерево рисуют на плоскости, все дуги должны быть направлены сверху вниз. То есть для каждой дуги из u в v должно выполняться: yu > yv. Вам даны координаты всех вершин дерева. Ваша задача — соединить эти вершины дугами так, чтобы получилось бинарное корневое дерево, и суммарная длина дуг была минимальна. Все дуги построенного дерева должны быть направлены сверху вниз. Выходные данные Если невозможно построить бинарное дерево на данных точках, выведите «-1». Иначе выведите одно вещественное число — суммарную длину дуг в минимальном бинарном дереве. Ответ будет засчитан, если абсолютная или относительная погрешность не превосходит 10 - 6. | |
![]()
|
|
C. Игра на дереве
Деревья
математика
реализация
Теория вероятностей
*2200
У Мумиджу есть корневое дерево, состоящее из n вершин. Вершины дерева пронумерованы целыми числами от 1 до n. Корень дерева имеет номер 1. Мумиджу решил поиграть в игру на этом дереве. Игра состоит из нескольких шагов. На каждом шаге Мумиджу выбирает одну из оставшихся вершин дерева (обозначим ее v) и удаляет из дерева все вершины поддерева с корнем в вершине v. Сама вершина v тоже удаляется. Игра заканчивается, когда в дереве не остается вершин. Другими словами, игра заканчивается после шага, на котором выбрана вершина с номером 1. Каждый раз Мумиджу выбирает новую вершину равновероятно среди всех оставшихся вершин. Ваша задача — найти математическое ожидание количества шагов в описанной игре. Выходные данные Выведите единственное вещественное число — математическое ожидание количества шагов в описанной игре. Ответ будет считаться правильным, если его относительная или абсолютная погрешность не превышает 10 - 6. Примечание В первом тестовом примере возможны два случая. Первый — это сразу удалить корень, второй — удалить корень после одного шага. Таким образом, математическое ожидание количества шагов равно: 1 × (1 / 2) + 2 × (1 / 2) = 1.5Второй пример более сложный. Два случая из трех приводят нас к задаче, эквивалентной первому тестовому примеру, третий случай — удалить корень на первом шаге. Таким образом, математическое ожидание количества шагов равно: 1 × (1 / 3) + (1 + 1.5) × (2 / 3) = (1 / 3) + (5 / 3) = 2 | |
![]()
|
|
E. Максимизация Сосиски
битмаски
Деревья
Структуры данных
*2200
Необъяснимый народ эти битландцы. У них свои проблемы и свои решения. Свои мысли и свои убеждения, свои ценности и свои идеалы. Свои тарелки и свои сосиски! В Битландии сосиска — это массив целых чисел! Аппетитность сосиски равна побитовому исключающему ИЛИ (операция xor) всех элементов сосиски. Как-то раз, когда Mr. Bitkoch (местный повар) уже закрывал свой ресторан BitRestaurant, BitHaval и BitAryo (самые известные жители Битландии) зашли в ресторан и заказали по сосиске. У Mr. Bitkoch осталась ровно одна сосиска. Поэтому он решил отрезать начало сосиски (сколько-то, возможно ноль, первых чисел массива) и отдать его BitHaval-у, BitAryo же достанется некоторый конец сосиски (сколько-то, возможно ноль, последних чисел массива). Обратите внимание, что оба куска сосиски одновременно или по отдельности могут быть пустыми. Конечно, отрезанные куски не должны пересекаться (никакой элемент массива не может содержаться в обоих кусках). Удовольствие, которое получат BitHaval и BitAryo от ужина, равно побитовому исключающему ИЛИ аппетитностей их сосисок. Аппетитность пустой сосиски равна нулю. Найдите способ отрезать BitHaval-у и BitAryo по куску сосиски, чтобы максимизировать их удовольствие от ужина. Выходные данные Выведите единственное целое число — максимальное удовольствие, которое могут получить BitHaval и BitAryo от ужина. | |
![]()
|
|
D. Пингвин Поло и дерево
Деревья
Комбинаторика
поиск в глубину и подобное
*2400
У маленького пингвина Поло есть дерево — неориентированный связанный ациклический граф, в котором n вершин и n - 1 ребро. Будем считать, что вершины дерева пронумерованы целыми числами от 1 до n. Сегодня Поло интересует следующая задача: найти количество пар путей, у которых нет ни одной общей вершины. Более формально, нужно найти количество четверок целых чисел a, b, c и d таких, что: - 1 ≤ a < b ≤ n;
- 1 ≤ c < d ≤ n;
- не существует такой вершины, которая одновременно лежит на кратчайшем пути от вершины a до вершины b и от вершины c до вершины d.
Под кратчайшим путем между двумя вершинами подразумевается путь, кратчайший по количеству ребер. Помогите Поло, решите эту задачу. Выходные данные В единственной строке выведите целое число — ответ на задачу. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-битных чисел на С++. Рекомендуется использовать потоки cin, cout или спецификатор %I64d. | |
![]()
|
|
D. Муравей на дереве
Деревья
Конструктив
поиск в глубину и подобное
*2000
Дерево — это связный неориентированный граф без циклов. Деревья представляют собой широкий класс графов, интересный не только людям, но и муравьям. В корне одного дерева стоит муравей. Он видит, что в дереве n вершин, и они соединены n - 1 ребрами так, что от любой вершины можно дойти до любой другой. Лист в дереве — это отличная от корня вершина, которая соединена ровно с одной другой вершиной. Муравей хочет обойти все вершины дерева и вернуться назад к корню, пройдя по каждому ребру ровно два раза. При этом он хочет обойти все листья в заданном порядке. Ваша задача найти любой возможный путь муравья. Выходные данные Если искомого порядка обхода всех n вершин не существует, выведите -1. Иначе выведите 2n - 1 чисел — сам обход. Каждый раз, когда муравей приходит в вершину, выводите номер этой вершины. | |
![]()
|
|
C. WTF?
*особая задача
Деревья
Паросочетания
реализация
*1700
HAI
I HAS A TUX
GIMMEH TUX
I HAS A FOO ITS 0
I HAS A BAR ITS 0
I HAS A BAZ ITS 0
I HAS A QUZ ITS 1
TUX IS NOW A NUMBR
IM IN YR LOOP NERFIN YR TUX TIL BOTH SAEM TUX AN 0
I HAS A PUR
GIMMEH PUR
PUR IS NOW A NUMBR
FOO R SUM OF FOO AN PUR
BAR R SUM OF BAR AN 1
BOTH SAEM BIGGR OF PRODUKT OF FOO AN QUZ AN PRODUKT OF BAR BAZ AN PRODUKT OF FOO AN QUZ
O RLY?
YA RLY
BAZ R FOO
QUZ R BAR
OIC
IM OUTTA YR LOOP
BAZ IS NOW A NUMBAR
VISIBLE SMOOSH QUOSHUNT OF BAZ QUZ
KTHXBYE
Выходные данные Выведите единственное вещественное число. Ответ будет считаться правильным, если его абсолютная или относительная погрешность не превышает 10 - 4. | |
![]()
|
|
E. Близкие вершины
Деревья
разделяй и властвуй
Структуры данных
*2700
Дано взвешенное дерево из n вершин. Каждое ребро имеет неотрицательный вес. Длиной пути между двумя вершинами дерева называется количество ребер в пути. Весом пути называется суммарный вес всех входящих в него ребер. Две вершины называются близкими, если существует путь между двумя этими вершинами длины не более l и также существует путь между ними веса не более w. Посчитайте количество пар вершин v, u (v < u), таких, что вершины v и u близкие. Выходные данные Выведите единственное целое число — количество близких пар. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-х битовых чисел на С++. Рекомендуется использовать потоки cin, cout или спецификатор %I64d. | |
![]()
|
|
E. Шаасс Великий
Деревья
дп
*2300
Великий Шаасс коронован как новый император Драхта. В империи есть n городов, их соединяет n - 1 двусторонних дорог. У каждой дороги есть определенная длина, каждая дорога соединяет пару городов. Каждую пару городов соединяет единственный простой путь. Его величество великий Шаасс решил разрушить одну из дорог и построить другую дорогу той же длины между некоторой парой городов. Он должен построить дорогу так, чтобы было все еще возможно путешествовать из каждого города в любой другой по дорогам империи. Вы как его советник должны помочь ему найти способ выполнить описанное действие. Вы должны найти такой способ, который минимизирует общую сумму попарных расстояний между городами. Вычислите минимальную сумму. Выходные данные В единственной строке выведите минимальную попарную сумму расстояний между городами. Пожалуйста, не используйте спецификатор %lld для чтения и записи 64-битных чисел на С++. Рекоммендуется использовать потоки cin, cout или спецификатор %I64d. | |
![]()
|
|
C. Баланс
графы
Деревья
Конструктив
поиск в глубину и подобное
*2500
Имеется система из n сосудов с водой, некоторые пары которых соединены трубками с клапанами и механизмами для переливания. Через трубки, соединяющие сосуды, можно переливать целое число литров из одного сосуда в другой (в любом направлении). Два сосуда могут быть соединены более чем одной трубкой. Общее количество трубок равно e. Объемы всех сосудов одинаковы и равны v, и объем воды в сосудах, разумеется, не должен превышать объема сосуда в процессе переливаний. Известны начальные объемы ai воды в сосудах и объемы bi, которые требуется получить. Найдите последовательность переливаний, которая выполняет эту задачу. Число переливаний не должно превышать 2·n2. Выходные данные Выведите «NO» (без кавычек), если такой последовательности переливаний не существует. Иначе выведите любую подходящую последовательность переливаний в следующем формате. В первой строчке выведите число переливаний k (k не должно превышать 2·n2). В последующих строчках выведите переливания по одному на строке в формате x y d (переливание d литров из сосуда номер x в сосуд номер y, x и y должны быть различны). Для всех операций число d должно быть целым неотрицательным. | |
![]()
|
|
C. Командир Ciel
Деревья
жадные алгоритмы
Конструктив
поиск в глубину и подобное
разделяй и властвуй
*2100
Лиса Ciel становится командиром Древоземелья. В Древоземелье, как это следует из названия, есть n городов, соединенных n - 1 ненаправленными дорогами, а между любыми двумя городами существует путь по дорогам Древоземелья. Лиса Ciel должна назначить каждому городу офицера. У каждого офицера есть ранг — буква от 'A' до 'Z'. Таким образом, имеется 26 различных рангов, самый высокий — 'A', самый низкий — 'Z'. У Ciel имеется достаточно офицеров каждого ранга. Но не все так просто, должно быть выполнено особое условие: если x, y — два различных города и у их офицеров одинаковые ранги, то на простом пути между x и y должен быть город z, имеющий офицера более высокого ранга. Таким образом, общение между офицерами одного ранга будет гарантированно проходить под присмотром офицера более высокого ранга. Помогите Ciel составить подходящий план назначения офицеров городам. Если это невозможно, выведите «Impossible!». Выходные данные Если подходящий план существует, выведите n символов, разделенных пробелами — i-ый символ обозначает ранг офицера в городе i. В противном случае, выведите «Impossible!». Примечание В первом примере для любых двух офицеров ранга 'B', офицер с рангом 'А' будет на пути между ними. То есть, такое решение подходит. | |
![]()
|
|
D. Книга Зла
Деревья
дп
поиск в глубину и подобное
разделяй и властвуй
*2000
Паладин Манао напал на след древней Книги Зла в одной болотистой местности. Всего в этой местности расположено n населенных пунктов, пронумерованных числами от 1 до n. Из-за того, что передвигаться по местности очень сложно, люди вытоптали ровно n - 1 тропинок, каждая из которых соединяет некоторую пару населенных пунктов. По каждой из этих тропинок можно передвигаться в обоих направлениях. Из любого населенного пункта можно попасть в любой другой, перейдя по одной или нескольким тропинкам. Назовем расстоянием между двумя населенными пунктами наименьшее количество тропинок, которые надо пересечь, чтобы попасть из одного пункта в другой. Манао известно, что у искомой им Книги Зла радиус действия d. Это означает, что если Книга Зла находится в некотором населенном пункте, то ее пагубное влияние (например, явление привидений и оборотней) распространяется в населенных пунктах на расстоянии d или меньше от него. Манао услышал, что влияние Книги Зла было замечено в m населенных пунктах с номерами p1, p2, ..., pm. Заметим, что Книга возможно влияет и на другие населенные пункты, просто этого еще никто не заметил. Он хочет определить, в каких из населенных пунктов может находиться эта Книга. Помогите ему в этой непростой задаче. Выходные данные Выведите единственное число — количество населенных пунктов, в которых может находиться Книга Зла. Возможно, что информация, дошедшая до Манао, противоречива и не существует такого населенного пункта, где может находиться Книга. В таком случае выведите 0. Примечание Пример 1. Радиус действия Книги Зла равен 3-ем, а ее воздействие было замечено в населенных пунктах 1 и 2. Таким образом, она может находиться в населенных пунктах под номерами 3, 4 и 5.  | |
![]()
|
|
E. Дерево делителей
Деревья
Перебор
теория чисел
*2200
Дерево делителей — это корневое дерево, для которого выполняются следующие условия: - В каждой из вершин дерева записано целое положительное число.
- В листьях дерева записаны простые числа.
- Для любой внутренней вершины произведение чисел, записанных в ее сыновьях, равно числу, записанному в этой вершине.
У Манао есть n различных чисел a1, a2, ..., an. Он пытается построить такое дерево делителей, в вершинах которого каждое из ai будет встречаться хотя бы по одному разу. Манао любит компактность, но деревья у него получаются уж слишком большие. Помогите Манао определить минимальное возможное количество вершин в искомом дереве делителей. Выходные данные Выведите единственное число — минимальное количество вершин в дереве делителей, содержащем каждое из чисел ai. Примечание Пример 1. Самое маленькое дерево делителей выглядит так:  Пример 2. В этом случае можно построить следующее дерево делителей:  Пример 3. Дерево может состоять из единственной вершины. | |
![]()
|
|
D. Ксюша и битовые операции
Деревья
Структуры данных
*1700
У начинающего программиста Ксюши есть последовательность a, состоящая из 2n неотрицательных целых чисел: a1, a2, ..., a2n. Сейчас Ксюша изучает битовые операции. Чтобы лучше понять как они работают, Ксюша решила подсчитать некоторое значение v по a. А именно, значение v считается в несколько итераций. На первой итерации, Ксюша записывает новую последовательность a1 or a2, a3 or a4, ..., a2n - 1 or a2n, состоящую из 2n - 1 элементов. Другими словами, она записывает побитовое ИЛИ соседних элементов последовательности a. На второй итерации, Ксюша записывает побитовое исключающее ИЛИ соседних элементов полученной после первой итерации последовательности. На третьей итерации Ксюша записывает побитовое ИЛИ соседних элементов последовательности, полученной после второй итерации. И так далее операции побитовое исключающее ИЛИ и побитовое ИЛИ чередуются. В конце концов получится последовательность, состоящая из одного элемента, этот элемент и равен v. Рассмотрим пример, пусть последовательность a = (1, 2, 3, 4). Тогда запишем все преобразования (1, 2, 3, 4) → (1 or 2 = 3, 3 or 4 = 7) → (3 xor 7 = 4), в итоге v = 4. Вам задана изначальная последовательность Ксюши. Но посчитать значение v по заданной последовательности было бы слишком просто, поэтому Вам дополнительно заданы m запросов. Каждый запрос — это пара целых чисел p, b. Запрос p, b означает, что нужно выполнить присвоение ap = b. После каждого запроса, нужно вывести новое значение v посчитанное по новой последовательности a. Выходные данные Выведите m целых чисел — i-ое число обозначает значение v посчитанное для последовательности a после выполнения i-ого запроса. Примечание Для справок по битовым операциям вы можете использовать информацию по ссылке: http://ru.wikipedia.org/wiki/Битовые_операции | |
![]()
|
|
E. Ксюша и дерево
Деревья
разделяй и властвуй
Структуры данных
*2400
У программиста Ксюши есть дерево, состоящее из n вершин. Будем считать, что вершины дерева пронумерованы от 1 до n. Также будем считать, что первоначально вершина номер 1 покрашена в красный цвет, а остальные вершины покрашены в синий цвет. Расстоянием между двумя вершинами дерева v и u будем называть количество ребер в кратчайшем пути между v и u. Ксюше нужно научиться быстро выполнять запросы двух видов: - покрасить заданную синюю вершину в красный цвет;
- посчитать, какая красная вершина ближе всего к заданной и вывести кратчайшее расстояние до ближайшей красной вершины.
Ваша задача — написать программу, которая будет выполнять описанные запросы. Выходные данные Для каждого запроса второго типа выведите ответ на отдельной строке. | |
![]()
|
|
D. Водяное дерево
графы
Деревья
поиск в глубину и подобное
Структуры данных
*2100
Безумный ученый Майк построил корневое дерево, которое состоит из n вершин. Каждая вершина представляет собой резервуар, который может быть либо пуст, либо заполнен водой. Вершины дерева пронумерованы числами от 1 до n. Корень дерева находится в вершине 1. Резервуары детей каждой вершины расположены ниже резервуара этой вершины, при этом вершина соединена с каждым из детей трубой, по которой вниз может стекать вода. Майк хочет выполнять с деревом следующие операции: - Заполнить водой вершину v. Тогда v и все ее потомки (дети, дети детей, и так далее) заполняются водой.
- Опустошить вершину v. Тогда v и все ее предки становятся пустыми.
- Определить, заполнена ли вершина v водой в данный момент.
Изначально все вершины дерева пусты. Майк уже составил полный список операций, которые он хочет выполнить по порядку. Перед испытанием дерева Майк решил провести симуляцию этих действий. Помогите Майку определить, какие результаты он получит в результате выполнения всех операций. Выходные данные Для каждой операции типа 3 выведите на отдельной строке 1, если вершина заполнена, и 0, если вершина пуста. Ответы на запросы выводите в том порядке, в котором запросы даны во входных данных. | |
![]()
|
|
E. Насосные станции
графы
Деревья
жадные алгоритмы
Перебор
поиск в глубину и подобное
Потоки
разделяй и властвуй
*2900
Безумный ученый Майк устроился на работу. Его задача — управлять системой насосных станций для перекачки воды. Система состоит из n насосных станций, которые пронумерованы целыми числами от 1 до n. Некоторые пары станций соединены двунаправленными трубами, по которым может течь вода в том или другом направлении (но одновременно только в одном). Для каждой трубы задана пропускная способность — наибольшее количество литров воды, которое может через нее протекать в течение одного часа. Каждая насосная станция может перекачивать входящую воду из одних станций в другие станции по трубам при условии, что за один час общее входящее в эту станцию количество литров воды равняется общему исходящему из этой станции количеству литров воды. В обязанности Майка входит перекачивание воды между станциями. Из станции a в станцию b по трубам (возможно, через другие станции) в течение одного часа можно пустить какое-то количество литров воды согласно правилам, описанным выше. В течение этого времени вода из других станций не может втекать в станцию a, и не может вытекать из станции b, при том из станции a может вытекать любое количество воды, и в станцию b может втекать любое количество воды. Если из станции a за час в общем было выкачано x литров воды, то Майк получает к зарплате x бублей. Чтобы получить зарплату, Майк по контракту должен работать n - 1 дней. В первый день он выбирает две станции v1 и v2, и в течение одного часа перекачивает определённое количество воды из v1 в v2. Далее в i-тый день Майк выбирает до этого ни разу не выбранную станцию vi + 1, и в течение одного часа перекачивает определенное количество воды из станции vi в станцию vi + 1. При этом количество перекачиваемой воды в i-тый день не зависит от количества перекачиваемой воды в (i - 1)-ый день. Для своих проектов Майку нужно заработать как можно больше бублей. Помогите Майку найти такую перестановку номеров станций v1, v2, ..., vn, при которой Майк может заработать наибольшую возможную зарплату. Выходные данные В первой строке выведите одно целое число — наибольшее значение зарплаты, которую может получить Майк. В второй строке через пробелы выведите перестановку из n чисел от 1 до n — номера станций последовательности v1, v2, ..., vn. Если существует несколько ответов, выведите любой. | |
![]()
|
|
B. Яблоня
Деревья
поиск в глубину и подобное
теория чисел
*2100
Дано корневое дерево, состоящее из n вершин. В каждом листе дерева записано ровно одно число — количество яблок в этом листе. Весом поддерева назовем сумму чисел в листьях этого поддерева. В частности, вес поддерева, соответствующего некоторому листу — это число, которое записано в этом листе. Дерево называется сбалансированным, если для каждой вершины дерева v все поддеревья, соответствующие сыновьям вершины v, имеют одинаковый вес. Какое минимальное количество яблок нужно удалить из дерева (точнее из некоторых его листьев), чтобы сделать дерево сбалансированным? Обратите внимание, что цель всегда можно достигнуть, удалив все яблоки. Выходные данные Выведите единственное целое число — минимальное количество яблок, которое нужно удалить, чтобы сбалансировать дерево. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-битных чисел на С++. Рекомендуется использовать потоки cin, cout или спецификатор %I64d. | |
![]()
|
|
E. Пилигримы
Деревья
дп
поиск в глубину и подобное
*2800
Долгое время назад жили-были люди в стране Dudeland. Эта страна состояла из n городов, соединенных n - 1 двунаправленными дорогами. Города пронумерованы от 1 до n, и известно, что из любого города можно попасть в любой другой, двигаясь по дорогам страны. В Dudeland есть m монастырей, расположенных в m различных городах. В каждом монастыре живет пилигрим. В начале года, каждый пилигрим записывает, какой монастырь находится дальше всего от того монастыря, в котором он живет. Если существует более одного такого монастыря, то он записывает все подходящие монастыри. В день Большого Лебовски каждый пилигрим выбирает наугад город из своего списка и начинает туда идти. Уолтер ненавидит пилигримов и поэтому хочет прервать путь как можно большего числа пилигримов. Он планирует уничтожить ровно один город, в котором нет монастыря. Пилигрим огорчается, если все монастыри из его списка становятся недостижимыми из его монастыря. Найдите максимальное количество пилигримов, которых Уолтер может огорчить. Также найдите количество способов, которым Уолтер может этого достигнуть — количество городов, которые он может удалить. Выходные данные Выведите два целых числа: максимальное количество пилигримов, которых Уолтер может огорчить, и количество способов, которыми он может осуществить свой план. | |
![]()
|
|
C. Валера и выборы
графы
Деревья
поиск в глубину и подобное
*1600
В городе, где живет Валера, скоро состоятся выборы в Городскую Думу. Всего в городе есть n районов и n - 1 двусторонняя дорога. При этом известно, что из любого района существует путь по дорогам в любой другой район. Пронумеруем все районы в городе некоторым образом целыми числами от 1 до n включительно. Для каждой дороги жители определили, является ли она проблемной или нет. Проблемная дорога — это дорога, которая нуждается в ремонте. На выборы баллотируются n кандидатов. Пронумеруем всех кандидатов некоторым образом целыми числами от 1 до n включительно. Если кандидат с номером i будет избран в Городскую Думу, то он выполнит ровно одно обещание — отремонтировать все проблемные дороги на пути от района с номером i до района с номером 1, в котором расположена Городская Дума. Помогите Валере и найдите множество кандидатов, после избрания которых в Городскую Думу все проблемные дороги в городе будут отремонтированы. Если же существует несколько таких множеств, следует выбрать множество, состоящее из минимального количества кандидатов. Выходные данные В первой строке выведите одно целое неотрицательное число k — минимальный возможный размер искомого множества. Во второй строке выведите k целых чисел a1, a2, ... ak — номера кандидатов, которые образуют искомое множество. Если существует несколько решений, то разрешается вывести любое. | |
![]()
|
|
C. Древнеберляндский язык
Деревья
жадные алгоритмы
Структуры данных
*1900
Берляндские ученые знают, что в древнеберляндском языке было ровно n слов. Эти слова имели длины l1, l2, ..., ln букв. В словах древнеберляндцы использовали две буквы, 0 и 1. Древние берляндцы говорили быстро и не делали пауз между словами, но при этом всегда могли однозначно понять друг друга. Это было возможно потому, что никакое слово не было префиксом никакого другого (префиксом строки называется некоторая её подстрока, начинающаяся с первого символа). Помогите ученым определить, можно ли восстановить все слова из древнеберляндского языка, и если можно, выведите сами слова. Выходные данные Если такого набора слов не существует, в единственной строке выведите NO. Иначе, в первой строке выведите YES, а в следующих N строках выведите сами слова в том порядке в каком даны их длины во входном файле. Если решений несколько, выведите любое. | |
![]()
|
|
D. Сосуды
Деревья
реализация
снм
Структуры данных
*1800
Есть система из n сосудов, расположенных один над другим так, как показано на рисунке ниже. Представим, что сосуды пронумерованы числами от 1 до n в порядке от самого верхнего к самому нижнему, объем i-го сосуда равен ai литров.  Изначально все сосуды пустые. В некоторые сосуды наливают воду, при этом вся вода, не поместившаяся в i-й сосуд, переливается в (i + 1)-й. Жидкость, не поместившаяся в n-й сосуд, выливается на пол. Ваша задача состоит в том, чтобы промоделировать наливание воды в сосуды. Для этого вам потребуется обрабатывать два типа запросов: - Долить в pi-й сосуд xi литров воды;
- Вывести, сколько воды находится в ki-м сосуде.
При ответе на второй запрос можно считать, что вся вода, налитая до этого момента, уже успела перелиться между сосудами. Выходные данные На каждый запрос второго типа в отдельной строке выведите количество воды в соответствующем сосуде. | |
![]()
|
|
D. Весело выбирать поддерево
Бинарный поиск
Деревья
поиск в глубину и подобное
Структуры данных
*2600
Дано дерево, состоящее из n вершин. Вершины пронумерованы от 1 до n. Определим длину отрезка [l, r] величиной r - l + 1. Счет поддерева данного дерева равняется максимальной длине такого отрезка [l, r], что вершины с номерами l, l + 1, ..., r принадлежат поддереву. Рассмотрим все поддеревья данного дерева размером не больше k, выведите максимальный счет поддерева среди рассматриваемых. Обратите внимание, что в данной задаче дерево не корневое, поэтому поддерево — это любой связный подграф дерева. Выходные данные Выведите единственное целое число — максимальный возможный счет. Примечание В первом примере имеется поддерево размера не больше 6, включающее тройку последовательных номеров вершин. Например, поддерево, состоящее из {1, 3, 4, 5, 7, 8} или из {1, 4, 6, 7, 8, 10}, включает тройку последовательных номеров вершин. Однако не существует поддерева, размер которого не больше 6, включающего 4 или более последовательных номеров вершин. | |
![]()
|
|
D. Инна и последовательность
Бинарный поиск
Деревья
дп
Структуры данных
*2000
Дима долго думал, что подарить Инне, и подарил ей пустую последовательность w. Теперь ребята хотят заполнить последовательность w нулями и единицами вместе. Для этого они решили поиграть в забавную игру. Перед началом игры Дима загадывает m целых чисел a1, a2, ..., am (1 ≤ a1 < a2 < ... < am). Далее Инна и Дима начинают играть, то есть добавлять числа в последовательность w. Каждое новое число ребята дописывают в конец последовательности. В некоторые моменты времени Дима решает, что игра слишком близится к концу, поэтому (он же хочет играть с Инной как можно дольше) Дима сильно стукает кулаком по столу. При этом a1-е, a2-е, a3-е, ..., ak-е числа от начала одновременно вылетают из последовательности (в последовательности становится на k чисел меньше). Здесь k — такое максимальное число, что значение ak не превосходит текущей длины последовательности. Если число a1 больше текущей длины w, то из последовательности ничего не вылетает. Вам дана хронологическая последовательность событий в игре. Каждое событие — это либо добавление числа в конец последовательности w, либо стук Димы по столу. Определите чему будет равна последовательность после того, как все эти события произойдут. Выходные данные В единственной строке выведите последовательность из 0 и 1 — содержимое w после всех событий. Элементы последовательности должны быть выведены в порядке от начала к концу последовательности. Если после всех событий последовательность w окажется пустой, выведите «Poor stack!». | |
![]()
|
|
D. Дерево и запросы
Деревья
поиск в глубину и подобное
Структуры данных
*2400
Задано корневое дерево, состоящее из n вершин. Каждая вершина дерева имеет определенный цвет. Будем считать, что вершины дерева пронумерованы целыми числами от 1 до n. Тогда цвет вершины v будем обозначать cv. Корнем дерева является вершина с номером 1. В задаче вам требуется ответить на m запросов. Каждый запрос характеризуется двумя целыми числами vj, kj. Ответ на запрос vj, kj — это количество таких цветов вершин x, что в поддереве вершины vj содержится как минимум kj вершин цвета x. Определение корневого дерева можно прочитать по ссылке: http://ru.wikipedia.org/wiki/Дерево_(теория_графов). Выходные данные Выведите m целых чисел — ответы на запросы в порядке появления запросов во входных данных. Примечание Поддерево вершины v в корневом дереве с корнем r — это множество вершин дерева {u : dist(r, v) + dist(v, u) = dist(r, u)}. Где dist(x, y) — это длина кратчайшего по количеству ребер пути между вершинами x и y. | |
![]()
|
|
F. Новогоднее дерево
Деревья
разделяй и властвуй
Структуры данных
*2400
Вы — программист, и у вас есть новогоднее дерево (нет, не елка) — дерево из четырех вершин: одна вершина степени три (имеет номер 1), связанная с тремя листами (имеют номера от 2 до 4). На новый год программисты обычно веселятся, вот и вы решили повеселиться, добавляя вершины в свое дерево. При этом одна операция добавления выглядит следующим образом: - Сначала выбирается некоторой лист дерева с номером v.
- Обозначим количество вершин в дереве на данный момент переменной n, тогда в дерево добавляются две вершины с номерами n + 1 и n + 2, а также ребро между вершинами v и n + 1 и ребро между вершинами v и n + 2.
Как и полагается, ваша задача не просто промоделировать процесс добавления вершин в дерево, но и после каждой операции добавления выводить диаметр текущего дерева. Вперед, на решение новогодней задачи! Выходные данные Выведите q целых чисел — диаметр текущего дерева после каждой операции. | |
![]()
|
|
D. Ксюша и пешки
графы
Деревья
поиск в глубину и подобное
реализация
*2200
У Ксюши есть шахматная доска размером n × m. На каждой клетке этой шахматной доски нарисован один из символов: «<», «>», «^», «v», «#». Клетки, на которых нарисован символ «#», Ксюша называет заблокированными. Известно, что все клетки шахматной доски, которые касаются ее границы, являются заблокированными. Ксюша играет с двумя пешками на этой шахматной доске. Изначально она ставит пешки на шахматную доску. Причем в одной клетке шахматной доски в один момент времени могут стоять две пешки тогда и только тогда, когда эта клетка заблокированная. В других случаях две пешки не могут находиться в одной клетке. Игра начинается, когда Ксюша поставила пешки на доску. За один ход Ксюша перемещает каждую из пешек на соседнюю по стороне клетку в направлении стрелки, нарисованной на клетке, на которой стоит соответствующая пешка (если пешка стоит на «#», она не двигается). Считайте, что Ксюша двигает пешки одновременно (смотрите второй тестовый пример). Конечно, Ксюша играет на очки. Как же посчитать очки за игру? Очень просто! Давайте посчитаем сколько перемещений совершила первая пешка и сколько вторая, просуммируем эти два числа — это и будет являться результирующим количеством очков игры. Ксюше очень интересно, какое максимальное количество очков она может заработать (для этого одна должна оптимально разместить пешки в самом начале игры). Помогите ей, найдите это число. Выходные данные Если Ксюша может заработать бесконечно большое количество очков, выведите -1. Иначе выведите максимальное количество очков, которое она может заработать. | |
![]()
|
|
C. Дерево подвижных сумм
Деревья
поиск в глубину и подобное
Структуры данных
*2000
Яхуб очень любит деревья. Недавно он обнаружил интересное дерево под названием «дерево подвижных сумм». Дерево состоит из n вершин, пронумерованных от 1 до n, каждая вершина i содержит начальное значение ai. Корень дерева — вершина 1. Это дерево имеет особое свойство: когда значение val добавляется к значению вершины i, значение -val добавляется ко всем значениям детей вершины i. Обратите внимание, что когда вы добавляете значение -val ребенку вершины i, вы также добавляете -(-val) ко всем детям этого ребенка вершины i и так далее. Для того, чтобы лучше понять описанное свойство, обратите внимание на пояснение к первому тесту. Дерево поддерживает два типа запросов: - «1 x val» — добавить значение val к значению вершины x;
- «2 x» — вывести текущее значение вершины x.
Чтобы помочь Яхубу лучше понять дерево, надо ответить на m запросов описанных типов. Выходные данные Для каждого запроса второго типа (вывод текущего значения вершины) надо вывести ответ на запрос на отдельной строке. Ответы на запросы выводите в порядке следования запросов во входных данных. Примечание Изначально значения в вершинах равны [1, 2, 1, 1, 2]. Затем значение 3 добавляется к вершине 2. Вершина 2 передает значение -3 своим сыновьям, и далее значение -3 добавляется к вершинам 4 и 5. Дальше значение никуда не передается. После этого запроса значения в вершинах равны [1, 5, 1, - 2, - 1]. Затем значение 2 добавляется к вершине 1. Вершина 1 передает значение -2 своим сыновьям: вершине 2 и вершине 3. Из вершины 2 значение 2 передается вершинам 4 и 5. Вершина 3 не имеет сыновей, следовательно из нее значение не передается. После этого запроса значения в вершинах становятся равны [3, 3, - 1, 0, 1]. С основными определениями, связанными с корневыми деревьями, можно ознакомиться по ссылке: http://ru.wikipedia.org/wiki/Дерево_(теория_графов) | |
![]()
|
|
C. О меняющемся дереве
графы
Деревья
Структуры данных
Дано корневое дерево, состоящее из n вершин, пронумерованных от 1 до n. Корень дерева находится в вершине с номером 1. Изначально во всех вершинах записано число 0. Далее приходят q запросов, каждый из которых имеет один из следующих двух видов: - Формат запроса: 1 v x k. В ответ на запрос нужно к числу, записанному в вершине v, добавить x; к числам, записанным в потомках вершины v на расстоянии 1, добавить x - k; и так далее, к числам, записанным в потомках на расстоянии i, нужно добавить x - (i·k). Расстоянием между двумя вершинами считается длина кратчайшего по количеству ребер пути между этими вершинами.
- Формат запроса: 2 v. В ответ на запрос требуется вывести, какое число сейчас записано в вершине v по модулю 1000000007 (109 + 7).
Выполните заданные во входных данных запросы. Выходные данные Для каждого запроса второго типа на отдельной строке выведите число, записанное в вершине, обозначенной в запросе, по модулю 1000000007 (109 + 7). Примечание О корневом дереве можно прочитать здесь: http://ru.wikipedia.org/wiki/Дерево_(теория_графов). | |
![]()
|
|
E. Два корневых дерева
Деревья
реализация
Структуры данных
*2900
У вас есть два корневых неориентированных дерева, каждое из которых содержит по n вершин. Пронумеруем вершины каждого дерева целыми числами от 1 до n. Корень каждого дерева находится в вершине 1. Ребра первого дерева окрашены в синий цвет, ребра второго — в красный цвет. Для удобства будем говорить, что первое дерево — синее, а второе — красное. Ребро {x, y} называется плохим для ребра {p, q} если выполнены два условия: - Цвет ребра {x, y} отличен от цвета ребра {p, q}.
- Рассмотрим дерево того же цвета, что и ребро {p, q}. Ровно одна из вершин x, y лежит как в поддереве вершины p, так и в поддереве вершины q.
В этой задаче вам нужно промоделировать процесс, который описан далее. Процесс состоит из нескольких этапов: - На каждом этапе удаляются ребра ровно одного цвета.
- На первом этапе удаляется ровно одно синее ребро.
- Пусть на этапе с номером i были удалены ребра {u1, v1}, {u2, v2}, ..., {uk, vk}. Тогда на этапе с номером i + 1 будут удалены все еще не удаленные плохие ребра для ребра {u1, v1}, затем все еще не удаленные плохие ребра для ребра {u2, v2}, и так далее до ребра {uk, vk}.
Для каждого этапа удаления ребер определите, какие ребра будут удалены на данном этапе. Обратите внимание, что в определении плохого ребра всегда рассматривается изначальное дерево — дерево, в котором еще не удалено ни одно ребро. Выходные данные Для каждого этапа удаления ребер выведите его описание. Каждое описание должно состоять ровно из двух строк. Если на данном этапе будет происходить удаление синих ребер, тогда в первой строке описания этапа должно содержаться слово Blue, иначе слово Red. Во второй строке выведите индексы ребер, которые будут удалены на данном этапе, в порядке возрастания. Примечание Для удобства представим, что все ребра корневого дерева получили некоторое направление, причем так, что все вершины достижимы из вершины с номером 1. Тогда поддеревом вершины v будем называть множество вершин, достижимых из вершины с номером v в полученном ориентированном графе (сама вершина v тоже входит в это множество). | |
![]()
|
|
D. Скалолазание
геометрия
Деревья
поиск в глубину и подобное
*2200
Эта задача никак не связана с маленьким Крисом. Здесь надо лазать по скалам (это в круг интересов Криса уж точно не входит). В ряд расположены n гор, каждая из которых имеет форму вертикального отрезка, один конец которого находится на земле. Горы пронумерованы слева направо целыми числами от 1 до n. Гора под номером i находится в точке xi, а ее вершина — на высоте yi. Для каждых двух гор a и b, если вершину горы a можно видеть с вершины горы b, их вершины связаны веревкой. Формально, вершины двух гор соединены, если отрезки, соединяющие вершины, не пересекаются или не соприкасаются с любыми другими отрезками гор. С помощью этих веревок скалолазы могут взбираться на горы. Есть m команд, в каждой ровно по два скалолаза. Первый и второй скалолаз из i-й команды стоят на вершинах ai-й и bi-й скалы, соответственно. Они хотят встретиться на вершине некоторой горы. Теперь каждый из двух скалолазов двигается согласно следующему алгоритму: - если один скалолаз находится на вершине горы, где его партнер уже находится сам, либо рано или поздно придет туда, то первый скалолаз остается ждать на этой горе;
- в противном случае, скалолаз выбирает самую правую скалу справа от его текущей скалы, до которой он может добраться по веревке; взбирается на эту скалу и продолжает процесс (скалолаз может взобраться и на гору, которая ниже его текущей).
 Для каждой команды определите номер скалы, где участники этой команды встретятся! Выходные данные В единственной строке выведите m целых чисел через пробел, где i-е число — номер скалы, на которой встретятся скалолазы из i-й команды. | |
![]()
|
|
D. Машмох и резервуары с водой
Бинарный поиск
Деревья
жадные алгоритмы
Структуры данных
*2300
Машмох играет в новую игру. В начале у него есть k литров воды и p монеток. Также у него есть корневое дерево (неориентированный связный ациклический граф), состоящее из m вершин. Каждая вершина дерева содержит резервуар с водой, изначально пустой. Игра начинается с того, что Машмох выбирает несколько (не более k) таких резервуаров (кроме того, что находится в корне) и льет в каждый ровно 1 литр воды. Затем следующий процесс продолжается, пока в резервуарах не остается воды. - Процесс состоит из нескольких итераций.
- В начале каждой итерации Машмох открывает крышки всех резервуаров. Затем он закрывает крышки некоторых резервуаров (ему нельзя закрывать крышку корневого резервуара) на время этой итерации. Пусть некоторый резервуар содержал w литров воды и был закрыт на данной итерации, тогда Машмох платит w монеток за закрытие этого резервуара.
- Обозначим через x1, x2, ..., xm список вершин дерева, отсортированный в порядке неубывания по глубине. Будем рассматривать вершины из этого списка одну за одной. Сперва опустошается резервуар в вершине x1 (то есть, корень). Затем для каждой вершины xi (i > 1), если ее резервуар закрыт, вершина пропускается, иначе вся вода переливается из резервуара вершины xi в резервуар ее родителя (несмотря на то, что резервуар родителя может быть закрытым).
Предположим, что до опустошения всех резервуаров дерева произошло l итераций. Обозначим количество воды в резервуаре корня после i-й итерации как wi. В результате описанного процесса Машмох выиграет max(w1, w2, ..., wl) долларов. Машмох хочет знать, какое максимальное количество долларов он может выиграть, сыграв приведенную выше игру. Он просит вас найти для него это значение. Выходные данные Выведите единственное целое число — число, которое Машмох попросил вас найти. Примечание Дерево в первом примере показано на рисунке внизу. Черный, красный и синий цвета соответствуют вершинам с 0, 1, 2 литрами воды.  Один из способов заработать максимальное количество денег — залить 1 литр воды в каждую из вершин, 3 и 4. Начальное состояние указано на рисунке ниже.  Затем первым ходом Машмох заплатит одну монетку за закрытие двери резервуара в третьей вершине. Дерево после первого хода показано на рисунке ниже.  После второго хода в корне будет 2 литра воды.  | |
![]()
|
|
D. Большие проблемы организаторов
графы
Деревья
Структуры данных
*2800
Финал «Russian Code Cup» 2214 года будет проводиться в n гостиницах. При этом в двух гостиницах, назовем их главными, будут проводиться всевозможные мероприятия, а в остальных поселят участников. Сеть дорог устроена таким образом, что гостиницы соединены n - 1 дорогой, при этом из любой гостиницы можно попасть в любую. Организаторам интересно, за какое минимальное количество времени все участники доберутся до главных гостиниц, если каждый участник едет в ближайшую к нему главную гостиницу, а перемещение между двумя гостиницами, соединенными дорогой, занимает одну единицу времени. Сейчас организаторы еще окончательно не определились, какие гостиницы должны быть главными, поэтому они рассматривают различные варианты расположения главных гостиниц. Для каждого рассматриваемого расположения помогите организаторам посчитать минимальное время. Выходные данные На каждый запрос организаторов выведите одно целое число — время, которое понадобится, чтобы все участники добрались до главных гостиниц. | |
![]()
|
|
E. Военные и Володя
графы
Деревья
поиск в глубину и подобное
*2700
Володя — мастер искажений. Он обладает уникальной способностью — строить портальчики! Имея два местоположения в пространстве, Володя может построить портальчик, позволяющий перемещаться между ними в любом из двух направлений. К сожалению, такое действие не обходится Володе даром, и при каждом строительстве редеет на несколько волос его и так, скажем откровенно, не очень-то густая шевелюра. Из-за своих экстраординарных способностей, Володя привлек внимание военных. Ему поручено особо важное задание. Но обо всем по порядку. Военная база представляет собой несколько подземных объектов, некоторые из которых соединены между собой двусторонними тоннелями, причем так, что между любыми двумя объектами есть путь по тоннелям. Ровно два объекта имеют выходы на поверхность. Для охраны тоннелей действует патрульный, который каждый день спускается в любой из объектов, имеющих выход, обходит все тоннели и выходит на поверхность через любой из объектов, имеющих выход. Он может входить и выходить через один и тот же объект, а может через разные. Руководство военной базы заметило, что патрульный проходит через некоторые тоннели по несколько раз, и решило оптимизировать схему патрулирования. Перед военными встала задача: построить систему портальчиков между объектами так, чтобы патрульный мог совершать свой обход, проходя по каждому тоннелю ровно один раз. При этом через портальчики патрульный может проходить неограниченное число раз. Здесь-то и вступает в дело Володя: планирование и постройку системы порталов решили поручить именно ему. К несчастью для Володи, из-за строгой секретности ему не сообщили расположения тоннелей, но потребовали, чтобы система порталов выполняла задачу в любом случае. Тем не менее, некоторой информацией Володя располагает: ему известно, между какими парами объектов он может построить порталы и во сколько волос они обойдутся. Более того, завтра Володе обещают сообщить, какие два объекта имеют выходы на поверхность. Конечно же, Володя решил не терять времени и посчитать минимальные стоимости постройки для нескольких вероятных, по его мнению, пар объектов. Помогите ему! Выходные данные Выведите q строк, по одной для каждого запроса. В i-ой строке должно содержаться одно число — ответ на i-ый (в порядке перечисления во входных данных) запрос: минимальная стоимость (в волосах) системы порталов, позволяющей совершать обход для любой системы тоннелей, удовлетворяющей условиям, когда ai-ый и bi-ый объекты имеют выходы на поверхность, или "-1", если построить такую систему порталов нельзя. | |
![]()
|
|
A. Дерево XOR
Деревья
поиск в глубину и подобное
*1300
Сегодня Яхуб изобрел новое дерево под названием дерево XOR. После этого революционного открытия юноша изобрел игру для детей на деревьях XOR. Игра проходит на корневом дереве с n вершинами, пронумерованными от 1 до n. Каждая вершина i имеет начальное значение initi, равное 0 или 1. Корень дерева — вершина с номером 1. Во время игры нужно выполнить несколько (возможно, ноль) операций с деревом. Единственный доступный тип операции — выбрать вершину x. Как только вершина x выбрана, значение в ней меняется на противоположное (с 1 на 0, а с 0 на 1), значения сыновей вершины x не меняются, значения сыновей сыновей вершины x меняются на противоположные, значения сыновей сыновей сыновей вершины x остаются прежними и так далее. Цель игры — присвоить каждой вершине i значение goali. Вам же надо достигнуть цели игры за минимальное количество операций. Выходные данные В первой строке выведите целое cnt, которое обозначает минимальное количество операций. В каждой из следующих cnt строк надо вывести целое число xi, обозначающее, что на i-м ходу вы выбрали вершину xi. | |
![]()
|
|
C. Угадай дерево
битмаски
Деревья
дп
жадные алгоритмы
Конструктив
*2300
Яхуб и Яхубина пошли на пикник. Зашли они в густой лес. Не прошло и пяти минут, как Яхуб вспомнил про деревья в информатике. Более того, он придумал новую задачу, и Яхубине надо ее решить, а не то Яхуб ее не покормит. Яхуб спрашивает у Яхубины: можешь ли ты построить такое корневое дерево, что - каждая внутренняя вершина дерева (вершина, имеющая хотя бы одного сына) имеет по меньшей мере двух сыновей;
- у вершины i в поддереве содержится ci вершин?
Яхубина должна придумать описанное дерево. Она девушка умная и поняла, что, возможно, описанного дерева вовсе не существует. Тогда вся еда достанется Яхубу. Вы должны помочь Яхубине: определите, есть ли хотя бы одно дерево, удовлетворяющее ограничениям Яхуба. Требуемое дерево должно состоять из n вершин. Выходные данные Выведите в первой строке «YES» (без кавычек), если хотя бы одно дерево удовлетворяет ограничениям Яхуба, в противном случае выведите «NO» (без кавычек). | |
![]()
|
|
C. k-дерево
Деревья
дп
реализация
*1600
Совсем недавно креативный студент Леша прослушал лекцию по деревьям. После лекции Леша был вдохновлен и придумал собственное дерево, которое он назвал k-дерево. k-дерево — это бесконечное корневое дерево, в котором: - каждая вершина имеет ровно k сыновей;
- каждое ребро имеет некоторый вес;
- если рассмотреть ребра из некоторой вершины в ее сыновей (ровно k ребер), то их веса будут равны 1, 2, 3, ..., k.
На рисунке ниже представлен фрагмент 3-дерева.  Как только Дима, хороший друг Леши, узнал про это дерево, его сразу заинтересовал вопрос: «Сколько существует путей с суммарным весом ребер равным n, которые начинаются в корне k-дерева, а также содержат хотя бы одно ребро веса не меньше d?». Помогите Диме узнать ответ на его вопрос. Так как количество путей может быть достаточно большим, найдите остаток от деления ответа на 1000000007 (109 + 7). Выходные данные Выведите единственное целое число — ответ на задачу по модулю 1000000007 (109 + 7). | |
![]()
|
|
E. Дерево Фурукава Нагисы
Бинарный поиск
Деревья
разделяй и властвуй
сортировки
*3000
Однажды Оказаки Томоя купил дерево на день рождения Фурукава Нагисы. Дерево было немного странное, у каждой вершины дерева было написано значение. Обозначим значение у i-й вершины переменной vi. Теперь Фурукава Нагиса и Оказаки Томоя хотят сыграть в игру с деревом. Пусть (s, e) — путь из вершины s к вершине e дерева, тогда можно записать последовательность значений вершин на пути (s, e) и обозначить эту последовательность как S(s, e). Определим функцию G от последовательности S(s, e) следующим образом. Предположим, что последовательность равна z0, z1...zl - 1, где l — длина последовательности. Определим G(S(s, e)) = z0 × k0 + z1 × k1 + ... + zl - 1 × kl - 1. Если путь (s, e) удовлетворяет  , тогда путь (s, e) принадлежит Фурукава Нагисе, в противном случае он принадлежит Оказаки Томоя. , тогда путь (s, e) принадлежит Фурукава Нагисе, в противном случае он принадлежит Оказаки Томоя. Считать, у кого больше путей, слишком легко, поэтому ребята хотят поиграть во что-то посложнее. Фурукава Нагиса выдвинула гипотезу: - если пути (p1, p2) и (p2, p3) принадлежат ей, то и путь (p1, p3) тоже принадлежит ей;
- если пути (p1, p2) и (p2, p3) принадлежат Оказаки Томоя, то и путь (p1, p3) тоже принадлежит Оказаки Томоя.
Конечно, описанное выполняется не для всех троек (p1, p2, p3). Итак, теперь Фурукава Нагиса хочет узнать, сколько троек (p1, p2, p3) удовлетворяют ее условию — и это ваша задача. Выходные данные Выведите единственное целое число — количество троек, удовлетворяющих гипотезе Фурукава Нагисы. | |
![]()
|
|
C. Dungeons and Candies
графы
Деревья
жадные алгоритмы
снм
*1800
Во время запуска игры «Dungeons and Candies» требуется получить по сети от сервера описания k уровней игры. Каждое описание — карта клетчатого прямоугольного поля n × m, в клетках которого расположены конфеты (в каждой клетке находится не более одной конфеты). Пустая клетка обозначается символом «.», если же в клетке находится конфета, то она кодируется буквой латинского алфавита. Уровень может содержать одинаковые конфеты, в таком случае буквы в соответствующих клетках карты будут одинаковы.  При передачи по сети требуется минимизировать трафик — суммарный размер переданных данных. Уровни можно передавать в любом порядке. Существует два способа передать очередной уровень A: - Можно передать уровень A целиком. Этот способ требует передачи n·m байтов по сети.
- Можно передать разницу между уровнем A и каким-то ранее переданным уровнем B, если такой существует; эта операция требует передачи dA, B·w байтов, где dA, B обозначает количество клеток поля, которые отличаются в A и B, а w — константа. Обратите внимание, что при вычислении dA, B сравниваются соответствующие друг другу клетки уровней A и B. При этом карты уровней нельзя преобразовывать, например, поворачивать или смещать относительно друг друга.
Ваша задача — найти способ передать все k уровней, минимизировав трафик. Выходные данные В первой строке выведите искомое минимальное количество переданных байтов. Далее выведите k пар целых чисел x1, y1, x2, y2, ..., xk, yk, описывающих способ передачи уровней. Пара xi, yi обозначает, что уровень xi нужно передавать способом yi. Если yi равно 0, значит, уровень нужно передавать первым способом, иначе yi должно быть равно номеру ранее переданного уровня, разницу по сравнению с которым нужно передать, т. е. вы передадите уровень xi, передавая разницу между уровнями xi и yi. Пары выводите в порядке передачи уровней. Уровни пронумерованы от 1 до k в порядке их описания во входных данных. Если существует несколько оптимальных решений, разрешается вывести любое. | |
![]()
|
|
D. Адам и дерево
Деревья
Структуры данных
*2600
Когда у Адама появляется корневое дерево (связный неориентированный граф без циклов), он сразу начинает его раскрашивать. Более формально, каждому ребру он сопоставляет некоторый цвет таким образом, чтобы выполнялись два условия: - Не существует вершины, у которой больше двух инцидентных ребер покрашены в один цвет.
- Для любых двух вершин, у которых есть инцидентные ребра, покрашенные в один цвет (скажем, c), путь между ними содержит ребра только цвета c.
Не все раскраски дерева нравятся Адаму одинаково. Рассмотрим путь от некоторой вершины до корня. Количество различных цветов на этом пути назовем стоимостью вершины. Стоимостью раскраски дерева будем называть максимальную стоимость среди всех вершин дерева. Помогите Адаму определить минимальную стоимость раскраски дерева. Изначально дерево Адама состоит из одной вершины, которая имеет номер один и является корнем. За один ход Адам подвешивает к уже существующей вершине новую, которая получает номер, равный наименьшему положительному целому не занятому числу. После каждой операции вам нужно сообщать минимальную стоимость раскраски получившегося дерева. Выходные данные Выведите n целых чисел — минимальные стоимости раскраски дерева после каждого добавления. Примечание На картинке изображен один из возможных вариантов раскраски дерева из примера в самый последний момент. Стоимость вершин с номерами 11 и 12 равна трем. 
| |
![]()
|
|
E. DZY любит садоводство
Бинарный поиск
Деревья
снм
*2700
DZY любит садоводство, поэтому он обожает решать задачи про деревья. У DZY есть взвешенное дерево (связный неориентированный граф без циклов), состоящее из n вершин (пронумерованных от 1 до n). Определим функцию g(x, y) (1 ≤ x, y ≤ n) как длину самого длинного ребра в кратчайшем пути между вершинами x и y. В частности, g(z, z) = 0 для любого z. Для каждой целочисленной последовательности p1, p2, ..., pn (1 ≤ pi ≤ n), определим f(p) как  . . DZY хочет найти такую последовательность p, что f(p) принимает максимальное возможное значение. Есть еще одно ограничение: элемент j может встречаться в p не более xj раз. Пожалуйста, помогите DZY, найдите максимальное возможное f(p) при описанных ограничениях. Выходные данные Выведите единственное целое число — ответ на задачу. Примечание В первом примере одна из оптимальных последовательностей p равна [4, 3, 2, 1]. | |
![]()
|
|
B. Ломаная на четырех точках
геометрия
Деревья
Конструктив
Перебор
*1800
Вам дана прямоугольная сетка с целочисленными точками с координатами от (0, 0) до (n, m) включительно. Вам надо выбрать ровно 4 разных точки и построить из них ломаную, возможно, с самопересечениями и самокасаниями. Ваша задача — найти самую длинную такую ломаную. Ломаная линия, построенная из точек p1, p2, p3, p4, состоит из трех отрезков p1 p2, p2 p3, p3 p4, и ее длина определена как сумма длин этих отрезков. Выходные данные Выведите 4 строки, по два целых числа на каждой — координаты точек p1, p2, p3, p4, образующих самую длинную ломаную соответственно. Проверяющая программа сравнивает длину ответа участника и длину ответа жюри с точностью 10 - 6. | |
![]()
|
|
B. Много игр
Деревья
дп
игры
поиск в глубину и подобное
реализация
Строки
*1900
Андрей, Федя и Леша — очень изобретательные ребята. В очередной раз они придумали игру для двоих игроков со строками. Задан набор, состоящий из n непустых строк. Во время игры два игрока вместе строят слово, изначально это слово пустое. Игроки ходят по очереди. За свой ход игрок должен дописать в конец слова одну букву так, чтобы полученное слово было префиксом хотя бы одной строки из заданного набора. Проигрывает тот, кто не может сделать ход. Андрей и Леша решили сыграть в эту игру k раз. Причем, игрок, проигравший в i-й игре, делает первый ход в (i + 1)-й игре. Ребята решили, что победителем по сумме всех игр будет считаться тот, кто победил в последней (k-й) игре. Андрей и Леша уже начали играть, а Федя в это время решил посчитать: кто будет победителем, если оба игрока будут играть оптимально. Помогите ему. Выходные данные Если победит игрок, который ходит первым, то выведите «First», иначе выведите «Second» (кавычки выводить не нужно). | |
![]()
|
|
C. Цивилизация
Деревья
дп
поиск в глубину и подобное
снм
Тернарный поиск
*2100
Андрей играет в игру «Цивилизация». Дима помогает ему. В игре «Цивилизация» n городов и m двусторонних дорог. Города пронумерованы целыми числами от 1 до n. Между любой парой городов либо существует единственный путь, либо не существует никакого пути. Путем называется последовательность различных городов v1, v2, ..., vk, в которой между любыми двумя соседними городами vi и vi + 1 (1 ≤ i < k) есть дорога. Длина такого пути равна (k - 1). Давайте говорить, что два города лежат в одной области тогда и только тогда, когда существует путь между этими двумя городами. В процессе игры происходят события двух типов: - Андрей спрашивает у Димы длину самого длинного пути в области, в которой лежит город x.
- Андрей просит Диму объединить область, в которой лежит город x, с областью, в которой лежит город y. Если города лежат в одной области, то объединять области не нужно. Иначе нужно объединить области следующим образом: выбрать город в первой области, город во второй области и связать их дорогой так, чтобы минимизировать длину самого длинного пути в полученной области. Если существует несколько оптимальных способов соединить области, то разрешается выбрать любой.
Диме очень сложно выполнять просьбы Андрея, поэтому он обращается к вам за помощью. Помогите Диме. Выходные данные Для каждого события первого типа выведите ответ на него в отдельной строке. | |
![]()
|
|
F. Простая задача о деревьях
Деревья
дп
жадные алгоритмы
игры
*3200
Pieguy и Piegirl играют в игру. У них есть корневое бинарное дерево, которое обладает следующим свойством: каждая вершина дерева либо лист, либо имеет ровно два сына. Каждый лист имеет некоторое значение, ассоциированное с ним. Во время игры игроки по очереди делают ходы. На своем ходу игрок выбирает два листа, имеющих общего непосредственного предка, и удаляет их. При этом он ассоциирует с общим предком листов (после удаления он станет листом) какое-то одно из ассоциированных с ними значений на свой выбор. Игра заканчивается, когда в дереве остается ровно одна вершина — корень дерева. Pieguy ходит первым и его цель — максимизировать значение, которое будет ассоциировано с корнем в конце игры. Piegirl, наоборот, хочет минимизировать это значение. Считая, что оба игрока играют оптимально, вычислите значение, которое будет ассоциировано с корнем в конце игры. Выходные данные Для каждого теста в отдельной строке выведите ответ на задачу. | |
![]()
|
|
B. Яблов и дерево
Деревья
дп
поиск в глубину и подобное
*2000
У Яблова есть дерево, состоящее из n вершин. Некоторые вершины (по крайней мере одна) покрашены в черный цвет, остальные вершины покрашены в белый цвет. Рассмотрим множество, состоящее из k (0 ≤ k < n) ребер этого дерева. Если Яблов удалит эти ребра из дерева, то дерево распадется на (k + 1) частей. Каждая часть также будет представлять из себя дерево с покрашенными вершинами. Теперь Яблову интересно, сколько существует множеств, в результате удаления ребер которых в каждой получившейся части будет ровно одна черная вершина? Выведите это количество по модулю 1000000007 (109 + 7). Выходные данные Выведите единственное целое число — количество требуемых множеств по модулю 1000000007 (109 + 7). | |
![]()
|
|
E. Caisa и дерево
Деревья
математика
Перебор
поиск в глубину и подобное
теория чисел
*2100
Caisa сейчас дома и его сын придумал для него простую задачку. Задано корневое дерево, состоящее из n вершин, пронумерованных от 1 до n (вершина 1 — корень дерева). В каждой вершине записано некоторое значение. Требуется ответить на q запросов. Каждый запрос является одним из следующих: - Формат запроса «1 v». Выпишем последовательность вершин вдоль пути от корня до вершины v: u1, u2, ..., uk (u1 = 1; uk = v). Выведите такую вершину ui, что gcd(значение вершины ui, значение вершины v) > 1 и i < k. Если существует несколько таких вершин, выведите вершину с максимальным значением i. Если таких вершин вовсе нет, выведите -1.
- Формат запроса «2 v w». Нужно изменить значение, записанное в вершине v, на w.
Вам заданы все запросы, помогите Caisa справиться с этой задачей. Выходные данные Для каждого запроса первого типа выведите ответ на него. Примечание Запись gcd(x, y) обозначает наибольший общий делитель целых чисел x и y. | |
![]()
|
|
E. Граф информаций
графы
Деревья
поиск в глубину и подобное
снм
*2100
В компании «X» работает n сотрудников (для удобства пронумеруем их от 1 до n). Изначально, не было никаких отношений между сотрудниками. В каждый из m следующих дней происходило одно из событий: - либо сотрудник y стал начальником сотрудника x (при этом у сотрудника x не было начальника до этого события);
- либо сотруднику x передают пакет документов и он подписывает их; затем передает их своему начальнику, затем начальник подписывает документы и передает их своему начальнику и так далее (последний человек, подписавший документы, отправляет их в архив);
- либо приходит запрос вида «определить, подписывался ли сотрудник x на определенных документах».
Ваша задача написать программу, которая по заданным событиям будет отвечать на запросы, описанного вида. При этом гарантируется, что на протяжении всего времени работы компании не было циклических зависимостей. Выходные данные Для каждого запроса третьего типа выведите «YES», если сотрудник подписывал пакет документов, и «NO» в ином случае. Все слова выводите без кавычек. | |
![]()
|
|
D. Уроки дизайна задач: обратные задачи
Деревья
кратчайшие пути
поиск в глубину и подобное
снм
*1900
Помимо прочего, можно придумывать новые задачи, решая обратные задачи к старым задачам. Обратная задача — это когда в качестве входных данных даются выходные данные исходной задачи и нужно сгенерировать в качестве выходных данных такие входное данные, что решение исходной задачи на них выдавало бы заданные входные данные. Самая сложная задача Topcoder Open 2014 раунда 2C, InverseRMQ, является хорошим примером такого подхода. Попробуем придумать новую задачу таким способом. В качестве основы используем следующую задачу: задано дерево; подсчитайте расстояние между всеми парами его вершин. Да, это просто. Но обратная версия этой задачи куда сложнее: задана матрица расстояний размера n × n. Определите, может ли данная матрица быть матрицей всех попарных расстояний между вершинами взвешенного дерева (все веса должны быть целыми положительными числами). Выходные данные Если такое дерево существует, выведите «YES», в противном случае выведите «NO». Примечание В первом примере необходимое дерево существует. Оно состоит из ребра между вершинами 1 и 2 с весом 2 и ребра между вершинами 1 и 3 с весом 7. Во втором примере дерево не существует, потому что d1, 1 должно равняться 0, а оно равняется 1. В третьем примере дерево не существует, потому что d1, 2 должно равняться d2, 1. | |
![]()
|
|
E. Столбы
Бинарный поиск
Деревья
дп
сортировки
Структуры данных
*2000
Сурок нашел ряд из n столбов. Высота i-ого столба равняется hi метрам. Начиная с некоторого столба i1, Сурок хочет пропрыгать по столбам i2, ..., ik. (1 ≤ i1 < i2 < ... < ik ≤ n). Сурок может перепрыгнуть со столба i на столб j, только если i < j и |hi - hj| ≥ d, где |x| — абсолютное значение числа x. Сурок просит вас найти последовательность прыжков максимальной длины и вывести её. Выходные данные В первой строке должно быть записано одно целое число k — максимальная длина последовательности прыжков. Во второй строке должно быть записано k целых чисел i1, i2, ..., ik (1 ≤ i1 < i2 < ... < ik ≤ n) — номера столбов из максимально длинной последовательности прыжков. Если есть несколько последовательностей прыжков максимальной длины, выведите любую из них. Примечание В первом примере Сурок выбирает столбы 1, 2, 3, 5 с высотами 1, 3, 6, 4. Ещё одна последовательность прыжков длины 4 такова: 1, 2, 4, 5. | |
![]()
|
|
G. Галактический Союз
Деревья
дп
*2700
В одной далекой галактике n обитаемых планет, пронумерованных числами от 1 до n. Однажды независимо друг от друга президенты всех n планет пришли к идее о создании Галактического Союза. Теперь необходимо поделиться этой прекрасной идеей с собратьями по разуму, поэтому каждый из президентов занят разработкой проекта переговоров с остальными президентами. Для переговоров между некоторыми парами планет существуют двунаправленные каналы связи, каждый из которых характеризуется «временем дозвона» ti, которое, как правило, занимает несколько часов и значительно превышает время разговора. Всего в галактике n каналов связи, и они объединяют все планеты в единую сеть. Это означает, что с любой планеты u можно дозвониться до любой планеты v, возможно, через некоторые промежуточные планеты v1, v2, ..., vm при помощи существующих каналов между u и v1, v1 и v2, ..., vm - 1 и vm, vm и v. При этом время дозвона с u до v будет равно суммарному времени дозвона задействованных каналов. Итак, каждому президенту необходимо поговорить по очереди с президентами остальных n - 1 планет. При этом переговоры проходят строго последовательно, и пока переговоры с очередной планетой не завершатся, дозвон до следующей не начинается. Поскольку дело очень срочное, из различных способов дозвона до нужной планеты каждый раз выбирается самый быстрый. Для убеждения другого президента в ценности Галактического Союза не требуется много времени, поэтому время переговоров с каждой планетой можно считать равным времени дозвона до нее. Так как президенты ничего не подозревают о намерениях друг друга, они не учитывают в своих планах, что, например, нужный президент может позвонить сам или уже знать о создающемся Галактическом Союзе из других источников. Правительства всех n планет обратились к вам для разработки плана переговоров. В первую очередь вам предстоит выяснить для каждого президента, сколько времени займут его предполагаемые переговоры. Выходные данные В первой строке выведите n целых чисел — времена предполагаемых переговоров для каждого из президентов. Числа разделяйте пробелами. | |
![]()
|
|
B. Интересный массив
Деревья
Конструктив
Структуры данных
*1800
Будем считать массив из n неотрицательных целых чисел a[1], a[2], ..., a[n] интересным, если он удовлетворяет m ограничениям. i-е из m ограничений состоит из трех целых чисел li, ri, qi (1 ≤ li ≤ ri ≤ n), которые означают, что величина  в точности равна qi. в точности равна qi. Ваша задача — найти любой интересный массив из n элементов, либо сообщить, что такого не существует. Выражение x&y означает побитовое И чисел x и y. В языках программирования C++, Java и Python эта операция обозначается как «&», на Pascal она обозначается как «and». Выходные данные Если интересный массив существует, выведите «YES» (без кавычек) в первой строке, а во второй строке выведите n целых чисел a[1], a[2], ..., a[n] (0 ≤ a[i] < 230) — описание интересного массива. Если существует несколько ответов, разрешается вывести любой. Если не существует интересного массива, выведите «NO» (без кавычек) в единственной строке. | |
![]()
|
|
D. Случайная функция и дерево
Деревья
дп
Комбинаторика
*2700
У вас есть корневое дерево, состоящее из n вершин. Пронумеруем вершины дерева целыми числами от 1 до n включительно. Корень дерева находится в вершине 1. Для каждого i > 1 непосредственным предком вершины i является вершина pi. Назовём вершину i ребёнком вершины pi. Изначально вы покрасили все вершины в красный цвет. Кроме этого, вы любите перекрашивать некоторые вершины дерева. Для этого вы используете функцию paint, которую вы вызываете от корня дерева. Ниже приведен псевдокод этой функции:
count = 0 // глобальная целочисленная переменная
rnd() { // эта функция используется в коде paint
вернуть 0 или 1 с равной вероятностью 50%
}
paint(s) {
if (count четное) then покрасить вершину s в белый цвет
else покрасить вершину s в черный цвет
count = count + 1
if rnd() = 1 then children = [массив из детей вершины s в порядке возрастания номеров]
else children = [массив из детей вершины s в порядке убывания номеров]
for child in chilren { // проходим по элементам массива child
if rnd() = 1 then paint(child) // выполняем рекурсивный вызов функции paint
}
}
В результате выполнения этой функции некоторые вершины могут изменить свой цвет на белый или чёрный, а некоторые — остаться красными. Ваша задача — определить количество различных возможных раскрасок вершин дерева. Будем считать раскраску возможной, если существует ненулевая вероятность получить эту раскраску с помощью одного вызова функции paint(1). Будем считать раскраски различными, если существует пара вершин, которые покрашены в различные цвета в этих раскрасках. Поскольку искомое количество может быть очень большим, найдите остаток от деления этого количества на 1000000007 (109 + 7). Выходные данные Выведите единственное целое число — ответ на задачу по модулю 1000000007 (109 + 7) Примечание Ниже приведены все возможные покраски первого примера.  | |
![]()
|
|
E. ELCA
Деревья
Структуры данных
*3200
У вас есть корневое неориентированное дерево, состоящее из n вершин. Пронумеруем вершины дерева целыми числами от 1 до n. Корень дерева находится в вершине 1. У каждой вершины (кроме корня дерева 1) есть непосредственный предок pv. Кроме того, в каждой вершине дерева v написано ее значение — целое число sv. Необходимо последовательно обрабатывать следующие запросы: - P v u (u ≠ v). Если вершина u не лежит в поддереве v, необходимо присвоить pv = u. В противном случае, необходимо присвоить pu = v. Обратите внимание, после выполнения запроса граф всегда остается неориентированным деревом из n вершин.
- V v t. Необходимо присвоить sv = t.
Ваша задача — до начала выполнения запросов, а также после выполнения каждого запроса выводить математическое ожидание значения, написанного на наименьшем общем предке двух равновероятно выбранных вершин i, j дерева. Под наименьшим общим предком вершин i и j понимается наиболее удалённая от корня вершина среди тех, которые лежат и на пути от корня до i, и на пути от корня до j. Обратите внимание, что i и j могут совпадать (в таком случае их наименьший общим предок совпадает с ними). Выходные данные Выведите q + 1 число — соответствующие математические ожидания. Ваш ответ будет считаться правильным, если абсолютная или относительная погрешность каждого числа не превышает 10 - 9. Примечание Обратите внимание, что в запросе P v u в случае, если u лежит в поддереве v, требуется присвоить pu = v. Пример такого случая — последний запрос в примере. | |
![]()
|
|
D. Допустимые множества
Деревья
дп
математика
поиск в глубину и подобное
*2100
Как вы, наверное, знаете, неориентированный связный граф с n вершинами и n - 1 ребрами называется деревом. Вам дано целое число d и дерево, состоящее из n вершин. С каждой вершиной i связано её значение ai. Назовем множество S вершин дерева допустимым, если выполняются следующие условия: - S является непустым множеством.
- S является связным множеством. Иными словами, если вершины u и v содержатся во множестве S, то все вершины, лежащие на простом пути между u и v должны также лежать в S.
-
 . .
Ваша задача — посчитать количество допустимых множеств. Так как результат может быть очень большим, выведите его остаток по модулю 1000000007 (109 + 7). Выходные данные Выведите количество допустимых множеств по модулю 1000000007. Примечание В первом примере можно найти ровно 8 допустимых множеств: {1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {3, 4} и {1, 3, 4}. Множество {1, 2, 3, 4} не является допустимым, поскольку оно не отвечает третьему условию. Множество {1, 4} отвечает третьему условию, но противоречит второму условию. | |
![]()
|
|
E. Туристы
графы
Деревья
поиск в глубину и подобное
Структуры данных
*3200
В Киберленде n городов, пронумерованных от 1 до n и соединенных m двунаправленных дорогами. j-я дорога соединяет города aj и bj. В каждом городе Киберленда продаются сувениры для туристов. В частности, город i продает сувениры по цене wi. Вам надо обработать q запросов. Запросы бывают двух типов: - "C a w": Цена в городе a меняется на w.
- "A a b": Турист едет из города a в город b. Для этого он выбирает путь, при этом, турист не хочет посетить никакой город дважды. Он собирается купить сувениры в том городе, где сувениры самые дешевые (возможно, прямо в городе a или b). Вам следует вывести наименьшую возможную цену, по которой он может купить сувениры, путешествуя по некоторому простому пути.
Более формально, можно определить пути следующим образом: - Путь — это последовательность городов [x1, x2, ..., xk], где k — некоторое положительное число.
- Для любых 1 ≤ i < j ≤ k, xi ≠ xj.
- Для любого 1 ≤ i < k есть дорога, соединяющая xi и xi + 1.
- Наименьшая стоимость на пути равна min(wx1, wx2, ..., wxk).
- Искомый ответ — это наименьшее значение наименьших стоимостей на всех корректных путях из a в b.
Выходные данные Для каждого запроса типа "A" выведите соответствующий ответ. Примечание Во втором примере оптимальные пути таковы: Из 2 в 3 — [2, 3]. Из 6 в 4 — [6, 5, 1, 2, 4]. Из 6 в 7 — [6, 5, 7]. Из 3 в 3 — [3].  | |
![]()
|
|
F. Турне по Древляндии
Деревья
дп
поиск в глубину и подобное
Структуры данных
*2200
Группа ДТП планирует беспрецедентное турне по Древляндии. Фанаты ДТП предвкушают событие и делают ставки, как много концертов даст любимая группа. Древляндия состоит из n городов, некоторые пары из которых соединены двусторонними дорогами. Всего в этой стране n - 1 дорога. Известно, что из любого города можно добраться до любого другого. Города пронумерованы от целыми числами 1 до n. Про каждый город известна величина ri — количество жителей в нем. Достоверно известно, что музыканты проедут по некоторому пути, давая концерты в некоторых городах вдоль этого пути. Путь музыкантов не будет проходить по одному городу дважды, каждый раз они будут переезжать в ранее не посещенный город. Таким образом музыканты проедут по некоторому пути (не посещая никакой город дважды) и в каких-то (необязательно всех) городах вдоль пути дадут концерты. По мере турне группа планирует собирать все большие стадионы и концертные площадки, поэтому каждый раз они будут выступать в городе с большим количеством жителей, чем в городе предыдущего выступления. Иными словами, последовательность численностей населения в городах, где будут концерты, будет строго возрастающей. В недавнем интервью лидер группы ДТП пообещал фанатам, что группа даст концерты в максимальном возможном количестве городов! Таким образом группа проедет по некоторой цепочке городов Древляндии и даст концерты в некоторых из этих городов так, что численности будут возрастать, а количество концертов будет максимально возможным. Фанаты Древляндии судорожно пытаются понять, сколько концертов даст «ДТП» в Древляндии. Кажется, без помощи настоящего программиста не обойтись! Помогите фанатам найти искомое количество концертов. Выходные данные Выведите количество городов, в которых «ДТП» даст концерты. | |
![]()
|
|
D. День рождения
Деревья
дп
поиск в глубину и подобное
Структуры данных
*2700
Али — младший брат Хамеда, у него завтра день рождения. Хамед хочет подарить брату подарок. Для этого он дал ему задачу по программированию и сказал, что если Али её решит, то он получит новенький ноутбук. Али ещё не такой талантливый программист как Хамед, и, хотя он обычно не жульничает, этот случай — исключение. Всё-таки на кону новенький ноутбук. Поэтому он решил в тайне от него попросить вас помочь ему. Пожалуйста, решите для Али следующую. Вам дано взвешенное корневое дерево из n вершин. Вершина номер 1 является корнем дерева. Определим d(u, v) как сумму длин рёбер на кратчайшем пути между вершинами u и v. В частности, определим d(u, u) = 0. Также, определим S(v) для каждой вершины v как множество, содержащее все вершины u, такие, что d(1, u) = d(1, v) + d(v, u). Затем определим функцию f(u, v) по следующей формуле:  Ваша задача — вычислить f(u, v) для каждой из q данных пар вершин. Так как ответ может быть довольно большим, выведите его по модулю 109 + 7. Выходные данные Выведите q строк. В i-й строке выведите значение f(ui, vi) по модулю 109 + 7. | |
![]()
|
|
D. Новогоднее взаимодействие Санта-Клаусов
графы
Деревья
Комбинаторика
поиск в глубину и подобное
*1900
В Древесном мире наступает Новый год! В этом мире, как понятно из названия, есть n городов, соединенных n - 1 дорогой, и между каждыми двумя различными городами всегда существует путь. Города пронумерованы целыми числами от 1 до n. Дороги пронумерованы целыми числами от 1 до n - 1. Определим d(u, v) как суммарную длину дорог на пути между городом u и городом v. Отдавая дань традиции, народ в Древесном мире ремонтирует ровно по дороге в год. В результате длина этой дороги уменьшается. Известно, что в i-м году длина ri-й дороги станет wi, что короче прежней длины этой же дороги. Предположим, что текущий год — это год 1. Три Санта-Клауса планируют раздавать подарки всем детям Древесного мира ежегодно. Для этого им надо подготовиться, в целях чего они выберут три различных города c1, c2, c3, и создадут в каждом из этих городов по одному складу: k-й (1 ≤ k ≤ 3) Санта-Клаус будет отвечать за склад в городе ck. Трем Санта-Клаусам очень скучно сидеть на складах поодиночке. Поэтому они решили построить сеть сообщения, предназначенную только для Сант! Затраты, необходимые для того, чтобы построить подобную сеть, равны d(c1, c2) + d(c2, c3) + d(c3, c1) долларам. Санты слишком заняты, чтобы искать лучшее место, так что они решили выбрать c1, c2, c3 случайно равновероятно среди всех троек различных чисел от 1 до n. Санты хотели бы знать математическое ожидание цены, необходимой для построения сети. Однако, как мы сказали, каждый год длина ровно одной дороги уменьшается. Таким образом, Санты хотят просчитать математическое ожидание после каждого изменения длины. Помогите им посчитать требуемые значения. Выходные данные Выведите q чисел. После каждого из изменений выведите строку с математическим ожиданием цены, необходимой для постройки сети сообщения в Древесном мире. Ответ будет считаться корректным, если его абсолютная или относительная погрешность не превышают 10 - 6. Примечание Рассмотрим первый пример. Есть 6 троек: (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1). Так как n = 3, затраты на построение сети всегда равны d(1, 2) + d(2, 3) + d(3, 1) для всех троек. Таким образом, матожидание стоимости равняется d(1, 2) + d(2, 3) + d(3, 1). | |
![]()
|
|
G. Новогодний забег
Деревья
теория чисел
*3200
На Древесном острове наступает Новый год! На этом острове, как понятно из названия, есть n городов, соединенных n - 1 дорогами, причём между каждыми двумя различными городами всегда существует путь. Каждому человеку на Древесном острове требуется ровно минута на прохождение одной дороги. Есть на Древесном острове причудливая новогодняя традиция под названием «экстремальный забег». Традицию эту можно описать следующим образом. Некоторый бегун выбирает два различных города, a и b. Для простоты, обозначим кратчайший путь из города a в город b как p1, p2, ..., pl (в частности, p1 = a и pl = b). Затем происходит следующее: - бегун стартует из города a;
- он следует из города a в город b по кратчайшему пути;
- когда бегун прибывает в город b, он немедленно разворачивается (на это времени не требуется) и бежит в город a по кратчайшему пути;
- когда бегун прибывает в город a, он немедленно разворачивается (на это времени не требуется) и бежит в город b по кратчайшему пути;
- шаги 3 и 4 повторяются до бесконечности.
Иными словами, маршрут бегуна выглядит так:   Два бегуна, JH и JY, решили совершить «экстремальный забег» в честь Нового года. JH выбрал два города u и v, а JY выбрал два города x и y. Ребята решили начать бежать в одно и то же время и бежать до тех пор, пока они впервые не встретятся в одном городе. Встреча посреди дороги не считается. Они хотят знать, сколько времени им предстоит бегать. JH и JY не смогли это определить, так что они просят вас помочь им. Выходные данные Для каждого тестового примера выведите целое число, описывающее количество времени, необходимое для пробега в минутах. Если ребятам придётся бежать бесконечно долго (иными словами, если бегуны никогда не встретятся в одном городе), выведите -1. Если ребята встретятся в момент начала забега, выведите 0. Примечание Пример выглядит так:  | |
![]()
|
|
C. Миша и лес
Деревья
жадные алгоритмы
Конструктив
сортировки
Структуры данных
*1500
Назовем лесом неориентированный граф без циклов (петли и кратные рёбра также запрещены). Однажды Миша играл с лесом из n вершин. Для каждой вершины v от 0 до n - 1 он записал два числа degreev и sv, где первое число — количество вершин, смежных с вершиной v, а второе — XOR-сумма номеров вершин, смежных с v (в случае, если смежных вершин не было, он записал 0). На следующий день Миша не смог вспомнить, какой граф у него был изначально. У Миши остались значения degreev и sv. Помогите ему найти количество ребер и сами ребра исходного графа. Гарантируется, что существует лес, которому соответствуют выписанные Мишей числа. Выходные данные В первой строке выведите число m, количество ребер графа. Далее выведите m строк, каждая из которых содержит два различных числа a и b (0 ≤ a ≤ n - 1, 0 ≤ b ≤ n - 1), соответствующие ребру (a, b). Рёбра могут быть выведены в любом порядке; вершины одного ребра также могут быть выведены в любом порядке. Примечание XOR-суммой чисел называется результат побитового сложения чисел по модулю 2. Данная операция существует во многих современных языках программирования, например, в языках C++, Java и Python она обозначается как «^», а в Pascal — как «xor». | |
![]()
|
|
E. Миша и LCP на дереве
Бинарный поиск
Деревья
поиск в глубину и подобное
строковые суфф. структуры
хэши
*3000
У Миши есть дерево с написанными на вершинах символами. Он может выбрать две вершины s и t этого дерева и записать символы, соответствующие вершинам дерева, лежащим на пути из s в t. Будем говорить, что такая строка соответствует паре (s, t). У Миши есть m запросов вида: дано 4 вершины a, b, c, d; необходимо найти наибольший общий префикс строк, соответствующих парам (a, b) и (c, d). Ваша задача — помочь ему. Выходные данные На каждый запрос выведите длину наибольшего общего префикса в отдельной строке. | |
![]()
|
|
C. Угадай, где выход!
Деревья
математика
реализация
*1700
Amr купил новую компьютерную игру "Угадай, где выход!". Цель игры— найти выход из лабиринта, похожего на полное двоичное дерево высоты h. Изначально игрок стоит в корне дерева, выход из дерева расположен в некотором листе дерева. Пронумеруем все листы слева направо числами от 1 до 2h. Выход расположен в некоторой вершине n, где 1 ≤ n ≤ 2h. Amr пользуется следующим простым алгоритмом выбора пути. Рассмотрим бесконечную строку "LRLRLRLRL..." (состоящую из чередующихся символов 'L' и 'R'). Amr последовательно выполняет символы строки по следующим правилам: - Символ 'L' означает "перейти к левому сыну текущей вершины";
- Символ 'R' означает "перейти к правому сыну текущей вершины";
- Если вершину, в которую ведёт текущая команда, Amr уже это этого посещал, то он пропускает текущую команду, в противном случае он переходит в эту вершину;
- Если Amr пропустил две последовательные команды, то он возвращается к предку текущей вершины перед тем, как выполнять следующую команду;
- Если он оказался в листе, который не является выходом, он сразу возвращается к предку текущей вершины;
- Если он достиг выхода, игра заканчивается.
Теперь Amr интересно: если он будет следовать этому алгоритму, сколько вершин он посетит до того, как достичь выхода? Выходные данные Выведите единственное целое число, обозначающее количество вершин (не включая лист, в котором расположен выход), которые Amr посетит перед тем, как добраться до выхода, следуя этому алгоритму. Примечание Полное двоичное дерево высоты h— это двоичное дерево, состоящее из h + 1 уровня. Уровень 0 состоит из единственной вершины, которая называется корень, уровень h состоит из 2h вершин, которые называются листьями. Каждая вершина, не являющаяся листом, имеет ровно двух потомков, левого и правого. Следующая картина иллюстрирует третий тест из условия. Вершины помечены в порядке их посещения. 
| |
![]()
|
|
F. Контроль успеваемости
Деревья
дп
*2300
На одной из своих контрольных работ по информатике Дмитрий Олегович решил дать следующую задачу: Пусть дано дерево T на n вершинах, заданное своей матрицей смежности a[1... n, 1... n]. Какую последовательность чисел выведет следующий псевдокод?
used[1 ... n] = {0, ..., 0};
procedure dfs(v):
print v;
used[v] = 1;
for i = 1, 2, ..., n:
if (a[v][i] == 1 and used[i] == 0):
dfs(i);
dfs(1);
Чтобы было легче проверять работы студентов, Дмитрий Олегович решил придумать такое дерево T, чтобы в ответе получилась его любимая последовательность b. С другой стороны, Дмитрий Олегович не хочет давать студентам одинаковые данные в контрольной работе — ведь в таком случае не миновать списывания. Поэтому у Дмитрия Олеговича возник следующий вопрос: сколько существует таких деревьев, что при запуске данного псевдокода на них выведенная последовательность в точности совпадает с последовательностью b? Два дерева на n вершинах считаются различными, если их матрицы смежности a1 и a2 не совпадают, то есть существует такая пара (i, j), что 1 ≤ i, j ≤ n и a1[i][j] ≠ a2[i][j]. Выходные данные Выведите одно число — остаток от деления количества подходящих деревьев на 109 + 7. | |
![]()
|
|
F. Гусеница
графы
Деревья
дп
поиск в глубину и подобное
*2800
Неориентированный граф называется гусеницей, если он является связным графом без циклов, и в нем существует такой путь, что любая вершина находится на расстоянии не более 1 от него. Гусеница может содержать петли, но не может содержать кратных ребер. На рисунке изображен пример гусеницы:  Вам задан неориентированный граф G с которым можно производить операцию сжатия двух вершин в одну. Для этого выбираются любые две вершины графа a и b (a ≠ b). Из графа удаляются обе эти вершины вместе с их ребрами (инцидентными хотя бы одной из вершин a или b), но добавляется новая вершина w вместе с ребрами вида (x, w) для каждого ребра (a, w) и (b, w). Если в графе существовало ребро (a, b), то оно преобразуется в петлю (w, w). В результате операции слияния могут появляться кратные ребра и петли. Заметим, что эта операция уменьшает количество вершин графа на 1, но оставляет неизменным количество ребер в графе. Операция сжатия двух вершин может быть неформально описана как объединение двух вершин графа в одну, с естественным преобразованием ребер графа. С помощью последовательного применения описанной операции можно любой заданный неориентированный граф сделать гусеницей. Напишите программу, которая выведет наименьшее количество операций сжатия, чтобы заданный граф сделать гусеницей. Выходные данные Выведите искомое наименьшее число операций. | |
![]()
|
|
D. Лиса и путешествие
Деревья
дп
*2900
Лиса Ciel собирается в путешествие по Фокслендам этим летом. На Фокслендах n достопримечательностей, соединенных m двусторонними дорогами. Две достопримечательности называются соседними, если они соединены дорогой. У Ciel есть k дней на исследование Фокслендов, и она собирается потратить каждый день на посещение ровно одной достопримечательности. На Фокселндах есть одно важное правило: вы не можете посетить достопримечательность, если у неё более одной соседней достопримечательности, которую вы ещё не посетили. В начале путешествия Ciel не посетила ни одной достопримечательности. В процессе путешествия она может перемещаться произвольным образом между достопримечательностями. После осмотра достопримечательности a она может отправиться осматривать любую ещё не осмотренную достопримечательность b, удовлетворяющую условию выше, в том числе не достижимую из a по дорогам (Ciel использует катер для перемещения между достопримечательностями, поэтому у неё есть такая возможность). Ciel хочет знать, сколько существует различных маршрутов для её путешествия. Более того, определите остаток от деления на 109 + 9 от их количества для каждого k от 0 до n, так как лиса ещё не определилась, на сколько дней она отправится на Фоксленды. Выходные данные Выведите n + 1 целых чисел: количество возможных маршрутов путешествия по модулю 109 + 9 для всех k от 0 до n. Примечание В первом тесте из условия для k = 3 существует 4 маршрута: {1, 2, 3}, {1, 3, 2}, {3, 1, 2}, {3, 2, 1}. Во втором тесте из условия Ciel не может начать ни с одной достопримечательности в первый же день, так что для k > 0 ответ равен 0. В третьем тесте из условия Фоксленды выглядят следующим образом:  | |
![]()
|
|
D. Drazil и утренняя зарядка
Деревья
дп
поиск в глубину и подобное
снм
*2800
Drazil и Varda — дождевые черви. Они хотят подыскать хорошее местечко, чтобы растить детей. И вот нашли они подходящую почву с хорошей природной норой. Нора состоит из множества комнат, некоторые пары которых соединены маленькими туннелями, по которым могут перемещаться черви. Рассмотрим комнаты и туннели как вершины и ребра в графе. Этот граф представляет собой дерево. Иными словами, между любой парой вершин существует единственный простой путь. Каждая комната, являющаяся листом этого дерева, соединена с поверхностью вертикальным туннелем. Здесь, под листом мы подразумеваем вершину, смежную ровно с одним ребром в дереве. В каждой комнате хватает места для проживания не более одного червя. Дождевой червь не может жить в туннеле. Drazil и Varda подумывают воспитывать своих деток по следующему плану. Им хочется, чтобы все их дети сразу после подъема делали утреннюю зарядку! Когда наступает утро, все червячки просыпаются в одно и то же время, затем каждый из них выбирает самый длинный путь к поверхности на собрание (как и любые дети, они ленятся делать зарядку, поэтому им всем хочется приступить к упражнениям как можно позже). Drazil и Varda хотят, чтобы разница между моментами появления на поверхности первого и последнего червячка не превышала l (в противном случае детишки расползутся по земле и их будет сложно собрать на зарядку). Есть дополнительное условие — комнаты, которые занимают детки, должны формировать связное множество. Иными словами, для любых двух комнат, которые занимают червячки, все комнаты, лежащие на пути из одной комнаты в другую, тоже должны быть заняты червячками. Какое максимальное количество детей может быть у Drazil и Varda, чтобы удовлетворить всем вышеприведенным условиям? Drazil и Varda хотят знать ответ для многих различных вариантов l. (Drazil и Varda не живут в одной норке со своими детьми) Выходные данные Выведите q строк, каждая из которых содержит единственное целое число, обозначающее ответ для очередного значения l. Примечание В первом примере нора выглядит следующим образом. Комнаты 1 и 5 представляют из себя листы, так что в них содержится по вертикальному туннелю, связывающему их с поверхностью. Длины наидлиннейшего пути из комнат 1 – 5 наружу равняются 12, 9, 7, 9, 12, соответственно. При l = 1 мы можем выбрать любую одну комнату. При l = 2..4 мы можем выбрать в качестве ответа комнаты 2, 3, и 4. При l = 5 мы можем выбрать все комнаты.  | |
![]()
|
|
E. A и B и аудитории
Бинарный поиск
Деревья
дп
поиск в глубину и подобное
Структуры данных
*2100
A и B готовятся к олимпиадам про программированию. Университет, в котором учатся A и B, представляет собой множество аудиторий, соединенных между собой переходами. Всего в университете n аудиторий, соединённых n - 1 переходом таким образом, что из любой аудитории можно дойти до любой по переходам. Аудитории пронумерованы от 1 до n. Каждый день А и B пишут контесты в некоторых аудиториях своего университета, и после каждого контеста они собираются вместе в одной аудитории и обсуждают задачи. A и B хотят, чтобы расстояния от аудитории, где они будут обсуждать задачи, до аудиторий, где они пишут контесты, были равны. Расстоянием между двумя аудиториями является количество ребер на кратчайшем пути между ними. Так как каждый день они пишут контесты в новых аудиториях, то они попросили вас помочь им найти количество возможных аудиторий для обсуждения задач на каждый из ближайших m дней. Выходные данные В i-й (1 ≤ i ≤ m) строке выведите количество аудиторий, равноудаленных от аудиторий, в которых A и B пишут контест в i-й день. Примечание В первом примере из условия на одинаковом расстоянии от аудиторий с номерами 2 и 3 находится только одна аудитория — аудитория с номером 1. | |
![]()
|
|
A. Репосты
*особая задача
графы
Деревья
дп
поиск в глубину и подобное
*1200
Однажды Поликарп опубликовал в социальной сети смешную картинку с опросом про цвет своего хэндла. Многие из его друзей стали репостить шутку Поликарпа себе в ленту. Некоторые из них репостили репосты и так далее. Эти события заданы в виде последовательности строк «name1 reposted name2» где name1 — это имя того, кто репостнул, а name2 — имя того, с чей ленты репостнули шутку. Гарантируется, что для каждой строки «name1 reposted name2» пользователь «name1» еще не имел эту шутку в свой ленте, а «name2» уже имел ее в своей ленте к моменту репоста. Поликарп зарегистрирован под именем «Polycarp», и изначально шутка есть только в его ленте. Поликарп измеряет успешность шутки как длину наибольшей цепочки репостов. Выведите успешность шутки Поликарпа. Выходные данные Выведите единственное целое число — максимальную длину цепочки репостов. | |
![]()
|
|
G. Коварный план пауков
Деревья
жадные алгоритмы
*3300
Пауки — старые враги Ам Няма. Они не меньше его любят есть леденцы, и поэтому они постоянно пытаются не дать монстрику добраться до любимой сладости. Они придумали коварный план, чтобы заманить Ам Няма в ловушку.  Рассмотрим верёвочную конструкцию из n узелков и n - 1 тросика, соединяющего эти узелки. Конструкция образует единое целое, таким образом, тросы с узелками представляют собой дерево. Каждый тросик образованной конструкции имеет свою длину. К узелку x конструкции привязан леденец, который хочет съесть Ам Ням. Ему стараются в этом помешать y пауков. Они решили опутать леденец и некоторую часть конструкции паутиной, приклеив его таким образом к как можно большей части верёвочного сооружения. Каждый паук может покрыть паутиной все тросики на пути между двумя произвольными узелками a и b. Таким образом, y пауков могут покрыть множество тросиков, которое является объединением y путей в данном дереве, причём эти y путей могут произвольным образом пересекаться друг с другом. Пауки хотят, чтобы: - узелок, содержащий леденец, был смежен хотя бы одному тросику, покрытому паутиной
- покрытые паутиной тросики образовывали связную конструкцию (зачем покрывать паутиной части, не связанные с леденцом?)
- суммарная длина тросов, покрытых паутиной, была как можно больше
Пауки ещё не решили, к какому узелку конструкции будет привязан леденец, и сколько пауков будет покрывать конструкцию паутиной, поэтому они обратились к вам за помощью. Помогите им посчитать оптимальный план для нескольких значений x и y. Выходные данные На каждый вопрос пауков выведите в отдельной строке одно целое число Ansi — суммарную длину тросов, опутанных паутиной в оптимальном плане. | |
![]()
|
|
E. Тавас в пути
Деревья
разделяй и властвуй
Структуры данных
*3100
Тавас живет в Тавасполисе. В Тавасполисе n городов, пронумерованных от 1 до n, соединенных n - 1 двунаправленными дорогами. Между любыми двумя городами есть путь. Также у каждой дороги есть длина.  Любимые строки Таваса — двоичные строки (содержащие только 0 и 1). Для любой двоичной строки типа s = s1s2... sk, определим T(s) — значение этой строки. T(s) вычисляется следующим способом: Предположим, что в строке s ровно m блоков цифр 1 (блок цифр 1 — это максимальная подстрока s, которая содержит только единицы) длинами x1, x2, ..., xm. Определим  , где f — данная последовательность чисел (в частности, если m = 0, то T(s) = 0). , где f — данная последовательность чисел (в частности, если m = 0, то T(s) = 0). Тавас любит запросы. Он просит Вас ответить на q запросов. В каждом запросе он дает вам числа v, u, l, а вам следует вывести следующее число: Рассмотрим дороги на пути из города v в город u: e1, e2, ..., ex. Построим бинарную строку b длины x, такую, что: bi = 1 тогда и только тогда, когда l ≤ w(ei), где w(e) — длина дороги e. Результатом запроса является строка T(b). Выходные данные Выведите ответ на каждый запрос на отдельной строке. | |
![]()
|
|
E. Бесконечные инверсии
Бинарный поиск
Деревья
реализация
сортировки
Структуры данных
*2100
Есть бесконечная последовательность, состоящая из всех положительных целых чисел в порядке возрастания: p = {1, 2, 3, ...}. К ней последовательно применили n операций swap. Операция swap(a, b) меняет местами элементы последовательности на позициях a и b. Требуется найти количество инверсий в получившейся последовательности, т.е. количество таких пар индексов (i, j), что i < j и pi > pj. Выходные данные Выведите единственное целое число — количество инверсий в получившейся последовательности. Примечание В первом примере последовательность меняется следующим образом:  . В ней 4 инверсии, их образуют пары индексов (1, 4), (2, 3), (2, 4) и (3, 4). . В ней 4 инверсии, их образуют пары индексов (1, 4), (2, 3), (2, 4) и (3, 4). | |
![]()
|
|
D. Улучшение дорог
Деревья
дп
*2300
В стране есть n городов и n - 1 двусторонняя дорога, причем из каждого города можно добраться до любого другого города, двигаясь только по дорогам. Города пронумерованы целыми числами от 1 до n включительно. Все дороги изначально плохие, однако правительство хочет улучшить состояние некоторых дорог. Будем считать, что граждане довольны улучшением дорог, если на пути от столицы, расположенной в городе x, до любого города не более одной плохой дороги на пути. Ваша задача — для каждого возможного x определить количество способов улучшить качество некоторых дорог так, чтобы удовлетворить требованиям граждан. Поскольку искомые значения могут быть очень большими, нужно подсчитать остаток от деления каждого количества на 1 000 000 007 (109 + 7). Выходные данные Выведите n целых чисел a1, a2, ..., an, где ai, где ai — искомое количество способов улучшить качество дорог по модулю 1 000 000 007 (109 + 7), если столица страны находится в городе с номером i. | |
![]()
|
|
E. Майк и друзья
Деревья
Строки
строковые суфф. структуры
Структуры данных
*2800
What-The-Fatherland — это странная страна! Все номера телефонов там представляют собой строки, состоящие из строчных букв латиницы. Вдвойне странно то, что один номер телефона может относиться к нескольким медведям! В этой стране есть рок-группа под названием CF, состоящая из n медведей (включая Майка), пронумерованных от 1 до n.  Номер телефона i-го члена CF — si. 17 мая в стране выходной под названием День звонков. В последний День Звонков каждый медведь позвонил по всем номерам, являющимся построками его номера (возможно, по некоторому номеру пришлось позвонить несколько раз). В частности, каждый позвонил себе (это действительно странная страна!). Обозначим как call(i, j) количество раз, которое i-й участник CF позвонил j-ому участнику CF. У Майка есть q запросов, которые он хочет задать вам. В каждом запросе он дает вам номера l, r и k, а вы должны назвать ему число  Выходные данные Выведите ответ на каждый запрос на отдельной строке. | |
![]()
|
|
E. Дело о компьютерной сети
графы
Деревья
поиск в глубину и подобное
*2800
Андроид Андреид — известный на всю галактику детектив. Сейчас он занимается подготовкой защиты от возможной атаки хакеров на важную компьютерную сеть. В этой сети n узлов, некоторые пары узлов связаны m двусторонними каналами связи. По этой сети планируется передать q важных сообщений, i-е из которых должно быть отправлено из узла si в узел di с помощью одного или нескольких каналов связи, возможно через некоторые промежуточные узлы. Для защиты от нападения был разработан специальный алгоритм. К сожалению его можно применить только к сети, состоящей из односторонних каналов связи. Поэтому, так как новые каналы связи создавать нельзя, было принято решение для каждого из существующих двусторонних каналов оставить возможность передавать данные только в одном из двух существующих направлений. Перед Вами стоит задача определить, возможно ли так задать направление для каждого канала связи, чтобы каждое из q сообщений можно было успешно передать. Выходные данные Если решение существует, выведите в единственной строке "Yes" (без кавычек). Иначе выведите "No" (без кавычек). Примечание В первом тесте из условия каналам можно задать направление, например, следующим образом: 1 → 2, 1 → 3, 3 → 2, 4 → 3. Тогда для первого сообщения будет путь 1 → 3, а для второго — 4 → 3 → 2. В третьем тесте из условия каналам можно задать направление, например, следующим образом: 1 → 2, 2 → 1, 2 → 3. Тогда для первого сообщения будет путь 1 → 2 → 3, а для второго — 2 → 1. | |
![]()
|
|
E. Аня и полупалиндром
графы
Деревья
дп
Строки
строковые суфф. структуры
Структуры данных
*2300
Завтра Ане предстоит сдавать самый сложный экзамен по программированию, на котором ей необходимо получить отличную оценку. На последнем теоретическом занятии преподаватель ввел понятие полупалиндрома. Строка t является полупалиндромом, если для всех нечетных позиций i ( ) выполняется условие ti = t|t| - i + 1, где |t| — длина строки t, а нумерация позиций начинается с единицы. Например, строки "abaa", "a", "bb", "abbbaa" являются полупалиндромами, а строки "ab", "bba" и "aaabaa" — нет. ) выполняется условие ti = t|t| - i + 1, где |t| — длина строки t, а нумерация позиций начинается с единицы. Например, строки "abaa", "a", "bb", "abbbaa" являются полупалиндромами, а строки "ab", "bba" и "aaabaa" — нет. Аня узнала, что на экзамене она получит строку s, состоящую только из латинских символов a и b, а также число k. Для получения отличной оценки ей необходимо будет найти k-ю в лексикографическом порядке подстроку данной строки s среди тех подстрок, которые являются полупалиндромами. При этом, каждая подстрока в этом порядке учитывается столько раз, сколько раз она встречается в s. Преподаватель гарантирует, что данное число k не превышает количества подстрок данной строки, которые являются полупалиндромами. А вы сможете справиться с такой задачей? Выходные данные Выведите подстроку заданной строки, которая является k-й в лексикографическом порядке из тех подстрок заданной строки, которые являются полупалиндромами. Примечание По определению, строка a = a1a2... an лексикографически меньше строки b = b1b2... bm, если либо a является префиксом b и не совпадает с b, либо существует такое i, что a1 = b1, a2 = b2, ... ai - 1 = bi - 1, ai < bi. В первом примере подстроками-полупалиндромами являются следующие строки — a, a, a, a, aa, aba, abaa, abba, abbabaa, b, b, b, b, baab, bab, bb, bbab, bbabaab (список задан в лексикографическом порядке). | |
![]()
|
|
D. Деревянные запросы
Бинарный поиск
битмаски
графы
Деревья
Конструктив
поиск в глубину и подобное
*2200
Роман посадил дерево из n вершин. В каждой вершине записана строчная английская буква. Вершина 1 является корнем дерева, у каждой из n - 1 оставшихся вершин есть предок в дереве, с которым вершина соединена ребром. Предком вершины i является вершина pi, причём номер предка всегда меньше, чем номер вершины (то есть, pi < i). Глубина вершины — это количество вершин на пути по рёбрам от корня до v. В частности, глубина корня равна 1. Скажем, что вершина u лежит в поддереве вершины v, если мы можем попасть из u в v, переходя из вершины в предка. В частности, вершина v лежит в своём поддереве. Рома даёт вам m запросов, i-й из которых задаётся двумя числами vi, hi. Рассмотрим вершины, лежащие в поддереве vi, и находящиеся на глубине hi. Определите, можно ли из букв, записанных в этих вершинах, составить строку, являющуюся палиндромом? Буквы, записанные в вершинах, можно переставить в произвольном порядке для составления палиндрома. Выходные данные Выведите m строк. В i-й строке выведите «Yes» (без кавычек), если в i-м запросе возможно составить палиндром из букв, написанных на вершинах, иначе выведите «No» (без кавычек). Примечание Строка s является палиндромом, если она одинаково читается слева направо и справа налево. В частности, пустая строка является палиндромом. Пояснение к тесту из условия. В первом запросе существует единственная вершина 1, подходящая под все условия, мы можем составить палиндром "z". Во втором запросе вершины 5 и 6 удовлетворяют условиям, на этих вершинах написаны буквы "с" и "d". Составить палиндром невозможно. В третьем запросе не существует ни одной вершины на глубине 1 в поддереве вершины 4. Мы можем составить пустой палиндром. В четвертом запросе не существует вершин в поддереве 6 на глубине 1. Мы можем составить пустой палиндром. В пятом запросе вершины 2, 3 и 4 удовлетворяют условиям, на этих вершинах написаны буквы a, с и с. Мы можем составить палиндром "cac" | |
![]()
|
|
D. Кампус
Бинарный поиск
Деревья
снм
Структуры данных
*3100
В городе Осколково есть кампус, состоящий из n студенческих общежитий, n университетов и n военкоматов. Изначально i-е общежитие принадлежит i-му университету и приписано к i-му военкомату. Жизнь бурлит, и в кампусе постоянно происходят изменения. Изменения бывают четырех типов: - Университет под номером aj объединяется с университетом bj, после чего все общежития, которые принадлежали университету bj, переходят под контроль университета aj, а университет bj перестает существовать.
- Военкомат под номером cj объединяется с военкоматом dj, после чего все общежития, которые были приписаны к военкомату dj, переходят под контроль военкомата cj, а военкомат dj перестает существовать.
- Университет под номером xj производит заселение. Путь kxj — количество общежитий, которые принадлежат этому университету в момент заселения. Тогда количество студентов в каждом общежитии университета xj увеличивается на kxj (обратите внимание, чем больше общежитий принадлежат университету, тем больше студентов заселяется в каждое общежитие университета).
- Военкомат под номером yj производит облаву на все подконтрольные ему общежития и забирает из них всех студентов.
Таким образом, в любой момент времени каждое общежитие относится только к одному университету и одному военкомату. Изначально все общежития пусты. Вам требуется обрабатывать изменения, происходящие в кампусе, а также отвечать на запросы, сколько человек живёт в общежитии qj в данный момент времени. Выходные данные В i-й строке выведите ответ на i-й запрос количества человек в общежитии. Примечание Рассмотрим первый тестовый пример: - При первом запросе университету 1 принадлежит только общежитие номер 1, значит после запроса в общежитии 1 будет жить 1 студент.
- После третьего запроса университету номер 1 принадлежат общежития 1 и 2.
- Четвертый запрос увеличивает на 2 количество студентов, живущих в общежитиях 1 и 2, принадлежащих университету номер 1. После этого в первом общежитии живет 3 студента, а во втором — 2 студента.
- При пятом запросе обнуляется количество студентов, живущих в общежитии номер 1, приписанном к военкомату номер 1.
| |
![]()
|
|
C. Мишка и рисование
Деревья
Конструктив
поиск в глубину и подобное
*2300
Лимак — маленький мишка, который учится рисовать. Люди обычно начинают с домиков, заборов и цветов, ну а мишкам с чего бы так делать? Лимак живет в лесу и решает нарисовать дерево. Напомним, что деревом называется связный граф, состоящий из n вершин и n - 1 ребра (n ≥ 1). Лимак выбрал дерево, состоящее из n вершин. У него есть бесконечная полоска бумаги с двумя параллельными рядами точек. Маленький мишка хочет сопоставить вершины дерева некоторым n различным точкам так, чтобы рёбра могли пересекаться только в своих конечных точках — иными словами, должно получиться планарное изображение дерева. Ниже приведен один из корректных рисунков к первому тесту.  Сможет ли Лимак нарисовать выбранное дерево? Выходные данные Выведите "Yes" (без кавычек), если Лимак может нарисовать выбранное дерево. В противном случае, выведите "No" (без кавычек). | |
![]()
|
|
B. Взятки
графы
Деревья
поиск в глубину и подобное
*2200
В стране Руритании дорожная сеть организована из рук вон плохо, это не радует дальнобойщиков, которым постоянно надо что-то перевозить. Некоторые дороги являются односторонними, некоторые — двусторонними. Оказывается, что иногда невозможно добраться из одного города до другого законно — однако взятка, данная правильному человеку, может помочь добраться куда угодно! К счастью для нас, полицейские позволят дальнобойщику нарушить правила и проехать в запрещённом направлении при условии, что машине ДПС будет предоставлено соответствующее вознаграждение. На каждой дороге расположено по одной машине ДПС и они просят 1000 рирутанских динаров за проезд в запрещенном направлении. Но патрульные — жадные ребята, и каждый раз, когда они замечают, что один и тот же дальнобойщик нарушает правила, они запрашивают вдвое большую сумму, чем которую они запрашивали в прошлый раз на этой конкретной дороге. Борна — дальнобойщик, сумевший раскусить всю эту схему. Ему надо сделать K остановок в некоторых городах по всей Руритании, и ему надо совершить эти остановки в некотором порядке. Дано N городов (пронумерованных от 1 до N) в Руритании и известно, что изначально Борна находится в столице, то есть городе 1. Так получилось, что он знает, какие дороги из N - 1 Руританских дорог на данный момент односторонние, но он не может подсчитать минимальное количество денег, которое надо подготовить на взятки ДПС. Помогите Борне, предоставьте ему ответ и вас щедро вознаградят. Выходные данные Выведите единственное целое число: наименьшее количество тысяч Руританских динаров, необходимое Борне для взяток, по модулю 109 + 7. Примечание Борна сперва идет по пути 1 → 5 и должен оплатить 1000 динаров. Затем он идет по пути 5 → 1 → 2 → 3 → 4 и в этот раз ничего не платит. Однако когда ему придется вернуться через 4 → 3 → 2 → 1 → 5, ему нужно подготовить 3000 (1000+2000) динаров. Затем дорога до 2 через 5 → 1 → 2 ничего не будет ему стоить. Наконец, ему не даже надо выезжать из города 2, чтобы добраться до 2, так что дополнительную взятку готовить не надо. Таким образом, всего он подготовит 4000 динаров. | |
![]()
|
|
B. Инвариантность дерева
Деревья
жадные алгоритмы
Конструктив
поиск в глубину и подобное
*2100
Деревом размера n называется неориентированный связный граф из n вершин без циклов. Рассмотрим некоторое дерево из n вершин. Назовем дерево инвариантным относительно перестановки p = p1p2... pn, если для любых двух вершин дерева u и v выполняется утверждение: «Вершины u и v соединены ребром тогда и только тогда, когда вершины pu и pv соединены ребром». Вам дана перестановка p размера n. Найдите какое-нибудь дерево размера n, инвариантное относительно данной перестановки. Выходные данные Если искомого дерева не существует, то выведите «NO» (без кавычек). Иначе выведите «YES», а затем выведите n - 1 строку, в каждой из которых находится по два целых числа — концы очередного ребра искомого дерева. Вершины нумеруются с единицы, порядок следования рёбер и порядок следования вершин внутри ребра не имеет значения. Если решений несколько, выведите любое из них. Примечание В первом тесте из условия, при применении к ребру перестановки, ребро (4, 1) перейдет в ребро (1, 4), ребро (4, 2) перейдет в ребро (1, 3), а ребро (1, 3) перейдет в ребро (4, 2). Все эти ребра есть в ответе. Можно заметить, что во втором тесте из условия, ни одно дерево не подходит под ограничения. | |
![]()
|
|
F. Коробка с зеркалами
Деревья
матрицы
*3200
Вам дана зеркальная коробка. Коробка представляет собой сетку размера n × m. Каждая ячейка сетки содержит зеркало, расположенное в форме '\' или ' / ' (т. е. под 45 градусов к горизональной или вертикальной прямой). Но, к сожалению, некоторые ячейки содержат разбитые зеркала. Вы хотите поместить новые зеркала в эти ячейки таким образом, чтобы выполнялись следующие два условия: - Если пустить луч света горизонтально/вертикально в середину любого единичного отрезка, являющегося стороной некоторой граничной ячейки, то луч света выйдет из одноги из соседних с ним единичных отрезков.
- Каждый единичный отрезок сетки, образующей коробку с зеркалами, может быть достигнут лучом света, пущенным в соответствие с правилами из предыдущего абзаца.
 Когда вы попробовали вставить несколько зеркал, вы обнаружили, что это можно сделать многими способами. Сколько существует возможных способов вставить зеркала на разбитые места, удовлетворяя условию задачи? Ответ может быть большим, поэтому выведите остаток от его деления на простое число MOD. Выходные данные Выведите ответ по модулю MOD. Примечание Единственный способ для первого примера показан на левой картинке в условии. Единственный способ для второго примера показаны на правой картинке в условии. Для третьего примера есть 5 возможностей, приведенных ниже: 1. 

2. 

3. 

4. 

5. 

| |
![]()
|
|
C. Кефа и парк
графы
Деревья
поиск в глубину и подобное
*1500
Кефа решил отпраздновать свой первый крупный заработок походом в ресторан. Он живет возле необычного парка. Парк представляет из себя подвешенное дерево из n вершин c корнем в вершине 1. В вершине 1 также находится дом Кефы. К сожалению для нашего героя, в парке также находятся коты. Кефа уже выяснил номера вершин, в которых находятся коты. В листовых вершинах парка находятся рестораны. Кефа хочет выбрать ресторан, в который он пойдет, но, к сожалению, он очень боится котов, поэтому он ни за что не пойдёт в ресторан, на пути к которому от его дома найдётся более m подряд идущих вершин с котами. Ваша задача — помочь Кефе посчитать количество ресторанов, в которые он может сходить. Выходные данные Одно целое число — количество различных листьев дерева, на пути от дома Кефы до которых не больше m подряд идущих вершин с котами. Примечание Напомним, что дерево — это связный граф на n вершинах, состоящий из n - 1 ребра. Подвешенное дерево — это дерево с особой выделенной вершиной, корнем. В подвешенном дереве из любых двух вершин, соединённых ребром, одна называется предком (та из них, что ближе к корню), а оставшаяся — ребёнком. Вершина называется листом, если у неё нет детей. Пояснение к первому тесту из условия:  Красным цветом отмечены вершины в которых находятся коты. Рестораны находятся в вершинах 2, 3, 4. Кефа не может сходить только в ресторан, находящийся в вершине 2. Красным цветом отмечены вершины в которых находятся коты. Рестораны находятся в вершинах 2, 3, 4. Кефа не может сходить только в ресторан, находящийся в вершине 2. Пояснение ко второму тесту из условия:  Рестораны находятся в вершинах 4, 5, 6, 7. Кефа не может попасть в рестораны 6, 7. Рестораны находятся в вершинах 4, 5, 6, 7. Кефа не может попасть в рестораны 6, 7. | |
![]()
|
|
F. Зубликанцы и мумократы
Деревья
дп
*2400
В Берляндии наступила пора выборов. Фаворитами конечно являются партии зубликанцев и мумократов. Предвыборные кампании обеих партий включают в себя многочисленные митинги на n главных площадях столицы Берляндии. На каждой из n площадей конечно может митинговать только одна партия, иначе это может привести к беспорядкам. С другой стороны обе партии подали заявки на проведение огромного количества митингов так, что на всех площадях обязательно пройдут митинги. Теперь руководству столицы предстоит распределить площади между двумя партиями. Некоторые пары площадей соединены (n - 1) двусторонними дорогами таким образом, что между любой парой площадей существует единственный способ попасть с одной площади на другую. Некоторые площади находятся на окраинах столицы, поэтому соединены дорогой лишь с одной другой площадью, такие площади называются тупиковыми. Мэр столицы поручил распределить все площади между партиями таким образом, чтобы в тупиковых площадях было одинаковое количество митингов первой и второй партии. Гарантируется, что количество тупиковых площадей города чётно. Для предотвращения возможных конфликтов между зубликанцами и мумократам было решено минимизировать количество дорог соединяющих площади с разными партиями. Вам как разработчику отдела распределения площадей предстоит определить это наименьшее количество. Выходные данные Выведите единственное число — минимальное количество дорог, соединяющих площади с митингами разных партий. | |
![]()
|
|
C. Duff в армии
Деревья
Структуры данных
*2200
На днях Duff стала солдатом армии. Malek — её командир. В их стране, Andarz Gu, есть n городов (пронумерованных от 1 до n) и n - 1 дорог. Каждая дорога соединяет два различных города. Между любыми двумя городами существует уникальный путь. Также в Andarz Gu живут m людей (пронумерованных от 1 до m). У каждого человека есть номер. Номер i-го человека равен i, и он/она живет в городе номер ci. Обратите внимание, в одном городе могут жить несколько людей, либо не жить вовсе.  Malek любит отдавать приказы. Поэтому он попросил Duff ответить на q запросов. В каждом запросе он дает ей числа v, u и a. Чтобы ответить на запрос: Предположим, что x людей живут в городах, лежащих на пути из города v в город u. Предположим, что номера этих людей — p1, p2, ..., px, если выписать их в возрастающем порядке. Пусть k = min(x, a). Duff должна назвать Malek'у числа k, p1, p2, ..., pk, именно в таком порядке. Иными словами, Malek хочет знать a минимумов на этом пути (или меньше, если дано меньше a людей). Duff сейчас очень занята, так что она попросила тебя помочь ей ответить на запросы. Выходные данные Для каждого запроса выведите числа k, p1, p2, ..., pk через пробел в одной строке. Примечание В тесте из условия страна Andarz Gu имеет следующий вид (номера людей, живущих в каждом городе, подписаны рядом с соответствующим городом):  | |
![]()
|
|
D. Супер М
графы
Деревья
дп
поиск в глубину и подобное
*2200
На самом деле Ари — не совсем обычное чудовище. Она представляет собой скрытую личность Супер М, одного из главных супергероев Байтфорсес. Байтфорсес — это страна, состоящая из n городов, соединенных n - 1 дорогами. Каждая дорога соединяет ровно два различных города, и вся дорожная система разработана так, что можно добраться от любого города до любого другого города, используя только данные дороги. На m городов напали злые люди. И вот, Ари... то есть, Супер М должен немедленно направиться в каждый из атакуемых городов, чтобы прогнать злых людей. Супер М может перемещаться между городами только используя данные дороги. Более того, перемещение по любой из дорог занимает у неё ровно один крон (единица времени, используемая в Байтфорсес).  Однако, сейчас Супер М не в Байтфорсес — она посещает тренировочный лагерь, расположенный в близлежащей стране Кодфорсес. К счастью, в Кодфорсес есть особый прибор, позволяющий мгновенно телепортировать девушку из Кодфорсес в любой город Байтфорсес. Обратный путь слишком долог, так что в рамках данной задачи телепортация используется ровно один раз. Вам следует помочь Супер М и вычислить город, в который она должна телепортироваться в начале, чтобы завершить свою работу за минимальное время (измеряемое в кронах). Также сообщите ей это время, чтобы она могла распланировать дорогу обратно в Кодфорсес. Выходные данные Сперва выведите номер города, куда надо телепортироваться Супер М. Если оптимальных ответов несколько, выведите город с наименьшим номером. Затем выведите наименьшее возможное время, необходимое для того, чтобы распугать всех людей в атакуемых городах, измеренное в кронах. Обратите внимание, что правильный ответ всегда единственен. Примечание В первом примере есть две возможности завершить работу Супер М за 3 крона:  and and  . .
Однако вам следует выбрать первый вариант, так как он начинается в городе с меньшим номером. | |
![]()
|
|
D. Деревянный День Рождения
графы
Деревья
математика
поиск в глубину и подобное
Структуры данных
*2400
У Богдана сегодня День Рождения и мама подарила ему дерево, состоящее из n вершин. На ребре i было написано число xi. Напомним, что деревом называется связный неориентированный граф без циклов. После этого на вечеринку к Богдану последовательно приходят m гостей. Когда приходит i-й гость, он делает ровно одну из двух операций: - Выбирает некоторое число yi, а так же две вершины ai и bi. После этого двигаясь по рёбрам дерева проходит от вершины ai до вершины bi кратчайшим путём (такой путь в дереве, конечно, единственный). Каждый раз проходясь по какому-то ребру j, он заменяет своё текущее число yi на
 , то есть на целую часть деления yi на xj. , то есть на целую часть деления yi на xj. - Выбирает некоторое ребро pi, и заменяет написанное на нём значение xpi на целое положительное число ci < xpi.
Богдан заботится о своих гостях и решил автоматизировать данный процесс. Напишите программу, которая проделает все применяемые гостями операции, и каждому гостю выбравшему операцию первого типа сообщит результирующее значение yi. Выходные данные Для каждого гостя, выбравшего операцию первого типа, выведите результирующее значение для выбранного им yi. Примечание Изначально дерево выглядит так:  На первый запрос ответом будет  = 2 = 2 После изменения третьего ребра дерево выглядит так:  На второй запрос ответом будет  = 4 = 4 В третьем запросе начальная и конечная вершина совпадает, то есть ответом будет исходное число 20. После изменения четвертого ребра дерево выглядит так:  В последнем запросе ответом будет  = 3 = 3 | |
![]()
|
|
E. Сэнди и Орешки
битмаски
Деревья
дп
*2600
Корневым деревом называется связный граф без циклов с выделенной вершиной. В рамках данной задачи будем считать, что корнем дерева всегда является вершина с номером 1. Наименьшим общим предком вершин u и v называется наиболее удалённая от корня дерева вершина, лежащая как на пути от корня до u, так и на пути от корня до v. Будем обозначать наименьшего общего предка вершин u и v как LCA(u, v). У белочки Сенди было корневое дерево, состоявшее из n вершин, в которых она хранила свои орешки. К несчастью, подводный шторм разрушил это дерево, и теперь Сенди никак не может его восстановить. Она смогла назвать m рёбер своего дерева и q троек чисел ai, bi и ci, про которые она полагает, что LCA(ai, bi) = ci. Помогите Сенди посчитать, сколько существует деревьев с корнем в вершине 1, про которые верна вся информация, названная Сенди. Если же она что-то напутала, и таких деревьев не существует, то выведите 0. Два корневых дерева считаются различными, если существует хотя бы одно ребро, принадлежащее одному из этих деревьев и не принадлежащее другому. Выходные данные Выведите количество деревьев размера n с корнем в вершине 1, таких что для них верна вся информация, которую помнит Сенди. Примечание Во втором примере правильный ответ выглядит так:  В третьем примере возможны два правильных ответа:   В четвёртом примере несложно заметить, что информация, предоставленная Сенди, противоречива. | |
![]()
|
|
E. Экспозиция
Бинарный поиск
Деревья
снм
Структуры данных
*1900
До пятидесятилетия известного писателя Берляева осталось несколько дней. По этому поводу в местной библиотеке решили организовать выставку сочинений известного фантаста. Также было решено, что необходимо выбрать все книги, изданные автором за какой-то интервал времени. Понятно, что если книги будут очень сильно различаться по размерам, то посетителям это не понравится. Поэтому, посовещавшись, организаторы пришли к мнению, что высота самой низкой и самой высокой книг, отобранных для экспозиции, должны отличаться не более чем на k миллиметров. В библиотеке имеется n томов произведений Берляева, расположенных в хронологическом порядке выпуска в свет. Про каждую книгу известна ее высота в миллиметрах hi. Поскольку юбиляр является очень уважаемым в городе человеком, то организаторы хотят представить на выставке наибольшее число его книг, а также узнать, какие при этом периоды творчества писателя они смогут охватить. Помогите организаторам справиться с этой нелегкой задачей. Выходные данные В первую строку выходных данных выведите через пробел два числа a и b. Число a означает наибольшее количество книг, которое организаторы смогут представить на выставке, а число b — количество интервалов времени таких, что в каждый из них писатель Берляев издал a книг, и самая высокая из этих книг превосходит самую низкую не более чем на k миллиметров. В последующие b строк выведите по два целых числа через пробел — номер первого и последнего тома каждого из искомых периодов творчества Берляева. | |
![]()
|
|
E. Lomsat gelral
Деревья
поиск в глубину и подобное
снм
Структуры данных
*2300
Задано корневое дерево с корнем в вершине 1. Каждая вершина покрашена в некоторый цвет. Будем говорить, что цвет c доминирует в поддереве вершины v, если нет другого цвета, который встречается в поддереве вершины v большее количество раз, чем цвет c. Таким образом, возможно два или более цвета одновременно доминируют в одном поддереве. Поддерево вершины v — это сама вершина v и все такие вершины, путь от которых до корня обязательно проходит через вершину v. Вам нужно для каждой вершины v определить сумму доминирующих цветов в поддереве вершины v. Выходные данные Выведите n целых чисел — суммы доминирующих цветов, для каждой вершины. | |
![]()
|
|
D. Ациклические органические составляющие
Деревья
поиск в глубину и подобное
снм
Строки
Структуры данных
хэши
*2400
Дано дерево T состоящее из n вершин (пронумерованных целыми числами от 1 до n). В каждой вершине записана некоторая буква. Корень дерева расположен в вершине 1. Рассмотрим поддерево дерево Tv некоторой вершины v. Вдоль любого просто пути, начинающегося в v и заканчивающегося в некоторой вершине  (возможно, в самой v), можно прочитать некоторую строку. Обозначим количество различных строк, которые можно прочитать таким способом как (возможно, в самой v), можно прочитать некоторую строку. Обозначим количество различных строк, которые можно прочитать таким способом как  . . Дополнительно: для каждой вершины v дано целое число cv. Нас интересуют вершины, в которых значение  как можно больше. как можно больше. Вы должны вычислить две величины — максимальное значение  и количество вершин v с максимальным и количество вершин v с максимальным  . . Выходные данные Выведите два числа — значение  для всех 1 ≤ i ≤ n и количество вершин v, для которых для всех 1 ≤ i ≤ n и количество вершин v, для которых  . . Примечание В первом примере дерево выглядит следующим образом: 
Наборы строк, которые могут быть прочитаны из вершин: 
Наконец, значения  таковы: таковы: 
Во втором примере значения  таковы: (5, 4, 2, 1, 1, 1).Различные строки, которые можно прочитать из вершины 2 таковы: таковы: (5, 4, 2, 1, 1, 1).Различные строки, которые можно прочитать из вершины 2 таковы:  ; обратите внимание, что ; обратите внимание, что  может быть прочитано как на пути до вершины 3, так и на пути до вершины 4. может быть прочитано как на пути до вершины 3, так и на пути до вершины 4. | |
![]()
|
|
E. Пастушеские странности
Деревья
математика
разделяй и властвуй
снм
Структуры данных
*3000
В стране Бурении есть n пастбищ, но нет дорог, их соединяющих. Конечно, это ужасная ситуация, поэтому Кевин Сан планирует исправить её, построив m двунаправленных дорог. Каждая дорога соединит какую пару пастбищ. Для того чтобы перемещение по дорогам было более эффективным, он также планирует замостить некоторые из этих новых дорог булыжником. Кевин очень дотошен в вопросе мощения путей. Так как он любит нечётные числа, то хочет, чтобы к каждому пастбищу вело нечётное число мощеных дорог. Назовём замощение дорог солнечным, если каждому пастбищу инцидентно нечётное количество замощёных дорог. Кроме того, короткие дороги нравятся Кевину больше, чем длинные, поэтому он хочет, чтобы самая длинная мощёная дорога была как можно короче. После добавления очередной дороги Кевин хочет знать, может ли он добиться солнечного замощения дорог Бурении, и если это так, то надо найти минимальную возможную длину самой длинной дороги, которую он замостит. Выходные данные Выведите m целых чисел, i-е из которых обозначает минимальную возможную длину самой длинной дороги в солнечном замощении после добавления первых i дорог. Если не существует такого замощения, что каждое пастбище инцидентно нечётному количеству мощёных дорог, то выведите - 1. Обратите внимание, что каждый раз рассматривается только гипотетическое замощение — ваш ответ после добавления i-й дороги не должен никак зависеть от ваших предыдущих ответов. Примечание В первом примере после добавления i-й дороги пути Кевин должен вымостить следующие из них: - Никакой набор дорог не подходит.
- Дорога номер 1 (длина 4) и номер 2 (длина 8).
- Дорога номер 1 (длина 4) и номер 2 (длина 8).
- Дорога номер 3 (длина 2) и номер 4 (длина 3).
Во втором примере нет ни одного солнечного замощения. | |
![]()
|
|
D. Могучее Дерево
Деревья
Структуры данных
*2600
Геос и Сайтама пошли покупать новогодние ёлки, но их внимание привлекло необыкновенное Могучее Дерево. Могучее Дерево изначально состоит из единственной корневой вершины, имеющей номер 1. Могучее дерево иногда растёт благодаря волшебному феномену, известному как обновление. Во время обновления к дереву добавляется один новый лист. Каждой вершине дерева (корню и всем добавленным вершинам) присвоено некоторое значение vi. Мощность вершины определяется как сила мультимножества, составленного из значения данной вершины (то есть числа vi) и значений мощностей её непосредственных детей. Сила мультимножества определяется как сумма всех элементов в мультимножестве, умноженная на их количество, то есть для некоторого мультимножества S:  Сайтама знает, какие обновления произойдут с данным деревом, так что он решил проверить Геноса и задать ему вопросы о мощности разных вершин дерева во время его роста. Каждое обновление имеет вид 1 p v, что означает добавление новой вершины со значением v, как непосредственного потомка вершины p. Каждый запрос имеет вид 2 u, что означает, что Генос должен назвать мощность вершины u в текущий момент. Пожалуйста, помогите Геносу ответить на все вопросы Сайтама. Ответ выводите по модулю 109 + 7. Выходные данные Для каждого запроса выведите мощность указанной вершины в данный момент по модулю 109 + 7. Примечание В первом примере после всех обновлений дерево будет выглядеть следующим образом: 1 — 2 — 3 — 4 — 5 Вершинам будут присвоены следующие значения: 2 — 3 — 5 — 7 — 11 Мощности вершин будут, соответственно, равны: 344 — 170 — 82 — 36 — 11 | |
![]()
|
|
E. Минимальное остовное дерево по каждому ребру
графы
Деревья
поиск в глубину и подобное
снм
Структуры данных
*2100
Дан связный неориентированный взвешенный граф без петель и кратных ребер, состоящий из n вершин и m ребер. Для каждого ребра графа (u, v) найдите вес такого остовного дерева, что это ребро (u, v) входит в него, и при этом вес этого остовного дерева минимален. Весом остовного дерева называется сумма весов ребер, входящих в остовное дерево. Выходные данные Выведите m строк: i-я строка должна содержать минимальный вес такого остовного дерева, содержащего i-ое ребро. Ребра нумеруются от 1 до m в порядке их появления во входных данных. | |
![]()
|
|
D. Великая победа
графы
Деревья
жадные алгоритмы
кратчайшие пути
поиск в глубину и подобное
*1800
Шапур победил Валериана. Эта победа была так важна, что Шапур решил вырезать на скале сцену поражения Валериана. Теперь ему нужно было найти наилучшее место и увековечить там свою победу! Он решил посетить все n городов Персии чтобы найти наиболее подходящую скалу. Но недавняя война утомила его, и он не хотел много путешествовать. Поэтому он хотел посетить каждый из этих n городов хотя бы один раз. При этом пройденное расстояние должно быть как можно меньше. Персидские города соединены двусторонними дорогами. Из каждого города можно дойти до любого другого, причем единственным способом. Все города пронумерованы от 1 до n. Шапур сейчас в городе 1, и он хочет посетить все остальные города, пройдя как можно меньше. Шапур может закончить свое путешествие в любом городе. Найдите расстояние, которое Шапур пройдет. Выходные данные Выведите одно число — минимальную длину пути Шапура. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-х битовых чисел на С++. Рекомендуется использовать поток cout (также вы можете использовать спецификатор %I64d). | |
![]()
|
|
E. Противник слаб
Деревья
Структуры данных
*1900
Римляне снова наступают. На этот раз их гораздо больше чем персов, но Шапур готов победить их. Он говорит: «Лев никогда не испугается сотни овец». Не смотря на это, Шапур должен найти слабость римской армии чтобы победить ее. Как вы помните, Шапур — математик, поэтому он определяет насколько слаба армии как число — степень слабости. Шапур считает, что степень слабости армии равна количеству таких троек i, j, k, что i < j < k и ai > aj > ak, где ax — сила человека, стоящего в строю на месте с номером x. Армия римлян обладает одной особенностью — силы всех людей в ней различны. Помогите Шапуру узнать, насколько слаба армия римлян. Выходные данные Выведите одно число — степень слабости римской армии. Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-х битовых чисел на С++. Рекомендуется использовать поток cout (также вы можете использовать спецификатор %I64d). | |
![]()
|
|
D. Королевство и его города
графы
Деревья
дп
поиск в глубину и подобное
разделяй и властвуй
сортировки
*2800
В королевстве К готовились к свадьбе дочери Короля. Однако, чтобы не ударить в грязь лицом перед будущими родственниками, Королю сперва необходимо провести реформу королевства. Так как Королю не терпится выдать свою дочь замуж, этот вопрос ему нужно решить как можно скорее. Королевство в данный момент состоит из n городов. Города соединены с помощью n - 1 двунаправленной дороги, причём из каждого города можно добраться до любого другого города. Поскольку в былые времена Королю приходилось много экономить, между любыми двумя городами есть ровно один простой путь. В чём же суть реформы? Выяснилось, что для максимально эффективного управления ключевые функции государственного аппарата необходимо вынести в различные города (назовем такие города важными). Однако из-за того, что существует риск атаки со стороны варваров, это необходимо сделать осторожно. Король составил несколько планов, каждый из которых описывается набором важных городов, и теперь интересуется, какой же план лучше. Варвары могут захватывать некоторые города, не являющиеся важными (уж те-то, разумеется, будут достаточно укреплены), после этого через захваченный город становится невозможно проехать. В частности, интересной характеристикой плана является минимальное количество городов, которое необходимо захватить варварам, чтобы все важные города оказались попарно изолированы друг от друга, то есть ни из какого важного города нельзя было доехать ни до какого другого важного города. Помогите Королю посчитать эту характеристику для каждого своего плана. Выходные данные Для каждого плана выведите единственное число — минимальное количество городов, которое потребуется захватить варварам, или - 1, если все попытки варваров изолировать важные города обречены на провал. Примечание В первом тесте в первом и третьем плане варварам достаточно захватить город 3. Во втором и четвёртом плане все попытки будут обречены на провал. Во втором тесте варварам достаточно захватить города 3 и 5. | |
![]()
|
|
C. Беговой трек
Деревья
дп
жадные алгоритмы
Строки
*2000
На планете AMI-1511 живёт мальчик Айрат. У каждого из жителей этой планеты есть свое хобби, в частности, Айрат любит бегать, причём не просто так — он мечтает превратить бег в настоящее искусство. Для начала Айрат хочет сконструировать беговой трек с полотном t. Полотно для трека на AMI-1511 — последовательность из цветных блоков, где каждый блок обозначается строчной английской буквой. Таким образом, любое полотно представляется как строка некоторой длины. К сожалению, блоки отсутствуют в свободной продаже. Айрат нашёл в магазине неограниченное количество полотен для трека s, а ещё у него есть ножницы и клей. Айрат может купить некоторое количество полотен s, после чего вырезать из каждого ровно один непрерывный кусок (подстроку) и приклеить его в конец своего полотна, при этом он может развернуть новый кусок перед приклеиванием. Помогите Айрату посчитать, сколько минимум полотен s ему нужно купить, какие куски из них вырезать и в каком порядке склеить, чтобы получить желанное полотно t. Выходные данные В первой строке выведите минимальное число полотен n или -1, если собрать желанное полотно не представляется возможным. Если ответ не -1, то в следующих n строках выведите по два числа xi и yi — номера крайних блоков в вырезаемом куске. xi ≤ yi означает, что кусок приклеивается в исходном порядке, а xi > yi — что в развёрнутом. Куски выводите в том порядке, в котором их следует склеивать, чтобы получить строку t. Примечание В первом примере строка "cbaabc" = "cba" + "abc". Во втором примере: "ayrat" = "a" + "yr" + "at". | |
![]()
|
|
D. Гамильтоново остовное дерево
Деревья
дп
жадные алгоритмы
Паросочетания
поиск в глубину и подобное
*2200
Группа из n городов связана сетью дорог. Первоначально между любой парой городов есть двунаправленная дорога, таким образом суммарное количество дорог равно  . Чтобы проехать по любой из этих дорог, требуется ровно y секунд. . Чтобы проехать по любой из этих дорог, требуется ровно y секунд. Остовным деревом называется такое подмножество дорог размера n - 1, что между любой парой городов можно проехать, используя только эти дороги. Было выбрано некоторое остовное дерево. После этого время проезда по каждой дороге остовного дерева было изменено с y на x. Обратите внимание, не гарантируется, что x меньше y. Вы хотели бы посетить все города по одному разу, используя кратчайший путь. Вам даны числа n, x, y и описание выбранного остовного дерева. Определите минимальное время, необходимое, чтобы посетить каждый город ровно один раз, если разрешается начать маршрут в любом городе и закончить также в любом городе. Выходные данные Выведите единственное целое число — минимальное количество секунд, которое придётся потратить на путь, проходящий через каждый город ровно один раз. Примечание В первом примере дороги в остовном дереве требуют 2 секунд, в то время как на другие дороги уходит 3 секунды. Один из примеров оптимального пути:  . . Во втором примере нам дано такое же остовное дерево, но дороги в нём требуют 3 секунд, в то время как остальные дороги требуют 2 секунд. Один из примеров оптимального пути:  . . | |
![]()
|
|
E. Новогодняя ёлка
битмаски
Деревья
Структуры данных
*2100
Новый год прошёл, но Resha решил не убирать ёлку, а немного переукрасить её. К нему пришли его друзья Kerim и Gural, чтобы помочь переукрасить ёлку. Ёлка представляет собой обычное неориентированное дерево из n вершин с корнем в вершине 1. Вам требуется обрабатывать запросы двух типов: - Перекрасить все вершины из поддерева вершины v в цвет c.
- Найти количество различных цветов в поддереве вершины v.
Выходные данные Для каждого запроса второго типа выведите одно целое число a — количество различных цветов в поддереве вершины, заданной в запросе. Числа нужно выводить в отдельных строках, в порядке появления запросов во входных данных. | |
![]()
|
|
F. Ксоры на подотрезке
Деревья
Строки
Структуры данных
*2800
Вам задан массив из n целых чисел ai, а также m запросов. Каждый запрос описывается с помощью двух целых чисел (lj, rj). Определим функцию  . Функция определена только для u ≤ v. . Функция определена только для u ≤ v. Для каждого запроса выведите наибольшее значение функции f(ax, ay) по всем lj ≤ x, y ≤ rj, ax ≤ ay. Выходные данные Для каждого запроса выведите в отдельной строке целое число aj — наибольшее значение функции f(ax, ay) по всем lj ≤ x, y ≤ rj, ax ≤ ay. | |
![]()
|
|
E. Муравьи в листьях
Деревья
жадные алгоритмы
поиск в глубину и подобное
сортировки
*2200
Связный граф без циклов называется деревом. Листом дерева называется любая вершина, которая связана ровно с одной другой вершиной. Задано дерево из n вершин с корнем в вершине 1. В каждом листе дерева находится один муравей. За одну секунду несколько муравьёв могут одновременно перейти в предка вершины в которой они находятся. Два муравья не могут находиться одновременно в одной вершине, за исключением корня дерева. Определите наименьшее время за которое все муравьи смогут попасть в корень дерева. Обратите внимание, что исходно муравьи находятся только в листьях дерева. Выходные данные Выведите целое число t — наименьшее время, необходимое, чтобы все муравьи попали в корень дерева. | |
![]()
|
|
D. Тестирование дерева
Бинарный поиск
графы
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
*2600
На уроке информатики Якоб построил модель дерева из шариков и палочек. Модель соответствует некоторому дереву, состоящему из n вершин. На создание i-го шарика Якоб потратил ai минут. Учительница будет оценивать качество модели по количеству усилий, потраченных Якобом на создание шариков. У неё нет времени рассматривать их все, поэтому она посмотрит только на k первых шариков в порядке DFS-обхода дерева. Оценкой Якоба будет минимальное ai среди k рассмотренных шаров. У Якоба уже не хватит времени переделать модель, но он может сам выбрать корневую вершину, из которой учительница начнёт обход. Более того, для каждой вершины Якоб может переупорядочить список её соседей как захочет. Помогите Якобу определить, какую максимальную оценку он может получить. Порядок DFS-обхода — это последовательность номеров вершин, выписанная рекурсивной процедурой DFS. Будучи вызванной от вершины v, процедура делает следующее: - Напечатать v.
- Пройтись по списку соседей вершины v и вызвать процедуру DFS от всех из них по очереди. Не вызывать процедуру DFS от вершины u, если мы пришли в вершину v непосредственно из u.
Выходные данные Выведите одно целое число — максимальную оценку, которую может получить Якоб, если правильно выберет корневую вершину и переупорядочит списки соседей. Примечание В первом примере Якоб может назначить корнем вершину 2 и переупорядочить список её соседей следующим образом: 4, 1, 5. В результате этого порядок DFS-обхода станет 2, 4, 1, 3, 5, минимальное значение ai среди первых трёх вершин равняется 3. Во втором примере любой порядок обхода будет содержать вершину 1 на первом или втором месте, поэтому Якоб не может получить оценку больше чем 1. | |
![]()
|
|
F. Островной пазл
графы
Деревья
поиск в глубину и подобное
снм
*3400
В далёком островном государстве насчитывается n островов, соединённых мостами с двухсторонним движением. Текущая система мостов образует дерево. Другими словами, всего мостов n - 1, каждый мост соединяет одну пару различных островов, и от любого острова можно дойти до любого другого, используя только эти мосты. В центре каждого острова расположен пьедестал. На всех пьедесталах всех островов, кроме одного, находится очень хрупкая статуя, причём все статуи различны. У оставшегося острова пьедестал пуст. Жители островов договорились переупорядочить статуи определённым образом. Единственная доступная им операция — это выбрать какой-то остров, непосредственно соединённый мостом с островом с пустым пьедесталом, и аккуратно перенести статую с одного пьедестала на свободный пьедестал. Разумеется, очень часто статуи невозможно переупорядочить требуемым образом, используя только описанную выше операцию переноса. Островитяне хотят построить ещё один дополнительный мост, такой что после этого станет возможным перенести все статуи. При этом они, конечно, хотели бы выполнить как можно меньше переносов. Помогите им определить, какой мост необходимо построить и какое минимальное количество действий выполнить, чтобы добиться желаемого расположения статуй. Выходные данные Возможные варианты вывода: Если переупорядочить статуи требуемым образом можно и без постройки дополнительно моста, то выведите 0 t, где t равняется минимальному требуемому количеству действий. В противном случае выведите u, v и t (1 ≤ u < v ≤ n) — концы нового моста и минимальное количество действий, необходимое, чтобы добиться желаемого расположения статуй. Если переставить статуи невозможно, даже построив новый мост, выведите - 1. Примечание В первом примере островитяне могут соединить мостом острова 1 и 3, после чего выполнить следующую последовательность действий: передвинуть статую 1 с острова 1 на остров 2, передвинуть статую 2 с острова 3 на остров 1, передвинуть статую 1 с острова 2 на остров 3. Желаемое расположение статуй будет достигнуто за 3 действия. Во втором примере можно просто передвинуть статую 1 с острова 1 на остров 2. Строить новых мостов не требуется. В третьем примере переставить статуи желаемым образом невозможно, даже построив новый мост. | |
![]()
|
|
E. Фома Дор и дороги
Деревья
дп
Комбинаторика
поиск в глубину и подобное
Структуры данных
Теория вероятностей
*2300
Карта города, в котором живёт Фома Дор, представляет собой дерево (неориентированный связный граф без простых циклов), поэтому гости зовут его Древоградом. В городе n перекрёстков, соединённых n - 1 дорогой. По всем дорогам можно перемещаться в обоих направлениях. В городе живёт m друзей Фомы Дора, i-й из них живёт рядом с перекрёстком ui, а работает рядом с перекрёстком vi. Все жители города несчастны, потому что между из домом и работой существует ровно один простой путь. Фома Дор хочет построить ровно одну новую дорогу, которую он выберет случайно среди всех n·(n - 1) / 2 возможных дорог. Обратите внимание, что он вполне может построить новую дорогу между какой-то парой перекрёстков, уже соединённых друг с другом дорогой. Фома знает, что каждый из его друзей будет счастлив, если после построения новой дороги будет путь из его дома до работы и обратно, который не проходит по одной дороге дважды. Формально, в графе будет существовать простой цикл, на котором лежат ui и vi. Более того, если какой-то друг становится счастлив, то уровень его радости определяется как длина этого пути (несложно заметить, что эта длина определяется однозначно). Для каждого своего друга Фома хочет вычислить математическое ожидание значения уровня радости, то есть математическое ожидание длины цикла, если этот цикл содержит ui и vi. Выходные данные Для каждого друга Фомы Дора вычислите математическое ожидание его уровня радости, при условии, что он будет счастлив. Ваш ответ будет считаться правильным, если его абсолютная или относительная ошибка не будет превосходить 10 - 6. А именно: пусть ваш ответ равен a, а ответ жюри — b. Проверяющая программа будет считать ваш ответ правильным, если  . . Примечание Рассмотрим второй пример. - Подходят дороги (1, 2) и (2, 3), поэтому математическое ожидание равняется
 - Построение дорог (1, 3) и (2, 3) сделает второго друга счастливым. Как и для друга 1, ответ равен 2.5
- Единственный способ сделать третьего друга счастливым — это построить дорогу (2, 3), поэтому ответ равен 3
| |
![]()
|
|
F. Волшебная матрица
графы
Деревья
матрицы
Перебор
разделяй и властвуй
*2400
Вам задана матрица A размера n × n. Будем называть матрицу с неотрицательными элементами волшебной, если она симметрична (то есть aij = aji), aii = 0 и aij ≤ max(aik, ajk) для всех троек i, j, k. Заметим, что i, j, k не обязательно различны. Определите является ли матрица волшебной. Рекомендуется для ввода и вывода данных использовать функции scanf, printf в языке C++, поскольку они работают значительно быстрее чем cin, cout. Аналогично, рекомендуется использовать классы BufferedReader, PrintWriter вместо Scanner, System.out в языке Java. Выходные данные Выведите ''MAGIC" (без кавычек) если матрица A является магической. В противном случае выведите ''NOT MAGIC". | |
![]()
|
|
F. Шоколадное веселье
графы
Деревья
дп
поиск в глубину и подобное
*2600
У Алисы и Боба есть дерево (неориентированный связный ацикличный граф). В i-й вершине дерева лежит ai шоколадок. Сперва ребята выбирают себе стартовые вершины (Алиса выбирает первой) и забирают себе все шоколадки, которые там лежат. Затем Алиса и Боб ходят по очереди, на каждом ходу выбирая одну вершину и забирая все лежащие там шоколадки. Чтобы разнообразить процесс, они договорились, что каждый из них может выбирать только среди вершин, которые являются соседними по отношению к выбранной этим игроком вершиной на предыдущем ходу. Более того, можно выбирать только вершины, не выбранные до этого никем другим. Если в какой-то момент времени один из игроков не может сделать ход, он просто ожидает, пока другой игрок сделает все свои ходы. Процесс заканчивается, когда ни Алиса, ни Боб не могут больше сделать ни одного хода. Поскольку Алиса и Боб — большие сладкоежки, они хотят собрать как можно больше шоколадок. Однако они ещё и друзья, поэтому их волнует только суммарное количество шоколадок, которое они соберут вместе. Найдите это значение, если ребята действуют оптимально. Выходные данные Выведите, сколько шоколадок смогут собрать Алиса и Боб, если они будут действовать оптимально. Примечание В первом примере Алиса начнёт в вершине 9, а Боб в вершине 8. Затем Алиса сделает ход в вершину 1, и Боб будет вынужден остаться на месте. Алиса сделает ход в вершину 7, и игра закончится. Во втором примере они сразу выберут две вершины и заберут их них все шоколадки. | |
![]()
|
|
C. Ремонт дорог
*особая задача
графы
Деревья
жадные алгоритмы
поиск в глубину и подобное
*1800
В Берляндии есть n городов и n - 1 дорога с двусторонним движением. Каждая дорога соединяет какую-то пару городов, при этом от любого города можно доехать до любого другого, используя только данные дороги. В каждом городе есть ровно одна ремонтная бригада. Чтобы отремонтировать какую-то дорогу, необходима одновременная работа в течение одного дня двух бригад, базирующихся в городах, которые эта дорога соединяет. Обе бригады занимаются ремонтом одной дороги весь день и не могут в этот день участвовать в ремонте других дорог, а вот ничего не делать в течение дня ремонтная бригада вполне может. Определите минимальное количество дней, в течение которых можно отремонтировать все дороги. Бригады не могут менять города, в которых расположены изначально. Выходные данные Сначала выведите число k — минимальное количество дней, за которое возможно отремонтировать все дороги Берляндии. В следующих k строках выведите описание дорог, которые должны быть отремонтированы в каждый из k дней. В i-й строке выведите сначала число di — количество дорог, которые должны быть отремонтированы в i-й день, а затем через пробел выведите di целых чисел — номера дорог, которые должны быть отремонтированы в i-й день. Дороги нумеруются согласно порядку во входных данных, начиная с единицы. Если вариантов ответа несколько, разрешается вывести любой из них. Примечание В первом примере отремонтировать все дороги можно за два дня, например, отремонтировать дороги 1 и 2 в первый день, а дорогу 3 — во второй. | |
![]()
|
|
B. Медвежонок и забытое дерево 3
графы
Деревья
Конструктив
*1600
Деревом называется связный неориентированный граф состоящий из n вершин и n - 1 ребра. Вершины пронумерованы от 1 до n. У полярного медвежонка Лимака было дерево, пока его не украл злой Радевуш. Медвежонок очень расстроился, потому что он помнит о дереве только три числа n, d и h: - Дерево состояло ровно из n вершин.
- Диаметр дерева был равен d. Другими словами, d это максимальное расстояние между какой-то парой вершин дерева.
- Также Лимак помнит, что если сделать корнем дерева вершину 1, то его высота будет равна h. Другими словами, h это максимальное расстояние от 1 до какой-то другой вершины.
Расстоянием между двумя вершинами дерева называется количество рёбер на простом пути между ними. Помогите Лимаку найти какое-нибудь дерево, удовлетворяющее всем условиям и выведите его рёбра в произвольном порядке. Если подходящего дерева не существует, то выведите «-1». Выходные данные Если не существует ни одного дерева подходящего под описание Лимака, то выведите «-1» (без кавычек). В противном случае выведите дерево, подходящее под описание Лимака. В n - 1 строке выведите пары вершин, соединённых рёбрами. Если подходящих деревьев несколько, разрешается вывести любое из них. Рёбра можно выводить в произвольном порядке. Примечание Ниже приведены рисунки для первого и третьего примеров.  | |
![]()
|
|
F. Медведь и химия
графы
Деревья
поиск в глубину и подобное
Структуры данных
*3300
Умный бурый мишка Лимак обожает химию, особенно ему нравятся химические реакции превращения элементов друг в друга. В Беарляндии (родине Лимака) есть n химических элементов, пронумерованных от 1 до n. Также там существуют специальные машины, которые превращают элементы друг в друга. Каждая машина описывается парой чисел ai и bi (не обязательно различных), означающей что машина может превратить элемент ai в bi и наоборот, превратить элемент bi в ai. Машины в Беарляндии очень ненадёжные и каждая из них может быть использована не более одного раза. Допустимо, что ai = bi или несколько машин преобразуют одну и ту же пару ai и bi. Радевуш — главный соперник Лимака, и он решил проверить его знание химии. Завтра они встретятся, и каждый принесёт с собой все имеющиеся у него машины. У Лимака есть m машин, но о машинах Радевуша он ничего не знает. Оно договорились, что Радевуш выберет два различных элемента x и y. Лимак начинает с элемента x и должен перевести его в элемент y используя имеющиеся машины, а затем перевести элемент обратно в x. Для выполнения задачи Лимак может использовать как свои машины, так и машины Радевуша, но каждую машину можно применить не более одного раза. Известно, что у Радевуша есть непустое множество любимых элементов, и он обязательно выберет x и y из этого множества. Лимак не знает ни элементов в этом множестве, ни какие машины есть у Радевуша, но до него дошли q слухов, каждый из которых содержит описание машин Радевуша и его любимого множества. Теперь для каждого слуха Лимак хочет знать, правда ли, что используя свои машины и машины Радевуша (согласно слуху) он сможет успешно выполнить преобразование для любой пары различных элементов x и y из множества любимых элементов Радевуша (опять же, согласно слуху). Входные данные В первой строке входных данных записаны три числа n, m и q (1 ≤ n, q ≤ 300 000, 0 ≤ m ≤ 300 000) — количество элементов, количество машин Лимака и количество слухов соответственно. В каждой из последующих m строк записаны два числа ai и bi (1 ≤ ai, bi ≤ n), описывающие i-ю машину Лимака. Затем следует q описаний слухов. В первой строке каждого описания i-го слуха записаны два числа ni и mi (1 ≤ ni ≤ 300 000, 0 ≤ mi ≤ 300 000). Во второй строке описания записы ni различных чисел xi, 1, xi, 2, ..., xi, ni (1 ≤ xi, j ≤ n) — любимые элементы Радевуша согласно данному слуху. Обратите внимание, что если ni = 1, то Лимак автоматически выигрывает, поскольку нельзя выбрать ни одной пары различных x и y (и ответ «YES»). В следующих mi строках записаны по два числа ai, j, bi, j (1 ≤ ai, j, bi, j), описывающие Машины Радевуша в i-м слухе. Гарантируется, что сумма всех ni не превосходит 300 000. Аналогично, сумма всех mi тоже не превосходит 300 000. Важно! Поскольку мы хотели бы, чтобы вы обрабатывали слухи один за другим, получить очередной запрос можно только узнав ответ на предыдущий. Для этого необходимо ко всем числам, описывающим множество любимых элементов Радевуша и его машины применить следующую функцию: int rotate(int element)
{
element=(element+R)%n;
if (element==0) {
element=n;
}
return element;
}
Здесь R изначально равняется 0 и увеличивается на порядковый номер запроса каждый раз, когда ответом является «YES». Запросы нумеруются начиная с 1 в порядке, в котором они встречаются во входных данных. Выходные данные Выведите q строк, для i-го запроса выведите «YES» (без кавычек), если для i-го слуха Лимак сумеет успешно перевести друг в друга любую пару элементов x и y из множества xi, 1, xi, 2, ..., xi, ni. В противном случае выведите «NO». Примечание Рассмотрим первый пример. В первом слухе любимым множеством Радевуша является {4, 2} и у него нет машин. Лимак может преобразовать элемент 4 в элемент 2, а затем 2 в 3 и 3 в 4. Таким образом, ответ «YES» и R увеличивается на 1. Во втором слухе задач набор {6, 2} и машина (3, 4), но поскольку R = 1, то реально требуется рассмотреть множество {1, 3} и машину (4, 5). Ответ «NO» и значение R не меняется. В третьем слухе множество {6, 4, 3} и машины (2, 5) и (4, 6) переводятся в {1, 5, 4}, (3, 6) и (5, 1) Рассмотрим возможный выбор Радевуша: - Если выбрать элементы 1 и 5, то Лимак может перевести 1 в 5, затем 6 в 3, 3 в 2 и, наконец, 2 в 1.
- Если он выберет элементы 5 и 4, то Лимак может перевести 5 в 6, 6 в 3, 3 в 4, а затем 4 в 2, 2 в 1, 1 в 5.
- Наконец, если выбрать элементы 1 и 4, то Лимак может превратить 1 в 2, потом 2 в 4, 4 в 3, 3 в 6, 6 в 5 и 5 в 1.
Таким образом Лимак может выполнить задачу для любой пары x и y и ответ «YES», а значение R увеличивается на 3 и становится равно 4. В последнем слухе {1, 2} и (1, 2) переводятся в {5, 6} и (5, 6). Имеются две машины (5, 6) и Лимак легко справляется с заданием. | |
![]()
|
|
E. Медвежонок и уничтожение поддеревьев
Деревья
дп
математика
Теория вероятностей
*2700
Лимак — это маленький медвежонок гризли. Однажды он нападёт на страну оленей, но пока что он занимается уничтожением деревьев в компьютерной ролевой игре. Лимак начинает с дерева, состоящего из одной вершины. Эта вершина имеет индекс 1 и является корнем дерева. Время от времени игра выбирает некоторое поддерево, и Лимак атакует его. Когда Лимак атакует поддерево, он разрушает каждое его ребро независимо с вероятностью  . Штрафом Лимака после атаки на поддерево является целое число, равное высоте поддерева после атаки. Высотой поддерева называется самый длинный простой путь, начинающийся в корне поддерева и заканчивающийся в какой-нибудь вершине поддерева. . Штрафом Лимака после атаки на поддерево является целое число, равное высоте поддерева после атаки. Высотой поддерева называется самый длинный простой путь, начинающийся в корне поддерева и заканчивающийся в какой-нибудь вершине поддерева. Вам требуется обрабатывать запросы двух типов. - 1 v обозначает запрос первого типа. В дерево добавляется новая вершина, и её родителем является вершина v. Вершина получает минимальный свободный индекс (таким образом, вершины получают номера 2, 3, ...).
- 2 v обозначает запрос второго типа. Предположим, Лимак атакует поддерево вершины v. Чему в таком случае равно математическое ожидание штрафа, который он получит?
В запросах второго типа только предполагается, что Лимак атакует поддерево, но на самом деле никакие рёбра не разрушаются, и этот запрос никак не влияет на последующие. Выходные данные Для каждого запроса второго типа выведите одно вещественное число — математическое ожидание штрафа Лимака после атаки на соответствующее поддерево. Ваш ответ будет считаться правильным, если его абсолютная или относительная ошибка не будет превосходить 10 - 6. А именно: пусть ваш ответ равен a, а ответ жюри — b. Проверяющая программа будет считать ваш ответ правильным, если  . . Примечание На рисунке ниже представлен первый пример. Красными кружочками обозначены запросы второго типа.  | |
![]()
|
|
E. Часовой механизм
Деревья
жадные алгоритмы
поиск в глубину и подобное
снм
Структуры данных
*3200
Меня зовут Джим ди Гриз, я самый ловкий мошенник и авантюрист во всей галактике. По мотивам моих похождений написано множество книг, а ограблениям, совершённым мною, нет числа. Однако вы смогли застать меня в весьма неприятной ситуации. Не обнаружив себя перед камерами, перехитрив десяток охранников и обойдя множество ловушек, я смог добраться до желанного ящика с сокровищами. Отворив его крышку, я активировал бомбу с часовым механизмом, который уже отсчитывает секунды до неминуемого взрыва! К счастью, мне уже приходилось сталкиваться с бомбами подобной модели, и я знаю, что часовой механизм можно остановить, если правильно соединить проводами контакты на панели управления. Передо мной n контактов, соединённых n - 1 проводами. Контакты пронумерованы целыми числами от 1 до n. Бомба устроена таким образом, что если некоторый набор из k ≥ 2 контактов c1, c2, ..., ck соединён по циклу, то есть между парами контактов c1 и c2, c2 и c3, ..., ck и c1 есть k различных проводов, то срабатывает проверка безопасности, и заряд мгновенно детонирует, не оставляя от неудачливого взломщика и следа. В том числе, если два контакта соединены более чем одним проводом, то на них образуется цикл длины 2, и бомба также взрывается. Соединять контакт с самим собой запрещается. С другой стороны, если я отсоединю одновременно более чем один провод (иными словами, в какой-то момент времени будет подключено менее n - 2 проводов), то сработает другая проверка безопасности, которая приведёт к такому же плачевному результату. Таким образом, всё, что мне остаётся, это последовательно вытаскивать провод и вставлять его в новое место, следя, чтобы не образовалось цикла, связывающего контакты. Я знаю, как надо расположить провода, чтобы остановить часовой механизм. Но у меня остаётся всё меньше и меньше времени на это! Помогите мне выбраться из передряги: найдите кратчайшую последовательность безопасных операций, каждая из которых представляет собой отключение определённого провода и его подключение в новое место, а также выстраивает провода требуемым образом. Выходные данные В первой строке выведите число k (k ≥ 0) — минимальное количество проводов, которые потребуется переподключить. В последующих k строках выведите четвёрки чисел ai, bi, ci, di, означающих, что на i-м шаге нужно отсоединить провод, соединяющий контакты ai и bi, и соединить им контакты ci и di. Разумеется, к этому моменту времени провод между контактами ai и bi должен присутствовать на схеме. Если оптимальных последовательностей несколько, то выведите любую из них. Если требуемой последовательности операций не существует, выведите одно число -1. Примечание Картинка с пояснением к тестам из условия:  | |
![]()
|
|
E. В погоне за артефактами
графы
Деревья
поиск в глубину и подобное
снм
*2300
Павел снова играет в одну известную компьютерную игру. Игроку предоставлена в распоряжение целая страна, где можно свободно путешествовать, выполнять квесты и набирать опыт. В этой стране n островов и m мостов, расположенных между островами так, что от каждого острова можно добраться до каждого. В середине некоторых мостов лежат древние могущественные артефакты. Павлу сами по себе артефакты не нужны, зато он может неплохо заработать, продав хотя бы один такой артефакт. В начале игры Павел находится на острове a, а торговец артефактами — на острове b (возможно, на том же самом, что и Павел). Павел хочет найти артефакт, прийти к торговцу и продать его. Проблема осложняется тем, что мосты между островами очень старые и разрушаются сразу после того, как по ним пройти. Так как персонаж Павла не умеет плавать, летать и телепортироваться, задача становится не такой и простой! Обратите внимание, что Павел не может пройти половину моста, забрать артефакт и вернуться на тот же остров. Определите, сможет ли Павел найти артефакт и принести его к торговцу. Выходные данные Если Павел сможет добыть артефакт и продать его торговцу, выведите «YES» (без кавычек). Иначе выведите «NO» (без кавычек). | |
![]()
|
|
E. Медвежонок и забытое дерево 2
графы
Деревья
поиск в глубину и подобное
снм
*2400
Деревом называется связный неориентированный граф, состоящий из n вершин и n - 1 ребра. Вершины пронумерованы целыми числами от 1 до n. У полярного медвежонка Лимака было дерево, но он его потерял. Однако он всё ещё помнит о нём некоторые факты. Вам даны m пар вершин (a1, b1), (a2, b2), ..., (am, bm). Лимак точно помнит, что между вершинами ai и bi не было ребра. Помимо этого, он помнит, что в дереве было ровно k рёбер инцидентных вершин 1 (степень вершины 1 равнялась k). Проверьте, существует ли хотя бы одно дерево, подходящее под описание Лимака. Выходные данные Если существует хотя бы одно дерево, подходящее под описание Лимака, то выведите «possible» (без кавычек). В противном случае выведите «impossible» (без кавычек). Примечание В первом примере дерево состоит из 5 вершин. Степень вершины 1 должна быть равна 2. Все условия будут выполнены для дерева, состоящего из рёбер 1 - 5, 5 - 2, 1 - 3 и 3 - 4. Во втором примере Лимак помнит, что не существовало рёбер 1 - 2, 1 - 3, 1 - 4, 1 - 5 и 1 - 6. Таким образом, вершина 1 не могла быть соединена ни с одной другой вершиной, и подходящего дерева не существует. | |
![]()
|
|
E. Красивые подмассивы
Деревья
разделяй и властвуй
Строки
Структуры данных
*2100
Однажды ZSCoder выписал массив целых чисел a с элементами a1, a2, ..., an. Будем называть подмассивом массива a последовательность al, al + 1, ..., ar для некоторой пары целых чисел (l, r) таких, что 1 ≤ l ≤ r ≤ n. ZSCoder считает подмассив красивым, если значение операции побитового исключающего или (xor) по всем элементам подмассива не меньше k. Помогите ZSCoder-у найти количество красивых подмассивов массива a! Выходные данные Выведите одно целое число c — количество красивых подмассивов массива a. | |
![]()
|
|
D. Построение дерева
Деревья
Структуры данных
*1800
Васе задали по информатике сложную задачу. К сожалению, Вася не умеет программировать и не смог найти решение в Интернете. Поэтому он обратился за помощью к Вам. У нас есть последовательность \(a\) из \(n\) различных чисел, с помощью которой строится бинарное дерево поиска. Опишем правила построения формально. - Первое число \(a_1\) становится корнем дерева.
- Последовательно добавляются все элементы \(a_2, a_3, \ldots, a_n\). При добавлении элемента \(a_i\) выполняется спуск по дереву от корня вниз, по следующим правилам:
- Изначально текущей вершиной является корень.
- Если значение \(a_i\) больше значения в текущем элементе, то правый сын текущей вершины становится текущей вершиной. В противном случае текущей вершиной становится левый сын.
- В момент когда требуемый переход в сына невозможен (то есть такой сын отсутствует) создаётся новая вершина, в которую записывается число \(a_i\). Эта вершина становится соответствующим сыном текущей вершины.
Выходные данные Выведите \(n - 1\) число. Для всех \(i > 1\) выведите значение, записанное в вершине являющей предком вершины с числом \(a_i\). | |
![]()
|
|
D. Подарки по списку
графы
Деревья
Конструктив
поиск в глубину и подобное
*2000
Саша живет в большой дружной семье. В Мужской День мужчины из этой семьи собираются вместе и празднуют его, следуя своей особой традиции. В семье Саши n мужчин, поэтому для простоты будем нумеровать их от 1 до n. Каждый мужчина имеет не более одного отца, но может иметь произвольное количество сыновей. Мужчина с номером A является предком мужчины с номером B, если выполняется хотя бы одно из утверждений: - A = B;
- мужчина с номером A — отец мужчины с номером B;
- существует такой номер C, что мужчина с номером A — предок мужчины с номером C, а мужчина с номером C — отец мужчины с номером B.
Конечно же, если мужчина с номером A является предком мужчины с номером B, причём A ≠ B, то мужчина с номером B не может являться предком мужчины с номером A. На Мужской День в семье Саши принято дарить подарки. Просто так дарить подарки скучно, поэтому в этой семье процесс дарения каждый год выглядит следующим образом. - Определяется список кандидатов, в котором перечислены некоторые из n мужчин в определённом порядке.
- Каждый из n мужчин решает сделать подарок.
- Чтобы сделать кому-нибудь подарок, мужчина выбирает из составленного списка первого члена семьи, который является его предком, и делает ему подарок. В частности, он может сделать подарок сам себе.
- Если в списке нет ни одного предка какого-нибудь мужчины, то он расстраивается и покидает праздник, так и не подарив никому подарок.
В этом году вы решили помочь с организацией праздника и узнали у каждого из n мужчин, кому из своих предков он хочет сделать подарок. Сможете ли вы построить список кандидатов таким образом, чтобы удовлетворить желание каждого? Выходные данные В первой строке выведите целое число k (1 ≤ k ≤ n) — количество мужчин в списке кандидатов. Затем выведите k различных неотрицательных целых чисел — номера мужчин в списке кандидатов в порядке, определяющем необходимый выбор каждого из n мужчин, — по одному в строке. Если подходящих списков несколько, выведите любой из них. Если подходящего списка не существует, выведите - 1 в единственной строке выходных данных. Примечание Пояснение к первому примеру: - если в списке не будет 1, то желания первого и третьего мужчины не сбудутся (a1 = a3 = 1);
- если в списке не будет 2, то желание второго мужчины не сбудется (a2 = 2);
- если разместить в ответе 1 перед 2, то второму мужчине придется дарить подарок первому мужчине, а не себе (a2 = 2);
- если же разместить мужчину с номером 2 перед мужчиной с номером 1, то третьему мужчине придется дарить подарок второму мужчине, а не первому (a3 = 1).
| |
![]()
|
|
C. Алёна и дерево
графы
Деревья
дп
поиск в глубину и подобное
*1600
Алёна решила сесть на диету и пошла в лес за яблоками. Внезапно она обнаружила волшебное корневое дерево с корнем в вершине 1, на каждом ребре и в каждой вершине которого записаны некоторые числа. Девочка заметила, что некоторые вершины дерева грустят, поэтому она решила с ними поиграть. Назовем вершину v грустной, если в ее поддереве найдется вершина u, такая что dist(v, u) > au, где au — число, записанное в вершине u, а dist(v, u) — сумма чисел на ребрах на пути от v до u. Листьями дерева называются вершины, соединенные ребром ровно с одной вершиной, а корень дерева является листом тогда и только тогда, когда дерево состоит из единственной вершины-корня. Алёна решила удалять листья дерева до тех пор, пока все вершины не перестанут грустить. Какое минимальное количество листьев нужно удалить Алёне? Выходные данные Выведите минимальное количество листьев, которое требуется удалить Алёне, чтобы не осталось ни одной грустной вершины. Примечание Процесс удаления листьев дерева из первого примера может выглядеть так:  | |
![]()
|
|
B. Кай и снежинки
Деревья
дп
поиск в глубину и подобное
Структуры данных
*1900
После того как Каю в глаз попал осколок дьявольского зеркала, его уже не трогала красота роз. Зато он начал любоваться снежинками. Однажды в сад прилетела большая снежинка, имеющая форму корневого дерева (связного графа без циклов) на n вершинах. Корнем дерева является вершина номер 1. Кай очень заинтересовался его структурой. После долгого изучения Каю стали интересны ответы на некоторые запросы про q вершин. А именно: для i-го запроса ему интересно, какой номер имеет центроид поддерева vi-й вершины. Ваша задача — ответить на все запросы Кая. Поддеревом вершины называется часть дерева, состояющая из этой вершины, а также всех её потомков. Другими словами, поддерево вершины v состоит из таких вершин u, что v обязательно присутствует на пути от u до корня дерева. Центроидом дерева называется вершина, при удалении которой дерево развалится на компоненты связности, каждая из которых не превосходит по количеству вершин половину числа вершин исходного дерева. Выходные данные На каждый запрос выведите номер центроида соответствующего поддерева в отдельной строке. Если центроидов в поддереве несколько, выведите любой. Гарантируется, что у каждого поддерева заданного дерева есть хотя бы один центроид. Примечание  Первый вопрос спрашивает о центроиде всего дерева — это вершина 3, её удаление оставит четыре компоненты связности, две размера 1 и две размера 2. Поддерево второй вершины состоит только из неё самой, поэтому ответ 2. Вершина 3 также является центроидом собственного поддерева. Центроидами поддерева 5 являются вершины 5 и 6 — оба этих ответа являются корректными. | |
![]()
|
|
C2. Мозговая сеть (средняя)
графы
Деревья
поиск в глубину и подобное
*1500
Дальнейшие исследования мыслительных процессов зомби дали интересные результаты. Как мы знаем из предыдущей задачи, нервная система зомби состоит из n мозгов и m мозговых соединений, связывающих их воедино. Было замечено, что интеллектуальные способности зомби сильно зависят от топологии нервной системы. Точнее, определим как расстояние между двумя мозгами u и v (1 ≤ u, v ≤ n) как минимальное количество мозговых соединений, которые потребуется использовать, чтобы передать мысль между этими двумя мозгами. Мозговая задержка зомби определяется как максимальное расстояние между какой-нибудь парой мозгов. Ученые подозревают, что мозговая задержка является ключевым параметром определяющим, насколько умён данный зомби. Помогите им протестировать их гипотезу, написав программу для вычисления мозговой задержки данной нервной системы. В данной задаче вы можете считать, что данная вам во входных данных мозговая система является правильной, то есть удовлетворяет пунктам (1) и (2) из лёгкой версии данной задачи. Выходные данные Выведите одно число — мозговую задержку данной нервной системы. | |
![]()
|
|
C3. Мозговая сеть (сложная)
Деревья
*2200
Срочные новости из неврологии зомби! Оказывается — в отличие от того как считалось ранее — что каждый зомби рождён с одним мозгом, и только потом мозг развивается в сложную структуру. На деле, каждый раз когда зомби съедает один мозг, новый мозг появляется в его нервной систему и сразу соединяется с одним из уже существующих мозгов единственной мозговой связью. Исследователи хотели бы отслеживать мозговую задержку после каждого такого изменения. Вам поставлена задача написать программу, которая по истории эволюции нервной системы конкретного зомби вычислит мозговую задержку на каждом шаге. Выходные данные Выведите n - 1 число — мозговую задержку после добавления мозга с номером k для k = 2, 3, ..., n. | |
![]()
|
|
F2. Древо жизни (средняя)
Деревья
Конструктив
хэши
*2700
Хайди устала расшифровывать древние пророчества и решила отправиться в штаб, чтобы отдохнуть и попытаться снова. Разумеется, она не может выкорчевать дерево и взять его с собой, поэтому он сделала точный рисунок дерева на бумаге. Подумав ещё, она сделала ещё несколько рисунков, которых суммарно получилось n (по числу вершин в Древе Жизни) — кто знает что может случиться? В самом деле, по пути назад Хайди была атакована группой зомби. Хотя она и смогла с ними справиться, рисункам был причинён очень странный урон: с i-й копии пропала вершина с номером i, вместе со всеми своими рёбрами. На каждом рисунке зомби также стёрли номера вершин и перенумеровали оставшиеся n - 1 вершину произвольными числами от 1 до n (по крайней мере, номера вершин всё ещё различны). Более того, рисунки были случайным образом переупорядочены. Теперь Хайди хочет восстановить Древо Жизни по имеющемся у неё описаниям и рисункам (спискам рёбер). Выходные данные Если рисунки Хайди никак не могут описывать одно и то же дерево, то выведите NO. В противном случае выведите слово YES и n - 1 строку с описанием любого дерева, которое могло послужить первоисточником для рисунков Хайди. Для каждого ребра выведите два целых числа — индексы соединённых вершин. Если подходящих решений несколько, разрешается вывести любое. | |
![]()
|
|
F3. Древо жизни (сложная)
Деревья
*3200
Для увеличения олимпиадности задачи зомби забрали все рисунки кроме двух! Помогите Хайди восстановить описание Древа жизни только по двум имеющимся рисункам. Выходные данные Совпадает со средней версией данной задачи. | |
![]()
|
|
A. Лоренцо Фон Маттерхорн
Деревья
Перебор
реализация
Структуры данных
*1500
Барни живет в Нью-Йорке. Нью-Йорк содержит бесконечное число перекрестков, пронумерованных целыми числами, начиная с 1. Известно, что в городе существует дорога, соединяющая перекрестки с номерами i и 2i, и дорога, соединяющая перекрестки с номерами i и 2i + 1, для любого целого положительного i. Все дороги в городе двусторонние. Легко убедиться, что между любыми двумя перекрестками существует ровно один кратчайший путь.  Изначально передвижение по любой дороге является бесплатным, однако, так как намечается «День пощечедавания», в ближайшее время произойдет q последовательных событий: 1. Правительство издает новое правило, определяемое тройкой целых чисел v, u и w, согласно которому стоимость передвижения по всем дорогам на кратчайшем пути от u до v увеличивается на w долларов. 2. Барни идет из перекрестка v до перекрестка u, где хочет обниматься с девушкой. Барни всегда использует кратчайший путь (по количеству посещенных вершин и дорог) для перемещения между перекрестками. Теперь правительству нужна ваша помощь: каждый раз, когда Барни отправляется обниматься с девушкой, вам нужно сообщать, сколько долларов Барни должен заплатить (т.е. суммарную стоимость передвижения по всем дорогам, которые он пройдет). Выходные данные Для каждого события второго типа выведите суммарную стоимость прохождения дорог, которые Барни пройдет на своем пути. Ответы выводите в том же порядке, что и соответствующие им запросы. Примечание В запросах первого примера:  - Перекрестки на пути — 3, 1, 2 и 4.
- Перекрестки на пути — 4, 2 и 1.
- Перекрестки на пути — 3 и 6.
- Перекрестки на пути — 4, 2, 1 и 3. Стоимости прохождения по дорогам равны 32, 32 и 30 в порядке прохождения. Ответ равен 32 + 32 + 30 = 94.
- Перекрестки на пути — 6, 3 и 1.
- Перекрестки на пути — 3 и 7. Стоимость прохождения по дороге между ними равна 0.
- Перекрестки на пути — 2 и 4. Стоимость прохождения по дороге между ними равна 32 (увеличенная на 30 после первого события и на 2 после второго).
| |
![]()
|
|
A. Лоренцо Фон Маттерхорн
Деревья
Перебор
реализация
Структуры данных
*1500
Барни живет в Нью-Йорке. Нью-Йорк содержит бесконечное число перекрестков, пронумерованных целыми числами, начиная с 1. Известно, что в городе существует дорога, соединяющая перекрестки с номерами i и 2i, и дорога, соединяющая перекрестки с номерами i и 2i + 1, для любого целого положительного i. Все дороги в городе двусторонние. Легко убедиться, что между любыми двумя перекрестками существует ровно один кратчайший путь.  Изначально передвижение по любой дороге является бесплатным, однако, так как намечается «День пощечедавания», в ближайшее время произойдет q последовательных событий: 1. Правительство издает новое правило, определяемое тройкой целых чисел v, u и w, согласно которому стоимость передвижения по всем дорогам на кратчайшем пути от u до v увеличивается на w долларов. 2. Барни идет из перекрестка v до перекрестка u, где хочет обниматься с девушкой. Барни всегда использует кратчайший путь (по количеству посещенных вершин и дорог) для перемещения между перекрестками. Теперь правительству нужна ваша помощь: каждый раз, когда Барни отправляется обниматься с девушкой, вам нужно сообщать, сколько долларов Барни должен заплатить (т.е. суммарную стоимость передвижения по всем дорогам, которые он пройдет). Выходные данные Для каждого события второго типа выведите суммарную стоимость прохождения дорог, которые Барни пройдет на своем пути. Ответы выводите в том же порядке, что и соответствующие им запросы. Примечание В запросах первого примера:  - Перекрестки на пути — 3, 1, 2 и 4.
- Перекрестки на пути — 4, 2 и 1.
- Перекрестки на пути — 3 и 6.
- Перекрестки на пути — 4, 2, 1 и 3. Стоимости прохождения по дорогам равны 32, 32 и 30 в порядке прохождения. Ответ равен 32 + 32 + 30 = 94.
- Перекрестки на пути — 6, 3 и 1.
- Перекрестки на пути — 3 и 7. Стоимость прохождения по дороге между ними равна 0.
- Перекрестки на пути — 2 и 4. Стоимость прохождения по дороге между ними равна 32 (увеличенная на 30 после первого события и на 2 после второго).
| |
![]()
|
|
A. Лоренцо Фон Маттерхорн
Деревья
Перебор
реализация
Структуры данных
*1500
Барни живет в Нью-Йорке. Нью-Йорк содержит бесконечное число перекрестков, пронумерованных целыми числами, начиная с 1. Известно, что в городе существует дорога, соединяющая перекрестки с номерами i и 2i, и дорога, соединяющая перекрестки с номерами i и 2i + 1, для любого целого положительного i. Все дороги в городе двусторонние. Легко убедиться, что между любыми двумя перекрестками существует ровно один кратчайший путь.  Изначально передвижение по любой дороге является бесплатным, однако, так как намечается «День пощечедавания», в ближайшее время произойдет q последовательных событий: 1. Правительство издает новое правило, определяемое тройкой целых чисел v, u и w, согласно которому стоимость передвижения по всем дорогам на кратчайшем пути от u до v увеличивается на w долларов. 2. Барни идет из перекрестка v до перекрестка u, где хочет обниматься с девушкой. Барни всегда использует кратчайший путь (по количеству посещенных вершин и дорог) для перемещения между перекрестками. Теперь правительству нужна ваша помощь: каждый раз, когда Барни отправляется обниматься с девушкой, вам нужно сообщать, сколько долларов Барни должен заплатить (т.е. суммарную стоимость передвижения по всем дорогам, которые он пройдет). Выходные данные Для каждого события второго типа выведите суммарную стоимость прохождения дорог, которые Барни пройдет на своем пути. Ответы выводите в том же порядке, что и соответствующие им запросы. Примечание В запросах первого примера:  - Перекрестки на пути — 3, 1, 2 и 4.
- Перекрестки на пути — 4, 2 и 1.
- Перекрестки на пути — 3 и 6.
- Перекрестки на пути — 4, 2, 1 и 3. Стоимости прохождения по дорогам равны 32, 32 и 30 в порядке прохождения. Ответ равен 32 + 32 + 30 = 94.
- Перекрестки на пути — 6, 3 и 1.
- Перекрестки на пути — 3 и 7. Стоимость прохождения по дороге между ними равна 0.
- Перекрестки на пути — 2 и 4. Стоимость прохождения по дороге между ними равна 32 (увеличенная на 30 после первого события и на 2 после второго).
| |
![]()
|
|
A. Лоренцо Фон Маттерхорн
Деревья
Перебор
реализация
Структуры данных
*1500
Барни живет в Нью-Йорке. Нью-Йорк содержит бесконечное число перекрестков, пронумерованных целыми числами, начиная с 1. Известно, что в городе существует дорога, соединяющая перекрестки с номерами i и 2i, и дорога, соединяющая перекрестки с номерами i и 2i + 1, для любого целого положительного i. Все дороги в городе двусторонние. Легко убедиться, что между любыми двумя перекрестками существует ровно один кратчайший путь.  Изначально передвижение по любой дороге является бесплатным, однако, так как намечается «День пощечедавания», в ближайшее время произойдет q последовательных событий: 1. Правительство издает новое правило, определяемое тройкой целых чисел v, u и w, согласно которому стоимость передвижения по всем дорогам на кратчайшем пути от u до v увеличивается на w долларов. 2. Барни идет из перекрестка v до перекрестка u, где хочет обниматься с девушкой. Барни всегда использует кратчайший путь (по количеству посещенных вершин и дорог) для перемещения между перекрестками. Теперь правительству нужна ваша помощь: каждый раз, когда Барни отправляется обниматься с девушкой, вам нужно сообщать, сколько долларов Барни должен заплатить (т.е. суммарную стоимость передвижения по всем дорогам, которые он пройдет). Выходные данные Для каждого события второго типа выведите суммарную стоимость прохождения дорог, которые Барни пройдет на своем пути. Ответы выводите в том же порядке, что и соответствующие им запросы. Примечание В запросах первого примера:  - Перекрестки на пути — 3, 1, 2 и 4.
- Перекрестки на пути — 4, 2 и 1.
- Перекрестки на пути — 3 и 6.
- Перекрестки на пути — 4, 2, 1 и 3. Стоимости прохождения по дорогам равны 32, 32 и 30 в порядке прохождения. Ответ равен 32 + 32 + 30 = 94.
- Перекрестки на пути — 6, 3 и 1.
- Перекрестки на пути — 3 и 7. Стоимость прохождения по дороге между ними равна 0.
- Перекрестки на пути — 2 и 4. Стоимость прохождения по дороге между ними равна 32 (увеличенная на 30 после первого события и на 2 после второго).
| |
![]()
|
|
A. Лоренцо Фон Маттерхорн
Деревья
Перебор
реализация
Структуры данных
*1500
Барни живет в Нью-Йорке. Нью-Йорк содержит бесконечное число перекрестков, пронумерованных целыми числами, начиная с 1. Известно, что в городе существует дорога, соединяющая перекрестки с номерами i и 2i, и дорога, соединяющая перекрестки с номерами i и 2i + 1, для любого целого положительного i. Все дороги в городе двусторонние. Легко убедиться, что между любыми двумя перекрестками существует ровно один кратчайший путь.  Изначально передвижение по любой дороге является бесплатным, однако, так как намечается «День пощечедавания», в ближайшее время произойдет q последовательных событий: 1. Правительство издает новое правило, определяемое тройкой целых чисел v, u и w, согласно которому стоимость передвижения по всем дорогам на кратчайшем пути от u до v увеличивается на w долларов. 2. Барни идет из перекрестка v до перекрестка u, где хочет обниматься с девушкой. Барни всегда использует кратчайший путь (по количеству посещенных вершин и дорог) для перемещения между перекрестками. Теперь правительству нужна ваша помощь: каждый раз, когда Барни отправляется обниматься с девушкой, вам нужно сообщать, сколько долларов Барни должен заплатить (т.е. суммарную стоимость передвижения по всем дорогам, которые он пройдет). Выходные данные Для каждого события второго типа выведите суммарную стоимость прохождения дорог, которые Барни пройдет на своем пути. Ответы выводите в том же порядке, что и соответствующие им запросы. Примечание В запросах первого примера:  - Перекрестки на пути — 3, 1, 2 и 4.
- Перекрестки на пути — 4, 2 и 1.
- Перекрестки на пути — 3 и 6.
- Перекрестки на пути — 4, 2, 1 и 3. Стоимости прохождения по дорогам равны 32, 32 и 30 в порядке прохождения. Ответ равен 32 + 32 + 30 = 94.
- Перекрестки на пути — 6, 3 и 1.
- Перекрестки на пути — 3 и 7. Стоимость прохождения по дороге между ними равна 0.
- Перекрестки на пути — 2 и 4. Стоимость прохождения по дороге между ними равна 32 (увеличенная на 30 после первого события и на 2 после второго).
| |
![]()
|
|
A. Лоренцо Фон Маттерхорн
Деревья
Перебор
реализация
Структуры данных
*1500
Барни живет в Нью-Йорке. Нью-Йорк содержит бесконечное число перекрестков, пронумерованных целыми числами, начиная с 1. Известно, что в городе существует дорога, соединяющая перекрестки с номерами i и 2i, и дорога, соединяющая перекрестки с номерами i и 2i + 1, для любого целого положительного i. Все дороги в городе двусторонние. Легко убедиться, что между любыми двумя перекрестками существует ровно один кратчайший путь.  Изначально передвижение по любой дороге является бесплатным, однако, так как намечается «День пощечедавания», в ближайшее время произойдет q последовательных событий: 1. Правительство издает новое правило, определяемое тройкой целых чисел v, u и w, согласно которому стоимость передвижения по всем дорогам на кратчайшем пути от u до v увеличивается на w долларов. 2. Барни идет из перекрестка v до перекрестка u, где хочет обниматься с девушкой. Барни всегда использует кратчайший путь (по количеству посещенных вершин и дорог) для перемещения между перекрестками. Теперь правительству нужна ваша помощь: каждый раз, когда Барни отправляется обниматься с девушкой, вам нужно сообщать, сколько долларов Барни должен заплатить (т.е. суммарную стоимость передвижения по всем дорогам, которые он пройдет). Выходные данные Для каждого события второго типа выведите суммарную стоимость прохождения дорог, которые Барни пройдет на своем пути. Ответы выводите в том же порядке, что и соответствующие им запросы. Примечание В запросах первого примера:  - Перекрестки на пути — 3, 1, 2 и 4.
- Перекрестки на пути — 4, 2 и 1.
- Перекрестки на пути — 3 и 6.
- Перекрестки на пути — 4, 2, 1 и 3. Стоимости прохождения по дорогам равны 32, 32 и 30 в порядке прохождения. Ответ равен 32 + 32 + 30 = 94.
- Перекрестки на пути — 6, 3 и 1.
- Перекрестки на пути — 3 и 7. Стоимость прохождения по дороге между ними равна 0.
- Перекрестки на пути — 2 и 4. Стоимость прохождения по дороге между ними равна 32 (увеличенная на 30 после первого события и на 2 после второго).
| |
![]()
|
|
A. Лоренцо Фон Маттерхорн
Деревья
Перебор
реализация
Структуры данных
*1500
Барни живет в Нью-Йорке. Нью-Йорк содержит бесконечное число перекрестков, пронумерованных целыми числами, начиная с 1. Известно, что в городе существует дорога, соединяющая перекрестки с номерами i и 2i, и дорога, соединяющая перекрестки с номерами i и 2i + 1, для любого целого положительного i. Все дороги в городе двусторонние. Легко убедиться, что между любыми двумя перекрестками существует ровно один кратчайший путь.  Изначально передвижение по любой дороге является бесплатным, однако, так как намечается «День пощечедавания», в ближайшее время произойдет q последовательных событий: 1. Правительство издает новое правило, определяемое тройкой целых чисел v, u и w, согласно которому стоимость передвижения по всем дорогам на кратчайшем пути от u до v увеличивается на w долларов. 2. Барни идет из перекрестка v до перекрестка u, где хочет обниматься с девушкой. Барни всегда использует кратчайший путь (по количеству посещенных вершин и дорог) для перемещения между перекрестками. Теперь правительству нужна ваша помощь: каждый раз, когда Барни отправляется обниматься с девушкой, вам нужно сообщать, сколько долларов Барни должен заплатить (т.е. суммарную стоимость передвижения по всем дорогам, которые он пройдет). Выходные данные Для каждого события второго типа выведите суммарную стоимость прохождения дорог, которые Барни пройдет на своем пути. Ответы выводите в том же порядке, что и соответствующие им запросы. Примечание В запросах первого примера:  - Перекрестки на пути — 3, 1, 2 и 4.
- Перекрестки на пути — 4, 2 и 1.
- Перекрестки на пути — 3 и 6.
- Перекрестки на пути — 4, 2, 1 и 3. Стоимости прохождения по дорогам равны 32, 32 и 30 в порядке прохождения. Ответ равен 32 + 32 + 30 = 94.
- Перекрестки на пути — 6, 3 и 1.
- Перекрестки на пути — 3 и 7. Стоимость прохождения по дороге между ними равна 0.
- Перекрестки на пути — 2 и 4. Стоимость прохождения по дороге между ними равна 32 (увеличенная на 30 после первого события и на 2 после второго).
| |
![]()
|
|
A. Лоренцо Фон Маттерхорн
Деревья
Перебор
реализация
Структуры данных
*1500
Барни живет в Нью-Йорке. Нью-Йорк содержит бесконечное число перекрестков, пронумерованных целыми числами, начиная с 1. Известно, что в городе существует дорога, соединяющая перекрестки с номерами i и 2i, и дорога, соединяющая перекрестки с номерами i и 2i + 1, для любого целого положительного i. Все дороги в городе двусторонние. Легко убедиться, что между любыми двумя перекрестками существует ровно один кратчайший путь.  Изначально передвижение по любой дороге является бесплатным, однако, так как намечается «День пощечедавания», в ближайшее время произойдет q последовательных событий: 1. Правительство издает новое правило, определяемое тройкой целых чисел v, u и w, согласно которому стоимость передвижения по всем дорогам на кратчайшем пути от u до v увеличивается на w долларов. 2. Барни идет из перекрестка v до перекрестка u, где хочет обниматься с девушкой. Барни всегда использует кратчайший путь (по количеству посещенных вершин и дорог) для перемещения между перекрестками. Теперь правительству нужна ваша помощь: каждый раз, когда Барни отправляется обниматься с девушкой, вам нужно сообщать, сколько долларов Барни должен заплатить (т.е. суммарную стоимость передвижения по всем дорогам, которые он пройдет). Выходные данные Для каждого события второго типа выведите суммарную стоимость прохождения дорог, которые Барни пройдет на своем пути. Ответы выводите в том же порядке, что и соответствующие им запросы. Примечание В запросах первого примера:  - Перекрестки на пути — 3, 1, 2 и 4.
- Перекрестки на пути — 4, 2 и 1.
- Перекрестки на пути — 3 и 6.
- Перекрестки на пути — 4, 2, 1 и 3. Стоимости прохождения по дорогам равны 32, 32 и 30 в порядке прохождения. Ответ равен 32 + 32 + 30 = 94.
- Перекрестки на пути — 6, 3 и 1.
- Перекрестки на пути — 3 и 7. Стоимость прохождения по дороге между ними равна 0.
- Перекрестки на пути — 2 и 4. Стоимость прохождения по дороге между ними равна 32 (увеличенная на 30 после первого события и на 2 после второго).
| |
![]()
|
|
B. Puzzles
Деревья
математика
поиск в глубину и подобное
Теория вероятностей
*1700
Барни живет в USC (United States of Charzeh). USC состоит из n городов с номерами от 1 до n и n - 1 дорог между ними. Города и дороги в USC формируют корневое дерево (и Барни понятия не имеет, почему оно корневое). Корню дерева соответствует город номер 1. Таким образом, начиная в городе 1, по дорогам можно добраться до любого другого города.  Незнакомка завладела сердцем Барни, и теперь он хочет ее найти. Он начинает поиски в городе номер 1, и, (так как он Барни Стинсон, а не кто-то еще), и для поисков использует случайный поиск в глубину. Этот алгоритм можно описать с помощью следующего псевдокода:
let starting_time be an array of length n
current_time = 0
dfs(v):
current_time = current_time + 1
starting_time[v] = current_time
shuffle children[v] randomly (each permutation with equal possibility)
// children[v] is vector of children cities of city v
for u in children[v]:
dfs(u)
Как было сказано ранее, Барни начинает свое путешествие в корне дерева (что эквивалентно вызову dfs(1)). Теперь Барни нужно собрать рюкзак, и поэтому он хочет знать больше о предстоящем путешествии: для каждого города i Барни хочет знать математическое ожидание величины starting_time[i]. Барни — друг Джона Сноу, и поэтому ничего не знает, в связи с чем просит вас ему помочь. Выходные данные В единственной строке выведите n чисел, значение i-го из которых равно математическому ожиданию величины starting_time[i]. Ответ для каждого города будет засчитан, если его абсолютная или относительная погрешность не превосходит 10 - 6. | |
![]()
|
|
E. ...Подожди...
Деревья
снм
Структуры данных
*3000
Барни ищет девушку своей мечты. Он живет в Нью-Йорке, который состоит из n перекрестков с номерами от 1 до n, соединенных n - 1 дорогами. Будем рассматривать Нью-Йорк как ориентированное дерево с корнем в перекрестке 1. В Нью-Йорке живут m девушек, i-я из них живет рядом с перекрестком номер ci, а ее вес исходно равен i килограмм.  Барни считает, что девушка x лучше девушки y тогда и только тогда, когда: вес девушки x строго меньше веса девушки y, либо же они весят одинаково, но номер перекрестка, рядом с которым живет девушка x строго меньше соответствующего номера для девушки y, то есть cx < cy. Таким образом, среди любой пары девушек одна из них всегда лучше другой. В следующие q дней происходит по одному событию в день. Всего типов событий два: - Барни идет от перекрестка v до перекрестка u. На пути он подбирает не более k лучших девушек, которых он еще не приглашал и приглашает к себе домой, чтобы проверить, не является ли кто-то из них девушкой его мечты. Если на пути Барни находятся меньше чем k еще не приглашенных девушек, то Барни приглашает их всех.
- Девушки, живущие возле перекрестков в поддереве перекрестка v (включая сам перекресток v) набирают вес. В результате вес каждой из них увеличивается на k килограмм.
Ваша задача — для каждого события первого типа сообщить Барни номера девушек, которых он пригласит к себе домой во время этого события. Выходные данные Для каждого события первого типа выведите число t и t целых чисел g1, g2, ..., gt в одной строке, означающих, что во время этого события Барни пригласит t девушек, номера которых равны g1, ..., gt в порядке от лучшей к худшей по меркам Барни. Примечание В первом примере из условия:  Описание событий: - Веса девушек в поддереве перекрестка 4 увеличиваются на 3. Номера этих девушек: 1, 3, 5, 4, 7.
- Барни идет от перекрестка 2 до перекрестка 1. На его пути встречаются девушки с номерами 1, 2, 3, 5, 6, 7 и весами 4, 2, 6, 8, 6, 10 соответственно. Он приглашает девушек 2 и 1.
- Барни идет от перекрестка 4 до перекрестка 2. На его пути встречаются девушки с номерами 3, 5, 7 и весами 6, 8, 10 соответственно. Барни приглашает девушку 3.
- Веса девушек в поддереве перекрестка 2 увеличиваются на 10. Неприглашенных девушек это не касается, и ничего интересного не происходит.
- Веса девушек в поддереве перекрестка 1 увеличиваются на 10. Номера этих девушек равны 4, 5, 6, 7.
- Барни идет от перекрестка 2 до перекрестка 4. На его пути встречаются девушки с номерами 5, 7 и весами 18, 20 соответственно. Барни приглашает девушку с номером 5.
- Барни идет от перекрестка 2 до перекрестка 3. На его пути нет девушек.
- Веса девушек в поддереве перекрестка 5 увеличиваются на 2. Единственная девушка там имеет номер 4.
- Веса девушек в поддереве перекрестка 4 увеличиваются на 9. Номера этих девушек: 4, 6, 7.
- Барни идет от перекрестка 3 до перекрестка 5. Единственная девушка на его пути имеет номер 4.
- Барни идет от перекрестка 1 до перекрестка 2. Девушки на его пути имеют номера 6, 7 и веса 16, 29 соответственно.
| |
![]()
|
|
B. Исправление дерева
графы
Деревья
Конструктив
поиск в глубину и подобное
снм
*1700
Дерево — это неориентированный связный граф без циклов. Рассмотрим корневое неориентированное дерево, состоящее из n вершин, пронумерованных от 1 до n. Существует несколько способов представлять такие деревья. Одним из наиболее популярных является массив предков, состоящий из n чисел p1, p2, ..., pn, где pi означает предка вершины i (в рамках данной задачи корень дерева считается предком самого себя).  Для данного корневого дерева массив p равен [2, 3, 3, 2]. Для данного корневого дерева массив p равен [2, 3, 3, 2]. По данной последовательности p1, p2, ..., pn легко восстановить дерево: - Существует ровно один индекс r, такой что pr = r. Вершина r является корнем дерева.
- Для всех остальных n - 1 вершины i существует ребро между вершинами i и pi.
Последовательность p1, p2, ..., pn является корректной, если описанная выше процедура определяет некоторое (произвольное) корневое дерево. Например, для n = 3 последовательности (1,2,2), (2,3,1) и (2,1,3) не являются корректными. Вам дана последовательность a1, a2, ..., an, не обязательно являющаяся корректной. Вам требуется изменить минимальное количество элементов, чтобы последовательность стала корректной. Выведите минимальное необходимое количество изменений и пример любого ответа, который можно получить с их помощью. Если существует несколько корректных последовательностей, достижимых за минимальное количество изменений, то разрешается вывести любую. Выходные данные В первой строке выведите минимальное количество изменений, которое надо сделать, чтобы получить корректную последовательность. Во второй строке выведите любую корректную последовательность, которая может быть получена из (a1, a2, ..., an) за минимальное количество изменений. Если существует несколько таких последовательностей, то выведите любую. Примечание В первом примере достаточно изменить один элемент. В приведённом примере вывода последовательность представляет корневое дерево с корнем в вершине 4 (потому что p4 = 4), которое можно увидеть на левом рисунке. Одним из корректных решений будет являться последовательность 2 3 3 2, определяющая дерево с корнем в вершине 3 (правый рисунок). На обоих рисунках корни выделены красным.  Во втором примере данная во входных данных последовательность уже является корректной. | |
![]()
|
|
E. Информационная реформа
Деревья
дп
реализация
*2700
Несмотря на то, что уже XXI век на дворе, СМИ в Моржландии не сильно распространены. Оповещение городов ведется с помощью гонцов которые могут путешествовать только по дорогам. Сеть дорог в Моржландии устроена так, что от каждого города до любого другого можно добраться ровно одним способом, и длины дорог равны между собой. Решением правителя Северного Полюса было принято провести информационную реформу. Было решено выбрать несколько городов и назначить их областными центрами. На обслуживание областного центра приходится тратить k рыбликов (местная валюта) в год. Считается, что областной центр всегда имеет информацию о последних новостях. Каждому городу, не являющемуся областным центром, было принято решение назначить областной центр, который будет отвечать за информированность этого города. В таком случае затраты на обслуживание равняются dlen рыбликам в год, где len — расстояние от города до соответствующего областного центра, измеряемое в количестве дорог, которые надо проехать. Ваша задача минимизировать расходы на проведение реформы. Выходные данные В первой строке выведите минимальное количество рыбликов, затрачиваемых на обслуживание за один год. Во второй строке выведите n чисел, где i-ое число будет обозначать номер областного центра, который был назначен i-ому городу. Если i-й город сам является областным центром, то следует вывести число i. Если решений несколько, выведите любое. | |
![]()
|
|
B. Соединяя университеты
графы
Деревья
дп
поиск в глубину и подобное
*1800
Древляндия — это страна в которой n городов, соединенных n - 1 двусторонней дорогой так, что из любого города можно проехать в любой другой по дорогам. В Древляндии 2k университетов, расположенных в разных городах. Недавно Президент подписал указ о соединении университетов высокоскоростной сетью. Министерство образования по своему поняло этот указ, решив что для экономии усилий достаточно каждый университет соединить кабелем с некоторым другим. Формально, указ окажется выполнен! Для того, чтобы в бюджет заложили максимальную сумму в министерстве решили так разбить университеты на пары, что суммарная длина потраченного кабеля будет максимальна. Иными словами, сумма расстояний между университетами в k парах должна быть как можно больше. Помогите министерству найти искомую максимальную сумму расстояний. Конечно, каждый университет должен попасть ровно в одну пару. Считайте, что все дороги равны по длине между собой и имеют длины равные 1. Выходные данные Выведите искомую максимальную сумму расстояний при делении университетов на пары. Примечание На рисунке ниже представлено одно из возможных оптимальных разбиений на пары для первого тестового примера. Если соединить кабелем университеты номер 1 и 6 (отмечены красным цветом) и университеты номер 2 и 5 (отмечены синим цветом), то суммарное расстояние будет равно 6, что является максимальной суммой для данного примера.  | |
![]()
|
|
E. Железный человек
геометрия
Деревья
Структуры данных
*3300
Тони Старк играет со своими костюмами, которые теперь оснащены автопилотом. Он живёт в Малибу. Малибу представляет из себя n перекрёстков, пронумерованных целыми числами от 1 до n, соединённых с помощью n - 1 двусторонних дорог таким образом, что от любого перекрёстка можно добраться до любого другого, используя данные дороги (да, граф Малибу является деревом). У Тони есть m костюмов, для каждого из которых разработан специальный план. Костюм номер i появится в момент времени ti на перекрёстке vi и будет двигаться в направлении перекрёстка ui по кратчайшему пути со скоростью ci дорог в секунду (пересечение перекрёстка происходит мгновенно), а затем исчезнет, как только достигнет перекрёстка ui. Если костюм достигает перекрёстка ui непосредственно в момент времени q, то он доступен там в этот момент времени, но не позже. Костюмы передвигаются непрерывно, например, если vi ≠ ui, то в момент времени  костюм находится на середине дороги. Обратите внимание, что vi = ui означает, что костюм будет доступен на перекрёстке vi только в момент времени ti и затем исчезнет. костюм находится на середине дороги. Обратите внимание, что vi = ui означает, что костюм будет доступен на перекрёстке vi только в момент времени ti и затем исчезнет. Если в какой-либо момент времени два костюма оказываются в одной точке (это может быть как на перекрёстке, так и на какой-нибудь дороге непосредственно после появления или перед исчезновением), то там происходит взрыв. Тони просит вас определить момент самого первого взрыва (если это вообще произойдёт). Выходные данные Если никаких взрывов так и не произойдёт, то выведите -1 в первой и единственной строке входных данных. В противном случае выведите момент времени первого взрыва. Ваш ответ будет считаться правильным, если его относительная или абсолютная погрешность не превзойдёт 10 - 6. | |
![]()
|
|
D. Мультимножество Василия
Бинарный поиск
битмаски
Деревья
Структуры данных
*1800
У автора уже закончились истории про Василия, поэтому он просто написал формальную постановку задачи. У вас есть q запросов и мультимножество A, изначально содержащее только число 0. Запросы бывают трёх видов: - «+ x» —добавить в мультимножество A число x.
- «- x» —удалить одно вхождение числа x из мультимножества A. Гарантируется, что хотя бы одно число x в этот момент присутствует в мультимножестве.
- «? x» —вам даётся число x, требуется вычислить
 , то есть максимальное значение побитового исключающего ИЛИ (также известно как XOR) числа x и какого-нибудь числа y из мультимножества A. , то есть максимальное значение побитового исключающего ИЛИ (также известно как XOR) числа x и какого-нибудь числа y из мультимножества A. Мультимножество — это множество, в котором разрешается несколько одинаковых элементов. Выходные данные На каждый запрос типа «?» выведите единственное целое число — максимальное значение побитового исключающего ИЛИ для числа xi и какого-либо числа из мультимножества A. | |
![]()
|
|
C. Центроиды
графы
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
Структуры данных
*2300
Деревом называется связный неориентированный граф без циклов. Вам дано дерево, состоящее из n вершин, тогда центроидом дерева называется любая вершина, такая что при её удалении размер любой компоненты связности не будет превосходить  . . Вам дано дерево размера n и разрешается выполнить не более одной операции перестановки ребра. Перестановкой ребра называется удаление одного ребра из дерева (без удаления инцидентных вершин) и добавление одного нового ребра (без добавления новых вершин) таким образом, что граф остаётся деревом. Требуется для каждой вершины дерева определить, правда ли, что её можно сделать центроидом, выполнив не более одной перестановки ребра. Выходные данные Выведите n чисел, i-е из которых равно 1, если i-ю вершину можно сделать центроидом, выполнив не более одной перестановки ребра, и 0 в противном случае. Примечание В первом тестовом примере любую вершину можно сделать центроидом. Например, чтобы сделать центроидом вершину 1, нужно заменить ребро (2, 3) на ребро (1, 3). | |
![]()
|
|
C. Цифровое дерево
Деревья
поиск в глубину и подобное
разделяй и властвуй
снм
*2700
У Кодера ZS'а есть большое дерево. Его можно представить как неориентированный связный граф из n вершин, пронумерованных от 0 до n - 1, и n - 1 ребер между ними. На каждом ребре записана одна ненулевая цифра. Однажды, Кодер ZS заскучал и решил исследовать некоторые параметры дерева. Он выбрал целое положительное M, которое является взаимно простым с 10, т.е.  . . ZS считает упорядоченную пару различных вершин (u, v) интересной, когда если бы он проследовал по кратчайшему пути от вершины u до вершины v и выписывал цифры, которые он встречает на своем пути, в том же порядке, он получил бы десятичную запись целого числа, делящегося на M. Формально, ZS считает упорядоченную пару различных вершин (u, v) интересной, если верно следующее: - Пусть a1 = u, a2, ..., ak = v — последовательность вершин на кратчайшем пути от u до v в порядке их встречи;
- Пусть di (1 ≤ i < k) — цифра, записанная на ребре между вершинами ai и ai + 1;
- Целое число
 делится на M. делится на M. Помогите Кодеру ZS'у найти количество интересных пар! Выходные данные Выведите единственное целое число — количество интересных (по мнению Кодера ZS'а) пар. Примечание В первом примере из условия интересными являются пары (0, 4), (1, 2), (1, 5), (3, 2), (2, 5), (5, 2), (3, 5). Числа, образуемые этими парами — 14, 21, 217, 91, 7, 7, 917 соответственно, все они кратны 7. Заметьте, что (2, 5) и (5, 2) считаются различными. 
Во втором примере из условия интересными являются пары (4, 0), (0, 4), (3, 2), (2, 3), (0, 1), (1, 0), (4, 1), (1, 4), и 6 из этих пар дают число 33, а 2 из них дают число 3333, и все они кратны 11. 
| |
![]()
|
|
D. Андрей и задача по химии
Деревья
дп
хэши
*2900
На уроке химии Андрей узнал, что насыщенные углеводороды (алканы) вступают в реакцию радикального хлорирования. При этом образуется смесь различных хлорпроизводных. Андрей — очень любопытный мальчик, поэтому его заинтересовало, сколько существует различных монохлорпроизводных для заданного алкана. Для небольших молекул Андрей легко справился с этой задачей, но с большими молекулами у него возникли трудности, поэтому он попросил вас решить эту задачу. Формально, вам дано дерево, состоящее из n вершин, такое что степень каждой вершины не превосходит 4. Требуется посчитать количество различных с точностью до изоморфизма деревьев, которые можно получить путем добавления к данному дереву одной вершины и одного ребра так, чтобы граф оставался деревом и степень каждой вершины не превосходила 4. Два дерева называются изоморфными, если существует биекция f(v), такая что вершины u и v соединены ребром, если и только если вершины f(v) и f(u) соединены ребром. Выходные данные Выведите одно число — ответ на задачу. Примечание В первом примере к каждой вершине можно добавить новую, но при этом деревья, полученные добавлением новой вершины к вершинам 1, 3, 4 будут изоморфными, поэтому ответ 2. Во втором примере к первой вершине добавить новую вершину нельзя так как степень вершины уже равна четырем. А все деревья, полученные добавлением новой вершины к вершинам 2, 3, 4, 5 будут изоморфными, поэтому ответ 1. | |
![]()
|
|
D. Генерация наборов
Бинарный поиск
Деревья
жадные алгоритмы
поиск в глубину и подобное
Строки
Структуры данных
*1900
Вам задан набор Y из n различных целых положительных чисел y1, y2, ..., yn. Назовём набор X из n различных целых положительных чисел x1, x2, ..., xn генератором для Y, если из набора X можно получить набор Y, применяя к элементам набора X следующие две операции: - Умножить произвольное число xi на два, то есть заменить xi на 2·xi.
- Умножить произвольное число xi на два и прибавить единицу, то есть заменить xi на 2·xi + 1.
Обратите внимание, не требуется, чтобы все числа в наборе X были различны после выполнения каждой операции. Наборы в данной задаче сравниваются как множества чисел. Другими словами, два набора различных чисел X и Y совпадают, если, выписав оба набора в отсортированном порядке, мы получим одинаковые массивы. Заметьте, что любой набор чисел (или его перестановка) сам является одним из своих генераторов. По заданному набору Y найдите его генератор, в котором максимальное число минимально. Выходные данные Выведите n чисел — генератор для заданного набора Y, в котором максимальное число как можно меньше. Если подходящих наборов несколько, разрешается вывести любой из них. | |
![]()
|
|
F. Равномерно ветвистые деревья
Деревья
дп
Комбинаторика
*2700
Деревом называется связный граф без циклов. Два дерева, состоящих из n вершин, называются изоморфными, если существует перестановка p: {1, ..., n} → {1, ..., n} такая, что ребро (u, v) присутствует в первом дереве тогда и только тогда, когда ребро (pu, pv) присутствует во втором. Вершина дерева называется внутренней, если её степень больше либо равна двум. Посчитайте количество различных неизоморфных деревьев, состоящих из n вершин, таких что степень каждой внутренней вершины в точности равна d. Ответ выведите по заданному простому модулю mod. Выходные данные Выведите одно число — количество деревьев, удовлетворяющих условию задачи, взятое по модулю mod. | |
![]()
|
|
G. Xor-матическое число графа
битмаски
графы
Деревья
математика
теория чисел
*2600
Вам дан неориентированный граф, состоящий из n вершин и m ребер. На каждом ребре написано целое неотрицательное число. Назовем тройку чисел (u, v, s) интересной, если 1 ≤ u < v ≤ n и между вершинами u и v существует путь (необязательно простой, то есть может содержать какие-то вершины и рёбра по несколько раз), такой что xor чисел, написанных на рёбрах этого пути, равен s. При вычислении значения s для какого-нибудь пути, каждое ребро участвует в xor столько раз, сколько раз оно встречает на данном пути. Нетрудно доказать, что таких троек конечное количество. Посчитайте сумму по модулю 109 + 7 значений числа s по всем интересным тройкам. Выходные данные Выведите единственное число, равное искомой сумме по модулю 109 + 7. Примечание В первом примере существует 6 интересных троек: - (1, 2, 1)
- (1, 3, 2)
- (1, 4, 3)
- (2, 3, 3)
- (2, 4, 2)
- (3, 4, 1)
Искомая сумма равна 1 + 2 + 3 + 3 + 2 + 1 = 12. В втором примере существует 12 интересных троек: - (1, 2, 1)
- (2, 3, 2)
- (1, 3, 3)
- (3, 4, 4)
- (2, 4, 6)
- (1, 4, 7)
- (1, 4, 8)
- (2, 4, 9)
- (3, 4, 11)
- (1, 3, 12)
- (2, 3, 13)
- (1, 2, 14)
Искомая сумма равна 1 + 2 + 3 + 4 + 6 + 7 + 8 + 9 + 11 + 12 + 13 + 14 = 90. | |
![]()
|
|
F. Недовольство автомобилистов
графы
Деревья
снм
Структуры данных
*2200
В одном королевстве имеется n городов и m двусторонних дорог. Каждая дорога соединяет пару городов, причём для каждой дороги известен уровень недовольства ею автомобилистами — величина wi. Для каждой дороги известна величина ci — сколько надо потратить лямзиков, чтобы уменьшить уровень недовольства этой дорогой на единицу. Таким образом, чтобы уменьшить недовольство i-й дорогой на k, надо потратить k·ci лямзиков. При этом допустимо, чтобы недовольство стало нулевым или даже отрицательным. В соответствии с приказом короля, необходимо выбрать n - 1 дорогу, сделав их главными дорогами. Должно выполняться важное условие: из любого города должно быть возможно проехать в любой другой по главным дорогам. У министерства дорог есть бюджет S лямзиков на проведение реформы. Министерство планирует потратить этот бюджет на ремонт некоторых дорог (то есть уменьшить недовольство ими), а уже затем выбрать n - 1 главную дорогу. Помогите потратить бюджет так, а затем и произвести выбор главных дорог, чтобы суммарное недовольство главными дорогами было как можно меньше. При этом величина недовольства некоторыми дорогами может стать отрицательной. Не обязательно тратить весь бюджет S полностью. Гарантируется, что из любого города королевства можно добраться по дорогам в любой другой город королевства. Каждая дорога в королевстве — двусторонняя. Выходные данные В первой строке выведите K — минимально возможное суммарное недовольство главными дорогами. В следующих n - 1 строках выведите по два целых числа x, vx — означающих, что дорога x является главной, и дорога x после реформы имеет уровень недовольства vx. Считайте, что дороги пронумерованы от 1 до m в порядке их задания во входных данных. Номера рёбер можно выводить в произвольном порядке. Если решений несколько, выведите любое. | |
![]()
|
|
E. Антон и дерево
Деревья
дп
поиск в глубину и подобное
*2100
Антон посадил в своём саду дерево. Напоминаем, что дерево — это связный неориентированный граф, не содержащий циклов. Вскоре дерево выросло. Каждая из его n вершин оказалась покрашена либо в чёрный, либо в белый цвет. Однако, Антону не нравятся разноцветные деревья, и поэтому он решил покрасить дерево так, чтобы оно было либо полностью белым, либо полностью чёрным. Для изменения цвета вершин дерева Антону доступна только одна операция, обозначим её как paint(v), где v — некоторая вершина дерева. Эта операция перекрашивает в противоположный цвет все такие вершины u, что на кратчайшем пути от u до v все вершины покрашены в один цвет (при этом сами вершины u и v также учитываются). Например, дерево  после применения операции paint(3) станет следующим:  Антону стало интересно, за какое минимальное количество операций покраски ему удастся сделать так, чтобы дерево стало покрашено в один цвет. Помогите ему найти это число! Выходные данные В единственной строке выходных данных выведите единственное число — минимальное количество операций покраски, которое необходимо Антону, чтобы дерево стало либо полностью белым, либо полностью черным. Примечание В первом примере дерево такое же, как и на рисунке в условии. Если применить к нему сначала операцию paint(3), потом операцию paint(6), то оно будет полностью покрашено в черный цвет, поэтому ответ — 2. Во втором примере дерево уже и так полностью покрашено в белый цвет, и к нему не придется применять ни одной операции покраски, поэтому ответ — 0. | |
![]()
|
|
E. Остап и дерево
Деревья
дп
*2500
Остап поселился в предместье Рио-де-Жанейро и сразу же начал выращивать у себя в саду дерево. Напомним, деревом называется связный неориентированный граф без циклов. Сейчас в дереве Остапа n вершин. Он хочет покрасить некоторые вершины дерева в чёрный цвет таким образом, чтобы для любой вершины дерева u существовала хотя бы одна чёрная вершина v, удалённая от неё не более, чем на k. Расстоянием между двумя вершинами в дереве называется минимальное количество рёбер на пути между ними. Поскольку количество способов покрасить дерево соответствующим образом может быть достаточно велико, Остап попросил вас вычислить его по модулю 109 + 7. Два способа покрасить дерево считаются различными, если существует вершина, которая покрашена в чёрный цвет в одном способе и не покрашена в другом. Выходные данные Выведите одно целое число — остаток от деления количества способов корректно покрасить вершины дерева в чёрный цвет на 1 000 000 007 (109 + 7). Примечание В первом примере необходимо покрасить в чёрный цвет обе вершины дерева. Во втором примере достаточно покрасить только одну из двух, поэтому ответ 3: покрасить только вершину 1, покрасить только вершину 2, покрасить и вершину 1, и вершину 2. В третьем примере подходящими будут покраски следующих множеств вершин: {1, 3}, {1, 4}, {2, 3}, {2, 4}, {1, 2, 3}, {1, 2, 4}, {1, 3, 4}, {2, 3, 4}, {1, 2, 3, 4}. | |
![]()
|
|
B. Алёна и дерево
Бинарный поиск
графы
Деревья
поиск в глубину и подобное
Структуры данных
*1900
У Алёны есть дерево из n вершин. Корень дерева — вершина с номером 1. В вершину с номером i Алёна записала положительное целое число ai. Также, девочка записала на каждом ребре дерева какое-то положительное целое число (возможно, различные числа на различных ребрах). Определим dist(v, u) как сумму чисел, записанных на ребрах, которые лежат на кратчайшем пути из v в u. Вершина дерева v контролирует вершину u (v ≠ u), если u лежит в поддереве v и dist(v, u) ≤ au. Девочка хочет поселиться в некоторой вершине дерева. Для этого она хотела бы знать для каждой вершины v, сколько в дереве есть вершин u таких, что вершина v контролирует вершину u. Выходные данные Выведите в одной строке n чисел — i-е из этих чисел должно равняться количеству вершин, которое контролируется вершиной с номером i. Примечание В тесте из условия вершина 1 контролирует вершину 3, также вершина 3 контролирует вершину 5 (обратите внимание, отсюда не следует, что вершина 1 контролирует вершину 5). | |
![]()
|
|
D. Помеченное буквами дерево Arpa и забавные пути Mehrdad
Деревья
поиск в глубину и подобное
Структуры данных
*2900
Если вдруг кто-то пропустил, у нас в стране Arpa чудесные девушки. У Arpa есть подвешенное дерево (связный ациклический граф), состоящее из n вершин. Вершины пронумерованы от 1 до n, вершина 1 является корнем. На каждом ребре дерева написана некоторая буква. Mehrdad — фанат самовлюбленных вещей. Он называет строку самовлюбленной, если возможно переставить местами символы строки так, чтобы она стала палиндромом.  Он спросил Arpa про каждую вершину v, какая наибольшая длина среди простых путей в поддереве вершины v таких, что буквы на пути образуют самовлюбленную строку. Выходные данные Выведите n чисел. i-е из них должно быть равно наибольшей длине среди простых путей в поддереве вершины i таких, что буквы на пути образуют самовлюбленную строку. | |
![]()
|
|
D. Хлоя и приятные подарки
графы
Деревья
дп
поиск в глубину и подобное
*1800
Щедрые спонсоры олимпиады, в которой участвуют Хлоя и Владик, разрешили всем участникам выбрать себе приз самостоятельно. Так как близится Новый год, спонсоры решили нарядить новогоднюю елку своими призами. Они взяли n подарков для участников и на каждом подарке написали его уникальный номер (целое число от 1 до n). Подарок с номером i характеризуется целым числом ai — приятностью подарка. Приятность подарка может быть как положительным, так и отрицательным числом, а так же нулем. Подарок с номером 1 отправился на вершину елки. Все остальные подарки привязываются веревкой к одному из других подарков так, что каждый подарок в итоге оказывается подвешенным к первому подарку, возможно цепочкой из веревок и других подарков. Более формально, подарки формируют корневое дерево из n вершин. Раздача подарков происходит таким образом: очередной участник подходит к елке, выбирает любой подарок из оставшихся и отрезает веревку, которой был привязан этот подарок. Обратите внимание, что все веревки, которыми другие подарки были привязаны к подарку, выбранному участником, не отрезаются. Таким образом, участник забирает выбранный подарок, а так же все множество подарков, подвешенное к нему, возможно цепочкой из веревок и других подарков. Наши герои, Хлоя и Владик, поделили между собой на олимпиаде первое место и они, вопреки правилам раздачи подарков, будут выходить за подарком вместе! Чтобы не поссориться, они решили выбрать себе два таких различных подарка, что множества подарков, подвешенное к ним цепочкой из веревок и других подарков, не имеют пересечения. Иначе говоря, не должно быть подарка, который был бы подвешен к подарку Хлои и подарку Владика одновременно. Из всех возможных вариантов они выберут такую пару подарков, что сумма приятностей всех подарков, которые достанутся им после того, как они отрежут веревки, максимальна. Найдите максимальную сумму приятностей, которую могут забрать себе Хлоя и Владик. Если это по каким-то причинам невозможно, выведите Impossible. Выходные данные Если Хлоя и Владик смогут выбрать себе подарки, не поссорившись, выведите одно число — максимальную сумму приятностей, которую они смогут забрать в таком случае. Иначе выведите строку Impossible. | |
![]()
|
|
G. Новые дороги
графы
Деревья
Конструктив
*2100
В Берляндии есть n городов, каждый из которых имеет свой уникальный номер — целое число от 1 до n, причём столица имеет номер 1. В Берляндии в настоящий момент совсем плохо с дорогами — их нет. По этой причине было решено построить n - 1 дорогу так, чтобы между каждой парой городов существовал ровно один путь по дорогам. В плане на постройку дорог было указано t чисел a1, a2, ..., at, где t равно расстоянию от столицы до самого удаленного города, если добираться до него только по новым дорогам, а ai равно количеству городов, которые должны находиться на расстоянии i от столицы. Под расстоянием понимается количество дорог, которые нужно преодолеть на пути от одного города до другого. Также было решено, что среди всех городов, исключая столицу, должно быть ровно k городов, к которым примыкает ровно одна дорога. Такие города являются тупиковыми и не могут быть экономически привлекательными. При подсчете таких городов столица не учитывается независимо от количества примыкающих дорог к ней. Перед вами стоит задача предложить план постройки дорог, удовлетворяющий всем описанным условиям, либо сообщить, что это невозможно. Выходные данные Если построить дороги, удовлетворяющие всем условиям, невозможно, выведите -1. В противном случае, выведите в первую строку одно целое число n — количество городов в Берляндии. В следующей n - 1 строке выведите по два целых числа — номера городов, которые соединяет очередная дорога. Каждая дорога должна быть выведена ровно один раз. Порядок вывода дорог и соединяемых дорогой городов неважен. Если решений несколько, выведите любое. Помните, что столица имеет номер 1. | |
![]()
|
|
F. Санта-Клаусы и чемпионат по футболу
графы
Деревья
Конструктив
поиск в глубину и подобное
*2300
В Древляндии n городов, соединенных между собой n - 1 дорогой так, что из каждого города можно по дорогам добраться до любого другого. В следующем году в Древляндии пройдет чемпионат по футболу среди команд, состоящих из Санта-Клаусов. Всего в чемпионате примут участие 2k команд из 2k различных городов. На первом этапе команды разобьются на k пар, каждая пара сыграет два матча: один в городе первой команды из пары, другой — в городе второй команды из пары. Таким образом, в каждом из 2k городов участников будет проведен ровно один матч. Однако как разбить команды на пары, пока не решено. Перед организаторами также стоит задача определить, в каких городах расселить участников на время чемпионата. Организаторы хотят поселить команды в как можно меньшее число городов, чтобы Санта-Клаусы побольше общались друг с другом и обменивались опытом. Никакая из команд не хочет чересчур много передвигаться во время турнира, поэтому если команда будет играть в городах u и v, то жить она хочет в городе, лежащем на кратчайшем пути из u в v (в том числе, возможно, в городе u или городе v). Также команды из одной пары необходимо расселить в одном городе. Таким образом, организаторы турнира хотят разбить 2k команд на пары и расселить участников по минимально возможному числу m городов так, чтобы команды из одной пары жили в одном городе, и чтобы для каждой команды город, в котором она будет жить во время турнира, лежал на кратчайшем пути между городами, в которых она будет играть. Выходные данные В первой строке выведите целое число m — минимальное количество городов, по которым можно расселить участников. Во второй строке выведите m различных чисел чисел d1, d2, ..., dm (1 ≤ di ≤ n) — номера городов, в которых будут жить участники. Далее выведите k строк. В j-й из них выведите 3 числа uj, vj, xj, где uj и vj — города, в которых будет играть j-я пара, а xj — номер города, в котором будут жить команды этой пары. Каждое из чисел c1, c2, ..., c2k должно встретиться среди чисел uj и vj ровно один раз. Каждое из чисел xj должно принадлежать множеству {d1, d2, ..., dm}. Если оптимальных ответов несколько, выведите любой из них. Примечание В первом тесте из условия можно расселить всех участников в один город с номером 2. Разбить на пары можно любым образом, при этом все условия всегда будут выполнены, т. к. город 2 лежит на кратчайшем пути между любой парой городов из множества {2, 4, 5, 6}. | |
![]()
|
|
D. Максимальная сумма
Деревья
дп
жадные алгоритмы
математика
реализация
Структуры данных
*2000
Ахмед и Мостафа участвуют в соревнованиях по программированию уже много лет. Однажды их тренер Фегла попросил их решить одну непростую задачу. Конечно же, Ахмед справился, а Мостафа — нет. Эта задача похожа на классическую задачу, но имеет другую структуру и ограничения. В классической задаче дан массив целых чисел, требуется найти такой подмассив данного массива, что сумма чисел в нем максимальная возможная. Подмассив — последовательность из одного или нескольких подряд идущих элементов данного массива. Но в данной задаче дано n маленьких массивов. Из них получается один большой массив — конкатенацией одного или нескольких экземпляров маленьких массивов (каждый маленький массив может встречаться в большом более одного раза). Большой массив задан в виде массива индексов (1-индексированных) маленьких массивов. Конкатенация должна быть выполнена в том же порядке, в котором числа записаны в массиве. После конкатенации на большом массиве решается описанная выше классическая задача. Например, пусть маленькие массивы — {1, 6, -2}, {3, 3} и {-5, 1}. Индексы большого массива — {2, 3, 1, 3}. Так, после конкатенации большой массив будет {3, 3, -5, 1, 1, 6, -2, -5, 1}. В этом примере максимальная сумма равна 9. Помогите Мостафе решить эту задачу. Выходные данные Выведите одно число — наибольшую сумму на каком-либо подмассиве сформированного большого массива. Учтите, что подмассив суммирования не может быть пустым, то есть он должен включать в себя хотя бы один элемент. Пожалуйста, не используйте спецификатор %lld для записи 64-х битовых чисел на С++. Рекомендуется использовать поток cout (также вы можете использовать спецификатор %I64d). | |
![]()
|
|
F. Новый год и поиск корня
Деревья
интерактив
Конструктив
реализация
*2800
Это интерактивная задача. В секции «Протокол взаимодействия» вы найдёте информацию о том, как сбрасывать буфер вывода (делать операцию 'flush'). Новогоднее дерево высоты h является полным двоичным деревом, вершины которого некоторым образом пронумерованы от 1 до 2h - 1. В данной задаче мы будем считать, что h не меньше 2. Рисунок ниже изображает пример новогоднего дерева высоты 3:  Полярные медведи очень любят украшать новогодние деревья, и Лимак конечно же не исключение. Чтобы украсить дерево, ему требуется сначала найти его корень, то есть вершину у которой ровно два соседа (предполагая, что h ≥ 2). Маленькому медвежонку будет крайне непросто это сделать, так как он не может окинуть взглядом всё дерево. Сможете ли вы ему помочь? Входных данные содержат t тестовых примеров. В начале каждого тестового примера на ввод подаётся единственное число h. Далее вы можете сделать не более 16 запросов в формате «? x», где x — некоторое целое число от 1 до 2h - 1 включительно. В качестве ответа вам будет дан список всех соседей вершины x (подробнее смотрите секцию «Протокол взаимодействия»). Например если про дерево с картинки выше сделать запрос «? 1», то в качестве ответа будут получены 3 его соседа: 4, 5 и 7. Ваша задача — найти индекс корневой вершины y и сообщить его в формате запроса «! y». Вы сможете считать значение h для следующего тестового примера только после вывода ответа для предыдущего примера и выполнения операции 'flush'. В каждом тестовом примере дерево фиксировано с самого начала и не изменяется в зависимости от запросов. Протокол взаимодействия Чтобы запросить список соседей вершины x выведите «? x» (без кавычек) в отдельной строке. Не забудьте вывести символ конца строки и выполнить операцию 'flush' чтобы получить ответ. Ответ на запрос состоит из двух строк. В первой из них записано целое число k (1 ≤ k ≤ 3) — количество соседей вершины x. Во второй строке записаны k различных целых чисел t1, ..., tk (1 ≤ t1 < ... < tk ≤ 2h - 1) — индексы вершин смежных вершине x, перечисленные в порядке возрастания. Сделав не более 16 запросов для одного тестового примера вы должны сообщить y — индекс корня дерева. Выведите «! y» (без кавычек) и символ конца строки, после чего выполните операцию 'flush'. В каждом тестовом примере дерево фиксировано с самого начала и не изменяется в зависимости от запросов. Если вы ничего не выведите или забудете сделать операцию 'flush', то можете получить вердикт Idleness Limit Exceeded. Для сброса буфера вывода (то есть для операции 'flush') сразу после вывода числа или ответа и перевода строки можно сделать: - fflush(stdout) в языке C++;
- System.out.flush() в Java;
- stdout.flush() в Python;
- flush(output) в Pascal;
- смотрите документацию для других языков.
Если в любой момент ваша программа считает h = 0 или k = 0 она должна немедленно завершиться с нулевым кодом возврата (например, вызовом exit(0)). Это означает, что проверяющая программа обнаружила некорректный запрос или вывод и вывела 0, так как не может дальше обрабатывать запросы. В этом случае вы получите вердикт «Wrong Answer», но если ваша программа не завершится после считывания h = 0 или k = 0 то это может привести к получению вердиктов «Runtime Error», «Time/Memory limit exceeded» или любых других поскольку ваша программа продолжит считывать мусор из уже закрытого потока ввода. Взломы. Для взломов не разрешается использовать мультитест. Чтобы совершить взлом, используйте следующий формат входных данных: В первой строке следует записать одно целое число t равное 1. Во второй строке должно быть записано одно целое число h. В каждой из последующих 2h - 2 строк должна быть записана пара целых чисел ai и bi (1 ≤ ai, bi ≤ 2h - 1), означающая что две вершины с данными индексами соединены ребром. Выведенный набор рёбер должен задавать полное двоичное дерево высоты h. Разумеется, это описание дерева не будет доступно взламываемому участнику. Примечание В первом примере дерево соответствует изображённому на рисунке в условии. Второй пример состоит из двух наборов входных данных. Дерево в первом из них имеет высоту 2 и содержит 3 вершины. Дерево во втором примере имеет высоту 4 и содержит 15 вершин. Оба дерева изображены на рисунке ниже.  | |
![]()
|
|
E. Даша и циклическая таблица
битмаски
бпф
Деревья
Перебор
Строки
*2600
Даша увлекается всякими сложными головоломками — кубик Рубика 3 × 3 × 3, 4 × 4 × 4, 5 × 5 × 5 и тому подобное. На этот раз у неё есть циклическая таблица размера n × m клеток из строчных букв латинского алфавита. Каждая клетка таблицы имеет координаты (i, j) (0 ≤ i < n, 0 ≤ j < m). Цикличность этой таблицы заключается в том, что правее клетки (i, j) находится клетка  , а ниже находится клетка , а ниже находится клетка  . . Также у Даши есть шаблон. Шаблоном является нециклическая таблица размера r × c клеток. Каждая клетка шаблона является либо строчной буквой латинского алфавита либо символом вопроса. Каждая клетка шаблона имеет координаты (i, j) (0 ≤ i < r, 0 ≤ j < c). Задачей головоломки является определение всех позиций вхождения шаблона в циклическую таблицу. Определим позицию вхождения шаблона в циклическую таблицу. Позиция (i, j) циклической таблицы является позицией вхождения, если для каждого (x, y), что 0 ≤ x < r и 0 ≤ y < c, выполняется одно из двух условий: - Клетка шаблона с координатами (x, y) является символом вопроса.
- Клетка циклической таблицы с координатами
 равняется клетке шаблона с координатами (x, y). равняется клетке шаблона с координатами (x, y). Даша прекрасно справилась с решением этой головоломки, впрочем как и со всеми остальными головоломками. Посмотрим, сможете ли вы это сделать. Выходные данные Выведите n строк. Каждая из этих n строк должна содержать по m символов. Каждый из этих символов должен быть равен '0' или '1'. На позиции j строки i (0-индексация) выходных данных должен находиться символ '1', если позиция (i, j) является позицией вхождения, иначе символ '0'. | |
![]()
|
|
C. Польшар и Лес
графы
Деревья
интерактив
поиск в глубину и подобное
снм
*1300
Польшар и его семья живут в лесу. Лес состоит из деревьев. Деревом называется неориентированный ациклический граф с k вершинами и k - 1 ребрами, где k — некоторое целое число. Заметьте, что изолированная вершина является корректным деревом. В каждой вершине каждого дерева живет ровно один родственник, они пронумерованы от 1 до n. Для каждого шара i нам известен номер самого дальнего от него родственника, живущего на том же дереве. Если существует несколько таких родственников, нам известен лишь наименьший номер среди них. Сколько же деревьев в лесу? Выходные данные Выведите число деревьев в лесу, где живет Польшар. Протокол взаимодействия Технически данная задача является интерактивной. Однако, это никак не влияет на вас (кроме взломов), т. к. никакого взаимодействия нет. Примечание В первом примере лес выглядит так: 1-2 3-4-5. Всего здесь 2 дерева. Во втором примере единственный возможный граф это одна вершина и ни одного ребра. Поэтому здесь всего одно дерево. | |
![]()
|
|
G. Может ли Баш выйти из положения?
графы
Деревья
разделяй и властвуй
Структуры данных
*3400
Вау! Вы отлично помогли команде Р поймать всех покемонов, посланных Башем. Мяут, член частью команды Р, уже выучил человеческий язык, и теперь хочет обучиться программированию. Он согласился освободить покемонов, если Баш ответит на его вопросы. В начале Мяут дает Башу взвешенное дерево из n вершин и последовательность a1, a2..., an, которая является перестановкой чисел 1, 2, ..., n. Теперь Мяут задает q запросов в одной из следующих форм: - 1 l r v значит, что Баш должен посчитать
 , где dist(a, b) — длина кратчайшего пути от вершины a до вершины b в данном дереве. , где dist(a, b) — длина кратчайшего пути от вершины a до вершины b в данном дереве. - 2 x значит, что Баш должен поменять местами ax и ax + 1 в заданной последовательности. Новая последовательность будет использоваться для следующих запросов.
Помогите Башу ответит на запросы! Выходные данные Для каждого запроса типа 1 выведите единственное число в отдельной строке — ответ на запрос. Примечание В примере запросы следующие: - 1 1 5 4
- 1 1 3 3
- 2 3
- 2 2
- 1 1 3 3
| |
![]()
|
|
E. Сломанное дерево
графы
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
*2600
Вам дано дерево, состоящее из n вершин, пронумерованных числами от 1 до n, где вершина с номером один — корень дерева. У каждого ребра есть собственные вес wi и прочность pi. Ботаник Иннокентий, единственный член жюри олимпиады по информатике, очень не любит сломанные деревья. Дерево является сломанным, если существует такое ребро, прочность которого меньше суммы весов рёбер поддерева, в которое оно ведёт. Разрешается уменьшать вес любого ребра на целую величину, но тогда прочность этого ребра уменьшается на ту же величину. То есть если вес ребра 10, а прочность 12, то при уменьшении веса на 7 его вес станет равным 3, а прочность станет равной 5. Увеличивать вес ребра нельзя. Ваша задача: уменьшая веса рёбер заданного дерева, получить дерево, которое не является сломанным, а также все рёбра в нём должны иметь положительный вес, причём суммарный вес всех рёбер должен быть наибольшим. Очевидно, что прочность рёбер не может быть отрицательной, однако она может равняться нулю, если вес поддерева равен нулю. Выходные данные Если из заданного дерева нельзя получить несломанное, то выведите в единственной строке -1. Иначе, выходные данные должны содержать n строк: В первой строке выведите число n — количество вершин в дереве. В следующих n - 1 строках выведите описание рёбер конечного дерева. Каждая строка должна содержать четыре целых числа x, y, w, p (1 ≤ x, y ≤ n, 1 ≤ w ≤ 109, 0 ≤ p ≤ 109), где x и y — вершины, которые соединяет ребро (вершина под номером x — предок вершины под номером y), w и p — новые вес и прочность ребра соответственно. Выводите рёбра в том же порядке, в каком они заданы во входных данных, то есть первые два числа каждой строки должны оставаться неизменёнными. | |
![]()
|
|
A. Подарок
графы
Деревья
снм
сортировки
*2200
В королевстве Олимпия находится N городов и M двусторонних дорог, каждая из которых соединяет ровно два города. Между двумя городами может быть более одной дороги. Дорога может соединять город с самим собой, образуя петлю. Все дороги постоянно грабятся разбойниками. В последнее время разбойникам надоело тратить силы на грабеж и они обратились к могущественному и справедливому королю Олимпии с коммерческим предложением. Согласно этому предложению король должен отправить разбойникам подарок, состоящий из золотых и серебряных монет. В ответ на любезность короля разбойники прекратят грабить определенные дороги. Для каждой из дорог установлено: gi — минимальное количество золотых и si — минимальное количество серебряных монет в подарке, чтобы ее грабеж закончился. То есть, если в подарке a золотых и b серебряных монет, то прекращается грабеж всех дорог, для которых gi ≤ a и si ≤ b. В казне короля нет ни одной золотой или серебряной монеты, но есть Олимпийские Тугрики. Цена одной золотой монеты в тугриках — G, а серебряной — S. Король хочет, чтобы после отправки подарка разбойникам между каждой парой городов существовал хотя бы один безопасный путь, который, возможно, проходит через другие города. Ваше задание найти минимальное количество тугриков, которую нужно потратить королю для того, чтобы получить безопасные пути между каждой парой городов в королевстве. Выходные данные Единственная строка должна содержать минимальное количество тугриков, которое нужно потратить королю на покупку золотых и серебряных монет, чтобы достичь своей цели. Выведите  , в случае, если никакое количество тугриков не поможет. , в случае, если никакое количество тугриков не поможет. | |
![]()
|
|
E. Даша и головоломка
графы
Деревья
жадные алгоритмы
Конструктив
поиск в глубину и подобное
*2000
После решения задачи, Даша решила отдохнуть. Она уже была готова приступить к своему любимому занятию — оригами, но вспомнила о головоломке которую не смогла решить.  Дерево — это неориентированный связный граф без циклов. В частности, в дереве из n вершин всегда n - 1 ребро. Головоломка заключалась в расположении вершин в точках декартовой плоскости с целочисленными координатами, так чтобы проведенные отрезки между вершинами соединенными ребрами были параллельны осям координат. Также пересечение отрезков допускается только на их концах. Различным вершинам должны соответствовать различные точки. Помогите Даше найти любой из искомых способов расположения вершин дерева на плоскости. Гарантируется, что если можно расположить вершины дерева на плоскости не нарушив условия выше, то это можно сделать воспользовавшись точками с целочисленными координатами по модулю не превышающими 1018. Выходные данные Если головоломка не имеет решения, то в единственной строке выходных данных выведите «NO». Иначе, первая строка выходных данных должна содержать «YES». В следующих n строках должна содержаться пара чисел xi, yi (|xi|, |yi| ≤ 1018) — координаты точки соответствующей i-ой вершине дерева. Если решений несколько, выведите любое. Примечание В первом примере одним из возможных размещений дерева будет следующее:  | |
![]()
|
|
F. Вложение дерева
графы
Деревья
Комбинаторика
*2800
Даны два дерева (связных неориентированных графа без циклов) S и T. Требуется посчитать количество поддеревьев (связных подграфов) дерева S, изоморфных дереву T. Так как это число может быть достаточно большим, выведите его по модулю 109 + 7. Два поддерева дерева S считаются различными, если хотя бы одна вершина S входит ровно в одно из этих поддеревьев. Дерево G называется изоморфным дереву H, если существует биекция f из множества вершин дерева G в множество вершин дерева H, обладающая следующим свойством: если в дереве G есть ребро между вершинами A и B, то в дереве H должно быть ребро между вершинами f(A) и f(B), и наоборот — если в дереве H есть ребро между вершинами A и B, то в дереве G должно быть ребро между вершинами f - 1(A) и f - 1(B). Выходные данные На единственной строке выведите одно целое число — ответ на задачу по модулю 109 + 7. | |
![]()
|
|
A. Тимофей и береза
графы
Деревья
дп
поиск в глубину и подобное
реализация
снм
*1600
Каждый Новый Год Тимофей и его друзья рубят в лесу дерево из n вершин и приносят его домой. Чтобы получше его украсить, они превращают его в березу. Береза — дерево из n вершин, каждая вершина i которого покрашена в какой-то цвет ci. Но вот настал день рождения, и мама Тимофея попросила его вынести березу. Тимофей выносит березу так: хватает за какую-то вершину, остальные вершины опускаются вниз, и дерево становится подвешенным за вершину, за которую он схватил. После этого он идет с ним на улицу и выкидывает. Попытавшись ухватить березу, Тимофей понял, что его раздражают разноцветные переливы. Поддерево раздражает Тимофея, если в нем есть вершины разных цветов. Он хочет найти, за какую вершину ему нужно взяться, чтобы ни одно поддерево не раздражало его. При этом он не рассматривает все дерево целиком как поддерево, потому что он не видит цвет корневой вершины. Поддерево некоторой вершины — это подграф, содержащий эту вершину и всех ее потомков. Определите, есть ли вершина, схватившись за которую, Тимофей не будет раздражен. Выходные данные В первой строке выведите «NO», если Тимофей не может взять березу так, чтобы его ничто не раздражало. В противном случае выведите «YES», а в следующей строке выведите номер вершины, за которую Тимофею нужно схватить березу. Если существует несколько ответов, выведите любой. | |
![]()
|
|
D. Тимофей и плоское дерево
графы
Деревья
кратчайшие пути
Структуры данных
хэши
*2900
У маленького Тимофея есть большое дерево — неориентированный связный граф из n вершин, не содержащий ни одного простого цикла. Он очень любит по нему гулять. Дерево Тимофея плоское и когда он гуляет по нему, он видит всё дерево целиком. Вполне естественно, что, находясь в вершине, он видит дерево подвешенным за эту вершину. Тимофей считает, что чем больше в дереве вершин, поддеревья которых попарно неизоморфны, тем лучше выглядит подвешенное дерево. Под поддеревом вершины подвешенного дерева он понимает подграф, состоящий из этой вершины и всех ее потомков. Помогите ему встать в такую вершину, что размер максимального подмножества вершин, поддеревья которых попарно неизоморфны при подвешивании за эту вершину, был максимально возможным. Поддеревья вершин u и v изоморфны, если число сыновей у u и v совпадают, и можно так упорядочить сыновей, что поддерево первого сына u изоморфно поддереву первого сына v, поддерево второго сына u изоморфно поддереву второго сына v, и так далее. В частности, поддеревья, состоящие из одной вершины, всегда изоморфны друг другу. Выходные данные Выведите одно число — номер вершины, в которую надо встать Тимофею. Если ответов несколько, можно вывести любой. Примечание В первом примере можно встать в вершину 1 или вершину 3, тогда все поддеревья будут неизоморфны. Если же встать в вершину 2, то поддеревья вершин 1 и 3 будут изоморфны друг другу. Во втором примере, если встать в вершину 1, то только поддеревья вершин 4 и 5 будут изоморфны. В третьем примере, если встать в вершину 1, то поддеревья вершин 2, 3, 4, 6, 7 и 8 будут изоморфны друг другу. Если же встать в вершину 2, то изоморфны будут только воддеревья вершин 3, 4, 6, 7 и 8. А если, например, встать в вершину 5, то будут изоморфны поддеревья вершин 2, 3, 4, 6, 7 и 8, а также поддеревья вершин 1 и 9:
1 9
/\ /\
7 8 4 2
| |
![]()
|
|
E. Складывание дерева
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
реализация
*2200
Ваня хочет уменьшить дерево. Для этого он может произвольное количество раз выполнять следующую операцию. Сначала Ваня выбирает вершину v и два пути одной длины, идущих из неё и не имеющих никаких общих вершин, кроме v. Обозначим эти пути за a0 = v, a1, ..., ak и b0 = v, b1, ..., bk. Кроме того, у вершин a1, ..., ak, b1, ..., bk не должно быть других соседей, кроме соседних вершин в соответствующем пути. После этого Ваня может «наложить» один путь на другой, тем самым, фактически, удалив вершины b1, ..., bk:  Помогите Ване определить, можно ли последовательным применением этой операции получить из дерева путь. Если ответ положительный, также определите минимально возможную длину такого пути. Выходные данные Если получить путь невозможно, выведите -1. Иначе выведите минимально возможное число ребер в пути. Примечание В первом примере можно получить путь из трех ребер после наложения путей 2 - 1 - 6 и 2 - 4 - 5. Во втором примере нельзя совершить ни одной корректной операции. Например, нельзя склеить пути 1 - 3 - 4 и 1 - 5 - 6, поскольку у вершины 6 есть сосед 7, которого нет в соответствующем пути. | |
![]()
|
|
E. Махмуд и xor-поездка
битмаски
Деревья
дп
Конструктив
математика
поиск в глубину и подобное
Структуры данных
*2100
Махмуд и Ехаб живут в стране, в которой n городов, пронумерованных от 1 до n, соединенных n - 1 двунаправленными дорогами. Гарантируется, что из любого города можно добраться в любой другой используя только эти дороги. Про каждый город известна некоторая величина ai. Определим расстояние от города x до города y как xor чисел, известных про города на пути от x до y (включая как x, так и y). Другими словами, если мы выпишем все величины городов на пути от x до y в массив p длины l, то расстояние между ними будет равно  , где , где  — операция побитовый xor. — операция побитовый xor. Махмуд и Ехаб хотят выбрать два города и проехать от одного до другого. Номер города, в котором они стартуют, всегда не больше номера города, в котором они финишируют (они могут стартовать и закончить в одном и том же городе, тогда расстояние будет равно величине, известной про этот город). Они никак не могут выбрать эти два города, поэтому они попробуют каждый город как старт и каждый город с не меньшим индексом как финиш. Определите суммарное расстояние между всеми этими парами городов. Выходные данные Выведите одно число — суммарное расстояние между всеми возможными парами городов. Примечание Операция побитовый xor принимает два целых битовых числа одинаковой длины и выполняет логическую операцию xor на каждой паре соответсвующих бит. Результат в позиции равен 1, если и только если только первый бит 1 или только второй бит 1, и результат равен 0 если оба бита 0 или оба бита 1. Больше информации о побитовом xor можно найти здесь: https://ru.wikipedia.org/wiki/Битовые_операции#.D0.98.D1.81.D0.BA.D0.BB.D1.8E.D1.87.D0.B0.D1.8E.D1.89.D0.B5.D0.B5_.D0.98.D0.9B.D0.98_.28XOR.29. В первом тесте из примера возможные пути следующие: - из города 1 в него самого, расстояние 1,
- из города 2 в него самого, расстояние 2,
- из города 3 в него самого, расстояние 3,
- из города 1 в город 2, расстояние
 , , - из города 1 в город 3, расстояние
 , , - из города 2 в город 3, расстояние
 . . Суммарное расстояние равно 1 + 2 + 3 + 3 + 0 + 1 = 10. | |
![]()
|
|
C. Гирлянда
графы
Деревья
жадные алгоритмы
поиск в глубину и подобное
*2000
Однажды под Новый Год Диме приснилось, что ему подарили сказочную гирлянду. Гирлянда — это набор лампочек, некоторые пары которых соединены проводами. Дима запомнил, что она представляла из себя единое целое, то есть любая пара лампочек была связана некоторой последовательностью проводов. Еще он заметил, что проводов было ровно на один меньше, чем лампочек. Необычность гирлянды состояла в том, что яркость каждой лампочки зависела от температуры этой лампочки, которая могла быть как отрицательной, так и положительной! У Димы есть два друга, и он захотел поделиться с ними сказочным подарком. Для этого он планирует разрезать два разных провода так, чтобы гирлянда распалась на три части. Дима хочет, чтобы все три части светились одинаково, то есть чтобы в каждой из них суммарная температура лампочек совпадала. Конечно же, каждая из частей должна быть непустой, то есть в ней должна быть хотя бы одна лампочка.  Помогите ему найти способ, как это сделать, либо определите, что такого не существует. Осматривая гирлянду, Дима поднял ее, взяв за какую-то лампочку. Таким образом, каждая лампочка, кроме той, за которую он взял, оказалась висящей на некотором проводе. Поэтому в качестве ответа вам нужно вывести номера двух различных лампочек, что будет означать, что Диме нужно разрезать провода, за которые они подвешены. Соответственно, в ответ не может входить лампочка, за которую Дима взял гирлянду. Выходные данные Если решения не существует, выведите ровно одно число -1. В противном случае выведите одну строку из двух различных чисел — номеров искомых лампочек. Если правильных ответов несколько, выведите любой. Примечание Схема гирлянды и разрезаний к первому примеру из условия:  | |
![]()
|
|
C. Боброжуй-0xFF
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
снм
*2100
«Съел бобра — спас дерево!» — именно под таким девизом пройдёт срочный слёт экологов в городе Бобруйске. А всё дело в том, что популяция бобров на земном шаре достигла невероятных размеров! Каждый день их количество увеличивается в разы, а они даже и не догадываются, какой ущерб приносит природе и человечеству их нездоровая любовь к древесине. Количество кислорода в атмосфере упало до 17 процентов, и, как считают лучшие умы мира, это далеко не предел. В середине 50-х годов прошлого века группа советских учёных смогла спрогнозировать ситуацию с бобрами и разработала секретную технологию по очистке территории под таинственным названием «Боброжуй-0xFF». Теперь судьба планеты лежит на хрупких плечах всего нескольких людей, отдавших свою жизнь науке. Прототип уже готов, теперь нужно срочно проводить его испытания в полевых условиях. Вам дано дерево, сплошь усеянное бобрами. Дерево состоит из n вершин, в i-ой вершине расположилось ki бобров. Напомним, дерево — это связный неориентированный граф без циклов. «Боброжуй-0xFF» работает по следующему принципу: находясь в некоторой вершине u, он может перейти к вершине v, если они соединены ребром, и съесть ровно одного бобра из тех, что находятся в вершине v. Переместиться в вершину v невозможно, если в ней не осталось бобров. «Боброжуй-0xFF» не может просто так стоять в какой-то вершине и есть там бобров. Он должен двигаться без остановок. Почему «Боброжуй-0xFF» работает именно так? Потому что разработчики не предусмотрели место в нём для аккумулятора, а поедание бобров необходимо для перегона их массы в чистую энергию. Гарантируется, что бобры будут находиться в шоке от происходящего, поэтому не смогут перемещаться по дереву. В свою очередь, «Боброжуй-0xFF» может перемещаться по каждой ветке в обоих направлениях сколько угодно раз, пока условия, описанные выше, выполняются. Корень дерева находится в вершине s. Это значит, что «Боброжуй-0xFF» начинает свою миссию в вершине s и обязательно должен в неё же вернуться в конце испытания, потому что снимать его с большой высоты никто не намерен. Определите максимальное количество бобров, которое сможет съесть «Боброжуй-0xFF», вернувшись при этом в стартовую вершину. Выходные данные Нужно вывести единственное число — максимальное возможное число бобров, съеденных «Боброжуем-0xFF». Пожалуйста, не используйте спецификатор %lld для записи 64-х битовых чисел на С++. Рекомендуется использовать поток cout (также вы можете использовать спецификатор %I64d). | |
![]()
|
|
C. Мишка и прыжки по дереву
Деревья
дп
поиск в глубину и подобное
*2100
Деревом называется неориентированный ациклический связный граф. Расстоянием между двумя вершинами называется число ребер на простом пути между ними. Лимак — маленький полярный мишка. Он живет на дереве, состоящем из n вершин, вершины дерева пронумерованы от 1 до n. Недавно Лимак научился прыгать. Он может прыгнуть из некоторой вершины в любую вершину на расстоянии не дальше k. Для пары вершин (s, t) определим f(s, t) как минимальное число прыжков, которое требуется Лимаку, чтобы попасть из вершины s в вершину t. Найдите сумму величин f(s, t) по всем парам вершин (s, t) таким, что s < t. Выходные данные Выведите одно число — сумму величин f(s, t) по всем парам вершин (s, t) таким, что s < t. Примечание В первом примере дерево состоит из 6 вершин и показано на рисунке ниже. Лимак может прыгать в любую вершину на расстоянии не больше 2 от текущей. Например, из вершины 5 он может прыгнуть в вершины 1, 2 и 4 (а также в саму вершину 5).  Всего есть  пар вершин (s, t) таких, что s < t. Для 5 из этих пар Лимаку понадобится два прыжка, это пары (1, 6), (3, 4), (3, 5), (3, 6), (5, 6). Для остальных 10 пар вершин достаточно одного прыжка. Таким образом, ответ равен 5·2 + 10·1 = 20. пар вершин (s, t) таких, что s < t. Для 5 из этих пар Лимаку понадобится два прыжка, это пары (1, 6), (3, 4), (3, 5), (3, 6), (5, 6). Для остальных 10 пар вершин достаточно одного прыжка. Таким образом, ответ равен 5·2 + 10·1 = 20. В третьем примере Limak может прыгать из любой вершины в любую. Всего есть 3 пары вершин (s < t), поэтому ответ равен 3·1 = 3. | |
![]()
|
|
E. Верифицируем Королевство
Бинарный поиск
Деревья
интерактив
разделяй и властвуй
*3200
Эта задача является интерактивной. Жюри загадало полное корневое бинарное дерево с n листьями. Полное бинарное дерево — такое дерево, каждая вершина которого имеет либо 0, либо 2 ребенка. Вершины с 0 детьми называются листьями. Так как дерево полное бинарное, то всего в нем 2n - 1 вершина. Листья загаданного дерева имеют индексы от 1 до n. Вы хотите построить дерево, изоморфное дереву жюри. Чтобы это сделать, вы можете спрашивать некоторые вопросы. Вопрос состоит из трех различных листьев a1, a2, a3. Пусть глубина вершины равна кратчайшему расстоянию от вершины до корня дерева. Пусть LCA(a, b) означает вершину с максимальной глубиной такую, что эта вершина является общим предком вершин a и b. Пусть X = LCA(a1, a2), Y = LCA(a2, a3), Z = LCA(a3, a1). Жюри ответит вам, какая из вершин X, Y, Z имеет наибольшую глубину. Заметьте, что ответ определен однозначно, так как дерево бинарное. Формально, если наибольшую глубину имеет X (или Y, Z соответственно), жюри ответит строкой «X» (или «Y», «Z» соответственно). Вы можете задать не более 10·n вопросов. Выходные данные Чтобы вывести угаданное дерево, выведите число «-1» на отдельной строке. Следующая строка должна содержать 2n - 1 целых чисел. i-е из этих чисел должно равняться индексу родителя i-й вершины, или -1, если это корень. Ваш ответ будет считаться правильным, если ваше дерево изоморфно загаданному. В частности, листья не обязаны быть пронумерованы от 1 до n. Изоморфность означает, что существует такая перестановка π, что вершина i является родителем вершины j в загаданном дереве если и только если вершина π(i) является родителем вершины π(j) в вашем дереве. Протокол взаимодействия Чтобы задать вопросы, выведите три различных целых числа a1, a2, a3. Эти числа должны быть от 1 до n включительно. Программа жюри ответит единственным символом: «X», «Y» или «Z». Если ответ равен «X» (или «Y», «Z», соответственно), то пара (a1, a2) (или (a2, a3), (a3, a1), соответственно) имеет наиболее глубокий LCA среди всех трех пар. Вы можете задать не более 10·n вопросов, иначе вы получите вердикт Неправильный ответ. Когда вы будете готовы вывести ответ, выведите число «-1» на отдельной строке. Следующая строка должна содержать 2n - 1 целых чисел. i-е из этих чисел должно равняться индексу родителя i-й вершины, или -1, если это корень. Не забудьте сделать операцию flush после вывода ответа тоже. Вывод ответа не учитывается при подсчете количества вопросов. Вы получите вердикт Неправильный ответ, если - Ваш вопрос или ответ не соответствует формату, описанному в условии.
- Вы спросили строго больше 10·n вопросов.
- Ваш вопрос содержит повторяющиеся индексы.
- Ваше дерево не изоморфно дереву жюри.
Вы получите вердикт Решение «зависло», если не будете ничего выводить, или забудете сделать операцию flush после вывода вопроса или ответа (смотрите ниже информацию, как сделать flush). Чтобы выполнить операцию flush, можете использовать (сразу после вывода чисел и перевода строки): - fflush(stdout) в C++;
- System.out.flush() в Java;
- stdout.flush() в Python;
- flush(output) в Pascal;
- Смотрите документацию для других языков.
Если в любой момент ваша программа считывает -1 как ответ, она должна немедленно нормально завершиться (например, вызовом exit(0)). Вы получите вердикт Неправильный ответ, и это будет означать, что вы задали больше вопросов, чем разрешено, или сделали некорректный вопрос. Если вы проигнорируете это, то можете получить любой вердикт, так как ваша программа продолжит читать из закрытого потока ввода. Взломы Чтобы взломать кого-нибудь, используйте следующий формат.
n
p_1 p_2 ... p_{2n-1}
Это описывает дерево, где родителем вершины i является вершина pi (pi = - 1 or n < pi ≤ 2n - 1). Значение pi, равное -1 означает, что вершина i является корнем. Эти данные должны описывать корректное полное бинарное дерево. Конечно, взламываемая программа не будет иметь доступ к этим данным. Примечание В первом примере загаданное дерево выглядит так: 
Взаимодействие в более удобном формате:  Последняя строка также может быть равной 8 6 9 8 9 7 -1 6 7. | |
![]()
|
|
F. Пари Шерлока и Мориарти
геометрия
графы
Деревья
Конструктив
разделяй и властвуй
реализация
Структуры данных
*2800
Шерлок и Мориарти встретились для финальной битвы умов. Шерлок дал Мориарти правильный выпуклый n-угольник. Кроме того, он дал ему некоторые диагонали в этом многоугольнике, которые разделяют его на регионы. Гарантируется, что диагонали не пересекаются во внутренних точках. Шерлок посчитал для каждого региона его важность. Важность региона, образованного вершинами многоугольника с номерами a1, a2, ... , ax, равна 2a1 + 2a2 + ... + 2ax. Затем Шерлок упорядочил регионы в порядке увеличения важности. После этого он присвоил каждому региону уникальный номер от 1 до k, где k — количество регионов, а номер региона это его позиция в упорядоченном по важности списке. Шерлок хочет, чтобы Мориарти раскрасил регионы, используя не более чем 20 цветов так, чтобы все простые пути между двумя одноцветными регионами проходили через хотя бы один регион, покрашенный в цвет с номером меньше, чем номер цвета данных регионов. Простой путь между двумя регионами f и h это последовательность регионов r1, r2, ... rt такая, что r1 = f, rt = h, для каждого 1 ≤ i < t регионы ri и ri + 1 имеют общую сторону, а также ri = rj если и только если i = j. Мориарти не смог ответить и спросил решение у Шерлока. Помогите Шерлоку предоставить ответ Мориарти. Выходные данные Пусть число регионов равно k. Выведите k целых чисел, каждое от 1 до 20 — цвета регионов в порядке увеличения важности. Если существует несколько решение, выведите любое из них. Можно показать, что существует хотя бы одно решение. Примечание Во втором примере регионы будут в таком порядке: (1, 2, 3), (1, 3, 4), (1, 4, 5), (1, 5, 6), т. е. регион (1, 2, 3) будет первым, затем регион (1, 3, 4) и так далее. Мы можем покрасить регионы 1 и 3 в один цвет, так как регион 2 будет на пути из 1 в 3, и его цвет равен 1, что меньше, чем цвет регионов 1 и 3, который равен 2. | |
![]()
|
|
C. Петрович — полиглот
Деревья
Перебор
поиск в глубину и подобное
снм
Строки
хэши
*2500
Петрович обожает изучать новые языки, но самое любимое его увлечение — составление своих собственных. Языком Петрович называет множество слов, а словом — последовательность маленьких букв латинского алфавита. Каждое утро Петрович составляет свой новый язык. Хранить все языки в явном виде очень сложно, поэтому Петрович придумал веник — специальную структуру данных для хранения языка, представляющую собой подвешенное дерево, на ребрах которого написаны буквы. Перед придумыванием языка веник представляет одну вершину — корень. При добавлении нового слова в язык Петрович встает в корень веника и обрабатывает буквы слова по одной. Пусть Петрович стоит в вершине u. Если из u есть ребро, на котором написана текущая буква, он переходит по нему. Иначе же, Петрович добавляет ребро из u в новую вершину v, пишет на нем текущую букву и переходит по этому ребру. Размером веника Петрович называет количество вершин в нем. Вечером, приходя со смены, Петрович не может понять язык, придуманный утром: он ему кажется слишком сложным. Тогда Петрович старается упростить свой язык. Упрощением языка Петрович называет удаление букв из некоторых слов языка. Формально, Петрович фиксирует некоторое целое положительное число p, берет все слова, содержащие хотя бы p букв, и выкидывает из каждого из них букву с номером p. Буквы в слове Петрович предпочитает нумеровать, начиная с 1. Петрович считает, что при упрощении языка хотя бы одно слово должно измениться, то есть в языке должно быть хотя бы слово с длиной хотя бы p. Так как Петрович стремится сделать язык, придуманный утром, как можно проще, он старается подобрать число p таким образом, чтобы минимизировать размер веника, в котором он будет хранить язык. Петровичу надоело заниматься одним и тем же каждый вечер, поэтому он обратился за помощью к вам. Напишите программу, которая будет находить минимальный размер веника, который может получиться в результате упрощения языка, придуманного Петровичем, и число p, которое нужно выбрать, чтобы получить такой размер. Выходные данные В первой строке выведите минимальный возможный размер веника, который может получиться в результате упрощения языка. Во второй строке выведите число p, которое следует выбрать Петровичу для получения минимального размера. Если таких чисел p несколько, выведите минимальное из них. Примечание 
Веник из второго примера может быть составлен из множества слов «piece», «of», «pie», «pretty», «prefix». После упрощения языка с p = 2 получается язык из слов «pece», «o», «pe», «petty», «pefix». Этот язык и задаёт веник минимального возможного размера. | |
![]()
|
|
C. Андрюша и разноцветные шарики
графы
Деревья
жадные алгоритмы
поиск в глубину и подобное
*1600
Андрюша каждый день с самого детства ходит через городской парк. Дорожки и полянки парка все время казались ему слишком одинаковыми, и однажды он решил украсить их и сделать разнообразными. Парк состоит из n полянок, которые соединены между собой (n - 1) двусторонними дорожками, причем от каждой полянки можно дойти по дорожкам до любой другой. Андрюша решил на каждой полянке повесить один цветной шарик. Цвета шариков задаются целыми положительными числами, начиная с 1. Чтобы парк стал более разнообразным, Андрюша решил выбирать цвета шариков по-особенному. А именно, он хочет развесить шарики так, чтобы для любых трех попарно различных полянок a, b и c таких, что a и b соединены дорожкой, и b и c соединены дорожкой, цвета шариков на этих полянках были попарно различными. Чтобы не тратить много денег на покупку шариков, Андрюша хочет использовать как можно меньше различных цветов. Так как Андрюша не очень силен в программировании, он просит вас помочь ему решить эту задачу. Выходные данные В первой строке выведите одно целое число k — минимальное количество цветов, которое необходимо использовать Андрюше. Во второй строке выведите n целых чисел, i-е из которых равняется цвету шарика, который нужно повесить на i-й полянке. Каждое из чисел должно быть в пределах от 1 до k. Примечание В первом примере из условия парк состоит из трех полянок, которые последовательно соединены: 1 → 3 → 2. Значит, цвета шариков на каждой полянке должны быть попарно различны.  Иллюстрация к первому примеру. Иллюстрация к первому примеру. Во втором примере в парке можно найти следующие тройки полянок, соединенных последовательно: - 1 → 3 → 2
- 1 → 3 → 4
- 1 → 3 → 5
- 2 → 3 → 4
- 2 → 3 → 5
- 4 → 3 → 5
Отсюда мы видим, что каждая пара полянок лежит в какой-нибудь тройке, а значит цвета шариков на всех полянках должны быть попарно различны.  Иллюстрация ко второму примеру. Иллюстрация ко второму примеру. В третьем примере есть следующие тройки: - 1 → 2 → 3
- 2 → 3 → 4
- 3 → 4 → 5
Это значит, что одного или двух цветов недостаточно, а для трех цветов ответ существует и приведен в примере.  Иллюстрация к третьему примеру. Иллюстрация к третьему примеру. | |
![]()
|
|
D. Бог рэпа
Деревья
поиск в глубину и подобное
Строки
Структуры данных
хэши
*3400
Рик влюблен в Юнити. Но и мистер Мисикс также любит Юнити. Поэтому Рик и мистер Мисикс «любовные соперники». Юнити нравится рэп, поэтому было решено, что они должны участвовать в рэп игре (баттле), чтобы выбрать лучшего. Рик слишком ботаник, поэтому вместо этого он собирается сделать свой текст используя его оригинальный алгоритм на лирике песни «Rap God».  Его алгоритм немного сложен. Он делает дерево с n вершинами, пронумерованными от 1 до n. На каждом ребре дерева написана маленькая латинская буква. Он определил str(a, b), как строку сформированную написанием всех букв, одну за другой, на кратчайшем пути от a до b (длина строки равна расстоянию от a до b). Заметьте, что str(a, b) это, записанная задом наперед, строка str(b, a). Также строка str(a, a) является пустой строкой. Чтобы сделать лучший текст, ему необходимо отвечать на некоторые запросы, но он не ученый-компьютерщик и не может ответить на эти запросы, поэтому он просит вас помочь ему. Каждый запрос характеризуется двумя вершинами x и y (x ≠ y). Ответом на этот запрос является кол-во таких вершин z, что z ≠ x, z ≠ y и str(x, y) лексикографически больше, чем str(x, z). Строка x = x1x2...x|x| лексикографически больше, чем строка y = y1y2...y|y|, если |x| > |y| и x1 = y1, x2 = y2, ..., x|y| = y|y|, или существует такое r (r < |x|, r < |y|), что x1 = y1, x2 = y2, ..., xr = yr и xr + 1 > yr + 1. Символы сравниваются, как их ASCII коды (или как их позиции в алфавите). Помогите Рику заполучить девушку. Выходные данные Для каждого запроса выведите ответ в одну строку. Примечание Дерево для первого теста из условия:  Дерево для второго теста из условия:  В этом тесте: - str(8, 1) = poo
- str(8, 2) = poe
- str(8, 3) = po
- str(8, 4) = pop
- str(8, 5) = popd
- str(8, 6) = popp
- str(8, 7) = p
Поэтому для первого запроса  и для третьего запроса и для третьего запроса  это ответ. это ответ. | |
![]()
|
|
E. Альт
графы
Деревья
Потоки
Структуры данных
*3200
Альт — планета в галактике «Энкор». Люди управляют этой планетой, но по некоторым причинам здесь нет собак, на их планете. Поэтому люди в депрессии и грустят. Рик и Морти вселенские филантрописты и они хотят сделать людей на планете Альт счастливыми. Альт имеет n городов пронумерованных от 1 до n и n - 1 двунаправленных дорог, пронумерованных от 1 до n - 1. От любого города до любого можно доехать используя эти дороги. На Альте есть два типа людей: - Стражи. Страж живет в доме вдоль дороги и охраняет дорогу.
- Граждане. Гражданин живет дома, внутри города, и работает в офисе, в другом городе.
Каждый человек на Альте является либо стражем либо гражданином. Вдоль каждой дороги живет один страж.  Рик и Морти обратились ко всем людям на Альте, и вот что они получили: - m граждан живет на Альте.
- Гражданин номер i живет в городе номер xi и работает в городе номер yi.
- Каждый день гражданин едет по дорогам вдоль кратчайшего пути от его дома на работу.
- Гражданин будет счастлив, если и только если он будет иметь щенка, или все стражи вдоль пути на его работу будут иметь щенка (он видит щенков у стражей на каждой дороге и он счастлив).
- Страж всегда счастлив.
Вам необходимо сказать Рику и Морти минимальное количество щенков необходимое, чтобы сделать всех на Альте счастливыми, и также предоставить оптимальный путь раздать щенков. Выходные данные В первой строке выведите целое число k — суммарное необходимое количество щенков (1 ≤ k ≤ n). Во второй строке выведите число q — количество щенков, которых необходимо раздать гражданам, за которым следует q различных чисел a1, a2, ..., aq — номера граждан, которым необходимо раздать щенков (0 ≤ q ≤ min(m, k), 1 ≤ ai ≤ m). В третьей строке выведите число e — количество щенков, которых необходимо раздать стражам, за которым следует e различных целых чисел b1, b2, ..., be — номера дорог, стражам которых необходимо раздать щенков (0 ≤ e ≤ min(n - 1, k), 1 ≤ bi ≤ n - 1). Сумма q и e должна быть равна k. Примечание Карта Альта для первого тестового примера (числа, написанные на дорогах, это их номера):  Карта Альта для второго тестового примера (числа, написанные на дорогах, это их номера):  | |
![]()
|
|
D. Пути в полном бинарном дереве
битмаски
Деревья
*1900
Пусть T — полное бинарное дерево, состоящее из n вершин. Это означает, что ровно одна вершина является его корнем и у каждой вершины либо ровно два сына (левый и правый), либо нет сыновей (вершина является листом). Все листы полного бинарного дерева находятся на одинаковом расстоянии от корня. Очевидно, число n таково, что n + 1 обязательно является степенью числа 2. На рисунке ниже изображен пример полного бинарного дерева для n = 15.  Вершины дерева будем нумеровать от 1 до n специальным образом. Нумерацию будем производить рекурсивным образом: сначала рекурсивно назначим номера вершинам левого поддерева (если оно есть), затем дадим очередной номер текущей вершине, а после этого рекурсивно назначим номера вершинам правого поддерева (если оно есть). Номера на рисунке выше назначены именно таким образом. Отметим, что описанный способ однозначно определяет номера вершин. Такой порядок обхода бинарного дерева называется симметричным. Напишите программу, которая по заданному числу n и q запросам возвращает ответ на каждый из них. Каждый из запросов — это целое число ui (1 ≤ ui ≤ n) и строка si, где ui — номер вершины, а si — описание пути из этой вершины. Строка si содержит исключительно буквы 'L', 'R' и 'U', которые обозначают переход к левому сыну, переход к правому сыну и переход к родительской вершине соответственно. Символы в строке si следует обрабатывать последовательно слева направо, считая стартовой вершину ui. Если переход невозможен, то его следует проигнорировать. Ответом на запрос является номер вершины, в которой будет завершен путь si. Например, если ui = 4 и si = «UURL», то ответом будет вершина 10. Выходные данные Выведите q чисел, i-е из них должно быть равно ответу на i-й запрос. | |
![]()
|
|
E. Проблемы отделений
Деревья
дп
Конструктив
поиск в глубину и подобное
*2900
Раньше, когда не было интернета, у каждого банка было множество отделений по всему городу Банкополису, что вызывало множество проблем. А именно, в каждом отделении нужно было каждый день проводить инкассацию. Однажды Олег услышал разговор двух инкассаторов одного банка. Они каждый день объезжали все отделения и офисы этого банка, причем двигались они по строго определенной схеме. Инкассаторы выезжали из центрального офиса, и каждый раз перемещались по специальной дороге либо между двумя офисами, либо между каким-то офисом и каким-то отделением, в итоге возвращаясь обратно в центральный офис. Известно, что всего отделений и офисов было было n, а специальных дорог — на одну меньше, то есть n - 1. Иными словами, система специальных дорог образовывала корневое дерево, корнем которого являлся центральный офис, все листья дерева были отделениями, а все внутренние вершины — офисами. Инкассаторы всегда объезжали офисы и отделения по одному и тому же маршруту, число дорог в котором было минимально возможным, то есть 2n - 2. Один из инкассаторов утверждал, что между посещениями отделения a и отделения b (в таком порядке) они посещают столько же отделений, что и между посещениями отделений b и затем a. Другой инкассатор утверждал, что между посещениями отделения c и отделения d они посещают столько же отделений, что и между посещениями отделений d и затем c. Интересной особенностью разговора было то, что кратчайший путь по специальным дорогам между любой парой отделений из a, b, c и d проходил через центральный офис. Зная схему дорог и номера отделений a, b, c и d, определите, могла ли происходить ситуация, описанная инкассаторами, или нет. Выходные данные Если ситуация, описанная инкассаторами, возможна, выведите «YES». Иначе выведите «NO». Примечание В первом примере возможен следующий маршрут инкассаторов  . Можно заметить, что между посещениями отделений a и b инкассаторы посещают столько же отделений, сколько между посещениями отделениями b и a; аналогичная ситуация с отделениями c и d (маршрут инкассаторов является бесконечным и периодичным, но порядок посещения офисов и отделений не меняется изо дня в день и всегда строго фиксирован). . Можно заметить, что между посещениями отделений a и b инкассаторы посещают столько же отделений, сколько между посещениями отделениями b и a; аналогичная ситуация с отделениями c и d (маршрут инкассаторов является бесконечным и периодичным, но порядок посещения офисов и отделений не меняется изо дня в день и всегда строго фиксирован). Во втором примере не существует такого порядка посещения офисов и отделений, что между посещениями c и d инкассаторы заедут в столько же отделений, что между посещениями d и c, а значит, ответа не существует. В третьем примере маршрут, удовлетворяющий условию задачи, такой:  . . | |
![]()
|
|
C. Взлом банков
Деревья
дп
Конструктив
Структуры данных
*1900
Несмотря на то, что Инзейн нашел свою кость, его хозяин Зейн еще не вернулся. Чтобы найти Зейна, Инзейну потребуется много денег, которых у него сейчас совсем нет. Чтобы стправиться с этим, он решил взломать банки.  Всего есть n банков, пронумерованных от 1 до n. Банки соединены n - 1 проводами. все банки изначально находятся в состоянии онлайн. У каждого банка есть изначальная защита: защита банка i изначально равна ai. Определим некоторые понятия перед тем, как продолжить. Банки i и j называются соседними, если и только если между ними существует провод напрямую. Банки i и j называются полу-соседними, если и только если существует такой онлайн банк k, что банки i и k являются соседними, и банки k и j являются соседними. Когда некоторый банк взломан, он переходит в состояние оффлайн (и никогда не возвращается в онлайн), а другие банки, которые являются соседними или полу-соседними к взломанному, увеличивают свою защиту на 1. Вначале Инзейн выберет банк, который он взломает первым. Конечно, защита этого банка не должна превышать мощности его компьютера. После этого, он будет выбирать для взлома некоторый банк до тех пор, пока не будут взломаны все банки, но он может выбрать для взлома банк номер x если и только если все следующие условия выполнены: - Банк x находится в состоянии онлайн. То есть, банк x еще не взломан.
- Банк x является соседним к какому-то оффлайн банку.
- Защита банка x не превосходит мощности компьютера Инзейна.
Определите минимальную необходимую мощность компьютера, с помощью которого Инзейн сможет взломать все банки. Выходные данные Выведите одно число — минимальная мощность компьютера, с которым Инзейн сможет взломать все банки. Примечание В первом примере Инзейн может взломать все банки, используя компьютер мощности 5: - Изначально защиты банков равны [1, 2, 3, 4, 5].
- Он взламывает банк 5, силы банков становятся равными [1, 2, 4, 5, - ].
- Он взламывает банк 4, силы банков становятся равными [1, 3, 5, - , - ].
- Он взламывает банк 3, силы банков становятся равными [2, 4, - , - , - ].
- Он взламывает банк 2, силы банков становятся равными [3, - , - , - , - ].
- Он взламывает банк 1 и достигает своей цели.
Во втором примере Инзейн может взламывать банки в порядке 4, 2, 3, 1, 5, 7 и 6. Таким образом, ему достаточно компьютера мощностью 93. | |
![]()
|
|
D. Посты полиции
графы
Деревья
дп
Конструктив
кратчайшие пути
поиск в глубину и подобное
*2100
Инзейн наконец-то нашел Зейна, и у них еще много денег! Поэтому они решили создать собственную страну. Правление страной — непростая задача. Бандиты и террористы постоянно пытаются разрушить покой. Чтобы бороться с этим, Зейн и Инзейн разработали следующее правило: от каждого города должно быть возможно достичь пост полиции, проехав не более d километров по дорогам.  В стране n городов, пронумерованных от 1 до n, соединенных n - 1 дорогами. Все дороги имею длину 1 километр. Возможно добраться от любого города до любого другого, используя эти дороги. Кроме того, есть k постов полиции, расположенных в некоторых городах. Расположение постов полиции удовлетворяет закону, описанному выше. Заметьте, что некоторые посты могут быть расположены в одном и том же городе. Однако, Зейн считает, что n - 1 дорога это слишком много. Страна испытывает финансовый кризис, поэтому необходимо закрыть как можно больше дорог. Помогите Зейну определить максимальное число дорог, которое можно закрыть, не нарушая закон. Кроме того, найдите эти дороги. Выходные данные В первой строке выведите одно целое число s, означающее максимальное число дорог, которое можно закрыть. Во второй строке выведите s различных чисел — номера дорог, для которых это верно. Если ответов несколько, выведите любой из них. Примечание Во втором примере, если закрыть дорогу номер 5, то от всех городов по-прежнему можно будет достичь пост полиции, проехав не более k = 4 километров. Во втором примере, несмотря на то, что множество дорог, которые можно закрыть, единственно, вы можете вывести 4 5 или 5 4 во второй строке. | |
![]()
|
|
J. Отправьте Дурака Дальше! (простая)
графы
Деревья
поиск в глубину и подобное
*1400
Друг Хайди Дженни просит ее доставить важное письмо их общему другу. Поскольку Дженни ирландка, Хайди считает, что это может быть шутка. Точнее, она подозревает, что сообщение, которое она попросила доставить, гласит: «Отправьте дурака дальше!», и, читая его, получатель попросит Хайди передать то же сообщение другому другу (общему для получателя и Хайди), и так далее. Хайди считает, что ее друзья хотят избежать неловких ситуаций, поэтому она не сможет дважды посетить одного и того же человека (включая Дженни). Она также знает, какова стоимость путешествий между любыми двумя друзьями, которые знают друг друга. Она хочет знать: какова максимальная сумма денег, которую она потратит на путешествие, если это действительно шутка? У Хайди есть n друзей, пронумерованных от 0 до n - 1, и их дружеские связи образуют дерево. Другими словами, каждые двое из ее друзей a и b знают друг друга, возможно, косвенно (то есть существует последовательность друзей, начинающаяся с a и заканчивающаяся b такая, что каждые два последовательных друга в этой последовательности знают друг друга напрямую). Есть ровно n - 1 пара друзей, которые знают друг друга напрямую. Дженни имеет номер 0. Выходные данные Выведите единственное число — максимальная сумма денег, которую Хайди может потратить на путешествия между друзьями. Примечание Во втором примере наихудший сценарий выглядит следующим образом: Дженни отправляет Хайди к другу, помеченному номером 2 (Хайди расходует на это 100). Потом друг 2 отправляет Хайди к другу 1 (Хайди тратит на это 3). Затем 1 направляет ее к другу 4 (Хайди расходует на это 2). | |
![]()
|
|
K. Отправьте Дурака Дальше! (средняя)
Деревья
дп
*2100
Спасибо, что помогаете Хайди! Сегодня второе апреля, но ее снова вызвала Дженни. Шутка еще не закончилась... Тем временем Хайди решила, что больше не доверяет своим друзьям. Во всяком случае, не слишком доверяет. Ее относительное отсутствие доверия проявляется следующим образом: в то время как ранее ей не пришлось бы посещать одного и того же человека дважды, теперь она может быть уверена лишь в том, что ее не заставят посетить одного и того же друга более чем k раз. В случае с Дженни первое её посещение в начале учитывается. Ситуация с простой версией задачи соответствует случаю для k = 1. Это не так плохо, как кажется, поскольку один билет на маршрут между двумя друзьями позволяет Хайди путешествовать между этой парой друзей целый день (в обоих направлениях). Другими словами, как только она платит за путешествие между парой друзей, все дальнейшие путешествия между этой парой бесплатны. Каково максимальная сумма денег, которые Хайди может потратить на путешествия между друзьями? Выходные данные Выведите одно целое число — максимальную сумму денег, которые Хайди может потратить на путешествия между друзьями. Примечание В первом пример худший сценарий для Хайди - посетить друзей в следующем порядке: 0, 1, 5, 1, 3, 1, 0, 2, 6, 2, 7, 2, 8. Обратите внимание, что ни один друг не посещается более чем 3 раза. | |
![]()
|
|
L. Отправьте Дурака Дальше! (сложная)
Деревья
дп
математика
поиск в глубину и подобное
*2400
Хайди в ужасе от шутки, и она сочла нереальным, что ее друзья будут специально загонять её в долги. Она ожидает, что фактически, каждый человек просто выберет случайного друга, чтобы отправить Хайди. Из этого следует, что теперь Хайди может посещать одного и того же друга произвольное количество раз. Более того, если у человека есть ровно один общий друг с Хайди (то есть он является листом дерева), тогда этот человек не отправит Хайди обратно (то есть путешествие Хайди закончится в некоторой точке). Хайди также кажется нереальным то, что она сможет совершить свое путешествие за один день. Поэтому теперь она предполагает, что каждый раз, когда она путешествует по маршруту между двумя друзьями, ей нужно покупать новый билет. Она хочет знать математическое ожидание суммы денег, которые она потратит на путешествия. Полагайте, что у Дженни есть по крайней мере два друга. Выходные данные Предположим, что ожидаемая стоимость путешествий записывается как несократимая дробь a / b (то есть, a и b являются взаимно простыми). Хайди просит вас вывести величину  . То есть, выводимое число должно быть в пределах от 0 до 109 + 6, включительно. . То есть, выводимое число должно быть в пределах от 0 до 109 + 6, включительно. Примечание В первом примере с вероятностью 1 / 2 Хайди пойдет в 1 из 0, и с вероятностью 1 / 2 она пойдет в 2. В первом случае стоимость будет 10, а во второй она будет 20. Достигнув 1 или 2 она остановится, так 1 и 2 являются листьями дерева. Следовательно, ожидаемые расходы Хайди на путешествия составляют 10·1 / 2 + 20·1 / 2 = 15. В третьем примере ожидаемая стоимость составляет 81 / 5. Поэтому нужно вывести число 400000019. В ходе своих путешествий Хайди узнала интригующий факт о структуре своих дружеских связей. Она сообщает вам следующее: Таинственный определитель, о котором вы могли бы подумать, таков, что он не вызывает странных ошибок в вашем разумном решении... Мы упоминали, что Хайди - странная корова? | |
![]()
|
|
D. Матожидание диаметра дерева
Бинарный поиск
Деревья
дп
Перебор
поиск в глубину и подобное
сортировки
*2500
Паша — прилежный студент, один из лучших друзей Моджака. Он всегда размышляет над какой-то задачей. Сегодня они разговаривали о следующей задаче. Дан лес (ациклический неориентированный граф) из n вершин и m ребер. Также есть q запросов, на которые необходимо ответить. В каждом запросе даны две вершины v и u. Пусть V — множество вершин в компоненте связности, к которой принадлежит v, а U — множество вершин в компоненте связности, к которой принадлежит u. Добавим ребро между некоторой вершиной  и некоторой вершиной и некоторой вершиной  и вычислим величину d получившейся компоненты. Если получившаяся компонента — дерево, то величина d равна диаметру компоненты, иначе она равна -1. Найдите математическое ожидание величины d, если вершины a и b выбираются из множеств равновероятно случайным образом. и вычислим величину d получившейся компоненты. Если получившаяся компонента — дерево, то величина d равна диаметру компоненты, иначе она равна -1. Найдите математическое ожидание величины d, если вершины a и b выбираются из множеств равновероятно случайным образом. Можете помочь Паше решить эту задачу? Диаметром компоненты называется максимальное расстояние между парой вершин в компоненте. Расстоянием между двумя вершинами называется минимальное число ребер на пути между ними. Заметьте, что запросы не добавляют ребер в изначальный лес. Выходные данные Для каждого запроса выведите математическое ожидание величины d в соответствии с условием задачи. Ваш ответ будет засчитан, если его абсолютная или относительная ошибка не превосходит10 - 6. Формально, пусть ваш ответ равен a, а ответ жюри равен b. Ваш ответ будет засчитан, если  . . Примечание В первом примере вершины 1 и 3 лежат в одной компоненте, поэтому ответ на первый запрос равен -1. Во втором запросе есть два исхода: добавить ребро 1 - 2, или добавить ребро 2 - 3. В обоих случаях диаметр равен 2, поэтому ответ равен 2. Во втором примере ответ на первый запрос равен -1. Ответ на второй запрос — среднее по трем случаям: Если добавлены ребра 1 - 2 или 1 - 3, то диаметр будет равен 3, а если добавлено ребро 1 - 4, то диаметр равен 2. Поэтому ответ равен  . . | |
![]()
|
|
E. Удиви меня!
Деревья
математика
разделяй и властвуй
теория чисел
*3100
Устав от скучных свиданий, Леха и Нура решили сыграть в игру. Леха раздобыл дерево из n вершин, пронумерованных от 1 до n. Напомним, что дерево — это связный неориентированный граф без циклов. На каждой вершине v дерева записано некоторое число av. Совершенно случайно оказалось, что все значения, записанные на вершинах, различны и являются натуральными числами от 1 до n. Игра происходит следующим образом. Нура случайно и равновероятно выбирает некоторую вершину u дерева и передает ход Лехе. Леха, в свою очередь, случайно и равновероятно выбирает некоторую вершину v из оставшихся вершин дерева (v ≠ u). Как несложно догадаться, существует n(n - 1) вариантов выбора вершин игроками. Затем игроки вычисляют значение функции f(u, v) = φ(au·av) · d(u, v) от выбранных вершин, где φ(x) — функция Эйлера, а d(x, y) — кратчайшее расстояние между вершинами x и y в дереве. Совсем скоро игра наскучила Нуре, поэтому Леха, чтобы разрядить обстановку, решил посчитать математическое ожидание значения функции f по всем вариантам выбора вершин u и v в надежде хоть как-то удивить девушку. Леха просит вас помочь ему посчитать искомое математическое ожидание. Пусть данное значение представимо в виде несократимой дроби  . Чтобы еще больше удивить Нуру, он хочет назвать ей значение . Чтобы еще больше удивить Нуру, он хочет назвать ей значение  . . Помогите Лехе! Выходные данные В единственной строке выведите число, равное P·Q - 1 по модулю 109 + 7. Примечание Функция Эйлера φ(n) — это количество таких i, что 1 ≤ i ≤ n, что gcd(i, n) = 1, где gcd(x, y) — наибольший общий делитель чисел x и y. В первом примере существует 6 вариантов выбора вершин Лехой и Нурой: - u = 1, v = 2, f(1, 2) = φ(a1·a2)·d(1, 2) = φ(1·2)·1 = φ(2) = 1
- u = 2, v = 1, f(2, 1) = f(1, 2) = 1
- u = 1, v = 3, f(1, 3) = φ(a1·a3)·d(1, 3) = φ(1·3)·2 = 2φ(3) = 4
- u = 3, v = 1, f(3, 1) = f(1, 3) = 4
- u = 2, v = 3, f(2, 3) = φ(a2·a3)·d(2, 3) = φ(2·3)·1 = φ(6) = 2
- u = 3, v = 2, f(3, 2) = f(2, 3) = 2
Искомое математическое ожидание равно  . Значение, которым Леха хочет удивить Нуру, равно 7·3 - 1 = 7·333333336 = 333333338 . Значение, которым Леха хочет удивить Нуру, равно 7·3 - 1 = 7·333333336 = 333333338  . . Во втором примере математическое ожидание равно  , следовательно, Лехе придется удивлять Нуру числом 8·1 - 1 = 8 , следовательно, Лехе придется удивлять Нуру числом 8·1 - 1 = 8  . . | |
![]()
|
|
E. По парам
графы
Деревья
дп
поиск в глубину и подобное
реализация
снм
*2700
В классе у Поликарпа учится n человек (включая его самого). Недавно все ученики класса писали сочинение «Мой лучший друг». Сочинение каждого ученика было посвящено одному из учеников класса — лучшему другу. Заметим, что вовсе не обязательно у ученика b лучшим другом является ученик a, если у a лучший друг — b. А сейчас учительница ведет весь класс в музей истории спортивного программирования. Учеников ждут захватывающие истории о легендарных героях: tourist, Petr, tomek, SnapDragon — вот о ком пойдет речь! Учительница решила разбить учеников на пары так, чтобы каждая пара состояла из ученика и его лучшего друга. Возможно, ей не удастся разбить всех учеников на пары, не беда — она хочет выделить наибольшее количество таких пар. Если существует более одного варианта сделать это, она хочет выделить пары так, чтобы пар мальчик-девочка было как можно больше. Конечно, каждый ученик должен входить не более чем в одну пару. Выходные данные В первую строку выведите два числа t, e, где t — максимальное количество образованных пар, а e — максимальное количество среди них пар вида мальчик-девочка. Далее выведите t строк, каждая из строк должна содержать пару ai, bi (1 ≤ ai, bi ≤ n) — номера учеников в i-ой паре. Пары выводите в любом порядке. Числа в парах выводите в любом порядке. Если существует несколько решений, выведите любое. Примечание Рисунок ниже соответствует первому примеру. На нем ромбы обозначают мальчиков, а квадраты — девочек. Стрелки ведут от ученика к его лучшему другу, жирные (не пунктирные) обозначают пары из ответа.  | |
![]()
|
|
D. Сахир и детский сад
графы
Деревья
поиск в глубину и подобное
реализация
*2700
Сахир работает в детском саду. Всего в саду n детей и m различных игрушек. Чтобы поиграть с игрушками, дети должны следовать определенному протоколу: - У каждого ребенка есть набор любимых игрушек. Он запрашивает эти игрушки по одной в различные моменты времени. Ребенок начинает играть, только когда у него окажутся все игрушки из любимого набора.
- Если ребенок начал играть, то рано или поздно он отдаст все игрушки обратно. Никто не будет держать игрушки вечно.
- Дети запрашивают игрушки в различные моменты времени, никакие два ребенка не запрашивают игрушки одновременно.
- Если ребенку дали запрашиваемую игрушку, то он не отдаст ее, пока не закончит играть со своим любимым набором.
- Если ребенку не дали запрашиваемую игрушку, то он будет ждать, пока ее ему дадут. Он не может запросить другую игрушку, пока ждет. То есть, каждый ребенок в каждый момент времени ждет не более одной игрушки.
- Если два ребенка ждут одну и ту же игрушку, то сначала ее получит тот, кто запросил ее раньше.
Дети не любят играть друг с другом, поэтому они никогда не делятся игрушками. Когда ребенок запрашивает игрушку, то решение дать ему ее или нет зависит от того, свободна игрушка, или нет. Если игрушка свободна, Сахир даст ее ребенку. Иначе ребенок будет ждать ее и не сможет запрашивать другие игрушки, пока ждет. Дети умные и замечают, если случилось так, что им придется ждать запрошенных игрушек бесконечно долго. В таких случаях они начинают плакать. Другими словами, группа плачущих детей это такая группа детей, в которой каждый ребенок ждет игрушку, которая находится у кого-то другого из этой группы. У вас есть сценарий, в котором все дети запрашивают все игрушки из их любимых наборов, кроме одного ребенка x, который запросит еще одну игрушку. Сценарий таков, что после выполнения запросов из сценария некоторые дети начнут играть, а некоторые будут ждать последнюю игрушку, но никто не будет плакать. Если ребенок x будет ждать какую-то игрушку, то он сделает свой оставшийся запрос после ее получения. Иначе, он сразу же запросит ее. Когда ребенок x это сделает, сколько детей начнут плакать? Вам дан сценарий и q независимых запросов. Каждый запрос будет иметь форму x y, что означает, что оставшийся запрос ребенка x — это игрушка y. Ваша задача — помочь Сахиру определить размер максимальной плачущей группы детей после того, как ребенок x сделает свой последний запрос. Выходные данные Для каждого запроса выведите на отдельной строке число детей, которые начнут плакать после того, как ребенок x сделает свой последний запрос (игрушку y). Заметьте, что все варианты последнего запроса независимы. Примечание В первом примере ребенок 1 ждет игрушку 2, которая находится у ребенка 2, а ребенок 2 ждет игрушку 3, которая находится у ребенка 3. Когда ребенок 3 сделает свой последний запрос (он может сделать это сразу), то игрушка, которую он запросит, будет у ребенка 1. Каждый из трех детей будет ждать игрушку, которая находится у другого ребенка, и никто не будет играть, поэтому все трое начнут плакать. Во втором примере после исполнения сценария у ребенка номер i будет находиться игрушка i для 1 ≤ i ≤ 4. Дети 1 и 3 уже собрали свой любимый набор. После того, как они закончат играть, игрушка 3 освободится, а игрушку 1 отдадут ребенку 2, и он соберет любимый набор. После того, как он закончит играть, игрушки 1 и 2 освободятся, и ребенок 5 возьмет игрушку 1. Итак: - В первом варианте ребенок 5 возьмет игрушку 3, и когда он закончит играть, сможет играть ребенок 4.
- Во втором варианте ребенок 5 запросит игрушку 4, которая находится у ребенка 4. В то же время ребенок 4 ждет игрушку 1, которая сейчас находится у ребенка 5. Никто из них не сможет начать играть, и они оба заплачут.
| |
![]()
|
|
E. Сахир и дерево с яблоками
Деревья
игры
*2300
Сахир играет со своим лучшим другом Солиманом. Он принес дерево из n вершин, пронумерованных от 1 до n, корнем дерева является вершина 1. Вершина номер i изначально содержит ai яблок. У дерева есть особенность: длина всех путей от корня к любому из листьев имеет одну и ту же четность (т.е. все пути имеют четную длину, или все пути имеют нечетную длину). Сахир и Солиман будут ходить по очереди. Солиман будет ходить первым. Игрок, который не может сделать ход, проигрывает. На каждом ходу текущий игрок выберет одну из вершин, возьмет ненулевое количество яблок из нее и сделает одно из следующих действий: - съест эти яблоки, если вершина — лист.
- переместит все эти яблоки в одного из сыновей выбранной вершины, если эта вершина не является листом.
Перед тем, как Солиман сделает первых ход, Сахир сделает ровно одно изменение в дереве. А именно, он выберет две различные вершины u и v и поменяет местами яблоки в вершине u и в вершине v. Помогите Сахиру посчитать количество способов сделать это изменение (т.е. выбрать вершины u и v) таких, что при оптимальной игре обоих игроков на полученном дереве выиграет он. (u, v) и (v, u) считаются одной и той же парой. Выходные данные На единственной строке выведите число различных пар вершин (u, v), u ≠ v таких, что если друзья начнут играть после того, как поменяют местам яблоки в этих вершинах, Сахир выиграет. (u, v) и (v, u) считаются одной и той же парой. Примечание В первом примере Сахир может выиграть только если он поменяет яблоки в вершине 1 с яблоками в вершине 3. В таком случае в обоих листьях будет по 2 яблока. Если Солиман сделает ход в листе, то Сахир сделает такой же ход в другом листе. Если Солиман передвинет яблоки из корня, то Сахир съест эти яблоки. Когда-нибудь у Солимана не будет хода. Во втором примере нет такого изменения, чтобы Сахир выиграл. Заметьте, что Сахир должен сделать изменение, даже если он выигрывает с изначальным деревом. | |
![]()
|
|
D. Ночные танцы на дискотеке
геометрия
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
*2000
Теснота на дискотеке никогда не помешает веселиться нашим друзьям, но побольше места не помешает, не правда ли? Дискотека может быть представлена как бесконечная плоскость xy, на которой находятся n танцоров. Как только кто-то начинает двигаться, он будет перемещаться только в своей зоне движения, которая представляет из себя круг Ci с центром в (xi, yi) и радиусом ri. Никакие две границы зон не имеют более, чем одну общую точку, то есть для каждой пары (i, j) (1 ≤ i < j ≤ n) либо зоны Ci и Cj не пересекаются, либо одна лежит полностью в другой. Заметьте, что возможно такое, что две границы зон имеют ровно одну общую точку, однако, никакие два танцора не имеют совпадающие зоны. Цукихи, один из танцоров, определяет просторность как площадь, покрытая нечетным числом зон движений танцоров. Пример показан на рисунке ниже, затемненные регионы определяют просторность, если все танцуют одновременно.  К счастью, никто не танцует всю ночь, поэтому ночь разделена на две части: до полуночи и после полуночи. Каждый танцор одну половину времени танцует, а другую — сидит с друзьями, не занимая площади. Просторность каждой половины времени вычисляется отдельно, и танцоры хотят, чтобы их сумма была максимально возможна. Следующий рисунок показывает оптимальное разделение примера выше.  Возможны различные варианты разделить танцоров на две части: кто танцует в первой половине, а кто — во второй, которые ведут к различным суммам просторности в двух половинах. Вам предстоит определить максимально возможное значение этой суммы. Выходные данные Выведите одно число — максимально возможную сумму просторностей двух половин ночи. Ответ будет считаться верным, если его относительная или абсолютная ошибка не превосходит 10 - 9. Иными словами, пусть ваш ответ равен a, а ответ жюри равен b. Тогда ваш ответ будет зачтен, если  . . Примечание Первый пример соответствует рисунку из условия. | |
![]()
|
|
C. Карен и супермаркет
Деревья
дп
Перебор
*2400
На пути домой Карен решила зайти в супермаркет за продуктами.  Ей нужно купить много продуктов, но, так как она еще учится, ее бюджет ограничен. Она может потратить не более b долларов. В супермаркете есть n товаров. Товар номер i может быть куплен за ci долларов. Конечно, каждый товар может быть куплен только один раз. Супермаркет хочет расширяться, поэтому Карен получила n купонов. Если Карен купит i-й товар, то она может использовать i-й купон для того, чтобы уменьшить цену этого товара на di. Конечно, купон не может быть использован без покупки соответствующего товара. Однако, на использование купонов накладывается ограничение. Для всех i ≥ 2, чтобы использовать купон номер i, Карен должна использовать также купон номер xi (для использования которого может понадобиться использовать другие купоны, чтобы выполнить условие). Карен хочет узнать, сколько максимум товаров она может купить, не превысив своего бюджета b? Выходные данные Выведите одно целое число: количество товаров, которые Карен может купить, не превысив бюджет. Примечание В первом примере Карен может купить следующие 4 товара: - Используя первый купон для покупки первого товара за 10 - 9 = 1 доллар.
- Используя третий купон для покупки третьего товара за 12 - 2 = 10 долларов.
- Используя четвертый купон для покупки четвертого товара за 20 - 18 = 2 доллара.
- Купив шестой товар за 2 доллара.
Суммарная стоимость равна 15, что не превышает бюджета. Заметьте, например, что она не может использовать купон на шестой товар, так как тогда она должна будет использовать пятый купон и купить пятый товар, что она не сделала. Во втором примере у Карен достаточно денег, чтобы использовать все купоны для покупки всех товаров. | |
![]()
|
|
E. Выбор командира
битмаски
Деревья
Структуры данных
*2000
Как вы, может быть, помните по предыдущему раунду, Вова играет в стратегическую компьютерную игру Rage of Empires. Вове удалось создать большую армию, но он забыл о самом главном человеке в армии - командире. Сейчас он пытается нанять командира для своей армии. У каждого воина в армии Вовы есть свой характер, обозначаемый числом pi. У каждого командира два параметра — характер командира pj и лидерство lj (оба параметра — целые числа). Воин i уважает командира j только в том случае, если  ( ( — побитовое исключающее ИЛИ чисел x и y). — побитовое исключающее ИЛИ чисел x и y). Изначально армия Вовы пуста. С ней происходит последовательность событий трёх типов: - 1 pi — один воин с характером pi присоединяется к армии;
- 2 pi — один воин с характером pi покидает армию;
- 3 pi li — Вова пытается нанять командира с характером pi и лидерством li.
Для каждого события третьего типа Вова хочет знать, сколько воинов (считая только тех, кто присоединился к армии и не покинул её до этого события) уважают командира, которого он пытается нанять. Выходные данные Для каждого события третьего типа выведите одно число — кол-во воинов, которые уважают командира, которого пытается нанять Вова в соответствующем событии. Примечание В первом тесте после первых двух событий армия Вовы состоит из двух воинов с характерами 3 и 4. Затем Вова пытается нанять командира с характером 6 и лидерством 3, и один воин уважает этого командира ( , и 2 < 3, но , и 2 < 3, но  , и 5 ≥ 3). Затем воин с характером 4 уходит, и когда Вова снова пытается нанять того же командира, ни один воин не уважает его. , и 5 ≥ 3). Затем воин с характером 4 уходит, и когда Вова снова пытается нанять того же командира, ни один воин не уважает его. | |
![]()
|
|
F. Запросы на MEX
Бинарный поиск
Деревья
Структуры данных
*2300
Дано множество целых чисел, изначально пустое. Ваша задача — обработать n запросов. Запросы бывают трех типов: - 1 l r — Добавить все отсутствующие числа из интервала [l, r]
- 2 l r — Удалить все присутствующие числа из интервала [l, r]
- 3 l r — Инвертировать интервал [l, r] — добавить все отсутствующие и удалить все присутствующие числа из интервала [l, r]
После каждого запроса выведите MEX множества — наименьшее положительное (MEX ≥ 1) целое число, которого нет во множестве. Выходные данные Выведите MEX множества после каждого запроса. Примечание Рассмотрим содержимое множества после каждого из запросов первого примера: - {3, 4} — интервал [3, 4] добавлен
- {1, 2, 5, 6} — числа {3, 4} из интервала [1, 6] удалены, а остальные добавлены
- {5, 6} — числа {1, 2} удалены
| |
![]()
|
|
C. Окабэ и коробки
Деревья
жадные алгоритмы
Структуры данных
*1500
Окабэ и хакер Дару складывают коробки в стопку одну поверх другой. Всего есть n коробок, пронумерованных от 1 до n. Изначально коробок в стопке нет. Окабэ, любящий командовать, дает Дару 2n команд: n из них — добавить некоторую коробку на верх стопки, а n оставшихся — убрать верхнюю коробку из стопки и выкинуть ее. Окабэ хочет, чтобы Дару выкидывал коробки в порядке от 1 до n. Конечно, это означает, что возможно такое, что Дару не сможет выполнить некоторые из команд убрать, потому что необходимая коробка находится не наверху стопки. Поэтому Дару может иногда, когда Окабэ отвернется, переупорядочить коробки в стопке как ему захочется. Он может сделать это в любой момент между командами Окабэ, но он не может добавлять или удалять коробки в процессе переупорядочивания. Скажите Дару, сколько минимум раз ему необходимо переупорядочивать коробки, чтобы он мог успешно выполнить все команды Окабэ. Гарантируется, что каждая коробка добавляется в стопку раньше, чем потребуется ее убрать. Выходные данные Выведите, какое минимальное число раз Дару должен переупорядочивать коробки, чтобы успешно выполнить все команды Окабэ. Примечание В первом примере Дару должен переупорядочивать коробки после добавления коробки 3 в стопку. Во втором примере Дару должен переупорядочивать коробки после добавления коробки 4 и коробки 7 в стопку. | |
![]()
|
|
F. Безумие
Деревья
Конструктив
поиск в глубину и подобное
*2500
В университете Павлополиса начинается второй семестр. После отдыха в Вичкополисе Нура вынуждена вернуться в Павлополис и продолжить обучение. Иногда (или достаточно часто) встречаются преподаватели, которым вы не нравитесь. Вот и у Нуры есть такой. Зовут его Юрий Дмитриевич и он преподает теорию графов. Нура совсем не нравится Юрию Дмитриевичу, поэтому он всегда даёт девушке самые сложные задания. Так случилось и на этот раз. Преподаватель даёт Нуре дерево из n вершин. Вершины пронумерованы целыми числами от 1 до n. Длины всех ребер этого дерева равны 1. Нура выбирает некоторое множество простых путей, которые попарно не пересекаются по ребрам. При этом каждая вершина должна принадлежать хотя бы одному из выбранных путей. Для каждого из выбранных путей выполняется следующее: - Выбирается ровно одно ребро (u, v), которое принадлежит пути.
- На выбранном ребре (u, v) отмечается точка на некотором выбранном расстоянии x от вершины u и расстоянии 1 - x от вершины v. При этом расстояние x выбирается Нурой произвольно, то есть может быть различным для разных ребер.
- Выбирается одна из вершин u или v — именно к выбранной вершине точка начнет свое движение.
Поясним, как происходит движение точки на примере. Пусть путь состоит из двух ребер (v1, v2) и (v2, v3), точка изначально стоит на ребре (v1, v2) и начнет свое движение к вершине v1. Достигнет v1, затем «развернётся», так как был достигнут конец пути, начнет движение к v2, оттуда к v3, там снова «развернётся», переместится к v2 и так далее. При этом скорость движения точек равна 1 ребро в секунду. Например, за 0.5 секунды точка перемещается на длину половины ребра. В каждую вершину дерева помещается секундомер. Время, которое показывают секундомеры в начальный момент времени, равно 0 секунд. Затем в начальный момент времени все точки одновременно начинают движения с выбранных позиций в выбранные направления по выбранным путям, а секундомеры одновременно запускаются. Когда какая-то из точек достигает вершины v, секундомер в вершине v автоматически обнуляется, то есть начинает считать время с нуля. Обозначим за resv — максимальное время, которое покажет секундомер в вершине v, если процесс движения точек будет продолжаться бесконечно. Нуру просят выбрать пути и точки на них так, чтобы res1 было минимально возможным. Если вариантов сделать это несколько, необходимо минимизировать res2, затем res3, res4, ..., resn. Помогите Нуре выполнить задание преподавателя. Для лучшего понимания условия задачи смотрите пояснение к примерам. Выходные данные В первой строке выведите одно целое число paths — количество путей, которые вы хотите выбрать. В последующих paths строках выведите описания путей: - Одно целое число len — количество ребер в текущем пути.
- len целых чисел — номера ребер, входящих в текущий путь. Ребра нумеруются от 1 до n - 1 в том порядке, в котором они следуют во входном файле.
- Два целых числа u и v — это будет означать, что вы поставили точку на ребро между вершинами u и v (очевидно, что оно должно принадлежать пути) и точка начнет движение по направлению к вершине v. Обратите внимание, что важен порядок, в котором вы выведите эти два числа. Например, если вы выведите «1 2» (без кавычек), то точка начнет движение по направлению к вершине с номером 2; если же вывести «2 1» (без кавычек), то точка начнет движение по направлению к вершине с номером 1.
- Одно вещественное число x (0 ≤ x ≤ 1) — расстояние между точкой и вершиной u (той самой, номер которой вы вывели первым в пункте 3).
Система оценки Система проверки сгенерирует массив res по выходным данным, предоставленным участником. Кроме того, система проверки сгенерирует массив resOptimal по ответу жюри. Ваше решение будет считаться корректным, если для каждого целого i (1 ≤ i ≤ n)  . . Примечание Рассмотрим пример. В начальный момент времени точки расположены следующим образом: 
Красным выделен первый путь, синим — второй, зеленые круги обозначают выбранные точки, а коричневые числа внутри вершин — текущее значение секундомера. Фиолетовые стрелочки показывают направление, куда будет двигаться точка. Через 0.(3) секунд точки будут расположены следующим образом (до обнуления секундомеров): 
После обнуления секундомеров: 
Через 1.0 секунду после начала движения: 
Через 1.(3) секунд после начала движения (после обнуления секундомеров): 
Наконец, через 2 секунды после начала движения точки вернутся на исходные позиции: 
Такой процесс движения будет продолжаться бесконечно. | |
![]()
|
|
G. Запросы на дереве
графы
Деревья
поиск в глубину и подобное
*2500
Дано дерево из n вершин (пронумерованных от 1 до n). Изначально все вершины белого цвета. Необходимо обработать q запросов двух типов: - 1 x — покрасить вершину x в чёрный цвет. Гарантируется, что первый запрос будет такого типа.
- 2 x — для вершины x найти минимальный индекс y, такой, что вершина с индексом y принадлежит простому пути от x до некоторой чёрной вершины (простой путь — такой путь, который проходит через каждую вершину не более одного раза).
Выведите ответ на каждый запрос типа 2. Обратите внимание, что запросы задаются в модифицированном виде. Выходные данные Выведите ответ на каждый запрос типа 2. | |
![]()
|
|
D. Лучший вес для ребра
графы
Деревья
поиск в глубину и подобное
Структуры данных
*2700
Дан связный неориентированный взвешенный граф с n вершинами и m ребрами. Граф не содержит петель и мультиребер. Рассмотрим некоторое ребро с номером i. Для него определим наибольший возможный вес, который можно присвоить этому ребру, чтобы оно содержалось во всех минимальный покрывающих деревьях данного графа. Требуется для каждого ребра посчитать максимальный вес по описанным правилам. При этом для каждого ребра ответ должен считаться независимо, то есть в графе может существовать максимум одно ребро с измененным весом. Выходные данные В единственной строке выведите через пробел искомые веса ребер в том порядке, в котором они заданы во входных данных. Если ребро при любом весе будет содержаться во всех покрывающих деревьях, выведите для него -1. | |
![]()
|
|
D. Миша, Гриша и метро
графы
Деревья
поиск в глубину и подобное
*1900
Миша и Гриша — веселые ребята, поэтому они любят кататься на новом метро. В метро есть n станций, соединенных n - 1 перегонами так, что каждый перегон соединяет две станции, и от каждой станции до любой другой можно добраться по перегонам. Ребята решили повеселиться и затеяли кое-что. А именно, в какой-нибудь день утром Миша проезжает кратчайшим путем от станции s до станции f, и на каждой из станций, мимо которых он проехал (включая s и f), он рисует баллончиком корявую надпись «Здесь был Миша». После чего вечером того же дня, Гриша едет со станции t до станции f кратчайшим путем и считает количество станций, на которых обнаружит надпись Миши. После этого ночью этого же дня работники метро смывают все эти надписи, потому что метро должно быть чистым. Ребята уже выбрали на несколько дней вперед по три станции a, b и c, одна из которых должна стать станцией s, другая — станцией f, а третья — станцией t в каждый из дней. Им стало интересно, как нужно выбрать из этих трех станций s, f, t так, чтобы число, которое насчитает Гриша, было максимально возможным. Они просят вас помочь им. Выходные данные Выведите q строк. В i-й строке выведите максимальное число, которое может насчитать Гриша при оптимальном выборе s, t и f из трех станций в i-й день. Примечание В первом примере в первый день при s = 1, f = 2, t = 3, Миша поедет по маршруту 1  2, а Гриша по маршруту 3 2, а Гриша по маршруту 3  1 1  2. Он увидит надпись на станциях 1 и 2. Во второй день при s = 3, f = 2, t = 3, оба мальчика едут по маршруту 3 2. Он увидит надпись на станциях 1 и 2. Во второй день при s = 3, f = 2, t = 3, оба мальчика едут по маршруту 3  1 1  2. Гриша видит надпись на 3 станциях. 2. Гриша видит надпись на 3 станциях. Во втором примере при s = 1, f = 3, t = 2, Миша поедет по маршруту 1  2 2  3, а Гриша по маршруту 2 3, а Гриша по маршруту 2  3 и увидит надпись на обеих станциях. 3 и увидит надпись на обеих станциях. | |
![]()
|
|
D. Красно-черная паутина
Деревья
разделяй и властвуй
реализация
Структуры данных
*2800
 Сластене очень нравится наблюдать за жизнью обитателей тенистой рощи, находящейся неподалеку от Мармеладного замка. На этот раз ее вниманием завладел странный красно-черный желейный паук, восседающий в центре огромной паутины. Паутина странного паука представляет собой набор из n узлов, соединенных прочными нитями, каждая из которых покрашена либо в красный, либо в черный цвет. Используя эти нити, паук перемещается между узлами паутины, причем ни одна нить не соединяет узел с самим собой и для любых двух различных узлов существует единственная последовательность нитей, их соединяющая. Как настоящий энтузиаст, Сластена начала исследовать замечательные свойства паутины. После нескольких часов наблюдения Сластена заметила, что каждая нить имеет собственное значение клейкости x, что само по себе удивительный факт. Но больше всего Сластену интересует желейность данной паутины. Рассмотрим те из кратчайших путей между всеми парами узлов в паутине, на которых количество нитей каждого цвета отличается не более, чем вдвое. Для каждого такого пути посчитаем произведение клейкостей всех нитей на пути. Желейностью паутины Сластена называет произведение всех полученных величин по всем путям. Из путей, отличающихся только направлением движения, учитывается только один. Естественно, данное число очень большое, а Сластена большие числа не любит. Поэтому она просит вас посчитать желейность данной паутины и вывести ответ по модулю 109 + 7. Выходные данные Выведите единственное число — желейность паутины по модулю 109 + 7. Если не существует путей таких, что число красных и черных нитей отличается не более, чем вдвое, выведите 1. Примечание В первом примере существует 4 пары узлов, количество нитей двух цветов между которыми отличается не более, чем вдвое. Это пары (1, 3) с произведением клейкостей на пути 45, (1, 5) с произведением клейкостей на пути 45, (3, 4) с произведением клейкостей на пути 25 и (4, 5) с произведением клейкостей на пути 25. Желейность такой паутины равняется 1265625. | |
![]()
|
|
F. Дороги в королевстве
графы
Деревья
дп
поиск в глубину и подобное
*2500
В королестве К. есть n городов, занумерованных целыми числами от 1 до n. Города соединены n двусторонними дорогами, занумерованными целыми числами от 1 до n. i-я дорога соединяет города ui и vi и имеет длину li. Между двумя городами не бывает более одной дороги. Также не бывает дорог, которые соединяют город с самим собой. Назовём неудобством дорог максимальное из кратчайших расстояний между всеми парами городов. В связи с нехваткой денег было решено отказаться от одной из дорог, при этом после её удаления все города должны быть достижимы друг из друга. Вам необходимо узнать, какое минимальное неудобство дорог можно получить после отказа от одной из дорог. Выходные данные Выведите одно целое число — минимально возможное неудобство дорог после отказа от одной из дорог. | |
![]()
|
|
B. Расходящиеся направления
Деревья
поиск в глубину и подобное
Структуры данных
*2100
Вам дан ориентированный взвешенный граф из n вершин и 2n - 2 ребер. Вершины пронумерованы от 1 до n, а ребра пронумерованы от 1 до 2n - 2. Ребра графа могут быть разделены на две группы. - Первые n - 1 ребер образуют корневое основное дерево, вершина 1 является корнем. Все ребра направлены от корня.
- Последние n - 1 ребер идут от i к 1, для всех 2 ≤ i ≤ n.
Вам дано q запросов. Есть два типа запросов - 1 i w: Изменить вес i-го ребра на w;
- 2 u v: Вывести длину кратчайшего пути между вершинами u и v.
По данным запросам выведите длины кратчайших путей. Выходные данные Для каждого запроса второго типа, выведите длину кратчайшего пути на отдельной строке. | |
![]()
|
|
C. Путешествие
графы
Деревья
дп
поиск в глубину и подобное
Теория вероятностей
*1500
В Семи Королевствах n городов и n - 1 дорога, каждая дорога соединяет два города, и возможно достичь каждый город из каждого, передвигаясь по дорогам. Теон и Яра Грейджой начинают путешествовать на лошади по дорогам из первого города. Из-за тумана они не видят, куда лошадь их везет. Когда лошадь входит в город (в том числе в первый), она направляется в один из городов, соединенных с ним. Но это странная лошадь, поэтому она пойдет только в город, в котором до этого не была. Она идет равновероятно в каждый из таких городов и останавливается, если таких городов нет. Пусть длина каждой дороги 1. Путешествие начинается в городе 1. Чему равно математическое ожидание длины их путешествия? Формально, математическое ожидание — это ожидаемое (то есть среднее) значение. Подробнее можно прочесть по ссылке https://ru.wikipedia.org/wiki/Математическое_ожидание. Выходные данные Выведите одно число — математическое ожидание длины путешествия. Путешествие начинается в городе 1. Ваш ответ будет считаться правильным, если его абсолютная или относительная точность не превосходит 10 - 6. А именно, если ваш ответ равен a, а ответ жюри равен b, то ваш ответ будет зачтен, если  . . Примечание В первом примере путешествие может закончиться в городах 3 или 4 с равной вероятностью. Расстояние до городов 3 и 4 равно 1 и 2, соответственно, поэтому матожидание длины равно 1.5. Во втором примере путешествие может закончиться в городах 4 или 5. Расстояние до обоих городов 2, поэтому матожидание равно 2. | |
![]()
|
|
E. В ловушке
Деревья
*3200
Леха попал в дерево из n вершин с корнем в вершине под номером 1. На каждой вершине i написано целое число ai. Его не выпустят пока он не ответит на q запросов вида u v. Ответ на запрос это максимальное значение  , среди всех вершин i на пути от u до v, включая u и v, где dist(i, v) — количество рёбер на пути от i до v. Так же гарантируется, что вершина u является предком вершины v. Лехины вкусы очень специфичны: Он считает, что вершина является предком самой себя. , среди всех вершин i на пути от u до v, включая u и v, где dist(i, v) — количество рёбер на пути от i до v. Так же гарантируется, что вершина u является предком вершины v. Лехины вкусы очень специфичны: Он считает, что вершина является предком самой себя. Помогите Лехе выйти. Выражение  означает применение побитового исключающего ИЛИ к числам x и y. означает применение побитового исключающего ИЛИ к числам x и y. Напомним, что вершина u является предком вершины v, если вершина u лежит на пути от корня до вершины v. Выходные данные Выведите q строк — ответы на запросы. | |
![]()
|
|
C. Илья и дерево
графы
Деревья
математика
поиск в глубину и подобное
теория чисел
*2000
Илья очень любит графы, особенно деревья. Во время последнего похода в лес Илья нашел очень интересное дерево с корнем в вершине 1, в каждой вершине i которого записано одно целое число ai. Красотой вершины x Илья называет наибольший общий делитель всех чисел в вершинах на пути от корня до x включительно. При этом Илья может изменить число в одной произвольной вершине на 0, либо оставить все вершины неизменными. Теперь Илью интересует, какая максимальная красота может быть у каждой вершины. Для каждой вершины ответ нужно считать независимо. Красота корня равна числу, записанному на нем. Выходные данные В единственной строке через пробел выведите n чисел, где i-е по порядку числу — максимальная красота вершины i. | |
![]()
|
|
E. Никита и игра
Бинарный поиск
графы
Деревья
поиск в глубину и подобное
разделяй и властвуй
*2800
Никита играет в новую компьютерную игру. Всего в игре m уровней. На каждом уровне появляется новый класс, который наследуется от класса yi (и yi является родителем нового класса). Таким образом, классы образуют дерево. Изначально существует только один класс с номером 1. Поменять класс на его соседа в дереве стоит 1 монету, причем обратно класс поменять нельзя. Стоимость смены класса a на класс b равна суммарной стоимости изменений классов на пути от a до b в дереве классов. Пусть на i-м уровне максимальная стоимость смены одного класса на другой равна x. Выведите для каждого уровня количество классов, для которых существует такой класс y, что смена с этого класса на y стоит x. Выходные данные Пусть на i -ом уровне максимальная стоимость смены одного класса на другой равна x. Выведите для каждого уровня количество классов, для которых существует такой класс y, что смена с этого класса на y стоит x. | |
![]()
|
|
C. Переподвешивание дерева
графы
Деревья
Конструктив
математика
поиск в глубину и подобное
*2600
Вам дано дерево размера n и разрешается выполнить не более 2n операций над ним. Операция заключается в выборе трех вершин x, y, y', удалении ребра (x, y) и добавлении ребра (x, y'). Операцию x, y, y' можно выполнить в случае, если выполнены все условия: - Ребро (x, y) присутствует в дереве.
- После операции граф останется деревом.
- При удалении ребра (x, y) дерево распадается на две компоненты связности. Обозначим множество вершин в одной компоненте с вершиной x множеством Vx, а в одной компоненте с вершиной y — множеством Vy. Тогда должно выполняться условие |Vx| > |Vy|, т.е. размер компоненты с x должен быть строго больше размера компоненты с y.
Вам требуется минимизировать сумму квадратов расстояний между всеми парами вершин в итоговом дереве, полученном после не более чем 2n операций, а также предоставить последовательность операций, с помощью которых можно получить итоговое дерево из исходного. Обратите внимание, что минимизировать количество операций не нужно. Нужно минимизировать исключительно сумму квадратов расстояний. Выходные данные В первой строке выведите число k (0 ≤ k ≤ 2n) — количество операций, которые нужно провести, чтобы минимизировать сумму квадратов расстояний между различными парами вершин. В следующих k строках выведите по три целых числа x, y, y' — номера вершин, участвующих в очередной операции. Операции, в которых y = y', разрешены (хоть ничего и не меняют), если выполнены условия операции. Если возможных ответов несколько, выведите любой из них. Примечание Иллюстрация изменений графа во втором примере из условия. Темным обозначены ребра после операции, пунктиром — до. 
| |
![]()
|
|
E. Берляндская химия
Деревья
жадные алгоритмы
поиск в глубину и подобное
*2300
Игорь — аспирант химического факультета Берляндского Государственного Университета (БерГУ). Он должен провести сложный эксперимент для написания научной работы, но в лаборатории БерГУ не хватает некоторых веществ для проведения эксперимента. К счастью, законы химии позволяют преобразовывать одни вещества в другие (да, химия в Берляндии сильно отличается от химии в нашем мире). Но правила преобразования достаточно странные. Берляндским химикам известно n веществ, пронумерованных в порядке их открытия. Каждый материал можно преобразовать в какой-то другой материал (и обратно). Формально, для каждого i (2 ≤ i ≤ n) существуют два числа xi и ki, обозначающие возможное преобразование: ki килограмма вещества xi можно превратить в 1 килограмм вещества i, а 1 килограмм вещества i можно превратить в 1 килограмм вещества xi. Химическое оборудование в БерГУ позволяет проводить только такие преобразования, в результате которых получается целое число килограммов нового вещества. Для каждого i (1 ≤ i ≤ n) Игорю известно, что эксперимент требует ai килограммов вещества i, а в лаборатории есть bi килограммов этого вещества. Можно ли после некоторых преобразований (или вообще без них) провести эксперимент? Выходные данные Выведите YES, если Игорь сможет провести эксперимент. Иначе выведите NO. | |
![]()
|
|
L. Компьютерная сеть Берляндского ГУ
графы
Деревья
Конструктив
поиск в глубину и подобное
хэши
*2400
В компьютерной сети Берляндского государственного университета имеется n маршрутизаторов, пронумерованных от 1 до n. Некоторые пары маршрутизаторов соединены коммутационными шнурами (патч-кордами). Информация по патч-корду может передаваться в любом из двух направлений. Сеть устроена таким образом, что между любыми двумя маршрутизаторами возможна передача информации (непосредственно или через другие маршрутизаторы). В сети отсутствуют циклы, поэтому между каждой парой маршрутизаторов существует единственный путь по патч-кордам. К сожалению, точная топология сети была утеряна администраторами. С целью её восстановления была собрана следующая вспомогательная информация. Для каждого патч-корда p, непосредственно присоединённого к маршрутизатору i, известны все маршрутизаторы, находящиеся за патч-кордом p относительно i. Иными словами, известны все маршрутизаторы, путь от которых до маршрутизатора i включает в себя патч-корд p. Таким образом, для каждого маршрутизатора i составлены ki списков, где ki — количество патч-кордов, подключенных к i. Например, пусть сеть состоит из трех маршрутизаторов, соединённых в цепочку 1 - 2 - 3. Тогда: - маршрутизатор 1: для единственного патч-корда, присоединённого к первому маршрутизатору, составлен единственный список, который содержит два маршрутизатора: 2 и 3;
- маршрутизатор 2: для каждого из патч-кордов, присоединённых ко второму маршрутизатору, составлено по списку: один из них содержит маршрутизатор 1, а другой — маршрутизатор 3;
- маршрутизатор 3: для единственного патч-корда, присоединённого к третьему маршрутизатору, составлен один список, который содержит два маршрутизатора: 1 и 2.
Помогите администраторам компьютерной сети БГУ восстановить топологию сети, то есть определить все пары маршрутизаторов, непосредственно соединенные патч-кордами. Выходные данные Если решения не существует, выведите -1. В противном случае в первую строку выведите число n - 1 — количество патч-кордов в сети. В каждой из следующих n - 1 строк выведите по два целых числа — описания патч-кордов в виде номеров соединяемых ими маршрутизаторов. Информация о каждом патч-корде должна быть выведена ровно один раз. Примечание Первый пример разобран в условии. Ответ для второго примера изображён на рисунке.  На нём мы можем видеть, что у первого маршрутизатора один список, в котором встречаются все остальные маршрутизаторы. У второго маршрутизатора три списка: в первом — маршрутизатор 4, во втором — маршрутизатор 1, а в третьем — маршрутизаторы 3 и 5. У третьего маршрутизатора один список, в котором встречаются все остальные маршрутизаторы. У четвёртого маршрутизатора тоже один список, в котором встречаются все остальные маршрутизаторы. У пятого маршрутизатора два списка: в первом — маршрутизатор 3, а во втором — маршрутизаторы 1, 2 и 4. | |
![]()
|
|
C. Петя и дерево
Бинарный поиск
Деревья
поиск в глубину и подобное
сортировки
Теория вероятностей
*2200
Однажды после тяжелого рабочего дня Пете приснился страшный сон. И было в том сне большое бинарное дерево поиска. Но не дерево пугало Петю, а то, что не получалось у Пети искать в этом дереве элементы. Сколько ни пробовал Петя загадывать ключ и искать его в дереве, каждый раз приходил куда-то не туда. Долго мучился Петя, много загадывал ключей, и все одно и то же. Отчание стало охватывать Петю, как вдруг на него снизошло озарение: каждый раз, когда он искал ключ, этого ключа не было в дереве, и при этом случалась ровно одна ошибка. "Не беда!" — подумал Петя, — "А посчитаю-ка я матожидание значения элемента, который находится при поиске данного ключа." Только он собрался это сделать, как, вдруг, проснулся. Итак, вам дано бинарное дерево поиска, то есть дерево, у которого в каждой вершине записано некоторое число, называемое ключом вершины. Количество сыновей у каждой вершины дерева равно либо 0, либо 2. Вершины, имеющие 0 сыновей, называются листьями, а вершины, имеющие 2 сыновей, называются внутренними. У внутренней вершины есть левый сын, то есть сын, у которого ключ меньше ключа текущей вершины, и правый сын, у которого ключ больше ключа текущей вершины. Потомками некоторой вершины называются все вершины, достижимые из нее. То есть это непосредственные сыновья вершины, сыновья сыновей, и так далее. Левые потомки вершины — потомки ее левого сына. Аналогично, правые потомки вершины — потомки ее правого сына. По свойству дерева поиска, ключ любой вершины строго больше всех ключей левых потомков вершины и строго меньше всех ключей правых потомков вершины. Так же вам задан набор ключей поиска, все из которых различны и отличаются от ключей вершин, имеющихся в дереве. Для каждого ключа из набора выполняется его поиск в дереве. Поиск устроен следующим образом: изначально мы находимся в корне дерева, если ключ текущей вершины больше нашего ключа поиска, то мы переходим в левого сына вершины, иначе переходим в правого сына вершины, и процесс повторяется. Так как ключ поиска гарантированно не содержится в дереве, поиск всегда будет останавливаться в листьях дерева. Ключ, лежащий в листе, объявляется результатом поиска. Достоверно известно, что в ходе этого поиска мы ровно один раз ошибемся в сравнении, то есть пойдем не туда куда надо, а дальше ошибаться не будем. Все возможные ошибки равновероятны, то есть рассматриваются все такие поиски, в которых происходит ровно одна ошибка. Ваша задача — для каждого ключа поиска найти математическое ожидание (среднее значение) результата поиска, при условии что в этом поиске происходит ровно одна ошибка. То есть, надо для набора путей, в которых содержится ровно одна ошибка поиска заданного ключа, посчитать среднее значение ключей, находящихся в листьях этих путей. Выходные данные Выведите k действительных чисел, являющихся матожиданиями ответов для ключей, заданных во входе. Ответ должен отличаться от правильного с относительной или абсолютной погрешностью не более 10 - 9. Примечание В первом сэмпле поиск ключа 1 с одной ошибкой порождает в дереве два пути: (1, 2, 5) и (1, 3, 6), в скобках перечислены номера вершин от корня к листу. Ключи в листьях этих путей равны 6 и 10 соответственно, поэтому ответ равен 8. | |
![]()
|
|
I. Брачное агенство
графы
Деревья
Перебор
поиск в глубину и подобное
*2300
Эта история происходит в городе BubbleLand. В этом городе есть n домов. В каждом из этих n домов живет мальчик или девочка. В этом городе люди действительно любят числа, и у каждого есть свое любимое число f. Это означает, что мальчик или девочка, живущие в городе в i-м доме, имеют свое любимое число, равное fi. Дома пронумерованы числами от 1 до n. Дома соединены n - 1 двунаправленными дорогами, от любого дома возможно добраться до любого другого. Между каждой парой домов есть ровно один путь. Новое брачное агенство открыло свои офисы в этом странном городе, и жители были восхищены. Они сразу же отправили q запросов в агенство, каждый запрос был в следующем формате: - a b — спрашивает, сколько есть способов выбрать пару (мальчик и девочка) такую, что они имеют одинаковое любимое число и живут в домах, находящимся на уникальном пути от дома a до дома b.
Помогите брачному агенству ответить на запросы и расширить их бизнес. Выходные данные Для каждого из q запросов выведите единственное число — ответ на этот запрос. Примечание В первом вопросе на пути от дома 1 до дома 3 потенциальными парами являются (1, 3) и (6, 3). Во втором вопросе на пути от дома 7 до дома 5 потенциальными парами являются (7, 6), (4, 2) и (4, 5). | |
![]()
|
|
C. Чаша Пенелоппы Пуффендуй
Деревья
дп
*2000
Гарри, Рон и Гермиона обнаружили, что чаша Пенелоппы Пуффендуй является крестражем. В результате встречи с Белатриссой Лестрейндж Гермиона узнала, что чаша находится в семейном хранилище Лейстренджей в банке Гринготтс. Волшебный банк представляет собой дерево из n хранилищ, каждое из которых имеет тип, определяемый целым числом от 1 до m. Деревом называется неориентированный связный граф без циклов. Хранилища с идеальной охраной имеют тип k, все хранилища с типом k имеют идеальную охрану. В банке может быть не более x хранилищ с идеальной охраной. Кроме того, если хранилище имеет идеальную охрану, все соседние хранилища не имеют идеальной охраны, а их тип строго меньше k. Гарри хочет рассмотреть все возможные варианты устройства банка. Он знает расположение хранилищ, поэтому его интересует количество возможных вариантов назначить хранилищам типы, чтобы все условия выполнялись. Выходные данные Выведите единственное число — количество способов назначить хранилищам типы для выполнения всех условий по модулю 109 + 7. Примечание В примере 1, не может быть хранилищ с идеальной охраной, так тип хранилища с идеальной охраной равен 1, что значит, что соседние хранилища должны иметь тип меньше чем 1, что невозможно. Поэтому единственно возможный вариант — когда все хранилища имеют тип 2. | |
![]()
|
|
D. Диадема Кандиды Когтевран
Деревья
*2500
Гарри, расспросив призрак Елены Когтевран, узнал, что она рассказала Тому Риддлу, или Сами-знаете-кому, о диадеме Кандиды Когтевран, и он украл ее. Гарри считает, что Том спрятал диадему в Выручай-комнате, так как думал, что только он нашел ее. Потому Гарри собирается проникнуть в Выручай-комнату, ведь он знает, что диадема является крестражем. Однако ему необходимо решить задачку перед тем, как попасть в комнату. Ему дано n объектов, пронумерованных от 1 до n. Некоторые объекты имеют родительский объект, имеющий меньший номер. Формально, объект i может иметь родительский объект parenti такой, что parenti < i. У каждого отношения «объект — родительский объект» имеется тип, который может быть равен 1 или 2. Отношение типа 1 означает, что дочерний объект является особым случаем родительского объекта. Отношение типа 2 означает, что дочерний объект всегда является частью родительского и всех его особых случаев. Обратите внимание, если объект b является специальным случаем объекта a, а объект c является специальным случаем объекта b, то объект c является специальным случаем объекта a. То же самое верно для отношений второго типа: если объект b является частью объекта a, а объект c является частью объекта b, то объект c является частью объекта a. Кроме того. обратите внимание, что если объект b является частью объекта a, а объект c является особым случаем a, то объект b является частью c. Никакой объект не является ни особым случаем себя, ни частью себя. Гарри должен отвечать на два типа запросов: - 1 u v: он должен ответить, является ли объект v особым случаем объекта u.
- 2 u v: он должен ответить, является ли объект v частью объекта u.
Выходные данные Выведите q строк, в каждой выведите «YES», если ответ на очередной запрос утвердительный, и «NO» иначе. Вы можете выводить каждую из букв в любом регистре (строчную или заглавную). Примечание В примере 1 объект 2 является особым случаем объекта 1, а объект 3 является особым случаем объекта 2, поэтому объект 3 является особым случаем объекта 1. В примере 2 объект 2 является особым случаем объекта 1, а объект 1 содержит объект 3 как часть, поэтому объект 2 тоже содержит объект 3 как часть. Это потому, что если общий случай (объект 1) содержит объект 3 как часть, то его особый случай (object 2) тоже содержит объект 3. | |
![]()
|
|
G. Гарри против Волан-де-Морта
графы
Деревья
дп
поиск в глубину и подобное
*3300
После того, как Гарри уничтожил все крестражи Волан-де-Морта, началась их решающая битва. Они кидают друг в друга заклинания, исходящие из волшебных палочек, и заклинания сталкиваются. Битва происходит в Хогвартсе, который можно представить в виде дерева. В Хогвартсе есть n локаций, соединённых n - 1 двунаправленной дорогой. Рону, наблюдающему за битвой между Гарри и Волан-де-Мортом, стало интересно, сколько существует троек локаций (u, v, w), таких что если Гарри находится в локации u, а Волан-де-Морт в локации v, их заклинания могут столкнуться в локации w. Это возможно только если u, v и w попарно различны и существуют путь из u в w и путь из v в w, не проходящие по одной и той же дороге. В хаосе битвы в Хогвартсе стали появляться новые дороги. Вам необходимо вычислять величину, интересующую Рона, после каждого добавления дороги. Формально, задано дерево из n вершин и n - 1 ребер. q новых рёбер добавляются между вершинами дерева. После каждого добавления необходимо вычислять число троек вершин (u, v, w), таких что u, v и w попарно различны и существуют два пути, один из которых между вершинами u и w, а другой — между v и w, такие, что у них нет общих рёбер. Выходные данные В первой строке выведите число троек до всех добавлений. После этого выведите q строк, в каждой из которых выведите число ansi, показывающее число троек после i-го запроса о добавлении дороги. Примечание В первом примере для изначального дерева только (1, 3, 2) и (3, 1, 2) являются возможными тройками локаций (u, v, w). После добавления ребра из 2 в 3, возможны тройки локаций (1, 3, 2), (3, 1, 2), (1, 2, 3) и (2, 1, 3). | |
![]()
|
|
B. Похожие слова
Деревья
дп
Строки
хэши
*2300
Назовем словом непустую последовательность, состоящую из строчных букв латинского алфавита. Префиксом слова x называется слово y, которое можно получить из x удалением нуля или более последних букв x. Назовем два слова похожими, если одно из них можно получить из другого, удалив в нем первую букву. Дано множество слов S. Требуется найти размер максимального множества непустых слов X, удовлетворяющего следующим условиям: - каждое слово из X является префиксом некоторого слова из S;
- в X нет двух похожих слов.
Выходные данные Для каждого теста выведите на отдельной строке число m — размер максимального искомого множества X. | |
![]()
|
|
D. Кактусомания
Деревья
дп
*2400
Маша очень любит кактусы. В детстве Маша посадила дерево, и сейчас оно стало достаточно большим. Маша хочет из своего дерева сделать самый красивый кактус. Напомним, что дерево — это неориентированный связный граф, в котором нет циклов. А кактус — это неориентированный связный граф, через каждую вершину которого проходит не более одного простого цикла. У Маши есть дополнительные ребра, которые она может добавить к дереву. Для каждого ребра Маша знает, какие вершины оно должно соединять, и красоту этого ребра. Маша может добавить некоторые из этих ребер к дереву, если после их добавления получившийся граф будет кактусом. Красота полученного графа равна сумме всех значений красоты добавленных ребер. Помогите Маше выяснить, какую максимальную красоту итогового кактуса Маша может получить. Выходные данные Выведите одно целое число — максимально возможную суммарную красоту кактуса, которую Маша может получить. | |
![]()
|
|
D. Сумасшествие третьего месяца
Деревья
дп
Теория вероятностей
*2100
Приближается ежегодное школьное соревнование по спортболу, по причинам копирайта назовем его «Сумасшествие третьего месяца». Всего будут участвовать 2N команд, пронумерованных от 1 до 2N. В турнире будет N раундов, в каждом раунде половина команд будет выбывать. Первый раунд будет состоять из 2N - 1 игр, пронумерованных с 1. В игре номер i команда 2·i - 1 сыграет с командой 2·i. Проигравший выбывает, а победитель проходит в следующий раунд (ничьих не бывает). В каждом последующем раунде вдвое меньше игр, чем в предыдущем, и в игре номер i играет победитель игры номер 2·i - 1 предыдущего раунда против победителя игры номер 2·i предыдущего раунда. Каждый год в офисе проходит соревнование по построению лучшей турнирной сетки. Турнирная сетка — это набор предсказаний победителя в каждой игре. Для игр первого раунда можно любую из двух команд выбрать победителем, а для игр из более поздних раундов необходимо, чтобы предсказанный победитель был также предсказанным победителем в предыдущем раунде. Заметьте, что турнирная сетка строится перед тем, как начнутся игры. Правильные предсказания в первом раунде дают составителю 1 очко, а правильные предсказания в каждом последующем раунде дают в два раза больше очков, чем в предыдущем. Таким образом, правильное предсказание в финале дает 2N - 1 очков. Для каждой пары команд среди участников вы оценили вероятность победы каждой игры, если эти команды сыграют между собой. Теперь вы хотите построить турнирную сетку с максимальным математическим ожиданием суммарного количества очков. Выходные данные Выведите максимально возможное математическое ожидание суммарного числа очков среди всех возможных турнирных сеток. Ваш ответ должен быть правильным с абсолютной или относительной точностью 10 - 9. Формально, пусть ваш ответ равен a, а ответ жюри равен b. Ваш ответ будет считаться правильным, если  . . Примечание В первом примере вы должны выбрать команды 1 и 4 как победителей в раунде 1, и команду 1 как победителя в раунде 2. Обратите внимание, победитель в раунде 2 должен быть победителем в раунде 1. | |
![]()
|
|
E. Беспорядок на рабочих местах
графы
Деревья
Комбинаторика
поиск в глубину и подобное
снм
*2100
Привезли новые рабочие столы, и нужно с ними поскорее разобраться, так как в офисе стало очень тесно! Вам нужно составить новую рассадку инженеров в офисе. Столы пронумерованы, и вы провели опрос среди инженеров, выяснив, за каким столом они работают сейчас, и за каким столом они хотели бы работать (может совпадать с тем столом, за которым они сейчас работают). Каждый инженер должен либо остаться на своем месте, либо переместиться на то место, которое он обозначил как желаемое. Никакие два инженера не работают сейчас за одним столом, и после пересадки никакие два инженера также не должны работать за одним столом. Сколько существует способов рассадить инженеров так, чтобы удовлетворить описанным ограничениям? Ответ может быть большим, поэтому выведите его по модулю 1000000007 = 109 + 7. Выходные данные Выведите число способов рассадить всех инженеров по модулю 1000000007 = 109 + 7. Примечание Следующие рассадки возможны в первом примере: - 1 5 3 7
- 1 2 3 7
- 5 2 3 7
- 1 5 7 3
- 1 2 7 3
- 5 2 7 3
| |
![]()
|
|
C. Генная инженерия
Деревья
дп
строковые суфф. структуры
*2500
«Многомерные пространства нынче не в моде, а вот генные алгоритмы — очень даже», — подумал физик Воль и переквалифицировался в биоинформатика. Исследуя любезно предоставленные ему результаты секвенирования, он столкнулся со следующей задачей, касающейся цепочек ДНК. Далее мы будем считать, что цепочка ДНК — это произвольная строка, состоящая из заглавных букв «A», «C», «G» и «T» (разумеется, это упрощенная интерпретация). Пусть есть длинная цепочка ДНК w и набор s1, s2, ..., sm коротких цепочек. Будем говорить, что набор фильтрует w, если цепочками набора можно покрыть w. Естественно, подстроки для разных позиций могут пересекаться между собой и даже накрывать друг друга. Формально это условие означает следующее: пусть строка w имеет длину |w|, ее символы пронумерованы от 1 до |w|, и для каждой позиции i в строке w найдется такая пара индексов l, r (1 ≤ l ≤ i ≤ r ≤ |w|), что подстрока w[l ... r] является элементом набора s1, s2, ..., sm. Воль заметил, что цепочек фиксированной длины, фильтрующихся конкретным набором, может быть очень много, и как посчитать их количество — не знает. Помогите физику! Ваша задача — для заданной длины n и набора {si} найти количество различных цепочек ДНК длины n, фильтрующихся данных набором. Ответ может быть очень большим, поэтому выведите его по модулю 1000000009. Выходные данные Выведите единственное целое число: ответ по модулю 1000000009 (109 + 9). Примечание В первом примере строка должна фильтроваться символом «A». Ясно, что такая строка единственна: «AA». Во втором примере существуют ровно две различные строки, удовлетворяющие условию (см. картинки).   | |
![]()
|
|
E. Аркадий и человек-никто
Деревья
поиск в глубину и подобное
Структуры данных
*2700
Аркадий работает в крупной компании. Всего в компании n сотрудников, при этом действует жесткая иерархия. А именно, у каждого сотрудника, кроме директора, есть ровно один непосредственный начальник, а директор является начальником (через цепочку непосредственных подчиненных) всех сотрудников. У каждого сотрудника есть ранг, выраженный целым числом. У директора ранг равен 1, а каждый другой сотрудник имеет ранг на 1 больший, чем ранг его непосредственного начальника. У Аркадия неплохая позиция в компании, однако он чувствует, что он — никто в структуре компании, и есть много людей, которые могут заменить его. Он ввел понятие заменяемости. Рассмотрим сотрудника a и сотрудника b, который является начальником a (не обязательно непосредственным). Тогда заменяемостью r(a, b) сотрудника a относительно начальника b называется количество подчиненных (не обязательно непосредственных) данного начальника b, ранг которых не превосходит ранга данного подчиненного a. Кроме заменяемости, Аркадий ввел еще и понятие ничтожности. Ничтожность za сотрудника a равна сумме его заменяемостей относительно всех его начальников, то есть  , где сумма берется по всем его начальникам b. , где сумма берется по всем его начальникам b. Аркадию интересна не только своя ничтожность, но и ничтожность всех остальных сотрудников компании. Найдите для Аркадия ничтожность каждого из сотрудников. Выходные данные Выведите n целых чисел — ничтожности всех сотрудников в порядке их нумерации: z1, z2, ..., zn. Примечание Рассмотрим первый пример. Тогда: - У директора нет начальников, поэтому z1 = 0.
- r(2, 1) = 2 (сотрудники 2 и 4 подходят, сотрудник 3 имеет слишком большой ранг). Поэтому z2 = r(2, 1) = 2.
- Аналогично, z4 = r(4, 1) = 2.
- r(3, 2) = 1 (сотрудник 3 является подчиненным 2 и имеет необходимый ранг). r(3, 1) = 3 (подходят сотрудники 2, 3, 4). Поэтому z3 = r(3, 2) + r(3, 1) = 4.
| |
![]()
|
|
B. Махмуд, Ехаб и двудольность
графы
Деревья
поиск в глубину и подобное
*1300
Махмуд и Ехаб продолжают свои приключения! Каждый житель Злой Страны знает, что Доктор Зло любит двудольные графы, особенно деревья. Дерево — это связный граф без циклов. Двудольный граф — это граф, вершины которого можно разбить на 2 множества таким образом, что для любого ребра (u, v) графа вершины u и v лежат в разных множествах. Более формальное определение дерева и двудольного графа дано ниже. Доктор Зло дал Махмуду и Ехабу дерево, состоящее из n вершин и сказал добавлять рёбра таким образом, чтобы граф оставался двудольным, а также в нём не было петель и кратных рёбер. Какое максимальное число рёбер они могут добавить? Выходные данные Выведите одно число — максимальное число рёбер, которые Махмуд и Ехаб могут добавить в граф. | |
![]()
|
|
F. Экскурсии по городам
графы
Деревья
поиск в глубину и подобное
*2700
В Берляндии есть n городов. Некоторые пары городов соединены m односторонними дорогами. Из одного города в другой можно добраться только по этим дорогам. При этом нет дорог, соединяющих город с самим собой. Для любой пары городов (x, y) может быть не более одной дороги из x в y. Путь из города s в город t представляет собой последовательность городов p1, p2, ... , pk, где p1 = s, pk = t, где из города pi идет дорога в город pi + 1 для все i от 1 до k - 1. Через любой из городов, кроме последнего города t пути, путь может проходить многократно. Через город t многократно путь проходить не может. Путь p из s в t называется идеальным, если он является лексикографически минимальным таким путем. Иными словами, p — идеальный путь из s в t, если для любого другого пути q из s в t pi < qi, где i — наименьший индекс такой, что pi ≠ qi. В стране работает туристическое агенство, которое предоставляет q необычных экскурсий: j-я экскурсия начинается в городе sj и заканчивается в городе tj. Помогите туристическому агентству для каждой пары sj, tj проанализировать идеальный путь из sj в tj. Заметим, что идеальный путь из sj в tj может не существовать. Такое возможно по двум причинам: - из города sj невозможно добраться по дорогам в город tj;
- из города sj возможно добраться по дорогам в город tj, но для любого такого пути p найдется другой путь q из sj в tj, что pi > qi, где i — первый индекс, что pi ≠ qi.
Анализ идеального пути из sj в tj состоит в нахождении города, который является kj-м в этом пути (при следовании из sj в tj). Напишите программу, которая для каждой тройки sj, tj, kj (1 ≤ j ≤ q) определит, существует ли идеальный путь из sj в tj и выведет kj-й город пути, если таковой есть. Выходные данные В j-ю строку выходных данных выведите город, который расположен kj-м в идеальном пути из sj в tj. Если идеального пути из sj в tj не существует или число kj больше длины этого пути, выведите в j-ю строку '-1' без кавычек. | |
![]()
|
|
E. Полицейский и дерево
графы
Деревья
дп
*2700
Дано дерево (связный неориентированный граф без циклов), его вершины пронумерованы от 1 до n, длина i-го ребра wi. В вершине s стоит полицейский, также в вершинах x1, x2, ..., xm (xj ≠ s) расположены m преступников. Полицейский ходит по ребрам со скоростью 1, преступники могут перемещаться со сколь угодно большой скоростью. Если преступник в какой-то момент находится в одной точке с полицейским, его мгновенно ловят. Определите время, за которое можно поймать всех преступников, если преступники и полицейский действуют оптимально (т.е. преступники максимизируют это время, а полицейский — минимизирует). В любой момент времени все знают текущие положения всех остальных людей. Выходные данные Если полицейский не сможет поймать всех преступников, выведите в единственную строку «Terrorists win» (без кавычек). Иначе выведите одно число — время, за которое полицейский поймает всех преступников. Примечание В первом примере один из оптимальных сценариев такой. Преступник 2 перемещается в вершину 3, а преступник 4 — в вершину 4. Полицейский идет в вершину 4 и ловит двух преступников. После этого преступник 1 перемещается в вершину 2. Полицейский идет в вершину 3 и ловит преступника 2, потом идет в вершину 2 и ловит оставшегося преступника. | |
![]()
|
|
D. Красивая дорога
графы
Деревья
дп
поиск в глубину и подобное
реализация
снм
сортировки
*2300
Давным давно где-то в Азии в одной стране шли междоусобные войны. Каждый из n городов хотел захватить власть, поэтому иногда один город собирал армию и отправлял ее в поход против другого города. Прокладывание дорог было делом трудным, поэтому их в стране было мало, а именно n - 1. Также из любого города до любого другого можно было добраться по этим дорогам. Даже во время войны жители Востока остаются людьми духовно богатыми и ценящими красоту природы. И, дабы оставить на века память о своем великом походе, на дороге, на которой в пути армия провела больше всего времени, сажали одно красивое дерево. Жители Востока любят природу, поэтому если таких дорог было несколько, то по одному дереву сажалось на каждой. Недавно, когда были обнаружены летописи той войны, выяснилось, что каждый город напал на каждый ровно по одному разу. Всего было ровно n(n - 1) походов. Всем стало интересно, какая дорога после тех войн стала самой красивой, то есть на какой дороге посадили больше всего красивых деревьев. Выходные данные В первой строке выведите два числа — количество красивых деревьев на самой красивой дороге и количество самых красивых дорог. Во второй строке выведите список самых красивых дорог, в порядке возрастания номеров. Дороги пронумерованы от 1 до n - 1 в том порядке, в котором они даны во входных данных. Пожалуйста, не используйте спецификатор %lld для записи 64-х битовых чисел на С++. Рекомендуется использовать поток cout (также вы можете использовать спецификатор %I64d). | |
![]()
|
|
E. Точки, прямые и неоригинальные названия
графы
Деревья
поиск в глубину и подобное
снм
*2300
На плоскости дано n различных точек с целыми координатами. Для каждой точки можно выполнить одно из трех действий: провести через нее вертикальную прямую, провести через нее горизонтальную прямую или ничего не делать. Если рассматривать несколько совпадающих прямых как одну, то сколько различных картинок может получиться? Ответ вывести по модулю 109 + 7. Выходные данные Вывести количество различных картинок по модулю 109 + 7. Примечание В первом примере через точки проходят две вертикальные и две горизонтальные прямые. Существуют способы получить картинку из любого набора этих прямых. В частности, получить картинку на которой нарисованы все четыре прямые можно двумя способами (каждый отрезок обозначает прямую, которой отрезок принадлежит). Первый способ:  Второй способ: Второй способ:  Во втором примере для каждой точки можно независимо выполнить одно из трех действий. Количество картинок равно 32 = 9. | |
![]()
|
|
E. Восстановление дерева
графы
Деревья
жадные алгоритмы
*2900
У Пети было дерево, состоящее из n вершин, пронумерованных целыми числами от 1 до n. Но по стечению обстоятельств он своё дерево потерял. Петя помнит о k вершинах из своего дерева информацию о расстоянии от каждой из них до всех n вершин дерева. Перед вами стоит задача восстановить любое дерево, удовлетворяющее информации, которую помнит Петя, либо сообщить, что это невозможно. Выходные данные Если не существует подходящего дерева, выведите -1. В противном случае, выведите в n - 1-й строке по два целых числа — концы очередного ребра. Вы можете выводить ребра и концы ребер в любом порядке. Вершины дерева пронумерованы от 1 до n. Если ответов несколько, разрешается вывести любой из них. Примечание Иллюстрация к первому примеру:  | |
![]()
|
|
E. Данил и подработка
битмаски
Деревья
Структуры данных
*2000
Данил решил заработать денег, поэтому нашел подработку. Собеседование прошло хорошо, и его взяли на очень ответственную должность переключателя света. Данил будет работать в корневом дереве (связном неориентированном графе без циклов) из n вершин, корнем которого является вершина 1. В каждой вершине находится комната, в которой может гореть свет. В обязанности Данила входит переключение света во всех комнатах поддерева вершины. Это значит, что если в какой-то комнате поддерева горит свет, он должен выключить его, иначе он должен включить его. К сожалению (или к счастью), Данил очень ленивый. Он знает, что его начальник не собирается лично проверять выполнение работы. Вместо этого он будет присылать Данилу задания через личные сообщения на Workforces. Задания бывают двух типов: - pow v обозначает задание на переключение света в поддереве вершины v
- get v обозначает задание на подсчет количества комнат в поддереве v, в которых горит свет. Данил должен отправить начальнику ответ личным сообщением на Workforces.
Под поддеревом вершины v понимается все вершины, кратчайший путь от которых до корня дерева проходит через вершину v. В частности, сама вершина v лежит в поддереве вершины v. Данил не собирается выполнять свою работу. Вместо этого он просит написать вас программу, которая будет отвечать начальнику за него. Выходные данные На каждый запрос get v выведите одно целое число — количество комнат в поддереве v, в которых горит свет. Примечание  Дерево до задания pow 1. Дерево до задания pow 1. Дерево после задания pow 1. Дерево после задания pow 1.
| |
![]()
|
|
C. Петя и катакомбы
Деревья
жадные алгоритмы
реализация
снм
*1300
Однажды Петя — очень храбрый исследователь — решил заняться изучением великих парижских катакомб. Так как Петя не очень опытный в этом деле, его исследование заключается в хождении по катакомбам. Катакомбы представляют из себя набор комнат, некоторые из которых соединены переходами, переход может соединять комнату с самой собой, по переходам можно ходить в любую сторону. Переходы могут находиться на разных глубинах, что позволяет им не пересекаться. Каждую минуту Петя выбирает произвольным образом переход из комнаты, в которой он находится, и проходит его за одну минуту. Когда он заходит в комнату в минуту i, он делает в журнал запись — число ti: - Если Петя уже был в этой комнате, он записывает минуту, когда он был в этой комнате в предыдущий раз;
- Иначе Петя записывает в журнал произвольное неотрицательное целое число, строго меньшее текущей минуты i.
Изначально Петя находился в какой-то из комнат в минуту 0, при этом число t0 он не записывал. В какой-то момент Петя устал, бросил журнал и пошёл домой (не обязательно в той же комнате, из которой он начинал). Вася нашёл этот журнал, и теперь ему интересно: какое наименьшее количество комнат может быть в катакомбах, согласно журналу Пети? Выходные данные В первой строке выведите единственное число — минимальное возможное количество комнат в парижских катакомбах. Примечание В первом тестовом примере последовательность комнат, по которым прошёл Петя, могла быть 1 → 1 → 2 или 1 → 2 → 1, или, например, 1 → 2 → 3. Минимальное число комнат равно 2. Во втором тестовом примере эта последовательность могла быть 1 → 2 → 3 → 1 → 2 → 1. | |
![]()
|
|
D. Лень
Деревья
дп
Паросочетания
поиск в глубину и подобное
*3100
Лень — это плохо, не так ли? Поэтому мы решили приготовить задачу, чтобы наказать ленивых. Вам дано дерево, вы должны посчитать количество способов убрать одно ребро, а затем добавить одно ребро так, чтобы получившийся граф был деревом, и в нем существовало совершенное паросочетание. Два способа считаются различными, если удаленные или добавленные ребра не совпадают. Добавленное ребро может совпадать с удаленным. Совершенным паросочетанием называется подмножество ребер такое, что каждая вершина графа является концом ровно одного ребра. Выходные данные Выведите одно целое число — ответ на задачу. Примечание В первом примере имеются 8 вариантов: - ребро между 2 и 3 заменить на ребро между 1 и 3,
- ребро между 2 и 3 заменить на ребро между 1 и 4,
- ребро между 2 и 3 заменить на ребро между 2 и 3,
- ребро между 2 и 3 заменить на ребро между 2 и 4,
- ребро между 1 и 2 заменить на ребро между 1 и 2,
- ребро между 1 и 2 заменить на ребро между 1 и 4,
- ребро между 3 и 4 заменить на ребро между 1 и 4,
- ребро между 3 и 4 заменить на ребро между 3 и 4.
| |
![]()
|
|
F. Минимум в поддереве
Деревья
Структуры данных
*2300
Дано корневое дерево, состоящее из n вершин. В каждой вершине записано некоторое число: в i-й вершине — ai. Определим расстояние между вершинами i и j в дереве — d(i, j) (количество ребер на кратчайшем пути из i в j). Также определим поддерево глубины k вершины x — набор вершин y такой, что выполняются следующие условия: - x является предком y (каждая вершина считается своим предком);
- d(x, y) ≤ k.
Заданы m запросов к дереву. i-й запрос представляется двумя числами xi и ki. Ответ на запрос — минимальное значение aj среди таких вершин j, что j принадлежат поддереву глубины ki вершины xi. Напишите программу, которая быстро обработает такие запросы. Обратите внимание, что запросы подаются в особом виде. Выходные данные Выведите m чисел. i-е из них должно быть ответом на i-й запрос. | |
![]()
|
|
D. Ральф и его поездки по Бинарной стране
Деревья
Перебор
Структуры данных
*2200
Ральф находится в Бинарной стране. Бинарная страна состоит из n городов и (n - 1) двунаправленной дороги, соединяющей города. Дороги пронумерованы от 1 до (n - 1), где i-я дорога соединяет город номер  (здесь ⌊ x⌋ обозначает x, округленный вниз к ближайшему целому) и город номер (i + 1), а длина i-й дороги равна Li. (здесь ⌊ x⌋ обозначает x, округленный вниз к ближайшему целому) и город номер (i + 1), а длина i-й дороги равна Li. Ральф дал вам m запросов. В каждом запросе он указал некоторый город Ai и целое число Hi. Он хочет сделать несколько поездок, начинающихся в указанном городе. Он может выбрать любой город (включая Ai) в Бинарной стране в качестве конца поездки. От такой поездки он получит (Hi - L) единиц счастья, где L — расстояние между городом Ai и конечным городом маршрута. Ральфу интересны все поездки из Ai, в которых он может получить положительное количество единиц счастья. Для каждого запроса посчитайте суммарное количество получаемых единиц счастья по всем таким поездкам. Ральф никогда не проедет по одному и тому же маршруту дважды или больше (в одном запросе), также, он никогда не посетит один город дважды или больше за одну поездку. Выходные данные Выведите m строк, на i-й из них выведите одно целое число — ответ на i-й запрос. Примечание Далее следует пояснение ко второму примеру. Первый запрос Ральфа — начинать поездки в городе 2, а Hi равно 4. Вот варианты поездок, которые у него есть: - Закончить поездку в городе 5. Так как расстояние между городами 5 и 2 равно 3, он получит 4 - 3 = 1 единицу счастья.
- Закончить поездку в городе 4, тогда он получит 3 единицы счастья.
- Закончить поездку в городе 1, тогда он получит 2 единицы счастья.
- Закончить поездку в городе 3, тогда он получит 1 единицу счастья.
- Обратите внимание, он может закончить поездку в городе 2, тогда он получит 4 единицы счастья.
- Ральф не может закончить поездку в городе 6, так как расстояние между городом 6 и городом 2 равно 5, что приводит к отрицательному количеству единиц счастья.
Поэтому ответ на первый запрос равен 1 + 3 + 2 + 1 + 4 = 11. | |
![]()
|
|
A. Хешируем деревья
Деревья
Конструктив
*1500
Саша участвует в соревновании по программированию. В очередной задаче ей нужно уметь проверять корневые деревья на изоморфизм. Она никогда не сталкивалась с этой задачей раньше, но, будучи опытной участницей, быстро догадалась, что для этого стоит сопоставить каждому дереву некоторую последовательность и сравнивать уже эти последовательности, а не деревья. Саша хочет поставить в соответствие дереву такую последовательность a0, a1, ..., ah, где h — высота дерева, что ai равно числу вершин, находящихся на расстоянии i рёбер от корня. К сожалению, в этот раз интуиция подвела Сашу, и оказалось, что такая последовательность может не однозначно задавать дерево. Чтобы это показать, вы должны написать программу, которая по заданной последовательности ai предоставит два неизоморфных корневых дерева, которым соответствует такая последовательность, или скажет, что такое дерево единственно. Два корневых дерева считаются изоморфными, если можно так перенумеровать вершины одного из них, чтобы оно стало равно второму, при этом корень первого дерева должен получить номер корня второго дерева. Высотой дерева будем называть наибольшее число рёбер в пути от корня до какой либо другой вершины. Выходные данные Если последовательность однозначно задаёт дерево, выведите «perfect». Иначе в первую строку выведите «ambiguous». Во вторую и третью строчки выведите описания двух деревьев в следующем формате: в одну строку выведите  чисел, k-е из них должно задавать предка вершины k или быть равным нулю, если k-я вершина является корнем дерева. чисел, k-е из них должно задавать предка вершины k или быть равным нулю, если k-я вершина является корнем дерева. Эти два дерева должны быть неизоморфны и должны соответствовать заданной последовательности. Примечание Единственное дерево к первому примеру и два выведенных дерева ко второму: 
| |
![]()
|
|
F. Разрушение дерева
графы
Деревья
жадные алгоритмы
Конструктив
поиск в глубину и подобное
*2400
Задано невзвешенное дерево с n вершинами. С ним производят n - 1 операцию. Каждая из операций состоит в следующем: - выбирается два листа в дереве;
- к ответу добавляется длина простого пути между этими листами;
- выбирается один из этих двух листов и удаляется из дерева.
До проведения операций ответ равен 0. Очевидно, что после n - 1 проведённой операции в дереве останется одна вершина. Вам необходимо посчитать, какого максимального ответа можно добиться, если действовать оптимально, и вывести, каким образом необходимо действовать. Выходные данные В первой строке выведите одно целое число — максимальный ответ, которого можно достигнуть. В следующих n - 1 строках выведите действия в порядке их совершения в формате ai, bi, ci, где ai, bi — пара листов, выбранных на текущем шаге (1 ≤ ai, bi ≤ n), ci (1 ≤ ci ≤ n, ci = ai или ci = bi) — выбранный лист, который удаляется на текущем шаге. Посмотрите в примеры для лучшего понимания. | |
![]()
|
|
B. Новогодняя елка
Деревья
реализация
*1200
Рассмотрим корневое дерево. В корневом дереве есть одна выделенная вершина — корень. Все ребра ориентированы по направлению от корня. Вершина u является ребенком вершины v, а вершина v является родителем вершины u, если существует ориентированное ребро из v в u. Листом корневого дерева называется вершина, у которой нет детей, и есть родитель. Назовем корневое дерево елкой, если у каждой вершины, не являющейся листом, хотя бы 3 ребенка являются листами. Вам дано корневое дерево, проверьте, является ли оно елкой. Определение корневого дерева можно прочитать по ссылке. Выходные данные Выведите «Yes», если дерево является елкой, и «No» иначе. Примечание Первый пример: 
Второй пример: 
Это не елка, потому что у вершины 1, которая не является листом, только 2 ребенка являются листьями. Третий пример: 
| |
![]()
|
|
E. Палиндромы в дереве
битмаски
Деревья
разделяй и властвуй
Структуры данных
*2400
Дано дерево (связный ациклический граф) на n вершинах. Вершины пронумерованы от 1 до n и на каждой вершине записана буква английского алфавита от a до t. Путь в дереве называется палиндромным, если из букв, записанных на нём, можно составить палиндром (буквы можно произвольным образом переставлять). Для каждой вершины выведите количество палиндромных путей, проходящих через неё. Учтите, что путь из вершины u в вершину v и путь из вершины v в вершину u считаются одинаковыми, такие пути должны учитываться ровно один раз. Выходные данные Выведите n чисел, где i-е число обозначает количество палиндромных путей, проходящих через вершину i. Примечание В первом тестовом примере следующие пути являются палиндромными: 2 - 3 - 4 2 - 3 - 5 4 - 3 - 5 Кроме того, все пути, состоящие из одной вершины, являются палиндромными. А следующие пути палиндромными не являются: 1 - 2 - 3 1 - 2 - 3 - 4 1 - 2 - 3 - 5 | |
![]()
|
|
H. Деревянная игра Эмбера и Шторма
Деревья
дп
игры
Комбинаторика
*3400
Эмбер и Шторм играют в игру. Вначале, Эмбер выбирает помеченное дерево T на n вершинах, такое что степень каждой вершины не превосходит d. Затем Шторм выбирает две различные вершины u и v в этом дереве и выписывает номера вершин на пути из u в v как последовательность a1, a2... ak. Наконец Эмбер выбирает произвольный индекс i (1 ≤ i < k) и выполняет одну из следующих операций ровно один раз: - перевернуть подотрезок [i + 1, k] и прибавить ai ко всем числам на нём. После этого последовательность приобретает вид a1, ... ai, ak + ai, ak - 1 + ai, ... ai + 1 + ai
- Заменить все числа на подотрезке [i + 1, k] на противоположные и прибавить ai к ним. После этого последователньость приобретает вид a1, ... ai, - ai + 1 + ai, - ai + 2 + ai, ... - ak + ai
Эмбер выигрывает, если после произведённой операции массив монотонно возрастает или убывает, иначе выигрывает Шторм. Игра может быть представлена набором (T, u, v, i, op), где op — это «перевернуть» или «выполнить отрицаение» в зависимости от действия, которое Эмбер выполнил на последнем шаге. Найдите количество наборов, которые могут образоваться в результате оптимальной игры Эмбера и Шторма. Если они играют оптимально и у игрока есть несколько ходов, которые гарантируют победу, игрок может воспользоваться любым из них. Также если у игрока нет ни одного хода, гарантирующего победу, он может воспользоваться любым ходом. Выведите ответ по модулю m. Выходные данные Выведите единственное число — количество возможных наборов по модулю m. Примечание В первом тестовом примере существует только одно возможное дерево. Можно выбрать два пути: из 1 в 2 и из 2 в 1. Для обоих путей i может быть равно только 1, а op может принимать оба возможных значения. Поэтому ответ равен 4. Во втором тестовом примере подходящих деревьев нет. В третьем тестовом примере есть три возможных дерева. | |
![]()
|
|
F. Несбалансированность дерева
графы
Деревья
снм
Структуры данных
*2400
Задано дерево T, состоящее из n вершин. На каждой вершине записано число; на i-й — ai. Определим функцию I(x, y) — разница между максимальным и минимальным значением ai на простом пути между вершинами x и y. Ваша задача — вычислить  . . Выходные данные Выведите одно число —  . . | |
![]()
|
|
D. Джейми и список дел
Деревья
интерактив
Структуры данных
*2200
Почему мне надо делать так много домашних заданий??? У Джейми очень много дел в школе. Он начинает забывать, какие домашние задания ему надо сделать, поэтому он решил записывать их в список дел. Каждому заданию он присваивает некоторый приоритет так, что чем приоритет меньше, тем важнее задание. Таким образом он сможет решить, на какие задания тратить больше времени. Через несколько дней Джейми обнаружил, что его список дел настолько большой, что он не может им пользоваться самостоятельно. Так как вы дружите с Джейми, помогите ему и напишите программу, которая выполняет следующий операции со списком дел: - set ai xi — Добавить задание ai в список дел, если оно ещё не в списке, и назначить ему приоритет равный xi. Если задание ai уже в списке дел, его приоритет станет равен xi.
- remove ai — Удалить задание ai из списка дел, если оно в нём есть.
- query ai — Выведите количество заданий, которые важнее (имеют меньший приоритет), чем задание ai, чтобы Джейми смог лучше распределить своё время. Выведите - 1 если задания ai в списке дел нет.
- undo di — Отменить все изменения, сделанные за последние di дней (не включая день текущей операции)
В день с номером 0 список дел пуст. В каждый из следующих q дней Джейми будет делать ровно одну операцию одного из четырёх типов. Если операция — это query, то необходимо вывести ответ на запрос до начала обработки запроса, соответствующего следующему дню, чтобы Джейми смог заранее спланировать свой день. Выходные данные Для каждого запроса типа query, выведите одно целое число — количество заданий, которые имеют приоритет меньше, чем ai, или - 1, если задания ai нет в списке дел. Протокол взаимодействия Если операцимя имеет тип query, вам необходимо вывести ответ на запрос и сбросить буфер вывода до начала обработки следующей операции. В противном случае Вы можете получить вердикт Idleness Limit Exceed. Для того, чтобы узнать, как сбросить буфер вывода, обратитесь к документации по Вашему языку программирования. Ниже приведён код для некоторых популярных языков программирования: - C: fflush(stdout);
- C++: cout « flush;
- Java: System.out.flush();
| |
![]()
|
|
E. Джейми и дерево
Деревья
Структуры данных
*2400
Трудно поверить, но Джейми — финальный босс! У Джейми есть дерево на n вершинах, пронумерованных от 1 до n. Изначально корнем дерева является вершина с номеров 1. Кроме того, на каждой вершине дерева записано число. Вам необходимо обрабатывать запросы трёх типов: 1 v — Сделать вершину с номером v корнем дерева. 2 u v x — Прибавить x к значению каждой вершины наименьшего по размеру поддерева, содержащего вершины u и v. 3 v — Найти сумму значений вершин в поддереве вершины v. Поддерево вершины v — это множество вершин, для которых v лежит на кратчайшем пути от этой вершины до корня. Обратите внимание, что поддерево вершины может измениться в результате изменения корня дерева. Покажите Джейми вашу мощь и выполните все запросы! Выходные данные Для каждого запроса третьего типа выведите ответ на него. Гарантируется, что в тесте есть хотя бы один запрос третьего типа. Примечание Картинка ниже иллюстрирует изменения дерева в первом тестовом примере.  | |
![]()
|
|
D. Очень странные деревья
Деревья
дп
математика
матрицы
*2600
Сознание Уилла связано с сознанием монстра с Обратной стороны, поэтому Уиллу известно все, о чем думает монстр. Неожиданно Уилл начал рисовать без остановок, страницу за страницей. Его мама Джойс и шериф Хоппер сложили все рисунки вместе и поняли, что это помеченное дерево!  Деревом называется связный ациклический граф. В дереве Уилла n вершин. Джойс и Хоппер не знают, что означает это дерево, поэтому они решили его исследовать, а также исследовать похожие деревья. Для каждого k такого, что 0 ≤ k ≤ n - 1, они собираются исследовать все такие помеченные деревья из n вершин, у которых ровно k ребер совпадают с ребрами дерева Уилла. Два помеченных дерева различны, если и только если существует пара вершин (v, u) такая, что в одном дереве существует ребро между вершинами v и u, а в другом — нет. Хоппер и Джойс хотят узнать, сколько работы им предстоит, поэтому они просят вас посчитать для каждого k число помеченных деревьев из n вершин, у которых ровно k ребер совпадают с ребрами в дереве Уилла. Так как ответ может быть большим, выведите ответы по модулю 1000000007 = 109 + 7. Выходные данные Выведите n целых чисел на одной строке. i-е из этих чисел должно быть равно числу помеченных деревьев из n вершин таких, что ровно i - 1 ребро совпадает с ребрами в дереве Уилла, по модулю 1000 000 007 = 109 + 7. | |
![]()
|
|
E. Обратная сторона
Деревья
Строки
строковые суфф. структуры
Структуры данных
*3400
Все знают, что Одиннадцать обладает некоторыми сверхспособностями. Поэтому Хоппер уговорила ее закрыть врата на Обратную сторону силой мысли. Монстры с Обратной стороны любят перемещаться между мирами, поэтому они собираются атаковать Хоппер и Одиннадцать, чтобы остановить их. Монстры живут на дереве из n вершин, пронумерованных от 1 до n. На каждом ребре написана строчная латинская буква.  Обратная сторона — магический мир. В нем живут m видов монстров, пронумерованных от 1 до m. У каждого вида монстров есть специальное слово, которое дает ему силу. Специальное слово вида i равно si. Всего на Обратной стороне q монстров. Каждый сейчас находится в одной вершине и собирается дойти до некоторой другой вершины. Если монстр типа k идет от вершины i до вершины j, его сила увеличивается на количество раз, когда он видел свое специальное слово (sk) как подстроку на своем пути. Более формально: Пусть f(i, j) — строка, которую мы получим, если выпишем все буквы на ребрах на кратчайшем пути из i в j. Тогда сила монстра увеличивается на количество вхождений sk в f(i, j). Хоппер и Одиннадцать хотят подготовиться, поэтому для каждого монстра они хотят определить силу, которую приобретет монстр после передвижения. Выходные данные Выведите q строк. В i-й из этих строк выведите силу i-го монстра после передвижения. | |
![]()
|
|
C. Идеальная защита
Деревья
жадные алгоритмы
Строки
Структуры данных
*1800
У Алисы есть важное сообщение M, состоящее из нескольких неотрицательных целых чисел, которое она хочет сохранить в тайне от Евы. Алиса знает, что единственный теоретически защищенный способ шифрования — использование одноразового ключа. Алиса сгенерировала случайный ключ K с длиной, равной длине сообщения. Алиса затем вычислила побитовое исключающее ИЛИ каждого соответствующего элемента массива и ключа ( , где , где  обозначает операцию побитового исключающего ИЛИ) и сохранила зашифрованное сообщение A. Алиса умная. Будь как Алиса. обозначает операцию побитового исключающего ИЛИ) и сохранила зашифрованное сообщение A. Алиса умная. Будь как Алиса. Например, пусть Алиса хочет сохранить сообщение M = (0, 15, 9, 18), и она сгенерировала ключ K = (16, 7, 6, 3). Тогда зашифрованное сообщение равно A = (16, 8, 15, 17). Алиса понимает, что она не может хранить ключ вместе с зашифрованным сообщением. Поэтому Алиса послала ключ K Бобу и удалила свою копию. Алиса умная. Действительно, будь как Алиса. Боб понимает, что зашифрованное сообщение защищено только до тех пор, пока ключ является секретным. Поэтому Боб случайным образом поменял местами элементы ключа перед тем, как сохранить его. Боб думает, что в таком случае, даже если Ева получит и зашифрованное сообщение, и ключ, она не сможет прочитать исходное сообщение. Боб не умный. Не будь как Боб. В примере выше Боб мог, например, выбрать перестановку (3, 4, 1, 2), перемешать элементы в соответствии с ней и сохранить ключ P = (6, 3, 16, 7). Прошел год, и Алиса теперь хочет расшифровать свое сообщение. Только сейчас Боб понял, что это невозможно. Так как он поменял местами элементы ключа случайным образом, сообщение утеряно навсегда. Мы уже сказали, что Боб не очень умный? Боб хочет получить хотя бы какую-то информацию из сообщения. Так как он не очень умный, он попросил у вас помощи. Вам известны зашифрованное сообщение A и произвольно перемешанный ключ P. Каково лексикографически минимальное сообщение, которое могло быть зашифровано подобным образом? Формально, по данным A и P найдите лексикографически минимальное сообщение O такое, что существует перестановка π такая, что  для всех i. для всех i. Напомним, что последовательность S лексикографически меньше последовательности T, если существует такая позиция i, что Si < Ti, а для всех j < i выполняется Sj = Tj. Выходные данные Выведите одну строку с N целыми числами — лексикографически минимально возможное сообщение O. Напомним, что все числа в нем должны быть неотрицательны. Примечание В первом примере решением является (10, 3, 28), потому что  , ,  и и  . Другие возможные перестановки ключа дают сообщения (25, 6, 10), (25, 3, 15), (10, 21, 10), (15, 21, 15) и (15, 6, 28), все из которых лексикографически больше, чем оптимальное решение. . Другие возможные перестановки ключа дают сообщения (25, 6, 10), (25, 3, 15), (10, 21, 10), (15, 21, 15) и (15, 6, 28), все из которых лексикографически больше, чем оптимальное решение. | |
![]()
|
|
F. Общественный транспорт
графы
Деревья
Конструктив
*3200
В стране Боба N городов, соединенных дорогами. Между некоторыми парами городов можно проехать на общественном транспорте. Есть две конкурирующие компании: Бобавто возит пассажиров на автобусах, а Бобжд управляет пассажирскими поездами. Чтобы проехать из города A в город B, пассажир сначала должен выбрать вид транспорта, который он будет использовать (автобус или поезд), и затем отправиться в путь. Для каждой пары городов существует ровно два способа добраться из одного города в другой, не посещая ни один город дважды: один способ использует автобусы, другой — поезда. Кроме того, никакая пара городов не соединена одновременно автобусной линией и железной дорогой напрямую. У вас есть схемы обеих сетей. К сожалению, каждая компания использует различные названия для одних и тех же городов. А именно, автобусная компания нумерует города от 1 до N, а железнодорожная — от N + 1 до 2N. Найдите какое-либо возможное соответствие между этими нумерациями такое, что никакая пара городов не соединена одновременно автобусным и железнодорожным маршрутом напрямую. Обратите внимание на то, что различным городам на одной схеме должны соответствовать различные города другой схемы. Выходные данные Если решения нет, выведите единственную строку, содержащую слово «No». Если решение существует, выведите две строки. В первой строке выведите слово «Yes». Во второй строке выведите N целых чисел P1, P2, ..., PN (N + 1 ≤ Pi ≤ 2N) — соответствие между двумя схемами. А именно, для i ≠ j должно выполняться Pi ≠ Pj, и для всех автобусных маршрутов (i, j) не должно быть прямого железнодорожного маршрута (Pi, Pj). Если существует несколько решений, выведите любое. Примечание Первый пример показан на рисунке (автобусные линии красные, железнодорожные — синие): 
| |
![]()
|
|
E. Майские праздники
Деревья
Структуры данных
*2900
Во Флатландии наступил месяц май, который длится \(m\) дней. Несмотря на то, что майские праздники давным-давно отменили для повышения производительности трудящихся, работники одной софтверной компании по старой памяти продолжают брать короткие и длинные отпуска в мае, чтобы съездить в путешествие или отметить начало дачно-огородного сезона за городом. Разумеется, это не может не тревожить руководителей компании. В компании \(n\) сотрудников, объединённых в древовидную структуру подчинения — каждому сотруднику назначен номер \(i\) от \(1\) до \(n\), а также у каждого сотрудника \(i\) (за исключением самого главного начальника, имеющего номер 1) есть ровно один непосредственный руководитель, номер которого есть \(p_i\). В структуре подчинения нет циклов, то есть, если мы начнём переходить от любого сотрудника к его начальнику, затем к его начальнику и так далее, то мы рано или поздно дойдём до самого главного начальника. Будем считать, что сотрудник \(u\) является подчинённым сотрудника \(v\), если \(v\) — непосредственный руководитель \(u\), либо если непосредственный руководитель \(u\) является подчинённым сотрудника \(v\). Обозначим за \(s_i\) количество подчинённых сотрудника \(i\) (например, \(s_1 = n - 1\) в соответствии с данным определением). У каждого сотрудника \(i\) есть предел терпения \(t_i\), выражающийся целым числом от \(0\) до \(s_i\), обозначающий максимальное количество одновременно пребывающих в отпуске подчинённых сотрудника \(i\), которое тот готов терпеть. Если в какой-то момент времени у сотрудника \(i\) в отпуске находится более, чем \(t_i\) подчинённых, и при этом сотрудник \(i\) не находится в отпуске сам, то он становится недовольным. В каждый из последующих \(m\) дней случается ровно одно событие одного из двух видов — либо некоторый сотрудник уходит в отпуск с текущего дня, либо возвращается из отпуска с текущего дня. Вам известна последовательность событий, происходящих в каждый из \(m\) майских дней. Ваша задача — определить, сколько сотрудников компании являются недовольными в каждый из \(m\) дней. Выходные данные Выведите последовательность из \(m\) целых чисел \(a_1, a_2, \ldots, a_m\), где \(a_i\) — количество недовольных сотрудников компании в \(i\)-й день. Примечание В первом тесте из условия после ухода сотрудника 2 в отпуск в первый день недовольным становится самый главный начальник, который не готов терпеть отпуск ни одного из сотрудников компании кроме себя. В четвёртый день недовольным становится сотрудник 5, у которого в отпуск уходит последний его подчинённый, имеющий номер 7. В пятый день из отпуска возвращается сотрудник 2, но это не меняет число недовольных сотрудников, так как сотрудники 5 и 1 по-прежнему недовольны. В шестой день из отпуска возвращается сотрудник 3, в результате чего сотрудник 5 перестаёт быть недовольным, а в последний день самый главный начальник номер 1 сам уходит в отпуск, в результате чего недовольных людей не остаётся. | |
![]()
|
|
D. Автодополнение
*особая задача
Деревья
Строки
*1900
Аркадий работает копирайтером. Сегодня ему нужно написать некоторый текст, который он уже продумал до мельчайших подробностей, но еще не набрал. Для набора текста Аркадий использует свою любимый текстовый редактор. Аркадий набирает слова, знаки препинания и пробельные символы один за другим, для набора каждой буквы и каждого знака (в том числе перевода строки) требуется одно нажатие клавиши на клавиатуре. При этом, когда Аркадий набрал непустой префикс некоторого слова (в том числе слово полностью), его редактор подсказывает возможное автоматическое дополнение для текущего слова: слово из числа тех, которые Аркадий набрал до этого, префикс которого совпадает с текущим набранным префиксом, если такое слово уникально. Например, если Аркадий уже набрал слова «codeforces», «coding» и еще раз «codeforces», то, если он наберет префикс «cod», то редактор ему ничего не подскажет, а если он наберет префикс «code», редактор подскажет «codeforces». При этом не важно, собирается ли Аркадий набрать слово «codeforces» или, например, «codebest». Одним нажатием клавиши Аркадий может использовать подсказку, то есть дополнить текущий префикс до слова, предложенного редактором, при этом никаких других символов после слова автоматически не ставится и можно продолжить набирать слово. Какое минимальное число нажатий на клавиши необходимо Аркадию для того, чтобы набрать текст, если он не может перемещать курсор и стирать уже написанные буквы и другие символы? Формально словом называется непрерывная последовательность латинских букв, с обоих концов ограниченная пробелами, знаками препинания, началом или концом строки или текста. Аркадий использует только строчные буквы. Например, в тексте «it's well-known that tic-tac-toe is a paper-and-pencil game for two players, x and o.» 20 слов. Выходные данные Выведите одно целое число — минимальное количество нажатий на клавиши, которое должен сделать Аркадий. Примечание В первом примере нужно воспользоваться автодополнением для первого слова «snowboarding» после того, как набран префикс «sn», и для второго слова «snowboarding» после того, как набран префикс «snowb». Суммарно это экономит 7 нажатий. Во втором примере все равно, пользоваться автодополнением, или нет. В третьем нужно можно воспользоваться автодополнением для второго слова после набора «t», для третьего слова — после набора «t», затем набрать его до конца, далее слова «thun» надо набирать полностью, а для набора «thunder» необходимо набирать «thund», затем пользоваться автодополнением, кроме того, надо пользоваться автодополнением для вторых слов «lightning» и «feel» после набора одной буквы. | |
![]()
|
|
A. Необычная яблоня
графы
Деревья
поиск в глубину и подобное
*1500
У Аркадия в саду есть одна необычная яблоня, с которой иногда необходимо собирать яблоки. Так как яблоня необычная, на ней есть n соцветий, они пронумерованы от 1 до n. Соцветие номер 1 находится около корня дерева, любое другое соцветие с номером i (i > 1) расположено на верхнем конце ветки, нижний конец которой расположен в соцветии pi, при этом pi < i. Когда яблоки созревают, одновременно появляется ровно по одному яблоку в каждом соцветии. В тот же момент все яблоки начинают скатываться вниз по веткам к корню дерева. Каждую секунду все яблоки, кроме находящегося в первом соцветии, одновременно скатываются на одну ветку ближе к корню, то есть, например, из соцветия a яблоко попадет в соцветие pa. Яблоки, находившиеся в первом соцветии, забирает Аркадий. Яблоня необычная, поэтому, если в какой-то момент в одном соцветии оказываются два яблока, они аннигилируют. Так происходит с каждой парой, например, если в соцветие попадет одновременно 5 яблок, то останется только одно яблоко, а если в соцветие попадет одновременно 8 яблок, то не останется ни одного яблока. Таким образом, в каждом соцветии в любой момент времени находится не более одного яблока. Помогите Аркадию, подсчитайте, сколько яблок он сможет забрать из первого соцветия за один урожай. Выходные данные Выведите количество яблок, которые Аркадий сможет забрать из первого соцветия за один урожай. Примечание В первом примере Аркадий соберет всего одно яблоко, которое изначально находилось в соцветии номер 1. Через секунду в это соцветие попадёт еще два яблока из соцветий 2 и 3, но они аннигилируют между собой и Аркадий не сможет собрать ни одно из них. Во втором примере Аркадий соберет три яблока. Первым он соберет то яблоко, которое изначально находится в соцветии один. Через секунду в соцветие 1 попадет яблоко из соцветия 2 (которое Аркадий тоже соберет), а в соцветия 2 попадут три яблока из соцветий 3, 4 и 5, два из которых аннигилируют между собой, и в соцветии 2 останется всего одно яблоко, которое еще через секунду попадёт в соцветие 1, и Аркадий его соберёт. | |
![]()
|
|
D. Дерево
Бинарный поиск
Деревья
дп
*2200
Дана вершина дерева с номером 1 и весом 0. Обозначим за cnt количество вершин в дереве в любой момент (изначально cnt равно 1). Необходио обработать Q запросов, каждый из которых имеет один из двух типов: -
 Добавить новую вершину (с номером cnt + 1) и весом W и провести ребро между вершиной R и этой вершиной. Добавить новую вершину (с номером cnt + 1) и весом W и провести ребро между вершиной R и этой вершиной. -
 Выведите максимальную длину последовательности вершин такой, что она Выведите максимальную длину последовательности вершин такой, что она - Начинается с вершины R.
- Каждая следующая вершина является предком предыдущей вершины
- Сумма весов вершин в последовательности не превосходит X.
- Для любой пары i, j вершин, которые являются соседними в последовательности и вершина i является предком вершины j, выполнено w[i] ≥ w[j], а также не существует вершины k на простом пути из i в j такой, что w[k] ≥ w[j]
Дерево подвешено за вершину 1 в любой момент. Учтите, что запросы заданы в зашифрованном виде. Выходные данные Для каждого запроса второго типа выведите ответ на него в отдельной строке. Примечание В первом тестовом примере, last = 0 - Запрос 1: 1 1 1, Вершина 2 с весом 1 подвешивается к вершине 1. - Запрос 2: 2 2 0, Никакая последовательность вершин, начинающаяся с вершины 2, не имеет сумму весов не более 0. last = 0 - Запрос 3: 2 2 1, Ответ равен 1, так как требуемая последователньость равна {2}. last = 1 - Запрос 4: 1 2 1, Вершина 3 с весом 1 подвешивается к вершине 2. - Запрос 5: 2 3 1, Ответ равен 1, так как требуемая последовательность равна {3}. Вершина 2 не может быть добавлена к последовательности, так как сумма весов должна быть не более 1. last = 1 - Запрос 6: 2 3 3, Ответ равен 2, так как требуемая последовательность будет равна {3, 2}. last = 2 | |
![]()
|
|
E. Фафа и древняя математика
Деревья
дп
поиск в глубину и подобное
*2300
Известно, что древние Египтяне были сильными математиками. Древнеегипетский математик Ахмес любил писать некие арифметические выражения на листе папируса, которые он называл Ахмесовы арифметические выражения. Ахмесово арифметическое выражение можно определить как: - «d» является Ахмесовым арифметическим выражением, где d — это положительное число, состоящее из одной цифры;
- «(E1 op E2)» является Ахмесовым арифметическим выражением, где E1 и E2 — корректные Ахмесовы арифметические выражения (без пробелов) и op это плюс ( + ) или минус ( - ).
Например 5, (1-1) и ((1+(2-3))-5) — корректные Ахмесовы арифметические выражения. Во время своей поездки в Египет, Фафа нашел кусочек папирусной бумаги, на которой было написано одно из корректных Ахмесовых арифметических выражений. Кусочек папируса очень состарился и все операции стерлись, оставив только числа и скобки. Так как Фафа любит математику, он решил бросить себе вызов следующей задачей. Дано количество операций плюс и минус в исходном выражении, найдите максимальное возможное значение выражения, поставив плюсы и минусы вместо стертых операций. Выходные данные Выведите одну строку, содержащую ответ на задачу. Примечание - Ответом на первый тест из условия будет (1 + 1) = 2.
- Ответом на второй тест из условия будет (2 + (1 - 2)) = 1.
- Ответом на третий тест из условия будет ((1 - (5 - 7)) + ((6 + 2) + 7)) = 18.
- Ответом на четвертый тест из условия будет ((1 + (5 + 7)) - ((6 - 2) - 7)) = 16.
| |
![]()
|
|
F. Кучи
Деревья
дп
*2600
Дано дерево на n вершинах с корнем в вершине 1. Скажем, что в вершине u содержится k-ичная куча глубины m, если выполняется следующее: - При m = 1 вершина u сама является k-ичной кучей глубины 1.
- При m > 1 вершина u является k-ичной кучей глубины m, если хотя бы k из ее детей являются k-ичными кучами глубины не менее m - 1.
Определим dpk(u) как максимальную глубину k-ичной кучи по всем вершинам в поддереве u (включая u). Требуется посчитать значение  . . Выходные данные В единственной строке выведите одно число — ответ на задачу. Примечание Рассмотрим первый пример. Для k ≥ 3 все значения dpk будут равны 1. При k = 2 dpk равняется 2 при  и 1 в противном случае. и 1 в противном случае. При k = 1 значения dpk равны (3, 1, 2, 1). Таким образом, сумма равняется 4·1 + 4·1 + 2·2 + 2·1 + 3 + 1 + 2 + 1 = 21. | |
![]()
|
|
B2. Maximum Control (medium)
графы
Деревья
жадные алгоритмы
поиск в глубину и подобное
Структуры данных
*2200
The Resistance is trying to take control over as many planets of a particular solar system as possible. Princess Heidi is in charge of the fleet, and she must send ships to some planets in order to maximize the number of controlled planets. The Galaxy contains N planets, connected by bidirectional hyperspace tunnels in such a way that there is a unique path between every pair of the planets. A planet is controlled by the Resistance if there is a Resistance ship in its orbit, or if the planet lies on the shortest path between some two planets that have Resistance ships in their orbits. Heidi has not yet made up her mind as to how many ships to use. Therefore, she is asking you to compute, for every K = 1, 2, 3, ..., N, the maximum number of planets that can be controlled with a fleet consisting of K ships. Output On a single line, print N space-separated integers. The K-th number should correspond to the maximum number of planets that can be controlled by the Resistance using a fleet of K ships. Note Consider the first example. If K = 1, then Heidi can only send one ship to some planet and control it. However, for K ≥ 2, sending ships to planets 1 and 3 will allow the Resistance to control all planets. | |
![]()
|
|
C. Махмуд, Эхаб и неправильный алгоритм
Деревья
Конструктив
*1500
Махмуд пытался решить задачу вершинного покрытия на дереве. Эта задача формулируется так. По данному неориентированному дереву, состоящему из n вершин, найдите минимальное число вершин, которые покрывают все рёбра. Формально, нам необходимо найти такой набор вершин, что для каждого ребра (u, v), принадлежащего дереву, или u, или v принадлежит этому набору, или они оба принадлежат ему. Махмуд нашёл следующий алгоритм для решения задачи: - Возьмём за корень дерева вершину 1.
- Посчитаем количество вершин на чётной глубине и назовём её evenCnt.
- Посчитаем количество вершин на нечётной глубине и назовём её oddCnt.
- Ответом будет являться минимальное из чисел evenCnt и oddCnt.
Глубиной вершины называется число рёбер в кратчайшем пути между этой вершиной и корнем. Глубина корня равна 0. Эхаб сказал Махмуду, что данный алгоритм неверен, но Махмуд не поверил ему, поскольку он тестировал этот алгоритм на множестве разных деревьев и он всегда выводил правильный ответ. Поэтому Эхаб просит вас помочь найти два таких дерева, состоящих из n вершин, что алгоритм Махмуда выведет неправильный ответ для первого дерева и правильный — для второго. Выходные данные Вывод должен состоять из 2 независимых частей, каждая из которых содержит дерево. Алгоритм Махмуда должен получать неправильный ответ для дерева в первой части и правильный — для дерева во второй части. Если по какой-либо причине корректного дерева для какой-то части не существует, выведите -1 только для данной части. Если ответ для какой-то части существует, он должен содержать n - 1 строку, в каждой из которых должно содержаться 2 целых числа u и v (1 ≤ u, v ≤ n), разделённых пробелами, что будет означать, что между вершинами u и v есть неориентированное ребро. Если выданный вашей программой граф не будет являться деревом или не будет следовать формату выходных данных, ваше решение получит вердикт «Неправильный ответ». Если существует несколько правильных ответов, выведите любой из них. Примечание В первом примере существует всего одно дерево с двумя вершинами (вершина 1, соединённая с вершиной 2). Алгоритм всегда получит на нём правильный ответ, поэтому мы вывели - 1 в первой секции, но заметьте, что мы вывели это дерево во второй секции. Во втором примере: В первом дереве алгоритм выведет ответ с 4 вершинами, но существует следующий ответ с 3 вершинами:  Во втором дереве алгоритм найдёт ответ с 3 вершинами, который верен: Во втором дереве алгоритм найдёт ответ с 3 вершинами, который верен:  | |
![]()
|
|
D. Запросы для полного бинарного дерева
Деревья
Перебор
реализация
*2100
У вас есть полное бинарное дерево с бесконечным количеством уровней. В каждой вершине записано значение. Если в вершине записано значение x, то в ее левом потомке записано значение 2·x, а в правом потомке — значение 2·x + 1. Значение, записанное в корне, равно 1. Вам нужно обработать Q запросов. Всего есть 3 типа запросов: - Циклически сдвинуть на K значения, записанные во всех вершинах, которые находятся на одном уровне с вершиной, в которой записано значение X. (Вершины и значения, записанные в вершинах, на других уровнях остаются без изменений).
- Циклически сдвинуть на K вершины, которые находятся на одном уровне с вершиной, в которой записано значение X. (Поддеревья сдвигаемых вершин двигаются вместе с ними).
- Вывести значения, записанные в каждой из вершин, которые встречаются на простом пути из вершины, в которой записано значение X, до корня.
Положительное K означает циклический сдвиг вправо, а отрицательное K означает циклический сдвиг влево. Гарантируется, что среди запросов есть хотя бы один, который имеет тип 3. Выходные данные Для каждого запроса типа 3 выведите в порядке убывания значения, записанные во всех вершинах, встречающихся на пути. Примечание На картинках ниже изображены первые 4 уровня дерева для первого примера: Изначальное дерево:  Дерево после запроса 1 2 1:  Дерево после запроса 2 4 -1:  | |
![]()
|
|
E. Знакопеременное дерево
Деревья
дп
Комбинаторика
поиск в глубину и подобное
разделяй и властвуй
Теория вероятностей
*2300
Вам дано дерево с \(n\) вершинами, пронумерованными с \(1\) до \(n\). В вершине \(i\) записано значение \(V_i\). Если простой путь от вершины \(u_1\) до вершины \(u_m\) состоит из \(m\) вершин, а именно из \(u_1 \rightarrow u_2 \rightarrow u_3 \rightarrow \dots u_{m-1} \rightarrow u_{m}\), то знакопеременная сумма для этого пути \(A(u_{1},u_{m})\) определяется как \(A(u_{1},u_{m}) = \sum\limits_{i=1}^{m} (-1)^{i+1} \cdot V_{u_{i}}\). Путь может содержать \(0\) рёбер, т. е. \(u_{1}=u_{m}\). Вычислите сумму знакопеременных сумм для всех различных простых путей в дереве. Обратите внимание, пути ориентированны: два пути считаются различными, если у них различное начало или различный конец. Так как ответ может быть большим, выведите остаток от деления его на \(10^{9}+7\). Выходные данные Выведите сумму знакопеременных сумм по всем различным простым путям в дереве по модулю \(10^{9}+7\). Примечание Рассмотрим первый пример. Знакопеременная сумма для простого пути из вершины \(1\) в вершину \(2\): \(1 \rightarrow 2\) равна \(A(1,2) = 1 \cdot (-4)+(-1) \cdot 1 = -5\). Знакопеременная сумма для простого пути из вершины \(1\) в вершину \(3\): \(1 \rightarrow 3\) равна \(A(1,3) = 1 \cdot (-4)+(-1) \cdot 5 = -9\). Знакопеременная сумма для простого пути из вершины \(2\) в вершину \(4\): \(2 \rightarrow 1 \rightarrow 4\) равна \(A(2,4) = 1 \cdot (1)+(-1) \cdot (-4)+1 \cdot (-2) = 3\). Простой путь из вершины \(1\) в вершину \(1\) содержит только вершину \(1\), поэтому \(A(1,1) = 1 \cdot (-4) = -4\). Аналогично, \(A(2, 1) = 5\), \(A(3, 1) = 9\), \(A(4, 2) = 3\), \(A(1, 4) = -2\), \(A(4, 1) = 2\), \(A(2, 2) = 1\), \(A(3, 3) = 5\), \(A(4, 4) = -2\), \(A(3, 4) = 7\), \(A(4, 3) = 7\), \(A(2, 3) = 10\), \(A(3, 2) = 10\). Поэтому ответ равен \((-5) + (-9) + 3 + (-4) + 5 + 9 + 3 + (-2) + 2 + 1 + 5 + (-2) + 7 + 7 + 10 + 10 = 40\). | |
![]()
|
|
H. Подарок Санты
Деревья
Структуры данных
*3100
У Санты есть бесконечное число конфет каждого из \(m\) вкусов. Вам дано корневое дерево с \(n\) вершинами. Корень дерева — вершина с номером \(1\). Каждая вершина содержит ровно одну конфету, \(i\)-я вершина содержит конфету вкуса \(f_i\). Иногда Санта боится, что конфеты вкуса \(k\) испортились. Он выбирает любую вершину \(x\) случайным образом и посылает поддерево вершины \(x\) кондитерам на замену. Во время замены все конфеты вкуса \(k\) в поддереве заменяются на новые конфеты того же вкуса, а конфеты не вкуса \(k\) остаются неизменными. После замены дерево возвращается в состояние, в котором оно было до замены. Настоящая цена замены одной конфеты вкуса \(k\) равна \(c_k\) (дана для каждого \(k\)). Однако, для простоты вычислений кондитеры берут за каждое посланное им поддерево одинаковую сумму \(C\) вне зависимости от того, какое поддерево выбрано, сколько конфет в поддереве и какого вкуса они. Предположим, что для заданного вкуса \(k\) вероятность выбора каждой вершины Сантой для посылки на замену одинакова для всех вершин. Вам нужно найти математическое ожидание ошибки в подсчёте стоимости замены конфет вкуса \(k\). Ошибка в подсчёте стоимости вычисляется так: \(\) Ошибка\ E(k) =\ (настоящая\ стоимость\ замены\ –\ цена,\ взятая\ кондитерами) ^ 2.\(\) Обратите внимание, что настоящая стоимость замены равна стоимости замены одной конфеты вкуса \(k\), умноженной на количество конфет этого вкуса в поддереве. Иногда Санта заменяет конфету в вершине \(x\) на конфету некоторого вкуса из его кармана. Ваша программа должна уметь обрабатывать два типа запросов: - Изменить вкус конфеты в вершине \(x\) на вкус \(w\).
- Подсчитайте математическое ожидание ошибки подсчёта стоимости замены конфет для заданного вкуса \(k\).
Входные данные Первая строка входных данных содержит четыре целых числа \(n\) (\(2 \leqslant n \leqslant 5 \cdot 10^4\)), \(m\), \(q\), \(C\) (\(1 \leqslant m, q \leqslant 5 \cdot 10^4\), \(0 \leqslant C \leqslant 10^6\)) — число вершин в графе, количество различных вкусов конфет, число запросов и цена, которую кондитеры берут за замену поддерева? соответственно. Вторая строка содержит \(n\) целых чисел \(f_1, f_2, \dots, f_n\) (\(1 \leqslant f_i \leqslant m\)), где \(f_i\) — изначальный вкус конфеты в \(i\)-й вершине. В третьей строке содержится \(n - 1\) целое число \(p_2, p_3, \dots, p_n\) (\(1 \leqslant p_i \leqslant n\)), где \(p_i\) — родитель \(i\)-й вершины. Следующая строка содержит \(m\) целых чисел \(c_1, c_2, \dots c_m\) (\(1 \leqslant c_i \leqslant 10^2\)), где \(c_i\) — стоимость замены одной конфеты со вкусом \(i\). Следующие \(q\) строк описывают запросы. Каждая строка начинается с целого числа \(t\) (\(1 \leqslant t \leqslant 2\)) — типа запроса. Если \(t = 1\), тогда эта строка описывает запрос первого типа. За ним следует два целых числа \(x\) и \(w\) (\(1 \leqslant x \leqslant n\), \(1 \leqslant w \leqslant m\)) — Санта заменяет конфету в вершине \(x\) на конфету вкуса \(w\). Иначе, если \(t = 2\), строка описывает запрос второго типа и после него следует целое число \(k\) (\(1 \leqslant k \leqslant m\)) — выведите математическое ожидание ошибки в подсчёте стоимости замены конфет для данного вкуса \(k\). Вершины пронумерован с \(1\) до \(n\). Вершина \(1\) является корнем. Выходные данные Выведите ответ на каждый запрос второго типа в отдельной строке. Ваш ответ будет принят, если его относительная или абсолютная погрешность не превышает \(10^{-6}\). Формально, пусть ваш ответ равен \(a\), а ответ жюри равен \(b\). Ваш ответ будет засчитан, если и только если \(\frac{|a-b|}{max(1,b)}\leqslant 10^{-6}\). Примечание Для \(1\)-го запроса ошибка в подсчёте стоимости замены для вкуса \(1\) равна \(66^2\), \(66^2\) и \((-7)^2\), если выбран \(1\), \(2\) и \(3\) соответственно. Так как вероятность выбора каждой из вершин одинакова, математическое ожидание ошибки равно \(\frac{66^2+66^2+(-7)^2}{3}\). Аналогично, для \(2\)-го запроса ожидаемое значение ошибки равно \(\frac{41^2+(-7)^2+(-7)^2}{3}\). После \(3\)-го запроса, вкус конфеты на вершине \(2\) изменится с \(1\) на \(3\). Для \(4\)-го запроса ожидаемое значение ошибки равно \(\frac{(-7)^2+(-7)^2+(-7)^2}{3}\). Аналогично для \(5\)-го запроса ожидаемое значение ошибки равно \(\frac{89^2+41^2+(-7)^2}{3}\). | |
![]()
|
|
F. Рёбра на простых циклах
графы
Деревья
поиск в глубину и подобное
*2400
Задан неориентированный граф, состоящий из \(n\) вершин и \(m\) рёбер. Граф не обязательно связный. Гарантируется, что в графе нет кратных рёбер и петель. Цикл в графе называется простым, если он содержит каждую свою вершину ровно один раз (под своими вершинами цикла понимаются все вершины, которые входят в этот цикл). Определите рёбра, которые лежат ровно на одном простом цикле. Выходные данные В первую строку выведите количество рёбер, которые лежат ровно на одном простом цикле. Во вторую строку выведите номера рёбер, лежащих ровно на одном простом цикле, в порядке возрастания. Рёбра нумеруются начиная с единицы в том же порядке, в котором заданы во входных данных. | |
![]()
|
|
G. Видимые черные области
геометрия
Деревья
снм
Структуры данных
*2800
У Пети есть многоугольник, состоящий из \(n\) вершин. Все стороны многоугольника Пети параллельны осям координат, а каждые две смежные стороны многоугольника Пети — перпендикулярны. Гарантируется, что многоугольник простой, то есть не имеет самопересечений и самокасаний. Вся внутренняя часть (границы не учитываются) многоугольника была покрашена Петей в черный цвет. Также у Пети есть прямоугольное окно, заданное своими координатами, через которое он смотрит на свой многоугольник. Прямоугольное окно задается своими координатами и не может быть перемещено. Стороны прямоугольного окна параллельны осям координат.  Синим цветом изображена граница многоугольника, красным — окно. Ответ в этом случае равен 2. Синим цветом изображена граница многоугольника, красным — окно. Ответ в этом случае равен 2. Определите количество черных связных областей многоугольника Пети, которые можно увидеть через прямоугольное окно. Выходные данные Выведите количество черных связных областей многоугольника Пети, которые можно увидеть через прямоугольное окно. Примечание Пример из условия соответствует картинке выше. | |
![]()
|
|
B. Уничтожение дерева
Деревья
дп
жадные алгоритмы
Конструктив
поиск в глубину и подобное
*2000
Дано дерево (граф состоящий из n вершин, соединенных n - 1 ребрами, в котором от каждой вершины можно добраться до каждой, двигаясь только по ребрам). Вершину можно уничтожить если из нее выходит четное число ребер, при этом уничтожаются все ребра, выходящие из нее. Требуется уничтожить все вершины в дереве, либо сказать, что это невозможно. Выходные данные Если уничтожить все вершины возможно, выведите «YES» (без кавычек), иначе выведите «NO» (без кавычек). Если возможно уничтожить все вершины, в следующих n строках выведите номера вершин в порядке, в котором их надо уничтожать. Если существует несколько способов удалить все вершины, выведите любой. Примечание В первом примере сначала нужно уничтожить вершину с номером 1 (при ее уничтожении удалятся ребра (1, 2) и (1, 4)), затем 2-ю (удаляются ребра (2, 3) и (2, 5)). После этого в дереве не остается ребер, поэтому оставшиеся вершины можно уничтожать в любом порядке.  | |
![]()
|
|
E. Короткий код
Деревья
дп
жадные алгоритмы
Строки
Структуры данных
*2200
Код Аркадия содержит \(n\) переменных. Каждая переменная имеет уникальное имя, состоящее только из английских строчных (маленьких) букв. Однажды Аркадий решил укоротить свой код. Он хочет заменить имя каждой переменной его непустым префиксом таким образом, что новые имена останутся попарно различными (но новое имя какой-либо переменной может совпадать со старым именем этой или другой переменной). Среди всех таких возможных замен он хочет найти такую, для которой суммарная длина названий переменных будет минимальной. Строка \(a\) является префиксом строки \(b\), если вы можете удалить несколько (возможно, ни одного) символа с конца строки \(b\) и получить \(a\). Найдите минимальную возможную суммарную длину новых имён. Выходные данные Выведите одно целое число — минимально возможную суммарную длину новых названий переменных. Примечание В первом примере одним из наилучших вариантов будет сокращение имён в порядке их ввода до "cod", "co", "c". Во втором примере можно укоротить последнее имя до "aac" и первое имя до "a" без изменения других имён переменных. | |
![]()
|
|
E. Лидеры
графы
Деревья
поиск в глубину и подобное
снм
*2200
После революции в Берляндии новый диктатор столкнулся с неожиданной проблемой — страной надо как-то управлять. Диктатор является очень эффективным менеджером, однако не может раздавать приказы всему населению лично, поэтому он решил выбрать некоторое множество подконтрольных ему лидеров, которые и будут управлять людьми непосредственно. Однако оказалось, что лидерская эффективность может очень сильно варьироваться от человека к человеку, поэтому диктатор обратился за помощью к всемирно известным берляндским ученым. Ученые предложили инновационную идею — лидеры должны работать парами. Граф взаимоотношений — некоторый неориентированный граф с вершинами, соответствующими людям. Путь называется простым, если вершины в нем не повторяются. В результате многодневных и очень дорогих исследований было выяснено, что пара людей обладает наиболее высокими лидерскими качествами, если между ними в графе взаимоотношений есть простой путь с нечетным количеством ребер. Ученые решили называть такие пары различных людей лидерскими. Спецслужбы выдали ученым граф взаимоотношений, так что дело осталось за малым — надо научиться отвечать диктатору, являются ли лидерскими заданные пары людей. Помогите ученым справиться с этой задачей. Выходные данные Для каждого запроса ученых в отдельной строке выведите «Yes», если между парой людей существует простой нечетный путь, иначе выведите «No». Примечание Пояснение к примеру: 1) Между вершинами 1 и 2 есть всего 2 различных простых пути: 1-3-2 и 1-4-2. Оба состоят из четного количества ребер. 2) Вершины 1 и 3 соединены ребром, поэтому простой нечетный путь для них: 1-3. 5) Вершины 1 и 5 находятся в разных компонентах связности, между ними нет ни одного пути. | |
![]()
|
|
C. Куро и прогулочный маршрут
Деревья
поиск в глубину и подобное
*1600
Куро живёт в стране Уберляндии, состоящей из \(n\) городов, пронумерованных от \(1\) до \(n\), и \(n - 1\) двусторонняя дорога, соединяющих эти города. Из каждого города можно добраться до любого другого. Каждая дорога соединяет два города \(a\) и \(b\). Куро любит пешие прогулки и поэтому планирует устроить пеший марафон — она выберет пару городов \((u, v)\) (\(u \neq v\)) и пройдёт от \(u\) до \(v\) по кратчайшему пути (заметим, что пары \((u, v)\) и \((v, u)\) считаются различными). Как ни странно, в Уберляндии есть два особых города, один из которых — Цветниса (обозначается индексом \(x\)), а другой — Пчелополис (обозначается индексом \(y\)). Цветниса — город, в котором растёт много сильнопахнущих растений, а в Пчелополисе живёт много пчёл. Куро будет избегать такие пары городов \((u, v)\), если на пути от \(u\) до \(v\) он достигнет Пчелополиса после того, как он побывал в Цветнисе, поскольку пчёлы будут привлечены цветочным запахом и ужалят Куро. Куро хочет узнать, сколько пар городов \((u, v)\) он может выбрать для своей пробежки. Так как задача нетривиальна, она обратилась за помощью к вам. Выходные данные Выведите одно целое число — количество пар городов \((u, v)\), которые Куро может использовать для пешего марафона. Примечание В первом примере Куро может выбрать следующие пары городов: - \((1, 2)\): её маршрутом будет \(1 \rightarrow 2\),
- \((2, 3)\): её маршрутом будет \(2 \rightarrow 3\),
- \((3, 2)\): её маршрутом будет \(3 \rightarrow 2\),
- \((2, 1)\): её маршрутом будет \(2 \rightarrow 1\),
- \((3, 1)\): её маршрутом будет \(3 \rightarrow 2 \rightarrow 1\).
Куро не может выбрать пару \((1, 3)\), так как её маршрутом будет \(1 \rightarrow 2 \rightarrow 3\), в котором Куро сначала посетит город \(1\) (Цветнису), после чего посетит город \(3\) (Пчелополис), что запрещено (заметьте, что пара \((3, 1)\) является разрешённой, поскольку хотя Куро и посетила и Цветнису, и Пчелополис, она не посетила их в этом порядке). Во втором примере, Куро может выбрать следующие пары городов: - \((1, 2)\): её маршрутом будет \(1 \rightarrow 2\),
- \((2, 1)\): её маршрутом будет \(2 \rightarrow 1\),
- \((3, 2)\): её маршрутом будет \(3 \rightarrow 1 \rightarrow 2\),
- \((3, 1)\): её маршрутом будет \(3 \rightarrow 1\).
| |
![]()
|
|
D. Куро, НОД, побитовое исключающее ИЛИ, сумма и все-все-все
Бинарный поиск
битмаски
Деревья
дп
жадные алгоритмы
математика
Перебор
снм
Строки
Структуры данных
теория чисел
*2200
Куро играет в обучающую игру про числа. Основные математические операции в этой игре — наибольший общий делитель, побитовое исключающее ИЛИ и сумма двух чисел. Куро так любит эту игру, что проходит уровень за уровнем изо дня в день. К сожалению, Куро уезжает в отпуск и будет неспособна продолжить череду решений. Поскольку Кэти — надёжный человек, Куро попросил её прийти к нему домой в этот день и поиграть за него. Изначально дан пустой массив \(a\). Игр состоит из \(q\) запросов двух разных типов. Запросы первого типа просят Кэти добавить число \(u_i\) в массив \(a\). Запросы второго типа просят Кэти найти такое число \(v\), принадлежащее массиву \(a\), что \(k_i \mid GCD(x_i, v)\), \(x_i + v \leq s_i\), и \(x_i \oplus v\) максимально, где \(\oplus\) обозначает операцию побитового исключающего ИЛИ, \(GCD(c, d)\) обозначает наибольший общий делитель целых чисел \(c\) и \(d\), а \(y \mid x\) означает, что \(x\) делится на \(y\), или же вывести -1, если таких чисел в массиве нет. Поскольку вы программист, Кэти просит вас написать программу, которая будет автоматически и точно выполнять внутриигровые запросы, чтобы выполнить поручения Куро. Давайте поможем ей! Выходные данные Для каждого запроса типа \(2\) выведите запрашиваемое число \(v\) или -1, если таких чисел не найдено, в отдельной строке. Примечание В первом примере необходимо выполнить пять запросов: - Первый запрос просит вас добавить \(1\) в \(a\). Теперь \(a\) — \(\left\{1\right\}\).
- Второй запрос просит вас добавить \(2\) в \(a\). Теперь \(a\) — \(\left\{1, 2\right\}\).
- Третий запрос просит вас найти ответ с \(x = 1\), \(k = 1\) и \(s = 3\). И \(1\), и \(2\) удовлетворяют условиям на \(v\), так как \(1 \mid GCD(1, v)\) и \(1 + v \leq 3\). Поскольку \(2 \oplus 1 = 3 > 1 \oplus 1 = 0\), ответом на этот запрос будет \(2\).
- Четвёртый запрос просит вас найти ответ с \(x = 1\), \(k = 1\) и \(s = 2\). Только \(v = 1\) удовлетворяет условия \(1 \mid GCD(1, v)\) и \(1 + v \leq 2\), поэтому ответом на этот запрос будет \(1\).
- Пятый запрос просит вас найти ответ с \(x = 1\), \(k = 1\) и \(s = 1\). В \(a\) нет удовлетворяющих условиям элементов, поэтому мы выводим -1 как ответ на этот запрос.
| |
![]()
|
|
B. Помогите Царю
Деревья
реализация
Теория вероятностей
*2200
Это модификация задачи, использованной на официальном раунде. К сожалению, авторское решение к оригинальной формулировке оказалось неверным, поэтому задача была изменена специально для архива. Жил да был в Тридевятом царстве Царь, и была у него прекрасная дочь Василиса. Жили они не тужили, пока не случилась беда лихая: налетел на Тридевятое царство злобный Змей Горыныч и украл Василису. Закручинился Царь, однако собрал своих храбрых молодцев, и пообещал полцарства и руку дочери тому, кто спасет его дочь от супостата иноземного. Долго ли, коротко ли, нашли молодцы логово Змея Горыныча, и завалились в него спасать Василису Прекрасную всей толпой. Каждый из них плюнул в супостата один раз, и, будучи очень нежным и легкоранимым существом, бедный Змей Горыныч умер от разрыва сердца. Храбры же молодцы доставили Василису Прекрасную Царю и передрались из-за того, кому же достанется ее рука. Поскольку все храбры молодцы были одинаково храбры и одинаково красивы, а Василиса все равно не хотела выходить замуж ни за кого из них, то Царь, будучи очень мудрым, дабы не обидеть никого, решил определить, кому достанется его дочь, случайным образом — бросанием монетки. Однако оказалось, что добрых молодцев целых n человек, а у монетки — только две стороны, но зато каждая выпадает при подбрасывании с равной вероятностью. Царю стало интересно, как можно выбрать одного добра молодца с помощью этой монетки таким образом, чтобы у всех добрых молодцев вероятность быть выбранным совпадала (и равнялась, соответственно, 1 / n). Перво-наперво Царь хочет узнать матожидание количества раз, которое потребуется бросить монетку, чтобы определить победителя, следуя оптимальной стратегии подбрасывания (то есть такой, которая это матожидание минимизирует). Помогите Царю в его непростой задаче. Выходные данные Выведите искомое матожидание количества подбрасываний в виде несократимой дроби вида «a/b» (без кавычек) без лидирующих нулей. | |
![]()
|
|
E. Народные игры
Деревья
жадные алгоритмы
Структуры данных
*2200
Государство Панел проводит ежегодное шоу «Народные игры», в котором каждый дистрикт будет представлять один участник. В государстве \(n\) дистриктов, пронумерованных от \(1\) до \(n\), причём от каждого дистрикта до любого другого есть ровно один путь. Число фанатов участника игр из дистрикта \(i\) равно \(2^i\). В этом году президент решил снизить затраты на проведение Народных игр. По этой причине он хочет убрать \(k\) участников из соревнования, но есть проблема — дистрикты, участники из которых будут убраны из соревнования, будут в бешенстве и не дадут никому пересекать их границы. Президент хочет, чтобы все оставшиеся в играх участники были из дистриктов, которые можно достичь друг из друга. Он также хочет, чтобы суммарное количество фанатов оставшихся участников было максимальным. Каких участников должен убрать президент? Выходные данные Выведите \(k\) целых чисел, разделённых пробелами — номера дистриктов, участники из которых должны быть убраны, в порядке возрастания номера дистрикта. Примечание В первом примере максимально достижимое число фанатов равно \(2^2 + 2^5 + 2^6 = 100\). Этого можно достичь, убрав участников из кварталов 1, 3 и 4. | |
![]()
|
|
F. От кактуса до дерева
графы
Деревья
дп
*2900
Вам дан специальный связный неориентированный граф, в котором каждая вершина принадлежит максимум к одному простому циклу. Ваша задача — убрать из этого графа столько рёбер, сколько необходимо, чтобы превратить этот граф в дерево (связный граф без циклов). Для каждой вершины независимо выведите максимальное расстояние от неё до листа в результирующем дереве, предполагая, что рёбра были убраны так, чтобы минимизировать данное расстояние. Выходные данные Выведите \(n\) целых чисел, разделённых пробелами, \(i\)-е из которых обозначает максимальное расстояние между вершиной \(i\) и листом дерева, если убранные рёбра были выбраны таким образом, что это расстояние минимально среди всех возможных вариантов убирания рёбер. Примечание В первом примере один из возможных путей минимизации максимального расстояния от вершины \(1\) — убирание отмеченных на следующем изображении рёбер:  Обратите внимание, что для минимизации ответа для разных вершин можно убирать разные ребра. | |
![]()
|
|
C. Полезная декомпозиция
Деревья
реализация
*1400
Рамзес — мастер решения задач про деревья (неориентированные связные графы без циклов)! Он придумал новую, очень полезную декомпозицию дерева, но, так как обычно он решает задачи только в уме, он не знает, как её найти, и просит вашей помощи! Его декомпозиция заключается в разбиении ребер дерева на простые пути так, что любая пара путей в декомпозиции будет иметь хотя бы одну общую вершину. Каждое ребро дерева должно войти в ровно один путь. Помогите Рамзесу, найдите такую декомпозицию данного дерева, или сообщите, что её не существует. Выходные данные Если необходимой декомпозиции не существует, в единственной строке выведите «No». В противном случае в первой строке выведите «Yes», а во второй целое число \(m\) — число путей в декомпозиции. Следующие \(m\) строк должны содержать по два целых числа \(u_i\), \(v_i\) (\(1 \leq u_i, v_i \leq n\), \(u_i \neq v_i\)), разделенных пробелом, обозначающие, что очередной путь декомпозиции — путь между вершинами \(u_i\) и \(v_i\). Любая пара путей в декомпозиции должна иметь хотя бы одну общую вершину, а каждое ребро дерева должно присутствовать ровно в одном пути. Пути и концы каждого пути можно выводить в любом порядке. Если существует несколько подходящих декомпозиций, выведите любую. Примечание Дерево из первого примера изображено на картинке ниже:  Рядом с каждым ребром указан номер, к которому принадлежит это ребро в декомпозиции, несложно видеть, что данная декомпозиция удовлетворяет условиям задачи. Рядом с каждым ребром указан номер, к которому принадлежит это ребро в декомпозиции, несложно видеть, что данная декомпозиция удовлетворяет условиям задачи. Дерево из второго примера изображено на картинке ниже:  Можно доказать, что для данного дерева не существует искомой декомпозиции. Можно доказать, что для данного дерева не существует искомой декомпозиции. Дерево из третьего примера изображено на картинке ниже:  Рядом с каждым ребром указан номер, к которому принадлежит это ребро в декомпозиции, несложно видеть, что данная декомпозиция удовлетворяет условиям задачи. Рядом с каждым ребром указан номер, к которому принадлежит это ребро в декомпозиции, несложно видеть, что данная декомпозиция удовлетворяет условиям задачи. | |
![]()
|
|
C. Удали их всех!
графы
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
*1500
Дано дерево из \(n\) вершин. Необходимо ответить на следующий вопрос: какое максимальное количество ребер можно удалить из дерева так, чтобы все получившиеся компоненты связности содержали в себе четное количество вершин? Выходные данные Выведите единственное число \(k\) — максимальное количество ребер, которое можно удалить, чтобы все компоненты связности имели четное число вершин, или \(-1\), если нельзя удалить ребра так, чтобы все компоненты связности имели четное число вершин. Примечание В первом тестовом примере можно удалить ребро, соединяющее вершины \(1\) и \(4\), тогда граф распадется на две компоненты связности, в каждой из которых по две вершины. Во втором тестовом примере нельзя удалить ребра так, чтобы все компоненты связности имели четное число вершин, поэтому ответ \(-1\). | |
![]()
|
|
D. Акула
Деревья
Перебор
снм
Структуры данных
*1900
Уже давно ученые наблюдают занятное поведение акул. Акулы, как и многие другие живые существа, в поисках пищи чередуют перемещения на маленькие отрезки внутри одной локации с переходами на более длительные расстояния между локациями. Максу, начинающему биологу, досталась распечатка, содержащая перемещения акулы за каждый из \(n\) последовательных дней в течение года. Длины всех передвижений оказались различными. По этим данным Макс решил посчитать, какое же количество локаций посетила морская хищница. Он предположил, что существует такое число \(k\), что, если за один день акула переместилась на расстояние, строго меньшее \(k\), то она не поменяла локацию; если же акула переместилась на расстояние, большее или равное \(k\), то в этот день она перемещалась на новую локацию. При этом перемещение на новую локацию могло занять несколько дней, в каждый из которых акула переместилась на расстояние, не меньшее \(k\). Акула никогда не возвращается на старую локацию после того, как она ушла из нее. Таким образом, в последовательности из \(n\) дней можно выделить отрезки, в течение которых акула перемещалась на расстояния, меньшие \(k\): это соответствует одной локации. Аркадий хочет выбрать такое \(k\), чтобы длины всех таких отрезков были одинаковы. Найдите такое целое число \(k\), что количество локаций в перемещениях акулы максимально возможно. Если существует несколько таких \(k\), выведите минимальное. Выходные данные Выведите целое число \(k\) такое, что: - на каждой локации акула провела равное количество дней;
- среди вариантов, удовлетворяющих первому условию, число локаций максимально возможное;
- среди вариантов, удовлетворяющих первому и второму условию, \(k\) минимально возможное.
Примечание В первом тестовом примере перемещения по локации являются перемещения в \(1\)-й и \(2\)-й дни (первая локация), в \(4\)-й и \(5\)-й (вторая локация), в \(7\)-й и \(8\)-й (третья локация). Таким образом, всего локаций три. Во втором примере перемещений по локации является только перемещение во \(2\)-й день. Всего одна локация. | |
![]()
|
|
E. Страна NN
Бинарный поиск
Деревья
Структуры данных
*2800
В стране NN \(n\) городов, пронумерованных от \(1\) до \(n\), и \(n - 1\) дорога. Существует путь по дорогам между любыми двумя городами. Между городами проложено \(m\) двухсторонних автобусных маршрутов. Автобусы ездят между двумя городами по кратчайшему пути, останавливаясь во всех промежуточных городах. На автобусе можно проехать от любой остановки маршрута до любой другой. Вы можете перемещаться между городами только на автобусах. Вас интересует \(q\) вопросов: возможно ли добраться из одного города в другой и какое минимальное число автобусов необходимо для этого использовать. Выходные данные Выведите ответ на каждый вопрос в отдельной строке. Если не существует способа добраться из одного в другой, выведите \(-1\). Иначе выведите минимальное число автобусов. Примечание  На рисунке показаны маршруты автобусов из первого примера. На рисунке показаны маршруты автобусов из первого примера. | |
![]()
|
|
E. Задача Принца
Деревья
математика
Перебор
Структуры данных
теория чисел
*2800
Действующими лицами этой задачи будут герои какого-нибудь недавно вышедшего в прокат фильма. Кажется, в последнее время много мемов по «Мстители: Война бесконечности». Я не смотрел ни одной части, поэтому лишь смутно знаю героев. Впрочем, это не помешает мне использовать их в задаче. Пусть героями нашей задачи будут Танос и Доктор Стрендж. Итак, Танос и Доктор Стрендж занимаются своими супергеройскими и суперзлодейскими делами, как вдруг они наталкиваются на обычную задачу по спортивному программированию. Есть дерево размера \(n\). В каждой вершине \(v\) записано целое положительное число \(a_{v}\). Нужно ответить на \(q\) запросов. Запрос задаётся в виде \(u\) \(v\) \(x\). Нужно посчитать \(\prod_{w \in P} gcd(x, a_{w}) \mod (10^{9} + 7)\), где \(P\) — множество вершин, лежащих на пути из \(u\) в \(v\). Иными словами, вычислите произведение \(gcd(x, a_{w})\) для всех вершин \(w\) на пути от \(u\) до \(v\). Так как произведение может быть большим, выведите его по модулю \(10^9+7\). Здесь \(gcd(s, t)\) обозначает наибольший общий делитель \(s\) и \(t\). Обратите внимание, что сами числа в вершинах не изменяются. Думаю, вам интереснее было бы смотреть на супергеройские похождения Доктора Стренджа и Таноса, чем на то, как они решают задачку. Поэтому вам предлагается решить задачу вместо них. Выходные данные Выведите \(q\) чисел в отдельных строках — ответы на запросы в том порядке, в котором они заданы во входных данных. Выведите каждый ответ по модулю \(10^9+7 = 1000000007\). | |
![]()
|
|
F. Управление потоками
Деревья
дп
жадные алгоритмы
поиск в глубину и подобное
*2400
Вам необходимо настроить очень сложную водораспределительную систему. Система состоит из \(n\) узлов и \(m\) труб, \(i\)-я труба соединяет узлы \(x_i\) и \(y_i\). Вам нужно всего лишь подобрать настройки труб. Требуется выбрать \(m\) целых чисел \(f_1\), \(f_2\), ..., \(f_m\) для того, что использовать их в качестве настроек соответствующих труб. \(i\)-я труба будет пересылать \(f_i\) единиц воды в секунду из узла \(x_i\) в узел \(y_i\) (если \(f_i\) отрицательно, то труба будет пересылать \(|f_i|\) единиц воды из узла \(y_i\) в узел \(x_i\)). Разрешается выставлять \(f_i\) значение от \(-2 \cdot 10^9\) до \(2 \cdot 10^9\). Для корректной работы системы необходимо также соблюдать следующие ограничения: для каждого \(i \in [1, n]\), \(i\)-му узлу присвоено число \(s_i\), означающее, что разница между входным и выходным потоками для \(i\)-го узла должна быть ровно \(s_i\) (если \(s_i\) неотрицательно, то \(i\)-й узел должен принимать \(s_i\) единиц воды; если отрицательно, то \(i\)-й узел должен отдавать \(|s_i|\) единиц воды другим узлам). Можно ли выбрать целые числа \(f_1\), \(f_2\), ..., \(f_m\) таким образом, чтобы все ограничения на входные и выходные потоки соблюдались? Выходные данные Если можно выбрать целые числа \(f_1, f_2, \dots, f_m\) таким образом, что все ограничения на входные и выходные потоки соблюдаются, то выведите «Possible» в первой строке. После выведите \(m\) строк, в \(i\)-й строке должно быть записано число \(f_i\) — выбранные настройки труб. Трубы пронумерованы в порядке, в котором появляются во входных данных. В противном случае выведите «Impossible» в единственной строке. | |
![]()
|
|
G. Подсчёт GCD
Деревья
дп
разделяй и властвуй
снм
теория чисел
*2400
Дано дерево из \(n\) вершин. На каждой вершине дерева записано число; на \(i\)-й вершине записано число \(a_i\). Определим функцию \(g(x, y)\) как наибольший общий делитель всех чисел, записанных на вершинах на простом пути от вершины \(x\) до вершины \(y\) (включая эти две вершины). Для каждого целого числа от \(1\) до \(2 \cdot 10^5\) подсчитайте количество таких пар \((x, y)\) \((1 \le x \le y \le n)\), что \(g(x, y)\) равен этому числу. Выходные данные Для каждого целого числа \(i\) от \(1\) до \(2 \cdot 10^5\) необходимо сделать следующее: если не существует таких пар \((x, y)\), что \(x \le y\) и \(g(x, y) = i\), не выводите ничего; иначе выведите два числа: \(i\) и количество описанных пар. Значения \(i\) нужно выводить в возрастающем порядке. Посмотрите примеры для лучшего понимания. | |
![]()
|
|
F. Зарплаты в комуупании
Деревья
дп
Комбинаторика
математика
*2700
Аллен выпустился из Муусского техмулогоческого института (MIT) и основал стартап! Аллен — президент стартапа. Он нанял \(n-1\) работника, у каждого из которых есть один непосредственный начальник. Если \(u\) является начальником \(v\), а \(v\) является начальником \(w\), то \(u\) является начальником \(w\). Кроме того, нет таких \(u\) и \(v\), что \(u\) является начальником \(v\) и \(v\) является начальником \(u\). У Аллена нет начальников. Аллен — сотрудник номер \(1\), все остальные пронумерованы от \(2\) до \(n\). Наконец, Аллен должен назначить каждому в компании, включая себя, зарплату. Из-за бюджетных ограничений зарплата каждого из сотрудников должна быть между \(1\) и \(D\) включительно. Кроме того, никто не может получать больше, чем его начальник. Помогите Аллену найти количество способов назначить сотрудникам зарплаты. Эта величина может быть достаточно большой, поэтому выведите ее по модулю \(10^9 + 7\). Выходные данные Выведите одно целое число: количество способов назначить зарплаты по модулю \(10^9 + 7\). Примечание В первом примере сотрудники с номерами 2 и 3 подчиняются непосредственно Аллену. Три зарплаты по порядку могут быть \((1,1,1)\), \((2,1,1)\), \((2,1,2)\), \((2,2,1)\) или \((2,2,2)\). Во втором примере сотрудник 2 подчиняется Аллену, а сотрудник 3 подчиняется сотруднику 2. Возможные зарплаты равны \((1,1,1)\), \((2,1,1)\), \((2,2,1)\), \((2,2,2)\), \((3,1,1)\), \((3,2,1)\), \((3,2,2)\), \((3,3,1)\), \((3,3,2)\), \((3,3,3)\). | |
![]()
|
|
D. Циклы в произведении
Деревья
Комбинаторика
разделяй и властвуй
*2900
Рассмотрим дерево (то есть неориентированный связный граф без циклов) \(T_1\) и дерево \(T_2\). Определим их декартово произведение \(T_1 \times T_2\) следующим образом. Пусть \(V\) — множество вершин \(T_1\), а \(U\) — множество вершин \(T_2\). Тогда множеством вершин \(T_1 \times T_2\) является \(V \times U\), то есть множество упорядоченных пар вершин, где первая вершина из \(V\), а вторая из \(U\). Проведём ребра следующего вида: - Между \((v, u_1)\) и \((v, u_2)\) есть неориентированное ребро, если \(u_1\) и \(u_2\) смежны в графе \(U\).
- Аналогично между \((v_1, u)\) и \((v_2, u)\) есть неориентированное ребро, если \(v_1\) и \(v_2\) смежны в графе \(V\).
Обратите внимание на пояснения к примерам, они содержат картинки для произведения деревьев для тестов из примеров. Рассмотрим граф \(T_1 \times T_2\). Вычислите количество циклов в этом графе (не обязательно простых) длины \(k\). Выведите остаток при делении найденного количества на \(998244353\). Циклом называется последовательность вершин \(w_1\), \(w_2\), ..., \(w_k\), где \(w_i \in V \times U\), такая что любые две соседние вершины смежны, а также \(w_1\) смежно с \(w_k\). Циклы отличающиеся только циклическим сдвигом или направлением обхода всё равно считаются различными. Выходные данные Выведите одно число — количество циклов по модулю \(998244353\). Примечание Следующие три картинки иллюстрируют графы, которые получаются в результате произведения в тестах из условия. В первом примере список циклов длины \(2\) следующий: - «AB», «BA»
- «BC», «CB»
- «AD», «DA»
- «CD», «DC»
   | |
![]()
|