| | | |
|
Сумма на отрезке
Префиксные суммы(минимумы, ...)
Дан неизменяемый массив длины n и q запросов типа “вычислить сумму подотрезка массива с l по r”. Выведите ответ на каждый запрос.
Входные данные
В первой строке дано число n – размер массива (\(1 <= n <= 10^5\)). Во второй строке дано n чисел – элементы массива. Числа по модулю не превосходят \(10^9\). В третьей строке дано число q – кол-во запросов (\(1 <= q <= 10^5\)). Далее дано q строк, в каждой из которых дано 2 числа: l и r (\(1 <= l <= r <= n\)).
Выходные данные
Выведите ответы на все запросы, каждый в отдельной строке.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
1 2 3 4 5
3
1 2
3 3
2 5
|
3
3
14 |
| |
![]()
|
|
Тихий Дон №3
Префиксные суммы(минимумы, ...)
Наталья Коршунова очень скучает по Григорию Мелехову и хочет вернуться к нему. Но, к сожалению, Григорий любит Аксинью, поэтому Наталья решила доказать любимому, что она лучше нее.
Для этого Наталья отправилась к Григорию и заявила, что она может решить любую задачу, какую бы он ни предложил. Мелехов принял вызов.
Григорий дает Наталье массив A, состоящий из n целых неотрицательных чисел. Затем он просит ее сделать q однотипных операций, заключающихся в следующем: "Даны числа l, r и k. Далее для каждого индекса i от l до r происходит подстановка числа k вместо числа Ai и считается побитовое исключающее “или” всех чисел на отрезке \([l;r]\), после чего на iое место опять возвращается число Ai".
Таким образом, происходит \(r – l + 1\) независимых подстановок, не меняющих массив, и соответственно \(r – l + 1\) результатов побитового исключающего “или”. Наталье необходимо сообщить Григорию побитовое исключающее “или” всех результатов подстановок (для лучшего понимания ознакомьтесь с примерами).
Помогите Наталье Коршуновой справиться с этой задачей! Тогда Григорий точно вернется к ней!
Входные данные
В первой строке дано целое число n (\(1 <= n <= 10^5\)) – количество элементов массива.
Во второй строке содержится n целых неотрицательных чисел, не превышающих по значению \(10^8\).
В третьей строке дано целое число q (\(1 <= q <= 10^5\)) – количество запросов.
Далее содержится q строк, в каждой из которых содержится 3 целых числа: l, r, k (\(1 <= l <= r <= n\), \(0 <= k <= 10^8\)).
Выходные данные
Вам необходимо вывести q ответов на каждый запрос в одной строке через пробел.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
1 2 3 4 5
2
1 3 7
4 5 10
|
7 1 |
Пояснение
Первый запрос:
1) 7 ⊕ 2 ⊕ 3 = 6
2) 1 ⊕ 7 ⊕ 3 = 5
3) 1 ⊕ 2 ⊕ 7 = 4
6 ⊕ 5 ⊕ 4 = 7
Ответ: 7.
Второй запрос:
1) 10 ⊕ 5 = 15
2) 4 ⊕ 10 = 14
15 ⊕ 14 = 1
Ответ: 1.
| |
![]()
|
|
Тихий дон №2
"Два указателя"
Префиксные суммы(минимумы, ...)
Аксинья любит Григория, но она замужем за Степаном. Со своим мужем она несчастна, поэтому время, которое она проводит с ним можно характеризовать отрицательным показателем счастья Аксиньи (\(a_i < 0\)), а то время, которое она проводит с Григорием, - положительным показателем счастья (\(a_i > 0\)). Известно, что Аксинья проводит один день либо с мужем, либо с Григорием.
Найдите максимальное суммарное счастье за L дней, в которые Аксинья будет проводить с мужем не более C дней.
Входные данные
В первой строке подается 3 числа: N – кол-во дней, L и C (\(1 <= L, C <= N <= 1 000 000\)).
Во второй строке содержится N чисел a_i (\(1 <= |a_i| <= 1 000 000 000\)).
Входные данные
Требуется вывести ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 3 3
1 -1 2 -2 3 |
3 |
| |
![]()
|
|
Рубка деревьев
Префиксные суммы(минимумы, ...)
Чубатый учит Григория Мелехова выполнять баклановский удар шашкой. В качестве целей, они используют n деревьев, стоящих в ряд и пронумерованных от 1 до n. Чубатый, оценил прочность всех деревьев натуральными числами, и записал их. За каждое дерево, которое Мелехов смог разрубить, он получает количество очков равное числу, записанному на дереве, а если не смог - то теряет столько же.
Чубатый просит Григория выполнить удары на деревьях с l по r, в порядке возрастания их номеров. Мелехов недавно ушиб плечо, потому он может успешно срубить дерево через раз, т. е. если он срубил дерево с номером i, то он не сможет срубить дерево с номером i + 1, но сможет срубить дерево с номером i + 2 и т. д.
Чубатый m раз попросил Григория выполнить удары, но он забыл, какие деревья Мелехов смог срубить. Помогите ему определить, сколько очков набрал Григорий за каждую попытку.
Входные данные
В первое строке содержатся 2 числа n и m (\(1 <= n, m <= 100000\))
Во второй строке содержатся n чисел - прочность всех деревьев, где на позиции i написана прочность дерева i.
В следующих m строках содержатся пары чисел l и r (\(1 <= l <= r <= n\)), означающие какой отрезок деревьев попросил срубить Чубатый.
Выходные данные
На каждый запрос выведите сколько очков в эту попытку заработал Григорий.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6 6
1 2 3 4 5 6
1 6
1 5
2 6
2 5
2 4
2 2
|
-3
3
4
-2
3
2
|
| |
![]()
|
|
Банды Фомина №2
Остатки
Быстрое возведение в степень
Префиксные суммы(минимумы, ...)
Малая теорема Ферма
Банда Фомина состоит из n групп, в каждой из которых ai человек. Планируется провести q рейдов. В i-ом рейде будет участвовать ровно один разбойник из каждой группы, номер которой лежит в отрезке \([l_i, r_i]\).
Мелехов тоскует, поэтому для каждого рейда он решил посчитать количество возможных отрядов по модулю \(10^9 + 7\). Однако Григорий постоянно находится в раздумьях о смысле жизни и поиске правды, поэтому он не может сконцентрироваться на расчетах и просит вас помочь.
Входные данные
В первой строке дано число n (\(1 <= n <= 10^5\)) – количество групп в банде Фомина.
Во второй строке дано n натуральных чисел ai (\(1 <= a_i <= 10^6\)) – количество человек в i-ой группе.
В третьей строке дано число q – количество рейдов.
Далее дано q строк, в каждой из которых дано два числа – li и ri (\(1 <= l_i <= r_i <= n\)) – номера групп, участвующих в i-ом рейде.
Выходные данные
Выведите q чисел, каждое в отдельной строке – ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6
1 3 7 1 4 100
3
1 3
3 4
2 6 |
21
7
8400 |
| |
![]()
|
|
Банды Фомина
Префиксные суммы(минимумы, ...)
Банда Фомина состоит из n групп, в каждой из которых ai человек. Планируется провести q рейдов. В i-ом рейде будет участвовать ровно один разбойник из каждой группы, номер которой лежит в отрезке \([l_i, r_i]\).
Мелехов тоскует, поэтому для каждого рейда он решил посчитать количество возможных отрядов по модулю \(10^9 + 7\). Однако Григорий постоянно находится в раздумьях о смысле жизни и поиске правды, поэтому он не может сконцентрироваться на расчетах и просит вас помочь.
Входные данные
В первой строке дано число n (\(1 <= n <= 10^5\)) – количество групп в банде Фомина.
Во второй строке дано n натуральных чисел ai (\(1 <= a_i <= 2\)) – количество человек в i-ой группе.
В третьей строке дано число q – количество рейдов.
Далее дано q строк, в каждой из которых дано два числа – li и ri (\(1 <= l_i <= r_i <= n\)) – номера групп, участвующих в i-ом рейде.
Выходные данные
Выведите q чисел, каждое в отдельной строке – ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6
1 2 1 1 2 2
3
1 3
3 4
2 6
|
2
1
8 |
| |
![]()
|
|
Кот Гусь и случайная матрица
Куча
Префиксные суммы(минимумы, ...)
Кот Гусь подготовил для Ника Фьюри прямоугольную таблицу a размера \(n \cdot m\), содержащую числа от 0 до p−1. Ник Фьюри сразу понял, что каждое число в этой таблице выбрано случайно равновероятно от 0 до p−1, независимо от остальных.
Ваша задача — найти прямоугольную подматрицу этой таблицы, в которой сумма делится на p. Среди всех таких подматриц нужно найти ту, в которой сумма элементов максимальна.
Формально, вам необходимо найти такие \(1 <= i_1 <= i_2 <= n\), \(1 <= j_1 <= j_2 <= m\), что сумма ax,y по всем \(i_1 <= x <= i_2\), \(j_1 <= y <= j_2\) делится на p, и среди таких имеет максимальную сумму.
Входные данные
В первой строке расположено три целых числа n, m, p (\(1 <= n·m, p <= 1 000 000\)) — размерности матрицы и число, на которое должна делится сумма подматрицы.
В следующих n строках расположено по m целых чисел, j-е число в i-й строке равно ai,j (\(0 <= a_{i,j} <= p ? 1\)).
Гарантируется, что каждое число в a выбрано независимо случайно равновероятно от 0 до p−1.
Выходные данные
Выведите одно целое число — максимальную сумму прямоугольной подматрицы, в которой сумма делится на p. Если таких нет, выведите 0.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6 7 5
0 0 3 0 1 0 4
0 2 3 0 2 2 1
2 4 1 4 4 0 3
1 1 0 2 0 3 2
3 0 3 1 0 1 2
1 2 0 0 3 3 1
|
65 |
| |
![]()
|
|
Достаточно зеленого
Префиксные суммы(минимумы, ...)
Пастбище Фермера Джона может рассматриваться как NхN решётка (\(1<=N<=500\)) квадратных ячеек с травой (как большая шахматная доска). Из-за изменчивости почвы, трава в некоторых ячейках зеленее, чем в других. Каждая ячейка (i,j) описывается целым числом - уровнем зелёности G(i,j), в интервале \(1…200\).
Фермер Джон хочет сделать фотографию прямоугольной подрешётки своего пастбища. Он хочет, чтобы минимальная из величин G на его фотографии была ровна 100. Помогите ему посчитать, сколько таких различных фотографий он сможет сделать. Подрешётка может быть размером от всего пастбища и до одной ячейки. Всего существует \(N^2(N+1)^2/4\) различных подрешёток, для хранения такого числа используйте 64-битное целое (типа long long в C++).
Входные данные
Первая строка содержит N. Каждая из следующих N строк содержит N целых чисел и все вместе они описывают величины G(i,j) для пастбища NхN .
Выходные данные
Выведите количество различных фотографий, которые может сделать Фермер Джон, т.е. количество прямоугольных подрешёток, в которых минимальный уровень "зелёности" ровно 100.
Заметим, что для ответа требуется использовать 64-битную целую переменную типа long long в C++.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
57 120 87
200 100 150
2 141 135 |
8 |
| |
![]()
|
|
Выбор цветов для букета
Бинарный поиск в массиве
Префиксные суммы(минимумы, ...)
Володя хочет красиво поздравить свою жену с годовщиной их свадьбы и собирается подарить ей букет из n цветов.
Придя в цветочный магазин, Володя обнаружил, что букет можно составлять из цветов m различных видов, причём количество цветов каждого вида не ограничено. Володя знает, что от первого цветка i-го вида в букете его супруга становится счастливее на ai, а от каждого следующего цветка
такого вида она становится счастливее на bi. То есть, если в букете xi > 0 цветов вида i, то от цветов этого вида жена Володи становится счастливее на ai + (xi − 1) · bi.
Как любой любящий муж, Володя хочет как можно сильнее порадовать свою супругу. Поэтому ему хочется знать, на какую максимальную величину может увеличиться её счастье от букета, набранного из доступных в магазине цветов.
Формат входных данных
В первой строке вводятся два целых числа n и m (1 ≤ n ≤ 109 , 1 ≤ m ≤ 100 000) — требуемое
количество цветов в букете и количество доступных видов цветов.
Каждая из следующих m строк описывает i-й вид цветов и содержит два целых числа ai и bi (0 ≤ ai , bi ≤ 109 ) — увеличение счастья от первого цветка i-го вида и увеличение счастья от каждого последующего цветка этого вида.
Формат выходных данных
В единственной строке выведите одно число — максимальное увеличение счастья, которое может получить жена Володи от букета из n цветов.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 3
5 0
1 4
2 2 |
14 |
| 2 |
5 3
5 2
4 2
3 1 |
16 |
| |
![]()
|
|
Практический тест
Массивы
Динамическое программирование: один параметр
Префиксные суммы(минимумы, ...)
У нас есть сетка с H строками и W столбцами. Квадрат в i-й строке и j-м столбце будет называться Square(i, j). Целые числа от 1 до H·W записаны по всей сетке, а целое число, записанное в Square(i, j), равно Ai,j.
Вы - волшебник (волшебница), и можете телепортировать фигуру, помещенную на Square(i, j) в Square(x, y), потратив \(|x-i|+|y-j|\) маджиков (магических монет).
Теперь вам нужно пройти Q практических тестов на свои способности как волшебника (волшебницы). I-е испытание будет проводиться следующим образом:
- первоначально фигура располагается в квадрате, где записано целое число Li;
- пусть x будет целым числом, записанным в квадрате, занятом фигурой. Неоднократно переместите фигуру в квадрат, где написано целое число x+D, пока x не станет равен Ri. Тест заканчивается, когда x = Ri .
Гарантируется, что Ri- Li делится на D.
Для каждого теста найдите сумму маджиков, израсходованных во время этого теста.
Входные данные
В первой строке заданы три целых числа: H, W и D (\(1\leq H,W \leq 300\), \(1 \leq D \leq H \cdot W\)).
В следующих H строках записано по W чисел Ai,j (\(1 \leq A_{i,j} \leq H \cdot W\), \(A_{i,j} \neq A_{x,y} ((i,j) \neq (x,y))\).
В следующей строке записано целое число Q (\(1 \leq Q \leq 10^5\)).
В последних Q строках записано по 2 целых числа: Li и Ri (\(1 \leq L_i \leq R_i \leq H \cdot W\)), \((R_i-L_i)\) кратно D.
Выходные данные
Для каждого теста выведите сумму маджиков, израсходованных во время этого теста. Вывод должен быть в порядке проведения тестов.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснения |
| 1 |
3 3 2
1 4 3
2 5 7
8 9 6
1
4 8 |
5 |
- 4 записано Square (1,2).
- 6 записано в Square (3,3).
- 8 записано in Square (3,1).
Таким образом, сумма магических очков, израсходованных во время одного теста, составляет:
\((|3-1|+|3-2|)+(|3-3|+|1-3|)=5\).
|
| 2 |
4 2 3
3 7
1 4
5 2
6 8
2
2 2
2 2 |
0
0 |
Обратите внимание, что может быть тест, в котором фигура вообще не перемещается, и может быть несколько идентичных тестов. |
| 3 |
5 5 4
13 25 7 15 17
16 22 20 2 9
14 11 12 1 19
10 6 23 8 18
3 21 5 24 4
3
13 13
2 10
13 13 |
0
5
0 |
|
| |
![]()
|
|
Длина подстроки
Динамическое программирование: один параметр
Префиксные суммы(минимумы, ...)
У вас есть строка s. Вы хотите сделать новую строку, записывая в ней каждую букву количество раз равное порядковому номеру этой буквы в алфавите. Например, s = "abcdc", новая строка s_new = "abbcccddddccc". Нам стало интересно, какая получится у вас длина строки, если выписать все символы исходной строки, начиная с символа l и заканчивая символом r. Всего у нас k запросов к вам.
Входные данные
В первой строке программа получает на вход два числа n и k (1<=n<=106, 1<=k<=106), где n - длина строки, k - количество запросов. Во второй строке записана строка s длиной n. В следующих k строках расположены границы отрезков l и r (1 <= l <= r <= n). l, r - порядковые номера символов в строке, начиная с 1.
Выходные данные
Для каждого запроса выведите длину строки, которая у вас получилась. По одному числу в строке. Всего k строк.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 3
abcdc
1 5
2 3
3 5 |
13
5
10 |
| |
![]()
|
|
Получите OK
Строки
Префиксные суммы(минимумы, ...)
Дана строка S длины N, состоящая из символов S, T, O и K. Дайте ответ на Q запросов следующего вида.
Запрос i(1 <= i <= Q): для заданных целых чисел li и ri (1 <= li< ri <= N), рассматривается подстрока S, начинающаяся с индекса li и заканчивающася индексом ri (оба включительно). Необходимо определить, сколько раз в этой строке втречается OK как подстрока?
Пояснение
Подстрока строки - это строка, полученная удалением нуля или более символов из начала и конца строки исходной строки. Например, для строки KOTS подстроками будут строки KO, KOT, OT, OTS, (пустая строка) и другие, но не OK.
Входные данные
В первой строке записаны два числа N (2<=N<=105) и Q (1<=Q<=105). Во второй строке записана строка S длины N. Каждый символ строки это S, T, O или K. Далее идут Q строк по 2 числа в каждой: li и ri (1 <= li< ri <= N).
Выходные данные
Выведите Q строк. I-я строка должна содержать ответ на i-й запрос.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
8 3
OKOKTOKS
3 7
2 3
1 8 |
2
0
3 |
| |
![]()
|
|
Гармоничная последовательность
Бинарный поиск
Префиксные суммы(минимумы, ...)
Цикл лекций в университете Флатландии посвящен изучению последовательностей.
Профессор называет последовательность целых чисел \(a_1, a_2, ..., a_n\) гармоничной, если каждое число, кроме \(a_1\) и \(a_n\), равно сумме соседних: \(a_2 = a_1 + a_3, a_3=a_2+a_4, ..., a_{n-1}=a_{n-2}+a_n\). Например, последовательность [1,2,1,–1] является гармоничной, поскольку 2=1+1, и 1=2+(–1) .
Рассмотрим последовательности равной длины: \(A=[a_1,a_2, ... a_n]\) и \(B=[b_1,b_2, ... b_n]\). Расстоянием между этими последовательностями будем называть величину \(d(A,B)= |a_1-b_1|+|a_2-b_2|+...+|a_n-b_n|\) . Например, \(d([1,2,1,–1][1,2,0,0])=|1–1|+|2–2|++|1–0|+|–1–0|=0+0+1+1=2 \)
В конце лекции профессор написал на доске последовательность из n целых чисел \(B=[b_1,b_2, ... b_n]\)и попросил студентов в качестве домашнего задания найти гармоничную последовательность \(A=[a_1,a_2, ... a_n]\), такую, что \(d(A, B)\) минимально. Чтобы облегчить себе проверку, профессор просит написать в качестве ответа только искомое минимальное расстояние \(d(A,B)\) .
Требуется написать программу, которая по заданной последовательности B определяет, на каком минимальном расстоянии от последовательности B найдется гармоничная последовательность A.
Входные данные
Первая строка входного файла содержит целое число n – количество элементов в последовательности ( \(3 \le n \le 300 000\)).
Вторая строка содержит n целых чисел \(b_1, b_2, …, b_n (–10^9 \le b_i \le 10^9 )\) .
Выходные данные
Выходной файл должна содержать одно целое число: минимальное возможное расстояние от последовательности во входном файле до гармоничной последовательности.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4
1 2 0 0 |
2 |
| |
![]()
|
|
Подпоследовательность длиной L
"Два указателя"
Префиксные суммы(минимумы, ...)
Дана последовательность из N чисел. Рассматриваются все её непрерывные подпоследовательности, в которых количество отрицательных чисел не превышает С. Найдите среди них подпоследовательность с максимальной суммой, длины L. В ответе укажите сумму найденной подпоследовательности.
Входные данные
В первой строке записаны 3 числа: количество чисел N (1 <= N <= 1 000 000), L и C (\(1 <= L, C <= N <= 1 000 000\)). Каждая из следующих N строк содержит одно число, не превышающее по модулю 1 000.
Пример организации исходных данных во входном файле (для L = 3 и С = 3):
5 3 3
1
-1
2
-2
3
В этом наборе можно выбрать несколько последовательностей, но с максимальной суммой равной 3 будет: 2+(-2)+3.
Ответ (для С = 3 и L = 3): 3.
| |
![]()
|
|
Нет времени рисовать
Стек
Префиксные суммы(минимумы, ...)
Беси недавно получила набор красок, и она хочет разрисовать длинную изгородь с одной стороны её пастбища. Изгородь состоит из N последовательных 1-метровых сегментов (1≤N≤105). У Беси есть краски 26 различных цветов, которые она пометила буквами от 'A' до Z' в порядке возрастания темноты ('A' - самый светлый цвет, 'Z' - самый тёмный). Поэтому она может описывать раскраску изгороди как строку из N символов (где каждый символ один из - от 'A' до Z').
Изначально все сегменты изгороди не раскрашены. Беси может раскрасить любой непрерывный диапазон сегментов одним цветом за одно прикосновение кисти, также она никогда не красит более светлым поверх более темного (она может красить более темным поверх более светлого).
Например, изначально не покрашенный отрезок длины 4 она может покрасить так:
.... -> BBB. -> BBLL -> BQQL
Ограниченная во времени, Беси может оставить некоторые последовательные отрезки не покрашенными. Сейчас она рассматривает Q кандидатов отрезков (1≤Q≤105), каждый задаётся двумя целыми числами (a,b) (1≤a≤b≤N), указывающих индексы конечных точек отрезка, которые должны остаться не раскрашенными.
Для каждого кандидата укажите минимальное количество прикосновений, которое требуется, чтобы раскрасить все сегменты вне этого диапазона с желаемым цветом, оставляя сегменты внутри диапазона не раскрашенными. Заметим, что Беси в реальности ничего не раскрашивает, поэтому ответы для каждого диапазона-кандидата независимы.
Входные данные
Первая строка содержит N и Q.
Следующая строка содержит N, представляющих желаемый цвет каждого сегмента изгороди.
Каждая из следующих Q строк содержит два разделённых пробелом целых числа a и b представляющих диапазон сегментов, которые возможно останутся не раскрашенными.
Выходные данные
Для каждого из Q кандидатов выведите ответ на новой строке.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
8 2
ABBAABCB
3 6
1 4
|
4
3 |
В этом примере, исключение диапазона соответствует желаемому образцу В этом примере исключение диапазона BAAB требует четыре прикосновения для раскраски, а исключение диапазона ABBA - только три.
.... -> AA.. -> ABBB -> ABCB |
| |
![]()
|
|
Подстроки в строке
Префиксные суммы(минимумы, ...)
Хеш
Дана строка S = s1s2...sn и множество запросов вида (l1, r1, l2, r2). Для каждого запроса требуется ответить, равны ли подстроки sl1...sr1 и sl2...sr2.
Входные данные:
В первой строке дана строка S (1 <= |S| <= 105), состоящая из строчных латинских букв.
Во второй строке дано натуральное число q (1 <= q <= 105) - количество запросов.
В следующих q строках дано по 4 натуральных числа - l1, r1, l2, r2 (1 <= l1 <= r1 <= |S|, 1 <=l2 <= r2 <= |S|).
Выходные данные:
Для каждого запроса выведите '+', если подстроки равны, и '-', в противном случае.
Примеры:
| Входные данные |
Выходные данные |
abacaba
4
1 1 7 7
1 3 5 7
3 4 4 5
1 7 1 7 |
++-+ |
| |
![]()
|
|
Том Сойер и слово на заборе
Префиксные суммы(минимумы, ...)
Хеш
Жадный алгоритм
Во время покраски забора Том Сойер написал на нем слово s. Однако затем он решил, что слова-палиндромы смотрятся красивее.
Теперь он хочет дописать к имеющемуся слову s справа другое слово g так, чтобы получившееся слово sg было палиндромом. Однако в целях экономии краски длина g должна быть как можно меньше.
Помогите Тому Сойеру определить слово g.
Входные данные:
В первой строке дано слово s (1 <= |s| <= 200000), состоящее из строчных латинских букв.
Выходные данные:
Выведите минимально возможное по длине слово g, которое нужно дописать, чтобы слово sg на заборе стало палиндромом. Если дописывать ничего не надо, то выведите '-'.
Примеры:
| Входные данные |
Выходные данные |
| abc |
ba |
| a |
- |
| |
![]()
|
|
Чтение вслух
Бинарный поиск
Бинарный поиск по ответу
Префиксные суммы(минимумы, ...)
Хеш
Том Сойер и Гекльберри Финн вместе читают вслух вырезку из газеты. Но получилось так, что Том Сойер начал читать с i-ого символа, а Гекльберри Финн с j-ого.
Сколько букв они смогут прочитать, прежде чем обнаружат, что начали читать с разных мест или пока оба не дочитают до конца?
Входные данные:
В первой строке дана строка S (1 <= |S| <= 105), состоящая из строчных латинских букв - надпись из газетной вырезки.
В следующей строке дано натуральное число q - количество запросов.
В следующих q строках дано по два натуральных числа i и j - позиции, с которых начинают читать Том Сойер и Гекльберри Финн соответственно.
Выходные данные:
Выведите q строк, в каждой из которых должно быть одно целое число - количество символов, совпадающих при чтении подстрок, начинающихся с i-ого и j-ого символа.
Примеры:
| Входные данные |
Выходные данные |
abacaba
4
1 5
3 5
4 2
2 6 |
3
1
0
2 |
| |
![]()
|
|
Гекльберри Финн и две строки
Перебор
Префиксные суммы(минимумы, ...)
Хеш
У Гекльберри Финна есть две строки s и t одинаковой длины n.
Гекльберри Финну нравится, когда у строк одинаковые префиксы (начала), поэтому он может поменять местами два символа в строке s, чтобы общий префикс строк s и t стал больше.
Однако этот трюк довольно утомительный, поэтому Гекльберри Финн либо совсем не будет его делать, либо сделает ровно один раз.
Помогите Гекльберри Финну определить наибольшую длину общего префикса строк s и t, которую он может получить.
Входные данные:
В первой строке дано натуральное число n (1 <= n <= 200000) - длина строк s и t
Во второй строке дана строка s, состоящая из строчных латинских букв.
В третьей строке дана строка t, состоящая из строчных латинских букв.
Выходные данные:
Выведите одно натуральное число - наибольшую длину общего префикса s и t, которую можно получить, применив операцию обмена двух символов в строке s не более одного раза.
Примеры:
| Входные данные |
Выходные данные |
3
wai
add |
1 |
5
qdyid
xreac |
0 |
| |
![]()
|
|
Культурный контакт
Перебор
Префиксные суммы(минимумы, ...)
Хеш
В начале XVIII века группа европейских исследователей прибыла на остров, населённый группой племён, никогда не вступавших в контакт с представителями европейской цивилизации.
Для успешного налаживания контактов с аборигенами руководитель группы планирует делать подарок вождю каждого встреченного племени. С этой целью он привёз длинную цепочку из стекляшек, похожих на драгоценные камни.
Представим цепочку как строку s, состоящую из маленьких букв английского алфавита, где каждая буква означает тип кусочка стекла на соответствующей позиции.
Исследователи собираются разрезать цепочку на некоторые фрагменты, после чего вручать ровно один фрагмент вождю каждого встреченного группой племени. Руководитель исследователей решил разделить цепочку на фрагменты согласно следующим правилами:
- Чтобы не тратить на разрезания много времени, каждый фрагмент должен являться группой соседних стекляшек цепочки, то есть подстрокой строки s.
- Все стекляшки должны быть использованы, то есть каждая стекляшка должна оказаться включённой ровно в один фрагмент.
- Поскольку исследователи не знают, как аборигены оценят те или иные виды стекляшек, они хотят, чтобы каждому вождю достался один и тот же набор стекляшек без учёта порядка. Иными словами, для любого типа стекляшек количество стекляшек этого типа должно быть одинаковым в каждом из фрагментов.
- Исследователи не знают, сколько племён обитает на острове, поэтому количество подготовленных фрагментов должно быть максимальным.
Помогите руководителю определить максимальное количество фрагментов, которое может получиться.
Входные данные:
В первой строке дана строка s (1 <= |s| <= 5000000).
Выходные данные:
Выведите одно число - максимально возможное количество фрагментов, на которое исследователи могут разрезать имеющуюся у них цепочку, не нарушая ни одного из условий, сформулированных руководителем группы.
Примеры:
| Входные данные |
Выходные данные |
| abbabbbab |
3 |
| aabb |
1 |
Пояснения:
В первом примере исследователи могут разбить цепочку 'abbabbbab' на фрагменты 'abb', 'abb', 'bab', тогда вождю каждого встреченного ими племени достанется по одной стекляшке типа 'a' и по две стекляшки типа 'b'.
Во втором примере строку невозможно поделить цепочку больше чем на один фрагмент, соблюдая все условия.
| |
![]()
|
|
Максимальные вопросы
Динамическое программирование
Префиксные суммы(минимумы, ...)
У Макс в блокноте были записаны две строки s длины n и t длины m, состоящие из букв «a» и «b» латинского алфавита. Причем Макс знает, что строка t имеет вид «abab...», то есть на нечетных позициях строки стоит буква «a», а на четных — «b».
Вдруг утром Макс обнаружила, что кто-то испортил ее строку s. Некоторые буквы s были заменены на символ «?».
Назовем последовательность позиций i, i + 1, ..., i + m - 1 вхождением строки t в s, если 1 ≤ i ≤ n - m + 1 и t1 = si, t2 = si + 1, ..., tm = si + m - 1.
Красота строки s оценивается как максимальное количество непересекающихся вхождений строки t в нее. Макс может заменить некоторые из символов «?» на «a» или «b» (символы на разных позициях можно заменять на разные буквы). Макс хочет произвести замены так, чтобы красота строки s была максимально возможной. Из всех таких вариантов она хочет заменить как можно меньше символов «?». Найдите, сколько замен она должна сделать.
Входные данные:
Первая строка содержит одно целое число n (1 ≤ n ≤ 105) — длину строки s.
Вторая строка входных данных содержит строку s длины n, состоящую только из букв «a» и «b» латинского алфавита, а также символов «?».
Третья строка содержит целое число m (1 ≤ m ≤ 105) — длину строки t. Сама строка t содержит «a» на нечетных позициях, и «b» на четных.
Выходные данные:
Выведите единственное целое число — минимальное количество замен, которое должен сделать Вася, чтобы сделать красоту строки s максимально возможной.
Примеры:
| Входные данные |
Выходные данные |
5
bb?a?
1 |
2 |
9
ab??ab???
3 |
2 |
Пояснения:
В первом примере строка t имеет вид «a». Единственный оптимальный вариант — заменить все символы «?» на «a».
Во втором примере используя две замены можно получить строку «aba?aba??». Больше двух вхождений получить нельзя.
| |
![]()
|
|
Количество чисел на диапазоне
Бинарный поиск
Префиксные суммы(минимумы, ...)
Вам даны N целых чисел A1, ..., AN.
На каждый из Q запросов, заданных в формате L R X, выведите количество элементов среди AL, ..., AR, значения которых равны X.
Входные данные
В первой строке задано целое число N (1 <= N <= 2·105).
Вторая строка содержит N целых чисел Ai (1 <= Ai <= N, 1 <= i <= N).
В третьей строке задано одно целое число Q (1 <= Q <= 2·105).
Каждая из следующих Q строк содержит три целых числа L, R, X (1 <= L <= R <= N, 1 <= X <= N).
Выходные данные
Выведите на экран Q строк, i-я строка содержит ответ на i-й запрос.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
3 1 4 1 5
4
1 5 1
2 4 3
1 5 2
1 3 3
|
2
0
0
1
|
| |
![]()
|
|
XOR и любимое число
Префиксные суммы(минимумы, ...)
Алгоритм Мо
У Эвана есть любимое число k и массив ai длины n. Теперь он просит вас ответить на m запросов.
Для каждого запроса, задаваемого парой чисел l и r, требуется найти количество пар целых чисел i и j таких, что l ≤ i ≤ j ≤ r и xor чисел ai, ai + 1, ..., aj равен k.
Входные данные:
В первой строке даны целые числа n, m и k (1 ≤ n, m ≤ 105, 0 ≤ k ≤ 106) — длина массива, количество запросов и любимое число Эвана соответственно.
Во второй строке записаны n целых чисел ai (0 ≤ ai ≤ 106) — имеющийся у Эвана массив.
Дальше идут m строк. В i-й строке записаны числа li и ri (1 ≤ li ≤ ri ≤ n), определяющие i-й запрос.
Выходные данные:
Выведите m строк, ответы на запросы в порядке их появления во входных данных.
Примеры:
| Входные данные |
Выходные данные |
6 2 3
1 2 1 1 0 3
1 6
3 5 |
7
0 |
5 3 1
1 1 1 1 1
1 5
2 4
1 3 |
9
4
4 |
| |
![]()
|
|
Отрезок с максимальной суммой
Префиксные суммы(минимумы, ...)
В одномерном массиве, заполненном произвольными целыми числами, за один проход найдите непрерывный кусок, сумма чисел в котором максимальна.
Примечание. Фактически требуется найти такие i и j (i≤j), что сумма всех элементов массива от ai до aj включительно будет максимальна.
Входные данные
На вход программе сначала подается натуральное n ≤100000 — количество элементов в массиве. Далее, по одному в строке расположены сами элементы массива — целые числа, по модулю не превосходящие 30 000.
Выходные данные
Выдайте пару искомых значений индексов. Если таких пар несколько, то j должно быть минимально возможным, а при равных j значение i должно быть максимально возможным.
Примеры
| входные данные |
выходные данные |
5
-1
2
3
-2
2
|
2
3
|
7
2
-2
3
-1
5
-2
7
|
3
7
|
| |
![]()
|
|
Сумма подряд идущих
Префиксные суммы(минимумы, ...)
Дан массив целых чисел a[1], a[2], ..., a[n] и натуральные числа k и m.
Укажите минимальное значение i, для которого a[i] + a[i+1] + ... + a[i + k] = m (то есть сумма k + 1 подряд идущих элементов массива равна m).
Если такого значения нет, то выведите 0. Вложенные циклы и дополнительные массивы не использовать (требуется решить задачу за один проход исходного массива).
Входные данные
На вход программе сначала подаются значения n, k и m (m <= 1000000000, 0 < k < n <= 100000; n - количество элементов в массиве). В следующей строке входных данных расположены сами элементы массива - целые числа, по модулю не превосходящие 100.
Выходные данные
Выведите ответ на задачу.
Примеры
входные данные
4 1 22
9 13 10 -11
выходные данные
1
| |
![]()
|
|
Торговля акциями
Префиксные суммы(минимумы, ...)
В настоящее время на бирже при торговле акциями активно применяются компьютерные системы, которые упрощают и автоматизируют процесс покупки и продажи акций. Некоторые из них даже позволяют вести торговлю вообще без участия человека.
Разумеется, основным критерием, по которому такие системы оцениваются, является прибыль, которую приносит торговля с их применением. Для того, чтобы ее повысить при построении этих систем применяются различные математические методы и модели, такие, как, например, квадратичное программирование, нейронные сети, генетические алгоритмы и т. д.
Основной трудностью при создании таких систем является то, что они должны некоторым образом учитывать изменение стоимости акций в будущем, а также его прогнозировать. Ваша задача несколько проще — курсы продажи и покупки акций за весь период из n дней уже известны, необходимо лишь разработать оптимальную стратегию продаж и покупок. При этом для простоты будем считать, что за эти n дней купить акции можно не более одного раза и продать акции можно также не более одного раза.
Кроме этого, будем считать, что продажа и покупка будет осуществляться только с акциями одного типа. На начало этого периода вы располагаете суммой в x рублей. Для каждого из дней известна цена ai (от ask — цена предложения), по которой можно купить одну акцию, и цена bi (от bid — цена спроса), по которой можно одну акцию продать. При этом в соответствии с действующими правилами торгов на бирже разрешается продавать и покупать только целое число акций (например, если у вас есть 5 рублей, а акция стоит 2 рубля, то вы можете купить не более двух акций).
Требуется написать программу, которая по имеющимся данным о стоимости акций в каждый из дней, найдет оптимальную стратегию покупки и продажи акций.
Входные данные
Первая строка входного файла содержит два целых числа n и x (1 ≤ n ≤ 100000, 1 ≤ x ≤ 106).
Вторая строка входного файла содержит n целых чисел a1, . . . , aт. Третья строка входного файла содержит n целых чисел b1, . . . , bт. Для каждого индекса i (1 ≤ i ≤ n) выполняются неравенства 1 ≤ bi ≤ ai ≤ 1000.
Выходные данные
В первой строке выходного файла выведите максимальную сумму, которой вы можете обладать по окончании рассматриваемого периода. Во второй строке выведите два числа — номер дня d1, в который следует купить акции, и номер дня d2, в который эти акции следует продать (должно выполняться неравенство d2 > d1). При этом подразумевается, что покупается столько акций, сколько их можно купить на x рублей, а потом они все продаются. Если в найденной вами стратегии продавать и покупать акции не требуется, то выведите выведите во второй строке «-1 -1».
Если существует несколько вариантов оптимальной стратегии, то выведите любой из них
Примеры
| входные данные |
выходные данные |
5 1000
2 3 1 4 3
1 2 1 2 3
|
3000
3 5 |
5 1000
10 9 8 7 6
9 8 7 6 5
|
1000
-1 -1 |
| |
![]()
|
|
Клиппи и Мерлин грабят банк
Префиксные суммы(минимумы, ...)
Клиппи и Мерлин решили грабить банк «Документы», который представляет из себя N расположенных в ряд банковских ячеек, пронумерованных последовательно числами от 1 до N .
С помощью своего друга Ровера, который работал в банке сторожевым псом, они добыли ключи от всех ячеек, а так же узнали, как много ценностей хранится в каждой ячейке.
Чтобы не вызывать лишних подозрений, Клиппи и Мерлин решили ограбить всего две ячейки "— по одной на каждого. Также, чтобы охрана банка не почуяла неладного, они решили работать далеко друг от друга "— между ними должно быть не меньше K банковских ячеек.
Входные данные
В первой строке вводятся два числа "— N ( 2 ≤ N ≤ 10 5 ) и K ( 0 ≤ K < N - 1 ) соответственно. В второй строке вводятся N чисел a i ( 0 ≤ a i ≤ 10 9 ) "— стоимости хранимых ценностей в ячейках от 1 до N соответственно.
Выходные данные
Выведите два числа в возрастающем порядке "— номера ячеек, которые нужно ограбить, чтобы суммарно украсть как можно более дорогие ценности, не вызвав при этом лишних подозрений. Если вариантов несколько выберите тот, в котором меньший номер вскрываемой ячейки был как можно ближе к единице, чтобы в экстренном случае покинуть банк как можно скорее. Если и таких вариантов несколько, выберите тот, в котором и больший номер вскрываемой ячейки был как можно меньше.
Примеры
входные данные
6 2
2 4 3 1 4 4
выходные данные
2 5
| |
![]()
|
|
Бинарная сортировка
Префиксные суммы(минимумы, ...)
Вы решили съездить проведать своего друга из Озерска. Однако на въезде в город вас остановили и попросили решить задачу, чтобы удостовериться, что вы действительно можете проехать на территорию закрытого города.
Бинарная строка это строка, состоящая только из символов 0 и 1. Полицейский дал вам бинарную строку s1s2 ... sn. Нужно отсортировать эту строку (то есть превратить ее в строку вида 00 ... 0011 ... 11) за наименьшее количество операций. За одну операцию вы можете сделать следующее:
• Выбрать произвольный индекс в строке 1 <= i <= n;
• Для всех j >= i поменять значение в j-й позиции на противоположное, то есть если sj = 1, то сделать sj = 0, и наоборот.
Входные данные
Каждый тест состоит из нескольких наборов входных данных. Первая строка содержит целое число t (1 <= t <= 104) количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит единственное целое число n (1 <= n <= 105) длину строки.
Вторая строка каждого набора входных данных содержит бинарную строку s длины n.
Гарантируется, что сумма n по всем наборам входных данных не превосходит 2 ·105.
Выходные данные
Для каждого набора входных данных выведите единственное целое число минимальное количество операций, которое потребуется сделать, чтобы отсортировать строку.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6
1
1
2
10
3
101
4
1100
5
11001
6
100010 |
0
1
2
1
2
3 |
Замечание
В первом наборе входных данных строка уже отсортирована.
Во втором наборе входных данных можно выбрать i = 1 и после этого s = 01.
В третьем наборе входных данных можно выбрать i = 1 и получить s = 010, а после этого выбрать i = 2. В результате получим s = 001, то есть отсортированную строку.
В шестом наборе входных данных можно на первой итерации выбрать i = 5 и получить s = 100001. Затем выбрать i = 2 тогда s = 111110. Дальше выбираем i = 1, получая отсор-
тированную строку s = 000001.
| |
![]()
|
|
Дартс
Префиксные суммы(минимумы, ...)
Петя и Ваня решили придумать свои правила для игры Дартс. Они взяли круглое игровое поле и поделили его на сектора. Сектора нумеруются натуральными числами. Каждому сектору назначили количество очков, которое можно получить, если попасть дротиком в него. Перед началом игры выбирается нулевой сектор, который служит точкой отсчета: количество очков, которое набирает игрок, попадая в сектор, считается как количество очков, указанное в секторе, умноженное на расстояние (количество секторов) от нулевого сектора. При попадании в нулевой сектор количество очков равно нулю.
Поскольку заранее неизвестно, в какие именно сектора попадут игроки, нулевой сектор следует выбирать так, чтобы при однократном попадании во все сектора игрового поля игрок набирал максимальное количество очков.
Определите, какой сектор необходимо выбрать нулевым.
Входные данные
Первая строка входных данных содержит число N — количество секторов, на которые разделено игровое поле.
Следующие N строк содержат по одному числу — количество очков, которые набирают игроки, попадая в соответствующий сектор, начиная с сектора с номером 1.
Выходные данные
Выведите одно число — номер сектора, который необходимо выбрать как нулевой.
Примеры
| № |
Входные данные |
Выходные данные |
Примечание |
| 1 |
6
8
20
5
13
7
19 |
3 |
Для данного примера ответ — 3 (5 * 0 + 20 * 1 + 13 * 1 + 8 * 2 + 7 * 2 + 19 * 3 = 120) |
| |
![]()
|
|
Два мусоровоза
Префиксные суммы(минимумы, ...)
На каждом километре кольцевой автодороги с двусторонним движением установлены контейнеры для мусора. Длина кольцевой автодороги равна N километров. Нулевой километр и N-й километр автодороги находятся в одной точке. Известно количество мусора, которое накапливается ежедневно в каждом из контейнеров.
На автодороге работают два мусоровоза. Один едет по часовой стрелке, другой против. Оба мусоровоза выезжают из центра переработки одновременно навстречу друг другу и встречаются возле одного из контейнеров. Из одного контейнера вывезти мусор может только один мусоровоз. Время доставки мусора вычисляется как произведение количества мусора на расстояние от пункта до центра переработки. Центр переработки отходов открыли в одном из пунктов сбора мусора таким образом, чтобы общее время сбора мусора двумя мусоровозами было минимально.
Определите, возле контейнера с каким номером необходимо поставить центр переработки, чтобы потребовалось минимальное время мусоровозам для сбора мусора.
Входные данные
Первая строка входных данных содержит число N (1 <= N <= 10 000 000) – количество пунктов сбора мусора на кольцевой автодороге. В каждой из следующих N строк находится число – количество мусора в контейнере (все числа натуральные, количество мусора в каждом пункте не превышает 1000). Числа указаны в порядке расположения контейнеров на автомагистрали, начиная с первого километра.
Выходные данные
Выведите на экран одно число - ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
7
8
20
5
13
7
19
21 |
7 |
При таких исходных данных необходимо открыть центр переработки возле контейнера с номером 7:
Первый мусоровоз собирает мусор: 0 * 21 + 1 * 19 + 2 * 7 + 3 * 13 = 72
Второй мусоровоз потратит времени: 0 * 21 + 8 * 1 + 20 * 2 + 3 * 5 = 63
Итоговое время, которое потратят два мусоровоза: 72 |
| |
![]()
|
|
Непрерывная подпоследовательность
Префиксные суммы(минимумы, ...)
Дана последовательность из N натуральных чисел. Известно, что сумма всех чисел последовательности не превышает 109. Рассматриваются все её непрерывные подпоследовательности, в которых количество нечётных чисел кратно K = 7. Найдите наибольшую сумму такой подпоследовательности.
Входные данные
Первая строка входных данных содержит одно число N (1 <= N <= 1 000 000) - количество чисел. Каждая из следующих N строк содержит одно натуральное число, не превышающее 1 000.
Входные данные
Выведите ответ на задачу
Пример организации исходных данных во входном файле (для К=4):
6
8
17
3
13
11
21
В этом наборе можно выбрать последовательности 8+17+3+13+11 (сумма 52) и 3+13+11+21 (сумма 48).
Ответ (для K = 4): 52.
| |
![]()
|
|
Призы
Префиксные суммы(минимумы, ...)
Алиса и Боб стали победителями телевикторины, и теперь им предстоит выбрать себе призы. На выбор предлагается n призов, пронумерованных от 1 до n.
Распределение призов происходит следующим образом. Организаторы телевикторины сообщают победителям целое положительное число k (1 ≤ k ≤ n / 3). Сначала Алиса выбирает себе любые k подряд идущих номеров призов. Потом Боб выбирает себе k подряд идущих номеров призов, при этом он не может выбирать номера, которые уже выбрала Алиса. После этого победители забирают выбранные ими призы.
Алиса хорошо знает Боба, и для каждого приза выяснила его ценность для Боба, которая является целым положительным числом. Алиса обижена на Боба и хочет выбрать свои призы так, чтобы суммарная ценность призов, которые достанутся Бобу, была как можно меньше. При этом Алису не волнует, какие призы достанутся ей.
Требуется написать программу, которая по информации о ценности призов и значению k определит, для какого минимального значения x Алиса сможет добиться того, чтобы Боб не смог выбрать призы с суммарной ценностью больше x.
Формат входного файла
Первая строка входного файла содержит два целых числа: n — общее количество призов и k — количество подряд идущих номеров призов, которое должен выбрать каждый из победителей (3 ≤ n ≤ 100 000, 1 ≤ k ≤ n / 3). Вторая строка содержит n целых положительных чисел: a1, a2, …, an. Для каждого приза указана его ценность для Боба (1 ≤ ai ≤ 109 ).
Формат выходного файла
Выходной файл должен содержать одно число — минимальное значение x, для которого Алиса сможет добиться того, чтобы Боб не смог выбрать призы с суммарной ценностью больше x.
Пример
Ввод:
10 2
1 2 4 5 2 4 2 2 1 6
Вывод:
7
Пояснение к примеру
В приведенном примере Алиса может, например, выбрать 4-й и 5-й призы. После этого для Боба оптимально выбрать 9-й и 10-й призы с суммарной ценностью 7.
| |
![]()
|
|
Кладовка из Простоквашино
Динамическое программирование
Динамическое программирование: один параметр
Префиксные суммы(минимумы, ...)
Сразу же после заселения в новый дом в Простоквашино кот Матроскин, Шарик и дядя Фёдор затеяли ремонт. Непосредственно перед его началом они обнаружили, что в доме отсутствует кла- довка для стройматериалов, и наспех пристроили её к дому. Как только вспомогательное строение было готово, встал вопрос о необходимости провести туда электричество и повесить лампочку.
Обсудив вопросы электрификации новых помещений с почтальоном Печкиным, наши герои узна- ли много полезной информации. Чтобы посетители не мучились с выбором, в деревенском магазине продаётся только один вид лампочек, зато в неограниченных количествах. Стоит одна лампочка ни дорого, ни дёшево, а ровно C рублей. Правда, лампочки в магазине не самые качественные, и вклю- чить каждую из них можно только K раз, а на K + 1 включение она перегорает. Недостаток этот компенсируется тем, что во включенном состоянии лампочка перегореть не может. К сожалению, электроэнергия в Простоквашино недешевая, и каждая минута работы лампочки обойдется дяде Фёдору и его друзьям в D рублей.
Узнав всё это, экономный Матроскин составил поминутный график из N предполагаемых посе- щений кладовки. Каждый визит в новое помещение задаётся моментом входа ai и моментом выхода bi . Таким образом, i-й визит продолжается ровно bi − ai минут.
Разумеется, во время посещения свет в кладовке должен быть включён. Если в начале очередного визита лампочка не горит, то посетитель сразу её включает, а вот уходя он может как выключить свет, так и оставить его включенным. Если во время очередного включения лампочка перегорает, то её приходится немедленно заменить. Теперь Матроскина интересует минимальное количество рублей, которое придётся потратить, чтобы выполнить все запланированные визиты в кладовку. Изначально в помещении уже висит новая лампочка в выключенном состоянии.
Формат входных данных
В первой строке входных данных записаны четыре целых числа N, K, C, D — количество пла- нируемых посещений кладовки, количество успешных включений для одной лампочки, стоимость покупки лампочки и стоимость минуты работы лампочки соответственно (1 <= N, K <= 200 000, 1 <= C, D <= 109 ). В следующих N строках даны по два целых положительных числа ai и bi , описывающих пред- полагаемые визиты в кладовку (1 <= ai < bi <= 109 ). Посещения не пересекаются по времени и упорядочены, то есть bi < ai+1.
Формат выходных данных
Выведите одно целое число — минимальное количество рублей, которое придётся потратить жителям дома, чтобы выполнить все запланированные визиты в кладовку при свете.
| Ввод |
Вывод |
1 2 5 6
3 5 |
12 |
3 1 15 10
1 3
4 5
30 35 |
105 |
Замечание
Замечание В первом примере достаточно заплатить только за электроэнергию: лампочка должна быть включена на третьей минуте и выключена на пятой, стало быть, суммарные затраты составляют (5 − 3) × 6 = 12.
Во втором примере выгодно не выключать лампочку между первым и вторым посетителем, а для третьего использовать уже новую лампочку
| |
![]()
|
|
Падающее домино
Структуры данных
Префиксные суммы(минимумы, ...)
Разбор случаев
Вася обожает выставлять сложные фигуры из костяшек домино и, толкнув одну из них, смот- реть, как вся конструкция падает. Однако, он сделал уже так много фигур, что решил придумать что-то новое.
Для своей новой идеи он использует костяшки не только длиной 2, но и более длинные (и более короткие). Все костяшки выстраиваются в одну линию на расстоянии 1, а цель игры опрокинуть все костяшки толкнув наименьшее количество костяшек.
Каждую костяшку можно толкнуть влево или вправо, падая она опрокидывает все костяшки, находящиеся на расстоянии строго меньшем высоты падающей костяшки. При этом те костяшки, которые упали в результате падения на них других костяшек также падают в ту же сторону и, в свою очередь, могут опрокидывать и другие костяшки и так далее.
Формат входных данных
В первой строке записано натуральное число N (0 <= N <= 1 000 000) количество костяшек. Во второй строке записано N натуральных чисел Hi (1 <= Hi <= 1 000 000) высоты костяшек.
Формат выходных данных
Выведите число M наименьшее количество костяшек, которые нужно толкнуть, чтобы вся конструкция упала.
В следующих M строках выведите описание костяшек, которые необходимо толкнуть: номер костяшки (нумерация начинается с единицы и идет слева-направо), а также направление толчка: букву L для толчка влево и R для толчка вправо. Номер костяшки и букву разделяйте пробелом.
Порядок вывода костяшек, которые нужно толкнуть, может быть произвольным. Если решений несколько выведите любое из них
Система оценки
Решения, верно работающие при N <= 1000, будут набирать не менее половины баллов.
| Ввод |
Вывод |
6
1 2 1 4 1 3 |
1
6 L |
7
1 2 4 1 2 3 2 |
2
3 R
2 L |
Замечание
В первом примере последняя костяшка толкается влево, опрокидывая костяшки с номерами 4 и 5 (их высоты 4 и 1 соответственно). Костяшка номер 4 также падает налево и опрокидывает костяшки с номерами 1, 2 и 3.
Во втором примере костяшка номер 3 толкается вправо, опрокидывая костяшки номер 4, 5 и 6.
Костяшка номер 6 также падает вправо и опрокидывает костяшку номер 7. После этого костяшка
номер 2 толкается влево и опрокидывает костяшку номер 1.
| |
![]()
|
|
Двумерный дождь
Линейные структуры
Префиксные суммы(минимумы, ...)
Игра PitCraft происходит в двумерном мире, который состоит из блоков размером 1 на 1 метр.
Остров игрока представляет собой набор столбцов различной высоты, состоящих из блоков камня и окруженный морем.
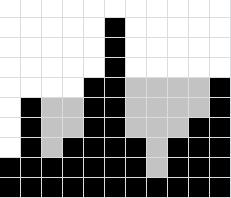
Над островом прошёл сильный дождь, который заполнил водой все низины, а не поместившаяся в них вода стекла в море, не увеличив его уровень. По ландшафту острова определите, сколько блоков воды осталось после дождя в низинах на острове.
Формат входных данных
В первой строке записано натуральное число N (0 <= N <= 100 000) количество столбцов, задающих ландшафт острова.
Во второй строке записано N натуральных чисел Hi (1 <= Hi <= 109) высоты столбцов.
Формат выходных данных
Выведите одно число количество блоков занятых водой.
Система оценки
Решения, верно работающие при N <= 100, будут набирать не менее половины баллов.
| Ввод |
Вывод |
11
2 5 2 3 6 9 3 1 3 4 6 |
18 |
Замечание
Пример соответствует рисунку. Черным цветом обозначен камень, серым вода.
| |
![]()
|
|
Воздушные потоки
Деревья
Наименьший общий предок
Структуры данных
Префиксные суммы(минимумы, ...)
Разреженные таблицы (sparse table)
Колобок ушёл от бабушки и поехал путешествовать. Неожиданно для себя он забрёл в страну Ивэнлэнд. Первые трудности встали на его пути: Колобка и вход в страну отделял огромный ров с водой, которая, как известно, не очень хорошо влияет на нашего героя. К счастью, повсюду рас- положены воздушные потоки, которые могли поднимать того, кто на них встает, на определённую высоту. Страна не просто так названа Ивэнлэнд, поэтому все высоты, на которые могут поднять героя воздушные потоки — это чётные числа.
Представим воздушные потоки как массив h[1..n] из n натуральных чисел — высот потоков. Для каждого 1 ≤ i ≤ n посчитаем G[i] — индекс ближайшего элемента слева, строго большего h[i]. Более формально, g[i] = max{j | j < i и h[j] > h[i]}. Если i = 1 или до h[i] нет ни одного элемента больше него, то G[i] считается равным 0.
Колобок считает, что оптимальность расположения воздушных потоков определяется суммой
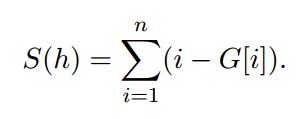
Чем меньше сумма, тем расположение оптимальнее. Всё, что может сейчас сделать Колобок — это увеличить высоту одного из воздушных потоков не более чем на m. После этого действия высота потока должна остаться целым числом, но может, если необходимо, стать и нечётной.
Помогите Колобку сделать оптимальное изменение, которое позволит добиться, чтобы сумма S(h), описанная выше, после проделанного действия была минимальна.
Формат входного файла
В первой строке входного файла даны числа n, m (1 ≤ n ≤ 105 , 1 ≤ m ≤ 109 ) — количество воздушных потоков и максимальное значение, на которое можно увеличить высоту одного из них. Во второй строке даны высоты воздушных потоков h[i] (1 ≤ h[i] ≤ 109 ). Гарантируется, что все высоты — чётные числа.
Формат выходного файла
В единственной строке выходного файла выведите одно целое число — минимальную искомую сумму.
| Ввод |
Вывод |
3 100
4 2 6 |
4 |
3 2
4 2 6 |
5 |
3 10
2 2 2 |
4 |
| |
![]()
|
|
Путь в никуда
Бинарный поиск
Деревья
Деревья
Структуры данных
Префиксные суммы(минимумы, ...)
Разреженные таблицы (sparse table)
Колобку снится странный сон.
В нём Колобок находится на клетчатом поле размера n × m в клетке с координатами (x, y).
Изначально Колобок смотрит вдоль положительного направления оси X. Затем он начинает идти по полю со следующей закономерностью:
• Пройти на одну клетку вперед. Повернуть на 90o вправо.
• Пройти на одну клетку вперед. Повернуть на 90o вправо.
• Пройти на две клетки вперед. Повернуть на 90o вправо.
• Пройти на две клетки вперед. Повернуть на 90o вправо.
• Пройти на три клетки вперед. Повернуть на 90o вправо.
• Пройти на три клетки вперед. Повернуть на 90o вправо.
• Пройти на четыре клетки вперед. Повернуть на 90o вправо.
• И так далее...
Движение продолжается до тех пор, пока Колобок не выйдет за границы поля. После этого Колобок просыпается.
Утром Колобок решил проанализировать свой сон. Он догадался, что в каждой клетке он был максимум один раз, но никак не может вспомнить, сколько клеток он посетил. Колобок просит вас написать программу, которая посчитает количество посещённых им клеток.
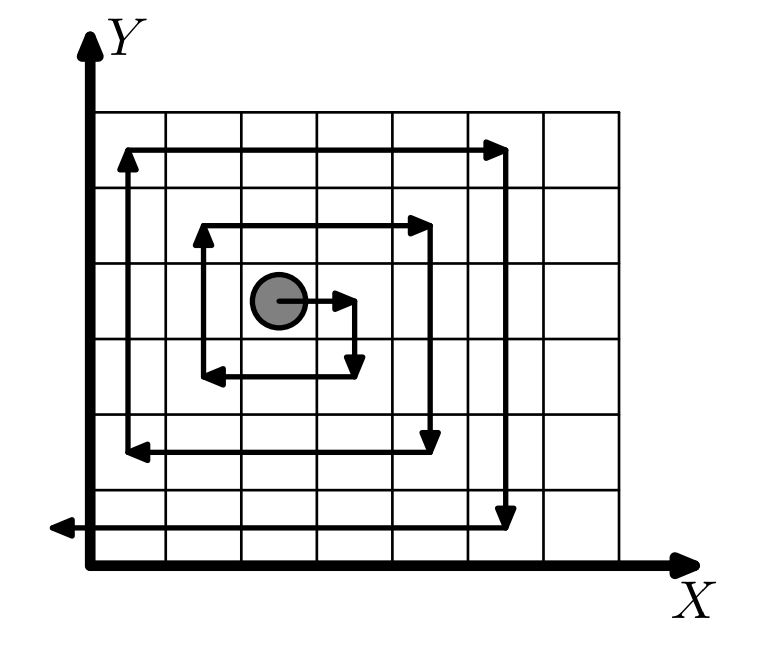
Формат входного файла
В первой строке входного файла находятся два натуральных числа n, m (1 ≤ n, m ≤ 109 ) — размеры доски вдоль оси X и оси Y соответственно. Во второй строке находятся два натуральных числа x, y (1 ≤ x ≤ n; 1 ≤ y ≤ m) — координаты стартовой позиции колобка.
Формат выходного файла
В выходной файл выведите одно число — количество клеток, посещенных Колобком во сне.
| Вывод |
Ввод |
7 6
3 4 |
36 |
2 2
1 1 |
2 |
2 2
1 2 |
4 |
Комментарий
На рисунке наглядно показан первый пример.
| |
![]()
|
|
Modern Art
Префиксные суммы(минимумы, ...)
Picowso - новый гений!
Picowso рисует особым способом. Она начинает на пустом холсте размером N×N ячеек, представленном решёткой из N×N нолей, где ноль обозначает пустую ячейку холста. Затем она рисует N2 прямоугольников на холсте каждым из N2 цветов последовательно пронумерованных 1…N2. Например, она может начать рисовать прямоугольник цветом 2 и получится такой холст:
2 2 2 0
2 2 2 0
2 2 2 0
0 0 0 0
Затем она может нарисовать прямоугольник цветом 7:
2 2 2 0
2 7 7 7
2 7 7 7
0 0 0 0
А затем она может нарисовать маленький прямоугольник цветом 3:
2 2 3 0
2 7 3 7
2 7 7 7
0 0 0 0
Каждый прямоугольник имеет стороны, параллельные сторонам холста, и прямоугольник может быть таким большим как весь холст или таким маленьким как одна ячейка. Каждый цвет из 1…N2 используется ровно один раз, хотя более поздние цвета могут полностью перекрыть более ранние цвета.
По заданному финальному состоянию холста определите сколько из N2 цветов могли быть первым, использованным при рисовании.
ФОРМАТ ВВОДА:
Первая строка ввода содержит N, размер холста (1≤N≤1000). Следующие N строк описывают финальную картину на холсте, каждая строка содержит N целых чисел в интервале 0…N2. Гарантируется, что картина была нарисована способом описанным выше, рисованием прямоугольников различных цветов.
ФОРМАТ ВЫВОДА:
Выведите количество цветов, которые могли быть использованы первыми.
| Ввод |
Вывод |
|
4
2 2 3 0
2 7 3 7
2 7 7 7
0 0 0 0
|
14 |
В этом примере цвет 2 мог быть использован первым. Цвет 3 был использован после цвета 7, а цвет 7 был использован после цвета 2. Поскольку мы не видим других цветов, мы делаем вывод, что они также могли быть использованы первыми (а потом перекрашены). | |
![]()
|
|
Сумма подотрезка
Префиксные суммы(минимумы, ...)
Дан неизменяемый массив длины n и q запросов типа “вычислить сумму подотрезка массива с l по r”. Выведите ответ на каждый запрос.
Входные данные
В первой строке дано число n – размер массива (\(1 <= n <= 10^5\)). Во второй строке дано n чисел – элементы массива. Числа по модулю не превосходят \(10^9\). В третьей строке дано число q – кол-во запросов (\(1 <= q <= 10^5\)). Далее дано q строк, в каждой из которых дано 2 числа: l и r (\(1 <= l <= r <= n\)).
Выходные данные
Выведите ответы на все запросы, каждый в отдельной строке.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
1 2 3 4 5
3
1 2
3 3
2 5 |
3
3
14 |
| |
![]()
|
|
Разность сумм
Префиксные суммы(минимумы, ...)
Дан массив целых чисел (nums) с индексацией, начинающейся с 0. Сформируйте новый массив целых чисел (ans), в котором i-й элемент вычисляется по формуле:
ans[i] = |leftSum[i] - rightSum[i]|.
Где:
leftSum[i] - сумма элементов, стоящих слева от элемента nums[i]. Если таких элементов нет, то leftSum[i] = 0.
rightSum[i] - сумма элементов, стоящих справа от элемента nums[i]. Если таких элементов нет, то rightSum[i] = 0.
Выведите элементы нового массива на экран в одну строку, разделяя элементы одним пробелом. Количество элементов нового массива должно быть равно количеству элементов исходного.
Формат входных данных
Первая строка содержит число n (n <= 105). Во второй строке записаны n целых чисел numsi - элементы массива nums (|numsi| < 106).
Формат выходных данных
Выведите на экран n чисел - элементы нового массива на экран в одну строку, разделяя элементы одним пробелом.
| |
![]()
|
|
Средний индекс массива
Префиксные суммы(минимумы, ...)
Дан массив целых чисел nums (первый элемент массива имеет индекс 0). Найдите наименьший "средний" индекс массива.
Средний индекс - это индекс, для которого выполняется условие: сумма элементов слева от индекса равна сумме элементов справа от индекса (не включая сам элемент со средним индексом). То есть
leftSum[middle] = rightSum[middle].
Где:
middle - средний индекс массива.
leftSum[middle] - сумма элементов, стоящих слева от элемента nums[middle]. Если таких элементов нет, то leftSum[middle] = 0.
rightSum[middle] - сумма элементов, стоящих справа от элемента nums[middle]. Если таких элементов нет, то rightSum[middle] = 0.
Формат входных данных
Первая строка содержит натуральное число N (1 <= N <= 105) - количество элементов в массиве nums. Вторая строка содержит N чисел numsi - элементы массива nums (|numsi|<=1000, 0 <= i < N).
Формат выходных данных
Выведите одно число - наименьший "средний" индекс массива. Если такого индекса нет, то выведите -1.
| |
![]()
|
|
Подсчет прибыли
Префиксные суммы(минимумы, ...)
ЕГЭ - вычислительные задачи
Финансовый аналитик компании "Хлебосушки" анализирует прибыль компании на протяжении N месяцев. Аналитику поставили задачу найти интервал длиной не менее K месяцев с максимальной прибылью. Месяцы имеют сквозную нумерацию, начиная с 1 (с месяца открытия компании).
Вы - ведущий программист компании. Вам дали задачу написать программу, которая бы находила максимальную прибыль в непрерывном интервале длиной не менее K месяцев.
Формат входных данных
Первая строка содержит натуральное число N (1 < N ≤ 1 000 000) – количество месяцев существования компании и натуральное число K (1 < K < N) – минимально допустимый интервал. В каждой из следующих N строк находится одно целое число profiti, не превышающее по модулю 10 000 000: прибыль компании за iй месяц.
Формат выходных данных
Выведите одно число - максимальную прибыль в интервале длиной не менее K месяцев. Гарантируется, что ответ к задаче не превышает 109.
| |
![]()
|
|
Опорная точка
Префиксные суммы(минимумы, ...)
Назовем опорным числом последовательности натуральных чисел - целое число x, такое что:
- Сумма всех элементов между
1 и x включительно равна сумме всех элементов между x и n включительно.
Например, для числовой последовательности из 8 элементов (числа от 1 до 8 включительно) опорным числом будет число 6 (1+2+3+4+5+6 = 6+7+8).
Для заданного натурального числа n, найдите минимальную опорную точку последовательности натуральных чисел от 1 до n.
Формат входных данных
Программа получает на вход натуральное число n (1 <= n <= 2000).
Формат выходных данных
Выведите минимальную опорную точку последовательности натуральных чисел от 1 до n. Если такой точки не существует, вернуть -1.
| |
![]()
|
|
Битовый баланс двоичной строки
Префиксные суммы(минимумы, ...)
Битмен ищет битовый баланс у двоичной строки (строки, состоящей только из 0 и 1). Чтобы найти битвой баланс, Битмен разбивает строку на две непустые подстроки (левую подстроку и правую подстроку). Затем Битмен считает сумму количества нулей в левой подстроке и количества единиц в правой подстроке. Битовый баланс двоичной строки равен максимальной сумме, полученной после какого-либо разбиения строки на подстроки.
Формат входных данных
На вход подается строка (2 <= длина строки <= 1000). Строка состоит только из символов 0 и 1.
Формат выходных данных
Выведите одно число - битовый баланс строки.
Примечание
В тестовом примере все возможные способы разить строку на 2 непустые строки следующие:
left = "0" и right = "11101", сумма = 1 + 4 = 5
left = "01" и right = "1101", сумма = 1 + 3 = 4
left = "011" и right = "101", сумма = 1 + 2 = 3
left = "0111" и right = "01", сумма = 1 + 1 = 2
left = "01110" и right = "1", сумма = 2 + 1 = 3
Битовый баланс равен максимальному значению суммы, следовательно ответ 5.
| |
![]()
|
|
Вася и Петя
Префиксные суммы(минимумы, ...)
Друзья Вася Л. и Петя П. — талантливые мальчики, которые любят писать песни собственного сочинения. В будущем они хотят стать популярными музыкантами. Ребята знают: чтобы добиться успеха, нужно регулярно тренироваться. Именно поэтому они каждый день пишут по новой песне, совершенствуя свое мастерство.
Однажды Петя в очередной раз написал грустную песню про любовь и поспешил показать ее Васе. Песня представляет собой строку из маленьких букв английского алфавита. У Васи сразу возникло \(q\) вопросов про эту песню. Каждый вопрос представляет собой некоторый отрезок песни с позиции \(l\) до позиции \(r\) включительно. Вася рассматривает подстроку, образованную символами на этом отрезке, а затем повторяет каждую букву в этой подстроке \(k\) раз, где \(k\) — порядковый номер соответствующей буквы в алфавите. Например, если Вася выбрал подстроку <<abbcb>>, то он повторит букву <<a>> один раз, каждую из букв <<b>> — по два раза, букву <<c>> — три раза, и полученная строка будет равна <<abbbbcccbb>>, ее длина равна 10. Вася интересуется именно длиной полученной строки.
Помогите Пете ответить Васе на его вопросы, а именно, для каждого из заданных вопросов определите длину строки, которую выпишет Вася.
Формат входных данных
В первой строке вводятся числа \(n, q\) (\(1\leq n\leq 100\,000, 1\leq q \leq 100\,000\)) — длина песни и количество вопросов.
Во второй строке дана строка \(s\) — сама песня, представляющая собой строку длины \(n\) из маленьких букв английского алфавита.
В следующих \(q\) строках даны описания вопросов. Каждое описание состоит из двух чисел \(l\) и \(r\) \((1 \leq l \leq r \leq n)\) — границы каждого из вопросов.
Формат выходных данных
Выведите \(q\) строк — для каждого вопроса выведите длину строки, которую выпишет Вася.
Примечание
В первом примере Васю интересуют три вопроса. В первом вопросе Вася рассматривает подстроку <<aba>>, которая превратится в <<abba>>, а значит, ответ на этот вопрос равен 4. Во втором вопросе Вася рассматривает подстроку <<baca>>, которая превратится в <<bbaccca>>, а значит, ответ на этот вопрос будет равен 7. В третьем вопросе Вася рассматривает всю строку <<abacaba>>, которая превратится в <<abbacccabba>> — строку длины 11.
Для получение номера буквы можно использовать следующий код:
-
В языке python3 или pypy3 выражение ord(x) - 96, например ord(a) - 96 равно 1, а ord(x) - 96 равно 24.
-
В языке c++ выражение x - 96, например a - 96 равно 1, а x - 96 равно 24.
-
В языке pascal выражение ord(x) - 96, например ord(a) - 96 равно 1, а ord(x) - 96 равно 24.
| |
![]()
|
|
Длина последовательности
"Два указателя"
Префиксные суммы(минимумы, ...)
Рассмотрим отрезок целых неотрицательных чисел от \(l\) до \(r\). Запишем их подряд в десятичной системе счисления, получив строку \(a\). Например, если \(l=3\), \(r=10\), то \(a=345678910\).
Найдите такой отрезок подряд идущих неотрицательных чисел \([l,r]\) (\(0 \le l \le r \le 10^{18}\)), что записанная для него строка \(a\) имеет длину ровно \(S\), а количество чисел на отрезке \([l,r]\) максимально.
Формат входных данных
Первая строка содержит одно целое число \(S\) (\(1 \le S \le 10^{18}\)).
Формат выходных данных
В первой строке выведите длину отрезка \([l,r]\). Если решения не существует, выведите одно целое число \(-1\).
Если решение существует, во второй строке выведите искомые границы отрезка \(l\) и \(r\).
Если существуют несколько решений, выведите любое из них.
| |
![]()
|