| | | |
|
Bovine Genomics №3
Двумерные массивы
У Фермера Джона есть N коров с пятнами и N коров без пятен. ФД, как генетик, знает, что пятна на коровах вызваны мутациями в одной позиции коровьего генома.
За большие деньги ФД выписал геномы своих коров. Каждый геном есть строка длины M, построенная из четырёх символов A, C, G, T. Когда он выписал их, у него получилась такая таблица (для N=3):
Позиция: 1 2 3 4 5 6 7 ... M
Пятнистая корова 1: A A T C C C A ... T
Пятнистая корова 2: G A T T G C A ... A
Пятнистая корова 3: G G T C G C A ... A
Без пятен корова 1: A C T C C C A ... G
Без пятен корова 2: A C T C G C A ... T
Без пятен корова 3: A C T T C C A ... T
Внимательно проанализировав эту таблицу, он предположил, что позиция 2 есть потенциальное место в геноме, которое отвечает за пятнистость. Потому что в этой позиции у коров без пятен находится один и тот же символ С, а у пятнистых коров находятся символы A или G. Причём G больше никогда не появлялось на позиции 2. Позиция 1 не может объяснять пятнистость, поскольку A в этой позиции есть и у пятнистых коров.
По заданным геномам коров ФД, посчитайте количество позиций, которые потенциально могли бы объяснять пятнистость.
ФОРМАТ ВВОДА:
Первая строка ввода содержит N и M, оба - положительные целые числа не более 100. Каждая из следующих N строк содержит по M символов. Они описывают геномы пятнистых коров. Следующие N строк описывают геномы коров без пятен.
ФОРМАТ ВВОДА:
Вычислите количество позиций генома (целое число в интервале от 0…M), которые потенциально могут объяснять пятнистость. Такие позиции можно предсказывать по заданной информации.
| Ввод |
Вывод |
|
3 8
AATCCCAT
GATTGCAA
GGTCGCAA
ACTCCCAG
ACTCGCAT
ACTTCCAT
|
1 |
| |
![]()
|
|
Заполнение по диагоналям
Двумерные массивы
Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.
Входные данные: Программа получает на вход два числа n и m (1 <= n, m <= 15).
Выходные данные: Программа должна вывести полученный массив, отводя на вывод каждого числа ровно 3 символа.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 10 |
0 1 3 6 10 14 18 22 26 30
2 4 7 11 15 19 23 27 31 34
5 8 12 16 20 24 28 32 35 37
9 13 17 21 25 29 33 36 38 39
|
| |
![]()
|
|
12.25б
Двумерные массивы
Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.
Формат входных данных
Программа получает на вход два числа n и m.
Формат выходных данных
Программа должна вывести полученный массив, отводя на вывод каждого числа ровно 3 символа.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 5 |
1 5 9 13 17
2 6 10 14 18
3 7 11 15 19
4 8 12 16 20
|
| |
![]()
|
|
12.25г
Двумерные массивы
Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.
Формат входных данных
Программа получает на вход два числа n и m.
Формат выходных данных
Программа должна вывести полученный массив. Элементы строки должны разделяться одним пробелом, кроме этого, одно число необходимо записывать в трех знакоместах.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 5 |
4 8 12 16 20
3 7 11 15 19
2 6 10 14 18
1 5 9 13 17
|
| |
![]()
|
|
Заполнение матрицы - 1
Двумерные массивы
Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.
Формат входных данных
Программа получает на вход два числа n и m.
Формат входных данных
Программа должна вывести полученный массив. Элементы строки должны разделяться одним пробелом, кроме этого, одно число необходимо записывать в трех знакоместах.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 5 |
5 4 3 2 1
10 9 8 7 6
15 14 13 12 11
20 19 18 17 16
|
| |
![]()
|
|
12.25ж
Двумерные массивы
Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.
Формат входных данных
Программа получает на вход два числа n и m.
Формат выходных данных
Программа должна вывести полученный массив, отводя на вывод каждого числа ровно 3 символа.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 5 |
16 17 18 19 20
11 12 13 14 15
6 7 8 9 10
1 2 3 4 5
|
| |
![]()
|
|
Заполнение матрицы - 2
Двумерные массивы
Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.
Формат входных данных
Программа получает на вход два числа n и m.
Формат выходных данных
Программа должна вывести полученный массив. Элементы строки должны разделяться одним пробелом, кроме этого, одно число необходимо записывать в трех знакоместах.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 5 |
17 13 9 5 1
18 14 10 6 2
19 15 11 7 3
20 16 12 8 4
|
| |
![]()
|
|
12.25и
Двумерные массивы
Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.
Формат входных данных
Программа получает на вход два числа n и m.
Формат выходных данных
Программа должна вывести полученный массив. Элементы строки должны разделяться одним пробелом, кроме этого, одно число необходимо записывать в трех знакоместах.
| |
![]()
|
|
12.25к
Двумерные массивы
Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.
Формат входных данных
Программа получает на вход два числа n и m.
Формат выходных данных
Программа должна вывести полученный массив. Элементы строки должны разделяться одним пробелом, кроме этого, одно число необходимо записывать в трех знакоместах.
| |
![]()
|
|
12.25д
Двумерные массивы
Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.
Формат входных данных
Программа получает на вход два числа n и m.
Формат выходных данных
Программа должна вывести полученный массив. Элементы строки должны разделяться одним пробелом, кроме этого, одно число необходимо записывать в трех знакоместах.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 5 |
1 2 3 4 5
10 9 8 7 6
11 12 13 14 15
20 19 18 17 16
|
| |
![]()
|
|
12.25е
Двумерные массивы
Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.
Входные данные: Программа получает на вход два числа n и m.
Выходные данные: Программа должна вывести полученный массив, отводя на вывод каждого числа ровно 3 символа.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 5 |
1 8 9 16 17
2 7 10 15 18
3 6 11 14 19
4 5 12 13 20
|
| |
![]()
|
|
12.25л
Двумерные массивы
Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.
Формат входных данных
Программа получает на вход два числа n и m.
Формат выходных данных
Программа должна вывести полученный массив. Элементы строки должны разделяться одним пробелом, кроме этого, одно число необходимо записывать в трех знакоместах.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 5 |
20 19 18 17 16
11 12 13 14 15
10 9 8 7 6
1 2 3 4 5
|
| |
![]()
|
|
12.25м
Двумерные массивы
Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.
Формат входных данных
Программа получает на вход два числа n и m.
Формат выходных данных
Программа должна вывести полученный массив. Элементы строки должны разделяться одним пробелом, кроме этого, одно число необходимо записывать в трех знакоместах.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 5 |
5 4 3 2 1
6 7 8 9 10
15 14 13 12 11
16 17 18 19 20
|
| |
![]()
|
|
12.25н
Двумерные массивы
Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.
Формат входных данных
Программа получает на вход два числа n и m.
Формат выходных данных
Программа должна вывести полученный массив. Элементы строки должны разделяться одним пробелом, кроме этого, одно число необходимо записывать в трех знакоместах.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 5 |
17 16 9 8 1
18 15 10 7 2
19 14 11 6 3
20 13 12 5 4
|
| |
![]()
|
|
12.25о
Двумерные массивы
Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.
Формат входных данных
Программа получает на вход два числа n и m.
Формат выходных данных
Программа должна вывести полученный массив. Элементы строки должны разделяться одним пробелом, кроме этого, одно число необходимо записывать в трех знакоместах.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 5 |
4 5 12 13 20
3 6 11 14 19
2 7 10 15 18
1 8 9 16 17
|
| |
![]()
|
|
12.25п
Двумерные массивы
Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.
Формат входных данных
Программа получает на вход два числа n и m.
Формат выходных данных
Программа должна вывести полученный массив. Элементы строки должны разделяться одним пробелом, кроме этого, одно число необходимо записывать в трех знакоместах.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 5 |
16 17 18 19 20
15 14 13 12 11
6 7 8 9 10
5 4 3 2 1
|
| |
![]()
|
|
12.25р
Двумерные массивы
Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.
Формат входных данных
Программа получает на вход два числа n и m.
Формат выходных данных
Программа должна вывести полученный массив. Элементы строки должны разделяться одним пробелом, кроме этого, одно число необходимо записывать в трех знакоместах.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 5 |
20 13 12 5 4
19 14 11 6 3
18 15 10 7 2
17 16 9 8 1
|
| |
![]()
|
|
Таблица чемпионата - 1
Двумерные массивы
Дана таблица некоторого чемпионата. Элементы главной диагонали равны 888. Каждый элемент массива, находящийся не на главной диагонали, может быть либо однозначным либо двузначным числом, запись которых образована цифрами, обозначающими колмичество забитых (первая цифра числа) и количество пропущенных (вторая цифра числа) в данном матче.
Например: 32 - три забитых, два пропцщенных.
0 - ноль забитых, ноль пропущенных
5 - ноль забитых, пять пропущенных
Входные данные: Программа получает на вход число N <= 15, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет N строк по N чисел, являющихся элементами массива.
Выходные данные: Программа должна вывести N строк по 2 числа в каждой: общее количество забитых и общее количество пропущенных каждой командой мячей
| № |
Входные данные |
Выходные данные |
| 1 |
3
888 29 37
92 888 57
73 75 888
|
5 16
14 9
14 8
|
| |
![]()
|
|
Таблица чемпионата - 2
Двумерные массивы
Дана таблица некоторого чемпионата. Элементы главной диагонали равны 8. Каждый элемент массива, находящийся не на главной диагонали, может принимать следующие значения: 3 - если данная команда выиграла игру, 0 - если проиграла, 1 - если игра закончилась в ничью.
Входные данные: Программа получает на вход число N <= 15, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет N строк по N чисел, являющихся элементами массива.
Выходные данные: Программа должна вывести N строк по 3 числа в каждой: количество выигрышей, количество ничьих и количество проигрышей для каждой команды. Первая строка соответствует первой команде и т.д.
| № |
Входные данные |
Выходные данные |
| 1 |
3
8 0 3
3 8 1
0 1 8
|
1 0 1
1 1 0
0 1 1
|
| |
![]()
|
|
Минимальный на диагоналях
Двумерные массивы
В квадратном массиве размером NxN, где N - нечетное число. Наименьший элемент среди стоящих на главной и побочной диагоналях поменять местами с элементом, расположенным в левом нижнем углу массива. Если наименьших элементов несколько, то поменять тот у которого номер строки и столбца меньше.
Входные данные
Программа получает на вход число N <= 15, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет N строк по N чисел, являющихся элементами массива.
Выходные данные
Программа должна вывродить на экран измененный массив.
| № |
Входные данные |
Выходные данные |
| 1 |
3
80 10 22
81 90 13
37 79 80
|
80 10 37
81 90 13
22 79 80
|
| |
![]()
|
|
Наибольший на диагоналях
Двумерные массивы
В квадратном массиве размером NxN, где N - нечетное число. Наибольший элемент среди стоящих на главной и побочной диагоналях поменять местами с элементом, стоящим на пересечении этих диагоналей. Если наибольших элементов несколько, то поменять тот у которого номер строки и столбца меньше.
Входные данные: Программа получает на вход число N <= 15, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет N строк по N чисел, являющихся элементами массива.
Выходные данные: Программа должна вывродить на экран измененный массив
| № |
Входные данные |
Выходные данные |
| 1 |
3
89 10 79
42 7 5
94 32 68
|
89 10 79
42 94 5
7 32 68
|
| |
![]()
|
|
Сумма максимума и минимума
Двумерные массивы
Входные данные: Программа получает на вход число N <= 15, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет N строк по N чисел, являющихся элементами массива.
Выходные данные: Программа должна вывести одно число - сумму максимального элемента главной диагонали и минимального элемента побочной диагонали
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
11 24 19
8 21 10
16 24 14
|
37 |
| |
![]()
|
|
Сумма на диагоналях
Двумерные массивы
Входные данные: программа получает на вход число N <= 15, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет N строк по N чисел, являющихся элементами массива.
Входные данные: программа должна вывести
1) слово YES - если сумма элементов, расположенных на главной диагонали, больше суммы элементов расположенных на побочной диагонали
2) слово NO - если условие 1 не выполняется
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
24 23 5
27 19 6
15 16 25
|
YES |
| 2 |
3
17 20 18
25 9 26
30 4 11
|
NO |
| |
![]()
|
|
Среднее арифметическое на побочной диагонали
Двумерные массивы
Входные данные: программа получает на вход число N <= 15, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет N строк по N чисел, являющихся элементами массива.
Выходные данные: программа должна вывести одно число - среднее арифметическое элементов побочной диагонали двумерного массива.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
5 26 17
20 5 29
29 23 14
|
17.000000 |
| |
![]()
|
|
Среднее арифметическое на главной диагонали
Двумерные массивы
Входные данные: программа получает на вход число N <= 15, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет N строк по N чисел, являющихся элементами массива.
Выходные данные: программа должна вывести одно число - среднее арифметическое элементов главной диагонали двумерного массива.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
23 23 2 5 24
7 21 15 12 18
14 16 6 19 15
23 5 23 9 24
5 7 12 18 28
|
17.400000 |
| |
![]()
|
|
Сумма диагональных элементов
Двумерные массивы
Входные данные: программа получает на вход число N <= 15, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет N строк по N чисел, являющихся элементами массива.
Выходные данные: программа должна вывести строку, в которой через пробел указаны числа являющиеся суммой тех двух элементов каждой строки, которые принадлежат главной и побочной диагоналям
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
16 17 29 17 30
26 12 14 12 2
23 6 30 27 13
15 7 28 20 2
11 16 21 26 24
|
46 24 30 27 35 |
| |
![]()
|
|
Симметричный массив
Двумерные массивы
Проверьте, является ли двумерный массив симметричным относительно главной диагонали. Главная диагональ — та, которая идёт из левого верхнего угла двумерного массива в правый нижний.
Входные данные: программа получает на вход число N <= 15, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет n строк по N чисел, являющихся элементами массива.
Выходные данные: программа должна выводить слово yes для симметричного массива и слово no для несимметричного.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
0 1 2
1 2 3
2 3 4 |
yes |
| 2 |
3
0 1 2
1 8 3
2 4 9 |
no |
| |
![]()
|
|
Обработка столбца в матрице - 2
Двумерные массивы
Дан двумерный массив A[N][M] ( 2<=N<=20; M 2<=M<=20).
В первой строке вводятся через пробел количество строк - число от 0 до N-1, и количество столбцов - число от 0 до M-1.
Во второй строке вводится число s (0<=s<=20)
Далее идет ввод элементов массива построчно
Определить cумму всех элементов s-го столбца массива.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 2
1
5 5
1 2 |
7 |
| 2 |
2 3
0
1 5 2
3 4 0 |
4 |
| |
![]()
|
|
Поиск требуемой строки
Двумерные массивы
В метании молота состязается n спортcменов. Каждый из них сделал m бросков. (n<=20, m<=20)
Победителем считается тот спортсмен, у которого сумма результатов по всем броскам максимальна.
Если перенумеровать спортсменов числами от 0 до n-1, а попытки каждого из них – от 0 до m-1, то на вход программа получает массив A[n][m], состоящий из неотрицательных целых чисел (0<A[n][m]<500). Программа должна определить номер строки с максимальной суммой чисел и вывести на экран эту сумму и номер строки, для которой достигается эта сумма.
Входные данные: Программа получает на вход два числа n и m, являющиеся числом строк и столбцов в массиве. Далее во входном потоке идет n строк по m чисел, являющихся элементами массива.
Выходные данные: Программа должна вывести 2 числа: сумму и номер строки, для которой эта сумма достигается. Если таких строк несколько, то выводится номер наименьшей из них.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 3
5 6 7
6 6 7
7 6 6
4 3 5 |
19 1 |
| |
![]()
|
|
Метание молота
Двумерные массивы
В метании молота состязается n спортcменов. Каждый из них сделал m бросков. Победителем соревнований объявляется тот спортсмен, у которого максимален наилучший результат по всем броскам. Таким образом, программа должна найти значение максимального элемента в данном массиве, а также его индексы.
Формат входных данных
Программа получает на вход два числа n и m (1<=n<=20; 1<=m<=20), являющиеся числом строк и столбцов в массиве. Далее во входном потоке идет n строк по m чисел в каждой, являющихся элементами массива.
Формат выходных данных
Программа должна вывести значение максимального элемента, затем индекс строки и индекс столбца, в котором он встречается. Если в массиве несколько максимальных элементов, то нужно вывести минимальный индекс строки, в которой встречается такой элемент, а если в этой строке таких элементов несколько, то нужно вывести минимальный индекс столбца.
| |
![]()
|
|
Игра "Жизнь". Простой вариант
Двумерные массивы
Алгоритмы обработки
В некоторых клетках квадрата \( N\ х\ N\) живут микроорганизмы (не более одного в одной клетке). Каждую секунду происходит следующее:
– все микроорганизмы, у которых менее 2-х соседей, умирают от скуки (соседями называются микроорганизмы, живущие в клетках, имеющих общую сторону или вершину);
– все микроорганизмы, у которых более 3-х соседей, умирают от перенаселенности;
– на всех пустых клетках, у которых ровно в трех соседних клетках жили микроорганизмы, появляются новые микроорганизмы.
Все изменения происходят одновременно, то есть для каждой клетки сначала выясняется ее судьба, а затем происходят изменения сразу во всех клетках.
Требуется по данной конфигурации определить, во что она превратится через \(T\) секунд.
Входные данные: В первой строке вводятся два натуральных числа –\( N\) (\(1 \leq N \leq 10\)) и \(T\) (\(1 \leq T \leq 100\)). Далее записано \( N\) строчек по \( N\) чисел, описывающих начальную конфигурацию (0 – пустая клетка, 1 – микроорганизм). Числа в строках разделены пробелами.
Выходные данные: Требуется вывести \( N\) строк по \( N\) чисел – описание конфигурации через T секунд (в том же формате, как и во входных данных).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 1
1 0 1
1 0 1
1 0 1 |
0 0 0
1 0 1
0 0 0 |
| 2 |
2 2
1 1
1 1 |
1 1
1 1 |
| 3 |
5 10
1 0 1 1 0
0 1 0 0 0
0 0 0 1 0
0 0 0 0 0
0 1 0 1 0 |
0 1 1 0 0
0 1 1 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0 |
| |
![]()
|
|
Обработка строки в матрице - 2
Двумерные массивы
Дан двумерный массив A[N][M] ( 2<=N<=20; M 2<=M<=20).
В первой строке вводятся через пробел количество строк - число от 0 до N-1, и количество столбцов - число от 0 до M-1.
Во второй строке вводится число k
Далее идет ввод элементов массива построчно
Определить среднее арифметическое элементов k-ой строки массива.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 2
1
5 5
1 2 |
1.500000 |
| 2 |
2 3
0
1 5 2
3 4 0 |
2.666666 |
| |
![]()
|
|
Обработка строки в матрице - 1
Двумерные массивы
Дан двумерный массив A[N][M] ( 2<=N<=20; M 2<=M<=20).
В первой строке вводятся через пробел количество строк - число от 0 до N-1, и количество столбцов - число от 0 до M-1.
Во второй строке вводится число k
Далее идет ввод элементов массива построчно
Определить количество элементов из последней строки кратных k.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 2
1
5 5
1 2 |
2 |
| 2 |
2 3
2
1 5 2
3 4 0 |
2 |
| |
![]()
|
|
Обработка столбца в матрице - 2
Двумерные массивы
Дан двумерный массив A[N][M] ( 1<=N<=20; M 1<=M<=20).
В первой строке вводятся через пробел количество строк - (строки массива нумеруются от 0 до N-1), и количество столбцов - (столбцы массива нумеруются от 0 до M-1)
Далее идет ввод элементов массива построчно
Определить количество двухзначных чисел из последнего столбца.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 2
5 15
11 22 |
2 |
| 2 |
2 3
11 15 2
3 4 10 |
1 |
| |
![]()
|
|
Поиск в матрице
Двумерные массивы
Напишите программу, которая определяет, сколько раз встречается в матрице элемент, равный K .
Формат входных данных
В первой строке записаны через пробел размеры матрицы: количество строк N и количество столбцов M (1<=N, M <= 100). В следующих N строках записаны строки матрицы, в каждой – по M натуральных чисел, разделённых пробелами. В последней строке записано целое число K.
Формат выходных данных
Программа должна вывести количество элементов матрицы, равных K.
| |
![]()
|
|
Минимум и максимум в матрице
Двумерные массивы
Напишите программу, которая находит минимальный и максимальный элементы в матрице. Если в матрице есть несколько одинаковых минимальных (максимальных) элементов, нужно найти индексы первого такого элемента в порядке обхода по строкам: слева направо, сверху вниз.
Формат входных данных
В первой строке записаны через пробел размеры матрицы: количество строк N и количество столбцов M (1 <= N, M <= 100). В следующих N строках записаны строки матрицы, в каждой – по M натуральных чисел, разделённых пробелами.
Формат выходных данных
В первой строке программа должна вывести индексы минимального элемента (строку и столбец), а затем – его значение. Нумерация строк и столбцов начинается с единицы. Все числа разделены пробелами. Во второй строке выводится информация о максимальном элементе в том же формате.
| |
![]()
|
|
Вывод столбцов с максимумом
Двумерные массивы
Напишите программу, которая находит в матрице столбцы, в которых есть элемент, равный максимальному.
Формат входных данных
В первой строке записаны, через пробел, размеры матрицы: количество строк N и количество столбцов M (1<= N, M <= 100). Далее идут N строк, в каждой записано по M натуральных чисел, разделённых пробелами - элементы матрицы.
Формат выходных данных
Программа должна вывести все столбцы, в которых есть элемент, равный максимальному элементу матрицы. Каждый столбец выводится в одну строку, элементы разделяются пробелами. Столбцы должны следовать в том порядке, в котором они стоят в матрице.
| |
![]()
|
|
Строка с минимальной суммой
Двумерные массивы
Напишите программу, которая находит в матрице строку с минимальной суммой.
Формат входных данных
В первой строке записаны через пробел размеры матрицы: количество строк N и количество столбцов M (1<=N, M <= 100). В следующих N строках записаны строки матрицы, в каждой – по M натуральных чисел, разделённых пробелами.
Формат выходных данных
Программа должна вывести все элементы найденной строки с минимальной суммой, разделив их пробелами. Если строк с одинаковой минимальной суммой несколько, нужно выбрать из них строку с минимальным индексом.
| |
![]()
|
|
Подсчет по сумме
Двумерные массивы
Напишите программу, которая определяет, сколько в матрице есть K -значных чисел, сумма цифр каждого из которых кратна R .
Формат входных данных
В первой строке записаны, через пробел, размеры матрицы: количество строк N и количество столбцов M (1 <= N, M <= 100). В следующих N строках записаны строки матрицы, в каждой – по M натуральных чисел, разделённых пробелами. Затем в двух разных строках вводятся числа K и R .
Формат выходных данных
Программа должны вывести одно число – количество K -значных чисел, сумма цифр каждого из которых кратна R .
| |
![]()
|
|
Магический квадрат?
Двумерные массивы
Магическим квадратом называется квадратная матрица размера NхN, такая что суммы по каждому столбцу, каждой строке и каждой из двух больших диагоналей равны между собой. Напишите программу, которая проверяет, является ли заданная квадратная матрица магическим квадратом.
Формат входных данных
В первой строке вводится размер матрицы N (0 < N <= 100) . В следующих N строках вводятся строки матрицы, по N значений в каждой, разделённые пробелами.
Формат выходных данных
Программа должна вывести слово 'YES', если матрица является магическим квадратом, и слово 'NO', если не является.
| |
![]()
|
|
Нестандартное заполнение - 1. Диагонали
Двумерные массивы
Напишите программу, которая заполняет матрицу неотрицательными числами по диагоналям (см. пример). Значение элемента матрицы равно расстоянию от левого верхнего угла матрицы.
Формат входных данных
Во входной строке записаны через пробел размеры матрицы: количество строк N и количество столбцов M (1 <= N, M <= 100).
Формат выходных данных
Программа должна вывести полученную матрицу по строкам.
| |
![]()
|
|
Нестандартное заполнение - 2. Змейка
Двумерные массивы
Напишите программу, которая заполняет матрицу из N строк и M столбцов натуральными числами змейкой, как показано в примере.
Формат входных данных
Входная строка содержит числа N и M, разделённые пробелом (5 <= N, M <= 20).
Формат выходных данных
Программа должна вывести матрицу, заполненную заданным способом.
| |
![]()
|
|
Простая задача
Двумерные массивы
Дан двумерный массив N*M (0 < N, M <= 20).
Значения элементов массива вводятся с клавиатуры
Вывести в первой строке все угловые элементы массива, начиная с левого верхнего угла и далее, двигаясь по часовой стрелке.
Формат входных данных
В первой строке задается размер массива. N - количество строк, M - количество столбцов (\(0<N,M<=20\))
Далее идут N строк по M чисел в каждой строке - элементы двумерного массива (каждый элемент по модулю не больше 50)
Формат выходных данных
Вывести четыре числа, через один пробел, - все угловые элементы массива, начиная с левого верхнего угла и далее, двигаясь по часовой стрелке.
| |
![]()
|
|
Квадратная матрица
Двумерные массивы
Дано число n. Создайте двумерный массив размером nхn и заполните его по следующему правилу. На главной диагонали должны быть записаны числа 0. На двух диагоналях, прилегающих к главной, числа 1. На следующих двух диагоналях числа 2 и т.д.
Формат входных данных
На вход подается одно единственное число n (n<=10).
Формат выходных данных
Выведите на экран заполненную матрицу.
| |
![]()
|
|
Побочная диагональ
Двумерные массивы
Дано число n. Создайте массив размером nхn и заполните его по следующему правилу:
Числа на диагонали, идущей из правого верхнего в левый нижний угол, равны 1.
Числа, стоящие выше этой диагонали, равны 0.
Числа, стоящие ниже этой диагонали, равны 2.
Полученный массив выведите на экран. Числа в строке разделяйте одним пробелом.
Формат входных данных
На вход подается одно число n (n<=100).
Формат выходных данных
Выведите на экран, заполненную матрицу.
| |
![]()
|
|
Симметричный массив
Двумерные массивы
Дано число n и двумерный массив размером nхn. Проверьте, является ли этот двумерный массив симметричным относительно главной диагонали. Выведите слово “YES”, если двумерный массив симметричный, и слово “NO” - в противном случае.
Формат входных данных
В первой строке задается число n - размер двумерного массива (n <= 10). Далее идут n строк по n чисел в каждой - элементы двумерного массива.
Формат выходных данных
Выведите на экран слово "YES", если массив симметричен, или "NO" - в противном случае
| |
![]()
|
|
Диагональ ниже главной
Двумерные массивы
Дан квадратный двумерный массив размером nхn и число k. Выведите элементы k-й по счету диагонали ниже главной диагонали (т.е. если k=1, то нужно вывести элементы первой диагонали, лежащей ниже главной, если k=2, то второй диагонали и т.д.).
Значение k может быть отрицательным, например, если k=−1, то нужно вывести значение первой диагонали, лежащей выше главной. Если k=0, то нужно вывести элементы главной диагонали.
Формат входных данных
Программа получает на вход число n (n <= 10), затем идут элементы массива n строк по n символов в каждой строке, затем с новой строки, число k (все элементы и значение k по модулю не больше 100).
Формат выходных данных
Элементы k-й по счету диагонали ниже главной диагонали, через пробел, в одной строке.
| |
![]()
|
|
Обмен диагоналей
Двумерные массивы
Дана квадратная матрица. Поменяйте местами элементы, стоящие на главной и побочной диагоналях, при этом каждый элемент должен остаться в том же столбце (то есть в каждом столбце нужно поменять местами элемент на главной диагонали и на побочной диагонали).
Формат входных данных
На вход подается число n - размер квадратного массива (n <= 10). Далее идут n строк по n чисел в каждой - элементы массива.
Формат выходных данных
Выведите на экран матрицу после преобразования.
| |
![]()
|
|
Квадранты
Двумерные массивы
Заполните квадратную матрицу целыми числами по образцу. На главной и побочных диагоналях стоят нули, эти диагонали делят массив на четыре части. В верхней части записаны единицы, в правой записаны двойки, в нижней записаны тройки, в левой записаны четверки.
Формат входных данных
На вход подается одно число n - размер квадратного массива (n <= 100).
Формат выходных данных
Выведите на экран заполненную квадратную матрицу.
| |
![]()
|
|
Замена столбца на элементы массива
Двумерные массивы
Дана матрица размером NxM и массив чисел размером N. В данной матрице заменить все элементы столбца с максимальной суммой элементов на элементы заданного массива чисел. Если таких столбцов несколько, то заменить элементы в столбце с меньшим индексом.
Входные данные
В первой строке задаются числа N и M (\(0<N,M<=10\)). Далее идут N строк по M чисел в каждой. Каждое число по модулю не более 100. В последней строке идут N чисел массива.
Выходные данные
Выведите на экран преобразованную матрицу, отводя под каждый элемент три знакоместа. После вывода каждого числа должен следовать знак пробела.
Пример
| № |
Входные данные |
Выходные данные |
| 1 |
3 4
52 16 61 93
5 5 33 41
37 34 14 16
76 69 26 |
52 16 61 76
5 5 33 69
37 34 14 26
|
| |
![]()
|
|
Обмен строк
Двумерные массивы
Дана матрица размером NxM и два числа k1 и k2. Поменяйте местами строки с индексами k1 и k2.
Входные данные
В первой строке задаются числа N и M (\(0<N,M<=10\)). Далее идут N строк по M чисел в каждой. Каждое число по модулю не более 100. Далее с новой строки идут два числа k1, k2 (\(0<k1,k2<=N\)).
Выходные данные
Выведите на экран преобразованную матрицу, отводя под каждый элемент три знакоместа.
Пример
| № |
Входные данные |
Выходные данные |
| 1 |
4 5
72 50 18 79 74
48 93 27 9 76
33 76 69 59 58
19 65 53 90 77
2 0 |
33 76 69 59 58
48 93 27 9 76
72 50 18 79 74
19 65 53 90 77
|
| |
![]()
|
|
Удаление строк
Двумерные массивы
Двумерные массивы
В двумерном массиве хранятся результаты (время в минутах), показанные каждым из N автогонщиков на каждом из 10-ти этапов соревнований "Формула-1" (в нулевой строке - результаты первого гонщика, в первой - второго и т.д.). После десятого этапа гонщик с порядковым номером K выбыл из соревнований. Судейской коллегией было принято решение удалить результаты данного участника из таблицы.
Измените массив соответствующим образом и выведите его на экран.
Под удалением строки в двумерном массиве будем понимать:
1) исключение этой строки из массива путем смещения всех следующих за ней строк на одну вверх;
2) присваивание всем элементам последней строки значения 0 (или уменьшение количества строк на 1).
Входные данные
В первой строке задаётся число N (\(0<N<=30\)). Далее идут N строк по 10 чисел в каждой. Каждое число по модулю не более 100. Далее с новой строки идет число K (\(1<=K<=N\)).
Выходные данные
Выведите на экран преобразованную матрицу, отводя под каждый элемент три знакоместа.
Пример
| № |
Входные данные |
Выходные данные |
| 1 |
5
38 43 82 95 20 100 99 83 77 42
94 92 74 30 93 75 99 6 79 68
4 20 25 54 15 31 81 39 79 76
62 97 14 40 70 31 3 84 33 74
99 30 91 15 41 54 87 31 71 74
3 |
38 43 82 95 20 100 99 83 77 42
94 92 74 30 93 75 99 6 79 68
62 97 14 40 70 31 3 84 33 74
99 30 91 15 41 54 87 31 71 74
|
| |
![]()
|
|
Удаление строк
Двумерные массивы
Двумерные массивы
В двумерном массиве хранятся результаты (время в минутах), показанные каждым из N автогонщиков на каждом из 10-ти этапов соревнований "Формула-1" (в нулевой строке - результаты первого гонщика, в первой - второго и т.д.). После десятого этапа гонщик с порядковым номером K выбыл из соревнований. Судейской коллегией было принято решение удалить результаты данного участника из таблицы.
Измените массив соответствующим образом и выведите его на экран.
Под удалением строки в двумерном массиве будем понимать:
1) исключение этой строки из массива путем смещения всех следующих за ней строк на одну вверх;
2) присваивание всем элементам последней строки значения 0 (или уменьшение количества строк на 1).
Входные данные
В первой строке задаётся число N (\(0<N<=30\)). Далее идут N строк по 10 чисел в каждой. Каждое число по модулю не более 100. Далее с новой строки идет число K (\(1<=K<=N\)).
Выходные данные
Выведите на экран преобразованную матрицу, отводя под каждый элемент три знакоместа.
Пример
| № |
Входные данные |
Выходные данные |
| 1 |
5
38 43 82 95 20 100 99 83 77 42
94 92 74 30 93 75 99 6 79 68
4 20 25 54 15 31 81 39 79 76
62 97 14 40 70 31 3 84 33 74
99 30 91 15 41 54 87 31 71 74
3 |
38 43 82 95 20 100 99 83 77 42
94 92 74 30 93 75 99 6 79 68
62 97 14 40 70 31 3 84 33 74
99 30 91 15 41 54 87 31 71 74
|
| |
![]()
|
|
Удаление столбцов
Двумерные массивы
В двумерном массиве хранятся результаты (время в минутах), показанные каждым из \(N\) велогонщиков на каждом из 12-ти этапов соревнований (в нулевом столбце - результаты первого этапа, в первом - второго и т.д.) Судейской коллегией результаты K-го этапа были признаны недействительными и были удалены из таблицы.
Измените массив соответствующим образом и выведите его на экран.
Под удалением столбца в двумерном массиве будем понимать:
1) исключение этого столбца из массива путем смещения всех следующих за ним столбцов на один влево;
2) присваивание всем элементам последнего столбца значения 0 (или уменьшение количества столбцов на 1).
Входные данные
В первой строке задаётся число N (0<N<=30). Далее идут N строк по 12 чисел в каждой. Каждое число по модулю не более 100. Далее с новой строки идет число K (1<=K<=12).
Выходные данные
Выведите на экран преобразованную матрицу, отводя под каждый элемент три знакоместа.
Пример
| № |
Входные данные |
Выходные данные |
| 1 |
4
65 2 22 62 41 18 80 15 35 20 21 27
7 28 35 98 15 27 87 95 73 45 26 28
1 99 11 69 11 13 80 78 3 53 76 73
87 37 11 85 72 33 59 79 61 53 80 67
4 |
65 2 22 41 18 80 15 35 20 21 27
7 28 35 15 27 87 95 73 45 26 28
1 99 11 11 13 80 78 3 53 76 73
87 37 11 72 33 59 79 61 53 80 67
|
| |
![]()
|
|
Циклический сдвиг построчно
Двумерные массивы
Каждую строку заданной прямоугольной матрицы NxM сдвинуть циклически вправо на количество позиций, равных номеру строки (нумерация строк и столбцов с 0). Вывести на экран преобразованную матрицу.
Входные данные
В первой строке находятся два числа N и M (\(0 < N,M <= 10\)). Далее идут N строк по M чисел в каждой - элементы матрицы (каждый элемент не более 100 по модулю).
Выходные данные
Вывести измененную матрицу. Каждый элемент матрицы выводится в 3 знакоместах и с одним пробелом после него.
Оформите сдвиг вправо на K позиций в виде подпрограммы.
Пример
| № |
Входные данные |
Выходные данные |
| 1 |
3 4
47 63 22 75
69 69 12 70
70 90 13 31 |
47 63 22 75
70 69 69 12
13 31 70 90
|
| |
![]()
|
|
Обмен столбцов
Двумерные массивы
Дана матрица размером NxM и два числа k1 и k2. Выполните циклическую перестановку столбцов влево, находящихся между столбцами k1 и k2 (включая столбцы k1 и k2, т.е. столбец k1 должен оказаться на месте столбца k2, столбец k2 не месте столбца k2-1 и т.д.).
Входные данные
В первой строке задаются числа N и M (\(0<N,M<=10\)). Далее идут N строк по M чисел в каждой. Каждое число по модулю не более 100. Далее с новой строки идут два числа k1, k2 (\(0<= k1<=k2< M\)).
Выходные данные
Выведите на экран преобразованную матрицу, отводя под каждый элемент три знакоместа.
Пример
| № |
Входные данные |
Выходные данные |
| 1 |
3 4
56 32 94 12
15 72 51 60
43 4 97 38
0 2 |
32 94 56 12
72 51 15 60
4 97 43 38
|
| |
![]()
|
|
Вставка столбцов
Двумерные массивы
В двумерный массив записаны годовые оценки по десяти предметам каждого из N учеников класса (в нулевом столбце - оценки по первому предмету, в первом - по второму и т.д.), но по ошибке забыли вписать в массив оценки еще по одному предмету, который должен находиться в столбце K. Измените массив так, чтобы он был заполнен надлежащим образом.
Под добавлением столбца в двумерный массив будем понимать:
1) увеличение числа столбцов массива на 1;
2) смещение всех столбов после K-го на один вправо;
3) присваивание заданных значений элементам K-го столбца.
Входные данные
В первой строке задаётся число N (0<N<=30). Далее идут N строк по 10 чисел в каждой. Каждое число в диапазоне от 2 до 5. В следующей строке идет число K (1<=K<=10). Далее, в последней строке (без пропуска строк) идет N чисел, оценки соответствующего ученика по новому предмету.
Выходные данные
Выведите на экран преобразованную матрицу, отделяя каждый элемент одним пробелом.
Пример
| № |
Входные данные |
Выходные данные |
| 1 |
5
5 3 4 2 4 1 3 3 4 4
3 3 1 2 3 4 3 2 4 3
2 4 5 4 2 1 4 2 2 4
1 3 5 1 1 1 5 3 4 1
3 4 2 1 5 3 3 5 2 1
1
5 5 3 5 3 |
5 5 3 4 2 4 1 3 3 4 4
5 3 3 1 2 3 4 3 2 4 3
3 2 4 5 4 2 1 4 2 2 4
5 1 3 5 1 1 1 5 3 4 1
3 3 4 2 1 5 3 3 5 2 1
|
| |
![]()
|
|
Изменение строки с максимумом
Двумерные массивы
В матрице размером NхM заменить на значение -1 все элементы тех строк, в которых находится максимальный элемент.
Формат входных данных
В первой строке находятся два числа N и M (\(0 < N,M <= 10\)). Далее идут N строк по M неотрицательных чисел в каждой - элементы матрицы (каждый элемент меньше 100).
Формат выходных данных
Вывести измененную матрицу. На каждый элемент в выводе отводить ровно 3 символа (знакоместа). После вывода каждого числа должен следовать знак пробела.
Пример
| № |
Входные данные |
Выходные данные |
| 1 |
5 5
15 68 54 79 89
91 57 21 70 24
14 22 5 26 76
51 59 92 98 96
50 62 50 58 1 |
15 68 54 79 89
91 57 21 70 24
14 22 5 26 76
-1 -1 -1 -1 -1
50 62 50 58 1
|
| |
![]()
|
|
Комфорт для коров
Двумерные массивы
Циклы
Пастбище Фермера Джона может быть представлено как огромная 2D-решётка ячеек (огромная шахматная доска). Изначально пастбище пустое.
Фермер Джон добавит N (1≤N≤105) коров на пастбище одну за одной. i-ая корова занимает ячейку (xi,yi), которая отличается от ячеек, занятых всеми другими коровами (0≤xi,yi≤1000).
Говорят, что корове "комфортабельно", если по горизонтали и вертикали она имеет ровно три других коровы. Фермер Джон хочет посчитать, скольким коровам комфортабельно на его пастбище. Для каждого i в интервале 1…N, выведите общее количество коров, которым комфортабельно после того, как i-ая корова добавлена на пастбище.
Входные данные:
Первая строка содержит одно целое число N. Каждая из последующих N строк содержит два разделённых пробелом целых числа, указывающих (x,y) - координаты ячейки коровы. Гарантируется, что все ячейки различны.
Выходные данные:
i-ая строка вывода должна содержать общее количество коров, которым комфортабельно после добавления i-ой коровы на пастбище.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
8
0 1
1 0
1 1
1 2
2 1
2 2
3 1
3 2 |
0
0
0
1
0
0
1
2 |
После того, как добавлены первые 4 коровы, корове в ячейке (1,1) стало комфортабельно.
После того, как добавлены первые 7 коров, корове в ячейке (2,1) стало комфортабельно.
После того, как добавлены первые 8 коров, корове в ячейках (2,1) и (2,2) стало комфортабельно. |
| |
![]()
|
|
Шахматная доска
Двумерные массивы
Клеточная геометрия
Из шахматной доски по границам клеток выпилили связную (не распадающуюся на части) фигуру без дыр. Требуется определить ее периметр.
Входные данные
Сначала вводится число N (1 ≤ N ≤ 64) – количество выпиленных клеток. В следующих N строках вводятся координаты выпиленных клеток, разделенные пробелом (номер строки и столбца – числа от 1 до 8). Каждая выпиленная клетка указывается один раз.
Выходные данные
Выведите одно число – периметр выпиленной фигуры (сторона клетки равна единице).
Примеры
| № |
Входные данные |
Выходные данные |
Пояснения |
| 1 |
3
1 1
1 2
2 1 |
8 |
Вырезан уголок из трех клеток. Сумма длин его сторон равна 8. |
| 2 |
1
8 8 |
4 |
Вырезана одна клетка. Ее периметр равен 4. |
| |
![]()
|
|
Шахматное домино
Двумерные массивы
Комплект шахматного домино состоит из 32 костяшек 2x1, каждая из квадратов которой окрашен в черный или белый цвет (часть костяшек состоит из двух белых квадратов, часть – из двух черных, а часть из одного белого и одного черного). Комплект такого домино выложен на шахматную доску. Разрешается поворачивать костяшки домино на 180 градусов (менять местами их квадраты), оставляя каждую костяшку на своем месте. Требуется выяснить, можно ли так повернуть часть костей домино, чтобы в каждом горизонтальном ряду были квадраты только одного цвета.
Входные данные
Вводится 8 строк по 8 чисел. Каждое число соответствует номеру доминошки, которая покрывает данную клетку. Число положительное, если квадрат доминошки белый и отрицательное – если черный.
Выходные данные
Требуется вывести одно слово – YES или NO (заглавными буквами).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 2 2 7 7 8 8 9
1 3 6 10 10 11 11 9
4 3 6 31 31 24 23 12
4 5 5 30 32 24 23 12
28 29 29 30 32 25 22 13
28 27 27 26 26 25 22 13
18 19 19 20 20 21 21 14
18 17 17 16 16 15 15 14 |
YES |
Примечание:
Доминошки нумеруются числами от 1 до 32 в произвольном порядке.
| |
![]()
|
|
Магический квадрат
Двумерные массивы
Магическим квадратом называют таблицу, в которой записаны числа 123… по одному разу, так что сумма чисел в каждой строке и в каждом столбце равные. Мы расскажем вам об одном из методов построения магических квадратов (его называют сиамским). Он годится только для построения квадратов с нечетной стороной (3355…) .
Поставим число 1 в верхнюю клетку центрального столбца. Далее будем двигаться по диагонали вправо-вверх, расставляя в клетки последовательно числа 234… . Если мы вышли за пределы таблицы вверх, то нужно перейти к нижней клетке того же столбца и продолжить с нее. Если мы вышли за правую границу, нужно перейти к левой клетке той строки, куда мы должны были попасть. Если же мы одновременно вышли и вверх, и вправо, то нужно перейти в левую нижнюю клетку квадрата.
Если в следующей клетке на нашем пути уже стоит число, то вместо хода “вправо-вверх” нужно сделать ход “вниз” (опять же, если мы при этом выйдем за границы квадрата, нужно перейти к верхней клетке того же столбца). Примеры для квадратов 33 и 55 показаны на рисунках.
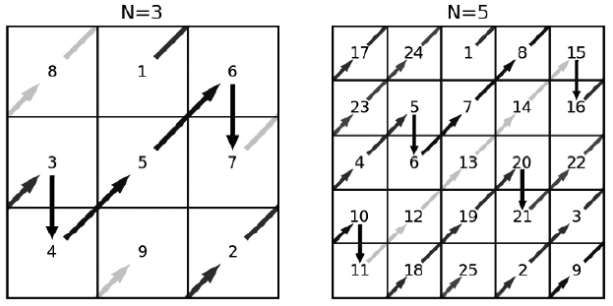
Входные данные
На вход подается одно натуральное нечетное число N, не превосходящее 30 – размер квадрата.
Выходные данные
Выведите числа, записанные в квадрате. Выравнивать числа по столбцам не обязательно. Обратите внимание: требуется вывести именно магический квадрат, полученный применением указанного метода.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 |
8 1 6
3 5 7
4 9 2 |
| 2 |
5 |
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9 |
| |
![]()
|
|
Муравьиная ферма
Двумерные массивы
На прошлый день рождения Олегу подарили муравьиную ферму и трех больших муравьев для нее. Ферма представляет собой поле размером a × b клеток. Клетка с координатой (1, 1) находится в левом верхнем углу. Вскоре он заметил, что передвигаясь по своему вольеру, муравьи оставляют на белом песке следы разных цветов. На протяжении нескольких месяцев Олег наблюдал за своей фермой и, наконец, смог строго описать происходящее в вольере.
Клетки бывают четырех цветов:
- белая (это значит, что клетка не покрашена ни одним из муравьев, обозначается цифрой 0)
- красная (это — цвет следа первого муравья, обозначается цифрой 1)
- желтая (это — цвет следа второго муравья, обозначается цифрой 2)
- зеленая (это — цвет следа третьего муравья, обозначается цифрой 3)
Муравей умеет оставлять на клетке свой след, стирать с нее все следы, поворачиваться и делать шаг вперед. То, как он изменит цвет клетки и куда он повернется, зависит только от цвета клетки, на которой он сейчас стоит. Опишем один ход муравья.
Если муравей стоит на белой клетке, то он:
- красит ее в свой цвет
- поворачивается на 90° вправо и делает шаг вперед
Если же муравей стоит не на белой клетке, то он:
- стирает с нее след (то есть красит клетку в белый цвет)
- поворачивается на 90º влево и делает шаг вперед
Если на пути муравья встречается граница фермы, шаг вперед он не делает.
Каждую минуту все три муравья по очереди делают один ход, причем сначала ходит первый, потом второй, потом третий.
Утром, уходя в школу, Олег чистит вольер так, что в начальный момент времени песок на всей ферме белый (то есть на нем нет никаких следов). Однако перемещения муравьев такие интересные, что мальчик не может нормально учиться, а вместо этого думает о своих любимцах. Сидя на занятиях, он старается понять, какой узор он увидит, когда вернется домой. Перед тем, как уйти на учебу, он записывает координаты всех своих питомцев. Олегу известно, что дома он будет ровно через T минут. Для того, чтобы Олег не отвлекался во время занятий на размышления о муравьях, напишите программу, которая сама воспроизведет рисунок, который получится на песке вольера через T минут.
Входные данные
В первой строке вводятся 3 числа a, b, T (1 ≤ a ≤ 100, 1 ≤ b ≤ 100, 1 ≤ T ≤ 103) — высота вольера, ширина вольера и время, которое Олега не будет дома, соответственно. Следующие три строки содержат описание положения муравьев. В каждой строке записано по 2 числа i, j (1 ≤ i ≤ a, 1 ≤ j ≤ b) — координаты муравьев (сначала записан номер строки, а затем номер столбца), причем в первой из строчек записаны координаты первого муравья, во второй — второго, а в третьей — третьего. Гарантируется, что в одной и той же клетке изначально не находилось двух муравьев. Изначально все муравьи смотрят вверх.
Выходные данные
Выведите состояние поля на момент времени T: a строк по b чисел в каждой через пробел. Каждое число обозначает цвет следа, оставленного в данной клетке вольера.
| |
![]()
|
|
"Сапер" с подсказками
Двумерные массивы
На весенних каникулах Оля долго обдумывала свое поведение и решила в четвертой четверти заниматься учебой побольше. Но уже первый урок биологии в новой четверти уничтожил все Олины благие намерения. Оле скучно, просто невыносимо скучно. От нечего делать она начала играть на своем телефоне в известную игру «Сапер».
На всякий случай напомним, в чем заключается эта игра. Игра происходит на поле размером N × M клеток, некоторые из которых «заминированы». Целью игры является открытие всех клеток, не содержащих мины.
Игрок открывает клетки, стараясь не открыть клетку с миной. Открыв клетку с миной, он проигрывает. Если под открытой ячейкой мины нет, то в ней появляется число, показывающее, сколько ячеек, соседствующих с только что открытой, «заминировано». Клетки считаются соседствующими, если у них есть общая сторона или общая вершина. Клетки, которые игрок считает «заминированными», можно пометить флажком, чтобы случайно не открыть их.
Оля играет в версию «Сапера» со встроенными подсказками. Одна из подсказок, «Показать ошибки», работает следующим образом. Если по соседству с клеткой, в которой записано некоторое число, находится больше флажков, чем может соседствовать с этой клеткой (то есть больше флажков, чем число, записанное в клетке), все флажки вокруг этой клетки подсвечиваются желтым цветом. Другие ошибки эта подсказка находить не умеет, иначе играть было бы совсем не интересно.
Ваша задача — по текущему состоянию игрового поля определить, какие флажки окажутся подсвечены желтым после запуска подсказки.
Входные данные
В первой строке содержатся два числа N и M, разделенные пробелами — высота и ширина таблицы соответственно (1 ≤ N ≤ 15, 1 ≤ M ≤ 15). В следующих N строчках содержится по M символов в каждой. Эти строчки задают игровое поле. Используются следующие обозначения:
F — флажок;
* — закрытая клетка;
Цифра от 0 до 8 — открытая клетка. Сама цифра обозначает, сколько суммарно мин находится в клетках, соседствующих с данной.
Выходные данные
В первой строке выведите количество флажков, которые окажутся подсвечены желтым, а в следующих N строчках выведите для каждого такого флажка его координаты — номер строки, а затем номер столбца, в котором стоит флажок. Флажки можно выводить в любом порядке.
Если подсвеченных флажков не будет, выведите единственное число 0
Примеры
| № |
Входные данные |
Выходные данные |
Пояснения |
| 1 |
2 3
FFF
*2* |
3
1 2
1 3
1 1 |
В тесте в клетке с координатами (2, 2) записано число 2, а касается она трех флажков, что больше двух. Значит, все эти три флажка будут подсвечены. |
| |
![]()
|
|
Остров
Двумерные массивы
На клетчатой бумаге нарисована карта острова (клетки острова закрашены). При этом остров является клетчато-выпуклой фигурой, то есть каждая горизонтальная или вертикальная линия на карте либо не пересекает остров, либо пересекает его по отрезку (линия пересечения не содержит разрывов). Также остров является связной фигурой, то есть любые две клетки острова соединены путём, каждые две соседние клетки которого имеют общую сторону.
Клетка считается соседней с островом, если она не принадлежит острову, но имеет общую сторону или угол с одной из клеток острова. Например, на следующей карте клетки острова закрашены, а соседние с островом клетки отмечены звёздочками.
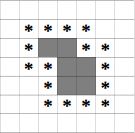
Самолёт должен облететь вокруг острова по соседним с ним клеткам, не вторгаясь на территорию острова. Программа должна составить маршрут полёта самолёта. Самолёт начинает облёт острова в одной из соседних клеток с островом и должен побывать во всех клетках, соседних с островом, ровно один раз. При этом самолёт может перемещаться из одной клетки в другую клетку, только если эти клетки имеют общую сторону.
Выходные данные
Программа получает на вход два числа N и M, записанные в отдельных строках, — количество строк и столбцов карты острова (3 ≤ N ≤ 100, 3 ≤ M ≤ 100). Далее записана карта острова — N строк, каждая содержащая M символов. Каждый символ карты может быть либо символом «.», что означает клетку, не принадлежащую острову, либо символом «#», что означает клетку острова. При этом остров не касается края карты.
Введём на карте систему координат. Первая координата является номером строки, строки нумеруются сверху вниз числами от 1 до N. Вторая координата — номер столбца, столбцы нумеруются слева направо числами от 1 до M.
Входные данные
Программа должна вывести координаты клеток карты в порядке их облёта самолётом. Каждая строка вывода должна содержать два числа x и y — координаты самолёта, записанные через пробел (1 ≤ x ≤ N, 1 ≤ y ≤ M). Самолёт должен побывать в каждой соседней с островом клетке ровно один раз. Каждые две клетки, идущие подряд в выводе, должны иметь общую сторону. Можно вывести любой возможный маршрут облёта острова.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6
7
.......
.......
.......
.###...
.###...
.......
|
3 1
3 2
3 3
3 4
3 5
4 5
5 5
6 5
6 4
6 3
6 2
6 1
5 1
4 1 |
| |
![]()
|
|
Луч света в темном царстве
Двумерные массивы
Задачи на моделирование
Темное царство представляет собой лабиринт NxM, некоторые клетки которого окружены зеркальными стенами, а остальные — пустые. Весь лабиринт также окружен зеркальной стеной. В одной из пустых клеток лабиринта поставили светофор, который испускает лучи в 4 направлениях: под 45 градусов относительно стен лабиринта. Требуется изобразить траекторию этих лучей.
Когда луч приходит в угол, через который проходят зеркальные стены, дальше он идет так, как показано на рисунках (серым цветом показаны клетки, которые окружены зеркальными стенами). Аналогичным образом луч ведет себя, когда приходит на границу лабиринта.

Входные данные
В первой строке входного файла записаны два натуральных числа N и M — число строк и столбцов в лабиринте (каждое из чисел не меньше 1 и не больше 100). В следующих N строках записано ровно по M символов в каждой — карта лабиринта. Символ * (звездочка) обозначает клетку, окруженную зеркальными стенками, . (точка) — пустую клетку, символ X (заглавная латинская буква X) — клетку, в которой расположен светофор (такая клетка ровно одна).
Выходные данные
В выходной файл выведите N строк по M символов в каждой — изображение лабиринта с траекториями лучей. Здесь, как и раньше, * (звездочка) должна обозначать клетки, окруженные зеркальными стенами, . (точка) — пустые клетки, через которые лучи света не проходят, / (слеш) — клетки, через которые луч света проходит из левого нижнего угла в правый верхний (или обратно — из правого верхнего в левый нижний), \ (обратный слеш) — клетки, через которые луч проходит из левого верхнего угла в правый нижний (или обратно), а символ X (заглавная латинская буква X) — клетки, через которые лучи проходят по обеим диагоналям.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 5
X....
.....
.....
|
XXXXX
XXXXX
XXXXX
|
| 2 |
3 3
...
..X
...
|
/X\
X.X
\X/
|
| |
![]()
|
|
Флаг
Двумерные массивы
Иннокентий работает на блошином рынке, продавая посетителям всякий хлам необычные вещи. Недавно он нашёл у себя на складе старое прямоугольное покрывало. Как оказалось, это покрывало имеет сетчатую форму, то есть покрывало состоит из nm цветных лоскутков, разбитых на n строк и m столбцов.
Цветные лоскутки привлекли внимание Иннокентия, и он сразу же придумал, как можно заработать на своей находке. Если вырезать из покрывала подпрямоугольник, состоящий из трёх цветных полос, то потом этот подпрямоугольник можно будет продать как флаг какой-нибудь страны. В частности, Иннокентий считает, что подпрямоугольник будет достаточно похож на флаг какой-нибудь страны, если он будет состоять из трёх одноцветных полос одинаковой высоты, находящихся друг под другом. Разумеется, цвет верхней полосы не должен совпадать с цветом средней полосы, а цвет средней не должен совпадать с цветом нижней.
Иннокентий пока не знает из какой части покрывала будет вырезать флаг, однако он точно решил, что будет вырезать флаг только по линиям сетки, при этом покрывало ни в коем случае нельзя поворачивать. Помогите Иннокентию и посчитайте количество различных подпрямоугольников, которые можно вырезать из покрывала и продать как флаг. Подпрямоугольники, образующие одинаковые флаги, однако расположенные в разных местах покрывала, считаются различными.
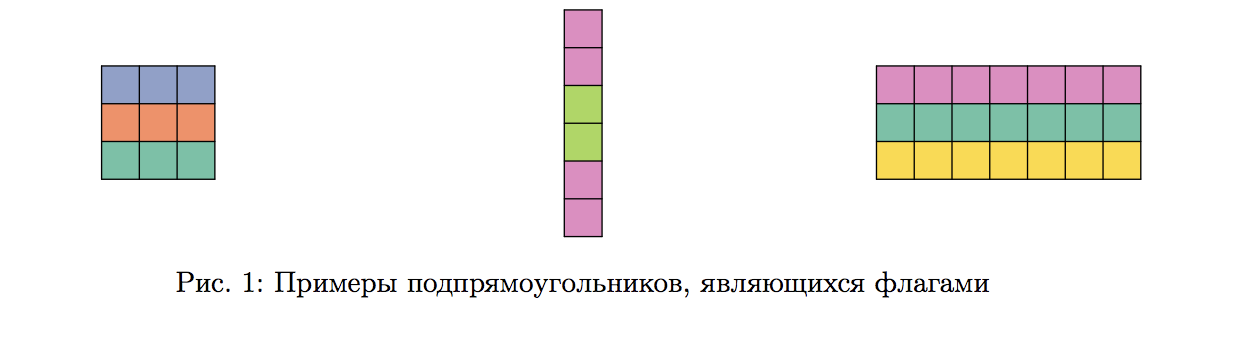
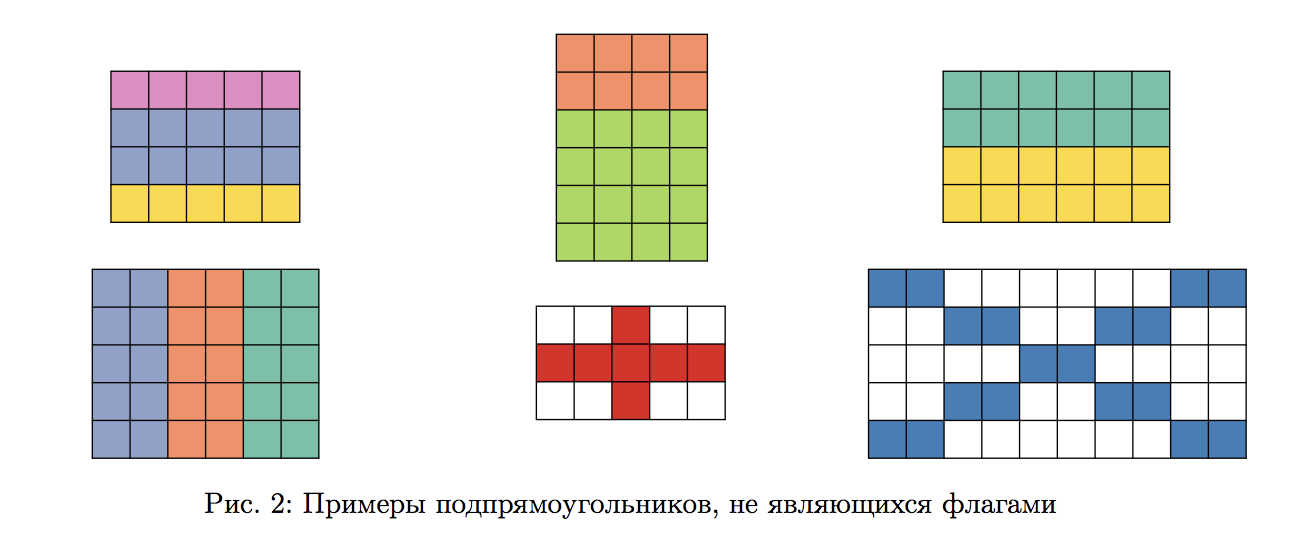
Входные данные
Первая строка содержит два целых числа n и m (1 ≤ n, m ≤ 1000 ) — количество строк и столбцов в покрывале.
Каждая из следующих n строк описывает очередную строку покрывала и состоит из m строчных латинских букв от « a » до « z », где одинаковым цветам соответствуют одинаковые буквы, а разным цветам — разные буквы.
Выходные данные
В единственной строке выведите одно целое число — количество подпрямоугольников, являющихся флагами.
Примечание
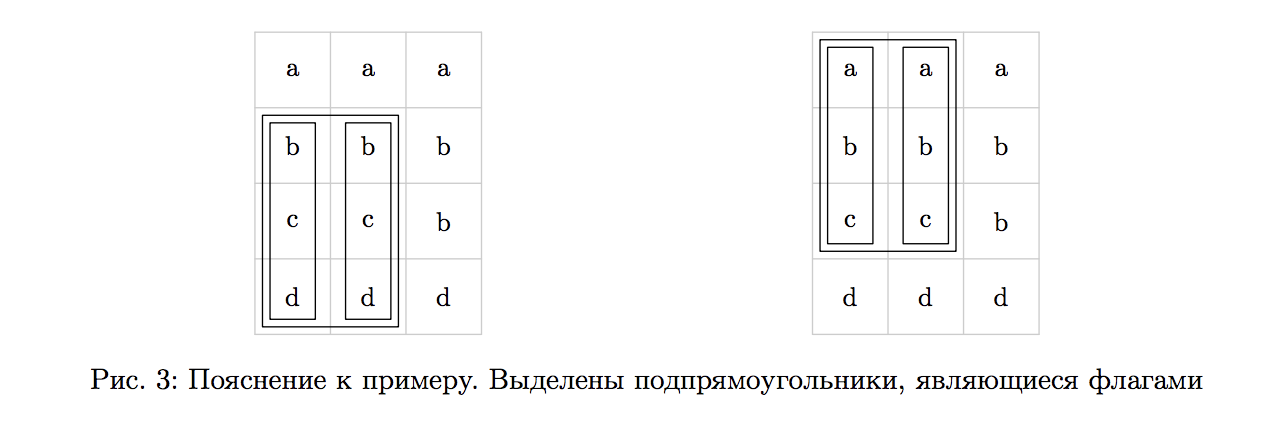
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 3
aaa
bbb
ccb
ddd |
6 |
| |
![]()
|
|
Мирные ладьи
Массивы
Двумерные массивы
На шахматной доске размером N × N расставлено N шахматных ладей не бьющих друг друга, то есть на каждой вертикали и каждой горизонтали стоит ровно одна ладья.
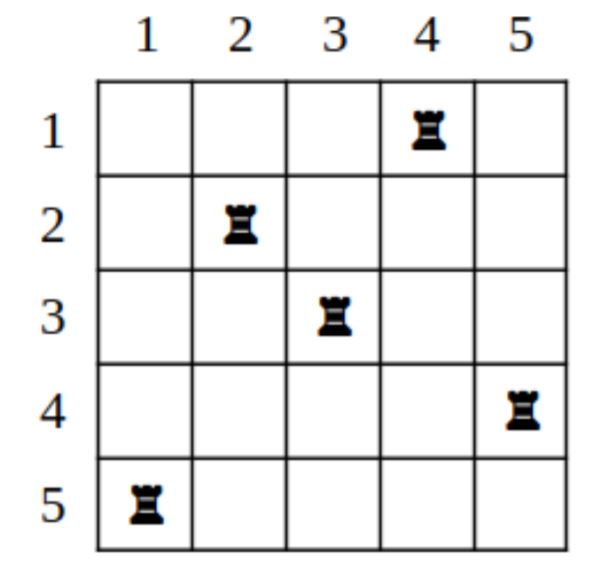
Шахматную доску повернули на 90° по часовой стрелке. Выведите получившуюся расстановку ладей.
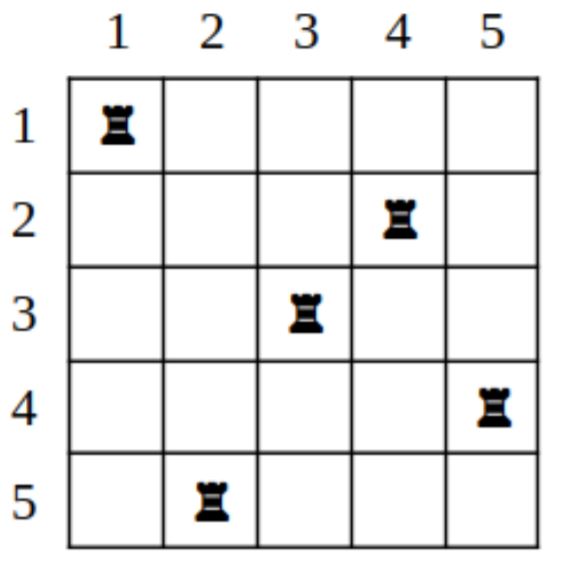
Входные данные
Первая строка входных данных содержит целое число N, 1 ≤ N ≤ 105 — размер доски. Следующие N строк содержат по одному числу от 1 до N, а именно, в i-й строке записано число ai — номер вертикали, в которой стоит ладья на i-й горизонтали. В этой задаче горизонтали нумеруются числами от 1 до N сверху вниз, вертикали нумеруются числами от 1 до N слева направо (см.рисунок).
Выходные данные
Программа должна вывести N чисел — расстановку ладей после поворота в таком же формате.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
4
2
3
5
1 |
1
4
3
5
2 |
Замечание
Пример в условии соответствует рисункам. Первоначально ладьи стояли в столбцах 4, 2, 3, 5, 1
при перечислении их по строкам сверху вниз. После поворота ладьи стоят в столбцах 1, 4, 3, 5, 2.
| |
![]()
|
|
Гипер-минимум
Двумерные массивы
Имеется 4-мерный массив X, каждый индекс которого может принимать значения от 1 до N. Вы должны построить новый 4-мерный массив Y , элементы которого должны принимать следующие значения: Y [i1, i2, i3, i4] = min(X[j1, j2, j3, j4]), где 1 ≤ ik ≤ N − M + 1, ik ≤ jk ≤ ik + M − 1, а M - заданное число.
Входные данные
В первой строке входного файла задаются N и M (1 ≤ M ≤ N). Остальные строки файла содержат элементы массива X. Количество элементов не будет превышать 1500000 и сами они будут целыми числами, не превышающими по абсолютному значению 109. Они расположены в таком порядке, что считать их можно с помощью псевдокода:
for i = 1 to N:
for j = 1 to N:
for k = 1 to N:
for l = 1 to N:
read X[i, j, k, l]
Выходные данные
Выведите искомый массив Y в том же формате, в котором был дан массив X.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 1
1 |
1 |
| 2 |
3 2
3 1 4 -4 0 4 0 0 -3 0 -2 -5 5 3 5 -4 4 -3 -5 -4 -4 5 -1 0 -3 -2 -1 2 -5 -5 -1 1 1 -4 3 5 3 -3 -3 3 0 1 4 -1 -2 3 -2 5 4 -1 -5 3 -4 0 -3 -1 3 -1 4 4 -1 -5 -3 4 -4 5 1 5 -4 3 2 2 -2 -2 4 2 -4 -3 1 3 1 |
-5 -5 -4 -3 -5 -5 -4 -5 -5 -5 -5 -5 -4 -5 -4 -5 |
| |
![]()
|
|
Игра с фишками
Двумерные массивы
Обход в ширину
Вы являетесь одним из разработчиков новой компьютерной игры. Игра происходит на прямоугольной доске, состоящей из W×H клеток. Каждая клетка может либо содержать, либо не содержать фишку (см. рисунок).
Важной частью игры является проверка того, соединены ли две фишки путем, удовлетворяющим следующим свойствам:
1. Путь должен состоять из отрезков вертикальных и горизонтальных прямых.
2. Путь не должен пересекать других фишек.
При этом часть пути может оказаться вне доски. Например:
Фишки с координатами (1, 3) и (4, 4) могут быть соединены. Фишки с координатами (2, 3) и (5, 3) тоже могут быть соединены. А вот фишки с координатами (2, 3) и (3, 4) соединить нельзя — любой соединяющий их путь пересекает другие фишки.
Вам необходимо написать программу, проверяющую, можно ли соединить две фишки путем, обладающим вышеуказанными свойствами, и, в случае положительного ответа, определяющую минимальную длину такого пути (считается, что путь имеет изломы, начало и конец только в центрах клеток (или “мнимых клеток”, расположенных вне доски), а отрезок, соединяющий центры двух соседних клеток, имеет длину 1).
Формат входных данных
Первая строка входного файла содержит два натуральных числа: W — ширина доски, H — высота доски (1 ≤ W, H ≤ 75). Следующие H строк содержат описание доски: каждая строка состоит ровно из W символов: символ “X” (заглавная английская буква “экс”) обозначает фишку, символ “.” (точка) обозначает пустое место. Все остальные строки содержат описания запросов: каждый запрос состоит из четырех натуральных чисел, разделенных пробелами — X1, Y1, X2, Y2, причем 1 ≤ X1, X2 ≤ W, 1 ≤ Y1, Y2 ≤ H. Здесь (X1, Y1) и (X2, Y2) — координаты фишек, которые требуется соединить (левая верхняя клетка имеет координаты (1, 1)). Гарантируется, что эти координаты не будут совпадать (кроме последнего запроса). Последняя строка содержит запрос, состоящий из четырех чисел 0; этот запрос обрабатывать не надо. Количество запросов не превосходит 20.
Формат выходных данных
Для каждого запроса необходимо вывести одно целое число на отдельной строке — длину кратчайшего пути, или 0, если такого пути не существует.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 4
XXXXX
X...X
XXX.X
.XXX.
2 3 5 3
1 3 4 4
2 3 3 4
0 0 0 0
|
5
6
0 |
| 2 |
4 4
XXXX
.X..
..X.
X...
1 1 3 1
0 0 0 0
|
4 |
| |
![]()
|
|
Состязания
Двумерные массивы
В метании молота состязается n спортcменов. Каждый из них сделал m бросков. Победитель определяется по лучшему результату. Определите количество участников состязаний, которые разделили первое место, то есть определите количество строк в массиве, которые содержат значение, равное наибольшему.
Входные данные
Программа получает на вход два числа n и m, являющиеся числом строк и столбцов в массиве. Далее во входном потоке идет n строк по m чисел, являющихся элементами массива.
Выходные данные
Программа должна вывести одно число - количество победителей соревнования.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 3
3 1 2
1 3 4
3 3 3 |
1 |
| |
![]()
|
|
Таблица умножения
Двумерные массивы
Даны два числа n и m. Создайте двумерный массив A[n][m], заполните его таблицей умножения A[i][j]=i*j и выведите на экран. При этом нельзя использовать вложенные циклы, все заполнение массива должно производиться одним циклом.
Входные данные
Программа получает на вход два числа n и m – количество строк и столбцов, соответственно.
Выходные данные
Программа должна вывести полученный массив. Числа разделяйте одним пробелом.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 3 |
0 0 0
0 1 2
0 2 4 |
| |
![]()
|
|
Треугольник Паскаля
Двумерные массивы
Даны два числа n и m. Создайте двумерный массив размерностью nхm и заполните его по следующему правилу:
- числа, стоящие в строке 0 или в столбце 0 равны 1 (A[0][j]=1, A[i][0]=1);
- значения остальных элементов массива должны быть равны сумме элементов, стоящих на один слобец левее и на одну строку выше от этого элемента.
Входные данные
Программа получает на вход два числа n и m.
Выходные данные
Выведите на экран получившийся массив.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 3
|
1 1 1
1 2 3
1 3 6
|
| |
![]()
|
|
Спираль
Двумерные массивы
Задачи на моделирование
Робот перемещается по клетчатой плоскости и рисует спираль. Исходно он находится в клетке (0, 0) и направлен в сторону увеличения первой координаты.
Далее он действует по следующему алгоритму: совершает d перемещений вперед, затем поворачивает налево и снова делает d перемещений вперед. После этого он поворачивает налево и умножает значение d на k. Затем робот повторяет описанный процесс. Робот останавливается, сделав суммарно ровно n перемещений.
Требуется вывести картинку, на которой отмечены клетки, на которых побывал робот.
Входные данные
На вход подаются целые числа n, d и k (1 ≤ n ≤ 1000, 1 ≤ d ≤ 100, 2 ≤ k ≤ 5).
Выходные данные
Пусть минимальный прямоугольник из клеток, содержащий все посещенные роботом клетки, имеет высоту h и ширину w. На первой строке выведите числа h и w, разделенные пробелом. Следующие h строк должны содержать по w символов, выведите «*» для клетки, посещенной роботом и «.» для не посещенной.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
13 2 2 |
5 5
*****
*...*
*.***
*....
**...
|
| |
![]()
|
|
Матрицы. Введение
Двумерные массивы
Объявите в программе три матрицы с начальными значениями
- матрицу A размером 5 на 6 элементов, в которой первый элемент каждой строки равен номеру строки, остальные элементы строки - нули
- матрицу B размером 10 на 10, заполненную нулями
- матрицу С размером 2 на 2, где каждый элемент равен сумме номера строки и номера столбца
| |
![]()
|
|
Златопольский 12.5
Двумерные массивы
Формат входных данных
В первой строке вводятся через пробел количество строк N (1<=N<=20) и количество столбцов M(1<=M<=20) двумерного массива.
Далее идет N строк по M элементов в строке - элементы двумерного массива. Все элементы двумерного массива по модулю не превышают 50.
Далее идет число k (1<=k<=N)
Формат выходных данных
Вывести на экран k-ю строку (считая, что нумерация элементов массива начинается с 1, т.е. для первой строки k=1).
Все элементы выводить в одну строку через 1 пробел между элементами
| |
![]()
|
|
Златопольский 12.3
Двумерные массивы
Формат входных данных
В первой строке вводятся через пробел количество строк N (1<=N<=20) и количество столбцов M (1<=M<=20) двумерного массива.
Далее идет N строк по M элементов в строке - элементы двумерного массива. Все элементы двумерного массива по модулю не превышают 50.
Далее, через пробел, идут два числа k и h (1<=k<=N, 1<=h<=M)
Формат выходных данных
Вывести на экран элемент, расположенный на позиции h в строке k (считая, что нумерация элементов массива начинается с 1, т.е. для левого верхнего элемента массива считается, что k=1 и h=1).
| |
![]()
|
|
Златопольский 12.2б
Двумерные массивы
Формат входных данных
В первой строке вводятся через пробел количество строк N(1<=N<=20) и количество столбцов M (1<=M<=20) двумерного массива.
Далее идет N строк по M элементов в строке - элементы двумерного массива. Все элементы двумерного массива по модулю не превышают 50.
Формат выходных данных
Вывести на экран элемент, расположенный в левом верхнем углу.
| |
![]()
|
|
Златопольский 12.2а
Двумерные массивы
Формат входных данных
В первой строке вводятся через пробел количество строк N (1<=N<=20) и количество столбцов M (1<=N<=20) двумерного массива.
Далее идет N строк по M элементов в строке - элементы двумерного массива. Все элементы двумерного массива по модулю не превышают 50.
Формат выходных данных
Вывести на экран элемент, расположенный в правом нижнем углу.
| |
![]()
|
|
Златопольский 12.1б
Двумерные массивы
Формат входных данных
В первой строке вводятся через пробел количество строк N (1<=N<=20) и количество столбцов M (1<=N<=20) двумерного массива.
Далее идет N строк по M элементов в строке - элементы двумерного массива. Все элементы двумерного массива по модулю не превышают 50.
Формат выходных данных
Вывести на экран элемент, расположенный в левом нижнем углу.
| |
![]()
|
|
Златопольский 12.1а
Двумерные массивы
Формат входных данных
В первой строке вводятся через пробел количество строк N (1<=N<=20) и количество столбцов M (M 1<=M<=20) двумерного массива.
Далее идет N строк по M элементов в строке - элементы двумерного массива. Все элементы двумерного массива по модулю не превышают 50.
Формат выходных данных
Вывести на экран элемент, расположенный в правом верхнем углу.
| |
![]()
|
|
7118
Двумерные массивы
Дано натуральное число N (N<=15). Заполните и выведите на экран квадратный двумерный массив размером NxN по следующему правилу:
0 0 0 1 1
0 0 1 1 1
0 0 0 1 1
0 0 0 0 1
Каждый элемент массива отделяется от другого одним пробелом, каждая строка массива выводится с новой строки
Пример входных и выходных данных
|
№ теста |
Входные данные |
Выходные данные |
|
1 |
5 |
0 0 0 0 1
0 0 0 1 1
0 0 1 1 1
0 0 0 1 1
0 0 0 0 1
|
| |
![]()
|
|
7117
Двумерные массивы
Дано натуральное число N (N<=15). Заполните и выведите на экран квадратный двумерный массив размером NxN по следующему правилу:
1 1 0 1 1
1 1 1 1 1
1 1 0 1 1
1 0 0 0 1
Каждый элемент массива отделяется от другого одним пробелом, каждая строка массива выводится с новой строки
Пример входных и выходных данных
|
№ теста |
Входные данные |
Выходные данные |
|
1 |
5 |
1 0 0 0 1
1 1 0 1 1
1 1 1 1 1
1 1 0 1 1
1 0 0 0 1
|
| |
![]()
|
|
7116
Двумерные массивы
Дано натуральное число N (N<=15). Заполните и выведите на экран квадратный двумерный массив размером NxN по следующему правилу:
1 0 0 0 0
1 1 0 0 0
1 1 1 0 0
1 1 0 0 0
1 0 0 0 0
Каждый элемент массива отделяется от другого одним пробелом, каждая строка массива выводится с новой строки
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 |
1 0 0 0 0
1 1 0 0 0
1 1 1 0 0
1 1 0 0 0
1 0 0 0 0
|
| |
![]()
|
|
23073
Двумерные массивы
Дано натуральное число N (N<=15). Заполните и выведите на экран квадратный двумерный массив размером NxN по следующему правилу:
1 2 3 4 5 6
2 3 4 5 6 1
3 4 5 6 1 2
4 5 6 1 2 3
5 6 1 2 3 4
6 1 2 3 4 5
Каждый элемент массива отделяется от другого одним пробелом, каждая строка массива выводится с новой строки
Пример входных и выходных данных
|
№ теста |
Входные данные |
Выходные данные |
|
1 |
6 |
1 2 3 4 5 6
2 3 4 5 6 1
3 4 5 6 1 2
4 5 6 1 2 3
5 6 1 2 3 4
6 1 2 3 4 5
|
| |
![]()
|
|
23072
Двумерные массивы
Дано натуральное число N (N<=15). Заполните и выведите на экран квадратный двумерный массив размером NxN по следующему правилу:
1 1 1 1 1 1
1 2 3 4 5 6
1 3 6 10 15 21
1 4 10 20 35 56
1 5 15 35 70 126
1 6 21 56 126 252
Каждый элемент массива отделяется от другого одним пробелом, каждая строка массива выводится с новой строки
Пример входных и выходных данных
|
№ теста |
Входные данные |
Выходные данные |
|
1 |
6 |
1 1 1 1 1 1
1 2 3 4 5 6
1 3 6 10 15 21
1 4 10 20 35 56
1 5 15 35 70 126
1 6 21 56 126 252
|
| |
![]()
|
|
7115
Двумерные массивы
Дано натуральное число N (N<=15). Заполните и выведите на экран квадратный двумерный массив размером NxN по следующему правилу:
1 1 1 1 1
0 1 1 1 0
0 0 1 0 0
0 0 0 0 0
0 0 0 0 0
Каждый элемент массива отделяется от другого одним пробелом, каждая строка массива выводится с новой строки
Пример входных и выходных данных
|
№ теста |
Входные данные |
Выходные данные |
|
1 |
5 |
1 1 1 1 1
0 1 1 1 0
0 0 1 0 0
0 0 0 0 0
0 0 0 0 0
|
| |
![]()
|
|
7114
Двумерные массивы
Дано натуральное число N (N<=15). Заполните и выведите на экран квадратный двумерный массив размером NxN по следующему правилу:
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
1 |
1 |
1 |
1 |
Каждый элемент массива отделяется от другого одним пробелом, каждая строка массива выводится с новой строки
Пример входных и выходных данных
|
№ теста |
Входные данные |
Выходные данные |
|
1 |
5 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
1 |
1 |
1 |
1 |
|
| |
![]()
|
|
7113
Двумерные массивы
Дано натуральное число N (N<=15). Заполните и выведите на экран квадратный двумерный массив размером NxN по следующему правилу:
|
1 |
3 |
3 |
3 |
3 |
|
10 |
4 |
3 |
3 |
3 |
|
10 |
10 |
9 |
3 |
3 |
|
10 |
10 |
10 |
16 |
3 |
|
10 |
10 |
10 |
10 |
25 |
Каждый элемент массива отделяется от другого одним пробелом, каждая строка массива выводится с новой строки
Пример входных и выходных данных
|
№ теста |
Входные данные |
Выходные данные |
|
1 |
5 |
|
1 |
3 |
3 |
3 |
3 |
|
10 |
4 |
3 |
3 |
3 |
|
10 |
10 |
9 |
3 |
3 |
|
10 |
10 |
10 |
16 |
3 |
|
10 |
10 |
10 |
10 |
25 |
|
| |
![]()
|
|
7112
Двумерные массивы
Дано натуральное число N (N<=15). Заполните и выведите на экран квадратный двумерный массив размером NxN по следующему правилу:
- числа на диагонали, идущей из левого нижнего в правый верхний угол, равны 1;
- числа, стоящие ниже этой диагонали, равны 0;
- числа, стоящие выше этой диагонали, равны 2.
Каждый элемент массива отделяется от другого одним пробелом, каждая строка массива выводится с новой строки
Пример входных и выходных данных
|
№ теста |
Входные данные |
Выходные данные |
|
1 |
4 |
2 2 2 1
2 2 1 0
2 1 0 0
1 0 0 0
|
| |
![]()
|
|
Квадратная матрица
Двумерные массивы
Дано натуральное число N (N<=15). Заполните и выведите на экран квадратный двумерный массив размером NxN по следующему правилу:
- числа на диагонали, идущей из правого верхнего в левый нижний угол, равны 1;
- числа, стоящие выше этой диагонали, равны 0;
- числа, стоящие ниже этой диагонали, равны 2.
Каждый элемент массива отделяется от другого одним пробелом, каждая строка массива выводится с новой строки
| |
![]()
|
|
12.41
Двумерные массивы
В двумерном массиве хранится информация о зарплате N человек за каждый из 12 месяцев года (в строках находится информация о людях, в столбцах о месяцах). Составить программу для расчета общей суммы, выплаченной работникам за K-й месяц года (месяцы нумеруются с 1).
Входные данные
В первой строке задается число N (0< N <= 25). Далее идут N строк по 12 чисел в каждой (каждое число - натуральное число, не более 150). В последней строке задается число K (1 <= K <= N).
Выходные данные
Выведите на экран отве на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
148 16 121 82 35 27 109 99 79 100 66 100
22 62 154 66 134 98 32 60 112 55 65 42
55 138 115 39 154 151 113 116 104 85 127 108
8 |
275 |
| |
![]()
|
|
12.39
Двумерные массивы
В зрительном зале N рядов, в каждом из которых M мест (кресел). Информация о проданных билетах хранится в двумерном массиве, номера строк соответсвуют номерам рядов, а номера столбцов - номерам мест. Если билет продан на то или иное место, то соответствующий элемент массива имеет значение 1, в противном случае - 0. Составить программу, определяющую число проданных билетов на места в K-м ряду.
Входные данные: в первой строке задаются два числа N (0<N<=15) и M (0<M<=25)
Далее идут N строк по M чисел в каждой (каждое число равно 0 или 1)
В последней строке идет число K (1<=K<=N)
Выходные данные: выведите ответ на задачу
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 5
1 1 1 0 1
0 0 0 1 1
1 1 1 1 1
3 |
5 |
| |
![]()
|
|
Обработка строки в матрице - 3
Двумерные массивы
В двумерном массиве хранится информация о баллах, полученных спортсменами-пятиборцами в каждом из пяти видов спорта (в нулевой строке - информация о баллах первого спортсмена, в первой - второго и т.д.). Общее число спорстменов \(N\). Определите общую сумму баллов, набранных \(K\)-м спортсменом.
Входные данные: в первой строке задается число \(N\) (\(0<N<=20\)).
Далее идут N строк по 5 чисел в каждой - баллы, полученные спортсменами (каждое число - натуральное, не более 50)
В последней строке задается число \(K\)
Выходные данные: выведите на экран ответ на задачу
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
13 3 15 12 26
1 28 17 17 27
18 18 50 21 27
3 |
134 |
| |
![]()
|
|
37097
Двумерные массивы
В зрительном зале N рядов, в каждом из которых по M мест (кресел). Информация о проданных билетах хранится в двумерном массиве, номера строк которого соответствуют номерам рядов, а номера столбцов - номерам мест (места нумеруются с 1). Если билет на то или иное место продан, то в массив записывается значение 2, если забронирован - 1, в противном случае - 0. Определить номера мест, на которые чаще всего продаются билеты. Обртите внимание, что забронированный билет не считается проданным, ведь его могут не выкупить.
Входные данные
В первой строке задаются числа N и M (0 <= N, M <= 25). Далее идет N строк по M чисел в каждой. Каждое число может быть равно 0, 1 или 2.
Выходные данные
Выведите на экран номера всех мест (в одну строку, через один пробел), которые продаются чаще всего (выводить номера в порядке возрастания).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 4
0 1 2 2
1 2 2 2
2 1 1 1 |
3 4 |
| |
![]()
|
|
37095
Двумерные массивы
В зрительном зале N рядов, в каждом из которых по M мест (кресел). Информация о проданных билетах хранится в двумерном массиве, номера строк которого соответствуют номерам рядов, а номера столбцов - номерам мест. Если билет на то или иное место продан, то в массив записывается значение 2, если забронирован - 1, в противном случае - 0. Определить номера мест, которые чаще всего бронируют и/или выкупают зрители.
Входные данные
В первой строке задаются числа N и M (0<=N, M<=25). Далее идет N строк по M чисел в каждой. Каждое число может быть равно 0, 1 или 2.
Выходные данные
Выведите на экран номера всех мест (в одну строку, через один пробел), которые продаются или бронируются чаще всего (нумерация мест начинается с 1). Номера выводить в порядке возрастания.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 4
0 1 2 1
1 2 2 0
2 2 1 1 |
2 3 |
| |
![]()
|
|
12.98а
Двумерные массивы
Информация о количестве жильцов в каждой из M квартир каждого этажа 12-этажного дома хранится в двумерном массиве (в нулевой строке - информация о количестве жителей в квартирах первого этажа, в первой - второго и т.д.). Определите на каком этаже проживаем меньше всего людей. Выведите это количество и номера всех таких этажей.
Входные данные: в первой строке подается число M (0<M<=25)
Далее идут 12 строк по M чисел в каждой (целое число, не превосходящее 10)
Выходные данные: выведите на экран сначала требуемое количество людей, затем с новой строки через пробел номера всех таких этажей (в порядке возрастания)
| |
![]()
|
|
12.98б
Двумерные массивы
Информация о количестве жильцов в каждой из M квартир каждого этажа 12-этажного дома хранится в двумерном массиве (в нулевой строке - информация о квартира первого этажа, в первой - второго и т.д.). Определите на каком этаже проживает больше всего людей. Выведите это количество и номера всех таких этажей.
Входные данные: в первой строке подается число M (0<M<=25)
Далее идут 12 строк по M чисел в каждой (целое число, не превосходящее 10)
Выходные данные: выведите на экран сначала требуемое количество людей, затем с новой строки через пробел номера всех таких этажей (в порядке возрастания)
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4
1 0 2 0
1 1 2 0
0 0 2 0
0 0 1 2
2 0 1 1
1 2 2 0
2 2 0 0
2 1 2 2
2 1 2 1
2 2 1 2
2 1 0 2
1 2 0 2 |
7
8 10 |
| |
![]()
|
|
Поиск требуемой строки - 2
Двумерные массивы
В метании молота состязается n спортcменов. Каждый из них сделал m бросков. Побеждает спортсмен, у которого максимален наилучший бросок. Если таких несколько, то из них побеждает тот, у которого наилучшая сумма результатов по всем попыткам. Если и таких несколько, победителем считается спортсмен с минимальным номером. Определите номер победителя соревнований.
Входные данные: Программа получает на вход два числа n и m (20<=n,m<=20), являющиеся числом строк и столбцов в массиве. Далее во входном потоке идет n строк по m чисел, являющихся элементами массива.
Выходные данные: Программа должна вывести одно число - номер победителя соревнований. Не забудьте, что строки (спортсмены) нумеруются с 0.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 3
8 8 8
5 9 3
9 4 7
6 6 2 |
2 |
| |
![]()
|
|
Под побочной диаганалью
Двумерные массивы
Дан двумерный массив размером nxn (n<=10). Сформировать одномерный массив из элементов заданного массива, расположенных под побочной диагональю.
Входные данные
Программа получает на вход число n <= 10, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет n строк по n чисел, являющихся элементами массива.
Выходные данные
Программа должна вывести одномерный массив, элементами которого являются значения элементов двумерного массива (через пробел), расположенные ПОД побочной диагональю.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
888 29 37
92 888 57
73 75 888
|
57 75 888 |
| |
![]()
|
|
Под главной диагональю
Двумерные массивы
Дан двумерный массив размером nxn (n<=10). Сформировать одномерный массив из элементов заданного массива, расположенных под главной диагональю.
Входные данные
Программа получает на вход число n <= 10, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет n строк по n чисел, являющихся элементами массива.
Выходные данные
Программа должна вывести одномерный массив, элементами которого являются значения элементов двумерного массива (через пробел), расположенные ПОД главной диагональю.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
888 29 37
92 888 57
73 75 888
|
92 73 75 |
| |
![]()
|
|
Над побочной диагональю
Двумерные массивы
Дан двумерный массив размером nxn (n<=10). Сформировать одномерный массив из элементов заданного массива, расположенных над побочной диагональю.
Входные данные
Программа получает на вход число n <= 10, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет n строк по n чисел, являющихся элементами массива.
Выходные данные
Программа должна вывести одномерный массив, элементами которого являются значения элементов двумерного массива (через пробел), расположенные НАД побочной диагональю.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
888 29 37
92 888 57
73 75 888
|
888 29 92 |
| |
![]()
|
|
Над главной диагональю
Двумерные массивы
Дан двумерный массив размером nxn (n<=10). Сформировать одномерный массив из элементов заданного массива, расположенных над главной диагональю.
Входные данные
Программа получает на вход число n <= 10, являющееся числом строк и столбцов в массиве. Далее во входном потоке идет n строк по n чисел, являющихся элементами массива.
Выходные данные
Программа должна вывести одномерный массив, элементами которого являются значения элементов двумерного массива (через пробел), расположенные НАД главной диагональю.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
888 29 37
92 888 57
73 75 888
|
29 37 57 |
| |
![]()
|
|
Третья планета от Солнца
Двумерные массивы
На третью планету от Солнца отправили n космических кораблей для сбора различных объектов для изучения. На каждом корабле было размещено по m контейнеров различного объема. После изучения планеты, отобрано n·m экземпляров. Командный состав решил взять несколько экземпляров самого большого объема. Необходимо определить какой объем должен иметь самый большой экземпляр, чтобы его можно было вывезти с планеты, а также количество кораблей и их номера, на которые можно поместить самые большие экземпляры. Все корабли пронумерованы, начиная с нуля.
Входные данные
Первая строка содержит два целых числа n и m: n - количество кораблей, отправленных на третью планету (1 <= n <= 100), m - количество контейнеров на каждом корабле. В следующих n строках содержат по m чисел, каждое из которых показывает объем контейнера (1 <= m <= 100, каждое число - неотрицательное не более 100).
Выходные данные
Выведите в первой строке - количество космических кораблей, которыми можно привезти самый большой экземпляр, через пробел максимальный объем, который можно вывезти с планеты. На следующей строке выведите через пробел номера кораблей (нумеруются с нуля), на которые можно загрузить самый большой экземпляр.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 3
1 2 3
3 5 4
5 2 2
|
2 5
1 2
|
| |
![]()
|
|
Заполнение спиралью
Двумерные массивы
Дано натуральное число n. Создайте массив A[2*n+1][2*n+1] и заполните его по спирали, начиная с числа 0 в центральной клетке A[n+1][n+1]. Спираль выходит вверх, далее закручивается против часовой стрелки.
Формат входных данных
Программа получает на вход число n.
Формат выходных данных
Программа должна вывести полученный массив. Каждый элемент массива необходимо записывать в трех знакоместах.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 |
12 11 10 9 24
13 2 1 8 23
14 3 0 7 22
15 4 5 6 21
16 17 18 19 20
|
| |
![]()
|
|
Максимальная строка
Двумерные массивы
В матрице найти номер строки, сумма чисел в которой максимальна.
Входные данные
Во входном файле записаны числа N и M - количество строк и столбцов матрицы (каждое из них - из диапазона от 1 до 100),
а затем сама матрица. Элементы матрицы - числа из целые числа, по модулю не превышающие 106.
Выходные данные
В выходной файл вывести номер строки, сумма чисел в которой максимальна. Если таких строк несколько,
вывести первую из них.
| |
![]()
|
|
Двумерный вектор
Двумерные массивы
Создайте двумерный массив размером n×m и заполните его натуральными числами от 1 до nxm по вертикали (см. пример).
Входные данные
Даны два натуральных числа: n и m, не превышающие 1010.
Выходные данные
Выведите заполненный двумерный массив
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 4
|
1 4 7 10
2 5 8 11
3 6 9 12
|
| |
![]()
|
|
Седловая точка
Двумерные массивы
Седловая точка – это элемент матрицы, который одновременно является наибольшим в своем столбце и наименьшим в своей строке. Напишите программу, которая находит индексы всех седловых точек матрицы. Нумерация строк и столбцов матрицы начинается с единицы.
Входные данные
В первой строке записаны через пробел размеры прямоугольной матрицы N и N (количество строк и количество столбцов, 1 <= N, M <= 100). В следующих N строках записаны строки матрицы, в каждой – по M натуральных чисел, разделённых пробелами.
Выходные данные
Программа должна вывести индексы всех седловых точек матрицы в порядке обхода по строкам (сверху вниз, слева направо). Номер строки и номер столбца каждой седловой точки разделяются пробелами. Нумерация начинается с единицы. Если в матрице нет ни одной седловой точки, нужно вывести число 0.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 5
1 2 3 4 5
6 7 8 9 10
11 12 13 14 15
9 17 18 19 20
|
3 1
|
| |
![]()
|
|
Сортировка строк
Двумерные массивы
Алгоритмы сортировки
Напишите программу, которая переставляет строки матрицы так, чтобы значения в столбце K шли в порядке убывания. Строки, у которых значения в столбце K равны, должны быть выведены в том же порядке, в котором они стояли в исходной матрице.
Входные данные
В первой строке записаны через пробел размеры матрицы: количество строк N и количество столбцов M ( 1 <= N , M <= 100 ). В следующих N строках записаны строки матрицы, в каждой – по M натуральных чисел, разделённых пробелами. В последней строке вводится номер столбца K .
Выходные данные
Программа должна вывести получившуюся матрицу, в которой строки переставлены так, чтобы значения в столбце K шли в порядке убывания.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 5
21 22 23 24 25
26 12 18 29 33
11 37 31 14 39
16 17 18 5 20
1
|
26 12 18 29 33
21 22 23 24 25
16 17 18 5 20
11 37 31 14 39
|
| |
![]()
|
|
Цветовое преобразование
Двумерные массивы
Яркости пикселей рисунка закодированы числами от 0 до 255 в виде матрицы. Преобразовать рисунок в черно-белый по следующему алгоритму:
- вычислить среднюю яркость пикселей по всему рисунку
- все пиксели, яркость которых меньше средней, сделать черными (записать код 0), а остальные -– белыми (код 255)
Входные данные
В первой строке записаны через пробел размеры матрицы: количество строк N и количество столбцов M ( 1 <= N , M <= 100 ). В следующих N строках записаны строки матрицы, в каждой – по M натуральных чисел в диапазоне от 0 до 255, разделённых пробелами.
Выходные данные
Программа должна вывести в первой строчке среднее значение яркости для заданного рисунка с точностью 4 знака в дробной части. В следующих N строчках выводится построенная матрица, соответствующая чёрно-белому изображению.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 4
12 14 67 45
32 87 45 63
69 45 14 11
40 12 35 15
|
37.8750
0 0 255 255
0 255 255 255
255 255 0 0
255 0 0 0
|
| |
![]()
|
|
Посещение театра
Двумерные массивы
Учащиеся театрального кружка школы любят посещать театр. В очередной раз они пошли в театр, в котором n рядов по m мест в каждом. Руководитель кружка пришла за билетами и хочет купить билеты всем учащимся в одном ряду на соседние места.
По имеющейся информации о проданных билетах на спектакль определите, сможет ли руководитель купить билеты всем учащимся и себе в одном ряду.
Информация о проданных билетах записана в двумерный массив (единицы означают, что на данное место билет продан, ноль - что место свободно). Руководителю кружка вместе с детьми необходимо k билетов.
Входные данные
В первой строке входных данных находятся числа n, m, k <= 100. В следующих n строках входных данных расположены по m чисел (0 и 1), разделенных пробелами.
Выходные данные
Выведите YES или NO в зависимости от ответа на вопрос задачи.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 4 2
0 1 0 1
1 0 0 1
1 1 1 1
|
YES
|
| |
![]()
|
|
Путешествие ферзя
Двумерные массивы
Алиса часто играет в шахматы. Причем так как она любит путешествовать по другим галактикам, она знает много разновидностей этой древней игры. Иногда она просто решает головоломки, созданные на шахматной доске. Шахматная доска Алисы может иметь самые разные размеры, не только 8×8.
Сейчас Алиса решает шахматную головоломку, суть которой заключается в следующем. На одно из полей доски размером m×n записывается некоторое положительное целое число и затем на него ставится ферзь. После этого ферзь делает k ходов. Ходит ферзь по стандартным шахматным правилам. Ферзь не может ходить на поля, на которых уже был. Также, перед там как выполнить ход, на выбранном поле пишется целое число, причем такое, что оно больше всех других чисел, уже записанных на доске.
Решение головоломки заключается в том, чтобы восстановить маршрут ферзя по числам, записанным на доске. Возможно записанные числа не дают решения.
Для решения этой головоломки Алиса написала программу, которая может быстро ее решать при больших значениях m, n и k.
Напишите и вы такую программу.
В стандартных шахматных правилах ферзь может переместиться на любое поле доски, находящееся на одной вертикали, горизонтали или диагонали с тем полем, на котором он находится.
Входные данные
В первой строке вводятся числа m, n и k ( 1< = m, n <= 300, 0 <= k < mn). Следующие m строк содержат по k целых чисел и описывают поля доски (пустому полю соответствует число 0, а полю, на котором записано число – это число). Все числа, записанные на доске, положительные, целые и не превышают 10 9.
Выходные данные
Если головоломка составлена с ошибкой и записанные на ней числа не дают решения, то вывелите « Wrong Board».
В противном случае выведите m строк по n чисел – для каждого поля выведите номер хода, перед которым ферзь побывал на этом поле, а для последнего поля, на котором он оказался – число k + 1. Для полей, на которые ферзь не попадал, выведите число 0.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 4 7
10 20 0 100
30 0 0 40
0 0 0 0
45 42 0 70
|
1 2 0 8
3 0 0 4
0 0 0 0
6 5 0 7
|
| 2 |
2 4 4
10 20 30 40
0 50 0 0
|
Wrong Board
|
| 3 |
2 2 2
1 2
4 3
|
Wrong Board
|
| |
![]()
|
|
Ральф любит пончики
Двумерные массивы
Громила Ральф вот уже 30 лет живёт в игровом автомате, и вы его можете увидеть на экране того самого автомата.
Сегодня Ральф гуляет по экрану, на котором отображается прямоугольное изображение, разбитое на N x N клеток. В каждой клетке находится тарелка с его любимыми блинчиками (на всех тарелках разное количество блинчиков). Ральф начинает перемещаться с левой нижней клетки прямоугольника. Съев все блинчики в текущей клетке, он перемещается на одну клетку вправо или на одну клетку вверх, всегда выбирая ту из клеток, где больше блинчиков в тарелке (за пределами прямоугольника тарелок с блинчиками нет). В конце концов Ральф приходит в правую верхнюю клетку. Вам же предстоит определить, сколко всего блинчиков съел Ральф пока путешествовал по экрану. Блинчики в начальной и конечной клетках Ральф тоже съел с большим удовольствием.
Входные данные
Программа получает на вход в первой строке целое число N – размер изображения (2 <= N <= 10). В следующих N строках задаются через пробел числа, обозначающие количество блинчиков на тарелках, начиная с верхнего ряда и заканчивая нижним. Все числа – различные, натуральные, не превосходящие 100.
Выходные данные
Выведите одно число - количество блинчиков, которое съест Ральф, добравшись до правой верхней клетки.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2
37 82
23 52
|
157
|
| |
![]()
|
|
Параллельное программирование
Двумерные массивы
Миша занимается параллельным программированием. Сегодня он пишет программу для исполнителя "Квадратик". Исполнитель "Квадратик" живет на клетчатом поле размера N х M, размер одной клетки 1х1. Перемещаясь он закрашивает клетку, на которой побывал. Клетку, на которой он начал движение и на которой остановился он также закрашивает.
Миша установил на поле K "Квадратиков". Каждый "Квадратик" будет двигаться в указанном Мишей направлении и останавливаться дойдя до конца поля. После окончании движения всех "Квадратиков", Миша хочет узнать сколько клеток поля получились закрашенными. Так как задача подсчета не относится к параллельному программированию, а размер поля может быть очень большим, Миша попросил вас написать программу для подсчета таких клеток.
Входные данные
Программа получает на вход несколько строк. Первая строка содержит целые числа M и N - размеры поля исполнителя "Квадратик" (1 <= M, N <= 106). Во второй строке записано число K - количество "Квадратиков" на поле (0 <= K <= 103). Далее идут K строк, каждая из которых описывает положение определенного "Квадратика" и направление, в котором он будет перемещаться. Формат каждой из таких строк: два целых числа, записанных через один пробел и один символ {N, E, S, W} - начальные координаты и направление движения соответствующего "Квадратика". Символ отделен от чисел ровно одним пробелом.
Символами обозначены следующие направления движения: N - вверх, S - вниз, W - влево, Е - вправо.
Выходные данные
Выведите количество закрашенных клеток поля, после окончания движения всех "Квадратиков".
Пояснения
Поле исполнителя и расположение "Квадратиков" для первого примера, показаны на рисунке ниже. Стрелочкой обозначено направление движения соответствующего "Квадратика".
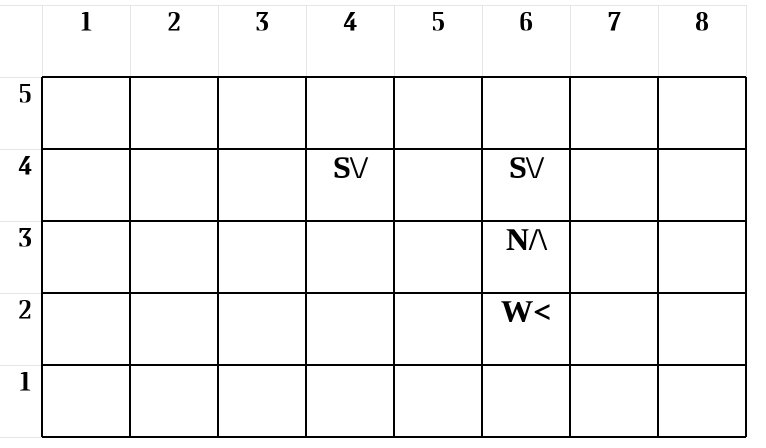
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
8 5
4
4 4 S
6 2 W
6 3 N
6 4 S
|
13
|
| |
![]()
|
|
2048
Двумерные массивы
В ожидании олимпиады школьники решили развлечься и поиграть в игру. Они вспомнили о своей любимой игре 2048, в которую постоянно играли на уроках. Ребята взяли лист бумаги и придумали себе развлечение на основе своей любимый игры. Правила в ней получились очень простыми. Ведущий загадывает какую-то позицию из игры 2048 и выписывает ее на лист. Игрок, который первым назовет наилучший ход, выигрывает. После нескольких раундов вы поняли, что выиграть по-честному у вас никак не выходит, поэтому вы решили пойти на хитрость и написать программу, решающую данную головоломку за вас.
Напомним правила игры 2048. На поле 4 × 4 разбросаны числа, являющиеся степенями двойки от 2 до 1024, некоторые клетки могут быть пустыми. Каждый ход игрок может сдвинуть все плитки игрового поля в одну сторону. Если при сдвиге две плитки одного номинала «налетают» одна на другую, то они слипаются в одну, номинал которой равен сумме соединившихся плиток. За каждое соединение игровые очки увеличиваются на номинал получившейся плитки. Плитка, получившаяся при слипании двух других, не может больше участвовать в слипании.
Входные данные
Программа получает на вход четыре строки, в каждой из которых записано четыре числа. Числа являются степенями двойки от 2 до 1024. В некоторых клетках записано число 0, означающий, что данная клетка пуста.
Выходные данные
Выведите единственное число — максимальное количество очков, которое можно получить за один ход из данной позиции.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 0 0 0
2 0 0 0
2 0 0 0
0 0 0 0
|
4
|
| 2 |
2 0 0 0
2 0 0 0
2 0 0 0
2 0 0 0
|
8
|
| 3 |
2 2 4 0
0 0 0 0
0 0 0 0
0 0 0 0
|
4
|
| 4 |
2 2 4 0
0 2 2 2
0 2 4 0
2 4 4 0
|
16
|
Примечания
Внимательно прочитайте этот раздел для лучшего понимания правил игры.
Наилучший ответ на первый тест достигается движением вниз.
0 0 0 0
0 0 0 0
2 0 0 0
4 0 0 0
Наилучший ответ на второй тест достигается движением вниз.
0 0 0 0
0 0 0 0
4 0 0 0
4 0 0 0
Наилучший ответ на третий тест достигается движением влево.
4 4 0 0
0 0 0 0
0 0 0 0
0 0 0 0
Наилучший ответ на четвертый тест достигается движением вниз.
0 0 0 0
0 2 4 0
0 4 2 0
4 4 8 2
| |
![]()
|
|
Диагональки
Двумерные массивы
В квадратной таблице NxN подсчитать суммы чисел, стоящих на диагоналях.
Входные данные
В первой строке содержится число N (1<=N<=100), а затем матрица NxN. Элементы матрицы - числа, не превосходящие по модулю 32767.
Выходные данные
Вывелите сначала сумму чисел на главной, а затем, через один пробел, - на побочной диагонали.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
1 2 3
4 5 6
10 9 8
|
14 18 |
| |
![]()
|
|
Вытаскивание минимума
Двумерные массивы
В массиве требуется найти минимальный элемент, и поставить его на первое место, а то, что стояло на 1-м месте - на его место.
Если минимальных чисел несколько, то надо менять с первым из них. Если минимальное число уже стоит на 1-м месте, ничего изменять не нужно.
Входные данные
Вводится число N - количество элементов массива (1<=N<=100), а затем - элементы массива (числа от 1 до 10000).
Выходные данные
Требуется вывести N чисел - элементы массива после перестановки.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
3 5 4 1 4
|
1 5 4 3 4 |
| |
![]()
|
|
Хождение за золотом - 1
Двумерные массивы
Однажды царь решил вознаградить одного из своих мудрецов за хорошую работу. Он привел его в прямоугольную комнату размром NxM, в каждой клетке которой лежало несколько килограммов золота. Царь разрешил мудрецу сделать обойти несколько клеток (переходя с клетки, где сейчас находится мудрец, в одну из четырех с ней соседних), и собрать все золото, которое попадется на его пути.
Вам дан маршрут мудреца. Требуется определить, сколько килограммов золота он собрал.
Входные данные
Входные данные содержат план комнаты и маршрут мудреца. Сначала записано количество строк N, затем - количество столбцов M (1<=N<=20,1<=M<=20).
Затем записано N строк по M чисел в каждой - количество килограммов золота, которое лежит в данной клетке (число от 0 до 50).
Далее записано число X - сколько клеток обошел мудрец. Далее записаны координаты этих клеток (координаты клетки - это два числа: первое определяет номер строки, второе - номер столбца, верхняя левая клетка на плане имеет координаты (1,1), правая нижняя - (N,M)).
Гарантируется, что мудрец не проходил по одной и той же клетке дважды.
Выходные данные
В выходной файл выведите количество килограммов золота, которое собрал мудрец.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 4
1 2 3 4
5 6 7 8
9 10 11 12
5
1 1
2 1
2 2
2 3
1 3
|
22 |
| |
![]()
|
|
Хождение за золотом - 2
Двумерные массивы
Однажды царь решил вознаградить одного из своих мудрецов за хорошую работу. Он привел его в прямоугольную комнату размром NxM, в каждой клетке которой лежало несколько килограммов золота. Царь разрешил мудрецу сделать обойти несколько клеток (переходя с клетки, где сейчас находится мудрец, в одну из четырех с ней соседних), и собрать все золото, которое попадется на его пути.
Мудрецу разрешено более одного раза проходить по одной и той же клетке. Золото с нее он берет при этом только один раз - когда проходит по клетке в первый раз.
Вам дан маршрут мудреца. Требуется определить, сколько килограммов золота он собрал.
Входные данные
Входные данные содержат план комнаты и маршрут мудреца. Сначала записано количество строк N, затем - количество столбцов M (1<=N<=20,1<=M<=20).
Затем записано N строк по M чисел в каждой - количество килограммов золота, которое лежит в данной клетке (число от 0 до 50).
Далее записано число X - сколько клеток обошел мудрец. Далее записаны координаты этих клеток (координаты клетки - это два числа: первое определяет номер строки, второе - номер столбца, верхняя левая клетка на плане имеет координаты (1,1), правая нижняя - (N,M)).
Число пройденных мудрецом клеток не превышает 10000.
Выходные данные
В выходной файл выведите количество килограммов золота, которое собрал мудрец.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 4
1 2 3 4
5 6 7 8
9 10 11 12
9
1 1
2 1
2 2
2 3
1 3
1 2
1 1
1 2
2 2
|
24 |
| |
![]()
|
|
Хождение за золотом - 3
Двумерные массивы
Однажды царь решил вознаградить одного из своих мудрецов за хорошую работу. Он привел его в прямоугольную комнату размром Nx M, в каждой клетке которой лежало несколько килограммов золота. Царь разрешил мудрецу сделать обойти несколько клеток (переходя с клетки, где сейчас находится мудрец, в одну из четырех с ней соседних), и собрать все золото, которое попадется на его пути.
Мудрецу разрешено более одного раза проходить по одной и той же клетке. Золото с нее он берет при этом только один раз - когда проходит по клетке в первый раз.
Вам дан маршрут мудреца. Требуется определить, сколько килограммов золота он собрал.
Входные данные
Входные данные содержат план комнаты и маршрут мудреца. Сначала записано количество строк N, затем - количество столбцов M (1<=N<=20,1<=M<=20).
Затем записано N строк по M чисел в каждой - количество килограммов золота, которое лежит в данной клетке (число от 0 до 50).
Далее записано число X - сколько клеток обошел мудрец (1<=X<=10000).
Известно, что мудрец начал с клетки с координатами (1, 1). Далее записано X-1 число: куда перемещался мудрец:
- число
1 обозначает, что мудрец делал шаг вправо,
- число
2 обозначает, что мудрец делал шаг вверх,
- число
3 обозначает, что мудрец делал шаг влево,
- число
4 обозначает, что мудрец делал шаг вниз.
Известно, что мудрец не выходил из лабиринта, при этом он мог через одну и ту же клетку пройти несколько раз.
Выходные данные
В выходной файл выведите количество килограммов золота, которое собрал мудрец.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 4
1 2 3 4
5 6 7 8
9 10 11 12
9
4 1 1 2 3 3 1 4
|
24 |
| |
![]()
|
|
Сумма положительных и отрицательных
Двумерные массивы
Дан двумерный массив A размерностью NxM. Напишите программу, которая добавляет к элементам каждой строки такой новый элемент, чтобы сумма положительных элементов строки стала бы равна модулю суммы отрицательных элементов строки.
Входные данные
В первой строке входных данных записаны через один пробел два натуральных числа N и M ( 0 < N, M <= 25). Далее идут N строк по M положительных целых чисел в каждой - элементы матрицы A (каждый элемент матрицы не превышает 105).
Выходные данные
Выведите результирующий массив A размерностью Nx(M+1) на экран. Все элементы строки должны быть разделены одним пробелом.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 5
-10 2 10 -3 4
-5 3 6 -8 8
12 -10 3 -8 4
1 2 3 -1 -2 |
-10 2 10 -3 4 -3
-5 3 6 -8 8 -4
12 -10 3 -8 4 -1
1 2 3 -1 -2 -3 |
| |
![]()
|
|
Сортировка главной диагонали
Двумерные массивы
Алгоритмы сортировки
Напишите программу, которая переставляет элементы квадратной матрицы, расположенные на главной диагонали, в порядке возрастания. Остальные элементы матрицы должны остаться на своих местах.
Входные данные
В первой строке записано одно число N размер квадратной матрицы ( 1 <= N <= 100 ). В следующих N строках записаны строки матрицы, в каждой – по N натуральных чисел, разделённых пробелами.
Выходные данные
Программа должна вывести получившуюся матрицу, в которой элементы главной диагонали расположены в порядке возрастаниия.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
1 11 11 5 10
2 9 2 10 2
12 9 10 9 15
6 15 14 1 11
11 12 4 9 3
|
1 11 11 5 10
2 1 2 10 2
12 9 3 9 15
6 15 14 9 11
11 12 4 9 10
|
| |
![]()
|
|
Сортировка массива (сложная) - 1
Двумерные массивы
Квадратичные сортировки
Дан массив целых чисел. Отсортируйте массив по невозрастанию суммы цифр каждого числа. При равенстве суммы цифр двух чисел, числа должны следовать в порядке убывания.
Формат входных данных
Программа получает на вход в первой строке натуральное число n - размер массива. Вторая строка содержит n целых чисел ai - элементы массива (1 <= n <= 103, 1 <= ai <= 104).
Формат выходных данных
Выведите результирующий массив.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4
1 43 12 10 |
43 12 10 1 |
| |
![]()
|
|
Сортировка побочной диагонали
Двумерные массивы
Квадратичные сортировки
Напишите программу, которая переставляет элементы квадратной матрицы, расположенные на побочной диагонали, в порядке убывания, начиная с правого верхнего угла. Остальные элементы матрицы должны остаться на своих местах.
Входные данные
В первой строке записано одно число N размер квадратной матрицы ( 1 <= N <= 100 ). В следующих N строках записаны строки матрицы, в каждой – по N натуральных чисел, разделённых пробелами.
Выходные данные
Программа должна вывести получившуюся матрицу, в которой элементы побочной диагонали расположены в порядке возрастаниия.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
12 4 8 13 13
1 12 1 4 15
2 3 5 2 3
6 5 13 12 14
14 9 15 4 12
|
12 4 8 13 14
1 12 1 13 15
2 3 5 2 3
6 5 13 12 14
4 9 15 4 12
|
| |
![]()
|
|
Сортировка двумерного массива
Двумерные массивы
Квадратичные сортировки
Напишите программу, которая сортирует двумерный массив целых чисел. При этом самое маленькое число должно оказаться в первом элементе первой строки, а самое большое в последнем элементе последней строки.
Входные данные
В первой строке записаны через пробел размеры двумерного массива: количество строк N и количество столбцов M ( 1 <= N , M <= 100 ). В следующих N строках записаны строки двумерного массива, в каждой – по M натуральных чисел, разделённых пробелами.
Выходные данные
Программа должна вывести отсортированный двумерный массив.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 7
13 5 1 8 4 14 5
5 13 10 9 3 7 7
3 3 9 6 3 7 5
10 8 11 2 1 1 13
1 12 13 15 9 11 4
|
1 1 1 1 2 3 3
3 3 4 4 5 5 5
5 6 7 7 7 8 8
9 9 9 10 10 11 11
12 13 13 13 13 14 15
|
| |
![]()
|
|
Перекраска клеток
Двумерные массивы
Информатика
Список
Система непересекающихся множеств
Дано клетчатое поле N x M, все клетки поля изначально белые. Автомат умеет:
закрасить клетку (i,j) в черный цвет.
для клетки (i,j) узнать её ближайших белых соседей по вертикали и горизонтали.
Дана последовательность команд для автомата. Требуется выполнить эти команды в указанной последовательности, и для каждой команды запроса ближайших белых соседей указать результат ее выполнения.
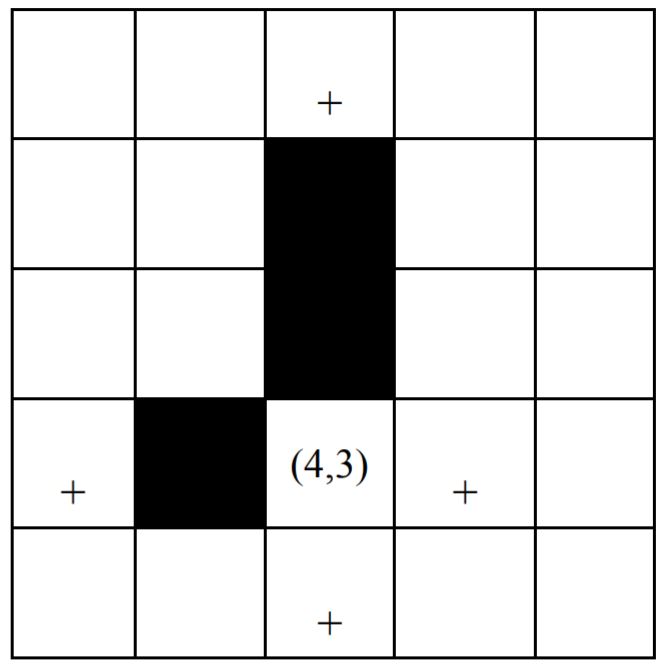
Входные данные
Сначала вводятся размеры поля N и M (1 ≤ N ≤ 20, 1 ≤ M ≤ 50000), затем количество команд K (1 ≤ K ≤ 105), а затем сами команды. Команды записаны по одной в строке в следующем формате:
Color i j — окраска клетки (i,j) в черный цвет;
Neighbors i j — нахождение белых соседей для БЕЛОЙ клетки (i,j).
1 ≤ i ≤ N, 1 ≤ j ≤ M.
Выходные данные
На каждый запрос Neighbors требуется вывести сначала количество ближайших белых соседей (или 0, если ни с одной из сторон белых клеток не осталось), а затем их координаты (соседей можно перечислять в произвольном порядке). Если запросов Neighbors нет, ничего выводить не надо.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 5 6
Color 4 2
Neighbors 4 3
Color 2 3
Color 3 3
Neighbors 4 3
Neighbors 5 1 |
4
4 1
4 4
3 3
5 3
4
4 1
4 4
1 3
5 3
2
5 2
4 1 |
| |
![]()
|
|
Крестики-нолики
Двумерные массивы
Простые игры
Задача на реализацию
Пете и Васе стало очень скучно на уроке биологии, и они решили поиграть в любимую всеми школьниками игру в крестики-нолики до пяти в ряд на бесконечном поле.
Рассмотрим кратко правила игры. Игра происходит на бесконечном клетчатом поле, два игрока делают ходы по очереди, первый игрок ходит крестиками, а второй — ноликами. В свой ход игрок
выбирает свободную клетку поля и ставит туда свой символ. Если после хода очередного игрока на поле есть пять его символов подряд по вертикали, горизонтали или диагонали, то сделавший такой ход игрок объявляется победителем и игра заканчивается.
Петя и Вася уже довольно долго играют в игру. Сейчас должен ходить Петя, который играет крестиками. Петя надеется побыстрее завершить игру и хочет выиграть не более чем за два, а лучше
за один ход. Петя называет ход оптимальным, если для этого хода выполнено одно из двух:
• этот ход приводит к немедленной победе Пети;
• не существует хода, который приводит к немедленной победе Пети, но если Петя сделает этот ход, то Вася не выиграет следующим ходом и, вне зависимости от ответного хода Васи, у Пети
будет следующий ход, который приведет к его немедленной победе.
Помогите Пете найти количество оптимальных ходов.
Формат входных данных
В первой входного файла находятся два натуральных числа n, m (1 ≤ n,m ≤ 200) — размеры прямоугольника, содержащего все уже поставленные на поле крестики и нолики.
Следующие n строк содержат по m символов, каждый из которых равен одному из следующих:
«.» (точка), «X» (заглавная латинская буква «икс») или «0» (ноль). При этом «.» обозначает пустую клетку, «X» обозначает крестик, а «0» обозначает нолик. Гарантируется, что на поле находится
равное число крестиков и ноликов, и ни один игрок еще не одержал победу.
Формат выходных данных
Выведите одно число — количество оптимальных ходов Пети.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 3
...
000
XXX
...
...
|
2 |
| 2 |
4 4
..0.
.XX0
.0X.
....
|
0 |
| 3 |
5 6
......
.XXX..
.0000.
..X...
......
|
0 |
| |
![]()
|
|
Пираты!
Двумерные массивы
Использование сортировки
Использование сортировки
Использование сортировки
В настолькой игре "Пираты!" задача одного из игроков состоит в том, чтобы провести торговый корабль с ценным грузом через море, на островах которого базируются пираты.
Поле представляют собой прямоугольник, состоящий из квадратных клеток. Игрок может за один ход перейти в одну из четырех соседних по стороне клеток, не выходя при этом за пределы поля. Торговый корабль начинает свой путь в любой клетке самого левого столбца и должен попасть в любую клетку самого правого столбца игрового поля.
Пиратские базы расположены на островах, которые также занимают одну клетку игрового поля, их расположение известно.
Вася выяснил, что чем больше расстояние от пиратской базы, тем безопаснее маршрут. расстояние считается как количество ходов по клеткам от пиратских баз до каждой из клеток маршрута.
Помогите ему определить, на какое минимальное расстояние придјтся подойти к пиратской базе, двигаясь по самому безопасному маршруту.
Формат входных данных
В первой строке записано натуральные числа N и M (1 <= N, M <= 1 000 000) количество строк и столбцов на игровом поле.
Во второй строке записано натуральное число K (1 <= K <= 500) количество пиратских баз.
В следующих K строках записаны пары чисел Ri , Ci (1 <= Ri <= N, 1 <= Ci <= M) координаты пиратских баз (строка, столбец).
Формат выходных данных
Выведите одно число минимальное расстояние, на которое придется приближаться к пиратской базе на самом безопасном маршруте.
Система оценки
Решения, верно работающие при N, M 6<=500, будут набирать не менее половины баллов.
| Ввод |
Вывод |
10 10
4
2 2
5 3
5 9
8 8 |
3 |
Замечание
Пример одного из безопасных маршрутов показан на рисун ке. Пиратские базы обозначены чјрным, клетки маршрута серым. Минимальное расстояние от пиратской базы до маршрута 3 хода.
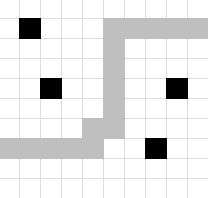 | |
![]()
|
|
Организация конференции (С, B')
Двумерные массивы
Задача на реализацию
Задача на реализацию
Недавно в солнечный весенний день директору Летней Флатландской Компьютерной Школы (ЛФКШ) Сергею Александровичу пришла в голову идея организовать первую флатландскую конференцию для школьников по программированию. Теперь перед ним стоит задача выбрать место проведения.
Флатландия представляет собой прямоугольник из m строк и n столбцов, в каждой из клеток которого расположен один город? Сергей Александрович уже посчитал для каждого города количество желающих принять участие в конференции. Известно, что флатландцы не любят далеко ездить, так что в каком бы городе она проводилась, в конференции смогут принять участие только школьники из самого города и соседних с ним по стороне городов. Формально говоря, если конференция проводится в городе, находящемся в i-ой строке и j-ом столбце, то в этой конференции будут участвовать школьники из городов (i, j), (i − 1, j) ( при условии, что i > 1) , (i + 1, j) (при условии, что i < m), (i, j − 1) (при условии, что j > 1) , и (i, j + 1) , (при условии, что j < n).
Сейчас Сергей Александрович хочет понять, в каких городах возможно поселить всех приезжих участников. Пока он выясняет количество доступных мест в гостиницах Флатландии, вам предстоит посчитать для каждого из возможных городов проведения, скольким школьникам потребуется предоставить жиль на время конференции.
Обратите внимание на то, что школьникам, живущим в том же городе, в котором проводится конференция, поселение не нужно.
Формат входных данных
В первой строке записаны два числа m и n (1 <= m, n <= 350) - размеры Флатландии. В каждой из последующих m строк содержатся по n чисел.
В i-ой стоке и j-ом столбце содержится число ai,j ( 0<= ai,j <=10000) - количество школьников из города (i, j), желающих принять участие в конференции.
Формат выходных данных
Выведите m строк по n чисел в каждой. Число в строке с номером i и стобце с номером j должно равняться количеству приезжих участников конференции, если местом проведения будет
выбран город, с координатами (i, j).
| Ввод |
Вывод |
3 4
1 0 3 2
5 6 1 2
1 1 0 11 |
5 10 3 5
8 7 11 14
6 7 13 2 |
1 1
5 |
0 |
| |
![]()
|
|
Modern Art #3
Двумерные массивы
Конструктив
Недавно вошла в моду корова-художница Picowso.
Picowso рисует особым образом. Она начинает на чистом холсте N×N, представленной матрицей N×N нолей, где ноль означает пустую ячейку холста. Затем она рисует до 9 прямоугольников на холсте, каждый одним из 9 цветов (последовательно пронумерованных 1…9). Например, она может начать рисовать прямоугольник цветом 2, получая такое промежуточное состояние холста:
2220
2220
2220
0000
Затем она может нарисовать прямоугольник цветом 7:
2220
2777
2777
0000
Затем она может нарисовать прямоугольник цветом 3:
2230
2737
2777
0000
Каждый прямоугольник имеет стороны, параллельные сторонам холста и самый большой прямоугольник может быть размером с весь холст, а самый маленький размером в одну ячейку. Каждый цвет из 1…9 используется ровно один раз, хотя впоследствии любой цвет может полностью покрыть некоторые из ранних цветов.
По заданному конечному положению холста вычислите сколько из ещё видимых цветов могли быть первым нарисованным цветом.
ФОРМАТ ВВОДА:
Первая строка ввода содержит N, размер холста (1≤N≤10). Следующие N строк описывают финальную картинку холста, каждая содержит по N чисел в интервале 0…9. Гарантируется, что такой ввод был получен рисованием как описано выше с использованием различных цветов.
ФОРМАТ ВЫВОДА:
Выведите количество цветов, которые могли быть использованы первым, из всех цветов, которые видны на финальном рисунке.
| Ввод |
Вывод |
|
4
2230
2737
2777
0000
|
1 |
| |
![]()
|
|
Building a Ski Course
Массивы
Двумерные массивы
Конструктив
Фермер Джон помогает превратить его большое поле в лыжный маршрут для предстоящих Му-олимпийских игр. Поле имеет размеры M x N (1 <= M,N <=100) и его целевое финальное состояние описывается решеткой из M x N символов таких как:
RSRSSS
RSRSSS
RSRSSS
Каждый символ описывает состояние снега на этом участке R – грубый, S – гладкий (организаторы считают, что в таком случае - чередования грубых и гладких участков, гонка будет интересней).
Для выполнения этой задачи ФД планирует модифицировать свой трактор так, чтобы тот мог «отштамповать» любой фрагмент размером B x B (B<=M,B<=N) грубым снегом или гладким снегом.
ФД хочет сделать B как можно большим. С B=1 он может подготовить поле, штампуя индивидуально квадраты в соответствии с заданным финальным состоянием. Однако для бОльших значений B может оказаться невозможным выполнить задачу. Каждый квадрат поля должен быть обработан трактором. Невозможно оставить ячейку поля в исходном состоянии.
Помогите ФД определить максимально возможное значение B, которое он сможет успешно использовать.
INPUT FORMAT:
* Строка 1: Два разделённых пробелом целых числа M и N.
* Строки 2..M+1: M строк ровно по N символов (каждый R или S),
описывающих желаемое финальное состояние поля.
OUTPUT FORMAT:
* Строка 1: Максимальное значение B, которое ФД может использовать, чтобы создать нужное поле.
| Ввод |
Вывод |
|
3 6
RSRSSS
RSRSSS
RSRSSS
|
3 |
OUTPUT DETAILS:
ФД может отштамповать R колонках 1-3, затем S в колонках 2-4, затем R в колонках 3-5, и наконец, S в колонках 4-6.
| |
![]()
|
|
Вывод столбца
Двумерные массивы
Формат входных данных
В первой строке вводятся через пробел количество строк N (1<=N<=20) и количество столбцов M (1<=M<=20) двумерного массива.
Далее идет N строк по M элементов в строке - элементы двумерного массива. Все элементы двумерного массива по модулю не превышают 50.
Далее идет число k (1<=k<=N)
Формат выходных данных
Вывести на экран k-й столбец (считая, что нумерация элементов массива начинается с 1, т.е. для первого столбца k=1).
Все элементы выводить в одну строку через 1 пробел между элементами.
| |
![]()
|
|
min/max в матрице - 1
Двумерные массивы
Дана матрица numsi,j размером nxm. Заменить каждый элемент матрицы, оканчивающийся на 12, на минимальный элемент матрицы.
Формат входных данных
Программа получает на вход в первой строке два числа n, m - количество строк и столбцов в матрице. В каждой из следующих n+1 строке записаны по m чисел - элементы матрицы numsi,j. (1<= n, m <= 15, -105 <= numsi,j<=105)
Формат выходных данных
Выведите измененную матрицу на экран. Элементы в строке должны разделяться одним пробелом.
| |
![]()
|
|
min/max в матрице - 2
Двумерные массивы
Дана матрица numsi,j размером nxm. Заменить каждый элемент матрицы, оканчивающийся на 43, на максимальный элемент матрицы.
Формат входных данных
Программа получает на вход в первой строке два числа n, m - количество строк и столбцов в матрице. В каждой из следующих n+1 строке записаны по m чисел - элементы матрицы numsi,j. (1<= n, m <= 15, -105 <= numsi,j<=105)
Формат выходных данных
Выведите измененную матрицу на экран. Элементы в троке должны разделяться одним пробелом.
| |
![]()
|
|
Строки с min/max
Двумерные массивы
Дана матрица numsi,j размером nxm. Вывести те строки матрицы, в которых имеется хотя бы один элемент, равный минимальному элементу матрицы.
Формат входных данных
Программа получает на вход в первой строке два числа n, m - количество строк и столбцов в матрице. В каждой из следующих n+1 строке записаны по m чисел - элементы матрицы numsi,j. (1<= n, m <= 15, -105 <= numsi,j<=105)
Формат выходных данных
Выведите строки матрицы, которые удовлетворяют условию задачи. Строки необходимо выводить в том же порядке, в котором они записаны в матрице.
| |
![]()
|
|
Столбцы с min/max
Двумерные массивы
Дана матрица numsi,j размером nxm. Вывести те столбцы матрицы, в которых имеется хотя бы один элемент, равный минимальному элементу матрицы.
Формат входных данных
Программа получает на вход в первой строке два числа n, m - количество строк и столбцов в матрице. В каждой из следующих n+1 строке записаны по m чисел - элементы матрицы numsi,j. (1<= n, m <= 15, -105 <= numsi,j<=105)
Формат выходных данных
Выведите столбцы матрицы, которые удовлетворяют условию задачи. Элементы столбцов необходимо выводить в одной строке, столбцы выводить в том же порядке, в котором они записаны в матрице.
| |
![]()
|
|
Бинарная картина для Алисы
Двумерные массивы
Дед Мороз принёс Алисе новогодний подарок - Бинарную картину, которая представляет собой матрицу размером n x n, где каждое значение равно 0 или 1. Однако, перед тем как положить его под елку, Дед Мороз заметил, что полученная картина немного отличается от той, которую она заказывала.
Чтобы получить картинку, которую хотела Алиса, нужно выполнить следующие два шага:
- Отразить картинку горизонтально: перевернуть каждую строку матрицы.
- Инвертировать каждый пиксель: заменить каждое значение
0 на 1 и каждое значение 1 на 0.
У Деда Мороза осталось совсем немного времени, чтобы изменить ошибочную картину. Для этого необходимо просто записать в его волшебный посох программу, которая бы изменила текущую.
Помогите Деду Морозу написать программу для посоха, иначе дети могут остаться без новогодних подарков!
Формат входных данных
Программа получает на вход в первой строке число n - размер картины (1 <= n <= 20). В каждой из следующих n строк написано по n чисел 0 или 1.
Формат выходных данных
Выведите бинарную картину, которую хотела получить на Новый год Алиса. Элементы в строке разделяются одним пробелом.
| |
![]()
|
|
Максимальный в области 1
Двумерные массивы
Напишите программу, которая выводит максимальный элемент в заштрихованной области квадратной матрицы.

| |
![]()
|
|
Магический квадрат подрядка N
Двумерные массивы
Магическим квадратом порядка N называется квадратная матрица размера NхN, составленная из чисел 1, 2, ..., N2 так, называется квадратная матрица размера NхN, такая что суммы по каждому столбцу, каждой строке и каждой из двух больших диагоналей равны между собой. Напишите программу, которая проверяет, является ли заданная квадратная матрица магическим квадратом.
Формат входных данных
В первой строке вводится размер матрицы N (0 < N <= 100). В следующих N строках вводятся строки матрицы, по N значений в каждой, разделённые пробелами.
Формат выходных данных
Программа должна вывести слово 'YES', если матрица является магическим квадратом, и слово 'NO', если не является.
| |
![]()
|
|
Сортировка массива (сложная) - 2
Двумерные массивы
Квадратичные сортировки
Дан массив целых чисел. Отсортируйте массив по невозрастанию чисел составленных из последних двух цифр каждого значения (в том же порядке следования). При равенстве чисел, составленных из двух последних цифр, числа должны следовать в порядке возрастания.
Формат входных данных
Программа получает на вход в первой строке натуральное число n - размер массива. Вторая строка содержит n целых чисел ai - элементы массива (1 <= n <= 103, -104 <= ai <= 104).
Формат выходных данных
Выведите результирующий массив.
| |
![]()
|
|
Сортировка массива (сложная) - 3
Двумерные массивы
Квадратичные сортировки
Дан массив целых чисел. Отсортируйте массив по неубыванию количества четных цифр в значении каждого элемента массива. При равенстве количества четных цифр у двух элементов, числа должны следовать в порядке убывания.
Формат входных данных
Программа получает на вход в первой строке натуральное число n - размер массива. Вторая строка содержит n целых чисел ai - элементы массива (1 <= n <= 103, -104 <= ai <= 104).
Формат выходных данных
Выведите результирующий массив.
| |
![]()
|
|
Сортировка массива (сложная) - 4
Двумерные массивы
Квадратичные сортировки
Дан массив целых чисел. Отсортируйте массив по неубыванию количества нечетных цифр в значении каждого элемента массива. При равенстве количества нечетных цифр у двух элементов, числа должны следовать в порядке убывания.
Формат входных данных
Программа получает на вход в первой строке натуральное число n - размер массива. Вторая строка содержит n целых чисел ai - элементы массива (1 <= n <= 103, -104 <= ai <= 104).
Формат выходных данных
Выведите результирующий массив.
| |
![]()
|
|
Вирус
Двумерные массивы
Двумерные массивы
Обход в ширину
Способы задания графа
Задача на реализацию
В лаборатории биоинформатики ученые проводят эксперименты по распространению искусственно созданных вирусов. Для эксперимента используется специальная лабораторная установка, представляющая собой таблицу из n × m ячеек. В каждую ячейку помещается живая клетка. Ученые заражают вирусом некоторые клетки, всего исходно заражается не более 8 клеток.
Каждую секунду среди незараженных клеток, имеющих зараженную клетку в соседней по стороне ячейке, ровно одна клетка заражается вирусом.
Ученые заинтересовались, какие конфигурации зараженных клеток могут получиться через t секунд. Для начала они хотят посчитать число таких конфигураций. Помогите им это сделать.
Формат входных данных
В первой строке входного файла находятся целые числа n, m и t (1 ≤ n, m ≤ 100, 1 ≤ t ≤ 6) — размеры таблицы и количество секунд. Каждая из следющих n строк содержит m символов. Символ «.» означает, что в изначальной конфигурации клетка не заражена, а символ «*» — что заражена. Количество «*» в таблице не превышает 8. Гарантируется, что незараженных клеток в исходной конфигурации не меньше t.
Формат выходных данных
Выведите количество различных возможных конфигураций таблицы после t секунд.
| Ввод |
Вывод |
2 2 1
*.
.. |
2 |
2 2 2
*.
.. |
3 |
2 2 3
*.
.. |
1 |
| |
![]()
|
|
Вирус
Двумерные массивы
Двумерные массивы
Обход в ширину
Способы задания графа
Задача на реализацию
В лаборатории биоинформатики ученые проводят эксперименты по распространению искусственно созданных вирусов. Для эксперимента используется специальная лабораторная установка, представляющая собой таблицу из n × m ячеек. В каждую ячейку помещается живая клетка. Ученые заражают вирусом некоторые клетки, всего исходно заражается не более 8 клеток.
Каждую секунду среди незараженных клеток, имеющих зараженную клетку в соседней по стороне ячейке, ровно одна клетка заражается вирусом.
Ученые заинтересовались, какие конфигурации зараженных клеток могут получиться через t секунд. Для начала они хотят посчитать число таких конфигураций. Помогите им это сделать.
Формат входных данных
В первой строке входного файла находятся целые числа n, m и t (1 ≤ n, m ≤ 100, 1 ≤ t ≤ 6) — размеры таблицы и количество секунд. Каждая из следющих n строк содержит m символов. Символ «.» означает, что в изначальной конфигурации клетка не заражена, а символ «*» — что заражена. Количество «*» в таблице не превышает 8. Гарантируется, что незараженных клеток в исходной конфигурации не меньше t.
Формат выходных данных
Выведите количество различных возможных конфигураций таблицы после t секунд.
| Ввод |
Вывод |
2 2 1
*.
.. |
2 |
2 2 2
*.
.. |
3 |
2 2 3
*.
.. |
1 |
| |
![]()
|
|
Сортировка строк
Двумерные массивы
Алгоритмы сортировки
Напишите программу, которая переставляет строки матрицы так, чтобы значения в столбце K шли в порядке убывания. Строки, у которых значения в столбце K равны, должны быть выведены в том же порядке, в котором они стояли в исходной матрице.
Входные данные
В первой строке записаны через пробел размеры матрицы: количество строк N и количество столбцов M ( 1 <= N , M <= 100 ). В следующих N строках записаны строки матрицы, в каждой – по M натуральных чисел, разделённых пробелами. В последней строке вводится номер столбца K .
Выходные данные
Программа должна вывести получившуюся матрицу, в которой строки переставлены так, чтобы значения в столбце K шли в порядке убывания.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 5
21 22 23 24 25
26 12 18 29 33
11 37 31 14 39
16 17 18 5 20
1
|
26 12 18 29 33
21 22 23 24 25
16 17 18 5 20
11 37 31 14 39
|
| |
![]()
|
|
Изображение перекрестка
Двумерные массивы
Вложенные циклы
Необходимо изобразить в текстовом формате перекресток двух дорог.
Изображение должно иметь размер \(n \times n\), ширина дорог должна быть \(l\). Центр перекрестка должен быть в центре изображения. Для клеток дороги следует использовать символ <<*>>, для клеток вне дороги символ <<.>>.
Формат входных данных
На первой строке дано целое число \(n\). На второй строке дано первое число \(l\). (\(3 \le n \le 100\), \(1 \le l < n\), \(l\) и \(n\) имеют одинаковую четность)
Формат выходных данных
Выведите \(n\) строк, изображение перекрестка.
| |
![]()
|
|
Рамки
Двумерные массивы
Сеня решил написать операционную систему. Для начала он планирует написать подпрограмму, которая будет рисовать рамки окон.
Поле для рисования представляет собой прямоугольник \(h \times w\) пикселей, строки занумерованы сверху вниз от 1 до \(h\), столбцы — слева направо от 1 до \(w\).
На поле последовательно рисуются \(n\) рамок, \(i\)-я рамка представляет собой границы прямоугольника с противоположными углами в точках \((r_{i,1}, c_{i,1})\) и \((r_{i,2}, c_{i,2})\).
Требуется вывести получившееся изображение в виде \(h\) рядов по \(w\) символов, пискель, который не был использован при изображении рамок, следует вывести с использованием символа <<.>>, а пиксели \(i\)-й рамки с использованием \(i\)-го символа латинского алфавита (первая рамка изображается буквами <<a>>, вторая — <<b>>, и т.д.)
Формат входных данных
Первая строка содержит целые числа \(h\), \(w\) и \(n\) — размеры поля и число рамок (\(2 \le h, w \le 80\), \(1 \le n \le 26\)). Следующие \(n\) строк содержат по четыре целых числа каждая: \(r_{i,1}, c_{i,1}, r_{i,2}\) и \(c_{i,2}\) (\(1 \le r_{i,1} < r_{i,2} \le h\),. \(1 \le c_{i,1} < c_{i,2} \le w\)).
Формат выходных данных
Выведите результат вывода описанных во вводе рамок.
| |
![]()
|
|
Подматрица - 2
Двумерные массивы
У Фили есть квадратная матрица \(A\) размера \(N \times N\), но она кажется ему слишком большой. Ему гораздо больше нравятся матрицы размера \(k \times k\) (\(k < N\)).
Филя хочет получить матрицу нужного размера взяв некоторую подматрицу исходной матрицы. Подматрицей \(k \times k\) матрицы \(A\) в данном случае Филя считает матрицу \(B\) такую, что \(b_{i, j} = a_{i + x, j + y}\), для всех \(i\), \(j\) от \(1\) до \(k\). Из данного определения можно заметить, что подматрица исходной матрицы задается парой чисел (\(x\), \(y\)).
Для того, чтобы выбрать наиболее интересную для себя подматрицу, Филя хочет узнать, сколько есть способов выбрать из исходной матрицы две различные (характеризующие пары (\(x\), \(y\)) отличаются хотя бы в одной позиции) неравные подматрицы \(k \times k\). Две матрицы \(Q\) и \(P\) размера \(k \times k\) считаются равными, если для любых \(i, j: 1 \le i, j \le k\) выполняется \(q_{i, j} = p_{i, j}\). Если условия равенства не выполняется, матрицы считаются неравными.
Формат входных данных
В первой строке входного файла содержатся два натуральных числа \(N\) и \(k\) — размеры исходной и нужной матрицы. (\(1 \le k < N \le 10\)). В следующих \(N\) строках заданы через пробел по \(N\) натуральных чисел \(a_{i, j}\) — элементы исходной матрицы (\(1 \le a_{i, j} < 10\)).
Формат выходных данных
В единственной строке выходного файла выведите одно число — количество способов выбрать из исходной матрицы две различные неравные подматрицы размера \(k \times k\).
| |
![]()
|
|
Подматрица - 1
Двумерные массивы
У Фили есть квадратная матрица \(A\) размера \(N \times N\), но она кажется ему слишком большой. Ему гораздо больше нравятся матрицы размера \(k \times k\) (\(k < N\)).
Филя хочет получить матрицу нужного размера взяв некоторую подматрицу исходной матрицы. Подматрицей \(k \times k\) матрицы \(A\) в данном случае Филя считает матрицу \(B\) такую, что \(b_{i, j} = a_{i + x, j + y}\), для всех \(i\), \(j\) от \(1\) до \(k\). Из данного определения можно заметить, что подматрица исходной матрицы задается парой чисел (\(x\), \(y\)).
Для того, чтобы выбрать наиболее интересную для себя подматрицу, Филя хочет узнать, сколько есть способов выбрать из исходной матрицы две различные (характеризующие пары (\(x\), \(y\)) отличаются хотя бы в одной позиции) равные подматрицы \(k \times k\). Две матрицы \(Q\) и \(P\) размера \(k \times k\) считаются равными, если для любых \(i, j: 1 \le i, j \le k\) выполняется \(q_{i, j} = p_{i, j}\). Если условия равенства не выполняется, матрицы считаются неравными.
Формат входных данных
В первой строке входного файла содержатся два натуральных числа \(N\) и \(k\) — размеры исходной и нужной матрицы. (\(1 \le k < N \le 10\)). В следующих \(N\) строках заданы через пробел по \(N\) натуральных чисел \(a_{i, j}\) — элементы исходной матрицы (\(1 \le a_{i, j} < 10\)).
Формат выходных данных
В единственной строке выходного файла выведите одно число — количество способов выбрать из исходной матрицы две различные равные подматрицы размера \(k \times k\).
| |
![]()
|
|
Состязания - 2
Двумерные массивы
В метании молота состязается n спортcменов. Каждый из них сделал m бросков. Победителем соревнований объявляется тот спортсмен, у которого максимален наилучший результат по всем броскам. Таким образом, программа должна найти значение максимального элемента в данном массиве, а также его индексы (то есть номер спортсмена и номер попытки).
Входные данные
Программа получает на вход два числа n и m, являющиеся числом строк и столбцов в массиве. Далее во входном потоке идет n строк по m чисел, являющихся элементами массива.
Выходные данные
Программа выводит значение максимального элемента, затем номер строки и номер столбца, в котором он встречается. Если в массиве несколько максимальных элементов, то нужно вывести минимальный номер строки, в которой встречается такой элемент, а если в этой строке таких элементов несколько, то нужно вывести минимальный номер столбца. Не забудьте, что все строки и столбцы нумеруются с 0.
| |
![]()
|
|
Состязания - 3
Двумерные массивы
В метании молота состязается n спортcменов. Каждый из них сделал m бросков. Побеждает спортсмен, у которого максимален наилучший бросок. Если таких несколько, то из них побеждает тот, у которого наилучшая сумма результатов по всем попыткам. Если и таких несколько, победителем считается спортсмен с минимальным номером. Определите номер победителя соревнований.
Входные данные
Программа получает на вход два числа n и m, являющиеся числом строк и столбцов в массиве. Далее во входном потоке идет n строк по m чисел, являющихся элементами массива.
Выходные данные
Программа должна вывести одно число - номер победителя соревнований. Не забудьте, что строки (спортсмены) нумеруются с 0.
| |
![]()
|
|
Заполнение диагоналями
Двумерные массивы
Даны числа n и m. Создайте массив A[n][m] и заполните его, как показано на примере.
Входные данные
Программа получает на вход два числа n и m.
Выходные данные
Программа должна вывести полученный массив.
| |
![]()
|
|
Цифровое табло
Двумерные массивы
Задачи на моделирование
В комнате у Аркадия Семеновича Тапкина стоят электронные часы. Цифры на этих часах показываются в специальной псевдографике. А именно каждое поле, на котором изображается цифра, состоит из \(w\) ячеек в ширину и \(h\) ячеек в высоту (при этом ячейки на поле имеют форму квадратов).
Но недавно у Аркадия Семеновича появилась проблема. Последнее время он стал плохо видеть. В связи с этим он хочет увеличить изображение этих цифр. Он уже приладил старый \(19''\) монитор к часам, и теперь дело осталось за малым. Осталось написать программу, которая будет рисовать цифры на дисплее. Аркадий Семенович хочет увеличить изображение в \(k\) раз и сделать толщину линий равной \(d\). Помогите ему в этом.
Опишем более формально понятие <<увеличить в \(k\) раз>>. Занумеруем ячейки поля \(w \times h\) сверху вниз и слева направо. Таким образом, верхняя левая ячейка имеет координаты \((0, 0)\), правая нижняя — \((w - 1, h - 1)\), правая верхняя — \((w - 1, 0)\), левая нижняя — \((0, h - 1)\). Кроме этого, введем декартову прямоугольную систему координат так, что начало координат находится в центре верхней левой ячейки, ось \(Ox\) направлена вправо, ось \(Oy\) — вниз, длину единичного отрезка примем равной длине стороны ячейки. Таким образом, координаты центра ячейки совпадают с ее координатами во введенной нумерации.
Каждая десятичная цифра задается набором составляющих ее изображение отрезков. Для простоты каждый из отрезков либо параллелен одной из координатных осей, либо идет под углом в 45 градусов к ней.
Увеличенная в \(k\) раз цифра рисуется на поле размером \((w - 1) \cdot (k - 1) + w\) ячеек по горизонтали на \((h - 1) \cdot (k - 1) + h\) ячеек по вертикали.
При увеличении некоторой цифры в \(k\) раз производятся следующие операции. Координаты точек, являющихся концами отрезков, составляющих цифру, умножаются на \(k\). После этого закрашиваются те ячейки, через центры которых проходят эти отрезки. Эти ячейки будем называть основными.
После этого, для того, чтобы получить толщину линий равную \(d\), дополнительно закрашиваются те ячейки, центры которых располагаются на расстоянии, не превышающем \((d - 1)\) от центров основных ячеек. Расстоянием между точками \(A(x_A, y_A)\) и \(B(x_B, y_B)\) будем называть число \(\rho(A, B) = |x_A - x_B| + |y_A - y_B|\).
По описанию цифры и параметрам \(k\) и \(d\) выведите изображение цифры, увеличенное в \(k\) раз, с толщиной линий \(d\).
Формат входных данных
Первая строка содержит целые числа \(k\) и \(d\) (\(1 \le k \le 100\), \(1 \le d \le 500\)). Вторая строка содержит целые числа \(w\) и \(h\) (\(1 \le w, h \le 10\)).
Третья строка содержит целое число \(n\) (\(1 \le n \le 100\)) — количество отрезков в описании цифры. Далее следуют \(n\) строк, каждая из которых описывает один отрезок. Описание отрезка состоит из четырех целых чисел: \(x_1\), \(y_1\), \(x_2\), \(y_2\) (\(0 \le x_1, x_2 < w\), \(0 \le y_1, y_2 < h\)) — координат концов отрезка.
Каждый из отрезков либо параллелен одной из координатных осей, либо идет под углом в 45 градусов к ней. Все отрезки имеют ненулевую длину.
Формат выходных данных
Выходные данные должны содержать ровно \((h - 1) \cdot (k - 1) + h\) строк по \((w - 1) \cdot (k - 1) + w\) символов в каждой, \(j\)-ый символ \(i\)-ой строки должен быть равен символу <<*>> (звездочка), если ячейка с центром в точке \((j,i)\) закрашена, и символу <<.>> (точка) — иначе.
| |
![]()
|
|
Матрица
Двумерные массивы
Условный оператор
Дан набор натуральных чисел: a1, …, aN. По этому набору строится таблица чисел размером N x N по следующему правилу: в клетку i-го столбца j-й строки записывается большее из чисел ai и aj при i ≠ j (если ai = aj, то записывается это число); на пересечении i-го столбца и i-й строки записывается число 0.
Дана таблица чисел. Требуется определить, могла ли она быть построена по данным правилам из какого-либо набора чисел a1, …, aN.
Входные данные
В первой строке входных данных задается натуральное число N – размер таблицы (1 ≤ N ≤ 500). В следующих N строках содержится по N чисел – числа соответствующей строки из таблицы (все числа целые неотрицательные и не превосходят 1 000).
Выходные данные
В одну строку выведите через пробел числа a1, …, aN. Если решений несколько, выведите любое из них. Если набора, удовлетворяющего данной таблице, не существует, выведите одно число "-1".
| |
![]()
|
|
Жизнь в квадрате
Двумерные массивы
В некоторых клетках квадрата N x N
живут микроорганизмы (не более одного в одной клетке). Каждую секунду происходит следующее:
– все микроорганизмы, у которых менее 2-х соседей, умирают от скуки (соседями называются микроорганизмы, живущие в клетках, имеющих общую сторону или вершину);
– все микроорганизмы, у которых более 3-х соседей, умирают от перенаселенности;
– на всех пустых клетках, у которых ровно в трех соседних клетках жили микроорганизмы, появляются новые микроорганизмы.
Все изменения происходят одновременно, то есть для каждой клетки сначала выясняется ее судьба, а затем происходят изменения сразу во всех клетках.
Требуется по данной конфигурации определить, во что она превратится через T
секунд.
Входные данные
В первой строке вводятся два натуральных числа – N (1 ≤ N ≤ 10) и T (1 ≤ T ≤ 100). Далее записано N строчек по N чисел, описывающих начальную конфигурацию (0 – пустая клетка, 1 – микроорганизм). Числа в строках разделены пробелами.
Выходные данные
Требуется вывести N строк по N чисел – описание конфигурации через T секунд (в том же формате, как и во входных данных).
| |
![]()
|
|
Мурка ест траву
Двумерные массивы
Пастбище представляет собой прямоугольник, разбитый на N x N клеток. В каждой клетке растет трава, имеющая свою калорийность (во всех клетках калорийность травы разная). В левой нижней клетке стоит корова Мурка. Съев всю траву в своей клетке, она перемещается на одну клетку вправо или на одну клетку вверх, всегда выбирая ту из клеток, калорийность травы в которой больше (за пределами поля трава не растет). В конце концов корова приходит в правую верхнюю клетку. Требуется определить, сколько всего калорий получит корова (считая калории травы в первой и в последней клетках).
Входные данные
Сначала вводится число N – размер поля (2 ≤ N ≤ 10). В следующей строке вводятся через пробел числа, задающие количество калорий в клетках верхнего ряда, в следующей – количество калорий в клетках следующего ряда, …, в последней – количество калорий в клетках нижнего ряда. Все числа – различные, натуральные, не превосходящие 100.
Выходные данные
Требуется вывести количество калорий, которое получит корова.
| |
![]()
|
|
Монстры
Двумерные массивы
В одной секретной лаборатории вывели новый вид маленьких монстров, размером чуть больше суслика. В ходе исследований ученые решили поставить следующий эксперимент. В центре комнаты устанавливается прямоугольный стол, поверхность которого разбита на N
х M клеток размера 1 х 1. В начальный момент времени на некоторых его клетках располагаются монстры, смотрящие параллельно сторонам стола. По команде экспериментатора монстры начинают двигаться по прямой в ту сторону, в которую они смотрят, доходят до края стола и спрыгивают на пол. Там их собирает лаборант Петя и относит в клетку.
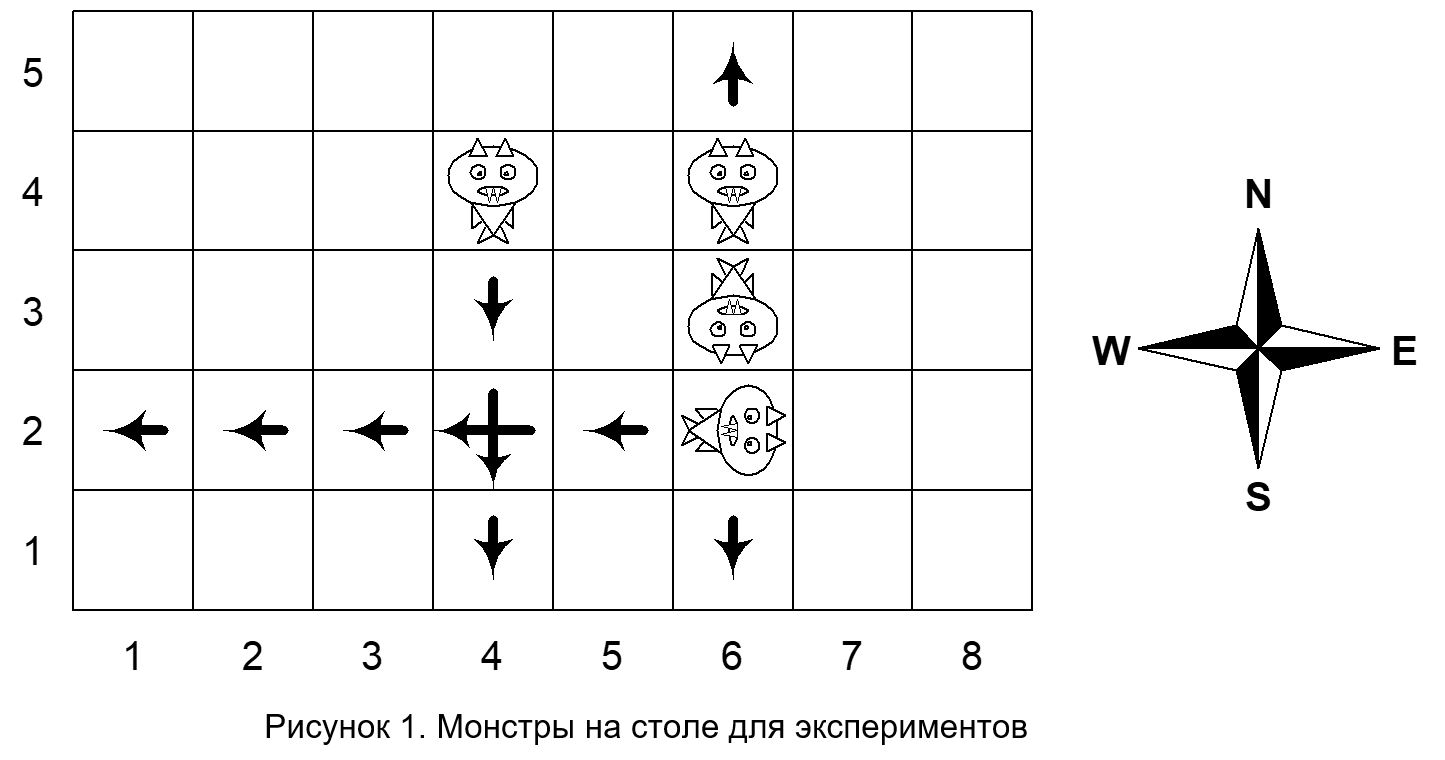
Поскольку у монстров очень грязные лапки, они оставляют следы на тех клетках, на которых они побывали. Так как отмывать стол придется лаборанту Пете, его заинтересовал вопрос - в каком количестве клеток побывают монстры. Помогите ему решить эту сложную задачу.
Входные данные
Программа получает на вход несколько строк. Первая строка содержит целые числа M и N - размеры лабораторного стола (1 <= M, N <= 106). Во второй строке записано число K - количество монстров (0 <= K <= 103). Следующие K строк содержат описания монстров - два целых числа и один символ из множества {N, E , S, W} - начальные координаты и направление соответствующего монстра (соответствие направлений и координат приведено на рисунке 1). Символ отделен от чисел ровно одним пробелом.
Символами обозначены следующие направления движения: N - вверх, S - вниз, W - влево, Е - вправо.
Выходные данные
Выведите единственное число - количество клеток стола, на которых побывают монстры.
Пояснения
Поле исполнителя и расположение "Квадратиков" для первого примера, показаны на рисунке ниже. Стрелочкой обозначено направление движения соответствующего "Квадратика".

Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
8 5
4
4 4 S
6 2 W
6 3 N
6 4 S
|
13
|
| |
![]()
|
|
Столица
Двумерные массивы
Порядковые статистики
В некотором царстве, в некотором государстве было N городов, и все они, судя по главной карте императора, имели целые координаты. В те годы леса были дремучие, дороги же строить умели только параллельно осям координат, так что расстояние между двумя городами определялось как |x1 - x2| + |y1 - y2|.
Император решил построить N+1-ый город и сделать его столицей своего государства, при этом координаты столицы также должны быть целыми. Место для столицы следует выбрать так, чтобы среднее арифметическое расстояний между столицей и остальными городами было как можно меньше. Однако, разумеется, столицу нельзя строить на месте существующего города.
Нелегкая задача выбрать место для столицы поручена Вам.
Входные данные
В первой строке вводится число N - количество городов (1 <= N <= 100). Следующие N строк содержат координаты городов - пары целых чисел, не превышающих 1000 по абсолютной величине.
Выходные данные
Выведите два целых числа - координаты точки, где следует построить столицу. Если решений несколько, выведите любое.
| |
![]()
|
|
Блокада
Двумерные массивы
Обход в глубину
Государство Флатландия представляет собой прямоугольник размером M × N, состоящий из единичных квадратиков. Флатландия разделена на K провинций (2 <= K <= 100). Каждая провинция представляет собой связное множество квадратиков, т.е. из каждой точки провинции можно дойти до любой другой ее точки, при этом разрешается переходить с квадратика на квадратик, только если они имеют общую сторону (общей вершины недостаточно). Во Флатландии нет точки, которая граничила бы более чем с тремя провинциями (т.е. четыре квадратика, имеющие общую вершину, не могут принадлежать четырем разным провинциям).
Каждая провинция имеет свой символ. Столица Флатландии находится в провинции, которой принадлежит символ A (заглавная латинская буква A). Провинция называется пограничной, если она содержит граничные квадратики. Провинция, в которой находится столица Флатландии, не является пограничной.
Король соседнего с Флатландией королевства Ректилания решил завоевать Флатландию. Для этого он хочет захватить столицу Флатландии. Однако он знает, что сил его армии недостаточно, чтобы сделать это сразу. Поэтому сначала он хочет окружить столичную провинцию, чтобы ослабить силы противника долгой блокадой, а потом захватить столицу.
Чтобы окружить провинцию, требуется захватить все провинции, с которыми она граничит. Две провинции граничат, если существует два квадратика, имеющие общую сторону, один из которых принадлежит первой из них, а другой - второй. Чтобы захватить провинцию, надо чтобы выполнялось одно из двух условий: либо она пограничная, либо граничит с какой-либо уже захваченной провинцией.
Чтобы сберечь силы своей армии, король Ректилании хочет установить блокаду столичной провинции, захватив как можно меньше провинций. Помогите ему выяснить, сколько провинций требуется захватить. Захватывать столичную провинцию нельзя, поскольку для этого сил армии Ректилании пока недостаточно.
Входные данные
В первой строке вводятся числа M и N (3 <= M, N <= 200). Следующие M строк содержат N символов каждая и задают карту Флатландии. Символ, находящийся в i + 1-й строке входных данных на j-м месте, представляет собой символ провинции, которой принадлежит квадратик (i, j). Все символы имеют ASCII-код больше 32 (пробела).
Выходные данные
Выведите единственное число - количество провинций, которые требуется захватить. Если установить блокаду невозможно, выведите "-1".
| |
![]()
|
|
Электронные часы
Двумерные массивы
Битовые операции
Дата и время
Циферблат новых электронных часов, установленных на главном здании офиса фирмы Macrohard, состоит из 4 прямоугольных панелей, каждая из которых состоит из 6 рядов по 5 лампочек в каждом. Первые две панели отображают цифры, из которых складываются часы, а следующие две - минуты. (Если сейчас меньше 10 часов, первая панель отображает 0).
К сожалению, лампочки, установленные на панелях, были произведены компанией Sveta.Net, которая известна своим принципом , вследствие чего на следующий день люди, проходя мимо офиса компании, видели лишь некоторое подобие цифр, поскольку некоторые лампочки больше не горели.
Петя живет в доме, стоящем прямо напротив офиса компании Macrohard. В первый день после установки часов он зарисовал у себя в блокноте, как выглядят все цифры на панелях (панели однотипные, поэтому одна и та же цифра на различных панелях выглядит одинаково). Теперь Петя хочет узнать, можно ли по текущему изображению на часах однозначно определить, сколько сейчас времени. Помогите ему!
Входные данные
Входные данные содержат 6 строк по 20 символов в каждой - текущее изображение на часах. Первый прямоугольник задает первую панель, следующий - вторую, следующий - третью и последний - четвертую.
Выходные данные
Если можно точно определить время, которое сейчас отображается на часах, выведите это время в формате hh:mm. Если время нельзя определить однозначно, выведите AMBIGUITY. Если же в часах точно сломалось еще что-то, например, центральный процессор, который управляет лампочками, выведите ERROR.
| |
![]()
|
|
Клетка для хомячка
Двумерные массивы
Обход в глубину
Простые задачи на перебор
Андрюше на день рождения подарили хомячка. Пока Андрюша не купил для него клетку, он решил сделать ему клетку из подручных средств. Для изготовления клетки он решил использовать набор кубиков, подаренный ему на прошлый день рождения. Однако, неожиданно выяснилось, что сестра Андрюши склеила кубики суперклеем, и отделить их друг от друга не представляется возможным.
Все кубики оказались склеены в две фигуры. Любые два кубика в каждой из фигур либо не имеют общих точек, либо имеют общую грань, либо имеют общее ребро, но в последнем случае есть кубик, с которым каждый из них имеет общую грань. Каждую фигуру можно положить на стол так, что каждый кубик будет касаться стола одной из своих граней.
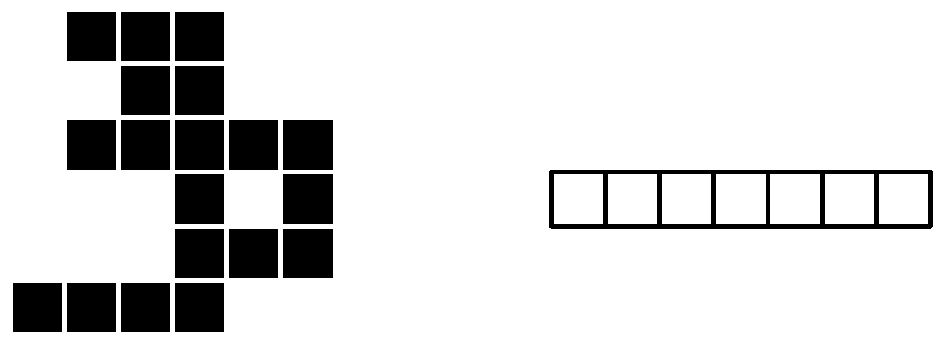
Теперь Андрюша хочет положить эти две фигуры на стол так, чтобы получилась клетка для хомячка. Фигуры должны быть положены таким образом, чтобы каждый кубик касался стола гранью. Стороны нижних граней кубиков должны быть параллельны сторонам стола. Любые два кубика, принадлежащие различным фигурам, должны либо не касаться друг друга, либо иметь общую грань, либо иметь общее ребро. Фигуры разрешается поворачивать и переворачивать.
Положив фигуры, Андрюша собирается выпустить хомячка на стол. Чтобы он не упал со стола, у него не должно быть возможности добраться от точки, в которую Андрюша его выпустит, до края стола. Хомячок не может перелезать через кубики, и, в частности, не может пролезть между двумя кубиками, имеющими общее ребро. Стол существенно больше каждой из фигур.
Андрюша хочет, чтобы площадь, по которой может бегать хомячок, была как можно больше. Помогите ему выяснить, какая максимальная площадь может быть у территории, до которой сможет добраться хомячок. Площадь грани кубика будем считать равной единице.
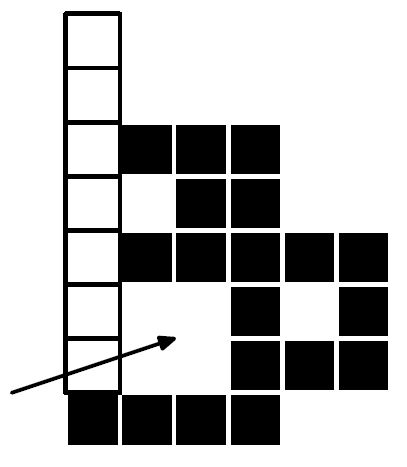
Например, две фигуры, показанные на рисунке выше, можно расположить как показано на следующем рисунке. Если выпустить хомячка в точку, отмеченную стрелкой, то доступная ему территория будет иметь площадь, равную четырем.
Входные данные
В первой строке вводятся два числа: h1 и w1 (1 <= h1, w1 <= 10). Следующие h1
строк содержат по w1 символов и описывают первую фигуру, вид сверху. Каждый из этих символов - либо "*" (звездочка), либо "." (точка), звездочка обозначает кубик, а точка – пустое место.
Далее в отдельной строке вводятся два числа: h2 и w2 (1 <= h2, w2 <= 10). Следующие h2 строк содержат по w2 символов и описывают вторую фигуру в формате, аналогичном формату первой. Каждая из фигур связна и содержит хотя бы один кубик.
Выходные данные
Выведите одно число – максимальную площадь, которая может быть доступна хомячку. Если сделать клетку для хомячка невозможно, выведите 0.
| |
![]()
|
|
Восстанови многоугольник
Двумерные массивы
Клеточная геометрия
Вася нарисовал на клетчатой бумаге многоугольник, все стороны которого проходят по линиям сетки. После этого в каждой клетке он написал число, равное количеству сторон данной клетки, которые принадлежат сторонам многоугольника. Затем он стер многоугольник так, что остался листок бумаги, в каждой клетке которого написано число.
Восстановите нарисованный Васей многоугольник.
Входные данные
В первой строке входных данных содержатся два натуральных числа: Y - количество строк и X - количество столбцов листа (3 <= Y <= 1000, 3 <= X <= 1000). В каждой из следующих Y строк задается по X целых неотрицательных чисел, не превосходящих 4. Ни одна из сторон многоугольника не проходит по границе листа бумаги.
Выходные данные
Выведите искомый многоугольник в следующем формате.
Выходные данные должны содержать Y строк по 2X-1 символов в каждой (по одному символу на клетку и линию между клетками).
В первой строке выведите вертикальные отрезки в верхнем ряду клеток, обозначая их символом | (вертикальная черта - символ с кодом 124) и горизонтальные отрезки, отделяющие первый ряд клеток от следующего, обозначая их символом _ (подчеркивание). Если соответствующий отрезок в данном многоугольнике отсутствует, выведите вместо него символ . (точка). Во второй строке выведите в том же формате вертикальные отрезки во втором ряду и горизонтальные отрезки, отделяющие второй ряд от третьего. И т.д. В каждой строке на нечетных местах могут стоять только символы точка или подчеркивание, на четных местах - символы точка или вертикальная черта.
Гарантируется, что хотя бы одно решение существует. Если решений несколько, выведите любое из них.
| |
![]()
|
|
Спираль
Двумерные массивы
Вывести квадрат, состоящий из N*N клеток, заполненных числами от 1 до N2 по спирали (см. примеры).
Входные данные
В первой строке находится единственное число N. 2 <= N <= 100.
Выходные данные
Выводится N строк по N чисел, разделённых пробелами. Не допускается начинать спираль в ином, кроме верхнего левого, углу, закручивать спираль против часовой стрелки или изнутри наружу.
| |
![]()
|
|
Змейка
Двумерные массивы
Вывести квадрат, состоящий из NxN ячеек, заполненных числами от 1 до N2 "змейкой" (см. примеры).
Входные данные
В первой строке находится единственное число N. 2 <= N <= 100.
Выходные данные
Выводится N строк по N чисел, разделённых пробелами. Не допускаются начало змейки в другом углу или другое её направление.
| |
![]()
|
|
Ближайшее число
Двумерные массивы
Дана матрица A размером N*N, заполненная неотрицательными целыми числами. Расстояние между двумя элементами Ai j и Ap q определено как |i - p| + |j - q|.
Требуется заменить каждый нулевой элемент матрицы ближайшим ненулевым. Если есть две или больше ближайших ненулевых ячейки, нуль должен быть оставлен.
Ограничения: 1 <= N <= 200, 0 <= Ai j <= 1 000 000.
Входные данные
В первой строке содержится число N. Затем идут N строк по N чисел, разделённых пробелами и представляющих собой матрицу.
Выходные данные
Выводится N строк по N чисел, разделённых пробелами, - модифицированная матрица.
| |
![]()
|
|
Крестики
Двумерные массивы
Перебор
Требуется расставить в некоторые клетки таблицы 3 x 3 крестики так, чтобы в каждой строке и в каждом столбце было заданное количество крестиков.
Входные данные
Вводятся 6 чисел (от 0 до 3) – требуемое количество крестиков в первом, втором, третьем столбце, в первой, второй, третьей строке.
Выходные данные
Требуется выдать количество возможных таблиц или 0, если таких таблиц нет.
| |
![]()
|
|
Поворот
Двумерные массивы
Дана картинка. Требуется повернуть ее на 90 градусов по часовой стрелке вокруг центра.
Картинка представляет собой квадрат, разбитый на N x N маленьких квадратиков. Каждый маленький квадратик закрашен в свой цвет. Цвета имеют номера от 0 до 255.
Входные данные
В первой строке вводится число одно натуральное число N, не превосходящее 100.
В следующих N строках записано по N чисел – цвета соответствующих квадратиков.
Выходные данные
Выведите N строк по N чисел, разделенных пробелами – цвета квадратиков после поворота картинки.
| |
![]()
|
|
Крепкий дом
Двумерные массивы
Джон Доу хочет построить крепкое здание, чтобы никто и никогда не нашел его. У него есть кирпичи 1х2, 1х3 и "уголки", то есть квадратики 2х2, у которых отсутствует одна клетка. Для уточнения смотрите на рисунки.
Стеной назовем клеточный прямоугольник, который заполняют кирпичи. Кирпичи должны ложиться по линиям сетки, их можно как угодно поворачивать. Кирпичи не могут накладываться друг на друга и на каждой клетке должен лежать кирпич.
Джон считает стену крепкой, если нельзя провести такую прямую, что по обе стороны от нее есть кирпичи и она не пересекает ни одного кирпича. Касание кирпичей не считается пересечением. Вам требуется спроектировать крепкую стену, величиной NхM. Можно поворачивать кирпичи на углы, кратные 90 градусам.
Формат входных данных
Вводятся числа N и M (1 <=N, M <= 100) высота и ширина требуемой стены.
Формат выходных данных
Выведите N строк, содержащих по M символов от «A» до «Z», описывающие стену. Каждый кирпич должен описываться одинаковыми символами (кирпичи, имеющие общую сторону должны описываться различными символами). Не должно существовать прямой, по обе стороны которой были бы кирпичи и она не пересекала бы ни один из кирпичей. Если стену с заданными ограничениями построить невозможно, выведите «impossible».
Частичные решения, работающие при N, M <=6 получат не менее 40 баллов.
| |
![]()
|
|
Экзамен
Двумерные массивы
Цикл for
Даны две таблицы. В первой записана информация о школьниках (фамилия, имя и номер школы), а во второй – информация о результатах экзамена (фамилия, имя школьника и его оценка за экзамен). Требуется составить сводную таблицу, в которой будет указан номер школы и средняя оценка за экзамен всех учеников из этой школы (средняя оценка – это среднее арифметическое всех оценок, округленное до ближайшего сверху числа).
Входные данные
В первой строке вводится одно натуральное число N, не превосходящее 50 – количество школьников.
В следующих N строках вводится информация о школьниках в формате
Фамилия Имя Номер_Школы
Фамилия и имя не содержат пробелов, а номер школы – натуральное число, не превосходящее 2007.
В следующих N строках вводится информация об экзамене в формате
Фамилия Имя Оценка
Порядок учеников может быть иным, но имена и фамилии школьников такие же, как в предыдущем списке. Оценка – натуральное число от 2 до 5.
Гарантируется, что любые два школьника отличаются именем или фамилией.
Выходные данные
Вывести список, отсортированный по возрастанию номера школы, каждая строка которого имеет формат
Номер_Школы Средняя_Оценка
| |
![]()
|
|
Преобрзование матрицы
Двумерные массивы
Введем следующие операции надо прямоугольной таблицей символов. Пусть нам дана матрица А, состоящая из m строк (первый индекс) и n столбцов (второй индекс). Определим результирующую матрицу В для каждой из операций следующим образом:
- Транспозиция относительно главной диагонали (код операции '1'): Bj,i=Ai,j
- Транспозиция относительно другой диагонали (код операции '2'): Bn-j+1,m-i+1=Ai,j
- Горизонтальное отражение (код операции 'H'): Bm-i+1,j=Ai,j
- Горизонтальное отражение (код операции 'V'): Bi,n-j+1=Ai,j
- Поворот на 90 ('A'), 180 ('B'), или 270 ('C') градусов по часовой стрелке: Bj,m-i+1=Ai,j (для 90º)
- Поворот на 90 ('X'), 180 ('Y'), или 270 ('Z') градусов против часовой стрелки: Bn-j+1,i=Ai,j (для 90º)
Вам дана последовательность не более 100000 операций над исходной матрицей. Выведите полученную в результате этих операций матрицу.
Входные данные
В первой строке входных данных находятся значения m и n (0<m,n≤300). В каждой из следующих m строк находятся по n печатных символов (т.е. не используются символы с кодами от 33 до 126).
Последняя строка содержит описание операций, которые были выполнены над этой матрицей, путем записи без пробелов из кодов. Операции выполняются по порядку слева направо.
Выходные данные
Выведите сначала два целых числа − число строк и столбцов в результирующей матрице. Затем выведите саму матрицу в том же формате, что и во входных данных.
| |
![]()
|
|
Шашки
Двумерные массивы
Петя и Вася играли в шашки по описанным ниже правилам. В какой-то момент забежавший в комнату кот перевернул доску, на которой играли Петя и Вася. К счастью, у них осталась запись сделанных ходов, используя которую можно восстановить расположение шашек к моменту, когда забежал кот.
Напишите программу, которая выведет положение шашек на доске после выполнения описанных ходов.
Правила игры
Игра происходит на стандартной доске (8х8), которая располагается так, что у игрока, играющего белыми, левая нижняя клетка является черной, и с нее начинается нумерация как строк, так и столбцов. Строки доски нумеруются числами от 1 до 8, столбцы — латинскими буквами от a до h.
| 8 |
|
|
|
|
|
|
|
|
| 7 |
|
|
|
|
|
|
|
|
| 6 |
|
|
|
|
|
|
|
|
| 5 |
|
|
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
|
|
| 1 |
|
|
|
|
|
|
|
|
|
a |
b |
c |
d |
e |
f |
g |
h |
В начале игры каждый из двух игроков имеет по 12 шашек своего цвета (белого или черного соответственно). Белые шашки располагаются на клетках a1, a3, b2, c1, c3, d2, e1, e3, f2, g1, g3, h2. Черные шашки располагаются на клетках a7, b6, b8, c7, d6, d8, e7, f6, f8, g7, h6, h8.
Игроки совершают ходы по очереди. Игрок, играющий белыми, ходит первым.
Шашки в процессе игры бывают двух видов: обычная шашка и дамка. В начале игры все шашки обычные. Белая шашка становится дамкой, если она оказывается в строке 8. Соответственно, черная шашка становится дамкой, если она оказывается в строке 1.
Шашка может совершать ходы двух типов:
1. Простой ход заключается в перемещении одной из шашек на одну клетку вперед по диагонали. Например, белая шашка с e3 может сходить на d4 или f4 (если соответствующая клетка свободна). А черная шашка с e3 может сходить на d2 или f2.
2. Рубка заключается в том, что шашка перепрыгивает через шашку (или дамку) противника, находящуюся в диагонально соседней с ней клетке при условии, что следующая клетка этой диагонали свободна. Шашка противника, которую срубили, убирается с доски. Если сразу после окончания рубки та же самая шашка может продолжить рубку, она ее продолжает этим же ходом. Рубка возможна в любом из 4-х диагональных направлений. Если в процессе рубки шашка оказывается в 1-й строке (для черных) или в 8-й (для белых), она становится дамкой.
Дамка может совершать следующие ходы:>
3. Простой ход заключается в перемещении дамки по диагонали на любое число клеток (при этом все клетки, через которые происходит перемещение, должны быть свободны).
4. Рубка заключается в том, что шашка перепрыгивает через шашку (или дамку) противника, находящуюся на той же диагонали, что и рубящая дамка. Это можно делать при условии, что все клетки между рубящей дамкой и шашкой, которую рубят, а также клетка, следующая за шашкой, которую рубят, свободны. После рубки дамка может встать на любую клетку данной диагонали за клеткой, на которой стояла срубленная шашка (при условии, что все клетки на ее пути свободны). Если из своего нового положения дамка может совершить рубку, она должна ее совершить этим же ходом.
Входные данные
В первой строке входного файла записано одно число N — количество ходов, которое было сделано с начала партии. Это количество не превышает 1000.
В каждой из следующих N строк записаны описания ходов (нечетные ходы совершались белыми, четные — черными). Описание каждого хода занимает ровно одну строку и записывается в следующем виде.
Простой ход записывается в виде <начальная клетка>–<конечная клетка>. Например, ход с c3 на d4 записывается как c3-d4.
Рубка записывается в виде <начальная клетка>:<клетка после рубки>. Если рубка продолжается, то ставится еще одно двоеточие, и записывается клетка, где окажется шашка после следующей рубки и т.д. Например, e3:c5:e7 (шашка, изначально расположенная на e3, рубит шашку на d4 и оказывается на c5, после чего рубит шашку на d6 и оказывается на e7).
Рубка a1:h8 может быть осуществлена только дамкой (например, дамка с a1 рубит шашку, стоящую в c3, и заканчивает ход в h8). Рубка дамкой может быть и такой a1:d4:f6:h4 (дамка рубит шашку, стоящую на b2, затем продолжает рубку и рубит шашку на e5, и, наконец, рубит шашку на g5). При этом после каждой рубки указывается клетка, на которой останавливается дамка перед следующей рубкой.
Строки с описанием ходов не содержат пробельных символов.
Выходные данные
В выходной файл выведите изображение доски с расположенными на ней шашками. В первой строке выходного файла должна быть выведена 8-я строка доски, во второй — 7-я и т.д. В каждой строке должно быть ровно 8 символов, описывающих клетки столбцов с a по h.
Белая клетка должна быть изображена символом “.” (точка), пустая черная клетка — символом “–“ (минус). Черная клетка, в которой стоит белая шашка — символом “w” (маленькая латинская буква w), а клетка с белой дамкой — символом “W” (заглавная латинская буква W). Аналогично клетка с черной шашкой должна быть изображена символом “b” (маленькая латинская буква b), а клетка с черной дамкой — символом “B” (большая латинская буква B)
| |
![]()
|
|
Сапер
Двумерные массивы
Условный оператор
Мальчику Васе очень нравится известная игра "Сапер" ("Minesweeper").
В "Сапер" играет один человек. Игра идет на клетчатом поле (далее будем называть его картой) NxM (N строк, M столбцов). В K клетках поля стоят мины, в остальных клетках записано либо число от 1 до 8 — количество мин в соседних клетках, либо ничего не написано, если в соседних клетках мин нет. Клетки являются соседними, если они имеют хотя бы одну общую точку, в одной клетке не может стоять более одной мины. Изначально все клетки поля закрыты. Игрок за один ход может открыть какую-нибудь клетку. Если в открытой им клетке оказывается мина — он проигрывает, иначе игроку показывается число, которое стоит в этой клетке, и игра продолжается. Цель игры — открыть все клетки, в которых нет мин.
У Васи на компьютере есть эта игра, но ему кажется, что все карты, которые в ней есть, некрасивые и неинтересные. Поэтому он решил нарисовать свои. Однако фантазия у него богатая, а времени мало, и он хочет успеть нарисовать как можно больше карт. Поэтому он просто выбирает N, M и K и расставляет мины на поле, после чего все остальные клетки могут быть однозначно определены. Однако на определение остальных клеток он не хочет тратить свое драгоценное время. Помогите ему!
По заданным N, M, K и координатам мин восстановите полную карту.
Входные данные
В первой строке входного файла содержатся числа N, M и K (1≤N≤200, 1≤M≤200, 0≤K≤N≤M). Далее идут K строк, в каждой из которых содержится по два числа, задающих координаты мин. Первое число в каждой строке задает номер строки клетки, где находится мина, второе число — номер столбца. Левая верхняя клетка поля имеет координаты (1,1), правая нижняя — координаты (N,M).
Выходные данные
Выходной файл должен содержать N строк по M символов — соответствующие строки карты. j-й символ i-й строки должен содержать символ ‘*‘ (звездочка) если в клетке (i,j) стоит мина, цифру от 1 до 8, если в этой клетке стоит соответствующее число, либо ‘.‘ (точка), если клетка (i,j) пустая.
| |
![]()
|
|
Робот K-79
Двумерные массивы
Петя написал программу движения робота К-79. Программа состоит из следующих команд:
- S — сделать шаг вперед
- L — повернуться на 90º влево
- R — повернуться на 90º вправо
Напишите программу, которая по заданной программе для робота определит, сколько шагов он сделает прежде, чем впервые вернется на то место, на котором уже побывал до этого, либо установит, что этого не произойдет.
Входные данные
Во входном файле записана одна строка из заглавных латинских букв S, L, R, описывающая программу для робота. Общее число команд в программе не превышает 200, при этом команд S — не более 50.
Выходные данные
В выходной файл выведите, сколько шагов будет сделано (то есть выполнено команд S) прежде, чем робот впервые окажется в том месте, через которое он уже проходил. Если такого не произойдет, выведите в выходной файл число –1.
| |
![]()
|
|
Квадрат
Двумерные массивы
Жадный алгоритм
Требуется в каждую клетку квадратной таблицы размером NxN поставить ноль или единицу так, чтобы в любом квадрате размера KxK было ровно S единиц.
Входные данные
Во входных данных записаны три числа — N, K, S (1 ≤ N ≤ 100, 1 ≤ K ≤ N, 0 ≤ S ≤ K2).
Выходные данные
Выведите заполненную таблицу. Числа в строке должны разделяться пробелом, каждая строка таблицы должна быть выведена на отдельной строке файла. Если решений несколько, выведите любое из них.
| |
![]()
|