| | | |
|
Сломанный робот
Элементарная геометрия
Конструктив
В 2037-м году для создания научно исследовательской базы на Марс высадился отряд роботов, один из которых отправился собирать информацию о районе дислокации. В данный момент роботу из-за отказа некоторых узлов срочно необходимо вернуться в место закладки будущей базы.
Поверхность Марса в районе высадки десанта можно условно представить в виде плоскости с введенной на ней системой координат, такой, что база находится в точке (0, 0). Робот же остановился в точке (x0, y0). Он может перемещаться в четырёх направлениях:
• «R» — вправо, при этом координата x робота увеличивается на 1;
• «L» — влево, при этом координата x робота уменьшается на 1;
• «U» — вверх, при этом координата y робота увеличивается на 1;
• «D» — вниз, при этом координата y робота уменьшается на 1.
Из-за неисправности робот не может совершить два перемещения подряд в одном направлении.
Помогите роботу вернуться на базу. Робот должен сделать не более 10000 передвижений, иначе он разрядится и не доедет до базы!
Входные данные
В единственной строке входных данных находятся два целых числа x0 и y0 — изначальные координаты робота (−1000 ≤ x0, y0 ≤ 1000).
Выходные данные
В первой строке выведите целое число, не большее 10000 — количество операций, которые должен сделать робот. Во второй строке выведите сами операции. Каждая операция задаётся одной буквой:
вправо — «R» влево — «L», вверх — «U», вниз — «D». Символы необходимо выводить без пробелов между ними.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 1 |
5
DLULD |
Замечание
Вы не обязаны выводить кратчайший маршрут. Например, в приведенном примере кратчайший
маршрут состоит из 3 передвижений: влево, вниз, влево.
Иллюстрация к тесту из примера:
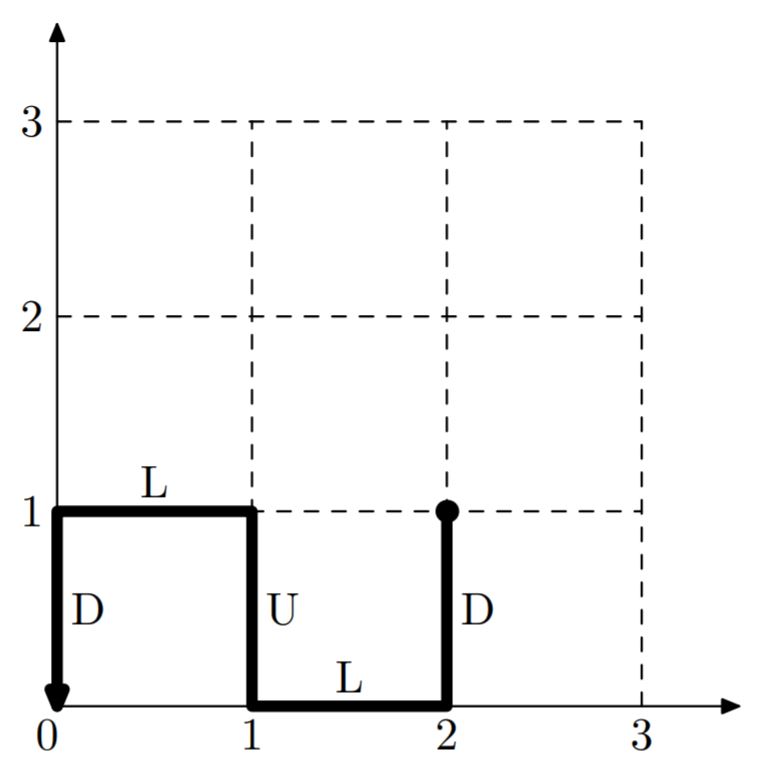
| |
![]()
|
|
Строки
Строки
Конструктив
Даны три строки, состоящие из строчных латинских букв. С этими строками можно производить следующие операции: либо заменить один символ строки на два таких же символа (например, заменить символ «a» на «aa»), либо, наоборот, заменить два подряд идущих одинаковых символа на один такой же символ.
Необходимо при помощи этих операций сделать все три строки равными какой-то другой общей строке S либо определить, что это сделать невозможно. При этом нужно минимизировать общее количество операций.
Входные данные
Программа получает на вход три строки, состоящие из строчных букв латинского алфавита. Длина каждой строки не превышает 100 символов.
Выходные данные
Если при помощи указанных операций возможно сделать все три строки равными, выведите такую строку S , что суммарное число операций, необходимых для преобразования всех трёх данных строк к строке S , будет минимальным. Если этого сделать нельзя, программа должна вывести одно слово IMPOSSIBLE (заглавными буквами).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
aaaza
aazzaa
azzza |
aazza |
| 2 |
xy
xxyy
yx |
IMPOSSIBLE |
| |
![]()
|
|
Ох уж эти палиндромы
Конструктив
Назовём палиндромом непустую строку, которая читается одинаково справа налево и слева направо. Например, « abcba », « a » и « abba » являются палиндромами, а « abab » и « xy » не являются.
Назовём подстрокой строки строку, полученную отбрасыванием некоторого (возможно, нулевого) количества символов с начала и с конца строки. Например, « abc », « ab » и « c » являются подстроками строки « abc », а « ac » и « d » не являются.
Назовем палиндромностью строки количество её подстрок, которые являются палиндромами. Например, палиндромность строки « aaa » равна 6, так как все её подстроки являются палиндромами, а палиндромность строки « abc » равна 3, так как только подстроки длины 1 являются палиндромами.
Вам дана строка s. Вы можете произвольным образом переставлять символы в ней. Требуется получить строку, имеющую максимальную палиндромность.
Входные данные
В первой строке задано целое число n (1 ≤ n ≤ 100000) — длина строки s.
Во второй строке задана строка s, состоящая из n строчных букв латинского алфавита.
Выходные данные
Выведите строку t, которая состоит из тех же символов (с учётом кратностей), что и s, и имеет максимальную палиндромность среди всех строк, которые могут быть получены из s перестановкой символов.
Если подходящих строк несколько, выведите любую.
Примечание
В первом примере у строки « ololo » есть 9 подстрок-палиндромов: « o », « l », « o », « l », « o », « olo », « lol », « olo », « ololo ». Обратите внимание, что некоторые подстроки совпадают, но учитываются несколько раз.
Во втором примере палиндромность строки « abccbaghghghgdfd » равна 29.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
oolol |
ololo |
| 2 |
16
gagadbcgghhchbdf |
abccbaghghghgdfd |
| |
![]()
|
|
Гуляй и телепортируйся
Конструктив
На линии, идущей с востока на запад, есть N городов. Города пронумерованы от 1 до N в порядке с запада на восток. Каждая точка на линии имеет одномерные координаты, а точка, которая находится дальше на восток, имеет большее значение координаты. Координата города i - Xi. Вы находитесь в городе 1 и хотите посетить все остальные города. У вас есть два способа путешествовать:
- Ходить по линии. Ваш уровень усталости увеличивается на A каждый раз, когда вы путешествуете на расстояние 1, независимо от направления.
- Телепортируйтесь в любое место по вашему выбору. Ваш уровень усталости увеличивается на B независимо от пройденного расстояния.
Найдите минимально возможное общее повышение уровня вашей усталости, когда вы посетите все города этими двумя способами.
Входные данные
В первой строке заданы три целых числа N (\(2<=N<=10^5\)), A (\(1<=A<=10^9\)), B (\(1<=B<=10^9\)). Во второй строке заданы координаты городов Xi (\(1<=X_i<=10^9\)), для всех i \(X_i <X_{i+1}\)(\(1<=i<=N-1\)).
Выходные данные
Выведите на экран ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
4 2 5
1 2 5 7 |
11 |
Из города 1 пройдите расстояние 1 до города 2, затем телепортируйтесь в город 3, затем пройдите расстояние 2 до города 4.
Общее увеличение вашего уровня усталости в этом случае составляет 2 × 1 + 5 + 2 × 2 = 11, что является минимально возможным значением. |
| 2 |
7 1 100
40 43 45 105 108 115 124 |
84 |
Из города 1 пройдите пешком до города 7.
Общее увеличение вашего уровня усталости в этом случае составляет 84, что является минимально возможным значением. |
| 3 |
7 1 2
24 35 40 68 72 99 103 |
12 |
Посетите все города в любом порядке, телепортировавшись шесть раз.
Суммарное повышение уровня утомляемости в этом случае составляет 12, что является минимально возможным значением. |
| |
![]()
|
|
Еще одна игра в кости
Конструктив
Ушан решил сыграть шестигранным кубиком. На каждой из шести сторон изображено целое число от 1 до 6, а два числа на противоположных сторонах всегда в сумме дают 7. Ушан сначала кладет кубик на стол произвольной стороной вверх, а затем повторно выполняет следующую операцию. Поверните кубик на 90 ° в одном из следующих направлений: влево, вправо, вперед (кубик приблизится) и назад (кубик уйдет дальше), затем получите y очков, где y - это число, написанное на стороне, обращенной вверх.
Например, давайте рассмотрим ситуацию, когда сторона, показывающая 1, обращена вверх, ближняя сторона показывает 5, а правая сторона показывает 4, как показано на рисунке (исходное положение для нашего примера).
Если кубик повернуть вправо, как показано на рисунке, сторона, показывающая 3, будет обращена вверх. Если из исходного положения кубик повернуть влево, сторона, показывающая 4, будет смотреть вверх. Вверху будет сторона, показывающая 2, если кубик из исходного положения повернуть вперед, а сторона, показывающая 5, будет обращена вверх, если кубик повернуть назад из исходного положения.
Найдите минимальное количество операций, которое Ушан должен выполнить, чтобы набрать в сумме не менее x баллов.
Входные данные
На вход подается целое число x (\(1<=x<=10^{15}\)).
Выходные данные
Выведите на экран ответ.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
7 |
2 |
| 2 |
149696127901 |
27217477801 |
| |
![]()
|
|
Пожиратель карт
Конструктив
Сортировка подсчетом
Ушан решил сыграть в карточную игру. У него есть колода, состоящая из N съедобных карт. На i-й карте сверху написано целое число Ai. Ушан выполняет описанную ниже операцию ноль или более раз, так что значения, записанные на оставшихся карточках, будут попарно различны.
Найдите максимально возможное количество оставшихся карт. Здесь N нечетное, что гарантирует сохранение хотя бы одной карты.
Операция: вынуть из колоды три произвольные карты. Из этих трех карт съешьте две: одну с наибольшим значением, а другую с наименьшим значением. Затем верните оставшуюся одну карту в колоду.
Входные данные
В первой строке записано нечетное число N (\(3<=N<=10^5\)). Во второй строке записаны N чисел Ai (\(1<=A_i<=10^5\))
Выходные данные
Выведите максимально возможное количество оставшихся карт.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснения |
| 1 |
5
1 2 1 3 7 |
3 |
Оптимальное решение - выполнить операцию один раз, вынув две карты с 1 и одну карту с 2. Одна карта с 1 и другая с 2 будут съедены, а оставшаяся карта с 1 будет возвращена в колоду.
Тогда значения, написанные на оставшихся картах в колоде, будут попарно различными: 1, 3 и 7. |
| 2 |
15
1 3 5 2 1 3 2 8 8 6 2 6 11 1 1 |
7 |
|
| |
![]()
|
|
Голосование
Циклы
Конструктив
Разбор случаев
Коротышки решили взять в полет на Луну либо Незнайку либо Пончика. Не сумев договориться, они решили проголосовать. Незнайка и Пончик наблюдают краткий отчет о голосовании. Коротышки показывают Незнайке и Пончику соотношение текущего количества голосов, полученных Незнайкой и Пончиком, но не фактическое количество голосов. Незнайка и Пончик посмотрели отчет N раз, и когда они смотрели его в i-й (1<=i<=N) раз, соотношение было Pi:Ni. Известно, что Незнайка и Пончик имели хотя бы один голос, когда впервые увидели отчет. Найдите минимально возможное общее количество голосов, полученных Незнайкой и Пончиком, когда они проверили отчет в N-й раз. Можно предположить, что количество голосов, полученных Незнайкой и Пончиком, никогда не уменьшается.
Входные данные
В первой строке задается целое число N (1<=N<=1000). В следующих N строках записано по 2 числа Pi и Ni (1<=Pi,Ni<=1000). Pi и Ni - взаимно простые числа.
Выходные данные
Выведите минимально возможное общее количество голосов. Гарантируется, что правильный ответ - не более 1018.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
3
2 3
1 1
3 2 |
10 |
Количество голосов, полученных Пончиком и Незнайкой, изменяется так 2,3 → 3,3 → 6,4.
Общее количество голосов в конце составляет 10, что является минимально возможным числом. |
| 2 |
4
1 1
1 1
1 5
1 100 |
101 |
Возможно, что ни Пончик ни Незнайка не получили голосов между моментом, когда они смотрели отчет, и моментом, когда они смотрели его в следующий раз. |
| 3 |
5
3 10
48 17
31 199
231 23
3 2 |
6930 |
|
| |
![]()
|
|
Сортировщик Томми
"Два указателя"
Жадный алгоритм
Конструктив
У Томми есть детская игрушка «cортировщик», с расположенными подряд n колышками. На каждом колышке сейчас не более одного диска (то есть на каком-то колышке диск есть, а на каком-то его нет). Томми хочет переложить имеющиеся диски на колышках таким образом, чтобы они образовывали неубывающую последовательность при просмотре слева направо. То есть на каждом следующем колышке количество дисков должно быть не меньше, чем на предыдущем. Какое минимальное количество дисков Томми необходимо переложить?
Обратите внимание, что какие- то колышки по окончанию сортировки могут быть пустыми. Какие-то колышки могут содержать более 1 диска.
Входные данные
Программа получает на вход в первой строке целое число n (1 <= n <= 105), количество колышек на «cортировщике». Следующая строка содержит n целых чисел a1, a2, ... an – наличие диска на соответствующем колышке (0 <= ai <= 1). число 0 означает, что на i-м колышке нет диска, 1 – диск есть.
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
8
0 0 1 1 1 1 1 1
|
0
|
| 2 |
11
1 1 0 0 1 0 0 1 1 1 0
|
3
|
| |
![]()
|
|
Чемпионат по поиску в сети Меганет
Структуры данных
Строки
Динамическое программирование
Конструктив
Задача на реализацию
Для проведения чемпионата мира по поиску в сети Меганет организаторам необходимо ограничить доступ к некоторым адресам. Адрес в сети Меганет представляет собой строку, состоящую из имени сервера и имени раздела.
Имя сервера представляет собой строку, содержащую от одной до пяти частей включительно. Каждая часть представляет собой непустую строку, состоящую из строчных букв латинского алфавита. Части разделены точкой. Примеры корректных имен сервера: «a», «ab.cd», «abacaba», «a.b.c.d.e».
Имя раздела представляет собой строку, которая может быть либо пустой, либо содержать от одной до пяти частей включительно. Каждая часть начинается с символа «/», после которого следует одна или несколько строчных латинских букв. Примеры корректных имен разделов: «», «/a», «/aba», «/a/b/c/d/e». Адрес формируется приписыванием имени раздела в конец имени сервера. Например, корректными адресами являются строки: «a», «aba/d/f/g/h», «a.b», «aba.caba/def/g», «c.d.e.f.g/a/b/c/d/e».
Для ограничения доступа к некоторым адресам сети Меганет организаторы чемпионата подготовили несколько фильтров. Фильтр, как и адрес, состоит из двух частей: фильтра сервера и фильтра раздела.
Фильтр сервера состоит из имени сервера, перед которым может также идти строка «*.». Если фильтр сервера представляет собой только имя сервера, то этому фильтру соответствует только сервер, имеющий точно такое же имя. Если фильтр сервера представляет собой строку «*.S », где S — имя сервера, то ему соответствуют сервера, удалением нуля или более начальных частей от имени которых можно получить строку S.
Аналогично, фильтр раздела представляет собой имя раздела, после которого может идти строка «/*». Фильтру раздела, который представляет собой просто имя раздела R, соответствуют только разделы, в точности совпадающие с R. Если фильтр раздела представляет собой строку «R/*», то ему соответствуют все разделы, удалением от имен которых нуля или более конечных частей можно получить строку R. Адрес соответствует фильтру, если его имя сервера соответствует фильтру сервера, а его имя раздела соответствует фильтру раздела.
Примеры фильтров и соответствующих им адресов приведены в таблице ниже.
| ab.c/d/e |
ab.c/d/e |
| *.a |
a ax.a efg.a |
| *.a/b/c |
a/b/c x.a/b/c e.fg.a/b/c |
| x.yz/a/* |
x.yz/a x.yz/a/b/c x.yz/a/xyz |
| *.a/* |
a x.a e.fg.a
a/b/c x.a/ddd/c e.fg.a/b/c/g/haha/i |
| *.a/b/c/* |
a/b/c x.a/b/c e.fg.a/b/c
a/b/c/xxx e.fg.a/b/c/d/e/f |
| |
|
Требуется написать программу, которая по заданному набору фильтров и списку адресов определяет для каждого адреса, какому числу фильтров соответствует этот адрес.
Пример:
Ввод:
2 0
a.bb/c
bb/c/d
4
a.bb
bb/c/d
a.bb/c/d
bb/c
Вывод:
0
1
0
0
Вывод:
4 0
*.bb/c
*.bb/c/*
bb/c/*
bb/c/*
6
bb
bb/c
bb/c/d
a.bb
a.bb/c
a.bb/c/d
Вывод:
0
4
3
0
2
1
| |
![]()
|
|
Пляжный волейбол
Конструктив
Вера очень много работала в этом году, подавая своим коллегам пример настоящего труженика. На восьмое марта за прекрасное исполнение служебных обязанностей Вера получила подарок — долгожданный отпуск в Теплой Стране! Тяжелые трудовые будни закончились, и Вера уже нежится на пляже на берегу Теплого Моря.
Любимое хобби Веры — пляжный волейбол, и как же Вера ждала момента, когда она сможет испытать невероятный азарт этой игры! Вера уже познакомилась с несколькими симпатичными волейболистами, но она пока не решила, какая же команда достойна иметь в своем составе такого замечательного игрока.
Каждый из N капитанов команд мечтает заполучить Веру в состав своей команды, поэтому они хотят максимально проявить себя. Так как поиграть хотят все, они решили действовать следующим образом: все N команд выстроились в очередь. Первый матч иг- рается между двумя командами, которые стоят в очереди раньше остальных. Победитель игры остается на площадке, а проигравший отправляется в конец очереди. В каждом из следующих матчей победитель предыдущего играет с первой командой из очереди, а про- игравший в очередной встрече опять становится в конец очереди. Каждая команда имеет некоторую силу, причем для простоты будем предполагать, что силы всех команд различ- ны, а победителем в матче является команда, сила которой больше. Матчей может быть как угодно много.
Вера решила для себя, что она будет действовать по самому справедливому принципу «считалочки»: она будет играть с одной из двух команд, играющих матч с соответствую- щем считалке номером K. Но затем Вера поняла, что уже выбрала себе команду, в которой хотела бы играть, причем ориентируясь не только на ее силу. Ей известны Q считалок, соответствующих различным значениям K. Для каждого из этих чисел Ki необходимо узнать, а кто же именно будет сражаться за столь ценный приз, то есть какие две коман- ды будут играть в матче с номером Ki.
Формат входного файла
Первая строка входных данных содержит единственное целое число N — количество команд (2 <= N <= 100 000). Вторая строка содержит N различных чисел от 1 до N — силы команд: первое число — сила команды, стоящей в начале очереди, второе — сила следующей по очереди команды, ..., последнее — сила команды, стоящей в конце очереди. Третья строка содержит единственное целое число Q (1 <= Q <= 100 000) — коли- чество известных Вере считалок. Каждая из следующих Q строк содержит число Ki (1 <= Ki <= 1018) — номер очередного интересующего Веру матча. Обратите внимание, Ki может быть больше N. Формат выходного файла Выведите Q строк: для каждого интересующего Веру числа Ki два числа в любом порядке — силы команд, сыграющих на Ki-м шаге. Первая строка должна содержать ответ на первый запрос, вторая — на второй и так далее.
Примеры
| Ввод |
Вывод |
4
1 3 2 4
1
3 |
3 4 |
4
2 1 4 3
3
1
5
2 |
2 1
4 2
2 4 |
Комментарии
Разберем первый тест из условия:
| |
Кто играет |
Состояние очереди |
Победитель |
Проигравший |
Матч № 1
Матч № 2
Матч № 3 |
1 3
3 2
3 4 |
2 4
4 1
1 2 |
3
3
4 |
1
2
3 |
Таким образом, в единственном интересующем Веру третьем матче сыграют команды с силами 4 и 3.
| |
![]()
|
|
Little Difference
Динамическое программирование: последовательности
Конструктив
Little Lidia likes playing with numbers. Today she has a positive integer n, and she wants to decompose it to the product of positive integers.
Because Lidia is little, she likes to play with numbers with little difference. So, all numbers in decomposition should differ by at most one. And of course, the product of all numbers in the decomposition must be equal to n. She considers two decompositions the same if and only if they have the same number of integers and there is a permutation that transforms the first one to the second one.
Write a program that finds all decompositions, which little Lidia can play with today.
Input
The only line of the input contains a single integer n (1 ≤ n ≤ 1018).
Output
In first line output the number of decompositions of n, or −1 if this number is infinite. If number of decompositions is finite, print all of them one per line. In each line first print number ki of elements in decomposition. Then print ki integers in this decomposition in any order. Don’t forget that decompositions which are different only in order of elements are considered the same.
| Input |
Output |
| 12 |
3
1 12
3 2 3 2
2 4 3 |
| 1 |
-1 |
In the second example 1 can be represented as product of any number of ones.
| |
![]()
|
|
Consonant Fencity
Конструктив
Строки
There are two kinds of sounds in spoken languages: vowels and consonants. Vowel is a sound, produced with an open vocal tract; and consonant is pronounced in such a way that the breath is at least partly obstructed. For example, letters a and o are used to express vowel sounds, while letters b and p are the consonants (e.g. bad, pot).
Some letters can be used to express both vowel and consonant sounds: for example, y may be used as a vowel (e.g. silly) or as a consonant (e.g. yellow). The letter w, usually used as a consonant (e.g. wet) could produce a vowel after another vowel (e.g. growth) in English, and in some languages (e.g. Welsh) it could be even the only vowel in a word.
In this task, we consider y and w as vowels, so there are seven vowels in English alphabet: a, e, i, o, u, w and y, all other letters are consonants.
Let’s define the consonant fencity of a string as the number of pairs of consecutive letters in the string which both are consonants and have different cases (lowercase letter followed by uppercase or vice versa). For example, the consonant fencity of a string CoNsoNaNts is 2, the consonant fencity of a string dEsTrUcTiOn is 3 and the consonant fencity of string StRenGtH is 5.
You will be given a string consisting of lowercase English letters. Your task is to change the case of some letters in such a way that all equal letters will be of the same case (that means, no letter can occur in resulting string as both lowercase and uppercase), and the consonant fencity of resulting string is maximal.
Input
The only line of the input contains non-empty original string consisting of no more than 106 lowercase English letters.
Output
Output the only line: the input string changed to have maximum consonant fencity.
| Input |
Output |
| consonants |
CoNsoNaNts |
| destruction |
dEsTrUcTiOn |
| strength |
StRenGtH |
| |
![]()
|
|
Boolean Satisfiability
Алгоритмы на графах
Конструктив
Комбинаторика
Boolean satisfiability problem (SAT) is known to be a very hard problem in computer science. In this problem you are given a Boolean formula, and you need to find out if the variables of a given formula can be consistently replaced by the values true or false in such a way that the formula evaluates to true. SAT is known to be NP-complete problem. Moreover, it is NP-complete even in case of 3-CNF formula (3-SAT). However, for example, SAT problem for 2-CNF formulae (2-SAT) is in P.
#SAT is the extension of SAT problem. In this problem you need to check if it is possible, and count the number of ways to assign values to variables. This problem is known to be #P-complete even for 2-CNF formulae. We ask you to solve #1-DNF-SAT, which is #SAT problem for 1-DNF formulae.
You are given a Boolean formula in 1-DNF form. It means that it is a disjunction (logical or) of one or more clauses, each clause is exactly one literal, each literal is either variable or its negation (logical not). Formally:
 Your task is to find the number of ways to replace all variables with values true and false (all occurrences of the same variable should be replaced with same value), such that the formula evaluates to true.
Input
The only line of the input file contains a logical formula in 1-DNF form (not longer than 1000 symbols). Logical operations are represented by ‘|’ (disjunction) and ‘~’ (negation). The variables are ‘A’ . . . ‘Z’ and ‘a’ . . . ‘z’ (uppercase and lowercase letters are different variables). The formula contains neither spaces nor other characters not mentioned in the grammar.
Output
Output a single integer — the answer for #SAT problem for the given formula
| Input |
Output |
| a |
1 |
| B|~B |
2 |
| c|~C |
3 |
| i|c|p|c |
7 |
| |
![]()
|
|
Коды Грея
Задача на реализацию
Рекурсия
Конструктив
На занятиях по дискретной математике Сереже рассказали про двоичные коды Грея — это такое упорядочение всех 2n различных двоичных векторов длины n, что любые два соседних, а также первый и последний, вектора различаются ровно в одном разряде.
Для закрепления материала преподаватель задал им следующее задание: в коде Грея в каждом двоичном векторе ровно один бит заменен на знак вопроса «?». Требуется заменить обратно все знаки вопроса «?» на «0» или «1», чтобы получился код Грея.
Преподаватель обещал бонус на экзамене тому из студентов, кто первым справится с заданием. Помогите Сереже решить задачу или скажите, что это невозможно, и преподаватель задал нераз- решимое задание.
Формат входных данных
В первой строке содержится целое число n — длина двоичных векторов. Следующие 2n строк содержат двоичные вектора длины n, в каждом из которых ровно один символ заменен на знак вопроса «?».
Формат выходных данных
В первой строке выведите «YES», если решение существует, и «NO» — в противном случае. В случае положительного ответа выведите исходный код Грея, если возможных вариантов ответа несколько, выведите любой.
| Ввод |
Вывод |
2
0?
0?
1?
1? |
YES
00
01
11
10 |
3
?00
0?1
01?
0?0
?10
1?1
10?
1?1 |
NO |
Система оценки
| Номер подзадачи |
Баллы |
Ограничения |
Комментарии |
| 1 |
37 |
1<=n<=4 |
Баллы начисляются, если все тесты пройдены. |
| 2 |
63 |
1<=n<=12 |
Баллы начисляются, если все тесты этой и предыду- щих подзадач пройдены. |
| |
![]()
|
|
Modern Art 2
Стек
Конструктив
Линейные структуры
Picowso решила переключиться на 1-мерный стиль.
Теперь её картины могут описываться 1-мерным массивом цветов длины NN (1≤N≤100,000). А вот стиль у неё остался прежний: Он начинает на пустом отрезке и рисует отрезками. Она использует каждый из цветов 1…N ровно один раз, хотя некоторые из цветов могут быть полностью скрыты к концу рисования.
Moonet, соперник Picowso, придумал, как копировать картины Picowso. Он рисует множество не соединяющихся интервалов и т.д. Moonet может рисовать не более одного интервала каждого цвета во время всего процесса. Вычислите количество таких раундов, которые требуются Moonet, чтобы скопировать 1-мерную картину Picowso.
ФОРМАТ ВВОДА:
Первая строка ввода содержит N, и следующие N строк содержат целое число в интервале 0…N, указывающее цвет каждой ячейки на 1-мерном холсте (0 для пустой ячейки).
ФОРМАТ ВЫВОДА:
Выведите минимальное количество раундов, которое требуется для копирования заданного рисунка или -1, если невозможно повторить этот рисунок стилем, аутеничным стилю Picowso (то есть, её нельзя нарисовать слоями последовательностей интервалов, по одному каждого цвета).
| Ввод |
Вывод |
|
7
0
1
4
5
1
3
3
|
2 |
Примечание
В данном примере интервал цвета 1 должен быть закрашен в более раннем раунде, чем интервалы цветов 4 и 5, поэтому необходимо как минимум два раунда.
| |
![]()
|
|
Modern Art #3
Двумерные массивы
Конструктив
Недавно вошла в моду корова-художница Picowso.
Picowso рисует особым образом. Она начинает на чистом холсте N×N, представленной матрицей N×N нолей, где ноль означает пустую ячейку холста. Затем она рисует до 9 прямоугольников на холсте, каждый одним из 9 цветов (последовательно пронумерованных 1…9). Например, она может начать рисовать прямоугольник цветом 2, получая такое промежуточное состояние холста:
2220
2220
2220
0000
Затем она может нарисовать прямоугольник цветом 7:
2220
2777
2777
0000
Затем она может нарисовать прямоугольник цветом 3:
2230
2737
2777
0000
Каждый прямоугольник имеет стороны, параллельные сторонам холста и самый большой прямоугольник может быть размером с весь холст, а самый маленький размером в одну ячейку. Каждый цвет из 1…9 используется ровно один раз, хотя впоследствии любой цвет может полностью покрыть некоторые из ранних цветов.
По заданному конечному положению холста вычислите сколько из ещё видимых цветов могли быть первым нарисованным цветом.
ФОРМАТ ВВОДА:
Первая строка ввода содержит N, размер холста (1≤N≤10). Следующие N строк описывают финальную картинку холста, каждая содержит по N чисел в интервале 0…9. Гарантируется, что такой ввод был получен рисованием как описано выше с использованием различных цветов.
ФОРМАТ ВЫВОДА:
Выведите количество цветов, которые могли быть использованы первым, из всех цветов, которые видны на финальном рисунке.
| Ввод |
Вывод |
|
4
2230
2737
2777
0000
|
1 |
| |
![]()
|
|
Building a Ski Course
Двумерные массивы
Конструктив
Массивы
Фермер Джон помогает превратить его большое поле в лыжный маршрут для предстоящих Му-олимпийских игр. Поле имеет размеры M x N (1 <= M,N <=100) и его целевое финальное состояние описывается решеткой из M x N символов таких как:
RSRSSS
RSRSSS
RSRSSS
Каждый символ описывает состояние снега на этом участке R – грубый, S – гладкий (организаторы считают, что в таком случае - чередования грубых и гладких участков, гонка будет интересней).
Для выполнения этой задачи ФД планирует модифицировать свой трактор так, чтобы тот мог «отштамповать» любой фрагмент размером B x B (B<=M,B<=N) грубым снегом или гладким снегом.
ФД хочет сделать B как можно большим. С B=1 он может подготовить поле, штампуя индивидуально квадраты в соответствии с заданным финальным состоянием. Однако для бОльших значений B может оказаться невозможным выполнить задачу. Каждый квадрат поля должен быть обработан трактором. Невозможно оставить ячейку поля в исходном состоянии.
Помогите ФД определить максимально возможное значение B, которое он сможет успешно использовать.
INPUT FORMAT:
* Строка 1: Два разделённых пробелом целых числа M и N.
* Строки 2..M+1: M строк ровно по N символов (каждый R или S),
описывающих желаемое финальное состояние поля.
OUTPUT FORMAT:
* Строка 1: Максимальное значение B, которое ФД может использовать, чтобы создать нужное поле.
| Ввод |
Вывод |
|
3 6
RSRSSS
RSRSSS
RSRSSS
|
3 |
OUTPUT DETAILS:
ФД может отштамповать R колонках 1-3, затем S в колонках 2-4, затем R в колонках 3-5, и наконец, S в колонках 4-6.
| |
![]()
|
|
Задачи на печать!
Конструктив
Арифметические алгоритмы (Теория чисел)
Олимпиады бывают не только личные, но и командные. В командной олимпиаде по программированию обычно принимают участие команды из трёх человек, которым предоставляется один компьютер и один комплект условий задач, причём задач обычно существенно больше, чем в личных олимпиадах.
Условие каждой из задач помещается на одной, двух или трёх страницах. При этом условие может быть напечатано на двух сторонах одного листа, но для удобства команд на одном листе может располагаться условие только одной из задач. Для экономии бумаги, если условие задачи занимает две страницы, оно должно быть напечатано на двух сторонах одного листа, а если из трёх страниц - на двух сторонах одного листа и на одной стороне другого листа, вторая сторона которого останется чистой. При этом можно напечатать первую страницу такой задачи отдельно на чистом листе, а оставшиеся две страницы - на одном листе или, наоборот, первые две страницы распечатать на одном листе, а третью - на чистом листе. Задачи и все их страницы печатаются последовательно.
Условия всех задач распечатываются на принтере в виде нескольких последовательных заданий. Для каждого задания необходимо задать диапазон печати: номера первой и последней страниц, которые будут напечатаны в этом задании (будут напечатаны все страницы в этом диапазоне), а также тип печати - односторонняя или двусторонняя.
Вам необходимо минимизировать количество заданий для печати условий.
Формат входных данных
Первая строка входных данных содержит целое число n (1 ≤ n ≤ 106) - количество задач в олимпиаде.
Вторая строка входных данных содержит целое число n (1 ≤ xi ≤ 3) - количество страниц в i-й задаче.
Формат выходных данных
Выведите единственное число - минимальное количество последовательных диапазонов, каждый из которых можно напечатать одной командой односторонней или двусторонней печати так, что условия всех задач будут напечатаны в удобном для командной олимпиады виде.
Замечание
В первом примере на олимпиаду предложены 4 задачи, условия которых состоят из 1, 3, 2 и 1 страниц соответственно. Всего необходимо распечатать 7 страниц. Их можно распечатать за два задания: cтраницы 1-2 - односторонней печатью (это единственная страница первой задачи и первая из трёх страниц второй задачи), оставшиеся страницы 3-7 - двусторонней.
Во втором примере на олимпиаду предложены 2 задачи, условия которых состоят из 3 страниц каждая. Всего необходимо распечатать 6 страниц. Их можно распечатать за два задания: cтраницы 1-1- односторонней печатью (это первая из трёх страниц первой задачи), оставшиеся страницы 2-6 - двусторонней. При этом в первой задаче первая страница будет напечатана на одной стороне, потому что она напечатана односторонней печатью, а во второй задаче последняя страница будет напечатана на одной стороне, потому что в этом задании нечётное число страниц печатается на двух сторонах, поэтому вторая сторона этого листа будет пустой.
| |
![]()
|
|
Пират Серёжа
Конструктив
Задача на реализацию
Участникам, использующим язык Python3, рекомендуется отправлять решения на проверку с использованием интерпретатора PyPy3.
Маленький пират Серёжа скачал игру с разными видами головоломок. Среди них ему понравилась лишь одна, самая сложная.
Головоломка представляет из себя таблицу из \(n\) строк и \(m\) столбцов, в ячейках которой записаны числа от \(1\) до \(n \cdot m\) по одному разу.
Чтобы собрать головоломку, нужно выбрать последовательность клеток таблицы, в которой любые две подряд идущие клетки соседние по стороне в таблице. Последовательность может иметь произвольную длину, и каждая клетка может встречаться в последовательности произвольное число раз. Для клетки со значением \(i\) рассмотрим позицию \(t_i\) — позицию первого вхождения клетки с таким значением в последовательность. Последовательность решит головоломку, если каждая клетка таблицы встречается в ней, и \(t_1 < t_2 < \dots < t_{nm}\). Другими словами, последовательность должна в первый раз посетить клетку со значением \(x\) до клетки со значением \(x + 1\) для всех \(x\).
Назовем головоломку решаемой, если для нее существует хотя бы одна подходящая последовательность.
Серёжа понял, что не любая головоломка решаемая, так как подходящей последовательности может не существовать. Ему стало интересно, можно ли немного изменить головоломку, чтобы ее можно было решить. На это Серёже не хватило таланта, поэтому ему нужна ваша помощь.
За одно действие Сережа может выбрать две произвольных клетки (не обязательно соседние по стороне) и поменять числа, записанные в них. Он хотел бы знать минимальное число действий, которое потребуется, чтобы головоломка стала решаемой, но очень нетерпелив. Поэтому найдите, равняется ли минимальное число действий \(0\), \(1\), или же не менее \(2\). В случае, когда потребуется ровно \(1\) действие, найдите также количество подходящих пар клеток для обмена чисел.
Формат входных данных
В первой строке вводятся два целых положительных числа \(n, m\) (\(1 \leq n \cdot m \leq 400\,000\)) — длины сторон таблицы.
В каждой из следующих \(n\) строках вводятся \(m\) целых чисел \(a_{i1}, a_{i2}, \dots, a_{im}\) (\(1 \le a_{ij} \le n \cdot m\)).
Гарантируется, что каждое число от \(1\) до \(n \cdot m\) встречается ровно один раз.
Формат выходных данных
Пусть \(a\) — минимальное число действий, после которых головоломка станет решаемой.
Если \(a = 0\), выведите \(0\).
Если \(a = 1\), выведите \(1\), а также количество подходящих пар клеток.
Если \(a \ge 2\), выведите \(2\).
В первом примере из условия последовательность клеток \((1, 2), (1, 1), (1, 2), (1, 3), (2, 3), (3, 3)\), \((2, 3), (1, 3), (1, 2), (1, 1), (2, 1), (2, 2), (3, 2), (3, 1)\) решает головоломку, поэтому ответ \(0\).
Головоломка во втором примере из условия не решается, но будет решаться после любого из трех обменов клеток со значениями \((1, 5), (1, 6), (2, 6)\).
В третьем примере из условия потребуется не менее двух обменов, поэтому ответ равен \(2\).
| |
![]()
|
|
Посадка в самолет
Конструктив
Задача на реализацию
В самолетах авиакомпании Битавиа кресла расположены в \(n\) рядов, при этом в каждом ряду по шесть мест, между третьим и четвертым местом находится проход. Некоторые пассажиры регистрируются заранее онлайн, другие пассажиры регистрируются на стойке регистрации в аэропорту.
При онлайн-регистрации пассажир может выбрать любое место и не может его затем менять. Например, при \(n = 6\) рассадка в самолете после онлайн-регистрации может выглядеть так (крестиками отмечены занятые места):
На стойку регистрации придут \(m\) пассажиров. По правилам Битавиа нужно рассадить их в самолете таким образом, чтобы итоговая рассадка в самолете была симметрична относительно прохода. То есть, если в некотором ряду на первом кресле сидит пассажир, то в том же ряду на шестом кресле тоже должен сидеть пассажир. То же самое справедливо для второго и пятого, третьего и четвертого кресел, соответственно. При этом пересаживать пассажиров, прошедших онлайн-регистрацию нельзя. В исходную рассадку, показанную на рисунке выше, можно добавить семь пассажиров, удовлетворив условие симметрии, например, следующим образом:
Вам дана рассадка пассажиров после онлайн-регистрации. Требуется рассадить \(m\) пассажиров так, чтобы итоговая рассадка в самолете была симметрична относительно прохода, или определить, что это невозможно.
Формат входных данных
В первой строке содержатся два целых числа \(n\) и \(m\) — количество рядов в самолете и количество пассажиров, которые придут на стойку регистрации (\(1 \le n \le 1000\), \(0 \le m \le 6000\)).
В следующих \(n\) строках задана изначальная рассадка в самолете после онлайн-регистрации. В каждой строке содержится по шесть символов, при этом \(i\)-й символ \(j\)-й строки равен <<X>> (заглавная английская X), если \(i\)-е место в \(j\)-м ряду уже занято и <<.>> (точка) иначе.
Формат выходных данных
Если искомой рассадки не существует, выведите <<Impossible>>.
Иначе выведите \(n\) строк по шесть символов — итоговую рассадку в самолете. При этом \(i\)-й символ \(j\)-й строки должен быть равен <<X>>, если место занято, и <<.>>, если свободно. Если существует несколько решений, разрешается вывести любое.
Ниже приведены пять примеров входных данных.
-
В первом примере \(m = 0\), а рассадка в самолете симметрична, поэтому итоговая рассадка совпадает с исходной.
-
Во втором примере есть только один способ рассадить пассажиров симметрично.
-
В третьем примере существовало бы решение, при \(m = 1\), но при \(m = 2\) не существует способа рассадить всех пассажиров симметрично.
-
В четвертом примере требуется рассадить больше пассажиров чем свободных мест в самолете.
-
Пятый примере соответствует ситуации, рассмотренной на рисунках в тексте условия. В этом примере существует несколько решений, приведено одно из них.
| |
![]()
|
|
Лабиринт
Динамическое программирование
Конструктив
Маленький Влад решил создать собственную компьютерную игру. Игра будет проходить на карте, состоящей из комнат, соединённых коридорами. По каждому коридору можно будет передвигаться в обе стороны. Кроме того, Влад планирует создать карту, в которой коридоров будет ровно на один меньше, чем комнат, а также между любой парой комнат можно будет пройти, используя только коридоры. Для того, чтобы пройти игру, игроку необходимо выполнять квесты.
Все квесты в игре имеют одинаковую структуру. Пусть на карте расположены \(m\) комнат. Тогда каждый квест задаётся парой комнат \(u\) и \(v\) (\(1 \le u \le v \le m\)). Для прохождения этого квеста игроку нужно переместиться из комнаты \(u\) в комнату \(v\). Для усложнения игры в каждой комнате, через которую пройдёт игрок (включая начальную и конечную комнату) необходимо решить загадку. Влад называет сложностью квеста минимальное количество загадок, которые надо решить, чтобы его пройти. В частности, сложность квеста, у которого начальная и конечная комната совпадает, равна \(1\), а сложность квеста, в котором начальная и конечная комнаты соединены коридором равна \(2\). Также Влад называет квест трудным, если не существует квеста с большей сложностью, чем данный.
Интересностью игры Влад называет количество трудных уровней. Влад решил создать игру с интересностью ровно \(n\). Поскольку Владу сложно придумывать новые загадки, помогите ему составить карту с минимальным числом комнат, которое может быть в игре с интересностью \(n\).
Формат входных данных
В первой строке задано целое число \(n\) (\(1 \le n \le 500\)) — требуемое количество трудных уровней.
Формат выходных данных
В первой строке выведите целое число \(m\) — минимальное количество комнат на карте.
В следующих \(m - 1\) строках выведите через пробел пары целых чисел \(u\) и \(v\), обозначающие коридор, между комнатами \(u\) и \(v\).
Если подходящих карт с минимальным числом комнат несколько, выведите любую из них.
Примечание
В первом примере карта выглядит так:
На этой карте есть 10 квестов. Обозначим за (u, v) квест, который начинается в комнате с номером u и заканчивается в комнате с номером v. Сложность квестов (1, 1), (2, 2), (3, 3) и (4, 4) равна 1, сложность квестов (1, 2), (1, 3) и (1, 4) равна 2, а сложность квестов (2, 3), (2, 4) и (3, 4) равна 3. Таким образом, трудными квестами являются квесты (2, 3), (2, 4) и (3, 4). Трудных квестов 3, значит интересность игры на данной карте равна 3.
Во втором тестовом примере карта выглядит так:
На этой карте есть 4 трудных квеста (2, 5), (2, 6), (3, 5) и (3, 6). Их сложность равна 4.
В третьем тестовом примере карта выглядит так:
На этой карте есть 5 трудных квестов (2, 8), (3, 8), (4, 8), (5, 8), (6, 8) со сложностью 4.
| |
![]()
|
|
Федя и массив
Конструктив
Недавно Феде на день рождения подарили массив из \(n\) целых чисел, записаных по кругу, в котором для каждой пары соседних элементов (\(a_1\) и \(a_2\), \(a_2\) и \(a_3\), \(\ldots\), \(a_{n - 1}\) и \(a_n\), \(a_n\) и \(a_1\)) модуль их разности равен \(1\) (два соседних элемента отличаются ровно на \(1\)).
Назовём локальным максимумом элемент, который больше обоих соседних элементов. Также назовём локальным минимумом элемент, который меньше обоих соседних элементов. Обратите внимание, что элементы \(a_1\) и \(a_n\) являются соседними.
К сожалению, Федя потерял массив, но он запомнил в нём сумму локальных максимумов \(A\) и сумму локальных минимумов \(B\).
По заданным \(A\) и \(B\) помогите найти любой из подходящих массивов.
Формат входных данных
В первой строке вводится целое число \(A\) (\(-10^{18} \leqslant A \leqslant 10^{18}\)).
Во второй строке вводится целое число \(B\) (\(-10^{18} \leqslant B \leqslant 10^{18}\), \(B < A\)).
В третьей строке вводится целое число \(t\) (\(0 \leqslant t \leqslant 1\)) — если \(t = 0\), то от вас требуется вывести только длину массива.
Гарантируется, что при \(t = 1\) выполняется \(A - B \leqslant 10^{5}\).
Обратите внимание, что входные данные могут быть больше, чем возможное значение 32-битной целочисленной переменной, поэтому необходимо использовать 64-битные целочисленные типы данных (тип int64 в языке Pascal, тип long long в C и C++, тип long в Java и C#). Язык Python будет корректно работать и с типом int.
Формат выходных данных
В первой строке выведите одно число \(n\) — длину массива. При \(t = 0\) должно быть верно, что найдется хотя бы один подходящий массив с такой длиной.
Если \(t = 1\), то выведите во второй строке \(n\) чисел \(a_1, a_2, \ldots, a_n\) (\(-10^{18} \leqslant a_i \leqslant 10^{18}\)) — элементы массива.
Гарантируется, что при \(t = 1\) существует массив, размер которого не превосходит \(4 \cdot 10^5\).
Если \(t = 0\), то во второй строке выводить ничего не нужно.
Примечание
В первом примере локальными максимумами являются числа на позициях \(3\) и \(10\), а локальными минимумами числа на позициях \(6\) и \(8\).
| |
![]()
|
|
Даша и поиски
Конструктив
Структуры данных
Как вы знаете, девочка Даша постоянно что-то ищет. На этот раз ей дали перестановку, и она хочет найти такой её подотрезок, что ни один из элементов на его концах не является ни минимумом, ни максимумом всего подотрезка. Более формально, вас просят найти такие числа \(l\) и \(r\) \((1 \leqslant l \leqslant r \leqslant n)\), что \(a_l \neq \min(a_l, a_{l + 1}, \ldots, a_r)\), \(a_l \neq \max(a_l, a_{l + 1}, \ldots, a_r)\) и \(a_r \neq \min(a_l, a_{l + 1}, \ldots, a_r)\), \(a_r \neq \max(a_l, a_{l + 1}, \ldots, a_r)\).
Напомнима, что перестановкой длины \(n\) называется массив, состоящий из \(n\) различных целых чисел от \(1\) до \(n\), выписанных в произвольном порядке. Например, \([2,3,1,5,4]\) является перестановкой, но \([1,2,2]\) не является перестановкой (\(2\) встречается дважды в массиве) и \([1,3,4]\) тоже не является перестановкой (\(n=3\), но \(4\) присутствует в массиве, а \(2\) отсутствует).
Помогите Даше найти такой подотрезок, либо скажите, что такого подотрезка не существует.
Формат входных данных
В первой строке входных данных вам дано одно целое число \(n\) (\(1 \leqslant n \leqslant 200\,000\)) — размер перестановки.
Во второй строке входных данных вам дано \(n\) целых чисел \(a_1, a_2, \ldots a_n\) (\(1 \leqslant a_i \leqslant n\)) — элементы перестановки.
Формат выходных данных
Если искомого подотрезка не существует, выведите \(-1\).
Иначе выведите такие два числа \(l\) и \(r\) \((1 \leqslant l \leqslant r \leqslant n)\), что \([a_l, a_{l + 1}, \ldots, a_r]\) удовлетворяет условиям задачи.
Если искомых подотрезков несколько, выведите любой из них.
| |
![]()
|
|
Заколдованное зеркало
Конструктив
Алисе нравятся две вещи — ее зеркало и ее кубики. Кубики были предназначены для изучения детьми алфавита, то есть на их сторонах написаны некоторые буквы. Алиса любит играть с кубиками возле зеркала.
Входные данные
Когда Алиса учила алфавит, она заметила, что с ее зеркалом что-то не так! Кубик в зеркале мог показывать не ту букву, что изображена на нем, но всегда одну и ту же. Алиса придумала новую игру, пытаясь составить смешные слова из реальных кубиков и из кубиков в зеркале одновременно.
Игра имела следующие правила. Алиса выкладывала из кубиков слово S1. Эти же буквы в зеркале показывали слово S2, которое могло отличаться от отражения S1, так как зеркало было заколдованным. Но длина каждого слова равнялась N.
Затем Алиса проделывала следующие шаги. Она выбирала два кубика i и j и меняла их местами. В зеркале при этом менялись изображения кубиков N – i + 1 и N – j + 1 соответственно.
Цель игры — получить из слова S1 слово T1, которое будет выглядеть в зеркале как слово T2. Алиса не знает, когда это возможно, а когда нет. Помогите ей ответить на этот вопрос.
Входные данные
Во входном файле находятся 4 слова S1, S2, T1 и T2, каждое в отдельной строке. Все слова имеют одну и ту же длину N (1 ≤ N≤ 100) и состоят только из заглавных латинских букв.
Выходные данные
Выведите Yes или No в зависимости от ответа на вопрос задачи.
| |
![]()
|
|
Сломанный принтер
Циклы
Задача на реализацию
Конструктив
Сломанный цветной принтер, печатая цифры, закрашивает все замкнутые области в красный цвет. Например, в цифрах 0, 4, 6, 9 одна замкнутая область. В цифре 8 - 2 замкнутых области. В других цифрах нет замкнутых областей, которые закрашиваются. В принтере красной краски осталось на покраску h замкнутых областей. Найдите минимальное неотрицательное число, напечатав которое в принтере закончится красная краска. Число не должно содержать ведущих нулей. Если в принтере отсутствует красная краска, то он не может напечатать цифру с замкнутой областью.
Входные данные
На вход подается число h (0 <= h <= 510).
Выходные данные
Выведите число, которое необходимо напечатать.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
15 |
48888888 |
| 2 |
70 |
88888888888888888888888888888888888 |
| |
![]()
|
|
Важные переключатели
Конструктив
Коля купил новую материнскую плату для своего компьютера, но ему кажется, что она работает некорректно. Возможно неправильно выставлены переключатели на ее разъеме, которые могут находиться в двух состояниях — включен или выключен. Коля хочет узнать текущее состояние переключателей.
К несчастью, переключатели не являются доступными. Но Коля нашел сокет, каждый пин которого соединен с одним из переключателей через некоторую схему. Коля нашел эту схему в Интернете. Он обозначил переключатели маленькими латинскими буквами, а пины сокета — большими буквами. После этого он выписал логическую формулу для каждого пина. Согласно этой формуле включенный переключатель представляется значением true, а выключенный —false.
Коля использует в формуле следующие обозначения (операции перечислены от высшего приоритета к нисшему):
- Обозначение пина — буква от ‘A’ до ‘K’ ;
- Скобки обозначают, что если E >— это формула, то (E) — тоже формула;
- Отрицание — ~E— это формула для любой формулы E;
- Конъюнкция — E1 & E2 &…&En;
- Дизъюнкция — E1| E2| … | En;
- Импликация Е1 => E2 =>… => En. Импликации выполняются справа налево: Е1 => E2 => E3 означат Е1 => (E2 => E3);
- Эквивалентность — Е1 <=> E2 <=> … <=> En. Такое выражение вычисляется так: (Е1 <=> E2) &(Е2<=> E3) & … &(En-1 <=> En)..
Коля может построить новую схему, соответствующую любой формуле. Переменными в этой формуле будут состояния пинов сокета. Для начала он хочет построить схему, в которой входными значениями будут состояния всех пинов сокета, а в качестве выхода мы получим значение единственного переключателя, который при любых входных значениях будет находится в состоянии включено. Напишите программу, которая поможет Коле написать соответствующую формулу.
Входные данные
Первая строка входных данных содержит единственное целое число n — количество пинов у сокета (1 < n < 10). Следующие n строк содержат описания каждого пина. Одно описание состоит из обозначения пина и соответствующей формулы, отделенной от обозначения символами ‘:=’. Пин обозначен заглавной латинской буквой. Его формула расположена в одной строке и состоит из элементов ‘a’..‘k’, ‘(’, ‘)’, ‘~’, ‘&’, ‘ |’, ‘=>’ и ‘<=>’. Элементы формулы могут быть отделены друг от друга произвольным числом пробелов. Описание каждого пина содержит не более 1000 символов.
Выходные данные
Если требуемая схема существует, то выведите в первой строке Yes и No в противном случае.
В первом случае в следующей строке выведите формулу для переключателя, которая всегда истинна. Имя каждого пина должно входить в нее по крайней мере один раз. Имен переключателей она содержать не должна. Длина формулы не должна превосходить 1000 символов.
| |
![]()
|
|
Сосны
Перестановки
Конструктив
Массивы
В городе П для подготовки к празднику решили украсить аллею. Для этого наняли две бригады, одна отвечает за освещение аллеи, а вторая "— за озеленение аллеи, закупку саженцев сосны.
Аллею можно представить как прямую, и её решили украсить следующим образом — начать с сосны, чередовать лампы и сосны. В итоге на аллее будет высажено \(n + 1\) сосен и установлено \(n\) ламп.
Лампы поставили почти сразу же, причём двух типов — <<A>> и <<B>>. Лампы типа <<B>> светят всегда белым светом, а цвет лампы типа <<A>> зависит от её окружения. Если дерево, которое стоит слева от лампы, выше, чем дерево, которое стоит справа от лампы, то она загорается красным цветом, иначе синим.
Когда наконец-то доставили саженцы сосен, оказалось, что высоты всех саженцев попарно различны и принимают значения от \(1\) до \(n + 1\). Решено было разместить сосны так, чтобы количество красных и количество синих ламп были как можно ближе друг к другу.
Помогите ответственным за деревья разместить все \(n + 1\) саженцев так, чтобы разница между количеством красных и синих ламп была минимальна. Формально, если после высадки сосен будет \(r\) красных и \(b\) синих ламп, необходимо минимизировать величину \(|r-b|\).
Формат входных данных
В первой строке вводится одно единственное число \(n\) — количество ламп (\(1 \leq n \leq 2 \cdot 10^5\)). Во второй строке вводится \(n\) символов, \(i\)-й из которых равен <<A>> или <<B>> — тип \(i\)-й лампы.
Формат выходных данных
Выведите \(n + 1\) различных чисел от \(1\) до \(n + 1\) — высоты сосен при оптимальном размещении. Если оптимальных ответов несколько, можно вывести любой из них.
Иллюстрация ко второму примеру
Для наглядности, на иллюстрации красные лампы имеют формулу пятиугольника, а синие имеют форму звезды.
Тогда \(r = 1\), \(b = 1\), \(|r - b| = 0\) и это размещение будет одним из оптимальных.
| |
![]()
|
|
Магия Копперфильда
Простые игры
Конструктив
Всемирно известный маг Дэвид Копперфильд любит показывать следующий трюк. Квадрат из N столбцов и N строк, в каждой клетке которого находится какая-нибудь картинка, появляется на экране телевизора. Пусть все картинки пронумерованы следующим образом:
| 1 |
2 |
… |
N |
| N+1 |
N+2 |
… |
2*N |
| : |
: |
… |
: |
| N*(N–1)+1 |
N*(N–1)+2 |
… |
N*N |
Дэвид просит каждого зрителя поставить палец на левую верхнюю картинку (то есть в клетку номер 1), и Магия начинается: маг просит зрителей сдвинуть свой палец K1 раз в произвольном направлении (сдвигать палец разрешается только на соседнюю картинку по горизонтали или по вертикали, оставлять палец на месте запрещено, при этом если, допустим, Дэвид попросил сдвинуть палец 3 раза, то можно, например, сдвинуть палец на одну клетку вправо, затем — на одну клетку вниз, затем — на одну вверх). Затем со словами "Ваш палец не здесь" Дэвид убирает некоторые картинки, и — что удивительно, пальцы телезрителей действительно не указывают на те картинки, которые убирает Дэвид. Затем он просит сделать K2 ходов, и так далее (если Дэвид уже убрал какую-то картинку, то ходить через эту клетку нельзя). В конце, Дэвид убирает все картинки, кроме одной, и, улыбаясь, говорит: "Вы здесь" (аплодисменты).
Дэвиду приходится довольно часто повторять этот трюк, и, чтобы не ошибиться, он попросил написать программу, которая будет ему сообщать, сколько ходов должны делать телезрители, и какие картинки нужно убирать. Напишите такую программу.
Входные данные
Во входном файле записано одно число N — размер квадрата (2<=N<=100).
Выходные данные
В выходной файл ваша программа должна печатать следующие строки чисел:
K1 X1,1 X1,2 … X1,m1
K2 X2,1 X2,2 … X2,m2
…
Ke Xe,1 Xe,.2 … Xe,me
где Ki — это число ходов, которые должны сделать телезрители, а Xi,1 … Xi,mi — номера картинок, которые Дэвид должен убрать с экрана после этого. При этом все Ki должны удовлетворять условию 2N<=Ki<=10000 и все Ki должны быть различны. Каждая картинка (кроме той, которая останется) должна убираться ровно один раз. После каждой просьбы зрителей сделать Ki ходов, Дэвид должен убирать хотя бы одну картинку. Каждое Ki должно печататься в начале новой строки. Ситуаций, когда телезритель остался на клетке, у которой нет соседних, а его просят куда-нибудь ходить, возникать не должно.
| |
![]()
|
|
Кластеры роботов
Обход в глубину
Жадный алгоритм
Конструктив
Деревья
На производстве расположены \(n\) роботов, пронумерованных от \(1\) до \(n\). Любая пара роботов может быть либо соединена проводом, либо нет. Всего на производстве \(m\) проводов и \(i\)-й из них сейчас соединяет роботов с номерами \(a_i\) и \(b_i\).
Вы находитесь рядом с роботом номер \(1\). Роботом номер \(t\) можно управлять, если он связан с первым некоторой цепочкой проводов, то есть
-
либо если \(t = 1\);
-
либо если существуют такие \(i_1, \ldots, i_k\), что \(i_1 = 1\), \(i_k = t\), и любые два соседних в этой последовательности робота \(i_j\) и \(i_{j + 1}\) связаны проводом.
Любому из роботов, которыми можно управлять, можно послать команду <<извлеки второй конец подключенного к себе провода и подключи его к другому роботу>>. Иными словами, если роботом номер \(t\) можно управлять, и есть провод, соединяющий его с роботом номер \(x\), то можно заменить провод \((t, x)\) на провод \((t, y)\) для любого \(y \neq t\), еще не связанного проводом с \(t\). Обратите внимание, что после этого вы можете потерять управление над \(t\)-м роботом, если единственная связь \(t\)-го с первым проходила через \(x\)-й.
Ваша задача — получить управление над максимально возможным количеством роботов на производстве. Найдите это количество и самую короткую последовательность действий, приводящую к такому исходу.
Формат входных данных
В первой строке записано целое число \(T\) (\(1 \le T \le 1000\)) — количество наборов входных данных в тесте.
Первая строка каждого набора входных данных содержит целые числа \(n\) и \(m\) (\(1 \leq n \leq 10^5\); \(0 \leq m \leq 1.5 \cdot 10^5\)) — количество роботов и количество проводов, соответственно.
В следующих \(m\) строках дано описание проводов: в \(i\)-й строке даны целые числа \(a_i\) и \(b_i\) (\(1 \leq a_i, b_i \leq n\); \(a_i \neq b_i\)) — номера роботов, соединенных \(i\)-м проводом. Гарантируется, что никакие два провода не соединяют одну и ту же пару роботов.
Также гарантируется, что сумма \(n\) по всем наборам входных данных не превосходит \(10^5\) и сумма \(m\) по всем наборам входных данных не превосходит \(1.5 \cdot 10^5\).
Формат выходных данных
Для каждого набора входных данных выведите в первой строке через пробел максимальное количество роботов, управление над которыми можно получить, и количество действий \(k\), которое для этого понадобится.
В следующих \(k\) строках выведите сами описания действий по одному на каждой строке. Описание действия должно состоять из трех целых чисел \(t\), \(x\) и \(y\) (\(1 \leq t, x, y \leq n\); \(x \neq y\)), означающих, что робот номер \(t\) меняет провод \((t, x)\) на провод \((t, y)\).
Если возможных ответов несколько, выведите любой. Обратите внимание, что \(k\) при этом обязано быть наименьшим, при котором можно подключить максимальное количество роботов.
| |
![]()
|
|
Кластеры роботов - 2
Деревья
Жадный алгоритм
Конструктив
Обход в глубину
На производстве расположены \(n\) роботов, пронумерованных от \(1\) до \(n\). Любая пара роботов может быть либо соединена проводом, либо нет. Известно, что \(i\)-й робот соединен с \(k_i\) другими роботами с номерами \(v_{i,1}, \ldots, v_{i,k_i}\). Провода двухсторонние, то есть если \(i\) связан с \(j\), то \(j\) связан с \(i\) (иными словами, \((i, j)\) и \((j, i)\) — это один и тот же провод).
Вы находитесь рядом с роботом номер \(n\). Роботом номер \(t\) можно управлять, если он связан с \(n\)-м некоторой цепочкой проводов, то есть
-
либо если \(t = n\);
-
либо если существуют такие \(i_1, \ldots, i_k\), что \(i_1 = n\), \(i_k = t\), и любые два соседних в этой последовательности робота \(i_j\) и \(i_{j + 1}\) связаны проводом.
Любому из роботов, которыми можно управлять, можно послать команду <<извлеки второй конец подключенного к себе провода и подключи его к другому роботу>>. Иными словами, если роботом номер \(t\) можно управлять, и есть провод, соединяющий его с роботом номер \(x\), то можно заменить провод \((t, x)\) на провод \((t, y)\) для любого \(y \neq t\), еще не связанного проводом с \(t\). Обратите внимание, что после этого вы можете потерять управление над \(t\)-м роботом, если единственная связь \(t\)-го с \(n\)-м проходила через \(x\)-й.
Ваша задача — получить управление над максимально возможным количеством роботов на производстве. Найдите это количество и самую короткую последовательность действий, приводящую к такому исходу.
Формат входных данных
В первой строке записано целое число \(T\) (\(1 \le T \le 1000\)) — количество наборов входных данных в тесте.
Первая строка каждого набора входных данных содержит одно целое число \(n\) (\(1 \leq n \leq 10^5\)) — количество роботов.
Затем следуют \(n\) строк, в \(i\)-й из которых записаны числа \(k_i\) (\(0 \le k_i \le n - 1\)) и \(v_{i,1}, \ldots, v_{i,k_i}\) (\(1 \le v_{i,j} \le n\); \(v_{i,j} \neq i\)) — количество проводов, подключенных к \(i\)-му роботу, и номера роботов на противоположных концах этих проводов. Гарантируется, что данные корректны: никакие два провода не соединяют одну и ту же пару роботов, и если \(j \in v_i\), то \(i \in v_j\).
Также гарантируется, что сумма \(n\) по всем наборам входных данных не превосходит \(10^5\) и сумма количества проводов по всем наборам входных данных не превосходит \(1.5 \cdot 10^5\).
Формат выходных данных
Для каждого набора входных данных выведите в первой строке через пробел максимальное количество роботов, управление над которыми можно получить, и количество действий \(k\), которое для этого понадобится.
В следующих \(k\) строках выведите сами описания действий в формате <<\(y\) + \(t\) - \(x\)>> (\(1 \leq t, x, y \leq n\); \(x \neq y\)). Каждая такая строка соответствует замене провода \((t, x)\) на провод \((t, y)\).
Если возможных ответов несколько, выведите любой. Обратите внимание, что \(k\) при этом обязано быть наименьшим, при котором можно подключить максимальное количество роботов.
| |
![]()
|