| | | |
|
Вычисление факториала
Рекурсия
Составить программу с рекурсивной функцией для расчета факториала.
Входные данные
В первой строке вводится натуральное число N ( N<=12 ).
Выходные данные
Выведите факториал числа.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 |
1 |
| 2 |
2 |
2 |
| |
![]()
|
|
Сумма битов
Рекурсия
Составить программу с рекурсивной функцией для расчета суммы битов в натуральном числе.
Входные данные
В первой строке вводится натуральное число N ( N<=109 ).
Выходные данные
Выводите сумму битов.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
16 |
1 |
| 2 |
7 |
3 |
| |
![]()
|
|
Произведение битов
Рекурсия
Составить программу с рекурсивной функцией для расчета произведения битов в натуральном числе.
Входные данные
В первой строке вводится натуральное число N ( N<=109 ).
Выходные данные
Выводите произведение битов.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
16 |
0 |
| 2 |
7 |
1 |
| |
![]()
|
|
Звездочки
Рекурсия
Дана строка, содержащая только английские буквы (большие и маленькие). Добавить символ ‘*’ (звездочка) между буквами (перед первой буквой и после последней символ ‘*’ добавлять не нужно).
Входные данные
Вводится строка ненулевой длины. Известно также, что длина строки не превышает 1000 знаков.
Выходные данные
Вывести строку, которая получится после добавления символов '*'.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
LItBeoFLcSGBOFQxMHoIuDDWcqcVgkcRoAeocXO |
L*I*t*B*e*o*F*L*c*S*G*B*O*F*Q*x*M*H*o*I*u*D*D*W*c*q*c*V*g*k*c*R*o*A*e*o*c*X*O |
| |
![]()
|
|
Количество цифр
Рекурсия
Дана строка, содержащая цифры и английские буквы (большие и маленькие). Найти и вывести количество цифр.
Входные данные
Вводится строка ненулевой длины. Известно также, что длина строки не превышает 1000 знаков.
Выходные данные
Выведите количество цифр, которые присутствуют в строке.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
74kz31n8pn26f2iv10c7u8x356gl73jlka67i929z08i5mnn35h0n |
28 |
| |
![]()
|
|
Наибольшая строка
Рекурсия
Дана строка, содержащая только десятичные цифры. Напишите программу с использованием рекурсии для нахождения наибольшей цифры.
При решении этой задачи запрещено использовать циклы и слово max.
Входные данные
Вводится строка ненулевой длины. Известно также, что длина строки не превышает 1000 знаков и строка содержит только десятичные цифры.
Выходные данные
Выведите максимальную цифру, которая встречается во введенной строке.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
11111111 |
1 |
| |
![]()
|
|
Сумма чисел от 1 до n
Рекурсия
Напишите программу, содержащую рекурсивную функцию, которая решает задачу нахождения суммы чисел от 1 до n (n <= 100)
Нельзя в программе использовать циклы и формулу суммы арифметической прогрессии
Основная программа должна содержать ввод исходных данных, вызов функции и вывод ответа
На вход программе подается число n
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 |
15 |
| |
![]()
|
|
Сумма делителей
Рекурсия
Для данного натурального числа n вычислите сумму всех его натуральных делителей, включая 1 и само число. Решение оформите в виде РЕКУРСИВНОЙ функции с одним параметром. Основная программа должна содержать ввод исходных данных, вызов функции и вывод ответ
Запрещено использовать циклы в программе
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6 |
12 |
| |
![]()
|
|
Степень числа
Рекурсия
Напишите программу, содержащую рекурсивную функцию, которая решает задачу возведения числа x в натуральную степень n.
Основная программа должна содержать ввод исходных данных, вызов функции и вывод результата
Запрещено использовать встроенные функции (и операции) возведения числа степень, а также циклы
На вход программе подаются два числа x и n
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 5 |
32 |
| |
![]()
|
|
Только квадраты
Рекурсия
Напишите рекурсивную функцию, которая выбирает из полученной последовательности квадраты целых чисел и выводит их в обратном порядке. Использовать массив для хранения последовательности не разрешается. Запрещено использовать циклы.
Основная программа должна содержать вызов функции и вывод результата
Входные данные: Во входных строках записаны целые числа, по одному в каждой строке. В последней строке записано число 0.
Выходные данные: Программа должна вывести элементы полученной последовательности, которые представляют собой квадраты целых чисел, в обратном порядке в одну строчку, разделив их пробелами. Если таких нет, программа должна вывести число 0.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1
2
3
4
0 |
4 1 |
| |
![]()
|
|
Сумма элементов последовательности
Рекурсия
Напишите рекурсивную функцию, которая вычисляет сумму элементов последовательности целых чисел, поданных не её вход. Ввод заканчивается числом 0. Основная программа должна содержать вызов функции и вывод результата. Запрещено использовать циклы
Входные данные: Во входных строках записаны целые числа, по одному в каждой строке. В последней строке записано число 0.
Выходные данные: Программа должна вывести одно число – сумму всех элементов последовательности.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1
2
3
0 |
6 |
| |
![]()
|
|
Максимум последовательности
Рекурсия
Напишите рекурсивную функцию, которая вычисляет максимальное значение из последовательности целых чисел, поданных не её вход. Ввод заканчивается числом 0. Основная программа должна содержать вызов функции и вывод результата. Запрещено использовать циклы
Входные данные: Во входных строках записаны целые числа, по одному в каждой строке. В последней строке записано число 0.
Выходные данные: Программа должна вывести одно число – максимальное значение из всех элементов последовательности (не считая числа 0).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1
3
2
0 |
3 |
| |
![]()
|
|
Длинный НОД
Рекурсия
НОД и алгоритм Евклида
Даны два числа. Найти их наибольший общий делитель.
Входные данные: Вводятся два натуральных числа, не превышающих 10^9, (запись 10^9 обозначает "10 в 9-й степени", то есть 1000000000).
Выходные данные: Выведите НОД введенных чисел
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
42 12 |
6 |
| |
![]()
|
|
Функция Аккермана
Рекурсия
В теории вычислимости важную роль играет функция Аккермана A(m,n), определенная следующим образом:
\(\begin{equation*} A(n, m) = \begin{cases} n+1 &\text{ $m = 0$}\\ A(m-1, 1) &\text{ $m>0, n=0$}\\ A(m-1, A(m, n-1)) &\text{ $m>0, n> 0$} \end{cases} \end{equation*}\)
Даны два целых неотрицательных числа m и n, каждое в отдельной строке. Выведите A(m,n).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2
2 |
7 |
| |
![]()
|
|
Функция
Рекурсия
Функция f(n) с натуральными аргументами и значениями определена так:
f(0) = 0
f(1) = 1
f(2n) = f(n)
f(2n + 1) = f(n) + f(n + 1)
Составить программу вычисления f(n) по заданному n.
Входные данные
Дано одно число n (1 <= n <= 1018).
Выходные данные
Выведите f(n).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
10 |
3 |
| |
![]()
|
|
Функция - 2*
Рекурсия
Описана рекурсивная функции с тремя параметрами F(a, b, c):
F(a, b, c) = 1, если a ≤ 0 или b ≤ 0 или c ≤ 0;
F(a, b, c) = F(20, 20, 20), если a > 20 или b > 20 или c > 20;
F(a, b, c) = F(a, b, c-1) + F(a, b-1, c-1) - F(a, b-1, c), если a < b и b < c;
F(a, b, c) = F(a-1, b, c) + F(a-1, b-1, c) + F(a-1, b, c-1) - F(a-1, b-1, c-1), во всех остальных случаях.
Входные данные
Входные данные содержат три целых числа a, b, c - параметры функции F (-104 ≤ a,b,c ≤ 104).
Выходные данные
В ответе выведите значение функции F(a, b, c).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 1 1 |
2 |
| 2 |
2 2 2 |
4 |
| 3 |
10 4 6 |
523 |
| 4 |
50 50 50 |
1048576 |
| |
![]()
|
|
Заполнение конем
Рекурсия
Обход в глубину
Дана шахматная доска nхn. Пусть конь стоит на клетке (1,1). Необходимо найти такую последовательность ходов коня, при которой он побывает на каждой клетке доски ровно по одному разу.
Входные данные
На вход программе подается натуральное число n (n ≤ 8).
Выходные данные
Если обход невозможен, то выведите в выходной файл 0, если возможен, то 1, а на следующих строчках выведите матрицу nn, иллюстрирующую порядок обхода. Выравнивать числа по столбцам не обязательно.
Примечание. Скорость работы рекурсивной программы в этой задаче существенно зависит от порядка, в каком будут рассматриваться варианты хода коня из очередной клетки. Одним из удачных порядков является размещение всех восьми вариантов хода "по кругу".
| Ввод |
Вывод |
| 3 |
0 |
| 5 |
1
1 20 17 12 3
16 11 2 7 18
21 24 19 4 13
10 15 6 23 8
25 22 9 14 5
|
| |
![]()
|
|
Разложение на слагаемые
Рекурсия
Требуется вывести все различные представления натурального числа N в виде суммы натуральных чисел. Представления, отличающиеся друг от друга порядком слагаемых, не являются различными.
Входные данные
Входная строка содержит целое число N (2 ≤ N ≤ 40).
Выходные данные
В ответе выведите все различные представления числа N без повторов в виде суммы по одному на отдельной строке. Как слагаемые, так и сами суммы могут следовать в произвольном порядке.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 |
|
| 2 |
5 |
1 1 1 1 1
1 1 1 2
1 1 3
1 2 2
2 3
1 4
5
|
| |
![]()
|
|
Лесенки
Рекурсия
Лесенкой называется набор кубиков, в котором каждый более верхний
слой содержит кубиков меньше, чем предыдущий.
---
| |
---------
| | | | |
-----------
| | | | | |
-----------------
| | | | | | | | |
-----------------
Подсчитать число лесенок, которое можно построить из N кубиков.
Входные данные
Во входном файле записано число N (1<=N<=100).
Выходные данные
В выходной файл вывести искомое число лесенок.
Пример
Пример входного файла
3
Пример выходного файла
2
| |
![]()
|
|
Монетки
Рекурсия
Рекурсивный перебор
В Волшебной стране используются монетки достоинством A1, A2,..., AM. Волшебный человечек пришел в магазин и обнаружил, что у него есть ровно по две монетки каждого достоинства. Ему нужно заплатить сумму N. Напишите программу, определяющую, сможет ли он расплатиться без сдачи.
Входные данные
На вход программы сначала поступает число N (1 <= N <= 109), затем - число M (1 <= M <= 15) и далее M попарно различных чисел A1, A2,..., AM (1 <= Ai <= 109).
Выходные данные
Сначала выведите K - количество монет, которое придется отдать Волшебному человечку, если он сможет заплатить указанную сумму без сдачи. Далее выведите K чисел, задающих достоинства монет. Если решений несколько, выведите вариант, в котором Волшебный человек отдаст наименьшее возможное количество монет. Если таких вариантов несколько, выведите любой из них.
Если без сдачи не обойтись, то выведите одно число 0. Если же у Волшебного человечка не хватит денег, чтобы заплатить указанную сумму, выведите одно число -1 (минус один).
| Ввод |
Вывод |
100 6
11 20 30 40 11 99 |
3
40 30 30 |
| |
![]()
|
|
Сумма кубов
Рекурсия
Известно, что любое натуральное число можно представить в виде суммы не более чем четырех квадратов натуральных чисел. Вася решил придумать аналогичное утверждение для кубов - он хочет узнать, сколько кубов достаточно для представления любого числа. Его первая рабочая гипотеза - восемь.
Выяснилось, что почти все числа, которые Вася смог придумать, представляются в виде суммы не более чем восьми кубов. Однако число 239, например, не допускает такого представления. Теперь Вася хочет найти какие-либо другие такие числа, а также, возможно, какую-либо закономерность в представлениях всех остальных чисел, чтобы выдвинуть гипотезу относительно вида всех чисел, которые не представляются в виде суммы восьми кубов.
Помогите Васе написать программу, которая проверяла бы, возможно ли представить данное натуральное число в виде суммы не более чем восьми кубов натуральных чисел, и если это возможно, то находила бы какое-либо такое представление.
Входные данные
Вводится натуральное число N <= 2*109.
Выходные данные
Требуется вывести не более восьми натуральных чисел, кубы которых в сумме дают N. Если искомого представления не существует, то в выходной файл необходимо вывести слово IMPOSSIBLE.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
239 |
IMPOSSIBLE |
| 2 |
17 |
2 2 1 |
| |
![]()
|
|
Троечные последовательности
Рекурсия
Вводится число N. Сгенерируйте в анти-лексикографическом порядке все последовательности длины N (1≤N≤9), состоящие из чисел 3, 4, 5, в которых количество троек не превосходит двух.
В "анти-лексикографическом" обозначает "в порядке, обратном к лексигографическому" (см. пример).
В "лексикографическом порядке" обозначает, что если на первых X местах две последовательности совпадают, а на месте X+1 - различаются, то раньше должна идти та из них, в которой число на месте X+1 меньше.
В анти-лексикографическом, соответственно, наоборот.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 |
5 5 5
5 5 4
5 5 3
5 4 5
5 4 4
5 4 3
5 3 5
5 3 4
5 3 3
4 5 5
4 5 4
4 5 3
4 4 5
4 4 4
4 4 3
4 3 5
4 3 4
4 3 3
3 5 5
3 5 4
3 5 3
3 4 5
3 4 4
3 4 3
3 3 5
3 3 4
|
| |
![]()
|
|
Перебор строк №4
Рекурсия
В алфавите языке племени «тумба-юмба» четыре буквы: «K», «L», «M» и «N». Нужно вывести на экран все возможные слова, состоящие из n букв, в которых есть по крайней мере две одинаковые буквы, не обязательно стоящие рядом. Программа не должна строить другие слова, не соответствующие условию.
(c) К.Ю. Поляков
| |
![]()
|
|
Перебор строк №3
Рекурсия
В алфавите языке племени «тумба-юмба» четыре буквы: «K», «L», «M» и «N». Нужно вывести на экран все возможные слова, состоящие из K букв (K<10), в которых есть по крайней мере две одинаковые буквы, стоящие рядом. Подсчитайте количество таких слов. Программа не должна строить другие слова, не соответствующие условию.
Автор задачи: К.Ю. Поляков
| |
![]()
|
|
Перебор строк №2
Рекурсия
В алфавите языке племени «Тумба-Юмба» четыре буквы: «K», «L», «M» и «N». Нужно вывести на экран все возможные слова, состоящие из n букв (n > 1), в которых вторая буква «K». Подсчитайте количество таких слов.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 |
KK
LK
MK
NK
4 |
(c) К.Ю. Поляков
| |
![]()
|
|
Чётные цифры
Рекурсия
Напишите рекурсивную функцию, которая считает количество чётных цифр введённого числа.
Основная программа должна содержать ввод исходных данных, вызов функции и вывод результата
Запрещено использовать циклы
Входные данные: Входная строка содержит одно натуральной число N .
Выходные данные: Программа должна вывести количество чётных цифр введённого числа.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
123456 |
3 |
| 2 |
13579 |
0 |
| |
![]()
|
|
Все числа от n до 1
Рекурсия
Напишите программу, содержащую рекурсивную функцию, которая по натуральному числу n, выводит все числа от n до 1. Основная программа должна содержать ввод исходных данных (число n) и вызов функции.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6 |
6 5 4 3 2 1 |
| |
![]()
|
|
Как поделить картошку
Рекурсия
Вася и Петя пошли копать картошку. В конце дня они накопали N мешков с картошкой весом W1, W2, ... WN. Как им поделить мешки с картошкой между собой, чтобы разница масс была минимальной.
Входные данные
В первой строке записано число N – количество мешков (1 ≤ N ≤ 18). Во второй строке через пробел перечислены массы мешков W1, W2 , … WN (1 ≤ Wi ≤ 105).
Выходные данные
В единственную строку нужно вывести одно неотрицательное целое число – минимально возможную разницу между массами двух куч с мешками.
| |
![]()
|
|
Двоичные последовательности
Рекурсия
Вводится число N (1<=N<=9). Сгенерируйте в лексикографическом порядке все последовательности длины N, состоящие из чисел 2, 4, 5, в которых количество двоек не больше двух.
В "лексикографическом порядке" обозначает, что если на первых X местах две последовательности совпадают, а на месте X+1 - различаются, то раньше должна идти та из них, в которой число на месте X+1 меньше.
| |
![]()
|
|
Ханойские башни
Рекурсия
Головоломка “Ханойские башни” состоит из трех стержней, пронумерованных числами 1, 2, 3. На стержень 1 надета пирамидка из n дисков различного диаметра в порядке возрастания диаметра. Диски можно перекладывать с одного стержня на другой по одному, при этом диск нельзя класть на диск меньшего диаметра. Необходимо переложить всю пирамидку со стержня 1 на стержень 3 за минимальное число перекладываний.
Напишите программу, которая решает головоломку; для данного числа дисков n печатает последовательность перекладываний в формате a b c, где a — номер перекладываемого диска, b — номер стержня с которого снимается данный диск, c — номер стержня на который надевается данный диск.
Например, строка 1 2 3 означает перемещение диска номер 1 со стержня 2 на стержень 3. В одной строке печатается одна команда. Диски пронумерованы числами от 1 до n в порядке возрастания диаметров.
Входные данные
Вводится натуральное число n ( 0 < n < 11).
Выходные данные
Программа должна вывести минимальный (по количеству произведенных операций) способ перекладывания пирамидки из данного числа дисков.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 |
1 1 2
2 1 3
1 2 3
|
| |
![]()
|
|
Быстрое возведение в степень
Рекурсия
Возводить в степень можно гораздо быстрее, чем за n умножений! Для этого нужно воспользоваться следующими рекуррентными соотношениями:
\(a^n=(a^2)^{n/2},\ при \ четном \ n, \\ a^n=a \cdot a^{n-1},\ при \ нечетном \ n.\)
Реализуйте алгоритм быстрого возведения в степень. Если вы все сделаете правильно, то сложность вашего алгоритма будет O(logn) .
Входные данные
Программа получает на вход вещественное число a и целое число n (a > 0, 0 <= n <= 109). Каждое число в отдельной строке.
Выходные данные
Выведите \(a^n\) с точностью не менее 5 знаком после запятой.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2
7 |
128 |
| 2 |
1.00001
100000 |
2.71827 |
| |
![]()
|
|
Скобки-2
Рекурсия
Вывести все правильные скобочные выражения длиной N, состоящие из круглых и квадратных скобок.
Входные данные
В первой строке находится единственное число N. \(1 <= N <= 14\), N - чётное.
Выходные данные
Каждое выражение выводится в отдельной строке.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 |
()
[]
|
| 2 |
4 |
(())
[[]]
[()]
()[]
[]()
()()
([])
[][]
|
| |
![]()
|
|
Взвешивание
Рекурсия
Перебор
Даны двухчашечные весы и набор гирек. На левую чашу весов положили взвешиваемый предмет весом K граммов. Можно ли привести весы в состояние равновесия, и если можно, то определите для каждой чаши весов, какие гирьки на нее для этого нужно положить. Имеющиеся гирьки разрешается класть на любую из чаш весов (каждая гирька имеется только в одном экземпляре, некоторые гирьки можно не использовать).
Входные данные
Вводится сначала K — вес предмета, который положили на левую чашу (1≤K≤50). Далее записано общее количество гирек N (1≤N≤10). Далее записано N различных натуральных чисел, не превышающих 50, — веса гирек.
Выходные данные
В первой строке выведите веса гирек, которые нужно поместить на левую чашу весов, во второй строке — гирьки, которые нужно поместить на правую чашу. Если на какую-то чашу ни одной гирьки помещать не нужно — выведите в этой строке число 0. Если с помощью данных гирек привести весы в равновесие нельзя, выведите одно число –1. Если вариантов несколько, выведите любой из них.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
2
3 5 |
0
5 |
| 2 |
5
3
6 3 4 |
4
3 6 |
| 3 |
5
1
2 |
-1 |
| |
![]()
|
|
Разбиение на невозрастающие слагаемые, лексикографический порядок
Рекурсия
Разбиения
Дано натуральное число N. Рассмотрим его разбиение на натуральные слагаемые. Два разбиения, отличающихся только порядком слагаемых, будем считать за одно, поэтому можно считать, что слагаемые в разбиении упорядочены по невозрастанию.
Входные данные
Задано единственное число N. (N ≤ 40)
Выходные данные
Необходимо вывести все разбиения числа N на натуральные слагаемые в лексикографическом порядке.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 |
1 1 1 1 1
2 1 1 1
2 2 1
3 1 1
3 2
4 1
5 |
| |
![]()
|
|
Площадь комнаты
Рекурсия
Обход в глубину
Требуется вычислить площадь комнаты в квадратном лабиринте.
Входные данные
В первой строке вводится число N – размер лабиринта (3 <= N <= 10). В следующих N строках задан лабиринт (‘.’ – пустая клетка, ‘*’ – стенка). И наконец, последняя строка содержит два числа – номер строки и столбца клетки, находящейся в комнате, площадь которой необходимо вычислить. Гарантируется, что эта клетка пустая и что лабиринт окружен стенками со всех сторон.
Выходные данные
Требуется вывести единственное число – количество пустых клеток в данной комнате.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
*****
**..*
*.*.*
*..**
*****
2 4
|
3 |
| |
![]()
|
|
Счастливого Нового Года!
Рекурсия
Перебор
Рекурсивный перебор
В каком-то другом мире сегодня 31 декабря. Дед Кокованя решил приготовить многомерный бургер, который так любит Дарёна. Бургер уровня L (L - целое число, большее или равное 0) готовится следующим образом:
- Бургер нулевого уровня - это котлета.
- Бургер с уровнем
L (L >= 1) - это булочка, бургер с уровнем (L-1), котлета, бургер с другим уровнем (L-1) и еще одна булочка, уложенные вертикально в указанном порядке, считая снизу.
Например, бургер уровня 1 и бургер уровня 2 выглядят как БКККБ и ББКККБКБКККББ (повернутые на 90 градусов), где Б и К обозначают булочку и котлету.
Бургер, который приготовит дед Кокованя, - это бургер уровня N. Дарёна всегда съедает только Х слоев нижней части бургера (слой - это котлета или булочка). Сколько котлет она съест?
Входные данные
Программа получает на вход 2 целых числа через пробел: N и X (1 <= N <= 50, 1 <= X <= (общее количество слоев в бургере N-го уровня)).
Выходные данные
Выведите количество котлет в самых нижних X слоях, считая от нижней части бургера уровня N.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
2 7 |
4 |
В самых нижних 7 слоях бургера второго уровня ( ББКККБКБКККББ) находятся 4 котлеты. |
| 2 |
1 1 |
0 |
|
| 3 |
50 4321098765432109 |
2160549382716056 |
Бургер 50-го уровня довольно толстый настолько, что количество его слоев не укладывается в 32-битное целое число. |
| |
![]()
|
|
+3 or +5
Рекурсия
Маленький Гриша научился выполнять с любым числом две операции: прибавлять к числу 3 и прибавлять к числу 5. Но, к сожалению, он еще не знает, что таким путем он не cможет из числа 1 получить любое число. Помогите Грише понять, сможет ли он из числа 1 получить число N или нет.
Входные данные
Программа получает на вход натуральное число N (N <= 200).
Выходные данные
Выведите слово YES, если число N можно получить из числа 1, или NO - в противном случае.
Примечание
Число 1 можно получить всегда, не выполняя при этом никаких действий.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 |
NO |
| 2 |
1 |
YES |
| |
![]()
|
|
Степень двойки (рекурсивно)
Рекурсия
Дано натуральное число N. Выведите слово YES, если число N является точной степенью двойки, или слово NO в противном случае.
Операцией возведения в степень пользоваться нельзя!
Входные данные
Вводится натуральное число N (N < 109).
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 |
YES |
| 2 |
4 |
YES |
| 3 |
5 |
NO |
| |
![]()
|
|
Перевод числа в десятичную систему счисления (рекурсивно)
Рекурсия
Информатика
Системы счисления
Напишите программу, которая переводит число N из системы счисления с основанием r в десятичную систему счисления.
Входные данные
Программа получает на вход два натуральных числа: N и r (2 <= r <= 9). Гарантируется, что число N является правильной записью числа в системе счисления c основанием r (то есть содержит цифры от 0 до r-1).
Выходные данные
Выведите на экран число в десятичной системе счисления.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
100 2 |
4 |
| |
![]()
|
|
Все ПСП
Рекурсия
Динамическое программирование
Перебор
Перебор с возвратом
Дано число n. Вам необходимо сгенерировать все правильные скобочные последовательности, содержащие n пар скобок.
Входные данные
В первой строке дано натуральное число n (1 <= n <= 8).
Выходные данные
Выведите все правильные скобочные последовательности по возрастанию в лексикографическом порядке. Каждую в отдельной строке.
| |
![]()
|
|
КП189
Рекурсия
ЕГЭ_информатика
(А. Богданов) Обозначим операцию целочисленного деления с округлением вниз как «//», а нахождения остатка деления через «%». Например, 8 // 3 == 2 и 7 % 3 == 1.
Алгоритм вычисления функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = n, если n < 2,
F(n) = F(n // 2) + F(n % 2), если n >= 2.
Определите количество натуральных чисел, меньших 230, для которых F(n) = 27?
| |
![]()
|
|
КП188
Рекурсия
ЕГЭ_информатика
(А. Рогов) Алгоритм вычисления функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = n, если n > 3000,
F(n) = 2 + F(n + 2), если n ≤ 3000.
Чему равно значение выражения F(40) – F(43)?
| |
![]()
|
|
КП187
Рекурсия
ЕГЭ_информатика
(Е. Джобс) Алгоритм вычисления функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = n, если n ≥ 2022,
F(n) = 7 + F(n + 5), если n < 2022.
Чему равно значение выражения F(45) – F(49)?
| |
![]()
|
|
КП186
Рекурсия
ЕГЭ_информатика
(ЕГЭ-2023) Алгоритм вычисления функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 3, если n < 3,
F(n) = 2n + 5 + F(n –2), если n ≥ 3.
Чему равно значение выражения F(3027) – F(3023)?
| |
![]()
|
|
КП185
Рекурсия
ЕГЭ_информатика
(ЕГЭ-2023) Алгоритм вычисления функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 7, если n < 7,
F(n) = n + 1 + F(n –2), если n ≥ 7.
Чему равно значение выражения F(2024) – F(2020)?
| |
![]()
|
|
КП184
Рекурсия
ЕГЭ_информатика
(ЕГЭ-2023) Алгоритм вычисления функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = n, если n < 11,
F(n) = n + F(n –1), если n ≥ 11.
Чему равно значение выражения F(2024) – F(2021)?
| |
![]()
|
|
КП183
Рекурсия
ЕГЭ_информатика
(Е. Джобс) Алгоритм вычисления функций F(n) и G(n), где n – натуральное число, задан следующими соотношениями:
F(n) = 1 , если n ≥ 3210,
G(n) = n, если n < 10.
F(n) = F(n+3) + 7, если n<3210,
G(n) = G(n–3) + 5, если n ≥ 10.
Чему равно значение выражения F(15) – G(3000)?
| |
![]()
|
|
КП182
Рекурсия
ЕГЭ_информатика
(Е. Джобс) Алгоритм вычисления функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n)= n, если n ≥ 2025,
F(n)=F(n+1) – F(n+2) + 7, если n < 2025.
Чему равно значение выражения F(15) – F(24)?
| |
![]()
|
|
КП180
Рекурсия
ЕГЭ_информатика
(А. Богданов) Обозначим частное от деления натурального числа a на натуральное число b как a // b, а остаток как a%b. Алгоритм вычисления функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = n // 3 + n % 3, если n < 9;
F(n) = F(n // 9) + F(n % 9), если n ≥ 9.
Определите количество значений n < 99, для которых функция F(n) = 33.
| |
![]()
|
|
КП179
Рекурсия
ЕГЭ_информатика
(А. Богданов) Обозначим частное от деления натурального числа a на натуральное число b как a // b, а остаток как a%b. Алгоритм вычисления функции F(n), где n – натуральное число, задан следующими соотношениями:
F(n) = n, если n < 2;
F(n) = n % 2 + 10· F(n//2), если n ≥ 2.
Определите значение n, для которого функция F(n) = 100000100001000100101.
| |
![]()
|
|
Задача Магистра Математикуса
Рекурсия
Магистр Математикус обладает волшебными способностями, которые позволяют ему превращать положительные числа в 1 с помощью следующих операций:
- Если число четное, он может разделить его на 2.
- Если число нечетное, он может увеличить его на 1 или уменьшить на 1.
Сегодня Магистр Математикус задумался над вопросом, какое минимальное количество операций ему необходимо выполнить для превращения числа n в 1 с использованием его волшебных способностей. Помогите ему ответить на этот вопрос.
Входные данные
Программа получает на вход целое число n.
Ограничения на входные данные
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
8 |
3 |
| 2 |
7 |
4 |
| |
![]()
|
|
Коды Грея
Рекурсия
Конструктив
Задача на реализацию
На занятиях по дискретной математике Сереже рассказали про двоичные коды Грея — это такое упорядочение всех 2n различных двоичных векторов длины n, что любые два соседних, а также первый и последний, вектора различаются ровно в одном разряде.
Для закрепления материала преподаватель задал им следующее задание: в коде Грея в каждом двоичном векторе ровно один бит заменен на знак вопроса «?». Требуется заменить обратно все знаки вопроса «?» на «0» или «1», чтобы получился код Грея.
Преподаватель обещал бонус на экзамене тому из студентов, кто первым справится с заданием. Помогите Сереже решить задачу или скажите, что это невозможно, и преподаватель задал нераз- решимое задание.
Формат входных данных
В первой строке содержится целое число n — длина двоичных векторов. Следующие 2n строк содержат двоичные вектора длины n, в каждом из которых ровно один символ заменен на знак вопроса «?».
Формат выходных данных
В первой строке выведите «YES», если решение существует, и «NO» — в противном случае. В случае положительного ответа выведите исходный код Грея, если возможных вариантов ответа несколько, выведите любой.
| Ввод |
Вывод |
2
0?
0?
1?
1? |
YES
00
01
11
10 |
3
?00
0?1
01?
0?0
?10
1?1
10?
1?1 |
NO |
Система оценки
| Номер подзадачи |
Баллы |
Ограничения |
Комментарии |
| 1 |
37 |
1<=n<=4 |
Баллы начисляются, если все тесты пройдены. |
| 2 |
63 |
1<=n<=12 |
Баллы начисляются, если все тесты этой и предыду- щих подзадач пройдены. |
| |
![]()
|
|
Овечка Толя (C, B')
Рекурсия
Задача на реализацию
Задача на реализацию
Овечка Толя умеет клонироваться - тогда рядом с ней появляется такая же овечка с той же логикой и привычками.
Когда овечка встречает n стогов сена то происходит следующее:
- Если n меньше 4 то овечка выкидывает эти n стогов сена в ближайший овраг. Иначе:
- Если n делится на 5, то овечка сбрасывает n/5 стогов сена в ближайший овраг; клонируется;
сама обрабатывает 3n/5 стогов сена с помощью этой же процедуры, а ее клон обрабатывает
оставшиеся n/5 стогов сена с помощью этой же процедуры. Иначе:
- Овечка съедает 4 стога сена и обрабатывает оставшиеся n-4 стогов с помощью этой же процедуры.
Овечка Толя однажды увидела n стогов сена - это число вам дано. Сколько стогов сена будет
съедено ей и всеми е клонами при описанном процессе ?
Формат входных данных
В первой строке содержится натуральное число n <= 6 n <= 106
Формат выходных данных
Выведите количество, стогов съеденных в итоге Толей и клонами
| |
![]()
|
|
Прямоугольное поле чудес (В, А',A)
Рекурсия
Задача на реализацию
Коля попал на телеигру "Прямоугольное поле чудес". В финале этой игры Коле показали прямоугольное поле размера n х m клеток, в каждое клетке которого записано целое число. Коля может
заменить числа в некоторых клетках на противоположные (т.е. вместо числа x записать в клетку число −x). Коля выиграет автомобиль, если сумма чисел в каждой строке и в каждом столбце будет равна нулю. Помогите Коле найти нужную расстановку чисел, либо определите, что ее не существует и Коля не сможет выиграть.
Формат входных данных
В первой строке записано два целых числа n и m (1 <= n, m <= 5) - размеры поля.
В следующих n строках записано по m целых чисел, разделенных пробелами - числа, записанные в клетках поля. Все числа по модулю не превосходят 106.
Формат выходных данных
Если ответ существует, в первой строке выведите YES, в следующих n строках выведите по m чисел через пробел - числа в клетках поля после изменений/
Если ответа не существует, в первой строке выведите NO.
| Ввод |
Вывод |
3 3
1 1 2
2 2 4
3 3 6 |
YES
1 1 -2
2 2 -4
-3 -3 6 |
| |
![]()
|
|
Circular Barn
Рекурсия
Динамическое программирование
Динамическое программирование: два параметра
Задача на реализацию
У Фермера Джона круглый амбар. Амбар состоит из кольца из n комнат, пронумерованных 1…n по периметру (3≤n≤1,000). Каждая комната имеет двери в две соседние комнаты и одну дверь во внешний мир.
ФД хочет разместить ровно ri коров в комнате i (1≤ri≤1,000,000). Он планирует открыть k внешних дверей (1≤k≤7), через которые коровы будут входить в амбар. Каждая корова затем идёт по часовой стрелке, пока не добредёт до нужной комнаты. ФД хочет открыть двери так, чтобы все коровы вместе прошли как можно меньшее расстояние. Коровы предварительно могут собраться как им выгоднее перед этими незакрытыми дверями (эти перемещения не входят в общее расстояние, учитываемое в задаче). Определите минимальное суммарное расстояние, которое придётся пройти коровам, если ФД наилучшим образом выберет какие k открыть.
ФОРМАТ ВВОДА:
Первая строка ввода содержит n и k. Последующие n строк содержат r1…rn.
ФОРМАТ ВВОДА:
Выведите минимальное суммарное расстояние пройденное коровами.
| Ввод |
Вывод |
|
6 2
2
5
4
2
6
2
|
14 |
ФД может открыть двери 2 и 5. 11 коров войдут в двери 2 и пройдут суммарное расстояние 8 чтобы попасть в комнаты 2,3,4. 10 коров войдут в дверь 5 и пройдут общее расстояние 6, чтобы попасть в комнаты 5,6,1.
| |
![]()
|
|
XOR-cумма массива
Рекурсия
Перебор с возвратом
Рекурсивный перебор
XOR-cумма массива определяется как побитовое XOR всех его элементов или 0, если массив пуст.
Например, XOR-сумма массива [2,5,6] равна 2 XOR 5 XOR 6 = 1.
Для заданного массива nums, верните сумму всех XOR-сумм для каждого подмножества nums.
Примечание: подмножества, состоящие из одинаковых элементов, считаются различными и должны подсчитываться несколько раз.
Массив a является подмножеством массива b, если a может быть получено из b путем удаления некоторых (возможно не удалением никаких) элементов b.
Входные данные
Программа получает на вход в первой строке натуральное число n - количество элементов массива nums. Во второй строке записаны n чисел numsi.
Ограничения
1 <= n <= 121 <= numsi <= 20
Выходные данные
Выведите ответ на задачу.
Пояснения к тестовым примерам
В первом примере
В [1,3] существует 4 подмножества:
- Пустое подмножество имеет XOR-сумму 0.
- [1] имеет XOR-сумму, равную 1.
- [3] имеет XOR-сумму, равную 3.
- В [1,3] сумма XOR равна 1 XOR 3 = 2.
0 + 1 + 3 + 2 = 6
Во втором примере
В [5,1,6] 8 подмножеств:
- Пустое подмножество имеет XOR-сумму 0.
- [5] имеет XOR-сумму, равную 5.
- [1] имеет XOR-сумму, равную 1.
- [6] имеет XOR-сумму, равную 6.
- [5,1] имеет XOR-сумму 5 XOR 1 = 4.
- [5,6] имеет XOR-сумму 5 XOR 6 = 3.
- [1,6] имеет XOR-сумму 1 XOR 6 = 7.
- [5,1,6] имеет XOR-сумму 5 XOR 1 XOR 6 = 2.
0 + 5 + 1 + 6 + 4 + 3 + 7 + 2 = 28
| |
![]()
|
|
Все сочетания из n по k
Рекурсия
Перебор с возвратом
Рекурсивный перебор
Даны два целых числа n и k, выведите все возможные комбинации из k чисел, выбранных из диапазона [1, n]. Порядок элементов в одной комбинации не важен. То есть комбинация (1, 2, 3) и (3, 2, 1) считается одинаковой.
Выведите на экран все такие комбинации в лексикографическом порядке.
Входные данные
В первой строке записано целое число n, во второй - целое число k.
Ограничения
Выходные данные
Выведите в лексикографическом порядке все возможные комбинации из k чисел, выбранных из диапазона [1, n]. Каждая комбинация чисел должна выводиться в отдельной строке, числа в одной комбинации разделяются одним пробелом.
| |
![]()
|
|
Полные квадраты
Рекурсия
Целые числа
Разбор случаев
Вывод формулы
С целью поиска закономерностей иногда полезно сгенерировать длинную последовательность по определенным правилам. Известно, например, что последовательность 0, 0+ 1, 0+ 1+ 3, 0+ 1+ 3+ 5,
. . . , 0 + 1 + 3 + . . . + (2n − 1), . . ., составленная из сумм нескольких первых нечетных натуральных чисел, состоит из квадратов целых чисел: 0, 1, 4, 9, . . . , n2, . . ..
Обобщим эту последовательность следующим образом: будем использовать вместо начального значения не ноль, а число k. Получим последовательность: k, k + 1, k + 1 + 3, k + 1 + 3 + 5, . . . ,k+ 1+ 3+. . .+ (2n−1), . . .. В отличие от случая k = 0, в этой последовательности могут встречаться не только полные квадраты. Необходимо найти минимальное целое неотрицательное число, квадрат которого встречается в этой последовательности.
Требуется написать программу, которая по заданному целому числу k определяет, квадрат какого минимального неотрицательного целого числа встречается в описанной последовательности,
либо выясняет, что в ней вообще не встречается полных квадратов.
Формат входных данных
В единственной строке содержится целое число k — начальное число в последовательности
(−1012 <= k <= 1012).
Обратите внимание, что для считывания и хранения такого большого числа необходимо использовать 64-битный тип данных.
Формат выходных данных
Выведите минимальное неотрицательное целое число, квадрат которого встречается в описанной
последовательности. Если в последовательности не встречается квадратов целых чисел, выведите
«none».
| Ввод |
Вывод |
| 0 |
0 |
| -5 |
2 |
| 2 |
none |
| |
![]()
|
|
Последовательность
Рекурсия
Целые числа
Арифметические алгоритмы (Теория чисел)
Последовательность 011212201220200112… строится следующим образом: сначала пишется 0, затем повторяется следующее действие: уже написанную часть приписывают справа с заменой 0 на 1, 1 на 2, 2 на 0, и т.д.
Требуется написать программу, которая по заданному натуральному числу N определяет, какое число стоит на N-ом месте.
Входные данные
Дано натурально число число N (1 ≤ N ≤ 1018).
Выходные данные
Выведите число, которое стоит на k-ом месте в последовательности.
| |
![]()
|
|
XOR и сумма
Рекурсия
Битовые операции
Динамическое программирование
Вам дано положительное целое число N (\(1<=N<=10^{18}\)). Найдите количество пар целых чисел u и v (\(0<=u, v<=N\)) таких, что существуют два неотрицательных целых числа a и b, удовлетворяющих \(a\ xor\ b=u\) и \(a+b=v\). Здесь xor обозначает побитовое исключающее ИЛИ. Поскольку ответ может быть очень большим, вычислите его по модулю \(10^9+7\).
Входные данные
На вход подается положительное целое число N (\(1<=N<=10^{18}\)).
Выходные данные
Выведите количество возможных пар целых чисел u и v (\(0<=u, v<=N\)) , по модулю \(10^9+7\).
Примеры
| № |
Входные данные |
Выходные данные |
Пояснения |
| 1 |
3 |
5 |
u=0,v=0 (Пусть a=0,b=0, тогда 0 xor 0=0, 0+0=0)
u=0,v=2 (Пусть a=1,b=1, тогда 1 xor 1=0, 1+1=2)
u=1,v=1 (Пусть a=1,b=0, тогда 1 xor 0=1, 1+0=1)
u=2,v=2 (Пусть a=2,b=0, тогда 2 xor 0=2, 2+0=2)
u=3,v=3 (Пусть a=3,b=0, тогда 3 xor 0=3, 3+0=3) |
| 2 |
1422 |
52277 |
|
| 3 |
1000000000000000000 |
787014179 |
|
| |
![]()
|
|
Непростые разбиения
Рекурсия
Динамическое программирование
Рассмотрим разбиения целого положительного числа \(n\) в сумму целых положительных чисел. Будем называть разбиение непростым, если слагаемые в нем упорядочены по неубыванию, причем среди слагаемых нет простых чисел.
Например, для \(n=5\) существует два непростых разбиения: \(1+1+1+1+1\) и \(1+4\).
Задано число \(n\). Выведите все его непростые разбиения на слагаемые.
Формат входных данных
На вход подается число \(n\) (\(1 \le n \le 70\)).
Формат выходных данных
Выведите все непростые разбиения \(n\) на слагаемые. Слагаемые разделяйте знаком <<+>>. Не выводите пробелы. Разбиения можно вывести в любом порядке.
| |
![]()
|
|
Интересные разбиения
Рекурсия
Недавно на кружке по математике Миша узнал про разбиения на слагаемые. Разбиением числа \(n\) на слагаемые называется представление его в виде суммы неубывающего набора натуральных чисел. Например, \(9=1+2+2+4\) является разбиением числа 9 на слагаемые.
Миша называет разбиение интересным, если никакие два слагаемых в наборе не равны и не отличаются ровно на 1. Так, например, разбиение, приведенное выше не является интересным, а разбиение \(9=1+3+5\) — является.
Помогите Мише вывести все интересные разбиения числа \(n\) на слагаемые.
Формат входных данных
На ввод подается одно целое число \(n\) (\(1 \le n \le 80\)).
Формат выходных данных
Выведите все интересные разбиения числа \(n\) на слагаемые. Разбиения можно выводить в любом порядке. Соблюдайте формат из примера.
| |
![]()
|
|
Оптимизация акции
Рекурсия
Динамическое программирование
Жадный алгоритм
В сети магазинов <<Мир>> при оплате карточкой Weeza действует акция. При оплате покупки, состоящей не менее чем из \(10\) товаров, плата за самый дешевый товар не берется. Если товаров не меньше 20, то не оплачиваются уже два самых дешевых товара и т.д.
Например, при одновременной покупке \(17\) товаров, покупатель потратит сумму денег равную стоимости только \(16\) самых дорогих из них, а при покупке \(20\) и \(37\) товаров придется заплатить только за \(18\) и \(34\) самых дорогих товара, соответственно.
Миша хочет купить в магазине <<Мир>> \(n\) дисков с альбомами его любимой музыкальной группы. Подобрав подходящие диски, Миша выложил их на ленту в супермаркете в некотором порядке. Так как Миша не только меломан, но и математик, он понял, что ему, возможно, удастся сэкономить, если платить не за все \(n\) товаров одновременно, а разбить их на несколько покупок и оплатить каждую покупку отдельно. Миша решил привлекать к себе как можно меньше внимания и, в частности, не менять порядок товаров на ленте. Таким образом, Миша может только разбивать товары на ленте на группы подряд идущих и платить за каждую группу в отдельности.
Миша, конечно, математик, но вот с арифметикой у него всегда были проблемы. Помогите Мише и скажите, за какую минимальную стоимость он сможет купить \(n\) дисков, разбивая товары на ленте на группы подряд идущих товаров и оплачивая каждую группу отдельно. При этом разные группы могут быть разной длины.
Формат входных данных
В первой строке находится одно число \(n\) (\(1 \leq n \leq 100\,000\)) — количество дисков на ленте.
Следующая строка содержит \(n\) чисел \(a_i\) (\(1 \leq a_i \leq 10^9\)) — стоимости дисков в порядке расположения на ленте.
Формат выходных данных
Выведите наименьшую возможную стоимость покупки всех дисков с учетом акции при оптимальном разбиении дисков на группы.
Примечание
В первом примере Мише в любом случае придется оплатить все диски, так как суммарное количество товаров меньше \(10\).
Во втором тестовом примере оптимально во время первой покупки оплатить первые два диска, а за остальные диски заплатить во время второй покупки. Тогда не придется заплатить за диск стоимостью \(9\).
| |
![]()
|
|
Быстрое возведение в степень
Рекурсия
Задачи на процедуры и функции
Напишите функцию быстрого возведения в степень. Количество действий должно быть пропорционально двоичному логарифму n.
Входные данные
Вводится 2 числа - a (вещественное) и n (целое неотрицательное).
Выходные данные
Необходимо вывести значение an.
| |
![]()
|
|
Ханойские башни
Рекурсия
Головоломка "Ханойские башни" состоит из трех колышков, пронумерованных числами 1, 2, 3. На колышек 1 надета пирамидка из n дисков различного диаметра в порядке возрастания диаметра. Диски можно перекладывать с одного колышка на другой по одному, при этом диск нельзя класть на диск меньшего диаметра. Необходимо переложить всю пирамидку с колышка 1 на колышек 2 за минимальное число перекладываний.
Напишите программу, которая решает головоломку для данного числа дисков n.
Входные данные
Вводится 1 число n.
Выходные данные
Необходимо вывести последовательность перекладываний в формате "Disk 1 move from 1 to 2" (диск 1 переложить c колышка 1 на колышек 2), печатая по одной инструкции в строке. Диски пронумерованы числами от 1 до n в порядке возрастания диаметров.
| |
![]()
|
|
Дерево игры
Рекурсия
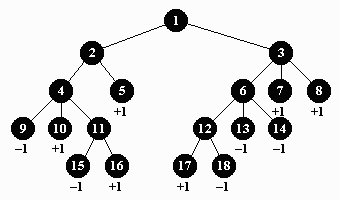
Игра для двух игроков определяется её деревом. Соперники делают ходы по очереди. Первый игрок начинает игру. Игра кончается или вничью, или победой одного из игроков. Листья дерева этой игры могут иметь значения, равные одному из трёх чисел: +1 - победа первого игрока, -1 - победа второго игрока, 0 - ничья. Ваша задача - определить, кто выиграет, если оба противника следуют правильной стратегии.
Входные данные
Узлы дерева пронумерованы последовательными целыми числами. Корень дерева всегда имеет номер 1. Первая строка входного файла содержит целое N - число узлов в дереве игры. Следующая N - 1 строка описывает узлы - одна строка для каждого узла (за исключением первого). Вторая строка содержит описание второго узла дерева, третья - третьего узла и т.д. Если узел является листом, первый символ строки - L, затем идёт пробел, затем номер родительского узла, ещё пробел и результат игры (+1 - победа первого игрока, -1 - победа второго, 0 - ничья). Если узел внутренний, то строка содержит N - первый символ, затем пробел и номер родительского узла. 2 <= N <= 1000.
Выходные данные
Выводится +1, если выигрывает первый игрок, -1, если второй, и 0 - в случае ничейного исхода.
| |
![]()
|
|
Умножение многочленов
Рекурсия
Ввести в символьной форме два многочлена от x с целыми коэффициентами и вывести их произведение в порядке убывания степеней - также в символьной форме.
Ограничения: степень исходных многочленов не более 10, коэффициенты исходных многочленов по модулю не более 104.
Входные данные
В двух строках находятся многочлены.
Выходные данные
В единственной строке выводится многочлен.
| |
![]()
|
|
Быстро возрастающее разбиение
Рекурсия
Перебор с возвратом
Рассмотрим все представления числа \(n\) в виде суммы различных целых возрастающих слагаемых: \(n = a_1 + a_2 + \ldots + a_k\), \(a_1 < a_2 < \ldots < a_k\).
Будем называть такое разбиение быстро возрастающим, если для него выполнено следующее условие: для любых трех подряд идущих слагаемых разница между большим и средним строго больше, чем между средним и меньшим, иначе говоря, \(a_{i+2} - a_{i+1} > a_{i+1} - a_i\).
Задано число \(n\). Выведите все его быстро возрастающие разбиения на слагаемые.
Формат входных данных
На ввод подается целое число \(n\) (\(1 \le n \le 100\)).
Формат выходных данных
Выведите все быстро возрастающие разбиения на слагаемые числа \(n\). Разбиения можно выводить в любом порядке. Выводите слагаемые в каждом разбиении, разделяя их знаком <<+>> без пробелов.
| |
![]()
|
|
Определение символа в позиции
Рекурсия
Строки, состоящие из последовательностей цифр, формируются следующим образом. Первая строка состоит из четырех единиц. Каждая из последующих строк создается следующим действием: берется предыдущая строка и после каждой ее цифры вставляется цифра на единицу большая. Вот первые 3 строки, созданные по этому правилу:
(1) 1111
(2) 12121212
(3) 1223122312231223
Какая цифра будет стоять в позиции 100 в строке (9)?
Первая цифра слева стоит на позиции 1
| |
![]()
|
|
Определение символа в позиции - 2
Рекурсия
Строки, состоящие из последовательностей цифр, формируются следующим образом. Первая строка состоит из четырех единиц. Каждая из последующих строк создается следующим действием: берется предыдущая строка и после каждой ее цифры вставляется цифра на единицу большая. Вот первые 3 строки, созданные по этому правилу:
(1) 1111
(2) 12121212
(3) 1223122312231223
Какая цифра будет стоять в позиции 479 в строке (9)?
Первая цифра слева стоит на позиции 1
| |
![]()
|
|
Определение символа в позиции - 3
Рекурсия
Строки, состоящие из последовательностей цифр, формируются следующим образом. Первая строка состоит из четырех единиц. Каждая из последующих строк создается следующим действием: берется предыдущая строка и перед каждой ее цифрой вставляется цифра на единицу большая. Вот первые 3 строки, созданные по этому правилу:
(1) 1111
(2) 21212121
(3) 3221322132213221
Какая цифра будет стоять в позиции 479 в строке (9)?
Первая цифра слева стоит на позиции 1
| |
![]()
|
|
Определение символа в позиции - 4
Рекурсия
Строки, состоящие из последовательностей цифр, формируются следующим образом. Первая строка состоит из одной единицы. Каждая из последующих строк создается следующим действием: берется предыдущая строка и после каждой ее цифры вставляется цифра на единицу большая и затем еще раз исходная цифра. Вот первые 3 строки, созданные по этому правилу:
(1) 1
(2) 121
(3) 121232121
(4) 121232121232343232121232121
Какая цифра будет стоять в позиции 1094 в строке (9)?
Первая цифра слева стоит на позиции 1
| |
![]()
|
|
Определение символа в позиции - 5
Рекурсия
Строка формируется из заглавных английских букв следующим образом
-
Начинаем с "A".
-
Каждый следующий шаг: к предыдущей строке приписываем новую строку, в которой каждый символ предыдущей строки сдвинут вправо на 1 по алфавиту (A→B, B→C и т. д. Z→A).
Вот первые четыре шага:
Шаг 1: A
Шаг 2: AB
Шаг 3: ABBC
Шаг 4: ABBCBCCD
Какой символ стоит на 100-й позиции после 8-го шага?
Первый символ слева стоит на позиции 1.
| |
![]()
|
|
Определение символа в позиции - 6
Рекурсия
Строка формируется из заглавных английских букв следующим образом
-
Начинаем с "A".
-
Каждый следующий шаг: к предыдущей строке приписываем новую строку, в которой каждый символ предыдущей строки сдвинут вправо на 2 по алфавиту (A→C, B→D, ..., Y→A, Z→B).
Вот первые четыре шага:
Шаг 1: A
Шаг 2: AС
Шаг 3: AССE
Шаг 4: ACCECEGG
Какой символ стоит на 50-й позиции после 7-го шага?
Первый символ слева стоит на позиции 1.
| |
![]()
|
|
Непизанские кролики (2024-2025, 11)
Рекурсия
Рекуррентные последовательности
Дана блок-схема алгоритма, реализованного в виде рекурсивно вызываемой функции:

Известно, что 𝐴, 𝐵 и 𝐶 - натуральные числа и что 𝐴 < 𝐵 < 𝐶.
Петя вызывает эту функцию, передавая ей в качестве входного параметра натуральное число. Известно, что для некоторого 𝑘 функция возвращает следующие значения:
𝐹(𝑘) = 50890368413;
𝐹(𝑘 + 1) = 93601980590;
𝐹(𝑘 + 2) = 172160883161.
Определите значения 𝐴, 𝐵 и 𝐶, при которых это возможно. Если таких вариантов несколько, выберите вариант с наименьшей суммой 𝐴, 𝐵 и 𝐶. В ответе введите в указанном порядке значения 𝐴, 𝐵 и 𝐶, разделённые пробелом.
| |
![]()
|
|
Рекурсивное закрашивание (2024-2025, 11)
Рекурсия
Разбирая старые задачи олимпиады, Петя наткнулся на алгоритм рекурсивного закрашивания растрового изображения. У Пети есть черно-белое (bitmap) изображение размером 13 на 13 пикселей. На изображении присутствует замкнутый контур, как приведено на рисунке. Пиксели внутри контура пронумерованы.

Традиционно для компьютерной графики, система координат имеет начало в верхнем левому углу, ось X направлена слева направо, а ось Y – сверху вниз.
Алгоритм рекурсивного закрашивания заключается в рекурсивном вызове процедуры «Закрасить», которой передаются два параметра – координаты X и Y пикселя.
Процедура Закрасить(X, Y), может быть описана следующим образом:
1. Если цвет пикселя с координатами (X, Y) белый, то:
a. Изменить цвет пикселя с этими координатами на черный;
b. Вызвать процедуру Закрасить(X+1, Y);
c. Вызвать процедуру Закрасить(X, Y+1);
d. Вызвать процедуру Закрасить(X-1, Y);
e. Вызвать процедуру Закрасить(X, Y-1);
2.Иначе завершить процедуру.
Известно, что последний закрашенный пиксель, перед завершением процедуры, имел номер 29. Сколько существует пикселей внутри контура, в которых можно исходно вызвать процедуру «Закрасить» так, чтобы получить такой результат?
В ответе укажите целое число.
| |
![]()
|
|
Проверка гипотезы (2024-2025, 11)
Рекурсия
Дана блок-схема алгоритма, реализованного в виде рекурсивно вызываемой функции:
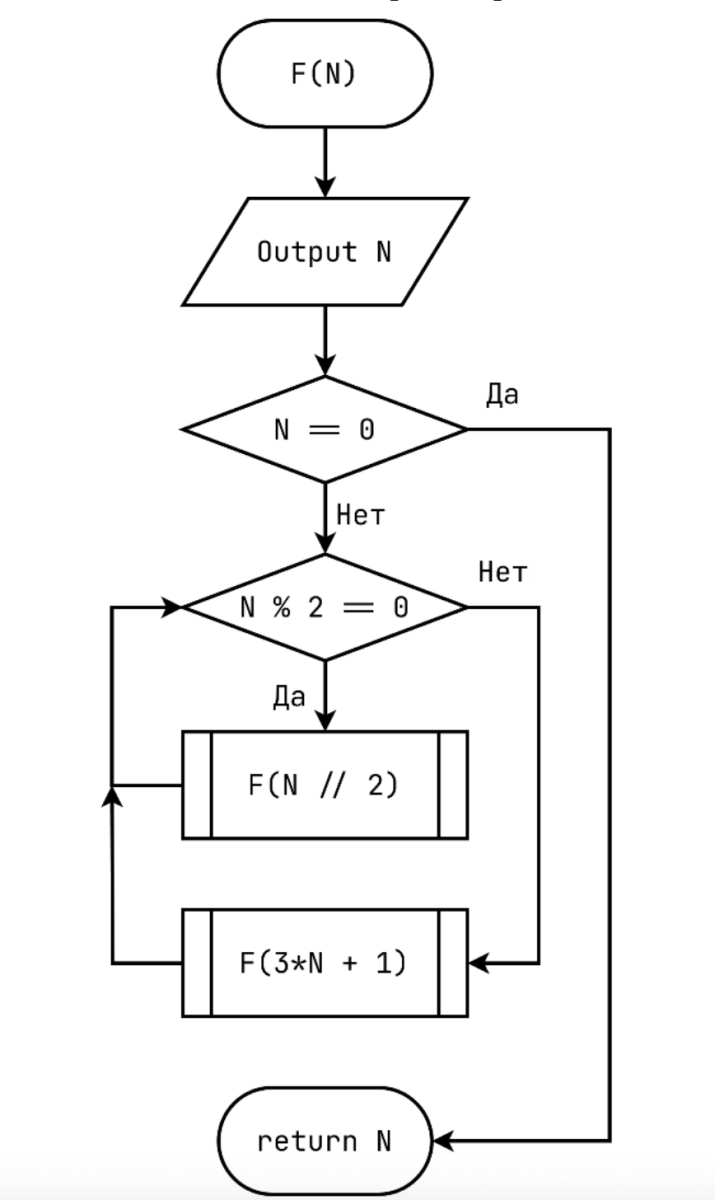
Определите сумму первых 1010 чисел, которые выведутся при запуске алгоритма с 𝑁 = −3159
| |
![]()
|
|
Гномы и сокровища
Рекурсия
В подземелье живут гномы. У них есть древняя традиция деления золота:
Когда гном получает N монет:
1. Если N = 0, гном грустит и ничего не делает
2. Если N = 1, гном оставляет монету себе и кричит "МОЁ!"
3. Если N > 1:
- Гном берёт себе 1 монету и кричит "МОЁ!"
- Остальные (N-1) монет делит пополам
- Левую половину (N-1)/2 отдаёт левому ученику-гному
- Правую половину (N-1) - (N-1)/2 отдаёт правому ученику-гному
- Каждый ученик делает то же самое по традиции
Подсчитайте, сколько раз прозвучит крик "МОЁ!" при делении N монет.
Формат входных данных
Одно число N (0 ≤ N ≤ 10^9) - начальное количество монет.
Формат выходных данных
Одно число - сколько раз прозвучит "МОЁ!"
| |
![]()
|
|
Рекурсия - 4
Рекурсия
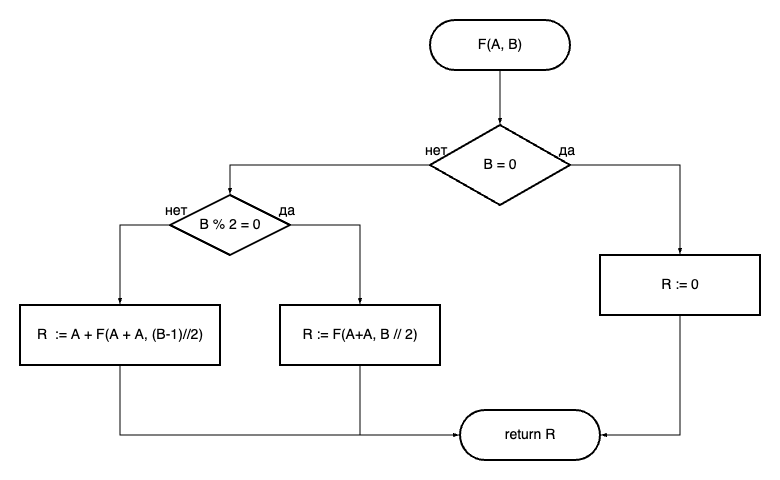
Дана блок-схема алгоритма F(A, B)
Найдите такую пару целых положительных чисел A и B (известно, что B > 1), чтобы вызов F(A, B) вернул число 1594323. Если таких пар существует несколько, найдите ту, у которой максимальное значение A. В ответе укажите через пробел сначала значение A и затем значение B.
| |
![]()
|
|
Рекурсия - 3
Рекурсия
Дана блок-схема алгоритма F(A, B)
Найдите такую пару целых положительных чисел A и B (известно, что B > 1), чтобы вызов F(A, B) вернул число 2097152. Если таких пар существует несколько, найдите ту, у которой максимальное значение A. В ответе укажите через пробел сначала значение A и затем значение B.

| |
![]()
|
|
Рекурсия - 2
Рекурсия
Дана блок-схема алгоритма F(A, B)
Найдите такую пару целых положительных чисел A и B (известно, что B > 1), чтобы вызов F(A, B) вернул число 1240029. Если таких пар существует несколько, найдите ту, у которой максимальное значение A. В ответе укажите через пробел сначала значение A и затем значение B.

| |
![]()
|