| | | |
|
Космическая флотилия
Циклы
Громозека и Алиса путешествуют по космосу и наткнулись на флотилию из M космических кораблей. Они решили, что для создания впечатляющего зрелища корабли должны выстроиться в форме квадрата, то есть число кораблей должно быть точным квадратом. Однако число M может быть не точным квадратом, поэтому они решили разделить корабли на несколько эскадр, каждая из которых будет выстраиваться в форме квадрата. Для красоты все эскадры должны быть одинакового размера, также размер каждой эскадры должен быть как можно больше.
Определите максимально возможный размер эскадры, чтобы они создали наиболее впечатляющее образование.
Входные данные
Программа получает на вход одно целое положительное число M, не превосходящее 2×109, – количество участников парада.
Выходные данные
Программа должна вывести одно число – максимально возможный размер эскадры.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
180
|
36
|
| |
![]()
|
|
Таблицы
Циклы
Вася записывает в клетки квадратной таблицы NxN натуральные числа по порядку, сначала заполняя первую строку слева направо, затем вторую и т.д. (см. рисунок слева). Петя заполняет такую же таблицу, расставляя числа сначала в первый столбец сверху вниз, затем во второй столбец и т.д.
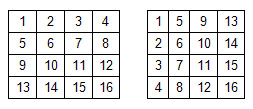
При этом оказалось, что некоторые числа и Вася, и Петя записали в одну и ту же клетку (например, число 6 записано во вторую строку второго столбца обеих таблиц).
Вам требуется написать программу, выводящую все числа, которые в обеих таблицах записаны в одних и тех же клетках.
Входные данные
Вводится одно число - размер таблицы.
Выходные данные
Программа должна вывести все числа, которые в обеих таблицах стоят на одном и том же месте, в порядке возрастания, через пробел.
Размер таблицы - натуральное число, не превосходящее 100.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 |
1 6 11 16 |
| |
![]()
|
|
Кузнечики
Циклы
На прямой тропинке на расстоянии 1 метр друг от друга сидят два кузнечика. Время от времени один из кузнечиков прыгает на несколько сантиметров влево или вправо. Требуется узнать, каково было минимальное расстояние, на которое сближались кузнечики в процессе прыжков. (Расстояние считается только в те моменты, когда оба кузнечика сидят на земле).
Входные данные: В первой строке вводится одно число N (1 <= N <= 100) – общее количество прыжков, а затем N чисел, описывающих прыжки. Модуль числа равен длине прыжка в сантиметрах; число отрицательное, если кузнечик начинал этот прыжок по направлению к другому кузнечику, и положительное – если от другого кузнечика. Числа по модулю не превосходят 100 и все отличны от 0. (Кузнечики могут перепрыгивать друг через друга. Гарантируется, что кузнечики не приземляются друг на друга.)
Выходные данные: Требуется вывести одно число – минимальное расстояние в сантиметрах, на которое сближались кузнечики.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
1
2
3
4
5 |
100 |
| |
![]()
|
|
Ёлочка
Циклы
Вам требуется нарисовать на экране ёлочку высоты H.
Входные данные: Вводится одно натуральное число H, не превосходящее 20.
Выходные данные: Выведите ёлочку из звёздочек (см. примеры).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 |
*
***
|
| 2 |
4 |
*
***
*****
*******
|
| |
![]()
|
|
Вложенные циклы - 1
Цикл for
Цикл while
Циклы
Вводятся два числа N и K. Выведите количество чисел из диапазона от 1 до N (включительно) таких, что их сумма цифр делится на K.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
100 3 |
33 |
| 2 |
22 4 |
5 |
| |
![]()
|
|
Найти карточку
Циклы
Для настольной игры используются карточки с номерами от 1 до N (N – натуральное число, не превышающее 106). Одна карточка потерялась. Найдите ее.
Входные данные: Дано N, далее N-1 номеров оставшихся карточек.
Выходные данные: Требуется вывести номер потерянной карточки.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
1
2
3
4 |
5 |
| 2 |
4
3
2
4 |
1 |
| |
![]()
|
|
Клад
Циклы
Строки
Путь к кладу задан в виде указаний, какое количество шагов нужно пройти в одном из четырёх направлений: север (N), юг (S), запад (W), восток (E). Весь маршрут записан в виде строки, содержащей последовательность из чисел и следующих за числами букв, указывающих направление перемещения. Например, строка «7N5E2S3E» означает "пройти 7 шагов на север, 5 шагов на восток, 2 шага на юг, 3 шага на восток». В маршруте может быть много команд перемещения, поэтому каждый такой маршрут можно сократить.
Например, ранее приведённый маршрут можно сократить до «5N8E". По данному маршруту до клада сократите его до строки минимальной длины.
Программа получает на вход строку, состоящую из целых неотрицательных чисел, не превосходящих 107 каждое, и одной буквы (N, S, W, E ) следующей за каждым
числом. Других символов (в том числе пробелов), кроме цифр и букв направлений, в строке нет. Длина строки не превосходит 250 символов. Гарантируется, что начальная
и конечная точки маршрута различаются.
Программа должна вывести маршрут, ведущий в ту же точку, записанный в таком же виде, как во входных данных, используя минимальное число символов. Если ответов
несколько, программа должна вывести один (любой) из них.
| Ввод |
Вывод |
Примечание |
| 7N5E2S3E |
5N8E |
Правильным ответом будет также «8E5N» |
| 10N30W20N |
30N30W |
Правильным ответом будет также «30W30N» |
| |
![]()
|
|
Второй максимум
Циклы
Дано N целых чисел. Найти второй по величине максимальный элемент последовательности (элемент, который бы стоял предпоследним, если бы входные данные отсортировали по неубыванию).
Входные данные
В первой строке задается число N (\(2<=N<=10^4\)). Далее идут N строк, в каждой строке по одному целому числу, не превышающему 105 по модулю.
Выходные данные
Выведите второй максимальный элемент.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
7
10
15
20
35
14
35
10 |
35 |
| 2 |
5
10
5
7
11
9 |
10 |
| |
![]()
|
|
Комфорт для коров
Циклы
Двумерные массивы
Пастбище Фермера Джона может быть представлено как огромная 2D-решётка ячеек (огромная шахматная доска). Изначально пастбище пустое.
Фермер Джон добавит N (1≤N≤105) коров на пастбище одну за одной. i-ая корова занимает ячейку (xi,yi), которая отличается от ячеек, занятых всеми другими коровами (0≤xi,yi≤1000).
Говорят, что корове "комфортабельно", если по горизонтали и вертикали она имеет ровно три других коровы. Фермер Джон хочет посчитать, скольким коровам комфортабельно на его пастбище. Для каждого i в интервале 1…N, выведите общее количество коров, которым комфортабельно после того, как i-ая корова добавлена на пастбище.
Входные данные:
Первая строка содержит одно целое число N. Каждая из последующих N строк содержит два разделённых пробелом целых числа, указывающих (x,y) - координаты ячейки коровы. Гарантируется, что все ячейки различны.
Выходные данные:
i-ая строка вывода должна содержать общее количество коров, которым комфортабельно после добавления i-ой коровы на пастбище.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
8
0 1
1 0
1 1
1 2
2 1
2 2
3 1
3 2 |
0
0
0
1
0
0
1
2 |
После того, как добавлены первые 4 коровы, корове в ячейке (1,1) стало комфортабельно.
После того, как добавлены первые 7 коров, корове в ячейке (2,1) стало комфортабельно.
После того, как добавлены первые 8 коров, корове в ячейках (2,1) и (2,2) стало комфортабельно. |
| |
![]()
|
|
Преферанс
Циклы
Перебор
В некоторой карточной игре используется колода, в которой 4 туза. В игре принимает участие 4 игрока, каждому из которых раздается равное число карт, а две карты откладываются в прикуп.
Каждый игрок похвастал, сколько у него тузов. Определите, сколько игроков заведомо солгали.
Например, они сказали 1, 1, 1, 2. Следовательно, заведомо солгал 1 игрок. (Какие-то трое могли сказать правду, но все четверо правду сказать не могли, так как тузов всего 4).
Входные данные
Вводятся 4 числа (от 0 до 9 каждое), разделенных пробелом – количество тузов по словам первого, второго, третьего и четвертого игроков.
Выходные данные
Выведите одно число – минимальное количество игроков, которые заведомо солгали. Если все одновременно могли сказать правду, выведите число 0.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 1 1 2 |
1 |
| 2 |
1 1 1 1 |
0 |
| |
![]()
|
|
Детский сад
Условный оператор
Циклы
В младшей группе детского сада «Телепузики» всего n детей. Каждый из них, как и любой четырехлетка, легко может начать плакать просто из-за того, что его одногруппники тоже плачут. Ну и что, что он не знает, в чем дело? Товарищи же не могут ошибаться.
Воспитательница работает в детском саду уже много лет, и отлично разбирается в детском настроении. Ей достаточно посмотреть на ребенка, чтобы понять, насколько он сегодня плаксив: заплачет ли он сегодня сам из-за того, что компот невкусный, разрыдается ли из-за того, что Катя и Ваня уже плачут, а он еще нет, или же будет сосредоточенно играть c кубиками, не обращая внимание на слезы и сопли товарищей.
Зная сегодняшнюю плаксивость каждого из детей, определите, будет ли сегодня рыдать вся группа одновременно, или обойдется без массовой истерики.
Входные данные
В первой строке дано целое число n (1n1000) — количество детей в группе. В следующей строке через пробел перечислены n чисел, причем i-е по счету число qi (0qin−1 ) обозначает плаксивость i-го ребенка. Число qi обозначает количество детей, которые должны заплакать, чтобы этот ребенок тоже заплакал. Если qi = 0, значит, этот ребенок точно сегодня заплачет просто так, вне зависимости от своих товарищей. Считается, что ребенок не может начать плакать, если вокруг него не плачет нужное количество детей. Если ребенок начал плакать, то он уже не успокоится до вечера.
Выходные данные
Выведите «YES», если вся группа будет плакать одновременно, или «NO» иначе.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4
1 0 1 2 |
YES |
| 2 |
3
1 1 1 |
NO |
| |
![]()
|
|
Башни
Циклы
Егор очень любит Москву и часто ходит на прогулку, чтобы полюбоваться ее видами.
Москва в представлении Егора представляет собой длинное прямое шоссе, вдоль которого расположено n башен, пронумерованных в порядке их следования числами от 1 до n. Все башни имеют различные высоты, которые выражаются целыми числами от 1 до n . Высота башни с номером i составляет hi .
Однако Егор не любит возрастающие последовательности. Его разочаровывают тройки башен, таких что с возрастанием их индексов их значения тоже возрастают. Более формально, тройка башен с номерами i , j и k разочаровывает Егора, если i < j < k и hi < hj < h k .
Егор заранее знает высоты всех башен в Москве и хочет узнать, сильно ли он разочаруется на прогулке. Помогите ему определить, сколько есть троек башен, которые его разочаруют.
Входные данные
Первая строка входных данных содержит единственное число n — количество башен в Москве ( 1 ≤ n ≤ 8000 ).
Вторая строка входных данных содержит n различных натуральных чисел, i -е из них h i — высота i -й башни ( 1 ≤ hi ≤ n ).
Выходные данные
Выведите одно число — количество троек башен, которые разочаруют Егора.
Обратите внимание, что ответ может не поместиться в стандартный 32-битный тип данных. Надо использовать 64-битный тип, в паскале он называется « int64 », в C++ « long long », в Java « long ».
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
1 3 4 2 5 |
5 |
| 2 |
3
3 1 2 |
0 |
| |
![]()
|
|
Дома и магазины
Одномерные массивы
Циклы
На Новом проспекте построили подряд 10 зданий. Каждое здание может быть либо жилым домом, либо магазином, либо офисным зданием.
Но оказалось, что жителям некоторых домов на Новом проспекте слишком далеко приходится идти до ближайшего магазина. Для разработки плана развития общественного транспорта на Новом проспекте мэр города попросил вас выяснить, какое же наибольшее расстояние приходится преодолевать жителям Нового проспекта, чтобы дойти от своего дома до ближайшего магазина.
Входные данные
Программа получает на вход десять чисел, разделенных пробелами. Каждое число задает тип здания на Новом проспекте: число 1 обозначает жилой дом, число 2 обозначает магазин, число 0 обозначает офисное здание. Гарантируется, что на Новом проспекте есть хотя бы один жилой дом и хотя бы один магазин.
Выходные данные
Выведите одно целое число: наибольшее расстояние от дома до ближайшего к нему магазина. Расстояние между двумя соседними домами считается равным 1 (то есть если два дома стоят рядом, то между ними расстояние 1, если между двумя домами есть еще один дом, то расстояние между ними равно 2 и т.д.)
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
2 0 1 1 0 1 0 2 1 2 |
3 |
В примере из условия дальше всего идти до ближайшего магазина жителям четвертого дома: ближайший к их дому магазин находится в первом доме, и им нужно пройти три дома до него. Жителям других домов придется пройти меньшее расстояние до ближайшего магазина, поэтому ответ 3. |
| |
![]()
|
|
Блины
Цикл while
Одномерные массивы
Циклы
Мы все знаем, что начавшаяся зима скоро закончится, и на праздновании Масленицы все будут есть блины. Об этом и будет наша задача.
N гостей сидят за столом, и перед каждым стоит тарелка с блинами. На тарелке i-го гостя лежит ai блинов. Каждый гость съедает один блин за одну минуту, таким образом, время, когда закончит есть блины последний человек, равно наибольшему значению из ai.
Неожиданно к ним присоединился ещё один человек, и теперь все присутствующие могут переложить часть своих блинов (в том числе могут переложить все свои блины, а могут не перекладывать ни одного блина) вновь пришедшему человеку. Перекладывание блинов происходит одновременно и моментально.
Гости хотят переложить блины таким образом, чтобы после перекладывания они съели все блины за минимальное время (которое равно наибольшему числу блинов на тарелках у гостей, включая нового гостя). Определите, за какое наименьшее время гости смогут съесть свои блины после перекладывания.
Программа получает на вход натуральное число N, не превосходящее 100.000, – первоначальное количество гостей. Следующие N строк содержат натуральные числа ai – количество блинов на тарелке i-го человека. Значения ai даны в порядке неубывания, то есть ai ≤ ai+1. Сумма значений всех ai не превосходит 2·109.
Программа должна вывести одно целое число – минимальное время, за которое все гости закончат есть свои блины после перекладывания части блинов на тарелку нового гостя.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
4
1
3
5
6 |
4 |
За столом сидят 4 человека, у них на тарелках 1, 3, 5, 6 блинов. Новому гостю последний гость отдаст 2 блина, а предпоследний – 1 блин, и тогда у всех, включая нового гостя, будет не более 4 блинов. |
| |
![]()
|
|
Раскраска кеглей
Циклы
Комбинаторика
В ряд ставятся N кеглей. Громозека красит каждую из них в один из K цветов из своих банок с краской. Из эстетических соображений любые две соседних кегли должны быть окрашены в разные цвета. Найдите количество возможных способов раскрасить кегли.
Входные данные
Входная строка содержит два целых числа N и K (\(1<=N<=1000\), \(2<=K<=1000\)).
Выходные данные
Выведите на экран ответ на задачу. Гарантируется, что верный ответ не превышает \(2^{31}-1\).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 2 |
2 |
| 1 |
1 10 |
10 |
| |
![]()
|
|
Соревнование с напитками
Циклы
Громозека собирается принять участие в финальном раунде STCoder Contest. В этом соревновании N задач, пронумерованных от 1 до N. Громозека знает, что на решение задачи i (\(1<=i<=N\)) требуется Ti секунд. Кроме того, участникам предлагается M видов напитков, пронумерованных от 1 до M. Если Громозека выпьет напиток i (\(1 <= i <= M\)), его мозг будет стимулироваться и время, необходимое ему для решения задачи Pi станет Xi секунд. Это не влияет на время решения других задач.
Участнику разрешается выпить ровно один из напитков до начала конкурса. Для каждого напитка Громозека хочет знать, сколько секунд ему понадобится, чтобы решить все задачи, если он выпьет этот напиток. Предположим, что время, необходимое ему для решения всех задач, равно сумме времени, необходимого для решения отдельных задач. Ваша задача - написать вместо Громозеки программу для расчета времени.
Входные данные
На вход подаются целые числа. В первой строке число N (\(1<=N<=100\)), во второй строке N чисел Ti (\(1<=T_i<=10^5\)). В третьей строке задано число M (\(1<=M<=100\)). Далее идет M строк, в каждой из которых задана пара Pi,Xi (\(1<=P_i<=N\), \(1<=X_i<=10^5\)).
Выходные данные
Для каждого напитка подсчитайте, сколько секунд потребуется Громозеке, чтобы решить все задачи, если он выпьет этот напиток, и выведите результаты, по одному в строке.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснения |
| 1 |
3
2 1 4
2
1 1
2 3 |
6
9 |
Если Громозека выпьет напиток под номером 1, время, необходимое ему для решения каждой задачи, составит 1, 1 и 4 секунды, соответственно, всего 6 секунд.
Если Громозека выпьет напиток 2, время, необходимое ему для решения каждой задачи, составит 2, 3 и 4 секунды, соответственно, всего 9 секунд. |
| 2 |
5
7 2 3 8 5
3
4 2
1 7
4 13 |
19
25
30 |
|
| |
![]()
|
|
Сумма трех целых
Циклы
Вложенные циклы
Вам даны два целых числа K и S. Три переменные X, Y и Z принимают целые значения, удовлетворяющие условию \(0<=X,Y,Z<=K\). Сколько существует различных значений X, Y и Z, таких что \(X+Y+Z=S\)?
Входные данные
На вход подается два целых числа K (\(2<=K<=2500\)) и S (\(0<=S<=3\cdot K\)).
Выходные данные
Выведите количество троек X, Y и Z, удовлетворяющих условию.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснения |
| 1 |
2 2 |
6 |
Есть шесть троек X, Y и Z, которые удовлетворяют условию:
Х = 0, Y = 0, Z = 2
Х = 0, Y = 2, Z = 0
Х = 2, Y = 0, Z = 0
Х = 0, Y = 1, Z = 1
Х = 1, Y = 0, Z = 1
Х = 1, Y = 1, Z = 0 |
| 2 |
5 15 |
1 |
Лишь одна тройка удовлетворяют условию задачи:
Х = 5, Y = 5, Z = 5 |
| |
![]()
|
|
Уменьшим-увеличим
Строки
Циклы
У вас есть целочисленная переменная x. Первоначально \(x = 0\). Кто-то дал вам строку S длины N, и, используя эту строку, вы выполнили следующую операцию N раз. В i-й операции вы увеличили значение x на 1, если Si = I, и уменьшили значение x на 1, если Si = D. Найдите максимальное значение, которое принимает x во время операций (в том числе до первой операции и после последней операции).
Формат входных данных
В первой строке задается число N (\(1<=N<=100\)), во второй - строка S. Длина строки N. Строка содержит только символы I и D.
Формат выходных данных
Выведите максимальное значение x, полученное во время операций.
| |
![]()
|
|
Снежный покров
Цикл for
Циклы
В некоторой деревне есть 999 башен высотой 1, (1 + 2), (1 + 2 + 3), ..., (1 + 2 + 3 + ... + 999) метров с запада на восток. Расстояние между двумя соседними башнями 1 метр. Некоторое время шел снег, прежде чем он наконец прекратился. Для двух соседних башен, расположенных на расстоянии 1 метра друг от друга, мы измерили длины частей этих башен, которые не покрыты снегом, и получили a метров для западной башни и b метров для восточной башни. Предполагая, что толщина снежного покрова и высота над уровнем моря одинаковы во всем населенном пункте, найдите общую глубину снежного покрова. Предположим также, что глубина снежного покрова всегда составляет не менее 1 метра.
Входные данные
Во входной строке содержится два целых чисел a и b (\(1\leq a<b<499500=1+2+3+...+999\)). Все входные данные удовлетворяют условию задачи.
Выходные данные
Выведите глубину снежного покрова.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
8 13 |
2 |
Высота двух башен - 10 метров и 15 метров соответственно. Таким образом, мы видим, что глубина снежного покрова составляет 2 метра. |
| 2 |
54 65 |
1 |
|
| |
![]()
|
|
День программиста
Целые числа
Циклы
Вложенные циклы
Перед празднованием Дня программиста офис IT компании украсили последовательностью чисел длины N, a = {a1, a2, a3, ..., aN}. Багз Хантер, сотрудник отдела тестирования, хотел бы поиграть с этой последовательностью. В частности, он хотел бы повторить следующую операцию как можно больше раз.
Для каждого i, удовлетворяющего 1<=i<=N, выполните одно из следующих действий: «разделить ai на 2» и «умножить ai на 3». Нельзя выполнять «умножить ai на 3» сразу для каждого i в течении одной операции, значение ai после любого действия должно быть целым числом.
Одну операцию Багз Хантер делает за 1 секунду независимо от количества чисел в последовательности. Определите максимум через сколько секунд Багз Хантер вернется к своей работе?
Входные данные
В первой строке записано целое число N (1<=N<=10000). Во второй строке записаны N целых чисел ai (1<=ai<=109).
Выходные данные
Выведите одно число - максимальное количество секунд, через которое Багз Хантер вернется к своей работе.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
3
5 2 4 |
3 |
Последовательность изначально 5,2,4.
Три операции можно выполнить следующим образом:
- сначала умножьте a1 на 3, умножьте a2 на 3 и разделите a3 на 2. Теперь последовательность 15,6,2;
- затем умножьте a1 на 3, разделите a2 на 2 и умножьте a3 на 3. Теперь последовательность 45,3,6;
- наконец, умножьте a1 на 3, умножьте a2 на 3 и разделите a3 на 2. Теперь последовательность 135,9,3.
Далее, с каждым числом можно выполнить только умножение на 3, но это действие недопустимо сразу для всех чисел ai.
Поэтому ответ 3. |
| 2 |
4
631 577 243 199 |
0 |
|
| 3 |
10
2184 2126 1721 1800 1024 2528 3360 1945 1280 1776 |
39 |
|
| |
![]()
|
|
Сумма цифр числа
Целые числа
Циклы
Для целых чисел b ( b >= 2 ) и n ( n >= 1 ) пусть функция f(b, n) определяется следующим образом:
\(f (b, n) = n, когда\ n < b \\
f (b, n) = f (b, floor (n / b)) + (n \ mod \ b), когда \ n >= b\)
Здесь
floor(n / b) обозначает наибольшее целое число, не превышающее n / b;
n mod b обозначает остаток от n, деленный на b.
Менее формально f(b, n) равно сумме цифр n, записанных в базе b. Например, справедливо следующее:
\(f (10,87654) = 8 + 7 + 6 + 5 + 4 = 30\\
f (100,87654) = 8 + 76 + 54 = 138\)
Вам даны целые числа n и s. Определите, существует ли целое число b (b >= 2) такое, что f(b, n) = s. Если ответ положительный, найдите наименьшее из таких b.
Входные данные
В первой строке вводится целое число n (1 <= n <= 1011). Во второй строке - целое число s (1 <= s <= 1011).
Выходные данные
Выведите ответ на задачу. Если ответа нет, то выведите -1.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
87654
30 |
10 |
| 2 |
87654
138 |
100 |
| 3 |
87654
45678 |
-1 |
| 4 |
31415926535
1 |
31415926535 |
| 5 |
1
31415926535 |
-1 |
| |
![]()
|
|
Путешествие Громозеки
Циклы
Массивы
У Громозеки есть следующие два личных принципа: он никогда не преодолевает расстояние больше L за один день. Он никогда не спит под открытым небом. То есть он должен находться в отеле в конце дня.
На планете Блук N отелей и все расположены на одной улице. Координата i-го отеля (1<=i<=N) равна xi.
Путешествуя по планете Блук, Громозека запланировал Q переездов. Каждым переездом он планирует менять отель aj на bj (1<=j<=Q). Для каждого переезда найдите минимальное количество дней, которое нужно Громозеке, чтобы добраться от aj-го отеля до bj-го, следуя его принципам.
Гарантируется, что он всегда может поехать из aj-го отеля до bj-го отеля.
Входные данные
В первой строке задается целое число N (2<=N<=105) - количество отелей на планете Блук. Во второй строке - N чисел xi - координаты i-го отеля (1<=x1<x2<...<xN<=109 , xi+1−xi<=L). В третьей строке записано число L (1<=L<=109). В четвертой строке - число Q (1<=N<=105).
В последних Q строчках находится по два различных числа aj и bj (1<=aj,bj<=N). Все числа целые.
Выходные данные
Выведите Q строк. В j-й строке (1<=j<=Q) должно быть указано минимальное количество дней, которое Громозеке нужно, чтобы добраться из aj-го отеля до bj -го отеля.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
9
1 3 6 13 15 18 19 29 31
10
4
1 8
7 3
6 7
8 5 |
4
2
1
2 |
По 1-му переезду он может проехать от 1-го отеля до 8-го за 4 дня следующим образом:
День 1: Переезд из 1-го отеля во 2-й отель. Пройденное расстояние - 2.
День 2: Переезд из 2-го отеля в 4-й. Пройденное расстояние - 10.
День 3: Переезд из 4-го отеля в 7-й. Пройденное расстояние - 6.
День 4: Переезд из 7-го отеля в 8-й. Пройденное расстояние - 10. |
| |
![]()
|
|
Голосование
Циклы
Конструктив
Разбор случаев
Коротышки решили взять в полет на Луну либо Незнайку либо Пончика. Не сумев договориться, они решили проголосовать. Незнайка и Пончик наблюдают краткий отчет о голосовании. Коротышки показывают Незнайке и Пончику соотношение текущего количества голосов, полученных Незнайкой и Пончиком, но не фактическое количество голосов. Незнайка и Пончик посмотрели отчет N раз, и когда они смотрели его в i-й (1<=i<=N) раз, соотношение было Pi:Ni. Известно, что Незнайка и Пончик имели хотя бы один голос, когда впервые увидели отчет. Найдите минимально возможное общее количество голосов, полученных Незнайкой и Пончиком, когда они проверили отчет в N-й раз. Можно предположить, что количество голосов, полученных Незнайкой и Пончиком, никогда не уменьшается.
Входные данные
В первой строке задается целое число N (1<=N<=1000). В следующих N строках записано по 2 числа Pi и Ni (1<=Pi,Ni<=1000). Pi и Ni - взаимно простые числа.
Выходные данные
Выведите минимально возможное общее количество голосов. Гарантируется, что правильный ответ - не более 1018.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
3
2 3
1 1
3 2 |
10 |
Количество голосов, полученных Пончиком и Незнайкой, изменяется так 2,3 → 3,3 → 6,4.
Общее количество голосов в конце составляет 10, что является минимально возможным числом. |
| 2 |
4
1 1
1 1
1 5
1 100 |
101 |
Возможно, что ни Пончик ни Незнайка не получили голосов между моментом, когда они смотрели отчет, и моментом, когда они смотрели его в следующий раз. |
| 3 |
5
3 10
48 17
31 199
231 23
3 2 |
6930 |
|
| |
![]()
|
|
Найдите отсутствующего
Циклы
Однажды на дистанционном уроке, проводимом при помощи какого-то сервиса видеоконференций, учитель заметил, что отсутствует один из N учащихся класса. Чтобы понять, кто именно отсутствует, учитель попросил каждого присутствующего ученика написать в чат его номер в классном журнале: число от 1 до N. Тогда после окончания урока, просмотрев сохранённый чат, учитель сможет понять, какой из учеников не написал свой номер. Помогите ему - напишите программу, которая сделает это.
Входные данные
В первой строке входных данных записано целое число N (1 <= N <= 105 ) — количество учеников в классе. Следующие N-1 строк содержат по одному числу — номера присутствовавших на уроке учеников в произвольном порядке. Среди этих чисел каждое число от 1 до N, кроме какого-то одного, встречается ровно один раз.
Выходные данные
Программа должна вывести одно число — номер отсутствовавшего ученика.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
2
5
1
3 |
4 |
| |
![]()
|
|
До до Нового года!
Циклы
В каком-то другом мире сегодня 29 декабря. Дарёна с дедом Кокованей решили купить N товаров в универмаге для веселого празднования Нового года. Обычная цена i-го товара (1 <= i <= N) - pi серебряных камушек, причем pi всегда чётное. У деда Коковани есть купон на скидку, и он может купить один товар по самой высокой цене за половину обычной цены. Оставшиеся N − 1 позиции стоят по своей обычной цене. Сколько раз необходимо ударить Серебряному копытцу, чтобы Дарёна с дедом могли расплатиться за товар? За один удар из под копытца вылетает один серебреный камушек.
Входные данные
В первой строке задано целое число N (2 <= N <= 105). В следующих N строках расположены целые положительные четные числа pi (100 <= pi <= 106), каждое число в отдельной строке.
Выходные данные
Выведите на экран ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
4980
7980
6980
|
15950
|
| |
![]()
|
|
Снежик Сугробович - 2
Циклы
Массивы
В некотором мире сейчас 31 декабря и все веселье только начинается. Снежик Сугробович слепил N больших снежков и расположил их в ряд слева направо. На каждом i-м снежке, если считать слева (1 <= i <= N), он написал целое число ai. Он предлагает вам сыграть в игру. Снежик Сугробович разрешил сломать не более N − 1 снежков по вашему выбору.
Допустим, осталось K снежков. Снежик Сугробович будет удовлетворен и подарит вам хороший подарок, если для каждого целого числа i (1<=i<=K) на i-м снежке, если считать слева оставшиеся снежки, будет написано целое число i.
Найдите минимальное количество снежков, которое вам нужно сломать, чтобы получить подарок. Если не получится, то выведите -1.
Входные данные
В первой строке программа получает на вход целое число N (1 <= N <= 200000). Во второй строке - N натуральных чисел ai (1<=ai<=N).
Выходные данные
Выведите минимальное количество снежков, которые нужно сломать, чтобы получить подарок, или выведите -1, если это невозможно сделать.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
3
2 1 2 |
1 |
Сломайте первый снежок, числа на остальных снежках будут удовлетворять условию Снежика Сугробовича |
| 2 |
3
2 2 2 |
-1 |
|
| 3 |
10
3 1 4 1 5 9 2 6 5 3 |
7 |
|
| 4 |
1
1 |
0 |
|
| |
![]()
|
|
До Нового года - 1
Циклы
Комбинаторика
Снежик Сугробович положил в ряд N ёлочных шаров, для того чтобы их покрасить. Он решил, что каждый шар будет одним из K цветов. При этом Снежик Сугробович хочет, чтобы любые два соседних ёлочных шара были окрашены в разные цвета. Найдите количество возможных способов раскрасить ёлочные шары.
Входные данные
Входная строка содержит два целых числа N и K (\(1<=N<=1000\), \(2<=K<=1000\)).
Выходные данные
Выведите на экран ответ на задачу. Гарантируется, что верный ответ не превышает \(2^{31}-1\).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 2 |
2 |
| 1 |
1 10 |
10 |
| |
![]()
|
|
Треугольная последовательность
Циклы
Дана монотонная последовательность, в которой каждое натуральное число k встречается ровно k раз: 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, ...
По данному натуральному n выведите первые n членов этой последовательности. В задаче разрешается использовать только один цикл.
Входные данные
Вводится натурально число n.
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 |
1 2 |
| 2 |
5 |
1 2 2 3 3 |
| |
![]()
|
|
Сломанный принтер
Циклы
Задача на реализацию
Конструктив
Сломанный цветной принтер, печатая цифры, закрашивает все замкнутые области в красный цвет. Например, в цифрах 0, 4, 6, 9 одна замкнутая область. В цифре 8 - 2 замкнутых области. В других цифрах нет замкнутых областей, которые закрашиваются. В принтере красной краски осталось на покраску h замкнутых областей. Найдите минимальное неотрицательное число, напечатав которое в принтере закончится красная краска. Число не должно содержать ведущих нулей. Если в принтере отсутствует красная краска, то он не может напечатать цифру с замкнутой областью.
Входные данные
На вход подается число h (0 <= h <= 510).
Выходные данные
Выведите число, которое необходимо напечатать.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
15 |
48888888 |
| 2 |
70 |
88888888888888888888888888888888888 |
| |
![]()
|
|
Среднее значение последовательности
Циклы
Дана непустая последовательность целых чисел, оканчивающаяся нулем. Ноль в последовательность не входит, служит признаком ее окончания. Определите среднее значение всех элементов последовательности.
Входные данные
Вводится последовательность целых чисел, оканчивающаяся числом 0 (само число 0 в последовательность не входит, а служит как признак ее окончания).
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4
2
7
0 |
4.333333333333333 |
| |
![]()
|
|
Машина для печенья
Циклы
Вывод формулы
Машина для изготовления печенья производит B печенья в следующие моменты времени: A секунд, 2A секунд, 3A секунд и каждое последующее число, кратное A секундам после включения. Определите сколько печенья будет изготовлено машиной к моменту времени T+0,5 секунд после включения.
Входные данные
Программа получает на вход одну строку, содержащую три числа A, B и T. 1 <= A, B, T <= 20, A <= T. Все числа целые положительные.
Выходные данные
Выведите одно число - ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 5 7 |
10 |
| 2 |
3 2 9 |
6 |
| |
![]()
|
|
Первоклассное сложение
Циклы
Первоклассник Фёдор любит складывать числа столбиком, но только если примеры легкие. Легкими он считает такие примеры, в которых не нужно делать переносов из младшего разряда в старшие. Все остальные примеры он считает трудными.
Вам даны положительные целые числа А и B. Посчитайте A+B (в десятичной системе счисления). Если это не связано с переносом в каком-либо разряде, выведите Easy, в противном случает выведите Hard.
Входные данные
Программа получает на вход одну строку, содержащую два целых числа А и B (1 <= A, B <= 1018).
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
229 390 |
Hard |
| 2 |
123456789 9876543210 |
Easy |
| |
![]()
|
|
Числовая последовательность - 5
Циклы
Вычислить
\(P = (1 + \sin 0.1 ) \cdot (1 + \sin 0.2 ) \cdot ...\cdot (1 + \sin 1 )\)
Входные данные
Нет.
Выходные данные
Вывести число P.
| |
![]()
|
|
Числовая последовательность - 4
Циклы
Дано вещественное число х. Вычислить
\(s = {{(x-1)\cdot(x-3)\cdot(x-7)\cdot...\cdot(x-63)}\over{(x-2)\cdot(x-4)\cdot(x-8)\cdot...\cdot(x-64)}}\)
Входные данные
Вводится вещественное число х (-50 <= х <= 50). Гарантируется, что для заданного х решение существует.
Выходные данные
Выведите значение S.
| |
![]()
|
|
Числовая последовательность - 3
Циклы
Дано натуральное число N, вещественное число А. Вычислить
\(S = {{1 \over A} + {1 \over {A^2}} + {1 \over A^4} +... + {1 \over A^{2\cdot N - 2}} }\)
Входные данные
В первой строке вводится натуральное число N (0 < N <= 10). Во второй строке вводится вещественное число А (-5 <= А<= 5, А!=0).
Выходные данные
Выведите значение S.
| |
![]()
|
|
Числовая последовательность - 2
Циклы
Дано натуральное число N, вещественное число А. Вычислить
\(P = A \cdot (A - N) \cdot (A - 2 \cdot N) \cdot...\cdot (A - N^2)\)
Входные данные
В первой строке вводится натуральное число N (0<N<=10). Во второй строке вводится вещественное число А (-10<=А<=10).
Выходные данные
Вывести число P.
| |
![]()
|
|
Числовая последовательность - 1
Циклы
Дано натуральное число N, вещественное число А. Вычислить
\(P = A \cdot (A + 1) \cdot...\cdot (A + N - 1)\)
Входные данные
В первой строке вводится натуральное число N (0<N<=10). Во второй строке вводится вещественное число А (-100<=А<=100).
Выходные данные
Вывести число P.
| |
![]()
|
|
Сумма ряда - 1
Циклы
Дан числовой ряд и малая величина eps=0.001. С точностью eps (то есть, если сумма при очередном добавлении слагаемого будет отличаться на величину меньшую чем 0.001 от предыдущей, то это слагаемое считается последним) найти сумму ряда, общий член которого задан формулой (n>0):
\(a_n = {(-1)^{n-1} \over{n^n}}\)
Выведите на экран сумму такого ряда.
| |
![]()
|
|
Сумма ряда - 2
Циклы
Дан числовой ряд и малая величина eps=0.001. С точностью eps (то есть, если сумма при очередном добавлении слагаемого будет отличаться на величину меньшую чем 0.001 от предыдущей, то это слагаемое считается последним) найти сумму ряда, общий член которого задан формулой (n>0):
\(a_n = {{1\over 2^n} + {1 \over 3^n}}\)
Выведите на экран сумму такого ряда.
| |
![]()
|
|
Сумма ряда - 3
Циклы
Дан числовой ряд и малая величина eps=0.001. С точностью eps (то есть, если сумма при очередном добавлении слагаемого будет отличаться на величину меньшую чем 0.001 от предыдущей, то это слагаемое считается последним) найти сумму ряда, общий член которого задан формулой (n>0):
\(a_n = {{2\cdot n-1} \over{2^n}}\)
Выведите на экран сумму такого ряда.
| |
![]()
|
|
Сумма ряда - 4
Циклы
Дан числовой ряд и малая величина eps=0.001. С точностью eps (то есть, если сумма при очередном добавлении слагаемого будет отличаться на величину меньшую чем 0.001 от предыдущей, то это слагаемое считается последним) найти сумму ряда, общий член которого задан формулой (n>0):
\(a_n = {1 \over{(3 \cdot n - 2)\cdot(3\cdot n+1)}}\)
Выведите на экран сумму такого ряда.
| |
![]()
|
|
Сумма ряда - 5
Циклы
Дан числовой ряд и малая величина eps=0.001. С точностью eps (то есть, если сумма при очередном добавлении слагаемого будет отличаться на величину меньшую чем 0.001 от предыдущей, то это слагаемое считается последним) найти сумму ряда, общий член которого задан формулой (n>0):
\(a_n = {{n!} \over{(2\cdot n)!}}\)
Выведите на экран сумму такого ряда.
| |
![]()
|
|
Сумма ряда - 6
Циклы
Дан числовой ряд и малая величина eps=0.001. С точностью eps (то есть, если сумма при очередном добавлении слагаемого будет отличаться на величину меньшую чем 0.001 от предыдущей, то это слагаемое считается последним) найти сумму ряда, общий член которого задан формулой (n>0):
\(a_n = {n! \over{n^n}}\)
Выведите на экран сумму такого ряда.
| |
![]()
|
|
Сумма ряда - 7
Циклы
Дан числовой ряд и малая величина eps=0.001. С точностью eps (то есть, если сумма при очередном добавлении слагаемого будет отличаться на величину меньшую чем 0.001 от предыдущей, то это слагаемое считается последним) найти сумму ряда, общий член которого задан формулой (n>0):
\(a_n = {2^n \cdot n! \over{n^n}}\)
Выведите на экран сумму такого ряда.
| |
![]()
|
|
Сумма ряда - 8
Циклы
Дан числовой ряд и малая величина eps=0.001. С точностью eps (то есть, если сумма при очередном добавлении слагаемого будет отличаться на величину меньшую чем 0.001 от предыдущей, то это слагаемое считается последним) найти сумму ряда, общий член которого задан формулой (n>0):
\(a_n = {n! \over{3 \cdot n^n}}\)
Выведите на экран сумму такого ряда.
| |
![]()
|
|
Сумма ряда - 9
Циклы
Дан числовой ряд и малая величина eps=0.001. С точностью eps (то есть, если сумма при очередном добавлении слагаемого будет отличаться на величину меньшую чем 0.001 от предыдущей, то это слагаемое считается последним) найти сумму ряда, общий член которого задан формулой (n>0):
\(a_n = {{n!} \over{(2^n)!}}\)
Выведите на экран сумму такого ряда.
| |
![]()
|
|
Сумма ряда - 10
Циклы
Дан числовой ряд и малая величина eps=0.001. С точностью eps (то есть, если сумма при очередном добавлении слагаемого будет отличаться на величину меньшую чем 0.001 от предыдущей, то это слагаемое считается последним) найти сумму ряда, общий член которого задан формулой (n>0):
\(a_n = {(2)^{n} \over{(n-1)!}}\)
Выведите на экран сумму такого ряда.
| |
![]()
|
|
Громозека и Алиса - 2
Задача на реализацию
Одномерные массивы
Циклы
Алиса и Громозека пошли гулять по городу. Заходя в первое кафе, Алиса посмотрела на часы и запомнила время входа. Далее она запоминала только количество минут, которое они с Громозекой тратили между двумя посещенными кафе (от входа в одно кафе, до входа в другое). По окончании прогулки, Алиса решила восстановить хронологию - время входа в очередное кафе.
Напишите программу, которая определит, в какое время Алиса и Громозека заходили в очередное кафе.
Входные данные
В первой строке задан, момент времени, в который Громозека и Алиса вошли в первое кафе. Формат времени: часы (число от 00 до 23), далее идет двоеточие, затем минуты (число от 00 до 59). Строка времени записана без пробелов.
Во второй строке записано натуральное число N (2 <= N <= 1000) - количество посещенных кафе (включая кафе из которого они вышли в начальный момент времени и последнее кафе). В третьей строке записано N-1 число: первое показывает время в минутах от входа в первое кафе до входа во второе, второе - время от входа во второе кафе до входа в третье и т.д. Каждое из этих чисел натуральное и не превышает 1000.
Выходные данные
Выведите для каждого кафе время входа Алисы и Громозеки. Формат времени должен быть такой же, как и во входных данных.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
07:00
4
10 5 3 |
07:00
07:10
07:15
07:18 |
| |
![]()
|
|
Количество подпоследовательностей
ЕГЭ_информатика
Циклы
Дана последовательность из N натуральных чисел. Рассматриваются все её непрерывные подпоследовательности, начинающиеся с первого элемента последовательности. Найдите количество подпоследовательностей, сумма которых кратна K.
Входные данные
В первой строке записаны два числа: количество чисел в последовательности N (1 <= N <= 108) и число K (1 <= K <= 100). Далее идет N строк, по одному натуральному числу в строке. Каждое число не превышает 10000.
Выходные данные
Выведите на экран ответ на задачу
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 3
33
41
19
22
40 |
2 |
| |
![]()
|
|
Соревнование по шахматной композиции
Циклы
На соревнованиях по шахматной композиции каждому участнику дается 10 задач для решения. За каждую задачу можно получить от 0 до 5 баллов. За правильно решенную задачу участнику начисляется 5 баллов. Если задача решена не полностью или не верно, то участнику дается вторая попытка. В этом случае за задачу участник получает балл равный среднему баллу за две попытки, округленный по правилам математики.
Баллы выставляются по порядку от первой до последней решенной задачи.
Маленький Витя Ч., участвуя на своем первом в жизни соревновании, забыл сколько задач он решил. Витя Ч. помнит, что получил всего 10 оценок, а также сами оценки по порядку.
Определите сколько всего задач решил Витя Ч., за сколько задач он получил максимальный балл с первой попытки, а также общую сумму баллов, которую он набрал.
Входные данные
Программа получает 10 строк, в каждой из которых записано по одному неотрицательному числу от 0 до 5.
Выходные данные
Выведите в первой строке количество задач, которые Витя Ч. успел решить, во второй строке - количество задач, которые решил с первой попытки на максимальный балл, в третьей строке - общее количество набранных баллов.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2
5
2
5
0
5
5
2
5
5 |
6
2
25 |
| |
![]()
|
|
Меню для школьника
Циклы
Вещественные числа
Питание школьника, при грамотной организации, должно обеспечивать содержание белков, жиров и углеводов в соотношении 10%:30%:60% (допускается погрешность +/- 1%). Детский лагерь составляет меню, состоящее из N различных продуктов. Для каждого продукта известна энергетическая ценность в белках (P), жирах (F) и углеводах (C), а также количество каждого вида продукта в меню (K).
Определите, является ли составленное меню сбалансированным или нет.
Входные данные
Программа получает на вход несколько строк. В первой строке записано число натуральное число N (N <= 100) количество различных продуктов. В каждой из следующих N строк записаны по 4 числа: Pi, Fi, Ci и Ki. Все числа вещественные, не превосходят 103.
Выходные данные
Выведите YES, если меню сбалансированное, и NO в противном случае.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
0 1 1 2
1 2 7 1
3 7 13 1 |
YES |
| |
![]()
|
|
Середина отрезка
Циклы
Целые числа
Громозека и Алиса играют в следующую игру. Изначально, они ставят на числовую прямую три точки в целые координаты. Затем, один из них стирает любую крайнюю точку и ставит ее посередине между двумя оставшимися в координату с целым числом. Если между оставшимися точками четное количество целых чисел, то можно поставить точку в любую из них.
Например, если изначально стояли точки в координатах 3, 6, 8, то первым ходом можно стереть точку с координатой 3 и поставить ее в координату 7. Или стереть точку с координатой 8 и поставить ее в координату 4 или 5.
Чтобы долго не думать, Громозека и Алиса решили, что на каждый ход они будут тратить не более двух секунд.
Вас просят вычислить, какое максимальное количество секунд будет продолжаться игра, если известно начальное расположение трех точек.
Входные данные
Программа получает на вход три целых числа A, B и C (1<=A < B < C <= 1000). Каждое число записано с новый строки.
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
6
8 |
4 |
| |
![]()
|
|
Водолей
Циклы
Цикл while
У исполнителя “Водолей” есть два сосуда, первый объемом A литров, второй объемом B литров, а также кран с водой. Водолей может выполнять следующие операции:
- Наполнить сосуд A (обозначается >A).
- Наполнить сосуд B (обозначается >B).
- Вылить воду из сосуда A (обозначается A>).
- Вылить воду из сосуда B (обозначается B>).
- Перелить воду из сосуда A в сосуд B (обозначается как A>B).
- Перелить воду из сосуда B в сосуд A (обозначается как B>A).
Команда переливания из одного сосуда в другой приводят к тому, что либо первый сосуд полностью опустошается, либо второй сосуд полность наполняется.
Входные данные
Программа получает на вход три натуральных числа A, B, N, не превосходящих 104.
Выходные данные
Необходимо вывести алгоритм действий Водолея, который позволяет получить в точности N литров в одном из сосудов, если же такого алгоритма не существует, то программа должна вывести текст Impossible.
Количество операций в алгоритме не должно превышать 105. Гарантируется, что если задача имеет решение, то есть решение, которое содержит не более, чем 105 операций.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
5
1
|
>A
A>B
>A
A>B
|
| 2 |
3
5
6
|
Impossible
|
| |
![]()
|
|
Кривая дракона
Циклы
Арифметические алгоритмы (Теория чисел)
Сегодня мальчик Саша на уроке математики узнал про фракталы. Учитель показывал так называемую «кривую дракона». Она представляет собой геометрическую фигуру, которая строится следующим образом: на первом шаге проводится отрезок из начала координатной плоскости в точку (0; 1). Далее на каждом шаге из конца фрактала повторяется уже нарисованная часть фигуры, повернутая на 90 градусов против часовой стрелки (см. рисунок).
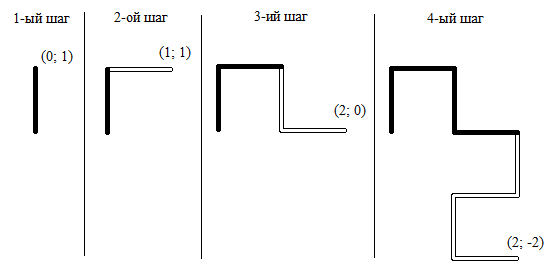
После уроков Саша попробовал сам изобразить «кривую дракона», и теперь он хочет знать, в какой точке координатной плоскости он закончил рисовать фрактал, проделав описанные выше N шагов. Требуется написать программу, которая по заданному числу N определяет координаты конца фрактала после выполнения N шагов.
Входные данные
Вводится одно целое число N (1 <= N <= 30).
Выходные данные
Выведите два числа через пробел - координаты конца фрактала.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 |
1 1 |
| 2 |
4 |
2 -2 |
| |
![]()
|
|
Сигналы из космоса
Циклы
Профессор Селезнёв анализирует сигналы из космоса. Он записывает в журнал интенсивность сигнала каждую секунду в виде целого числа. Делает это он до тех пор, пока сигнал не затухнет. Поэтому каждая запись его наблюдений заканчивается числом 0. Теперь он бы хотел узнать максимальную продолжительность по времени сигнала одной и той же интенсивности. Наблюдать сигналы Селезнёв может достаточно большой промежуток времени и посчитать максимальную продолжительность такого сигнала ему будет довольно сложно вручную. Помогите ему определить данный временной промежуток.
Входные данные
На вход программе подаются целые числа, по одному числу в строке. Последняя строка содержит число 0. (Число 0 - признак ее окончания).
Выходные данные
Максимальную продолжительность в секундах сигнала одной и той же интенсивности.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2
2
2
3
3
1
1
1
1
0 |
4 |
| |
![]()
|
|
Громозека и валерьянка
Цикл for
Циклы
Простые задачи на перебор
Задача на реализацию
Громозека очень любит валерьянку. На его родной планете Чумароза можно купить за k чумриков (местная валюта) первую упаковку валерьянки, за 2·k чумриков - вторую и так далее (иными словами, за i-ю упаковку надо заплатить i·k чумриков). Громозека хочет купить w упаковок валерьянки. У него есть n чумриков. Сколько чумриков ему придется взять в кредит в чумарозском банке, чтобы купить w упаковок валерьянки?
Входные данные
В первой строке записано три положительных целых числа k, n, w (1 <= k, w <= 1000, 0 <= n <= 109), стоимость первой упаковки, изначальное количество чумарозиков у Громозеки и количество упаковок валерьянки, которые он хочет купить.
Выходные данные
Выведите единственное целое число - количество чумарозиков, которое Громозеке необходимо взять в кредит в банке. Если брать кредит не надо, выведите 0.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 17 4 |
13 |
| |
![]()
|
|
Айвен делит кристалл
Циклы
Айвен обладает волшебной палочкой, которая может делить кристаллы с волшебной силой N на несколько кристаллов. При этом, мощность исходного кристалла кратна мощности каждого нового кристалла, полученного в результате деления, а также, все мощности новых кристаллов уникальны и меньше мощности исходного кристалла . Например, если исходный кристалл имеет волшебную силу 12, то Айвен может разделить его на кристаллы мощностью 1, 2, 3, 4, 6
Для кристалла с волшебной силой N выведите в порядке возрастания мощность всех кристаллов, полученных в результате деления.
Если кристалл не возможно поделить по указанным правилам, то выведите -1.
Входные данные
Программа получает на вход натуральное число N - мощность исходного кристалла (N <= 100).
Выходные данные
Выведите в порядке возрастания мощность всех кристаллов, полученных после деления. Все значения необходимо вывести в одну строку, разделяя одним пробелом.
Если кристалл не возможно поделить по указанным правилам, то выведите -1.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
12 |
1 2 3 4 6 |
| |
![]()
|
|
Бобы Айвена - 2
Циклы
В перерывах между отработкой заклинаний, Айвен любит лакомиться бобами. Бобы в волшебной школе имеют свою особенность. На каждом бобе написано некоторое целое число. Сегодня Айвен принес мешок, в котором лежит N бобов. Айвен хочет съесть только два боба, но такие чтобы произведение чисел, которые записаны на бобах было бы наименьшим среди всех пар бобов (пару образовывают любые два боба, лежащие в его мешке).
Определите это произведение.
Входные данные
В первой строке вводится число N (2 ≤ N ≤105) - количество бобов в мешке Айвена, а затем N целых чисел, по одному в строке - числа, записанные на бобах, в том порядке, в котором их доставал Айвен (каждое число мо модулю не превосходит 40000).
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
1
-3
2 |
-6 |
| |
![]()
|
|
Отсутствующий волшебник
Циклы
Каждый юный волшбеник в течении первого учебного года прокачивает свою волшебную палочку. В конце года каждый волшебник отправляет своему главному магу свой идентификационный номер и мощность своей волшебной палочки. Далее, все списки от всех магов объединяются и получается единый список. Но, в процессе передачи была утерена информация об одном из идентификационных номеров. Вас просят помочь определить потерянный номер.
Всего в школе волшбеников N учащихся. Каждый учащийся имеет уникальный номер от 1 до N.
Входные данные
В первой строке входных данных записано целое число N (1 <= N <= 105 ) — количество юных волшебников. Следующие N-1 строк содержат по одному числу — идентификационные номера, которые попали в общий список в произвольном порядке. Среди этих чисел каждое число от 1 до N, кроме какого-то одного, встречается ровно один раз.
Выходные данные
Программа должна вывести одно число — потерянный идентификационный номер.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
2
5
1
3 |
4 |
| |
![]()
|
|
Айвен делит кристаллы
Циклы
Айвен обладает волшебной палочкой, которая может делить кристаллы с волшебной силой N на несколько кристаллов. Айвен может одновременно поделить сразу два кристалла. В этом случае, они делятся на кристаллы, мощность которых строго больше 1 и, при этом, мощность каждого нового кристалла уникальна и кратна сразу мощностям исходных кристаллов.
Например, если исходные кристаллы имеют волшебную силу 12 и 6, то Айвен может разделить их на кристаллы мощностью 2, 3, 6
Для двух кристаллов с мощностями N и M выведите количество кристаллов, которые получатся после их деления.
Входные данные
Программа получает на вход два натуральных числа N и M - мощности исходных кристаллов (1<= N, M <= 1000). Каждое число вводится в отдельной строке.
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
12
6 |
3 |
| 2 |
25
30 |
1 |
| |
![]()
|
|
Магические порталы
Алгоритмы на графах
Задача на реализацию
Циклы
В некотором королевстве есть n городов, соединенных магическими порталами. Каждая пара различных городов соединена ровно одним магическим порталом, позволяющим мгновенно перемещаться из одного города в другой.
Из-за свойств магии, определяющей работу порталов, каждый портал можно использовать только в одну сторону. Для каждой пары городов A и B известно, можно ли воспользоваться порталом для перемещения напрямую из A в B или из B в A.
Из-за особенностей магических порталов иногда при перемещении жителей королевства из одного города в другой приходится использовать несколько порталов. Также могут существовать такие пары городов, что из одного города в другой нельзя добраться, используя только магические порталы.
Жители королевства называют город совершенным, если из него можно добраться до любого другого города в королевстве, используя только магические порталы. Пусть изначально количество совершенных городов в королевстве равно k.
Недавно король принял решение выбрать пару городов и изменить разрешенное направление перемещения по порталу, соединяющему их, на противоположное. Для выбора лучшего варианта король хочет понять, какое количество совершенных городов может оказаться в королевстве после перенастройки ровно одного портала.
Для получения этой информации король планирует запросить в министерстве транспорта соответствующий отчет. Король может запросить либо частичный, либо полный отчет. Содержимое отчета зависит от параметра L, для частичного отчета L = k + 1, для полного отчета L = 1.
Отчет содержит для каждого целого числа m, такого что m ≥ L, число таких пар городов A и B, для которых выполняются следующие условия:
- исходно магический портал позволяет перемещаться напрямую из города A в город B;
- если изменить направление перемещения этого магического портала на противоположное, чтобы он позволял напрямую перемещаться из города B в город A, то количество совершенных городов в королевстве станет равным m.
Таким образом, частичный отчет содержит информацию только о тех способах перенастройки одного портала, которые строго увеличивают количество совершенных городов в королевстве. Полный отчет содержит информацию обо всех способах перенастройки одного портала.
Требуется написать программу, которая по информации о разрешенных направлениях перемещения с использованием магических порталов, и информации о том, требуется предоставить частичный или полный отчет, формирует соответствующий отчет и выводит его в описанном ниже формате.
Формат входного файла
Первая строка входного файла содержит два целых числа: n — количество городов в королевстве (2 ≤ n ≤ 2000) и p, равное либо 0, если требуется вывести частичный отчет, либо 1, если требуется вывести полный отчет. Последующие n строк содержат по n символов, каждый из которых может быть «+», «–» или «.», и i-я из этих строк описывает магические порталы, соединяющие i-й город с другими городами.
В i-й строке j-й символ равен «+», если магический портал позволяет напрямую перемещаться из i-го города в j-й, равен «–», если магический портал позволяет напрямую перемещаться из j-го города в i-й, и равен «.», если i = j.
Формат выходного файла
Первая строка выходного файла должна содержать одно целое число k — количество совершенных городов в королевстве.
Если требуется частичный отчет (p = 0), то вторая строка выходного файла должна содержать (n – k) целых неотрицательных чисел, разделенных пробелами, где i-е из этих чисел должно быть равно количеству пар городов, изменение направления портала между которыми на противоположное приводит к тому, что количество совершенных городов в королевстве станет равным (k + i). Если при этом k = n, то вторая строка может отсутствовать, либо быть пустой.
Если требуется полный отчет (p = 1), то вторая строка должна содержать n целых неотрицательных чисел, разделенных пробелами, где i-е из этих чисел должно быть равно количеству пар городов, изменение направления портала между которыми на противоположное приводит к тому, что количество совершенных городов в королевстве станет равным i.
Пример:
| Ввод |
Вывод |
5 0
.-+++
+.+++
--.+-
---.+
--+-. |
1
0 0 0 3 |
5 1
.-+++
+.+++
--.+-
---.+
--+-. |
1
7 0 0 0 3 |
Пояснение к примерам
В приведенных примерах изначально совершенным является только город 2.
Изменив направление порталов, соединяющих пары городов (2, 3), (2, 4) или (2, 5), можно сделать все города совершенными. Изменение направление любого другого портала делает совершенным один город.
| |
![]()
|
|
Эпическое соревнование
Циклы
Эпическое соревнование проводится по почти олимпийской системе. Среди n команд, в несколько туров определяют единственную команду-победительницу по следующим правилам.
- Если количество команд, участвующих в очередном туре, четное, то команды разбиваются по парам. Эти пары соревнуются между собой (т.е. проводится
n/2 матчей) и в следующий раунд выходит ровно половина команд (команды всегда соревнуются между собой до победы какой-либо команды);
- Если количество команд, участвующих в очередном туре нечетное, то перед началом этого тура проводится лотерея, которая определит ту одну удачливую команду, которая получит пропуск в следующий раунд. Оставшиеся команды опять разбиваются на пары и соревнуются между собой (т.е. сыграют между собой
n/2 матчей).
Вас же просят определить количество матчей, сыгранных в соревновании до определения победителя.
Входные данные
Программа получает на вход натуральное число n (1 <= n <= 200) - количество команд, которое участвует в соревновании.
Выходные данные
Выведите единственное число - ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
7 |
6 |
| |
![]()
|
|
Интересные числа (С', C)
Вывод формулы
Циклы
Арифметические алгоритмы (Теория чисел)
Маленький Вася очень любит числа, а особенно сильно он любит интересные числа. Вася считает число x интересным, если сумма квадратов его цифр делится на число 7. Например, число 123 -
интересное, потому что 1 2 + 2 2 + 3 2 = 14 делится на 7, а число 16 - нет, потому что 1 2 + 6 2 = 37 не делится на 7. Однажды Вася увидел на доске число x, он сразу же захотел узнать величину минимального интересного числа, которое строго больше чем x. Так как Вася еще слишком юн, он обратился к вам за помощью в решение этой задачи.
Формат входных данных
Во входном файле содержится единственное целое число x - число, написанное на доске 0<= x <= 105
Формат выходных данных
В единственную строку выходного файла выведите минимальное интересное число, которое строго больше чем x.
| |
![]()
|
|
Парад
Циклы
В параде принимают участие M военных. Командование парада решило, что наиболее эффектное построение военных – в форме квадрата, то есть число участников построения должно быть точным квадратом. Но поскольку число M может не быть точным квадратом, разрешается разбить военных на несколько полков, каждый из которых строится в форме квадрата. Для красоты все полки должны быть одинакового размера, также командование парада хочет, чтобы размер каждого полка был как можно больше. Определите максимально возможный размер полка.
Входные данные
Программа получает на вход одно целое положительное число M, не превосходящее 2×109, – количество участников парад.
Выходные данные
Программа должна вывести одно число – максимально возможный размер полка.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
180
|
36
|
| |
![]()
|
|
Сломанный автомат
Целые числа
Циклы
Громозека является одним из ведущих в Галактике космических археологов. Возвращаясь домой с очередной археологической экспедиции, он решил привезти своим четырем детям их любимые печенья. Ему осталось только вбить необходимое количество килограмм на экране терминала, и автомат сразу выдаст ему печенье . Но, вот незадача, на терминале сломались все кнопки с цифрами и буквами. Работают только цифры 0 и 1. Громозека в задумчивости, как же ему заказать ровно n килограмм. Он придумал, что может сделать несколько заказов таким образом, чтобы каждый заказ мог состоять только из цифр 0 и 1. Вот только Громозека очень торопится, потому что до старта корабля осталось совсем немного времени. Помогите Громозеке определить минимальное число раз, которым ему придется воспользоваться автоматом, чтобы купить ровно n килограмм и порадовать своих детей!
Например, чтобы купить 12 киллограмм печенья Громозека может воспользоваться автоматом дважды, купив сначала 11 килограмм печенья, затем - 1 килограмм.
Входные данные
Программа получает на вход целое число n (1 <= n <= 109).
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1234
|
4
|
| |
![]()
|
|
Волшебные кристаллы Летовца
Циклы
Любой Летовец, окончивший курс магических наук, умеет делить одновременно два волшебных кристалла, каждый из которых обладает своей магической силой. При воздействии заклинания, оба кристалла одновременно делятся на новые кристаллы (возможно только на один), мощность которых строго больше 1 и, при этом, мощность каждого нового кристалла уникальна и кратна сразу мощностям исходных двух кристаллов.
Например, если исходные кристаллы имеют мощности 12 и 6, то Летовец может разделить их на кристаллы с мощностями 2, 3, 6
Для двух кристаллов с магическими силами N и M выведите количество кристаллов, которые получатся после их деления.
Формат входных данных
Программа получает на вход два натуральных числа N и M - мощности исходных кристаллов (1<= N, M <= 1000). Каждое число вводится в отдельной строке.
Формат выходных данных
Выведите ответ на задачу.
| |
![]()
|
|
Сеня наблюдает за кузнечиками
Условный оператор
Циклы
На прямой тропинке на расстоянии 1 метр друг от друга сидят два кузнечика. Время от времени один из кузнечиков прыгает на несколько сантиметров влево или вправо. Требуется узнать, каково было минимальное расстояние, на которое сближались кузнечики в процессе прыжков. (Расстояние считается только в те моменты, когда оба кузнечика сидят на земле).
Входные данные
В первой строке вводится одно число N (1 ≤ N ≤ 100) – общее количество прыжков, а затем N чисел, описывающих прыжки. Модуль числа равен длине прыжка в сантиметрах; число отрицательное, если кузнечик начинал этот прыжок по направлению к другому кузнечику, и положительное – если от другого кузнечика. Числа по модулю не превосходят 100 и все отличны от 0. (Кузнечики могут перепрыгивать друг через друга. Гарантируется, что кузнечики не приземляются друг на друга.)
Выходные данные
Требуется вывести одно число – минимальное расстояние в сантиметрах, на которое сближались
| |
![]()
|
|
Печенье Муми-мамы
Циклы
Вывод формулы
 Мумми-мама решила испечь печенье к празднику. Она печет по Мумми-мама решила испечь печенье к празднику. Она печет по B печений за один раз, и печёт их в следующие моменты времени: A минут, 2A минут, 3A минут и каждое последующее число, кратное A минутам после начала выпечки. Определите, сколько печений будет испечено Мумми-мамой к празднику, который наступит через T+0,5 после начала выпечки.
Формат входных данных
Программа получает на вход одну строку, содержащую три числа A, B и T. 1 <= A, B, T <= 20, A <= T. Все числа целые положительные.
Формат выходных данных
Выведите одно число - ответ на задачу.
| |
![]()
|
|
Красная Шапочка на болоте
Циклы
Красная Шапочка отправилась на болото для сбора клюквы, чтобы испечь пирожки для бабушки. Клюквенное болото представляет собой координатную прямую. Берег, на котором стоит девочка, имеет координату 0, а клюквенная поляна — координату N + 1. В точках с координатами 1, 2, . . . , N расположены кочки. Первоначально у девочки E единиц энергии. Красная Шапочка может прыгнуть из точки x в точку y (x < y), потратив на это (y − x) единиц энергии, то есть затраченная энергия равна расстоянию между кочками. После того, как девочка приземлится на кочке с координатой i, она получает ai единиц энергии (при этом значение ai может оказаться отрицательным, тогда энергия Красной Шапочки уменьшится при приземлении). Нельзя, чтобы энергия Красной Шапочки в какой-либо момент оказалась меньше нуля. Например, Красная Шапочка не может прыгнуть с кочки 1 на кочку 3, имея одну единицу энергии, вне зависимости от того, сколько энергии она получит на 3-й кочке, так как для осуществления такого прыжка необходимо две единицы энергии.
Так как Красной Шапочке ещё надо вернуться обратно, девочке интересно, какое максимальное количество энергии у неё может оказаться, когда она достигнет поляны (точки с координатой N +1).
Формат входных данных
Первая строка входных данных содержит целое число E — первоначальный запас энергии Красной Шапочки, 1 ≤ E ≤ 109 . Вторая строка входных данных содержит целое число N — количество кочек на болоте, 1 ≤ N ≤ 105 . Следующие N строк содержат по одному целому числу ai — энергия, которую получает Красная Шапочка на i-й кочке, −2000 ≤ ai ≤ 2000.
Формат выходных данных
Программа должна вывести одно число — максимальное количество единиц энергии, которое останется у Красной Шапочки после достижения клюквенной поляны. Если девочка не сможет достигнуть цели, выведите одно число «-1» (без кавычек).
Замечание
В первом примере три кочки и первоначально 2 единицы энергии у Красной Шапочки. Она прыгает на кочку 1, что требует 1 единицу энергии, и у неё остаётся 1 единица энергии. На кочке 1 девочка получает 1 единицу энергии, и у неё становится 2 единицы энергии. Затем она прыгает с кочки 1 на кочку 3, потратив 2 единицы энергии, и у неё становится 0 энергии. Приземлившись на кочку 3, Красная Шапочка получает 1 единицу энергии, этого достаточно, чтобы перепрыгнуть с кочки 3 на поляну в точке 4, после чего у Красной Шапочки останется 0 единиц энергии.
Во втором примере у Красной Шапочки первоначально только 1 единица энергии, поэтому она может прыгнуть только на кочку 1, но значение a1 = −1, то есть после приземления на кочку 1 у Красной Шапочки энергия станет отрицательной, и она не сможет продолжить свой путь.
| |
![]()
|
|
65984
Строки
Циклы
Условный оператор
Прибор передает результаты измерений блоками информации. Каждый блок представляет собой набор цифр в шестнадцатеричной системе счисления (0123456789ABCDEF). Последняя цифра пятеричной записи суммы цифр блока показывает код ошибки, где 0 означает корректную передачу данных. Предпоследняя цифра пятеричной записи суммы цифр блока показывает тип результата:
0: «Излучение»
1: «Вспышка»
2: «Нагрев»
3: «Охлаждение»
4: «Перегрузка»
Определите количество результатов «Перегрузка», которые были переданы без ошибок после приема n блоков данных.
Формат ввода
В первой строке программе подается на вход число натуральное число n, не превышающее 1000.
Далее в каждой из n строк идет блок данных – набор цифр в шестнадцатеричной системе счисления (0123456789ABCDEF), длина блока не превышает 100 знаков.
Формат вывода
Вывести одно число – количество результатов «Перегрузка», которые были переданы без ошибок после приема n блоков данных.
| |
![]()
|
|
66172
Словари
Использование сортировки
Циклы
Арифметические операции
Белочка живет в дубовом парке. Каждый день до обеда она собирает ровно К желудей и складывает их в дупле одного из дубов. Последнее время вечером каждого воскресенья в парк приходит мальчик Витя. Он обнаружил дупло, в котором белочка хранит жёлуди. Для своих игр он каждый раз забирает Т желудей из дупла.
Известно, что после последнего прихода Вити в парк, в дупле осталось Х желудей. Необходимо определить через сколько дней после этого прихода Вити, белочка сможет собрать не менее М желудей в дупле.
Формат ввода
На вход программе в одной строке подается четыре целых числа, записанные через пробел К, M, Т, Х (1≤ К, M, Т, Х ≤109).
Формат вывода
Вывести одно целое число – количество дней, через которое белочка сможет собрать необходимое число желудей.
Если белочка не сможет собрать нужное число желудей никогда, вывести число -1.
| |
![]()
|
|
66180
Циклы
Условный оператор
Натуральные числа, которые можно выразить в виде суммы двух или более последовательных натуральных чисел, называются вежливыми числами. С другой стороны, натуральные числа, которые нельзя выразить подобным образом, называются невежливыми.
Ваша задача не только определить является натуральное число вежливым, но и подсчитать количество способов, которыми число можно выразить в виде суммы последовательных натуральных чисел. Для невежливых чисел это значение будет равно одному, а для вежливых - двум и более.
Например, число 42 - вежливое, и его можно выразить как
а) 3+ 4 + 5 + 6 + 7 + 8 + 9;
б) 9 + 10 + 11 + 12;
в) 13 + 14 + 15;
г) 42.
Число 512 будет невежливым, так как для него существует единственное представление
а) 512
Входные данные
Одно натуральное число N (N <= 106)
Выходные данные
Одно натуральное число - количество представлений N в виде суммы последовательных натуральных чисел
| |
![]()
|
|
Задача 1
Циклы
Макс надеялся, что всё лето будет гулять и играть в футбол. Но схватил тройку по алгебре за год, и мама посадила его решать задачи. В знак протеста Макс рисует в тетради повторяющиеся узоры из знаков «плюс» и «минус».
Есть число n. Выведите узор из n частей, если одна его часть выглядит так:
-+-+-
+-+-+
Скопируйте узор из условия, чтобы не ошибиться.
| |
![]()
|
|
Задача 2
Циклы
Мама Макса наконец отпустила его поиграть в мяч с приятелем. Она втайне гордится его футбольными успехами, поэтому следит за ним через окно и записывает, кто забивает гол. Когда Макс, она пишет «М», а когда приятель — «П».
Есть строка с результатами игры. Выведите, сколько голов забил Макс.
| |
![]()
|
|
Задача 3
Циклы
Макс покормил уличного котёнка. Тот запомнил Макса и намяукал о нём всем собратьям в округе. Стоит мальчику показаться в парке, как к нему за едой сбегается толпа усатых.
В 1-ю неделю Макс скормил котятам 3 кусочка колбасы, во 2-ю — 9 кусков, а в третью — 27. В k-тую неделю ненасытные котята получили 3 ** k кусков.
Есть число n. На какой неделе общее количество кусков колбасы, которые съели котята, впервые стало строго больше n?
Примечание: за первую неделю котята получили 3 куска, за первую и вторую 3 + 9 = 12 кусков (12 больше 11), после третьей 3 + 9 + 27 = 39 кусков (39 больше 12).
| |
![]()
|
|
Задача 4
Циклы
Вечером в парке Макс увидел очень странную собаку. Она шла вдоль аллеи и лаяла на фонари — но не на все подряд, а только на каждый 4-й (через 3). Всего фонарей n, и на последний собака залаяла.
Есть число n. Выведите произведение номеров всех фонарей, на которые лаяла собака.
Примечание: для n = 8 из фонарей 1 2 3 4 5 6 7 8 собака лаяла на 4-й и 8-й фонари. Произведение их номеров равно 4 x 8 = 32. Для n = 5: 1 2 3 4 5 собака лаяла на 1-й и 5-й фонари. Произведение равно 1 x 5 = 5.
| |
![]()
|
|
Задача 5
Циклы
Макс с Алисой играют в компьютерную игру.
Есть запись их результатов за несколько партий: сколько очков набрала Алиса в 1-й партии, сколько набрал Макс в 1-й партии, сколько набрала Алиса во 2-й , и так далее. В конце — два нуля.
Выиграла ли Алиса хотя бы одну партию? Выведите "ДА" или "НЕТ".
Пояснение: в первом тесте были две игры с результатами 4:2, 4:3. Алиса выиграла оба раза. Во втором тесте Алиса проигрывала каждый день со счётом 0:10.
| |
![]()
|
|
Задача 6
Циклы
Алиса пишет Васе в мессенджере сначала сообщение с текстом «Угадай, куда я еду!», а потом — одну строку с обратным отсчётом (разделённые многоточиями числа в обратном порядке: n, n - 1, …, 1). После драматичной паузы Алиса сообщает: «На Байкал!».
Есть число n. Выведите строку с отсчётом, которую написала Алиса.
Обратите внимание, что после единицы Алиса тоже ставит многоточие.
| |
![]()
|
|
Задача 7
Циклы
Всё лето Соня подбирает на улице хвосты ящериц и приносит их домой.
Каждые 2 дня Соня прячет хвосты в тайниках, а каждый 3-й день Вася находит часть и выбрасывает.
В 1-й день каникул Соня спрятала 1 хвост, во 2-й — 2 хвоста. На 3-й день каникул Вася выбросил 3 хвоста. На 4-й Соня спрятала 4 хвоста, на 5-й — 5 хвостов. На 6-й Вася выбросил 6 хвостов и т. д.
На какой день хвостов в доме впервые стало строго больше n?
Примечание:
Последовательность количества оставшихся хвостов по дням такая:
1 : 1 = 1
2 : 1 + 2 = 3
3 : 1 + 2 - 3 = 0
4 : 1 + 2 - 3 + 4 = 4
5 : 1 + 2 - 3 + 4 + 5 = 9
Впервые оставшееся число хвостов стало (строго) больше 4 на 5-й день.
| |
![]()
|
|
Задача 8
Циклы
Летней ночью Макс и Эмилия жарят на костре картошку, играют на гитаре и переписываются с Алисой и Васей. «Мы сидим под воооот такой ёлкой, а вы?» — пишет Макс и рисует в чате «ёлочку» из знаков «плюс» и «минус».
«Ёлочка» высотой в 3 строки выглядит так:
--+--
-+++-
+++++
Для данного n (n всегда больше или равно 2), выведите «ёлочку» с высотой n.
| |
![]()
|
|
Задача 9
Циклы
Эмилия собралась объяснить Максу задачу по алгебре и даже нарисовала числовую прямую. Чтобы увильнуть от скучных примеров, Макс предложил игру: пусть Эмилия отмечает точки-корабли на прямой, а Макс «взрывает» либо все корабли с положительными координатами, либо все с отрицательными. Макс выигрывает, если ему удалось взорвать всё.
Есть последовательность (ненулевых) чисел, заканчивающаяся нулем. Выиграл ли Макс? Выведите "ДА", если все они с одним знаком, и "НЕТ", если среди них есть и положительные, и отрицательные.
| |
![]()
|
|
Задача 10
Циклы
Вася, Соня и Алиса играют в настольный теннис. Соня записывает, кто выиграл партию. Она пишет «Вася», «Алиса» или «я». Пробелов Соня не ставит.
Есть строка, в которой без пробелов записаны имена победителей. У кого больше побед — у Васи, Алисы или Сони? Известно, что победитель точно есть. Выведите его имя.
| |
![]()
|