| | | |
|
Acowdemia I
Использование сортировки
Беси учится на PhD в компьютерных науках. Она опубликовала N статей (1≤N≤105) и её i-ую статью цитировали ci раз (0≤ci≤105).
Беси слышала что академические успехи измеряются h-индексом. h-индекс - это наибольшее число h такое, что ученый имеет не менее h статей, каждая из которых цитируется не менее h раз. Например, учёный у которого четрые статьи с количествами цитат (1,100,2,3) имеет h-индекс равный 2, а ученый с количествами цитат (1,100,3,3) имеет h-индекс равный 3.
Чтобы повысить свой h-индекс Беси планирует написать обзорную статью, цитирующую некоторые из её прошлых статей. В связи с ограничением на количество страниц, она может включить не более L цитат в свой обзор (0≤L≤105), т конечно она может процитировать каждую из своих статей не более одного раза.
Помогите Беси определить максимальный h-индекс, который она может достичь написанием своей обзорной статьи.
Заметим, что научный руководитель должен был предупредить Беси, что написание статьи исключительно с целью увеличения своего h-индекса сомнительно с этической точки зрения.
ФОРМАТ ВВОДА
Первая строка ввода содержит N и L.
Вторая строка ввода содержит N разделённых одиночными пробелами целых чисел c1,…,cN.
ФОРМАТ ВЫВОДА
Максимальный h-индекс, который Беси может получить написанием обзорной статьи.
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
4 0
1 100 2 3 |
2 |
Беси не может цитировать свои статьи. Как указано ранее её h-индекс для (1,100,2,3) равен 2. |
| 2 |
4 1
1 100 2 3 |
3 |
Если Беси процитирует третью статью, её количества цитирований станут (1,100,3,3). Как отмечено ранее, h в этом случае равен 3.
|
| |
![]()
|
|
Маша и матрёшки
Использование сортировки
Маше на день рождения подарили набор матрёшек!
Теперь Маша сидит и вкладывает их одну в другую. Она заметила, что матрёшки отличаются по размеру, и одна помещается внутри другой, только если ее размеры строго меньше. Так, если есть две матрёшки i и j , а их размеры ai и aj соответственно, то матрёшка i вкладывается внутрь матрёшки j тогда и только тогда, когда ai < aj . Разумеется, непосредственно внутрь матрёшки можно вложить только одну другую матрёшку, иначе получится неаккуратно, а Маша — очень аккуратная девочка.
Маше особенно нравится, если она может, вкладывая матрёшки друг в друга, добиться того, что все они оказываются внутри одной самой большой матрёшки. Но, к сожалению, это не всегда возможно. Поэтому Маша решила убрать часть матрёшек в шкаф, оставив такой набор, чтобы их все можно было вложить друг в друга. Помогите Маше понять, какое максимальное количество матрёшек может быть в таком наборе.
Входные данные
В первой строке находится число n — количество матрёшек, подаренных Маше ( 1 ≤ n ≤ 1000 ). В следующей строке через пробел находятся n чисел — размеры матрёшек. Число ai , стоящее на месте i , задает размер матрёшки с номером i ( 1 ≤ ai ≤ 10 000 ).
Выходные данные
Выведите одно число — максимальное количество матрёшек, которые можно вложить друг в друга.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
2 10 2 |
2 |
| 2 |
6
2 1 2 1 3 4 |
4 |
| 3 |
4
3 1 4 2 |
4 |
| |
![]()
|
|
Нужно больше конфет!
Одномерные массивы
Использование сортировки
У Карлсона дома есть набор из n банок с конфетами. Банки пронумерованы от 1 до n , в i -й из них лежит a i конфет. Карлсон считает набор банок симпатичным , если в этом наборе нет трех банок с разным числом конфет.
У Карлсона есть неограниченный запас конфет в карманах, поэтому он может добавить в любую банку произвольное число конфет. Помогите ему определить, какое минимальное общее число конфет ему придется добавить, чтобы набор банок с конфетами стал симпатичным.
Входные данные
Первая строка входных данных содержит натуральное число n ( 1 ≤ n ≤ 105 ) — количество банок в наборе Карлсона.
Вторая строка входных данных содержит n целых чисел ai ( 0 ≤ ai ≤ 109 ) — число конфет в банках. Соседние числа отделены друг от друга одним пробелом.
Выходные данные
Выведите одно число — минимальное общее количество конфет, которое придется добавить, чтобы Карлсон считал набор банок симпатичным.
Примечание
В первом тесте из примера Карлсон может добавить в первую банку две конфеты, а во вторую банку — одну конфету. Тогда в первой и четвертой банках будет лежать по 7 конфет, а во второй и третьей — по 2 конфеты.
Во втором тесте из примера набор банок исходно является симпатичным, добавлять конфеты не требуется.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4
5 1 2 7 |
3 |
| 2 |
3
1 1 1 |
0 |
| |
![]()
|
|
Минимальное число
Использование сортировки
Дано натуральное четырехзначное число. Найдите минимальное натуральное четырехзначное число, состоящее из тех же цифр, что и заданное. Заметим, что четырехзначные числа не могут начинаться с нуля.
Входные данные
Вводится натуральное четырехзначное число.
Выходные данные
Выведите минимальное натуральное четырехзначное число, состоящее из тех же цифр.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1513 |
1135 |
| |
![]()
|
|
Сортировка точек
Структуры
Использование сортировки
Элементарная геометрия
Выведите все исходные точки в порядке возрастания их расстояний от начала координат.
Создайте структуру Point и сохраните исходные данные в массиве структур Point.
Входные данные
Программа получает на вход набор точек на плоскости. Сначала задано количество точек n, затем идет последовательность из n строк, каждая из которых содержит два числа: координаты точки. Величина n не превосходит 100, все исходные координаты – целые числа, не превосходящие 103.
Выходные данные
Необходимо вывести все исходные точки в порядке возрастания их расстояний от начала координат. Программа выводит только координаты точек, их количество выводить не надо.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2
1 2
2 3 |
1 2
2 3 |
| |
![]()
|
|
Печаль Громозеки
Одномерные массивы
Алгоритмы сортировки
Использование сортировки
Громозека имеет последовательность целых чисел A длины N. Он свободно выбирает целое число b. Здесь ему станет грустно, если Ai и b+i находятся далеко друг от друга. Точнее, печаль Громозеки рассчитывается следующим образом:
\(abs(A_1-(b+1))+abs(A_2-(b+2))+...+abs(A_N-(b+N))\).
Здесь \(abs(x) \)- это функция, которая возвращает абсолютное значение x. Найдите минимально возможную печаль Громозеки.
Входные данные
В первой строке записано целое число N (\(1<=N<=2 \cdot 10^5\)). Во второй строке записано N целых чисел Ai (\(1<=A_i<=10^9\)).
Выходные данные
Выведите на экран минимально возможную печаль Громозеки.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
5
2 2 3 5 5 |
2 |
Если мы выберем b = 0, печаль Громозеки будет \(\)
abs (2- (0 + 1)) + abs (2-(0 + 2))+ abs (3-(0 + 3)) + abs (5- (0 + 4)) + abs(5-(0 + 5)) = 2.
Любой другой выбор b не делает печаль Громозеки меньше 2, поэтому ответ - 2. |
| 2 |
9
1 2 3 4 5 6 7 8 9 |
0 |
|
| 3 |
6
6 5 4 3 2 1 |
18 |
|
| 4 |
7
1 1 1 1 2 3 4 |
6 |
|
| |
![]()
|
|
Число
Использование сортировки
Алгоритмы на строках
Вася написал на длинной полоске бумаги большое число и решил похвастаться своему старшему брату Пете этим достижением. Но только он вышел из комнаты, чтобы позвать брата, как его сестра Катя вбежала в комнату и разрезала полоску бумаги на несколько частей. В результате на каждой части оказалось одна или несколько идущих подряд цифр.
Теперь Вася не может вспомнить, какое именно число он написал. Только помнит, что оно было очень большое. Чтобы утешить младшего брата, Петя решил выяснить, какое максимальное число могло быть написано на полоске бумаги перед разрезанием. Помогите ему!
Формат входных данных
Входные данные состоят из одной или более строк, каждая из которых содержит последовательность цифр. Количество строк не превышает 100, каждая строка содержит от 1 до 100 цифр. Гарантируется, что хотя бы в одной строке первая цифра отлична от нуля.
Последняя строка входного потока содержит число -1 - признак окончания данных.
Формат выходных данных
Выведите одну строку – максимальное число, которое могло быть написано на полоске перед разрезанием.
| |
![]()
|
|
Количество чисел с суммой не больше S
Использование сортировки
ЕГЭ_информатика
В файле записаны целые положительные числа. В первой строке файла записано число N - количество чисел, и натуральное число S. В следующих N строках записаны сами числа.
Укажите в ответе два числа через пробел: сначала максимальное количество чисел, которые необходимо сложить, чтобы сумма была не больше числа S, затем, значение полученной суммы.
| |
![]()
|
|
Замена чисел
Использование сортировки
ЕГЭ_информатика
В наборе чисел N замените одно число на число из набора чисел M таким образом, чтобы сумма чисел в наборе N была как можно ближе к числу S. Выведите три числа, каждое в отдельной строке:
1 строка - число, которое заменили из набора N;
2 строка - число из набора M, которым заменили;
3 строка - полученную сумму чисел из набора N.
Гарантируется, что такую замену сделать можно. Если возможных замен несколько, то выбрать ту, в которой число из набора N меньше.
Входные данные
В первой строке вводится через пробел 3 числа: n (10<=N<=105) - количество чисел в наборе N, m (10<=M<=105) - количество чисел в наборе M, S (10<=S<=109) S>sum(N), где sum(N) - сумма всех чисел набора N.
Во второй строке записан набор чисел N: n чисел, разделенных одним пробелом (каждое число по модулю не превышает 105).
Во третьей строке записан набор чисел M: m чисел, разделенных одним пробелом (каждое число по модулю не превышает 105).
Выходные данные
Выведите на экран ответ на задачу, как указано в условии.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 2 10
2 4
1 3 |
2
3
7 |
| |
![]()
|
|
Демо-2022. Разбор задачи
Использование сортировки
ЕГЭ_информатика
Системный администратор раз в неделю создаёт архив пользовательских файлов. Однако объём диска, куда он помещает архив, может быть меньше, чем суммарный объём архивируемых файлов. Известно, какой объём занимает файл каждого пользователя. По заданной информации об объёме файлов пользователей и свободном объёме на архивном диске определите максимальное число пользователей, чьи файлы можно сохранить в архиве, а также максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей. Напишите программу, которая вычисляет наибольшее число пользователей, чьи файлы могут быть помещены в архив, а также максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Входные данные:
В первой строке находятся два числа: S – размер свободного места на диске (натуральное число, не превышающее 100 000) и N – количество пользователей (натуральное число, не превышающее 10000). В следующих N строках находятся значения объёмов файлов каждого пользователя (все числа натуральные, не превышающие 100), каждое в отдельной строке.
Выходные данные:
Выведите два числа в одной строке через пробел: сначала наибольшее число пользователей, чьи файлы могут быть помещены в архив, затем максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Пример
| № |
Входные данные |
Выходные данные |
| 1 |
100 4
80
30
50
40 |
2 50 |
При таких исходных данных можно сохранить файлы максимум двух пользователей. Возможные объёмы этих двух файлов 30 и 40, 30 и 50 или 40 и 50. Наибольший объём файла из перечисленных пар – 50, поэтому ответ для приведённого примера: 2 50
| |
![]()
|
|
Бонус за результат. Тренировочное задание - 1
Использование сортировки
ЕГЭ_информатика
В quizzz "Сдай ЕГЭ на 100 баллов" можно набрать до 10 000 очков. По окончании игры, первые K участников, набравшие наибольшее количество баллов, получают бонус к своим очкам в виде +30% от набранных. Вам известна информация о том, сколько очков набрал каждый участник игры. Определите максимальное количество очков, на которое не распространился бонус, а также целую часть от общей суммы бонуса, полученную игроками.
Входные и выходные данные
В первой строке входного файла находятся два числа, записанные через пробел: N – общее количество игроков (натуральное число, не превышающее 10 000) и K – количество игроков, которые получают бонус. В следующих N строках находятся результаты каждого участника (количество набранных очков - все числа натуральные, не превышающие 10 000), каждое в отдельной строке.
Запишите в ответе два числа: сначала максимальное количество очков, на которое не распространился бонус, а затем целую часть от суммы всех надбавок.
Пример входного файла:
12 4
370
580
3000
1310
1700
2810
1660
1250
1870
1340
1400
1260
При таких исходных данных ответ должен содержать два числа – 1660 2814.
| |
![]()
|
|
Яркость гирлянды. Тренировочное задание - 2
Использование сортировки
ЕГЭ_информатика
На фабрике Деда Мороза изготавливаются лампочки различного веса и яркости. Вес лампочки не превосходит 100 грамм, яркость лампочки не превосходит 10000 люменов.
Для изготовления новогодней гирлянды выбираются K самых ярких лампочек. Если яркость у двух лампочек одинаковая и они все не помещаются в гирлянду, то помещают лампочку с меньшим весом.
Известна информация о весе и яркости каждой лампочки, завезенной в мастерскую для формирования новогодней гирлянды.
Определите суммарный вес лампочек в гирлянде и среднюю яркость всей гирлянды.
Входные и выходные данные
В файле в первой строке через пробел записаны числа N - количество лампочек, завезенный в мастерскую (натуральное число, не превышающее 1000) и K – количество лампочек в гирлянде (натуральное число, не превосходящее 100). В каждой из последующих N строк через пробел записаны два числа – вес и яркость каждой лампочки.
Запишите в ответе два числа – сначала суммарный вес лампочек в гирлянде, затем среднюю яркость всей гирлянды (только целую часть).
Пример организации исходных данных во входном файле:
9 4
50 600
60 480
45 540
30 300
15 180
70 560
30 360
91 910
40 320
Ответ: 256 652
| |
![]()
|
|
Суперстадион
Использование сортировки
ЕГЭ_информатика
ЕГЭ-26. Обработка массива целых чисел. Сортировка
На планете Блук находится самый большой суперстадион Галактики. На суперстадионе 10 000 рядов, пронумерованных начиная с 1. В каждом ряду 10 000 мест, пронумерованных начиная с 1. К текущему моменту, на концерт Суперзвезды продали N билетов. В файле указана информация о проданных билетах: номер ряда и номер места в данном ряду. Определите, в каком ряду больше всего свободных мест, находящихся рядом. Если таких мест одинаковое количество в нескольких рядах, то укажите минимальный номер ряда. А также укажите минимальный номер места, с которого начинаются такие свободные места.
Входные данные
Первая строка входного файла содержит целое число N – общее количество проданных билетов. Каждая из следующих N строк содержит 2 целых числа: номер ряда и номер места в данном ряду.
В ответе запишите два целых числа: номер ряда, в котором больше всего свободных мест, находящихся рядом, затем – минимальный номер места, с которого начинаются такие свободные места.
Пример организации исходных данных во входном файле (при 5 рядах и 5 местах в ряду):
17
1 2
2 3
2 4
3 1
3 2
4 1
4 2
4 3
5 1
5 5
5 4
5 2
5 3
3 4
3 5
4 5
1 5
Ответ: 1 3
Файл к заданию
| |
![]()
|
|
Гошина последовательность
Использование сортировки
ЕГЭ_информатика
ЕГЭ-26. Обработка массива целых чисел. Сортировка
Любитель математики Гоша придумал свою собственную последовательность. Правила в его последовательности следующие:
1) все числа в последовательности имеют свой номер;
2) первый элемент последовательности имеет номер 1;
3) каждое число в последовательности должно делится на свой номер;
4) число с большим номером, должно быть не меньше, чем число с меньшим номером.
Пример Гошиной последовательности: 1 4 6 8 10 18 21.
По заданному набору чисел определите какое максимальное количество чисел можно выбрать, чтобы составить Гошину последовательность, а также, какое максимальное число в ней может быть.
Входные данные
В первой строке входного файла содержится число N - количество чисел в файле. Далее идет N натуральных чисел (N <= 105), каждое - в отдельной строке.
Запишите в ответе: сначала максимальное количество чисел, которые можно выбрать, чтобы составить Гошину последовательность, затем - максимальное число, которое может быть в этой последовательности.
Пример входного файла:
12
25
17
20
15
6
9
10
12
5
3
4
1
Ответ: 5 25
Файл к заданию
| |
![]()
|
|
Закупка болтов и гаек - 04
Использование сортировки
ЕГЭ_информатика
Магазин производит закупку болтов (bolt), гаек (nut), гвоздей (pin), шайб (shim) и винтов (screw), на которую выделена определённая сумма денег. У метизного завода есть в наличии различные модификации этих изделий по розничной цене. При покупке менеджер руководствуется следующими правилами:
- Нужно купить как можно больше изделий, независимо от их типа и модификации.
- Если можно разными способами купить максимальное количество двух различных изделий, нужно выбрать тот способ, при котором будет куплено как можно больше болтов.
- Если можно разными способами купить максимальное количество изделий с одинаковым количеством других товаров, нужно выбрать тот способ, при котором вся покупка будет дешевле.
Определите, сколько всего будет куплено болтов и какая сумма останется неиспользованной.
Входные данные
Программа получает на вход несколько строк. В первой строке расположены два числа через пробел: N - общее количество болтов, гаек, гвоздей, шайб и винтов у метизного завода и M - сумма выделенных на закупку денег (в рублях). Каждая из следующих N строк содержит целое число (цена изделия в рублях) и тип изделия. Все данные в строках отделены одним пробелом.
Выходные данные
В ответе запишите два целых числа: сначала количество закупленных болтов, затем оставшуюся неиспользованной сумму денег. (в одной строке через один пробел)
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6 1650
600 screw
750 bolt
750 shim
450 pin
300 nut
150 bolt |
2 0 |
| |
![]()
|
|
Закупка болтов и гаек - 01
Использование сортировки
ЕГЭ_информатика
Магазин производит закупку болтов (bolt) и гаек (nut), на которую выделена определённая сумма денег. У метизного завода есть в наличии различные модификации этих изделий по розничной цене. При покупке менеджер руководствуется следующими правилами:
- Нужно купить как можно больше изделий, независимо от их типа и модификации.
- Если можно разными способами купить максимальное количество изделий, нужно выбрать тот способ, при котором будет куплено как можно больше гаек.
- Если можно разными способами купить максимальное количество изделий с одинаковым количеством гаек, нужно выбрать тот способ, при котором вся покупка будет дешевле.
Определите, сколько всего будет куплено гаек и какая сумма останется неиспользованной.
Входные данные
Программа получает на вход несколько строк. В первой строке расположены два числа через пробел: N - общее количество болтов и гаек у метизного завода и M - сумма выделенных на закупку денег (в рублях). Каждая из следующих N строк содержит целое число (цена изделия в рублях) и тип изделия (bolt - болт, nut - гайка). Все данные в строках отделены одним пробелом.
Выходные данные
В ответе запишите два целых числа: сначала количество закупленных гаек, затем оставшуюся неиспользованной сумму денег.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6 6500
1500 bolt
500 bolt
3500 nut
3000 nut
2500 bolt
1000 nut |
2 500 |
| |
![]()
|
|
Закупка болтов и гаек - 03
Использование сортировки
ЕГЭ_информатика
Магазин производит закупку болтов (bolt), гаек (nut), гвоздей (pin), шайб (shim) и винтов (screw), на которую выделена определённая сумма денег. У метизного завода есть в наличии различные модификации этих изделий по розничной цене. При покупке менеджер руководствуется следующими правилами:
- Нужно купить как можно больше изделий, независимо от их типа и модификации.
- Если можно разными способами купить максимальное количество двух различных изделий, нужно выбрать тот способ, при котором будет куплено как можно больше гаек.
- Если можно разными способами купить максимальное количество изделий с одинаковым количеством гаек, нужно выбрать тот способ, при котором вся покупка будет дешевле.
Определите, сколько всего будет куплено гаек и какая сумма останется неиспользованной.
Входные данные
Программа получает на вход несколько строк. В первой строке расположены два числа через пробел: N - общее количество болтов и гаек у метизного завода и M - сумма выделенных на закупку денег (в рублях). Каждая из следующих N строк содержит целое число (цена изделия в рублях) и тип изделия. Все данные в строках отделены одним пробелом.
Выходные данные
В ответе запишите два целых числа: сначала количество закупленных болтов, затем оставшуюся неиспользованной сумму денег. (в одной строке через один пробел)
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6 1650
600 screw
750 bolt
750 nut
450 pin
300 nut
150 bolt |
2 0 |
| |
![]()
|
|
Закупка болтов и гаек - 02
Использование сортировки
ЕГЭ_информатика
Магазин производит закупку болтов (bolt) и гаек (nut), на которую выделена определённая сумма денег. У метизного завода есть в наличии различные модификации этих изделий по розничной цене. При покупке менеджер руководствуется следующими правилами:
- Нужно купить как можно больше изделий, независимо от их типа и модификации.
- Если можно разными способами купить максимальное количество изделий, нужно выбрать тот способ, при котором будет куплено как можно больше болтов.
- Если можно разными способами купить максимальное количество изделий с одинаковым количеством болтов, нужно выбрать тот способ, при котором вся покупка будет дешевле.
Определите, сколько всего будет куплено болтов и какая сумма останется неиспользованной.
Входные данные
Программа получает на вход несколько строк. В первой строке расположены два числа через пробел: N - общее количество болтов и гаек у метизного завода (1 <= N <= 105) и M - сумма выделенных на закупку денег (в рублях) (1 <= M <= 109). Каждая из следующих N строк содержит целое число (цена изделия в рублях) и тип изделия (bolt - болт, nut - гайка). Все данные в строках отделены одним пробелом.
Выходные данные
В ответе запишите два целых числа: сначала количество закупленных болтов, затем оставшуюся неиспользованной сумму денег. (в одной строке через один пробел)
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6 6500
1500 nut
500 nut
3500 bolt
3000 bolt
2500 nut
1000 bolt |
2 500 |
| |
![]()
|
|
Гошина последовательность
Использование сортировки
ЕГЭ_информатика
Любитель математики Гоша придумал свою собственную последовательность. Правила в его последовательности следующие:
1) все числа в последовательности имеют свой номер;
2) первый элемент последовательности имеет номер 1;
3) каждое число в последовательности должно делится на свой номер;
4) число с большим номером, должно быть больше, чем число с меньшим номером.
Пример Гошиной последовательности: 1 4 6 8 10 18 21.
По заданному набору чисел определите какое максимальное количество чисел можно выбрать, чтобы составить Гошину последовательность, а также какое максимальное число в ней может быть.
Входные данные
В первой строке записано число N - количество чисел в файле (N <= 105). Далее идет N натуральных чисел (не больше 106), каждое - в отдельной строке.
Входные данные
Выведите два числа через пробел: сначала максимальное количество чисел, которые можно выбрать, чтобы составить Гошину последовательность, затем - максимальное число, которое может быть в этой последовательности.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
12
25
17
20
15
6
9
10
12
5
3
4
1 |
5 25 |
| |
![]()
|
|
Скупщик шоколада
Алгоритмы сортировки
Использование сортировки
Услышав, что шоколад полезен для мозга и нервной системы, ученик Василий решает купить M плиток шоколада. В городе есть N магазинов, которые продают различный шоколад. В i-м магазине Василий может купить не более Bi плиток шоколада по Ai рублей каждая. Помогите Василию определить, какую минимальную сумму денег ему необходимо накопить, чтобы купить M плиток шоколада?
Гарантируется, что располагая нужной суммой, Василий всегда сможет купить M плиток шоколада.
Входные данные
В первой строке заданы два числа: N и M (1 <= N, M <= 105). Следующие N строк содержат по 2 числа: Ai (1 <= Ai <= 109) и Bi (1 <= Вi <= 105). \(B_1 + B_2 +... + B_N >= M\).
Выходные данные
Выведите минимальную сумму денег, необходимую Василию для покупки M плиток шоколада.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 5
4 9
2 4 |
12 |
| 2 |
4 30
6 18
2 5
3 10
7 9 |
130 |
| 3 |
1 100000
1000000000 100000 |
100000000000000 |
| |
![]()
|
|
Ресторан
Бинарный поиск в массиве
Использование сортировки
Динамическое программирование
Ресторан получил n заказов на проведение банкета. Каждый заказ характеризуется двумя величинами: моментом начала банкета li и моментом конца ri (li ≤ ri).
Руководство ресторана может либо принять заказ, либо отвергнуть его. Какое наибольшее количество заказов может быть принято?
Никакие два принятых заказа не могут пересекаться, то есть не должно существовать момента времени, который принадлежит сразу двум принятым заказам. Если один из заказов начинается в момент, когда заканчивается другой, то они не могут быть приняты вместе.
Входные данные:
В первой строке находится целое число n (1 ≤ n ≤ 200000) — количество заказов. В каждой из следующих n строк находится пара целых чисел li, ri (0 ≤ li ≤ ri ≤ 109).
Выходные данные:
Выведите наибольшее количество заказов, которые могут быть приняты.
Примеры:
| Входные данные |
Выходные данные |
2
7 11
4 7 |
1 |
5
1 2
2 3
3 4
4 5
5 6 |
3 |
6
4 8
1 5
4 7
2 5
1 3
6 8 |
2 |
| |
![]()
|
|
Меняю конфеты на ноутбук
Одномерные массивы
Порядковые статистики
Использование сортировки
Динамическое программирование
Динамическое программирование: один параметр
Антон Б., суперспособный ученик 8 класса, обладает неудивительными математическими способностями. Побывав однажды на экскурсии в Колоколамске, он понял, что легко может написать программу, которая бы предсказывала стоимость его любимых конфет на любой промежуток дней вперед.
Используя эту программу, Антон Б. решил приобрести на все свои карманные деньги конфеты (а их у него было всего 10 рублей), затем, чуть позже, продать все купленные им конфеты. Таким образом, Антон Б. хочет заработать как можно больше денег на новый ноутбук.
Так как Антон Б. еще несовершеннолетний и один ездить в другие города не может, ему нужно понять, в какие из двух дней попросить старшего брата отвезти его в Колоколамск. Старший брат совершеннолетний и очень любит своего младшего брата, поэтому всегда готов ему помочь.
Так как Антон Б. очень торопится на кружок по информатике, он просит вас определить эти два дня в ближайшие N дней.
Входные данные
В первой строке записано число N (2 <= N <= 100000) количество дней, на которые Антон Б. делает прогноз. Вторая строка содержит N целых положительных чисел ai (1 <= i <= N , 1 <= ai <= 5000 ), где ai - предсказанная стоимость конфет в i-й день.
Выходные данные
Выведите два числа: первое число - номер дня, в который Антон Б. поедет покупать конфеты, второе - номер дня, в который он поедет продавать конфеты. В случае, если таких вариантов дней несколько, выведите любой из них. Если Антон Б. в итоге не сможет получить прибыль ни при каких вариантах, то выведите два нуля.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6
10 3 5 3 11 9
|
2 5
|
| 2 |
4
5 5 5 5
|
0 0
|
| |
![]()
|
|
Радостная фигура
Использование сортировки
Жадный алгоритм
Маленький Миша любит играть счетными палочками. Счетные палочки он берет у своей сестры первоклассницы. Так как он редко возвращает их назад, маме приходится часто покупать новые палочки. Поэтому не все палочки у Миши одинаковые, но все палочки имеют целочисленную длину.
Сегодня Миша строит из палочек следующую фигуру. Он начал из угла комнаты. Мы с вами обозначим, условно, этот угол координатой (0, 0). Дальше Миша выкладывает палочку параллельно одной из двух стен, исходящей из данного угла. Будем считать, что стены ровные и образуют друг с другом в точке (0, 0) угол 90 градусов. При этом, Миша никогда не выкладывает две подряд палочки одновременно параллельно одной и той же стене (другими словами, он всегда чередует направление палочек).
Миша, хоть и маленький и не знает геометрии, но все же всегда радуется, если конец его фигуры находится как можно дальше от стартового угла. Помогите Мише выложить фигуру, которая его обрадует. Любые две палочки, которые выкладывает Миша всегда имеют минимум одну точку касания или пересечения.
Входные данные
Программа получает на вход несколько строк. Первая строка содержит целое число n (1<= n <= 100000) — количество палочек, которые есть у Миши. Вторая строка содержит n целых чисел a1,...,an (1 <= ai <= 10000) - длины Мишиных палочек.
Выходные данные
Выведите одно целое число — квадрат максимального расстояния от угла с координатой (0,0) до конечной точки фигуры, которую построил Миша.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
1 2 3 |
26 |
| 2 |
4
1 1 2 2 |
20 |
| |
![]()
|
|
Мишины кубики
"Два указателя"
Использование сортировки
Простые задачи на перебор
Жадный алгоритм
Задача на реализацию
У маленького Миши есть кубики, на каждом из которых написана одна английская строчная буква. Вчера он выкладывал кубики в два ряда. В первом ряду у Миши n кубиков с буквами, во втором - m кубиков с буквами. Так получилось, что в двух этих рядах нет совпадающих букв. Другими словами, ни одна буква не содержится одновременно в обоих рядах.
Сегодня маленький Миша решил продолжить играть с кубиками. Но теперь он берет один любой кубик из какого-либо ряда и составляет из них третий ряд, добавляя кубик всегда в конец. Маленький Миша никогда не берет более k кубиков подряд из одного и того же ряда. Миша закончил играть тогда, когда у него закончились кубики в каком-то одном ряду (в первом или во втором).
Наблюдавший за игрой папа заметил, что играя таким образом у Миши получилась лексикографически наименьшая строка. По известным двум строкам, которые образуются путем прочтения букв первого и второго ряда и числу k определите строку, которую получил маленький Миша.
Строка x лексикографически меньше строки y только и только тогда, когда выполняется одно из следующих условий:
- x является префиксом y, но x != y;
- в первой позиции, где x и y различаются, в строке x находится буква, которая стоит в алфавите раньше, чем соответствующая буква y.
Входные данные
Программа получает на вход несколько строк. В первой строке записаны три числа: n - количество кубиков в первом ряду, m - количество кубиков во втором ряду, k - целое число(1 <= n, m, k <= 100). Во второй строке записана строка a длиной n - строка, образованная прочтением букв, написанных на кубиках первого ряда. В третьей строке - строка b длиной m - строка, образованная прочтением букв, написанных на кубиках второго ряда.
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6 4 2
aaaaaa
bbbb |
aabaabaa |
| |
![]()
|
|
Раскраска отрезков
Использование сортировки
Сканирующая прямая
У Джона Доу есть n отрезков на прямой. Отрезок (a, b) (a < b) — это множество точек x, таких, что a < x < b. Говорят, что отрезки (a1, b1) и (a2, b2) пересекаются, если существует такая точка c, что a1 < c < b1 и a2 < c < b2.
Джон хочет покрасить каждый отрезок в чёрный или белый цвет так, чтобы никакие два отрезка одного цвета не пересекались. Он хочет узнать, сколько существует различных способов покрасить отрезки таким образом.
Две покраски считаются различными, если существует отрезок, который в одной покраске покрашен в белый цвет, а в другой — в чёрный.
Пусть количество способов покрасить отрезки равно x. Выведите остаток от деления x на 106 + 3.
Входные данные
В первой строке записано целое число n (1 ≤ n ≤ 105) — количество отрезков у Джона. В следующих n строках находится описание отрезков. В i-й из них записано два числа li и ri (0 ≤ li < ri ≤ 109) — координаты концов i-го отрезка.
Выходные данные
Выведите остаток от деления x (количество способов покрасить отрезки) на 106 + 3.
Примеры тестов
Входные данные
Входные данные
3
1 2
1 3
1 4
Входные данные
4
1 2
2 3
3 4
4 5
Примечание
Тесты поделены на группы, но оцениваются отдельно.
- n ≤ 3 — 10 баллов
- n ≤ 15 — 30 баллов
- n ≤ 100 — 20 баллов
- ai ≤ 106 — 20 баллов
- Без дополнительных ограничений — 20 баллов
| |
![]()
|
|
ПИРАМИДА
Использование сортировки
Для строительства двухмерной пирамиды используются прямоугольные блоки, каждый из которых характеризуется шириной и высотой. Можно поставить один блок на другой, только если ширина верхнего блока строго меньше ширины нижнего. Самым нижним в пирамиде может быть блок любой ширины.
По заданному набору блоков требуется определить, пирамиду какой наибольшей высоты можно построить из них.
Формат входных данных
В первой строке входных данных задается число N – количество блоков ( 1 <= N <= 100000 ). В следующих N строках задаются пары целых чисел wi и hi ( 1<= wi , hi <= 109), разделенные пробелом – ширина и высота блока, соответственно.
Формат выходных данных
Целое число – максимальная высота пирамиды.
| Ввод |
Вывод |
3
3 1
2 2
3 3 |
5 |
Замечание.
В приведенном примере пирамида будет состоять из двух блоков: нижним будет блок с номером 3, а верхним – блок с номером 2. Блок с номером 1 нельзя использовать для строительства пирамиды, т.к. его ширина совпадает с шириной нижнего блока.
| |
![]()
|
|
Пираты!
Двумерные массивы
Использование сортировки
Использование сортировки
Использование сортировки
В настолькой игре "Пираты!" задача одного из игроков состоит в том, чтобы провести торговый корабль с ценным грузом через море, на островах которого базируются пираты.
Поле представляют собой прямоугольник, состоящий из квадратных клеток. Игрок может за один ход перейти в одну из четырех соседних по стороне клеток, не выходя при этом за пределы поля. Торговый корабль начинает свой путь в любой клетке самого левого столбца и должен попасть в любую клетку самого правого столбца игрового поля.
Пиратские базы расположены на островах, которые также занимают одну клетку игрового поля, их расположение известно.
Вася выяснил, что чем больше расстояние от пиратской базы, тем безопаснее маршрут. расстояние считается как количество ходов по клеткам от пиратских баз до каждой из клеток маршрута.
Помогите ему определить, на какое минимальное расстояние придјтся подойти к пиратской базе, двигаясь по самому безопасному маршруту.
Формат входных данных
В первой строке записано натуральные числа N и M (1 <= N, M <= 1 000 000) количество строк и столбцов на игровом поле.
Во второй строке записано натуральное число K (1 <= K <= 500) количество пиратских баз.
В следующих K строках записаны пары чисел Ri , Ci (1 <= Ri <= N, 1 <= Ci <= M) координаты пиратских баз (строка, столбец).
Формат выходных данных
Выведите одно число минимальное расстояние, на которое придется приближаться к пиратской базе на самом безопасном маршруте.
Система оценки
Решения, верно работающие при N, M 6<=500, будут набирать не менее половины баллов.
| Ввод |
Вывод |
10 10
4
2 2
5 3
5 9
8 8 |
3 |
Замечание
Пример одного из безопасных маршрутов показан на рисун ке. Пиратские базы обозначены чјрным, клетки маршрута серым. Минимальное расстояние от пиратской базы до маршрута 3 хода.
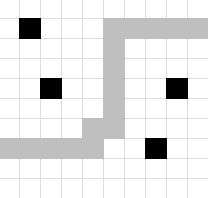 | |
![]()
|
|
Пираты!
Двумерные массивы
Использование сортировки
Использование сортировки
Использование сортировки
В настолькой игре "Пираты!" задача одного из игроков состоит в том, чтобы провести торговый корабль с ценным грузом через море, на островах которого базируются пираты.
Поле представляют собой прямоугольник, состоящий из квадратных клеток. Игрок может за один ход перейти в одну из четырех соседних по стороне клеток, не выходя при этом за пределы поля. Торговый корабль начинает свой путь в любой клетке самого левого столбца и должен попасть в любую клетку самого правого столбца игрового поля.
Пиратские базы расположены на островах, которые также занимают одну клетку игрового поля, их расположение известно.
Вася выяснил, что чем больше расстояние от пиратской базы, тем безопаснее маршрут. расстояние считается как количество ходов по клеткам от пиратских баз до каждой из клеток маршрута.
Помогите ему определить, на какое минимальное расстояние придјтся подойти к пиратской базе, двигаясь по самому безопасному маршруту.
Формат входных данных
В первой строке записано натуральные числа N и M (1 <= N, M <= 1 000 000) количество строк и столбцов на игровом поле.
Во второй строке записано натуральное число K (1 <= K <= 500) количество пиратских баз.
В следующих K строках записаны пары чисел Ri , Ci (1 <= Ri <= N, 1 <= Ci <= M) координаты пиратских баз (строка, столбец).
Формат выходных данных
Выведите одно число минимальное расстояние, на которое придется приближаться к пиратской базе на самом безопасном маршруте.
Система оценки
Решения, верно работающие при N, M 6<=500, будут набирать не менее половины баллов.
| Ввод |
Вывод |
10 10
4
2 2
5 3
5 9
8 8 |
3 |
Замечание
Пример одного из безопасных маршрутов показан на рисун ке. Пиратские базы обозначены чјрным, клетки маршрута серым. Минимальное расстояние от пиратской базы до маршрута 3 хода.
 | |
![]()
|
|
Пираты!
Двумерные массивы
Использование сортировки
Использование сортировки
Использование сортировки
В настолькой игре "Пираты!" задача одного из игроков состоит в том, чтобы провести торговый корабль с ценным грузом через море, на островах которого базируются пираты.
Поле представляют собой прямоугольник, состоящий из квадратных клеток. Игрок может за один ход перейти в одну из четырех соседних по стороне клеток, не выходя при этом за пределы поля. Торговый корабль начинает свой путь в любой клетке самого левого столбца и должен попасть в любую клетку самого правого столбца игрового поля.
Пиратские базы расположены на островах, которые также занимают одну клетку игрового поля, их расположение известно.
Вася выяснил, что чем больше расстояние от пиратской базы, тем безопаснее маршрут. расстояние считается как количество ходов по клеткам от пиратских баз до каждой из клеток маршрута.
Помогите ему определить, на какое минимальное расстояние придјтся подойти к пиратской базе, двигаясь по самому безопасному маршруту.
Формат входных данных
В первой строке записано натуральные числа N и M (1 <= N, M <= 1 000 000) количество строк и столбцов на игровом поле.
Во второй строке записано натуральное число K (1 <= K <= 500) количество пиратских баз.
В следующих K строках записаны пары чисел Ri , Ci (1 <= Ri <= N, 1 <= Ci <= M) координаты пиратских баз (строка, столбец).
Формат выходных данных
Выведите одно число минимальное расстояние, на которое придется приближаться к пиратской базе на самом безопасном маршруте.
Система оценки
Решения, верно работающие при N, M 6<=500, будут набирать не менее половины баллов.
| Ввод |
Вывод |
10 10
4
2 2
5 3
5 9
8 8 |
3 |
Замечание
Пример одного из безопасных маршрутов показан на рисун ке. Пиратские базы обозначены чјрным, клетки маршрута серым. Минимальное расстояние от пиратской базы до маршрута 3 хода.
 | |
![]()
|
|
Детские подарки
Использование сортировки
Вы замечательный родитель и хотите подарить детям подарки. Но, чтобы не избаловать своих детей, вы должны дать каждому ребенку не более одного подарка.
Каждый ребенок i имеет уровень ожидания равный g[i] - целое число, показывающее минимальный размер подарка, получив который ребенок обрадуется. Каждый подарок j имеет размер s[j].
Посчитайте, какое максимальное количество детей вы сможете обрадовать.
Входные данные
Первая строка содержит целое число n - количество детей. Вторая строка содержит n целых чисел g[i] - уровень ожидания i-го ребенка. В третьей строке записано число m - количество подарков. Четвертая строка содержит m целых чисел s[j] - размер j-го подарка.
Ограничения
1 <= n <= 3 * 1040 <= m <= 3 * 1041 <= g[i], s[j] <= 231 - 1
Выходные данные
Выведите одно число. Ответ на задачу
Пояснения к примерам
1. В первом примере у вас есть 3 ребенка и 2 подарка. Уровни ожидания детей равны 1, 2, 3, соответственно. Имея 2 подарка размером 1, вы можете обрадовать только того ребенка, чей уровень ожидания равен 1.
Количество таких детей равно одному. Ответ 1.
2. Во втором примере у вас есть 2 ребенка и 3 подарка. Уровни ожидания детей равны 1, 2, соответственно. 3 подарка имеют достаточно большие размеры, чтобы обрадовать всех детей. Ответ 2.
| |
![]()
|
|
Вечер кёрлинга
Использование сортировки
Жадный алгоритм
Сегодня вечером по телевизору на разных каналах будут показывать n матчей по кёрлингу, причём i-й матч начинается в момент времени li и заканчивается в момент времени ri.
Василиса хочет посмотреть как можно больше матчей от начала до конца. При этом если какой-то матч заканчивается в момент времени ri, то она может после него посмотреть любой матч j, который начинается не раньше момента времени ri, то есть lj > ri (Василиса может моментально переключить каналы в момент окончания матча и начать смотреть новый матч). Также она хочет сделать перерыв длины хотя бы t между какими-то двумя играми, чтобы поужинать, то есть должны найтись два последовательных матча i и j, которые просмотрит Василиса, удовлетворяющие условию lj - ri => t. Перерыв не может быть до или после всех просмотренных игр.
Помогите Василисе составить набор, содержащий максимальное количество матчей, которые она сможет просмотреть полностью и при этом сделать перерыв продолжительностью не менее t между какими-то матчами, или определите, что такого набора не существует.
Формат входных данных
Первая строка входных данных содержит число n (2 ≤ n ≤ 100 000) - количество показываемых матчей.
Вторая строка входных данных содержит число t (1 ≤ n ≤ 109) - минимальная длина перерыва, который должна сделать Василиса.
В следующих n строках содержится по два числа li и ri ( 1 ≤ li < ri ≤ 109) - начало и конец i-го матча.
Формат выходных данных
Программа должна вывести число m - максимально возможное количество матчей, которые просмотрит Василиса. Во второй строке выведите m чисел через пробел - номера матчей, которые должна посмотреть Василиса, в порядке просмотра.
Если Василиса не может составить расписание хотя бы из двух матчей так, чтобы между какими-то двумя матчами был перерыв хотя бы t, то выведите число -1.
Замечание
В первом примере ответом будет последовательность матчей 6, 3, 5. Василиса сначала посмотрит матч 6,
который заканчивается в момент времени 4, потом переключится на матч 3, который продолжается с 4 до 6.
Затем она сделает перерыв с 6 по 10, после чего просмотрит матч номер 5 с 10 до 12. Получилось расписание из 3 матчей с перерывом, продолжительность которого равна 4. Заметим, что в данном примере правильным ответом также будет последовательность матчей 6, 4, 5, в этом случае продолжительность перерыва между матчами 4 и 5 будет равна 3.
Во втором примере всего два матча, первый заканчивается в 5, а второй начинается в 9, то есть составить расписание, в котором был бы перерыв продолжительностью не менее t=5, нельзя.
| |
![]()
|
|
Ноутбук за печеньки
Одномерные массивы
Порядковые статистики
Использование сортировки
Динамическое программирование
Динамическое программирование: один параметр
Летовец обладает неудивительными математическими способностями. Его способности на столько велики, что он легко может просчитать стоимость его любимых печенек, которые продаются на другом конце города. К сожалению, Летовец не может по максимуму воспользоваться всеми своими способностями, потому что вчера у него сломался ноутбук и теперь он не может писать программы.
Чтобы купить себе новый ноутбук, Летовец решил потратить все свои карманные деньги (а это всего лишь 10 рублей) на покупку своих любимых печенек, а чуть позже, продать все купленные им печеньки.
Так как Летовец еще несовершеннолетний и один ездить на другой конец города не может, ему нужно понять, в какие из двух дней попросить маму отвезти его на другой конец города. Мама всегда готова ему помочь.
Отсутствие ноутбука очень угнетает юного Летовца, поэтому он просит вас определить эти два дня в ближайшие N дней.
Формат входных данных
В первой строке записано число N (2 <= N <= 100000) количество дней, на которые Летовец делает прогноз. Вторая строка содержит N целых положительных чисел ai (1 <= i <= N , 1 <= ai <= 5000 ), где ai - предсказанная стоимость печенек в i-й день.
Формат выходных данных
Выведите два числа: первое число - номер дня, в который Летовей поедет покупать печеньки, второе - номер дня, в который он поедет продавать печеньки. В случае, если таких вариантов дней несколько, выведите любой из них. Если Летовец в итоге не сможет получить прибыль ни при каких вариантах, то выведите два нуля.
| |
![]()
|
|
Минимизируем число
Использование сортировки
У Незнайки есть одно натуральное четырехзначное число. Он решил подарить его Гуньке. Но, так как Гунька любит минимальные числа, Незнайке нужно составить из цифр его числа новое число, чтобы оно было как можно меньше. Помогите Незнайке составить из цифр его числа новое число, чтобы оно было минимальным.
Заметим, что четырехзначные числа не могут начинаться с нуля.
Формат входных данных
Вводится натуральное четырехзначное число.
Формат выходных данных
Выведите минимальное натуральное четырехзначное число, состоящее из тех же цифр.
| |
![]()
|
|
Такси
Использование сортировки
Наши люди до метро на такси не ездят!
После затянувшегося совещания директор фирмы решил заказать такси, чтобы развезти сотрудников по домам. Он заказал N машин — ровно столько, сколько у него сотрудников. Однако когда они подъехали, оказалось, что у каждого водителя такси свой тариф за 1 километр.
Директор знает, какому сотруднику сколько километров от работы до дома (к сожалению, все сотрудники живут в разных направлениях, поэтому нельзя отправить двух сотрудников на одной машине). Теперь директор хочет определить, какой из сотрудников на каком такси должен поехать домой, чтобы суммарные затраты на такси (а их несет фирма) были минимальны.
Формат входных данных
Сначала во входном файле записано натуральное число N (1 ≤ N ≤ 1000) — количество сотрудников компании (совпадающее с количеством вызванных машин такси). Далее записано N чисел, задающих расстояния в километрах от работы до домов сотрудников компании (первое число — для первого сотрудника, второе — для второго и т.д.). Все расстояния — положительные целые числа, не превышающие 1000. Далее записано еще N чисел — тарифы за проезд одного километра в такси (первое число — в первой машине такси, второе — во второй и т.д.). Тарифы выражаются положительными целыми числами, не превышающими 10000.
Формат входных данных
В выходной файл выведите N чисел. Первое число — номер такси, в которое должен сесть первый сотрудник, второе число — номер такси, в которое должен сесть второй и т.д., чтобы суммарные затраты на такси были минимальны. Если вариантов рассадки сотрудников, при которых затраты минимальны, несколько, выведите любой из них.
| |
![]()
|
|
Обувной магазин
Квадратичные сортировки
Использование сортировки
В обувном магазине продается обувь разного размера. Известно, что одну пару обуви можно надеть на другую, если она хотя бы на три размера больше. В магазин пришел покупатель. Требуется определить, какое наибольшее количество пар обуви сможет предложить ему продавец так, чтобы он смог надеть их все одновременно?
Формат входных данных
Сначала вводится размер ноги покупателя (обувь меньшего размера он надеть не сможет), затем количество пар обуви в магазине и размер каждой пары. Размер — натуральное число, не превосходящее 100, количество пар обуви в магазине - неотрицательное число, не превосходит 1000.
Формат выходных данных
Выведите единственное число — максимальное количество пар обуви.
| |
![]()
|
|
Наибольший отрезок, не содержащий точек
Квадратичные сортировки
Использование сортировки
На числовой прямой отмечено N точек с целочисленными координатами. Определите наибольшую длину отрезка, внутри которого нет ни одной точки.
Формат входных данных
В первой строке записано натуральное число N - количество отмеченных точек (2 <= N <= 103). Во второй строке записано N целых чисел - координаты точек (каждое число по модулю не больше 109).
Формат выходных данных
В первой строке выведите максимальную длину искомого отрезка. Во второй строке выведите координаты его концов (сначала левую координату, затем через пробел правую). Если таких отрезков несколько, то выведите тот отрезок, у которого наименьшая левая координата.
| |
![]()
|
|
Лифт
Множества
Использование сортировки
Сортировка событий
Структуры данных
Задача на реализацию
В современном многоэтажном офисе крупной компании установлен новый лифт. В
компании работает n сотрудников. Для проверки эффективности системы управления
лифтом требуется провести моделирование его работы в конце рабочего дня, когда все
сотрудники должны покинуть здание и спуститься на первый этаж.
В здании m этажей, пронумерованных от 1 до m снизу-вверх. Известно, что i-й
сотрудник подходит к лифту в секунду ti на этаже ai, чтобы спуститься на первый этаж.
На каждом этаже могут находиться люди, ожидающие лифт. Когда очередной
сотрудник подходит к лифту, он вызывает лифт, если на этом этаже лифт еще не вызван,
либо присоединяется к ожидающим лифт. Таким образом, помимо вызвавшего лифт, вместе
с ним лифт могут ожидать и другие сотрудники.
В каждый момент времени не более одного вызова является активным.
Изначально лифт свободен и находится на первом этаже. Когда поступает первый
вызов, этот вызов становится активным и лифт отправляется на соответствующий этаж. Если
несколько вызовов поступает одновременно, активным становится вызов от сотрудника с
меньшим номером.
Лифт перемещается между этажами со скоростью один этаж в секунду. Когда лифт
оказывается на этаже, откуда был сделан активный вызов, в него заходят все, кто уже
ожидает лифт на этом этаже, и лифт отправляется вниз на первый этаж, со скоростью один
этаж в секунду.
При движении вниз лифт останавливается на тех этажах, в которых был сделан вызов
на момент проезда лифта мимо этого этажа. Все ожидающие лифт сотрудники заходят в него
и вызов на этом этаже сбрасывается. Когда лифт завершает движение на первом этаже, все
люди выходят из лифта, а лифт ожидает следующего вызова.
Если в момент, когда лифт освободился, есть хотя бы один необслуженный вызов,
активируется вызов, который поступил раньше других. Если несколько вызовов поступило
одновременно, активируется вызов от сотрудника с меньшим номером. Лифт продолжает
обслуживание описанным образом, пока все n сотрудников не окажутся на первом этаже.
Будем считать, что люди входят и выходят из лифта мгновенно. Каждую секунду
сначала люди подходят и вызывают лифт, а затем выполняются соответствующие действия
(лифт перемещается на соседний этаж, в него входят или из него выходят люди, принимается
решение, на какой вызов лифт должен отреагировать).
Требуется написать программу, которая по описанию вызовов лифта для каждого
сотрудника определяет, в какой момент этот сотрудник окажется на первом этаже.
Формат входных данных
Первая строка входных данных содержит целые числа n и m — количество людей,
вызывающих лифт, и количество этажей в здании (1 ≤ n ≤ 105, 2 ≤ m ≤ 109).
Следующие n строк описывают сотрудников, i-я из этих строк содержит два целых
числа ti и ai — секунду, в которую i-й сотрудник подходит к лифту, и номер этажа, на
котором это происходит (1 ≤ t1 ≤ t2 ≤ … ≤ tn ≤ 109, 2 ≤ ai ≤ m)
Формат выходных данных
Выходные данные должны содержать n целых чисел, для каждого сотрудника
требуется вывести секунду, в которую он выйдет из лифта на первом этаже.
| Ввод |
Вывод |
|
5 4
2 3
2 4
5 2
5 3
9 3
|
6
12
6
12
12
|
Пояснение к примеру
Пример работы лифта по шагам показан в следующей таблице.
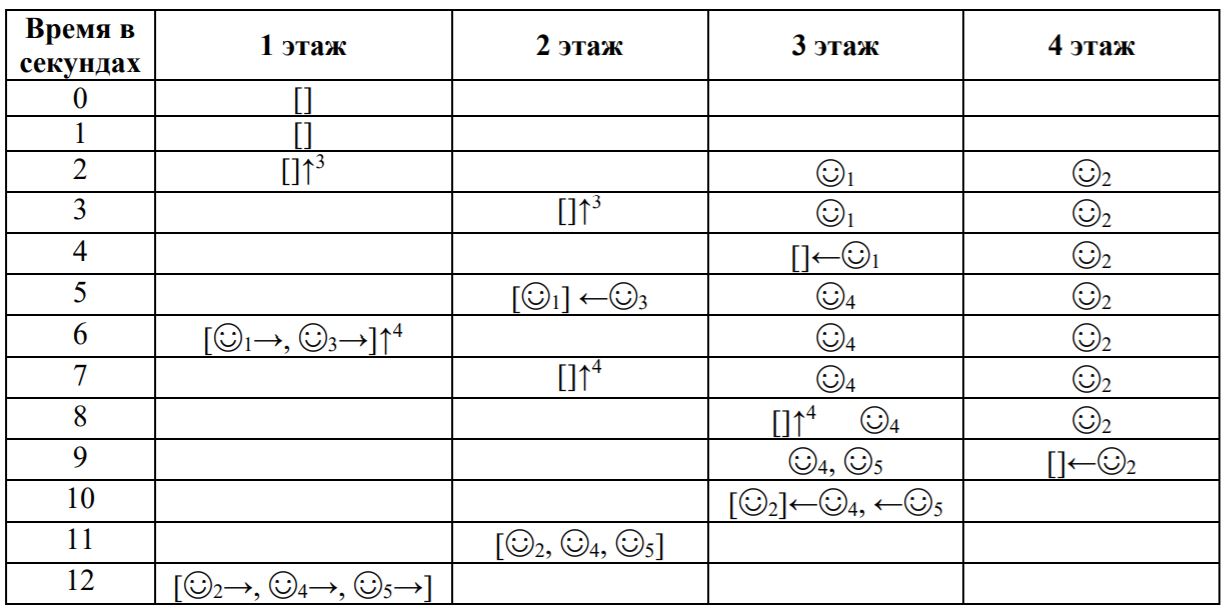
Использованные в пояснении к примеру обозначения
 | |
![]()
|
|
Чтение книг
Бинарный поиск по ответу
Использование сортировки
Жадный алгоритм
У Максима есть n книг различных жанров. В i-й книге ai страниц. Сегодня он хочет прочитать не менее xj страниц, при этом, чтобы не запутаться в историях, он хочет прочитать как можно меньше книг.
Помогите Максиму определить минимальное количество книг, которые он должен прочитать, чтобы общее число прочитанных страниц было не менее xj. Если это невозможно, выведите -1. Максим не может читать одну и ту же книгу дважды.
Формат входных данных
Первая строка содержит натуральное число n (1 ≤ 𝑛 ≤ 105) - количество книг, которые есть у Максима. Вторая строка содержит n целых чисел a1, a2, ..., an (1≤ ai ≤104) - количество страниц в i-й книге. Третья строка содержит натуральное число xj (1 ≤ xj ≤ 2⋅109) - количество страниц, которое хочет прочитать Максим.
Формат выходных данных
Выведите ответ на задачу.
| |
![]()
|
|
Спортивная акция
Использование сортировки
Организаторы спортивных соревнований закупают товары для награждения в спортивном магазине. В магазине проходит акция. На K товаров с самой высокой ценой установлена скидка. Организаторы не хотят дарить товары, купленные по акции.
Ваша задача - помочь организаторам спланировать бюджет и определить цену самого дорогого товара, который не попадает под акцию.
Входные данные
В первой строке вводят два числа, записанные через пробел: N – общее количество товаров (натуральное число, не превышающее 100 000) и K – количество товаров (1 < K < N). В следующих N строках находятся значения цены каждого из товаров (все числа натуральные, не превышающие 10 000), каждое в отдельной строке.
Выходные данные
Выведите одно число - ответ на задачу.
| |
![]()
|
|
Спортивная акция - 2
Использование сортировки
В магазине спортивных товаров проходит акция. На K товаров с самой высокой ценой установлена скидка в размере d%. Причем, от каждой цены, после применения скидки, отбрасываются копейки. Администрация магазина хочет узнать, какую сумму они получат от продажи всех товаров по акции.
Входные данные
В первой строке вводят три числа, записанные через пробел: N – общее количество товаров (натуральное число, не превышающее 100 000), K – количество товаров (1 < K < N), d - размер скидки в процентах (5 < d < 50). В следующих N строках находятся значения цены каждого из товаров (все числа натуральные, не превышающие 10 000), каждое в отдельной строке. Гарантируется, что ответ не превышает 109.
Выходные данные
Выведите одно число - ответ на задачу.
Примечание
Стоимость товара со скидкой выисляется по следующей формуле:
Цена со скидкой = Исходная цена - Исходная цена * (Процент скидки / 100).
| |
![]()
|
|
Радиация
Использование сортировки
Космический аппарат "Звезда" выполняет задачу по фиксации показаний уровня космической радиации. Каждое показание записывается в виде целого числа. В процессе первоначальной обработки данных, для устранения потенциально неточных результатов, убирают из списка K наибольших и K наименьших показаний.
Исходя из списка полученных показаний и количестве исключаемых показаний, определите самое высокое точное показание и целую часть среднего арифметического всех точных показаний.
Формат входных данных
В первой строке записаны два числа через пробел: N – общее количество показаний (натуральное число, не превышающее 10 000) и K – количество исключаемых минимальных и максимальных показаний. В следующих N строках находятся значений каждого показания (все числа натуральные, не превышающие 10000), каждое в отдельной строке.
Формат выходных данных
Запишите в ответе два числа: сначала наибольшего точного показания, а затем целую часть среднего арифметического всех точных показаний.
| |
![]()
|
|
Курьер
Использование сортировки
Жадный алгоритм
Курьеру Васе поручили доставить n посылок. Вася начинает работать в первый день и каждый день может доставить ровно одну посылку. Про каждую посылку известен последний день, когда ее можно доставить di, и штраф wi, который придется заплатить, если посылка не будет доставлена в срок.
Помогите Васе решить, в каком порядке доставлять посылки, чтобы суммарный штраф был как можно меньше.
Например, если есть 3 посылки, первую необходимо доставить в первый день и штраф за опоздание 2, вторую также необходимо доставку в первый день и штраф за опоздание 3, а третью необходимо доставить не позже третьего дня и штраф за опоздание 1, то оптимально доставить сначала вторую, потом третью, а затем первую посылку. В этом случае не в срок доставлена только первая посылка и штраф составляет 2. Доставить одновременно первую и вторую посылку в срок невозможно.
Формат ввода
Формат вывода
В первой строке выведите единственное число, равное минимально возможному суммарному штрафу. Во второй строке через пробел выведите n чисел, где i-е число — день, в который необходимо доставить i-ю посылку.
Если возможно несколько оптимальных расписаний, выведите любое из них.
Пример
| Ввод |
Вывод |
3
1 2
1 3
3 1
|
2
3 1 2
|
| |
![]()
|
|
День рождения
Использование сортировки
У ковбоя Влада день рождения! На праздник собрались n детей. Чтобы поздравить ковбоя, дети решили водить вокруг Влада хоровод. Среди детей, пришедших к Владу, есть и высокие, и низкие, поэтому если они встанут в хороводе как угодно, многим из них может быть неудобно, потому что если в хороводе рядом стоят очень высокий и очень низкий ребёнок, им трудно держаться за руки. Поэтому дети решили встать в хоровод так, чтобы максимальная разность ростов двух соседних детей была минимальной.
Более формально, пусть n детей выстроились в хоровод. Пронумеруем их целыми числами от 1 до n так, чтобы справа от ребёнка с номером i стоял ребёнок с номером i+1, а справа от ребёнка с номером n стоял ребёнок с номером 1. Тогда неудобством этого хоровода назовём максимальную разность между ростом детей, которые стоят рядом. Обратите внимание, что разностью в росте двух детей называется разность между ростом более высокого и более низкого ребёнка, таким образом, разность в росте двух детей всегда неотрицательна.
Помогите детям и определите, в каком порядке им надо выстроиться в круг, чтобы минимизировать неудобство получившегося хоровода. Обратите внимание, что все n детей должны оказаться в хороводе.
Входные данные
В первой строке содержится одно целое число n (2 ≤ n≤ 105) — количество детей, которые пришли на день рождения ковбоя Влада.
Во второй строке заданы n целых чисел ai (1≤ai≤109) — рост каждого из детей. Рост детей задан в нанометрах и уменьшен на 109, таким образом, рост ребёнка с ai=1 чуть выше метра, а рост ребёнка с ai=109 составляет два метра.
Выходные данные
Выведите n целых чисел — значения роста детей в порядке, в котором они должны встать в хоровод. В этом порядке соседними будут дети с номерами i и i+1, а также дети с номерами 1 и n. Если оптимальных хороводов несколько, то выведите любой из них.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснения |
| 1 |
5
2 1 1 3 2 |
1 2 3 2 1 |
Здесь неудобство хоровода равно 1, так как разность в росте между соседними детьми равна 1, 1, 1, 1 и 0 соответственно. Обратите внимание, что последовательности [23211] , [32112] задают те же хороводы и отличаются только выбором ребёнка с номером 1. |
| 2 |
3
30 10 20 |
10 30 20 |
Неудобство хоровода равно 20, так как разность в росте детей высотой 10 и 30 равна 20. |
| |
![]()
|
|
Киноакадемия
Использование сортировки
Жадный алгоритм
В финал конкурса Киноакадемии вышли \(n\) лучших кинофильмов 2014 года. В конкурсе награждаются фильмы в двух номинациях: лучшая режиссура и лучший сценарий. По правилам конкурса в каждой номинации должен быть награжден ровно один фильм, причём в разных номинациях — разные фильмы.
В ходе многочисленных опросов зрителей и кинокритиков удалось собрать данные, показывающие, какой уровень ликования вызовет победа каждого фильма в каждой из номинаций. Дотошные журналисты на этом не остановились и дополнительно выяснили, каким будет уровень ликования, если тот или иной фильм не выиграет ни в одной из номинаций.
Требуется написать программу, которая по результатам опросов определяет наибольший суммарный уровень ликования, которого можно добиться выбором фильмов для награждения в указанных номинациях.
Формат входных данных
В первой строке задано целое число \(n\) — количество кинофильмов, участвующих в финале конкурса Киноакадемии. В следующих \(n\) строках содержатся по три целых числа \(a_i\), \(b_i\), \(c_i\) — уровень ликования, если \(i\)-й фильм не выиграет ни в одной из номинаций, уровень ликования, если этот фильм выиграет в номинации на лучшую режиссуру, и уровень ликования, если этот фильм выиграет в номинации на лучший сценарий.
Формат выходных данных
Первая строка должна содержать одно число — наибольший возможный суммарный уровень ликования. Вторая строка должна содержать два целых числа — номера фильмов-победителей в номинациях лучшая режиссура и лучший сценарий соответственно. Фильмы нумеруются натуральными числами от 1 до \(n\). Если оптимальных способов выбора награждаемых фильмов несколько, можно вывести любой из них.
Пояснение к примеру
В приведенном примере наибольший суммарный уровень ликования равен \(3 + 5 + 9 = 17\).
| |
![]()
|
|
Шоссе
Использование сортировки
Способы задания графа
Элементарная геометрия
Во Флатландии \(n\) городов, расположенных в различных точках плоскости. Известно, что никакие три города не лежат на одной прямой.
Правительство решило построить в стране сеть сверхскоростных шоссе. Сеть шоссе должна быть такой, чтобы из любого города можно было проехать в любой другой по построенным шоссе. А в целях экономии средств было решено, что путь, соединяющий любые два города, должен быть единственным. Каждое шоссе представляет собой отрезок, соединяющий некоторую пару городов.
Завод, выполняющий этот госзаказ, подготовил проект сети шоссе. Проект представляет собой описание \(n - 1\) шоссе. Каждое шоссе задается городами, которые оно соединяет. В целях секретности вместо названий городов в проекте были использованы коды — числа от 1 до \(n\).
Однако когда дело дошло до реализации проекта, выяснилось, что документ, в котором было указано соответствие номеров городам, утерян. Поскольку проект приурочен к пятисотлетию культурной столицы Флатландии, переделывать проект полностью оказалось невозможно. Поэтому было решено установить некоторое новое соответствие номеров городам.
При попытке это сделать разработчики проекта столкнулись со следующей проблемой. В соответствии с техническими нормами строительства, недопустимо, чтобы шоссе пересекались вне городов. Поэтому не любое сопоставление номеров городам допустимо. После пары бессонных ночей главный инженер завода решил поручить спасение проекта вам.
Ваша задача — таким образом сопоставить числам от 1 до \(n\) города, чтобы после реализации проекта шоссе не пересекались вне городов, которые они соединяют.
Формат входных данных
В первой строке содержится целое число \(n\) — количество городов во Флатландии (\(2 \le n \le 1500\)).
Далее следует \(n\) описаний городов. Описание каждого города состоит из двух строк. Первая строка содержит название города — строку, состоящую из символов с ASCII-кодами от 33 до 127. Названия различных городов не совпадают. Длина названия города не превышает 60 символов. Вторая строка описания города содержит два целых числа \(x\) и \(y\) — координаты города. Координаты не превышают \(10^4\) по абсолютной величине.
Далее следуют \(n - 1\) строк, которые описывают проект строительства сети шоссе в его текущем состоянии. Каждая строка содержит по два целых числа — номера городов, соединенных шоссе в проекте. Никакое шоссе в проекте не соединяет город сам с собой, никакие два города не соединены более чем одним шоссе.
Формат выходных данных
Выведите \(n\) строк, \(i\)-я из этих строк должна содержать название города, который следует сопоставить числу \(i\) в проекте. Если решений несколько, выведите любое.
Если решения не существует, выведите <<No solution>>.
Иллюстрация к примеру
| |
![]()
|
|
Найди пару
Строки
Использование сортировки
Друзья играют в интересную игру со словами, суть которой заключается в разбиении слов на пары.
У друзей есть \(n\) слов одинаковой длины. Они хотят выбрать такое наибольшее число \(k\), чтобы можно было разбить слова на пары так, чтобы в каждой паре у слов совпадало хотя бы \(k\) первых букв.
Помогите друзьям найти искомое максимальное значение \(k\).
Формат входных данных
В первой строке входных данных находится целое число \(n\) — количество слов (\(1 \leqslant n \leqslant 2\cdot 10^5\), \(n\) — четное).
В следующих \(n\) строках заданы слова, которые есть у друзей. Гарантируется, что все строки имеют одинаковую длину и суммарная длина строк не превышает \(2 \cdot 10^6\).
Формат выходных данных
В единственной строке выведите число \(k\) — искомое максимальное значение.
| |
![]()
|
|
Шоколадная мудрость
Алгоритмы сортировки
Использование сортировки
Шоколад помогает развивать ум и укреплять дух! Старец Летовец после своих занятий угощает своих учеников шоколадом. На следующем занятии у него будет M учеников и каждому из них Старец хочет дать по одной плитке шоколада.
Чтобы купить нужное количество шоколада, старец отправил своего праправнука Летовёнка разузнать, какое минимальное количество денег ему понадобится.
Оказывается, каждый магазин продаёт шоколад по разной цене. В i-м магазине можно купить не более Bi плиток шоколада по цене Аi рублей за плитку. Летовец хочет потратить как можно меньше денег, но при этом купить ровно M плиток шоколада.
Помогите Летовёнку посчитать какую минимульную сумму на шоколад потратит старец Летовец.
Формат входных данных
В первой строке заданы два числа: N и M (1 <= N, M <= 105). Следующие N строк содержат по 2 числа: Ai (1 <= Ai <= 109) и Bi (1 <= Вi <= 105). \(B_1 + B_2 +... + B_N >= M\).
Формат выходных данных
Выведите минимальную сумму денег, необходимую для покупки M плиток шоколада.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 5
4 9
2 4 |
12 |
| 2 |
4 30
6 18
2 5
3 10
7 9 |
130 |
| 3 |
1 100000
1000000000 100000 |
100000000000000 |
| |
![]()
|
|
65813
Использование сортировки
В школе в очередной раз заболел преподаватель физкультуры Виктор Дмитриевич. Поэтому директор принял решение, что кто-то из свободных учителей проведёт занятие. После долгих размышлений, самым свободным оказался учитель информатики Анатолий Иванович, который очень любит алгоритмы сортировки, что вызвало сразу проблему у учеников. Ведь Анатолий Иванович первым делом сказал ребятам построиться в шеренгу, но не как обычно (по убыванию роста, ), а так, чтобы каждое нечётное место было отсортировано по росту по убыванию (первое место - самый высокий ученик, третье место выше пятого, пятое выше седьмого и так далее)), а каждое чётное по возрастанию (второе место - самый низкий ученик, четвёртый второй по росту среди всех, шестой - третий по росту среди всех и так далее) (учеников Анатолий Иванович нумеровал с 1).
Помогите ученикам получить правильный порядок, как встать им в шеренгу так, чтобы Анатолий Иванович оказался доволен.
Формат входных данных
На первой строке подаётся число N (1 <= N <= 121)– количество учеников в классе.
На N последующих строках подаются строки вида имя-рост (например, «Ivan 175»), где на первом месте указывается имя ученика – оно всегда одним словом на английском языке, без пробелов, а в конце указывается рост ученика (целое число от 100 до 220).
Формат выходных данных
Выведите имена учеников в одну строку через пробел, как они должны встать на уроке физкультуры.
Примечание:
Имена учеников у всех уникальны, рост ни у кого не повторяется.
| |
![]()
|
|
66172
Словари
Циклы
Использование сортировки
Арифметические операции
Белочка живет в дубовом парке. Каждый день до обеда она собирает ровно К желудей и складывает их в дупле одного из дубов. Последнее время вечером каждого воскресенья в парк приходит мальчик Витя. Он обнаружил дупло, в котором белочка хранит жёлуди. Для своих игр он каждый раз забирает Т желудей из дупла.
Известно, что после последнего прихода Вити в парк, в дупле осталось Х желудей. Необходимо определить через сколько дней после этого прихода Вити, белочка сможет собрать не менее М желудей в дупле.
Формат ввода
На вход программе в одной строке подается четыре целых числа, записанные через пробел К, M, Т, Х (1≤ К, M, Т, Х ≤109).
Формат вывода
Вывести одно целое число – количество дней, через которое белочка сможет собрать необходимое число желудей.
Если белочка не сможет собрать нужное число желудей никогда, вывести число -1.
| |
![]()
|
|
66173
Одномерные массивы
Цикл for
Использование сортировки
Автомат получает на вход последовательность натуральных чисел и работает с ними по следующим правилам:
1)Если число кратно 3, автомат добавляет его значение в первуюконтрольную сумму.
2)Если число не кратно 3, автомат добавляет его значение вовторую контрольную сумму.
После обработки последовательности автомат удваивает большую контрольную сумму, утраивает меньшую контрольную сумму, складывает их и выводит результат.
Располагая последовательностью, определите, какой результат выведет автомат.
Формат ввода
На вход программе в первой строке подается натуральное число N (5 ≤ N ≤ 10000) – количество чисел. Далее в N строках подаётся по одному натуральному числу, не превышающему 1000.
Формат вывода
Вывести одно целое число – результат обработки последовательности, который можно получить по правилам, описанным в условии задачи.
| |
![]()
|