| Условие задачи | | Прогресс | Попытки, все/успешные |
|
Темы:
Простые задачи на перебор
В процессе установки турникетов в автобусах, разработчики столкнулись с проблемой проверки подлинности билета. Для ее решения был придуман следующий способ защиты от подделок.
Информация, записанная на билете, кодируется K числами (0 или 1). При этом непосредственно на билете записывается последовательность из N чисел (N>=K) так, что числа, записанные на расстоянии K, совпадают. Таким образом, для проверки подлинности билета достаточно проверить, что все числа на расстоянии K совпадают. К сожалению, при считывании информации с билета иногда могут происходить ошибки — считается, что одно из чисел может исказиться (то есть 0 заменится на 1, или 1 — на 0). Такой билет все равно нужно считать подлинным. Во всех остальных случаях билет считается поддельным.
Напишите программу, которая по информации, считанной с билета, устанавливает его подлинность, и указывает, при считывании какого из чисел могла произойти ошибка.
Входные данные
В первой строке входного файла записаны числа N и K (1<=N<=50000, 1<=K<=1000, K<=N). Во второй строке записано N чисел, каждое из которых является 0 или 1 — информация, считанная с билета.
Выходные данные
В первой строке выходного файла должно быть записано одно из двух сообщений — OK или FAIL (первое сообщение обозначает, что билет признан подлинным, второе — поддельным). В случае, если билет подлинный, во второй строке выведите 0, если все числа были считаны правильно, или номер числа, в котором при считывании произошла ошибка. Если возможных ответов несколько, выведите любой из них (в частности, если для признания билета подлинным можно считать, что ошибок при считывании не было, а можно считать, что была ошибка в одном из чисел — правильным является любой из вариантов ответа).
| |
![]()
|
8/
1
|
|
Темы:
Простые задачи на перебор
На склад, который имеет форму прямоугольного параллелепипеда, привезли ноутбуки, упакованные в коробки. Каждая коробка также имеет форму прямоугольного параллелепипеда.
По правилам хранения коробки с ноутбуками должны быть размещены на складе с выполнением следующих двух условий:
Стороны коробок должны быть параллельны сторонам склада
Коробку при помещении на склад разрешается расположить где угодно (с выполнением предыдущего условия), в том числе на другой коробке, но все коробки должны быть ориентированы одинаково (т.е. нельзя одну коробку расположить «стоя», а другую – «лежа»)
Напишите программу, которая по размерам склада и размерам коробки с ноутбуком определит максимальное количество ноутбуков, которое может быть размещено на складе.
Входные данные
Вводится шесть натуральных чисел. Первые три задают длину, высоту и ширину склада. Следующие три задают соответственно длину, высоту и ширину коробки с ноутбуком. Каждое из чисел не превышает 1000.
Выходные данные
Выведите одно число — максимальное количество ноутбуков, которое может быть размещено на складе.
| |
![]()
|
1/
1
|
|
Темы:
Простые задачи на перебор
На базаре есть ряд из N мест, где продаются семечки подсолнечника. Потенциальные покупатели идут вдоль ряда, затем в некоторый момент останавливаются и покупают семечки. Качество семечек от места к месту различается незначительно, так что разницы только в цене семечек и положении места.
Перед тем как выйти на рынок в качестве ещё одного продавца семечек, Вы провели исследование рынка, чтобы найти зависимость числа покупателей от двух названных факторов. Исследование показывает, что большинство покупателей следуют одному и тому же шаблону. Они проходят мимо нескольких мест, замечая и запоминая цены, а затем после обхода K мест, возвращаются к месту с наименьшей замеченной ценой, совершают там покупку, затем покидают базар. Если есть несколько мест с одинаковой ценой, покупатель выбирает ближайшее.
Предположим, что есть пять мест с ценами 37, 34, 34, 35, 33. Если покупатель с K = 4 идёт слева направо, он видит семечки по ценам 37, 34, 34, 35. В этот момент он решает, что видел достаточно, возвращается к третьему месту и покупает семечки там. Хотя на втором месте цена та же, что и на третьем, покупателю до него идти дальше. Если бы тот же покупатель зашёл справа, он бы увидел цены 33, 35, 34, 34, затем остановился и вернулся бы к пятому месту.
Число мест, пройденных до принятия решения (K), является функцией жадности и терпеливости покупателя, и, очевидно, различается у разных покупателей. Исследование выявило средний процент BK покупателей для всех значений K (1 <= K <= N, 0 <= BK <= 99, сумма всех BK равна 100).
Вам следует определить оптимальную стратегию на этом рынке (то есть цену и положение нового места, которое максимизирует ожидаемый средний доход) в предположении, что половина клиентов идёт в направлении от первого места к N-му, а другая половина - от N-го места к первому, и они следуют описанному шаблону.
Входные данные
В первой строке находится число существующих мест N, во второй строке - N целых чисел - цены на каждом месте, в третьей строке - N целых чисел в диапазоне от 0 до 99 - значения BK для каждого K. Все числа в строках разделены пробелами.
Ограничения: 2 <= N <= 100, исходные цены - целые числа от 1 до 9999.
Выходные данные
Выводятся два целых числа - L и P. L (0 < L < N) - это число существующих мест, после которых должно быть размещено новое (Вам не разрешается устанавливать своё место первым или последним). Число P - оптимальная цена. Если существует более чем одно оптимальное решение, Вы должны выбрать решение с минимальным L, а среди них - с минимальным P.
| |
![]()
|
1/
1
|
|
Темы:
Двумерные массивы
Обход в глубину
Простые задачи на перебор
Андрюше на день рождения подарили хомячка. Пока Андрюша не купил для него клетку, он решил сделать ему клетку из подручных средств. Для изготовления клетки он решил использовать набор кубиков, подаренный ему на прошлый день рождения. Однако, неожиданно выяснилось, что сестра Андрюши склеила кубики суперклеем, и отделить их друг от друга не представляется возможным.
Все кубики оказались склеены в две фигуры. Любые два кубика в каждой из фигур либо не имеют общих точек, либо имеют общую грань, либо имеют общее ребро, но в последнем случае есть кубик, с которым каждый из них имеет общую грань. Каждую фигуру можно положить на стол так, что каждый кубик будет касаться стола одной из своих граней.
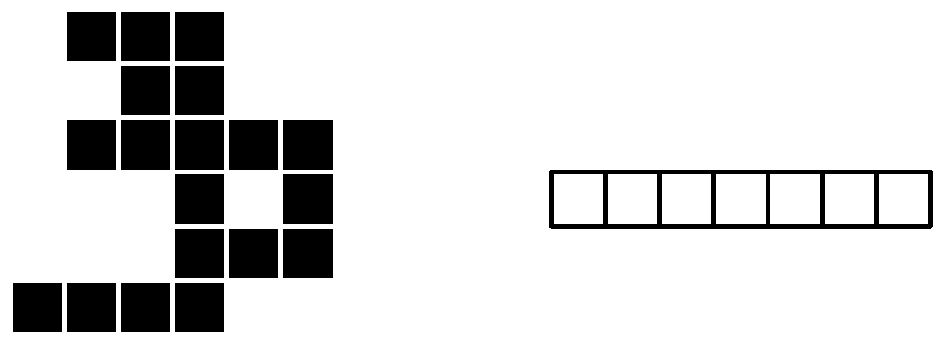
Теперь Андрюша хочет положить эти две фигуры на стол так, чтобы получилась клетка для хомячка. Фигуры должны быть положены таким образом, чтобы каждый кубик касался стола гранью. Стороны нижних граней кубиков должны быть параллельны сторонам стола. Любые два кубика, принадлежащие различным фигурам, должны либо не касаться друг друга, либо иметь общую грань, либо иметь общее ребро. Фигуры разрешается поворачивать и переворачивать.
Положив фигуры, Андрюша собирается выпустить хомячка на стол. Чтобы он не упал со стола, у него не должно быть возможности добраться от точки, в которую Андрюша его выпустит, до края стола. Хомячок не может перелезать через кубики, и, в частности, не может пролезть между двумя кубиками, имеющими общее ребро. Стол существенно больше каждой из фигур.
Андрюша хочет, чтобы площадь, по которой может бегать хомячок, была как можно больше. Помогите ему выяснить, какая максимальная площадь может быть у территории, до которой сможет добраться хомячок. Площадь грани кубика будем считать равной единице.
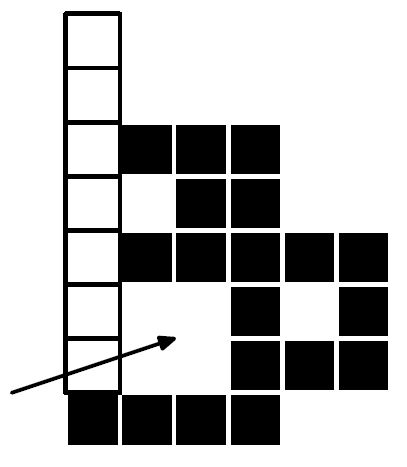
Например, две фигуры, показанные на рисунке выше, можно расположить как показано на следующем рисунке. Если выпустить хомячка в точку, отмеченную стрелкой, то доступная ему территория будет иметь площадь, равную четырем.
Входные данные
В первой строке вводятся два числа: h1 и w1 (1 <= h1, w1 <= 10). Следующие h1
строк содержат по w1 символов и описывают первую фигуру, вид сверху. Каждый из этих символов - либо "*" (звездочка), либо "." (точка), звездочка обозначает кубик, а точка – пустое место.
Далее в отдельной строке вводятся два числа: h2 и w2 (1 <= h2, w2 <= 10). Следующие h2 строк содержат по w2 символов и описывают вторую фигуру в формате, аналогичном формату первой. Каждая из фигур связна и содержит хотя бы один кубик.
Выходные данные
Выведите одно число – максимальную площадь, которая может быть доступна хомячку. Если сделать клетку для хомячка невозможно, выведите 0.
| |
![]()
|
1/
1
|
|
Темы:
Целые числа
Простые задачи на перебор
Входные данные
Вводятся 5 чисел: a, b, c, d и e.
Выходные данные
Найдите все целые решения уравнения ( ax3 + bx2 + cx + d ) / ( x - e ) = 0 на отрезке [0,1000] и выведите их количество.
| |
![]()
|
1/
1
|
|
Темы:
Простые задачи на перебор
Входные данные
Вводятся 4 числа: a, b, c и d.
Выходные данные
Найдите все целые решения уравнения ax3 + bx2 + cx + d = 0 на отрезке [0,1000] и выведите их в порядке убывания. Если на данном отрезке нет ни одного решения, то ничего выводить не нужно.
| |
![]()
|
1/
1
|
|
Темы:
Условный оператор
Простые задачи на перебор
Дед Мороз решил проверить фабрику игрушек, все ли подарки для детей готовы. Чтобы дойти до места хранения игрушек, ему необходимо пройти по узкому секретному коридору. В коридоре на каждом метре пути указано число метров от двери. У двери, возле которой стоит Дед Мороз, записано число 0. По коридору можно двигаться как влево, так и вправо. При движении влево числа отрицательные, при движении вправо - положительные.
Так как место засекречено, завод постоянно меняет вход в хранилище игрушек.
Дед Мороз знает, что вход в фабрику сегодня расположен у двери с числом X. Также известно, что в коридоре, рядом с числом Y находится дверь, перекрывающая проход по коридору. Чтобы ее открыть необходимо взять ключ, который располагается на стене на полке в коридоре рядом с числом Z.
Определите сможет ли Дед Мороз сам добраться до двери к игрушкам. Если сможет, определите минимальное расстояние, которое необходимо будет пройти Деду Морозу. Если не сможет, то выведите -1.
Входные данные
Программа получает на вход строку, содержащую 3 различных ненулевых числа: X, Y, Z (-103 <= X, Y, Z <= 103).
Выходные данные
Выведите минимальное расстояние, которое необходимо пройти Деду Морозу от двери, у которой он стоит, до двери, за которой расположено место хранения игрушек. Если Дед Мороз не сможет добраться до этой двери, выведите -1.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
10 -10 1 |
10 |
| 2 |
20 10 -10 |
40 |
| 3 |
100 1 1000 |
-1 |
| |
![]()
|
649/
98
|
|
Темы:
"Два указателя"
Использование сортировки
Простые задачи на перебор
Жадный алгоритм
Задача на реализацию
У маленького Миши есть кубики, на каждом из которых написана одна английская строчная буква. Вчера он выкладывал кубики в два ряда. В первом ряду у Миши n кубиков с буквами, во втором - m кубиков с буквами. Так получилось, что в двух этих рядах нет совпадающих букв. Другими словами, ни одна буква не содержится одновременно в обоих рядах.
Сегодня маленький Миша решил продолжить играть с кубиками. Но теперь он берет один любой кубик из какого-либо ряда и составляет из них третий ряд, добавляя кубик всегда в конец. Маленький Миша никогда не берет более k кубиков подряд из одного и того же ряда. Миша закончил играть тогда, когда у него закончились кубики в каком-то одном ряду (в первом или во втором).
Наблюдавший за игрой папа заметил, что играя таким образом у Миши получилась лексикографически наименьшая строка. По известным двум строкам, которые образуются путем прочтения букв первого и второго ряда и числу k определите строку, которую получил маленький Миша.
Строка x лексикографически меньше строки y только и только тогда, когда выполняется одно из следующих условий:
- x является префиксом y, но x != y;
- в первой позиции, где x и y различаются, в строке x находится буква, которая стоит в алфавите раньше, чем соответствующая буква y.
Входные данные
Программа получает на вход несколько строк. В первой строке записаны три числа: n - количество кубиков в первом ряду, m - количество кубиков во втором ряду, k - целое число(1 <= n, m, k <= 100). Во второй строке записана строка a длиной n - строка, образованная прочтением букв, написанных на кубиках первого ряда. В третьей строке - строка b длиной m - строка, образованная прочтением букв, написанных на кубиках второго ряда.
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6 4 2
aaaaaa
bbbb |
aabaabaa |
| |
![]()
|
141/
28
|
|
Темы:
Циклы
Цикл for
Простые задачи на перебор
Задача на реализацию
Громозека очень любит валерьянку. На его родной планете Чумароза можно купить за k чумриков (местная валюта) первую упаковку валерьянки, за 2·k чумриков - вторую и так далее (иными словами, за i-ю упаковку надо заплатить i·k чумриков). Громозека хочет купить w упаковок валерьянки. У него есть n чумриков. Сколько чумриков ему придется взять в кредит в чумарозском банке, чтобы купить w упаковок валерьянки?
Входные данные
В первой строке записано три положительных целых числа k, n, w (1 <= k, w <= 1000, 0 <= n <= 109), стоимость первой упаковки, изначальное количество чумарозиков у Громозеки и количество упаковок валерьянки, которые он хочет купить.
Выходные данные
Выведите единственное целое число - количество чумарозиков, которое Громозеке необходимо взять в кредит в банке. Если брать кредит не надо, выведите 0.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 17 4 |
13 |
| |
![]()
|
608/
160
|
|
Темы:
Условный оператор
Простые задачи на перебор
Разбор случаев
Ужасная болезнь поражает коров. Фермер Джон хочет их защитить.
Амбар ФД - это узкое длинное здание, содержащее N стойл в ряд (2≤N≤105). Некоторые из этих стойл уже заняты коровами, некоторые - свободны. Прочитав о необходимости социального дистанцирования, ФД хочет максимизировать D, где D, это расстояние между двумя ближайшими занятыми стойлами. Например, если стойла 3 и 8 ближайшие, которые заняты, тогда D=5.
Две новых коровы пополнили стадо ФД и он должен решить, в какое не занятое стойло разместить каждую из них. Определите, ка к он должен разместить этих коров, чтобы в результате D, стало максимальным из возможных. ФД не может передвигать никакую из имеющихся коров, он может только назначить стойла новым коровам.
Входные данные
Первая строка ввода содержит N. Следующая строка содержит строку длиной N из 0 и 1, описывающая последовательность стойл в амбаре. 0 означает пустое стойло, 1 означает занятое стойло. В строке имеется как минимум два нуля, что достаточно для размещения двух коров.
Выходные данные
Выведите наибольше значение D (наименьшее расстояние между двумя занятыми стойлами), которое ФД может получить добавлением двух новых коров оптимальным образом.
Примеры
| № |
Входные данные |
Выходные данные |
|
| 1 |
14
10001001000010 |
2 |
В этом примере ФД может добавить коров так: 10x010010x0010 где x показывает новых коров. В этом случае D=2. Невозможно разметить коров так, чтобы получить D больше. |
| |
![]()
|
2/
1
|
|
Темы:
Обход в глубину
Простые задачи на перебор
Петя нарисовал на бумаге n кружков и соединил некоторые пары кружков линиями. После этого он раскрасил каждый кружок в один из трех цветов – красный, синий или зеленый.
Теперь Петя хочет изменить их раскраску. А именно – он хочет перекрасить каждый кружок в некоторый другой цвет так, чтобы никакие два кружка одного цвета не были соединены линией. При этом он хочет обязательно перекрасить каждый кружок, а перекрашивать кружок в тот же цвет, в который он был раскрашен исходно, не разрешается.
Помогите Пете решить, в какие цвета следует перекрасить кружки, чтобы выполнялось указанное условие.
Входные данные
В первой строке вводятся два целых числа n и m – количество кружков и количество линий, которые нарисовал Петя, соответственно (1 ≤ n ≤ 1 000, 0 ≤ m ≤ 20 000).
Следующая строка содержит n символов из множества {'R', 'G', 'B'} – i-й из этих символов означает цвет, в который раскрашен i-й кружок ('R' – красный, 'G' – зеленый, 'B' – синий).
Далее в m строках задается по два целых числа – пары кружков, соединенных отрезками.
Выходные данные
Выведите одну строку, состоящую из n символов из множества {'R', 'G', 'B'} – цвета кружков после перекраски. Если решений несколько, выведите любое.
Если решения не существует, выведите слово "Impossible''.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 5
RRRG
1 3
1 4
3 4
2 4
2 3 |
BBGR |
| 2 |
4 5
RGRR
1 3
1 4
3 4
2 4
2 3 |
Impossible |
| |
![]()
|
129/
25
|
|
Темы:
Простые задачи на перебор
Дана функция \(z(x) = ax^3 + bx^2 + cx + d\). Для заданных чисел a, b, c и d, выведите все целые значения x из диапазона от 0 до 1000, при которых функция z(x) принимает нулевое значение.
Входные данные
Программа получает на вход 4 числа: a, b, c и d. Каждое число записано в отдельной строке.
Выходные данные
Выведите все значение x, которые удовлетворяют условию задачи в порядке возрастания.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1
-5
6
0 |
0 2 3 |
| |
![]()
|
203/
65
|
|
Темы:
Строки
Простые задачи на перебор
Вам дана строка S, состоящая из цифр от 1 до 9 включительно. Вы можете вставить символ + в некоторые позиции (возможно, ни в одну) между двумя цифрами в этой строке. Здесь знак + не должен появляться последовательно после вставки (т.е. не должно быть два и больше знака + подряд). Все строки, которые можно получить таким образом, можно оценить как формулы. Оцените все возможные формулы и распечатайте сумму результатов, полученных при вычислении всех возможных формул.
Входные данные
На вход подается непустая строка S, состоящая из цифр от 1 до 9 включительно. Длина строки не более 10 символов.
Выходные данные
Выведите сумму результатов, полученных при вычислении всех возможных формул.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
125 |
176 |
Всего можно получить 4 формулы: 125, 1 + 25, 12 + 5 и 1 + 2 + 5.
Результат после вычисления каждой формулы:
125
1 + 25 = 26
12 + 5 = 17
1 + 2 + 5 = 8
Таким образом, сумма 125 + 26 + 17 + 8 = 176. |
| 2 |
9999999999 |
12656242944 |
|
| |
![]()
|
15/
8
|
|
Темы:
Способы задания графа
Простые задачи на перебор
Штирлиц ехал на машине, увидел голосующего Бормана, и проехал мимо. Через некоторое время он снова увидел голосующего Бормана, и снова проехал мимо. Вскоре он опять увидел голосующего Бормана.
- Издевается! - подумал Борман.
- Кольцевая! - догадался Штирлиц.
В городе N площадей. Любые две площади соединены между собой ровно одной дорогой с двусторонним движением. В этом городе живет Штирлиц. У Штирлица есть хобби - он любит воскресным утром выйти из дома, сесть в машину, выбрать какой-нибудь кольцевой маршрут, проходящий ровно по трем площадям (то есть сначала он едет с какой-то площади на какую-то другую, потом - на третью, затем возвращается на начальную, и опять едет по этому маршруту). Он воображает, что где-то на этом пути стоит Борман. И так вот ездит Штирлиц все воскресенье, пока голова не закружится, и радуется...
Естественно, что Штирлицу хочется проезжать мимо точки, в которой, как он воображает, стоит Борман, как можно чаще. Для этого, естественно, выбранный Штирлицем маршрут должен быть как можно короче. Напишите программу, которая выберет оптимальный для Штирлица маршрут.
Входные данные
В первой строке задается число N (3 <= N <= 100). В последующих строках содержится матрица NxN расстояний между площадями (число в позиции i,j обозначает длину дороги, соединяющей i-ую и j-ую площади). Все числа в матрице (кроме стоящих на главной диагонали) - натуральные, не превышающие 1000. Матрица симметрична относительно главной диагонали, на главной диагонали стоят 0.
Выходные данные
Требуется вывести три числа — номера площадей в оптимальном маршруте. Если маршрутов несколько, выведите любой из них.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
0 1 9 9 2
1 0 9 9 9
9 9 0 9 9
9 9 9 0 9
2 9 9 9 0 |
1 2 5 |
| |
![]()
|
57/
32
|
|
Темы:
Простые задачи на перебор
Представьте данное число n в виде суммы двух кубов.
Входные данные
Программа получает на вход одно натуральное число n (n <= 1028).
Выходные данные
Программа должна вывести 2 целых неотрицательных числа (в порядке убывания), сумма кубов которых равна n. Если это невозможно, выведите строку impossible.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
9 |
2 1 |
| 2 |
3 |
impossible |
| |
![]()
|
254/
37
|
|
Темы:
Простые задачи на перебор
Теорема Лагранжа утверждает, что любое натуральное число можно представить в виде суммы четырех точных квадратов. По данному числу n найдите такое представление: напечатайте от 1 до 4 натуральных чисел, квадраты которых дают в сумме данное число.
Входные данные
Программа получает на вход одно натуральное число n < 10000.
Выходные данные
Программа должна вывести от 1 до 4 натуральных чисел, квадраты которых дают в сумме данное число.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 |
1 1 1 |
| 2 |
7 |
2 1 1 1 |
| |
![]()
|
32/
9
|
|
Темы:
Цикл for
Простые задачи на перебор
Весельчак У любит дарить алмазных черепашек. У него в сумке лежат черепашки либо трех цветов: розовый, белый и зеленый, либо четырех цветов: розовый, белый, зеленый и желтый. Он по очереди дарил черепашек из сумки, цвет i-й черепашки был Si. Цвета представлены следующим образом: P - розовый, W - белый, G - зеленый, Y - желтый. Если количество цветов черепашек в сумке было три, выведите Three; если цветов было четыре, выведите Four.
Входные данные
В первой строке записано число N (\(1<=N<=100\)) - количество Черепашек, которое вынимал Весельчак У. Во второй строке содержатся N символов Si - цвета, вынимаемых черепашек. Каждый символ Si равен P, W, G или Y. Всегда существуют такие i, j и k, что Si = 'P', Sj = 'W' и Sk = 'G'.
Выходные данные
Если количество цветов черепашек в сумке было три, выведите Three; если цветов было четыре, выведите Four.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6
G W Y P Y W |
Four |
| 2 |
9
G W W G P W P G G |
Three |
| 3 |
8
P Y W G Y W Y Y |
Four |
| |
![]()
|
44/
18
|
|
Темы:
Простые задачи на перебор
Во время недавних раскопок на Марсе были обнаружены листы бумаги с таинственными символами на них. После долгих исследований ученые пришли к выводу, что надписи на них на самом деле могли быть обычными числовыми равенствами. Если бы этот вывод оказался верным, это доказало бы не только то, что на Марсе много лет назад были разумные существа, но и то, что они уже умели считать…
Ученые смогли понять, что в этом случае означают найденные символы, и перевели эти равенства на обычный язык — язык цифр, скобок, знаков арифметических действий и равенства. Кроме того, из других источников было получено веское доказательство того, что марсиане знали только три операции — сложение, умножение и вычитание (марсиане никогда не использовали “унарный минус”: вместо “–5” они писали “0–5”). Также ученые доказали, что марсиане не наделяли операции разным приоритетом, а просто вычисляли выражения (если в них не было скобок) слева направо: например, 3 + 3*5 у них равнялось 30, а не 18.
К сожалению, символы арифметических действий марсиане почему-то наносили специальными чернилами, которые, как оказалось, были не очень стойкими, и поэтому в найденных листках между числами вместо знаков действий были пробелы. Если вся вышеизложенная теория верна, то вместо этих пробелов можно поставить знаки сложения, вычитания и умножения так, чтобы равенства стали верными. Например, если был найден лист бумаги с надписью “18=7 (5 3) 2”, то возможна такая расстановка знаков: “18=7+(5–3)*2” (помните про то, в каком порядке марсиане вычисляют выражения!). В то же время, если попался лист с надписью “5=3 3”, то марсиане явно не имели в виду числового равенства, когда писали это…
Вы должны написать программу, находящую требуемую расстановку знаков или сообщающую, что таковой не существует.
Формат входных данных
Первая строка входного файла состоит из натурального (целого положительного) числа, не превосходящего 230, знака равенства, и последовательности натуральных чисел (не более десяти), произведение которых также не превосходит 230. Некоторые группы чисел (одно или более) могут быть окружены скобками. Длина входной строки не будет превосходить 80 символов, и других ограничений на количество и вложенность скобок нет. Между двумя соседними числами, не разделенными скобками, всегда будет хотя бы один пробел, во всех остальных местах может быть любое (в том числе и 0) число пробелов (естественно, внутри числа пробелов нет).
Формат выходных данных
В выходной файл необходимо вывести одну строку, содержащую полученное равенство (т.е., исходное равенство со вставленными знаками арифметических действий). В случае если требуемая расстановка знаков невозможна, вывести строку, состоящую из единственного числа “–1”. Выходная строка не должна содержать пробелов.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
18=7 (5 3) 2 |
18=7+(5–3)*2 |
| 2 |
5= 3 3 |
-1 |
| |
![]()
|
4/
4
|
|
Темы:
Перебор
Простые задачи на перебор
У Пети имеется игровое поле размером 3x3, заполненное числами от 1 до 9. В начале игры он может поставить фишку в любую клетку поля. На каждом шаге игры разрешается перемещать фишку в любую соседнюю по стороне клетку, но не разрешается посещать одну и ту же клетку дважды. Петя внимательно ведет протокол игры, записывая в него цифры в том порядке, в котором фишка посещала клетки. Пете стало интересно, какое максимальное число он может получить в протоколе. Помогите ему ответить на этот вопрос.
Входные данные
Входной файл содержит описание поля — 3 строки по 3 целых числа, разделенных пробелами. Гарантируется, что все девять чисел различны и лежат в диапазоне от 1 до 9.
Выходные данные
Выведите одно целое число — максимальное число, которое могло получиться в протоколе при игре на данном поле.
Ответ можно выводить не в виде числа, а в виде строки или в виде последовательности отдельных цифр (но не разделяя их пробелами).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 2 3
4 5 6
7 8 9 |
987456321 |
| |
![]()
|
32/
9
|
|
Темы:
Простые задачи на перебор
Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку [2385177; 2385437] простые числа. Выведите все найденные простые числа в порядке возрастания, слева от каждого числа выведите его номер по порядку (каждое число с номером выводите с новой строки).
| |
![]()
|
67/
31
|
|