Вывод формулы Автоматизированная система генерации тестов

Обувная фабрика собирается начать выпуск элитной модели ботинок. Дырочки для шнуровки будут расположены в два ряда, расстояние между рядами равно a, а расстояние между дырочками в ряду b. Количество дырочек в каждом ряду равно N. Шнуровка должна происходить элитным способом “наверх, по горизонтали в другой ряд, наверх, по горизонтали и т.д.” (см. рисунок). Кроме того, чтобы шнурки можно было завязать элитным бантиком, длина свободного конца шнурка должна быть l. Какова должна быть длина шнурка для этих ботинок?

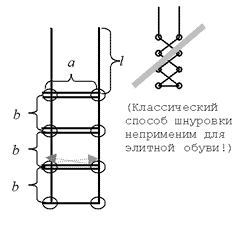
Формат входных данных
Программа получает на вход четыре натуральных числа a, b, l и N.

Формат выходных данных
Программа должна выводить одно число – искомую длину шнурка.

Улица

По одну сторону улицы находятся дома с нечётными номерами (1, 3, 5, …), по другую сторону – с чётными (2, 4, 6, …). Дом № 1 находится напротив дома № 2, дом № 3 – напротив дома № 4 и т. д. До соседнего дома нужно идти вдоль по улице одну минуту, неважно, с какой стороны улицы он находится (то есть от дома № 1 нужно идти одну минуту как до дома № 3, так и до дома № 4). До дома, стоящего напротив, идти не нужно.

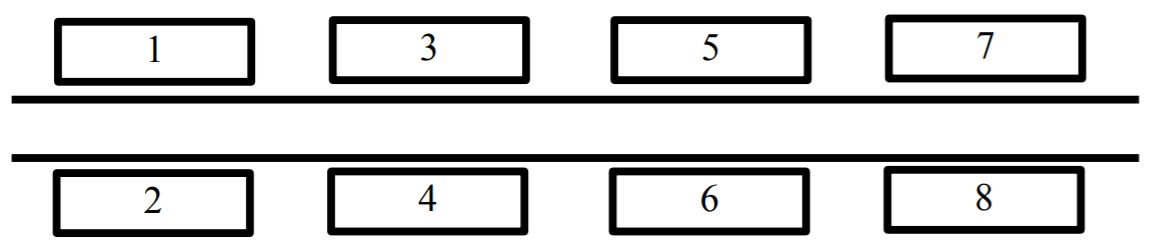
Человек вышел на улицу из дома номер A и должен дойти до дома номер B. Определите, сколько минут ему нужно идти вдоль по улице. Программа получает на вход два различных целых положительных числа A и B, не превосходящие 2×10⁹ , – номера домов. Программа должна вывести одно число – искомое количество минут.

Входные данные
Программа получает на вход два различных целых положительных числа A и B,не превосходящие 2×10⁹, – номера домов.

Выходные данные
Программа должна вывести одно число – искомое количество минут.

Примеры

№	Входные данные	Выходные данные
1	1 8	3

Периметр треугольника

Вывод формулы

С клавиатуры вводятся два целых числа - катеты прямоугольного треугольника. Напишите программу определения периметра такого треугольника.

Пример

№	Входные данные	Выходные данные
1	3 4	12.000000

Гипотенуза треугольника

Вывод формулы

С клавиатуры вводятся два целых числа - катеты прямоугольного треугольника. Напишите программу определения гипотенузы такого треугольника.

Пример

№	Входные данные	Выходные данные
1	3 4	5.000000

Периметр прямоугольника и длина диагонали

Вывод формулы

С клавиатуры вводятся два целых числа - стороны прямоугольника. Напишите программу нахождения его периметра и длины диагонали. Выведите в первой строке периметр прямоугольника, во второй строке - длину его диагонали.

Пример

№	Входные данные	Выходные данные
1	2 13	30 13.152946

Лифт

Вывод формулы Условный оператор

Петру необходимо попасть с этажа A на этаж B. Для вызова лифта на всех этажах офисного здания, кроме первого и последнего, есть две кнопки – для перемещения вниз и перемещения вверх. В тот момент, когда Петр нажал нужную кнопку вызова, лифт находился на этаже C и вез одного пассажира на этаж D. Если лифт проезжает мимо этажа, на котором нажата кнопка вызова, и лифт движется в подходящем направлении, то лифт останавливается, чтобы посадить дополнительного пассажира. Лифт перемещается между соседними этажами за одну единицу времени, также одну единицу времени занимает остановка лифта на этаже для высадки или посадки пассажиров.

Напишите программу, вычисляющую, через сколько времени Петр доберется до этажа B, при условии, что никто больше не будет вызвать лифт.

Первая строка ввода содержит четыре целых числа A, B, C и D, разделенных одним пробелом (1 ≤ A, B, C, D ≤ 20, A≠B, C≠D, A≠C).

Вывести одно целое число – количество единиц времени от момента вызова лифта до момента, когда Петр выйдет из лифта на этаже B.

Ввод	Вывод
3 9 2 5	10
3 9 5 2	13

Примечание:

Пояснение к примеру 1

Лифт за 1 единицу времени доедет до 3-го этажа, остановится на 1 единицу времени, чтобы Петр сел в лифт, затем через 2 единицы времени доедет до 5-го этажа и остановится на 1 единицу времени для высадки предыдущего пассажира, через 4 единицы времени лифт довезет Петра до 9-го этажа, и через 1 единицу времени Петр выйдет из лифта.

*Король-пекарь

Королевская кухня покрыта кухонным фартуком, который разбит на квадраты со стороной A см. Роланд хочет повесить на фартук картину с изображением своей семьи. Он знает точку, с которой соприкасается левый нижний угол картины, а также ширину и высоту самой картины. И тут ему захотелось узнать количество квадратов, которые будут частично или полностью закрыты картиной.

Формат входных данных
Первая строка содержит число A – сторону одного квадрата кухонного фартука. Вторая и третья строки - числа X и Y – координаты левого нижнего угла картины. Четвёртая и пятая строки - числа W и H – ширина и высота картины. Ось OX направлена вправо, ось OY направлена вверх. Левый нижний угол одного из квадратов кухонного фартука находится в начале координат. Все числа целые, не превосходящие 2×10⁹ , числа A, W, H – положительные, числа X и Y – положительные или равны 0. Стороны картины параллельны осям координат.

Формат выходных данных
Вывести одно число – количество плиток, полностью или частично закрытых картиной.
Квадрат считается закрытым картиной, если пересечение картины и квадрата имеет ненулевую площадь, то есть касание картины и квадрата не считается перекрытием.

Примечание

В первом тестовом примере сторона квадрата (сторона клетки на рисунке) А = 10. Левый нижний угол картины имеет координаты (15, 5), картина имеет ширину 35 см и высоту 20 см. Картина полностью или частично закрывает 12 квадратов

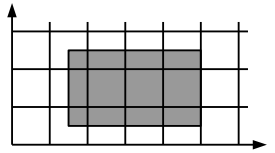
Сложная формула - 1

С клавиатуры вводятся два целых числа: сначала x, затем y (оба числа не больше 1000).
Составьте программу для вычисления значений z и q по формулам.

$z = \frac {x + \frac {2+y} {x^2}} {y+ \frac 1 {\sqrt{x^2+10}}}$ и $q = 2,8 \cdot sin(x) + \vert y \vert$

Входные данные
На вход подаются 2 целых числа x и y (оба числа по модулю не больше 1000).

Выходные данные
Выведите на экран значения z и q, в виде
z=значение q=значение

Примеры

№	Входные данные	Выходные данные
1	5 3	z=1.64088 q=0.315012

Полоски радуги

В школе № 2007 на уроке информатики в системе SilverTests Васе попалась следующая задача: «В младшей группе одного объединённого детского сада воспитательница изучала с детишками порядок цветов радуги. Она отыскала семь соответствующих цветных мелков и начала рисовать полоски, не нарушая последовательности цветов. Начала она с красной полоски. Когда доходила до фиолетовой полоски, опять рисовала красную. Воспитательница успела нарисовать N полосок, когда у неё закончились мелки. Напишите программу, которая вычисляет количество полосок каждого цвета». Вася взялся писать программу, но тут обнаружилось, что на клавиатуре отсутствует клавиша с буквой «i». Помогите Васе написать программу с учётом этого обстоятельства.

Входные данные: Вводится одно целое положительное число N > 0.
Выходные данные: Выведите ответ на задачу.

Если в коде программы встречается буква «i» система выдаст сообщение: Использование запрещенных операторов

Примеры

№	Входные данные	Выходные данные
1	3	'red - 1' 'orange - 1' 'yellow - 1' 'green - 0' 'blue - 0' 'sky - 0' 'purple - 0'

Совпадение стрелок

Вывод формулы

На вход программе подаются два целых числа n, m, каждое в отдельной строке $0<n<=12, 0<=m<60$ , указывающие момент времени "n часов m минут". Определите наименьшее число полных минут, которое должно пройти до того момента, когда часовая и минутная стрелки ни циферблате совпадут, не обязательно на каком-то делении. Вещественную арифметику не использовать.

Задачу необходимо решить без использования условных операторов (в том числе без тернарного оператора ?: в С++) и\или циклов. Кроме того, нельзя использовать операции сравнения и логический (булевский) тип данных.

Примеры

№	Входные данные	Выходные данные
1	2 50	26
2	3 0	16

Чётные – нечётные

Вывод формулы

Маша любит чётные числа, а Миша – нечётные. Поэтому они всегда радуются, если встречают числа, которые им нравятся.
Сегодня им встретились все целые числа от A до B включительно. Маша решила посчитать сумму всех чётных чисел от A до B, а Миша – сумму всех нечётных, после чего они начали спорить, у кого получилась сумма больше. Помогите им – найдите разность
между суммой Маши и суммой Миши.
Программа получает на вход два целых положительных числа A и B, не превосходящие 2×10⁹.
Программа должна вывести одно число – разность между суммой чётных чисел и суммой нечётных чисел от A до B.

Примеры

№	Входные данные	Выходные данные	Пояснение
1	3 6	2	Сумма чётных чисел равна 4 + 6 = 10, сумма нечётных чисел равна 3 + 5 = 8, разность равна 2.
2	3 7	-5	Сумма чётных чисел равна 4 + 6 = 10, сумма нечётных чисел равна 3 + 5 + 7 = 15, разность равна −5.

Покупка

Вывод формулы

Ручка стоила K рублей. Первого сентября стоимость ручки увеличилась ровно на P процентов. Определите, сколько ручек можно купить на S рублей после подорожания.
Программа получает на вход три целых положительных числа. Первое число K – стоимость ручки в рублях до подорожания. Второе число P – величина подорожания ручки
в процентах. Третье число S – имеющаяся сумма денег. Числа K и S не превосходят 10⁷ , число P не превосходит 100.

Примеры

№	Входные данные	Выходные данные	Пояснение
1	33 5 100	2	Ручка стоила 33 рубля. После подорожания на 5 % ручка будет стоить 34 рубля 65 копеек (заметим, что, поскольку первоначальная цена ручки была целым числом рублей, после подорожания стоимость ручки будет выражаться целым числом рублей и копеек). На 100 рублей после подорожания можно купить 2 ручки.

Между А и В

Вывод формулы

Вам даны неотрицательные целые числа a и b (a<=b) и положительное целое число x. Сколько целых чисел от a до b включительно делятся на x?

Входные данные
В одной строке задаются три числа a, b и x ($0<=a<=b<=10^{18}$, $1<=x<=10^{18}$).

Выходные данные
Выведите на экран ответ на задачу.

Примеры

№	Входные данные	Выходные данные	Пояснение
1	4 8 2	3	Есть три целых числа от 4 до 8 включительно, которые делятся на 2: 4, 6 и 8.
2	0 5 1	6	Есть шесть целых чисел от 0 до 5 включительно, которые делятся на 1: 0, 1, 2, 3, 4 и 5.
3	9 9 2	0	Нет целого числа от 9 до 9 включительно, которое делится на 2.
4	1 1000000000000000000 3	333333333333333333	Остерегайтесь целочисленных переполнений!

Черепашка

Черепашка ползет по полу, который уложен квадратной плиткой со стороной A см. Начало пути Черепахи в точке X. Черепашка успела проползти расстояние D см, прежде чем хозяин взял ее на руки. Определите сколько клеток (частично или целых) успела проползти Черепашка.

Входные данные
Первая строка содержит число A – длина стороны одной плитки. Вторая строка содержит число X - координата точки, с которой Черепашка начала свой путь. Третья строка - число D - расстояние, которое проползла Черепаха. Ось OX направлена вправо. Крайняя плитка в ряду, по которому ползет Черепашка находится в начале координат. Все числа целые, не превосходящие $2\cdot10^9 $, числа A, D – положительные, число X – положительное или равно 0.

Выходные данные
Вывести одно число – количество плиток, которые Черепашка полностью или частично успела проползти.
Считается, что Черепашка проползла плитку, если условно проведенная линия пути Черепашки имеет ненулевую длину, то есть касание линии пути и края плитки не считается.

Примеры

№	Входные данные	Выходные данные	Пояснение
1	10 15 35	4	Сторона плитки (сторона клетки на рисунке) А = 10. Черепашка начала движение с координаты Х = 15, и прошла 35. Черепаха прошла полностью или частично 4 плитки.

Оставшееся время

Громозека любит соревнования по программированию. Сегодня он примет участие в конкурсе в STCoder. На этой площадке используются 24-часовые часы. Например, 21:00. обозначается как «21 o'clock».
Текущее время - A часов, а соревнование начнется ровно через B часов. Определите время начала соревнования? Ответ дайте в 24-часовом формате.

Входные данные
Во входной строке содержится два целых числа A и B ($0<=A,B<=23$), записанных через один пробел.

Выходные данные
Выведите час начала конкурса в 24-часовом формате.

Примеры

№	Входные данные	Выходные данные
1	9 12	21
2	19 0	19
3	23 2	1

Две кнопки

Вывод формулы Отрезки Пересечение множеств

Алиса и Боб управляют роботом. У каждого из них есть по одной кнопке, которая управляет роботом. Алиса начала удерживать кнопку через A секунд после запуска робота и отпустила кнопку через B секунд после запуска. Боб начал удерживать кнопку через C секунд после запуска и отпустил кнопку через D секунд после запуска. Сколько секунд Алиса и Боб удерживали свои кнопки одновременно?

Входные данные
На вход 4 целых числа: A, B, C и D ($1<=A<B<=100$, $1<=C<D<=100$).

Выходные данные
Выведите продолжительность времени (в секундах), в течение которого Алиса и Боб удерживали свои кнопки одновременно.

Примеры

№	Входные данные	Выходные данные	Пояснения
1	0 75 25 100	50	Алиса начала удерживать кнопку через 0 секунд после запуска робота и отпустила ее через 75 секунд после запуска. Боб начал удерживать кнопку через 25 секунд после запуска и отпустил ее через 100 секунд после запуска. Следовательно, время, когда они оба удерживали свои кнопки, составляет 50 секунд от 25 секунд после запуска до 75 секунд после запуска.
2	0 33 66 99	0	Алиса и Боб не удерживали кнопки одновременно, поэтому ответ - ноль секунд.
3	10 90 20 80	60

Минимизация

Вывод формулы

Имеется последовательность длины N: A₁, A₂, ..., A_N. Изначально эта последовательность представляет собой перестановку 1, 2, ..., N. В этой последовательности Алиса может выполнить следующую операцию:
1) выбрать K последовательных элементов в последовательности;
2) затем заменить значение каждого выбранного элемента минимальным значением среди выбранных элементов.
Алиса хочет уравнять все элементы в этой последовательности, повторяя указанную выше операцию некоторое количество раз.
Найдите минимальное количество необходимых операций.
Можно доказать, что при ограничениях этой проблемы эта цель всегда достижима.

Входные данные
В первой строке задаются два целых числа N и K (2<=K<=N<=100000). Во второй строке задается последовательность целых чисел A₁, A₂, ..., A_N- перестановка чисел от 1 до N (каждое число в последовательности различно, 1<=A_i<=N).

Выходные данные
Выведите минимальное количество необходимых операций.

Примеры

№	Входные данные	Выходные данные
1	4 3 2 3 1 4	2
2	3 3 1 2 3	1
3	8 3 7 3 1 8 4 6 2 5	4

Ускорение Незнайки

Вывод формулы

Незнайка тренировался у Торопыжки быстрее ходить. До тренировки он проходил путь длиной S метров за t₁ секунд. После тренировки скорость Незнайки увеличилась на P%. Напишите программу, которая определяет, какой путь (в метрах) будет проходить Незнайка за t₂секунд после тренировки с Торопыжкой.

Входные данные
На вход четыре целых числа: S (1<=S<=100), t₁(1<=t₁<=100), P (1<=P<=100) и t₂(1<=t₂<=100).

Выходные данные
Выведите одно число - ответ на задачу.

Пример

№	Входные данные	Выходные данные
1	20 5 40 10	56.0

Автомобили Винтика и Шпунтика

Вывод формулы

Винтик и Шпунтин тестировали новые автомобили. Расстояние вокруг Цветочного города автомобиль Винтика проехал за t₁ секунд, спидометр всю дорогу показывал скорость V м/с. Автомобиль Шпунтика такое же расстояние вокруг Цветочного города прошел за t₂ секунд, при этом спидометр у Шпунтика был сломан. Помогите Шпунтику определить с какой скоростью (в м/с) он ехал.

Входные данные
На вход 3 целых числа: t₁(1<=t₁<=100), V(1<=V<=100) и t₂(1<=t₂<=100).

Выходные данные
Выведите одно число - ответ на задачу.

Пример

№	Входные данные	Выходные данные
1	10 12 15	8.0

Камень-Ножница-Бумага. Без "Ножниц"

Вывод формулы

Незнайка и его друг Гунька играют в игру. Игра состоит из N ходов. На каждом ходу каждый игрок играет одним из двух жестов, Камень и Бумага, как в «Камень-ножницы-бумага», при следующих условиях:
- После каждого хода
(количество раз, когда игрок играл Бумагу) <= (количество раз, когда игрок играл Камень).
- Счет каждого игрока рассчитывается по формуле:
(количество ходов, на которых игрок выигрывает) - (количество ходов, на которых игрок проигрывает),
где результат каждого хода определяется по правилам «камень-ножницы-бумага».

Для тех, кто не знаком с игрой "Камень-нужница-бумага": если один игрок играет Камень, а другой играет Бумагу, последний игрок выиграет, а первый проиграет. Если оба игрока играют одним и тем же жестом, раунд считается ничейным, и ни один из игроков ни выиграет ни проиграет.

Используя волшебную палочку Незнайка смог предвидеть жест, который Гунька будет использовать в каждом из N ходов перед началом игры. Распланируйте жесты Незнайки на каждом шагу, чтобы максимизировать его счет.
Жест, который Гунька будет воспроизводить на каждом ходу, задается строкой s. Если i-й (1 <= i <= N) символ в s равен g, то Гунька будет играть "Камень" на i-м ходу. Аналогично, если i-й (1 <= i <= N) символ s в p, Гунька будет играть Бумага на i-м ходу.

Входные данные
На вход подается одна строка s длиной N. Каждый символ в строке s - это g или p. Жесты, представленные s, удовлетворяют условию игры.

Выходные данные
Выведите максимально возможный счет Незнайки.

Примеры

№	Входные данные	Выходные данные	Пояснение
1	gpg	0	Выполнение одного и того же жеста с противником на каждом этапе дает 0 очков, что является максимально возможным результатом.
2	ggppgggpgg	2	Например, рассмотрите возможность воспроизведения жестов в следующем порядке: Камень, Бумага, Камень, Бумага, Камень, Камень, Бумага, Бумага, Камень, Бумага. Эта стратегия приносит три победы и одно поражение, в результате чего получается 2, что является максимально возможным результатом.

Белые клетки

Вывод формулы

Клетчатое поле состоит из белых клеток. Размер поля - H строк и W столбцов. Вам необходимо выбрать h строк и w столбцов и закрасить все ячейки, содержащиеся в этих строках или столбцах. Сколько белых клеток останется после закрашивания?

Входные данные
В первой строке записаны 2 числа: H и W (1 <= H, W <= 20). Во второй строке записаны 2 числа: h и w (1 <= h <= H, 1 <= w <= W).

Выходные данные
Выведите ответ на задачу.

Примеры

№	Входные данные	Выходные данные
1	3 2 2 1	1
2	5 5 2 3	6
3	2 4 2 4	0

Часовое дерево

Обход в глубину Вывод формулы

Новый амбар Фермера Джона состоит из N комнат (2 ≤ N ≤ 2500), последовательно пронумерованных 1…N, и N−1 коридоров. Каждый коридор соединяет пару комнат таким образом, что возможно пройти из лбой комнаты в любую через серию коридоров.
Каждая комната в амбаре имеет круглые часы на стене со стандартным размещением цифр 1…12 на лицевой стороне. Однако на этих часах имеется только одна стрелка, которая всегда показывает точно на одно из целых чисел (она никогда не показывает между двумя из этих чисел).

Корова Беси хочет синхронизировать все часы в амбаре, чтобы они все показывали на число 12. Но со своим коровьим мышлением, каждый раз, когда она входит в комнату, она перемещает стрелку вперёд на одну позицию. Например, если стрека показывала на 5, Беси переводит стрелку на 6. Если часы указывали на 12, она переводит стрелку на 1. Если Беси входит в комнату несколько раз, она переводит стрелку при каждом входе.

Определите номера комнат, в которых Беси может начинать путешествие по амбару чтобы установить все стрелки на 12. Заметим, что Беси не переводит стрелку в стартовой комнате в начале пути и переводит при каждом последующем входе в неё. Стрелки сами по себе не двигаются. Беси входя в коридор должна дойти до конца и войти в комнату в конце коридора. Она не может повернуть назад внутри коридора, чтобы снова войти в комнату из которой вышла.

Входные данные
Первая строка ввода содержит N. Следующая строка содержит N целых чисел, каждое в интервале 1…12, указывающих начальные положения стрелок в каждой комнате. Каждая из следующих N−1 строк описывает коридор двумя целыми числам a и b, каждое в интервале 1…N, и задающих номера комнат, соединённых этим коридором.

Выходные данные
Выведите номера комнат, в которых Беси может начинать, чтобы установить все часы на 12.

Примеры

№	Входные данные	Выходные данные	Пояснение
1	4 11 10 11 11 1 2 2 3 2 4	1	В этом примере Беси может установить все стрелки на 12, тоько в том случае, если она начнёт в комнате 2 (например перемещаясь так: 1, 2, 3, 2, 4.

Треугольники - 2

Алгоритмы сортировки Вывод формулы

Фермер Джон хочет создать треугольное пастбище для своих коров.
Всего имеется N столбов забора (3 ≤ N ≤ 10⁵) как различных (X₁,Y₁)…(X_N,Y_N) точек на карте фермы. Он может выбрать три из них чтобы сформировать вершины треугольного пастбища, но так чтобы одна из сторон была параллельна оси x, а другая - параллельно оси y.

Какова сумма площадей всех возможных пастбищ, которые может сформировать ФД?

Входные данные
Первая строка содержит N.
Каждая из последующих N строк содержит два целых числа Xi и Yi, каждое в интервале −10⁴…10⁴ включительно, описывающих положение столба.

Выходные данные
Поскольку сумма площадей может быть числом не целым и очень большим, выведите остаток от деления удвоенной суммы площадей на 10⁹+7.

Примеры

№	Входные данные	Выходные данные	Пояснение
1	4 0 0 0 1 1 0 1 2	3	Точки (0,0), (1,0), (1,2) образуют треугольник с площадью 1. Точки (0,0), (1,0), (0,1) образуют треугольник с площадью 0.5. Поэтому ответ 2⋅(1+0.5)=3.

Раз-два-три-четыре-пять корову поменять

Вывод формулы Быстрое возведение в степень Перестановки

N коров (1 ≤ N ≤ 10⁵) Фермера Джона стоят в ряд. i-ая корова слева имеет метку i (1 ≤ i ≤ N).
ФД дал коровам M пар целых чисел s (L₁,R₁)…(L_M,R_M), где 1 ≤ M ≤ 100. Затем он сказал коровам повторить ровно K (1 ≤ K ≤ 10⁹) раз процесс из M шагов:

Для каждого i от 1 до M:
Последовательность коров на позициях Li…Ri слева реверсивно меняют свой порядок.
Выведите метки всех коров слева направо для каждого i, (1 ≤ i ≤ N) после завершения описанного процесса.

Входные данные
Первая строка содержит числа N, M, K. Для каждого 1 ≤ i ≤ M строка i+1 содержит L_i и R_i, два целых числа в интервале 1…N, где L_i<R_i.

Выходные данные
На i-ой строке вывода, выведите i-ый элемент массива после выполнения всех инструкций K раз.

Примеры

№	Входные данные	Выходные данные	Пояснение
1	7 2 2 2 5 3 7	1 2 4 3 5 7 6	Изначально порядок коров слева направо такой [1,2,3,4,5,6,7] После первого шага процесса порядок станет таким [1,5,4,3,2,6,7] После второго шага процесса порядок станет таким [1,5,7,6,2,3,4]. Повторив оба шага ещё раз получим результат, приведенный в выводе.

Bovine Genomics №2

Вывод формулы Перебор

У Фермера Джона есть N коров с пятнами и N коров без пятен. Как генетик, ФД уверен, что пятна на его коровах вызваны мутацией коровьего генома.

За большие деньги ФД выписал геномы своих коров. Каждый геном - это строка длины M, состоящая из четырёх символов A, C, G, T. Когда он выписал геномы всех коров, он получил таблицу, представленную ниже для N=3:

Позиция: 1 2 3 4 5 6 7 ... M

Пятнистая корова 1: A A T C C C A ... T

Пятнистая корова 2: G A T T G C A ... A

Пятнистая корова 3: G G T C G C A ... A

Корова без пятен 1: A C T C C C A ... G

Корова без пятен 2: A G T T G C A ... T

Корова без пятен 3: A G T T C C A ... T

Посмотрев внимательно на эту таблицу он предположил, что позиции 2 и 4 могут отвечать за пятнистость. Поскольку, глядя на символы в этих позициях, ФД может предсказать, какая из его коров пятнистая, а какая - нет (например, если он видит G и С - значит, корова не пятнистая).

ФД предположил, что может быть объяснена множеством из трёх различных позиций. Помогите ему посчитать количество трёх различных позиций, которые могут объяснять пятнистость.

ФОРМАТ ВВОДА:

Первая строка ввода содержит NN (1≤N≤500) и MM (3≤M≤50). Каждая из следующих N строк содержит по M символов. Это описание геномов пятнистых коров. Следующие N строк описывают геномы коров без пятен.

ФОРМАТ ВЫВОДА:

Вычислите количество множеств из трёх различных позиций, которые могут объяснять пятнистость. Множество из трёх различных позиций может объяснять пятнистость, если пятнистость может быть предсказана абсолютно точно для популяции коров ФД, при анализе этих трёх позиций генома.

Ввод	Вывод
3 8 AATCCCAT GATTGCAA GGTCGCAA ACTCCCAG ACTCGCAT ACTTCCAT	22

Три четыре пять корову поменять

Вывод формулы Задача на реализацию Задачи на моделирование

N коров (1 ≤ N ≤ 100) Фермера Джона выстроены в ряд. i-ая корова слева имеет метку i, для всех 1≤i≤N.
ФД приказал коровам повторить ровно K (1 ≤ K ≤10⁹) раз следующий двухшаговый процесс:

Последовательность коров в позициях A1…A2 слева реверсивно меняют свой порядок (1≤A₁<A₂≤N).
Затем последовательность коров в позициях B1…B2 слева реверсивно меняют свой порядок (1≤B₁<B₂≤N).
Выведите получившийся порядок коров для всех i 1 ≤ i ≤ N после выполнения этого процесса ровно K раз.

Входные данные
Первая строка содержит N и K. Вторая строка содержит A₁ и A₂, третья строка содержит B₁ и B₂.
Выходные данные
На i-ой строке выведите метку i-ой коровы слева после завершения процесса всех обменов.

Примеры

№	Входные данные	Выходные данные	Пояснение
1	7 2 2 5 3 7	1 2 4 3 5 7 6	Изначально порядок коров слева направо такой [1,2,3,4,5,6,7] После первого шага процесса порядок станет таким [1,5,4,3,2,6,7] После второго шага процесса порядок станет таким [1,5,7,6,2,3,4]. Повторив оба шага ещё раз получим результат, приведенный в выводе.

Треугольники

Вывод формулы Перебор

Фермер Джон хочет создать треугольное пастбище для своих коров.
Всего имеется N столбов забора (3 ≤ N ≤ 100) как различных (X₁,Y₁)…(X_N,Y_N) точек на карте фермы. Он может выбрать три из них чтобы сформировать вершины треугольного пастбища, но так чтобы одна из сторон была параллельна оси x, а другая - параллельно оси y.

Какова сумма площадей всех возможных пастбищ, которые может сформировать ФД?

Входные данные
Первая строка содержит N.
Каждая из последующих N строк содержит два целых числа Xi и Yi, каждое в интервале −10⁴…10⁴ включительно, описывающих положение столба.

Выходные данные
Поскольку сумма площадей может быть числом не целым и очень большим, выведите остаток от деления удвоенной суммы площадей на 10⁹+7.

Примеры

№	Входные данные	Выходные данные	Пояснение
1	4 0 0 0 1 1 0 1 2	3	Точки (0,0), (1,0), (1,2) образуют треугольник с площадью 1. Точки (0,0), (1,0), (0,1) образуют треугольник с площадью 0.5. Поэтому ответ 2⋅(1+0.5)=3.

Голодная пешка

Строки Условный оператор Вывод формулы

Громозека уважает игры на шахматной доске. На обычной доске размером 8х8 у Громозеки стоит голодная пешка. Голодная пешка каждым ходом съедает какую-либо фигуру соперника (т.е. она может пойти по диагонали вперед на 1 клетку вправо или влево, назад пойти она не может). Громозека, не глядя на доску, научился определять, может ли голодная пешка попасть с одной клетки доски на другую. Превращаться в ферзя голодной пешке нельзя.
Напишите программу, с помощью которой вы могли бы также легко проверить Громозеку.

Входные данные
Программа получает на вход две клетки шахматной доски в шахматной нотации. Сначала клетка, где стоит голодная пешка, а затем, через пробел, клетка, куда голодная пешка должна попасть.

Выходные данные
Выведите слово YES (заглавными буквами), если голодная пешка может попасть из первой клетки во вторую, и NO в противном случае.
Доска имеет размер 8x8, вертикали нумеруются маленькими латинскими буквами от a до h, горизонтали - числами от 1 до 8. Исходная и конечная клетки не совпадают.

Примеры

№	Входные данные	Выходные данные
1	a1 b2	YES
2	b2 a1	NO
3	a1 h7	NO

Коровы в стойле

Вывод формулы

У Фермера Джона есть N коров (1 ≤ N ≤ 20) с высотами a₁…a_N. Его амбар имеет N стойл с максимальными высотами b₁…b_N (поэтому например, b₅=17 означает, что коров с высотой не более 17 можно разместить в стойле 5). Сколькими различными способами ФД может разместить коров по стойлам, так чтобы ограничение по высоте было выполнено для каждого стойла.

Входные данные
Первая строка содержит N. Вторая строка содержит N разделённых одиночными пробелами чисел a₁, a₂,…,a_N. Третья строка содержит N разделённых одиночными пробелами чисел b₁,b₂,…,b_N. Все величины - целые числа в интервале [1,10⁹].

Выходные данные
Количество способов, которыми ФД может разместить коров в стойлах, так чтобы для каждого стойла был удовлетворён лимит по высоте. Заметьте, что ответ может быть очень большим, поэтому для него требуется использовать 64-битную целую переменную, такую как "long long" в C++.

Примеры

№	Входные данные	Выходные данные	Пояснение
1	4 1 2 3 4 2 4 3 4	8	В этом примере мы не можем разместить третью корову в первое стойло, поскольку 3=a₃>b₁=2. Аналогично, мы не можем разместить 4-ую корову в 1-ое или 3 -е стойло. Один из 8 способов размещения: корову 1 в стойло 1, корову 2 в стойло 2, корову 3 в стойло 3 корову 4 в стойло 4.

Еще больше странных фотографий

Вывод формулы

Фермер Джон фотографирует N своих коров (2≤N≤1000).
Каждая корова имеет целое число - "ID породы" в интервале 1…100. ФД разбить всех коров на несвязные группы (другими словами, поместить каждую корову ровно в одну группу) и затем выставить группы так, чтобы сумма "ID породы" коров в первой группе была чётной, во второй - нечётной и т.д., чередуя чётные и нечётные.

Какое максимальное количество групп может сформировать ФД?

Входные данные
Первая строка ввода содержит число N. Следующая строка содержит N разделённых пробелом целых чисел, представляющих "ID породы".
Выходные данные
Максимально возможное количество групп на фото ФД. Можно доказать, что хотя бы одна группа будет всегда.

Примеры

№	Входные данные	Выходные данные	Пояснения
1	7 1 3 5 7 9 11 13	3	В этом примере один из способов сформировать максимальное количество (3) групп так: 1 группа: 1 3 2 группа: 5 7 9 3 группа: 11 13
2	7 11 2 17 13 1 15 3	5	В этом примере один из способов сформировать максимальное число (5) групп так: 1 группа: 2 2 группа: 11 3 группа: 13 1 4 группа: 15 5 группа: 17 3.

Хэш двойной строки

Хеш Вывод формулы

Вам дано t запросов, в каждом из которых вам дана строка s, состоящая из строчных латинских букв, число p и число mod.
Для каждого запроса вычислите полиномиальный хэш с основанием p по модулю mod от строки, являющейся строкой s, где каждая буква продублирована. То есть, если s = "isaac", то нужно посчитать хэш от строки "iissaaaacc".

Входные данные:
В первой строке дается число t - количество запросов.
Далее идет t строк, в каждой из которых через пробел даны s (1 <= |s| <= 20), p (1 <= p <= 10⁵) и mod (1 <= mod <= 10⁸).

Выходные данные:
Выведите ответы на запросы, каждый в отдельной строке.

Пример:

Входные данные	Выходные данные
2 isaac 12345 87654321 newton 54321 12345678	8829000 9632318

Мощный массив

Алгоритм Мо Вывод формулы

Имеется массив натуральных чисел a₁, a₂, ..., a_n. Рассмотрим некоторый его подмассив a_l, a_l + 1, ..., a_r, где 1 ≤ l ≤ r ≤ n, и для каждого натурального числа s обозначим через K_s число вхождений числа s в этот подмассив. Назовем мощностью подмассива сумму произведений K_s·K_s·s по всем различным натуральным s. Так как количество различных чисел в массиве конечно, сумма содержит лишь конечное число ненулевых слагаемых.

Необходимо вычислить мощности каждого из t заданных подмассивов.

Входные данные
Первая строка содержит два целых числа n и t (1 ≤ n, t ≤ 200000) — длина массива и количество запросов соответственно.
Вторая строка содержит n натуральных чисел ai (1 ≤ a_i ≤ 10⁶) — элементы массива.
Следующие t строк содержат по два натуральных числа l и r (1 ≤ l ≤ r ≤ n) — индексы левого и правого концов соответствующего подмассива.

Выходные данные
Выведите t строк, где i-ая строка содержит единственное натуральное число — мощность подмассива i-го запроса.

Примеры:

Входные данные	Выходные данные
3 2 1 2 1 1 2 1 3	3 6
8 3 1 1 2 2 1 3 1 1 2 7 1 6 2 7	20 20 20

Лабораторные столы

На кафедру "Прикладной информатики" университета N в новом учебном году набрали три группы первокурсников. Для практических занятий необходимо оборудовать новую аудиторию лабораторными столами. За каждым таким столом могут сидеть не более четырех студентов, причем все студенты обязаны быть из одной группы. Аудитория имеет возможность одновременно разместить студентов сразу трех групп одновременно.
Определите минимальное количество столов, которые необходимо закупить.

Входные данные
Программа получает на вход три натуральных числа (по одному числу в строке): количество студентов каждой из трех групп.

Выходные данные
Выведите ответ на задачу.

Примеры

№	Входные данные	Выходные данные
1	15 20 24	15

Разность времен

Даны значения двух моментов времени, принадлежащих одним и тем же суткам: часы, минуты и секунды для каждого из моментов времени. Известно, что второй момент времени наступил не раньше первого. Определите, сколько секунд прошло между двумя моментами времени.

Входные данные
Программа на вход получает три целых числа — часы, минуты, секунды, задающие первый момент времени и три целых числа, задающих второй момент времени.

Выходные данные
Выведите число секунд между этими моментами времени.

Примеры

№	Входные данные	Выходные данные
1	1 1 1 2 2 2	3661
2	1 2 30 1 3 20	50

Машина для печенья

Циклы Вывод формулы

Машина для изготовления печенья производит B печенья в следующие моменты времени: A секунд, 2A секунд, 3A секунд и каждое последующее число, кратное A секундам после включения. Определите сколько печенья будет изготовлено машиной к моменту времени T+0,5 секунд после включения.

Входные данные
Программа получает на вход одну строку, содержащую три числа A, B и T. 1 <= A, B, T <= 20, A <= T. Все числа целые положительные.

Выходные данные
Выведите одно число - ответ на задачу.

Примеры

№	Входные данные	Выходные данные
1	3 5 7	10
2	3 2 9	6

Приключения Максимуса

Вывод формулы

Однажды Максимус услышал о загадочной пещере, которая находится на вершине высокой горы. Говорят, что в этой пещере скрывается невероятное сокровище. Максимус преодолевает опасности и достигает пещеры. Но в пещере его встречает Старец, который просит по заданным двум числам num и t назвать ему максимальное супер-число. Число x называется супер-числом, если его можно сделать равным num, применяя следующую операцию t раз:

увеличьте или уменьшите x на 1 и одновременно увеличьте или уменьшите num на 1.

Максимум очень устал пока поднимался к загадочной пещере и очень просит вас написать для него программу, которая будет сразу показывать ему ответ для любых двух чисел, которые назовет ему Старец.

Можно доказать, что существует хотя бы одно супер-число.

Входные данные
В первой строке записано число num, во второй - число t.

Ограничения

1 <= num, t <= 50

Выходные данные
Выведите ответ на задачу.

Примеры

№	Входные данные	Выходные данные
1	4 1	6
2	3 2	7

Улица

По одну сторону улицы находятся дома с нечётными номерами (1, 3, 5, …), по другую сторону – с чётными (2, 4, 6, …). Дом № 1 находится напротив дома № 2, дом № 3 – напротив дома № 4 и т. д. До соседнего дома нужно идти вдоль по улице одну минуту, неважно, с какой стороны улицы он находится (то есть от дома № 1 нужно идти одну минуту как до дома № 3, так и до дома № 4). До дома, стоящего напротив, идти не нужно.

Громозека вышел на улицу из дома номер A и должен дойти до дома номер B. Определите, сколько минут ему нужно идти вдоль по улице.

Запрещено использовать какие-либо алгоритмические конструкции для решения данной задачи. Можно использовать только арифметические операции (без использования встроенных функций).

Входные данные
Программа получает на вход два различных целых положительных числа A и B,не превосходящие 2×10⁹, – номера домов.

Выходные данные
Программа должна вывести одно число – искомое количество минут.

Примеры

№	Входные данные	Выходные данные
1	1 8	3

Подъемник

Вывод формулы Условный оператор

На стройку многоэтажного дома завезли инструменты. Прорабу необходимо доставить инструменты с этажа A на этаж B. Для вызова подъемника на всех этажах строящегося здания, кроме первого и последнего, есть две кнопки. Кнопка вниз перемещает подъемник вниз, кнока вверх - перемещает вверх. Когда прораб нажал нужную кнопку, подъемник находился на этаже С и вез груз на этаж D. Работает подъемник следующим образом:

если подъемник проезжает мимо этажа, на котором нажата кнопка вызова, и, при этом, движется в подходящем направлении, то подъемник останавливается и в него можно зайти.

Подъемник перемещается между соседними этажами за одну единицу времени, также одну единицу времени занимает остановка подъемника на этаже для загрузки или разгрузки.

Определите сколько времени необходимо прорабу, чтобы доставить инструменты до этажа B, при условии, что никто больше не будет вызывать подъемник.

Входные данные
Первая строка ввода содержит четыре целых числа A, B, C и D, разделенных одним пробелом (1 <= A, B, C, D <= 20, A≠B, C≠D, A≠C).

Выходные данные
Вывести одно целое число – количество единиц времени, которое пройдет с момента вызова подъемника до момента, когда инструменты разгрузят из подъемника на этаже B.

Примеры

№	Входные данные	Выходные данные
1	3 9 2 5	10
2	3 9 5 2	13

Примечание

Пояснение к примеру 1

Подъемник за 1 единицу времени доедет до 3-го этажа, остановится на 1 единицу времени, чтобы прораб смог погрузить инструменты на подъемник, затем через 2 единицы времени доедет до 5-го этажа и остановится на 1 единицу времени для разгрузки груза, через 4 единицы времени подъемник довезет инструменты до 9-го этажа, и через 1 единицу времени инструменты рагрузят.

Поиграем в камушки

Вывод формулы

Магистр Максимус со своим верным другом фокусником Феликсом играют в игру камушки. Правила этой игры описаны ниже.

Вначале на столе лежит куча камней.
Ходы Максимуса и Феликса чередуются по очереди, причем Максимус всегда ходит первым.
На каждом ходу тот, чья очередь подошла, убирает от 1 до 3 камней из кучи.
Побеждает тот, кто уберет последний камень.

Учитывая n - количество камней в куче, верните имя того, кто победит в игре, при условии, что и Максимус, и Феликс всегда играют оптимально.

Входные данные
Программа получает на вход натуральное число n - количество камней в куче (1<= n <= 2³¹ - 1).

Выходные данные
Выведите одну из английских букв: M, если победит в игре Максимус и F - если победит Феликс.

Примеры

№	Входные данные	Выходные данные
1	4	F
2	2	M

Василий собирает ягоды

Цикл while Целые числа Бинарный поиск по ответу Вывод формулы

Медведь Василий собирает ягоды. Он будет счастлив, если ягод малины в его корзинке окажется не менее трети от общего числа ягод. Медведь Василий уже собрал N ягод, из них K штук малины. Василий уже изрядно устал собирать ягоды, поэтому помогите ему понять, какое минимальное число ягод малины ему необходимо собрать, чтобы быть счастливым.

Входные данные
Программа получает на вход два целых числа N и K (N > 0, 0 ≤ K ≤ N, K<=10⁹, N<=2*10⁹), записанные в отдельных строках, — текущее количество ягод в корзинке медведя Василия и количество ягод малины в корзинке.

Выходные данные
Выведите единственное число — минимальное число ягод малины, которое необходимо собрать.

Примеры

№	Входные данные	Выходные данные	Примечание
1	27 7	3	В примере всего ягод в корзинке 27, из которых малины 7 ягод. Если в собрать ещё 3 ягоды малины, то в корзинке станет 30 ягод, из которых малины будет 10.

Intelligence in Perpendicularia

Вывод формулы

There are only two directions in Perpendicularia: vertical and horizontal. Perpendicularia government are going to build a new secret service facility. They have some proposed facility plans and want to calculate total secured perimeter for each of them.
The total secured perimeter is calculated as the total length of the facility walls invisible for the perpendicularly-looking outside observer. The figure below shows one of the proposed plans and corresponding secured perimeter.

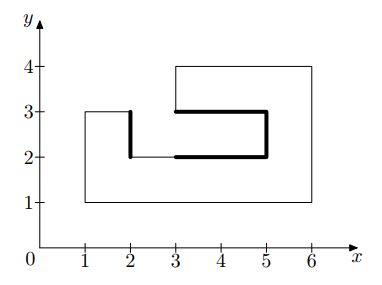Write a program that calculates the total secured perimeter for the given plan of the secret service facility.

Input
The plan of the secret service facility is specified as a polygon. The first line of the input contains one integer n — the number of vertices of the polygon (4 ≤ n ≤ 1000). Each of the following n lines contains two integers xi and yi – the coordinates of the i-th vertex (−10⁶ ≤ x_i , y_i ≤ 10⁶ ). Vertices are listed in the consecutive order. All polygon vertices are distinct and none of them lie at the polygon’s edge. All polygon edges are either vertical (x_i = x_i+1) or horizontal (y_i = y_i+1) and none of them intersect each other.

Output
Output a single integer — the total secured perimeter of the secret service facility.

Input	Output
10 1 1 6 1 6 4 3 4 3 3 5 3 5 2 2 2 2 3 1 3	6

Auxiliary Project

Разбор случаев Вывод формулы

Anna has just finished her course project. She has a lot of seven-segment LED displays as leftovers and a small power source. Each display consumes power proportionally to the number of lit segments, e.g. ‘9’ consumes twice more power than ‘7’.

Anna wonders what is the maximum possible sum of digits she is able to achieve, if her power source is able to light n segments, and she wants to light exactly n segments.
Input
The single line of the input contains one integer n — the number of segments that should be lit (2 ≤ n ≤ 10⁶ ).
Output
Output a single integer — the maximum possible sum of digits that can be displayed simultaneously.

Input	Output
4	4
7	11
6	14

In the first example, a single ‘4’ should be displayed (‘7’ has greater value, but has only three segments). In the second example ‘4’ and ‘7’ should be displayed, in the third one — two ‘7’s.

Время полета

Вывод формулы

При полутах на самолетах в качестве времени вылета и прилета используется местное время аэропортов вылета и прилета.

Часовые пояса характеризуются разницей во времени с меридианом, на котором расположена Гринвичская обсерватория. Для каждого часового пояса вводится отклонение от UTC (Всемирного координированного времени).

Например, Москва расположена в часовом поясе UTC+3, а Новосибирск в часовом поясе UTC+7. Если вылететь из Москвы рейсом в 11:15 и временем полјта ровно в 4 часа, то прилет будет в Новосибирск будет в 19:15 (4 часа полёта и 4 часа разницы во времени).

Например, Москва расположена в часовом поясе UTC+3, а Новосибирск в часовом поясе UTC+7. Если вылететь из Москвы рейсом в 11:15 и временем полјта ровно в 4 часа, то прилјт будет в Новосибирск будет в 19:15 (4 часа полёта и 4 часа разницы во времени).

Часовые пояса могут изменяться от UTC-11 (Американское Самоа) до UTC+14 (острова Лайн, Кирибати).

По заданному времени вылета и времени полёта, а также по часовым поясам аэропортов вылета и прилёта, вам необходимо определить местное время прилёта и количество дней, прошедших в

пути.

Формат входных данных

В первой строке записаны целые числа H_D, M_D (0 <= H_D <= 23, 0 <= M_D <= 59) время вылета.

Во второй строке записаны целые числа H_F , M_F (0 <= H_F <= 10⁹, 0 <= M_F <= 59) время полёта.

В третьей строке записаны целые числа D, A (-11 6 D, A <= 14) часовые пояса аэропорта вылета и прилёта.

Формат выходных данных

Выведите три числа H_A;M_A; Days время прилёта в часах и минутах, а также разницу в датах между датой вылета и датой прилёта.

Система оценки

Решения, верно работающие для рейсов, дата вылета и прилјта которых не отличаются, будут набирать не менее половины баллов.

Ввод	Вывод
11 15 4 0 3 7	19 15 0
12 0 1 0 -10 13	12 0 1

Замечание

Первый тест соответствуте разобранному в условии примеру с Москвой и Новосибирском.

Второй тест соответствует, например, часовому перелету из Американского Самоа на Самоа.

Самолет вылетает в 12:00, летит в течение часа и приземляется в 12:00 местного времени. Т.к. он пересёк линию перемены даты, то на Самоа уже наступил следующий день.

В реальности существуют часовые пояса, которые отличаются от UTC на нецелое число часов, однако в задаче они не рассматриваются.

Дилемма Кубратова

Вывод формулы

Маленькому Егору в школе задали простую задачу: вывести абсолютное значение числа. Посмотрим, сможет ли он справится с этим без использования строк (даже в выводе).

Формат входных данных:

В единственной строке выходных данных содержится целое число M (-2^63 <= M < 2^63)

Формат выходных данных:

Выведите число, равное модулю числа M.

Пример:

Ввод	Вывод
5	5
-7	7

P.S. Задача была проверена неоднократно. Все тесты верные. Ошибок быть не может.

P.P.S Все имена вымышлены, все совпадения с реальными людьми случайны.

(c) Ярослав Свиридов и Владимир Линд

Денежная система (С, В')

Вывод формулы

Денежная система Небритании развивалась на протяжении многих лет, изначально небританцы пользовались пшиллингами 0-го уровня - обычными монетками.

Во время правления Генриха 1-го были введены пшиллинги 1-го уровня, которые равнялись 10 пшиллингам 0-го уровня.
Во время правления Генриха 2-го были введены пшиллинги 2-го уровня, которые равнялись 20 пшиллингам 1-го уровня.
Во время правления Генриха 3-го были введены пшиллинги 3-го уровня, которые равнялись 30 пшиллингам 2-го уровня.
И так далее, а именно, во время правления Генриха k-го были введены пшиллинги k-го уровня, которые равнялись 10k пшиллингам (k − 1)-го уровня.

Сейчас в казне Небритании огромная сумма, равная n пшиллингам 0-го уровня. Запишите ее фразой вида "столько-то пшиллингов такого-то уровня, столько-то пшиллингов такого-то уровня

и т. д.", причем суммарное количество упомянутых вами пшиллингов всех уровней должно быть минимальным.

Формат входных данных

В первой строке содержится натуральное число n ( 1<= n <= 10¹⁵).

Формат выходных данных

Выведите несколько пар целых чисел, по одной на строке. При этом пара (a, b) означает фразу

" a пшиллингов b-го уровня".

Номера уровней в вашей фразе должны строго убывать. Можно совсем не использовать пшилинги какого-то уровня, в этом случае не нужно выводить про них ничего. Количество пшиллингов

каждого упомянутого вами уровня должно быть положительно (a > 0).

Ввод	Вывод
7777	1 3 8 2 17 1 7 0
6030	1 3 3 1

Интересные числа (С', C)

Вывод формулы Циклы Арифметические алгоритмы (Теория чисел)

Маленький Вася очень любит числа, а особенно сильно он любит интересные числа. Вася считает число x интересным, если сумма квадратов его цифр делится на число 7. Например, число 123 -

интересное, потому что 1² + 2² + 3² = 14 делится на 7, а число 16 - нет, потому что 1² + 6² = 37 не делится на 7. Однажды Вася увидел на доске число x, он сразу же захотел узнать величину минимального интересного числа, которое строго больше чем x. Так как Вася еще слишком юн, он обратился к вам за помощью в решение этой задачи.

Формат входных данных

Во входном файле содержится единственное целое число x - число, написанное на доске 0<= x <= 10⁵

Формат выходных данных
В единственную строку выходного файла выведите минимальное интересное число, которое строго больше чем x.

Ввод	Вывод
1	7
0	7
35	70

Шнурки

Обувная фабрика собирается начать выпуск элитной модели ботинок. Дырочки для шнуровки будут расположены в два ряда, расстояние между рядами равно a, а расстояние между дырочками в ряду b. Количество дырочек в каждом ряду равно N. Шнуровка должна происходить элитным способом “наверх, по горизонтали в другой ряд, наверх, по горизонтали и т.д.” (см. рисунок). Кроме того, чтобы шнурки можно было завязать элитным бантиком, длина свободного конца шнурка должна быть l. Какова должна быть длина шнурка для этих ботинок?
Запрещено использовать операторы if, while, for, repeat-until (Паскаль)

Входные данные: Программа получает на вход четыре натуральных числа a, b, l и N.

Выходные данные: Программа должна выводить одно число – искомую длину шнурка.

Примеры
входные данные
2
1
3
4
выходные данные
26

Ферзь

Вывод формулы

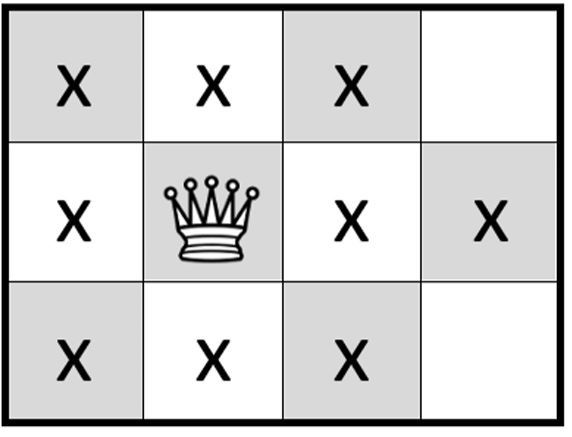
Пётр любит шахматы и математику. Он знает, что самая мощная фигура в шахматах - это ферзь, потому что он ходит и как ладья, на все клетки на одной с ним вертикали или горизонтали, и как слон, на все клетки по диагоналям. Ферзя можно поставить на доску 8 X 8 так, чтобы он контролировал (то есть мог переместиться в эти клетки за один ход) целых 27 клеток доски!

Петра заинтересовало, какое максимальное количество клеток может контролировать ферзь на прямоугольных досках самых разных размеров. Помогите ему в решении этой задачи.

Формат входных данных
Первая строка входных данных содержит целое число n (1 ≤ n ≤ 10⁹) - размер доски по вертикали.
Вторая строка входных данных содержит целое число m (1 ≤ m ≤ 10⁹) - размер доски по горизонтали.
Формат выходных данных

Программа должна вывести одно целое число - максимальное количество клеток, которое может контролировать ферзь на доске n x m.

Обратите внимание на то, что ответ в этой задаче может превышать возможное значение 32-битной целочисленной переменной, поэтому необходимо использовать 64-битные целочисленные типы данных (тип long long в языке C++, тип int64 в Pascal, тип long в Java и C#).

Замечание
Второй пример из условия приведён на рисунке. Крестиками обозначены клетки, которые контролирует ферзь.

Два массива

Сортировка слиянием Вывод формулы Разбор случаев

Алиса со своим отцом профессором Селезневым записывают на листочке числа определенной последовательности. У Алисы каждый i-й член последовательности равен i², у профессора Селезнева i-й член последовательности равен i³. Они решили создать новую возрастающую последовательность путем объединения двух своих последовательностей. При этом, если в обоих последовательностях есть одинаковое число, то в новой последовательности оно присутствует только один раз.

Алиса и профессор просят вас угадать i-е число в новой объединенной последовательности.

Входные данные

В единственной строке входного файла дано натуральное число i (1 <= i <= 10⁷).

Выходные данные

Выведите i-е число новой последовательности.

Примеры

№	Входные данные	Выходные данные
1	1	1
2	2	4
3	4	9

Василий собирает ягоды

Цикл while Целые числа Бинарный поиск по ответу Вывод формулы

Летовец набирает себе предметы, которые он будет изучать в текущем учебном году. Он будет счастлив, если количество его любимых предметов в учебном плане окажется не менее трети от общего числа предметов. Летовец уже выбрал N предметов, из них K любимых. Теперь он хочет посчитать, какое минимальное количество любимых предметов ему осталось выбрать, чтобы быть весь учебный год счастливым.

Формат входных данных
Программа получает на вход два целых числа N и K (N > 0, 0 ≤ K ≤ N, K<=10⁹, N<=2*10⁹), записанные в отдельных строках, — текущее количество предметов и количество любимых предметов, которые Летовец уже выбрал.

Формат выходных данных
Выведите единственное число — минимальное число любимых предметов, которые необходимо выбрать.

Примечение
В примере всего предметов 27, из которых любимых 7.
Если в выбрать ещё 3 любимых предмета, то всего станет 30 предметов, из которых любимых будет 10.

Улучшение успеваемости

Бинарный поиск Целые числа Вывод формулы

В лицее на уроках информатики ответы учеников оцениваются целым числом баллов от 2 до 5. Итоговая оценка по информатике выставляется как среднее арифметическое оценок на всех уроках, округленное до ближайшего целого числа. Если среднее значение находится ровно посередине между двумя целыми числами, то оценка округляется вверх.

Примеры округления оценок приведены в таблице.

Оценки на уроках	Среднее арифметическое	Итоговая оценка
2, 3, 5	${ {2 + 3 + 5} \over 3 }= 3 {1 \over 3}$	3
3, 3, 4, 4	${ {3 + 3 + 4 + 4} \over 4 }= 3 {1 \over 2}$	4
5, 5, 5, 3, 5	${ {5 + 5 + 5 + 3 + 5} \over 5 }= 4 {3 \over 5}$	5

Все ученики лицея стремятся получить итоговую оценку по информатике не ниже 4 баллов. К сожалению, один из учеников получил на уроках a двоек, b троек и c четверок.Теперь он планирует получить несколько пятерок, причем хочет, чтобы итоговая оценка была не меньше 4 баллов. Ему надо понять, какое минимальное количество пятерок ему необходимо получить, чтобы добиться своей цели.

Требуется написать программу, которая по заданным целым неотрицательные числам a, b и c определяет минимальное количество пятерок, которое необходимо получить ученику, чтобы его итоговая оценка по информатике была не меньше 4 баллов.

Входные данные

Входные данные содержат три строки. Первая строка содержит целое неотрицательное число a, вторая строка содержит целое неотрицательное число b, третья строка содержит целое неотрицательное число c (0 ≤ a, b, c ≤ 10¹⁵, a + b + c ≥ 1).

Выходные данные

Выходные данные должны содержать одно число: минимальное число пятерок, которое необходимо получить ученику, чтобы итоговая оценка была не меньше 4 баллов.

Ввод	Вывод
2 0 0	2

Старая книга

Бинарный поиск "Два указателя" Вывод формулы

Группа юных археологов работает на раскопках здания древней библиотеки. Летом

они обнаружили остатки старой книги и, изучив их, сделали следующие выводы.

Книга содержит несколько страниц, каждая страница содержит либо текст, либо

иллюстрацию. Первые k страниц книги точно содержат иллюстрации. Все страницы книги

пронумерованы, но номер страницы написан только на страницах, содержащих текст. Сумма

номеров страниц с текстом равна s.

К сожалению, ни общее количество страниц в книге, ни количество иллюстраций

установить не удалось. Тем не менее, юных археологов заинтересовал вопрос, какое

минимальное количество иллюстраций могло быть в книге.

Например, если k = 1, а s = 8, то страницы книги могли иметь следующее содержание

(буквой «Т» обозначена страница, содержащая текст, а буквой «И» — страница, содержащая

иллюстрацию):

- И Т И И И Т, пронумерованы страницы 2 и 6, 4 иллюстрации;

- И И Т И Т, пронумерованы страницы 3 и 5, 3 иллюстрации;

- И И И И И И И Т, пронумерована страница 8, 7 иллюстраций.

Минимальное количество иллюстраций равно 3.

Требуется написать программу, которая по заданным целым числам k и s определяет

минимальное количество иллюстраций, которое могло быть в книге.

Формат входных данных

Первая строка входных данных содержит целое число k (0 ≤ k ≤ 10⁹).

Вторая строка входных данных содержит целое число s (k + 1 ≤ s ≤ 10¹²).

Формат выходных данных

Требуется вывести одно целое число — минимальное количество иллюстраций в

книге.

Ввод	Вывод
1 8	3

Полные квадраты

Разбор случаев Целые числа Вывод формулы Рекурсия

С целью поиска закономерностей иногда полезно сгенерировать длинную последовательность по определенным правилам. Известно, например, что последовательность 0, 0+ 1, 0+ 1+ 3, 0+ 1+ 3+ 5,

. . . , 0 + 1 + 3 + . . . + (2n − 1), . . ., составленная из сумм нескольких первых нечетных натуральных чисел, состоит из квадратов целых чисел: 0, 1, 4, 9, . . . , n², . . ..

Обобщим эту последовательность следующим образом: будем использовать вместо начального значения не ноль, а число k. Получим последовательность: k, k + 1, k + 1 + 3, k + 1 + 3 + 5, . . . ,k+ 1+ 3+. . .+ (2n−1), . . .. В отличие от случая k = 0, в этой последовательности могут встречаться не только полные квадраты. Необходимо найти минимальное целое неотрицательное число, квадрат которого встречается в этой последовательности.

Требуется написать программу, которая по заданному целому числу k определяет, квадрат какого минимального неотрицательного целого числа встречается в описанной последовательности,

либо выясняет, что в ней вообще не встречается полных квадратов.

Формат входных данных

В единственной строке содержится целое число k — начальное число в последовательности

(−10¹² <= k <= 10¹²).

Обратите внимание, что для считывания и хранения такого большого числа необходимо использовать 64-битный тип данных.

Формат выходных данных

Выведите минимальное неотрицательное целое число, квадрат которого встречается в описанной

последовательности. Если в последовательности не встречается квадратов целых чисел, выведите

«none».

Ввод	Вывод
0	0
-5	2
2	none

Плитка

Вывод формулы

Стена покрыта квадратной плиткой со стороной M см. На стену повесили картину, известны координаты левого нижнего угла картины, её ширина и высота. Определите количество плиток, которые оказались частично или полностью закрыты картиной.

Первая строка входных данных содержит число M – сторону плитки. Вторая и третья строки содержат числа X и Y – координаты левого нижнего угла картины. Четвёртая и пятая строки содержат числа W и H – ширину и высоту картины. Ось OX направлена вправо, ось OY направлена вверх. Левый нижний угол одной из плиток находится в начале координат. Все числа целые, не превосходящие 2×10⁹ , числа M, W, H – положительные, числа X и Y – положительные или равны 0.

Программа должна вывести одно число – количество плиток, полностью или частично закрытых картиной. Плитка считается закрытой картиной, если пересечение картины и плитки имеет ненулевую площадь, то есть касание картины и плитки не считается перекрытием.

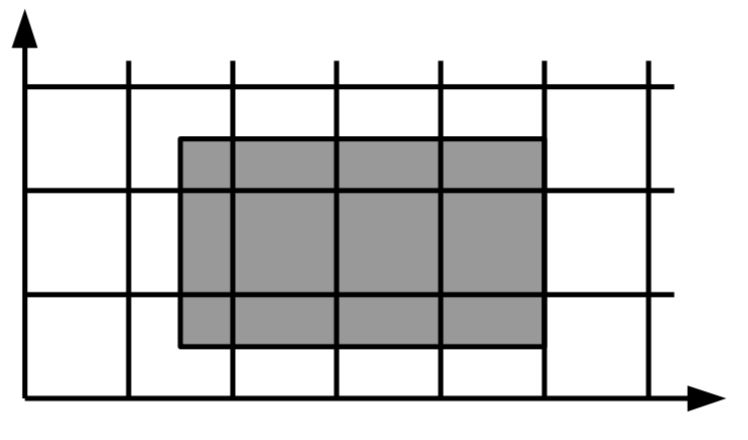
Ввод	Вывод	Примечание
10 15 5 35 20	12	Пример соответствует рисунку. Сторона плитки (сторона клетки на рисунке) M = 10. Левый нижний угол картины имеет координаты (15, 5), картина имеет ширину 35 см и высоту 20 см. Картина полностью или частично закрывает 12 плиток.

Сажени, аршины, пяди, вершки

Вывод формулы

Древнерусская мера длины сажень состояла из трёх аршин. Один аршин делился на четыре пяди. Одна пядь состояла из 4 вершков.
Купец привез на рынок рулон сукна длиной N вершков, но для уплаты пошлины ему нужно указать длину сукна в саженях, аршинах, пядях и вершках. Помогите ему – переведите длину сукна, записанного в вершках в сажени, аршины, пяди и вершки.
Программа получает на вход одно натуральное число N, не превосходящее 2×10⁹ , – длину сукна в вершках.
Программа должна вывести 4 целых неотрицательных числа S, A, P, V – количество саженей, аршин, пядей и вершков, в сумме дающих ровно N вершков, при этом значение A должно быть меньше 3 (т. к. 3 аршина дают одну сажень), значение P должно быть меньше 4 (четыре пяди дают один аршин), значение V должно быть меньше 4 (четыре вершка дают одну пядь).

Ввод	Вывод	Примечание
30	0 1 3 2	30 вершков это 0 саженей, 1 аршин, 3 пяди и 2 вершка

Замок

Вывод формулы

Замок имеет форму большого квадрата, составленного из N × N маленьких квадратиков. Внешние квадратики являются башнями, именно они играют основную роль в защите замка от неприятеля. Например, если замок имеет размер 4 × 4, то у него 12 башен (смотрите второй рисунок, башни на нем выделены серым цветом).

Замок охраняет K полков, которые необходимо разместить по башням. В одной башне можно разместить несколько полков, но при этом в каждой башне должен находиться хотя бы один полк, иначе неприятель легко захватит эту башню. Если все башни защищены, то неприятель выбирает для атаки одну из четырех сторон замка, которую защищает наименьшее число полков (то есть суммарное число полков во всех башнях данной стороны квадрата минимально).

Определите, как нужно разместить полки для наилучшей защиты замка.

Входные данные

Первая строка входных данных содержит число N — размер замка (2 ≤ N ≤ 100). Вторая строка входных данных содержит число K — количество полков, охраняющих замок (0 ≤ K ≤ 100).

Выходные данные

Выведите единственное число — количество полков на наименее укрепленной стороне замка при наилучшем размещении полков. Если имеющихся полков недостаточно для защиты всех башен, выведите число 0.

Ввод	Вывод	Примечание
2 5	2	башни четыре, а полков пять, поэтому на одну из башен можно поставить два полка, но все равно найдется сторона, которую защищает всего два полка.
4 15	5	можно расположить полки так, что каждую сторону будет защищать 5 полков. Защитить каждую сторону не менее, чем шестью полками не удастся.

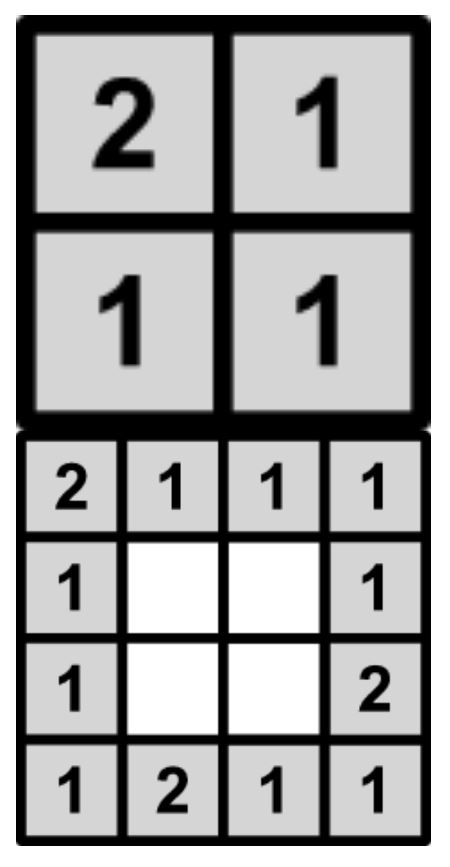
Составление МОШ

Вывод формулы

Для МОШ по информатике было придумано и подготовлено $n$ задач. Всего в олимпиаде будут учавствовать $k$ школьников. И вот до олимпиады осталась всего неделя! Но, как вы знаете, некий <<Турист>> очень любит придумывать задачи и потом давать их на разные олимпиады. А так как <<Турист>> ну уж очень умный, то он явно придумает и даст все задачи, которые придумало жюри МОШа. В рамках подготовки к олимпиаде, школьники будет решать задачи <<Туриста>>. Причём вы знаете, что каждый из участников прорешает за неделю не менее $a$ и не более $b$ задач из тех, что собираются дать на МОШ. Жюри даст на олимпиаду все задачи, которые не решал никто из участников ранее. Скажите минимальное и максимальное количество задач, которые могут быть даны на МОШ из заранее подготовленных.

Формат входных данных
В первой строке вводится число $n$ $(1 \leqslant n \leqslant 10^9)$ — количество задач, подготовленных для МОШ по информатике.

Во второй строке вводится число $k$ $(1 \leqslant k \leqslant 10^9)$ — число участников МОШ.

В третьей строке вводится число $a$ $(1 \leqslant a \leqslant n)$ — минимальное число задач, которое прорешает каждый из участников в течение недели.

В третьей строке вводится число $b$ $(a \leqslant b \leqslant n)$ — максимальное число задач, которое может прорешать каждый из участников в течение недели.

Формат выходных данных
Выведите два числа – минимальное и максимальное число задач, которые жюри может дать на МОШ.

Ещё одна акция - 2

Вывод формулы

В знаменитом магазине <<Двоечка>> продукты продаются всего два дня в неделю — понедельник и вторник — причём в разные дни по разным ценам. Вы захотели купить $n$ килограммов картофеля на неделю. По понедельникам один килограмм картофеля стоит $a$ рублей, а по вторникам — $b$ рублей. Чтобы упростить работу кассирам, в <<Двоечке>> можно покупать только целое число килограммов.

Вам крупно повезло, ведь в <<Двоечке>> проходит акция: каждый понедельник за каждые $m$ килограммов купленного картофеля дарят ещё один!

Найдите минимальную сумму, за которую можно приобрести хотя бы $n$ килограммов картофеля на неделю.

Формат входных данных
В первой строке вводится целое число $a$ $(1 \leqslant a \leqslant 10^9)$ — цена одного килограмма картофеля в понедельник.

Во второй строке вводится целое число $b$ $(1 \leqslant b \leqslant 10^9)$ — цена одного килограмма картофеля во вторник.

В третьей строке вводится целое число $n$ $(1 \leqslant n \leqslant 10^9)$ — желаемое количество килограммов картофеля.

В четвертой строке вводится целое число $m$ $(1 \leqslant m \leqslant 10^9)$ — количество килограммов картофеля, участвующее в акции.

Формат выходных данных
Выведите одно целое число — минимальное число рублей, которое придется заплатить, чтобы купить хотя бы $n$ килограммов картофеля.

Обратите внимание, что ответ может быть больше, чем возможное значение 32-битной целочисленной переменной, поэтому необходимо использовать 64-битные целочисленные типы данных (тип int64 в языке Pascal, тип long long в C и C++, тип long в Java и C#). Язык Python будет корректно работать и с типом int.

Примечание

В первом примере выгодно купить один килограмм в понедельник за 5 рублей, получить еще один килограм в подарок и купить килограмм во вторник за 4 рубля. Купить три килограмма дешевле не получится.

Во втором примере выгодно купить три килограмма в понедельник и получить один килограмм в подарок.

В третьем примере акцией пользоваться невыгодно.

В четвертом примере выгодно купить шесть килограммов в понедельник, получить по акции три килограмма и купить еще один килограмм во вторник.

Ещё одна акция

Вывод формулы

Найдите минимальную сумму, за которую можно приобрести хотя бы $n$ килограммов картофеля на неделю.

Во второй строке вводится целое число $b$ $(1 \leqslant b \leqslant 10^9)$ — цена одного килограмма картофеля во вторник.

В третьей строке вводится целое число $n$ $(\mathbf{1 \leqslant n \leqslant 10^6})$ — желаемое количество килограммов картофеля.

В четвертой строке вводится целое число $m$ $(1 \leqslant m \leqslant 10^6)$ — количество килограммов картофеля, участвующее в акции.

Формат входных данных
Выведите одно целое число — минимальное число рублей, которое придется заплатить, чтобы купить хотя бы $n$ килограммов картофеля.

Примечание

Во втором примере выгодно купить три килограмма в понедельник и получить один килограмм в подарок.

В третьем примере акцией пользоваться невыгодно.

Кубооктаэдр

Вывод формулы Цикл for

Возьмем кубик и приклеим к его граням еще по такому же кубику. В результате получим фигуру, представленную на втором рисунке. К свободным граням полученной фигуры, приклеим еще кубики. На рисунке представлены "кубооктаэдры" степеней 0, 1, 2.

Кубооктаэдром степени N назовем фигуру, полученную в результате N-го доклеивания кубиков. Составить программу, подсчитывающую, количество кубиков для кубооктаэдра N-й степени.

Входные данные
Содержит единственное число - степень кубооктаэдра 0 <= N <= 100000

Выходные данные
Вывести одно число - количество кубиков для кубооктаэдра степени N.

Забор

Вывод формулы

Том Сойер получил важное задание по покраске забора. Забор состоит из n досок. Он когда-то был покрашен, однако с некоторых участков забора краска облупилась. Эти доски Тому и необходимо покрасить. Так как забор большой, пришлось подвезти к забору целую цистерну с краской. Цистерна была помещена у края забора и не может перемещаться. У Тома есть ведерко, набрав краски в которое, Том может покрасить k
досок забора. При этом Том может в любой момент вернуться за краской к цистерне.

Изначально Том находится у цистерны. Соседние доски находятся на расстоянии 1 фута друг от друга, цистерна находится на расстоянии 1 фута от первой доски. По окончании работы Том должен положить кисточку и ведерко на свою исходную позицию рядом с цистерной.

Требуется выяснить, какое минимальное расстояние Тому необходимо пройти, чтобы покрасить забор.

Входные данные
Первая строка содержит количество досок в заборе n (1 ≤ n ≤ 10⁹) и вместимость ведерка k (1 ≤ k ≤ 100). Во второй строке содержится количество неокрашенных отрезков забора m (1 ≤ m ≤ 50).
Далее следуют m строк, в каждой из которых описан один неокрашенный отрезок. Отрезок описывается своей левой границей li и правой границей ri (1 ≤ l_i ≤ r_i ≤ n). Такое описание означает, что не покрашены l_i-я, (l_i+1)-я, …, (r_i–1)-я, r_i-я доски забора (доски нумеруются от 1 до n). Гарантируется, что неокрашенные отрезки, заданные во входном файле, не пересекаются.

Выходные данные
Выведите одно число — минимальное расстояние в футах, которое необходимо пройти Тому для выполнения своего ответственного задания.

Праздники

Перебор с отсечением Дата и время Вывод формулы

Парламент некоторой страны принял новый закон о праздничных днях. Согласно этому закону первые K дней года, а также 23 февраля (День олимпиады по информатике) и 8 марта объявляются праздничными, а все остальные праздники отменяются. При этом все выходные (суббота и воскресенье), попавшие на праздничные дни, переносятся на следующие за этими праздниками рабочие дни.

В зависимости от того, на какой день недели приходится 1 января, количество нерабочих дней, которые идут подряд, может меняться.

Требуется определить, какое наибольшее количество нерабочих дней может идти подряд.

Входные данные
На вход подается единственное число K (1≤K≤50).

Выходные данные
Требуется вывести единственное число — наибольшее количество нерабочих дней, идущих подряд.

Печенье Муми-мамы

Циклы Вывод формулы

Мумми-мама решила испечь печенье к празднику. Она печет по B печений за один раз, и печёт их в следующие моменты времени: A минут, 2A минут, 3A минут и каждое последующее число, кратное A минутам после начала выпечки. Определите, сколько печений будет испечено Мумми-мамой к празднику, который наступит через T+0,5 после начала выпечки.

Формат входных данных
Программа получает на вход одну строку, содержащую три числа A, B и T. 1 <= A, B, T <= 20, A <= T. Все числа целые положительные.

Формат выходных данных
Выведите одно число - ответ на задачу.

Интересные числа

Комбинаторика Динамическое программирование Вывод формулы

Будем назвать натуральное число интересным, если в его десятичной записи первая цифра совпадает с последней.

Дано число $n$. Найдите количество интересных чисел, не превышающих $n$.

Формат входных данных
На ввод подается целое число $n$ ($1 \le n \le 10^{18}$).

Обратите внимание, что для считывания этого числа вам может понадобиться 64-битный тип данных (<<long long>> в C++, <<long>> в Java, <<int64>> в Паскале).

Формат выходных данных
Выведите одно целое число — количество интересных натуральных чисел, не превышающих $n$.

Кузнечик 2D

Вывод формулы

В левом-нижнем углу квадратной клетчатой доски размером $n\times m$ стоит $k$-кузнечик. За один ход $k$-кузнечик перемещается по доске вправо, вверх или вправо-вверх по диагонали не более чем на $k$ клеток.

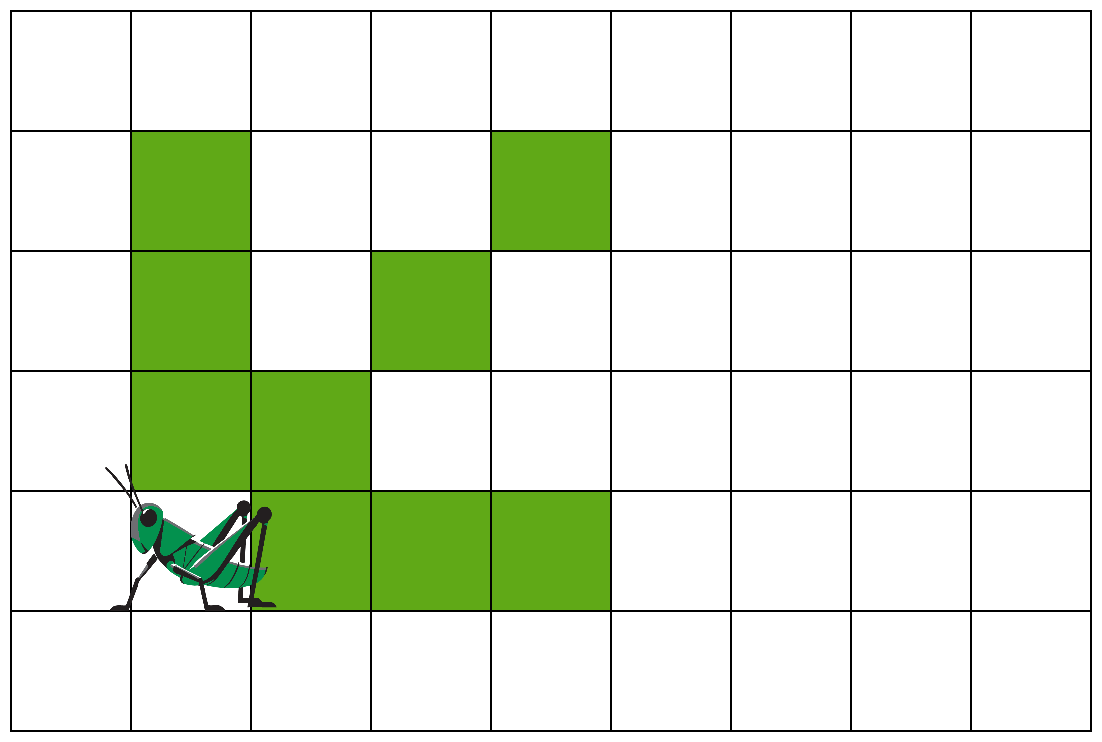
Возможные ходы $k$-кузнечика для $k = 3$.

Необходимо передвинуть $k$-кузнечика в правый верхний угол доски в клетку $(n, m)$. За какое минимальное число ходов можно передвинуть $k$-кузнечика из клетки $(1, 1)$ в клетку $(n, m)$?

Формат входных данных
В первой строке заданы три целых числа $n$, $m$ и $k$ — размеры сторон доски и максимальное число клеток, на которое может ходить $k$-кузнечик, соответственно ($1 \le n, m, k \le 10^9$).

Формат выходных данных
Выведите одно число — минимальное число ходов, необходимое, чтобы передвинуть $k$-кузнечика из клетки $(1, 1)$ в клетку $(n, m)$.

Экзамен

Вывод формулы

В самом лучшем университете России есть специальный предмет, который называется <<Теория Лени>>. Вы очень любите этот предмет и стараетесь постоянно использовать то, чему вас там научили.

Но, как и везде, на нём есть устный экзамен. Всего есть $n$ билетов, из которых вы выучили ровно $a$ (ваша лень не позволяет вам выучить больше).

Экзамен проходит в стандартном формате: есть стопка с билетами, каждый билет встречается в ней ровно один раз, и каждый студент случайно выбирает себе один билет. При этом, когда студент достал билет, то он забирает его себе и не возвращает обратно в стопку.

Вы знаете, что до вас отвечали уже $b$ человек, а это значит, что стопка содержит уже на $b$ билетов меньше. Так как вас интересует не только <<Теория Лени>>, но и математика (и даже чуть-чуть информатика!), вы хотите узнать, какое минимальное и максимальное количество билетов из оставшихся вы можете знать.

Формат входных данных
Первая строка содержит одно целое число $n$ ($1 \leq n \leq 10^9$) — количество билетов на экзамене.

Вторая строка содержит одно целое число $a$ ($1 \leq a \leq n$) — количество билетов, которые вы выучили.

Третья строка содержит одно целое число $b$ ($0 \leq b < n$) — количество людей, которые уже взяли свой билет до вас.

Формат выходных данных
Вывод вашей программы должен состоять из двух строк.

Первая строка должна содержать единственное целое число — минимальное количество билетов, которое вы можете знать из оставшихся.

Вторая строка должна содержать единственное целое число — максимальное количество билетов, которое вы можете знать из оставшихся.

В первом примере давайте считать, что вы знаете билеты с номерами $1, 2, 3, 4$. Тогда, если люди до вас вытянули билеты с номерами $1, 2, 3$, то остался только $1$ билет, который вы знаете. А если люди до вас вытянули билеты с номерами $4, 5, 6$, то вы знаете $3$ билета из оставшихся.

Урок физкультуры

Вывод формулы

В известной школе прошёл урок физкультуры. Как полагается, всех построили в шеренгу и попросили рассчитаться на <<первый–$k$-й>>.

Как известно, расчёт на <<первый–$k$-й>> происходит следующим образом: первые $k$ человек имеют номера $1, 2, 3, \ldots, k$, следующие $k - 1$ человек имеют номера $k - 1, k - 2, \ldots, 1$, следующие $k - 1$ человек имеют номера $2, 3, \ldots, k$ и т.д. Таким образом, расчёт повторяется через каждые $2k - 2$ позиции. Примеры расчёта приведены в разделе <<Замечание>>.

Мальчик Вася постоянно всё забывает. Например, он забыл позицию, которую занимал в шеренге. Но он помнит число $k$, описанное выше, номер, который он получил при расчёте, а также, что его позиция в шеренге была не больше $n$. Другими словами, если Вася стоял на позиции $y$ в шеренге, то $y \leq n$. Помогите Васе понять, сколько есть различных позиций в ряду, где он мог стоять.

Формат входных данных
Первая строка содержит одно целое число $k$ ($2 \leq k \leq 10^9$) — характеристика расчёта, описанная в условии.

Вторая строка содержит одно целое число $x$ ($1 \leq x \leq k$) — номер, который Вася получил при расчёте.

Третья строка содержит одно целое число $n$ ($x \leq n \leq 10^9$) — верхнее ограничение на позицию Васи.

Формат выходных данных
Выведите единственное целое число – количество различных позиций, которые подходят под данные ограничения.

Замечание

В первом примере подходят позиции равные $2, 4, 6, 8, 10$.

Во втором примере подходят позиции равные $2, 4, 6, 8, 10$.

В третьем примере подходят позиции равные $3$ и $7$.

Пример расчёта для $k = 2$, $k = 3$ и $k = 5$:

k\№	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$	$9$	$10$
$2$	$1$	$2$	$1$	$2$	$1$	$2$	$1$	$2$	$1$	$2$
$3$	$1$	$2$	$3$	$2$	$1$	$2$	$3$	$2$	$1$	$2$
$5$	$1$	$2$	$3$	$4$	$5$	$4$	$3$	$2$	$1$	$2$

Разрез прямоугольника

Вывод формулы

У Пети есть прямоугольник размера $a \times b$ с целыми сторонами, хотя бы одна из которых больше $1$. Он пробует разрезать этот прямоугольник на два прямоугольника с целыми сторонами, сделав разрез, параллельный какой-то из сторон исходного прямоугольника. Затем Петя пытается из двух получившихся прямоугольников сложить какой-то отличный от исходного прямоугольник, при этом он может как угодно поворачивать и двигать эти два прямоугольника. Если у него получается это сделать, то он называет прямоугольник $a \times b$ интересным.

Обратите внимание, что если два прямоугольника отличаются поворотом на $90^{\circ}$, то они считаются одинаковыми. Например, прямоугольники $6 \times 4$ и $4 \times 6$ считаются одинаковыми.

Таким образом, прямоугольник $2 \times 6$ является интересным, потому что его можно разрезать на два прямоугольника $2 \times 3$, после чего из этих двух прямоугольников сложить прямоугольник $4 \times 3$, который отличается от прямоугольника $2 \times 6$.

При этом прямоугольник $2 \times 1$ не является интересным, потому что его можно разрезать только на два прямоугольника $1 \times 1$, а из них можно сложить только прямоугольники $1 \times 2$ и $2 \times 1$, которые считаются одинаковыми с исходным.

Также у Пети есть некоторое целое число $n$. Он хочет узнать, сколько существует различных интересных прямоугольников со сторонами, которые являются целыми числами, не превосходящими $n$. Помогите ему это сделать.

Формат входных данных
Первая и единственная строка содержит одно целое число $n$ ($2 \le n \le 2 \cdot 10^9$) — ограничение на длину сторон прямоугольника.

Формат выходных данных
Выведите одно целое число — количество различных интересных прямоугольников с длинами сторон, не превышающими $n$.

Замечание

В первом примере только прямоугольник $2 \times 2$ является интересным: его можно разрезать на два прямоугольника $1 \times 2$, а из них можно сложить прямоугольник $1 \times 4$. Обратите внимание, что прямоугольник $1 \times 1$ не является интересным, потому что хотя бы одна сторона должна быть больше $1$.

Во втором примере прямоугольники $2 \times 2$ и $2 \times 3$ являются интересными. Прямоугольник $2 \times 3$ можно разрезать на два прямоугольника $1 \times 3$, а из них можно сложить прямоугольник $1 \times 6$. Прямоугольник $3 \times 3$ не является интересным, потому что его можно разрезать только на два прямоугольника $1 \times 3$ и $2 \times 3$, но из них можно сложить только прямоугольник $3 \times 3$. Обратите внимание, что прямоугольники $2 \times 3$ и $3 \times 2$ считаются одинаковыми, поэтому в ответе их нужно учесть только один раз.

Урок физкультуры - 2

Вывод формулы Арифметические алгоритмы (Теория чисел)

В известной школе прошёл урок физкультуры. Как полагается, всех построили в шеренгу и попросили рассчитаться на <<первый–$k$-й>>, где $k > 1$.

Мальчик Вася постоянно всё забывает. Например, он забыл число $k$, описанное выше. Но он помнит позицию, которую занимал в шеренге, а также какой номер он получил при расчёте. Помогите Васе понять, сколько натуральных чисел $k$ подходят под данные ограничения.

Обратите внимание, что не существует расчёта для $k = 1$.

Формат входных данных
Первая строка содержит одно целое число $n$ ($2 \leq n \leq 10^9$) — позиция Васи в ряду в нумерации, начинающейся с $1$.

Вторая строка содержит одно целое число $x$ ($1 \leq x < n$) — номер, который Вася получил при расчёте.

Формат выходных данных
Выведите единственное целое число — количество различных $k > 1$, которые подходят под данные ограничения.

Можно доказать, что при данных ограничениях ответ является конечным.

Примечание
В первом примере подходят $k$ равные $2, 3, 5, 6$.

Пример расчёта для этих $k$:

k\№	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$	$9$	$10$
$2$	$1$	$2$	$1$	$2$	$1$	$2$	$1$	$2$	$1$	$2$
$3$	$1$	$2$	$3$	$2$	$1$	$2$	$3$	$2$	$1$	$2$
$5$	$1$	$2$	$3$	$4$	$5$	$4$	$3$	$2$	$1$	$2$
$6$	$1$	$2$	$3$	$4$	$5$	$6$	$5$	$4$	$3$	$2$

Суммы модулей

Комбинаторика Вывод формулы Структуры данных

Для последовательности целых чисел $a_1, a_2, \ldots, a_n$ и целого числа $x$ обозначим через $f(a, x)$ количество таких целых $i$ от $1$ до $n$, что $a_i \le x$.

Для пары последовательностей целых чисел $a_1, a_2, \ldots, a_n$ и $b_1, b_2, \ldots, b_n$ обозначим через $g(a, b, c)$ сумму значений $|f(a, x)-f(b, x)|$ по всем целым $x$, лежащим в отрезке $[0, c]$. Более формально, $g(a, b, c) = \sum_{x=0}^c |f(a, x)-f(b, x)|$.

Вам даны два целых числа $n$ и $c$, а также две последовательности целых чисел $a_1, a_2, \ldots, a_n$ и $b_1, b_2, \ldots, b_n$, все элементы которых лежат в отрезке $[-1, c]$. Известно, что ни в $a$, ни в $b$ нет двух подряд идущих элементов, равных $-1$.

Скажем, что пара последовательностей целых чисел $a_1', a_2', \ldots, a_n'$ и $b_1', b_2', \ldots, b_n'$, все элементы которых лежат в отрезке $[0, c]$, соответствует шаблону $(a, b)$, если выполняются следующие условия:

Для всех $i$ ($1 \le i \le n$), таких, что $a_i \ne -1$, выполняется $a_i'=a_i$.
Для всех $i$ ($1 \le i \le n$), таких, что $b_i \ne -1$, выполняется $b_i'=b_i$.
Для всех $i$ ($1 \le i \le n-1$) выполняется $a_i' \le a_{i+1}'$.
Для всех $i$ ($1 \le i \le n-1$) выполняется $b_i' \le b_{i+1}'$.

Обозначим через $h(a, b, c)$ сумму значений $g(a', b', c)$ по всем парам последовательностей $(a', b')$, соответствующих шаблону $(a, b)$. Вы должны посчитать $h(a, b, c)$. Также вы должны обработать $q$ запросов изменения последовательностей $a$ и $b$ и посчитать $h(a, b, c)$ после каждого изменения. Обратите внимание, что ни в $a$, ни в $b$ нет двух подряд идущих элементов, равных $-1$, ни до всех запросов, ни после какого-либо запроса.

Формат входных данных
Первая строка содержит три целых числа $n$, $c$ и $q$ ($1 \le n \le 100\,000$, $0 \le c \le 10^9$, $0 \le q \le 100\,000$) — длина последовательностей $a$ и $b$, ограничение на значения элементов $a$ и $b$ и количество запросов, соответственно.

Вторая строка содержит $n$ целых чисел $a_1, a_2, \ldots, a_n$ ($-1 \le a_i \le c$) — последовательность $a$.

Третья строка содержит $n$ целых чисел $b_1, b_2, \ldots, b_n$ ($-1 \le b_i \le c$) — последовательность $b$.

В следующих $q$ строках заданы запросы изменения. Каждый запрос задается тройкой целых чисел $t$, $p$, $x$ ($1 \le t \le 2$, $1 \le p \le n$, $-1 \le x \le c$). Если $t=1$, то данный запрос меняет $a_p$ на $x$. Если $t=2$, то данный запрос меняет $b_p$ на $x$.

Гарантируется, что до всех изменений и после каждого изменения ни в $a$, ни в $b$ нет двух подряд идущих элементов, равных $-1$.

Формат выходных данных
Выведите $(q+1)$ строку. В $(i+1)$-й строке ($0 \le i \le q$) выведите одно целое число — значение $h(a, b, c)$ по модулю $10^9+7$ после применения первых $i$ запросов изменения.

Примечание
Рассмотрим первый тест из примера. В нем $n=3$, $c=4$, $q=3$. До всех запросов $a=[-1, 1, 3]$, $b=[1, -1, 2]$. Шаблону $(a, b)$ соответствуют следующие пары последовательностей:

$a'=[0, 1, 3], b'=[1, 1, 2]$, $g(a, b, 4)=2$.
$a'=[0, 1, 3], b'=[1, 2, 2]$, $g(a, b, 4)=3$.
$a'=[1, 1, 3], b'=[1, 1, 2]$, $g(a, b, 4)=1$.
$a'=[1, 1, 3], b'=[1, 2, 2]$, $g(a, b, 4)=2$.

Таким образом, ответ на задачу до всех запросов равен $h(a, b, 4)=2+3+1+2=8$.

В первом запросе $t=1$, $p=1$, $x=2$. Этот запрос меняет $a_1$ с $-1$ на $2$. Таким образом, после этого запроса $a=[2, 1, 3]$, $b=[1, -1, 2]$. В последовательности $a$ нет $-1$, поэтому в любой паре последовательностей $(a', b')$, соответствующей шаблону $(a, b)$, последовательность $a'$ должна совпадать с $a$. В последовательности $a$ не выполняется условие $a_1 \le a_2$, поэтому не существует ни одной пары последовательностей, соответствующей шаблону, а тогда $h(a, b, 4)=0$ после первого запроса.

Качели

Бинарный поиск по ответу Вывод формулы

Трое друзей — Аня, Боря и Саша — пришли на детскую площадку, чтобы покачаться на качеляхбалансире. Качели представляют собой длинную балку, закреплённую в центре, на которую дети садятся с разных концов.

Массы детей равны A, B и C кг. Чтобы держать баланс на качелях, разница масс на двух концах качелей должна быть не более D кг. Друзьям повезло: рядом с площадкой оказалась груда достаточно тяжёлых камней. Один из детей может взять с собой любой камень, чтобы сделать разность масс на концах качелей допустимой. Помогите друзьям определить минимальную массу камня, благодаря которому они смогут покачаться на качелях.

Формат входных данных
Программа получает на вход три числа A, B, C, записанных в отдельных строках, — массы друзей. В четвёртой строке записано число D — наибольшая допустимая разница масс на концах качелей. Все числа — целые, положительные и не превосходящие 10⁹ .

Формат выходных данных
Программа должна вывести одно целое число — минимальную необходимую массу камня, которую нужно добавить на одну из сторон качелей, чтобы друзья смогли покачаться на них, сев оптимально. Если камень им не понадобится, программа должна вывести число 0.

Замечание
В первом примере Аня и Саша сядут на одну сторону, их суммарная масса будет равна 65 кг. На другую сторону сядет Боря, взяв 15-килограммовый камень, тогда масса Бори с камнем составит 55 кг. Разница весов на концах качелей примет значение 10 кг. Во втором примере Аня и Боря сядут на одну сторону (50 кг), Саша — на другую сторону (45 кг). Разница весов будет равна 5 кг, поэтому камень не понадобится.

АиП-6

Вывод формулы

Фотограф выкладывает свои фотографии в интернет и предлагает подписчикам создавать мемы, накладывая на фотографии забавные подписи.
Какой подход позволит фанатам на законных основаниях создавать мемы с фотографиями?

Фотограф должен написать: «Эта работа распространяется на условиях лицензии Creative Commons Attribution без производных работ» (CC BY-ND).
Фотограф должен написать: «Эта работа распространяется на условиях лицензии Creative Commons Attribution».
Фотограф должен подписывать каждую свою фотографию так: «Авторские права © 2019 Имя».
Фотограф должен разместить на странице галереи ссылку на лицензию с открытым исходным кодом (например, лицензию MIT).

Ситуационная задача - 1

Вывод формулы

Вы набираете текст: «Диапазон цен от 500 – 1000 рублей». Какое правило вы нарушили?

Правило использования неразрывного пробела.
Правило написания числовых диапазонов.
Правило написания денежных единиц.
Правило использования дефиса вместо тире.

Пробелы-2

Вывод формулы

Какой знак препинания и с какой отбивкой используется для обозначения прямой речи?

Длинное тире с неразрывным пробелом с обеих сторон.
Короткое тире без пробелов.
Длинное тире, которое ставится сразу после слова без пробелов.
Дефис с неразрывным пробелом после него.

44199

Вывод формулы

Математической моделью является:

1) модель автомобиля;
2) сборник правил дорожного движения;
3) формула закона всемирного тяготения;
4) номенклатура списка товаров на складе.

44198

Вывод формулы

Сколько моделей может соответствовать одному объекту?

1) 1
2) 2
3) 10
4) много

44195

Вывод формулы

Новый объект, который отражает существенные с точки зрения цели моделирования признаки изучаемого предмета, процесса или явления.

1) предмет
2) знак
3) модель
4) образ

24647

Вывод формулы

Публичный наглядный способ предствления информации называется

1. мультимедиа технологией
2. фильмом
3. презентацией
4. монтажом

23544

Вывод формулы

Кто является создателем телеграфа?

1. Хартли
2. Шеннон
3. Колмогоров
4. Морзе

23527

Вывод формулы

Как определяется понятие информации в нейрофизиологии?

1. содержание генетического кода – структуры молекул ДНК, входящих в состав клетки живого организма
2. содержание сигналов электрохимической природы, передающихся по нервным волокнам организма.
3. содержание сигналов, передаваемых по каналам связи в системах управления
4. знания, сведения

23526

Вывод формулы

Кто является основателем кибернетики?

1. Клод Шеннон
2. Билл Гейтс
3. Норберт Винер
4. Владимир Путин

21994

Вывод формулы

Наибольшей наглядностью при определении долей и процентов обладает

1. круговая диаграмма
2. гистограмма
3. график
4. пузырьковая диаграмма

21945

Вывод формулы

Какая из ссылок является смешанной?

1. F2
2. $F$3
3. F$3
4. $F$4

21944

Вывод формулы

Какая из ссылок является относительной?

1. F2
2. $F$3
3. F$3
4. $F4

21943

Вывод формулы

Какая из ссылок является абсолютной?

1. F2
2. $F$3
3. F$3
4. $F4

21925

Вывод формулы

Если раскопировать формулу влево или вправо, то в формуле будет меняться

1. номер столбца
2. номер строки
3. номер столбца и номер строки
4. в зависимости от направления копирования

21924

Вывод формулы

Если раскопировать формулу вниз или вверх, то в формуле будет меняться

1. номер столбца
2. номер строки
3. номер столбца и номер строки
4. в зависимости от направления копирования

21923

Вывод формулы

К каому типу относится данная ссылка: $А$2

1. абсолютная
2. относительная
3. смешанная
4. гиперссылка

21922

Вывод формулы

К каому типу относится данная ссылка: $А2

1. абсолютная
2. относительная
3. смешанная
4. гиперссылка

21921

Вывод формулы

К каому типу относится данная ссылка: А2

1. абсолютная
2. относительная
3. смешанная
4. гиперссылка

21918

Вывод формулы

Какую информацию удобно представлять в табличной форме?

1. список продуктов
2. классный журнал
3. стихотворение
4. реферат

21743

Вывод формулы

Написание конспекта является процессом

1. сбора информации
2. обработки информации
3. хранения информации
4. передачи информации

21742

Вывод формулы

Телефонный разговор является процессом

1. сбора информации
2. обработки информации
3. хранения информации
4. передачи информации

21741

Вывод формулы

Работа на поисковом сервере является процессом

1. сбора информации
2. обработки информации
3. хранения информации
4. передачи информации

21740

Вывод формулы

Чтение книги является процессом

1. сбора информации
2. обработки информации
3. хранения информации
4. передачи информации

21632

Вывод формулы

Что из перечисленного относится к формальным языкам?

1. дорожный знак
2. звук флейты
3. ничего из перечисленного
4. все перечисленное

21631

Вывод формулы

Что из перечисленного относится к естественным языкам?

1. дорожная карта
2. звук флейты
3. рычание тигра
4. все выше перечисленное

21621

Вывод формулы

Информация, отражающая действительное положение дел называется

1. верной
2. достоверной
3. избыточной
4. объективной

21620

Вывод формулы

Информация, представленная на понятном пользователю языке называется

1. точной
2. актуальной
3. нужной
4. понятной

21610

Вывод формулы

Деятельность человека, связанную с процессами получения, преобразования, накопления и передачи информации, называется

1. информационная деятельность
2. информационный процесс
3. информационный объект
4. информационная связь

21603

Вывод формулы

К информационным процессам относятся

1. хранение, передача, изменение
2. хранение, обработка, передача
3. сохранение, открытие, вырезание
4. хранение, восприятие, удаление

21581

Вывод формулы

Процесс передачи данных о состоянии исполнителя называется

1. обратная связь
2. сообщение
3. связь
4. прямая связь

21576

Вывод формулы

Какая концепция характеризует информацию как сферу общения?

1. коммуникационная
2. общественная
3. коммуникативная
4. классическая

21572

Вывод формулы

Как переводится латинское слово informatio?

1. информатика
2. письмо
3. сообщение, объяснение
4. информация

21453

Вывод формулы

Что такое информация?

1. отражение внешнего мира с помощью знаков и сигналов
2. то, что мы видим и слышим
3. тексты, аудиоинформация и картинки
4. файлы компьютерной системы

21449

Вывод формулы

Свойство объекта, которое может быть представлено конкретным значением называется

1. числовое значение
2. характеристика
3. определение
4. параметр

1728

Вывод формулы

Вопрос 1
Ответы
1 2 3 4

1571

Вывод формулы

Абак - это

1) музыкальный инструмент
2) счеты
3) устройство для работы по заданной программе
4) первая механическая машина

1563

Вывод формулы

Что общего между машиной Беббиджа, современным компьютером и человеческим мозгом?

1) способность обрабатывать числовую информацию;

2) способность обрабатывать текстовую информацию;

3) способность обрабатывать звуковую информацию;

4) способность обрабатывать графическую информацию.

1541

Вывод формулы

Когда появилась первая ЭВМ в России?

1) 1946
2) 1955
3) 1951

1240

Вывод формулы

Дан фрагмент ЭТ в режиме отображения формул:

Чему будут равны значения в ячейках В2 и В3, если в них скопировать содержимое ячейки В1?

1) 30 и 30;
2) 50 и 70;
3) 50 и 30;
4) 30 и 50

1236

Вывод формулы

Какая формула будет получена при копировании в ячейку С3, формулы из ячейки С2:

=A1*A2+B2;
=$A$1*$A$2+$B$2;
=$A$1*A3+B3;
=$A$2*A3+B3;?

1234

Вывод формулы

При перемещении или копировании в электронной таблице абсолютные ссылки:

1. не изменяются;
2. преобразуются вне зависимости от нового положения формулы;
3. преобразуются в зависимости от нового положения формулы;
4. преобразуются в зависимости от правил указанных в формуле.

955

Вывод формулы

Назначение дорожного знака - информацию, в основном

Ответ: 1) хранить 2)передавать 3)обрабатывать 4)получать

836

Вывод формулы

Дайте самый полный ответ

Информация – это…

Ответ: 1) сведения об окружающем мире 2)то, что передают по телевизору в выпусках новостей 3)прогноз погоды 4)то, что печатают в газете

639

Вывод формулы

Калькулятор информацию, в основном

Ответ: 1) обрабатывает 2)передает 3)хранит 4)получает

Большой квадрат

Вывод формулы

Даны два прямоугольника размера $a\times b$ и $c\times d$. Можно соединить их вместе, приложив сторону одного прямоугольника к стороне другого и склеив место соединения. Прямоугольники можно поворачивать перед склеиванием. После этого из полученной фигуры нужно вырезать квадрат со сторонами, параллельными сторонам прямоугольника. Определите максимальное возможное значение стороны квадрата.

На рисунке изображены два прямоугольника со сторонами $8\times 3$ и $6\times 2$, из которых можно вырезать квадрат со стороной 5 (заштрихован).

Программа получает на вход натуральные числа $a$, $b$, $c$, $d$, каждое в отдельной строке — стороны первого и второго прямоугольников. Все числа не превосходят $10^9$.

Программа должна вывести одно целое число — максимальную возможную сторону квадрата.

Номерки

Вывод формулы

В Отеле все комнаты пронумерованы числами длины $n$ (возможно, с ведущими нулями). Как и заведено во всех отелях, при заселении Вам выдали ключ, на котором написан номер, также состоящий из $n$ цифр (возможно, с ведущими нулями).

В Отеле ключ открывает комнату, только если выполнено следующее условие. Для каждого $1 \le i < n$, сумма $i$-й и $(i+1)$-й цифры номера комнаты должна быть равна $i$-й цифре ключа по модулю 10. Помимо этого, последняя цифра ключа должна быть равна сумма первой и последней цифры номера комнаты по модулю 10.

Найдите все номера комнат, которые открывает имеющийся у Вас ключ.

Формат входных данных
На первой строке дано число $n$ ($2 \le n \le 100\,000$) — количество цифр в номерах комнат.

Во второй строке написан номер ключа, гарантируется, что это строка длины $n$, состоящая только из цифр.

Формат выходных данных
На первой строке выведите количество комнат, открываемых ключом.

На каждой следующей строке выведите каждый из номеров этих комнат, по одному номеру в строке. Каждый номер комнаты должен представлять собой строку длины $n$, состоящую только из цифр.

Поясним второй пример. Ключ с номером 25575 открывает комнату 57870 так как: \[2 = (5 + 7) \mod 10\] \[5 = (7 + 8) \mod 10\] \[5 = (8 + 7) \mod 10\] \[7 = (7 + 0) \mod 10\] \[5 = (0 + 5) \mod 10\]

Можно проверить аналогичные равенства и для комнаты 02325. Утверждается, что больше никакие комнаты этим ключом открыть нельзя.

Transforming Pairs

Вывод формулы

п»ї

Р‘РµСЃРё СЃС‚РѕРёС‚ РїРµСЂРµ РґРІСѓРјСЏ СЃС‚РѕРіР°РјРё СЃРµРЅР°. РџРµСЂРІС‹Р№ СЃРѕРґРµСЂР¶РёС‚ $a$ СЃРЅРѕРїРѕРІ, РІС‚РѕСЂРѕР№ - $b$ СЃРЅРѕРїРѕРІ $1\le a,b\le 10^{18}$).

РћРЅР° РґРѕР»Р¶РЅР° РїСЂРµРІСЂР°С‚РёС‚СЊ РёС… РІ СЃС‚РѕРіРё СЃ $c$ Рё $d$ СЃРЅРѕРїР°РјРё - РЅРё Р±РѕР»СЊС€Рµ, РЅРё РјРµРЅСЊС€Рµ.

Р‘РµСЃРё РјРѕР¶РµС‚ РІС‹РїРѕР»РЅСЏС‚СЊ С‚РѕР»СЊРєРѕ С‚Р°РєРёРµ РґРІР° Р·Р°РєР»РёРЅР°РЅРёСЏ:

РЈРІРµР»РёС‡РёС‚СЊ СЂР°Р·РјРµСЂ РїРµСЂРІРѕРіРѕ СЃС‚РѕРіР° РЅР° РєРѕР»РёС‡РµСЃС‚РІРѕ СЃРЅРѕРїРѕРІ РІРѕ РІС‚РѕСЂРѕРј СЃС‚РѕРіРµ.
РЈРІРµР»РёС‡РёС‚СЊ СЂР°Р·РјРµСЂ РІС‚РѕСЂРѕРіРѕ СЃС‚РѕРіР° РЅР° РєРѕР»РёС‡РµСЃС‚РІРѕ СЃРЅРѕРїРѕРІ РІ РїРµСЂРІРѕРј СЃС‚РѕРіРµ.

РћРЅР° РґРѕР»Р¶РЅР° РІС‹РїРѕР»РЅСЏС‚СЊ РѕРїРµСЂР°С†РёРё РїРѕСЃР»РµРґРѕРІР°С‚РµР»СЊРЅРѕ, РЅРѕ РѕРЅР° РјРѕР¶РµС‚ РІС‹РїРѕР»РЅСЏС‚СЊ РёС… Р»СЋР±РѕРµ РєРѕР»РёС‡РµСЃС‚РІРѕ СЂР°Р· Рё РІ Р»СЋР±РѕРј РїРѕСЂСЏРґРєРµ. РћРЅР° РґРѕР»Р¶РЅР° РїРѕР»СѓС‡РёС‚СЊ СЂРѕРІРЅРѕ $c$ СЃРЅРѕРїРѕРІ РІ РїРµСЂРІРѕРј СЃС‚РѕРіРµ Рё $d$ РІРѕ РІС‚РѕСЂРѕРј ($1\le c,d\le 10^{18}$).

Р”Р»СЏ РєР°Р¶РґРѕРіРѕ РёР· $T$ ($1\le T\le 10^4$) РЅРµР·Р°РІРёСЃРёРјС‹С… РїРѕРґС‚РµСЃС‚РѕРІ, РІС‹РІРµРґРёС‚Рµ РјРёРЅРёРјР°Р»СЊРЅРѕРµ РєРѕР»РёС‡РµСЃС‚РІРѕ РѕРїРµСЂР°С†РёР№, С‡С‚РѕР±С‹ РґРѕР±РёС‚СЊСЃСЏ РЅСѓР¶РЅРѕРіРѕ СЂРµР·СѓР»СЊС‚Р°С‚Р°, РёР»Рё РµСЃР»Рё СЌС‚Рѕ РЅРµРІРѕР·РјРѕР¶РЅРѕ, РІС‹РІРµРґРёС‚Рµ -1.

Р¤РћР РњРђРў Р’Р’РћР”Рђ (СЃ РєР»Р°РІРёР°С‚СѓСЂС‹ / stdin):

РџРµСЂРІР°СЏ СЃС‚СЂРѕРєР° СЃРѕРґРµСЂР¶РёС‚ $T$.

РљР°Р¶РґР°СЏ РёР· СЃР»РµРґСѓСЋС‰РёС… $T$ СЃС‚СЂРѕРє СЃРѕРґРµСЂР¶РёС‚ С‡РµС‚С‹СЂРµ С†РµР»С‹С… С‡РёСЃР»Р° $a,b,c,d$.

Р¤РћР РњРђРў Р’Р«Р’РћР”Рђ (РЅР° СЌРєСЂР°РЅ / stdout):

Р’С‹РІРµРґРёС‚Рµ $T$ СЃС‚СЂРѕРє, РѕС‚РІРµС‚ РЅР° РєР°Р¶РґС‹Р№ РїРѕРґС‚РµСЃС‚.

РџР Р�РњР•Р Р’Р’РћР”Рђ:

РџР Р�РњР•Р Р’Р«Р’РћР”Рђ:

-1
3
-1
0

Р’ РїРµСЂРІРѕРј РїРѕРґС‚РµСЃС‚Рµ РЅРµРІРѕР·РјРѕР¶РЅРѕ, РїРѕСЃРѕРєР»СЊРєСѓ РёР·РЅР°С‡Р°Р»СЊРЅРѕ $b>d$, СЂР°Р·СЂРµС€С‘РЅРЅС‹Рµ РѕРїРµСЂР°С†РёРё РјРѕРіСѓС‚ С‚РѕР»СЊРєРѕ СѓРІРµР»РёС‡РёРІР°С‚СЊ $b$.

Р’Рѕ РІС‚РѕСЂРѕРј РїРѕРґС‚РµСЃС‚Рµ РёР·РЅР°С‡Р°Р»СЊРЅРѕ СЃС‚РѕРіРё РёРјРµСЋС‚ $(5, 3)$ СЃРЅРѕРїРѕРІ. Р‘РµСЃРё РјРѕР¶РµС‚ СѓРІРµР»РёС‡РёС‚СЊ РїРµСЂРІС‹Р№ СЃС‚РѕРі РЅР° РєРѕР»РёС‡РµСЃС‚РІРѕ СЃРЅРѕРїРѕРІ РІРѕ РІС‚РѕСЂРѕРј РїРѕР»СѓС‡РёС‚ $(8, 3)$. Р—Р°С‚РµРј СѓРІРµР»РёС‡РёС‚ РєРѕР»РёС‡РµСЃС‚РІРѕ РІС‚РѕСЂРѕР№ СЃС‚РѕРі РЅР° РЅРѕРІРѕРµ РєРѕР»РёС‡РµСЃС‚РІРѕ СЃРЅРѕРїРѕРІ РІ РїРµСЂРІРѕРј, РїРѕР»СѓС‡РёС‚ $(8, 11)$ Р—Р°С‚РµРј СЃРґРµР»Р°РµС‚ СЌС‚Сѓ РѕРїРµСЂР°С†РёСЋ РµС‰С‘ СЂР°Р· Рё РїРѕР»СѓС‡РёС‚ $(8, 19)$ Р� СЌС‚Рѕ РјРёРЅРёРјР°Р»СЊРЅРѕРµ РєРѕР»РёС‡РµСЃС‚РІРѕ РѕРїРµСЂР°С†РёР№, С‡С‚РѕР±С‹ РїРѕР»СѓС‡РёС‚СЊ РґР°РЅРЅС‹Р№ СЂРµР·СѓР»СЊС‚Р°С‚.

Р—Р°РјРµС‚РёРј, С‡С‚Рѕ РІ С‚СЂРµС‚СЊРµРј РїРѕРґС‚РµСЃС‚Рµ РѕС‚РІРµС‚ РЅРµ С‚Р°РєРѕР№ РєР°Рє РІРѕ РІС‚РѕСЂРѕРј, РїРѕС‚РѕРјСѓ, С‡С‚Рѕ $c$ Рё $d$ РїРѕРјРµРЅСЏРЅС‹ РјРµСЃС‚Р°РјРё (РїРѕСЂСЏРґРѕРє РєСѓС‡ РёРјРµРµС‚ Р·РЅР°С‡РµРЅРёРµ).

Р’ С‡РµС‚РІРµСЂС‚РѕРј РїРѕРґС‚РµСЃС‚Рµ РЅРµ С‚СЂРµР±СѓРµС‚СЃСЏ РІС‹РїРѕР»РЅСЏС‚СЊ РѕРїРµСЂР°С†РёРё.

РџР Р�РњР•Р Р’Р’РћР”Рђ:

1
1 1 1 1000000000000000000

РџР Р�РњР•Р Р’Р«Р’РћР”Рђ:

999999999999999999

РћР¦Р•РќР�Р’РђРќР�Р•:

РўРµСЃС‚С‹ 3-4: $\max(c, d) \le 20 \cdot\min(a, b)$
РўРµСЃС‚С‹ 5-7: $T \le 10$ and $a,b,c,d\le 10^6$
РўРµСЃС‚С‹ 8-12: РќРµС‚ РґРѕРїРѕР»РЅРёС‚РµР»СЊРЅС‹С… РѕРіСЂР°РЅРёС‡РµРЅРёР№

РђРІС‚РѕСЂ: Benjamin Qi

Transforming Pairs

Вывод формулы

Ответьте на $Q$ ($1\le Q\le 10^5$) независимых запроса следующего вида:

Вам даны четыре целых числа $a,b,c,d$ ($-10^{18}\le a,b,c,d\le 10^{18}$). За одну операцию Вы можете сделать либо $a\mathrel{+}=b$, или $b\mathrel{+}=a$ Определите минимальное количество операций чтобы трансформировать $(a,b)$ в $(c,d)$, если это невозможно сделать, выведите $-1$.

ФОРМАТ ВВОДА (с клавиатуры / stdin):

Первая строка содержит $Q$.

Каждая из следующих $Q$ строк содержит четыре целых числа $a,b,c,d$.

ФОРМАТ ВЫВОДА (на экран / stdout):

Ответ для каждого запроса на отдельной строке

Roundabout Rounding

Вывод формулы

Беси вернулась в школу. Она начала делать домашнюю работу по математике, в которой требуется округлить положительные целые числа до степени $10$.

Чтобы округлить положительное целое число $a$ к ближайшему $10^b$, где $b$ положительное целое число, Беси сначала находит $b$-ую цифру справа. Пусть $x$ обозначает эту цифру.

Если $x \geq 5$, Беси добавляет $10^b$ к $a$.

Затем Беси устанавливает в $0$ все цифры вправо от $b$-ой цифры.

Например, если Беси хочет округлить $456$ к ближайшей $10^2$ (сотне), Беси сначала находит 2-ую цифру справа - это $5$. То есть, $x = 5$. Затем, поскольку $x \geq 5$, Беси прибавляет $100$ к $a$. Наконец Беси устанавливает в $0$ все цифры справа начиная со второй, получается $500$.

Однако если Беси станет округлять $446$ до ближайшей $10^2$, она получит $400$.

Посмотрев на домашнюю работу Беси, Эльза придумала новый тип округления: цепочечное округления. Чтобы цепочечно округлить до ближайшего $10^b$, Эльза сначала округляет до ближайшего $10^1$, затем до ближайшего $10^2$, и т.д. до ближайшего $10^b$.

Беси думает, что Эльза ошибается, но она сильно занята со своей домашней работой, чтобы подтвердить свои подозрения. Она просит Вас посчитать сколько целых чисел $x$, начиная с $2$ и до $N$ ($1 \leq N \leq 10^{9}$) таких, что округление его до ближайшего $10^P$ отличается от цепочечного округления к ближайшему $10^P$, где $P$ - минимальное целое такое, что $10^P \geq x$.

ФОРМАТ ВВОДА (с клавиатуры / stdin):

Вы должны дать ответ на множество подтестов.

Первая строка ввода содержит целое число $T$ ($1 \leq T \leq 10^5$) обозначающее количество подтестов. Далее следуют $T$ подтестов.

Первая и единственная строка ввода для каждого подтеста содержит целое число $N$. Все $N$ различны.

ФОРМАТ ВЫВОДА (на экран / stdout):

Выведите $T$ строк, $i$-ая строка содержит ответ на $i$-ый подтест. Каждая строка должна быть целым числом обозначающим сколько целых чисел от $2$ до $N$ включительно различаются в двух методах округления.

Farmer John Actually Farms

Жадный алгоритм Задачи на моделирование Вывод формулы

Фермер Джон вырастил $N$ ($1 \leq N \leq 2\cdot 10^5$) аспарагусов на своей ферме. Однако некоторые из этих растений имеют генетические отличия, поэтому некоторые растения растут быстрее чем другие. Изначальная высота $i$-го растения равна $h_i$ дюймов и после каждого дня $i$-ое растение вырастает на $a_i$ дюймов.

ФД любит некоторые растения больше чем другие, и он хочет, чтобы некоторые растения были выше чем другие. Он дал Вам массив различных целых чисел $t_1,\dots,t_N$, содержащих все целые числа от $0$ до $N-1$ и хочет, чтобы $i$-ое растение имело ровно $t_i$ растений, которые выше этого. Определите минимальное количество дней, чтобы требование ФД было удовлетворено или укажите, что это невозможно.

ФОРМАТ ВВОДА (с клавиатуры):

Первая строка состоит из целого числа $T$, обозначающего количество независимых тестов $(1 \leq T \leq 10)$.

Первая строка каждого теста состоит из целого числа $N$.

Вторая строка состоит из $N$ целых чисел $h_i$ $(1 \leq h_i \leq 10^9)$, обозначающих изначальную высоту $i$-го растения в дюймах.

Третья строка состоит из $N$ целых чисел $a_i$ $(1 \leq a_i \leq 10^9)$, обозначающих количество дюймов, на которые $i$-ое растение вырастает каждый день.

Четвёртая строка содержит $N$ различных целых чисел $t_i$, обозначающих массив, который ФД даст Вам.

Гарантируется, что сумма всех $N$ по всем тестам не превысит $2\cdot 10^5$.

ФОРМАТ ВЫВОДА (с клавиатуры):

Выведите $T$ строк, ответ на каждый тест на отдельной строке. Если невозможно, выведите -1.

Заметим, что тесты этой задачи могут потребовать использования 64-битного целого типа (например, "long long" в C/C++).

COW Operations

Вывод формулы

Имеется строка $s$ длиной не более $2 \cdot 10^5$ символов (только трёх 'C', 'O', 'W'). Требуется узнать, можно ли её превратить в одну букву 'C', используя следующие операции:

1. Выбрать два соседних одинаковых символа и удалить их.

2. Выбрать один символ и заменить его на два других символа в любом порядке.

В задаче требуется дать ответ для $Q$ ($1\le Q\le 2\cdot 10^5$) подстрок строки $s$.

ФОРМАТ ВВОДА (с клавиатуры / stdin):

Первая строка содержит $s$.

Вторая строка содержит $Q$.

Каждая из последующих $Q$ строк содержит два целых числа $l$ и $r$ ($1\le l\le r\le |s|$, где $|s|$ означает длину строки $s$).

ФОРМАТ ВЫВОДА (на экран / stdout):

Строка длины $Q$, где $i$-ый символ есть 'Y', если $i$-ая подстрока может быть сокращена до 'C'. и 'N' в противном случае.

Range Reconstruction

Вывод формулы

У Беси есть массив $a_1, \ldots, a_N$, где $1 \leq N \leq 300$ и $0 \leq a_i \leq 10^9$ для всех $i$. Она не хочет сообщать Вам сам массив $a$, но может отвечать на ваши запросы то есть для каждой пары индексов $i \leq j$, Беси скажет Вам $r_{i, j} = \max a[i\ldots j] - \min a[i\ldots j]$. По заданным значениям $r$ сконструируйте массив, который мог бы быть оригинальным массивом Беси. Значения в этом массиве должны быть в интервале $[-10^9, 10^9]$.

ФОРМАТ ВВОДА (с клавиатуры / stdin):

Первая строка содержит число $N$.

Далее следуют $N$ строк. $i$-ая из этих строк содержит число $r_{i, i}, r_{i, i + 1}, \ldots, r_{i, N}$.

Гарантируется, что существует некоторый массив с числами в интервале $[0, 10^9]$ такой, что для всех $i \leq j$, $r_{i, j} = \max a[i\ldots j] - \min a[i\ldots j]$.

ФОРМАТ ВЫВОДА (на экран / stdout):

Выведите одну строку, содержащую $N$ целых чисел $b_1, b_2, \ldots, b_N$ в интервале $[-10^9, 10^9]$ представляющих Ваш массив. Они должны удовлетворять $r_{i, j} = \max b[i\ldots j] - \min b[i\ldots j]$ для всех $i \leq j$.

Circus

графы Деревья Вывод формулы

$N$ коров из цирка Фермера Джона ($1 \leq N \leq 10^5$) готовят своё представление. Оно будет происходить на дереве с вершинами помеченными $1\ldots N$. "Стартовое состояние" представления определяется числом $1 \leq K \leq N$ и назначением коров $1\dots K$ вершинам на дереве так, что никакие две коровы не размещаются в одной и той же вершине.

Во время представления коровы выполняют произвольно большое количество "шагов". Во время "шага" корова перемещается из своей текущей вершины в соседнюю незанятую вершину. Два стартовых состояния называются эквивалентными, если одно из них может быть достигнуто из другого некоторой последовательностью шагов.

Для каждого $1 \leq K \leq N$, помогите коровам определить количество классов эквивалентности стартовых состояний: то есть максимальное количество стартовых состояний, которое они могут выбрать, так что никакие два из них не будут эквивалентными. Поскольку эти числа могут быть очень большими, выведите их остатки по модулю $10^9 + 7$.

ФОРМАТ ВВОДА (файл circus.in):

Строка $1$ содержит $N$.

каждая из строк $2\le i\le N$ содержит да целых числа $a_i$ и $b_i$ обозначающих ребро в дереве между вершинами $a_i$ и $b_i$.

ФОРМАТ ВЫВОДА (файл circus.out):

Для кажого $1\le i\le N,$ $i$-ая строка вывода должна содержать ответ для $K=i$ по модулю $10^9+7$.

MooBuzz

Вывод формулы

Коровы фермера Джона недавно стали поклонниками простой числовой игры под названием «FizzBuzz». Правила игры просты: стоя в кругу, коровы последовательно отсчитывают от одного, каждая корова произносит одно число, когда наступает ее очередь. Однако, если корова достигнет числа кратного 3, она должна сказать «Fizz» вместо этого числа. Если корова достигает кратного 5, она должна сказать «Buzz» вместо этого числа. Если корова достигает кратного 15, она должна сказать «FizzBuzz» вместо этого числа. Поэтому расшифровка первой части игры:

1, 2, Fizz, 4, Buzz, Fizz, 7, 8, Fizz, Buzz, 11, Fizz, 13, 14, FizzBuzz, 16

Имея немного более ограниченный словарный запас, версия FizzBuzz, которую играют коровы, включает в себя выражение «Moo» вместо Fizz, Buzz и FizzBuzz. Поэтому начало коровьей версии игры

1, 2, Moo, 4, Moo, Moo, 7, 8, Moo, Moo, 11, Moo, 13, 14, Moo, 16

По заданному числу $ N $ ($ 1 \ leq N \ leq 10 ^ 9 $), определите $ N $-ое число, которое говорят в этой игре.

ОЦЕНИВАНИЕ

Тесты 2-5 удовлетворяют $ N \ le 10 ^ 6. $

ФОРМАТ ВВОДА (файл moobuzz.in):

Ввод состоит из единственного целого числа, $ N $.

ФОРМАТ ВЫВОДА (файл moobuzz.out):

Выведите $ N $-ое число, которое произнесли во время игры.

Sprinklers

Вывод формулы

У Фермера Джона есть большое поле, и он собирается посадить в некоторых его местах сладкую пшеницу. ФД представил поле квадратом с размерами $(N-1) \times (N-1)$. Юго-западный угол поля имеет координаты $(0,0)$, а северо-восточный конец поля имеет координаты $(N-1,N-1)$.

В некоторых целочисленных координатах имеются двухглавые разбрызгиватели, оба разбразгивают воду и удобрения. Разбрызгиватель в координатах $(i,j)$ разбрызгивает воду на часть поля к северу и востоку от себя и разбрызгивает удобрения к югу и западу от себя. Формально, он поливает водой все вещественные координаты $(x,y)$ для которых $N \geq x \geq i$ и $N \geq y \geq j$, и удобряет все вещественные координаты $(x,y)$ для которых $0 \leq x \leq i$ and $0 \leq y \leq j$.

Фермер Джон хочет засадить сладкой пшеницей некоторые прямоугольные области, параллельные осям координат, с углами в целочисленных координатах. Однако, чтоыб сладкая пшеница росла, надо чтобы все точки такого прямоугольника поливались и удобрялись. И конечно, прямоугольник должен иметь положительную площадь.

Помогите ФД определить количество прямоугольников с положительной площадью, на которых он может растить сладкую пшеницу. Поскольку число может быть очень большим, выводите его по модулю $10^9 + 7$.

ФОРМАТ ВВОДА (файл sprinklers.in):

Первая строка ввода содержит целое число $N$, определяющее размер поля. ($1 \leq N \leq 10^5$).

Каждая из последующих $N$ строк содержит два разделённых пробелом целых числа $i$ и $j$, ($0 \leq i,j \leq N-1$), они обозначают, что разбрызгиватель находится в позиции $(i,j)$.

Гарантируется, что ровно один разбрызгиватель находится в каждой колонке и ровно один разбрызгиватель находится в каждой строке. То есть, никакие два разбрызгивателя не имеют одинаковую $x$-координату, и никакие два разбрызгивателя не имеют одинаковую $y$-координату.

ФОРМАТ ВЫВОДА (файл sprinklers.out):

Вывод должен содержать одно целое число - количество прямоугольников положительной площади, которые полностью поливаются и удобряются, по модулю $10^9 + 7$.

Cow Gymnasts

Комбинаторика Вывод формулы теория чисел

Соскучившись от жизни на ферме, коровы ушли в бродячий цирк. И с ними готовится новое шоу.

Сцена для шоу представляет $N$ платформ, размещённых по кругу. На каждой платформе от $1$ до $N$ коров формируют стек (корова становится на корову). По сигналу главного на манеже, все стеки параллельно "падают" по часовой стрелке так, что нижняя корова стека не движется, корова на ней движется на одну платформу по часовой стрелке, следующая корова - на две платформы и т.д. В результате получаются новые стеки коров.

Главный на манеже думает, что шоу будет лучше, если после того, как стеки упадут, новый стек на каждой платформе будет содержать такое же количество коров, что и исходный стек на манеже. Мы называем конфигурацию стеков на манеже "магической", если она удовлетворяет этому условию. Вычислите количество "магических" конфигураций. Поскольку это число может быть очень большое, выведите его остаток по модулю $10^9 + 7$.

Две конфигурации считаются различными, если существует платформа, для которых у этих двух конфигураций различное количество коров.

ФОРМАТ ВВОДА (файл gymnasts.in):

Ввод - олдно целое число, $N$ ($1 \leq N \leq 10^{12}$).

ФОРМАТ ВЫВОДА (файл gymnasts.out):

Одно целое число - количество магических конфигураций по модулю $10^9 + 7$.

Bessie Goes Moo

Вывод формулы

Фермер Джон и корова Беси в свободное время любят обмениваться математическими головоломками. Последняя головоломка, которую ФД дал Беси была очень сложной и Беси не смогла решить ей. Теперь она хочет дать ФД очень сложную головоломку.

Беси даёт ФД выражение $(B+E+S+S+I+E)(G+O+E+S)(M+O+O)$, содержащее семь переменных $B,E,S,I,G,O,M$ (the "$O$" это переменная, а не 0). Для каждой из переменных она даёт ФД список до 500 целых значений, которые та может принять. Она просит ФД посчитать количество способов, получить результат, кратный числу 7.

Заметим, что ответ на эту задачу может быть слишком большим, чтобы пометситься в 32-битную переменную, рекомендуется использовать 64-битную переменную типа long long в С/С++.

ФОРМАТ ВВОДА (файл bgm.in):

Первая строка ввода содержит целое число $N$. Каждая из последующих $N$ строк содержит переменную и возможное значение этой переменной. Каждая переменная появится в этом списке не менее одного и не более 500 раз. Для одной и той же переменной никакие значения не повторяются. Все возможные значения находятся в диапазоне $-10^5$ до $10^5$.

ФОРМАТ ВЫВОДА (файл bgm.out):

Выведите одно целое число, задающее количество способов, которыми ФД может назначить значения переменным, чтобы в результате вычислений получить выражение, кратное семи.

Bessie Gets Even

Вывод формулы

Фермер Джон и корова Беси в свободное время любят обмениваться математическими пазлами. Последний пазл, который ФД дал Беси, был довольно сложный и Беси не смогла решить его. Теперь она хочет дать ФД очень сложный пазл.

Беси даёт ФД выражение $(B+E+S+S+I+E)(G+O+E+S)(M+O+O)$, содержащее семь переменных $B,E,S,I,G,O,M$ ( "$O$" это переменная, а не 0). Для каждой переменной она даёт ФД список до 20 целых чисел, которые эта переменная может принять. Беси просит ФД посчитать количество различных способов назначить значения переменным, чтобы вычисленное выражение было чётным числом.

ФОРМАТ ВВОДА (файл geteven.in):

Первая строка ввода содержит целое число $N$. Каждая из $N$ следующих строк содержит переменную и возможное значение для этой переменной. Каждая переменная появится в этом списке не менее одного раза и не более 20 раз. Для одной и той же переменной все задаваемые значения различны. Все значения находятся в диапазоне $-300$ to $300$.

ФОРМАТ ВЫВОДА (файл geteven.out):

Выведите единственное целое число, задающее количество способов, которыми ФД может назначить значения переменным, чтобы выражение давало чётный результат.

Code Breaking

графы Деревья Вывод формулы

Фермер Джон спрятал ключи от трактора в сейфе. Коровы пытаются взломать этот сейф. Сейф защищён сложной парольной системой. Она организована как корневое дерево из N (1 <= N <= 20,000) вершин, каждая из которых требует цифру от 0 до 9. Вершины пронумерованы от 0 до N-1.
Единственная информация, которой владеют коровы – что определённая последовательность длины 5 не случается на путях в этом дереве.
Например, предположим, то дерево выглядит так (с корнем в A):
A <- B <- C <- D <- E ^ | F
Коровы могут знать, что последовательность 01234 не случится начиная от F, И что последовательность 91234 не случится, начиная от E. Эта информация приводит к тому, что возможными остаются 19 паролей, все такого вида:
The cows might know that the sequence 01234 does not occur starting at F, and that the sequence 91234 does not occur starting at E. This information rules out 19 possible passcodes: all those of the form
4 <- 3 <- 2 <- 1 <- * ^ | 0
или
4 <- 3 <- 2 <- 1 <- 9 ^ | *
Что даёт 19 паролей, поскольку такой
4 <- 3 <- 2 <- 1 <- 9 ^ | 0
появится дважды
По заданным M (1 <= M <= 50,000) последовательностям длины 5, вместе с их стартовой позицией в дереве помогите коровам вычислить сколько паролей будет подходить. Вы должны выводить свой ответ по модулю 1234567.

PROBLEM NAME: code
Формат ввода:
* Строка 1: Два разделённых пробелом целых числа, N и M.
* Строки 2..N: Строка i+1 содержит одно целое число p(i), означающее родителя вершин I в дереве (0 <= p(i) < i).
* Строки N+1..N+M: Строка N+i описывает i-ую последовательность про которую известно, что она не произойдёт в коде. Строка содержит v(i) и s(i), разделённые пробелом. Здесь v(i) - стартовая вершина последовательности, s(i) – строка из 5 цифр, которая не встретится в шифре начиная с вершины v(i) если двигаться вверх по дереву. Гарантируется, что корень дерева находится не менее чем в 4 шагах от v(i).

B. Три матрицы

матрицы Вывод формулы реализация

Прямо сейчас Вася изучает линейные уравнения. Он придумал неплохую задачу. В этой задаче вам дана матрица W размера n × n, состоящая из целых чисел, ваша задача — найти две матрицы A и B размера n × n, при этом должны выполняться все следующие условия:

A_ij = A_ji, для всех i, j (1 ≤ i, j ≤ n);
B_ij = - B_ji, для всех i, j (1 ≤ i, j ≤ n);
W_ij = A_ij + B_ij, для всех i, j (1 ≤ i, j ≤ n).

А вам по силам эта задачка?

Входные данные

В первой строке записано целое число n (1 ≤ n ≤ 170). Каждая из следующих n строк содержит n целых чисел: j-ое число в i-ой строке равняется W_ij (0 ≤ |W_ij| < 1717).

Выходные данные

В первых n строках должна быть записана матрица A. В следующих n строках должна быть записана матрица B. Выведите матрицы в формате, равном формату матрицы W во входных данных. Гарантируется, что ответ существует. Если правильных ответов несколько, можете вывести любой из них.

Ответ будет считаться корректным, если его абсолютная или относительная погрешность не превосходит 10^- 4.

A. Nineteen

Вывод формулы

Алисе очень нравится слово "nineteen". У нее есть строка s, и она хочет, чтобы строка содержала как можно больше таких слов. Для этого она может переставлять местами буквы в строке.

Например, если есть строка "xiineteenppnnnewtnee", то Алиса может получить из нее строку "xnineteenppnineteenw", содержащую два таких слова (словоупотребления выделены). Более формально, слово "nineteen" содержится в строке столько раз, сколько раз можно прочесть его, начиная от некоторой буквы строки. При прочтении пропускать буквы запрещается.

Помогите Алисе определить: какое максимальное количество слов "nineteen" она может получить в своей строке?

Входные данные

Первая строка содержит непустую строку s, состоящую только из строчных букв английского алфавита. Длина строки s не превосходит 100.

Выходные данные

Выведите единственное целое число — максимальное количество слов "nineteen", которое Алиса может получить в своей строке.

E1. Три дерева

графы Деревья Вывод формулы

Задача состоит из двух подзадач: за решение подзадачи E1 вы получите 11 баллов, за решение подзадачи E2 вы получите 13 баллов.

Деревом называется неориентированный связный граф, не содержащий циклов. Расстояние между двумя вершинами в дереве определяется как наименьшее количество ребер, которые надо пройти, чтобы попасть из одной из этих вершин в другую.

Вам дано 3 дерева, которые нужно объединить в одно посредством добавления двух ребер между данными деревьями. Каждое из этих ребер может соединять любую пару вершин из двух деревьев. После соединения деревьев, будут вычислены расстояния между всеми парами вершин в едином дереве. Найдите максимальное возможное значение суммы этих расстояний.

Входные данные

В первой строке через пробел записаны три целых числа n₁, n₂ и n₃ — количества вершин в первом, втором и третьем дереве соответственно. Следующие n₁ - 1 строк описывают первое дерево. Каждая из этих строк содержит два разделенных пробелом целых числа — номера вершин, соединенных ребром. Следующие n₂ - 1 строк описывают второе дерево в том же формате. Далее следуют n₃ - 1 строк, описывающие третье дерево в том же формате. Вершины в каждом из деревьев пронумерованы от 1 до количества вершин в соответствующем дереве.

Задача состоит из двух подзадач, которые отличаются друг от друга ограничениями на входные данные. За решение каждой подзадачи вы получите определенное количество баллов. Описание подзадач следует ниже.

В подзадаче E1 (11 баллов), количество вершин в каждом дереве будет между 1 и 1000, включительно.
В подзадаче E2 (13 баллов), количество вершин в каждом дереве будет между 1 и 100000, включительно.

Выходные данные

Выведите единственное целое число — наибольшую возможную сумму расстояний между всеми неупорядоченными парами вершин в объединенном дереве.

Примечание

Рассмотрим первый пример. Есть два дерева, состоящих из двух вершин, и одно дерево с тремя вершинами. Наибольший ответ получается, когда все деревья соединены в одну цепочку из 7 вершин.

Во втором примере для получения максимального ответа можно вставить новые ребра следующим образом:

Соединить вершину 3 первого дерева с вершиной 1 второго;
Соединить вершину 2 третьего дерева с вершиной 1 второго;

Сумма натуральных чисел не меньшее N

Цикл while Вывод формулы Цикл for

По данному натуральному числу N найдите наименьшее натуральное число k, такое что сумма всех натуральных чисел от 1 до k (включительно) не меньше N.

Формат входных данных
Во входной строке записано одно натуральное число N (N <= 10⁹)

Формат выходных данных
Выведите одно число - искомое число k.

Устный опрос

Вывод формулы

В классе $N$ учеников. Учитель опрашивает сначала всех учащихся с нечётными номерами (1, 3, 5, ...), затем — всех с чётными номерами (2, 4, 6, ...). Вася, имеющий номер $K$ по журналу, хочет узнать, какой по порядку вопрос достанется ему. Напишите программу, вычисляющую номер вопроса по данным $N$ и $K$.

Вводятся два целых числа $N$ и $K$, каждое в отдельной строке ($1 \le N \le 2 \cdot 10^9$, $1 \le K \le N$).

Выведите одно целое число — номер вопроса, который достанется Васе.

Решения, правильно работающие при $N \le 1000$, будут оцениваться в 50 баллов.

В примерах из условия $N = 10$, и ученики вызываются в следующем порядке: $1$, $3$, $5$, $7$, $9$, $2$, $4$, $6$, $8$, $10$. Если $K=7$, то Вася выйдет 4-м по счёту, если $K=6$, то Вася выйдет 8-м.

Робот

На бесконечной в обе стороны клетчатой полоске в клетке с нулевой координатой стоит робот.

Робот делает 1 шаг вправо, затем 2 шага влево, 3 шага вправо, 4 шага влево и так далее. Сделав суммарно N шагов, робот останавливается. Определите координату клетки, в которой окажется робот после остановки.
Формат входных данных
В единственной строке задано целое число N (0 ≤ N ≤ 10¹⁸). Обратите внимание, что значения переменных в этой задаче могут превышать возможные значения 32-битной целочисленной переменной, поэтому необходимо использовать 64-битные целочисленные типы данных (тип int64 в языке Pascal, тип long long в C++, тип long в Java и C#).
Формат выходных данных
Выведите единственное число координату клетки, в которой окажется робот после остановки.

Обои и дипломы

Родители Андрея решили поклеить на одну из стен в его комнате новые обои. Высота стены n сантиметров, а ширина m сантиметров. К сожалению, обои, выбранные родителями, Андрею не понравились, и он решил их чем-нибудь закрыть. Так как он участвовал в большом количестве олимпиад, у него накопилось много дипломов. Все дипломы у Андрея одинаковые это прямоугольники высотой a сантиметров и шириной b сантиметров. Помогите Андрею узнать, сколько квадратных сантиметров обоев он сможет завесить дипломами, если не будет их разрезать и переворачивать. Все дипломы должны целиком размещаться внутри стены и не накладываться друг на друга.
Формат входных данных
В первой строке входных данных находится целое число n (1 n ≤ 2 ·10⁹) высота стены.
Во второй строке находится целое число m (1 ≤ m ≤ 2 · 10⁹) ширина стены.
В третьей строке находится целое число a (1 ≤ a ≤ 2 ·10⁹) высота диплома.
В четвёртой строке находится целое число b (1 ≤ b ≤ 2 · 10⁹) ширина диплома.
Формат выходных данных
Выведите одно целое число площадь части стены, которая будет закрыта дипломами, если их не поворачивать, не обрезать и не накладывать друг на друга.
Обратите внимание, что значение ответа в этой задаче может превышать возможное значение 32-битной целочисленной переменной, поэтому необходимо использовать 64битные целочисленные типы данных (тип int64 в языке Pascal, тип long long в С и С++, тип long в Java и С#).

Замечание
В примере из условия можно разместить 6 дипломов, суммарная площадь которых равна 12 квадратным сантиметрам. Большее число дипломов разместить нельзя, они будут вылезать за границы стены.

Прожектора

На дискотеке в ряд стоят три прожектора, которые поочерёдно светят в следующем порядке: левый, средний, правый, средний, левый, средний, правый, средний и т.д. (слева направо, затем налево, опять направо, ...). Каждый прожектор горит в течение одной секунды.

Известно, что лампа левого прожектора имеет ресурс A секунд горения, среднего – B секунд, правого – С секунд. Определите, сколько времени сможет продолжаться этот процесс горения прожекторов.

Входные данные

Программа получает на вход три целых неотрицательных числа A, B, C – время горения левого, среднего, правого прожектора.

Выходные данные

Программа должна вывести одно целое число.

Пояснение к примеру
Прожектора горят в следующем порядке: левый, средний, правый, средний, левый, средний, правый. После этого должен загореться средний прожектор, но он уже выработал ресурс и загореться не сможет. Поэтому процесс обрывается после 7 с.

Осторожно, злые числа!

Двоичная система счисления Вывод формулы

Злым числом в математике называется неотрицательное целое число с чётным числом единиц в его двоичной записи (например, число 5 — злое, в его двоичной записи две единицы). Они используются в теории чисел при исследовании последовательности Морса–Туэ и применяются в алгоритмах фрактального сжатия изображений. Натуральное число будем называть очень злым, если само оно чётное и количество единиц в его двоичной записи также чётное. Это такие числа, как 6, 10, 12, 18, 20 и так далее. По данному n определите количество очень злых чисел, не превосходящих n.

Формат входных данных
Единственная строка входного файла содержит натуральное число n (1 ≤ n ≤ 10⁹ ).

Формат выходных данных
Выведите одно неотрицательное целое число — количество очень злых натуральных чисел, не превосходящих n.

Обработка заявлений

На столе у большого начальника лежит стопка из N заявлений, пронумерованных сверху вниз от 1 до N. Первое заявление он подписывает и убирает из стопки, второе — выбрасывает в мусорную корзину, третье — кладёт вниз стопки. Далее процесс продолжается аналогично, пока заявления в стопке не закончатся. Определите, будет ли заявление с номером K подписано или выброшено, а также номер шага, на котором это произойдёт. Одним шагом является каждая из трёх операций, описанных выше.

Формат входных данных
Первая строка входных данных содержит целое число N, вторая строка — целое число K (1 ≤ N ≤ 10⁹ , 1 ≤ K ≤ N).
Формат выходных данных
В первой строке выведите «Yes», если заявление с номером K будет подписано, и «No», если оно будет выброшено. Во второй строке выведите номер шага, на котором это произойдёт.

Замечание
В первом примере из условия в стопке находятся 4 заявления: (1, 2, 3, 4). Заявление 1 подписывается, заявление 2 выкидывается, заявление 3 перекладывается в конец. После выполнения трёх шагов в стопке будут заявления (4, 3). Поэтому на пятом шаге заявление 3 будет выброшено.
Во втором примере из условия стопка имеет вид (1, 2, 3, 4, 5). После выполнения трёх шагов стопка будет иметь вид (4, 5, 3). За следующие три шага заявление 4 будет подписано, заявление 5 будет выброшено, а заявление 3 — переложено в конец стопки (в которой ничего не будет, кроме заявления 3). Поэтому после шести шагов стопка будет иметь вид (3). На седьмом шаге заявление 3 будет подписано.

Беспилотная аэрологистика

Жадный алгоритм Использование сортировки Вывод формулы

На всероссийской олимпиаде по информатике 2224 года, которая проходит в Иннополисе, доставкой занимаются роботы нового поколения, которые способны создавать своих клонов. Доставку можно получить прямо через окно, не выходя из дома.

Изначально есть только один робот-доставщик. В любой момент верхний робот может создать одного или нескольких новых роботов прямо над собой. Так образуется колонна роботов. Высота каждого робота равна высоте одного этажа.

В процессе доставки колонна одинаковых роботов-клонов перемещается вдоль корпусов общежития слева направо. В базе данных у роботов содержится список сделанных заказов, для каждого из которых известно окно, в которое его нужно доставить. Когда колонна роботов проходит мимо окна, соответствующего какому-то заказу, она может произвести доставку, если в колонне есть робот, расположенный на уровне окна.

Во время перемещения конструкция из роботов может натолкнуться на препятствие. После препятствия движение продолжают только те экземпляры роботов, которые находились выше препятствия. Они оказываются на земле непосредственно за препятствием, по прежнему в виде вертикальной колонны, и могут продолжать движение, создавать новых клонов и доставлять заказы.

Расстояние между препятствиями и окнами достаточно большое, поэтому во время переезда через препятствие роботы не будут проезжать мимо окна.

За доставку одного заказа компания-организатор доставки получает $p$ крипторублей. Стоимость создания одного нового робота равна $c$ крипторублей. Итоговая прибыль равна суммарному доходу от доставки заказов за вычетом суммарной стоимости создания всех роботов. Компания хочет максимизировать свою прибыль. При этом, она не обязана выполнить все заказы, а роботы могут в любой момент остановиться, и прекратить процесс доставки.

Определите максимальную прибыль, которую может получить компания.

Формат входных данных
В первой строке входных данных находятся четыре целых числа $n$, $m$, $c$, $p$ ($0 \le n, m \le 100\,000$, $1 \le c, p \le 10^6$) — количество препятствий, количество заказов в базе, стоимость создания клона робота и стоимость доставки одного заказа, соответственно.

В следующих $n+m$ строках идёт описание препятствий и окон, в которые нужно доставить заказы, в порядке следования колонны роботов вдоль общежитий слева направо. Каждая строка содержит два целых числа $t_i$ и $h_i$ ($1 \le t_i \le 2$, $1 \le h_i \le 10^6$) — тип объекта $t_i$ ($1$ для препятствия и $2$ для окна) и $h_i$ "— высота препятствия в этажах или этаж, на котором находится окно.

Гарантируется, что ровно $n$ объектов имеют тип $1$, и оставшиеся $m$ объектов имеют тип $2$.

Формат выходных данных
Выведите одно число — максимальную величину прибыли, которую можно получить.Одна из оптимальных стратегий доставки заказов из первого примера изображена на девяти рисунках ниже, при этом выполнение второго заказа не увеличивает прибыль.

Пояснения к примерам

Одна из оптимальных стратегий доставки заказов из первого примера изображена на девяти рисунках ниже, при этом выполнение второго заказа не увеличивает прибыль.

Во втором примере достаточно один раз клонировать робота для доставки первого заказа, полученной системой роботов доставить второй заказ, а производить дополнительное клонирование для доставки третьего заказа экономически невыгодно.

Змейка

Вывод формулы

Успешно решив раньше времени контрольную работу по математике, Тимофей выбрал на клетчатой бумаге квадрат со стороной n клеток и стал заполнять его «змейкой» от левого верхнего угла так, как показано на рисунке. Определите длину проведённых линий.

Формат входных данных
Единственная строка входных данных содержит натуральное число n (1 ≤ n ≤ 10⁹ ).
Формат выходных данных
Выведите одно натуральное число — ответ на вопрос задачи.
Обратите внимание, что значение ответа в этой задаче может превышать возможное значение 32-битной целочисленной переменной, поэтому необходимо использовать 64- битные целочисленные типы данных (тип int64 в языке Pascal, тип long long в C++, тип long в Java и C#).

Треугольники

Вывод формулы Комбинаторика

Дана клетчатая сетка, состоящая из $n \times m$ клеток со стороной 1, в каждой клетке проведены обе диагонали.

Например, сетка $1 \times 2$ выглядит следующим образом:

Назовём прямоугольник на данной сетке подходящим, если его вершины расположены в узлах сетки, а длины его стороны равны $1$ или $2$ (то есть подходящими являются прямоугольники $1\times1$, $1\times2$, $2\times1$, $2\times2$).

Треугольник называется хорошим, если его стороны образованы сторонами и/или диагоналями сетки и он целиком лежит в каком-то подходящем прямоугольнике.

Посчитайте количество хороших треугольников на данной сетке.

Формат входных данных
Программа получает на вход два числа $n$ и $m$, записанных в отдельных строках, — размеры сетки, $1 \le n \le 10^{8}$, $1 \le m \le 10^{8}$.

Формат выходных данных
Программа должна вывести одно целое число — количество искомых треугольников.

Обратите внимание на то, что ответ в этой задаче может превышать возможное значение 32-битной целочисленной переменной, поэтому необходимо использовать 64-битные целочисленные типы данных (тип long long в языке C++, тип int64 в Pascal, тип long в Java и C#).

В данной задаче $20$ тестов помимо тестов из условия, каждый из них оценивается в $5$ баллов. При этом в 4 тестах (помимо тестов из условия) $n$ или $m$ равно 1, в 4 других тестах $n$ или $m$ равно 2.

Все треугольники из первого примера:

Речные прогулки

Вывод формулы Бинарный поиск значения функции

Вдоль течения реки размещены $n$ пристаней, пронумерованных числами от 1 до $n$. Пристань номер 1 находится выше всех остальных по течению реки, пристань номер $n$ находится в устье реки, расстояние между соседними пристанями равно 1 км.

Для развития туризма решено открыть два прогулочных речных маршрута. Маршруты будут начинаться на одной из промежуточных пристаней (пристани номер 1 или $n$ не могут быть начальными точками маршрутов), один маршрут будет идти вверх по течению реки к пристани номер 1, другой маршрут будет идти вниз по течению к пристани номер $n$. Промежуточных остановок на маршрутах нет.

Для подъёма вверх по течению реки судно тратит $a$ минут на один километр, а для спуска вниз по течению реки — $b$ минут на один километр. Определите, на какой пристани должны начинаться оба маршрута, чтобы их продолжительности различались как можно меньше. Это значит, что необходимо минимизировать модуль разности времени в пути двух маршрутов.

Формат входных данных
Первая строка входных данных содержит целое число $n$ ($3\le n\le 2\cdot 10^9$) — общее количество пристаней на маршруте. Вторая строка содержит число $a$ — время подъёма судна на один километр вверх по течению реки, третья строка содержит число $b$ — время спуска на один километр вниз по течению, $1\le b < a\le 2\cdot 10^9$.

Формат выходных данных
Программа должна вывести одно число — номер пристани, на которой необходимо организовать начальный пункт маршрутов. Если возможных подходящих ответов несколько, можно вывести любой из них.

Примечание
В примере из условия начальным пунктом маршрутов нужно сделать пристань 3. Тогда вверх по течению судно поднимется за $(3-1)\times 7=14$ минут, а вниз по течению реки спустится за $(8-3)\times3=15$ минут. Разница в продолжительности маршрутов составит 1, меньшей разности в данном примере достичь невозможно.

Числа Летовёнка

Остатки Вывод формулы

У Старца Летовца есть маленький прапраправнук по имени Летовёнок. Летовёнок очень любознательный и уже с ранних лет увлёкся математикой. Старец Летовец подарил ему набор чисел из натурального ряда, чтобы Летовёнок мог учиться считать. Но Летовёнок уже давно умеет считать и уже даже изучает делимость числа на три.

У Старца Летовца есть набор чисел. Эти числа можно склеивать друг с другом (или не склеивать вовсе), чтобы получать новые числа. Например, из набора чисел 12, 2 и 10 можно склеить число 12210, а можно 10212 — вариантов много, но выбрать придётся только один, потому что все числа в наборе в единственном виде.
Летовёнок задумался: какое максимальное количество чисел, делящихся на три, можно получить из этого набора?

Помогите ему решить эту задачу.

Формат входных данных

В первой строке ввода дано единственное число n (1<= n <=1000). Во второй строке ввода через пробел даны n чисел num_i (1<=num_i<=1000).

Формат выходных данных
Выведите одно число - максимальное количество чисел, кратных трём, которые можно получить из набора.

Примечание
В первом тестовом примере можно склеить числа 2 и 10 (получить 210 или 102) и в итоге получится 2 числа, кратные трём.

Во втором тестовом примере ничего склеивать не надо, так как. все числа уже кратны трём.

Вывод формулы

Совсем как огуречик

теория чисел Динамическое программирование: один параметр Вывод формулы

На числовой прямой в точке с координатой $0$ сидит кузнечик. За одно действие он может выбрать любое целое неотрицательное число $k$ и прыгнуть влево или вправо на расстояние $2^k$.

Помогите кузнечику определить, какое минимальное количество действий ему понадобится выполнить, чтобы из точки с координатой $0$ попасть в точку с координатой $x$.

Формат входных данных
В первой строке дано одно целое число $t$ — количество наборов входных данных ($1 \le t \le 100\,000$).

Каждый набор входных данных состоит из единственной строки, в которой дано целое число $x$ — координата точки, в которую хочет попасть кузнечик ($-10^{18} \le x \le 10^{18}$).

Формат выходных данных
Для каждого набора входных данных выведите одно целое число — минимальное количество действий, которое кузнечику понадобится совершить.

Счастливый билетик

Динамика по подмножествам Задача на реализацию Вывод формулы

В стране Лаккиландии очень развит общественный транспорт. Проезд в нем бесплатный, но при этом каждому пассажиру при входе выдают билетик с уникальным номером. Особенно ценятся так называемые счастливые билетики.

Билетик называется счастливым, если сумма цифр на четных позициях в его номере равна сумме цифр на нечетных позициях.

Ване известно, что билеты выдаются подряд в порядке возрастания номеров. В очередной раз войдя в автобус Ваня получил свой очередной билет и тут ему стало интересно, какой существует минимальный счастливый билетик с номером, большим номера Ваниного билетика. Помогите Ване узнать ответ на этот вопрос.

Входные данные
В единственной строке входного файла задан номер Ваниного билетика − натуральное число, имеющее в своей десятичной записи не более 100 цифр.

Выходные данные
В выходной файл выведите минимальный номер счастливого билетика, который больше номера Ваниного билетика.

Провода

Вывод формулы

В 2222 году экспедиция на планету XZ-238 в звездной системе ню Малой Медведицы обнаружила в одной из пещер загадочное устройство. Вдоль стены по прямой расположены n треугольных и n круглых гнезд. Расшифровка инструкций, расположенных рядом на стене, показала, что эти гнезда следует соединить проводами: каждое треугольное гнездо должно быть соединено с каким-либо круглым, расположенным правее.

Были изготовлены n треугольных и n круглых штекеров, которые можно соединять проводами. Однако никакой маркировки нет, поэтому понять какое гнездо следует соединить с каким не удается. Начальник экспедиции хочет заказать с Земли провода. Решено было заказать один большой моток кабеля, который затем нарезать на соединительные провода. Поскольку доставка грузов с Земли дорога, необходимо заказать как можно меньше кабеля. С другой стороны, поскольку неизвестно какое гнездо требуется соединить с каким, нужно заказать такое количество кабеля, чтобы при любом способе соединения длины кабеля хватило на изготовление соединительных проводов. Помогите руководству экспедиции по заданному расположению гнезд вычислить, кабель какой длины следует заказать. Гарантируется, что хотя бы один способ соединить гнезда описанным образом существует.

Например, рассмотрим расположение гнезд, изображенное на рисунке.

Можно соединить треугольное гнездо 1 с круглым гнездом A, а треугольное гнездо 2 − с круглым гнездом B. Для такого соединения необходимы провода длины 5 и 4, суммарная длина − 9. Можно также соединить 1 с B и 2 с A, в этом случае необходимы провода длины 7 и 2, суммарная длина также 9. Таким образом необходимо заказать с Земли кабель длиной 9 метров.

В случае же, показанном на следующем рисунке, есть лишь один способ соединить гнезда: 1 с A, а 2 с B. Гнездо 2 нельзя соединить с A, поскольку A расположено левее. Так что в этом случае необходимо 2 метра кабеля.

Входные данные
Первая строка входного файла содержит число n (1≤n≤1000). Вторая строка содержит n целых чисел, i-е число означает расстояние от начала стены до i-го треугольного гнезда. Третья строка также содержит n целых чисел, i-е число означает расстояние от начала стены до i
-го круглого гнезда. Все числа во второй и третьей строках различны и лежат в диапазоне от 0 до 10⁵.

Выходные данные
Выведите одно число − кабель какой длины необходимо заказать с Земли.

Робот

Линейные алгоритмы Вывод формулы

В левом нижнем углу доски размером NxM клеток стоит Робот. Он может ходить на одну клетку по горизонтали, вертикали или диагонали. Требуется переместить Робота в правый верхний угол за наименьшее количество ходов.

Формат входных данных

Вводятся два натуральных числа N (высота доски) и M (ширина доски), не превышающие 100.

Формат выходных данных

Выведите последовательность ходов в одном из возможных кратчайших путей. Каждый ход обозначается заглавной латинской буквой:
U – вверх,
R – вправо,
D – вверх и вправо.
Буквы выводятся без пробелов в одной строке.

Площадь

Вывод формулы

Какую наибольшую площадь может иметь прямоугольник периметра P, нарисованный на клетчатой бумаге по линиям сетки (сторона клетки равна 1)?

Входные данные
Вводится одно четное натуральное число P (4 ≤ P ≤ 600).

Выходные данные
Выведите одно число – наибольшую возможную площадь.

Статическая сложность

Вывод формулы Разбор выражений Задача на реализацию

Анализ временной сложности алгоритмов - важный инструмент создания эффективных программ. Алгоритмы, выполняемые за линейное время, как правило, значительно быстрее алгоритмов, требующих для выполнения той же задачи квадратичного времени, так что предпочтение должно быть отдано первым.

Обычно определяют время выполнения алгоритма по отношению к n - "размеру" входных данных. Это может быть число объектов, которые нужно отсортировать, число точек многоугольника и т.п. Поскольку определение формулы зависимости временной сложности алгоритма от n - непростая задача, было бы замечательно, если бы её можно было автоматизировать. К сожалению, в общем случае это невозможно. Но в этой задаче мы будем рассматривать программы очень простой природы, над которыми это можно проделать. Рассматриваемые программы записаны согласно следующим правилам БНФ, где <число> может быть любым неотрицательным целым числом:

<Программа> ::= "BEGIN" <Список операторов> "END"
<Список операторов> ::= <Оператор> | <Оператор> <Список операторов>
<Оператор> ::= <Оператор LOOP> | <Оператор OP>
<Оператор LOOP> ::= <Заголовок LOOP> <Список операторов> "END"
<Заголовок LOOP> ::= "LOOP" <число> | "LOOP n"
<Оператор OP> ::= "OP" <число>

Время выполнения такой программы может быть вычислено следующим образом: выполнение оператора OP требует столько единиц времени, сколько указано в его параметре. Список операторов, заключённый в оператор LOOP, выполняется столько раз, сколько указано в параметре оператора, то есть или заданное константное число раз, если задано число, или n раз, если параметром является n. Время выполнения списка операторов равно сумме времени выполнения его частей. Таким образом, время выполнения программы в целом зависит от n.

Входные данные
В первой строке находится целое число k - число программ во входном файле. Затем идут k программ, удовлетворяющих приведённой грамматике. Пробелы и переводы строк могут встречаться везде в программе, но не в ключевых словах BEGIN, END, LOOP и OP, нет их и в целых числах.

Выходные данные
Для каждой программы сначала идёт строка с номером программы. В следующей строке записывается время работы программы в терминах n - многочлен степени не более 10. Многочлен должен быть записан обычным способом, то есть подобные слагаемые должны быть приведены, слагаемое с большей степенью должно предшествовать слагаемому с меньшей степенью, слагаемые с коэффициентом 0 не записываются, множители 1 не записываются. Общий вид второй строки "Runtime = a*n^10+b*n^9+...+i*n^2+j*n+k". Если время выполнения нулевое, нужно вывести "Runtime = 0". За строкой с многочленом должна следовать пустая строка.

Ограничения: вложенность операторов LOOP не превышает 10, размер входного файла не более 2 Кбайт, коэффициенты многочлена в ответе не превышают 50 000.

Последовательность Фибоначчи

Рекуррентные последовательности Вывод формулы

{F_k} - бесконечная последовательность целых чисел, которая удовлетворяет условию Фибоначчи F_k = F_k - 1 + F_k - 2 (для любого целого k). Даны i, F_i, j, F_j, n (i <> j). Найти F_n. Пример части последовательности:

k	-2	-1	0	1	2	3	4	5	6
F_k	-5	4	-1	3	2	5	7	12	19

Ограничения: -1000 <= i, j, n <= 1000, -2 000 000 000 <= F_k <= 2 000 000 000 (k = min(i, j, n) ... max(i, j, n)).

Входные данные
В первой строке находятся числа i, F_i, j, F_j, n.

Выходные данные
Вывести одно число F_n.

Двойная решетка

Две бесконечные равномерные прямоугольные решётки заданы размерами ячеек x₁ y₁ и x₂ y₂. Решётки расположены на плоскости параллельно друг другу и координатным осям так, что смещение одного из узлов второй решётки относительно узла первой составляет Dx по горизонтали и Dy по вертикали. В результате наложения образуется новая, "составная" решётка с более мелкими ячейками различного размера. Требуется вывести в порядке возрастания все различные площади ячеек составной решётки.

Ограничения: 1 <= x₁, y₁, x₂, y₂ <= 100, 0 <= D_x < x₁, 0 <= D_y < y₁, все числа целые.

Входные данные
В первой строке находятся числа x₁, y₁, x₂, y₂, D_x, D_y, разделённые пробелами.

Выходные данные
В первой строке вывести N - количество получившихся площадей, в следующих N строках - сами площади.

Гирлянда

Бинарный поиск значения функции Вывод формулы

Гирлянда состоит из N лампочек на общем проводе. Один её конец закреплён на заданной высоте A мм (H₁ = A). Благодаря силе тяжести гирлянда прогибается: высота каждой неконцевой лампы на 1 мм меньше, чем средняя высота ближайших соседей (H_i = (H_i - 1 + H_i + 1) / 2 - 1 для 1 < i < N). Требуется найти минимальную высоту второго конца B (B = H_N) при условии, что ни одна из лампочек не должна лежать на земле (H_i > 0 для 1 <= i <= N).

Ограничения: 3 <= N <= 1000 - целое, 10 <= A <= 1000 - вещественное.

Входные данные
В первой строке находятся два числа, N и A.

Выходные данные
Вывести одно вещественное число B с двумя знаками после запятой.

Волшебная последовательность

Вывод формулы Конструктив

Недавно Петя научился считать. Он тут же заметил, что число 2 обладает замечательным свойством - 2 + 2 = 2 × 2. Его старший брат Ваня тут же объяснил ему, что дело не в двойке.

"Дело в том, что последовательность 2, 2 - волшебная," - сказал Пете Ваня. - "Волшебная последовательность - это такая последовательность натуральных чисел, что сумма ее членов равна их произведению. Например последовательность 1, 2, 3 - тоже волшебная."

Петя тут же сложил 1, 2 и 3, потом перемножил их и обрадовался.

Теперь Петя хочет найти более длинные волшебные последовательности. Помогите ему!

Входные данные
В первой строке входных данных содержится целое число N (2 <= N <= 100).

Выходные данные
Выведите любую волшебную последовательность длины N. Разделяйте числа пробелами. Члены последовательности не должны превышать 10⁹. Если такой волшебной последовательности длины N не существует, выведите единственное число - "-1".

Коля решает уравнение

Помогите Коле решить уравнение Уравнение. a / x²+ b / x + c = 0

Входные данные
Вводятся три числа a, b, c, разделенные пробелами. Все числа целые и по модулю не превосходят 100.

Выходные данные
Требуется вывести все различные корни уравнения (по одному разу в любом порядке). Выведенные корни должны отличаться от точного ответа не более, чем на 0,01. Если уравнение не имеет корней, вывести No solution.

Если уравнение имеет больше 10 корней, вывести Many solutions.

Сложное уравнение

Решить в целых числах уравнение ( ax + b ) : ( cx + d ) = 0.

Входные данные
Вводятся 4 числа: a, b, c и d; c и d не равны нулю одновременно.

Выходные данные
Необходимо вывести все целочисленные решения, если их число конечно, “NO” (без кавычек), если целочисленных решений нет, и “INF” (без кавычек), если их бесконечно много.

Красивый шарф

Алиса решила поздравить своего друга с началом нового учебного года. Впереди холодная осень, поэтому она решила связать для него собственными руками шарф.

Незаметно для друга Алиса узнала, что ему большего всего нравятся $k$ различных цветов. Алиса приняла решение связать шарф размером $n \times m$, в котором будут чередоваться полоски различных цветов. Её друг никогда не ищет легких путей, поэтому она решила, что шарф с горизонтальными или вертикальными полосками покажется ему слишком <<примитивным>>. Алиса решила, что полоски определённо должны быть диагональными!

Закончив вязать шарф, Алиса вспомнила, что один из $k$ цветов её друг считает особенным! Это цвет $c$, который по его мнению приносит школьникам удачу на олимпиадах по информатике. И Алисе стало невероятно интересно, сколько фрагментов шарфа имеют именно такой цвет. Шарф получился очень большим, Алиса очень устала, пока его вязала, поэтому сама она уже не может ответить на этот вопрос и просит вас о помощи...

Более формально шарф можно представить в виде таблицы размером $n \times m$, каждая клетка которой покрашена в один из $k$ цветов. Цвета нумеруются от $1$ до $k$.

Первая строка таблицы покрашена в цвета $1$, $2$, ..., $k$, $1$, $2$, ..., $k$ и т.д. Каждая следующая строка получена из предыдущей сдвигом влево на одну клетку. Таким образом, таблица состоит из диагональных полос.

При $n = 4$, $m = 8$ и $k = 3$ таблица будет иметь следующий вид:

По данным числам $n$, $m$, $k$ и $c$ определите, сколько всего клеток покрашено в цвет $c$.

Формат входных данных
Первая строка входных данных содержит натуральное число $n$ — ширину шарфа.

Вторая строка входных данных содержит натуральное число $m$ — длину шарфа.

Третья строка входных данных содержит натуральное число $k$ — количество любимых цветов друга Алисы.

Числа $n$, $m$ и $k$ не превосходят $10^9$.

Четвёртая строка входных данных содержит натуральное число $c$ — номер особенного цвета ($1\le c \le k$).

Формат выходных данных
Программа должна вывести одно целое число — количество клеток шарфа, которые покрашены в цвет $c$.

Обратите внимание, что ответ в этой задаче может превышать возможное значение 32-битной целочисленной переменной, поэтому необходимо использовать 64-битные целочисленные типы данных (тип int64 в языке Pascal, тип long long в C++, тип long в Java и C#).

Замечание

Картинка соответствует примеру из условия. Шарф имеет размеры $4\times8$ и состоит из клеток трёх цветов. В цвет $1$ покрашены $11$ клеток.

Речной бой

Поле в игре <<Речной бой>> представляет собой полоску длины $n$ клеток и шириной в одну клетку. Где-то на поле расположен корабль из $k$ клеток ($k \le n$). Какое наименьшее число выстрелов необходимо, чтобы гарантированно потопить корабль? После каждого выстрела сообщается его результат: <<мимо>>, <<ранен>> или <<убит>>.

Формат входных данных
Первая строка входных данных содержит целое число $n$ ($1 \le n \le 10^9$).

Вторая строка входных данных содержит целое число $k$ ($1 \le k \le n$).

Формат выходных данных
Выведите одно целое число — количество выстрелов.

Замечание

В первом примере поле состоит из $n=4$ клеток, корабль имеет длину $k=2$. Первый выстрел нужно сделать в одну из двух центральных клеток. Если результатом будет <<ранен>>, то вторая клетка корабля находится в одной из двух соседних клеток, и за два выстрела мы гарантированно потопим корабль Если результатом первого выстрела будет <<мимо>>, то корабль занимает две единственные свободные смежные клетки, которые тоже можно подбить двумя выстрелами. Итого нужно 3 выстрела. Двух выстрелов недостаточно, так как всегда есть шанс промахнуться первым выстрелом.

Пара-тройка конфет

У Алисы сегодня день рождения, и она хочет угостить своих одноклассников конфетами. В магазине, в который она успеет зайти перед школой, есть сладости двух видов: шоколадные и карамельные. Они продаются наборами по 3 штуки, причем в упаковке есть конфеты каждого из двух видов (то есть в одной упаковке лежат две конфеты одного вида и одна конфета другого вида). По внешнему виду упаковки нельзя понять, какие конфеты лежат внутри.

Чтобы никого не обидеть, всем в классе нужно раздать конфеты одного вида, а оставшиеся девочка заберёт домой. Алисе нужно собираться в школу, поэтому она попросила вас посчитать, какое минимальное число упаковок нужно купить, чтобы конфет хватило на всех.

Формат входных данных
В единственной строке задано число $n$ ($1 \le n \le 10 ^ 9$) — количество человек в классе.

Формат выходных данных

Выведите единственное число — количество упаковок, которое должна купить Алиса.

Замечание

В первом примере Алиса купит две упаковки с конфетами. В первой упаковке лежат 2 конфеты одного вида, и 1 конфета другого вида. Если вторая упаковка будет такая же, как и первая, то у Алисы окажется 4 конфеты одного вида и 2 конфеты другого вида. Если вторая упаковка будет отличаться от первой, то у Алисы будет по 3 конфеты каждого вида. В любом случае у Алисы найдётся 3 конфеты одного вида.

Как видно из первого примера, для того, чтобы гарантированно получить 4 конфеты одного вида, недостаточно купить две упаковки.

Новый год в детском саду

В детском саду готовятся к новому году, и воспитательница решила организовать детей, чтобы они подготовили украшения и отправили их Санте Клаусу для украшения своих оленей.

Дети с интересом восприняли идею и вырезали из бумаги $a$ звездочек и $b$ снежинок. Теперь они планируют отправить их Санте Клаусу по почте. Им так понравились вырезанные ими украшения, что они, возможно, решат оставить себе часть. Таким образом, дети могут отправить Санте $x$ звездочек и $y$ снежинок, где $0 \le x \le a$ и $0 \le y \le b$. Чтобы Санта не расстроился, дети должны отправить ему хотя бы одно украшение. То есть должно выполняться также условие $x + y > 0$.

Чтобы все олени выглядели красиво, на каждом должно оказаться одинаковое количество украшений. Известно, что у Санты $n$ оленей, поэтому если будут отправлены $x$ звездочек и $y$ снежинок, величина $x+y$ должна делиться на $n$.

Воспитательница заинтересовалась: а сколько есть всего различных способов составить посылку Санте Клаусу. Два способа считаются различными, если в них отличается количество звездочек или количество снежинок.

Формат входных данных

В одном наборе входных данных содержатся несколько тестов. Каждый тест следует решить независимо.
Первая строка входных данных содержит целое число $t$ — количество тестов ($1 \le t \le 10^5$).

Следующие строки описывают тесты, по одному на строке. Описание теста состоит из трех целых чисел $n$, $a$ и $b$ — количество оленей у Санты, количество звездочек и количество снежинок, вырезанных детьми ($4 \le n \le 10^9$; $0 \le a, b \le 10^9$).

Формат выходных данных
Выведите $t$ чисел. Для каждого теста выведите одно число: количество способов составить посылку для Санты Клауса.

Замечание
В первом тесте у Санты $4$ оленя, а дети вырезали $2$ звездочки и $2$ снежинки. Здесь подходит только один набор — нужно отправить все вырезанные украшения.

Во втором тесте у Санты также $4$ оленя, но дети вырезали $4$ звездочки и $4$ снежинки. Здесь подходит 6 наборов: 0 звездочек и 4 снежинки, 1 звездочка и 3 снежинки, 2 звездочки и 2 снежинки, 3 звездочки и 1 снежинка, 4 звездочки и 0 снежинок, а также 4 звездочки и 4 снежинки.

Ёлочки

Вывод формулы

На сегодняшнем уроке ИЗО весь класс рисует зимний лес. К сожалению, с передачей художественных образов изобразительными методами дела у Тимофея обстоят из рук вон плохо. Но хоть что-то нарисовать нужно, поэтому Тимофей рисует елочки по клеточкам.

Каждая елочка имеет свою красоту, равную количеству ветвей с одной стороны ствола и (так уж совпало) длине самой нижней ветви. Каждая следующая верхняя ветка на одну клетку короче предыдущей. Между ветвями, а также под самой нижней и над самой верхней ветвями, находится ствол дерева шириной ровно в одну клетку. На рисунке вы видите елки кисти Тимофея красотой от 0 до 5 включительно.

Поскольку с математическими формулами Тимофей дружит гораздо сильнее, чем с акварельными красками, его заинтересовал вопрос, какую площадь занимает клетчатая елка определенной красоты. Тимофей без труда решил эту задачу. А вы сможете?

Входные данные

Программа получает на вход одно целое число n — красоту ёлки (0 ≤ n ≤ 2×10⁹).

Обратите внимание, что при данных ограничениях ответ может быть больше, чем возможное значение 32-битной целочисленной переменной, поэтому необходимо использовать 64-битные числа (тип int64 в языке Pascal, тип long long в C и C++, тип long в Java и C#).

Выходные данные

Программа должна вывести одно целое число — площадь елки красоты n.

Расклейка афиш

НОД и алгоритм Евклида Вывод формулы

С утра по Васюкам ходил высокий худой старик в золотом пенсне и в коротких, очень грязных, испачканных клеевыми красками сапогах. Он наклеивал на стены рукописные афиши.

И.Ильф, Е.Петров. <<Двенадцать стульев>>.

Ипполит Матвеевич Воробьянинов ходит вдоль улицы из $n$ домов, пронумерованных числами от $1$ до $n$, и расклеивает афиши. Сначала он наклеил афиши на каждый дом, номер которого делился без остатка на $a$. Поскольку афиш осталось еще много, вторым проходом он наклеил афиши на каждый дом, номер которого делился без остатка на $b$. При этом, если на доме уже была наклеена афиша, новую Воробьянинов не клеил. Сколько всего афиш расклеил бывший предводитель дворянства?

Формат входных данных
Три строки содержат три натуральных числа: $n$ — количество домов на улице, $a$ и $b$ — выбранные Воробьяниновым числа. Все числа не превосходят $10^9$.

Формат выходных данных
Выведите одно неотрицательное целое число — количество расклеенных афиш.

Замечание
В первом примере на улице $10$ домов. Ипполит Матвеевич первым проходом расклеил пять афиш на дома, номера которых делятся на $2$, то есть на дома с номерами $2$, $4$, $6$, $8$, $10$. Вторым проходом он расклеил две афиши на дома, номера которых делятся на $3$, то есть на дома с номерами $3$ и $9$. Дом номер $6$ он пропустил — на нем афиша уже висит. Всего наклеено $7$ афиш.

Во втором примере Воробьянинов не наклеит ни одной афиши.

Пары

Задано четыре числа: $a$, $b$, $c$ и $d$. Требуется разбить их на две пары, чтобы сумма произведений в этих парах была максимальна.

Например, если заданы числа 2, 3, 4 и 5, то оптимально разбить их на пары $(2, 3)$ и $(4, 5)$, в этом случае искомая сумма равна $2 \times 3 + 4 \times 5 = 26$.

Формат входных данных
На вход подаются четыре числа: $a$, $b$, $c$ и $d$. Все числа по модулю не превышают 1000.

Формат выходных данных
Выведите искомую максимальную сумму.

Смешивание напитков

Бинарный поиск по ответу Дерево отрезков, RSQ, RMQ Вывод формулы

После тяжелого контеста бывает полезно выпить немного кофе. У настоящих программистов есть множество различных сортов кофе, которые постепенно добавляются в одну кружку. При этом мы будем рассматривать кофе с определенной особенностью: разные сорта кофе держатся в кружке <<слоями>> и не перемешиваются.

Напиток из таких сортов кофе можно описать следующим образом: всего в кружку налито $n$ сортов, $i$-й сорт характеризуется уровнем крепости $p_i$ и высотой слоя, который он занимает в кружке, $h_i$. При этом если $i < j$, то слой кофе $i$-го сорта находится ниже кофе $j$-го сорта. Также известно, что высота кружки равна $\sum\limits_{i=1}^n h_i$, то есть верхний край самого верхнего слоя кофе находится ровно на уровне верхней границы кружки.

Для разнообразия иногда хочется получить из такого <<коктейля>> напиток определенного суммарного уровня крепости. Суммарный уровень крепости определяется как среднее взвешенное уровней налитых в кружку сортов, то есть как \[P = \frac{\sum\limits_{i=1}^n p_i \cdot h_i}{\sum\limits_{i=1}^n h_i} \text{.}\]

Чтобы как-то изменять $P$, можно

выбрать трубочку произвольной высоты $h$;
один или более раз выполнить следующее: погрузить ее в напиток на любую глубину от $0$ до $h$ включительно относительно верхнего края кружки (не относительно текущего уровня жидкости) и отпить произвольное (не обязательно целое) количество кофе с того уровня, на который попал нижний конец трубочки.

При выпивании какого-то количества кофе из одного слоя высота этого слоя уменьшается на соответствующую величину, а все верхние слои опускаются на ту же величину вниз.

Ваша задача — ответить на запросы вида: можно ли из текущего напитка сделать напиток крепости $t_i$, и если можно, то какая минимальная высота трубочки для этого понадобится. Поскольку идеально точную необходимую высоту трубочки вычислить может быть сложно, достаточно определить минимальное количество верхних слоев кофе, достаточное, чтобы, отпив какое-то количество кофе из некоторых из них, можно было добиться суммарной крепости напитка $t_i$.

Формат входных данных
В первой строке ввода даны два целых числа $n$ и $q$ — количество слоев кофе в кружке и количество запросов ($1 \le n, q \le 2 \cdot 10^5$).

Следующие $n$ строк содержат по два целых числа $p_i$ и $h_i$ — уровень крепости и высоту $i$-го снизу кружки слоя кофе ($1 \le p_i, h_i \le 10^9$). Гарантируется, что сумма $p_i \cdot h_i$ по всем $i$ не превосходит $10^{18}$.

В $i$-й из следующих $q$ строк дано единственное целое число $t_i$, определяющее $i$-й запрос ($1 \le t_i \le 10^9$).

Формат выходных данных
Выведите $q$ строк, в $i$-й из которых содержится единственное целое число от $0$ до $n$ — ответ $i$-й запрос. Если для какого-то запроса ответ такой, что нельзя добиться требуемого уровня крепости, выведите в качестве ответа на этот запрос число $-1$.

Замечание
Для примера из условия:

В первом запросе, чтобы получить напиток крепости $1$, достаточно выпить верхние два слоя кофе.
Во втором запросе достаточно выпить часть кофе со второго сверху слоя.
В третьем запросе понадобится выпить первый и третий слой кофе.
В четвертом запросе невозможно добиться уровня крепости $4$.

Старт олимпиады

Пандемия охватила все страны мира, и Берляндия не стала исключением. Даже на Всеберляндской олимпиаде по информатике были введены противовирусные меры.

Всего в олимпиаде участвуют $n$ человек, и, чтобы соблюсти все предписания руководства, жюри олимпиады решило приглашать участников на тур по одному с интервалом $x$ минут. Таким образом первый участник начнёт тур в момент времени $0$, второй участник начнёт тур в момент времени $x$, третий — в момент времени $2 \cdot x$ и так далее.

Несмотря на разное время начала, длительность тура для каждого участника составляет ровно $t$ минут. Из-за этого некоторые участники заканчивают писать тур раньше остальных. Когда участник заканчивает писать тур, величина недовольства организацией олимпиады для этого участника равна числу других участников, которые в текущий момент времени еще пишут или только начинают писать тур, но еще не закончили его.

Помогите организаторам олимпиады выяснить, чему равно суммарное недовольство всех участников олимпиады.

Формат входных данных
В первой строке вводится единственное целое число $n$ ($1 \le n \le 2 \cdot 10^9$) — число участников олимпиады.

Во второй строке вводится единственное целое число $x$ ($1 \le x \le 2 \cdot 10^9$) — интервал в минутах между временами начала тура для участников.

В третей строке вводится единственное целое число $t$ ($1 \le t \le 2 \cdot 10^9$) — длительность тура.

Формат выходных данных
В единственной строке выведите одно число — суммарное недовольство всех участников олимпиады.

Примечание

В первом примере первый участник начнёт писать тур в момент времени $0$ и закончит в момент времени $5$. К этому времени второй и третий участники уже начнут писать тур, поэтому недовольство первого участника будет равно $2$.

Второй участник начнёт писать в момент времени $2$ и закончит в момент времени $7$. К этому моменту третий и четвёртый участники уже начнут писать тур, поэтому недовольство второго будет равно $2$.

Третий участник начнёт писать тур в момент времени $4$ и закончит в момент времени $9$. К этому времени четвёртый участник уже начнёт писать тур, поэтому недовольство третьего будет равно $1$.

Четвёртый участник начнёт писать тур в момент времени $6$ и закончит в момент времени $11$. В момент времени $9$ уже никто не будет писать тур, поэтому недовольство четвёртого будет равно $0$.

Таким образом, суммарное недовольство всех участников будет равно $2+2+1+0=5$.

Во втором примере первый участник начнёт писать тур в момент времени $0$ и закончит в момент времени $2$. К этому моменту второй участник уже будет писать тур, а третий участник как раз начнёт в момент времени $2$. Поэтому недовольство первого участника будет равно $2$.

Второй участник начнёт в момент времени $1$ и закончит в момент времени $3$. К этому моменту только третий участник будет всё ещё писать тур.

Таким образом, суммарное недовольство всех участников будет равно $2+1=3$.

Разноцветные диагонали

Задача на реализацию Вывод формулы

Миша увлекается компьютерной графикой. Он хочет нарисовать на экране квадрат размером $n\times n$ пикселей разными цветами.

Монитор Миши поддерживает 26 цветов. Для обозначения цветов будем использовать строчные буквы латинского алфавита от <<a>> до <<z>>. Миша хочет нарисовать каждый пиксель некоторым цветом, который зависит от расстояния от пикселя до ближайшей диагонали.

А именно, клетки на диагоналях квадрата он хочет нарисовать цветом <<a>>, соседние с ними клетки — цветом <<b>>, соседние с ними, но еще не покрашенные — цветом <<c>>, и так далее. После цвета <<z>> Миша снова переходит к цвету <<a>>.

По заданному $n$ выведите картинку, которая получится у Миши.

Формат входных данных
Входные данные содержат одно целое число $n$ ($1 \le n \le 100$).

Формат выходных данных
Выведите $n$ строк по $n$ символов — картинку, которая получится у Миши.

Номера по диагонали

Пронумеруем клетки прямоугольной таблицы с $r$ строками и $c$ столбцами, начиная с левого верхнего угла. Нумерацию будем вести по диагоналям, идущим справа-сверху налево-вниз, клетки одной диагонали будем нумеровать сверху вниз.

Например, для таблицы $3 \times 5$ клетки будут пронумерованы следующим образом:

1	2	4	7	10
3	5	8	11	13
6	9	12	14	15

Задано $q$ номеров клеток. Для каждого номера найдите, в какой клетке он находится.

Формат входных данных
Первая строка ввода содержит три целых числа: $r$, $c$ и $q$ ($1 \le r, c \le 10^9$, $1 \le q \le 100$).

Вторая строка содержит $q$ целых чисел $1 \le n_1 < n_2 < \ldots < n_q \le r\cdot c$.

Формат выходных данных
Выведите $q$ строк. Для каждого числа $n_i$ выведите два числа: номер строки и номер столбца, где находится соответствующая клетка. Строки нумеруются с 1 сверху вниз. Столбцы нумеруются с 1 слева направо.

Конфеты для первоклассников

Старшеклассники Андрей и Аня планируют прийти на празднование 1 сентября у первоклассников. Они решили принести конфеты, чтобы раздать ребятам. Им известно, что на празднике будет $n$ первоклассников. Каждый из старшеклассников готов купить от $a$ до $b$ конфет, включительно. Они хотели бы купить в сумме такое число конфет, чтобы их можно было поделить между всеми первоклассниками поровну. Если же такое число конфет купить не получается, то они хотят, чтобы после деления поровну между первоклассниками осталось как можно меньше конфет.

Если есть несколько способов выбрать, сколько конфет купят Андрей и Аня, они решили выбрать такой способ, в котором Андрей купит как можно больше конфет. А если по прежнему есть несколько способов, то чтобы Аня купила как можно больше конфет. Помогите Андрею и Ане понять, сколько конфет нужно купить каждому из них.

Формат входных данных
На ввод подаются три натуральных числа, по одному на строке: $n$ — число первоклассников, $a$ и $b$ — минимальное и максимальное число конфет, которое согласен купить каждый из старшеклассников ($1 \le n \le 10^9$, $1 \le a \le b \le 10^9$).

Формат выходных данных
Выведите два целых числа $x$ и $y$ — число конфет, которые купят Андрей и Аня, соответственно.

Лестница из чисел

Валентин выписывает натуральные числа, начиная с 1, в виде лестницы: на первой строке он пишет одно число, на второй — два, на третьей — три, и так далее.

После этого он стирает все числа на каждой строке, кроме первых $k$. Если в строке меньше $k$ чисел, он оставляет их все.

Заданы целые числа $a$ и $b$, а также число $k$. Выведите строки с $a$-й по $b$-ю, которые получились у Валентина.

Формат входных данных

На ввод подаются три строки: первая содержит число $a$, вторая содержит число $b$, третья содержит число $k$ ($1 \le a \le b \le 10^9$, $b - a \le 100$, $1 \le k \le 100$).

Формат выходных данных
Выведите строки с $a$-й по $b$-ю, которые получились у Валентина. Числа в строках разделяйте пробелами.

Класс

В классе, в котором ведет уроки географии Иван Петрович, $n$ мальчиков и $m$ девочек. Иван Петрович рассаживает учеников по по два человека за парту, кроме, возможно, одной парты, за которую приходится посадить одного ученика, если число учеников нечётно.

Иван Петрович заметил, что если за одной партой сидят два мальчика или две девочки, они отвлекаются во время урока. А если за одной партой сидят мальчик и девочка, или за партой сидит один ученик, то они слушают урок внимательно.

Помогите Ивану Петровичу выяснить, какое максимальное число учеников может внимательно слушать урок, если он правильно рассадит их за парты.

Формат входных данных
Первая строка ввода содержит целое число $n$ ($0 \le n \le 30$).

Вторая строка ввода содержит целое число $m$ ($0 \le m \le 30$).

Формат выходных данных
Выведите одно целое число: максимальное количество учеников, которые могут внимательно слушать урок.

Примечание
В примере Иван Петрович может посадить за 3 парты мальчика и девочку, и за четвертую парту двух мальчиков, тогда 6 учеников будут внимательно слушать урок.

Устный счет

реализация Вывод формулы

Отвлечемся от задач про программистов и перенесемся в совершенно обыкновенные ясли, где мальчик Вова (3 годика) практикуется в устном счете, а если точнее — в вычислении арифметических выражений по модулю $10^9 + 7$.

Совсем недавно Вова придумал длинное и очень красивое арифметическое выражение. Выражение состяло из $n$ целых неотрицательных чисел, меньших $10^9 + 7$, и знаков сложения и умножения между ними. Первым же делом он вычислил это выражение по модулю $10^9 + 7$, после чего выписал само выражение и результат на лист бумаги. Все числа он выписал без ведущих нулей.

Пока шел тихий час, Вова спал, а хулиганы стерли несколько цифр в выражении и заменили их на другие. Менять знаки или результат вычисления выражения хулиганы не решились, даже для них это слишком низко. Когда Вова проснулся, он обнаружил рядом с его листочком ластик и карандаш. У Вовы есть принципы — если хулиганы изменили не более двух цифр, то он их простит, иначе они будут наказаны по всей строгости ясельных законов.

К сожалению, чтобы понять, сколько цифр изменили хулиганы, Вове явно понадобится ваша помощь. Определите, могло ли данное выражение быть получено из верного равенства заменой не более двух цифр, и если да, то в каких числах и какие цифры были изменены.

Формат входных данных
Единственная строка входного файла содержит выражение, которое обнаружил Вова у себя на листке. Выражение состоит из двух частей, разеделенных знаком ‘=’.

Первая часть содержит $n$ целых неотрицательных чисел, разделенных знаками сложения (‘+’) и умножения (‘*’) ($1 \le n \le 10^5$). Вторая часть — целое неотрицательное число, означающее результат вычисления выражения.

Числа и все знаки разделяются одним пробелом. Гарантируется, что все числа строго меньше $10^9 + 7$ и записаны без ведущих нулей.

Формат выходных данных
В случае, если данное выражение не может быть получено из верного равенства заменой не более двух цифр, выведите <<NO>>.

В противном случае в первой строке выведите <<YES>>. На следующей строке выведите целое число $k \leq 2$ — количество чисел, которые были изменены.

В следующих $k$ строках выведите по два числа — позицию измененнного числа в выражении (от $1$ до $n$) и его исходное значение.

Суммарно должно быть изменено не более двух цифр. В процессе замены в числах не должны появиться ведущие нули и числа должны остаться меньше $10^9 + 7$. Если существует несколько вариантов ответа, выведите любой из них.

SpamGPT-4

Вывод формулы Вычисление по заданной формуле Задачи на моделирование

Для тестирования отказоустойчивости двух лучших спам-ботов компании <<LinkedOut>> было решено настроить их на взаимодействие друг с другом и посмотреть, как долго они проработают в таком режиме без ошибок.

После старта оба бота отправляют друг другу по одному сообщению, после чего первый бот отправляет новое сообщение каждые $a$ секунд, а второй — каждые $b$ секунд. Иными словами, первый бот отправляет новое сообщение на секундах $0$, $a$, $2a$, и так далее, а второй — на секундах $0$, $b$, $2b$, и так далее.

Помимо этого, оба бота отправляют ответ на каждое полученное сообщение ровно спустя секунду после получения. Сообщения отправляются без задержки и приходят моментально после отправки. В частности, если в момент времени $t$ первый бот отправит сообщение, то в момент времени $t + 1$ он получит ответ на него, а в момент времени $t + 2$ — отправит свой ответ. Также боты отлично выполняют параллельные задачи параллельно и могут отправлять любое количество сообщений одновременно (например, если надо одновременно отправить новое сообщение и ответы на полученные).

Вам даны параметры ботов $a$ и $b$. Определите, сколько сообщений каждый из ботов должен будет отправить к моменту времени $T$, если они оба будут работать без ошибок.

Формат входных данных
В единственной строке ввода через пробел даны три целых числа $a$, $b$ и $T$ — периодичности отправки новых сообщений и время работы ботов ($1 \le a, b, T \le 10^9$).

Формат выходных данных
Выведите через пробел два целых числа — количество сообщений, отправленных к моменту $T$ первым и вторым ботом, соответственно. Если какие-то сообщения должны быть отправлены в $T$-ю секунду, их тоже следует учесть в ответе.

Замечание
Пояснение ко второму примеру:

в момент времени $0$ первый бот отправляет второму сообщение A, а второй первому — B;
в момент времени $1$ боты отправляют друг другу ответы на полученные на нулевой секунде сообщения: первый второму B(1) (ответ на B), а второй первому — A(1);
в момент времени $2$ новых сообщений не появляется, и они отправляют друг другу ответы на полученные на первой секунде сообщения: A(2) (ответ на A(1)) и B(2);
в момент времени $3$ будут отправлены B(3) и A(3), и одновременно с этим второй бот отправит первому новое сообщение C;
в момент времени $4$ первый отправит второму новое сообщение D, C(1) (ответ на C) и A(4), а второй первому — B(4);
в момент времени $5$ новых сообщений нет, боты отправляют друг другу ответы на полученные секунду назад сообщения;
в момент времени $6$ будут отправлены ответы на сообщения с предыдущей секунды, а также второй бот отправит первому новое сообщение E.

Итого, первый бот отправил: A, B(1), A(2), B(3), D, C(1), A(4), B(5), D(2), C(3) и A(6), всего 11 сообщений.

Второй бот тоже отправил ровно 11 сообщений: B, A(1), B(2), C, A(3), B(4), D(1), C(2), A(4), E и B(6).

Игра в напёрстки

Вывод формулы

В свободное время Бомбослав любит наблюдать из окна как ребята во дворе играют “на интерес” в известную игру в напёрстки. Для игры требуется два человека, ведущий и игрок. Ведущий берёт три одинаковых непрозрачных напёрстка и прячет под один из них шарик. Затем он несколько раз меняет некоторые пары напёрстков местами, после чего игрок должен угадать, под каким напёрстком сейчас находится шарик.

Бомбослав заметил, что ребята во дворе не очень изобретательны в своих действиях, и всегда меняют местами левый напёрсток со средним на нечётных действиях (то есть на первом, третьем, пятом и так далее) и средний с правым на чётных действиях (то есть на втором, четвёртом и так далее).

Пронумеруем напёрстки от $0$ до $2$ слева направо. То есть левый напёрстком имеет номер $0$, средний номер $1$, а правый номер $2$. Бомбослав не успел увидеть начало игры, но посчитал, что ведущий совершил $n$ действий и в итоге шарик оказался под напёрстком $x$. Под каким напёрстком находился шарик в самом начале?

Формат входных данных
В первой строке входных данных записано одно цело число $n$ ($1 \leq n \leq 2 \cdot 10^9$) — количество действий, совершённых ведущим.

Во второй строке записано одно целое число $x$ ($0 \leq x \leq 2$) — номер напёрстка, под которым оказался шарик через $n$ действий.

Формат выходных данных
Выведите одно целое число от $0$ до $2$, означающее номер напёрстка, под которым находился шарик в самом начале.

Замечание

В первом примере шарик изначально мог лежать под средним напёрстком и ведущий совершил четыре действия.

Первым действием ведущий поменял местами левый и средний напёрстки. В результате шарик оказался под левым напёрстком.
Вторым действием ведущий поменял местами средний и правый напёрстки. Шарик остался под левым напёрстком.
Третьим действием ведущий снова поменял местами левый и средний напёрстки. В результате шарик снова оказался посередине.
Последним четвёртым действием ведущий опять поменял местами средний и правый напёрстки и шарик оказался под правым напёрстком.

В данной задаче 50 тестов, помимо тестов из условия, каждый из них оценивается в 2 балла. Результаты работы ваших решений на всех тестах будут доступны сразу во время соревнования.

Решения, верно работающие при $n \leq 100\,000$ будут набирать не менее 50 баллов.

Генераторы квадратов

Перебор Вывод формулы реализация

Множество $A = \{a_1, a_2, \ldots, a_k\}$ различных натуральных чисел с суммой $a_1+a_2+\ldots+a_k=n$ называется генератором квадратов, если сумма любых $k-1$ элементов этого множества является полным квадратом целого числа.

Например, множество $\{1, 22, 41, 58\}$ является генератором квадратов, так как $1 + 22 + 41 = 64 = 8^2$, $1 + 22 + 58 = 81 = 9^2$, $1 + 41 + 58 = 100 = 10^2$, $22 + 41 + 58 = 121 = 11^2$.

По заданным $n$ и $k$ постройте множество из $k$ различных натуральных чисел с суммой $n$, которое является генератором квадратов, либо выясните, что такого нет.

Формат входных данных
На ввод подаются два целых числа $n$ и $k$ ($2 \le n \le 200\,000$, $2 \le k \le 30$).

Формат выходных данных
Если искомый генератор квадратов существует, выведите <<YES>> на первой строке, а на второй строке выведите $k$ натуральных чисел "— искомое множество.

Если генератора квадратов с заданными параметрами не существует, выведите <<NO>>.

Граничные клетки

Вывод формулы

У Ани есть клетчатый листок бумаги, на котором она нарисовала прямоугольник размером $m \times n$.

После этого она раскрасила клетки прямоугольника, которые лежат на его границе.

Сколько клеток раскрасила Аня?

Формат входных данных

На первой строке ввода задано целое число $m$ ($1 \le m \le 10^8$).

На второй строке ввода задано целое число $n$ ($1 \le n \le 10^8$).

Формат выходных данных
Выведите одно целое число — сколько клеток раскрасила Аня.

В этой задаче 10 тестов, каждый оценивается независимо в 10 баллов.

Шлюзы

Вывод формулы Бинарный поиск в массиве Задача на реализацию

Участникам, использующим язык Python3, рекомендуется отправлять решения на проверку с использованием интерпретатора PyPy3.

Недавно в Диваново построили огромную шлюзовую систему. Всего было построено $n$ шлюзов, $i$-й из них имеет объем $v_i$ литров. Изначально все шлюзы пусты. В каждый шлюз ведет труба, при открытии которой в шлюз будет поступать по $1$ литру воды в секунду. Исходно все трубы закрыты.

Шлюзовая система устроена так, что если доливать воду в $i$-й шлюз сверх его объема, она будет моментально моментально переливаться в шлюз с номером $i + 1$. Если шлюз c номером $i + 1$ тоже заполнен, вода будет переливаться дальше. Вода из последнего шлюза будет выливаться в озеро.

Рисунок показывает $5$ шлюзов с открытыми трубами к шлюзам $1$ и $3$. Так как шлюзы $1$, $3$ и $4$ уже заполнены, фактически вода идет в шлюзы $2$ и $5$.

Для того, чтобы шлюзы начали функционировать, необходимо заполнить каждый из них. Мэра Дивановской области интересует $q$ независимых запросов. Для каждого запроса предположим, что изначально все шлюзы пусты и все трубы закрыты, затем одновременно открываются несколько труб. Для $j$-го запроса мэр хочет знать, какое минимальное число труб надо включить, чтобы не позже чем через $t_j$ секунд все шлюзы стали заполнены.

Помогите мэру справиться с этой сложной задачей и ответьте на все его запросы!

Формат входных данных
В первой строке вводится одно целое число $n$ ($1 \le n \le 200\,000$) — количество шлюзов.

Во второй строке вводятся $n$ целых чисел $v_1, v_2, \dots, v_n$ ($1 \le v_i \le 10^9$) — объемы шлюзов.

В третьей строке вводится одно целое число $q$ ($1 \le q \le 200\,000$) — число запросов.

В следующих $q$ строках вводится по одному целому числу $t_i$ ($1 \le t_j \le 10^9$) — время, за которое нужно наполнить все шлюзы в $j$-м запросе.

Формат выходных данных
Выведите $q$ чисел, $j$-е из них должно быть равно минимальному числу труб, которое нужно открыть, чтобы наполнить все шлюзы за время $t_j$. Если за это время наполнить всю шлюзы невозможно, выведите $-1$.

В первом примере $6$ запросов:

В запросах $1, 3, 4$ ответ $-1$. Чтобы заполнить первый шлюз нужно подождать $4$ секунды, даже если открыты все трубы.

В шестом запросе можно открыть трубы в шлюзах $1, 3$, и $4$. Тогда через $4$ секунды заполнятся шлюзы $1$ и $4$. Через $1$ секунду $1$ литр воды перельётся в шлюзы $2$ и $5$. Шлюз $3$ будет заполнен своей трубой.

Аналогично во втором запросе можно открыть трубы в шлюзах $1, 3$ и $4$.

В пятом запросе можно открыть трубы в шлюзах с номерами $1, 2, 3, 4$.

Рамка для рисунка

Вывод формулы Задача на реализацию Задачи на моделирование

У Алексея есть набор, который состоит из n палочек длины 1 и m палочек длины 2. Палочки можно соединять между собой, либо выстраивая их в линию, либо под прямым углом.

Алексей хочет собрать из имеющихся палочек рамку прямоугольной формы, чтобы потом вставить в эту рамку лист бумаги и нарисовать красивый пейзаж для мамы на Новый год.

При этом Алексей считает, что чем больше будет площадь прямоугольника, тем значимей будет его подарок. Поэтому ему важно определить максимальную площадь прямоугольника, границу которого можно собрать из имеющихся палочек.

Формат входных данных
Первая строка входных данных содержит целое число n - количество палочек длины 1 (1 ≤ n ≤ 10⁹).
Вторая строка входных данных содержит целое число m - количество палочек длины 2 (1 ≤ n ≤ 10⁹).

Формат выходных данных
В единственной строке выведите единственное целое число - максимальную площадь прямоугольника, который можно сложить из имеющихся палочек. Если из имеющихся палочек невозможно сложить никакой прямоугольник, то выведите число 0.

Замечание
В первом примере есть 5 палочек длины 1. Из них можно сложить квадрат со стороной 1, его площадь равна 1, при этом одна палочка останется.
Во втором примере есть 4 палочки длины 1 и 3 палочки длины 2. Из них можно сложить прямоугольник размера 2 x 3.
В третьем примере есть 3 палочки длины 1, из них невозможно сложить прямоугольник.

Массив сумм

Юля выписала на доску n последовательных натуральных чисел a, a+1, …, a+n−1 и написала под каждым из них сумму его цифр в десятичной записи, под i-м числом было выписано sum_i.

После этого Юра стёр исходные числа и оставил только их суммы цифр. От вас требуется восстановить первое число в исходной последовательности a.

Входные данные

В первой строке содержится одно целое число n (2 <= n <= 100000) - длина исходной последовательности.

В следующей строке содержатся n целых чисел sum₁, sum₂, …, sum_n (1 <= sum_i<= 90) - суммы цифр чисел исходной последовательности.

Гарантируется, что для всех тестов существует подходящее a, такое что 1 <= a <= 10¹⁸.

Выходные данные
Выведите одно число a (1 <= a <= 10¹⁸) - первое число исходной последовательности. В случае, если существует несколько подходящих a, можно вывести любое.

Примечание

В первом тестовом примере сумма цифр 1 равняется 1, сумма цифр 2 равняется 2, сумма цифр 3 равняется 3, что соотносится с массивом sum, поэтому a = 1 подходит под условие задачи.

Во втором тестовом примере сумма цифр 77 равняется 14, сумма цифр 78 равняется 15, сумма цифр 79 равняется 16, сумма цифр 80 равняется 8, сумма цифр 81 равняется 9, что соотносится с массивом sum, поэтому a = 77 подходит под условие задачи.

Примеры

№	Входные данные	Выходные данные
1	3 1 2 3	1
2	5 14 15 16 8 9	77

Олимпиада по выживанию

В некоторой стране каждый год проходит олимпиада по выживанию. В финале участвуют по 4 человека от каждой из n провинций. По результатам соревнования составляется рейтинг, в который входят все 4n участников в порядке убывания баллов, равных баллов у участников не бывает. Дипломами награждаются ровно 50 % лучших участников (то есть если общее число участников было равно m, то награждаются m/2 первых участников из общего рейтинга).
После публикации предварительного рейтинга тренеры команд могут подавать апелляции против каких-то других провинций, обвинив участников из этой провинции в нарушении правил олимпиады. Каждый тренер может не подавать аппеляции или подать апелляцию на одну или несколько команд соперников.
Если жюри удовлетворит апелляцию против команды, то все участники из данной провинции будут дисквалифицированы и удалены из таблицы результатов. При этом общее число количество участников уменьшится на 4, а количество призёров олимпиады уменьшится на 2.
Тренеры команд каждой из провинций хотят улучшить результаты участников из своей провинции (то есть сделать так, чтобы количество участников олимпиады из этой провинции, которые стали призёрами, увеличилось хотя бы на одного). Для этого они планируют подать апелляции против команд других провинцией. Для каждой провинции определите, какое минимальное количество аппеляций должно удовлетворить жюри, чтобы количество участников из этой провинции, награждённых дипломами, увеличилось. Обратите внимание на то, что вы должны дать ответ для каждой провинции независимо, то есть без учёта возможных апелляций, поданных другими командами.

Входные данные
В первой строке входных данных содержится одно целое число n (1 ≤ n ≤ 25000) — количество провинций, участвовавших в олимпиаде. Следующие 4·n строк содержат рейтинг участников олимпиады, в порядке от лучшего участника к худшему. В i-й строке содержится число от 1 до n — номер команды i-го по рейтингу участника олимпиады. Гарантируется, что в списке участников каждое число от 1 до n встречается ровно 4 раза.
Выходные данные
Программа должна вывести n строк. В i-й строке необходимо вывести минимальное число апелляций, которое должно удовлетворить жюри, чтобы количество награждённых дипломами участников из i-й команды увеличилось. Если улучшить результаты i-й команды путём подачи апелляций нельзя, то в i-й строке должно быть записано число −1.

Примеры

№	Входные данные	Выходные данные
1	2 1 1 1 2 2 2 2 1	-1 1
2	2 1 1 2 2 2 2 1 1	-1 -1
3	3 3 3 2 2 1 3 3 2 2 1 1 1	2 1 -1

Замечание
В первом примере из условия в олимпиаде участвовали две команды, и рейтинг участников выглядит так: 1, 1, 1, 2, 2, 2, 2, 1. По предварительному рейтингу дипломами награждаются три участника команды 1 и один участник команды 2. Команда 1 не может улучшить свои результаты, так как если команда 2 будет дисквалифицирована, то дипломы будут выданы всего 2 участникам из 4, но первоначально у команды 1 было 3 диплома. А вторая команда может увеличить количество призёров до 2, подав апелляцию против команды 1.
Во втором примере у обеих команд уже есть по 2 диплома, а при удалении одной из команд останется всего 2 призовых места, то есть при подаче апелляции против другой команды у каждой команды количество дипломов не изменится.
В третьем примере участвовали 3 команды и первоначально дипломами награждались участники из команд 3, 3, 2, 2, 1, 3. Команда 1 может улучшить свои результаты, если подаст две апелляции: против команд 2 и 3. Тогда останется только 4 участника (все они из команды 1), из них дипломами будет награждено двое. Команда 2 может улучшить свои результаты, если подаст одну апелляцию против команды 3. Тогда останется 8 участников и дипломами будут награждены 4 из них: 2, 2, 1, 2, — и у команды 2 станет 3 призёра вместо 2. Команда номер 3 не может улучшить свой результат при помощи апелляций.

Самолёт

В салоне самолёта в одном ряду находится n кресел. Для удобства прохода и обсуживания пассажиров вдоль салона делается один или два прохода. Например, в салоне самолёта Sukhoi Superjet 100 в ряду 5 кресел и один проход (с одной стороны прохода два кресла, с другой стороны — три), а в самых больших современных самолётах — 10 кресел и два прохода (по три кресла по бокам салона у иллюминаторов и четыре кресла между проходами).

Предположим, что в будущем появятся самолёты большего размера, поэтому количество проходов придётся увеличить. Определите, какое минимальное число проходов должно быть в самолёте, в одном ряду салона которого находится n кресел. По бокам салона (у иллюминаторов) может находиться не более 3 кресел, а между двумя проходами — не более 4 кресел. При этом в салоне должен
быть хотя бы один проход.
Входные данные
Программа получает на вход одно натуральное число n, не превосходящее 2 · 10⁹ , — количество кресел в одном ряду салона.
Выходные данные
Программа должна вывести единственное целое число — минимальное количество проходов, которое должно быть в салоне самолёта с n креслами в одном ряду.

Примеры

№	Входные данные	Выходные данные
1	10	2

Спираль

В левом верхнем углу прямоугольного поля размера N ×M сидит Черепашка. Она хочет закрасить некоторые клетки по спирали, закручивающейся к центру, как на рисунке:

Определите, сколько клеток ей придётся закрасить.
Входные данные
Первая строка входных данных содержит число N — высоту прямоугольника, вторая строка содержит число M — ширину прямоугольника. Все числа — целые положительные и не превосходят 2 × 10⁹.
Выходные данные
Программа должна вывести одно целое число — количество клеток, закрашенных Черепашкой.
Обратите внимание, что ответ в этой задаче может превышать возможное значение 32-битной целочисленной переменной, поэтому необходимо использовать 64-битные целочисленные типы данных (тип int64 в языке Pascal, тип long long в C++, тип long в Java и C#).

Примеры

№	Входные данные	Выходные данные
1	5 6	20
2	1 5	5

Заказ в магазине

Решив запастись ручками на весь новый учебный год, Игорь подсчитал, что ему нужно M ручек.
В его любимом интернет-магазине есть удобная функция — он может сразу добавить в заказ упаковку из любого числа ручек от 1 до N. Правда, оказалось, что нельзя добавить в заказ две упаковки одного размера. Например, если Игорю нужно купить M = 12 ручек, а максимальное число ручек в упаковке N = 10, то Игорь может добавить в заказ упаковку из 7 ручек и упаковку из 5 ручек, но не сможет добавить две упаковки из 6 ручек.
Сформируйте заказ на M ручек, используя минимальное число различных упаковок.

Входные данные
Первая строка входных данных содержит число N — максимальный размер одной упаковки (1 ≤ N ≤ 10⁹ ). Вторая строка входных данных содержит целое число M — необходимое количество ручек в заказе (1 ≤ M ≤ 10⁹ ).

Выходные данные
Программа должна вывести одно или несколько чисел от 1 до N — размеры выбранных упаковок в любом порядке. Есть имеется несколько возможных решений, то выведите любое из них. Если решения не существует, необходимо вывести одно число «0».

Примеры

№	Входные данные	Выходные данные
1	10 12	5 7
2	2 5	0

Центральные квадраты

Вывод формулы

Дан прямоугольник из N ×M квадратов. Назовём квадраты на границе прямоугольника крайними. Расстоянием от какого-либо квадрата до края назовём количество перемещений, которое нужно сделать из данного квадрата в соседний по стороне квадрат, чтобы добраться от данного квадрата до крайнего квадрата. Квадраты с максимальным расстоянием до края, будем называть центральными. При этом квадрат может быть одновременно и крайним, и центральным.
На рисунке изображён прямоугольник для N = 7 и M = 8, в каждом квадрате которого записано расстояние от этого квадрата до края. У этого прямоугольника два центральных квадрата.

По данным N и M определите количество центральных квадратов в прямоугольнике.

Примеры

№	Входные данные	Выходные данные
1	7 8	2

Лягушка и кузнечик

В крайних клетках полоски шириной в одну клетку и длиной в N клеток сидят лягушка и кузнечик: лягушка в клетке № 1, кузнечик в клетке № N. Каждую секунду лягушка прыгает в сторону кузнечика, и одновременно кузнечик прыгает в сторону лягушки. Лягушка может прыгать только на две или на три клетки, кузнечик — только на одну или на две клетки. За какое наименьшее время они смогут оказаться в одной клетке?

Входные данные
Единственная строка входных данных содержит целое число N — длину клетчатой полосы (2 ≤ N ≤ 2 · 10⁹ ).
Выходные данные
Если лягушка и кузнечик могут оказаться в одной клетке, требуется вывести одно целое число — минимальное количество секунд, через которое они встретятся. Если они не смогут оказаться в одной клетке, требуется вывести число «-1» (без кавычек).

Примеры

№	Входные данные	Выходные данные
1	5	1
2	9	2

Замечание
В первом примере лягушка может прыгнуть из клетки 1 в клетки 3 и 4, а кузнечик может прыгнуть из клетки 5 в клетки 3 и 4. Поэтому через 1 секунду они могут оказаться в одной клетке.
Во втором примере лягушка и кузнечик могут встретиться через 2 секунды. Например, лягушка прыгает в клетку 3, затем в клетку 6, а кузнечик прыгает в клетку 8, затем в клетку 6.

Чебаркульские спортсмены

Вывод формулы Комбинаторика

Алексей Юрьевич и Михаил Леонидович — тренера чебаркульской сборной по американскому футболу. Сегодня им нужно заполнить очень важную анкету на чемпионат мира, в которой необходимо указать всех членов команды в порядке возрастания их силы.
Для решения этой непростой задачи были собраны все игроки сборной, и каждый из спортсменов сказал несколько (возможно ноль) фраз вида: «Я сильнее, чем игрок k» (k может отличаться от высказывания к высказыванию, ни один спортсмен не говорил одинаковых фраз). Когда опрос был окончен, тренера поняли, что теперь могут однозначно упорядочить спортсменов по силе, соответствуя всем высказываниям.
Сразу после того, как Алексей Юрьевич и Михаил Леонидович написали ответ организаторам олимпиады, они задумались, а что было бы, если бы футболисты отвечали иначе? Ведь далеко не во всех случаях можно восстановить единственно возможный порядок игроков.
Теперь им интересно, сколько наборов ответов спортсменов однозначно задают их порядок? Так как это число может быть слишком большим, они просят найти лишь его остаток от деления на 10⁹+7.
Входные данные
Во входных данных записано единственное число n — количество спортсменов в сборной (1 <= n <= 10⁵) .
Выходные данные
Выведите единственное число — количество наборов ответов спортсменов, однозначно позволяющих упорядочить их по силе.

Примеры

№	Входные данные	Выходные данные
1	2	2

Замечание
В данном тесте вариантов ответов всего 2: первый сказал, что сильнее второго, второй не сказал ничего, или первый не сказал ничего и второй сказал, что он сильнее первого.

Лекция по товароведению

Гена Букин приехал в Златоуст провести управленческую лекцию в обувном магазине. Зайдя в магазин, Гена увидел полнейший бардак: коробки обуви хаотично валялись в куче посреди зала.
Конечно же, его эта ситуация не устроила, и он решил, что нужно показать, как правильно расставлять коробки. Он заметил, что в магазине есть коробки только двух типов: красные имеют высоту x сантиметров, их a штук; синие имеют высоту y сантиметров, их b штук.
Гена хочет взять несколько коробок из кучи и составить из них башню. Однако из каких-то личных представлений об эстетике Гена не ставит две коробки одинакового цвета друг на друга, в башне он может только чередовать цвета.
Попробовав все возможные способы построения башни, Гена запомнил, сколько различных высот конструкции он смог получить. А сможете ли вы определить, сколько существует различных высот h > 0, что можно построить башню из коробок высотой h, удовлетворяя требованиям о чередовании цветов?
Входные данные
В единственной строке через пробел вводятся 4 целых числа x, y, a, b — высота красной коробки, высота синей коробки, количество красных коробок, количество синих коробок (1<= x,y,a,b <=10⁹).
Выходные данные
Выведите одно число — количество различных высот башен из коробок.

Примеры

№	Входные данные	Выходные данные
1	1 2 3 3	9

Ящики

математика Вывод формулы Задача на реализацию

Саша Белый давно планировал переехать в Кыштым. И вот настал день X. Саша собрал все свои вещи в ящики и вынес их на улицу. Ящики были распределены на n стопок, расположенных вдоль одной прямой, следующим образом: a₁ ящиков в первой стопке стоят непосредственно у газели, a₂ ящиков во второй стопке – правее первой на метр, следующие a₃ еще через метр и т.д. Теперь Белому нужно переставить все ящики как можно ближе к газели, а именно, все ящики из второй, третьей и т.д. стопок должны быть переставлены в первую стопку к исходным a₁ ящикам.
Саша за этот день уже очень устал. Но, к счастью, мимо проходили n мальчишек. Ребята согласились перенести ящики. Каждый из них, ввиду своей выносливости, переносит грузы следующим образом:
1. i-й мальчик проходится по стопкам, номера которых делятся на i, справа налево.
2. Он берет из первой стопки на своем пути ровно один ящик (эта стопка обязана быть непустой).
3. Пройдя i метров налево (то есть до следующей стопки, номер которой делится на i), он снова берет один ящик со стопки, рядом с которой он стоит (исходя из этого, в стопке обязательно должен быть хотя бы один ящик), пройдя еще i метров налево он снова берет ящик и так далее.
4. Когда i-й мальчик доходит до стопки с номером i, он кладет все ранее взятые ящики в эту стопку.

Каждый из ребят может делать сколько угодно проходов. Мальчики могут делать проходы в любом порядке (например, возможна ситуация, когда сначала проходится второй
мальчик, потом первый и снова второй).
Теперь Саша Белый хочет знать, получится ли у них переставить все ящики в начало. Скажите ему ответ на вопрос.

Входные данные
В первой строке входных данных записано целое число n количество стопок ящиков (1 <= n <= 10⁵).
Во второй строке через пробел записаны n целых чисел di количество ящиков в i-й стопке (1 <= d_i <= 10⁹).
Выходные данные
Выведите YES, если существует способ, при котором ребята перенесут все ящики к газели в первую стопку, или NO, если такого способа нет.

Примеры

№	Входные данные	Выходные данные
1	5 2 1 3 5 3	YES
2	4 1 5 2 3	NO

Замечание
В первом примере сначала второй мальчик пройдется два раза, таким образом перенеся два ящика из четвертой стопки во вторую. После этого шага d = (2,3,3,3,3). Потом первый мальчик пройдется 3 раза, перетащив все ящики в первую стопку.
Во втором примере мальчикам не удастся перенести все ящики в первую стопку.

Пробежка

Выходя на пробежку Рита берёт с собой телефон для прослушивания музыки и беспроводные наушники. Перед каждой пробежкой Рита заряжает наушники, и этой зарядки хватает на A минут прослушивания музыки. Рита решила, что каждый день она будет тренироваться на минуту дольше, чем в предыдущий день. То есть если в первый день Рита бегала и слушала музыку в течение B минут, во второй день она будет бегать B + 1 минуту, в третий день — B + 2 минуты и т.д.
Если заряда наушников хватает на большее время, чем продолжительность пробежки, то неиспользованный заряд накапливается и может быть использован в последующие дни. Емкость аккумулятора наушников можно считать неограниченной.
Определите, в какой день Рите впервые не хватит заряда для прослушивания музыки во время всей пробежки.

Входные данные
Первая строка входных данных содержит целое число A (1 <= A <= 10⁹ ) — величина ежедневного заряда аккумулятора (в минутах прослушивания музыки). Вторая строка входных данных содержит целое число B (1 <= B <= 10⁹ ) — продолжительность пробежки в первый день.

Выходные данные
Программа должна вывести одно целое число — номер дня, на который Рите впервые не хватит
заряда наушников на всю пробежку

Примеры

№	Входные данные	Выходные данные
1	42 40	6

Подарки

В новогодний сладкий подарок нужно положить ровно N конфет. На складе хранятся конфеты, собранные по одной штуке и по три штуки в одной упаковке. Всего имеется A упаковок по одной конфете и B упаковок по три конфеты. Определите, какое наибольшее число подарков можно собрать из имеющихся конфет, если упаковки из трёх конфет нельзя вскрывать и разделять на отдельные конфеты.

Входные данные
Первая строка входных данных содержит целое положительное число N — количество конфет в одном подарке. Вторая строка входных данных содержит целое неотрицательное число A — количество упаковок из одной конфеты. Третья строка содержит целое неотрицательное число B — количество упаковок из трёх конфет.
Чиcло N и общее число конфет на складе не превосходят 2 × 10⁹.

Выходные данные
Программа должна вывести единственное целое число — максимальное число подарков, которое можно собрать из имеющихся конфет

Примеры

№	Входные данные	Выходные данные
1	4 8 2	3

Замечание
В примере из условия на складе имеются 8 упаковок из одной конфеты и 2 упаковки из трёх конфет. В один подарок необходимо положить 4 конфеты. Два подарка можно собрать, используя 1 упаковку из одной конфеты и 1 упаковку из трёх конфет. Ещё один подарок можно собрать из 4 упаковок из одной конфеты. Всего было использовано 6 упаковок из одной конфеты и 2 упаковки из трёх конфет, осталось 2 упаковки из одной конфеты, которых не хватит на дополнительный подарок.

Морской бой

Чтобы разнообразить игру «морской бой» Боря решил добавить в неё новый тип кораблей. Эти корабли состоят из двух прямоугольников. Первый прямоугольник имеет ширину w₁ и высоту h₁, а второй прямоугольник - w₂ и h₂ соответственно. Прямоугольники располагаются один над другим и выровнены по левому краю (см. рисунки примеров): введём на поле систему координат так, чтобы левая нижняя клеточка первого прямоугольника имела координаты (1,1). Тогда верхняя правая клеточка первого прямоугольника имеет координаты (w₁,h₁), левая нижняя клеточка второго прямоугольника имеет координаты (1,h₁+1), а правая верхняя клеточка второго прямоугольника имеет координаты (w₂,h₁+h₂).

По правилам морского боя, после уничтожения корабля необходимо отметить все клеточки, соседние по стороне или углу с клеточками, в которых есть корабль, потому что в этих клеточках уже не могут стоять другие корабли. При этом отмечаются только не принадлежащие кораблю клетки.

Определите, сколько клеток надо будет отметить после уничтожения корабля, придуманного Борей. Поле, на котором, происходит игра, бесконечно во все стороны.

Входные данные
В четырёх строках заданы четыре целых числа w₁,h₁,w₂ и h₂ (1<=w₁,h₁,w₂,h₂<=10⁸) - ширина первого прямоугольника, высота первого прямоугольника, ширина второго прямоугольника и высота второго прямоугольника, соответственно.

Выходные данные
Выведите одно целое число — количество клеток, которые необходимо закрасить после уничтожения корабля.

Примечание

В первом примере поле выглядит так (красным обозначен первый прямоугольник, синим обозначен второй прямоугольник, зеленым обозначены отмеченные точки):

Во втором примере поле выглядит так:

Примеры

№	Входные данные	Выходные данные
1	2 1 2 1	12
2	2 2 1 2	16

Порядочные числа

У Миши развитое эстетическое чувство. Он считает, что не все числа одинаково порядочные. Когда ему грустно, он начинает придумывать числа и приводить их в порядок.

Миша очень любит рассматривать сумму цифр числа. Для того чтобы привести в порядок число A, он сначала записывает само число. Потом он пишет сумму цифр этого числа. Затем — сумму цифр суммы цифр и так далее, до тех пор, пока очередное число не станет однозначным. Он считает, что результатом приведения в порядок числа A является сумма всех выписанных чисел, включая само число A.

Миша настолько любит этот процесс, что он даже заменяет ему счёт овец, когда долго не получается заснуть. Он помнит, что вчера ночью, когда он в уме привёл в порядок число A, у него получилось число B. Но вот беда — он не помнит, какое именно он взял число A! Помогите ему в отыскании этого числа.

Входные данные
На ввод подаётся единственное целое число B (1 ≤ B ≤ 10⁹ )

Выходные данные
Если существует такое число A, что после приведения его в порядок, получается B, то выведите любое такое число. Если же Миша где-то ошибся в расчётах и такого числа не существует, то выведите -1.

Примеры

№	Входные данные	Выходные данные
1	42	29
2	20	-1

Тюрьма для Зедда

Вывод формулы Задача на реализацию Разбор случаев

Черный рейнджер нашел в жерле заброшенного вулкана n прямоугольных листов металла разного размера, i-й лист имеет размер a_i на b_i метров.
Зордон поручил построить Черному рейнджеру тюрьму для злобного генерала Зедда, и эта находка оказалась для него просто подарком судьбы. Тюрьма должна иметь вид прямоугольного параллелепипеда каждая грань которого представляет собой цельный лист металла. Так что рейнджер собирается взять 6 из найденных им листов металла, сложить из них параллелепипед, и показать его Зордону. Листы нельзя гнуть или разрезать, листы, из которых будет сложена тюрьма не должны выступать за её края.
Поскольку чем больше тюрьма, чем надежнее, параллелепипед должен иметь максимальный возможный объем. Помогите герою выбрать 6 листов прямоугольников так, чтобы собрать из них самую большую тюрьму.
Листы можно поворачивать, таким образом, например, листы 4 на 7 метров и 7 на 4 метра считаются одинаковыми.

Формат входных данных
В первой строке дано одно число n — количество листов металла у Черного Рейнджера (6 ≤ n ≤ 200 000).
В следующих n строках даны пары чисел a_i; b_i — размеры i-го куска металла (1 ≤ a_i; b_i ≤ 10⁶).

Формат выходных данных
Выведите одно целое число — максимальный объем прямоугольного параллелепипеда, который можно собрать из этих кусков металла.
Если из данных листов невозможно собрать прямоугольный параллелепипед, выведите -1.

Примеры

№	Входные данные	Выходные данные
1	6 3 6 6 9 9 3 6 3 3 9 9 6	162
2	6 1 1 1 1 1 1 1 1 1 1 1 1	1
3	6 1 2 2 3 3 4 4 5 5 6 6 1	-1

Мегазорды

Мегазорд — необходимая вещь для защиты Земли. Для сборки одного мегазорда, необходимо ровно три зорда: зеленый, красный и синий.
Зеленому, красному и синему рейнджеру стало интересно, сколько у них есть различных способов собрать мегазорд. Для каждого рейнджера известен набор зордов, которыми он обладает. У зеленого рейнджера есть зеленые зорды, у красного рейнджера — красные, а у синего — синие.
При сборке мегазорда необходимо соблюдать три правила:

Первая цифра номера модели красного зорда должна быть равна последней цифре модели зеленого.
Последняя цифра номера модели красного зорда должна быть равна первой цифре модели синего.
Все три использованных зорда должны иметь разные номера моделей.

Два способа собрать мегазорд считаются различными, если хотя бы один из рейнджеров использует при сборке другой зорд, возможно той же модели.
Для каждого рейнджера вам известны номера моделей его зордов. У одного рейнджера могут быть несколько зордов одной модели.
Помогите рейнджерам понять, сколько у них есть различных способов собрать мегазорд.

Входные данные
В первой строке входного файла заданы числа g, r и b — количество зордов у зеленого, красного и синего рейнджера соответственно (1 ≤ g, r, b ≤ 10⁵).
В следующей строке находится g чисел x_i — номера моделей, которые есть у зеленого рейнджера (0 ≤ x_i ≤ 10⁹).
В следующей строке находится r чисел y_i — номера моделей, которые есть у красного рейнджера (0 ≤ y_i ≤ 10⁹).
В следующей строке находится b чисел z_i — номера моделей, которые есть у синего рейнджера (0 ≤ z_i ≤ 10⁹).

Выходные данные
Выведите одно число — количество различных мегазордов, которые можно собрать.

Примеры

№	Входные данные	Выходные данные
1	3 3 2 101 11 52 11 23 23 31 13	3

Замечание
Различные мегазорды из первого примера: 101 + 11 + 13, 52 + 23 + 31, 52 + 23 + 31. Последний мегазорд встречается дважды, так как красный ренжер мог взять либо второй, либо третий зорд. Обратите внимание, что собрать мегазорд 11+11+13 нельзя, так как при этом одна и та же модель будет использована дважны.

Железная дорога

Порядковые статистики Вывод формулы

Вите на день рождения подарили Очень Большую Игрушечную Железную Дорогу. Она представляет собой два параллельных пути, по которым движутся поезда во встречных направлениях. В центре находится станция, а железная дорога очень большая, поэтому можно считать пути бесконечными в обе стороны. Витя расставил поезда на железной дороге и одновременно запустил их, включив электропитание. Все поезда движутся с одинаковыми скоростями в одном из двух возможных направлений. Но когда-нибудь поезда придётся остановить и убрать игру, а поскольку поезд не может развернуться и начать движение в противоположном направлении, Вите придётся самому собирать поезда руками и переносить их на станцию. Витя хочет выбрать такой момент остановки всех поездов, чтобы ему пришлось потратить минимальное число усилий для того, чтобы собрать после этого все поезда на станции вместе, то есть в этот момент времени сумма расстояний всех поездов до станции была бы минимальной.

Входные данные
Введём на железной дороге координаты, считая, что станция находится в начале координат, а все поезда первоначально находятся в целочисленных точках координатной прямой. Сами поезда также будем считать точками. За одну секунду координаты всех поездов изменяются на +1 или на −1. Поезда движутся с равными скоростями, первоначально никакие два поезда, движущиеся в одном направлении, не находятся в одной точке. Первая строка входных данных содержит целое число N — количество поездов, движущихся в положительном направлении. Вторая строка входных данных содержит целое число M — количество поездов, движущихся в отрицательном направлении. Ограничения: N > 0, M > 0, 1 <= N + M <= 10⁵ . Следующие N строк содержат N чисел ai (|ai | <= 10⁹ ) — первоначальные координаты поездов, движущихся в положительном направлении. Все числа ai различны и заданы в порядке возрастания. Следующие M строк содержат M чисел bj (|bj | <= 10⁹ ) — первоначальные координаты поездов, движущихся в отрицательном направлении. Все числа bj различны и заданы в порядке возрастания.

Выходные данные
Программа должна вывести единственное целое число t — момент времени в секундах после запуска игры, в который суммарное расстояние всех поездов до станции будет минимальным. Если возможных правильных ответов несколько, то программа должна вывести любой из них. Если после старта игры суммарное расстояние всех поездов до станции будет всегда больше, чем в момент запуска игры, то правильным ответом будет t = 0.

Пример

№	Входные данные	Выходные данные	Пояснение
1	3 2 -5 -2 4 1 4	2	В примере из условия 3 поезда движутся в положительном направлении, 2 поезда движутся в отрицательном направлении. Начальные координаты поездов, движущихся в положительном направлении равны −5, −2, 4, движущихся в отрицательном направлении равны 1 и 4. Запишем, что при t = 0 координаты поездов (−5, −2, 4, 1, 4). Суммарное расстояние всех поездов до станции равно 16. В момент t = 1 координаты поездов будут (−4, −1, 5, 0, 3), суммарное расстояние до станции равно 13. В момент t = 2 координаты поездов будут (−3, 0, 6, −1, 2), суммарное расстояние до станции равно 12. В момент t = 3 координаты будут (−2, 1, 7, −2, 1), суммарное расстояние до станции равно 13. Ответ на этот тест t = 2.

Не был предателем ...

Поиск подстроки в строке Вывод формулы

Гриша уже несколько несколько недель отрабатывает свои навыки в новомодной онлайн-игре про команду космического корабля, вычисляющую предателей среди них. Так как игра очень популярна, появились игроки, которые договариваются между собой о каких-то способах коммуницировать заранее. Таких людей называют заговорщиками.
Заговорщики действуют по следующему алгоритму. В начале игры каждый из заговорщиков пишет в общий чат строку T — ключ шифрования. Далее в течение игры игрок придумывает строку S, записывает её N раз подряд и отправляет в чат. Для того, чтобы получить зашифрованное сообщение, остальным заговорщикам нужно посчитать, сколько раз в этой повторённой N раз строке S встречается ключ шифрования T. Чат обновляется слишком быстро и Гриша не успевает это сделать руками. Помогите Грише решить эту задачу.

Входные данные
В первой строке входных данных записана строка T, содержащая не более 300 символов — ключ шифрования. Во второй строке записана строка S, её длина также не превосходит 300. В третьей строке записано целое число N, 1 <= N <= 5 × 10⁶ — количество повторений строки S. Все строки состоят только из заглавных английских букв.

Выходные данные
Программа должна вывести единственное целое число — количество вхождений строки T в строку S, повторённую N раз. Под одним вхождением подразумевается один способ выбрать подстроку, то есть несколько подряд идущих символов строки, совпадающих со строкой T, не меняя порядок следования этих символов.

Примеры

№	Входные данные	Выходные данные	Пояснение
1	MON AMONGUS 3	3
2	ABA BABA 3	5	Если строку BABA повторить 3 раза, получится BABABABABABA. В полученной строке подстрока ABA встречается 5 раз: BABABABABABA, BABABABABABA, BABABABABABA, BABABABABABA, BABABABABABA

Кинотеатр

В кинотеатре места часто расставляют со сдвигом соседних рядов для удобства зрителей. Пусть в таком кинотеатре N мест в 1-м, 3-м, 5-м и всех нечётных рядах и N + 1 место во 2-м, 4-м и всех чётных рядах. Места в рядах нумеруются от 1 до N в нечётных рядах и от 1 до N + 1 в чётных рядах. Касса продаёт билеты подряд: сначала в 1-й ряд на места с 1-го по N-е, потом — во 2-й ряд на места с 1-го по N + 1-е, затем в 3-й ряд с 1-го места и т.д. Определите номер ряда и номер места для K-го проданного билета.

Входные данные
Программа получает на вход два целых числа. В первой строке записано число N (1 <= N <= 10⁹ ) — количество мест в 1-м ряду кинотеатра. Во второй строке записано число K — порядковый номер проданного билета (1 <= K <= 2 × 10⁹ ).

Выходные данные
Программа должна вывести два числа в одной строке через пробел: номер ряда и номер места K-го проданного билета.

Примеры

№	Входные данные	Выходные данные	Пояснение
1	10 25	3 4	Билеты с 1 по 10 будут проданы в первый ряд. Билеты с 11 по 21 будут проданы во второй ряд. В третий ряд будут проданы билеты, начиная с 22-го, 25-й билет окажется на 4-м месте 3-го ряда.

Удаление данных

Вывод формулы

Случилась беда — шпиона Сергея раскрыли, и теперь ему нужно срочно бежать! Но перед побегом он должен удалить все компрометирующие данные со своего компьютера.
На компьютере Сергея сохранены N файлов, пронумерованных числами от 1 до N. У каждого из файлов есть размер в байтах: a₁, a₂, . . . , a_N. Все данные на компьютере Сергея хорошо зашифрованы. Шпион определил, что для удаления файла с номером i понадобится минимум из a_i−1 и a_i+1 секунд (для удаления первого файла потребуется a₂ секунд, а для удаления последнего — a_N−1 секунд). Когда остается всего один файл, он удаляется мгновенно. После удаления файла с номером i остальные файлы перенумеровываются последовательно.
У Сергея осталось очень мало времени, а ему еще нужно собрать вещи, поэтому он просит у вас помощи. Определите, какое минимальное время понадобится шпиону, чтобы удалить все файлы.
Сергей может удалять файлы последовательно в любом порядке.

Входные данные
В первой строке выходных данных записано одно целое число N (1 ≤ N ≤ 10⁵) — количество файлов на компьютере шпиона.
В каждой из следующих N строк записано по одному целому числу a_i (1 ≤ a_i ≤ 10⁴) — размер файла с номером i на компьютере Сергея.

Выходные данные
В единственной строке выведите одно число — минимальное время, которое понадобится Сергею для удаления всех файлов.

Примеры

№	Входные данные	Выходные данные
1	5 1 2 3 1 100	4
2	1 1	0

Замечание
В первом примере у Сергея есть файлы с размерами 1, 2, 3, 1, 100. Один из вариантов решения приведен ниже:
1. Удалим последний файл. Это займет одну секунду.
2. Затем удалим файл размера 2 за одну секунду.
3. Далее удалим файл размера 3 за одну секунду.
4. Теперь удалим любой из оставшихся двух файлов за одну секунду.
5. Последний файл моментально удалится сам.
Итого, Сергею понадобится 1 + 1 + 1 + 1 = 4 секунды.
Во втором примере у Сергея изначально есть всего один файл, который сразу же удалится.

Странное устройство

По приезде Василий с Петром обнаружили в своем номере в гостинице странный прибор. Он был оснащен дисплеем, на котором показывалось число 0, и двумя кнопками. Василий сразу понял, что первая кнопка увеличивает число на дисплее на 1, а вторая умножает его на K. В этот момент Петр обнаружил на своей кровати листок бумаги, на котором было написано единственное число N.
Теперь друзья хотят воспроизвести число N на дисплее найденного ими устройства, и, поскольку их ждет еще множество дел, им интересно минимальное число нажатий на кнопки устройства для получения числа N.

Входные данные
В первой строке входных данных записано целое неотрицательное число N (1 ≤ N ≤ 10⁹ ).
Во второй строке входных данных записано целое положительное число K (2 ≤ K ≤ 10⁹ ).

Выходные данные
Выведите единственное число — минимальное количество нажатий на кнопки устройства для получения на его дисплее числа N.

Примеры

№	Входные данные	Выходные данные
1	4 2	3

Замечание
В примере из условия Василий и Петр хотят воспроизвести число 4. Кнопка умножает на 2 число, которое показывается на дисплее. Первой операцией друзья увеличивают текущее число на 1, нажимая первую кнопку, после чего оно становится равно 1. Затем они умножают его на 2, нажимая вторую кнопку. Текущее число становится равно 2. После чего, для получения на дисплее числа 4 достаточно один раз нажать вторую кнопку и умножить текущее число (то есть 2) на 2. Несложно показать, что меньше, чем за три операции, получить число 4 невозможно. Таким образом, минимальное число действий равняется трем.

Финансовая реформа

Вывод формулы математика

Однажды после олимпиады по экономике Мише приснился очень красочный и необычный сон.
Мальчик оказался министром финансов Берляндии. Осознав свою значимость, он тут же решил произвести в стране реформу. Раньше в Берляндии использовались банкноты с номиналами 1, 10, 100 и 1 000 бурлей. Мише данная система показалась крайне банальной, поэтому он решил придумать что-то свое.
Мальчик выбрал два целых числа x и y (x ≤ y) и заявил, что теперь в Берляндии будут использоваться только банкноты с номиналами x, x + 1, x + 2, . . . , y бурлей. Вскоре реформа была принята и вступила в силу, однако населению страны это совсем не понравилось. Недовольства начались из-за того, что теперь, используя новые банкноты, можно было набрать далеко не любую сумму.
Например, если Мишей были выбраны числа x = 5 и y = 7, то невозможно набрать суммы 1, 2, 3 и 4 бурлей. Также не получится набрать суммы 8 и 9 бурлей. Если же выбрать числа x = y = 2, то невозможно будет набрать любую нечетную сумму.
Миша, находясь на грани увольнения, решил успокоить население Берляндии и предъявить такое минимальное число N, что при помощи новых банкнот возможно набрать любую сумму, начиная с N. Таким образом, должно быть возможно набрать суммы N бурлей, N + 1 бурлей, N + 2 бурлей, и так далее. Помогите Мише найти искомое число N и избежать увольнения.

Входные данные
В первой строке входных данных записано целое число x — минимальный номинал новых банкнот.
Во второй строке записано целое число y (1 ≤ x ≤ y ≤ 2 · 10⁹ ) — максимальный номинал новых банкнот.

Выходные данные
Выведите одно натуральное число N — минимальное число, такое, что при помощи банкнот с номиналами x, x + 1, x + 2, . . . , y можно набрать любую сумму, начиная с N бурлей. Если такого числа не существует, в качестве ответа выведите −1.

Примеры

№	Входные данные	Выходные данные	Пояснение
1	5 7	10	Имеются банкноты трех номиналов: 5, 6 и 7 бурлей. Ниже перечислены суммы, которые можно набрать при помощи данных банкнот: • 5 = 5, • 6 = 6, • 7 = 7, • 10 = 5 + 5, • 11 = 5 + 6, • 12 = 5 + 7, • 13 = 6 + 7, • . . . Можно показать, что при помощи банкнот данных номиналов возможно набрать любую сумму, начиная с 10 бурлей.
2	2 2	-1	Есть банкноты всего одного номинала: 2 бурля. При помощи данных банкнот можно набрать только любую чётную сумму: 2, 4, 6, .... Таким образом, искомого числа N не существует.
3	1900000000 2000000000	36100000000

Ну все, я попрыгал!

Вывод формулы математика Задача на реализацию

Персонаж известной компьютерной игры Марио постарел и почти перестал прыгать. Но совсем недавно он увидел спуск из N ступенек, и его накрыло ностальгией. Марио встал на самую верхнюю ступеньку и решил преодолеть этот спуск при помощи прыжков.
Когда-то Марио знал тысячи различных видов прыжков, но теперь он смог вспомнить только два: короткие и длинные. Короткий прыжок позволяет спуститься на произвольное число ступенек, не большее X, а длинный — на произвольное число, не большее Y (X < Y ). Но в силу возраста Марио не может делать два длинных прыжка подряд и вынужден между ними совершать хотя бы один короткий. При этом Марио не хочет слишком уж сильно ухудшить свои прошлые результаты и поэтому постарается обойтись как можно меньшим числом прыжков.
Помогите Марио посчитать минимальное количество прыжков, требующееся для преодоления всех N ступенек.

Входные данные
В первой строке входных данных записано целое число X — максимальная длина короткого прыжка.
Во второй строке записано целое число Y (1 ≤ X < Y ≤ 10¹⁸) — максимальная длина длинного прыжка.
В третьей строке записано целое число N (1 ≤ N ≤ 10¹⁸) — количество ступенек в спуске.

Выходные данные
В единственной строке выведите целое число — минимальное число прыжков, необходимое Марио для спуска.

Примеры

№	Входные данные	Выходные данные
1	2 3 5	2
2	1 2 4	3
3	1 100 1000000000000000000	19801980198019801

Замечание
На изображениях ниже приведены возможные способы решения первых двух тестов из условия:

Починка блюдца

Вывод формулы

Придя домой, уставший Константин захотел выпить свой любимый чай. Для этого ему нужно было достать с высокой полки самое красивое блюдце, которое представляет собой клетчатое поле N × N. Но, так как Константин не очень аккуратен, он блюдце разбил.
В спешке Костя начал думать, как же починить столь ценную вещь. И тогда он заметил, что блюдце распалось ровно на клетчатые квадраты K × K! Более того он обнаружил, что N делится на K без остатка.
Восстановив исходное блюдце из кусочков, Костя понял, что ему также нужно купить клей, чтобы склеить все соприкасающиеся кусочки в исходное клетчатое поле N × N. Он тут же посчитал, что, для того чтобы проклеить границу между двумя соприкасающимися клетками длины 1, необходима ровно одна банка клея.
Помогите Косте посчитать, сколько банок клея ему нужно купить, чтобы склеить его любимое блюдце.

Входные данные
В первой строке входных данных записано одно целое число N (1 ≤ N ≤ 10⁴ ) — размер квадратного блюдца.
Во второй строке записано одно целое число K (1 ≤ K ≤ N, N делится на K без остатка) — размер квадратного осколка блюдца.

Выходные данные
В единственной строке выведите одно число — количество банок клея, которые Косте понадобится купить, чтобы починить блюдце.
Если на самом деле блюдце не разбилось, и Костя зря паниковал, выведите число 0.

Примеры

№	Входные данные	Выходные данные	Пояснения
1	2 1	4	Различными цветами обозначены различные части блюдца, изначально имевшего размер 2 × 2. Между частями белым цветом обозначен клей, который Костя купил и намазал, чтобы починить блюдце. Каждая часть блюдца имеет размер 1 × 1.
2	3 3	0	Костя зря паниковал, и на самом деле он не разбил блюдце!

Разнообразное питание - 2

Увлекшись машинным обучением, Вася совсем забыл про свои экзамены в университете, завалил их и пошел служить в армию. Однако, и тут ему пригодились его навыки программиста — у работников столовой возникла проблема с тем, что блюда постоянно повторяются, и солдаты начали слишком этому возмущаться. Узнав, что Вася разбирается в программировании, работники попросили его написать программу, которая сделает распределение блюд.
Работники столовой считают, что единственное, что характеризует распределение блюд — их «степень немонотонности» — число разных блюд, которые даются в последовательные приемы пищи. То есть, если представить расписание блюд как массив a, то «степень немонотонности» будет равна количеству индексов i, таких что $a_i \neq a_{i-1}$ . Для начала вас просят найти не само распределение блюд, а хотя бы максимальную возможную «степень немонотонности», которую можно было бы получить некоторой перестановкой заданного набора блюд. Помогите армейской столовой!
Входные данные
В первой строке содержится число n — количество блюд, которые должны войти в расписание (1 ≤ n ≤ 100).
В следующей строке содержится n чисел a_i — блюда (1 ≤ a_i ≤ 100). Одинаковые блюда обозначены одинаковыми числами, разные — разными.
Выходные данные
В единственной строке выведите одно число — максимальное возможное значение «степени немонотонности».

Ввод	Вывод
5 1 2 3 1 1	4
4 1 1 1 2	2

Под контролем слонов

Расставьте на шахматной доске размером N x N минимальное количество шахматных слонов так, чтобы они контролировали все поле (любая клетка должна находиться на одной диагонали хотя бы с одним слоном; считается, что слон контролирует и ту клетку, на которой стоит).

Входные данные
Вводится одно число - размер поля.

Выходные данные
Программа должна вывести одно число - минимальное количество слонов, которые можно расставить на данной доске так, чтобы они контролировали все поле.

Примеры

№	Входные данные	Выходные данные
1	3	3
2	1	1

Дипломы в папках

Жадный алгоритм Вывод формулы реализация

В этом году Иван заканчивает школу и поступает в вуз. За время своей учебы он часто участвовал в олимпиадах по информатике и у него накопилось много дипломов. Иван раскладывал дипломы по папкам совершенно бессистемно, то есть любой диплом мог оказаться в любой из папок. К счастью, Иван помнит, сколько дипломов лежит в каждой из папок.

Иван хочет принести в приемную комиссию выбранного вуза папку, в которой находится диплом Московской олимпиады по программированию (такой диплом у Ивана ровно один). Для того чтобы понять, что в данной папке нужного диплома нет, Ивану нужно просмотреть все дипломы из этой папки. Чтобы открыть одну папку Ивану нужно потратить одну секунду, просмотр одного диплома занимает у него также одну секунду, и он может мгновенно переходить к следующей папке после окончания просмотра предыдущей. Порядок просмотра папок Иван может выбирать. То, что в пустых папках диплом можно не искать, Ивану очевидно.

По заданному количеству дипломов в каждой из папок требуется определить, за какое наименьшее время в худшем случае Иван поймет, в какой папке содержится нужный ему диплом.

Входные данные
В первой строке входного файла записано целое число N (1 ≤ N ≤ 10⁵) - количество папок. Во второй строке записаны N целых чисел a₁, a₂, ..., a_N (0 ≤ a_i ≤ 10⁵) - количество дипломов в каждой из папок.

Выходные данные
Выведите одно число - минимальное количество секунд, необходимое Ивану в худшем случае для определения того, в какой папке содержится диплом.

Примечание
В первом примере Иван может открыть и просмотреть папку 2 за 2 секунды и, не найдя там диплома, понять, что диплом находится в папке 1.

Во втором примере Иван за 2 секунды просмотрит папку 1, потом за 2 секунды просмотрит папку 4, а если ни в одной из них диплома не встретилось, он поймет, что диплом в папке 3.

Примеры

№	Входные данные	Выходные данные
1	2 2 1	2
2	4 1 0 2 1	4

Построение

Вывод формулы Разбор случаев Задача на реализацию

N учащихся класса, удобно пронумеровали числами от 1 до N. На линейке 1 сентября они стояли в ряд, но теперь не уверены в том, в каком порядке они стояли. Однако каждый запомнил следующий факт: абсолютную разницу между количеством учащихся, стоявших слева от этого человека, и количеством учащихся, которые стояли справа от этого человека. Согласно их отчетам, разница для человека i равна A_i . На основании этих отчетов, найдите количество возможных расстановок, в которых они стояли. Поскольку ответ может быть очень большим, выведите его по модулю $10^9+7$. Обратите внимание, что отчеты могут быть неправильными и, следовательно, не может быть согласованного порядка. В таком случае выведите 0.

Входные данные
В первой строке задается число N ($1<=N<=10^5$). Во второй строке N чисел A_i ($0<=A_i<=N-1$).

Выходные данные
Выведите количество возможных расстановок по модулю $10^9+7$.

Примеры

№	Входные данные	Выходные данные	Пояснение
1	5 2 4 4 0 2	4	Возможны 4 расстановки учащихся, а именно: 2 ,1 ,4 ,5 ,3 2 ,5 ,4 ,1 ,3 3 ,1 ,4 ,5 ,2 3 ,5 ,4 ,1 ,2
2	7 6 4 0 2 4 0 2	0	Любая расстановка не совместима с отчетами. Поэтому ответ 0.
3	8 7 5 1 1 7 3 5 3	16

Трансформация чисел

Вычисление по заданной формуле Вывод формулы

У Громозеки есть N целых чисел a₁,a₂,..,a_N. Его цель - получить N равных целых чисел, преобразовав некоторые из них. Он может преобразовать каждое целое число не более одного раза. Преобразование целого числа x в другое целое число y стоит ему $(x-y)^2 $ рублей. Даже если $a_i = a_j$ ($i \neq j$) он должен отдельно оплатить стоимость преобразования каждого из них (см. пример 2).
Найдите минимальную общую стоимость для достижения цели Громозеки.

Входные данные
В первой строке задается число N ($1<=N<=100$). Во второй строке числа a₁,a₂,..,a_N($100<=a_i<=100$).

Выходные данные
Выведите минимальную общую стоимость для достижения цели Громозеки.

Примеры

№	Входные данные	Выходные данные	Пояснения
1	2 4 8	8	Минимальная по сумме трансформация обоих чисел - это преобразование каждого числа в 6 будет: (4-6)²+(8-6)²=8 рублей.
2	3 1 1 3	3	Трансформируем все числа в 2: (1-2)²+(1-2)²+(3-2)²=3 рубля. Громозека обязан заплатить $(1-2)^2$ рубля за каждое преобразованное число 1.
3	3 4 2 5	5	Трасформируем 2 и 5 в число 4: (2-4)²+(5-4)²=5 рублей.
4	4 -100 -100 -100 -100	0	Ничего не надо преобразовывать.

Конфеты

В детском саду Сластена N детей. Анна Николаевна выстраивает детей в линию, затем раздает 1 конфету первому ребенку, 2 конфеты второму ребенку, ..., N конфет N-му ребенку. Сколько всего конфет потребуется Анне Николаевне?

Входные данные
На вход подается целое число N ($1 <= N <=100$).

Выходные данные
Выведите на экран ответ на задачу.

Примеры

№	Входные данные	Выходные данные
1	3	6

Таблица

Бесконечную таблицу, строки и столбцы которой пронумерованы целыми числами начиная с 1 сверху вниз и слева направо, заполняют целыми числами 1, 2, 3 и т.д. Числа выписываются в
соседние клетки по границам квадратов увеличивающегося размера (см. рисунок).

Формат входных данных
Программа получает на вход одно целое число n, 1 ≤ n ≤ 10¹⁸
Формат выходных данных
Программа должна вывести два целых числа: номер строки и номер столбца, в которых находится число n в этой таблице. Запись выводимых чисел должна содержать только цифры, вывод
действительных чисел в ответе считается неверным.

Примеры

№	Входные данные	Выходные данные
1	15	4 2

Перевернутые родословные

Вывод формулы Разбор случаев Задача на реализацию

Учёный Иван Иванович изучает перевёрнутые родословные. Перевёрнутая родословная представляет собой набор людей, про каждого из которых известны либо оба его родителя, либо не известен ни один родитель. Кроме того, известно, что у всех людей из родословной есть ровно один
ребёнок, кроме одного человека, у которого детей вовсе нет. Поэтому, если пронумеровать людей целыми числами от 1 до n, то можно обозначить за s_i номер ребёнка человека с номером i и сказать, что s_i = 0 в случае, если у человека с номером i детей нет.
Будем считать, что человек a входит в родословную человека b, если либо a = b, либо если у b известны родители, и a входит в родословную одного из родителей b.

Будем считать, что произошёл перекос родословной с участием некоторого человека, если известны оба его родителя и количество людей в родословной одного из его родителей хотя бы вдвое больше, чем количество людей в родословной второго родителя.
Иван Иванович посчитал количество перекосов родословной и получил число k, но, конечно же, он делал это вручную и мог ошибиться. Помогите проверить Ивану Ивановичу его вычисления: по числам n и k скажите, существует ли родословная из n людей с k перекосами, и если существует, то приведите пример подобной родословной.

Формат входных данных
В единственной строке заданы два целых числа n и k (1 ≤ n ≤ 100 000, 0 ≤ k ≤ n) — количество людей в родословной и количество перекосов в ней.

Формат выходных данных
В первой строке выведите «YES» (без кавычек), если существует родословная с n людьми и k перекосами, и «NO» (без кавычек) в противном случае.
Если требуемая родословная существует, то во второй строке выведите n целых чисел s1, s2, . . . , sn (0 ≤ s_i ≤ n), задающих номера детей каждого из n человек в родословной. Если искомых родословных несколько, выведите любую.

Примеры

№	Входные данные	Выходные данные
1	3 0	YES 0 1 1
2	5 1	YES 0 1 1 3 3
3	3 2	NO

Замечание

В первом примере подойдет единственная родословная, которую можно составить из трёх человек (человек и два его родителя).

Во втором примере подойдет следующая родословная:

В этом случае в родословную человека 1 входят пять человек (люди 1, 2, 3, 4, 5), в родословную человека 2 входит один человек (только 2), в родословную человека 3 входят три человека (3, 4, 5), в родословную человека 4 входит один человек (только 4) и в родословную человека 5 входит один
человек (только 5). В этом случае происходит перекос родословной в человеке 1.
В третьем примере можно показать, что не существует родословной из трёх людей с двумя перекосами.

Подготовка к экзамену

Среди открытого банка задач ЕГЭ по математике есть следующая: по заданным натуральным числам l, r и m вас просят найти целые числа a, b и c, каждое из которых не меньше l и не больше r, и такие, что будет существовать натуральное число n (целое число, большее нуля) такое, что
n · a + b − c = m.
Паша еще только начал готовиться к ЕГЭ и не совсем понимает, как решать подобную задачу. Помогите ему для разных вариантов этой задачи находить подходящие a, b и c.

Формат входных данных
В единственной строке заданы три целых числа l, r и m (1 ≤ l ≤ r ≤ 500 000, 1 ≤ m ≤ 1010).

Формат выходных данных
Выведите три целых числа a, b и c такие, что l ≤ a, b, c ≤ r и существует такое натуральное число n, что n · a + b − c = m. Гарантируется, что такие числа существуют. Если подходящих решений несколько, выведите любое из них.

Примеры

№	Входные данные	Выходные данные
1	4 6 13	4 6 5
2	2 3 1	2 2 3

Замечание
В первом примере можно выбрать n = 3, тогда n · 4 + 6 − 5 = 13 = m. Так же возможны такие ответы: a = 4, b = 5, c = 4 (при этом n = 3); a = 5, b = 4, c = 6 (при этом n = 3); a = 6, b = 6, c = 5 (при этом n = 2); a = 6, b = 5, c = 4 (при этом n = 2).
Во втором примере n = 1, тогда n · 2 + 2 − 3 = 1 = m. Число n = 0 не могло быть выбрано, так как число n обязательно должно быть натуральным.

Разделение числа

Сегодня Дима целый день старался и выписывал на длинную бумажную ленту своё любимое целое положительное число n, состоящее из l цифр. К сожалению, лента получилась настолько длинной, что в итоге не влезла в Димин шкаф.

Чтобы справиться с этой неприятностью, Дима решил разрезать ленту на две непустые части, на каждой из которых записано целое положительное число без ведущих нулей, после чего сложить числа, написанные на получившихся частях, а полученную сумму записать на новую ленту.

Дима хочет, чтобы полученное число было как можно меньше, ведь это повышает шансы на то, что хотя бы сумма в шкаф влезет. Помогите Диме определить, какое минимальное число он может получить.

Входные данные
Первая строка содержит одно целое число l (2 ≤ l ≤ 100000) — длину любимого числа Димы.

Вторая строка содержит целое положительное число n, изначально записанное на ленте — любимое число Димы.

Число n состоит ровно из l цифр, при этом запись не содержит ведущих нулей. Также Дима гарантирует, что существует хотя бы один способ разрезать число, удовлетворяющий всем требованиям выше.

Выходные данные
Выведите одно целое число — минимальное число, которое может получить Дима.

Примечание
В первом примере Дима может разрезать число 1234567 на числа 1234 и 567. Их сумма равна 1801.

Во втором примере Дима может разрезать число 101 на числа 10 и 1. Их сумма равна 11.

Примеры

№	Входные данные	Выходные данные
1	7 1234567	1801
2	3 101	11

Держать строй - 2

В воинской части города Шатров продолжаются занятия по строевой подготовке. Молодой прапорщик Андрей Юрьевич уже приноровился проводить эти занятия, но тут его начальник Павел Андреевич стал давать ему новые, более сложные задания.

Как известно, обычно все солдаты выстраиваются в шеренгу по росту, начиная с самого низкого. Но Павлу Андреевичу это показалось слишком скучным и он потребовал от Андрея Юрьевича выстроить солдат в другом порядке. Случайный порядок ему показался слишком хаотичным, поэтому он потребовал построения, в котором будет ровно k инверсий. Инверсией называется такая пара солдат, что более высокий из них стоит в шеренге раньше более низкого.

К счастью для Андрея Юрьевича, все солдаты разного роста и для каждого он знает, какой он по росту среди всех солдат. Исходя из этого, каждому солдату Андрей Юрьевич присвоил номер: первый номер получил самый низкий, а последний — самый высокий солдат.

Например, в построении (3, 1, 2) есть две инверсии — пары (3, 1) и (3, 2), в которых более высокий солдат стоит раньше более низкого.

Андрей Юрьевич поручил Вам помочь ему в построении солдат в требуемом порядке, и для этого вы должны написать программу, находящую расстановку n солдат в порядке, в котором есть ровно k инверсий.

Входные данные
Первая и единственная строка входного файла содержит два целых числа n и k (1 ≤ n ≤ 100 000) — количество солдат в строю и требуемое количество инверсий.

Гарантируется, что существует построение солдат с требуемым числом инверсий, то есть 0 ≤ k ≤ n(n - 1) / 2.

Выходные данные
В выходной файл выведите n целых чисел — построение солдат в требуемом порядке.

Примеры

№	Входные данные	Выходные данные
1	3 2	3 1 2
2	3 0	1 2 3

Двухтуровая олимпиада

Как известно, личная олимпиада по информатике проходит в два тура. На каждом из туров участники получают какие-то баллы, при этом итоговый балл определяется как сумма полученных баллов. Известны баллы, которые каждый участник получил на каждом из туров. Жюри хочет фальсифицировать итоги олимпиады так, чтобы победил «нужный» участник.

При этом жюри может делать следующие «подтасовки» (можно делать несколько «подтасовок» применительно как к одному и тому же, так и к разным турам):

Прибавить к результатам всех участников по одному из туров одно и то же положительное число.
Умножить результаты участников по одному из туров на некоторый коэффициент, больший 1.
При этом должна сохраниться правдоподобность результатов, которая заключается в том, что никто из участников не должен получить больше 100 баллов за каждый из туров.

Определите список участников, которые в результате таких фальсификаций могут оказаться победителями олимпиады (то есть в сумме за два тура иметь не меньше баллов, чем каждый из остальных участников).

Входные данные
Во входном файле записано сначала число участников N (1 ≤ N ≤ 1000), затем N пар чисел — результаты каждого участника за 1-й и за 2-й туры (результат участника за тур — это вещественное число от 0 до 100) не более, чем с 3 знаками после десятичной точки.

Выходные данные
В выходной файл выведите сначала количество участников, которые смогут стать победителями олимпиады, а затем в возрастающем порядке их номера.

Примеры

№	Входные данные	Выходные данные
1	4 45 90 70 80 0 0 75 75	2 2 4

Гирьки

У ювелира есть весы с двумя чашками, он может определять равны ли массы грузов, лежащих на двух чашках, а если не равны – то на какой чашке лежит более лёгкий груз.

Масса ювелирного изделия, которую нужно определить ювелиру, является целым числом от 1 до N. Ювелир должен запасти набор гирек (их массы также должны быть целыми числами), используя которые ювелир может определить любую возможную массу от 1 до N. Для определения массы ювелир может производить любое число взвешиваний, может использовать все гирьки или только некоторые из них, может класть гирьки на разные чашки весов.

Определите набор гирек, содержащий минимальное возможное число гирек, используя который можно определить любую возможную целочисленную массу от 1 до N.

Программа получает на вход натуральное число N (2 ≤ N ≤ 10⁸) – максимально допустимую массу ювелирного изделия.

Программа должна вывести несколько натуральных чисел, не превосходящих 10⁹, – массы гирек в минимальном требуемом для решения задачи наборе (допускается использовать гирьки массой, больше, чем N, если их масса не превосходит 10⁹).

Если задача имеет множество решений, необходимо вывести любое из них.

Примеры

№	Входные данные	Выходные данные	Пояснение
1	3	2	Пусть x – изделие, массу которого необходимо определить. Нужно на одну чашу весов положить x, а на другую чашу весов – гирьку в 2. Если x будет легче, то x = 1, при равенстве – x = 2, если x тяжелее, то x = 3.
2	5	3 4	Покажем, как при помощи гирек в 3 и 4 определить все массы от 1 до 5. Массы 3 и 4 можно определить при помощи равенств x = 3 и x = 4. Массу 1 можно определить при помощи равенства x + 3 = 4 (на одну чашу кладется изделие и гирька массой 3, на другую чашу – гирька массой 4). Массу 2 можно определить, например, по условию x < 3 (на одну чашу весов кладется изделие, на другую – гирька массой 3), а также проверив при помощи ранее описанного алгоритма, что x ≠ 1 . Массу 5 можно определить при помощи взвешивания x > 4.

Жук в деревне

Однажды утром во время традиционной инспекции картофельного поля кот Матроскин обнаружил на одном из кустиков колорадского жука. Придя в ужас, он тут же помчался расспрашивать дядю Фёдора (как наиболее образованного из друзей) о том, как эти жуки размножаются и как с ними бороться.

Картофельные поля обычно очень аккуратно устроены: кусты картофеля рассажены на них так, что образуют клетчатое поле, где каждая клетка — картофельный куст. Как только на каком-то из кустов появляется колорадский жук, он начинает активно есть и размножаться. Поэтому каждый час на каждый куст будет добавляться столько же жуков, сколько соседних с ним по стороне кустов, уже зараженных жуками. Например, если у куста ровно один сосед, на котором уже есть жуки, то на него добавится один жук, а если все четыре соседа заражены жуками, то на куст добавится четыре новых жука. И если жуков не остановить, они заполнят собой все поле. Но к счастью, когда-то давно дядя Фёдор, прочитав статью в «Мурзилке», сделал отпугиватель колорадских жуков...

Если честно, Матроскин не очень понял, как работает этот отпугиватель. Но главное он запомнил: его надо установить на один из кустиков картофеля, и как только на этом кустике окажется ровно k колорадских жуков, что-то (вот этого Матроскин и не понял) произойдет и все жуки сбегут с поля.

Зная координаты куста картофеля, на который Матроскин установил отпугиватель, посчитайте, через сколько часов после появления первого колорадского жука на поле он подействует. Матроскин поставил ловушку в первый час после появления жука на поле.

Входные данные
Вам даны три числа: x и y — координаты кустика картофеля, на который Матроскин установил отпугиватель, и k — параметр отпугивателя (1<=k<=10⁹, |x|<=10⁹, |y|<=10⁹ ). Тот из кустов, на котором был найден первый жук, имеет координаты (0, 0) . Координаты всех кустов поля не превосходят 10⁹+1 по модулю.

Выходные данные
Выведите одно целое число: через сколько часов ловушка сработает. Если же ловушка никогда не сработает, выведите −1.

Примеры

№	Входные данные	Выходные данные
1	0 0 1	0
2	0 0 5	2

Считаем графы

графы Обход в ширину Вывод формулы

У Маши есть связный ненаправленный граф G с N вершинами, помеченными 1…N и M ребрами ($1 \leq N \leq10^2$, $N-1 \leq M \leq \frac {N^2+N}{2}$). G может содержать петли (ребра из вершины в неё же), но не имеет параллельных ребер (несколько ребер, соединяющих одни и те же конечные точки).
Пусть $f_G(a,b)$ это булевская функция, которая отвечает истина, если существует путь от вершины 1 до вершины a, который проходит ровно b ребер, для $1 \leq a \leq N$ и $0 \leq b$, и ложь иначе. Если по ребру проходим множество раз, это число включается в ответ.
Даша хочет повторить за Машей. В частности, она хочет сконструировать ненаправленный граф G′ такой, что $f_{G'}(a,b)=f_G(a,b)$ для всех a и b.

Посчитайте количество различных графов G′, которые Даша может создать, по модулю $10^9+7$. Как и G, G′ может содержать петли но не может иметь параллельные ребра (это означает, что имеется всего $2^{ \frac {N^2+N} {2}}$ различных графов на N вершинах).
Каждый ввод содержит T ($1 \leq T \leq \frac {10^5}{4}$) тестов, которые должны решаться независимо. Гарантируется, что сумма $N^2$ по всем тестам не превысит $10^5$.

Входные данные
Первая строка ввода содержит T, количество тестов.
Первая строка каждого теста содержит два целых числа N и M.
Следующие M строк каждого теста содержат два целых числа x и y ($1 \leq x \leq y \leq N$), обозначающих ребро между x и y в G.

Тесты разделены пустой строкой для читабельности.

Выходные данные
Для каждого теста выведите количество различных G′ по модулю $10^9+7$ на отдельной строке.

Примеры

№	Входные данные	Выходные данные	Примечание
1	1 5 4 1 2 2 3 1 4 3 5	3	`G′` может быть равен `G′` или одному из двух следующих графов: 5 4 1 2 1 4 3 4 3 5 5 5 1 2 2 3 1 4 3 4 3 5
2	7 4 6 1 2 2 3 3 4 1 3 2 4 1 4 5 5 1 2 2 3 3 4 4 5 1 5 5 7 1 2 1 3 1 5 2 4 3 3 3 4 4 5 6 6 1 2 2 3 3 4 4 5 5 6 6 6 6 7 1 2 2 3 1 3 1 4 4 5 5 6 1 6 10 10 1 1 1 2 1 3 1 4 1 5 1 6 1 7 1 8 1 9 1 10 22 28 1 2 2 3 3 4 4 5 5 6 6 7 1 7 1 8 3 9 8 10 10 11 10 12 10 13 10 14 11 15 12 16 13 17 14 18 9 15 9 16 9 17 9 18 15 19 19 20 15 20 16 21 21 22 16 22	45 35 11 1 15 371842544 256838540	Это пример более крупного теста. Обязательно выводите ответ по модулю $10^9+7$. Обратите внимание, что ответ для предпоследнего теста - $2^{45}\ \ (mod\ 10^9 + 7)$.

Площадь

Городская площадь имеет размер n х m и покрыта квадратной плиткой размером 1 х 1. При плановой замене плитки выяснилось, что новой плитки недостаточно для покрытия всей площади, поэтому было решено покрыть плиткой только дорожку по краю площади, а в центре площади разбить прямоугольную клумбу (см. рисунок к примеру). При этом дорожка должна иметь одинаковую ширину по всем сторонам площади. Определите максимальную ширину дорожки, которую можно выложить из имеющихся плиток.

Формат входных данных
Первая и вторая строки входных данных содержат по одному числу n и m (3 ≤ n ≤ 2 x 10⁹ , 3 ≤ m ≤ 2 x 10⁹) - размеры площади.
Третья строка содержит количество имеющихся плиток t, 1 ≤ t < nm.
Формат выходных данных
Программа должна вывести единственное число - максимальную ширину дорожки, которую
можно выложить из имеющихся плиток.

Ввод	Вывод
6 7 38	2

Замечание
Пояснение к примеру. Площадь имеет размеры 6 х 7, из 38 плиток можно выложить дорожку шириной в 2 плитки.

Игра для Пети и Вани

игры НОД и алгоритм Евклида Вывод формулы

Некоторые уроки в школе для Вани и Пети очень скучны. На этих уроках Петя и Ваня придумали игру. Сначала мальчики записывают на листке два различных натуральных числа a и b .
Ход игры заключается в следующем: среди записанных чисел выбирают p и q такие, что модуля их разности $| p - q |$ еще нет на листке, и дописывают его.
Проигрывает тот, кто не может сделать ход.
Определите, кто из ребят окажется победителем при правильной игре обоих. Ваня вежливый мальчик, поэтому всегда ходит вторым.

Входные данные: В первой и единственной строке записано два различных натуральных числа 1 <= a , b <= 10^9 , разделенные пробелом - два исходных числа на листке.

Выходные данные: Выведите имя победителя в этой игре (Petya или Vanya)

Примечание: В первом примере Петя первым ходом допишет на листок число |6−2| = 4 . Больше ходов нет, поэтому выигрывает Петя. Во втором примере первым ходом на листок будет дописано число |4−1| = 3 . Затем Ваня может записать |3−1| = 2 , тогда у Пети ходов не останется. Побеждает Ваня.

Примеры

№	Входные данные	Выходные данные
1	6 2	Petya
2	4 1	Vanya

Задача для Пети и Вани

НОД и алгоритм Евклида Вывод формулы

Пятиклассники Петя и Ваня изучили на уроках математики следующий алгоритм Евклида:

Пусть a, b — числа, НОД которых надо найти.
Если b = 0, то число a — искомый НОД.
Если b > a, то необходимо поменять местами числа a и b.
Присвоить числу a значение a – b.
Вернуться к шагу 2.

Маша придумала для них задачу на закрепление. Она попросила мальчиков придумать такие числа a, b, c и d, что в процессе реализации алгоритма Евклида для заданной пары чисел (a, b) наступает такой момент, когда перед исполнением шага 2 число a будет равно c, а число b будет равно d.

Напишите для Маши программу, которая проверит, удовлетворяют ли числа a, b, c, d условиям Маши.

Входные данные: Первая строка входных данных содержит количество наборов входных данных K ($1 <= K <= 100$). Далее идут описания этих наборов. Каждое описание состоит из двух строк. Первая из них содержит два целых числа: a, b ($1 <= a,\ b <= 10^{18}$). Вторая строка – два целых числа: c, d ($1 <= c,\ d <= 10^{18}$).
Все числа в строках разделены пробелом.

Выходные данные: Для каждого набора входных данных выведите слово «YES», если в процессе применения алгоритма Евклида к паре чисел (a, b) в какой-то момент получается пара (c, d). В противном случае выведите слово «NO».

Примеры

№	Входные данные	Выходные данные
1	2 20 10 10 10 10 7 2 4	YES NO

Следующий палиндром

Строки Вывод формулы

Натуральное число называется палиндромом, если его запись в десятичной системе счисления одинаково читается как слева направо, так и справа налево. По данному натуральному числу N определите следующее за ним натуральное число (то есть наименьшее число, которое превосходит N), являющееся палиндромом.
Программа получает на вход одно натуральное число N.
Программа должна вывести наименьшее натуральное число, которое больше N и является палиндромом.

Ввод	Вывод
4321	4334

Переливания

Имеется 10 колб с водой и известен объем воды в каждой из них. За одно «касание» можно взять одну колбу и часть воды (или всю воду) из этой колбы разлить по одной или нескольким другим колбам в любом количестве. За какое наименьшее количество «касаний» можно уравнять объемы воды во всех колбах? Каждая колба может вместить любой объем воды.
Формат входных данных
Программа получает на вход 10 целых чисел a_i , каждое записанное в отдельной строке — объем воды в каждой из колб. Все числа — целые, от 0 до 100.
Формат выходных
данных Выведите одно целое число — минимальное количество «касаний», за которое можно уравнять объемы воды во всех колбах.

Ввод	Вывод
30 26 2 3 4 5 6 7 8 9	2

Примечание В примере можно из первой колбы перелить 20 во вторую, оставляя в первой колбе 10. Затем из второй колбы разлить воду по всем остальным колбам так, чтобы в каждой из колб оказалось по 10.

Заработная плата

В некоторой компании работают три сотрудника — Алексей, Виктор и Сергей. Их месячный оклад составляет A, B и C рублей соответственно. При этом Алексей работает на полную ставку, а Виктор и Сергей — на половину ставки, то есть работают вдвое меньше, чем Алексей.

По итогам месяца директор компании хочет распределить между этими сотрудниками премиальный фонд, который составляет N рублей. При этом директор хочет распределить премиальный фонд таким образом, чтобы итоговая зарплата (сумма оклада и премии) у этих сотрудников оказалась пропорциональна проведённому на работе времени, то есть зарплата Алексея должна оказаться ровно в два раза больше, чем зарплата Виктора и Сергея. Более формально, если премия Алексея составит x рублей, премия Виктора — y рублей, премия Сергея — z рублей, то A + x = 2 (B + y) = 2 (C + z), x + y + z ≤ N. При этом бухгалтерия требует, чтобы размер премии (как и размер оклада) выражался целым числом рублей, а директор хочет распределить максимально большую часть премиального фонда, то есть сумма x + y + z должна быть максимально возможной, не превышая при этом N.

Напишите программу, которая определит, какую премию нужно назначить каждому из сотрудников.
Программа получает на вход сначала три целых числа A, B, С, записанные в отдельных строках, — размеры окладов Алексея, Виктора и Сергея (A > 0, B > 0, С > 0). В четвёртой строке входных данных записано одно целое число N — размер премиального фонда (N ≥ 0).
Программа должна вывести три числа — размер премии Алексея, Виктора и Сергея. Если премиальный фонд нельзя распределить так, чтобы выполнялись требуемые условия, программа должна вывести одно число 0.

Ввод	Вывод	Примечание
7 3 4 12	5 3 2	С учетом премии зарплата Алексея составит 12 рублей, Виктора и Сергея — 6 рублей.
20 10 11 2	0	Добиться нужного соотношения премиальных выплат невозможно.

Лифт в бизнес-центре - 2

В прошлом году на муниципальном этапе была задача про сотрудников бизнесцентра, которые вечером выходят с работы. Теперь решите задачу про сотрудников бизнесцентра, которые утром приходят на работу.

Бизнес-центр представляет собой N-этажное здание, этажи пронумерованы от 1 до N снизу вверх. На каждом этаже работает ровно один сотрудник. Все сотрудники утром приезжают на парковку, которая расположена в подвальном помещении, на один этаж ниже первого. Бизнес-центр оборудован лифтом, который вмещает неограниченное число людей, но вредный лифтёр сегодня готов отвезти всех сотрудников только на один какой-то этаж.

У каждого сотрудника есть выбор: он может пойти вверх пешком по лестнице, на подъём на один этаж при этом будет уходить A секунд. Либо он может сесть в лифт, который отвезёт всех сотрудников на какой-то выбранный ими вместе этаж. Выйдя из лифта, сотрудник может подняться до своего этажа (также тратя A секунд на подъём на один этаж), либо спуститься до нужного этажа вниз, тратя B секунд на спуск на один этаж. Лифт тратит C секунд на подъём на один этаж.
Определите минимальное время, за которое все сотрудники разойдутся по своим этажам, если они наилучшим образом выберут этаж, на который едет лифт, и свою стратегию поведения (подниматься по лестнице или ехать на лифте, а затем идти по лестнице).

Первая строка входных данных содержит число N – количество этажей в бизнесцентре. Следующие три строки содержат числа A, B, С – время, необходимое сотруднику на подъём на один этаж, на спуск на один этаж и время, необходимое лифту на подъём на один этаж. Все числа – целые положительные, не превосходящие 2×10⁹ , при этом A ≥ B, A ≥ С. Программа должна вывести единственное целое число – минимальное время, за которое все сотрудники могут добраться до своего этажа.

Ввод	Вывод	Примечание
6 20 10 5	45	В здании 6 этажей. Сотрудник поднимается на один этаж за 20 секунд, спускается за 10 секунд. Лифт поднимается на один этаж за 5 секунд. Чтобы быстрее всем добраться до мест, лифт едет на 5-й этаж за 25 секунд. Сотрудник, который работает на 6-м этаже, выходит из лифта и поднимается за 20 секунд, всего его путь занимает 45 секунд. Сотрудник, работающий на 3-м этаже, едет на лифте и спускается на 2 этажа, это также занимает 45 секунд. Сотрудники с 4 и 5-го этажей также едут на лифте, их путь будет быстрее 45 секунд. На 1 и 2-й этажи сотрудники поднимаются пешком по лестнице за 20 и 40 секунд соответственно. Итого все сотрудники добираются до своих этажей не более чем за 45 секунд.

Книга по полкам

Линейные алгоритмы Вывод формулы

На полки нужно расставить N книг. На каждую полку можно поставить не более K книг. Сколько минимально потребуется полок? Написать программу: вводятся два целых числа N и K; вывести одно число - ответ на задачу.

Примеры

№	Входные данные	Выходные данные
1	40 10	4

Симметричное число

Вывод формулы

Дано число, на запись которого отведено 4 знакоместа. Определите, является ли десятичная запись этого числа симметричной. Если число симметричное, то выведите 1, иначе выведите любое другое целое число. Число может иметь меньше четырех цифр, тогда нужно считать, что его десятичная запись дополняется слева незначащими нулями.

Входные данные
Программа получает на вход неотрицательное число.

Выходные данные
Выведите ответ на задачу.

Запрещено использовать какие-либо алгоритмические конструкции для решения данной задачи. Можно использовать только арифметические операции (без использования встроенных функций)

Примеры

№	Входные данные	Выходные данные
1	2007	8
2	2002	1

Вося и Доша

Папа Воси покупал ёлочку 31 декабря, поэтому ему впихали последнюю и очень странную. У этой ёлочки всего 2 ветки, и каждая из них разветвляется ещё на две ветки, и эти ветки ещё на две, и ещё, и ещё... и так N раз.
Вося захотел повесить на бедное дерево свои любимые ёлочные игрушки: разноцветные шарики с красивой надписью "С++". Но Восе удобно вешать свои шарики только на "конечные" веточки (веточки, которые не разветвляются), и ему даже не лень стало из сосчитать. В итоге Вося повесил на ёлочку K шариков и пошёл помогать маме стругать оливье.
Тогда до ёлочки добралась его сестра, начинающий математик Доша. Она захотела украсить ёлочку мишурой, наматывая её на каждую ветку (одна мишура на одну ветку). Считать она, однако, умеет только до 100, поэтому позвонила своему другу, то есть вам, с просьбой сказать, сколько мишуры ей нужно.
Считайте, что вы следили за этой ёлочкой, поэтому знаете и N, и K (0 < N, K <= 10^9). Помогите Доше как можно быстрее, ведь ей пора бежать за тазиком для оливье.

Ввод	Вывод
90 84	173

кунтер-струк

В игре кунтер-струк: локальное отступление добавили новое НЕЛЕТАЛЬНОЕ оружие с названием ХАХАЙКА. Суть ХАХАЙКИ заключается в том, что она заставляет обрадоваться каждого персонажа на N секунд. Число секунд высчитывается по определённой формуле, которая состоит из модуля произведения округленного вверх корней уравнения ax2+bx+c=0 и умноженного на количество секунд удержания сочетаний клавиш “Alt + f4”=m. От вас требуется найти количество N секунд, если это невозможно, то вывести на экран -1;

Формат входных данных

На вход подаются числа a,b,c,m -10*100^4 ≤ a, b, c ≤ 10*100^4; 1 ≤ m ≤ 10*100^4

Выводится одно целое число, количество N секунд.

Ввод	Вывод
1 -2 1 5	5
1 3 2 4	8

Ануфрий

Вывод формулы математика

Жил дотер по имени Ануфрий. И вдруг случилось так, что его заботливая мама отрубила ему интернет. И как назло на компьютере Ануфрия была всего одна офлайновая игра – Minecraft.

Во время увлекатейнешего разрушения своего разума мальчик не знал что в этой версии игры надо думать о еде. И тут ему пришла интереснейшая мысль насчет своей еды: так как у него был только торт(как ни странно он круглый), каким образом он может получить максимальное количество кусков торта при разрезаний n. Но так как, как типичный игрок в Dota 2, Ануфрий не отличался сообразительностью. HELP HIM!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Гарантируется, что меч, которым он режет торт, прямой. Так как Ануфрий не учит математику, а играет в доту, то не гарантируется n – натуральное(если такое произошло то выведите смайлик «

-1»).

На вход подается n.

На выходе вы должны вывести ответ на задачу)))

Ввод	Вывод
-2	-1
0	0
3	7

(с) Тимченко А., 2018 г.

три оленя

Элементарная геометрия Вывод формулы

Однажды на огород к Ивану Петровичу (сыну Деда Мороза и Снегурочки) забежало целых три оленя. Известно, что олени — весьма агрессивное нечто, особенно когда речь идет о борьбе за вкусную зелень. Поэтому каждый из трех оленей, заметив других козлов, замер на месте и начал наблюдать за оставшимися оленями: одним глазом за одним оленем, другим — за оленем номер 2. Естественно, для этого оленю нужно “косить” глазами.

Определите наибольший угол, на который пришлось “раскосить” глазами этим странным животным. Причём тут Иван Петрович и мы, и как олени “раскосили” глаза, мы в душе не знаем. Своего дилера мы не сдадим.

Программа получает на вход координаты трех точек, в которых стоят олени (сначала координаты первого оленя, затем — второго и третьего). Координаты — пара целых чисел, не превосходящих 104 по модулю.

Ввод	Вывод
0 0 3 0 0 4	90.000000

(с) Манаев И., Кашукова М., 2018 г.

Танец

Для исполнения большого танца в круг выстроилось N танцоров (N чётное). Пронумеруем танцоров числами от 1 до N начиная от подиума по часовой стрелке. На каждом шаге танца танцоры разбиваются на пары (пару образуют два соседних по кругу танцора), и танцоры в паре меняются местам, причём на первом и всех последующих нечётных шагах танцор, стоящий в начале круга, образует пару с танцором, стоящим рядом с ним по часовой стрелке. Также пару образуют два танцора, следующие за ними по часовой стрелке, и т. д. На втором шаге и всех шагах с чётными номерами танцор, стоящий в начале

круга, образует пару с танцором, стоящим рядом с ним против часовой стрелки. Два танцора, следующие за ними против часовой стрелки, также образуют пару и т. д.

На рисунке изображена начальная расстановка для N = 6 танцоров и два следующих шага танца. Расположение подиума отмечено точкой.
Определите, кто будет стоять рядом с танцором номер P через K шагов.

Программа получает на вход три целых числа N, P, K, записанные в отдельных строках. Первое число N – количество танцоров в кругу, N чётное. Второе число P – номер танцора, 1 ≤ P ≤ N. Третье число K – количество сделанных шагов после начала танца, 1 ≤ K. Максимальные значения для N и K <= 10⁹.

Программа должна вывести два целых числа в порядке возрастания – номера танцоров, которые будут стоять рядом с танцором номер P после K шагов танца.

Ввод	Вывод	Примечание
6 5 2	2 4	Рисунок выше соответствует этому примеру.

Преобразование дроби

Дана правильная рациональная несократимая дробь a / b. С этой дробью выполняется следующая операция: к числителю и знаменателю дроби прибавляется 1, после чего дробь сокращается. Определите, можно ли при помощи таких операций из дроби a / b получить другую правильную дробь c / d.

Программа получает на вход четыре целых числа a, b, c, d, причём 0 < a < b ≤ 10⁵, 0 < с < d ≤ 10⁵, числа a и b взаимно простые, числа с и d взаимно простые, a / b ≠ c / d.

Программа должна вывести одно натуральное число – сколько описанных операций нужно применить, чтобы из дроби a / b получить дробь с / d. Если это сделать невозможно, программа должна вывести число 0.

Ввод	Вывод	Примечание
1 3 2 3	2	Дана дробь 1 / 3. После первой операции получается дробь 2 / 4, которая сокращается до 1 / 2. После второй операции получается дробь 2 / 3.
2 3 1 3	0	Получить из дроби 2 / 3 дробь 1 / 3 невозможно.

Разбиение последовательности

Последовательность натуральных чисел от 1 до `N` нужно разбить на две части от 1 до `K` и от `K+1` до `N` так, чтобы абсолютное значение разности суммы чисел в первой и второй части последовательности было как можно меньше. То есть нужно найти такое `K`, что значение выражения `|\ sum_{i=1}^K\ i\ -\ sum_{i=K+1}^N\ i\ |` минимально. Например, для последовательности чисел от 1 до 4 разбиение будет минимальным для `K=3`, так как `|\ (1+2+3)-(4)\ |\ =\ 2`, что меньше значения разности для `K=1` равного `|\ (1)-(2+3+4)\ |\ =\ 8` и для `K=2` равного `|\ (1+2)-(3+4)\ |\ =\ 4`.

Напишите программу, которая для заданного `N` находит минимальное разбиение.

Первая строка ввода содержит одно целое число `N` (`2\ ≤\ N\ ≤\ 10^9`).

Вывести одно целое число `K`. Если существует несколько вариантов разбиения, то вывести меньшее из возможных `K`.

Ввод	Вывод
4	3

Кинотеатр

В первом ряду кинотеатра N + 2 мест, крайние места заняты персоналом кинотеатра, но N мест посередине свободно. K школьников входят в зрительный зал по очереди, и, конечно же, каждый школьник достаёт спиннер и начинает его крутить до начала сеанса. Поэтому каждый школьник выбирает себе место как можно дальше от уже занятых мест. А именно, школьник находит самый большой свободный участок в ряду (любой, если таких несколько) и садится посередине него. Если число свободных мест на этом участке было нечётно, то школьник садится точно посередине участка, тогда слева и справа от него остаётся поровну свободных мест. Если же это число чётно, то школьник выбирает одно из двух свободных мест посередине, тогда с одной стороны от школьника будет на одно свободное место больше, чем с другой стороны.

По данным числам N и K определите, сколько мест осталось свободными с двух сторон от школьника, который занял место последним (K-м по счёту).

Программа получает на вход два целых числа N и K, 1 ≤ K ≤ N ≤ 10¹⁸, и должна вывести два целых числа в порядке неубывания – количество свободных мест с двух сторон от школьника, который последним занял место в ряду.

Ввод	Вывод	Примечание
10 1	4 5	В зале 10 свободных мест, первый школьник сел посередине, с одной стороны от него 4 места, с другой стороны – 5.
10 2	2 2	Второй вошедший в зал школьник садится посередине группы из 5 свободных мест, с каждой стороны от него остаётся по 2 свободных места.
10 3	1 2	После того, как два школьника сели на места, в зале остались группы свободных мест из 4, 2, 2 мест. Третий школьник садится посередине группы из 4 мест, поэтому с одной стороны от него 1 место, с другой стороны – 2 места.

Спиннеры

Спиннер – модная игрушка c подшипником в основании, к которому прикреплены лопасти. Афанасий открыл бизнес по производству спиннеров. Он выяснил, что за спиннер, у которого N лопастей, покупатели готовы платить A + B × N рублей, но при этом покупатель не станет покупать спиннер, если его цена будет выше C рублей. Определите максимальное число лопастей спиннера, который согласится приобрести покупатель. Программа получает на вход три числа A, B, C (стоимость основания спиннера, стоимость одной лопасти и максимальная стоимость всего спиннера). Все числа – целые положительные, не превосходящие 2×10⁹ , при этом A ≤ C.

Программа должна вывести одно число – максимальное число лопастей спиннера.

Ввод	Вывод	Примечание
20 10 55	3	Спиннер с 3 лопастями будет стоить 50 рублей, а с 4 лопастями – 60 рублей. Максимальная возможная стоимость спиннера – 55 рублей, поэтому максимальное число лопастей равно 3.

RAID

Битовые операции Вывод формулы

При хранении данных одна из основных задач – соблюдение баланса между расходами на количество дисков и надёжностью записи. Одним из компромиссных по надёжности и стоимости хранения данных является RAID-3 – избыточный массив независимых дисков с выделенным диском для хранения блоков чётности. Наш RAID-3 состоит из пяти дисков, на четырёх из которых содержится информация, а на пятом – блоки контрольных битов чётности. При записи четырёх байтов (по байту на каждый из четырёх дисков) вычисляется контрольный байт четности, составленный из контрольных битов. Для каждого из восьми разрядов вычисляется сумма значений битов в этих разрядах во всех байтах данных, при этом значение контрольного бита выбирается так, чтобы сумма значений во всех разрядах (включая контрольный) была чётной. Например, у нас есть два основных диска и на них записывается байты 10010010 и 01110111. Тогда значение контрольного байта равно 11100101 – в каждом разряде сумма получается чётной.

Один из четырёх основных дисков в RAID-3 вышел из строя. Известны значения байтов в трёх оставшихся дисках и значение байта на контрольном диске. Какой байт был записан на сломавшемся диске? Все числа приведены в десятичной системе счисления.

– значения на первых трех дисках: 177, 177, 177, контрольный байт: 177;

– значения на первых трех дисках: 79, 79, 79, контрольный байт: 0;

– значения на первых трех дисках: 46, 56, 248, контрольный байт: 90;

– значения на первых трех дисках: 255, 0, 150, контрольный байт 96;

– значения на первых трех дисках: 137, 232, 23, контрольный байт 212.

Ответы также следует привести в десятичной системе счисления. Ответы разделять

пробелом.

Уравнение

Вывод формулы

Курбат Егоров очень любит математику, особенно уравнения. Он решает их все свободное время. Но он не любит решать уравнеия, которые он не может решить, ибо это пустая трата времени, поэтому Курбат попросил Вас написать программу, которая будет определять, может ли он решить это уравнение. Курбат, как победитель всероса по информатике, разумеется, может написать эту программу сам, но у него совершенно нет на это времени - ему же нужно решать уравнения!

Входные данные

На вход подается одна строка без пробелов и знаков переноса строки.

В ней могут содержаться такие символы:

x - переменная, относительно которой Курбат должен решить

уравнение. Может стоять где угодно.

+-*/= - соответствующие знаки арифметических операций. НЕ могут стоять в начале уравнения. Могут стоять после икса или констант.

^ - возведение в степень. Может стоять только после икса. После может стоять только константа.

Числа от -10^1000 до 10^1000 - константы. Могут стоять после иксов,

знаков арифметических операций и знака возведения в степень.

Выходные данные

Если курбат может решить уравнение, то выведите "Yes", иначе выведите "No".

Ввод	Вывод
10x+x=7	Yes

(с) Григорьев Е., 2017

Задача №3

Вывод формулы

Пионер угрюмо сидел в своей темной комнате. По совершенно непонятной причине лампочка тускло помигивала вместо того, чтобы ярко светить непеременным светом. Пионер находился в раздумьях. Кровавые лужи давно были вытерты со стола, но все же остались багровые следы. Они слегка раздражали внимание пионера. Но это отвлекало не так сильно, как гудок столовой и хруст костей, которые постоянно шумели в его разуме и не давали покоя. Но пионер уже давно привык к ним.
Он думал, чем бы ему заняться. Казалось за 47953 круга он переделал все, что только можно было. Но вдруг пионер осознал, что он никогда не считал сумму слегка избыточных чисел на отрезке. Он решил немедленно заняться этим.

Слегка избыточное число — число, сумма собственных делителей( всех делителей кроме исходного числа) которого на единицу больше самого числа.

P.S. Делитель числа x – натуральное число, на которое x делится без остатка.

Входные данные

Даны два целых числа l, r ( 0 <= l, r, <= 10^9) – границы запроса

Выходные данные

Выведите одно число – сумму слегка избыточных чисел, лежащих на отрезке [l, r].

(c) Егор Курбатов, 10и

Идеальный сад

Элементарная геометрия Вывод формулы

Один успешный бизнесмен Василий после двух долгих лет непрерывной работы ушел в долгожданный отпуск. Желая расслабиться, у него

возникла идея завести сад из синих и красных цветов на заднем дворе своего коттеджа. Ежедневная работа с таблицами ему изрядно надоела,

поэтому он хотел видеть сад круглой формы. Однако чтобы созерцание сада, сидя на кресле, было максимально расслабляющим,

граница между синими и красными должна быть на одинаковом расстоянии L от него.

Василий нанял садовника для создания сада. Садовник закупил одинаковое количество красных и синих цветов, Но потом вспомнил последнее

условие бизнесмена. Ему было жаль выкидывать так много цветов, поэтому он решил что граница между разными цветами должна делить сад

на две равные по площади части. Тогда он сможет посадить все цветы. Не владея высокими знаниями геометрии, садовник смог посчитать

радиус сада R, но расстояние от кресла на веранде до центра сада он попросил посчитать Вас.

Входной файл содержит целое число R - радиус сада (1 < R < 10000) и целое число L - расстояние от кресла до границы между синими и красными

цветами (1 < L < 10000). Ваша задача вывести расстояние от кресла на веранде до центра сада. Ответ округлите до сотых, или выведите -1,

если построить такой сад невозможно. Обратите внимание, что кресло может находится как за пределами сада, так и в саду.

Входные данные:

12 15

Выходные данные:

13.262

Входные данные:

100 1

Выходные данные:

-1

(с) Линд Владимир

Разности