| | | |
|
Цепочка слов
Обход в глубину
Бор
Цепочкой слов длины n назовем последовательность слов w1, w2, ..., wn такую, что для 1 ≤ i ≤ n слово wi является собственным префиксом слова wi + 1.
Напомним, что слово u длины k называется собственным префиксом слова v длины l, если l > k и первые k букв слова v совпадают со словом u.
Задано множество слов S = {s1, s2, ..., sm}. Найдите максимальную длину цепочки слов, которую можно построить, используя (возможно, не все) слова этого множества.
Входные данные
Первая строка входного файла содержит целое число m(1 ≤ m ≤ 255). Каждая из последующих m строк содержит по одному слову из множества S.
Все слова не пусты, имеют длину, не превосходящую 255 символов, и состоят только из строчных букв латинского алфавита.
Выходные данные
В выходной файл выведите ответ на задачу.
| Ввод |
Вывод |
|
3
a
ab
abc
|
3 |
|
5
a
ab
bc
bcd
add
|
2 |
| |
![]()
|
|
Type Printer
Бор
Обход в глубину
Вам нужно напечатать N слов на Movable Type Printer. Movable Type Printers — это старые принтеры, для работы которых требуется ставить маленькие металлические кусочки (каждый из кусочков содержит одну букву) в определенном порядке, образуя таким образом слова. Потом все они вдавливаются в лист бумаги. Таким образом печатается одно слово. Ваш принтер позволяет делать следующие операции:
- Добавить букву в конец слова, находящегося сейчас на принтере.
- Удалить последнюю букву из слова, находящегося сейчас на принтере. Эту операцию можно делать, только если слово содержит хотя бы одну букву.
- Напечатать слово, находящееся на принтере.
Изначально на принтере содержится пустое слово. В конце печати на принтере можно оставить непустое слово. Слова, которые вам даны, вы можете печатать в произвольном порядке.
Каждая из трёх операций занимает одну единицу времени. Вам нужно найти последовательность операций, которая печатает данные N слов за минимальное время. Если минимальных последовательностaей несколько, выведите любую.
Входные данные
Ваша программа должна считать следующие входные данные:
На первой строке число N (1<=N<=25000).
На следующих N строках слова, состоящие из маленьких букв латинского алфавита. Длина каждого слова не превышает 20. Все слова различны.
Выходные данные
Ваша программа должна вывести следующие данные:
На первой строке M — число операций.
На следующих M строках по одному символу — описание операций. Каждая операция описывается одним символом:
Добавление символа обозначается собственно символом.
Удаление символа обозначается символом «-» (минус, ASCII-код 45).
Операция «напечатать текущее слово» обозначается символом «P» (заглавная латинская буква P).
| Ввод |
Вывод |
|
3
print
the
poem
|
20
t
h
e
P
-
-
-
p
o
e
m
P
-
-
-
r
i
n
t
P
|
| |
![]()
|
|
Топологическая сортировка
Обход в глубину
Топологическая сортировка
Дан ориентированный невзвешенный граф. Необходимо его топологически отсортировать.
Входные данные: В первой строке содержатся два натуральных числа n и m (1≤n≤105, 1≤m≤105) — количество вершин и рёбер в графе соответственно. Далее в m строках перечислены рёбра графа. Каждое ребро задаётся парой чисел — номерами начальной и конечной вершин соответственно (нумерация вершин начинается с 1).
Выходные данные: Вывести любую топологическую сортировку графа в виде последовательности номеров вершин. Если граф невозможно топологически отсортировать, требуется вывести −1.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 4
1 4
4 3
4 2
3 2 |
1 4 3 2 |
| |
![]()
|
|
Обход графа. Компонента связности
Обход в глубину
Дан неориентированный невзвешенный граф. Для него вам необходимо найти количество вершин, лежащих в одной компоненте связности с данной вершиной (считая эту вершину).
Входные данные: В первой строке входных данных содержатся два числа: N и S (1 ≤ N ≤ 100; 1 ≤ S ≤ N), где N – количество вершин графа, а S – заданная вершина. В следующих N строках записано по N чисел – матрица смежности графа, в которой 0 означает отсутствие ребра между вершинами, а 1 – его наличие. Гарантируется, что на главной диагонали матрицы всегда стоят нули.
Выходные данные: Выведите одно целое число – искомое количество вершин.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 1
0 1 1
1 0 0
1 0 0 |
3 |
| |
![]()
|
|
Компоненты связности
Обход в глубину
В неориентированном графе посчитать количество компонент связности. В графе могут быть петли и кратные ребра.
Входные данные: В первой строке записаны сначала два числа N и M, задающие соответственно количество вершин и количество ребер (1<=N<=100, 0<=M<=10000), а затем перечисляются ребра. Каждое ребро задается двумя номерами вершин, которые оно соединяет.
Выходные данные: Выведите одно число - количество компонент связности
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 4
1 1
1 2
1 3
2 3
|
1 |
| 2 |
5 3
1 1
1 2
2 1
|
4 |
| 3 |
5 0 |
5 |
| |
![]()
|
|
Баобаб
Обход в глубину
Дан неориентированный невзвешенный граф. Необходимо определить, является ли он деревом.
Формат входных данных
В первой строке содержится одно натуральное число N (N ≤ 100) - количество вершин в графе. Далее в N строках по N чисел - матрица смежности графа: в i-ой строке на j-ом месте стоит 1, если вершины i и j соединены ребром, и 0, если ребра между ними нет. На главной диагонали матрицы стоят нули. Матрица симметрична относительно главной диагонали.
Формат выходных данных
Вывести "YES", если граф является деревом, и "NO" иначе.
| |
![]()
|
|
Банкет
Обход в глубину
На банкет были приглашены N Очень Важных Персон (ОВП). Были поставлены 2 стола. Столы достаточно большие, чтобы все посетители банкета могли сесть за любой из них. Проблема заключается в том, что некоторые ОВП не ладят друг с другом и не могут сидеть за одним столом. Вас попросили определить, возможно ли всех ОВП рассадить за двумя столами.
Входные данные: В первой строке входных данных содержатся два числа: N и M (1 <= N,M <= 100), где N – количество ОВП, а M – количество пар ОВП, которые не могут сидеть за одним столом. В следующих M строках записано по 2 числа – пары ОВП, которые не могут сидеть за одним столом.
Выходные данные: Если способ рассадить ОВП существует, то выведите YES в первой строке и номера ОВП, которых необходимо посадить за первый стол, во второй строке. В противном случае в первой и единственной строке выведите NO.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 2
1 2
1 3
|
YES
1 |
| |
![]()
|
|
Поиск циклов в графе
Обход в глубину
Дан ориентированный невзвешенный связный граф. Требуется определить, содержит ли он циклы.
Входные данные: Первая строка содержит одно натуральное число n — количество вершин (0 ≤ n ≤ 1 111).
Следующие n строк содержат матрицу смежности графа. Если в позиции (i, j) квадратной матрицы стоит единичка, то i-ый и j-ый ребра соединены ребрами, а если нолик, то не соединены. При этом ребро направленно из i-ого в j-ое ребро графа, и j-ое и i-ое ребро не соеденены ребрами.
Выходные данные: Первая строка должна содержать YES, если граф содержит цикл и NO — в противном случае.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
8
0 1 1 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 0 0 1 0 0 0
0 1 1 0 0 0 0 0
0 0 0 0 1 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 0
|
YES |
| |
![]()
|
|
Рекурсивный DFS
Обход в глубину
Дана матрица N (1 <= N <= 100) на M (1 <= M <= 100). В матрице имеются ‘.’ – пустые клетки и ‘#’ – клетки, которые нельзя посетить. Ходить можно только вверх, вниз, влево и вправо. Дано q запросов: номер строки и номер столбца, если эта клетка – ‘#’, то она станет ‘.’, иначе – ‘#’. Для каждого из q запросов определить, достижима ли из клетки (Sx; Sy) клетка (tx; ty). Вывести на каждой строчке “Yes”, если достижима, и “No” - иначе.
Гарантируется, что клетка (Sx; Sy) и клетка (tx; ty)не являются ‘#’ клеткой в каждом запросе.
Формат входных данных
На первой строчке вводятся числа Sx (1 <= Sx <= 100), Sy (1 <= Sy <= 100), tx (1 <= tx <= 100), ty (1 <= ty <= 100), N (1 <= N <= 100), M(1 <= M <= 100) и q (1 <= q <= 100). На следующих N строках дается матрица, где ‘.’ – пустая клетка и ‘#’ – клетка, которую нельзя посетить. На следующих q строках дан номер строки и номер столбца, которые надо изменить.
Формат выходных данных
Вывести на каждый из q запросов “Yes”, если из клетки (Sx; Sy) в клетку (tx; ty) можно попасть, “No” – иначе.
Пояснение
В тестовом примере после первого запроса матрица будет такой:
..#
##.
###
Из точки (1; 1) в (2; 3) нет прохода, следовательно, выводим “No”.
После второго запроса матрица будет такой:
..#
#..
###
Из точки (1; 1) в (2; 3)есть проход, следовательно, выводим “Yes”. Выделен путь, по которому мы сможем идти.
| |
![]()
|
|
Грядки*
Обход в глубину
Прямоугольный садовый участок шириной N и длиной M метров разбит на квадраты со стороной 1 метр. На этом участке вскопаны грядки. Грядкой называется совокупность квадратов, удовлетворяющая таким условиям:
* из любого квадрата этой грядки можно попасть в любой другой квадрат этой же грядки, последовательно переходя по грядке из квадрата в квадрат через их общую сторону;
* никакие две грядки не пересекаются и не касаются друг друга ни по вертикальной, ни по горизонтальной сторонам квадратов (касание грядок углами квадратов допускается).
Подсчитайте количество грядок на садовом участке.
Входные данные
В первой строке находятся числа N и M через пробел, далее идут N строк по M символов. Символ # обозначает территорию грядки, точка соответствует незанятой территории. Других символов в исходном файле нет. 1 ≤ N, M ≤ 200.
Выходные данные
Вывести одно число - количество грядок на садовом участке.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 10
##..#####.
.#.#.#....
###..##.#.
..##.....#
.###.#####
|
5 |
| |
![]()
|
|
*Производство деталей
Обход в глубину
Топологическая сортировка
Предприятие «Авто-2010» выпускает двигатели для известных во всём мире автомобилей. Двигатель состоит ровно из n деталей, пронумерованных от 1 до n, при этом деталь с номером i изготавливается за pi секунд. Специфика предприятия «Авто-2010» заключается в том, что там одновременно может изготавливаться лишь одна деталь двигателя. Для производства некоторых деталей необходимо иметь предварительно изготовленный набор других деталей.
Генеральный директор «Авто-2010» поставил перед предприятием амбициозную задачу — за наименьшее время изготовить деталь с номером 1, чтобы представить её на выставке.
Требуется написать программу, которая по заданным зависимостям порядка производства между деталями найдёт наименьшее время, за которое можно произвести деталь с номером 1.
Входные данные
Первая строка входного файла содержит число n (1≤ n ≤ 100000) — количество деталей двигателя. Вторая строка содержит n натуральных чисел p1, p2, pn, определяющих время изготовления каждой детали в секундах. Время для изготовления каждой детали не превосходит 109 секунд.
Каждая из последующих n строк входного файла описывает характеристики производства деталей. Здесь i-я строка содержит число деталей ki, которые требуются для производства детали с номером i, а также их номера. В i-й строке нет повторяющихся номеров деталей. Сумма всех чисел ki не превосходит 200000.
Известно, что не существует циклических зависимостей в производстве деталей.
Выходные данные
В первой строке выходного файла должны содержаться два числа: минимальное время (в секундах), необходимое для скорейшего производства детали с номером 1 и число k деталей, которые необходимо для этого произвести. Во второй строке требуется вывести через пробел k чисел — номера деталей в том порядке, в котором следует их производить для скорейшего производства детали с номером 1.
| Ввод |
Вывод |
3
100 200 300
1 2
0
2 2 1 |
300 2
2 1 |
2
2 3
1 2
0 |
5 2
2 1 |
4
2 3 4 5
2 3 2
1 3
0
2 1 3 |
9 3
3 2 1 |
| |
![]()
|
|
Есть ли цикл?
Обход в глубину
Алгоритм Флойда
Дан ориентированный граф. Требуется определить, есть ли в нем цикл.
Входные данные
В первой строке вводится число вершин N≤ 50. Далее в N строках следуют по N чисел, каждое из которых – 0 или 1. j-ое число в i-ой строке равно 1 тогда и только тогда, когда существует ребро, идущее из i-ой вершины в j-ую. Гарантируется, что на диагонали матрицы будут стоять нули.
Выходные данные
Выведите 0, если в заданном графе цикла нет, и 1, если он есть.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
0 1 0
0 0 1
0 0 0
|
0 |
| 2 |
3
0 1 0
0 0 1
1 0 0
|
1 |
| |
![]()
|
|
Лабиринт Tac Toe
Применение обхода в глубину
Обход в глубину
Беси любит искать пути в лабиринтах и играть в "крестики-нолики". Фермер Джон придумал для неё способ играть в обе игры одновременно!
Первое - "крестики-нолики" - вместо размещения X и O на решётке 3×3, коровы играют с М и О на решётке 3×3. Во время хода корова может поставить М или О в любую пустую ячейку (в отличие от стандартной игры, где один игрок всегда ставит X, а другой всегда О). Победитель этой игры тот, кто первый получит слово 'MOO' горизонтально, вертикально или по диагонали. В обратном порядке тоже засчитывается, то есть 'OOM' тоже выигрышная комбинация. Как и в стандартной игре, возможно заполнить всё поле и никто не выиграл. Ход в игре указывается 3 символами 'Mij' или 'Oij', где i и j в интервале 1…3 и указывают строку и столбец, в которые ставится соответствующий символ 'M' или 'O'.
Фермер Джон спроектировал для Беси квадратный лабиринт, представляющий решётку из N×N ячеек (3≤N≤25). Некоторые ячейки, включая все граничные ячейки, содержат большие стоги сена, предотвращающие Беси от захода в эти ячейки. Беси может свободно двигаться во все другие ячейки лабиринта предпринимая шаги в в обычных направлениях -север, юг, запад, восток. Некоторые ячейки содержат листок бумаги, на котором написан ход для "крестиков ноликов". По ходу тго, как Беси двигается по лабиринту, каждый раз, когда она попадает на такую ячейку, она должна сделать соответствующий ход в игре "крестики-нолики", в которую она играет параллельно с движением по лабиринту. Если соответствующая ячейка в "крестиках-ноликах" уже занята, то она не предпринимает никаких действий. У неё нет противника в игре "крестики-нолики", но некоторые из ячеек лабиринта могут противоречить её цели составить слово 'MOO'.
Если Беси останавливает игру "крестики-нолики" сразу после победы, определите количество различных выигрышных конфигураций в "крестиках-ноликах", которые она может сгенерировать, двигаясь соответственно в лабиринте.
ФОРМАТ ВВОДА
Первая строка содержит N.
Лабиринт определяется следующими N строками, каждая из которых содержит 3N символов. Каждая ячейка описывается блоком из 3 символов: '###' для стены, '...' для пустой ячейки, 'BBB' для ячейки в которой стартует Беси, ход для "крестиков-ноликов". Ровно одна ячейка содержит 'BBB'.
ФОРМАТ ВЫВОДА
Выведите количество различных выигрышных комбинаций для "крестиков-ноликов" (возможно 0), которые Беси может сгенерировать движением по лабиринту, остановившись после победы.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
7
#####################
###O11###...###M13###
###......O22......###
###...######M22######
###BBB###M31###M11###
###...O32...M33O31###
#####################
|
8 |
В этом примере имеется 8 выигрышных комбинаций, которые Беси может достичь:
O.M
.O.
MOM
O..
.O.
.OM
O.M
.O.
.OM
O..
.O.
MOM
O..
...
OOM
..M
.O.
OOM
...
.O.
OOM
...
...
OOM
Пояснения к одной из них:
O..
...
OOM
Здесь Беси сначала посещает ячейку O11, затем двигается в нижний коридор, посещая O32, M33, O31. Игра прекращается, поскольку Беси выиграла. |
| |
![]()
|
|
Выбор гурмана
Динамическое программирование на графах
Обход в глубину
Система непересекающихся множеств
Гурман Яблочков работает редактором известного гастрономического издания. Он разъезжает по всему миру, дегустируя новые изыски именитых шеф-поваров самых фешенебельных ресторанов высокой кухни. У Яблочкова есть свой фирменный способ ревью: в каждом заведении Яблочков заказывает два набора блюд в разные дни. Все заказанные блюда разные, так как Яблочков не любит есть одно и то же. Для каждой пары блюд из разных наборов он точно помнит, какое из них лучше по его ощущениям, или что они одинаковы по вкусовым качествам. Затем гурман оценивает каждое блюдо положительным целым числом.
Однажды, во время очередной ревизии, ресторан кельтской средневековой кухни «Пуассон», подающий суп из каштанов с пихтой, теплый содовый хлеб, пряный лимонный пирог и другую народную еду, очень приятно удивил гурмана своим разнообразным меню, и эксперт заказал слишком много. Поэтому ему нужна помощь в оценке блюд.
Гурман в первый день дегустировал набор из n блюд, во второй день набор из m блюд. Он составил таблицу ощущений a размером nm, в которой описал свои впечатления. Если по мнению эксперта блюдо i из первого набора лучше блюда j из второго набора, то aij равно « > », в противоположном случае aij равно « < ». Блюда также могут быть равны по уровню, тогда aij равно « = ».
Теперь Яблочков хочет, чтобы вы помогли ему оценить каждое блюдо в наборах целым положительным числом. Так как Яблочков очень строгий дегустатор, то постарается оценить блюда так, чтобы максимальная из оценок была как можно меньше. В то же время Яблочков очень справедливый, поэтому никогда не оценивает блюда так, чтобы это шло вразрез с его ощущениями. Другими словами, если aij равно « < », то оценка блюда i из первого набора должна быть меньше оценки блюда j из второго набора, если aij равно « > », то должна быть больше, а если aij равно « = », то должна совпадать.
Помогите Яблочкову выставить оценки каждому блюду из обоих наборов так, чтобы это согласовывалось с его ощущениями, или определите, что это невозможно.
Входные данные
В первой строке заданы два целых числа n и m (1 ≤ n, m ≤ 1000 ) — количества блюд в каждый из двух дней.
Каждая из следующих n строк содержит строку из m символов. j-й символ в i-й строке задаёт значение aij. Все строки состоят только из символов « < », « > » и « = ».
Выходные данные
В первой строке выведите « Yes » (без кавычек), если можно сделать корректную оценку всем блюдам и « No » (без кавычек), если иначе.
В случае, если сделать корректную оценку можно, во второй строке выведите n целых чисел — оценки блюд первого набора, а в третьей строке m целых чисел — оценки блюд второго набора.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснения |
| 1 |
3 4
>>>>
>>>>
>>>> |
Yes
2 2 2
1 1 1 1 |
Все блюда первого дня лучше всех блюд второго дня. Значит, самой высокой оценкой будет 2 для всех блюд первого дня. |
| 2 |
3 3
>>>
<<<
>>> |
Yes
3 1 3
2 2 2 |
|
| 3 |
3 2
==
=<
== |
No |
Таблица противоречива: нет ни одного набора оценок, который удовлетворял бы ей. |
| |
![]()
|
|
Введите одностороннее движение
Обход в глубину
В Тридевятом Царстве было N городов, некоторые из которых были соединены дорогами. К сожалению, в последнее время добраться из одного города в другой стало очень сложно из-за возникших автомобильных пробок. В целях борьбы с пробками было решено все дороги сделать односторонними, т.е. разрешить проезд по каждой дороге только в одном направлении. При этом требуется, чтобы по-прежнему можно было из любого города попасть в любой другой.
Входные данные
Во входном файле записано сначала число N — количество городов (1≤N≤1000). Затем записано число M — количество дорог (1≤M≤100000). Далее идет M пар чисел, задающих дороги (каждая дорога описывается номерами городов, которые она соединяет). Не бывает дорог из некоторого города в тот же город. Между двумя городами может быть несколько дорог. Гарантируется, что до введения одностороннего движения можно было попасть из любого города в любой другой.
Выходные данные
В выходной файл нужно выдать M пар чисел, соответствующих дорогам (дороги должны быть выданы в том же порядке, в котором они заданы во входном файле). Для каждой дороги сначала должен быть записан номер города, из которого по ней можно будет уехать после введения одностороннего движения, а затем — номер города, куда эта дорога ведет.
Если ввести одностороннее движение так, чтобы можно было из любого города попасть в любой другой, нельзя, выходные данные содержать одно число 0.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4
6
1 2
1 2
2 3
2 4
4 3
1 4 |
2 1
2 1
3 2
4 2
4 3
1 4 |
| |
![]()
|
|
Перегоны
Обход в глубину
На некоторой железнодорожной ветке расположено N станций, которые последовательно пронумерованы числами от 1 до N. Известны расстояния между некоторыми станциями. Требуется точно вычислить длины всех перегонов между соседними станциями или указать, что это сделать невозможно (то есть приведенная информация является противоречивой или ее недостаточно).
Входные данные
Во входном файле записаны сначала числа N — количество станций (2 ≤ N ≤ 100) и E — количество пар станций, расстояния между которыми заданы (0 ≤ E ≤ 10000). Далее идет E троек чисел, первые два числа каждой тройки задают номера станций (это числа из диапазона от 1 до N), а третье — расстояние между этими станциями (все эти расстояния заданы точно и выражаются вещественными неотрицательными числами не более чем с 3-я знаками после десятичной точки).
Выходные данные
В случае, когда восстановить длины перегонов можно однозначно, в выходной файл выведите сначала число 1, а затем N–1 вещественное число. Первое из этих чисел должно соответствовать расстоянию от 1-й станции до 2-й, второе — от 2-й до 3-й, и так далее. Все числа должны быть выведены с точностью до 3-х знаков после десятичной точки.
Если приведенная информация о расстояниях между станциями является противоречивой или не позволяет однозначно точно восстановить длины перегонов, выведите в выходной файл одно число 2.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 3
1 1 0
2 2 0
2 1 2.5 |
1
2.500 |
| 2 |
15 13
1 2 1
1 3 2
1 4 3
1 5 4
1 6 5
1 7 6
1 8 7
1 9 8
1 10 9
1 11 10
1 12 11
1 13 12
15 14 13 |
2 |
| |
![]()
|
|
Кодовый замок
Обход в глубину
Компания «Замки и замки» недавно разработала новый тип кодового замка, для размещения на воротах замков. Панель замка представляет собой прямоугольник шириной w ячеек и высотой h ячеек. В некоторых из них расположены кнопки.
Код на этом замке вводится одновременным нажатием k кнопок. Для того, чтобы код было легче запомнить, используемые в нем кнопки должны образовывать связную область. Область называется связной, если из любой клетки области можно добраться до любой другой, перемещаясь только между клетками этой области с общей стороной. Важным критерием надежности замка является число различных кодов, которые на нем можно набрать.
Для оценки надежности замков требуется написать программу для вычисления указанной величины.
Выходные данные
В первой строке находятся три целых числа h, w и k (1 ≤ h, w ≤ 30; 1 ≤ k ≤ 10). Каждая из последующих h строк содержит w символов. Символ «#» обозначает кнопку, а «.» — ее отсутствие.
Выходные данные
Выведите единственное число — количество кодов, удовлетворяющих указанным требованиям.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 2 2
.#
##
|
2 |
| 2 |
5 6 7
.#....
##.##.
..#.#.
.####.
.....#
|
3 |
| |
![]()
|
|
Деревни
Динамическое программирование
Алгоритмы на графах
Обход в глубину
Динамическое программирование на графах
В тридесятом государстве есть N деревень. Некоторые пары деревень соединены дорогами. В целях экономии, “лишних” дорог нет, т.е. из любой деревни в любую можно добраться по дорогам единственным образом.
Новейшие исследования показали, что тридесятое государство находится в сейсмически опасной зоне. Поэтому глава государства захотел узнать, какой именно ущерб может принести его державе землетрясение. А именно, он хочет узнать, какое минимальное число дорог должно быть разрушено, чтобы образовалась изолированная от остальных группа ровно из P деревень такая, что из любой деревни из этой группы до любой другой деревни из этой группы по-прежнему можно будет добраться по неразрушенным дорогам (группа изолирована от остальных, если никакая неразрушенная дорога не соединяет деревню из этой группы с деревней не из этой группы).
Вы должны написать программу, помогающую ему в этом.
Формат входных данных
Первая строка входного файла содержит два числа: N и P (1 ≤ P ≤ N ≤ 150). Все остальные строки содержат описания дорог, по одному на строке: описание дороги состоит из двух номеров деревень (от 1 до N), которые эта дорога соединяет. Все числа во входном файле разделены пробелами и/или переводами строки.
Формат выходных данных
В выходной файл выведите единственное число — искомое количество дорог.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
3 2
1 2
3 2 |
1 |
|
| 2 |
11 6
1 2
1 3
1 4
1 5
2 6
2 7
2 8
4 9
4 10
4 11 |
2 |
группа деревень (1, 2, 3, 6, 7, 8) окажется изолированной от остальных, если разрушить дороги 1–4 и 1–5. |
| |
![]()
|
|
Построение
Обход в глубину
Топологическая сортировка
Группа солдат-новобранцев прибыла в армейскую часть N666. После знакомства с прапорщиком стало очевидно, что от работ на кухне по очистке картофеля спасти солдат может только чудо.
Прапорщик, будучи не в состоянии запомнить фамилии, пронумеровал новобранцев от 1 до N. После этого он велел им построиться по росту (начиная с самого высокого). С этой несложной задачей могут справиться даже совсем необученные новобранцы, да вот беда, прапорщик уверил себя, что знает про некоторых солдат, кто из них кого выше, и это далеко не всегда соответствует истине.
После трех дней обучения новобранцам удалось выяснить, что знает (а точнее, думает, что знает) прапорщик. Помогите им, используя эти знания, построиться так, чтобы товарищ прапорщик остался доволен.
Входные данные
Сначала на вход программы поступают числа N и M (1 < N <= 100, 1 <= M <= 5000) – количество солдат в роте и количество пар солдат, про которых прапорщик знает, кто из них выше. Далее идут эти пары чисел A и B по одной на строке (1 <= A,B <= N), что означает, что, по мнению прапорщика, солдат A выше, чем B. Не гарантируется, что все пары чисел во входных данных различны.
Выходные данные
В первой строке выведите "Yes" (если можно построиться так, чтобы прапорщик остался доволен) или "No" (если нет). После ответа "Yes" на следующей строке выведите N чисел, разделенных пробелами, - одно из возможных построений.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 5
1 2
2 3
3 4
1 4
4 1 |
No |
| |
![]()
|
|
Площадь комнаты
Обход в глубину
Рекурсия
Требуется вычислить площадь комнаты в квадратном лабиринте.
Входные данные
В первой строке вводится число N – размер лабиринта (3 <= N <= 10). В следующих N строках задан лабиринт (‘.’ – пустая клетка, ‘*’ – стенка). И наконец, последняя строка содержит два числа – номер строки и столбца клетки, находящейся в комнате, площадь которой необходимо вычислить. Гарантируется, что эта клетка пустая и что лабиринт окружен стенками со всех сторон.
Выходные данные
Требуется вывести единственное число – количество пустых клеток в данной комнате.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
*****
**..*
*.*.*
*..**
*****
2 4
|
3 |
| |
![]()
|
|
Бусинки
Обход в глубину
Маленький мальчик делает бусы. У него есть много пронумерованных бусинок. Каждая бусинка имеет уникальный номер - целое число в диапазоне от 1 до N. Он выкладывает все бусинки на полу и соединяет бусинки между собой произвольным образом так, что замкнутых контуров не образуется. Каждая из бусинок при этом оказывается соединенной с какой-либо другой бусинкой. Требуется определить, какое максимальное количество последовательно соединенных бусинок присутствует в полученной фигуре.
Входные данные
В первой строке записано число N (1 ≤ N ≤ 2500) - количество бусинок . В последующих N - 1 строках по два целых числа - номера, соединенных бусинок.
Выходные данные
Вывести одно число - искомое количество бусинок.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2
1 2 |
2 |
| 2 |
5
2 1
2 3
2 4
2 5 |
3 |
| |
![]()
|
|
Одностороннее движение
Обход в глубину
В городе, построенном во времена средневековья, ширина улиц стала препятствовать движению транспорта, которое изначально было двусторонним по каждой из улиц. Для решения этой проблемы было предложено сделать движение по каждой из улиц односторонним. Мэр поручил эту задачу своему первому заму. После долгих размышлений тот доложил, что на некоторых улицах движение придется оставить двусторонним, в противном случае будет невозможно проехать из любого места в городе в любое другое. По данной схеме города требуется найти все такие улицы.
Входные данные
В первой строке входного файла находятся числа N - количество площадей в городе и М - количество улиц их соединяющих (1 <= N <= 20000, 1 <= M <= 200000). Площади имеют номера от 1 до N. В каждой из следующих M строк находится пара натуральных чисел, описывающая между какими двумя площадями проходит соответствующая улица (две площади соединяются не более чем одной улицей).
Выходные данные
На первой строке выведите число B - количество улиц, на которых организовать одностороннее движение невозможно. На следующей строке выведите B целых чисел - номера этих улиц в возрастающем порядке. Улицы нумеруются с единицы в том порядке, в котором они заданы во входном файле.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
10 16
2 6
3 7
6 5
5 9
5 4
1 2
9 8
6 4
2 10
3 8
7 9
1 4
2 4
10 5
1 6
6 10 |
1
4 |
| |
![]()
|
|
Премьер министр
Обход в глубину
Новый премьер-министр решил проехать по России от Москвы до Владивостока по железной дороге, а затем вернуться обратно. Он поручил своим помощникам разработать маршрут так, чтобы не пришлось два раза проезжать через один и тот же город. Однако помощники сообщили, что для Российских железных дорог это невозможно. Определите, в каких городах премьер-министр будет вынужден побывать дважды.
Входные данные
В первой строке входного файла находятся числа N - количество российских городов, соединенных железными дорогами в единую сеть и М - количество железнодорожных перегонов, соединяющих пары городов (1 <= N <= 20000, 1 <= M <= 200000). Города имеют номера от 1 до N. В каждой из следующих M строк находится пара натуральных чисел, описывающая между какими двумя городами проходит соответствующая железнодорожная ветка. В последней строке находятся два целых числа S и Е (1 <= S != E <= N) - номера Москвы и Владивостока по версии РЖД.
Выходные данные
В первой строке выведите число B - количество городов, которые премьер-министру придется посетить дважды. В следующих В строках выведите B целых чисел - номера этих городов в возрастающем порядке.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 2
1 2
2 3
3 1 |
1
2 |
| |
![]()
|
|
Раскраска в три цвета
Обход в глубину
Простые задачи на перебор
Петя нарисовал на бумаге n кружков и соединил некоторые пары кружков линиями. После этого он раскрасил каждый кружок в один из трех цветов – красный, синий или зеленый.
Теперь Петя хочет изменить их раскраску. А именно – он хочет перекрасить каждый кружок в некоторый другой цвет так, чтобы никакие два кружка одного цвета не были соединены линией. При этом он хочет обязательно перекрасить каждый кружок, а перекрашивать кружок в тот же цвет, в который он был раскрашен исходно, не разрешается.
Помогите Пете решить, в какие цвета следует перекрасить кружки, чтобы выполнялось указанное условие.
Входные данные
В первой строке вводятся два целых числа n и m – количество кружков и количество линий, которые нарисовал Петя, соответственно (1 ≤ n ≤ 1 000, 0 ≤ m ≤ 20 000).
Следующая строка содержит n символов из множества {'R', 'G', 'B'} – i-й из этих символов означает цвет, в который раскрашен i-й кружок ('R' – красный, 'G' – зеленый, 'B' – синий).
Далее в m строках задается по два целых числа – пары кружков, соединенных отрезками.
Выходные данные
Выведите одну строку, состоящую из n символов из множества {'R', 'G', 'B'} – цвета кружков после перекраски. Если решений несколько, выведите любое.
Если решения не существует, выведите слово "Impossible''.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 5
RRRG
1 3
1 4
3 4
2 4
2 3 |
BBGR |
| 2 |
4 5
RGRR
1 3
1 4
3 4
2 4
2 3 |
Impossible |
| |
![]()
|
|
Часовое дерево
Обход в глубину
Вывод формулы
Новый амбар Фермера Джона состоит из N комнат (2 ≤ N ≤ 2500), последовательно пронумерованных 1…N, и N−1 коридоров. Каждый коридор соединяет пару комнат таким образом, что возможно пройти из лбой комнаты в любую через серию коридоров.
Каждая комната в амбаре имеет круглые часы на стене со стандартным размещением цифр 1…12 на лицевой стороне. Однако на этих часах имеется только одна стрелка, которая всегда показывает точно на одно из целых чисел (она никогда не показывает между двумя из этих чисел).
Корова Беси хочет синхронизировать все часы в амбаре, чтобы они все показывали на число 12. Но со своим коровьим мышлением, каждый раз, когда она входит в комнату, она перемещает стрелку вперёд на одну позицию. Например, если стрека показывала на 5, Беси переводит стрелку на 6. Если часы указывали на 12, она переводит стрелку на 1. Если Беси входит в комнату несколько раз, она переводит стрелку при каждом входе.
Определите номера комнат, в которых Беси может начинать путешествие по амбару чтобы установить все стрелки на 12. Заметим, что Беси не переводит стрелку в стартовой комнате в начале пути и переводит при каждом последующем входе в неё. Стрелки сами по себе не двигаются. Беси входя в коридор должна дойти до конца и войти в комнату в конце коридора. Она не может повернуть назад внутри коридора, чтобы снова войти в комнату из которой вышла.
Входные данные
Первая строка ввода содержит N. Следующая строка содержит N целых чисел, каждое в интервале 1…12, указывающих начальные положения стрелок в каждой комнате. Каждая из следующих N−1 строк описывает коридор двумя целыми числам a и b, каждое в интервале 1…N, и задающих номера комнат, соединённых этим коридором.
Выходные данные
Выведите номера комнат, в которых Беси может начинать, чтобы установить все часы на 12.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
4
11 10 11 11
1 2
2 3
2 4
|
1 |
В этом примере Беси может установить все стрелки на 12, тоько в том случае, если она начнёт в комнате 2 (например перемещаясь так: 1, 2, 3, 2, 4. |
| |
![]()
|
|
Where's Bessie?
Обход в глубину
Перебор
Задача на реализацию
Фермер Джон тестирует новую камеру, которая может "схватить картинку" и автоматически вычислить положение коров. К несчастью, у камеры не очень хороший алгоритм поиска коров и ФД нуждается в Вашей помощи.
Картинка, получаемая камерой, может быть описана решёткой из N×N символов, каждый в интервале A…Z, представляющих один из 26 возможных различных цветов. ФД считает наилучшим такой алгоритм распознавания коров: PCL (возможное размещение коровы) - это прямоугольник на решётке (возможно вся решётка) со сторонами параллельными сторонам решётки, не содержащий внутри других PCL и обладающий следующим свойством: внутри этого прямоугольника должны присутствовать ровно два цвета, один формирует непрерывный регион, а другой формирует два или более непрерывных регионов.
Например, такой образ
AAAAA
ABABA
AAABB
есть PCL, поскольку символы A формируют непрерывный регион, символы B форрмируют более одного непрерывного региона. Интерпретация - это корова с цветом A и с пятнами цвета B.
Регион является непрерывным, если вы может пройти его весь, перемещаясь из одной клетки в другую соседнюю по направлениям вверх, вниз, влево, вправо.
По заданному образу камеры ФД определите количество PCL.
ФОРМАТ ВВОДА:
Первая строка ввода содержит N, размер решётки (1≤N≤20). Следующие N строк описывают образ, каждая состоит из N символов.
ФОРМАТ ВЫВОДА:
Количество PCL в образе.
| Ввод |
Вывод |
|
4
ABBC
BBBC
AABB
ABBC
|
2 |
| |
![]()
|
|
Танцевальные движения
Обход в глубину
Перестановки
Коровы Фермера Джона танцуют.
Сначала все N коров (2≤N≤105) стоят в ряд и корова i находится на позиции i. Последовательность танцевальных движений задаётся K (1≤K≤2⋅105) парами позиций (a1,b1),(a2,b2),…,(aK,bK). Каждую минуту i=1…K танца коровы на позициях ai и bi меняются местами. Такие же K обменов делаются на минутах K+1…2K, затем опять на минутах 2K+1…3K, и т.д. Другими словами,
на минуте 1 меняются местами коровы на позициях a1 и b1.
на минуте 2 меняются местами коровы на позициях a2 и b2.
...
На минуте K меняются местами коровы на позициях aK и bK swap.
На минуте K+1, меняются местами коровы на позициях a1 и b1.
На минуте K+1, меняются местами коровы на позициях a2 и b2.
и т.д. ...
Для каждой коровы определите количество уникальных позиций, которые она посетит во время бесконечного танца.
Входные данные
Первая строка ввода содержит целые числа N и K. Каждая из последующих K строк содержит (a1,b1)…(aK,bK) (1≤ai<bi≤N).
Выходные данные
Выведите N строк, где i-ая строка содержит количество уникальных позиций, которые посетит корова i.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
5 4
1 3
1 2
2 3
2 4
|
4
4
3
4
1
|
- Корова 1 достигнет позиций {1,2,3,4}.
- Корова 2 достигнет позиций {1,2,3,4}.
- Корова 3 достигнет позиций {1,2,3}.
- Корова 4 достигнет позиций {1,2,3,4}.
- Корова 5 не будет двигаться, и не покинет позицию 5.
|
| |
![]()
|
|
Игра со строками
Бор
Обход в глубину
Игры и выигрышные стратегии
Дана игра для двоих игроков со строками.
Задан набор, состоящий из n непустых строк. Во время игры два игрока вместе строят слово, изначально это слово пустое. Игроки ходят по очереди. За свой ход игрок должен дописать в конец слова одну букву так, чтобы полученное слово было префиксом хотя бы одной строки из заданного набора. Проигрывает тот, кто не может сделать ход.
По задданому набору строк определите, кто будет победителем, если оба игрока будут играть оптимально.
Входные данные:
Первая строка содержит целое число n (1 ≤ n ≤ 105).
Каждая из n следующих строк содержит непустую строку из заданного набора. Суммарная длина всех строк из набора не превышает 105. Все строки из набора состоят только из строчных латинских букв.
Выходные данные:
Если победит игрок, который ходит первым, то выведите «First», иначе выведите «Second» (кавычки выводить не нужно).
Примеры:
| Входные данные |
Выходные данные |
3
a
b
c |
First |
1
ab |
Second |
| |
![]()
|
|
Orders
Обход в глубину
Перебор
Бор
Блейз отправляет приказы на перемещение своим войскам, собранным из жителей одной из теней. К сожалению, они не понимают амберский язык, поэтому Блейзу приходится отправлять им сообщения на их родном языке.
В этом и заключается проблема: Амберийский принц плохо знает орфографию этого языка, поэтому иногда он делает ошибки в словах, но не более одной ошибки в слове.
В языке очень много слов, поэтому если в слове изменится хотя бы одна буква, то его смысл может кардинально измениться. Если армия не правильно поймет приказ, то вся военная кампания может провалиться. Поэтому Блейзу очень важно проверять правильность в написании слов. Он решил попросить вас помочь ему.
Вы должны создать программу, которая будет выводить в лексикографическом порядке все возможные слова, которые Блейз мог пытаться написать с учетом того, что он мог ошибиться 1 раз.
Входные данные
В первой строке на вход подается числа n и m - количество приказов, которые отдал Блейз, и количество команд, которые понимают его войска соответственно. (1 <= n, m <= 5000)
В следующей строке на вход подаются m слов - команды, которые понимают войска Блейза.
В следующих n строках на вход подаются слова - приказы, которые отдает Блейз.
Все строки длиной не превышают 100.
Выходные данные
Выведите n строк: в строке номер i содержится ответ на задачу для приказа Блейза номер i. Строки, являющиеся ответом на этот запрос, выводятся через пробел в одну строку.
Пример
Ввод
5 5
is in if on of
it
in
of
ij
op
Вывод
if in is
if in is on
if of on
if in is
of on
(с) Евгений Григорьев
| |
![]()
|
|
Заполнение конем
Рекурсия
Обход в глубину
Дана шахматная доска nхn. Пусть конь стоит на клетке (1,1). Необходимо найти такую последовательность ходов коня, при которой он побывает на каждой клетке доски ровно по одному разу.
Входные данные
На вход программе подается натуральное число n (n ≤ 8).
Выходные данные
Если обход невозможен, то выведите в выходной файл 0, если возможен, то 1, а на следующих строчках выведите матрицу nn, иллюстрирующую порядок обхода. Выравнивать числа по столбцам не обязательно.
Примечание. Скорость работы рекурсивной программы в этой задаче существенно зависит от порядка, в каком будут рассматриваться варианты хода коня из очередной клетки. Одним из удачных порядков является размещение всех восьми вариантов хода "по кругу".
| Ввод |
Вывод |
| 3 |
0 |
| 5 |
1
1 20 17 12 3
16 11 2 7 18
21 24 19 4 13
10 15 6 23 8
25 22 9 14 5
|
| |
![]()
|
|
Switch Grass
Минимальный каркас
Структуры данных
Дерево отрезков, RSQ, RMQ
Обход в глубину
Алгоритмы на графах
Фермер Джон обнаружил, что разные типы коров любят разные типы травы. Однако он должен правильно их высаживать, чтобы не навредить.
Ферма Джона состоит из NN (1≤N≤200,000), полей, и MM пар полей соединены двунаправленными дорожками (1≤M≤200,000). Используя эти дорожки, можно пройти от любого поля к любому другому полю. Каждая дорожка имеет целочисленную длину в интервале 1…1,000,000. Любая пара полей соединена не более чем одной прямой дорожкой.
В каждом поле ФД изначально посадил один из KK типов травы (1≤K≤N). Через некоторое время, однако, он может решить изменить тип травы на некоторых из полей. Он называет это операцией "обновления".
После каждого обновления, ФД хочет знать длину кратчайшего пути между двумя полями, имеющими различные типы травы. То есть, среди всех пар полей, имеющих различные типы травы, он хочет узнать, какие два поля ближайшие друг к другу. Гарантируется, что всегда имеется как минимум одна пара полей с различными типами травы.
В 30 процентах тестов каждое поле непосредственно соединено не более чем с 10 дорожками.
ФОРМАТ ВВОДА:
Первая строка ввода содержит четыре целых числа N, M, K, Q, где Q - количество операций обновления (1≤Q≤200,000). Следующие M строк описывают дорожки. Каждая строка содержит три целых числа A, B, L, указывающих, что есть дорожка между полями A, B и её длина L. (A, B - целые числа в интервале 1…N). Следующая строка указывает начальный тип травы для каждого поля (N целых чисел в интервале 1…K). Затем идут Q строк, каждая из которых описывает одну операцию обновления двумя целыми числами A и B, означающими, что на поле A типе травы изменён на B.
ФОРМАТ ВЫВОДА:
Для каждой операции обновления выведите длину кратчайшего пути между двумя полями с различными типами травы, после применения этой операции обновления.
| Ввод |
Вывод |
|
3 2 3 4
1 2 3
2 3 1
1 1 2
3 3
2 3
1 2
2 2
|
1
3
3
1
|
| |
![]()
|
|
Возрастающие пути
Алгоритмы на графах
Арифметические алгоритмы (Теория чисел)
Применение обхода в глубину
Обход в глубину
Дано дерево на n вершинах (связный неориентированный ациклический граф c n−1 рёбрами), где у каждого ребра есть вес w. Назовём простой путь длины k возрастающим , если существует такое целое x>=2, что вес первого ребра пути делится на x, второго ребра — делится на x2, ……, вес k-го ребра делится на xk.
Требуется найти максимальную длину k возрастающего пути, где k — количество рёбер в нём.
Входные данные
В первой строке вводится единственное целое число n (1 <= n <= 100000) - число вершин в дереве.
В следующих n−1 строках вводятся по три целых числа u, v, w ( 1<= v <= n, 1<= w <= n, u ≠ v, 1 <= w <= 107) - номера вершин, которые соединяет очередное ребро, и его вес.
Выходные данные
Выведите одно целое число k - максимальную длину возрастающего пути.
Примечание
Простым путем называется такой путь, что все вершины в нем различны.
В 1-м примере есть путь длины 2: 3 — 1 — 2. Тогда для него подходящий x = 2. Можно показать, что возрастающего пути большей длины не существует.
Во 2-м примере есть путь длины 3: 3 — 4 — 5 — 6. Тогда для него подходящий x = 2. Можно показать, что возрастающего пути большей длины не существует.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4
1 2 8
1 3 6
1 4 3
|
2
|
| 2 |
6
1 2 2
2 3 4
3 4 2
4 5 4
5 6 8
|
3
|
| |
![]()
|
|
Эвакуация
Обход в глубину
Через T минут армия читаури под предводительством Локи атакует Землю. Мстители никак не успевают помешать открытию портала в Нью-Йорке, поэтому Капитан Америка принял решение эвакуировать из города всех его жителей. Ему необходимо выяснить, успеют ли жители города эвакуироваться до начала вторжения.
Окрестности Нью-Йорка можно представить как набор небольших городов, связанных между собой дорогами с односторонним движением. Каждая дорога характеризуется своей длиной и пропускной способностью. Длина дороги l означает, что въехав на нее в момент времени t, автомобиль окажется в конце этой дороги через l минут, в момент времени t + l. Пропускная способность дороги s означает, что каждую минуту на эту дорогу могут въехать не больше, чем s автомобилей. Приехав в какой-нибудь город, любой автомобиль может сразу продолжить путь, въехав на какую-то дорогу, выходящую из этого города, а может остановиться в этом городе на любое количество минут, и только потом уехать из него.
Капитан Америка уже решил, в каком именно городе должны оказаться жители Нью-Йорка после эвакуации. Также ему известно, сколько автомобилей необходимо для эвакуации всего города. Теперь ему необходимо выяснить успеют ли все жители эвакуироваться до прибытия захватчиков и, если да, какое минимальное количество времени у них на это уйдет, а если нет какому минимальному числу автомобилей с горожанами не удастся доехать до безопасного города.
Формат входного файла
Первая строка входного файла содержит четыре целых числа n, m, K и T (1 ≤ n x T ≤ 10 000, 1 ≤ m, K ≤ 10 000) количество городов в окрестностях Нью-Йорка, количество дорог между ними, количество автомобилей, которым необходимо попасть из Нью-Йорка в безопасный город и время до вторжения захватчиков соответственно. Следующие m строк содержат описания дорог между городами.
Каждая дорога описывается четырьмя целыми числами u, v, l и s (1 ≤ u, v ≤ n, u != v, 1 ≤ s ≤ 3 000, 1 ≤ l ≤ 200) город, из которого выходит эта дорога, город, в который она ведет, ее длина и пропускная способность соответственно.
Между двумя городами может существовать только одна дорога, ведущая в каком-то направлении. Нью-Йорком считается город с номером 1, а безопасным городом город с номером n. в момент времени 0 все автомобили находятся в Нью-Йорке.
Формат выходного файла
Если все жители Нью-Йорка успеют добраться до безопасного города не более, чем за T минут, выведите в выходной файл минимальное количество минут, которое им на это понадобится. В противном случае выведите минимальное количество автомобилей, которым не удастся попасть в безопасное место за T минут. Да, не нужно выводить, какой из этих случаев имеет место :-).
| Ввод |
Вывод |
5 5 10 10
1 2 2 2
2 3 1 1
2 4 1 1
4 5 2 4
3 5 2 4 |
9 |
| |
![]()
|
|
Олег и двоичные последовательности
Обход в глубину
Применение обхода в глубину
Разбор случаев
Олег очень любит двоичные последовательности — последовательности из нулей и единиц. Совсем недавно он написал в тетради очередную двоичную последовательность из n элементов.
Для выписанной последовательности Олег посчитал Z-функцию.
Z-функцией последовательности s1, . . . , sn называется массив z[1..n], в котором:
• z[1] = 0;
• Если i > 1, то z[i] равно длине наибольшего общего префикса последовательности s и суффикса последовательности s, начинающегося с i-й позиции. Иначе говоря, z[i] равно максимальному k, такому что s1 = si , s2 = si+1, . . . , sk = si+k−1.
Например, для последовательности s = h0, 0, 1, 1, 0, 0, 1i Z-функция следующая: z = h0, 1, 0, 0, 3, 1, 0i.
Записав в тетради последовательность и ее Z-функцию, Олег лег спать. Пока он спал, его младший брат Егор прокрался в комнату и закрасил фломастером последовательность и некоторые значения Z-функции. Проснувшись, Олег заинтересовался, сколько различных двоичных последовательностей он мог вечером написать в тетради, чтобы незакрашенные значения Z-функции были правильными.
Найдите число искомых последовательностей и выведите его по модулю 109 + 7. Заметьте, что Олег мог и ошибиться при вычислении Z-функции, в этом случае ни одна последовательность не подходит и ответ равен 0.
Формат входных данных
В первой строке входного файла находится целое число n — длина исходной двоичной последовательности (1 ≤ n ≤ 1000). Во второй строке входного файла находятся n целых чисел z[1], . . . , z[n], где z[i] — значение Z-функции в позиции i, или −1, если значение в i-й позиции было закрашено (−1 ≤ z[i] ≤ n).
Формат выходных данных
В выходной файл выведите единственное число — остаток от деления числа подходящих двоичных последовательностей на число 109 + 7.
| Ввод |
Вывод |
3
0 0 1 |
2 |
4
0 0 1 0 |
0 |
3
0 3 -1 |
0 |
3
-1 -1 -1 |
8 |
Пояснение
В первом примере подходят последовательности {0, 1, 0 } и { 1, 0, 1 }.
Во втором примере не существует ни одной двоичной последовательности длины 4 с заданной Z-функцией.
В третьем примере z[2] = 3, что противоречит определению Z-функции, поэтому ответ 0.
В четвертом примере подходит любая двоичная последовательность длины 3.
| |
![]()
|
|
Гномы и Одинокая гора
Обход в глубину
Применение обхода в глубину
Применение обхода в глубину
Обход в глубину
Деревья
Гномы продолжают искать золото предков в недрах Одинокой горы. Недра Одинокой горы представляют собой n пещер, некоторые из которых соединены двусторонними переходами. При этом из каждой пещеры в любую другую можно попасть по переходам, причем это можно сделать единственным способом.
Гномы разделились на два отряда, которые начали свои поиски с пещер u0 и v0, соответственно. Гномы каждого из отрядов перемещаются вместе. На обследование пещеры у отряда гномов уходит ровно одна минута, после чего каждый отряд быстро перемещается по переходу в одну из соседних пещер. При этом гномы никогда не заходят в пещеру, если они или другой отряд в ней уже побывали. Оба отряда никогда не заходят в одну и ту же пещеру. Если хотя бы один из отрядов гномов не может переместиться в соответствии с этими правилами, оба отряда сразу прекращают поиски сокровищ.
Чтобы как можно лучше обследовать недра Одинокой горы, гномы хотят, чтобы поиски продолжались как можно дольше. По заданной карте пещер в Одинокой горе и начальному положению отрядов гномов определите, какое максимальное время могут продолжаться поиски сокровищ.
Формат входных данных
В первой строке число n (2 ≤ n ≤ 200 000) — число пещер в Одинокой горе. В следующих n−1 строках заданы переходы между пещерами. В каждой строке записаны номера двух пещер v и u, соединенных переходом (1 ≤ v, u ≤ n). В следующей строке заданы номера пещер v0 и u0, в которых исходно находятся два отряда гномов (1 ≤ v0, u0 ≤ n, v0 != u0).
Формат выходных данных
Выведите максимальное число минут, которое могут продолжаться поиски сокровищ.
| Ввод |
Вывод |
Пояснение |
6
1 2
2 3
3 4
4 5
5 6
4 5 |
2 |
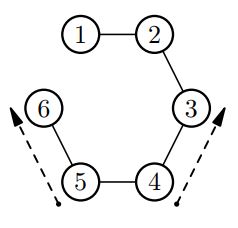 |
8
1 2
2 3
3 4
2 5
5 6
3 7
7 8
1 8 |
4 |
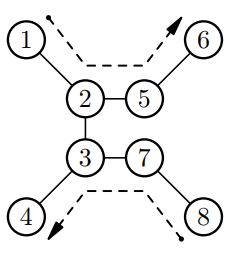 |
| |
![]()
|
|
Гномы и Одинокая гора
Обход в глубину
Применение обхода в глубину
Применение обхода в глубину
Обход в глубину
Деревья
Гномы продолжают искать золото предков в недрах Одинокой горы. Недра Одинокой горы представляют собой n пещер, некоторые из которых соединены двусторонними переходами. При этом из каждой пещеры в любую другую можно попасть по переходам, причем это можно сделать единственным способом.
Гномы разделились на два отряда, которые начали свои поиски с пещер u0 и v0, соответственно. Гномы каждого из отрядов перемещаются вместе. На обследование пещеры у отряда гномов уходит ровно одна минута, после чего каждый отряд быстро перемещается по переходу в одну из соседних пещер. При этом гномы никогда не заходят в пещеру, если они или другой отряд в ней уже побывали. Оба отряда никогда не заходят в одну и ту же пещеру. Если хотя бы один из отрядов гномов не может переместиться в соответствии с этими правилами, оба отряда сразу прекращают поиски сокровищ.
Чтобы как можно лучше обследовать недра Одинокой горы, гномы хотят, чтобы поиски продолжались как можно дольше. По заданной карте пещер в Одинокой горе и начальному положению отрядов гномов определите, какое максимальное время могут продолжаться поиски сокровищ.
Формат входных данных
В первой строке число n (2 ≤ n ≤ 200 000) — число пещер в Одинокой горе. В следующих n−1 строках заданы переходы между пещерами. В каждой строке записаны номера двух пещер v и u, соединенных переходом (1 ≤ v, u ≤ n). В следующей строке заданы номера пещер v0 и u0, в которых исходно находятся два отряда гномов (1 ≤ v0, u0 ≤ n, v0 != u0).
Формат выходных данных
Выведите максимальное число минут, которое могут продолжаться поиски сокровищ.
| Ввод |
Вывод |
Пояснение |
6
1 2
2 3
3 4
4 5
5 6
4 5 |
2 |
 |
8
1 2
2 3
3 4
2 5
5 6
3 7
7 8
1 8 |
4 |
 |
| |
![]()
|
|
Число пар районов
Обход в глубину
В Сильвертауне есть N районов, пронумерованных от 1 до N, и M дорог, пронумерованных от 1 до M. Дорога i ведет из района Ai в район Bi, но вы не можете воспользоваться ею, чтобы попасть из района Bi в район Ai.
Максимус планирует прогулки по районам города. Он начинает в некотором районе, проходит по нулю или более дорог и заканчивает в некотором районе.
Сколько пар районов могут быть отправной и конечной точкой прогулки Максимуса?
Мы различаем пары с одинаковым набором районов, расположенных в разном порядке.
Формат входных данных
Первая строка содержит два целых числа N и M. Далее идет M строк, в каждой из которых записано по 2 числа: Ai и Bi.
Ограничения
2 ≤ N ≤ 20000 ≤ M ≤ min(2000, N*(N-1)1 ≤ Ai, Bi ≤ NAi не равно Bi.Пары (Ai,Bi) уникальны.Все значения во входных данных целые числа.
Формат выходных данных
Выведите ответ на задачу.
Примечание
В первом тестовом примере есть семь пар районов, которые могут быть отправной точкой и пунктом назначения (1,1),(1,2),(1,3),(2,2),(2,3),(3,2),(3,3)
| |
![]()
|
|
Красота фейерверка
Обход в глубину
Применение обхода в глубину
Динамическое программирование
Динамическое программирование
Динамическое программирование на поддеревьях
В лаборатории теоретической пиротехники изучают новые технологии организации
фейерверков. Фейерверк представляется как корневое дерево, а поскольку в мощном
фейерверке его элементы также взрываются, порождая новые фейерверки, то ученые вводят
операцию возведения корневого дерева в степень.
Корневое дерево содержит одну или несколько вершин. Одна из вершин выделена и
называется корнем дерева, для каждой из остальных вершин ровно одна другая вершина
является родителем. При этом от любой вершины можно добраться до корня,
последовательно переходя от вершины к ее родителю. Вершина, которая не является
родителем никакой другой вершины, называется листом. Если вершина x является
родителем вершины y, то вершина y является ребенком вершины x. Будем говорить, что
вершина и ее родитель соединены ребром.
На рис. 1 показан пример корневого дерева с корнем в вершине 1. Родителем вершин
2 и 3 является вершина 1, родителем вершины 4 является вершина 2. Вершины 2 и 3 — дети
вершины 1, а вершина 4 — ребенок вершины 2. Листьями являются вершины 3 и 4.
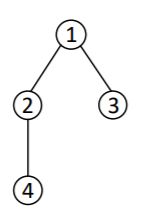
Рис. 1. Пример корневого дерева с корнем в вершине 1, листьями 3 и 4.
Фейерверк задается своим базовым деревом T и мощностью m. Фейерверк представляется деревом, которое получается в результате возведения дерева T в степень m. Операция возведения дерева в степень устроена следующим образом. Если m = 1, то результат T 1 — само дерево T. Для m > 1 рассмотрим дерево T m – 1 . Выполним следующую операцию: для каждого листа x дерева T m – 1 создадим копию дерева T и назначим лист x родителем корня соответствующей копии. Получившееся дерево будет деревом T m .
На рис. 2 показано дерево, представленное на рис. 1, в степенях 1, 2 и 3.
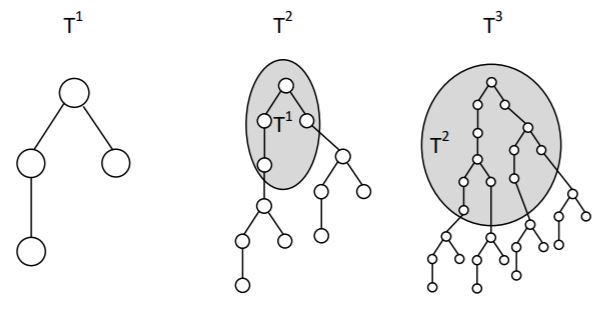
Рис. 2. Пример возведения дерева в степени 1, 2 и 3
Путем в дереве называется последовательность вершин, в которой две соседние
вершины соединены ребром. Все вершины в пути должны быть различны.
Для того, чтобы оценить красоту фейерверка, необходимо определить, какое
максимальное количество вершин может содержать путь в дереве, которым представляется
фейерверк. На рис. 3 приведен путь в дереве T2, содержащий максимальное количество
вершин. Таким образом, красота фейерверка с базовым деревом T и мощностью 2 равна 10.
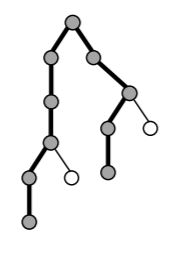
Рис. 3. Путь в дереве T 2 , содержащий максимальное количество вершин.
Требуется написать программу, которая по описанию дерева T и натуральному числу m определяет красоту фейерверка с базовым деревом T и мощностью m.
Формат входных данных
Первая строка входных данных содержит два натуральных числа n и m — количество
вершин в базовом дереве фейерверка T и его мощность (3 ≤ n ≤ 200 000, 1 ≤ m ≤ 200 000).
Вторая строка описывает дерево T и содержит (n – 1) целых чисел: p2, p3, …, pn —
номера родителей вершин 2, 3, …, n, соответственно (1 ≤ pi ≤ i – 1).
Формат выходных данных
Требуется вывести одно целое число — красоту фейерверка, представляемого
деревом Tm.
| |
![]()
|
|
Breaking News
Деревья
Обход в глубину
Жизнь завода по производству олимпиадных задач монотонна и однообразна: каждый день происходит одно и то же, вечера похожи как две снежинки и каждое утро всё начинается сначала - ничего не меняется на заводе по производству олимпиадных задач.
В частности, давно известно, когда в течение дня пара сотрудников встречается между собой.
При встрече сотрудники делятся друг с другом новостями.
Утром перед работой сотрудник номер 1 узнал нежелательную новость. Конечно же, он делится с ней при встрече со всеми остальными сотрудниками и они тоже узнают новость и начинаются делиться ей с другими. Если встречаются два сотрудника и один из них знает новость, то начиная с этого момента второй из них также знает новость. Ни один сотрудник не может встречаться с двумя или более сотрудниками одновременно (из соображений секретности). Пара сотрудников может встречаться несколько раз в течение дня.
Вы можете помешать ровно одной встрече за весь день. Выберите такую встречу, отмена которой приведёт к тому, что как можно меньше сотрудников завода узнают новость.
Входные данные
В первой строке входного файла задано два целых числа N (2 ≤ N ≤ 1000) и D (1 ≤ D ≤ 100000) — количество сотрудников и встреч соответственно. В следующих D строках заданы описания встреч. Каждое описание встречи состоит из трех
чисел Ai, Bi и Ti (1 ≤ Ai, Bi ≤ N, 1 ≤ Ti ≤ 109) — пара номеров сотрудников и время встречи.
Выходные данные
Выведите описание встречи, которую необходимо отменить в том же формате, который используется во входных данных. Если ответов несколько — выведите любой.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 5
2 3 1
1 2 4
4 2 110
2 3 5
3 4 4 |
1 2 4 |
| |
![]()
|
|
Удаление клеток
Обход в ширину
Обход в глубину
Из прямоугольного листа клетчатой бумаги (M строк, N столбцов) удалили некоторые клетки. На сколько кусков распадётся оставшаяся часть листа? Две клетки не распадаются, если они имеют общую сторону.
Входные данные
В первой строке находятся числа M и N, в следующих M строках - по N символов. Если клетка не была вырезана, этому соответствует знак #, если вырезана - точка. 1 <= M, N <= 100.
Выходные данные
Вывести одно число.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 10
##..#####.
.#.#.#....
###..##.#.
..##.....#
.###.#####
|
5
|
| |
![]()
|
|
Путешествия в реальности
Обход в глубину
Каждый раз, когда в мире происходит значимое событие, наша реальность разветвляется на несколько — в зависимости от исхода этого события. После этого существует уже не только наша основная реальность, но и ответвившиеся от неё в моменты появления разных исходов.
Однажды один архимаг решил сделать мир лучше. Такая грандиозная задача не под силу одному архимагу, поэтому он решил найти самого себя ещё в \(K\) реальностях и выполнить эту задачу вместе. Проведённое теоретическое исследование показало, что, кроме реальности, в которой находится именно он, существует ещё \(N - 1\) реальностей. Для удобства они были занумерованы числами от \(1\) до \(N\), при этом его собственная реальность имеет номер \(1\), а посетить ему необходимо реальности с номерами \(2, 3, \ldots, K + 1\).
Как уже говорилось, каждая реальность когда-то ответвилась от некоторой другой, за исключением одной Начальной реальности, которая существовала всегда (её номер может оказаться каким угодно; считается, что она появилась в момент времени \(0\)). Исследование показало, что реальность с номером \(i\) ответвилась от реальности с номером \(P_i\) в момент времени \(T_i\). Из каждой реальности с номером \(i\) архимаг может переместиться
-
в любую ответвившуюся от неё, то есть в любую \(j\), такую что \(P_j = i\);
-
в \(P_i\), если \(i\) — не Начальная реальность.
Другими словами, возможны лишь переходы вида \(i \leftrightarrows P_i\). На каждый такой переход в любую сторону архимаг затрачивает \(T_i-T_{P_i} > 0\) условных единиц энергии.
Требуется найти минимальное количество энергии, которое потребуется архимагу, чтобы, начав в реальности с номером \(1\), посетить все реальности с номерами от \(2\) до \(K + 1\) (в любом порядке) и затем вновь вернуться в \(1\). Любую реальность при этом разрешается посещать сколько угодно раз.
Формат входных данных
Сначала вводятся два целых числа \(N\) и \(K\) (\(0 \leqslant K < N \leqslant 100\,000\)): количество доступных реальностей и количество реальностей, которые необходимо посетить. Далее идёт \(N\) пар целых чисел, \(i\)-я пара — это \(P_i\) и \(T_i\) (\(1 \leqslant P_i \leqslant N\), \(0 \leqslant T_i \leqslant 10^6\); для Начальной реальности \(P_i=T_i=0\)).
Гарантируется, что ответвившаяся реальность появилась строго позже породившей (\(T_i > T_{P_i})\), и что маг может при желании добраться до любой из \(N\) реальностей.
Формат выходных данных
Выведите единственное число \(E\) — минимальную возможную энергию, которая потребуется архимагу для путешествия.
| |
![]()
|
|
Спелестология
Обход в глубину
Спелестологический клуб «Залезь и посмотри» часто привлекается к поиску заблудившихся в каменоломнях незадачливых путешественников. Заблудившиеся в темноте и тесноте паникуют, хаотично перемещаются, ходят кругами и осложняют этим поисковые работы. Гораздо удобнее было бы, если бы потерявшиеся сидели в каком-нибудь зале и никуда не двигались.
Каменоломни представляют собой набор из N залов, занумерованных числами от 1 до N и M проходов между ними. Проходы могут быть как двусторонними, так и односторонними (например, с сильным вертикальным уклоном). Ни один проход не соединяет зал сам с собой. Пара залов может соединяться максимум одним проходом. Гарантируется, что двигаясь только по односторонним проходам, нельзя попасть в тот зал, из которого вышли путешественники.
Чтобы избежать хождения заблудившихся по кругу, члены клуба решили нанести на двусторонние проходы специальные аварийные стрелки так, чтобы идя по этим стрелкам нельзя было попасть в уже посещенное место, откуда бы ни началось движение и, в итоге, потерявшиеся оказались бы в одном из залов, из которого нельзя уйти, двигаясь по стрелочкам — там их и найдут спелестологи.
Для каждого двустороннего прохода определите допустимое направление движения.
Формат входных данных
В первой строке входных данных задается два числа N (2 ≤ N ≤ 100000) и M (1 ≤ M ≤ 100000) — количество залов и проходов между ними.
В следующих M строках задаются описания проходов. Каждое описание состоит из трёх чисел A, B и D (1 ≤ A, B ≤ N). Числа A и B задают номера соединенных проходом залов. Если D = 1, то проход односторонний из зала A в зал B. Если D = 2, то проход двусторонний.
Формат выходных данных
Для каждого двустороннего прохода из входных данных выведите пару чисел, описывающих соединяемые этим проходом залы. Движение может осуществляться из первого зала во второй.
Если правильных ответов несколько — выведите любой из них. Порядок вывода описания проходов не важен. Гарантируется, что ответ всегда существует.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 5
1 2 1
2 4 2
2 3 1
3 4 1
4 1 2 |
2 4
1 4 |
| |
![]()
|
|
Робот-курьер
Обход в глубину
Это интерактивная задача. Ваше решение должно взаимодействовать с программой-интерактором по описанному ниже протоколу.
На вас возложили ответственную задачу по управлением роботом-курьером. Карта, по которой перемещается робот, представляет из себя поле размера \(n \times m\) (\(n\) строк и \(m\) столбцов). Каждая клетка поля может быть либо тротуаром (‘.’), либо проезжей частью дороги (‘+’).
Ровно \(k\) клеток проезжей части содержат регулируемые пешеходные переходы. Гарантируется, что для любого пешеходного перехода ровно две противоположные относительно него соседние с ним по стороне клетки (то есть верхняя и нижняя или левая и правая) являются клетками тротуара. Соответственно, с обоих концов каждого пешеходного перехода расположен светофор.
Робот может перемещаться только по тротуарам и пешеходным переходам. Для определения цвета светофора робот обладает камерой с разрешением \(h \times w\) (где \(w\) четно). Для управления роботом вы можете передавать ему следующие команды:
-
<<turn \(c\)>>, где \(c \in \{\text{`{L}'}, \text{`{U}'}, \text{`{R}'}, \text{`{D}'}\}\), означает поворот в соответствующую сторону (влево, вверх, вправо или вниз);
-
<<move>> означает перемещение на одну клетку вперед относительно текущего направления;
-
<<camera>> означает получение изображения с камеры; в ответ на эту команду вы получаете таблицу из \(h \times w\) символов, каждый из которых описывает преобладающий цвет (‘r’, ‘g’ или ‘b’ — красный, зеленый или синий) в соответствующей области пространства перед роботом;
-
<<wait \(t\)>> означает ожидание в течение \(t\) секунд.
На поворот или перемещение требуется ровно одна секунда. Получение изображения с камеры времени не требует. Каждый светофор горит одним цветом в течение фиксированного периода времени, после чего моментально переключается и горит другим цветом то же время (и так далее). Этот период времени вам неизвестен и может быть разным у разных светофоров, однако гарантируется, что он не превышает \(10^6\).
Светофоры могут находиться на разной высоте и на разном расстоянии сбоку от соответствующего перехода. Если робот находится около перехода с \(i\)-м светофором и смотрит в его направлении, на изображении с камеры светофор будет занимать две клетки в \(a_i\)-й и \((a_i + 1)\)-й снизу строках в столбце на расстоянии \(b_i\) от центра (слева от центра, если \(b_i < 0\), и справа, если \(b_i > 0\)). Для светофора, горящего красным, нижняя из этих двух клеток равна ‘b’, а верхняя равна ‘r’. Для зеленого светофора нижняя клетка равна ‘g’, а верхняя — ‘b’. Остальные клетки на изображении могут любого из трех цветов.
Требуется переместить робота из клетки \((i_1, j_1)\) (\(i_1\)-я сверху строка, \(j_1\)-й слева столбец) в клетку \((i_2, j_2)\). Начинать пересекать пешеходные переходы можно только если на соответствующем светофоре горит зеленый сигнал. Если движение по переходу начато, когда на светофоре горит зеленый сигнал, можно считать, что как минимум в течение еще двух секунд находиться на переходе безопасно, то есть можно гарантированно переместиться на тротуар на противоположной стороне дороги.
Напишите программу, сообщающую роботу команды, безопасно приводящие его из стартовой клетки в конечную. Минимизировать затраченное в пути время не требуется. В изначальной клетке робот находится в направлении <<вверх>> (‘U’).
Каждый тест состоит из нескольких наборов входных данных. В первой строке ввода дано единственное целое число \(t\) — количество наборов входных данных в тесте (\(1 \le t \le 50\)).
Наборы входных данных поступают вам на ввод последовательно: для каждого набора сначала вводится информация о карте и роботе, а затем сразу запускается протокол взаимодействия с интерактором (см. ниже).
В первой строке описания карты даны два целых числа \(n\) и \(m\) — размеры карты (\(1 \le n, m \le 50\)). Следующие \(n\) строк содержат по \(m\) символов каждая и описывают карту. Символ на \(j\)-й позиции \(i\)-й строки описывает клетку с координатами \((i, j)\) и равен ‘.’, если это клетка тротуара, и ‘+’, если это клетка проезжей части.
В следующей строке даны три целых числа \(k\), \(h\) и \(w\) — количество переходов со светофорами и разрешение камеры, соответственно (\(k \le n \cdot m\); \(2 \le h, w \le 8\); \(w\) четно).
Следующие \(3k\) строк описывают светофоры: по три на каждый из \(k\) переходов. В первой строке для \(i\)-го светофора дано положение соответствующего ему перехода \((r_i, c_i)\) (\(1 \le r_i \le n\); \(1 \le c_i \le m\)). Во второй строке дано описание светофора с одного из двух концов перехода в формате <<\(d_{i,1}\) \(a_{i,1}\) \(b_{i,2}\)>>, где \(d_1\) указывает на направление перехода, соответствующее этому светофору, а \(a_{i,1}\) и \(b_{i,1}\) — его высота и расстояние от центра перехода, соответственно (\(d_{i,1} \in \{\text{`{L}'}, \text{`{U}'}, \text{`{R}'}, \text{`{D}'}\}\); \(1 \le a_{i,1} < h\); \(1 \le |b_{i,1}| \le \frac{w}{2}\)). В третьей строке в том же формате описывается светофор с противоположной стороны перехода.
Наконец, в последней строке набора входных данных даны четыре целых числа \(i_1\), \(j_1\), \(i_2\) и \(j_2\) — координаты стартовой и конечной клеток, соответственно (\(1 \le i_1, i_2 \le n\); \(1 \le j_1, j_2 \le m\)).
Гарантируется, что все \((r_i, c_i)\) различны, а описания светофоров корректны: направления \(d_{i,1}\) и \(d_{i,2}\), указанные во вводе, противоположны и соответствуют направлениям, в которых от этого перехода расположен тротуар. Также гарантируется, что конечная клетка достижима из стартовой.
После прочтения вашей программой входных данных для очередного набора запускается протокол взаимодействия с интерактором.
Взаимодействие с интерактором заключается в сообщении вашей программой интерактору очередного действия робота, после чего интерактор будет выводить результат выполнения этого действия. Для большего понимания обратите внимание на пример теста в условии.
-
Чтобы повернуть робота, выведите <<turn \(c\)>>, где \(c \in \{\text{`{L}'}, \text{`{U}'}, \text{`{R}'}, \text{`{D}'}\}\). В результате выполнения этого действия робот повернется <<лицом>> в соответствующем направлении, и интерактор выведет <<OK>> на отдельной строке.
-
Чтобы переместить робота, выведите <<move>>. В таком случае робот переместится на одну клетку вперед в том направлении, в котором он повернут. Если это действие успешно, интерактор выведет <<OK>> на отдельной строке. Если при этом робот достиг конечной клетки \((i_2, j_2)\), интерактор перейдет к рассмотрению следующего набора входных данных и подаст соответствующие входные данные на ввод вашей программе (либо завершится и засчитает ваше решение, если это был последний набор входных данных).
Если же робот при таком перемещении попадает в непроходимую клетку, выходит за пределы карты или выезжает на пешеходный переход на красный свет, интерактор выведет <<FAIL>> и завершится с вердиктом Wrong Answer. Во избежание получения некорректного вердикта, считав <<FAIL>>, ваше решение также должно завершиться.
-
Чтобы сделать снимок, выведите <<camera>>. В ответ интерактор выведет \(h\) строк по \(w\) символов каждая. Каждый символ равен ‘r’, ‘g’ или ‘b’ и задает цвет соответствующего <<пикселя>>. Если непосредственно перед роботом не находится пешеходный переход, все символы будут случайными. Если же робот стоит у перехода, то два символа, соответствующие положению на <<изображении>> светофора напротив, будут отражать цвет этого светофора как описано в условии.
-
Чтобы подождать \(t\) секунд (\(1 \le t \le 2 \cdot 10^6\)), выведите <<wait \(t\)>>. В ответ интерактор выведет <<OK>> на отдельной строке и обновит состояние всех светофоров, цвет которых за это время поменяется.
Запрещается делать более \(25\) команд ожидания в одной и той же клетке поля. Если ваше решение совершает хотя бы \(26\) запросов ожидания из одной и той же клетки, интерактор в ответ выведет <<FAIL>> и завершится с вердиктом Wrong Answer.
Вывод каждой команды ваша программа должна завершать выводом символа перевода строки (endl, ‘\n’) и сбросом буфера вывода. Сбросить буфер можно с помощью
-
<<fflush(stdout)>> в C и C++, или <<cout.flush()>> только в C++,
-
<<System.out.flush()>> в Java,
-
<<sys.stdout.flush()>> в Python,
-
и <<Console.Out.Flush()>> в C#.
-
В Pascal и Delphi сброс буфера при выводе в стандартный поток вывода происходит автоматически.
Решение, не выполняющее эти действия, может получить произвольный вердикт (скорее всего, Time Limit Exceeded или Idleness Limit Exceeded).
В примере из условия добавлены лишние пустые строки, чтобы проиллюстрировать взаимодействие с интерактором и порядок ввода-вывода при этом взаимодействии. В решении выводить эти пустые строки не надо.
Пояснение к примеру
Во втором наборе входных данных в примере:
-
В клетке \((3, 2)\) нет перехода, поэтому по ней нельзя перемещаться;
-
При пересечении перехода в \((1, 2)\) в направлении ‘R’ светофор находится на высоте \(2\) и на расстоянии \(-2\) от центра: соответственно, его клетки на изображении располагаются в первом столбце во второй и третьей снизу строках. Для данного снимка они равны ‘b’ в верхней строке и ‘g’ во второй, поэтому его сразу можно пересекать.
-
При пересечении перехода в \((2, 3)\) в направлении ‘D’ светофор находится на высоте \(1\) и на расстоянии \(2\) от центра, то есть в четвертом столбце в двух нижних строках. На первом изображении он горит красным, а после ожидания (<<wait 10>>) — зеленым.
| |
![]()
|
|
Автомат с игрушками
Обход в глубину
В развлекательном центре Е-города был установлен игровой автомат нового поколения. В автомат можно бросить монету и следить за её продвижением сверху вниз по разветвляющемуся лабиринту из трубок. В лабиринте есть \(n\) узлов, которые пронумерованы числами от 1 до \(n\). При бросании монета попадает в первый узел. Каждый узел лабиринта, кроме первого, имеет одну входящую сверху трубку, по которой монета может в него попасть. Из каждого узла выходит не более двух трубок, идущих вниз, одна из которых ведет налево, а другая "— направо. Каждая трубка имеет некоторую ширину. Монета проваливается в более широкую трубку, а в случае равенства ширины трубок "— в левую.
После прохождения монеты по трубке ширина этой трубки уменьшается на 1. Монета не может пройти по трубке ширины 0. Если монета достигла узла, из которого она не может дальше двигаться вниз, автомат останавливается и ждёт, когда в него бросят следующую монету.
Изначально в каждом узле лабиринта находится по игрушке. Когда монета попадает в узел первый раз, игрушка, находящаяся в этом узле, достаётся игроку, бросившему эту монету.
Панкрату понравилась игрушка, которая находится в узле с номером \(v\).
Требуется написать программу, которая определяет, сколько монет должен бросить в автомат Панкрат, чтобы получить игрушку из узла \(v\).
Формат входных данных
В первой строке задано число \(n\) — количество узлов в лабиринте. В последующих \(n\) строках заданы описания всех узлов, в \(k\)-й из этих строк описан узел с номером \(k\).
Описание \(k\)-го узла состоит из четырех целых чисел: \(a_k\), \(u_k\), \(b_k\), \(w_k\). Если из \(k\)-го узла выходит левая трубка, то \(a_k\) — номер узла, в который она ведет (\(k < a_k \leqslant n\)), а \(u_k\) — её ширина. Если левой трубки нет, то \(a_k = u_k = 0\). Если из \(k\)-го узла выходит правая трубка, то \(b_k\) — номер узла, в который она ведет (\(k < b_k \leqslant n\)), а \(w_k\) — её ширина. Если правой трубки нет, то \(b_k = w_k = 0\).
В последней строке задано целое число \(v\) (\(1 \leqslant v \leqslant n\)) — номер узла, в котором находится игрушка, понравившаяся Панкрату.
Гарантируется, что во все узлы, кроме первого, входит ровно одна трубка.
Формат выходных данных
Выходные данные должны содержать одно число — количество монет, которое необходимо бросить в автомат Панкрату, чтобы получить игрушку, которая находится в узле \(v\). Если получить выбранную игрушку невозможно, выведите число \(-1\).
Пояснение к примеру
В первом примере первая монета пройдет лабиринт по следующему пути, и игрок получит игрушки из вершин 1, 3 и 4:
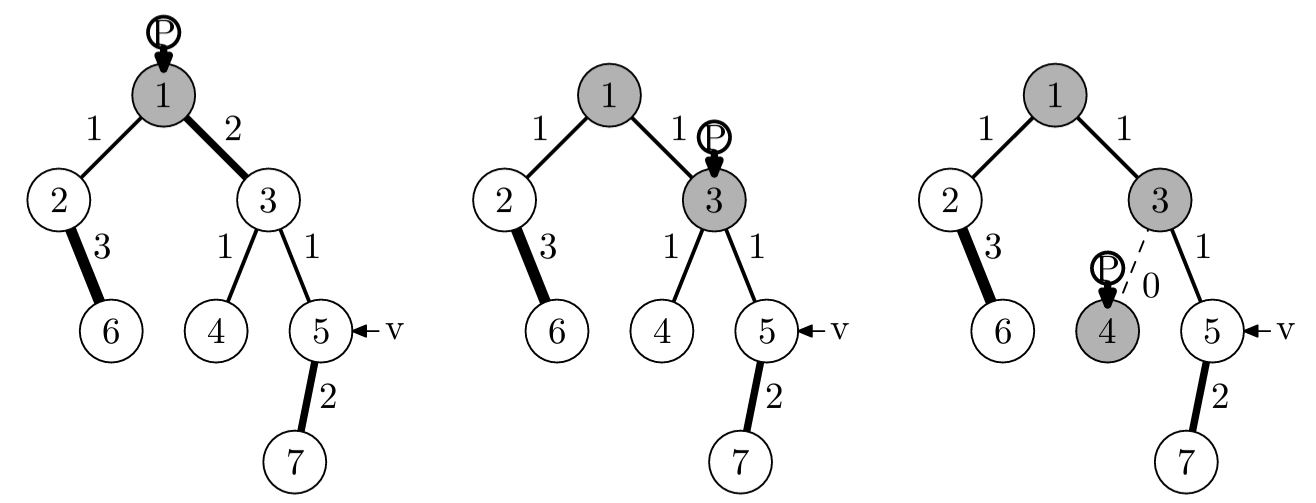
Вторая монета пройдет лабиринт по следующему пути, и игрок получит игрушки из вершин 2 и 6:
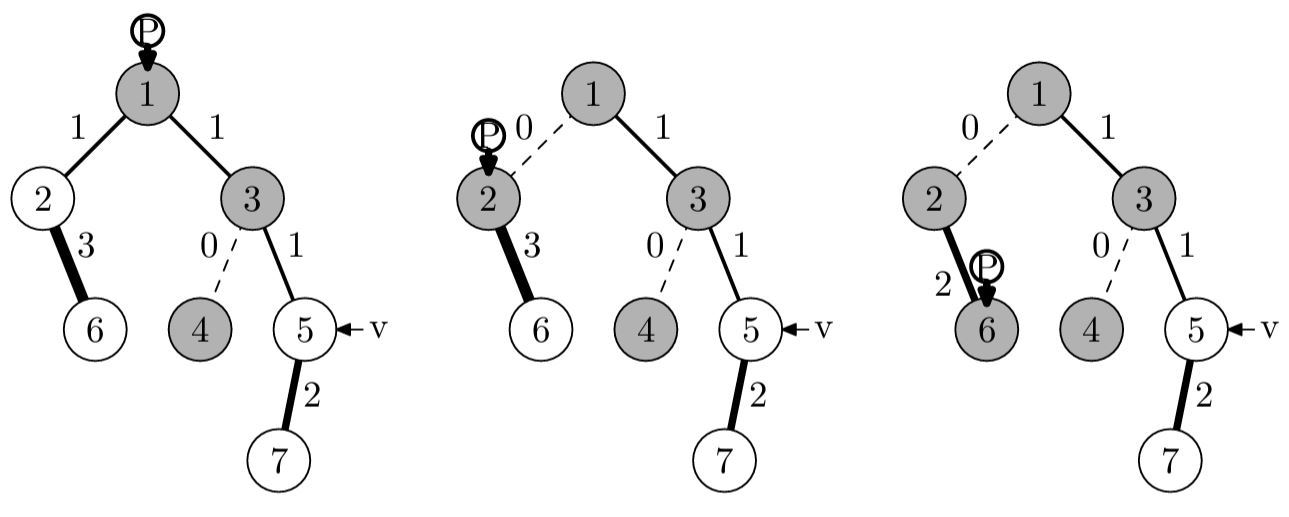
Третья монета пройдет лабиринт по следующему пути, и игрок получит игрушки из вершин 5 и 7:
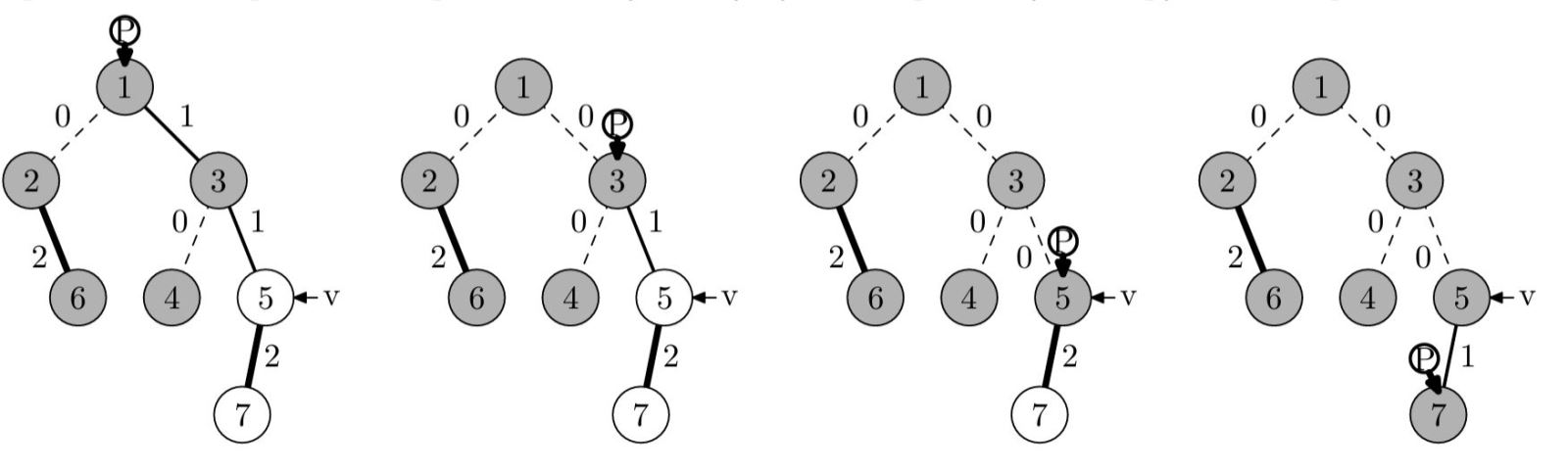
| |
![]()
|
|
Электрички на перегонах не меняют
Способы задания графа
Обход в глубину
На пригородной железной дороге N станций и M соединяющих их перегонов. Любые две станции соединены не более чем одним перегоном. Сеть перегонов устроена так, что, отправившись от любой станции, можно вернуться на нее, только проехав хотя бы один перегон дважды. На железной дороге организовано движение электричек. Каждая электричка ходит в обоих направлениях по своему маршруту между двумя конечными станциями и останавливается на всех промежуточных станциях
Для удобства пассажиров руководство железной дороги решило ввести новую систему оплаты проезда. По этой системе каждой станции присваивается некоторое целое число, называемое тарифным номером этой станции. Стоимость проезда между двумя станциями без пересадок определяется модулем разности тарифных номеров этих станций. Тарифные номера станций вдоль маршрута каждой электрички должны изменяться монотонно, то есть при движении в каком-либо направлении строго возрастать и, следовательно, строго убывать при движении в обратном направлении. Это обеспечивает рост стоимости проезда с увеличением количества пройденных перегонов.
Требуется написать программу, которая назначит каждой станции тарифный номер.
 |
4 станции, 3 перегона: 1-4, 2-4, 3-4
Маршруты: 1-4-2, 2-4-3, 3-4-1.
Ответ: решения нет
|
 |
5 станций, 4 перегона: 1-5, 2-5, 3-5, 4-5
Маршруты: 1-5-2, 2-5-3, 3-5-4, 4-5-1.
Ответ: решение есть; например, следующее: номер станции: 1 2 3 4 5
тарифный номер: 1 4 1 5 3
Замечание: тарифные номера разных станций могут совпадать.
|
Формат входных данных
В первой строке входных данных содержатся два целых числа: N — количество станций (2 ≤ N ≤ 100 000), и M — количество перегонов между ними (1 ≤ M ≤ N – 1). В последующих M строках записаны пары целых чисел a, b (a ≠ b, 1 ≤ a ≤ N, 1 ≤ b ≤ N), означающие наличие перегона между станциями a и b. За ними в отдельной строке записано единственное целое положительное число K — количество маршрутов электричек. В последующих K строках идут описания маршрутов электричек, по одному на строке. Каждое описание представляет собой последовательность целых чисел — номеров всех станций маршрута в порядке одного из двух возможных направлений следования электрички. Описание маршрута заканчивается числом 0.
Все номера станций в описании маршрута различны. Количество станций в каждом маршруте не менее двух. Любые две последовательные станции в маршруте каждой электрички соединены перегоном. Суммарное количество станций в описаниях всех маршрутов не превосходит 200 000. Могут быть станции и перегоны, через которые не проходит ни одна электричка.
Формат выходных данных
В первую строку выведите «NO», если искомого назначения тарифных номеров не существует. В противном случае в первую строку выведите «YES», а в следующей строке — N целых положительных чисел, где i-е число — тарифный номер i-й станции. Тарифный номер каждой станции должен находиться в диапазоне от 1 до N.
Если существует несколько решений, необходимо вывести любое из них.
| |
![]()
|
|
Монополия
Обход в глубину
В Тридесятом государстве есть N фирм, занимающихся разработкой программного обеспечения. Однажды известный олигарх Тридесятого государства Иванушка решил монополизировать эту отрасль. Для этого он хочет купить максимальное число программистских фирм Тридесятого государства.
Он разослал предложения всем N компаниям и через некоторое время получил от каждой их них согласие или отказ. Однако он знает, что в бизнесе очень многое зависит от взаимного доверия партнеров.
В результате небольшого исследования Иванушка установил, между какими компаниями существует взаимное доверие (причем всегда если компания доверяет компании B, то компания B доверяет компании A).
Теперь, при желании, Иванушка может повторно разослать предложения всем компаниям, включив в письма список компаний, давших согласие участвовать в его проекте. При этом каждая компания, независимо от своего первоначального мнения дает согласие, если в списке есть хотя бы одна компания, которой она доверяет, и отказ в противном случае. Таким образом, некоторые компании, которые изначально не согласились участвовать в проекте, могут теперь дать свое согласие, а некоторые из давших согласие — наоборот отказаться. В результате этого у Иванушки формируется новый список, который он опять может разослать фирмам. Он может сколь угодно долго повторять операцию, каждый раз рассылая текущий список. Иванушка может остановить процесс в любой момент и заключить договора с теми, кто после последней рассылки дал согласие.
Напишите программу, которая определит, какое максимальное число компаний может объединить Иванушка под своим началом.
Будем считать, что Иванушка — честный предприниматель и он никогда не подтасовывает рассылаемые им списки.
Входные данные
В первой строке входных данных содержится число N — количество фирм (1≤N≤2000). Далее идут N чисел, описывающих ответ фирмы на первое предложение Иванушки (1 — согласие, 0 — отказ). Далее задается число M (0≤M≤200000) — количество пар компаний, между которыми существует доверие. Далее следуют M пар чисел, задающих номера фирм, между которыми существует взаимное доверие (числа в паре не могут быть одинаковыми). Любая пара компаний упоминается в этом списке не более одного раза.
Выходные данные
Выведите одно число — максимальное число фирм, которое сможет купить Иванушка.
| |
![]()
|
|
Формула - 3
Обход в глубину
Сканирующая прямая
Элементарная геометрия
В ежегодном чемпионате Флатландии (которая, естественно, является плоским миром) по космическим гонкам "Формула-3" участвуют N космических скутеров, имеющие форму треугольников. До начала гонок скутеры занимают положение в стартовой зоне согласно результатам жеребьевки.
Скутеры стартуют строго по порядку. Каждый скутер,получив команду «старт», уезжает в положительном направлении оси Ox. Следующий скутер стартует лишь тогда, когда предыдущий покинет стартовую зону. Скутеры уезжают строго параллельно оси Ox, скутеры в стартовой зоне не поворачивают и не разворачиваются.
Естественно, что если в момент старта на пути скутера окажется другой скутер, то произойдет авария (даже если скутер заденет лишь угол другого скутера своим углом).
Для уменьшения опасности столкновения скутеров на старте строго соблюдается следующее правило: прямые, параллельные оси Ox и пересекающие какой-то скутер, должны в совокупности пересекать не более 100 других скутеров (прямая, проходящая через одну точку скутера также считается прямой, пересекающей скутер). Например, на приведенном рисунке прямые, параллельные Ox и пересекающие скутер 2, проходят через 2 других скутера (1 и 3), а прямые, проходящие через скутер 1, проходят только через один другой скутер (номер 2).
Главный Судья гонок хочет определить порядок, в котором должны стартовать скутеры, чтобы аварии не произошло. Например, в ситуации, приведенной на рисунке, сначала должен стартовать скутер номер 2 (если попытается стартовать скутер номер 1 или 3, то он столкнется со скутером номер 2). После этого скутеры 1 и 3 могут стартовать в любом порядке (они друг другу не мешают).
Помогите Главному Судье — напишите программу, которая определит какой-нибудь порядок старта скутеров, чтобы аварии не произошло.
Входные данные
В первой строке вводится натуральное число N( 1 ≤ N ≤ 30 000).
В каждой из следующих N строк содержится по 6 чисел: x1, y1, x2, y2, x3, y3 – координаты трех вершин скутера на старте, целые числа, не превосходящие по модулю 106. В начальный момент скутеры не задевают друг друга.
Выходные данные
Выведите через пробел N чисел – номера скутеров в том порядке, в котором они могут стартовать. Если решений несколько, выведите одно любое из них. Если решений нет, выведите одно число -1.
Примечание
Первый тест соответствует приведенному рисунку. Ответ 2 3 1 в этом тесте также является правильным
| |
![]()
|
|
Автобусы
Бинарный поиск по ответу
Обход в глубину
В столице одной Очень Демократической Страны все жители в 8 часов утра одновременно выходят со станций метро, ближайших к месту своей работы, и дальше добираются до работы на автобусах. Мэр города хочет построить еще одну станцию метро так, чтобы после этого время, к которому все люди доберутся до места своей работы (то есть время, когда последний работник окажется на работе), было наименьшим возможным.
Автобусное сообщение в столице устроено следующим образом. Есть N автобусных остановок, в частности, возле каждой станции метро расположено по остановке. Между N – 1 парой остановок постоянно курсируют автобусы, время движения от одной остановки до другой – 1 минута. Временем ожидания и пересадки можно пренебречь. Автобусное сообщение в столице организовано так, что от любой автобусной остановки до любой другой можно добраться на автобусах (возможно, с пересадками).
Входные данные
В первой строке входных данных содержатся два числа N и M – количество автобусных остановок и станций метро соответственно (2 ≤ N ≤ 50 000, 1 ≤ M ≤ 1 000, M < N).
Во второй строке задаются через пробел M чисел – номера автобусных остановок, рядом с которыми есть станции метро (каждая – не более одного раза).
В следующих N – 1 строках записано по два числа – номера автобусных остановок, между которыми курсирует автобус. (Автобус ходит в обоих направлениях. Каждый маршрут указан один раз.)
Выходные данные
Выведите два числа – сначала наибольшее время за которое кто-то будет и после строительства добираться на работу, а затем номер автобусной остановки, рядом с которой следует построить новую станцию метро. (Строить можно возле тех автобусных остановок, возле которых еще нет станций метро). Если решений несколько, выведите одно из них.
| |
![]()
|
|
Блокада
Обход в глубину
Двумерные массивы
Государство Флатландия представляет собой прямоугольник размером M × N, состоящий из единичных квадратиков. Флатландия разделена на K провинций (2 <= K <= 100). Каждая провинция представляет собой связное множество квадратиков, т.е. из каждой точки провинции можно дойти до любой другой ее точки, при этом разрешается переходить с квадратика на квадратик, только если они имеют общую сторону (общей вершины недостаточно). Во Флатландии нет точки, которая граничила бы более чем с тремя провинциями (т.е. четыре квадратика, имеющие общую вершину, не могут принадлежать четырем разным провинциям).
Каждая провинция имеет свой символ. Столица Флатландии находится в провинции, которой принадлежит символ A (заглавная латинская буква A). Провинция называется пограничной, если она содержит граничные квадратики. Провинция, в которой находится столица Флатландии, не является пограничной.
Король соседнего с Флатландией королевства Ректилания решил завоевать Флатландию. Для этого он хочет захватить столицу Флатландии. Однако он знает, что сил его армии недостаточно, чтобы сделать это сразу. Поэтому сначала он хочет окружить столичную провинцию, чтобы ослабить силы противника долгой блокадой, а потом захватить столицу.
Чтобы окружить провинцию, требуется захватить все провинции, с которыми она граничит. Две провинции граничат, если существует два квадратика, имеющие общую сторону, один из которых принадлежит первой из них, а другой - второй. Чтобы захватить провинцию, надо чтобы выполнялось одно из двух условий: либо она пограничная, либо граничит с какой-либо уже захваченной провинцией.
Чтобы сберечь силы своей армии, король Ректилании хочет установить блокаду столичной провинции, захватив как можно меньше провинций. Помогите ему выяснить, сколько провинций требуется захватить. Захватывать столичную провинцию нельзя, поскольку для этого сил армии Ректилании пока недостаточно.
Входные данные
В первой строке вводятся числа M и N (3 <= M, N <= 200). Следующие M строк содержат N символов каждая и задают карту Флатландии. Символ, находящийся в i + 1-й строке входных данных на j-м месте, представляет собой символ провинции, которой принадлежит квадратик (i, j). Все символы имеют ASCII-код больше 32 (пробела).
Выходные данные
Выведите единственное число - количество провинций, которые требуется захватить. Если установить блокаду невозможно, выведите "-1".
| |
![]()
|
|
Яблоко от яблони…
Способы задания графа
Обход в глубину
У Пети в саду растет яблоня. Воодушевленный историей об Исааке Ньютоне, который, как известно, открыл закон всемирного тяготения после того, как ему на голову упало яблоко, Петя с целью повысить свою успеваемость по физике часто сидит под яблоней.
Однако, поскольку по физике у Пети твердая тройка, яблоки с его яблони падают следующим образом. В какой-то момент одно из яблок отрывается от ветки, на которой оно висит, и начинает падать строго вниз. Если в некоторый момент оно задевает другое яблоко, то то тоже отрывается от своей ветки и начинает падать вниз, при этом первое яблоко не меняет направление своего падения. Вообще, если любое падающее яблоко заденет другое яблоко на своем пути, то оно также начнет падать.
Таким образом, в любой момент каждое яблоко либо висит на ветке, либо падает строго вниз, причем все яблоки кроме первого, чтобы начать падать, должны сначала соприкоснуться с каким-либо другим падающим яблоком.
Выясните, какие яблоки упадут с Петиной яблони.
Входные данные
В первой строке вводится число N - количество яблок на Петиной яблоне (1 <= N <= 200). Следующие N строк содержат описания яблок. Будем считать все яблоки шарами. Каждое яблоко задается координатами своей самой верхней точки (той, где оно исходно прикреплено к дереву, длиной черенка пренебрежем) xi, yi и zi и радиусом ri ( -10000 <= xi, yi, zi <= 10000, 1 <= ri <= 10000, все числа целые). Гарантируется, что изначально никакие яблоки не пересекаются (даже не соприкасаются). Ось OZ направлена вверх.
Выходные данные
В первой строке выведите количество яблок, которые упадут с яблони, если начнет падать первое яблоко. В следующей строке выводите номера упавших яблок. Яблоки нумеруются, начиная с 1, в том порядке, в котором они заданы во входных данных.
| |
![]()
|
|
Запрещенный подграф
Обход в глубину
Два неориентированных графа G и H называются изоморфными , если:
- они имеют одинаковое количество вершин;
- существует такое однозначное соответствие между их вершинами, что любые две различные вершины графа G соединены ребром тогда и только тогда, когда соединены ребром соответствующие вершины графа H.
Например, следующие два графа изоморфны, хотя выглядят по-разному:
Возможным однозначным соответствием, показывающим, что эти два графа изоморфны, является {a-1, b-6, c-8, d-3, g-5, h-2, i-4, j-7}, хотя существуют и другие подобные соответствия.
Подграфом графа G называется граф, множества вершин и ребер которого являются подмножествами множеств вершин и ребер графа G. Заметьте, что граф G является также и своим подграфом. На рисунке показаны граф и один из его подграфов:
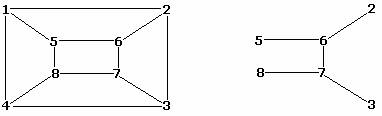
Говорят, что граф G содержит другой граф H , если существует хотя бы один подграф H ’ графа G , который изоморфен H . Следующий рисунок показывает граф G , который содержит граф H .
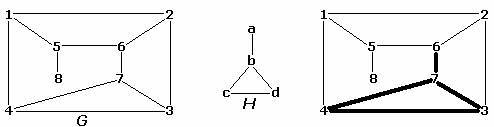
ЗАДАНИЕ
По двум заданным неориентированным графам G и H постройте подграф G’ графа G такой, что:
количество вершин в графах G и G’ одинаково;
H не содержится в G’ .
Естественно, может быть много подграфов графа G’ с перечисленными свойствами. Постройте подграф с как можно большим количеством ребер.
БАЗОВЫЙ АЛГОРИТМ
Возможно, наиболее простой стратегией при решении этой задачи будет следующая: рассматривать ребра графа G в порядке, в котором они представлены во входных данных, после чего пытаться добавлять ребра одно за другим в граф G’, проверяя на каждом шаге, входит ли граф H в граф G’ или нет. Правильная реализация этого жадного алгоритма наберет некоторое количество очков, хотя существуют гораздо лучшие стратегии.
ОГРАНИЧЕНИЯ
3 ≤ m ≤ 4 m – количество вершин в H.
3 ≤ n ≤ 1000 n – количество вершин в G .
ВВОД
Вы получите 10 тестов каждый со следующими данными:
|
Пример ввода
|
ОПИСАНИЕ
|
|
3 5
0 1 0
1 0 1
0 1 0
0 1 0 0 0
1 0 1 0 0
0 1 0 1 0
0 0 1 0 1
0 0 0 1 0
|
СТРОКА 1: Содержит два целых числа, разделенных пробелом, соответственно m и n.
СЛЕДУЮЩИЕ m СТРОК: Каждая строка содержит m целых чисел, разделенных пробелами, и представляет одну вершину из H в порядке 1, ..., m . i -ый элемент j -ой строки в этой секции равняется 1, если вершины i и j соединены ребром в H , и равняется 0 в противном случае.
СЛЕДУЮЩИЕ n СТРОК : Каждая строка содержит n целых чисел, разделенных пробелами, и представляет одну вершину из G в порядке 1, ..., n . i -ый элемент j -ой строки в этой секции равняется 1, если вершины i и j соединены ребром в G , и равняется 0 в противном случае.
|
Заметьте, что за исключением строки 1, приведенные входные данные представляют собой матрицы смежности графов H и G .
ВЫВОД
Вы должны создать 10 выводов по одному на каждый входной. Каждый тест должен содержать следующие данные:
|
Пример вывода
|
ОПИСАНИЕ
|
|
#FILE forbidden K
5
0 1 0 0 0
1 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
|
СТРОКА 1: Заголовок файла. Заголовок файла должен содержать
#FILE forbidden K
где K – это число между 1 и 10, которое соответствует решенному входному файлу.
СТРОКА 2: Содержит одно целое число : n .
СЛЕДУЮЩИЕ n СТРОК : Каждая строка содержит n целых чисел, разделенных пробелом, и представляет одну вершину из G’ в порядке 1, ..., n . i -ый элемент j -ой строки в этой секции равняется 1, если вершины i и j соединены ребром в G’ , и равняется 0 в противном случае.
|
Заметьте, что за исключением строк 1 и 2, приведенные входные данные представляют собой матрицу смежности графа G’. Обратите внимание, что есть много вариантов ответа, и приведенный вариант является корректным, но не оптимальным.
| |
![]()
|
|
Клетка для хомячка
Двумерные массивы
Обход в глубину
Простые задачи на перебор
Андрюше на день рождения подарили хомячка. Пока Андрюша не купил для него клетку, он решил сделать ему клетку из подручных средств. Для изготовления клетки он решил использовать набор кубиков, подаренный ему на прошлый день рождения. Однако, неожиданно выяснилось, что сестра Андрюши склеила кубики суперклеем, и отделить их друг от друга не представляется возможным.
Все кубики оказались склеены в две фигуры. Любые два кубика в каждой из фигур либо не имеют общих точек, либо имеют общую грань, либо имеют общее ребро, но в последнем случае есть кубик, с которым каждый из них имеет общую грань. Каждую фигуру можно положить на стол так, что каждый кубик будет касаться стола одной из своих граней.
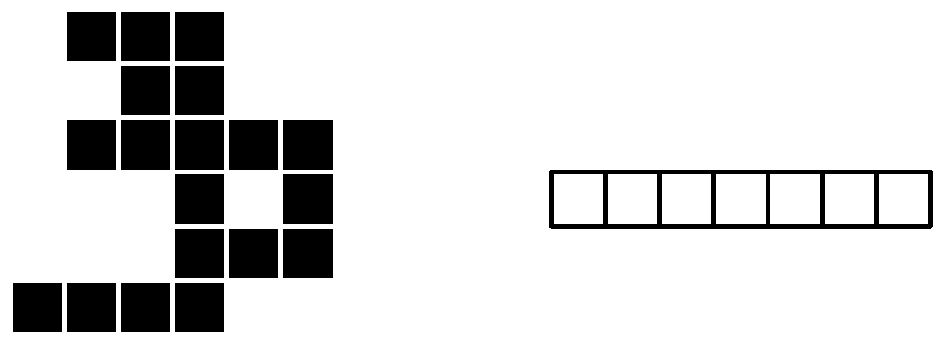
Теперь Андрюша хочет положить эти две фигуры на стол так, чтобы получилась клетка для хомячка. Фигуры должны быть положены таким образом, чтобы каждый кубик касался стола гранью. Стороны нижних граней кубиков должны быть параллельны сторонам стола. Любые два кубика, принадлежащие различным фигурам, должны либо не касаться друг друга, либо иметь общую грань, либо иметь общее ребро. Фигуры разрешается поворачивать и переворачивать.
Положив фигуры, Андрюша собирается выпустить хомячка на стол. Чтобы он не упал со стола, у него не должно быть возможности добраться от точки, в которую Андрюша его выпустит, до края стола. Хомячок не может перелезать через кубики, и, в частности, не может пролезть между двумя кубиками, имеющими общее ребро. Стол существенно больше каждой из фигур.
Андрюша хочет, чтобы площадь, по которой может бегать хомячок, была как можно больше. Помогите ему выяснить, какая максимальная площадь может быть у территории, до которой сможет добраться хомячок. Площадь грани кубика будем считать равной единице.
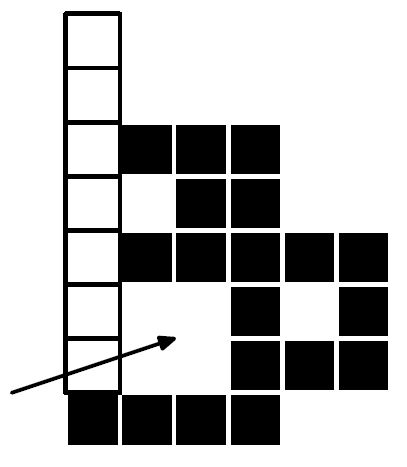
Например, две фигуры, показанные на рисунке выше, можно расположить как показано на следующем рисунке. Если выпустить хомячка в точку, отмеченную стрелкой, то доступная ему территория будет иметь площадь, равную четырем.
Входные данные
В первой строке вводятся два числа: h1 и w1 (1 <= h1, w1 <= 10). Следующие h1
строк содержат по w1 символов и описывают первую фигуру, вид сверху. Каждый из этих символов - либо "*" (звездочка), либо "." (точка), звездочка обозначает кубик, а точка – пустое место.
Далее в отдельной строке вводятся два числа: h2 и w2 (1 <= h2, w2 <= 10). Следующие h2 строк содержат по w2 символов и описывают вторую фигуру в формате, аналогичном формату первой. Каждая из фигур связна и содержит хотя бы один кубик.
Выходные данные
Выведите одно число – максимальную площадь, которая может быть доступна хомячку. Если сделать клетку для хомячка невозможно, выведите 0.
| |
![]()
|
|
Развлечения с измерителем
Способы задания графа
Обход в глубину
Дима обнаружил у папы на столе специальный чертежный прибор, похожий на циркуль - измеритель. Измеритель отличается от обычного циркуля тем, что в обеих его ножках находятся иголки (у обычного циркуля в одной ножке находится иголка, а в другой - грифель).
Дима взял клетчатый лист бумаги, установил между иглами измерителя некоторое расстояние, прочно зафиксировав его, и начал втыкать измеритель в лист бумаги. Каждый раз Дима втыкал в лист обе иглы измерителя, при этом он всегда делал это так, что дырочки получались в точках пересечениях линий, которыми лист разлинован на клетки. При этом в одну и ту же дырку Дима мог вставлять измеритель несколько раз.
Вечером папа нашел лист, с которым развлекался Дима, и решил выяснить, какое расстояние между иглами измерителя Дима мог установить. Все, что знает папа - координаты дырок, проделанных иглами измерителя. Помогите Папе решить поставленную задачу.
Входные данные
В первой строке вводится число n
- количество дырок (2 <= n <= 1000). Следующие n строк содержат по два целых числа - координаты дырок. Координаты не превышают 104
по абсолютной величине.
Выходные данные
В первой строке выведите k
- количество различных расстояний, которые Дима мог установить между иглами измерителя. Следующие k строк должны содержать искомые расстояния, по одному вещественному числу в строке. Расстояния должны быть выведены в возрастающем порядке. Каждое число должно быть выведено с точностью не менее, чем 10-9.
Гарантируется, что существует по крайней мере одно расстояние, которое Дима мог установить между иглами измерителя.
| |
![]()
|
|
Похожие матрицы
Остатки
Обход в глубину
Рассмотрим таблицу, состоящую из N строк и M столбцов. Если в каждой ячейке такой таблицы стоит целое число, назовем такую таблицу целочисленной матрицей. Скажем, что эта матрица кратна чиcлу p, если все числа в ее ячейках кратны p.
Рассмотрим теперь суммы элементов матрицы по строкам и столбцам соответственно. Обозначим сумму чисел i-й строки за Hi, а сумму чисел j-го столбца за Vj. Упорядоченный набор чисел (H1, H2, …, HN, V1, V2, …, VM) назовем профилем матрицы. Скажем, что матрица почти кратна p, если все числа, входящие в ее профиль, кратны p. Почти кратная 5 матрица и ее профиль изображены на рисунке 1.
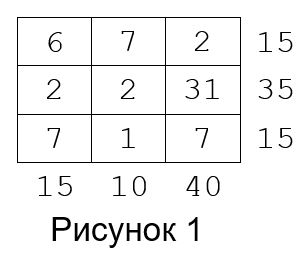
Если две матрицы A и B имеют одинаковый размер, причем элемент, стоящий на пересечении i-й строки и j
-го столбца в матрице A отличается от соответствующего элемента матрицы B не более чем на p, скажем, что A отличается от B не более чем на p. Скажем, что матрица B похожа на матрицу A относительно числа p, если
1. отличается от не более чем на p
2. профили B и A совпадают.
На рисунке 2 изображены две похожие относительно числа 5 матрицы, первая из них почти кратна 5, а вторая кратна 5. Третья матрица на рисунке 2 тоже кратна 5, но непохожа на первую (хотя похожа на вторую).
Дано число p и почти кратная p матрица A. Ваша задача - найти такую матрицу B, чтобы она была кратна p и похожа на A относительно p.
Входные данные
В первой строке входных данных задаются целые числа p (1 <= p <= 10), N и M (1 <= N, M <= 30). Следующие N строк содержат по M целых неотрицательных чисел, не превышающих 1000, которые являются элементами исходной матрицы A.
Выходные данные
Выведите матрицу B по строкам - сначала M элементов первой строки, затем M элементов второй, и т. д. Разделяйте числа пробелами и/или переводами строк. Заботиться о красивом форматировании таблицы не надо. Если искомой матрицы не существует, выведите единственное число - "-1". Если решений несколько, выведите любое из них.
| |
![]()
|
|
Свинки-копилки
Способы задания графа
Обход в глубину
У Васи есть N свинок-копилок, свинки занумерованы числами от 1 до N. Каждая копилка может быть открыта единственным соответствующим ей ключом или разбита.
Вася положил ключи в некоторые из копилок (он помнит, какой ключ лежит в какой из копилок). Теперь Вася собрался купить машину, а для этого ему нужно достать деньги из всех копилок. При этом он хочет разбить как можно меньшее количество копилок (ведь ему еще нужно копить деньги на квартиру, дачу, вертолет…). Помогите Васе определить, какое минимальное количество копилок нужно разбить.
Входные данные
В первой строке содержится число N — количество свинок-копилок (1≤N≤100000). Далее идет N строк с описанием того, где лежит ключ от какой копилки: в i-ой из этих строк записан номер копилки, в которой находится ключ от i-ой копилки.
Выходные данные
Выведите единственное число: минимальное количество копилок, которые необходимо разбить.
Примечание
Ключи от первой и третьей копилки лежат в копилке 2, ключ от второй — в первой, а от четвертой — в ней самой.
Чтобы открыть все копилки, достаточно разбить, например, копилки с номерами 1 и 4.
| |
![]()
|
|
Трехцветные таблицы
Способы задания графа
Обход в ширину
Обход в глубину
Прямоугольную таблицу, состоящую из N строк и M столбцов, раскрашивают следующим образом. Каждый столбец таблицы и каждую строку красят либо в синий, либо в желтый цвет. В итоге клетки, оказавшиеся на пересечении синего столбца и синей строки оказываются синими, желтого столбца и желтой строки — желтыми, а клетки на пересечении синего столбца и желтой строки, или, наоборот, желтого столбца и синей строки — зелеными.
Раскраска всех клеток таблицы (или просто сама таблица) называется правильной, если она может быть получена описанным выше способом.
Вам дана прямоугольная таблица, которую нужно раскрасить таким образом. Про некоторые клетки известно, какого цвета они должны быть, а остальные клетки могут в итоге быть любого цвета. Определите, сколько существует различных правильных таблиц, в которых нужные клетки покрашены в нужный цвет.
Входные данные
Вводятся числа N и M — количество строк и столбцов таблицы (1≤N≤30, 1≤M≤30). Далее записано N строк по M чисел в каждой, задающие цвета, в которые должны быть окрашены клетки:
0 — клетка может в итоге быть любого цвета
1 — клетка должна быть синей
2 — клетка должна быть желтой
3 — клетка должна быть зеленой
Выходные данные
Выведите одно число — количество различных правильных таблиц, в которых нужные клетки покрашены в нужный цвет. Обратите внимание, что если два или более способов раскраски столбцов и строк таблицы приводят к одинаковой раскраске самой таблицы, то это нужно считать как один вариант раскраски таблицы (см. пример 2).
| |
![]()
|
|
Свинки-копилки
Способы задания графа
Обход в глубину
У Васи есть N свинок-копилок, свинки занумерованы числами от 1 до N. Каждая копилка может быть открыта единственным соответствующим ей ключом или разбита.
Вася положил ключи в некоторые из копилок (он помнит, какой ключ лежит в какой из копилок). Теперь Вася собрался купить машину, а для этого ему нужно достать деньги из всех копилок. При этом он хочет разбить как можно меньшее количество копилок (ведь ему еще нужно копить деньги на квартиру, дачу, вертолет…). Помогите Васе определить, какое минимальное количество копилок нужно разбить.
Входные данные
В первой строке содержится число N — количество свинок-копилок (1≤N≤100000). Далее идет N строк с описанием того, где лежит ключ от какой копилки: в i-ой из этих строк записан номер копилки, в которой находится ключ от i-ой копилки.
Выходные данные
Выведите единственное число: минимальное количество копилок, которые необходимо разбить.
Примечание
Ключи от первой и третьей копилки лежат в копилке 2, ключ от второй — в первой, а от четвертой — в ней самой.
Чтобы открыть все копилки, достаточно разбить, например, копилки с номерами 1 и 4.
| |
![]()
|
|
Путь к файлу
Обход в глубину
В операционной системе Xunil информация обо всех файлах и директориях хранится в специальном файле в следующем формате:
emoh
vonavi
a.doc
b.doc
vortep
.bashrc
vorodis
onrop
1.avi
2.avi
rav
bil
Имена файлов, и только они, содержат точку.
Требуется по данному имени файла найти путь к нему. Если таких файлов несколько, вывести путь к файлу, который записан выше.
Входные данные
В первой строке вводится имя искомого файла. Во второй строке вводится общее количество файлов и директорий. В остальных строках вводится информация о файлах и директориях в указанном выше формате (директория или файл, находящиеся внутри другой директории, отделяются одним дополнительным пробелом в начале строки). Количество строк в файле и количество символов в каждой строке не превосходит 100.
Выходные данные
Выведите путь к файлу в формате /директория/директория/…/файл
Гарантируется, что такой файл есть.
Гарантируется, что длина строки ответа не превосходит 255.
| |
![]()
|
|
Сад пчел
Обход в глубину
Элементарная геометрия
В саду Бена расположено n ульев. Некоторые из них соединены друг с другом или с домом Бена прямыми дорожками. Бен гуляет только по дорожкам, переходя с одной на другую только возле очередного улья. Ни дом Бена, ни какой-либо улей не расположены на дорожке, соединяющей другие два улья. Дорожки организованы таким образом, что Бен может дойти от дома до любого улья только единственным способом.
Каждую неделю Бен делает обход ульев. Он начинает от своего дома и идет по дорожкам, посещая каждый улей по крайней мере один раз, минимизируя при этом общий путь. Сын Бена решил помочь своему стареющему отцу и проложить еще одну прямую дорожку между двумя ульями, так чтобы путь Бена от дома через все ульи с возвращением к дому стал как можно короче. Она, как и старые дорожки, проходить мимо дома или другого улья не должна.
Входные данные
На вход сначала подается число n — количество ульев (1≤n≤200).
Введем координаты так, что дом Бена будет располагаться в точке (0, 0). В следующих n строках входных данных записаны координаты ульев в саду Бена. Они не превосходят 10000 по абсолютному значению. Никакие два улья не совпадают, и нет ульев, расположенных в точке (0, 0). Будем считать, что они пронумерованы от 1 до n.
Следующие n строк описывают дорожки — каждая дорожка описывается номерами объектов, которые она соединяет. Дом Бена имеет номер 0.
Выходные данные
Выведите два числа — номера объектов, которые надо соединить дополнительной дорожкой. Если требуемой прямой дорожки, сокращающей общий путь Бена не существует, то выведите –1.
| |
![]()
|
|
Водостоки
Обход в ширину
Обход в глубину
Карту местности условно разбили на квадраты, и посчитали среднюю высоту над уровнем моря для каждого квадрата.
Когда идет дождь, вода равномерно выпадает на все квадраты. Если один из четырех соседних с данным квадратом квадратов имеет меньшую высоту над уровнем моря, то вода с текущего квадрата стекает туда (и, если есть возможность, то дальше), если же все соседние квадраты имеют большую высоту, то вода скапливается в этом квадрате.
Разрешается в некоторых квадратах построить водостоки. Когда на каком-то квадрате строят водосток, то вся вода, которая раньше скапливалась в этом квадрате, будет утекать в водосток.
Если есть группа квадратов, имеющих одинаковую высоту и образующих связную область, то если хотя бы рядом с одним из этих квадратов есть квадрат, имеющий меньшую высоту, то вся вода утекает туда, если же такого квадрата нет, то вода стоит во всех этих квадратах. При этом достаточно построить водосток в любом из этих квадратов, и вся вода с них будет утекать в этот водосток.
Требуется определить, какое минимальное количество водостоков нужно построить, чтобы после дождя вся вода утекала в водостоки.
Входные данные
Во входном файле записаны сначала числа N и M, задающие размеры карты — натуральные числа, не превышающие 100. Далее идет N строк, по M чисел в каждой, задающих высоту квадратов карты над уровнем моря. Высота задается натуральным числом, не превышающим 10000. Считается, что квадраты, расположенные за пределами карты, имеют высоту 10001 (то есть вода никогда не утекает за пределы карты).
Выходные данные
В выходной файл выведите минимальное количество водостоков, которое необходимо построить.
| |
![]()
|
|
Есть ли цикл? - Флойдом
Обход в глубину
Алгоритм Флойда
Дан ориентированный граф. Используя алгоритм Флойда определите, есть ли в заданном графе цикл.
Формат входных данных
В первой строке вводится число вершин N≤ 50. Далее в N строках следуют по N чисел, каждое из которых – 0 или 1. j-ое число в i-ой строке равно 1 тогда и только тогда, когда существует ребро, идущее из i-ой вершины в j-ую. Гарантируется, что на диагонали матрицы будут стоять нули.
Формат выходных данных
Выведите 0, если в заданном графе цикла нет, и 1, если он есть.
| |
![]()
|
|
Кластеры роботов
Обход в глубину
Жадный алгоритм
Конструктив
Деревья
На производстве расположены \(n\) роботов, пронумерованных от \(1\) до \(n\). Любая пара роботов может быть либо соединена проводом, либо нет. Всего на производстве \(m\) проводов и \(i\)-й из них сейчас соединяет роботов с номерами \(a_i\) и \(b_i\).
Вы находитесь рядом с роботом номер \(1\). Роботом номер \(t\) можно управлять, если он связан с первым некоторой цепочкой проводов, то есть
-
либо если \(t = 1\);
-
либо если существуют такие \(i_1, \ldots, i_k\), что \(i_1 = 1\), \(i_k = t\), и любые два соседних в этой последовательности робота \(i_j\) и \(i_{j + 1}\) связаны проводом.
Любому из роботов, которыми можно управлять, можно послать команду <<извлеки второй конец подключенного к себе провода и подключи его к другому роботу>>. Иными словами, если роботом номер \(t\) можно управлять, и есть провод, соединяющий его с роботом номер \(x\), то можно заменить провод \((t, x)\) на провод \((t, y)\) для любого \(y \neq t\), еще не связанного проводом с \(t\). Обратите внимание, что после этого вы можете потерять управление над \(t\)-м роботом, если единственная связь \(t\)-го с первым проходила через \(x\)-й.
Ваша задача — получить управление над максимально возможным количеством роботов на производстве. Найдите это количество и самую короткую последовательность действий, приводящую к такому исходу.
Формат входных данных
В первой строке записано целое число \(T\) (\(1 \le T \le 1000\)) — количество наборов входных данных в тесте.
Первая строка каждого набора входных данных содержит целые числа \(n\) и \(m\) (\(1 \leq n \leq 10^5\); \(0 \leq m \leq 1.5 \cdot 10^5\)) — количество роботов и количество проводов, соответственно.
В следующих \(m\) строках дано описание проводов: в \(i\)-й строке даны целые числа \(a_i\) и \(b_i\) (\(1 \leq a_i, b_i \leq n\); \(a_i \neq b_i\)) — номера роботов, соединенных \(i\)-м проводом. Гарантируется, что никакие два провода не соединяют одну и ту же пару роботов.
Также гарантируется, что сумма \(n\) по всем наборам входных данных не превосходит \(10^5\) и сумма \(m\) по всем наборам входных данных не превосходит \(1.5 \cdot 10^5\).
Формат выходных данных
Для каждого набора входных данных выведите в первой строке через пробел максимальное количество роботов, управление над которыми можно получить, и количество действий \(k\), которое для этого понадобится.
В следующих \(k\) строках выведите сами описания действий по одному на каждой строке. Описание действия должно состоять из трех целых чисел \(t\), \(x\) и \(y\) (\(1 \leq t, x, y \leq n\); \(x \neq y\)), означающих, что робот номер \(t\) меняет провод \((t, x)\) на провод \((t, y)\).
Если возможных ответов несколько, выведите любой. Обратите внимание, что \(k\) при этом обязано быть наименьшим, при котором можно подключить максимальное количество роботов.
| |
![]()
|
|
Кластеры роботов - 2
Деревья
Жадный алгоритм
Конструктив
Обход в глубину
На производстве расположены \(n\) роботов, пронумерованных от \(1\) до \(n\). Любая пара роботов может быть либо соединена проводом, либо нет. Известно, что \(i\)-й робот соединен с \(k_i\) другими роботами с номерами \(v_{i,1}, \ldots, v_{i,k_i}\). Провода двухсторонние, то есть если \(i\) связан с \(j\), то \(j\) связан с \(i\) (иными словами, \((i, j)\) и \((j, i)\) — это один и тот же провод).
Вы находитесь рядом с роботом номер \(n\). Роботом номер \(t\) можно управлять, если он связан с \(n\)-м некоторой цепочкой проводов, то есть
-
либо если \(t = n\);
-
либо если существуют такие \(i_1, \ldots, i_k\), что \(i_1 = n\), \(i_k = t\), и любые два соседних в этой последовательности робота \(i_j\) и \(i_{j + 1}\) связаны проводом.
Любому из роботов, которыми можно управлять, можно послать команду <<извлеки второй конец подключенного к себе провода и подключи его к другому роботу>>. Иными словами, если роботом номер \(t\) можно управлять, и есть провод, соединяющий его с роботом номер \(x\), то можно заменить провод \((t, x)\) на провод \((t, y)\) для любого \(y \neq t\), еще не связанного проводом с \(t\). Обратите внимание, что после этого вы можете потерять управление над \(t\)-м роботом, если единственная связь \(t\)-го с \(n\)-м проходила через \(x\)-й.
Ваша задача — получить управление над максимально возможным количеством роботов на производстве. Найдите это количество и самую короткую последовательность действий, приводящую к такому исходу.
Формат входных данных
В первой строке записано целое число \(T\) (\(1 \le T \le 1000\)) — количество наборов входных данных в тесте.
Первая строка каждого набора входных данных содержит одно целое число \(n\) (\(1 \leq n \leq 10^5\)) — количество роботов.
Затем следуют \(n\) строк, в \(i\)-й из которых записаны числа \(k_i\) (\(0 \le k_i \le n - 1\)) и \(v_{i,1}, \ldots, v_{i,k_i}\) (\(1 \le v_{i,j} \le n\); \(v_{i,j} \neq i\)) — количество проводов, подключенных к \(i\)-му роботу, и номера роботов на противоположных концах этих проводов. Гарантируется, что данные корректны: никакие два провода не соединяют одну и ту же пару роботов, и если \(j \in v_i\), то \(i \in v_j\).
Также гарантируется, что сумма \(n\) по всем наборам входных данных не превосходит \(10^5\) и сумма количества проводов по всем наборам входных данных не превосходит \(1.5 \cdot 10^5\).
Формат выходных данных
Для каждого набора входных данных выведите в первой строке через пробел максимальное количество роботов, управление над которыми можно получить, и количество действий \(k\), которое для этого понадобится.
В следующих \(k\) строках выведите сами описания действий в формате <<\(y\) + \(t\) - \(x\)>> (\(1 \leq t, x, y \leq n\); \(x \neq y\)). Каждая такая строка соответствует замене провода \((t, x)\) на провод \((t, y)\).
Если возможных ответов несколько, выведите любой. Обратите внимание, что \(k\) при этом обязано быть наименьшим, при котором можно подключить максимальное количество роботов.
| |
![]()
|
|
66151
Дата и время
Обход в глубину
Коля очень мечтал поступить в лучший ВУЗ – МГТУ им. Н.Э. Баумана и у него это получилось. Однако, ему не хватило 1 балла для того, чтобы ему предоставили общежитие, потому ему придётся добираться до института на электричках, благо институт находится не только у метро, но и у станции электричек, от которой идти всего 20 минут пешком.
Коля очень пунктуальный мальчик, потому, он каждый раз вечером садится и выписывает расписание электричек на следующий день, чтобы понять, как ему лучше всего добраться до института, чтобы успеть к нужной паре. Но есть проблема, Коле приходится добираться на нескольких электричках, так как он живёт уж очень далеко.
Коля хоть и пунктуальный мальчик, но он, как и все, очень любит поспать, поэтому он решил рассчитать во сколько он доберётся до института в самом оптимистичном случае.
Стоит учесть тот момент, что иногда электрички сбиваются с расписания и могут прийти раньше до 10 минут (включительно), но время в пути у них неизменно.
Помогите Коле рассчитать, во сколько ему нужно встать, по самому оптимистическому сценарию, чтобы приехать к паре вовремя, если известно время начала пары и расписание электричек на каждой станции, с которой он будет отправляться.
Входные данные
На первой строке задаётся время начала пары, к которой Коля должен успеть в формате (hh:mm).
На второй строке задаётся количество станций, с которых будет отправляться Коля (1 <= N <= 10).
На третьей строке задаётся N целых чисел через пробел (1 <= M_1, M_2, …, M_n <= 20) – количество отправлений поездов для каждой станции.
Далее следует N блоков данных по M строк в каждой из которых задано время отправления электрички со станции по расписанию и время в пути до нужной Коле станции (через точку с запятой) (например, 12:10;30, что означает, что электричка отправляется в 12:10, в пути она 30 минут.
Выходные данные
Вывести на одной строке время в формате hh:mm (например, 08:10 или 12:13), в которое Коля должен быть уже на первой станции электричек, чтобы отправиться в институт, притом в самом оптимистичном варианте.
Примечание:
•на вход подаются расписания электричек со станций в порядке,в котором Коля должен на них прибывать;
•гарантируется, что Коля 100% может успеть на пару вовремя.
| |
![]()
|