| | | |
|
Сборка компьютера
Динамическое программирование
Для сборки компьютера необходимо T компонентов различного типа (видеокарта, жесткий диск, монитор и т.д.). В магазине продаются N компонентов. Каждый компонент относится к определенному типу и имеет некоторую стоимость и рейтинг по обзорам в журналах.
Напишите программу, определяющую из каких компонентов нужно собрать компьютер, чтобы его стоимость не превышала B, в составе были по одному компоненту каждого типа, а суммарный рейтинг использованных компонентов был максимальным.
Первая строка ввода содержит одно целое число – количество типов компонентов T (1 ≤ T ≤ 5). Вторая строка ввода содержит одно целое число – количество компонентов в магазине N (1 ≤ N ≤ 1000). Далее следует N строк, содержащих по три целых числа, разделенных пробелами – стоимость i-го компонента Ci (1 ≤ Ci ≤ 3000), его рейтинг Ri (1 ≤ Ri ≤ 3000) и его тип ti (1 ≤ ti ≤ T). Далее следует строка, содержащая одно целое число – бюджет на покупку компьютера B (1 ≤ B ≤ 3000).
Вывести в первой строке одно целое число – максимальный суммарный рейтинг использованных компонент. Во второй строке вывести T целых чисел – i-е число означает номер компонента типа i, выбранного для сборки. Если существует несколько вариантов с максимальным суммарным рейтингом, то из них вывести вариант с минимальной стоимостью, а среди таких вариантов можно вывести любой. Если не существует варианта сборки компьютера в рамках указанного бюджета, то вывести в первой строке одно число –1
|
Ввод |
Вывод |
|
2
5
10 6 1
5 7 1
6 10 2
1 5 1
11 11 2
16
|
18
2 5 |
| |
![]()
|
|
Шаблон с ? и *
Динамическое программирование
Шаблоном называется строка, состоящая из английских букв (a, ..., z, A, ..., Z) и символов ? и *. Каждый из символов ? разрешается заменить на одну произвольную букву, а каждый из символов * – на произвольную (возможно пустую) последовательность букв. Про любую строку из букв, которую можно получить из шаблона такими заменами, будем говорить, что она удовлетворяет этому шаблону.
Имеются два шаблона. Требуется найти строку минимальной длины, которая удовлетворяет обоим шаблонам, либо выдать сообщение, что такой строки не существует.
Входные данные
Заданные шаблоны записаны в первых двух строках входных данных. Длина каждого шаблона не превосходит 80 символов.
Выходные данные
Выведите строку минимальной длины, удовлетворяющую обоим шаблонам, либо сообщение " No solution!"
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
AB?
*BC
|
ABC |
| |
![]()
|
|
Садовник-художник
Динамическое программирование
Садовник посадил N деревьев в один ряд. После посадки деревьев садовнику нужно их покрасить. В его распоряжении есть краска трех цветов: белая, синяя и оранжевая. Сколько способов покраски деревьев есть у него, если никакие два соседних дерева нельзя красить в одинаковый цвет?
Входные данные
В единственной строке записано одно натуральное число - количество деревьев N (1 ≤ N ≤ 50).
Выходные данные
В единственную строку нужно вывести одно число - количество способов покраски.
| |
![]()
|
|
Ход конем_1
Динамическое программирование
Динамическое программирование: два параметра
Дана прямоугольная доска N × M (N строк и M столбцов). В левом верхнем углу находится шахматный конь, которого необходимо переместить в правый нижний угол доски. При этом конь может ходить ТОЛЬКО на две клетки вниз и на одну клетку вправо, либо на две клетки вправо и на одну клетку вниз (смотри рисунок).
Необходимо определить, сколько существует различных маршрутов, ведущих из левого верхнего в правый нижний угол.
Входные данные
Во входной строке находятся два натуральных числа N и M (\(1 <= N,\ M <= 50\)).
Выходные данные
Выведите единственное число количество способов добраться конём до правого нижнего угла доски.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 4 |
2 |
| |
![]()
|
|
Ход конем - 2
Динамическое программирование
Динамическое программирование: два параметра
Дана прямоугольная доска N × M (N строк и M столбцов). В левом верхнем углу находится шахматный конь, которого необходимо переместить в правый нижний угол доски. При этом конь может ходить только так, как показано на рисунке:
Необходимо определить, сколько существует различных маршрутов, ведущих из левого верхнего в правый нижний угол.
Входные данные
Во входной строке находятся два натуральных числа N и M (\(1 <= N,\ M <= 15\)).
Выходные данные
Выведите единственное число количество способов добраться конём до правого нижнего угла доски.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 4 |
2 |
| 2 |
7 15 |
13309 |
| |
![]()
|
|
Уравнение с пропущенными цифрами
Динамическое программирование
Динамическое программирование по подстрокам
Задано уравнение вида A+B=C, где A, B и C - неотрицательные целые числа, в десятичной записи которых некоторые цифры заменены знаками вопроса (?). Примером такого уравнения является ?2+34=4?. Требуется так подставить вместо знаков вопроса цифры, чтобы это равенство стало верным, либо определить, что это невозможно. Найти только одно из возможных решений.
Входные данные
Вводится строка, представляющая собой заданное уравнение без пробелов. Длина уравнения не превышает 80 символов.
Выходные данные
Требуется вывести верное равенство, полученное из исходного уравнения заменой знаков вопроса цифрами, либо сообщение "No solution".
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
??2?4+9?=355 |
00264+91=355 |
| |
![]()
|
|
Муравьиная ферма
Динамическое программирование
Динамическое программирование на таблицах
У мальчика Пети есть муравьиная ферма. На ферме есть участок прямоугольной формы, состоящий из NxM квадратов. В правом нижнем квадрате данной области имеется дырка, благодаря которой можно сбежать с фермы. Каждый день очередной муравьишка начинает свой путь с левой верхней клетки. Далее он перемещается в соседнюю клетку либо вправо, либо вниз (влево и вверх перемещаться он не может), и двигается так до достижения правой нижней клетки. Затем он выбирается наружу. Каждый муравьишка двигается своим уникальным путем (т.е. никакой муравей не повторяет ни один путь другого). Если муравей не может пойти по своему уникальному пути, то он остается на ферме. Посчитайте, сколько муравьев сбежит с фермы и поселится в комнате Пети.
Входные данные
Вводятся два числа N и M - размеры таблицы ( \(1<=N<=10\), \(1<=M<=10\)).
Выходные данные
Выведите искомое количество способов.
Примечание
При указанных ограничениях число способов входит в тип Longint.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 10 |
1 |
| |
![]()
|
|
Дамка
Динамическое программирование
Динамическое программирование на таблицах
Домовой Кузьма очень любит играть в шашки на доске 8х8. Когда никто не хочет с ним играть, он просто сидит и думает. Например, сейчас он пытается посчитать сколько есть вариантов провести белую шашку в дамки, если она находится одна на доске?
(Белая шашка ходит по диагонали на одну клетку вверх-вправо или вверх-влево. Шашка проходит в дамки, если попадает на верхнюю горизонталь.)
Входные данные
Вводятся два числа от 1 до 8: номер номер столбца (считая слева) и строки (считая снизу), где изначально стоит шашка.
Выходные данные
Выведите одно число - количество вариантов.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 7 |
2 |
| 2 |
1 8 |
1 |
| 3 |
3 6 |
4 |
| |
![]()
|
|
Максимальная сумма смежных элементов
Динамическое программирование
ЕГЭ - вычислительные задачи
На вход программы подается натуральное число N, а затем N целых чисел. Необходимо определить максимальную сумму смежных элементов последовательности. N не превышает 1000000, каждый элемент последовательности не превосходит по модулю 100.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
9
-2
1
-3
4
-1
2
1
-5
4
|
6 |
Пояснения: для заданной последовательности чисел (-2 1 -3 4 -1 2 1 -5 4) наибольшую сумму можно получить для смежной последовательности элементов: 4 -1 2 1.
Решение на 2 балла начисляются при прохождении программой 50% тестов, 3 балла - при прохождении программой 75% тестов.
| |
![]()
|
|
Лесопилка
Остатки
Динамическое программирование
Недавно на лесопилку, где работает Вася, поступил новый заказ. Для постройки нового дома мэру соседнего города требуется a досок длины x футов и b досок длины y футов.
Поскольку на лесопилке имеется только неограниченный запас досок длины z футов, Васе поручили исполнить заказ клиента, распилив имеющиеся доски на меньшие. Вася хочет закончить работу как можно быстрее, поэтому он хочет выполнить заказ, сделав как можно меньше распилов. При этом количество использованных досок длины z роли не играет, кроме того, часть досок, образовавшихся в результате распила, может не требоваться для заказа и остаться на лесопилке.
Например, если на лесопилке имеются доски длины 80, а клиенту требуется две доски длины 30 и семь досок длины 20, то достаточно сделать семь распилов: одну доску распилить двумя распилами на доски длины 20, 30 и 30, одну тремя распилами на четыре доски длины 20 и одну двумя распилами на доски длины 20, 20 и 40. Доска длины 40 клиенту не нужна, она останется на лесопилке, остальные доски будут отправлены клиенту.
Входные данные
На вход программы поступают числа a, x, b, y и z. Все числа положительны и не превышают 300, x<=z, y<=z, x!=y.
Выходные данные
Выведите минимальное количество распилов, которые требуется сделать для того, чтобы выполнить заказ.
| Ввод |
Вывод |
| 2 30 7 20 80 |
7 |
| |
![]()
|
|
Подсчёт коров
Динамическое программирование
Коровы Фермера Джона разбрелись по огромному пастбищу, представленному в виде 2D-решётки (шахматной доски). Размещение коров весьма занимательно. Для каждой ячейки (x,y) с \(x>=0\) и \(y>=0\), существует корова в ячейке (x,y), если для всех целых чисел \(k>=0\), остатки \(\lfloor {\frac {x}{3^k} }\rfloor\) и \(\lfloor {\frac {y}{3^k} }\rfloor\) по модулю 3 имеют одну и ту же четность. Другими словами оба эти остатка нечётные (равны 1) или оба чётные (равны 0 или 2). Например, ячейки для \(0<=x,y<9\), которые содержат коров обозначены цифрой 1 на рисунке ниже.
x
012345678
0 101000101
1 010000010
2 101000101
3 000101000
y 4 000010000
5 000101000
6 101000101
7 010000010
8 101000101
Ферме Джон интересуется сколько коров присутствует в определённом квадратном регионе его пастбища. Он задаёт Q вопросов, кажый содержит три целых числа xi,yi,di. Для каждого вопроса Фермер Джон хочет знать, сколько коров в ячейках с (xi, yi) до (xi+di, yi+di) (включая конечные точки).
Входные данные
Первая строка содержит Q (\(1<=Q<=10^4\)) - количество вопросов.
Каждая из следующих Q строк содержит 3 целых числа di, xi, и yi (\(0<=x_i,y_i,d_i<=10^{18}\)).
Выходные данные
Q строк, по одной для каждого вопроса - одно целое число - ответ.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
8
10 0 0
10 0 1
9 0 2
8 0 2
0 1 7
1 1 7
2 1 7
1000000000000000000 1000000000000000000 1000000000000000000 |
11
0
4
3
1
2
2
1000000000000000001 |
| |
![]()
|
|
Современное искусство - 3
Динамическое программирование
Наскучившись стандартными двумерными произведениями искусства (а также разочаровавшись тем, что другие копируют ее работы), великая художница Пикоусо решила перейти к более минималистичному, одномерному стилю. Ее последняя картина может быть описана одномерным массивом цветов длины N (\(1<=N<=300\)), где каждый цвет указывается целым числом в интервале \(1…N\).
К великому разочарованию Пикоусо, ее конкурент Муне, похоже, придумал, как копировать даже эти одномерные картины! Муне закрашивает один интервал одним цветом, ждет, пока он высохнет, затем красит другой интервал и так далее. Муне может использовать каждый из N цветов столько раз, сколько пожелает (возможно ни одного).
Вычислите минимальное количество движений кисти одним цветом, которое потребуется Муне, чтобы скопировать картину Пикоусо.
Входные данные
Первая строка содержит число N. Следующая строка содержит N целых чисел в интервале \(1…N\), указывающих цвет каждой ячейки в картине Пикоусо.
Выходные данные
Выведите минимальное количество движений кисти, чтобы скопировать картину.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
10
1 2 3 4 1 4 3 2 1 6 |
6 |
Пояснение
В этом примере Муне может скопироват картину так: (незакрашенные ячейки обозначены цветом 0).
Изначально весь массив не закрашен:
0 0 0 0 0 0 0 0 0 0
Муне закрашивает первые 9 ячеек цветом 1:
1 1 1 1 1 1 1 1 1 0
Муне закрашивает интервал цветом 2:
1 2 2 2 2 2 2 2 1 0
Муне закрашивает интервал цветом 3:
1 2 3 3 3 3 3 2 1 0
Муне закрашивает интервал цветом 4:
1 2 3 4 4 4 3 2 1 0
Муне закрашивает одну ячейку цветом 1:
1 2 3 4 1 4 3 2 1 0
Муне закрашивает последнюю ячейку цветом 6:
1 2 3 4 1 4 3 2 1 6
Заметим, что на первом движении кисти можно было закрасить цветом 1 и десятую ячейку. Это не изменило бы финальное состояние.
| |
![]()
|
|
Деревни
Динамическое программирование
Динамическое программирование на графах
Алгоритмы на графах
Обход в глубину
В тридесятом государстве есть N деревень. Некоторые пары деревень соединены дорогами. В целях экономии, “лишних” дорог нет, т.е. из любой деревни в любую можно добраться по дорогам единственным образом.
Новейшие исследования показали, что тридесятое государство находится в сейсмически опасной зоне. Поэтому глава государства захотел узнать, какой именно ущерб может принести его державе землетрясение. А именно, он хочет узнать, какое минимальное число дорог должно быть разрушено, чтобы образовалась изолированная от остальных группа ровно из P деревень такая, что из любой деревни из этой группы до любой другой деревни из этой группы по-прежнему можно будет добраться по неразрушенным дорогам (группа изолирована от остальных, если никакая неразрушенная дорога не соединяет деревню из этой группы с деревней не из этой группы).
Вы должны написать программу, помогающую ему в этом.
Формат входных данных
Первая строка входного файла содержит два числа: N и P (1 ≤ P ≤ N ≤ 150). Все остальные строки содержат описания дорог, по одному на строке: описание дороги состоит из двух номеров деревень (от 1 до N), которые эта дорога соединяет. Все числа во входном файле разделены пробелами и/или переводами строки.
Формат выходных данных
В выходной файл выведите единственное число — искомое количество дорог.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
3 2
1 2
3 2 |
1 |
|
| 2 |
11 6
1 2
1 3
1 4
1 5
2 6
2 7
2 8
4 9
4 10
4 11 |
2 |
группа деревень (1, 2, 3, 6, 7, 8) окажется изолированной от остальных, если разрушить дороги 1–4 и 1–5. |
| |
![]()
|
|
Скайлайн
Динамическое программирование
Вы хотите, чтобы небоскребы в вашем городе имели красивый вид. Решено построить N небоскребов в ряд. У небоскреба с номером i должно быть ровно h[i] этажей.
У Вас есть предложения от различных строительных компаний. Первая из них предлагает строить один этаж в любом из небоскребов за 3 миллиона евро. Вторая предлагает строить по одному этажу в каждом из двух соседних небоскребов за 5 миллионов евро. Заметим, что не имеет значения, находятся ли эти этажи на одинаковой высоте или нет. Третья компания предлагает строить по одному этажу в каждом из трех последовательных небоскребах за 7 миллионов евро.
Вы можете построить этажи в любом порядке. Вычислите минимальную необходимую сумму денег для строительства.
Входные данные
Первая строка содержит одно целое число N (1 ≤ N ≤ 300). Вторая строка содержит N целых чисел h[1], h[2] ..., h[N], 1 ≤ h[i] ≤ 200.
Выходные данные
В единственной строке выведите одно целое число: минимальную сумму денег для строительства, в миллионах.
| |
![]()
|
|
Подстроки подпоследовательностей
Динамическое программирование
Динамическое программирование: один параметр
Дерево отрезков, RSQ, RMQ
Дерево Фенвика
Назовем подпоследовательностью массива a непустой массив b такой, что он может быть получен из массива a удалением нескольких (возможно, никаких) элементов массива a. Например, массив [1,3] является попоследовательностью массива [1,2,3] , но [3,1] не является.
Назовем подотрезком массива a непустой массив b такой, что он может быть получен путем удаления нескольких (возможно, никаких) первых и последних элементов массива a. Например, [1,2] является подотрезком массива [1,2,3] , а [1,3] не является. Несложно заметить, что у массива длины n ровно \( {n(n+1) \over 2}\) подотрезков.
Назовем массив a длины n возрастающим , если для любого 1 ≤ i ≤ n выполняется ai ≤ ai+1.
Монотонностью массива назовем количество его возрастающих подотрезков.
Дан массив a длины n. Посчитайте сумму монотонностей по всем его подпоследовательностям. Так как ответ может быть очень большим, выведите его по модулю 109+7.
Входные данные
В первой строке задано целое число n (1 ≤ n ≤ 200000) — длина массива a.
Во второй строке заданы n целых чисел (1 ≤ ai ≤ 200000) — элементы массива a.
Выходные данные
Выведите одно целое число — сумму монотонностей всех подпоследовательностей по модулю 109+7.
Примечание
В первом тестовом примере у массива есть 7 подпоследовательностей:
- У массива [1] есть ровно один подотрезок и он является возрастающим.
- У массива [2] есть ровно один подотрезок и он является возрастающим.
- У массива [3] есть ровно один подотрезок и он является возрастающим.
- У массива [1,2] есть три подотрезка ([1], [2], [1,2] ) и все они являются возрастающими.
- У массива [1,3] есть три подотрезка ([1], [3], [1,3] ) и все они являются возрастающими.
- У массива [3,2] есть три подотрезка ([3], [2], [3, 2] ), но только два из них ([3] и [2] ) являются возрастающими.
- У массива [1,3,2] есть шесть подотрезков ([1], [3], [2], [1,3], [3,2], [1,3,2] ) и четыре из них ([1], [3], [2], [1,3] ) являются возрастающими.
Во втором тестовом примере все возрастающие подотрезки всех подпоследовательностей имеют длину 1.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
1 3 2 |
15 |
| 2 |
3
6 6 6 |
12 |
| |
![]()
|
|
Путешествие по строке
Динамическое программирование
Суффиксный массив
Дерево отрезков, RSQ, RMQ
sqrt декомпозиция
Хеш
Хеш
Скажем, что последовательность строк t1 , ..., tk является путешествием длины k , если для всех i > 1 ti является подстрокой ti - 1 строго меньшей длины. Например, { ab , b } является путешествием, а { ab , c } или { a , a } — нет.
Определим путешествие по строке s как путешествие t1 , ..., tk , все строки которого могут быть вложены в s так, чтобы существовали (возможно, пустые) строки u1 , ..., uk + 1 , такие, что s = u1t1u2 t2 ... uk tk uk + 1 . К примеру, { ab , b } является путешествием по строке для abb , но не для bab , так как соответствующие подстроки расположены справа налево.
Назовём длиной путешествия количество строк, из которых оно состоит. Определите максимально возможную длину путешествия по заданной строке s .
Входные данные
В первой строке задано целое число n ( 1 ≤ n ≤ 500 000 ) — длина строки s .
Во второй строке содержится строка s , состоящая из n строчных английских букв.
Выходные данные
Выведите одно число — наибольшую длину путешествия по строке s .
Примечание
В первом примере путешествием по строке наибольшей длины является { abcd , bc , c } .
Во втором примере подходящим вариантом будет { bb , b } .
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
7
abcdbcc |
3 |
| 2 |
4
bbcb |
2 |
| |
![]()
|
|
Бургеры в McDuck's
Динамическое программирование
Динамическое программирование: два параметра
Популярная сеть быстрого питания «McDuck's» открыла новый филиал в Берляндии. В ресторане установлено k плит. Для того чтобы приготовить бургер, надо жарить котлету в течение минуты на одной из плит, поэтому ресторан может готовить не более k бургеров в минуту.
Известно, что в «McDuck's» придут n клиентов. i-й из них придёт в момент времени ti, закажет xi бургеров и будет готов заплатить за них ci бурлей. Каждый клиент готов ждать заказ в течение w минут и, если через w минут после прихода он не получил xi бургеров, он не заплатит ничего. При этом каждый клиент готов получать только свежие бургеры, то есть только те, котлеты для которых были поджарены не раньше времени ti. Из-за таких сложных требований ресторан не всегда сможет выполнить все заказы всех клиентов.
Менеджеров ресторана заинтересовало, какую максимальную прибыль может получить «McDuck's». Помогите им ответить на этот непростой вопрос. Можно считать, что на готовку бургеров не расходуется никаких денег.
Входные данные
В первой строке содержатся три целых числа n, k и w (1 ≤ n ≤ 100000, 1 ≤ k ≤ 10, 1 ≤ w ≤ 60) — число клиентов, число плит и время ожидания клиента, соответственно.
Следующие n строк содержат описания клиентов, состоящие из трёх целых чисел — ti, xi, ci (1 ≤ ti, xi, ci ≤ 109) — время (в минутах) прихода i-го клиента, число бургеров, которые он закажет и число бурлей, которые он готов заплатить, соответственно. Клиенты перечислены в порядке возрастания времени прихода, то есть для любого i > 1 верно, что ti−1 ≤ ti.
Выходные данные
В единственной строке выведите одно число — максимальную прибыль ресторана.
Примечание
В первом тестовом примере первую котлету можно поставить жариться в момент времени 0 и тогда в момент времени 1 она будет готова и её можно будет дать в бургере первому клиенту. В момент времени 1 можно поставить жариться ещё одну котлету, она будет готова в момент времени 2 и её можно будет дать в бургере второму клиенту.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 1 1
1 1 5
1 1 7 |
12 |
| 2 |
3 2 2
1 6 8
2 5 10
3 4 4 |
12 |
| |
![]()
|
|
Числовые печеньки - 2
Динамическое программирование
Комбинаторика
У Громозеки N печенек. На i-й (1<=i<=N) печеньке написано целое число xi. Он выбирает одну или несколько из этих печенек, так чтобы среднее значение целых чисел, записанных на выбранных печеньках, было равно А.
Какими способами он может сделать свой выбор?
Входные данные
В первой строке вводятся два целых числа N (1<=N<=50) и A (1<=A<=50). Во второй строке N целых чисел - xi (1<=xi<=50).
Выходные данные
Выведите одно число - количество способов выбрать такие печеньки, чтобы среднее значение всех записанных чисел на печеньках было ровно A.
Примеры
| № |
Входные данные |
Выходные данные |
Примечение |
| 1 |
4 8
7 9 8 9 |
5 |
Ниже приведены 5 способов выбрать печеньки так, чтобы в среднем было 8.
1) Выберите 3-ю печеньку.
2) Выберите 1-ю и 2-ю печеньки.
3) Выберите 1-ю и 4-ю печеньки.
4) Выберите 1-ю, 2-ю и 3-ю печеньки.
5) Выберите 1-ю, 3-ю и 4-ю печеньки. |
| 2 |
3 8
6 6 9 |
0 |
|
| 3 |
8 5
3 6 2 8 7 6 5 9 |
19 |
|
| 4 |
33 3
3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 |
8589934591 |
Ответ может не соответствовать 32-битному целому числу. |
| |
![]()
|
|
Количество сообщений
Динамическое программирование
В сообщении, состоящем из одних русских букв и пробелов, каждую букву заменили её порядковым номером в русском алфавите (А – 1, Б – 2, …, Я – 33), а пробел – нулем.
Требуется по заданной последовательности цифр найти количество исходных сообщений, из которых она могла получиться.
Входные данные:
В первой строке содержится последовательность из не более чем 70 цифр.
Выходные данные:
Выведите одно число - количество возможных сообщений.
Пример:
| Входные данные |
Выходные данные |
| 1025 |
4 |
| |
![]()
|
|
Комфортная поездка Макс
Динамическое программирование
Макс находится на начальной станции поезда, и сейчас в него хотят зайти n человек (включая саму Макс). Они уже выстроились в некотором порядке, и для каждого из них известен код города ai, в который они направляются.
Начальник поезда выбирает некоторое количество непересекающихся отрезков исходной последовательности людей (отрезки не обязаны покрывать всю последовательность). Люди, находящиеся в одном и том же отрезке, будут находиться в одном и том же вагоне поезда. Отрезки выбираются так, что если в город X едет как минимум один человек, то все люди, которые направляются в город X должны будут находиться в одном вагоне. Это обозначает, что они не имеют права принадлежать разным отрезкам. Следует заметить, что все люди, которые едут в город X, либо едут в него и находятся в одном вагоне, либо вовсе не едут никуда.
Комфортность поездки в поезде с людьми на отрезке с l по r равна XOR-у различных кодов городов у людей на отрезке с l по r. Операция XOR также известна как исключающее побитовое ИЛИ.
Общая комфортность выбранных отрезков вычисляется как сумма комфортности каждого отдельного отрезка.
Помогите Макс узнать максимальную достижимую общую комфортность.
Входные данные:
Первая строка содержит натуральное число n - число людей (1 <= n <= 5000).
Вторая строка содержит n целых чисел ai (0 <= ai <= 5000) - код города, в который направляется i-й человек.
Выходные данные:
Выведите одно целое число - максимальную общую комфортность.
Примеры:
| Входные данные |
Выходные данные |
6
4 4 2 5 2 3 |
14 |
9
5 1 3 1 5 2 4 2 5 |
9 |
| |
![]()
|
|
Сумма минимумов
Динамическое программирование
Дерево отрезков, RSQ, RMQ
Вам дан массив из n целых чисел. Вам необходимо разделить его на k непустых подотрезков (последовательность подряд идущих элементов) так, чтобы:
1) Каждый элемент массива входил ровно в один подотрезок.
2) Если для каждого подотрезка выбрать минимальное в нем число, то сумма всех минимумов должна быть максимально возможной.
Сообщите сумму минимумов значений в подотрезках этого разбиения.
Входные данные:
В первой строке дается два натуральных числа - n (1 <= n <= 500) и k (1 <= k <= n).
Во второй строке дается n целых чисел - элементы массива ai (1 <= ai <= 105).
Выходные данные:
Выведите одно число - ответ на задачу.
Пример:
| Входные данные |
Выходные данные |
5 3
4 2 5 1 3 |
8 |
Пояснение:
Одно из подходящих разбиений: [4, 2], [5], [1, 3]. Сумма минимумов в каждом подотрезке равна 2 + 5 + 1 = 8.
| |
![]()
|
|
Сжатие строки
Динамическое программирование
Z-функция. Префикс-функция
Хлоя хочет написать письмо своей подруге. Письмо - строка s, состоящая из строчных латинских букв.
К сожалению, как только Хлоя начала писать письмо, она поняла, что оно слишком длинное, и писать его целиком придётся очень долго. Поэтому она хочет написать сжатую версию строки s вместо самой строки.
Сжатая версия строки s — последовательность строк c1, s1, c2, s2, ..., ck, sk, где ci — десятичная запись числа ai (без лидирующих нулей), а si — некоторая строка из строчных латинских букв. Если Хлоя запишет строку s1 ровно a1 раз, потом s2 ровно a2 раз, и так далее, у нее получится строка s.
Длина сжатой версии равна |c1| + |s1| + |c2| + |s2|... |ck| + |sk|. Среди всех сжатых версий Хлоя хочет выбрать такую, что её длина минимальна. Помогите Хлое определить минимально возможную длину.
Входные данные:
В единственной строке входных данных записана строка s, состоящая из строчных латинских букв (1 ≤ |s| ≤ 5000).
Выходные данные:
Выведите одно целое число — минимальную длину сжатой версии строки s.
Примеры:
| Входные данные |
Выходные данные |
| aaaaaaaaaa |
3 |
| abcab |
6 |
| cczabababab |
7 |
Пояснения:
В первом примере Хлоя выберет следующую версию: c1 — 10, s1 — a.
Во втором примере Хлоя выберет следующую версию: c1 — 1, s1 — abcab.
В третьем примере Хлоя выберет следующую версию: c1 — 2, s1 — c, c2 — 1, s2 — z, c3 — 4, s3 — ab.
| |
![]()
|
|
Ресторан
Бинарный поиск в массиве
Использование сортировки
Динамическое программирование
Ресторан получил n заказов на проведение банкета. Каждый заказ характеризуется двумя величинами: моментом начала банкета li и моментом конца ri (li ≤ ri).
Руководство ресторана может либо принять заказ, либо отвергнуть его. Какое наибольшее количество заказов может быть принято?
Никакие два принятых заказа не могут пересекаться, то есть не должно существовать момента времени, который принадлежит сразу двум принятым заказам. Если один из заказов начинается в момент, когда заканчивается другой, то они не могут быть приняты вместе.
Входные данные:
В первой строке находится целое число n (1 ≤ n ≤ 200000) — количество заказов. В каждой из следующих n строк находится пара целых чисел li, ri (0 ≤ li ≤ ri ≤ 109).
Выходные данные:
Выведите наибольшее количество заказов, которые могут быть приняты.
Примеры:
| Входные данные |
Выходные данные |
2
7 11
4 7 |
1 |
5
1 2
2 3
3 4
4 5
5 6 |
3 |
6
4 8
1 5
4 7
2 5
1 3
6 8 |
2 |
| |
![]()
|
|
Максимальные вопросы
Динамическое программирование
Префиксные суммы(минимумы, ...)
У Макс в блокноте были записаны две строки s длины n и t длины m, состоящие из букв «a» и «b» латинского алфавита. Причем Макс знает, что строка t имеет вид «abab...», то есть на нечетных позициях строки стоит буква «a», а на четных — «b».
Вдруг утром Макс обнаружила, что кто-то испортил ее строку s. Некоторые буквы s были заменены на символ «?».
Назовем последовательность позиций i, i + 1, ..., i + m - 1 вхождением строки t в s, если 1 ≤ i ≤ n - m + 1 и t1 = si, t2 = si + 1, ..., tm = si + m - 1.
Красота строки s оценивается как максимальное количество непересекающихся вхождений строки t в нее. Макс может заменить некоторые из символов «?» на «a» или «b» (символы на разных позициях можно заменять на разные буквы). Макс хочет произвести замены так, чтобы красота строки s была максимально возможной. Из всех таких вариантов она хочет заменить как можно меньше символов «?». Найдите, сколько замен она должна сделать.
Входные данные:
Первая строка содержит одно целое число n (1 ≤ n ≤ 105) — длину строки s.
Вторая строка входных данных содержит строку s длины n, состоящую только из букв «a» и «b» латинского алфавита, а также символов «?».
Третья строка содержит целое число m (1 ≤ m ≤ 105) — длину строки t. Сама строка t содержит «a» на нечетных позициях, и «b» на четных.
Выходные данные:
Выведите единственное целое число — минимальное количество замен, которое должен сделать Вася, чтобы сделать красоту строки s максимально возможной.
Примеры:
| Входные данные |
Выходные данные |
5
bb?a?
1 |
2 |
9
ab??ab???
3 |
2 |
Пояснения:
В первом примере строка t имеет вид «a». Единственный оптимальный вариант — заменить все символы «?» на «a».
Во втором примере используя две замены можно получить строку «aba?aba??». Больше двух вхождений получить нельзя.
| |
![]()
|
|
Межрегиональная олимпиада
Бинарный поиск в массиве
Динамическое программирование
Жадный алгоритм
На межрегиональной олимпиаде по программированию роботов соревнования проводятся в один тур и в необычном формате. Задачи участникам раздаются последовательно, а не все в самом начале тура, и каждая i-я задача (1 ≤ i ≤ n) становится доступной участникам в свой момент времени si. При поступлении очередной задачи каждый участник должен сразу определить, будет он ее решать или нет. В случае, если он выбирает для решения эту задачу, то у него есть ti минут на то, чтобы сдать ее решение на проверку, причем в течение этого времени он не может переключиться на решение другой задачи. Если же участник отказывается от решения этой задачи, то в будущем он не может к ней вернуться. В тот момент, когда закончилось время, отведенное на задачу, которую решает участник, он может начать решать другую задачу, ставшую доступной в этот же момент, если такая задача есть, или ждать появления другой задачи. При этом за правильное решение i-й задачи участник получает ci баллов.
Артур, представляющий на межрегиональной олимпиаде один из региональных центров искусственного интеллекта, понимает, что важную роль на такой олимпиаде играет не только умение решать задачи, но и правильный стратегический расчет того, какие задачи надо решать, а какие пропустить. Ему, как и всем участникам, до начала тура известно, в какой момент времени каждая задача станет доступной, сколько времени будет отведено на ее решение и сколько баллов можно получить за ее решение. Артур является талантливым школьником и поэтому сможет успешно решить за отведенное время и сдать на проверку любую задачу, которую он выберет для решения на олимпиаде.
Требуется написать программу, которая определяет, какое максимальное количество баллов Артур сможет получить при оптимальном выборе задач, которые он будет решать, а также количество и перечень таких задач.
Входные данные
Первая строка содержит одно целое число n (1 ≤ n ≤ 105) количество задач на олимпиаде.
Последующие n строк содержат описания задач, по три числа на каждой строке: si момент появления i-й задачи в минутах, ti время, отведенное на ее решение в минутах, и ci сколько баллов получит участник за решение этой задачи (1 ≤ si, ti, ci ≤ 109).
Выходные данные
Первая строка должна содержать одно число – максимальное количество баллов, которое сможет получить Артур на олимпиаде.
Вторая строка должна содержать одно целое число m - количество задач, которые надо решить при оптимальном выборе.
Третья строка должна содержать m разделенных пробелом целых чисел - номера этих задач в порядке их решения. Задачи пронумерованы, начиная с единицы, в порядке их описания во входном файле.
Если оптимальных ответов несколько, необходимо вывести любой из них.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2
1 1 1
2 2 2 |
3
2
1 2 |
| 2 |
3
1 2 1
3 2 1
2 4 3 |
3
1
3 |
| |
![]()
|
|
Игра-заливка
Динамическое программирование
Вам дана полоска из клетчатой бумаги из n раскрашенных квадратов, пронумерованных от 1 до n слева направо. Квадрат под номером i изначально покрашен в цвет ci.
Скажем, что квадраты i и j лежат в одной компоненте, если ci = cj и ci = ck для всех k, удовлетворяющих i < k < j. Иначе говоря, все квадраты на отрезке от i до j должны иметь одинаковый цвет.
Например, у полоски [3,3,3] есть 1 компонента связности, а у [5,2,4,4] их 3.
Игра «заливка» играется на этой полоске следующим образом:
В начале игры вы выбираете один произвольный стартовый квадрат (это не считается за ход).
Затем, в каждый ход, вы меняете цвет компоненты связности, содержащей стартовый квадрат на любой другой цвет.
Выясните минимальное количество ходов, которое нужно, чтобы перекрасить всю полоску в один цвет.
Входные данные:
Первая строка содержит одно целое число n (1 ≤ n ≤ 5000) — количество квадратов.
Вторая строка содержит целые числа c1,c2,…,cn (1 ≤ ci ≤ 5000) — изначальные цвета квадратов.
Выходные данные:
Выведите одно целое число — минимальное количество ходов, которое нужно сделать.
Примеры:
| Входные данные |
Выходные данные |
4
5 2 2 1 |
2 |
8
4 5 2 2 1 3 5 5 |
4 |
1
4 |
0 |
Пояснение:
Один из оптимальных способов в первом примере: [5, 2, 2, 1] -> [5, 2, 2, 2] -> [5, 5, 5, 5]
| |
![]()
|
|
Zuma
Динамическое программирование
Хлоя недавно установила на свой телефон игру «Zuma». Игроку даётся ряд из n драгоценных камней, i-й из которых имеет цвет ci. Цель игры — уничтожить все камни за как можно меньшее количество секунд.
За одну секунду Хлоя может выбрать любую подстроку (последовательность стоящих рядом камней), являющуюся палиндромом, и удалить её. После удаления данной подстроки оставшиеся камни сдвигаются, чтобы снова образовать непрерывный ряд. Какое минимальное количество секунд необходимо, чтобы уничтожить всю строку?
Напомним, что строка (или подстрока) является палиндромом, если она одинаково читается как слева направо, так и справа налево. В данном случае это означает, что цвет первого камня равен цвету последнего камня, цвет второго равен цвету предпоследнего и так далее.
Входные данные:
В первой строке входных данных записано единственное число n (1 ≤ n ≤ 500) — количество камней в изначальном ряду.
Во второй строке записано n целых чисел, i-е из которых равно ci (1 ≤ ci ≤ n) — цвет i-го камня в изначальном ряду.
Выходные данные:
Выведите единственное целое число — минимальное количество секунд, необходимое чтобы удалить все камни.
Примеры:
| Входные данные |
Выходные данные |
3
1 2 1 |
1 |
3
1 2 3 |
3 |
7
1 4 4 2 3 2 1 |
2 |
Пояснения:
Последовательность в третьем примере: [1, 4, 4, 2, 3, 2, 1] -> [1, 4, 4, 1] -> []
| |
![]()
|
|
Удаление пар
Динамическое программирование
Дана строка, состоящая из прописных латинских букв. Можно удалять из этой строки все пары соседних одинаковых букв, включая пары, образовавшиеся после удаления других пар. Нужно заменить в заданной строке 0 или более букв так, чтобы после удаления всех пар строка стала пустой.
Входные данные:
Первая строка содержит одну строку четной длины от 2 до 200, состоящую из строчных букв латинского алфавита.
Выходные данные:
В первой строке вывести минимальное количество замен букв.
Пример:
| Входные данные |
Выходные данные |
| baddaacc |
1 |
Пояснение:
Можно заменить шестую букву на b, тогда процесс удаления будет выглядеть следующим образом: baddabcc -> baddab -> baab -> bb -> .
| |
![]()
|
|
Меняю конфеты на ноутбук
Одномерные массивы
Порядковые статистики
Использование сортировки
Динамическое программирование
Динамическое программирование: один параметр
Антон Б., суперспособный ученик 8 класса, обладает неудивительными математическими способностями. Побывав однажды на экскурсии в Колоколамске, он понял, что легко может написать программу, которая бы предсказывала стоимость его любимых конфет на любой промежуток дней вперед.
Используя эту программу, Антон Б. решил приобрести на все свои карманные деньги конфеты (а их у него было всего 10 рублей), затем, чуть позже, продать все купленные им конфеты. Таким образом, Антон Б. хочет заработать как можно больше денег на новый ноутбук.
Так как Антон Б. еще несовершеннолетний и один ездить в другие города не может, ему нужно понять, в какие из двух дней попросить старшего брата отвезти его в Колоколамск. Старший брат совершеннолетний и очень любит своего младшего брата, поэтому всегда готов ему помочь.
Так как Антон Б. очень торопится на кружок по информатике, он просит вас определить эти два дня в ближайшие N дней.
Входные данные
В первой строке записано число N (2 <= N <= 100000) количество дней, на которые Антон Б. делает прогноз. Вторая строка содержит N целых положительных чисел ai (1 <= i <= N , 1 <= ai <= 5000 ), где ai - предсказанная стоимость конфет в i-й день.
Выходные данные
Выведите два числа: первое число - номер дня, в который Антон Б. поедет покупать конфеты, второе - номер дня, в который он поедет продавать конфеты. В случае, если таких вариантов дней несколько, выведите любой из них. Если Антон Б. в итоге не сможет получить прибыль ни при каких вариантах, то выведите два нуля.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6
10 3 5 3 11 9
|
2 5
|
| 2 |
4
5 5 5 5
|
0 0
|
| |
![]()
|
|
Dank numbers
Динамическое программирование
Число является dank number, если все его цифры идут в неубывающем порядке. Чтобы получить dank kush, Bonkisilver должен назвать все n-значные dank numbers. Вас не просят узнать все такие числа, Вам лишь нужно вывести их количество.
Входные данные
На вход подается число n (0 <= n <= 50).
Выходные данные
Выведите одно число - количество n-значных dank number.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
9 |
24310 |
| |
![]()
|
|
MLG pro
Динамическое программирование
Динамическое программирование: один параметр
Bonkisilver очень хочет стать MLG pro и попасть в FaZe clan. Для этого он каждый день практикуется в стрельбе из снайперской винтовки. В качестве поощрения, за каждый noscope он получает 2 пачки doritos, а за каждый quickscope - одну. Сколько вариантов сделать выстрелы было у Bonkisilver, если в итоге у него была n-1 пачка.
Входные данные
На вход подается число n (1 <= n <= 50).
Выходные данные
Выведите одно число - количество вариантов сделать выстрелы.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 |
2 |
| |
![]()
|
|
MTN DEW
Динамическое программирование
Рекуррентные последовательности
Динамическое программирование: один параметр
Чтобы подготовиться к предстоящей битве Bonkisilver должен прокачать свой скил, а, как известно, лучшим способом это сделать, является употребление mtn dew при прослушивании дабстепа в 4:20 по МСК. Полученный скилл вычисляется по формуле:
f(n) = f(n - 1) + f(n - 2) + f(n / 2),
где n - количество литров mtn dew, выражаемое целым числом. Операция n/2 означает целочисленное деление числа n на 2.
Также, известно, что
f(1) = 1 microCoinZ
f(x) = 0 microCoinZ, при x < 1.
Помогите Bonkisilver сосчитать полученное количество microCoinZ.
Входные данные
На вход подается число n (0 <= n <= 70).
Выходные данные
Выведите одно число - полученный скилл.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 |
1 |
PS: Mountain Dew, также MTN DEW — безалкогольный сильногазированный прохладительный напиток, торговая марка американской компании PepsiCo.
| |
![]()
|
|
Числа Фибоначчи
Динамическое программирование
Рекуррентные последовательности
Числа Фибоначчи определяются рекуррентной формулой:
\(F_0 = F_1 = 1, \\ F_n = F_{n-1} + F_{n-2}, \text{ при}\ n \ge 2\)
Входные данные
В единственной строке входных данных записано натуральное число n (\(1<=n<=45\)).
Выходные данные
Вывести одно n-е число Фибоначчи - Fn.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 |
1 |
| 2 |
7 |
21 |
| |
![]()
|
|
Завоевание
Динамическое программирование
Лорд Петир собирает армию для похода на соседнее королевство. Он хочет, чтобы в его армию вошли все воины каждого из n городов его королевства. Петир выяснил, что в i-м городе ищут работу ai воинов, которых он может завербовать в свою армию.
Исходно в армии Лорда нет ни одного воина. Чтобы воин вошел в армию, Петир может заплатить этому воину. Для вербовки одного воина из i-го города, необходимо заплатить ему ci золотых монет. При этом воины из больших городов ценят свою работу дороже, поэтому если для i-го и j-го города выполнено ai < aj , то ci ≤ cj . Однако есть еще один способ добиться того, чтобы воины присоединились к армии. Если в какой-то момент оказывается, что в армии Лорда Петира уже строго больше воинов, чем осталось в некотором городе, то все воины этого города бесплатно присоединяются к армии Лорда.
Помогите Лорду Петиру выяснить, какое минимальное количество золотых монет он должен заплатить воинам, чтобы все воины из всех городов оказались в его армии.
Входные данные
В первой строке входного файла находится целое число n (1 ≤ n ≤ 1000) — количество городов, в которых Лорд Петир намерен набирать себе воинов. В следующих n строках входного файла находится по два целых числа ai и ci (1 ≤ ai ≤ 100, 1 ≤ ci ≤ 10 000) — количество воинов в i-м городе и число монет, которое необходимо заплатить одному воину в этом городе, чтобы он присоединился к армии. Для всех пар i и j выполнено условие, что если ai < aj , то ci ≤ cj .
Выходные данные
В выходной файл выведите одно целое число — минимальное количество монет, которые Лорду Петиру придется заплатить, чтобы все воины вошли в его армию.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
1 1
2 2
4 3
|
5 |
В приведенном примере Лорду необходимо действовать следующим образом. Сначала он платит 2 монеты воину из второго города, и 3 монеты воину из третьего города, чтобы они присоединились
к его армии. Теперь в армии Лорда 2 воина, а в городах осталось 1, 1 и 3 воина, соответственно. Воины из первого и второго городов бесплатно присоединяются к армии Лорда Петира, в его армии становится 4 воина, после чего и оставшиеся 3 воина из третьего города бесплатно присоединяются к его армии.
| |
![]()
|
|
Упорядочите шарики
Динамическое программирование
Динамическое программирование: последовательности
При игре в новую игру (некоторый гибрид боулинга и бильярда) используется N шариков, пронумерованных числами от 1 до N. В начале игры эти шарики должны быть выложены в линию в порядке своих номеров. В процессе игры их порядок может меняться.
Для того, чтобы упорядочить шарики перед началом следующей партии, используется следующее устройство. Это устройство состоит из головки, которая, перемещаясь над шариками, может «засасывать» и «выплевывать» шарики. Чтобы получить большее представление об этом устройстве, представьте себе пылесос, который может засасывать шарики, перемешаться в нужное место, и там, включаясь на продув в обратном направлении, шарики «выплевывать».
При засасывании шарика все шарики, которые находились правее засасываемого, сдвигаются влево. «Выплюнуть» шарик можно между любыми двумя шариками (а также перед первым шариком или после последнего), тогда выплевываемый шарик вставляется между этими шариками, и все шарики, которые находятся правее вставляемого, сдвигаются вправо.
В устройство может быть одновременно засосано больше одного шарика, при этом при выплевывании шарика первым выплевывается последний засосанный шарик, затем - предпоследний и т.д. (т.е. устройство работает по принципу стека). Шарики выплевываются по одному, т.е. можно выплюнуть только один шарик, остальные оставив внутри устройства (при этом дальше можно как продолжать «выплевывать» шарики в том же или в другом месте, так и засасывать новые шарики).
Наиболее энергоемкой из описанных операций является операция засасывания шарика, поэтому хочется минимизировать количество именно таких операций.
Напишите программу, которая по данному начальному расположению шариков определит минимальное количество операций засасывания, которое нужно, чтобы расположить шарики в порядке их номеров.
Входные данные
Во входном файле задано сначала число N — количество шариков (1<= N <= 1000). Далее идет N чисел, задающих номера шариков в порядке слева направо в их текущем расположении (каждое число — от 1 до N, и каждое из чисел встречается в последовательности ровно один раз).
Выходные данные
В выходной файл выведите одно число — минимальное количество операций засасывания шарика, которое потребуется, чтобы расположить шарики в порядке их номеров.
Комментарии к примерам тестов
1.Можно засосать, например, шарик номер 2 и выплюнуть его между 1-м и 3-м шариком.
2. Можно действовать, например, так. Сначала засосем шарик номер 1, затем – шарик номер 2. Затем переместимся в начало и перед 4-м шариком выплюнем шарик (это будет шарик номер 2). Дальше засосем шарик номер 3, и выплюнем его между шариками 2 и 4. Дальше переместимся в начало и там выплюнем шарик номер 1. Впрочем, это не единственный возможный вариант упорядочения шариков в этом примере.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
2 1 3 |
1 |
| 2 |
4
4 3 2 1 |
3 |
| |
![]()
|
|
Кузнечик и лягушки
Динамическое программирование
Рекуррентные последовательности
Динамическое программирование: один параметр
Кузнечик прыгает по столбикам, расположенным на одной линии на равных расстояниях друг от друга. Столбики имеют порядковые номера от 1 до N . В начале Кузнечик сидит на столбике с номером 1. Он может прыгнуть вперед на расстояние от 1 до K столбиков, считая от текущего.
На некоторых столбиках сидят лягушки, которые едят кузнечиков (Кузнечик не должен попадать на эти столбики!). Определите, сколькими способами Кузнечик может безопасно добраться до столбика с номером N. Учитывайте, что Кузнечик не может прыгать назад.
Входные данные
Входная строка содержит натуральные числа N и K , разделённые пробелом. Гарантируется, что 1 <= N, K <= 32 . Во второй строке записано число лягушек L ( 0 <= L <= N - 2 ). В третьей строка записано L натуральных чисел: номера столбиков, на которых сидят лягушки (среди них нет столбиков с номерами 1 и N ).
Выходные данные
Программа должна вывести одно число: количество способов, которыми Кузнечик может безопасно добраться до столбика с номером N .
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6 4
2
2 4 |
3 |
| |
![]()
|
|
Черепаха
Динамическое программирование
Динамическое программирование на таблицах
Черепаха хочет переползти из левого верхнего угла поля размером N на M клеток ( 1 ≤ N , M ≤ 16 ) в правый нижний. За один шаг она может переместиться на соседнюю клетку вправо или на соседнюю клетку вниз. Определите, сколькими различными способами Черепаха может добраться до цели.
Входные данные
Входная строка содержит два натуральных числа: размеры поля N и M , разделённые пробелом ( 1 ≤ N , M ≤ 16 ).
Выходные данные
Программа должна вывести одно число: количество различных маршрутов из левого верхнего угла поля в правый нижний.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 3 |
6 |
| |
![]()
|
|
Все ПСП
Рекурсия
Динамическое программирование
Перебор
Перебор с возвратом
Дано число n. Вам необходимо сгенерировать все правильные скобочные последовательности, содержащие n пар скобок.
Входные данные
В первой строке дано натуральное число n (1 <= n <= 8).
Выходные данные
Выведите все правильные скобочные последовательности по возрастанию в лексикографическом порядке. Каждую в отдельной строке.
| |
![]()
|
|
Числа Фибоначчи: Мемоизация рекурсии (C++)
Динамическое программирование
Динамическое программирование: один параметр
Числа Фибоначчи, обозначаемые обычно F(n) образуют последовательность, называемую последовательностью Фибоначчи, такую, что каждое число является суммой двух предыдущих, начиная с 0 и 1. То есть,
F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), для n > 1.
По заданному n, вычислите F(n) (0 <= n <= 80).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 |
1 |
| 2 |
3 |
2 |
| 3 |
4 |
3 |
| |
![]()
|
|
Числа Фибоначчи: Мемоизация рекурсии (Python)
Динамическое программирование
Динамическое программирование: один параметр
Числа Фибоначчи, обозначаемые обычно F(n) образуют последовательность, называемую последовательностью Фибоначчи, такую, что каждое число является суммой двух предыдущих, начиная с 0 и 1. То есть,
F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), для n > 1.
По заданному n, вычислите F(n) (0 <= n <= 80).
(в коде программы длина одного отступа равна 4 пробелам!)
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 |
1 |
| 2 |
3 |
2 |
| 3 |
4 |
3 |
| |
![]()
|
|
N-е число Трибоначчи (рекурсивно)
Динамическое программирование
Динамическое программирование: один параметр
Последовательность чисел Трибоначчи (Tn) определяется следующим образом:
T0 = 0,
T1 = 1,
T2 = 1, и Tn+3 = Tn + Tn+1 + Tn+2 при n >= 0.
Для заданного числа n, определите значение Tn.
Входные данные
Программа получает на вход натуральное число n (0 <= n <= 37). Ответ гарантированно укладывается в рамки 32-разрядного целого числа, т.е. ответ <= 231 - 1.
Выходные данные
Выведите значение Tn.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 |
4 |
| 2 |
25 |
1389537 |
| |
![]()
|
|
Подняться на вершину горы (снизу-вверху)
Динамическое программирование
Динамическое программирование: один параметр
Робот Сильвер занимается терроформированием на планете Шелезяка. Сейчас робот находится перед лестницей, ведущей на вершину горы. Лестница состоит из n ступенек. Робот, поднимаясь вверх, может пойти на одну или сразу две ступеньки.
Пока робот поднимается на вершину, вы хотите определить, сколько существует различных способов, которыми он может добраться до последней ступеньки этой лестницы и тем самым оказаться на вершине горы.
Входные данные
Программа получает на вход одно целое число n - количество ступенек в лестнице (1 <= n <= 45).
Выходные данные
Выведите одно число - количество способов добраться до вершины горы.
Попробуйте решить эту задачу без использования массивов и других структур данных! Другими словами, ваша программа должна использовать фиксированный объем памяти, не зависящий от входных данных (О(1)).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 |
2 |
| 2 |
3 |
3 |
| |
![]()
|
|
Числа Фибоначчи. Динамика снизу вверх
Динамическое программирование
Динамическое программирование: один параметр
Числа Фибоначчи, обозначаемые обычно F(n) образуют последовательность, называемую последовательностью Фибоначчи, такую, что каждое число является суммой двух предыдущих, начиная с 0 и 1. То есть,
F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), для n > 1.
По заданному n, вычислите F(n) (0 <= n <= 80).
Попробуйте решить эту задачу без использования массивов и других структур данных! Другими словами, ваша программа должна использовать фиксированный объем памяти, не зависящий от входных данных (О(1)).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 |
1 |
| 2 |
3 |
2 |
| 3 |
4 |
3 |
| |
![]()
|
|
Подняться на вершину горы (рекурсивно)
Динамическое программирование
Динамическое программирование: один параметр
Робот Сильвер занимается терроформированием на планете Шелезяка. Сейчас робот находится перед лестницу, ведущей на вершину горы. Лестница состоит из n ступенек. Робот, поднимаясь вверх, может пойти на одну или сразу две ступеньки.
Пока робот поднимается на вершину, вы хотите определить, сколько существует различных способов, которыми он может добраться до последней ступеньки этой лестницы и тем самым оказаться на вершине горы.
Входные данные
Программа получает на вход одно целое число n - количество ступенек в лестнице (1 <= n <= 45).
Выходные данные
Выведите одно число - количество способов добраться до вершины горы.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
2 |
2 |
| 2 |
3 |
3 |
| |
![]()
|
|
N-е число Трибоначчи (снизу-вверх)
Динамическое программирование
Динамическое программирование: один параметр
Последовательность чисел Трибоначчи (Tn) определяется следующим образом:
T0 = 0,
T1 = 1,
T2 = 1, и Tn+3 = Tn + Tn+1 + Tn+2 при n >= 0.
Для заданного числа n, определите значение Tn.
Входные данные
Программа получает на вход натуральное число n (0 <= n <= 37). Ответ гарантированно укладывается в рамки 32-разрядного целого числа, т.е. ответ <= 231 - 1.
Выходные данные
Выведите значение Tn.
Попробуйте решить эту задачу без использования массивов и других структур данных! Другими словами, ваша программа должна использовать фиксированный объем памяти, не зависящий от входных данных (О(1)).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4 |
4 |
| 2 |
25 |
1389537 |
| |
![]()
|
|
Стоимость проезда
Динамическое программирование
Динамическое программирование: один параметр
Робот Сильвер движется по платному шоссе на планете Шелезяка. На каждом километре шоссе расположен пункт оплаты. Всего на шоссе n пунктов оплаты. Первый пункт оплаты находится в самом начале шоссе, n-й пункт оплаты находится в начале последнего километра шоссе. Заплатив нужную сумму в i-м пункте оплаты, робот может двигаться дальше либо до следующего пункта оплаты, либо же до того, который находится через 2 километра (то есть, если робот находится в пункте i, то он может двигаться либо до пункта i+1, либо до пункта i+2). Первую оплату можно сделать либо в первом пункте, либо во втором (на выбор). Если оплаты была произведена в предпоследнем (n-1) пункте, то можно просто доехать до конца шоссе, не оплачивая проезд в последнем пункте.
Зная стоимость, которую необходимо заплатить в определенном пункте оплаты, помогите роботу Сильверу найти наименьшую сумму, которую он заплатит, проехав через все шоссе.
Формат входных дынных
В первой строке записано количество пунктов оплаты n (2 <= n <= 1000). Во второй строке записыны n целых чисел (costi) - стоимость проезда через i-й пункт оплаты (1 <= i <= n, 0 <= costi <= 999).
Формат выходных дынных
Выведите одно число - ответ на задачу.
| |
![]()
|
|
Маршрут наименьшей стоимости
Динамическое программирование
Динамическое программирование: один параметр
Робот Сильвер движется по платному шоссе на планете Шелезяка. На каждом километре шоссе расположен пункт оплаты. Всего на шоссе n пунктов оплаты. Первый пункт оплаты находится в самом начале шоссе, n-й пункт оплаты находится в начале последнего километра шоссе. Заплатив нужную сумму в i-м пункте оплаты, робот может двигаться дальше либо до следующего пункта оплаты, либо же до того, который находится через 2 километра (то есть, если робот находится в пункте i, то он может двигаться либо до пункта i+1, либо до пункта i+2). Первую оплату можно сделать либо в первом пункте, либо во втором (на выбор). Если оплаты была произведена в предпоследнем (n-1) пункте, то можно просто доехать до конца шоссе, не оплачивая проезд в последнем пункте.
Зная стоимость проезда через определенный пункт оплаты, помогите роботу Сильверу найти наименьшую стоимость проезда через все шоссе, которую должен будет заплатить Сильвер, а также пункты оплаты, на которых ему необходимо будет остановиться.
Входные данные
В первой строке записано количество пунктов оплаты n (2 <= n <= 1000). Во второй строке записыны n целых чисел (costi) - стоимость проезда через i-й пункт оплаты (1 <= i <= n, 0 <= costi <= 999).
Выходные данные
Выведите в первой строке наименьшую стоимость проезда через шоссе.
Во второй строке выведите через пробел номера пунктов оплаты (по возрастанию), на которых роботу придется остановиться, чтобы оплатить проезд. Если вариантов маршрута с остановками в пунктах оплаты несколько, то выведите любой из них.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3
10 15 20 |
15
2 |
| 2 |
10
1 100 1 1 1 100 1 1 100 1 |
6
1 3 5 7 8 10 |
| |
![]()
|
|
Калькулятор с восстановлением ответа
Динамическое программирование
Динамическое программирование: один параметр
Имеется калькулятор, который выполняет три операции:
- Прибавить к числу
X единицу.
- Умножить число
X на 2.
- Умножить число
X на 3.
Определите кратчайшую последовательность операций, необходимую для получения из числа 1 заданное число N.
Входные данные
Программа получает на вход одно число X, не превосходящее 10 6.
Выходные данные
Выведите строку, состоящую из цифр "1", "2" или "3", обозначающих одну из трех указанных операций, которая получает из числа 1 число N за минимальное число операций. Если возможных минимальных решений несколько, выведите любое из них.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1 |
|
| 2 |
5 |
121 |
| 3 |
562340 |
3333312222122213312 |
| |
![]()
|
|
Путешествия Аркадия
Динамическое программирование
Магистр Аркадий любит путешествовать на поезде. Он собирается отправиться в множество поездок в течение года и заранее знает, в какие дни он поедет.
Аркадий может купить билеты по разным тарифам:
- 1-дневный тариф стоит
C1 рублей;
- 7-дневный тариф стоит
C2 рублей;
- 30-дневный тариф стоит
C3 рублей.
Каждый билет начинает действовать с того дня, когда был куплен.
Например, если Аркадий купит 7-дневный билет на 2-й день путешествия, то он сможет путешествовать 7 дней: 2, 3, 4, 5, 6, 7 и 8 дни.
Помогите Аркадию найти минимальную стоимость, за которую можно купить билет(ы), чтобы он мог отправиться путешествовать в любой из запланированных дней.
Входные данные
Первая строка содержит натуральное число n - количество дней, в которые Аркадий планирует путешествовать. Вторая строка содержит порядковые номера дней, в которые Аркадий планирует путешествовать (daysi). Третья строка содержит три числа: C1, C2, C3.
Ограничения:
1 <= n <= 3651 <= daysi <= 365- Порядковы номера дней
daysi даются в строго возрастающем порядке.
1 <= С1, С2, С3 <= 1000
Выходные данные
Выведите минимальное количество рублей, которое Аркадию придется заплатить за билеты.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
6
1 4 6 7 8 20
2 7 15
|
11
|
| 2 |
12
1 2 3 4 5 6 7 8 9 10 30 31
2 7 15
|
17
|
| |
![]()
|
|
Чемпионат по поиску в сети Меганет
Строки
Динамическое программирование
Структуры данных
Конструктив
Задача на реализацию
Для проведения чемпионата мира по поиску в сети Меганет организаторам необходимо ограничить доступ к некоторым адресам. Адрес в сети Меганет представляет собой строку, состоящую из имени сервера и имени раздела.
Имя сервера представляет собой строку, содержащую от одной до пяти частей включительно. Каждая часть представляет собой непустую строку, состоящую из строчных букв латинского алфавита. Части разделены точкой. Примеры корректных имен сервера: «a», «ab.cd», «abacaba», «a.b.c.d.e».
Имя раздела представляет собой строку, которая может быть либо пустой, либо содержать от одной до пяти частей включительно. Каждая часть начинается с символа «/», после которого следует одна или несколько строчных латинских букв. Примеры корректных имен разделов: «», «/a», «/aba», «/a/b/c/d/e». Адрес формируется приписыванием имени раздела в конец имени сервера. Например, корректными адресами являются строки: «a», «aba/d/f/g/h», «a.b», «aba.caba/def/g», «c.d.e.f.g/a/b/c/d/e».
Для ограничения доступа к некоторым адресам сети Меганет организаторы чемпионата подготовили несколько фильтров. Фильтр, как и адрес, состоит из двух частей: фильтра сервера и фильтра раздела.
Фильтр сервера состоит из имени сервера, перед которым может также идти строка «*.». Если фильтр сервера представляет собой только имя сервера, то этому фильтру соответствует только сервер, имеющий точно такое же имя. Если фильтр сервера представляет собой строку «*.S », где S — имя сервера, то ему соответствуют сервера, удалением нуля или более начальных частей от имени которых можно получить строку S.
Аналогично, фильтр раздела представляет собой имя раздела, после которого может идти строка «/*». Фильтру раздела, который представляет собой просто имя раздела R, соответствуют только разделы, в точности совпадающие с R. Если фильтр раздела представляет собой строку «R/*», то ему соответствуют все разделы, удалением от имен которых нуля или более конечных частей можно получить строку R. Адрес соответствует фильтру, если его имя сервера соответствует фильтру сервера, а его имя раздела соответствует фильтру раздела.
Примеры фильтров и соответствующих им адресов приведены в таблице ниже.
| ab.c/d/e |
ab.c/d/e |
| *.a |
a ax.a efg.a |
| *.a/b/c |
a/b/c x.a/b/c e.fg.a/b/c |
| x.yz/a/* |
x.yz/a x.yz/a/b/c x.yz/a/xyz |
| *.a/* |
a x.a e.fg.a
a/b/c x.a/ddd/c e.fg.a/b/c/g/haha/i |
| *.a/b/c/* |
a/b/c x.a/b/c e.fg.a/b/c
a/b/c/xxx e.fg.a/b/c/d/e/f |
| |
|
Требуется написать программу, которая по заданному набору фильтров и списку адресов определяет для каждого адреса, какому числу фильтров соответствует этот адрес.
Пример:
Ввод:
2 0
a.bb/c
bb/c/d
4
a.bb
bb/c/d
a.bb/c/d
bb/c
Вывод:
0
1
0
0
Вывод:
4 0
*.bb/c
*.bb/c/*
bb/c/*
bb/c/*
6
bb
bb/c
bb/c/d
a.bb
a.bb/c
a.bb/c/d
Вывод:
0
4
3
0
2
1
| |
![]()
|
|
Кладовка из Простоквашино
Динамическое программирование
Динамическое программирование: один параметр
Префиксные суммы(минимумы, ...)
Сразу же после заселения в новый дом в Простоквашино кот Матроскин, Шарик и дядя Фёдор затеяли ремонт. Непосредственно перед его началом они обнаружили, что в доме отсутствует кла- довка для стройматериалов, и наспех пристроили её к дому. Как только вспомогательное строение было готово, встал вопрос о необходимости провести туда электричество и повесить лампочку.
Обсудив вопросы электрификации новых помещений с почтальоном Печкиным, наши герои узна- ли много полезной информации. Чтобы посетители не мучились с выбором, в деревенском магазине продаётся только один вид лампочек, зато в неограниченных количествах. Стоит одна лампочка ни дорого, ни дёшево, а ровно C рублей. Правда, лампочки в магазине не самые качественные, и вклю- чить каждую из них можно только K раз, а на K + 1 включение она перегорает. Недостаток этот компенсируется тем, что во включенном состоянии лампочка перегореть не может. К сожалению, электроэнергия в Простоквашино недешевая, и каждая минута работы лампочки обойдется дяде Фёдору и его друзьям в D рублей.
Узнав всё это, экономный Матроскин составил поминутный график из N предполагаемых посе- щений кладовки. Каждый визит в новое помещение задаётся моментом входа ai и моментом выхода bi . Таким образом, i-й визит продолжается ровно bi − ai минут.
Разумеется, во время посещения свет в кладовке должен быть включён. Если в начале очередного визита лампочка не горит, то посетитель сразу её включает, а вот уходя он может как выключить свет, так и оставить его включенным. Если во время очередного включения лампочка перегорает, то её приходится немедленно заменить. Теперь Матроскина интересует минимальное количество рублей, которое придётся потратить, чтобы выполнить все запланированные визиты в кладовку. Изначально в помещении уже висит новая лампочка в выключенном состоянии.
Формат входных данных
В первой строке входных данных записаны четыре целых числа N, K, C, D — количество пла- нируемых посещений кладовки, количество успешных включений для одной лампочки, стоимость покупки лампочки и стоимость минуты работы лампочки соответственно (1 <= N, K <= 200 000, 1 <= C, D <= 109 ). В следующих N строках даны по два целых положительных числа ai и bi , описывающих пред- полагаемые визиты в кладовку (1 <= ai < bi <= 109 ). Посещения не пересекаются по времени и упорядочены, то есть bi < ai+1.
Формат выходных данных
Выведите одно целое число — минимальное количество рублей, которое придётся потратить жителям дома, чтобы выполнить все запланированные визиты в кладовку при свете.
| Ввод |
Вывод |
1 2 5 6
3 5 |
12 |
3 1 15 10
1 3
4 5
30 35 |
105 |
Замечание
Замечание В первом примере достаточно заплатить только за электроэнергию: лампочка должна быть включена на третьей минуте и выключена на пятой, стало быть, суммарные затраты составляют (5 − 3) × 6 = 12.
Во втором примере выгодно не выключать лампочку между первым и вторым посетителем, а для третьего использовать уже новую лампочку
| |
![]()
|
|
Выборы
Простые числа и разложение на множители
Динамическое программирование
Динамическое программирование: один параметр
Алгоритмы на графах
Скоро в Соединенных Штатах Берляндии пройдут выборы президента. На эту ответственную должность претендуют два кандидата: Дядя Сэм и Дядя Фродо. Вы работаете аналитиком в пред- выборном штабе Дяди Сэма, и вам поручено помочь ему победить конкурента. Раздуть газетный скандал из одержимости оппонента бросанием колец в жерла вулканов не получилось, так что при- дётся воспользоваться математикой.
Казалось бы, чтобы выиграть, необходимо убедить проголосовать за нашего кандидата более половины пришедших на выборы. Оказывается, что иногда нужно гораздо меньше! Для того чтобы понять, как это возможно, рассмотрим подробнее процедуру голосования.
Как вы знаете, Соединенные Штаты Берляндии разделены на несколько административных ре- гионов первого уровня — штатов. Сначала в каждом из штатов проходят местные выборы, по итогам которых каждый штат отдаёт свой голос за одного из кандидатов. Если не менее половины штатов выбрало Дядю Сэма, то выигрывает он (в случае равенства голосов Дядя Сэм имеет преимущество как действующий президент), иначе побеждает Дядя Фродо. Все штаты, в свою очередь, состоят из административных регионов второго уровня, каждый из которых представлен выборщиком из административных регионов третьего уровня и так далее. Последний уровень состоит из отдельных жителей Берляндии. Всего в Берляндии N жителей и K уровней административных единиц. Одним из ключевых принципов этой страны является равенство, так что любой регион i-го уровня делится на одинаковое число регионов следущего уровня (в том числе содержит одинаковое число граждан).
Так получилось, что делением на регионы поручили заняться именно вам, то есть в ваших руках назначить, на сколько именно административных единиц i-го уровня делится (i−1)-ая администра- тивная единица.
Также у вас есть сильный инструмент влияния на выбор людей — нефтяные бурли. Чтобы заста- вить одного избирателя отдать свой голос за Дядю Сэма, достаточно дать ему скромный подарок в размере одного нефтяного бурля.
К несчастью, изначально все N жителей Соединённых Штатов Берляндии собираются отдать свой голос за Дядю Фродо. Требуется определить минимальное количество нефтяных бурлей, ко- торое достаточно потратить для победы на выборах.
Формат входных данных
В единственной строке ввода находятся два целых числа N и K (1 <= N <= 1015 , 1 <= K <= 10).
Формат выходных данных
Требуется вывести единственное число — минимальное количество нефтяных бурлей, которое придётся потратить на предвыборные подарки при наилучшем разбиении на регионы.
Примеры
Замечание
Берляндские законы не запрещают, чтобы страна состояла из одного штата, а город — одного жителя. Аналогично с остальными типами регионов.
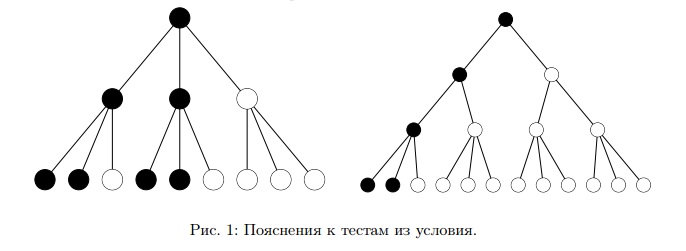
На рисунке 1 черным цветом отмечены те регионы, в которых победил Дядя Сэм. На нижнем уровне черными изображены вершины, соответствущие подкупленным конкретным жителям.
| |
![]()
|
|
Постройка забора
Динамическое программирование
Динамическое программирование: один параметр
После побега Колобка Дед и Баба решили построить забор вокруг своего дома, чтобы не допустить повторения истории.
Забор представляет собой многоугольник ненулевой площади, сторонами которого являются доски. Пилить или ломать доски нельзя. Например, из трех досок с длинами 10, 11 и 12 можно построить забор, а из четырех досок с длинами 100, 1, 2 и 3 — нельзя.
У Деда нашлось целых n досок, поэтому они с Бабой задались вопросом: а сколько различных способов выбрать несколько досок из имеющихся, чтобы из них затем можно было построить забор? Способы считаются различными, если существует доска, которая используется в одном из них, но не используется в другом.
Пожилым людям надо помогать, так что вам не составит труда решить для них эту задачу! Количество способов может быть довольно большим, поэтому выведите остаток от деления этого количества на число 109 + 7.
Формат входного файла
В первой строке входного файла находится одно натуральное число n (1 ≤ n ≤ 4000) — количе- ство досок. Во второй строке дано n чисел li (1 ≤ li ≤ 4000) — длины досок.
Формат выходного файла
В выходной файл выведите одно число — количество способов выбрать доски для постройки забора, взятое по модулю 109 + 7.
| Ввод |
Вывод |
3
10 11 12 |
1 |
4
100 1 2 3 |
0 |
4
5 5 5 5 |
5 |
| |
![]()
|
|
Наибольшая возрастающая подпоследовательность за O(n*log(n))
Динамическое программирование
Динамическое программирование: последовательности
Динамическое программирование: последовательности
Числовая последовательность задана рекуррентной формулой: ai+1=(k * ai + b) mod m. Найдите длину её наибольшей возрастающей подпоследовательности.
mod - операция вычисления остатка от деления
Входные данные
Программа получает на вход пять целых чисел: длину последовательности n (1≤n≤105), начальный элемент последовательности a1, параметры k, b, m для вычисления последующих членов последовательности (1≤m≤104, 0≤k<m, 0≤b<m, 0≤a1<m).
Выходные данные
Требуется вывести длину наибольшей возрастающей подпоследовательности данной последовательности.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5 41 2 1 100
|
3
|
| |
![]()
|
|
По крышам!
Динамическое программирование
Динамическое программирование
Структуры данных
В городе будущего Иннополис еще во всю идет стройка, но уже сейчас построено n зданий. Крышу каждого здания можно представить как прямоугольник со сторонами, параллельными осям координат. Никакие здания не касаются и не пересекаются.
Инна любит гулять по крышам. Она стоит на крыше здания с номером 1 и хочет попасть на крышу здания с номером n.
Инну можно представить как точку на плоскости. Она может перемещаться по крыше, не выходя за ее границы, но не может находиться на границе крыши. Также она умеет прыгать с крыши на крышу, но только в направлениях, параллельных осям координат. В целях безопасности Инна не может перепрыгивать здания, то есть в любой момент прыжка под ней не должно находиться здание.
Помогите Инне посчитать, какое минимальное количество раз она должна прыгнуть с одной крыши на другую, чтобы попасть на здание с номером n.
Формат входных данных
В первой строке задано натуральное число n — число зданий в Иннополисе (n<= 105). В следующих n строках заданы крыши зданий. Каждая из этих строк содержит четыре целых числа xi1, yi1, xi2 и yi2 — координаты противоположных вершин прямоугольника, описывающего крышу здания (xi1 < xi2; yi1 < yi2) Гарантируется, что никакие два прямоугольника не имеют общих точек. Все координаты — неотрицательные целые числа и <= 109
Формат выходных данных
Выведите одно целое число — минимальное количество прыжков, которые Инна должна совер- шить, чтобы добраться с крыши здания 1 до крыши здания n. Если же Инна не может добраться до крыши n-го здания, выведите -1.
| Ввод |
Вывод |
4
0 0 3 2
1 6 4 8
1 3 4 5
7 7 10 9 |
3 |
3
0 0 3 2
1 3 4 5
7 7 10 9 |
-1 |
| |
![]()
|
|
По крышам!
Динамическое программирование
Динамическое программирование
Структуры данных
В городе будущего Иннополис еще во всю идет стройка, но уже сейчас построено n зданий. Крышу каждого здания можно представить как прямоугольник со сторонами, параллельными осям координат. Никакие здания не касаются и не пересекаются.
Инна любит гулять по крышам. Она стоит на крыше здания с номером 1 и хочет попасть на крышу здания с номером n.
Инну можно представить как точку на плоскости. Она может перемещаться по крыше, не выходя за ее границы, но не может находиться на границе крыши. Также она умеет прыгать с крыши на крышу, но только в направлениях, параллельных осям координат. В целях безопасности Инна не может перепрыгивать здания, то есть в любой момент прыжка под ней не должно находиться здание.
Помогите Инне посчитать, какое минимальное количество раз она должна прыгнуть с одной крыши на другую, чтобы попасть на здание с номером n.
Формат входных данных
В первой строке задано натуральное число n — число зданий в Иннополисе (n<= 105). В следующих n строках заданы крыши зданий. Каждая из этих строк содержит четыре целых числа xi1, yi1, xi2 и yi2 — координаты противоположных вершин прямоугольника, описывающего крышу здания (xi1 < xi2; yi1 < yi2) Гарантируется, что никакие два прямоугольника не имеют общих точек. Все координаты — неотрицательные целые числа и <= 109
Формат выходных данных
Выведите одно целое число — минимальное количество прыжков, которые Инна должна совер- шить, чтобы добраться с крыши здания 1 до крыши здания n. Если же Инна не может добраться до крыши n-го здания, выведите -1.
| Ввод |
Вывод |
4
0 0 3 2
1 6 4 8
1 3 4 5
7 7 10 9 |
3 |
3
0 0 3 2
1 3 4 5
7 7 10 9 |
-1 |
| |
![]()
|
|
Билеты в театр
Динамическое программирование
Динамическое программирование: два параметра
Не так давно в городе будущего Иннополис достроили первый театр. После тяжелой рабочей недели студенты университета решили сходить в театр. Утром они приехали к открытию кассы театра, чтобы успеть купить билеты. Билет в театр стоит 100 рублей.
Оказалось, что у каждой девочки есть ровно одна банкнота номиналом 100 рублей, а у каждого мальчика — номиналом 1000 рублей. До ребят еще никто не успел купить билет, поэтому касса пуста. Это значит, что кассир выдает сдачу только теми банкнотами, которые получил от других ребят, стоявших раньше в очереди. Кассир обслуживает всех по очереди и не начинает обслуживать следующего человека, если еще не продал билет или не выдал требуемую сдачу предыдущему.
Ребята начали выстраиваться в очередь таким образом, чтобы каждый мог купить билет. Пока они думали, как создать такую очередь, кассир задался вопросом, а сколько всего существует спосо- бов расставить девочек и мальчиков так, чтобы каждый смог купить билет. Помогите ему ответить на этот вопрос.
Способы считаются различными, если существует такое место в очереди, что в одном из них на этом месте стоит девочка, а в другом — мальчик.
Формат входных данных
В первой строке задано два целых неотрицательных числа n и m, где n — количество девочек, m — количество мальчиков (1<= n + m < 104).
Формат выходных данных
Выведите остаток от деления числа способов расставить студентов в очередь, чтобы все смогли купить билет, на 109 + 7.
| Ввод |
Вывод |
| 18 2 |
10 |
| 8 1 |
0 |
| 12 1 |
4 |
| |
![]()
|
|
Кристаллы максимуса
Динамическое программирование
Динамическое программирование: последовательности
Задача о рюкзаке
 Максимус очень любит коллекционировать кристаллы. Среди всех кристаллов у него есть один самый любимый с магической силой равной Максимус очень любит коллекционировать кристаллы. Среди всех кристаллов у него есть один самый любимый с магической силой равной n. Также у него есть коллекция совершенных кристаллов. Совершенный кристалл - это кристалл, магическая сила которого равна квадрату натурального числа.
У Максимуса выдался свободный вечер, и он задумался: сколько нужно ему совершенных кристаллов, чтобы сумма их магических сил равнялась бы магической силе его любимого кристалла?
Квадратом натурального числа является число, которое получается умножением натурального числа на себя. Например, 1, 4 и 9 - это квадраты натуральных чисел, а 2, 3 и 5 - нет.
Ваша задача - помочь Максимусу найти минимальное количество совершенных кристаллов, сумма магических сил которых равна n.
Входные данные
Программа получает на вход натуральное число n (n < 104).
Выходные данные
Выведите ответ на задачу.
Примеры
| № |
Входные данные |
Выходные данные |
Примечание |
| 1 |
12
|
3
|
12 = 4 + 4 + 4 |
| 2 |
13 |
2 |
13 = 4 + 9 |
| |
![]()
|
|
Магическая подпоследовательность Айвена
Динамическое программирование
Динамическое программирование: последовательности
Юный волшебник Айвен считает последовательность символов магической, если она является палиндромом (то есть читается одинаково как слева направо, так и справа налево). Айвену попалась в руки последовательность символов s. Он хочет удалить из нее любое (возможно нулевое) количество символов, чтобы получить из нее самую длинную магическую подпоследовательность.
Определите длину самой длинной магической подпоследовательности, которую сможет получить Айвен.
Входные данные
Программа получает на вход последовательность символов s (1<= |s| <= 1000), состоящую из строчных английских букв.
Выходные данные
Выведите одно число - длину самой длинной магической подпоследовательности.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
bbbab
|
4
|
| |
![]()
|
|
Сумма фишек
Динамическое программирование
Задача о рюкзаке
Задача о рюкзаке
Алиса и Громозека играют в фишки по следюущим правилам. Громозека загадывает определенное число, а Алиса должна использовать свои фишки, чтобы составить сумму, равную этому числу. У Алисы есть фишки, на каждой из которых записано определенное число. Алиса имеет неограниченный запас фишек с каждым числом. Если Алиса сможет составить нужную сумму, используя свои фишки, она победит.
Ваша задача - определить, сможет ли Алиса победить Громозеку и если да, то сколько различных комбинаций у нее есть для достижения победы. Если Алиса не сможет победить Громозеку, то вы должны вывести число 0.
Входные данные
Программа получает в первой строке два числа: n - количество различных чисел, которые записаны на фишках, num - число, которое загадал Громозека. Во второй строке записаны n различных чисел ci - числа, каждое из которых может быть записано на фишке. На каждой фишке записано только одно число из набора чисел ci. При этом, количество фишек с числом ci не ограниченно. Все фишки с одинаковым числом, считаются одинаковыми. Другими словами, комбинация фишек 2+1 и 1+2 считается одной комбинацией.
Ограничения
1 <= n <= 3001 <= ci <= 5000- Все значения
ci уникальны.
0 <= num <= 5000
Выходные данные
Выведите одно число - количество комбинаций, которым Алиса может выиграть Громозеку. Если Алиса не может выиграть, то выведите на экран 0.
Примечание
В первом примере есть 4 способа набрать сумму, равную 5:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
| |
![]()
|
|
Айвен собирает кристаллы
Динамическое программирование
Задача о рюкзаке
Юный волшебник Айвен отправляется в волшебный лес, чтобы набрать волшебных кристаллов. Каждый кристалл, растущий в данном лесу, обладает своей массой. Айвен имеет рюкзак, который может выдержать определенный вес M. Айвен хочет использовать свой рюкзак по максимуму и набрать кристаллов такое количество, чтобы суммарно их вес равнялся в точности весу, который может выдержать его рюкзак.
Вам стали известны массы кристаллов, которые растут в волшебном лесу. Выведите "YES", если Айвен сможет набрать кристаллов суммарным весом ровно M, иначе выведите "NO".
Входные данные
В первой строке вводится натуральное число N, не превышающее 100 и натуральное число M, не превышающее 104. Во второй строке вводятся N натуральных чисел mi, не превышающих 100.
Выходные данные
Выведите YES или NO.
| |
![]()
|
|
Фишки-палочки
Динамическое программирование
Динамическое программирование: последовательности
Алиса и Громозека играют в фишки-палочки. У каждого из них есть набор фишек, на каждой фишке записано одно целое число. Каждый из них выкладывает свои фишки вдоль двух параллельных горизонтальных линий. Следующим шагом Алиса соединяет палочкой две фишки, расположенные на разных горизонтальных линиях, то есть соединяет одну свою фишку с одной из фишек Громозеки по следующим правилам:
- числа, на фишке Алисы и на фишке Громозеки равны;
- соединяющая палочка не должна пересекать другие палочки;
- две палочки не могут указывать на одну и ту же фишку.
Далее, Громозека считает сколько палочек выложила Алиса. После этого, Алиса убирает свои палочки и фишки соединяет Громозека по тем же правилам. Выигрывает тот, кто выложит по данным правилам больше всего палочек.
Вас, как наблюдателя за этой игрой, просят определить максимальное количество палочек, которые можно выложить по указанным правилам.
Входные данные
Первая строка входных данных содержит число n - количество фишек Алисы. Вторая строка содержит n чисел nums1i - числа на фишках Алисы, в том порядке, в котором она их выложила. Третья строка содержит число m - количество фишек Громозеки. Четвертая строка содержит m чисел nums2j - числа на фишках Громозека, в том порядке, в котором он их выложил.
Ограничения
1 <= n, m <= 5001 <= nums1[i], nums2[j] <= 2000
Выходные данные
Выведите одно число - максимальное количество палочек, которые можно выложить по указанным в условии задачи правилам игры.
Примечание
Рисунок к первому тестовому примеру
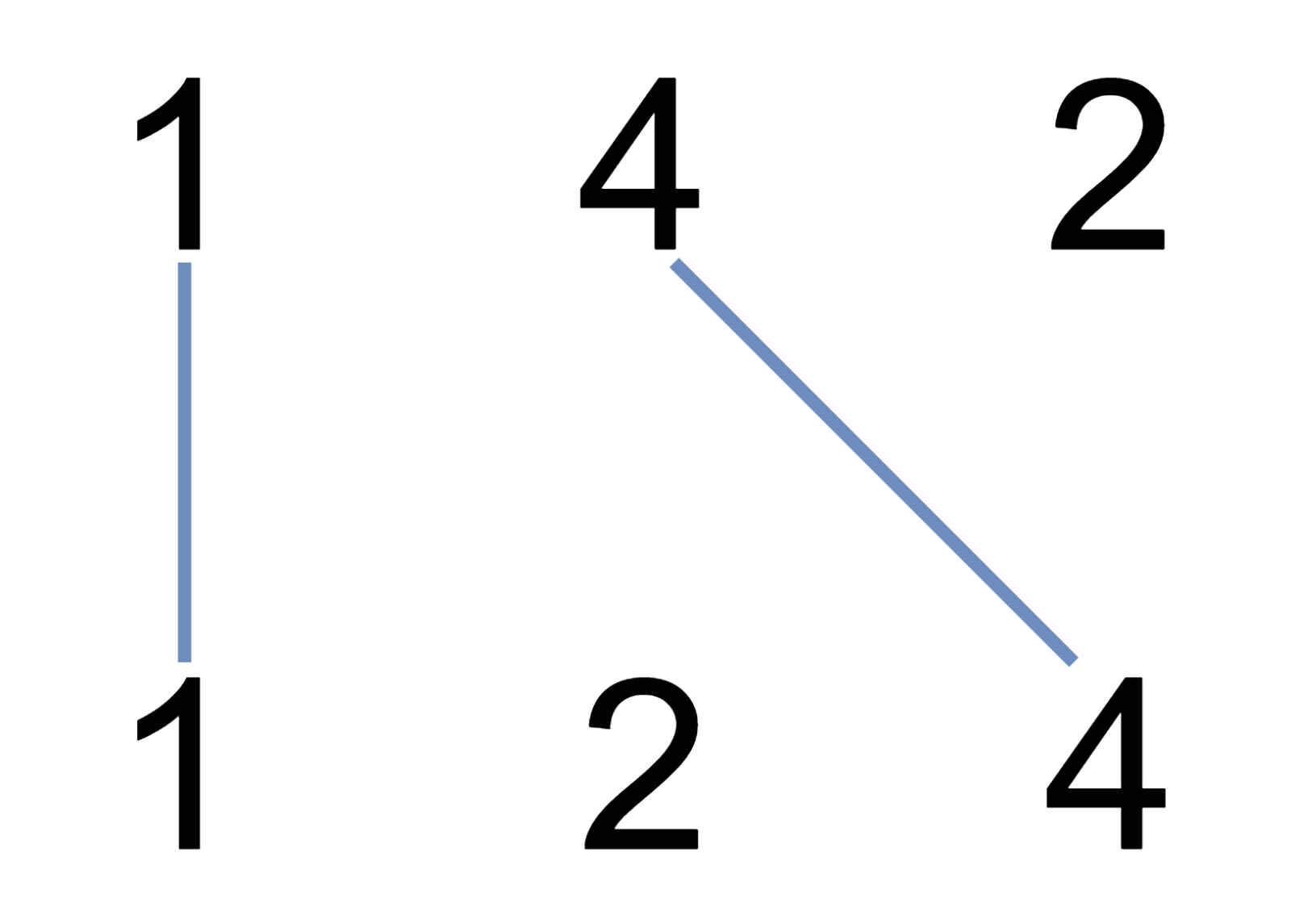
| |
![]()
|
|
Palindromic Paths
Строки
Динамическое программирование
Динамическое программирование: два параметра
Комбинаторика
Ферма Джона представлена решёткой N×N полей (1≤N≤500). Каждое поле представлено символом латинского алфавита. Например:
ABCD
BXZX
CDXB
WCBA
Каждый день корова Беси прогуливается из верхнего левого угла в правый нижний, каждый раз двигаясь на один шаг вправо или вниз. Беси записывает в строку буквы, по которым прошлась. Она огорчится, если у неё получится палиндром (слово, которое читается одинаково слева направо и справа налево), поскольку тогда она запутается, в каком направлении двигалась.
Пожалуйста, помогите Беси определить количество различных маршрутов которыми она может получить палиндромы. Различные пути, которыми получаются одинаковые палиндромы учитывать множество раз. Выведите свой ответ по модулю 1,000,000,007.
ФОРМАТ ВВОДА:
Первая строка ввода содержит N, и последующие N строк содержат N строк решётки, описывающей поля. Каждая строка содержит N символов в интервале A..Z.
ФОРМАТ ВЫВОДА:
Выведите количество различных путей Беси, формирующих палиндромы по модулю 1,000,000,007.
| Ввод |
Вывод |
|
4
ABCD
BXZX
CDXB
WCBA
|
12 |
Беси может сделать следующие палиндромы:
1 x "ABCDCBA"
1 x "ABCWCBA"
6 x "ABXZXBA"
4 x "ABXDXBA"
| |
![]()
|
|
Trapped in the Haybales
Динамическое программирование
Динамическое программирование: один параметр
Структуры данных
Дерево отрезков, RSQ, RMQ
Фермер Джон получили груз из N больших стогов сена (1≤N≤100,000), и разметил их в различных положениях вдоль дороги, ведущей к амбару. К несчастью, он полностью забыл, что корова Беси пасётся вдоль дороги и может попасть в ловушку между стогами сена.
Каждый стог j имеет размер Sj и позицию Pj определяющую его положение вдоль дороги. Беси может двигаться вдоль дороги вплоть до позиции стога, но не может пересечь эту позицию. Исключение – если она прошла в этом направлении D единиц расстояния, тогда она набрала достаточно скорости, чтобы протаранить стог любого размера строго меньше чем D. Конечно после этого она может продолжить движение и таранить другие стога.
Беси может выйти на свободу если она в конце концов протаранит протаранит самый левый или самый правый стог. Вычислите общий размер участка дороги, состоящий из возможных точек старта Беси, из которых она не сможет выбраться.
ФОРМАТ ВООДА:
Первая строка ввода содержит N. Каждая из последующих N строк описывает стог, и содержит два целых числа определяющих размер и позицию в диапазоне 1…109. Все позиции различны.
ФОРМАТ ВЫВОДА:
Выведите одно целое число – размер области дороги, откуда Беси не сможет выбраться.
| Ввод |
Вывод |
|
5
8 1
1 4
8 8
7 15
4 20
|
14 |
| |
![]()
|
|
Cow Hopscotch
Динамическое программирование
Динамическое программирование: один параметр
Динамическое программирование: два параметра
Комбинаторика
Фермер Джон придумал игру для своих коров
Она играется на решётке R*C (2 <= R <= 750, 2 <= C <= 750), где каждый квадрат помечен целым числом от 1 до K (1 <= K <= R*C). Коровы выполняют последовательность прыжков, начиная в левом верхнем квадрате и заканчивая в правом нижнем квадрате и прыжок является корректным если и только если:
1) Вы прыгаете на квадрат c другим числом
2) Квадрат, куда Вы прыгаете, как минимум на одну строку ниже квадрата, в котором Вы сейчас стоите
3) Квадрат, в который Вы прыгаете как минимум на одну колонку правее квадрата, в котором Вы сейчас стоите
Пожалуйста, помогите коровам вычислить количество возможных различных последовательностей корректных прыжков из левого верхнего квадрата в правый нижний.
INPUT FORMAT:
Первая строка ввода содержит целые числа R, C, K. Каждая из следующих R строк содержит C целых чисел, каждое в интервале 1..K.
OUTPUT FORMAT:
Выведите количество различных способов пропрыгать из левого верхнего угла в правый нижний, по модулю 1000000007.
| Ввод |
Вывод |
|
4 4 4
1 1 1 1
1 3 2 1
1 2 4 1
1 1 1 1
|
5 |
| |
![]()
|
|
Cow Curling
Динамическое программирование
Вычислительная геометрия
Структуры данных
В коровий кёрлинг вовлечены две команды, каждая из которых двигает N тяжёлых камней (3 <= N <= 50,000) по льду. В конце игры имеется 2N камней на льду, каждый из которых расположен в различной точке
плоскости.
Подсчёт очков в коровьем кёрлинге ведётся следующим образом:
Камень считается «захваченным», если он содержится внутри треугольника, по углам которого находятся камни противника (камень, который находится на границе такого треугольника, также считается захваченным). Счёт команды есть количество камней команды противника, которые «захвачены».
Вычислите финальный счёт матча по коровьему кёрлингу, по заданному расположению всех камней.
INPUT FORMAT:
* Строка 1: Целое число N.
* Строки 2..1+N: Каждая строка содержит 2 целых числа, указывающих x и y координаты камня команды A (каждая координата лежит в диапазоне -40,000 .. +40,000).
* Строки 2+N..1+2N: Каждая строка содержит 2 целых числа, указывающих x и y координаты камня команды B (каждая координата лежит в диапазоне -40,000 .. +40,000).
OUTPUT FORMAT:
* Строка 1: Два разделённых пробелом целых числа, представляющих счета команд A и B
SAMPLE:
| Ввод |
Вывод |
4
0 0
0 2
2 0
2 2
1 1
1 10
-10 3
10 3 |
1 2 |
INPUT DETAILS:
У каждой команды по 4 камня.
Команда A имеет камни (0,0), (0,2), (2,0), (2,2).
Команда B имеет камни (1,1), (1,10), (-10,3), (10,3).
OUTPUT DETAILS:
Команда A захватила камень противника в точке (1,1).
Команда B захватила камни противника в точках (0,2) и (2,2).
| |
![]()
|
|
Circular Barn
Рекурсия
Динамическое программирование
Динамическое программирование: два параметра
Задача на реализацию
У Фермера Джона круглый амбар. Амбар состоит из кольца из n комнат, пронумерованных 1…n по периметру (3≤n≤1,000). Каждая комната имеет двери в две соседние комнаты и одну дверь во внешний мир.
ФД хочет разместить ровно ri коров в комнате i (1≤ri≤1,000,000). Он планирует открыть k внешних дверей (1≤k≤7), через которые коровы будут входить в амбар. Каждая корова затем идёт по часовой стрелке, пока не добредёт до нужной комнаты. ФД хочет открыть двери так, чтобы все коровы вместе прошли как можно меньшее расстояние. Коровы предварительно могут собраться как им выгоднее перед этими незакрытыми дверями (эти перемещения не входят в общее расстояние, учитываемое в задаче). Определите минимальное суммарное расстояние, которое придётся пройти коровам, если ФД наилучшим образом выберет какие k открыть.
ФОРМАТ ВВОДА:
Первая строка ввода содержит n и k. Последующие n строк содержат r1…rn.
ФОРМАТ ВВОДА:
Выведите минимальное суммарное расстояние пройденное коровами.
| Ввод |
Вывод |
|
6 2
2
5
4
2
6
2
|
14 |
ФД может открыть двери 2 и 5. 11 коров войдут в двери 2 и пройдут суммарное расстояние 8 чтобы попасть в комнаты 2,3,4. 10 коров войдут в дверь 5 и пройдут общее расстояние 6, чтобы попасть в комнаты 5,6,1.
| |
![]()
|
|
Ноутбук за печеньки
Одномерные массивы
Порядковые статистики
Использование сортировки
Динамическое программирование
Динамическое программирование: один параметр
Летовец обладает неудивительными математическими способностями. Его способности на столько велики, что он легко может просчитать стоимость его любимых печенек, которые продаются на другом конце города. К сожалению, Летовец не может по максимуму воспользоваться всеми своими способностями, потому что вчера у него сломался ноутбук и теперь он не может писать программы.
Чтобы купить себе новый ноутбук, Летовец решил потратить все свои карманные деньги (а это всего лишь 10 рублей) на покупку своих любимых печенек, а чуть позже, продать все купленные им печеньки.
Так как Летовец еще несовершеннолетний и один ездить на другой конец города не может, ему нужно понять, в какие из двух дней попросить маму отвезти его на другой конец города. Мама всегда готова ему помочь.
Отсутствие ноутбука очень угнетает юного Летовца, поэтому он просит вас определить эти два дня в ближайшие N дней.
Формат входных данных
В первой строке записано число N (2 <= N <= 100000) количество дней, на которые Летовец делает прогноз. Вторая строка содержит N целых положительных чисел ai (1 <= i <= N , 1 <= ai <= 5000 ), где ai - предсказанная стоимость печенек в i-й день.
Формат выходных данных
Выведите два числа: первое число - номер дня, в который Летовей поедет покупать печеньки, второе - номер дня, в который он поедет продавать печеньки. В случае, если таких вариантов дней несколько, выведите любой из них. Если Летовец в итоге не сможет получить прибыль ни при каких вариантах, то выведите два нуля.
| |
![]()
|
|
Пазл
Динамическое программирование
Динамическое программирование
Паросочетания
Жадный алгоритм
Участникам, использующим язык Python3, рекомендуется отправлять решения на проверку с использованием интерпретатора PyPy3.
Школьники Алиса и Ибрагим — лучшие друзья. У Ибрагима скоро день рождения, и по этому поводу Алиса решила подарить ему новый пазл. Пазл можно представить в виде матрицы из \(2\) строк и \(n\) столбцов, каждый элемент которой \(0\) или \(1\). За один ход можно поменять местами два элемента, стоящие в соседних клетках.
Более формально, будем считать, что строки матриц пронумерованы сверху вниз от \(1\) до \(2\), а столбцы — слева направо от \(1\) до \(n\). Обозначим клетку на пересечении строки \(x\) и столбца \(y\) за \((x, y)\). Будем считать две клетки \((x_1, y_1)\) и \((x_2, y_2)\) соседними, если \(|x_1 - x_2| + |y_1 - y_2| = 1\).
Алисе не нравится, какой рисунок образуют клетки пазла в данный момент. Она придумала свой рисунок, с которым и планирует подарить Ибрагиму новый пазл, но для этого нужно привести пазл в соответствующее состояние.
В конце учебного года у Алисы очень плотное расписание, и она не хочет тратить на эту задачу много времени. Помогите Алисе найти минимальное количество ходов, за которое она может получить свой рисунок, или скажите, что это невозможно.
Формат входных данных
В первой строке вводится одно целое число \(n\) (\(1 \leq n \leq 200\,000\)) — количество столбцов в пазле.
Следующие две строки описывают рисунок, образованный пазлом в данный момент. В каждой строке вводятся \(n\) целых чисел, каждое из которых равно \(0\) или \(1\).
Следующие две строки описывают желаемый рисунок Алисы в том же формате.
Формат выходных данных
Если Алиса не ошиблась и её рисунок можно получить, найдите и выведите минимальное необходимое количество ходов, иначе выведите \(-1\).
В первом примере из условия подойдет следующая последовательность обменов:
\((2, 1), (1, 1)\)
\((1, 2), (1, 3)\)
\((2, 2), (2, 3)\)
\((1, 4), (1, 5)\)
\((2, 5), (2, 4)\)
Можно показать, что меньшим числом обменов обойтись нельзя, поэтому ответ равен \(5\).
Во втором примере из условия никакая последовательность ходов не приводит пазл к нужному виду.
| |
![]()
|
|
Пазл
Динамическое программирование
Динамическое программирование
Паросочетания
Жадный алгоритм
Участникам, использующим язык Python3, рекомендуется отправлять решения на проверку с использованием интерпретатора PyPy3.
Школьники Алиса и Ибрагим — лучшие друзья. У Ибрагима скоро день рождения, и по этому поводу Алиса решила подарить ему новый пазл. Пазл можно представить в виде матрицы из \(2\) строк и \(n\) столбцов, каждый элемент которой \(0\) или \(1\). За один ход можно поменять местами два элемента, стоящие в соседних клетках.
Более формально, будем считать, что строки матриц пронумерованы сверху вниз от \(1\) до \(2\), а столбцы — слева направо от \(1\) до \(n\). Обозначим клетку на пересечении строки \(x\) и столбца \(y\) за \((x, y)\). Будем считать две клетки \((x_1, y_1)\) и \((x_2, y_2)\) соседними, если \(|x_1 - x_2| + |y_1 - y_2| = 1\).
Алисе не нравится, какой рисунок образуют клетки пазла в данный момент. Она придумала свой рисунок, с которым и планирует подарить Ибрагиму новый пазл, но для этого нужно привести пазл в соответствующее состояние.
В конце учебного года у Алисы очень плотное расписание, и она не хочет тратить на эту задачу много времени. Помогите Алисе найти минимальное количество ходов, за которое она может получить свой рисунок, или скажите, что это невозможно.
Формат входных данных
В первой строке вводится одно целое число \(n\) (\(1 \leq n \leq 200\,000\)) — количество столбцов в пазле.
Следующие две строки описывают рисунок, образованный пазлом в данный момент. В каждой строке вводятся \(n\) целых чисел, каждое из которых равно \(0\) или \(1\).
Следующие две строки описывают желаемый рисунок Алисы в том же формате.
Формат выходных данных
Если Алиса не ошиблась и её рисунок можно получить, найдите и выведите минимальное необходимое количество ходов, иначе выведите \(-1\).
В первом примере из условия подойдет следующая последовательность обменов:
\((2, 1), (1, 1)\)
\((1, 2), (1, 3)\)
\((2, 2), (2, 3)\)
\((1, 4), (1, 5)\)
\((2, 5), (2, 4)\)
Можно показать, что меньшим числом обменов обойтись нельзя, поэтому ответ равен \(5\).
Во втором примере из условия никакая последовательность ходов не приводит пазл к нужному виду.
| |
![]()
|
|
Мониторинг труб
Строки
Динамическое программирование
Алгоритмы на графах
Деревья
Газораспределительная система одного региона устроена следующим образом. Она
содержит n узлов, пронумерованных от 1 до n, некоторые узлы соединены односторонними
трубами. Узел с номером 1 соответствует центральному газохранилищу.
Система узлов описывается числами от p2, p3, …, pn. Для всех i от 2 до n узел с
номером pi соединен односторонней трубой с узлом i, газ по этой трубе передается от узла pi
к узлу i. Известно, что возможно доставить газ по трубам от центрального газохранилища до
любого узла системы (возможно, с использованием промежуточных узлов). В системе
используются трубы различных типов, тип трубы обозначается буквой английского алфавита
от «a» до «z». Труба, соединяющая узел pi с узлом i, имеет тип ci.
Для проверки качества труб используется специальный робот. Он помещается в
систему труб в одном из узлов и перемещается по трубам, каждый раз проверяя трубу, по
которой он перемещается. Робот может перемещаться по трубам только в том же
направлении, в котором по трубе передается газ. Совершив одно или несколько
перемещений по трубам между узлами, робот извлекается из системы труб.
Каждый запуск робота должен соответствовать одной из m заданных спецификаций,
пронумерованных от 1 до m. Спецификация с номером t представляет собой строку st,
состоящую из строчных букв английского алфавита. Запуск соответствует спецификации st,
если количество перемещений робота по трубам во время запуска совпадает с длиной st, и
для всех j от 1 до длины st на j-м шаге робот перемещается по трубе, тип которой совпадает с
st[j] —символом на позиции j в спецификации.
Если запуск робота соответствует спецификации с номером t, то стоимость этого
запуска составляет wt. Оператору системы необходимо проверить все трубы, для этого
можно запускать робот несколько раз. Каждый раз выбирается спецификация и маршрут
робота по трубам, соответствующие выбранной спецификации. Необходимо проверить все
трубы так, чтобы суммарная стоимость запусков робота для проверки качества труб была
минимальна. Одну и ту же трубу можно проверять несколько раз.
Требуется написать программу, которая по описанию системы труб и списку
спецификаций определяет минимальную суммарную стоимость запусков робота, в
результате которых все трубы будут проверены, а также список необходимых для этого
запусков (по требованию).
Формат входных данных
В первой строке входных данных находятся три целых числа n, m и t — количество
узлов системы труб, количество спецификаций запусков робота и параметр, указывающий,
требуется ли вывести список запусков робота или только их минимальную суммарную
стоимость (1 ≤ n ≤ 500, 1 ≤ m ≤ 105, t равно 0 или 1).
В последующих (n – 1) строках содержится информация о трубах, (i – 1)-я из этих
строк содержит разделенные пробелом значения pi и ci, где pi — целое число, задающее
номер узла, из которого ведет труба в i-й узел, а ci — строчная буква английского алфавита,
задающая тип этой трубы (1 ≤ pi ≤ i – 1).
В последующих m строках содержится информация о спецификациях, i-я из этих
строк содержит разделенные пробелом целое число wi — стоимость запуска робота в
соответствии с этой спецификацией, и состоящую из строчных букв английского алфавита
строку si — саму спецификацию (1 ≤ wi ≤ 10 9). Суммарная длина строк si не превышает 10 6.
Формат выходных данных
Первая строка выходных данных должна содержать одно число — минимальную
суммарную стоимость запусков робота, в результате которых все трубы будут проверены.
Если проверить все трубы невозможно, требуется вывести «–1».
Если t = 0, то больше ничего выводить не требуется.
Если t = 1 и проверить трубы возможно, то далее следует вывести список описаний
запусков робота. В этом случае вторая строка выходных данных должна содержать
число k — количество запусков робота, которое необходимо выполнить для проверки труб. В
следующих k строках необходимо вывести по три целых числа ai, bi и ci — номер узла, в
котором начинается запуск, номер узла, в котором заканчивается запуск, и номер
спецификации, которой соответствует запуск.
Если оптимальных способов проверки несколько, требуется вывести любой из них.
| Ввод |
Вывод |
|
3 3 0
1 a
2 b
3 a
4 b
2 a
|
6 |
|
7 3 1
1 a
2 a
3 b
3 b
1 b
6 b
3 aab
5 b
2 ab
|
15
4
1 4 1
2 5 3
1 6 2
6 7 2
|
Пояснение к примеру
Система труб, заданная во втором примере входных данных, и оптимальный способ
проверки всех труб для этого случая приведены на рисунке ниже.
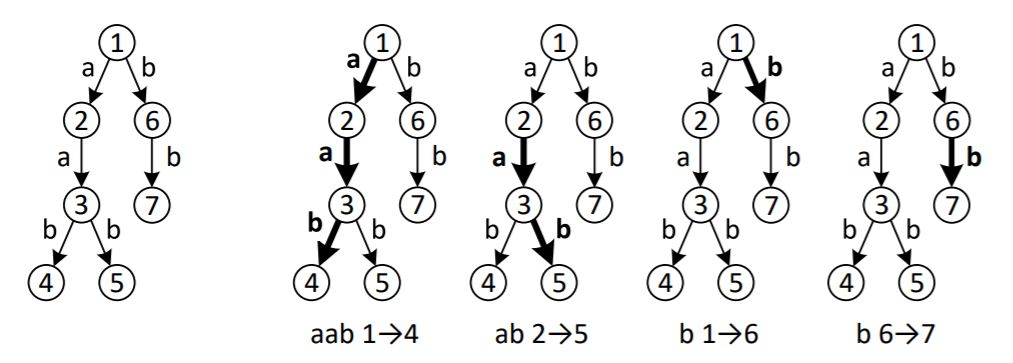
Необходимо обратить внимание на следующие моменты:
- трубу можно проверять несколько раз, так в приведенном примере дважды
проверена труба из узла 2 в узел 3;
- одну и ту же спецификацию разрешается использовать несколько раз, в
приведенном примере вторая спецификация используется дважды, для
проверки труб из узла 1 в узел 6 и из узла 6 в узел 7;
- робот может перемещаться по трубам только в том же направлении, по
которому по трубе передается газ, спецификацию «ab» нельзя использовать
для проверки труб по маршруту 2→1→6, так как робот не может
переместиться из узла 2 в узел 1.
| |
![]()
|
|
Красота фейерверка
Динамическое программирование
Динамическое программирование
Динамическое программирование на поддеревьях
Обход в глубину
Применение обхода в глубину
В лаборатории теоретической пиротехники изучают новые технологии организации
фейерверков. Фейерверк представляется как корневое дерево, а поскольку в мощном
фейерверке его элементы также взрываются, порождая новые фейерверки, то ученые вводят
операцию возведения корневого дерева в степень.
Корневое дерево содержит одну или несколько вершин. Одна из вершин выделена и
называется корнем дерева, для каждой из остальных вершин ровно одна другая вершина
является родителем. При этом от любой вершины можно добраться до корня,
последовательно переходя от вершины к ее родителю. Вершина, которая не является
родителем никакой другой вершины, называется листом. Если вершина x является
родителем вершины y, то вершина y является ребенком вершины x. Будем говорить, что
вершина и ее родитель соединены ребром.
На рис. 1 показан пример корневого дерева с корнем в вершине 1. Родителем вершин
2 и 3 является вершина 1, родителем вершины 4 является вершина 2. Вершины 2 и 3 — дети
вершины 1, а вершина 4 — ребенок вершины 2. Листьями являются вершины 3 и 4.
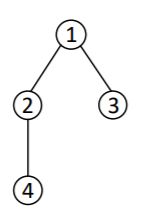
Рис. 1. Пример корневого дерева с корнем в вершине 1, листьями 3 и 4.
Фейерверк задается своим базовым деревом T и мощностью m. Фейерверк представляется деревом, которое получается в результате возведения дерева T в степень m. Операция возведения дерева в степень устроена следующим образом. Если m = 1, то результат T 1 — само дерево T. Для m > 1 рассмотрим дерево T m – 1 . Выполним следующую операцию: для каждого листа x дерева T m – 1 создадим копию дерева T и назначим лист x родителем корня соответствующей копии. Получившееся дерево будет деревом T m .
На рис. 2 показано дерево, представленное на рис. 1, в степенях 1, 2 и 3.
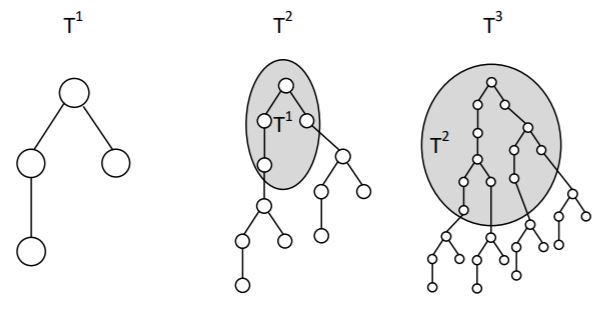
Рис. 2. Пример возведения дерева в степени 1, 2 и 3
Путем в дереве называется последовательность вершин, в которой две соседние
вершины соединены ребром. Все вершины в пути должны быть различны.
Для того, чтобы оценить красоту фейерверка, необходимо определить, какое
максимальное количество вершин может содержать путь в дереве, которым представляется
фейерверк. На рис. 3 приведен путь в дереве T2, содержащий максимальное количество
вершин. Таким образом, красота фейерверка с базовым деревом T и мощностью 2 равна 10.
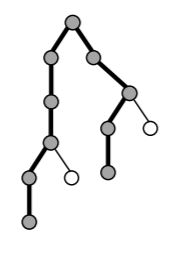
Рис. 3. Путь в дереве T 2 , содержащий максимальное количество вершин.
Требуется написать программу, которая по описанию дерева T и натуральному числу m определяет красоту фейерверка с базовым деревом T и мощностью m.
Формат входных данных
Первая строка входных данных содержит два натуральных числа n и m — количество
вершин в базовом дереве фейерверка T и его мощность (3 ≤ n ≤ 200 000, 1 ≤ m ≤ 200 000).
Вторая строка описывает дерево T и содержит (n – 1) целых чисел: p2, p3, …, pn —
номера родителей вершин 2, 3, …, n, соответственно (1 ≤ pi ≤ i – 1).
Формат выходных данных
Требуется вывести одно целое число — красоту фейерверка, представляемого
деревом Tm.
| |
![]()
|
|
Красота фейерверка
Динамическое программирование
Динамическое программирование
Динамическое программирование на поддеревьях
Обход в глубину
Применение обхода в глубину
В лаборатории теоретической пиротехники изучают новые технологии организации
фейерверков. Фейерверк представляется как корневое дерево, а поскольку в мощном
фейерверке его элементы также взрываются, порождая новые фейерверки, то ученые вводят
операцию возведения корневого дерева в степень.
Корневое дерево содержит одну или несколько вершин. Одна из вершин выделена и
называется корнем дерева, для каждой из остальных вершин ровно одна другая вершина
является родителем. При этом от любой вершины можно добраться до корня,
последовательно переходя от вершины к ее родителю. Вершина, которая не является
родителем никакой другой вершины, называется листом. Если вершина x является
родителем вершины y, то вершина y является ребенком вершины x. Будем говорить, что
вершина и ее родитель соединены ребром.
На рис. 1 показан пример корневого дерева с корнем в вершине 1. Родителем вершин
2 и 3 является вершина 1, родителем вершины 4 является вершина 2. Вершины 2 и 3 — дети
вершины 1, а вершина 4 — ребенок вершины 2. Листьями являются вершины 3 и 4.

Рис. 1. Пример корневого дерева с корнем в вершине 1, листьями 3 и 4.
Фейерверк задается своим базовым деревом T и мощностью m. Фейерверк представляется деревом, которое получается в результате возведения дерева T в степень m. Операция возведения дерева в степень устроена следующим образом. Если m = 1, то результат T 1 — само дерево T. Для m > 1 рассмотрим дерево T m – 1 . Выполним следующую операцию: для каждого листа x дерева T m – 1 создадим копию дерева T и назначим лист x родителем корня соответствующей копии. Получившееся дерево будет деревом T m .
На рис. 2 показано дерево, представленное на рис. 1, в степенях 1, 2 и 3.

Рис. 2. Пример возведения дерева в степени 1, 2 и 3
Путем в дереве называется последовательность вершин, в которой две соседние
вершины соединены ребром. Все вершины в пути должны быть различны.
Для того, чтобы оценить красоту фейерверка, необходимо определить, какое
максимальное количество вершин может содержать путь в дереве, которым представляется
фейерверк. На рис. 3 приведен путь в дереве T2, содержащий максимальное количество
вершин. Таким образом, красота фейерверка с базовым деревом T и мощностью 2 равна 10.

Рис. 3. Путь в дереве T 2 , содержащий максимальное количество вершин.
Требуется написать программу, которая по описанию дерева T и натуральному числу m определяет красоту фейерверка с базовым деревом T и мощностью m.
Формат входных данных
Первая строка входных данных содержит два натуральных числа n и m — количество
вершин в базовом дереве фейерверка T и его мощность (3 ≤ n ≤ 200 000, 1 ≤ m ≤ 200 000).
Вторая строка описывает дерево T и содержит (n – 1) целых чисел: p2, p3, …, pn —
номера родителей вершин 2, 3, …, n, соответственно (1 ≤ pi ≤ i – 1).
Формат выходных данных
Требуется вывести одно целое число — красоту фейерверка, представляемого
деревом Tm.
| |
![]()
|
|
Обработка больших данных
Множества
Динамическое программирование
Структуры данных
В научной лаборатории разрабатывается новая архитектура суперкомпьютера,
позволяющая эффективно обрабатывать большие объемы данных.
Суперкомпьютер имеет 2k ячеек памяти, пронумерованных от 0 до 2k– 1. Отрезком
[L, R] называется последовательность подряд идущих ячеек памяти с номерами от L до R,
включительно.
Некоторые отрезки памяти являются корректными. Отрезок памяти [L, R] является
корректным, если его длина (R – L + 1) равна 2i для некоторого i, а число L делится на 2i.
Например, если k = 3, то ячейки памяти пронумерованы от 0 до 7, а корректными являются
отрезки [0, 7], [0, 3], [4, 7], [0, 1], [2, 3], [4, 5], [6, 7], [0, 0], [1, 1], [2, 2], [3, 3], [4, 4], [5, 5], [6,
6] и [7, 7].
Ключевой операцией в новой архитектуре является операция STORE, которая за одно
действие присваивает одно и то же значение всем ячейкам памяти некоторого корректного
отрезка.
Исходно все ячейки памяти содержат значение 0. В лаборатории планируют запустить
на суперкомпьютере программу обработки данных, но перед её запуском необходимо
инициализировать память определенным образом. А именно: первые с1 ячеек памяти
необходимо заполнить значениями v1, следующие c2 ячеек — значениями v2, и так далее,
последние cn ячеек памяти необходимо заполнить значениями vn, где 1 ≤ vi ≤ m.
Ученым надо выяснить, какое минимальное количество операций STORE необходимо
выполнить, чтобы проинициализировать память требуемым образом.
Например, если k = 3, n = 3, m = 2, c1 = 1, v1 = 1, c2 = 2, v2 = 2, c3 = 5, v3 = 1, то итоговое
содержимое памяти должно быть следующим: [1, 2, 2, 1, 1, 1, 1, 1]. В этом случае для
инициализации памяти достаточно трех операций STORE:
- STORE([0, 7], 1), после этой операции все ячейки памяти содержат значение 1;
- STORE([1, 1], 2), после этой операции содержимое памяти [1, 2, 1, 1, 1, 1, 1, 1];
- STORE([2, 2], 2) , после этой операции содержимое памяти [1, 2, 2, 1, 1, 1, 1, 1],
как и требуется.
Заметим, что операцию STORE([1, 2], 2) выполнить нельзя, потому что [1, 2] не
является корректным отрезком памяти.
Требуется написать программу, которая по заданному содержимому памяти
определяет минимальное количество операций STORE, которое необходимо выполнить для
инициализации памяти заданным образом.
Формат входных данных
Первая строка входных данных содержит три целых числа: k, n и m (0 ≤ k ≤ 30,1 ≤ n ≤ 10
5, 1 ≤ m ≤ 109).
Следующие n строк содержат по два целых числа, i-я из этих строк содержит числа ci
и vi (1 ≤ ci ≤ 2k, 1 ≤ vi ≤ m, c1 + c2 + … + cn = 2k).
Формат выходных данных
Требуется вывести одно целое число – минимальное количество операций STORE,
которое необходимо выполнить для инициализации памяти заданным образом.
| Ввод |
Вывод |
|
3 3 2
1 1
2 2
5 1
|
3 |
| |
![]()
|
|
XOR и сумма
Рекурсия
Битовые операции
Динамическое программирование
Вам дано положительное целое число N (\(1<=N<=10^{18}\)). Найдите количество пар целых чисел u и v (\(0<=u, v<=N\)) таких, что существуют два неотрицательных целых числа a и b, удовлетворяющих \(a\ xor\ b=u\) и \(a+b=v\). Здесь xor обозначает побитовое исключающее ИЛИ. Поскольку ответ может быть очень большим, вычислите его по модулю \(10^9+7\).
Входные данные
На вход подается положительное целое число N (\(1<=N<=10^{18}\)).
Выходные данные
Выведите количество возможных пар целых чисел u и v (\(0<=u, v<=N\)) , по модулю \(10^9+7\).
Примеры
| № |
Входные данные |
Выходные данные |
Пояснения |
| 1 |
3 |
5 |
u=0,v=0 (Пусть a=0,b=0, тогда 0 xor 0=0, 0+0=0)
u=0,v=2 (Пусть a=1,b=1, тогда 1 xor 1=0, 1+1=2)
u=1,v=1 (Пусть a=1,b=0, тогда 1 xor 0=1, 1+0=1)
u=2,v=2 (Пусть a=2,b=0, тогда 2 xor 0=2, 2+0=2)
u=3,v=3 (Пусть a=3,b=0, тогда 3 xor 0=3, 3+0=3) |
| 2 |
1422 |
52277 |
|
| 3 |
1000000000000000000 |
787014179 |
|
| |
![]()
|
|
Непростые разбиения
Рекурсия
Динамическое программирование
Рассмотрим разбиения целого положительного числа \(n\) в сумму целых положительных чисел. Будем называть разбиение непростым, если слагаемые в нем упорядочены по неубыванию, причем среди слагаемых нет простых чисел.
Например, для \(n=5\) существует два непростых разбиения: \(1+1+1+1+1\) и \(1+4\).
Задано число \(n\). Выведите все его непростые разбиения на слагаемые.
Формат входных данных
На вход подается число \(n\) (\(1 \le n \le 70\)).
Формат выходных данных
Выведите все непростые разбиения \(n\) на слагаемые. Слагаемые разделяйте знаком <<+>>. Не выводите пробелы. Разбиения можно вывести в любом порядке.
| |
![]()
|
|
Трамвай
Динамическое программирование
Вася идет из школы домой вдоль проспекта, по которому ходят трамваи. Мама считает, что ему после школы полезно дышать свежим воздухом, поэтому настаивает, чтобы не менее \(K\) метров он прошел пешком. Вася при этом хочет попасть домой как можно быстрее (обязательно выполнив требование мамы).
Вдоль проспекта расположено \(N\) трамвайных остановок, которые находятся в точках \(a_1, a_2, \ldots, a_N\) (все координаты задаются в метрах). Школа находится около 1-й остановки, а дом — около остановки номер \(N\). Мальчик идет пешком со скоростью \(v\) метров в минуту. Трамвай едет со скоростью \(w\) метров в минуту (временем стоянки трамвая на остановках пренебрежем). В нулевой момент времени и далее с интервалом \(T\) минут от первой остановки в сторону Васиного дома отправляются трамваи. Вася выходит из школы также в момент времени 0. Сесть в трамвай и выйти из него можно только на остановке. При этом, если Вася приходит на остановку раньше трамвая, на который хочет сесть, то ему придется подождать, пока тот не подъедет. Вася идет пешком и едет на трамвае только в направлении от школы к дому.
Напишите программу, которая определит, когда Вася сможет оказаться дома.
Формат входных данных
Сначала вводится число \(N\) — количество остановок (\(1 \leqslant N \leqslant 2000\)). Далее заданы координаты остановок \(a_1, a_2, \dots, a_N\) (\(0 \leqslant a_1 < a_2 < \ldots < a_N \leqslant 10^9\)). Далее вводится интервал движения трамваев \(T\) (\(1 \leqslant T \leqslant 2000\)). Затем расстояние, не меньше которого Вася должен пройти пешком \(K\) (\(0 \leqslant K \leqslant 2000\)). Затем заданы скорости Васи \(v\) и трамвая \(w\) (\(1 \leqslant v \leqslant w \leqslant 10\,000\)). Все вводимые числа целые. \(K\) не превышает длины пути от школы до дома.
Формат выходных данных
В первую строку выведите не менее чем с пятью знаками после десятичной точки одно число — минимальное время, когда Вася сможет оказаться дома, пройдя пешком не менее \(K\) метров. Далее нужно вывести информацию о пути Васи. Занумеруем промежутки между соседними остановками числами от 1 до \(N-1\) (то есть промежуток между первой и второй остановками имеет номер 1, между второй и третьей — 2 и так далее). Следующая строка должна содержать количество промежутков, пройденных Васей пешком. Далее выведите номера этих промежутков в возрастающем порядке.
| |
![]()
|
|
Сумма минимумов
Динамическое программирование
У Саши есть блокнот, состоящий из \(n\) листочков, пронумерованных от 1 до \(n\). На \(i\)-м листочке написано целое число \(a_i\).
Аня собирается разорвать блокнот на \(k\) частей, для этого она выбирает \(k-1\) число \(1 \le r_1 < r_2 < \ldots < r_{k-1} < n\) и разрывает блокнот так, что листки с 1 по \(r_1\)-й оказываются в первой части, листки с \((r_1+1)\)-го по \(r_2\)-й оказываются во второй части, и т.д., последняя \(k\)-я часть содержит листки с \((r_{k-1}+1)\)-го по \(n\)-й.
После того, как Аня разорвет блокнот, Саша найдет минимальное число в каждой из получившихся частей и сложит их. Аня хочет разорвать блокнот таким образом, чтобы получившаяся сумма была как можно больше. Помогите ей выбрать способ разорвать блокнот, чтобы максимизировать сумму минимальных значений.
Формат входных данных
Первая строка ввода содержит два числа: \(n\) и \(k\) (\(2 \le k \le n \le 300\)). Вторая строка содержит \(n\) целых чисел: \(a_1, a_2, \ldots, a_n\) (\(1 \le a_i \le 10^9\)).
Формат выходных данных
На первой строке выведите максимальное значение суммы, которое удастся достичь Ане. На второй строке выведите значения \(r_1, r_2, \ldots, r_{k-1}\), которые ей необходимо выбрать. Если вариантов разорвать блокнот, чтобы максимизировать искомую сумму несколько, выведите любой из них.
Примечание
В приведенном примере Аня разорвала блокнот на части \([1, 10, 2]\), \([8]\), \([9]\), \([3, 5, 4]\) и \([7, 6]\). Искомая сумма равна \(1 + 8 + 9 + 3 + 6 = 27\).
| |
![]()
|
|
Сумма
Динамическое программирование
Задано целое положительное число \(n\). Требуется найти число способов представить его в виде суммы нечетных слагаемых. При этом разбиения, отличающиеся только порядком слагаемых, считаются одинаковыми.
Например, число 6 можно представить следующими способами: \(1+1+1+1+1+1\), \(1+1+1+3\), \(3+3\), \(1+5\).
Формат входных данных
На вход подается число \(n\) (\(1 \le n \le 1000\)).
Формат выходных данных
Выведите число способов представить \(n\) в виде суммы нечетных слагаемых.
| |
![]()
|
|
Перевозки
Динамическое программирование
В связи с приближающимся завершением эпидемии коронавируса правительство города Энска приняло решение отправить на южные морские курорты отличников школ города - N отдыхающих.
В авиакомпаниях для перевозки имеются K типов самолётов с различным количеством пассажирских мест (P1, P2,...,Pk). Необходимо решить логистическую задачу: зарезервировать необходимое количество рейсов (R1, R2,...,Rk).
Суммарное количество посадочных мест не может быть меньше, чем количество пассажиров, а общее количество незанятых пассажирских мест (V) должно быть минимальным. Если будет обнаружено несколько вариантов, одинаковых по количеству незанятых мест, то следует выбрать вариант с меньшим общим количеством рейсов самолётов. Если и таких вариантов будет несколько, то нужно вывести любой из них.
Входные данные
в первой строке через пробел записаны 2 натуральных числа N и K, во второй - K натуральных чисел P1 P2 … Pk. N не превышает 10000, K не превышает 20, любое Pi меньше 500.
Выходные данные
в первой строке вывести число V, во второй через пробел вывести R1 R2 … Rk. Порядок количеств рейсов должен соответствовать исходному порядку типов самолётов.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1000 3
300 220 150 |
30 0
0 4 1 |
| 2 |
80 4
100 50 40 30 |
0
0 1 0 1 (вариант - 0 0 2 0) |
| |
![]()
|
|
Наша Таня громко плачет
Задачи на моделирование
Динамическое программирование
Тяжела жизнь системного администратора в крупной компании! То у одного из сотрудников не работает принтер, то у другого отключился интернет. Передохнуть нельзя ни секунды.
Сегодня рабочий день системного администратора Миши начался со звонка секретаря Тани, которая в очередной раз не справилась с редактированием документа. Миша моментально пришёл к Тане и узнал, что в результате ошибки в папке на ее компьютере оказалось n копий документа, над которым она сейчас работает. Других документов в папке нет. Таня просит Мишу удалить лишние копии, чтобы у неё осталась ровно одна копия нужного файла.
Таня работает в операционной системе Bububuntu, в которой есть две команды, позволяющие удалять файлы. Первая команда удаляет один произвольный файл с компьютера. На выполнение этой команды Миша тратит A секунд. Вторая команда рассчитана как раз на случай, подобный Таниному, и позволяет уменьшить количество копий файла в k раз. В силу технический особенностей Bububuntu эта команда работает, только если количество файлов в папке делится на k без остатка. На выполнение этой команды Миша тратит B секунд.
Для решения Таниной проблемы Миша решил по очереди использовать эти команды таким образом, чтобы в конце в папке остался ровно один документ.
У Миши сегодня много других дел, поэтому он хочет справиться с проблемой как можно быстрее. Помогите Мише и скажите, за какое минимальное количество секунд он сможет решить Танину проблему, если будет действовать оптимально.
Входные данные
В первой строке содержится целое число n ( 1 <= n <= 2*109 ) - количество копий документа в папке у Тани.
Во второй строке содержится целое число k ( 1 <= k <= 2*109 ) - количество раз, в которое уменьшает количество файлов вторая команда.
В третьей строке содержится целое число A ( 1 <= A <= 2*109 ) - количество секунд, которое Миша тратит на выполнение первой команды.
В четвёртой строке содержится целое число B ( 1 <= B <= 2*109 ) - количество секунд, которое Миша тратит на выполнение второй команды.
Выходные данные
Выведите единственное число - минимальное количество секунд, которое придётся потратить Мише на решение проблемы.
Примечание
В первом тестовом примере оптимальная стратегия Миши такова:
- За 3 секудны удалить один файл, в результате чего в папке останется 8 файлов. Обратите внимание, что Миша не мог использовать вторую команду, потому что 9 не делится на 2 .
- За 1 секунду уменьшить число файлов в 2 раза. После этой операции в папке останется 4 файла.
- За 1 секунду уменьшить число файлов в 2 раза. После этой операции в папке останется 2 файла.
- За 1 секунду уменьшить число файлов в 2 раза. После этого в папке останется 1 файл и цель Миши будет выполнена.
На выполнение этих четырёх операций Миша потратит 6 секунд. Можно показать, что Миша не сможет удалить лишние файлы меньше, чем за 6 секунд.
Во втором тестовом примере Мише выгодно 4 раза удалить один файл. Так как на одно удаление Миша тратит 2 секунды, на выполнение всего задания Миша потратит 4·2 = 8 секунд. Кроме того, Миша мог бы удалить лишние файлы, один раз воспользовавшись второй командой, но, так как её выполнение занимает 20 секунд, Мише это не выгодно.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
9
2
3
1 |
6 |
| 2 |
5
5
2
20 |
8 |
| 3 |
19
3
4
2 |
12 |
| |
![]()
|
|
Оптимизация акции
Рекурсия
Динамическое программирование
Жадный алгоритм
В сети магазинов <<Мир>> при оплате карточкой Weeza действует акция. При оплате покупки, состоящей не менее чем из \(10\) товаров, плата за самый дешевый товар не берется. Если товаров не меньше 20, то не оплачиваются уже два самых дешевых товара и т.д.
Например, при одновременной покупке \(17\) товаров, покупатель потратит сумму денег равную стоимости только \(16\) самых дорогих из них, а при покупке \(20\) и \(37\) товаров придется заплатить только за \(18\) и \(34\) самых дорогих товара, соответственно.
Миша хочет купить в магазине <<Мир>> \(n\) дисков с альбомами его любимой музыкальной группы. Подобрав подходящие диски, Миша выложил их на ленту в супермаркете в некотором порядке. Так как Миша не только меломан, но и математик, он понял, что ему, возможно, удастся сэкономить, если платить не за все \(n\) товаров одновременно, а разбить их на несколько покупок и оплатить каждую покупку отдельно. Миша решил привлекать к себе как можно меньше внимания и, в частности, не менять порядок товаров на ленте. Таким образом, Миша может только разбивать товары на ленте на группы подряд идущих и платить за каждую группу в отдельности.
Миша, конечно, математик, но вот с арифметикой у него всегда были проблемы. Помогите Мише и скажите, за какую минимальную стоимость он сможет купить \(n\) дисков, разбивая товары на ленте на группы подряд идущих товаров и оплачивая каждую группу отдельно. При этом разные группы могут быть разной длины.
Формат входных данных
В первой строке находится одно число \(n\) (\(1 \leq n \leq 100\,000\)) — количество дисков на ленте.
Следующая строка содержит \(n\) чисел \(a_i\) (\(1 \leq a_i \leq 10^9\)) — стоимости дисков в порядке расположения на ленте.
Формат выходных данных
Выведите наименьшую возможную стоимость покупки всех дисков с учетом акции при оптимальном разбиении дисков на группы.
Примечание
В первом примере Мише в любом случае придется оплатить все диски, так как суммарное количество товаров меньше \(10\).
Во втором тестовом примере оптимально во время первой покупки оплатить первые два диска, а за остальные диски заплатить во время второй покупки. Тогда не придется заплатить за диск стоимостью \(9\).
| |
![]()
|
|
Лабиринт
Динамическое программирование
Конструктив
Маленький Влад решил создать собственную компьютерную игру. Игра будет проходить на карте, состоящей из комнат, соединённых коридорами. По каждому коридору можно будет передвигаться в обе стороны. Кроме того, Влад планирует создать карту, в которой коридоров будет ровно на один меньше, чем комнат, а также между любой парой комнат можно будет пройти, используя только коридоры. Для того, чтобы пройти игру, игроку необходимо выполнять квесты.
Все квесты в игре имеют одинаковую структуру. Пусть на карте расположены \(m\) комнат. Тогда каждый квест задаётся парой комнат \(u\) и \(v\) (\(1 \le u \le v \le m\)). Для прохождения этого квеста игроку нужно переместиться из комнаты \(u\) в комнату \(v\). Для усложнения игры в каждой комнате, через которую пройдёт игрок (включая начальную и конечную комнату) необходимо решить загадку. Влад называет сложностью квеста минимальное количество загадок, которые надо решить, чтобы его пройти. В частности, сложность квеста, у которого начальная и конечная комната совпадает, равна \(1\), а сложность квеста, в котором начальная и конечная комнаты соединены коридором равна \(2\). Также Влад называет квест трудным, если не существует квеста с большей сложностью, чем данный.
Интересностью игры Влад называет количество трудных уровней. Влад решил создать игру с интересностью ровно \(n\). Поскольку Владу сложно придумывать новые загадки, помогите ему составить карту с минимальным числом комнат, которое может быть в игре с интересностью \(n\).
Формат входных данных
В первой строке задано целое число \(n\) (\(1 \le n \le 500\)) — требуемое количество трудных уровней.
Формат выходных данных
В первой строке выведите целое число \(m\) — минимальное количество комнат на карте.
В следующих \(m - 1\) строках выведите через пробел пары целых чисел \(u\) и \(v\), обозначающие коридор, между комнатами \(u\) и \(v\).
Если подходящих карт с минимальным числом комнат несколько, выведите любую из них.
Примечание
В первом примере карта выглядит так:
На этой карте есть 10 квестов. Обозначим за (u, v) квест, который начинается в комнате с номером u и заканчивается в комнате с номером v. Сложность квестов (1, 1), (2, 2), (3, 3) и (4, 4) равна 1, сложность квестов (1, 2), (1, 3) и (1, 4) равна 2, а сложность квестов (2, 3), (2, 4) и (3, 4) равна 3. Таким образом, трудными квестами являются квесты (2, 3), (2, 4) и (3, 4). Трудных квестов 3, значит интересность игры на данной карте равна 3.
Во втором тестовом примере карта выглядит так:
На этой карте есть 4 трудных квеста (2, 5), (2, 6), (3, 5) и (3, 6). Их сложность равна 4.
В третьем тестовом примере карта выглядит так:
На этой карте есть 5 трудных квестов (2, 8), (3, 8), (4, 8), (5, 8), (6, 8) со сложностью 4.
| |
![]()
|
|
Московские гориллы
Динамическое программирование
Зимой обитателям Московского зоопарка очень скучно, в частности, это касается горилл. Вы решили развлечь их и принесли в зоопарк перестановку \(p\) длины \(n\).
Напомним, что перестановкой длины \(n\) называется последовательность целых чисел от \(1\) до \(n\), в которой каждое такое число встречается ровно один раз. Например, последовательности \([3, 1, 2]\) и \([1, 4, 2, 3]\) являются перестановками, а последовательности \([3, 4]\) и \([1, 2, 2, 3]\) нет.
У горилл помимо вашей оказалась и своя перестановка \(q\) длины \(n\). Они предложили вам посчитать количество пар целых чисел \(l, r\) (\(1 \le l \le r \le n\)), таких что \(\operatorname{MEX}([p_l, p_{l+1}, \ldots, p_r])=\operatorname{MEX}([q_l, q_{l+1}, \ldots, q_r])\).
Вы не хотите отказать гориллам, поэтому попытаетесь решить эту задачу.
\(\operatorname{MEX}\) последовательности — это минимальное целое положительное число, отсутствующее в этой последовательности. Например, \(\operatorname{MEX}([1, 3]) = 2\), \(\operatorname{MEX}([5]) = 1\), \(\operatorname{MEX}([3, 1, 2, 6]) = 4\).
Формат входных данных
Первая строка содержит одно целое число \(n\) (\(1 \le n \le 2 \cdot 10^5\)) — длину перестановок.
Вторая строка содержит \(n\) целых чисел \(p_1, p_2, \ldots, p_n\) (\(1 \le p_i \le n\)) — элементы перестановки \(p\).
Третья строка содержит \(n\) целых чисел \(q_1, q_2, \ldots, q_n\) (\(1 \le q_i \le n\)) — элементы перестановки \(q\).
Формат выходных данных
Выведите одно целое число — ответ на задачу.
Обратите внимание, что ответ может быть больше, чем возможное значение 32-битной целочисленной переменной, поэтому необходимо использовать 64-битные целочисленные типы данных (тип int64 в языке Pascal, тип long long в C и C++, тип long в Java и C#). Язык Python будет корректно работать и с типом int.
| |
![]()
|
|
Велепин и маркетинг
Динамическое программирование
Знаменитый писатель Велепин очень продуктивен. Совсем недавно он подписал контракт с известным изданием, и теперь за \(i\)-й год ему нужно написать \(k_i\) романов. Для него это вообще не проблема: он может сколько угодно писать о самураях, космосе, пустоте, насекомых и оборотнях.
У него есть \(n\) постоянных читателей, каждый из которых в \(i\)-й год прочитает один из \(k_i\) романов, выпущенных Велепиным. Читатели очень любят обсуждать новинки, поэтому \(j\)-й из них будет доволен в течение года, если такой же роман, как и он, прочитают как минимум \(a_j\) человек, включая его самого.
Издание, с которым подписал контракт Велепин, очень современно: у него есть возможность контролировать, какое произведение прочитает каждый из поклонников. Оно не хочет издавать романы просто так, поэтому хотя бы один экземпляр каждого романа должен попасть в руки читателя. Издание надеется выиграть награду <<Издание \(q\)-летия>>, поэтому отдел маркетинга хочет узнать, какое максимальное количество постоянных читателей можно сделать довольными в течение каждого года, оптимально распределяя романы между ними. Так как в отделе маркетинга нет никого, кто мог бы это сделать, он обратился к вам за помощью.
Формат входных данных
В первой строке дано одно целое число \(n\) \((2 \leqslant n \leqslant 300\,000)\) — количество постоянных читателей Велепина.
Во второй строке дано \(n\) целых чисел \(a_1, a_2, \ldots, a_n\) \((1 \leqslant a_j \leqslant n)\) — количество людей, которые должны читать тот же роман, что и \(j\)-й, чтобы он был доволен.
В третьей строке дано одно целое число \(q\) (\(1 \leqslant q \leqslant 300\,000\)) — количество лет, которые нужно проанализировать.
В каждой из следующих \(q\) строк дано по одному целому числу \(k_i\) \((2 \leqslant k_i \leqslant n)\) — количество романов, которые Велепин должен написать в \(i\)-й год.
Формат выходных данных
Выведите \(q\) строк, в каждой из них ровно одно число — максимальное количество человек, которые могут быть довольны в \(i\)-й год, если Велепин выпустит \(k_i\) романов.
Примечание
В первом примере в первый год оптимальным является разделение \(1, 1, 1, 2, 2\) (первый роман читают первые три человека, а два последних — второй). Во второй год оптимальным решением является \(1, 1, 2, 2, 3\) (первый роман читает первый и второй человек, второй роман читает третий и четвертый человек, третий роман читает пятый человек). В третий год оптимальным будет разбиение \(1, 2, 2, 4, 3\). Соответственно количество довольных людей по годам будет \(5, 5, 3\).
| |
![]()
|
|
Ребрендинг
Динамическое программирование
sqrt декомпозиция
Костя и Женя — создатели группы <<Бумага>> — после выпуска легендарного альбома решили создать новое музыкальное объединение <<дневные грузчики>>, для этого им нужно найти двух новых людей.
Они пригласили на кастинг \(n\) человек. Кастинг продлится \(q\) дней. В \(i\)-й из дней Костя и Женя хотят найти двух человек на отрезке с \(l_i\) по \(r_i\), которые больше всего подходят их объединению. Так как <<дневные грузчики>> занимаются современным искусством, музыкальные навыки им не важны, и они смотрят лишь на внешние признаки: им хочется, чтобы разница роста двух людей была как можно меньше.
Помогите им, и для каждого дня укажите минимальную разницу роста людей с кастинга на данном отрезке!
Формат входных данных
В первой строке вам дано два числа \(n, q\) (\(2 \leqslant n \leqslant 4 \cdot 10^5, 1 \leqslant q \leqslant 10^6\)) — количество людей, которые пришли на кастинг, а также количество дней кастинга.
Во второй строке вам даны \(n\) чисел \(a_1, a_2, a_3, \ldots, a_n\) (\(1 \leqslant a_i \leqslant n\)) — рост каждого из кандидатов.
Также гарантируется, что все \(a_i\) различны.
В следующих \(q\) строках даны по \(2\) числа \(l_i, r_i\) (\(1 \leqslant l_i < r_i \leqslant n\)) — отрезок людей для рассмотрения в \(i\)-й день кастинга.
Формат выходных данных
Выведите \(q\) строк. В \(i\)-й строке должна быть минимальная разница роста между двумя кандидатами на отрезке в \(i\)-й день кастинга.
Примечание
В первом примере минимальная разность на отрезке \([1, 2]\) составляет \(2\) (\(3 - 1 = 2\)), на отрезке \([2, 3]\) – \(1\), на отрезке \([1, 3]\) также \(1\).
В третьем примере минимальную разность на отрезке \([4, 6]\) составляют числа \(3, 5\) (\(5 - 3 = 2\)). На отрезке \([1, 2]\) минимальную разность имеют числа \(2, 6\) (\(6 - 2 = 0\)). На отрезке \([3, 6]\) минимальную разность имеют числа \(1, 3\) (\(3 - 1 = 2\)). На отрезке \([1, 3]\) минимальную разность образуют числа \(1, 2\) (\(2 - 1 = 1\)).
| |
![]()
|
|
Загадка у костра
Динамическое программирование
Алгоритмы на графах
Комбинаторика
Однажды Юрик оказался в лесу у костра, где собрались \(n\) человек. Оказалось, что некоторые из них знакомы друг с другом. Для удобства пронумеруем людей целыми числами от \(1\) до \(n\). Обозначим как \(d_i\) количество людей, сидящих у костра, с которыми знаком \(i\)-й человек. Неожиданно оказалось, что два человека с номерами \(i\) и \(j\) (\(i \ne j\)) знакомы друг с другом тогда и только тогда, когда \(d_i = d_j\).
Вернувшись домой, Юрик задумался, какое минимальное количество пар людей могли быть знакомы, чтобы выполнялось это условие?
Формат входных данных
Единственная строка содержит одно целое число \(n\) (\(1 \le n \le 5\,000\)) — количество людей.
Формат выходных данных
Выведите одно целое число — минимальное количество пар знакомых людей.
Замечание
Рассмотрим первый пример из условия. Возможны следующие варианты:
-
Любые два человека знакомы друг с другом. В этом случае количество пар знакомых людей равно \(\frac{4 \cdot 3}{2} = 6\).
-
Некоторые три человека попарно знакомы друг с другом, четвертый человек не знаком ни с кем. В этом случае количество пар знакомых людей равно \(3\).
| |
![]()
|
|
Игра "Даты"
Динамическое программирование
Играют двое. Задаётся какая-то дата 2020 года. Каждый игрок на своём ходе называет более позднюю дату, увеличивая на 1 или 2 либо день в месяце, либо месяц, но не то и другое сразу. При этом сочетание дня и месяца должно оставаться датой. Игрок, назвавший 31 декабря, проигрывает. Оба играют наилучшим образом. Исходя из заданной даты вывести, кто выиграет.
Входные данные
В первой строке находятся числа, обозначающие день и месяц.
Выходные данные
Вывести 1, если выигрывает первый (начинающий) игрок, или 2 - в противном случае.
| |
![]()
|
|
Формирование поезда
Динамическое программирование
Компания, занимающаяся железнодорожными перевозками, получила заказ сформировать поезд, состоящий из определённого числа вагонов. Проблема в том, что у компании есть вагоны, выпущенные в разное время, так что каждый из вагонов может иметь один из двух видов сцеплений на каждом конце. У компании также есть один локомотив.
Сцепления и для локомотива, и для вагонов обозначены буквой A или B. Повернуть вагон или локомотив противоположной стороной невозможно.
Дана информация о вагонах и локомотиве. Требуется найти число способов сформировать разные поезда заданной длины из имеющихся видов вагонов. Дополнительным требованием является то, что тип сцеплений на каждом конце состава должен соответствовать типу сцеплений локомотива.
Поезда считаются различными, если при их сравнении от одного конца к другому выявляется хотя бы одно отличие.
Пример 1. Пусть у компании есть вагоны AA, AA, AB, BA, BA и локомотив AB. В поезде должно быть 4 вагона. Из данных вагонов можно сформировать только два различных поезда: BAAAABBA и BAABBAAA. Локомотив можно присоединить к поезду как с левого (используя сцепление B), так и с правого конца (используя сцепление A).
Пример 2. Пусть у компании есть только по одному вагону каждого типа (AA, AB, BA, BB) и локомотив AA, а поезд должен состоять из трёх вагонов. Существует три способа сформировать поезд: AAABBA, ABBAAA и ABBBBA.
Входные данные
В первой строке через пробел N - число вагонов, находящихся в распоряжении компании, и K - требуемая длина поезда в вагонах. Вторая строка описывает тип сцеплений локомотива. Следующие N строк описывают типы сцеплений вагонов. Описания даны как AB, AA, BB или BA.
Ограничения: 1 <= K <= N <= 40.
Выходные данные
В первой строке выводится слово "YES", если можно сформировать хотя бы один поезд, или "NO" - в противном случае.
Если поезд сформировать возможно, во второй строке должно указываться число способов это сделать.
| |
![]()
|
|
Не в билетах счастье, а в их количестве
Динамическое программирование
Люди, покупающие какие-либо билеты, часто пытаются понять, на сколько счастливый билет им попался. При этом определения счастья бывают различные. В общественном транспорте Кирова для нумерации билетов используются числа от 1 до n. Витя считает билет счастливым, если его номер делится на сумму его цифр. Помогите Вите определить количество счастливых билетов.
Входные данные
На вход подается число n (1 ≤ n ≤ 1012).
Выходные данные
Выведите количество счастливых билетов в диапазоне от 1 до n.
| |
![]()
|
|
Интересные числа
Динамическое программирование
Вывод формулы
Комбинаторика
Будем назвать натуральное число интересным, если в его десятичной записи первая цифра совпадает с последней.
Дано число \(n\). Найдите количество интересных чисел, не превышающих \(n\).
Формат входных данных
На ввод подается целое число \(n\) (\(1 \le n \le 10^{18}\)).
Обратите внимание, что для считывания этого числа вам может понадобиться 64-битный тип данных (<<long long>> в C++, <<long>> в Java, <<int64>> в Паскале).
Формат выходных данных
Выведите одно целое число — количество интересных натуральных чисел, не превышающих \(n\).
| |
![]()
|
|
Простоватые числа
Динамическое программирование
Назовём число простоватым, если произведение цифр этого числа в десятичной системе счисления является простым числом. Например, простоватым является число 12, а число 29 не является.
Требуется посчитать количество простоватых чисел от \(l\) до \(r\).
Напомним, что целое число \(p > 1\) называется простым, если оно имеет ровно два делителя: \(1\) и \(p\).
Формат входных данных
Первая строка содержит одно целое число \(l\) (\(1 \le l \le 10^{100\,000}\)).
Вторая строка содержит одно целое число \(r\) (\(l \le r \le 10^{100\,000}\)).
Обратите внимание, что числа во вводе не помещаются в стандартные типы данных для целых чисел в большинстве языков программирования, в частности, в C++. Необходимо каким-либо специальным образом считывать входные данные, например, в виде строки.
Формат выходных данных
Выведите количество простоватых чисел от \(l\) до \(r\).
| |
![]()
|
|
Модообразная последовательность
Динамическое программирование
Даны два целых числа \(x\) и \(y\). Назовем последовательность \(a\) длины \(n\) модообразной, если \(a_1=x\), и для всех \(1 < i \le n\) значение \(a_{i}\) равно либо \(a_{i-1} + y\), либо \(a_{i-1} \bmod y\). Здесь \(x \bmod y\) обозначает остаток от деления \(x\) на \(y\).
Определите, существует ли модообразная последовательность длины \(n\), сумма элементов которой равна \(S\), и если существует, то найдите любую такую последовательность.
Формат входных данных
Первая и единственная строка содержит четыре целых числа \(n\), \(x\), \(y\) и \(S\) (\(1 \le n \le 200\,000\), \(0 \le x \le 200\,000\), \(1 \le y \le 200\,000\), \(0 \le S \le 200\,000\)) — длина последовательности, параметры \(x\) и \(y\), и необходимая сумма элементов последовательности.
Формат выходных данных
Если искомая последовательность существует, выведите в первой строке <<Yes>> (без кавычек). Далее, во второй строке выведите \(n\) целых чисел \(a_1, a_2, \ldots, a_n\) через пробел — элементы последовательности \(a\). Если подходящих последовательностей несколько, выведите любую из них.
Если же последовательность не существует, выведите в единственной строке <<No>>.
Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Например, строки <<yEs>>, <<yes>>, <<Yes>> и <<YES>> будут приняты как положительный ответ.
Замечание
В первом примере условиям удовлетворяет последовательность \([8, 11, 2, 5, 2]\). Таким образом, \(a_1 = 8 = x\), \(a_2 = 11 = a_1 + 3\), \(a_3 = 2 = a_2 \bmod 3\), \(a_4 = 5 = a_3 + 3\), \(a_5 = 2 = a_4 \bmod 3\).
Во втором примере первый элемент последовательности должен равняться \(5\), поэтому последовательность \([2, 2, 2]\) не подходит.
| |
![]()
|
|
Гигантский дракон
Динамическое программирование
Деревья
Вычислительная геометрия
Канеки смотрит на неориентированный граф на плоскости из \(n\) вершин и \(m\) ребер. В этом графе ему интересно найти самого большого дракона.
Назовем сегментом дракона три ребра графа \(AL\), \(AB\) и \(AR\), имеющие общую вершину \(A\), и обладающие следующими свойствами:
-
\(0 < \measuredangle (BAL) < 45^\circ\) и направление поворота от \(\overrightarrow{AB}\) к \(\overrightarrow{AL}\) — по часовой стрелке;
-
\(0 < \measuredangle (BAR) < 45^\circ\) и направление поворота от \(\overrightarrow{AB}\) к \(\overrightarrow{AR}\) — против часовой стрелки;
-
\(|AB| \geqslant |AL|\) и \(|AB| \geqslant |AR|\), то есть \(AB\) — максимальное по длине из трех ребер.
При выполнении всех указанных условий вершины \(A\) и \(B\) называются началом и концом сегмента, а ребра \(AL\), \(AB\) и \(AR\) — левой лапой, основанием и правой лапой сегмента, соответственно.
Определим дракона как последовательность сегментов, в которой
-
начало первого сегмента \(A_1\), также называемое головой дракона, находится в вершине \(S\);
-
\(A_{i} = B_{i-1}\) для всех \(i > 1\), то есть начало каждого следующего сегмента совпадает с концом предыдущего;
-
\(\left|\measuredangle \left(\overrightarrow{A_{i-1} B_{i-1}}, \overrightarrow{A_i B_i}\right)\right| < 45^\circ\), то есть угол между векторами оснований соседних сегментов строго меньше \(45^\circ\);
-
\(\left|\measuredangle \left(\overrightarrow{A_1 A_i}, \overrightarrow{A_i B_i}\right)\right| < 45^\circ\), то есть угол между вектором от головы дракона \(A_1\) до начала сегмента и основанием сегмента строго меньше \(45^\circ\).
Обратите внимание, что здесь углы взяты по модулю, то есть каждый следующий сегмент может быть повернут относительно предыдущего на менее чем \(45^\circ\) как по, так и против часовой стрелки.
Мощностью дракона будем считать сумму квадратов длин оснований его сегментов, то есть \(\sum |A_i B_i|^2\). В заданном графе помогите Канеки найти дракона максимальной мощности с головой в вершине \(S\).
Формат входных данных
В первой строке входных данных даны три числа \(n, m, S\) (\(2 \leqslant n \leqslant 2\cdot 10^5\); \(1 \leqslant m \leqslant 4\cdot 10^5\); \(1 \leqslant S \leqslant n\)) — количество вершин и ребер в заданном графе и номер вершины, являющейся головой дракона.
В следующих \(n\) строках дано описание вершин графа. Каждая строка содержит два целых числа \(x_i\) и \(y_i\) — координаты \(i\)-й вершины (\(0 \leqslant x_i, y_i \leqslant 10^9\)). Гарантируется, что все вершины графа различны, то есть не существует двух вершин, обе координаты которых совпадают.
Далее следует пустая строка.
В следующих \(m\) строках дано описание ребер графа. Каждая строка содержит два целых числа \(u_i\) и \(v_i\) — номера вершин, соединенных \(i\)-м ребром (\(1 \leqslant u_i, v_i \leqslant n\); \(u_i \neq v_i\)). Гарантируется, что граф не содержит кратных ребер.
Формат выходных данных
В первой строке выходных данных выведите два числа \(k\) и \(ans\) — количество сегментов в драконе, имеющем максимальную мощность, и само значение его мощности.
В следующих \(k\) строках выведите описание сегментов в том порядке, в котором они образуют дракона. В качестве описания сегмента \(i\) выведите номера вершин \(L_i\), \(B_i\) и \(R_i\).
Будем считать, что дракон может состоять только из вершины \(S\). В таком случае количество сегментов и его мощность следует считать нулями.
Замечание
Графы, данные в первом, втором и третьем тесте условий, выглядят следующим образом.
-
В первом тесте в качестве максимального дракона можно взять весь граф целиком;
-
Во втором тесте ни одна тройка ребер не может быть взята в сегмент, так как не выполняется одно из обязательных условий;
-
В третьем тесте максимальный дракон состоит из двух сегментов с основаниями \(9 \to 5\) и \(5 \to 1\) с лапами \((9 \to 8, 9 \to 7)\) и \((5 \to 3, 5 \to 2\)).
| |
![]()
|
|
Зоомагазин-2
Динамическое программирование
Динамическое программирование: два параметра
В зоомагазине нужно расставить в один ряд клетки с кошками и собаками. В ряд помещается N клеток, при этом есть одно ограничение: нельзя ставить подряд три клетки с животными одного вида (иначе они передерутся). Предполагается, что в магазине есть неограниченное количество клеток с кошками и собаками. Определите, сколькими безопасными способами можно расставить N клеток в ряд.
Входные данные
Входная строка содержит одно натуральное число – количество клеток в ряду N .
Выходные данные
Программа должна вывести количество безопасных способов расстановки N клеток в ряд.
| |
![]()
|