| Условие задачи | | Прогресс | Попытки, все/успешные |
|
Темы:
Задача на реализацию
реализация
сортировки
матрицы
Космическая станция «Орион» принимает сигналы от спутников-разведчиков. Приёмная матрица станции имеет размер 640 строк на 480 позиций. При получении каждого сигнала в журнал записываются координаты активированного элемента матрицы: номер строки и номер позиции в строке.
Элемент матрицы, который принял хотя бы один сигнал, считается активным. Элемент, который не принял ни одного сигнала, считается неактивным.
Для анализа качества связи нужно найти наибольшую непрерывную цепочку активных элементов в одной строке.
Определите наибольшую длину цепочки активных элементов, расположенных подряд в одной строке, и номер этой строки. Если таких строк несколько, укажите максимальный из их номеров.
Формат входных данных
В первой строке записано целое число N — количество принятых сигналов (1 ≤ N ≤ 10000).
В каждой из следующих N строк записаны по два числа через пробел:
- номер строки (целое число от 1 до 640)
- номер позиции в строке (целое число от 1 до 480)
Один и тот же элемент матрицы может получить несколько сигналов (координаты могут повторяться).
Формат выходных данных
Два целых числа через пробел: наибольшая длина цепочки активных элементов и номер строки, в которой она находится.
| |
![]()
|
14/
5
|
|
Темы:
Задача на реализацию
ЕГЭ_информатика
реализация
матрицы
В новом датацентре «Кибер-Облако» серверы размещаются в стойках, которые расположены рядами. Ряды пронумерованы натуральными числами. Слоты в каждом ряду также пронумерованы натуральными числами начиная с единицы.
По данным инвентаризации известно, в каких рядах и в каких слотах уже установлены серверы. Администратору нужно разместить новое оборудование: кластер из ровно 25 серверов, которые должны располагаться в соседних слотах одного ряда.
Для надёжной работы кластера требуется, чтобы непосредственно слева и справа от него в том же ряду уже были установлены работающие серверы (они будут выполнять роль шлюзов).
Найдите ряд с наибольшим номером, в котором есть ровно 25 свободных слотов подряд, ограниченных занятыми слотами с обеих сторон.
Гарантируется, что существует хотя бы один ряд, удовлетворяющий условию.
Формат входных данных
В первой строке находится число N — количество установленных серверов (натуральное число, не превышающее 20000).
Каждая из следующих N строк содержит два натуральных числа, не превышающих 10000:
- номер ряда
- номер слота в этом ряду
Формат выходных данных
Два целых числа через пробел: наибольший номер ряда и наименьший номер слота в выбранной последовательности из 25 свободных мест.
| |
![]()
|
4/
3
|
|
Темы:
Массивы
ЕГЭ - вычислительные задачи
Задача на реализацию
реализация
Космическая Академия «Звёздный Путь» проводит ежегодный набор курсантов. Отбор кандидатов происходит по сумме баллов трёх вступительных испытаний (физическая подготовка, математика, астронавигация) и собеседования с приёмной комиссией.
На заранее известное количество мест отбираются кандидаты, набравшие наибольшую сумму баллов по результатам трёх испытаний. Все кандидаты, набравшие определённую сумму баллов или больше, зачисляются на имеющиеся места. Такой балл называется проходным.
Если после заполнения имеющихся мест кандидатами с проходным баллом остаются незаполненные места, но кандидатов, набравших следующую сумму баллов, больше, чем вакантных мест, набранная этими кандидатами сумма баллов называется полупроходным баллом.
Из числа кандидатов, набравших полупроходной балл, на имеющиеся места принимаются кандидаты, имеющие более высокий балл за собеседование. Если два кандидата с полупроходным баллом имеют одинаковый балл за собеседование, то проходит тот кандидат, значение ID которого выше.
Для данного множества кандидатов определите полупроходной балл, а также ID кандидата с полупроходным баллом, который будет зачислен последним (займёт последнее свободное место).
Формат входных данных
В первой строке находятся два числа:
- N — количество кандидатов (натуральное число, не превышающее 10000)
- S — количество имеющихся мест (натуральное число, S ≤ N)
Каждая из следующих N строк содержит пять чисел:
- ID кандидата (натуральное число, не превышающее 10 000 000)
- три оценки по испытаниям (целые неотрицательные числа, не превышающие 100)
- балл за собеседование (целое неотрицательное число, не превышающее 10)
Гарантируется, что в исходных данных существует полупроходной балл.
Формат выходных данных
Два целых числа через пробел: полупроходной балл и ID кандидата с полупроходным баллом, занявшего последнее место.
Примечание
В первом тестовом примере
- ID=1001: сумма экзаменов = 270, собеседование = 10 → проходит (проходной балл)
- ID=1002: сумма = 240, собеседование = 8 → полупроходной балл, проходит
- ID=1003: сумма = 240, собеседование = 5 → не проходит (собеседование меньше)
- ID=1004: сумма = 210, собеседование = 10
Мест: 2. Кандидат с ID=1001 проходит автоматически. Осталось 1 место, но с суммой 240 — два кандидата. Это полупроходной балл. Между ними выбираем по собеседованию: ID=1002 (собес 8) > ID=1003 (собес 5).
Во втором тестовом примере
Все кандидаты имеют одинаковую сумму баллов (240) и одинаковый балл за собеседование (5). Мест: 2. Выбираем по ID в порядке убывания: сначала 503, затем 502. Последний зачисленный — кандидат с ID=502.
| |
![]()
|
1/
1
|
|
Темы:
Массивы
ЕГЭ - вычислительные задачи
Задача на реализацию
реализация
На подводной исследовательской станции «Нептун-7» требуется установить новый научный модуль. Станция состоит из M уровней (пронумерованных от 1 до M сверху вниз, где уровень 1 ближе всего к поверхности) и K отсеков на каждом уровне.
Некоторые отсеки уже заняты оборудованием. По требованиям безопасности, новый модуль нужно разместить так, чтобы над ним (на уровнях с меньшими номерами) было как можно больше подряд идущих свободных отсеков с тем же номером — это обеспечивает путь аварийной эвакуации к поверхности.
Если несколько отсеков имеют одинаковое максимальное количество свободных отсеков над ними, выбирается отсек на уровне ближе к поверхности (с меньшим номером уровня).
Гарантируется, что хотя бы один свободный отсек на станции существует.
Формат входных данных
В первой строке находятся три числа:
- N — количество занятых отсеков (1 ≤ N ≤ 10 000)
- M — количество уровней (1 ≤ M ≤ 100 000)
- K — количество отсеков на каждом уровне (1 ≤ K ≤ 100 000)
В следующих N строках находятся пары натуральных чисел: номер уровня и номер отсека занятого места соответственно.
Формат выходных данных
Два целых числа через пробел:
- Номер уровня выбранного отсека
- Количество свободных отсеков над ним (подряд, с тем же номером)
| |
![]()
|
/
|
|
Темы:
Массивы
ЕГЭ - вычислительные задачи
Задача на реализацию
реализация
На орбитальной станции «Галактика-7» завершился ежегодный технический осмотр космических кораблей. По его результатам каждый корабль получил:
- Оценки трёх бортовых систем: двигательной, навигационной и системы жизнеобеспечения (по шкале от 2 до 5, где 2 — критическая неисправность, 5 — отличное состояние)
- Статус лицензии пилота: действующая или просроченная
Корабль допускается к полётам, если выполнены оба условия:
- Все три бортовые системы имеют оценку 3 или выше
- Лицензия пилота действующая
Корабль не допущен к полётам, если хотя бы одно из условий не выполнено.
Руководство станции решило предоставить возможность экстренного ремонта одной системы одному из кораблей. Корабль может претендовать на ремонт, если:
- Лицензия пилота действующая
- Ровно одна система имеет критическую неисправность (оценка 2), а две другие системы исправны (оценка 3 или выше)
Если таких кораблей несколько, выбирается тот, у которого наибольшая сумма оценок всех трёх систем (такой корабль ближе всего к допуску).
Гарантируется, что ровно один корабль удовлетворяет всем критериям отбора.
Формат входных данных
В первой строке находится число N — количество кораблей (1 ≤ N ≤ 1000).
Каждая из следующих N строк содержит пять целых чисел через пробел:
- ID — бортовой номер корабля (натуральное число, не превышающее 108)
- S1, S2, S3 — оценки трёх бортовых систем (каждая от 2 до 5)
- L — статус лицензии пилота (1 — действующая, 0 — просроченная)
Формат выходных данных
Выведите два числа через пробел:
- Количество кораблей, не допущенных к полётам
- Бортовой номер корабля, который получит возможность экстренного ремонта
| |
![]()
|
17/
7
|
|
Темы:
Задача на реализацию
Радиоуправляемый робот умеет перемещаться по клетчатому полю размером \(n \times m\) (\(n\) строк и \(m\) столбцов) и красить клетки в один из четырех цветов (красный, зеленый, синий и белый). Будем обозначать клетку на пересечении \(i\)-й сверху строки и \(j\)-го слева столбца как \((i, j)\).
Робот выполняет команды пользователя, при этом перемещаясь по полю в соответствии с заданными настройками и ограничениями.
Настройки представляют собой матрицу \(S\) размера \(n \times m\), каждый элемент которой — либо \(\varnothing\), либо пара из координат клетки и цвета. Если \(S_{i,j} = ((i', j'), c)\), то после того, как робот красит клетку \((i, j)\) в какой-либо цвет, он сразу же перемещается в клетку \((i', j')\) и красит ее в цвет \(c\). Если для новой покрашенной клетки \(S_{i',j'} \neq \varnothing\), процесс продолжается по тем же правилам.
Ограничения бывают двух типов:
-
ограничение на минимальное требуемое число клеток цвета \(c\);
-
запрет наличия на поле квадрата \(2 \times 2\), покрашенного цветами \(\begin{pmatrix} c_{1,1} & c_{1,2} \\ c_{2,1} & c_{2,2} \end{pmatrix}\).
Пользователю доступны следующие команды для взаимодействия с роботом:
-
<<fill \(i\) \(j\) with \(c\)>> — закрасить клетку \((i, j)\) в цвет \(c\), после чего выполнять действия в соответствии с настройками; процесс останавливается, когда
-
очередное перемещение привело робота за границу поля;
-
очередное перемещение привело робота в клетку, которую он уже красил в процессе выполнения текущей команды;
-
для очередной клетки \(S_{i',j'} = \varnothing\);
-
с очередной покраской перестанет выполняться какое-то из ограничений.
Обратите внимание, что если первая же покраска клетки \((i, j)\) в цвет \(c\) приводит к нарушению какого-то из ограничений, робот остановится сразу же, не покрасив ни одну клетку.
-
<<at-least \(x\) \(c\)>> — выставить ограничение на минимальное число клеток цвета \(c\) в \(x\). Если в настоящий момент на поле меньше \(x\) клеток цвета \(c\), команда игнорируется и ограничение не меняется. Для каждого цвета в каждый момент времени действует только последнее введенное на него ограничение на число клеток.
-
<<no-squares \(c_{1,1}\) \(c_{1,2}\) \(c_{2,1}\) \(c_{2,2}\)>> — запретить появление квадратов \(2 \times 2\), раскрашенных цветами \(\begin{pmatrix} c_{1,1} & c_{1,2} \\ c_{2,1} & c_{2,2} \end{pmatrix}\). Если в настоящий момент на поле уже есть квадрат, раскрашенный таким образом, команда игнорируется и ограничение не добавляется.
-
<<allow-squares \(c_{1,1}\) \(c_{1,2}\) \(c_{2,1}\) \(c_{2,2}\)>> — аналогично, отменить запрет на раскрашенные соответствующим образом квадраты \(2 \times 2\), если такой запрет сейчас есть.
-
<<move \(i\) \(j\) to \(i'\) \(j'\) \(c\)>> — выставить настройки для клетки \((i, j)\) в значение \(((i', j'), c)\), где \((i', j')\) — клетка, в которую надо переместиться, а \(c\) — цвет, в который затем надо ее покрасить.
-
<<no-move \(i\) \(j\)>> — выставить настройки для клетки \((i, j)\) в значение \(\varnothing\), соответствующее отсутствию перемещения после покраски клетки \((i, j)\).
Еще раз повторим, что робот никогда не красит одну и ту же клетку дважды во время исполнения одной команды, а также останавливается до момента первого нарушения какого-либо ограничения. Например, если \(S_{1,1} = ((1, 2), \mathtt{red})\), \(S_{1,2} = ((2, 2), \mathtt{blue})\), \(S_{2,2} = ((2, 1), \mathtt{green})\) и \(S_{2,1} = ((1, 1), \mathtt{red})\), то при поступлении команды <<fill \(1\) \(1\) with blue>>, робот покрасит \((1, 1)\) в синий, \((1, 2)\) в красный, \((2, 2)\) в синий и \((2, 1)\) в зеленый. Затем робот остановится, так как клетка \((1, 1)\) уже была покрашена при исполнении этой команды.
Изначально все настройки равны \(\varnothing\), никакие ограничения не введены, а все клетки поля покрашены в белый цвет. Вам дан список из \(q\) команд пользователя, которые были последовательно отправлены роботу. Выведите раскраску поля после применения всех этих команд.
Формат входных данных
В первой строке записано целое число \(t\) (\(1 \le t \le 1000\)) — число наборов входных данных в тесте.
В первой строке каждого набора данных даны три целых положительных числа \(n\), \(m\) и \(q\) — размеры поля и число команд. Гарантируется, что сумма \(n \cdot m \cdot q\) по всем наборам входных данных не превосходит \(10^5\).
В следующих \(q\) строках дано описание команд, посланных роботу в формате, описанном в условии. Цвета задаются строками <<red>> (красный), <<green>> (зеленый), <<blue>> (синий) и <<white>> (белый).
Формат выходных данных
Для каждого набора входных данных выведите итоговую раскраску поля, полученную после обработки всех команд. Для обозначения красного, зеленого или синего цвета используйте первую букву его английской записи (‘r’, ‘g’ или ‘b’); для обозначения белого цвета используйте символ ‘.’.
Примечание
В первом примере из условия
-
Команда <<fill 1 1 with red>> красит \((1, 1)\) в красный, после чего из-за \(S_{1,1} = ((2, 1), \mathtt{red})\) клетка \((2, 1)\) тоже красится в красный, а из-за \(S_{2,1} = ((3, 1), \mathtt{red})\) затем и \((3, 1)\) красится в красный.
-
При выполнении <<fill 2 1 with green>> робот красит \((2, 1)\) в зеленый. \(S_{2,1}\) в этот момент уже равно \(((2, 2), \mathtt{blue})\), поэтому после этого клетка \((2, 2)\) должна быть покрашена в синий, но это бы нарушило ограничение <<at-least 3 white>>, поэтому процесс останавливается до этого.
-
После этого поле выглядит как
-
Затем <<fill 2 2 with R>> должен покрасить \((2, 2)\) в красный (ограничение на число белых уже снято), но это бы привело к получению квадрата с цветами r.gr, который запрещен, поэтому выполнение команды сразу останавливается.
-
Последняя команда покраски <<fill 2 2 with B>> выполняется. После чего, в соответствии с \(S_{2,2} = ((1, 2), \mathtt{green})\), клетка \((1, 2)\) красится в зеленый.
-
Итоговый рисунок:
| |
![]()
|
1/
1
|
|
Темы:
Задача на реализацию
Радиоуправляемый робот умеет перемещаться по клетчатому полю размером \(n \times m\) (\(n\) строк и \(m\) столбцов) и красить клетки в один из четырех цветов (красный, зеленый, синий и белый). Будем обозначать клетку на пересечении \(i\)-й сверху строки и \(j\)-го слева столбца как \((i, j)\).
Робот выполняет команды пользователя, при этом перемещаясь по полю в соответствии с заданными настройками и ограничениями.
Настройки представляют собой матрицу \(S\) размера \(n \times m\), каждый элемент которой — либо \(\varnothing\), либо пара из направления (вправо, вверх, влево, вниз) и цвета. Если \(S_{i,j} = (d, c)\), то после того, как робот красит клетку \((i, j)\) в какой-либо цвет, он сразу же смещается на одну клетку в направлении \(d\) и красит ее в цвет \(c\). Если для новой покрашенной клетки \(S_{i',j'} \neq \varnothing\), процесс продолжается по тем же правилам.
Ограничения бывают двух типов:
-
ограничение на максимальное разрешенное число клеток цвета \(c\);
-
запрет наличия на поле квадрата \(2 \times 2\), покрашенного цветами \(\begin{pmatrix} c_{1,1} & c_{1,2} \\ c_{2,1} & c_{2,2} \end{pmatrix}\).
Пользователю доступны следующие команды для взаимодействия с роботом:
-
<<color \(i\) \(j\) \(c\)>> — закрасить клетку \((i, j)\) в цвет \(c\), после чего выполнять действия в соответствии с настройками; процесс останавливается, когда
-
очередное перемещение привело робота за границу поля;
-
очередное перемещение привело робота в клетку, которую он уже красил в процессе выполнения текущей команды;
-
для очередной клетки \(S_{i',j'} = \varnothing\);
-
с очередной покраской перестанет выполняться какое-то из ограничений.
Обратите внимание, что если первая же покраска клетки \((i, j)\) в цвет \(c\) приводит к нарушению какого-то из ограничений, робот остановится сразу же, не покрасив ни одну клетку.
-
<<limit \(c\) \(x\)>> — выставить ограничение на максимальное число клеток цвета \(c\) в \(x\). Если в настоящий момент на поле уже больше \(x\) клеток цвета \(c\), команда игнорируется и ограничение не меняется. Для каждого цвета в каждый момент времени действует только последнее введенное на него ограничение на число клеток.
-
<<block \(c_{1,1}\) \(c_{1,2}\) \(c_{2,1}\) \(c_{2,2}\)>> — запретить появление квадратов \(2 \times 2\), раскрашенных цветами \(\begin{pmatrix} c_{1,1} & c_{1,2} \\ c_{2,1} & c_{2,2} \end{pmatrix}\). Если в настоящий момент на поле уже есть квадрат, раскрашенный таким образом, команда игнорируется и ограничение не добавляется.
-
<<allow \(c_{1,1}\) \(c_{1,2}\) \(c_{2,1}\) \(c_{2,2}\)>> — аналогично, отменить запрет на раскрашенные соответствующим образом квадраты \(2 \times 2\), если такой запрет сейчас есть.
-
<<settings \(i\) \(j\) \(d\) \(c\)>> — выставить настройки для клетки \((i, j)\) в значение \((d, c)\), где \(d\) — направление перемещения, а \(c\) — цвет, в который затем будет раскрашена клетка, в которую робот переместится.
-
<<settings \(i\) \(j\) none>> — выставить настройки для клетки \((i, j)\) в значение \(\varnothing\), соответствующее отсутствию перемещения после покраски клетки \((i, j)\).
Еще раз повторим, что робот никогда не красит одну и ту же клетку дважды во время исполнения одной команды, а также останавливается до момента первого нарушения какого-либо ограничения. Например, если \(S_{1,1} = (\rightarrow, \mathtt{red})\), \(S_{1,2} = (\downarrow, \mathtt{blue})\), \(S_{2,2} = (\leftarrow, \mathtt{green})\) и \(S_{2,1} = (\uparrow, \mathtt{red})\), то при поступлении команды <<color \(1\) \(1\) blue>>, робот покрасит \((1, 1)\) в синий, \((1, 2)\) в красный, \((2, 2)\) в синий и \((2, 1)\) в зеленый. Затем робот остановится, так как клетка \((1, 1)\) уже была покрашена при исполнении этой команды.
Изначально все настройки равны \(\varnothing\), никакие ограничения не введены, а все клетки поля покрашены в белый цвет. Вам дан список из \(q\) команд пользователя, которые были последовательно отправлены роботу. Выведите раскраску поля после применения всех этих команд.
Формат входных данных
В первой строке записано целое число \(t\) (\(1 \le t \le 1000\)) — число наборов входных данных в тесте.
В первой строке каждого набора данных даны три целых положительных числа \(n\), \(m\) и \(q\) — размеры поля и число команд. Гарантируется, что сумма \(n \cdot m \cdot q\) по всем наборам входных данных не превосходит \(10^5\).
В следующих \(q\) строках дано описание команд, посланных роботу в формате, описанном в условии. Направления задаются строками <<right>> (вправо), <<up>> (вверх), <<left>> (влево), <<down>> (вниз). Цвета задаются заглавными буквами ‘R’ (красный), ‘G’ (зеленый), ‘B’ (синий) и ‘W’ (белый).
Формат выходных данных
Для каждого набора входных данных выведите итоговую раскраску поля, полученную после обработки всех команд.
Примечание
В первом примере из условия
-
Команда <<color 1 1 R>> красит \((1, 1)\) в красный, после чего из-за \(S_{1,1} = (\downarrow, \mathtt{red})\) клетка \((2, 1)\) тоже красится в красный, а из-за \(S_{2,1} = (\downarrow, \mathtt{red})\) затем и \((3, 1)\) красится в красный.
-
При выполнении <<color 2 1 G>> робот красит \((2, 1)\) в зеленый. \(S_{2,1}\) в этот момент уже равно \((\rightarrow, \mathtt{blue})\), поэтому после этого клетка \((2, 2)\) должна быть покрашена в синий, но это бы нарушило ограничение <<limit B 0>>, поэтому процесс останавливается до этого.
-
После этого поле выглядит как
-
Затем <<color 2 2 R>> должен покрасить \((2, 2)\) в красный, но это бы привело к получению квадрата с цветами RWGR, который запрещен, поэтому выполнение команды сразу останавливается.
-
Последняя команда покраски <<color 2 2 B>> отрабатывает корректно, так как до этого было разрешено иметь на поле не больше \(1\) синей клетки. После чего, в соответствии с \(S_{2,2} = (\uparrow, \mathtt{green})\), клетка \((1, 2)\) красится в зеленый.
-
Итоговый рисунок:
| |
![]()
|
20/
3
|
|
Темы:
Задача на реализацию
На жидкокристаллическом дисплее с разрешением \(h\times w\) используются пиксели трех цветов: красного, зеленого и синего. Будем обозначать их заглавными английскими буквами ‘R’, ‘G’ и ‘B’, соответственно.
Поскольку человеческий глаз имеет максимальную чувствительность к зеленому цвету, зеленых пикселей на дисплее примерно в два раза больше, чем красных и чем синих. Пиксели в каждой строке чередуются: каждый второй пиксель зеленый, а среди остальных чередуются красные и синие пиксели.
В первой строке первый пиксель <<R>>, а каждая следующая строка сдвинута на один налево относительно предыдущей: во второй первый пиксель <<G>>, а второй <<B>>, в третьей первый пиксель <<B>>, в четвертой первый пиксель <<G>>, а второй <<R>>, и так далее.
Выведите, как расположены пиксели на экране.
Формат входных данных
На вход подаются целые числа \(h\) и \(w\), по одному на строке (\(1 \le h, w \le 100\)).
Формат выходных данных
Выведите \(h\) строк по \(w\) символов — цвета пикселей на дисплее.
| |
![]()
|
45/
21
|
|
Темы:
Задача на реализацию
У Вовы есть любимый магнит. Вове очень нравится играть с ним на большой поляне, которую можно представить в виде прямоугольника \(n\) на \(m\) клеток.
Однажды он пришел играть на поляну с магнитом и потерял его в одной из клеток. Вова очень расстроился, но нашел решение — в каждую клетку поляны он положил компас, стрелка которого может принимать 8 положений: вверх, вверх-вправо, вправо, вниз-вправо, вниз, вниз-влево, влево и вверх-влево. Каждому положению стрелки соответствует его номер:
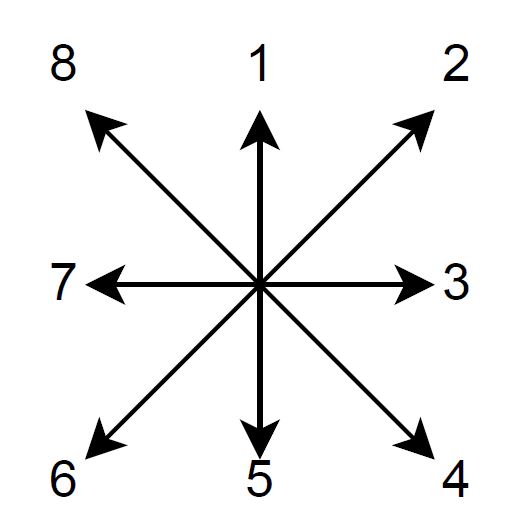
Стрелки принимают направление, близкое к направлению на магнит: если магнит лежит строго по диагонали от компаса, то его стрелка примет диагональное положение, иначе — более близкое к направлению на магнит из вертикального и горизонтального. Стрелка компаса в клетке с магнитом может быть направлена куда угодно.
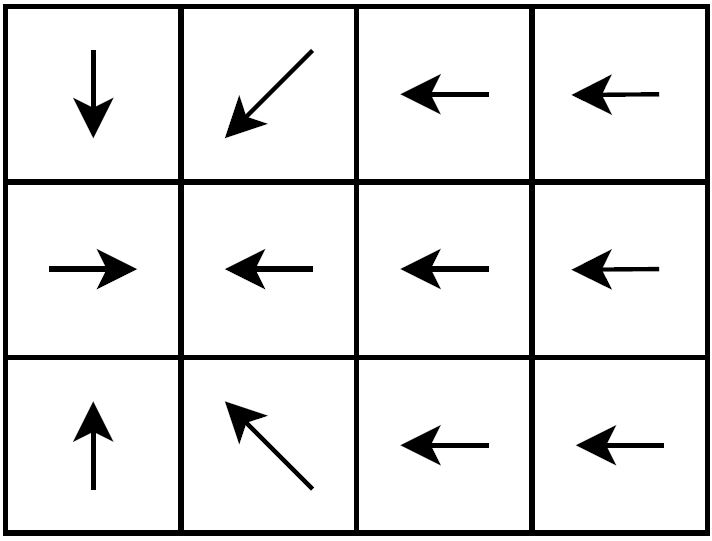
Рисунок для примера из входных данных, стрелки всех компасов направлены на магнит.
Вова уже был готов к поискам, но тут вспомнил, что на поляне есть аномалия, которая инвертирует показания компасов вдоль ровно одной горизонтали и ровно одной вертикали. У компасов, которые лежат в зоне действия аномалии, стрелка смотрит строго в противоположном направлении тому, в котором она должна указывать.
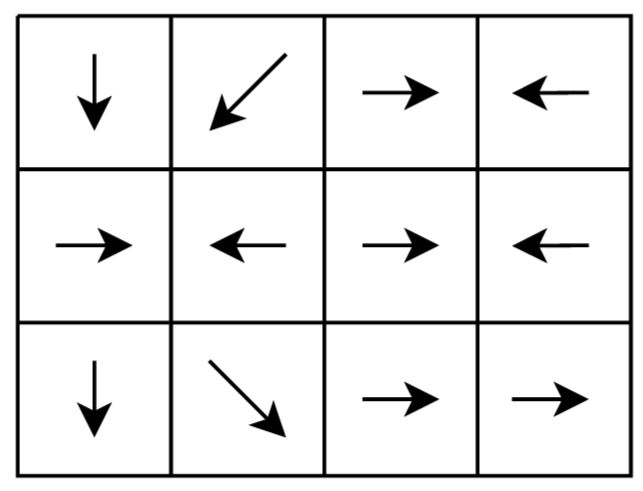
Рисунок для примера из входных данных с учетом аномалии.
Теперь Вова не знает, как ему найти свой магнит, и просит помощи у вас.
Формат входных данных
В первой строке входных данных записаны два целых числа через пробел \(n\) и \(m\) — размеры поляны (\(2 \le n, m \le 1500, nm \ge 6\)).
В следующих \(n\) строках описываются компасы на поляне.
В \(i\)-й строке записаны \(m\) целых чисел \(a_{i,j}\) (\(1 \le a_{i,j} \le 8\)), \(j\)-е число в \(i\)-й строке обозначает направление стрелки компаса в \(j\)-й клетке \(i\)-й строки.
Формат выходных данных
В первой строке выведите два числа \(x\) и \(y\) через пробел — номер строки и столбца клетки, в которой лежит магнит.
Во второй выведите два числа \(a\) и \(b\) через пробел — номера горизонтали и вертикали, в которых действует аномалия.
Замечание
В данном тесте магнит лежит в клетке \((2, 1)\), инвертируется горизонталь номер \(3\) и вертикаль номер \(3\).
| |
![]()
|
5/
1
|
|
Темы:
Разбор случаев
Задача на реализацию
Петя живёт в Санкт-Петербурге и увлекается метеорологией. Из научного интереса он решил подтвердить или опровергнуть мнение о том, что в Санкт-Петербурге постоянно идёт дождь. Для этого Петя завёл дневник дождя и раз в неделю в воскресенье оставляет в нём запись с информацией о том, идёт ли дождь. Каждую запись Петя подписывает номером текущего дня в месяце, дни в месяце нумеруются с 1 до числа дней в этом месяце (от 28 до 31 в разных месяцах).
Сегодня Петя открыл дневник, чтобы сделать очередную запись, и обнаружил, что он сделал последнюю запись две недели назад, а в прошлое воскресенье забыл занести информацию в дневник. Петя помнит, что неделю назад шёл дождь, и он решил сделать две записи: за сегодняшний день и за прошлое воскресенье. Он знает номер текущего дня в месяце \(n\) и видит, каким числом \(m\) подписана запись две недели назад. Каким числом Петя должен подписать запись за прошлую неделю?
Формат входных данных
В первой строке вывода даны два целых числа \(n\) и \(m\) (\(1 \le n, m \le 31\)) — номер текущего дня месяца и число, которым подписана запись две недели назад.
Формат выходных данных
Выведите единственное число – каким числом должна быть подписана запись неделю назад.
| |
![]()
|
236/
82
|
|
Темы:
Задача на реализацию
Даны две строки \(S\) и \(T\) из строчных букв английского алфавита.
Посмотрим на следующий процесс. Рассмотрим не более одного раза каждый символ, хотя бы где-то входящий в первую строку. После чего, для рассматриваемого символа \(x\) определим другой символ \(p(x) \neq x\) и заменим некоторые вхождения \(x\) в \(S\) на \(p(x)\). Определите, возможно ли в ходе такого процесса получить из строки \(S\) строку \(T\). При этом разные символы можно заменять на один и тот же символ или на символ, который заменяться не будет.
Например, пусть \(S =\) <<aabab>>, \(T =\) <<abbbc>>. Из \(S\) можно получить \(T\), если выбрать p(‘a’) = ‘b’, p(‘b’) = ‘c’ и заменить второе и третье вхождение ‘a’ на p(‘a’), второе вхождение ‘b’ на p(‘b’).
А если \(S =\) <<aabaс>>, \(T =\) <<bbbbb>>, то все вхождения ’a’ и ’c’ были заменены на ’b’.
Формат входных данных
В первой строке вам дано число \(n\) \((1 \leqslant n \leqslant 200\,000)\). Во второй строке задана \(S\). В третьей строке задана \(T\). Обе строки имеют длину \(n\) и состоят только из букв от ‘a’ до ‘z’.
Формат выходных данных
Если возможно осуществить описанный процесс так, чтобы из \(S\) получилась \(T\), выведите <<YES>>, на следующей строке выведите \(m\) – количество различных символов \(S\), которые хотя бы раз заменялись. Обозначим эти символы за \(c_1,\ c_2,\ \ldots \ c_m\). После чего выведите \(m\) строк. На \(i\)-й строке необходимо вывести символы \(c_i\) и \(p(c_i)\) через пробел. Если это сделать невозможно, выведите <<NO>>.
| |
![]()
|
3/
3
|
|
Темы:
Задача на реализацию
Вы создали очередную платформу для проведения онлайн соревнований по программированию. После первого контеста вы изучили решения участников и заметили, что некоторые списывают друг у друга. После этого вам захотелось написать программу, чтобы быстрее обнаруживать списывания и блокировать нечестных участников.
Пусть есть две строки, описывающие решения. Рассмотрим не более одного раза каждый символ, хотя бы где-то входящий в первую строку. После этого для рассматриваемого символа \(x\) определим другой символ \(p(x) \neq x\) и заменим некоторые вхождения \(x\) в первое решение на \(p(x)\). Если в ходе такого процесса из первого решения возможно получить второе, то скажем, что второе решение списано с первого.
Иными словами, участник копирует чужое решение и, чтобы списывание не было таким очевидным, один раз рассматривает некоторые различные символы \(x\), которые хотя бы раз встречаются в первом решении. Для каждого такого символа \(x\) он выбирает, на какой другой символ \(p(x)\) он будет заменять его вхождения, после чего проходит по строке и заменяет в ней \(x\) на \(p(x)\), но на некоторых позициях забывает это сделать (или там замена невозможна).
Значения \(p(x)\) участником выбираются независимо для разных \(x\), поэтому они могут и совпасть.
Напишите программу, которая позволит обнаружить списывания такого рода.
Кроме платформы вы создали язык программирования S++ и, чтобы его популяризировать, вы решили разрешить сдавать задачи в своей системе только на нем. Одной из особенностью языка является то, что любая программа записывается в одну строку и может состоять только из строчных и заглавных букв английского алфавита (a-z, A-Z), цифр (0-9), скобок (‘(’, ‘)’, ‘{’, ‘}’ ‘[’, ‘]’), знаков сравнения (‘<’, ‘>’, ‘=’) и символов ‘+’, ‘-’, ‘*’, ‘/’, ‘;’.
Формат входных данных
В первой строке вам дано число \(n\) \((1 \leqslant n \leqslant 200\,000)\), равное длине каждой из программ.
Во второй строке вам дана программа первого участника на языке S++.
В третьей строке вам дана программа второго участника на языке S++.
Формат выходных данных
Если вторая программа списана с первой, выведите <<YES>> (без кавычек), на следующей строке выведите \(m\) – количество различных символов в первой программе, которые хотя бы раз заменялись. Обозначим эти символы за \(c_1,\ c_2,\ \ldots, \ c_m\). После этого выведите \(m\) строк. На \(i\)-й строке необходимо вывести символы \(c_i\) и \(p(c_i)\) через пробел. Если вторая программа не списана с первой, то выведите <<NO>> (без кавычек).
Примечание
В первом примере списывающий заменил все вхождения ‘i’ на ‘j’ и вхождения ‘n’ на ‘m’.
Во втором примере участник заменял ‘a’ на ‘e’, ‘b’ на ‘f’, ‘с’ на g’ и ‘-’ на ‘+’.
В третьем примере невозможно осуществить процесс замен так, чтобы из первой строки получилась вторая.
В четвертом примере участник списал, заменив некоторые вхождения ‘a’ на ‘b’.
В пятом примере участник списал, заменив некоторые вхождения ‘a’ на ‘b’ и все вхождения ‘c’ на ‘a’.
| |
![]()
|
10/
2
|
|
Темы:
Бинарный поиск
Задача на реализацию
Квартира Максима еще не прошла реновацию, поэтому температура в ней сильно зависит от температуры на улице. Для поддержания комфортной температуры он купил обогреватель и установил систему <<Умный дом>>. В соответствующую программу Максим заложил два целых числа \(t_{min} \leq t_{max}\) и следующий алгоритм использования обогревателя:
-
Если в течение последних пяти дней до текущего дня включительно обогреватель каждый день был выключен, и в каждый из этих дней температура на улице была строго меньше \(t_{min}\), то надо включить обогреватель в этот день и считать, что он был включен весь день. Обогреватель остается включенным и в последующие дни до тех пор, пока программа его не выключит.
-
Если в течение последних пяти дней до текущего дня включительно обогреватель каждый день был включен, и в каждый из этих дней температура на улице была строго больше \(t_{max}\), то надо выключить обогреватель в этот день и считать, что он был выключен весь день. Обогреватель остается выключенным и в последующие дни до тех пор, пока программа его не включит.
Из-за кратковременного отключения электроэнергии программу необходимо настроить заново. Сами значения \(t_{min}\) и \(t_{max}\) Максим забыл, зато у него остались записи программы о температуре и состоянии обогревателя в каждые из \(n\) дней использования системы.
Максим помнит, что \(t_{min}\) и \(t_{max}\) были целыми числами, по модулю не превосходящими \(10^9\) и \(t_{min} \leq t_{max}\), также он помнит, что программа не учитывала дни до первого дня использования системы и не включала обогреватель в течение первых четырех дней. Наконец, Максим помнит, что он выбирал \(t_{min}\) и \(t_{max}\) как можно более близкими друг к другу.
Помогите найти два подходящих значения \(t_{min}\) и \(t_{max}\), не превосходящих \(10^9\) по абсолютной величине, таких, что выполняются правила использования обогревателя в каждые из \(n\) дней, \(t_{min}\) не превосходит \(t_{max}\) и величина \(t_{max} - t_{min}\) минимальна.
Гарантируется, что записи программы правильные, и такие два числа существуют.
Формат входных данных
В первой строке задано целое число \(n\) (\(5 \leq n \leq 10^5\)) — количество дней, в течение которых работала система.
Во второй строке входных данных задаются \(n\) целых чисел \(t_1, \dots, t_n\) (\(-10^9 \leq t_i \leq 10^9\)) — температуры на улице в каждый из \(n\) дней.
В третьей строке входных данных задается строка из \(n\) символов, состоящая из 0 и 1 — если в \(i\)-й позиции данной строки записан 0, то это значит, что в \(i\)-й день обогреватель был выключен, а если 1, — то включен.
Формат выходных данных
В единственной строке выведите два целых числа \(t_{min}\) и \(t_{max}\) (\(t_{min} \leq t_{max}\)), по модулю не превосходящих \(10^9\) — значения температур, при вставке которых в программу обогреватель будет включен и выключен в те же дни, в которые он был включен и выключен при исходных значениях, а значение \(t_{max} - t_{min}\) минимально.
Если подходящих пар значений несколько, выведите любую из них.
Примечание
В первом тестовом примере первые пять дней температура строго меньше \(7\) градусов, при этом до пятого дня обогреватель был в каждый из четырех дней выключен, следовательно в пятый день программа его включила. На данный тест корректен любой ответ удовлетворяющий условию \(6 \leq t_{min} = t_{max} \leq 10^9\).
| |
![]()
|
4/
1
|
|
Темы:
Строки
Задача на реализацию
Московские библиотеки имеют электронный сервис, с помощью которого можно бесплатно получить издание, несколько лет не востребованное читателями. Андрея заинтересовала красочная энциклопедия, правда изданная в прошлом веке на неизвестном ему языке.
Получив желаемое издание, он стал его изучать, открывая в произвольных местах. На одной из открытых страниц было всего две статьи, название первой из них можно было легко прочитать, так как оно было записано английскими буквами, а буквы в названии второй из них оказались практически затертыми. Легко определить было только что остались следы от \(k\) букв. Очевидно также, что второе название стоит в алфавитном порядке позже, чем первое. Это означает, что либо первая не совпадающая в написании двух слов буква в первом слове стоит в алфавите раньше, чем соответствующая буква второго слова, либо начало второго слова полностью совпадает с первым словом, но при этом второе слово длиннее первого (содержит еще какие то буквы).
Андрей не знает язык, на котором написана энциклопедия, поэтому он предположил, что второе слово состоит из тех же букв, что и первое. Чтобы проверить свое предположение, он собирается искать предполагаемое слово в интернете.
Помогите Андрею найти первое следующее в алфавитном порядке слово, состоящее из тех же букв, что и заданное слово, и состоящее ровно из \(k\) букв. Гарантируется, что такое слово существует.
Формат входных данных
В первой строке задано целое число \(n\) (\(1 \leq n \leq 100\,000\)) — количество букв в первом слове.
Во второй строке задано слово, состоящее из \(n\) строчных букв английского алфавита.
В третьей строке задано целое число \(k\) (\(1 \leq k \leq 100\,000\)) — количество букв в искомом слове.
Формат выходных данных
Выведите искомое слово, состоящее из \(k\) букв, входящих в первое слово.
Примечание
В первом тестовом примере требуемое слово должно состоять из букв a, b и c. Следующим после abc в алфавитном порядке будет слово abca, но оно состоит из 4 букв, а не из 3. Следующим после abc в алфавитном порядке состоящим из букв a, b и c и имеющим длину 3 будет слово aca.
В данной задаче \(50\) тестов, помимо тестов из условия.
Не менее чем в 15 тестах первое слово будет состоять только из букв abc, причем каждая из трех букв будет встречаться.
Решения, работающие при \(1 \leq n, k \leq 3\) будут набирать не менее \(10\) баллов.
Решения, работающие при \(1 \leq n, k \leq 10\) будут набирать не менее \(30\) баллов.
Решения, работающие при \(1 \leq n, k \leq 5\,000\) будут набирать не менее \(60\) баллов.
| |
![]()
|
10/
5
|
|
Темы:
Задача на реализацию
В самолетах авиакомпании Битавиа кресла расположены в \(n\) рядов, при этом в каждом ряду по шесть мест, между третьим и четвертым местом находится проход. Некоторые пассажиры регистрируются заранее онлайн, другие пассажиры регистрируются на стойке регистрации в аэропорту.
При онлайн-регистрации пассажир может выбрать любое место и не может его затем менять. Например, при \(n = 6\) рассадка в самолете после онлайн-регистрации может выглядеть так (крестиками отмечены занятые места):
На стойку регистрации придут \(m\) пассажиров. По правилам Битавиа нужно рассадить их в самолете таким образом, чтобы итоговая рассадка в самолете была симметрична относительно прохода. То есть, если в некотором ряду на первом кресле сидит пассажир, то в том же ряду на шестом кресле тоже должен сидеть пассажир. То же самое справедливо для второго и пятого, третьего и четвертого кресел, соответственно. При этом пересаживать пассажиров, прошедших онлайн-регистрацию нельзя. В исходную рассадку, показанную на рисунке выше, можно добавить семь пассажиров, удовлетворив условие симметрии, например, следующим образом:
Вам дана рассадка пассажиров после онлайн-регистрации. Требуется рассадить \(m\) пассажиров так, чтобы итоговая рассадка в самолете была симметрична относительно прохода, или определить, что это невозможно.
Формат входных данных
В первой строке содержатся два целых числа \(n\) и \(m\) — количество рядов в самолете и количество пассажиров, которые придут на стойку регистрации (\(1 \le n \le 1000\), \(0 \le m \le 6000\)).
В следующих \(n\) строках задана изначальная рассадка в самолете после онлайн-регистрации. В каждой строке содержится по шесть символов, при этом \(i\)-й символ \(j\)-й строки равен <<X>> (заглавная английская X), если \(i\)-е место в \(j\)-м ряду уже занято и <<.>> (точка) иначе.
Формат выходных данных
Если искомой рассадки не существует, выведите <<Impossible>>.
Иначе выведите \(n\) строк по шесть символов — итоговую рассадку в самолете. При этом \(i\)-й символ \(j\)-й строки должен быть равен <<X>>, если место занято, и <<.>>, если свободно. Если существует несколько решений, разрешается вывести любое.
Ниже приведены пять примеров входных данных.
-
В первом примере \(m = 0\), а рассадка в самолете симметрична, поэтому итоговая рассадка совпадает с исходной.
-
Во втором примере есть только один способ рассадить пассажиров симметрично.
-
В третьем примере существовало бы решение, при \(m = 1\), но при \(m = 2\) не существует способа рассадить всех пассажиров симметрично.
-
В четвертом примере требуется рассадить больше пассажиров чем свободных мест в самолете.
-
Пятый примере соответствует ситуации, рассмотренной на рисунках в тексте условия. В этом примере существует несколько решений, приведено одно из них.
| |
![]()
|
80/
13
|
|
Темы:
Строки
Перебор
Задача на реализацию
Камила и Динара играют в <<Wordle>>. Камила загадала слово длины \(n\), состоящее из различных латинских букв. Динара сделала одну попытку угадать и назвала слово длины \(n\), также состоящее из различных латинских букв. Камила раскрасила буквы в догадке Динары в соответствии со следующими правилами:
-
Буква, совпадающая с буквой в загаданном слове, красится в зеленый цвет и обозначается G.
-
Буква, которая присутствует в загаданном слове, но стоит не своей позиции, красится в жёлтый цвет и обозначается Y.
-
Буква, отсутствующая в загаданном слове, красится в белый цвет и обозначается W.
Например, если было загадано слово ALERT, а догадка была ALONE, то буквы будут раскрашены в цвета GGWWY. Первые две буквы в словах совпадают, поэтому они зеленые. Буква E есть в загаданном слове, но находится на другой позиции, поэтому она жёлтая. Остальные буквы белые, так как их нет в загаданном слове.
Проснувшись следующим утром, Динара увидела, что буквы в ее слове не разобрать, так как они закрашены гуашью. Динара поняла, что забыла свою догадку. Помогите ей и определите, существует ли слово из различных букв, которое было бы раскрашено таким образом, и если существует, выведите любое такое слово.
В первой строке вводится одно целое число \(n\) \((1 \le n \le 10)\) — длина загаданного слова.
Во второй строке вводится строка длины \(n\), состоящая из заглавных латинских букв — загаданное слово. Гарантируется, что все буквы в нем различны.
В третьей строке вводится строка длины \(n\), состоящая из букв G, Y, W — цвета, в которые были раскрашены буквы в слове Динары.
Если подходящих слов не существует, выведите No.
Если хотя бы одно подходящее слово существует, в первой строке выведите Yes, во второй — любое подходящее слово.
Разберем первый пример из условия.
Буквы H и G не встречаются в загаданном слове, поэтому они белые.
Буквы E и B встречаются, но на других позициях, поэтому они жёлтые
Буквы C и D совпадают с буквами на соответствующих позициях в загаданном слове, поэтому они зелёные.
Есть и другие ответы, любой правильный ответ будет зачтен.
Обратите внимание, что строка HECDBH не является ответом, так как в ней есть совпадающие буквы.
| |
![]()
|
55/
8
|
|
Темы:
Конструктив
Задача на реализацию
Участникам, использующим язык Python3, рекомендуется отправлять решения на проверку с использованием интерпретатора PyPy3.
Маленький пират Серёжа скачал игру с разными видами головоломок. Среди них ему понравилась лишь одна, самая сложная.
Головоломка представляет из себя таблицу из \(n\) строк и \(m\) столбцов, в ячейках которой записаны числа от \(1\) до \(n \cdot m\) по одному разу.
Чтобы собрать головоломку, нужно выбрать последовательность клеток таблицы, в которой любые две подряд идущие клетки соседние по стороне в таблице. Последовательность может иметь произвольную длину, и каждая клетка может встречаться в последовательности произвольное число раз. Для клетки со значением \(i\) рассмотрим позицию \(t_i\) — позицию первого вхождения клетки с таким значением в последовательность. Последовательность решит головоломку, если каждая клетка таблицы встречается в ней, и \(t_1 < t_2 < \dots < t_{nm}\). Другими словами, последовательность должна в первый раз посетить клетку со значением \(x\) до клетки со значением \(x + 1\) для всех \(x\).
Назовем головоломку решаемой, если для нее существует хотя бы одна подходящая последовательность.
Серёжа понял, что не любая головоломка решаемая, так как подходящей последовательности может не существовать. Ему стало интересно, можно ли немного изменить головоломку, чтобы ее можно было решить. На это Серёже не хватило таланта, поэтому ему нужна ваша помощь.
За одно действие Сережа может выбрать две произвольных клетки (не обязательно соседние по стороне) и поменять числа, записанные в них. Он хотел бы знать минимальное число действий, которое потребуется, чтобы головоломка стала решаемой, но очень нетерпелив. Поэтому найдите, равняется ли минимальное число действий \(0\), \(1\), или же не менее \(2\). В случае, когда потребуется ровно \(1\) действие, найдите также количество подходящих пар клеток для обмена чисел.
Формат входных данных
В первой строке вводятся два целых положительных числа \(n, m\) (\(1 \leq n \cdot m \leq 400\,000\)) — длины сторон таблицы.
В каждой из следующих \(n\) строках вводятся \(m\) целых чисел \(a_{i1}, a_{i2}, \dots, a_{im}\) (\(1 \le a_{ij} \le n \cdot m\)).
Гарантируется, что каждое число от \(1\) до \(n \cdot m\) встречается ровно один раз.
Формат выходных данных
Пусть \(a\) — минимальное число действий, после которых головоломка станет решаемой.
Если \(a = 0\), выведите \(0\).
Если \(a = 1\), выведите \(1\), а также количество подходящих пар клеток.
Если \(a \ge 2\), выведите \(2\).
В первом примере из условия последовательность клеток \((1, 2), (1, 1), (1, 2), (1, 3), (2, 3), (3, 3)\), \((2, 3), (1, 3), (1, 2), (1, 1), (2, 1), (2, 2), (3, 2), (3, 1)\) решает головоломку, поэтому ответ \(0\).
Головоломка во втором примере из условия не решается, но будет решаться после любого из трех обменов клеток со значениями \((1, 5), (1, 6), (2, 6)\).
В третьем примере из условия потребуется не менее двух обменов, поэтому ответ равен \(2\).
| |
![]()
|
4/
1
|
|
Темы:
Строки
Задача на реализацию
Участникам, использующим язык Python3, рекомендуется отправлять решения на проверку с использованием интерпретатора PyPy3.
Однажды во время прогулки Алина увидела длинное число, которое кто-то написал на асфальте. Алина захотела найти положительное число такой же длины без ведущих нулей, чтобы сумма этих двух чисел была палиндромом.
Число называется палиндромом, если оно читается одинаково справа налево и слева направо. Например, числа \(121, 66, 98989\) являются палиндромами, а \(103, 239, 1241\) — нет.
После некоторых размышлений Алина поняла, что такое число всегда можно найти. Помогите Алине найти подходящее число!
Формат входных данных
В первой строке вводится одно целое число \(n\) (\(2 \leq n \leq 100\,000\)) — длина числа, которое увидела Алина.
Во второй строке вводится одно положительное целое число длины \(n\). Гарантируется, что оно не содержит ведущих нулей.
Формат выходных данных
Выведите ответ на задачу — положительное целое число без ведущих нулей длины \(n\), такое что его сумма с числом из входных данных будет палиндромом.
Если таких чисел несколько, вы можете вывести любое из них.
В первом примере из условия \(99 + 32 = 131\) — палиндром. Число \(12\) также будет являться ответом, так как \(99 + 12 = 111\).
Во втором примере из условия \(1023 + 8646 = 9669\).
В третьем примере из условия \(385 + 604 = 989\).
| |
![]()
|
33/
5
|
|
Темы:
Строки
Линейный поиск
Задача на реализацию
Саша недавно начала регистровать компанию по разработке чат ботов и уже подала необходимые документы. Но добрые люди рассказали Саше, что в телефонном справочнике компании располагаются в лексикографически возрастающем порядке их названий. Что такое телефонный справочник, Саша не знает, но решила учесть рекомендации и поменять название своей компании, чтобы оно было как можно раньше в телефонном справочнике. Поскольку Саша уже подала документы, она не может полностью поменять название компании, но может сказать, что допустила опечатку, и поменять любые две буквы в названии местами. Помогите Саше выбрать новое название компании или оставить текущее.
Формат входных данных
В единственной строке содержится одно слово, состоящее из строчных латинских букв от "a" до "z" (2 ≤ n ≤ 106)
Формат выходных данных
Выведите одно слово - новое название компании. Если название не~изменилось, выведите изначальное название.
| |
![]()
|
552/
94
|
|
Темы:
Структуры данных
Задача на реализацию
Алгоритмы обработки
Линейные алгоритмы
В компьютерной игре есть n башен, высота i-й башни равна ai метров. Определим расстояние между двумя башнями с индексами i и j как |i−j|. Разрешается прыгнуть с i-й башни на j-ю башню тогда и только тогда, когда не существует такого индекса 1 <= k <= n, такого, что расстояние от i-й до j-й башни не меньше расстояния от i-й башни до k-й башни, и k-я башня имеет большую высоту, чем j-я. Башня j достижима из башни i если существует последовательность корректных прыжков, которая начинается в i-й башне и заканчивается в j-й. Посчитайте для каждой башни количество достижимых из неё башен, включая её саму.
Входные данные
Первая строка входных данных содержит одно целое число n (1 <= n <= 500000) - количество башен.
Вторая строка входных данных содержит n чисел a1, a2, ..., an (1 <= an <= 109) - высоты башен.
Выходные данные
Выведите n чисел, i-е из которых должно быть равным количеству башен, достижимых из i-й башни.
Примечание
В первом примере с 1-й башни можно прыгнуть на башни 1 и 5. Любая другая башня имеет меньшую высоту, чем башня 1, поэтому туда нельзя прыгнуть (в качестве k можно выбрать 1). Множество достижимых из 1-й башни также состоит из башен 1 и 5. Со второй башни можно прыгнуть на башни 1, 2, и 5, они же являются множеством достижимых. С третьей башни можно прыгнуть на башни 2, 3, 5. Однако, башня 1 также является достижимой, поскольку можно сделать два прыжка: 3→2→1. Таким образом, получается 4 достижимые башни. С 4-й башни можно прыгнуть на башни 4 и 5, они же являются единственными достижимыми. Из 5-й башни достижима только она сама.
Во втором примере из 1-й и из 2-й башни достижимы башни 1,2,3,4,5. Из 3-й башни достижимы башни 3,4,5. Из 4-й и 5-й башни достижимы башни 4,5. Из 6-й башни достижимы башни 4,5,6. Из 7-й башни достижимы башни 4,5,6,7.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
5
7 6 3 4 10
|
2 3 4 2 1
|
| 2 |
7
1 1 1 2 2 1 1
|
5 5 3 2 2 3 4
|
| |
![]()
|
6/
3
|
|